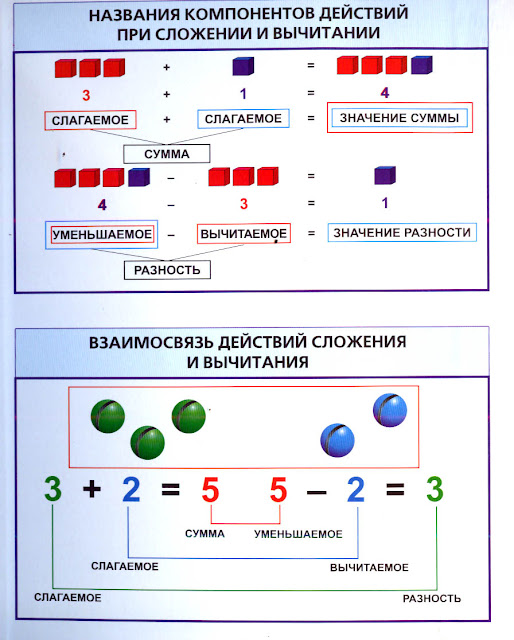
Выучить компоненты по математике 3 класс: Названия компонентов 3 класс
Урок по математике 3 класс по теме: «Компоненты арифметических действий» | План-конспект урока по математике (3 класс) на тему:
Урок по математике 3 класс
Тема: Компоненты арифметических действий
Цели:
• развивать внимание, логическое мышление учащихся, наблюдательность, способность видеть различные варианты решения задач, классификации примеров, способность сравнивать, самостоятельно проводить анализ, делать выводы;
• создать условия для уяснения зависимости компонентов от значения арифметического действия при классификации и при решении простых уравнений;
• закреплять умение составлять и решать уравнения.
Оборудование: дидактический материал для устного счёта, карточки для самостоятельной работы, веер цифр и знаков арифметических действий, карточки контроля «Да» и «Нет».
Ход урока
I. Организационный момент.
– Мы начинаем наш урок.
– Скажите, какими качествами нужно обладать, чтобы на уроке сделать для себя маленькое открытие? (Нужно быть внимательным, наблюдательным, активным, уметь поддержать товарища. )
)
II. Постановка цели и сообщение темы урока.
Игра «Живые числа».
Сейчас 11 ребят возьмут карточки с числами и построятся у доски. Контролёр станет около меня. («Числа» занимают свое место.)
– Числа, назовите себя. (Каждый из учеников, изображающих числа, называет себя: 10, 15, 18, 27, 44, 55, 62, 77, 82, 99, 100.)
– Контролёр, как ты думаешь, на какие группы можно разделить данные числа? Сейчас мы это узнаем у ребят. Я начну фразу, а вы закончите:
Числа делятся на… (чётные и нечётные; однозначные и двузначные).
Теперь я дам задание «числам», а контролер проследит, верно ли они его выполнили:
Двузначные числа, встаньте вдоль доски в порядке возрастания!
(«Числа» строятся. Число 100 оказалось «лишним».)
У ч и т е л ь (обращается к числу 100). Почему ты оказалось лишним?
Число 100. Потому что я трехзначное число, а не двузначное.
(«Лишнее» число и контролёр занимают свои места.)
Учитель (обращается к ребятам-числам). Переверните, пожалуйста, свои карточки – на обратной стороне записаны буквы. Что получилось?
Переверните, пожалуйста, свои карточки – на обратной стороне записаны буквы. Что получилось?
10 | 15 | 18 | 27 | 44 | 55 | 62 | 77 | 82 | 99 |
К | О | М | П | О | Н | Е | Н | Т | Ы |
(Получилось слово КОМПОНЕНТЫ. )
)
– Что такое компоненты? (Так можно назвать числа при сложении, вычитании, умножении, делении.)
– Верно, так называются числа участники арифметических действий: сложения, вычитания, умножения, деления.
– При выполнении каких заданий мы можем встретиться с математическими компонентами? (При решении задач, примеров.)
– Вы правы. О чём мы будем говорить на уроке, в чём упражняться?
Дети отвечают.
Действительно, тема нашего урока «Название чисел в записях действий». Мы будем упражняться в их правильном чтении и учиться их находить.
III. Чистописание.
– В чём мы упражняемся на чистописании? Для чего мы это делаем? (Мы упражняемся в письме цифр. Мы это делаем, чтобы правильно и красиво писать числа.)
– Действительно, мы учимся красиво и правильно записывать цифры.
– Скажите, а чем отличается цифра от числа? (Цифр всего десять. Чисел множество. С помощью цифр записываются любые числа.)
Задание. Перепишите в тетрадь цифры, с помощью которых записаны все числа на карточках.
Запишите в тетради данные цифры в порядке убывания.
Проверка на слух. Взаимопроверка.
(1, 0, 5, 8, 2, 7, 4, 6, 9.)
(9, 8, 7, 6, 5, 4, 2, 1, 0.)
IV. Минутка теории.
1. Веер знаков арифметических действий.
а) Чтобы узнать, «сколько всего», нужен знак… (Дети показывают «+».)
б) Для того чтобы сравнить два числа, применяют знак… (Дети показывают «-».)
в) Чтобы увеличить число на несколько единиц, надо использовать знак… (Дети показывают «+».)
г) Чтобы уменьшить число на несколько единиц, надо… (Дети показывают «—».)
е) Чтобы увеличить число в несколько раз, используют… (Дети показывают знак «х».)
ж) Чтобы уменьшить число в несколько раз, нужен знак…
(«:»).
з) Чтобы узнать, во сколько раз одно число больше или меньше другого, нужен знак … («:»).
2. Компоненты записей арифметических действий.
– Повторим названия чисел в записях арифметических действий.
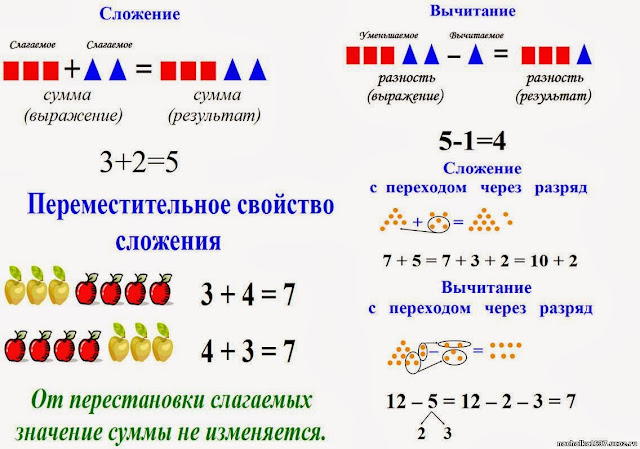
– Участники действия «сложение» называются.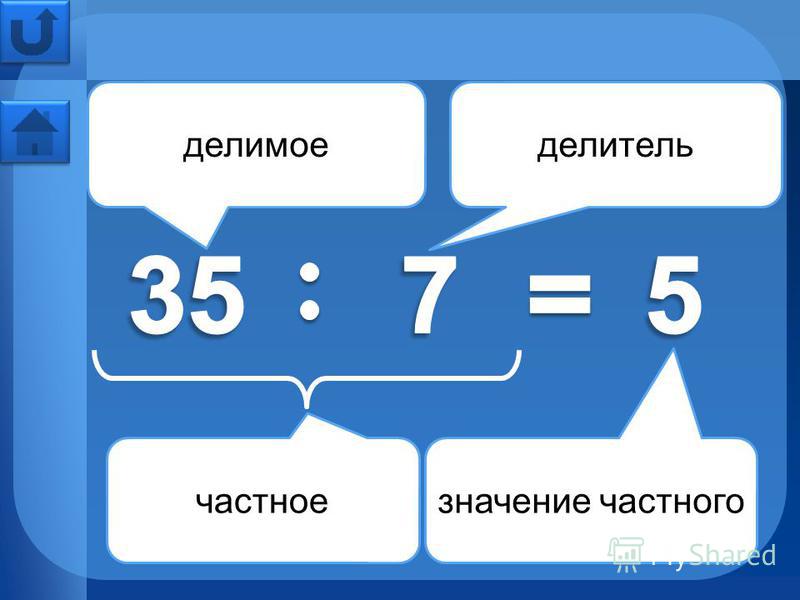 .. (слагаемые и сумма). Числа, которые складываются – … (слагаемые). Результат сложения – … (сумма).
.. (слагаемые и сумма). Числа, которые складываются – … (слагаемые). Результат сложения – … (сумма).
– Участники действия «вычитание» называются… (делимое, делитель, частное).
И так далее.
– Как вы думаете, почему мы повторяем правила? (Нам пригодятся эти правила при решении примеров, уравнений, задач.)
Физкультминутка.
Учитель. Поднимает руки класс.
Дети. Это раз! (Поднимают правую руку).
Учитель. Повернулась голова.
Дети. Это два/ (Поворот головы влево.)
Учитель. Руки вниз, вперед смотри.
Дети. Это три! (Руки опустили вниз, смотрят вперед.)
Учитель. Руки в стороны пошире.
Дети. Развернули на «четыре»! (Руки в стороны.)
Учитель. С силой их к плечам прижать.
Дети. Это пять!
Учитель. Всем ребятам тихо сесть.
Дети. Это шесть!
V. Устный счет.
Ну-ка, в сторону карандаши!
Ни костяшек, ни ручек, ни мела.
Устный счет! Мы творим это дело
Только силой ума и души.
– Итак, пришло время устного счета.
1. «Цепочка».
1) Посмотрите на доску:
3 × 3 × 2 : 3 × 5 : 10 × 8 : 4 × 2 : 4 =
– Какое задание нужно выполнить? (Нужно решить цепочку.)
– Какие знания нам в этом помогут? Что повторим? (Повторим таблицу умножения. Она поможет нам решить цепочку.)
– Какая цифра нам не понадобилась для записи наших «живых чисел»? (Это цифра 3.)
2) Давайте вспомним таблицу умножения и деления на 3:
а) повторим таблицу умножения по порядку;
б) повторим таблицу деления в любом порядке.
3) Применим знания таблицы умножения и решим «цепочку».
4) Объясните вычислительный приём, который применяли. Дети отвечают.
2. Цифровой веер.
– Примеры читаем, ответ показываем.
78 – 26 = 32 + 49 =
56 + 34 = 36 – 19 =
24 + 9 = 100 – 75 =
3. Игра «Молчанка».
Учащиеся слушают задание. Ответ показывают при помощи веера.
1) Сумму чисел 3 и 2 увеличить в 3 раза.
2) Произведение чисел 2 и 10 уменьшить на 20.
– Подведем итог. Что повторяли? В чем упражнялись? Когда пригодятся эти знания? (Мы повторят компоненты арифметических действий, таблицу умножения и деления. Эти знания пригодятся при решении задач, примеров.)
VI. Решение задач.
1. Математический диктант.
– Я буду диктовать задачу, вы будете решать и решение записывать в тетрадь.
1) Лошади различают 4 цвета (красный, жёлтый, зелёный, синий), а кошки на 2 цвета больше. Сколько цветов различают кошки?
Решение: 4 + 2 = 6 (цв.).
2) Речной рак живёт 20 лет, а рабочая пчела – в 4 раза меньше. Сколько лет живёт рабочая пчела?
Решение: 2 0:4 = 5 (лет).
3) Вася решил 7 примеров, а Петя отвлекался и решил 4. Кто решил примеров больше и почему? На сколько больше?
Решение: 7-4 = 3 (пр.).
– Подведем итог. У кого эта работа сегодня получилась? VII. Закрепление изучаемого материала.
1. Работа по цепочке: решение уравнений.
– Посмотрите на доску. Какое задание нужно выполнить?
25 + = 45; 38 – = 28;
× 4= 12; : 6 = 7.
(Нужно восстановить примеры. Можно вставить числа. Молено проговорить правила. Можно «окошечко» заменить буквой и получится уравнение.)
Ученики по цепочке решают уравнения, проговаривая выполняемые действия.
Первый заменяет «окошечко» буквой и читает получившееся
уравнение.
Второй с места проговаривает правило.
Третий подсчитывает и записывает, чему равно неизвестное число.
2. Самостоятельная работа (задание на выбор).
– Каждый выбирает задание по силам:
вариант а), б) или в),
а) Работа у доски по карточкам.
– Решить простое уравнение.
3 + х + 7 16 – у = 10
Проверка решения на доске коллективная (с помощью карточек «Да» или «Нет»).
б) В тетради самостоятельно.
– Решить составное уравнение.
х – (34 + б) = 15;
х = 55.
Решение составного уравнения записано на доске. В конце работы доска открывается для самопроверки.
в) Совместно с учителем.
– Придумать уравнение, в котором учитель заранее оговаривает, какой компонент в уравнении нужно определить.
Образцы заданий.
• Придумать уравнение, в котором неизвестным компонентом является слагаемое, (х + 5 = 10.)
• Неизвестное число можно найти сложением. Какой это компонент? (у-25 = 5.)
• Неизвестный компонент можно найти делением, и он должен равняться двум. Прочитайте свое уравнение.
(6 : х = 3) или (4 × а = 8).
– Подведем итог. В чём упражнялись? (Ответы ребят.)
Физкультминутка.
Раз – подняться, потянуться.
Два – согнуться, разогнуться.
Три – в ладоши три хлопка,
Головою три кивка.
На четыре – руки шире,
Пять – руками помахать.
Шесть – за парту тихо сесть,
Сказку можно вам прочесть.
VIII. Работа по учебнику (у доски).
1) Сумму чисел 3 и 5 увеличь в 8 раз.
2) Произведение 7 и 5 уменьши на 5.
3) Разность 46 и 16 уменьши в 6 раз.
4) Выполни действия:
(100-50)-20= (45 + 5) + 5 =
60 + (40-10)= (30 + 80)-20 =
– Подведем итог. В чём упражнялись? (Ответы детей.)
IX. Математический диктант по правилам.
«Проверь себя».
– Рядом с номером прочитанного выражения поставь нужный знак арифметического действия.
1. Чтобы найти слагаемое, нужно… («-» – вычесть).
2. Уменьшаемое находим… («+» – сложением).
3. Множитель находим… («:» – делением).
4. Чтобы найти вычитаемое, нужно… («—» ~ вычесть).
5. Для того чтобы найти делимое, нужно… («х» – умножить).
6. Для того чтобы найти делитель, нужно… («:» -разделить).
Самопроверка.
– Поставьте буквы «J1» или «Т» на полях.
– Кому нужно еще поработать с правилами?
X. Итог урока.
В чём упражнялись на уроке? Что повторяли?
Домашнее задание.
– Какое домашнее задание вы хотели бы получить сегодня? Дети предлагают варианты домашнего задания. Например,
Например,
решить уравнения, задачу, примеры…
ВЫЧИТАЕМОЕ |
РАЗНОСТЬ |
” Название компонентов и результата деления” 2 класс.

Конспект урока по математике . 2 класс. (12.03.2018)
Тема урока: Название компонентов и результатов действия деления
Цель урока: ввести названия компонентов и результата действия деления.
Задачи урока:
совершенствовать устные вычислительные навыки;
закрепить знания компонентов и результатов изученных арифметических действий;
закреплять умения работы по алгоритму;
совершенствовать навыки осознанного выбора арифметического действия при решении задач изученных видов;
развивать навык устного счета;
развивать математическую речь учащихся, внимание, логическое мышление;
развивать умение правильно формулировать свои мысли в процессе общения;
воспитывать активную личность, умеющую работать самостоятельно и в коллективе.
Средства обучения:
ПК, мультимедийный проектор;
презентация Power Point к уроку;
карточки для групповой работы.
Ход урока
I. Организационно-мотивационный момент.
Долгожданный дан звонок –
Начинается урок.
Тут затеи, и задачи,
Игры, шутки, всё для вас!
Пожелаем вам удачи –
За работу, в добрый час!
– Ребята, сегодня у нас необычный урок. Мы отправимся в космическое путешествие. Как вы думаете, а почему именно сегодня мы полетим в космос?(Какой праздник отмечает наша страна в апреле?)
.– Что вы знаете об этом дне?
12 апреля 1961 года Ю.А.Гагарин впервые в истории полетел в космос на космическом корабле «Восток». Он совершил один оборот вокруг нашей планеты и благополучно вернулся на Землю.
– О полёте Ю.Гагарина мы ещё поговорим, а сейчас я хочу проверить, готовы ли вы отправиться в путь. А чтобы наше путешествие прошло успешно, вам нужно внимательно слушать, думать и правильно считать.
II. Устный счёт. Повторение.
1. Найдите закономерность и продолжите ряд чисел:
9, 12, 16, 21, 27, 34, …, …, … . | РА | /42, 51, 61/ |
13, 15, 19, 25, 33, …, …, … . | КЕ | /43, 55, 69/ |
81, 84, 80, 83, 79, …, …, … . | ТА | /82, 78, 81/ |
– И так, мы будем путешествовать на ракете.
– Оцените свою работу.
2. – Займите свои места в ракете. Откройте бортовые журналы – тетради и запишите сегодняшнее число.
3. Математический диктант.
– Записывает только ответы, в строчку через клеточку.
1 слагаемое 40, второе 16. Найдите значение суммы.
Уменьшаемое 80, вычитаемое 7. Найдите значение разности.
Найдите сумму чисел 63 и 8.
1 множитель 6, второй множитель 3. Найдите значение произведения.
Найдите разность чисел 75 и 21.
Найдите произведение чисел 8 и 4.
Отрезок длиной 12 см разделили на 4 равные части. Чему равна длина каждой части?
Чему равна длина каждой части?
– Поменяйтесь тетрадями, проверьте ответы.
56 | 73 | 71 | 18 | 54 | 32 | 3 |
Т | ! | Ь |
| У | П | В |
Запишите эти числа в порядке возрастания и прочитайте команду.
3 | 18 | 32 | 54 | 56 | 71 | 73 |
В |
| П | У | Т | Ь | ! |
– Какую команду получили?
– Какие знания вы применили?
– Какими арифметическими действиями пользовались во время устных вычислений?
– Оцените свою работу.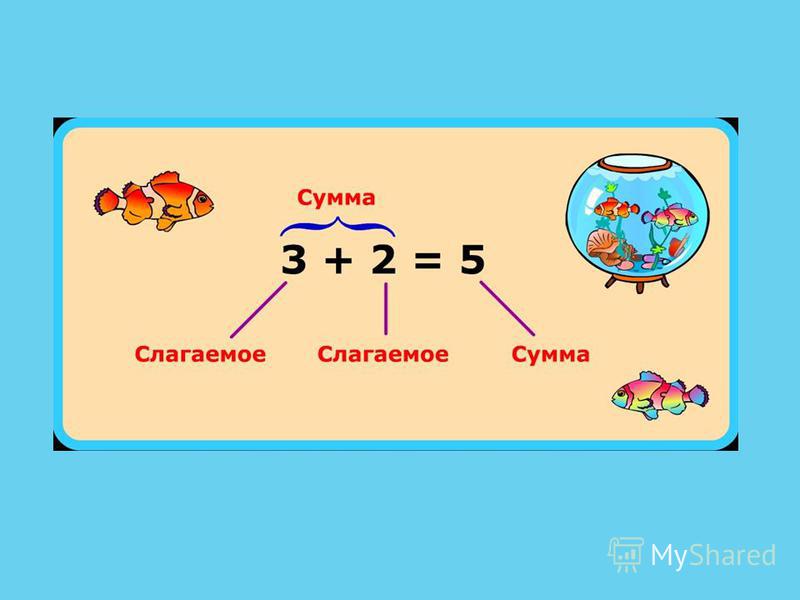
III. Актуализация имеющихся знаний. Постановка проблемы.
1. – Назовите компоненты и результат действия сложения.
– Назовите компоненты и результат действия вычитания?
– Назовите компоненты и результат действия умножения?
– Что бы вы хотели узнать сегодня на уроке?
IV. Сообщение темы. Объяснение нового материала.
– Верно, сегодня мы узнаем название компонентов и результата действия деления.
– Пока вы вспоминали названия компонентов и результатов различных арифметических действий, наша ракета приблизилась к первой космической станции «Запоминай-ка», на которой мы и познакомимся с названием компонентов и результата действия деления.
– Прочитайте выражение: 6 : 2 = 3 . /6 разделить на 2, получится 3/
– А как бы вы назвали эти числа?
– Первый компонент – первое число при делении, что мы с ним делаем? /делим/
– Как можно его назвать? делимое
– Второй компонент указывает на сколько разделили?
– Как можно его назвать? делитель
– Результат действия деления – это значение части?
– Как можно его назвать? частное
– Повторим и запомним. Как называется число, которое делим? делимое
Как называется число, которое делим? делимое
– Как называется число, на которое делим? делитель
– Как называется результат действия деления? частное
– Как называется само выражение? частное
– Давайте вместе прочитаем запись, используя новые термины, хором. Делимое 6, делитель 2, частное 3.
– А как можно прочитать по другому? Частное чисел 6 и 2 равно 3.
– Оцените свою работу.
– Молодцы! Держим путь дальше!
V. Физ. минутка.
– В космосе есть понятие «состояние невесомости».
– Кто знает, что это такое?
– Да, это когда все предметы находятся в движении, они невесомы.
– Расстегните ремни! Встаньте!
– Давайте сейчас под музыку изобразим состояние невесомости.
VI. Закрепление нового материала.
1. – Молодцы, для закрепления новых терминов отправимся на станцию «Закрепляй-ка».
– Прочитайте выражение. 16 : 2
– Чему равно его значение? 8
– Вспомните названия компонентов действия деления.
– Прочитайте по – разному.
– Запишите в свои бортовые журналы числовые выражения: делимое 10, делитель 5. Что надо найти? частное
– Чему равно частное? Частное равно 2. 10 : 5 = 2
– Прочитайте по-другому. Частное чисел 10 и 2 равно 5
– Запишите примеры: делимое 18, делитель 6. 18 : 6 = 3
– Прочитайте по-другому.
2. Работа по учебнику.
– Откройте учебники на стр.62, №1.
– Запишите в свои бортовые журналы числовые выражения во 2 столбик самостоятельно. 6:3=2
– Прочитайте по-другому. 12:6=2
– Оцените свою работу.
VII. Повторение изученного.
– Мы прибыли на станцию «Решай-ка». Запишите – «задача».
– Возьмите карточки, которые лежат у вас на столе.
– Работая в парах, по памятке решите задачу.
Для освещения космического корабля потребовалось 12 ламп. Сколько отсеков на корабле, если в каждом отсеке по 4 лампы?
Памятка:
Прочитай задачу и представь себе то, о чём говорится.
Обозначь каждую лампу кружком и запиши задачу кратко(выбери и начерти рисунок, который подходит к данной задаче).
Объясни, что показывает каждое число, и повтори вопрос задачи.
Выбери выражение, которое является решением задачи.
Запиши решение и ответ задачи.
1. 12 – 4 = 8 (л.)
2. 12 : 4 = 3( отс.)
3. 12 : 4 = 3(л.)
12 : 4 = 3 ( отс.)
– Прочитайте решение задачи, называя компоненты действия деления.
Ответ: на корабле 3 отсека.
VIII. Итог урока.
– Наше путешествие подходит к концу.
– Расскажите мне по схеме, что вам дал сегодняшний урок математики?
Я узнал. Я представил. Я смог.
IX. Рефлексия.
– При помощи солнышка и тучки, поставьте оценку за урок себе? Всему классу?
X. Домашнее задание. Выучить название компонентов деления.
стр. 62 № 3, 8 (с промежуточными результатами), по желанию – разгадать магические квадраты на полях учебника.
Тест: Знание компонентов – Математика 3 класс
Тест: Знание компонентов – Математика 3 классАнглийский язык
Астрономия
Белорусский язык
Биология
География
ИЗО
Информатика
История
Итальянский язык
Краеведение
Литература
Математика
Музыка
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
ОРКСЭ
Русский язык
Технология
Физика
Физкультура
Химия
Черчение
Для учителей
Дошкольникам
VIP – доступ
- Предметы »
- Математика »
- 3 класс »
- Знание компонентов
Знание компонентов
Знание компонентов
Математика 3 класс | Автор: Калинина Г. В. | ID: 4395 | Дата: 15.3.2015
В. | ID: 4395 | Дата: 15.3.2015
Помещать страницу в закладки могут только зарегистрированные пользователи
Вопрос №
1
Как называются числа при сложении?
слагаемое, слагаемое сумма
уменьшаемое, вычитаемое, разность
множитель, множитель, произведение
делимое, делитель, частное
Вопрос №
2
Как называются числа при вычитании?
слагаемое, слагаемое сумма
уменьшаемое, вычитаемое, разность
делимое, делитель, частное
множитель, множитель, произведение
Вопрос №
3
Как называются числа при делении?
слагаемое, слагаемое сумма
уменьшаемое, вычитаемое, разность
делимое, делитель, частное
множитель, множитель, произведение
Как называются числа при умножении?
делимое, делитель, частное
слагаемое, слагаемое сумма
уменьшаемое, вычитаемое, разность
множитель, множитель, произведение
Вопрос №
5
С помощью какого действия можно увеличить число в несколько раз?
сложения
умножения
деления
вычитания
Вопрос №
6
С помощью какого действия можно уменьшить число на несколько единиц?
сложения
умножения
вычитания
деления
Вопрос №
7
С помощью какого действия можно увеличить число на несколько единиц?
умножения
сложения
вычитания
деления
Вопрос №
8
С помощью какого действия можно уменьшить число в несколько раз?
умножения
деления
вычитания
сложения
Вопрос №
9
Каким действием найти неизвестное слагаемое?
сложением
вычитанием
умножением
делением
Вопрос №
10
Каким действием найти неизвестное уменьшаемое?
сложением
вычитанием
умножением
делением
Вопрос №
11
Каким действием найти неизвестное вычитаемое?
умножением
делением
вычитанием
сложением
Вопрос №
12
Каким действием найти неизвестный множитель?
сложением
вычитанием
умножением
делением
Вопрос №
13
Каким действием найти неизвестное делимое?
сложением
вычитанием
умножением
делением
Вопрос №
14
Каким действием найти неизвестный делитель?
сложением
вычитанием
умножением
делением
Показать ответы
Получение сертификата
о прохождении теста
Доступно только зарегистрированным пользователям
© TestEdu. ru 2013-2022
ru 2013-2022
E-mail администратора: [email protected]
Свойства умножения и деления. Распределительное и переместительное свойство
Свойства умножения
Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.
Узнаем, какие бывают свойства умножения и как их применять.
Переместительное свойство умножения
От перестановки мест множителей произведение не меняется. |
То есть, для любых чисел a и b верно равенство: a * b = b * a.
Это свойство можно применять к произведениям, в которых больше двух множителей.
Примеры:
- 6 * 5 = 5 * 6 = 30;
- 4 * 2 * 3 = 3 * 2 * 4 = 24.
Сочетательное свойство умножения
Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением. |
То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).
Пример:
- 3 * 2 * 5 = 3 * (2 * 5) = 3 * 10 = 30
- 3 * 2 * 5 = (3 * 2) * 5 = 6 * 5 = 30.
или
Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.
Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты. |
То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.
Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.
С учетом переместительного свойства умножения можно переформулировать правило так:
Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить. |
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе. |
То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.
С учетом переместительного свойства умножения можно переформулировать правило так:
Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе. |
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю. |
То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.
Свойство единицы при умножении
Если умножить любое целое число на единицу, то в результате получится это же число. |
То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Свойства деления
Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.
Основные свойства деления целых чисел
|
И еще одно важное свойство деления, которое проходят в 5 классе:
Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится. |
В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.
Применим свойства деления на практике.
Пример 1
Вычислить: 500 * (100 : 5).
Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.
Ответ: 500 * (100 : 5) = 10000.
Пример 2
Упростить выражение: 27a – 16a.
Как решаем: 27a – 16a = a * 27 – a * 16 = a * (27 – 16) = a * 11 = 11a.
Ответ: 11a.
Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.
Программа по математике за 3 класс – Справочник
3 класс тема по математике
Материалы программы 3 класса по математике включает в себя как повторение уже пройденного материала, так и изучение нового. Изучаются таблицы умножения и деления чисел в пределах первых двух десятков и связь между ними. Рассматриваются числовые выражения, содержащие до трех действий, и изучается порядок выполнения действий в них.
Изучаются таблицы умножения и деления чисел в пределах первых двух десятков и связь между ними. Рассматриваются числовые выражения, содержащие до трех действий, и изучается порядок выполнения действий в них.
Рассматриваются основные единицы стоимости, массы и времени. Между различными изученными единицами измерения устанавливаются соответствия. Изучаются задачи в два действия, в том числе задачи на стоимость.
Помимо основ арифметики, включены основы геометрии. В третьем классе на уроках математики школьники знакомятся с понятиями окружности и круга.
Ниже представлена программа по математике за 3 класс. Каждая страница содержит развернутый ответ, который поможет лучше понять данную тему.
В третьем классе на уроках математики школьники знакомятся с понятиями окружности и круга.
Www. nado5.ru
04.06.2020 3:11:10
2020-06-04 03:11:10
Источники:
Https://www. nado5.ru/e-book/matematika-3
Математика, 3 класс | План-конспект урока по математике (3 класс) на тему: | Образовательная социальная сеть » /> » /> . keyword { color: red; }
keyword { color: red; }
3 класс тема по математике
Тип урока: Урок изучения нового материала.
Скачать:
| matematika_3_klass. docx | 18.22 КБ |
Предварительный просмотр:
Учебный предмет: Математика.
Автор УМК: М. И. Моро (УМК «Школа России»).
Тема урока: «Деление с остатком».
Тип урока: Урок изучения нового материала.
- Научить выполнять деление с остатком; делать вывод, что при делении остаток всегда меньше делителя. Совершенствовать вычислительные навыки, умение решать задачи.
- Развивать логическое мышление при выполнении заданий в учебнике. Развивать внимание, наблюдательность, при выполнении заданий. Развивать мыслительные операции сравнения, анализа, при выполнении заданий. Развивать речь, при ответе на вопросы учителя и при проверки выполнения заданий.
- Воспитывать аккуратность, при работе с рабочей тетрадью, с учебником.

Универсальные учебные действия (метапредметные):
— Учить самостоятельно выделять и формулировать познавательную цель.
— Выделять необходимую информацию, при работе с учебником.
— Осознанно строить речевые высказывания.
— Овладение навыком ориентироваться в учебнике.
— Самостоятельное определение и высказывание самых простых, общих для всех людей правил поведения.
— Уметь оценивать свою работу и работу одноклассников.
— Контроль способа выполнения действия.
— Внесение необходимых дополнений и коррективов в план выполнения действия (в случае необходимости).
— Выделение и осознание того, что уже усвоено и что еще нужно усвоить.
— Умение оформлять свои мысли в устной и письменной формах.
— Планирование, сотрудничество с учителем и сверстниками.
— Построение простого речевого высказывания.
— Умение в рамках совместной учебной деятельности слушать других.
Для учителя: учебник М. И. Моро, наглядное пособие.
Для учащихся: учебник М. И. Моро, тетрадь, рабочая тетрадь по математике на печатной основе, пенал.
I. Организационный момент. (1 – 2 мин.)
— Здравствуйте, ребята. Садитесь. Я приветствую вас на уроке математики. Всё ли готово к уроку? Давайте проверим. Я буду называть, что нам понадобится на уроке, а вы кладите руку на названный мной предмет: учебник, тетрадь, рабочая тетрадь на печатной основе, пенал.
— Хорошо, молодцы. Тогда начинаем наш урок.
Встало солнышко давно,
Заглянуло к нам в окно,
На урок торопит нас
Пожелаем всем удачи –
За работу в добрый час!
II. Актуализация опорных знаний. (5 – 7 мин.)
— Начнем урок с устного счета. Я буду читать задачи, а вы должны будете назвать только ответ:
1) В кинозале находятся 78 кресел. Для проведения концерта принесли ещё 7 кресел. Сколько кресел стало в кинозале? (85)
2) Вчера туристический автобус проехал 12 км, а сегодня проехал ещё 14 км. Сколько километров проехал туристический автобус за 2 дня? (26)
3) Коля за весь день собрал 23 кг картофеля. А его брат собрал на 30 кг больше. Сколько кг собрал брат Коли? Сколько они собрали вместе? (53, 76)
А его брат собрал на 30 кг больше. Сколько кг собрал брат Коли? Сколько они собрали вместе? (53, 76)
4) В кафе стоят 16 стульев. После ремонтов кафе расширилось в 3 раза. Сколько стульев стало после ремонта? (48)
5) На заводе есть 56 станков. 4 часть из них отправили на ремонт. Сколько станков оставили на ремонт и сколько осталось на заводе? (14, 42)
6) На рынке продавец продавал ягоды. За день продал половину ягод. Сколько всего он продал кг ягод, если всего у него было 68 кг ягод? (34)
— Ребята, с какой темой мы познакомились на прошлом уроке? ( Деление с остатком. )
— Сегодня мы с вами продолжим работать над этой темой и откроем много нового.
III. Объяснение нового материала. (12 – 15 мин.)
— Откройте свои тетради. Запишите число, классная работа. Не забывайте, что в тетрадях нужно писать красиво и аккуратно. Тетради положите правильно, спинки прямые.
На доске записаны числа 2, 3, 4, 5, 6, 7, 8, 9.
— Посмотрите на доску. Разделите числа, записанные на доске на 2.
2 : 2 = 4 6 : 2 = 3
3 : 2 = 1 (ост. 1) 7 : 2 = 3 (ост. 1)
4 : 2 = 2 8 : 2 = 4
5 : 2 = 2 (ост. 1) 9 : 2 = 4 (ост. 1)
— Что вы заметили? (Либо числа делятся на 2 без остатка, либо в остатке получается 1)
— Разделите на 3 следующие числа: 21, 22, 23, 24, 25, 26.
21 : 3 = 7 24 : 3 = 8
22 : 3 = 7 (ост. 1) 25 : 3 = 8 (ост. 1)
23 : 3 = 7 (ост. 2) 26 : 3 = 8 (ост. 2)
— Что вы заметили? (При делении на 3 в остатке получается 1 или 2)
— А при делении на 3 может в остатке получиться 3? Почему? (Остаток должен быть меньше делителя, в ином случае деление можно выполнить еще раз.)
— Значит, какой можно сделать вывод, какое правило при делении с остатком? (При делении остаток всегда должен быть меньше делителя.)
— Молодцы! Откройте свои учебники на стр. 27. Прочитайте правило в красной рамочке.
— Это правило нужно выучить.
— Давайте немного отдохнем.
Ветер дует нам в лицо,
А деревцо все выше-выше!
IV. Первичное закрепление. (5 – 7 мин.)
Первичное закрепление. (5 – 7 мин.)
— Выполним задание № 3.
— Прочитайте задачу. Что известно в задаче? (Всего затратил 25 мин, на решение задачи – 10 мин, на решение каждого уравнения по 5 минут.)
— Что нужно узнать? (Сколько уравнений решил ученик.)
— А как узнать, сколько времени ученик затратил на решение уравнений? (25 – 10 = 15)
— Запишем краткую запись. (1 ученик у доски.)
Уравнения — ? шт, по 5 мин.
1) 25 – 10 = 15 (мин) – время, затраченное на уравнения.
2) 15 : 5 = 3 (шт) – решил уравнений.
Ответ: 3 уравнения.
V. Подведение итогов урока, домашнее задание. (2 – 3 мин.)
— Чему новому научились на уроке?
— Что было трудно?
— Что больше всего понравилось делать?
— Что нового узнали?
Учебник: № 4, стр. 27. Рабочая тетрадь: № 88, стр. 34
VI. Рефлексия учебной деятельности на уроке. (2 – 3 мин.)
— Понравилось ли вам на уроке?
— Что показалось самым интересным на уроке?
— С каким правилом познакомились на уроке? (При делении остаток всегда должен быть меньше делителя. )
)
— Молодцы, ребята! Закрываем тетради, урок окончен!
— Спасибо за урок!
По теме: методические разработки, презентации и конспекты
Предмет: математика Класс 1 Тема «Сложение» Программа традиционная «Гармония»
Разъяснить смысл сложения и познакомить младших школьников с той терминологией, которая употребляется в математике при сложении (выражение, сумма, слагаемые, значение суммы, равенство) на.
Предмет: математика Класс: 1б Учебник: УМК «Планета знаний» Тема урока: Больше на … Меньше на …
Предмет математика, класс 1, учебник «Планета знаний», тип урока — изучение и первичное закрепление новых знаний, оборудование: проектор, компьютер, карточки для самооценивания, карточки для теста, ка.
Урок математики Класс: 4 Тема: Задачи на движение УМК «Начальная школа 21 века»
Урок изучения новой темы. На уроке используются различные формы работы :индивидуальная и парная. На заключительном этапе проводится рефлексия с помощью оценочных листов.
Математика. Класс 3 . Учебник: Аргинская И. И. ОКРУЖНОСТЬ
Урок математики в 3 классе, обучающемся по развивающей системе Л. В.Занкова, по теме «Окружность» построен с учетом новых требований ФГОС с использованием системно-деятельностного подхода.
Тип урока: Урок изучения нового материала.
| matematika_3_klass. docx | 18.22 КБ |
— Уметь оценивать свою работу и работу одноклассников.
Nsportal. ru
15.03.2020 21:34:15
2020-03-15 21:34:15
Источники:
Https://nsportal. ru/nachalnaya-shkola/matematika/2018/09/23/matematika-3-klass
Уроки по математике 3 класс » /> » /> .keyword { color: red; }
3 класс тема по математике
Уроки по математике 3 класс и другие полезные материалы Для учителя математики, которые вы можете выбрать и скачать бесплатно в этом разделе.
«Задачи на кратное и разностное сравнение»
Уроки
Предмет: математика Класс: 3 Тема раздела: Табличное умножение и деление Тема урока: Задачи на кратное и разностное сравнение Тип урока: урок открыти
Технологическая карта урока на тему » Алгоритм письменного деления трехзначного числа на однозначное»
Уроки
Предметные: продолжить работу над формированием умения самостоятельно применять полученные знания. Метапредметные: Познавательные: извлекать информац
Метапредметные: Познавательные: извлекать информац
Конспект урока по математическому развитию на тему «Широкий, узкий».
Уроки
Контрольная работа по математике для 3 класса. Тема :»Трёхзначные числа»
Уроки
Решение геометрических задач
Уроки
Урок математики,3 класс
Уроки
Тема урока Проверка деления умножением Урок построен по технологии проблемного обучения Е. Мельниковой
Конспект урока математики в 3 классе. Тема: «Умножение и деление на 7».
Уроки
Данные задания предназначены для учеников общеобразовательной школы 3 класса или для учеников 2 класса, 3 года обучения, интегрированного обучения и в
Нахождение неизвестных компонентов. Выражения на порядок действий. Деление с остатком. Решение задач на сравне
Уроки
Продолжить работу по формированию умения находить неизвестные компоненты выражений, выполнять деление с остатком; совершенствовать вычислительные навы
Письменное деление двузначного числа на однозначное без перехода через разряд.
 Закрепление. Великие математики
Закрепление. Великие математикиУроки
Краткосрочный план урока по математике
Уроки
КР Психологический настрой Ребята! Какое у вас сегодня настроение? Вы настроены на учебу? Молодцы! Давайте поприветствуем друг — друга! Повернитесь дру
Получите свидетельство о публикации сразу после загрузки работы
Получите бесплатно свидетельство о публикации сразу после добавления разработки
Серия олимпиад «Весна — лето 2022»
Комплекты учителю
Качественные видеоуроки, тесты и практикумы для вашей удобной работы
Вебинары для учителей
Бесплатное участие и возможность получить свидетельство об участии в вебинаре.
© 2014 – 2022, Общество с ограниченной ответственностью «ИНТОЛИМП»
Свидетельство выдано Администрацией Ленинского района г. Могилева 01.09.2014
212030, РБ, г. Могилев ул. Ленинская д. 63 оф. 502
УНП 790945001, ОКПО 302890157000
Банк: ОАО «Приорбанк» ЦБУ 300 БИК PJCBBY2X г. Могилев ул. Первомайская, д. 63
Могилев ул. Первомайская, д. 63
Время приёма заявок — круглосуточно. Режим работы офиса: 8:00 — 17:00
Служба поддержки privet@intolimp. org
Телефон: +375 29 225 71 36
Уроки
Тема Трёхзначные числа.
Intolimp. org
30.05.2020 8:54:41
2020-05-30 08:54:41
Источники:
Https://intolimp. org/publication/matematika/uroki-1/3-class/
Разжигание любопытства, подпитка осмысления, активизация движения учителя
ССЫЛКИ :
«Задавайте вопросы и продвигайте беседу». Национальный совет учителей математики, www.nctm.org/Conferences-and-Professional-Development/Tips-for-Teachers/Asking-Questions-and-Promoting-Discourse/.
Брюс, К. (2014a). «Пространственность» учебного плана по математике: новые перспективы, новые рамки. Материалы 38-й конференции Международной группы психологии математического образования. Ванкувер, Британская Колумбия: PME.
Клементс, Д., и Сарама, Дж. (2009). Изучение и преподавание ранней математики: подход траекторий обучения. Нью-Йорк, штат Нью-Йорк: Рутледж.
Нью-Йорк, штат Нью-Йорк: Рутледж.
Дреер, Аника и Кунце, Себастьян и Лерман, Стивен. (2015). Зачем использовать несколько представлений на уроке математики? Взгляды учителей английского и немецкого языков. Int J of Sci and Math Educ. 1-20. 10.1007/s10763-015-9633-6.
Дюрксен, Трейси и Уэй, Дженнифер и Бобис, Джанетт и Андерсон, Джуди и Скиллинг, Карен и Мартин, Эндрю. (2017). Мотивация и участие в математике: качественная основа для взаимодействия учителя и ученика. Журнал исследований в области математического образования. 29. 10.1007/с13394-017-0199-1.
Evertson, Carolyn M., et al. «Связь между поведением в классе и результатами учащихся на уроках математики и английского языка». Американский журнал исследований в области образования, том. 17, нет. 1, 1980, стр. 43–60. JSTOR, www.jstor.org/stable/1162507. По состоянию на 28 января 2020 г.
Фоснот, Кэтрин Туми и Виллем Уиттенбогаард. Мини-уроки по расширению умножения и деления: годовой ресурс. Pearson Education, 2008.
Хетика, Хетика и Фарида, Ида и Приатнасари, Йени. (2018). Думайте о парном обмене (TPS) как о методе повышения мотивации учащихся к обучению и успеваемости. Динамика Пендидикан. 12. 125-135. 10.15294/дп.v12i2.13561.
Киллиан, Шон. «8 способов использовать модель I Do WE Do YOU Do для улучшения результатов учащихся». Evidence, 22 ноября 2019 г., www.evidencebasedteaching.org.au/the-i-do-we-do-you-do-model-explained/.
Кинг, А. (1994). Руководство по построению знаний в классе: результаты обучения детей тому, как задавать вопросы и как объяснять. Американский журнал исследований в области образования, 31 (2), 338–368. https://doi.org/10.3102/00028312031002338
Лоуренс Вайнштейн и Адамс, Джон. Предположение. (Издательство Принстонского университета, 2008 г.).
Лойцингер, Л. П., Ратмелл, Э. К., и Урбатч, Т. Д. «Развитие навыков оценивания в начальных классах». В Estimation and Mental Computation: (Ежегодник 1986 г., под редакцией HL Schoen и MJ Zweng, 1986, 82–92. Рестон, Вирджиния) Национальный совет учителей математики.
Рестон, Вирджиния) Национальный совет учителей математики.
Лильедал, Питер. «Создание класса мышления по математике». Edutopia, Образовательный фонд Джорджа Лукаса, 17 октября 2017 г., www.edutopia.org/article/building-thinking-classroom-math.
Лильедал, Питер и Дариен Аллан. «СТУДЕНЧЕСТВО: ДЕЛО «ТЕПЕРЬ ПОПРОБУЙТЕ ОДИН»». 2013 г., http://www.peterliljedahl.com/wp-content/uploads/PME-2013-Studenting-2.pdf
Маккуиви, Джеймс. (2008). Как видео завоюет мир: что означает появление OmniVideo для профессионалов в области потребительской стратегии.
https://www.forrester.com/report/How+Video+Will+Take+Over+The+World/-/E-RES44199
Мейер, Дэн. «Три акта математической истории». Dy/Dan, 6 августа 2016 г., blog.mrmeyer.com/2011/the-three-acts-of-a-mathematical-story/.
Малвахилл, Элизабет. «10 забавных альтернатив Think-Pair-Share». WeAreTeachers, 29 августа 2019 г., www.weareteachers.com/think-pair-share-alternatives/.
Национальный исследовательский совет. 2001. Добавление: помощь детям в изучении математики. Вашингтон, округ Колумбия: Издательство национальных академий. https://doi.org/10.17226/9822.
2001. Добавление: помощь детям в изучении математики. Вашингтон, округ Колумбия: Издательство национальных академий. https://doi.org/10.17226/9822.
Ньюкомб, Северная Каролина (2010). Представьте себе: повышение уровня обучения математике и естественным наукам за счет улучшения пространственного мышления. Американский педагог, 34, 29–35.
Орр, Джон и Пирс, Кайл. «Эпизод № 21: Класс мышления: интервью с Питером Лильедалом». Сделайте Math Moments, 22 апреля 2019 г., makemathmoments.com/episode21.
Орр, Джон и Пирс, Кайл. «Эпизод № 24: Пейзажи обучения: интервью с Кэти Фоснот». Make Math Moments, 13 мая. 2019 г., makemathmoments.com/episode24.
Орр, Джон и Пирс, Кайл. «Эпизод № 24: 5 практик: интервью с Пег Смит». Make MathMoments, 15 июля 2019 г., makemathmoments.com/episode33.
Орр, Джон. «Создание устойчивых и целеустремленных студентов-математиков». Мистер Орр — гик, 25 февраля 2018 г., mrorr-isageek.com/building-resilient-determined-math-students.
Орр, Джон. «Переполох по периметру», мистер Орр — гик, 20 декабря 2016 г., tapintoteenminds.com/3act-math/candles-burning.
Орр, Джон. «Прикладная математика Spiralling Grade 9», г-н Орр — гик, 4 февраля 2015 г., mrorr-isageek.com/spiralling-grade-9-applied-math/.
Пирс, Кайл. «Candle Burning» Tap In Teen Minds, 14 октября 2013 г., tapintoteenminds.com/3act-math/candles-burning.
Пирс, Кайл. «Запоминание умножения больше вредит, чем помогает?» Tap In Teen Minds, 20 мая. 2016, tapintoteenminds.com/memorizing-multiplication-tables-hurt-help.
Пирс, Кайл. «Рулетка Doritos: горячо или нет?» Tap Into Teen Minds, 31 марта 2015 г., tapintoteenminds.com/3act-math/doritos-roulette-hot-or-not.
Пирс, Кайл. «Мармеладные черви» проникают в умы подростков, 1 января 2018 г., tapintoteenminds.com/3act-math/gummy-worms.
Пирс, Кайл. «Полное руководство по расширению учебной программы по математике» Tap In Teen Minds, 20 мая. 2016 г., tapintoteenminds. com/spiralling-guide.
com/spiralling-guide.
Пирс, Кайл. «Использование задач для преподавания уроков» Прикоснитесь к подростковому разуму, 26 декабря 2017 г., tapintoteenminds.com/tasks-teach-lessons.
Пирс, Кайл. «Почему я прошу учащихся замечать и удивляться», «Прикоснитесь к мыслям подростков», 13 ноября 2017 г., tapintoteenminds.com/notice-wonder.
Прессфилд, Стивен. «Трехактная структура». Стивен Прессфилд, 15 апреля 2011 г., stevenpressfield.com/2011/04/three-act-structure/.
Путри, Хафизиани и Миснарти, Миснарти и Саптини, Риа. (2018). ВЛИЯНИЕ КОНКРЕТНО-ИЗОБРАЖЕННО-РЕФЕРАТНОГО (КИП) ПОДХОДА НА ПОВЫШЕНИЕ МАТЕМАТИЧЕСКИХ СПОСОБНОСТЕЙ МЛАДШИХ ШКОЛЬНИКОВ. 10. 61. 10.17509/эх.v10i2.10915.
Рейс, Роберт Э., Мэрилин Н. Суйдам, Мэри М. Линдквист и Нэнси Л. Смит. Помощь детям в изучении математики (Пятое издание). (Нидхэм-Хайтс, Массачусетс: Allyn & Bacon, 1998).
Сэмпсел, Ариана, «Выявление влияния «думай-пары-поделись» на уверенность и участие учащихся» (2013). Проекты с отличием. 28. https://scholarworks.bgsu.edu/honorsprojects/28
Проекты с отличием. 28. https://scholarworks.bgsu.edu/honorsprojects/28
Шиммер, Т. (2016). Выставление оценок изнутри наружу: обеспечение точности оценок учащихся с помощью мышления, основанного на стандартах. Блумингтон, Индиана: Solution Tree Press.
Скиллинг, Карен. (2014). Практика учителей: как они способствуют или препятствуют вовлечению учащихся в математику.
Смит, Маргарет С. и Мэри К. Стейн. 5 практик организации продуктивных математических дискуссий. Рестон, Вирджиния: Национальный совет учителей математики, 2011. Печать.
Тейлор-Кокс, Дж. 2001. «Сколько шариков в банке? Оценка в младших классах». Обучение детей математике, 8, 208-214.
Уилер, Лора. «Погружаемся в #ThinkingClassroom @Pgliljedahl». Твиттер, 25 февраля 2017 г., twitter.com/wheeler_laura/status/8355109606402.
HMH ВПЕРЕД, математика! Программа | K-6 Math Curriculum
Доступен на испанском языке
Создан для успеха учителей и учащихся
Вперед, математика! для классов K–6 сочетает в себе проверенный контент, практику и игры с удобными инструментами, направленными на то, чтобы направлять каждого учащегося к мастерству.
Запрос информации
Получить образецИнструменты для вовлечения учащихся на всех уровнях
Займитесь математикой! предоставил надежный контент для более чем семи миллионов студентов по всему миру. Теперь мы внедрили больше вспомогательных средств, чтобы каждый учитель мог уверенно преподавать математику. Программа подчеркивает простоту использования, объединяя оценку, персонализированную и адаптивную практику, а также профессиональное обучение по требованию в одной управляемой системе.
Единая платформа для экономии времени
Математика! настраивает учителей на успех с практической дорожной картой для ежедневного планирования уроков, оцениванием, которое автоматически помещает учащихся в персонализированную, адаптивную практику, и доступом к богатым ресурсам профессионального развития — и все это на одной платформе.

Динамическая персонализация
Встроенные занятия Waggle ® , доступные на английском и испанском языках, обеспечивают динамическое персонализированное обучение на основе результатов учащихся по шкале HMH Growth Measure ™ .
Готовые ресурсы
Наш настольный флипчарт расширяет возможности обучения математике в небольших группах с помощью готовых мини-уроков для целенаправленной поддержки навыков.
 Кроме того, Займитесь математикой! предлагает обширные ресурсы для центров, дифференцированное обучение математике, а уровни 2 и 3 помогают учителям знать и доверять.
Кроме того, Займитесь математикой! предлагает обширные ресурсы для центров, дифференцированное обучение математике, а уровни 2 и 3 помогают учителям знать и доверять.
Внимание, текущий
Займитесь математикой! КлиентыНаш новый и улучшенный Займитесь математикой! Учебная программа для классов K–6 прибыла и готова удовлетворить требования современных классов. Будьте уверены, мы все еще здесь, чтобы поддержать учителей, использующих текущую версию программы.
Вход в программу Получить поддержку
Испытайте захватывающую эффективность
Займитесь математикой! Послушайте, как учитель описывает, как Займитесь математикой! помог учащимся с разным уровнем подготовки добиться успеха в математике.
Студенческий опыт
Аутентичные обучающие связи
Займись математикой! разработан с использованием проверенной учебной модели 5E, которая помогает учащимся достичь мастерства, опираясь на их прежнее понимание математических концепций. Встроенные формирующие математические оценки гарантируют, что учащиеся получат необходимую им поддержку.
Математическая беседа для совместной работы
Embedded Math Обсуждение и совместная деятельность поощряют живую дискуссию.
 Учащиеся всех языков чувствуют себя в безопасности, участвуя в математическом сообществе. Math Talk, новые уроки запуска, математические центры и игры предлагают интересные возможности для исследований и дискуссий.
Учащиеся всех языков чувствуют себя в безопасности, участвуя в математическом сообществе. Math Talk, новые уроки запуска, математические центры и игры предлагают интересные возможности для исследований и дискуссий.Ускорение для каждого учащегося
Waggle выходит за рамки адаптивной практики, дополняя ежедневные уроки, помогая учащимся всех уровней владения языком, с тщательно подобранными практическими и учебными мероприятиями, направленными на устранение индивидуальных пробелов в навыках.
В прошлом году у меня было 63 ученика разного уровня.
Из этих 63 детей 100 процентов сдали экзамен. Мой директор сказал, что никогда не видел ничего подобного.
Даниэль Лафонтан
Учитель 5-го класса, школы округа Броуард, Флорида
Опыт учителя
Упрощенная инструкция
Настраиваемые презентации уроков
Наше упрощенное планирование уроков, которое включает в себя готовые редактируемые презентации уроков в классе, экономит часы работы учителей.

Ресурсы Wida-Aligned
Поддержка многоязычных учащихся
Займись математикой! теперь включает в себя обширную, согласованную с WIDA поддержку для многоязычных учащихся на каждом уроке, а дополнительная поддержка уровня владения языком для малых групп доступна через настольный флипчарт.
Пути успеха учителя
Неограниченная поддержка внедрения
Встроенное обучение по запросу и еженедельное руководство по планированию всего за 30 дней вселяют в учителей уверенность, открывая им четкий путь к успеху.

Сила онлайн-обучения и преподавания
Ed , учебная платформа HMH, предлагает онлайн-обучение для Go Math! , где оценивание информирует о персонализированной практике, а учителя получают необходимую им поддержку, когда они в ней нуждаются, — и все это в единой бесшовной системе.
- Сравнительная оценка
- Индивидуальная практика навыков
- Профессиональное обучение
Узнайте, как
Займитесь математикой! повышает успеваемость учителей и учеников.
Запрос информации
Получить образецИнформация и ресурсы
- Статьи
- Исследования
7 стратегий преподавания математики изучающим английский язык
Эти стратегии ELL для обучения математике помогут вам в обучении математике изучающих английский язык и в поддержке изучения математики для многоязычных учащихся.
Ричард Бланкман
Фасонный РедакторТехнологии и персонализированное обучение
Откройте для себя преимущества технологий и персонализированного обучения в классе, а также цифровые инструменты, которые могут автоматизировать персонализированный процесс обучения.
Аойф Демпси
Старший вице-президент по управлению продуктами, HMHОбучение математическим знаниям для преподавания
Чтобы хорошо преподавать математику, учителям необходим специальный тип знаний, называемый математическими знаниями для преподавания.
Д-р Сью Чепмен
Консультант по профессиональному обучению, Heinemann
GO Math!: База данных исследований
- Тип отчета: База научных данных
- Уровень: Начальный, средний
- Демонстрирует обоснование
- Математика
GO Math!: Исследование эффективности для начальных классов 2015 г.

- Тип отчета: Исследование эффективности, исследование, проведенное третьей стороной
- Уровень: Начальный, средний
- Регион: Средний Запад, Северо-Восток, Запад
- Район Город: Городской, пригородный, сельский
- Демонстрирует обоснование
- Математика
GO Math!: рандомизированное контрольное исследование (РКИ), двухлетнее исследование, 1, 2 и 3 классы
- Тип отчета: Исследование эффективности, исследование, проведенное третьей стороной
- Уровень: Элементарный
- Регион: Средний Запад, Северо-Восток, Юго-Запад, Запад
- Район Город: Пригородный, сельский
- Умеренные доказательства
- Математика
GO Math!: Квазиэкспериментальное исследование (QED), 3, 4 и 5 классы
- Тип отчета: Исследование эффективности, исследование, проведенное третьей стороной
- Уровень: Элементарный
- Район Город: Городской, Пригородный
- Многообещающие доказательства
- Математика
GO Math!: исследование эффективности, 2–4 классы
- Тип отчета: Исследование эффективности, исследование, проведенное третьей стороной
- Уровень: Элементарный
- Регион: Средний Запад, Северо-Восток
- Район Город: Пригородный, сельский
- Демонстрирует обоснование
- Математика
Узнайте, как Займитесь математикой! повышает успеваемость учителей и учеников.
Запросить информацию
Получить образецПодписаться
Математика, уровень 3, базовый набор
Описание
Обзор изучения творчества с помощью математики, уровень 3
Практическая интерактивная учебная программа по математике для начальных классов «Исследуя творение с помощью математики, уровень 3» была разработана для того, чтобы побудить вашего ребенка взмывать к новым высотам в радостном путешествии, открывающем новые вещи о мире и его Творце. На уровне 3 учащиеся изучают сложение, вычитание, умножение, деление, сбор данных и построение графиков, дроби и геометрию. Эта учебная программа, наполненная заданиями, проектами и играми, которые помогут вашему ребенку понять, как использовать числа в повседневной жизни, также побуждает вашего ребенка размышлять о творчестве на новом уровне.
Родителям нравится эта учебная программа:
«Эта математика изменила правила игры в нашем доме! Я бы так много спорил со своей дочерью из-за математики. Теперь она просит сделать это первой и иногда делает больше, чем требуется! Спасибо за выпуск продукта, который вселил в меня уверенность, что мы можем продолжать домашнее обучение без борьбы каждый день».
«Мне нравится макет книги «Исследуя мироздание с помощью математики». Каждый урок включает в себя мастерство со спиральным повторением. Это идеальная смесь для моего сына без перегрузки».
«Спасибо за создание такой фантастической программы по математике! Apologia Math идеально подходит для нашей дочери!»
«Мы купили книгу «Исследуя творение с помощью математики, уровни 1 и 2» для двух моих детей. В прошлом году моя дочь часто плакала, когда занималась математикой. Однако в этом году она взволнована, когда начинает свой урок; она любит это! Спасибо!”
«Нам очень понравилась эта учебная программа! Простота использования и подготовки! Такой естественный подход к математике! Я перепробовал так много учебных программ по математике для 1-го класса. Этот – мой любимый!”
Этот – мой любимый!”
«Эта учебная программа (Изучение творчества с помощью математики) представляет собой идеальный баланс практических задач и практических занятий. Дочке понравились все игры. Очень рекомендую!”
«У нас уже несколько недель, как наша книга «Апология математики», и моя дочь умоляет сделать еще один урок в конце каждого дня! Спасибо за такое веселое математическое приключение».
«Большое спасибо за написание этой программы по математике. Моему сыну это очень ОЧЕНЬ нравится, и нам так весело вместе. Математика — его любимый предмет, и он с нетерпением ждет его каждый день».
«Я рекомендую ваши учебники по математике всем мамам, обучающимся на дому. Спасибо за все, что вы вносите в мир домашнего обучения. Мы благодарны!»
Что включено в базовый набор «Исследуя творчество с помощью математики», уровень 3
Базовый набор включает в себя учебник и рабочую тетрадь для учащихся «все в одном» на спирали, а также руководство для преподавателя и ключ к ответам.
Изучение творчества с помощью математики, уровень 3, учебник и рабочая тетрадь для учащихся «все в одном»
Этот курс представляет собой подробное введение в элементарную математику. Обложки уровня 3:
- Сложение и вычитание
- Умножение
- Подразделение
- Дроби
- Время, Вес
- Данные и графики
- Периметр, Участок
В серии «Исследуя мироздание с помощью математики» используется мастерский подход с большим количеством обзоров. Автор, Кэтрин Гомес, связывает темы, используя встроенный обзор, с разделами по отработке навыков. Практические проекты глубже знакомят и укрепляют концепции.
Автор перемещается по материалу, следуя определенной последовательности и четырехступенчатому подходу. Каждый урок использует проблемы и проекты и начинается с осязаемой презентации, затем проходит через графическое представление концепции, затем следует абстрактная презентация и заканчивается прикладной деятельностью. В проектах математика применяется в жизни учащихся, чтобы привить им любовь к математике и помочь им с нетерпением ждать занятий математикой каждый день.
В проектах математика применяется в жизни учащихся, чтобы привить им любовь к математике и помочь им с нетерпением ждать занятий математикой каждый день.
Руководство по размещению
Просмотрите наше руководство по математике, чтобы определить, какой уровень лучше всего подходит вашему ребенку.
Просмотреть руководство по трудоустройству
5 ключевых компонентов Apologia Math для начальных классов
Множество практических навыков
Каждый день в программе «Изучение творчества с помощью математики» учащийся тратит 5–10 минут на повторение ранее изученных навыков. Мы предоставляем соответствующие варианты для родителей и учащихся, чтобы рассмотреть в зависимости от их потребностей. На начальном уровне значительную часть содержания составляют математические факты, которые необходимо запомнить. В дополнение к ежедневным урокам, студентам также назначается отработка навыков на каждый день. Игры и занятия, которые легко настроить, перечислены в Руководстве для преподавателей и Ключе ответов. Эти практические занятия гарантируют, что учащиеся останутся хорошо подготовленными и уверенными в своих текущих знаниях, когда учатся использовать новые концепции.
Игры и занятия, которые легко настроить, перечислены в Руководстве для преподавателей и Ключе ответов. Эти практические занятия гарантируют, что учащиеся останутся хорошо подготовленными и уверенными в своих текущих знаниях, когда учатся использовать новые концепции.
Христианские связи
Хотя изучение математики ради математики — это замечательно, Апология считает, что вы не должны изучать математику, чтобы сдать тест, преуспеть в школьном предмете или даже продвинуться по карьерной лестнице. Истинная цель математики — узнать больше о Боге, создавшем ее. Математика является частью Творения и как таковая отражает аспекты Бога. Мы можем стать свидетелями Его красоты, верности и любви, изучая числа. Каждый модуль в серии «Изучение творения с помощью математики» помогает учащимся установить эти связи, поскольку он начинается с разделов «Видеть нашего Творца», которые связывают учащегося с началом математического пути.
Весело и увлекательно
Если вы связываете числа со страницами уравнений, вы не смотрели заголовок Apologia Exploring Creation with Mathematics. Сочетая цвет, фотографии, практические занятия, увлекательные проекты и множество игр, дизайн каждого урока представляет математику как доступный и увлекательный предмет. Давайте заглянем в эти книги. План уроков на уровнях с 1 по 3 и тщательно продуманные задания представляют математику как доступный и увлекательный предмет. Каждый курс «Исследуя творчество с помощью математики» проведет вашего ребенка через основательный и тщательный год изучения математики. Кульминацией каждого раздела в «Исследовании творчества с помощью математики» являются заключительные проекты, которые укрепляют математику, которую учащийся изучил в реальных сценариях. Мы постепенно переходим к сложным концепциям, каждый день ставя перед собой достаточно задач.
Сочетая цвет, фотографии, практические занятия, увлекательные проекты и множество игр, дизайн каждого урока представляет математику как доступный и увлекательный предмет. Давайте заглянем в эти книги. План уроков на уровнях с 1 по 3 и тщательно продуманные задания представляют математику как доступный и увлекательный предмет. Каждый курс «Исследуя творчество с помощью математики» проведет вашего ребенка через основательный и тщательный год изучения математики. Кульминацией каждого раздела в «Исследовании творчества с помощью математики» являются заключительные проекты, которые укрепляют математику, которую учащийся изучил в реальных сценариях. Мы постепенно переходим к сложным концепциям, каждый день ставя перед собой достаточно задач.
Простота использования
Структура исследования творчества с помощью математики, уровни 1, 2 и 3 разработана с максимальной гибкостью, чтобы семьи могли корректировать задания по мере необходимости и при этом добиваться успеха. Каждый день учащиеся проходят урок и отрабатывают навыки, перечисленные в ежедневном расписании, которое можно найти в прилагаемом Руководстве для преподавателей и Ключе ответов. Родители могут легко проверить ответы своих учеников с помощью эскизов каждого рабочего листа. Ответы четко видны для простоты использования.
Каждый день учащиеся проходят урок и отрабатывают навыки, перечисленные в ежедневном расписании, которое можно найти в прилагаемом Руководстве для преподавателей и Ключе ответов. Родители могут легко проверить ответы своих учеников с помощью эскизов каждого рабочего листа. Ответы четко видны для простоты использования.
Бонусный контент онлайн
Каждое издание Apologia имеет собственный веб-сайт. Эти дополнения к книгам содержат дополнительные материалы, которые помогут родителям и учащимся добиться успеха.
- Соответствующие веб-сайты, такие как электронные игры или места для создания собственных рабочих листов
- Печатный PDF-файл всех расходных страниц, найденных в Руководстве для преподавателей и Ключе ответов
- Дополнительные рабочие листы в формате PDF для печати для учащихся, которые борются с концепцией и могут нуждаться в дополнительной поддержке.
- Красочные и соответствующие возрасту макеты уроков и дизайн страниц делают обучение более привлекательным для вашего ученика
- Предоставляются варианты и предложения по корректировке урока, если ваш ребенок испытывает затруднения или если ваш ребенок быстро продвигается по материалу
- Также приводятся списки материалов, ответы на задачи, советы по обучению и предложения по дальнейшему выполнению задания.

- Что вы найдете внутри, исследуя творение с помощью математики
Каждый из первых трех уровней начальной математической программы Apologia состоит из 2 компонентов:
- Расходный материал, учебник и рабочая тетрадь для учащихся «все в одном» на спирали
- Учебное пособие в мягкой обложке и ключ для ответов
Каждый уровень рабочей тетради для учащихся имеет одинаковый дизайн:
- Единицы открываются разделом «Видение нашего Создателя» по математике. Они также включают «Отработку навыков», которую учащиеся будут повторять при работе над новыми материалами. Единицы разделены на отдельные главы.
- Главы охватывают отдельные концепции и разделены на отдельные ежедневные уроки.
- Ежедневные уроки состоят из начального практического занятия, в котором используются обычные предметы домашнего обихода, текстовые материалы для объяснения любых новых понятий и практический рабочий лист. Практические занятия включают в себя игры и проекты с использованием прилагаемых листов с заданиями и повседневных предметов домашнего обихода, которые дают вашему ребенку ощутимую связь с изученными абстрактными понятиями.
Изучение творчества с помощью руководства по обучению математике и ответов, уровни 1, 2 и 3 содержит:
- 28-недельный план занятий, разбитый на 4 дня в неделю. Этот рекомендуемый ежедневный график был разработан с продуманным шагом с помощью концепций, которые отражают систематический переход от одного навыка к другому, что наиболее важно для устранения разочарования. Также предоставляются
- заметок для учителя по каждому разделу, включая советы по обучению и предложения по дальнейшему выполнению задания.
- Список поставок для каждого устройства (также доступен полный список поставок)
- Практические советы и идеи
- Заметки учителя для индивидуальных уроков, где необходимо
- Предоставляются варианты и предложения по корректировке урока, если ваш ребенок испытывает затруднения или если ваш ребенок быстро продвигается по материалу.
- Ключ быстрого ответа для каждой страницы книги
- Рабочие листы для расходных материалов (копии также находятся на сайте Book Extras для каждого издания)
Подробнее о ежедневном расписании и расходных материалах
Изучение творчества с помощью математики, уровень 3, содержит следующий план урока:
- 7 единиц
- 13 глав
- 100 уроков
- 340 страниц
Рекомендуемое ежедневное расписание, включенное в каждый курс, основано на четырех днях в неделю в течение 28 недель. Мы рекомендуем вам адаптировать его к потребностям вашего ребенка и расписанию вашей семьи. В среднем каждое занятие занимает от 30 до 45 минут. Однако это время может варьироваться, если ваш ребенок немного продвинулся в практическом проекте или ему нужно немного больше времени для отработки навыков. В обычный день ваш ученик потратит от 5 до 10 минут на повторение ранее изученных концепций, примет участие в увлекательном практическом занятии, знакомящем с новой концепцией, а затем применит новую концепцию, работая с практическими рабочими листами. Вам также нужно будет собрать некоторые обычные предметы домашнего обихода и купить несколько обычных математических манипулятивных предметов, чтобы в полной мере использовать этот курс. Обычные предметы домашнего обихода включают такие вещи, как сухие бобы для счета. Математические манипуляции включают такие элементы, как набор десятичных блоков. Полный список доступен для каждого класса, а материалы повторно используются в разных классах в зависимости от изучаемых понятий.
Мы рекомендуем вам адаптировать его к потребностям вашего ребенка и расписанию вашей семьи. В среднем каждое занятие занимает от 30 до 45 минут. Однако это время может варьироваться, если ваш ребенок немного продвинулся в практическом проекте или ему нужно немного больше времени для отработки навыков. В обычный день ваш ученик потратит от 5 до 10 минут на повторение ранее изученных концепций, примет участие в увлекательном практическом занятии, знакомящем с новой концепцией, а затем применит новую концепцию, работая с практическими рабочими листами. Вам также нужно будет собрать некоторые обычные предметы домашнего обихода и купить несколько обычных математических манипулятивных предметов, чтобы в полной мере использовать этот курс. Обычные предметы домашнего обихода включают такие вещи, как сухие бобы для счета. Математические манипуляции включают такие элементы, как набор десятичных блоков. Полный список доступен для каждого класса, а материалы повторно используются в разных классах в зависимости от изучаемых понятий.
Что включено?
Учебное пособие по математике, уровень 3 и ключи ответов
Это учебное пособие и ключ к ответу для Изучение творчества с помощью математики s, уровень 3.
Учебник по математике для учащихся 3-го уровня и рабочая тетрадь
Изучение творчества с помощью математики, уровень 3 Учебник и рабочая тетрадь «Все в одном» со спиральным переплетом была разработана, чтобы побудить вашего ребенка к восхождению на новые высоты в радостном путешествии, открывающем новые вещи о мире и его Творце. На уровне 3 учащиеся изучают сложение, вычитание, умножение, деление, сбор данных и построение графиков, дроби и геометрию. Эта практическая интерактивная учебная программа также побуждает вашего ребенка размышлять о творчестве на новом уровне. Обратите внимание, что эта учебная программа делает , а не , включает руководство по обучению и ключ для ответов.
Обратите внимание, что эта учебная программа делает , а не , включает руководство по обучению и ключ для ответов.
Концептуальные уроки: KEMS — Национальная сеть обучения
Перейти к содержимомуУроки, основанные на концепциях: KEMSEvelyn Dufner2022-06-30T18:00:18-04:00
Ключевые элементы успешного обучения математике (KEMS)
Каждый уровень обучения KEMS состоит из концептуальных уроков, которые поддерживают обучение с использованием нескольких представления для развития глубокого концептуального понимания. Эти уроки предназначены для работы в сочетании с любой математической программой. Издание KEMS для учителей включает блоки для моделирования, которые служат руководством для учителей при обучении от конкретного к абстрактному. На протяжении всего урока учащиеся работают совместно и получают значимый опыт работы с концептом на конкретно-графическом-словесном и абстрактном уровнях. Этот процесс способствует обучению учащихся и помогает учащимся увидеть важную связь между несколькими представлениями. Учителям выдаются карты и модули для размещения всей информации, которая им понадобится для поддержки их обучения.
Этот процесс способствует обучению учащихся и помогает учащимся увидеть важную связь между несколькими представлениями. Учителям выдаются карты и модули для размещения всей информации, которая им понадобится для поддержки их обучения.
Раскрытие возможностей KEMS:
- Студенты строят концептуальное понимание путем исследования.
- Учащиеся устанавливают связи о своем обучении, используя манипуляции, графические изображения и диаграммы.
- Учащиеся проходят реальную практику и применяют решения с помощью SOLVE, парадигмы решения проблем NTN.
- Учащиеся учатся систематизировать , а объясняют свои мысли о математических концепциях, используя графические органайзеры, таблицы и диаграммы.
- Учащиеся рассказывают о своем математическом мышлении в совместных учебных группах, участвуя в увлекательных учебных мероприятиях.
- Студенты участвуют в содержательной практике.

- Учащиеся могут продемонстрировать понимание с помощью мини-оценки, которая может ежедневно предоставлять учителям данные формирующей оценки и стандартные вопросы.
Доступные ресурсы
Чтобы связаться с нами напрямую, используйте следующую информацию:
Телефон : 1-855-NTN-MATH
Время работы : 8:00 – 17:00 EST
Адрес : PO Box 36,
Summerfield, NC для получения номера
9000 Бесплатное домашнее задание
Посмотреть обзорное видео
Посмотреть видео урока
Каковы ключевые элементы успеха в математике?
Национальная учебная сеть предоставляет ресурсы для конкретных классов под названием «Ключевые элементы успеха в математике» — KEMS для 3–8 классов. Каждый уровень обучения состоит из уроков, которые поддерживают обучение, помогая формировать концептуальное понимание содержания каждого уровня, соответствующего стандарту. к СССС. Учительское издание для этого ресурса включает блоки для моделирования на протяжении каждого урока. Эти блоки моделирования служат руководством для учителей, когда они шаг за шагом продвигаются по процессу построения концептуального понимания. На протяжении всего урока учащиеся получают осмысленный опыт работы с понятием на конкретно-образно-словесном и абстрактном уровнях. Этот опыт помогает формировать учебный опыт и помогает учащимся увидеть важные связи между представлениями. Ключевые слова из математического словаря интегрированы на протяжении всего урока, чтобы помочь учащимся установить связи с ранее изученными понятиями. Коробки для моделирования также демонстрируются в видеороликах онлайн-уроков, размещенных на веб-сайте NTN www.ntnmath.com, вместе с электронной копией конспектов уроков из Издания для учителей 9.0005
к СССС. Учительское издание для этого ресурса включает блоки для моделирования на протяжении каждого урока. Эти блоки моделирования служат руководством для учителей, когда они шаг за шагом продвигаются по процессу построения концептуального понимания. На протяжении всего урока учащиеся получают осмысленный опыт работы с понятием на конкретно-образно-словесном и абстрактном уровнях. Этот опыт помогает формировать учебный опыт и помогает учащимся увидеть важные связи между представлениями. Ключевые слова из математического словаря интегрированы на протяжении всего урока, чтобы помочь учащимся установить связи с ранее изученными понятиями. Коробки для моделирования также демонстрируются в видеороликах онлайн-уроков, размещенных на веб-сайте NTN www.ntnmath.com, вместе с электронной копией конспектов уроков из Издания для учителей 9.0005
РЕШЕНИЕ задач (пятиступенчатая парадигма решения проблем):
Каждая задача открывается и закрывается задачей РЕШИТЬ, чтобы установить обучение на день, используя шаг «S», и завершить урок, используя шаги «OLVE». Это способствует применению концепции на реальном примере.
Это способствует применению концепции на реальном примере.
Манипуляторы:
В комплект KEMS входят все манипуляторы, необходимые для проведения уроков, чтобы учащиеся могли получить опыт моделирования с помощью математики.
Графические органайзеры:
Инструкции и рекомендации по использованию графических органайзеров включены в уроки.
Увлекательные занятия:
Большинство уроков включают в себя игру или задание, которое позволит учащимся отработать концепцию урока и навыки. Включены инструкции учителя, а занятия также дают возможность критически мыслить и общаться с другими, чтобы защитить и объяснить свое мышление.
Практика домашних заданий:
Каждый урок KEMS включает в себя домашние задания, которые можно использовать для закрепления обучения на протяжении всего раздела.
Викторины:
Каждый урок KEMS включает в себя 10 вопросов викторины, чтобы дать учителям возможность для постоянной формирующей оценки.
Дополнительные материалы
Национальная сеть обучения разработала дополнительные материалы для поддержки уроков KEMS и методологий Национальной сети обучения.
КАРТЫ УРОВНЕЙ (необязательно):
Каждая Карта уровней обучения разделена на 12 модулей. MAP может использоваться для долгосрочного планирования и определяет уроки KEMS, которые подходят для каждого модуля на основе общих базовых стандартов. Ежедневные цели обучения включены.
Модули уровня обучения (необязательно):
Каждый уровень обучения KEMS состоит из 12 модулей. Модули предназначены для помощи в планировании уроков и предоставления учителям различных ресурсов для поддержки уроков KEMS. Каждый модуль содержит следующее:
- Тема или большая идея модуля
- Словарь для модуля
- Предварительное обучение
- Основные вопросы, компетенции и распространенные заблуждения
- Список уроков KEMS для модулей, который включает информацию о дополнительных занятиях и викторинах.
- Ссылки на стандартные соответствующие практические задания.
- Вопросы, которые напрямую соответствуют стандартам.
Оценки модулей на уровне класса:
Национальная сеть обучения разработала набор из двенадцати формирующих оценок модулей для 3–8 классов, чтобы помочь классным руководителям, тренерам-инструкторам и администраторам контролировать успеваемость.
- Целью оценки модуля NTN является предоставление информации классному учителю, учащимся и другому школьному персоналу о понимании и применении учащимися стандартов/концепций из модуля. Поскольку оценивание является неотъемлемой частью цикла обучения, обратная связь от модульных оценок NTN помогает учителям анализировать, размышлять и принимать меры для поддержки обучения учащихся.
- Каждая модульная оценка состоит из трех разделов: часть 1, часть 2 и часть 3 с 13 вопросами с несколькими вариантами ответов и 3 вопросами с открытыми ответами, что в сумме дает 20 баллов.
 Дизайн модульного оценивания ссылается на основные, вспомогательные и дополнительные стандарты, а также на типы вопросов (открытые и с множественным выбором), которые учащиеся увидят при оценивании в конце класса.
Дизайн модульного оценивания ссылается на основные, вспомогательные и дополнительные стандарты, а также на типы вопросов (открытые и с множественным выбором), которые учащиеся увидят при оценивании в конце класса. - Оценка модулей может использоваться в классе различными способами: в качестве предварительной оценки для определения предшествующего опыта и/или понимания учащимися понятий раздела, в качестве последующей оценки для повторной оценки учащихся по конкретным предметам. стандарты или для моделирования ожиданий для вопросов с открытым ответом.
Другие важные примечания:
- KEMS 3 класса включает в себя программу Fact Masters для сложения и вычитания, чтобы у учителей были ресурсы для работы с учащимися, которым может потребоваться дополнительное повторение и подкрепление фактов сложения и вычитания.
- KEMS 4 класса включает в себя программу Fact Masters для умножения и деления, чтобы у учителей были ресурсы для работы с учащимися, которым может потребоваться дополнительный обзор и закрепление фактов об умножении и делении.

- KEMS Grade 6 включает в себя урок «Набор дробей» для ознакомления с понятиями дробей с учащимися перед делением дробей на дроби.
Ресурсы для конкретных классов, поддерживающие обучение и концептуальное понимание
Fact MastersПовышайте беглость учащихся к основным математическим фактам, устанавливая понимание смысла фактов
05
05
9 Fact Masters Видео по запросу
Видеоматериалы о профессиональном развитии для конкретных классов с ключевыми математическими понятиями
Заполните мою онлайн-форму.
Ссылка для загрузки страницы Перейти к началуМатематика
Ожидания в учебной программе по математике разделены на шесть отдельных, но связанных направлений: A. Социально-эмоциональное обучение (SEL) Навыки в области математики и математических процессов; Б. Номер; С. Алгебра; Д. Данные; E. Пространственное чувство; и F. Финансовая грамотность.
Финансовая грамотность.
Программа для всех классов разработана таким образом, чтобы учащиеся заложили прочную основу по математике и развили положительную математическую идентичность, соединяя и применяя математические концепции различными способами. Для поддержки этого процесса учителя используют имеющиеся у учащихся знания, навыки и опыт; интегрировать концепции из разных направлений; и часто применяют математику, которую изучают учащиеся, к типам ситуаций, которые могут возникнуть за пределами классной комнаты.
Следующая диаграмма показывает поток обучения в рамках учебной программы и взаимосвязь между ее различными компонентами.
| Прядь B. Номер | Strand C. Алгебра | Прядь D. Данные | Прядь E. Пространственное чувство | Strand F. Финансовая грамотность |
В1.
В2. Операции
| С1. Паттерны и отношения
С2. Уравнения и неравенства
С3. Код
С4. Математическое моделирование | Д1. Грамотность данных
Д2. Вероятность | Е1. Геометрические и пространственные рассуждения
Е2.
| С 1 по 8 классы: Ф1. Деньги
Классы с 4 по 8: Ф1. Финансы
|
Имеются убедительные доказательства того, что развитие социально-эмоциональных навыков обучения в школе способствует общему здоровью и благополучию всех учащихся, а также их успешной успеваемости. Он также поддерживает положительное психическое здоровье, а также способность учащихся учиться, повышать устойчивость и развиваться. Развитие социально-эмоциональных навыков обучения в школьные годы поможет всем учащимся стать более здоровыми и успешными в повседневной жизни и стать полезными членами общества. Во всех классах обучение, связанное с ожиданиями в этом направлении, происходит в контексте обучения, связанного с другими пятью направлениями, и оценивается и оценивается в этих контекстах.
Во всех классах обучение, связанное с ожиданиями в этом направлении, происходит в контексте обучения, связанного с другими пятью направлениями, и оценивается и оценивается в этих контекстах.
Социально-эмоциональные навыки обучения можно развивать по всем предметам учебной программы, включая математику, а также во время различных школьных мероприятий, дома и в обществе. Эти навыки помогают учащимся в понимании математических концепций и в применении математических процессов, которые являются ключевыми для изучения и выполнения математических действий. Они помогают всем учащимся – да и вообще всем учащимся, включая педагогов и родителей – развивать уверенность в себе, справляться с трудностями и критически мыслить. Это, в свою очередь, позволяет им улучшать и демонстрировать математические знания, концепции и навыки в различных ситуациях. Социально-эмоциональные навыки обучения помогают каждому учащемуся развить положительную идентичность как способного «ученика математики».
Во всех классах направление А включает одно общее ожидание и таблицу, в которой перечислены социально-эмоциональные навыки обучения, математические процессы и ожидаемые результаты, когда учащиеся используют эти навыки и процессы, чтобы продемонстрировать свое понимание и применение математического содержания. Развитие обучения от класса к классу показано в примерах, которые связаны с каждым социально-эмоциональным навыком обучения в каждом классе и подчеркивают, как навыки могут быть интегрированы с обучением в других пяти направлениях. Содержание и применение обучения меняются по мере развития и взросления учащихся. Применение учащимися социально-эмоциональных навыков обучения и математических процессов должно быть оценено и оценено как часть их достижения общих ожиданий в каждом из направлений для каждого класса.
Развитие обучения от класса к классу показано в примерах, которые связаны с каждым социально-эмоциональным навыком обучения в каждом классе и подчеркивают, как навыки могут быть интегрированы с обучением в других пяти направлениях. Содержание и применение обучения меняются по мере развития и взросления учащихся. Применение учащимися социально-эмоциональных навыков обучения и математических процессов должно быть оценено и оценено как часть их достижения общих ожиданий в каждом из направлений для каждого класса.
Диаграмма в группе А описывает социально-эмоциональные навыки обучения, математические процессы и ожидаемые результаты, когда учащиеся применяют одновременно знания и занятия по математике. Взаимодействие навыков и процессов является переменным: различные социально-эмоциональные навыки обучения могут применяться в разное время в связи с различными математическими процессами для достижения результатов.
Социально-эмоциональные навыки обучения: ключевые компоненты и примеры стратегий
В следующей таблице представлена подробная информация о каждом из навыков, включая ключевые идеи и примеры стратегий.
Навыки Какие навыки? Как они помогают? Как они выглядят в математике? | Ключевые компоненты и примеры стратегий |
Идентификация и управление эмоциями Студенты часто испытывают целый ряд эмоций в течение дня в школе. Они могут чувствовать себя счастливыми, грустными, злыми, разочарованными или взволнованными, или любое количество эмоций в сочетании. Учащимся, и особенно детям младшего возраста, может быть трудно определить и правильно выразить свои чувства. Обучение распознаванию различных эмоций и эффективному управлению ими может помочь учащимся функционировать и взаимодействовать более успешно. Когда учащиеся понимают влияние мыслей и эмоций на поведение, они могут улучшить качество своего взаимодействия. В математике, по мере того как они изучают новые математические концепции и взаимодействуют с другими при решении задач, учащиеся имеют много возможностей для развития осознания своих эмоций и использования коммуникативных навыков, чтобы выражать свои чувства и конструктивно реагировать, когда они распознают эмоции других. |
|
Управление стрессом и преодоление стресса Каждый день учащиеся сталкиваются с целым рядом проблем, которые могут способствовать чувству стресса. По мере того, как они учатся управлению стрессом и навыкам преодоления стресса, они приходят к пониманию того, что стресс является частью жизни и что с ним можно справиться. Мы можем научиться реагировать на вызовы, которые позволят нам «прийти в себя» и, таким образом, укрепить устойчивость перед лицом жизненных препятствий. Со временем, при поддержке, практике, обратной связи, размышлениях и опыте, учащиеся начинают создавать набор личных стратегий преодоления трудностей, которые они могут носить с собой на протяжении всей жизни. В математике учащиеся решают сложные задачи, понимая, что их находчивость в использовании стратегий выживания помогает им повысить личную устойчивость. Мы можем научиться реагировать на вызовы, которые позволят нам «прийти в себя» и, таким образом, укрепить устойчивость перед лицом жизненных препятствий. Со временем, при поддержке, практике, обратной связи, размышлениях и опыте, учащиеся начинают создавать набор личных стратегий преодоления трудностей, которые они могут носить с собой на протяжении всей жизни. В математике учащиеся решают сложные задачи, понимая, что их находчивость в использовании стратегий выживания помогает им повысить личную устойчивость. |
|
Позитивная мотивация и настойчивость Навыки положительной мотивации и настойчивости помогают учащимся «дальновидно смотреть» и сохранять надежду, даже когда их личные и / или непосредственные обстоятельства трудны. При регулярном использовании практики и привычки ума, которые способствуют положительной мотивации, помогают учащимся подходить к жизненным проблемам с оптимистичным и позитивным мышлением и пониманием того, что за большинством успехов стоит борьба и что повторные усилия могут привести к успеху. Эти практики включают в себя замечание сильных сторон и положительных аспектов опыта, переосмысление негативных мыслей, выражение благодарности, практику оптимизма и практику настойчивости — оценку ценности практики, совершения ошибок и процесса обучения. В математике учащиеся имеют регулярные возможности применять эти методы при решении задач и развивают способность учиться на ошибках как часть учебного процесса. При регулярном использовании практики и привычки ума, которые способствуют положительной мотивации, помогают учащимся подходить к жизненным проблемам с оптимистичным и позитивным мышлением и пониманием того, что за большинством успехов стоит борьба и что повторные усилия могут привести к успеху. Эти практики включают в себя замечание сильных сторон и положительных аспектов опыта, переосмысление негативных мыслей, выражение благодарности, практику оптимизма и практику настойчивости — оценку ценности практики, совершения ошибок и процесса обучения. В математике учащиеся имеют регулярные возможности применять эти методы при решении задач и развивают способность учиться на ошибках как часть учебного процесса. |
|
Навыки здоровых отношений Когда учащиеся позитивно и осмысленно взаимодействуют с другими, взаимно уважая разнообразие мыслей и выражений, усиливается их чувство принадлежности к школе и сообществу. Изучение навыков здоровых отношений помогает учащимся установить положительные модели общения и вдохновляет на здоровые отношения сотрудничества. Эти навыки включают в себя способность понимать и ценить точку зрения другого человека, сопереживать другим, внимательно слушать, быть настойчивым и применять навыки разрешения конфликтов. В математике учащиеся имеют возможность развивать и практиковать навыки, которые поддерживают позитивное взаимодействие с другими, когда они работают вместе в небольших группах или в парах, чтобы решать математические задачи и решать задачи. Развитие этих навыков помогает учащимся общаться с учителями, сверстниками и семьей о математике, ценя красоту и чудо математики. |
|
Самосознание и чувство идентичности Знание того, кто мы есть, и наличие чувства цели и смысла в нашей жизни позволяет нам функционировать в мире как самосознательные личности. Наше чувство идентичности позволяет нам делать выбор, который поддерживает наше благополучие, и позволяет нам общаться и иметь чувство принадлежности к различным культурным и социальным сообществам. Педагоги должны учитывать, что для учащихся из числа коренных народов, метисов и инуитов термин «чувство идентичности и принадлежности» может также означать принадлежность к определенному сообществу и/или нации и идентификацию с ним. Навыки самосознания и идентичности помогают учащимся понять, кто они есть, их сильные стороны, трудности, предпочтения, интересы, ценности и амбиции, а также то, как их социальный и культурный контекст повлиял на них. В математике, осваивая новые навыки, учащиеся используют навыки самосознания, чтобы следить за своим прогрессом и определять свои сильные стороны; в процессе они формируют свою личность как способные ученики по математике. Педагоги играют ключевую роль в утверждении того, что все — учащиеся, преподаватели и родители — изучают математику, а также в разделении понимания красоты и чудес математики. Наше чувство идентичности позволяет нам делать выбор, который поддерживает наше благополучие, и позволяет нам общаться и иметь чувство принадлежности к различным культурным и социальным сообществам. Педагоги должны учитывать, что для учащихся из числа коренных народов, метисов и инуитов термин «чувство идентичности и принадлежности» может также означать принадлежность к определенному сообществу и/или нации и идентификацию с ним. Навыки самосознания и идентичности помогают учащимся понять, кто они есть, их сильные стороны, трудности, предпочтения, интересы, ценности и амбиции, а также то, как их социальный и культурный контекст повлиял на них. В математике, осваивая новые навыки, учащиеся используют навыки самосознания, чтобы следить за своим прогрессом и определять свои сильные стороны; в процессе они формируют свою личность как способные ученики по математике. Педагоги играют ключевую роль в утверждении того, что все — учащиеся, преподаватели и родители — изучают математику, а также в разделении понимания красоты и чудес математики. |
|
Критическое и творческое мышление Навыки критического и творческого мышления позволяют нам выносить обоснованные суждения и решения на основе ясного и полного понимания идей и ситуаций и их последствий в различных условиях и контекстах. Студенты учатся задавать вопросы, интерпретировать, предсказывать, анализировать, синтезировать, выявлять предвзятость и различать альтернативы. Они практикуются в установлении связей, постановке целей, создании планов, принятии и оценке решений, а также в анализе и решении проблем, для которых может не быть четко определенных ответов. Исполнительные функциональные навыки — навыки и процессы, которые позволяют нам проявлять инициативу, сосредотачиваться, планировать, сохранять и передавать знания, а также определять приоритеты — также поддерживают критическое и творческое мышление. Во всех аспектах учебной программы по математике учащиеся имеют возможность развивать навыки критического и творческого мышления. Студенты имеют возможность опираться на предыдущие знания, углубляться и устанавливать личные связи с помощью реальных приложений. Они практикуются в установлении связей, постановке целей, создании планов, принятии и оценке решений, а также в анализе и решении проблем, для которых может не быть четко определенных ответов. Исполнительные функциональные навыки — навыки и процессы, которые позволяют нам проявлять инициативу, сосредотачиваться, планировать, сохранять и передавать знания, а также определять приоритеты — также поддерживают критическое и творческое мышление. Во всех аспектах учебной программы по математике учащиеся имеют возможность развивать навыки критического и творческого мышления. Студенты имеют возможность опираться на предыдущие знания, углубляться и устанавливать личные связи с помощью реальных приложений. |
|
Понимание того, как работают числа, лежит в основе многих аспектов математики. Распознавание и понимание числовых свойств является основой для понимания таких разделов математики, как арифметика и алгебра. В разделе «Числа» учащиеся с 1 по 8 классы узнают о различных типах чисел и о том, как эти числа ведут себя при применении к ним различных операций.
Распознавание и понимание числовых свойств является основой для понимания таких разделов математики, как арифметика и алгебра. В разделе «Числа» учащиеся с 1 по 8 классы узнают о различных типах чисел и о том, как эти числа ведут себя при применении к ним различных операций.
Жизненно важным аспектом работы с числами в начальных классах является развитие того, что часто называют числовым чувством, когда учащиеся развивают способность гибко связывать числа и связывать вычисления. Учащиеся, у которых развито чувство числа, регулярно используют числовые отношения, чтобы понять смысл вычислений и оценить обоснованность чисел, используемых для описания ситуаций, например, в средствах массовой информации.
Учащиеся учатся эффективно считать, а затем свободно владеют математическими фактами, чтобы эффективно и точно выполнять вычисления в уме или с помощью алгоритмов на бумаге. Это направление основано на убеждении, что важно развивать автоматизм, т. е. способность использовать математические навыки или выполнять математические действия практически без умственных усилий. Автоматизм с математическими фактами позволяет учащимся участвовать в критическом мышлении и решении проблем.
Автоматизм с математическими фактами позволяет учащимся участвовать в критическом мышлении и решении проблем.
Большинство учащихся изучают математические факты постепенно в течение нескольких лет, подключаясь к предшествующим знаниям, используя инструменты и калькуляторы. Мастерство приходит с практикой, а практика помогает развить беглость и глубину речи. Учащиеся опираются на свою способность применять математические факты при работе с алгебраическими выражениями, уравнениями и неравенствами. Умственные математические способности включают в себя способность выполнять математические вычисления, не полагаясь на карандаш и бумагу. Они позволяют учащимся оценивать ответы на расчеты и, таким образом, точно и эффективно работать над повседневными задачами и оценивать обоснованность ответов, к которым они пришли с помощью вычислений. Чтобы разработать эффективные стратегии ментальной математики, все учащиеся должны иметь сильные навыки в смысле чисел и твердое концептуальное понимание операций.
Несмотря на то, что отдельные учащиеся могут прогрессировать с разной скоростью, в целом, факты сложения/вычитания должны быть усвоены к концу 3-го класса, а факты умножения/деления – к концу 5-го класса. Однако все учащиеся должны продолжать узнать об эффективных стратегиях, а также практиковать и расширять свое мастерство в операциях в классах и в контексте обучения по всем направлениям учебной программы по математике.
В этом направлении учащиеся развивают алгебраические рассуждения, работая с шаблонами, переменными, выражениями, уравнениями, неравенствами, кодированием и процессом математического моделирования.
По мере прохождения классов учащиеся изучают различные закономерности, в том числе и те, что встречаются в реальной жизни. Учащиеся учатся выявлять закономерности в числовых и нечисловых закономерностях и классифицировать их на основе характеристик этих закономерностей. Они создают и переводят шаблоны, используя различные представления. Учащиеся определяют правила шаблонов для различных шаблонов, чтобы расширить их, сделать близкие и дальние прогнозы и определить недостающие элементы. Они развивают рекурсивное и функциональное мышление, а также аддитивное и мультипликативное мышление, когда работают с линейными паттернами, и используют это мышление для разработки общих терминов паттернов для поиска неизвестных значений. Понимание закономерностей и определение взаимосвязи между двумя переменными во многом связано с наукой и лежит в основе дальнейшей математики. В начальных классах учащиеся сосредотачиваются на понимании того, какие величины остаются неизменными, а какие могут изменяться в повседневных условиях, и на том, как установить равенство между числовыми выражениями. В младших и средних классах учащиеся работают с переменными в алгебраических выражениях, уравнениях и неравенствах в различных контекстах.
Они развивают рекурсивное и функциональное мышление, а также аддитивное и мультипликативное мышление, когда работают с линейными паттернами, и используют это мышление для разработки общих терминов паттернов для поиска неизвестных значений. Понимание закономерностей и определение взаимосвязи между двумя переменными во многом связано с наукой и лежит в основе дальнейшей математики. В начальных классах учащиеся сосредотачиваются на понимании того, какие величины остаются неизменными, а какие могут изменяться в повседневных условиях, и на том, как установить равенство между числовыми выражениями. В младших и средних классах учащиеся работают с переменными в алгебраических выражениях, уравнениях и неравенствах в различных контекстах.
По мере того, как учащиеся продвигаются по классам, их опыт кодирования также улучшается: от представления движений в сетке до решения задач, связанных с оптимизацией, и до манипулирования моделями, чтобы найти, какая из них лучше всего соответствует данным, с которыми они работают, чтобы делать прогнозы. Кодирование может быть включено во все направления и дает учащимся возможность применять и расширять свое математическое мышление, рассуждения и общение.
Кодирование может быть включено во все направления и дает учащимся возможность применять и расширять свое математическое мышление, рассуждения и общение.
Учащиеся всех классов также участвуют в процессе математического моделирования.
Процесс математического моделирования
Математическое моделирование обеспечивает подлинную связь с реальными жизненными ситуациями. Процесс начинается с плохо определенных, часто запутанных реальных проблем, которые могут иметь несколько разных решений, и все они являются правильными. Математическое моделирование требует от моделиста критического и творческого подхода, а также принятия решений, предположений и решений. В ходе этого процесса они создают математическую модель, описывающую ситуацию с помощью математических концепций и языка, которую можно использовать для решения проблемы или принятия решений, а также для углубления понимания математических концепций.
Процесс математического моделирования состоит из четырех ключевых компонентов, которые взаимосвязаны и применяются итеративно, когда учащиеся могут перемещаться между ними, а также возвращаться к каждому из четырех компонентов по мере изменения условий для наблюдения за новыми результатами до тех пор, пока модель готова к совместному использованию и действию. При прохождении этих компонентов по мере необходимости применяются социально-эмоциональные навыки обучения и математические процессы.
При прохождении этих компонентов по мере необходимости применяются социально-эмоциональные навыки обучения и математические процессы.
1. Понять проблему
- На какие вопросы нужно ответить?
- Какая информация необходима?
2. Проанализируйте ситуацию
- Какие предположения я делаю о ситуации?
- Что меняется, что остается прежним?
3. Создание математической модели
- Какие представления, инструменты, технологии и стратегии помогут построить модель?
- Какие математические знания, понятия и навыки могут быть задействованы?
4. Проанализируйте и оцените модель
- Может ли эта модель обеспечить решение?
- Что такое альтернативные модели?
Связанные темы статистики и вероятности, которые рассматриваются в этом разделе, очень важны для реальной жизни. Общественность бомбардируется данными через рекламу, опросы общественного мнения, политику, демографические тенденции и научные открытия, и это лишь некоторые из них. Таким образом, одним из ключевых направлений этого направления является поддержка учащихся в развитии навыков критического мышления на протяжении всего развития их грамотности в отношении данных, чтобы они могли анализировать, синтезировать, понимать, генерировать и использовать данные как в качестве потребителей, так и производителей.
Таким образом, одним из ключевых направлений этого направления является поддержка учащихся в развитии навыков критического мышления на протяжении всего развития их грамотности в отношении данных, чтобы они могли анализировать, синтезировать, понимать, генерировать и использовать данные как в качестве потребителей, так и производителей.
Основной целью сбора и систематизации данных является сбор информации для ответа на вопросы. Когда вопросы стимулируют любопытство учащихся, они начинают собирать, систематизировать и интерпретировать данные, которые дают ответы на их вопросы. Соответствующие вопросы часто возникают в ходе дискуссий в классе; классные мероприятия, вопросы и тематические мероприятия; и темы в различных предметных областях. Когда учащиеся собирают и систематизируют данные, у них есть возможность больше узнать о себе, своем окружении, проблемах в своей школе или сообществе и так далее. Учебная деятельность должна помочь учащимся понять процессы, связанные с формулированием вопросов, поиском соответствующей информации и осмысленной организацией этой информации. Вовлечение студентов в сбор и организацию данных позволяет им участвовать в принятии решений, которые требуются на разных этапах процесса.
Вовлечение студентов в сбор и организацию данных позволяет им участвовать в принятии решений, которые требуются на разных этапах процесса.
По мере прохождения классов у учащихся появляется понимание качественных данных, а также дискретных и непрерывных количественных данных, и они используют это понимание для выбора подходящих способов организации и отображения данных. Учащиеся изучают основы статистики и развивают навыки визуализации и критического анализа данных, включая выявление любых возможных систематических ошибок в данных. Начиная с младших классов, учащиеся делают осознанный выбор при создании инфографики, чтобы представить ключевую информацию о наборе данных для конкретной аудитории и участвовать в критической интерпретации данных. Кроме того, студенты узнают, как использовать данные, чтобы привести убедительные аргументы по интересующим вопросам.
Изучение этого направления также помогает учащимся развивать вероятностные рассуждения. По мере того, как учащиеся продвигаются по классам, они начинают понимать взаимосвязь между вероятностью и данными, а также то, как данные используются для прогнозирования населения. Интуитивное понимание вероятности у учащихся формируется в младших классах, чтобы помочь им связать свой предыдущий опыт с вероятностью в повседневной жизни, начиная с простого понимания того, что некоторые события могут произойти, а другие маловероятны. Со временем учащиеся начинают понимать и представлять эти вероятности в виде дробей, десятичных знаков и процентов. С 5 по 8 класс учащиеся сравнивают экспериментальные вероятности, связанные с независимыми и зависимыми событиями, со своими теоретическими вероятностями и используют эти меры для предсказания событий.
Интуитивное понимание вероятности у учащихся формируется в младших классах, чтобы помочь им связать свой предыдущий опыт с вероятностью в повседневной жизни, начиная с простого понимания того, что некоторые события могут произойти, а другие маловероятны. Со временем учащиеся начинают понимать и представлять эти вероятности в виде дробей, десятичных знаков и процентов. С 5 по 8 класс учащиеся сравнивают экспериментальные вероятности, связанные с независимыми и зависимыми событиями, со своими теоретическими вероятностями и используют эти меры для предсказания событий.
В этом разделе сочетаются области геометрии и измерения, чтобы подчеркнуть взаимосвязь между двумя областями и подчеркнуть роль пространственного мышления в их развитии. Обучение в этом направлении предоставляет учащимся язык и инструменты для анализа, сравнения, описания и навигации по окружающему миру. Это ворота к профессиям в других дисциплинах STEM (наука, технология, инженерия и математика) и формирует базовые навыки, необходимые для строительства, архитектуры, инженерии, исследований и дизайна.
На этом этапе учащиеся анализируют свойства фигур — элементы, которые определяют форму и делают ее уникальной, — и используют эти свойства для определения, сравнения и построения форм и объектов, а также для изучения взаимосвязей между свойствами. Студенты начинают с интуиции в отношении своего окружения и объектов в нем и учатся визуализировать объекты с разных точек зрения. Со временем у учащихся развивается все более сложное понимание размера, формы, местоположения, движения и изменений как в двух, так и в трех измерениях. Они понимают и выбирают соответствующие единицы для оценки, измерения и сравнения атрибутов, а также используют соответствующие инструменты для проведения измерений. Они применяют свое понимание отношений между формами и измерениями для разработки формул для расчета длины, площади, объема и многого другого.
Всем учащимся Онтарио необходимы навыки и знания, чтобы взять на себя ответственность за управление своим личным финансовым благополучием с уверенностью, компетентностью, критическим и сострадательным отношением к окружающему миру.
Финансовая грамотность является отдельным направлением в программе начальной математики. Финансовая грамотность — это больше, чем просто знание денег и финансовых вопросов и умение работать с этими знаниями. Учащиеся развивают уверенность и способность успешно применять необходимые знания, концепции и навыки в различных соответствующих контекстах реальной жизни и для различных целей. Они также развивают способность принимать обоснованные решения как потребители и граждане, принимая во внимание этические, социальные, экологические и личные аспекты этих решений.
В классах с 1 по 3 учащиеся демонстрируют понимание ценности и использования денег, распознавая канадские монеты и банкноты, представляющие различные суммы, и вычисляя сдачу в простых транзакциях. В 4–8 классах учащиеся расширяют свое обучение, приобретая знания, концепции и навыки, необходимые для принятия обоснованных финансовых решений, соответствующих их жизненному опыту, и планирования простых примерных бюджетов. Учащиеся начинают развивать потребительское и гражданское сознание в младших и средних классах. Связываясь с тем, что они изучают в разделе «Медиаграмотность» языковой программы, а также в программе социальных наук, истории и географии, учащиеся становятся информированными потребителями и узнают о более широких экономических системах в своих местных сообществах, сообществах в других глобальных контекстах, которые их семьи связаны с и за его пределами. Педагоги рассматривают и реагируют на ряд вопросов справедливости, связанных с разнообразными обстоятельствами и жизненным опытом учащихся и их семей.
Учащиеся начинают развивать потребительское и гражданское сознание в младших и средних классах. Связываясь с тем, что они изучают в разделе «Медиаграмотность» языковой программы, а также в программе социальных наук, истории и географии, учащиеся становятся информированными потребителями и узнают о более широких экономических системах в своих местных сообществах, сообществах в других глобальных контекстах, которые их семьи связаны с и за его пределами. Педагоги рассматривают и реагируют на ряд вопросов справедливости, связанных с разнообразными обстоятельствами и жизненным опытом учащихся и их семей.
Эта ветвь во многом связана с другими ветвями математики, такими как применение знаний, концепций и навыков, связанных с:
- числами и операциями для вычисления сдачи;
- процентов для расчета налога с продаж и процентов;
- математическое моделирование для понимания реальных финансовых ситуаций, включая финансовые приложения линейных ставок;
- расценок за единицу для сравнения товаров и услуг, а также математические вычисления в уме для быстрого определения тех, которые имеют наибольшую ценность;
- социально-эмоциональное обучение, чтобы стать уверенными и критически настроенными потребителями, а также настойчиво управлять своим финансовым благополучием.

Учебная программа по математике в начальных и неполных средних классах – Энциклопедия TIMSS 2015
Главная/Страны/САР Гонконг/Учебная программа по математике в начальных и неполных средних классах
средний уровень был введен в 2002 и 2001 годах соответственно. В дополнение к подчеркиванию важности приобретения предметных знаний и навыков, учебные программы по математике на уровне начального и младшего (младшего) среднего образования направлены на то, чтобы помочь учащимся развить общие навыки и сформировать положительное отношение к математике, а также сделать упор на надлежащее использование информационных технологий. 17Руководства по учебным программам по математике, опубликованные CDC, четко определяют цели начального и среднего математического образования. 18,19 Цели начальной программы по математике:
- Стимулировать интерес к изучению математики
- Помогите учащимся понять и усвоить основные математические понятия и вычислительные навыки
- Помогите учащимся развить творческие способности и способность думать, общаться и решать проблемы
- Помогите учащимся развить числовое и пространственное чувство, а также способность оценивать закономерности и структуры чисел и форм
- Повышение способности учащихся к обучению на протяжении всей жизни за счет базовых математических знаний
Учебная программа охватывает пять предметных областей на начальном уровне: числа; Форма и пространство; Измерение; обработка данных; и алгебра. 20 Алгебра вводится в 5 классе (начальный 5 класс). В приложении 1 представлены темы по математике, преподаваемые в каждой предметной области на начальном уровне.
20 Алгебра вводится в 5 классе (начальный 5 класс). В приложении 1 представлены темы по математике, преподаваемые в каждой предметной области на начальном уровне.
Приложение 1: Темы по математике, преподаваемые в начальной школе, 1–6 классы (1–6 классы начальной школы)
| Область содержимого | темы |
| Номер |
|
| Форма и пространство |
|
| Измерение |
|
| Обработка данных |
|
| Алгебра* |
|
| *Введено в 5 классе (5 класс) | |
Учебная программа средней школы по математике преследует следующие цели:
- Дать возможность учащимся развить навыки математического осмысления, исследования, рассуждения и общения, а также способность использовать математику для формулирования и решения задач в повседневной жизни, а также в математическом контексте
- Разрешить учащимся манипулировать числами, символами и другими математическими объектами
- Помогите учащимся развить чувство числа, символа и пространства, а также чувство меры и способность оценивать структуры и узоры
- Помогите учащимся развить позитивное отношение к математике и способность ценить эстетический характер и культурные аспекты математики
В младших классах средней школы учебная программа по математике дополнительно объединяет пять предметных областей, изучаемых в начальных классах, в три основных области обучения: число и алгебра; Измерение, форма и пространство; и обработка данных. 21 В приложении 2 представлены темы по математике, преподаваемые в каждой предметной области на уровне младшей (младшей) средней школы.
21 В приложении 2 представлены темы по математике, преподаваемые в каждой предметной области на уровне младшей (младшей) средней школы.
Приложение 2: Темы математики, преподаваемые на младших (младших) уровнях средней школы, 7–9 классы (1–3 классы средней школы)
| Область содержимого | темы |
| Числа и алгебра |
|
| Измерение, форма и пространство |
|
| Обработка данных |
|
‘;
number.

 Я хочу учиться. Я очень хочу учиться. Я готов к работе. Работаю!
Я хочу учиться. Я очень хочу учиться. Я готов к работе. Работаю!
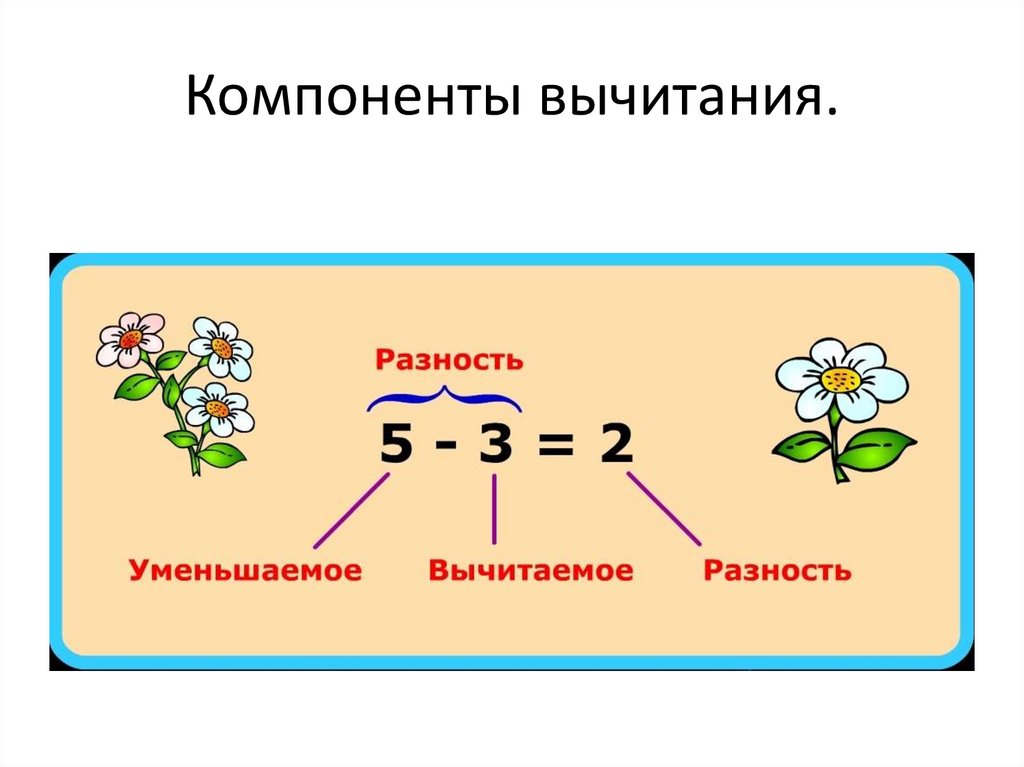
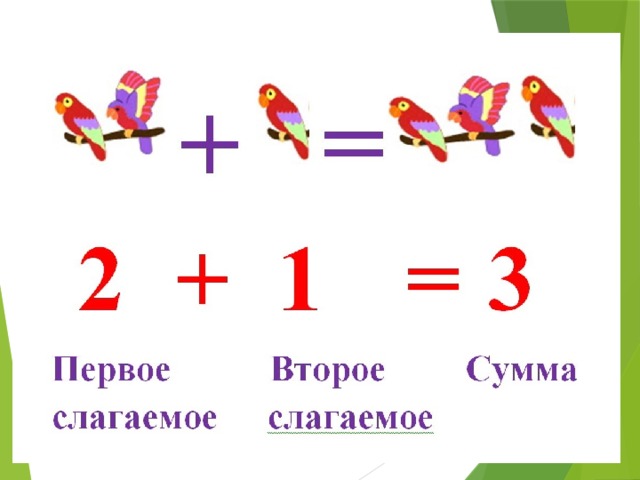 (Вычитаем)
(Вычитаем) )
)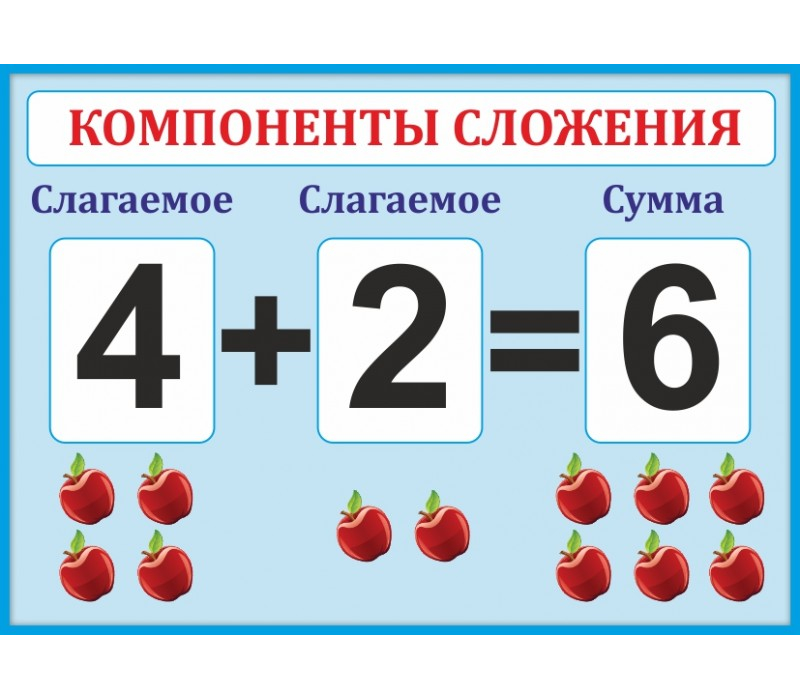 Сравните с первым. Можете ли что-нибудь отметить? (Точки отмечены разные, значит, результаты будут неравны.)
Сравните с первым. Можете ли что-нибудь отметить? (Точки отмечены разные, значит, результаты будут неравны.)



