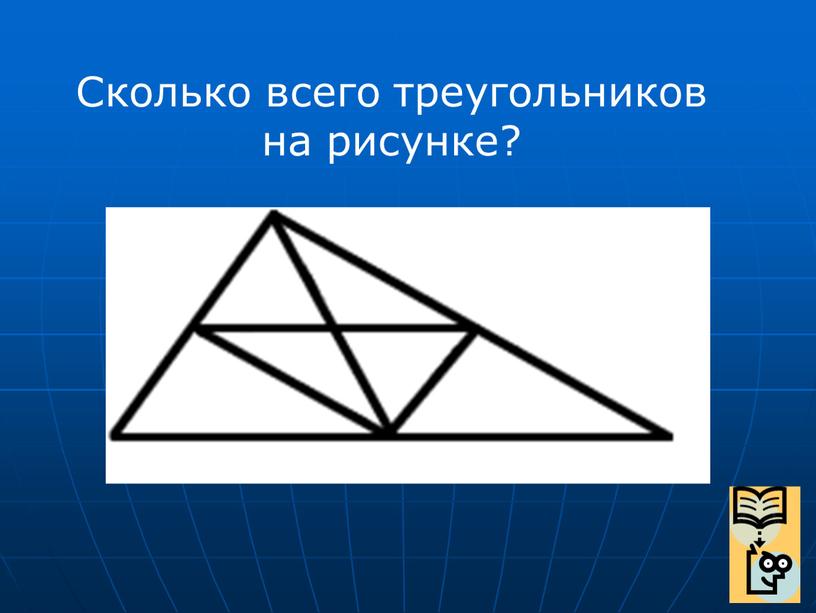
Треугольник на что похож: Что похоже на треугольник – презентация онлайн
Большая энциклопедия школьника
Большая энциклопедия школьникауникальное издание, содержащее весь свод знаний, необходимый ученикам младших классов. Для детей, собирающихся в 1-й класс, она послужит незаменимым помощником для подготовки к школе. В этой энциклопедии ребенок сможет найти любую интересующую его информацию, в понятном и простом для него изложении. Вы подбираете слова и определения для простых вещей, которые надо объяснить ребенку? Сомневаетесь в формулировках? Просто возьмите «Большую энциклопедию школьника» и найдите нужный ответ вместе с малышом!
Математика в стихах
Развитие речи
Азбука в картинках
Игры на развитие внимания
Как правильно выбрать школу
Ваш ребенок левша
Как готовить домашнее задание
Контрольные и экзамены
Большая энциклопедия школьника – это твой надёжный путеводитель в мире знаний.
| Ребенок не хочет учить буквы Ребенок не хочет учить буквы
– Понимаете, ведь надо что-то делать! – с тревогой говорила мне полная, хорошо одетая дама, едва умещающаяся на стуле. Ее ноги в аккуратных лодочках были плотно сжаты (юбка до середины колена казалась слегка коротковатой для такой монументальной фигуры), руки сложены на коленях. | Past continuous passive Страдательный залог образуется с помощью вспомогательного глагола ‘to be’. Страдательный залог глагола ‘to repair’ в группе ‘continuous’ : To be repaired = Быть исправленным. The road is being repaired = Дорогу чинят. The road is not being repaired = Дорогу не чинят. Is the road being repaired? = Чинят ли дорогу? The road was being repaired = Дорогу чинили. The road was not being repaired = Дорогу не чинили. Was the road being repaired? = Чинили ли дорогу? Страдательный … |
| Определение формулы органического вещества по его молярной массе Задание: Определить формулу углеводорода, если его молярная масса равна 78 г. | У У
ЗВУК (У).
1) Удобная буква!
Удобно в ней то,
Что можно на букву
Повесить пальто.
У – сучок,
В любом лесу
Ты увидишь букву У.
2) ФОНЕТИЧЕСКАЯ ЗАРЯДКА.
– Как воет волк! ( у – у – у )
3) ЗАДАНИЯ.
а) Подними руку, если услышишь звук (у):
паук, цветок, лужа, диван, стол, стул, голуби, курица. |
Ромб на что похож
Презентация была опубликована 4 года назад пользователемАнтон Шиловский
Похожие презентации
Презентация на тему: ” Найдем предметы, похожие на круг А что похоже на треугольник?” — Транскрипт:
4 Найдем предметы, похожие на круг
6 А что похоже на треугольник?
8 Где на картинке квадратные предметы?
10 Что похоже на овал?
12 Где на картинке прямоугольные предметы?
14 Здесь есть предметы, похожие на ромб. Где они?
Похожие презентации
Найдем предметы, похожие на круг А что похоже на треугольник?
Найдем предметы, похожие на круг А что похоже на треугольник?
КВАДРАТ КРУГ ПРЯМОУГОЛЬНИК ОВАЛ ТРЕУГОЛЬНИК РОМБ.
29.07.20151. Все эти предметы похожи на квадрат. Какие ещё предметы квадратной формы ты знаешь? 29. 07.20152.
07.20152.
ФИГУРЫ ОВАЛ ПРЯМОУГОЛЬНИК КРУГ ТРАПЕЦИЯ РОМБ.
Картинка 1 Картинка 2 Картинка 3 Картинка 4 Картинка 5.
37 92 74 22 19 53 49 55 26 37 19 49 26 92 74 53.
Форма 22 44 55 77 55. Посмотри на эти фигуры. Они все разные. Здесь ты узнаешь, как они называются, и выполнишь интересные задания. 24.07.20152.
? ? ? ? ? ? ? ВЫСОТА ? ? ? БИССЕКТРИСА ЕДИАНАМ ? ? ? ?
квадрат прямоугольник равнобедренный треугольник.
Автор: Ходжаян В.Н. МОУ СОШ 2 ст Старощербиновская.
Презентация «Геометрические фигуры» к ООД по ФЭМП для детей 5-7 лет.
Почему квадрат? В. А. Дегтярь – Новоазовская ОШ ı-ııı ст.2.
основные фигуры квадрат прямоугольник треугольник.
Открытый урок на тему «Геометрические фигуры» учительницы 1 «З» класса полной средней школы4 г.Гянджа Байрамовой Сабины. 22 44 55 77 55.
НА ЧТО ПОХОЖ КРУГ? Это круг Это – Земля, она тоже круглая.
Лазарева Лидия Андреевна, учитель начальных классов, Рижская основная школа «ПАРДАУГАВА», Рига, 2008 ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ 1 класс.
Соотношения между сторонами и углами в прямоугольном треугольнике.
АЗБУКА в картинках ЦИФРЫ (1-20) ФИГУРЫ ЦВЕТА в картинках.
Poznavatel nih psihicheskih protsessov/vnimanie/.
С давних времен люди пытались предсказать свою судьбу по руке и узнать, что означают линии на ладони. На наших ладонях засекречены разные фигуры, которые имеют определенное значение. Кроме треугольников, звезд и ромбов, существуют и другие формы, такие как трезубец, полумесяц, рыба и крест.
Посмотри внимательно на свою ладонь. Что ты видишь?
Треугольник: На твоей ладони треугольник? Тогда ты обладаешь мега-талантом! Треугольник любого размера указывает на наличие особого таланта. И чем больше треугольник, тем больше у тебя шансов стать очень уважаемым человеком в обществе.
Звезда: Если на твоей ладони красуется форма звезды, которая состоит из пересечения мелких линий, ты обладатель могущественных и специфических способностей. Расположение звезды вверху линии жизни под указательным пальцем говорит о тебе как о человеке больших умственных способностей, посвященному науке, философии или религии.
Расположение звезды вверху линии жизни под указательным пальцем говорит о тебе как о человеке больших умственных способностей, посвященному науке, философии или религии.
Ромб: Линия судьбы на ладони образует одну из граней ромба, это говорит о безудержном духе авантюризма и желании познавать неизвестное. Такие люди отличаются невероятной смелостью и даже безрассудством. Ты видишь у себя ромб? Тогда ты исследователь, который любит рисковать. Но мы же знаем, что риск — благородное дело!
Рыба: Эта форма очень похожа на ромб. Однако, особенность таится в треугольнике ниже основной формы, который похож на хвост рыбы. Человек, который найдет у себя этот символ, очень религиозный.
Полумесяц: Если у тебя имеются 2 линии, которые при пересечении образуют серп или полумесяц, ты буквально можешь предсказывать будущее. Твоя интуиция настолько сильна, что близкие не раз обращались к тебе за советом. Узнаешь себя?
Трезубец: Линия жизни на ладони делится на три части, образуя трезубец: ты в буквальном смысле обладатель божественной защиты и ничто не может причинить тебе боль.
Крест: Этот символ показывает, что человек является духовным, но не склонен исследовать пределы человеческого духа. Это в большей мере человек, который имеет некоторые специфические духовные знания.
Ответ
Тем, что они оба параллелограммы. И у них все стороны равны между собой, а противолежащие — параллельны (т.к. у параллелограммов противолежащие стороны параллельны)
«>
Загадки про фигуры – Математика для детей Мама7я
Загадки про геометрические фигуры
Загадки про геометрические фигуры позволят понять и изучить все фигуры в математике. Закрепляя знания в форме игры ребенок быстро будет осваивать геометрические фигуры и применять свои знания решая примеры. Загадки про геометрические фигуры раскрывают все особенности своих форм.
В разделе загадки про геометрические фигуры собраны:
- Загадки про круг
- Загадки про треугольник
- Загадки про полукруг
- Загадки про прямоугольник
- Загадки про квадрат
- Загадки про ромб
- Загадки про линию
- Загадки про луч
- Загадки про куб
- Загадки про окружность
- Загадки про шар
- Загадки про прямую
- Загадки про угол
- Загадки про точки
- Загадки про отрезок
- Загадки про конус
- Загадки про призму
- Загадки про цилиндр
- Загадки про трапецию
- Загадки про параллелепипед
- Загадки про пирамиду
- Загадки про овал
- Загадки про прямоугольник
- Загадки про многоугольник
- Загадки про пятиугольник
- Загадки про шестиугольник
- Загадки про восьмиугольник
- Загадки про Сферу.

Загадки про геометрические фигуры для детей и дошкольников
***
У батона колбасы
Мы отрезали носы,
Он теперь – мужская шляпа
Удивительной красы.
Правильный ответ: Цилиндр
***
В шаре мышь жила, как в норке,
Съела мякоть всю до корки –
Таковы ее манеры.
Шар же превратился в ___.
Правильный ответ: Сфера
Эта форма у клубка
У планеты, колобка
Но сожми ее, дружок
И получится ____
(Кружок)
***
Четыре палочки сложили
И фигуру получили.
Он давно знаком со мной,
Каждый угол в нем — прямой.
Все четыре стороны
Одинаковой длины.
Вам его представить рад,
А зовут его ____
(квадрат)
***
Из него мы строим дом
И окошко в доме том
За него в обед садимся
В час досуга веселимся
Ему каждый в доме рад
И зовут его — ____
(Квадрат)
***
Ноги очень интересны
У таинственного друга:
Если первая на месте,
То другая ходит кругом!
(циркуль)
***
На полу квадратном крыша
Всех вокруг барханов выше,
И под нею фараон
Свой загробный смотрит сон.
Правильный ответ: Пирамида
***
Горы на него похожи
Во дворе все горки схожи
А еще на крышу дома
Очень сильно он похож
Что же загадала я?
_____ то, друзья!
(Треугольник)
***
Вот кирпич, учебник новый,
Пастила, журналов тюк.
Назови их форму словом
Из четырнадцати букв!
Правильный ответ: Параллелепипед
***
Шесть квадратов подружились
И в него навек сложились.
Правильный ответ: Куб
***
У круга есть одна подруга,
Знакома всем ее наружность!
Она идет по краю круга
И называется ____
(окружность)
***
Вечеринки гость всегдашний,
Но не шар и не флажок,
Он похож на крышу башни
И на вафельный рожок.
Правильный ответ: Конус
***
Он и мячик, и клубок,
И Луна, и колобок.
Правильный ответ: Шар
***
Треугольник сунул нос
В реактивный пылесос.
А без носа он, – о, боже! –
Стал на юбочку похожим.
Интереснее всего,
Как теперь зовут его.
Правильный ответ: Трапеция
***
Эти фигуры по городу мчат
В садик и школу развозят ребят
Похож на автобус, троллейбус, трамвай
Дружок, на дороге ты не зевай
На дома похожи
С какой фигурой они схожи?
(Прямоугольник)
***
Восемь мух на крае блюдца
Над паучиком смеются –
Привязал он их по кругу
Паутинками друг к другу.
Паутинок восемь тоже.
Кто назвать фигуру сможет?
Правильный ответ: Восьмиугольник
***
Треугольник с полукругом
Круг дразнили «толстым другом».
Круг, расстроившись до слез,
Уже стал и вверх подрос.
Кто же угадает тут,
Как теперь его зовут.
Правильный ответ: Овал
***
Встал квадрат на уголок –
Ткнулся носом в потолок.
Вверх он рос еще дней пять.
Как теперь его назвать?
Правильный ответ: Ромб
***
Кубик в краску окуни,
Приложи и подними.
Вася десять раз так сделал –
Отпечатались они.
Правильный ответ: Квадраты
***
Злая рыба хвост-лопата
Откусила полквадрата –
Целый угол, верь не верь!
Кто ж он, бедненький, теперь?
Правильный ответ: Треугольник
***
Два квадрата-близнеца –
Половинки их отца.
Сторонами приложи,
Имя их отца скажи.
Правильный ответ: Прямоугольник
***
Для пчелы фигуры этой
В целом мире лучше нету.
Правильный ответ: Шестиугольник
***
Обведи кирпич мелком
На асфальте целиком,
И получится фигура –
Ты, конечно, с ней знаком.
Правильный ответ: Прямоугольник
***
На мяче футбольном нашем
Черным цветом он закрашен.
Правильный ответ: Пятиугольник
***
Мы встречаем их везде
На лугу и на воде
И на всем воздушном шаре
Их так много, мы же знаем
Вокруг нас они везде
В каждом доме и в траве
Все мы формы узнаем
С ними вместе мы живем
(Фигуры)
***
Ни угла, ни стороны,
А родня – одни блины.
Правильный ответ: Круг
***
Козья ножка танцевала
И ее нарисовала.
Правильный ответ: Окружность
***
Не овал я и не круг,
Треугольнику я друг,
Прямоугольнику я брат,
Ведь зовут меня…
Правильный ответ: Квадрат
***
Нет углов у меня,
И похож на блюдце я,
На тарелку и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья?
Правильный ответ: Круг
***
Три вершины тут видны,
Три угла, три стороны, —
Ну, пожалуй, и довольно! —
Что ты видишь? — …
Правильный ответ: Треугольник
***
А братишка мой, Сережа,
Математик и чертежник —
На столе у бабы Шуры
Чертит всякие…
Правильный ответ: Фигуры
***
Шесть тупых углов внутри
На фигуре рассмотри
И представь, что из квадрата
Получили его брата.
Слишком много здесь углов,
Ты назвать его готов?
(Многоугольник)
***
Нет углов у меня
И похож на блюдце я,
На медаль, на блинок,
На осиновый листок.
Людям я старинный друг.
Называют меня
(круг)
***
Прикатилось колесо,
Ведь похожее оно,
Как наглядная натура
Лишь на круглую фигуру.
Догадался, милый друг?
Ну, конечно, это …
(круг)
***
Хорошо живется мне
В вышине и в глубине.
Отгадать меня вам просто –
Пять углов тупых, пять острых.
(Звезда)
***
Вроде круг, но дело в том,
Что иначе мы зовем
Нарисованный кружок.
В чем секрет? Скажи, дружок!
Эта странная наружность
Называется…
(окружность)
***
Он похожий на яйцо
Или на твое лицо.
Вот такая есть окружность —
Очень странная наружность:
Круг приплюснутым стал.
Получился вдруг…
(овал)
***
Если взял бы я окружность,
С двух сторон немного сжал,
Отвечайте дети дружно —
Получился бы …
(овал)
***
Три вершины,
Три угла,
Три сторонки –
Кто же я?
(Треугольник)
***
Три угла, три стороны.
Могут разной быть длины.
Если стукнешь по углам,
То скорей подскочишь сам!
(Треугольник)
***
Три моих стороны
Могут разной быть длины.
Где стороны встречаются –
Угол получается.
Что же вышло? Посмотри!
Ведь углов-то тоже три.
На меня вы посмотрите,
Мое имя назовите.
(Треугольник)
***
Пес Барбос и пес Пират
Тянут за углы квадрат.
Коль сейчас не прекратят,
То во что же превратят?
(в ромб, если тянут за противоположные углы)
(в трапецию, если за соседние)
***
Ты на меня внимательно смотри –
Ведь у меня всего по три.
Три стороны и три угла,
Три пика – острия.
Теперь быстрее дай ответ,
Кто же я?
(Треугольник)
***
На фигуру посмотри
И в альбоме начерти
Три угла. Три стороны
Меж собой соедини.
Получился не угольник,
А красивый…
(треугольник)
***
Четыре угла и четыре сторонки,
Похожи точно родные сестренки.
В ворота его не закатишь, как мяч,
И он за тобою не пустится вскачь.
Фигура знакома для многих ребят.
Его вы узнали? Ведь это …
(Квадрат)
***
Он давно знакомый мой,
Каждый угол в нем прямой,
Все четыре стороны
Одинаковой длины.
Вам его представить рад.
А зовут его…
(квадрат)
***
«Я, – сказал он спозаранку, –
Самый замечательный!
Я и пончик, и баранка,
Я и круг спасательный!»
(тор)
***
Вы подумайте, скажите …
Только помнить вы должны:
Стороны фигуры этой
Противоположные равны.
(Прямоугольник)
***
Растянули мы квадрат
И представили на взгляд,
На кого он стал похожим
Или с чем-то очень схожим?
Не кирпич, не треугольник —
Стал квадрат…
(прямоугольник)
***
Если встали все квадраты
На вершины под углом бы,
То бы видели ребята
Не квадраты мы, а …
(ромб)
***
Чуть приплюснутый квадрат
Приглашает опознать:
Острый угол и тупой
Вечно связаны судьбой.
Догадались дело в чем?
Как фигуру назовем?
(Ромб)
***
Как его нам не вертеть
Равных граней ровно шесть.
С ним в лото сыграть мы сможем,
Только будем осторожны:
Он не ласков и не груб
Потому что это…
(куб)
***
Вновь беремся мы за дело,
Изучаем снова тело:
Может мячиком он стать
И немного полетать.
Очень круглый, не овал.
Догадались? Это…
(шар)
***
Египтяне их сложили
И так ловко смастерили,
Что стоят они веками.
Догадайтесь, дети, сами
Что же это за тела,
Где вершина всем видна?
Догадались? Из-за вида
Всем известна…
(пирамида)
***
Треугольник подпилили
И фигуру получили:
Два тупых угла внутри
И два острых – посмотри.
Не квадрат, не треугольник,
А похож на многоугольник.
(Трапеция)
***
Присмотрись, стоит ведро —
Сверху крышка, снизу дно.
Два кружка соединили
И фигуру получили.
Как же тело называть?
Надо быстро отгадать.
(Цилиндр)
***
Это, вроде бы, ведро,
Но совсем другое дно:
Не кружок, а треугольник
Или даже шестиугольник.
Очень тело уж капризно,
Потому что это…
(призма)
***
Вот колпак на голове –
Это клоун на траве.
Но колпак не пирамида
Это сразу, братцы, видно:
Круг в основе колпака.
Как же звать его тогда?
(Конус)
***
Часть от линии возьмем
И фигуру назовем
Не куском – уж слишком резко,
А, наверное,…
(отрезком)
***
В математике она
Пригождается всегда:
Без хвоста от запятой
Всем нам кажется простой.
И в конце, закончив строчку,
Мы поставим, братцы,…
(точку)
***
Эта странная фигура,
Ну, совсем миниатюра!
И на маленький листочек
Мы поставим сотни …
(точек)
***
Он и острый, да не нос,
И прямой, да не вопрос,
И тупой он, да не ножик, —
Что еще таким быть может?
(угол)
***
Он от солнца прилетает,
Пробивая толщу туч
И в тетрадочке бывает,
А зовется просто — …
(луч)
***
По фигуре пролегла
Очень тонкая игла:
Не черта и не прямая,
Что ж за линия такая?
В математике живуч
Этот очень ровный…
(луч)
***
Едет ручка вдоль листа
По линеечке, по краю —
Получается черта,
Называется …
(прямая)
***
Прикатилось колесо,
Ведь похожее оно,
Как наглядная натура
Лишь на круглую фигуру.
Догадался, милый друг?
Ну, конечно, это … (круг).
***
Я фигура – хоть куда,
Очень ровная всегда,
Все углы во мне равны
И четыре стороны.
Кубик – мой любимый брат,
Потому что я…. (квадрат).
***
Под линейку я рисую
Очень ровную, простую
Всем заметную черту.
Как фигуру назову?
Не спеши, а рассуждай
И ответ скорее дай. (Линия).
***
Все фигуры повторяем
И спокойно называем:
Вот овал, окружность, круг…
Продолжай-ка, милый друг!
***
Книгу с мячиком возьмем —
Их телами назовем.
А фигуры нарисуем —
Круг с овалом и лучом.
Продолжаем рисовать
Ромб, отрезок и квадрат.
Отгадали или нет
Геометрии секрет?
Нарисованный рисунок
Может много рассказать,
Надо главное запомнить
И секрет его понять:
Тело может быть объемным,
Круглым или трехсторонним.
В руки тело можно взять,
А фигуры – рисовать
Сможем мы, иль начертить
И на плоскость разместить.
Сколько есть на белом свете
Удивительных секретов.
Все нам хочется узнать,
Мир премудростей познать.
***
А братишка мой, Сережа,
Математик и чертежник —
На столе у бабы Шуры
Чертит всякие ___
(Фигуры)
***
Он похож на колесо
В серединке буква О
По дороге катится
И в ромашке прячется
Нрав его совсем не крут
Догадались? Это — ____
(Круг)
Как называется белка с тремя, пятью, шестью или более углами?
Ответ после небольшого исследования, вызванного комментарием Waruyama .
Обращение к ним как к многоугольникам Реуло, например, треугольнику Реуло , может куда-то вас привести. На мой взгляд, эти многоугольники гораздо ближе к внешнему виду, чем многоугольники со скругленными углами (которые, на мой взгляд, совершенно различны и совсем не являются достаточным описанием этих форм). Тем не менее, этот термин имеет ряд проблем:
Он недостаточно известен за пределами геометрии и конкретных технических областей (например, они используются в некоторых движках), и название ни на что не намекает.

Полигоны Reuleaux – это очень специфические математические формы с особыми свойствами. Вы не можете просто взять многоугольник, немного искривить стороны и заявить, что это многоугольник Reuleaux, который относится только к многоугольнику с очень специфическими кривыми по сторонам.
Только полигоны с нечетным числом углов могут быть правильно названы полигонами Ройло. Таким образом, белка не может быть многоугольником Reuleaux, независимо от того, насколько тщательно вы изогните стороны.
И в этом отношении эти углы острые, а не закругленные. Хотя, говоря «многоугольник Reuleaux с закругленными углами », вы можете обойти это.
Наконец, кажется, что есть компания под названием Reuleaux, которая продает атрибутику для вейпинга и имеет тенденцию доминировать в результатах поиска, что вызовет проблемы в понимании и обнаружении.
Тем не менее, чтение связанной страницы Википедии дает ссылку на круговой треугольник , и этот термин имеет гораздо большие перспективы: это общий термин для треугольников, образованных из круговых кривых. Треугольник Reuleaux один, но этот термин может также охватывать множество других форм. Фактически, он может охватывать формы, которые мы не считаем такими же, как ваш «треугольник», поскольку образующие его кривые могут быть выпуклыми или вогнутыми. На этих фигурах все они выпуклые, что, согласно статье, может быть связано с «выпуклым круговым треугольником».
Треугольник Reuleaux один, но этот термин может также охватывать множество других форм. Фактически, он может охватывать формы, которые мы не считаем такими же, как ваш «треугольник», поскольку образующие его кривые могут быть выпуклыми или вогнутыми. На этих фигурах все они выпуклые, что, согласно статье, может быть связано с «выпуклым круговым треугольником».
Поскольку мы также не очень разборчивы в отношении наших кривых – на самом деле они не обязательно являются круговыми кривыми – мы можем обобщить и этот термин. Ответ AAGD предполагает «выпуклый эллиптический треугольник», где эллипс является более общим термином для кривых, которые включают в себя круги, так что это шаг в правильном направлении, но тогда мы также не обязательно ссылаемся на эллиптические кривые (и это может также столкнуться с некоторой путаницей с эллиптической геометрией, которая снова выглядит похожей, но не совсем эти формы).
Поэтому я собираюсь предложить, чтобы мы могли использовать термин «треугольники с выпуклой кривой», а в более общем смысле – «многоугольники с выпуклой кривой».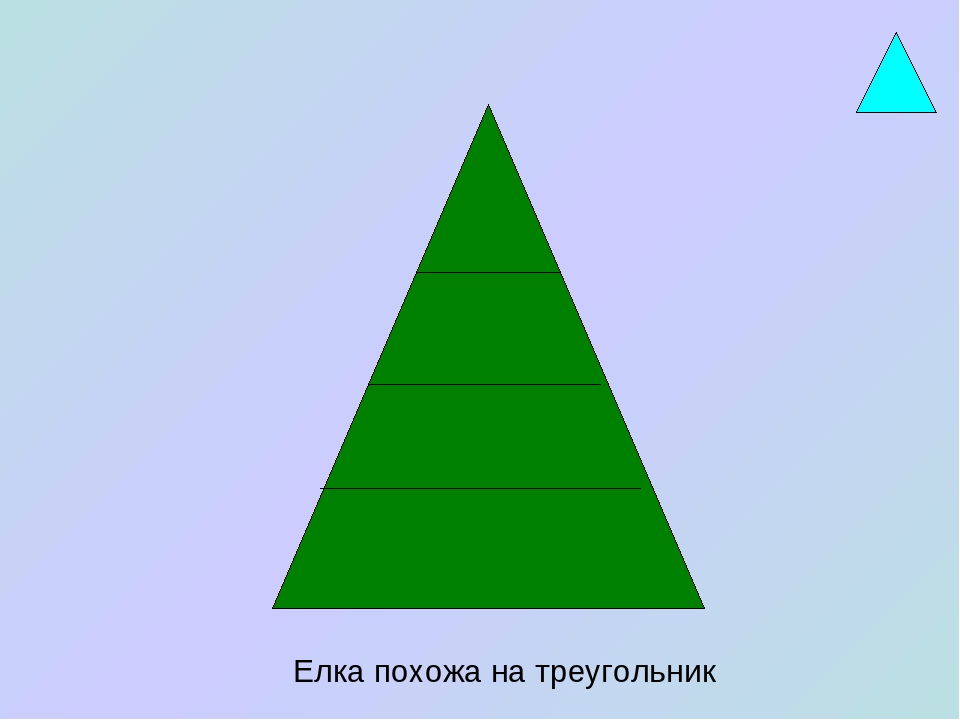 Вероятно, «с закругленными углами». Это будет охватывать именно те формы, о которых идет речь.
Вероятно, «с закругленными углами». Это будет охватывать именно те формы, о которых идет речь.
Это также в принципе неслыханно. Google находит 6 результатов для "convex curve triangle". Один продает ювелирные изделия с камнями, вырезанными в соответствующую форму, а другой выглядит как художественная галерея с геометрическим изгибом, и оба используют этот термин для обозначения «треугольника», поэтому, по крайней мере, мы не противоречим тому, что мало использование там есть , но это не говорит много. "convex curve polygon"получает 10 результатов, но все они кажутся высокотехнологичными исследовательскими работами по геометрии.
Наконец, я хотел бы отметить, что термин, который был наиболее точным для этих фигур, хотя и находился в сфере «люди на самом деле используют этот термин», был «круговые многоугольники», из которых мы можем ясно увидеть фактическое происхождение белка: квадрат-круг стал коротышкой Точно так же треугольный круг становится треугольником, пятиугольный круг становится пятиугольником или пятиугольником или чем-то еще, и так далее. Таким образом, хотя эти имена используются не часто, как отмечено в вопросе, они оба являются точными (как сокращение терминов «круговой многоугольник») и явным расширением более известного «короткого замыкания». Поэтому мой вывод, в конечном счете, таков: повторить ответ Филипа и предположить, что эти имена являются лучшим выбором для регулярного использования.
Таким образом, хотя эти имена используются не часто, как отмечено в вопросе, они оба являются точными (как сокращение терминов «круговой многоугольник») и явным расширением более известного «короткого замыкания». Поэтому мой вывод, в конечном счете, таков: повторить ответ Филипа и предположить, что эти имена являются лучшим выбором для регулярного использования.
Перевернутый треугольник вызывает страх
Человек быстрее замечает в толпе злые, неприятные лица, чем доброжелательные и нейтральные. Ему трудно игнорировать чужую внешность, если она вызывает тревогу и страх. Британские психологи решили выяснить, что за механизм лежит в основе такого предпочтения, пишет livestream.ru.
Ученые из Уорикского университета (Великобритания) пригласили для участия в эксперименте добровольцев, которым нужно было смотреть на экран со сменяющимися картинками. Добрые, злые и нейтральные лица были перемешаны с разного вида треугольниками.
Предыдущие исследования этой же группы учёных показали, что геометрические фигуры могут ассоциироваться с положительными и отрицательными эмоциями. На этот раз им удалось выяснилось, что страх и тревогу вызывает перевёрнутый треугольник. На него очень похожи лица мультяшных злодеев со сведёнными к переносице бровями и острым выступающим подбородком.
На этот раз им удалось выяснилось, что страх и тревогу вызывает перевёрнутый треугольник. На него очень похожи лица мультяшных злодеев со сведёнными к переносице бровями и острым выступающим подбородком.
Любая черта, делающая лицо похожим на перевёрнутый треугольник – приподнятые края бровей, складки у рта, острый нос и острый подбородок – будет замечена в первую очередь.
КСТАТИ
А О ЧЕМ РАССКАЖЕТ ВЗГЛЯД?
– Человек, смотрящий собеседнику прямо в глаза, выдерживающий чужой взгляд, является мужественным и смелым, он относится к себе с уважением, но невысокого мнения о других, считает психолог Илья Щеголев. – Манера смотреть поверх головы собеседника говорит о чрезмерной гордости, заносчивости, тщеславии.
Если человек смотрит на собеседника, несколько склонив голову, то в его характере есть скромность, желание найти общее решение, излишняя осторожность, иногда переходящая в беспокойство.
У некоторых людей есть привычка не смотреть прямо в глаза, а лишь бросать быстрые взгляды.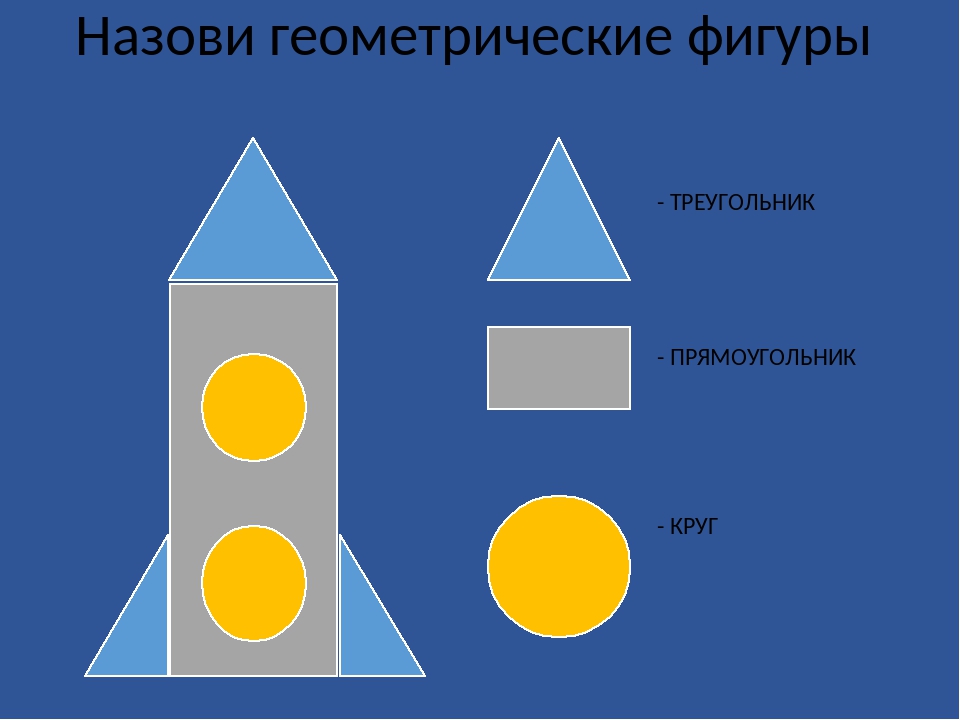 Обычно такие люди что-то замышляют, они сильно «себе на уме». Такие взгляды характерны для жуликов и насильников.
Обычно такие люди что-то замышляют, они сильно «себе на уме». Такие взгляды характерны для жуликов и насильников.
Иногда человек нарочито отводит взгляд. Он, возможно, что-то замышляет, либо ему стыдно за какие-то свои действия, либо он очень неуверен в себе и боится, что прочтут его мысли.
Встречаются люди, у которых взгляд постоянно перебегает с предмета на предмет. Такие люди отличаются повышенной восприимчивостью, они легко отвлекаются. Им очень трудно доводить дело до конца, поэтому они немногого и достигают.
С другой стороны, человек, который фокусирует свой взгляд на собеседнике, долго и внимательно его разглядывает, обладает аналитическими способностями, знает свои цели и пути их реализации. Такие люди очень упорны, но им часто не хватает гибкости и скорости принятия решений.
ЗАГЛЯНИ ВНУТРЬ ЗНАКОМЫХ ГЛАЗ
В зависимости от ширины глазной щели, глазного яблока, вида бровей и ресниц физиономисты определяют шесть типов глаз.
Тип глаза. «Вытаращенный»: выпуклый белок с кровавыми прожилками и желтоватым оттенком, ресницы короткие, брови топорщатся и расположены высоко.
«Вытаращенный»: выпуклый белок с кровавыми прожилками и желтоватым оттенком, ресницы короткие, брови топорщатся и расположены высоко.
Характер. Это человек раздражительный и вспыльчивый, но по жизни – добрейшей души весельчак.
Тип глаза. «Близорукий»: глаз находится в продольной, узко прорезанной глазной щели, внешний угол век приподнят. Брови приподняты к вискам, ресницы густые и короткие.
Характер. Наблюдательный, скрытный, хитрый, лицемерный. Отличается большой выдержкой, эгоизмом и гиперсексуальностью.
Тип глаза. «Узкий»: глаз находится в узкой глазной щели, без блеска, зрачок со слабой реакцией на свет. Брови в виде правильной дуги, ресницы длинные и редкие.
Характер. Бесстрастная, проницательная, серьезная и справедливая до жестокости натура.
Тип глаза. «Сонный»: заключен как бы в опухших веках, невыразителен, зрачок крупный. Брови и ресницы густые и длинные.
Характер. Характерен для ленивой, апатичной натуры, однако не лишенной душевной мягкости.
Тип глаза. «Открытый»: глаз широко открыт, взгляд направлен в упор на слушателя. Брови сильно изогнуты и опускаются к виску. Ресницы загнуты круто кверху.
Характер. Человек энергичный, решительный. Благодаря смелости очень правдив. Не терпит промедлений при исполнений просьб и приказаний
Тип глаза. «Свиной»: маленький глаз находится в очень узкой глазной щели, веки тяжелые, зрачок «бегающий». Брови и ресницы небольшие, редкие.
Характер. Характерен для мелочно-хитрой и практично-сметливой натуры. Отличается эгоизмом и ханжеством.
Еще больше о себе и своих близких вы узнаете из книг Светланы Кузиной.
Занятие по развитию элементарных представлений “Круг, квадрат, треугольник” в средней группе
Цель: совершенствовать умение
различать и называть геометрические фигуры
(круг, квадрат, треугольник) независимо от их
размера и цвета. Развивать наблюдательность и
воображение.
Развивать наблюдательность и
воображение.
В гости к детям пришёл Ванечка (большая кукла). Он не знает ещё геометрические фигуры. Хочет посмотреть, как дети играют, и поучиться у них.
“На что похож?”
Дети стоят в кругу. Передают мяч друг другу и называют, на что похож круг, квадрат, треугольник.
“Будь внимателен”
На доске – круг, квадрат, треугольник. Предлагаю рассмотреть фигуры и запомнить их расположение. Затем прошу детей закрыть глаза, а сама в это время убираю одну фигуру. Открыв глаза, дети говорят, что изменилось.
“Найди фигуру”
Показываю детям по одной карточке, на которых нарисованы предметы (колесо, платок, палатка, мяч, телевизор и т.д.). Назовите фигуру такой же формы (круг, квадрат, треугольник).
“Перепутались“
Говорю, что несла детям фигуры показать, но они все перепутались в коробочке. Надо их разделить и разложить по тарелочкам. (Треугольники, квадраты и круги).
“Найди домик”
У детей по одной фигуре. Даю задание разойтись по группе, и найти такую фигуру на стене, на шкафу и т.д.
“Поиграем с фигурами”
Выложить рисунок геометрическими фигурами. Раздаю детям карточки, и предлагаю положить фигурки на нужное место. Задаю вопросы:
– Сколько треугольников? Сколько кругов? Сколько квадратов?
“Раскрась”
Я знаю, что все дети и взрослые любят подарки. Давайте Ванечке сделаем подарок. Подарим ему карточки с геометрическими фигурами.
Чтобы они были красивыми, их надо раскрасить. Квадраты в красный цвет, круги в зелёный, а треугольники в синий.
Ванечка благодарит детей за игры, за подарки и говорит, что он теперь никогда не перепутает фигуры.
“Наша группа”
XAML WPF многоугольник (треугольник) с границей только на 2/3 сторон
У меня есть нарисованный многоугольник в WPF/XAML, как это:
<Polygon
HorizontalAlignment="Right"
VerticalAlignment="Top" Margin="0,0,0,0"
Points="0 2,0,0 2,1"
Fill="Transparent"
Stretch="Fill" Stroke="#FFFFFF" StrokeThickness="1" />
Это ставит белую границу на всех трех сторонах треугольника. Однако мне нужна только белая кайма с двух сторон (а не с левой, плоской). С третьей стороны, я вообще не хочу никакой границы (это будет выглядеть как открытый треугольник. .. вроде как знак больше, чем>). Есть ли способ сделать это? Я безрезультатно играл с толщиной Штриха (не позволяет указать каждую сторону).
.. вроде как знак больше, чем>). Есть ли способ сделать это? Я безрезультатно играл с толщиной Штриха (не позволяет указать каждую сторону).
Поделиться Источник swinkel 04 января 2017 в 14:32
2 ответа
- Box2D: треугольник, вызывающий ” многоугольник вырождается”
В настоящее время я портирую небольшой игровой движок на Linux Ubuntu 14.04.4 . Все работает отлично, но я столкнулся с проблемой с Box2D . Я использую Poly2Tri для триангуляции своих фигур. Эта библиотека возвращает треугольники против часовой стрелки, с помощью которых я затем создаю Box2D…
- Треугольник с CSS с границей
Во-первых, вот fiddle: http://jsfiddle.net/krish7878/kuG6X/3 / Мне нужен треугольник css с простой границей для текстового пузыря, фон должен быть прозрачным. Код: HTML: <div class=arrow-up> </div> CSS: .
 arrow-up { position:absolute; top:50px; left:5px; width: 0; height: 0;…
arrow-up { position:absolute; top:50px; left:5px; width: 0; height: 0;…
3
Один из способов-использовать путь, а не полигон. Что-то вроде:
<Path Stroke="White">
<Path.Data>
<GeometryGroup>
<LineGeometry StartPoint="10,10" EndPoint="30,35"></LineGeometry>
<LineGeometry StartPoint="30,35" EndPoint="10,55"></LineGeometry>
</GeometryGroup>
</Path.Data>
</Path>
Возможно, вам придется немного подправить конечные точки, но это должно привести вас довольно близко к тому, что вам нужно.
Поделиться sous2817 04 января 2017 в 15:14
2
Чтобы создать заполненную фигуру с частично заглаженными краями, используйте PathGeometry, как это:
<Path StrokeThickness="1" Stroke="White" Fill="Transparent">
<Path. Data>
<PathGeometry>
<PathFigure StartPoint="0,0">
<PolyLineSegment Points="10,10 0,20"/>
<LineSegment Point="0,0" IsStroked="False"/>
</PathFigure>
</PathGeometry>
</Path.Data>
</Path>
Data>
<PathGeometry>
<PathFigure StartPoint="0,0">
<PolyLineSegment Points="10,10 0,20"/>
<LineSegment Point="0,0" IsStroked="False"/>
</PathFigure>
</PathGeometry>
</Path.Data>
</Path>
Поделиться Clemens 04 января 2017 в 16:13
Похожие вопросы:
Как нарисовать многоугольник WPF с отверстиями?
У меня есть коллекция пользовательских объектов PlanarMember, раскрывающих свойства границ и отверстий. Свойство Boundary – это пользовательский класс Polygon, предоставляющий доступ к вершинам,…
Нарисуйте сплошной цветной треугольник, используя только XAML
Можно ли нарисовать заполненный треугольник только с помощью XAML (а не кода, стоящего за решением)? Треугольник должен быть похож на изображение ниже, чтобы представлять направление сортировки. ..
..
Отзывчивый треугольник с границей по высоте и ширине контейнера
Проблема Мне нужно создать контейнер, содержащий контур треугольника, который реагирует на размер контейнера, вот пример изображения, так как он намного проще: Требования Треугольник должен…
Box2D: треугольник, вызывающий ” многоугольник вырождается”
В настоящее время я портирую небольшой игровой движок на Linux Ubuntu 14.04.4 . Все работает отлично, но я столкнулся с проблемой с Box2D . Я использую Poly2Tri для триангуляции своих фигур. Эта…
Треугольник с CSS с границей
Во-первых, вот fiddle: http://jsfiddle.net/krish7878/kuG6X/3 / Мне нужен треугольник css с простой границей для текстового пузыря, фон должен быть прозрачным. Код: HTML: <div class=arrow-up>…
Многоугольник треугольник с изогнутой гипотенузой
Я могу создать полигон со следующим XAML: <Polygon Grid.Row=1 Grid.Column=1 Fill={StaticResource GreenBrush} Points=0,1 1,1 1,0 Stretch=Fill /> В результате получается прямоугольный. ..
..
Как нарисовать треугольник с границей с помощью Java графики
Я пытаюсь нарисовать треугольник с границей, используя метод Graphics.drawPolygon() Треугольник нарисован правильно,но как я могу вычислить 3 точки границы? Я уже сделал это с кругом, но, похоже, не…
Многоугольник, разделенный на равнобедренный треугольник в python
Я хотел нарисовать многоугольник, разделенный на равнобедренный треугольник в python году. Я попробовал этот код ниже, но, похоже, в переменной inside angle есть ошибка. почему стрелка движется…
Как нарисовать треугольник с трех сторон JS?
У меня будет 3 входа и кнопка. При нажатии на эту кнопку Вы должны нарисовать треугольник, в котором длины 3 сторон равны значениям во входных данных. Как это организовать? Я нашел это:…
Нарисуйте треугольник с заданными 3 сторонами
Я хочу нарисовать треугольник только с длиной сторон 3. (В C# Winforms) Пример: S1(3), S2(4), S3(5) с SN(x) в качестве длины каждой стороны. Я пытался сделать это, и в результате получился не…
Я пытался сделать это, и в результате получился не…
типов треугольников – объяснения и примеры
В геометрии треугольник является наиболее важной формой , определяемой как замкнутая двумерная диаграмма, содержащая 3 стороны, 3 угла и 3 вершины. Проще говоря, треугольник – это многоугольник с 3 сторонами. Слово «треугольник» происходит от латинского слова «triangulus», что означает треугольник.
В древние времена астрономы создали метод, называемый триангуляцией, для определения расстояний до далеких звезд.Они измеряют расстояние от двух разных мест, а затем измеряют угол, образованный сдвигом или параллаксом, образованным движением наблюдателя между двумя точками. Затем они применяли закон синусов для вычисления необходимого расстояния.
Египтяне создали пирамиды около 2900 г. до н. Э. Его форма на самом деле напоминает трехмерную пирамиду с треугольными гранями. Это идеально спроектированная модель, длина и углы которой одинаковы со всех сторон. Милет (624 г. до н.э. – 547 г. до н.э.), греческий математик, перенял геометрию Египта и был доставлен в Грецию.
Милет (624 г. до н.э. – 547 г. до н.э.), греческий математик, перенял геометрию Египта и был доставлен в Грецию.
Аристарх (310 г. до н.э. – 250 г. до н.э.), греческий математик, использовал вышеуказанный метод, чтобы найти расстояние между Землей и Луной. Эратосфен (276 г. до н.э. – 195 г. до н.э.) снова использовал тот же метод для определения расстояния вокруг поверхности Земли (называемого окружностью).
В этой статье будет обсуждаться значение треугольника , различных типов треугольников и их свойства, а также их практическое применение.
Что такое треугольник?
Треугольник – это двумерная замкнутая фигура с 3 сторонами.Это многоугольник с тремя углами, тремя вершинами и тремя углами, соединенными вместе, которые образуют замкнутую диаграмму. Мы используем символ ∆ для обозначения треугольника.
Рисунки A и B представляют собой треугольники.
Различные типы треугольников
Типы треугольников классифицируются на основе:
- Длины их сторон
- Внутренние углы
Классификация треугольников по величине внутренних углов
Согласно Что касается внутренних углов, мы можем разделить треугольники на три категории:
- Острый угол
- Тупоугольный
- Прямоугольный
Острый треугольник
Треугольник с острым углом – это треугольник, в котором все три внутренние углы менее 90 градусов.
Каждый из углов a, b и c меньше 90 градусов.
Тупой треугольник
Тупой треугольник – это треугольник, в котором один из внутренних углов больше 90 градусов.
Угол a более тупой, а углы b и c острые.
Прямой треугольник
Прямоугольный треугольник – это треугольник, в котором один из углов равен точно 90 градусам. Гипотенуза – это сторона прямоугольного треугольника с наибольшей длиной.
На рисунке выше угол a = 90 градусов, а углы b и c являются острыми углами.
Классификация треугольников по длине сторон
В зависимости от длины сторон треугольники можно разделить на 3 типа:
- Скален
- Равнобедренный
- Равносторонний
Равнобедренный треугольник
Равнобедренный треугольник – это треугольник, в котором две стороны и два угла равны. Треугольники одинаковой длины показаны по дуге с каждой стороны.
На диаграмме выше , длина стороны AB = AC и ∠ ABC = ∠ ACB.
Равносторонний треугольник
У равностороннего треугольника все три стороны равны, и все три внутренних угла также равны. В этом случае каждый внутренний угол равностороннего треугольника составляет 60 градусов. Равносторонний треугольник иногда называют равносторонним треугольником, потому что все три угла равны.
В равностороннем треугольнике стороны AB = BC = AC и ∠ ABC = ∠ ACB = ∠ BAC
Обратите внимание, что углы равностороннего треугольника не зависят по длинам сторон.
Масштабный треугольник
Разносторонний треугольник – это треугольник, в котором все стороны имеют разные размеры, и все внутренние углы также разные.
Свойства треугольника
Свойства треугольников широко используются. Многие математики использовали его при решении своих задач. Евклидова геометрия и тригонометрия широко используют свойства треугольников.
Вот несколько основных свойств треугольника:
- Треугольник – это двумерный многоугольник
- Треугольник имеет 3 стороны, 3 угла и 3 вершины.
- Сумма длин любых двух сторон треугольника больше длины оставшейся стороны.
- Сумма длин трех сторон дает периметр треугольников.
- Площадь треугольника равна произведению основания на высоту.
Рабочие примеры на различных типах треугольников
Пример 1
Найдите значение угла x в треугольнике ниже.
Решение
Это равнобедренный треугольник, в котором две стороны равны, а также два угла равны.Следовательно,
x = (180 ° – 70 °) / 2
x = 110 ° / 2
= 55 °
Пример 2
Найдите угол y в прямоугольном треугольнике, показанном ниже.
Решение
Один угол прямоугольного треугольника равен 90 °. Итак, мы;
y + 50 + 90 = 180
y = (180 – 140) °
y = 40 °
Пример 3
Классифицируйте следующий треугольник.
Решение
Это разносторонний треугольник, потому что все стороны и углы имеют разные размеры.Точно так же треугольник также можно классифицировать как тупой треугольник, потому что один угол тупой.
Пример 4
Классифицируйте треугольник, показанный ниже.
Решение
Это равнобедренный треугольник. Две стороны равны, и два угла равны по размеру.
Применение треугольников
Давайте рассмотрим некоторые из реальных приложений треугольников:
- Дорожные знаки. Большинство дорожных знаков отображаются на треугольных структурах.
- Пирамиды Египта: пирамиды – древние памятники, построенные египтянами. Пирамиды имеют треугольную форму.
- Ферма: Фермы крыш или мостов изготавливаются треугольной формы, потому что треугольник считается самой прочной формой.
- Бермудский треугольник: Бермудский треугольник – это треугольная область в Атлантическом океане, где считается, что любое судно или самолет, проходящие через точку, проглатываются.
 Считается, что в Бермудском треугольнике загадочным образом исчезли 50 кораблей и 20 самолетов.
Считается, что в Бермудском треугольнике загадочным образом исчезли 50 кораблей и 20 самолетов. - Глобальная система позиционирования (GPS) работает с алгоритмами триангуляции для определения долготы и широты объекта.
- Лестница, прислоненная к стене, имеет форму треугольника.
- Эйфелева башня имеет треугольную форму.
- Концепция треугольников рассчитывает высоту или высоту высоких объектов, таких как флагштоки, горы, здания и т. Д.
- Сэндвичи и кусочки пиццы имеют треугольную форму.
Треугольники – равносторонние, равнобедренные и чешуйчатые
Треугольник имеет три стороны и три угла | ||
Три угла всегда складываются в 180 ° |
Равносторонний, равнобедренный и чешуйчатый
Треугольникам даны три специальных имени, которые показывают, сколько сторон (или углов) равны.
Может быть 3 , 2 или Нет равных сторон / углов:
Равносторонний треугольник Три равных сторон | |
Равнобедренный треугольник Две равные стороны | |
Чешуйчатый треугольник Нет равные стороны |
Как запомнить? По алфавиту идут 3, 2, нет:
- Равносторонний : “равный” – боковой (боковой означает сторона), поэтому у них все равные стороны
- Равнобедренный : означает «равные ноги», а у нас две ноги , верно? Также i SOS celes имеет два одинаковых “S ides”, соединенных стороной “ O dd”.

- Scalene : означает «неровный» или «нечетный», поэтому нет равных сторон.
Какой тип угла?
Треугольники также могут иметь имена, которые сообщают вам, какой тип угла находится внутри :
Острый треугольникВсе углы меньше 90 ° | |
Прямой треугольникИмеет прямой угол (90 °) | |
Тупой треугольникИмеет угол более 90 ° |
Объединение имен
Иногда у треугольника будет два имени, например:Равнобедренный прямоугольный треугольникИмеет прямой угол (90 °), а также два равных угла. Вы можете угадать, что такое равные углы? |
Поиграй с ним…
Попробуйте перетащить точки и составить разные треугольники:
Вы также можете поиграть с Интерактивным треугольником.
Уголки
Три внутренних угла всегда составляют 180 °
Периметр
Периметр – это расстояние по краю треугольника: просто сложите три стороны:
Площадь
Площадь составляет , половина базовой, умноженная на высоту .
- “b” – расстояние по основанию
- “h” – высота (измеренная под прямым углом к основанию)
Площадь = ½ × ш × в
Формула работает для всех треугольников.
Примечание: более простой способ записать формулу – bh / 2
Пример: Какова площадь этого треугольника?
(Примечание: 12 – это высота , а не длина левой стороны)
Высота = h = 12
База = b = 20
Площадь = ½ × b × h = ½ × 20 × 12 = 120
Основание может быть любой стороной. Убедитесь, что высота измеряется под прямым углом к основанию. :
(Примечание: вы также можете рассчитать площадь, исходя из длин всех трех сторон, используя формулу Герона.)
Почему область «половина bh»?
Представьте, что вы «удвоили» треугольник (перевернули его вокруг одного из верхних краев), чтобы получилась квадратная форма (параллелограмм), которую можно преобразовать в простой прямоугольник:
ЗАТЕМ вся площадь составляет bh , что соответствует обоим треугольникам, поэтому только один будет ½ × bh .
10 реальных примеров треугольника – StudiousGuy
Разве большинство из нас не увлечено геометрическими формами? В повседневной жизни можно встретить множество геометрических форм.Кровать, стекло, зеркало, ноутбук, духовка и другие предметы повседневного обихода имеют четкую геометрическую форму. Часто можно встретить разные продукты или вещи треугольной формы. От бутербродов, которые вы едите на завтрак, геометрических вычислений высокого уровня, которые вы делаете в школе, до опасного Бермудского треугольника – почти все имеет треугольную форму. Давайте узнаем больше об этой геометрической форме, которая присутствует почти на всех участках в нашем районе.
Треугольник – это трехсторонняя и двумерная замкнутая конструкция.Это многоугольник с тремя углами, вершинами и тремя углами, соединенными вместе, образуя замкнутую структуру.
Давайте рассмотрим реальные примеры треугольника:
1. Бермудский треугольникБермудский треугольник, также известный как треугольник Дьявола, представляет собой нечетко определенную треугольную область в Атлантическом океане, где, как утверждается, загадочным образом исчезли более 50 кораблей и 20 самолетов. Это нечетко очерченный треугольный регион между Флоридой, Бермудскими островами и Великими Антильскими островами.
2. Дорожные знакиДорожные знаки – наиболее часто встречающиеся примеры треугольника в нашей повседневной жизни. Знаки имеют форму равностороннего треугольника; Это означает, что все три стороны имеют одинаковую длину и равные углы.
3. ПирамидыПирамиды – древние памятники, построенные египтянами. Они имеют четырехгранную форму, т. Е. Имеют четыре треугольные стороны, которые сходятся в одну точку наверху.Они до сих пор остаются загадкой для человечества. Опять же, форма пирамид – равносторонний треугольник.
4. Фермовые мостыФермовые мосты имеют несущие конструкции треугольной формы. Треугольники используются для поддержки конструкции мостов, потому что они равномерно распределяют вес без изменения пропорций. Когда сила прикладывается к прямоугольной форме, она расплющивается. Раньше мосты были очень слабыми и не могли выдерживать большой вес, пока в их конструкцию не вошли треугольные формы.
5. Парусная лодкаСегодня почти каждая лодка имеет треугольный парус. В первые годы парусные корабли имели квадратную форму. Благодаря треугольной конструкции паруса стало возможным двигаться против ветра, используя технику, известную как лавирование. Лодка позволяет лодке двигаться вперед с ветром, перпендикулярным лодке.
6. КрышаКрыши домов выполнены в форме треугольника.Ферма крыши представляет собой тупоугольный треугольник. В этом типе треугольника любой из трех углов больше 90 градусов. Ферма крыши построена потому, что она не позволяет воде или снегу дольше оставаться на крыше.
7. Лестница и лестницаСтроительство лестницы требует знания прямых углов. Лестница построена в форме треугольника, чаще всего прямоугольного. Более того, лестница, поставленная под любым углом к стене, тоже образует треугольник.
8. Здания, памятники и башниМногие здания имеют треугольную форму, чтобы сделать их более привлекательными и интересными. Башни, включая сетевые башни и самую известную Эйфелеву башню, также имеют треугольную форму. Треугольная форма придает башне прочность, так как образует прочное основание. Высота Эйфелевой башни составляет 1063 фута. Эйфелева башня состоит примерно из 186 треугольников.
9. Определение высоты полюса или горыПонятие прямого угла снова используется всякий раз, когда нам нужно найти угол возвышения, высоту столба или горы.Более того, мы также можем рассчитать расстояние корабля от конкретной башни, используя треугольную геометрию.
10. Бутерброды или кусочки пиццыБольшинство из нас начинают свой день с бутербродов треугольной формы. Наши мамы делают сэндвич треугольной формы, потому что он выглядит аппетитнее, а из-за треугольной формы бутерброды пригодятся. Было проведено исследование, в котором говорится, что дети предпочитают бутерброды треугольной формы, чем бутерброды нетреугольной формы.
Что такое скаленовый треугольник? [Определение, факты и пример]
Что такое скаленовый треугольник?
Треугольник – это многоугольник, состоящий из трех сторон и трех углов.
Мы можем классифицировать треугольники по длине их сторон.
(i) Равносторонний треугольник : Если все стороны треугольника равны, то он называется равносторонним треугольником.
(ii) Равнобедренный треугольник : Если две стороны треугольника равны, то он называется равнобедренным треугольником.
(iii) Масштабный треугольник : если ни одна из трех сторон треугольника не равны друг другу, он называется разносторонним треугольником.
Свойства разностороннего треугольника:
| Все углы разностороннего треугольника неравны. | Разносторонний треугольник не имеет линии симметрии. | Угол, противоположный самой длинной стороне, будет наибольшим углом, и наоборот. |
У данного разностороннего треугольника все стороны не равны. | Данный треугольник нельзя разделить на две одинаковые половины. Нет линии симметрии. | В этом треугольнике угол E будет наибольшим углом, поскольку он противоположен наибольшей стороне GO, а угол O будет наименьшим углом, поскольку он противоположен наименьшей стороне GE. |
Разносторонний треугольник может быть остроугольным, тупоугольным или прямоугольным.
| Тупой разносторонний треугольник | Острый разносторонний треугольник | Правый разносторонний треугольник |
Примеры из жизни
Интересные факты
|
Треугольник и его типы – MathsTips.com
Треугольник – это геометрическая плоская фигура. Форма треугольника выглядит как на рисунке ниже:
Треугольник имеет три стороны и три угла. Это замкнутая фигура с тремя отрезками в качестве границы. Эти отрезки называются сторонами. У него есть три угла, называемые вершинами. Обозначение треугольника Δ
.Три вершины обычно называются тремя последовательными алфавитами, такими как A, B и C или X, Y и Z.Треугольник с вершинами A, B и C обозначим ΔABC.
Треугольник означает три, поэтому у Треугольника три угла. Эти углы образованы двумя сторонами в каждом из углов. Угол, образованный в вершине A двумя сторонами AB и AC, называется
.Три стороны и три угла треугольника вместе называются шестью частями или элементами треугольника.
Теперь посмотрите на диаграмму ниже
Сторона BC противоположна вершине A и также кратко обозначается буквой «a».Стороны, противоположные B и C, записываются как b и c. Таким образом, стороны BC = a, AC = b и AB = c
Свойства треугольника
- Сумма трех углов любого треугольника всегда равна 180 градусам.
- Любой угол треугольника всегда больше нуля и меньше 180 °
- Не более одного угла может составлять 90 ° и более.
- Сумма длин любых двух сторон всегда будет больше длины третьей стороны.
- Это замкнутая плоская фигура.
Типы треугольников
Треугольник можно классифицировать либо по его сторонам, либо по углу.
(A) Треугольник подразделяется на три типа: разносторонний, равнобедренный или равносторонний треугольник в зависимости от его сторон.
1. Равносторонний треугольник
Треугольник, у которого все стороны равны, называется равносторонним треугольником. Все углы тоже равны. Так как сумма трех углов треугольника равна 180 °, каждый угол равностороннего треугольника равен 60 °.
2. Равнобедренный треугольник
Треугольник, у которого две стороны равны, называется равнобедренным треугольником. Углы, противоположные равным сторонам, также равны.
3. Скаленовый треугольник
Треугольник, у которого все стороны различаются по длине, называется разносторонним треугольником.
На рисунке выше стороны a ≠ b ≠ c. Значит, это разносторонний треугольник.
(B) Треугольник подразделяется на три типа: острый, прямой или тупой треугольник в зависимости от его углов:
1.Острый треугольник
Треугольник, все углы которого меньше 90 °, называется острым треугольником.
В приведенном выше треугольнике три угла составляют 50 °, 60 ° и 70 °. Все три меньше 90 °. Следовательно, это острый треугольник.
2. Тупой треугольник
Треугольник с одним углом более 90 ° называется тупым треугольником.
В треугольнике выше три угла составляют 25 °, 35 ° и 120 °. Один из углов больше 90 °.Следовательно, это тупой треугольник.
3. Правый треугольник
Если любой угол треугольника равен 90 °, треугольник называется прямоугольным. Треугольник ниже представляет собой прямоугольный треугольник, так как Сторона, противоположная прямому углу, называется гипотенузой . Гипотенуза больше двух других сторон.На диаграмме выше AB – гипотенуза, противоположная прямому углу Прямоугольный треугольник обладает особым свойством, известным как теорема Пифагора. Квадрат длины гипотенузы равен сумме квадратов длин двух других сторон. . Теорема Пифагора названа в честь греческого математика Пифагора, который доказал эту взаимосвязь в 570–495 годах до нашей эры. Теорема находит широкое применение в высшей математике. Что следует помнить о треугольниках Вопрос 1: Решение: Вопрос 2: Какие элементы (части) ΔPQR? Решение: ΔPQR имеет три стороны и три угла.Три стороны – это PQ, QR и PR, а три угла – Вопрос 3: Два угла треугольника – 60 ° и 45 °. Что такое измерение третьего угла? Решение: Пусть Сумма трех углов любого треугольника всегда равна 180 градусам. Эти четыре части треугольника объединяются в формулу для площади треугольника: A = (1/2) b h , где b = длина основания и h = высота (или высота над уровнем моря) Например, если треугольник имеет длину основания 4 сантиметра и высоту 10 сантиметров, то мы можем найти площадь треугольника, вставив b = 4 и h = 10 в формулу и упрощение. A = (1/2) (4) (10) = 20 Мы видим, что площадь описанного треугольника составляет 20 квадратных сантиметров. Когда дело доходит до высоты треугольника, есть один тип треугольника, в котором высота может быть одной из сторон, и это прямоугольный треугольник. Прямоугольный треугольник имеет угол 90 градусов, поэтому две его стороны перпендикулярны. Если мы рассматриваем одну из перпендикулярных сторон как основание, тогда другая перпендикулярная сторона перпендикулярна основанию и проходит через угол напротив основания, делая его высотой. Другой треугольник с особой высотой – это равносторонний треугольник. Высота равностороннего треугольника делит основание ровно пополам и разделяет треугольник на два равных прямоугольных треугольника Есть также очень важное свойство прямоугольных треугольников, которое связывает длины сторон треугольника вместе. Это называется теорема Пифагора. Давайте обсудим! В прямоугольном треугольнике мы называем самую длинную сторону треугольника гипотенузой , а две короткие стороны – катетами .Теорема Пифагора показывает взаимосвязь между этими длинами сторон и утверждает, что если катеты прямоугольного треугольника имеют длину a и b , а длина гипотенузы c , то a 2 + b 2 = c 2 Например, предположим, что есть болото, заполненное аллигаторами, через которое вы хотите построить мост. Вы, конечно, не собираетесь идти в болото, чтобы измерить длину моста, поэтому вы рассматриваете равносторонний треугольник, высота которого равна длине моста.Одна сторона треугольника полностью находится на суше, поэтому вы можете измерить ее как 100 футов в длину. Поскольку это равносторонний треугольник, основание должно иметь ту же длину, что и измеренная сторона (или 100 футов), а высота создает два прямых угла внутри треугольника. Кроме того, мы знаем, что высота разрезает основание прямо пополам, поэтому мы знаем, что гипотенуза прямоугольного треугольника составляет 100 футов, а длина одного из катетов – 50 футов. Мы просто подставляем a = 50 и c = 100 в формулу, а затем решаем для a , и у нас есть длина моста. Теорема Пифагора говорит нам, что мост будет примерно 86,6 футов в длину. Напомним, что треугольник – это трехсторонний трехугольный многоугольник. Существует ряд различных типов треугольников, таких как равносторонних треугольников , прямоугольных треугольников , разносторонних треугольников , тупых треугольников , острых треугольников и равнобедренных треугольников .Все эти треугольники имеют четыре общие черты: основания, высоты, высоты и площади, и они связаны в формуле для площади треугольника. Еще одно важное свойство треугольников связано именно с прямоугольными треугольниками, и это теорема Пифагора , которая утверждает, что если прямоугольный треугольник имеет катеты с длиной , a и b , а гипотенуза длиной c , затем a 2 + b 2 = c 2 Знание типов и свойств треугольников оказывается очень полезным как в абстрактных, так и в реальных приложениях треугольников, поэтому рекомендуется поместить их на память и продолжать практиковаться с этими свойствами. Вопросы и ответы
Теорема Пифагора
Резюме урока

 № п/п
Последовательность действий
Выполнение действий
1.
Записать общую формулу углеводорода.
Общая формула углеводорода СхНу
2.
Найти молярную массу углеводорода в общем виде.
М(СхНу)=12х +у
3.
Приравнять найденное в общем виде значение молярной массы к данному в …
№ п/п
Последовательность действий
Выполнение действий
1.
Записать общую формулу углеводорода.
Общая формула углеводорода СхНу
2.
Найти молярную массу углеводорода в общем виде.
М(СхНу)=12х +у
3.
Приравнять найденное в общем виде значение молярной массы к данному в …
