Составы чисел: Что такое – состав числа ?

Конспект открытого урока по математике на тему “Состав чисел 16, 17, 18”

• Сорокина Светлана Анатольевна

Разделы: Математика

---

Цели урока:

1. Разобрать состав чисел 16, 17, 18; закрепить умение складывать однозначные числа и вычитать из двузначного числа однозначные с переходом через разряд.
2. Развивать наблюдательность, внимание, логическое мышление.
3. Воспитывать чувство взаимопомощи, коллективизма, уважение к товарищам, самостоятельность.

Ход урока

I. Орг. момент.

Здравствуйте, дети! Садитесь.

Математика пришла,
Занимай свои места.
Найди для головы полезное занятье!
Чтоб от безделья не зевать,
Полезно голову ломать!

Учитель.

Как вы понимаете выражение “ломать голову”? Сегодня на уроке нас ждет интересная и разноплановая работа. Я предлагаю вам проверить свои математические способности, проявить всю смекалку, рассудительность. Для того чтобы нам пройти все испытания, мы вспомним правила работы в коллективе:

Учитель.

Проверим готовность к урокУчитель. Хозяин на уроке – учебник, его помощники: тетрадь, ручка, карандаш.

II. Постановка учебных задач.

1. Запись даты и “классная работа”.

На доске появляется запись: 14, 12, 9,19, 15, 13, 11.

Учитель.

Посмотрите, подумайте и ответьте какое число лишнее и почему?

Посмотрите внимательно на двузначные числа. В правильном порядке они записаны?

Давайте запишем их в порядке возрастания. Что значит в порядке возрастания?

Запишите самостоятельно числа в порядке возрастания. Проверьте, так ли у вас?

11, 12, 13, 14, 15, 19.

– Каких чисел не хватает? (16, 17, 18.)

На доске появляется запись:

Учитель.

Посмотрите на схемы. Поставьте учебные задачи.

Д. Сегодня рассмотрим состав чисел 16, 17, 18.

III. Новый материал.

1.

Учитель.

Запомним состав чисел из однозначных слагаемых. (Прочитать хором)

2. № 123 – с комментированием у доски.

3. Физминутка.

А теперь, ребята, встать,
Руки медленно поднять.
Пальцы сжать, потом разжать.

Руки вниз и так стоять.
Наклонитесь вправо, влево
И беритесь вновь за дело.

4. № 124. 1 столбик с комментированием у доски. 2 столбик – самостоятельно. (Взаимопроверка)

У.

Поменяйтесь друг с другом тетрадями. Сейчас каждый из вас станет учителем и оценит правильность выполнения задания соседа по парте. Если решено правильно, возле выражения ставьте знак «+», Если нет – «-».

На столах у вас лежат белые листки с вашими фамилиями и квадратики трех цветов (красные, желтые, синие). Выберите нужный квадратик и прикрепите его на листик.

На доске появляется запись:

Все «+» –
Есть «+» и «-» –
Все «-» –

5. № 121. 1 и 2 выражения с комментированием с места. 3, 4, 5 – самостоятельно. (Самопроверка) Выберите нужный квадратик и прикрепите его на листик.

6. Индивидуальный разноуровневый материал. (Самопроверка)

а) На розовых карточках I уровень:

7 + 3 + 4 = …

5 + 5 + 3 = …

4 + 6 + 1 = …

15 – 5 – 7 =…

12 – 2 – 4 = …

14 – 4 – 3 = …

б)

На желтых карточках II уровень:

6 + 9 = …

5 + 6 = …

7 + 7 = …

13 – 8 = …

12 – 9 = …

15 – 6 = …

в)

На синих карточках III уровень:

7 + … = 15

… + 6 = 12

8 + … = 13

14 – … = 8

… – 4 = 7

12 – … = 8

На доске появляется запись с ответами:

14	15	8
13	11	6
11	14	5
3	5	6
6	3	11
7	9	4

После самопроверки дети выбирают нужный квадратик и прикрепляют его на листик.

IV. Итог урока.

Учитель. Чему учились на уроке?

Учитель. Оцени свою работу на уроке. – Урок прошел для меня хорошо, с пользой. Я научился и могу помочь другим складывать и вычитать однозначные числа с переходом через разряд – красный цвет. – Я научился складывать и вычитать однозначные числа с переходом через разряд, но мне еще нужна помощь – желтый цвет. - Мне было трудно на уроке – синий цвет.

V. Д/з. с. 45 № 122, т. с.25 № 58

3.03.2008

Состав чисел 2, 3, 4, 5

Макинская средняя школа

Открытый урок

по математике

«Состав чисел 2, 3, 4, 5»

Подготовила:

учитель начальных классов

Садриева В. Д.

2015-2016 учебный год

Дата:

№ урока:

Тема: Состав чисел 2,3,4,5

Цель: учить соотносить количество предметов с цифрой; закрепить навыки количественного и порядкового счета; повторить числа 1-5: образование, написание, состав; научить отгадывать математические загадки; развивать внимание, сообразительность, точность, речь, логическое мышление, моторику пальчиков; воспитывать познавательный интерес.

Оборудование: компьютер, интерактивная доска, слайды, “домики”- для повторения состава чисел; по 5 кружков красного и зелёного цвета, цифры 1-10, мягкая проволока

Ход урока

1.Орг. момент

Встали все у парт красиво, 
Поздоровались учтиво,
Тихо сели, спинки прямо.
Мы легонечко вздохнем
Урок математики начнем.

– Сегодня мы продолжим увлекательное путешествие в страну «Математики» И закрепим полученные знания о числах 1,2,3,4,5 .

2. Введение в тему

– Сопровождать нас на протяжении урока будут жители страны «Математика». Отгадайте, о ком пойдет речь в веселых стихах.

Вид ее – как запятая 
Хвост крючком, и не секрет: 
Любит всех она лентяев,
А лентяи ее нет. 

(На доске появляется цифра 2)

Пять – сестра родная двойки.
В дневнике одни пятерки.
Чтобы двойку написать – 
Вверх ногами ставим пять.

(На доске появляется цифра 5)

Этот месяц дугой
Ниже месяц дугой,
А теперь посмотри: 
Получилась цифра 3

(на доске появляется цифра 3)

Гляди, четыре – это стул,
Который я перевернул. 

(На доске появляется цифра 4)

На длинной ножке,
3астыв до поры, 
Отдыхает палочка после игры

(На доске появляется цифра 1)

На доске получился ряд цифр 2,5,3,4,1

– Назовите самое маленькое число.(1)

– Назовите самое большое число.(2)

3.Устный счет

1)Назови геометрические фигуры(слайд)

2)Веселые задачи(слайд)

1. Я маме в подарок картинку рисую. 
Сначала одну,  а потом – (вторую)

2. На полке было два куска мыла. 
Возьмем один только. 
Останется сколько? (2-1)

3. На поляне два зайчонка 
В чехарду играли. 
Прибежал еще зайчонок. 
Сколько всех, узнали? (2+1)

4. Трое зайчат на поляне гуляли. 
Вдруг одного мама с папой позвали. 
Сколько зайчат на полянке гуляет,
Может быть, кто-то из вас сосчитает? (3-1)

5. Трех медвежат и медведицу маму
Шишкин, художник, нарисовал.
Сколько медведей всего на картине,
Кто,  их не видя, уже сосчитал? (3+1)

3)Сравни

– Пересчитайте красные шары. Сколько их? 3

– Пересчитайте синие шары. Сколько их? 4

– Каких шаров меньше? Каких шаров больше?

– Пересчитайте слонов. Сколько их? 5

– Пересчитайте улиток. Сколько их? 3

– Каких зверей меньше? Каких зверей больше?

– Пересчитайте курочек. Сколько их? 4

– Пересчитайте цыплят. Сколько их? 9

– Каких птиц меньше? Каких птиц больше?
– Сколько жёлтых звездочек? (5)
– Сколько голубых звездочек? (4)
– Каких больше? Каких меньше?

4. Образование и запись чисел 1-5. Счет до 5.

А) Игра “День – ночь”.

На интерактивной доске появляется слайд с изображением мышки-норушки.

– Дети, кто пришёл к нам в гости?

– Сколько у нас гостей? (1)

– Я говорю вам “ночь”, вы закрываете глаза, будто спите.

На интерактивной доске появляется слайд с изображением лягушки-квакушки.

– День! Открываете глаза. Что изменилось?

– Сколько теперь героев сказки? (2)

– Ночь!

Дети “спят”, появляется слайд с изображением зайчика-побегайчика.

– День! Что теперь изменилось?

– Сколько стало героев сказки? (3)

-Ночь!

Дети “спят” – появляется слайд с изображением лисички-сестрички.

– День! Что сейчас изменилось?

– Сколько теперь стало героев сказки? (4)

– Ночь!

Дети “спят” – появляется слайд волчок серый бочок.

– День! Что изменилось сейчас?

– Сколько теперь стало героев? (5)

б) Игра “Волшебная проволочка”. Пальчиковая гимнастика.

Конструирование из проволоки соответствующей цифры. У каждого ребенка “волшебная проволочка”.

– Покажите с помощью “волшебной проволочки” цифру. Дети конструируют с помощью мягкой проволочки цифры 3, 2, 1

Физминутка

Раз – подняться, потянуться,
Два – согнуться, разогнуться,
Три – в ладоши три хлопка,
На четыре – руки шире,
Пять – руками помахать,
Шесть – за парту тихо сесть.

5. Закрепление представлений о составе чисел 2-5.

(работа по слайду)

– Посмотрите на картинку. Подумайте, почему рядом с божьей коровкой в кружочке цифра 2?

– (На одном крыле 1 кружок и на другом 1 кружок, а вместе -2.)

– Как можно составить число два? (1+1=2 )

– Почему у двух следующих жучков рядом стоит цифра 3?

– (На одном крылышке 1 кружок, а на другом 2 кружка. А у другого -наоборот – 2 кружка на первом крылышке и 1 кружок на втором. А вместе будет 3.)

– Как можно составить число три?

– (1+2=3 2+1=3 )

– Рассмотрите божьих коровок, рядом с которыми стоит цифра четыре.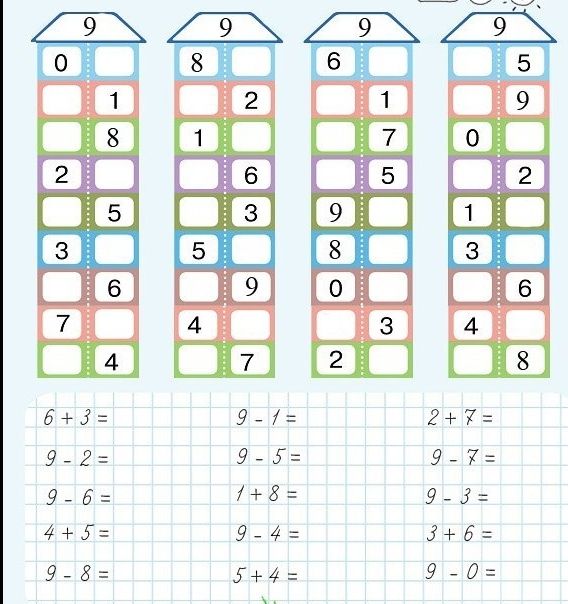 – (На одном крылышке 1 кружок, а на другом 3 кружка. А у другого 2 кружка на первом крылышке и 2 кружка на втором. У третьей божьи коровки 3 кружка на первом крылышке и 1 кружок на втором. А вместе будет 4. )

– Как можно составить число четыре?

– (1+3=4 2+2=4 3+1=4 )

– Рассмотрите жучков, рядом с которыми стоит цифра 5. – (На одном крылышке 1 кружок, а на другом 4 кружка. А у другого 2 кружка на первом крылышке и 3 кружка на втором. У третьей божьи коровки 3 кружка на первом крылышке и 2 кружка на втором. У четвертой божьи коровки на первом крылышке 4 кружка, а на втором 1 кружок. А вместе будет 5. )

– (1+4=5 2+3=5 3+2=5 4+1=5)

6. Запись и состав чисел 1-5.

7. Итог урока

– Молодцы! Работали дружно, старались. Были активны в работе.

Я  приготовила вам шарики: если вам понравился урок, у вас всё получилось и у вас хорошее настроение – дорисуйте шарику УЛЫБКУ. А если урок не понравился и вас плохое настроение – нарисуйте грустные губки.

Резерв:

Работа в тетради:

Дорисовывать такое количество квадратиков, которое соответствует записанной цифре.

Изучаем состав чисел (для детей 5-6 лет) – МНОГОКНИГ.ee

Изучаем состав чисел (для детей 5-6 лет) – МНОГОКНИГ.ee – Книжный интернет-магазин

категории

книги

НовинкиАкции %АвтомобилиДетективы, боевикиДетская литератураДом, быт, досугИностранные языки, словариИстория, политикаКомпьютерные технологииЛюбовный романМедицина и здоровьеПодарочные изданияПсихология, философияПутеводители, атласыСовременная и классическая литератураСпорт, оружие, рыбалкаСувениры. АксессуарыФантастикаЭзотерика, астрология, магияЭкономическая литература

Подарочные карты

игры, игрушки

Игрушки Книги-игры Настольные игры Развивающие игры

товары для малышей

Прорезыватели и пустышки Шезлонги и качели Автокресла Аксессуары для защиты ребенка Вигвам Детская мебель Детская одежда Детские кроватки Кровать для путешествий Купание малыша Матрасы Подушки для беременных Развивающие игрушки для малышей Текстиль Товары для кормления Уход за малышом Ходунки

товары для праздника

Все открытки Карнавальные костюмы, маски и аксессуары Одноразовая посуда Подарочные коробки Подарочные пакеты Свечи Шарики

товары для школы

Бумажная продукция Глобусы Канцелярские товары Папки Пеналы Товары для творчества Школьные ранцы

товары для живописи, рукоделия и хобби

Декорирование Жемчуг эффект для декупажа Живопись Контур по стеклу и керамике Контур по ткани Краски для свечей Маркеры для скетчинга Моделирование Прочее Рукоделие

традиционные товары

Костровые чаши и очаги Матрёшки Платки Самовары Фарфоровые фигурки

другие товары

Аксессуары для девочек Аксессуары для мальчиков Товары для пикника Фотоальбомы

издательство

Об издательстве Многоразовые наклейки Настольные игры Рабочие тетради для дошкольников Рабочие тетради для школьников Развивающее лото Раскраски для девочек Раскраски машины и техника Раскрась водой! Учебные пособия для дошкольников

Код: 9785978008913

Купить

Автор: БОРТНИКОВА Е.
Издательство: оитур
Серия: Рабочая тетрадь
Год издания: 2017
Примечание:
Е-бург: Литур (А4-5/бр), ДЕТСАД

Мягкая обложка
Автор
Елена Бортникова
Формат издания
170×240 мм (средний формат)
Количество страниц
32

Под заказ

В данной тетради представлены задания, направленные на развитие математических способностей у детей 5-6 лет. Важный этап в успешной подготовке ребенка к школе и основная ступенька в закреплении устных вычислительных навыков – изучение состава чисел первого десятка. Запомнив состав чисел, он легко будет находить значения выражений на сложение и вычитание и вскоре начнет безошибочно складывать и вычитать двухзначные и трехзначные числа.

Тетрадь рассчитана на совместную работу взрослых и детей.

генерирующих функций – количество композиций n

задано 9 лет, 3 месяца назад

Изменено 8 лет, 9 месяцев назад

Просмотрено 734 раза

$\begingroup$

Докажите, что для $n\ge2$ количество композиций $n$, где первая часть равна 1, равно количеству композиций $n$, где первая часть больше 1.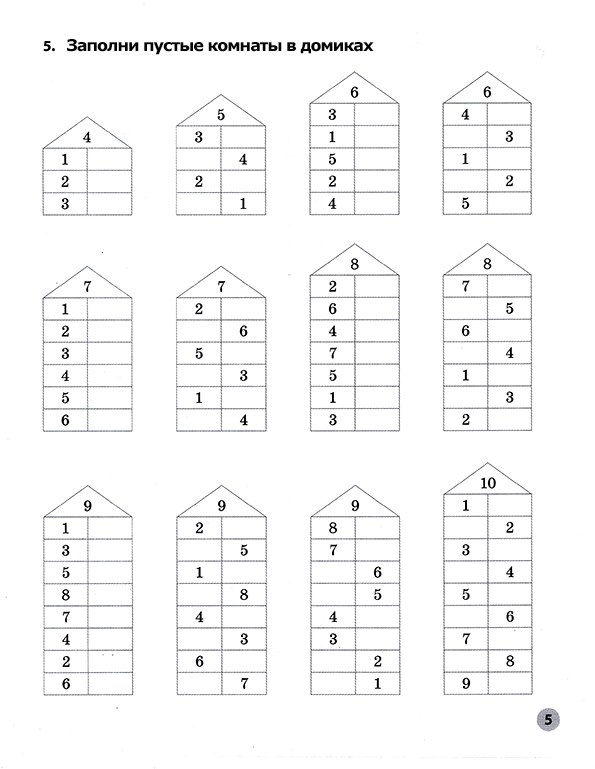 2}$$ но я не знаю, как показать, что они равны друг другу.

Кто-нибудь может мне помочь?

• производящие функции

$\endgroup$

$\begingroup$

Другой подход: Biject между $1+a_1+a_2+\cdots+a_k$ и $(1+a_1)+a_2+\cdots+a_k$.

$\endgroup$

1

$\begingroup$

У нас есть $n$ копий X подряд, например: $$ \text{X}\quad\text{X}\quad\text{X}\quad\text{X}\quad\text{X}\quad\text{X}\quad\text{X}\ quad\text{X}\quad\text{X}\quad\text{X}\quad\text{X}\quad\text{X}\quad\text{X}\quad\text{X}$$ 9{n-2}$ композиции, начинающиеся с числа больше $1$.

Примечание: Производящая функция, упомянутая в OP для количества композиций с первым элементом больше $1$, неверна.

$\endgroup$

$\begingroup$

Я проголосовал за биективный ответ vadim123 (который, я думаю, является лучшим способом увидеть это), но если вы хотите сделать это с помощью вашего оригинального подхода к генерирующим функциям, обратите внимание, что второй, который вы написали, неверен.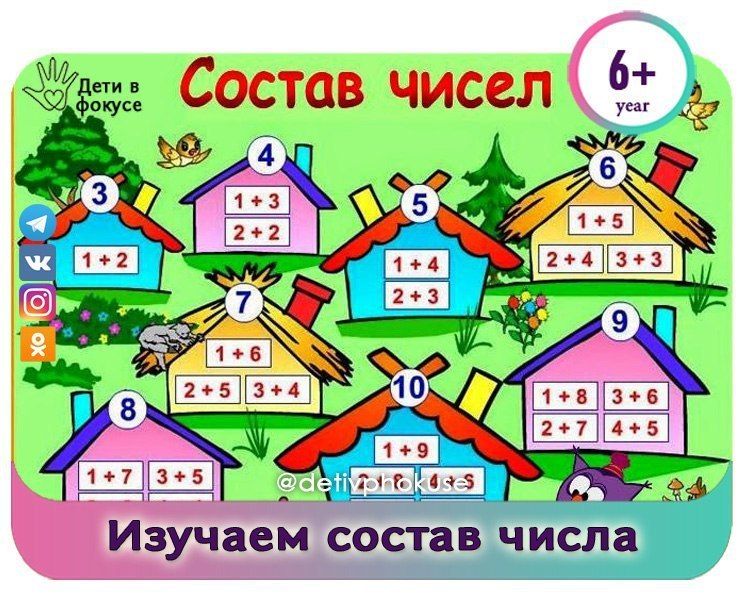

Композиция, в которой первая часть равна $1$, или, другими словами, нечто, имеющее форму «$1$», за которой следует последовательность положительных целых чисел, может быть обозначена (следуя обозначениям книги «Аналитическая комбинаторика ») как $ \mathcal{Z} \times \operatorname{S\scriptsize EQ}(\mathcal{I})$, где $\mathcal{I}$ обозначает класс целых положительных чисел $\{1, 2, 3, \dots\} $ (где «размер» целого числа является самим этим целым числом). Другими словами, $\mathcal{I} = \operatorname{S\scriptsize EQ}_{\ge 1}(\mathcal{Z})$ и имеет производящую функцию $\frac{z}{1-z}$, что означает, что ПФ для композиций с первой частью $1$ равен $$z \frac{1}{1-\frac{z}{1-z}} = \frac{z(1-z)}{1-2z},$$ как вы получили. 9n$ для всех $n$.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Фотокомпозиции по номерам | Креативный фотограф

---

Примечание редактора: наша октябрьская распродажа проходит на mastering-lightroom.com! Получите скидку 30% на все наши электронные книги, пресеты и видеокурсы Lightroom Classic с кодом ml30 . Кликните сюда, чтобы узнать больше. Спасибо за прочтение, Андрей.

---

Дискуссии о фотокомпозиции часто основаны на идее размещения, то есть, где вы должны разместить в кадре главный объект или фокус фотографии. Но бывают случаи, когда у вас может быть два, три или даже больше фокусных точек, особенно в более сложных композициях. Это дает вам возможность создавать интересные и динамичные фотографии. Давайте посмотрим, как это работает.

Группы из трех и фотографическая композиция

Включение трех фокусных точек в фотографию позволяет вам использовать два обычных композиционных приема — создание треугольников и создание узора.

Треугольники в композиции

Треугольники придают композиции динамичность. Взгляд зрителя перемещается между точками, следуя сторонам треугольника, охватывая разные части кадра.

На фото ниже хороший пример. Я наткнулся на эту сцену в приморском городке на юге Чили. Мне понравились яркие цвета и то, как рыбак раскрашивал лодку.

Вы видели треугольник? Должен признаться, что я не видел этого, когда делал фото, но когда смотрю сейчас, это становится ясно.

В следующем примере группа из трех состоит из статуи в центре рамы и цветочных горшков по бокам. Они создают симметричный треугольник, который переводит взгляд с одной стороны кадра на другую.

Фото ниже я сделал во время прогулки по городу на северо-западе Аргентины. На улице играли три девушки. Я спросил, могу ли я сделать фото, и они сказали, что да. Три грани образуют динамичный треугольник, который побуждает взгляд перемещаться по кадру от лица к лицу.

Группы из трех и узор

Иногда группы из трех могут располагаться в ряд, а не в треугольник. Это фото хороший пример. Группа из трех становится образцом повторяющихся форм и форм.

Когда глаз перемещается между объектами в группе, он создает своего рода ритм. Стрелки ниже показывают, как глаз перемещается по группе из трех.

На этом фото три красных цветка образуют еще один узор. Ему вторит меньший зеленый цветок в левой части кадра, который имеет ту же форму.

Пары и фотографическая композиция

Группы из двух фокусов или объектов также интересны по композиции.

Пары и симметрия

Три фотографии ниже показывают, как пары могут создавать интересные симметричные композиции. На каждой фотографии есть два одинаковых или похожих предмета.

Симметрия интересна, когда она нарушена. Когда я сделал фотографию двух шаров Баодин, я поместил их в рамку, чтобы расположить шары под углом, создав диагональную линию, которая проходит через кадр из левого нижнего угла в правый верхний.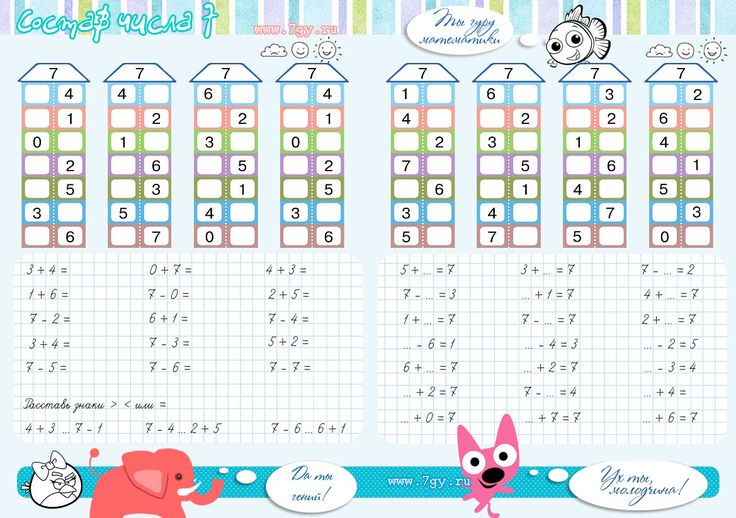 Это добавляет динамичный элемент в композицию.

На фото две головы будды, одна синяя, а другая красная. Это также нарушает симметрию и делает композицию более интересной. Это побуждает зрителя переводить взгляд с одного на другое, сравнивать их и замечать различия.

Пары и контрапункты

Пара образует контрапункт, когда она дает вам два различных фокуса, на которые можно смотреть. В любом фото с парой есть элемент контрапункта, потому что для глаза естественно перемещаться между ними. Но вы можете использовать его намеренно, чтобы помочь глазу перемещаться по кадру.

На этом пейзажном снимке два маяка образуют контрапункт. Взгляд переходит от одного к другому. Это помогает создать ощущение глубины, потому что по разнице в размерах зритель может увидеть, что второй маяк находится дальше.

Это уличное фото, сделанное в Пекине, демонстрирует еще один контрапункт. Две женщины не знали друг друга и действовали независимо друг от друга. Но их объединяет сходство в действиях и позициях.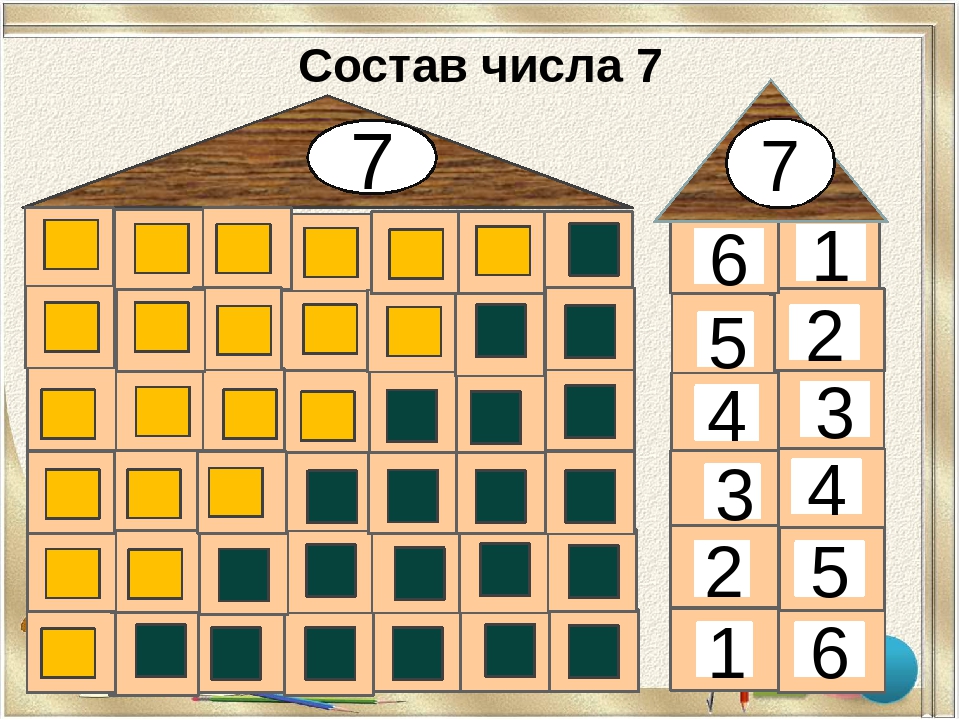

Большие группы и фотокомпозиции

Возможно, вы сталкивались с таким понятием в композиции, как правило шансов — идея о том, что включение группы с нечетным числом субъектов лучше, чем с четным числом. Я знаю, что некоторым фотографам нравятся правила, поскольку они дают простые рекомендации, которым нужно следовать, но как концепция эта не имеет большого значения.

Давайте рассмотрим пример. Сколько инструментов вы видите на этом фото?

Если вы пересчитаете их точно, то увидите, что их 16. Какая разница, если их будет 15 или 17? Я так не думаю. Все, что имеет значение, это то, что есть группа инструментов, расположенных в ряд, который создает интересный узор.

Не имеет большого значения, четное или нечетное число в группе. Но это помогает создать более сильную композицию, если вы можете использовать форму, рисунок и ритм.

Фото ниже я сделал на уличном рынке в Уругвае. На базарном прилавке пять половинок тыквы.

Трое в центре составляют группу из трех, с треугольной композицией. Если бы на фото не было других половинок тыквы, получилась бы сильная композиция.

В целом пять половинок тыквы образуют спираль, которая переносит взгляд через рамку.

На последней фотографии, еще одной уличной фотографии, которую я сделал в Пекине, запечатлена группа из четырех человек. Они позировали другому фотографу, но самое забавное, что пока они втроем смотрят на фотографа, девочка просто хотела поиграть со своей игрушкой. Четыре человека сгруппированы вместе, и в их промежутках есть ритм. Но это также показывает динамическое взаимодействие, которое происходит, когда вы собираете группы людей вместе. Контраст между действиями девушки и другими людьми делает фото более интересным.

Заключение

Группы объектов или людей открывают множество интересных возможностей, когда дело доходит до фотографической композиции. Это дает вам возможность исследовать закономерности, формы, симметрию и отношения между предметами. Это также поможет вам создать более интересную композицию, расположив фотографию таким образом, чтобы глаза двигались по кадру.

Дополнительная литература

• Композиция и заполнение кадра

• Обрамление, размещение и композиция

• Разоблачение правила третей

Об Эндрю С. Гибсоне

Эндрю С. Гибсон — писатель, издатель, путешественник, руководитель семинаров и фотограф из Великобритании. Он начал писать о фотографии во время путешествия по Боливии и публиковался во многих престижных фотожурналах, включая журнал EOS, где он работал писателем и техническим редактором в течение двух лет. Его вдохновляют встречи с новыми людьми, посещение новых мест и получение новых впечатлений. Ознакомьтесь с его электронными книгами по фотографии здесь.

Просмотреть все сообщения Эндрю С. Гибсона

Композиция (комбинаторика) – HandWiki

Из HandWiki

Пространства имен

• Page
• Обсуждение

Страница Действия

• Читать
• Просмотр Источник
• ИСТОРИЯ
• ZWI Export

2 В Mathematics

ZWI

2. запись n в виде суммы последовательности (строго) положительных целых чисел. Две последовательности, различающиеся порядком членов, определяют разный состав их суммы, хотя считается, что они определяют одну и ту же часть этого числа. Каждое целое число имеет конечное число различных композиций. Отрицательные числа не имеют композиций, а 0 имеет одну композицию — пустую последовательность. Каждое положительное целое число n имеет 2 ^{n −1} различных составов.

Биекция между 3-битными двоичными числами и композициями из 4

Слабая композиция целого числа n аналогична композиции n , но позволяет элементам последовательности быть равными нулю: это способ записать n как сумму последовательности неотрицательных целых чисел. Как следствие, каждое натуральное число допускает бесконечно много слабых композиций (если их длина не ограничена). Добавление ряда терминов 0 к и слабого состава обычно не считаются определяющими другой слабый состав; другими словами, предполагается, что слабые композиции неявно бесконечно расширяются с помощью терминов 0.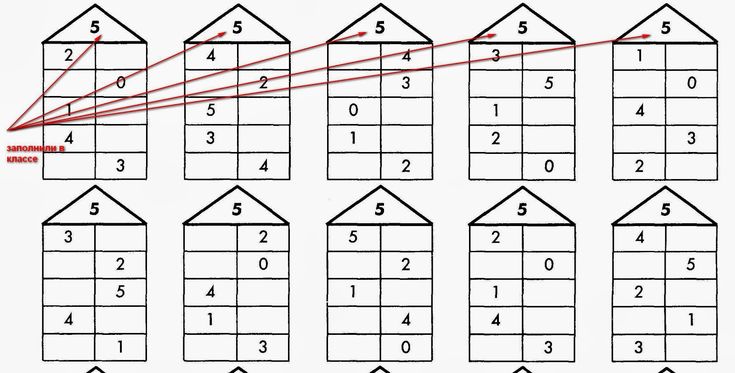

Обобщая далее, A -ограниченная композиция целого числа n для подмножества A целых чисел (неотрицательных или положительных) является упорядоченным набором одного или нескольких элементов в A сумма которых равна n . ^[1]

Содержимое

• 1 Пример
• 2 Количество композиций
• 3 Однородные многочлены
• 4 См. также
• 5 Каталожные номера
• 6 Внешние ссылки

Примеры

32 композиции из 6

1 + 1 + 1 + 1 + 1 + 1
2 + 1 + 1 + 1 + 1
1 + 2 + 1 + 1 + 1
. . .
1 + 5
6

11 разделов по 6

1 + 1 + 1 + 1 + 1 + 1
2 + 1 + 1 + 1 + 1
3 + 1 + 1 + 1
. . .
3 + 3
6

Шестнадцать композиций из 5:

• 5
• 4 + 1
• 3 + 2
• 3 + 1 + 1
• 2 + 3
• 2 + 2 + 1
• 2 + 1 + 2
• 2 + 1 + 1 + 1
• 1 + 4
• 1 + 3 + 1
• 1 + 2 + 2
• 1 + 2 + 1 + 1
• 1 + 1 + 3
• 1 + 1 + 2 + 1
• 1 + 1 + 1 + 2
• 1 + 1 + 1 + 1 + 1.

Сравните это с семью разделами из 5:

• 5
• 4 + 1
• 3 + 2
• 3 + 1 + 1
• 2 + 2 + 1
• 2 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1.

Можно накладывать ограничения на части композиций. Например, пять композиций из 5 в отдельные термины:

• 5
• 4 + 1
• 3 + 2
• 2 + 3
• 1 + 4.

Сравните это с тремя разбиениями числа 5 на отдельные термины:

• 5
• 4 + 1
• 3 + 2.

Количество композиций

Количество композиций n  +1 в k  +1 упорядоченные разбиения образуют треугольник Паскаля композиции n , например, количество способов, которыми можно подняться по лестнице длиной n , делая одну или две ступеньки за раз

Обычно пустая композиция считается единственной композицией 0, и есть нет композиций отрицательных целых чисел. Есть 2 9п\, \большой) }[/math]

производит уникальную композицию n . И наоборот, каждая композиция n определяет назначение плюсов и запятых. Поскольку имеется n  − 1 бинарных вариантов, результат следующий. Тот же аргумент показывает, что количество композиций n ровно на k частей (a k -композиция ) определяется биномиальным коэффициентом [math]\displaystyle{ {n-1\choose k-1 } }[/математика]. Заметим, что суммируя все возможные количества частей, мы получаем 2 9{н-1}. }[/math]

Для слабых композиций число равно [math]\displaystyle{ {n+k-1\choose k-1} = {n+k-1 \choose n} }[/math], поскольку каждой k -композиции n + k соответствует слабая композиция n по правилу

[математика]\displaystyle{ a_1+a_2+ \ldots + a_k = n +k \quad \mapsto \quad (a_1 -1) + (a_2-1) + \ldots + (a_k – 1) = n }[/math]

Из этой формулы следует, что количество слабых композиций 9{d_n} }[/math] такое, что [math]\displaystyle{ d_1 + \ldots + d_n = d }[/math].