Сложные задачи по математике 4 класс с ответами: Задания для городской олимпиады по математике (4 класс). | Олимпиадные задания по математике (4 класс) по теме:
Математическая олимпиада для 4 класса с ответами
В стародавние времена издавались познавательные журналы для детей с интересными замысловатыми заданиями, которые учителя использовали в своей работе, подготавливая по ним олимпиады. Ох и интересно было разгадать, какой ответ скрывается под сложной логической задачкой. Мы надеемся, что и сейчас остались еще такие учителя, которые специально ищут интересные задания, чтобы увлечь учеников математикой, и такие детки, которым интересно найти разгадки на загадки. Для тех и других, учителей и учеников четвертого класса, наша математическая олимпиада.
Задания олимпиады с ответами
Задание №01. Шаг Дяди Фёдора в три раза больше шага Матроскина. Сначала по прямой дорожке прошёл Матроскин, а потом – Фёдор, начав с того же места, что и Матроскин. Наступая на след Матроскина, Фёдор стирает этот след. Потом Шарик насчитал 17 следов Матроскина. Сколько следов Фёдора было на дорожке?
Ответ: 9
Задание №02. У Винни-Пуха есть 11 больших горшков с мёдом и 10 маленьких.
Комментарий. Все коробки одинаковые. Другие способы упаковки Винни Пуху неизвестны. Вместо больших горшков можно класть маленькие или не наполнять коробки полностью. Все большие горшки одинаковы и все маленькие тоже одинаковы.
Ответ: 3
Задание №03. Вдоль тропинки вбиты колышки на расстоянии одного метра друг от друга. Между первым и последним колышками 8 метров. Сколько всего колышков вдоль тропинки?
Ответ: 9
Задание №04. Найди неизвестное число:
709 / 7 / 153
499 / 11 / 218
568 / ? / 312
Ответ: 13
Задание №05. В трёхзначном нечётном числе сумма цифр равна 3. Известно, что все цифры различные. Найдите это число.
Ответ: 201
Задание №06. Школьник написал все числа от 1 до 1000. Сколько цифр написал школьник?
Ответ: 2893
Задание №07. На какое однозначное число, не равное нулю, надо умножить 142857, чтобы получилось число, записанное одинаковыми цифрами.
На какое однозначное число, не равное нулю, надо умножить 142857, чтобы получилось число, записанное одинаковыми цифрами.
Ответ: 7
Задание №08. 15 человек, отдыхающих в доме отдыха, любят играть в уголки. Они провели между собой соревнование. После каждой партии выбывал проигравший. Впервый день состоялось 5 партий, во второй 6, а в третий день соревнование закончилось. Сколько партий состоялось в третий день?
Ответ: 3
Задание №09. На школьном дворе играют 14 девочек и 17 мальчиков. Какое наименьшее количество учеников должны к ним присоединиться, чтобы их можно было разбить на 6 групп с одинаковым числом школьников в каждой?
Ответ: 5
Задание №10. У коллекционера 4000 марок. Половина всех марок – о млекопитающих. Четверть – о птицах. Половина остатка – о рыбах. Остальные – о рептилиях. Сколько марок с рептилиями у коллекционера?
Ответ: 500
Задание №11. Ученик загадал число. Известно, что загаданное число больше 8 ровно на половину этого загаданного числа. Чему равно число, которое загадал ученик?
Чему равно число, которое загадал ученик?
Ответ: 16
Задание №12. У школьника было 5 целых груш, 6 половинок да 8 четвертинок. Сколько всего было груш у школьника?
Ответ: 10
Задание №13. К числу 8 слева и справа приписали одну и ту же цифру так, что полученное число делилось без остатка на 6. В ответе укажите число, полученное после приписывания цифры. Если таких чисел может быть несколько, то необходимо указать наименьшее из них.
Ответ: 282
Задание №14. Масса ящика с конфетами 37 килограммов. Какова масса (в килограммах) пустого ящика, если после продажи половины всех конфет ящик имел массу 19 килограммов?
Ответ: 1
Задание №15. В пакете лежат апельсины, мандарины, лимоны – всего 20 штук. Апельсинов в 6 раз больше, чем лимонов. Мандаринов меньше, чем апельсинов. Сколько мандаринов в пакете?
Ответ: 6
Задание №16. В магазине картофель расфасовали в 24 пакета: по 5 кг и по 3 кг. Масса всех пакетов по 5 кг оказалась равна массе всех пакетов по 3 кг. Сколько получилось пакетов по 3 кг?
Сколько получилось пакетов по 3 кг?
Ответ: 15
Задание №17. Чему равно число, если двенадцатая его часть равна 3?
Ответ: 36
Задание №18. Какое наибольшее двузначное число делится на 7 без остатка?
Ответ: 98
Задание №19. Группа учеников состоит из 18 человек. Они учатся говорить по-французски и/или по-немецки. 13 человек учат немецкий, 9 человек – французский. Сколько человек учат сразу два языка: немецкий и французский?
Ответ: 4
Задание №20. Врач прописал больному порошки, указав, что их надо принимать через каждые 2 часа. Больному необходимо выпить 8 порошков. Через какое время (в часах) после начала приёма больной выпьет последний порошок?
Ответ: 14
Задачи на скорость, время, расстояние 4 класс | Движение
Тут есть простые и сложные задачи на движение для 4 класса! На встречное движение, на движение в разных направлениях и другое.
Задачи на нахождение времени
Из одной точки в разные стороны выехали 2 машины. Их скорости – 70 и 140 км/ч. Через 4 часа машина с наибольшей скоростью развернулась и принялась догонять другую. (Все машины ехали). И догнала. Сколько часов транспорт был в пути?
Их скорости – 70 и 140 км/ч. Через 4 часа машина с наибольшей скоростью развернулась и принялась догонять другую. (Все машины ехали). И догнала. Сколько часов транспорт был в пути?
На расстоянии 350 км навстречу друг другу выплыли 2 лодки. Их скорости – 30 и 40 км/ч. Они плыли 4 часа. Оставшееся время до встречи они двигались со скоростями по 35 км/ч. Сколько часов они плыли, пока не встретились?
3Вы должны войти, чтобы пройти эту викторину.
Задачи на нахождение расстояния и скорости
Однажды папа и дедушка решили поспорить, что быстрее: машина или автобус. Начальная скорость у машины – 100 км/ч, а у автобуса – 60 км/ч. И вот они стартовали. При этом известно, что у машины каждый час скорость уменьшается на 10 км, а у автобуса на 10 км увеличивается. Кто будет раньше через 5 часов, если оба начали с одного места и едут в одном направлении?Котик и собачка с одного места в разных направлениях пробежали по 66 километров. Собачка за 2 часа, а котенок – за 3. С такой же скоростью они вернулись обратно. И с этой же скоростью они бежали в разных направлениях 2 часа. А сколько метров они пробежали вместе?
Собачка за 2 часа, а котенок – за 3. С такой же скоростью они вернулись обратно. И с этой же скоростью они бежали в разных направлениях 2 часа. А сколько метров они пробежали вместе?
Папа едет со скоростью 180 км/час. Когда он проехал 45 км, поменял скорость на 120 км/час. Сколько надо времени, чтобы проехать 105 км?
Первые 3 часа папа ехал со скоростью 160 км/ч, а потом снизил скорость в 2 раза. Сколько км он проедет, если время его поездки составляет 5 часов?
Решайте больше задач на движение на этих страницах:
https://matsharik.ru/vremya-skorost-rasstoyanie-3-klass/
4 класс | Олимпиадные задания
Содержание Задача 4.1 Задача 4.2 Задача 4.3 Задача 4.4 Задача 4.5 Задача 4.6 Задача 4.7 Задача 4.8 Задача 4.1 Винни-Пух и Пятачок договорились утром пойти в гости к Кролику. Пятачок встал пораньше и решил сначала дойти до домика Винни-Пуха, а потом вместе с другом к полудню быть у Кролика. Какое расстояние прошёл Пятачок до полудня, […]
7378
17. 11.2020
11.2020
Содержание Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 1 Какая звезда самая яркая на небе Земли? Канопус Вега Полярная Арктур Солнце Денеб Бетельгейзе Сириус Ответ: 5 (2 балла) За ответ (8) – 1 балл. Комментарий: Солнце – тоже звезда. Задание 2 Назовите тело Солнечной системы, […]
3052 29.10.2020
Содержание Part 1 (15 minutes) Part 2 «Reading» (15 minutes) Part 3 «Use of English» (30 minutes) Task 1 Task 2 Task 3 Audioscript KEYS Part 1. Listening Part 2. Reading Part 3. Use of English Part 1 (15 minutes) Maximum points – 5 Listening Listen to Helena and her father talking about her school […]
14372 17.09.2020
Содержание Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 1 На доске в ряд выписаны цифры 1 1 1 2 2 2 5 5 5 : Между ними можно расставить несколько плюсов, чтобы получившийся результат заканчивался на цифру один: 1 + 1 + 12 + 2 + 25 + 5 + 5 […]
17144
26. 09.2019
09.2019
32356 19.09.2019
Содержание Задание № 1 (5 баллов) Модель ответа и критерии Задание № 2 (4 балла) Модель ответа и критерии Задание № 3 (5 баллов) Модель ответа и критерии Задание № 4 (4 балла) Модель ответа и критерии Задание № 5 (4 балла) Модель ответа и критерии Задание № 6 (5 баллов) Модель ответа и критерии […]
22238 10.11.2017
Содержание Задание 1 (7 баллов) Задание 2 (7 баллов) Задание 3 (7 баллов) Задание 4 (7 баллов) Задание 5. (7 баллов) Задание 1 (7 баллов) Содержание ↑ Расставьте скобки так, чтобы получилось верное равенство: 90 — 72 : 6 + 3 = 82 .
31222 30.10.2017
Прочитайте текст и выполните задания 1–10 (1)Город Углич на юго-западе Ярославской области стоит на крутом берегу Волги. (2)Здесь река делает резкий поворот и получается острый угол, отсюда и название города. (3)Углич – один из самых древних городов России. (4)Он основан в 937 г. (5)В 14 веке здесь построили деревянный Кремль. Это был пограничный укреплённый город […]
6792 02.02.2017
Задание 1 (7 баллов) Замените звёздочки цифрами так, чтобы равенство стало верным и все семь цифр были различными: ** + ** = 175. Возможные ответы 92 + 83 = 175 82 + 93 = 175 93 + 82 = 175 83 + 92 = 175 Дополнительных объяснений не требуется. Критерии проверки Приведён любой из возможных […]
11939 27.12.2016
Нестандартные задачи.
 (факультатив, математика 4 класс)
(факультатив, математика 4 класс)Факультатив по математике
Урок №25 6.12.2017
Тема урока: Нестандартные задачи.
Цели: -закрепить навыки умения решать разнотипные сложные задачи в 3-4 действия
– умение работать самостоятельно
– работа над развитием логического мышления учащихся
Оборудование: – учебник, доска, тетради, дидактический и наглядный материал
по математике.
Ход урока.
Оргмомент.
Психологический настрой на урок.
Работа над пройденной темой.
– закрепление знания таблицы умножения в игровой форме
«Подводный мир» (карточки с примерами)
Работа над новой темой.
– сегодня мы порешаем задачки в 3-4 действия
Решить выражения на порядок действий:
307975 – 27648:8 + 253 = 304 772
Решение задач:
В 6 одинаковых мешках 288 кг картофеля. Сколько кг картофеля в 5-ти таких же мешках. На сколько меньше в 5 мешках, чем в 6 мешках?
Сколько кг картофеля в 5-ти таких же мешках. На сколько меньше в 5 мешках, чем в 6 мешках?
Масса 1 мешка кол-во мешков общая масса
Одина- 6м 288 кг
ковая 5 м ? – на ? меньше
288:6 = 48 (кг)в 1 мешке
48*5 = 240 (кг)
288 – 240 = 48 (кг)
Один товарный поезд шёл со скоростью 43 км/ч и прошёл 1634 км, а другой со скоростью 42 км/ч и прошёл 1680 км. На сколько часов второй поезд был в пути больше, чем первый?
Скорость время расстояние
1 поезд 43 км/ч ? 1634 км
На ? больше
2 поезд 42 км/ч ? 1680 км
1634 : 43 = 38 (ч)
1680 : 42 = 40 (ч)
40-38 = 2 (ч)
С одного аэродрома вылетели одновременно в противоположных направлениях два самолёта. Скорость одного из них 600 км/ч, а другого 720 км/ч. На каком расстоянии находились самолёты через 3 часа?
Скорость время расстояние
1 самолёт 600 км/ч ?
3 часа ?
2 самолёт 720 км/ч 7
600*3 = 1800 (км)
720*3 = 2160 (км)
1800 + 2160 = 3960 (км)
Коммерческая задача:
Охотник Тигров добыл за сезон 48 шкур белок. Каждые 4 шкуры он может обменять на 1 мешок пшеницы, каждые 2 шкуры – на 8 подков. Хватит ли ему добытых шкурок для того, чтобы подковать 4 лошади и получить 3 мешка пшеницы?
Каждые 4 шкуры он может обменять на 1 мешок пшеницы, каждые 2 шкуры – на 8 подков. Хватит ли ему добытых шкурок для того, чтобы подковать 4 лошади и получить 3 мешка пшеницы?
Решение:
всего – 48 шкур 1 лошадь -4 подковы
4 шкуры – 1 мешок пшеницы 4 лошади – 16 подков
2 шкуры -8 подков
3 мешка пшеницы – 12 шкур
4 лошади – 16 подков – 4 шкуры
12 +4 = 16 48 -16 = 32 шкуры останется
48-4-4-4=36 36-2-2 = 32
Работа по карточкам самостоятельно на выбор учащихся
Обобщение
Итоги занятия.
Задачи на пропорции по математике — примеры с ответами
Понятие пропорции
Чтобы решать задачи на тему пропорции, вспомним главное определение.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин.
Главное свойство пропорции: Произведение крайних членов равно произведению средних. a : b = c : d, где a, b, c, d — члены пропорции, a, d — крайние члены, b, c — средние члены. |
Вывод из главного свойства пропорции:
- Крайний член равен произведению средних, которые разделены на другой крайний. То есть для пропорции a/b = c/d:
- Средний член равен произведению крайних, которые разделены на другой средний. То есть для пропорции a/b = c/d:
Решить пропорцию — значит найти неизвестный член. Свойство пропорции — главный помощник в решении.
Запомним!
Равенство двух отношений называют пропорцией.
Рассмотрим легкие и сложные задачи, которые можно решить с помощью пропорции. 5, 6, 7, 8 класс — неважно, всем школьникам полезно проанализировать занимательные задачки.
Задачи на пропорции с решением и ответами
Свойства пропорции придумали не просто так! С их помощью можно найти любой из членов пропорции, если он неизвестен. Решим 10 задач на пропорцию.
Задание 1. Найти неизвестный член пропорции: x/2 = 3/1
Как решаем:
В этом примере неизвестны крайние члены, поэтому умножим средние члены и разделим полученный результат на известный крайний член:
x = (2 * 3)/1 = 6
Ответ: x = 6.
Задание 2. Найти неизвестный член: 1/3 = 5/y
Как решаем:
y = (3 * 5)/1 = 15
Ответ: y = 15.
Задача 3. Решить пропорцию: 30/x = 5/8
Как решаем:
x = (30 * 8)/5 = 48
Ответ: x = 48.
Задание 4. Решить: 7/5 = y/10
Как решаем:
y = (7 * 10)/5 = 14
Ответ: y = 14.
Задание 5. Известно, что 21x = 14y. Найти отношение x — к y
Как решаем:
- Сначала сократим обе части равенства на общий множитель 7: 21x/7 = 14y/7.
Получим: 3x = 2y.
- Теперь разделим обе части на 3y, чтобы в левой части убрать множитель 3, а в правой части избавиться от y: 3x/3y = 2y/3y.
- После сокращения отношений получилось: x/y = 2/3.
Ответ: 2 к 3.
На следующем примере мы узнаем как составить пропорцию по задаче💡
Задание 6. Из 300 подписчиков в инстаграм 108 человек — поставили лайк под постом. Какой процент всех подписчиков составляют те, кому понравился пост и они поставили лайк?
Как решаем:
- Примем всех подписчиков за 100% и запишем условие задачи кратко:
300 — 100%
108 — ?%
- Составим пропорцию: 300/108 = 100/x.

- Найдем х: (108 * 100) : 300 = 36.
Ответ: 36% всех подписчиков поставили лайк под постом.
Задание 7. Подруга Гарри Поттера при варке оборотного зелья использовала водоросли и пиявки в отношении 5 к 2. Сколько нужно водорослей, если есть только 450 грамм пиявок?
Как решаем:
- Составим пропорцию: 5/2 = x/450.
- Найдем х: (5 * 450) : 2 = 1125.
Ответ: на 450 грамм пиявок нужно взять 1125 гр водорослей.
Задание 8. Известно, что арбуз состоит на 98% из воды. Сколько воды в 5 кг арбуза?
Как решаем:
Вес арбуза (5 кг) составляет 100%. Вода — 98% или х кг.
Составим пропорцию:
5 : 100 = х : 98
х = (5 * 98) : 100
х = 4,9
Ответ: в 5 кг арбуза содержится 4,9 кг воды.
Перейдем к примерам посложнее. Рассмотрим задачу на пропорции из учебника по алгебре за 8 класс.
Задание 9. Папин автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Как рассуждаем:
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
Обозначим:
- v1 = 75 км/ч
- v2 = 52 км/ч
- t1 = 13 ч
- t2 = х
Как решаем:
- Составим пропорцию: v1/v2 = t2/t1.
Соотношения равны, но перевернуты относительно друг друга.
- Подставим известные значения: 75/52 = t2/13
t2 = (75 * 13)/52 = 75/4 = 18 3/4 = 18 ч 45 мин
Ответ: 18 часов 45 минут.
Задание 10. 24 человека за 5 дней раскрутили канал в телеграм. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
Как рассуждаем:
1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.
3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:
Как решаем:
- Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию:
30 : 24 = 5 : х
- Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член:
х = 24 * 5 : 30
х = 4
- Значит, 30 человек раскрутят канал за 4 дня.
Ответ: за 4 дня.
Давайте практиковаться еще! Приходите на интерактивные уроки по математике в онлайн-школу Skysmart. Мы создали тысячи увлекательных заданий, чтобы учеба не вгоняла в тоску, а вдохновляла и приносила приятные оценки в дневник.
На бесплатном вводном уроке расскажем, как у нас все устроено и наметим план развития школьника.
Олимпиадные задания (математика) – Олимпиада школьников «Высшая проба» – Национальный исследовательский университет «Высшая школа экономики»
В старых версиях браузеров сайт может отображаться некорректно. Для оптимальной работы с сайтом рекомендуем воспользоваться современным браузером.
Мы используем файлы cookies для улучшения работы сайта НИУ ВШЭ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь, наши правила обработки персональных данных – здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом НИУ ВШЭ и согласны с нашими правилами обработки персональных данных. Вы можете отключить файлы cookies в настройках Вашего браузера.
✖Обычная версия сайта
2020/2021 учебный год
Для младших классов: максимальная оценка за всю работу – 100 баллов. Если сумма баллов, набранных участником по всем задачам, превосходит 100, его итоговая оценка равна 100.
Если сумма баллов, набранных участником по всем задачам, превосходит 100, его итоговая оценка равна 100.
Для старших классов: итог подводится по трём задачам, по которым достигнуты наилучшие результаты; баллы за пункты одной задачи суммируются.
2019/2020 учебный год
Для младших классов: максимальная оценка за всю работу – 100 баллов. Если сумма баллов, набранных участником по всем задачам, превосходит 100, его итоговая оценка равна 100.
Для старших классов: итог подводится по трём задачам, по которым достигнуты наилучшие результаты; баллы за пункты одной задачи суммируются.
2018/2019 учебный год
| Задания | Решения и критерии |
2017/2018 учебный год
2016/2017 учебный год
2015/2016 учебный год
2014/2015 учебный год
2013/2014 учебный год
2012/2013 учебный год
Задания 8 класс (задачи 1 и 2 имеют вес 16 баллов, остальные — 17 баллов)
Задания 9 класс (все задачи имеют равный вес (кроме 4): 17 баллов, задача 4 — 15 баллов)
Задания 10 класс (все задачи имеют равный вес (кроме 2): 17 баллов, задача 2 — 15 баллов)
Задания 11 класс (все задачи имеют равный вес (кроме 3): 17 баллов, задача 3 — 15 баллов)
2011/2012 учебный год
Страница не найдена
16 май
Трагедия в Казани, где 19-летний Ильназ Галявиев расстрелял школьников и их учителей, унесла жизни девяти человек, ещё 23 получили ранения. В пермском селе Вильгорт подобное преступление предотвратила мать 14-летнего подростка. В 2019 году женщина обратилась в правоохранительные органы, заметив агрессию и странности в поведении сына. Оказалось, что молодой человек говорил о планах убить своих одноклассников и учителей. Летом 2020 года его приговорили к трём годам лишения свободы. Специальный корреспондент RT Екатерина Винокурова пообщалась с родственниками и знакомыми осуждённого подростка и выяснила подробности неслучившейся трагедии.
В пермском селе Вильгорт подобное преступление предотвратила мать 14-летнего подростка. В 2019 году женщина обратилась в правоохранительные органы, заметив агрессию и странности в поведении сына. Оказалось, что молодой человек говорил о планах убить своих одноклассников и учителей. Летом 2020 года его приговорили к трём годам лишения свободы. Специальный корреспондент RT Екатерина Винокурова пообщалась с родственниками и знакомыми осуждённого подростка и выяснила подробности неслучившейся трагедии.
16 май
В России снижается качество подготовки выпускников вузов, что связано также и с уровнем образования в школах, заявил в ходе всероссийского форума «Молодёжь и наука» президент Российской академии наук (РАН) Александр Сергеев.
14 май
Директор петербургского Президентского физико-математического лицея №239, заслуженный учитель России Максим Пратусевич прокомментировал систему контроля на ЕГЭ.
14 май
Ильназ Галявиев, напавший на казанскую гимназию №175 11 мая, был тихим и неконфликтным студентом. Об этом RT рассказал одногруппник обвиняемого в убийстве девяти человек. Впрочем, староста группы, в которой учился Галявиев, отметил, что однажды тот предложил одному из учеников «вступить в свою секту», однако тогда это сочли шуткой. Ранее ректор университета, при котором находится колледж, заявила, что последние полтора года Галявиев жил один, потому что родители и старший брат переехали от него на другую квартиру.
Задачи по математике для 4-х классов
К четвертому классу у большинства учеников развиваются навыки чтения и анализа. Тем не менее, они все еще могут быть напуганы математическими задачами со словами. Они не должны быть такими. Объясните ученикам, что для решения большинства задач со словами в четвертом классе обычно требуется знание основных математических операций – сложение, вычитание, умножение и деление – и понимание того, когда и как использовать простые математические формулы для улучшения математических навыков.
Они не должны быть такими. Объясните ученикам, что для решения большинства задач со словами в четвертом классе обычно требуется знание основных математических операций – сложение, вычитание, умножение и деление – и понимание того, когда и как использовать простые математические формулы для улучшения математических навыков.
Объясните ученикам, что вы можете узнать скорость (или скорость), с которой кто-то путешествует, если вы знаете расстояние и время, которое он проехал.И наоборот, если вы знаете скорость (скорость), с которой человек движется, а также расстояние, вы можете рассчитать время, в течение которого он путешествовал. Вы просто используете базовую формулу: скорость, умноженная на время, равна расстоянию, или r * t = d (где « * » – символ времени). В приведенных ниже таблицах учащиеся решают задачи и заполняют свои ответы на предоставленных пустых местах. Ответы предоставляются вам, учителю, на дублированном листе, к которому вы можете получить доступ и распечатать на втором слайде после рабочего листа учащихся.
На этом листе ученики ответят на такие вопросы, как: «Ваша любимая тетя летит к вам домой в следующем месяце. Она летит из Сан-Франциско в Буффало. Это 5-часовой перелет, и она живет в 3060 милях от вас. самолет идет? ” и «Сколько подарков получила« Настоящая любовь »за 12 дней Рождества? (Куропатка на грушевом дереве, 2 горлицы, 3 французские курицы, 4 кричащие птицы, 5 золотых колец и т. д.). Работа?”
Эта форма для печати является копией рабочего листа на предыдущем слайде с ответами на проблемы.Если учащиеся испытывают трудности, объясните им первые две задачи. Для первой задачи объясните, что ученикам дается время и расстояние, на которое летит тетя, поэтому им нужно только определить скорость (или скорость).
Скажите им, что, поскольку они знают формулу r * t = d , им просто нужно настроить, чтобы выделить « r ». Они могут сделать это, разделив каждую часть уравнения на « t », что дает пересмотренную формулу r = d ÷ t (скорость или скорость передвижения тети = пройденное ею расстояние, деленное на время). Затем просто введите цифры: r = 3060 миль ÷ 5 часов = 612 миль / ч .
Затем просто введите цифры: r = 3060 миль ÷ 5 часов = 612 миль / ч .
Для второй задачи студентам просто нужно перечислить все подарки, полученные за 12 дней. Они могут спеть песню (или спеть ее всем классом) и перечислить количество подарков, дарованных каждый день, или найти песню в Интернете. Если сложить количество подарков (1 куропатка на грушевом дереве, 2 горлицы, 3 курицы, 4 кричащие птицы, 5 золотых колец и т. Д.), Получим ответ 78 .
Второй рабочий лист предлагает задачи, требующие некоторых рассуждений, например: «У Джейд 1281 бейсбольная карточка.У Кайла 1535. Если Джейд и Кайл объединят свои бейсбольные карточки, сколько карточек будет? Оценка ___________ Ответ ___________. «Чтобы решить задачу, ученики должны оценить и указать свой ответ в первом бланке, а затем сложить фактические числа, чтобы увидеть, насколько близко они подошли.
Чтобы решить задачу, указанную на предыдущем слайде, учащимся необходимо знать округление. Для этой задачи вы округлите 1281 либо до 1000, либо до 1500, и вы округлите 1535 до 1500, получив расчетные ответы от 2500 до 3000 (в зависимости от того, каким образом ученики округлили 1281).Чтобы получить точный ответ, студенты просто складывают два числа: 1,281 + 1,535 = 2,816 .
Для этой задачи вы округлите 1281 либо до 1000, либо до 1500, и вы округлите 1535 до 1500, получив расчетные ответы от 2500 до 3000 (в зависимости от того, каким образом ученики округлили 1281).Чтобы получить точный ответ, студенты просто складывают два числа: 1,281 + 1,535 = 2,816 .
Обратите внимание, что эта сложная задача требует переноски и перегруппировки, поэтому просмотрите этот навык, если ваши ученики не могут понять концепцию.
БЕСПЛАТНЫХ заданий по математике для 4-го класса
Помогите своим детям получить дополнительную практику по математике с помощью этих бесплатных распечатываемых листов по математике для 4-го класса. Эти бесплатные распечатываемые листы для 4-го класса не требуют подготовки, загрузите файл в формате pdf… распечатайте….идти! Эти бесплатные рабочие листы домашнего обучения идеально подходят для летнего обучения, математических центров и дополнительной практики с по математике для 4 класса , а также для того, чтобы помочь детям овладеть математикой в четвертом классе.
Задания по математике для 4-го класса
Мы всегда ищем забавные способы для наших учеников 4-х классов практиковать математику. Это настолько важно не только для более продвинутой математики, но и для их жизни, что они получают много практики, чтобы сформировать прочную основу и достичь беглости в математике. Поэтому мы стараемся сделать это увлекательным, чтобы они с нетерпением ждали и получали удовольствие от занятий математикой.Эти рабочие листы по математике для 4-го класса можно использовать как бесплатные задания по математике или превратить в бесплатную математическую игру для отработки сложения, вычитания, умножения, деления, дроби, задач со словами и многого другого.
Рабочие листы 4-го класса
Родителям, учителям или ученикам на дому – вам понравится, что эти распечатанных математических листов помогают детям практиковать различные навыки, такие как сложение (включая трехзначное сложение), вычитание (включая трехзначное вычитание), умножение, деление. , дроби, задачи со словом, счет денег и многое другое по математике для четвертого класса.Используйте их в математическом центре в качестве дополнительной практики, работы с сиденьями, математической игры для четвертого класса или летнего обучения, чтобы помочь детям избежать потери учебы летом.
, дроби, задачи со словом, счет денег и многое другое по математике для четвертого класса.Используйте их в математическом центре в качестве дополнительной практики, работы с сиденьями, математической игры для четвертого класса или летнего обучения, чтобы помочь детям избежать потери учебы летом.
Получите эту бесплатную услугу, прокрутив до конца сообщения, в соответствии с условиями использования, и щелкнув текстовую ссылку, которая гласит >> Загрузить <<. PDF-файл откроется в новом окне, чтобы вы могли распечатать и сохранить бесплатные рабочие листы 4-го класса. Вам понравится, что эти черно-белые рабочие листы не требуют подготовки! Страницы с черной линией идут от самых простых до самых сложных и включают в себя также листы для ответов.
Ищете больше из наших бесплатных заданий по математике ? Попробуйте эти:
Бесплатные задания по математике для 4-го класса
Это математическое задание БЕЗ ПОДГОТОВКИ отлично подходит для превращения заданий по математике в математическую игру. Просто дайте учащимся один из заданий (они идут в порядке сложности), и вы готовы к 4-му классу математики.
Просто дайте учащимся один из заданий (они идут в порядке сложности), и вы готовы к 4-му классу математики.
Хотя вы, безусловно, можете использовать эти математические рабочие листы традиционным способом – раздайте их детям, а дети решают математические уравнения, а затем вы их проверяете… мы предпочитаем развлечь их с помощью MAD MINUTES !
4-й класс по математике
Бесплатные рабочие листы по математике для 4-го класса делают занятия математикой увлекательными, увлекательными и запоминающимися для учеников 4-го класса не только практиковать математику , но и улучшать запоминание и беглость .Студенты будут лучше запоминать их, повторяя одни и те же задачи изо дня в день, пока им не станет лучше – и они вернутся, чтобы исправить свою работу, чтобы повысить точность.
Задания по математике для 4-го класса
Полные инструкции для этих бесплатных рабочих листов по математике для 4-го класса включены в загрузку, но вот суть. Вы даете своему четверокласснику лист «Безумные минуты» лицевой стороной вниз. Установите таймер на 3-5 минут, и когда вы скажете «ИДТИ», они перевернут Рабочий лист «Безумные минуты» и начнут решать математические задачи. Напомните им, что цель – это не только скорость, но и точность.
Вы даете своему четверокласснику лист «Безумные минуты» лицевой стороной вниз. Установите таймер на 3-5 минут, и когда вы скажете «ИДТИ», они перевернут Рабочий лист «Безумные минуты» и начнут решать математические задачи. Напомните им, что цель – это не только скорость, но и точность.
Рабочие листы для печати по математике
Когда таймер подает звуковой сигнал, они останавливаются. Теперь перейдите к правильным ответам. ( В конце рабочих листов есть ключи для ответов). Сколько они закончили? Сколько они получили права?
Продолжайте использовать те же рабочие листы, пока они не заполнят не менее 90% с точностью 90% за 3-5 минут.
Вам понравится, что в каждый рабочий лист включен ключ с ответом!
Умножение Факты игры
Деятельность отдела
Ищете еще веселые бесплатные распечатанные игры на деление для детей, чтобы они могли практиковать математику и научиться бегло говорить? Вам понравятся эти листы деления, распечатанные игры на деление и многое другое!
Рабочие листы 4-го класса
Скачивая с моего сайта, вы соглашаетесь со следующим:
- Это только для личного пользования (учителя, пожалуйста, смотрите мой магазин TPT)
- Запрещается продавать, размещать, воспроизводить или хранить на любом другом сайте (включая блог, Facebook, Dropbox и т.
 Д.))
Д.)) - Все загруженные материалы защищены авторским правом. См. Условия использования.
- Я предлагаю бесплатные печатные издания, чтобы благословить моих читателей И обеспечить свою семью. Ваши частые посещения моего блога и поддержка покупок по партнерским ссылкам и рекламе заставляют светиться, так сказать. Спасибо!
>> Скачать Минуты безумия 4-го класса
<<Обучение студентов обоснованию ответов в математике
Обучение студентов обоснованию своего ответа в математике может быть трудным, но, к счастью, это не обязательно.Я хочу поделиться с вами некоторыми идеями, как научить студентов обосновывать ответы по математике, а также некоторыми из моих любимых ресурсов для обеспечения столь необходимой практики с математическими задачами и задачами со словами.
Каждый раз, когда мои ученики с чем-то борются, мне нравится внимательно смотреть на то, с чем они борются, чтобы увидеть, смогу ли я разбить это и прояснить для них. Что касается обучения студентов тому, как обосновывать ответы, я пытался придумать все способы, которыми студенты могли бы оправдать свою работу.Вот таблица якоря, которая показывает некоторые способы, которыми мои ученики могли и обосновывали свои ответы в прошлом. Я предлагаю вам иметь в виду то, что вы ищете, но обсудить со студентами и получить их мнение. Лучшим сценарием будет создание таблицы вместе, и если студенты «помогут» вам придумать различные способы, которыми они могут обосновать свои ответы.
Что касается обучения студентов тому, как обосновывать ответы, я пытался придумать все способы, которыми студенты могли бы оправдать свою работу.Вот таблица якоря, которая показывает некоторые способы, которыми мои ученики могли и обосновывали свои ответы в прошлом. Я предлагаю вам иметь в виду то, что вы ищете, но обсудить со студентами и получить их мнение. Лучшим сценарием будет создание таблицы вместе, и если студенты «помогут» вам придумать различные способы, которыми они могут обосновать свои ответы.
Я знаю, что первый в этой таблице (маркировка вашей работы) технически не помогает оправдать их ответ, но определенно помогает им оставаться организованными и сосредоточенными.Мы также говорим о том, что демонстрация всей вашей работы является ключом к процессу обоснования. За последние два года у меня было все больше и больше студентов, которые стирали свои математические задания после того, как нашли ответ. Это поразило меня, когда я продолжал наблюдать, как они делают это снова и снова, и мне потребовалось около месяца, чтобы избавиться от этой привычки. Я всегда говорю им, что их работа так же важна, как их ответ и их объяснение.
Я всегда говорю им, что их работа так же важна, как их ответ и их объяснение.
Говоря об объяснении, мне также нравится очень осторожно учить их, как объяснять свой ответ.Как вы можете видеть из таблицы, я показываю им, как объяснить, как они получили свой ответ, как они выбрали конкретную операцию и как они узнают, что их ответ правильный. Я люблю давать студентам основы предложений всякий раз, когда могу, чтобы помочь им тоже. И, наконец, я пытаюсь выдвинуть несколько представлений, чтобы учащиеся различными способами обосновывали свой ответ.
После того, как мои ученики заполнили эту таблицу, я хотел бы дать им версию для печати, которую они могут наклеить в свои интерактивные блокноты и вспомнить, когда они решают математические задачи и задачи самостоятельно.Моим студентам особенно помогает, когда у них есть четкий список, который они могут просмотреть, чтобы убедиться, что они оправдали свою работу.
Чтобы получить бесплатную распечатку, показанную выше, щелкните изображение ниже.
После того, как вы сформулировали четкие ожидания для своих учеников, следующий шаг – предоставить им несколько возможностей попрактиковаться в обосновании своих ответов. Если вы ищете ресурсы, которые можно использовать для практики своих учеников, вот несколько моих любимых.
Дифференцированные математические задачи с построенным ответом, состоящим из нескольких частей: Этот ресурс посвящен математическим задачам, состоящим из нескольких частей, которые дифференцированы и разделены по навыкам. Раздел ответов каждой задачи (а не сами задачи) разделен на три уровня, чтобы помочь учащимся эффективно организовать свои ответы и обоснования. Нажмите здесь, чтобы получить бесплатную возможность опробовать этот пост, или посмотрите их в моем магазине TpT, нажав здесь.
Задачи Word для интерактивных тетрадей по математике: Следующая задача нравится студентам и учителям.Мои ученики всегда любят математические интерактивные тетради. Помня об этом, я создал набор задач из интерактивной тетради по математике для каждого из основных математических стандартов. Чтобы прочитать подробный пост об этом ресурсе, нажмите здесь. Студентам они нравятся, потому что они могут раскрасить графику, когда они закончены, и они занимают половину страницы, что делает их менее опасными. Я люблю их, потому что они хранятся в их записных книжках, чтобы студенты могли к ним обращаться в течение года. Щелкните здесь, чтобы увидеть версию для четвертого класса.Ознакомьтесь с версией для пятого класса, нажав здесь.
Помня об этом, я создал набор задач из интерактивной тетради по математике для каждого из основных математических стандартов. Чтобы прочитать подробный пост об этом ресурсе, нажмите здесь. Студентам они нравятся, потому что они могут раскрасить графику, когда они закончены, и они занимают половину страницы, что делает их менее опасными. Я люблю их, потому что они хранятся в их записных книжках, чтобы студенты могли к ним обращаться в течение года. Щелкните здесь, чтобы увидеть версию для четвертого класса.Ознакомьтесь с версией для пятого класса, нажав здесь.
Математические задачи с построенным ответом: Я также регулярно в течение года использую стандартные математические задачи с построенным ответом, поэтому у моих учеников есть много возможностей попрактиковаться в обосновании и объяснении своих ответов. Делая это в течение года (примерно раз в две недели или около того), мои ученики становятся в этом профи. Государственное испытание в конце года – это просто продолжение всей работы, которую они проделали в течение года. Я обычно использую их как больше для оценки, чем два других примера ресурсов, которыми я поделился выше. Нажмите на уровень обучения, который вы хотите видеть в моем магазине TeachersPayTeachers, чтобы увидеть больше. Кроме того, в предварительных просмотрах каждого уровня есть бесплатные подарки, так что вы можете попробовать их со своими учениками!
Я обычно использую их как больше для оценки, чем два других примера ресурсов, которыми я поделился выше. Нажмите на уровень обучения, который вы хотите видеть в моем магазине TeachersPayTeachers, чтобы увидеть больше. Кроме того, в предварительных просмотрах каждого уровня есть бесплатные подарки, так что вы можете попробовать их со своими учениками!
4 класс
5 класс
Как вы помогаете своим ученикам научиться решать текстовые задачи и обосновывать свои ответы?
Сохранить
15 самых сложных вопросов по SAT математике
Хотите проверить себя, отвечая на самые сложные вопросы по математике SAT? Хотите знать, что делает эти вопросы такими сложными и как их лучше всего решать? Если вы готовы по-настоящему погрузиться в математический раздел SAT и нацелиться на этот высший балл, то это руководство для вас.
Мы собрали то, что мы считаем , из 15 самых сложных вопросов для текущего SAT , со стратегиями и ответами на каждый из них. Все это сложные вопросы SAT Math из практических тестов SAT College Board, а это значит, что их понимание – один из лучших способов учиться для тех из вас, кто стремится к совершенству.
Все это сложные вопросы SAT Math из практических тестов SAT College Board, а это значит, что их понимание – один из лучших способов учиться для тех из вас, кто стремится к совершенству.
Изображение: Соня Севилья / Викимедиа
Краткий обзор SAT Math
Третий и четвертый разделы SAT всегда будут математическими .Первый математический подраздел (с меткой «3») не позволяет использовать калькулятор , , а не , а второй математический подраздел (с меткой «4») разрешает использование калькулятора. Однако не беспокойтесь о разделе без калькулятора: если вам не разрешено использовать калькулятор для ответа на вопрос, это означает, что вам не нужен калькулятор, чтобы ответить на него.
Каждый математический подраздел расположен в порядке возрастания сложности (где чем больше времени требуется на решение задачи и чем меньше людей ответят на нее правильно, тем сложнее).В каждом подразделе вопрос 1 будет «легким», а вопрос 15 – «сложным». Однако возрастающая сложность сбрасывается с простого на сложный на сетке.
Однако возрастающая сложность сбрасывается с простого на сложный на сетке.
Таким образом, вопросы с несколькими вариантами ответов расположены по возрастающей сложности (вопросы 1 и 2 будут самыми легкими, вопросы 14 и 15 будут самыми сложными), но уровень сложности сбрасывается для секции сетки (то есть вопросы 16 и 17 снова будут будьте «легкими», и вопросы 19 и 20 будут очень сложными).
Таким образом, за очень немногими исключениями, наиболее сложные математические задачи SAT будут сгруппированы в конце сегментов с несколькими вариантами ответов или во второй половине вопросов сетки. Однако, помимо места в тесте, у этих вопросов есть еще несколько общих черт. Через минуту мы рассмотрим примеры вопросов и способы их решения, а затем проанализируем их, чтобы выяснить, что общего у этих типов вопросов.
Но сначала: стоит ли вам прямо сейчас сосредоточиться на самых сложных математических вопросах?
Если вы только начинаете подготовку к учебе (или если вы просто пропустили этот первый, важный шаг), обязательно остановитесь и пройдите полный практический тест, чтобы определить свой текущий уровень оценок. Ознакомьтесь с нашим руководством по всем бесплатным практическим тестам SAT, доступным в Интернете, а затем сядьте, чтобы пройти все сразу.
Ознакомьтесь с нашим руководством по всем бесплатным практическим тестам SAT, доступным в Интернете, а затем сядьте, чтобы пройти все сразу.
Абсолютно лучший способ оценить свой текущий уровень – просто пройти практический тест SAT, как если бы он был настоящим, соблюдая строгий график и работая без перерывов (мы знаем – вероятно, это не ваш любимый способ провести субботу) . Как только вы получите хорошее представление о своем текущем уровне и процентильном рейтинге, вы можете установить контрольные точки и цели для получения окончательного результата по SAT Math.
Если вы в настоящее время набираете баллы в диапазоне 200–400 или 400–600 по SAT Math, лучше всего сначала ознакомиться с нашим руководством по повышению своего балла по математике , чтобы он постоянно был на уровне 600 или выше, прежде чем начинать. в попытке решить самые сложные математические задачи на тесте.
Если, однако, вы уже набрали больше 600 баллов по математике и хотите проверить свои способности на реальном SAT, то обязательно переходите к остальной части этого руководства. Если вы стремитесь к совершенству (или близкому к нему), вам необходимо знать, как выглядят самые сложные вопросы по математике SAT и как их решать.И, к счастью, именно этим мы и займемся.
Если вы стремитесь к совершенству (или близкому к нему), вам необходимо знать, как выглядят самые сложные вопросы по математике SAT и как их решать.И, к счастью, именно этим мы и займемся.
ПРЕДУПРЕЖДЕНИЕ: Поскольку количество официальных практических тестов SAT ограничено, вы можете подождать, чтобы прочитать эту статью, пока не попробуете все или большую часть первых четырех официальных практических тестов (поскольку большинство вопросов, приведенных ниже, были приняты из этих тестов). Если вы беспокоитесь о том, чтобы испортить эти тесты, прекратите читать это руководство сейчас; вернитесь и прочтите, когда вы их закончите.
А теперь перейдем к нашему списку вопросов (ууу)!
Изображение: Niytx / DeviantArt
15 самых сложных вопросов SAT по математике
Теперь, когда вы уверены, что должны попытаться ответить на эти вопросы, давайте приступим прямо к делу! Мы собрали 15 самых сложных вопросов по SAT Math, которые вы можете попробовать, ниже, а также пошаговые инструкции, как получить ответ (если вы в тупике).
Нет калькулятора Вопросы по SAT Math
Вопрос 1
$$ C = 5/9 (F-32) $$
Приведенное выше уравнение показывает, как температура $ F $, измеренная в градусах Фаренгейта, соотносится с температурой $ C $, измеренной в градусах Цельсия. Основываясь на уравнении, какое из следующих утверждений должно быть верным?
- Повышение температуры на 1 градус по Фаренгейту эквивалентно повышению температуры на 5/9 градусов Цельсия.
- Повышение температуры на 1 градус Цельсия эквивалентно повышению температуры на 1.8 градусов по Фаренгейту.
- Повышение температуры на 5 долларов / 9 градусов по Фаренгейту эквивалентно повышению температуры на 1 градус Цельсия.
A) только I
B) только II
C) только III
D) только I и II
ОБЪЯСНЕНИЕ ОТВЕТА: Думайте об уравнении как об уравнении для линии
$$ y = mx + b $$
, где в данном случае
$$ C = {5} / {9} (F − 32) $$
или
$$ C = {5} / {9} F – {5} / {9} (32) $$
Вы можете видеть, что наклон графика составляет $ {5} / {9} $, что означает, что при увеличении на 1 градус по Фаренгейту увеличение составляет $ {5} / {9} $ на 1 градус Цельсия.
$$ C = {5} / {9} (F) $$
$$ C = {5} / {9} (1) = {5} / {9} $$
Следовательно, утверждение I верно. Это эквивалентно тому, что увеличение на 1 градус Цельсия равно увеличению на $ {9} / {5} $ градусов по Фаренгейту.
$$ C = {5} / {9} (F) $$
$$ 1 = {5} / {9} (F) $$
$$ (F) = {9} / {5} $$
Поскольку $ {9} / {5} $ = 1.8, утверждение II верно.
Единственный ответ, в котором и утверждение I, и утверждение II являются истинными, – это D , но если у вас есть время и вы хотите быть абсолютно внимательными, вы также можете проверить, соответствует ли утверждение III (увеличение на $ {5} / { 9} $ градус Фаренгейта равен увеличению температуры на 1 градус Цельсия) верно:
$$ C = {5} / {9} (F) $$
$$ C = {5} / {9} ({5} / {9}) $$
$$ C = {25} / {81} (\ which \ is ≠ 1) $$
Увеличение на 5 долларов / 9 градусов по Фаренгейту приводит к увеличению на {25} / {81} долларов, а не на 1 градус Цельсия, и поэтому утверждение III неверно.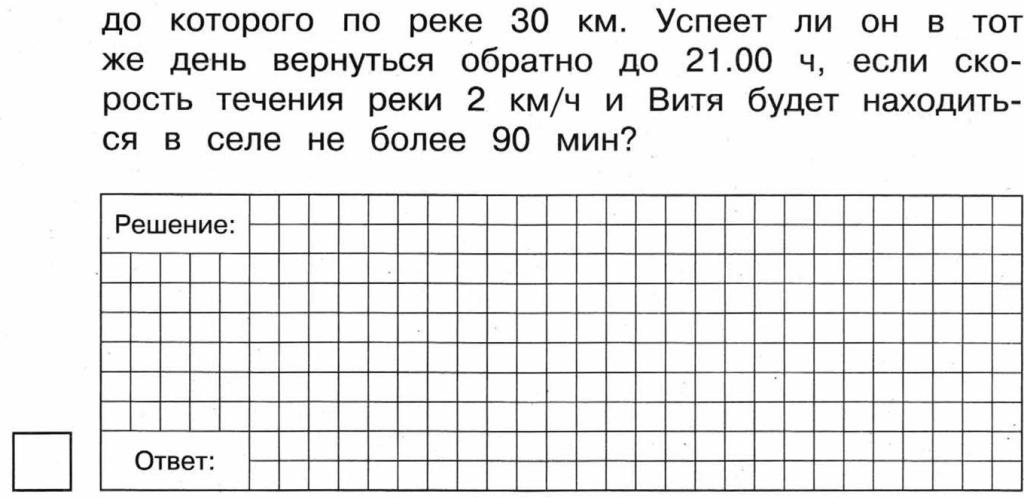 2 $
2 $
D) Значение не может быть определено на основании предоставленной информации.12 $$
Окончательный ответ: A.
Вопрос 4
Точки A и B лежат на окружности радиуса 1, а дуга $ {AB} ↖⌢ $ имеет длину $ π / 3 $. Какая часть окружности окружности равна длине дуги $ {AB} ↖⌢ $?
ОБЪЯСНЕНИЕ ОТВЕТА: Чтобы выяснить ответ на этот вопрос, вам сначала нужно знать формулу для определения длины окружности.
Длина окружности $ C $ равна $ C = 2πr $, где $ r $ – радиус окружности.Для данной окружности радиусом 1 длина окружности равна $ C = 2 (π) (1) $ или $ C = 2π $.
Чтобы узнать, какая часть окружности составляет длину $ {AB} ↖⌢ $, разделите длину дуги на длину окружности, что даст $ π / 3 ÷ 2π $. Это деление можно представить как $ π / 3 * {1/2} π = 1/6 $.
Дробь $ 1/6 $ также может быть переписана как $ 0,166 $ или 0,167 $.
Окончательный ответ: 1/6 доллара, 0,166 доллара или 0,167 доллара.
Вопрос 5
$$ {8-i} / {3-2i} $$
Если приведенное выше выражение переписать в форме $ a + bi $, где $ a $ и $ b $ – действительные числа, каково значение $ a $? (Примечание: $ i = √ {-1} $)
ОБЪЯСНЕНИЕ ОТВЕТА: Чтобы переписать $ {8-i} / {3-2i} $ в стандартной форме $ a + bi $, вам нужно умножить числитель и знаменатель $ {8-i} / {3- 2i} $ сопряженным, $ 3 + 2i $.2 = -1 $, последняя дробь может быть уменьшена упрощенно до
$$ {24 + 16i-3i + 2} / {9 – (- 4)} = {26 + 13i} / {13} $$
, что упрощается до 2 + i $. Следовательно, когда $ {8-i} / {3-2i} $ переписывается в стандартную форму a + bi, значение a равно 2.
Окончательный ответ: A.
Вопрос 6
В треугольнике $ ABC $ мера $ ∠B $ равна 90 °, $ BC = 16 $ и $ AC $ = 20. Треугольник $ DEF $ похож на треугольник $ ABC $, где вершины $ D $, $ E $ и $ F $ соответствуют вершинам $ A $, $ B $ и $ C $ соответственно, а также каждой стороне треугольника $.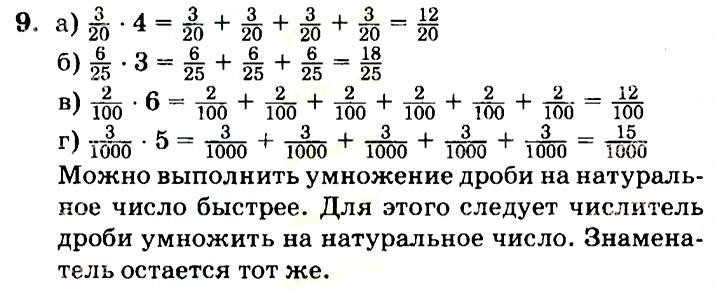 DEF $ составляет $ 1/3 $ длины соответствующей стороны треугольника $ ABC $.2} = √ {400-256} = √ {144} = 12 $$
DEF $ составляет $ 1/3 $ длины соответствующей стороны треугольника $ ABC $.2} = √ {400-256} = √ {144} = 12 $$
Поскольку треугольник DEF подобен треугольнику ABC, с вершиной F, соответствующей вершине C, мера $ \ angle ∠ {F} $ равна мере $ \ angle ∠ {C} $. Следовательно, $ sin F = sin C $. От сторон треугольника ABC,
$$ sinF = {\ Against \ side} / {\ hypotenuse} = {AB} / {AC} = {12} / {20} = {3} / {5} $$
Следовательно, $ sinF = {3} / {5} $.
Окончательный ответ: {3} / {5} $ или 0,6.
Вопросы SAT по математике, разрешенные калькулятором
Вопрос 7
Неполная таблица выше суммирует количество учащихся-левшей и учащихся-правшей с разбивкой по полу для учащихся восьмых классов средней школы им. Кейзеля.Учениц-правшей в 5 раз больше, чем учениц-левшей, и учеников-правшей в 9 раз больше, чем учащихся-левшей. Если в школе всего 18 учеников-левшей и 122 ученика-правшей, что из следующего наиболее близко к вероятности того, что случайно выбранный ученик-правша будет женщиной? (Примечание: предположим, что ни один из восьмиклассников не является одновременно правшой и левшой.)
А) 0.410
B) 0,357
C) 0,333
D) 0,250
ОБЪЯСНЕНИЕ ОТВЕТА: Чтобы решить эту проблему, вы должны создать два уравнения, используя две переменные ($ x $ и $ y $) и предоставленную вам информацию. Пусть $ x $ будет количеством учениц-левшей и пусть $ y $ будет количеством учениц-левшей. Используя информацию, приведенную в задаче, количество учащихся-правшей будет составлять 5 долларов США, а количество учащихся-правшей будет составлять 9 лет.Поскольку общее количество студентов-левшей составляет 18, а общее количество студентов-правшей – 122, система уравнений ниже должна быть верной:
$$ x + y = 18 $$
$$ 5x + 9y = 122 $$
Когда вы решаете эту систему уравнений, вы получаете $ x = 10 $ и $ y = 8 $. Таким образом, из 122 учащихся-правшей 5 * 10, или 50, – девушки. Следовательно, вероятность того, что случайным образом выбранный студент-правша будет женщиной, составляет {50} / {122} $, что с точностью до тысячных составляет 0,410.
Окончательный ответ – А.Вопросы 8 и 9
Используйте следующую информацию как для вопроса 7, так и для вопроса 8.
Если покупатели входят в магазин со средней скоростью $ r $ покупателей в минуту и каждый остается в магазине в течение среднего времени T $ минут, среднее количество покупателей в магазине, N $, в любой момент времени равно задается формулой $ N = rT $. Эта связь известна как закон Литтла.
По оценкам владельца магазина Good Deals Store, в рабочее время в магазин заходит в среднем 3 покупателя в минуту, и каждый из них остается в среднем на 15 минут.Владелец магазина использует закон Литтла, чтобы оценить, что в магазине одновременно находится 45 покупателей.
Вопрос 8
Закон Литтла может применяться к любой части магазина, например к определенному отделу или кассовым линиям. Владелец магазина определяет, что в рабочее время примерно 84 покупателя в час совершают покупку, и каждый из этих покупателей проводит в очереди в кассе в среднем 5 минут. Сколько в среднем покупателей в любое время в рабочее время ожидают в очереди у кассы, чтобы совершить покупку в магазине Good Deals Store?
ОБЪЯСНЕНИЕ ОТВЕТА: Поскольку в вопросе говорится, что закон Литтла может применяться к любой отдельной части магазина (например, только к кассе), тогда среднее количество покупателей, $ N $, в очереди к кассе в любой time равно $ N = rT $, где $ r $ – это количество покупателей, заходящих в кассу в минуту, а $ T $ – это среднее количество минут, которое каждый покупатель проводит в очереди.
Поскольку 84 покупателя в час совершают покупку, 84 покупателя в час входят в кассу. Однако это необходимо преобразовать в количество покупателей в минуту (для использования с $ T = 5 $). Поскольку в часе 60 минут, тариф составляет $ {84 \ shoppers \ per \ hour} / {60 \ minutes} = 1,4 $ покупателя в минуту. Используя данную формулу с $ r = 1,4 $ и $ T = 5 $, получаем
$$ N = rt = (1.4) (5) = 7 $$
Таким образом, среднее количество покупателей, $ N $, в очереди на кассу в любое время в рабочее время равно 7.
Окончательный ответ 7.
Вопрос 9
Владелец магазина Good Deals Store открывает новый магазин в другом конце города. По оценкам владельца нового магазина, в рабочее время в него заходят в среднем 90 покупателей в час, и каждый из них остается в среднем на 12 минут. Среднее количество покупателей в новом магазине в любой момент времени на какой процент меньше среднего количества покупателей в исходном магазине в любое время? (Примечание: игнорируйте символ процента при вводе ответа.Например, если ответ 42,1%, введите 42,1)
ОБЪЯСНЕНИЕ ОТВЕТА: Согласно исходной информации, расчетное среднее количество покупателей в исходном магазине в любой момент времени (N) составляет 45. В вопросе говорится, что в новом магазине менеджер оценивает, что в среднем 90 покупателей в час (60 минут) заходят в магазин, что эквивалентно 1,5 покупателям в минуту (r). Менеджер также подсчитал, что каждый покупатель остается в магазине в среднем 12 минут (T).Таким образом, по закону Литтла в каждый момент времени в новом магазине в среднем находится $ N = rT = (1.5) (12) = 18 $ покупателей. Это
$$ {45-18} / {45} * 100 = 60 $$
На% меньше, чем среднее количество покупателей в исходном магазине в любое время.
Окончательный ответ – 60.
Вопрос 10
На плоскости $ xy $ точка $ (p, r) $ лежит на прямой с уравнением $ y = x + b $, где $ b $ – константа. Точка с координатами $ (2p, 5r) $ лежит на прямой с уравнением $ y = 2x + b $.Если $ p ≠ 0 $, каково значение $ r / p $?
A) 2/5 долларов США
B) 3/4 $
C) 4/3 долл. США
D) $ 5/2 $
ОБЪЯСНЕНИЕ ОТВЕТА: Поскольку точка $ (p, r) $ лежит на прямой с уравнением $ y = x + b $, точка должна удовлетворять уравнению. Подстановка $ p $ вместо $ x $ и $ r $ вместо $ y $ в уравнение $ y = x + b $ дает $ r = p + b $, или $ \ bi b $ = $ \ bi r- \ bi p $.
Аналогично, поскольку точка $ (2p, 5r) $ лежит на прямой с уравнением $ y = 2x + b $, точка должна удовлетворять уравнению.Замена $ 2p $ на $ x $ и $ 5r $ на $ y $ в уравнении $ y = 2x + b $ дает:
$ 5r = 2 (2p) + b $
$ 5r = 4p + b $
$ \ bi b $ = $ \ bo 5 \ bi r- \ bo 4 \ bi p $.
Затем мы можем установить два уравнения, равных $ b $, равным друг другу и упростить:
$ б = р-п = 5р-4п $
$ 3p = 4r $
Наконец, чтобы найти $ r / p $, нам нужно разделить обе части уравнения на $ p $ и на $ 4 $:
$ 3p = 4r $
3 доллара США = {4r} /
доллара США на человека$ 3/4 = р / п $
Правильный ответ: B , 3/4 доллара.
Если вы выбрали варианты A и D, возможно, вы неправильно сформировали свой ответ из коэффициентов в пункте $ (2p, 5r) $. Если вы выбрали вариант C, возможно, вы перепутали $ r $ и $ p $.
Обратите внимание, что пока он находится в разделе калькулятора теста SAT, вам совершенно не нужен калькулятор для его решения!
Вопрос 11
Зерновой бункер состоит из двух правых круглых конусов и правого круглого цилиндра с внутренними размерами, представленными на рисунке выше. 2h $$
можно использовать для определения общего объема силоса.2) (5) = ({4} / {3}) (250) π $$
, что примерно равно 1047,2 кубических футов.
Окончательный ответ – D.
Вопрос 12
Если $ x $ – среднее (среднее арифметическое) для $ m $ и $ 9 $, $ y $ – это среднее значение для $ 2m $ и $ 15 $, а $ z $ – это среднее значение для $ 3m $ и $ 18 $, то что есть среднее значение $ x $, $ y $ и $ z $ в пересчете на $ m $?
A) $ m + 6 $ 90 102 B) $ m + 7 $ 90 102 C) $ 2m + 14 $ 90 102 D) $ 3m + 21 $
ОБЪЯСНЕНИЕ ОТВЕТА: Поскольку среднее (среднее арифметическое) двух чисел равно сумме двух чисел, деленных на 2, уравнения $ x = {m + 9} / {2} $, $ y = {2m +15} / {2} $, $ z = {3m + 18} / {2} $ верны.2-x- {11} / {4} $$
и
$$ y = k $$
Реальное решение системы двух уравнений соответствует точке пересечения графиков этих двух уравнений на плоскости $ xy $.
График $ y = k $ – это горизонтальная линия, которая содержит точку $ (0, k) $ и трижды пересекает график кубического уравнения (поскольку оно имеет три действительных решения). Учитывая график, единственная горизонтальная линия, которая трижды пересекала бы кубическое уравнение, – это линия с уравнением $ y = −3 $ или $ f (x) = −3 $.2 $$
Динамическое давление $ q $, создаваемое жидкостью, движущейся со скоростью $ v $, можно найти с помощью приведенной выше формулы, где $ n $ – постоянная плотность жидкости. Инженер-авиастроитель использует формулу для определения динамического давления жидкости, движущейся со скоростью $ v $, и той же жидкости, движущейся со скоростью 1,5 $ v $. Каково отношение динамического давления более быстрой жидкости к динамическому давлению более медленной жидкости?
ОБЪЯСНЕНИЕ ОТВЕТА: Чтобы решить эту проблему, вам необходимо задать уравнения с переменными.2 = (2.25) q_1 $$
Следовательно, коэффициент динамического давления более быстрой жидкости равен
$$ {q2} / {q1} = {2.25 q_1} / {q_1} = 2.25 $$
Окончательный ответ – 2,25 или 9/4.
Вопрос 15
Для полинома $ p (x) $ значение $ p (3) $ равно $ -2 $. Что из следующего должно быть истинным относительно $ p (x) $?
A) $ x-5 $ – множитель $ p (x) $.
B) $ x-2 $ является множителем $ p (x) $.
C) $ x + 2 $ является множителем $ p (x) $.
D) Остаток от деления $ p (x) $ на $ x-3 $ равен -2 $.1 $ и не выше), остаток – действительное число.
Следовательно, $ p (x) $ можно переписать как $ p (x) = (x + k) q (x) + r $, где $ r $ – действительное число.
В вопросе указано, что $ p (3) = -2 $, поэтому должно быть верно, что
$$ – 2 = p (3) = (3 + k) q (3) + r $$
Теперь мы можем включить все возможные ответы. Если ответ A, B или C, $ r $ будет $ 0 $, а если ответ D, $ r $ будет $ -2 $.
A. $ -2 = p (3) = (3 + (-5)) q (3) + 0 $ 90 102 $ -2 = (3-5) q (3) 90 $ 102 $ -2 = (- 2 ) q (3) $
Это могло быть правдой, но только если $ q (3) = 1 $
Б.$ -2 = p (3) = (3 + (-2)) q (3) + 0 $
$ -2 = (3-2) q (3) $
$ -2 = (-1) q ( 3) $
Это могло быть правдой, но только если $ q (3) = 2 $
C. $ -2 = p (3) = (3 + 2) q (3) + 0 $ 90 102 $ -2 = (5) q (3)
$Это могло быть правдой, но только если $ q (3) = {- 2} / {5} $
D. $ -2 = p (3) = (3 + (-3)) q (3) + (-2) $ 90 102 $ -2 = (3 – 3) q (3) + (-2) $
-2 = (0) q (3) + (-2) 9000 3 долл. США
всегда будет истинным независимо от того, что такое $ q (3) $.
Из вариантов ответа единственное, что должно быть верным относительно $ p (x) $, – это D, а остаток от деления $ p (x) $ на $ x-3 $ равен -2.
Окончательный ответ – D.
Хотите улучшить свой результат SAT на 160 баллов? Мы написали руководство о 5 лучших стратегиях, которые вы должны использовать, чтобы улучшить свой результат. Скачать бесплатно сейчас:
Вы заслуживаете того, чтобы вздремнуть, задав эти вопросы.
Что общего у самых сложных вопросов по SAT Math?
Важно понимать, что делает эти сложные вопросы «сложными». Таким образом, вы сможете понять и решить похожие вопросы, когда вы увидите их в день тестирования, а также получите лучшую стратегию для выявления и исправления ваших предыдущих математических ошибок SAT.
В этом разделе мы рассмотрим, что общего у этих вопросов, и дадим примеры каждого типа.Некоторые из причин, по которым самые сложные вопросы по математике являются самыми сложными вопросами по математике, заключаются в том, что они:
# 1: Проверить несколько математических понятий одновременно
Здесь мы должны иметь дело с мнимыми числами и дробями одновременно.
Секрет успеха: Подумайте, какую применимую математику вы могли бы использовать для решения задачи, выполняйте по одному шагу за раз и пробуйте каждый метод, пока не найдете тот, который работает!
# 2: задействовать множество шагов
Помните: чем больше шагов вам нужно предпринять, тем легче где-то напортачить!
Мы должны решить эту проблему поэтапно (делая несколько средних), чтобы разблокировать остальные ответы в эффекте домино.Это может сбивать с толку, особенно если вы в стрессе или у вас не хватает времени.
Секрет успеха: Не торопитесь, делайте шаг за шагом и перепроверяйте свою работу, чтобы не ошибиться!
# 3: Проверьте концепции, с которыми вы мало знакомы
Например, многие учащиеся менее знакомы с функциями, чем с дробями и процентами, поэтому большинство функциональных вопросов считаются задачами “высокой сложности”.
Если вы не разбираетесь в функциях, это может быть сложной проблемой.
Секрет успеха: Просмотрите математические концепции, с которыми вы не так хорошо знакомы, например, функции. Мы предлагаем использовать наши отличные бесплатные руководства по тестированию SAT Math.
# 4: написаны необычным или запутанным образом
Может быть сложно точно определить, какие вопросы задает , не говоря уже о том, как их решить. Это особенно верно, когда вопрос находится в конце раздела, а у вас не хватает времени.
Поскольку в этом вопросе содержится так много информации без диаграммы, может быть сложно разобраться в этом за ограниченное время.
Секрет успеха: Не торопитесь, проанализируйте, что от вас просят, и нарисуйте диаграмму, если это вам поможет.
# 5: Используйте много разных переменных
При таком большом количестве различных переменных очень легко запутаться.
Секрет успеха: Не торопитесь, проанализируйте, что от вас просят, и подумайте, является ли включение цифр хорошей стратегией для решения проблемы (это не относится к вопросу выше, но может быть ко многим другим. SAT переменные вопросы).
Итоги
SAT – это марафон, и чем лучше вы к нему подготовитесь, тем лучше вы будете себя чувствовать в день теста. Знание того, как отвечать на самые сложные вопросы, которые может бросить вам тест, сделает сдачу настоящего SAT намного менее сложной задачей.
Если вы считаете, что эти вопросы были легкими, не стоит недооценивать влияние адреналина и усталости на вашу способность решать проблемы. Продолжая учиться, всегда придерживайтесь надлежащих рекомендаций по времени и старайтесь проходить полные тесты, когда это возможно. Это лучший способ воссоздать реальную среду тестирования, чтобы вы могли подготовиться к реальной сделке.
Если вы считаете, что эти вопросы были сложными, обязательно укрепит свои математические знания, ознакомившись с нашими индивидуальными руководствами по математическим темам для SAT. Здесь вы увидите более подробные объяснения рассматриваемых тем, а также более подробную разбивку ответов.
Что дальше?
Почувствовали, что эти вопросы оказались сложнее, чем вы ожидали? Взгляните на все темы, затронутые в разделе SAT по математике, а затем отметьте, какие разделы были для вас особенно трудными.Затем взгляните на наши индивидуальные руководства по математике, которые помогут вам укрепить любую из этих слабых сторон.
Не хватает времени на сдачу экзамена по математике? Наш гид поможет вам выиграть время и увеличить свой счет.
Хотите набрать высший балл? Ознакомьтесь с нашим руководством о том, как набрать 800 баллов по математике в разделе SAT, написанном отличным игроком.
Хотите улучшить свой результат SAT на 160 баллов?
Посетите наши лучшие в своем классе онлайн-классы подготовки к SAT.Мы гарантируем возврат ваших денег , если вы не улучшите свой результат SAT на 160 или более баллов.
Наши классы полностью онлайн, и их ведут эксперты SAT. Если вам понравилась эта статья, вам понравятся наши классы. Наряду с занятиями под руководством экспертов вы получите индивидуальное домашнее задание с тысячами практических задач, организованных по индивидуальным навыкам, чтобы вы учились наиболее эффективно. Мы также дадим вам пошаговую индивидуальную программу, которой вы будете следовать, чтобы вы никогда не запутались, что изучать дальше.
Попробуйте без риска сегодня:
Книги по математике для детей
Программа Problemoids была создана для студентов, изучающих математику на продвинутом уровне. Он основан на объеме и последовательности государственных учебных программ по математике и основан на работе выдающегося математика профессора Джорджа Поля (1887–1985) по решению задач. Программа требует более высокого уровня мышления, чем типичная учебная программа, поэтому она идеально подходит для одаренных детей.Он предназначен для детей 4, 5, 6 и выше классов.
Problemoids фокусируется на разработке и использовании стратегий решения проблем, а не на запоминании или операциях. Подсказки и листы решений предназначены для ознакомления, обучения и закрепления 19 стратегий решения проблем.
Программа предоставляет студентам возможность самостоятельно проверять наиболее сложную часть своей работы. Он состоит из трех компонентов: рабочие тетради для учащихся под названием Math Challenge , которые включают 50 задач и несколько уровней подсказок на основе стратегии для каждой задачи; отдельный лист решения для каждой проблемы, со стратегиями решения проблем, подробно проиллюстрированными, чтобы учащиеся могли проверить свою работу; и руководство для учителя под названием Math Mentor , которое объясняет программу и содержит ответы на задачи.Руководства и листы решений разработаны таким образом, чтобы минимизировать непосредственное участие инструктора в реализации.
Problemoids предназначен для студентов, которые преуспевают в математике и могут работать в своем собственном темпе. Когда ученик решает задачу, инструктор просто проверяет ответ и дает ученику лист решения. Студент может сравнить свой метод решения задачи с предложенным авторами. И подсказки, и листы решений подчеркивают стратегии решения проблем.
В задачах используются множества, числа и нумерация, операции, геометрия, измерения, алгебра, вероятность и статистика.
Книга наставника для каждого уровня содержит сетку, которая показывает, какие проблемы на этом уровне связаны с каждой концепцией и получает ли эта концепция основное или второстепенное внимание при решении проблемы.
Программа Problemoids была создана для студентов, изучающих математику на продвинутом уровне. Он основан на объеме и последовательности государственных учебных программ по математике и основан на работе выдающегося математика профессора Джорджа Поля (1887–1985) по решению задач.Программа требует более высокого уровня мышления, чем типичная учебная программа, поэтому она идеально подходит для одаренных учеников. Он предназначен для учащихся 4, 5, 6 и выше классов.
Problemoids фокусируется на разработке и использовании стратегий решения проблем, а не на запоминании или операциях. Подсказки и листы решений предназначены для ознакомления, обучения и закрепления 19 стратегий решения проблем.
Программа предоставляет студентам возможность самостоятельно проверять наиболее сложную часть своей работы.Он состоит из трех компонентов: рабочие тетради для учащихся под названием Math Challenge , которые включают 50 задач и несколько уровней подсказок на основе стратегии для каждой задачи; отдельный лист решения для каждой проблемы, со стратегиями решения проблем, подробно проиллюстрированными, чтобы учащиеся могли проверить свою работу; и руководство для учителя под названием Math Mentor , которое объясняет программу и содержит ответы на проблемы. Пособия и листы с решениями призваны свести к минимуму непосредственное участие учителя в реализации.
Problemoids предназначен для студентов, которые преуспевают в математике и могут работать в своем собственном темпе. Когда ученик решает задачу, учитель просто проверяет ответ и дает ученику лист с решением. Студент может сравнить свой метод решения задачи с предложенным авторами. И подсказки, и листы решений подчеркивают стратегии решения проблем.
В задачах используются множества, числа и нумерация, операции, геометрия, измерения, алгебра, вероятность и статистика.
Книга наставника для каждого уровня содержит сетку, которая показывает, какие проблемы на этом уровне связаны с каждой концепцией и получает ли эта концепция основное или второстепенное внимание при решении проблемы.
Что заставляет учащихся испытывать трудности с математикой?
Многие дети плохо разбираются в математике, но некоторым школьникам это труднее, чем другим. Это могут быть в остальном умные дети, у которых есть острое чувство логики и рассуждений, но которые все равно плохо справляются с домашними заданиями, тестами и викторинами.
Со временем повторяющаяся неуспеваемость по математике может привести к тому, что ученик потеряет мотивацию и поверит, что он или она «глуп» или плохо разбирается в предмете.
Более того, поскольку математика накапливается, отставание может означать, что учащийся пропускает большую часть того, чему его учат, до конца учебного семестра. Базовые математические навыки важны независимо от карьеры, которую выбирает человек.
Вот почему так важно выявлять проблемы на ранней стадии. При правильном сочетании условий в классе и стратегий обучения каждый ученик может полностью раскрыть свой потенциал в математике.
Есть ряд причин, по которым у ребенка могут быть проблемы с математикой в школе, от низкой мотивации, вызванной математическим беспокойством, до плохого понимания того, как применять и выполнять математические операции. Но иногда первопричина недостаточной успеваемости кроется в чем-то другом, например, в различиях в обучении или проблемах с моторикой.
Наиболее часто ассоциированным заболеванием является дискалькулия , при котором люди испытывают трудности с выполнением основных вычислений и имеют проблемы с манипулированием числами так же, как и их сверстники.
Тем не менее, ученики с дислексией также могут испытывать трудности с математикой в школе из-за трудностей с чтением чисел и проблем с пониманием слов. Они могут менять порядок цифр при выполнении работы на бумаге или правильно решать задачи, но записывать свои ответы неправильно.
Дети с СДВГ / СДВГ могут броситься вперед и пропустить шаг или с трудом сосредоточиться и быть не в состоянии проверить свою работу, когда они решат проблему.
Учащиеся с дисграфией и диспраксией , которым трудно писать от руки, могут настолько отвлечься на формирование чисел, что они сделают неосторожные ошибки или выполнят шаги в уравнении в неправильном порядке.
Наконец, дети с расстройствами зрительной обработки могут не обладать навыками визуально-пространственной обработки, которые им необходимы для выравнивания чисел, чтения графиков и выполнения основных геометрических операций.
Как мы относимся к математике
Математика – один из тех предметов, которые плохо понимают как дети, так и взрослые. Это связано с тем, что в то время как дошкольная математика заключается в решении практических задач, обнаружении закономерностей, распознавании форм в вашей среде и обучении счету, обучение математике в средней и старшей школе становится более абстрактным.Он часто фокусируется на заучивании наизусть и решении уравнений в книгах – подумайте об арифметике и таблицах умножения – что может оттолкнуть студентов и заставить их поверить, что математические навыки не имеют отношения к их повседневной жизни.
На самом деле, многие студенты жалуются, что математика скучна. Они могут не видеть смысла в изучении алгебры, геометрии или математического анализа в школе. Или они могут спросить, почему им нужно уметь выполнять основные арифметические операции, такие как сложение, вычитание, умножение и деление, вручную, когда ответы можно легко найти с помощью калькулятора или компьютера.
Ответ на этот последний вопрос тройной. Во-первых, у вас не всегда может быть калькулятор; во-вторых, даже если вы это сделаете, понимание того, как и почему нужно делать это для себя, дает более прочную основу для будущего обучения, и в-третьих, выполнение арифметики – это умственная тренировка, которая укрепляет вашу рабочую память.
Числа окружают нас повсюду, и возможность работать с ними быстро и эффективно – это важный жизненный навык. Учтите, что быстрота в арифметике также весьма практична во многих профессиях, от плотника до розничной торговли, ракетостроения и обеспечения своевременного движения поездов!
Однако математика – это гораздо больше, чем арифметика.Многое из того, что входит в решение многоступенчатых задач со словами, – это идентификация проблемы, выбор подходящего подхода к ее решению (их может быть несколько) и соблюдение правильного порядка действий.
Уяснить фактическую арифметику – ту часть, на которую способен калькулятор – гораздо проще. Это одна из причин, по которой детей просят показывать свою работу, когда они делают домашнее задание или отвечают на тесте по математике.
В некоторых случаях учителя могут поставить за хорошую работу больше, чем за правильный ответ.Это потому, что именно в развернутой рукописной работе педагоги могут увидеть, как происходит «математическое мышление».
Однако такой подход может оскорбить очень способного ребенка, который интуитивно подскакивает к правильному решению, но не анализирует, как он к нему пришел, или ребенка, которому трудно писать от руки. Признание индивидуальных потребностей и сильных сторон учащихся лежит в основе передового опыта в обучении.
Кто борется с математикой?
- Учащиеся с математической тревогой
Исследования показали, что математика – это предмет, в котором на успех сильно влияют психологические факторы, включая тревогу.Тревога – это больше, чем просто чувство беспокойства – это химическая реакция в мозгу, которая может подавлять когнитивные процессы и вызывать физические симптомы, включая учащенное дыхание, учащенное сердцебиение и потоотделение.
Беспокойство по математике может привести к тому, что люди, которые в остальном являются сильными учениками, замирают на школьной викторине или экзамене.
У них могут быть трудности с поиском решения проблемы, неправильное прочтение вопросов или выполнение гораздо меньшего количества задач, чем они способны. Многие учащиеся с тревогой совершают небрежные ошибки из-за стресса, который они испытывают в данный момент, и, как правило, их оценочная работа по расписанию хуже по качеству, чем классные занятия или домашние задания.
Тревога по поводу математики не обязательно связана с плохими математическими способностями, она может влиять на учащихся с любым уровнем способностей – даже на одаренных детей. Тем не менее, это обычно приводит к снижению оценок, что подрывает уверенность учащегося.
Это несоответствие между оценками и знаниями / навыками может как обескураживать, так и демотивировать учащихся. В худшем случае ребенок может начать проявлять признаки избегания математики и проявлять негативное отношение к школе и обучению в результате беспокойства.
Стоит отметить, что некоторые учащиеся унаследовали от родителей тревогу и / или избегание математики. В западных обществах нередко можно услышать, как люди выражают неприязнь к математике. Фактически, это стало общепринятым способом обсуждения предмета в США и Великобритании. Это может повлиять на учащихся, которые начинают обесценивать его как предмет или считают приемлемым заниженные ожидания от себя, когда дело касается математики в школе.
Также имейте в виду, что для некоторых учащихся беспокойство по поводу математики является результатом плохой успеваемости из-за неучтенных проблем с обучением или моторикой либо пробелов в их истории обучения.
- Дети с дискалькулией
Учащиеся с дискалькулией плохо справляются с основами арифметики и могут с трудом усваивать математические факты. Как и в возрасте до 5 лет, им, возможно, потребовалось больше времени, чем их сверстникам, чтобы овладеть счетом.
Дискалькулия также может влиять на оценочные способности и пространственное мышление; эти ученики могут быть не в состоянии определять время на часах, делать сравнительные суждения о размерах или определять математические символы. Дискалькулия часто сочетается с другими специфическими различиями в обучении, такими как дислексия, а также с проблемами внимания.
СОВЕТ: Калькуляторы – разумная настройка. Поскольку учащиеся с дискалькулией могут быть не в состоянии надежно выполнять вычисления сложения, вычитания, умножения и pision, им может потребоваться использовать калькулятор для решения сложных математических задач.
- Студенты с дислексией
Дислексия – это другой способ обработки в мозгу, который может повысить вероятность того, что ученики переворачивают цифры и буквы, меняют числа или меняют их порядок.Например, копирование многозначного числа из одной строки в другую может привести к тому, что учащийся уронит цифру или добавит цифру, которой там не было.
Проблемы могут возникать и при обработке письменной речи, поскольку дислексия влияет на способность ребенка слышать звуки, из которых состоят слова. Это затрудняет чтение и может повлиять на понимание текстовых задач.
Студентам с дислексией может потребоваться перечитать абзац несколько раз, чтобы понять его, они могут легко потерять свое место, выполняя упражнения вручную, и им может потребоваться гораздо больше времени, чем их сверстникам, чтобы пройти начальные этапы понимания подсказки.Следовательно, у них останется меньше времени для выполнения фактических вычислений, необходимых для поиска решения.
- Лица с диспраксией
Диспраксия может повлиять на мелкую моторику, необходимую для того, чтобы держать ручку или карандаш. Поскольку большая часть длинных форм математики выполняется вручную, учащиеся с диспраксией могут с трудом показать шаги, которые они использовали, чтобы прийти к ответу.
Человек может легко отвлечься или расстроиться из-за боли от почерка и с большей вероятностью бросит или оставит вопрос, прежде чем его решит.Диспраксия также может влиять на планирование и организационные навыки. Поскольку решение более сложных проблем требует определенного планирования того, как вы придете к ответу, учащимся с диспраксией может быть трудно начать.
Они также могут бороться с последовательностью шагов и правильным порядком операций в математике.
- Дети с СДВ / СДВГ
Проблемы с вниманием могут повлиять на математические навыки по-разному. Во-первых, им труднее уделять внимание в классе.Решение математической задачи требует от вас выполнения нескольких шагов; ответ на одну строку сообщает следующую.
Если ученик отвлекается и теряет внимание, ему может быть очень сложно проследить за демонстрацией учителя и понять, как было получено определенное число. Сохранение концентрации также является проблемой при выполнении работы вручную и проверке работы после того, как проблема решена .
ПОЛЕЗНЫЙ СОВЕТ: Учащиеся с проблемами внимания могут быть более восприимчивыми к эффектам привязки.Когда вы впервые сталкиваетесь с математической задачей, вам нужно сначала сосредоточиться на понимании того, что от вас просят. Частью сбора важных битов является блокирование любых эффектов привязки от чисел, которые появляются постоянно и пытаются привлечь ваше внимание. Эти числа обычно указываются намеренно, чтобы отвлекать внимание, но они могут быть проблематичными для некоторых учащихся. Вы можете научить детей следить за этими числами, чтобы они могли активно подавлять свои инстинкты и использовать их в качестве ответа.
Дети с СДВГ и гиперактивностью могут спешить с математическими задачами и в результате пропускать шаги или ошибаться с арифметикой. Они могут импульсивно записывать ответы, или их рукописные работы могут быть запутанными и трудными для чтения.
Сложные для расшифровки числа могут сбить с толку как учащегося, так и учителя – узнайте больше о том, как трудности с письмом влияют на учащихся с СДВ / СДВГ.
- Учащиеся с дисграфией
Одна из самых важных частей решения математической задачи – это способность изложить свои мысли на бумаге.Это сделано для того, чтобы вы могли работать поэтапно, потому что одновременное удержание в голове нескольких вычислений создает нагрузку на когнитивные ресурсы и увеличивает вероятность ошибки.
Однако для учащихся с дисграфией записать «математическое мышление» может быть непросто. Студенты-дисографы могут испытывать трудности с формированием чисел и символов, их пространственной организацией и копированием текста с доски при ведении заметок.
У них может быть беспорядочная и неорганизованная письменная работа, которую им может быть трудно читать и из-за которой они получат неправильный ответ, даже если выбранный ими подход был правильным.Узнайте больше о дисграфии.
- Лица с нарушениями обработки зрения
Учащиеся с нарушениями визуальной обработки могут иметь трудности с математическими задачами, которые включают пространственное мышление, включая геометрию, чтение таблиц, чтение карт, а также различение и идентификацию различных чисел. Узнайте больше о нарушениях обработки зрения.
Как учителя могут сделать занятия по математике более инклюзивными
Сделайте математику актуальной.Мотивируйте учащихся, показывая им реальные ситуации, связанные с использованием математики вне школьных классов. Объясните, как работает математика, убедите учащихся, что дело не только в арифметике, и побудите их попробовать и почувствовать себя комфортно, пробуя различные подходы к решению проблем, даже если это означает, что они не всегда получают правильный ответ.
Обучайте мультисенсорным способом.Учитель дает устные объяснения, показывает работу на доске и, если возможно, использует тактильные приспособления, которые ученики могут коснуться и передвигать.Мультисенсорный ввод может помочь в обучении, облегчая учащимся участие в уроке, а также может закрепить материал в памяти. Это особенно важно для облегчения понимания предмета, который может быть довольно абстрактным.
Упражнение по словарю заранее.Некоторым учащимся, особенно тем, кто борется с грамотностью, возможность попрактиковаться в чтении, правописании и наборе математической лексики и определений может облегчить и ускорить выполнение урока, чтение учебника или понимание проблемы в домашнем задании. или в викторинах.
ПОЛЕЗНЫЙ СОВЕТ. Вы когда-нибудь задумывались о том, как слепой ввод может помочь учащимся с математикой? Попробуйте читать и писать по буквам с помощью сенсорного ввода.
Узнать больше
Назначьте друзей для ведения заметок.Иногда записывать информацию и одновременно обрабатывать ее может утомительно. Также может случиться так, что копирование с доски может привести к тому, что числа будут перенесены или записаны таким образом, что работа больше не имеет смысла. Может быть полезно разрешить ребенку делать заметки с помощью компьютера или объединить их с другом, который ведет заметки.
Разрешить доступ к жилым помещениям.Если учащемуся диагностировали трудности в обучении, такие как дискалькулия, дислексия или дисграфия, вы можете разрешить им использовать калькулятор для выполнения основных арифметических операций или компьютер, чтобы печатать и отправлять работы. Слепой набор на компьютере часто бывает проще для детей, которым сложно научиться писать от руки.
Дайте учащимся больше времени.Потребность в времени на обработку в математике может варьироваться между учащимися, но детям с трудностями в обучении часто полезно иметь больше времени, чтобы понять концепцию и посмотреть, как она работает.Это также помогает разбить работу на небольшие этапы и дать каждому учащемуся время, необходимое для осмысления линии, на которой он находится, прежде чем перейти к следующей. Увеличение ограничения по времени также может помочь уменьшить беспокойство по поводу математики.
Быстрая замена крышки:
Учащиеся с дискалькулией, дислексией, диспраксией, проблемами с вниманием, дисграфией, проблемами обработки изображений и тревогой могут бороться с математикой.
- Дети с дискалькулией могут затруднить основы арифметики и счета
- Учащиеся с трудностями обработки и ADD / ADHD могут иметь проблемы после объяснений учителя в классе
- Учащимся с диспраксией может быть сложно выбрать лучший подход к решению проблемы
- Запись, интерпретация и преобразование решения могут быть сложными для учащихся с дислексией и дисграфией
- Учащиеся с по математике с тревогой могут испытывать трудности с выполнением заданий по оценке по времени или испытывать недостаток мотивации из-за низкой самооценки или неуверенности в себе
Сенсорное чтение и написание
Touch-type Read and Spell – это мультисенсорная программа набора текста, которая учит печатать с использованием всего слова и подхода, основанного на звуке.Учащиеся могут использовать модули набора текста по математике, созданные учителями для соответствия учебной программе на разных уровнях обучения. Математические модули TTRS обучают основным определениям и помогают укрепить навыки чтения с листа для ключевых слов. Подход работает как для детей, так и для взрослых, которые испытывают трудности с математикой.
Используйте наши предметы по математике, чтобы подготовиться к предстоящему году, поддержать обучение в классе или просмотреть ранее изученный материал. Печатание может дать учащимся с трудностями в обучении уверенность и навыки, необходимые для достижения успеха!
Тест по математике для 4-го класса
Перед тем, как начать, распечатайте свой тест по математике для 4-го класса.Постарайтесь ответить на все вопросы.
Имя ________________ Дата: _____________________
Решите следующие проблемы
1.
a. Какая дробь не эквивалентна двум другим? ___________
Эквивалентные фракции
2. У Jetser дела идут неважно. В пятницу он заработал 468 долларов. В субботу он заработал 459. Во вторник он заработал 432 доллара. Сколько денег он заработал в четверг?
А.424 B. 414 C. 314 D. 451
3. Посмотрите на блоки с основанием 10 ниже и скажите, какое число они представляют. Внимательно посмотрите, прежде чем отвечать!
Базовые 10 блоковA. 363 B. 164 C. 451 D. 300
4. Округлите 846 до ближайшей сотни _____________ и 3756 до ближайшей тысячи _____________
5. Какое число совпадает с пятью тысячами двадцать двумя?
A. 5200 B. 502 C. 5202 D. 5022
6.Запишите десятичные дроби 0,25 и 0,4 прописью и дробями
0,25: ___________________________________________ ______________
0,4: ___________________________________________ ______________
7. Какое число больше 5678, но меньше 5708?
A. 5677 B. 5707 C. 5800 D. 0
8. Какое значение имеет символ #? ________________
6 + # = 14
9.Сколько блоков из 100 и 10 вы можете сделать с 3250?
A. 325 и 1 B. 32 и 5 C. 30 и 50 D. 3 и 55
10. 1 четверть, 3 дайма, 2 никеля и 6 центов равны
A. 0,70 доллара B. 0,71 доллара C. 0,75 доллара D. 0,69 доллара
11. Умножьте 235 на 13 ________________
A. 4322 B. 3078 C. 3055 D. 566
12. Какая дробь больше 2/3?
А.1/3 B. 4/5 C. 4/6 D. 2/6
13. Найдите 4 задачи умножения, которые совпадают с 12 + 12 + 12
14. Заштрихованная дробь равна
A. две девятые B. девять-три C. четыре восьмых D. три девятых
15. Выполните следующие операции сложения и вычитания
64837 + 4598 =?
92345 –
=?
16.
Как лучше всего назвать геометрическую фигуру, похожую на мусорный бак? ______________________
Какую из следующих форм вы, вероятно, могли бы использовать для описания формы вашего глазного яблока?
А.Куб B. Сфера C. Цилиндр D. Конус
Какую из следующих форм вы, вероятно, могли бы использовать, чтобы описать форму холодильника в вашем доме?
A. Куб B. Сфера C. Цилиндр D. прямоугольная призма
17. Предположим, у вас в кармане 3 четверти, 5 центов, 2 пенни и 1 цент. Вы говорите другу выбрать только одну монету. Какую монету ваш друг, скорее всего, выберет? Кратко объясните, почему
18.Запишите прописью следующие числа:
5669 ___________________________________________
8765 ___________________________________________
19. Выполните следующее деление в столбик
20. Какие два круга при добавлении дадут вам целое?
Вариант 1: A и C Вариант 2: B и C Вариант 3: A и B Вариант 4: B и D
21. Обведите круг. Разбейте круг на 4 равные части.Затем заштрихуйте две четверти круга.
22. Сделайте два круга. Разбейте оба круга на 4 равные части. Затем заштрихуйте три четверти первого круга и одну четверть второго круга
a. Что такое три четверти минус одна четверть? _______________________
б. Что такое три четверти плюс одна четверть? _________________________
23. Замените символы * и # числами, чтобы сбалансировать уравнение
6 + * = 10 + # + #
24. Какая математическая задача (задачи) означает, что то же самое, что 40+ (100 + 300)? ______________
А.140 + 300 Б. 40 + 500 В. 40 × 11 Д. 40 × 100 + (30)
25. Навыки решения проблем. Калькулятора нет. Не исключение! На самом деле, для решения этого математического теста для 4-го класса вообще не следует использовать калькулятор.
У вас 6700 долларов в кармане. Вы хотите купить 7 ноутбуков по 800 долларов каждый.
Сколько будут стоить 7 ноутбуков? _________
Объясните, как вы использовали таблицу умножения и математические факты, чтобы быстро получить ответ
Сколько денег у вас осталось после оплаты калькуляторов? _________
Объясните Опять же, как вы использовали математические факты, чтобы очень быстро получить ответ.
Вы хотите равномерно разделить оставшиеся деньги между вами и 10 друзьями.Сколько денег получит каждый? ____________
26. Если 5 книг стоят 100 долларов, какова цена 2 книг? (Предположим, вы купили 5 таких же книг)
27. Площадь фигуры ниже
A. 14 квадратных единиц B. 17 квадратных единиц C. 10 квадратных единиц × 11 D. 16 квадратных единиц
28. В пространстве ниже нарисуйте 2 параллельные линии и третью линию, перпендикулярную параллельным линиям
29. Нарисуйте 2 одинаковые формы и 2 похожие формы на пустом месте ниже:
30.Дополнить следующими двумя числами
4, 20, 100, ________, ___________
Что вам нужно знать об этом тесте по математике для 4-го класса
Примечание. Результат 25 или более баллов в этом тесте по математике для 4-го класса является хорошим показателем того, что большинство навыков, которым обучали в 4-м классе, были освоены.
Если у вас много проблем с тестом по математике для 4-го класса, попросите кого-нибудь помочь вам.