Решение примеров со скобками 2 класс: Выражения со скобками – 2 класс, примеры, порядок действия

Порядок выполнения действий, правила, примеры. Порядок выполнения математических действий Примеры в 2 действия без скобок

Мы рассмотрим в этой статье три варианта примеров:

1. Примеры со скобками (действия сложения и вычитания)

2. Примеры со скобками (сложение, вычитание, умножение, деление)

3. Примеры, в которых много действий

1 Примеры со скобками (действия сложения и вычитания)

Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:

Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.

*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.

Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:

В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.

А теперь — тренажеры!

1) Примеры со скобками в пределах до 20. Онлайн тренажер.

2) Примеры со скобками в пределах до 100. Онлайн тренажер.

3) Примеры со скобками. Тренажер №2

4) Вставь пропущенное число — примеры со скобками. Тренажер

2 Примеры со скобками (сложение, вычитание, умножение, деление)

Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.

Сначала рассмотрим примеры без скобок:

Есть одна хитрость, как не запутаться при решении примеров на порядок действий.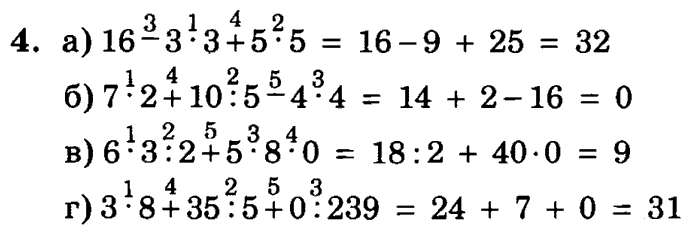 Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:

Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:

3 Примеры, в которых много действий

Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).

Эти знаки и будут делить наш пример на блоки:

Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.

А теперь закрепляем решение примеров на порядок действий на тренажерах!

Если у вас не открываются игры или тренажёры, читайте .

На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.

В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот.

Но нельзя сначала уйти в школу, а потом надеть одежду.

А в математике обязательно ли выполнять арифметические действия в определенном порядке?

Давайте проверим

Сравним выражения:
8-3+4 и 8-3+4

Видим, что оба выражения совершенно одинаковы.

Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий

В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.

Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.

Видим, что значения выражений получаются разные.

Сделаем вывод: порядок выполнения арифметических действий менять нельзя .

Узнаем правило выполнения арифметических действий в выражениях без скобок.

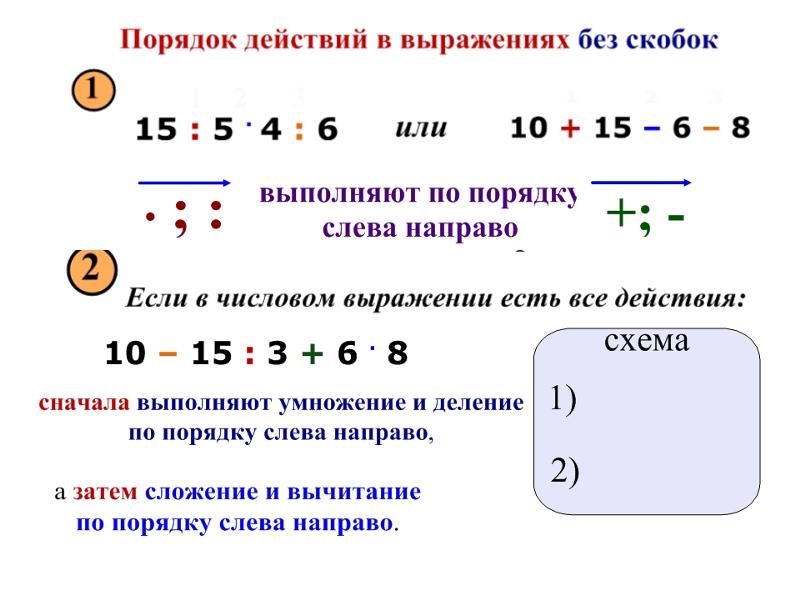
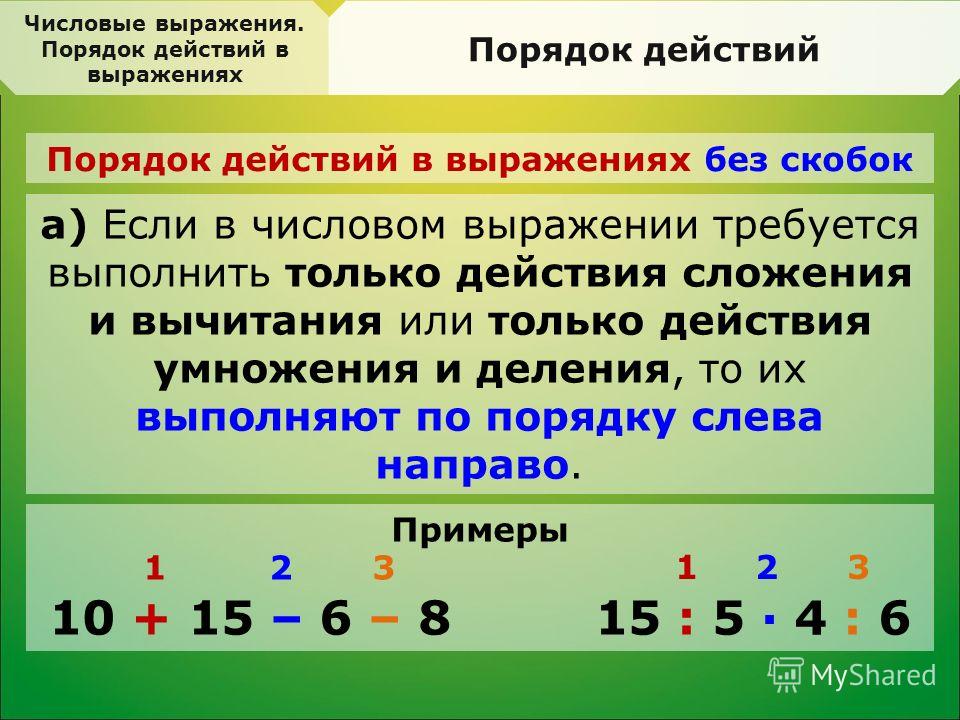
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.

Потренируемся.

Рассмотрим выражение

В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .

Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий

Рассмотрим второе выражение

В этом выражении имеются только действия умножения и деления – это действия второй ступени.

Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий

В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Рассмотрим выражение.

Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.

Вычислим значение выражения.

18:2-2*3+12:3=9-6+4=3+4=7

В каком порядке выполняются арифметические действия, если в выражении имеются скобки?

Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.

Рассмотрим выражение.

30 + 6 * (13 – 9)

Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.

30 + 6 * (13 – 9)

Вычислим значение выражения.

30+6*(13-9)=30+6*4=30+24=54

Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?

Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:

1. действия, записанные в скобках;

2. умножение и деление;

3. сложение и вычитание.

Схема поможет запомнить это несложное правило (рис. 4).

Рис. 4. Порядок действий

Потренируемся.

Рассмотрим выражения, установим порядок действий и выполним вычисления.

43 – (20 – 7) +15

32 + 9 * (19 – 16)

Будем действовать по правилу. В выражении 43 – (20 – 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 – (20 – 7) +15 =43 – 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 – 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 – 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.

2*9-18:3=18-6=12

Узнаем, правильно ли определен порядок действий в следующих выражениях.

37 + 9 – 6: 2 * 3 =

18: (11 – 5) + 47=

7 * 3 – (16 + 4)=

Рассуждаем так.

37 + 9 – 6: 2 * 3 =

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37

Продолжаем рассуждать.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

18:(11-5)+47=18:6+47=3+47=50

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

7*3-(16+4)=7*3-20=21-20=1

Выполним задание.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

1. Festival.1september.ru ().
2. Sosnovoborsk-soobchestva.ru ().
3. Openclass.ru ().

Домашнее задание

1. Определи порядок действий в данных выражениях. Найди значение выражений.

2. Определи, в каком выражении такой порядок выполнения действий:

1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.

3. Составь три выражения, в которых такой порядок выполнения действий:

1. умножение; 2. сложение; 3. вычитание

1. сложение; 2. вычитание; 3. сложение

1. умножение; 2. деление; 3. сложение

Найди значение этих выражений.

Сегодня мы поговорим о порядке выполнения математических действий . Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.

Итак, вспомним о том, что сначала вычисляются выражения в скобках

38 – (10 + 6) = 22 ;

1) в скобках: 10 + 6 = 16 ;

2) вычитание: 38 – 16 = 22 .

Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.

10 ÷ 2 × 4 = 20 ;

Порядок выполнения действий :

1) слева направо, сначала деление: 10 ÷ 2 = 5 ;

2) умножение: 5 × 4 = 20 ;

10 + 4 – 3 = 11 , т.е.:

1) 10 + 4 = 14 ;

2) 14 – 3 = 11 .

Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.

18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7

Порядок выполнения действий:

1) 18 ÷ 2 = 9 ;

2) 2 × 3 = 6 ;

3) 12 ÷ 3 = 4 ;

4) 9 – 6 = 3 ; т.е. слева направо – результат первого действия минус результат второго;

5) 3 + 4 = 7 ; т.е. результат четвертого действия плюс результат третьего;

Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.

30 + 6 × (13 – 9) = 54 , т.е.:

1) выражение в скобках: 13 – 9 = 4 ;

2) умножение: 6 × 4 = 24 ;

3) сложение: 30 + 24 = 54 ;

Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:

1) действия, заключенные в скобках;

2) умножение и деление;

3) сложение и вычитание.

Если вы хотите получать анонсы наших статей подпишитесь на рассылку “ “.

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

1. Все действия выполняются слева направо.
2. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Пример 1

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Пример 3

Условие: подсчитайте, сколько будет 17 − 5 · 6: 3 − 2 + 4: 2 .

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6: 3 − 2 + 4: 2 = 7 .

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

Определение 2

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Определение 3

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Пример 4

Условие: вычислите, сколько будет 5 + (7 − 2 · 3) · (6 − 4) : 2 .

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7:

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2: 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + (7 − 2 · 3) · (6 − 4) : 2 = 6 .

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Пример 5

Условие: вычислите, сколько будет 4 + (3 + 1 + 4 · (2 + 3)) .

Решение

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · (2 + 3) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + (3 + 1 + 4 · (2 + 3)) = 28 .

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет (4 + (4 + (4 − 6: 2)) − 1) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 – 1 , результатом которой будет 7 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Пример 6

Условие: найдите, сколько будет (3 + 1) · 2 + 6 2: 3 − 7 .

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид (3 + 1) · 2 + 36: 3 − 7 .

(3 + 1) · 2 + 36: 3 − 7 = 4 · 2 + 36: 3 − 7 = 8 + 12 − 7 = 13

Ответ: (3 + 1) · 2 + 6 2: 3 − 7 = 13 .

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .

В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.

Навигация по странице.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :

• действия выполняются по порядку слева направо,
• причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.

Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.

Пример.

Выполните действия 7−3+6 .

Решение.

Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .

Кратко решение можно записать так: 7−3+6=4+6=10 .

Ответ:

7−3+6=10 .

Пример.

Укажите порядок выполнения действий в выражении 6:2·8:3 .

Решение.

Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.

Ответ:

Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.

Пример.

Вычислите значение выражения 17−5·6:3−2+4:2 .

Решение.

Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 – значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .

Ответ:

17−5·6:3−2+4:2=7 .

На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .

Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание – следует придерживаться и при работе с буквенными выражениями.

Действия первой и второй ступени

В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.

Определение.

Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .

В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Пример.

Выполните указанные действия 5+(7−2·3)·(6−4):2 .

Решение.

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .

Ответ:

5+(7−2·3)·(6−4):2=6 .

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Пример.

Выполните действия в выражении 4+(3+1+4·(2+3)) .

Решение.

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 .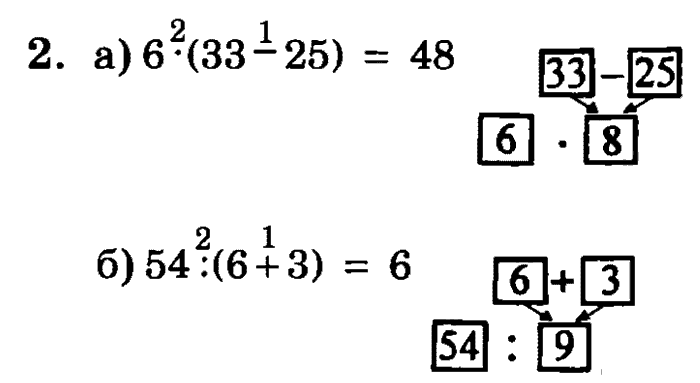 В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .

Ответ:

4+(3+1+4·(2+3))=28 .

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .

Урок матемтаики 2 класс “Порядок действий. Скобки” | План-конспект урока по математике (2 класс):

Конспект урока по математике.

Класс: 2

Программа: Школа России.

Тема: Порядок выполнения действий. Скобки.

Тип урока: урок изучения и первичного закрепления новых знаний

Цели: познакомить с порядком выполнения действий при вычислениях; учить находить значения выражений со скобками; развивать умение решать текстовые задачи и задачи логического характера; совершенствовать вычислительные навыки.

Планируемые результаты:

Регулятивные:

–  определять цель деятельности на уроке с помощью учителя;

–  находить и формулировать проблему совместно с учителем;

–  планировать учебную деятельность на уроке;

-оценивать полученный результат.

Познавательные:

-добывать новые знания в учебнике;

-перерабатывать полученную информацию, наблюдать и делать выводы.

Коммуникативные:

-слушать и понимать речь других;

– участвовать в беседе на уроке.

Предметные:

– использовать в своей речи название компонентов действий сложения и вычитания;

-осознанно следовать алгоритму выполнения действий в выражениях со скобками;

-находить значение выражений в двух действиях;

-уметь читать числовые выражения.

Этапы урока:

Оборудование: учебник «Математика» 2 класс, М.И. Моро, М.А.Бантова, проектор, экран, презентация.

---

Ход урока:

1. Организационный момент.

– Здравствуйте, дети. Давайте проверим, все ли необходимые предметы у вас на партах.

2. Актуализация знаний.

1) Каллиграфическая минутка.

 – Начнём работу с каллиграфической минутки:

– Запишите число, в котором 7 десятков и 6 единиц. Пропиши его до конца строки. Ниже представьте это число в виде суммы разрядных слагаемых.

2) Устный счет.

– Решите примеры. (на доске)

5+8	56-5     56-50
3     3+5	4+3      4+34
15      15-5	78-8    78-8

5+8=13      56-50=6

3+5=8        4+34=38

15-5=10     78-8=70

-Я задумала число, и прибавила к нему 2, получила 19. Какое число я задумала? (17)

– Я задумала число, и прибавила 3, получила 35.

Какое число я задумала? (32)

– Я задумала число, и вычла 3, получила 40.

Какое число я задумала? (43)

-Запишите число, следующее за числом 49. (50)

– Запишите число, предшествующее числу 25. (24)

3.Самоопределение к деятельности.

(На доске записаны примеры.)

20-9+8=19

20-9+8=3

-Рассмотрите примеры. Сравните. Чем они похожи? Чем отличаются?

-Какое равенство верно? (Первое.)

– Как выполняли действия? (Сначала выполнили вычитание, а потом сложение.)

– В каком порядке нужно выполнить действия во втором равенстве, чтобы оно стало верным? (Сначала сложить 9 и 3, а затем из 20 вычесть их сумму.)

 Для чего нам нужно знать порядок действий? Правильно выполнять вычисления в длинных выражениях.

 -Сформулируйте тему урока. Тема урока: Порядок действий.

– Мы поняли, как нужно решать эти примеры. А как показать это другим?

– Чего мы не знаем? (Как показать, в каком порядке нужно выполнять действия в некоторых примерах. )

– О чём сейчас говорили? (О порядке выполнения действий.)

– Какая тема урока? (Порядок выполнения действий.)

-Какова цель нашего урока? (Научиться обозначать в записи порядок действий.)

– Откройте учебник на странице 38 и проверьте, правильно ли вы догадались.

4.Работа по теме урока.

Учитель вместе с учащимися формулируют правило: «Действия, записанные в скобках, выполняются первыми.» (на слайд)

На слайде два примера:

10-(5+2)

(10-5) +2

-Чем похожи эти выражения, а чем различаются? (Похожи-набором чисел и знаков, различаются-порядком скобок)

Учащиеся составляют алгоритм решения выражении со скобками с помощью учителя.

Алгоритм: (на слайде по порядку)

1. Выполняется действия, записанные в скобках.
2. Выполняется сложение и вычитание, действие по порядку слева направо.

-Одинаковое ли значение получилось в этих выражениях? (нет)

После данной работы учащиеся формулируют вывод: «Скобки изменяют порядок действий в выражениях и их значения. » (На слайд)

5.Физминутка.

6. Закрепление изученного материла.

1) Работа по учебнику.

– Мы получили новое знание. Проверим, правильно ли мы сделали выводы.

Сравним наше новое знание с научным в учебнике. Прочитайте на с.38 выделенное в рамочку.

– выполним задание №1 на стр.38. Что нужно сделать? (Коллективное выполнение с комментированием. Выходят к доске.)

2) Работа с карточками.

– для закрепления полученных знаний поработаем парами с карточками.

– прочитайте задание. (приложение №1)

ЗАДАНИЕ: Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой.

10-6+3   10 –(2+3)

5+3+2     4+(8-2)

9-9+5      5+(4-2)

– Проверьте ответы. (слайд)

10-6+3        10 –(2+3)

5+3+2          4+(8-2) 

9-9+5           5+(4-2)

– Оцените свою работу в парах. Если выполнили всё правильно-то весёлый смайлик, если допустили ошибки- то серьёзный, не улыбающийся, а если ничего не получилось – грустный.

---

7. Повторение пройденного материала.

– Обратимся к задаче на стр.39 №5.

– Прочитайте. (Дети читают задачу сначала про себя, а затем один ученик  читает её вслух).

– О ком говорится в задаче?

– Чем занимался Коля?

– Какую пользу приносит людям посещение бассейна? ( Укрепляет здоровье человека.)

– Вы тоже должны укреплять своё здоровье, заниматься спортом.

– Что известно в задаче?

– Что нужно найти в задаче?

– Давайте обратимся к чертежу задачи.

– Что обозначают числа 100? 60?

– Как ответить на вопрос задачи?

– Запишите решение и ответ. (Один ученик работает у доски).

– Молодцы, справились с заданием.

8.Рефлексия.

«Проверь себя», стр. 39

9. Итог урока.

– что нового вы узнали на уроке? (о порядке выполнения действий в выражении со скобками и без скобок)

– что запомнили? (действия, записанные в скобках, выполняют первыми)

– чему научились? (решать примеры со скобками)

– оцените свою работу на уроке с помощью сигнальных карточек (зелёный-всё понял; жёлтый- некоторые моменты остались мне непонятны; красный- ничего не понял, мне нужна помощь)

9.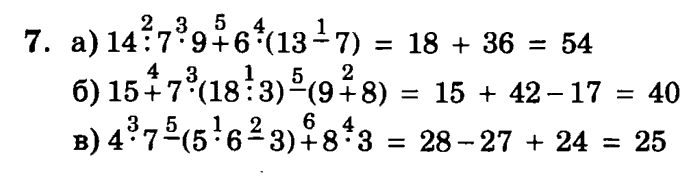 Домашнее задание.

– дома предлагаю ещё раз повторить правило о порядке выполнения действий и потренироваться в решении выражений со скобками. Стр. 38 № 1, №6

---

Приложение 1

Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3   10 –(2+3) 5+3+2     4+(8-2) 9-9+5      5+(4-2)	Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3   10 –(2+3) 5+3+2     4+(8-2) 9-9+5      5+(4-2)
Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3   10 –(2+3) 5+3+2     4+(8-2) 9-9+5      5+(4-2)	Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3   10 –(2+3) 5+3+2     4+(8-2) 9-9+5      5+(4-2)
Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3   10 –(2+3) 5+3+2     4+(8-2) 9-9+5      5+(4-2)	Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3   10 –(2+3) 5+3+2     4+(8-2) 9-9+5      5+(4-2)
Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3   10 –(2+3) 5+3+2     4+(8-2) 9-9+5      5+(4-2)	Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3   10 –(2+3) 5+3+2     4+(8-2) 9-9+5      5+(4-2)
Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3   10 –(2+3) 5+3+2     4+(8-2) 9-9+5      5+(4-2)	Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3   10 –(2+3) 5+3+2     4+(8-2) 9-9+5      5+(4-2)
Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3   10 –(2+3) 5+3+2     4+(8-2) 9-9+5      5+(4-2)	Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3   10 –(2+3) 5+3+2     4+(8-2) 9-9+5      5+(4-2)

“Порядок выполнения действий в выражениях. Скобки”

• Шевцова Елена Викторовна

Разделы: Начальная школа, Конкурс «Учение с увлечением, или Как полюбить математику?»

Класс: 2

Ключевые слова: математика, Порядок выполнения действий в выражениях

---

Тип урока: Урок «открытия» новых знаний.

Цель: создать условия для формирования умения определять порядок действий в выражениях, использовать скобки.

Планируемые результаты.

Предметные:

• дети научатся определять порядок действий в выражениях со скобками и применять алгоритм выполнения действий на практике;
• читать выражения со скобками и без скобок.

Метапредметные.

Познавательные УУД:

• дети будутсравнивать выражения с целью выделения признаков сходства и различия;
• аргументировать свои ответы;
• находить необходимую информацию в учебнике;
• проводить анализ и синтез в результате решения выражений со скобками и без скобок.

Регулятивные УУД:

• принимать и удерживать цель на протяжении всего урока;
• выполнять самопроверку по образцу;
• оценивать свою работу;
• действовать по намеченному плану.

Коммуникативные УУД:

• включаться и поддерживать учебный диалог;
• уметь слушать и понимать других.

Личностные УУД:

• самоопределение;
• смыслообразование («какое значение, смысл имеет для меня умение учиться, зачем мне знать порядок выполнения действий в выражениях со скобками»).

Оборудование: учебник – Истомина Н.Б. «Математика 2 класс» Смоленск: «Ассоциация XXI век», 2012; карточки для индивидуальной работы; презентация.

Описание урока

Урок открытия новых знаний.

Используется проблемно-диалогическая технология Е.Л.Мельниковой. Для постановки проблемы использую прием № 1, для этого  предъявляю противоречивые факты. Для решения поиска проблемы использую подводящий диалог, работу в парах.

Результатом этапа поиска решения является формулирование темы и целей урока, составление алгоритма определения порядка действий в выражениях.

Используя полученные знания и алгоритм, учащиеся выполняли продуктивные задания учебника.

Это первый урок в группе уроков по данной теме. На данном уроке учащиеся изучили правило порядка действий в выражениях.

При планировании урока были учтены все особенности класса. Осуществляя индивидуальный подход, учащиеся были распределены в пары так, чтобы в каждой были и «слабые», и «сильные» ученики, так, чтобы «слабый» оказался в ситуации успеха и «сильный» участвовал в поиске правильных ответов.

Высокая работоспособность достигнута сменой деятельности, наличием наглядности в виде презентации и проведением двух динамических пауз.
Использовались различные приемы устной и письменной работы, фронтального опроса, самостоятельной работы с самопроверкой в классе.

Этапы урока	Ход урока
1. Мотивация к учебной деятельности	– Всем, всем – Добрый день! Прочь с дороги наша лень. Не мешай трудиться, Не мешай учиться. В математику-страну Вас сегодня всех зову. Встретим мы своих друзей. Назовем их поскорей. (на доске карточки с равенствами и неравенствами, арифметическими действиями) Ученики называют известные им математические термины. (сумма, разность, равенство, неравенство, схема, рисунок, арифметические действия +, – и т.д.) – Сегодня на уроке мы будем использовать термины: выражение, равенство, сумма, разность, вычесть, прибавить, порядок, действия и … узнаем новые математические знаки.
2. Актуализация знаний	– У вас на столах – карточки. (Приложение 1) Что на них записано? (выражения) Как вы думаете, какое задание я вам предложу сделать с данными выражениями? (найти, вычислить значения данных выражений) – Сейчас возьмите маркеры и вычислите значения данных выражений. (дети вычисляют) (карточки А4, вложены в файлы, дети работают маркерами, которые потом легко стираются) – Сравните свои ответы с ответами на доске, если есть ошибки, зачеркните и напишите верный ответ. – Поставьте: – 5, если все правильно, – 4 – если 1 ошибка, – 3 – если 2 ошибки. Сдайте тихонько карточки. (С целью проверки самостоятельной работы учитель затем располагает рядом с примерами карточки с ответами, на обратной стороне которых записаны буквы.)
3. Выявление места и причины затруднения и постановка учебной задачи (работа на доске и в тетради) — Расположите ответы, полученные каждым вариантом, по убыванию и прочитайте словосочетание. («Порядок действий».) — О чем будем говорить на уроке? (О порядке действий.) Тема нашего урока: “Порядок действий“. Учитель выполняет на доске записи: 8-3+4=9 8-3+4=1 — Что вас удивило? (Почему у одинаковых выражений получились разные значения. )
4. Построение проекта выхода из затруднении («открытие детьми нового знания» (подводящий диалог) — Давайте рассуждать: если отличаются правые части равенства, то… (Должны отличаться и левые.) – Чем могут отличаться левые части? – Как получили число 9? (Сначала выполнили вычитание, а затем сложение.) – Как получили число 1? (Сначала выполнили сложение, а затем вычитание.) -Чем отличаются выражения? (Порядком действий.) – Мы поняли, как нужно решать эти выражения. А как показать это другим? – Чего мы не знаем? Что надо узнать? Чему научиться? (Как показать, какое действие надо выполнить первым?) Узнать … Как показать, какое действие надо выполнить первым? Научиться … определять порядок действий в выражениях (со скобками и применять алгоритм выполнения действий на практике.) и находить значения этих выражений -Для определения порядка действий иногда не хватает специального знака. (Если ученики затрудняются сделать этот вывод, то можно задать наводящий вопрос) – «Как водитель на дороге узнает, куда надо ехать и с какой скоростью?» – Какой бы вы использовали знак с этой целью? Учащиеся предлагают свои варианты. – Математики всего мира много лет назад тоже столкнулись с этой проблемой, поэтому они договорились обозначать действие, которое надо выполнить первым, скобками. Что показывают скобки в выражении? (Какое действие выполняется первым.) – Давайте откроем учебник на с. 66 и подтвердим правильность наших выводов. Еще сегодня мы будем учиться правильно читать выражения со скобками и без них. – Прочтем текст под условным знаком «новая информация» (учебник с.66) Вывод: 1. Если в выражении стоят скобки, то действие, записанное в них, нужно выполнить вначале. 8 – (3+4) Прочтем наше выражение – В этом выражении есть скобки, значит, сначала мы должны выполнить действие, которое в скобках. (найдем сумму 3 и 4 =7, из 8 вычтем 7= 1	2. Если в выражении нет скобок, то действия выполняются по порядку, слева направо. (пример на доске 8-3+4 ) – Прочтем наше выражение (к разности 8 и 3 прибавить 4) – В этом выражении нет скобок, поэтому действия выполняются в порядке, в котором они записаны (слева направо). сначала найдем разность 8 и 3=5, теперь к 5 прибавим 4=9)
5. Первичное закрепление во внешней речи	Первичное закрепление Ученики открывают учебник на с. 67 и анализируют № 223 и 224. (проговаривание хором и индивидуально) – Давайте рассуждать. 18 – (6-4) – В этом выражении есть скобки, значит, сначала мы должны выполнить действие, которое в скобках. Ставим над скобками 1, потом 2. (найдем разность 6 и 4 =2, из 18 вычтем 2= 16 18-6-4 – В этом выражении нет скобок, поэтому действия выполняются в порядке, в котором они записаны (слева направо). (сначала найдем разность 18 и 6=12,теперь из 12 вычтем 4 =8) (на экране расставляем порядок действий, считаем самостоятельно, проверяем, ответ появляется на экране) Физкультминутка 1) 1 хлопок учителя – поднимаются или опускаются руки, 2 хлопка – действие для ног (встать или присесть)
6. Самостоятельная работа с самопроверкой по эталону	Самостоятельная работа с самопроверкой по образцу. Давайте вспомним, чему мы сегодня должны научиться… – Определять порядок действий в выражениях со скобками и находить значения выражений (применять алгоритм выполнения действий на практике.)
Работа в группах	– Сейчас мы попробуем составить памятку №3 «Как определить порядок действий?» Для этой работы мы разобьемся на группы. Цель: составление алгоритма определения порядка действий. Группы по 4 человека выполняют работу на листах А4,  которые вывешиваются на доску и выбирается верное решение. Представители групп, которые справились, озвучивают получившийся результат. (по 1 пункту, каждая группа) Все вместе собирается в одну памятку. ПАМЯТКА №3 Как определить порядок действий? 1. Прочитай выражение. 2. Потом посмотри: есть ли скобки? «Нет» – выполняю действия по порядку. «Да» – первое действие в скобках. (Памятку дети вкладывают в папку для памяток по математике) – Как будем действовать, чтобы определить порядок? Алгоритм: 1) Прочитать выражение. 2) Скобки есть? «Нет» – выполняем действия в том порядке, как записаны. «Да» – первое действие в скобках. Действуя по памятке 3, ученики выполняют №225 (1,2,3,4) 1, 2 с комментированием, 3, 4 – самостоятельно.
Работа в парах Обсудить в парах: в каких парах выражений значения одинаковые, а в каких разные. – Какой вывод можно сделать? Вывод: – При использовании скобок в выражении всегда меняется порядок действий, а значение может остаться без изменений.	Физминутка. 2) Мы ногами – топ-топ, мы руками – хлоп-хлоп, Мы плечами – чик-чик, мы глазами – миг-миг. Раз – присели¸ два – привстали, Три, четыре – поскакали. Пять – нагнулись, разогнулись. Шесть – друг другу улыбнулись. Семь – за парту тихо сесть, А на восемь – лень отбросим.
7. Включение в систему знаний и повторение	Карточки для индивидуальной работы 1. Подчеркни выражение, где правильно расставлен порядок действий. 2. Расставь порядок действий. (9 + 2) – 5 16 – (7+ 3) 3. Найди ответ в первом действии. (5 + 6 ) – 3 – 2 7 + 4 – (8 + 4 ) 12 – (5 + 8 ) + 2 Проверить (если будет время)
8. Рефлексия учебной деятельности	Что должны были узнать?… Чему научиться?…
9. Самооценка	«Дорожка успеха» (см. Приложение 2)
10. Домашнее задание	1. №225 (5-8), тпо №103, 105 2. Составить 6 выражений со скобками для своих одноклассников (по желанию)

2.11.2020

Типы, использование, правило BODMAS, решенные проблемы и часто задаваемые вопросы

Первый вопрос, который студент получает по этой теме: «Как мы можем определить скобки». При вычислении выражения, содержащего заключенное в квадратные скобки подвыражение, скобки обозначают тип группировки, операторы в подвыражении имеют приоритет над окружающими его. Кроме того, для различных скобок существует множество применений и определений.

 

Типы кронштейнов

Часто используемые типы кронштейнов:

• Parentheses ( )

• Square brackets [ ]

• Curly brackets { }

• Angle brackets ⟨ ⟩

 

Parentheses

Among the four different types of brackets used, parentheses являются наиболее часто используемым типом скобок. В математических задачах скобки в основном используются для группировки чисел. Используйте порядок операций для решения проблемы, когда мы видим несколько чисел и операций в скобках.

 

Скобки используются в математике по трем основным причинам:

Чтобы разделить числа для пояснения, можно использовать круглые скобки.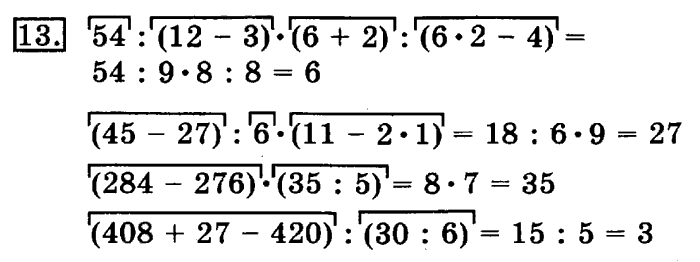 Например, если у нас есть дополнительная проблема с отрицательным числом, чтобы различить два знака, будут использоваться круглые скобки. Чтобы отличить число от его показателей, также можно использовать круглые скобки. Как правило, это происходит, если мы поднимаем отрицательное число до контроля.

 

Квадратные скобки

В математике квадратные скобки [ ] используются в различных ситуациях:

• Квадратные скобки иногда используются вместо скобок (или в дополнение к ним) в очень сложных выражениях, особенно в качестве знака группы вне внутреннего набора скобок.

• Они могут означать то же, что и скобки, но предназначены для облегчения чтения. Все зависит от ситуации.

• Квадратные скобки используются для включения номера, который он охватывает при работе с включением.

• Их также можно использовать для обозначения наименьшего общего кратного 

Фигурные скобки (также известные как фигурные скобки)

Левые фигурные скобки и правые фигурные скобки используются вместе в математических выражениях. Их можно заменить квадратными скобками или круглыми скобками. Во вложенной фразе с тремя уровнями группировки круглые скобки обычно используются в самых внутренних группировках. В группе следующего более высокого уровня используются квадратные скобки, в то время как фигурные скобки используются в самых внешних группах (см. « Вложенные выражения » для примера).

Угловые кронштейны

Внутреннее произведение двух функций представлено угловой скобкой, состоящей из бра и кет (бра+кет = скобка). Поскольку угловые скобки напоминают знаки «меньше» и «больше», некоторым учащимся они могут показаться запутанными. Но вы освоитесь, как только начнете время от времени использовать их в своей математической практике.

 

Для чего нужны скобки?

Пример: 5 * (2 + 4) равно 30, (5 * 3) + 2 равно 30.

• Скобки часто используются в математических выражениях, чтобы обозначить группировку, где это уместно, чтобы предотвратить двусмысленность и повысить ясность.

• В декартовой системе координат скобки используются для обозначения координат точки.

Пример: (4,8) обозначает точки в системе координат x-y, где координата x равна 4, а координата y равна 8.

Пример: f(x), g(x).

Пример: [0,8) обозначает полузамкнутый интервал, включающий все действительные числа, кроме 8 от 0 до 8.

• Широкие круглые скобки вокруг двух чисел обозначают биномиальный коэффициент, один над другим.

• Как и в (a,b,c), круглые скобки вокруг набора из двух или более чисел обозначают набор из n чисел, которые связаны определенным образом.

• Матрица обозначается широкими скобками вокруг массива чисел.

• Для обозначения наибольшего общего делителя используются круглые скобки.

 

Правило BODMAS

Скобки находят свое основное применение в правиле BODMAS или PEMDAS, где последовательность операций должна выполняться при разрешении выражения. BODMAS или PEMDAS означает:

B — скобки, P — круглые скобки

O — порядок, E — показатели степени

D — деление

M — умножение

A — сложение

S — вычитание

выполнять до тех пор, пока выражение не будет разрешено. Согласно закону БОДМАСА, если в выражении есть скобки ((), {},), мы сначала должны преодолеть или упростить скобку, а затем порядок, затем делить, умножать, складывать и вычитать слева направо. В неправильном порядке решение проблемы приведет к неправильному ответу.

 

Проще говоря, четыре операции имеют решающее значение для обучения арифметике, и подростки, которые не знают, в какой последовательности их выполнять, не смогут двигаться вперед с годами.

 

Еще одна причина, по которой BODMAS преподается на уроках математики, заключается в том, что учащимся намного легче запомнить, какую операцию выполнять при столкновении со сложными уравнениями.

 

Основные задачи на скобки и их применение:

1) Решить (2 + 4) – (6 – 3)

Ответ: В данном выражении задействованы две круглые скобки. Мы можем решить обе из них по отдельности по правилу БОДМАСа, а затем объединить их результаты.

(2 + 4) = 6……….(1)

(6 – 3) = 3………..(2)

Теперь вычитая (1) с (2), получаем

( 2 + 4) – (6 – 3) = 6 – 3 = 3

 

2) Решите (3 + (5 * 4)) – ((4 * 6) – 10)

Ответ: задействовано четыре скобки в заданном выражении.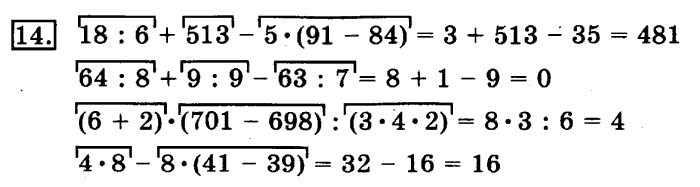 Мы решим это, используя правило BODMAS, чтобы найти ответ.

Первые круглые скобки: (5 * 4) = 20………………………………..(1)

Вторые круглые скобки: (3 + (5*4))=(3 + 20) =23 ………(2)

Третья скобка (4 * 6) = 24……………………………(3)

Четвертая скобка ((4 * 6) – 10) = (24 – 10) = 14……(4)

Теперь вычитаем (2) и (4) получаем

(3+(5*4))-((4*6)-10)=23-14=9.

Порядок операций: примеры

PEMDASan Issue

Purplemath

Большинство проблем с упрощением порядка операций возникает из-за вложенных скобок, экспонент и знаков «минус». Итак, в следующих примерах я покажу, как работать с такими выражениями.

(Приведены ссылки для дополнительного ознакомления с работой с отрицаниями, символами группировки и степенями.)

Продолжение содержания ниже

MathHelp.com

Порядок действий

Я буду упрощать изнутри: сначала круглые скобки , затем квадратные скобки, не забывая, что знак «минус» на цифре 3 перед скобками идет с цифрой 3.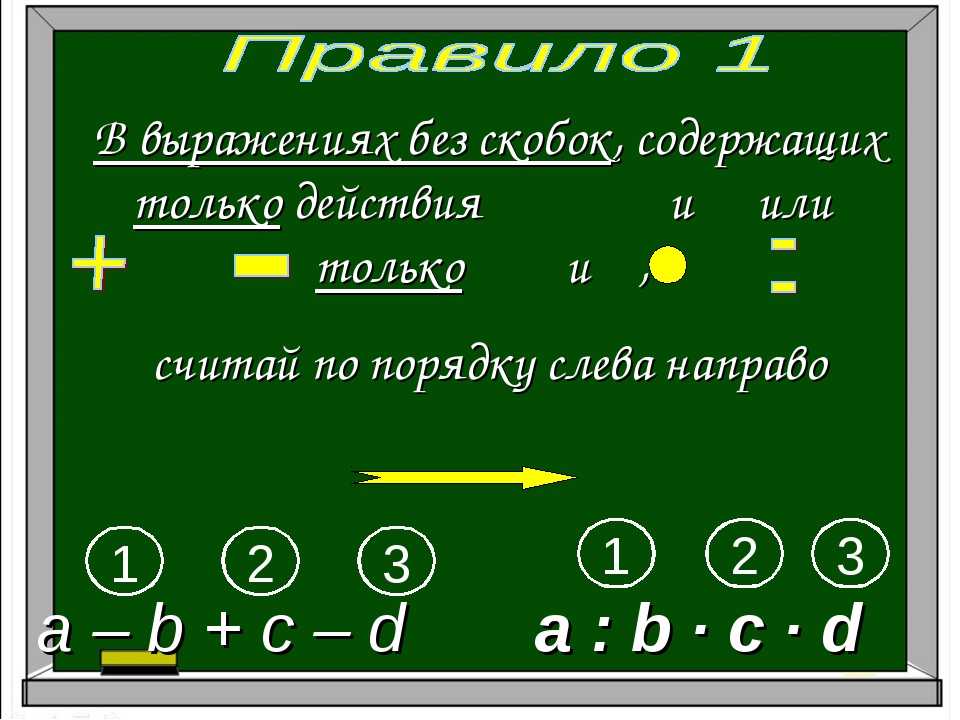 Только после того, как части группировки будут выполнены, я сделаю деление, а затем добавлю 4.

4 − 3[4 −2(6 − 3)] ÷ 2

4 − 3[4 − 2(3)] ÷ 2

4 − 3[4 − 6] ÷ 2

4 − 3[ −2] ÷ 2

4 + 6 ÷ 2

4 + 3

7

Помните, что вместо группирующих символов, говорящих об обратном, деление стоит перед сложением, поэтому это выражение упрощено в конец, вплоть до «4 + 3», а не «10 ÷ 2».

(Если вас не устраивают все эти знаки «минус», просмотрите «Негативы».)

---

Я должен не забыть упростить в скобках перед I в квадрате, потому что (8 − 3) ² — это , а не , то же самое, что 8 ² — 3 ² .

16 – 3 (8 – 3) ² ÷ 5

16 – 3 (5) ² ÷ 5

16 – 3 (25) ÷ 5

16 – 75 ÷ 5

16-151717178 16.

1

---

Если вы узнали о переменных и комбинировании «подобных» терминов, вы также можете увидеть такие упражнения:

Если у меня возникают проблемы с вычитанием через круглые скобки, я могу превратить его в умножение на минус 1. через круглые скобки (обратите внимание на выделенную красным «1» ниже):

14 х + 5[6 − (2 х + 3)]

14 х + 5[6 − 1(2 х + 3)]

5

14 90 6 − 2 x − 3]

14 x + 5[3 − 2 x ]

14 x + 15 − 10 x

4 x + 15

---

I нужно помнить об упрощении на каждом этапе, комбинируя одинаковые термины, когда и где я могу:

− {2 x − [3 − (4 − 3 x )] + 6 x }

-1{2 x – 1[3 – 1(4 – 3 x )] + 6 x }

-1{2 x – 1[3 – 4 + 3 х ] + 6 х }

-1 {2 х – 1[- 1 + 3 х ] + 6 х }

-1 х 902 1 {2 902 x + 6 x }

−1 {2 x + 6 x – 3 x + 1}

–1 (5 x + 1}

–1 (5 x + 10003

–1 (5 x + 10003

– − 1

(Дополнительные примеры такого рода см. в разделе Упрощение в скобках.)

---

Выражения, содержащие дробные формы, также могут вызвать путаницу. Но, пока вы работаете с числителем (то есть верхним) и знаменателем (то есть нижним) отдельно, пока они сначала полностью не упростятся, а уж потом комбинируете (или уменьшаете), если это возможно, то вы все должно быть в порядке. Если дробная форма добавляется или вычитается из другого термина, дробного или иного, убедитесь, что вы полностью упростили и сократили дробную форму, прежде чем пытаться выполнить сложение или вычитание.

Прежде чем я смогу добавить два термина, я должен упростить.

[45]/[8(5 − 4) − 3] + [3(2) ² ]/[5 − 3]

[45]/[8(1) − 3] + [3(4)]/[2]

[45]/[8 − 3] + [12]/[2]

[45]/[5] + 6

9 + 6

15

---

Это работает так же, как и в предыдущих примерах. Мне просто нужно работать с «верхом» и «низом» отдельно, пока я не получу дробь, которую я могу (возможно) уменьшить.

[(3 – 2) + (1 + 2) ² ]/[5 + (4 – 1)]

[(1) + (3) ² ]/[5 + (3)]

[1 + 9]/[8]

8/10

5/4

(Для примеров с большим количеством степеней см. раздел Упрощение с степенями.)

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении, используя порядок операций. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Упростить» или «Оценить» во всплывающем окне, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления. ) никогда не возникает, но когда возникает, кажется, что спорам нет конца. (Публиковать их на Facebook стало раздражать.)

Упрощаю обычным способом:

16 ÷ 2[8 − 3(4 − 2)] + 1

16 ÷ 2[8 − 3(2)] + 1

16 ÷ 2[8 − 6] + 1

16 ÷ 2[ 2] + 1 (**)

16 ÷ 4 + 1

4 + 1

5

Непонятная часть приведенного выше расчета заключается в том, как “16 разделить на 2[2] + 1” (в строке, отмеченной с двойной звездой) становится «16 разделить на 4 + 1» вместо «8 умножить на 2 + 1».

Это потому, что, несмотря на то, что умножение и деление находятся на одном уровне (поэтому должно применяться правило слева направо), круглые скобки, кажется, каким-то образом опережают деление, поэтому первые 2 в отмеченной звездочкой строке часто рассматриваются как идущие с [2], который следует за ним, а не с предшествующим ему «16 разделить на». То есть умножение, обозначенное помещением в круглые скобки (или квадратные скобки и т. д.), часто рассматривается (специалистами) как «более сильное», чем «обычное» умножение, которое обозначается каким-либо символом, например как «×».

Набор всей задачи в графическом калькуляторе подтверждает существование этой иерархии, по крайней мере, в некоторых программах:

Обратите внимание, что разные пакеты программ будут обрабатывать это выражение по-разному ; даже разные модели графических калькуляторов Texas Instruments будут обрабатывать это выражение по-разному. Среди математиков общее мнение состоит в том, что «умножение путем сопоставления» (то есть умножение путем простого размещения элементов рядом друг с другом, а не с использованием знака «×») указывает на то, что сопоставленные значения должны быть умножены вместе перед обработкой других операций. Но не все программы запрограммированы таким образом, и иногда учителя смотрят на вещи по-разному. Если сомневаетесь, спрашивайте! И, печатая что-то боком, будьте очень осторожны со скобками и ясным смыслом, чтобы избежать именно этой двусмысленности.

(Пожалуйста, не присылайте мне электронное письмо с просьбой или предложением окончательного вердикта по этому вопросу. Насколько мне известно, такого окончательного вердикта не существует. Сказать мне, чтобы я делал что-то по-вашему, , а не решит проблема!) (Для примера того, какие электронные письма я получаю, перейдите на следующую страницу, которая также содержит больше примеров дробной формы.)

---

---

---

URL: https://www.purplemath .com/modules/orderops2.htm

Страница 1 Страница 3

Порядок операций – BODMAS

Операции

“Операции” означают такие вещи, как сложение, вычитание, умножение, деление, возведение в квадрат и т. д. Если это не число, то, вероятно, это операция.

Но когда вы видите что-то вроде…

7 + (6 × 5 ² + 3)

… какую часть следует вычислить в первую очередь?

Начать слева и идти направо?
Или идти справа налево?

Предупреждение: Вычислите их в неправильном порядке, и вы можете получить неправильный ответ!

Итак, люди давно договорились следовать правилам при расчетах, а они таковы:

Порядок операций

Сначала сделайте что-нибудь в скобках

		4 × (5 + 3)	=	4 × 8	=	32
		4 × (5 + 3)	=	20 + 3	=	23	(неверно)

Экспоненты (степени, корни) перед умножением, делением, сложением или вычитанием

		5 × 2 2	=	5 × 4	=	20
		5 × 2 2	=	10 2	=	100	(неверно)

Умножьте или разделите перед сложением или вычитанием

		2 + 5 × 3	=	2 + 15	=	17
		2 + 5 × 3	=	7 × 3	=	21	(неверно)

В противном случае просто идите слева направо

		30 ÷ 5 × 3	=	6 × 3	=	18
		30 ÷ 5 × 3	=	30 ÷ 15	=	2	(неверно)

Как мне все это запомнить.

.. ? БОДМАС!

Б	B ракетки первые
О	O заказы (т. е. степени и квадратные корни и т. д.)
ДМ	D ivision и M умножение (слева направо)
КАК	Добавление A и удаление S (слева направо)

Разделить и умножить ранги одинаково (и идти слева направо).

Прибавлять и вычитать ранги поровну (и идти слева направо)

Итак, сделайте так:

После того, как вы сделали «B» и «O», просто идите слева направо, выполняя любые «D» или «M», как вы их найдете.

Затем идите слева направо, выполняя любую букву «А» или «S», как вы их найдете.

Примечание: единственное странное название – “Приказы”. Вы можете предпочесть GEMS ( G rouping, E xponents, M умножить или разделить, добавить или S вычесть). Или в США, где вместо квадратных скобок говорят «круглые скобки», значит, это «PEMDAS».

Примеры

Пример: Как вычислить

3 + 6 × 2 ?

M Ультипилизация перед A DDITION:

Первый 6 × 2 = 12 , затем 3 + 12 = 15

9045

Пример: как вы работаете

444444444444444444 4. ?

B сначала ракетки:

Сначала (3 + 6) = 9 , затем 9 × 2 = 18

0444 ?

M умножение и D ivision имеют одинаковый ранг, поэтому просто идите слева направо:

Сначала 12/6 = 2 , затем 2 × 3 = 6 , затем 39 2 = 39043 6/044

Практический пример:

Пример: Сэм бросил мяч прямо вверх со скоростью 20 метров в секунду, какое расстояние он пролетел за 2 секунды?

Сэм использует специальную формулу, включающую гравитацию:

высота = скорость × время — (1/2) × 9,8 × время ²

Сэм подставляет скорость 20 метров в секунду и время 2 секунды:

высота = 20 × 2 − (1/2) × 9,8 × 2 ²

Теперь расчеты!

Начните с: 20 × 2 − (1/2) × 9,8 × 2 ²

Первые скобки: 20 × 2 − 0,5 × 9,8 × 2 ²

= Затем заказы (2 ^{2 4) :20 × 2 − 0,5 × 9,8 × 4}

Затем умножить: 40 − 19,6

Вычесть и ГОТОВО! 20,4

Мяч достигает 20,4 метра через 2 секунды

Экспоненты экспонентов .