Ребус на слово математика: Ребусы по математике
Математические ребусы | Образовательная социальная сеть
Оглавление
Введение………………………………………………………………………………………………2
1. Типы математических ребусов…………………………………………………………………….3
2. Примеры математических ребусов
2.1.Сложение ………………………………………………………………………………………5
2.2.Вычитание……………………………………………………………………………………..6
2.3.Умножение ……………………………………………………………………………………6
3. Ребусы в стихах……………………………………………………………………………………6
4. Ребусы с ключевыми словами ……………………………………………………………………7
5. Способы решения некоторых ребусов. ………………………………………………………….9
6. Ребусы различных видов …………………………………………………………………………11
7. Комплекс математических ребусов для учащихся……………………………………………..12
8. Заключение ……………………………………………………………………………………….14
9.Список литературы ……………………………………………………………………………….15
Введение
В древности одним из важнейших достоинств человека считали владение математическими знаниями. В Индии, например, только тот юноша считался подготовленным к жизни, кто овладел искусством решения задач, физических упражнений и стихосложения.
Непрерывно возрастают роль и значение математики в современной жизни. В условиях научно-технического прогресса труд приобретает все более творческий характер и к этому надо себя готовить за школьной партой.
Необходимость выполнять арифметические действия (вычислять) так же, как и считать, диктуется практикой, самой жизнью.
Понятие арифметических действий в разные времена у разных пародов было различным. Древние египтяне к арифметическим действиям относили сложение, удвоение и деление пополам. Позже некоторые европейские ученые (XIII в.) насчитывали 9 арифметических действий, в том числе и нумерацию. В первом учебнике по математике для «российского юношества» «Арифметике» – Л. Ф. Магницкого (1703) нумерация чисел тоже относилась к арифметическим действиям.
Для обозначения арифметических действий сначала употреблялись слова, затем – буквы. Знаки «+», « — » и точка как знак умножения впервые употреблены в учебниках по арифметике в XV в., а знак деления (две т очки) – в XVII в.
, но окончательно все эти знаки утвердились в работах выдающегося немецкого ученого Г. В. Лейбница (XVII в.).
При разгадке математических ребусов надо не только уметь хорошо вычислять, используя знания об арифметических действиях их свойствах, но и проявить смекалку, терпение, выдержку и настойчивость.
Объект исследования: математические ребусы различных видов.
Цели и задачи работы:
– найти занимательные математические ребусы различных видов;
– исследовать возможные пути решения ребусов;
Актуальность.
Необходимость выполнять арифметические действия (вычислять) так же, как и считать, диктуется практикой, самой жизнью.
Эффективное развитие математических способностей учащихся невозможно без использования в учебном процессе задач на сообразительность, задач-шуток, математических ребусов и головоломок, что вызывает естественный интерес к изучаемой теме, осознание необходимости её изучения и соответствующий настрой к преодолению предстоящих на пути приобретения новых знаний трудностей.
Я считаю, что моя работа будет способствовать развитию математического мышления и творческой активности школьников 5-8 классов.
Методы исследования:
Для выполнения поставленной задачи я провела анализ материалов, в которых рассмотрено огромное разнообразие математических ребусов.
Типы математических ребусов.
Математические ребусы одновременно относят к нестандартным и занимательным задачам. Ребусы можно отнести к задачам с неполным составом условия и к задачам с несколькими решениями.
Математический (числовой) ребус – задание на восстановление записей вычислений. Математические ребусы обычно используются для развития логического мышления у школьников, поскольку их решение построено на логических рассуждениях. Кроме того, происходит совершенствование вычислительных навыков. Существует два типа математических ребусов.
Ребусы первого типа – это задачи, удовлетворяющие следующим требованиям:
- в тексте задачи приведена буквенная запись;
- в вопросе задачи требуется определить цифры, при подстановке которых в эту запись вместо букв выполняется условие, сформулированное в тексте задачи.
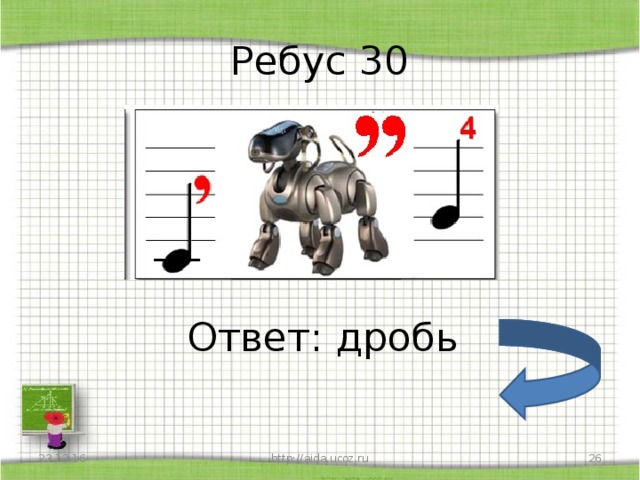
При решении ребусов этого типа следует помнить, что разные буквы заменяются разными цифрами, а одинаковые буквы – одинаковыми цифрами.
Ребусы второго типа – это задачи, удовлетворяющие следующим требованиям:
- дана запись, в которой встречаются звездочки;
- в вопросе задачи требуется определить набор цифр, при подстановке которых вместо звездочек выполнится условие, сформулированное в тексте задачи. При этом звездочку можно заменять любой цифрой, независимо от того, использована ли она в другом месте.
Решить ребус означает найти все возможные наборы цифр, удовлетворяющие условию задачи. Очевидно, что решение даже самого простого ребуса методом полного перебора приведет к большим временным затратам. Основная причина – большое количество неизвестных, каждая из которых может принимать до десяти значений.
Для того чтобы найти свойство, позволяющее упростить процедуру полного перебора, рассмотрим отдельно ребусы первого и второго типов.
В ребусах первого типа каждая буква заменяет свою цифру. Следовательно, выполнено следующее утверждение:
Утверждение 1. Если в записи используется 10 различных букв, значит, в числовом выражении использованы все 10 цифр; если используется более 10 букв, то ребус не имеет решения.
Это утверждение позволяет ограничить варианты перебора по количеству переменных. Отметим, что для ребусов второго типа это ограничение неприменимо, так как звездочки в разных местах можно заменять одной и той же цифрой.
Перечислим несколько простых утверждений, позволяющих ограничить перечень значений, которые может принимать каждая из переменных. Эти утверждения используют расположение буквы или звездочки в записи.
Утверждение 2. Если в записи числа буква расположена в старшем разряде, то ее значение не может равняться нулю.
Утверждение 3. Если А и В – количество единиц в некотором разряде в слагаемых, а С – количество единиц в сумме, то возможны следующие варианты:
- А+В=С, в этом разряде нет переноса; из этого разряда нет переноса;
- А+В+1=С, в этот разряд есть перенос; из этого разряда нет переноса;
- А+В=С+10, в этот разряд нет переноса; из этого разряда есть перенос;
- А+В+1=С+10, в этот разряд есть перенос; из этого разряда есть перенос.
Это утверждение удобно применять, если известно, есть ли перенос в рассматриваемый разряд или известно есть ли перенос из рассматриваемого разряда.
Утверждение 4. Если количество разрядов в сумме больше количества разрядов в каждом из двух слагаемых, то старший разряд в сумме содержит 1 единицу.
Утверждение 5. Если буква в каком-то разряде суммы совпадает с буквой в том же разряде одного из слагаемых, то в этом разряде второго слагаемого 0 или 9 единиц. Если этот разряд единиц, то в разряде единиц второго слагаемого 0 единиц.
Утверждение 6. Если количество разрядов в сумме больше числа разрядов в одном из слагаемых и на 2 больше числа разрядов в другом слагаемом, то:
- Вторая слева цифра суммы равна 0;
- У большего слагаемого в старшем разряде 9 единиц.
Утверждение 7. Если в одном из слагаемых, получаемых при умножении, все буквы совпадают с буквами в множимом, то соответствующий разряд множителя содержит 1 единицу.
Утверждение 8. Если отсутствует одно из слагаемых, получаемых при умножении, то соответствующий разряд множителя содержит 0 единиц.
Пример 1. Решите ребус: WIND * OF=CHANGE.
Решение. Заметим, что в записи ребуса использовано 11 различных букв. Следовательно, заменить их различными цифрами невозможно.
Ответ. Нет решений.
Пример 2. решите ребус: СОРОК + ОДИН = ТРИСТА
Решение. По утверждению 4, Т=1, а по утверждению 6, Р=0, С=9. поставим полученные значения в ребус: 9О0ОК +ОДИН=10И91А. применим утверждение 3 к разряду сотен. Варианты 0+Д=10+9 и 0+Д+1=10+9 невозможны, так как в этих случаях Д>9. Остаются варианты 0+Д=9 и 0+Д+1=9. Первый из них невозможен, так как в этом случае Д=9=С. Итак, Д=8.
Применим теперь утверждение 3 к разряду тысяч. При этом учтем, что из разряда сотен в разряд тысяч переноса нет, а из разряда тысяч в разряд десятков тысяч – есть. Следовательно, О+О=10+И, откуда О≥5. поскольку цифры 8 и9 уже использованы, О=5 или О=6, или О=7.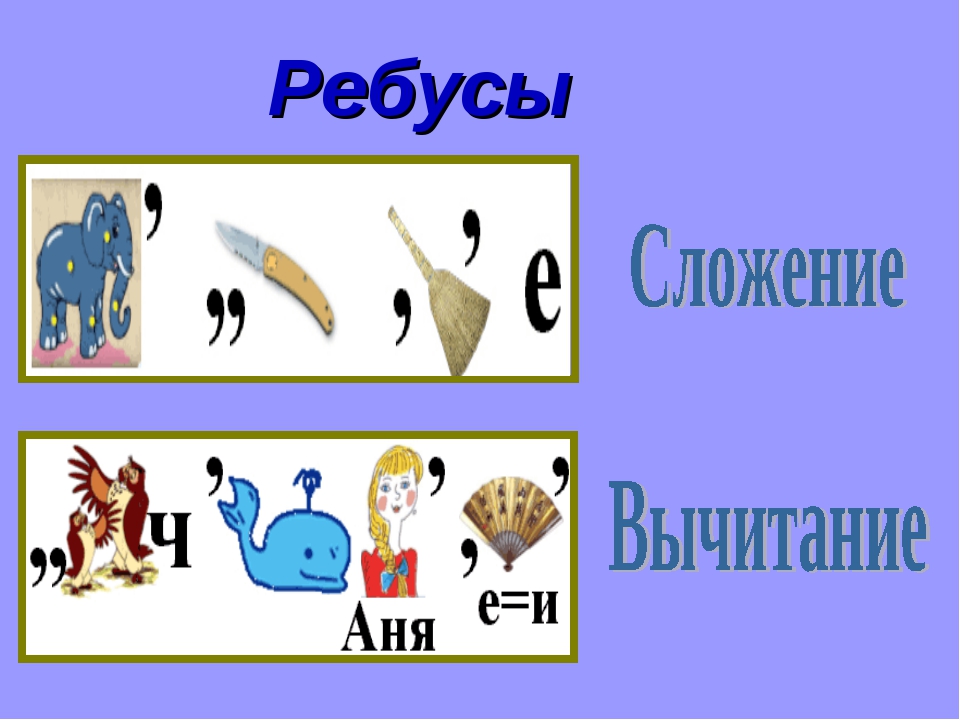
- О=5. Тогда И=О+О-10=0=Р, что невозможно.
- О=6. Тогда И=О+О-10=2, и ребус примет вид: 96606К+682Н=10291А. Заметим, что в разряде десятков не выполнено ни одного из соотношений утверждения 3. Следовательно, этот случай невозможен.
- О=7. Тогда И=О+О-10=4, и ребус примет вид: 9707К+784Н=10491А. Неиспользованными остались цифры 2, 3, 5 и 6. Буквы К, Н и А надо заманить на какие-то из этих цифр так, чтобы выполнялось равенство К+Н=А. Очевидно, это возможно сделать двумя способами 2+3=5 и 3+2=5. Итак, получаем два решения ребуса: 97072+7843=104915 и 97073+7842=104916.
Ответ. 97072+7843=104915 и 97073+7842=104916.[1]
Примеры математических ребусов
Рассмотрим задачи, где требуется восстановить первоначальный вид арифметического примера. Расшифровать ребус – это значит восстановить первоначальную запись примера.
При решении, задач такого типа требуется внимательность к очевидным арифметическим действиям и умение вести нить логических рассуждений.
Сложение
1) А 6 2) СИНИЦА 342457 3) КАФТАН 364768
+ АБ + 67 + СИНИЦА + 342457 + КАФТАН + 364768
АБВ 674 ПТИЧКИ 684914 ТРИШКА 729536
БВБ 747
4) ОХОХО 90909 5) ТРИ 769 6) БУЛОК 87130
+ АХАХА + 10101 + ДВА + 504 + БЫЛО + 8213
АХАХАХ 101010 ПЯТЬ 1273 МНОГО 95343
7) ХОД + ХОД + ХОД + ХОД + ХОД = МАТ
имеет много решений, например:
123 + 123 + 123 + 123 + 123 = 615
146 + 146 + 146 + 146 + 146 = 730
152 + 152 + 152 + 152 + 152 = 760
8) Б 2 9) АБВГ 1085 10) АБВГ 9541
АААА 9999 + ФГЕТ + 9567 + ВБВА + 4549
+ АААА + 9999 АБЕГР 10652 ГВДАД 14090
АААА 9999
БАААА 29999
Вычитание
1) ТРИ 769 2) ПОДАЙ 10652 3) ПЯТЬ 1273
– ДВА – 504 – ВОДЫ – 9067 – ТРИ – 769
ЯРД 265 ПАША 1585 ДВА 504
Умножение
1) ДВА 209 2) ТРИ 153 3) ГГГГ 2222
* ДВА * 209 * ТРИ * 153 * ГГГ * 222
ОЛЛО 1881 СРО 459 АААА 4444
+ ЧОЯ + 418__ + ПАР + 765 + АААА + 4444
ЧИСЛО 43681 ТРИ___ 153__ АААА 4444
ЧИСЛО 23409 АБВВГДА 493284
Ребусы в стихах
Задание 1.
Веселый клоун Нибумбум
Сегодня мрачен и угрюм.
Что огорчает Нибумбума?
Пример решал он восемь раз,
И каждый раз другая сумма!
Печальный случай! (А у вас?)
При решенье не забудьте
(В том-то вся и четкость смысла!)
Одинаковые буквы – одинаковые цифры!
КОШКА
+ КОШКА
КОШКА
СОБАКА
Обратив внимание на то, что последние две буквы (цифры) слагаемых и суммы одинаковы, постараемся их расшифровать. Понятно, что одна из этих букв (или А, или К) означает 0, а другая-5. Может ли А = 5, чтобы К = 0? Остальные буквы рассматриваемые справа налево, расшифровываются в зависимости от этих двух.
Сумма трёх А оканчивается на А, поэтому А= 0 или а = 5. Но, если А = 5, тогда (К + К + К + 1) не может оканчиваться на К. Следовательно А = 0, К = 5. Так как ( Ш + Ш + Ш + 1) оканчивается на А = 0, то Ш = 3.
Так как К + К + К = 15, то С = 1. Имеем
5*350 56350 57350
+ 5*350 + 56350 + 57350
5*350 56350 или 57350
1**050 169050 172050
Задание 2.
ЗАДАЧА ОЧЕНЬ НЕПРОСТА –
НАЙТИ НЕ КАЖДЫЙ СМОЖЕТ:
ЧЕМУ РАВНЯЕТСЯ ЗВЕЗДА,
ВЕЛОСИПЕД И ЁЖИК?
Данный ребус интересен тем, что слова обозначают только 1 цифру.
ВЕЛОСИПЕД ЕЖИК 7
+ ЗВЕЗДА ЕЖИК 4
6 ВЕЛОСИПЕД ЕЖИК
1 ВЕЛОСИПЕД 0 ЗВЕЗДА
Расшифровку ребусов попробуем начать с рассмотрения средней колонки слагаемых и их суммы. При сложении двух одинаковых чисел и третьего, отличного от них, при условии передачи единицы из низшего разряда получаем число, оканчивающееся цифрой 0.
Какой же может быть сумма
ЕЖИК + ЕЖИК + ВЕЛОСИПЕД?
Из двух значений удовлетворяет лишь одно. Имея сумму трёх слагаемых (ЕЖИК, ЕЖИК, ВЕЛОСИПЕД), устанавливаем, какие слагаемые удовлетворяют условию задачи. Получив «ключ» легко откроем «замок».
(ЕЖИК + ЕЖИК + ВЕЛОСИПЕД + 1) оканчивается цифрой 0. Значит, (ЕЖИК + ЕЖИК + ВЕЛОСИПЕД) = 9 (или 19). Равенство ЕЖИК + ЕЖИК + ВЕЛОСИПЕД = 19 невозможно. Значит, возможна сумма 9, тогда из случаев 1 + 1 + 7 = 9, 2 + 2 + 5 = 9, 3 + 3 + 3 = 9, 4 + 4 + 1 = 9 подходит только 2 + 2 + 5 = 9. В результате ЕЖИК = 2, ЗВЕЗДА = 3, ВЕЛОСИПЕД = 5:
Ответ: 527 + 324+ 652 =1503
Ребусы с ключевыми словами
Ниже представлены ребусы, в которых цифры зашифрованы буквами, причем разным цифрам соответствуют и разные буквы. Между зашифрованными числами поставлены математические знаки, показывающие действия по горизонталям и по вертикалям. Путем рассуждений нужно восстановить числовые значения букв так, чтобы выполнить указанные действия.
Расставив буквы соответственно их числовому значению (от 1 до 9 включая 0), получаем ключевое слово.
1) ТА+ ИТ = ЛЕТ 2) КРА + ОЛИ = ИАЯ
X – + X : –
ЕС х СН = ЛЛАС Л х АР= КЯИ
ЛЕАА + ЕЦ = ЛЕЕЦ ОИИ + АЛ = РКА
3) СТУН + САРН + ЕАТД = ДНЕЕ
– – + –
ЛОЕН-ЛЕУН +САРН = СЕТН
ЕЛОА – ЛДСА + ТЛТТ = ТОУТ
4) УЕИ – ЕАС = СЕУ 5) ИЦГ-УАЕ = ЕИН
: + – : + –
БЕ х Т = НЕ ИГ х Е = СЕЕ
ПП+ЕАЦ=ЕУС ГГ + УГА = УУГ
6) ВЕОЬ : МЕ = ОК 7) МЕЛ : СЛ -= СП
– х + – х +
СВС + В Р = ССА ЕФФ + ЛС = ЕРА
ВСВВ-КМО = СМК РАО – ОАС=САЛ
8) АЕО – КЦЦ = ИСЕ
: – –
Л X КОН = ЛИЦ
ЛКЕ + НО = ЛИН
Ответы: 1) Лестница; 2) Калория ; 3) Лесотундра; 4) Беспутница; 5) Гусеница;
6) Восьмерка; 7) Лесоферма; 8) Колесница.
Существуют числовые ребусы в виде примеров деления. Делимое и делитель выглядят как обычные слова. Частное и промежуточные выкладки представляют неосмысленные сочетания букв. Решив ребус, расположите буквы в порядке их цифровых значений (от 1 до 9 и включая 0) -получится третье слово, которое является ответом и называется ключом ребуса.
Загадывающий задумывает слово, состоящее из 10 неповторяющихся букв, например «трудолюбие», «специально», «просвещать». Приняв буквы задуманного слова за цифры, загадывающий изображает посредством этих букв какой-нибудь случай деления. Если задумано слово просвещать, то можно взять такой пример деления:
просвещать 123564 3548 провес овса
12345657809 10644 34 пьесс ос
17124 пщпрс
17192 пспрс
2932 ртор
Делимое – провес, 123564
Делитель – овса, 3548
Можно взять и другие слова:
восстать свет
свет ппета
щщвт
свет
оптьа
рщспс
сстст
сппрт
оараь
оеввр
пщра
делимое – восстать 53449890
делитель – свет 4569
трудолюбие блюдо труд
1234567890 блуб юе
уло
делимое – блюдо, 86745
делитель – труд, 1234
Способы решения некоторых ребусов
Среди математических задач и развлечений часто встречаются числовые ребусы или криптарифмы.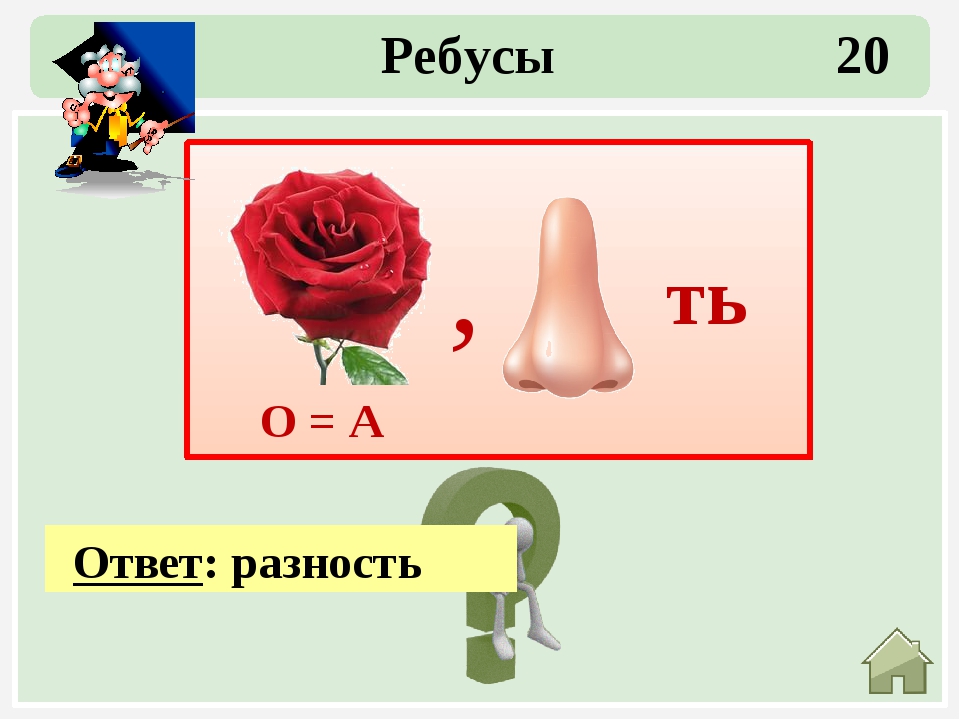
Вот несколько из них. В этих примерах все цифры заменены буквами.
Одинаковыми буквами обозначены одинаковые цифры, а разными буквами – неодинаковые цифры. Требуется восстановить первоначальный вид примера.
Задание 1
УРАН
+ УРАН
НАУКА
Решение подобных задач достигается не механическим перебором вариантов, а строго логически. Можно рассуждать, например, так:
сумма двух четырехзначных чисел равна пятизначному. Это возможно, если буква Н обозначает 1: УР21
Значит, буква А обозначает цифру 2: + УР21
12УК2
6Р21
Далее, буква У обозначает цифру 6: + 6Р21
126К2
Таким образом, буква Р обозначает цифру 3, буква К- цифру 4.
Окончательно:
6321
+ 6321
12642
Решение единственное. Задание 2. Восстановить цифры в примере (число СТО делится на 139).
ВОРОН
+ СТАЯ
ЛЕТЕЛА
Решение. Заметим, что сумма пятизначного и четырехзначного чисел может быть шестизначной только когда первая цифра суммы 1, вторая цифра 0, а первая цифра пятизначного числа 9.
9ОРОН
Поэтому данный пример принимает вид + СТАЯ
10Т01А
Так как СТО делится на 139, то оно является одним из следующих чисел: 139, 278, 417, 556, 695, 834, 973, и поскольку разные буквы обозначают разные числа, то надо рассмотреть только два случая: СТО = 278 и СТО = 834.
В первом случае в разряде тысяч «сверху вниз» стоят цифры 8, 2, 7, но при сложении 8 + 2 даже при переносе единицы из разряда сотен не может получиться цифра 7, и, следовательно, этот случай невозможен, т.е. = 834.
Теперь пример принимает вид:
94Р4Н
+ 83АЯ .
10301А
Ясно, что при сложении в разряде десятков переносится единица, и по этому Р = 6, и из того же разряда десятков видно, что А = 7. Для букв Н и Я остаются две возможности: одна из них 2 другая 5.
Таким образом, данный пример расшифровывается двумя способами:
103017 103017
– 8375 – 8372
94642 94645
Задание 3. ДВА
* ДВА
****
+ ***В
Е***
ЧЕТЫРЕ
Решение: буква А обозначает не единицу, не пятёрку и не шестёрку, так как последние цифры множителей и произведения разные. Значит, второе частное произведение
ДВА * В = ***В
Может оканчиваться буквой В, только если она обозначает пятёрку, а буква А- какую-то нечётную цифру.
Из столбца шестого разряда видно, что Е меньше Ч. Следовательно, Е не может обозначать девятку, поэтому А не может быть тройкой или семёркой.
Отсюда А = 9, Е = 1. После этого несложно найти, что Ч = 2, Д = 4.
Окончательно, 459
* 459
4131
+ 2295
1836
210681
Решение единственное.
Ребусы различных видов
Задание 1. Расшифруйте числовой ребус
СЛОВ,О + СЛОВ,О = ПЕСНЯ
Обратив внимание на то, что при сложении двух одинаковых дробей получаем целое число, определяем цифру, обозначенную буквой О. Определяется также сразу цифра, обозначенная буквой П, так как в целой части каждого слагаемого по 4 цифры, а в полученном результате 5. Так как Н = 1 то для Н остаётся одно значение. Какое? Методом проб определяем остальные цифры.
Запишем выражение в столбик
СЛОВ,О
+ СЛОВ,О
ПЕСНЯ
Так как в результате получим целое число, то О = 5.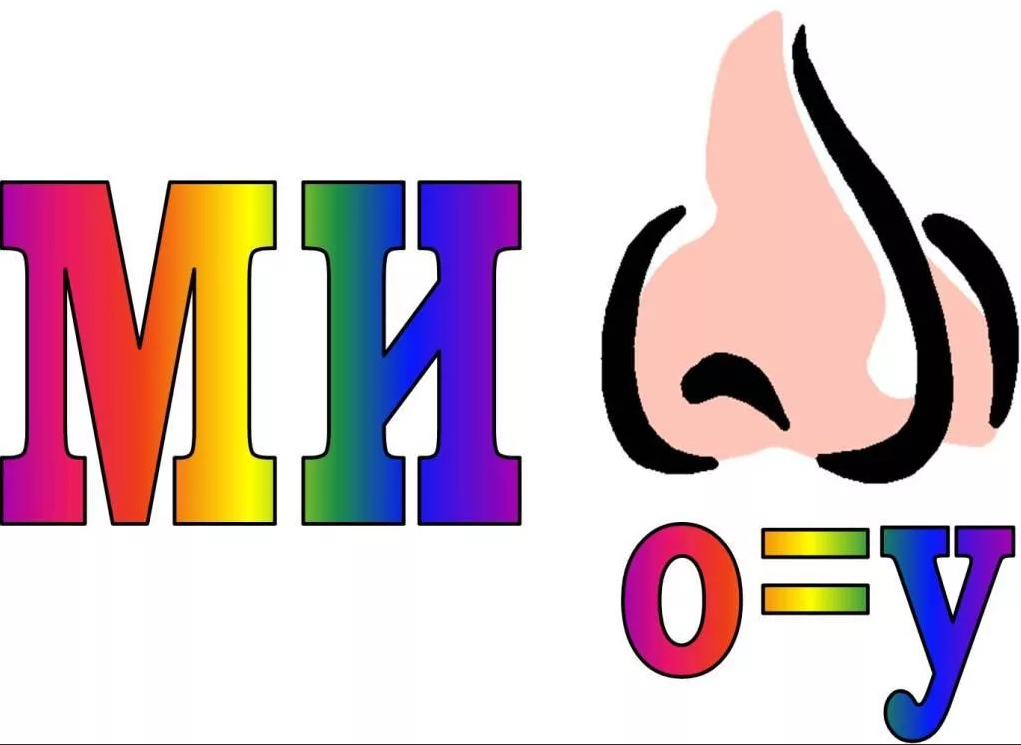
Буква П может обозначать только цифру 1, тогда Н = 0. Так как С 5, то методом проб находим С = 9, Л = 4 и тд.
Получаем 9453,5 + 9453,5 = 18907.
Задание 2. Расшифруйте ребус возведения числа в степень.
(АР) М =МИР (16) 2 =256
Комплекс математических ребусов для учащихся.
Задания для учащихся 4 -7классов.
- (КА-СИ=СА)+(8-Р=3)=(3Р-СР=КИ)
- (КГ+ГК=ББ) – (Б+Г=А)=(1А+КС=4В)
- ДА + ДА + ДА = ЕДА
- 4*36* + 12*7 = *2*98
- 5*6* + *0*4 = 10981
- ТРИ+ТРИ+ТРИ=ДЫРА
- РЛОРЕ+РККРК=ЛКЕККЕ
- AB0 + AB = X27
- ра + ра + ра = ура
- КТО * 2 = ТОК
- КО х КО х КО = ТРИКО
Заключение
Выводы
Математический ребус – задание на восстановление записей вычислений.
Математические ребусы обычно используются для развития логического мышления у школьников, поскольку их решение построено на логических рассуждениях.
С детского возраста нужно решать ребусы, это поможет развить математические способности
Задачи, представленные в занимательной форме, очень интересны. Их хочется решать, они увлекают своей необычностью, неочевидностью ответа. Появляется желание совершить пусть даже нелёгкий путь поиска решения. Занимательность и строгость вполне совместимы. Каждое самостоятельно решенное задание – это возможно, небольшая, но всё же победа.
Практическое применение работы:
Материал данной работы может быть использован на уроках, на занятиях математического кружка и для подготовки к олимпиадам.
Список литературы
- Кудряшова Т.Г. Методы решения математических задач, 2008.
- Коваленко В.Г. Дидактические игры на уроках математики – М.: Просвещение, 1990.
- Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: пособие для учащихся. – 4-е изд., перераб. и доп. – М.: Просвещение,1984.
- Шейнина О.С., Соловьёва Г.М. Математика. Занятия школьного кружка. 5 – 6 кл. – М.: Изд-во НЦ ЭНАС, 2005.
- Клименченко Д.В. Задачи по математике для любознательных. – ср. шк. – М.: Просвещение, 1992.
- Перельман Я.И. Занимательная арифметика. Загадки и диковинки в мире чисел. Издательство Русанова, состав. 1994
- Терентьева Л.П. Решение нестандартных задач учебное пособие. М.: 2002
- Фарков. Математические олипиады.5-6 классы: учебно-методическое пособие для учителей математики общеобразовательных школ.-5 изд, перераб. и доп.- М : Издательство «Экзамен», 2011.
Занятия школьного кружка. 5 – 6 кл. – М.: Изд-во НЦ ЭНАС, 2005.[1] Методы решения математических задач. Кудряшова Т.Г., 2008. с.100
Считай, смекай, отгадывай — Белоиванова Марина Александровна
Прямая, луч, отрезок
Leave a comment
Если мы остро отточенным карандашом прикоснемся к листу бумаги, то на нём останется круглый след, который называют точкой.
В качестве имени точкам присваивают заглавные латинские буквы: А, В, С и т.д. При объединении множества точек получаются геометрическая фигура. Например, если точки выстроятся вдоль натянутого шнура, то получившаяся фигура даёт представление о прямой линии. С той лишь разницей, что прямая линия является бесконечной, то есть она неограниченно распространяется как в одну,…
Read More >>
Движение вдогонку
Рассмотрим задачу, в которой объекты, двигаясь в одном направлении, будут сближаться. Жаба, обнаружила пропажу Дюймовочки, и бросилась догонять уносимый быстрым течением лист кувшинки, на котором сидела девочка. Чтобы определить, как ежесекундно изменялось расстояние между ними, то есть их относительная скорость, заполним таблицу зависимости координат Жабы и Дюймовочки от времени, где x1 — координата Дюймовочки, x2 — координата Жабы, d — расстояние между ними.
Расстояние между объектами уменьшалось каждую…
Read More >>
Движение с отставанием
Leave a comment
Чтобы понять, от чего зависит относительная скорость объектов, двигающихся в одном направлении, необходимо учесть, что при этом они могут сближаться, но могут и удаляться. Например, рассмотрим такую задачу. Волк объяснил Красной Шапочке, как пройти в бабушкину деревню. Девочка остановилась на полянке с координатой равной пяти и стала собирать для бабушки ягодки и цветочки. Когда она отправилась к бабушке, Волк был уже в точке с координатой 20. И Красная Шапочка, и…
Read More >>
Движение в противоположных направлениях
Leave a comment
Проиллюстрируем движение объектов в противоположных направлениях на следующей задаче.
Read More >>
Встречное движение
Leave a comment
Рассмотрим такую задачу. Курочка бежит навстречу к своему цыплёнку со скоростью 2 м/с. А цыплёнок приближается к курице со скоростью 1 м/с. Если заполнить таблицу зависимости координат курицы и цыплёнка от времени, где t – время их совместного встречного движения, x1 – соответствующая координата курицы, x2 – координата цыплёнка, то можно заметить, как ежесекундно изменялось расстояние d между ними.
Read More >>
Скорость, время, расстояние
Leave a comment
Быстрота передвижения Окружающий нас мир находится в постоянном развитии и движении. И людям часто приходится оценивать быстроту перемещения различных объектов наблюдения. Проще это делать, указывая пройденные ими расстояния за равные промежутки времени. Скорость Например, заяц может пробежать за один час 60 км, страус за час – 80 км, гепард за час – 120 км. Говорят, что скорость зайца 60 км в час, страуса – 80 км в час, гепарда –…
Read More >>
Единицы времени
Leave a comment
Год, месяц, неделя и сутки – это общеизвестные меры времени.
Как они возникли? Посмотрите пояснения на рисунках. Месяцы имеют разную длину. Как определить длину месяца? Почему происходит смена дня и ночи? А как же исчисляется время в течение суток? На циферблате часов расположены числа от 1 до 12, а в сутках 24 часа. Чтобы различить о каком времени суток идёт речь, обычно уточняют: семь часов утра или семь часов вечера….
Read More >>
Задание на лето
Leave a comment
Память имеет уникальное свойство вытеснять информацию, которой мы длительное время не пользуемся. Из-за этого каждый год в сентябре и дети, и учителя испытывают огромные трудности, поскольку приходится много времени уделять повторению. При этом текущая программа требует продолжения изучения новых тем. Но всё повторить невозможно, поэтому у многих учеников образуются белые пятна в знаниях или так называемые пробелы.
Особенно это заметно в математике, где новые навыки вырабатываются на имеющейся у ребенка…
Read More >>
Разрядные слагаемые
Leave a comment
Если начать считать предметы по порядку: один, два, три, четыре, пять и т. д., то есть, добавляя по единичке к каждому предыдущему числу, чтобы перейти к последующему, то дойдя до последнего однозначного числа 9, мы далее получим наименьшее двузначное число – 10. У двузначных чисел мы имеем две позиции для цифр: справа – разряд единиц, слева – разряд десятков. При счёте каждые 10 единичек объединяются в десяток, 10 десятков –…
Read More >>
Деление с остатком
Leave a comment
Сказка о том, как Белка к зиме готовилась Собрала как-то белка 16 грибов и решила посушить их на зиму.
«Развешу я их поровну на этих трёх ветках, – подумала она. – Красиво будет». Буду действовать так. Сначала на каждую веточку нанижу по одному грибочку, потом по два, потом по три, четыре, пять. У меня останется 1 грибок, но веток 3. Значит, дальше поровну распределить грибы не получится. Развешено по 5…
Read More >>
Площади
Сегодня мы познакомимся с понятием площади, со способами сравнения площадей и их единицами измерения. В математике площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией, занимающая какое-то место. В быту под словом площадь подразумевают большое и ровное место. Например, в городе или в селе площадь – это незастроенное пространство, от которого обычно расходятся в разные стороны улицы.
Посевная площадь – это пространство, предназначенное для посева, жилая площадь –…
Read More >>
Виды треугольников
Leave a comment
Какие же треугольники все разные! Есть ли какие-нибудь свойства, по которым можно было бы их различать? Да, их различают по особенностям углов и длинам сторон. Построение треугольника Как же получить эту фигуру? Поставим три точки на листе бумаги так, чтобы через них нельзя было провести одну прямую линию. Назовём эти точки, например, буквами А, К, М. Обычно точки обозначают заглавными латинскими буквами. Соединим эти точки кусочками прямых линий. Говорят –…
Read More >>
Родительское собрание
Leave a comment
Уважаемые родители! Наше родительское собрание посвящается итогам 2 четверти 2020/2021 учебного года.
Read More >>
Образование и сравнение долей
Leave a comment
Разделим апельсин, например, на 8 равных частей. Эти равные части называются долями (апельсиновыми дольками). В нашем случае каждый кусочек – восьмая доля апельсина. Если взять три кусочка – будет три доли. Все, что мы проделали, записывается с помощью чисел, разделенных черточкой.
Эту запись назвали обыкновенной дробью: 3/8. Читают дробь так: три восьмых. Запись дробей Для того чтобы записать взятые доли, нужно выполнять действия по следующему правилу: посчитать, на сколько равных долей…
Read More >>
математических ребусов | Математические шутки 4 Мати Фолк
Математические ребусы
15 декабря 2011 г., 9:16
Какое слово или фраза изображены на следующей картинке?
Нога в могиле.
Подобные головоломки иногда называют головоломками с пиктограммами, головоломками со словами или иероглифами.
Кевин Стоун из BrainBashers называет их мозговыми летучими мышами.
Многие называют их головоломками Ребус. И хотя я не думаю, что это совсем правильно (то, что я считаю ребусом, можно найти здесь), это слово я тоже буду использовать, потому что оно самое короткое.
Как угодно. Наслаждайтесь MJ4MF Rebus Quiz .
Обратите внимание, что каждая картинка так или иначе является математической, даже если ответ не является таковым.
Загрузить викторину MJ4MF Rebus Quiz (PDF)
Если вы школьный учитель, то страшный день перед каникулами быстро приближается. MJ4MF Rebus Quiz — отличное занятие для студентов, у которых слишком много энергии, чтобы сидеть на месте, и слишком мало внимания, чтобы чему-то научиться. (Разрешается использовать викторину MJ4MF Rebus Quiz со студентами в некоммерческих образовательных целях.)
Ключ к ответу и копию экзамена можно найти по адресу http://mathjokes4mathyfolks.com/rebus.html.
Оценить:
Нравится:
Нравится Загрузка…
Заявка подается в рубрике: Без рубрики. Теги: могила, математика, postweek2011, головоломка, ребус.
144 Gross Jokes The Book of Tebow
О MJ4MF
Математические шутки 4 Блог Mathy Folks — это онлайн-расширение книги Math Jokes 4 Mathy Folks .
Блог содержит шутки, присланные читателями, новые шутки, обнаруженные автором, подробности о выступлениях и семинарах, а также другую случайную информацию, которая может быть интересна странным людям, которым нравятся математические шутки.
Math Jokes 4 Mathy Folks можно приобрести в Amazon, Borders, Barnes & Noble, NCTM, Robert D. Reed Publishers и других поставщиках исключительной литературы.
Прошлые сообщения| М | Т | Вт | Т | Ф | С | С |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | |
Введите свой адрес электронной почты, чтобы подписаться на блог MJ4MF и получать новые сообщения по электронной почте.
Адрес электронной почты:
Присоединяйтесь к 481 другому подписчику
Местоположения посетителейСловесные ребусы с ответами
Мемориальная табличка №531
Следующая «Мозговая летучая мышь» означает «Замедление».
S
L
O
W
Используя ту же логику, можете ли вы сказать нам, что означает следующее Brain Bat? 95
Опубликовано в РЯДдом №533
Сможете ли вы составить число 24, используя числа 1, 3, 4 и 6? Вы должны использовать одно число только один раз, и вы можете использовать символы математических операций в любое время в любом месте.
Посмотреть ответ Обсудить
6/(1 – 3/4) = 24
Опубликовано в УРАВНЕНИЕМемориальная табличка №534
Может ли мужчина жениться на сестре своей вдовы в Индии на законных основаниях?
Посмотреть ответ Обсудить
Нет, он не может. Если его жена вдова, значит, он уже умер.
дом №535
Водитель такси двигался в неправильном направлении по дороге с односторонним движением. Рядом стоял полицейский. Он заметил водителя, но отпустил его.
Почему полицейский не оштрафовал его и не остановил?
Посмотреть ответ Обсудить
Это потому, что таксист был пешком. В вопросе не упоминается, что таксист вел свою машину, и это имеет смысл.
Опубликовано в ЮМОР ЗАГАДКАдом №536
В математике существует специальное целое число, которое показывает особое свойство. Если вы вычтете любое число из этого целого числа, результат всегда будет полностью делиться на преемника этого числа.
Вы знаете, что это за число?
Посмотреть ответ Обсудить
Требуемое целое число равно -1.
Например, вычтем 7 из -1.
-1 – 7 = -8
Теперь последующее число 7 равно 8, а (-8) точно делится на 8.
Вы можете попробовать это для любого числа, и оно останется верным.
Мемориальная табличка №537
Можете ли вы выяснить, какие варианты лучше всего подходят для отсутствующего столбца?
Посмотреть ответ Обсудить
Вариант «d» впишется в отсутствующее место.
Что здесь происходит? В каждом следующем столбце порядок меняется на противоположный, а самая младшая цифра опускается.
Опубликовано в РЯД РИСУНОКдом №538
В ящике рядом с кроватью три оранжевых, два розовых и пять фиолетовых шаров. Электричества нет, в комнате совершенно темно. Сколько шаров вы должны вынуть, чтобы убедиться, что у вас есть хотя бы по одному шару каждого цвета.
Посмотреть ответ Обсудить
9
2 Чтобы узнать необходимое количество шаров, возьмите единицу вместо наименьшего числа (т.е. возьмите один розовый шар), а затем прибавьте к нему все большие числа (т.е. три оранжевых и пять фиолетовых шаров).
Необходимое количество шаров = 1 + 3 + 5 = 9.