Развитие математических представлений у детей дошкольного возраста: Развитие элементарных математических представлений у детей дошкольного возраста через разнообразные формы работы. | Консультация по математике (подготовительная группа):
Развитие математических представлений у дошкольников
Автор: Смолянова Татьяна Львовна
Рубрика: Педагогика
Опубликовано в Молодой учёный №29 (215) июль 2018 г.
Дата публикации: 23.07.2018 2018-07-23
Статья просмотрена: 7895 раз
Скачать электронную версию
Скачать Часть 2 (pdf)
Библиографическое описание: Смолянова, Т. Л. Развитие математических представлений у дошкольников / Т. Л. Смолянова. — Текст : непосредственный // Молодой ученый. — 2018. — № 29 (215). — С. 167-171. — URL: https://moluch.ru/archive/215/52106/ (дата обращения: 10.12.2022).
Л. Смолянова. — Текст : непосредственный // Молодой ученый. — 2018. — № 29 (215). — С. 167-171. — URL: https://moluch.ru/archive/215/52106/ (дата обращения: 10.12.2022).
Статья посвящена проблеме развития математических представлений у дошкольников. Рассмотрены современные требования в соответствии с федеральным государственным образовательным стандартом дошкольного образования к математической подготовке дошкольников. Дается сравнительный анализ реализации программы по развитию математических представлений у дошкольников в контрольной и исследуемой группе. Указаны условия оптимального математического развития детей дошкольного возраста, на основе деятельностного и интегративного подходов.
Ключевые слова: математическое представление у дошкольников; познавательные процессы; эксперимент; математические задачи.
Введение. Развитие математических представлений у детей дошкольного возраста на ознакомительном уровне имеет большую ценность для интенсивного интеллектуального их развития.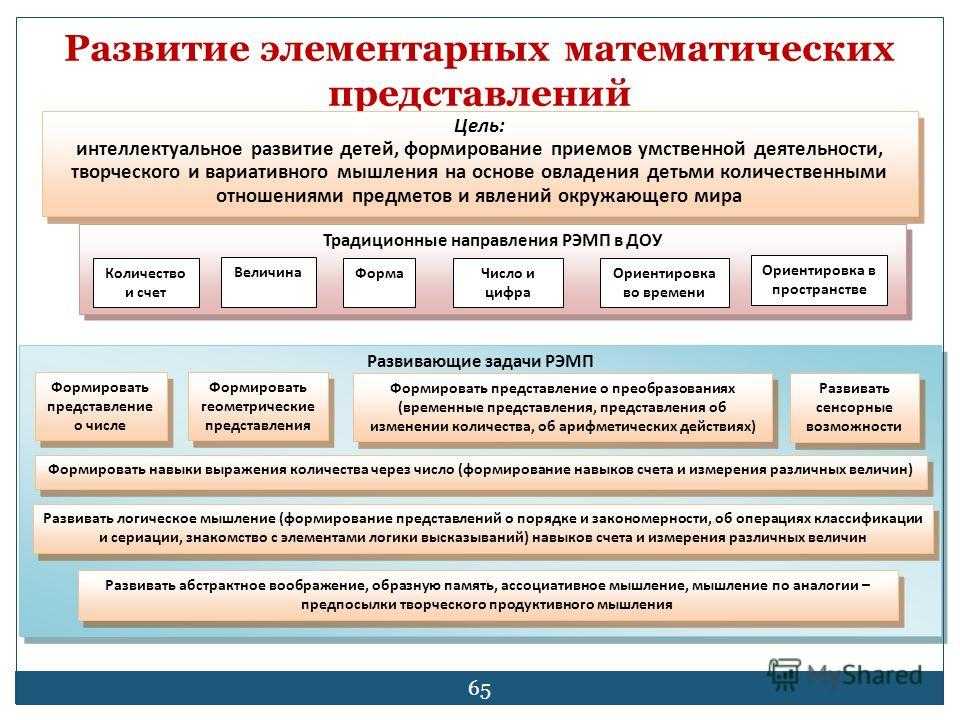
Актуальность исследования на педагогическом уровне вызвана реформированием дошкольного образования на основе взаимодействия рациональной и когнитивной составляющих новой образовательной концепции, которая характеризуется смещением акцентов с социального заказа и требований науки на самореализацию личности ребенка.
Посредством развития математических представлений у дошкольников закладываются предпосылки успешной учебной адаптации.
Исследованию возможностей детей дошкольного возраста, их возрастных особенностей посвятили свои научные труды А. В. Брушлинский, Л. С. Выготский, И. В. Дубровина, А. Н. Колмогоров, B. В. Давыдов, Ю. М. Колягин, С. Л. Рубинштейн и др.
Л. Рубинштейн и др.
Ими отмечены такие особенности мыслительного процесса у средних и старших дошкольников как гибкость мышления, критичность мышления, умение искать неординарные способы решения познавательной проблемы.
Среди ученых педагогов, которые исследовали и разрабатывали методологию обучения математическим навыкам дошкольников, можно назвать Т. И. Ерофееву [3], А. Белошистую, Н. В. Ломову, З. А. Грачеву, М. А. Габову [2], Махину Н. С. [4] и др.
Развитие математических представлений дошкольников не может быть рассмотрено в отрыве от исследования основных тенденций развития психических познавательных процессов. Поэтому основными ориентирами в решении актуальных проблем развития математических представлений дошкольников являются труды Я. А. Коменского, И. Г. Песталоцци, К. Д. Ушинского, Ф. Фребеля и др.
В соответствии с Федеральным государственным стандартом дошкольного образования содержание образовательной деятельности должно обеспечивать развитие первичных представлений детей о свойствах и отношениях объектов окружающего мира, т. е. сформировать картину Мира. При этом центральное место отводится обогащению сенсорного опыта детей путем ознакомления с цветовой гаммой, величиной, формой, пространством и обучение строится по принципу постепенного движения от конкретному к абстрактному, от чувственного познания у логическому, от практического к теоретическому.
е. сформировать картину Мира. При этом центральное место отводится обогащению сенсорного опыта детей путем ознакомления с цветовой гаммой, величиной, формой, пространством и обучение строится по принципу постепенного движения от конкретному к абстрактному, от чувственного познания у логическому, от практического к теоретическому.
Анализируя исследования В. В. Давыдова, А. В. Запорожца, делаем вывод, что дошкольный возраст самоценен тем, что он позволяет ребенку осуществлять разные виды свободной деятельности, проявлять инициативу. Развивающие и образовательные задачи в дошкольном возрасте должны решаться в игровой форме, опосредованным образом. Доказано, что такой подход позволяет избежать значительных проблем в будущем школьном обучении детей [5, с.23].
Целью исследование явилось создание педагогических условий для развития математических представлений у дошкольников.
Задачи исследования:
- Разработка программы для развития математических представлений у дошкольников;
- Реализация программы Развития математических представлений у дошкольников в средней и в старшей группе дошкольной образовательной организации;
- Провести сравнительный анализ математических представлений у детей в контрольной и эмпирической группе.

Методика исследования и испытуемые
В исследовании приняли участие дошкольники двух старших и двух средних групп МБДОУ «ЦРР -детский сад № 172» города Воронежа. Разработанную программу развития математических представлений у дошкольников использовали в эмпирических группах. В контрольных группах был проведен мониторинговый срез математических представлений.
Для развития математических представлений у дошкольников воспитателями исследуемых групп были подготовлены математические задания для обучения детей в игровой форме. Например, стихи известных поэтов использовались для построения математической задачи. Некоторые из них.
Средняя группа | Старшая группа |
Из-за леса, из-за гор Едет дедушка Егор: Сам на лошадке, Вопрос: сколько ног шагало по земле? Ответ: 8 ног. | Лиса по лесу ходила, Громким голосом вопила. Лиса лычки драла, Лиса лапотки плела: Мужу — двое, себе — трое… Вопрос: сколько пар лаптей сплела лиса? А сколько штук? Ответ: 5 пар, 10 штук. |
У Аленки в гостях Два цыпленка в лаптях, Петушок в сапожках, Курочка в сережках, Селезень в кафтане, Утка в сарафане, А корова в юбке, В теплом полушубке. Вопрос: сколько всего гостей было у Аленки. Ответ: 7 гостей | Дедушка Ежок, Не ходи на бережок Там растаял снежок, Заливает лужок. Ты промочишь ножки, Красные сапожки. Вопрос: сколько сапожек может промочить дедушка Ежок? Ответ: 4 сапога. |
Жили у бабуси Два веселых гуся. Вопрос: сколько крыльев было у гусей? Сколько хвостов? Ответ: 4 крыла, 2 хвоста. | Ехали медведи На велосипеде… Вопрос: сколько ехало медведей? Ответ: не известно, в стихах о количестве медведей ничего не сказано |
Потеряли котятки На дороге перчатки И в слезах прибежали домой. Вопрос: сколько перчаток потеряли котята? | Дама сдавала в багаж: Диван, чемодан, саквояж, Картину, корзину, картонку И маленькую собачонку. Вопрос: сколько вещей дама сдавала в багаж? Ответ: 6 вещей (1 животное). |
Задача на развитие логического мышления Дети играли в одних трусиках и майках. пошел сильный снег. Но дети не замерзли и не промокли. Почему? Ответ: дети играли в комнате. | Задача на развитие логического мышления По морю плыли две подводные лодки и вдруг они ушли на дно. Сколько подводных лодок было в море? Ответ: 2 подводные лодки, только они ушли на дно. |
Развитие математических представлений и усиление концентрации слухового внимания. Даны три числа 1; 2; 1. От второго числа вычли третье число и прибавили к разности первое число. Вопрос. Назовите сумму. Ответ. 2 | Развитие математических представлений и усиление концентрации слухового внимания. Назовите первую букву первого весеннего месяца и вторую букву в слове МАМА Ответ: М; А, |
Программа по развитию математических представлений дошкольников содержит методические разработки, направленные на коррекцию и развитие познавательных процессов. Дошкольники с интересом решают лабиринты, картинки «Нелепицы», корректурную пробу «Вычеркни цифру», интерактивные игры «Чего не стало», «Что прибавилось», «Занимательная геометрия», «Считалочка», «Приключения сказочных героев в стране «Математика» и др.
Дошкольники с интересом решают лабиринты, картинки «Нелепицы», корректурную пробу «Вычеркни цифру», интерактивные игры «Чего не стало», «Что прибавилось», «Занимательная геометрия», «Считалочка», «Приключения сказочных героев в стране «Математика» и др.
Проведенный эксперимент показал, что систематические занятия по программе развития математических представлений дают хорошие образовательные результаты. Дошкольники средней и старшей группы, которые приняли участие в эксперименте, меньше допускали ошибок при решении контрольных задач. Они быстрее ориентировались в задачах, где требуется логическое и критическое мышление, безошибочно выполняли задачи с условием в косвенной форме, решали головоломки и анаграммы, соответствующие возрастным данным.
Тренируя слуховую память, внимание, восприятие, воспитатель развивает математическое представление. Слуховая память у детей, принявших участие в эксперименте, развита на уровне выше среднего и высоком.
Отмечено, что дети, занимающиеся по программе развития математического представления более успешны в подвижных играх, более сообразительные и ловкие на физкультурно-оздоровительных занятиях с инструктором по физической культуре.
Таким образом, процесс развития математических представлений определяется следующими закономерностями: зависимость проектирования от успешности отражения всех компонентов математического образования; зависимость программы от учета адаптационной функции развития математических представлений.
Из закономерностей процесса планирования и реализации программы развития математических представлений вытекают принципы проектирования математического образования дошкольников, предусмотренного ФГОС ДО: учет этапов развития мышления дошкольников; учет возрастных особенностей; взаимосвязь игровой и познавательной деятельности; учет адекватности и адаптивности программы развития математических представлений дошкольников; преемственность детский сад — школа.
Разработанная программа и предложенная методология ее реализации позволили создать проект математического образования дошкольников. Для этого разработано методическое обеспечение, включающее учебные и методические пособия, примерное содержание мультимедийного обучающего материала, материальное оснащение на прогулочных площадках и в группах образовательной организации.
Анализ результатов экспериментальной работы, качественные и количественные методы диагностики и статистический метод обработки результатов подтвердили эффективность предлагаемой программы развития математических представлений дошкольников.
Литература:
- Вербенец, A. M. Моделирование как средство познания свойств и отношений предметов детьми среднего дошкольного возраста (на математическом содержании) [Текст].: дис.. канд. пед. наук / A. M. Вербенец. — СПб, 2001.-209 с.
- Габова М. А. Математическое развитие детей дошкольного возраста: теория и технологии. [Текст]/ — М.:Директ-Медиа, -2014, 534 с.
- Ерофеева Т. И. Математика для дошкольников. [Текст] / Книга для воспитателя детского сада./ Т. И. Ерофеева, Л. Н. Павлова, В. П. Новикова.-М.; Просвещение, 1992. — 191 с.
- Махина Н. С. Формирование исторических представлений младших школьников о родном крае средствами краеведения. [Текст]/ дисс…к.п.н., 2010 г, -231 с.

- Михайлова З. А., Полякова М. Н., Непомнящая Р. Л., Вербенец А. М. Математическое развитие дошкольников. [Текст] /:СПб., 1998, 184 с.
Основные термины (генерируются автоматически): представление, дошкольный возраст, математическое представление дошкольников, развитие, дошкольник, ответ, ребенок, дошкольное образование, математическое представление, старшая группа.
Ключевые слова
эксперимент, познавательные процессы, математическое представление у дошкольников, математические задачиматематическое представление у дошкольников, познавательные процессы, эксперимент, математические задачи
Похожие статьи
Формирование элементарных
математических представлений.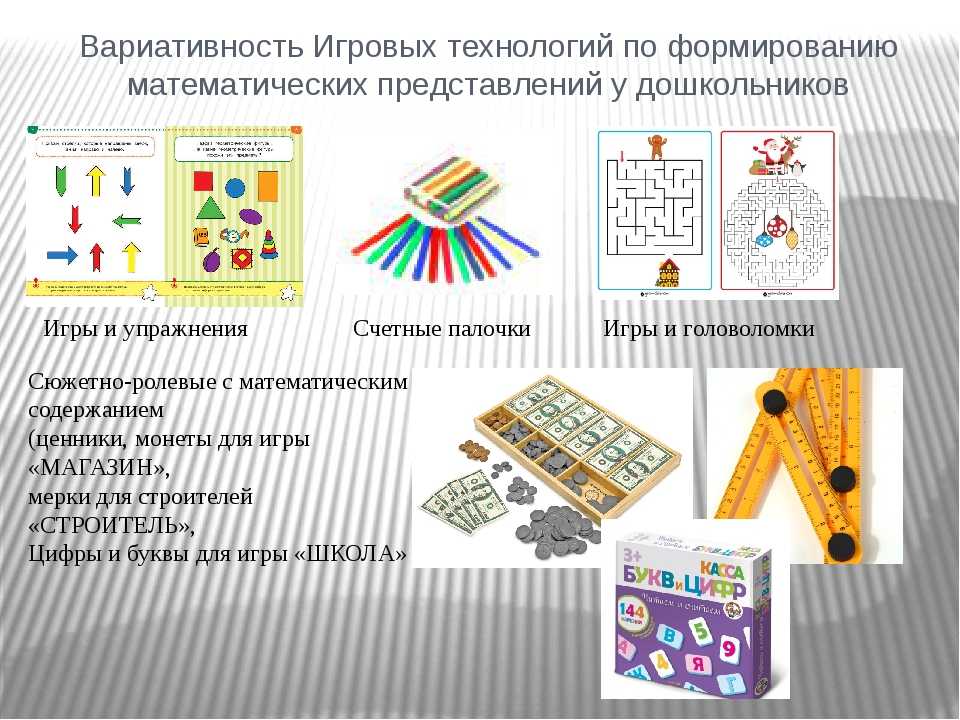 ..
..Формирование математических представлений у детей старшего дошкольного возраста через дидактические игры.
ребенок, логическое мышление, дошкольный возраст, задача, теория решения, математическое развитие, детский сад, игра, знание, Число.
Развитие математических способностей у детей дошкольного…Создать условия для усвоения дошкольниками математических представлений, обеспечить успешное развитие познавательных способностей и логического мышления у детей старшего дошкольного возраста
Формирование
математических представлений у детей. ..
..Формирование математических представлений у детей старшего дошкольного возраста через дидактические игры.
воспитатель, ребенок, дошкольный возраст, Какое число, игра, буква, Ответ детей, математическое развитие, детский сад, представление.
Влияние дидактической игры на формирование
математических…игра, ребенок, дидактическая игра, дошкольный возраст, представление, день недели, задание, фигура, лист бумаги, детский сад.
ребенок, игра, логическое мышление, предмет, старший дошкольный возраст, признак, развитие, детское мышление, группа предметов. ..
..
Использование ТРИЗ в
математическом развитии детей…воспитатель, ребенок, дошкольный возраст, Какое число, игра, буква, Ответ детей, математическое развитие, детский сад, представление. Формирование математических представлений у детей старшего…
Организация индивидуального подхода к
дошкольнику…общее образование, начальная школа, дошкольное образование, уровень, детский сад, дошкольный возраст, ребенок
Развитие математических способностей дошкольника. ребенок, палочка, игра
ребенок, палочка, игра
Формирование математических представлений у детей старшего…
КВН по
математике (ФЭМП) для старшего дошкольного возраста− Систематизировать представления детей в математическом образовании и развитии
ПРЕДСТАВЛЕНИЕ КОМАНД.
(Подготовительная группа). РАЗМИНКА. (За каждый правильный ответ команда получает флажок).
Развитие количественных представлений у детей старшего…Изучив методическую литературу, по данной теме мы подобрали игровой комплекс (ряд компьютерных игр и игровых упражнений) по развитию количественных представлений детей старшего дошкольного возраста.
Программа для обучения
детей старшего дошкольного возраста…дошкольный возраст, ребенок, программа, игра, математическое развитие дошкольников, преобразующий элемент, использование компьютера
Преемственность в математическом развитии детей… школа, учебная деятельность, ребенок, детский сад, дошкольно-школьная…
Похожие статьи
Формирование элементарных
математических представлений…Формирование математических представлений у детей старшего дошкольного возраста через дидактические игры.
ребенок, логическое мышление, дошкольный возраст, задача, теория решения, математическое развитие, детский сад, игра, знание, Число.
Развитие математических способностей у детей дошкольного…Создать условия для усвоения дошкольниками математических представлений, обеспечить успешное развитие познавательных способностей и логического мышления у детей старшего дошкольного возраста
Формирование
математических представлений у детей…Формирование математических представлений у детей старшего дошкольного возраста через дидактические игры.
воспитатель, ребенок, дошкольный возраст, Какое число, игра, буква, Ответ детей, математическое развитие, детский сад, представление.
Влияние дидактической игры на формирование
математических…игра, ребенок, дидактическая игра, дошкольный возраст, представление, день недели, задание, фигура, лист бумаги, детский сад.
ребенок, игра, логическое мышление, предмет, старший дошкольный возраст, признак, развитие, детское мышление, группа предметов…
Использование ТРИЗ в
математическом развитии детей…воспитатель, ребенок, дошкольный возраст, Какое число, игра, буква, Ответ детей, математическое развитие, детский сад, представление. Формирование математических представлений у детей старшего…
Формирование математических представлений у детей старшего…
Организация индивидуального подхода к
дошкольнику…общее образование, начальная школа, дошкольное образование, уровень, детский сад, дошкольный возраст, ребенок
Развитие математических способностей дошкольника. ребенок, палочка, игра
Формирование математических представлений у детей старшего…
КВН по
математике (ФЭМП) для старшего дошкольного возраста− Систематизировать представления детей в математическом образовании и развитии
ПРЕДСТАВЛЕНИЕ КОМАНД.
(Подготовительная группа). РАЗМИНКА. (За каждый правильный ответ команда получает флажок).
Развитие количественных представлений у детей старшего…Изучив методическую литературу, по данной теме мы подобрали игровой комплекс (ряд компьютерных игр и игровых упражнений) по развитию количественных представлений детей старшего дошкольного возраста.
Программа для обучения
детей старшего дошкольного возраста…дошкольный возраст, ребенок, программа, игра, математическое развитие дошкольников, преобразующий элемент, использование компьютера
Преемственность в математическом развитии детей. .. школа, учебная деятельность, ребенок, детский сад, дошкольно-школьная…
.. школа, учебная деятельность, ребенок, детский сад, дошкольно-школьная…
Развитие математических представлений у детей дошкольного возраста в условиях вызовов новой реальности
Каличак Людмила Петровна,воспитатель высшей квалификационной категории МКДОУ д/с № 388 г. Новосибирска |
Курасова Софья Леонидовна,воспитатель первой квалификационной категории МКДОУ д/с № 388 г. Новосибирска |
Формирование элементарных математических представлений отнесено ФГОС к образовательной области «Познавательное развитие». Целевые ориентиры предполагают: владение ребёнка общими приёмами умственной деятельности (классификация, сравнение, обобщение и другие), простейшими графическими навыками и умениями, математической терминологией; умение считать, измерять, моделировать; умение ориентироваться в количественных, пространственных и временных отношениях окружающей действительности.
С математикой мы всё время сталкиваемся в детском саду. Дети естественным образом изучают её в течение дня. Она есть в их повседневной жизни. Ребята играют, не подозревая, что осваивают знания и умения. Малыши охотно участвуют в играх, узнавая о разных предметах: об их свойствах, таких, как форма, цвет, величина, вес, качество материала, пространство. Не всем дошкольникам освоение этой науки даётся легко, особенно ребятам с ограниченными возможностями здоровья. У некоторых нет желания заниматься математикой. А вот играть готовы каждую минуту, даже в дидактические игры. Наша задача – «пробудить» познавательный интерес, сделать обучение занимательным.
В своей книге «Математика в детском саду» Лидия Васильевна Михайлова-Свирская пишет: «Математика связана прежде всего с понятием «порядок». Он появляется благодаря применению основных математических понятий: классификация, сортировка, категоризация». Поэтому в группе всегда следим, чтобы вещи были убраны на свои места. Во время утреннего круга с ребятами считаем: сколько детей сегодня пришло? Сколько отсутствует? Структурируем и классифицируем: кто выступает первым с сообщением? Кто будет вторым, третьим? Во время игры, например, предлагаем настольные игры-бродилки, где каждый ход определяется кубиком. Определяем направление движения и положения вещей в пространстве: между, рядом, вперёд… Знакомимся с понятием «скорость»: быстрее, медленнее. Постоянно ищем числа в окружающей обстановке, формы: какие числа вы нашли? Для чего они тут? Кто нашёл круг? Мы измеряем, сравниваем. Например, какой высоты это дерево? Сколько шагов надо сделать до определённого места? Сколько этажей в доме? Применяем временные понятия и объясняем их: какой день был вчера, а какой сегодня?
Определяем направление движения и положения вещей в пространстве: между, рядом, вперёд… Знакомимся с понятием «скорость»: быстрее, медленнее. Постоянно ищем числа в окружающей обстановке, формы: какие числа вы нашли? Для чего они тут? Кто нашёл круг? Мы измеряем, сравниваем. Например, какой высоты это дерево? Сколько шагов надо сделать до определённого места? Сколько этажей в доме? Применяем временные понятия и объясняем их: какой день был вчера, а какой сегодня?
Математика – не просто сухие цифры и строгие фигуры, это ключ к сообразительности. Для дошкольников она должна быть осязаемой. Они приемлют только игры и наглядные задания. Несомненна роль дидактических игр в умственном воспитании детей.
Дидактические игры по формированию математических представлений можно разделить на следующие группы.
1. Игры с цифрами и числами.
2. Игры-путешествия во времени.
3. Игры на ориентировку в пространстве.
4. Игры с геометрическими фигурами.
5. Игры на логическое мышление.
Ценными в ДОУ являются игры, сделанные своими руками. Это забота и внимание мастера. Материалы для создания: подручные – ткань, пряжа, пуговицы; природное сырьё – листья, цветы, жёлуди, каштаны, палочки; канцелярия: клей, цветная бумага, картон. Воображение – это самая главная составляющая.
Насыщенности среды уделяем особое внимание. Приобретены игры: конструктор «Магнитный», умные пчёлки и мыши – роботы «Bee bot», развивающие игры Никитина. Оформили картотеки с заданиями к доске «Геоборд», математическому планшету, по логическим блокам Дьенеша, палочкам Кьюзенера и другие.
Современный этап развития общества предполагает широкое применение в образовании ИКТ: используем развивающие компьютерные игры, сеть Интернет как источник дополнительной информации, иллюстративный материал, мультимедийные средства, например, презентации.
Родители наших воспитанников являются активными участниками образовательного процесса. Изготавливают своими руками дидактические игры и пособия по развитию математических представлений у детей, готовят с детьми презентации, книжки-малышки, подбирают материал для мини-музеев, выставляют коллекционные материалы. Используем в работе с семьями и папки-передвижки, например, «Игры для развития математических способностей детей», буклеты.
Используем в работе с семьями и папки-передвижки, например, «Игры для развития математических способностей детей», буклеты.
Дети растут, набираются опыта. Мы находимся в постоянном поиске материалов, пробуждающих у детей любопытство. В нашей подготовительной группе пополнился математический уголок. Оформлен и вызвал интерес математический лэпбук «Мудрая совушка». Организован мини-музей денег «Юный финансист», по теме «Время» представлена коллекция «Ручные часы», накоплен «Сундучок измерительных приборов» (измерение длины, массы, времени) и другие вещи, которые необходимы для занятий творчеством в бытовых условиях и могут использоваться в математическом уголке в практических целях.
Математические навыки очень важны, и необходимо искать игровые и увлекательные способы обучения. Созданные для этого в группе ДОУ условия пробуждают у детей наблюдательность и любознательность, познавательную активность.
Список литературы.
1. Арапова-Пискарева Н.А. Формирование элементарных математических представлений. – М.: Мозаика-Синтез, 2006.
2. Белошистая А.В. Формирование математических способностей: пути и формы // Ребенок в детском саду, 2001. № 1. е. 5-17; № 2. с. 9-25.
3. Белошистая А.В. Обучение математике в ДОУ: Методическое пособие. – М.: Айрис-пресс, 2005. 320 с.
4. Бостельман Антже. Математика в любое время! Практическое руководство по раннему обучению математике. ФГОС ДО. Издательство: «Национальное образование», 2016.
5. Михайлова-Свирская Л. В. Математика в детском саду. Учебно-практическое пособие для педагогов ДО. ФГОС ДО. Издательство: «Национальное образование», 2015.
6. Нищева Н. В. Развитие математических представлений у дошкольников с ОНР (с 6 до 7 лет). Издательство: Детство-Пресс, 2016.
| Количество просмотров: 1526 |
SCIRP Открытый доступ
Издательство научных исследований
Журналы от A до Z
Журналы по темам
- Биомедицинские и биологические науки.

- Бизнес и экономика
- Химия и материаловедение.
- Информатика. и общ.
- Науки о Земле и окружающей среде.
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные науки. и гуманитарные науки
Журналы по тематике
- Биомедицина и науки о жизни
- Бизнес и экономика
- Химия и материаловедение
- Информатика и связь
- Науки о Земле и окружающей среде
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные и гуманитарные науки
Публикация у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Публикуйте у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp. org org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
| Недавно опубликованные статьи |
| Недавно опубликованные статьи |
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp. org org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
Бесплатные информационные бюллетени SCIRP
Copyright © 2006-2022 Scientific Research Publishing Inc. Все права защищены.
верхнийВведение в поддержку начальной математики в ECE
Дети удивительно мотивированы и способны участвовать в математическом мышлении и решении задач еще до того, как они начнут формальное школьное обучение. Они изучают математику самостоятельно, играя и неформально общаясь со своими учителями и сверстниками. Считается, что дети уже с рождения интуитивно понимают некоторые математические понятия, например, сравнение размеров наборов и выполнение простых арифметических действий с группами объектов. Другие концепции, такие как изучение названий чисел и письменных цифр, то, как они отображаются на соответствующие группы объектов, и как числовые символы сравниваются по величине и могут быть объединены арифметически, требуют большего опыта и подробных инструкций от учителей, других взрослых и т. д. продвинутые сверстники. Педагоги дошкольного возраста могут помочь детям дошкольного возраста развить математические знания, сочетая свободную игру и методы управляемой игры, такие как игры.
Другие концепции, такие как изучение названий чисел и письменных цифр, то, как они отображаются на соответствующие группы объектов, и как числовые символы сравниваются по величине и могут быть объединены арифметически, требуют большего опыта и подробных инструкций от учителей, других взрослых и т. д. продвинутые сверстники. Педагоги дошкольного возраста могут помочь детям дошкольного возраста развить математические знания, сочетая свободную игру и методы управляемой игры, такие как игры.
В этом руководстве описываются некоторые основные математические навыки, которые дети готовы освоить и демонстрировать в раннем детстве, как определить, когда дети тренируют эти навыки самостоятельно во время игры, а также идеи о том, как включить вспомогательное обучение математике с руководством и без руководства в день. Намерение состоит не в том, чтобы выступать за формальное или рутинное обучение математике в условиях дошкольного образования, а в том, чтобы предложить способы, с помощью которых учителя могут замечать и реагировать на возникающий у детей интерес к математике и понимание математики, поддерживая их в дальнейшем развитии этих интересов и понимания через игру.
Счет относится к способности рассуждать и применять простые числовые понятия. Базовые навыки счета включают способность идентифицировать и понимать числа, выполнять простые арифметические операции (например, сложение и вычитание) и сравнивать числовые величины.
Несимволические отношения и комбинации: Люди и даже некоторые животные с рождения способны думать о числах несимволически, поскольку они способны различать и сравнивать относительную величину одного набора объектов с другим. В младенчестве дети демонстрируют раннее представление о числе, поскольку они могут довольно точно различать представления малых величин, могут приблизительно различать большие величины, различающиеся числом, и даже распознавать основные понятия арифметики с небольшими наборами элементов. Точность этих способностей оттачивается по мере развития ребенка и предсказывает его более поздние математические достижения.
Распознавание s Знакомство и идентификация символических представлений: В раннем и дошкольном возрасте дети в странах с формальными системами счисления переходят к более точному представлению чисел посредством овладения символической системой счисления. Они учатся произносить цифры (“четыре”) и писать их (“4”). Они могут считать последовательно (‘1, 2, 3’) и начинают узнавать свои первые написанные цифры. По мере взросления дети все больше способны распознавать и называть написанные цифры, как маленькие (1–3), так и большие (4–10), а также расширять диапазон своего списка счетных слов.
Соединение символических и несимволических представлений: По мере приближения к пятилетнему возрасту у детей развивается способность связывать вместе символические и несимволические представления чисел. Например, они начинают ассоциировать числовые слова, которые впервые выучили в детстве, с определенными наборами видимых объектов, которые они представляют. При изучении этого навыка дети этого возраста работают над однозначным соответствием или способностью назначать отдельные исчисляемые слова отдельным объектам в наборе. Однако, когда их просят обозначить установленный размер объектов, они могут не определить последнее число в своей последовательности подсчета как установленный размер или предоставить соответствующее количество объектов по запросу (принцип кардинальности). Они также будут неточно оценивать уместность некоторых стратегий подсчета, которые могут привести к правильному ответу, но являются нетрадиционными (например, подсчет предметов справа налево).
При изучении этого навыка дети этого возраста работают над однозначным соответствием или способностью назначать отдельные исчисляемые слова отдельным объектам в наборе. Однако, когда их просят обозначить установленный размер объектов, они могут не определить последнее число в своей последовательности подсчета как установленный размер или предоставить соответствующее количество объектов по запросу (принцип кардинальности). Они также будут неточно оценивать уместность некоторых стратегий подсчета, которые могут привести к правильному ответу, но являются нетрадиционными (например, подсчет предметов справа налево).
Еще одним важным компонентом соединения символических и несимволических знаний о числах является важность способности детей понимать арабские цифры, называемые цифрами или числовыми знаниями . Это понимание влечет за собой способность как распознавать письменные цифры (и связывать их с соответствующими словесными названиями чисел), так и напрямую связывать числовые символы с их соответствующими количествами. Дети дошкольного возраста, приближающиеся к пятилетнему возрасту, учатся связывать эти символы с соответствующими несимволическими наборами массивов объектов (или объектов, расположенных в строках и/или столбцах). Приобретение числовых знаний считается последним важным шагом в переходе от опоры на несимволические представления чисел к способности полностью символически представлять числа. Кроме того, он предсказывает успехи детей в математике в начальной и поздней начальной школе.
Дети дошкольного возраста, приближающиеся к пятилетнему возрасту, учатся связывать эти символы с соответствующими несимволическими наборами массивов объектов (или объектов, расположенных в строках и/или столбцах). Приобретение числовых знаний считается последним важным шагом в переходе от опоры на несимволические представления чисел к способности полностью символически представлять числа. Кроме того, он предсказывает успехи детей в математике в начальной и поздней начальной школе.
Символические отношения и комбинации: Последний аспект развития чисел в раннем детстве включает повышенную способность решать задачи на символьные числа. Именно в этой области дети демонстрируют свое концептуальное понимание чисел, поскольку они могут выйти за рамки обычного ответа на вопрос «сколько?» и применить свои базовые знания к более новым ситуациям. Например, они могут определить, какое из двух числовых слов или письменных цифр больше, или найти сумму или разность двух чисел (сложение и вычитание). Чтобы решить эти задачи, дети должны помнить о величине задействованных чисел, их порядке в последовательности счета и, в случае арифметики, о том, как можно объединить две числовые величины, чтобы создать новое, большее число. Исследования показали, что развитие этих навыков в дошкольном возрасте важно, потому что они в значительной степени предсказывают более поздние достижения детей в математике.
Чтобы решить эти задачи, дети должны помнить о величине задействованных чисел, их порядке в последовательности счета и, в случае арифметики, о том, как можно объединить две числовые величины, чтобы создать новое, большее число. Исследования показали, что развитие этих навыков в дошкольном возрасте важно, потому что они в значительной степени предсказывают более поздние достижения детей в математике.
Учителя могут помочь детям развить эти базовые навыки счета в игре разными способами. Например, использование игрушечных весов может помочь детям сравнивать величины наборов объектов. Драматические игры, декоративно-прикладное искусство и блоки также могут способствовать знакомству детей с предметами разных размеров, особенно потому, что дети остро настроены на количество игрушек и материалов, которые есть у других детей, по сравнению с их собственным запасом. Простое выполнение действий с участием большого количества объектов будет побуждать детей проводить эти сравнения самостоятельно. Кроме того, перераспределение игрушек и материалов, которое часто является результатом конфликта из-за неравного распределения игрушек, – это возможность испытать несимволическую арифметику.
Кроме того, перераспределение игрушек и материалов, которое часто является результатом конфликта из-за неравного распределения игрушек, – это возможность испытать несимволическую арифметику.
Маленьким детям редко требуется подсказка для подсчета предметов. Фактически, они будут искать элементы в своей среде, чтобы количественно определить, были ли эти элементы предоставлены намеренно или нет. Но детская игра может выиграть от воздействия большого количества мелких объектов, которые различаются по характеристикам восприятия, таким как цвет и форма (например, наборы шнурков и бусинок). Детям часто нравится сортировать предметы по схожим характеристикам, а затем считать эти группы предметов, поэтому наличие множества предметов увеличивает возможности счета.
Дети также могут знакомиться с письменными цифрами во многих играх. Игра в «магазины» с игрушечными деньгами и кассовыми аппаратами позволяет знакомиться с цифрами в культурно значимом контексте. Это поддерживает знания о числах, мотивируя детей ассоциировать эти числа с ценами и конкретным количеством продуктов питания. Детям также могут быть представлены модифицированные игральные карты с точками и их соответствующим количеством либо на одной карте, либо на разных картах. Дети могут практиковаться в сопоставлении карточек с цифрами и точками (если они разные) или изучать связь между количеством точек и цифрами на одних и тех же карточках. Головоломки с числами и таблицы с числами 100, которые отображают цифры, чтобы помочь детям узнать величину цифр, помогая им сравнивать разные цифры друг с другом.
Детям также могут быть представлены модифицированные игральные карты с точками и их соответствующим количеством либо на одной карте, либо на разных картах. Дети могут практиковаться в сопоставлении карточек с цифрами и точками (если они разные) или изучать связь между количеством точек и цифрами на одних и тех же карточках. Головоломки с числами и таблицы с числами 100, которые отображают цифры, чтобы помочь детям узнать величину цифр, помогая им сравнивать разные цифры друг с другом.
Считается, что пространственные навыки необходимы для математических рассуждений и решения задач, и исследования показывают, что пространственные навыки маленьких детей предсказывают их дальнейшие успехи в математике. Это связано с тем, что они помогают детям мысленно визуализировать информацию (что полезно для выполнения арифметических действий) и изучать математические понятия (например, наблюдение и отслеживание преобразований размера набора, таких как добавление в группу объектов). В частности, пространственная визуализация (преобразование мысленных образов объектов) — это особенно сложный навык, который начинает развиваться в дошкольном возрасте и является пространственным навыком, который наиболее последовательно и тесно связан с одновременным и более поздним математическим знанием. Навык зрительно-пространственной рабочей памяти (запоминание и воспроизведение последовательностей местоположений объектов) также развивается в раннем детстве и связан с параллельными и более поздними математическими знаниями.
В частности, пространственная визуализация (преобразование мысленных образов объектов) — это особенно сложный навык, который начинает развиваться в дошкольном возрасте и является пространственным навыком, который наиболее последовательно и тесно связан с одновременным и более поздним математическим знанием. Навык зрительно-пространственной рабочей памяти (запоминание и воспроизведение последовательностей местоположений объектов) также развивается в раннем детстве и связан с параллельными и более поздними математическими знаниями.
Маленькие дети естественным образом тянутся к конструированию и формированию игр — двум видам деятельности, которые имеют основополагающее значение для пространственного развития. Детям можно предоставить фотографии моделей или предварительно собранные конструкции для воссоздания или оставить для создания своих собственных конструкций. Дошкольникам нравится использовать обычные деревянные блоки, которые требуют соблюдения устойчивости конструкции, а также игрушки, такие как Magformers или Lego, которые можно соединять друг с другом. Игра с блоками Tangram/шаблона и изображениями-моделями побуждает детей распознавать формы и помещать их в соответствующие места на картинках. Дети также могут собирать блоки танграма вместе, не полагаясь на изображения моделей. Эти действия подчеркивают важные свойства формы и требуют планирования, а также проб и ошибок, чтобы расположить фигуры в правильных местах на изображениях модели или, в случае с блоками танграма, таким образом, чтобы различные формы соответствовали друг другу.
Игра с блоками Tangram/шаблона и изображениями-моделями побуждает детей распознавать формы и помещать их в соответствующие места на картинках. Дети также могут собирать блоки танграма вместе, не полагаясь на изображения моделей. Эти действия подчеркивают важные свойства формы и требуют планирования, а также проб и ошибок, чтобы расположить фигуры в правильных местах на изображениях модели или, в случае с блоками танграма, таким образом, чтобы различные формы соответствовали друг другу.
Считается, что навыки шаблонов помогают находить и обобщать правила и закономерности, лежащие в основе математики, и исследования показывают, что навыки шаблонов детей дошкольного возраста предсказывают их более поздние достижения в математике и числовые знания. Создание паттернов считается важным для математического мышления, поскольку оно поддерживает то, как дети узнают правила о числах (например, следующее число в последовательности счета на единицу больше, чем предыдущее число, и если число появляется после другого в последовательности счета, оно должно быть больше по величине). Навыки узоров для маленьких детей сосредоточены на повторяющихся узорах или линейных массивах с повторяющимися единицами, такими как 9.0005 АББ АББББ. Примерно в трехлетнем возрасте у детей начинают формироваться явные знания о повторяющихся узорах и они способны распознавать примеры (например, полоски на рубашке). По мере взросления дети дошкольного возраста развивают все более сложные навыки построения узоров. Сначала они осваивают исправление паттернов (заполнение отсутствующих элементов) и дублирование или копирование повторяющихся паттернов модели. Затем они учатся расширять паттерны (продолжая существующий паттерн хотя бы на одну единицу повторения, например, ABCABC ABC ) и абстрагирование шаблонов (воссоздание шаблона модели с использованием другого набора материалов, например, ABBABB в CDDCDD с использованием красных/желтых и синих/зеленых блоков). В конце концов, дети могут озвучить и продемонстрировать, что делает последовательность повторяющимся паттерном (путем определения основной единицы, которая повторяется в паттерне).
Навыки узоров для маленьких детей сосредоточены на повторяющихся узорах или линейных массивах с повторяющимися единицами, такими как 9.0005 АББ АББББ. Примерно в трехлетнем возрасте у детей начинают формироваться явные знания о повторяющихся узорах и они способны распознавать примеры (например, полоски на рубашке). По мере взросления дети дошкольного возраста развивают все более сложные навыки построения узоров. Сначала они осваивают исправление паттернов (заполнение отсутствующих элементов) и дублирование или копирование повторяющихся паттернов модели. Затем они учатся расширять паттерны (продолжая существующий паттерн хотя бы на одну единицу повторения, например, ABCABC ABC ) и абстрагирование шаблонов (воссоздание шаблона модели с использованием другого набора материалов, например, ABBABB в CDDCDD с использованием красных/желтых и синих/зеленых блоков). В конце концов, дети могут озвучить и продемонстрировать, что делает последовательность повторяющимся паттерном (путем определения основной единицы, которая повторяется в паттерне).
Детям часто нравится находить и создавать закономерности, используя повседневные предметы. Дети могут делать ожерелья из бисера с повторяющимися или симметричными узорами, используя наборы бусин для шнуровки и нанизывания или другие материалы для декоративно-прикладного искусства, такие как пуговицы или помпоны, или создавать узоры из блоков, различающихся по цвету и форме. Если образцы рисунков уже показаны (например, настоящее ожерелье или изображение различных симметричных или повторяющихся рисунков из бусинок или блоков), дети могут скопировать эти узоры, используя те же или другие материалы (если намеренно предоставлены материалы, которые соответствуют или не соответствуют модели) или сделать свои собственные выкройки. Материалы также можно настроить таким образом, чтобы дети могли расширять узоры объектов с помощью бусинок или блоков (например, предоставить частично созданный узор ожерелья из бисера, закрепленный узлом, который можно построить на оставшейся нитке).
Дополнительная литература
Риттл-Джонсон, Б., Зипперт, Э.Л., и Бойс, К.Л. (2019). Роль построения моделей и пространственных навыков в раннем развитии математики. Ежеквартальное исследование раннего детства , 46 , 166-178.
Зипперт, Э.Л., Доберт, Э.Н., Скализ, Н.Р., Норин, Г.Д., и Рамани, Г.Б. (2019). «Нажми пробел номер три»: поощрение математических разговоров во время игры родителей и детей на планшете. Развивающая P психология , 55 (8), 1605–1614.
Зипперт, Э.Л., и Рамани, Г.Б. (2017). Оценки родителей навыков счета дошкольников связаны с вовлеченностью в домашнюю деятельность, связанную с числами. Развитие младенцев и детей , 26 (2).
Зипперт, Э.Л., и Риттл-Джонсон, Б. (2020). Домашняя математическая среда: больше, чем счет. Ежеквартальное исследование раннего детства, 50 , 4–15.
Доктор Эрика Зипперт
ПОДГОТОВЛЕН ДЛЯ ОБРАЗОВАТЕЛЬНОГО ЦЕНТРА BY
Д-р Эрика Зиппер
Д-р Эрика Зипперт — научный сотрудник Университета Пердью, получивший докторскую степень.

 ..
.. Вдруг
Вдруг