Примеры неравенства 2 класс: Верные и неверные равенства и неравенства — урок. Математика, 1 класс. – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Решение неравенств второй степени с одной переменной. Метод интервалов 9 класс онлайн-подготовка на Ростелеком Лицей |

Тема 6.

Решение неравенств второй степени с одной переменной. Метод интервалов.

Неравенства вида

ax² + bx + c > 0 и ax² + bx + c

где x – переменная, a, b и c – некоторые числа и a ≠ 0, называют неравенствами второй степени с одной переменной.

Решение неравенства ax² + bx + c > 0 или ax² + bx + c y = ax² + bx + c принимает положительные или отрицательные значения. Для этого достаточно проанализировать, как расположен график функции y = ax² + bx + c в координатной плоскости: куда направлены ветви параболы – вверх или вниз, пересекает ли парабола ось

x и если пересекает, то в каких точках.

Пример:

Решить неравенство: x² + 2x – 48

Введем функцию y = x² + 2x – 48.

Графиком этой функции является парабола, ветви которой направлены вверх, так как a = 1.

Выясним, как расположен график этой функции относительно оси x. Для этого решим квадратное уравнение x² + 2x – 48 = 0.

Это уравнение имеет два корня:

x₁ = -8 и x₂ = 6.

Значит, парабола y = x² + 2x – 48 пересекает ось x в двух точках, абсциссы которых равны -8 и 6. Схематично изобразим эту параболу.

Ответ: x∈-8;6

Решим неравенство:

–x

² + 2x + 15

График функции y = –x² + 2x + 15 – это парабола, ветви которой направлены вниз, так как a

Выясним, как расположен график функции y = –x² + 2x + 15 в координатной плоскости, пересекает ли он ось x и в каких точках.

Для этого решим уравнение:

–x² + 2x + 15 = 0

x₁=-3; x₂=5

Схематично изобразим эту параболу

Функция принимает отрицательные значения при x принадлежит -∞;-3 или 5;+∞.

Ответ: x∈-∞;-3∪5;+∞

Решим неравенство:

2x² – 3x + 8 > 0

Графиком функции y = 2x² – 3x + 8 является парабола, ветви которой направлены вверх, так как a > 0. Выясним, как располагается эта парабола относительно оси x. Для этого решим квадратное уравнение:

2x² – 3x + 8 = 0

D = 9 – 4 ∙ 2 ∙ 8 = -55

Данное уравнение не имеет корней, значит, парабола не пересекает ось x. Схематично покажем, как располагается эта парабола относительно оси x.

Из рисунка видно, что данная функция принимает положительные значения при любом значении x.

Ответ: -∞;+∞

Итак, для решения неравенств вида

ax² + bx + c > 0 и

ax² + bx + c

Выяснить имеет ли квадратный трехчлена ax² + bx + c имеет ли трехчлен корни;
Если трехчлен имеет корни, то отмечают их на оси x и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх, если a > 0 или вниз, если a a > 0 или в нижней полуплоскости при a
На оси x найти промежутки, для которых точки параболы расположены выше оси x (если решают неравенство ax² + bx + c > 0) или ниже оси x (если решают неравенство ax² + bx + c

Рассмотрим функцию

fx=x+1x-2x+3

Областью определения этой функции является множество всех чисел. Точки -3, -1 и 2 нули функции, которые разбивают область определения на промежутки -∞;-3,-3;-1,-1;2,2;+∞. Выясним знак функции в каждом из указанных промежутков.

Выражение (x + 1)(x – 2)(x + 3) представляет собой произведение трех множителей. Знак каждого из этих множителей в рассматриваемых промежутках указан в таблице.

	-∞;-3	-3;-1	-1;2	2;+∞
x + 3	–	+	+	+
x + 1	–	–	+	+
x – 2	–	–	–	+

Отсюда ясно, что:

Если x∈-∞;-3, то fx<0;

Если x∈-3;-1, то fx>0;

Если x∈-1;2, то fx<0;

Если x∈2;+∞, то fx>0;

Видно, что в каждом из промежутков

-∞;-3,-3;-1,-1;2,2;+∞ функция сохраняет знак, а при переходе через точки -3, -1 и 2 ее знак изменяется.

Вообще пусть функция задана формулой

fx=x-x1x-x2…x-xn, где x – переменная, а x₁, x₂, …, x_n не равные друг другу числа. Числа x₁, x₂, …, x_n являются нулями функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через ноль знак изменяется.

Это свойство используется для решений неравенств вида:

x-x1x-x2…x-xn>0,

x-x1x-x2…x-xn<0.

x-5x+3x+7>0

Введем функцию fx=x-5x+3x+7

Найдем нули функции: -7, -3 и 5

Определим знак функции в каждом из этих промежутков. В крайнем правом промежутке функция положительна, а далее знаки чередуются.

Ответ: -7;-3∪5;+∞

Итак, чтобы решить неравенство методом интервалов, надо:

Ввести функцию;
Найти нули этой функции;
Нанести нули функции на числовую прямую;
Определить знак в каждом промежутке;
Посмотреть знак и выделить нужный интервал.

Урок математики в 3 классе по теме: «Числовые равенства и неравенства»

Муниципальное бюджетное общеобразовательное учреждение Зимовниковская средняя общеобразовательная школа №1

Зимовниковский район, Ростовская область

Урок математики

в 3 классе

по теме: «Числовые равенства и неравенства»

разработала: учитель начальных классов

Московченко Галина Васильевна

класс: 3, 9 лет

п. Зимовники

2014 г.

ТЕМА: «Числовые равенства и неравенства»

Цели: создать условия для знакомства с терминами «равенство» и «неравенство», формирования навыков употребления в своей речи слов: «верное» и «неверное» равенство и неравенство; развития навыков математического счета, смекалки, мышления; воспитания положительных нравственных качеств.

Ход урока

1.Организационный момент.

Каждый день всегда, везде

На занятиях, в игре

Смело, четко говорим

И тихохонько сидим.

Ну-ка, проверь дружок,

Ты готов начать урок?

Всё ль на месте? Все в порядке

Книжка, ручка и тетрадка?

Все ли правильно сидят?

Все ль внимательно глядят?

Каждый хочет получать только лишь оценку пять.

2.Устный счёт

А сейчас посчитаем устно.

-Назовите числа в порядке возрастания:

61, 70, 68 , 62, 65, 63.

_ Посчитаем:

300 + 400 520 +4

254 – 54 738 -30

– Ребята « Книга – источник знаний»

-Что я произнесла? (пословицу, предложение)

-А как в математике мы называем такие предложения? (высказывания)

-Верно ли оно? Докажите. (книги учат жизни. много полезной информации)

– В выражении 24: 8 *9 нужно выполнить действия по порядку слева направо.

-Верно ли это высказывание? Найдите значение этого выражения.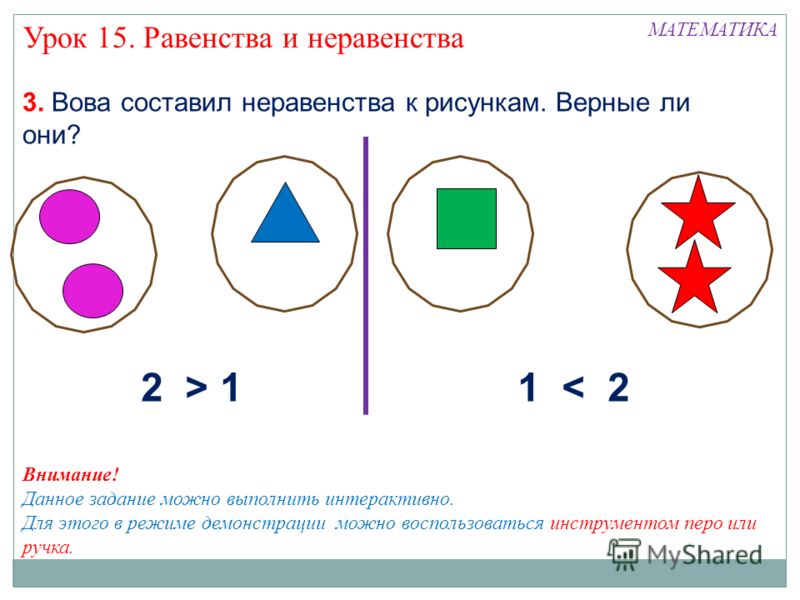 (27)

– В следующем выражении 64- 5*7 +5 сначала надо выполнить вычитание. Верно ли это высказывание. Почему? (надо выполнить сильное действие – умножение, а затем по порядку).

-Найдите значение этого выражения. (34)

3.Работа по теме урока.

А)Это дети, равенства, потому что стоит знак =.

Прочитайте тему нашего урока.

– Можете ли вы сказать, что такое числовое равенство и неравенство? (равенство ,когда стоит знак =: неравенство—знаки Б,М)

– Посмотрите на рисунок, скажите, в каком столбике записаны равенства, в каком неравенство? Почему?

– проверим (решаем по картинке)

Б) Совершенствование знаний.

№2,стр.4

– Что мы выписали? (мы выписали верные равенства)

№3.Читаем задание.

А почему неравенства? (потому что стоят знаки сравнения)

– Что мы выписывали? (мы выписывали верные неравенства)

4.Работа в парах.

А сейчас поиграете вдвоём, со своим соседом (соседкой): вы придумайте и запишите —1 ряд (верное равенство), 2 ряд (неверное равенство).

1 ряд (неверное неравенство), 2 ряд (верное неравенство).

Молодцы

5.Физминутка

Чья пара лучше справилась с заданием? Давайте поаплодируем.

6.Самостоятельная работа

– Сейчас выполните самостоятельно №4.

-Ваша задача проверить, верна ли каждая запись?

1вариант—1столбик

2 вариант —2столбик ПРОВЕРКА.

7.Повторение пройденного материала.

– Откройте рабочие тетради на стр.4,№9 (и выполним 3-4столбик)

8.Итог урока.

Подведем итог урока

—Я познакомилась с новыми терминами: числовые равенства и неравенства.

Я понял, что равенством называют тогда, когда стоит знак =,

А неравенством- когда стоят знаки больше и меньше.

Я научилась определять, когда равенство верно, а когда неверно.

А мне понравилось, когда помогает соседка.

Ребята спасибо вам за работу на уроке, вы были моими самыми лучшими друзьями и помощниками.

9.Домашнее задание.

Стр. 4(р.т.) №9(1,2 столбик)

Список литературы

Истомина Н.Б. Учимся решать комбинаторные задачи/ Н.Б. Истомина, Е.П. Виноградова. – Смоленск: Ассоциация XXI век, 2004.
Кравченко В.С. Устные упражнения по математике в 1-3 классах/ В.С. Кравченко. – М. Просвещение, 1979.
Рудницкая В.М. Математика 3 кл.: учебник для учащихся общеобразовательных учреждений: в 2 ч./В.М. Рудницкая, Т.В. Юдачева. – М.: Вентана-Граф, 2008.
Рудницкая В.М. Математика: рабочая тетрадь для 3 класса: № 2/ В.М. Рудницкая, Т.В. Юдачева. – М.: Вентана-Граф, 2008.
Энциклопедический словарь юного математика/ сост. Н.П. Ернылев. – М.: Педагогика, 1980.

Интернет-ресурсы

http://migranov.ru/photoalbum/fall/12.php

http://images.yandex.ru/yandsearch?text=смайлики веселые и грустные

Понятие равенства, знак равенства, связанные определения

Материал статьи позволит ознакомиться с математической трактовкой понятия равенства. Порассуждаем на тему сути равенства; рассмотрим его виды и способы его записи; запишем свойства равенства и проиллюстрируем теорию примерами.

Что такое равенство

Само понятие равенства тесно переплетено с понятием сравнения, когда мы сопоставляем свойства и признаки, чтобы выявить схожие черты. Процесс сравнения требует наличия двух объектов, которые и сравниваются между собой. Данные рассуждения наводят на мысль, что понятие равенства не может иметь место, когда нет хотя бы двух объектов, чтобы было что сравнивать. При этом, конечно, может быть взято большее количество объектов: три и более, однако, в конечном, счете, мы так или иначе придем к сравнению пар, собранных из заданных объектов.

Смысл понятия «равенство» в обобщенном толковании отлично определяется словом «одинаковые». О двух одинаковых объектах можно говорить – «равные». Например, квадраты и . А вот объекты, которые хоть по какому-то признаку отличаются друг от другу, назовем неравными.

Говоря о равенстве, мы можем иметь в виду как объекты в целом, так и их отдельные свойства или признаки. Объекты являются равными в целом, когда одинаковы по всем характеристикам. Например, когда мы привели в пример равенство квадратов, имели в виду их равенство по всем присущим им свойствам: форме, размеру, цвету. Также объекты могут и не быть равными в целом, но обладать одинаковыми отдельными признаками. Например: и . Указанные объекты равны по форме (оба – круги), но различны (неравны) по цвету и размеру.

Таким образом, необходимо заранее понимать, равенство какого рода мы имеем в виду.

Запись равенств, знак равно

Чтобы произвести запись равенства, используют знак равно (или знак равенства), обозначаемый как =.Такое обозначение является общепринятым.

Составляя равенство, равные объекты размещают рядом, записывая между ними знак равно. К примеру, равенство чисел 5 и 5 запишем как 5=5. Или, допустим, нам необходимо записать равенство периметра треугольника АВС 6 метрам: PАВС=6 м.

Определение 1

Равенство – запись, в которой использован знак равно, разделяющий два математических объекта (или числа, или выражения и т.

п.).

Когда возникает необходимость письменно обозначить неравенство объектов, используют знак не равно, обозначаемый как ≠, т.е. по сути зачеркнутый знак равно.

Верные и неверные равенства

Составленные равенства могут соответствовать сути понятия равенства, а могут и противоречить ему. По этому признаку все равенства классифицируют на верные равенства и неверные равенства. Приведем примеры.

Составим равенство 7=7. Числа 7 и 7, конечно, являются равными, а потому 7=7 – верное равенство. Равенство 7=2, в свою очередь, является неверным, поскольку числа 7 и 2 не равны.

Свойства равенств

Запишем три основных свойства равенств:

Определение 2

свойство рефлексивности, гласящее, что объект равен самому себе;
свойство симметричности: если первый объект равен второму, то второй равен первому;
свойство транзитивности: когда первый объект равен второму, а второй – третьему, тогда первый равен третьему.

Буквенно сформулированные свойства запишем так:

a=a;
если a=b, то b=a;
если a=b и b=c, то a=c.

Отметим особенную пользу второго и третьего свойств равенств – свойств симметричности и транзитивности – они дают возможность утверждать равенство трех и более объектов через их попарное равенство.

Двойные, тройные и т.д. равенства

Совместно со стандартной записью равенства, пример которой мы приводили выше, также часто составляются так называемые двойные равенства, тройные равенства и т.д. Подобные записи представляют собой как бы цепочку равенств. К примеру, запись 2+2+2=4+2=6 – двойное равенство, а |AB|=|BC|=|CD|=|DE|=|EF| – пример четвертного равенства.

При помощи таких цепочек равенств оптимально составлять равенство трех и более объектов. Такие записи по своему смыслу являются обозначением равенства любых двух объектов, составляющих исходную цепочку равенств.

Например, записанное выше двойное равенство 2+2+2=4+2=6 обозначает равенства: 2+2+2=4+2, и 4+2=6, и 2+2+2=6, а в силу свойства симметричности равенств и 4+2=2+2+2, и 6=4+2, и 6=2+2+2.

Составляя подобные цепочки, удобно записывать последовательность решения примеров и задач: такое решение становится наглядным и отражает все промежуточные этапы вычислений.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Решение неравенств примеры. Решите неравенство 2х больше.

Альфашкола
Статьи
Примеры решения неравенств

Как решать неравенства?

Пример 1. Решите $-x+3>\:2x+1$

$-x+3>\:2x+1$

$-3x>-2$

$x<\frac{2}{3}$ $–>$ $\frac{2}{3}=0,67$

Ответ:$(-∞;\frac{2}{3})$ .

Пример 2. Решите $-3<\:5-2x<\:9$

Решение:

$-3<\:5-2x<\:9$

$-8<\:-2x<\:4$

$-4<\:-x<\:2$

Знаки меняются при умножении на $-1$

$4>\:x>\:-2$

$-2<\:x<\:4$

Ответ: $(2;4)$.

Пример 3. Решите $\frac{\left(x+3\right)}{\left(x-5\right)}>\:0$

Решение:

$\frac{\left(x+3\right)}{\left(x-5\right)}>\:0$

$x<-3$ и $\:x>5$

Ответ: $\:\left(-\infty \:,\:-3\right)\cup \left(5,\:\infty \:\right)$.

Пример 4. Решите $5\left(6+3x\right)+7\ge \:127$

Решение:

$5\left(6+3x\right)+7\ge \:127$

$5\left(6+3x\right)\ge \:120$

$\frac{5\left(6+3x\right)}{5}\ge \frac{120}{5}$

$6+3x\ge \:24$

$3x\ge \:18$

$x\ge \:6$

Ответ: $[6,\:\infty \:)$

Пример 5. Решите $-17<\:3+10x\le \:33$

Решение:

$-17<\:3+10x\le \:33$

$-20<\:10x\le \:30$

$-2<\:x\le \:3$

Ответ: $\:(-2,\:3]$.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы “Альфа”. Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку “Записаться” принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Зоя Юрьевна Духненко

Репетитор по математике

Стаж (лет)

Образование:

Душанбинский государственный педагогический институт им. Т. Г. Шевченко

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике 5-9 классов и по физике 7-9 классы. Подготовка к ОГЭ. Я люблю математику и очень стараюсь привить эту любовь детям. Ведь без математики наша жизнь была бы скучной и однообразной, мы много бы не узнали об окружающем нас мире. К каждому ребенку нахожу индивидуальный подход. Объясняю доступно, легко и просто.

Kateryna Toprak

Репетитор по математике

Стаж (лет)

Образование:

Erciyes üniversitesi

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

6 yıldır Türkiye’ de yaşamaktayım. Rusça ve Ukraynaca dillerine ana dilim olması sebebiyle ve de Rus Dili Edebiyatı mezunu olmam sebebiyle hem teorik hem pratikte hakimim. 2018’ den bu yana Türklere Rusça öğretmenliği yapmaktayım. Derslerimizi hedeflerinize ve seviyenize göre hazırlamaktayım, (konuşma, dinleme ve okuma aktiviteleri uyguluyorum). Ana dilimi anlatmaktan çok keyif alıyorum ve eminim ki siz de alırsınız. 2019′ den bu yana yabancilara (Rusça bilenlere) Türkçe öğretmenliği yapmaktayım.

Дмитрий Владимирович Лобачевский

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 5-11 классов. В преподавании для меня важно: не выглядеть в глазах ребенка врагом или неизбежным мучением. И совместными усилиями (преподаватель + ученик + родители) добиться понимания предмета. Каждый ученик задает свой собственный темп, в котором мы максимально эффективно проводим занятия. С радостью жду всех на своих занятиях!

Числовые равенства и неравенства

Равенство может быть верным и неверным.

Для формирования представлений о верных и неверных равенствах в учебнике 1-го класса используются примеры с окошками.

Например, вставь в окошки подходящие числа:

5-1= ; + = 4

Методом подбора ученик находит подходящие числа и проверяет верность равенства вычислением.

Процесс сравнения чисел и обозначение отношений между ними с помощью знаков сравнения приводит к получению неравенств.

Если одно число больше (меньше) другого, или одно выражение имеет значение больше (меньше), чем другое выражение, то, соединённые соответствующим знаком, они образуют неравенство.

Неравенства также могут быть верными и неверными:

Подбери числа так, чтобы записи были верными:

Методом подбора ученик находит подходящие числа и проверяет верность неравенства.

Ознакомление с равенствами и неравенствами в начальных классах непосредственно связывается с изучением нумерации и арифметических действий.

1) Сравнение чисел. Начинается в дочисловой период первого класса

· Путём соотнесения множеств один к одному

3=3

· Путём счёта элемента множества.

Положи слева кружки, а справа – треугольники. Каких фигур меньше? (кружков так как 5<7)

· По месту числа в натуральном ряду. 7>5,так как 7 в натуральном ряду стоит после 5.

· При изучении многозначных чисел путём сравнения разрядов, начиная с высшего.

450<475, так как 5 десятков < 7 десятков.

52345>9276, так как количество разрядов больше

53275<53901, так как 2 сотни < 9 сотен.

2) Сравнение именованных чисел.Заданные величины выражают в одинаковых единицах измерения (чаще всего в меньших) и сравниваются полученные числа.

3 км 500 м > 3 км 050м

3500 м > 3050 м

Задания для сравнения должны быть разнообразными:

a) 7 км 300 м =мм м

5090 кг = ц кг

b) ч < мин

см = дм

c) Вставить наименование

16 мин >16 … (сек)

35км = 35000 … (м)

d) Сравни, проверь и исправь ошибки.

4 т 8 ц = 480 кг (>) 2 м 05 см = 250 см (<)

4800 кг >480 кг 205 см < 250 см

3) Сравнение выражения и числа. Объяснение в 1 классе при изучении нумерации первого десятка.

На наборном полотне 3 треугольника и 3 круга.

3=3

Каких фигур больше? (поровну)

К 3 треугольникам придвинь ещё 1. Сколько треугольников стало? (4) Как получили?

3+1 3

Прочитай выражение: 3+1 (сумма 3 и 1). Сравните сумму 3 и 1 и числа 3.

3+1>3

Прочитай полученное неравенство (сумма 3 и 1 больше, чем 3)

Доказательство: 3+1 > 3, так как 4 > 3

Аналогично решаются неравенства вида

3-1 < 3

3 3

3-1 < 3, так как 2 < 3

Позднее дети находят значение выражения и сравнивают его с числом.

5+3… 8

8>5

Полезно дать на сравнение следующие выражения:

19-0…19 8…1*8 0/5…0 0/5…5

При выборе знака сравнения ученик вычисляет значение выражения и сравнивает его с заданным числом, что отражается в выборе соответствующего знака.

Возможен и другой способ выбора знака сравнения – без ссылки на вычисления значения выражения.

Например:

7+2…7; 10-3…10

4) Сравнение двух выражений.

Сравнить 2 выражения – значит сравнить их значения. Вводится при изучении = и – в пределах 10, а затем при изучении действий во всех концентрах.

При выборе знака сравнения ученик вычисляет значения выражений и сравнивает их, что отражается в выборе соответствующего знака:

35*1…35*0+35; 48:4…52:4

Возможен другой способ выбора знака сравнения – без ссылки на вычисления значения выражения:

5+4… 5+3; 7-5…7-3

Для формирования представлений о верных и неверных равенствах и неравенствах используются задания вида:

Проверь, верны ли неравенства:

45- 18<42; 50-8<58-10; 27+15>32

Выпиши верные равенства и неравенства:

9дес.9ед. >100; 5см 6мм+65мм; 69+8=77; 90-7<89

Для проверки используется метод вычисления значений и сравнения полученных чисел.

Неравенства с переменной.

Неравенство с переменной – математическая запись, состоящая из

выражения с переменной и другого числа или выражения, соединённые знаками «>» или «<».

Подготовка: 6+4>… 7+4<7+…

После введения буквы для обозначения неизвестного числа такие неравенства приобретают привычный вид неравенства с переменной:

С+3 <5, 10-с > 5, с*4>12, 72/с < 36

Значения неизвестных чисел в таких неравенствах находятся методом подбора, а затем подстановкой проверяется каждое подобранное число:

· Сначала для облегчения подбора дается ряд чисел: а+24>40, где а=15.16,17,18

· Подбор чисел самостоятельно 6*с < 37,с = 0,1,2,3,4,5,6. Какое самое маленькое (большое) число?

Особенность данных неравенств состоит в том, что могут быть подобраны несколько чисел, подходящих к ним (дающих верное неравенство).

В случае бесконечного множества решений или большого количества решений неравенства ученик ограничивается подбором нескольких значений переменной, при которых неравенство является верным.

4. Процесс усвоения младшими школьниками понятия «уравнения» и способов его решения можно разделить на три этапа:

1) Подготовительный.

На этом этапе подготовка учащихся к решению уравнений осуществляется по двум направлениям. 1-ое направление связано с усвоением взаимосвязи между компонентами каждого арифметического действия (как найти неизвестное слагаемое, уменьшаемое, вычитаемое). 2-ое направление связано со специальными упражнениями, в процессе выполнения которых у учащихся формируется представление о переменной и о верном или неверном числовом равенстве («примеры с окошками»). В процессе выполнения упражнений ученики овладевают одним из способов решения уравнения – подбором числового значения, при котором уравнение обращается в верное числовое равенство.

Правильная организация учебной деятельности школьников существенно зависит от тех заданий, которые формулирует учитель, предлагая им «примеры с окошками».

3+ =7. Вставь в окошко нужное число.

Дети быстро дают ответ, опираясь на знание состава числа, а способ подстановки теряет свой алгебраический смысл.

Необходимо иначе формулировать задание:

· Какое число нужно вставить в окошко, чтобы получить верное равенство?

· Объясни, почему числа 1, 2, 3, 5 нельзя вставить в окошко?

· Какое равенство получим, если вставим в окошко число 6?

Поставленные таким образом вопросы подготавливают учащихся к осознанию такой операции, как проверка решения уравнения.

2) Знакомство с уравнением и овладение способами его решения.

Замена окошка латинской буквой (а, с, d), введение термина «неизвестное число», узнавание уравнений среди других математических записей (выражения, равенства, неравенства), ориентируясь на то, что уравнение– равенство, содержащее неизвестное число.

Сравнение двух записей вида:

6+ =9 и 6+с=9 позволяют учащимся самостоятельно справиться с решением уравнений способом подбора. Аналогично 6* =30; 6*а=30; 40: =5; 40:с=5.

Для того, чтобы учащиеся при решении уравнений использовали правила, раскрывающие взаимосвязь компонентов арифметических действий, надо предлагать упражнения, которые нельзя быстро решить методом подбора.

1сл. 2сл. сумма

Х + 13 = 71

Решить уравнение – значит найти такое значение неизвестного числа, при котором равенство будет верным. Это число называется корнем уравнения.Если значение неизвестного числа найдено верно, то получается верное равенство.

Тест-тренажёр по математике для 1 класс за 4 четверть с ответами!

Математика / 1 класс / Тесты

Онлайн-тест за IV четверть покажет, как ребенок научился решать примеры на сложение и вычитание, составлять и решать неравенства, узнавать геометрические фигуры.

Задания в тесте составлены с учетом пройденного материала. Ребенку будет предложено найти сумму, сравнить числовые выражения, составить неравенство, определить геометрическую фигуру, выполнить перевод мер длины, решить задачи в одно и два действия.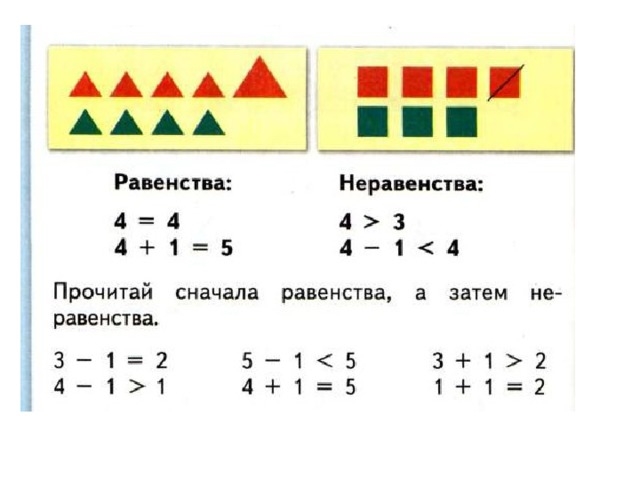

Результат теста:

Более 2500 заданий для развития математических способностей и логического мышления — в онлайн‑курсе ЛогикЛайк.

Предложите ребенку решить тест и узнайте, как маленький школьник усвоил материал по математике за 4 четверть. Тест поможет учителям и родителям определить уровень усвоения материала и выявить «слабые места» — темы, которые необходимо еще раз проработать с ребенком.

В четвертой четверти на уроках математики первоклассники учатся:

Читать, записывать, сравнивать, упорядочивать числа от 0 до 20;
Решать примеры на сложение и вычитание в пределах 20 устно и письменно;
Понимать связь между суммой и слагаемыми;
Применять переместительное свойство сложения;
Составлять и читать неравенства;
Использовать единицы измерения длины сантиметр, дециметр и знать соотношение между ними;
Выполнять измерение длины с помощью линейки;
Различать, называть геометрические фигуры: треугольник, прямоугольник (квадрат), круг; куб и шар;
Решать задачи в два действия;
Распознавать верные и неверные элементарные логические высказывания.

Тест составлен на основе программного материала по математике для учеников 1 класса и соответствует требованиям ФГОС.

Сумма каких чисел равна 9?

Варианты ответов:
а) 3 и 4
б) 2 и 7
в) 4 и 6
г) 8 и 2

Узнать ответ

Ответ: б) 2 и 7.

Сравни, выбери знак > 13 + 0 ☐ 12 + 1

Варианты ответов:
а) >
б) в) =

Узнать ответ

Ответ: в) =.

У Вани было две монеты по 5 копеек, а у Маши было три монеты по 3 копейки. У кого из детей было больше денег?

Варианты ответов:
а) у Вани
б) у Маши

Узнать ответ

Ответ: а) у Вани.

Выбери число, чтобы неравенство стало верным.
10 − 3

Варианты ответов:
а) 7
б) 6
в) 9

Узнать ответ

Ответ: в) 9.

Чтобы решать задачи, начните занятия онлайн!

Выбери квадрат.

Варианты ответов:
а) 1
б) 2
в) 3
г) 4

Узнать ответ

Ответ: б) 2.

Длина отрезка 20 см. Укажи длину этого отрезка в дециметрах.

Варианты ответов:
а) 2 дм
б) 12 дм
в) 20 дм
г) 10 дм

Узнать ответ

Ответ: а) 2 дм.

Верно ли, что разность чисел 5 и 2 равна 7?

Варианты ответов:
а) Да
б) Нет

Узнать ответ

Ответ: б) Нет.

Выбери число, чтобы равенство стало верным:
6 − 1 + ☐ = 9

Варианты ответов:
а) 7
б) 5
в) 4
г) 3

Узнать ответ

Ответ: в) 4.

В каком примере будет наибольшая сумма?

Варианты ответов:
а) 2 + 3 =
б) 9 − 2 =
в) 3 + 3 =

Узнать ответ

Ответ: б) 9 − 2 =.

Бабушка испекла 4 пирожка с капустой, 6 пирожков с картошкой и 5 пирожков с мясом. Сколько всего пирожков испекла бабушка?

Варианты ответов:
а) 10
б) 15
в) 16
г) 14

Узнать ответ

Ответ: б) 15.

Попробуйте пройти другие «Математические тесты для 1 класса».

Решение неравенств – объяснение и примеры

Что такое неравенство в математике?

Слово неравенство означает математическое выражение, в котором стороны не равны друг другу. По сути, неравенство сравнивает любые два значения и показывает, что одно значение меньше, больше или равно значению на другой стороне уравнения.

В основном существует пять символов неравенства, используемых для представления уравнений неравенства.

Символы неравенства

Эти символы неравенства: меньше ( < ), больше ( > ), меньше или равно ( ≤ ), больше или равно ( ≥ ) и символ не равно ( ≠ ). .

Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, удовлетворяющих условиям данной переменной.

Операции над неравенствами

Операции над линейными неравенствами включают сложение, вычитание, умножение и деление. Общие правила для этих операций показаны ниже.

Хотя мы использовали символ < для иллюстрации, вы должны отметить, что те же самые правила применяются к >, ≤ и ≥.

Символ неравенства не меняется, если к обеим сторонам неравенства прибавляется одно и то же число. Например, если a< b, то a + c < b +
Вычитание обеих частей неравенства на одно и то же число не меняет знак неравенства. Например, если a< b, то – c < b – c.
Умножение обеих частей неравенства на положительное число не меняет знак неравенства. Например, если a< b и c — положительное число, то a * c < b *
Деление обеих частей неравенства на положительное число не меняет знак неравенства. Если a< b и если c является положительным числом, то a/c < b/c
Умножение обеих частей уравнения неравенства на отрицательное число изменяет направление символа неравенства. Например, если a < b и c — отрицательное число, тогда a * c > b *
Аналогично, деление обеих частей уравнения неравенства на отрицательное число изменяет символ неравенства. Если a < b и c — отрицательное число, то a /c > b/c

Как решать неравенства?

Как и линейные уравнения, неравенства можно решать, применяя аналогичные правила и шаги за некоторыми исключениями. Единственным отличием при решении линейных уравнений является операция, включающая умножение или деление на отрицательное число. Умножение или деление неравенства на отрицательное число изменяет символ неравенства.

Линейные неравенства решаются с помощью следующих операций:

Сложение
Вычитание
Умножение
Деление
Распределение имущества

Решение линейных неравенств со сложением

Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.

Пример 1

Решите 3x – 5 ≤ 3 – x.

Решение

Начнем со сложения обеих частей неравенства на 5

3x – 5 + 5 ≤ 3 + 5 − x

3x ≤ 8 – x

Затем добавьте обе стороны на x.

3x + x ≤ 8 – x + x

4x ≤ 8

Наконец, разделите обе части неравенства на 4, чтобы получить;

x ≤ 2

Пример 2

Рассчитайте диапазон значений y, что удовлетворяет неравенству: Y – 4 <2y + 5.

Solution

ADD ADD ADD ADD + 5.

7777 9000

. обе части неравенства на 4.

у – 4 + 4 < 2у + 5 + 4

y < 2y + 9

Вычесть обе части на 2y.

y – 2y < 2y – 2y + 9

Y < 9 Умножьте обе части неравенства на −1 и измените направление символа неравенства. y > − 9

Решение линейных неравенств с вычитанием

Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.

Пример 3

Решите x + 8 > 5.

Решение

Изолируйте переменную x, вычитая 8 из обеих частей неравенства.

х + 8 – 8 > 5 – 8 => х > −3

Следовательно, х > −3.

Пример 4

Решение 5x + 10> 3x + 24.

Раствор

Вычтите 10 с обеих сторон неравности.

5x + 10 – 10 > 3x + 24 – 10

5x > 3x + 14.

Теперь вычитаем обе части неравенства в 3 раза.

5x – 3x > 3x – 3x + 14

2x > 14

x > 7

Решение линейных неравенств с умножением Ниже приведены несколько примеров, чтобы понять эту концепцию. Пример 50005

4 (x/4)> 5 x 4

x> 20

Пример 6

Solve -x/4 ≥ 100005

Раствор:

. стороны неравенства на 4.

4(-x/4) ≥ 10 x 4

-x ≥ 40

Умножьте обе части неравенства на -1 и измените направление символа неравенства.

x ≤ – 40

Решение линейных неравенств с делением

Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.

Пример 7

Решение неравенства: 8x – 2> 0.

Раствор

Сначала добавьте обе стороны из несравненного. + 2 > 0 + 2

8x > 2

Теперь решите, разделив обе части неравенства на 8, чтобы получить;

х > 2/8

х > 1/4

Пример 8

Решите следующее неравенство:

-5x> 100

Решение

Разделение обеих сторон неравенства на -5 и изменение именового и изменение. символ

= -5x/-5 < 100/-5

= x < - 20

Решение линейных неравенств с использованием свойства распределения

Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.

Пример

Решение: 2 (x – 4) ≥ 3x – 5

Решение

2 (x – 4) ≥ 3x – 5

Применить свойство распределения, чтобы удалить искажения.

⟹ 2x – 8 ≥ 3x – 5

Добавить обе стороны на 8.

⟹ 2x – 8 + 8 ≥ 3x – 5 + 8

⟹ 2x ≥ 3x + 3

Обегают обе стороны по 3.

⟹ 2x – 3x ≥ 3x + 3 – 3x

⟹ -x ≥ 3

⟹ x ≤ – 3

Пример 10

Студент набрал 60 баллов за первый тест и 45 баллов за второй тест итогового экзамена. Сколько минимальных баллов должен набрать учащийся в третьем тесте, чтобы в среднем было не менее 62 баллов?

Решение

Пусть в третьем тесте набрано x баллов.

(60 + 45 + x)/3 ≥ 62
105 + x ≥ 196
x ≥ 93
Таким образом, учащийся должен набрать 93 балла, чтобы поддерживать средний балл не менее 62 баллов.

Пример 11

Джастину требуется не менее 500 долларов для проведения вечеринки по случаю его дня рождения. Если он уже накопил 150 долларов и до этой даты осталось 7 месяцев. Какую минимальную сумму он должен откладывать ежемесячно?

Решение

Пусть минимальная сумма сэкономленной ежемесячно = x

150 + 7x ≥ 500

Решение для x

150 – 150 + 7x ≥ 500 – 150

x ≥ 500005

С. $50 или больше

Пример 12

Найдите два последовательных нечетных чисел, которые превышают 10 и имеют сумму менее 40,

Раствор

Пусть меньшее число нечетное = x

Следовательно, следующее число будет x + 2

x > 10 ………. больше 10

x + (x + 2) < 40 ……сумма меньше 40

Решите уравнения.

2x + 2 < 40

x + 1< 20

x < 19

Объедините два выражения.

10 < x < 19

Следовательно, последовательные нечетные числа равны 11 и 13, 13 и 15, 15 и 17, 17 и 19. и визуализировать числа – это числовая линия. Числовая линия определяется как прямая горизонтальная линия с числами, расположенными вдоль через равные сегменты или интервалы. Числовая линия имеет нейтральную точку посередине, известную как начало координат. Справа от начала координат на числовой прямой находятся положительные числа, а слева от начала координат — отрицательные числа.

Линейные уравнения также могут быть решены графическим методом с использованием числовой прямой. Например, чтобы изобразить x > 1 на числовой прямой, вы обводите цифру 1 на числовой прямой и рисуете линию, идущую от круга в направлении чисел, которая удовлетворяет утверждению о неравенстве. Пример 13 и заполните или заштрихуйте круг. Наконец, нарисуйте линию, идущую от заштрихованного круга в направлении чисел, которая удовлетворяет уравнению неравенства.

Пример 14

х ≥ 1

Пример 15

–2 < x <2

9004 . Пример 16

≤ . 40050449444444444494444944444444444444444444444444444444444444444444444444444444444444444494449.

944444444444444444494494494494494494494494449.

Example 17
–1 < x ≤ 2

Solving Inequalities
Sometimes we need to solve Inequalities like these:
Symbol
Слова
Пример
>
больше
х + 3 > 2
<
меньше
7x < 28
≥
больше или равно
5 ≥ х – 1
≤
меньше или равно
2 года + 1 ≤ 7
Решение
Наша цель состоит в том, чтобы иметь x (или любую другую переменную) сам по себе слева от знака неравенства:
Что-то вроде: х < 5
или: г ≥ 11
Мы называем это «решенным».
Пример: x + 2 > 12
Вычтем 2 из обеих сторон:
x + 2 − 2 > 12 − 2
Упростим:
x > 10
Решено!
Как решать
Решение неравенств очень похоже на решение уравнений … мы делаем почти то же самое …
… но мы также должны обратить внимание на направление неравенства .

Направление: Куда “указывает” стрелка
Некоторые вещи могут изменить направление !
< становится >
> становится <
≤ становится ≥
≥ становится ≤
номер с двух сторон
Умножить (или разделить) обе части на положительный номер
Упростить сторону
Пример: 3x
< 7+3
Мы можем упростить 7+3, не затрагивая неравенство:
3x < 10
пример):
Умножить (или разделить) обе части на отрицательное число
Поменять местами левую и правую стороны
Пример: 2y+7
< 12
Когда мы меняем местами левую и правую части, мы также должны изменить направление неравенства :
12 > 2y+7
Вот подробности:
Добавление или вычитание значения
Часто мы можем решать неравенства, добавляя (или вычитая) число с обеих сторон (так же, как во Введении в алгебру), например:
Пример: x + 3
< 7
Если мы вычтем 3 с обеих сторон, получаем:
x + 3 − 3 < 7 − 3
x < 4
И это наше решение: x < 4
Другими словами, любое значение меньше 4. x 9.

Что мы сделали?
Мы пошли от этого:

Сюда:

х+3 < 7

х < 4

И это хорошо работает для , добавляя и вычитая , потому что, если мы прибавим (или вычтем) одно и то же количество с обеих сторон, это не повлияет на неравенство
Пример: У Алекса больше монет, чем у Билли. Если и Алекс, и Билли получат по три монеты больше, у Алекса все равно будет больше монет, чем у Билли.
Что, если я решу это, но “x” окажется справа?
Неважно, просто поменяйте стороны местами, но перевернет знак , чтобы он все равно «указывал» на правильное значение!
Пример: 12
< x + 5
Если вычесть 5 из обеих частей, мы получим:
12 − 5 < x + 5 − 5
7 < x
Это решение!
Но нормально поставить “х” слева…
… так что давайте поменяем местами (и знак неравенства!):
x > 7
Видите, как неравенство знак по-прежнему «указывает» на меньшее значение (7) ?
Вот наше решение: x > 7
Примечание: “x” может быть справа, но людям обычно нравится видеть его слева.
Умножение или деление на значение
Еще мы делаем умножение или деление обеих частей на значение (так же, как в Алгебре – Умножение).
Но нам нужно быть немного осторожнее (как вы увидите).

Положительные значения
Все в порядке, если мы хотим умножить или разделить на положительное число :
Пример: 3y
< 15
Если мы разделим обе части на 3, мы получим:
3y 34 < 15 /3
y < 5
И это наше решение: y < 5

Отрицательные значения
Когда мы умножаем или делим на отрицательное число
мы должны обратить неравенство.

Почему?
Ну, вы только посмотрите на числовой ряд!
Например, от 3 до 7 это увеличение ,
, а от -3 до -7 это уменьшение.
−7 < −3 7 > 3
Видите, как меняется знак неравенства (с < на >)?
Рассмотрим пример:
Пример: −2y
< −8
Разделим обе части на −2 … и обратим неравенство !
−2y < −8
−2y /−2 > −8 /−2
y > 4
И это правильное решение: y > 4
(Обратите внимание, что я перевернул неравенство в той же строке Я разделил на отрицательное число.)
Итак, просто помните:
При умножении или делении на отрицательное число, перевернуть неравенство
Умножение или деление на переменные
Вот еще один (хитрый!) пример:
Пример: bx
< 3b
Кажется легким просто разделить обе части на b , что дает нам:
x < 3
. .. но подождите … если b равно отрицательному , нам нужно обратить неравенство следующим образом:
x > 39
Но мы не знаем, является ли b положительным или отрицательным, поэтому мы не можем ответить на этот вопрос !
Чтобы помочь вам понять, представьте себе замену b на 1 или −1 в примере bx < 3b :
, если b равно 1 , то ответ x < 3
, но если b равно −1 , то мы решаем −x < −3 , и ответ равен x > 3
.
Ответ может быть x < 3 или x > 3 , и мы не можем выбрать, потому что не знаем b .
Так:
Не пытайтесь делить на переменную для решения неравенства (если только вы не знаете, что переменная всегда положительна или всегда отрицательна).
Большой пример
Пример:
x−3 2 < −5
Во-первых, давайте удалим «/2», умножив обе части на 2.
Поскольку мы умножаем на положительное число , неравенства не изменятся.
x−3 2 ×2 < −5 ×2
x−3 < −10
Теперь прибавьте 3 к обеим сторонам: 1−0 9 + 3
x < −7
И это наше решение: x < −7
Два неравенства сразу!
Как мы можем решить что-то с двумя неравенствами сразу?
Пример:
−2 < 6−2x 3 < 4
Сначала удалим «/3», умножив каждую часть на 3.
Поскольку мы умножаем на положительное число, неравенства не выполняются. t change:
−6 < 6−2x < 12
Теперь из каждой части вычтем 6:
−12 < −2x < 6
Теперь разделим каждую часть на 2 (положительное число, так что снова неравенство не изменится):
−6 < −x < 3
Теперь умножим каждую часть на −1 . Поскольку мы умножаем на отрицательное число , неравенства меняют направление .
6 > x > −3
И это решение!
Но для аккуратности лучше иметь меньший номер слева, больший справа. Итак, поменяем их местами (и убедимся, что неравенства указывают правильно):
−3 < x < 6

Итог
Многие простые неравенства можно решить путем сложения, вычитания, умножения или деления обеих частей до тех пор, пока не останется переменная сама по себе.
Но эти вещи изменят направление неравенства:
Умножение или деление обеих частей на отрицательное число
Замена левой и правой сторон
Не умножайте и не делите на переменную (если только вы не знаете, что она всегда положительна или всегда отрицательна)

4.7 Решение линейных неравенств | Уравнения и неравенства
Предыдущий
4. 6 Буквенные уравнения
Следующий
4.8 Краткое содержание главы
4.7 Решение линейных неравенств (EMA3H)
Линейное неравенство похоже на линейное уравнение в том, что наибольший показатель степени переменной равен $\текст 1}$. Ниже приведены примеры линейных неравенств.
\начать{выравнивать*} 2х+2&\ле 1\ \frac{2 – x}{3x + 1} & \ge 2 \\ \frac{4}{3}x – 6 & < 7x + 2 \конец{выравнивание*}
Методы, используемые для решения линейных неравенств, аналогичны тем, которые используются для решения линейных уравнений. Единственный разница возникает, когда есть умножение или деление, которое включает знак минус. Например, мы знайте, что $8>6$. Если обе части неравенства разделить на $-\text{2}$, то получим $-4>-3$, что неверно. Следовательно, знак неравенства необходимо поменять местами, что дает $-4<-3$.
Чтобы сравнить неравенство с нормальным уравнением, мы сначала решим уравнение.
Решите $2x + 2 = 1$:
\начать{выравнивать*} 2х+2&=1\ 2х & = 1 – 2 \ 2х&=-1\ х & = -\фракция{1}{2} \конец{выравнивание*}
Если мы представим этот ответ на числовой прямой, мы получим:
Теперь найдем $x$ в неравенстве $2x + 2 \le 1$:
\начать{выравнивать*} 2х+2&\ле 1\ 2x&\le 1 – 2\ 2х&\ле-1\ х & \ le – \ гидроразрыва {1} {2} \конец{выравнивание*}
Если мы представим этот ответ на числовой прямой, мы получим:
Мы видим, что для уравнения существует только одно значение $х$, для которого уравнение верно. Однако, для неравенства существует диапазон значений, для которых неравенство верно. Это главное отличие между уравнением и неравенством.
Помните: когда мы делим или умножаем обе части неравенства на отрицательное число, направление изменения неравенства. Например, если $x<1$, то $-x>-1$. Также обратите внимание, что мы не можем разделить или умножить на переменную.
Следующее видео знакомит с линейными неравенствами.
Видео: 2FGH
Интервальное обозначение (EMA3J)
Примеры:
$\влево(4;12\вправо)$
Круглые скобки означают, что номер не включен. В этот интервал входят все действительные числа больше, но не равны $\text{4}$ и меньше, но не равны $\текст{12}$.
$\влево(-\infty ;-1\вправо)$
Круглые скобки всегда используются для положительной и отрицательной бесконечности. Этот интервал включает все действительные числа меньше, но не равны $-\text{1}$.
$\влево[1;13\вправо)$
Квадратная скобка означает, что число включено. В этот интервал входят все действительные числа больше или равные $\text{1}$ и меньше, но не равные $\текст{13}$.
Важно отметить, что это обозначение может использоваться только для представления интервала действительных чисел.
Мы представим приведенный выше ответ в интервальной нотации как $\left(-\infty ; -\frac{1}{2}\right]$
Рабочий пример 17: Решение линейных неравенств
Найдите $r$:
\[6 – г > 2\]
Ответ представить в числовой строке и в интервальной записи.
Переставить и решить для $r$
\начать{выравнивать*} -r & > 2 – 6 \\ -r & > -4 \конец{выравнивание*}
Умножение на $-\text{1}$ и обратный знак неравенства
\[г < 4\]
Представьте ответ в числовой строке
Представить ответ в интервальной нотации
\[\влево(-\infty ; 4\вправо)\]
Рабочий пример 18: Решение линейных неравенств
Найдите $q$:
\[4q + 3 < 2(q + 3)\]
Ответ представить в числовой строке и в интервальной записи.
Развернуть скобу
\начать{выравнивать*} 4q + 3 & < 2(q + 3) \\ 4q + 3 & < 2q + 6 \end{выравнивание*}
Переставить и решить для $q$
\начать{выравнивать*} 4q + 3 & < 2q + 6 \\ 4q - 2q & < 6 - 3 \\ 2q & < 3 \конец{выравнивание*}
Разделить обе стороны на $\text{2}$
\начать{выравнивать*} 2q & < 3 \\ д & < \ гидроразрыва {3} {2} \end{выравнивание*}
Представьте ответ в числовой строке
Представить ответ в интервальной нотации
$\left(-\infty ; \frac{3}{2}\right)$
температура текст
Рабочий пример 19: Решение сложных линейных неравенств
Найдите $x$:
\[5 \le x + 3 < 8\]
Ответ представить в числовой строке и в интервальной записи.
Вычесть $\text{3}$ из всех частей неравенства
\[\begin{массив}{ccccc} 5 – 3 &\le&x + 3 – 3 &< & 8 - 3 \\ 2 & \le & x & < & 5 \конец{массив}\]
Представьте ответ в числовой строке
Представить ответ в интервальной нотации
$\влево[2 ; 5\вправо)$
температура текст
Учебник Упражнение 4.6
$x < -1 \text{ и } x \ge 6 ; x \in \mathbb{R}$
$3 < x < 6 ; x \in \mathbb{R}$
$x \neq 3 ; x \neq 6 ; x \in \mathbb{R}$
$x > -10 ; x \in \mathbb{R}$
$3x + 4 > 5x + 8$
\начать{выравнивать*} 3х+4&>5х+8\ 3х – 5х & > 8 – 4\ -2х > 4\ 2х<-4\ х < -2 \конец{выравнивание*}
Представлено на числовой прямой:
В интервальной записи: $(-\infty; -2)$
$3(x – 1) – 2 \le 6x + 4$
\начать{выравнивать*} 3(х – 1) – 2 & \le 6x + 4 \\ 3х – 5 и \ле 6х + 4\ 3х – 6х &\ле 4+5\ -3х\ле 9\ х \ge -\frac{9}{3} \\ х \ гэ -3 \конец{выравнивание*}
Представлено на числовой прямой:
В интервальной записи: $[-3; \infty)$
$\dfrac{x – 7}{3} > \dfrac{2x – 3}{2} $
\начать{выравнивать*} \frac{x – 7}{3} & > \frac{2x – 3}{2} \\ 2(х – 7) & > 3(2х – 3) \\ 2х – 14 > 6х – 9\ -4х > 5\ х < -\фракция{5}{4} \конец{выравнивание*}
Представлено на числовой прямой:
В интервальной записи: $(-\infty; -\frac{5}{4})$
$-4(x – 1) < x + 2$
\начать{выравнивать*} -4 (х – 1) & < х + 2 \\ -4x + 4 & < х + 2 \\ -5х < -2\ х > \ гидроразрыва {2} {5} \конец{выравнивание*}
Представлено на числовой прямой:
В интервальной записи: $(\frac{2}{5}; \infty)$
$\dfrac{1}{2}x + \dfrac{1} {3}(x – 1) \ge \dfrac{5}{6}x – \dfrac{1}{3}$
\начать{выравнивать*} \frac{1}{2}x + \frac{1}{3}(x – 1) & \ge \frac{5}{6}x – \frac{1}{3} \\ \frac{1}{2}x + \frac{1}{3}x – \frac{1}{3} & \ge \frac{5}{6}x – \frac{1}{3} \ \ \frac{1}{2}x + \frac{1}{3}x – \frac{5}{6}x & \ge \frac{1}{3} – \frac{1}{3} \ \ \frac{3}{6}x + \frac{2}{6}x – \frac{5}{6}x & \ge 0 \\ 0x\ge 0 \конец{выравнивание*}
Неравенство верно для всех действительных значений $x$.
$-2 \le x – 1 < 3$
\[\begin{массив}{ccccc} -2 & \le & x – 1 & < & 3 \\ -1 & \le & x & < & 4 \конец{массив}\]
Представлено на числовой прямой:
В интервальной записи: $[-1; 4)$
$-5 < 2x - 3 \le 7$
\[\begin{массив}{ccccc} -5&<&2x - 3&\le&7\ -2 & < & 2x & \le & 10 \\ -1 & < & х & \ле & 5 \конец{массив}\]
Представлено на числовой прямой:
В интервальной записи: $(-1; 5]$
$7(3x + 2) – 5(2x – 3) > 7$
\начать{выравнивать*} 7 (3x + 2) – 5 (2x – 3) & > 7 \\ 21х + 14 – 10х + 15 и > 7\ 11х&>-22\ х & > -2 \конец{выравнивание*}
Представлено на числовой прямой:
В интервальной записи: $(-2; \infty)$
$\dfrac{5x – 1}{-6} \ge \dfrac{1 – 2x}{ 3}$
\начать{выравнивать*} \frac{5x – 1}{-6} & \ge \frac{1 – 2x}{3} \\ 5x – 1 & \ge -2(1 – 2x) \\ 5x – 1 & \ge -2 + 4x \ 5x – 4x & \ge -1\ х & \ ge -1 \конец{выравнивание*}
Представлено на числовой прямой:
В интервальной записи: $[-1; \infty)$
$3 \ле 4 – х \ле 16$
\[\begin{массив}{ccccc} 3&\ле&4 – х&\ле&16\ -1&\le&-x&\le&12\ 1 & \ge & x & \ge & -12 \конец{массив}\]
Представлено на числовой прямой:
В интервальной записи: $[1; 12]$
$\dfrac{-7y}{3} – 5 > -7$
\начать{выравнивать*} \frac{-7y}{3} – 5 & > -7 \\ -7у – 15 и > -21\ -7у&>-6\ у & < \ гидроразрыва {6} {7} \конец{выравнивание*}
Представлено на числовой прямой:
В интервальной записи: $(-\infty;\frac{6}{7})$
$1 \le 1 – 2y < 9$
\[\begin{массив}{ccccc} 1&\le&1 – 2у&<&9\ 0&\le&-2y&<&8\ 0 & \ge & y & > & -4 \\ -4 & < & у & \ле & 0 \конец{массив}\]
Представлено в числовой строке:
В интервальной записи: $(-4;0]$
$-2 < \dfrac{x - 1}{-3} < 7$
\[\begin{массив}{ccccc} -2 & < & \dfrac{x - 1}{-3} & < & 7 \\ 6&>&х-1&>&-21\ 7&>&х&>&-20\ -20 & < & х & < & 7 \конец{массив}\]
Представлено на числовой прямой:
В интервальной записи: $(-20;7)$
$2x -1 < 3(x+11)$
\begin{align*} 2 х -1 &< 3(х +11) \\ 2 х -1 &< 3 х +33 \\ 2 х -3 х &< 33 +1 \ -1 х &< 34\ \поэтому х &> -34 \end{выравнивание*}
\[\left(-34;\infty\right)\]
$x -1 < -4(x-6)$
\begin{align*} х-1 &<-4(х-6) \\ х -1 &< -4 х +24 \\ х +4 х &< 24 +1 \\ 5 х &< 25\ \поэтому х &< 5 \end{align*}
\[\left(-\infty;5\right)\]
$\dfrac{x-1}{8} \leq \dfrac{2(x-2)}{3}$
\начать{выравнивать*} \frac{x-1}{8} &\leq \frac{2(x-2)}{3} \\ 3(х-1) &\leq 16(х-2) \\ 3x-3 &\leq 16x-32\ 3x -16x &\leq -32 +3\ -13x &\leq -29\ \поэтому х &\geq\frac{29}{13} \конец{выравнивание*}
$\; x \in \left[ \frac{29}{13} ;\infty\right)$.
$\dfrac{x+2}{4} \leq \dfrac{-2(x-4)}{7}$
\начать{выравнивать*} \frac{x+2}{4} &\leq \frac{-2(x-4)}{7} \\ 7(х+2) &\leq -8(х-4) \\ 7x+14 &\leq -8x+32 \\ 7x +8x &\leq 32 -14\ 15x &\leq 18\\ \поэтому х &\leq\frac{6}{5} \конец{выравнивание*}
$\; x \in \left(-\infty; \frac{6}{5} \right]$.
$\dfrac{1}{5}x – \dfrac{5}{ 4}(x+2) > \dfrac{1}{4}x + 3$
\begin{align*} \frac{1}{5}x – \frac{5}{4}(x+2) &> \frac{1}{4}x +3 \\ 4x – 25(x+2) &> 5x +60 \\ 4х – 25х-50 &> 5х +60\ 4х – 25 х -5х &> 60 + 50\\ -26x &> 110\\ \следовательно, x &< -\frac{55}{13} \end{выравнивание*}
Интервал: \[\left(-\infty;-\frac{55}{13}\right)\]
$\dfrac{1}{5}x – \dfrac{2}{5}(x+3) \geq \dfrac{4}{2}x +3$
\begin{align*} \frac{1}{5}x – \frac{2}{5}(x+3) &\geq \frac{4}{2}x +3 \\ 2x – 4(x+3) &\geq 20x +30 \\ 2x – 4x-12 &\geq 20x+30\ 2x – 4 x -20x &\geq 30 + 12\\ -22x &\geq 42\\ \поэтому x &\leq -\frac{21}{11} \end{выравнивание*}
Интервал: \[\left(-\infty;-\frac{21}{11}\right]\]
$4x +3 < -3 \quad\text{or}\quad 4x +3 > 5$
Решите неравенство: \[\begin{массив}{rclcrcl} 4x +3 &<& -3 &\text{or}& 4x +3 &>& 5 \\ 4x &<& -3-3 &\text{or}& 4x &>& 5-3 \\ х &<& \frac{-3-3}{4} &\text{or}& x &>& \frac{5-3}{4} \\ x &<& - \frac{3}{2} &\text{or}& x &>& \frac{1}{2} \\ \конец{массив}\]
\[\left(-\infty; – \frac{3}{2}\right) \cup \left(\frac{1}{2}; \infty\right)\]
$4 \ ge -6x -6 \ge -3$
Решите неравенство: \[\begin{массив}{rcccl} 4 &\ge&-6x -6 &\ge&-3 \\ 4+6 &\ge& -6x &\ge& -3+6 \\ \frac{4+6}{-6} &\le& x &\le& \frac{-3+6}{-6} \\ – \frac{5}{3} &\le& x &\le& – \frac{1}{2} \\ \конец{массив}\]
\[\left[- \frac{5}{3}; – \frac{1}{2}\right]\]
$6b – 3 > b + 2 , ~b \in \mathbb{Z}$
\начать{выравнивать*} 6b – 3 > b + 2 , ~b \in \mathbb{Z}\\ 5б > 5\ б > 1 \конец{выравнивание*}
$3a – 1 < 4a + 6 , ~a \in \mathbb{N}$
\начать{выравнивать*} 3а – 1 < 4а + 6\ -а < 7\ а > -7 \конец{выравнивание*}
Однако нам говорят, что $a \in \mathbb{N}$ и, следовательно, $a > 0$.
$\dfrac{b-3}{2} + 1 < \dfrac{b}{4} - 4 , ~b \in \mathbb{R}$
\начать{выравнивать*} \frac{b-3}{2} + 1 < \frac{b}{4} - 4 \\ 2б - 6 + 4 < б - 16\ б < -14 \конец{выравнивание*}
$\dfrac{4a +7}{3} – 5 > a – \dfrac{2}{3} , ~a \in \mathbb{N}$
\начать{выравнивать*} \frac{4a +7}{3} – 5 > a – \frac{2}{3} \\ 4а + 7 – 15 > 3а – 2\ а > 6 \конец{выравнивание*}
Предыдущий
4.6 Буквенные уравнения
Оглавление
Следующий
4. 8 Краткое содержание главы
Реальные ситуации Образовательные ресурсы Обучение K12, выражения и уравнения, предварительная алгебра, планы уроков по математике, упражнения, эксперименты, помощь на дому 5 миллионов долларов. Каковы два возможных значения цены кольца? Как вы можете использовать числовое предложение для представления этой суммы?
Неравенства и уравнения постоянно используются в окружающем вас мире.
Прежде чем продолжить, если вы пропустили или хотели бы просмотреть предыдущий урок из этой серии Уравнения и неравенства , найдите его в разделе Связанные уроки на правой боковой панели.
Ситуации могут показаться вам не математическими, потому что вы с ними так хорошо знакомы. Если у вас есть мобильный телефон, у вас может быть определенное количество текстовых сообщений или телефонных звонков, которые вы можете использовать каждый месяц. На дорогах есть ограничения скорости, у некоторых фильмов есть ограничения по возрасту, а время, необходимое вам, чтобы дойти до парка, — все это примеры неравенства. Неравенство не представляет точную сумму, а вместо этого представляет собой предел того, что разрешено или что возможно. Уравнения представляют значения, которые равны .
Для начала посмотрите видеоклип MooMoo Math and Science, чтобы узнать о задачах на неравенство. Пока вы смотрите Решение неравенств — Задания на слова — Математика 6-го класса , запишите фразы, представляющие данный символ сравнения, в свой математический журнал (клип заканчивается на 0:57):
> ≥ < ≤

После просмотра видео просмотрите таблицу в этом интерактивном приложении, чтобы убедиться, что у вас есть все фразы из видео. Нажмите на каждый символ, чтобы прочитать фразы, которые представляют его в неравенстве:
Затем посмотрите Неравенства в текстовых задачах от Shmoop , чтобы узнать, как создать неравенство из текстовой задачи. Ответьте на следующие вопросы в своем дневнике по математике:
Какое значение стоит перед открытой частью символа сравнения?
В чем разница между символом «больше чем» и символом «больше или равно»?
Как вы думаете, в чем разница между неравенством и уравнением?
Обсудите приведенные выше вопросы с родителем или учителем после просмотра видеоклипа (окончание в 2:21):

Как вы видели в видеороликах выше, неравенства включают специальные знаки, указывающие, какая сторона больше или меньше. , или показать, что две стороны не равны. В уравнениях используется знак равенства (=), чтобы показать, что обе части уравнения равны друг другу. Открытая часть символа сравнения всегда обращена к большему значению.
Числовые предложения используются для представления уравнений и неравенств. А числовое предложение — это математическое предложение, написанное с использованием цифр и математических символов, таких как символы сравнения, знак равенства и символы операций. Символы операций указывают, какую операцию следует использовать для решения задачи: сложение, вычитание, умножение или деление. Если сумма неизвестна, для представления суммы используется переменная . Переменная — это любая буква. Вы можете выбрать букву, которая относится к проблеме слова, или выбрать любую букву, которую вы хотите.
Если символ содержит «равно», например «больше или равно» или «меньше или равно», выражения с обеих сторон символа должны быть равны друг другу. Если используется символ «меньше» или «больше», выражения не могут быть равны друг другу.
равно =
не равно ≠
меньше <
меньше или равно ≤
больше >
больше или равно ≥

Пример Переведите выражение в числовое предложение:
Таннер потратил более 24 долларов.
Фраза «более» 24 долларов США означает, что он не потратил ровно 24 доллара, поэтому «равно» нельзя использовать. Числовое предложение будет таким: t > $24.
Помните, что переменная может быть любой буквой, и это не обязательно должна быть буква «т». Если используемые символы и числа верны, вы можете использовать любую букву для переменной.
Фрэнки прошел 15 миль до школы.
Выражение не означает, что Фрэнки прошел больше или меньше 15 миль, поэтому можно предположить, что он прошел ровно 15 миль. Числовое предложение, представляющее это, будет следующим: w = 15,
.
Дети до 10 лет проходят на концерт бесплатно.
Фраза «10 и младше» указывает на то, что ребенку может быть 10 лет или меньше 10 лет. Возраст должен быть «меньше или равен 10», что записывается: a ≤ 10.
Пример В начале урока вам была предложена следующая задача:
Обручальное кольцо Бейонсе от Jay Z оценивается более чем в 5 миллионов долларов. Каковы два возможных значения цены кольца? Как вы можете использовать числовое предложение для представления этой суммы?
Поскольку стоимость кольца «более» 5 миллионов долларов, возможные значения должны быть больше 5 миллионов долларов. Есть много возможностей, но два примера могут быть 6 миллионов долларов или 5,5 миллионов долларов.
Ключевая фраза «больше чем», что означает, что вы будете использовать символ «больше чем». Числовое предложение, представляющее эту ситуацию, будет следующим: r > 5 миллионов долларов.
В своем математическом журнале напишите ответы на следующие вопросы:
Как вы можете определить, используете ли вы «равно» в своем сравнении неравенства?
Может ли уравнение со знаком равенства иметь более одного решения? Объяснять.
Теперь вы перейдете к Понял? Раздел , чтобы завершить интерактивную практику написания числовых предложений для реальных утверждений.
Математика 7 класс | Уравнения и неравенства
Учащиеся решают уравнения и неравенства с рациональными числами и сталкиваются с реальными ситуациями, которые можно смоделировать и решить с помощью уравнений и неравенств.
Раздел 4
7-й класс
Fishtank Plus для математики
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Узнать больше
Оценка
Следующие оценки сопровождают Раздел 4.
Предварительная часть
Предложите учащимся пройти предварительную оценку и самооценку учащихся перед началом модуля. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.
Промежуточный модуль
Предложите учащимся выполнить оценку промежуточного модуля после урока 4.
Послемодульный
Используйте приведенные ниже ресурсы для оценки усвоения учащимися содержания модуля и плана действий для будущих модулей.
Постмодальная оценка
Ключ к ответам после модульной оценки
Руководство по анализу послемодульной оценки
92F25A3F-8529-4314-9899-6EE68694E3D0
Пост-юнит самооценка
Расширенный пакет оценивания
Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить уровень владения учащимися базовыми навыками и понятиями, а также их прогресс в изучении содержания модуля.
Скачать образец
Подготовка блока
Интеллектуальная подготовка
Предложения по подготовке к обучению данного модуля
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950
Запуск модуля
Подготовьтесь к преподаванию этого модуля, погрузившись в стандарты, большие идеи и связи с предыдущим и будущим содержанием. Запуск модулей включает в себя серию коротких видеороликов, целевую литературу и возможности для планирования действий.
Обновление до Plus
Интернализация стандартов с помощью оценки после завершения обучения
Пройдите оценку после завершения обучения. Аннотировать для:
Стандарты, которым соответствует каждый вопрос
Стратегии и представления, используемые на ежедневных уроках
Связь с основными понятиями модуля
Уроки, на которые Оценка указывает
Интернализация траектории отряда
Прочитайте и аннотируйте сводку отряда.
Обратите внимание на последовательность понятий в модуле, используя карту урока.
Выполнить все целевые задачи. Аннотируйте целевые задачи для:
Основные понятия
Связь с вопросами послемодульной оценки
Определите ключевые возможности для вовлечения учащихся в академический дискурс. Прочтите наш Инструмент для учителя на Академический дискурс и ссылайтесь на него на протяжении всего модуля.
Интеллектуальная подготовка для конкретного модуля
Прочтите разделы 6-8, Выражения и уравнения, соответствующие стандарты в этой области Выражения и уравнения.
Прочтите следующую таблицу, в которой указаны модели, используемые во всем устройстве.
Модель Пример
Диаграмма ленты и уравнения
$$3(x+4)=45$$
$$3x+4=45$$
Основные понятия
Основные математические понятия, которые учащиеся поймут в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950
Уравнения и неравенства — это мощные инструменты, которые можно использовать для моделирования и решения реальных ситуаций с неизвестными величинами.
Уравнения можно решить, рассуждая об арифметике, необходимой для раскрытия значения неизвестного. Уравнения также можно решать алгебраически, используя свойства операций и равенства.
Неравенства имеют бесконечные решения, которые можно изобразить графически на числовой прямой. В контексте эти решения иногда ограничены тем, что имеет смысл в данной ситуации; например, при поиске максимального количества людей, которые могут поместиться в лодке, набор решений будет ограничен положительными целыми числами.
Запас слов
Термины и обозначения, которые учащиеся изучают или используют на уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950
уравнение
неравенство
решение
подстановка
лента
5
5
уравнение Чтобы увидеть весь словарный запас для модуля 4, просмотрите наш глоссарий лексики для 7-го класса.
Карта урока
Тема A: Решение и моделирование с помощью уравнений
Решите одношаговые уравнения с рациональными числами.
7.EE.B.4.A
Представляйте уравнения в формах $${px+q=r}$$ и $${p(x+q)=r}$$, используя ленточные диаграммы.
7.EE.B.4.A
Решите уравнения в формах $${px+q=r}$$ и $${p(x+q)=r}$$ , используя ленточные диаграммы.
7.EE.B.3 7.EE.B.4.A
Решите уравнения в формах $${px+q=r }$$ и $${p(x+q)=r}$$ алгебраически.
7.EE.B.4.A
Решите текстовые задачи, ведущие к уравнениям в формах $${px+q=r}$$ и $${p(x+q)=r}$$ (Часть 1).
7.EE.B.3 7.EE.B.4.A
Решите текстовые задачи, ведущие к уравнениям в формах $${px+q=r}$$ и $${p(x+q)=r }$$ (Часть 2).
7.EE.B.3 7.EE.B.4.A
Модель с уравнениями вида $${px+q=r}$$ и $${p(x+q)=r}$$.
7.EE.B.3 7.EE.B.4.A
Тема B: Решение и моделирование с помощью неравенств
Решить одношаговые неравенства и построить график.
7.EE.B.4.B
Напишите и решите неравенства в формах $${px+q>r}$$ или $${px+qr }$$ или $${ p(x+q)
7.EE.B.4.B
Решите неравенства с отрицательными коэффициентами.
7.EE.B.4.B
Решите текстовые задачи, ведущие к неравенствам в формах $${px+q>r}$$ или $${px+qr}$$ или $ ${p(x+q)
7.EE.B.4.B
Модель с неравенствами.
7.EE.B.3 7.EE.B.4.B
Общие базовые стандарты
Ключ
Основной кластер
Вспомогательный кластер
Дополнительный кластер
Основные стандарты
Стандарты содержания, рассматриваемые в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950
Выражения и уравнения
7. EE.B.3 — Решайте многоэтапные задачи из реальной жизни и математические задачи, связанные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. Применять свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает надбавку на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить перекладину для полотенец длиной 9 3/4 дюйма в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить перекладину примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
7.EE.B.4 — Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах.
7.EE.B.4.A — Решите текстовые задачи, ведущие к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?
7.EE.B.4.B — Решите текстовые задачи, ведущие к неравенствам вида px + q > r или px + q. Например: как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.
Основополагающие стандарты
Стандарты, описанные в предыдущих модулях или классах, которые являются важной основой для текущего модуля
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950
Выражения и уравнения
6. EE.B.5
6.EE.B.7
6.EE.B.8
Будущие стандарты
Стандарты будущих классов или разделов, которые связаны с содержанием данного раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950
Выражения и уравнения
8.EE.C.7
8.EE.C.8
Стандарты математической практики
CCSS.MATH.PRACTICE.MP1 – Разбираться в проблемах и настойчиво решать их.
CCSS.MATH.PRACTICE.MP2 — Рассуждайте абстрактно и количественно.
CCSS.MATH.PRACTICE.MP3 — Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
CCSS.MATH.PRACTICE.MP4 — Модель с математикой.
CCSS.MATH.PRACTICE. MP5 — Стратегически используйте соответствующие инструменты.
CCSS.MATH.PRACTICE.MP6 — Следите за точностью.
CCSS.MATH.PRACTICE.MP7 — Ищите и используйте структуру.
CCSS.MATH.PRACTICE.MP8 — Ищите и выражайте закономерность в повторяющихся рассуждениях.
значок/стрелка/вправо/крупная копия
Блок 3
Числовые и алгебраические выражения
значок/стрелка/вправо/большой
Блок 5
Проценты и масштабирование
Решение линейных неравенств с одной переменной , ≥ и >. это математическое утверждение, которое связывает линейное выражение как меньшее или большее, чем другое. Ниже приведены некоторые примеры линейных неравенств, все они решаются в этом разделе:
Решение линейного неравенстваВещественное число, которое дает истинное утверждение, когда его значение подставляется вместо переменной. это действительное число, которое даст истинное утверждение при замене переменной. Линейные неравенства либо имеют бесконечно много решений, либо не имеют решений. Если существует бесконечно много решений, нарисуйте набор решений на числовой прямой и/или выразите решение, используя обозначение интервала.
Пример 1
Являются ли x=−4 и x=6 решениями уравнения 5x+7<22?
Решение:
Подставьте значения вместо x , упростите и проверьте, получаем ли мы истинное утверждение.
Ответ: x=−4 является решением, а x=6 — нет.
Все методы решения линейных уравнений, кроме одного, применимы и к решению линейных неравенств. Вы можете прибавлять или вычитать любое действительное число к обеим сторонам неравенства, а также умножать или делить обе части на любое положительное действительное число, чтобы получить эквивалентные неравенства. Например:
10> −510−7> −5–7 Вычитание 7 с обеих сторон.3> −12 ✓ True
10> −5105> −55 Разделите обе стороны на 5,2> −1 ✓ TRU сторона и деление каждой стороны на положительные 5 приводит к истинному неравенству.
Пример 2
Решите и нарисуйте набор решений: 5x+7<22.
Решение:
5x+7<225x+7−7<22−75x<155x5<155x<3
Полезно потратить минуту и выбрать несколько значений из набора решений, подставить их в исходное неравенство, а затем проверить результаты. Как указано, вы должны ожидать, что x=0 решит исходное неравенство, а x=5 — нет.
Такая проверка показывает, что мы правильно решили неравенство.
Мы можем выразить это решение двумя способами: используя запись набора и запись интервала.
{x|x<3} Set notation (−∞,3) Interval notation
В этом тексте мы будем представлять ответы, используя интервальную запись.
Ответ: (−∞, 3)
При работе с линейными неравенствами при умножении или делении на отрицательное число применяется другое правило. Чтобы проиллюстрировать проблему, рассмотрим истинное утверждение 10>−5 и разделим обе части на −5.
10> −510–5> −5–5 Разделите обе стороны на −5,i2> 1 ✗ False
, делящие на -5, что приводит к ложному утверждению. Чтобы сохранить истинное утверждение, неравенство должно быть обращено.
10>−510−5<−5−5 Обратное неравенство.−2<1 ✓При умножении отрицательного числа на
возникает та же проблема. Это приводит к следующему новому правилу: при умножении или делении на отрицательное число инвертировать неравенство . Это легко забыть сделать, поэтому будьте особенно внимательны и следите за отрицательными коэффициентами. В общем, учитывая алгебраические выражения A и B , где c положительное ненулевое действительное число, мы имеем следующие свойства неравенств Свойства, используемые для получения эквивалентных неравенств и используемые в качестве средства для их решения.:
Мы используйте эти свойства, чтобы получить эквивалентное неравенство, которое имеет один и тот же набор решений, одно с тем же набором решений, где переменная изолирована. Процесс аналогичен решению линейных уравнений.
Пример 3
Решите и нарисуйте набор решений: −2(x+8)+6≥20.
Решение:
−2 (x+8)+6ц .20 Распределение. – 2x – 16+6≥20 Комбинируйте, как термины. – 2x – 10,20 Решайте для x.2x ≥30 Разделите обе стороны на 2. –2x – 2≤30–2 Обратите внимание на неравенство. X≤15
Ответ: Интервальная нотация (−∞, −15]
Пример 4
Решение и график набор решений: −2 (4x-5 )<9−2(x−2).
Решение: 9Обратное неравенство.x>−12
Ответ: Обозначение интервала (−12, ∞)
Пример 5
Решите и нарисуйте набор решений: 12x−2≥12(74x−9)+1.
Решение:
12x – 2≥12 (74x – 9) +1 12x – 2≥78x – 92+1 12x – 78x≥ – 72+2–38x–32 (−83) ( – 38x) ≤ ( −83)(−32) Обратное неравенство. x≤4
Ответ: Обозначение интервала: (−∞, 4]
Попробуйте! Решите и начертите набор решений: 10−5(2x+3)≤25.
Ответ: [−3, ∞);
(нажмите, чтобы посмотреть видео)
Составные неравенства
Ниже приведены некоторые примеры составных линейных неравенств:
Эти составные неравенства Два или более неравенства в одном утверждении, соединенные словом «и» или словом «или». на самом деле два неравенства в одном утверждении, соединенные словом и или словом или . Например, −13<3x−7<17 является составным неравенством, поскольку его можно разложить следующим образом: −13<3x−7 и 3x−7<17
Мы можем решить каждое неравенство по отдельности; пересечение двух наборов решений решает исходное составное неравенство. Хотя этот метод работает, есть еще один метод, который обычно требует меньшего количества шагов. Примените свойства этого раздела ко всем трем частям составного неравенства с целью выделения переменной в середине .0050 оператора для определения границ набора решений.
Пример 6
Решите и нарисуйте набор решений: −13<3x−7<17.
Решение:
−13<3x−7<17−13 +7<3x−7 +7<17 +7−6<3x<24−63<3x3<243−2
Ответ: Обозначение интервала: (−2,8)
Пример 7
Решите и нарисуйте набор решений: 56≤13(12x+4)<2.
Решение:
56≤13(12x+4)<256≤16x+43<26⋅(56)≤6⋅(16x+43)<6⋅(2)5≤x+8<125−8≤ х+8−8<12−8−3≤x<4
Ответ: интервальная запись [−3,4)
Важно отметить, что при умножении или делении всех трех частей составного неравенства на отрицательное число необходимо обратить все неравенства в утверждении. Например: −10<−2x<20−10−2>−2x−2>20−25> x >−10 Ответ выше можно записать в эквивалентной форме, где меньшие числа лежат слева, а большие числа лежат справа, как они появляются на числовой прямой. −10
Попробуйте! Решите и нарисуйте набор решений: −3≤−3(2x−3)<15.
Ответ: (−1,2];
(нажмите, чтобы посмотреть видео)
Для составных неравенств со словом « или » вы работаете с обоими неравенствами по отдельности, а затем рассматриваете объединение наборов решений. union решает любое неравенство
Пример 8
Решите и начертите набор решений: 4x+5≤−15 или 6x−11>7
Решение:
Решите каждое неравенство и сформируйте объединение, объединив наборы решений.
Ответ: Интервальное обозначение (−∞,−5]∪(3,∞)
Попробуйте! <1.
Ответ: (−∞,−1)∪(32, ∞)
(нажмите, чтобы посмотреть видео)
Применение линейных неравенств
Некоторые ключевые слова и фразы, указывающие на неравенства, приведены ниже. :
Как и во всех приложениях, внимательно прочитайте задачу несколько раз и найдите ключевые слова и фразы.Определите неизвестные и назначьте переменные.Затем переведите формулировку в математическое неравенство.Наконец,используйте изученные свойства для решения задачи неравенство и выразить решение графически или в интервальной записи.
Пример 9
Семь меньше, чем сумма числа, умноженная на 3, и 5 не больше 11. Найдите все числа, удовлетворяющие этому условию.
Решение:
Сначала выберите переменную для неизвестного числа и определите ключевые слова и фразы.
Пусть n представляют неизвестное, обозначенное как « число ».
Найти n .
3(n+5)−7≤113n+15−7≤113n+8≤113n≤3n≤1
Ответ: Любое число, меньшее или равное 1, будет удовлетворять утверждению.
Пример 10
Чтобы получить B по курсу математики, средний результат теста должен быть не менее 80% и менее 90%. Если учащийся набрал 92 %, 96 %, 79 % и 83 % на первых четырех тестах, сколько он должен набрать на пятом тесте, чтобы получить четверку?
Решение:
Задайте составное неравенство, в котором среднее значение теста находится в диапазоне от 80% до 90%. В этом случае включите нижнюю границу, 80.
Пусть x представляет результат пятого теста.
80≤испытание среднее<9080≤92+96+79+83+x5<905⋅80≤5⋅350+x5<5⋅
≤350+x<45050≤x<100
Ответ: Она должна набрать не менее 50% и менее 100%.
В предыдущем примере верхняя граница 100% не входила в набор решений. Что произойдет, если она заработает 100% на пятом тесте?
среднее=92+96+79+83+1005=4505=90
Как мы видим, ее среднее значение составит 90%, что принесет ей пятерку. решения. Решения представлены графически на числовой прямой или с использованием интервальной записи, или и того, и другого.
Все правила решения линейных неравенств, кроме одного, аналогичны правилам решения линейных уравнений. Если вы разделите или умножите неравенство на отрицательное число, переверните неравенство, чтобы получить эквивалентное неравенство.
Составные неравенства со словом «или» требуют, чтобы мы решили каждое неравенство и образовали объединение каждого множества решений. Это значения, которые решают хотя бы одно из заданных неравенств.
Составные неравенства со словом «и» требуют пересечения множеств решений для каждого неравенства. Это значения, которые решают оба или все заданные неравенства.
Общие рекомендации по решению текстовых задач применимы к приложениям, использующим неравенства. Помните о новом списке ключевых слов и фраз, которые указывают на математическую установку, включающую неравенства.
Тематические упражнения
Часть A. Линейные неравенства
Определить, является ли заданное значение решением.
5x-1<-2; х=−1
−3x+1>−10; х=1
2x−3<−5; х=1
5x−7<0; х=2
9y−4≥5; у=1
−6y+1≤3; у=-1
12а+3≤-2; а=-13
25а-2≤-22; а=-45
−10<2x−5<−5; х=-12
3x+8<−2 или 4x−2>5; х=2
Нанесите все решения на числовую прямую и задайте соответствующее обозначение интервала.
3x+5>−4
2x+1>−1
5–6 лет <–1
7−9 лет>43
6−a≤6
−2а+5>5
5x+63≤7
4x+116≤12
12 лет+54≥14
112г+23≤56
2(3x+14)<−2
5(2г+9)>−15
5-2(4+3г)≤45
−12+5(5−2x)<83
6(7−2а)+6а≤12
2а+10(4-а)≥8
9(2t−3)−3(3t+2)<30
−3(t−3)−(4−t)>1
12(5x+4)+56x>−43
25+16(2x−3)≥115
5x−2(x−3)<3(2x−1)
3(2x−1)−10>4(3x−2)−5x
−3y≥3(y+8)+6(y−1)
12≤4(у-1)+2(2у+1)
−2(5t−3)−4>5(−2t+3)
−7(3t−4)>2(3−10t)−t
12(х+5)−13(2х+3)>76х+32
−13(2x−3)+14(x−6)≥112x−34
4(3x+4)≥3(6x+5)−6x
1−4(3x+7)<−3(x+9)−9x
6−3(2a−1)≤4(3−a)+1
12-5(2а+6)≥2(5-4а)-а
Часть B: Составные неравенства
Нанесите все решения на числовую прямую и укажите соответствующее обозначение интервала.
−1<2x+1<9
−4<5x+11<16
−7≤6y−7≤17
−7≤3г+5≤2
−7<3x+12≤8
−1≤2x+73<1
−4≤11−5t<31
15<12−t≤16
−13≤16a+13≤12
−16<13a+56<32
5x+2<−3 или 7x−6>15
4x+15≤−1 или 3x−8≥−11
8x−3≤1 или 6x−7≥8
6x+1<−3 или 9x−20>−5
8x−7<1 или 4x+11>3
10x−21<9 или 7x+9≥30
7+2 года <5 или 20−3 года>5
5−y<5 или 7−8y≤23
15+2x<−15 или 10−3x>40
10−13x≤5 или 5−12x≤15
9−2x≤15 и 5x−3≤7
5−4x>1 и 15+2x≥5
7 лет−18<17 и 2 года−15<25
13 лет+20≥7 и 8+15 лет>8
5−4x≤9 и 3x+13≤1
17−5x≥7 и 4x−7>1
9 лет+20≤2 и 7 лет+15≥1
21−6y≤3 и −7+2y≤−1
−21<6(x−3)<−9
0≤2(2x+5)<8
−15≤5+4(2y−3)<17
5<8−3(3−2 года)≤29
5<5−3(4+t)<17
−3≤3−2(5+2t)≤21
−40<2(x+5)−(5−x)≤−10
−60≤5(x−4)−2(x+5)≤15
−12<130(x−10)<13
−15≤115(x−7)≤13
−1≤a+2(a−2)5≤0
0<5+2(а-1)6<2
Часть C: Приложения
Найдите все числа, удовлетворяющие заданному условию.
Три меньше, чем удвоенная сумма числа, а 6 не больше 13.
Сумма числа, умноженная на пять меньше, чем в 3 раза, и 4 не больше 10.
Пятикратная сумма числа и 3 не меньше 5.
Три раза разница между числом и 2 составляет не менее 12.
Сумма трех чисел, умноженных на 8, составляет от 2 до 20.
Число, меньшее, чем удвоенное число, составляет от -20 до -8.
Четыре вычитается из трех, умноженных на некоторое число от -4 до 14.
Девять вычитается из 5, умноженного на некоторое число от 1 до 11.
Составьте алгебраическое неравенство и решите его.
При членстве в гольф-клубе стоимостью 120 долларов в месяц каждый раунд игры в гольф стоит всего 35 долларов. Сколько раундов в гольф может сыграть участник, если он хочет сохранить свои расходы не более 270 долларов в месяц?
Аренда грузовика стоит 95 долларов в день плюс 0,65 доллара за милю. Сколько миль можно проехать за однодневную аренду, чтобы стоимость не превышала 120 долларов?
Марк заработал 6, 7 и 10 баллов из 10 в первых трех тестах. Что он должен набрать в четвертом тесте, чтобы в среднем было не менее 8?
Джо получил 78, 82, 88 и 70 баллов за свои первые четыре экзамена по алгебре. Что он должен набрать на пятом экзамене, чтобы средний балл был не менее 80?
Гимнастка набрала 13,2, 13,0, 14,3, 13,8 и 14,6 балла в первых пяти упражнениях. Что он должен набрать в шестом соревновании, чтобы средний балл был не менее 14,0?
Танцор получил 7,5 и 8,2 балла от первых двух судей. Какой должна быть ее оценка от третьего судьи, если она должна получить в среднем 8,4 или выше?
Если два раза угол составляет от 180 до 270 градусов, то каковы границы исходного угла?
Периметр квадрата должен быть от 120 до 460 дюймов. Найдите длины всех возможных сторон, удовлетворяющих этому условию.
Компьютер настроен на отключение, если температура превышает 45°C. Приведите эквивалентное утверждение, используя градусы Фаренгейта. Подсказка: C=59(F−32).
Определенный антифриз эффективен в диапазоне температур от −35°C до 120°C. Найдите эквивалентный диапазон в градусах Фаренгейта.
Часть D: Дискуссионная доска
Часто учащиеся обращают неравенство, решая 5x+2<−18? Как вы думаете, почему это распространенная ошибка? Объясните начинающему студенту алгебры, почему мы этого не делаем.
Выполните поиск в Интернете по запросу «решение линейных неравенств». Поделитесь ссылкой на веб-сайт или видеоурок, которые вы считаете полезными.
Напишите свои собственные 5 ключевых выводов для всей этой главы. Что вы считаете обзором, а что новым? Поделитесь своими мыслями на доске обсуждений.
Ответы
Да
№
Да
№
Да
(-3,∞);
(1,∞);
[0,∞);
(-∞,3];
[−2,∞);
(-∞,-5);
[−8,∞);
[5,∞);
(-∞,7);
(-1,∞);
(3,∞);
(-∞,-32];
(-∞,0);
[−2,∞);
(-1,4);
[0,4];
(−5,5];
(−4,3];
[−4,1];
(-∞,-1)∪(3,∞);
(-∞,12]∪[52,∞);
(-∞,5);
(-∞,-10);
[−3,2];
(-∞,5);
(-12,32);
[−1,3);
(-8,-4);
(-15,-5];
(-5,20);
[−13, 43];
(-∞,2]
[−2,∞)
(−2,4)
(0,6)
Участники могут сыграть 4 раунда или меньше.

\(\влево(4;12\вправо)\)	Круглые скобки означают, что номер не включен. В этот интервал входят все действительные числа больше, но не равны \(\text{4}\) и меньше, но не равны \(\текст{12}\).
\(\влево(-\infty ;-1\вправо)\)	Круглые скобки всегда используются для положительной и отрицательной бесконечности. Этот интервал включает все действительные числа меньше, но не равны \(-\text{1}\).
\(\влево[1;13\вправо)\)	Квадратная скобка означает, что число включено. В этот интервал входят все действительные числа больше или равные \(\text{1}\) и меньше, но не равные \(\текст{13}\).

Symbol	Слова	Пример
>	больше	х + 3 > 2
<	меньше	7x < 28
≥	больше или равно	5 ≥ х – 1
≤	меньше или равно	2 года + 1 ≤ 7

равно	=
не равно	≠
меньше	<
меньше или равно	≤
больше	>
больше или равно	≥

Решение неравенств второй степени с одной переменной. Метод интервалов 9 класс онлайн-подготовка на Ростелеком Лицей |

Урок математики в 3 классе по теме: «Числовые равенства и неравенства»

Понятие равенства, знак равенства, связанные определения

Что такое равенство

Запись равенств, знак равно

Верные и неверные равенства

Свойства равенств

Двойные, тройные и т.д. равенства

Решение неравенств примеры. Решите неравенство 2х больше.

Числовые равенства и неравенства

Тест-тренажёр по математике для 1 класс за 4 четверть с ответами!

Результат теста:

Решение неравенств – объяснение и примеры

Что такое неравенство в математике?

Символы неравенства

Операции над неравенствами

Как решать неравенства?

Решение линейных неравенств со сложением

Решение линейных неравенств с вычитанием

Решение линейных неравенств с умножением Ниже приведены несколько примеров, чтобы понять эту концепцию. Пример 50005

Решение линейных неравенств с делением

Решение линейных неравенств с использованием свойства распределения

944444444444444444494494494494494494494494449.

Solving Inequalities

Решение

Пример: x + 2 > 12

Как решать

Пример: 3x

Пример: 2y+7

Добавление или вычитание значения

Пример: x + 3

Что мы сделали?

Что, если я решу это, но “x” окажется справа?

Пример: 12

Умножение или деление на значение

Пример: 3y

Пример: −2y

Умножение или деление на переменные

Пример: bx

Большой пример

Пример:

Два неравенства сразу!

Пример:

Итог

4.7 Решение линейных неравенств | Уравнения и неравенства

4.7 Решение линейных неравенств (EMA3H)

Интервальное обозначение (EMA3J)

Рабочий пример 17: Решение линейных неравенств

Переставить и решить для \(r\)

Умножение на \(-\text{1}\) и обратный знак неравенства

Представьте ответ в числовой строке

Представить ответ в интервальной нотации

Рабочий пример 18: Решение линейных неравенств

Развернуть скобу

Переставить и решить для \(q\)

Разделить обе стороны на \(\text{2}\)

Представьте ответ в числовой строке

Представить ответ в интервальной нотации

Рабочий пример 19: Решение сложных линейных неравенств

Вычесть \(\text{3}\) из всех частей неравенства

Представьте ответ в числовой строке

Представить ответ в интервальной нотации

Математика 7 класс | Уравнения и неравенства

Оценка

Предварительная часть

Промежуточный модуль

Послемодульный

Подготовка блока

Интеллектуальная подготовка

Интернализация стандартов с помощью оценки после завершения обучения

Интернализация траектории отряда

Интеллектуальная подготовка для конкретного модуля

Основные понятия

Запас слов

Карта урока

Общие базовые стандарты

Основные стандарты

Выражения и уравнения

Основополагающие стандарты

Выражения и уравнения