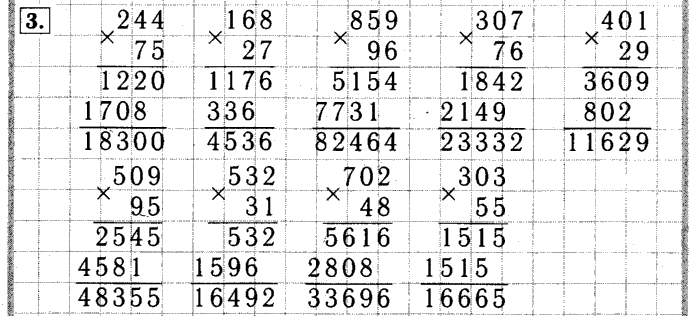
Примеры на деление трехзначных чисел на однозначные примеры: Деление трёхзначного числа на однозначное | Методическая разработка по математике (3 класс) по теме:

Математика Деление трехзначного числа на однозначное, когда в записи частного есть нуль

Материалы к уроку

• 8. Деление трехзначного числа на однозначное, когда в записи частного есть нуль.ppt

  5.52 MBСкачать

• 8. Деление трехзначного числа на однозначное, когда в записи частного есть нуль.doc

  57.5 KBСкачать

Конспект урока

8. Деление трехзначного числа на однозначное, когда в записи частного есть нуль
Организационный этап   Долгожданный дан звонок, Начинается урок. Все ли правильно сидят? Все ль внимательно глядят? Начинается урок, Он пойдёт ребятам впрок. Постарайтесь не зевать, Чтобы лучше всё понять!
Этап подготовки учащихся к активному сознательному усвоению знаний   Сегодня на уроке мы закрепим приёмы письменного деления трёхзначного числа на однозначное, будем учиться  делить трёхзначное число на однозначное, когда в записи частного есть нуль.
Устный счёт
Задание Поставьте арифметические знаки  между данными цифрами так, чтобы выражения стали верными  9     9     9    =    2 Проверьте себя. (9 + 9) : 9    =     2
Задание В первую строку запищите все трёхзначные числа, которые состоят из цифр 4, 5, 6 (цифры в записи чисел не повторяйте). Подчеркните нечётные числа. Во вторую строку запишите частные от деления чётных трёхзначных чисел первой строки на 2 и частные от деления чисел 456 и 564 на 4. Проверьте себя. 456, 465, 546, 564, 645, 654 228, 273, 282, 327, 114, 141 Если все вычисления вы сделали правильно, то во второй строке получились пары чисел, записанные одними и теми же цифрами: 228 и 282, 273 и 327, 114 и 141.
Задание Деревянный куб со стороной 30 см покрасили краской, а затем распилили на кубики со сторонами 10 см. Запишите в строчку, сколько среди них кубиков, окрашенных с трёх сторон?                С двух сторон?                С одной стороны?              Неокрашенных ни с одной стороны? Проверим. Кубики, окрашенные с трёх сторон Кубики, окрашенные с двух сторон Кубики, окрашенные с одной стороны Кубики, неокрашенные ни с одной стороны
Задание Найдите общую площадь окрашенных сторон куба. Проверьте себя. Для ответа на вопрос задания, надо найти площадь одной грани. Грань куба – это квадрат. Площадь квадрата находится умножением длин сторон – «а» умножить на «а». Длина стороны равна 30 см, значит при умножении 30 см на 30 см, получим 900 квадратных сантиметров. Всего у куба 6 граней. Чтобы найти общую площадь всех граней куба, нужно площадь одной грани умножить на количество граней. 900 см² ∙ 6 = 5400 см²
Этап усвоения новых знаний   Повторим пройденные приёмы письменного деления. Объясните решение примеров по плану. 872 : 4 948 : 3 526 : 2 825 : 5 Проверьте себя. 872 : 4 = 218 948 : 3 = 316 526 : 2 = 263 825 : 5 =165
Давайте познакомимся с новым случаем деления трёхзначного числа на однозначное. Разделим число 428 на 4. Первое неполное делимое – 4 сотни. Значит,  в частном будет три цифры – ставим три точки.                 Делим сотни: сотен 4, разделим их на 4 и получим в частном 1.                 Умножаем 1сотню  на 4, получаем 4 сотни.                 Из 4 сотен вычитаем 4 сотни, получаем 0. Делим десятки.                 Десятков 2. Делим два  на 4 и получаем нуль.                 Нуль умножаем на  4, получаем нуль.                 Вычитаем, получаем остаток два.                 Остаток меньше делителя. Теперь делим единицы. 28 разделим на 4 и получим 7. 7 умножим на 4, получим 28. Вычитаем, в остатке получаем нуль.
Закрепление материала   Задание Помогите Маше найти пример с ошибкой. 436 : 4 = 109 824 : 4 = 6                        924 : 3 = 38                      Решите примеры, в которых допущены ошибки, правильно. Проверьте себя. 824 : 4 = 206                    924 : 3 = 308   Задание Расшифруйте название самого медленного и редкого на планете вида крокодилов. А  654 : 6                    И  921 : 3 В  959 : 7                    Л  832 : 4 Г  981 : 3                     А  436 : 4 327 109 137 307 109 208             Давайте узнаем название этого интересного животного. 327 109 137 307 109 208 Г А В И А Л         ГАВИАЛ Гавиал – самые медленные и редкие крокодилы. В 1970 году они считались исчезнувшими животными, но благодаря программе по искусственному выведению животных, разработанной в Индии, они были выведены до 1500 особей. Теперь с полной гордостью можно сказать, что этот вид сохранился.   Задание Найдите значение Х.          Х  |                   – 34  |        : 6  |     + 92  |          ∙ 4  |      + 35 |                      851 |   А теперь проверим задание. Чтобы найти значение «х», нужно действовать от обратного, т.е. начинать решение надо с результата и все действия заменить на противоположные. От восьмиста пятидесяти одного вычитаем тридцать пять и получаем разность равную восьмистам шестнадцати. Далее, восемьсот шестнадцать необходимо разделить на четыре. Получим число двести четыре. Теперь от двухсот четырёх отнимаем 92. Разность равна ста двенадцати. В следующем действии сто двенадцать умножаем на шесть и получаем число шестьсот семьдесят два. 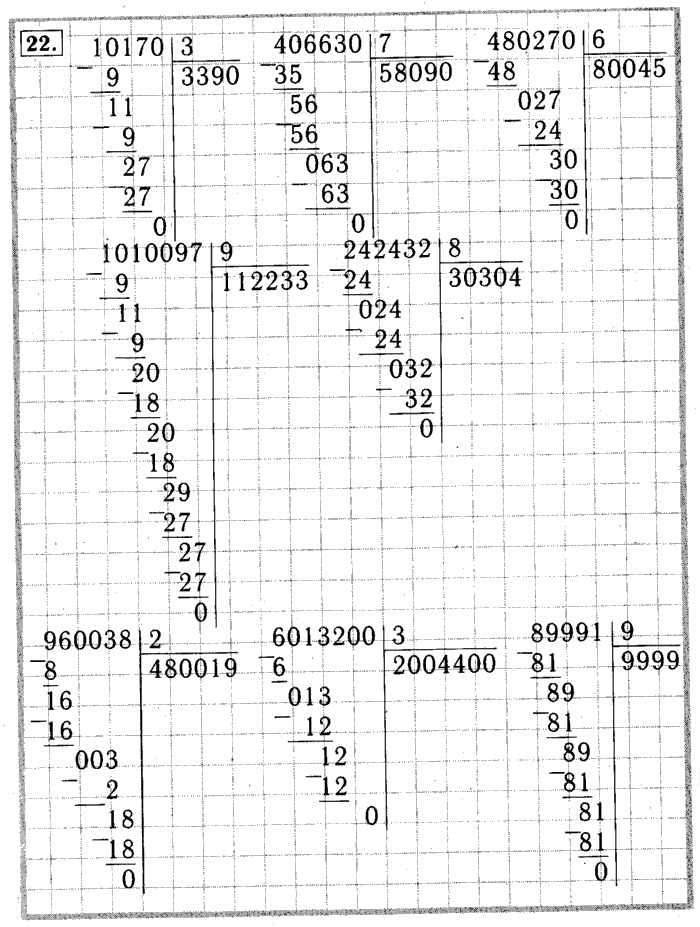Осталось выполнить последнее действие: к числу шестьсот семьдесят два прибавляем число 34 и получаем значение «х» – семьсот шесть.
Задание Решите задачу. В библиотеку привезли 615 учебников для 2 класса, а для 3 класса в три раза меньше, чем для второго. Для 4 класса привезли учебников  в два раза больше, чем для третьего класса. Сколько всего привезли учебников. Проверьте себя. Решение. 1) 615 : 3 = 205 (уч.) для 3 класса. 2) 205 ∙ 2 = 410 (уч.) для 4 класса. 3) 615 + 205 + 410 = 1230 (уч.) всего. Ответ: привезли 1230 учебников.   Этап подведения итогов   Закончите фразу. Сегодня на уроке я узнал… На уроке я научился… Мне легко далось… У меня вызвало затруднение…   Рефлексия   Нарисуйте в тетради маленький круг. Закрасьте его тем цветом, который соответствует вашему настроению

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитора

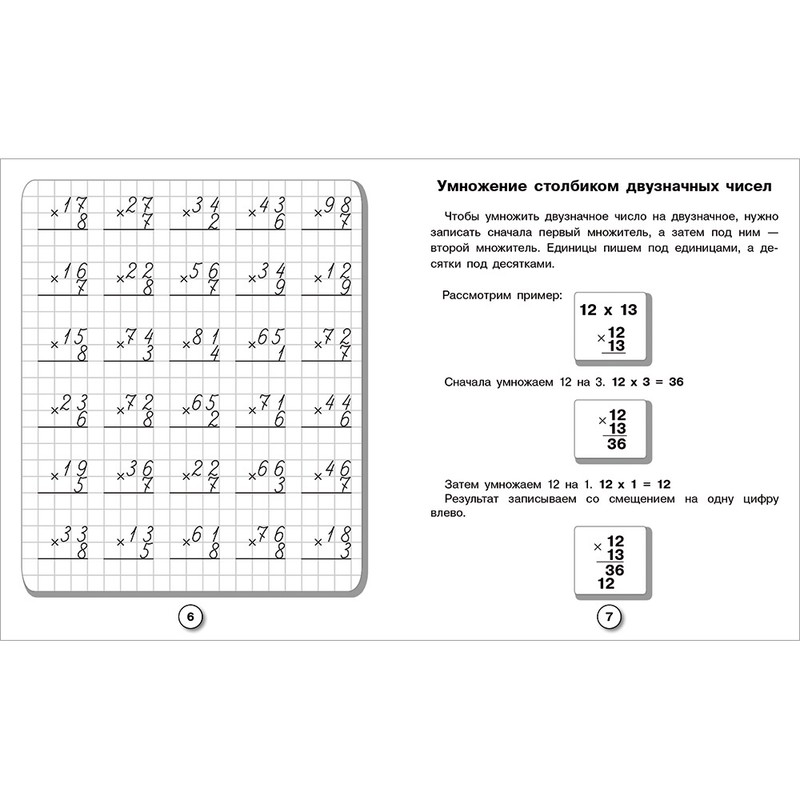
Примеры на деление трехзначных чисел на двузначное, как делить двухзначные на двухзначные с остатком? Разное

❤ 2531 , Категория: Разное,   ⚑ 03 Июн 2020г

---

Содержание

• 1 Деление столбиком на двузначное число
• 2 Алгоритм деления столбиком на двузначное число
• 3 Разбор примеров на деление столбиком на двузначное число
• 4 Пример на деление с остатком
• 5 Деление с нулем в частном
• 6 Примеры на деление для самопроверки
• 7 Деление на двузначное число — способы и примеры решений
• 8 Деление на двузначное число устно
• 9 Деление в столбик на двузначное число
• 10 Примеры деления в столбик на двузначное число
  • 10. 1 Пример 1
  • 10.2 Пример 2
  • 10.3 Пример 3
  • 10.4 Пример 4
  • 10.5 Пример 5
• 11 Письменное деление с остатком на двузначное число
  • • • 11.0.0.1 Этот видеоурок доступен по абонементу
  • 11.1 С помощью этого урока вы сможете пройти тему «Деление на двузначное число». В ходе урока учитель напомнит пройденный материал, когда в частном при делении будет находиться однозначное или двухзначное число. Далее расскажет о правилах письменного деления в случае, если частное представлено трехзначным числом.
• 12 Деление на двузначное число без остатка
• 13 Деление на двузначное число с остатком
• 14 Заключение

Деление столбиком на двузначное число

Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться.

Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.

Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.

Для начала повторим кратко, как делить столбиком на однозначное число:

А что если деление с остатком? Смотрим в следующем видео:

Алгоритм деления столбиком на двузначное число

Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.

1. Находим первое неполное делимое. Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.

Примеры 76 8:24. Первое неполное делимое 76
265 :53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.

2. Определяем количество цифр в частном. Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.

Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.

3. Находим цифры в каждом разряде частного. Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.

Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.

4. Находим остаток (если есть).

Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.

Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)

Разбор примеров на деление столбиком на двузначное число

Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.

— Найдем значение частного чисел 265 и 53.

Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.

Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.

Значение частного чисел 265 и 53 равно 5.

Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.

— Найдем значение частного чисел 184 и 23.

В частном будет однозначное число.

Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.

Значение частного чисел 184 и 23 равно 8.

Рассмотрим более сложные случаи деления.

— Найдем значение частного чисел 768 и 24.

Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.

Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.

Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.

Значение частного чисел 768 и 24 равно 32.

— Найдем значение частного чисел 15344 и 56.

Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.

Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.

Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414_10=41(ост.4). 41_5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.

Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.

Значение частного чисел 15344 и 56 равно 274.

Пример на деление с остатком

Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой

— Найдем значение частного чисел 15345:56

Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50.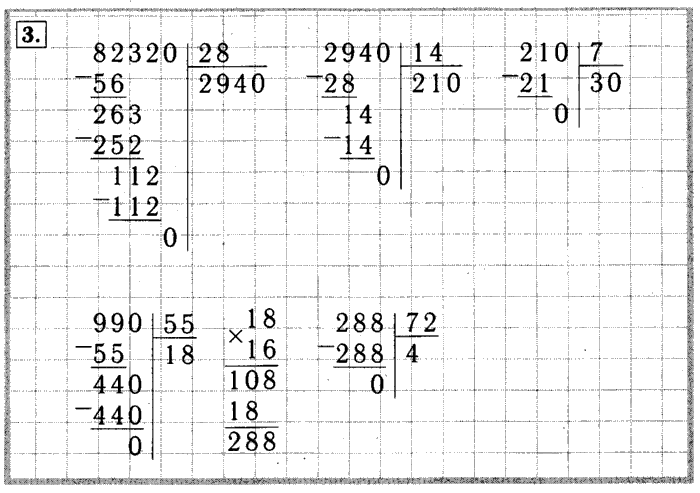 То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.

Значение частного чисел 15345 и 56 равно 274 (остаток 1).

Деление с нулем в частном

Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.

— Найдем значение частного чисел 2870:14

Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.

Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.

Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.

Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).

70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.

Значение частного чисел 2870 и 14 равно 205.

Деление нужно непременно проверить умножением.

Примеры на деление для самопроверки

Найдите первое неполное делимое и определите количество цифр в частном.

3432:66 2450:98 15145:65 18354:42 17323:17

Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.

1428 : 42 30296 : 56 254415 : 35 16514 : 718

2924 : 68 136576 : 64 710278 : 91 15830 : 293

Деление на двузначное число — способы и примеры решений

Деление на двузначное число похоже на тот же процесс с однозначным числом, но занимает больше времени. Однако есть немало методов, которые упрощают процесс. Научиться выполнять деление быстро помогут основные правила и серьезная практика.

Деление на двузначное число устно

Осуществляется такое деление методом подбора. Например, нужно разделить число 90 на двузначное число 15 без остатка.

Чтобы это сделать устно, нужно подобрать такое число, которое при умножении его на 5 (15 оканчивается на 5) даст число, оканчивающееся на 0 (так как 90 оканчивается на ноль).

Какое число при умножении на 5 даст в результате число с цифрой 0 на конце? Их несколько.

Теперь проверяем. Если цифра нам подходит, то, умножив ее на 15, получим 90:

Последняя цифра 6 подходит. Мы выполнили деление: 90 : 15 = 6.

Деление в столбик на двузначное число

Деление в столбик школьники проходят еще в младших классах на уроках математики. В дальнейшем его применяют как вспомогательное средство при решении задач. Но если не пройти в нормальном виде деление уголков, то могут возникнуть затруднения и с трехзначными числами.

На рисунке 1 показан принцип деления и названия основных элементов процесса. Как и при делении на однозначные числа, работает алгоритм перехода от крупных к мелким единицам.

Порядок действий опишем, взяв для примера вычисление, представленное на рисунке 1:

Выделить самое маленькое двузначное число 63, которое можно поделить на делитель 61. Оно всегда больше того, которое является делителем.

Делим 63 на 61. Сколько раз 61 поместится в 63? Один. Записываем под уголком единицу. Это первая цифра частного.

Умножаем делитель на эту первую цифру: 61 * 1 = 61, вычитаем из 63 число 61, проводим черту и пишем разность — 2.

Сносим следующую цифру делимого — 4. Получаем число 24. Оно не делится на 61, потому записываем ноль на место второй цифры частного (это место рядом с цифрой 1 в нашем примере).

Сносим следующую (последнюю в нашем примере) цифру, это 4. Получаем число 244. Делим его на 61. Применим правило устного деления, описанное выше. Нужно подобрать такую цифру, которая при умножении на последнюю цифру (у 61 последняя цифра 1) даст ответ, оканчивающийся на последнюю цифру делимого (у 244 последняя цифра 4, она нам и нужна). Т. е. 4 * 1 = 4. Проверка: 61 * 4 = 244. Мы подобрали цифру 4 и она нам подошла.

Вписываем 4 третьей цифрой частного в уголок, получаем 104. Умножаем 61 на 4 и вычитаем результат из 244. Получаем 0. Деление выполнено.

В данном примере делимое — трёхзначное число. В общем случае процесс сноса цифр делимого и деления их на делитель продолжается до тех пор, пока не закончатся все цифры делимого. Этот принцип подходит для трехзначных, четырехзначных и других многозначных чисел.

Примеры деления в столбик на двузначное число

Рассмотрим некоторые примеры. Они довольно простые и помогут понять основные моменты данного способа.

Пример 1

Найдём значение частного чисел 265 и 53:

Пример 2

Найдем результат деления чисел 624 и 52:

Пример 3

Рассмотрим более сложные случаи деления в столбик. Найдем значение частного чисел 1610 и 35:

Пример 4

Деление пятизначного числа на двузначное. Узнаем значение частного чисел 10150 и 35:

Пример 5

Деление многозначного числа на двузначное с остатком. Вычислим, чему будет равно частное чисел 1978 и 38:

Деление на двузначное число можно выполнять в столбик и устно, но многозначные числа устно считать намного сложнее. Немногие школьники могут похвастаться подобными умениями.

Освоение процесса деления поможет школьникам в дальнейшем обучении. Так же существует немало тренажеров и онлайн-калькуляторов, которые можно использовать в свою пользу.

Письменное деление с остатком на двузначное число

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

С помощью этого урока вы сможете пройти тему «Деление на двузначное число». В ходе урока учитель напомнит пройденный материал, когда в частном при делении будет находиться однозначное или двухзначное число. Далее расскажет о правилах письменного деления в случае, если частное представлено трехзначным числом.

Деление на двузначное число без остатка

Рассмотрим сначала, как выполнить деление на двузначное число без остатка.

В значении частного будет одна цифра. Чтобы легче было подобрать цифру частного, разделим 312 не на 52, а на 50:

(ост. )

6 – это пробная цифра, ее нельзя сразу записывать в частном, ведь мы делим не на 50, а на 52. Сначала нужно проверить, подойдет ли цифра 6. Умножим 52 на 6.

Цифра подошла. Значение частного будет 6.

Рассмотрим еще один случай деления.

В значении частного будет одна цифра. Чтобы легче было подобрать цифру частного, разделим 469 не на 67, а на 60.

7 – это пробная цифра, ее нельзя сразу записывать в частном, ведь мы 469 делим не на 60, а на 67. Сначала нужно проверить, подойдет ли цифра 7. Умножим 67 на 7.

Мы видим, что цифра 7 подходит. Значит, значение частного будет 7.

Деление на двузначное число с остатком

При делении на двузначное число с остатком рассуждать нужно так же.

1. Найдем частное.

В частном будет одна цифра. Чтобы легче было найти цифру частного, разделим 299 не на 34, а на 30.

(ост. 29)

9 – это пробная цифра частного, ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 34 на 9.

306 больше, чем делимое 299. Значит, цифра 9 не подходит. Проверим цифру 8.

Значит, цифра 8 подойдет. Остаток меньше, чем делитель. Записываем в частном цифру 8.

Значение частного чисел 299 и 34 – 8 и остаток 27.

2. Рассмотрим еще один случай деления.

В частном будет одна цифра. Чтобы легче было найти цифру частного, разделим 191 не на 46, а на 40.

(ост. 31)

4 – это только пробная цифра, ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 46 на 4.

Остаток 7 меньше, чем делитель 46. Значит, цифра частого 4 подходит, запишем ее.

Значение частного чисел 191 и 46 – 4 и остаток 7.

Заключение

На уроке мы учились выполнять деление на двузначные числа без остатка и с остатком.

Список литературы

1. Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова – М.: Просвещение, 2010.
2. Демидова Т.Е., Козлова С.А., Тонких А.П. Математика. 4 класс. Учебник в 3 ч. . 2-е изд., испр. – М.: 2013.; Ч.1 – 96 с., Ч.2 – 96 с., Ч.3 – 96 с.
3. Математика: учеб. для 4-го кл. общеобразоват. учреждений с рус. яз. обучения. В 2 ч. Ч. 1 / Т.М. Чеботаревская, В.Л. Дрозд, А.А. Столяр; пер. с бел. яз. Л.А. Бондаревой. – 3-е изд., перераб. – Минск: Нар. асвета, 2008. – 134 с.: ил.
4. Математика. 4 класс. Учебник. В 2 ч./Гейдман Б.П. и др. – 2010. – 120 с., 128 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

Выполните деление с остатком и без остатка.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

Источники:

http://7gy.ru/shkola/matematika/1312-delenie-stolbikom-na-dvuznachnoe-chislo.html
http://nauka.club/matematika/delenie-na-dvuznachnoe-chislo.html
http://interneturok.ru/lesson/matematika/4-klass/delenie-na-dvuznachnoe-chislo/pismennoe-delenie-s-ostatkom-na-dvuznachnoe-chislo

Статью нашли по запросам:

• деление трехзначнвх надвузначные методом под бора 3 класс ответы
• деление трехзначного на двузначное примеры 4 класс
• примеры деления трехзначного числа на двузначное без остатка
• примеры для 4 класса по математике на деление и умножение в столбик трехзначные на двузначные
• примеры на деление в столбик 4 класс трехзначные числа на двузначные

Как научить ребенка делению трехзначных чисел. Как научиться делить столбиком: примеры и решения

Алгоритм деления чисел в столбик, обучение ребёнка. Особенности деления многозначных чисел и многочленов.

Школа даёт ребёнку не только дисциплину, развитие талантов и навыков общения, но и знания по фундаментальным наукам. Одна из них — математика.

Хотя программа и нагрузка на учеников часто меняются, но деление в столбик чисел с разным количеством разрядов остаётся неприступной с первого захода вершиной для многих из них. Потому без тренировок дома с родителями часто не обойтись.

Дабы не упустить время и предотвратить образование кома непонятного у ребёнка в математике, освежите в памяти свои знания по делению чисел столбиком. Статья вам в этом поможет.

Как правильно делить числа в столбик: алгоритм деления

Для деления чисел столбиком следуйте по таким шагам:

• правильно запишите действие деления на бумаге. Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку. Так вы сохраните визуальную последовательность решения,
• разлинейте место между делимым и делителем.
  Вам поможет схема ниже.

• планируйте пространство для деления в столбик. Чем длиннее число, которое подлежит делению, и чем корове делитель, тем ниже на станице спуститься решение,
• первое действие деления совершайте с тем количеством цифр делимого, которое равно делителю. Например, если справа от разделительной линии у вас стоит однозначная цифра, то рассматривайте первую у делимого, если двухзначная — то 2 первых,
• перемножьте числа под и над чертой и запишите результат под цифрами делимого, которые вы обозначили для первого действия,
• завершайте действие вычитанием и определением остатка. Нарисуйте горизонтальную линию над ним, чтобы отделить первый шаг решения,
• допишите следующую цифру делимого к остатку и продолжайте решение,
• последний шаг деления — когда вы получите от вычитания 0 либо число, меньше делителя. Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.

Как объяснить ребенку деление и научить делить столбиком?

Во-первых, учтите ряд вводных факторов:

• ребёнок знает таблицу умножения
• хорошо разбирается и умеет применять на практике действия вычитания и сложения
• понимает разницу между целым и его составными элементами

• поиграйте с таблицей умножения. Положите её перед ребёнком и на примерах покажите удобство использования при делении,
• объясните расположение делимого, делителя, частного, остатка. Предложите ребёнку повторить эти категории,
• превратите процесс в игру, придумайте историю про цифры и действие деления,
• подготовьте наглядные предметы для обучения. Подойдут счётные палочки, яблоки, монеты, игрушки, очищенные сведение или апельсин. Предлагайте их распределить между разным количеством людей, например, между мамой, папой и ребенком,
• первым показывайте ребёнку действия с чётными числами, чтобы он видел результат деления, кратный двум.

Сам процесс освоения деления столбиком:

• запишите цифры, разделив их границами. Повторите с ребёнком расположение категорий деления,
• предложите ему проанализировать цифры делимого на предмет «больше-меньше» делителя. Помогайте вопросом — сколько раз одно число помещается во втором. В результате ребёнку следует выделить то число/числа, которые он будет применять для совершения первого действия,
• подскажите алгоритм определения разрядности частного. Её удобно изобразить точками, которые потом превратятся в цифры,
• помогите правильно определить и записать первое число в частное, совершите его умножение на делитель, запишите результат под делимым, выполните вычитание. Объясните, что результат вычитания всегда должен быть меньше делителя. В противном случае действие совершилось с ошибкой и его следует переделать,
• следующий шаг — анализ ситуации с добавлением второго числа от делимого и определения количества раз повторения делителя в нём,
• снова помогите с записью действия,
• продолжайте до момента, когда результат от разницы составит ноль. Это актуально только для деления чисел без остатка,
• закрепите знания у ребёнка еще несколькими примерами. Следите, чтобы он не устал, иначе дайте перерыв.

Как письменно делить в столбик двузначное число на однозначное и двузначное: примеры, объяснение

Приступим к пошаговому разбору примеров на деление в столбик.

Осуществите действие над цифрами 25 и 2:

• запишите их рядом и разделите линиями границы,
• определите нужное количество цифр делимого для первого действия,
• запишите значение под делителем и результат умножения под делимым,
• выполните вычитание,
• допишите вторую цифру делимого и повторите действия на умножение и вычитание.

Частично выполненное задание на деление столбиком двузначного числа на однозначное смотрите ниже:

Учтите, что деление столбиком двухзначного числа на однозначное возможно и в одно действие.

Второй пример. Разделите 87 на 26 в столбик.

Алгоритм аналогичен рассмотренному выше с той лишь разницей, что учитывать нужно сразу 2 числа делителя при определении количества раз повторения в делимом.

Чтобы облегчить задачу ребёнку, который только осваивается азы деления, предложите ему ориентироваться на первые цифры у делимого и делителя. Например, 8:2=4. Пусть ребёнок подставит это число под черту и выполнит умножение. Ему нужно увидеть своими глазами, что 4 много и нужно попробовать с тройкой.

Ниже пример деления столбиком двузначного числа на двузначное с остатком.

Третий пример. Как разделить число в столбик с нулем в ответе.

Вначале делим 15 на 15, в остатке 0, в ответ 1. Сносим 6, а оно на 15 не делится, значит ставим в ответе 0. Далее, 15 умноженное на 0, будет ноль и его отнимаем от 6. Сносим ноль, что в конце числа, получаем 60, которое делится на 15 и в ответ ставим 4.

Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение

Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.

Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.

Схематически он выглядит так:

В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.

Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.

Схема деления трехзначного на двузначное числа такая:

Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.

Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.

Схема деления трёхзначного на трёхзначное числа.

Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение

В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:

• определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
• появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
• проверку полученного результата посредством выполнения действия умножения. Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.

Ниже пример решения.

Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.

Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:

• количество знаков у частного, то есть результата
• цифры у делимого для первого действия
• правильность переноса остальных чисел

Примеры подробного решения ниже.

При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:

• у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
• для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
• совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов. Тогда их сократите и получится результат без остатка.

Ниже ряд подробных примеров с решениями.

Как делить в столбик с остатком?

Алгоритм деления в столбик с остатком аналогичен классическому. Разница лишь в появлении остатка, который меньше делителя. А значит первый остаётся без изменения.

Запишите его в ответе либо:

• как дробь, где в числителе остаток, а в знаменателе — делитель
• словами, например, 73 целых и 6 в остатке

Как делить столбиком десятичные дроби с запятой?

Существует несколько особенностей при подобном делении. Если вы совершаете действие с:

• десятичной дробью-делимым и целым числом-делителем, то действуйте по обычному алгоритму до тех пора, пока закончатся цифры у делимого перед запятой. Затем поставьте её в частном и продолжайте переносить цифры до окончания деления,
• числом, которое делится на 10, 100, 100 и т.д., то перенесите запятую в делимом влево на количество цифр, равное количеству нулей делителя. Например, 749,5:100=7,495,
• десятичными дробями одновременно и в делителе, и в делимом, то сначала избавьтесь от запятой у второго элемента. Для этого перенесите её вправо в обоих дробных числах на то количество знаков, которые отделены у делителя. Например, 416,788:5,3 преобразуйте в 4167,88:53 и совершите обычное деление в столбик.

Как делить столбиком меньшее число на большее?

При таком делении у вас частное будет начинаться с 0 и иметь после него запятую.

Чтобы ребёнок лучше усвоил подобное деление и не запутался в количестве нулей, месте постановки запятой в частном, дайте ему такой пример:

• первое действие на вычитание проведите с нулями, записанными по одному под делителем и в графе «частное»,
• поставьте запятую в частном, а остатка после разницы добавьте ноль и продолжайте обычное деление в столбик,
• когда остаток от вычитания опять будет меньше делителя, допишите первому ноль и продолжайте действие. Финальный итог — получение ноля от разницы верхнего и нижнего чисел либо повторения остатка. В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.

Ниже пример.

Как делить столбиком числа с нулями?

Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.

Из нюансов отметим:

• при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
• если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.

Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.

Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.

Практикуйте полученные знания и помогайте своему чаду осваивать математику.

Видео: как правильно делить числа в столбик?

Деление чисел с остатком или без него является самым трудным из четырех арифметических действий. С основами этого процесса ребенок знакомится еще в самом раннем детстве иногда малышу приходится поровну делить конфеты между плюшевым мишкой и куклой. Правильно разделить угощение на несколько кучек для ребенка обычно труда не составляет.

Однако позже могут возникнуть проблемы. Школьные задачи не всегда подразумевают деление нескольких предметов на количество людей. Это могут быть, например, задания на скорость – и часто они вводят ребенка в ступор.

В таком случае научить принципам деления числа обязаны родители. Математика не терпит пустоты – если ребенок что-то пропустил или просто не усвоил информацию, это может сильно затруднить изучение дальнейших тем, а также других дисциплин в более поздних классах.

Начальное обучение делению

1. Чем раньше родители объяснят ребенку принципы деления с остатком или без него – тем лучше он их усвоит. А чтобы процесс прошел легко, нужно это сделать в форме игры. Например, дать шесть конфет и попросить их поделить поровну между куклой, киской и папой. А теперь – между мамой и бабушкой. Естественно, у ребенка получатся разные результаты. Важно объяснить, почему так получилось.
2. Следует учесть, что для обучения лучше использовать бытовые, знакомые малышу предметы: игры со счетными палочками или бумажными квадратиками вряд ли будут ему интересны.
3. Следующим шагом можно попробовать объяснить деление с остатком – принцип тот же: игра. Пусть кроха попробует пятью орехами угостить Мишу и Свету. Он отдаст каждому по 2 орешка, а оставшийся сможет съесть сам.
4. Теперь ребенок сможет понять сам принцип деления: большее число делится на меньшее. Конечно, взрослые-то знают, что так происходит не всегда, но для ребенка в возрасте от 5 до 8 лет этой информации будет достаточно.

Обучение делению школьников младших классов

Если ребенок все прекрасно усвоил в игровой форме, то в школе ему придется применить свои знания и умения на практике. Именно в это время отход от привычных категорий – конфет, кукол и прочего – может вызвать серьезные затруднения.

1. В этом возрасте ребенок школьник должен уже знать первые три арифметических действия и уметь оперировать ими. Он должен понимать и знать таблицу умножения. Вот она, кстати, в некоторых случаях поможет объяснить ученику, что деление – это умножение наоборот. Родителю стоит сесть рядом с ребенком и, изучая напечатанную на обложке тетради таблицу умножения, объяснить, как это работает на практике. Например, 4х7=28. А если пойти наоборот? Уточнить, на пересечении какого числа с цифрой 7 находится 28. С 4. Вот и разделили.
2. Теперь ребенок должен сделать цифровую запись этого процесса: это способствует закреплению информации в памяти.

Деление столбиком

Лишь после того, как ученик освоил и хорошо запомнил предыдущие способы, можно переходить к делению столбиком, с остатком или без него.

Вначале необходимо, чтобы ребенок понял и заучил название компонентов процесса деления:

• делимое – то число, которое делят;
• делитель – то, на что делят;
• частное – конечный результат.

• вначале пишется делимое – пусть это будет 98;
• справа от него рисуют уголок, как перевернутую букву «Т», в нем записывают делитель – в нашем случае 7;
• теперь определяют наименьшее число в делимом, которое делится на 7 – это 9;
• цифра 7 в числе 9 может поместиться 1 раз – значит, в частном пишем 1;
• теперь нужно умножить делитель 7 на первую цифру частного 1 – получится 7. Его надо записать под 9;
• из 9 вычесть 7 – получится 2.

Обратите внимание: полученная разность никогда не сможет быть равна или больше делителя. Если это произошло, значит, было неверно определено количество 7 в 9.

• так как 2 на 7 не делится, сносят вниз следующую цифру из двузначного делимого – 8. Получили 28. Его можно поделить на 7 – получится 4;
• эту цифру нужно записать рядом с 1 – получится 14. Это и будет частным в данном примере;
• но правильно оформить решение все-таки нужно, поэтому 7 умножают на 4 – получают результат 28, который и пишут под 28. Вычитают 28 из 28 – получают 0. Его пишут под чертой, которой подводят итог решения.
• в случае если остаток не равен нулю, то это – деление с остатком.

В первый класс идет не только малыш – родители вместе с ним начинают и заканчивают школу. Учитель не всегда имеет возможность объяснить каждому ученику ту или иную тему. И вот тогда родители должны научить свое чадо, что такое умножение, деление с остатком двузначного числа на однозначное. При переходе в третий класс задание усложнится – научить нужно будет делению с остатком и трехзначного числа на двузначное. Главное, набраться терпения и не ругать ребенка из-за малейшей оплошности. Тогда все получится, и математика, возможно, станет любимым школьным предметом.

Поскольку операция деления простых чисел является одним из важных математических действий, многие родители задумываются о том, как научить ребенка делению.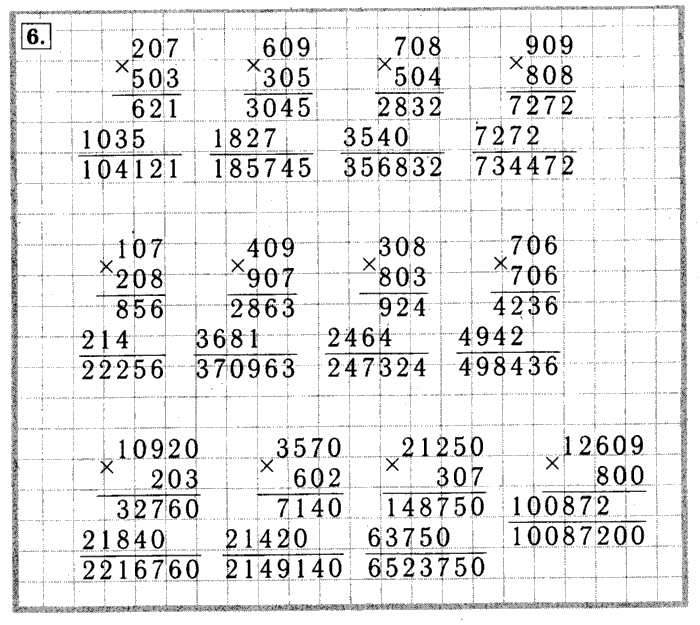 Перед тем, как приступить к обучению, вы должны убедиться в том, что малыш уже умеет вычитать, складывать и умножать числа. Лучше всего приступать к изучению деления столбиком, когда ребенок отправляется в третий класс. Очень важно объяснить, что деление представляет собой процесс, по ходу которого целое разбивают на отдельные части. Не забудьте учесть знания таблицы умножения – убедитесь в том, что кроха уверенно знает ее.

Перед тем, как серьезно приступить к обучению, попробуйте освоить эту нехитрую науку в игровой форме. Для того чтобы сформировать у малыша представление о том, что деление – это разбор целого на части, дайте ему несколько предметов и попросите разделить между членами семьи или игрушками. При этом эффективно использовать нечто целое – фрукт или овощ, например, который можно разрезать на кусочки.

Потренируйтесь на кубиках. Возьмите парное количество этих элементов и предложите ребенку разделить их поровну между собой и вами. Варьируйте задание. Добавьте такое количество кубиков, чтобы их общее количество делилось на три или шесть. Затем можно усложнить задачу и делить на восемь, семь или девять. После выполнения каждого задания тщательно анализируйте результат вместе с малышом. Он должен понимать сам процесс. Если что-то ему непонятно, постарайтесь доходчиво это объяснить. Не зацикливайтесь на определенных предметах. Постоянно меняйте их, чтобы ребенок приспосабливался делить любые объекты.

Вместе с этим ищут и читают:

Теперь вам необходимо решить, как научить ребенка делить. Если он уже перешел в третий класс, трудностей у вас возникнуть не должно. Для начала объясните малышу зависимость между делением и умножением. Продемонстрируйте ему, как правильно делить столбиком, используя таблицу умножения. Рассмотрим следующий пример: 3*4=12. Расскажите ребенку, что три и четыре – это множители, а двенадцать – произведение. Проиллюстрируйте ему это на наглядном примере. Покажите ему, что если двенадцать разделить столбиком на три, получится четыре.

Объясните ученику, который перешел в третий класс, что категории, описывающие деление, называются «делимое», «делитель», «частное». Продемонстрируйте это наглядно с помощью таблицы. Рассмотрите как можно больше примеров, чтобы малышу было понятнее. Это пригодится в дальнейшем, когда вы будете осваивать деление столбиком. По сути, вам необходимо научить кроху смотреть на таблицу умножения «наоборот».

Перед началом занятий еще раз вспомните категории деления. Теперь попробуем объяснить все наглядно. Например, разделим число девятьсот тридцать восемь на семь. Запишем числа, чтобы делить их столбиком. Если вы только начинаете обучение, то ребенку, который пошел в третий класс, будет проще для начала делить числа без остатка. Теперь показываем ученику числа делимого и предлагаем ему выбрать наименьшее число, которое будет больше, чем делитель. Выбираем число девять. Теперь предложите малышу ответить, сколько чисел семь может содержаться в числе девять? Правильный ответ – одно. Поэтому записываем единичку.

Умножаем семь на один, получаем семь. Этот результат мы записываем под девяткой из числа девятьсот тридцать восемь. Вычитаем от девятки семерку в столбик. В остатке получаем два. Аналогичным образом записываем результат. Полученное число меньше, чем делитель. Таким образом, нам необходимо его увеличить. Объединяем его со следующим неиспользованным числом – тройкой. «Плюсуем» тройку и двойку. Продолжаем процесс деления согласно с алгоритмом. В итоге мы получаем число – сто тридцать четыре.

Самое главное в процессе обучения малыша, который перешел в третий класс, чтобы он усвоил простой алгоритм. Развивайте наблюдательность у крохи, проводите аналогии с другими математическими действиями, больше играйте и наблюдайте за природой.

В классе много детей, и у учителя не всегда получается уделить внимание каждому. Однако если ребенок что-то пропустит или не поймет, то это затруднит изучение дальнейших тем. В этом случае на помощь ему должны прийти родители. К примеру, как научить ребенка делению? Сначала математический процесс лучше объяснять в игровой форме. Затем можно переходить к более сложным задачам.

Как научить ребенка делению в форме игры

Скучные учебники лучше отложить в сторону на время. Малыш быстро усвоит сложный материал, если мама или папа превратит обучение в интересную игру. Итак, как научить ребенка делению?

Для этого применяют упражнение:

1. Для проведения домашних занятий следует запастись конфетами или яблоками. Также понадобятся игрушки, с которыми любит возиться ученик. Нужно попросить малыша, чтобы он разделил четыре яблока или конфеты между двумя-тремя мишками или куклами. Затем количество предметов, подлежащих делению, увеличивается до шести, восьми, десяти.
2. Итак, игрушки «получили» конфеты или яблоки. Теперь ученик должен посчитать, сколько досталось каждому мишке или кукле. Обязательно следует подвести итог. Предположим, что игрушек было три и между ними были разделены шесть конфет. Следовательно, каждая «получила» по две. Нужно объяснить ребенку, что «разделить» означает всем раздать поровну.
3. Как научить ребенка делению дома? Для лучшего усвоения материала стоит изменить условия задачи. К примеру, нужно дать малышу шесть яблок и попросить распределить их между бабушкой, дедушкой и кошкой поровну. Затем это же количество предметов следует предложить ему поделить между бабушкой и животным. Обязательно следует объяснить ученику, почему результат оказался разным.

Деление с остатком

Итак, малыш хорошо справляется с простыми задачами. Это означает, что пора использовать более сложные примеры. Как научить ребенка делению с остатком? Скажем, можно дать ученику пять конфет и предложить угостить ими дедушку и бабушку в одинаковом количестве. Остается одно лакомство, которое малыш забирает себе.

На этом примере можно объяснить ребенку, что одна конфета и является остатком. Затем можно предложить малышу, к примеру, разделить между бабушкой, дедом и кошкой восемь конфет поровну.

На примере таблицы умножения

Как научить ребенка делению, если он уже знает умножение? Малыш должен понять, что этот процесс подразумевает действия, противоположные умножению:

1. Для начала пусть ученик умножит число 6 на 3. У него получится 18.
2. Далее нужно обратить внимание ребенка на то, что число 18 является результатом умножения вышеуказанных чисел.
3. Теперь следует разделить 18 на 6. Ребенок получит 3. Это станет для него наглядным примером того, что деление представляет собой действие, противоположное умножению.

Для закрепления материала непременно стоит рассмотреть примеры с другими цифрами. Деление освоится легко, если школьник хорошо знает умножение и сумеет понять связь между математическими действиями.

Определение понятий

Как научить ребенка делению чисел? Что ему необходимо знать? Малыш должен запомнить и названия чисел, которые участвуют в этом процессе.

1. Делимое. Так называется число, которое необходимо разделить.
2. Делитель. Это число, на которое разделяется делимое.
3. Частное. Так называется результат деления.

Для наглядности стоит вновь вернуться к примерам с лакомствами и игрушками. Ребенок должен понять, что делимое – это количество конфет или яблок, которое следует раздать. Делитель же – число игрушек, на которое они делятся.

Усложняем задачу

От простого следует переходить к сложному. Как научить ребенка делению в столбик? К обучению следует переходить уже тогда, когда малыш хорошо усвоит таблицу умножения. Предположим, что нужно разделить 110 на 5.

Эти числа необходимо написать на чистом листке бумаги, а затем разделить их перпендикулярными линиями.

1. Далее нужно объяснить ребенку, что число 110 является делимым, а число 5 – делителем.
2. Первая цифра числа 110 – 1, ее нельзя разделить на 5. Следовательно, необходимо взять следующую цифру. Получится число 11, в которое 5 может поместиться два раза.
3. В столбике под пятеркой нужно записать цифру 2. Далее необходимо попросить ученика умножить 5 на 2. У него получится 10. Эту цифру следует записать под числом 11.
4. Затем вместе с ребенком нужно вычесть число 10 из 11. Получится 1, возле этой цифры нужно записать оставшийся нолик в столбике. Получится 10.
5. Далее нужно разделить с малышом 10 на 5. Результат – 2, эту цифру нужно записать под пятеркой. Результатом деления является число 22.

Обучение лучше всего начинать с цифр, которые можно делить без остатка – однозначных, двузначных. Когда ребенок будет хорошо справляться с простыми операциями, задачу можно усложнить.

Алгоритм деления в столбик

Деление в столбик – задача, с которой поможет справиться знание простого алгоритма.

1. Для начала следует понять, где в примере делимое, а где делитель.
2. Далее делимое и делитель следует записать под «уголок». Чтобы ребенок не путался на начальном этапе обучения, можно сказать ему, что слева нужно записать большее число, а справа – меньшую цифру.
3. Затем нужно определить часть делимого, которую можно использовать для первичного деления.
4. Далее следует понять, сколько раз уменьшается в выбранной части делимого делитель. Можно обратить внимание ребенка на то, ответ не должен превышать 9.
5. Затем делитель нужно умножить на полученное число под «уголком». Результат вписывается под выбранную часть делимого.
6. Далее необходимо найти разницу (остаток).
7. Действия повторяются до тех пор, пока не удастся получить в остатке цифру 0.

Как быстро научить ребенка делению? Начинать процесс обучения необходимо с простейших задач. К примеру, малышу нужно разделить апельсин на дольки между членами семьи. Он начнет с того, что будет перекладывать по одной штучке. Уже после этого можно предложить ему подсчитать изначальное количество долек, а затем количество, которое должно достаться каждому.

Результат обучения зависит не только от умения родителей выбирать простые примеры. Также важно запастись терпением, так как путь предстоит долгий. Если ребенок не понимает какой-то момент, обязательно следует возвращаться к нему и повторять еще раз. Ни в коем случае нельзя ругать малыша, если у него что-то не получается. Если он допускает ошибку, необходимо спокойно поправить его.

Нужна ли таблица

Как сделать, чтобы малыш быстро освоил деление? Как научить ребенка решать примеры? Чтобы успешно справиться с этой задачей, необходимо знать таблицу умножения. Однако сейчас появились и таблицы деления, которыми пользуются некоторые учителя в процессе обучения.

Нужна ли таблица деления? Или достаточно, чтобы ребенок понял, что деление – это умножение наоборот? Второй вариант предпочтительнее, так как побуждает малыша думать. Однако вовсе не обязательно отказываться и от таблицы деления, когда ребенок уже проникнет в тайны этого процесса.

Не расстраивайтесь, если ваш ребенок не понял на уроке, как происходит процесс деления чисел. Учитель в школе не всегда может уделить внимание каждому ученику. Наберитесь терпения и станьте для школьника домашним педагогом. Математический процесс сначала объясняйте в игровой форме. Постепенно переходите к более сложным задачам. Ребенок все поймет и математика станет у него самым любимым предметом.

Объясняем ребенку деление в форме игры

Отложите в сторону скучные учебники. Превратите обучение в интересную игру:

• возьмите яблоки или конфеты. Попросите малыша, чтобы он разделил между двумя-тремя куклами или мишками четыре конфетки или яблока. Постепенно увеличивайте количество фруктов до восьми и десяти. Сначала ребенок будет раскладывать предметы медленно. Не кричите на него, запаситесь терпением. Если ошибается – спокойно поправьте. После того, как игрушки «получат» конфеты, пусть ребенок посчитает, сколько у каждой куклы их получилось. Подведите итог. Если было 6 конфет и их раздали трем куклам – каждой досталось по две. Объясните, что «разделить» – это значит, что всем нужно раздать поровну;
• другой игровой пример. Объясняем деление на цифрах. Скажите ребенку, что цифры являются теми же яблоками или конфетами. Объясните ему, что количество конфет, которое нужно разделить называется делимое. А количество человек, на которых делятся конфеты – делитель;
• дайте малышу 6 яблок. Попросите, чтобы он раздал их поровну бабушке, кошке и папе. Потом пусть он поделит это же количество предметов между котом и бабушкой. Объясните, почему получился разный результат;
• объясняем деление с остатком. Дайте малышу 5 орехов, и пусть он угостит в одинаковом количестве ими папу и бабушку. Оставшийся орешек малыш забирает себе. Объясните на этом примере, что один орешек и является остатком.

Вышеуказанные способы в игровой форме помогут ребенку понять процесс деления и то, что большее число делится на меньшее. Первое число – это количество яблок или конфет, а число второе – участники, между которыми делятся предметы. Для ребенка в возрасте от 5 до 8 лет этой информации хватит. Учите делению малыша еще до школы, ему будет легче усваивать уроки математики в будущем.

Объясняем ребенку деление на примере таблицы умножения

Этот способ обучения подойдет для учеников начальных классов, если они знают умножения. Расскажите, что деление – это та же таблица умножения, но в ней происходят противоположные умножению действия. Наглядный пример для ребенка:

• умножьте число 5 на 4. Получится 20;
• напомните школьнику, что число 20 – это результат умножения двух вышеуказанных чисел;
• разделите 20 на 5. Получите 4. Этим вы наглядно покажете, что деление является противоположным действием умножению.

Рассмотрите примеры с другими цифрами. Если школьник хорошо усвоил таблицу умножения и поймет связь между двумя математическими действиями – деление освоится легко.

Объясняем ребенку деление – определение понятий

Объясните ребенку названия чисел, участвующих в делении:

• делимое. Число, которое надо разделить;
• делитель. Число, на которое делимое разделяется;
• частное. Итог, полученный после деления.

Для наглядности используйте те же примеры с конфетами и людьми или игрушками, которых ребенок должен угостить сладостями.

Объясняем ребенку деление столбиком

Переходите к этому обучению только после того, как ребенок усвоил вышеуказанные способы.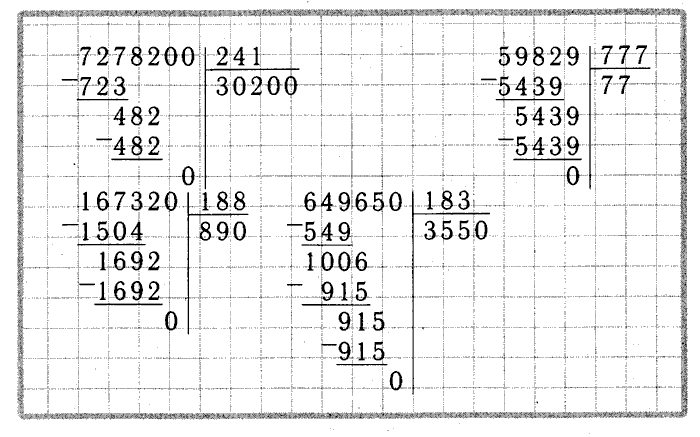 Также он должен знать, как умножаются в столбик числа. Берем простой пример: 110 делим на 5. Процесс объяснения:

• напишите на чистом листке бумаги эти числа;
• разделите их перпендикулярными линиями так, как будете делить в столбик;
• объясните, какое число является делителем, а какое – делимым;
• определите с ребенком, какое число может сначала использоваться для деления. Первая цифра – 1 на 5 не поделится. Значит, надо взять следующую цифру к ней и получится число 11. Цифра 5 может поместиться в 11 два раза;
• запишите цифру 2 в столбике под пятеркой. Попросите, чтобы ребенок умножил 5 на 2. Получится 10. Записываете эту цифру под числом 11;
• вычитаете с ребенком из 11 число 10. Получится 1. Пишете возле единицы оставшийся нолик в столбике. Получается 10;
• разделите с ребенком 10 на 5. Получится 2. Это число записываете под пятеркой, и конечный итог получается 22.

Начинайте обучение с двухзначных или даже однозначных цифр, которые можно делить без остатка. Постепенно усложняйте задачу.

Для легкого усвоения ребенком математики пробуждайте у него интерес к этому уроку. Сейчас появились таблицы деления. Но нужно ли ее запоминать ребенку, если он знает таблицу умножения и поймет, что деление – это процесс наоборот? Все зависит не только от школьного учителя, но и от ваших занятий со школьником.

УМНИКИ И УМНИЦЫ: ПРИМЕРЫ (ТРЕНАЖЕРЫ)

👌ГОТОВИМСЯ К ИТОГОВОЙ КОНТРОЛЬНОЙ РАБОТЕ

Выполни по действиям:

602 630 – 297 480 : 37 · 69 + 8 653 =

424 410 : 47 – 261 + 608 · 34 =

3 807 · 98 + ( 550 701 – 82 989 ) : 64 =

2 603 · 58 + ( 100 000 – 19 975 ) : 75 =

170 604 : 36 + ( 60 700 – 358 · 47 ) =

( 258 270 + 8 090 · 67 – 366 860 ) : 48 =

Реши уравнения:

у – 584= 425         856- с = 412

х + 147 = 231       к – 4523 = 2354

4824 : у = 12        х : 220 = 700

15 х у = 255         а х 28 = 1680 

Реши задачи:

😼Из города выехал автомобиль со скоростью  40  км/ч. Через  4  часа вслед за ним выехал второй автомобиль со скоростью  60  км/ч. Через сколько часов второй автомобиль догонит первый?

😼Из двух посёлков между которыми  5  км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди,  4  км/ч, а скорость пешехода, идущего позади  5  км/ч. Через сколько часов после выхода второй пешеход догонит первого?

😼С одного аэродрома одновременно в противоположных направлениях вылетели два самолёта. Один летел со скорость 420 км/ч, скорость другого на 80 км/ч меньше. Какое расстояние будет между ними через 3 часа?

😼Из гнезда одновременно в противоположных направлениях полетели две ласточки. Через 20 с расстояние между ними было 680 м. чему равна скорость одной из ласточек, если другая летела со скоростью

 16 м/с?

😼Два мальчика одновременно  вышли навстречу друг другу из своих домов. Один мальчик шёл со скоростью 50 м/мин, а другой со скоростью  65 м/мин. Через сколько минут они встретятся, если расстояние между домами 1035 м?

😼С двух льдин расстояние между которыми 1785 дм, одновременно навстречу друг другу поплыли два белых медведя . Скорость первого медведя 27 дм/с. С какой скоростью плыл второй медведь, если они встретятся через 35 с.?

😼Два автомобиля ехали с одинаковой скоростью. Один из них проехал 400 км, а другой – 480 км. Сколько часов был в пути каждый автомобиль, если первый был в пути на 2 часа меньше чем второй?

😼Два шофера возили зерно. Один из них сделал 3 рейса, другой – 5 рейсов за день. Второй шофер перевез на 30 т зерна больше, чем первый. Сколько зерна перевез каждый из шоферов по отдельности, если каждый рейс перевозилось одинаковое количество зерна?

😼Грузовики возили с базы муку в два разных магазина. В первый магазин отвезли 3 грузовика муки, а во второй 5. Сколько центнеров муки отправили в каждый магазин по отдельности, если в первый магазин отправили муки на 40 центнеров меньше, чем во второй?

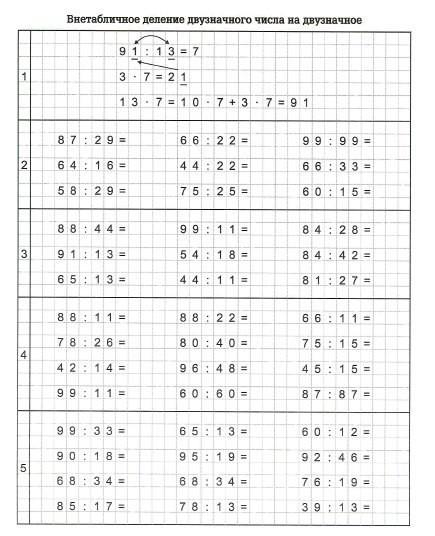
👌ДЕЛЕНИЕ НА ДВУЗНАЧНОЕ ЧИСЛО

6519 : 53 =	1127 : 49 =	4872 : 87 =	288 : 24 =
2805 : 33 =	5037 : 73 =	2812 : 76 =	2870 : 35 =
4268 : 44 =	18228 : 28 =	1450 : 25 =	735 : 15 =

243:14                 3912:12               6405:15              10104:12

6372:12              10914:34              3945:15              7800:24

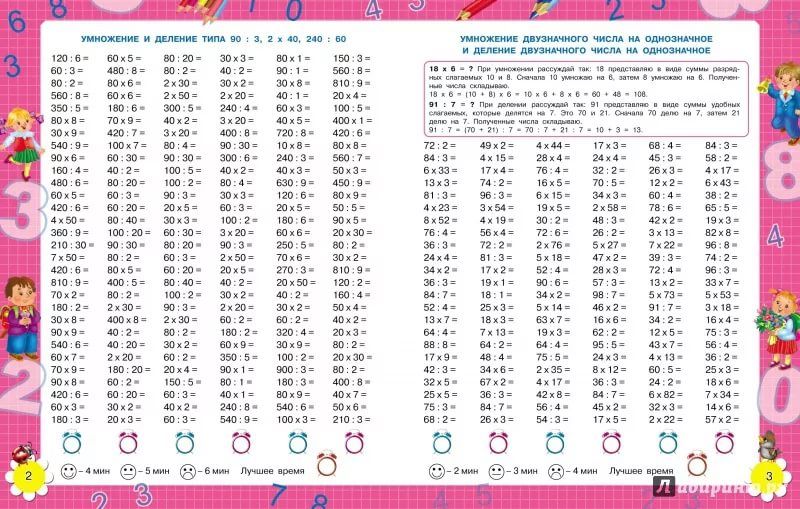
👌УМНОЖЕНИЕ НА ТРЕХЗНАЧНОЕ ЧИСЛО

👌УМНОЖЕНИЕ НА ДВУЗНАЧНОЕ ЧИСЛО

👌ВЕЛИЧИНЫ

1. Вырази в миллиметрах.

53 см =……..мм        6 м 46 см = ………мм        
3 м 5 дм 8 мм = ……….мм 6 м 4 дм 8 мм = ……….мм 

    38 см =……..мм     7 м 26 см = ……мм        

2. Переведи.

9000 м = ….. км                 6040 м = ….. км ….. м                       5001 м = ….. км …..м        730 см = ….. дм ….. см
 306 мм = ….. см ….. мм    9005 мм = ….. м ….. мм         

730 мм = ….. см ….. мм      39 см = ….. дм ….. см    
527 см = ….. дм…..              39 мм = ….. см ….. мм            
7030 мм = ….. м ….. мм        65200 м = …… км …… м
3. Напишите именованные числа в порядке возрастания.
10 см, 20 мм, 9 дм, 11 км, 43 см, 8 мм, 5 м, 62 м, 7 дм.

1. Вырази в центнерах.
6 т 4 ц                    5 т 200 кг         84000кг
2. Вырази в тоннах.
2600 ц                    57000 кг           69000ц
3. Сравни.
329т… 331 ц                  673ц… 375т 
1000 кг… 1т                   340 кг. .. 304 ц
901кг… 899 ц                 871кг… 817 ц
4. Переведи.
4000 г =… кг                      26 т65 ц = … ц 
62 т 5 ц = … ц                    30 ц = … кг

 

УМНОЖЕНИЕ И ДЕЛЕНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ 

Раздели заданные многозначные числа на однозначное число.

1)

37464

8

36830

5

39809

7

9314

1

16548

4

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

. ..

…

…

2)

7885

1

69616

8

12964

7

90369

9

6912

4

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

3)

9396

9

10126

1

50301

9

18819

9

22536

3

. ..

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

4)

5055

3

71010

9

75042

9

83862

9

13820

5

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

. ..

…

…

…

5)

52025

5

15230

2

14100

6

17346

7

2188

1

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

6)

25092

4

8126

2

16236

6

21352

2

23988

4

. ..

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

ЕДНИЦЫ ИЗМЕРЕНИЯ ПЛОЩАДИ 

И ПЕРЕВОД ВЕЛИЧИН

СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ

УМНОЖЕНИЕ И ДЕЛЕНИЕ КРУГЛЫХ МНОГОЗНАЧНЫХ ЧИСЕЛ

РЕШИ  

ДЕЛЕНИЕ ДВУЗНАЧНОГО НА ОДНОЗНАЧНОЕ

 ДЕЛЕНИЕ ДВУЗНАЧНОГО ЧИСЛА

  НА   ДВУЗНАЧНОЕ        

УМНОЖЕНИЕ И ДЕЛЕНИЕ             ТРЕХЗНАЧНЫХ ЧИСЕЛ

    ПИСЬМЕННОЕ ДЕЛЕНИЕ                                    ТРЕХЗНАЧНОГО ЧИСЛА 

                            НА  ОДНОЗНАЧНОЕ  

нажми сюда

👇

Видео “Письменное деление”

Примеры для тренировки: 855 : 5        568 : 2    879 : 3 

                                                   526 : 2       724 : 4    655 : 3   

                                                 847 : 7       966 : 6    968 : 4

жми сюда и решай

👇

Письменное деление

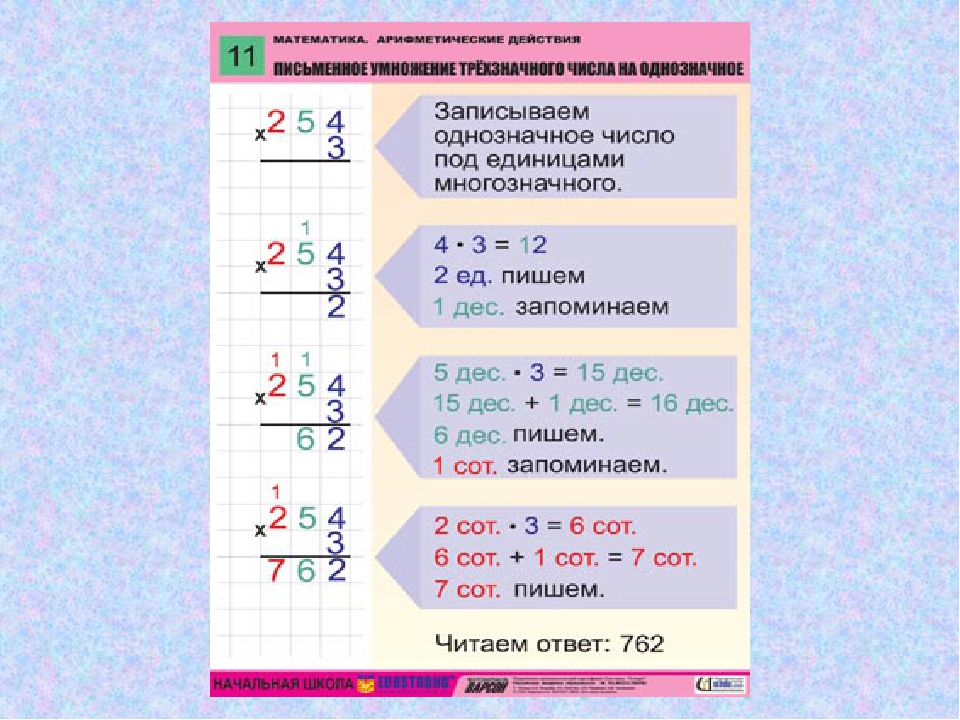
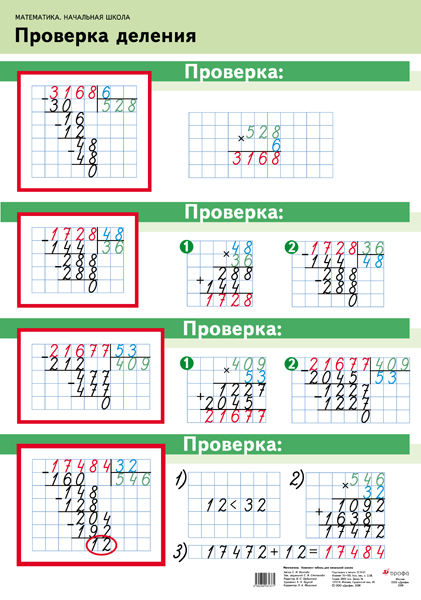
Конспект урока по математике 3 класс по теме ” Деление трехзначного числа на однозначное”

Конспект урока по математике 3 класс

 «Деление трёхзначного числа на однозначное».

Цель урока: Создание условий для усвоения алгоритма деления трёхзначного числа на однозначное через различные виды деятельности учащихся.

Задачи урока.

Образовательные:

-освоение алгоритма деления трёхзначного числа на однозначное; умение 
вычислять частное; совершенствование вычислительных навыков, навыков устного счёта; совершенствование умения работать в группе, в 
паре и самостоятельно.

Развивающие:

– развитие наблюдательности, внимания, памяти, логического мышления.

Воспитательные:

– воспитание умения слушать, общаться, стремление сознательно соблюдать дисциплину, воспитание ответственности и добросовестного отношения к 
работе, уважительных и доброжелательных отношений к одноклассникам, пропаганда здорового образа жизни.

Планируемые результаты:

Личностные результаты: 

устанавливать связь между целью деятельности и её результатом; определять общие для всех правила поведения; уметь осознанно и внимательно читать задания; выражать способность к самооценке на основе критерия успешности учебной деятельности.

Метапредметные результаты:

Регулятивные УУД: 
– работать по предложенному плану, инструкции; выдвигать свои гипотезы на основе учебного материала; осуществлять самоконтроль.

Познавательные УУД: 
– раскрывать значение понятия «частное», «произведение», «сумма», «разность» и использовать их в активном словаре;

– определять условия письменного деления трехзначного числа на однозначное без перехода через разряд и обосновывать свое мнение;

– -определять порядок письменного деления трехзначного числа на однозначное и обосновывать свое мнение;

Коммуникативные УУД: 
– формулировать высказывание, используя математические термины, в рамках учебного диалога;

– согласовывать позиции и находить общее решение.

Ход урока

1. Мотивирование к учебной деятельности. (1-2мин).

– Ребята, закройте глаза и представьте ту оценку, которую вы хотели бы получить на уроке, нарисуйте ее в воздухе перед собой.

– Очень захотите получить ее и приложите для этого все усилия.

– Я желаю вам удачи. Давайте вместе постараемся.

2. Актуализация знаний и фиксирование индивидуального затруднения в пробном действии. (4-5 мин).

– Откройте тетради, запишите число и классная работа.

– На следующей строчке запишите последнюю цифру вчерашнего числа 9

– В следующей клетке запишите цифру, показывающую порядковый номер текущего дня 2

-Рядом запишите цифру 5.

– Какое число у вас получилось? 925

– Что вы о нём можете сказать?

-Оно натуральное, некруглое, стоит на 925 месте в ряду натуральных чисел, ему предшествует число 924 за ним стоит число 926. Сумма цифр этого числа 16. Оно трехзначное. В нем 9 сотен, 2 десятка, 5 единиц.

Запишите самостоятельно другие трехзначные числа, используя эти цифры. Цифры в записи числа не должны повторяться. 

– Какие числа у вас получились? взаимопроверка

925 952  529 592 295 259 – доска

– Что означает цифра 9 в подчеркнутых числах?

952 925 529 592 295 259

– В числе 952 – сотни, 
-в числе 295 – десятки,
-в числе 529 – единицы.

 – Отчего это зависит?

– От места, которое цифра занимает в записи числа

– Чем похожи все эти числа?

-Они трехзначные.

– Какие задания вы можете предложить для выполнения с трехзначными числами?

– Назвать числа в порядке убывания и возрастания, назвать последующие и предыдущие числа, сравнить, сложить, вычесть, представить в виде суммы разрядных слагаемых.

-Запишите в порядке возрастания

259 295 529 592 925 952

-Запишите 259 в виде суммы разрядных слагаемых

259 =200+50+9

925=900+20+5

Взаимопроверка

3.Постановка цели и задач урока.

Расшифруйте слово

а	200	250	90	50	100	400	300
х	400	50	180	100	200	80	60
	д	е	л	е	н	и	е

х	200	50	400	80	180	60	100
	н	е	д	и	л	е	е

-Какое слово у вас получилось?

-Кто догадался какая будет тема урока?

-Какие цели мы поставим перед собой на уроке?

4.  Построение проекта выхода из затруднения. (7-8 мин)

Доска

40:2 153:9 420:60

974:2 72:9 952:2

-На какие две группы можно разбить данные выражения?

(табличное и внетабличное деление)

40:2=20 974:2=487 (учитель)

72:9=8 153:9=17 (ребенок)

420:60=7 952:2=476 (ребенок)

5. Физкультминутка. (динамическая пауза).

6. Реализация построенного проекта.

Открываем учебник и прочитаем алгоритм решения примера 248 и 2 столбиком.

Алгоритм письменного деления трехзначного числа на однозначное

1. Выделяем первое неполное делимое.

2. Определяем количество цифр в значении частного.

3. Подбираем первую цифру в значении частного.

4. Умножаем число, записанное этой цифрой, на делитель.

5. Вычитаем полученный результат из неполного делимого и находим остаток.

6. Убеждаемся , что остаток меньше делителя.

7. Записываем цифру следующего разряда делимого рядом с остатком.

8. Повторяем пункты 3, 4, 5, 6, 7.

7. Первичное закрепление с проговариванием во внешней речи.

– Используя алгоритм, решим примеры, записав действия столбиком.

696:3=232 609:3=203

864:2=432 840:4=210

-А сейчас решаем примеры у доски

8. Самостоятельная работа с самопроверкой по эталону (4-5 мин)

1)А теперь решим примеры на деление трёхзначных чисел, используя известный алгоритм

92:4=23

575:5=113

847:7=121

-Проверили результаты примеров на доске.

Тренировка по теме Деление трёхзначного числа на однозначное число

9. Включение в систему знаний и повторение (7-8 мин )
– Где нам может пригодиться умение делить трёхзначное число на однозначное?

1) Послушайте задачу.

За сезон одна пальма дала 128 литров кокосового сока, а вторая – в 2 раза меньше. Сколько всего литров сока собрали с двух пальм?

– О чем говорится в задаче?

– Прочитайте задачу еще раз, чтобы составить краткое условие.

– Что известно?

– Что запишем в краткое условие?

– Прочитай вопрос задачи.

– Можно ли сразу ответить на главный вопрос? Почему?

– А можно узнать? Как?

I  п.- 128 л – ? л

II п. – ? л в 2 р. м.

– Сколько всего литров сока собрали с двух пальм?

– Нет. Мы не знаем, сколько литров сока дала вторая пальма.

1) 128 : 2 = 64 (л) – со II пальмы

2) 128 + 64 = 291 (л)

Ответ: 291 л сока собрали с двух пальм.

Обсудите в паре решение и запишите в тетрадь.

2) Решение уравнения 
859 – а = 124 : 4

– Проверьте решение по образцу

859 – а = 124 : 4
859 – а = 31
а = 859 – 31
а = 828

859 – 828 = 124 :4

31=31
Ответ: а = 828

10. Рефлексия деятельности (2-3 мин)

Чему сегодня научились? 

– Что у вас получилось лучше всего?

– Что было интересного на уроке?

– Какое задание понравилось больше?

– Понравилось ли вам работать в группе?

– Как бы оценили своё настроение после урока?

11. Домашнее задание.

Детям раздается домашнее задание на разноцветных карточках разного уровня сложности. Дети самостоятельно выбирают для себя уровень сложности.

https://uchi.ru/teachers/stats/main

Тренировка по теме Деление трёхзначного числа на однозначное число

Методика изучения деления многозначных чисел — Мегаобучалка

А) Деление многозначного числа на однозначное

Умение делить многозначное число на однозначное фактически начинает формироваться при рассмотрении деления трехзначных чисел в разделе «Числа от 1 до 1000».

Изучение деления трехзначных чисел на однозначное число начина­ется с устных приемов. Вначале целесообразно вспомнить знакомые детям случаи деления двузначных чисел на однозначное. При этом следует вспомнить рассуждения для разных случаев:

48 : 4; 48 : 3. Обобщая, по­вторяем вывод: при делении двузначного числа на однозначное делим десятки, а затем делим единицы.

Приступая к делению трехзначных чисел, следует провести аналогии с рассмотренными ранее случаями:

48 : 4, 848 : 4= (800+40+8): 4; 48 : 3, 480 : 3 = (300 + 180) : 3.

Установив сходство и различия, подводим детей к основному выво­ду: делим, начиная с единиц высшего разряда, сначала делим сотни, затем десятки, затем единицы, то есть делим поразрядно.

Уже при устных вычислениях можно ввести некоторые новые для детей термины, которые будут употребляться в дальнейшем.

Например, в случае 480 : 3 = (300 +180): 3 = 300 : 3 +180 : 3, числа 300 и 180 называют неполными делимыми.

Переход к письменным приемам деления трехзначных чисел следует проводить с постепенным нарастанием сложности.

После решения нескольких примеров на деление устно целесообразно предложить детям случай, где выполнить вычисления устно будет труд­но. Например, 968: 4. Представляя делимое в виде суммы удобных сла­гаемых, то есть, выделяя неполные делимые, дети, естественно, будут испытывать трудности. Здесь следует напомнить детям, что, если трудно вычислять, можно записать столбиком. Однако запись в столбик при де­лении отличается от столбика при умножении. Поэтому вначале следует показать эту запись на знакомом детям материале, объясняя, где что за­писываем и как при этом рассуждаем:

8:2=4; 15:3=5; 13:4=3 (ост. 1).

_ 8 ∟2 _15 ∟3 _13 ∟4

8 4 15 5 12 3

0 0 1

Затем следует рассмотреть случай, записав его в столбик, когда каж­дый разряд делимого делится на делитель. Например, решая пример 846 : 2 = (800 + 40 + 6): 2 = 800 : 2 + 40 : 2 + 6 : 2 и повторив ход устных рассуждений, предлагается записать решение в столбик.

_ 846∟ 2При решении показывается и ход рассуждений:

8 423 1. Начинаем делить с сотен. Смотрим, сколько сотен в делимом (8). 8

_4 на 2 делится. Значит первое неполное делимое 8 сотен. Определяем,

4 сколько всего цифр будет в частном (3). Ставим 3 точки.

_6 Находим эти цифры частного. 8 сотен делимна 2 получим 4. В частном

6 пишем 4 на месте сотен. Узнаем, сколько сотен разделилось. 4 умножа

0 ем на 2, получим 8, за­писываем под сотнями. Из 8 вычесть 8 будет 0, его писать не будем. Сот­ни разделились все.

2. Делим десятки. 4 десятка – второе неполное делимое. 4 разделить на 2 будет 2. Пишем в частном цифру 2 на месте десятков. Узнаем, сколь­ко десятков разделилось. 2 умножим на 2, получим 4. Из 4 вычесть 4 получим 0. Десятки разделились все.

3. Делим единицы. 6 единиц – третье неполное делимое. 6 разделить на 2 будет 3. Пишем в частном 3. Узнаем, сколько единиц разделилось. 3 умножим на 2, получим 6. Из 6 вычесть 6 будет 0. Все число раздели­лось. Читаем ответ: 423.

Теперь следует вернуться к решению примера 984 : 4 в столбик и на нем повторить ход рассуждений, обращая внимание на некоторые новые моменты.

_948 ∟4 1. Делим сотни. 9 сотен делится на 4 с остатком. Значит

8 237 9 сотен – первое неполное делимое. В частном будет 3

_14 цифры, ставим три точки.

12 2. 9 делим на 4, возьмем по 2.

_28 3. Узнаем, сколько сотен разделилось. 2 умножим на 4,

28 получаем 8.

0 4. Из 9 вычесть 8, получаем 1. Остаток 1 меньше дели­теля. Можно делить дальше.

5. Делим десятки. 1 сотня да 4 десятка в делимом получаем 14 десят­ков – это второе неполное делимое и т.д.

Следующий элемент усложнения состоит в том, что первая цифра делимого может быть меньше делителя. Это значит, что первое неполное делимое будет образовано двумя первыми цифрами делимого. В частном получится цифр на 1 меньше, чем в делимом.

Пример. 348 : 4

Здесь следует обратить внимание детей на образование первого не­полного делимого.

Наиболее коварными для детей являются случаи деления, когда в се­редине или на конце частного получаются нули. В таких случаях дети часто допускают ошибки, теряя нули.

При решении первого такого примера запись следует выполнять под­робно, затем показать ее в сокращенном виде.

_915 ∟3 _915 ∟3

9 305 9 305

_1 … _15 …

0 15

_ 15 0

15

В качестве подготовительных упражнений, наряду с другими, с деть­ми обязательно следует вспомнить решение примеров, которые должны решаться при изучении деления с остатком

1:3=0 (ост. 1) 2:6=0 (ост. 2)

Чтобы облегчить детям усвоение алгоритма деления, рекомендуется использовать памятку вида:

1. Прочитай и запиши пример;

2. Установи высший разряд и число цифр в частном;

3. Раздели, чтобы найти цифру высшего разряда частного;

4. Умножь, чтобы узнать, сколько единиц этого разряда разделили;

5. Вычти, чтобы узнать, сколько единиц этого разряда осталось разделить;

6. Сравни остаток с делителем;

7. Если получился остаток, то вырази его в единицах следующего за ним низшего разряда и прибавь к ним единицы такого же разряда делимого;

8. Продолжай деление так же, пока не решишь пример до конца;

9. Проверь результат.

Вначале этой памяткой пользуется только учитель. При этом важно, чтобы объяснения давались им в той же последовательности. Затем с па­мяткой знакомятся учащиеся. В классе она вывешивается в виде таблицы, а для себя каждый ученик записывает на отдельном листке.

Начинают работать учащиеся с памяткой под руководством учителя, проговаривая каждое задание и ответ на него. Затем начинают пользо­ваться сами, проговаривая рассуждения про себя. И, наконец, выполня­ют операции самостоятельно в соответствии с заданиями.

Эта работа получает свое естественное продолжение в разделе “Чис­ла, которые больше 1000”. Здесь продолжается работа по формирова­нию у детей умения выполнять деление чисел в пределах миллиона.

Все случаи деления многозначных чисел изучаются в такой последо­вательности:

– деление многозначного числа на однозначное;

– деление многозначного числа на числа, оканчивающиеся нулями;

– деление многозначного числа на двузначное и трехзначное число. Приступая к рассмотрению первого случая деления, следует провес­ти работу по восстановлению в памяти детей необходимых сведений:

– смысл действия деления; названия компонентов и результата дей­ствия деления;

– связь умножения и деления;

– таблица умножения и деления;

– внетабличные случаи деления двузначного числа на однозначное;

– деление с остатком;

– деление трехзначных чисел на однозначное число (устные приемы

и письменные).

В результате этого, деление многозначного числа на однозначное бу­дет являться логическим продолжением начатой ранее работы.

Начинать следует с устных приемов. После решения примероввида:

84 : 2 и 484 : 2;

И 840 : 3,

следуетпредложить примеры:

6484:2= (6000+400+80+4): 2 ==6000:2+400:2+80:2+4:2 =3242;

8400 : 3 = (6000 + 2400) : 3 = 2800.

Проведя сравнение, установив сходство и различие, подводим детей к выводу:

– делим, начиная с единиц высшего разряда;

– делим поразрядно.

Приступая к рассмотрению письменных приемов деления многознач­ных чисел, естественно, повторить деление трехзначных чисел в столбик.

Случаи деления трехзначных чисел следует взять разные, начиная с легких, то есть таких, когда количество цифр в частном такое же, как и в делимом, а затем усложнить.

Пример.

_9648 ∟4

8 2412

_16

16

_4

4

_8

8

1964 ∟4 3624∟4 36240∟4

… … ….

При решении этих примеров надо обратить внимание детей на ход рассуждений, вспомнить памятку, а затем показать, как применить ее и при решении новых примеров.

Деление однозначных, двухзначных и трехзначных чисел (определение, типы и примеры)

Содержание

• Что такое деление?
• Что такое дивиденд, делитель, частное и остаток?
• Деление на однозначные числа
• Деление трехзначных чисел на двузначные числа
• Деление четырехзначного числа на двузначное число
• Решаемые примеры
• Часто задаваемые вопросы

Что такое деление?

В математике есть четыре основных действия: сложение, вычитание, умножение и деление. Деление — это процесс деления чисел на равные части или равные доли. Предположим, 25 студентов нужно разделить на баскетбольные команды по 5 игроков в каждой. Чтобы найти количество баскетбольных команд, мы делим 25 на 5 = 5. Это означает, что учеников можно разделить на 5 команд поровну. Здесь 25 известно как делимое, 5 известно как делитель, а результат 5 известен как частное.

Что такое делимое, делитель, частное и остаток?

Общая форма деления: \(\text{Дивиденд}\div \text{Дивизор}=\text{Частное}\)

Деление также может быть записано как \(\frac{\text{Дивиденд}} {\text{Делитель}}=\text{Частное}\)

Делимое — это число, которое делится в операции деления. Делитель — это число, на которое делится делимое. Частное есть результат операции деления.

 

Во многих случаях делитель не может полностью делить делимое. В таких случаях мы получаем остаток после операции деления. Остаток — это остаточное значение, которое мы получаем после операции деления.

 

 

 

Предположим, вы хотите раздать 15 файлов cookie поровну между 4 друзьями. Вы можете раздать своим друзьям только 12 файлов cookie, если хотите, чтобы каждый из них получил одинаковую долю. Оставшиеся 3 файла cookie представляют остаток. Результат операции деления можно записать как 3 R 3, где 3 — частное, а 3 — остаток.

Если есть остаток, то

 

\(\text{Дивиденд}=\text{Делитель}\times \text{Частное}+\text{Остаток}\)

 

Пример остатка:

 

Важно отметить, что делитель не может быть равен 0. В таких случаях операция деления не определена. То есть мы не можем выполнить деление, а значит, и результата не получим.

Деление на однозначные числа

Деление на однозначные числа можно выполнить с помощью длинной таблицы деления. Предположим, вы хотите разделить \(2048\div 5\).

Выполните следующие действия.

Сначала находим оценку \(2000\дел 5=400\)

 

 

Здесь делимое равно 2048, делитель равен 5, частное равно 409, а остаток равен

. проверить результат, мы можем умножить частное на делитель, добавить остаток и сравнить его с делимым. Если оба значения равны, это означает, что операция деления выполнена правильно.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=5\times 409+3 \)

\ (= 2045+3 \)

\ (= 2048 \)

\ (= \ text {dividend} \)

Следовательно, операция деления подтверждается

Отдел 3- digit Числа на двузначные числа

Деление трехзначных чисел на двузначные числа аналогично делению, которое мы выполняли ранее с однозначными числами. В этом случае единственное отличие состоит в том, что делимое будет трехзначным числом, а делитель — двузначным числом.

Давайте посмотрим, как мы можем разделить

\(369\дел 12\).

Сначала найдем оценку, так что \(300\div 10=30\)

В этом случае делимое равно 369, делитель равен 12, частное равно 30, а остаток равен 9. 

 

Чтобы проверить результат, мы можем умножить частное на делитель, добавить остаток и сравнить его с делимым. Если оба значения равны, это означает, что операция деления выполнена правильно.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=12\times 30+9\)

\ (= 360+9 \)

\ (= 369 \)

\ (= Dividend \)

Операция деления проверяется.

Деление четырехзначного числа на двузначное

Деление четырехзначного числа на двузначное также аналогично операциям деления, которые мы выполняли ранее. Разделим 4156 на 41,9.0005

Сначала мы находим оценку так \(4000\times 40=100\)

В этом примере делимое равно 4156, делитель равен 41, частное равно 101, а остаток равен 15. 

Проверить результат, мы можем умножить частное на делитель, добавить остаток и сравнить его с делимым. Если оба значения равны, это означает, что операция деления выполнена правильно.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=41\times 101+15\)

\ (= 4141+15 \)

\ (= 4156 \)

\ (= Dividend \)

Операция деления проверяется.

Решенные примеры

Пример 1: Разделите 418 ÷ 4 и проверьте результат.

 

Решение:

Найдем оценку \(400\дел 4=100\)

 

Мы можем проверить ответ, используя следующее уравнение.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=4{\times} 104+2=416+2=418=\text{Дивиденд}\)

 

Пример 2: Уильям разделил \(2149\div 7\) и получил частное как 306, а остаток как 6. Разумен ли этот ответ?

 

Решение:

Если операция деления верна, она должна удовлетворять следующему условию.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=\text{Дивиденд}\)

 

В этом случае делимое равно 2149, делитель равен 7, частное равно 306, а остаток равен 6.

Подставьте значения в уравнение:

\(7\times 306+6=2142+6=2148\)

\(2148\neq 2149\)

Следовательно, мы можем сделать вывод, что Вильям допустил ошибку в операции деления.

 

Пример 3: Две недели называются двумя неделями. Сколько двухнедель в году? (1 год = 365 дней)

 

Решение:  

1 год = 365 дней

1 две недели = 14 дней

Чтобы найти количество двух недель в году, нужно разделить количество дней в году на количество дней. через две недели. Это означает, что нам нужно найти \(300\div 10=30\).

Сначала находим оценку \(300\дел 10=30\)

 

Итак, в году 26 полных двухнедельников. Дополнительный 1, который мы получили в качестве остатка, можно считать дополнительным днем. Следовательно, в году 26 двухнедельников и один дополнительный день.

Здесь делимое равно 365, делитель равен 14, частное равно 26, а остаток равен 1. Чтобы проверить ответ, мы можем использовать следующее уравнение.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=\text{Дивиденд}\)

 

\(14\times 26+1=364+1=365 = Дивиденд\)

Следовательно, операция деления проверена

 

Пример 4: Франклин владеет кукурузным полем, и на нем работают 14 рабочих. Он передал 6200 долларов Куперу, который также работает на ферме. Франклин попросил Купера разделить деньги поровну и выплатить заработную плату всем рабочим. Если после деления заработной платы поровну останутся деньги, Франклин хочет, чтобы Купер купил всем закуски. Какова дневная заработная плата каждого рабочего? Сколько денег осталось на покупку напитков?

 

Решение:  

Общая заработная плата = $6200

Количество рабочих = 14

Чтобы найти дневную заработную плату каждого рабочего, нужно найти \(6200\div 14\). Сумма денег на угощение будет получена как оставшаяся часть этой операции разделения.

 

Сначала найдем оценку \(6000\дел 15=400\)

 

Здесь делимое равно 6200, делитель 14, частное 442, а остаток 9 1.0005

 

Это означает, что работники фермы получат по 442 доллара каждый, и у них есть 12 долларов на покупку напитков.

Часто задаваемые вопросы

Что осталось?

Остаток — это остаточное значение, которое мы получаем после выполнения операции деления. Во многих случаях делимое не может полностью делить делитель. Получаем остаток в таких операциях деления.

Как проверить результат операции деления?

Чтобы операция деления была корректной, она должна удовлетворять следующему условию.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=\text{Дивиденд}\)

 

Если мы не получим дивиденд при добавлении остатка к произведение делителя и частного, значит, операция деления пошла не так.

Почему результат операции деления можно проверить умножением?

Мы можем проверить результат операции деления с помощью умножения, потому что операция умножения обратна операции деления. Например, разделим 1 на 2.

\(1\div 2=\frac{1}{2}\)

Теперь умножим результат на 2.

\(\frac{1}{2 }{\times}2 =1\)

Выполнив умножение того же числа, мы получили исходное число. Это потому, что умножение обратно делению. Мы используем ту же логику для проверки результата длинной операции деления.

 

Где мы используем деление в реальной жизни?

Мы используем разделение в нашей повседневной жизни для различных целей. Разделение используется при разделении счета в ресторане, поровну делящихся закусками между друзьями, выделении времени для изучения разных предметов и т.д.

Ознакомьтесь с другими нашими курсами

Деление многозначного числа на однозначное

Эта тема может показаться запутанной в первый раз. Не отчаивайтесь и не отказывайтесь от обучения. Понимание придет в любом случае. Если не сразу, то чуть позже. Главное не сдаваться и продолжать усердно учиться.

В предыдущих примерах мы делили однозначное число на однозначное число, и это не доставляло нам особых хлопот. Теперь мы собираемся разделить многозначное число на однозначное число.

Если вы не понимаете, что такое однозначные и многозначные числа, советуем изучить предыдущий урок, который называется умножение.

Используя стандартный алгоритм

Чтобы разделить многозначное число на однозначное число, вы должны сначала посмотреть на первую цифру этого многозначного числа и посмотреть, больше ли она делителя. Если больше, то разделить, а если нет, то проверить, больше ли первые две цифры многозначного числа делителя. Если первые две цифры больше делителя, то разделить, а если нет, то проверить, больше ли первые три цифры многозначного числа делителя. И так до тех пор, пока не будет сделано первое деление.

Сложно? Вовсе нет, если мы посмотрим на некоторые примеры.

Пример 1.  Найти значение выражения 25 : 3

25 — многозначное число, а 3 — однозначное число. Примените правило. Посмотрите на первую цифру многозначного числа. Первая цифра 2. Два больше, чем три? Нет. Итак, мы смотрим на первые две цифры многозначного числа. Первые две цифры образуют число 25. Двадцать пять больше трех? Да, это больше. Итак, делим число 25 на 3. Запишем это выражение с помощью длинного деления и начнем делить:

Сколько троек в числе 25? Если ответ поначалу затруднен, можно посмотреть таблицу умножения на три. Там нужно найти произведение меньшее 25, но очень близкое к нему или равное ему. Если вы найдете такой продукт, вам нужно взять оттуда множитель, который дал такой продукт:

Это таблица умножения на три. В нем нужно найти произведение меньшее 25, но очень близкое к нему или равное ему. Очевидно, это произведение числа 24, которое выделено синим цветом. Из этого выражения нужно отнять тот множитель, который дал этот продукт. Это множитель 8, заштрихованный красным цветом.

Эта восьмерка отвечает на вопрос, сколько троек в числе 25. Запишите это так:

Теперь выньте остаток. Для этого умножьте частное на делитель (8 на 3) и под делителем запишите полученное число:

Теперь от делителя отнимите число 24 и получите 1. Это и будет остаток:

25 : 3 = 8 (1 осталось)

(8 x 3)  + 1 = 24  + 1 = 25

Последний остаток всегда меньше делителя. Если последний остаток больше делителя, значит, деление не завершено.

В приведенном выше примере последний остаток равен 1, а делитель равен 3. Один меньше трех, поэтому деление завершено. Последний остаток, меньший делителя, указывает на то, что он не содержит чисел, равных делителю.

В нашем примере, если вы зададите вопрос «сколько троек в единице?», ответ будет «ни одной», потому что единица не содержит троек, потому что она меньше тройки.

---

Пример 2.  Разделите 326 на 4.

Посмотрите на первую цифру числа 326. Первая цифра 3. Она больше делителя 4? Нет. Затем проверяем два разряда делителя. Две цифры делителя образуют число 32. Оно больше делителя 4? Да, это так. Вот почему мы разделяем это. Напишите такое выражение:

Теперь зададим вопрос: «Сколько четверок в числе 32? В числе 32 восемь четверок. Это можно увидеть в таблице умножения на четыре:

Эта восьмерка, выделенная красным, отвечает на вопрос, сколько четверок в числе 32. Запишите:

Теперь умножьте 8 на 4, чтобы получить 32, и запишите это число под делителем. Затем вычитаем это число из 32. Получаем 0. Поскольку решение еще не завершено, ноль не пишем:

Первое число 32 делится. Осталось разделить оставшиеся 6. Для этого снести ту шестерку:

Теперь разделить 6 на 4. Для этого зададим вопрос «Сколько четверок в шестерке?» В шестерке одна четверка; вы можете увидеть это, представив шестерку как шесть палочек:

Запишите единицу в правом углу нашего ответа:

Теперь умножьте нашу единицу на делитель (1 на 4) и запишите полученное число под шестеркой:

Затем из числа вычтем 4 6 и получаем число 2, которое является остатком:

Получили 326 : 4 = 81 (2 в остатке)

Проверка: (81 х 4) + 2 = 324 + 2 = 326

Процедура в котором мы ищем первое число для деления, сравнивая, больше ли оно делителя или меньше, называется нахождением первый неполный делитель .

Вернемся к предыдущему примеру 326 : 4. Первым неполным делителем в этом выражении был 32, потому что мы разделили его первым.

А в примере 25 : 3 первым неполным делителем было 25. неполный делитель . Первая цифра меньше делителя, поэтому проверяем две цифры. Две цифры вместе образуют число 38, которое больше делителя. Это число будет первый неполный делитель . Разделим сначала на делитель:

Сколько пятерок в числе 38? Если сложно ответить сразу, можно посмотреть таблицу умножения на пять и найти произведение меньшее 38, но очень близкое к нему или равное ему. Найдя такое произведение, нужно взять оттуда множитель, который ответит на наш вопрос:

Это таблица умножения на пять. Найдите произведение, которое меньше 38, но очень близко к нему или равно ему. Очевидно, это произведение числа 35, которое выделено синим цветом. Из этого выражения мы отнимаем множитель, который дал этот продукт. Это множитель 7, который выделен красным цветом.

Эта семерка отвечает на вопрос, сколько пятерок в числе 38. Напишите эту семерку в правом углу нашего примера:

Умножьте 7 на 5, чтобы получить 35, и запишите под 38:

Теперь из 38 вычесть 35, чтобы получить 3:

Эта тройка – остаток, который остался неразделенным при делении 38 на 5. Но, как видите, нам еще нужно разделить 4. Эту 4 мы снимаем и делим вместе с 3:

Вы видите, что после того, как мы убрали четверку, она вместе с тройкой образовала число 34. Разделим это число 34 на 5. Для этого снова зададим вопрос, “сколько пятерок в числе 34 ?” Вы можете еще раз посмотреть в таблицу умножения на пять и найти произведение меньшее 34, но очень близкое к нему или равное ему:

Вы можете видеть, что в таблице умножения на пять число 30 меньше чем наш 34, но близко к этому. Из этого выражения мы берем множитель 6, который отвечает на наш вопрос. Напишите эту шестерку в правом углу нашего примера:

Теперь умножьте 6 на 5, чтобы получить 30, и запишите это число под 34:

Теперь вычтите 30 из 34, и вы получите 4. Это четыре — остаток от деления 384 на 5.

384 002: 5 = 76 (и 4 осталось)

Проверка: (76 x 5) + 4 = 380 + 4 = 384

---

Пример 4.  Найти значение выражения 8642 : 4

Этот пример немного больше сложный. Напишите это выражение в углу:

Первая цифра числа 8 больше делителя. Эта восьмерка будет первым неполным делителем. Разделив 8 на 4, получим 2

Теперь умножьте 2 на 4 и получится 8. Запишите эту восьмерку под первым неполным делителем:

Вытяните остаток: 8 – 8 = 0. Остаток от деления 8 на 4 равно нулю. Ноль не пишем, так как решение примера не полное.

Далее сносим цифру 6 и делим на делитель, получаем 1

Умножьте 1 на 4, чтобы получить 4. Запишите эту четверку под снятой шестеркой. Затем вычитаем остаток, вычитая из шести четыре:

Остаток равен 2. Это остаток от деления 6 на 4.

Теперь вычитаем из делителя следующую цифру. Это цифра 4. Эта четверка вместе с предыдущим остатком 2 составляет 24. Делим ее на делитель. Получаем 6

Умножаем 6 на 4 и получаем 24. Запишем это число под 24

Вытяните остаток: 24 – 24 = 0. Ноль – это остаток от деления 24 на 4.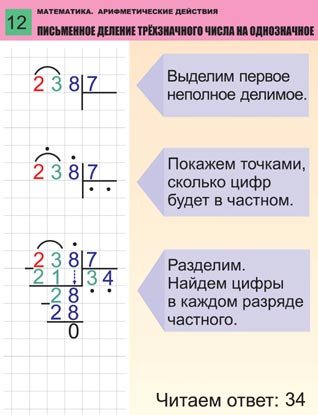 Ноль, как мы уже договорились, не записывается. Затем сносим последнюю цифру 2

Здесь начинается самое интересное. Двойка — это последняя цифра, которую мы записали, и ее надо разделить на делитель 4. Но дело в том, что двойка меньше четверки, а делитель должен быть больше делителя. Если мы зададим вопрос «сколько четверок в двойке?», то ответ будет нулевым, потому что двойка меньше четверки и не может содержать число больше себя.

Следовательно, два разделить на четыре равно нулю:

Умножьте 0 на 4, чтобы получить 0. Запишите, что 0 под 2:

Теперь найдите остаток: 2 – 0 = 2. Двойка это остаток

8642 : 4 = 2160 (2 лишние)

Проверка: (2160 x 4) + 2 = 8640 + 2 = 8642

---

4 1.

 Выполнить деление:

Решение:

Показать решение

Задача 2. Выполнение Отделение:

Решение:

Show Solution

Задача 3. Выполнение Дивизион:

Решение:

Показать решение

Видео урок

. Ведические математические приемы

Умственные математические приемы, чтобы стать человеком-калькулятором

На этом уроке вы изучите математический подход к умножению трехзначных чисел. В предыдущем уроке по двузначному умножению мы рассмотрели технику вертикального и крестообразного умножения или технику Урдхва Тирьяк из Ведической математики. Это тот же метод, который мы собираемся расширить для умножения на 3 цифры.

Цель этого урока – помочь вам умножить трехзначные числа в уме. Умственные вычисления осуществимы, если вы можете умножать слева направо, что снижает накладные расходы, связанные с переносом. Поскольку подход к технике трехзначного умножения, описанный в этом разделе, включает вычисления слева направо, он может значительно улучшить наши навыки вычисления в уме. Но помните, что умножение трехзначных чисел слева направо не так просто, так как требует значительной практики. Пожалуйста, используйте этот урок в качестве руководства для изучения подхода, и если вы хотите попрактиковаться, вы можете рассмотреть возможность использования нашего приложения на математических трюках.

К концу этого поста вы узнаете следующие приемы:

• Умножение 3 цифр на 1 цифру
• Умножение 3 цифр на 2 цифры
• Умножение 3 цифр на 3 цифры

Умножение чисел на 3

Подход к умножению трехзначных чисел объясняется в видеороликах ниже с помощью двух примеров. В первом примере основное внимание уделяется умножению трехзначных чисел без переноса, а во втором — с переносом.

• Пример 1

• Пример 2

Умножение на три цифры

цифры числа. Эта техника помогает нам легко умножать в уме трехзначные числа. Теперь давайте рассмотрим этот трюк с умножением, разделив подход к умножению на 3 цифры на следующие разделы:

• Как умножить два трехзначных числа
• Умножение трехзначного числа на двухзначное
• Как умножить трехзначное число на однозначное

Как умножить два трехзначных числа вычислить произведение двух чисел слева направо.

Однако он также может быть рассчитан справа налево. Но мы рекомендуем делать это слева направо, так как идея изучения этих трюков состоит в том, чтобы помочь улучшить наши навыки счета в уме. Прежде всего, умственный расчет — это расчет слева направо.

Итак, ниже приведен метод умножения трех цифр, который объясняется с помощью двух примеров. Подход, показанный в этих примерах, можно использовать для умножения любого трехзначного числа.

Пример 1: Произведение чисел 121 и 231

• Чтобы выполнить умножение на 3 цифры, разделим решение на 5 частей. Количество частей здесь получается как 2x$n$-1, где $n$ представляет значение в n-разрядном умножении. В случае трехзначного умножения n равно 3. Следовательно,

 121
x 231 
 ————————
? | ? | ? | ? | ?

• Самая левая часть получается путем умножения крайних левых цифр 1 из 121 и 2 из 231 => 1×2 = 2.

 121
x 231 
————————
2 | ? | ? | ? | ?

• Вторая часть получается путем перекрестного умножения первых двух цифр 1 и 3 и 2 и 2 с последующим сложением соответствующих произведений => 1×3 + 2×2 = 7

 121
x 231 
—— ——————
2 | 7 | ? | ? | ?

• Средняя часть получается путем перекрестного умножения трехзначного числа 1 и 1, 2 и 3, 1 и 2, а затем сложения соответствующих произведений => 1×1 + 2×3 + 1×2 = 9

 121
x 231 
————————
2 | 7 | 9 | ? | ?

• Четвертая часть получается путем перекрестного умножения двух последних цифр 2 и 1 и 1 и 3 с последующим сложением соответствующих произведений => 2×1 + 1×3 = 5

 121
x 231 
————————
2 | 7 | 9 | 5 | ?

• Правая часть получается путем умножения самых правых цифр в обоих числах => 1×1 = 1

 121
x 231 
———————
2 | 7 | 9 | 5 | 1

• Таким образом, результатом умножения трехзначных чисел 121 и 231 является 27951.

Пример 2: Произведение чисел 415 и 326

• Аналогично примеру 1, найдем произведение, разделив 5 частей:

 415
x 326
 ————————
? | ? | ? | ? | ?

• Первая часть получается произведением 4 и 3 => 4×3 = 12

 415
x 326 
————————
12 | ? | ? | ? | ?

• Теперь следующая часть получается путем перекрестного умножения первых двух цифр 4 и 2 и 1 и 3, а затем сложения соответствующих произведений => 4×2 + 1×3 = 11

 415
x 326 
————————
12 | 11 | ? | ? | ?

Примечание. За исключением левой части, все остальные части должны содержать только одну цифру, лишняя цифра, если таковая имеется, будет перенесена влево. Следовательно, избыток 1 из 11 будет перенесен в левую часть. Таким образом:

 415
x 326 
————————
13 | 1 | ? | ? | ?

• Затем третья часть получается путем перекрестного умножения трех цифр 4 и 6, 1 и 2, 5 и 3 и сложения соответствующих произведений => 4×6 + 1×2 + 5×3 = 41

415
x 326
————————
13 | 1 | 41 | ? | ?

=> 13 | 5 | 1 | ? | ?

• Теперь четвертая часть вычисляется путем перекрестного умножения двух последних цифр 1 и 6 и 5 и 2, а затем сложения соответствующих произведений => 1×6 + 5×2 = 16

 415
x 326 
————————

13 | 1 | 41 | 16 | ?

=> 13 | 5 | 2 | 6 | ?

• Последняя часть получается путем умножения самых правых цифр в обоих числах => 5×6 = 30

416
x 326
————————
13 | 5 | 2 | 6 | 30

 = 13 | 5 | 2 | 9 | 0

• Таким образом, мы вычислили трехзначное умножение 416 и 326, используя вертикальную и крестообразную технику слева направо без использования калькулятора.

 

Умножение трех цифр на две цифры

Умножение трех цифр на две можно выполнить путем преобразования ее в умножение трех цифр на три цифры. То есть мы в основном преобразуем двузначное число в трехзначное число, добавляя к нему 0. Если ABC — трехзначный множитель, а DE — двузначное множимое, то ABC x DE можно рассматривать как:

     A B C
x 0 D E
—————-
=====>

Пример: произведение 246 и 34

  246
x 034 

• Далее мы действуем аналогично умножению трех цифр выше

 246
x 034 
 ————————
? | ? | ? | ? | ?

• Вычислить большую часть слева: 2×0 = 0

 246
x 034 
————————
0 | ? | ? | ? | ?

• Затем вторая часть с использованием двух левых цифр => 2×3 + 4×0 = 6

 246
x 034 
————————
0 | 6 | ? | ? | ?

• Вычислите среднюю часть, используя вертикальное и поперечное умножение => 2×4 + 4×3 + 6×0 = 20. Поскольку в нем больше одной цифры, лишняя цифра 2 будет перенесена влево:

 246
x 034 
————————
0 | 6 | 20 | ? | ?

0 | 8 | 0 | ? | ?

• Затем вычислите четвертую часть, используя вертикальное и перекрестное умножение двух последних цифр, и сложите полученные произведения => 4×4 + 6×3 = 34

 246
x 034 
—————— ——
0 | 8 | 0 | 34 | ?

0 | 8 | 3 | 4 | ?

• Найти правую большую часть => 6×4 = 24

 246
x 034 
————————
0 | 8 | 3 | 4 | 24

0 | 8 | 3 | 6 | 4

 

Таким образом, путем преобразования 3-значного на 2-значное умножение в 3-значное на 3-значное умножение, мы вычислили произведение 246 и 34, что равно 8364

 

Трюк умножения трех цифр на одну цифру

Если ABC является трехзначным числом, которое нужно умножить на однозначное число, скажем D. Затем выполняется подход слева направо к умножению трех цифр на две цифры. путем умножения A на D, B на D и затем C на D.

A B C
x     D
————
=====>

Во время этого процесса умножения, если произведение B и D или C и D приводит к более чем 1 цифре, лишняя цифра будет перенесена влево.

Пример: Произведение 456 и 3

В 456 x 3 сначала умножьте крайнюю левую цифру 4 на 3 => 4×3 = 12

 4 5 6
x     3
————– 920661 | ? | ?

Затем умножьте вторую цифру 5 на 3 => 5×3 = 15. Перенесите лишнее 1 из 15 влево, как показано ниже:

  4 5 6
x     3
————–
12 | 15 | ?

13 | 5 | ?

Теперь умножьте цифру единиц 6 на 3: 6×3 = 18, а затем перенесите лишнюю 1 в среднюю часть. Таким образом, 5 становится 6. Следовательно, мы имеем 456 x 3 = 1368

  4 5 6
x      3
————–
13 | 5 | 18 

13 | 6 | 8 

 

Что дальше?

Как вы можете видеть в этом уроке, трехзначное умножение является простым расширением двузначного умножения. Этот трюк требует значительной практики. Но как только вы овладеете ею, вы будете поражены тем, насколько хорошей умственной тренировкой она окажется. Для практики вы можете начать с умножения 3 цифр на 1 цифру слева направо, что поможет вам попрактиковаться в расчете переноса в уме, а затем начать с умножения 3 цифр на 3 цифры.

Помните, что вы не сможете освоить умножение слева направо за одну ночь, но, приложив значительные усилия, вы обязательно влюбитесь в эту технику. Теперь пройдите тест ниже и упражнения, связанные с этим уроком, чтобы начать.

 

Викторина: Умножение 3-х цифр с ответами

Проверьте свои знания

Деление: Целые числа

Разделение это математическая операция, записанная с помощью символа ÷ , это можно рассматривать двумя способами: а ÷ б размер каждой группы, когда а объекты делятся на б группы одинакового размера, ИЛИ а ÷ б это количество групп, когда а объекты разбиты на группы б объекты каждый.

Например, 20 ÷ 4 можно найти, разделив 20 точки в 4 группы одинакового размера.

Мы находим, что каждая из четырех групп содержит 5 точки, так 20 ÷ 4 знак равно 5 .

В качестве альтернативы мы можем найти 20 ÷ 4 путем формирования групп 4 точки каждая, а затем подсчет количества групп:

Есть 5 группы.

Дивизия – это обратная операция умножения. То есть,

а ÷ б знак равно с если и только если с × б знак равно а .

Здесь а называется дивиденд , б называется делитель , а также с (результат) называется частное .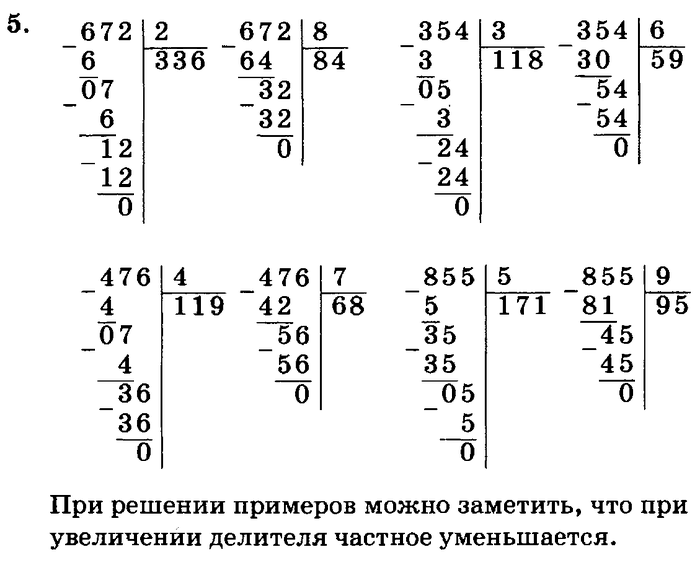

Разделение по 0 не определено; чтобы понять почему, замените б знак равно 0 в приведенных выше уравнениях. С с × 0 знак равно 0 независимо от того, какое значение с , так а также должен быть равен 0 ; и если а а также б оба 0 , с может равняться чему угодно!

Деление на целые числа может привести к остатку. Например, если мы разделим 20 ÷ 6 путем деления 20 на группы 6 , мы получаем 3 группы с 2 осталось:

Иногда мы пишем 20 ÷ 6 знак равно 3 р 2 , куда 2 это остаток .

Или мы можем записать один числовой ответ в виде дробная часть или десятичное.

Длинный дивизион

Чтобы разделить многозначное число на однозначное, мы можем использовать длинное деление.

Пример 1:

Разделять. 496 ÷ 8

Поместите делимое внутри символа деления, а делитель снаружи символа деления.

8 496

Здесь, 8 не может содержаться в 4 , так что рассмотрим и следующую цифру. Есть 6 восьмерки в 49 , так что пиши 6 в десятках частного.

Умножить 6 на делитель 8 и вычесть.

6 8 49 6 48 _ 1

Теперь снова 8 не может содержаться в 1 , поэтому опустите следующую цифру 6 .

6 8 49 6 48 _ 16

Там 2 восьмерки в 16 , так что пиши 2 на тех местах.

Умножить 2 на делитель 8 и вычесть.

6 2 8 496 48 _ 16 16 _ 0

Чтобы разделить многозначное число на многозначное число, процесс аналогичен.

Пример 2:

Разделять 1036 по 32 . Поместите делимое внутри символа деления, а делитель снаружи символа деления.

32 1036

Здесь, 32 не может содержаться в 1 , рассмотрим следующую цифру, еще 32 не может содержаться в 10 . Итак, рассмотрим также следующую цифру. Есть 3 тридцать два в 103 , так что пиши 3 в десятках частного.

Умножить 3 на делитель 32 и вычесть.

3 32 103 6 96 _ 7

Теперь снова 32 не может содержаться в 7 , поэтому опустите следующую цифру 6 .

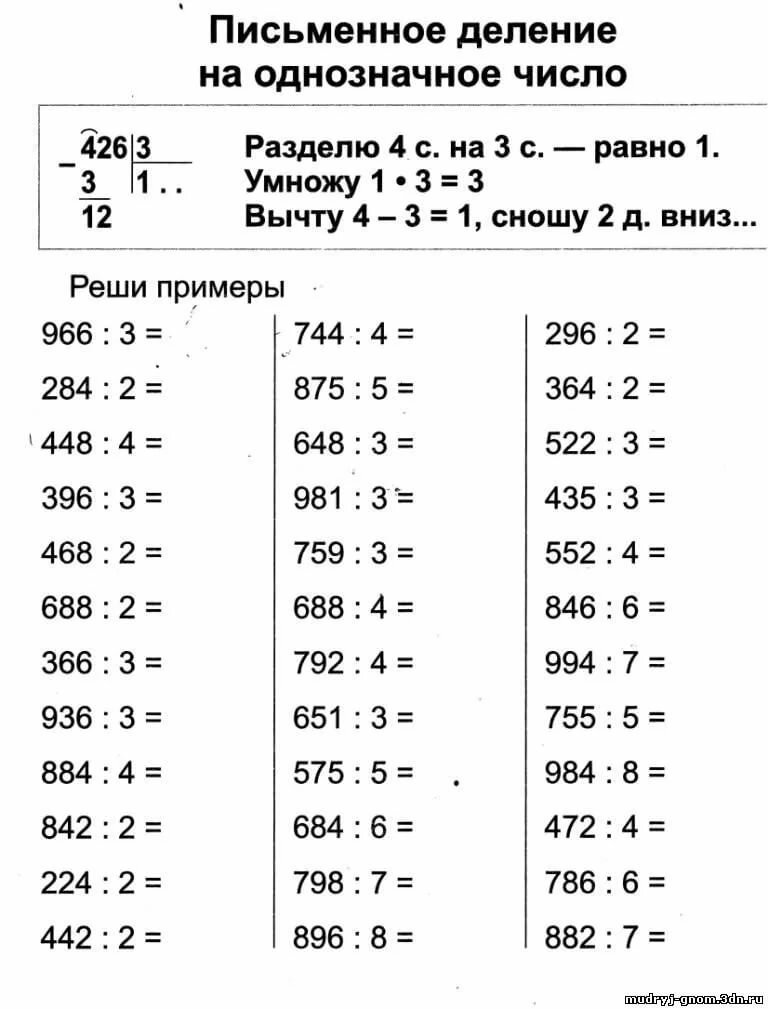
3 32 1036 96 _ 76

Там 2 тридцать два в 76 , так что пиши 2 на тех местах.

Умножить 2 на делитель 32 и вычесть.

Вот и остаток 12 .

3 2 32 103 6 96 _ 76 64 _ 12

В отличие от сложения и умножения, для вещественные числа , операция деления нет коммутативный . То есть порядок имеет значение: 40 ÷ 8 знак равно 5 , но 8 ÷ 40 знак равно 1 5 (дробное значение).

Точно так же деление нет ассоциативный ; то есть группировка имеет значение. Например,

( 80 ÷ 10 ) ÷ 2 знак равно 8 ÷ 2 знак равно 4 , но

80 ÷ ( 10 ÷ 2 ) знак равно 80 ÷ 5 знак равно 16 .

Глава 8: Отдел – Миссис. LONG’S 3RD CLASS

Math in Focus Chapter 8: Division

​ Trimester 2

*Привязать к зоне

Большая идея:  При делении на равные группы или при разделении поровну могут остаться остатки. Используйте связанные факты умножения для деления. Используйте шаблоны для деления чисел, кратных 10 и 100. Разделите однозначное или двузначное число на однозначное число с остатком или без него. Используйте разные стратегии для определения нечетных и четных чисел. Используйте десятичные блоки и разрядное значение для деления двузначных чисел без перегруппировки или остатка. Использование блоков с основанием 10 и разряда для деления двузначных чисел на однозначные числа с перегруппировкой, с остатком или без него Угадай и проверь Словарь глав: частное, остаток, четные числа, нечетные числа

Основные иллюстрации/упражнения: Учащиеся используют связанные факты умножения для деления. Они применяют обратное отношение умножения и деления, чтобы записать операторы деления из соответствующего предложения умножения. Учащиеся узнают, что при делении всегда есть частное и, возможно, остаток. Учащиеся изучают шаги вертикального деления на деление с перегруппировкой или без нее или с остатком. Предварительный просмотр урока: 8.1: ментальное разделение 8.2: Коэффициент и остаток 8.3: нечетные и четные номера 8.4: разделение без остатков и перегруппинг 8.5: Отделение с перегрузкой в ​​Tens и Ones 117 8.5.

Обучающие видео: Словарь деления ​Отношения деления и умножения ​ Basic Division – Math Antics Long Division – Math Antics Division Song Khan Academy Long Division Video (no remainders) Khan Academy Long Division Video: 280/5 Академия Хана, длинное видео (остатки) Игровые предложения для дивизии: Подразделение дрэг-рейсинга ​Division Derby ​Puzzle Picture Division ​Dino Park Division ​Cave Run Pirates Division Fruit Shoot Matching Division A+ Math Division Bingo ​ Факты отдела Практика длинного дивизиона: Dare to Share – Base 10 & Long Division Practice ​Snork’s Long Division ​Dividerama! Divide Pal: Long Division Made Easy Math Mountain Long Division Games Long Division (с остатком и без остатка) 1​ 0 8 60 60

Обучающие ссылки: Глава 8 Фоновое видео для родителей Раздел Факты Рабочие листы для разделов (для печати) ​ Задачи Word по темам Видео с рабочими тетрадями (от Дэниела Лу): Page 147-148 Page 149 Page 150 Page 151 Page 152 Page 153-154 ​Page 155 ​Страница 156 Страница 157 Страница 158 Сайт Даниэля Лу для рабочей тетради

Стандарты Common Core State:

Операции и алгебраическое мышление:
Представлять и решать задачи на умножение и деление.

• CCSS.MATH.CONTENT.3.OA.A.2
  Интерпретировать целочисленные частные целых чисел, например, интерпретировать 56 ÷ 8 как количество объектов в каждой доле, когда 56 объектов разделены поровну на 8 долей , или как количество долей, когда 56 объектов разбиты на равные доли по 8 объектов в каждой. Например, опишите контекст, в котором количество долей или количество групп можно выразить как 56 ÷ 8 .
• ​CCSS.MATH.CONTENT.3.OA.A.3
  Используйте умножение и деление в пределах 100 для решения текстовых задач в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например, с помощью рисунков и уравнений с символом для неизвестное число для представления задачи.1
• CCSS.MATH.CONTENT.3.OA.A.4
  Определите неизвестное целое число в умножении или уравнении деления, связывающем три целых числа. Например, определите неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ?

Понимать свойства умножения и связь между умножением и делением. Примеры: Если известно 6 × 4 = 24, то известно и 4 × 6 = 24. (Переместительное свойство умножения.) 3 × 5 × 2 можно найти по формуле 3 × 5 = 15, тогда 15 × 2 = 30, или по 5 × 2 = 10, тогда 3 × 10 = 30. (Ассоциативное свойство умножения. ) Зная, что 8 × 5 = 40 и 8 × 2 = 16, можно найти 8 × 7 как 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Дистрибутивное свойство.)

CCSS.MATH.CONTENT.3.OA.B.6
Понимание деления как задачи с неизвестным фактором. Например, найдите 32 ÷ 8, найдя число, которое дает 32 при умножении на 8 .

Умножать и делить в пределах 100.

• CCSS.MATH.CONTENT.3.OA.C.7
  Свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная, что 8 × 5 = 40, известно 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.
  

Обзор главы 8:

Семейное письмо:

Дополнительные ресурсы

из Math in Focus  Curriculum

Как делить числа

• Дом

• Узнать

• Базовая математика

• Дополнение
• Вычитание
• Умножение
• Подразделение
• Целые числа
• Натуральные числа
• Четное нечетное

коэффициенты и множители Ссылки

Предварительная алгебра Ссылки

Вычитание определенного количества объектов снова и снова — это деление.

Примечание:

•  Деление обозначается знаком «÷».
•  Результат выражается знаком «=».
• Используя таблицы, мы можем выполнять деление без вычитания объектов.

Пример

Если есть 10 шоколадок. Сколько групп можно составить из этих 10 конфет с поровну в каждой группе?

5 групп по 2 шоколадки в каждой

Объяснение :

 Сначала уберём 2 шоколадки из 10. Остаётся 8 шоколадок.
 Теперь, когда мы уберем 2 шоколадки из 8, останется 6 шоколадок.
 Когда из 6 уберём 2 шоколадки, останется 4 шоколадки.
 Из оставшихся 4, когда мы уберем 2 шоколадки, останется 2 шоколадки.
 Когда мы удаляем группу из 2 в пятый раз, конфет не остается.
Получаем 5 таких групп по 2 шоколадки в каждой.
 Таким образом, мы можем сказать, что 10÷2= 5

---

Таблицы сообщают нам результат во сколько раз число.
Если мы скажем, что 2 × 5 = 10. Это означает, что для получения 10 в качестве произведения скажем таблицу от 2 до 10, получаем 5.
Так что 10 ÷ 2= 5.

Примечание:

Делимое число и есть делимое. Число, на которое мы делим, и есть делитель.
Если 8 ÷ 2 = 4. Здесь делимое равно 8, делитель 2, частное 4 и остаток 0.

Простой пример

---

Раздел: задачи Word

Пример 1:

Пример 2:

В книге 64 страницы. Элизабет читает по 2 страницы каждый день. За сколько дней она завершит книга?

Элизабет заканчивает книгу за 32 дня.

Объяснение :

Чтобы найти дни для завершения книги, нужно разделить 64 на 2.
64 ÷ 2 = Сколько?
Чтобы разделить, сначала посмотрите на цифру слева в делимом. Скажи 2 раза стол до 6.
Две тройки шесть. Произведение 3 и 2 равно 6. Вычтите это произведение из 6 T. Осталось ноль десятков.
Запишите цифру 3 над чертой в разряде десятков делимого.
Запишите 4 единицы перед 0. Разделите 4 единицы на 2. Произнесите таблицу умножения на 2. до 4.
Частное равно 2. Произведение 2 на 2 равно 4. Вычтите это произведение из 4 U. Осталось ноль десятков.
Остаток 0.
Частное равно 32.
Таким образом, 64 ÷ 2 = 32.

---

Простой пример

---

Раздел: задачи Word

3876 рубашек расставлены на 17 полках. Если на каждом лежит одинаковое количество рубашек. полка, сколько рубашек на каждой полке?

На каждой полке 228 рубашек.

Объяснение :

Чтобы найти количество рубашек на каждой полке, разделите 3876 на 17.
Чтобы разделить, сначала посмотрите на разряд тысяч в делимом. что 3.
3 меньше делителя 17. 3 нельзя разделить на 17. Возьмите 38, чтобы разделить на 17.
Разделите 38 на 17. Вычтите 34 из 38. Частное равно 2. Остаток равен 4.
Запишите 7 десятков перед 4. Разделите 47 на 17. Вычтите 34 из 47.
Частное равно 2. Остаток равен 13.
Запишите 6 единиц перед 13. Разделите 136 единиц на 17.
Произнесите таблицу умножения на 17 до 136.
Частное равно 8. Вычтите это произведение из 136 U. Остаток 0,
. Частное равно 228.
Следовательно, 3876 ÷ 17 = 228

---

Набор фактов, связанных с делением, составляет семейств фактов.

•  Скажем, 35 ​​÷ 7. Получим 5.
•  А также 35 ÷ 5. Получим 7.
•  Таким образом, 5,7 и 35 составляют семью.

---

Что нужно помнить

Деление на 1

 Если мы разделим любое число на 1, мы получим само число.

Допустим, 78 ÷ 1. Получится 78.

Советы

•  Мы всегда должны начинать делить числа с первого места заданного числа.
•  Порядок деления некоторого числа: тысячи, сотни, десятки… и так далее…
•  При делении любого числа делитель должен быть меньше числа делимого.
•  Каждый раз вычитайте произведение из числа делимого, а затем берите следующее число, пока все число не закончилось.
•  Частное всегда пишется над чертой, а произведение — под числом делимого.

Думай

•   Ручки стоят 60, а сколько тогда стоит каждая ручка?
•  Если 20 000 ÷ 20 = 1000, чему равно 20 000 ÷ 200?
•  У Рупы 55 шоколадок. Она хочет раздать их своим друзьям как каждому другу можно получить 5 шоколадок.