Примеры кругов эйлера логика примеры: описание, примеры, для дошкольников, для школьников
1.6. Круговые схемы Эйлера. Логика. Учебное пособие
1.6. Круговые схемы Эйлера
Как мы уже знаем, в логике выделяется шесть вариантов отношений между понятиями. Два любых сравнимых понятия обязательно находятся в одном из этих отношений. Например, понятия писатель и россиянин находятся в отношении пересечения, писатель и человек – подчинения, Москва и столица России – равнозначности, Москва и Петербург – соподчинения, мокрая дорога и сухая дорога – противоположности, Антарктида и материк – подчинения, Антарктида и Африка – соподчинения и т. д. и т. п.
Надо обратить внимание на то, что если два понятия обозначают часть и целое, например месяц и год, то они находятся в отношении соподчинения, хотя может показаться, что между ними отношение подчинения, ведь месяц входит в год. Однако, если бы понятия месяц и год были подчиненными, то тогда надо было бы утверждать, что месяц – это обязательно год, а год – это не обязательно месяц (вспомним отношение подчинения на примере понятий 
Месяц – это не год, а год – это не месяц, но и то, и другое – отрезок времени, следовательно, понятия месяц и год, так же, как и понятия книга и страница книги, автомобиль и колесо автомобиля, молекула и атом и т. п., находятся в отношении соподчинения, т. к. часть и целое – не то же самое, что вид и род.
В начале говорилось о том, что понятия бывают сравнимыми и несравнимыми. Считается, что рассмотренные шесть вариантов отношений применимы только к сравнимым понятиям. Однако возможно утверждать, что все несравнимые понятия находятся между собой в отношении соподчинения. Например, такие несравнимые понятия, как пингвин и небесное тело возможно рассматривать как соподчиненные, ведь пингвин – это не небесное тело и наоборот, но в то же время объемы понятий пингвин и небесное тело входят в более широкий объем третьего понятия, родового по отношению к ним: это может быть понятие объект окружающего мира или форма материи (ведь и пингвин и небесное тело – это различные объекты окружающего мира или различные формы материи).
Если же одно понятие обозначает что-то материальное, а другое – нематериальное (например, дерево и мысль), то родовым для этих (как возможно утверждать) соподчиненных понятий является понятие форма бытия, т. к. и дерево, и мысль, и что угодно еще – это различные формы бытия.
Как нам уже известно, отношения между понятиями изображаются круговыми схемами Эйлера. Причем до сих пор мы изображали схематично отношения между двумя понятиями, а это можно сделать и с большим количеством понятий. Например, отношения между понятиями
Взаимное расположение кругов показывает, что понятия боксер и негр находятся в отношении пересечения (боксер может быть негром и может им не быть, а также негр может быть боксером и может им не быть), а понятия боксер и человек, так же как и понятия негр и человек находятся в отношении подчинения (ведь любой боксер и любой негр – это обязательно человек, но человек может не быть ни боксером, ни негром).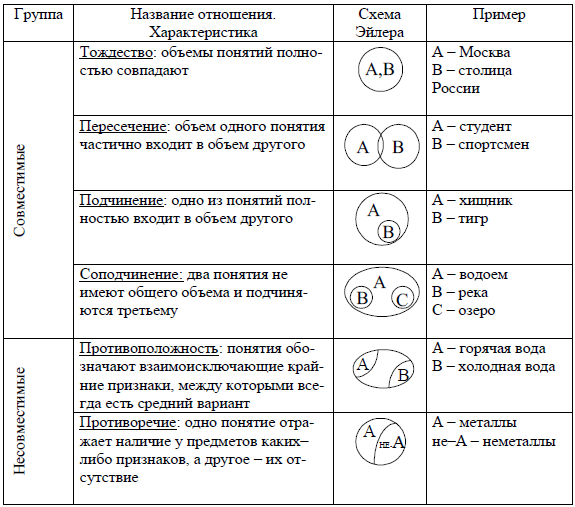
Рассмотрим отношения между понятиями дедушка, отец, мужчина, человек с помощью круговой схемы:
Как видим, указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; и, наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина. Отношения между понятиями хищник, рыба, акула, пиранья, щука, живое существо изображаются следующей схемой:
Попробуйте самостоятельно прокомментировать эту схему, установив все имеющиеся на ней виды отношений между понятиями.
Подытоживая сказанное, отметим, что отношения между понятиями – это отношения между их объемами. Значит, для того, чтобы было возможно установить отношения между понятиями, их объем должен быть резким, а содержание, соответственно, ясным, т. е. эти понятия должны быть определенными. Что касается неопределенных понятий, о которых шла речь выше, то установить точные отношения между ними достаточно сложно, фактически невозможно, ведь из-за неясности их содержания и нерезкости объема два каких-нибудь неопределенных понятия можно будет характеризовать как равнозначные или как пересекающиеся, или как подчиняющиеся и т.
Данный текст является ознакомительным фрагментом.
9.1. Графические схемы структуры аргументации
9.1. Графические схемы структуры аргументации
Всякая аргументация начинается с установления и обсуждения некоторых фактов, которые в дальнейшем будут называться данными, и с помощью которых выдвигается и обосновывается некоторое заключение.
Комментарии и схемы
Комментарии и схемы Учение, в основе которого лежит внутренняя работа личности, не могло бы пережить саму эту личность без приливов новой внутренней работы новых личностей. Тех, кто увидел для себя особый смысл в этом учении. Меняются условия существования, приходит
Нравственная философия Толстого и Достоевского в рамках ницшеанской схемы нигилизма
Нравственная философия Толстого и Достоевского в рамках ницшеанской схемы нигилизма Начиная с последней четверти прошлого века проблема нигилизма выходит на одно из первых мест в числе важнейших проблем западноевропейской философии. Своим «статусом» она прежде всего
СХЕМЫ ПРАВИЛЬНЫХ РАССУЖДЕНИЙ
СХЕМЫ ПРАВИЛЬНЫХ РАССУЖДЕНИЙ
Вот два примера дедуктивных выводов из рассказа русского юмориста начала века В.
Билибина. «Если бы на свете не существовало солнца, то пришлось бы постоянно жечь свечи и керосин. Если бы пришлось постоянно жечь свечи и керосин, то чиновникам
Теоретические схемы и абстрактные объекты технической теории
Теоретические схемы и абстрактные объекты технической теории Теоретические схемыпредставляют собой совокупность абстрактных объектов, ориентированных, с одной стороны, на применение соответствующего математического аппарата, а с другой, – на мысленный эксперимент,
2. Диалектика схемы, аллегории и символа
2. Диалектика схемы, аллегории и символа Какие же возможны вообще виды этого взаимоотношения? Их очень много. Но, следуя Шеллингу, можно указать три основных таких вида. При этом будем иметь в виду, что наши термины «внутреннее» и «внешнее» – очень общие термины и их можно
Иконография как система методов: схемы и угрозы
Иконография как система методов: схемы и угрозы
Сама практика иконографического анализа сформировала «проверенную схему» последовательных исследовательских действий.
Схема подразумевает:– уяснение исторического значения мотива – с точки зрения времени (момент
2.1.1. Нормы-схемы речевого общения: речевой этикет
2.1.1. Нормы-схемы речевого общения: речевой этикет Выбор первой проблемной области – речевого этикета – обусловлен следующим. При определении сущностных характеристик нормы мы начали движение от социальных норм, при этом заметили, что их существование в полной мере
2.1.2. Семиотически закрепленные нормы-схемы: жанры
2.1.2. Семиотически закрепленные нормы-схемы: жанры Основой противопоставления социально и семиотически закрепленных норм, как было сказано в главе I, является способ их закрепления в социокультурной практике. Первые – неписаные законы – становятся программами, схемами
почему один раз увидеть лучше, чем сто раз услышать
Если вы думаете, что ничего не знаете о кругах Эйлера, вы ошибаетесь.
На самом деле вы наверняка не раз с ними сталкивались, просто не знали, как это называется. Где именно? Схемы в виде кругов Эйлера легли в основу многих популярных интернет-мемов (растиражированных в сети изображений на определенную тему).
Давайте вместе разберемся, что же это за круги, почему они так называются и почему ими так удобно пользоваться для решения многих задач.
Происхождение термина
Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.
Пока не очень понятно, верно? Посмотрите на этот рисунок:
На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей).
Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.
Ну что, так стало понятнее? Именно поэтому круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.
Автор метода – ученый Леонард Эйлер (1707-1783). Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки.
До него подобным принципом при построении своих умозаключений руководствовался немецкий математик и философ Готфрид Лейбниц.
Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.
Свою лепту внес также немецкий математике Эрнест Шредер. Но главные заслуги принадлежат англичанину Джону Венну. Он был специалистом в логике и издал книгу «Символическая логика», в которой подробно изложил свой вариант метода (использовал преимущественно изображения пересечений множеств).
Благодаря вкладу Венна метод даже называют диаграммами Венна или еще Эйлера-Венна.
СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).
Зачем нужны круги Эйлера?
Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только.
Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение каких-то понятий (например, соотношение рода и вида) – мы их рассмотрели на примере в начале статьи.
А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера:
Забавно, правда? И главное, все сразу становится понятно. Можно потратить много слов, объясняя свою точку зрения, а можно просто нарисовать простую схему, которая сразу расставит все по местам.
Кстати, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором:
Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.
Решение задач с помощью кругов Эйлера
Давайте рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.
Вот на этом сайте – http://logika.vobrazovanie.ru/index.php?link=kr_e.html Елена Сергеевна Саженина предлагает интересные и несложные задачи, для решения которых потребуется метод Эйлера. Используя логику и математику, разберем одну из них.
Задача про любимые мультфильмы
Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым – «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».
Решение:
Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:
Выходит, что:
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Губка Боб Квадратные Штаны». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:
38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Теперь смело можем сложить все полученные цифры и выяснить, что:
мультфильм «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек.
Это и есть ответ на поставленный в задаче вопрос.
А еще давайте рассмотрим задачу, которая в 2011 году была вынесена на демонстрационный тест ЕГЭ по информатике и ИКТ (источник – http://eileracrugi.narod.ru/index/0-6).
Условия задачи:
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | Линкор | 7000 |
| Крейсер | 4800 |
| Линкор | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?
Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.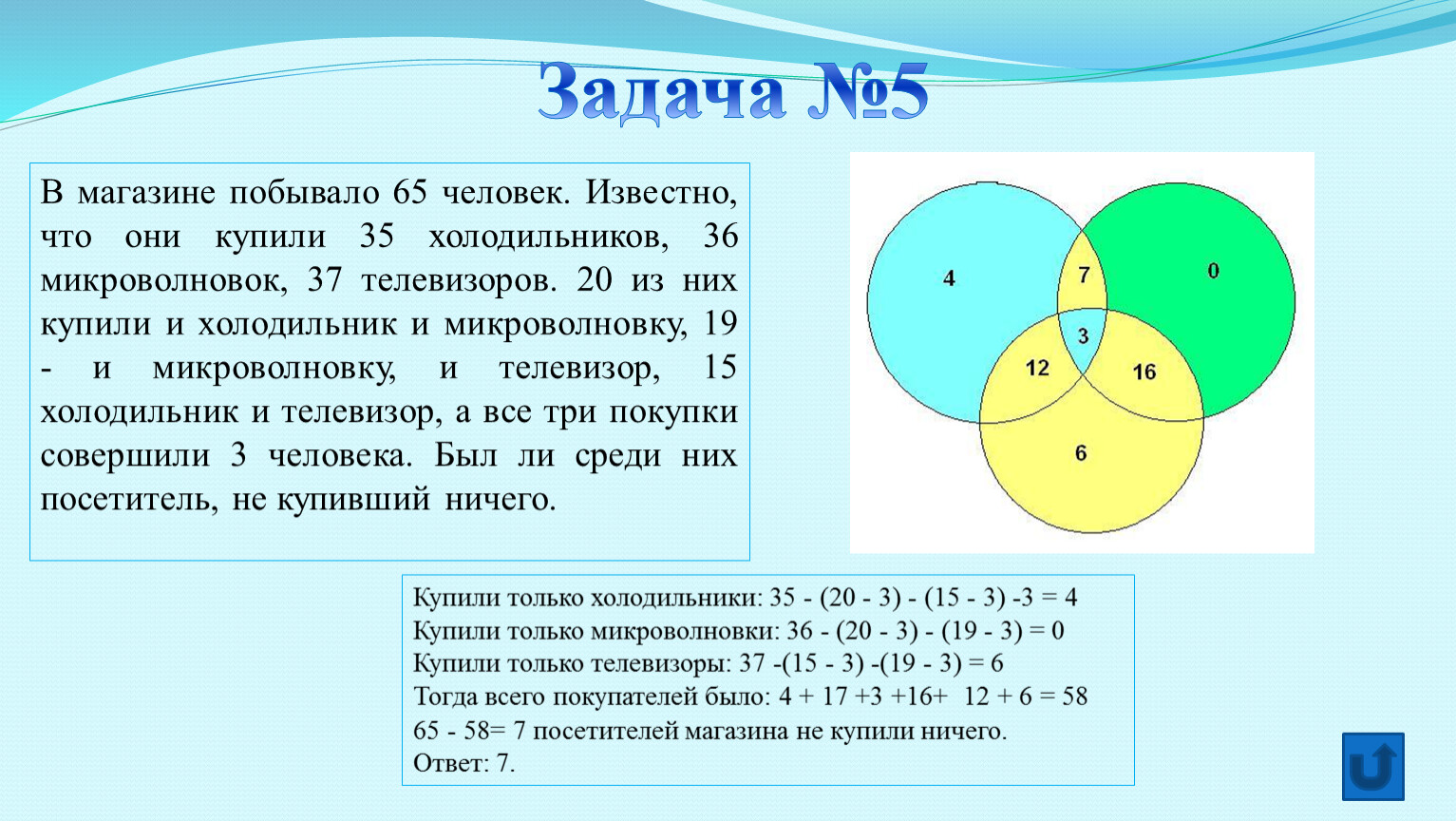
Решение:
При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.
Опираясь на условия задачи, составим уравнения:
- Крейсер | Линкор: 1 + 2 + 3 = 7000
- Крейсер: 1 + 2 = 4800
- Линкор: 2 + 3 = 4500
Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300.
Ответ: 2300 – количество страниц, найденных по запросу Крейсер & Линкор.
Как видите, круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
Заключение
Полагаю, нам удалось убедить вас, что круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач.
Причем не только абстрактных задач на школьный уроках, но и вполне себе житейских проблем. Выбора будущей профессии, например.
Вам еще наверняка будет любопытно узнать, что в современной массовой культуре круги Эйлера нашли отражение не только в виде мемов, но и в популярных сериалах. Таких, как «Теория большого взрыва» и «4исла».
Используйте это полезный и наглядный метод для решения задач. И обязательно расскажите о нем друзьям и одноклассникам. Для этого под статьей есть специальные кнопки.
Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил. Но если вдруг что-то еще непонятно – попробуй онлайн-занятие с репетитором (подробности тут + 🎁).
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
сек. 3.6 – Математика колледжа для начального образования
Глава 3, Раздел 6
Математические темы – Диаграммы Эйлера и логические аргументы, «Если… то» (условные) утверждения
Тема обучения – Какие типы представлений подходят?
youtube.com/embed/Di1F-wT05h8?version=3&rel=1&showsearch=0&showinfo=1&iv_load_policy=1&fs=1&hl=en&autohide=2&wmode=transparent” allowfullscreen=”true” sandbox=”allow-scripts allow-same-origin allow-popups allow-presentation”> Логические аргументы
В предыдущем разделе у нас был пример
Все кошки — животные. Флаффи — кот.
Если вы посмотрите на диаграмму (не привнося свои знания), на диаграмме также видно, что Пушистик должен быть животным.
Мы можем записать это как заключение логического рассуждения:
Все кошки — животные. Помещение 1 Флаффи — кот. Помещение 2 Следовательно, Пушистик — животное. Заключение
Первые две строки аргумента — это предпосылки, то, что мы принимаем за истину.
Последняя строка – заключение.
Быть девяткой0003 действительный аргумент, вывод должен следовать из двух посылок.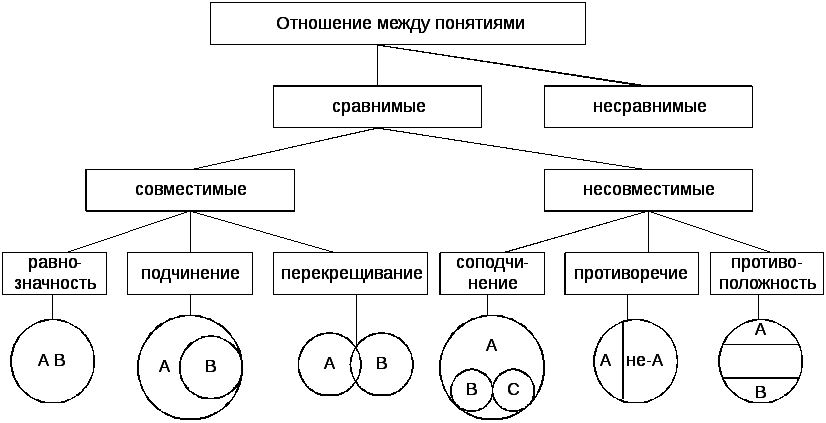
То есть, если мы за исключением того, что посылки верны, вывод должен быть истинным на основе посылок . Приведенный выше аргумент действителен.
Что сделало бы аргумент не действительным? Попробуем немного изменить набор предпосылок и выводов:
Все кошки — животные. Помещение 1 Дэн - животное. Помещение 2 Следовательно, Дэн - кот. Заключение
Чтобы проверить, является ли это аргументом, нарисуйте только помещения.
Даже не смотрите на вывод, когда рисуете!
Глядя на нашу картинку, мы видим, что вывод, что Дэн является котом , неверен. Дэн может быть котом, или Дэн может быть другим видом животных. На диаграмме показано, что D может находиться в двух возможных местах.
Это означает, что аргумент недействителен (недействителен).
Чтобы аргумент был действительным, мы должны быть на 100% уверены в том, что вывод верен на основе предпосылок.
Пример 1 Какой вывод верный?
Все квадраты четырехсторонние. Все квадраты четырехсторонние. М четырехгранный. Х - квадрат. Следовательно, М — квадрат. Следовательно, X четырехсторонний.
Чтобы принять решение, постройте диаграмму Эйлера, используя каждый набор предпосылок.
Помещения:
Все квадраты четырехсторонние. Все квадраты четырехсторонние. М четырехгранный. Х - квадрат.
Помните, что для построения диаграммы используйте только предпосылки, а не заключение.
Обратите внимание, что M может стоять в двух возможных местах. М должно быть в четырехстороннем круге вещей, потому что это первая предпосылка. M также может быть в круге квадратов, потому что это еще одно возможное место внутри четырехстороннего круга вещей.
Для X есть только одно возможное место внутри квадратного круга, так как это первая предпосылка этого аргумента. X не может быть вне этого круга, так как это означало бы, что X не был квадратом.
Помните, мы принимаем каждую из посылок за абсолютно истинных.
Теперь смотрим на выводы, чтобы увидеть, следуют ли они из посылок.
Верен ли вывод Следовательно, M является квадратом ?
№
Глядя на нашу диаграмму, мы видим, что M может быть квадратом, а может и не быть. M может быть за пределами круга квадратов и иметь только 4 стороны. Например, M может выглядеть так:
M — 4-сторонний.
Верен ли вывод Следовательно, X является четырехсторонним ?
Да, потому что X находится внутри четырехстороннего круга вещей. Все квадраты четырехсторонние.
Но когда вы указываете причину, по которой аргумент действителен, используйте первую часть причины, приведенную выше: «Да, потому что X находится внутри четырехстороннего круга вещей». Вторая часть, « Все квадрата четырехсторонние», просто повторяет предпосылку. Переформулировка посылки (даже курсивом или подтекстом!) не является достаточной причиной для поддержки вашего аргумента.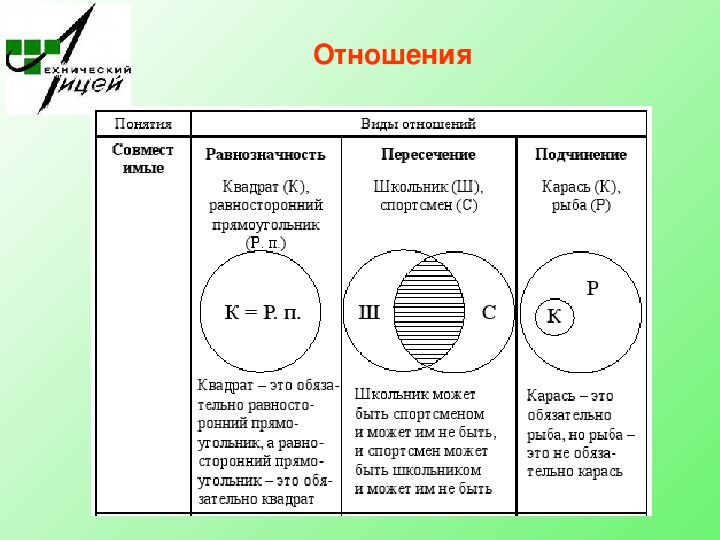
Вместо этого обратитесь к своей диаграмме и объясните, используя диаграмму.
Итог
НЕВЕРНЫЙ Аргумент и причина
Все квадраты четырехсторонние.
М четырехсторонний.
Следовательно, M — квадрат.
Недействительно, так как М может находиться в части круга вне квадратов
(см. схему).
ДЕЙСТВИТЕЛЬНО Аргумент и причина
Все квадраты четырехсторонние.
X — квадрат.
Следовательно, X четырехсторонняя.
Действителен, потому что X должен быть в круге квадратных вещей,
внутри четырехсторонних вещей, так что это автоматически делает X
также четырехсторонним (см. схему).
Условное
Другой способ показать логический аргумент — использовать символы вместо диаграмм Эйлера или в дополнение к ним.
Все кошки — животные — это то же самое, что сказать: Если — это кошка, , то — это животное.
Утверждение «if…then» известно как условное .
Мы используем стрелку для обозначения условного выражения: c → a, где c означает «это кошка, а a — это животное». Мы используем три точки, ∴, чтобы представить слово поэтому.
Допустимый аргумент
Использование «всех» Использование условных символов In Все кошки животные
| Использование «всех» | Использование условного обозначения | Символы |
| Если это кошка, то это животное. Это кошка. Следовательно, это животное. | c → a c ∴ a |
Обратите внимание, что когда мы используем условную стрелку, мы больше не называем кота Пушистиком.
Это делается для того, чтобы вторая посылка могла точно соответствовать первой части условного предложения.
В действительный ( не действительный) аргумент
| Использование «все» 900 04 | Использование условного обозначения | Символы |
| Все кошки – животные . Дэн — животное. Значит, Дэн – кот. | Если это кошка, то это животное. Это животное. Следовательно, это кошка. | с → а а ∴ с |
Посмотрите внимательно на порядок двух приведенных выше аргументов. Следуя этому шаблону, для оператора if-then типа A → B, какая вторая строка и вывод будут давать действительный аргумент?
| Допустимый аргумент (Modus Ponens) Порядок правильный | Неверный аргумент Порядок неправильный | А → В А ∴ В | А → В В ∴ А |
Официальное название действительной формы аргумента — латинская фраза modus ponens , но можно просто сказать «правильный порядок».
В правильном аргументе вторая посылка и заключение следуют в том же порядке, что и в условном выражении.
Ученик в моем классе указал, что порядок должен быть правильным, потому что условная стрелка не является коммутативной. То есть сказать A → B — это не то же самое, что сказать B → A. Или, вернувшись к нашему предыдущему примеру, если это кошка, то это животное это не то же самое, что сказать если это животное, то это кошка .
Мы можем использовать как диаграмму Эйлера , так и символическую логику , чтобы решить, является ли аргумент допустимым. Некоторым учащимся визуальное представление проще всего; для других студентов символическое представление является самым простым. Вот почему мы хотим всегда стараться дать нашим ученикам множество способов представления математики!
Пример 2 Верен или неверен следующий аргумент? Для принятия решения используйте диаграмму Эйлера и символическую логику с условным символом.
Все собаки дружелюбны.
Бонзо — собака.
Значит, Бонзо дружелюбен.
Чтобы принять решение, сначала перепишите аргумент в виде условного оператора («Если… то»). Посмотрите, к какому из приведенных выше шаблонов он подходит. Наконец, проверьте, нарисовав диаграмму Эйлера, чтобы визуально увидеть, действительна ли она.
| Использование «всех» | Использование условного обозначения | Символы |
| Если это собака, то она дружелюбная. Это собака. Поэтому он дружелюбный. | d → f d ∴ f |
Этот аргумент действителен , потому что порядок аргумента верен. У вас есть d → f в качестве первой посылки, за которой следует первая буква d, а заключение — вторая буква f.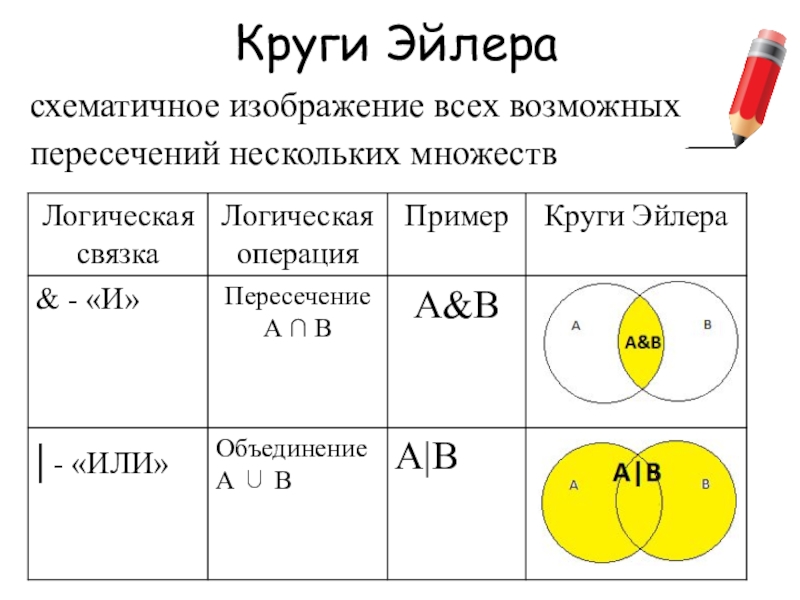
Итак, вторая посылка и заключение идут в том же порядке, что и условное в первой посылке.
Или, вместо букв d и f, вы можете думать о «собаках» как о A, а о «дружественных» как о B, и вы получите
A → B
A
∴ B
Это точное совпадение форму действительного аргумента, modus ponens, вверху этой страницы.
Диаграмма Эйлера подводит нас к тому же заключению. Аргумент действителен , потому что Бонзо находится внутри круга «Собаки», который, в свою очередь, находится внутри круга «дружеских вещей», что означает, что Бонзо находится внутри круга «дружественных вещей». ” круг.
Пример 3 Верен или недействителен следующий аргумент?
Все собаки дружелюбны.
Рекс дружелюбный.
Значит, Рекс — собака.
Чтобы решить, мы перепишем аргумент как условное, чтобы увидеть шаблон. Затем мы рисуем диаграмму Эйлера, чтобы визуально увидеть, верна ли она.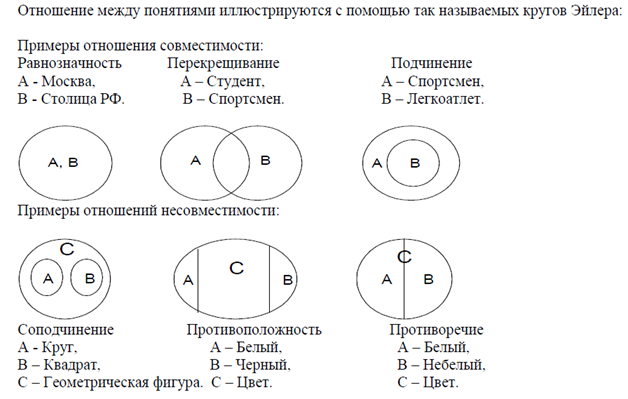
| Использование «все» | Использование условного | Символы |
| Все собаки дружелюбны. Рекс дружелюбен. Следовательно, Рекс — собака. | Если это собака, то она дружелюбная. Это дружелюбно. Следовательно, это собака. | d → f f ∴ d |
Этот аргумент недействителен – вы можете видеть, что порядок d → f, сначала d, затем f, не соблюдается, так как вторая посылка – f, за которой следует по заключению д. Если у нас есть d → f, правильный порядок будет иметь d в качестве первой посылки, за которой следует f. Но в этом аргументе сначала f, а затем d.
В качестве альтернативы вы можете думать о собаке как о A, а о дружелюбном как о B:
A → B
B
∴ A
Этот аргумент точно соответствует форме недопустимого аргумента в верхней части этой страницы.
Диаграмма Эйлера приводит нас к тому же заключению: аргумент неверен , потому что Рекс может быть в любом месте. Не факт, что Рекс находится внутри круга «Собаки». Чтобы быть действительным аргументом, вывод должен быть на 100% уверен.
Символ «не» в логических рассуждениях
В логических рассуждениях, если мы хотим сказать « не собака», мы будем использовать букву d, означающую «это собака», и мы поместим перед ним символ «не» ~: ~d означает «не собака». Этот символ подобен символу дополнения в наборах.
Пример 4 Верен или неверен следующий аргумент?
Если зеленый, то это не собака.
Зеленый.
Следовательно, это не собака.
Чтобы решить, пишем аргумент символами, чтобы увидеть закономерность. Мы также переписываем утверждение, чтобы мы могли нарисовать диаграмму Эйлера, чтобы визуально увидеть, верно ли оно.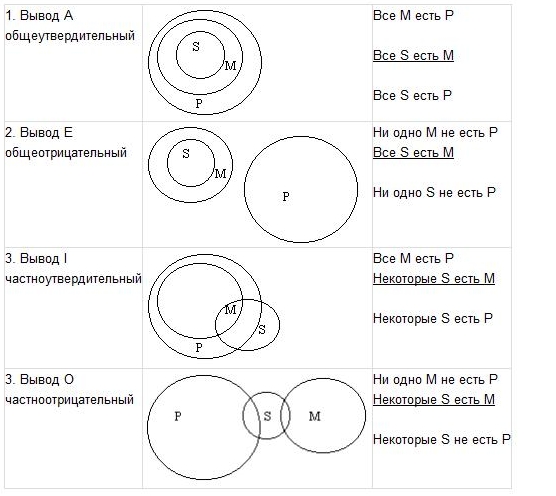
| Условное | Символы | Слова |
| Если оно зеленое, то это не собака. Зеленый. Следовательно, это не собака. | г → ~d г ∴ ~d | Нет зеленых собак Генри зеленый Следовательно, Генри не собака. |
Этот аргумент действителен: вторая посылка и заключение следуют в том же порядке, что и в условном (если… то). То есть в первой строке g → ~d, g стоит первой, а ~d — второй. Следующая посылка g и заключение ~d следуют в том же порядке.
С диаграммой Эйлера, Если зеленый, то это не собака переведет в два отдельных круга. Это то же самое, что нет зеленых собак .
Используя диаграмму Эйлера, мы видим, что аргумент действителен , так как Гарри находится в круге зеленых вещей, поэтому он не может быть в круге собак, так как они не пересекаются.
youtube.com/embed/sU4QGi1qyyo?version=3&rel=1&showsearch=0&showinfo=1&iv_load_policy=1&fs=1&hl=en&autohide=2&hd=1&wmode=transparent” allowfullscreen=”true” sandbox=”allow-scripts allow-same-origin allow-popups allow-presentation”> Логические аргументы с использованием «Некоторые» и «Нет»
Пример 5 Является ли следующий аргумент допустимым или недействительным?
Некоторые кошки являются домашними животными.
Пушистый кот.
Следовательно, Пушистик — домашнее животное.
Из предыдущего раздела мы знаем, что F можно поставить в двух местах: Пушистый может быть котом, который является домашним животным (в центре), или котом, который не является домашним животным (слева). Поскольку мы не знаем наверняка, что Пушистик находится в кошачьем круге, аргумент недействителен. Помните, чтобы аргумент был действительным, заключение должно следовать без сомнения из посылок.
В этом примере мы делаем , а не меняем аргумент на символы, потому что какой-то 9Оператор 0022 переводит , а не в условное выражение.
Некоторые кошки являются домашними животными не эквивалентно c → p, это будет все кошки являются домашними животными.
Важно уметь выбирать, какой тип представления — визуальный или символический — лучше всего использовать в данной ситуации.
Пример 6 Верен или неверен следующий аргумент? Используйте диаграмму Эйлера или символы, в зависимости от того, что лучше, чтобы решить.
Некоторые телешоу смешные.
Вебстер не смешной.
Следовательно, Вебстер — это не телешоу.
Для любого аргумента с «some» мы не можем использовать условное выражение , поэтому рисуем диаграмму Эйлера. Здесь у нас есть «Некоторые телешоу смешные».
Поскольку Вебстер не смешной, есть два возможных места, где можно поместить Вебстера, кроме «Забавных вещей». Одно из этих возможных мест находится внутри телешоу, поэтому вывод «Вебстер — это не телешоу» будет 9.0003 неверный .
Все отношения и Транзитивность
Какой вывод правильный, чтобы сказать нам о том, как связаны квадраты и четырехугольники?
Все квадрата являются прямоугольниками.
Все прямоугольники являются четырехугольниками (имеют четыре стороны).
Следовательно, все ____ являются _______.
Правильный вывод создаст действительный аргумент.
Используйте диаграмму, чтобы увидеть, какой набор будет подмножеством другого.
действительный вывод равен Следовательно, все квадраты четырехугольники (имеют четыре стороны).
Мы знаем, что это так, потому что на нашей диаграмме набор квадратов равен внутри набора четырехугольников.
Мы также можем использовать условное выражение и символы, чтобы понять, почему.
Условный Символы
Если это квадрат, то это прямоугольник. с → р
Если это прямоугольник, то это четырехугольник r → q
Следовательно, если это квадрат, то это четырехугольник. ∴ s → q
Символы по порядку: s → r, r → q. То есть s → r → q
Это образует непрерывную цепочку от s, хотя и r, до q. Таким образом, вывод s → q верен.
Этот тип аргумента,
A → B
B → C
∴ A → C
, называется действительным аргументом на транзитивность .
Он показывает цепочку, идущую от А к В, затем от В к С, следовательно, А идет к С. Если одно число на меньше другого на , мы пишем a < b . Например, 3 < 4.
Теперь предположим, что мы знаем, что a < b и мы знаем, что b < c.
Мы можем записать это как одно неравенство: a < b < c ( a меньше b меньше c ).
Мы можем заключить, что a должно быть на меньше, чем c , то есть a < c.
Написанное числами, это все равно, что сказать, что если 3 < 4 и 4 < 5, мы знаем, что 3 < 5. .
A → B
C → B
∴ A → C
– это , а не – допустимый аргумент по транзитивности.
, а не показывает цепочку, идущую от A к B, а затем от B к C. Вместо этого и A, и C ведут к B, поэтому ничего не связывает A с C.
Пример 7 Используйте ваше знание наборов чисел для создания действительного аргумента по транзитивности.
Все натуральные числа являются целыми числами. N → W
Все целые числа являются целыми числами W → I
Следовательно, все натуральные числа ____? ∴ N → ____?
Вы могли бы правильно заключить, что N → I.
Это следует из построения цепочки из посылок: N → W, W → I, значит имеем N → W → I
Пример 8 аргумент в силе?
Все целые числа являются целыми числами. W → I
Все натуральные числа являются целыми числами N → I
Следовательно, все целые числа являются натуральными числами ∴ W → N
Мы можем видеть, что этот аргумент недействителен , глядя на ту же диаграмму – множество целых чисел не входит в множество натуральных чисел,
Мы также можем видеть, что этот аргумент недействителен , взглянув на символы:
W → I, N → I
Цепочки от W до N нет, каждая стрелка указывает на I, ничто не указывает от до N.
Пример 9 Какие из следующих аргументов, показанных только символами, верны транзитивностью? Что недействительно? Совет: посмотрите, сможете ли вы найти цепочку, ведущую от одной буквы в заключении к другой.
Аргумент 1 Аргумент 2 Аргумент 3 Аргумент 4
p → q a → b
a → b m → r ~y → q c → b
д → г a → t q → m ∴ a → c
∴ p → r ∴ m → t ∴ x → q
Первый аргумент можно вывести в одну длинную строку, чтобы увидеть, что с чем связано. Имеем p → q, a → b, q → r. Мы можем избавиться от a → b, так как эта посылка не имеет ничего общего с остальными. Теперь у нас есть p → q, q → r, что дает нам цепочку: p → q → r, что означает, что p действительно приводит к r , p → r. Аргумент равен действительный .
Можно удалить из посылок аргумент, который не влияет на ваш вывод! Предположим, кто-то сказал вам: «Все свиньи быстрые» (p → q), все аллигаторы большие (a → b) и все быстрые существа быстрые (q → r).
Вы определенно можете проигнорировать эту часть об аллигаторах и сделать вывод, что все свиньи быстрые (p → r).
Для аргумента 2 имеем m → z, m → r, a → t. Поскольку в заключении m → t, мы ищем в посылках цепочку, связывающую m с t, например: m → ___ → ___ …→ t. Цепь, идущая от m к t, отсутствует. Вместо этого m переходит в z и в r, но ни z, ни r не ведут ни к чему другому. Аргумент неверный .
Для аргумента 3 имеем x → ~ y, ~ y → q и q → m в посылках. Поскольку вывод x → q, мы ищем в посылках цепочку, которая связывает x с q. У нас есть эта цепочка: у нас есть x → ~ y, ~ y → q, что становится x → ~ y → q, так что мы имеем x → q. Аргумент допустим .
Наконец, аргумент 4 равен недействителен , так как у нас нет цепочки, идущей от а к с в помещении. У нас есть a, идущий к b, и у нас также есть c, идущий к b. Нет ничего, что привело бы к c. Проблема в том, что вторая посылка — это наоборот .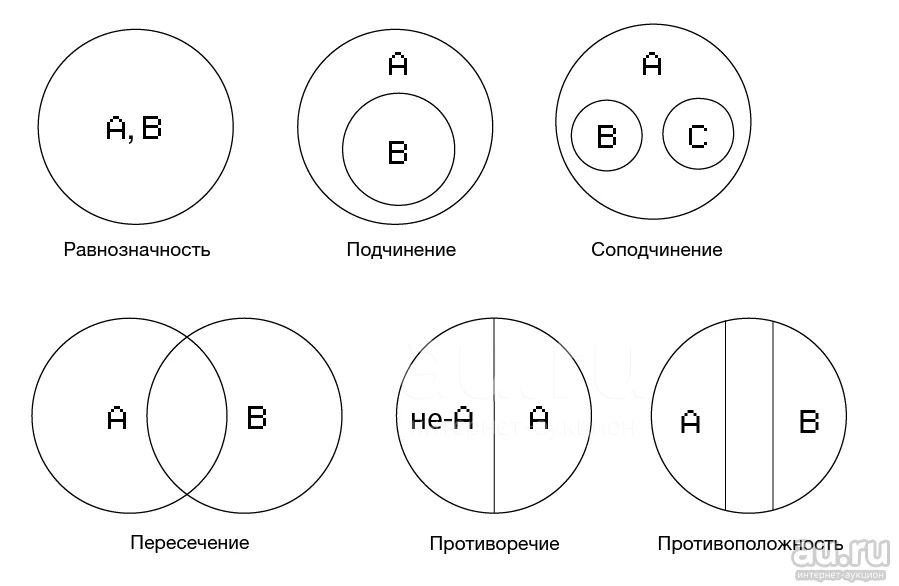
Если бы мы вместо этого имели a → b и b → c, то мы могли бы заключить, что ∴ a → c.
sec-3.6-homeworkСкачать
sec-3.6-homework-answersСкачать
Нравится:
Нравится Загрузка…
Диаграммы Венна и диаграммы Эйлера с примерами
Дата обновления:
Диаграммы Венна и диаграммы Эйлера выглядят очень похоже, поэтому понятно, что многие люди не могут определить разницу. Хотя оба типа диаграмм основаны на теории множеств, существуют некоторые тонкие различия, которые делают их уникальными. Надеюсь, эта статья рассеет ваши сомнения по поводу диаграмм Венна и диаграмм Эйлера, и я приведу несколько примеров, чтобы было понятнее.
Венн против Эйлера: определение
Что такое диаграмма Венна?
Проще говоря, диаграмма Венна иллюстрирует логическую связь между двумя или более наборами элементов. Он визуально представляет различия и сходства между двумя концепциями.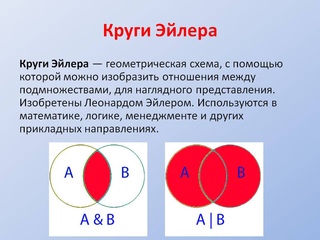
Что такое диаграмма Эйлера?
Диаграмма Эйлера — это еще одна диаграмма, которая представляет наборы и их отношения. Это похоже на диаграмму Венна, поскольку обе используют круги для создания диаграммы. Однако в то время как диаграмма Венна представляет все множество, диаграмма Эйлера представляет часть множества. Диаграмма Венна показывает пустое множество, затеняя его, тогда как на диаграмме Эйлера эта область может просто отсутствовать.
В чем разница между диаграммой Венна и диаграммой Эйлера?
Оба набора диаграмм основаны на теории множеств. Диаграмма Венна показывает все возможные логические отношения между наборами множеств. Но диаграмма Эйлера показывает только те отношения, которые существуют в реальном мире.
Хотя диаграммы Венна и диаграммы Эйлера являются инструментами, используемыми для представления множеств и их отношений, между ними есть некоторые важные различия.
| Функция | Диаграмма Венна | Диаграмма Эйлера |
| Перекрытие | Перекрытие между двумя или более наборами представлено общая область на диаграмме. | Может использовать перекрывающиеся или вложенные фигуры для представления взаимосвязей между наборами и может вообще не иметь общих областей. |
| Полнота | Разработаны, чтобы быть полными, что означает, что они показывают все возможные отношения между наборами. | Могут быть частичными или неполными, что означает, что они могут не отображать все возможные отношения между наборами. |
| Выразительность | Ограниченная в своей выразительности, так как они могут представлять установленные отношения только в терминах объединения, пересечения и различия. | Можно использовать перекрывающиеся и вложенные фигуры для представления более широкого диапазона отношений и зависимостей между наборами. |
| Сложность | Может стать сложным и трудным для чтения при представлении отношений между более чем тремя наборами. | Может быть разработан для обработки более сложных взаимосвязей, и в таких случаях его легче интерпретировать. |
В общем, диаграммы Венна идеально подходят для визуализации простых отношений множеств и могут быть полезны для обучения основным понятиям теории множеств. Однако диаграммы Эйлера более гибки и универсальны, поэтому их можно использовать для визуализации более широкого диапазона отношений между множествами. Это делает их полезными для более сложных ситуаций и приложений.
Диаграммы Венна против
Диаграммы Эйлера ПримерыНачнем с очень простого примера. Давайте рассмотрим надмножество Animals с млекопитающими и птицами в качестве подмножеств. Диаграмма Венна показывает пересечение двух множеств, хотя в реальном мире такой возможности не существует. Диаграмма Эйлера, с другой стороны, не показывает пересечения.
Диаграммы Венна показывают все возможные комбинации, даже если они не существуют в реальном сценарии Теперь давайте рассмотрим немного более сложный пример с колодой карт. Опять же, важно помнить о разнице между двумя типами диаграмм, все возможные комбинации против реальных комбинаций .
Возьмем карты как надмножество, а черные карты, красные карты и бубны — как подмножества.
Как видно из приведенного выше примера, диаграммы Венна показывают четыре пересечения, которые не содержат никаких данных, поскольку должны показывать все возможные комбинации.
Существуют различные методы преобразования диаграмм Венна в диаграммы Эйлера и наоборот. Посмотрите эту замечательную вики-статью о диаграммах Эйлера, в которой объясняются некоторые методы, которые вы можете использовать для преобразования диаграмм Венна в диаграммы Эйлера. Я надеюсь, что приведенные выше примеры помогли вам развеять ваши сомнения относительно диаграмм Венна и диаграмм Эйлера. Если у вас есть какие-либо вопросы, не стесняйтесь задавать их в разделе комментариев.
Рисуете ли вы диаграммы Венна или диаграммы Эйлера, Creately предоставляет вам все необходимые инструменты.