Правила по математике за 1 класс: Презентация по математике “Правила по математике для учащихся 1 класса”
Правила по математике 1 класс (программа “Школа XXI века”)
Свойства предметов: цвет, форма, размер, материал, количество, назначение, расположение и другие.
Сложить – это значит объединить части в одно целое.
Компоненты сложения:
3 + 1 = 4
слагаемое слагаемое сумма (результат)
сумма (выражение)
Равенство 3 + 1 = 4 можно прочитать так:
«Три плюс один равно четырём», или
«Сумма трёх и одного равна четырём», или
«К трём прибавить один получится четыре», или
«Первое слагаемое – 3, второе – 1, сумма – 4», или
«Части – 3 и 1, целое – 4».
Вычесть – это значит взять часть из целого и найти оставшуюся часть.
Компоненты вычитания:
4 – 1 = 3
уменьшаемое вычитаемое разность (результат)
разность (выражение)
Равенство 4 – 1 = 3 можно прочитать
«Четыре минус один равно трём», или
«Разность четырёх и одного равна трём», или
«Из четырёх вычесть один получится три», или
«Уменьшаемое – 4, вычитаемое – 1, разность – 3», или
«Целое – 4, части – 1 и 3».
Границей круга является окружность.
Ломаная линия. Многоугольник.
Незамкнутая Замкнутая
ломаная линия ломаная линия
Многоугольником называют замкнутую ломаную линию (без самопересечений).
треугольник четырёхугольник пятиугольник
Таблица сложения.
1 + 1 = 2 2 + 1 = 3 3 + 1 = 4 4 + 1 = 5 5 + 1 = 6
1 + 2 = 3 2 + 2 = 4 3 + 2 = 5 4 + 2 = 6 5 + 2 = 7
1 + 3 = 4 2 + 3 = 5 3 + 3 = 6 4 + 3 = 7 5 + 3 = 8
1 + 4 = 5 2 + 4 = 6 3 + 4 = 7 4 + 4 = 8 5 + 4 = 9
1 + 5 = 6 2 + 5 = 7 3 + 5 = 8 4 + 5 = 9
1 + 6 = 7 2 + 6 = 8 3 + 6 = 9
1 + 7 = 8 2 + 7 = 9
1 + 8 = 9
6 + 1 = 7 7 + 1 = 8 8 + 1 = 9
6 + 2 = 8 7 + 2 = 9
6 + 3 = 9
Связь
между компонентами сложения.
Чем больше слагаемое, тем больше сумма, и наоборот (если другое слагаемое одинаковое).
4 + 1 < 4 + 1, так как 1 < 3
Связь между компонентами вычитания.
Чем больше уменьшаемое, тем больше разность, и наоборот (если вычитаемое одинаковое).
6 – 3 > 5 – 3, так как 6 > 5
Чем больше вычитаемое, тем меньше разность, и наоборот (если уменьшаемое одинаковое).
6 – 3 < 6 – 2, так как 3 > 2
Сложение и вычитание с нулём.
а + 0 = а 0 + а = а а – а = 0 а – 0 = а
Римская нумерация
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
I | II | III | IV | V | VI | VII | VIII | IX | X |
Задача.
Из чего состоит задача
Условие | У Тани 4 гриба, у Саши 2 гриба. | Часть задачи, из которой узнают, что известно. |
Вопрос | Сколько грибов у Тани и Саши вместе? | Часть задачи, из которой узнают, что нужно найти. |
Что нам помогает ответить на вопрос задачи
Условный рисунок | |||||
Схема |
Таня Саша
4 гр.
| ||||
Выражение | 4 + 2 | ||||
Решение | 4 + 2 = 6 (гр.) | Запись, при помощи которой находят ответ на вопрос задачи. | |||
Ответ | 6 грибов | Запись, которая фиксирует ответ на вопрос задачи. | |||
Взаимно обратные задачи.
? в в
а б а ? ? б
а + б в – а в – б
Разностное сравнение чисел
Чтобы
узнать, на сколько одно число больше или меньше другого, можно из большего
числа вычесть меньшее.
б
р = б – м
? (б – большее число, м – меньшее число, р – разность)
м
Правило нахождения большего числа.
Чтобы найти большее число, можно к меньшему числу прибавить разность.
Правило нахождения меньшего числа.
Чтобы найти меньшее число, можно из большего числа вычесть разность.
Величины.
Длина.
Сантиметр (см), дециметр (дм)
1дм = 10 см
Масса.
Килограмм (кг)
Объём.
Литр (л)
Сравнивать, складывать и вычитать значения величин можно только тогда, когда они выражены в одинаковых единицах измерения.
Свойства величин:
Если а = б, то б =
а.
Если а > б, то б < а.
Если а = б, б = с, то а = с.
Если а > б, то б > с, то а > с.
Уравнения.
Уравнения вида х + а = б, а + х = б
5 + х = 9 х + 3 = 7
х = 9 – 5 х = 7 – 3
х = 4 х = 4
5 + 4 = 9 4 + 3 = 7
9 = 9 7 = 7
Чтобы найти неизвестную часть, надо из целого вычесть известную часть.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
Уравнения вида а – х = б
5 – х = 4 6 – х = 3
х = 5 – 4 х = 6 – 3
х = 1 х = 3
5 – 1 = 4 6 – 3 = 3
4 = 4 3 = 3
Чтобы найти
неизвестную часть, надо из целого вычесть известную часть.
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть значение разности.
Уравнения вида х – а = б
х – 6 = 3
х = 6 + 3
х = 9
9 – 6 = 3
3 = 3
Чтобы найти целое, части надо сложить.
Чтобы найти неизвестное уменьшаемое, надо к вычитаемому прибавить значение разности.
Круглые числа.
1 д = = 1 д. 0 ед. = 10 | десять |
2 д = = 2 д. 0 ед. = 20 | двадцать |
3 д = = 3 д. 0 ед. = 30 | тридцать |
4 д =
= 4 д. | сорок |
5 д = = 5 д. 0 ед. = 50 | пятьдесят |
6 д = = 6 д. 0 ед. = 60
| шестьдесят |
7 д = = 7 д. 0 ед. = 70 | семьдесят |
8 д = = 8 д. 0 ед. = 80 | восемьдесят |
9 д = = 9 д. 0 ед. = 90 | девяносто |
Числа до 20.
=
1 д. | десять |
. = 1 д. 1 ед. = 11 = 10 + 1 | одиннадцать |
: = 1 д. 2 ед. = 12 = 10 + 2 | двенадцать |
\ = 1 д. 3 ед. = 13 = 10 + 3 | тринадцать |
: : = 1 д. 4 ед. = 14 = 10 + 4 | четырнадцать |
: . : = 1 д. 5 ед. = 15 = 10 + 5 | пятнадцать |
: : : = 1 д. 6 ед. = 16 = 10 + 6 | шестнадцать |
: : : = 1 д. 7 ед. = 17 = 10 + 7 . | семнадцать |
: :
: = 1 д. . . | восемнадцать |
.. : : : = 1 д. 9 ед. = 19 = 10 + 9 . . . | девятнадцать |
= 2 д. 0 ед. = 20 = 10 + 10 | двадцать |
Натуральные числа служат для счёта предметов и единиц измерения величин.
Для записи натуральных чисел используют 10 цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральный ряд чисел: 1, 2, 3, 4, 5, 6, …
Сравнение двузначных чисел.
Любое двузначное число больше любого однозначного числа, и наоборот.
< >
Из двух двузначных чисел больше то, у которого десятков больше, и наоборот.
62 > 45, так как 6 д. > 4 д.
Если количество десятков одинаковое, то больше то число, у которого единиц больше, и наоборот.
31 < 37, так как 1 ед. < 7 ед.
Сложение и вычитание двузначных чисел.
Чтобы сложить двузначные числа, можно к десяткам прибавить десятки, а к единицам – единицы.
: : + : = : : :
24 + 12 = 36
Чтобы вычесть двузначные числа, можно из десятков вычесть десятки, а из единиц – единицы.
: : : – : : = :
46 – 14 = 32
Таблица сложения.
+ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
9 + 2 = 11 | 8 + 3 = 11 | 7 + 4 = 11 | 6 + 5 = 11 | 11 |
9 + 3 = 12 | 8 + 4 = 12 | 7 + 5 = 12 | 6 + 6 = 12 | 12 |
9 + 4 = 13 | 8 + 5 = 13 | 7 + 6 = 13 |
| 13 |
9 + 5 = 14 | 8 + 6 = 14 | 7 + 7 = 14 |
| 14 |
9 + 6 = 15 | 8 + 7 = 15 |
|
| 15 |
9 + 7 = 16 | 8 + 8 = 16 |
|
| 16 |
9 + 8 = 17 |
|
|
| 17 |
9 + 9 = 18 |
|
|
| 18 |
Сложение чисел с
переходом через десяток.
7 + 5 = 10 + 2 = 12
3 2
Алгоритм сложения:
1. Дополняю одно из слагаемых до 10.
2. Прибавляю остальные единицы.
Вычитание чисел с переходом через десяток.
12 – 5 = 10 – 3 = 7
2 3
Алгоритм вычитания:
1. Уменьшаю до 10.
2. Вычитаю остальные единицы.
Математические определения и понятия | |||||||||||||
Геометрические фигуры. Точка и прямая линия являются основными геометрическими фигурами. Геометрические фигуры бывают плоскими и объемными. Плоские геометрические фигуры – это четырехугольник, треугольник, многоугольник, квадрат, прямоугольник, круг, овал, ромб, трапеция и др. Объемные геометрические фигуры (геометрические тела) – это пирамида, шар, конус, куб, цилиндр, параллелепипед и др. | |||||||||||||
Точка. Линии. Точка – это самая малая геометрическая фигура. Линии бывают прямые, кривые, ломаные. Прямая линия – это геометрическая фигура, которая не имеет ни начала, ни конца, она бесконечна. | ·
| ||||||||||||
Отрезок. Отрезок – это часть прямой линии, которая имеет начало и конец. Длину можно измерить. | 3 см
| ||||||||||||
Луч. Луч – это часть прямой, которая имеет начало, но не имеет конца. |
| ||||||||||||
Углы. Угол — геометрическая фигура, образованная двумя лучами из одной точки. |
| ||||||||||||
Прямоугольник. Прямоугольник – это четырехугольник, у которого все углы прямые и противоположные стороны равны. Большую сторону называют длиной, меньшую шириной. |
| ||||||||||||
Квадрат. Квадрат – это четырехугольник, у которого все стороны и углы равны. |
| ||||||||||||
Выражения. Выражения – это записи из чисел и букв, соединенных знаками арифметических действий. Выражения бывают буквенные – в них встречаются буквы (а+3), числовые – составлены из чисел (5 – 2). | |||||||||||||
Высказывания. Высказывания – это верные и неверные предложения, относительно которого имеет смысл вопрос: истинно оно или ложно. | |||||||||||||
Равенство. Неравенство. Равенство – это высказывания, в записи которых используется знак =. Неравенство – это два числа или выражения, соединенные одним их знаков: >, Поставить один из этих знаков между числами или выражениями – значит, сравнить их. | |||||||||||||
Увеличение и уменьшение на.
| |||||||||||||
Компоненты при сложении. 1 слагаемое 2 слагаемое Сумма 4 + 2 = 6
сумма | Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое. | ||||||||||||
Компоненты при вычитании. Уменьшаемое вычитаемое разность 8 – 3 = 5 разность | Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность. | ||||||||||||
Уравнение. Уравнение – это равенство с переменной, значение которой надо найти. Решить уравнение- это значит найти все его корни. Алгоритм: 1. Выделить компоненты. 2. Применить правило. 3. Найти корень уравнения. 4. Сделать проверку. | 1с 2с С Х + 2 = 6 Х = 6 – 2 Х = 4 4 + 2 = 6 6 = 6 | ||||||||||||
Задача. | Для решения задач можно использовать – рисунок – схему – краткую запись У Тани 4 гриба, а у Саши 2 гриба. Сколько грибов у Тани и Саши?
| ||||||||||||
Целое и части. ?
Ищем целое. Чтобы найти целое, части надо сложить. |
? Ищем часть. Чтобы найти часть, надо из целого вычесть другую часть. | ||||||||||||
Задача на сравнение. У Тани 4 гриба, а у Саши 2 гриба. | |||||||||||||
| Схема Т. С. 4 гр. 2 гр.
на ? > | ||||||||||||
Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее. | |||||||||||||
Состав числа. | |||||||||||||
УМК «Школа России» 1 класс
УМК «Школа России» 1 класс состоит из следующих предметных УМК (учебники включены в федеральный перечень рекомендуемых учебников):
– Русский язык.
Азбука. 1 класс. Горецкий В.Г., Кирюшкин В.А., Виноградская Л.А. и др.
Русский язык. 1 класс. Канакина В.П., Горецкий В.Г.
– Литературное чтение. 1 класс. Климанова Л.Ф., Горецкий В.Г., Голованова М.В. и др.
– Математика. 1 класс. Моро М.И., Степанова С.В., Волкова С.И.
– Окружающий мир. 1 класс. Плешаков А.А.
– Изобразительное искусство. 1 класс. Неменская Л.А., Коротеева Е.И., Горяева Н.А. (под ред. Неменского Б.М.).
– Музыка. 1 класс. Критская Е.Д., Сергеева Г.П., Шмагина Т.С.
– Технология. 1 класс. Лутцева Е.А., Зуева Т.П.
– Физическая культура. 1-4 классы. Лях В.И.
– Физическая культура. Гимнастика. 1-4 классы. Винер И.А., Горбулина Н.М., Цыганкова О.Д. (Учебники могут использоваться в составе систем учебников «Школа России» и «Перспектива»).
На данной странице представлены УМК по русскому языку ( в том числе обучению грамоте), литературному чтению, математике, окружающему миру.
УМК по изобразительному искусству, музыке, технологии, физической культуре и дополнительная литература.
Быстрый переход:
Обучение грамоте
Русский язык
Литературное чтение
Математика
Окружающий мир
Обучение грамоте | |||||
| Азбука. Учебник. 1 класс. В 2-х частях Горецкий В.Г., Кирюшкин В.А., Виноградская Л.А. и др.
| |||||
| Прописи. 1 класс. В 4-х частях Горецкий В.  Г., Федосова Н.А. Г., Федосова Н.А.
| |||||
| Чудо-пропись. 1 класс. В 4-х частях Илюхина В.А.
| |||||
| Читалочка. Дидактическое пособие. 1 класс Абрамов А.В., Самойлова М.И.
| |||||
| Обучение грамоте. Тесты. 1 класс Игнатьева Т.В.
| |||||
| Тренажер по чтению. Букварный период. 1 класс Самойлова М.И.
| |||||
| Обучение грамоте. Методическое пособие с поурочными разработками. 1 класс. (В электронном виде на сайте издательства) Горецкий В.  Г., Белянкова Н.М. Г., Белянкова Н.М. | |||||
| Русский язык. Предметная линия учебников системы «Школа России» авторов В.П. Канакиной, В.Г. Горецкого. Примерные рабочие программы. 1-4 классы. (В электронном виде на сайте издательства) Канакина В.П., Горецкий В.Г., Бойкина М.В. и др. | |||||
| Наверх | |||||
Русский язык | |||||
| Русский язык. Учебник. 1 класс Канакина В.П., Горецкий В.Г.
| |||||
| Русский язык. Рабочая тетрадь. 1 класс Канакина В.  П. П.
| |||||
| Русский язык. Тетрадь учебных достижений. 1 класс Канакина В.П.
| |||||
| Русский язык. Проверочные работы. 1 класс Канакина В.П.
| |||||
Русский язык. Тесты. 1 класс Тесты. 1 классЗанадворова А. В.
| |||||
| Русский язык. Сборник диктантов и творческих работ. 1-2 классы Коробейникова Т.Н.
| |||||
| Русский язык. Методическое пособие с поурочными разработками. 1 класс. (В электронном виде на сайте издательства) Канакина В.П. | |||||
Русский язык. Предметная линия учебников системы «Школа России» авторов В. П. Канакиной, В.Г. Горецкого. Примерные рабочие программы. 1-4 классы. (В электронном виде на сайте издательства) П. Канакиной, В.Г. Горецкого. Примерные рабочие программы. 1-4 классы. (В электронном виде на сайте издательства)Канакина В.П., Горецкий В.Г., Бойкина М.В. и др. | |||||
| Пишу правильно. Орфографический словарь. Начальная школа Бондаренко А.А., Гуркова И.В. | |||||
| Рабочий словарик. 1 класс Бондаренко А.А.
| |||||
| Русский язык. Летние задания. Переходим во 2-й класс Никишенкова А.В. | |||||
Русский язык. Предварительный контроль, текущий контроль, итоговый контроль. 1 класс 1 класс Курлыгина О.Е., Харченко О.О.
| |||||
| Русский язык. Тетрадь летних заданий. 1 класс Михайлова С.Ю.
| |||||
| Русский язык. Тесты. 1 класс Бондаренко А.А. | |||||
| Русский язык. Проверочные работы. 1 класс Бондаренко А.А.
| |||||
| Наверх | |||||
Литературное чтение | |||||
| Литературное чтение. Учебник. 1 класс. В 2-х частях Климанова Л.Ф., Горецкий В.Г., Голованова М.В. и др.
| |||||
| Литературное чтение. Рабочая тетрадь. 1 класс Бойкина М.В., Виноградская Л.А.
| |||||
| Литературное чтение. Тетрадь учебных достижений. 1 класс Стефаненко Н.А.
| |||||
| Литературное чтение. Методическое пособие с поурочными разработками. 1 класс. (В электронном виде на сайте издательства) Климанова Л.Ф., Бойкина М.В. | |||||
| Литературное чтение. Предметная линия учебников системы «Школа России». Примерные рабочие программы. 1-4 классы. (В электронном виде на сайте издательства) Климанова Л.  Ф., Бойкина М.В. Ф., Бойкина М.В. | |||||
| Литературное чтение. Тетрадь по развитию речи. 1 класс Бойкина М.В., Бубнова И.А.
| |||||
| Литературное чтение. Предварительный контроль, текущий контроль, итоговый контроль. 1 класс Бойкина М.В.
| |||||
| Смысловое чтение. Рабочая тетрадь. 1 класс Бойкина М.В., Бубнова И.  А А
| |||||
| Смысловое чтение. Читаю, понимаю, узнаю. 1 класс Ульяхина Л.Г.
| |||||
| Литературное чтение. Читаем летом. 1 класс Фомин О.В.
| |||||
Литературное чтение. Дневник читателя. 1 класс Дневник читателя. 1 классБойкина М.В., Бубнова И.А. | |||||
| Наверх | |||||
Математика | |||||
| Математика. Учебник. 1 класс. В 2-х частях Моро М.И., Волкова С.И., Степанова С.В.
| |||||
| Математика. Рабочая тетрадь. 1 класс. В 2-х частях Моро М.И., Волкова С.И.
| |||||
Математика. Устные упражнения. 1 класс Устные упражнения. 1 класс Волкова С.И.
| |||||
| Математика. Проверочные работы. 1 класс Волкова С.И.
| |||||
| Математика. Тесты. 1 класс Волкова С.И.
| |||||
Математика. Тетрадь учебных достижений. 1 класс Тетрадь учебных достижений. 1 класс Волкова С.И.
| |||||
| Математика. Контрольные работы. 1-4 классы Волкова С.И.
| |||||
| Для тех, кто любит математику. 1 класс Моро М.И., Волкова С.И.
| |||||
| Математика и конструирование. Конструирование. 1 класс Волкова С.И., Пчелкина О.Л. | |||||
| Математика. Методические рекомендации. 1 класс. (В электронном виде на сайте издательства) Бантова М.А., Бельтюкова Г.В., Волкова С.И. и др. | |||||
| Математика. Предметная линия учебников «Школа России». Примерные рабочие программы. 1-4 классы. (В электронном виде на сайте издательства) Моро М.И., Волкова С.И., Степанова С.В. и др. | |||||
| Справочник младшего школьника. Правила по математике. 1-4 классы Глаголева Ю.И., Волковская И.И. | |||||
Математика. Предварительный контроль, текущий контроль, итоговый контроль. 1 класс 1 класс Глаголева Ю.И., Волковская И.И.
| |||||
| Математика. Летние задания. Переходим во 2-й класс Светин А.В. | |||||
| Математика. Тетрадь летних заданий. 1 класс Селькина Л.В., Худякова М.А.
| |||||
| Математика. Олимпиадные задания. 1-2 классы Глаголева Ю.И., Волковская И.  И., Буденная И.О. И., Буденная И.О.
| |||||
| Математика. Тесты. 1 класс Глаголева Ю.И. | |||||
| Математика. Проверочные работы. 1 класс Глаголева Ю.И.
| |||||
| Наверх | |||||
Окружающий мир | |||||
Окружающий мир. Учебник. 1 класс. В 2-х частях Учебник. 1 класс. В 2-х частях Плешаков А.А.
| |||||
| Окружающий мир. Рабочая тетрадь. 1 класс. В 2-х частях Плешаков А.А.
| |||||
| Окружающий мир. Проверочные работы. 1 класс Плешаков А.А., Плешаков С.А.
| |||||
| Окружающий мир. Тесты. 1 класс Плешаков А.А., Гара Н.Н., Назарова З.Д.
| |||||
| Окружающий мир. Тетрадь учебных достижений. 1 класс Плешаков А.А., Назарова З.Д.
| |||||
| Окружающий мир. Основы безопасности жизнедеятельности. Рабочая тетрадь. 1 класс Плешаков А.  А., Назарова З.Д. А., Назарова З.Д. | |||||
| Окружающий мир. Методические рекомендации. 1 класс. (В электронном виде на сайте издательства) Плешаков А.А., Ионова М.А., Кирпичева О.Б. и др. | |||||
| Окружающий мир. Предметная линия учебников системы «Школа России». Примерные рабочие программы. 1-4 классы. (В электронном виде на сайте издательства) Плешаков А.А. | |||||
| Энциклопедия путешествий. Страны мира. Книга для учащихся начальных классов Плешаков А.А., Плешаков С.А.
| |||||
От земли до неба. Атлас-определитель. Книга для учащихся начальных классов Атлас-определитель. Книга для учащихся начальных классов Плешаков А.А.
| |||||
| Великан на поляне, или Первые уроки экологической этики. Книга для учащихся начальных классов Плешаков А.А., Румянцев А.А.
| |||||
| Зеленые страницы. Книга для учащихся начальных классов Плешаков А.А.
| |||||
| Окружающий мир. Предварительный контроль, текущий контроль, итоговый контроль. 1 класс Глаголева Ю.И., Архипова Ю.И.
| |||||
| Окружающий мир. Летние задания. Переходим во 2-й класс Казанцева И.В., Архипова Ю.И., Глаголева Ю.И. | |||||
| Наверх | |||||
Если материал вам понравился, нажмите кнопку вашей социальной сети:
Поиск материала «Правила по математике в таблицах и схемах, 1-4 класс» для чтения, скачивания и покупки
Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
Search results:
- Математика 1–4 классы в схемах и таблицах | Книга по…
Правила, определения объединены в наглядные логические блоки, схемы, которые позволяют лучше понять и усвоить информацию. Пособие окажет неоценимую помощь в учебе, систематизируя полученные знания, а также будет полезным при подготовке к итоговому тестированию по
урок математики в 3 классе по теме “Закрепление таблицы умножения и деления на 2 и 3” представлен в виде путешествия, с применением слайдовой презентации. Путешествие по достопримечательностям с… Английский язык 1-4 классы в схемах и таблицах.
nsportal.ru
- Правила по математике в таблицах и схемах (1–4 классы) 2022
Тренажер по математике (1 класс) Основные правила орфографии и пунктуации.
 .
.vk.com
-
Купить эту книгу
- Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.
my-shop.ru
- И.С.Марченко. Математика в схемах и таблицах.1–4 классы.
Математика в схемах и таблицах.1-4 классы. учебно-методическое пособие по математике (2 класс) на тему. Опубликовано 20.12.2015 – 19:55 – Колодязная Надежда Петровна.
В издании в сжатой, концентрированной форме приводится основной теоретический материал, охватывающий курс математики начальной школы. Правила, определения объединены в наглядные логические блоки, схем…
nsportal.ru
- Математика в таблицах и схемах для 1–4 классов.
В этом документе собраны таблицы и схемы для уроков математики в начальной школе. Данное методическое пособие значительно облегчает для учителя объяснение нового материала.
Дидактический материал для 3 класса по математике, русскому языку, литературному чтению, окружающему миру (таблицы, блок-схемы) по УМК “Перспектива”. Дидактический материал предлагается использовать на уроках математики, русского язяка, окружающего мира, литературного чтения по УМК “Перспектива”, как на этапе актуализиции…
nsportal.ru
- Математика. 1–4 классы. В схемах и таблицах – Марченко И.С.
1-4 классы. В схемах и таблицах – Марченко И.С. В издании в сжатой, концентрированной форме приводится основной теоретический материал, охватывающий курс математики начальной школы. Правила, определения объединены в наглядные логические блоки, схемы, которые позволяют лучше понять и усвоить информацию.
 Пособие окажет неоценимую помощь в учебе, систематизируя полученные знания, а также будет полезным при подготовке к итоговому тестированию по математике за курс начальной школы.
Пособие окажет неоценимую помощь в учебе, систематизируя полученные знания, а также будет полезным при подготовке к итоговому тестированию по математике за курс начальной школы.11klasov.net
- Математика в таблицах и схемах (1–4 класс) | Скачать
Математика в таблицах и схемах (1-4 класс) учебно-методическое пособие (1, 2, 3, 4 класс). Опубликовано 30.01.2021 – 22:26 – Федоренко Татьяна Романовна.
Математика в таблицах и схемах для 1-4 классов… Конспект урока по математике «Составление таблицы умножения на 2» 2 класс (УМК «Школа России»). Тема: «Составление таблицы умножения на 2»Цели деятельности учителя: формирование умения реализовывать способы действия, помогающие вывести таблицу умножения и деления на 2; знакомст…
nsportal.ru
- таблицы по математике 1–4 класс | Методическая разработка по.
/3fa0d5fa597f86c.s.siteapi.org/img/d48671e05016c6f1f1632ec98bf0efee3bbf1ecf.png) ..
..Все необходимые таблицы по математике для учебного процесса в начальной школе, легко распечатать и склеить.
Конспект урока математики в 3 классе по теме:”Таблица умножения 9.Составление таблицы. Установление зависимости между изменяющимся множителем и цифрой в разряде десятков и в разряде единиц”….
nsportal.ru
- Правила по математике
ПРАВИЛА ПО МАТЕМАТИКЕ для начальной школы. Справочное пособие предназначено для учащихся начальных классов и подготовлено в соответствии с требованиями школьной программы. СОДЕРЖАНИЕ.
Частное от деления произведений двух множителей на число равно произведению одного из множителей на частное от деления второго множителя на это число.
www.klass39.ru
- Правила по математике для 1– 4 классов(наглядные схемы.
 ..)
..)Начальные классы, Методическая литература и другое, Правила по математике для 1- 4 классов(наглядные схемы и таблицы).
Благодаря готовым учебным материалам для работы в классе и дистанционно.
multiurok.ru
- Математика в схемах и таблицах (1 – 4 класс) – 138 фотографий
Математика в схемах и таблицах (1 – 4 класс). Сборник правил математики для учеников начальной школы. Roditeli.club.
vk.com
- Таблицы по математике 1–4 класс. | Картотека по математике на…
демонстрационные таблицы по математике 1-4 класс. Данный дидактический мптериал поможет учащимся начальной школы лучше усваивать изучаемый материал….
Все необходимые таблицы по математике для учебного процесса в начальной школе, легко распечатать и склеить.
 .. Конспект урока математики в 3 классе по теме:”Таблица умножения 9.Составление таблицы.Установление зависимости между изменяющимся множителем и цифрой в разряде десятков и в разряде единиц”.
.. Конспект урока математики в 3 классе по теме:”Таблица умножения 9.Составление таблицы.Установление зависимости между изменяющимся множителем и цифрой в разряде десятков и в разряде единиц”.nsportal.ru
- Математика в схемах и таблицах 1 – 4 класс. Обсуждение на…
Математика в схемах и таблицах 1 – 4 класс. Среда, 25 Апреля 2018 г. 10:42 + в цитатник.
Метки: математика 1-4класс схемы таблицы. Процитировано 50 раз Понравилось: 9 пользователям.
www.liveinternet.ru
- Скачать бесплатно Математика. 1–4 классы. В схемах…
1-4 классы. В схемах и таблицах – Марченко И.С. cкачать в PDF. В издании в сжатой, концентрированной форме приводится основной теоретический материал, охватывающий курс математики начальной школы.
 Правила, определения объединены в наглядные логические блоки, схемы, которые позволяют лучше понять и усвоить информацию. Пособие окажет неоценимую помощь в учебе, систематизируя полученные знания, а также будет полезным при подготовке к итоговому тестированию по математике за курс начальной школы.
Правила, определения объединены в наглядные логические блоки, схемы, которые позволяют лучше понять и усвоить информацию. Пособие окажет неоценимую помощь в учебе, систематизируя полученные знания, а также будет полезным при подготовке к итоговому тестированию по математике за курс начальной школы.fizikadlyvas.net
- Памятка по математике 1–4 классы | Картотека по математике на…
Скачать: Вложение.
Памятки по математике. 1-4 класс. Разрезной дидактический материал с опорными схемами, таблицами по основным темам
Памятка по математике содержит выбор действий, названия компонентов арифметических действий, правила для решения уравнений…
nsportal.ru
- Весь курс | математика
В38 Весь курс школьной программы в схемах и таблицах: математика, физика, химия, информатика, биология – СПб.
 : Тригон, 2007. – 624 с. Справочное пособие предназначено учащимся общеобразовательных школ. В наглядных таблицах и схемах изложен весь материал школьной про граммы по математике, физике, химии, информатике и биологии.
: Тригон, 2007. – 624 с. Справочное пособие предназначено учащимся общеобразовательных школ. В наглядных таблицах и схемах изложен весь материал школьной про граммы по математике, физике, химии, информатике и биологии.8х 2х. 4 (х-1)” 4(х-1)” х-1. За !
www.school2-lgov.ru
- Математика в таблицах и схемах для 1–4 классов | Материал по…
Дидактический материал для 3 класса по математике, русскому языку, литературному чтению, окружающему миру (таблицы, блок-схемы) по УМК “Перспектива”. Дидактический материал предлагается использовать на уроках математики, русского язяка, окружающего мира, литературного чтения по УМК “Перспектива”, как на этапе актуализиции знаний, так и на уроках си… Математика в таблицах и схемах для 1-4 классов. В этом документе собраны таблицы и схемы для уроков математики в начальной школе.
 Данное методическое пособие значительно…
Данное методическое пособие значительно…nsportal.ru
- Правила по математике в таблицах и схемах (1–4 классы)
Pravila_po_matematike_v_tablitsakh_i_skhemakh_1-4_klass.pdf.
vk.com
- демонстрационные таблицы по математике 1–4 класс | Материал…
Скачать
Демонстрационные таблицы по математике учителю начальных классов….
В документе “Таблицы по математике для 2 класса” представлены таблицы на следующие темы:Сложение с переходом через десяток;Вычитание с переходом через десяток;Задачи…
nsportal.ru
- Памятки по математике. 1–4 класс | Материал по математике по.
 ..
..Разрезной дидактический материал с опорными схемами, таблицами по основным темам начальной школы, которые можно использовать на этапах изучения нового материла, закрепления и повторения пройденного, а так же при работе над ошибками.
Памятка по математике содержит выбор действий, названия компонентов арифметических действий, правила для решения уравнений, соотношение мер длины и массы, формулы нахождения площади и периметра, некот…
nsportal.ru
- Правила по математике для 1–4 класса в таблицах
МАТЕМАТИКА. ПАМЯТКА №2. Правила вычисления.
znanio.ru
- Математика. В схемах и таблицах. 1–4 класс. Марченко И.С.
Подготовка к школе и начальные классы. Все фотографии.
 Математика. В схемах и таблицах. 1-4 класс. Марченко И.С.144.
Математика. В схемах и таблицах. 1-4 класс. Марченко И.С.144.vk.com
- Математика в схемах и таблицах 1 – 4 класс. Обсуждение на…
Математика в схемах и таблицах 1 – 4 класс. Среда, 25 Апреля 2018 г. 10:42 + в цитатник.
Метки: математика 1-4класс схемы таблицы. Процитировано 50 раз Понравилось: 9 пользователям.
www.liveinternet.ru
- Памятка (в помощь ученику) Математика (1–4 классы) скачать
уменьшаемое вычитаемое разность. 5 – 3 = 2. Таблица сложения. + 1. 2.
Буквенные выражения – это выражения, содер-. жащие не только числа, но и буквы. Помни, что в математике в буквенных выраже-. ниях используются буквы латинского алфавита: 8 + d (восемь плюс дэ)
uchitelya.
 com
com - Правила по математике в схемах и таблицах. 1–4 класс
Ученикам начальных классов трудно запомнить все правила по математике, а чтобы было легче запомнить и выучить их, я предлагаю изучать все правила в схемах и картинка. Так деткам легче усваивается информация и намного интереснее изучать все в картинках и схемах..
Просмотр содержимого документа “Правила по математике в схемах и таблицах. 1-4 класс”.
multiurok.ru
- Правила по математике в таблицах и схемах для 1–4 классов
. Начальные классы, 2 класс, Учебные пособия, учебники, методички .Начальная школа, Правила по математике в таблицах и схемах для 1-4 классов.

Благодаря готовым учебным материалам для работы в классе и дистанционно.
multiurok.ru
- Таблицы и схемы математика
Таблицы и схемы
Цветовая схема.
www.annachistova.natalinska-soch.edusite.ru
- Марченко 1–4 классы в схемах и таблицах математика 2011
Название: Математика в схемах и таблицах. Класс: 1-4. Читать онлайн: Да. Скачать бесплатно: Да. Формат книги: jpg.
Читать онлайн или скачать математику в схемах и таблицах Марченко 2011 года: Самые популярные статьи
gdz-online.ws
- Все правила по математике. 1–4 классы. Обсуждение на…
Цитата сообщения Ксю11111 Прочитать целикомВ свой цитатник или сообщество! Все правила по математике 1.
 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.www.liveinternet.ru
- Математика: 1–4 классы в схемах и таблицах [Ирина Марченко]…
Математика: 1-4 классы в схемах и таблицах читать онлайн. В издании в сжатой, концентрированной форме приводится основной теоретический материал, охватывающий курс математики начальной школы. Правила
Правила, определения объединены в наглядные логические блоки, схемы, которые позволяют лучше понять и усвоить информацию. Пособие окажет неоценимую помощь в учебе, систематизируя полученные знания, а также будет полезным при подготовке к итоговому тестированию по математике за курс начальной школы.
coollib.com
- Математика в таблицах и схемах 1–4 кл – часть 1 и часть 2
Отчеты: Посетители Поисковые фразы.
 Математика в таблицах и схемах 1-4 кл – часть 1 и часть 2. Воскресенье, 09 Сентября 2018 г. 18:01 + в цитатник. 32.
Математика в таблицах и схемах 1-4 кл – часть 1 и часть 2. Воскресенье, 09 Сентября 2018 г. 18:01 + в цитатник. 32.Серия сообщений “математика”: Часть 1 – Таблицы по математике Часть 2 – Математика в таблицах и схемах 1-4 кл – часть 1 и часть 2 Часть 3 – Быстро учимся решать уравнения 1-4 класс Часть 4 – Полная энциклопедия для начальной школы РУССКИЙ ЯЗЫК и МАТЕМАТИКА 1-4 класс …
www.liveinternet.ru
- Все правила по математике для начальной школы – Скачать…
Пособие содержит основные правила по математике, изучаемые в начальной школе. Объяснение правил сопровождается яркими иллюстрациями и наглядными схемами. Справочник будет полезен школьникам 1 – 4 классов при подготовке к уроку и выполнении домашних заданий, а также родителям и учителям при контроле знаний учащихся.
Арифметические действия. Сложение. Таблица сложения в пределах 20. Состав числа (первый десяток).
 Вычитание. Умножение. Таблица Пифагора.
Вычитание. Умножение. Таблица Пифагора.e-bookshelf.info
- Правила по математике в таблицах и схемах, 1–4 класс
▫ не могу скачать ▫ не могу скачать. ОЧЕНЬ ЖАЛЬ ▫ Дочитала. Сложно. Для детей бы по-проще. ▫ Не ветром ветреным – до – осени Снята гроздь. Ах, виноградарем – до – осени Пришел гость. Небесным странником – мне – страннице Предстал – ты.
▫ О реализации занятий внеурочной деятельности ▫ Строение нашей галактики ▫ Уважаемые педагоги! ▫ Нам нужна только одна Победа! ▫ Конкурс Культурные ▫ ГБОУ СОШ Санкт-Петербурга №310 Слово ПЛАН-КОНСПЕКТ УРОКА.
proshkolu.ru
На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Правила по математике в таблицах и схемах, 1-4 класс»
Для формирования результатов поиска документов использован сервис Яндекс. XML.
XML.
Нашлось 30 млн ответов. Показаны первые 32 результата(ов).
Дата генерации страницы:
Математика в 1 классе – что должен уметь ребенок?
Общемировое развитие не стоит на месте, поэтому требования к человеку и его возможностям постоянно возрастают. В том числе и к такой категории населения как школьники. Им необходимо трудится практически без отдыха, чтобы выдерживать конкуренцию своих ровесников.
Уровень знаний первоклассников также стал довольно высоким. У школ нет жестких требований к будущим ученикам, но все же вчерашние детсадовцы должны быть подготовлены к основным предметам. Ребенку будет легче учиться в первом классе, если он будет знать буквы и звуки, сможет читать по слогам, правильно держать ручку, а еще лучше уметь писать буквы и хорошо знать алфавит. Что касается математики в первом классе, то также есть некоторые требования: нужно знать простые геометрические фигуры, считать до 10, а лучше до 20, понимать, что такое прямой и обратный порядковый счет, ориентироваться на листе бумаги.
Важна как образовательная, так и моральная готовность детей. Родители волнуются за будущего первоклашку, ведь, даже зная все, что нужно, он может растеряться и занервничать. А школьные собеседования именно для того и проводятся, чтобы преподаватели могли понять, насколько способный и подготовленный ребенок.
Как помочь выучить ребенку школьную программу по математике в первом классе?
Многие родители с первого класса стремятся приучить детей учиться хорошо – получать одни пятерки. Но при этом забывают сделать акцент на том, что самое главное – это получать знания. Даже у первоклассников часто возникает проблема, что оценки хорошие, а знаний очень мало. Ведь несложно просто зазубрить материал, чтобы хорошо ответить у доски на следующий день. Сложно – понять и разобраться в теме, чтобы закрепить ее навсегда.
Поэтому родители должны донести до детей, что самое главное – понять математику, научиться применять ее в жизни, осознанно выполнять упражнения, не решать примеры на занятиях механически, а только с полным пониманием и без спешки. Для осознанного обучения также помогает развитие логики и нестандартного критического мышления. Благодаря им ученику будет легче понять математику и применять ее законы в жизни.
Для осознанного обучения также помогает развитие логики и нестандартного критического мышления. Благодаря им ученику будет легче понять математику и применять ее законы в жизни.
Задания по математике в 1 классе
Обучение первоклассников в основном строится на том, что дети изучали на уроках подготовки к школе. Повторяется уже пройденное, а усложнение материала происходит очень постепенно.
Задания по математике в 1 классе – это изучение прямой, точки, ломанной, простых геометрических фигур, счет как письменный, так и в уме. Учитывая, что основа алгебры – это таблица умножения, то в первом классе происходит подготовка к ее изучению: нарабатываются фундаментальные знания, которые во втором классе позволяют освоить таблицу умножения.
Кроме этого, конечно, ученики учатся находить фигуры в окружающем мире, расширяют свой кругозор, стараются применять в жизни счет, который уже освоили. Также они решают ребусы, головоломки, легкие занимательные задачи, самые простые примеры. Несмотря на то, что это школа, учителя стараются преподать материал интересно, а задания подобрать увлекательные и в игровой форме.
Несмотря на то, что это школа, учителя стараются преподать материал интересно, а задания подобрать увлекательные и в игровой форме.
Математические ребусы и задачи на сообразительность
Кроме изучения цифр, правил и обучения счету, важно давать малышу решать различные ребусы и головоломки. Именно нестандартные задачи помогают ребенку развивать свой мозг, научиться находить решение, не боятся трудностей, применять математические хитрости. Простые примеры помогут только отработать навык арифметических вычислений, а развиваться дальше можно только лишь используя нестандартное мышление.
Современная методика «Амаматика» от Академии развития интеллекта AMAKids включает в себя онлайн-платформу и игровые тренажеры по математике, которые позволяют развивать сразу все способности детей в области математики.
Чтобы научить учеников легко решать задачи любой сложности, а также применять «царицу наук» в жизни, в наших учебниках и пособиях предложены интересные задания с пропущенными числами, неизбитые кроссворды и головоломки, математические ребусы за 1 класс и для детей постарше, увлекательные лабиринты, задачи на сообразительность. Умея применять нестандартные способы решения, ребенок не испытывает страх перед заданиями повышенной сложности. Он с интересом берется за любую задачку.
Умея применять нестандартные способы решения, ребенок не испытывает страх перед заданиями повышенной сложности. Он с интересом берется за любую задачку.
Тренажер по математике 1 класс
Платформа и тренажер Амаматика помогут не только преуспевать в школе, но и научат находить подход к сложным заданиям, обучат финансовой грамотности и основам программирования, помогут развить аналитическое мышление, пространственное воображение. Математика – сложный предмет, но, если структурировано подходить к обучению и придерживаться проверенной методики, школьник сможет понять и закрепить даже самые непростые темы.
На нашей удобной онлайн-платформе ученики могут подтянуть любое математическое направление – нужно лишь зайти в требующийся раздел и начать выполнять упражнения. Тренажер по математике для первого класса обеспечит правильное понимание предмета и заложит необходимые азы для дальнейшего обучения.
Также на игровой платформе есть разделы с арифметикой, геометрией, задачами, а также заданиями по финансовой грамотности, программированию и играми на развитие логики, памяти и внимания. Амаматика – эффективные и удобные курсы для современных детей.
Амаматика – эффективные и удобные курсы для современных детей.
Правила начальных классов (с 1 по 4 класс)
Числа. Чтение, сравнение
3 класс – миллионов 2 класс – тысяч 1 класс единиц сотни мил-лионов десят-ки мил-лионов едини-цы мил-лионов сотни тысяч десят-ки тысяч едини-цы тысяч сотни десят-ки едини-цы 9 разряд 8 разряд 7 разряд 6 разряд 5 разряд 4 разряд 3 разряд 2 разряд 1 разряд
I = 1 V = 5 X = 10 L = 50 C = 100 D = 500 M = 1000 Примеры записи римских цифр. 1- I 2 – II 3 – III 4 – IV 5 – V 6 – VI 7 – VII 8 – VIII 9 – IX 10 – X 11 – XI 12 – XII 13 – XIII 14 – XIV 15 – XV 16 – XVII 17 – XVII 18 – XVIII 19 – XIX 20 – XX 21 – XXI 30 – XXX 40 – XL 50 – L 60 – LX 70 – LXX 80 – LXXX 90 – XC 99 – XCIX 100 – C 102 – CII 400 – CD 500 – D 800 – DCCC 900 – CM Арифметические действия и их свойства. Сложение 3+5=8 Знак +(плюс), действие- сложение, 3 – первое слагаемое, 5- второе слагаемое, 3+5 – сумма, 8 – значение суммы. Если из суммы вычесть одно слагаемое, то получится другое слагаемое. Вычитание 9-4=5 Знак-(минус), действие – вычитание, 9 – уменьшаемое, 4 – вычитаемое, 9 – 4 – разность, 5- значение разности. Если из уменьшаемого вычесть разность, то получится вычитаемое. Если к разности прибавить вычитаемое, то получится уменьшаемое. Умножение. 3•5=15 Знак •или х (умножить), действие- умножение, 3 – первый множитель,5- второй множитель, 3•5 – произведение, 15 – значение произведения. Если произведение разделить на один множитель, то получится другоймножитель. Деление. 20:4 = 5 Знак (:) – разделить, действие деление. 20 – делимое, 4 – делитель, 20:4 это частное, 20 – значение частного Если делимое разделить на частное, то получится делитель. Если частное умножить на делитель, то получится делимое.
Свойства и законы арифметических действий.
Свойства арифметических действий. Свойства 0 (нуля)
Свойства 1 (единицы)
Действия над числами.
Выражения. Выражения бывают числовые и буквенные.
Равенства и неравенства.
Порядок действий. Если в примере встречаются два и более арифметических действия, то их выполнение проводят в следующем порядке:
Минутная стрелка. Число на циферблате Количество минут Как прочитать 1 5 Пять минут (какого?) 2 10 Десять минут (какого?) 3 15 Пятнадцать минут (какого?) 4 20 Двадцать минут (какого?) 5 25 Двадцать пять минут (какого?) 6 30 Половина (какого?) 7 35 Без 25 минут (сколько?) 8 40 Без 20 минут (сколько?) 9 45 Без 15 минут (сколько?) 10 50 Без 10 минут (сколько?) 11 55 Без 5 минут (сколько?) 12 60 Ровно (сколько?) ЭТО НАДО ЗНАТЬ НАИЗУСТЬ !!! Таблица №1 1+1=2 2+1=3 3+1=4 2+2=4 4+1=5 3+2=5 5+1=6 4+2=6 3+3=6 6+1=7 5+2=7 4+3=7 7+1=8 6+2=8 5+3=8 4+4=8 8+1=9 7+2=9 6+3=9 5+4=9 9+1=10 8+2=10 7+3=10 6+4=10 5+5=10 Таблица №2 2+9=11 3+8=11 4+7=11 5+6=11 3+9=12 4+8=12 5+7=12 6+6=12 4+9=13 5+8=13 6+7=13 5+9=14 6+8=14 7+7=14 6+9=15 7+8=15 7+9=16 8+8=16 8+9=17 9+9=18 Таблица №3 2∙2=4 3∙2=6 3∙3=9 9∙9 = 81 4∙2=8 4∙3=12 4∙4=16 5∙2=10 5∙3=15 5∙4=20 5∙5=25 6∙2=12 6∙3=18 6∙4=24 6∙5=30 6∙6=36 7∙2=14 7∙3=21 7∙4=28 7∙5=35 7∙6=42 7∙7=49 8∙2=16 8∙3=24 8∙4=32 8∙5=40 8∙6=48 8∙7 =56 8∙8=64 9∙2=18 9∙3=27 9∙4=36 9∙5=45 9∙6=54 9∙7 =63 8∙9 = 72 Уравнения и способы их решения.
Уравнения на «+» Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. Все уравнения на «плюс» решаются обратным действием «минусом» Уравнения на «▪» Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. Все уравнения на «умножение» решаются обратным действием «делением» Уравнения на «-»
Уравнение на «:»
Величины и их измерения. Единицы времени. Секунда – с Минута – мин Час – ч Сутки – сут Неделя – нед Месяц – мес. Год (лет) – год (л) Век – век 1мин – 60 с 1ч – 60 мин 1 сут = 24 ч 1 нед = 7 сут 1 год = 365(366)сут 1 век = 100 л 1 мес = 31сут, 30 сут 28 или 29 сут (февраль) Январь – 31 Февраль – 28(29) Март – 31 Апрель – 30 Май – 31 Июнь – 30 Июль – 31 Август – 31 Сентябрь – 30 Октябрь – 31 Ноябрь – 30 Декабрь – 31 Дни недели: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье. 1.Для того, чтобы перевести из большей величины в меньшую, надо значение большей умножить на соотношение между ними. Например 1 час = 60минут. 7чсасов = 7 ∙60 = 420 минут. 2.Для того, чтобы перевести из меньшей величины в большую, надо меньшую величину разделить на соотношение между ними. Например. 1 сут – 24 часа. Тогда 48ч = 48 :24 = 2 сут. Единицы длины. Миллиметр – мм, сантиметр – см, дециметр – дм, метр – м, километр – км. 1см = 10мм 1дм = 10см = 100мм 1м = 10дм = 100см = 1 000мм 1км = 1 000м = 10 000дм = 100 000см = 1000 000мм Единицы массы Грамм – г Килограмм – кг Центнер – ц Тонна – т 1 кг = 1 000г 1 ц = 100 кг = 100 000 г 1 т = 10 ц = 1000 кг = 1000 000г Единицы площади 1см2 = 100мм2 1дм2 = 100см2 = 10000мм2 1м2 = 100дм2 = 10000см2 = 1000000мм2 1км2 = 1 000000м2 1а(ар) = 100м2 1га(гектар) = 10000м2 1 га = 100а Единицы объёма 1см3 = 1000мм3 1дм3= 1000см3 = 1000000мм3 1м3 = 1000дм3 = 1000000см3 1 км3 = 1000000000м3 Если перевод их одних величин в другие идет по стрелочке вперёд, то мы добавляем нужное количество нулей, если в обратном направлении, то убираем нужное количество нулей. Чтобы найти долю меньшей величины в большей, надо посмотреть на соотношение между ними. Если 1см = 10мм, то 1мм = десятая часть см. Если 1т = 1000000г, то 1г – миллионная часть тонны. Решение задач. Для того, чтобы текст был задачей, в нем должны быть: условие, вопрос, решение, ответ. Решение простых задач по вопросу Вид решения решение Вопрос «Сколько всего?» записывается в условии «уголком». Плюс(+) Вопрос «Сколько осталось?» записывается в условии !Ост-?». Минус(-) Вопрос « На сколько меньше?» или «На сколько больше?» записывается в условии стрелочкой. Это задачи на сравнения. От большего числа отнимаем меньшее Вопрос « Во сколько меньше?» или «Во сколько больше?» записывается в условии стрелочкой. Большее число делим на меньшее По условию с прямым сравнением Условие решение Если в условие сказано «на больше» Плюс(+) Если в условие сказано «на меньше» Минус(-) Если в условие сказано «в … раз больше» Умножить (•) Если в условие сказано «в … раз меньше» Разделить (:) По условию с косвенным сравнением Если в условии сказано … решение «это или что на больше» Минус(-) «это ил что на меньше» Плюс(+) «это или что в … раз больше» Разделить (:) «это или что в … раз меньше» Умножить (•) Решение задач, с записью условия в таблице. Цена (за 1 предмет) Количество Стоимость (Всего) Решение ? Цена=стоимость:количество ? Количество=стоимость:цену ? Стоимость = цена количесво Решение задач, с записью условия в таблице. Скорость (V) Время (t) Расстояние (S) Решение ? v =S t ? t = S :v ? S = v t Правило треугольника. Составные задачи.
Памятка по решению задач на движение. Одновременное встречное движение. Нахождение общего расстояния 1 способ 1.находим S1 = V1·• t 2 способ 1. находим Vсближения = V1 + V2 2. находим Sобщее = Vсближения ·• t Нахождение одной из скоростей. 1 способ. 1. находим S1 = V1·• t 2 способ. 1. находим Vсближения = Sобщее : t 2. находим V2 = Vсближения – V1 Нахождение времени. 1 способ 1.находим Vсближения = V1 + V2 Решение задач на движение вдогонку. Нахождение времени, через которое один объект догонит другой. 1.находим Vприближения = V1 – V2 1. находим Vприближения = V1 – V2 Обратные задачи. Задачи называются обратными, если то, что было неизвестно по условию в первой задаче, становится известным во второй. А то, что было известным в первой задаче, становится неизвестным во второй. Решениями этих задач являются обратные друг другу примеры. Геометрический материал. Прямая линия (нет ни начала, ни конца) Луч (есть начало, нет конца) Отрезок (есть начало и есть конец) Прямые линии могут быть параллельными (не пересекаются), пересекающимися, перпендикулярными (при пересечении все углы прямые) Углы. Прямой Острый Тупой Развёрнутый Острый угол меньше прямого, тупой угол больше прямого. Прямоугольник Прямоугольник – это четырёхугольник, у которого все углы прямые и противоположные стороны равны. Нахождение периметра. 4 угла, 4 вершины, 4 стороны
Нахождение стороны по периметру и другой стороне. а = (Р – b – b) : 2 или b = (Р – a – a) : 2 или Р:2 – а Например. Р = 24см, а = 7 см. Найти в. в = 24:2 – 7 = 5 см Нахождение площади S = a ∙ b Нахождение стороны прямоугольника по площади и известной стороне. a = S:b или b = S:a Нахождение площади по известному периметру и стороне. Сначала надо найти вторую сторону, затем по формуле площадь. Нахождение периметра по известной площади. Сначала надо найти сторону, затем площадь. Квадрат Квадрат – это прямоугольник, у которого все стороны равны. 4 угла, S = a ∙ a = a2 4 вершины, P = a+a+a+a 4 стороны. P = 4 ∙ a Нахождение стороны квадрата по известному периметру. Если P = 4 ∙ a, то а = Р : 4 (Чтобы найти сторону, надо периметр разделить на 4) Нахождение стороны квадрата по известной площади. Чтобы найти сторону квадрата по известной площади, надо подобрать произведение равных множителей, значение которого равно значению площади. 1 = 1 ∙ 1 4 = 2 ∙ 2 9 = 3 ∙ 3 16 = 4 ∙ 4 25 = 5 ∙ 5 36 = 6 ∙ 6 49 = 7 ∙ 7 64 = 8 ∙ 8 81 = 9 ∙ 9 100 = 10 ∙ 10 121 = 11 ∙ 11 400 = 20 ∙ 20 8100 = 90 ∙ 90 и так далее Нахождение площади, если известен периметр квадрата.
Треугольник 3 угла 3 вершины 3 стороны Периметр равен сумме трёх сторон. Круг и окружность. Окружность имеет длину. Круг имеет площадь Центр окружности или круга Радиус окружности или круга – Диаметр окружности или круга – Чтобы определить полное количество десятков в числе, надо зачеркнуть последний знак (единицы). В числе 6758 – 675 десятков. Чтобы определить количество сотен, надо зачеркнуть два знака 6758 – 67 сотен |
Основные правила математики
Правила добавления
Правило 1:
положительный + положительный = положительный = добавить
Результат будет отрицательным
Пример:
-3 + (-5) = -8
Правила вычитания
Правило 1:
Отрицательное + положительное = вычесть наибольшее значение
Принять знак числа 9 с абсолютным значением0005
Пример:
-3 + 5 = 2
Правило 2:
Положительный + Отрицательный = Вычесть
Взять знак числа с наибольшим абсолютным значением
Пример:
3 ()
Правила умножения
Правило 1:
Положительный x положительный = положительный
Пример:
3 x 5 = 15
Правило 2:
Отрицательный x Отрицательный = положительный
Пример:
(-3. ) х (-5) = 15
) х (-5) = 15
Правило 2:
Положительный x отрицательный = отрицательный
Пример:
3 x (-5) = -15
Правило 2:
Отрицательный x Положительный = отрицательный
Пример:
-3 x 5 = -15
Правила деления
Правило 1:
Положительный ÷ положительный = положительный
Пример:
20 ÷ 4 = 5
Правило 2:
Отрицательный ÷ отрицательный = положительный
:
(-20) ÷ (-4) = 5
Правило 2 :
Положительный ÷ Отрицательный = Отрицательный
Пример:
20 ÷ (-4) = -5
Отрицательный 900÷4 Правило 2 00: 5 = Отрицательный
Пример:
-20 ÷ 4 = -5
Правила показания
Правило 1:
x M ⋅ x N = x M+N
. Пример:
9 33
3
3
3
3
3
3
3
3
3
3
3 9000 3
3
3 9000 3 9000 3 M+N
. 4 ⋅ 3 5 = 3 4+5
4 ⋅ 3 5 = 3 4+5
3 4 ⋅ 3 5 = 3 9
Rule 2 :
x m ÷ x n = x m-n
Example :
3 7 ÷ 3 5 = 3 7-5
3 7 ÷ 3 5 = 3 2
Правило 3:
(x M ) N = x M ) N = X MN ) N = X MN ) N = X MN ) N = X M ) N = x M ) N = x M ) N . 2 ) 4 = 3 (2)(4)
(3 2 ) 4 = 3 8
Rule 4 :
(xy) m = x m ⋅ y m
Example :
(3 ⋅ 5) 2 = 3 2 ⋅ 5 2
(3 ⋅ 5) 2 = 9 ⋅ 25
(3 ⋅ 5) 2 = 225.
Правило 5:
(x/y) M = =
(x/y) x м /г м
Пример:
(3/5) 2 = 3 2 /5 2
(3/5) 2 = 9/25
Правило 6:
x -M = 1/x M
Пример:
3 -2 = 1000 28 2 2 3 -2 = 10009 28 28 28 2 2 -2 = 10004 28 28 2 3 -2 = 10004 2 3 -2 .
3 -2 = 1/9
Правило 7:
x 0 = 1
Пример:
3 0 = 1
Правило 8:
x 1 = 1
.
Пример :
3 1 = 3
Правило 9 :
x m/n = y —-> x = y N/M
Пример:
x 1/2 = 3
x = 3 2/1
x = 3 2
x = 3 2
x = 3 2
x = 3 2 9000
. x = 9
x = 9
Правило 10 :
(x/y) -m = (y/x) m
Пример:
(5/3) -2 ) 9 = (31/3) 2
(5/3) -2 = 3 2 /5 2
(5/3) -2 9 0 0 4 9 = 9/250005
A x = A Y —-> x = Y
Пример:
3 M = 3 5 —-> M = 5
Правило 12:
44129 —> M = 5
Правило 12:
44444444444 x a = y a —-> x = y
Пример:
k 3 = 5 3 = 5 3 = Операция 3s90MD
AS)
Это правило можно использовать для упрощения или вычисления сложных числовых выражений с более чем одной бинарной операцией.
Очень простой способ запомнить правило PEMDAS:
P —-> Круглая скобка
E —–> Экспоненты
M —-> Умножение
D —-> 5 Деление 9000 —-> Сложение
S —-> Вычитание
Важные примечания:
1. В конкретном упрощении, если у вас есть и умножение, и деление, выполняйте операции одну за другой в порядке слева направо. .
В конкретном упрощении, если у вас есть и умножение, и деление, выполняйте операции одну за другой в порядке слева направо. .
2. Умножение не всегда предшествует делению. Мы должны сделать один за другим в порядке слева направо.
3. В особом упрощении, если у вас есть и сложение, и вычитание, выполняйте операции одну за другой в порядке слева направо.
Примеры:
15 ÷ 3 x 2 = 5 x 2 = 10
24 – 8 + 5 = 16 + 5 = 21
В приведенном выше упрощении мы имеем как деление, так и умножение. Слева направо у нас сначала деление, а потом умножение.
Итак, сначала мы делаем деление, а потом умножение.
Для получения дополнительных примеров по PEMDAS нажмите здесь
Процентное уравнение
Процентное уменьшение/увеличение
Приведенную ниже формулу можно использовать для определения процентного увеличения или уменьшения значения.
Изменение может быть увеличением или уменьшением.
Здесь исходная сумма — это значение до увеличения или уменьшения.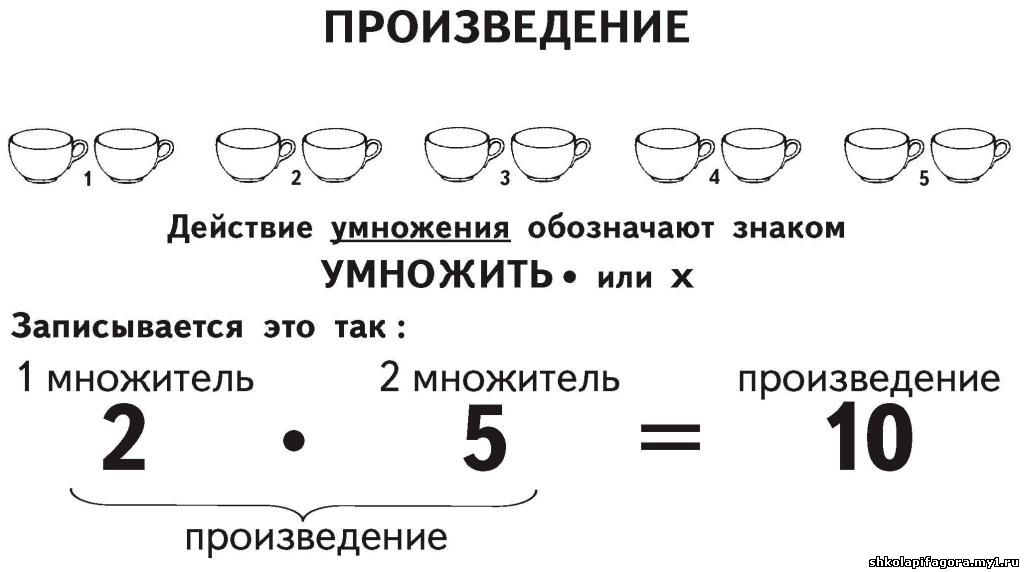
Для получения дополнительных примеров увеличения/уменьшения процентов,
нажмите здесь
Разрядное значение
Разрядное значение цифры в числе — это цифра, умноженная на тысячу или сотню, или в любом другом месте, где она расположена.
Пример:
В 2 5 486 разрядное значение числа 5 равно
= 5 ⋅ 1000
= 5000
. 5 находится на разряде тысяч.
Номинальная стоимость
Номинальная стоимость цифры в числе — это сама цифра.
Точнее, номинал цифры всегда остается одним и тем же, независимо от позиции, в которой она находится.
Пример:
В 2 5 486, номинальная стоимость 5 равна 5.
Разница между разрядной стоимостью и номиналом
Разница между разрядной стоимостью и номиналом показана на рисунке ниже.
У углы
Острый угол: менее 90 °
Тупой угла: более 90 °
ПРАВИТЬ ПРАВО: 90 °
Прямой угол: 180 °
Комплементарные углы:
составляет 90 градусов.
Дополнительные уголки:
Два угла, сумма мер которых равна 180 градусам.
Треугольники
Треугольники :
1. Сумма длин любых двух сторон треугольника больше третьей стороны.
2. Сумма всех трех углов треугольника равна 180°.
Равнобедренный треугольник:
Две равные стороны; два равных угла
Равносторонний треугольник:
Три равные стороны; три равных угла
Прямоугольные треугольники :
Теорема Пифагора :
a 2 + b 2 = c 2
, где a и b — меры катетов треугольника, а c — гипотенуза.
Статистика
Среднее (среднее):
Сумма всех значений, деленная на количество значений.
Медиана:
Среднее значение, когда значения расположены в числовом порядке.
Режим:
Наиболее часто встречающееся значение данных.
Вероятность
Вероятность события A :
P(A) = частота события A/общий объем выборки
Преобразование смешанных чисел в неправильную дробь
Преобразование неправильной дроби в смешанное число
Пожалуйста, отправьте свой отзыв по адресу v4formath@gmail.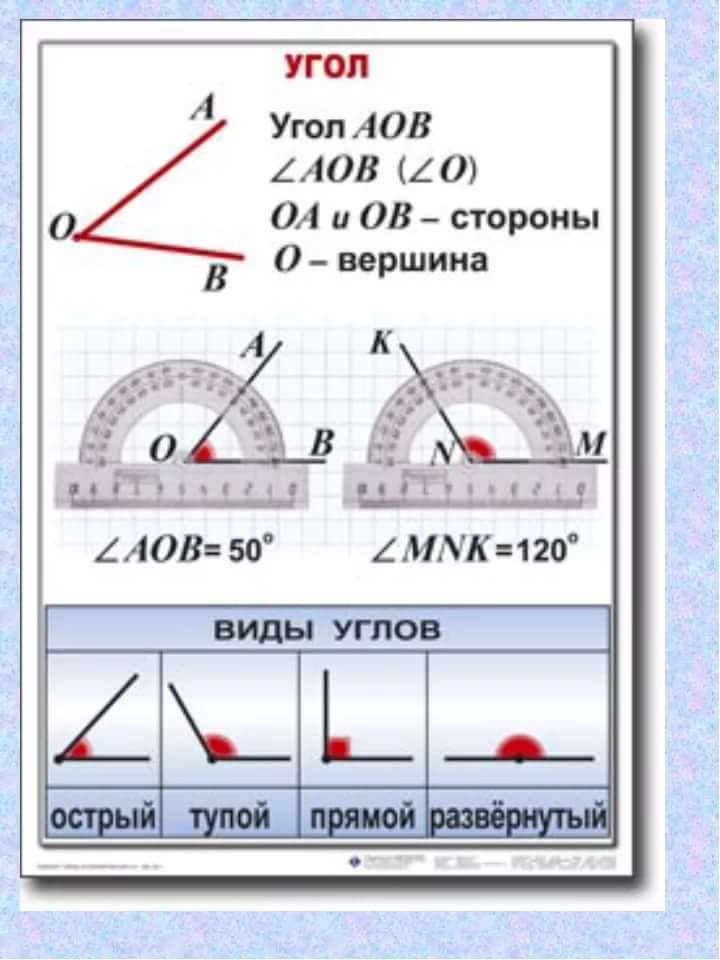 com
com
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Основные математические правила, которым должен учить каждый родитель
Чтобы изменить способ преподавания математики дома, вы должны сначала дать своим детям понять, что этот предмет выходит за рамки набора правил, концепций и процессов. Вместо этого математику следует воспринимать как способ распознавания закономерностей и корреляций, проведения рационального анализа и защиты своих теорий и выводов логичным и разумным способом.
Математика может быть очень творческим процессом, который может вселить в людей уверенность и ценные навыки для решения сложных проблем в повседневной жизни. Это также может превратить их в независимых мыслителей, иногда даже нестандартных мыслителей. Короче говоря, математика — это фантастическое средство, с помощью которого дети учатся думать. Вы все еще задаетесь вопросом, как подходить к обучению детей математике?
Что ж, какой бы непосильной задачей она ни казалась, существуют определенные базовые математические правила, которым каждый родитель должен научиться своих детей.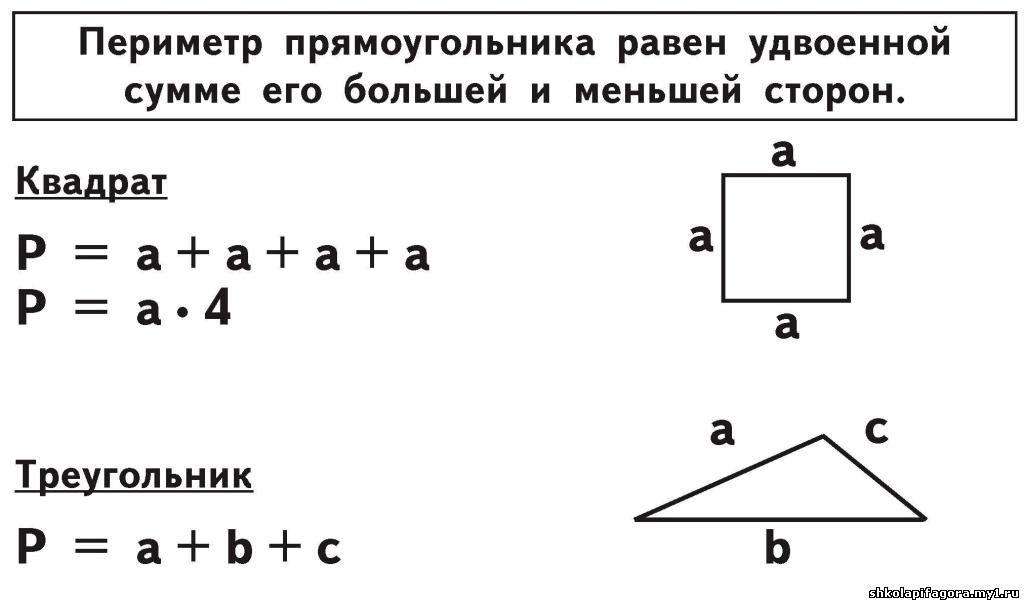 Эти правила применяются независимо от уровня обучения ваших детей и основаны на многолетних исследованиях в области преподавания и изучения математики. Это больше, чем правила, это способ подхода к предмету, который может иметь большое значение для воспитания умных, уверенных в себе и думающих людей. Давайте углубимся в некоторые из этих правил.
Эти правила применяются независимо от уровня обучения ваших детей и основаны на многолетних исследованиях в области преподавания и изучения математики. Это больше, чем правила, это способ подхода к предмету, который может иметь большое значение для воспитания умных, уверенных в себе и думающих людей. Давайте углубимся в некоторые из этих правил.
Начнем с основ. Математика может быть трудным предметом, осознание которого поначалу может показаться пугающим. Тем не менее, формирование позитивного мышления еще до начала изучения математики может быть весьма полезным. Когда дети сталкиваются с трудностями в математике, они могут легко прийти к выводу, что недостаточно хорошо разбираются в предмете. Родители играют значительную роль в устранении таких страхов и некоторых других, связанных с математикой. Многие дети могут полагать, что компетентность в математике — это одаренное качество, которым они не наделены. Другими словами, они могут думать, что не имеют большого контроля над своей способностью понимать математические понятия. Решение сложных проблем может показаться далеким. Такое мышление может оказаться для них большим недостатком.
Решение сложных проблем может показаться далеким. Такое мышление может оказаться для них большим недостатком.
Здесь могут вмешаться родители. Крайне важно дать детям понять, что, уделив немного больше внимания и много практики, они могут быть готовы справиться с большинством математических задач. Это может улучшить мышление детей и побудить их приложить все усилия. Дети, которых приучили к растущему мышлению, верят в то, что нужно прилагать искренние и постоянные усилия, чтобы познакомиться с предметом и расти в нем. Их нужно учить, что только упорным трудом и усилиями они могут решать сложные математические задачи. Это очень важно для родителей понять, потому что это означает, что благодаря позитивному мышлению они могут привести своих детей к успеху.
Переход от конкретного к абстрактному Для детей конкретный опыт является ступенькой на пути к абстрактному пониманию мира. Это справедливо и в отношении математики. Этого можно добиться с помощью грамотного использования манипуляторов, которые также помогают лучше запоминать математику. С помощью манипуляторов дети могут переходить от реальных примеров к более абстрактным идеям. Числа больше не просто символы; это реальные количества. Когда у них будет достаточно знаний, они смогут постепенно переходить к более абстрактным понятиям. Например, родители могут учить сложению путем перегруппировки, используя десятичные кубики. При выполнении сложения дети могут заменять блоки на 10 стержней по мере необходимости. При достаточной практике дети могут ознакомиться с традиционным алгоритмом решения задач, кроме перегруппировки с помощью только карандаша и листа бумаги. Таким образом, дети могут постепенно переходить от конкретного к абстрактному.
С помощью манипуляторов дети могут переходить от реальных примеров к более абстрактным идеям. Числа больше не просто символы; это реальные количества. Когда у них будет достаточно знаний, они смогут постепенно переходить к более абстрактным понятиям. Например, родители могут учить сложению путем перегруппировки, используя десятичные кубики. При выполнении сложения дети могут заменять блоки на 10 стержней по мере необходимости. При достаточной практике дети могут ознакомиться с традиционным алгоритмом решения задач, кроме перегруппировки с помощью только карандаша и листа бумаги. Таким образом, дети могут постепенно переходить от конкретного к абстрактному.
Еще одна важная вещь, которую родители должны попытаться сделать, это научить детей практическому использованию математики в повседневной жизни. Это делает математику более увлекательной и полезной для них. Поняв математические понятия, дети должны уметь использовать их в реальном мире.
Например, они могут сложить общую стоимость продуктов в своей продуктовой корзине, используя вычисления в уме. Они также могут посчитать огромное количество сгруппированных вещей с помощью умножения. Математика также очень полезна в других профессиях. Инженеры, архитекторы и другие используют математические концепции в своих областях. Дети также могут создавать и балансировать бюджет.
Чтобы дать им больше практического опыта в математике, вы можете вовлечь их в некоторые другие действия, например, позволить им измерить, когда вы что-то печете, попросить их вычислить, сколько миль вы все проедете за определенную поездку или какой длины трубка вам понадобится от носика возле калитки до середины сада. Благодаря таким занятиям дети будут чувствовать себя более вовлеченными и, следовательно, будут изучать математические понятия гораздо более практичным способом.
Обучение детей математике может показаться непростой задачей. Однако это существенно. Соблюдая некоторые основные правила, упомянутые выше, вы можете обеспечить своему ребенку отличное начало изучения предмета, который будет интересен и полезен. Пока вы этим занимаетесь, посетите блог BYJU FutureSchool, чтобы узнать больше о математике и о том, как помочь вашему ребенку изучать ее более увлекательно и весело.
Пока вы этим занимаетесь, посетите блог BYJU FutureSchool, чтобы узнать больше о математике и о том, как помочь вашему ребенку изучать ее более увлекательно и весело.
Ссылки:
- Помощь вашему ребенку в изучении математики . (1994). https://www2.ed.gov/parents/academic/help/math/math.pdf
- Sonnenschein, S., Galindo, C., Metzger, S.R., Thompson, J.A., Huang, H.C., & Lewis, H. (2012). Представления родителей о математическом развитии детей и участии детей в математических занятиях. Исследование детского развития , 2012 , 1–13. https://doi.org/10.1155/2012/851657
- Стандарты математической практики. Руководство для родителей . (н.д.). Получено 15 июля 2022 г. с http://www.debbiewaggoner.com/uploads/1/2/9/9/12998469/practices-4-5.pdf
- Как помочь ребенку с математикой | Понял . (н.д.). Получено 15 июля 2022 г. с https://www.understood.org/en/articles/how-to-help-your-child-with-math
Учиться с математикой, Математика
Об авторе
Больше, чем просто программирование и математика! Наша запатентованная учебная программа, основанная на деятельности, с обучением в режиме реального времени облегчает: Решение проблем. Креативное мышление. Песок. Уверенность. Связь
Вам также может понравиться
Онлайн-курс математики для начальной школы | Математика для 1 класса
Перейти к основному содержаниюНЕОБХОДИМОСТЬ ИНФОРМАЦИЯ
Найти школу
Чат
Свяжитесь с нами
Зарегистрироваться Родительский портал
Как зарегистрироваться
Требуется дополнительная информация
Найдите школу в своем штате
Купить этот индивидуальный курс
Обзор курса
Математика для первого класса предлагает опыт, который помогает учащимся развить формальное понимание чисел и математических понятий. Физические модели по-прежнему играют фундаментальную роль в связывании реального мира с символическими выражениями. Учащиеся продолжат развивать навыки сортировки и построения моделей; узнать основные факты сложения и соответствующие факты вычитания; распознавать и описывать двухмерные фигуры; и опираться на имеющиеся навыки решения проблем. Студенты будут:
Физические модели по-прежнему играют фундаментальную роль в связывании реального мира с символическими выражениями. Учащиеся продолжат развивать навыки сортировки и построения моделей; узнать основные факты сложения и соответствующие факты вычитания; распознавать и описывать двухмерные фигуры; и опираться на имеющиеся навыки решения проблем. Студенты будут:
- Работа с паттернами и последовательностями
- Практика сложения и вычитания
- Научитесь определять время и считать деньги
- Определить разрядность до сотен
- Практика измерения длины, объема и веса
- Работа с геометрическими фигурами
- Ознакомиться с концепцией симметрии
- Решайте задачи с помощью логических рассуждений, рисунков и моделей
- Начните развивать интуицию о вероятности и дробях
вернуться к началу
Краткое содержание курса
Числа до 12
- Считать, читать, писать, сравнивать и упорядочивать целые числа до 12
- Сравнить и упорядочить порядковые номера с первого по десятый
- Определить на единицу больше и на единицу меньше заданного числа
- Счет вперед и назад по числовой строке
- Решайте задачи, рисуя картинки и находя закономерности
Понимание сложения: факты к 6
- Показать значение сложения (соединение, соединение, увеличение)
- Знать дополнительные факты к 6
- Напишите числовые предложения с добавлением
- Поймите, что числа можно добавлять в любом порядке
- Определение и расширение простых числовых шаблонов для сложения
- Решайте проблемы, используя графики и разыгрывая проблемные ситуации
Понимание вычитания: факты до 6
- Показать значение вычитания (отнять, разделить)
- Знать факты вычитания до 6
- Напишите числовые предложения с вычитанием
- Понимание сложения и вычитания как обратных операций
- Сложение и вычитание с нулем
- Определение и расширение простых числовых шаблонов для вычитания
- Решайте задачи, выбирая операции и записывая числовые предложения
Дополнительные факты к номеру 12
- Узнайте дополнительные факты к номеру 12
- Развить понимание стратегий сложения, таких как использование числовой строки, шаблоны сложения, двойные и почти двойные числа
- Сложите три однозначных числа
- Поймите, что порядок группировки слагаемых не влияет на сумму
- Решайте проблемы, задавая вопросы и выбирая операции
Факты вычитания до 12
- Изучение фактов вычитания до 12
- Развить понимание стратегий вычитания, таких как использование числовой строки, а также выявление и использование шаблонов вычитания
- Используйте сложение для проверки вычитания
- Определить семейства фактов сложения и вычитания
- Решайте задачи, рисуя картинки и используя модели
Размещение значения до 100
- Чтение, счет, запись, сравнение и упорядочивание целых чисел до 100
- Понимание разрядности путем представления чисел до 100 в виде десятков и единиц
- Понимать и описывать пропуск счета до 100 двойками, пятерками и десятками
- Решать проблемы, используя стратегию «угадай и проверь» и логические рассуждения
Деньги и время
- Узнать ценность пенни, пятаков, десятицентовиков и четвертаков
- Сортировка, подсчет и нахождение стоимости группы монет
- Показать различные комбинации монет, которые равны по достоинству
- Сообщать время с точностью до получаса
- Привязка времени к событиям
- Определить продолжительность прошедшего времени
- Решайте проблемы, используя логические рассуждения и скрытую информацию
Геометрия, дроби и вероятности
- Определение общих плоских и объемных фигур и описание их атрибутов
- Распознавать линейную симметрию как равные части плоских фигур
- Распознавать конгруэнтные фигуры как фигуры одинакового размера и формы
- Узнавать, называть и писать 1/2, 1/3 и 1/4 как часть целого или части набора
- Изучить расположение объектов и понять вероятность простых событий
- Решение задач с помощью логических рассуждений, рисунков и моделей
Сложение и вычитание двузначных чисел
- Сложение и вычитание единиц и десятков
- Сложение и вычитание целых двузначных чисел и денежных сумм без перегруппировки
- Оценка двузначных целых чисел с точностью до десяти
- Использование моделей для сложения и вычитания двузначных целых чисел с перегруппировкой
- Решать задачи, выбирая операции и используя логические рассуждения
Измерение
- Измерение объекта путем определения единицы измерения и использования соответствующих инструментов
- Измерение, сравнение и оценка длины, емкости и веса/массы в английских и метрических единицах
- Измерение периметра с использованием нестандартных единиц измерения
- Считайте показания термометра, чтобы найти температуру в градусах по Фаренгейту
- Решайте проблемы с помощью карт и логических рассуждений
Факты сложения и вычитания до 18
- Изучение фактов сложения и вычитания до 18
- Определение семейств фактов
- Сложение и вычитание с использованием таких стратегий, как связанные факты, порядок свойств, удвоение и получение десяти
- Решайте проблемы, рисуя картинки и зная, когда игнорировать дополнительную информацию
Продолжение изучения математики
- Углубление понимания нумерации, разрядного значения и перегруппировки понятий и навыков
- Определить функциональные правила
- Поиск пропущенных номеров или неизвестных операций
- Изучение перегруппировки сложения и вычитания двузначных чисел
- Сложите три двузначных числа
- Понимать числа до 999 как сотни, десятки и единицы
- Решайте проблемы, составляя таблицы и используя стратегию «угадай-и-проверь»
вернуться к началу
Количество уроков и расписание
45 минут
Вы можете разделить уроки на более мелкие сегменты и делать перерывы по мере необходимости. Онлайн-система отслеживания уроков K12 позволяет вам продолжить с того места, где вы остановились на любом уроке.
Онлайн-система отслеживания уроков K12 позволяет вам продолжить с того места, где вы остановились на любом уроке.
Всего уроков: 182
наверх
Требуется дополнительная информация
* Обязательно.
* Имя *
* Фамилия *
* Эл. адрес *
* Телефон *
Состояние *
* Select State…InternationalAlabamaAlaskaArizonaArkansasCaliforniaColoradoConnecticutDistrict of ColumbiaDelawareFloridaGeorgiaHawaiiIdahoIllinoisIndianaIowaKansasKentuckyLouisianaMaineMarylandMassachusettsMichiganMinnesotaMississippiMissouriMontanaNebraskaNevadaNew HampshireNew JerseyNew MexicoNew YorkNorth CarolinaNorth DakotaOhioOklahomaOregonPennsylvaniaRhode IslandSouth CarolinaSouth DakotaTennesseeTexasUtahVermontVirginiaWashingtonWest VirginiaWisconsinWyoming
* Почтовый индекс *
* Какие марки вас интересуют? Выберите все подходящие варианты.
Да, я заинтересован в подготовке к карьере
У меня есть вопросы по следующим темам.
Виртуальное/онлайн-обучение
Участие учителя
Добавить личное примечание
Начать писать
Мой ребенок/дети уже зачислены в школу K12.
Предоставляя эту информацию, вы соглашаетесь получать звонки/текстовые сообщения от K12 или представителя школы или устройства, которое будет автоматически набирать предоставленный номер. Могут применяться тарифы на передачу сообщений и данных.
Требуется дополнительная информация *Обязательные поля
* Имя *
* Фамилия *
* Адрес электронной почты *
* Номер телефона *
Состояние *
* Select State. ..InternationalAlabamaAlaskaArizonaArkansasCaliforniaColoradoConnecticutDistrict of ColumbiaDelawareFloridaGeorgiaHawaiiIdahoIllinoisIndianaIowaKansasKentuckyLouisianaMaineMarylandMassachusettsMichiganMinnesotaMississippiMissouriMontanaNebraskaNevadaNew HampshireNew JerseyNew MexicoNew YorkNorth CarolinaNorth DakotaOhioOklahomaOregonPennsylvaniaRhode IslandSouth CarolinaSouth DakotaTennesseeTexasUtahVermontVirginiaWashingtonWest VirginiaWisconsinWyoming
..InternationalAlabamaAlaskaArizonaArkansasCaliforniaColoradoConnecticutDistrict of ColumbiaDelawareFloridaGeorgiaHawaiiIdahoIllinoisIndianaIowaKansasKentuckyLouisianaMaineMarylandMassachusettsMichiganMinnesotaMississippiMissouriMontanaNebraskaNevadaNew HampshireNew JerseyNew MexicoNew YorkNorth CarolinaNorth DakotaOhioOklahomaOregonPennsylvaniaRhode IslandSouth CarolinaSouth DakotaTennesseeTexasUtahVermontVirginiaWashingtonWest VirginiaWisconsinWyoming
* Почтовый индекс *
* Какие марки вас интересуют?
Выберите все подходящие варианты.
Да, я заинтересован в подготовке к карьере
У меня есть вопросы по следующим темам.
Виртуальное/онлайн-обучение
Участие учителя
Добавить личную заметку
Мой ребенок/дети уже зачислены в школу K12
Предоставляя эту информацию, вы соглашаетесь получать звонки/текстовые сообщения от K12 или представителя школы или устройства, которое будет автоматически набирать предоставленный номер. Могут применяться тарифы на передачу сообщений и данных.
Могут применяться тарифы на передачу сообщений и данных.
Мы хотим услышать от вас. Отправьте электронное письмо или позвоните нам по телефону 866.968.7512. *Обязательные поля
* Имя *
* Фамилия *
* Адрес электронной почты *
* Номер телефона *
* Сообщение *
Мой ребенок/дети уже зачислены в школу K12
Состояние *
* Select State…InternationalAlabamaAlaskaArizonaArkansasCaliforniaColoradoConnecticutDistrict of ColumbiaDelawareFloridaGeorgiaHawaiiIdahoIllinoisIndianaIowaKansasKentuckyLouisianaMaineMarylandMassachusettsMichiganMinnesotaMississippiMissouriMontanaNebraskaNevadaNew HampshireNew JerseyNew MexicoNew YorkNorth CarolinaNorth DakotaOhioOklahomaOregonPennsylvaniaRhode IslandSouth CarolinaSouth DakotaTennesseeTexasUtahVermontVirginiaWashingtonWest VirginiaWisconsinWyoming
* Почтовый индекс *
* Какие марки вас интересуют?
Выберите все подходящие варианты.
Да, я заинтересован в подготовке к карьере
У меня есть вопросы по следующим темам.
Виртуальное/онлайн-обучение
Участие учителя
Предоставляя эту информацию, вы соглашаетесь получать звонки/текстовые сообщения от K12 или представителя школы или устройства, которое будет автоматически набирать предоставленный номер. Могут применяться тарифы на передачу сообщений и данных.
Вы здесь
- Дом
- Список онлайн-курсов K-8
- Математика для первого класса
Обучение математическим навыкам с числовыми линиями: часть 1
Обычные детские сады и классы для первоклассников не были бы полными, если бы на стене с гордостью не висели алфавит и числовой ряд. Часто к верхней части парты каждого учащегося приклеивается ламинированная числовая строка, к которой учащийся может легко получить доступ. Почему числовые линии занимают такое видное место в классах? Числовые линии помогают обеспечить умственную стратегию сложения и вычитания; исследования показали, что числовые линии важны, потому что они способствуют хорошему умственному восприятию чисел и арифметическим стратегиям.
Почему числовые линии занимают такое видное место в классах? Числовые линии помогают обеспечить умственную стратегию сложения и вычитания; исследования показали, что числовые линии важны, потому что они способствуют хорошему умственному восприятию чисел и арифметическим стратегиям.
Мы все согласны с тем, что числовые линии важны. Итак, как мы учим понятиям числа и числа, особенно младших школьников с нарушениями зрения? Передовая практика для слабовидящих учащихся поддерживает использование манипулятивных средств для первоначального ознакомления с базовыми математическими навыками и концепциями восприятия чисел. В части 1 этой серии мы расскажем о различных основных действиях с числовыми линиями и проследим за тем, как молодой студент развивает базовое чувство чисел с помощью тактильных числовых линий.
Джессика Макдауэлл, опытный и творческий TVI, поделилась своими материалами и идеями, когда она преподает концепции числовых линий этой очаровательной первокласснице.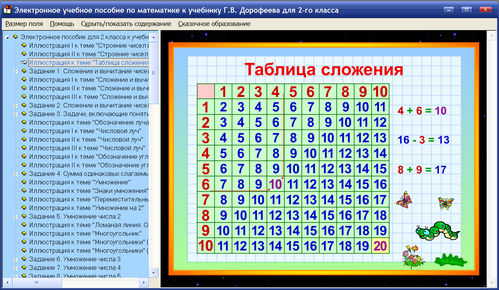 Логан умеет читать по Брайлю и получает доступ к своей математике с помощью шрифта Брайля. Первоначально Джессика познакомила Логана со стандартными линиями тактильных чисел APH (включая числовую строку APH, которая находится в диапазоне от 0 до 20), а также с меньшими числовыми линиями, созданными учителем. Его TVI предварительно научил, как получить доступ к тактильной числовой линии, и Логан последовал за своим основным классом, когда они научились использовать числовые линии для изучения основных математических понятий.
Логан умеет читать по Брайлю и получает доступ к своей математике с помощью шрифта Брайля. Первоначально Джессика познакомила Логана со стандартными линиями тактильных чисел APH (включая числовую строку APH, которая находится в диапазоне от 0 до 20), а также с меньшими числовыми линиями, созданными учителем. Его TVI предварительно научил, как получить доступ к тактильной числовой линии, и Логан последовал за своим основным классом, когда они научились использовать числовые линии для изучения основных математических понятий.
Базовые навыки работы с числовыми линиями
- Найдите точку, отмеченную на числе (и назовите точку)
- Поставьте точку в нужном месте
- Найдите нужное число под галочкой в числовой строке*
- Добавьте недостающий номер
- Узнайте, что числа справа больше, чем числа слева
- Определите, какое число больше, меньше или равно
- Измените диапазон числовой строки и повторите вышеуказанные навыки
- Создавайте числовые ряды, которые считают единицами, двойками, пятерками и десятками, и повторяйте описанные выше навыки .

*Примечание. Важно, чтобы строки с тактильными номерами были созданы с делениями и с числом, напечатанным шрифтом Брайля под делением. Студентов, изучающих шрифт Брайля, нужно научить пользоваться делениями (важно для сложения и вычитания) и тому, как физически проводить пальцем прямо вниз, чтобы найти число в шрифте Брайля.
Первоначальные проблемы для Логана
Класс провел много игр и упражнений по понятиям, не используя книгу и не выполняя задания с бумагой/карандашом. Многие из этих игр требовали модификации, чтобы быть доступными, или использовались замененные игры.
Примечание. Многие классы используют мотивирующие, но недоступные приложения для отработки навыков числового ряда.
В конце концов, ученики были оценены на бумаге, и у Логана не было много времени с тактильной графикой учебника для числовых линий до оценивания.
Интерактивные тактильные числовые линии
Ресурсы номерной строки
Создавайте веселые интерактивные игры с числовыми рядами, чтобы практиковать основные навыки работы с числовыми рядами, включая способность находить точку на числовом ряду.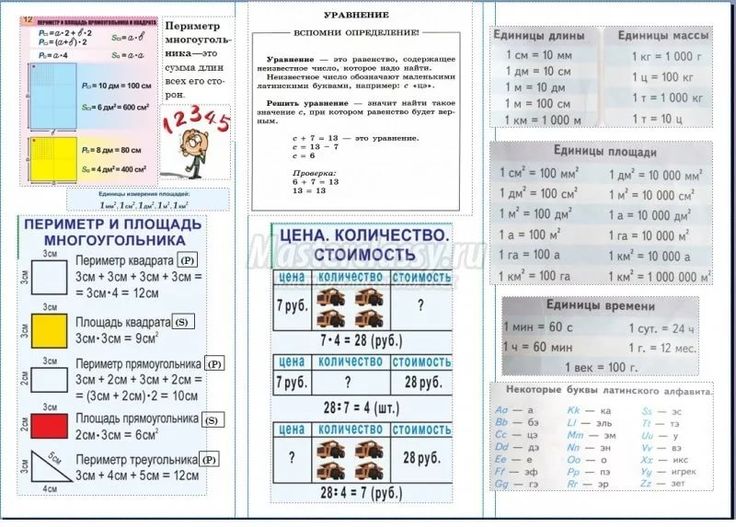 Начните с манипулятивных действий, таких как создание магнитной тактильной числовой строки и размещение забавной формы/объекта, магнитного на или чуть выше галочки в числовой строке Брайля. Добавьте тактильную цифру на пробковую доску и попросите ученика использовать огромную канцелярскую кнопку на отметке или чуть выше, чтобы отметить желаемое число. (См. пост «Упражнения с числовыми строками», чтобы узнать об упражнениях с пробковой доской и связанных с ними действиях с числовыми строками.) По мере продвижения ученик может наклеивать наклейки (наклейки из пеноматериала хорошо работают!) на созданную учителем числовую строку Брайля или числовую строку APH.
Начните с манипулятивных действий, таких как создание магнитной тактильной числовой строки и размещение забавной формы/объекта, магнитного на или чуть выше галочки в числовой строке Брайля. Добавьте тактильную цифру на пробковую доску и попросите ученика использовать огромную канцелярскую кнопку на отметке или чуть выше, чтобы отметить желаемое число. (См. пост «Упражнения с числовыми строками», чтобы узнать об упражнениях с пробковой доской и связанных с ними действиях с числовыми строками.) По мере продвижения ученик может наклеивать наклейки (наклейки из пеноматериала хорошо работают!) на созданную учителем числовую строку Брайля или числовую строку APH.
Основные понятия числовой линии
При вводе числовой строки объясните, что такое деления и почему они используются. Предложите учащемуся следить за отметками, чтобы найти кружок (или объект) на отметке. Как только объект найден, учащийся должен провести пальцем вниз по отметке и продолжить вниз, чтобы найти число Брайля, соответствующее этой отметке.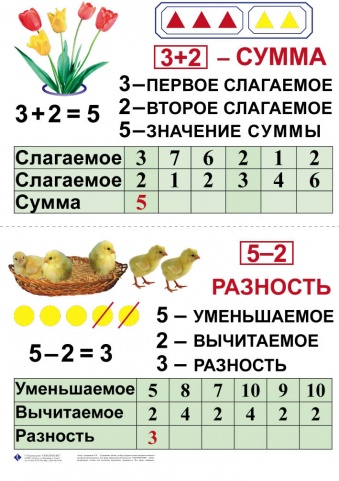
Предложите учащемуся определить диапазон числовой прямой и шкалы. Диапазон можно найти, указав число в крайнем левом углу и число в крайнем правом углу. Начните с единицы – каждое число и галочка увеличиваются на единицу. По мере продвижения ученика шкала может измениться на увеличение на двойки, пятерки, десятки и более.
Помните: цель состоит в том, чтобы научить ученика находить предмет по делениям (не по цифрам Брайля под числовой строкой); затем учащийся должен провести пальцем вниз, чтобы определить правильное число. (Причина: если учащийся привык следовать цифрам, а не галочкам, сложение и вычитание могут сбивать с толку, поскольку учащийся затем считает, одновременно следуя цифрам Брайля.)
Начало игры с числовой линией
Выберите простую числовую строку (в зависимости от ученика диапазон может быть от 1 до 5 или от 1 до 10). Используя одну из манипулятивных числовых линий, упомянутых выше (магнитная доска, пробковая доска и т. д.), попросите ученика исследовать тактильную числовую линию. Определите различные части и положение/взаимосвязь каждой части: деления, прямая горизонтальная линия и числа. Начните слева и двигайтесь вправо. Учащимся, возможно, придется сначала следовать по прямой горизонтальной линии, прежде чем они смогут следовать по отметкам. Попросите учащегося начать с левой стороны и подсчитать галочки (обязательно начните с того же числа — нуля или единицы — которое указано шрифтом Брайля для этой числовой строки). Затем попросите учащегося прочитать цифры Брайля под числовой строкой. Соответствовало ли количество его делений цифрам Брайля? Вернитесь назад и пересчитайте галочки.
Определите различные части и положение/взаимосвязь каждой части: деления, прямая горизонтальная линия и числа. Начните слева и двигайтесь вправо. Учащимся, возможно, придется сначала следовать по прямой горизонтальной линии, прежде чем они смогут следовать по отметкам. Попросите учащегося начать с левой стороны и подсчитать галочки (обязательно начните с того же числа — нуля или единицы — которое указано шрифтом Брайля для этой числовой строки). Затем попросите учащегося прочитать цифры Брайля под числовой строкой. Соответствовало ли количество его делений цифрам Брайля? Вернитесь назад и пересчитайте галочки.
Теперь незаметно добавьте магнитный объект или канцелярскую кнопку чуть выше деления; никогда не наклеивайте наклейку на число Брайля! (Сначала выбрал галочку в середине числовой строки, чтобы учащийся практиковался в том, чтобы следовать галочке, а затем считать ее.) Предложите учащемуся определить соответствующую цифру, проведя пальцем вниз к цифре Брайля.
С помощью 10-кадра ниже первоклассник Логан перемещает Пятно (трехмерную божью коровку вдоль 10-кадрового лотка, разрезанного вдоль пополам и превращенного в 1×10 (вместо 2×5). Джессика (TVI) добавлена ряд соответствующих чисел Брайля ниже десяти кадров (каждое число выровнено по центру каждого квадрата десяти кадров). На рисунке ниже соответствующие числа Брайля находятся в диапазоне от 1 до 10. Джессика сделала дополнительные соответствующие числовые строки, такие как 10 – 100 (считая на десятки), которые можно легко заменить. Внизу изображения находится числовая строка APH 0-20, которая не такая длинная, как числовая строка с 10 кадрами.0005
Джессика (TVI) добавлена ряд соответствующих чисел Брайля ниже десяти кадров (каждое число выровнено по центру каждого квадрата десяти кадров). На рисунке ниже соответствующие числа Брайля находятся в диапазоне от 1 до 10. Джессика сделала дополнительные соответствующие числовые строки, такие как 10 – 100 (считая на десятки), которые можно легко заменить. Внизу изображения находится числовая строка APH 0-20, которая не такая длинная, как числовая строка с 10 кадрами.0005
Благодаря действиям с божьей коровкой Логан научился считать квадраты, определяя квадрат, в котором находилась божья коровка.
Следующим шагом будет попросить вашего ученика найти и поместить маркер на желаемую отметку или немного выше нее. Используя рамку 1 × 10, Логан научился считать квадраты, чтобы поместить божью коровку в нужный квадрат. Перемещение божьей коровки при подсчете квадратов более конкретно, чем подсчет делений. Он также научился находить число Брайля под десятичной рамкой.
Студенческий прогресс
Время выполнения этих заданий с числовым рядом зависит от возраста и способностей учащегося. Некоторые учащиеся могут потратить неделю на каждую часть задания, в то время как другие учащиеся могут быстро выполнить многие из этих действий за один урок. Имейте в виду, что большинству младших школьников требуется время и практика — повторение одного и того же действия или подобных действий снова и снова, прежде чем они будут готовы перейти к следующему шагу. Для учащихся со зрением учителя обычно предлагают множество игр, которые предоставляют несколько возможностей повторить один и тот же навык, прежде чем перейти к следующему навыку.
Некоторые учащиеся могут потратить неделю на каждую часть задания, в то время как другие учащиеся могут быстро выполнить многие из этих действий за один урок. Имейте в виду, что большинству младших школьников требуется время и практика — повторение одного и того же действия или подобных действий снова и снова, прежде чем они будут готовы перейти к следующему шагу. Для учащихся со зрением учителя обычно предлагают множество игр, которые предоставляют несколько возможностей повторить один и тот же навык, прежде чем перейти к следующему навыку.
Примечание. Вводите основные понятия числовых рядов в том порядке, в котором их вводят в основной класс. Помните, цель состоит в том, чтобы учитель общего образования взял на себя ответственность за обучение ученика; Ответственность TVI состоит в том, чтобы модифицировать материалы и концепции предварительного обучения, которые являются уникальными для учащихся с нарушениями зрения, и поддерживать учителя общего образования.
Студенческие ожидания
Каждое задание поощряет максимальную самостоятельность учащихся. Ожидается, что Логан самостоятельно прочитает свою математическую задачу по Брайлю, объявит математическую задачу вслух, объявит по мере счета и будет иметь «план» того, как найти ответ. Он автоматически перемещает руки к своим манипулятивным и/или числовым линиям, чтобы выяснить проблему. Очень мало подсказок — если они вообще есть — даются. Логану разрешено делать ошибки, и, если необходимо, позже он получает дополнительные инструкции, чтобы исправить свою ошибку. Найдя ответ, Логану сначала предлагается переформулировать математическую задачу и ответить. (В части 2 этой серии Логан автоматически повторяет математическую задачу и отвечает без подсказок.) Также интересно отметить, что Логан может сидеть неподвижно во время работы, даже если у него много энергии, когда он физически не взаимодействует с манипуляторы или тактильные материалы.
Ожидается, что Логан самостоятельно прочитает свою математическую задачу по Брайлю, объявит математическую задачу вслух, объявит по мере счета и будет иметь «план» того, как найти ответ. Он автоматически перемещает руки к своим манипулятивным и/или числовым линиям, чтобы выяснить проблему. Очень мало подсказок — если они вообще есть — даются. Логану разрешено делать ошибки, и, если необходимо, позже он получает дополнительные инструкции, чтобы исправить свою ошибку. Найдя ответ, Логану сначала предлагается переформулировать математическую задачу и ответить. (В части 2 этой серии Логан автоматически повторяет математическую задачу и отвечает без подсказок.) Также интересно отметить, что Логан может сидеть неподвижно во время работы, даже если у него много энергии, когда он физически не взаимодействует с манипуляторы или тактильные материалы.
Чего не хватает? Активность
Счет является обязательным навыком перед введением в действие «Чего не хватает». Заполнение пробелов для последовательности чисел и в числовой сетке – это вопрос активности и оценки, который встречается в младших начальных классах. Студенты также должны уметь читать цифры Брайля. Сначала создайте простую страницу шрифта Брайля с цифрами от 1 до 10 (оставьте два пустых места между цифрами, чтобы дать учащемуся время обработать числа, которые он только что прочитал) и попросите учащегося прочитать числа, написанные Брайлем. Затем дайте учащемуся простую страницу шрифтом Брайля с цифрами от 1 до 10, без одной цифры. (При необходимости вначале можно оставить пустое место для пропущенного числа, чтобы помочь учащемуся самостоятельно определить пропущенное число.) Повторите игру со страницами Брайля, на которых есть несколько пропущенных чисел и/или разные диапазоны чисел. Хотите вызов? Меняйте числа, считая двойками, пятерками или десятками!
Студенты также должны уметь читать цифры Брайля. Сначала создайте простую страницу шрифта Брайля с цифрами от 1 до 10 (оставьте два пустых места между цифрами, чтобы дать учащемуся время обработать числа, которые он только что прочитал) и попросите учащегося прочитать числа, написанные Брайлем. Затем дайте учащемуся простую страницу шрифтом Брайля с цифрами от 1 до 10, без одной цифры. (При необходимости вначале можно оставить пустое место для пропущенного числа, чтобы помочь учащемуся самостоятельно определить пропущенное число.) Повторите игру со страницами Брайля, на которых есть несколько пропущенных чисел и/или разные диапазоны чисел. Хотите вызов? Меняйте числа, считая двойками, пятерками или десятками!
В следующем видео Логану дается созданная учителем страница Брайля с диапазоном чисел, заканчивающихся на 101; отсутствуют различные номера. Обеими руками Логан спокойно сидит и читает цифры на странице, определяя, каких цифр не хватает.
Как только учащийся поймет концепцию определения пропущенных чисел, дайте ему созданные учителем числовых строк с пропущенными числами.
Примечание. При выполнении задания с отсутствующей числовой строкой учащийся будет следить за числами Брайля, а не за галочками в числовой строке. Однако не забудьте указать учащемуся, что для большинства операций с числовыми строками, таких как сложение и вычитание, учащийся должен считать деления, а не числа Брайля.
Больше, равно, меньше активности
Спросите учащегося, «растут» ли числа (становятся больше) по мере того, как вы перемещаетесь вправо или влево по числовой строке. Обсудите идею о том, что чем больше вы двигаетесь вправо, тем выше число. Если вы двигаетесь влево (назад по числовой строке), числа становятся меньше.
Используйте желаемую манипулятивную числовую строку; в этом примере будет использоваться кадр Логана 1 × 10, 2 божьи коровки и 2 лягушки. На трех каталожных карточках напечатайте шрифтом Брайля один из следующих математических символов: Больше, Равно или Меньше. Разместите божью коровку и манипуляторы лягушки в разных квадратах; начните с того, что божья коровка больше лягушки. Обсудите, какое число больше, божья коровка или лягушка? Введите соответствующий математический символ «Больше чем». Составьте математическое уравнение, поместив вторую божью коровку на каталожную карточку (оставив место для карточки с математическими символами), а вторую лягушку — на другую карточку. Попросите учащегося поместить символ «Больше чем» между двумя жуками. Повторите это действие несколько раз со знаком «больше чем». Если ученик готов, замените вторую божью коровку и лягушку каталожными карточками, на которых указано соответствующее число. Пример: если божья коровка на 5, а лягушка на 2, учетная карточка со шрифтом Брайля 5 будет заменена на божью коровку, а учетная карточка со шрифтом Брайля номер два будет заменена на лягушку.
Обсудите, какое число больше, божья коровка или лягушка? Введите соответствующий математический символ «Больше чем». Составьте математическое уравнение, поместив вторую божью коровку на каталожную карточку (оставив место для карточки с математическими символами), а вторую лягушку — на другую карточку. Попросите учащегося поместить символ «Больше чем» между двумя жуками. Повторите это действие несколько раз со знаком «больше чем». Если ученик готов, замените вторую божью коровку и лягушку каталожными карточками, на которых указано соответствующее число. Пример: если божья коровка на 5, а лягушка на 2, учетная карточка со шрифтом Брайля 5 будет заменена на божью коровку, а учетная карточка со шрифтом Брайля номер два будет заменена на лягушку.
Представьте процесс с помощью математических символов «меньше чем», а затем «равно». Некоторым учащимся может быть полезно просто выбрать правильный математический символ, а не составлять математическое уравнение.
Ресурсы номерной строки APH
В APH есть несколько ресурсов тактильной числовой строки, которые могут оказаться полезными:
- Устройство номерной строки
- Расходные материалы APH, напечатанные крупным шрифтом, числовые строки
- Расходные материалы APH, числовые строки шрифта Брайля
- Устройство APH Number Line: виниловые весы, набор из 15 шт.

- APH Advances Desktop Stick-On Number Line
- Наклейки с цифрами для настольных ПК APH: крупный шрифт Брайля
Этот пост является частью серии постов Number Line.
- Обучение математическим навыкам с числовыми линиями: часть 2 (сложение и вычитание)
- Обучение навыкам работы с числовыми линиями: часть 3 (доступное приложение для числовых линий)
- Обучение навыкам работы с числовыми линиями: Часть 4 (Применение числовых линий и дополнительные навыки)
- Действия с числовыми линиями
Дайан Браунер
ПОДЕЛИТЕСЬ ЭТОЙ СТАТЬЕЙ
Изменения в учебном плане по математике в Сан-Франциско неоднозначны
Вкратце
Еще в 2014 году Сан-Франциско принял одну из основных идей предложенной штатом математической структуры. Пока результаты не совсем обнадеживающие.
Lea este artículo en español .
Джозелин Маррокин, первокурсница Линкольн Хай в Сан-Франциско, бросила себе вызов, посетив в этом году два урока математики.
Поскольку Объединенный школьный округ Сан-Франциско требует, чтобы учащиеся не сдавали Алгебру 1 до 9 класса, Джозелин записалась на Алгебру 1 и Геометрию одновременно, чтобы она могла сдать экзамен AP Calculus к старшему году обучения.
«Стресс, связанный с посещением двух занятий и выполнением домашних заданий по каждому, было трудно справиться, — сказала Джозелин. «Сначала было тяжело, но я привык».
В 2014 году власти округа решили отложить изучение алгебры 1 до 9-го класса в надежде снизить количество чернокожих, латиноамериканцев и учащихся из малообеспеченных семей, не сдавших алгебру 1 в 8-м классе. Цель состояла в том, чтобы научить этих студентов учиться на более высоких математических курсах и, в конечном итоге, сделать карьеру в области естественных наук, технологий, инженерии или математики. Это изменение помогло сократить количество учащихся, не проходящих курс, но совпало с падением результатов тестов в некоторых школах, обслуживающих учащихся с более высокими потребностями, что является предметом критики, относящимся ко всей Калифорнии, поскольку штат планирует рекомендовать одну и ту же политику для всех.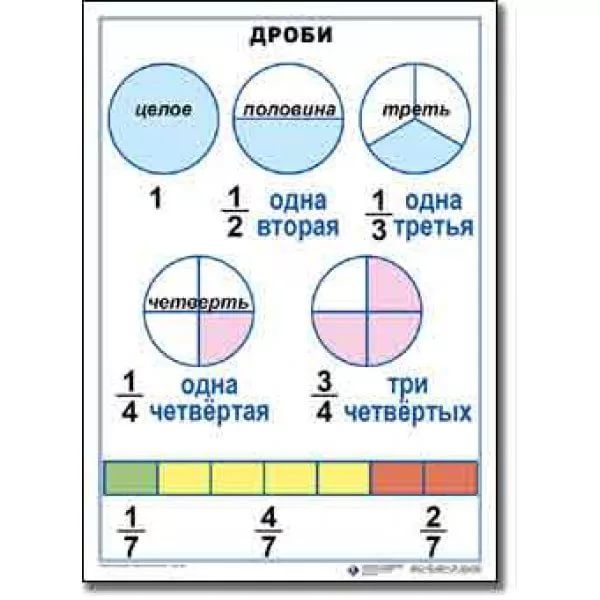 школьный округ по всему штату как часть новой математической структуры.
школьный округ по всему штату как часть новой математической структуры.
В то же время это изменение побудило семьи с такими ресурсами, как у Джозелин, найти способы помочь своим детям добиться успехов в математике, увековечив некоторые из неравенств, которые политика должна была устранить.
Чтобы убедиться, что Джозелин сможет пройти два урока математики в этом году, ее дедушка Рекс Риджуэй, курирующий образование Джозелин, заплатил 850 долларов за то, чтобы она записалась в первый класс алгебры летом после 8-го класса. Риджуэй, чернокожий, сказал, что надеется, что переход в старшую школу, уже зная алгебру 1, облегчит бремя двух занятий по математике.
«Я заставил ее сдать алгебру 1 летом, чтобы она могла освоить ее, когда снова будет сдавать ее по геометрии», — сказал Риджуэй. «У многих черных семей нет ресурсов, чтобы сделать то, что сделал я».
Джозелин Маррокин делает домашнее задание в парке в нескольких кварталах от своего дома в районе Бэй-Вью в Сан-Франциско, 2 декабря 2021 года. Нина Риджио для CalMatters Родители Франциско, такие как Риджуэй, выступили против этой меры почти восемь лет назад. После негативной реакции со стороны родителей и экспертов по математике штат выпустит пересмотренную структуру в январе, а в июле завершит работу над рекомендациями. Однако структура представляет собой набор предложений, и округа, которые решат ее игнорировать, не будут наказаны.
Нина Риджио для CalMatters Родители Франциско, такие как Риджуэй, выступили против этой меры почти восемь лет назад. После негативной реакции со стороны родителей и экспертов по математике штат выпустит пересмотренную структуру в январе, а в июле завершит работу над рекомендациями. Однако структура представляет собой набор предложений, и округа, которые решат ее игнорировать, не будут наказаны.Риджуэй сказал, что был в ярости, когда узнал о политике округа и стал искать способы научить Джозелин математическому анализу к 12-му классу и увеличить ее шансы на поступление в Калифорнийский университет в Лос-Анджелесе, школу ее мечты. То же самое сделали и другие родители в округе. Учителя не удивлены.
«Это привело к еще большему неравенству и загнало их в подполье», — сказала Элизабет Стэтмор, учитель математики в районной средней школе Лоуэлл, самой успешной государственной средней школе города. «Люди со средствами начали искать другие способы добиться успеха».
Просчитанный ход
Статус-кво Сан-Франциско до 2014 года был не самым лучшим.
«Наши дети вылетели из алгебры в 8-м классе, и я бы сказала, что это была проблема справедливости», — сказала Эмили Мурасе, которая была членом школьного совета в 2014 году. детей, которые провалили Алгебру 1».
Школы в округе придумали множество способов, позволяющих учащимся приступить к математическому анализу к 12-му классу, даже несмотря на изменение политики. Некоторые школы предлагают летний курс геометрии, на который приоритетно зачисляются учащиеся с низким доходом. В других школах учащиеся могут пройти годичный курс, который сочетает в себе алгебру 2 и предварительный анализ.
Лиззи Халл Барнс, отвечающая за преподавание математики в San Francisco Unified, сказала, что эти варианты учитываются при приеме в Калифорнийский университет и Калифорнийский государственный университет.
Это изменение означало, что все учащиеся с 6 по 8 классы будут посещать одни и те же уроки математики. В то же время школьный округ скорректировал учебные программы для классов математики в средних школах, чтобы они лучше соответствовали стандартам штата. «Алгебра 1» в 8-м классе, они все еще охватывают почти все понятия, которые у них были раньше, такие как линейные уравнения, пропорциональные отношения и системы уравнений. Они должны знать все, что им нужно, перед стандартизированным тестированием в 8-м классе.
«Алгебра 1» в 8-м классе, они все еще охватывают почти все понятия, которые у них были раньше, такие как линейные уравнения, пропорциональные отношения и системы уравнений. Они должны знать все, что им нужно, перед стандартизированным тестированием в 8-м классе.
Барнс сказал, что все учащиеся, особенно чернокожие, латиноамериканцы и учащиеся из малообеспеченных семей, лучше подготовлены к успеху в алгебре 1, если сосредоточатся на изучении этих основ в средней школе.
«Концепции из Алгебры 1 были разделены и перераспределены более продуманным образом», — сказала она. «Мы хотели прервать расистские результаты, связанные с математикой».
Здание объединенного школьного округа Сан-Франциско в Сан-Франциско, 2 декабря 2021 года. Нина Риджио для CalMatters Риджуэй и другие родители отличников заявили, что школьный округ сдерживает учащихся. Но Барнс сказал, что алгебра 1 теперь преподается в 9 классах.й класс является более продвинутым, чем тот, который преподавался в 8-м классе до 2014 года. Учебная программа теперь включает концепции из алгебры 2 и науки о данных.
Учебная программа теперь включает концепции из алгебры 2 и науки о данных.
В рамках школьного округа учащиеся могут решить, хотят ли они посещать более продвинутые курсы математики в старшей школе, как только они лучше поймут свои интересы и уровень знаний по математике. До 2014 года, по словам Барнса, студентов слишком рано помещали на дорожки или «дорожки».
«Я думаю, что самое главное, что мы хотим донести, это то, что студенты, которые хотят достичь более высокого уровня математики, могут это сделать», — сказал Барнс. «Мы ничего ни у кого не отнимаем».
Смешанные результаты по математике в Сан-Франциско
По данным округа, после того, как округ принял это правило в 2014 году, меньше учащихся из всех демографических групп не смогли сдать алгебру 1. Он сообщил, что с момента принятия этой политики все больше учащихся из всех расовых демографических групп записались как на высшую математику, так и получили больше кредитов по математике и естественным наукам во время своей карьеры в старшей школе.
«Это действительно помогло учащимся с низкими и средними баллами больше заниматься математикой», — сказал бывший член правления Мурасэ. «Большим сюрпризом стало то, что в результате студенты больше увлекались наукой. Это было непреднамеренным последствием».
Но стандартизированные тестовые данные рисуют более сложную картину.
В масштабах округа процент учащихся, достигших уровня математических знаний, который штат считает приемлемым, увеличился на 2,6 процентных пункта в период между 2014-15 и 2018-19 учебными годами. Процент чернокожих и латиноамериканских учащихся, отвечающих стандартам, также увеличился на 2,6 пункта. Но разрыв между процентом учащихся с низким доходом и процентом школьников, отвечающих стандартам округа, вырос на 2 пункта.
Школы с высоким процентом чернокожих и латиноамериканцев показали гораздо худшие результаты на стандартизированных тестах.
Средняя школа О’Коннелла зачислила самый высокий процент чернокожих учащихся среди общеобразовательных средних школ округа в 2018-19 учебном году. В 2014-15 учебном году, согласно стандартизированным тестам, всего 6% чернокожих учащихся школы соответствовали математическим стандартам. Как бы плохо это ни звучало, ситуация ухудшилась после того, как в округе изменили метод преподавания математики. В 2018-19 учебном году этот показатель снизился до 0%.
В 2014-15 учебном году, согласно стандартизированным тестам, всего 6% чернокожих учащихся школы соответствовали математическим стандартам. Как бы плохо это ни звучало, ситуация ухудшилась после того, как в округе изменили метод преподавания математики. В 2018-19 учебном году этот показатель снизился до 0%.
В средней школе Вилли Брауна в том же году был самый высокий процент зачисления чернокожих среди средних школ. С момента его открытия в 2015 году процент учащихся, отвечающих стандартам по математике, упал с 14% до 7,8% в 2019 году. Доля чернокожих учащихся, соответствующих стандартам, оставалась ниже 4% в течение всех четырех промежуточных лет. В 2018-19 учебном году только 1,5% из 84 чернокожих учеников школы соответствовали математическим стандартам.
В школе Джеймса Лика в 2018–2019 годах почти три четверти из 568 студентов были латиноамериканцами.учебный год, что делает ее школой с наибольшей долей латиноамериканских учащихся в округе. Однако в том году только 7% латиноамериканских студентов соответствовали математическим стандартам, что является пятилетним минимумом. Между тем, 18,16% соответствовали стандартам английского языка, что является пятилетним максимумом для латиноамериканских учащихся школы.
Между тем, 18,16% соответствовали стандартам английского языка, что является пятилетним максимумом для латиноамериканских учащихся школы.
В средних школах Президио и Рузвельта, двух средних школах с самым высоким процентом белых учащихся, результаты тестов значительно улучшились. Процент чернокожих и латиноамериканских учащихся, отвечающих стандартам, увеличился на двузначные числа в обеих школах.
Что касается различных взлетов и падений результатов тестов в San Francisco Unified, Поликофф сказал, что «существует миллион разных вещей, которые могут объяснить тенденции в результатах тестов».
Морган Поликофф, профессор педагогики Университета Южной Калифорнии, сказал, что если больше студентов посещают более сложные курсы и получают хорошие оценки, это может быть хорошим знаком. Но результаты стандартизированных тестов покажут, действительно ли учащиеся изучают материал.
«Стандарты оценок можно смягчить», — сказал он. «Но стандартизированный тест должен служить независимым доказательством».
Что касается различных взлетов и падений результатов тестов в San Francisco Unified, Поликофф сказал, что «существует миллион разных вещей, которые могут объяснить тенденции в результатах тестов». Чиновники San Francisco Unified отказались подробно обсудить данные результатов тестов.
Стандартизированные тесты в Калифорнии основаны на тех же стандартах, которые привели к изменению политики, поэтому предложение Алгебры 1 в 9-м классе теоретически должно было привести к более справедливым результатам на тестах штата.
Но Барнс сказал, что количество студентов, обучающихся математике более высокого уровня, является более эффективной мерой, и что данные о результатах тестов «не являются мерой, которую мы использовали бы для оценки воздействия.
«В старших классах тест сдают один раз в 11 классе», — сказала она. «Трудно использовать это как мерило успеха во всей математике».
Джозелин Маррокин делает домашнее задание в парке в нескольких кварталах от своего дома в районе Бэй-Вью в Сан-Франциско, 2 декабря 2021 года. не могут просто отклонить их, особенно потому, что они проверяют именно то, что учащиеся должны были изучить в соответствии с изменением политики округа.
не могут просто отклонить их, особенно потому, что они проверяют именно то, что учащиеся должны были изучить в соответствии с изменением политики округа.«Вы не можете сказать: «Мы собираемся принять эту политику, и мы не можем оценить ее с помощью тестов», — сказал он. «Это неприемлемо».
Мурасе утверждает, что результаты тестов были бы еще хуже, если бы San Francisco Unified придерживалась своих старых методов.
«Вам придется сравнить траекторию оценок по математике с тем, что было бы при старой системе», — сказала она. «Никто бы не подумал, что эти баллы были бы выше, если бы мы сохранили алгебру в 8-м классе».
Результаты на местном уровне, последствия для штата
Алгебра задержки 1 — одна из основных идей, рекомендованных Калифорнийской математической структурой. Рамки, представляющие собой набор необязательных рекомендаций по преподаванию математики в государственных школах штата, также рекомендуют использовать более инклюзивный язык в классе и больше примеров из реальной жизни на уроках математики с целью привлечения более разнообразного студенческого контингента к участию в обучении. математика.
математика.
Родители, педагоги и математики по всему штату выступают против этой структуры по целому ряду причин. Они обвиняют авторов в разбавлении математики уроками, ориентированными на социальную справедливость.
Родители также говорят, что система сдерживает отличников. Авторы фреймворка не согласны. Они сказали, что изменения будут включать более подробные рекомендации для продвинутых студентов.
В то время как предложенная Калифорнией математическая структура вызывает споры по всей стране, в Сан-Франциско она возродила гнев некоторых родителей, которые яростно выступали против этих идей еще в 2014 году.
Майя Кешаван — мать двух недавних выпускников округа и член семьи Сан-Франциско, группа родителей, борющихся против предложенной Калифорнией математической структуры. Кешаван и другие участники говорят, что структура не должна рекомендовать откладывать Алгебру 1 до 9.th на основании некоторых несоответствий, которые они обнаружили в сообщениях об успехах San Francisco Unified.
Джо Хонг
В отчете Families for San Francisco говорится, что округ опубликовал вводящие в заблуждение данные о том, как часто учащиеся должны были повторять алгебру 1: в то время как количество учащихся, повторно сдавших предмет, упало с 40% до 7% в год после того, как алгебра 1 была вытеснена до В 9-м классе округ также отменил вступительный тест по алгебре 1, который, по словам Families for San Francisco, вероятно, снизил уровень повторения, устранив дополнительное препятствие для перехода к следующему математическому классу.
Барнс сказал, что у округа нет данных, показывающих, сколько учеников должны были пересдать алгебру 1 только из-за вступительного теста.
Кешаван, цветная женщина, работающая инженером-электриком, сказала, что понимает необходимость различных точек зрения в области науки и техники. Но она сказала, что сомнительные данные, представленные округом, вызывают серьезные сомнения в целесообразности отсрочки первого курса алгебры до 9-го класса.
Но она сказала, что сомнительные данные, представленные округом, вызывают серьезные сомнения в целесообразности отсрочки первого курса алгебры до 9-го класса.
Авторы структуры состояния, тем не менее, ссылаются на меньшее количество студентов, повторяющих Алгебру 1, как на свидетельство успеха. Джо Боулер, один из авторов государственной структуры и профессор математического образования в Стэнфордском университете, написала в соавторстве редакционную статью, в которой цитирует эти сообщения об успехах в San Francisco Unified. Текущий проект концепции ссылается на эту редакционную статью.
Отвечая на вопрос об этих потенциально вводящих в заблуждение данных в San Francisco Unified, Боалер сказал, что предлагаемая структура штата никоим образом не основана на политике одного округа. Она сказала, что в отличие от политики округа, государственная структура требует, чтобы средние школы объединяли алгебру и геометрию, а не преподавали их как два отдельных класса.
Боалер также отказался комментировать снижение результатов тестов в округе. Бен Форд, еще один соавтор фреймворка, сказал, что вернется к ссылкам на San Francisco Unified в текущем проекте.
Бен Форд, еще один соавтор фреймворка, сказал, что вернется к ссылкам на San Francisco Unified в текущем проекте.
Дочь Кешавана, окончившая школу в 2020 году, была в одной из первых когорт, которым необходимо было сдать алгебру 1 в 9-м классе. Кешаван, однако, заплатила 700 долларов за то, чтобы ее дочь прошла курс алгебры 1 в частной компании в 8-м классе.
И, как и ее дочь, сказала она, учащиеся по всему штату из привилегированных семей будут иметь преимущество, когда дело доходит до поступления в колледж и начала карьеры в области естественных наук, технологий, инженерии и математики.
«Я знал, что должен обойти это для моей дочери», — сказал Кешаван. «По сей день я считаю несправедливым, что у нее есть преимущество в том, что она может платить за внешний класс».
Мы хотим услышать от вас
Хотите оставить комментарий гостя или реакцию на статью, которую мы написали? Вы можете найти наши правила подачи здесь. Пожалуйста, свяжитесь с CalMatters с любыми комментариями: commentary@calmatters. org
org
История, которую вы только что прочитали, была профинансирована такими же людьми, как вы.
CalMatters — это некоммерческий отдел новостей, и ваши не облагаемые налогом пожертвования помогают нам продолжать предоставлять вам и каждому жителю Калифорнии важную беспристрастную информацию.
пожертвовать сейчас
Поддержка некоммерческих и беспристрастных новостей — один из способов бороться с поляризацией журналистики .
Джонатан, Лагуна Нигель
Избранный участник программы CalMatters
Новый учебный план по математике для 1–8 классов
Обзор
Мы обновили учебный план по математике для 1–8 классов. Учителя начнут использовать новый учебный план с сентября 2020 года.
Новый учебный план по математике является частью четырехлетней математической стратегии предназначен для:
- повысить успеваемость учащихся по математике
- помочь учащимся решать повседневные математические задачи
- повысить возможности трудоустройства учащихся для получения работы в будущем
Содержание и структура
В учебной программе 2005 года учащимся было трудно совмещать обучение из года в год.
 Существуют разные ожидания для изучающих английский и французский языки.
Существуют разные ожидания для изучающих английский и французский языки.В учебной программе 2020 будут четкие связи, чтобы показать, как из года в год развиваются математические навыки. Будет одна учебная программа на английском и французском языках – одинаковый опыт обучения для всех учащихся Онтарио.
Реальные связи
В учебной программе 2005 года есть устаревшие примеры для учащихся.
В учебной программе 2020 будут актуальные примеры из реальной жизни, которые помогут связать математику с повседневной жизнью, например, разработка инфографики, составление бюджета, электронные переводы и обучение программированию.
Числовые факты
В учебной программе 2005 года учащиеся не обязаны запоминать ключевые числовые факты.
В учебной программе 2020 больше внимания будет уделяться фундаментальным математическим понятиям, таким как изучение фактов умножения от 0 × 0 до 12 × 12, для улучшения решения задач и умственной математики.

Пространственное чувство
В учебной программе 2005 года младшие классы имеют ограниченные знания о пространственных рассуждениях, например, о связи между измерениями и геометрией.
В учебном плане 2020 будут использоваться пространственные отношения и формы, чтобы помочь маленьким детям подготовиться к более позднему изучению математики. Во всех классах учащиеся будут понимать основные понятия чисел, закономерности и геометрические понятия.
Дроби
В учебной программе 2005 понятия дробей в младших классах сбивают с толку.
В учебной программе 2020 , начиная с 1 класса, будут введены концепции равного распределения, чтобы облегчить понимание дробей.
Уверенность в математике
В учебной программе 2005 подразумевается построение уверенности в математике.
В учебной программе 2020 будут инструменты и стратегии, которые являются частью учебной программы, чтобы помочь учащимся развить уверенность, справиться с трудностями и критически мыслить.
Кодирование
В учебной программе 2005 года нет явных ссылок на кодирование.
В учебной программе 2020 , начиная с 1 класса, будут представлены навыки кодирования для улучшения решения проблем и развития навыков владения технологиями.
Финансовая грамотность
В учебном плане 2005 года понятия финансовой грамотности ограничиваются базовым пониманием денег и монет.
В учебной программе 2020 будет обязательное обучение финансовой грамотности в классах с 1 по 8, включая понимание ценности и использования денег с течением времени, как управлять финансовым благополучием и значение составления бюджета.
Краткое изложение основных знаний и навыков
Учебная программа научит учащихся основным математическим навыкам и свяжет их с реальной жизнью, чтобы подготовить учащихся к успеху – сейчас и в будущем.
Новый учебный план описывает знания и навыки, которые учащиеся должны освоить в каждом классе.
 Он организован в пяти областях, где социально-эмоциональные навыки обучения и математические процессы преподаются и оцениваются во всех областях.
Он организован в пяти областях, где социально-эмоциональные навыки обучения и математические процессы преподаются и оцениваются во всех областях.Номер
Учащиеся узнают о мире чисел и развивают основные навыки, включая понимание основных фактов о числах, таких как 5 × 5 = 25, и способы решения математических задач в повседневной жизни.
Студенты будут:
- понимают основные понятия и навыки во всех начальных классах, поэтому они способны выполнять эффективные и точные математические вычисления как в уме, так и на бумаге навыки использования их для различных целей и приложений в реальной жизни
- начать использовать понятия дроби, соответствующие развитию, раньше
Алгебра
Учащиеся изучают закономерности и алгебраические выражения. Учащиеся анализируют ситуации из реальной жизни с помощью кодирования и применяют процесс математического моделирования. Например, в 1 классе учащиеся могут планировать и отслеживать пожертвования класса в продовольственный банк, а к 8 классу учащиеся могут разработать стратегию сокращения отходов в школе.
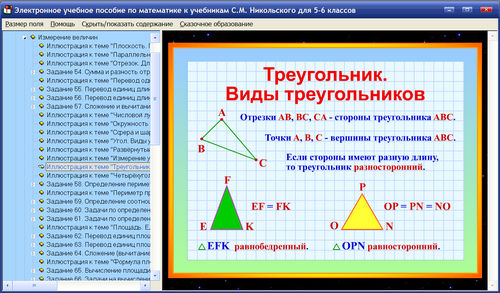
Учащиеся:
- познакомятся с математическим моделированием и узнают, как можно использовать математику для лучшего понимания и прогнозирования реальной жизни
- развивать навыки алгебраического мышления в течение всего класса, поскольку учащиеся работают с шаблонами, отношениями и выражениями
Данные
Учащиеся учатся собирать, систематизировать, отображать и анализировать данные, чтобы приводить убедительные аргументы, обоснованные решения и прогнозы.
Учащиеся:
- научатся быть критическими потребителями данных и тому, как определить, когда данные искажены
- разовьют навыки создания инфографики, чтобы рассказать историю с использованием данных
- установить связь между использованием данных и пониманием вероятности того, что что-то может произойти, например, прогнозы погоды
Пространственное чувство
Учащиеся изучают измерения и геометрию, что помогает им описывать и исследовать окружающий мир.
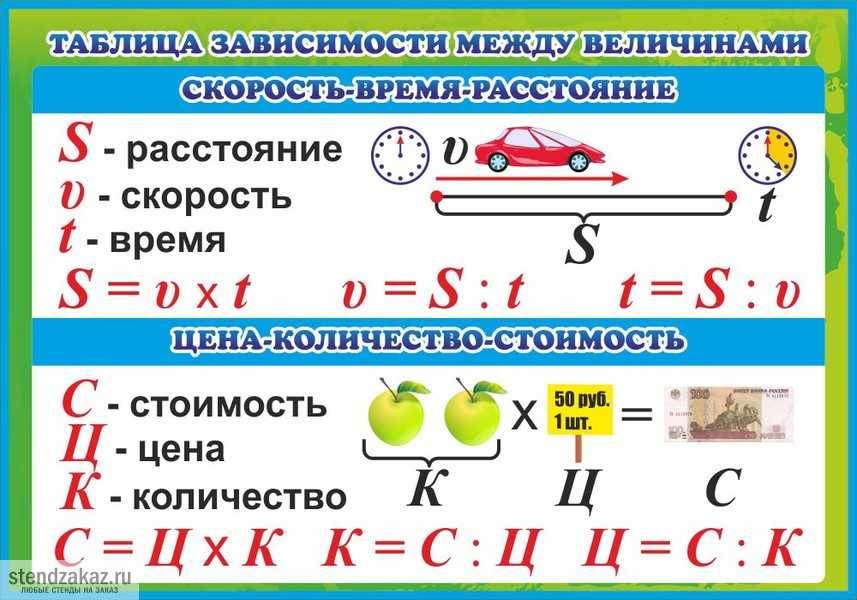
Учащиеся будут:
- устанавливать связи между измерениями и геометрией, чтобы описывать объекты и их отношения к пространству вокруг них
- понимать, как пространственное чувство влияет на графический дизайн, планирование структур и кодирование
- научиться оценивать меры и точно использовать инструменты измерения
- лучше понимать различные единицы измерения, на которые обычно ссылаются в современном цифровом мире, включая большие единицы измерения, такие как терабайты, и очень маленькие единицы измерения, такие как наносекунды
Финансовые грамотность
Учащиеся получат навыки и знания о ценности и использовании денег, о том, как решения влияют на личные финансы, а также разовьют потребительское и гражданское сознание.
Учащиеся:
- узнают, как ответственно управлять финансами, например, составлять бюджет, чтобы сэкономить достаточно денег, чтобы купить что-то, что они хотят, например, книгу, игрушку или видеоигру
- , начнут лучше осознавать себя как потребители и участники местной и более широкой экономической системы
Социально-эмоциональные навыки обучения и математические процессы
Социально-эмоциональные навыки обучения помогают учащимся развивать уверенность, справляться с трудностями и критически мыслить.
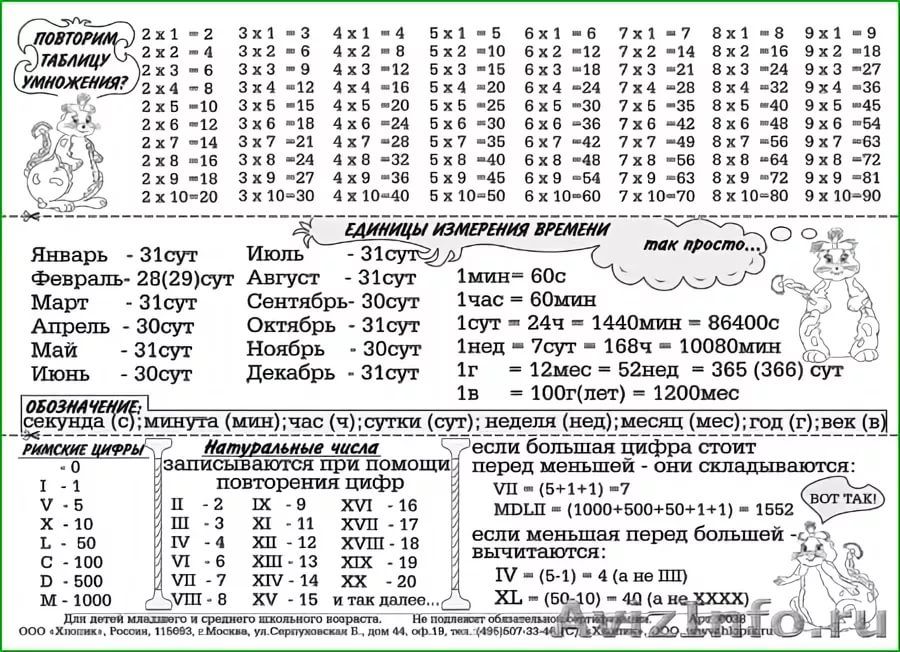 Это обучение отражает текущие исследования и приверженность правительства благополучию учащихся и формированию навыков, чтобы помочь учащимся увидеть себя способными и уверенными в себе учениками по математике.
Это обучение отражает текущие исследования и приверженность правительства благополучию учащихся и формированию навыков, чтобы помочь учащимся увидеть себя способными и уверенными в себе учениками по математике.Учащиеся будут развивать социально-эмоциональные навыки обучения и использовать математические процессы (например, решение задач и общение) в учебной программе по математике. Учащиеся научатся:
- устанавливать связи между математикой и повседневной жизнью, дома и в обществе
- распознавать ошибки и учиться на них
- использовать стратегии, чтобы проявлять изобретательность при решении сложных задач
поддерживать обучение вашего ребенка
Математика повсюду. Вы можете помочь своим детям установить связь между тем, что они изучают в школе, и повседневным опытом дома и в обществе, например:
- покупка чего-либо в магазине
- приготовление пищи дома
- управление деньгами
Вы можете изменить ситуацию и поддержать обучение своего ребенка, если будете положительно отзываться о математике и уверенности в своих силах.
 Узнайте больше о том, как сделать математику частью своего дня.
Узнайте больше о том, как сделать математику частью своего дня.Узнайте, чему учащиеся изучают класс за классом
Ключевые понятия и навыки, такие как сложение, вычитание, деление и умножение, помогают подготовить почву для более продвинутых навыков, таких как работа с десятичными дробями, данными и целыми числами.
Новые области, такие как кодирование, математическое моделирование и финансовая грамотность, помогут студентам получить базовые знания, необходимые для того, чтобы быть компетентными и преуспевать в современном мире. Приоритет их благополучия поможет дать учащимся инструменты и уверенность, чтобы подходить к математике позитивно, получать удовольствие и ценить математику, а также преодолевать любое беспокойство, которое они могут испытывать.
- Класс 1
- Класс 2
- Класс 3
- Класс 4
- Класс 5
- 6-й класс
- 7-й класс
- 8-й класс
1-й класс
Вот некоторые знания и навыки, которыми должны овладеть учащиеся.
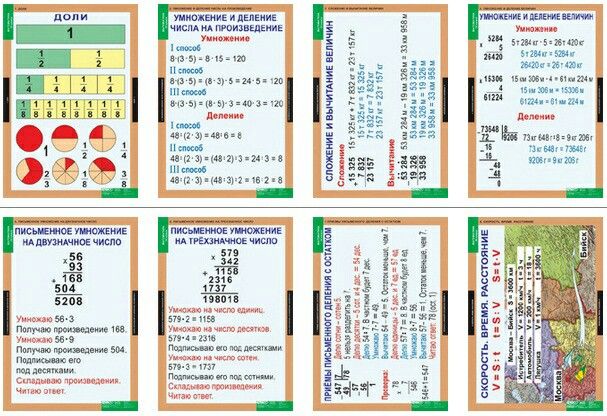
Номер
Учащиеся работают с числами до 50 и начинают понимать, как мы используем числа. Они также знакомятся с идеей дробей в контексте равного распределения вещей.
Алгебра
Учащиеся начинают изучать, как шаблоны можно использовать для прогнозирования. Также начинают прорабатывать мысль о том, что в числовом предложении (например, 2+2=4) обе части должны быть равны друг другу. Эти идеи лежат в основе работы по алгебре в более поздних классах. Студенты начнут писать код, чтобы упорядочить последовательность шагов. Они также познакомятся с математическим моделированием для анализа и создания решений для реальных ситуаций, таких как создание рассадки для классного мероприятия.
Данные
Учащиеся начинают развивать свое понимание данных, отвечая на интересующий их вопрос (например, «Какие животные нравятся моим одноклассникам?»). Они организуют эти данные по категориям, а затем отображают эту информацию, чтобы сделать выводы.
Пространственное чувство
Учащиеся развивают свое пространственное чувство, сравнивая длину, массу и вместимость различных объектов, а также изучая, как организованы календари для описания времени. Они также изучают специальный язык для описания различных форм.
Финансовая грамотность
Учащиеся учатся узнавать канадские монеты и банкноты и сравнивать их стоимость.
Социально-эмоциональные навыки обучения и математические процессы
Учащиеся узнают о положительной мотивации и о том, как использовать стратегии внутреннего диалога, такие как «Я делал это раньше, поэтому я знаю, что могу сделать это снова» в качестве поощрения, что они могут сделать это или поощрять сверстников при подсчете.
2 класс
Вот некоторые знания и навыки, которыми должны овладеть учащиеся.
Номер
Учащиеся работают с числами до 200. Они развивают и применяют свое растущее понимание чисел различными способами, например, решают задачи на сложение и вычитание.
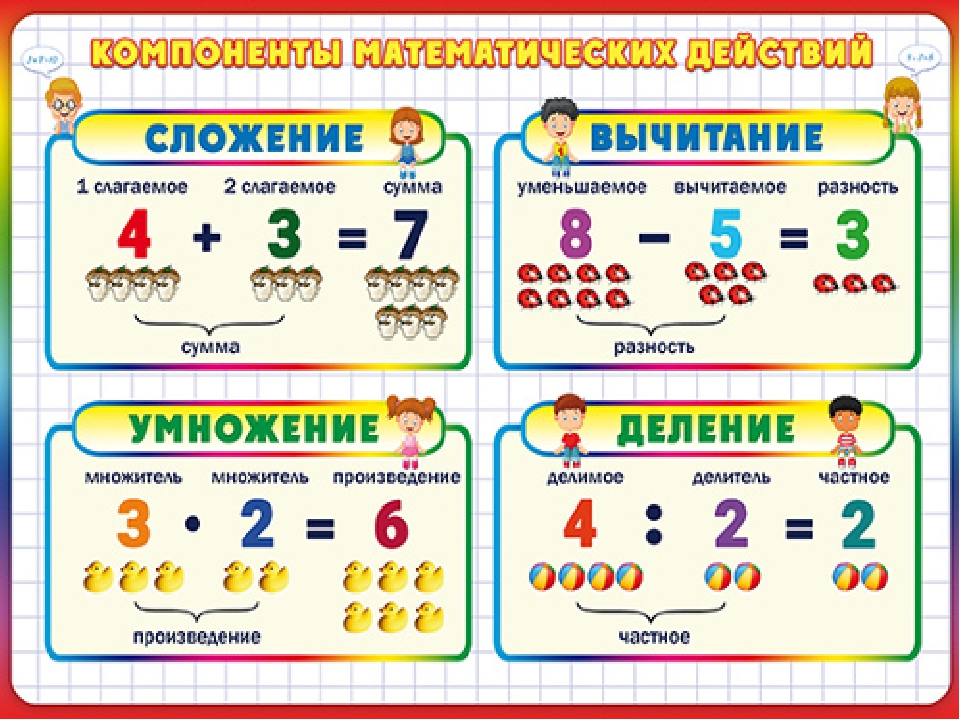 Они продолжают работать с дробями в контексте равного обмена вещами.
Они продолжают работать с дробями в контексте равного обмена вещами.Алгебра
Учащиеся используют фигуры и числа, чтобы продолжить изучение шаблонов и способов их расширения. Они также узнают о равенстве, корректируя пары операторов сложения и вычитания, чтобы сделать их равными. Учащиеся будут разрабатывать код для одновременного перемещения нескольких объектов из одного места в другое по сетке. Они также будут использовать математическое моделирование для анализа и создания решений для реальных ситуаций, таких как определение стоимости обеденной программы.
Данные
Учащиеся продолжают развивать свое понимание данных, изучая способы сбора, организации, отображения и интерпретации более сложных данных. Они узнают о вероятности наступления событий и о том, как это можно использовать для принятия обоснованных решений (например, «Если завтра будет дождь, я должен надеть резиновые сапоги»).
Пространственное чувство
Учащиеся продолжают развивать свое пространственное чувство, учась визуализировать, как выглядят различные формы, когда их переворачивают или разбирают.
 Они учатся распознавать и описывать более сложные формы и создавать простые карты знакомых мест. Такие инструменты, как линейки, будут использоваться для точного измерения длины объектов, а таймеры и часы — для измерения того, сколько времени прошло.
Они учатся распознавать и описывать более сложные формы и создавать простые карты знакомых мест. Такие инструменты, как линейки, будут использоваться для точного измерения длины объектов, а таймеры и часы — для измерения того, сколько времени прошло.Финансовая грамотность
Учащиеся опираются на свое понимание того, что деньги имеют ценность, и определяют различные способы представления одной и той же суммы денег. Например, как разные комбинации монет могут составить до 1 доллара, и как различные комбинации луни, мультяшек и банкнот могут составить до 100 долларов.
Социально-эмоциональные навыки обучения и математические процессы
Учащиеся практикуют критическое и творческое мышление. Например, в области финансовой грамотности учащиеся учатся разбивать деньги на разные номиналы и выбирать различные инструменты и стратегии, такие как составление списков различных комбинаций денег, рисование изображений различных групп и использование манипулятивных средств для разбивки сумм по-разному.

3 класс
Вот некоторые знания и навыки, которыми должны овладеть учащиеся.
Номер
Учащиеся работают с числами до 1000 и учатся разбивать числа разными способами. Например, как число 225 можно описать как 200 + 20 + 5 или 2 сотни, 2 десятка и 5 единиц. Учащиеся узнают, что дроби могут быть представлены более чем одним способом — например, половину можно представить как две четверти. Умножение вводится с использованием строк и столбцов, и ожидается, что учащиеся знают x 2, x 5 и x 10.
Алгебра
Учащиеся учатся определять и описывать, что повторяется в шаблоне, например, когда определенное событие происходит каждый понедельник или когда числовая последовательность увеличивается на 2 каждый раз. Учащиеся начинают находить равные уравнения умножения и деления, такие как 3 × 4 и 6 × 2. Учащиеся будут писать код для выполнения повторяющейся операции, например повторяющегося числового шаблона. Они также будут использовать математическое моделирование для анализа и создания возможных решений для реальных ситуаций, таких как сбор средств на благотворительность.

Данные
Учащиеся продолжают развивать свое понимание данных. Они узнают больше о способах сбора, организации, отображения и интерпретации данных, включающих большие числа. Они начинают использовать масштабы на своих графиках, чтобы представлять большие наборы данных, и использовать средние значения для сравнения данных.
Пространственное чувство
Учащиеся продолжают развивать свое пространственное чувство, узнавая и описывая трехмерные объекты и представляя, как эти объекты будут выглядеть, если их разобрать или перевернуть. Учащиеся продолжают измерять длину и знакомятся с измерением веса объекта или того, сколько он вмещает. Они измеряют площадь и сравнивают ее с длиной, а также учатся определять время как по цифровым, так и по аналоговым часам.
Финансовая грамотность
Учащиеся продолжают развивать свое понимание денег, вычисляя сдачу, необходимую для простых транзакций с целыми суммами в долларах.
Социально-эмоциональные навыки обучения и математические процессы
Учащиеся определяют и учатся управлять эмоциями, которые они могут испытывать, такими как гордость, замешательство, страх и волнение.
 Например, в алгебре они создают и выполняют код, представляющий математическую ситуацию.
Например, в алгебре они создают и выполняют код, представляющий математическую ситуацию.4 класс
Вот некоторые знания и навыки, которые должны получить учащиеся.
Номер
Учащиеся работают с числами до 10 000 и знакомятся с десятичными дробями. Они узнают, как десятичные числа используются в реальной жизни, например, при измерении температуры человека термометром, а также при выполнении и записи точных измерений. Учащиеся начнут делить двух- и трехзначные целые числа на однозначные целые числа, и ожидается, что они будут знать факты умножения от 1 x 1 до 10 x 10. Они также начнут решать задачи, требующие более одной операции с целыми числами. .
Алгебра
Учащиеся расширяют свои знания о построении паттернов по мере того, как они начинают классифицировать паттерны как повторяющиеся или увеличивающиеся. Они также начинают определять значения, которые делают алгебраические утверждения верными — например, если 91 662 n 91 663 + 3 = 10, то 91 662 n 91 663 должно быть равно 7.
 Учащиеся учатся писать и читать код для создания геометрических фигур. Они также будут использовать процесс моделирования для анализа и создания решений для реальных жизненных ситуаций, таких как сбор денег через прогулку.
Учащиеся учатся писать и читать код для создания геометрических фигур. Они также будут использовать процесс моделирования для анализа и создания решений для реальных жизненных ситуаций, таких как сбор денег через прогулку.Данные
Развитие понимания данных продолжается по мере того, как учащиеся собирают, систематизируют и отображают два или более набора данных, используя таблицы частот и гистограммы. Студенты начинают учиться создавать инфографику, чтобы они могли рассказать историю о данных.
Пространственное чувство
Учащиеся изучают характеристики и свойства прямоугольника, одной из самых распространенных форм в нашей повседневной жизни. Учащиеся узнают, как определить площадь прямоугольника и взаимосвязь между различными единицами метрической системы ̶ системы измерения, используемой в Канаде и большей части мира.
Финансовая грамотность
Учащиеся узнают, что существуют различные способы оплаты товаров и услуг.
 Студенты также узнают, как потребители определяют, является ли товар хорошим соотношением цены и качества.
Студенты также узнают, как потребители определяют, является ли товар хорошим соотношением цены и качества.Социально-эмоциональные навыки обучения и математические процессы
Чтобы узнать о положительной мотивации, учащиеся будут использовать различные инструменты и стратегии в пространственном смысле, поскольку они пробуют различные нестандартные единицы измерения площади столешницы, корректируя их по мере необходимости. они идут, чтобы найти решение.
5 класс
Вот некоторые знания и навыки, которыми должны овладеть учащиеся.
Номер
Учащиеся продолжают работать с числами до 100 000. Учащиеся знакомятся с процентами и продолжают развивать свое понимание десятичных дробей и дробей. Учащиеся знакомятся со сложением и вычитанием дробей с одинаковым знаменателем. Ожидается, что учащиеся знают факты умножения от 0 × 0 до 12 × 12. Они также решают задачи, включающие более одной операции с целыми и десятичными числами.
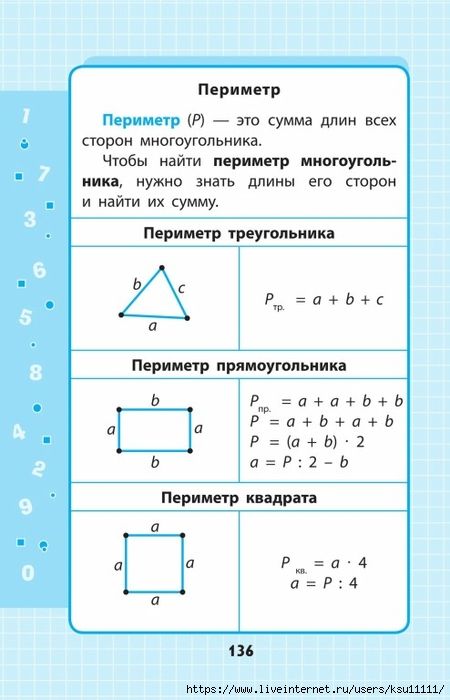
Алгебра
Учащиеся продолжают классифицировать модели как повторяющиеся, растущие и уменьшающиеся. Учащиеся начинают писать и решать алгебраические уравнения с целыми числами, например 3 + x = 24 – 5 . Учащиеся применяют свое понимание умножения и отношений для создания и выполнения кода для шаблонов, которые растут. Они используют процесс математического моделирования для решения задач, взятых из реальной жизни, таких как создание дизайна школьной игровой площадки и расчет стоимости выбранных ими игровых конструкций.
Данные
Учащиеся узнают о важности использования различных методов выборки для получения «хороших» данных. Они создают инфографику и учатся определять, когда графики вводят в заблуждение. Студенты начинают использовать эксперименты, чтобы понять концепцию вероятности.
Пространственное чувство
Развитие пространственного чувства продолжается по мере изучения треугольника. Учащиеся изучают характеристики и свойства различных видов треугольников, включая их углы и размеры.
 Продолжается работа по пониманию и использованию метрической системы для измерения длины, площади, массы и емкости, а также для преобразования более крупных единиц в более мелкие.
Продолжается работа по пониманию и использованию метрической системы для измерения длины, площади, массы и емкости, а также для преобразования более крупных единиц в более мелкие.Финансовая грамотность
Учащиеся узнают о различных способах перевода денег между людьми и организациями, таких как электронные переводы и чеки. Они рассчитывают общую стоимость и сдачу, необходимую для операций с наличными, включая товары, оцененные в долларах и центах, используя ментальную арифметику и другие стратегии. Учащиеся узнают, как определить наилучшую стоимость товара, например, пять яблок за 1 доллар США против трех яблок за 75 центов. Учащиеся готовят базовые бюджеты и узнают о понятиях кредита и долга.
Социально-эмоциональные навыки обучения и математические процессы
Учащиеся продолжают развивать навыки здоровых отношений, работая с числами. Учащиеся играют с одноклассниками в игры, в которых используются дроби, десятичные числа и целые числа.
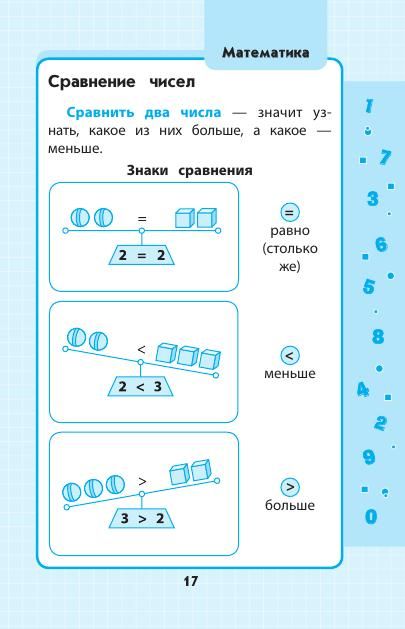 Они также узнают, как поддерживать позитивное взаимодействие и проявлять терпение по отношению к другим, поскольку ученикам требуется разное количество времени, чтобы найти ответ, когда наступает их очередь.
Они также узнают, как поддерживать позитивное взаимодействие и проявлять терпение по отношению к другим, поскольку ученикам требуется разное количество времени, чтобы найти ответ, когда наступает их очередь.6 класс
Вот некоторые знания и навыки, которыми должны овладеть учащиеся.
Число
Помимо работы с числами до 1 миллиона, учащиеся знакомятся с целыми числами, такими как -2, -1, 0, 1, 2. Они изучают правила делимости на 2, 3, 4. , 5, 6, 8, 9 и 10. Например, число делится на 5, если оно оканчивается на 5 или 0. Расширение операционных навыков включает деление целого числа на дробь или смешанное число, например 2½. Учащиеся также решают задачи, включающие более одной операции и использование целых чисел, десятичных дробей и дробей.
Алгебра
Учащиеся продолжают работать с закономерностями и начинают определять закономерности, которые растут с постоянной скоростью. Например, если кто-то едет со скоростью 100 километров в час, пройденное расстояние увеличивается на 100 километров за каждый час.
 Они решают алгебраические выражения, включающие целые числа и десятичные доли, и алгебраические уравнения, включающие несколько членов, например 2x + 3x = 5. Учащиеся используют код для решения задач, связанных с оптимизацией, таких как нахождение максимальной площади для заданного периметра. Они также используют процесс математического моделирования для решения задач, взятых из реальной жизни, таких как поиск нескольких различных способов максимизации игровой площади в дизайне игровой площадки и расчет стоимости каждого из них.
Они решают алгебраические выражения, включающие целые числа и десятичные доли, и алгебраические уравнения, включающие несколько членов, например 2x + 3x = 5. Учащиеся используют код для решения задач, связанных с оптимизацией, таких как нахождение максимальной площади для заданного периметра. Они также используют процесс математического моделирования для решения задач, взятых из реальной жизни, таких как поиск нескольких различных способов максимизации игровой площади в дизайне игровой площадки и расчет стоимости каждого из них.Данные
Учащиеся учатся различать дискретные данные, такие как количество учащихся, и непрерывные данные, такие как количество осадков в сантиметрах. Они могут выбирать, как отображать эти различные типы данных, включая использование ломаных графиков для отображения изменений во времени. Кроме того, студенты изучают различные способы описания вероятности. Например, шанс выиграть приз на школьной ярмарке развлечений составляет один к четырём, или вероятность дождя завтра составляет 40%.

Пространственное чувство
Продолжается развитие пространственного чувства с упором на четырехсторонние формы. Учащиеся изучают характеристики и свойства различных видов четырехгранных фигур и находят их площади. Они также строят трехмерные конструкции и учатся вычислять площадь поверхности. Студенты учатся переводить из одних единиц в другие в метрической системе. Они также сосредоточены на расширении своих возможностей измерения углов.
Финансовая грамотность
Исследованы преимущества и недостатки использования различных способов оплаты товаров и услуг. Учащиеся исследуют различные типы финансовых целей, выявляют и описывают факторы, которые могут повлиять на эти цели, и намечают шаги для их достижения. Учащиеся объясняют концепцию процентных ставок и определяют процентные ставки и сборы, предлагаемые банками и другими финансовыми учреждениями. Они также узнают, как торговля, кредитование, заимствование и пожертвование — это разные способы распределения ресурсов.

Социально-эмоциональные навыки обучения и математические процессы
Учащиеся продолжают углублять свое самоощущение. Учащиеся отслеживают различные аспекты, влияющие на их физическое и психическое здоровье, такие как количество шагов, которые они делают каждый день, количество минут экранного времени или самочувствие после физической активности. Они используют графики и инструменты визуализации данных, чтобы предоставить информацию для размышлений и обучения.
7 класс
Вот некоторые знания и навыки, которыми должны овладеть учащиеся.
Номер
Работая с числами до 1 миллиарда, учащиеся знакомятся с рациональными числами, такими как совершенные квадраты и квадратные корни. Ожидается, что они будут знать факты умножения от 0 × 0 до 12 × 12. Учащиеся начинают генерировать множители (например, множители 6 равны 1 и 6, 2 и 3), множители (например, кратные 6 равны 6, 12, 24 и т. д.), а также складывать и вычитать дроби, создавая эквивалентные дроби.
 Учащиеся исследуют задачи, требующие сложения и вычитания целых чисел (например, определение общего балла или изменение температуры).
Учащиеся исследуют задачи, требующие сложения и вычитания целых чисел (например, определение общего балла или изменение температуры).Алгебра
Учащиеся связывают свое понимание закономерностей целых чисел с закономерностями, включающими десятичные дроби. Они продолжают решать уравнения, включающие несколько членов, целые числа и десятичные числа, например 2x + 5 = 3x – 1 . Учащиеся пишут код для имитации вероятностного эксперимента и определения различных результатов в игре. Они также используют математическое моделирование, чтобы получить представление о реальных жизненных ситуациях, например, определить наилучшие варианты сбора средств для местной благотворительной организации.
Данные
Учащиеся узнают, как использовать круговые диаграммы для представления данных. Они начинают развивать критический взгляд на анализ данных, изучая графики, которые могут вводить в заблуждение. Учащиеся также определяют разницу между вероятностью независимых событий и зависимых событий.
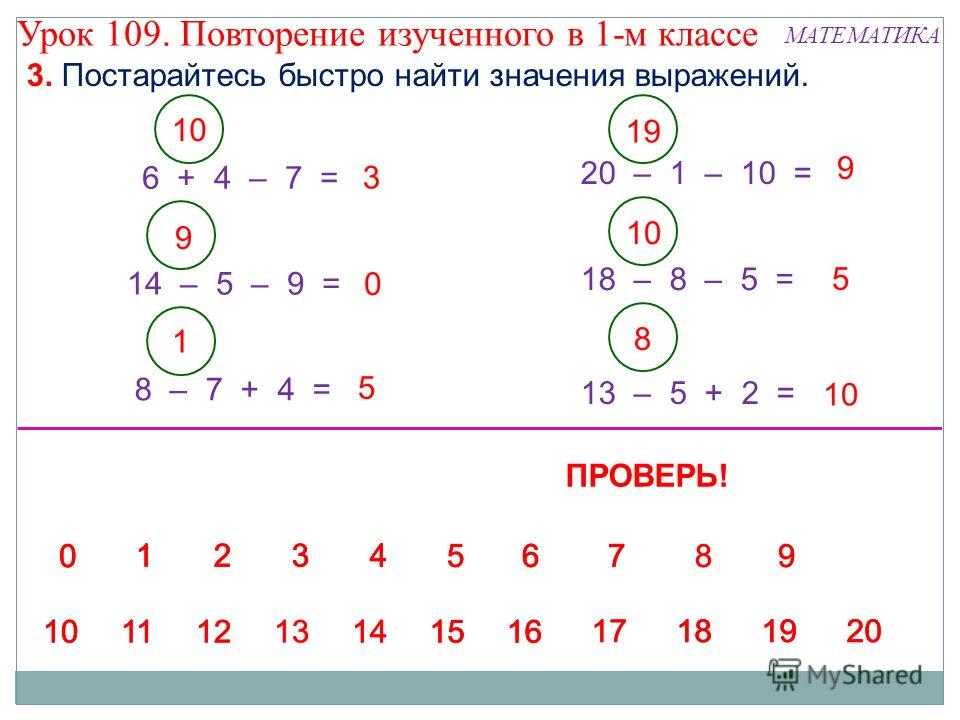 Например, как изменится вероятность, если из мешка вынуть два шарика с возвратом или без возврата.
Например, как изменится вероятность, если из мешка вынуть два шарика с возвратом или без возврата.Пространственное чувство
Учащиеся продолжают развивать пространственное чувство, изучая круг. Студенты учатся измерять различные аспекты кругов, такие как длина окружности, диаметр, радиус и площадь. Они используют эти и другие измерения для определения площади поверхности и объема цилиндров и других трехмерных объектов. Учащиеся также узнают, как расширять — увеличивать и уменьшать — форму.
Финансовая грамотность
Учащиеся начинают понимать, что международные валюты имеют другую стоимость по сравнению с канадскими долларами, и понимают, как работают обменные курсы. Они развивают понимание того, как планировать и достигать финансовых целей. Студенты строят свои знания о том, как процентные ставки могут повлиять на сбережения и инвестиции. Они также узнают о стоимости заимствования и сравнивают процентные ставки и сборы для различных типов счетов и кредитов, чтобы стать более информированными потребителями.

Социально-эмоциональные навыки обучения и математические процессы
Учащиеся учатся справляться со стрессом и решать сложные задачи. Студенты учатся разбивать задачу на более мелкие части, составлять план и выполнять ее шаг за шагом.
8 класс
Вот некоторые знания и навыки, которые должны получить учащиеся.
Номер
Учащиеся используют экспоненциальное представление, такое как 5,46 × 10 6 легче понимать, представлять и сравнивать очень большие и малые числа, что часто требуется в науке. Учащиеся взаимозаменяемо используют дроби, десятичные числа и проценты и должны уметь запоминать квадратные числа до 144 и их квадратные корни. Учащиеся решают задачи, связанные с пропорциями (например, определение процентного увеличения или уменьшения посещаемости шоу), целыми числами, дробями, десятичными знаками, целыми числами и показателями степени.
Алгебра
Учащиеся продолжают развивать свое понимание шаблонов, в том числе тех, которые связаны с целыми числами.
 Они используют алгебраическую запись, например, с = d/t , для представления отношения между скоростью, расстоянием и временем. Они решают алгебраические уравнения, включающие несколько терминов, целые числа и десятичные числа. Учащиеся пишут код для создания линии или кривой, попадающей между наибольшим числом точек данных. Они также используют моделирование для реальных жизненных ситуаций, таких как прогнозирование будущих сборов средств на основе средств, собранных в ходе прошлых сборов средств.
Они используют алгебраическую запись, например, с = d/t , для представления отношения между скоростью, расстоянием и временем. Они решают алгебраические уравнения, включающие несколько терминов, целые числа и десятичные числа. Учащиеся пишут код для создания линии или кривой, попадающей между наибольшим числом точек данных. Они также используют моделирование для реальных жизненных ситуаций, таких как прогнозирование будущих сборов средств на основе средств, собранных в ходе прошлых сборов средств.Данные
Учащиеся продолжают совершенствовать свои навыки работы с данными. Они анализируют данные, представленные более сложными способами, например, в виде точечных диаграмм, показывающих взаимосвязь между двумя переменными. Кроме того, учащиеся продолжают углублять свое понимание вероятности, сравнивая результаты более сложных экспериментов.
Пространственное чувство
Учащиеся продолжают развивать пространственное чувство, изучая прямоугольные треугольники.
 Они узнают, что если длины двух сторон известны, то длину третьей можно вычислить, не измеряя ее, используя теорию Пифагора. Учащиеся узнают, как вычислять неизвестные углы, применяя угловые свойства пересекающихся и параллельных линий. Учащиеся также строят свое понимание очень больших единиц, таких как терабайт, и очень маленьких единиц, таких как наносекунды, которые используются в современных технологиях.
Они узнают, что если длины двух сторон известны, то длину третьей можно вычислить, не измеряя ее, используя теорию Пифагора. Учащиеся узнают, как вычислять неизвестные углы, применяя угловые свойства пересекающихся и параллельных линий. Учащиеся также строят свое понимание очень больших единиц, таких как терабайт, и очень маленьких единиц, таких как наносекунды, которые используются в современных технологиях.Финансовая грамотность
Учащиеся учатся составлять план достижения финансовых целей и определять способы поддержания сбалансированного бюджета. Учащиеся сравнивают различные способы, с помощью которых потребители могут получить отдачу от своих денег при тратах, например, используя программы вознаграждений или пользуясь преимуществами распродаж. Учащиеся изучают концепции простых и сложных процентов с помощью технологий (например, программы для работы с электронными таблицами) и объясняют, как проценты влияют на долгосрочное финансовое планирование.
Социально-эмоциональные навыки обучения и математические процессы
Учащиеся продолжают развивать навыки здоровых взаимоотношений.
 Они будут использовать данные в инфографике, чтобы общаться и рассказывать истории, а также повышать осведомленность о других. Это поможет им понять, что у них общего со сверстниками и что делает разные группы уникальными.
Они будут использовать данные в инфографике, чтобы общаться и рассказывать истории, а также повышать осведомленность о других. Это поможет им понять, что у них общего со сверстниками и что делает разные группы уникальными.Как мы разработали новую учебную программу
Эта новая учебная программа была разработана на основе результатов общественных консультаций Онтарио в 2018 году с родителями, педагогами и заинтересованными сторонами относительно направлений деятельности, которые помогут улучшить успеваемость учащихся.
Учебная программа также основана на обширных исследованиях под руководством доктора Кристин Сууртамм, заместителя декана по исследованиям и профессиональному развитию и профессора математического образования педагогического факультета Оттавского университета, при участии ученых и экспертов в области образования в область изучения математики.
Чтобы понять современные подходы к обучению математике, мы изучили тенденции в регионах с высокими достижениями и рассмотрели передовой опыт в области математического образования.

 2 гр.
2 гр.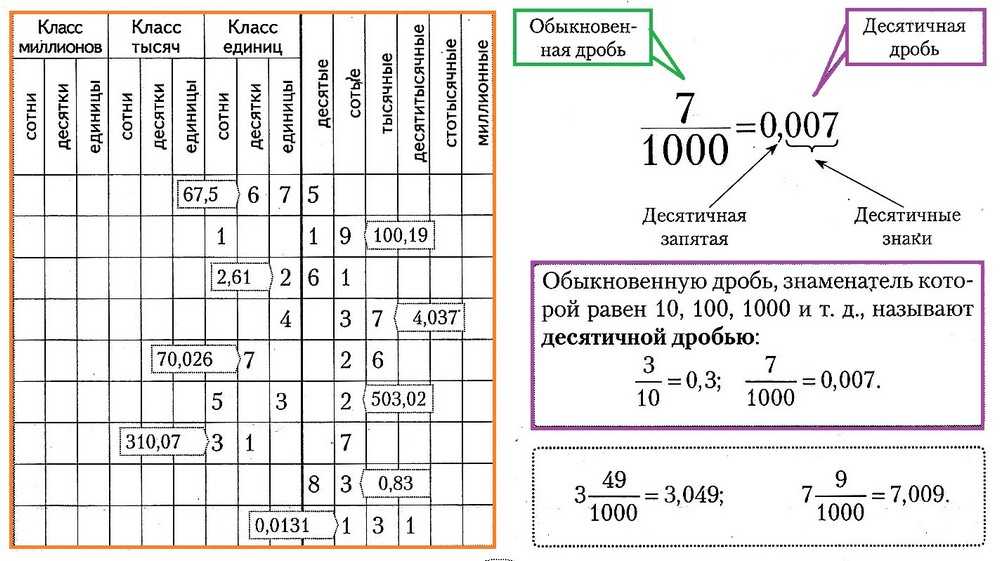 0 ед. = 40
0 ед. = 40 0 ед. = 10
0 ед. = 10 8 ед. = 18 = 10 + 8
8 ед. = 18 = 10 + 8 Простейшие геометрические фигуры – это отрезок, луч, ломаная линия.
Простейшие геометрические фигуры – это отрезок, луч, ломаная линия.


 На сколько больше грибов у Тани, чем у Саши?
На сколько больше грибов у Тани, чем у Саши? ru :
ru : ru :
ru : ru :
ru : ru :
ru : ru :
ru : ru :
ru :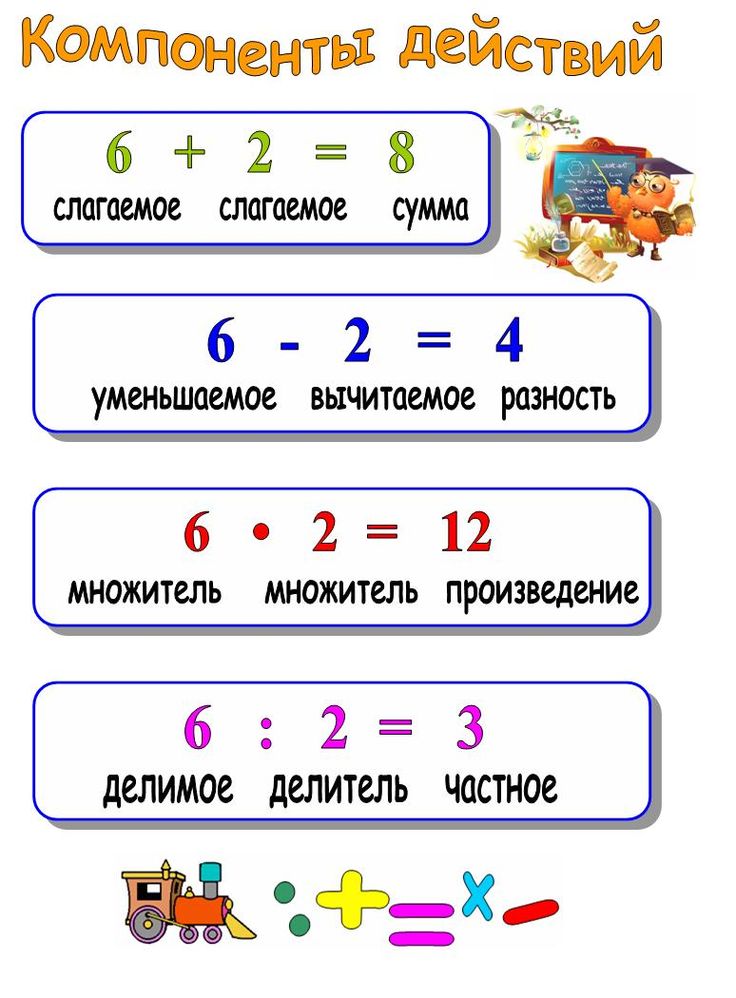 Она может обозначать единицы, десятки, сотни и т.д. Это десятичная система счисления.
Она может обозначать единицы, десятки, сотни и т.д. Это десятичная система счисления.
 В ней при записи числа применяются буквы латинского алфавита.
В ней при записи числа применяются буквы латинского алфавита. 

 От перестановки слагаемых, значение суммы не меняется. a + b = b + a
От перестановки слагаемых, значение суммы не меняется. a + b = b + a Для того, чтобы умножить сумму на число, надо это число умножить на каждое слагаемое, а произведения сложить. (a + b) ▪ c = a ▪ c + b ▪ c
Для того, чтобы умножить сумму на число, надо это число умножить на каждое слагаемое, а произведения сложить. (a + b) ▪ c = a ▪ c + b ▪ c


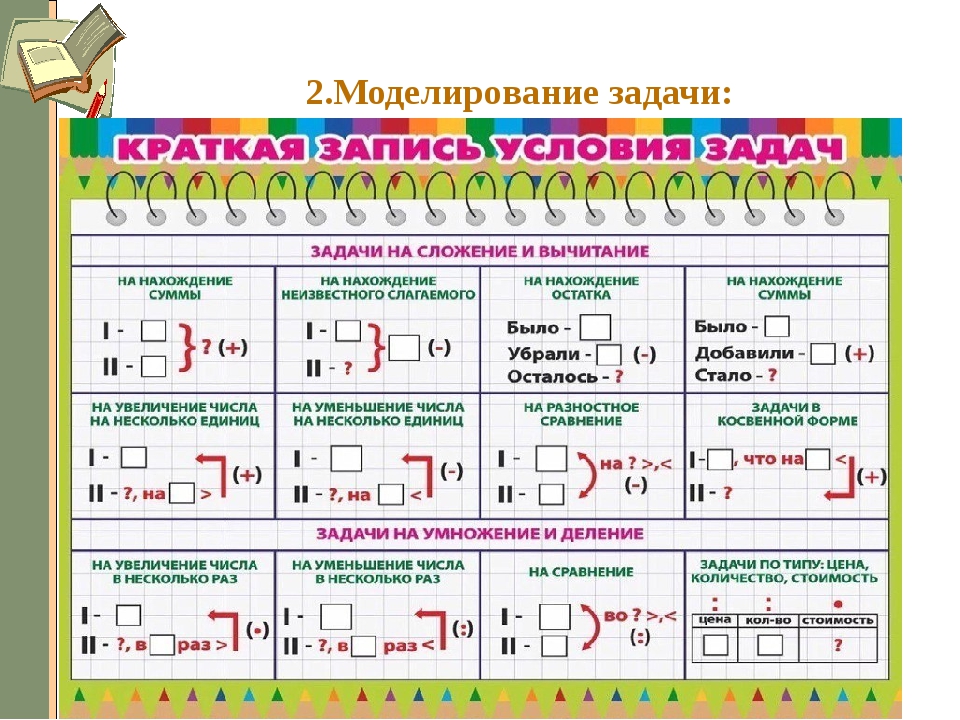
 Если в уравнении навычитание неизвестное число стоит на втором месте, то уравнение решается прямым действием – вычитанием.
Если в уравнении навычитание неизвестное число стоит на втором месте, то уравнение решается прямым действием – вычитанием. Для этого надо определить порядок действий в уравнении.
Для этого надо определить порядок действий в уравнении.
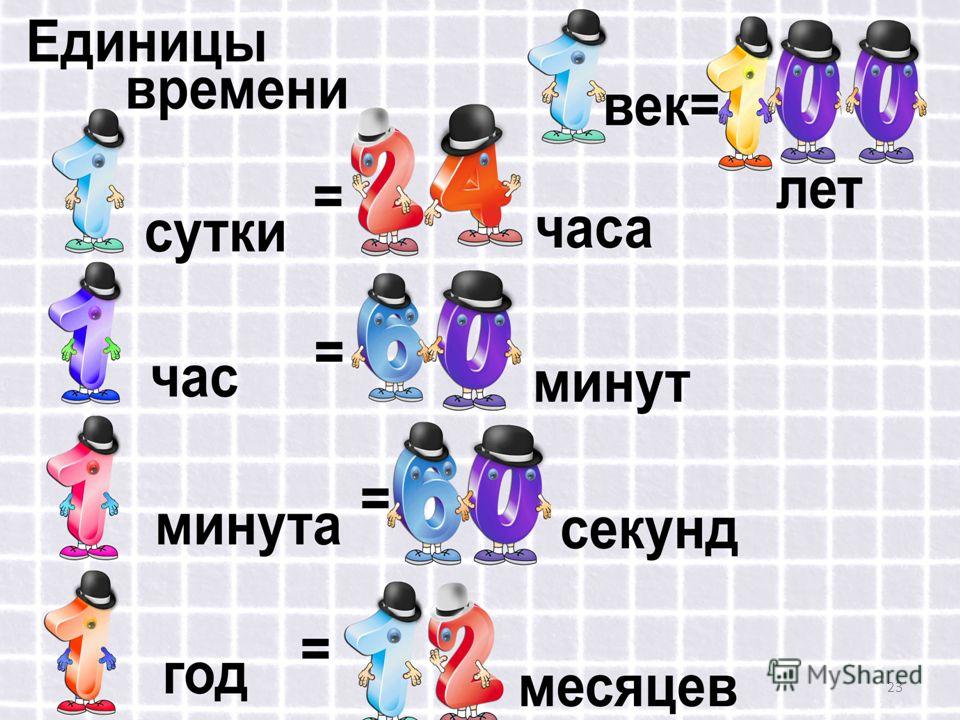 Например, 1 км = 1000м, тогда 4 км = 4000м. и 56000м= 56 км.
Например, 1 км = 1000м, тогда 4 км = 4000м. и 56000м= 56 км. Это задачи на сравнения.
Это задачи на сравнения.
 находим S2 = V2 ·• t
находим S2 = V2 ·• t