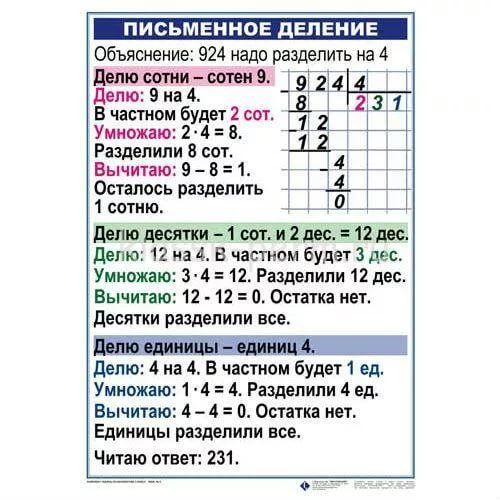
Правила математики 2 класс в таблицах и схемах распечатать: Математика в таблицах и схемах | Учебно-методическое пособие по математике (2 класс) на тему:

Основные правила по математике 2 класс | Учебно-методический материал по математике (2 класс) на тему:

	Вопрос	Правило	Пример
1	Компоненты сложения (как называются числа при сложении):	Слагаемое  +  слагаемое =  сумма	2 + 3 = 5
2	Как найти неизвестное слагаемое?	Чтобы найти неизвестное слагаемое надо из суммы вычесть известное слагаемое	? + 3 = 5 5 – 3 = 2
3	Компоненты вычитания (как называются числа при вычитании):	Уменьшаемое – вычитаемое = разность	7 – 4 = 3
4	Как найти уменьшаемое?	Чтобы найти уменьшаемое надо к разности прибавить вычитаемое.	? – 4 = 3 4 + 3 = 7
5	Как найти неизвестное вычитаемое?	Чтобы найти вычитаемое надо из уменьшаемого вычесть разность	7 – ? = 3 7 – 3 = 4
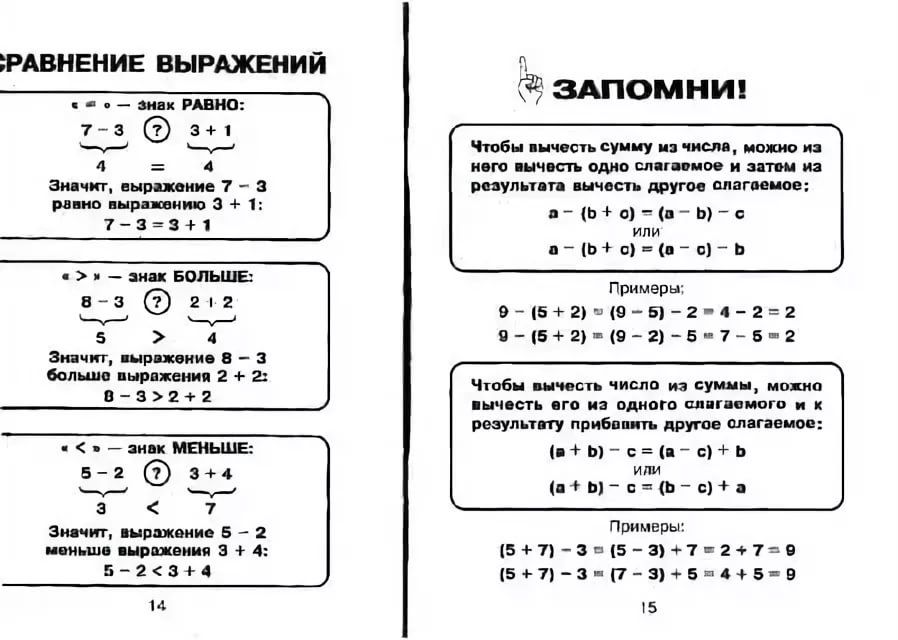
6	Как узнать,  на сколько одно число больше или меньше другого?	Чтобы узнать,  на сколько одно число больше или меньше другого надо из большего вычесть меньшее.	На сколько 8 больше 5? 8 – 5 = 3
7	Как уменьшить число?	Уменьшить  – действие вычитание	Уменьши 9 на 3 9 – 3 = 6
8	Как увеличить число?	Увеличить – действие сложение	Увеличь 2 на 6 2 + 6 = 8
9	Однозначные числа	Числа, которые записывают одной цифрой, называют  однозначными   (содержат только разряд единиц).	2, 3, 6. 8
10	Двузначные числа	Числа, которые записывают двумя цифрами, называют двузначными. (содержат  разряд десятков и разряд единиц)	24   =   2 десятка 4 единицы 50   =   5 десятков 0 единиц
11	Какие числа называют круглыми?	У круглых двузначных чисел в  разряде единиц записывают      0	10, 20, 30, 40, 50, 60, 70, 80, 90
12	Как к двузначному числу прибавить  двузначное число?	Чтобы сложить двузначные числа надо к десяткам прибавить десятки, к единицам – единицы	23 + 35 = 58 2 дес + 3 дес = 5  дес 3 ед + 5 ед = 8 ед 5 дес 8 ед = 58
13	Как из двузначного числа вычесть двузначное число?	Чтобы вычесть из  двузначного числа двузначное число надо из десятков вычесть десятки, из единиц – единицы	32 – 21 = 11 3 дес – 2 дес = 1  дес 2 ед – 1 ед = 1 ед 1 дес 1 ед = 11

Основные правила математики 6 класс(кратко).

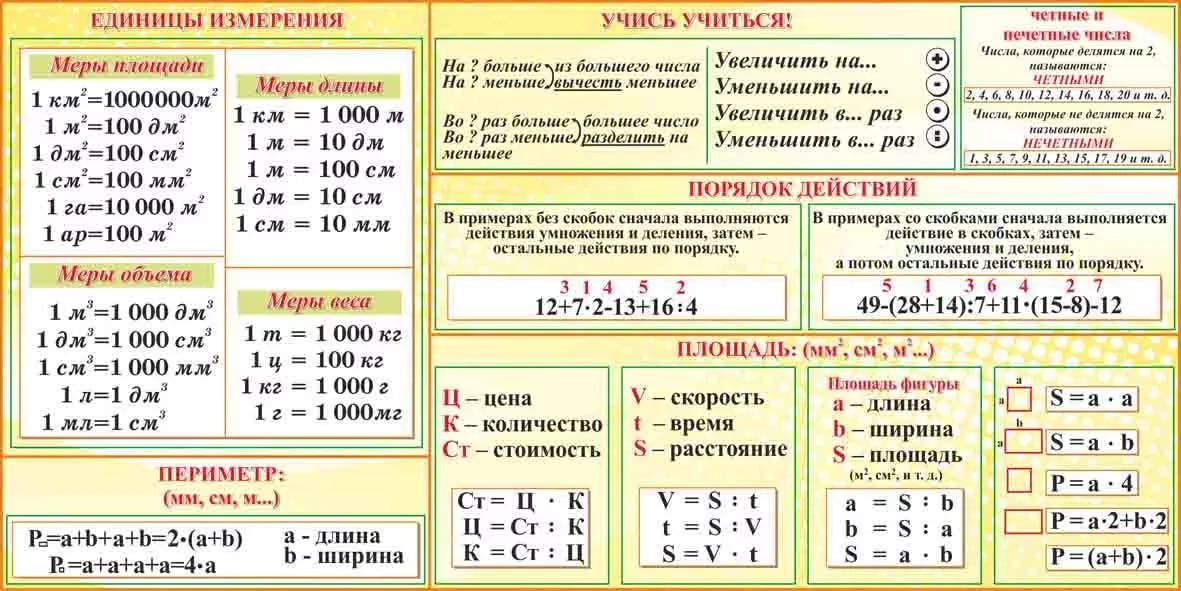
Основные правила математики 6 класс(кратко).

Содержание

• Делимость натуральных чисел
• Простые и составные числа
• Признаки делимости натуральных чисел
  
• Основное свойство дроби
• Сокращение дробей
• Приведение дробей к наименьшему общему знаменателю
• Целые числа. Рациональные числа
• Модуль числа
• Сложение и вычитание дробей
• Сложение и вычитание рациональных чисел
• Умножение. Свойства умножения
  
• Умножение обыкновенных дробей
• Умножение рациональных чисел

• Деление обыкновенных дробей
• Деление рациональных чисел
• Нахождение дроби от числа
• Нахождение числа по его дроби
• Степень числа
• Числовые и буквенные выражения
• Приведение подобных слагаемых
• Раскрытие скобок
• Свойства уравнений
• Отношения
• Пропорции
• Основное свойство пропорции
• Процентное отношение двух чисел
• Прямая и обратная пропорциональная зависимость

Делимость натуральных чисел

Если натуральное число делится нацело на натуральное чис­ло , то число   называют кратным числа , число — делителем числа

. Для любого натурального числа   каждое из чисел

a · 1, a · 2, a · 3,…

является кратным числа .

Наименьшим делителем любого натурального числа  является число , а наибольшим — само число .

Среди чисел, кратных , наибольшего нет, а наименьшее есть — это само число .

Если каждое из чисел и делится нацело на число ,то и сумма также делится нацело на число .

Если число  делится нацело на число ,  а число не делится на­цело на число , то сумма также не делится нацело на число .

Простые и составные числа

Натуральное число называют простым, если оно имеет только два разных делителя: единицу и само это число. Натуральное число, имеющее более двух делителей, называют составным.

Любое составное число можно представить в виде произведения простых чисел, то есть разложить на простые множители.

Если наибольший общий делитель двух натуральных чисел равен 1, то их называют взаимно простыми.

Признаки делимости натуральных чисел

Если запись натурального числа оканчивается цифрой 0, то это число делится нацело на 10.

Если запись натурального числа оканчивается любой цифрой, отличной от 0, то это число не делится нацело на 10.

Если натуральное число разделить на 10, то остаток равен числу, записанному последней цифрой этого числа.

Если запись натурального числа оканчивается четной цифрой, то это число делится нацело на 2.

Если запись натурального числа оканчивается нечетной цифрой, то это число не делится нацело на 2.

Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на 5.

Если запись натурального числа оканчивается любой цифрой, отличной от цифр 0 и 5, то это число не делится нацело на 5.

Если сумма цифр натурального числа делится нацело на 9, то и само число делится нацело на 9.

Если сумма цифр натурального числа не делится нацело на 9, то и само число не делится нацело на 9.

Если сумма цифр натурального числа делится нацело на 3, то и само число делится нацело на 3.

Если сумма цифр натурального числа не делится нацело на 3, то и само число не делится нацело на 3.

Основное свойство дроби

Если числитель и знаменатель данной дроби умножить на одно и то же натуральное число, то получим дробь, равную данной:

ab = a · nb · n

Если числитель и знаменатель данной дроби разделить на их общий делитель (или на одно и то же натуральное число), то получим дробь, равную данной:

a : nb : n = ab 

Сокращение дробей

Деление числителя и знаменателя дроби на их общий делитель, отличный от 1, называют сокращением дроби.

Дробь, числитель и знаменатель которой — взаимно простые числа, называют несократимой.

Если сократить дробь на наибольший общий делитель числителя и знаменателя, то получим несократимую дробь.

Приведение дробей к наименьшему общему знаменателю

Чтобы привести дроби к наименьшему общему знаменателю, надо:

• найти наименьший общий знаменатель данных дробей;
• найти дополнительные множители для каждой из дробей, разделив общий знаменатель на знаменатели данных дробей;
• умножить числитель и знаменатель каждой дроби на ее до­полнительный множитель.

Целые числа. Рациональные числа

Все натуральные числа, противоположные им числа и число 0 называют целыми числами.
Натуральные числа называют целыми положительными числами. Числа -1, -2, -3, … называют целыми отрицательными числами.
Объединив натуральные числа с целыми отрицательными и нулем, получим целые числа.
Объединив целые числа с дробными, получим рациональные числа.

Модуль числа

Модулем числа  называют расстояние от начала отсчета до точки, изображающей это число на координатной прямой.
Модуль числа обозначают так:

a

(читают: «модуль a»).
Модуль положительного числа равен этому числу; модуль отри­цательного числа равен числу, противоположному данному;

a = a, a≥0—a, a<0

Модуль числа принимает только неотрицательные значения. Модули противоположных чисел равны:

a = —a

Сложение и вычитание дробей

Чтобы сложить две дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же.
Чтобы найти разность двух дробей с одинаковыми знаменате­лями, надо из числителя уменьшаемого вычесть числитель вычи­таемого, а знаменатель оставить тот же.
Чтобы сложить (вычесть) две дроби с разными знаменателями, надо привести их к общему знаменателю, а потом применить пра­вило сложения (вычитания) дробей с одинаковыми знаменателями.

Сложение и вычитание рациональных чисел

Чтобы сложить два числа с разными знаками, надо:

• найти модули слагаемых;
• из большего модуля вычесть меньший модуль;
• перед полученным числом поставить знак слагаемого с боль­шим модулем.

Чтобы сложить два отрицательных числа, надо:

• найти модули слагаемых;
• сложить модули слагаемых;
• перед полученным числом поставить знак «-».

Сумма двух противоположных чисел равна нулю:

—a+a=0 или a—a=0

Для любого рационального числа

a+0 = 0+a = a

Чтобы найти разность двух чисел можно

к уменьшаемому при­бавить число, противоположное вычитаемому.

Умножение. Свойства умножения

Произведением числа на натуральное число не равное 1, называют сумму, состоящую из слагаемых, каждое из которых равно а:

a · b = a +a +a+…+a⏟b

Если один из двух множителей равен 1, то произведение равно второму множителю:

m · 1 = 1 · m = m

Если один из множителей равен нулю, то произведение равно нулю:

m · 0 = 0 · m = 0

Если произведение равно нулю, то хотя бы один из множителей равен нулю.

Умножение обыкновенных дробей

Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения:

ab·n=a·nb

Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

ab · cd = a · cb · d

Чтобы умножить смешанные числа, надо сначала записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

Умножение рациональных чисел

Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным произведением поставить знак «-».

Чтобы умножить два отрицательных числа, надо умножить их модули.

Для любого рационального числа :

a · (—1) = —a

Если произведение •   — положительное, то числа и имеют одинаковые знаки;

Если произведение • — отрицательное, то числа и имеют раз­ные знаки.

Деление обыкновенных дробей

Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:

ab : cd = ab · dc

Деление рациональных чисел

Чтобы найти частное двух чисел с разными знаками, надо мо­дуль делимого разделить на модуль делителя и перед полученным числом поставить знак «-».
Чтобы найти частное двух отрицательных чисел, надо модуль делимого разделить на модуль делителя.

Нахождение дроби от числа

Чтобы найти проценты от числа, можно представить проценты в виде дроби и умножить число на эту дробь.

Нахождение числа по его дроби

Чтобы найти число по его процентам, можно представить про­центы в виде дроби и разделить значение процентов на эту дробь.
[ads2]

Степень числа

Степенью числа с натуральным показателем , большим , на­зывают произведение множителей, каждый из которых равен :

an=a · a · a ·…·a⏟n

Число  при этом называют основанием степени.

Степенью числа с показателем называют само число

a1=a

Вторую степень числа называют также квадратом числа. Напри­мер, запись читают: « в квадрате». Третью степень называют кубом числа, а запись читают: « в кубе».

Если в числовое выражение входит степень, то сначала выпол­няют возведение в степень, а затем производят другие действия.

Числовые и буквенные выражения

Запись, составленную из чисел, знаков арифметических действий и скобок, называют числовым выражением. Запись, составленную из чисел, букв, знаков арифметических действий и скобок, называют буквенным выражением.

Приведение подобных слагаемых

Чтобы привести подобные слагаемые, надо сложить их коэффици­енты и полученный результат умножить на общую буквенную часть.

Раскрытие скобок

Если перед скобками стоит знак «-», то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, изменить на противоположные.
Если перед скобками стоит знак « + », то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, оставить без изменений.

Свойства уравнений

• Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, имеющее те же корни, что и данное.
• Если данное уравнение не имеет корней, то, прибавив к обе­им его частям одно и то же число, получим уравнение, тоже не имеющее корней.
• Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то по­лучим уравнение, имеющее те же корни, что и данное.
• Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.

Отношения

• Частное двух чисел и , не равных нулю, еще называют от­ношением чисел и , или отношением числа к числу .
• Отношение положительных чисел и показывает, во сколько раз число больше числа , или какую часть число составляет число .
• Отношение не изменится, если его члены умножить или раз­делить на одно и то же число, не равное нулю.

Пропорции

Равенство двух отношений называют пропорцией. В буквенном виде пропорцию можно записать так:

a : b =c : d или ab = cd

Числа и называют крайними членами пропорции, а чис­ла и — средними членами пропорции.

Основное свойство пропорции

Произведение крайних членов пропорции равно произведению ее средних членов:

ab = cd ⇒ ad = bc

Если , , и числа, не равные нулю, и • = • , то отношения

ab  и cd

могут образовывать пропорцию

ab = cd

Процентное отношение двух чисел

Процентное отношение двух чисел — это их отношение, вы­раженное в процентах. Оно показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отно­шение умножить на 100 и к результату дописать знак процента.

Прямая и обратная пропорциональная зависимость

Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Если величины и обратно пропорциональны, то их соответ­ствующие значения удовлетворяют равенству

y = kx

,  где  — число, постоянное для данных величин.

Данная информация составлена на базе УМК  А.Г.Мерзляк, В.Б.Полонский, М.С. Якир

Таблица умножения

для печати — Etsy.de

Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии.

Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.

ГЕРМАНИЯ Найдите уникальные предметы со всего мира, которые доставляются в Германию

(651 соответствующий результат)

карт.