Математика 4 класс без ответов: Математика 4 класс Моро
ГДЗ по математике 4 класс учебник Моро, Бантова 2 часть
- Тип: ГДЗ, Решебник.
- Автор: Моро М. И., Волкова С. И., Бантова М. А.
- Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
❤️️Ответ к странице 21. Математика 4 класс учебник 2 часть. Авторы: М.И. Моро, М.А. Бантова.
Решебник – страница 21Готовое домашнее задание
Номер 10.
Начерти окружность, проведи в ней диаметр и соедини концы диаметра с любой точкой окружности. Проверь, какого вида треугольник получился.
Ответ:
Получился прямоугольный треугольник.
Номер 11.
Вычисли значение выражения а : b, если: 1) а = 7020 и b = 6; 2) а = 17418 и b = 3.
Ответ:
Номер 12.
Два мальчика одновременно побежали навстречу друг другу по спортивной дорожке, длина которой 100 м.
Ответ:
1) 4 ∙ 10 = 40 (м) – пробежал первый мальчик.
2) 100 − 40 = 60 (м) – пробежал второй мальчик.
3) 60 : 10 = 6 (м/с)
II способ:
1) 100 : 10 = 10 (м/с) – скорость сближения.
2) 10 – 4 = 6 (м/с)
Ответ: 6 м/с скорость второго мальчика.
Номер 13.
Товарный поезд прошёл 315 км. Он был в пути до остановки 3 ч и после остановки 4 ч. Сколько километров прошёл поезд до остановки и сколько после, если он шёл с одинаковой скоростью?
Ответ:
1) 3 + 4 = 7 (ч) – поезд был в пути. 2) 315 : 7 = 45 (км/ч) – скорость поезда. 3) 45 ∙ 3 = 135 (км) – прошел до остановки. 4) 315 − 135 = 180 (км) – прошел после остановки. Ответ: 135 км, 180 км.
Номер 14.
Отрезок длиной 90 мм разделили сначала на 3 равные части, а затем каждую из них разделили на 2 равные части. На сколько равных частей разделили весь отрезок? Чему равна длина одной шестой части данного отрезка? Сделай по задаче чертёж и реши её.
На сколько равных частей разделили весь отрезок? Чему равна длина одной шестой части данного отрезка? Сделай по задаче чертёж и реши её.
Ответ:
Отрезок разделили на 6 равных частей. 90 : 6 = 15 (мм) – длина одной шестой части данного отрезка.
Номер 15.
Молочный завод отправил в магазин 56 ящиков сливочного масла, по 20 кг в каждом. За день продали одну седьмую часть этого масла. Сколько килограммов масла осталось?
Ответ:
Всего – 56 ящ. по 20 кг Продали – 1/7 часть Осталось – ? кг 1) 20 ∙ 56 = 1120 (кг) – отправили масла. 2) 1120 : 7 = 160 (кг) – продали. 3) 1120 − 160 = 960 (кг) – осталось. Ответ: 960 кг.
Номер 16.
Расстояние между городом и зимовкой 150 км. Из города к зимовке выехали аэросани и двигались со скоростью 60 км/ч. В это же время навстречу им из зимовки по той же дороге пошёл лыжник со скоростью 15 км/ч. На каком расстоянии от зимовки он встретил аэросани?
На каком расстоянии от зимовки он встретил аэросани?
Ответ:
1) 60 + 15 = 75 (км/ч) – скорость сближения. 2) 150 : 75 = 2 (ч) – время пути. 3) 15 ∙ 2 = 30 (км) – на таком расстоянии от зимовки лыжник встретил аэросани. Ответ: 30 километров.
Номер 17.
Найди ошибки в вычислениях и реши правильно.
Ответ:
1751 : 5 = 35 (ост. 1) решено неверно, так как первое неполное делимое 17, в частном должно быть 3 цифры.
1983 : 9 = 22 (ост. 3) решено неверно, так как первое неполное делимое 19, в частном должно быть 3 цифры.
40202 : 6 = 670 (ост. 2) решено неверно, так как первое неполное делимое 40, в частном должно быть 4 цифры.
Правильное решение:
Номер 18.
Ответ:
32340 : 10 = 3234 56400 : 100 = 564
Номер 19.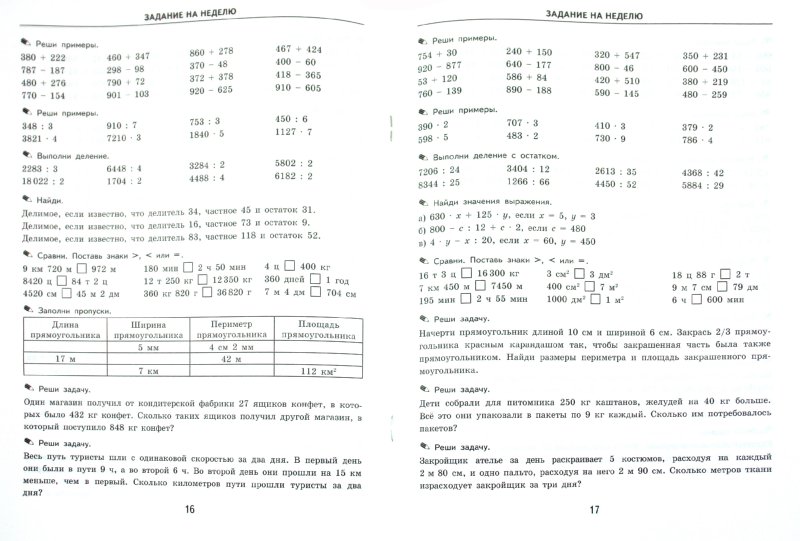
Запиши 5 чисел, каждое из которых делится без остатка и на 5, и на 9.
Ответ:
Ответ: 45, 90, 135, 180, 225.
Задание на полях страницы
Начерти узор
Ответ:
Рейтинг
Выберите другую страницу
| Учебник Моро | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 |
|---|
Ваше сообщение отправлено!
+
ВПР 4 класс математика
ВПР 4 класс математика- Математика
Официальная демоверсия ВПР 2023 по математике для 4 класса опубликована на сайте Федерального института оценки качества образования (ФИОКО).
- Математика
Весной 2022 года в очередной раз прошли всероссийские проверочные работы по математике в 4 классах.
- Математика
Официальная демоверсия ВПР 2022 по математике для 4 класса опубликована на сайте Федерального института оценки качества образования (ФИОКО).
- Математика
Весной 2021 года в проходят ВПР по математике в 4 классах в штатном порядке для всех школ страны.
- Математика
Демоверсию ВПР 2021 по математике для 4 класса опубликовал официальный сайт Федерального института оценки качества образования.
- Математика
ВПР 2020. Математика 4 класс. Варианты с ответами (реальные варианты заданий с критериями оценивания и ответами).
Математика 4 класс. Варианты с ответами (реальные варианты заданий с критериями оценивания и ответами).
- Математика
Тренировочная работа в формате ВПР по математике 4 класс 2019-2020 гг. от СтатГрад.
- Математика
Официальный сайт ФИОКО опубликовал демоверсии ВПР 2020 для 4 класса по математике. Расписание ВПР 2020
- Математика
ВПР 2019. Математика. 4 класс. Варианты с ответами (реальные варианты заданий с критериями оценивания и ответами)
- Математика
24 апреля 2018 года проведены всероссийские проверочные работы ВПР по математике в 4 классах.
Проверочная работа по математике включает 11 заданий, на ее выполнение отводится 45 минут. При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором.
Доступны новые образцы ВПР 2019 года по математике 4 класс
- Математика
ВПР в 4 классе по математике в 2019 году будет проходить в апреле. Ещё есть время подготовиться к написанию этой сложной проверочной работы. В нашей статье мы дадим ответы на основные вопросы родителей и учителей при выполнении ВПР по математике в 4 классе.
- Демоверсия ВПР 2019 по математике 4 класс
- Демоверсия ВПР по математике 4 класс 2018 год
- Задания по ВПР 4 класс математика 2018 – 2015 год
- Варианты ВПР по математике для 4 класса + ответы 2017 год
Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи в разделе контакты
Событие – Неразгаданная К-12 | MathPickle
Нерешенная K-12 Введение в конференцию и процесс выбора 13 задач – по одной для каждого класса K-12.
Детский сад – не окончательный отбор. Это оказалось нерешенной задачей 1 класса.
Детский сад — окончательный выбор Окончательный выбор для детского сада — это нерешенная проблема, поставленная в 1977 году Krishnamoorthy & Deo.
1 класс – не окончательный выбор Выбранная задача 1 класса – задача о жуке в среднем верхнем ряду.
2 класс – окончательный выбор Sum-Free Partitions by Isaii Schur, 1916
3 класс – не окончательный выбор Вторая задача на этом видео (1967) Graceful. . Игра Aggression, несомненно, станет победителем 3-го класса на предстоящей конференции Math Games K-12.
. Игра Aggression, несомненно, станет победителем 3-го класса на предстоящей конференции Math Games K-12.
4 класс — окончательный выбор Гипотеза Коллатца, 1937
5 класс — не окончательный выбор Окончательный выбор — нерешенная проблема, поставленная в 2013 году Брайаном Конри и его коллегами. о нетранзитивных костях. Вы увидите эту проблему, описанную в видео для 11 класса ниже.
6 класс – не окончательный отбор Гипотеза о простых числах-близнецах Евклида, 250 г. до н.э. является окончательным выбором. Опыт работы в классе будет основан на статье Полиа: Эвристические рассуждения в теории чисел. Вы можете увидеть гипотезу о простых числах-близнецах, описанную в видео для 7-го класса.
7 класс — не окончательный выбор. Задача Стюарта Андерсона о мозаике прямоугольника, 2013 г., является окончательным выбором.
8 класс – не окончательный выбор Гипотеза Эрдёша-Штрауса является окончательным выбором. На конференции Джошуа Цукер придумал такой способ представления проблемы, который был опубликован здесь, в New York Times.
9 класс – не окончательный выбор Катакомбы с простыми числами Уильяма Полсена, 2000 является окончательным выбором.
класс 10 -Задача окончательного выбора встроенный квадратный, Otto Toeplitz, 1911
Уровень 110006-Нефинальный отбор. Окончательный отбор-Markov numbers от 1897.
. не окончательный выбор Окончательный выбор — задача Стивена Кука P=NP из 1971 года.
Лиор Пахтер из Беркли самостоятельно решает нерешенные задачи в классе. Посмотрите на его идеи здесь.
Вот pdf-файл, в котором собраны нерешенные проблемы-победители.
Легенда о «неразрешимой математической задаче»
Требовать:
Учащийся принял примеры нерешенных статистических задач за домашнее задание и решил их.
Рейтинг:
Правда
Об этом рейтинге
Легенда о «неразрешимой математической задаче» сочетает в себе одну из величайших академических фантазий об исполнении желаний — студент не только доказывает, что он самый умный в своем классе, но и превосходит своего профессора и всех остальных ученых в своей области — с мотив «позитивного мышления», который встречается в других городских легендах: когда люди свободны в достижении целей, не стесненных предполагаемыми ограничениями того, что они могут достичь, они просто могут совершать некоторые экстраординарные подвиги, сочетая врожденный талант и тяжелую работу:
Молодой студент колледжа усердно работал над курсом математики для старших классов, опасаясь, что не сможет сдать экзамен. В ночь перед финалом он так долго учился, что проспал утро контрольной.
Когда он вбежал в класс с опозданием на несколько минут, он обнаружил на доске три уравнения.
Первые два прошли довольно легко, а третий казался невозможным. Он лихорадочно работал над этим, пока — всего за десять минут до дедлайна — не нашел работающий метод и не закончил задачи, как только было назначено время.
Студент сдал контрольную работу и ушел. В тот же вечер ему позвонил профессор. — Ты понимаешь, что ты сделал сегодня на контрольной? — крикнул он студенту.
«О нет, — подумал студент. Должно быть, я не сразу понял проблемы.
“Вы должны были решить только первые две задачи”, – объяснил профессор. «Это последнее уравнение было примером уравнения, которое математики со времен Эйнштейна безуспешно пытались решить. Я обсуждал его с классом перед началом теста. И вы только что решили его!»
И эта конкретная версия тем более интересна, что основана на реальном происшествии!
Однажды в 1939 году Джордж Бернард Данциг, докторант Калифорнийского университета в Беркли, опоздал на занятие по статистике для выпускников и обнаружил две задачи, написанные на доске. Не зная, что это примеры «нерешенных» статистических задач, он принял их за часть домашнего задания, записал и решил. (Уравнения, за которые взялся Данциг, более точно описываются не как неразрешимые проблемы, а скорее как недоказанные статистические теоремы, для которых он разработал доказательства.)
Не зная, что это примеры «нерешенных» статистических задач, он принял их за часть домашнего задания, записал и решил. (Уравнения, за которые взялся Данциг, более точно описываются не как неразрешимые проблемы, а скорее как недоказанные статистические теоремы, для которых он разработал доказательства.)
Шесть недель спустя профессор статистики Данцига уведомил его, что он подготовил одно из двух своих «домашних» доказательств для публикации, а Данциг был признан соавтором второй статьи несколько лет спустя, когда другой математик независимо разработал такое же решение для вторая проблема.
Джордж Данциг рассказал о своем подвиге в интервью 1986 года для College Mathematics Journal :
Это произошло потому, что во время моего первого года в Беркли я однажды опоздал на один из занятий [Ежи] Неймана. На доске было две задачи, которые, как я полагал, были заданы для домашнего задания. Я их скопировал. Через несколько дней я извинился перед Нейманом за то, что так долго делал домашнюю работу — задачи оказались немного сложнее, чем обычно.
Я спросил его, хочет ли он еще этого. Он сказал мне бросить его на стол. Я сделал это неохотно, потому что его стол был завален такой кучей бумаг, что я боялся, что моя домашняя работа потеряется там навсегда. Примерно шесть недель спустя, в одно воскресное утро около восьми часов, [моя жена] Энн и я проснулись от того, что кто-то стучал в нашу входную дверь. Это был Нейман. Он вбежал с бумагами в руках, весь взволнованный: «Я только что написал предисловие к одной из ваших статей. Прочтите ее, чтобы я мог сразу же отправить ее для публикации». В течение минуты я понятия не имел, о чем он говорит. Короче говоря, задачи на доске, которые я решил, думая, что это домашнее задание, на самом деле были двумя известными нерешенными задачами по статистике. Это было первое подозрение, что в них есть что-то особенное.
Год спустя, когда я начал беспокоиться о теме диссертации, Нейман только пожал плечами и сказал мне завернуть две задачи в папку, и он примет их как мою диссертацию.
Однако вторая из двух задач не была опубликована до окончания Второй мировой войны.
Это произошло так. Примерно в 1950 году я получил письмо от Абрахама Вальда, в котором были приложены окончательные корректуры его статьи, готовящейся к печати в «Анналах математической статистики» № . Кто-то только что указал ему, что основной результат в его статье совпадает со второй “домашней” задачей, решенной в моей диссертации. Я написал в ответ, предлагая опубликовать совместно. Он просто вставил мое имя как соавтора в гранку.
Доктор Данциг также объяснил, как его история перешла в разряд городских легенд:
На днях, когда я совершал раннюю утреннюю прогулку, меня окликнул Дон Кнут, когда он проезжал мимо на своем велосипеде. Он коллега по Стэнфорду. Он остановился и сказал: «Эй, Джордж, я недавно был в Индиане и слышал проповедь о тебе в церкви. Ты знаешь, что ты оказываешь влияние на христиан средней Америки?» Я посмотрел на него, пораженный. «После проповеди, — продолжал он, — подошел служитель и спросил меня, знаю ли я Джорджа Данцига в Стэнфорде, потому что так звали человека, о котором шла его проповедь».
Происхождение проповеди этого священника можно проследить до другого лютеранского священника, преподобного Шулера [так в оригинале] из Хрустального собора в Лос-Анджелесе. Он поделился со мной своими идеями о позитивном мышлении, а я рассказал ему свою историю о домашних заданиях и своей диссертации. Несколько месяцев спустя я получил от него письмо с просьбой разрешить включить мою историю в книгу, которую он писал о силе позитивного мышления. Опубликованная версия Шулера была немного искажена и преувеличена, но по существу верна. Мораль его проповеди была такова: если бы я знал, что задача не является домашним заданием, а на самом деле является двумя известными нерешенными задачами по статистике, я, вероятно, не думал бы положительно, впал бы в уныние и никогда бы не решил их.
Версия рассказа Данцига, опубликованная христианским телеевангелистом Робертом Шуллером, содержала много приукрашиваний и дезинформации, которые с тех пор распространялись в формах, похожих на городские легенды, таких как та, что цитируется в начале этой страницы: домашнего задания на «выпускной экзамен» с десятью задачами (восемь из которых были реальными, а две из них «неразрешимыми»), утверждал, что «даже Эйнштейн не смог раскрыть секреты» двух дополнительных задач, и ошибочно утверждал, что задача Данцига профессор был настолько впечатлен, что «дал Данцигу работу своим ассистентом, и с тех пор Данциг работает в Стэнфорде».
Джордж Данциг (сам сын математика) получил степень бакалавра в Мэрилендском университете в 1936 году и степень магистра в Мичиганском университете в 1937 году, прежде чем получить докторскую степень (прерванную Второй мировой войной) в Калифорнийском университете в Беркли в 1946 году. Позже он работал в ВВС, в 1952 году занял должность математика-исследователя в корпорации RAND, в 1960 году стал профессором исследования операций в Беркли, а в 1966 году поступил на факультет Стэнфордского университета, где преподавал и публиковался в качестве профессора операций. исследование до 1990-е. В 1975 году доктор Данциг был награжден Национальной медалью науки президентом Джеральдом Фордом.
Джордж Данциг скончался в своем доме в Стэнфорде в возрасте 90 лет 13 мая 2005 года.
Наблюдения: Эта легенда используется в качестве основы сюжета в фильме 1997 года Умница Уилл Хантинг . Кроме того, в одной из первых сцен фильма 1999 года « Рашмор, » главный герой мечтает решить неразрешимый вопрос и получить всеобщее одобрение.
