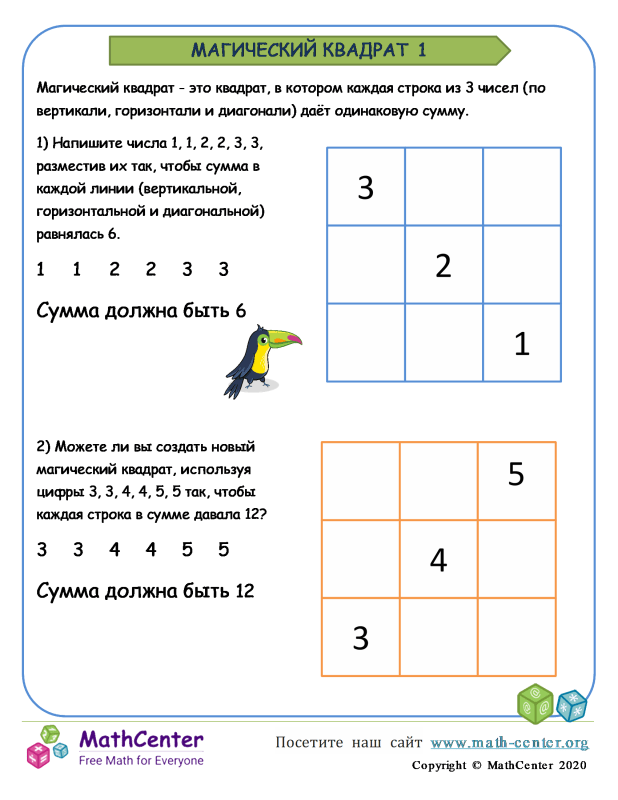
Магический квадрат 1 класс задания: Презентация по математике на тему “Магические квадраты”
Внеклассное занятие по теме “Магические квадраты – магия или наука”. 6‒8-й класс
Внеклассное мероприятие по математике для учащихся 6-8 классов найдет место при проведении предметной недели. Призвано способствовать повышению интереса к предмету математики, развитию мышления, познавательной и творческой активности учащихся. Построение магических квадратов является интересным и увлекательным занятием и одновременно служит хорошей гимнастикой для ума, а так же способствует большему интеллектуальному развитию учащихся. Использование групповой формы работы позволяет учащимся ставить вопросы, решать проблемы, распределять роли и сотрудничать, убеждать других, отвечать за себя.
Цели:
- пробуждение и развитие устойчивого познавательного интереса учащихся к предмету;
- формирование умение использовать знания в нестандартной ситуации;
- формирование товарищеского доброжелательного отношения к членам команды и соперникам,
- знакомство с различными магическими квадратами, их свойствами.
– Милостливый государь, я составил магический квадрат 21-го порядка!
– А я – рамочный 23-го!
(из переписки Баше де Мезириака и Рене Декарта)
Вступительное слово учителя
Среди занимательных задач теории чисел в число интереснейших входят те, которые связаны с магическими (волшебными) квадратами. Учение о них занимало значительное место в древние времена. Магический квадрат – древнекитайского происхождения. Согласно легенде, во времена правления императора Ю (ок. 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы, и эти знаки известны под названием ло-шу. В XI веке о магических квадратах узнали в Индии, а затем в Японии. В XVI веке Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7-ми планет. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы.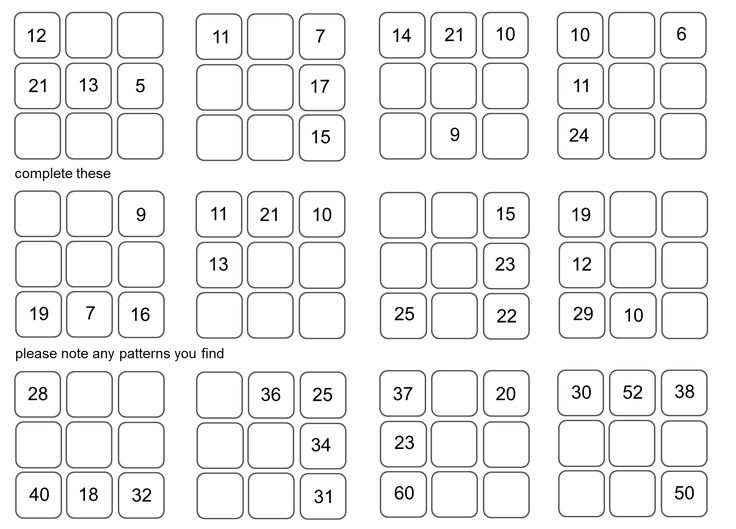
В работах XVII века магические квадраты выступили в роли математических развлечений.
Обратимся к Большой Советской энциклопедии: “Магический квадрат — квадрат, разделённый на равное число n столбцов и строк, со вписанными в полученные клетки первыми n2 натуральными числами, которые дают в сумме по каждому столбцу, каждой строке и двум большим диагоналям одно и то же число».
Разминка
Вставь недостающие цифры (цифры в квадрате от 1 до 9) в магический квадрат.
Своеобразная мозаика чисел действительно придает магическому квадрату волшебную силу произведения искусства. Этот факт привлек не только математиков, но и художников. В начале VI века выдающийся немецкий художник, математик, астроном и географ Альберт Дюрер (1471–1528), в одной из своих гравюр, названной «Меланхолия» (1514), за фигурой крылатой женщины воспроизвел магический квадрат из 16 клеток.
Рассмотрим внимательнее, изображенный магический квадрат. Интересно, что в двух средних клетках нижней строки указано время ее написания (1514 год).
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
В этом магическом квадрате таится немало загадочных свойств.
Задание 1. Работа в группах – 10 минут.
Найти как можно больше свойств магического квадрата.
Проверка и обсуждение.
Свойство 1. Сумма чисел в каждой строке, каждом столбце и на каждой из двух диагоналей одна и та же. Она равна 34.
Свойство 2. Сумма чисел, расположенных по углам квадрата, также равна 34.
Свойство 3. Суммы чисел в каждом из четырехклеточных квадратов, примыкающих к вершинам данного квадрата, и в таком же центральном квадрате из 4 клеток – одинаковы, каждая равна 34.
Свойство 4. В любой строке квадрата имеется два рядом стоящих числа, с суммами 15 и 19 соответственно.
При желании можно отыскать и другие свойства квадрата Дюрера.
Задание 2. Работа в группах – до 10 минут.
Клетки квадрата 4×4 пронумеровали так, что клетка в правом нижнем углу получила номер 1, а все остальные получили разные номера от 2 до 16. Оказалось, что суммы номеров клеток каждой строки, каждого столбца, а также каждой из двух диагоналей квадрата одинаковы («магический» квадрат).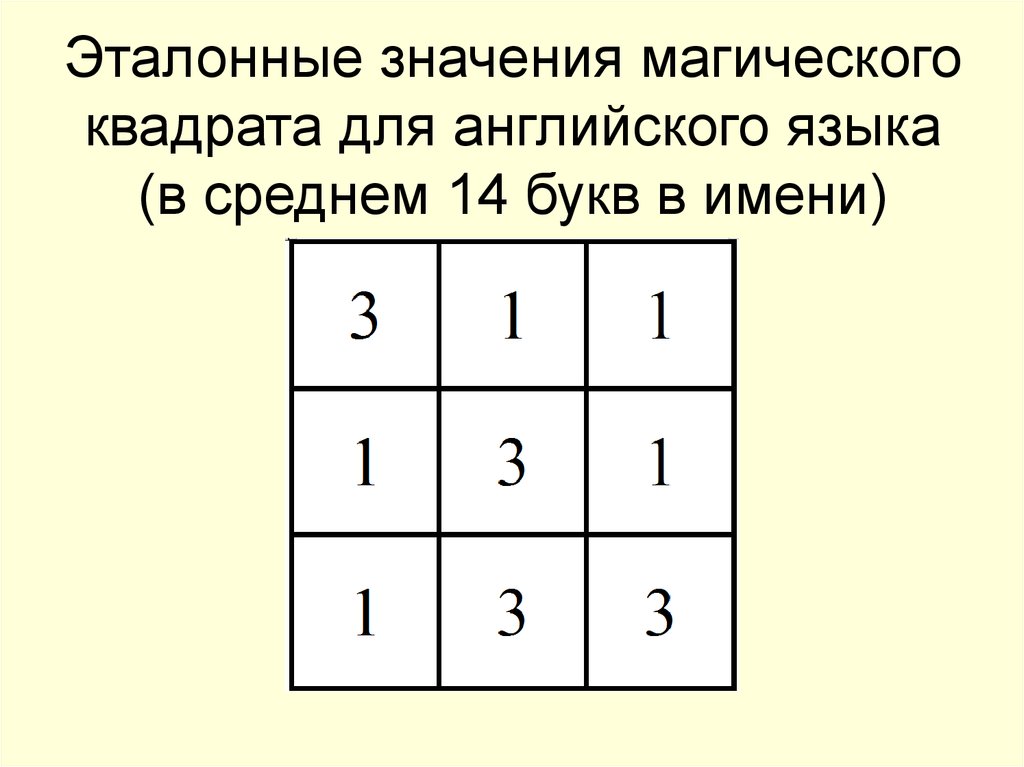
Клетки квадрата заполнили буквами некоторого сообщения так, что его первая буква попала в клетку с номером 1, вторая – в клетку с номером 2 и т. д. В результате построчного выписывания букв заполненного квадрата (слева направо и сверху вниз) получилась последовательность букв
Ы Р Е У С Т Е В Ь Т А Б Е В К П.
Восстановите магический квадрат и исходное сообщение.
Решение:
Сначала восстановим магический квадрат. Сумма чисел во всех клетках квадрата равна
1 + 2 + … +16 = 16 · 17 / 2 = 136,
значит, в каждом столбце (а также в строке, на диагонали) сумма чисел составляет 136:4=34. Попытаемся построить магические квадраты с суммой на линии, равной 34, и единицей в правом нижнем углу. Имеется несколько таких квадратов.
Расставляя буквы в соответствии с условием, только в одном случае, отвечающем четвертому квадрату, получаем читаемый текст: ПЕРЕСТАВЬТЕ БУКВЫ.
Остроумие и терпение привели математиков к построению рамочных квадратов, т.
е. таких, что если в них отбросить окаймляющие полосы шириной в одну или несколько клеток, то оставшийся квадрат не утратит своего свойства. Например: магический квадрат порядка 7 с магической суммой 175. Если удалить внешнюю рамку, то останется магический квадрат порядка 5 и магической суммой 125. При удалении второй рамки – квадрат окажется магическим с магической суммой – 75.
Широкое распространение в наши дни магические квадраты получили в виде популярной головоломки с числами – игра Судоку. Судоку развивает мышление и логику.
Итог занятияДля ответа на вопрос можно использовать следующие шаблоны:
- сегодня я узнал…
- мне было интересно…
- мне было трудно…
- я выполнял задания…
- я понял, что…
- теперь я могу…
- я почувствовал, что…
- я приобрел…
- я научился…
- у меня получилось …
- я смог…
- я попробую…
- меня удивило…
- мне захотелось…
Список литературы:
- Большая советская энциклопедия enc-dic. com/enc_sovet/Magicheski-kvadrat-34831.html
- А.Е. Малых Магические квадраты. // Живая математика, 2008, №1.
- В.А. Файнштейн Заполним магический квадрат // Математика в школе, 2000, №3.
com/enc_sovet/Magicheski-kvadrat-34831.htmlГлавная — Школа №619
Отделение дошкольного образования на Д. Бедного
Школа на Черкасова
Школа на Кондратьевском
Обучение с применением дистанционных образовательных технологий
Все выпуски школьного ТВ »
Добро пожаловать
Сегодня Школа № 619 Калининского района Санкт-Петербурга – лидер образования, интерактивная площадка, куда съезжаются для обмена опытом взрослые и дети из разных регионов России и других стран. Одно из самых ценных и значимых событий недавнего времени – заключение договора о сотрудничестве с ереванской школой №8 им. А. С Пушкина, с которого началась теплая и крепкая дружба двух школ. Для нас это страничка новой истории.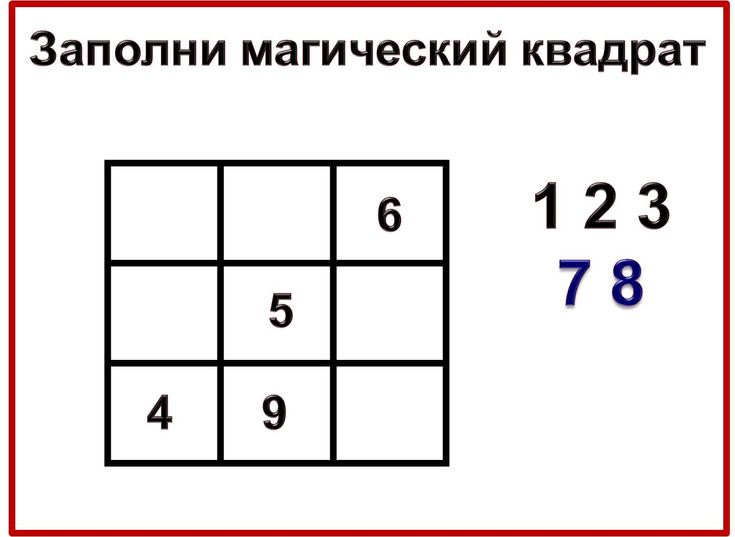
Один из слоганов школы, родившийся 25 лет назад – «Дети и взрослые, объединяйтесь!» – сегодня стал общим направлением движения: дети и взрослые вместе обсуждают вопросы совершенствования системы образования, вместе совершают научные открытия, вместе творят и выходят на сцену, – вместе идут к общему успеху!
Школа № 619 делает ставку на развитие личности ребенка. Здесь ребенок с первых дней ученичества пробует свои силы в разных видах творческой, научной, спортивной и общественной деятельности. В школе создано пространство, в котором ученику предоставлены все возможности для раскрытия своей индивидуальности.
Собственная научно-практическая конференция «Многогранная Россия» и STA-лаборатория, проект «Абитуриент», лидерское движение, Малые Олимпийские игры, студии танца и вокала, легоконструирование и робототехника, детский театр, студия КВН и школьное ТВ, многообразие спортивных секций и собственный литературно-художественный журнал, обучение с оздоровлением, поддержка одаренных учащихся, творческие выезды во время каникул – вот он, настоящий праздник интеллекта, творчества, здоровья, воображения.
Школа 619 – ты как оркестр, где каждый музыкант, инструмент ведет свою партию, а в целом – рождается искусство. Ведь только тогда, когда школа поднимается от ремесла до искусства, она способна дать достойное образование и воспитание.
28.02.2023
Приглашаем на Ученический пленум 2023
10.02.2023
Школа 619 – в “Движении первых”!
10.02.2023
11 февраля – День открытых дверей
10.02.2023
День науки: дорогу молодым!
10.02.2023
День Науки в корпусе на Черкасова
10.02.2023
Слова благодарности родителям 3Б класса за обновление Точки Активности!
Все новости »
- Инновационная деятельность
- Воспитательная система
- Реализация проекта АрктикЛаб в рамках грантовой поддержки (2022)
- Смешанный формат обучения
- Система наставничества
- Реализация проекта ГлобЛаб в рамках грантовой поддержки (2021)
- ШСК “Олимп”. Спортивная кафедра
- Бассейн
- Служба здоровья
- Концертный зал
- Загородная дача
- Столовая
- Информационно-библиотечный центр
Полезные ссылки
Версия для слабовидящих
Наши достижения
Участники профессиональных конкурсов 2021/2022
Киселева Мария, 5К
Бирцев Никита, 8М
Цинцкаладзе Дарий, 5К
Васильева Анна, 10К
Ребезов Иван, 5К
Борисиков Арсений, 5К
Ладыгина Маргарита, 5К
10.
02.2023
Официальный старт Года педагога и наставника в Школе 619
08.02.2023
День Науки в Школе 619
07.02.2023
На Черкасова объявляется Неделя науки!
07.02.2023
Родительские собрания для 5-х и 6-х классов на Черкасова
06.02.2023
Даем старт Году учителя в Школе 619!
06.02.2023
Сдали нормы ГТО!
03.02.2023
Результаты турнира “Январская классика”
02.02.2023
Погружение в науку продолжается!
01.02.2023
Удачи нашим педагогам!
31.01.2023
Итоги соревнований по волейболу на Кондратьевском
31.01.2023
9 февраля – прямой эфир главы администрации Калининского района
31.01.2023
Вперед, юные инженеры!
30.01.2023
Пульс моего города
27.01.2023
27 января – День полного снятия блокады Ленинграда
27.
Праздник со слезами на глазах
Все новости »
Волшебные квадраты
FutureLearn использует куки-файлы для повышения удобства использования веб-сайта. Все файлы cookie, кроме строго необходимых, в настоящее время отключены для этого браузера. Включите JavaScript, чтобы применить настройки файлов cookie для всех необязательных файлов cookie. Вы можете ознакомиться с политикой FutureLearn в отношении файлов cookie здесь.
В этой статье Йосси Эльран рассказывает нам о магических квадратах.
© Институт научного образования Дэвидсона, Институт науки Вейцмана
Магические квадраты очаровывали человечество на протяжении тысячелетий. Никто точно не знает происхождения магических квадратов, но многие историки считают, что они были изобретены в Древнем Китае.
Что такое магический квадрат?
Магический квадрат — это квадрат размером n x n , внутри каждой клетки которого записано целое число, так что сумма чисел в каждой строке, в каждом столбце и на каждой из главных диагоналей равна.
Это число называется магическое число . Главные диагонали – это те, которые тянутся из угла в угол. Изображение выше является примером магического квадрата 3 на 3 . Сумма каждой строки, каждого столбца и каждой из двух главных диагоналей равна 15, поэтому 15 — это магическое число этого магического квадрата. Это наименьший возможный магический квадрат (почему?), и он известен уже тысячи лет. У него даже есть специальное название: магический квадрат Ло Шу .
Квадрат Ло Шу
Китайские легенды гласят, что гигантская черепаха с выгравированным на спине магическим квадратом три на три вышла из реки Ло, чтобы спасти Китай от наводнения. Первые легенды, в которых упоминается об этом, были написаны в четвертом веке до нашей эры, но они утверждают, что потоп произошел в 23 веке до нашей эры. С тех пор, примерно до тысячи лет назад, китайцы считали магические квадраты действительно магическими. Они были особенно заинтригованы магическим квадратом Ло Шу и считали, что четные числа в квадрате представляют «инь» — женские вещи в мире, а нечетные числа представляют «ян» — мужские вещи.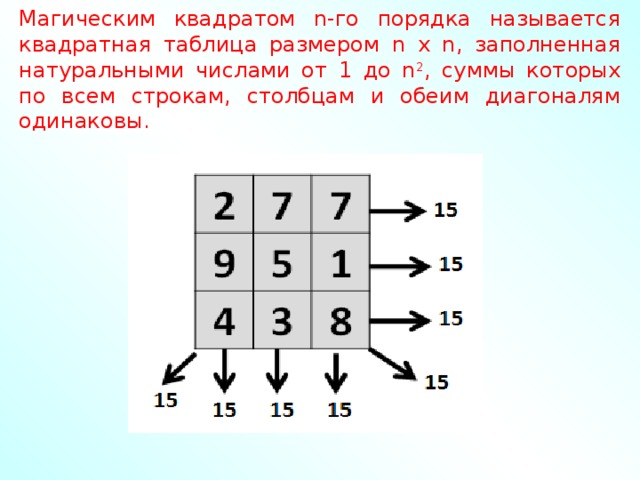
Магические квадраты Корнелия Агриппы
Магические квадраты стали очень популярны в Европе в средние века. Одним из главных действующих лиц, ответственных за это, был Корнелий Агриппа (1486-1535), весьма неординарный немец. В университете Агриппа тайно сформировал группу студентов, изучавших магию и алхимию. Некоторые из его друзей были фактически сожжены заживо на костре из-за того, что занимались черной магией. Помимо прочего, Агриппа изучал в университете право и теологию, а также философию, магию и каббалу, и написал много важных рукописей по всем этим предметам. Он был приговорен к смертной казни (несколько раз) церковью, но каким-то образом ему всегда удавалось бежать. Помимо всего этого, он также был высокопоставленным офицером в армии и личным врачом (врачом) короля Карла III.
Агриппа считал, что каждый магический квадрат каким-то мистическим образом связан со звездами, поэтому магические квадраты возрастающего размера (3×3, 4×4, 5×5 и т.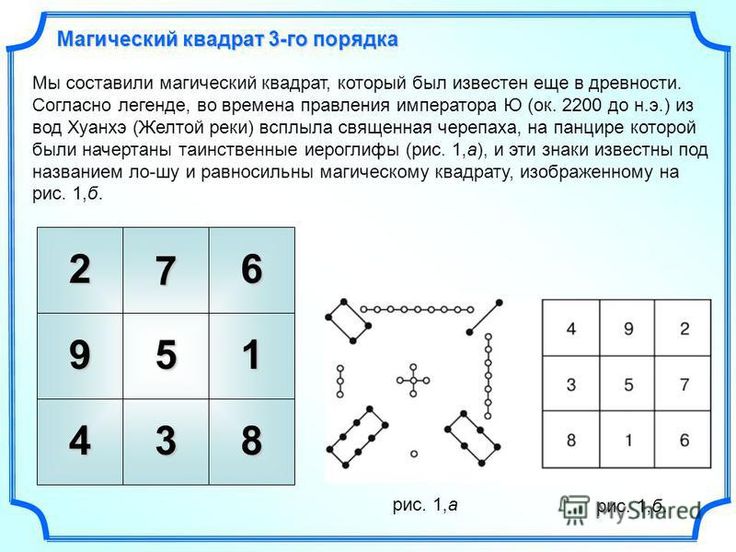
д.) он связывал с каждым из семи так называемых небесных тела (солнце, луна и пять видимых невооруженным глазом планет). Например, он назвал магический квадрат Ло Шу Сатурном. Вот магический квадрат Агриппы 9×9 «луна»:
Магический квадрат Альбрехта Дюрера
Другим известным немцем, который также был заинтригован магическими квадратами и жил в одно время с Корнелиусом Агриппой, был Альбрехт Дюрер, известный художник и математик. Дюрер включил в свои работы множество математических и геометрических тем, используя циркуль и линейку, чтобы его работы были очень точными. Он также был одним из первых художников, изучавших и использующих пропорции в своих рисунках. Одним из уникальных произведений искусства, созданных Дюрером, является гравюра под названием 9.0019 меланхолия . Он описывает отношение Дюрера к депрессии. Дюрер спрятал магический квадрат в правом верхнем углу меланхолии . Год, когда Дюрер выгравировал Меланхолия , 1514, спрятан в двух центральных ячейках нижнего ряда магического квадрата.
Магические квадраты сегодня
Многие другие влиятельные люди проявляли интерес к магическим квадратам, включая Бенджамина Франклина. Сегодня математики все еще изучают магические квадраты. Их интересуют такие вопросы, как: существует ли способ построения магических квадратов заданного размера? Методы строительства известны с древних времен, и их можно найти на соответствующих веб-сайтах, но на сегодняшний день не существует известного метода, позволяющего построить все возможные магических квадратов. Математики также даже не знают, сколько существует магических квадратов порядка n x n для n больше 5!
Видели ли вы где-нибудь примечательные магические квадраты? Если это так, пожалуйста, поделитесь этим с нами!
© Институт научного образования Дэвидсона, Институт науки Вейцмана
Эта статья взята из бесплатного онлайн-ресурса
Флексагоны и математика, стоящая за скрученной бумагой
Создано
Присоединяйся сейчас
Мы предлагаем широкий выбор курсов от ведущих университетов и учреждений культуры со всего мира.
Они предоставляются поэтапно и доступны на мобильных устройствах, планшетах и компьютерах, поэтому вы можете приспособить обучение к своей жизни.
Мы считаем, что обучение должно быть приятным, социальным опытом, поэтому наши курсы дают возможность обсудить то, что вы изучаете, с другими, помогая вам делать новые открытия и формировать новые идеи.
Вы можете открыть новые возможности с неограниченным доступом к сотням кратких онлайн-курсов в течение года, подписавшись на наш безлимитный пакет. Развивайте свои знания в ведущих университетах и организациях.
Узнайте больше о том, как FutureLearn меняет доступ к образованию
Затем они могут начать видеть, что есть 8 строк, которые должны иметь одинаковую сумму, поэтому им нужно 8 троек чисел (составленных из цифр от 1 до 9), которые в сумме дают одно и то же число. Что это может быть за число?
Четыре из этих линий проходят через один и тот же квадрат, центр, а это значит, что одно число должно быть в четырех тройках. Только 5 удовлетворяют этому условию, поэтому 5 должны быть в середине, и теперь мы знаем другие части каждой тройки, с которыми она выровнена по горизонтали, вертикали и по двум диагоналям. Мы еще не знаем, какая 5-я тройка входит в какую из этих линий, но, пробуя возможности и рассматривая тройки, которые должны быть следствиями в пограничных линиях, мы можем выяснить это.
Кроме того, просмотр верхнего набора показывает, что каждое решение — это решение слева от него, повернутое на 90 против часовой стрелки. Так что на самом деле есть только одно решение, и из него можно создать другие.
