Как в математике пишется знак больше и меньше: Больше, меньше, равно — урок. Математика, 1 класс.
Обозначение знака больше. Что означают символы знаков зодиака. Символика царства животных
В абстрактной алгебре повсеместно используются символы для упрощения и сокращения текста, а также стандартные обозначения для некоторых групп. Ниже приведён список наиболее часто встречающихся алгебраических обозначений, соответствующие команды в … Википедия
Математические обозначения это символы, используемые для компактной записи математических уравнений и формул. Помимо цифр и букв различных алфавитов (латинского, в том числе в готическом начертании, греческого и еврейского),… … Википедия
Статья содержит список общеупотребительных аббревиатур математических функций, операторов и др. математических терминов. Содержание 1 Аббревиатуры 1.1 Латиница 1.2 Греческий алфавит … Википедия
Юникод, или Уникод (англ. Unicode) стандарт кодирования символов, позволяющий представить знаки практически всех письменных языков. Стандарт предложен в 1991 году некоммерческой организацией «Консорциум Юникода» (англ.
Список используемых в математике специфических символов можно увидеть в статье Таблица математических символов Математические обозначения («язык математики») сложная графическая система обозначений, служащая для изложения абстрактных… … Википедия
У этого термина существуют и другие значения, см. Плюс минус (значения). ± ∓ Знак плюс минус (±) математический символ, который ставится перед некоторым выражением и означает, что значение этого выражения может быть как положительным, так и … Википедия
Необходимо проверить качество перевода и привести статью в соответствие со стилистическими правилами Википедии. Вы можете помочь … Википедия
Или математические символы знаки, которые символизируют определённые математические действия со своими аргументами. К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения в… … Википедия
Знаки операций или математические символы знаки, которые символизируют определённые математические действия со своими аргументами. К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения… … Википедия
К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения… … ВикипедияЗнаки зодиака названы по имени созвездий, которым они соответствовали в древние времена. В процессе становления науки астрологии стало понятно, что для удобства работы нужны специальные символы или обозначения знаков зодиака. Именно про них я расскажу в статье.
На мою почту поступил вопрос:
ПЕРСОНАЛЬНЫЙ ГОРОСКОП – теперь доступен на нашем сайте. Составляется по ВАШИМ индивидуальным данным рождения, то есть для вас ЛИЧНО. Вы узнаете, что говорят планеты о вашей личности.
Дарья, г. Саратов
Здравствуйте, Светлана. Давно хочу выяснить, что означают значки знаков зодиака? Откуда они взялись? Например, я — Рыбка, но значок своего знака до конца не понимаю. Заранее благодарю за ответ.
Овен
Овен традиционно открывает зодиак — именно здесь находится точка весеннего равноденствия, когда день становится равным ночи. Кстати, слово «овен» означает барана старше одного года.
Кстати, слово «овен» означает барана старше одного года.
Графический символ знака зодиака Овен чем-то напоминает латинскую букву «V». Считается, что она является изображением рогов барана. Не правда ли, есть сходство?
Существует и другая версия, согласно которой значок Овна представляет собой образ восхода солнца или взрыв.
Люди, рожденные под этим созвездием, обладают именно таким характером: они импульсивны, стремительны, смелы и стремятся быть первыми во всех сферах жизни.
Телец
Обозначением знака зодиака Телец выступает круг с дугой над ним. Это схематическое изображение головы быка.
Круг в этом значке отражает Солнце (Дух человека), а дуга — Луну (Душа). Так как здесь сверху находится значок души, то становится ясно, что в жизни Тельцов ведущую роль играет близость к Земле и природе, а не к Космосу и Богу.
Характер данного знака во многом напоминает черты быка — это упрямство, некоторая медлительность, мощь и большая природная сила.
Близнецы
Символ знака зодиака Близнецы представляет собой римскую цифру 2. Нетрудно догадаться, откуда возник такой образ. Само слово «близнецы» указывает на двоих людей — братьев или сестер.
В характере рожденных под этим созвездием также присутствует двойственность. Такие люди переменчивы, в их личности словно бы живут бок о бок два непохожих человека.
Кстати, обратите внимание на дуги сверху и снизу в обозначении Близнецов. Они символизируют растущую и убывающую Луну.
Соединяясь, они указывают на путь развития от прошлого к будущему.
Рак
Впервые увидев символ знака зодиака Рак, вы сразу поймете, о ком идет речь. Две «запятые» в данном значке очень похожи на клешни рака, который будто бы прикрывается ими от постороннего наблюдателя.
Этот знак действительно не любит быть на виду, предпочитает оставаться в своем закрытом и уютном мирке, где никто его не потревожит. Раки любят свой дом, который можно сравнить с раковиной.
Символ Рака напоминает нам также знак бесконечности. И действительно, эмоции представителей знака Рак настолько глубоки, что эта глубина кажется бесконечной. И еще одна расшифровка — это слияние Инь и Ян, мужского и женского начала, в результате которого наступает беременность. Рак связан с материнством.
Лев
Обозначением знака зодиака Лев выступает завитушка с кругом на конце. Она чем-то похожа на гриву льва, создающую яркий и заметный образ этого величественного животного в природе. Рожденные под данным созвездием также часто имеют роскошные, не очень послушные волосы.
Круг в символе указывает нам на Солнце, являющееся покровителем знака зодиака Лев. Оно отражает Дух и внутренний стержень, силу характера и яркие творческие способности.
Символ Льва может напомнить сперматозоид. Перед нами «мужской» знак, который, как и Рак, участвует в акте творения новой жизни.
Поэтому оба эти представителя зодиака признаны отличными воспитателями и очень заботливыми родителями.
Дева
Обозначение знака зодиака Дева неоднозначно. Некоторые утверждают, что в этом символе изображены 3 колоска пшеницы, бережно связанные между собой. Представители данного знака в самом деле близки к земле и трудолюбивы.
Есть другое — исторически обоснованное объяснение символа Девы. Знак представляет собой монограмму из букв «MV», составленную из инициалов Maria Virgo, то есть Дева Мария.
Дева являет собой чистоту и непорочность. И если о чистоте мы говорим в физическом смысле слова, то непорочность подразумевается скорее духовная.
Весы
Символ знака зодиака Весы в точности соответствует своему названию. Он отражает идеи правосудия и равновесия. Словно бы на весах, здесь взвешиваются разные точки зрения, в результате чего можно увидеть истину и рассудить людей.
Представители Весов наделены чувством меры и красоты. Они стремятся к равновесию и гармонии во всех сферах жизни, в том числе ищут баланс в отношениях, не любят конфликтов.
Другое значение символики Весов — это изображение заката, в противовес Овну, который являет собой восход солнца. Закат — чудесное, романтическое время суток, не так ли?
Закат — чудесное, романтическое время суток, не так ли?
Скорпион
Изображением знака зодиака Скорпион является латинская буква «m». Существует две версии значения стрелочки на конце символа:- она обозначает ядовитое жало Скорпиона;
- указывает на хвост этого животного.
В любом случае, наличие стрелки говорит о том, что Скорпион устремлен к активным действиям — он не останавливается на пути к желанной цели. Жало Скорпиона намекает на его мстительность. Кстати, вас может заинтересовать материал про .
Стрелец
Обозначением знака зодиака Стрелец выступает стрела, которую кентавр выпустил из лука. Стрела не случайно направлена вперед и вверх. Стрелец метится в будущее, он устремлен к высоким целям.
Представители этого знака не станут задерживаться на прошлом. Их взгляд направлен вдаль, куда-то туда, где светит путеводная звезда. Этой звездой выступает идеал, вдохновляющий кентавра.
Стрелец — это также знак путешествий и расширения горизонтов.
Он пускает свои стрелы в разные уголки мира, совершая вдали от дома удивительные открытия.
Козерог
Символ знака зодиака Козерог неоднозначен. Есть два варианта его расшифровки:
- в первом случае говорят об изображении затейливых рогов и хвоста горного козла, олицетворяющего данный зодиакальный знак;
- во втором случае предполагается, что в символе зашифрованы греческие буквы — «тау» и «ро» — первые две буквы в слове tragos, которое означает «козел».
Горный козел наделен такими качествами, как выносливость, стойкость, решительность и мужество. Ему с рождения приходится в поисках пастбищ карабкаться по горным склонам, обходя овраги и ущелья. В результате Козерог достигает горных вершин.
Водолей
Обозначением знака зодиака Водолей являются две ломаные линии. Они символизируют океанические волны, которые поднимаются, благодаря ветру. Ветер, как и сам Водолей, относится к Воздушной стихии.
Представители данного знака зодиака всегда стремятся быть в потоке. Они общительны, контактны, дружелюбны. Их разум, подобно волнам, постоянно занят какими-либо идеями или концепциями.
Они общительны, контактны, дружелюбны. Их разум, подобно волнам, постоянно занят какими-либо идеями или концепциями.
Невероятные факты
Каждый символ что-то означает и для чего-то предназначен. Мы видим их каждый день и даже не задумываясь, в большинстве случаев знаем, что они означают. Безусловно, они делают нашу жизнь проще.
Однако, мало кто из нас знает их происхождение и первоначальное значение. Ниже мы рассмотрим 10 всем известных символов и расскажем их историю.
Что значит знак сердца
10. Символ сердца
Символ в форме сердца известен во всём мире, и обычно он означает любовь и романтику. Но почему мы инстинктивно воспринимаем его как сердце, ведь он нисколько не похож на настоящее человеческое сердце?
Существует несколько теорий о том, откуда это символ появился и как стал таким, каким мы его знаем сегодня. Некоторые теории утверждают, что символ связан с всем известной частью человеческого тела.
Другие полагают, основываясь на древних рисунках этого символа, что “сердце” есть ничто иное, как изображение листьев плюща, растения, связанного с верностью.
Ещё более правдоподобное объяснение приходит от ныне вымершего растения сильфиума. Когда-то оно в изобилии росло на небольшом участке побережья Северной Африки. Оно почиталось как греками, так и римлянами за свои целебные свойства, а также было средством контроля над рождаемостью.
Греческая колония Кирине, расположенная в регионе, который сегодня принадлежит Ливии, разбогатела благодаря этому растению и даже отпечатала его на своих монетах. На них мы и видим всем известный символ.
Однако, из-за небольшой области обитания растения и большого спроса на него, к первому столетию до нашей эры оно вымерло.
Ещё одна теория происхождения этого символа родом из средневековья. Основываясь на писаниях Аристотеля, где он описывает сердце, как нечто, имеющее три камеры и впадину, итальянский врач 14 века Гвидо да Виджевано сделал серию анатомических рисунков, на которых изобразил сердце именно в таком виде.
Основываясь на писаниях Аристотеля, где он описывает сердце, как нечто, имеющее три камеры и впадину, итальянский врач 14 века Гвидо да Виджевано сделал серию анатомических рисунков, на которых изобразил сердце именно в таком виде.
Это изображение сердца обрело популярность в эпоху Возрождения, оно всё чаще стало появляться в религиозном искусстве. Оттуда оно и пришло к нам, как символ любви и привязанности.
Символ Инь-Ян
9. Инь-Ян
Символ Инь-Ян глубоко укоренился в китайской философии, а также является ключевым элементом в даосской религии в Китае. Сегодня его можно найти повсюду. Его смысл также прост, как и сложен.
О концепции инь и ян впервые заговорили в 3 веке до нашей эры, когда появился интерес к философии. И инь, и ян – это и хорошее, и плохое, это две стороны одной монеты. Инь может превращаться в ян и наоборот. Точка, с которой начинается каждый знак, представляет собой потенциал, противоположное семя.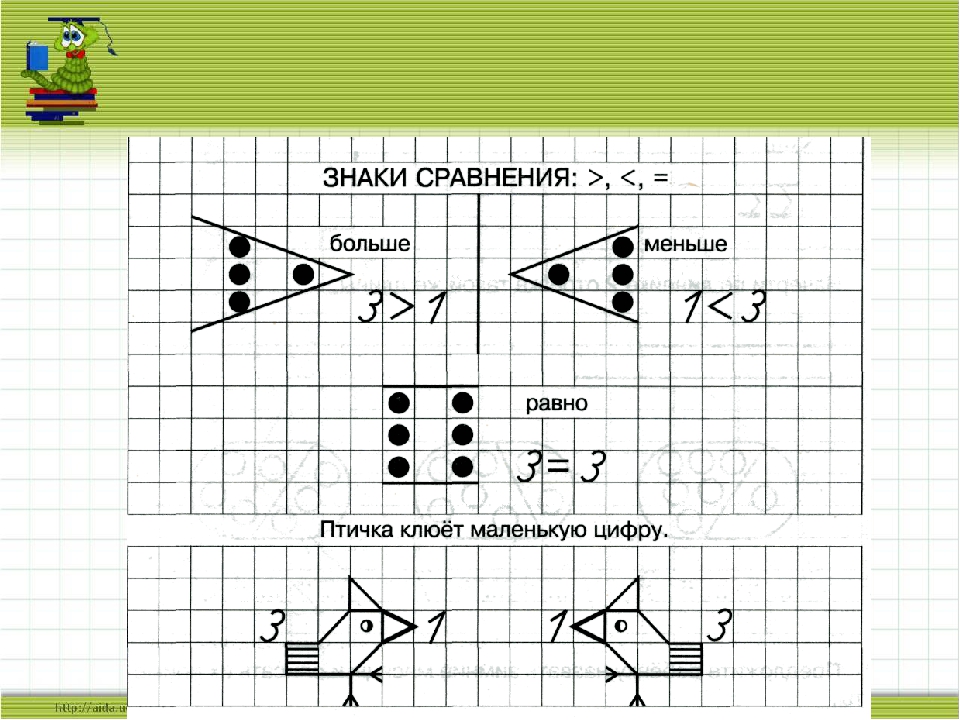
Инь – это женская сторона, в которой проявляются такие вещи, как темнота, вода, холод, мягкость, пассивность, север, трансформация, самоанализ, она даёт дух всему. С другой стороны, ян – это свет, горы, огонь, тепло, солнце, действие, движение, ян даёт форму всем вещам.
Даосизм верит в идею объятия обоих аспектов, чтобы во всём находить баланс. Чтобы понять, насколько сильна эта концепция в Китае, достаточно просто посмотреть на названия некоторых поселений.
Деревни на солнечной стороне долин и рек имеют такие имена, как Люян и Шиян, в то время, как те, которые расположились на противоположной стороне, носят имена подобные Цзяньгин.
Интересно, что Китай не был родиной инь-ян. Самая ранняя информация относится к использовании символа в доисторической культуре, занимавшей территорию части современной Молдовы, южной Украины и центральной Румынии.
Известная как Трипольская культура, это общество существовало в 5400 – 2700 годах до нашей эры. С символами инь-ян было обнаружено несколько предметов керамики той эпохи. Но так как письменного языка у них не было, мы не можем узнать, рассматривали ли они символ также, как китайцы, или это просто совпадение.
С символами инь-ян было обнаружено несколько предметов керамики той эпохи. Но так как письменного языка у них не было, мы не можем узнать, рассматривали ли они символ также, как китайцы, или это просто совпадение.
Значение символа Bluetooth
8. Символ Bluetooth
На первый взгляд нет никакой связи между этой беспроводной технологией и синим зубом (именно так переводится дословно с английского слово bluetooth). Но верите или нет, на самом деле связь есть.
Эта технология была изобретена ещё в 1994 году шведской телекоммуникационной компанией Ericsson. В соответствии с прошлым викингов в Швеции символ – это две руны, соединённые вместе. Руна Н и руна В, вместе они и образуют всем известный символ.
Но что общего у них с синим зубом? Это фамилия первого короля викингов Дании, Харальда Блотанда (Harald Blåtand). А шведское слово “blatand” в переводе означает «синий зуб». Харальд жил с 910 по 987 гг. нашей эры и за свою жизнь сумел объединить все датские племена, а позднее захватил и Норвегию, управляя ею вплоть до своей смерти.
нашей эры и за свою жизнь сумел объединить все датские племена, а позднее захватил и Норвегию, управляя ею вплоть до своей смерти.
Ему также приписывают и принятие датчанами христианства. Он сделал это больше по политическим и экономическим причинам, нежели по каким-то другим, что избежать движения Священной Римской империи на юг, а также сохранить своих торговых партнёров.
Происхождение его фамилии, Синий Зуб, является загадкой. Некоторые полагают, что возможно он любил ежевику, которая придавала его зубам синий оттенок. Однако, более правдоподобно звучащее объяснение заключается в том, что Синий Зуб – это фактически неверно истолкованные записи средневековых историков, и на самом деле его имя была больше похоже на “тёмный вождь”.
Значение флага планеты Земля
7. Международный флаг планеты Земля
Во время каждой космической миссии сегодня используются разные национальные флаги в зависимости от того, какая страна её финансирует.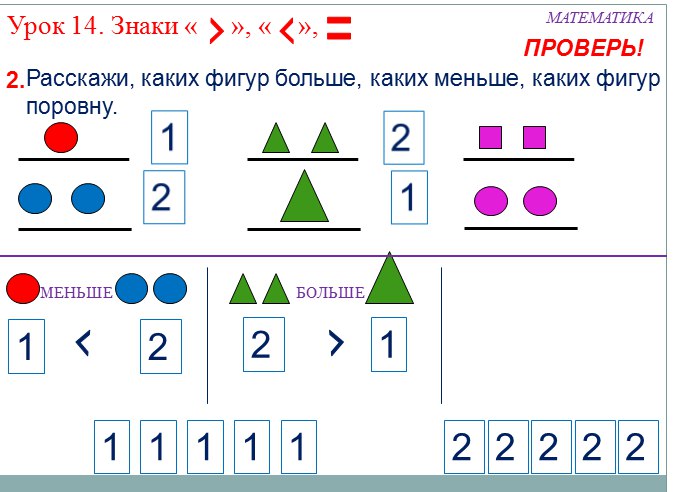 Всё это хорошо, но астронавты, независимо от страны происхождения, “выступают” за планету в целом, а не за государство, давшее средства на полёт.
Всё это хорошо, но астронавты, независимо от страны происхождения, “выступают” за планету в целом, а не за государство, давшее средства на полёт.
По этой причине был разработан флаг планеты Земля. Он состоит из семи белых переплетённых между собой колец на синем фоне. Кольца символизируют всю жизнь на нашей планете.
Однако, сам символ гораздо старше флага и более известен как “Семя Жизни”. Он считается частью “Священной геометрии”. Этот термин используется для обозначения универсальных геометрических узоров, часто встречающихся в природе. Семя Жизни имеет поразительное сходство с клеточной структурой во время эмбрионального развития.
Более того, Семя Жизни, также как и Большой Цветок Жизни, находили во многих местах мира. Самая старая находка была обнаружена в храме Осириса в Абидосе, в Египте, возрастом около 5000-6000 лет.
Подобный “дизайн” также использовался в буддийских храмах в Китае и Японии, в современной Турции, в Индии, по всей Европе, в Ираке и во многих других местах. Семя Жизни также играет важную роль в различных религиях. К примеру, в старых славянских религиях символ Семени Жизни обозначал солнце.
Семя Жизни также играет важную роль в различных религиях. К примеру, в старых славянских религиях символ Семени Жизни обозначал солнце.
Что значит серп и молот
6. Серп и молот
Советский “серп и молот”, возможно, один из самых узнаваемых политических символов, который стоит в одном ряду по узнаваемости с нацистской свастикой и американскими звёздами с полосами.
И хотя их смысл скорее всего прямолинеен, он может нести в себе скрытые сообщения. Молот может означать пролетариат (синих воротничков), а серп – крестьян. Вместе они являлись единством и силой советского государства. Однако, придумать эмблему было не так просто, как кажется.
С молотом ситуация была проще, так как он традиционно по всей Европе ассоциировался с рабочими. Со второй частью символа было посложнее, фигурировало несколько вариантов: молот был с наковальней, плугом, мечом, косой и гаечным ключом.
Интригует и сам дизайнер, Евгений Камзолкин.
Возможно, Камзолкин использовал серп и молот для передачи абсолютно другого сообщения, даже если его никто и не понял. К примеру, в индуистской и китайской культуре молот часто связывали с торжеством зла над добром. Серп в разных религиях ассоциировали со смертью.
Перед тем, как появилась коса, в средневековой Европе Смерть изображали с серпом, индуистские религии также изображали бога смерти с серпом в левой руке. Что именно имел ввиду Камзолкин, разрабатывая дизайн, никто не знает.
Все это домыслы, а правильный ответ никто так не спросил у дизайнера, который скончался ещё в 1957 году. Ключевым моментом в данном случае является интерпретация символа, потому что в зависимости от контекста, подобные эмблемы могут означать две абсолютно разные вещи.
Что означает знак пентаграммы
5. Пентаграмма
Пентаграмма
Сегодня этот символ ассоциируют с виккой (современное колдовство), сатанизмом и масонством. Но немногим известно, что пентаграмма гораздо старше любой из этих практик и используется с древних времён.
Пятиконечную звезду нашли еще на пещерной стене в Вавилонии, а древние греки полагали, что она обладает магическими свойствами. Предполагается, что пентаграмма – это путь, который Венера берёт на ночное небо по отношению к Земле в 8-летнем цикле.
Пентаграмма была даже печатью Иерусалима в течение некоторого времени, а в средние века она символизировала собой пять ран, которые получил Иисус во время своего распятия. Она также обозначала пропорции человеческого тела и пять его основных чувств.
Только в 20 веке пентаграмма начала ассоциироваться с сатанизмом, вероятно из-за того, что использовалась викканами. Ранее пять точек звезды представляли собой четыре стихии (земля, вода, воздух, огонь) и человеческий дух.
Однако, у викканов пентаграмма символизирует победу духа над четырьмя стихиями, в сатанизме же пятиконечная звезда ориентирована вниз. Это означает, что каждый человек в первую очередь материален.
Значение анархии
4. Символ анархии
Чтобы правильно понять символ анархии, нужно сначала знать, что такое анархия, и что она означает на самом деле. Анархия – это такая же политическая идеология, как демократия, монархия, олигархия, коммунизм или либерализм.
Она развивалась в Древней Греции наряду с демократией, и с древнегреческого это слово переводится как “без правителя”. Это означает, что анархия – это не беззаконие и хаос, а скорее это общество с надлежащими к выполнению правилами и положениями, введёнными в действие, но без наличия авторитарного правителя.
Анархия развивалась еще активнее и стала более совершенной во время периода Французской революции в конце 18 века. В тот же период анархия получает свои негативные коннотации, потому что правящая элита по понятным причинам была против такого режима.
В тот же период анархия получает свои негативные коннотации, потому что правящая элита по понятным причинам была против такого режима.
Здравствуйте, уважаемые читатели блога сайт. Не так давно мы с вами довольно подробно обсудили тему использования смайликов в социальной сети Вконтакте. Там же были приведены основные коды Emoji-смайлов (около тысячи — на все случаи жизни). Если вы с той публикацией еще не ознакомились, то настоятельно рекомендую это сделать:
Что значат текстовые смайлики составленные из символов?
Мы же с вами давайте продолжим изучать значения наиболее распространенных вариантов написания тех или иных смайликов с помощью обычных (невычурных) символов. Готовы? Ну, тогда поехали.
Изначально распространение получили, т.е. лежащие на боку (см. приведенные выше примеры смеющихся и грустящих лиц). Давайте посмотрим, какие еще комбинации могут встретиться вам в интернете и что они обозначают (как их расшифровать).
Обозначение символами смайликов эмоций
- Радость или улыбка 🙂 чаще всего изображается с помощью символов: 🙂 либо:-) либо =)
- Безудержный смех 😀 (эквивалент выражения ): 😀 либо:D либо)))) (недосмайл используемый в основном в рунете)
- Еще одно обозначение смеха, но больше походящее на насмешку 😆 (эквивалент ): XD либо xD либо >:-D (злорадство)
- Смех до слез, т.
 е. то, что значит смайл „слезы радости“ 😂: :”-) либо:”-D
е. то, что значит смайл „слезы радости“ 😂: :”-) либо:”-D - Коварная ухмылка 😏: }:-> либо ]:->
- Грустный или печальный смайлик 🙁 имеет текстовые значения: :-(либо =(либо:(
- Символьное обозначение очень грустного смайла 😩: :-C либо:C либо (((((опять же вариант недосмайла)
- Легкое неудовольствие, растерянность или озадаченность 😕: :-/ либо:-\
- Сильная злость 😡: D-:
- Текстовое обозначение смайлика нейтрального отношения 😐: 😐 либо:-I либо._. либо -_-
- Символьное значение смайлика восхищения 😃: *О* либо *_* либо **
- Расшифровка эмоции удивления 😵: :-() либо:- либо:-0 либо:O либо O: либо о_О либо oO либо o.O
- Варианты того, что может значить смайлик сильного удивления или недоумения 😯: 😯
либо =-O либо:- - Разочарование 😞: :-e
- Ярость 😠: :-E либо:E либо:-t
- Смущение 😖: :-[ либо %0
- Угрюмость: :-*
- Печаль: :-
Значение текстовых смайликов эмоциональных действий или жестов
- Что значит подмигивающий смайл в текстово-символьном исполнении 😉: 😉 либо;)
- Грустная шутка: ;-(
- Радостная шутка: 😉
- Варианты обозначение плачущего смайлика 😥 или 😭: :_(либо:~(либо:”(либо:*(
- Радостный плач (означает смайлик „слезы радости“ 😂): :~-
- Горестный плач 😭: :~-(
- Гневный крик: :[email protected]
- Поцелучик в текстовом обозначении 😚 или 😙 или 😗: :-* либо:-{}
- Обнимашки: {}
- Показать язык (значит дразнить) 😛 или 😜: 😛 либо:-p либо:-Ъ
- Рот на замок (значит тссс) 😶: :-X
- С души воротит (обозначение тошноты): :-!
- Выпимши или смущен (значит либо „я пьян“, либо „ты пьян“): :*)
- Ты олень: Э:-) либо 3:-)
- Ты клоун: *:O)
- Сердечко 💓:
- Текстовое обозначение смайлика „цветочек розы“ 🌹: @}->– либо @}~>~~ либо @-“-,”-,—
- Гвоздика: *->->–
- Старая шутка (значит баян): [:|||:] либо [:]/\/\/\[:] либо [:]|||[:]
- Крези (обозначает „у тебя крыша поехала“): /:-(либо /:-]
- Пятая точка: (_!_)
Что значат горизонтальные (японские) символьные смайлы?
Изначально так повелось, что большинство из придуманных и получивших распространение текстовых смайликов нужно было расшифровывать как бы „наклонив голову набок“. *)
*)
Естественно, что на многих блогах и форумах уже давным-давно имеется возможность добавлять смайлики в виде картинок (из готовых наборов), но многие по-прежнему продолжают использовать текстовые смайлы, ибо уже набили на этом руку и при этом нет необходимости отыскивать в каталоге нужную картинку.
Если хотите узнать, что значит тот или иной набор символов, являющийся текстовым смайликом, то пишите об этом в комментариях. Авось всем миром и разберемся…
Удачи вам! До скорых встреч на страницах блога сайт
Вам может быть интересно
Смайлики в Твиттере – как их вставляют и где можно скопировать картинки смайлов для Twitter
ЛОЛ – что это такое и что значит lOl в интернете
Файл – что это такое и как настроить file в Виндовс
Скрытые смайлы в Skype – где взять новые и секретные смайлики для Скайпа
Импонировать – что это (значение слова)
Что такое рофл и рофлить, или +1 к пониманию молодежного сленга
Флексить – что это значит и что такое флекс
Отзовик – сайт отзывов обо всем и как на нем можно зарабатывать
Символ собака – почему значок собачки @ так называют, история появления этого знака в адресе электронной почты и на клавиатуре
Аська и ее веб версия – старый, добрый бесплатный онлайн мессенджер с новыми возможностями
Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше , а также знак равно.
Однако, если с последним что-то напутать достаточно сложно, то о том, как и в какую сторону пишутся знаки больше и меньше (знак менее и знак более , как ещё их иногда называют) многие сразу после этой же школьной скамьи и забывают, т.к. они довольно редко используются нами в повседневной жизни.
Но практически каждому рано или поздно всё равно приходится столкнуться с ними, и “вспомнить” в какую сторону пишется нужный им символ получается лишь обратившись за помощью к любимой поисковой системе. Так почему бы не ответить развернуто на этот вопрос, заодно подсказав посетителям нашего сайта как запомнить правильное написание этих знаков на будущее?
Именно о том, как правильно пишется знак больше и знак меньше мы и хотим напомнить вам в этой небольшой заметке. Также будет не лишним рассказать и том, как набрать на клавиатуре знаки больше или равно и меньше или равно , т.к. этот вопрос тоже довольно часто вызывает затруднения у пользователей, сталкивающихся с такой задачей очень редко.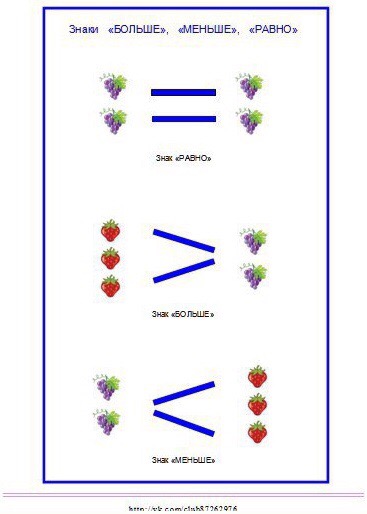
Перейдем сразу к делу. Если вам не очень интересно запоминать всё это на будущее и проще в следующий раз снова “погуглить”, а сейчас просто нужен ответ на вопрос “в какую сторону писать знак”, тогда для вас мы приготовили краткий ответ – знаки больше и меньше пишутся так, как показано на изображении ниже.
А теперь расскажем немного подробнее о том, как это понять и запомнить на будущее.
В общем и целом логика понимания очень проста – какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону – такой и знак. Соответственно, знак больше влево смотрит широкой стороной – большей.
Пример использования знака больше:
- 50>10 – число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.
Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной – меньшей, то перед вами знак меньше.
Пример использования знака меньше:
- 100
- на заседание явилось
Как видите, все довольно логично и просто, так что теперь вопросов о том, в какую сторону писать знак больше и знак меньше в будущем у вас возникать не должно.
Знак больше или равно/меньше или равно
Если вы уже вспомнили, как пишется необходимый вам знак, то дописать к нему одну черточку снизу вам не составит труда, таким образом вы получите знак “меньше или равно” или знак “больше или равно” .
Однако относительно этих знаков у некоторых возникает другой вопрос – как набрать такой значок на клавиатуре компьютера? В результате большинство просто ставят два знака подряд, к примеру, “больше или равно” обозначая как “>=” , что, в принципе, часто вполне допустимо, но можно сделать красивее и правильнее.
На самом деле для того, чтобы напечатать эти знаки, существуют специальные символы, которые можно ввести на любой клавиатуре. Согласитесь, знаки “≤” и “≥” выглядят значительно лучше.
Согласитесь, знаки “≤” и “≥” выглядят значительно лучше.
Знак больше или равно на клавиатуре
Для того, чтобы написать “больше или равно” на клавиатуре одним знаком даже не нужно лезть в таблицу специальных символов – просто поставьте знак больше с зажатой клавишей “alt” . Таким образом сочетание клавиш (вводится в английской раскладке) будет следующим.
Или же вы можете просто скопировать значок из этой статьи, если вам нужно воспользоваться им один раз. Вот он, пожалуйста.
≥
Знак меньше или равно на клавиатуре
Как вы наверное уже смогли догадаться сами, написать “меньше или равно” на клавиатуре вы можете по аналогии со знаком больше – просто поставьте знак меньше с зажатой клавишей “alt” . Сочетание клавиш, которое нужно вводить в английской раскладке, будет следующим.
Или просто скопируйте его с этой страницы, если вам так будет проще, вот он.
≤
Как видите, правило написания знаков больше и меньше довольно просто запомнить, а для того чтобы набрать значки больше или равно и меньше или равно на клавиатуре достаточно просто нажать дополнительную клавишу – всё просто.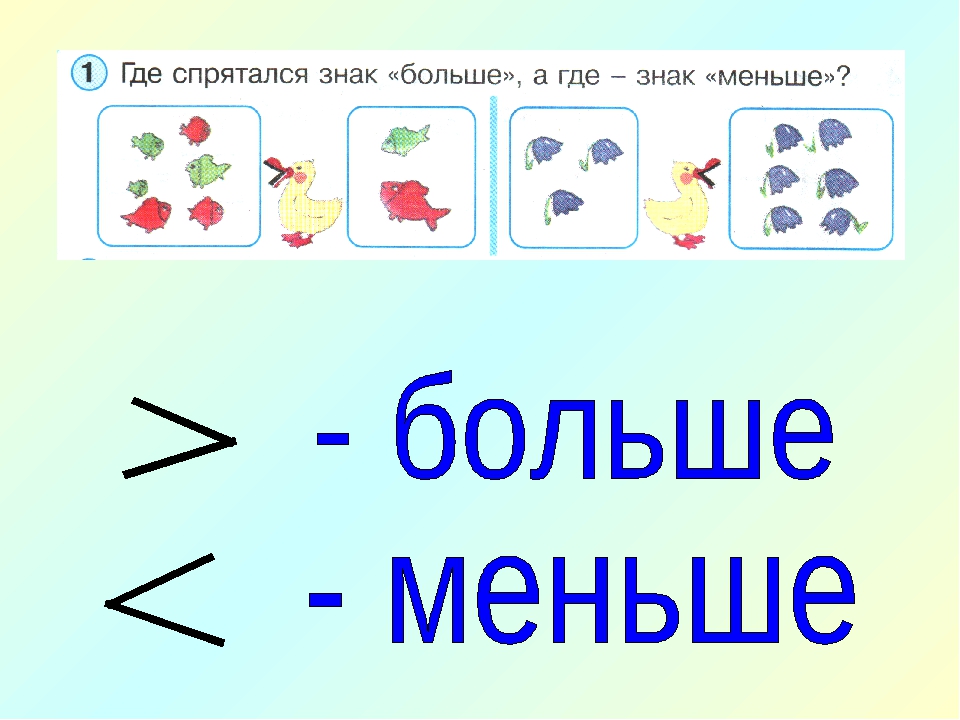
Как правильно ставить знак больше меньше
Вконтакте
Одноклассники
Как пишется знак больше и знак меньше?
При обучении математике детям обычно называют знаки больше и меньше клювиком, так им проще запоминать образное понятие. А вот чтобы запомнить в какую сторону пишется меньше, а в какую больше приводят другой пример — закрытый клювик всегда смотрит в сторону меньшего числа, открытый в сторону большего. То есть у нас получается такая жадная уточка, которая разевает клюв только на действительно стоящее. Возможно поэтому еще этот знак сравнивают с крокодилом. Теперь если слева стоит большее число, клювик к нему открыт и мы имеем знак quot;большеquot;, а если слева стоит меньшее число, клювик налево закрыт, то у нас получается знак quot;меньшеquot;.
Знак quot;большеquot; и quot;меньшеquot; при письме изображаются галочкой, которая поврнута на девяносто градусов. При этом если носик галочки смотрит направо, то это знак больше. В противном случае, если узкий кончик галочки смотри налево, то меньше.
В противном случае, если узкий кончик галочки смотри налево, то меньше.
В математике часто приходится сравнивать числа по величине, для чего и были придуманы графические символы. Вместо слова quot;большеquot; используется знак quot;>quot;, а вместо слова quot;меньшеquot; — символ quot;lt;quot;.
Если, например, нам нужно сравнить между собой цифры 5 и 3, то это будет выглядеть так: 5 > 3. Между цифрами стоит знак quot;большеquot;, который повернут своей открытой стороной в сторону большей величины. Запомнить обозначение очень просто: quot;носикquot; всегда повернут своим острием в сторону меньшего числа.
Математические знаки запомнить легко: вот этот знак quot;>quot; обращен к буквам перед ним широкой частью и означает quot;большеquot;, а этот знак quot;lt;quot; обращен тонким углом и означает меньше. Оба знака могут быть усложнены знаком равно.
Если вы хотите запомнить как пишется знак больше и знак меньше, то в первую очередь нужно запомнить о том, что у знака больше острый кончик направлен вправо:>.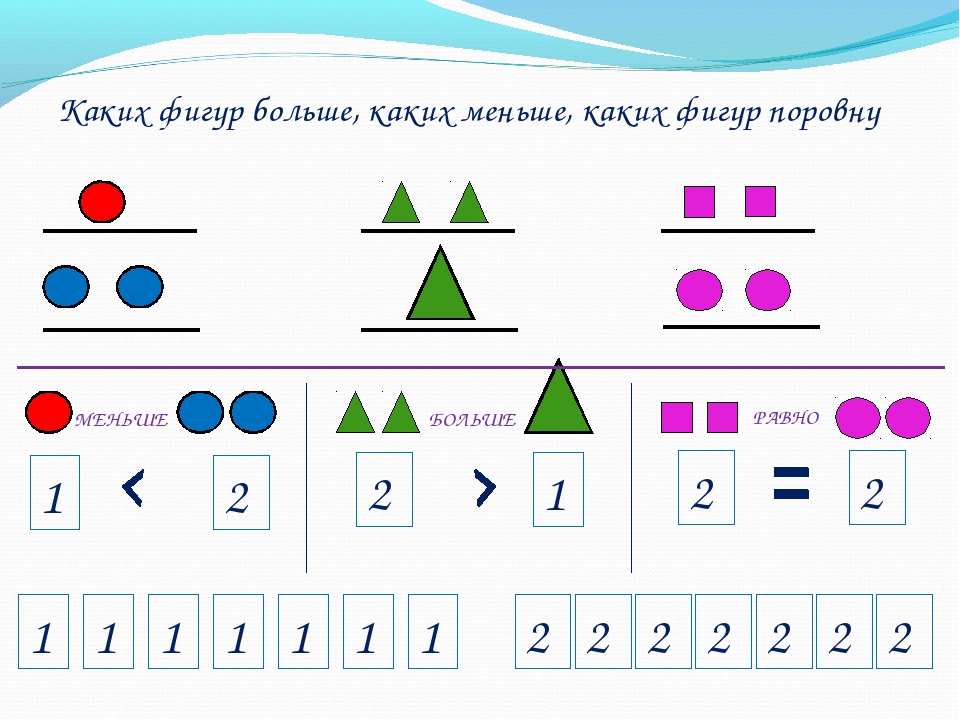 У знака меньше наоборот, острый кончик направлен влево: lt;.
У знака меньше наоборот, острый кончик направлен влево: lt;.
В первом классе нас учили (и я теперь так же 3х летней дочке легко объяснила), что этот знак похож на открытый клювик уточки, которая смотрит в сторону большего числа, то есть если левое число больше правого, то пишем > (больше), если наоборот- то lt; (меньше). Также можно запомнить что широкой (большой) своей стороной он смотрит в сторону большего числа.
Если quot;открытой пастьюquot; знак поврнут влево — это больше.
А если вправо — это знак меньше.
Запомнить легко, если считать, что quot;открытая пасть — большаяquot;, значит БОЛЬШЕ.
Острый угол на знаке показывает на число — маленькая стрелка — знак МЕНЬШЕ.
Так как в основном мы пишем слева направо и читаем так же, то нужно запомнить.
Знак quot;большеquot; и quot;меньшеquot; изображается в виде буквы V, которая упало влево или вправо.
Если этот знак упал влево, то есть два конца смотрят влево, а угол смотрит вправо, то это знак quot;большеquot; — quot; > quot;
Если наоборот — знак упал вправо, то знак quot;меньшеquot; — quot; lt; quot;.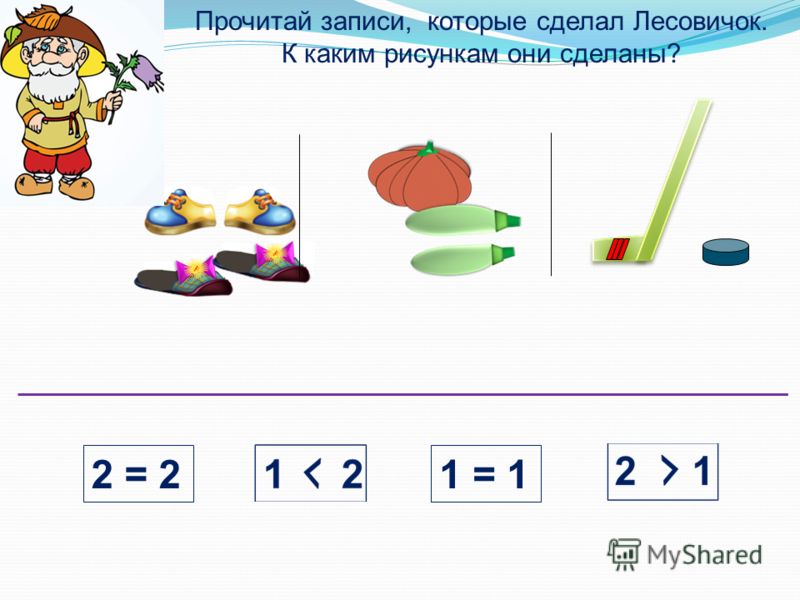
Угол этого знака всегда смотрит на ту цифру, которая меньше. Если цифры равны, то между ними ставится знак равенства quot; = quot;.
Знак больше и знак меньше в математике и статистике в формулах записываются с помощью специальных обозначений (значков):
Символ меньше: lt;
Прописью вы можете записать их при необходимости как:
Математические знаки больше и меньше практический одинаковые, вот только открывают свой ротик в разные стороны. Ротик этого знака открывается всегда в ту сторону, где стоит большее число, а уголочек знака всещда указывает на меньшее число.
7 lt; 9 — это знак меньше, потому что в левую сторону смотрит уголочек.
9 > 7 — это знак больше, потому что в оевуб сторону открыт ротик знака.
Пишутся знаки меньше и больше следующим образом:
quot;lt;quot; — это зак, который означает quot;меньшеquot;,
quot;>quot; — это знак, который означает quot;большеquot;.
Ориентируйтесь на сторону знака, широкая указывает на большее число, а угол — на меньшее.
Как правильно, в какую сторону направлен
В первом классе нас учили (и я теперь так же 3х летней дочке легко объяснила), что этот знак похож на открытый клювик уточки, которая смотрит в сторону большего числа, то есть если левое число больше правого, то пишем > (больше), если наоборот- то
В математике часто приходится сравнивать числа по величине, для чего и были придуманы графические символы. Вместо слова «больше» используется знак «>», а вместо слова «меньше» — символ » 3. Между цифрами стоит знак «больше», который повернут своей открытой стороной в сторону большей величины. Запомнить обозначение очень просто: «носик» всегда повернут своим острием в сторону меньшего числа.
Данные знаки (больше и меньше) используются в математике для составления неравенств. Я сам, когда учился в школе очень часто путал их друг с другом. На мой взгляд, единственный способ не путаться в них — это просто запомнить, без каких-либо ассоциаций.
На мой взгляд, единственный способ не путаться в них — это просто запомнить, без каких-либо ассоциаций.
Итак. знаки «больше» и «меньше» имеют форму перевернутой галочки. Основная ошибка: в какую именно сторону перевернут каждый из них.
Поэтому, бужет правильным, если я приведу здесь условное неравенство и потом напишу его так. как оно произносится.
Итак, первое неравенство:
неравенство вида a
неравенство вида a>b означает, что a больше,чем b.
Что еще можно сказать о неравенствах? Ну разве что только то, что есть еще знаки, которые называются «меньше или равно» и «больше или равно».Обозначаются они следующим образом: ≤ ≥ .
При обучении математике детям обычно называют знаки больше и меньше клювиком, так им проще запоминать образное понятие. А вот чтобы запомнить в какую сторону пишется меньше, а в какую больше приводят другой пример — закрытый клювик всегда смотрит в сторону меньшего числа, открытый в сторону большего. То есть у нас получается такая жадная уточка, которая разевает клюв только на действительно стоящее. Возможно поэтому еще этот знак сравнивают с крокодилом. Теперь если слева стоит большее число, клювик к нему открыт и мы имеем знак «больше», а если слева стоит меньшее число, клювик налево закрыт, то у нас получается знак «меньше».
Возможно поэтому еще этот знак сравнивают с крокодилом. Теперь если слева стоит большее число, клювик к нему открыт и мы имеем знак «больше», а если слева стоит меньшее число, клювик налево закрыт, то у нас получается знак «меньше».
Так как в основном мы пишем слева направо и читаем так же, то нужно запомнить.
Знак «больше» и «меньше» изображается в виде буквы V, которая упало влево или вправо.
Если этот знак упал влево, то есть два конца смотрят влево, а угол смотрит вправо, то это знак «больше» — » > «
Если наоборот — знак упал вправо, то знак «меньше» — «
Математические знаки больше и меньше практический одинаковые, вот только открывают свой ротик в разные стороны. Ротик этого знака открывается всегда в ту сторону, где стоит большее число, а уголочек знака всещда указывает на меньшее число.
7 7 — это знак больше, потому что в оевуб сторону открыт ротик знака.
Эти знаки используются в младших школьных классах в математике, для определения какое же число больше. Запомнить очень легко: у нас в школе этот знак звали «клювик» , это как-то по-детски и легче запомнить. И вот нам говорили: куда смотрит «клювик» значит это число меньше.
Запомнить очень легко: у нас в школе этот знак звали «клювик» , это как-то по-детски и легче запомнить. И вот нам говорили: куда смотрит «клювик» значит это число меньше.
Например: 5>1 — «клювик» смотрит на цифру один своей острой частью, получается это число меньше второго.
Также можно встретить знак больше или равно ,его не стоит пугаться , это совмещение знаков : и = . Приведу пример: 5 ≤ 5 , получается ,что неравенство имеет смысл ,при второй пятерки ,если она например 5 или 6 , и так до бесконечности.
Советую больше делать таких примеров и само собой запомниться без всяких «клювиков».
Цели урока:
- Образовательная: познакомить со знаками меньше « », равно «=» и записями вида 2 2, 4=4, повторить геометрический материал, состав чисел;
- Развивающая: развитие коммуникативных качеств личности (умение работать в паре, вести учебный диалог, проводить самооценку)
- Воспитательная: воспитание чувства сопереживания, взаимопомощи.
1. Орг. момент
Внимание, проверь дружок,
Готов ли ты начать урок?
Всёли на месте, всёли в порядке
Книга, ручка и тетрадки?
И цветные карандаши
Ты на парту положи,
И линейку не забудь
В математику держим путь!
А сейчас, ребята, поудобнее садитесь,
Не шумите, не вертитесь,
И внимательно считайте
А спрошу вас – отвечайте.
Вам условие понятно?
Это слышать мне приятно
Путешествие зовёт
Первоклашек на урок!
2. Основная часть:
Учитель: А совершим мы с вами сегодня полёт в неизведанное космическое пространство. Сегодня мы будем не учениками, а исследователями космического пространства. А чтобы полёт прошёл удачно давайте вспомним, чем мы занимаемся на уроках математики?
Ученики: Решаем, считаем, пишем, думаем…
Учитель: А как вы думаете, что мы будем делать сегодня?
Ученики: Считать, решать, отвечать, думать, чертить…
Учитель: Чтобы полёт прошёл удачно, необходимо быть:
- Внимательными
- Точно и правильно выполнять задания
- Не допускать ошибок, иначе ракета может потерпеть аварию.

В расчётное время, стартуя с Земли,
К загадочным звёздам
Летят корабли
Представим: чуть-чуть помечтали –
И все космонавтами стали.
Учитель: Итак, повышенное внимание! До старта ракеты осталось 10 секунд, давайте немного посчитаем. (Ученики ведут счёт)
- Счёт цепочкой до 10.
- Начинает учитель, дети продолжают.
- Отсчёт в обратном направлении.
- Отсчитываем секунды 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 пуск. Мы в полёте!
Учитель: Ребята, посмотрите на доску, она сегодня превратилась в «звёздное небо». Но какие необычные звёзды! Что они нам напоминают?
Ученики: геометрические фигуры.
Учитель: Что это за фигуры, назовите.
Ученики: отрезок, прямая, точки, ломаная, кривая.
Учитель: Пока мы смотрели на небо глазки устали, давайте сделаем для них зарядку.
Рисуй глазами треугольник,
Теперь его переверни
Вершиной вниз
И вновь глазами
Ты по периметру веди.
Рисуй восьмёрку вертикально
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води
И на бочок её клади.
Теперь следи горизонтально.
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец
Зарядка окончилась.
Ты молодец!
Учитель: Ребята, посмотрите, наш пульт управления находится в аварийном состоянии. Запали кнопки, необходимо исправить пульт.
- Какое число идёт при счёте за числом 3, 6, 9?
- Какое число стоит перед числом 2, 5, 8, 10?
- Назовите соседей числа 2, 7?
Но на пульте кроме цифр есть ещё различные знаки, они тоже стёрлись, давайте их восстановим (дети по очереди отвечают, остальные хлопают в ладоши, если верно)
Однажды решили Белочка и Ёжик проверить, что птицы любят есть больше всего: пшеничные зерна или крошки белого хлеба. На один пень насыпали зерна, а на другой крошки хлеба и стали наблюдать.
— Ежик, ну что ты там видишь?
— О, теперь вижу. Два воробья прилетели. Сейчас зерна будут клевать.
Два воробья прилетели. Сейчас зерна будут клевать.
— Ой. Ко второму пню, ну там где крошки, сорока наша прилетела.
— Так где птиц больше?
— На пне с зернышками птиц больше, чем около пня с крошками.
— Белочка, кажется дядя Филя прилетел.
— Ну, и где сейчас птиц стало больше?
— Теперь птиц стало одинаково.
— Любик, а ты знаешь, что в математике, чтобы сравнивать объекты или предметы используют специальные математические знаки: больше, меньше и равно.
Например, вот у нас одно яблоко и одна груша, т.е. яблок столько же сколько и груш. Значит между ними можно поставить знак равно. А записать это можно так: два равно двум.
Теперь мы сравним грибы: три боровика и две лисички. Что больше?
— Три боровика больше, чем две лисички.
— Правильно. В этом случае мы между грибами поставим знак больше. А записать это можно так: три больше чем два.
— А сейчас сравним жёлуди и орехи. Чего меньше?
— Ага… Желудей у нас три, а орехов пять. Значит желудей меньше, чем орехов.
Значит желудей меньше, чем орехов.
— Правильно, в этом случае мы поставим знак меньше. А записать это можно так: пять меньше чем три.
А теперь мы посмотрим, как пишутся эти знаки.
— Я помню как пишется знак равно. Он состоит из двух палочек, которые пишутся друг под другом. Вот.
— Правильно. Знаки больше и меньше тоже состоят из двух палочек. В знаке больше палочки расходятся к большему числу, а записывается этот знак так.
В знаке меньше палочки сходятся к меньшему числу и записывается он так.
— Ежик, допиши пожалуйста знаки в строчку, в пустые клеточки.
— Ага… Сейчас, сейчас. Сначала допишу знак равно, теперь больше и меньше.
А чтобы ты не запутался, запомни: левая рука, согнутая в локте даст нам знак меньше, а правая рука согнутая в локте даст нам знак больше.
Если между двумя числами поставить знак равно, то получится числовое равенство. А если между двумя числами поставить знаки больше или меньше, то получится числовые неравенства.
Ежик, а теперь проверь пожалуйста, верные ли равенства и неравенства.
Так, так, так. Ага. Два больше чем один – все верно, три больше, чем четыре…ага…
что-то не так, три обозначает большее количество предметов, чем четыре и при счете
идет раньше, чем четыре значит это неравенство не верное. Мы его зачеркнем.
— А давай лучше исправим, чтобы у нас не было ошибок.
— Давай. Значит здесь надо поставить знак меньше. Вот.
— Так-так. Пять равно пяти. Все верно.
— Ага, а здесь совсем сложно.
— Ничего сложного. Смотри, чтобы проверить, надо сначала посчитать, сколько будет два да один.
— А сколько будет два да три.
— Пять. Значит три меньше пяти. Здесь опять ошибка. Надо поставить знак меньше.
— Ну молодец Ежик. Ты все правильно выполнил. Итак, ты должен запомнить:
1. Чтобы сравнить числа в математике используют знаки больше, меньше или равно.
2. Знак больше, расходится палочками к большему числу. И если согнуть правую руку в локте, то получится знак больше. Выражение, в котором стоит знак больше называется неравенство.
И если согнуть правую руку в локте, то получится знак больше. Выражение, в котором стоит знак больше называется неравенство.
3. Знак меньше, сходится палочками к меньшему числу. И если согнуть левую руку в локте, то получится знак меньше. Выражение, в котором стоит знак меньше тоже называется неравенство.
4. Знак равно состоит из двух палочек, которые пишутся друг под другом, а выражение, в котором стоит знак равно называется числовым равенством.
— Белочка, а давай посмотрим, что там наши птицы делают?
— Все склевали и улетели. Да, теперь мы не сможем определить, что же птицы любят больше. Ничего не осталось.
— Наверное, Ежик, одни птицы больше любят есть зерна, а другие хлебные крошки.
Источники: http://info-4all.ru/obrazovanie/kak-pishetsya-znak-bolshe-i-znak-menshe/, http://www.bolshoyvopros.ru/questions/923688-kak-pishetsja-znak-bolshe-i-znak-menshe.html, http://xn--i1abbnckbmcl9fb.xn--p1ai/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/569979/, http://videouroki. net/video/13-znaki-bol-shie-mien-shie-ravno-ravienstvo-nieravienstvo.html
net/video/13-znaki-bol-shie-mien-shie-ravno-ravienstvo-nieravienstvo.html
Больше либо равно в ворде
Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше, а также знак равно.
Однако, если с последним что-то напутать достаточно сложно, то о том, как и в какую сторону пишутся знаки больше и меньше (знак менее и знак более, как ещё их иногда называют) многие сразу после этой же школьной скамьи и забывают, т.к. они довольно редко используются нами в повседневной жизни.
Но практически каждому рано или поздно всё равно приходится столкнуться с ними, и “вспомнить” в какую сторону пишется нужный им символ получается лишь обратившись за помощью к любимой поисковой системе. Так почему бы не ответить развернуто на этот вопрос, заодно подсказав посетителям нашего сайта как запомнить правильное написание этих знаков на будущее?
Именно о том, как правильно пишется знак больше и знак меньше мы и хотим напомнить вам в этой небольшой заметке. Также будет не лишним рассказать и том, как набрать на клавиатуре знаки больше или равно и меньше или равно, т.к. этот вопрос тоже довольно часто вызывает затруднения у пользователей, сталкивающихся с такой задачей очень редко.
Также будет не лишним рассказать и том, как набрать на клавиатуре знаки больше или равно и меньше или равно, т.к. этот вопрос тоже довольно часто вызывает затруднения у пользователей, сталкивающихся с такой задачей очень редко.
Содержание:
Перейдем сразу к делу. Если вам не очень интересно запоминать всё это на будущее и проще в следующий раз снова “погуглить”, а сейчас просто нужен ответ на вопрос “в какую сторону писать знак”, тогда для вас мы приготовили краткий ответ — знаки больше и меньше пишутся так, как показано на изображении ниже.
А теперь расскажем немного подробнее о том, как это понять и запомнить на будущее.
Как и в какую сторону пишется знак больше
В общем и целом логика понимания очень проста — какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону — такой и знак. Соответственно, знак больше влево смотрит широкой стороной — большей.
Пример использования знака больше:
- 50>10 — число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.
Как и в какую сторону пишется знак меньше
Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной — меньшей, то перед вами знак меньше.
Пример использования знака меньше:
- 100 =”, что, в принципе, часто вполне допустимо, но можно сделать красивее и правильнее.
На самом деле для того, чтобы напечатать эти знаки, существуют специальные символы, которые можно ввести на любой клавиатуре. Согласитесь, знаки “≤” и “≥” выглядят значительно лучше.
Знак больше или равно на клавиатуре
Для того, чтобы написать “больше или равно” на клавиатуре одним знаком даже не нужно лезть в таблицу специальных символов — просто поставьте знак больше с зажатой клавишей “alt”. Таким образом сочетание клавиш (вводится в английской раскладке) будет следующим.
Или же вы можете просто скопировать значок из этой статьи, если вам нужно воспользоваться им один раз. Вот он, пожалуйста.
Вот он, пожалуйста.
Знак меньше или равно на клавиатуре
Как вы наверное уже смогли догадаться сами, написать “меньше или равно” на клавиатуре вы можете по аналогии со знаком больше — просто поставьте знак меньше с зажатой клавишей “alt”. Сочетание клавиш, которое нужно вводить в английской раскладке, будет следующим.
Или просто скопируйте его с этой страницы, если вам так будет проще, вот он.
Как видите, правило написания знаков больше и меньше довольно просто запомнить, а для того чтобы набрать значки больше или равно и меньше или равно на клавиатуре достаточно просто нажать дополнительную клавишу — всё просто.
В Word можно вставлять математические символы в уравнения и текст.
На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.
В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.
Щелкните стрелку рядом с названием набора символов и выберите набор символов, который вы хотите отобразить.
Щелкните нужный символ.
Доступные наборы символов
В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.
Основные математические символы
Часто используемые математические символы, такие как > и
Почему мы используем знак «меньше», а не «меньше»
Английский – сложный для освоения язык, потому что в нем много правил. Возьмем, к примеру, «меньше» и «меньше». Оба слова означают, что количество уменьшилось в размере, но они не являются взаимозаменяемыми при правильном использовании. Используйте «меньше», когда вы имеете в виду количество, которое невозможно подсчитать, и «меньше», когда вы можете подсчитать количество. Например, вы не можете сосчитать «свет». Вы говорите: «У меня меньше света». Однако вы можете сосчитать «лампочки» и сказать: «У меня меньше лампочек.”
Так почему же в математике используется знак «меньше», чем знак «меньше»? Мы же считаем количество математикой, верно?
Ответ приходит с нескольких сторон: текущее состояние английского языка, история и идея чего-то «похожего на английский».
В английском языке есть исключения из правила подсчета, сообщает grammar.quickanddirtytips.com. Цитируя почтенного Фаулера Modern English Usage и dictionary.com, на сайте говорится: «Например, слово« меньше »принято использовать для описания времени, денег и расстояния.Например, можно сказать: «Свадебный прием длился менее двух часов. Я надеюсь, что они заплатили группе менее 400 долларов. «Так что имейте в виду, что время, деньги и расстояние – разные, но если вы будете придерживаться быстрых и грязных советов, которые меньше для массовых существительных и меньше для подсчета существительных, вы» в большинстве случаев буду прав “.
Другое объяснение исходит из самой истории. Английский язык боролся за «меньше» и «меньше». Блогер Марк Израэль (alt-usage-english.org/excerpts/fxlessvs.html говорит:
) Обычно встречается правило: используйте «меньше» для вещей, которые вы считаете (индивидуально), и «меньше» для вещей, которые вы измеряете: «меньше яблок», «меньше воды». Поскольку «меньше» также используется как наречие
Поскольку «меньше» также используется как наречие
(«менее успешный»), «меньше» помогает отличить «меньше успешных профессионалов» (меньше успешных профессионалов) от «менее успешных профессионалов» (менее успешных профессионалов).
(Такое различие невозможно с «больше», которое служит антонимом «меньше» и «меньше».) «Меньше» использовалось в смысле «меньше» со времен короля Альфреда Великого в
году. (9 век), и до сих пор распространен в этом смысле, особенно неофициально в США.S .; но в британском английском это стало настолько редким, что в 1-м издании [Oxford English Dictionary]
(в разделе, подготовленном в 1902 г.) не было цитирования более позднего, чем 1579 г., и была дана метка использования «Сейчас считается неправильным». Во 2-м издании OED добавлены две цитаты 19-го века и изменена метка использования на
«Часто встречается, но в целом считается неправильной».
При всей этой путанице неудивительно, что знак «меньше чем» впервые появился в книге Томаса Харриота «Алгебраические решения» (1560–1621), опубликованной посмертно в 1631 году. Если английский собирался бороться, математики выбирали имя и придерживались его. Тогда можно сказать, что язык математики «похож на английский». Современный пример – компьютерные языки, такие как COBOL. COBOL – это не совсем по-английски. Изучите этот синтаксис COBOL и обратите внимание на его точность:
Если английский собирался бороться, математики выбирали имя и придерживались его. Тогда можно сказать, что язык математики «похож на английский». Современный пример – компьютерные языки, такие как COBOL. COBOL – это не совсем по-английски. Изучите этот синтаксис COBOL и обратите внимание на его точность:
MOVE Source $ # il TO Destination $ # i…
«MOVE» и «TO» выглядят как английские, но эти слова должны использоваться в соответствии с правилами COBOL, а не английскими правилами. Компилятор не знал бы, что делать с оператором «MOVE THIS OVER THERE»: «THIS» нужно было бы объявить источником, а «THERE» – местом назначения, но «OVER» в этом утверждении не имеет значения.
Математика – это тоже отдельный язык. Да, мы все видели «проблемы со словами» с начальной школы, но цель не в том, чтобы приукрашивать английский язык. Намерение состоит в том, чтобы построить математическое уравнение – производное от английского языка (другой язык, очевидно, тоже подойдет) – для решения проблемы. Вот очень простая проблема:
Вот очень простая проблема:
Цена компьютера меньше 2000 долларов, цена принтера меньше 300 долларов, а цена сканера меньше 200 долларов. Какова общая ориентировочная стоимость трех предметов?
Здесь мы взяли с английского информацию, чтобы построить то, что нам нужно, чтобы получить наш ответ.Нас не интересует хорошая грамматика, плохая грамматика или то, стоит ли «меньше» перед «меньшим». Нам нужен ответ, и он у нас есть, и мы используем то название, которое символ носил уже около 450 лет.
Конечно, когда мы пишем по-английски, мы будем использовать «меньше» и «меньше» в соответствии с действующими правилами: если мы можем посчитать то, о чем пишем, мы будем использовать «меньше»; «Мы будем делать меньше ошибок». Когда мы не можем посчитать количество, мы будем использовать «меньше»; «Мы хотим меньше зла».
Где найти дополнительную информацию:
• Берчфилд, Р.Мы б. Современное английское употребление Нового Фаулера. Третье издание. Нью-Йорк: Оксфорд, 1996, стр. 295.
Нью-Йорк: Оксфорд, 1996, стр. 295.
• мало. Dictionary.com. Словарь английского языка American Heritage®, четвертое издание. Бостон: Houghton Mifflin Company, 2004. http://dictionary.reference.com/browse/few (дата обращения: 10 мая 2007 г.).
• grammar.quickanddirtytips.com/less-versus-fewer.aspx
• cobolprog.blogspot.com/2008/07/move-command.html
• www.onlinemathlearning.com/math-word-problems.html
• alt -использование-английский.org / excrpts / fxlessvs.html
Подробнее о журнале Electronic Products Magazine
математических цитат
«Это важный и популярный факт, что вещи не всегда такие, какими кажутся. Например, на планете Земля человек всегда считал, что он умнее дельфинов, потому что он многого достиг: колесо, Нью-Йорк, войны. […] Но, наоборот, дельфины всегда считали, что они намного умнее людей, по точно таким же причинам.”
«42. (Ответ на жизнь, вселенную и все остальное.)»
Дуглас Адамс ( Путеводитель по галактике, )
«Математика меньше связана с бухгалтерским учетом, чем с философией».
Леонард Адлеман (цитируется в статье Джины Колата в газете New York Times от 13 декабря 1994 г.)
«Что, если все иллюзия и ничего не существует? В таком случае я определенно переплатил за свой ковер».
Вуди Аллен
“Если вам не нравится ваш аналитик, обратитесь к местному алгебраисту!”
Герт Альмквист (основатель и директор Института алгебраической медитации)
Было доказано, что logloglog n стремится к бесконечности, но никогда не наблюдалось.”
«Кто угодно может посчитать семена в яблоке, но никто не может сосчитать яблоки в семени».
Аноним
“Вы можете добиться успехов только в том, что любите. Не зарабатывайте деньги
цель. Вместо этого занимайтесь тем, что вам нравится делать, и делайте их так хорошо, чтобы
люди не могут оторвать глаз от вас. Все остальные ощутимые награды придут
как результат.”
Maya Angleou
«Вероятное невозможное следует предпочесть невероятным возможностям».
Аристотель
“По моему опыту, доказательства с использованием матриц можно сократить на 50%, если выбросить матрицы.”
Э. Артин ( Геометрическая алгебра , стр. 14)
Комбинаторный анализ в тривиальном смысле манипулирования биномиальными и полиномиальными коэффициентами и формального расширения степеней бесконечных рядов с помощью приложений ad libitum и ad nauseamque полиномиальной теоремы представлял лучшее, что могла сделать академическая математика в Германии конца 18 века. . ”
“Если вещи хорошие, то, вероятно, есть веские причины, почему они хороши: и если вы делаете
Если вы не знаете хотя бы одну причину такой удачи, то вам еще есть над чем поработать.”
Ричард Аски ( Рамануджан и важные формулы , стр. 32, в Шриниваса
Рамануджан (1887-1920), Дань , К. Нагараджан и Т. Саундараджан, ред.,
Университет Мадурай Камарадж, 1987 г.)
“В свете дня математики проверяют свои уравнения и доказательства, не оставляя камня на камне.
непоколебимы в поисках строгости. Но ночью, под полной луной, они мечтают, они плывут
среди звезд и дивиться чуду небес. Они воодушевлены.Без мечты там
нет ни искусства, ни математики, ни жизни ».
Майкл Атия ( Уведомления AMS , 2010 г.)
«Проводить время с математиками – это очень весело. В результате игры я ужинал в полупьяном виде с математиками со всей страны. Я рекомендую этот опыт».
Дэвид Оберн (драматург Proof )
“Quapropter bono christiano, sive mathematici, sive quilibet impie divinantium, maxime dicentes vera, cavendi sunt,
ne consortio daemoniorum animam deceptam, pacto quodam societatis иррециант.”
(“Таким образом, добрый христианин должен остерегаться математиков и всех тех, кто делает ложные пророчества,
на самом деле они могут говорить правду; чтобы они, будучи в союзе с дьяволом, не обманули заблудшие души, заставив их делать общее дело “.)
Августин ( De genesis ad literam , Liber 2, Caput XVII, Nr. 37)
« Z сложный».
Эрик Бэбсон (ИИГС, 18.12.08)
“Неснижаемая цена обучения – это осознание того, что вы не знаете.”
Джеймс Болдуин
«Если« религия »определяется как система идей, содержащая недоказуемые утверждения, то Гёдель учил нас, что математика – это не только религия, это единственная религия, которая может доказать, что она таковая».
Джон Барроу
«Чтобы подсчитать целые очки, нужна деревня».
«Решетчатые точки похожи на тараканов. Если вы видите одного из них, вы знаете, что вокруг прячется много других».
«Доказано, что этот алгоритм работает, но никогда не наблюдалось, чтобы он работал» (о методе цепей Маркова Монте-Карло для приблизительного подсчета таблиц непредвиденных обстоятельств).
Александр Барвинок (Совместная летняя научная конференция, Snowbird, UT, 16.07.03, Коллоквиум по математике в Иллинойсе, 02/05, и Совместная летняя исследовательская конференция, Snowbird, UT, 15.06.06)
«Один, и один, и один – три».
Битлз ( Соберитесь вместе, )
«Очевидное – самое опасное слово в математике».
Э. Т. Белл
«Математика – это сборник дешевых уловок и грязных шуток».
Липман Берс
“Истоки теории графов скромны, даже легкомысленны.”
Н. Биггс, Э. К. Ллойд и Р. Дж. Уилсон ( Теория графов: 1736-1936, )
«Нет WLAN [Wi-Fi]. Пожалуйста, поговорите друг с другом и напивайтесь».
Доска возле бара на Кольвицштрассе, Берлин
“Жизнь – это двойное внутреннее движение композиции и разложения на
когда-то общий и непрерывный “.
Анри де Бленвиль ( Американский журнал медицинских наук ,
1858)
«В жизни многих американцев есть две версии математики: странный и скучный предмет, с которым они сталкиваются в классах, и интересный набор идей, который является математикой мира, который на удивление отличается и удивительно интересен.Наша задача – познакомить сегодняшних студентов со второй версией, увлечь их математикой и подготовить к будущему ».
Джо Булер ( Что с этим связано с математикой? , Penguin 2008)
«У 5 из 4 людей проблемы с дробями».
Доска
в Дэнби, Нью-Йорк
«Предположим, вы хотите научить концепции« кошка »очень маленького ребенка. Объясните ли вы, что кошка относительно
маленькое, в основном хищное млекопитающее с убирающимися когтями, характерным звуковым выходом и т. д.? Готов поспорить, нет. Ты
возможно, покажите малышу много разных кошек, каждый раз говоря «котенок», пока он не поймет. Чтобы сказать больше
как правило, обобщения лучше всего делать путем абстрагирования от опыта ».
Р. П. Боас ( Можем ли мы сделать математику неприемлемой? , American Mathematical Monthly 88 (1981), стр. 727-731)
«Мы все согласны с тем, что ваша теория безумна, но достаточно ли она безумна?»
Нильс Бор (1885-1962)
«Мое особое удовольствие в математике основывалось на ее чисто умозрительной части.”
Бернхард Больцано (1781-1848)
«Математика в том виде, в каком мы ее знаем и как она сформировала современную науку, никогда бы не появилась на свет без некоторого игнорирования опасностей бесконечности».
Дэвид Брессуд ( Радикальный подход к реальному анализу , MAA, 2007, стр. 22)
«Нет проблем, просто паузы между идеями».
Братство розы
«Есть три типа людей: те, кто умеет считать, и те, кто не умеет».
Наклейка на бампер на автомобиле в Итаке, штат Нью-Йорк
«Абстракция заключается в создании и использовании двусмысленности.”
«Логика движется в одном направлении, в направлении ясности, согласованности и структуры. Неоднозначность движется в другом направлении, в плавности, открытости и освобождении. Математика движется вперед и назад между этими двумя полюсами. взаимодействие между этими различными аспектами, которое придает математике ее силу ».
Уильям Байерс ( Как думают математики, , Princeton University Press, 2007)
“Слишком много людей думают о безопасности, а не о возможностях.Кажется, они больше боятся жизни, чем смерти ».
Джеймс Ф. Бирнс
«Сущность математики заключается в ее свободе».
«Задать правильный вопрос труднее, чем ответить на него».
Георг Кантор
«Алиса засмеялась:« Нет смысла пытаться, – сказала она, – нельзя поверить в невозможное ».
«Я полагаю, у вас не было большой практики», – сказала Королева. ‘Когда я был моложе, я всегда делал это для
полчаса в день. Иногда я верил в шесть невозможных вещей перед завтраком.'”
«С чего мне начать?» – спросил он. «Начни с начала, – сказал король, – и остановись, когда дойдёшь до конца».
«А что толку от книги, – подумала Алиса, – без картинок и разговоров?»
Льюис Кэрролл ( Алиса в стране чудес )
“Особый интерес магических квадратов и всего lusus numerorum в целом заключается в
тот факт, что они обладают очарованием таинственности. Кажется, они предают некоторые скрытые
интеллект, который по заранее составленному плану производит впечатление преднамеренного замысла,
явление, находящее близкий аналог в природе.”
Пол Карус (в W. S. Andrews, Magic Squares and Cubes , 1960)
«Сначала необходимо изучить факты, умножить количество наблюдений, а потом уже искать
формулы, которые связывают их, чтобы таким образом различить частные законы, управляющие определенным классом явлений.
В общем, только после того, как будут установлены эти конкретные законы, можно ожидать открытия
и сформулировать более общие законы, которые завершают теории, приводя множество, по-видимому, очень разных
явления вместе под единым управляющим принципом.”
Огюстен Луи Коши (1789-1857)
«Чтобы осуществить великую мечту, первое требование – это большая способность мечтать; второе – настойчивость».
Сезар Чавес
«Я математический оптимист: имею дело только с положительными целыми числами».
«Самое сложное в работе с математиком – это то, что у него всегда есть проблемы».
Tendai Chitewere
“Каждый, кто занимается исследованиями, должен иметь опыт работы с
лихорадочное и продолжительное стремление к написанию статьи, которую больше никто не будет
прочитать или решить проблему, которую никто не считает важной и которую
не принесет никакой мыслимой награды – что может только подтвердить общее
мнение, что исследователь тратит время на неактуальные.”
Ноам Хомский ( Обзор вербального поведения Б. Ф. Скиннера, , Language, 35, No. 1 (1959), 26-58)
«Пессимист видит трудности в каждой возможности; оптимист видит возможность в каждой трудности».
“Я видел, как можно увидеть прохождение Венеры, величина, проходящая через бесконечность и меняющая свой знак.
от плюса до минуса. Я точно видел, как это произошло … но это было после обеда, и я отпустил это “.
Уинстон Черчилль ( Моя молодость, , 1930)
“11:15 Переформулирую свои предположения:
1.Математика – это язык природы.
2. Все, что нас окружает, можно представить и понять с помощью чисел.
3. Если вы построите график этих чисел, вы увидите закономерности. Следовательно: В природе повсюду есть закономерности ».
Макс Коэн (играет Шон Гуллетт, Pi , фильм Даррена Аронофски)
«Для многих математика – это набор теорем. Для меня математика – это набор примеров; теорема – это утверждение о наборе примеров, а цель доказательства теорем – классифицировать и объяснять примеры… ”
Джон Б. Конвей ( Субнормальные операторы, , Pitman Advanced Publishing Program, 1981)
«Ненавижу алгебру».
Джон Х. Конвей (приглашенный адрес AMS, Торонто, 23.09.00)
«Я сфотографировал многих людей: художников, писателей и ученых, среди прочих. Говоря о своей работе, математики используют слова« элегантность »,« правда »и« красота »больше, чем все остальные вместе взятые».
Мариана Кук (в предисловии к ее книге Математики: внешний вид внутреннего мира с Клиффордом Ганнингом, Princeton University Press, 2009).
“Математический феномен всегда возникает из простой арифметики, столь полезной в повседневной жизни.
жизнь, из числа, это оружие богов: боги там, за стеной, в игре
с числами “.
Ле Корбюзье
«Математик – это слепой в темной комнате, который ищет черную кошку, которой там нет».
Чарльз Р. Дарвин
«Je serais reconnaissant a toute personne ayant, cette демонстрация de me l’expliquer».
«От [Гротендика] я также научился не гордиться трудностью доказательства: трудность означает, что мы не поняли.Идея состоит в том, чтобы уметь рисовать
пейзаж, в котором очевидны доказательства “.
Pierre Deligne ( Theorie des topos et cohomologie etale des schemas, Том 3, , стр. 584, и Notices of AMS 63 (2016), p. 250)
«Математики заботятся о логике не больше, чем логики о математике».
Огастес Де Морган
«По сути, то, что мы делали последние четыре недели, было многогранником быстрого датирования».
Джессика Де Силва (ИИГС-UP, 27 июля 2012 г.)
“Я, конечно, забочусь об оценке образовательных результатов.Но что такое «образовательный результат»? Мерцающие глаза моих учеников вместе с их искренними и красиво выраженными математическими аргументами – все, что мне нужно ».
Кейт Девлин (Угол Девлина)
«Самое главное – иметь возможность рассуждать задом наперед».
Артур Конан Дойл ( Этюд в алом цвете )
«Многие математики в той или иной степени немного странные. Это связано с творчеством».
Питер Дурен (Нью-Йорк Таймс, 26 мая 1996 г., стр.23)
«Предположим, что мы думаем о целых числах, выстроенных в ряд, как домино. Шаг индукции говорит нам, что они достаточно близки, чтобы каждое домино могло опрокинуть следующее, базовый случай говорит нам, что первое домино падает, вывод состоит в том, что они все опрокидываются. Ошибка в этой аналогии в том, что каждому домино требуется время, чтобы упасть, и поэтому домино, которое находится далеко вдоль линии, долго не упадет. Математическое значение находится вне времени ».
Питер Дж. Эклс ( Введение в математическое мышление, , стр.41)
«Я не потерпел неудачу. Я только что нашел 10 000 способов, которые не работают».
Томас Альва Эдисон (1847-1931)
«Самое прекрасное переживание – таинственное. Это источник истинного искусства и науки».
«Все надо делать как можно проще, а не проще».
«Чистая математика – это в своем роде поэзия логических идей».
«Не все, что можно подсчитать, имеет значение, и не все, что может быть подсчитано».
“Не беспокойтесь слишком сильно о своих трудностях в математике, могу вас заверить, что мои еще больше.”
«Я никогда не думаю о будущем – оно наступит достаточно скоро».
«Воображение важнее знаний».
«Дело не в том, что я такой умный. Просто я больше времени тратил на проблемы».
«Insofern sich die Sätze der Mathematik auf die Wirklichkeit beziehen, sind sie nicht sicher, und insofern sie sicher sind, beziehen sie sich nicht auf die Wirklichkeit».
“Wenn ein gewisses technisches Können erreicht ist, verschmelzen Wissenschaft und Kunst gern zur Ästhetik. Die grossen Wissenschaftler sind auch immer Künstler.”
Альберт Эйнштейн (1879-1955)
«Секрет образования – это уважение к ученику».
Ральф Уолдо Эмерсон
«Анализ – это искусство укрощения бесконечности».
Нил Фолкнер (Amer. Math. Monthly 116 (2009), стр. 658)
«Невозможно понять … универсальность законов природы, взаимосвязь вещей без понимания математики. Другого способа сделать это нет».
Ричард П. Фейнман
«Цель образования – заменить пустой ум открытым.”
Малькольм Форбс
«Кормление из ложки в конечном итоге не учит нас ничему, кроме формы ложки».
Э. М. Форстер
«Математика сравнивает самые разные явления и обнаруживает секретные аналогии, которые их объединяют».
Жан Батист Жозеф Фурье (1768-1830)
«В 1906 году было подсчитано, что каждый восьмой американец покупал открытку каждый день».
Джон Фриман ( Тирания электронной почты , стр. 46; в остальном книга неплохая)
«Когда я работаю над проблемой, я никогда не думаю о красоте.Я думаю только о том, как решить
проблема. Но когда я закончу, если решение не будет красивым, я знаю, что оно неправильное ».
«Все, что вы учили в школе как« очевидное », становится менее очевидным.
и менее очевиден, когда вы начинаете изучать Вселенную. Для
Например, во Вселенной нет твердых тел. Нет даже
предложение твердое. Абсолютных континуумов не существует.
Нет поверхностей. Прямых линий нет “.
Бакминстер Фуллер (1895-1983)
«Когда люди говорят вам, что что-то не так или не работает для них, они почти всегда правы.Когда они говорят вам, что именно они считают неправильным и как это исправить, они почти всегда
неправильный.”
Нил Гейман
“Философия написана в этой великой книге – я имею в виду вселенную, – которая постоянно открыта нашему взору,
но его нельзя понять, если сначала не научиться понимать язык и интерпретировать символы
в котором это написано. Он написан на языке математики, и его символы – треугольники,
круги и другие геометрические фигуры, без которых по-человечески невозможно понять ни единого слова.”
Галилео Галилей ( Il Saggiatore , 1623)
«Когда я читаю этот доклад перед физической аудиторией, я удаляю цитаты из своей« Теоремы »».
Брайан Грин (приглашенный доклад на Joint Math Meetings, Вашингтон, округ Колумбия, 19 января 2000 г.)
«За задержку с подготовкой статьи авторы приносят извинения своим читателям и друг перед другом».
Кертис Грин и Том Заславски ( Транзакции AMS 280 (1983), 97-126).
“Тот факт, что мы люди, действительно довольно ограничивает.Я имею в виду, мы не эволюционировали до
понимать структуру пространственно-временного континуума или делать что-то в 100000 измерениях. Мы
умеют держаться подальше от дождя и [не] быть съеденными животными ».
Рон Грэм
«Барт: Эй, Гудини! Почему ты не видел Мартина пополам?
Волшебник: О, я не из тех фокусников. Я математик!
[Дети стонут]
Волшебник: А теперь, приготовьтесь поразиться тайнам вселенной, пока я заставлю этот остаток исчезнуть.[пишет 7 переходит в 28 три раза]
Лиза: Но 7 переходит в 28 четыре раза.
Маг: Эээ, это магия 7. “
«Апу: На самом деле я могу назвать« пи »до 40000 знаков. Последняя цифра – единица!
Гомер: Мммм, пирог».
Гомер: В этот раз завтра ты будешь на высоких каблуках!
Нед: Нет, будешь.
Гомер: «Не пугайся.
Нед:« Так бояться! »
Гомер:« Не пугайся.
Нед: «Не пугайся». !
Гомер: «Бояться бесконечности!»
Нед: «Бояться бесконечности плюс один!»
Гомер: Ооо!
“Интернет-парень: Ваши акции на нуле”.
Барт: Но у меня 52 миллиона акций! Что 52 миллиона умножить на ноль ?! И не говори мне, что это ноль! ”
(Гомер скрылся в стене в гостиной.)
Лиза: Ну, а где мой отец?
Фринк: Ну, это должно быть очевидно даже самому тупому человеку, имеющему ученую степень в области гиперболической топологии, н’ги , что Гомер Симпсон наткнулся на … [свет гаснет] третье измерение
Лиза: [переворачивает выключатель света] Извини
Фринк: [рисует на доске] Вот обычный квадрат….
Виггам: Эй, стой – помедленнее, яйцеголовый!
Фринк: … но предположим, что мы продолжим квадрат за пределы двух измерений нашей Вселенной, вдоль гипотетической оси z, там.
Все: [задыхается]
Фринк: Это формирует трехмерный объект, известный как «куб» или «Фринкаэдр» в честь его первооткрывателя, н’эй, н’эй.
Голос Гомера: Помогите мне! Вы мне помогаете или продолжаете и продолжаете?
Фринк: Да, верно. И, конечно же, внутри мы находим обреченного человека ».
Мэтт Гроунинг (обязательно ознакомьтесь с «Руководством по математике и математикам» Эндрю Нестлера на The Simpsons !)
“Кратчайший путь между двумя истинами в реальной области проходит через сложную область.”
Жак Саломон Адамар (1865-1963)
«Комбинаторика – это не наука, это отношение».
Марк Хайман
«Единственный способ выучить математику – это заниматься математикой».
«Хороший набор примеров, насколько это возможно, необходим для полного понимания любой концепции, и когда я хочу узнать что-то новое, я первым делом создаю такое».
Пол Халмос
«Вы когда-нибудь замечали, что мы уделяем гораздо больше внимания мудрому отрывку, когда его цитируем, чем когда читаем его у первоначального автора?»
Филип Г.Hamerton
«Цель вычислений – понимание, а не числа».
«Между теми, кто работает с открытыми дверями, и теми, кто
в конечном итоге делают важные дела, хотя люди, которые работают с закрытыми дверями, часто работают усерднее “.
[из этого выступления]
Ричард Хэмминг (1915-1998)
«Вдохновение постоянно витает в воздухе. Нам нужно развить в себе чувствительность, чтобы уловить его».
Херби Хэнкок
«В обучении математическому анализу хорошо то, что у вас развивается жесткое отношение к повторению самих себя.”
Фил Хэнлон
«Я верю, что математическая реальность находится вне нас, что наша функция – обнаруживать или наблюдать ее, и что теоремы, которые мы доказываем и которые мы величественно называем нашими« творениями », являются просто записями наших наблюдений».
«Математические узоры, как и узоры художника или поэта, должны быть красивыми; идеи, такие как цвета или слова, должны гармонично сочетаться друг с другом».
Годфри Гарольд Харди
«Ученик, изучающий математику, должен развивать терпимость к двусмысленности.Педантизм может быть врагом проницательности ».
Гила Ханна (в издании Дэвида Талла, Продвинутое математическое мышление )
«Вся цель образования – превратить зеркала в окна».
Сидней Дж. Харрис
“Es ist eine Tatsache, dass die genauere Kenntnis des Verhaltens einer analytischen Funktion in der Nähe ihrer singulären Stellen eine Quelle von arithmetischen Sätzen ist.
Эрих Гекке ( Vorlesungen über die Theorie der algebraischen Zahlen , Kapitel VIII)
“Одно из самых больших заблуждений по поводу математики, которое мы совершаем в наших классах, заключается в том, что
Учитель, кажется, всегда знает ответ на любую обсуждаемую проблему.Это дает студентам
идея, что где-то есть книга со всеми правильными ответами на все интересные вопросы, и
учителя знают эти ответы. И если бы можно было достать книгу, можно было бы все
поселился. Это так непохоже на истинную природу математики ».
Леон Хенкин
«Я считаю, что числа и функции анализа не являются произвольным результатом нашего разума; я думаю, что они существуют вне нас, с тем же характером необходимости, что и вещи объективной реальности, и мы встречаемся с ними или открываем их, и изучаем их, как и физиков, химиков и зоологов.”
Чарльз Эрмит (цитируется в книге Морриса Клайна «Математическая мысль от древних до наших дней », Oxford University Press, 1972, стр. 1035)
«Я написал несколько статей по алгебрам Кошуля, но я действительно не понимаю определения алгебр Кошуля».
Такаюки Хиби (Совместная летняя исследовательская конференция, Snowbird, Юта, 15 июня 2006 г.)
«Математика для ленивых».
Питер Хилтон (Приглашенный адрес, Конференция студентов на реке Гудзон, 2000 г.)
“Die Mathematische Forschung besteht aus 10% Intuition und 90% Arbeit.”
Эдмунд Глава (DMV-Mitteilungen 2/99)
«Как только вы устраните невозможное, все, что останется, каким бы невероятным оно ни было, должно быть правдой».
“‘Данные! Данные! Данные!’ – нетерпеливо воскликнул он. – Я не могу делать кирпичи без глины ».
Шерлок Холмс (сэр Артур Конан Дойл, 1859-1930)
«Хорошее суждение приходит из опыта. Опыт приходит из плохого суждения».
Джим Хорнинг
«Здесь мы опишем, что задействовано в вычислениях, и перечислим наши ответы.Подробности можно получить у автора по запросу. Автор действительно надеется, что кто-то проверит расчеты, потому что он не очень верит в свою способность безошибочно провести детализацию. Однако он надеется, что ответы будут качественно правильными, как указано “.
Роджер Хоу (Proc. Indian Acad. Sci. Math. Sci. 97 (1987), стр. 85-109)
«Чтобы просмотреть список всех причин, по которым технологии не смогли улучшить качество жизни, нажмите три».
Алиса Кан
«Подсчет пар – старейший трюк комбинаторики… Каждый раз, считая пары, мы чему-то учимся ».
Гил Калаи
«Математика – это деятельность, управляемая теми же правилами, что и симфонии Бетховена, картины Да Винчи и поэзия Гомера».
Эдвард Каснер и Джеймс Ньюман ( Математика и воображение, , Саймон и Шустер, Нью-Йорк, 1940, стр. 362)
“Ubi materia, ibi geometria”.
«Геометрия – архетип красоты мира».
Иоганн Кеплер (1571-1630)
“Если вы сделали что-то дважды, вы, скорее всего, сделаете это снова.”
Брайан Керниган и Боб Пайк ( Среда программирования Unix, , стр. 97)
«Математика во многих отношениях является самым ценным ответом человеческого духа на призыв бесконечности».
Кассиус Дж. Кейзер ( Человеческая ценность строгого мышления: эссе и адреса , Columbia University Press, Нью-Йорк, 1925, стр. 59.)
«Хороший доклад не содержит доказательств; хороший доклад не содержит теорем».
«Математические доказательства должны сообщаться только наедине и с согласия взрослых.”
Виктор Клее
«Худшее, что вы можете сделать с проблемой, – это решить ее полностью».
«Если вы используете одну и ту же нотацию для всего, вы никогда не ошибаетесь».
Даниэль Клейтман
«Наука – это то, что мы понимаем достаточно хорошо, чтобы объяснить компьютеру, искусство – это все остальное».
«Я был счастливым человеком с 1 января 1990 года, когда у меня больше не было адреса электронной почты. Я использовал электронную почту примерно с 1975 года, и мне кажется, что 15 лет электронной почты – это достаточно для одной жизни.”
Дональд Э. Кнут
«В L_infinity много места для кратчайших векторов».
«Зафиксируем N, скажем, какое-нибудь небольшое число. [На доске записано N = 300000]»
Маттиас Кеппе (AIM 11.10.10 и 11.11.16)
«Самая большая награда для ученика – плохая оценка. Это готовность учителя его слушать».
Николай Константинов
«Нейн! Вир Синд Дихтер».
“Die ganzen Zahlen hat der liebe Gott geschaffen, alles andere ist Menschenwerk.”
«Теоретики чисел подобны пожирателям лотосов – попробовав эту пищу, они никогда не смогут отказаться от нее».
Леопольд Кронекер (1823-1891)
«Воображаемое число – прекрасный и чудесный ресурс человеческого духа, почти амфибия между бытием и небытием».
«Музыка – это удовольствие, которое человеческий разум испытывает от счета, не осознавая, что он считает».
Готфрид Вильгельм Лейбниц (1646-1716)
«Каждое измерение особенное».
Джефф Лагариас (Совместная летняя исследовательская конференция, Snowbird, UT, 13.07.03)
«Природа смеется над трудностями интеграции.”
Пьер-Симон де Лаплас
«Я не знаю, откуда пришли мои идеи. Я признаю, однако, что одним из ключевых ингредиентов является кофеин. Я наливаю себе пару чашек кофе, и странные вещи просто начинают происходить».
Гэри Ларсон ( Предыстория дальней стороны )
«Музыка – часть теории чисел. Сегодня, когда теоретик чисел подает заявку на грант, он говорит, что это хорошо для безопасности, но в те дни, задолго до Америки, он сказал, что это хорошо для музыки.Я не буду комментировать, продвинулись ли мы … “
” Рекреационная теория чисел […] – это та часть теории чисел, которую слишком сложно изучать. “
” Лекция по математике без доказательства подобна фильму без любовная сцена. [пауза] У этого выступления есть два доказательства ».
Хендрик Ленстра (совместные математические встречи, январь 2002 г.)
“Es ist unglaublich, wie unwissend die studirende Jugend auf Universitäten kommt, wenn ich nur 10 Minuten rechne oder geometrisire, so schläft 1/4 derselben sanfft ein.””
«Ich glaube, dass es, im Strengsten Verstand, für den Menschen nur eine einzige Wissenschaft gibt, und diese ist reine Mathematik. Hierzu bedürfen wir nichts weiter als unseren Geist».
“Die Mathematik ist eine gar herrliche Wissenschaft, aber die Mathematiker taugen oft den Henker nicht. Es ist fast mit der Mathematik wie mit der Theologie. So wie die letzteren Beflisenen, zumal wenn sieuf Kämtern bestehen, Ansinruden und eine nähere Verwandtschaft mit Gott machen, obgleich sehr viele darunter wahre Taugenichtse sind, so verlangt sehr oft der so genannte Mathematiker für einen tiefen Denker gehalten zu werden, ob es gleich darunter die gröpfessten gluderden Geschäft, das Nachdenken erfordert, wenn es nicht unmittelbar durch jene leichte Verbindung von Zeichen geschehen kann, die mehr das Werk der Routine, als des Denkens sind.”
Георг Кристоф Лихтенберг (1742-1799)
«Раньше давалось серьезное предупреждение, что изображения не являются строгими; это никогда не подвергалось блефу и постоянно пугало своих жертв, заставляя их играть из соображений безопасности».
Джон Эденсор Литтлвуд (1885-1977)
«Нет ничего более мечтательного и поэтичного, ничего более радикального, подрывного и психоделического, чем математика. Это не менее поразительно, чем космология или физика (математики придумали черных дыр задолго до того, как астрономы их обнаружили), и допускает больше свободы выражения, чем в поэзии, искусстве или музыке (что сильно зависит от свойств физической вселенной).Математика – самое чистое из искусств, а также самое неправильно понимаемое ».
Пол Локхарт (Плач математика)
«Образование – это самое мощное оружие, которое вы можете использовать, чтобы изменить мир».
Нельсон Мандела
«Der geistige Mensch hat die Wahl (soweit er die Wahl hat), entweder Ironiker oder Radikalist zu sein; ein Drittes ist anständigerweise nicht möglich».
Томас Манн
“Математика – единственное место, где истина и красота означают одно и то же.”
Даника МакКеллар
«Для каждой проблемы есть одно простое, изящное и неправильное решение».
Х. Л. Менкен (1880-1956)
«То, […] то, что мы, эволюционные биологи, не […] делаем в достаточной степени, […] это эмоциональные и моральные доводы в пользу изучения эволюции. Вчера вечером я завершил свое выступление цитатой из Дувра, креациониста из Пенсильвании. член школьного совета Уильям Бэкингем, который заявил: “Две тысячи лет назад кто-то умер на кресте. Неужели никто не может встать на его защиту?” Я ответил: «За последние две минуты кто-то умер от бактериальной инфекции.Мы встаем на его сторону ».
Майк безумный биолог
“Математические исследования и исследования очень напоминают альпинизм. Уимпер приложил несколько усилий, прежде чем он
поднялся на Маттерхорн в 1860-х годах, и даже тогда это стоило жизни четырем участникам его группы. Однако теперь любой турист может быть
поднимается за небольшую плату и, возможно, не оценивает сложность первоначального восхождения. Итак, в математике
может быть трудно осознать огромную первоначальную трудность сделать небольшой шаг, который теперь кажется таким естественным и очевидным,
и неудивительно, если такой шаг снова будет найден и потерян. # ers ass you want to know how to rhyme, you better learn how to add it Mathematics.”
Мос Деф ( Математика )
“Иногда хорошая идея приходит к вам, когда вы ее не ищете.
невероятное сочетание совпадения, наивности и удачных ошибок … ”
Кэри Муллис ( Необычное происхождение полимеразной цепной реакции, , Sci. Amer., Апрель 1990 г., стр. 445)
«Мир непрерывен, но разум дискретен».
Дэвид Мамфорд (пленарное выступление на ICM 2002, 21 августа 2002 г.).
«В математике вы ничего не понимаете.Вы просто привыкните к ним “.
«Если люди не верят, что математика проста, то только потому, что они не осознают, насколько сложна жизнь».
Джон фон Нейман (1903-1957)
“Все остальные поднимались бы на пик, ища тропу где-нибудь в горе. Нэш поднимался бы на другую
горы, и с этой далекой вершины луч прожектора снова попадет на первую вершину “.
Дональд Ньюман (1930-2007) (цитируется в A Beautiful Mind С.Насар, стр. 12)
«Если я и мог видеть дальше, то только потому, что стоял на плечах гигантов».
«Истину всегда можно найти в простоте, а не в множестве и беспорядке вещей».
«Похоже, я был всего лишь мальчиком, играющим на берегу моря и время от времени отвлекающимся на поиски более гладкого камешка или более красивой раковины, чем обычно, в то время как великий океан истины лежал передо мной совершенно неоткрытым».
Исаак Ньютон (1643-1727)
“Критикуйте эффективность вашего урока не по тому, что дают ученики, а по тем, какие вопросы они задают.”
Fawn Nguyen
«Те, кого видели танцующими, считались сумасшедшими теми, кто не мог слышать музыку».
Фридрих Ницше (1844-1900)
«Противоречие не является признаком лжи, а отсутствие противоречия – признаком истины».
«Не уверен, что все неопределенно».
«Свободно говорить о математике, я считаю это высшим упражнением духа; но в то же время я знаю, что это настолько бесполезно, что я мало делаю различие между человеком, который является всего лишь математиком, и обычным ремесленником.Кроме того, я называю это самой красивой профессией в мире; но это всего лишь профессия “.
«Нас обычно легче убедить по причинам, которые мы сами нашли, чем по тем, которые приходили в голову другим».
Блез Паскаль
«Это неправильно, это даже не так».
Вольфганг Паули (1900-1958), прочитав статью молодого физика
«Математики немного похожи на немногословного Вермонтера, который на вопрос, прожил ли он в этом штате всю свою жизнь, отвечает:« Еще нет.”
«Простые уравнения, порождающие запутанный фрактал Мандельброта, были названы самыми остроумными замечаниями из когда-либо сделанных».
Джон Аллен Паулос ( Irreligion , стр. Xii и Once Upon a Number , стр. 130-131)
“… и, вероятно, здесь есть какой-то секрет, который еще предстоит раскрыть.
обнаруженный.”
К. С. Пирс (цитируется Э. П. Вигнером в
необоснованная эффективность математики в естествознании, Сообщения по чистой и прикладной математике 13 (1960, 1-14)
«Лев, у тебя есть религия? Знаешь, религия, например, еврейская, или христианская, или математическая…? ”
Алон Перес, 6-летний сын Ювала Переса (цитируется в Amer. Math. Monthly 110, стр. 324)
«Компьютеры бесполезны. Они могут дать вам только ответы».
Пабло Пикассо
«Не допускайте никого, кто не разбирается в геометрии».
Надпись на дверях платоновской академии
«Математика – это искусство давать одно и то же имя разным вещам».
«Одна геометрия не может быть вернее другой; она может быть только удобнее».
“Мысль – всего лишь вспышка между двумя долгими ночами, но эта вспышка – все.”
“Наука – это факты; как дома сделаны из камня, так и наука.
сделано из фактов; но груда камней – это не дом, а собрание
факты не обязательно наука “.
Жюль Анри Пуанкаре (1854-1912)
«Геометрия – это наука о правильном рассуждении о неправильных числах».
«Однажды у Гильберта был студент-математик, который перестал приходить на его лекции, и ему наконец сказали, что молодой человек ушел, чтобы стать поэтом. Гильберт, как сообщается, заметил:« Я никогда не думал, что у него достаточно воображения, чтобы стать поэтом ». математик ».”
Георгий Поля (1887-1985)
«Теоремы доставляют удовольствие, особенно когда вы доказываете, но потом удовольствие исчезает.
Нас поддерживают нерешенные проблемы ».
Карл Померанс (приглашенный доклад MAA, 21.01.2000)
“Там, где сегодня такой калькулятор, как ENIAC, оснащен 18 000 электронных ламп.
и весит 30 тонн, компьютеры в будущем могут иметь всего 1000 электронных ламп.
и, возможно, весит всего 1 1/2 тонны “.
Popular Mechanics , март 1949 г., стр.258
«Макферсон сказал мне, что мою теорему можно рассматривать как бла-бла-бла-Гротендик-бла-бла-бла, что делает ее более респектабельной».
«Я думаю, что некоторая интуиция просачивается на каждом этапе индукционного доказательства».
Джим Пропп (выступление на специальной сессии AMS, 22.01.00)
«Откровенно говоря, учителя – единственная профессия, которая обучает наших детей».
Дэн Куэйл, 18.09.90
“Кембридж дал мне различные виды обучения и
надзором, но, возможно, наибольшее влияние оказал Джеффри
Голдстоуна и Питера Суиннертон-Дайера, которые побудили меня продолжать
думаю для себя и не относиться к техническим деталям слишком серьезно.”
Майлз Рид (в предсмертном некрологе)
«Математика – это стойкая интеллектуальная честность».
Моисей Ричардсон ( Математика и интеллектуальная честность , Amer. Math. Monthly 59 (1952), стр. 73)
«Больно думать о конвергенции, но иногда это действительно необходимо».
Sinai Robins (коллоквиум SUNY Binghamton 14.03.02)
“Мне нравится думать о математиках как о формировании нашей собственной нации, независимо от географического происхождения, расы, вероисповедания, пола, возраста или даже времени… все посвящены самым прекрасным из искусств и наук “.
Джулия Робинсон
«Бог создал бесконечность, а человек, неспособный понять бесконечность, создал конечные множества».
«Если мы не знаем, почему утверждение истинно, мы все равно можем доказать его по индукции».
«Природа имитирует математику».
«В каждой области есть свои табу. В алгебраической геометрии табу
(1) написание черновика, за которым может подписаться кто угодно, кроме двух или трех ближайших друзей,
(2) утверждение, что результат имеет приложения,
(3) упоминание слова «комбинаторный» и
(4) утверждение, что алгебраическая геометрия существовала и до Гротендика (разрешены лишь некоторые размахивающие рукой ссылки на «итальянцев» при условии, что они не подкреплены конкретными ссылками).”
«В статистике есть нечто, что очень похоже на астрологию».
Джан-Карло Рота
«Иногда идеи просто приходят ко мне. Иногда мне приходится вспотевать и почти истекать кровью, чтобы воплотить идеи в жизнь. Это загадочный процесс, но я надеюсь, что никогда не узнаю, как именно он работает».
Дж. К. Роулинг
“Это потому, что современное образование так редко вдохновляется великой надеждой, что оно так редко дает великий результат. Желание сохранить прошлое, а не надежда создать будущее доминирует в умах тех, кто контролирует обучение молодежи.”
«Во всех делах полезно время от времени вешать вопросительный знак на то, что вы давно принимаете как должное».
Бертран Рассел
«У нас нет денег, поэтому мы должны думать».
Эрнст Резерфорд
«Если вы хотите построить корабль, не призывайте людей собирать дрова и не поручайте им задания и работу, а научите их тосковать по бескрайним просторам моря».
«Взрослые никогда ничего не понимают для себя, и детям утомительно постоянно им что-то объяснять.”
Антуан де Сент-Экзюпери
«Всякая истина проходит три стадии. Во-первых, ее высмеивают. Во-вторых, ей жестоко противостоят. В-третьих, ее принимают как самоочевидную».
“Dass die niedrigstealler Tätigkeiten die arithmetische ist, wird dadurch belegt, dass sie die einzige ist, die auch durch eine Maschine ausgeführt werden kann. Nun läuft aber all analysis finitorum et infinitorum im Grunde doch doch. Mathematischen Tiefsinn ‘.”
Артур Шопенгауэр (1788-1860)
«Проблема в том, что мы склонны жить среди множества крошечных целых чисел и обычно игнорируем огромное количество более крупных. Как банально и ограничивающе наш взгляд!»
П. Д. Шумер ( Mathematical Journeys , Wiley, 2004)
«Удачная, но недоказанная гипотеза может иметь гораздо большее значение для математики, чем доказательство многих уважаемых теорем».
А. Сельберг ( Сборник статей , т. I (1989), стр.700)
“Мне кажется, что математическое письмо похоже на использование языка. Чтобы быть понятым, вы должны следовать некоторым грамматическим правилам. Однако в нашем случае никто не позаботился о написании грамматики; мы получаем ее, как ребенок, из родители, подражая другим. У некоторых математиков хороший слух, у некоторых – нет (а некоторые предпочитают жаргонные выражения, такие как «iff»). Такова жизнь ».
Жан-Пьер Серр
(см. также его лекцию
о том, как плохо писать математику)
«Мы научились быть счастливыми.Мы танцевали по залу.
И умение считать было ключом ко всему “.
Улица Сезам
“Мы научили вас, что земля круглая,
Это красное и белое делают розовым,
И еще кое-что, что имеет большее значение –
Мы научили вас думать ».
Доктор Сьюз ( Ура, День Диффендуфера )
«Хотя это безумие, но в этом есть метод».
«Не теряй времени на ветреные споры, но оставь дело в покое».
В. Шекспир
“log log log x уходит в бесконечность с большим достоинством.”
Дэн Шанкс ( Math. Comp. 13 (1959), 272-284)
«Он [Танияма] был одарен особой способностью совершать множество ошибок, в основном в правильном направлении. Я завидовал
ему в этом и пытались подражать ему, но было довольно трудно делать хорошие ошибки ».
Горо Шимура (программа Nova на FLT и Enigma Ферма Саймона Сингха, стр.174)
«Серьезные цифры всегда будут говорить с нами».
Пол Саймон ( Когда цифры становятся серьезными , 1983)
«Теоретически разницы между теорией и практикой нет.Но на практике это так ».
Ян Л.А. ван де Снепшют
«Сам термин« комбинаторные методы »носит оксюморонический характер».
Джоэл Спенсер ( Справочник по комбинаторике , стр. 1807)
«Математика – это наука о закономерностях, а природа использует практически все существующие закономерности».
Ян Стюарт ( Числа природы: Нереальная реальность математического воображения , Basic Books, Нью-Йорк, 1995, стр. 18)
“1 * 1 = 1, нецелевой вал.Aber 1 * 2 ist nicht 1, weil das Quadrat einer gegebenen Zahl grösser sein mss als die Zahl selbst. Die Wurzel aus 1 kann logischerweise nicht 1 sein, weil die Wurzel aus einer Zahl kleiner sein muss als die Zahl selbst. Aber Mathematisch oder Formal ist sqrt (1) = 1. Die Mathematik widerspricht in diesem Falle der Logik oder der reinen Vernunft, und darum ist die Mathematik in diesem Kardinalfalle vernunftwidrig. Auf dieser Sinnlosigkeit, der 1, bauen sich dann alle Werte auf, und in diesen falschen Werten fusst die Mathematische Wissenschaft, die ‘einzig exakte, unfehlbare’.Aber dies ist Mathematik! Ein artiges Spiel für Leute, die nichts zu tun haben “.
Август Стриндберг (1849-1912)
«Если вы думаете, что это просто, значит, вы неправильно поняли проблему».
Bjarne Strustrup (лекция в Temple U., 25.11.97)
«Единственная причина, по которой нам нравятся комплексные числа, – это то, что нам не нравятся действительные числа».
Бернд Штурмфельс (IAS / Математический институт Парк-Сити, 14.07.04)
«Чисто формальный язык геометрии адекватно описывает реальность пространства.В этом смысле можно сказать, что геометрия – это успешная магия. Я хотел бы сказать обратное: разве вся магия, если она успешна, не является геометрией? ”
Рене Том ( Структурная стабильность и морфогенез , В. А. Бенджамин, Рединг, Массачусетс, 1975, стр. 11)
«Сначала соберите свои факты, а затем вы можете искажать их сколько угодно».
«Мало что может быть труднее, чем хороший пример».
“Через двадцать лет вы будете еще больше разочарованы тем, что вы
не сделали, чем те, которые вы сделали.Так что сбрось боулинги, уплывай
из безопасной гавани ловите пассат в своих парусах. Проводить исследования. Мечтать.
Обнаружить.”
Марк Твен (1835-1910)
«Красивая проблема похожа на забавную шутку».
Даниэль Ульман ( Amer. Math. Monthly 105 (1998), стр. 292)
«Красивая проблема – не шутка!»
Марвин Кнопп (исправления к моей диссертации, апрель 2000 г.)
«Математика – это бегство от реальности».
Станислав Улам ( Приключения математика , UC Press, Беркли, 1991, стр.120)
Филлис объяснила ему, пытаясь передать свое более глубокое «я»: «Разве ты не находишь это таким прекрасным, математика? Как бесконечный лист золотых цепей, каждое звено заперто в предыдущее, теоремы и функции, одно делая следующее неизбежным. Это музыка, которая висит посреди пространства, означающая не что иное, как она сама, и поэтому движется … ‘”
«То, что мой мозг не совсем понимает, – настаивал Оуэн, возводя себя до уровня психической хрупкости Кантора, – вот почему это было так важно, когда Рассел и Гедель обнаружили эти внутренние противоречия или парадоксы, – как указывает Кляйн. , путаница в основном семантическая.Я не понимаю, какое отношение неразрешимость имеет к истории компьютера ». «Я имею в виду, – сказал он, – так что , что , если существует набор наборов, которые не являются членами самих себя, что делает его набором, который одновременно является и не является членом самого себя?» «Но, Оуэн, дорогой, – сказала Филлис, – антиномии – парадоксы – подрывают классическую логику, но то, как они должны быть сформулированы, приводит нас к символической логике, которая вводит булеву математику, машину и алгоритмы Тьюринга. Неразрешимость – это как знать, что у вас болото, и все равно изобретать методы, чтобы на нем строить.Это как Бэк-Бэй на всех сваях, – сказала она … »
Джон Апдайк ( Village , Альфред А. Кнопф, Нью-Йорк, 2004 г., стр. 93-96)
«Отсутствие серьезности привело ко множеству чудесных открытий».
Курт Воннегут
«Математик, который не является одновременно чем-то вроде поэта, никогда не станет законченным математиком».
Карл Вейерштрасс
“Каждый математик, достойный этого имени, хотя бы изредка испытывал состояние ясного
возвышение, в котором одна мысль сменяет другую, как бы чудесным образом, и в котором бессознательное
(как бы ни толковалось это слово), похоже, играет роль.”
“Gott existiert, weil die Mathematik widerspruchsfrei ist, und der Teufel existiert, weil wir das nicht beweisen können.”
Андре Вайль
«Это все хорошо на практике, но как это работает в теории?»
Шмуэль Вайнбергер (ИИГС, 05.09.06)
«Мои работы всегда пытались соединить истину с прекрасным, но когда мне приходилось выбирать одно или другое, я обычно выбирал прекрасное».
Герман Вейль
«Мы думаем в общих чертах, но живем в деталях.”
«Погоня за математикой – это божественное безумие человеческого духа».
«Фундаментальный прогресс связан с переосмыслением основных идей».
«Порядка недостаточно. Требуется нечто гораздо более сложное. Это порядок, вступающий в новизну; чтобы массивность порядка не переросла в простое повторение; и чтобы новизна всегда отражалась на фоне системы. . ”
Альфред Норт Уайтхед
“Жизнь слишком важна, что бы воспринимать ее серьезно.”
Оскар Уайльд
«Я никогда не использую компьютер».
Эндрю Уайлс (программа Nova на FLT и Enigma Ферма Саймона Сингха, стр. 211)
«Производящая функция – это бельевая веревка, на которую мы вешаем последовательность чисел для отображения».
«Вся прелесть производящих функций проявляется только при настройке на оба канала: дискретный и непрерывный».
“Индукция заставляет вас чувствовать себя виноватым за то, что вы получаете что-то из ничего, и это искусственно, но это одно из величайших
идеи цивилизации.”
Герберт Вильф
“Когда я поступил в аспирантуру, я выполнил инструкции, данные мне моим отцом, и постучал по обоим
Двери Мюррея Гелл-Манна и Фейнмана и спросили их, что они сейчас делают. Мюррей записал
статистической суммы для трехмерной модели Изинга и сказал, что было бы неплохо, если бы я мог ее решить (по крайней мере, так
Помню разговор). Фейнман ответил «ничего» ».
Кен Г. Уилсон (цитируется по J.2 имеет неприятную сингулярность при r = 0, но это не беспокоило Ньютона – Луна находится достаточно далеко ».
Эдвард Виттен (лекция AMS Гиббса, Балтимор, 7 января 1998 г.)
«Все средства (даже непрерывные) освящают дискретную цель». (электронное письмо в среду, 14 августа 2002 г., 16:29:35 -0400 (EDT))
“Много лет назад я однажды сказал в своем выступлении,
Прямое комбинаторное доказательство похоже на секс. Если хорошо, то отлично. Если плохо, то все равно лучше, чем ничего ».
Я больше в этом не уверен. Я по-прежнему считаю, что прямые комбинаторные доказательства похожи на секс, за исключением того, что и плохой секс, и плохие комбинаторные доказательства хуже, чем ничего.”(89-е мнение)
Дорон Зейлбергер
Математические знаки ≈ ∑ ⇒ ∈ ≤ ∞
В этом разделе собраны математические символы, которые нельзя правильно ввести с клавиатуры. Представленный набор можно разделить на несколько групп:
- знаки оператора: сложение, вычитание, деление, умножение, суммирование;
- интегральных знака: двойные, тройные, объемные, поверхностные, по и против часовой стрелки;
- символа неравенства: больше, меньше;
- знаков равенства: равно, не равно, примерно равно, равноценно, тождественно;
- геометрических символа: угол, пропорции, диаметр, перпендикуляр, параллельность, пересечение;
- геометрических фигуры: треугольник, дуга, параллелограмм, ромб;
- знак корня, степень числа;
- для теории множеств: пустое множество, принадлежит, подмножеству, объединению, пересечению;
- логическая связка: импликация и, или, отрицание, эквивалент;
- другие символы: бесконечность, существует, принадлежит, del или nabla, многоточие для матрицы, потолочные скобки, символы для теории групп.
Пример применения
Парабола: ƒ (x) = ax² + bx + c (a ≠ 0)
Представление исключительного ИЛИ: A⊕B: ⇔ (A⋁B) ∧¬ (A∧B)
Скорость тела, падающего с высоты h: V = √̅2̅g̅h̅
Использование этих значков – единственный способ вставить различные математические символы на веб-сайт или в сообщение, появляющееся в любой операционной системе. Нужно просто скопировать закодированный знак. Использование изображений для таких целей усложняет процесс: они требуют настройки при разработке или наполнении Интернет-сайта.Кроме того, мультимедийный контент занимает слишком много места на диске.
Математические знаки можно использовать в социальных сетях, чатах и форумах. Они также могут быть полезны веб-разработчикам.
Математика как язык всех наук не может существовать без системы письма. Его многочисленные концепции и операторы приобрели свои шрифты по мере развития науки. Поскольку стандартные алфавиты не включают их, набрать эти символы довольно проблематично. Вы можете легко скопировать их на нашем сайте и вставить.
КонсорциумUnicode включил в себя множество различных знаков. Если вы не можете найти то, что вам нужно, попробуйте наш поиск по сайту или просмотрите следующие разделы:
Математические операторы 2200–22FF
Разные математические символы-A 27C0–27EF
Разные математические символы-B 2980–29FF
Дополнительные математические операторы 2A00–2AFF
Буквы для формул:
Греческий и коптский 0370–03FF
Математические буквенно-цифровые символы 1D400–1D7FF
Возведение в степень и дробь
Мы сделали еще один набор для надстрочных и подстрочных чисел.2 \ ge 0] \ end {gather *} \] Математический символ может использоваться для разных целей от одного математического подполя к другому (например, $ \ sim $ как логическое отрицание и подобие треугольника), так же как несколько символов может использоваться для обозначения одного и того же понятия или отношения (например, $ \ times $ и $ \ cdot $ при умножении).
Базовое понимание математической терминологии необходимо для прочного фундамента высшей математики. С этой целью ниже приводится компиляция некоторых из наиболее хорошо адаптированных, широко используемых символов в математике.
Более того, эти символы дополнительно классифицируются по их функции в таблицы. Более полные списки символов – по категориям предмет и тип – также можно найти на соответствующих страницах ниже (или на панели навигации).
Предпочитаете версию в формате PDF?
Получите полный, исчерпывающий список математических символов в форме электронной книги – вместе с использованием каждого символа и кодом LaTeX.
Константы
В математике константы – это символы, которые используются для обозначения неизменяющихся объектов .Они могут включать ключевые числа, ключевые математические наборы, ключевые математические бесконечности и другие ключевые математические объекты (например, матрицу идентичности $ I $).
Математические константы часто принимают форму буквы алфавита или производной от нее. В некоторых случаях константа может рассматриваться как переменная в более широком контексте. В следующих таблицах представлены некоторые из наиболее часто используемых констант, а также их имя, значение и использование.
Ключевые математические числа
| Имя символа | Пояснение | Пример |
|---|---|---|
| $ 0 $ ( Ноль ) | $ Аддитивная идентификация общих чисел | |
| Мультипликативное тождество общих чисел | $ 5 \ times 1 = 5 $ | |
| $ \ sqrt {2} $ ( Квадратный корень из 2 $ ) | Положительное число, квадрат которого равен 2 доллара.2 = 2i $ |
Ключевые математические наборы
Для более полного списка см. ключевых математических наборов в алгебре .
| Имя символа | Пояснение | Пример |
|---|---|---|
| $ \ varnothing $ ( Пустой набор ) | Набор без элемента | $ | \ varnothing | = 0 $ |
| $ \ mathbb {N} $ ( N ) | Набор натуральных чисел | $ \ forall x, y \ in \ mathbb {N} $, $ x + y \ in \ mathbb {N} $ |
| $ \ mathbb {Z} $ ( Z ) | Набор целых чисел (Z означает zahlen, число на немецком языке) | $ \ mathbb {N} \ substeq \ mathbb {Z } $ |
| $ \ mathbb {Z} _ + $ ( Z-plus ) | Набор натуральных чисел | $ 3 \ in \ mathbb {Z} _ + $ |
| $ \ mathbb {Q } $ ( Q ) | Набор рациональных чисел (Q означает частное) | $ \ sqrt {2} \ notin \ mathbb {Q} $ |
| $ \ mathbb {R} $ ( R ) | Набор действительных чисел | $ \ forall x \ in \ mathbb {R}, x ^ 2 \ ge 0 $ |
| $ \ mathbb {R} _ + $ ( R-plus ) | Набор положительных действительных чисел | $ \ forall x, y \ in \ mathbb {R} _ + $, $ xy \ in \ mathbb {R} _ + $ |
| $ \ mathbb {C} $ ( C ) | Набор комплексных чисел | $ \ exists z \ in \ mathbb {C} \, (z ^ 2 + 1 = 0) $ |
| $ \ mathbb {Z} _n $ ( Zn ) | Набор целых чисел по модулю $ n $ | В мире $ \ mathbb {Z} _2 $, $ 1 + 1 = 0 $. {\ aleph_0} $ |
| $ \ omega $ ( Omega ) | Наименьшее бесконечное порядковое число | $ \ forall n \ in \ mathbb {N}, n <\ omega $ |
Для более полного списка см. символов, связанных с числом элементов .
Другие ключевые математические объекты
| Имя символа | Пояснение | Пример |
|---|---|---|
| $ \ mathbf {0} $ ( Ноль ) | Нулевой вектор | векторного пространства $ 909 \ \ mathbb {v} \ in V $, $ \ mathbf {v} + \ mathbf {0} = \ mathbf {v} $ |
| $ e $ ( E ) | Идентификационный элемент группы | $ e \ circ e = e $ |
| $ I $ ( I ) | Матрица идентичности | $ AI = IA = I $ |
| $ C $ ( C ) | Константа интеграция | $ \ displaystyle \ int 1 \, \ mathrm {d} x = $ $ x + C $ |
| $ \ top $ ( Тавтология ) | Предложение формальной логики, которое безусловно истинно | Для каждого предложения $ P $, $ P \ land \ top \ Equiv P $. |
| $ \ bot $ ( Противоречие ) | Безоговорочно ложное предложение формальной логики | Для каждого предложения $ P $, $ P \ land \ lnot P \ Equiv \ bot. $ |
| $ Z $ ( Z ) | Стандартное нормальное распределение | $ Z \ sim N (0,1) $ |
Переменные
Математическая переменная – это символ, который функционирует как заполнитель для различных выражений или штук .x = y) \ end {gather *} В некоторых случаях переменные можно рассматривать как константы , в более узком контексте (например, как параметры), в то время как в других случаях переменные используются вместе с индексами , чтобы составить из-за отсутствия букв (например, $ x_3 $).
Хотя переменные в математике часто используются для представления чисел , они также могут использоваться для представления других объектов, таких как векторы, функции и матрицы. В следующих таблицах описаны некоторые из наиболее распространенных соглашений для переменных, а также контекст, в котором они приняты и используются.
Переменные для чисел
| Символ (ы) | Используется для | Пример |
|---|---|---|
| $ m, n, p, q $ | $ Целые числа и натуральные числа If | mn $ нечетно, то и $ m $, и $ n $ нечетны.|
| $ a, b, c $ | Коэффициенты функций и уравнений | Линия вида $ ax + by = 0 $ проходит через начало координат. |
| $ x, y, z $ | Неизвестные в функциях и уравнениях | Если $ 2x + 5 = 3 $, то $ x = -1 $.2 $ |
Переменные в геометрии
Для получения дополнительных символов в геометрии и тригонометрии см. геометрические и тригонометрические символы .
| Символ (ы) | Используется для | Пример |
|---|---|---|
| $ P, Q, R, S $ | Вершины | $ \ overline {PQ} \ perp \ overline {QR } $ |
| $ \ ell $ | Линии | $ \ ell_1 \ parallel \ ell_2 $ |
| $ \ alpha, \ beta, \ gamma, \ theta $ | Углы | $ \ alpha + \ beta + \ theta = 180 ^ {\ circ} $ |
Переменные в исчислении
Для более полного списка см. {0}} {h} = 1 $
Переменные в линейной алгебре
Для более полного списка см. переменных в алгебре .
| Символ (ы) | Используется для | Пример |
|---|---|---|
| $ \ mathbf {u}, \ mathbf {v}, \ mathbf {w} $ | Векторы 37 | \ mathbf {u} +4 \ mathbf {v} = \ mathbf {w} $|
| $ A, B, C $ | Матрицы | $ AX = B $ |
| $ \ lambda $ | Собственные значения | $ A \ mathbf {v} = \ lambda \ mathbf {v} $ |
Переменные в теории множеств и логике
Для получения более подробных списков по темам см. переменных в логике и переменных в теории множеств .
| Символ (ы) | Используется для | Пример |
|---|---|---|
| $ A, B, C $ | Наборы | $ A \ subteq B \ cup C $ |
| Элементы | $ a \ in A $ | |
| $ P, Q, R $ | Предложения | $ P \ lor \ lnot P \ Equiv \ top $ |
Переменные в вероятности и статистике
Для более полного списка см. переменных в вероятности и статистике .
| Символ (ы) | Используется для | Пример |
|---|---|---|
| $ X, Y, Z $ | Случайные переменные | $ E (X + Y) = $ E ( X) + E (Y) $ |
| $ \ mu $ | Средства населения | $ H_0 \!: \ Mu = 5 $ |
| $ \ sigma $ | Стандартные отклонения населения | $ \ sigma_1 = \ sigma_2 $ |
| $ s $ | Стандартные отклонения образца | $ s \ ne \ sigma $ |
| $ n $ | Размеры выборки | If $ n ge 30 $, используйте нормальное распределение.2 = 0,5625 $. |
| $ \ pi $ | Пропорции населения | $ \ pi = 0,5 $ |
| $ p $ | Примерные пропорции | $ p = \ dfrac {X} {n} $ |
Разделители
Подобно знакам препинания в английском языке, разделители представляют собой набор символов, которые указывают границы между независимыми математическими выражениями. Они часто используются для указания области действия, для которой будет применяться операция или правило, и могут встречаться как в виде изолированного символа, так и в виде пары противоположно выглядящих символов.
Во многих сценариях разделители используются в основном для целей группировки . В следующей таблице представлены некоторые из наиболее часто используемых разделителей, а также их функции и использование.
| Символ (ы) | Функция | Пример |
|---|---|---|
| $. | Десятичный разделитель | $ 25.9703 $ |
| $, $ | Разделитель объектов | $ (3, 5, 12) $ |
| $ (), [], \ { \} $ | Индикаторы порядка работы | $ (a + b) \ times c $ |
| $ (), [] $ | Интервальные индикаторы | $ 3 \ notin (3, 4] $, $ 4 \ in (3,4] $.2 – 2 = 0 \} $ |
| $ | |, \ | \ | $ | Операторы, связанные с нормами | $ \ | (3, 4) \ | = 5 $ |
| $ \ begin {cases} \ end {cases} $ | Кусочно-функциональный маркер | $ f (x) = \ begin {cases} 1 & x \ ge 0 \\ 0 & x <0 \ end {cases} $ |
| $ \ langle \ rangle $ | Оператор внутреннего продукта | $ \ langle ka, b \ rangle = k \ langle a, b \ rangle $ |
| $ \ lceil \ rceil $ | Оператор потолка | $ \ lceil 2.476 \ rceil = 3 $ |
| $ \ lfloor \ rfloor $ | Оператор пола | $ \ lfloor \ pi \ rfloor = 3 $ |
Операторы
Оператор используется для обозначения символа операция – функция, которая переводит один или несколько объектов на другой аналогичный объект. Большинство операторов являются унарными и двоичными по своей природе (т. Е. Принимают один и два входных значения для намеченной цели, соответственно), причем наиболее распространенными из них являются арифметические операторы (например,г., $ + $).
Как и в случае с английским языком, операторы позволяют расширять лексикон математики , где существует только конечное число символов. В следующих таблицах представлены некоторые из наиболее часто используемых математических операторов, а также их использование и предполагаемое значение.
Общие операторы
| Символ (ы) | Пояснение | Пример |
|---|---|---|
| $ x + y $ | Сумма $ x $ и $ y | $ 2a + 3a + 3a 5a $ |
| $ xy $ | Разница $ x $ и $ y $ | $ 11-5 = 6 $ |
| $ -x $ | Инверсная добавка $ | $ -3 + 3 = 0 $ |
| $ x \ times y $, $ x \ cdot y $, $ xy $ | Продукт из $ x $ и $ y $ | $ (m + 1 ) n = mn + n $ |
| $ \ dfrac {1} {x}, x ^ {- 1} $ | Мультипликативный обратный / обратная величина от $ x $ | $ \ dfrac {1} {9 } \ times 9 = 9 \ times \ dfrac {1} {9} = 1 $ |
| $ x \ div y, x / y $ | Частное от $ x $ сверх $ y $ | $ 152 \ div 3 = 50.4 = 81 $ |
| $ x \ pm y $ | $ x $ плюс и минус $ y $ | $ \ dfrac {-b \ pm \ sqrt {\ Delta}} {2a} $ |
| $ \ sqrt {x} $ | Положительный квадратный корень из $ x | $ \ sqrt {2} \ приблизительно 1,414 $ |
| $ | x | | $Абсолютное значение $ x | $$ | x-3 | <5 |
| $ x \% | $$ x % | $ x \% \ doteq \ dfrac {x} {100} | $
Операторы, связанные с функциями
Для более полного списка см. символы, связанные с функциями .
| Символ | Пояснение | Пример |
|---|---|---|
| $ \ operatorname {dom} (f) $ | Домен функции $ f $ | Если $ g (x) = \ ln { x} $, тогда $ \ operatorname {dom} (g) = \ mathbb {R} _ + $. |
| $ \ operatorname {ran} (f) $ | Диапазон функции $ f $ | Если $ h (y) = \ sin y $, то следует, что $ \ operatorname {ran} (h ) = [-1,1] $. |
| $ f (x) $ | Изображение элемента $ x $ под функцией $ f $ | $ g (5) = g (4) + 3 $ |
| $ f (X) $ | Изображение набора $ X $ под функцией $ f $ | $ f (A \ cap B) \ substeq $ $ f (A) \ cap f (B) $ |
| $ f \ circ g $ | Составная функция ($ f $ из $ g $) | Если $ g (3) = 5 $ и $ f (5) = 8 $, то $ (f \ circ g) (3) = 8 $.2) = 2 \ ln {x} $ |
| $ \ log x $ | Логарифмическая функция по основанию 10 (или основанию $ e $) | $ \ log 10000 = 4 $ |
| $ \ log_b x $ | Логарифмическая функция по основанию $ b $ | $ \ log_2 x = \ dfrac {\ ln x} {\ ln 2} $ |
| $ \ sin x $ | Синусоидальная функция | $ \ sin \ pi = 0 $ |
| $ \ cos x $ | Функция косинуса | $ \ cos \ dfrac {\ pi} {4} = \ dfrac {\ sqrt {2}} {2 } $ |
| $ \ tan x $ | Касательная функция | $ \ tan x = \ dfrac {\ sin x} {\ cos x} $ |
Операторы, связанные с алгеброй
Для a более полный список, см. операторов в алгебре .
| Символ (ы) | Пояснение | Пример |
|---|---|---|
| $ \ gcd (x, y) $ | Наибольший общий множитель для $ x $ и $ y $ | $ {\ gcd (35,14) = 7} $ |
| $ \ lfloor x \ rfloor $ | Этаж $ x (наибольшее целое число, меньшее или равное $ x $) | $ \ lfloor 3.6 \ rfloor = 3 $ |
| $ \ lceil x \ rceil $ | Потолок $ x $ (наименьшее целое число, большее или равное $ x $) | $ \ lceil \ pi \ rceil = 4 $ |
| $ \ min (A) $ | Минимум из набора $ A $ | Если $ \ min (A) = 3 $, то $ \ min (A + 5) = 8 $.{\ pi i} | = 1 $ |
| $ \ operatorname {arg} (z) $ | Аргументы комплексного числа $ z $ | $ \ operatorname {arg} (1 + i) = \\ [0.3em] \ dfrac {\ pi} {4} + 2 \ pi n $ |
Операторы, связанные с геометрией
Дополнительные символы в геометрии и тригонометрии см. В разделе геометрические и тригонометрические символы .
| Символ (ы) | Пояснение | Пример |
|---|---|---|
| $ \ angle ABC $ | Угол , образованный вершинами $ A $, $ B $ и $ C $ | $ \ angle ABC = \ angle CBA $ |
| $ \ измеренный угол ABC $, $ m \ angle ABC $ | Измерьте угла, образованного вершинами $ A $, $ B $ и $ C $ | $ \ измеренный угол ABC = \ measureangle A’B’C ‘$ |
| $ \ overleftrightarrow {AB} $ | Бесконечная линия , образованная точками $ A $ и $ B $ | $ \ overleftrightarrow {AB} = \\ \ overleftrightarrow { BA} $ |
| $ \ overline {AB} $ | Отрезок линии между точками $ A $ и $ B $ | Если $ B \ ne B ‘$, то $ \ overline {AB} \ ne \ \ \ overline {AB ‘}.$ |
| $ \ overrightarrow {AB} $ | Луч из точки $ A $ в точку $ B $ | $ \ overrightarrow {AB} \ cong \\ \ overrightarrow {CD} $ |
| $ | AB | $ | Расстояние между точкой $ A $ и точкой $ B $ | $ | AB | <{| A'B '|} $ |
| $ \ треугольник ABC $ | Треугольник сформирован по вершинам $ A $, $ B $ и $ C $ | $ \ треугольник ABC \ cong \ треугольник A’B’C ‘$ |
| $ \ square ABCD $ | Четырехугольник , образованный вершинами $ A $ , $ B $, $ C $ и $ D $ | $ \ square ABCD = \ square DCBA $ |
Операторы, связанные с логикой
Для более полного списка см. 2 = – \ pi)} $
Операторы, связанные с множеством
Для более полного списка см. Операторы в теории множеств .c $
$ BA.$
Векторные операторы
Для более полного списка см. T) = \ operatorname {tr} (A) $
Операторы, связанные с вероятностью
Для более полного списка см. Операторы в вероятности и статистике .
| Символ (ы) | Пояснение | Пример |
|---|---|---|
| $ n! $ | Факториал из $ n $ | $ 4! = 4 \ cdot 3 \ cdot 2 \ cdot 1 $ |
| $ n P \, r $ | Перестановка ($ n $ перестановка $ r $) | $ 5 P \, 3 = 5 \ cdot 4 \ cdot 3 $ |
| $ \ displaystyle nCr, \ binom {n} {r} $ | Комбинация ($ n $ выберите $ r $) | $ \ displaystyle \ binom {5} {2 } = \ binom {5} {3} $ |
| $ P (E) $ | Вероятность события $ E $ | $ P (A \ cup B \ cup C) = 0.\ overline {3} $ |
| $ P (A \, | \, B) $ | Условная вероятность события $ A $ данное событие $ B $ | $ P (A \, | \, B ) = \ dfrac {P (A \ cap B)} {P (B)} $ |
| $ E (X) $ | Ожидаемое значение случайной величины $ X $ | $ E (X + Y ) = $ E (X) + E (Y) $ |
| $ V (X) $ | Вариация случайной величины $ X $ | $ V (5X) = 25V (X) | $
Операторы, связанные со статистикой
Для более полного списка см. статистических операторов .2} {n} $
Ключевые вероятностные функции и распределения
Для более полного списка см. операторы, связанные с распределением вероятностей .
| Символ (ы) | Пояснение | Пример |
|---|---|---|
| $ {\ operatorname {Bin} (n, p)} $ | Биномиальное распределение с $ n $ попытками и вероятностью успеха $ p $ | Если $ X $ означает количество орлов в 10 бросках монеты, то $ X \ sim \ operatorname {Bin} (10, 0.2_ {0,05, 30} \ приблизительно 43,77 $ |
| $ F _ {\ alpha, \ nu_1, \ nu_2} $ | F-оценка , связанная с уровнем значимости $ \ alpha $ и степенями свободы $ \ nu_1 $ и $ \ nu_2 $ | $ F_ {0,05, 20, 20} \ приблизительно 2.1242 $ |
Операторы, связанные с исчислением
Для более полного списка см. символов исчисления и анализа .
| Символ (ы) | Объяснение | Пример |
|---|---|---|
| $ \ displaystyle \ lim_ {n \ to \ infty} a_n $ | $ Предел последовательности $ a_n41 $ | \ lim_ {n \ to \ infty} \ dfrac {n + 3} {2n} = \ dfrac {1} {2} $|
| $ \ displaystyle \ lim_ {x \ to c} f (x) $ | Предел функции $ f $ при стремлении $ x $ к $ c $ | $ \ displaystyle \ lim_ {x \ to 3} \ frac {\ pi \ sin x} {2} = \\ [0.3 $. |
Реляционные символы
Реляционные символы используются для выражения математических отношений между несколькими объектами. Многие реляционные символы являются двоичными по своей природе, поскольку они принимают два объекта в качестве входных данных и превращают их в полные, осмысленные предложения (как в случае символа неравенства $ <$).
Поскольку символы отношения образуют строительные блоки математических предложений , они имеют фундаментальное значение в математике.В следующих таблицах описаны некоторые из наиболее часто используемых реляционных символов, а также их использование и значение.
Реляционные символы, основанные на равенстве
| Символ (ы) | Объяснение | Пример |
|---|---|---|
| $ x = y | $ x $ и $ y $ равны 37 | = 2x $|
| $ x \ ne y $ | $ x $ и $ y $ не равны | $ 2 \ ne 3 $ |
| $ x \ приблизительно y $ | $ x $ и $ y $ примерно равны | $ \ pi \ приблизительно 3. 2 \ ge 0 $ |
В зависимости от числа Реляционные символы
| Символ | Пояснение | Пример | ||
|---|---|---|---|---|
| $ m \ mid n $ | Целое число $ m $ делит целое число $ n $ | $ 101 \ mid $ | $ m \ perp n $Целые числа $ m $ и $ n $ взаимно просты | $ 31 \ perp 97 $ |
Связанные с геометрией символы отношений
Дополнительные символы в геометрии и тригонометрии см. и символы тригонометрии.
| Символ | Пояснение | Пример |
|---|---|---|
| $ \ ell_1 \ parallel \ ell_2 $ | Линии $ \ ell_1 $ и $ \ ell_2 $ параллельны P | $ \ parallel \ overline {RS} $ |
| $ \ ell_1 \ perp \ ell_2 $ | Линии $ \ ell_1 $ и $ \ ell_2 $ перпендикулярны | $ \ overrightarrow {AB} \ perp \ overrightarrow {BC } $ |
| $ F \ sim F ‘$ | Рисунок $ F $ аналогичен фигуре $ F $ | $ \ треугольник ABC \ sim \ треугольник DEF $ |
| $ F \ cong F ‘$ | Рисунок $ F $ равен фигуре и фигуре $ F’ $ | $ \ square ABCD \ cong \ square PQRS $ |
Связанные с множеством реляционные символы
Для более полного списка см. реляционные символы в теории множеств .
| Символ | Пояснение | Пример |
|---|---|---|
| $ a \ in A $ | Элемент $ a $ – это член r из набора $ A $ | $ \ dfrac {2} {2} { 3} \ in \ mathbb {R} $ |
| $ a \ notin A $ | Элемент $ a $ не является членом набора $ A $ | $ \ pi \ notin \ mathbb {Q} $ |
| $ A \ substeq B $ | Набор $ A $ – это подмножество набора $ B $ | $ A \ cap B \ substeq A $ |
| $ A = B $ | Набор $ A $ равно , чтобы установить $ B $ | Если $ A = B $, то $ A \ substeq B $. |
Реляционные символы, связанные с логикой
Более полный список см. В разделе реляционных символов в логике .
| Символ | Пояснение | Пример |
|---|---|---|
| $ {P \! \ подразумевает \! Q} $ | Предложение $ P $ подразумевает предложение $ Q $ | $ x $ является четным $ \ подразумевает $ $ 2 $ делит $ x $ |
| $ P \! \ impliedby \! Q $ | Предложение $ P $ – это , подразумеваемое предложением $ Q $ | $ x = 3 \ impliedby $ $ 3x + 2 = 11 $ |
| $ P \! \ Iff \! Q, $ $ P \ Equiv Q $ | Предложение $ P $ тогда и только тогда, когда предложение $ Q $ | $ x \ ne y \ iff $ $ (xy) ^ 2> 0 $ |
| $ P \, следовательно, Q $ | $ P $, следовательно $ Q $ | $ i \ in \ mathbb {C} \ следовательно $ $ \ exists z \, (z \ in \ mathbb {C}) $ |
| $ P \ потому что Q $ | $ P $, потому что $ Q $ | $ x = \ dfrac {\ pi} {2} \ потому что $ $ \ sin x = 1 $ и $ \ cos x = 0 $ |
Реляционные символы, связанные с вероятностью
Для более полного списка см. реляционных символов в вероятности и статистике .
| Символ | Пояснение | Пример |
|---|---|---|
| $ A \ perp B $ | События $ A $ и $ B $ независимы | Поскольку $ A \ perp B $, мы имеем что $ P (A \ cap B) = P (A) P (B). $ |
| $ X \ sim F $ | Случайная величина $ X $ следует за распределением $ F $ | $ Y \ sim \ operatorname {Bin} (30, 0.4) $ |
Реляционные символы, связанные с исчислением
Для более полного списка см. реляционных символов в асимптотическом анализе .2) $
Условные обозначения
Условные обозначения – это условное обозначение или сокращенное обозначение , роль которого отличается от роли константы, переменной, разделителя, оператора или символа отношения. Часто он просто описывает используемую систему обозначений и может даже относиться к концепциям, которые имеют мало отношения к какому-либо определенному математическому объекту (например, $ \ infty $). 2 $
$ A \ overset {f} {\ to} B $
Условные обозначения в геометрии и тригонометрии
Дополнительные символы в геометрии и тригонометрии см. x = 0 $
Условные обозначения в вероятности и статистике
Для более полного списка см. условных обозначений в вероятности и статистике .
Список символов, разделенных на тип и предмет , см. На соответствующих страницах ниже.
Предпочитаете версию в формате PDF?
Получите общую сводку математических символов в форме электронной книги – вместе с использованием каждого символа и кодом LaTeX.
Дополнительные ресурсы
Грамматика по Уэсту
Первый раздел статьи – это «Введение», которое должно мотивировать проблема, обсудить связанные результаты, изложить результаты более полно и возможно, кратко изложите методы или структуру статьи или важнейшие определения.
Введение должно также содержать любые заключительные замечания или ключевые домыслы. Как правило, в отдельном разделе Заключительные замечания. Такие замечания либо избыточны, либо содержат информацию. читатели обычно ищут во введении. Читатели, которые изучают детали доказательств не нуждаются в резюме в заключительном разделе. Читатели, которые не читают полную информацию, не хотят переходить к Заключительный раздел. Математическая исследовательская статья не читается как роман или даже эссе, которое стремится «убедить» читателя; это не нужен эпилог.
Определения. Определяемые слова следует выделять курсивом (или, возможно, жирным шрифтом в контекст учебника). Когда курсив используется для обозначения определяемого слова, нет необходимости использовать «назвал» или «сказал, чтобы быть»; использование курсива объявляет, что это термин, который определяется, и заменяет эти слова.Многие определения сформулированы как «Объект имеет свойство , термин выделен курсивом . , если условие выполняется. «Здесь мы используем слово« если », хотя впоследствии понимается, что объект удовлетворяет свойству, являющемуся определил тогда и только тогда, когда выполняется данное условие.Курсив предупреждает читателя об этой ситуации. Условие можно оправдать, сказав что свойство или объект на самом деле не существует до тех пор, пока определение не будет завершено, поэтому в определении еще не говорится, что названный свойство эквивалентно условию.
Определения, написанные не носителями языка, иногда содержат лишние запятые.
В каждом предложении ниже следует удалить запятую.
«Двудольный граф – это двухцветный граф».
«График двудольный , если он двухцветный».
Первый пример – ошибочное размещение запятой внутри предложения (см.
обсуждение запятых).
Обратите внимание на разницу в выделении курсивом выше. При написании как прилагательное-существительное комбинации, определяемый термин – это название структур, которые имеют имущество; следовательно, полный член двудольный граф выделен курсивом. Когда только свойство определяется и позиционируется как прилагательное-предикат, курсивом выделено только прилагательное.
Определения двойного назначения. Невозможно сделать заявление об объекте до того, как он будет определен. Точно так же нельзя использовать нотацию как часть формулы, делающей утверждение об обозначенном объекте, если обозначения не были определены ранее. В в частности, эти задачи не могут быть правильно выполнены одновременно с один экземпляр обозначения. Например, “Окрестность вершины v равна N (v) = {u: uv∈ E (G)} ” это неверно.С подлежащим и глаголом перед уравнением уравнение представляет собой единую единицу (смотрите выражения как единицы). Это предложение определяет соседство v как особое уравнение, и оно не определяет обозначение N (v) .Конечно, читателям, достаточно знакомым с контекстом, не составит труда понимая, что имеется в виду, но зачем лишать права голоса других читателей? Можно так же легко написать: «Окрестность вершины v , обозначенная N (v) , это {u: uv∈ E (G)} “.В качестве альтернативы можно ввести обозначение как аппозитив в общепринятом положение сразу после определенного термина: “Окрестности N (v) вершины v составляет {u: uv∈ E (G)} “.
Распространенное определение двойной функции: «Пусть G = (V, E) – граф». В Предложение определяет уравнение G = (V, E) как график. Конечно, писатель намеревается одновременно ввести обозначение для конкретного графа и его набор вершин и набор ребер, но это не то, о чем говорится в предложении.это лучше написать «Пусть G будет графом» и использовать операторы V и E для обозначения наборов вершин и ребер G как V (G) и E (G) (см. Также Операторы и константы.)
Более тонкий пример: «Для каждого 1≤ i≤ n ,». Вступление к обозначение i было потеряно, поскольку неравенства накладывают условия на нем до того, как он будет определен. Поскольку выражение является единицей, грамматически фраза относится к каждому неравенству, написанному таким образом.Верный альтернативы, которые выражают предполагаемое значение, включают “Для всех и таких что 1≤i≤n “,” Для i∈ [n] “и” Для 1≤i≤n “. Третий вариант немного отличается от остальных; это означает «всякий раз, когда и таковы, что условия выполняются», неявно вводя i в указанный диапазон, но избегая грамматических проблем.
Выражения в виде единиц. Является ли уравнение или неравенство существительной единицей или читается с реляционной символ как глагол? Если рассматривать символ как глагол, часто приходится перечитывать уточнить смысл, и часто хочется, чтобы в предложении был еще один глагол.По этим причинам лучше всего рассматривать условные выражения как отдельные объекты. (то есть существительные), за некоторыми исключениями. Например, «существует i
Исключения. Применение этого принципа с очень простыми выражениями приводит к
тяжеловесному письму. Вот два заметных исключения:
1) В разделе «Выберите x∈ V (G) так, чтобы x имел минимальную степень», мы
выбирают x , а не выражение « x∈ V (G) ».В
оправданием для этого исключения является то, что символ членства или сдерживания
читается как «in», что не является глаголом. (Нечленство можно рассматривать как
способ.)
2) «Пусть G ‘= G-x ». При введении обозначений для объекта или выражения
одним повелительным глаголом («позволить», «установить», «положить», «выбрать» и т. д.) мы читаем
Символ равенства, как глагол «равно», поистине исключение. Это исключение может
быть узнаваемым по отсутствию в предложении какого-либо английского глагола. Продолжая с
другой глагол, например, «Пусть G ‘= G-x будет… “, будет производить
Определение двойной обязанности.
Если вводная часть предложения длиннее, значит, у нас уже может быть существительное и глагол, и выражение снова становится единицей. Например, “Включить каждую вершину независимо с вероятностью p = ( ln n) / n ” должно быть “Включать каждую вершину независимо с вероятностью p , где p = ( ln n) / n “.
Математические символы на испанском языке | ИспанскийDict
математических символов = математических математических символов = математических символов
Как говорить о математике по-испански
Если вы все еще посещаете уроки математики в школе или вам просто нужно выяснить, как рассчитать чаевые на следующий счет в ресторане, умение говорить и выполнять математику является важным навыком на любом языке.В этой статье мы подготовили список наиболее употребительных слов, связанных с математикой, на испанском языке, чтобы помочь вам во всех ваших будущих расчетах!
