Как легко выучить таблица умножения: 5 легких способов от учителя математики

Рассказываем, как помочь ребёнку выучить таблицу умножения

Поделись с друзьями

В начальной школе дети начинают учить таблицу умножения. Многие родители хотят, чтобы на уроках детям было проще, поэтому предлагают им тренироваться летом. Mel.fm разбирается, как не превратить такие занятия в кошмар с бесконечными примерами, а запомнить всё быстро и без проблем.

Как объяснить ребёнку, зачем нужно знать таблицу умножения

Обычно школьники начинают изучать таблицу умножения во 2-м классе. Смысл умножения им объясняют через сложение: 6*3 — это всё равно что 6+6+6.

Чтобы подвести ребёнка к этой идее, летом можно вместе с ним группировать разные предметы: яблоки, ягоды, одежду. Предложите ему разложить равное количество фруктов в три тарелки. Затем объясните, что сумма всех фруктов равна их числу в тарелке, умноженному на количество тарелок.

Следующий этап — объяснить ребёнку, почему таблицу умножения полезно знать наизусть. Она понадобится и в магазине, где цена часто представлена за килограмм товара, и когда нужно распределить подарки между друзьями, и когда нужно скинуться на билеты в кино. Каждый раз считать через сложение долго, нудно, а доставать калькулятор — это не всегда удобно. Поэтому знание таблицы умножения может стать для ребёнка суперспособностью, которая помогает справляться с повседневными проблемами силой мысли.

Таблица умножения в схемах, карточках и стихах

«Мел» уже писал о том, что таблицу умножения быстро запомнить не так просто, как, например, стихотворение. Поэтому не надо требовать от ребёнка сразу учить её наизусть, не подглядывая в подсказку. Пойдите ему навстречу — нарисуйте красивую таблицу умножения вместе, чтобы по ней ребёнок мог легко ориентироваться. А заодно покажите ему специальную таблицу Пифагора.

Таблица Пифагора

Попробуйте вместе заполнить таблицу Пифагора. В её ячейках — произведения чисел, написанных по горизонтали и вертикали. Попробуйте начать с первых двух строчек: 1*1, 1*2, 1*3, 2*1, 2*2, 2*3. Пусть ребенок складывает цифры, чтобы получить результат. Постепенно он увидит важные закономерности:

• по диагонали из верхнего угла в правый нижний идут квадраты чисел;
• относительно этой диагонали таблица симметрична: от перемены мест множителей ответ не меняется;
• при умножении на 1 число сохраняется;
• при умножении на 10 на конце добавляется 0;
• при умножении на 5 числа всегда заканчиваются на 0 или 5.

Также вы можете создать с ребёнком аналог палочек Непера, в которых наглядно видно табличные значения. Потом по ним можно будет решать более сложные примеры.

Мемо с таблицей умножения

Когда вы изучите таблицу Пифагора, ребёнок поймёт, что на самом деле ему не нужно запоминать все табличные значения. Если отбросить умножение на 1, на 10 и зеркальную половину таблицы, останется всего 36 примеров.

Их и напишите на карточках: с одной стороны — пример без ответа, с другой — с ответом. Сначала дайте ребенку время запомнить сторону с ответом, он может проговаривать пример вслух или рисовать его в воздухе. Далее распределите карточки на порции, разложите первые 5–7 на столе и начинайте игру. Правила простые: ребёнок смотрит на пример и старается вспомнить ответ. Когда ответ дан, время перевернуть карточку и проверить правильность ответа.

Если ответ верный, карточку можно убрать в стопку выученных;
Если ответ неправильный, карточка отправляется в стопку еще не выученных.

Блогер «Мела» советует также играть с выученными карточками на время: если ребёнок быстро назвал ответ, карточка отправляется в специальный конверт или коробку, вернуться к ней можно будет спустя время. Так у ребёнка появится мотивация собрать как можно больше «призовых» карточек и он будет видеть результат своего труда. Такой тренажёр поможет быстро запомнить таблицу умножения.

Лайфхак по умножению на 9

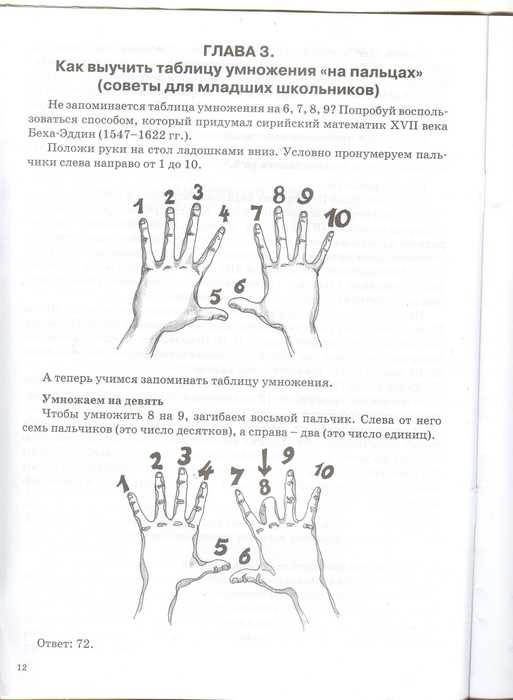
Умножать на 9 можно с помощью пальцев. Ребёнку нужно посмотреть на свои кисти рук и мысленно пронумеровать пальцы слева направо от 1 до 10 (если родители разрешат, можно даже оставить метки красками или фломастером). При умножении нужно загнуть палец, порядковый номер которого совпадает с числом, на которое мы умножаем девятку. Ответом будет число, состоящее из двух цифр: количество пальцев до загнутого и количество пальцев после него (в блоге «Мела» есть подробная схема). Например, умножаем 9 на 4, загибаем четвёртый палец (безымянный на левой руке). До него осталось 3 пальца, после — 6. Значит, ответ — 36.

Если с девяткой ребёнок справился, а остальные числа кажутся ему сложными, предложите учить таблицу умножения при помощи стихов. Это тот самый принцип, который помогает запомнить и правильные ударения в словах («это знает даже пума, верно говорить куркума» — помните?). У поэта Андрея Усачёва есть целый цикл «Таблица умножения в стихах», попробуйте выучить с ребёнком те числа, которые даются ему сложнее всего.

2×4=8

В пирог вонзилась пара вилок:

Два на четыре — восемь дырок.

6×6=36

Шесть старушек пряли шерсть:

Шестью шесть — тридцать шесть.

Из «Таблицы умножения в стихах» Андрея Усачёва

Игры на таблицу умножения

Когда ребёнок запомнил большинство комбинаций, можно добавлять в процесс больше игр, чтобы заучивание не становилось для него рутиной.

Можно снова использовать карточки: в одной колоде из 5 карт напишите примеры без ответов, в другой — ответы. Перемешайте каждую колоду и разложите в два сектора в перевернутом виде. Ребёнок должен сначала открыть рандомную карточку из левого сектора, затем — из правого. Если он случайно выбирает верный ответ для заданного примера, карточки остаются открытыми. Если ответ не совпал, карточки закрываются, но ребёнок должен запомнить, где какая была. В следующей попытке он откроет новый пример, который, возможно, совпадёт с только что закрытым ответом. Кон продолжается, пока не будут открыты все пары — тогда можно брать следующую десятку карточек.

Если ребёнок учит таблицу умножения вместе с другом, братом или сестрой, им можно предложить игру для двоих. Здесь отлично подойдут кости или домино — на них как раз нарисованы по два числа, которые можно перемножить. Мы уже писали, как, например, совместить таблицу умножения, игру в кости и тетрис или морской бой.

Другой вариант — предложить детям посоревноваться с калькулятором. Для этого понадобится не только вычислительный прибор, но и кости, колода игральных карт или опять же домино. Ведущий выбрасывает две карты, кости или домино. Задача одного игрока посчитать ответ на калькуляторе (да-да, набирать на приборе нужно даже самый простой пример, даже 2*2), другой в этот момент решает пример в уме. Тому, кто решает пример первым, достаётся призовое очко. Когда количество очков дошло до 10, игроки меняются ролями.

Для запоминания таблицы умножения существуют и мобильные приложения, и тематические настольные игры — их можно установить или купить, если ребёнок действительно заинтересовался темой (или, наоборот, если она ему неинтересна, а вот играть он любит).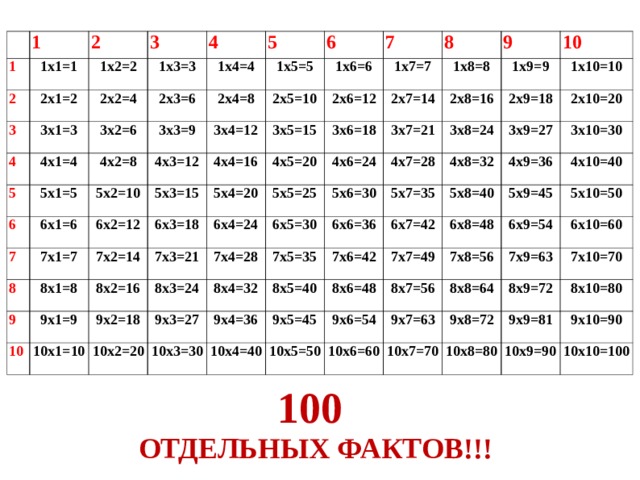 Поощряйте его интерес и старайтесь активно включаться в игры и изучение закономерностей: так заучивание таблицы умножения превратится из скучного занятия в интересный квест и сблизит вас с ребёнком. А это то, что нужно.

Подписывайтесь на наше Viber сообщество и телеграм канал, чтобы быть в курсе всех новостей.
Знаете новость? Пишите в наш Telegram-бот. @new_grodno_bot

как быстрее и легко выучить табличку умножения в 2023 году

Говоря о таблице умножения, у учеников возникает 2 вопроса – что это такое и как ее выучить. Поговорим об этом в контексте нашего урока.

Что такое таблица умножения Пифагора?

Таблица умножения (таблица Пифагора) – математическая таблица, используемая для определения операции умножения для алгебраических систем. Таблицу умножения можно отобразить как таблицу, заголовки строк и столбцов которой являются множителями, а ячейки – произведениями, полученными в результате умножения заголовков столбца и строки, на которых находится ячейка.

Вся таблица умножения на 10: как выглядит таблица Пифагора

На рисунке выше изображена таблица умножения от 1 до 10. Пользоваться ею достаточно просто – нужно найти сечение чисел, которые нужно умножить. Например, значение 4×7 = 28 находится на пересечении 4 и 7. В таблице не отражено умножение на 0, поскольку при умножении любого натурального числа на 0, в результате получим 0.

Кроме того, с помощью таблицы Пифагора легко изучить всю таблицу умножения, ведь результаты умножения являются зеркальными по отношению к основной диагонали, характеризующей переставной закон умножения:

Как легко выучить таблицу умножения?

Следует отметить, что таблица умножения – это основа или база математики, без которой не обойтись. Для того чтобы умножать двузначные, многозначные числа, нужно знать наизусть таблицу умножения до 10.

Умножение на 1

Если множитель равен единице, то при умножении числа на 1 произведение будет равно множимому.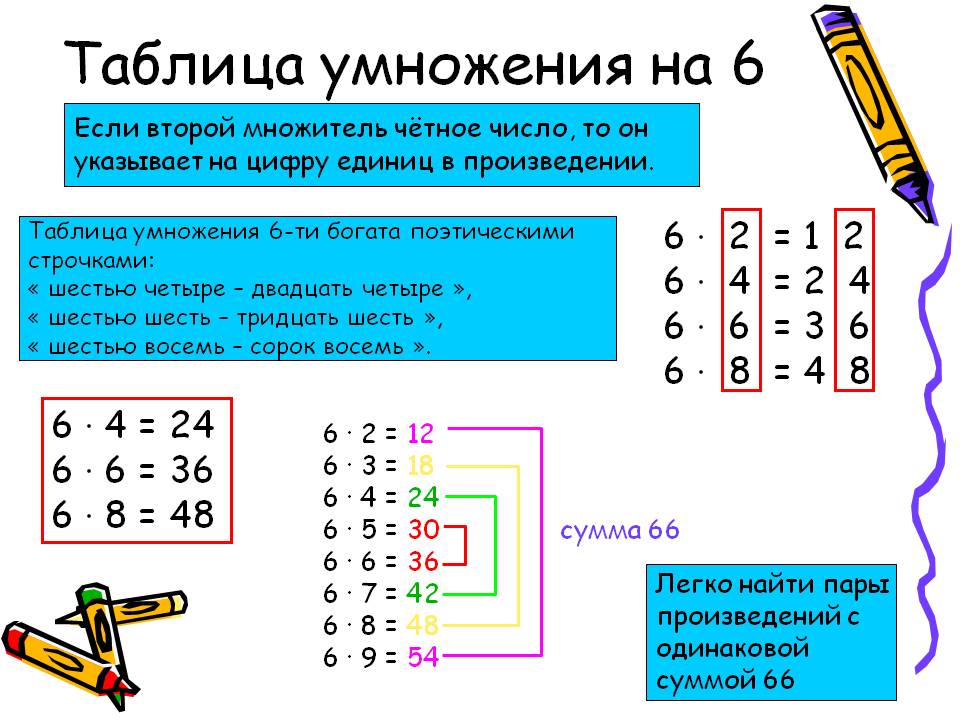 Поэтому легко запомнить таблицу умножения на 1:

1 × 1 = 1

1 × 2 = 1

1 × 3 = 1

1 × 4 = 4

1 × 5 = 5

1 × 6 = 6

1 × 7 = 7

1 × 8 = 8

1 × 9 = 9

1 × 10 = 10

Умножение на 2

Для изучения таблицы умножения на 2 и т.д. следует упомянуть определение действия умножения. Ведь умножение – это нахождение суммы одинаковых слагаемых: 2 × 2 = 2 + 2 = 4; 2 × 3 = 2 + 2 + 2 = 6; 2 × 4 = 2 + 2 + 2 + 2 = 8 и т.д. Изучая таблицу умножения на 2 последовательно, к каждому последующему произведению прибавляем 2.

2 × 1 = 2

2 × 2 = 4

2 × 3 = 6

2 × 4 = 8

2 × 5 = 10

2 × 6 = 12

2 × 7 = 14

2 × 8 = 16

2 × 9 = 18

2 × 10 = 20

Умножение на 3

3 × 1 = 3

3 × 2 = 6

3 × 3 = 9

3 × 4 = 12

3 × 5 = 15

3 × 6 = 18

3 × 7 = 21

3 × 8 = 24

3 × 9 = 27

3 × 10 = 30

Здесь также следует понимать принцип умножения: 3×2 – это то же, что 3 + 3 = 6; 3 × 3 = 3 + 3 + 3 = 9. Каждое последующее произведение будет больше на 3 от предыдущего.

Умножение на 4

4 × 1 = 4

4 × 2 = 8

4 × 3 = 12

4 × 4 = 16

4 × 5 = 20

4 × 6 = 24

4 × 7 = 28

4 × 8 = 32

4 × 9 = 36

4 × 10 = 40

Умножение на 5

Особенность умножения натуральных чисел на 5 состоит в том, что произведение заканчивается на 0 или 5. То есть разность между произведениями в таблице умножения составит 5.

5 × 1 = 5

5 × 2 = 10

5 × 3 = 15

5 × 4 = 20

5 × 5 = 25

5 × 6 = 30

5 × 7 = 35

5 × 8 = 40

5 × 9 = 45

5 × 10 = 50

Умножение на 6

Если вы изучили таблицу умножения до 5 и помните о переместительном законе умножения, то можно сказать, что половину таблицы умножения на 6 вы уже знаете. Ведь 6×1 = 1×6 = 6; 6×2 = 2×6 = 12 и т.д.

6 × 1 = 6

6 × 2 = 12

6 × 3 = 18

6 × 4 = 24

6 × 5 = 30

6 × 6 = 36

6 × 7 = 42

6 × 8 = 48

6 × 9 = 54

6 × 10 = 60

Умножение на 7

7 × 1 = 7

7 × 2 = 14

7 × 3 = 21

7 × 4 = 28

7 × 5 = 35

7 × 6 = 42

7 × 7 = 49

7 × 8 = 56

7 × 9 = 63

7 × 10 = 70

Умножение на 8

8 × 1 = 8

8 × 2 = 16

8 × 3 = 24

8 × 4 = 32

8 × 5 = 40

8 × 6 = 48

8 × 7 = 56

8 × 8 = 64

8 × 9 = 72

8 × 10 = 80

Умножение на 9

9 × 1 = 9

9 × 2 = 18

9 × 3 = 27

9 × 4 = 36

9 × 5 = 45

9 × 6 = 54

9 × 7 = 63

9 × 8 = 72

9 × 9 = 81

9 × 10 = 90

Умножение на 10

10 × 1 = 10

10 × 2 = 20

10 × 3 = 30

10 × 4 = 40

10 × 5 = 50

10 × 6 = 60

10 × 7 = 70

10 × 8 = 80

10 × 9 = 90

10 × 10 = 100

Проще всего запомнить таблицу умножения на 10, ведь при умножении 10 на число достаточно дописать в число один ноль справа: 10 × 8 = 80

Таким образом, для изучения таблицы умножения рекомендуем запомнить следующие основные свойства:

• при умножении числа на 1, произведение будет равно второму множителю;
• при умножении 10 на число произведение будет равно числу, к которому дописан один ноль справа;
• переставной закон умножения: 8×3 = 3×8 = 24;
• чтобы умножить число a на число b, необходимо b раз добавить число a. То есть 5×3 = 5 + 5 + 5 = 15

Как научить детей умножению 15 забавными и эффективными способами

Вы учитель математики в начальной школе? Вы пытаетесь понять, как научить своих учеников умножению? Что ж, тогда вы попали в нужный пост. Мы обсудим простые и забавные способы научить ваших юных учеников умножению.

Математика редко бывает любимым предметом школьников. Но он устанавливает основы большинства повседневных действий. Будь то измерение времени или подсчет денег, все это математика.

Среди четырех основных элементов математики (сложение, вычитание, умножение и деление) умножение является наиболее важным. Он закладывает основу для многих передовых математических понятий, таких как алгебра и исчисление.

Кроме того, обучающие столы улучшают память и математические способности детей. Таким образом, обучение ваших дошкольников беглому умножению дает им уверенность в решении сложных математических задач и совершенствовании их в математике.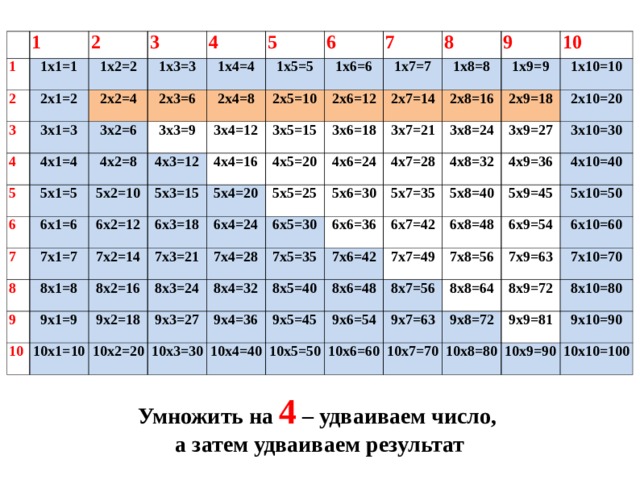 Кроме того, это дает студентам смелость заниматься математикой в ​​высших учебных заведениях.

Как учитель математики в начальной школе, вы должны сделать умножение веселым и увлекательным занятием для вашего класса. Если вы заинтересуете своих учеников математикой сейчас, вы можете дать им несколько успешных учебных лет вперед. Но не переживайте, мы здесь, чтобы помочь!

Как мы уже неоднократно говорили, игры и развлечения могут помочь учащимся учиться. Таким образом, вы также можете использовать забавные и инновационные стратегии, чтобы научить своих учеников умножению.

Давайте рассмотрим несколько увлекательных и простых способов научить дошкольников умножению.

   Дополнительная литература:    Как помочь детям с математикой: 6 инновационных подходов  

Как научить умножению за 9 простых шагов

Начальная школа — это ступенька в академическом развитии ребенка. Он учит жизненно важным предметам, таким как умножение, которые могут помочь выучить много новых предметов.

Поэтому учителя начальных классов должны сделать предмет интересным для учащихся. Поскольку основы умножения вращаются вокруг запоминания таблиц, учителя мало что могут сделать, чтобы сделать этот предмет интересным. Учащиеся должны изучать таблицы самостоятельно, чтобы продвигаться вперед в своих классах.

Но есть несколько стратегий, которые учителя могут использовать для упрощения обучения умножению в своем классе. Вот лучшие стратегии обучения умножению учащихся начальной школы:

Шаг 1: Препятствуйте запоминанию

Учащиеся часто борются с запоминанием. Им сложно изучить и реализовать все таблицы в задаче. Некоторые дети так боятся запоминания таблиц, что боятся заниматься математикой.

Чтобы предотвратить это, лучше всего показать вашему классу взаимосвязь между умножением и сложением. Эта стратегия также может помочь учащимся понять концепцию умножения, которая представляет собой просто повторяющееся сложение.

Используйте соответствующие примеры, чтобы показать вашему классу, как умножение основано на сложении. Поскольку ваш класс уже изучил сложение на предыдущих уроках, обучение умножению займет меньше времени.

Вы можете написать эти уравнения на доске, чтобы помочь учащимся, испытывающим трудности с визуализацией:

3 x 3 равно 3 + 3 + 3

Или

4 x 2 равно 4 + 4 

Шаг 2. Покажите волшебство Zero

Прежде чем приступить к комплексным числам, вы должны показать своим ученикам, как работает ноль в математике. Вы можете показать им, что прибавление числа к нулю не меняет его значения. Но умножение числа на ноль также делает его равным нулю.

Здесь вы можете использовать этот наглядный пример:

n + 0 = n

Но . . .

n x 0 = 0

Вы также можете использовать примеры, чтобы учащиеся поняли, как ноль действует при умножении. Например, попросите учащихся сосчитать количество стульев в классе, скажем, 25. После этого попросите их сосчитать стулья с обезьянами на них; это ноль.

Шаг 3: Определите свойство единицы

Как и ноль, единицу также легко умножить. Любое число, которое умножается на единицу, сохраняет свое значение: 

n x 1 = 1 

Вы можете использовать примеры из реальной жизни, чтобы показать своему классу свойство числа один. Например, строка в календаре показывает семь дней одной недели.

Шаг 4. Начните с простых чисел

Чтобы облегчить изучение таблиц, начните с простых чисел, которые учащиеся смогут быстрее запомнить.

Например, после обучения числу ноль и свойству единицы вы можете показать классу таблицы 10 и 11.

Итак, n x 10 = n0

Или

n x 11 = nn

Шаг 5 : Show Commutative Property

Умножение также является коммутативным, как и сложение. Это означает, что порядок факторов не меняет ответ.

Простыми словами, вы можете умножать два числа в любом порядке, и ответ будет одинаковым. Например, ответом для 2 x 5 или 5 x 2 будет одно и то же число 10. 

Это свойство может показать вашим ученикам, что умножение проще, чем кажется.

Шаг 6. Покажите взаимосвязь между таблицами

Еще один простой шаг в обучении умножению — показать вашему классу взаимосвязь между таблицами.

Например, вы можете выделить, что когда учащиеся изучают таблицы до 8, они автоматически изучают таблицу 9, поскольку число 9 встречается во всех таблицах, учащиеся могут пропустить изучение этой таблицы.

Это небольшое облегчение может помочь мотивировать учащихся, когда они борются с умножением.

Шаг 7. Расскажите им о логике умножения

Если дети попытаются запомнить таблицы, они тоже скоро их забудут. Поэтому вместо того, чтобы заставлять своих учеников запоминать таблицы, расскажите им о значении умножения, и они смогут использовать его в реальных ситуациях.

Например, вы можете принести своим ученикам коробку пончиков и попросить их подсчитать количество пончиков в коробке. Теперь покажите своим ученикам, что если они умножат количество строк на столбцы, они смогут вычислить пончики быстрее, чем считать каждый пончик.

Шаг 8: Разложите число

Если ваши ученики не умеют умножать большие числа, вы можете показать им, как разбивать числа.

Например, вместо умножения 8 x 9 они могут умножаться как 8 x (5 + 4).

Они также могут реализовать это свойство следующим образом: (8 x 5) + (8 x 4) : 40 + 32. 

Шаг 9. Используйте наглядные материалы

Многие исследования подтвердили, что учащиеся лучше учатся с помощью наглядных материалов. Таким образом, использование наглядных средств обучения является одним из лучших способов обучения умножению.

Например, учащиеся могут изучать умножение с помощью анимированных игр. Игры позволяют учащимся понять причину умножения. Кроме того, визуальные эффекты помогают быстрее выучить таблицы.

6 забавных способов научить отстающих учеников умножению

Чтобы упростить умножение для ваших учеников, вам нужно выйти за рамки обычных стратегий обучения. Чтобы сделать изучение умножения приятным и простым, вот несколько забавных учебных заданий:

Занятие №1: Веселые виртуальные игры

Сегодня невозможно оторвать детей от экранов. Таким образом, вы можете использовать экраны в своих интересах для обучения умножению.

Обращение к обучению на основе игр может сделать обучение умножению увлекательным. Эти игры могут улучшить уровень концентрации учащихся и математические навыки. Самое приятное то, что подобные игры устраняют страх неудачи, с которым борются многие ученики. Обучающие игры на умножение обеспечивают безопасную среду, в которой учащиеся могут ввести неправильный ответ, но при этом чувствовать мотивацию попробовать еще раз.

Увлекательное занятие №2: Умножение в классе

Вы можете избавиться от страха умножения в классе с помощью математических игр. Например, вы можете разыграть в своем классе простое упражнение «Константный калькулятор».

Предложите своим учащимся использовать константную функцию на калькуляторах, чтобы найти кратность любого числа, чтобы понять связь между сложением и умножением.

Вот как это работает: 

• Выберите число, например 7, и введите его в калькулятор.
• Сначала нажмите кнопку +, затем кнопку =. Калькулятор должен еще раз показать семь.
• Далее, продолжайте нажимать кнопку =. Семь будет непрерывно добавляться постоянной функцией, отображая возрастающие кратные числа (7, 14, 21, 28 и т. д.) 
• Вы можете попросить учащихся перечислить обнаруженные ими множители, а затем предложить им найти закономерности в своих список.

Забавное занятие №3: Умножение песен

Каждый ребенок любит музыку. И намного легче выучить все, что рифмуется и имеет биты. Итак, вы можете найти несколько хороших песен об умножении и проигрывать их в своем классе для увлекательного изучения математики. Вы даже можете предложить ученикам подпевать во время обучения.

На YouTube можно найти различные песни на умножение с анимированными видеороликами. Некоторые из лучших каналов песен и веб -сайтов умножений:

• Умножение Unplugged
• Песни для обучения
• Rock ‘n Learn
• Flocabulary Multiplaration Rap

Fun Activity Activity Aptaination Rap. лучший способ мотивировать учащихся. Вы можете провести в своем классе соревнование по умножению и предложить забавную награду, чтобы побудить учащихся изучить умножение.

Вот как это работает: 

• Разделите класс на две команды.
• Постройте две шеренги учеников, по одной шеренге, представляющей каждую команду, и поставьте их лицом друг к другу.
• Преподаватель может показать уравнение или назвать факт умножения.
• Ученик в первой паре (дети смотрят друг на друга) выкрикивает решение.
• Балл присуждается учащемуся, ответившему правильно первым.
• Преподаватель переходит к следующей паре, когда оба ученика садятся.
• Преподаватель продолжает в том же духе, пока не будут адресованы все ученики в очереди.
• Выигрывает ряд с наибольшим количеством очков.

Вы можете поручить роль счетовода ученику, если в вашем классе нечетное количество учеников. Объединение студентов одного академического уровня для соревнования друг с другом также может принести им пользу.

Увлекательное занятие №5: Карточные игры

Вы также можете использовать карточки для обучения своих учеников умножению. Multiplication War — это старая, но веселая автомобильная игра, которая может превратить обучение умножению в увлекательное занятие.

Вот как это работает:

В этой игре участвуют два игрока. Карты сдаются лицом вниз в две стопки одним учеником после того, как они перетасованы. Оба ученика переворачивают верхнюю карту из своей стопки лицевой стороной вниз после обратного отсчета (3, 2, 1, ВПЕРЕД!).

Набор выигрывает первый ученик, правильно умноживший оба числа на карточках. Когда все карточки будут использованы, побеждает студент с наибольшим количеством наборов.

Обязательно присвойте номера тузу, даме и королю, если вы планируете использовать их из колоды. Например, туз может стоить ноль, валет — один, дама — одиннадцать, а король — двенадцать. Не забудьте убрать джокеров!

Увлекательное занятие № 6: Умножение именных тегов

Это упражнение — отличный способ научить детей умножать. Это может помочь студентам выучить таблицы, даже не пытаясь.

Вот как это работает:

Сделайте бирки для умножения для себя и всех в классе. Каждый должен ходить по «имени» в течение дня. Чье-то имя на этот день было бы 24, если бы, например, на нем была бирка «8 x 3». Каждый день выделяйте определенное время, чтобы студенты могли встать и представиться друг другу. Доброе утро; меня зовут 80 (8 х 10) или 25 (5 х 5).

   Связанное чтение:    Простые способы сделать математику увлекательной для детей  

Заключение

Как видите, выяснение того, как научить умножению, — это не просто наука. Использование творческого подхода к обучению учащихся умножению поможет им выучить и запомнить концепции.

Инновационные методы могут сделать математику простой и интересной для учащихся. Итак, используйте визуальные эффекты, игры, занятия и различные стратегии, чтобы сделать умножение увлекательным.

Для игр на умножение вы всегда можете воспользоваться бесплатными играми SplashLearn. У нас есть широкий выбор бесплатных игр для дошкольников и учащихся начальной школы.

Часто задаваемые вопросы (FAQ)

Как я могу научить умножению учащихся, которые испытывают страх перед математикой?

1. Вот как научить умножению учащихся, которые кажутся перегруженными этой темой, за 4 простых шага:

Шаг 1. Разделите информацию на удобные части.

Шаг 2: Используйте простое визуальное представление, чтобы представить факт в контексте.

Шаг 3: Покажите учащемуся, как использовать более простые факты в качестве трамплина для более сложных.

Шаг 4: Работайте над освоением каждой таблицы отдельно.

Как я могу научить своих учеников с СДВ/СДВГ умножать?

Разложите карточки по одной, чтобы ваши ученики могли умножать их после того, как объясните, что вы хотите, чтобы они попрактиковали (например, 9 x таблиц), и установите таймер на одну минуту. Дайте им ответы на любые вопросы, в которых они ошиблись, чтобы у них было больше шансов ответить правильно в следующий раз, когда назовут этот номер.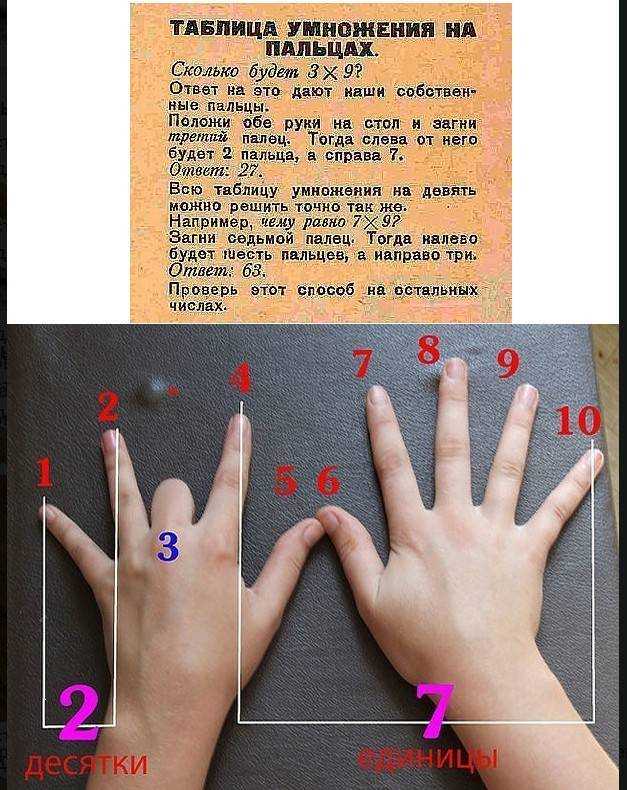

Ориентируйтесь на 20–30 фактов в минуту.

Как научить третьеклассника умножению?

Учащиеся могут решать задачи на умножение, используя массивы. Они могут использовать бусины, кубики, крышки от бутылок, скрепки или другие предметы, чтобы завершить их на сетке или просто на своих столах.

Когда ребенку следует начинать учить факты умножения?

Большинство экспертов сходятся во мнении, что дети начинают изучать свои таблицы в возрасте от пяти до восьми лет. Они могут начать понимать, как их числа взаимодействуют друг с другом, когда они начинают лучше осознавать свои числа.

Как запомнить таблицу умножения для улучшения математических навыков

Поделитесь историей

Если ваш ребенок учится в третьем классе, пришло время ему или ей столкнуться с этими ужасными таблицами умножения. Понимание концепции умножения необходимо для решения задач деления и решения более сложных математических задач. Проблема в том, что немногие дети учатся любить таблицу умножения.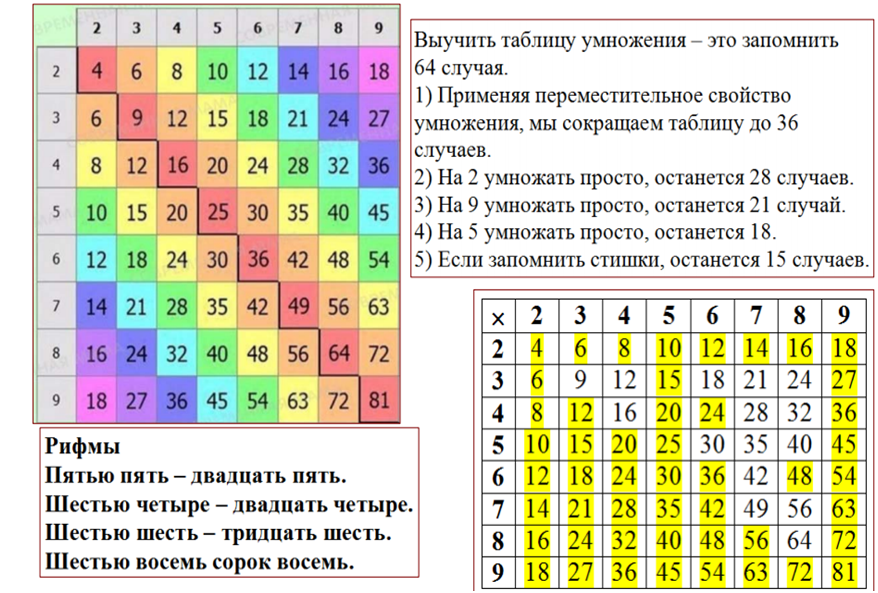

По мнению некоторых преподавателей математики, принуждение ребенка к запоминанию таблицы умножения может на самом деле подавить его способность развивать творческий подход к решению математических задач, помимо серьезного снижения его интереса к математике.

Содержание

Все больше педагогов считают, что нам следует отказаться от таблицы умножения, но хорошая ли это новость для вашего ребенка?

Математические факты, такие как 1✕1=1, являются фундаментальными предположениями, необходимыми для использования математики. Но механическое заучивание продуктов без понимания лежащего в их основе процесса не поможет вашему ребенку развить понимание числовых отношений.

Однако это не означает, что ваш ребенок должен игнорировать таблицы умножения, так как они описывают некоторые из основных строительных блоков математики — это было бы похоже на изучение языка без словаря. К счастью для детей, таблицы умножения не должны быть ужасными — все зависит от того, как мы подходим к задаче их обучения.

Итак, как вы можете помочь своему ребенку получить адекватное представление о таблице умножения, позволяя ему самостоятельно придумывать ответы?

Лучший способ выучить таблицу умножения

1. Начните с объяснения основных принципов умножения .

2✕3=6, 3✕2=6 : Даете ли вы три конфеты двум друзьям или две конфеты трем друзьям, у вас все равно останется 6 конфет.

1✕0=0, 2✕0=0, 0✕3=0, 1000✕0=0, 1✕2✕0=0, 5,5✕0=0: умножив любое число на 0, ответ будет всегда 0.

2. Используйте изображения и описательные объекты для лучшего понимания

Например, для 2✕2=4 : если в каждом пруду две утки и два пруда, то всего четыре утки .

3. Помогите ребенку понять группы и отношения

Покажите им, как счет с пропусками связан с таблицей умножения. Как только ваш ребенок сможет комфортно пропускать счет двойками, тройками, четверками и пятерками, ему будет легче освоить остальную часть таблицы умножения.

Например, когда ваш ребенок научится считать двойками, потренируйтесь удваивать ответы, чтобы понять умножение на 4. Как только он научится пропускать счет на четыре, снова удвойте ответы для умножения на 8. 

Повторите ту же концепцию для покажите соотношение между 3 и 6. 

4. Используйте другие числа, чтобы найти ответ

Помните, что 7✕9 может показаться вашему ребенку непосильным, но 7✕10=70 гораздо легче понять. Продемонстрируйте, как найти нужный им ответ, расширив то, что они уже знают; например: если 7✕10=70, мы можем вычесть «лишние» семь, чтобы решить 7✕9: 70-7=63.

Вот еще несколько примеров, использующих ту же стратегию для других сложных наборов факторов:

• 7✕8 равно 7✕10 минус две лишние семерки, поэтому 7✕8=70-14=56
• 7✕5 (или 5✕7) равносильно 5✕10 минус три лишние пятерки, поэтому 50-15=35
• 7✕4 двойное 7✕2, поэтому (7✕2=14)✕2=28

5. Используйте несколько трюков для дополнительного удовольствия!

Прием, описанный ниже, является примером упрощения понимания умножения за счет учета уникальных характеристик числовых комбинаций. Если вы посмотрите на продукты в 9таблицы умножения на множители от 1 до 10, можно заметить, что цифры всегда дают в сумме 9: 

9✕1 =  9 →    =    9

9✕2 = 18 → 1+8=9

2 9✕3 = 27 → 2+7=9

9✕4 = 36 → 3+6=9

9✕5 = 45 → 4+5=9

= 94 → 5+4=9

9✕7 = 63 → 6+3=9

9✕8 = 72 → 7+2=9

9=8+ 181 → 81 9

9✕10=90 → 9+0=9

Из-за этого аспекта таблицы умножения на 9 умножение 9 на коэффициент от 1 до 10 не только дает произведение, цифры которого всегда составляют 9, но и цифры которого в разряде десятков каждый увеличивается от 0 до 9, а разряд в разряде единиц уменьшается с 9 до 0: (09, 18, 27, 36, 45, 54, 63, 72, 81, 90). В результате мы можем использовать трюк с пальцем, чтобы сделать таблицу умножения на 9 проще и интереснее для изучения: 

В таблице умножения на 9 есть симпатичная палец трюк , чтобы помочь вашему ребенку.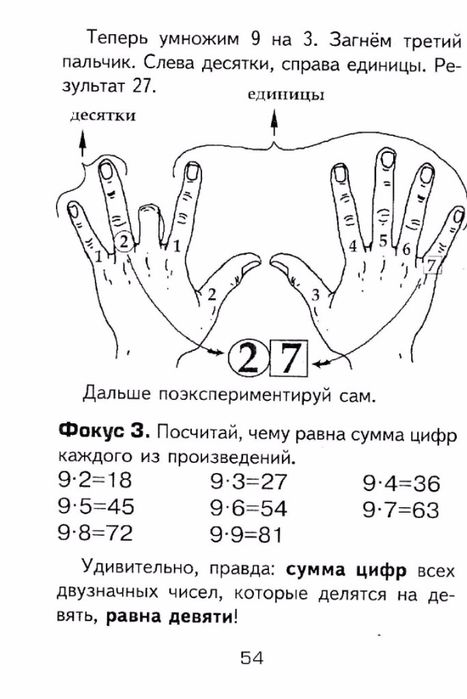

Раскройте обе ладони, обращенные к вам, мизинцы вместе. Теперь визуализируйте пальцы от слева направо , каждый из которых указывает числа от 1 до 10, которые будут умножены на 9. 

Например, сложите большой палец левой руки, чтобы показать 9✕1. Теперь вы видите 9 развернутых пальцев справа. 9✕1=9.

Затем, когда все 10 пальцев снова открыты, сложите только левый указательный палец, чтобы получилось 9✕2. Слева ваш развернутый большой палец, представляющий 1, а справа ваши остальные 8 открытых пальцев; вы читаете 1 и 8 как 18, поэтому 9✕2=18.

Для 9✕3 согните левый средний палец для числа 3. Теперь вы читаете открытый большой и указательный пальцы слева от сложенного среднего пальца как 2, а открытые пальцы справа как 7, чтобы получить 27

Сложив палец, представляющий каждый множитель от 1 до 10, вы получите все ответы для умножения их на 9. 

Заключение

неизбежно полезный инструмент для изучения математики, содержащий основные строительные блоки, необходимые вашему ребенку для понимания дальнейших математических понятий.