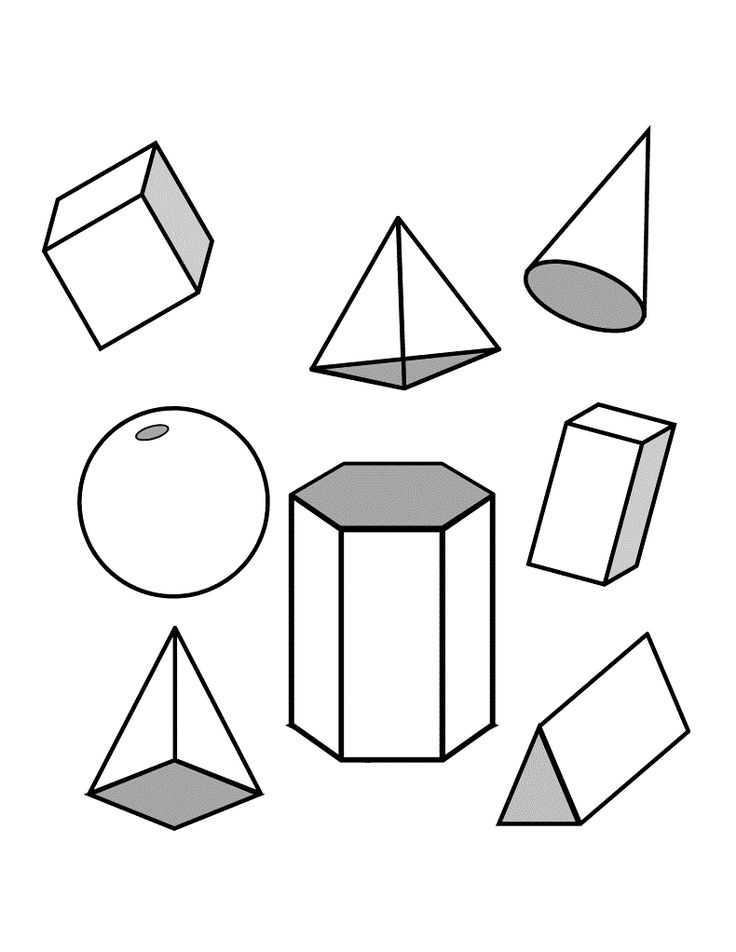
Геометрические фигуры картинки объемные: Объёмные геометрические тела (фигуры) и их названия.

Конспект занятия по ФЭМП в старшей группе. Тема: «Плоские и объёмные геометрические фигуры» | План-конспект занятия по математике (старшая группа):

Конспект занятия по ФЭМП в старшей группе.

Выполнила: воспитатель Светлана Викторовна И.

Тема: «Плоские и объёмные геометрические фигуры»

Цель: совершенствовать знания о геометрических фигурах и форме предметов.
Задачи: совершенствовать умение соотносить цифру с количеством; закреплять умения сравнивать предметы по длине, высоте; закреплять умения ориентироваться на листе бумаги развивать внимание, память, мышление; воспитывать интерес к математике;

Оборудование: картинки «Геометрические деревья», «Геометрическая улица», наборы геометрических фигур, альбомные листы (по колличеству детей), шар, куб; игрушка Старичка – лесовичка; строительный материал, карточки с изображением качели.

Ход занятия:

1. Мотивация

Организационный момент.

Игра-приветствие «Наши умные головки»

Наши умные головки
Будут думать много, ловко.
Ушки будут слушать,
Ротик четко говорить.
Ручки будут хлопать,
Ножки будут топать.
Спинки выпрямляются,
Друг другу улыбаемся,

Занятие начинается.

Воспитатель: – Внимание, ребята! Хочу вам сообщить, сегодня путешествие хотим мы совершить. Я знаю волшебные слова, которые помогут нам отправиться в путешествие в страну геометрических фигур.

2. Постановка цели

Воспитатель: Какие геометрические фигуры вы знаете? (ответы детей).

Воспитатель: Круг, овал, треугольник, прямоугольник, квадрат — это плоскостные фигуры. Еще есть фигуры объемные — куб, шар, цилиндр.

В геометрической стране геометрические фигуры везде-везде. А с нами пойдет Старичок – лесовичок, он все тропки в стране геометрических фигур знает. Нам много придется сегодня пройти и много задачек решить по пути. Итак, отправляемся в сказочное путешествие.

             «Ножкой топнем – в ладоши хлопнем

              Вокруг себя повернемся, дружно за руки возьмемся

              Глаза закроем – скажем «АХ» – и окажемся в гостях»

Вот мы и в стране геометрических фигур.

3. Совместная деятельность воспитателя с детьми

Наш первый привал. А называется он «Трудные задачки».

– На привале посидим, и задачки все решим.

Ребята, садитесь за столы.

Упражнение «Геометрические деревья»

Перед вами карточки, на которых изображены деревья с кронами, похожими на геометрические фигуры. Сосчитайте, сколько всего деревьев на рисунке? (Пять деревьев). Покажите дерево, с кроной похожей на круг (овал, треугольник, прямоугольник, квадрат).
Какое по счету дерево с круглой кроной (овальной, треугольной, прямоугольной, квадратной)?

Воспитатель: – Молодцы, ребята! Вы справились с заданием, и мы отправляемся дальше.

Шли мы, шли, шли мы, шли, на второй привал «Угадай – ка» пришли.

Этот привал находится на улице «Геометрическая».

– Рассмотрите дома геометрической страны.

– Как вы думаете, в каком доме живет какая геометрическая фигура?

– Чей дом самый высокий (низкий)?

– Чей дом самый широкий (узкий)?

– К чьему дому ведет самая длинная (короткая) дорожка?

4. Самостоятельная деятельность детей

Упражнение «Геометрические качели»

– В стране геометрических фигур есть волшебные качели. На качелях катаются геометрические фигуры. С левой стороны качелей посадите кататься три круга. А на правую сторону посадите квадратов, на один меньше, чем кругов. Что можно сделать, чтобы кругов и квадратов стало поровну? (Добавить один квадрат или убрать один круг.)

Шли мы, шли, шли мы, шли и на третий привал пришли.

Упражнение «Расставь геометрические фигуры на листе»

– А сейчас возьмите с края стола листы бумаги и приготовьте для работы картонные геометрические фигуры.

– Поставь квадрат в правый верхний угол.
– Поставь круг в середину листа.
– Поставьте треугольник в левый нижний угол.
– Поставьте овал в левый верхний угол.
– Поставьте треугольник в правый нижний угол.

– Молодцы ребята, вы отлично справились с заданием.

Динамическая пауза «Сосчитай и сделай»

А сейчас, ребята, давайте немного отдохнем.

Вставайте из-за столов и выходите ко мне.

Нас ждет физкультминутка!

Сколько точек в этом круге (5),                  
Столько раз поднимем руки.
Сколько палочек до точки (6),
Столько встанем на носочки.
Сколько ёлочек зелёных (4),
Столько сделаем наклонов.
Сколько здесь у нас кружков (7),
Столько сделаем прыжков.

5. Совместная деятельность воспитателя с детьми.

– В стране геометрических фигур Старичку-лесовичку очень нравится и ему бы хотелось здесь остаться. Он просит, чтобы вы помогли ему построить дом, а для строительства он принес материал. Вот, что он принес (показ строительного материала).

– Поможем построить дом для Старичка-лесовичка? (Ответ детей)

– Какие фигуры подойдут для строительства? Это кубы, они объёмные, у них есть углы, ребра, грани. Одна грань куба – квадрат.

– Чем куб отличается от квадрата? (Квадрат плоский, куб объемный)

– Чем куб отличается от шара? (Есть углы, не может катиться).

– Какое общее свойство у куба и шара? (Они оба объемные)

Воспитатель: – Почему из кубов удобно строить? (Они не катятся, объемные).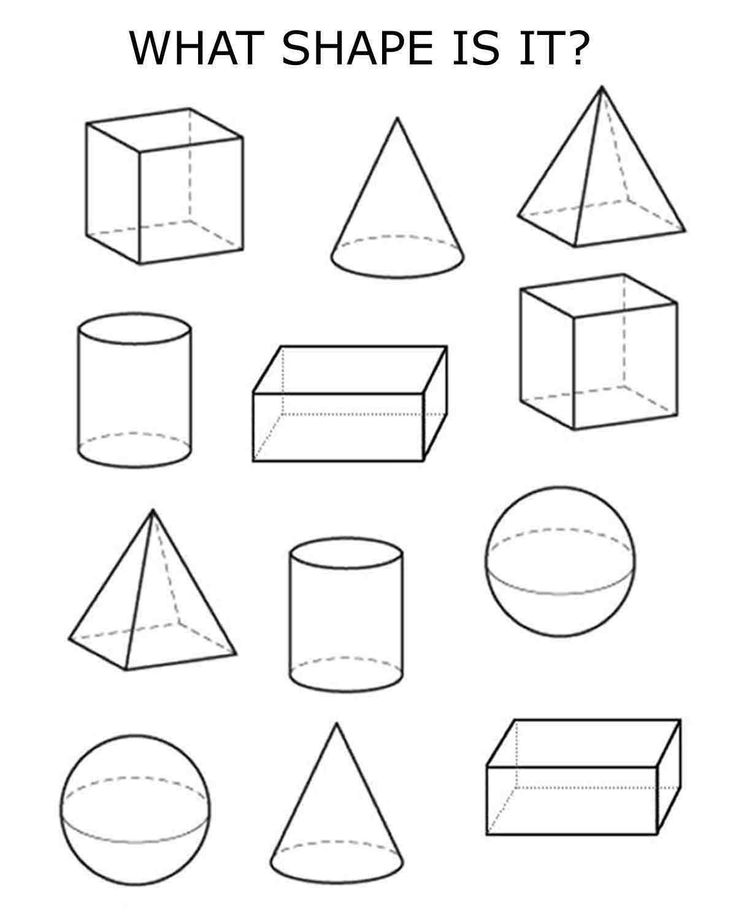

– Из каких фигур мы строили дом? (Ответы детей).

– Ребята, а кем были вы во время строительства домов? (Строителями). А кто такие строители? (Ответы детей)

Воспитатель: – Нелегкое дело – строительство дома. Устали вы, наверное, пока строили, давайте немного взбодримся.

Физкультминутка:

– 1, 2, 3, 4, 5 – хотим строителями стать (хлопки, руки в стороны)

Дружно доски поднимаем (руки вверх)

Быстро гвозди забиваем (кулачком об кулачок)

Кистью красим новый дом (поворот вокруг себя, «красят кистью»)

Чтоб уютно было в нём.

1, 2, 3, – дом построен – посмотри! (Прыжки, руки в стороны).

Воспитатель: – Ну как Старичок – лесовичок, ребята построили для вас дом?

– Молодцы, ребята! Старичок-лесовичок благодарит вас за помощь!

– Ну что ж, как не грустно, но нам пора возвращаться домой, все тропинки одолели без запинки.

– Закройте все глаза, а мы сосчитаем обратным счётом от 3 до 1. Вот мы и в группе, но я думаю, что мы ещё не раз побываем в замечательной стране геометрических фигур.

6. Рефлексия

Вы сегодня побывали в гостях у сказки, где все связано с математикой. Все вы старались, внимательно слушали, поэтому и справились со всеми заданиями.

– Какие задания вам показались интересными? Какие сложными? С какими заданиями вы справились быстрее.

– Занятие закончилось, спасибо Старичку-лесовичку за наше сказочное путешествие!

Геометрические фигуры в дизайне (64 фото)

1

Геометрическая абстракция

2

Объемная Геометрическая композиция

3

Композиция из геометрических фигу

4

Геометрическая абстракция

5

Графический дизайн геометрические фигуры

6

Композиция из геометрических фигур

7

Геометрический абстракционизм

8

Нео Мемфис стиль

9

Геометрические фигуры на стене

10

Объемные абстрактные фигуры

11

Необычные геометрические фигуры

12

Необычные геометрические фигуры

13

Графический дизайн геометрические фигуры

14

Акустические панели Aircone

15

Необычные геометрические формы

16

Постеры с геометрическим рисунком

17

Красивые геометрические формы

18

Дом геометрические фигуры

19

Дизайнерские геометрические фигуры

20

Украшение стены в геометрическом стиле

21

Абстрактная композиция из геометрических фигур

22

Геометрические паттерны

23

Геометрические фигуры натстенах

24

Панно из геометрических фигур

25

Дизайнерская композиция

26

Геометрический декор стен

27

Геометрические фигуры на стене

28

Абстрактные фигуры

29

Геометрическая абстракция на стене

30

Дизайнерская композиция

31

Геометрические фигуры Эстетика

32

Геометрические фигуры Минимализм

33

Композиция в треугольнике

34

Геометрические фигуры в архитектуре

35

Постеры с геометрическим рисунком

36

Графический дизайн геометрические фигуры

37

Геометрические фигуры необычной формы

38

Современное искусство геометрия

39

Геометрические фигуры на стене

40

Геометрические фигуры Графика

41

Красивые геометрические фигуры

42

Необычные геометрические фигуры

43

Абстрактные 3d фигуры

44

Необычные геометрические фигуры

45

Геометрические фигуры на стене

46

Объемная композиция

47

Геометрические фигуры на стене

48

Панно из геометрических фигур

49

Геометрические фигуры на стене

50

Необыкновенные геометрические фигуры

51

Сакральная геометрия трилистник

52

Объемные оптические иллюзии

53

Basic Shapes в иллюстраторе

54

Объемные абстрактные фигуры

55

Геометрические фигуры дизайн

56

Баланс Минимализм

57

Цветные геометрические узоры

58

Геометрические узоры

59

Геометрические фигуры в интерьере

60

Тату геометрические фигуры

61

Постеры в скандинавском стиле

62

Геометрический орнамент в интерьере

63

Нестандартные геометрические фигуры

64

3д палитра

Геометрические фигуры – Области

квадрат

Площадь квадрата может быть рассчитана как

A = A ² (1a)

Сточа квадрата может быть рассчитана как

. A = A ^1/2 (1B)

Диагональный квадрат можно рассчитать как

D = A 2 ^1/2 (1C)

прямоугольник

Площадь прямоугольника может быть рассчитана как

A = A B (2A)

Диагональ прямоугольника может быть рассчитана как

D = (A ² + B ² ) ^1/2 (2B)

Параллелограмм

Площадь параллелограммы может быть рассчитана как

A = A H

= A B SNIC α (3A) 9000

= A B SNIC α (3A) 9000

= A B SNIC α (3A) 9000

= A B SNIC α (3A)

= A B SNIN параллелограмм можно рассчитать как

D ₁ = ((A + H COT α ) ² + H ² ) ^1/2 (3B)

D ₂ = (A – – – – H COT α ) ² + H ² ) ^1/2 (3B)

ЭКОЛИЗАТЕЛЬНЫЙ ТРЕЗОН

ЭКОЛИЗАТЕЛЬНЫЙ КРЕЙНГЛ – это треугольник, в котором равны все три стороны.

Площадь равностороннего треугольника можно вычислить как

A = A ² /3 3 ^1/2 (4A)

Площадь равностороннего треугольника может быть рассчитана как

H = A/2 3 ^1/2 (4B)

Треугольник

Площадь треугольника может быть рассчитана как

A = A H / 2

= R S (5A)

R = A H / 2S (5B)

R = A H / 2S (5B)

R = A H / 2S (5B)

R = A H / 2S (5B)

.0014

R = B C / 2 H (5C)

S = (A + B + C) / 2 (5d)

X = S – A (5E)

Y = S = S – A (5E)

Y = S = S = S = S = S = S = S = S = S = S – A (5E)

Y = S = S = S = S = S = S = с. – B (5F)

Z = S – C (5G)

Трапезиоид

Площадь трапеции может быть рассчитана как

A = 1/2 (A + B) H

= M H (6A)

M = (A + B) / 2 (6B)

Hexagon

Область гексагона может быть рассчитана как

A = 3/2 A ² 3 ^1/2 (7A)

D = 2 A

= 2/3 ^1/2 S

= 1,1547005 S (7B)

= 1,1547005 S (7B)

= 1,1547005 S (7B)

= 1,1547005 S (7B)

= 1,1547005 S (7B)

= 1,1547005 S (7B)

= 1,1547005 S (7B) 0005

S = 3 ^1/2 /2 D

= 0,866025 D (7C)

Круг

Область круга может быть рассчитана как

. /4 d ²

  = π r ²  

  = 0.785.. d ²                       (8a)

C = 2 π r 

= π D (8b)

, где

C = округ

• Сколько кругов входит в прямого прямого?
• Сколько меньших кругов помещается в большом круге?

Сектор и сегмент круга

Сектор круга

Площадь сектора круга может быть выражена как

A = 1/2 θ _r r ² (9)

= 1/360 θ _D π r ²

, где

θ _R = Угол в Radians

_D = Угол в Radians

θ _D = Угол в Radians

θ _D = угла в Radians

_D = угла в Radians

θ _D .

Сегмент круга

Площадь сегмента круга может быть выражена как

A = 1/2 (θ _R – SIN θ _R ) R ²

= 10012 2

= 1/12).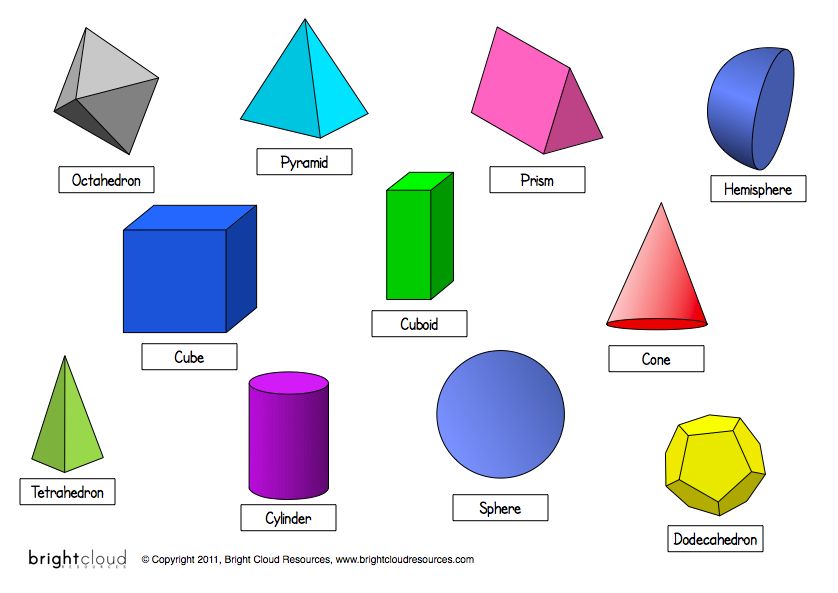 (π θ _д /180 – SIN θ _D ) R ² (10)

Правый круговой цилиндр

Площадь боковой поверхности правого круга может быть выражена как

A = 2 π R H (11)

5

где

h _{= высота цилиндра (м, фут)}

r = радиус основания (м, фут) выражается как

A = π R L

= π R (R ² + H ² ) ^1/2 (12)

, где

H _{= высота из CONESE (M.}

H _{= высота CONE of CONE of CONE (M.}

H _{= высота CONE of CON. , фут)}

r = радиус основания (м, фут)

l = наклонная длина (м, фут)

Сфера

Площадь боковой поверхности сферы может быть выражена как 9001 9 = 4 π r ²                                    (13)

геометрическая форма для более высоких структур в nLab

Пропустить навигационные ссылки | Домашняя страница | Все страницы | Последние версии | Обсудить эту страницу |

Контекст

Теория высших категорий

Теория высших категорий

• Теория категорий
• гомотопическая теория

Основные понятия

• k-морфизм, когерентность
• зацикливание и удаление циклов
• петля и подвеска

Основные теоремы

• гомотопическая гипотеза-теорема
• гипотеза-теорема о раскрытии цикла
• периодическая таблица
• гипотеза стабилизации-теорема
• гипотеза точности
• голографический принцип

Приложения

• приложения (высшей) теории категорий
• высшая категория теория и физика

Модели

• (n,r)-категория
  • Тета-пространство
  • ∞-категория/∞-категория
  • (∞,n)-категория
    • n-кратное полное пространство Segal
  • (∞,2)-категория
  • (∞,1)-категория
    • квазикатегория
      • алгебраическая квазикатегория
    • просто обогащенная категория
    • полный Segal space
    • категория модели
  • (∞,0)-категория/∞-группоид
    • Комплекс Кан
      • алгебраический комплекс Кана
      • симплициальный Т-комплекс
  • n-категория = (n,n)-категория
    • 2-категория, (2,1)-категория
    • 1-категория
    • 0-категория
    • (-1)-категория
    • (-2)-категория
  • n-посет = (n-1,n)-категория
    • poset = (0,1)-категория
    • 2-посет = (1,2)-категория
  • n-группоид = (n,0)-категория
    • 2-группоид, 3-группоид
• категоризация/декатегоризация
• геометрическое определение высшей категории
  • Комплекс Кан
  • квазикатегория
  • симплициальная модель для слабых ∞-категорий
    • дополнительный набор
    • слабый комплиментарный набор
• алгебраическое определение высшей категории
  • бикатегория
  • бигруппоид
  • три категории
  • тетракатегория
  • строгая ∞-категория
  • Батанин ∞-категории
  • Trimble ∞-категория
  • Grothendieck-Maltsiniotis ∞-категории
• стабильная гомотопическая теория
  • симметричная моноидальная категория
  • симметричная моноидальная (∞,1)-категория
  • стабильная (∞,1)-категория
    • dg-категория
    • Категория А-∞
    • триангулированная категория

Морфизмы

• k-морфизм
  • 2-морфизм
• трансформ
  • естественная трансформация
  • модификация

Функторы

• Функторы
• 2-функтор
  • псевдофунктор
  • функтор слабости
• (∞,1)-функтор

Универсальные конструкции

• 2-концевые
• (∞,1)-присоединение
• (∞,1)-расширение Кан
  • (∞,1)-предел
• (∞,1) – конструкция Гротендика

• космический куб
  • k-туплый моноидальный n-категории
  • строгая ∞-категория, строгий ∞-группоид
• стабильная (∞,1)-категория
• (∞,1)-топос

1-категориальные представления

• гомотопическая категория
• модель теории категорий
• расширенная теория категорий

Изменить эту боковую панель

Обзор

Работа с высшими структурами, такими как высшие категории, обычно предполагает представление их как конгломератов

клеток определенных форма .

Примеры возможных форм, используемых для моделирования более высоких категорий:

• глобуса;

• симплекса;

• призмы;

• куба;

• дерева;

• шаровидных клетки;

• опетопов, они же мультитопы.

Имеются соответствующие категории, чьи

• объекта — это «стандартные клеточные фигуры» данного сорта: глобусы, симплексы, кубы соответственно. Для глобусов, симплексов и кубов существует один объект для каждого натурального числа n∈ℕn \in \mathbb{N}, поэтому их обычно обозначают [n][n]. Для других видов фигур может быть несколько форм каждого измерения.

• морфизма генерируются из (некоторых) способов сопоставления этих стандартных клеточных форм друг с другом таким образом, что их клеточная структура сохраняется;

• , а композиция таких морфизмов подчинена отношениям, унаследованным от геометрического смысла этих отображений, который говорит, например, что левая граница верхней границы куба совпадает с верхней границей его левой границы — эти являются шаровыми тождествами , симплициальных тождеств и кубических тождеств соответственно.

Полученные категории основных форм ячеек:

• категория глобуса 𝔾\mathbb{G}

• симплексная категория Δ\Delta

• куб категории □\квадрат

• древовидная категория Ом\Омега

• категория opetope?

  𝕆\mathbb{O}

В общем случае в таких категориях есть два типа морфизма, называемые включениями граней (или когранями ) и вырождениями . Лицевые включения показывают низкоразмерную ячейку как «лицо» многомерной, в то время как вырождения схлопывают высокоразмерную ячейку до менее размерной. Все такие категории имеют включения граней (это действительно основные «структурные» карты, определяющие формы ячеек), но некоторые (например, Δ\Delta, □\square и Ω\Omega) включают вырождения, а некоторые (например, 𝔾\mathbb{G} и 𝕆\mathbb{O}) обычно не делают.

Общее понятие, включающее все эти категории, — это обобщенная категория Риди.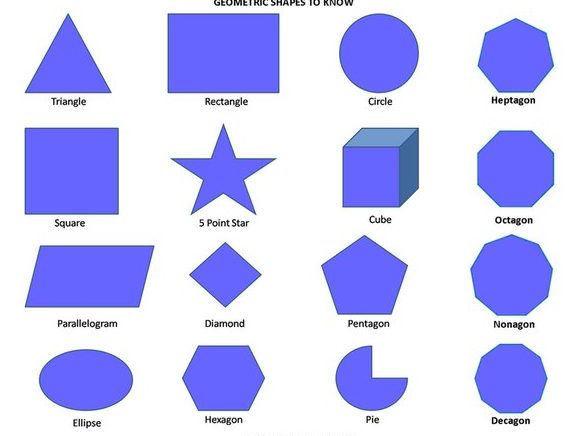 Если исключить вырождения, то мы получим более простое понятие (обобщенной) прямой категории.

Высшая структура, основанная на этих геометрических формах, представляет собой предпучок по одной из этих категорий. Они называются

• .

  шаровые наборы

• симплициальные наборы

• кубические комплекты

• дендроидные наборы

• опетопические наборы

соответственно.

Существуют также другие понятия геометрической формы, которые оказались полезными в теории высших категорий, такие как формы, инкапсулированные в дисковую категорию Джояла Θ\Theta (которые включают как глобусы, так и симплексы в качестве особых случаев).

Многие определения высших категорий даются одним из этих предварительных пучков

• либо оснащен дополнительными свойствами , в геометрическом определении более высоких категорий;

• или снабженный дополнительной структурой , в алгебраическом определении высших категорий.

Например, обычное определение строгих ∞-категорий основано на придании дополнительной структуры глобулярным множествам, как и слабая версия ∞-категории Батанина. Точно так же n-кратные категории придают дополнительную структуру кубическим множествам. С другой стороны, понятие квазикатегорий основано на симплициальных множествах, в то время как другие более «гомотопические» понятия более высокой категории основаны на кубических или мультисимплициальных методах. Вообще «геометрические» определения обычно можно рассматривать как нерв «алгебраических».

Иногда два определения, в которых используются разные формы, тем не менее охватывают эквивалентные понятия. Мы надеемся, что это верно для всех предлагаемых определений n-категории, хотя они используют множество различных форм. С другой стороны, иногда использование разных форм указывает на принципиально иную рассматриваемую структуру. Например, реберно-симметричные nn-кратные категории со связями дают то же понятие, что и глобулярные nn-кратные категории, а произвольные nn-кратные категории — совсем другое.