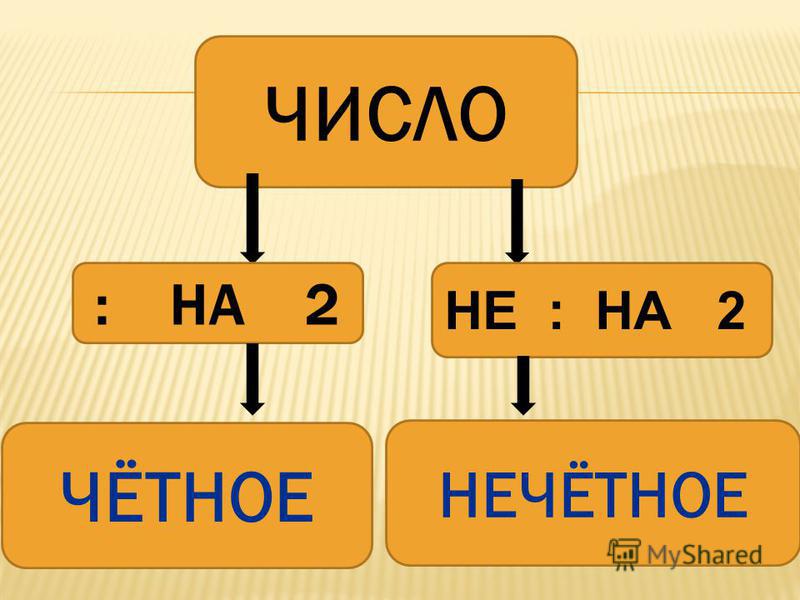
Четные и нечетные: Чётные и нечётные числа — урок. Математика, 2 класс.

Исследование: пчелы умеют различать четные и нечетные числа

Различия между людьми и другими животными меньше, чем считается?

С детства мы знаем, что числа могут быть как четными, так и нечетными. В новом исследовании, опубликованном в журнале Frontiers in Ecology and Evolution, показано, что и медоносные пчелы могут этому научиться. Кратко о результатах работы авторы рассказывают в Conversation.

Интересно, что люди, склонны, например, быстрее реагировать на четные числа действиями, выполняемыми правой рукой, а на нечетные числа — левой. Мы также быстрее и точнее находим четные числа по сравнению с нечетными. Исследования показали, что дети обычно ассоциируют слово «четный» с «правым», а «нечетный» — с «левым».

Эти исследования предполагают, что у людей могут быть базовые когнитивные установки в отношении нечетных и четных чисел, которые могли возникнуть в результате эволюции, культурной передачи либо их комбинации. Непонятно, почему четность может быть так важна для повседневной жизни, поэтому происхождение этих установок остается неясным.

Понимание того, могут ли другие животные и как распознавать нечетные и четные числа, могло бы рассказать нам больше о нас самих.

Предыдущие исследования показали, что медоносные пчелы могут научиться упорядочивать количества, выполнять простое сложение и вычитание, сопоставлять символы с количествами и соотносить понятия размера и числа.

Чтобы научить пчел различать четные и нечетные числа, насекомых разделили на две группы. Одна была обучена ассоциировать четные числа с сахарной водой и нечетные числа с горькой на вкус жидкостью (хинин). Другая — нечетные числа с сахарной водой и четные числа с хинином. Пчел обучали, показывая им карточки с напечатанными в количестве от 1 до 10 фигурами, до тех пор пока насекомые не выбирали правильный ответ с точностью 80%.

Примечательно, что группы учились с разной скоростью. Пчелы, обученные связывать нечетные числа с сахарной водой, научились быстрее.

Затем каждую пчелу проверили на новых числах. Насекомые классифицировали новые карточки из 11 или 12 элементов как нечетные или четные с точностью около 70%.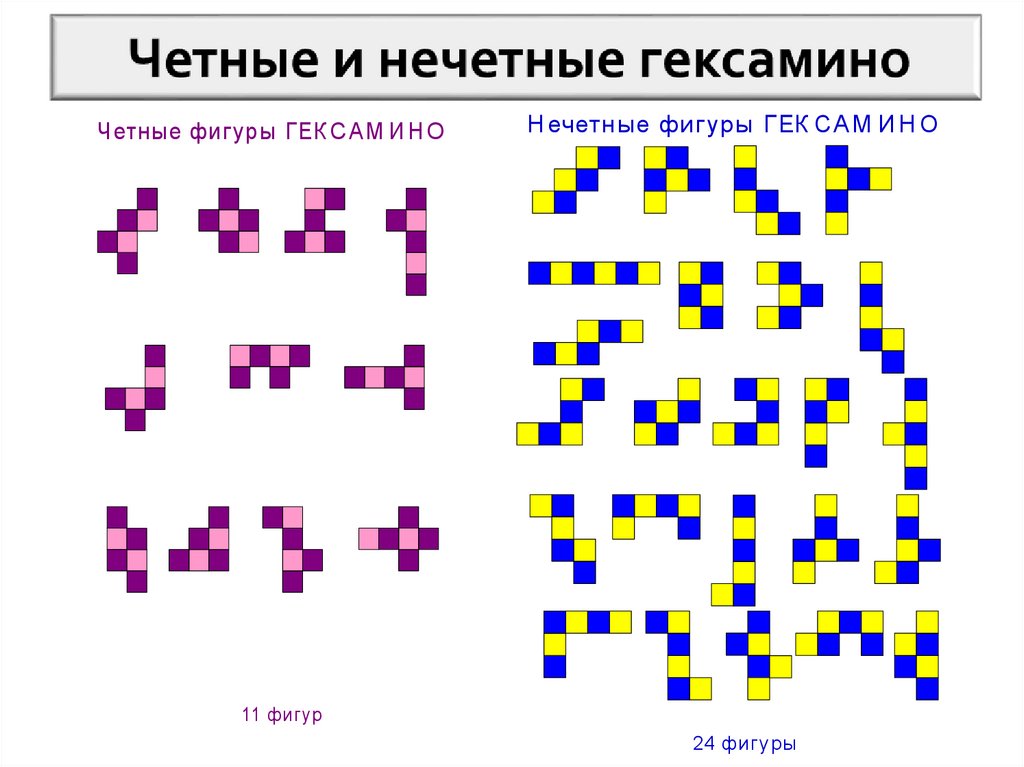

Результаты показали, что миниатюрный мозг медоносных пчел способен понимать понятия нечетного и четного. Означает ли это, что задача проверки четности оказалась менее сложной, чем думали ранее? Чтобы найти ответ, ученые обратились к биотехнологиям.

Построили простую искусственную нейронную сеть всего из пяти нейронов. Затем давали ей сигналы от 0 до 40 импульсов, которые она классифицировала как нечетные или четные. Несмотря на свою примитивность, нейронная сеть классифицировала количество пульсаций как нечетное или четное со 100% точностью. Однако все это не обязательно означает, что пчелы и простая нейронная сеть использовали один и тот же механизм для решения задачи.

Результаты исследования ставят новые вопросы. Является ли открытие математики неизбежным следствием интеллекта? Математика как-то связана с человеческим мозгом? Различия между людьми и другими животными меньше, чем считается?

Почему пчела умирает, когда жалит?

Пчела-блогер

На сайте могут быть использованы материалы интернет-ресурсов Facebook и Instagram, владельцем которых является компания Meta Platforms Inc. , запрещённая на территории Российской Федерации.

Самая низкая температура на Земле

Самая низкая температура на Земле

О городах-рекордсменах и о том, почему на одну и ту же температуру человек реагирует по-разному

Юлия Скопич

14 октября 2022

Самые северные города мира

Самые северные города мира

В каких условиях могут жить люди

13 октября 2022

Вопрос: что это?

Вопрос: что это?

Подсказка: время применения — 200 год до н. э.— 400 год н. э., место — Римская империя

12 октября 2022

РЖД запустят 200 дополнительных поездов на ноябрьские праздники

14 октября 2022

Палеонтологи нашли останки «адских рыб», вымерших вместе с динозаврами

14 октября 2022

«Суперхайвей» со следами древних людей и животных обнаружен в Британии

14 октября 2022

Древняя базилика поднялась из воды в Турции

14 октября 2022

Животные Красной книги России

Анонимное интервью: проводник поезда

Семь фактов про ворон и воронов

Сколько человек может прожить без сна

10 мест Туниса, где нельзя не побывать

Живыми или мертвыми: редкие животные России

Рекорды скорости

Мы используем cookie-файлы

ОАО «Моя Планета» использует cookie-файлы для улучшения работы и пользования сайта https://moya-planeta. ru/. Более подробную информацию о Политике ОАО «Моя Планета» по работе с cookie-файлами можно найти здесь, о Политике ОАО «Моя Планета» в отношении обработки персональных данных можно узнать здесь. Продолжая пользоваться сайтом https://moya-planeta.ru/, Вы подтверждаете, что были проинформированы об использовании cookie-файлов сайтом https://moya-planeta.ru/ и согласны с Политикой ОАО «Моя Планета» по работе с cookie-файлами. Вы можете отключить cookie-файлы в настройках Вашего браузера.

Четные и нечетные функции

Используй поиск, чтобы найти научные материалы и собрать список литературы

База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны

Содержание статьи

1. Четные функции

2. Нечетные функции

3. Функция общего вида

4. Пример задачи

Четные функции

Определение 1

Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть четной, если для всех точек из множества $X$ будет выполняться

\[f\left(x\right)=f(-x)\]

Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).

Рисунок 1.

Для исследования функции на четность необходимо в его аналитической записи заменить переменную $x$ на переменную $-x$, произвести, при необходимости элементарные преобразования, и проверить условие определения 1.

Нечетные функции

Определение 2

Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть нечетной, если для всех точек из множества $X$ будет выполняться

\[f\left(-x\right)=-f(x)\]

Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).

Рисунок 2.

Для исследования функции на нечетность необходимо в его аналитической записи заменить переменную $x$ на переменную $-x$, произвести, при необходимости элементарные преобразования, и проверить условие определения 2. 2+4}{x}$ следовательно, $f(x)$ — нечетная функция.

Изобразим её на графике:

Рисунок 5.

в) $f\left(x\right)=sinx+cosx$

$f\left(-x\right)={\sin \left(-x\right)\ }+{\cos \left(-x\right)\ }=cosx-sinx$ следовательно, $f\left(x\right)$ — функция общего вида.

Изобразим её на графике:

Рисунок 6.

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 04.07.2022

Выполнение любых типов работ по математике

Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами

Подбор готовых материалов по теме

Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

Сумма четных и нечетных чисел в Excel.

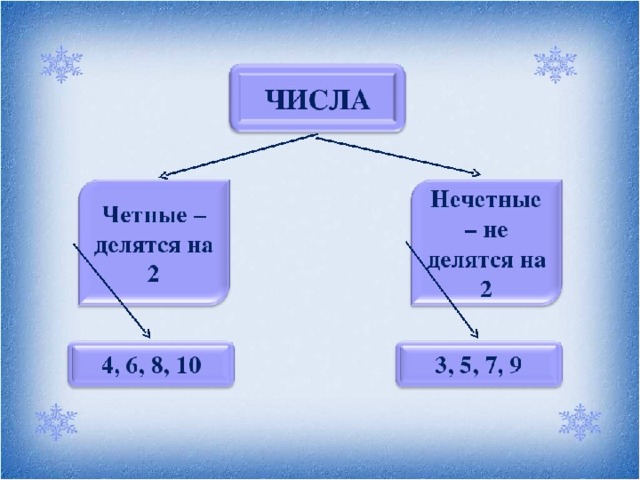
Как четные и нечетные числа выделить разным цветом в Excel Формулы для четных и нечетных чисел

· Четные числа – это те, которые делятся на 2 без остатка (например, 2, 4, 6 и т.п.). Каждое такое число можно записать в виде 2K, подобрав подходящее целое K (например, 4 = 2 х 2, 6 = 2 х 3, и т.д.).

· Нечетные числа – это те, которые при делении на 2 дают в остатке 1 (например, 1, 3, 5 и т.п.). Каждое такое число можно записать в виде 2K + 1, подобрав подходящее целое K (например, 3 = 2 х 1 + 1, 5 = 2 х 2 + 1, и т.д.).

• Сложение и вычитание:

• • Ч ётное ± Ч ётное = Ч ётное
  • Ч ётное ± Н ечётное = Н ечётное
  • Н ечётное ± Ч ётное = Н ечётное
  • Н ечётное ± Н ечётное = Ч ётное
• Умножение:
• • Ч ётное × Ч ётное = Ч ётное
  • Ч ётное × Н ечётное = Ч ётное
  • Н ечётное × Н ечётное = Н ечётное
• Деление:
• • Ч ётное / Ч ётное – однозначно судить о чётности результата невозможно (если результат целое число , то оно может быть как чётным, так и нечётным)
  • Ч ётное / Н ечётное -­– если результат целое число , то оно Ч ётное
  • Н ечётное / Ч ётное – результат не может быть целым числом, а соответственно обладать атрибутами чётности
  • Н ечётное / Н ечётное —если результат целое число , то оно Н ечётное

Сумма любого числа четных чисел – четно.

Сумма нечетного числа нечетных чисел – нечетно.

Сумма четного числа нечетных чисел – четно.

Разность двух чисел имеет ту же четность, что и их сумма .
(напр. 2+3=5 и 2-3=-1 оба нечетные)

Алгебраическая (со знаками + или -) сумма целых чисел имеет ту же четность, что и их сумма .
(напр. 2-7+(-4)-(-3)=-6 и 2+7+(-4)+(-3)=2 оба четны)

Идея четности имеет много разных применений. Самые простые из них:

1. Если в некоторой замкнутой цепочке чередуются объекты двух видов, то их четное число (и каждого вида поровну).

2. Если в некоторой цепочке чередуются объекты двух видов, а начало и конец цепочки разных видов, то в ней четное число объектов, если начало и конец одного вида, то нечетное число. (четное число объектов соответствует нечетному числу переходов между ними и наоборот !!! )

2″. Если у объекта чередуются два возможных состояния, а исходное и конечное состояния различны , то периодов пребывания объекта в том или ином состоянии – четное число, если исходное и конечное состояния совпадают – то нечетное . (переформулировка п.2)

3. Обратно: по четности длины чередующийся цепочке можно узнать, одного или разных видов ее начало и конец.

3″. Обратно: по числу периодов пребывания объекта в одном из двух возможных чередующихся состояний можно узнать, совпадает ли начальное состояние с конечным. (переформулировка п.3)

4. Если предметы можно разбить на пары, то их количество четно.

5. Если нечетное число предметов почему-то удалось разбить на пары, то какой-то из них будет парой к самому себе, причем такой предмет может быть не один (но их всегда нечетное число).

(!) Все эти соображения можно на олимпиаде вставлять в текст решения задачи, как очевидные утверждения.

Примеры:

Задача 1. На плоскости расположено 9 шестеренок, соединенных по цепочке (первая со второй, вторая с третьей… 9-я с первой). Могут ли они вращаться одновременно?

Решение: Нет, не могут. Если бы они могли вращаться, то в замкнутой цепочке чередовалось бы два вида шестеренок: вращающиеся по часовой стрелке и против часовой стрелки (для решения задачи не имеет никакого значения, в каком именно направлении вращается первая шестеренка ! ) Тогда всего должно быть четное число шестеренок, а их 9 штук?! ч. и.т.д. (знак “?!” обозначает получение противоречия)

Задача 2. В ряд выписаны числа от 1 до 10. Можно ли расставить между ними знаки + и -, чтобы получилось выражение, равное нулю?
Решение: Нет, нельзя. Четность полученного выражения всегда будет совпадать с четностью суммы 1+2+…+10=55, т.е. сумма всегда будет нечетной . А 0 – четное число?! ч.т.д.

Excel для Office 365 Excel для Office 365 для Mac Excel для Интернета Excel 2019 Excel 2016 Excel 2019 для Mac Excel 2013 Excel 2010 Excel 2007 Excel 2016 для Mac Excel для Mac 2011 Excel Starter 2010 Меньше

В этой статье описаны синтаксис формулы и использование функции ЕЧЁТН в Microsoft Excel.

Описание

Возвращает значение ИСТИНА, если число четное, и значение ЛОЖЬ, если число нечетное.

Синтаксис

ЕЧЁТН(число)

Аргументы функции ЕЧЁТН описаны ниже.

Число Обязательный. Проверяемое значение. Если число не является целым, оно усекается.

Замечания

Если значение аргумента “число” не является числом, функция ЕЧЁТН возвращает значение ошибки #ЗНАЧ!.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем – клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.

Например: -24, 0, 6, 38 — все это четные числа.

m = 2k — общая формула написания четных чисел, где k – целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.

Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.

Пример нечетных чисел: 3, 1, 7 и 35.

n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k – целое число.

Сложение и вычитание четных и нечетных чисел

В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.

Операция	Результат	Пример
Четное + Четное
Четное + Нечетное	Нечетное
Нечетное + Нечетное

Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.

Умножение четных и нечетных чисел

При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.

Операция	Результат	Пример
Четное * Четное
Четное * Нечетное
Нечетное * Нечетное	Нечетное

А теперь рассмотрим дробные числа.

Десятичная запись числа

Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.

Например: 3,14; 5,1; 6,789 — это все

С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.

Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.

Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.

А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом – дробную.

Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.

Стандартные функции

Первый способ возможен при использовании стандартных функций приложения. Для этого необходимо создать два дополнительных столбца с формулами:

• Четные числа – вставляем формулу «= ЕСЛИ (ОСТАТ(число;2) =0;число;0)», которая вернет число, в случае если оно делится на 2 без остатка.
• Нечетные числа – вставляем формулу «= ЕСЛИ (ОСТАТ(число;2) =1;число;0)», которая вернет число, в случае если оно не делится на 2 без остатка.

Затем необходимо определит сумму по двум столбцам с помощью функции «=СУММ()».

Плюсы данного способа в том, что он будет понятен даже тем пользователям, которые профессионально не владею приложением.

Минусы способа – приходится добавлять лишние столбцы, что не всегда удобно.

Пользовательская функция

Второй способ, является более удобным, чем первый, т.к. в нем применяется пользовательская функция, написанная на VBA – sum_num(). Функция возвращает сумму чисел в виде целого числа. Суммируются либо четные числа, либо нечетные, в зависимости от значения ее второго аргумента.

Синтаксис функции: sum_num(rng;odd):

1. Аргумент rng – принимает диапазон ячеек, по которым необходимо произвести суммирование.
2. Аргумент odd – принимает логическое значение ИСТИНА для четных чисел или ЛОЖЬ для нечетных.

Важно: Четными и нечетными числа могут являться только целые числа, поэтому числа, которые не соответствуют определению целого числа, игнорируются. Также, если значением ячейки является срока, то данная строка не участвует в расчете.

Плюсы: нет нужны добавлять новые столбцы; лучший контроль над данными.

Минусы заключаются в необходимости перевода файла в формат. xlsm для версий Excel, начиная с версии 2007. Также функция будет работать только в той книге, в которой она присутствует.

Использование массива

Последний способ является самым удобным, т.к. не требует создания дополнительных столбцов и программирования.

Его решение схоже с первым вариантом – они используют одни и те же формулы, но данный способ, благодаря использованию массивов, производит подсчет в одной ячейке:

• Для четных чисел – вставляем формулу «=СУММ (ЕСЛИ (ОСТАТ(диапазон_ячеек;2) =0;диапазон_ячеек;0))». После ввода данных в строку формул нажимаем одновременно клавиши Ctrl + Shift + Enter, чем сообщаем приложению, что данные необходимо обрабатывать как массив, и оно заключит их в фигурные скобки;
• Для нечетных чисел – повторяем действия, но изменяем формулу «=СУММ (ЕСЛИ (ОСТАТ(диапазон_ячеек;2) =1;диапазон_ячеек;0))».

Плюсом способа является то, что все рассчитывается в одной ячейке, без дополнительных столбцов и формул.

Минусом является лишь то, что неопытные пользователи могут не понять Ваших записей.

На рисунке видно,что все способы возвращают один и тот же результат, какой лучше, необходимо выбирать под конкретную задачу.

Скачать файл с описанными варианта можно по данной ссылке.

Когда нужно приготовить разного рода отчеты, иногда возникает потребность выделить все парные и непарные числа разными цветами. Для решения данной задачи наиболее рациональным способом является условное форматирование.

Как найти четные числа в Excel

Набор четных и нечетных чисел, которые следует автоматически выделить разными цветами:

Допустим парные числа нам нужно выделит зеленым цветом, а непарные – синим.

Две формулы отличаются только операторами сравнения перед значением 0. Закройте окно диспетчера правил нажав на кнопку ОК.

В результате у нас ячейки, которые содержат непарное число имеют синий цвет заливки, а ячейки с парными числами – зеленый.



Функция ОСТАТ в Excel для поиска четных и нечетных чисел

Функция =ОСТАТ() возвращает остаток от деления первого аргумента на второй. В первом аргументе мы указываем относительную ссылку, так как данные берутся из каждой ячейки выделенного диапазона. В первом правиле условного форматирования мы указываем оператор «равно» =0. Так как любое парное число, разделенное на 2 (второй оператор) имеет остаток от деления 0. Если в ячейке находится парное число формула возвращает значение ИСТИНА и присваивается соответствующий формат. В формуле второго правила мы используем оператор «неравно» 0. Таким образом выделяем синим цветом нечетные числа в Excel. То есть принцип работы второго правила действует обратно пропорционально первому правилу.

медоносных пчел умеют различать четные и нечетные числа так же, как и мы

В детстве мы знаем, что числа могут быть четными и нечетными. И есть много способов классифицировать числа как четные или нечетные.

Мы можем запомнить правило, согласно которому числа, оканчивающиеся на 1, 3, 5, 7 или 9, являются нечетными, а числа, оканчивающиеся на 0, 2, 4, 6 или 8, — четными. Или мы можем разделить число на 2, где любое целое число означает, что число четное, иначе оно должно быть нечетным.

Точно так же при работе с объектами реального мира мы можем использовать пары. Если у нас остался непарный элемент, значит, количество объектов было нечетным.

До сих пор нечетная и четная категоризация, также называемая классификацией по четности, никогда не демонстрировалась у нечеловеческих животных. В новом исследовании, опубликованном в пятницу в журнале Frontiers in Ecology and Evolution , мы показываем, что медоносные пчелы могут этому научиться.

Почему категоризация паритета особенная?

Задачи на четность (такие как нечетная и четная категоризация) считаются абстрактными и высокоуровневыми числовыми понятиями у людей.

Интересно, что люди демонстрируют предвзятость в отношении точности, скорости, языка и пространственных отношений, когда классифицируют числа как нечетные или четные.

Например, мы быстрее реагируем на четные числа действиями, выполняемыми правой рукой, и на нечетные числа действиями, выполняемыми левой рукой.

Мы также быстрее и точнее классифицируем числа как четные по сравнению с нечетными. Исследования показали, что дети обычно ассоциируют слово «четный» с «правым», а «нечетный» — с «левым».

Эти исследования предполагают, что люди могли усвоить предубеждения и/или врожденные предубеждения в отношении нечетных и четных чисел, которые могли возникнуть либо в результате эволюции, культурной передачи, либо их комбинации.

Неясно, почему четность может быть важна помимо ее использования в математике, поэтому происхождение этих предубеждений остается неясным.

Понимание того, могут ли и как другие животные распознавать (или могут научиться распознавать) нечетные и четные числа, могло бы рассказать нам больше о нашей собственной истории с четностью.

Обучение пчел обучению нечетным и четным числам

Исследования показали, что медоносные пчелы могут научиться упорядочивать количества, выполнять простое сложение и вычитание, сопоставлять символы с числами и связывать понятия размера и числа.

Чтобы научить пчел паритетной задаче, мы разделили особей на две группы. Один был обучен ассоциировать четные числа с сахарной водой и нечетные числа с горькой на вкус жидкостью (хинин). Другая группа была обучена связывать нечетные числа с сахарной водой и четные числа с хинином.

Иллюстрация того, как исследователи обучали пчел ассоциировать «четные» стимулы с вознаграждением. (Скарлетт Ховард)

Мы обучали отдельных пчел, сравнивая нечетные и четные числа (с карточками, представляющими от 1 до 10 печатных фигур), пока они не выбирали правильный ответ с точностью 80 процентов.

Примечательно, что соответствующие группы обучались с разной скоростью.

Пчелы, обученные ассоциировать нечетные числа с сахарной водой, научились быстрее.

Их склонность к обучению в пользу нечетных чисел была противоположностью людей, которые быстрее классифицируют четные числа.

Затем мы проверили каждую пчелу на новых числах, не показанных во время обучения. Впечатляет то, что они классифицировали новые числа из 11 или 12 элементов как нечетные или четные с точностью около 70 процентов.

Наши результаты показали, что миниатюрный мозг медоносных пчел способен понимать понятия нечетного и четного.

Таким образом, большой и сложный человеческий мозг, состоящий из 86 миллиардов нейронов, и миниатюрный мозг насекомого, содержащий около 960 000 нейронов, могут классифицировать числа по четности.

Означает ли это, что задача проверки четности оказалась менее сложной, чем мы думали ранее? Чтобы найти ответ, мы обратились к биотехнологиям.

Создание простой искусственной нейронной сети

Искусственные нейронные сети были одним из первых алгоритмов обучения, разработанных для машинного обучения. Вдохновленные биологическими нейронами, эти сети масштабируемы и могут решать сложные задачи распознавания и классификации, используя логику высказываний.

Мы построили простую искусственную нейронную сеть всего из пяти нейронов для выполнения теста на четность.

Мы дали сети сигналы от 0 до 40 импульсов, которые она классифицировала как нечетные или четные. Несмотря на свою простоту, нейронная сеть правильно классифицировала числа пульса как нечетные или четные со 100-процентной точностью.

Это показало нам, что в принципе паритетная категоризация не требует большого и сложного мозга, такого как человеческий.

Однако это не обязательно означает, что пчелы и простая нейронная сеть использовали один и тот же механизм для решения задачи.

Простой или сложный?

Мы еще не знаем, как пчелам удалось выполнить задание на четность. Объяснения могут включать простые или сложные процессы. Например, у пчел может быть:

1. парных элемента, чтобы найти непарный элемент

2. выполнял расчет деления, хотя деление ранее не демонстрировалось пчелами

3. подсчитал каждый элемент, а затем применил правило четной/нечетной классификации к общему количеству.

Обучая другие виды животных различать нечетные и четные числа и выполнять другие абстрактные математические действия, мы можем больше узнать о том, как математика и абстрактное мышление возникли у людей.

Является ли открытие математики неизбежным следствием интеллекта? Или математика как-то связана с человеческим мозгом? Различия между людьми и другими животными меньше, чем мы думали ранее?

Возможно, мы сможем почерпнуть эти интеллектуальные идеи, если только будем внимательно слушать.

Скарлетт Ховард, преподаватель Университета Монаш; Адриан Дайер, доцент Университета RMIT; Эндрю Гринтри, профессор квантовой физики и будущий член Австралийского исследовательского совета, Университет RMIT, и Джейр Гарсия, научный сотрудник Университета RMIT.

Эта статья перепечатана из The Conversation под лицензией Creative Commons. Прочитайте оригинальную статью.

5 способов учить нечетные и четные числа!

Некоторым из ваших детей трудно различать нечетные и четные числа? Как ни странно, , эта концепция может быть сложной для некоторых детей, даже , хотя кажется, что это должно быть совершенно очевидно! (Подмигивай, подмигивай!) Вот пять простых способов научить нечетные и четные числа!

1. Постройте детей в пары
Я думаю, что детям проще всего понять, что такое нечетное число, СНАЧАЛА выстраивая их в ряд по двое.  Если у вас действительно нечетное количество детей в классе, у одного из ваших учеников не будет партнера, и кто-то останется «лишним».  Как только я проделал это со своими учениками, дети, которые не знали четных и нечетных чисел, вдруг поняли все:  при четном числе каждый получает приятеля. При нечетном числе один человек остается без приятеля.

2. Объясните концепцию и спойте
На DVD-диске Musical Math Volume 2 есть песня Odds and Evens, в тексте которой это объясняется. Не только это, но и мои первоклассники и второклассники ПОЛЮБИЛИ эту песню в прошлом году!

Четные числа, четные числа,
Четные числа, кричите!
2, 4, 6, 8, 10!
Выстройте их по двое, а затем,
У всех парней есть друг!
2, 4, 6, 8, 10!
У всех вечеров есть друг.
Нечетные числа, нечетные числа,
Нечетные числа, кричите!
1, 3, 5, 7, 9!
При попытке группировки по двойке
Есть дополнительная функция, которую вы не можете использовать.
1, 3, 5, 7, 9!
Лишний человек, нет друга в очереди.

The Odds & Evens Song стала хитом в этом году с #firstgrade и #secondgrade!

Видео, опубликованное Хайди Буткус (@heidisongs) на 30 июня 2016 г. в 11:54 по тихоокеанскому времени

Эта песня из альбома HeidiSongs Musical Math Vol. 2 очень помогает научить детей различать нечетные и четные числа!

3. Ежедневно просматривайте это с помощью календаря
У меня есть держатель куба шансов и четов, который я использую с моим календарем, чтобы просматривать эту концепцию! Я нашел его на математической конференции много лет назад. Но даже без держателя, я думаю, вы могли бы попросить детей каждый день говорить вам, был ли номер дня нечетным или четным, верно? Вы также можете отметить это или указать как-то в своем календаре. В этом случае мы просто пишем цифры на кубиках унификса перманентным маркером, а затем каждый день спрашиваем детей, четные они или нечетные. Затем добавляем их в держатель. Дети могут легко увидеть, есть ли у числа партнер или нет. Это отличный маленький инструмент!

 

Этот уникальный маленький гаджет поступил от ClassroomStorageSupplies.com, но они либо переместили свой веб-сайт, либо прекратили свою деятельность! Я искал, но нигде не могу найти!

4. Спойте песню «Счет двойками» и запишите эти числа!
Я всегда говорил своим детям, что если мы используем число при счете двойками, то оно должно быть четным. Затем мы пели песню и пытались остановиться и написать эти числа на наших досках! Этот последний шаг очень полезен, потому что он соединяет песню с написанным номером! Эта песня входит в нашу новейшую АНИМИРОВАННУЮ версию Musical Math Vol. 1!

 

5. Попробуйте некоторые скрытые рабочие листы шансов и четов!
Эти рабочие листы со скрытыми шансами и четами являются новым дополнением к нашей коллекции скрытых рабочих листов, и я пробовал их в течение последнего учебного года. Я сделала их, когда увидела, что моим первоклассникам нужно немного больше практики. (Мои второклассники были достаточно старшей группой, и им действительно не нужно было это дополнительное подкрепление, слава богу!) И числа на этих листах имеют только двузначные числа.

Мне было интересно, не будет ли это слишком легко для детей, но, как вы можете видеть на картинке ниже, на самом деле это не так. Было несколько умных детей, которые не поняли его, хотя я думаю, что подсказки к ответу сделают все это действительно совершенно очевидным!

Помимо рабочих листов с числовыми словами, как вы видите выше, мы также сделали несколько листов с картинками, просто для развлечения. Страницы с картинками включают в себя клоунскую машину, тюленей, мячи, зонтики, енота, черепаху, божью коровку, иглу, кролика с яйцами и кексы! Всего есть десять рабочих листов, и набор стоит 3 доллара.

 

Надеюсь, вашим детям понравится!! Хороших выходных и счастливого 4 июля!!!

-Хайди

---

Следуй за мной! Вам понравился этот пост? Сделай мне одолжение и поделись этим с друзьями! И следите за этим блогом, подписавшись на обновления по электронной почте, или подпишитесь на Bloglovin’ или подпишитесь на меня на TPT! Я также на Pinterest, Facebook, Twitter, Instagram, Google+ и YouTube! Не забудьте подписаться на нашу рассылку по электронной почте (на левой боковой панели), чтобы получать специальные предложения и промокоды, о которых вы больше нигде не узнаете.

подсчет даже первый класс весело скрытый номер математика Музыкальная математика Числа шансы енот Распродажа Второй класс песни черепаха Без категории юнификс куб рабочие листы

Нечетные и четные числа | Математика Новой Зеландии

Цель

Целью этого раздела – изучить закономерность, занимающую центральное место в нашей системе счисления: нечетные и четные числа.

Цели достижения

NA2-7: Обобщите, что целые числа можно разделить разными способами.

Разработка AO и другие учебные ресурсы

NA2-8: Поиск правил для следующего члена в последовательном шаблоне.

Разработка АО и другие учебные ресурсы

Конкретные результаты обучения

• Распознавание четных и нечетных чисел.
• Самостоятельно исследуйте, распознавайте закономерности и характеристики четных и нечетных чисел и сообщайте о них.
• Сформулируйте обобщения о сложении и вычитании четных и нечетных чисел.
• Исследовать и распознавать результаты сложения и вычитания комбинаций четных и нечетных чисел.
• Применяйте обобщения о шаблонах нечетных и четных чисел к ситуациям решения задач.

Описание математики

Наша система счисления состоит из четных и нечетных чисел. Это фундаментальная или центральная структура паттерна, которая заслуживает пристального изучения учащимися.

Во многих младших и средних классах учащимся предоставляется возможность распознавать эти два набора чисел и часто считать вслух, используя эти разные наборы чисел, однако изучению их уникального поведения не всегда уделяется приоритетное внимание.

Члены каждого набора чисел ведут себя определенным образом, как и члены обоих наборов, когда они работают вместе в каждой из четырех числовых операций.

Цель этих уроков — помочь учащимся распознавать нечетные и четные числа и их характеристики, обобщать свое поведение при сложении или вычитании, а также уметь последовательно применять эти обобщения в контексте решения задач.

Упражнения, предлагаемые в этой серии уроков, могут стать основой для самостоятельных практических заданий. Также предполагается, что в течение учебного дня все члены класса, как ученики, так и учителя, будут искать и использовать возможности для применения знаний, включенных в эту единицу работы.

Возможности для адаптации и дифференциации

Возможности обучения в этом модуле можно дифференцировать, предоставляя или удаляя поддержку учащихся и изменяя требования к заданиям. Способы дифференциации включают:

• повторение действий по мере необходимости
• расширение примеров до больших чисел
• побуждает учащихся работать в парах или малых группах.

Упражнения в этом разделе можно адаптировать, чтобы сделать их более интересными, добавив в них знакомый контекст. Хотя основное внимание в обучении уделяется свойствам чисел, различные действия могут выполняться с любым оборудованием, интересующим ваших учащихся. Предложите своим ученикам рассказать о других местах в своей жизни, в которых они сталкиваются с нечетными и четными числами.

Требуемые ресурсы

• Пакеты упакованных предметов (например, батончики мюсли, изюм, банки с напитками и т. д.)
• Полоски с цифрами
• Цветные прозрачные пластиковые фишки
• Пластиковые кубики Multilink или unifix
• Сотни досок
• Карандаши и бумага

Упражнение

Сеанс 1 (Изучение четных чисел)

SLO:

• Распознавание четных чисел.
• Самостоятельно исследуйте, распознавайте закономерности и характеристики четных чисел и сообщайте о них.
• Сформулируйте обобщения о сложении и вычитании четных чисел.

Занятие 1

1. Предоставьте учащимся полоски с цифрами и цветные прозрачные фишки. Предложите учащимся работать в парах, используя полоску с числами и счетчики только одного цвета . (Используйте один цвет, чтобы лучше сфокусировать внимание учащихся на разрабатываемой концепции.)
    
2. Поместите перед учащимися набор расфасованных продуктов питания или напитков, которые содержат четное количество отдельных элементов содержимого.
   Предложите учащимся взять и проверить количество предметов в каждом пакете, а затем поместить счетчик на это число на полоске с номером. В результате на их числовой полосе будет несколько четных чисел, каждое из которых закрыто прозрачным счетчиком.
    
3. Запишите эти числа в таблицу занятий или в тетрадь по моделированию, и пусть учащиеся расскажут вам, что они заметили. Выясните у учащихся или скажите им, что это все четных чисел . Предложите учащимся назвать причины, по которым коммерческая упаковка в основном работает таким образом, и запишите их идеи. (например: «Так они аккуратнее», «Лишние не торчат», «Ряды равны», «Они парные» и т. д.) Согласитесь, что это все причины, по которым идентифицированные числа известны как четные числа .
    
4. Попросите учащихся поместить фишки одного цвета на каждое четное число на своей полосе с номерами. Пусть один учащийся прочитает вслух четные числа до двадцати, убирая при этом жетоны. Затем пусть другой учащийся начнет с двадцати и сосчитает в обратном порядке четными числами, заменяя при этом счетчики. При необходимости повторите. Распознайте закономерность, которую они создают: счетчики стоят на каждом -м секундном -м числе.

Деятельность 2

1. Сделайте доступными пластиковые кубики multilink или unifix.
   Предложите учащимся вместе построить модель куба из каждого из четных чисел не менее чем до 10, в зависимости от количества доступных кубиков. Попросите их обсудить (и записать) то, что они заметили.
   
    
2. Запишите все идеи учащихся в классную таблицу или в тетрадь по моделированию. Например: «вы продолжаете прибавлять 2», «это +2 каждый раз», «они идут парами», «они совпадают и имеют партнеров», «их называют даже потому, что ничего не осталось», «это мило». ярмарки» и др.). Признайте, что это закономерность, которая каждый раз увеличивается на +2.
    
3. Пусть каждый учащийся на своем листе бумаги или на доске нарисует четные числа. Для каждого числа попросите их записать количество пар .
   
   Предложите им обсудить в парах то, что они заметили в отношении четного числа, которое они вытянули, и количества пар, и записать свои идеи.
    
4. Предложите учащимся поделиться своими идеями и еще раз запишите их в карточке класса. Выявить важный язык «умножить на два», «двойной» и «половина». Например: «Число пар равно половине четного числа кубов», «Число в 2 раза больше или удваивает количество пар», «Это похоже на таблицу умножения на два», «Когда вы говорите 4 умножить на 2, это все равно, что говорить 4 пары».
    
5. Задайте вопрос: «Как узнать, верно ли это для всех четных чисел?» Примите все ответы и обсудите.
   Сделать доступными сотни досок.
   Предложите учащимся разместить фишки на четных числах больше 20.
   Запишите в классной таблице закономерности, которые они видят, и то, что они замечают в этих числах: «Все они заканчиваются на 0, 2, 4, 6 или 8».
   Дайте учащимся время изучить обобщения, сделанные на шаге 4 выше, «доказать» их, используя не менее трех чисел больше 20. Например: 48 — это 24 пары, 48 — это двойное 24, 24 — это половина 48, 24 x 2 = 48.
    
6. Предложите учащимся описать своему партнеру или классу четное число, которое они выбрали. Поощряйте их демонстрировать свое открытие, используя язык «умножить на два», «удвоить» и «пополам».

Действие 3

1. Обратитесь к пакетам в Упражнении 1, Шаг 1, которые имеют четное количество компонентов. Перечислите другие номера содержимого в таблице классов. Например: одна упаковка содержит: 6 баночек йогурта, 10 блоков льда, 8 банок с напитками, 2 упаковки супа, 12 упаковок изюма и т. д.
   Представьте это исследование:
   Сэм Шопперс говорит: «Независимо от того, какой из этих пакетов я положил в свою тележку для покупок, у меня всегда будет даже общее количество предметов ».
   Работа с партнером. Используйте доступное вам оборудование (кубики и доски сотен) и решите, согласны вы или нет с Сэмом Шоппером, что при сложении четных чисел всегда получается четное общее число.
   Объясните, что они должны быть готовы объяснить свою позицию классу и показать это с материалами, чтобы другие могли понять ваши мысли.
   Дайте учащимся время выполнить это задание, в том числе продемонстрировать свое обоснование с помощью кубиков .
    
2. Завершите это занятие, записав в классной таблице обобщение: При сложении четных чисел сумма всегда будет четным числом .

Занятие 4

Раздайте копию Приложения 1 каждому учащемуся. Попросите их индивидуально решить задачи, а затем обсудите их идеи с партнером.
Обсудите, что они замечают, и запишите в классной таблице их согласованные обобщения для вычитания и нуля.
Когда четное число вычитается из четного числа, всегда получается четное число.
Ноль — четное число. (Оно «вписывается» в структуру четных чисел, и когда к четному числу прибавляется или вычитается ноль, получается четное число.)

Занятие 5

Завершите занятие, попросив учащихся создать свой собственный плакат. , стихотворение или рассказ о четных числах. Подумайте о том, чтобы ученик выбрал несколько четных чисел и присвоил им характеры в письме (антропоморфизм). Например: «Даже Стивен любит…»
Предложите учащимся проверить упаковку продуктов дома или в супермаркете, чтобы убедиться, что все упаковки состоят из четных чисел. Попросите найти и записать названия всех найденных продуктов с нечетным количеством элементов контента.

Занятие 2 (Изучение нечетных чисел)

SLO:

• Распознавание нечетных чисел.
• Самостоятельно исследуйте, распознавайте закономерности и характеристики нечетных чисел и сообщайте о них.
• Сформулируйте обобщения о сложении и вычитании нечетных чисел.

Занятие 1

Начните с того, что учащиеся поделятся своими плакатами, стихами или рассказами о четных числах из Занятия 1, Занятия 5. ученик. Спросите, не находил ли кто-нибудь упаковку, в которой нечетных предметов. Укажите, что многие упаковки (пакеты) продуктов (например, морковь, помидоры) содержат нечетное количество предметов. Обсудите возможные причины. (например, предметы не всегда имеют одинаковый размер, и поэтому их может потребоваться нечетное количество, чтобы составить рекламируемый вес.)
 

Запишите в классную таблицу или книгу по моделированию, учащийся предсказания вещей, которые, по их мнению, они узнают о нечетных числах. Примите все предложения, включая возможные заблуждения, такие как нечетное число + нечетное число = нечетное число.
 

Сделайте доступными номерные полоски и прозрачный пластик, а также жетоны двух цветов .
Пусть они поработают индивидуально или в парах, набирая четные числа , при этом произнося числа вслух. Попросите их «заполнить пробелы» другим цветом, произнося числа вслух при этом. Определите их как нечетные числа .
Пусть они обсудят, что они заметили в том, как они расположены на полосе с номером.
 

Сделайте доступными пластиковые кубы multilink или unifix.
Предложите учащимся составить (или нарисовать) нечетные числа с помощью кубиков, замечая, сколько они каждый раз прибавляют, чтобы получить следующее нечетное число.

 

Предложите учащимся поделиться тем, что они замечают, и записать это в классной таблице. Выявите важные формулировки и ключевые идеи: «Один всегда торчит или остается», «Большинство в парах, а есть один нечетный без партнера», «Они называются нечетными, потому что не все в них». аккуратные пары», «Это уже не просто удвоение или умножение на два», «Это как удвоение чего-то плюс один».
 

Подчеркните, что особенностью четных чисел является то, что это шаблон плюс два (+2). Если это еще не было отмечено, попросите учащихся описать закономерность роста нечетных чисел.
Согласитесь (и обобщите), что набор нечетных чисел увеличивается на четное число, +2. Пусть учащиеся подтвердят это на полосе с цифрами и своими кубиками.

Действие 3

1. Сделать доступными сотни плат.
   Предложите учащимся поставить жетоны на нечетные числа больше 20.
   Запишите в классной таблице модели, которые они видят, и то, что они замечают в этих числах: «все они заканчиваются на 1, 3, 5, 7 или 9». со счетчиками на доске, для нечетных и четных чисел. (Столбцы нечетных чисел чередуются со столбцами четных чисел.)
    
2. Спросите, существуют ли другие типы целых чисел, кроме четных и нечетных. Запишите ответы, включая нечетные и четные отрицательные целые числа, если это обсуждение возникнет.
   
    
3. Предложите учащимся предложить нечетное количество продуктов (например, 11 морковок, 7 помидоров). Напишите в таблице класса. Предложите парам учащихся исследовать сложение и вычитание этих нечетных чисел, записывая при этом свои уравнения. Объясните, что они будут сообщать о своих выводах классу и должны будут объяснить и показать результаты своего исследования, используя оборудование или диаграмму.
    
4. После объяснений учащихся запишите в карточке обобщения:
   Когда одно нечетное число добавляется к другому нечетному числу, сумма получается четным числом.
   При сложении нечетного числа нечетных чисел получается нечетное число.
   При добавлении четного числа нечетных чисел результатом будет четное число.
   Когда из нечетного числа вычитается одно нечетное число, получается четное число.
   Убедитесь, что учащиеся демонстрируют каждое из этих обобщений с помощью материалов. Например. («s» — студенческое обозначение «запасного» куба. )
   

Занятие 4

Завершите занятие, попросив учащихся нарисовать собственную диаграмму сложения и вычитания пар нечетных чисел с соответствующим объяснением.

Занятие 3 (Изучение комбинаций нечетных и четных чисел)

SLO:

• Исследовать и распознавать результаты сложения и вычитания комбинаций нечетных и четных чисел.
• Сформулируйте обобщения о сложении и вычитании комбинаций четных и нечетных чисел.
• Применяйте обобщения о шаблонах нечетных и четных чисел к ситуациям решения задач.

Упражнение 1

В книге/диаграмме моделирования класса нарисуйте пустую диаграмму Венна с заголовками нечетных и четных чисел. Попросите учащихся интерпретировать задание и предложить, что они могут сделать. Подтвердите, что понятно следующее:
Они должны написать то, что они узнали о каждом наборе чисел, в правильном месте. Если что-то верно в отношении обоих множеств, оно принадлежит отрезку, который является пересечением обоих множеств (например, когда вы складываете два из этих чисел, сумма является четным числом).

Предложите учащимся поделиться и обсудить свои диаграммы Венна и обобщения. Достичь четкого соглашения.

Мероприятие 2

1. Предоставьте пластиковые кубики Multilink или Unifix.
   Напишите модель диаграммы записи в учебнике по моделированию. Например:

   Наше исследование нечетных и четных чисел
   Проблема	Пример/исследование	Результат
   четный + четный = ?	2 + 4 = 6	даже
   четный – четный = ?	8 – 4 = 4 продвижение диаграммы/картинки	даже

   
   Попросите пары учащихся составить свою собственную таблицу записи и исследовать сложение и вычитание комбинаций нечетных и четных чисел и записывать свои результаты.
    
2. Попросите пары учащихся поделиться результатами расследования с другой парой учащихся. Пусть они отметят на своей парной диаграмме, если их результат совпадает с результатом другой пары.
    
3. Предложите учащимся обсудить их всем классом и заполнить краткий обзор обобщений, который включает:

   Четный ± четный = четный	Нечетное ± нечетное = четное
   Чет ± нечет = нечет	Нечетное ± четное = нечетное

Задание 3

1. Убедитесь, что учащиеся могут увидеть копию обобщения «поведения» нечетных и четных чисел при применении числовых операций.
   Раздайте копию Приложения 2 каждому учащемуся. Попросите их индивидуально решить задачи, а затем обсудите их идеи с партнером. Подчеркните, что они должны использовать слова «нечетный» и «четный» в каждом из своих объяснений.
    
2. Когда учащиеся закончат, пусть они поиграют в парах, Нечетное и четное терпение .