Буквы по порядку с цифрами: Буква и ее номер в алфавите

Русский алфавит по порядку для детей, таблица транскрипции гласных и согласных

3.9

Средняя оценка: 3.9

Всего получено оценок: 141.

3.9

Средняя оценка: 3.9

Всего получено оценок: 141.

Чтобы записывать звучащую речь, требуются буквы. В русском современном языке 33 буквы, которые составляют русский алфавит. Вся необходимая информация об алфавите представлена в нашей статье.

Краткая история

Кто создал русский алфавит? Вопрос не такой уж очевидный. Ведь за древностию лет в него было внесено очень много изменений, проведено немало реформ.

На Руси алфавит – кириллица – появился в связи с принятием христианства, он и требовался в первую очередь в церкви. Каждая буква имела вое название (например, а – аз, б- буки, в – веди и т.д.) Цифры также обозначались буквами. Писали без пробелов и знаков препинания. Длинные и хорошо знакомые слова писали сокращенно, ставя над ними особый знак – титло. Чтобы обучаемым чтению монахам было легче запомнить алфавит по порядку, им предлагалась к заучиванию специальная молитва («азбучная»), где каждая строка начиналась на букву в алфавитном порядке (первая – на аз, вторая – на буки и т.

д.).

Нет сомнений, что создатели первой славянской азбуки – святые Кирилл и Мефодий. Вот только какая азбука первая? Есть мнение, что Кирилл создал глаголицу, а кириллица, положенная в основу современного алфавита, – творение ученика св. Кирилла, Климента Охридского.

Множество реформ русского алфавита было призвано приблизить его к тому, какие звуки на самом деле все еще используются в речи. Поэтому пропали буквы Ѯ, Ѱ, Ѳ, Ѵ и несколько других.

Первична устная речь, поэтому алфавит призван отражать ее фонетический состав.

Буквы русской азбуки

В основу русского, как и латинского, алфавита лег греческий. Многие буквы очень похожи и теперь. Например, β – в, π – п и т.д. Однако звуковой состав греческого языка отличается от славянского. Поэтому Кирилл и Мефодий несколько увеличили число букв, стремясь к тому, чтобы в азбуке были знаки для всех гласных и согласных. Нам не приходится прибегать к использованию особых значков или писать по 2-3 буквы, чтобы передать один звук.

Изучение алфавита

Буквы в русском, как и в любом другом, алфавите расположены в определенном порядке. Естественно, он случаен. Так надо ли заучивать русский алфавит по порядку? Конечно, нужно! Ведь именно в такой последовательности расположены слова в словаре и фамилии детей в школьном журнале, книги в библиотеке и статьи в энциклопедии – любые элементы любого списка. Конечно, в начале словаря обычно приводится алфавит для тех, кто так и не смог его запомнить, но всегда лучше знать самому, чем надеяться на подсказку.

Выучить алфавит несложно. Алфавит русского языка для детей в виде плаката с красочными картинками можно купить в любом магазине для школьников. Есть немало стихов и песенок для заучивания азбуки по порядку. Для иностранцев, изучающих русский язык, может быть полезна таблица транскрипции русского алфавита, которая предлагает не только начертание букв, но и их произношение.

Что мы узнали?

Из статьи мы узнали, что основой русского алфавита является его греческий аналог. Узнали кем и когда был придуман алфавит. Ответили на вопрос, зачем в повседневной жизни знать порядок расположения букв в алфавите.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

• I–Саша ПАВЛЕНКО

  5/5

• Светлана Дудко

  4/5

• Сергей Ефремов

  3/5

Оценка статьи

3.9

Средняя оценка: 3.9

Всего получено оценок: 141.

---

А какая ваша оценка?

Как оформлять перечни? – «Грамота.ру» – справочно-информационный Интернет-портал «Русский язык»

Техническое оформление текста

Как оформлять перечни?

Обратите внимание: в этой статье все приведенные перечни одновременно выступают в качестве примеров технического оформления.

Какой знак препинания ставится перед перечнем?

Фраза перед перечнем может оканчиваться двоеточием или точкой. Двоеточие ставится, если:

• в этой фразе содержится слово или словосочетание, указывающее на то, что далее последует перечень;

• перечень разъясняет то, о чем говорится в предшествующей ему фразе;

• перечень непосредственно продолжает текст.

Если данные условия не соблюдаются, то перед перечнем ставится точка.

Примечание.

Двоеточие перед перечнем может ставиться и в том случае, если элементы перечня начинаются с прописной буквы.

Как выделить элементы перечня?

Существует множество способов графического выделения элементов перечня. Вот основные:

1. Арабская или римская цифра с точкой.

2. Арабская цифра со скобкой.

3. Прописная буква с точкой.

4. Строчная буква со скобкой.

5. Тире.

6. Наборный знак (точка, квадрат, ромб, звездочка и т. д.).

Различают внутриабзацные перечни (элементы следуют в подбор) и перечни с элементами-абзацами (элементы перечня начинаются с красной строки).

В многоуровневых перечнях принято следующее разграничение:

• прописные буквы и римские цифры обозначают высший уровень членения;

• арабские цифры с точкой – средний уровень;

• арабские цифры со скобкой, буквы со скобкой и наборные знаки используются для обозначения низшего уровня членения.

Когда в перечнях используются прописные, а когда строчные буквы?

С прописной буквы начинается текст каждого элемента в перечне, если ему предшествует цифра с точкой или прописная буква с точкой.

1.  Язык. 2. Речь.

А. Язык. Б. Речь.

Со строчной буквы начинается текст каждого элемента в перечне, если ему предшествует

цифра со скобкой:

1) новое и старое;

2) старое и новое.

Аналогичным образом оформляются перечни, элементы которых начинаются строчной буквой со скобкой:

а) новое и старое;

б) старое и новое.

Какие знаки препинания ставятся после элементов перечня?

После абзацев – элементов перечня ставится:

а) запятая, если абзацы-элементы очень просты – из нескольких слов, без знаков препинания внутри, обозначены цифрой с закрывающей скобкой, строчной буквой с закрывающей скобкой, наборным знаком (например, тире) и начинаются со строчной буквы; но не будет ошибкой и постановка в подобных случаях после абзацев точки с запятой;

б) точка с запятой

, если элементы не совсем просты, со знаками препинания внутри, обозначены цифрой с закрывающей скобкой, строчной буквой с закрывающей скобкой, наборным знаком и начинаются со строчной буквы, т. е. строчной букве в начале элемента соответствует точка с запятой в конце его. Пример – настоящий перечень;

в) точка, если элементы обозначены цифрой с точкой или прописной буквой с точкой. Точке после обозначения элемента соответствует точка в конце элемента.

Что читать об оформлении перечней и рубрикации?

1. Правила русской орфографии и пунктуации. Полный академический справочник / Под ред. В. В. Лопатина. М., 2013. С. 282–286.

2. А. Э. Мильчин, Л. К. Чельцова. Справочник издателя и автора. 2-е изд., М., 2003. С. 38–44.

Как заполнить буквы алфавита в Excel тремя способами

от Ilker | 11 февраля 2021 г. | Советы и рекомендации по Excel

Вы можете легко вводить числа, названия месяцев или дней недели, перетаскивая мышь. Однако вы не можете заполнять буквы таким же образом. В этом руководстве мы покажем вам, как заполнить буквы алфавита в Excel, используя три разных метода.

Введение

Давайте сначала посмотрим, как наборы символов работают в Excel. Есть две встроенные функции, которые связаны с преобразованием чисел в символы:

• СИМВОЛ Функция
• КОД Функция

Мы можем использовать эти функции для преобразования чисел и букв друг в друга для заполнения букв в Excel.

Более простой метод

Прописные и строчные буквы в наборе символов ASCII находятся между числами 65–90 и 97–122 соответственно. 65 = A, 66 = B, 90 = Z, 106 = j и т. д. Используя формулы преобразования символов, такие как CHAR , мы можем преобразовать эти числа в соответствующие буквы.

Синтаксис

char (<число>)

Пример

= Чар (121) Возврат «Y»

. Задача для этого подхода генерирует номеров для Char функции. Как объяснялось в предыдущем разделе, вам нужны числа от 65 до 90 или от 97 до 122 для букв. Для этого на этом шаге можно использовать функцию SEQUENCE . Функция SEQUENCE может генерировать массив из последовательных номеров автоматически.

Все, что вам нужно сделать, это указать, сколько цифр вам нужно и с какой цифры начать.

Синтаксис

ПОСЛЕДОВАТЕЛЬНОСТЬ(строки,[столбцы],[начало],[шаг])

Пример

=ПОСЛЕДОВАТЕЛЬНОСТЬ(26,1,65) возвращает массив чисел от 690 до 40 90

Приведенная выше функция возвращает числа в 26 строк и в один столбец . Если вы хотите сгенерировать числа или буквы, как в нашем примере, вы можете использовать формулу вроде 9.0039 =ПОСЛЕДОВАТЕЛЬНОСТЬ(1,26,65) .

Давайте объединим обе функции, чтобы создать формулу для заполнения букв алфавита.

Синтаксис

=CHAR(SEQUENCE(26,1,<число, с которого начинаются буквы>))

Пример

Прописные буквы: =CHAR(SEQUENCE(26,1,65)) Строчные буквы: = CHAR(SEQUENCE(26,1,97))

Использование функции

CODE для заполнения букв алфавита

Excel имеет 9Функция 0012 CODE работает противоположно CHAR . Функция CODE просто возвращает соответствующий номер данного символа в наборе символов.

Синтаксис

КОД(текст)

Пример

КОД(“c”) возвращает 99

В результате сама функция может быть заменена символом1 КОД3. Ниже приведен пример использования этой формулы.

Синтаксис

=CHAR(SEQUENCE(CODE(<последний символ>)-CODE(<первый символ> )+1,1,CODE(<первый символ>)))

Пример

=CHAR (SEQUENCE(CODE(“Z”)-CODE(“A”)+1,1,CODE(“A”)))

Интервал динамического символа

Используя функцию CODE , мы можем улучшить модель следуя более динамичному подходу. Мы можем заменить жестко закодированные буквы, такие как «A» или «Z», на ссылки на ячейки, содержащие эти символы. Этот подход позволяет нам изменять начальные и конечные символы букв алфавита без обновления формулы.

Синтаксис

=СИМВОЛ(ПОСЛЕДОВАТЕЛЬНОСТЬ(КОД(<ячейка содержит последний символ>)-КОД(<ячейка содержит первый символ> )+1,1,КОД(<ячейка содержит первый символ> )))

Пример

=CHAR(SEQUENCE(CODE(I7)-CODE(I6)+1,1,CODE(I6)))

Использование функции LET для заполнения букв алфавита

Это необязательный шаг для заполнения букв алфавита в Excel. Относительно новый LET 9Функция 0013 позволяет создавать именованные диапазоны внутри контекста собственной формулы.

Синтаксис функции LET содержит фактическую формулу, в которой используются определенные пар “имя-значение” .

Синтаксис функции LET

LET(имя1, имя_значение1, [имя2], [имя_значение2], …, вычисление)

Синтаксис нашей модели с функцией LET

=LET(Start,CODE( <ячейка содержит первый символ>),Finish,CODE(<ячейка содержит последний символ>),CHAR(SEQUENCE(Start-Finish+1,1,Finish)))

Пример

=LET(Start,CODE(M7),Finish,CODE(M6),CHAR(SEQUENCE(Start-Finish+1,1,Finish)))

Мы определили именованные диапазоны для Start и Finish как CODE(M7) и CODE(M6) соответственно. Каждое имя заменяется соответствующим функциональным блоком CODE .

5.3: Перестановки – Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

40145

• Рупиндер Секон и Роберта Блум
• Колледж Де Анза

Цели обучения

В этом разделе вы научитесь:

• Выполнять вычисления с использованием факториалов.
• Подсчитайте количество возможных перестановок (упорядоченное расположение) n элементов, взятых по r за раз.
• Подсчитайте количество возможных перестановок при наличии условий, наложенных на расположение.

Предварительные навыки

Прежде чем начать, пройдите этот предварительный тест.

1. Сколько последовательностей слов из трех букв можно составить из букв { A, B, C }, если ни одна буква не повторяется?

Нажмите здесь, чтобы проверить свой ответ

Можно составить

\(6\) последовательностей.

Если вы пропустили эту проблему, просмотрите Раздел 5.2 . (Обратите внимание, что это откроется в новом окне.)

 

2. Номерной знак штата Калифорния состоит из цифры от 1 до 5, затем трех букв и любых трех цифр. Возможен повтор. Сколько таких пластин возможно?

Нажмите здесь, чтобы проверить свой ответ

\(87,880,000\) возможны разные номера.

Если вы пропустили эту проблему, просмотрите Раздел 5.2 . (Обратите внимание, что это откроется в новом окне.)

 

 

3. Сколько различных 4-буквенных позывных радиостанций можно составить, если первая буква должна быть K или W и ни одна буква не может повторяться?

Нажмите здесь, чтобы проверить свой ответ

Можно сделать

\(27 600\) имен станций.

Если вы пропустили эту проблему, просмотрите Раздел 5.2 . (Обратите внимание, что это откроется в новом окне.)

Факториалы

При работе с аксиомой умножения нам часто потребуется умножать последовательные убывающие числа, как мы это делали в примере 5.2.5. У нас есть специальное обозначение для этого вычисления, которое мы будем широко использовать как в этой, так и в следующей главе.

Определение: Факториал

\(n!\) читается как “n факториал”.

\[\mathrm{n} !=\mathrm{n}(\mathrm{n}-1)(\mathrm{n}-2)(\mathrm{n}-3) \cdots 3 \cdot 2 \ cdot 1\]

где \(n\) — натуральное число.

\(0! = 1\)

Пример \(\PageIndex{1}\)

Вычислить 5!

Решение

Используя определение факториала, \(5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1\). Умножение этих чисел дает значение \(120\).

Перестановки

В примере 5.2.6 нас попросили найти последовательности слов, образованные с использованием букв {A, B, C}, если ни одна буква не должна повторяться. Древовидная диаграмма дала нам следующие шесть расположений.

ABC, ACB, BAC, BCA, CAB и CBA.

Подобные расположения, в которых важен порядок и ни один элемент не повторяется, называются перестановками.

Определение: Перестановки

Перестановка набора элементов представляет собой упорядоченное расположение, в котором каждый элемент используется один раз.

Пример \(\PageIndex{2}\)

Сколько последовательностей слов из трех букв можно составить из букв { A, B, C, D }?

Решение

Есть четыре варианта первой буквы слова, три варианта второй буквы и два варианта третьей.

Применяя аксиому умножения, мы получаем \(4 \cdot 3 \cdot 2 = 24\) различных расположений.

Пример \(\PageIndex{3}\)

Сколько перестановок букв слова СТАТЬЯ имеет согласные на первой и последней позициях?

Раствор

В слове СТАТЬЯ 4 согласных.

Так как первая буква должна быть согласной, у нас есть четыре варианта для первой позиции, и как только мы используем согласную, остается только три согласных для последней позиции. Мы показываем следующим образом:

Поскольку ограничений больше нет, мы можем продолжить и сделать выбор для остальных позиций.

Пока мы израсходовали 2 буквы, поэтому осталось пять. Таким образом, для следующей позиции есть пять вариантов, для позиции после нее — четыре варианта и так далее. мы получаем

4

5

4

3

2

1

3

Таким образом, общее количество перестановок равно \(4 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 \cdot 3 = 1440\).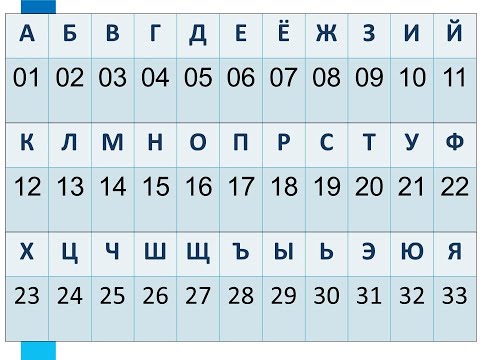

Пример \(\PageIndex{4a}\)

Даны пять букв { A, B, C, D, E }. Найдите следующее:

1. Количество последовательностей слов из четырех букв.
2. Количество последовательностей слов из трех букв.
3. Количество последовательностей двухбуквенных слов.

Решение

Задача легко решается с помощью аксиомы умножения, и ответы следующие:

1. Количество последовательностей слов из четырех букв равно \(5 \cdot 4 \cdot 3 \cdot 2 = 120\).
2. Количество последовательностей слов из трех букв равно \(5 \cdot 4 \cdot 3 = 60\).
3. Количество двухбуквенных последовательностей слов равно \(5 \cdot 4 = 20\).

Мы часто сталкиваемся с ситуациями, когда у нас есть набор из n объектов, и мы выбираем r объектов для формирования перестановок. Мы обозначаем это как перестановки n объектов, взятых r за раз , и мы обычно записываем это как нПр . n_r\) представляют перестановки.

Пример \(\PageIndex{4b}\)

Даны пять букв { A, B, C, D, E }. Используйте формулу перестановки, чтобы найти следующее:

1. Количество последовательностей слов из четырех букв.
2. Количество последовательностей слов из трех букв.
3. Количество последовательностей двухбуквенных слов.

Решение

Поскольку мы выбираем из 5 разных букв в наборе, \(n=5\). Значение для \(r\) — это количество букв, которые мы используем в каждой последовательности.

1. Количество последовательностей слов из четырех букв равно 5P4 = \( \dfrac{5!}{(5-4)!} = \dfrac{5 \cdot 4 \cdot  3 \cdot  2 \cdot  1}{1 } = 5 \cdot 4 \cdot 3 \cdot 2 = 120\)
2. Число последовательностей трехбуквенных слов равно 5P3 = \( \dfrac{5!}{(5-3)!} = \dfrac{5 \cdot 4 \cdot  3 \cdot  2 \cdot  1}{2 \cdot 1} = 5 \cdot 4 \cdot  3 = 60\)
3. Количество двухбуквенных последовательностей слов равно 5P2 = \( \dfrac{5!}{(5-2)!} = \dfrac{5 \cdot 4 \cdot  3 \cdot  2 \cdot  1}{3 \cdot 2 \cdot 1} = 5 \cdot 4 = 20\)

Пример \(\PageIndex{5}\)

Автосервис имеет 6 сотрудников и 3 рабочих места. Сколькими способами можно разместить сотрудников на трех участках, если на каждом участке будет только один сотрудник?

Решение

Мы будем определять \(n\) и \(r\) в каждом случае и решать, используя предоставленные формулы.

Поскольку у нас есть выбор из 6 сотрудников, \(n=6\). Поскольку мы размещаем только 3 из них за раз, \(r=3\). Поэтому мы пытаемся вычислить 6P3.

\( 6 \mathrm{P} 3=\frac{6 !}{(6-3) !}=\frac{6 !}{3 !}=\frac{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{3 \cdot 2 \cdot 1} = 6 \cdot 5 \cdot 4 = 120 \)

Далее мы рассмотрим еще несколько задач перестановки, чтобы лучше понять эти концепции.

Пример \(\PageIndex{6}\)

Сколькими способами можно рассадить 4 человек по прямой линии, если двое из них настаивают на том, чтобы сидеть рядом друг с другом?

Решение

Предположим, у нас есть четыре человека A, B, C и D. Далее предположим, что A и B хотят сесть вместе. Ради аргумента мы связываем А и Б вместе и относимся к ним как к одному человеку.

Четыре человека – это \(\boxed{AB}\) CD. Поскольку \(\boxed{AB}\) рассматривается как одно лицо, у нас есть следующие возможные варианты.

\[ \boxed{AB} CD, \boxed{AB} DC, C \boxed{AB}D, D\boxed{AB}C, CD \boxed{AB}, DC\boxed{AB} \nonumber\ ]

Обратите внимание, что существует еще шесть таких перестановок, потому что A и B также могут быть связаны в порядке BA. А их

\[ \boxed{BA}CD, \boxed{BA} DC, C\boxed{BA}D, D\boxed{BA}C, CD\boxed{BA}, DC \boxed{BA} \nonumber\ ]

Всего имеется 12 различных перестановок.

Давайте теперь решим задачу, используя аксиому умножения.

После того, как мы свяжем двух людей вместе и будем относиться к ним как к одному человеку, мы можем сказать, что у нас есть только три человека. Аксиома умножения говорит нам, что три человека могут сидеть на 3! способы. Так как два человека могут быть связаны вместе 2! способов, есть 3! 2! = 12 различных аранжировок

Пример \(\PageIndex{7}\)

У вас есть 4 учебника по математике и 5 учебников по истории, которые нужно поставить на полку с 5 слотами. Сколькими способами можно расставить книги по полкам, если первые три ячейки заняты учебниками по математике, а следующие две — учебниками по истории?

Решение

Сначала решим задачу, используя аксиому умножения.

Так как учебники по математике помещаются в первые три слота, есть 4 варианта для первого слота,
3 варианта для второго и 2 варианта для третьего.

Для четвертого слота требуется книга по истории и есть пять вариантов. Как только этот выбор сделан, остается 4 книги по истории и, следовательно, 4 варианта для последнего слота. Варианты показаны ниже.

4

3

2

5

4

Следовательно, число перестановок равно \(4 \cdot 3 \cdot 2 \cdot 5 \cdot 4 = 480\).

С другой стороны, мы можем видеть, что \(4 \cdot 3 \cdot 2\) действительно совпадает с 4P3, а \(5 \cdot 4\) – это 5P2.

Таким образом, ответ можно записать как (4P3) (5P2) = 480.

Очевидно, это имеет смысл. Для каждой перестановки трех книг по математике, помещенных в первые три слота, есть 5P2 перестановок книг по истории, которые можно поместить в два последних слота. Следовательно, применима аксиома умножения, и у нас есть ответ (4P3) (5P2).

Подытожим понятия этого раздела:

Примечание

1. Факториал

\[\mathrm{n} !=\mathrm{n}(\mathrm{n}-1)(\mathrm{n }-2)(\mathrm{n}-3) \cdots 3 \cdot 2 \cdot 1 \nonumber\]

Где \(n\) — натуральное число.

\[0! = 1 \nonumber\]

2. Перестановки

Перестановка набора элементов представляет собой упорядоченное расположение, в котором каждый элемент используется один раз.

3. Перестановки n объектов, взятых r одновременно

\[\mathrm{nPr}=\mathrm{n}(\mathrm{n}-1)(\mathrm{n}-2)(\mathrm{n}-3) \cdots(\mathrm{n }-\mathrm{r}+1) \nonumber\]

или

\[\mathrm{nPr}=\frac{\mathrm{n} !}{(\mathrm{n}-\mathrm{r} ) !} \nonumber\]

где \(n\) и \(r\) — натуральные числа.

---

Эта страница под названием 5.3: Permutations распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Рупиндер Сехон и Роберта Блум

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Метки

   1. факториал
   2. перестановка
   3. источник@https://www.