1 класс четные и нечетные числа: Четные и нечетные числа — как объяснить ребенку четные и нечетные числа?
конспект урока математики по теме “Чётные и нечётные числа” | План-конспект урока по математике (1 класс):
Муниципальное образование город Новороссийск Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 21 им. А.С. Пушкина города Новороссийска
Конкурс «Мой лучший урок»
Конспект урока математики
в 1 классе
по теме:
«Чётные и нечётные числа»
Учитель начальных классов
МБОУ СОШ № 21
Пролеева М. М.
Г. Новороссийск
Пояснительная записка
Данная работа представлена по первому направлению конкурса – начальная школа. Урок математики по теме «Чётные и нечётные числа» был разработан и проведён автором работы в 1 «Г» классе МБОУ СОШ № 21 города Новороссийска.
В классе 36 человек. Социальный уровень учащихся различный: учащиеся из благополучных семей, малообеспеченных семей, многодетных семей. Обучающиеся имеют различный уровень развития психических процессов: восприятия, мышления, произвольного внимания. Степень развития кругозора и общий жизненный опыт так же находится на разных стадиях формирования.
Следует заметить, что данный урок проводился в октябре (1 четверть). Данный период является адаптационным периодом обучения. Для обучающихся класса он проходит по-разному. У некоторых ребят к данному моменту ещё не сформирована (слабо сформирована) мотивация к обучению. Однако некоторые учащиеся уже на данном этапе обучения имеют положительную мотивацию к учению и высокий уровень развития произвольного внимания.
Урок строился на основе системно-деятельностного метода. Получение новых знаний проходило с помощью опоры на жизненный опыт детей, путём включения каждого в активную практическую разнообразную деятельность. На данном этапе у обучающихся преобладает конкретное мышление, поэтому опора на опыт, знакомые детям ситуации, а так же практическая деятельность (игра), представленная в различных видах, является наиболее эффективной формой работы для формирования математических понятий, а так же включения абсолютного большинства учащихся в процесс учения.
Данный урок проводился в рамках муниципального конкурса открытых уроков с применением системно-деятельностного подхода. Автор является победителем данного муниципального конкурса. (Приложение 7.)
Сценарий урока разработан в рамках работы по программе общеобразовательных учреждений «Начальная школа. 1-4 классы. Математика. УМК «Планета знаний» М. И. Башмаков, М.Г. Нефедовой – М.:Астрель,2012 год, 4 часа в неделю. Учебник: Математика, в 2-х частях,1 класс. М.И. Башмаков, М.Г. Нефедова – М., АСТ: Астрель,2012-2017 год.
ТЕМА:ЧЁТНЫЕ И НЕЧЁТНЫЕ ЧИСЛА
Тип урока: открытие нового знания | ||
Педагогические задачи: дать представление о чередовании на числовом луче четных и нечетных чисел; создать условия для знакомства с понятиями «четные» и «нечетные» числа; способствовать формированию умений называть четные и нечетные числа, выполнять сложение и вычитание. | ||
Планируемые результаты | ||
Предметные: познакомятся с понятиями «четные» и «нечетные» числа; научатся: называть четные и нечетные числа, выполнять сложение и вычитание чётных и нечётных однозначных чисел, опираясь на знания состава чисел первого десятка. | Метапредметные: Познавательные:общеучебные – располагать числа на числовом луче; постановка и решение проблем – формулировать проблему; логические – сравнивать числовые выражения. Регулятивные: вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок. Выполнять задания согласно условию. Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов. | Личностные: адекватно судить о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием. Понимать и удерживать цель деятельности. |
Образовательные ресурсы: учебник (с. 92‒93), мультимедийный проектор, электронный учебник, наборы фигур и лист с числовым рядом для организации работы в паре, инструменты для организации творческой деятельности. | ||
Организационная структура урока
Этап урока | Содержание деятельности учителя | Содержание деятельности обучающегося | Формируемые способы |
I. Актуализация опорных знаний. Устный счет. Интеллектуальная разминка | – Ответьте на вопросы: На тарелке три банана, Рядом с ними груша Сколько фруктов, сосчитай, Съест сейчас Андрюша? Запись на доске 3+1=4 (фр.) Мама яблоки купила, На тарелку положила. Их нетрудно сосчитать: Красных два и желтых пять. – Сколько яблок купила мама? Запись на доске 2+5=7 (яб.) – Ребята, Андрюша решил разделить свои фрукты с мамой поровну, чтобы никому не было обидно. -Перед вами на доске геометрические фигуры. Можно ли их разделить на группы по общему признаку? На доске фигуры Перед вами на доске натуральные числа. Можно ли их разделить на группы по общему признаку? На доске записаны числа 1 2 3 4 5 6 7 8 Ребята, эти числа можно разделить на группу чётных и группу нечётных чисел. Только вот какие числа, в какую группу отнести? | Фронатальная работа обучающихся ‒ Всего 4 фрукта: 3 + 1 = 4 . ‒ Мама купила 7 яблок: 2 + 5 = 7. 4 фрукта можно разделить между Андрюшей и его мамой поровну. Каждому по два. 7 яблок нельзя разделить поровну. Одно будет лишним. Фигуры можно разделить на четырёхугольники и треугольники | Выделять существенную информацию из текста задачи. Устанавливать закономерности и использовать их при выполнении заданий Сравнивать и классифицировать изображенные предметы и геометрические фигуры по заданным критериям. |
Затрудняются в определении общего признака и делении на группы Затрудняются в делении на группы чётных и нечётных чисел. | |||
II. Определение темы урока. Определение целей урока | –Сегодня на уроке нам предстоит это выяснить. – Попробуйте сформулировать тему нашего урока? ‒ Определите цели урока, используя опорные слова На доске опорные слова Узнаем… Научимся… | Тема урока – «Чётные и нечётные числа» ‒ Сегодня на уроке мы… Узнаем…(что такое чётные и нечётные числа) Научимся…(определять четность-нечётность, находить четные и нечётные числа) | Принимать и сохранять учебную цель и задачу |
III. Открытие нового знания, способа действия. Практическая работа | Работа с учебником и с электронным учебником посредством мультимедийной доски. Задание 1 (с. 92).(Приложение 2.) – Три супружеские четы отправились в кино. Сколько людей идет в кино? – Что такое супружеская чета? Это супружеская пара (мама и папа, муж и жена, бабушка и дедушка) – Сколько человек в паре? Давайте проследим цепочку понятий: пара- чета – чётные числа. Попробуйте продолжить утверждение: чётные числа те, которые можно… – Сколько пар составили 6 человек? – Число 6 – четноё или не чётное? Почему? – Когда мы с вами строимся в столовую, как вы становитесь? – Встать парами – это по сколько человек? Практическое задание: построиться парами (по рядам) – Если мы построились парами, и всем хватило пары, что можно сказать о числе человек в классе? – А если мы построились парами, и не всем хватило пары, каково число человек в классе? | – Шесть людей идут в кино. Затрудняются в определении понятия – Пара – это два человека – Чётные числа можно разделить на пары – Это три пары – Число 6- чётное, потому что его можно разделить на пары. – Мы встаём парами. – Пара – это два человека. Дети строятся парами – Если всем хватило пары, значит в классе чётное число детей. – Если кто-то остался без пары, значит в классе нечётное число детей | Планировать решение учебной задачи. Удерживать цель деятельности. Проявлять активность во взаимодействии. Делать логические выводы, проводить логические суждения. Исследовать свойства четных и нечетных чисел на геометрических моделях. Уметь договариваться при работе в паре и группе. Различать чётные и нечётные числа в числовом ряду на основе изученных свойств. Делить числа на пары, составлять из пар группы. Опираться на признаки чётности-нечётности при обоснованиях выбора.
Применять полученные знания о свойствах чётных и нечётных чисел в практической деятельности, в нестандартных условиях. Уметь ориентироваться в учебнике и тетради. Проводить самоконтроль после выполнения заданий. |
IV. Работа в паре | На партах у вас находятся набор фигур из бумаги и лист с отрезком натурального ряда чисел. – Сколько предметов перед вами на парте? – Работая в паре с соседом, составьте пары из предметов. Посчитайте, сколько фигур составляют то или иное количество пар. Подчеркните соответствующие числа в ваших листах. Аналогичная запись производится на доске учителем. – Как называются числа, которые вы подчеркнули? – Как называются числа, оставшиеся неподчёркнутыми? Что это за числа? – Сколько пар можно выделить в каждом нечётном числе? | – Всего 10 фигур Составляют пары кружков. Считают количество предметов в парах. 1 пара- 2 фигуры 2 пары-4 фигур 3 пары-6 фигур 4 пары-8 фигур 5 пар-10 фигур Дети подчёркивают числа 1 2 3 4 5 6 7 8 9 10 – Мы подчеркнули чётные числа. – Остались нечётные числа. Они не делятся на пары. Числа 1, 3, 5, 7, 9 – нечётные. Число 3- 1 пару и 1 останется лишним число5 – 2 пары 1 останется лишним число7- 3 пары и 1 останется лишним число9 – 4 пары и 1 останется лишним | |
ФИЗМИНУТКА Динамическая минутка-комплекс физических упражнений для снятия мышечной усталости | |||
Работа с учебником Закрепление нового понятия, запоминание терминов | Работа с учебником (Приложение 3.) – Как расположены четные и нечетные числа в ряду чисел? ‒ Назовите четные числа по порядку. Назовите их в обратном порядке. ‒ Назовите нечетные числа по порядку. Назовите их в обратном порядке | – Четные и нечетные числа в ряду чисел расположены через одно число. Называют четные и нечетные числа в прямом и обратном порядке | |
Самостоятельная работа | Самостоятельная работа. – Выполните сложение – Сколько пар можно выделить в числе 4? – В числе 6? – В числе 8? В числе 10? | Выполняют сложение. Запись: 2 + 2 = 4 2 + 2 + 2 + 2 = 8 2 + 2 + 2 = 6 2 + 2 + 2 + 2 + 2 = 10 Число 4- 2 пары число 6- 3 пары число 8- 4 пары число 10 – 5 пар | |
VСистематизация знаний на основе практического применения | Работа с учебником и с электронным учебником посредством мультимедийной доски. Задание 4 (с. 93) (Приложение 4.) – На доске перед вами фигуры, состоящие из клеток. Какие из этих фигур можно разделить на две части с одинаковым количеством клеток? – Что вы заметили? Сколько клеток в каждой из таких фигур? – Сделайте вывод: четное число можно разделить на пары и… …представить в виде суммы одинаковых слагаемых | Выходят к доске, указывают фигуру, поясняя, на какие части её можно разделить 1 + 1 = 2 4 + 4 = 8 2 + 2 = 4 5 + 5 = 10 3 + 3 = 6 – В этих фигурах чётное число клеток. – Четное число можно разделить пополам (на две одинаковые части). | Читать схемы, иллюстрирующие количество предметов. Соотносить количество изображенных предметов со схемой, схему – с числовым равенством, числовое равенство – с рисунком. Уметь договариваться при работе в малых группах. Проводить логические операции, делать логические выводы. Использовать полученные знания для решения нестандартных и творческих задач. Формировать творческое мышление. |
Решение задач | Работа по учебнику Задание 7 (с. 93) (Приложение 5.) – Сколько пар можно составить из 4 левых и 5 правых ботинок? Задание 8 (с. 93) – Сколько раз нужно переплыть речку, чтобы оказаться на том же берегу, где и одежда? | – Из них можно составить 4 пары ботинок. Один правый останется лишним. – Чётное число раз нужно переплыть речку, чтобы оказаться на том же берегу, где и одежда. | |
Работа в группе Творческая деятельность | -У вас на парте остались фигуры, из которых вы составляли пары. Объединитесь группами так, чтобы в каждой группе были два набора разных фигур: квадраты и круги, квадраты и треугольники, треугольники и круги. Составьте на лисе-основе узор из фигур так, чтобы фигур одного вида было чётное число, а фигур другого вида-нечётное число. На следующем уроке технологии мы завершим и оформим ваши узоры. – Сколько фигур каждого вида вы использовали для узора? – Каких фигур в вашем узоре чётное количество, а каких фигур – нечётное количество? | Обучающиеся делятся на группы. Составляют узор из геометрических фигур. (Приложение 6.) Члены групп сообщают количества фигур каждого вида и характеризуют числа о чётности-нечётности. 1 группа: у нас 5 кругов – нечётное число и 4 квадрата – чётное число. | |
VI. Итог урока. Рефлексия | – Что нового узнали на уроке? – Какие числа называют четными? Какие – нечетными? – Какими знаниями, полученными на уроке, вы хотели бы поделиться дома? – У кого возникли трудности На доске опорные слова На уроке я узнал… Я научился… Мне было сложно… Мне понравилось… | Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию. На уроке я узнал… Я научился… Мне было сложно… | Выражать доброжелательность и эмоционально-нравственную отзывчивость. Формировать адекватную оценку своих действий, своей работы. |
Приложение 1.
Урок строился на основе системно-деятельностного метода обучения. Получение новых знаний проходило с помощью опоры на жизненный опыт детей, путём включения каждого обучающегося в активную практическую деятельность разных видов.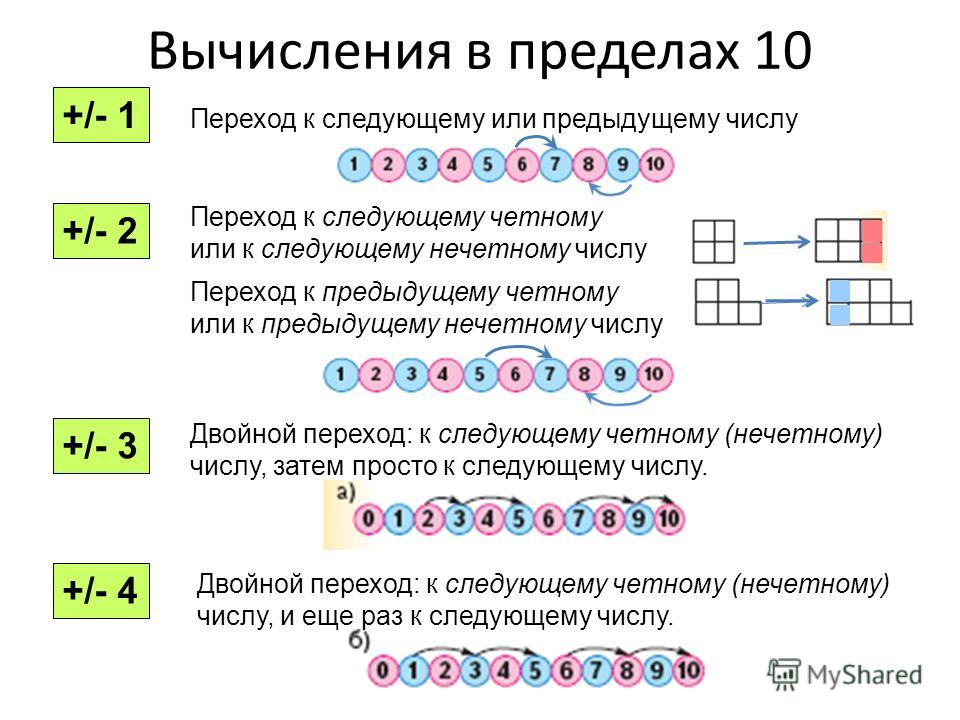 На данном этапе у обучающихся преобладает конкретное мышление, поэтому опора на опыт, знакомые детям ситуации, а так же конкретная практическая деятельность является наиболее эффективной формой работы. Системно-деятельностный подход, связь с жизнью и активное практическое применение полученных знаний способствуют повышению мотивации к учению.
На данном этапе у обучающихся преобладает конкретное мышление, поэтому опора на опыт, знакомые детям ситуации, а так же конкретная практическая деятельность является наиболее эффективной формой работы. Системно-деятельностный подход, связь с жизнью и активное практическое применение полученных знаний способствуют повышению мотивации к учению.
В ходе урока использовались различные виды организации деятельности учащихся: работа в парах, групповая работа, практическая деятельность, самостоятельная работа, творческая деятельность. Разнообразие видов организации деятельности связано с различными индивидуальными особенностями учащихся и дают возможность каждому поучаствовать и проявить себя в той форме, в которой ему наиболее комфортно работать. Это особенно важно, т.к. данный урок проходил в адаптационный период обучения в 1-м классе (1 четверть).Использование разнообразных виды практической деятельности направлено на обеспечение 100% активного участия детей в процессе учения. В каждом новом виде работы происходит включение вновь изученного материала в практическую работу. Это способствует лучшему пониманию теоретических аспектов изучаемого материала, запоминанию и правильному использованию математических терминов.
Это способствует лучшему пониманию теоретических аспектов изучаемого материала, запоминанию и правильному использованию математических терминов.
Реализация принципов наглядности и доступности осуществлялась путём использования мультимедийной доски (проектора) и ресурсов интерактивного образовательного ресурса – электронного учебника, которые значительно облегчают восприятие материала учащимися, а так же ориентирование на страницах учебника.
В рамках здоровьесберегающего направления работы проводилась физминутка в виде комплекса физических упражнений для снятия усталости и изменения статического положения тела. В рамках введения элементов самоуправления в классе, комплексы физических упражнений во время физминуток показывают сами обучающиеся. Такая форма проведения физминуток направлена на сплочение детского коллектива, а так же способствует повышению мотивации школьников.
Приложение 2.
Приложение 3.
Приложение 4.
Приложение 5.
Приложение 6.
Возможные варианты узоров
Урок математики во 2-м классе “Четные и нечетные числа”
Цели:
- Познакомить с понятием «чётные», «нечётные» числа.
- Отрабатывать знание таблиц «Умножения 2-х и Деление на 2».
Оборудование:
- Индивидуальные доски.
- Цифры от 1 до 10.
- «Чётные», «нечётные», «числа».
- Задание для работы в парах:
- (78-38)+(94-82)=
- 34+(99-66)-50=
Этапы урока:
- Банк знаний;
- Открытие темы;
- Знатоки;
- Всезнайки;
- Итог урока.
II. Активизация опорных знаний:Прозвенел звонок весёлый,
вы урок начать готовы?
Будем думать, вычислять
и заданья выполнять.
–
1 задание. Арифметический диктант.
*Дети показывают результат на индивидуальных досках, цифры выставляются на доске.
- Чему равна разность чисел, записанных в треугольниках?
- Найди частное чисел, записанных в квадратах.
- На сколько единиц число 43 больше, чем 40?
- Вычтите числа, записанные в квадратах.
- Чему равна разность чисел, записанных в прямоугольниках?
- Найди произведение чисел, записанных в треугольниках.
- Чему равно произведение чисел, записанных в кругах?
- Найди сумму чисел, записанных в кругах.
- Вычти из самого большого двузначного числа 9 десятков.

- 1-е слагаемое – 0, 2-е слагаемое – 10.Чему равна сумма?
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Открыватели.
– Посмотрите на числовой ряд, который у вас получился. На какие 2 группы можете разбить все эти числа?
– Кто знает, как называются числа, которые делятся на 2? А числа, которые не делятся на 2?
– Какая тема урока?
– А знакомились ли мы с этой темой ранее?
– Сформулируйте цель урока.
– Прослушайте математическую сказку.
Математическая сказка
Однажды в королевстве Математика произошла удивительная история. Числа, которые жили в этом королевстве, были очень дружные. Они часто ходили в гости друг к другу, собирались вместе и придумывали различные игры. Один раз они решили поиграть в такую игру: каждое число должно было разделиться на 2.Но в итоге все числа переругались и даже стали жить на разных сторонах улиц.
– Как вы думаете, что же произошло? (Не все числа делятся на 2)
– Верно, с тех пор, те числа, которые смогли разделиться на 2, стали жить на одной стороне улицы, а те, что не смогли разделиться на 2, стали жить на другой стороне.
– Давайте вместе попробуем расселить наши числа.
(На доске дома, дети разносят карточки с числами по улицам.)
- 2, 4, 6, 8, 10
- 1, 3, 5, 7, 9
- – Улица, на которой живут числа 2, 4, 6, 8, 10, которые смогли разделиться на 2, стала называться – ЧЁТНАЯ, а числа – чётными.
- – Улица, на которой живут числа 1, 3, 5, 7, 9, которые не смогли разделиться на 2, стала называться – НЕЧЁТНАЯ, а числа – нечётными.
– Сегодня на уроке мы познакомимся поближе с чётными и нечётными числами, а также повторим уже изученный материал.
– И в наше время для удобства нумерацию домов располагают в определённом порядке: чётные числа – на одной стороне улицы, а нечётные –на другой.
*Работа в парах по У.с.66 Правило(1)
– Как вы оцениваете своё понимание этой темы?
Физминутка «Чётные, нечётные».
III. Закрепление.2 задание.
– А можем ли мы продолжить этот числовой ряд?
(да, т.к. натуральный ряд чисел бесконечен)
– Запишите по порядку числа от 1 до 20 в строчку, через запятую.
– Подчеркните 1-ой линией – нечетные, 2-мя – чётные числа.
– Какой вывод вы сделали?
*Работа в парах по У. с. 66, Правило (2)
3 задание.
Самостоятельная работа по вариантам
1 вариант: Умножьте на 2 все чётные числа от 1 до 10
2 вариант: Умножьте на 2 все нечётные числа от 1 до 10
*Оцените работу на полях
* Сравните с эталоном:
| 1*2=2 | 2*2=4 |
| 3*2=6 | 4*2=8 |
| 5*2=10 | 6*2=12 |
| 7*2=14 | 8*2=16 |
| 9*2=18 |
*Оцените свою работу после проверки. У кого оценки совпали?
У кого оценки совпали?
– Какие числа получились в результате умножения четных чисел на 2?нечетных чисел на 2?
– Какой вывод можем сделать?
4 задание.
–
Следующее задание вы выберете себе сами.(На доске уравнения Х-45=27 ; А+32=45+2)
– Повторим алгоритм решения уравнения.
(Дети решают. На обратной стороне доски работают 2 ученика)
– Кто выбрал для решения первое уравнение? Кто выбрал второе уравнение? Какое уравнение легче? Какое сложнее? Почему?
(второе уравнение составное)
*Проверка.
– Каким числом является корень 1 уравнения? Второго?
5 задание. Выполнение вычислений в выражениях в несколько действий.
*Работа в парах. Повторение алгоритма работы в парах.
– Выберите выражение:
- (78-38)+(94-82)=
- 34+(99-66)-50=
*Проверяем по эталону.
– Какими числами являются полученные результаты? Докажите
ФИЗМИНУТКА
6 задание.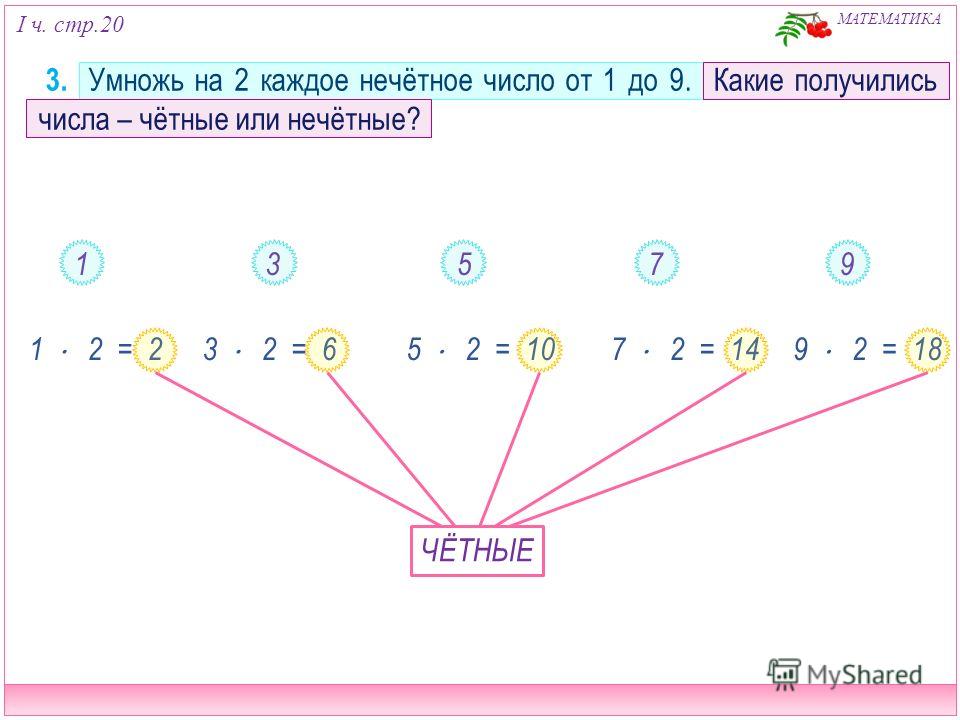
*Решение задачи. Работа с учебником с.67 № 5(а).
(1 ученик у доски, все в тетрадях)
– Как удобнее выполнить запись условия?
– 1 ребёнка обозначим кружком.
– Сколько человек было в каждой группе?
– Как изобразить на схеме?
– Какое действие мы выполняли, чтобы найти результат?
– Как записать решение?
Решение.
8:2 = 4 (гр.)
Ответ: 4 группы получилось.
– Какое это число чётное или нечётное?
– Действительно, вы – всезнайки.
IV. Итог урока. Рефлексия.– Какая тема нашего урока?
– Какие задания выполняли?
Игра «Продолжи предложение» (на дощечках).
– Числа, которые делятся на 2 называют…?
– Числа, которые не делятся на 2 называют…?
– Как вы оцениваете усвоение знаний по этой теме?
Д/з.
– Вы для себя уже сделали выводы, какие задания вызывают у вас затруднения. Поэтому, из учебника выберите 1 задание, которое по вашему мнению, следует повторить.
Поэтому, из учебника выберите 1 задание, которое по вашему мнению, следует повторить.
Конспект урока на тему “Чётные и нечётные числа”
Тема урока | Чётные и нечётные числа |
Тип урока | Урок открытия новых знаний |
Цель урока | Сформировать умение определять четные и нечетные числа. |
Задачи урока | Познакомить с понятиями четные и нечётные числа Развивать внимание, мышление, математическую речь Воспитывать усидчивость, внимательность, наблюдательность, активность, стремление к достижению цели, самостоятельность. |
Планируемые результаты | Предметные познакомить с понятиями чётные и нечётные числа; научить находить среди данных чисел четные и нечетные числа; закрепить таблицу умножения на 2 и соответствующие случаи деления; совершенствовать вычислительные навыки и умения решать текстовые задачи. |
Ресурсы урока | Учебник Моро М.И. Математика 3 класс (1 ч.), доска. |
Межпредметные связи | Математика-Литературное чтение-Геометрия |
Формы и методы обучения | Методы и формы работ: фронтальная и индивидуальная работы, проблемный метод, словесный, практический, наглядный. |
Основные понятия | Чётные числа, нечётные числа |
Этапы | Деятельность учителя | Деятельность учащихся | ||||||||||||||||||
Мотивация к учебной деятельности | -Здравствуйте ребята. Меня зовут Валерия Эдуардовна, и сегодня урок математики проведу у вас я. Прозвенел звонок веселый. Мы начать урок готовы. Будем слушать, считать, И друг другу помогать. Чему мы учимся на уроках математики? Я пожелаю вам хорошего настроения и очень хочу, чтобы такое хорошее настроение у вас оставалось до конца урока. | Приветствуют учителя Готовятся к уроку Настраиваются на предстоящую работу Считать, решать примеры и задачи… | ||||||||||||||||||
Актуализация знаний Устный счёт | Сейчас мы с вами проведем устный счет. Работа со всем классом Обратите внимание на доску. Решите примеры 39+6= 56+5= 66-9= 21-3= 32+9= 16-7= 46+8= 38+6= 73-4= 87-9= Найдите периметр прямоугольника, длины сторон которого 8 дм и 6 дм. -Что вы знаете о прямоугольнике? 6дм 8дм -Как найти периметр прямоугольника? – Молодцы! А теперь давайте найдем периметр нашего прямоугольника. Составьте пример. Внучка ехала на метро навестить бабушку. До пересадки она проехала 8 станций, после пересадки еще 7 . Сколько всего станций проехала внучка . -Можем ли мы сразу ответить на вопрос задачи? Каким действием? Как? Молодцы! – Молодцы, ребята. Вы были очень внимательны. | 39+6=45 56+5=61 66-9=57 21-3=18 32+9=41 16-7=9 46+8=54 38+6=44 73-4=69 87-9=78 – У прямоугольника все углы прямые ,четыре стороны, есть длина и ширина : длина большая сторона , ширина-меньшая – Периметр прямоугольника- это сумма длин всех сторон. (6+8)•2=28 -Да, можем 8+7=15(стан.)-всего проехала внучка . | ||||||||||||||||||
Выявление места и причины затруднения | – Ребята сейчас я вам расскажу одну удивительную историю, внимательно послушайте и скажите, о каких числах будет идти речь? – Однажды в Солнечном городе произошла удивительная история. Числа, которые жили в этом городе, были очень дружные. Они часто ходили в гости друг к другу, собирались вместе и придумывали различные игры. Один раз они решили поиграть в игру «Прятки», но в итоге все числа переругались и даже стали жить на разных сторонах улиц. Цифры 2,4,6,8,10 жили на одной улице, а цифры 1,3,5,7,9 на другой. -Что общего у чисел, которые живут на первой улице (2,4,6,8,10)? -А что общего у чисел, который живут на второй улице(1,3,5,7,9)? -Как вы думаете, как называются числа на первой улице? -А как на второй улице? Как вы думаете, какая тема урока? Хорошо. А вот как эти числа называются сейчас я вам открою секрет. | – Все числа делятся на 2 . -Эти числа не делятся на 2 Ответы детей. Затруднение Изучение чисел, которые делятся на 2 и которые не делятся на 2 | ||||||||||||||||||
Построение выхода из затруднений Реализация проекта выхода из затруднения | -Так вот, улица, на которой живут числа 2,4,6,8,10 называться будет– ЧЁТНАЯ, а числа называются чётными. Все эти числа делятся на 2 без остатка. -Улица, на которой живут числа1,3,5,7,9 стала называться–НЕЧЁТНАЯ, а числа – нечётными. Все эти числа не делятся на 2 без остатка. Откройте учебник на странице 20. Выполним № 1. -Кто прочитает первое задание? Сколько сахару положили в каждую чашку? -Какой вопрос в задании? -Как узнаем? -Правильно! Мы узнали , что на 4 чашки 8 кусков сахару хватило и ни одного куска не осталось . -А теперь причитаем второе задание? -Сколько у нас теперь кусков сахару? -Какой вопрос в задании? – Как узнаем? – Зачитайте правило. -Какие числа называют четными? Какие нечетными? -Кто может повторить правило? -Давайте откроем тетради, напишем дату, классная работа. Физкультминутка Буратино подтянулся, Раз нагнулся, два нагнулся, Руки в стороны развел, Видно ключик не нашел. Чтобы ключик отыскать, На носочки нужно встать! | В каждую чашку положили по 2 куску сахару. – На сколько чашек хватило 8 кусков сахару? – 8:2=4 -9 -На сколько чашек хватит 9 кусков сахару? Сколько кусков станется? -На 4 чашки и 1 кусок останется9:2=4 (1 ост) -Чётными называются числа, которые делятся на 2 без остатка. | ||||||||||||||||||
Первичное закрепление Самостоятельная работа с проверкой | – Ребята, а теперь посмотрите на № 2. Что необходимо сделать? Записывают числа в тетрадь( Кто-нибудь один у доски ) -Назовите числа, которые вы обвели в круг. Почему ты считаешь, что они четные? А какие подчеркнули? Почему они нечетные? Молодцы, вы хорошо справились -А теперь давайте узнаем, что необходимо сделать в № 3. (Кто-то выполняет у доски ) -Какие числа от 1 до 9 нечётные? -А теперь умножим эти числа на 2. Какие числа получились чётные или не чётные? Почему? -Молодцы! Обратите внимание на задачу под номером 4. Читаю задачу, затем читает кто-то из учащихся. -О чем говорится в задаче? – Сколько ящиков огурцов привезли в столовую? -Сколько огурцов было в каждом ящике? -Какой вопрос в задаче?
-Сможем ли мы сразу ответить на вопрос задачи? -Каким действием? Как? Запишите решение задачи и ответ. А теперь давайте придумаем две задачи обратные этой. (устно) -Каким действием решим эту задачу?
-А каким действием решим вторую задачу? -Посмотрите на №6. Это задание вы будете выполнять по вариантам. Верхнюю строку выполняет 1 вариант, а 2 строку 2 вариант. После выполнения проверим. Какой ответ у вас получился в первом примере? 1 вариант ? 2 Вариант? Какой ответ получился во втором примере? 1 вариант ? 2 вариант? В 3 примере? 1 вариант? 2 вариант? В 4 примере? 1 вариант? 2 вариант? Какой ответ в 5 примере? 1 вариант? 2 вариант? У кого ни одной ошибки? У кого одна ошибка? У кого 2 и более? Вы отлично справились. Молодцы, я думаю у вас самостоятельная работа не вызвала никаких затруднений, а если даже и вызвала мы разобрали ваши ошибки | Написать числа от 10до 19, а затем обвести кружками чётные числа и подчеркнуть нечётные. -В круг обвели 10,12,14,16,18 -Подчеркнули 11,13,15,17,19 Умножить каждое нечётное число от 1 до 9. 1•2=2 3•2=6 5•2=10 7•2=14 9•2=18 -Получились чётные числа -В задаче говорится о ящиках с огурцами которые привезли в столовую . -В столовую привезли 3 ящика с огурцами. – В каждом ящике было по 6 кг огурцов. -Сколько всего кг огурцов привезли в столовую. – Да -Действием умножения, 3•6= 18(кг) – 1) Всего в школу привезли 18 кг огурцов в 3 ящиках. Сколько кг было в каждом ящике? 18:3=6 (кг) 2) В школу привезли несколько ящиков с огурцами. Каждый ящик весит 6 кг. Всего привезли 18 кг огурцов. Сколько ящиков огурцов привезли? 18:6=3(ящ.) -Решить примеры Решают примеры 1 вариант 2•6=12 16:2=8 18:2=9 12:2•3=18 14:2•3=21 2 вариант 9•2=18 10:2=5 14:7=2 16:8•4=8 18:2•3=27 | ||||||||||||||||||
Рефлексия и итог урока | – Какую тему мы свами изучили на уроке? Какие числа называются четными? -Какие числа называются нечетными? – Оцените свою работу на уроке (лестница успеха). | – Ответы детей. Чётные и нечётные числа -Четными называются числа, которые без остатка делятся на 2.-Нечетные числа, те, которые не делятся без остатка на 2. -Оценивают свою деятельность на уроке . | ||||||||||||||||||
Домашняя работа | Откройте все свои дневники, запишите задание на дом: стр.20 №5 | |||||||||||||||||||
Организация учащихся на перемену | – Встаньте! На этом наш урок окончен, до свидания! | – До свидания! Прощаются с учителем. |
Колодкина Р.Н. _____________________________________ Манько Н.Н.______________________________
Четные и нечетные числа
Знакомство с четными и нечетными числами обычно происходит в старшем дошкольном возрасте. Если ваше чадо уже умеет считать в пределах двадцати, знает сложение и вычитание, то пришло время объяснить ему, как можно определить, четное число или нет. Это поможет в дальнейшем изучении арифметики и математики.
Содержание:
- Четные числа
- Нечетные числа
- Четность и нечетность: основные свойства
- Таблица четных и нечетных чисел
- 0 – это четное число или нет
- Игровые упражнения
Четные числа
Из школьного курса мы знаем, что четные числа – это те, которые делятся на два нацело. Малыши дошкольного возраста с делением чисел еще не знакомы, им лучше всего объяснять понятие четности и нечетности не в теории, а на примерах с конфетами, яблоками или игрушками.
Возьмите четыре конфеты и предложите ребенку поделить их на две равные кучки – для себя и для мамы. Обратите внимание малыша, что в этом случае каждому достанется по две конфеты.
Попросите малыша сделать то же самое с другими предметами для закрепления понимания. Можно раскладывать, например, карандаши, фишки, кубики и любое другое четное количество вещей.
Нечетные числа
Нечетные числа делятся на два с остатком. Возьмите три яблока и попросите кроху поделить их поровну между вами. Очень скоро малыш придет к выводу, что это невозможно.
Четность и нечетность: основные свойства
Объясните ребенку несколько простых лайфхаков:
- Нечетные и четные числа чередуются. Единица – нечетное, поэтому двойка – четное, тройка – нечетное и так далее.
- Понять, относится двузначное или многозначное число к четным, можно по последней цифре. Она должна быть 0, 2, 4, 6 или 8.
- У нечетных чисел в конце стоит 1, 3, 5, 7 или 9.

Если ребенок уже знаком с арифметикой, ему будет интересно узнать следующие свойства:
- При сложении двух четных чисел получается четное число: 4+2 = 6.
- Если к четному числу прибавить нечетное, то и результат будет нечетным: 2+1 = 3.
- Если умножить четное число на любое другое результат тоже будет четным: 2 х 3 = 6.
- Если умножить два нечетных числа, то получится нечетный результат: 3 х 5 = 15.
Таблица четных и нечетных чисел
Чтобы ребенок мог быстро определять, какое число перед вами, удобно использовать таблицу четных и нечетных чисел. В ней жирным в каждом ряду выделены четные элементы.
Дошкольники обычно умеют уверенно считать в пределах 20. Большая таблица будет их путать.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Для школьников подойдет таблица от 1 до 100.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
0 – это четное число или нет
Математическая теория утверждает, что ноль относится к четным числам. Ребенку этот факт можно объяснить тремя способами:
Ребенку этот факт можно объяснить тремя способами:
- Нечетные и четные числа чередуются, а ноль стоит перед единицей, которая является нечетным числом. Поэтому 0 – четное число.
- Если число оканчивается на ноль, то это признак четности. Соответственно и сам 0 относится к четным.
- Ноль делится на два без остатка. Поэтому его относят к четным числам.
Игровые упражнения
Чтобы закрепить знания, используйте понятия о четных и нечетных числах в играх и задачках. Например, сыграйте в «чет-нечет». Называйте числа и просите малыша хлопать в ладошки, если оно четное. А если вы назовете нечетное, он должен топать ногой.
На прогулке выясняйте у ребенка, четный или нечетный номер дома, автомобиля, городского автобуса или маршрутки. Распечатайте из интернета картинки с воздушными шариками или другими предметами, на которых изображены числа. Попросите закрасить предметы с четными числами синим цветом, а с нечетными – красным.
Рейтинг: 5/5 – 1 голосов
Конспект урока “Чётные и нечётные числа”
Тема: Чётные и нечётные числа
Тип урока: изучение нового материала.
Цели урока:
- Дать понятие “четные” и “нечетные” числа.
- Продолжать учить таблицу умножения числа 2 и соответствующих ей случаев деления.
- Совершенствовать вычислительные навыки и умения их применять.
- Развивать математическую смекалку и творческое мышление.
Оборудование: компьютер, презентация, карточки для устного счета, раздаточный материал (геометрические фигуры) учебник по математике 2 класс, рабочие тетради, картинка Знайка.
Ход урока
I. Организационный момент. Эмоциональный настрой.
У: Парам парейра! (2 хлопка)
Д: Парам парейра (2 хлопка)
У: Настроение каково?
Д: Во!
У: Все такого мнения?
Д: Да!
У: Все, без исключения?
Д: Ура!
У: Может вы уже устали?
Д: Мы с собой таких не брали!
У: Может ляжем отдохнем?
Д: Лучше мы урок начнем!!
К нам сегодня на урок
Пришел Знайка-педагог!
Значит, лениться нам никак нельзя!
У: Знайка и я, мы рады встречи, друзья!
И думаем, встретились мы не зря
Мы будем учиться сегодня решать,
Исследовать, сравнивать, рассуждать.
Но, сначала нас ждет
Увлекательный устный счет!
II. Актуализация знаний и мотивация учебной деятельности.
- Устный счет. Работаем с карточками
И вам задание- веселые задачки.
3 мартышки утром рано
Ссорясь, делят 6 бананов.
Поровну и без обмана
Разделите им бананы. (2)
Паслись на лугу
По 6 коров и телят.
«Я мал, – говорит пастушок,
Сосчитать не могу,
Сколько животных всего на лугу» (12)
Тихо белочки сидели,
Дружно ягодки делили.
8 ягод было там,
По 2 ровно всем.
Поглядеть бы надо нам
Сколько белок было там? (4)
Дарит бабушка лисица,
Трем внучатам рукавицы:
Это вам на зиму внуки,
Рукавичек по две штуки.
Берегите, не теряйте!
Сколько всех, пересчитайте! (6)
Если знаешь ты таблицу,
На вопрос ответишь смело:
Сколько птичек невеличек
На кормушку прилетело?
Воробьев драчливых пара,
И синичек тоже пара,
Пара сизых голубей
Ну и пара снегирей. (8)
(8)
У: Молодцы!
2) Пальчиковая гимнастика ( этот пальчик мама…)
Для начала разомнем наши пальцы
3) Работа в тетради. Повторение написания цифры 2.
Откройте свои рабочие тетради. Что мы в первую очередь запишем? Конечно сегодняшнее число. (Слайд 2) (Слайд 3)
А вот это цифра два.
Полюбyйтесь, какова:
Выгибает двойка шею,
Волочиться хвост за нею.
Ребята многие из вас умеют хорошо считать, могут сосчитать и свои игрушки, и своих друзей, и многое другое. А в далёкие времена люди с большим трудом научились считать сначала до двух и только через много-много лет начали продвигаться в счёте. Каждый раз за двойкой начиналось что-то неизвестное, загадочное. Когда считали “один, два, много”, то после двух было “все”.
У цифры “два” есть свой секрет
Она гордится этим.
А Знайка знает тот секрет,
О нем расскажет всем вам.
4. Работа со счетным материалом. Работа в паре
Наш герой очень любит геометрические фигуры. Возьмите 5 фигур (счетный материал) и разложите их по парам.
Что значит по парам? (По два)
Сколько пар получилось? (2 и еще 1 осталась)
Теперь возьмите 3 фигуры и разложите по две.
Сколько пар получили? (1 еще 1 осталась)
Что вы можете сказать о своей работе?
Вам удалось разложить по два? (Не совсем. В работе с числами 3,5, одна фигура остается без пары)
Вывод: То есть названные вами числа на 2 не делятся.
1 2 3 4 5 6 7 8 9 10
А как они расположены в числовом ряду? (Слайд 4)
(2-делится, 3– не делится, 4-делится, 5-не делится, 6 – делится, 7 – не делится, 8 – делится, 9 – не делится, 10 – делится)
Посмотрите, числа чередуются.
Мы с вами открыли секрет числа 2.
Взятые в кружочки числа называют четные.
Что их объединяет? (Эти числа делятся на 2)
А остальные нечетные.
Как определить в числовом ряду четные числа? (Если число делится на 2, то оно четное, а если не делится на 2, нечетное)
Молодцы!
III. Сообщение темы и целей урока.
Давайте сформулируем тему урока. (Четные и нечетные числа) (Слайд 5) А какую мы можем поставить перед собой цель? (Научиться распознавать четные и нечетные числа) (Слайд 6)
IV. Первичное закрепление знаний
- Работа с учебником.
Знайка с нами, а это значит –
Выполнять мы будем задания.
№ 1, 2, 3 – коллективно
- Работа в тетради. (Слайд 7)
- Решите задачу.
Восемь ребят разделились в группы по 2 человека. Сколько групп получилось?
- Вставь вместо «*» знаки «·» или «:». 2 человека у доски (Слайд 8)
8 * 2 = 4 2 * 5 = 10
6 * 2 = 12 4 * 2 = 2
7 * 2 = 14 18 * 9 = 2
16 * 8 = 2 3 * 2 = 6
V. Итог урока
Итог урока
– Вы помните, какую цель мы ставили перед собой? Научиться распознавать четные и нечетные числа
– Достигли ли мы этой цели? (Слайд 9)
– Кто испытывал трудности при выполнении заданий, но старался, быстро находил ошибки, тот говорит себе: «Я работал хорошо».
– Кому на уроке работать было трудно, и остались вопросы, скажите себе: «У меня обязательно всё получится».
– Кому всё было понятно, кто активно работал, скажите: «Я молодец!».
И Знайками вы стали,
И знанья обрели,
И я вам пожелаю
Удачи впереди!
– Урок окончен, всем спасибо за работу.
Четные и нечетные числа – определение, признаки и свойства
Одной из характеристик числа является его кратность двум. Простое арифметическое свойство стало основой для мистических верований древних людей, служит фундаментом для быстрых алгебраических вычислений и геометрических формул. Нечетные и четные числа широко используются современным человеком в повседневной жизни.
Содержание
- Арифметические свойства
- Характеристика парности у ноля
- Свойства группы для вычислений
- История и значение в культуре
- Практическое применение
Арифметические свойства
Четными называют числа, которые при делении на 2 образуют целое число. Нечетные при том же действии дают результат с остатком (дробное число). Чтобы быстро проверить на четность двузначную цифру, нужно определить параметр для последней его цифры в десятичной записи. Если она делится на два, число является четным, в противном случае — нечетным. Метод работает для любых многозначных чисел.
Арифметические правила четных и нечетных чисел при различных операциях описаны древнегреческим математиком Пифагором до нашей эры и используются для вычислений современниками. Они помогают составлять формулы для оптимизированных расчетов в задачах с большим рядом переменных. Алгоритмы многих онлайн-калькуляторов запрограммированы с помощью таких функций.
Закономерности арифметических операций с целыми числами:
Формула четного числа: m = 2k. Формула нечетного числа: m = 2k + 1.
При уменьшении или увеличении четного числа на единицу получается нечетное и наоборот. При начертании оси с нулем в центре будет сохраняться чередование четных и нечетных чисел. Наглядно продемонстрировать феномен школьникам можно, предложив записать последовательный ряд четных чисел через запятую.
Характеристика парности у ноля
Не бывает целых чисел, которые не принадлежат к одной из групп по признаку кратности двум. Ноль, который разделяет отрицательные и положительные значения последовательного ряда, не является целым. Из-за этого большинство предполагает, что ноль стоит особняком, т. е. не относится ни к одному виду или же одновременно представляет оба.
В науке ноль — это аддитивный нейтральный элемент четной группы. Он является логическим началом для рекурсии последовательного ряда кратных двум объектов. Исследования, проведенные в учебных заведениях Великобритании, показали, что 2/3 преподавателей не знают верного ответа, а ученики пятого класса ошибаются реже, чем из шестого и старше.
Признаки четности ноля:

Маленьким слушателям легче пояснить феномен с помощью двух таблиц — по одной для каждой группы. Элементы кратных схематически изображаются в первом столбце, во втором — остаток. Олицетворяемая нолем пустота при делении на два остается пустотой, что соответствует признаку кратности двум. Вышеприведенный список доказательств содержит другие примеры для наглядной демонстрации логики принадлежности знака к группе элементов, кратных двум.
Свойства группы для вычислений
Когда требуется вычислить сумму множества слагаемых из натурального ряда последовательных нечетных чисел, можно отказаться от длительных монотонных операций. Известно, что сумма любого количества элементов всегда соответствует квадрату их количества. Проверку можно осуществить путем сложения двух, трех и четырех элементов последовательного ряда. Аналогичное выражение можно составить для любого количества слагаемых.
youtube.com/embed/ZM966LdkTKI”>Алгоритм оптимизированного решения:
Количество складываемых элементов последовательного ряда некратных двум числительным всегда соответствует квадратному корню суммы.
Примеры логических задач для решения через характеристику парности:
Ответ на каждую из задач можно получить методом проб и подбора. Понимание законов парности позволяет существенно сократить время на поиск верного решения. Школьникам нравится изящное решение головоломки о маленьком кузнечике. Детям сообщают, что за один скачок он преодолевает 1 метр. Учащимся предлагают доказать, что насекомое совершило парное количество прыжков, если в результате движений оно оказалось в исходной точке.
Понимание законов парности позволяет существенно сократить время на поиск верного решения. Школьникам нравится изящное решение головоломки о маленьком кузнечике. Детям сообщают, что за один скачок он преодолевает 1 метр. Учащимся предлагают доказать, что насекомое совершило парное количество прыжков, если в результате движений оно оказалось в исходной точке.
Ответ становится очевидным при понимании, что пройденный путь, равен расстоянию, которое необходимо пройти для возвращения к стартовой позиции. Таким образом суммарное расстояние обязано быть парным.
История и значение в культуре
Неоценимое влияние на развитие арифметики оказали труды Пифагора. Ученый посвятил много труда и времени, чтобы выявить закономерности свойств чисел и объединить их в логичную систему. Математические законы и наблюдения он связал с мировосприятием и теорией самопознания человека.
Каждой цифре математик отвел свое значение. Нечетные обладают более сильными, активными характеристиками. Именно они в воссозданной мистической системе являлись олицетворением мужского начала, динамики и солнца. Четные же, наоборот, олицетворяли женское естество, статичность и луну.
Аналогичное деление характерно для китайской философии, в которой нечетные числительные относят к светлой мужской субстанции Ян, а Инь — к теневому, негативному, женскому. В учении о материи тайцзи противоположности представлены как единые и неделимые стороны одного целого.
У каждого этноса существуют свои поверья. Самое популярное суеверие у славян запрещает преподносить букеты с парным количеством цветов. В США и Европе такой подарок, наоборот, трактуется как пожелание счастья и благополучия. Нечетность приглашенных гостей, дней празднования, даты события также считается обязательным по свадебным традициям Руси.
Практическое применение
Возможность разделить все числительные на парные и непарные широко используется в повседневной жизни. В зависимости от того, кратен ли двум порядковый номер месяца, по правилам дорожного движения может быть запрещена или разрешена стоянка в определенных зонах. Четные и нечетные недели помогают запомнить расписание вузов с многочисленной аудиторией.
В зависимости от того, кратен ли двум порядковый номер месяца, по правилам дорожного движения может быть запрещена или разрешена стоянка в определенных зонах. Четные и нечетные недели помогают запомнить расписание вузов с многочисленной аудиторией.
В расписании железнодорожных поездов на кратности двум числа месяца завязаны маршруты с расписанием через день. Чтобы не нарушать установленный порядок, после 31 числа поезд может пропустить один выезд. Тот же принцип используется для нумерации вагонов — парность содержит информацию о направлении пути. В плацкартах и купе места с верхними полками всегда обозначены четным числом, а нижние — нечетным.
Парность строк помогает проверить созвучность стиха поэтам. Если мысленно пронумеровать слоги, можно подобрать слово в соответствии с ритмом произведения, так как ударные и безударные гласные являются основным ориентиром.
Предыдущая
МатематикаПараллельность плоскостей – способы, модели и примеры решения и построения
Следующая
МатематикаЧетырехугольник, вписанный в окружность – основные свойства, признаки и формулы
Как учить четные и нечетные числа
Поделись с друзьями!
0 акции
- Поделиться
- Твит
Четные и нечетные числа являются основным математическим понятием. Так как же научить их весело и запоминающимся образом? У нас есть методы для любого стиля обучения!
Так как же научить их весело и запоминающимся образом? У нас есть методы для любого стиля обучения!
Целые числа можно разделить на две категории: четные и нечетные. Признание разницы может помочь вам в делении и умножении, поэтому важно, чтобы вы знали, как их различать.
Обычно вы знакомите ребенка с этим понятием в первом или втором классе, а затем повторяете его в более поздних начальных классах. Чтобы понимать четные и нечетные числа, ребенок должен знать свои числа и уметь считать до 100.
Решая, как учить четные и нечетные числа, изучите варианты! Вот несколько способов преподавания этой концепции.
Как представить четные и нечетные числаЧтобы представить понятие четных и нечетных чисел, используйте маленькие счетчики. Съедобные жетоны, такие как M&Ms, особенно интересны!
Для юных учеников можно поставить две фигурки (это могут быть куклы, фигурки, мягкие игрушки и т. д.). Скажите: «Тебе когда-нибудь приходилось делиться со своим братом или сестрой? Вы хотите, чтобы обмен был справедливым; вы оба хотите одну и ту же сумму. Вот что происходит здесь с Фредом и Джинджер. Их родители оставили им немного M&Ms (или печенье, игрушки и т. д.) и сказали им поделиться».
д.). Скажите: «Тебе когда-нибудь приходилось делиться со своим братом или сестрой? Вы хотите, чтобы обмен был справедливым; вы оба хотите одну и ту же сумму. Вот что происходит здесь с Фредом и Джинджер. Их родители оставили им немного M&Ms (или печенье, игрушки и т. д.) и сказали им поделиться».
Пройдите через различные числа 1-10. Могут ли они поровну разделить 1 M&M? Не без разреза. Могут ли они разделить 2? Разделите их на 2 стопки, по одной перед каждой фигуркой. Да, 2 можно разделить поровну. Напишите цифру 2 на доске или листе бумаги.
В конце концов, у вас будет такой список чисел: 2, 4, 6, 8, 10. Объясните, что эти числа называются четными, потому что их можно разделить нацело, не разрезая на части. Остальные числа нечетные; они нечетные: 1, 3, 5, 7, 9. (Технически 0 также является четным числом, но не будем его рассматривать в этом базовом введении).
Как учить четные и нечетные числа с помощью цветов Мы устроены так, чтобы замечать закономерности, и дети не исключение. Помогите детям выучить нечетные и четные числа, используя цвет.
Помогите детям выучить нечетные и четные числа, используя цвет.
Вы можете использовать трехмерные цифры двух цветов или сделать свой собственный набор с маркерами на каталожных карточках (или использовать цифры, вырезанные из картона).
Выберите один цвет для нечетных чисел (красный) и один для четных (синий). Это особенно эффективный метод для визуалов.
Выложите на стол цифры от 0 до 10. Спросите: «Вы видите закономерность?» Они заметят, что цвета чередуются между красным и синим.
Назовите четные числа, а затем нечетные.
Повторите их (это особенно важный шаг для аудиалов).
Затем составьте двузначные нечетные и четные числа, ориентируясь на их последнюю цифру. «Это четное число, потому что оно заканчивается на 2».
Как обучать четным и нечетным числам с помощью счетчиков Этот метод обучения нечетным и четным числам особенно хорошо работает с кинестетиками. Вам понадобятся объемные буквы и фишки. Выстройте числа 1-10.
Под номером 2 положите две жетоны рядом. Скажите: «Видишь, у этого счетчика есть партнер? Мы называем номера, у которых есть партнеры, «четными номерами».
Теперь поместите одну фишку под номером 1, выровняв ее по левому краю, чтобы показать, где может стоять отсутствующая фишка. «У этого счетчика нет партнера. Это все в одиночку. Мы называем номера, в которых последний счетчик отсутствует партнером, «нечетными номерами».
Повторите этот процесс для номера 3. Поместите пару счетчиков непосредственно под номером 3 и один счетчик под этой парой. «Посмотрите на последний счетчик. Есть ли у него партнер? Нет? Тогда это нечетное число».
Повторите процесс с цифрой 4, поместите две пары жетонов под цифрой. Затем сделайте то же самое для 5, 6, 7 и т. д.
Как учить четные и нечетные числа с помощью числовой строки Старшие школьники могут визуализировать нечетные и четные числа с помощью числовой строки. Начните с числа 0. Объясните, что это четное начальное число. Теперь перепрыгните через 1, чтобы приземлиться на 2.
Объясните, что это четное начальное число. Теперь перепрыгните через 1, чтобы приземлиться на 2.
«Когда я прыгаю на 2 единицы, я приземляюсь на четное число».
Используя этот метод, вы можете отображать как положительные, так и отрицательные четные числа. Числа, которые вы пропускаете, являются нечетными числами!
Как учить с помощью числовой таблицыЭтот метод снова показывает взаимосвязь шаблонов, которые могут кристаллизовать понимание для некоторых учащихся (особенно для ваших визуалов и логически мыслящих).
Используйте диаграмму из 100 чисел, где числа перечислены в рядах по десять. Закрасьте четные числа в верхнем ряду (0-10). Повторите их несколько раз, чтобы запомнить. Затем раскрасьте четные числа во втором ряду (11-20). Видит ли ребенок узор?
Повторите это с оставшимися рядами.
В итоге диаграмма будет иметь вид 5 цветных столбцов. Укажите, что все числа, оканчивающиеся на 2, 4, 6, 8 и 0, четные; числа, оканчивающиеся на 1, 3, 5, 7 и 9, нечетны.
Независимо от стиля обучения, вы можете учить четные и нечетные числа так, чтобы они запоминались.
Вам также может понравиться:- Математические занятия для дошкольников
- Спасите спорт! {Математический цифровой квест}
- Как сделать математику увлекательной – используйте математические игры!
Поделись с друзьями!
0 акции
- Поделиться
- Твит
Как научить ребенка четным и нечетным числам?
Обучение вашего ребенка основам математики может показаться вам непосильным испытанием. Однако не стоит паниковать, так как малыши очень быстро усваивают простые понятия. Одна из таких концепций, которую вам нужно научить, — это нечетные и четные числа. «Как научить ребенка нечетным и четным числам?» — один из часто встречающихся запросов на многих родительских порталах.
Обычно большинство детей усваивают нечетные и четные числа в очень раннем возрасте. Все школы включают эту концепцию к первому или второму классу. Идеальная пара различных чисел является весьма важной концепцией в математике и чрезвычайно полезна при пропущенном счетном делении по мере взросления.
Слова «нечетный» и «четный» обеспечивают ребенка словарным запасом, который ему необходимо использовать, когда он начинает работать с этими понятиями.
При некоторой практике первоклассники обычно легко усваивают эту идею. Существует множество практических советов, которые помогут вашему ребенку легко понять четные и нечетные числа. Некоторые из этих забавных методов обязательно вызовут интерес у вашего ребенка и помогут ему быстро понять концепцию.
В этой статье
- Простое определение четных и нечетных чисел
- Упражнения, которые помогут вашему ребенку понять четные и нечетные числа
Простое определение нечетных и четных чисел
Сначала вам нужно объяснить, в чем разница между нечетными и четными числами. Самое простое объяснение состоит в том, что нечетные числа никогда нельзя разделить на две эквивалентные группы. С другой стороны, четные числа всегда можно разделить на две эквивалентные группы.
Самое простое объяснение состоит в том, что нечетные числа никогда нельзя разделить на две эквивалентные группы. С другой стороны, четные числа всегда можно разделить на две эквивалентные группы.
Хорошей идеей было бы представить мистера Эвена как джентльмена, который обычно делит все, что у него есть, поровну со своей семьей. С другой стороны, мистер Одд будет очень жадным и никогда не будет делиться поровну.
Дети усваивают такие понятия гораздо раньше, чем вы думаете. Это первая базовая концепция, которую ваш ребенок должен понять, знакомясь с концепцией четных и нечетных чисел. Затем вы можете продвигать концепцию с помощью некоторых интересных мероприятий.
Упражнения, которые помогут вашему ребенку понять четные и нечетные числа
Ниже приведены несколько простых упражнений, которые гарантированно помогут вашему ребенку быстро понять четные и нечетные числа:
1.
 Схемы хлопков и партнеры
Схемы хлопков и партнерыВсе, что вам нужно сделать, это попросить ребенка протянуть несколько пальцев и проверить, есть ли у каждого пальца партнер. Палец, у которого есть партнер, четный, а палец, у которого нет партнера, нечетный.
2. Счет до определенного числа Чередование щелчков и хлопков
Скажите им, что все щелчки — нечетные числа, а все хлопки — четные числа. Так ребенок без труда научится различать нечетные и четные числа.
3. Повторение чисел
Это еще один простой и эффективный метод, который поможет вашему ребенку выучить четные и нечетные числа без стресса. Попробуйте это и убедитесь, что это работает. Давайте повторять четные числа: 2, 4, 6, 8 и 0.
4. Теперь попробуем нечетные числа
1, 3,5,7,9. Также неплохо придумать простые рифмы, объясняющие четные и нечетные числа. Повторение этих стишков наверняка поможет вашему малышу.
5. Таблица сотен
Использование таблицы сотен – еще одна альтернатива для эффективного обучения четным и нечетным числам. Заставив вашего малыша раскрасить квадраты с четными числами определенного оттенка, а нечетные — другого цвета, вы, несомненно, поможете ему лучше различать четные и нечетные числа.
Заставив вашего малыша раскрасить квадраты с четными числами определенного оттенка, а нечетные — другого цвета, вы, несомненно, поможете ему лучше различать четные и нечетные числа.
6. Нечетное и четное многоборье
Просто поищите все, что можно сосчитать. Будь то подушки, монетки, чашки, ложки, тарелки, машинки или печенье. Попросите ребенка разбить их на пары и посмотреть, что осталось. Попросите его или ее записать это. Нравиться:
- Подушки – 5 (нечетные), печенье – 4 (четные): Им понравится выполнять это упражнение и одновременно изучать понятия четных и нечетных чисел.
- Игра «Крик и шепот»: Еще одно занятие, которое поможет вашему ребенку освоить четные и нечетные числа, состоит в том, чтобы заставить его считать до определенного числа, шепча четное число и выкрикивая нечетное число. Это упражнение также является отличной техникой, помогающей вашему ребенку быстро усвоить эту концепцию.

Вот несколько простых упражнений, которыми вам нужно часто заниматься с ребенком, чтобы он или она усвоили эту простую арифметическую концепцию.
Вышеупомянутые действия наверняка станут хитом. Всегда следите за тем, чтобы ваш ребенок знал основы, чтобы он или она могли определить четные и нечетные числа с первого взгляда.
Вы также можете сказать им, что последняя цифра в нечетных числах всегда будет 1,3,5,7 или 9. А когда дело доходит до четных чисел, они всегда заканчиваются на 2, 4, 6, 8 или 0.
Перестать беспокоиться о том, как научить моего ребенка четным и нечетным числам? Обязательно попробуйте эти удивительные занятия, чтобы научить вашего ребенка различать нечетные и четные числа.
Читайте также: 10 советов, как сделать сложение и вычитание простым и увлекательным
| План урока для Odd Vs. Раздел Тема: Математика Уровень обучения: первый класс Конкретный урок: четные и нечетные числа Цель урока:
Методы обучения
Учебные материалы
Теоретическая перспектива
Процедура
|
БЕСПЛАТНЫЕ снежки Математика с четными и нечетными числами
1-й класс • Математика 1-го класса • 2-й класс • Математика 2-го класса • 3-й класс • Математика 3-го класса • БЕСПЛАТНЫЕ распечатки • Математика • Математика Разное. • Зима16 января 2021 г.
Бет Горден
Помогите детям узнать о четных и нечетных числах с помощью этой супер милой математической игры в виде снежка , которую можно бесплатно распечатать. Бросай снежка в зависимости от того, являются ли они четными или нечетными числами в этом веселом математическом задании для детского сада , 1-го, 2-го и 3-го классов! Просто распечатайте PDF-файл с нечетными и четными числами , и вы готовы играть и учиться с веселыми зимние распечатки .
Pdd и даже игры для печати
Мы любим игривые детские математические игры в нашем доме. Математические задания для дошкольников не только помогают детям сохранять интерес и желание учиться, но и помогают детям лучше запоминать содержание! Это упражнение по сортировке четных или нечетных чисел помогает детсадовцам и ученикам 1-го класса практиковаться в определении того, являются ли числа четными или нечетными. Это действий с нечетными и четными числами — отличный способ помочь детям запомнить, какие числа четные, а какие нечетные.
Независимо от того, являетесь ли вы родителем, учителем или учеником на дому, эта зимняя математика наверняка доставит вам удовольствие дома, в качестве математического центра в вашем классе или в качестве дополнения к учебной программе по математике на дому.
Winter Printables
Начните с прокрутки вниз сообщения, под условиями использования, и нажмите на текстовую ссылку, которая говорит >> _____ <<. Файл PDF откроется в новом окне, чтобы вы могли сохранить халяву и распечатать шаблон.
Файл PDF откроется в новом окне, чтобы вы могли сохранить халяву и распечатать шаблон.
Зимняя математика
Просто распечатайте три страницы:
- Коврик для сортировки зимних сцен
- Пронумерованные снежки для сортировки
- Ключ ответа с объяснением четных/нечетных чисел
Вырежьте снежки, и вы готовы к игре. Его можно легко хранить в большом пакете с застежкой-молнией или в защитной пленке для страниц.
Математика снежковДля выполнения задания ваш ребенок будет сортировать пронумерованные снежки, стараясь, чтобы снежок «попал» в нужную крепость.
Например, если вы подняли 4 снежка, 4 будет четным. Вы бы «кинули» его в ровную снежную крепость.
Зимние развлечения
- Зимнее занятие по приготовлению снежной слизи для детей
- Как легко сделать снежную глину для рождественских украшений
- FUN Snowman Launcher – зимние развлечения для дошкольников
- Рецепт тающей слизи снеговика и задание
- Приготовление исторической снежной конфеты (с 2 рецептами!)
- Пистолет для рисования снега
- НЯМ! Как сделать снежное мороженое всего из 2 ингредиентов!
- Chilly Snow Dough Antarctica Занятия для дошкольников
- Занятия для детей от 30 января
- Поделка с рождественским украшением безделушка с БЕСПЛАТНЫМИ распечатками
- Деятельность Мартина Лютера Кинга
- Открытки ручной работы “Снеговик” Зимние поделки для детей
Зимняя наука
Ищете больше развлечений Зимние научные проекты для детей ? У нас есть много интересных идей, которые вы можете попробовать!
- Супер крутой снежный вулкан Научный эксперимент
- Эксперимент “Зимний тающий снеговик”
- Извержение снеговика с простым научным зимним экспериментом со снеговиком для детей
- Рецепт тающей слизи снеговика
- Легко взрывающийся снеговик — Зимний научный эксперимент
- Снеговик, измеряющий снегопад — зимнее задание STEM
- Зимние мраморные открытки, созданные с помощью науки
- Зимний научный эксперимент с извергающимся снегом
- Как сделать мороз в консервной банке- Зимний научный эксперимент
Распечатки со снеговиком
Ищете рабочие листы со снеговиком и идеи для занятий со снеговиком? Вам понравятся эти ресурсы!
Winter Printables
- Build-a-Snowman Winter CVC Words Activity
- Снеговик Части речи Зимние рабочие листы
- Игра «Зрение в словах для арктических животных»
- Игра «Горячий шоколад» или «Варежка: звуки начала»
- Hot Cocoa Winter Rhyming Words Puzzles, игра с зимними рифмованными словами или эти зимние рифмованные головоломки со словами в шляпе
- Снежинка Зимние составные слова Распечатки и упражнения
- Саморегулирующаяся игра «Азбука зимних ботинок»
- Пазлы из смеси варежек – зимние развлечения для детского сада
- Зимние слоги Печатная деятельность
- Рабочие листы слов “Взгляд пингвина”
Математика снеговика
- Зимняя математика Рассказ о времени Рабочие листы и упражнения
- Карточки со снеговиком
- Умножение снеговика Занятие
- Winter Snowballs Нечетные и четные игры для печати
- Счет карточек со снеговиком
- Снеговик по математике или эта сборка снеговика по математике для занятий сложением и вычитанием
- Занятия со снеговиком для дошкольников – посчитайте до 10
- Очень милые рабочие листы по зимнему счету для дошкольников
- Практическое занятие по счету снеговиков для юных учащихся
- Пазлы на умножение снеговиков
- Книга для подсчета снеговиков 9 для бесплатной печати0008
Зимняя математика
- Пазлы в форме милого снеговика
- Зимнее математическое задание с карточками с шаблонами Snap Cube
- Математика горячего шоколада – Семейства фактов сложения и вычитания
- Дополнение Математическая игра варежки для дошкольников
- Фракция Снежинки Активность
- Зимние цвета – игра «Собери пингвинов» или эта игра «Собери варежки»
- Коврики из зимнего пластилина варежки
- Карточки Penguin для печати с математическими клипами для счета до 20
- Зимняя математика — головоломки с пропуском счета
- Таблица сотен Зимняя раскраска по номерам или эти более простые рабочие листы зимней раскраски по номерам
- Рабочие листы Snowman, работающие над разрядным значением
- Полярные животные пропускают подсчет рабочих наборов
- Снеговик Набор рабочих листов с большим количеством страниц по математике, грамоте и многому другому для детей от 3 до 8 лет.

- Посмотрите еще больше идей в этой зимней теме
- Действия пингвинов в День осведомленности о пингвинах 20 января
- Простые зимние раскраски
- Зимние рабочие листы для дошкольников
- Не пропустите эти фантастические зимние книги для чтения вслух, веселые зимние книжки с картинками или эти зимние книги для дошкольников
- Листы с зимними упражнениями Roll and Dab или эти зимние распечатки для изучения цветных слов с помощью маркеров бинго
- Зимние рабочие листы для детского сада и дошкольников
- Рабочие листы «Животные Арктики» — огромный набор с заданиями по математике и грамотности для малышей, дошкольников, первоклассников и первоклассников
- Зимние птицы Рабочий лист для работы с буквами, счета, сложения и многого другого! (огромный пакет!)
- Страницы рабочего листа жизненного цикла пингвинов
- Последовательность Как построить снеговика. Листы
Четные и нечетные числа Snowball Math Activity
Используя ресурсы с моего сайта, вы соглашаетесь со следующим: этот пост, чтобы получить свою собственную копию) 4 сентября 2020 г. 25 сентября 2015 г. 7 сентября 2018 г. 6 апреля 2022 г. 10 июля 2021 г. 2 декабря 2013 г. 11 декабря 2018 г. 13 августа 2021 г. Бет Горден — творческий многозадачный создатель 123 Homeschool 4 Me. Будучи занятой матерью шести детей, занимающейся домашним обучением, она стремится создавать практические учебные задания и рабочие листы, которые детям понравятся, чтобы сделать обучение УДОВЛЕТВОРИТЕЛЬНЫМ! Она создала более 1 миллиона страниц печатных материалов, чтобы научить детей азбуке, естественным наукам, английской грамматике, истории, математике и многому другому! Бет также является создателем 2 дополнительных сайтов с еще большим количеством образовательных мероприятий и БЕСПЛАТНЫХ печатных материалов — www. Фильтр 3
1 класс 4
2 класс 5
3 класс 6
4 класс Сортировка: НовыеСтарыеНазвания (Я-А)Имя (А-Я)Цена (Высокая>Низкая)Цена (Низкая>Высокая) Показать: 15255075100 $4,50 Сортировка четных и нечетных чисел по программе Curriculum for Autism Нечетные или четные числа 1–100 Сортировка для учащихся с аутизмом и особыми образовательными потребностями. )… Уровни классов: 1-й класс, 2-й класс, 3-й класс Цели IEP: Имея до 10 однозначных или двузначных чисел для сортировки, СТУДЕНТ будет сортировать числа по нечетным или четным с точностью 80%, в 4 из 5 возможностей, МЕСЯЦ, ГОД. $3.00 Счет двойками | Группировка по 2 с НЕЧЕТНЫМ количеством объектов TASK BOX FILLER ACTIVITIES by AutismEducators Счет двойками и группировка по 2 с нечетным числом объектов КАРТОЧКА ЗАДАНИЙ набор задач Заполнитель коробки для использования в качестве ресурса раннего вмешательства по математике в вашем классе специального образования, математическом центре или для учащихся, которые переходят в класс общего образования для обучения математике. Уровни классов: 2-й класс, 3-й класс, 4-й класс Цели IEP: Учитывая НЕЧЕТНОЕ количество объектов до 20, (24) СТУДЕНТ сгруппирует объекты попарно и отметит/назовет правильный количество подсчитанных пар с точностью 80% в 4 из 5 возможностей, по МЕСЯЦАМ, ГОДАМ. $3.00 Счет двойками | Группировка по 2 с объектами | Действия по заполнению ящика задач by AutismEducators Счет двойками путем группировки по 2 с предметами КАРТОЧКИ С ЗАДАЧАМИ – задание для заполнения математических навыков. Считайте с помощью изображений предметов, чтобы научиться считать до 2, пропустите счет до 2 или сгруппируйте по 2 для расширенного счета для навыков умножения. Это сопряжение объектов из двух наборов карточек с заданиями соответствует государственным академическим стандартам. Уровни классов: 1-й класс, 2-й класс, 3-й класс, 4-й класс Цели IEP: Учитывая четное количество объектов до 20, (24) СТУДЕНТ сгруппирует объекты попарно и отметит/ скажем, правильное количество подсчитанных пар, с точностью 80%, в 4 из 5 возможностей, к МЕСЯЦУ, ГОДУ. 2,00 $ Сортировка нечетных и четных чисел – пауки by Curriculum for Autism Тема пауков Сортировка по нечетным и четным числам (числа 1-50) Доски задач/папки с файлами для учащихся с аутизмом и особыми образовательными потребностями. В этом наборе 5 досок с заданиями и 40 карточек с числами. Ваши ученики будут сортировать пауков по нечетным и четным числам до 50. Обратите внимание: для подготовки к этому занятию вам потребуются липучки. Доски и карточки с ответами имеют цветовую маркировку для облегчения освоения… Уровни классов: 1-й класс, 2-й класс, 3-й класс, 4-й класс Цели IEP: Имея сортировочные доски и числовые карточки от 1 до 50, СТУДЕНТ будет сортировать каждое число по четным и нечетным с точностью 80%. Примечание : Мелкие детали представляют опасность удушья и не подходят для детей в возрасте до пяти лет. Обязательно выбирайте материалы урока, отвечающие требованиям безопасности. д.)
д.) >> Четные нечетные снежки
<< Вам также может понравиться
Об авторе
Бет Горден
 kindergartenworksheetsandgames.com и www.preschoolplayandlearn.com
kindergartenworksheetsandgames.com и www.preschoolplayandlearn.com Четные или нечетные числа
Рассмотрите возможность поделиться этой страницей с другими, кому она может быть полезна.
 Считайте с картинками НЕЧЕТНОЕ количество предметов, чтобы научиться считать по 2, пропускать счет по 2 или группировать по 2 для расширенного счета.
Считайте с картинками НЕЧЕТНОЕ количество предметов, чтобы научиться считать по 2, пропускать счет по 2 или группировать по 2 для расширенного счета. Работайте с равными группами объектов, чтобы получить основу для умножения. УИЛЛ Т…
Работайте с равными группами объектов, чтобы получить основу для умножения. УИЛЛ Т… , в 4 из 5 возможностей по МЕСЯЦ, ГОД.
, в 4 из 5 возможностей по МЕСЯЦ, ГОД. Нечетное или четное – начальная математика.
Шаг 1: Соберите материалы.
Шаг 2. Введите действие.
количеству медведей? (Нет) Можем ли мы соединить каждого из медведей Салли с медведями Билли? (Нет) Так число пять четное или нечетное число?» (четный) Объясните , что при наличии даже предметов у вас и у вашего друга может быть равное количество этого предмета (вы можете соединить вещи в пары).
Объясните , что при наличии даже предметов у вас и у вашего друга может быть равное количество этого предмета (вы можете соединить вещи в пары).
Демонстрация : Попросите двух добровольцев. Используя четных манипуляций, дайте каждому ребенку предмет, считая , пока вы раздаете предметы. Произнесите : «У меня в руке четыре медведя. Я собираюсь подарить одного медведя Салли, одного медведя Билли, еще одного медведя Салли и еще одного медведя Билли. Все мои медведи ушли. Сколько медведей у меня было ДО ТОГО, как я отдал их Салли и Билли?» (Четыре) «Есть ли у Салли и Билли равных (одинаковых) медведей?» (Да) «Так четыре четное число или нечетное число ?» (четный) Последней цифрой нечетного числа будет 1, 3, 5, 7 или 9. Объясните , что если вы НАЧНЕТЕ с цифры 1 и посчитаете двойками, вы получите нечетных чисел . Начиная с единицы, посчитайте двойками. Объясните , что, когда есть нечетное количество предметов, вы и ваш друг не можете иметь равно количеству этого предмета (вы не можете соединить их в пару). Демонстрация : Попросите двух добровольцев. Используя нечетных манипуляций, дайте каждому ребенку предмет. Считая , когда вы раздаете предметы, говорит : «У меня в руке пять медведей. Я собираюсь подарить одного медведя Салли, одного медведя Билли, еще одного медведя Салли, еще одного медведя Билли и еще одного медведя Салли. Все мои медведи ушли. Сколько медведей у меня было до того, как я отдал их Салли и Билли? (5) У Салли и Билли есть по 9?0017 равно
Последней цифрой нечетного числа будет 1, 3, 5, 7 или 9. Объясните , что если вы НАЧНЕТЕ с цифры 1 и посчитаете двойками, вы получите нечетных чисел . Начиная с единицы, посчитайте двойками. Объясните , что, когда есть нечетное количество предметов, вы и ваш друг не можете иметь равно количеству этого предмета (вы не можете соединить их в пару). Демонстрация : Попросите двух добровольцев. Используя нечетных манипуляций, дайте каждому ребенку предмет. Считая , когда вы раздаете предметы, говорит : «У меня в руке пять медведей. Я собираюсь подарить одного медведя Салли, одного медведя Билли, еще одного медведя Салли, еще одного медведя Билли и еще одного медведя Салли. Все мои медведи ушли. Сколько медведей у меня было до того, как я отдал их Салли и Билли? (5) У Салли и Билли есть по 9?0017 равно
Шаг 3.
 Вовлеките детей в занятия на уроке.
Вовлеките детей в занятия на уроке.- Каждый ребенок получит 20 манипуляторов, сортировочный коврик и лист для записей с цифрами от 1 до 20.
- Объясните , что так же, как дети рассортировали медведей на даже и нечетные группы, теперь они будут работать индивидуально, чтобы отсортировать медведей и выяснить, какие из следующих чисел четные и какие из чисел нечетные .
- Объясните лист записи. Произнесите : «Вы поместите свои выводы на пустое место рядом с каждым числом. Например, мы уже знаем, что четыре — это (n)_____________ число». (Эвен) «Значит, вы бы написали даже рядом с цифрой 4».
- Для начала попросите детей назвать количество медведей, указанное в листе для записей. Они начнут с номера 1 и дойдут до номера 20 9.0008
- Когда все дети закончат, соберите их и просмотрите листы для записей.
 Используйте лист диаграммной бумаги, чтобы записать их выводы.
Используйте лист диаграммной бумаги, чтобы записать их выводы.
Дополнительные расширения
- Используйте числа выше 20 и далее объясните , что все числа, заканчивающиеся на 1, 3, 5, 7 и 9, являются нечетными и все числа, заканчивающиеся на 0, 2, 4, 6, 8 даже . Дайте детям большие числа, например 456 391, и пусть они решат, равно ли это число 9.0017 четный или нечетный , просто взглянув на число в разряде единиц. Спросите, могут ли они определить четное или нечетное, взглянув на последнее целое число (число в крайнем правом разряде).
Шаг 4: Словарь.
- Нечетное : число, которое не делится на два, например, числа, оканчивающиеся на 1, 3, 5, 7 и 9 (например, «Число 5 – нечетное число»).
- Четный : Число, которое делится на два, например числа, оканчивающиеся на 0, 2, 4, 6 и 8 (например, «Число 6 — это даже номер”)
- Равен : Быть одинаковым по количеству или сумме (например, «Есть ли у Салли и Билли равное количество медведей?»)
Глоссарий ранней математики
Шаг 5: Адаптируйте урок для малышей или дошкольников.

Адаптация урока для малышей
Малыши могут:
- Все еще работать над числовым соответствием один к одному
- Трудно различать нечетный и четный
Поставщики услуг по уходу за детьми могут:
- Использовать номера 1-10. Подсчитайте числа, взятые из ведра, и посчитайте, пока сортирует каждого из медведей в два круга
- Скажите детям, прежде чем они начнут сортировать медведей, какие числа четные и какие числа нечетные . Таким образом, после того, как они отсортируют , они смогут увидеть, что нечетное и даже выглядят.
Адаптированный урок для дошкольников
Дошкольники могут:
- Легко усвоить понятие четных и нечетных и чисел, делящихся на два
Поставщики услуг по уходу за детьми могут:
- Использовать числа больше 20 и далее объяснять , что все числа, заканчивающиеся на 1, 3, 5, 7 и 9, являются нечетными и все числа заканчиваются на 0, 2, 4, 6 , 8 равно даже .
 Дайте детям большие числа, например 456 391, и попросите их решить, является ли число четным или нечетным , просто взглянув на число в разряде единиц.
Дайте детям большие числа, например 456 391, и попросите их решить, является ли число четным или нечетным , просто взглянув на число в разряде единиц.
Предлагаемые книги
- One Odd Day Дорис Фишер (Pleasant, SC: Sylvan Dell Publishing, 2006)
- Мой четный день Дорис Фишер (Pleasant, SC: Sylvan Dell Publishing, 2006)
- Разделение стада: загон нечетных и четных Труди Харрис (Миннеаполис, Миннесота: Millbrook Pr Trade, 2008 г.)
Музыка и движение
- Эта песня знакомит детей с понятием четных чисел и учит их тому, что все четные числа можно «разделить пополам». Поставьте видео на паузу, чтобы спросить детей, четные или нечетные примеры. www.youtube.com/watch?v=Ei19HMn1BxM
- Эта песня учит нечетным цифрам и показывает, что любое число, оканчивающееся на нечетную цифру, также является нечетным .



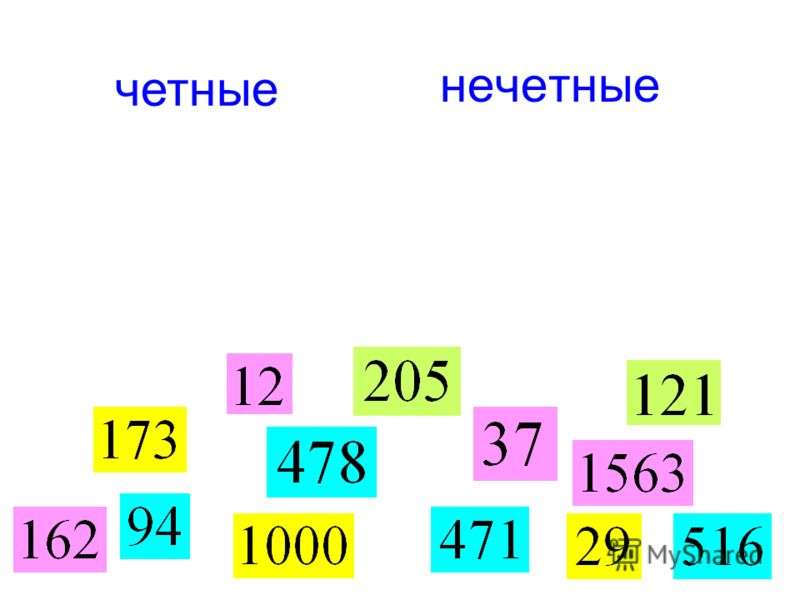
 Какую группу фруктов можно поделить между Андрюшей и мамой поровну?
Какую группу фруктов можно поделить между Андрюшей и мамой поровну?

 Включение нового знания в систему понятий
Включение нового знания в систему понятий
 Работа в тетради с. 54
Работа в тетради с. 54








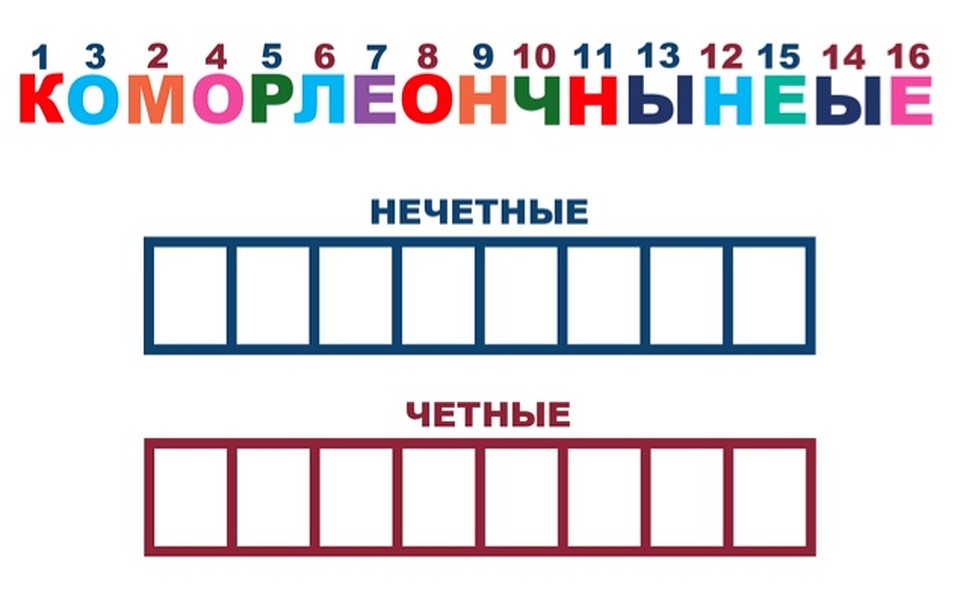
 Число 8 делится на 2 без остатка.
Число 8 делится на 2 без остатка. Нечетными называются числа, которые не делятся на 2 без остатка.
Нечетными называются числа, которые не делятся на 2 без остатка.
 ( Кто-то у доски)
( Кто-то у доски) Что необходимо сделать?
Что необходимо сделать? Какие числа получились – чётные или нечётные . – 1, 3,5,7,9
Какие числа получились – чётные или нечётные . – 1, 3,5,7,9 Если у вас на уроке не возникло трудностей нарисуйте человечка на самой верхней ступеньки. Если во время урока у вас возникли трудности нарисуйте на средней ступеньке . А если у вас нечего не получилось, то на самой первой ступеньке .
Если у вас на уроке не возникло трудностей нарисуйте человечка на самой верхней ступеньки. Если во время урока у вас возникли трудности нарисуйте на средней ступеньке . А если у вас нечего не получилось, то на самой первой ступеньке .