Задача на скорость время расстояние – КОНСПЕКТ УРОКА по математике “ЗАДАЧИ НА ДВИЖЕНИЕ. ВЗАИМОСВЯЗЬ МЕЖДУ ВЕЛИЧИНАМИ: СКОРОСТЬ, ВРЕМЯ, РАССТОЯНИЕ. (ЗАКРЕПЛЕНИЕ)”

Задачи на скорость, время и расстояние: примеры и решение

Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.

Разные объекты имеют разную скорость. Например, средняя скорость пешехода составляет 5 км в час, скорость велосипедиста – 12 км в час, а автомобиля – 80 км в час. При записи скорости, предлог в заменяют наклонной чертой – км/ч (например, 15 км/ч).

Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным. Далее будут рассмотрены задачи только на равномерное движение.

Нахождение скорости

Чтобы найти скорость по данному пути (расстоянию) и времени, надо путь разделить на время.

скорость = расстояние : время

Задача 1. Поезд проехал 320 км за 4 часа. Чему равна скорость поезда?

Решение: Чтобы найти скорость поезда, надо растояние, которое прошёл поезд (320 км), разделить на время поезда в пути (4 ч):

320 : 4 = 80 (км)

Ответ: Скорость поезда равна 80 км/ч.

Задача 2. Турист за 3 часа прошёл 12 км, а велосипедист за 2 часа проехал 24 км. Во сколько раз турист движется медленнее велосипедиста?

Решение: чтобы узнать во сколько раз скорость туриста меньше, чем у велосипедиста, надо узнать их скорость, разделив пройденные расстояния на затраченное время:

12 : 3 = 4 (км/ч) – скорость туриста

24 : 2 = 12 (км/ч) – скорость велосипедиста

Теперь осталось узнать на сколько медленнее движется турист, для этого надо большее число разделить на меньшее:

12 : 4 = 3

Ответ: Турист движется в 3 раза медленнее, чем велосипедист.

Нахождение времени

Чтобы найти время по данному расстоянию и скорости, надо расстояние разделить на скорость.

время = расстояние : скорость

Задача: Лодка преодолела путь в 100 км со скоростью 20 км/ч. Сколько времени плыла лодка?

Решение:

100 : 20 = 5 (ч)

Ответ: Лодка плыла 5 часов.

Нахождение расстояния

Чтобы найти расстояние по данным скорости и времени, надо скорость умножить на время.

расстояние = скорость · время

Задача: Грузовик ехал 12 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?

Решение:

70 · 12 = 840 (км)

Ответ: Грузовик за 12 часов проехал 840 км.

naobumium.info

Скорость, время, расстояние. Задачи по математике 3 класс



Задачи для 3 класса

Числа от 1 до 100

Контрольные работы

Тесты. 3 класс.

Примеры, уравнения



Задачи по математике для 3 класса



Задание 1

Автомобиль проехал 180 км за 3 часа.С какой скоростью он ехал?

Решение
• Всё время движения автомобиля – 3 часа, а пройденый путь – 180 км. Значит за один час он проезжал 180:3=60. Его скорось 60км/ч

Задание 2

Миша прошол на лыжах 80 м за 20 с,а Игорь 45 м за 15 с. Кто из них шёл быстрее?

Решение

Миша затратил больше времени, чем Иигорь,но он и прошёл больше расстояние. Чтобы узнать, кто шёл быстрее,надо сравнить расстояния которий каждый из ребят проходил за одну секунду: 80:20=4 45:15=3. Миша за одну секунду проходил 4 м, а Игорь только 3 м.Значит, Миша шёл быстрее, или с большей скоростью. Говорят так: Миша шёл 4 м в секунду,а Игорь 3 м в секунду.
80 : 20 = 4(м), 45 : 15 = 3(м)

Задание 3

Объясни смысл предложений:
• а) Самолёт летит со скоростью 800 км/ч.
• б) Скорость теплохода 45 км/ч.
• в) Человек идёт со скоростью 4 км/ч.
• г) Меч-рыба развивает скорость 100 км/ч.
• д) Земля движется по орбите со скоростью 30 км/с.
• е) Черепаха ползёт со скоростью 4 м/мин.
• ж) Поезд идёт со скоростью а км/ч. Какие значения может принимать а?
• Можно ли сравнить скорость движения человека со скоростью черепахи?

Решение
• а) Самолёт пролетает за 1 час 800км.
• б) Теплоход проплывает за 1 час 45км.
• в) Человек проходит за 1 час 4км.
• г) Меч-рыба развивает скорость 100 км/ч.
• д) Земля преодолевает расстояние в 30км. за 1 секунду.
• е) Черепаха проползает 4метра за 1 минуту
• ж) а может быть целым положительным числом
• Скорость черепахи можно сравнить со скоростью человека, если выразить эту скорость в одинаковых величинах, например км/ч



Задание 4

Найди:
• а) Скорость космического корабля, если он пролетел 56 км за 8 с.
• б) Скорость улитки, если она проползла 35 м за 7 ч.
• в) Скорость плота на реке, если он за 4 ч проплыл 16 км.
• г) Скорость автобуса, если он прошёл 120 км за 3 ч.
• д) Скорость велосипедиста, если он проехал 36 км за 2 ч.

Решение
• а) Скорость корабля 7 км/с
• б) Скорость улитки 5м/ч
• в) Скорость плота 4км/ч
• г) Скорость автобуса 40км/ч
• д) Скорость велосипеда 18км/ч

Задание 5

Решение
• Мальчик идет со скоростью 4км/ч
• Велосипедист едет со скоростью 18км/ч
• Электричка едет со оскоростью 90км/ч
• Скорость машины 60км/ч
• Скорость автобуса 45км/ч
• Скорость ракеты 6км/с
• Скорость самолета 900км/ч

Задание 6

Решение
• Волга едет со скоростью 100км/ч
• Жигули едут со скоростью 90км/ч
• Запорожец едет со скоростью 50км/ч

Задание 7

• а) Поезд прошёл 224 км за 4 часа. Его скорость в 3 раза меньше скорости вертолёта. Какова скорость вертолёта?
• б) Плот проплыл 27 км за 9 ч, а моторная лодка — 24 км за 2 ч. У кого из них скорость больше и на сколько?

Решение
• а) Скорость вертолета 168км/ч. Скорость поезда – 224 : 4 = 56км/ч, скорость вертолета в 3 раза больше поэтому 56 * 3 = 168.
• б) Скорость больше у моторной лодки на 9км/ч. Скорость плота 3км/ч = 27 : 9. Моторной лодки 12км/ч = 24 : 2. Значит 12-3=9.



Задание 8

Сравни:

5 ч 6 мин	56 мин
9 мин 20 с	560 с
1 сут. 15 ч	115 ч
108 мин	1ч8мин
734с	7мин 34 с
206ч	2 сут. 6ч

Решение:

5 ч 6 мин	>	56 мин
9 мин 20 с	=	560 с
1 сут. 15 ч	<	115 ч
108 мин	>	1ч8мин
734с	>	7мин 34 с
206ч	>	2 сут. 6ч

Задание 9

• а) Грузовая машина за 8 ч прошла 280 км, а легковая машина это же расстояние — за 4 ч. Во сколько раз скорость грузовой машины меньше скорости легковой?
• б) Велосипедист за 3 ч проехал 57 км, а мотоциклист за 2 ч проехал на 71 км больше. На сколько километров в час скорость велосипедиста меньше скорости мотоциклиста?

Решение
• a) Сначала узнаем скорость грузовика 280 : 8 = 35км/ч. Затем скорость легковой машины 280 : 4 = 70км/ч. Чтобы узнать во сколько раз скорость грузовой машины меньше чем легковой нужно скорость грузовой разделить на скорость легковой: 70 : 35 = 2. Ответ: В 2 раза.
• б) Сначала узнаем скорость велосипедиста 57 : 3 = 19км/ч. Узнаем сколько проехал мотоциклист 57 + 71 = 128км. Узнаем скорость мотоциклиста 128 : 2 = 64км/ч. Узнаем разницу в скорости велосипедиста и мотоциклиста 64 – 19 = 45км/ч. Ответ: 45км/ч.

Задание 10

Придумай задачу, в которой надо найти скорость по известному расстоянию и времени, и реши её.

Решение Задача:
• Из пункта а вышел поезд. Через 4 часа поезд прибыл в пункт б. Какова скорость поезда если расстояние от пункта а до пункта б 360км.
Решение задачи:
• 360 : 4 = 90км/ч. Скорость поезда 90км/ч.

Задание 11

Запиши множество делителей и множество кратных числа 14.

Решение
• Множество делителей: 1, 2, 7, 14.
• Множество кратных: 14, 28, 42, 56, 70, 84, 98, 102, 116, 130, 144, и так до бесконечности.

Задание 12

Реши уравнения с комментированием по компонентам действий:

• а) (40 • х): 10 = 28;
• б) у : 9 – 28 = 32;
• в) 39 + 490 : k = 46;
• г) (25 – а) • 7 = 63.

Решение
• а) Сначала узнаем значение выражения в скобках(40 • х) для этого надо 28 * 10 = 280, вычислем значение x = 280 : 40 = 70. x = 70.
• б) Сначала узнаем значение y : 9 для этого 32 + 28 = 60; узнаем значение y для этого 9 * 60 = 540.
• в) Сначала узнаем значение 490 : k для этого 46 – 39 = 7; что бы узнать значение k нужно 490 : 7 = 70. k = 70.
• г) Сначала узнаем значение выражения в скобках(25-а) для этого 63 : 7 = 9; Вычисляем значение а для этого 25 – 9 = 16. а равно 16.

Задание 13

Выполни сложение и вычитание. Сделай проверку:

• а) 547923 + 83699221;
• б) 483567823 + 998430;
• в) 4758036-50854;
• г) 2666990000 – 89607787.

Решение
• а) 84247144; проверка: 84247144 – 83699221 = 547923.
• б) 484566253; проверка: 484566253 – 483567823 = 998430.
• в) 4707182; проверка: 4707182 + 50854 = 4758036.
• г) 2577382213; проверка: 2577382213 + 89607787 = 2666990000.

Задание 14

По двору ходили гуси. Всего у них было 22 ноги. Подошли 3 утёнка и 4 козлёнка. Сколько ног гуляет теперь по двору?

Три утенка – это еще 6 ног, 4 козленка – это еще 16 ног потому что у козленка 4 ноги 4 * 4 =16. Теперь слаживаем все ноги: 22 + 6 + 16 = 44.
Ответ: 44 ноги гуляло по двору.



На странице использованы задачи и задания из книги Л. Г. Петерсон «Математика. 3 класс. Часть3.» 2008г. Ссылка на сайт автора: http://www.sch3000.ru

 

Простые задачи



Составные задачи



mat-zadachi.ru

Текстовые задачи. Задачи на движение с решениями

Задачи на движение с решениями

перейти к содержанию курса текстовых задач

1. Первый турист проехал 2 ч на велосипеде со скоростью 16 км/ч. Отдохнув 2 ч, он отравился дальше с прежней скоростью. Спустя 4 ч после старта велосипедиста ему вдогонку выехал второй турист на мотоцикле со скоростью 56 км/ч. На каком расстоянии от места старта мотоциклист догонит велосипедиста? Решение
2. Из пункта A в пункт B отправились три машины друг за другом с интервалом в 1 ч. Скорость первой машины равна 50 км/ч, а второй — 60 км/ч. Найти скорость третьей машины, если известно, что она догнала первые две машины одновременно. Решение
3. Поезд был задержан в пути на 12 мин, а затем на расстоянии 60 км наверстал потерянное время, увеличив скорость на 15 км/ч. Найти первоначальную скорость поезда. Решение
4. Расстояние между станциями A и B равно 103 км. Из A в B вышел поезд и, пройдя некоторое расстояние, был задержан, а потому оставшийся до B путь проходил со скоростью, на 4 км/ч большей, чем прежняя. Найти первоначальную скорость поезда, если известно, что оставшийся до B путь был на 23 км длиннее пути, пройденного до задержки, и что на прохождение пути после задержки было затрачено на 15 мин больше, чем на прохождение пути до нее. Решение
5. Скорость автомобиля по ровному участку на 5 км/ч меньше, чем скорость под гору, и на 15 км/ч больше, чем скорость в гору. Дорога из A в B идет в гору и равна 100 км. Определить скорость автомобиля по ровному участку, если расстояние от A до B и обратно он проехал за 1 ч 50 мин. Решение
6. Автобус проходит расстояние между пунктами A и B по расписанию за 5 ч. Однажды, выйдя из A, автобус был задержан на 10 мин в 56 км от A и, чтобы прибыть в B по расписанию, он должен был оставшуюся большую часть пути двигаться со скоростью, превышающей первоначальную на 2 км/ч. Найти скорость движения автобуса по расписанию и расстояние между пунктами A и B, если известно, что это расстояние превышает 100 км. Решение
7. Поезд проходит мимо платформы за 32 с. За сколько секунд поезд проедет мимо неподвижного наблюдателя, если длина поезда равна длине платформы? Решение
8. Два поезда отправляются навстречу друг другу с постоянными скоростями, один из А в В, другой из В в А. Они могут встретиться на середине пути, если поезд из А отправится на 1,5 ч раньше. Если бы оба поезда вышли одновременно, то через 6 ч расстояние между ними составило бы десятую часть первоначального. Сколько часов каждый поезд тратит на прохождение пути между А и В? Решение
9. От пристани А одновременно отправились вниз по течению катер и плот. Катер спустился вниз на 96 км, потом повернул обратно и вернулся в А через 14 ч. Найти скорость катера в стоячей воде и скорость течения, если известно, что катер встретил плот на обратном пути расстоянии 24 км от А. Решение
10. Пункт В находится по реке ниже пункта А. В одно и то же время из пункта А отплыли плот и первая моторная лодка, а из пункта В – вторая моторная лодка. Через некоторое время лодки встретились в пункте С, а плот за это время проплыл третью часть пути от А до С. Если бы первая лодка без остановки доплыла до пункта В, то плот за это время прибыл бы в пункт С. Если бы из пункта А в пункт В отплыла вторая лодка, а из пункта В в пункт А – первая лодка, то они встретились бы в 40 км от пункта А. Какова скорость обеих лодок в стоячей воде, а также расстояние между пунктами А и В, если скорость течения реки равна 3 км/ч? Решение
11. Два тела, двигаясь по окружности в одном направлении, встречаются через каждые 112 мин, а двигаясь в противоположных направлениях – через каждые 16 мин. Во втором случае расстояние между телами уменьшилось с 40 м до 26 м за 12 с. Сколько метров в минуту проходит каждое тело и какова длина окружности? Решение
12. Две точки, двигаясь по окружности в одном направлении, встречаются каждые 12 мин, причем первая обходит окружность на 10 с быстрее, чем вторая. Какую часть окружности проходит за 1 с каждая точка? Решение
13. Два тела движутся навстречу друг другу из двух точек, расстояние между которыми 390 м. Первое тело прошло в первую секунду 6 м, а в каждую последующую секунду проходило на 6 м больше, чем в предыдущую. Второе тело двигалось равномерно со скоростью 12 м/c и начало движение спустя 5 с после первого. Через сколько секунд после того, как начало двигаться первое тело, они встретятся? Решение

Задачи для самостоятельного решения

1. Дорога от A до D длиной в 23 км идет сначала в гору, затем — по ровному участку, а потом — под гору. Пешеход, двигаясь из A в D, прошел весь путь за 5 ч 48 мин, а обратно, из D в A, — за 6 ч 12 мин. Скорость его движения в гору равна 3 км/ч, по ровному участку — 4 км/ч, а под гору — 5 км/ч. Определить длину дороги по ровному участку. Ответ:  8 км
2. В 5 ч утра со станции A вышел почтовый поезд по направлению к станции B, отстоящей от A на 1080 км. В 8 ч утра со станции B по направлению к A вышел пассажирский поезд, который проходил в час на 15 км больше, чем почтовый. Когда встретились поезда, если их встреча произошла в середине пути AB? Ответ: в 5 ч дня
3. Из пункта A впунктB отправились три велосипедиста. Первый из них ехал со скоростью 12 км/ч. Второй отправился на 0,5 ч позже первого и ехал со скоростью 10 км/ч. Какова скорость третьего велосипедиста, который отправился на 0,5 ч позже второго, если известно, что он догнал первого через 3 ч после того как догнал второго? Ответ: 15 км/ч
4. Два поезда — товарный длиной в 490 м и пассажирский длиной в 210 м — двигались навстречу друг другу по двум параллельным путям. Машинист пассажирского поезда заметил товарный поезд, когда он находился от него на расстоянии 700 м; через 28 с после этого поезда встретились. Определить скорость каждого поезда, если известно, что товарный поезд проходит мимо светофора на 35 с медленнее пассажирского. Ответ:  36 км/ч; 54 км/ч
5. Турист A и турист B должны были выйти одновременно навстречу друг другу из поселка M ипоселкаN соответственно. Однако турист A задержался и вышел позже на 6 ч. При встрече выяснилось, что A прошел на 12 км меньше, чем B. Отдохнув, туристы одновременно покинули место встречи и продолжили путь с прежней скоростью. В результате A пришел в поселок N через 8 ч, а B пришел в поселок M через 9 ч после встречи. Определить расстояние MN и скорости туристов. Ответ:  84 км; 6 км/ч; 4 км/ч.
6. Пешеход, велосипедист и мотоциклист движутся по шоссе в одну сторону с постоянными скоростями. В тот момент, когда пешеход и велосипедист находились в одной точке, мотоциклист был на расстоянии 6 км позади них, а тот момент, когда мотоциклист догнал велосипедиста, пешеход отстал от них на 3 км. На сколько километров велосипедист обогнал пешехода в тот момент, когда пешехода настиг мотоциклист? Ответ: 2 км
7. Два туриста вышли одновременно из пункта A в пункт B.Первый турист проходил каждый километр на 5 мин быстрее второго. Пройдя 20% расстояния от A до B, первый турист повернул обратно, пришел в A, пробыл там 10 мин, снова пошел в B и оказался там одновремен-
   но со вторым туристом. Определить расстояние от A до B, если второй турист прошел его за 2,5 ч. Ответ: 10 км
8. Рыбак проплыл на лодке от пристани против течения 5 км и возвратился обратно на пристань. Скорость течения реки равна 2,4 км/ч. Если бы рыбак греб с той же силой в неподвижной воде озера на лодке с парусом, увеличивающим скорость на 3 км/ч, то он за то же время проплыл бы 14 км. Найти скорость лодки в неподвижной воде. Ответ:  9,6 км/ч
9. Моторная лодка проплыла по озеру, а потом спустилась вниз по реке, вытекающей из озера. Расстояние, пройденное лодкой по озеру, на 15% меньше расстояния, пройденного по реке. Время движения лодки по озеру на 2% больше, чем по реке. На сколько процентов скорость движения лодки вниз по реке больше скорости движения по озеру? Ответ: на 20%
10. Турист проплыл в лодке по реке из города A в город B и обратно, затратив на это 10 ч. Расстояние между городами равно 20 км. Найти скорость течения реки, зная, что турист проплывал 2 км против течения реки за такое же время, как 3 км по течению. Ответ: 5/6 км/ч
11. По окружности длиной 60 м равномерно в одном направлении движутся две точки. Одна из них совершает полный оборот на 5 с быстрее другой. При этом совпадение точек происходит каждый раз через 1 мин. Определить скорости точек. Ответ:  4 м/с; 3 м/с.
12. Из точек A и B одновременно начали двигаться два тела навстречу друг другу. Первое в первую минуту прошло 1 м, а в каждую последующую проходило на 0,5 м больше, чем в предыдущую. Второе тело проходило каждую минуту по 6 м. Через сколько минут оба тела встретились, если расстояние между A и B равно 117 м? Ответ: через 12 мин.
13. Два приятеля в одной лодке прокатились по реке вдоль берега и вернулись по одной и той же речной трассе через 5 ч с момента отплытия. Протяженность всего рейса составила 10 км. По их подсчетам получилось, что на каждые 2 км против течения в среднем потребовалось столько же времени, сколько на каждые 3 км по течению. Найти скорость течения реки, а также время проезда туда и время проезда обратно. Ответ:  5/12 км/ч; 2 ч и 3 ч.

 

Метки движение, текстовые задачи. Смотреть запись.

www.itmathrepetitor.ru

Задачи на движение с решениями

В задачах на движение  рассматриваются три взаимосвязанные величины:

S – расстояние (пройденный путь),

t – время движения и

V – скорость – расстояние, пройденное за единицу времени.

• Расстояние – это произведение скорости на время движения;

S = V t

• Скорость – это расстояние, которое тело проходит за единицу времени;
• Скорость  – это частное от деления расстояния на время движения;

V = S / t

• Время – это частное от деления расстояния на скорость движения

t = S / V

 

Какие могут быть ситуации?

 

Ситуация первая

Два объекта движение начинают одновременно навстречу друг другу.

Встречное  движение.

Ситуация вторая

Два объекта движение начинают одновременно в противоположных направлениях.

Движение в противоположных направлениях из одного пункта

Ситуация третья

Два объекта движение начинают одновременно в одном направлении.

При решении этих задач надо использовать понятия «скорость сближения» и « скорость удаления».

 

ЗАДАЧА 1

В данный момент расстояние между двумя таксистами 345 км. На каком расстоянии будут находиться таксисты через два часа, если скорость одного 72 км /ч., а другого  -68 км /ч., и они выезжают навстречу друг другу одновременно?

Первый способ решения
1) 72 + 68 =140 (км /ч.) – скорость сближения таксистов.
2) 140 * 2 = 280 (км) – на такое расстояние таксисты    приблизятся друг к другу за 2 часа.
3) 345 – 280 = 145 (км) – на таком расстоянии будут таксисты через 2 часа.
Ответ: 145 км.

Второй способ решения

1) 72 * 2 =144 (км) – такое расстояние проедет один таксист за 2 часа.

2)  68 * 2 = 136 (км) – такое расстояние проедет другой таксист за 2 часа.

3) 144+ 136 =280 (км) – на такое расстояние таксисты приблизятся друг к другу за 2 часа.

4) 345 – 280 = 145 (км) – на таком расстоянии будут таксисты через 2 часа.

Ответ: 145 км.

ЗАДАЧА 2

Расстояние между городами А и В 720км. Из А в В вышел скорый поезд со скоростью 80 км /ч. Через 2 часа навстречу ему  из В в А  вышел

пассажирский поезд  со  скоростью 60 км /ч. Через  сколько  часов после   выхода  пассажирского  поезда  эти  поезда встретятся?

Решение

1) 80*2=160(км) -прошёл скорый поезд за 2 часа.

2) 720-160=560(км) -осталось пройти поездам.

3) 80+60=140(км/ч) -скорость сближения 2 поездов.

4) 560:140=4(ч) -был в пути пассажирский поезд.

Ответ: 4часа.

ЗАДАЧА 3

Из двух пунктов навстречу друг другу одновременно выехали два автобуса.  Скорость  одного  автобуса  45 км /ч,  а скорость другого автобуса 72 км /ч. Первый автобус до встречи проехал 135км.
Найдите расстояние между пунктами.

Решение

Первый способ решения
1) 135 : 45 = 3 (часа) – ехали автобусы до встречи.
2) 72 * 3 = 216 (км) – проехал второй автобус до встречи.
3) 135 + 216 = 351 (км) – расстояние между пунктами.
Ответ: 351 км.

Второй способ решения

1) 135 : 45 = 3 (часа) – ехали автобусы до встречи.

2) 45 +72 = 117 (км/ ч.). – скорость сближения автобусов .

3) 117 * 3 = 351 (км) – расстояние между пунктами.

Ответ: 351 км.

Что такое скорость сближения?

ЗАДАЧА 4

Машина и автобус выехали из двух городов, находящихся на расстоянии 740 км навстречу друг другу со скоростями 70 км/ч и 50 км/ч.  Какое расстояние будет между машинами через 5 часов?

Решение

Первый способ решения

1) 50 * 5 = 250 (км) – проедет машина до встречи.

2) 70 * 5 = 350 (км) – проедет автобус до встречи.

3) 250 + 350 = 600 (км) – на такое расстояние они приблизятся друг к другу.

4) 740 -600 = 140 (км)  – такое расстояние будет между ними через 5 часов.

Ответ: 140 км.

Второй способ решения

1) 50 + 70 = 120 (км /ч.) – скорость сближения автобуса и машины.

2) 120 * 5 = 600 (км) – на такое расстояние они приблизятся друг к другу.

3) 740 – 600 = 140 (км) – такое расстояние будет между ними через 5 часов.

Ответ: 140 км.

ЗАДАЧА 5

Две гоночные машины выехали навстречу друг другу. Расстояние между ними было 660 км. Одна ехала со скоростью 100 км/ч, а другая 120 км/ч.  Через какое время они встретятся?

Решение

1) 100+120=220(км/ч)- скорость сближения машин .

2) 660:220=3(ч) -через такое время встретятся гоночные машины.

Ответ: через 3 часа.

ЗАДАЧА 6

Из одного логова одновременно в противоположных направлениях выбежало два тигра. Скорость одного тигра 48 км / ч.,  а  другого  – 54 км ч. Какое расстояние будет между тиграми через 3 часа?

Решение

Первый способ решения

1) 48 * 2 = 96 (км) – пробежит один тигр за 2 часа.

2) 54 * 2 = 108 (км) – пробежит другой тигр за 2 часа.

3) 96 + 108 = 204 (км) – будет между тиграми через 2 часа.

Ответ: 204 км.

Второй способ решения

1) 48 + 54 =102 (км /ч.) – скорость удаления тигров.

2) 102 * 2 =204 (км) – будет между тиграми через 2 часа.

Ответ: 204 км.

ЗАДАЧА 7

Максим и Саша вышли из школы со скоростью 50 м/мин. Рома вышел вслед за ними через 6 минут со скоростью 80 м/мин. Через сколько минут  Рома догонит Максима и Сашу?

Решение

1) 80 – 50 = 30 (км /ч.) –скорость сближения мальчиков.

2) 50 * 6 = 300 (км) – такое расстояние было между мальчиками перед выходом из школы Ромы.

3) 300 : 30 = 10 (мин.) – через такое время Рома догонит друзей.

Ответ: через 10 мин.

 

ИТОГИ

1) При решении задач на движении двух объектов применяются понятия «скорость сближения» и «скорость удаления».

2) При решении задач на встречное движение  и движение в противоположных направлениях скорость сближения и скорость удаления находятся сложением скоростей движущихся объектов.

3) При решении задач на движение в одном направлении скорость сближения и скорость удаления находятся вычитанием скоростей движущихся объектов.

iumka.ru

Математика: Простые задачи на движение

S – расстояние (путь); измеряется в км, м и т. д.

V – скорость (расстояние, преодолеваемое за единицу времени); измеряется в км/ч, м/мин и т.д.

t – время; измеряется в часах, минутах и т.д.

Чтобы найти расстояние, надо скорость умножить на время:

S = V • t

Чтобы найти скорость, надо расстояние разделить на время:

V = S : t

Чтобы найти время, надо расстояние разделить на скорость:

t = S : V

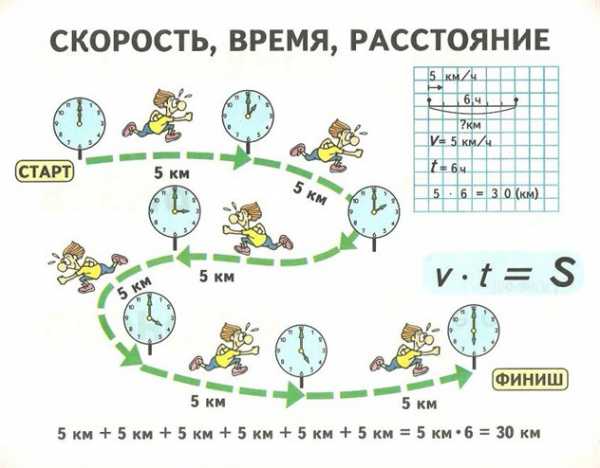
Пример 1. Задача на нахождение расстояния

Автомобиль двигается со скоростью 65 км/ч. Какое расстояние он пройдёт за 7 ч?

Схема к задаче:

 

Решение:

S = V • t

65 • 7 = 455 (км)

Ответ: 455 км.

Пример 2. Задача на нахождение скорости:

За 3 часа поезд проехал 195 км. С какой скоростью ехал поезд?

Схема к задаче:

 

Решение:

V = S : t

195 : 3 = 65 (км/ч)

Ответ: 65 км/ч.

Пример 3. Задача на нахождение времени:

Пешеход двигался со скоростью 5 км/ч и прошёл 15 км. Сколько часов пешеход был в пути?

Схема к задаче:

 

Решение:

t = S : V

15 : 5 = 3 (ч)

Ответ: 3 часа.

Задачи на движение Скорость велосипедиста 12 км / ч .

Сколько километров проедет велосипедист за 3 часа?

Пассажирский поезд за 8 часов прошёл 480 км.

За сколько часов он проедет 540 км при такой же скорости?

Скорость моторной лодки 28 км/ч. Какое расстояние пройдёт  моторная лодка за 4 часа? Автомобиль проехал 180 км за 3 часа. За сколько часов он проедет 240 км при той же скорости? Скорость автобуса 42 км/ч. Сколько км проедет автобус за 2 ч? Подводная лодка проплывает 200 км за 5 часов. За сколько часов она проплывёт 360 км? Скорость самолёта 800км/ч. Какое расстояние пролетит самолёт за 5 часов?

Грузовая машина за 6 часов прошла 240 км. За сколько часов она проедет 320 км при той же          скорости?

Теплоход прошёл за 6 часов 180 км. С какой скоростью шёл теплоход? Автобус едет со скоростью 50 км\ч.

Какое расстояние проедет автобус за 7 часов?

Моторная лодка прошла  90 км за 3 часа.Найди скорость моторной лодки.

Скорость самолёта 800 км/ч, а скорость подводной лодки 200 км/ч. Во сколько раз скорость самолёта больше, чем скорость подводной лодки?

Велосипедист проехал 30 км со скоростью 10 км/ч.Сколько часов был в пути велосипедист?

Скорость пассажирского поезда 70 км/ч, а скорость теплохода 50 км/ ч. На сколько скорость теплохода меньше скорости пассажирского поезда? 1.          Уж проплыл 48 дм со скоростью 8 дм/с. Сколько времени он плыл? 2.          Лодка плыла 4 ч со скоростью 7 км/ч. Какое расстояние проплыла лодка? 3.          Мотоциклист за 4 ч проехал 320 км. С какой скоростью ехал мотоциклист? 4.          Велосипедист 33 км проехал со скоростью 11 км/ч. Сколько времени он был в пути? 5.          Катер за 3 ч проплыл 96 км. С какой скоростью плыл катер? 6.          Вертолёт летел 2 ч со скоростью 200 км/ч. Какое расстояние пролетел вертолёт? 7.          Мышка, убегая от кота, пробежала 12 м со скоростью 3 м/с. Сколько времени ушло у неё на спасение? 8.          Паук за 2 с пробежал 60 см. С какой скоростью бежал паук? 9.          Жук за 2 ч пролетел 22 км. С какой скоростью летел жук? 10.      Слон бежал 2 ч со скоростью 40 км/ч. Какое расстояние пробежал слон? 11.      Белый медведь проплыл 40 км за 4 ч. С какой скоростью плыл медведь? 12.      Витя пробежал 20 м за 10 с.  С какой скоростью бежал Витя? 13.      Путь от дома до школы длиной 1200 м мальчик прошёл со скоростью 60 м/мин. Сколько времени мальчик шёл до школы? 14.      За какое время поезд пройдёт 210 км, если он будет идти со скоростью 70 км/ч? 15.      Лыжник шёл 5 ч со скоростью 14 км/ч. Какое расстояние прошёл лыжник? 16.      Антилопа 80 м бежала со скоростью 20 м/с. Сколько времени она затратила на этот путь? 17.      Самолёт пролетел 1800 км за 3 ч. С какой скоростью летел самолёт? 18.      За какое время сокол пролетел 78 м, если он летел со скоростью 26 м/с? 19.      Почтовый голубь за 3 ч пролетел 270 км. С какой скоростью летел почтовый голубь? 20.      Жираф бежал 60 с со скоростью 12 м/с. Какое расстояние пробежал жираф? 21.      Комар пролетел 16 дм со скоростью 4 дм/с. Сколько времени комар был в полёте? 22.      Самолёт пролетел 1800 км со скоростью 600 км/ч. Сколько времени он был в полёте? 23.      Скорый поезд ехал 5 ч со скоростью 90 км/ч. Какое расстояние проехал поезд? 24.      За 8 минут многоножка проползла 16 дм. С какой скоростью ползла многоножка? 25.      Поезд ехал 2 ч со скоростью 35 км/ч. Какое расстояние проехал поезд? 26.      За 4 с бегемот пробежал 48 м. С какой скоростью бежал бегемот? 27.      Кряква летела 3 мин со скоростью 2 км/мин. Какое расстояние проплыла кряква? 28.      Оса летела 40 км со скоростью 20 км/ч. Сколько времени она была в полёте? 29.      Ленивец сползал по стволу дерева со скоростью 2 м/мин. За какое время он проползёт 20 м? 30.       Мотоциклист ехал по шоссе  4 ч со скоростью 40 км/ч.  Какое расстояние проехал мотоциклист? 31.      Муха пролетела 75 м за 15 с. С какой скоростью летела муха? 32.      Ёжик пробежал 16 м со скоростью 2 м/с. Сколько времени бежал ёжик? 33.      Жираф бежал 600 м со скоростью 10 м/с. Сколько времени он был в пути? 34.      Вертолет летел 3 ч со скоростью 17 км/ч. Какое расстояние пролетел вертолёт? 35.      За какое время туристы проплывут на лодке 60 км со скоростью 12 км/ч? 36.      Какое расстояние пешеход пройдёт за 3 ч, идя со скоростью 5 км/ч? 37.      Велосипедист ехал 2 ч со скоростью 18 км/ч. Какое расстояние проехал велосипедист? 38.      Туристы за 5 ч проплыли на лодке 60 км. С какой скоростью плыли туристы? 39.      Лодка плыла 3 ч со скоростью 7 км/ч. Какое расстояние проплыла лодка? 40.      Туристы за 5 ч проплыли на лодке 60 км. С какой скоростью плыли туристы? 41.      За какое время пролетит муха расстояние в 75 м со скоростью 5 м/с? 42.      Крот бежал 7 с со скоростью 10 см/с. Какое расстояние проплыл плот? 43.      Оса за 2 ч пролетела 40 км. С какой скоростью летела оса? 44.      Жираф за 60 с пробежал 720 м. С какой скоростью бежал жираф 45.       Катер проплыл 96 км со скоростью  32 км/ч. Сколько времени был в пути катер? 46.      Рак ползёт со скоростью 18 м/мин. Какое расстояние он проползёт за 3 мин? 47.      Рыба-меч 3 ч плыла со скоростью 70 км/ч. Какое расстояние проплыла рыба? 48.      Лосось за 5 ч проплыл 150 км. С какой скоростью плыл лосось?

ymnyasha.blogspot.com

Как решать задачи на скорость?

Скорость, время и расстояние при движении связаны жёстким соотношением: S = v * t, где v – скорость движения, t – время, затраченное на движение, S – расстояние между начальной и конечной точкой движения. Об этом основном соотношении величин читайте в статье «Как решать задачи на движение?». Ниже мы поговорим о том, как можно найти скорость, расстояние или время в задаче.

Решаем задачи на скорость

Примеры подобных задач уже рассмотрены в статье Как найти скорость, время расстояние. Мы разберёмся в алгоритме решения задач на скорость и другие характеристики движения.

Как решать задачи: основные правила

• Прежде всего, надо учитывать, что скорость движения в таких задачах постоянна: нет ни торможения, ни ускорения. Поэтому часто говорят не просто о скорости, а о средней скорости, которая равна v = S / t.
• Нужно очень внимательно читать задачу и записать её в математическом виде, т.е. убрать всё лишнее. Уравнениям всё равно, идёт речь о Пете, поезде или лодке, что они делали и зачем. Главное – это движение, время, путь, скорость. Вот это всё и нужно записать.
• Решая задачи на движение, нужно обязательно сделать рисунок, на котором изобразить весь путь, расстояния, места встреч и т.п. Тогда сразу станет ясен характер движения, и будет понятно, что с этим нужно делать.
• Нельзя в задаче использовать одновременно метры и километры, секунды и часы. Все величины должны иметь одну размерность. Если в задаче сказано, что один объект был в дороге 10 часов, а другой – половину суток, нужно половину суток перевести в часы.

Пример решения задачи на скорость

Рассмотрим задачу. Расстояние от города до села 45 км. Из села в город вышел пешеход со скоростью 5 км/ч. Через час навстречу ему из города в село выехал велосипедист со скоростью 15 км/ч. Кто из них в момент встречи будет ближе к селу?

Внимательно читаем и записываем условия задачи:

• S = 45 км
• v1 = 5 км/ч.
• v2 = 15 км/ч.
• t1 – t2 = 1 ч. – пешеход вышел на час раньше, значит, до вст

elhow.ru

Урок математики по теме “Скорость, время, расстояние”. 5-й класс

Разделы: Математика

---

“Я люблю математику не только потому, что
она находит применение в технике, но и потому,
что она красива”.

Петер Ропсе

Цели урока: [Приложение 1]

1. Продолжать вырабатывать у учащихся умения и навыки решения задач с использованием деления натуральных чисел;
2. Развивать внимание, зрительную память, логическое и образное мышление, активность учащихся на уроках;
3. Продолжить развитие устной и письменной речи на уроках математики;
4. Прививать интерес и любовь к предмету;
5. Продолжить учиться видеть связь математики с реальной действительностью;
6. Продолжить учиться применять свои знания в нестандартных ситуациях.

План урока: [Приложение 1]

1. Организационный момент.
2. Скорость, время, расстояние – повтор формул.
3. Устная работа.
4. Составление задачи по рисунку.
5. Викторина.
6. Задача от дяди Степы-милиционера.
7. Олимпиадная задача.
8. Итоги урока.

Оборудование: картинки-пояснения к задачам; ксерокопии листов с домашним заданием; презентация к уроку; костюм для дяди Степы-милиционера.

Перед началом урока предлагается высказаться 5-6 ученикам словами великих людей о математике. (Высказывания ученики ищут дома и в библиотеке, это их домашнее задание)

Ход урока

1. Повторить, как найти расстояние, время, скорость, и решить задачи.

Дорогие ребята, в 4-м классе вы решали много задач по математике связанных с движением, для решения этих задач вы пользовались формулами нахождения скорости, времени или расстояния при равномерном движении. Эта формула выглядит так: <Рисунок 8> [Приложение 1]

S = V·t.

В данной формуле S – это путь, V – скорость, а t – время. Эта формула справедлива только для случаев, когда движение было с постоянной, т.е. не изменой скоростью.

Давайте рассмотрим пример [Приложение 1], грузовик ехал из одного города в другой 3 часа с постоянной скоростью 60 км/ч. [3] Тогда для того, чтобы узнать расстояние между городами нужно умножить 3 на 60 и получим 180 км.

Теперь рассчитаем, с какой скоростью следовало ехать грузовику, чтобы проехать этот путь за 2 часа. Для этого из формулы нужно выразить скорость:

V=S/t = 180/2=90 км/ч.

Аналогично предыдущему примеру узнаем время, за которое автомобиль преодолел то же расстояние, двигаясь со скоростью 120км/ч:

t=S/V = 180/120=1,5ч.

2. Устные упражнения.

На доске оформляются краткие и наглядные условия задач, полный текст задачи ребята видят на слайде презентации [Приложение 1]

1. Из пунктов А и В навстречу друг другу выехали автомобиль со скоростью 60 км/ч и велосипедист со скоростью 15 км/ч. Встретятся ли автомобиль и велосипедист через 2 часа, если расстояние между пунктами 160 км?[2] (Решить задачу двумя способами.)<Рисунок 1> [Приложение 1]

2. Из лагеря геологоразведчиков выехал вездеход со скоростью 30 км/ч. Через 2 часа вслед за ним был послан другой вездеход. С какой скоростью он должен ехать, чтобы догнать первый через 4 часа после своего выхода? [4] <Рисунок 2> [Приложение 1]

3. По рисунку составить задачу на движение и решить ее

. [1]

Рисунок задачи на слайде презентации [Приложение 1]

4. Викторина

(3 ряда – каждому ряду выдается по тексту задачи (всего 3 задачи) и карточки для наглядного составления краткой записи на доске, а также тексты всех трех задач выводятся на слайде [Приложение 1]). Ученикам необходимо решить задачу, представить наглядную краткую запись-схему у доски и предоставить ее решение.

Первый ряд: “Автомобиль “Москвич” за 3 часа может проехать 360 км. Бескрылая птица страус – лучший бегун в мире – развивает скорость до 120 км/ч. Сравните скорости автомобиля “Москвич” и страуса. [2] <Рисунок 3>

Второй ряд: “Скорость распространения света самая большая в природе – 300000 км/с. На Солнце произошла вспышка. Через какое время ее увидят на Земле, если расстояние от Земли до Солнца равно 150000000 км? [1] <Рисунок 4>

Третий ряд: “Пройденный путь пешехода S, его скорость v и время движения t связаны соотношением S = vt. Если пешеход за 4 часа прошел 24 км, то его скорость равна….? [3] <Рисунок 5>

5. Входит дядя Степа-милиционер

(Один из учеников класса, желательно посильнее который, с ним заранее разбираются задачи, и он их дома решает) и предлагает задачу из сборника задач по основам безопасности дорожного движения. <Рисунок 9>

Ширина проезжей части дороги 15 м, зеленый сигнал светофора горит 20 секунд. С какой наименьшей скоростью может двигаться пешеход с момента загорания светофора, чтобы благополучно перейти дорогу? [5] <Рисунок 6>

Решение:

1) 15 м = 1500 см
2) 1500 : 20 = 75 см/с.

Ответ: пешеход может двигаться со скоростью 75 см/с.

6. Решить олимпиадную задачу.

[Приложение 1]

Из пунктов А и В, расстояние между которыми 100 км, со скоростями 20 км/ч и 30 км/ч выезжают навстречу друг другу два велосипедиста. Вместе с ними со скоростью 50 км/ч вылетают две мухи, летят до встречи, поворачивают и летят обратно до встречи с велосипедистами, снова поворачивают и т. д. Сколько километров пролетит каждая муха в направлении от А до В до того момента, когда велосипедисты встретятся? [6] <Рисунок 7>

Решение: Велосипедисты встретятся через 2 часа на расстоянии 40 км/ч от А. За это время каждая муха пролетела 100 км. Муха, вылетевшая из А, пролетела в направлении от А до В на 40 км больше, чем в обратном направлении, и поэтому от АВ она пролетела 70 км. Аналогично, вторая муха в направлении от А к В пролетела на 60 км меньше, чем в обратном, то есть 20 км.

Ответ: первая муха в направлении от А к В пролетела 70 км, вторая – 20 км.

Запасная задача! (в зависимости от способностей учеников, если останется 3 минутки свободного времени на уроке) Мотоциклист едет со скоростью 95 км/ч, а скорость велосипедиста на 76 км/ч меньше. Во сколько раз скорость мотоциклиста больше скорости велосипедиста? Кому из них легче остановиться? [2]

Решение:

1) 95 – 76 = 19 км/ч
2) 95 : 19 = 5 раз.

Ответ: в 5 раз легче остановиться велосипедисту, так как при меньшей скорости короче тормозной путь.

Итог урока: выставление оценок наиболее отличившимся ученикам, вручение памятных дипломов каждому ряду за умение работать в группах.

Домашнее задание: [Приложение 1] ученикам раздаются ксерокопии заданий.[2,3]

1. Помогите французским девочкам. Однажды Жаннин и Моника поплыли по маленькой речке, отправившись из одного и того же места, но только Жаннин поплыла против течения, а Моника поплыла по течению. Оказалось, что Моника забыла снять большие деревянные бусы. Через четверть часа девочки повернули обратно. Кто же из них подберет бусы Моники: сама Моника или Жаннин? (Скорость обеих пловчих в неподвижной воде одинакова.)
2. Задача от дяди Степы. Скорость легкового автомобиля 60 км/ч, а грузовика 15 км/ч. Во сколько раз скорость легкового автомобиля больше скорости грузовика? Какой автомобиль опаснее для школьника, начавшего движение по пешеходному переходу?
3. Задание от “Знающего человека”. Заполнить таблицу.

Объект	Скорость v	Время t	Расстояние S
“Волга”	100 км/ч	5 ч
“Ока”	60 км/ч		420 км
“Москвич”		3 ч	240 км
Пчела	60 км/ч		180 км
Стрекоза		2 ч	200 км
Стриж	100 км/ч	4 ч
Меч-рыба	100 км/ч		300 км
Земля (вокруг Солнца)	30 км/ч	24 ч
Черепаха		6 мин	18 м
Улитка		7 ч	35 км
Верблюд	8 км/ч	5 ч
Почтовый голубь	50 км/ч		150 км

4. Составить по одной анаграмме.

Ответы для учителя.

Задача № 1

Скорости девушек относительно неподвижной воды одинакова. Но ведь по отношению к воде в реке бусы остаются неподвижными – они движутся в точности с такой же скоростью, что и вода (со скоростью течения). Пловчихи проплывают относительно воды одинаковое расстояние и по истечении получаса встречаются в том месте, где в этот момент находятся бусы. Таким образом, обе девушки могут подобрать бусы с равным основанием, так как встречаются в тот самый момент, когда подплывут бусы.

Задача № 2

Опаснее легковой автомобиль, так как у него скорость больше, кроме того, для водителя легкового автомобиля мальчик появится неожиданно, так как обзор будет закрыт грузовым автомобилем.

Список литературы:

1. Решение задач / Клустер Д. И. – М.: Просвещение. – 2005.
2. Задачи на движение/ Павлов Е. С. – красноярск. – 2002.
3. Решение задач на движение/ Кузнишина Т. Л. – Новосибирск. – 1990
4. Сборник задач/ Кравцова Е. Е. – М.: Просвещение.-2008.
5. Справочник по безопасности дорожного движения/ Сильянов В. В. – М.: Технополиграфцентр. – 2001
6. Сборник олимпиадных задач по математике/ Горбачев Н.В. – М.: МЦНМО. – 2004

17.06.2012

xn--i1abbnckbmcl9fb.xn--p1ai