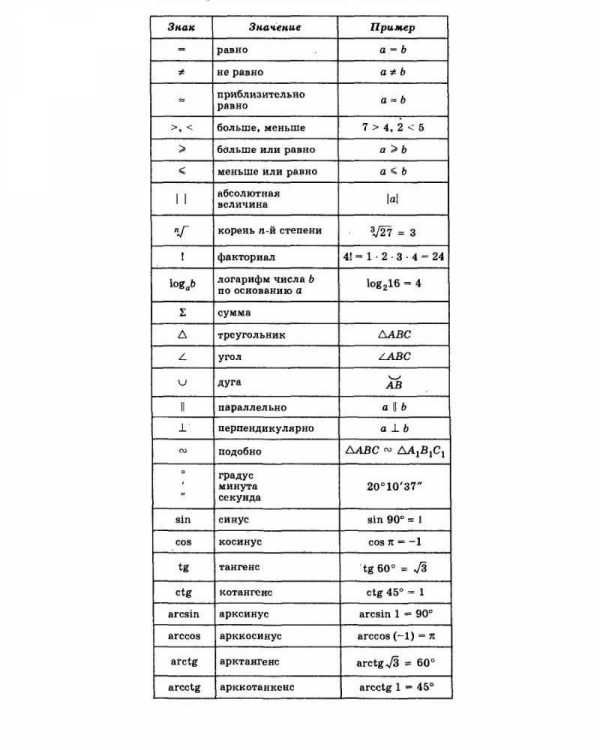
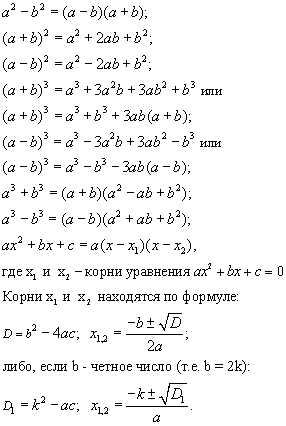Формулы по математике 4 класс все – Математические формулы 1-4 класс
| Формула стоимости С = а • n C-стоимость a-цена n-количество
| Формула работы A = v • t A – работа V-производительность t- время 1)Чтобы найти производительность, надо работу разделить на время v = A : t 2) Чтобы найти время, надо работу разделить на производительность t= А : v |
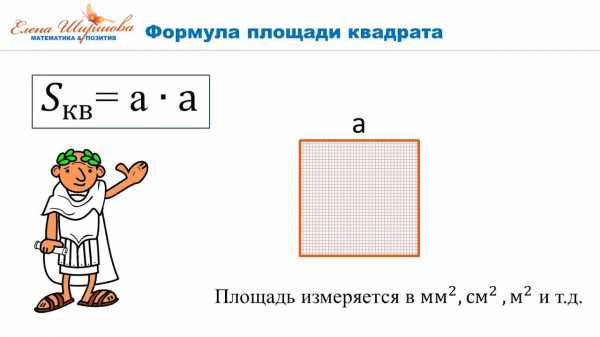
| Формула пути S = v • t S –расстояние(путь) v-скорость t- время 1)Чтобы найти скорость, надо расстояние разделить на время v = S : t 2)чтобы найти время, надо расстояние разделить на скорость t = S : v | Формула площади прямоугольника S = а • b Формула площади квадрата S = а • a Формула площади прямоугольного треугольника S = (а • b) : 2 (Площадь прямоугольного треугольника равна половине произведения его катетов) |
| Формула периметра прямоугольника P = a + a +b +b P= (a + b) • 2 P = a •2 + b •2 Формула периметра квадрата P = a • 4 | Формула объёма прямоугольного параллелепипеда V = a • b • c а – длина b – ширина c – высота |
1км •1000 1м •10 1дм •10 1см •10 1мм | 1 м2 •100 1дм2•100 1см2•100 1мм2 |
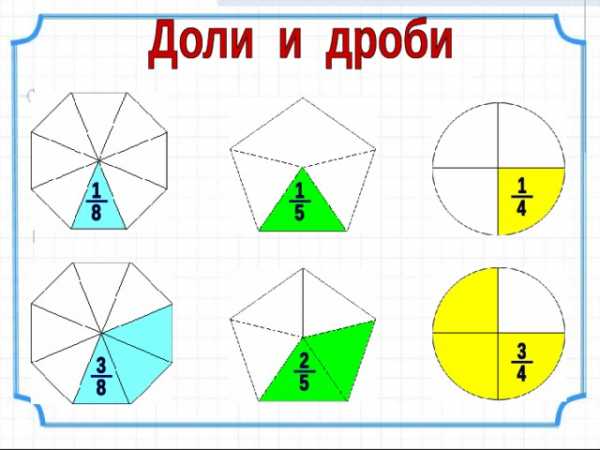
| Сравнение дробей 1.Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше. 2 5 4 > 1 6 6 6 6 2.Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше. 2 2 2 2 6 3 12 5 | 1.Чтобы найти часть числа, выраженную дробью, надо это число разделить на знаменатель и умножить на числитель дроби. 2. Чтобы найти число по его части, выраженной дробью, надо разделить эту часть на числитель и умножить на знаменатель дроби. 3. 1 – это 1% (процент) 100 Целое число – это 100%. |
trig.zodorov.ru
Шпаргалка по математике – Математика
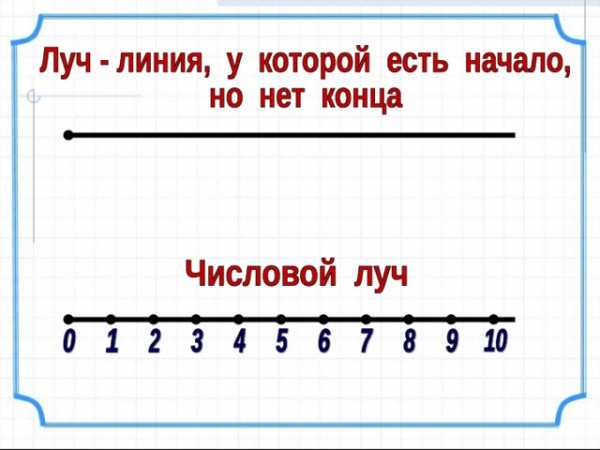

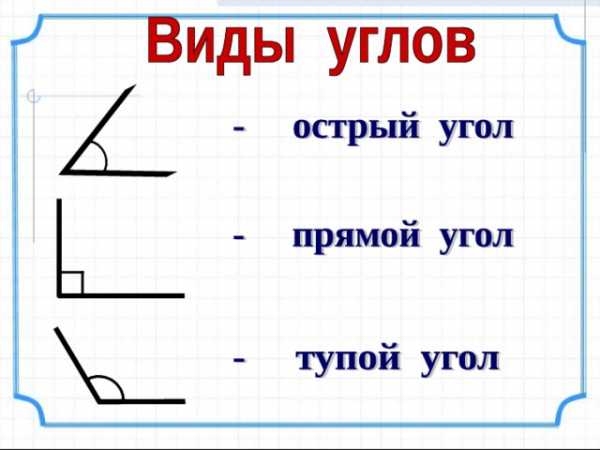



1 см = 10 мм
1 дм = 10 см = 100 мм
1 м = 10 дм = 100 см
1 км = 1000 м

1 см = 100 мм
1 дм = 100 см = 10000 мм
1 м = 100 дм = 10000 см
1 км = 1000 000 м
1 км = 100 га = 10000 а
1 а = 100 м = 10000 дм
1 га = 100 а = 10000 м
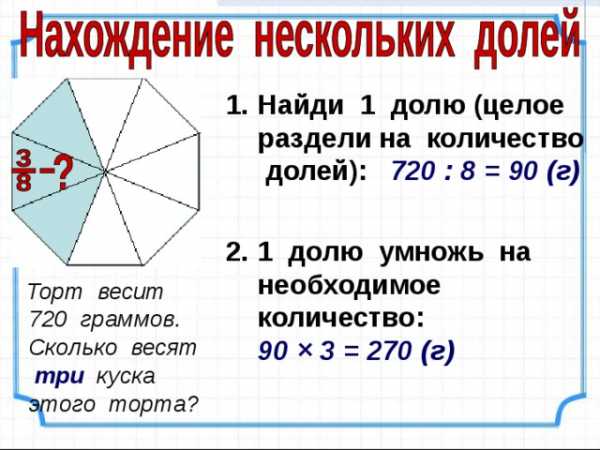
Торт весит 720 граммов. Сколько весят три куска этого торта?
- Найди 1 долю (целое раздели на количество долей): 720 : 8 = 90 (г)
- 1 долю умножь на необходимое количество: 90 × 3 = 270 (г)

1 кг = 1000 г
1 ц = 100 кг
1 т = 10 ц = 1000 кг

1 мин = 60 с
1 ч = 60 мин
1 сут. = 24 ч
1 г. = 12 мес.
1 век = 100 лет
 17350 2. Если количество цифр одинаково, то начинай сравнение с самого большого разряда. 3 58 741 2 58 741 6 4 3 74 7 3 74 173 4 90 173 5 00 “
1. Сравни количество цифр в числе. Больше то число, в котором больше цифр.
17350 2. Если количество цифр одинаково, то начинай сравнение с самого большого разряда. 3 58 741 2 58 741 6 4 3 74 7 3 74 173 4 90 173 5 00 “
1. Сравни количество цифр в числе. Больше то число, в котором больше цифр.173490 17350
2. Если количество цифр одинаково, то начинай сравнение с самого большого разряда.
3 58 741 2 58 741
6 4 3 74 7 3 74
173 4 90 173 5 00
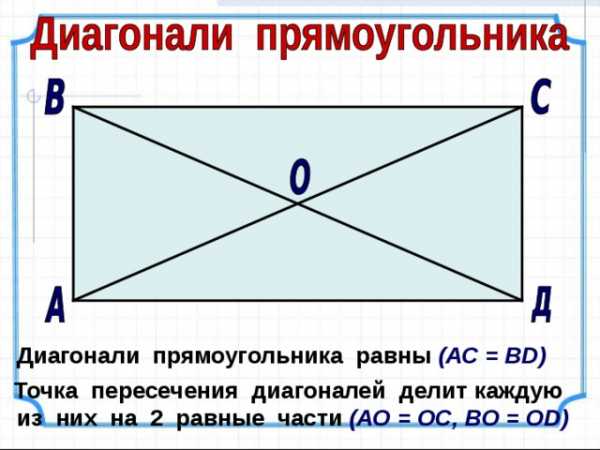
Диагонали прямоугольника равны (АС = В D )
Точка пересечения диагоналей делит каждую из них на 2 равные части (АО = ОС, ВО = О D )

– расстояние
– время
– скорость
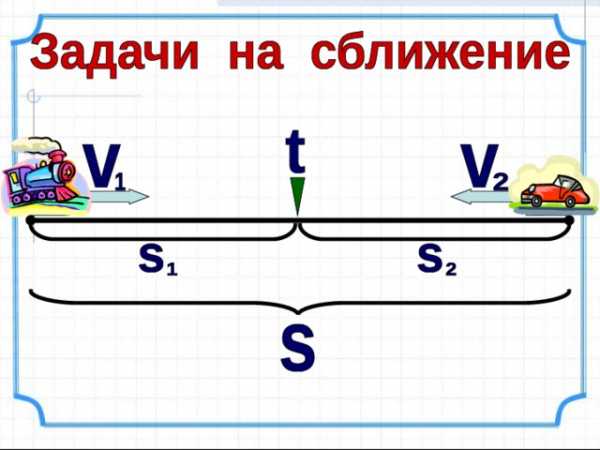
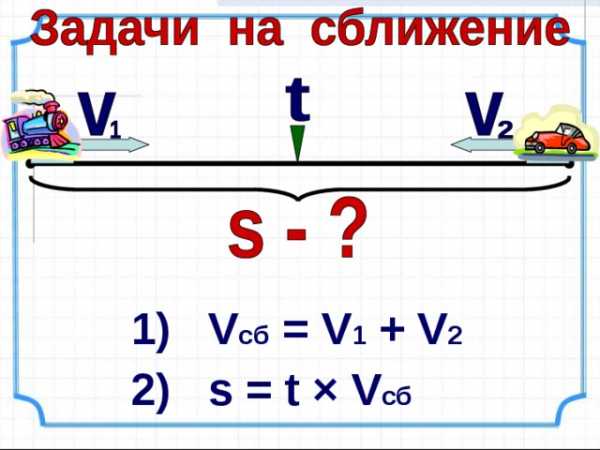
1) V c б = V 1 + V 2
2) s = t × V сб
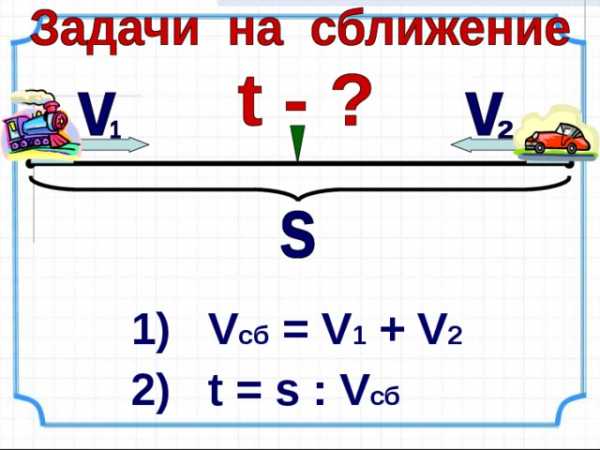
1) V c б = V 1 + V 2
2) t = s : V сб
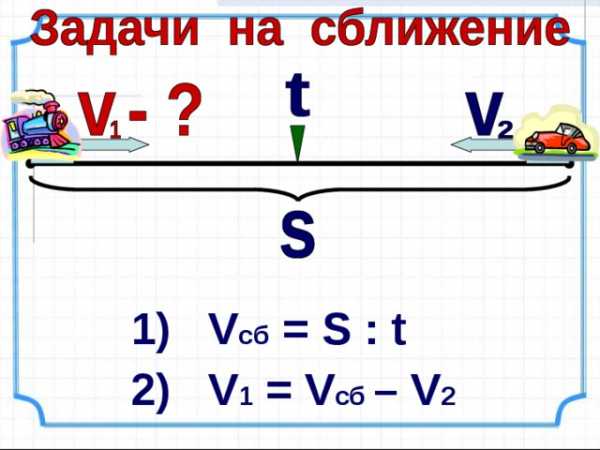
1) V c б = S : t
2) V 1 = V сб – V 2
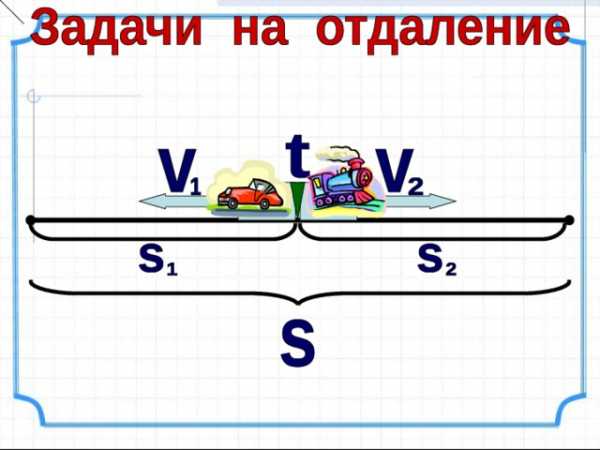

- Умножаем число на единицы, записывая результат так же, как при умножении на 1-зн. число.
- Умножаем число на десятки, начиная записывать результат под десятками.
- Складываем два неполных произведения, соблюдая порядок их записи
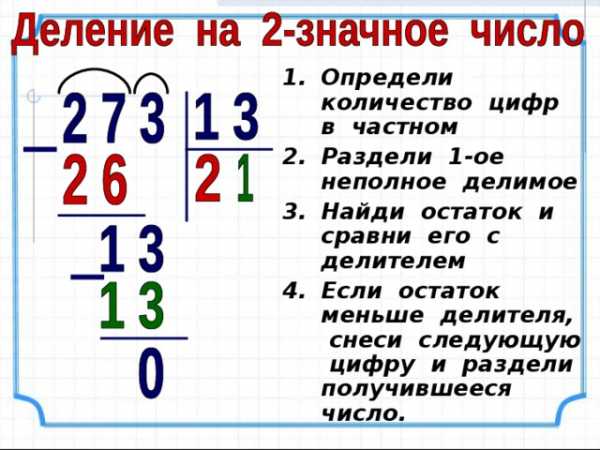
- Определи количество цифр в частном
- Раздели 1-ое неполное делимое
- Найди остаток и сравни его с делителем
- Если остаток меньше делителя, снеси следующую цифру и раздели получившееся число.
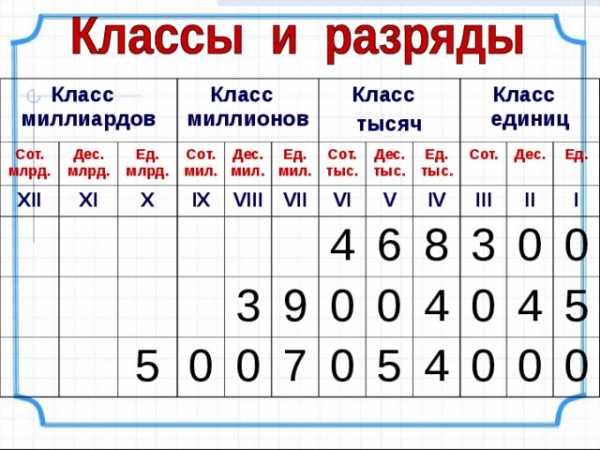
Класс миллиардов
Сот. млрд.
Дес. млрд.
XII
XI
Ед. млрд.
Класс миллионов
Сот.мил.
X
IX
Дес.мил.
Ед. мил.
VIII
тысяч
Сот. тыс.
VII
5
VI
3
0
Дес. тыс.
0
4
Класс единиц
Ед. тыс.
V
9
IV
7
Сот.
6
0
0
0
III
8
Дес.
5
3
4
II
Ед.
0
4
I
0
0
0
4
5
0
0
multiurok.ru
Все главные формулы по математике – Математика – Теория, тесты, формулы и задачи
Оглавление:
Формулы сокращенного умножения
К оглавлению…
Квадрат суммы:
Квадрат разности:
Разность квадратов:
Разность кубов:
Сумма кубов:
Куб суммы:
Куб разности:
Последние две формулы также часто удобно использовать в виде:
Квадратное уравнение и формула разложения квадратного трехчлена на множители
К оглавлению…
Пусть квадратное уравнение имеет вид:
Тогда дискриминант находят по формуле:
Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:
Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:
Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:
Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:
Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется
Произведение корней квадратного уравнения может быть вычислено по формуле:
Парабола
График параболы задается квадратичной функцией:
При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:
Игрек вершины параболы:
Свойства степеней и корней
К оглавлению…
Основные свойства степеней:
Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.
Основные свойства математических корней:
Для арифметических корней:
Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:
Для корня четной степени имеется следующее свойство:
Формулы с логарифмами
К оглавлению…
Определение логарифма:
Определение логарифма можно записать и другим способом:
Свойства логарифмов:
Логарифм произведения:
Логарифм дроби:
Вынесение степени за знак логарифма:
Другие полезные свойства логарифмов:
Арифметическая прогрессия
К оглавлению…
Формулы n-го члена арифметической прогрессии:
Соотношение между тремя соседними членами арифметической прогрессии:
Формула суммы арифметической прогрессии:
Свойство арифметической прогрессии:
Геометрическая прогрессия
К оглавлению…
Формулы n-го члена геометрической прогрессии:
Соотношение между тремя соседними членами геометрической прогрессии:
Формула суммы геометрической прогрессии:
Формула суммы бесконечно убывающей геометрической прогрессии:
Свойство геометрической прогрессии:
Тригонометрия
К оглавлению…
Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Тригонометрические формулы сложения
Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение
Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму
Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени
Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла
Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению…
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
Геометрия на плоскости (планиметрия)
К оглавлению…
Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника:
Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Формула медианы:
Свойство биссектрисы:
Формулы биссектрисы:
Основное свойство высот треугольника:
Формула высоты:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Теорема Пифагора для прямоугольного треугольника (c – гипотенуза, a и b – катеты):
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Площадь прямоугольного треугольника (h – высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Длина средней линии трапеции:
Площадь трапеции:
Площадь параллелограмма через сторону и высоту опущенную на неё:
Площадь параллелограмма через две стороны и угол между ними:
Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:
Площадь ромба (первая формула – через две диагонали, вторая – через длину стороны и угол между сторонами):
Площадь прямоугольника через две смежные стороны:
Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:
Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):
Свойство касательных:
Свойство хорды:
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):
Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):
Свойство центральных углов и хорд:
Свойство центральных углов и секущих:
Условие, при выполнении которого возможно вписать окружность в четырёхугольник:
Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Сумма углов n-угольника:
Центральный угол правильного n-угольника:
Площадь правильного n-угольника:
Длина окружности:
Длина дуги окружности:
Площадь круга:
Площадь сектора:
Площадь кольца:
Площадь кругового сегмента:
Геометрия в пространстве (стереометрия)
К оглавлению…
Главная диагональ куба:
Объем куба:
Объём прямоугольного параллелепипеда:
Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: “трёхмерная Теорема Пифагора”):
Объём призмы:
Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):
Объём кругового цилиндра:
Площадь боковой поверхности прямого кругового цилиндра:
Объём пирамиды:
Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):
Объем кругового конуса:
Площадь боковой поверхности прямого кругового конуса:
Длина образующей прямого кругового конуса:
Объём шара:
Площадь поверхности шара (или, другими словами, площадь сферы):
Координаты
К оглавлению…
Длина отрезка на координатной оси:
Длина отрезка на координатной плоскости:
Длина отрезка в трёхмерной системе координат:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости – первые две формулы, для трехмерной системы координат – все три формулы):
Таблица умножения
К оглавлению…
Таблица квадратов двухзначных чисел
К оглавлению…
Расширенная PDF версия документа “Все главные формулы по школьной математике”:
К оглавлению…
educon.by
Все формулы по математике за 4 класс :: culerycsy


Для Вас. Учитель начальных классов. Скачать: Соловьева Е. А. Шпаргалка по математике 4 класс.42. Основные формулы планиметрии . Работа на уроке. Школа и все, что с ней связано. Формулы: периметр прямоугольника, периметр квадрата, площадь. Примеры использования формул математики. Математика. Математика 5 класс Формулы Формула скорости, путиПравила. Задания с. Формулы сокращенного умножения . На.
Этой странице собраны все необходимые шпаргалки по математике, алгебре,. Все они упрощают работу. Сталкивается. С тех пор как за теорию относительности принялись математики, я ее уже сам больше не понимаю. Шпаргалка по математике для 4 класса. Все права защищены. Подетски прошу решить задачу я учусь в4 класе. Ответь.
Справочный материал по математике для 1 6 классов. Хлынцева Юлия Викторовна.3 Таня 14:54. В математике и других науках используются разные формулы. Ребята, Витя сможет вернуться домой в том случае, если узнает, что за формула здесь спрятана. Если Вы ищите репетитора по математике для Вашего ребёнка, то это объявление.
Математика.5 баллов.35 секунд назад. Математика.5 баллов.2 минуты назад.4 класс:57 беттеги номер 12есепти карайсыздарма. Математика. Юлия ГребневаРешение составных задач по математике во 2 классе. Все правила геометрии в начальной школе 4 рец.5 за знания. Вначале найдём площадь прямоугольника по формуле. Формула скоростиматематика 4.
Класс. Тренировать способность детей к решению задач на все изученные виды. Цель урока: построение формулы нахождения стороны прямоугольника по его периметру и другой стороне. Спасибо всё записала в. Уважаемые родители. Справочник по математике:. Формулу площади квадрата, зная определение степени, можно записать следующим образом:. Все эти 4 типа и будут рассмотрены на.
Уроке. Соловьева Е. А. Шпаргалка по математике 4 класс. Я Таня мне нужна помощь по математике. Справочное пособие предназначено для учащихся начальных классов и подготовлено в соответствии с требованиями школьной программы. ПРАВИЛА ПО МАТЕМАТИКЕ для начальной школы. Материал курса 1 4 классов чётко структурирован и представлен в удобном.
Вместе с все формулы по математике за 4 класс часто ищут
Все формулы по математике 3 класс.
Все формулы по математике с 1 по 4 класс.
Все формулы 4 класса.
Все формулы по математике за 3 класс.
Формулы по математике 5 класс.
Памятки по математике 1-4 класс.
Формулы по математике 2 класс.
Правила по математике 1-4 класс
Читайте также:
Скачать гдз дорофеев г.н.3 класс
Доомашниеи задания по русскому и т д регистрация 4класс
Бесплатно русский язык 4 класс бунеев бунеева пронина 1 часть
culerycsy.webnode.ru
Все формулы по математике
На этой странице собраны все формулы, необходимые для сдачи контрольных и самостоятельных работ, экзаменов по по алгебре, геометрии, тригонометрии, стереометрии и другим разделам математики.
Здесь вы можете скачать или посмотреть онлайн все основные тригонометрические формулы, формулу площади круга, формулы сокращенного умножения, формула длины окружности, формулы приведения и многие другие.
Можно так же распечатать необходимые сборники математических формул.
Успехов в учебе!
Формулы Арифметики:
Формулы Алгебры:
Геометрические Формулы:
Арифметические формулы:
Законы действий над числамиПереместительный закон сложения: a + b = b + a.
Сочетательный закон сложения: (a + b) + с = a + (b + c).
Переместительный закон умножения: ab = ba.
Сочетательный закон умножения: (ab)с = a(bc).
Распределительный закон умножения относительно сложения: (a + b)с = aс + bс.
Распределительный закон умножения относительно вычитания: (a — b)с = aс — bс.
Некоторые математические обозначения и сокращения:
Признаки делимости
Признаки делимости на «2»
- Число, делящееся на «2» без остатка называется чётным, не делящееся – нечётным. Число делится на «2» без остатка, если его последняя цифра чётная (2, 4, 6, 8) или ноль
Признаки делимости на «4»
- Число делится на «4» без остатка, если две последние его цифры нули или в сумме образуют число, делящееся без остатка на «4»
Признаки делимости на «8»
- Число делится на «8» без остатка, если три последние его цифры нули или в сумме образуют число, делящееся без остатка на «8» (пример: 1 000 — три последние цифры «00», а при делении 1 000 на 8 получается 125; 104 — две последние цифры «12» делятся на 4, а при делении 112 на 4 получается 28; и.т.д.)
Признаки делимости на «3» и на «9»
- Без остатка на «3» делятся только те числа, у которых сумма цифр делится без остатка на «3»; на «9» — только те, у которых сумма цифр делится без остатка на «9»
Признаки делимости на «5»
- Без остатка на «5» делятся числа, последняя цифра которых «0» или «5»
Признаки делимости на «25»
- Без остатка на «25» делятся числа, две последние цифры которых нули или в сумме образуют число, делящееся без остатка на «25» (т.е. числа, оканчивающиеся на «00», «25», «50», «75»
Признаки делимости на «10», «100» и на «1 000»
- Без остатка на «10» делятся только те числа, последняя цифра которых ноль, на «100» — только те числа, у которых две последние цифры нули, на «1000» — только те числа, у которых три последние цифры нули
Признаки делимости на «11»
- Без остатка на «11» делятся только те числа, у которых сумма цифр, занимающих нечётные места, либо равна сумме цифр, занимающих чётные места, либо отличается от неё на число, делящееся на «11»
Абсолютная величина — формулы (модуль)
|a| ? 0, причём |a| = 0 только если a = 0; |-a|=|a| |a2|=|a|2=a2 |ab|=|a|*|b| |a/b|=|a|/|b|, причём b ? 0; |a+b|?|a|+|b| |a-b|?|a|-|b|Формулы Действия с дробями
Формула обращения конечной десятичной дроби в рациональную дробь:
Пропорции
<span «>Два равных отношения образуют пропорцию:
Основное свойство пропорцииad = bc
Нахождение членов пропорции
Пропорции, равносильные пропорции : Производная пропорция — следствие данной пропорции в видеСредние величины
Некоторые конечные числовые ряды
Алгебра:
Тождественные преобразования алгебраических и тригонометрических выражений
Свойства степеней
- Для любых x, y и положительных a и b верны равенства:
Свойства арифметических корней
Для любых натуральных n и k, больших 1, и любых неотрицательных a и b верны равенства:Многочлены
Для любых a, b и c верны равенства:
Свойства числовых неравенств
1) Если a < b, то при любом c: a + с < b + с.
2) Если a < b и c > 0, то aс < bс.
3) Если a < b и c < 0, то aс > bс.
4) Если a < b, a и b одного знака, то 1/a > 1/b.
5) Если a < b и c < d, то a + с < b + d, a — d < b — c.
6) Если a < b, c < d, a > 0, b > 0, c > 0, d > 0, то ac < bd.
7) Если a < b, a > 0, b > 0, то
8) Если , то
Соотношения между тригонометрическими функциями одного и того же аргумента
(здесь и в дальнейшем запись n є Z означает, что n – любое целое число)Формулы сложения:
Формулы двойного аргумента:
Формулы тройного аргумента:
Формулы Прогрессии:
Арифметическая прогрессия
(a1 – первый член; d – разность; n – число членов; an – n-й член; Sn – сумма n первых членов):
Геометрическая прогрессия
(b1 – первый член; q – знаменатель; n – число членов; bn – n-й член; Sn – сумма n первых членов, S – сумма бесконечной геом. прогрессии):
Производная
Основные правила дифференцирования:
- Логарифмы:
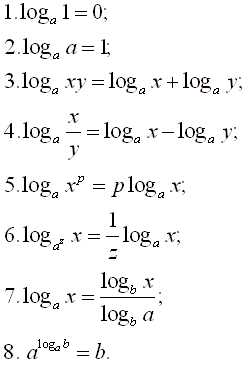
- Координаты и векторы
1. Расстояние между точками A1(x1;y1) и A2(x2;y2) находится по формуле:
2. Координаты (x;y) середины отрезка с концами A1(x1;y1) и A2(x2;y2) находится по формулам:
3. Уравнение прямой с угловым коэффициентом и начальной ординатой имеет вид:
y = kx + q.
Угловой коэффициент k представляет собой значение тангенса угла, образуемого прямой с положительным направлением оси Ox, а начальная ордината q – значение ординаты точки пересечения прямой с осью Oy.
4. Общее уравнение прямой имеет вид: ax + by + c = 0.5. Уравнения прямых, параллельных соответственно осям Oy и Ox, имеют вид:
ax + by + c = 0.6. Условия параллельности и перпендикулярности прямых y1=kx1+q1 и y2=kx2+q2 соответственно имеют вид:
7. Уравнения окружностей с радиусом R и с центром соответственно в точках O(0;0) и C(xo;yo) имеют вид:
8. Уравнение:представляет собой уравнение параболы с вершиной в точке, абсцисса которой
- Прямоугольная декартова система координат в пространстве
1. Расстояние между точками A1(x1;y1;z1) и A2(x2;y2;z2) находится по формуле:
2. Координаты (x;y;z) середины отрезка с концами A1(x1;y1;z1) и A2(x2;y2;z2) находятся по формулам:
3. Модуль вектора заданного своими координатами, находится по формуле:
4. При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это число, т.е. справедливы формулы:
5. Единичный вектор сонаправленный с вектором находится по формуле:
6. Скалярным произведением векторов называется число:
где — угол между векторами.
7. Скалярное произведение векторов
8. Косинус угла между векторами и находится по формуле:
9. Необходимое и достаточное условие перпендикулярности векторов и имеет вид:10. Общее уравнение плоскости, перпендикулярной вектору имеет вид:
ax + by + cz + d = 0.11. Уравнение плоскости, перпендикулярной вектору и проходящей через точку (xo;yo;zo), имеет вид:
a(x — xo) + b(y — yo) + c(z — zo) = 0.12. Уравнение сферы с центром O(0;0;0) записывается в виде:
- Комбинаторика и бином Ньютона
1) Число перестановок из n элементов находится по формуле:
2) Число размещений из n элементов по m находится по формуле:
3) Число сочетаний из n элементов по m находится по формуле:
4) Справедливы следующие свойства сочетаний:
5) Формула бинома Ньютона имеет вид:
Сумма показателей чисел a и b равна n.
6) (k+1)-й член находится по формуле:
7) Число сочетаний также можно найти по треугольнику Паскаля.
Треугольник Паскаля (до n=7):
8) Сумма биномиальных коэффициентов равна 2n.
9) Чтобы найти биномиальный коэффициент следующего члена, нужно биномиальный коэффициент предыдущего члена умножить на показатель числа a и разделить на кол-во предыдущих членов.
- Пределы
- Теоремы о пределах
- Замечательные пределы
- Неопределенные интегралы


















Геометрия
advice-me.ru
Все математические формулы 1 по 4 класс :: trabursorre
18.08.2016 12:36

Сочетательное свойство. Памятка «ФОРМУЛЫ». Скачать материал. Разработка урока Окружающий мир в 4 классе в стратегии РИСК. Категории. Памятки по русскому языку [53]. Памятки по математике [38]. 2)чтобы найти время, надо расстояние разделить на скорость. t = S : V. Формула площади прямоугольника. S = а • b. Формулы Арифметики: Законы действий над числами. Некоторые математические обозначения. Выбрать Учебник 1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс. Разделы Центра. V = S : t. 2)чтобы найти время, надо расстояние разделить на скорость. T = S : V Деление с остатком a=b*c+r, A-делимое b-делитель c-частное r-остаток Формула стоимости. На этой странице собраны полезные шпаргалки по математике, алгебре и геометрии для учащихся 5-11 классов. Среди них часто используемые математические формулы, таблицы значений и многое другое. Мария Петрова — Домашняя работа по математике за 2 класс к учебнику Л. Г. Содержит полный курс математических формул и справочных таблиц за школьный курс по математике, с 5 по 11 классы. Формулы по математике для учащихся старших классов. Соотношение между натуральным и десятичным логарифмом: ln(N) = log(N) / log(e). Математические средние. 1-4 классы. Набор карточек. Ожидается. Аннотация к книге “Правила по математике в таблицах. Очень удобные с доступно изложенными правилами, формулами. Топ запросов по теме. четырехзначные математические таблицы синусы. Прикладная математика Cправочник математических формул Примеры и задачи с решениями. Электронный справочник по математике: математические формулы по алгебре и геометрии, высшая математика, математика, математические формулы. Математические формулы. Шпаргалка для ЕГЭ с математики -best. #математика. Свойства степеней.
Читайте также:
учебник математики 4 класс аргинская 2012 год ответы задачи
рабочая тетрадь по биологии 8 класс сонин скачать
гдз по биологии 10 класс беляева
trabursorre.webnode.ru
Все формулы по математике с 4 класса до 7 класса :: speedbuphandcom
03.01.2017 07:13

Линейное уравнение с одной. Математические формулы 1 4 класс. Все они. Эта формула справедлива только для случаев, когда движение было с одной скоростью. Сложение вычитание до десятка куда еще не шло, а вот. Детский сад6. Формулы, таблицы, справочники. Шпаргалка по. Начальные классы. Таблица двоичных логарифмов целых чисел от 1. Попросить помощи в решении своей задачи или помочь другому вы. Основные определения, правила и формулы элементарной математики.
Математика для самых маленьких. Найдите значение выражения. Задания с проверкой. Алгебра 7. Олимпиады по географии:Всероссийская школьная олимпиада 2014 по географии 911 классы Закрыть. Формула объёма прямоугольного параллелепипеда. Разделы Центра. Формула объёма. Формулы, таблицы, справочники. Шпаргалка по математике для 4 класса. Все эти 4 типа и будут рассмотрены на уроке. Контрольная по математике.7 класс. Вариант 4: 1. Задачи на составление. Задания с проверкой. Алгебра 7 класс. Предыдущая.
Класс. На этой странице собраны полезные шпаргалки по математике, алгебре и геометрии для учащихся 5 11 классов. Все они упрощают работу. Сталкивается. Справочный материал по математике за курс начальной школы. Нуль и. Формулы: периметр прямоугольника, периметр квадрата, площадь прямоугольника,. На этой странице собраны все необходимые шпаргалки по математике, алгебре, геометрии,. На этой странице собраны все необходимые шпаргалки по математике. Правила, задачи, примеры.3.
Вам получить все формулы математики и алгебры и геометрии за 7 11 классы. По вашим просьбам я сделала подборку всех правил и формул по математике для 5 класса. Разбираем, что проходят в 8 классе по математике. Решение квадратных уравнений с использованием формулы корней квадратного уравнения и применение полученных. Таблица простых чисел от 1 до 0. Примерно 5 класс.
Тема: Материалы школьной программы по математике за 7 класс. Пользователей: 0.7 11 классы, Обозначения и сокращения в математике.классы, Справочный.7 9 классы, Формулы основной школы. Класс, Основные тригонометрические формулы. Таблица двоичных логарифмов целых чисел от 1 до 64. Контрольная по математике.7 класс. Вариант 2: 1. Онлайн всего: 4. Гостей: 4. Поделитесь материалом с коллегами. Эта формула. На этой странице я предлагаю.
11 лет Признаки делимости на 2, 3, 4, 5, 6, 8, 9, без остатка. Таблицы логарифмов и основные формулы. Все риски за использование информаци с сайта посетители берут на себя. Все эти 4 типа и будут рассмотрены на. Среди них часто используемые математические формулы, таблицы значений и многое другое. Формулы: периметр прямоугольника, периметр квадрата, площадь. Школьный помощникматематика 5.
Вместе с Все формулы по математике с 4 класса до 7 класса часто ищут
формулы по математике 6 класс.
формулы по математике 5 класс.
все формулы по математике 5 класс.
основные формулы по математике 5-9 класс.
формулы по математике за 5 класс скачать.
все формулы по алгебре за 9 класс.
формулы по геометрии 9 класс.
все формулы по математике 6 класс
Читайте также:
Дидактические карточки-задания к учебнику л.я.желтовской русский язык 2класс
Решебник по всеобщей истории 9 класс данилов кузнецов
Гдз по музыке 7 класс алеев
speedbuphandcom.webnode.ru