Задания математика 4 года: Математика для детей 4 лет, математические игры и задания для малышей онлайн
Развивающие задания на логику для детей 4-5 летучебно-методический материал по математике (средняя группа) на тему
Мультики развивающие по математике для детей 4 5 лет
По теме: методические разработки, презентации и конспекты
Развивающие задания для дошкольников подготовительной группы «Я готовлюсь к школе!» №1 Развиваем внимание, мышление, логику.
Материалы будут интересны воспитателям, педагогам-психологам в работе с дошкольниками и их родителям в период подготовки к школе. Презентации оформлены так, что выполняя задания, дети не только.
Развивающие задания в картинках для детей дошкольников 4-5 лет
Задания в картинка для детей 4-5 лет. Позновательные игры 4- 5 лет. логические игры 4-5 лет. Раскраски 4-5 лет.
Задания на логику, домашнее задание 26.01
Делать одно на выбор.
«Задания на логику для детей 5-7 лет»
Умственное развитие ребенка заключается не только в получении определенных знаний, но и развитие восприятия, памяти, мышления, воображения. У детей дошкольного возраста основной вид деятельности — игр.
У детей дошкольного возраста основной вид деятельности — игр.
Развивающие речь, память, логику задания для детей 3-4 года
Логические задачи, пальчиковые игры и многое другое.
06.02.2021г. Развивающие задания по математике для детей подготовительной группы
Предлагаю вам картотеку развивающих заданий по формированию элементарных математических представлений у детей старшего дошкольного возраста. Данный материал будет полезен воспитателям, педагогам допол.
Развивающие задания для дошкольников подготовительной группы «Я готовлюсь к школе!» №1 Развиваем внимание, мышление, логику.
Материалы будут интересны воспитателям, педагогам-психологам в работе с дошкольниками и их родителям в период подготовки к школе. Презентации оформлены так, что выполняя задания, дети не только.
Развивающие задания в картинках для детей дошкольников 4-5 лет
Задания в картинка для детей 4-5 лет. Позновательные игры 4- 5 лет. логические игры 4-5 лет. Раскраски 4-5 лет.
Раскраски 4-5 лет.
Задания на логику, домашнее задание 26.01
Делать одно на выбор.
«Задания на логику для детей 5-7 лет»
Умственное развитие ребенка заключается не только в получении определенных знаний, но и развитие восприятия, памяти, мышления, воображения. У детей дошкольного возраста основной вид деятельности — игр.
Развивающие речь, память, логику задания для детей 3-4 года
Логические задачи, пальчиковые игры и многое другое.
06.02.2021г. Развивающие задания по математике для детей подготовительной группы
Предлагаю вам картотеку развивающих заданий по формированию элементарных математических представлений у детей старшего дошкольного возраста. Данный материал будет полезен воспитателям, педагогам допол.
Развивающие речь, память, логику задания для детей 3-4 года.
Nsportal. ru
11.11.2018 12:52:05
2018-11-11 12:52:05
Источники:
Https://nsportal. ru/detskiy-sad/matematika/2017/01/28/razvivayushchie-zadaniya-na-logiku-dlya-detey-4-5-let
Развивающие задания для детей 4-5 лет » /> » /> . keyword { color: red; }
keyword { color: red; }
Мультики развивающие по математике для детей 4 5 лет
Данная серия заданий предназначена для групповых и индивидуальных занятий с детьми 4-5 лет. Все задания составлены в интересной игровой форме, красочно оформлены и соответствуют уровню знаний данной возрастной категории. Все эти задания направлены на Всестороннее развитие ребёнка:
— развитие логического мышления;
— развитие мелкой моторики рук;
— формирование элементарных математических знаний;
Для выполнения этих заданий вам понадобятся карандаши и фломастеры.
Задание 1
Раскрась узор на чайнике по заданному образцу.
Какие геометрические фигуры в этом узоре тебе знакомы?
Задание 2
Соедини линией предметы так, чтобы они образовали пары. Объясни свой выбор.
Задание 3
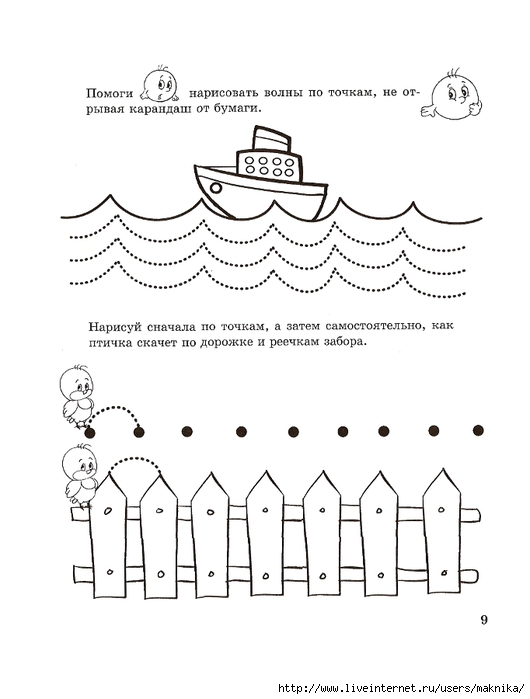
Пунктирные линии показывают, как передвигаются кузнечик, воробей и уточка. Обведи эти линии разноцветными фломастерами.
Обведи эти линии разноцветными фломастерами.
Задание 4
Помоги муравью найти выход из муравейника
Задание 5
Укрась зонт щенка жёлтыми и фиолетовыми полосками. Дорисуй зонтик.
Задание 6
В каком порядке должны стоять картинки?
Расскажи, что произошло.
Задание 7
Обведи предметы, названия которых начинаются на букву А.
Задание 8
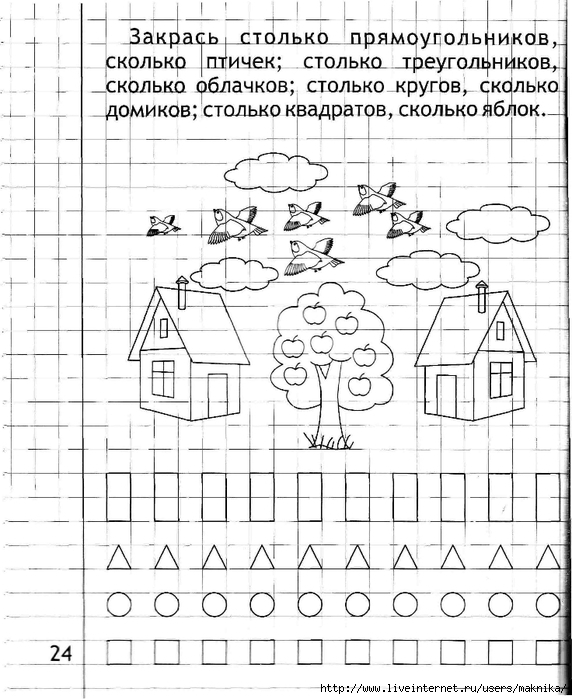
Сосчитай грибы, ягоды, яблоки и листочки.
Получившиеся ответы соедини с цифрами.
Задание 9
Продолжи узоры и раскрась их. На что они похожи?
Задание 10
Допиши цифры по образцу, называя их.
Задание 11
Соедини каждую тень со своим деревом.
Назови эти деревья.
Задание 12
Обведи дорожки, по которым поедут джип и велосипед.
Задание 13
Назови овощи, которые изображены на картинке.
Покажи линией, какие листья каким овощам принадлежат.
Задание 14
Дорисуй божьей коровке пятнышки и усики. Раскрась её.
Сосчитай, сколько у неё пятнышек и лапок.
Задание 15
Найди в каждом ряду лишний предмет и обведи его.
Как ты думаешь, почему он лишний?
Задание 16
Обведи предметы, животных и овощи, названия которых начинаются на букву О.
Задание 17
Внимательно рассмотри рисунок. Какие геометрические фигуры лежат в основе каждого из них?
Задание 18
Лисёнок повернулся к нам спиной. Раскрась правильно листья.
Задание 19
Обведи гриб и листья. Теперь раскрась рисунок, используя цифры-подсказки. Слева от картинки ты увидишь, какой цвет соответствует каждой цифре.
Задание 20
Найти в каждом ряду лишний рисунок и зачеркни его.
Объясни своё решение.
Задание 21
Баба-Яга пригласила на обед друзей. Сколько тарелок она должна поставить на стол? Нарисуй нужное количество тарелок. Кого из гостей Бабы-Яги ты знаешь?
Задание 22
Допиши цифры по образцу, называя их.
Задание 23
Проведи зверюшек к их любимой еде. Используй для каждого животного свой цвет.
Задание 24
Обведи и сосчитай жирафов, утят и зайчат. Ответы впиши в таблички.
Задание 25
Белочка отправилась в лес на прогулку. Помоги ей отыскать грибок, шишку и цветочек. Сделай дорожки разноцветными.
Какие геометрические фигуры в этом узоре тебе знакомы.
Alegri. ru
25.09.2017 13:38:32
2017-09-25 13:38:32
Источники:
Https://alegri. ru/deti/vospitanie-i-razvitie-rebenka/igry-dlja-detei/razvivayuschie-zadanija-dlja-detei-4-5-let. html
ПРОГРАММЫ обучающие — Обучалки и развивалки для детей — DetkiUch » /> » /> . keyword { color: red; }
keyword { color: red; }
Мультики развивающие по математике для детей 4 5 лет
«Кто под шляпой?» — это интуитивно простая компьютерная игра, которая поможет детям младшего возраста выучить названия разных животных и быстро развить свою память.
Это серия обучающих программно-методических комплексов по математике для начальной (2-6 классы) школы. Организация диагностического и коррекционного тестирования, контроль за усвоением учебного материала, выдача рекомендаций по устранению пробелов в знаниях.
Интересная игра для тех, кто хочет улучшить свои навыки набора на русской и английской клавиатуре
Scotland,
Реферат о Шотландии ( шотландская национальная одежда, элементы национального костюма ) для 6 класса по английскому языку
Формат: doc
Язык: английский
- Рефераты на татарском языке. 167 работ на русском и татарском языках. Курсовые, дипломные на татарском языке. 145 работ на русском и татарском языках.
 Курс татарского языка в институте.
Курс татарского языка в институте.Реферат для 7-го класса
Формат: ppt
Размер: 4 Mb
Подборка игр для разных возрастов. Развиваем ребенка в процессе игр.
Для детей и их родителей. Девочка Алиса через кроличью нору попадает в Страну чудес, где с ней происходят волшебные превращения и где она знакомится со странными существами: Чеширским Котом, Мартовским Зайцем и другими.
Самый известный и популярный персонаж детского писателя Сергея Козлова — Ёжик приглашает вас еще раз окунуться в волшебный и неповторимый мир сказок. В сборнике кроме всеми любимого Ёжика в тумане вас также ждут и другие сказки.
Тигренок отправляется в путешествие, находит себе новых друзей и познает как это здорово — «ДР-Р-Р-РУЖИТЬ. «
Популярная библиотека химических элементов (Вы не любите котов? — Да Вы просто не умеете их готовить..) То же можно сказать и про некоторые науки — взгляните на химию с более яркой её стороны. Обуздав эту науку не в школе, а дома и в окружающем мире.
Тренажёр по русскому языку с заданиями конкурса «Русский Медвежонок — языкознание для всех»
Эта программа-тренажер поможет школьникам подготовиться к конкурсу-олимпиаде по русскому языку, повторив задания прошлых лет, воскресить в памяти пройденный материал.
Надо только слушать и повторять!
Можно учить татарский язык дома или за рулем, на отдыхе или в спортзале
— везде, где есть проигрыватель компакт-дисков, Mp3-проигрыватель или компьютер.
Курс состоит из аудиоматериалов, самоучителя, словарей и разговорника.
Полные учебные словари, фонетика, книги:
* Русско-татарский словарь.
* Татарско-русский словарь.
* «Практическая фонетика татарского языка» (озвучено).
* Книга «Как писать курсовые, дипломы, диссертации. »
Компьютерный тренажер по русскому языку для старшеклассников и абитуриентов «Репетитор-Диктант»
После каждого диктанта программа проводит работу над ошибками — составляет текст из тех фраз, в которых Вы ошиблись, диктует грамматические диктанты — короткие фразы и отдельные слова.
UMS_9.9.5.2_online и UMS_5.0.1.3_RUS_Offline
Универсальный Математический Решатель (UMS) – замечательная программа и мечта любого школьника или студента — объясняет как «живой учитель».
Самая большая собранная коллекция Азбук для малышей.
Реферат для 7 класса по теме: «Использование геометрических фигур в реальной жизни»
Формат: ppt
Размер: 6,7 Mb
Большая коллекция детских обучающих познавательных презентаций со стихами разной тематики познакомит детишек с такими понятиями, как время года, чистота, а также со звуками, цветами, различными предметами и правилами поведения.
Искусство создания ароматов можно сравнить с созданием музыкальной гармонии. Духи состоят из трех нот: верхние ноты, средние, а еще глубина — базовые ноты. Верхние ноты являются наиболее неустойчивыми и быстро испаряются. Каждая из нот создает свой собственный аромат, но сливается с другими, чтобы создать запах, эмоции. Духи оптом в Москве.
Полные учебные словари, фонетика, книги:
Надо только слушать и повторять!
Можно учить татарский язык дома или за рулем, на отдыхе или в спортзале
— везде, где есть проигрыватель компакт-дисков, Mp3-проигрыватель или компьютер.
Курс татарского языка в институте.
Www. detkiuch. ru
21.06.2020 15:27:30
2017-12-10 00:58:58
Источники:
Https://www. detkiuch. ru/load/
Конспект занятия по математике для детей 4-5 лет
Конспект итогового занятия по математике в средней группе на тему:
“Путешествие в страну математики”
Воспитатель: Гильманова Лилия Клариковна
Возрастная категория: 4-5 лет
Цели занятия:
Образовательные:
· Продолжать формирование мыслительных операций (анализа, синтеза, сравнения, обобщения, классификации).
· Формировать представления о свойствах предметов: цвет, форма, размер. Умение выделять и объяснять признаки сходства и различия предметов, объединять их в группы по общему признаку. Умение находить “лишний” предмет.
·
Закрепить навыки порядкового и обратного счёта в пределах 10.
· Формировать навык полных ответов на вопросы.
Развивающие:
· Развивать речь, наблюдательность, мыслительную активность, умение высказывать и обосновывать свои суждения.
· Развивать слуховое и зрительное внимание, память, логическое мышление.
· Развивать конструктивные и творческие способности, фантазию, творческое воображение.
Воспитательные:
· Воспитывать интерес к математическим занятиям.
· Развивать самостоятельность, умение планировать свою работу.
· Воспитывать стремление оказывать помощь другим, которые оказались в трудной ситуации.
· Воспитывать дружеские взаимоотношения между детьми, привычку заниматься сообща.
Методы и приёмы:
Моделирование игровой ситуации с целью постановки проблемы и
создания мотивации, упражнения на логическое мышление и творческого характера,
вопросы к детям, использование дидактических пособий, наглядного материала,
физкультминутки, пальчиковой гимнастики.
Ход занятия.
Педагог. Ребята, когда я утром шла на работу, мне повстречался почтальон из страны «Математика» и передал для вас вот это письмо. А прислали его жители этой страны. Послушайте, что они пишут:
“Дорогие ребята, здравствуйте!
Очень хотим побывать у вас в гостях и пригласить в путешествие по удивительно красивой стране математики, но нас заколдовали, и не можем к вам прийти. В стране математики случилась беда – его захватили злые волшебники. Жителям нашей страны нужна помощь. Мы надеемся, что вы не оставите нас в беде, и пройдете все испытания, которые встретятся вам на пути, и сможете расколдовать нашу стану и освободить её жителей.
Жители страны математики.
Педагог. Ребята, а чтобы попасть в страну математики, нужно открыть вот эти ворота, подобрав ключ к замку. Но сначала давайте скажем волшебные слова.
Пальчиковая гимнастика.
На двери висит замок,
Кто его открыть бы мог?
Потянули, покрутили, постучали
И открыли…
Педагог. Вот из этой связки ключей
нужно подобрать тот, который бы мог открыть замок. Как вы думаете, какой ключ
подойдёт к замку? Почему? (Ответы детей).
Вот из этой связки ключей
нужно подобрать тот, который бы мог открыть замок. Как вы думаете, какой ключ
подойдёт к замку? Почему? (Ответы детей).
Скважина замка и шляпки ключей имеют определённую сложную геометрическую форму. Дети подбирают нужный ключик. Правильно выполненное задание позволяет открыть замок.
Педагог. Ключик подобран правильно, ворота открыты и мы оказываемся в стране математики. Идём дальше и посмотрим, что же ещё необычного ждёт нас впереди.
Игра “Где правая, где левая”.
Дети работают у мультимедийной доски. Слайды с изображением геометрических фигур. Ориентировка в пространстве.
Педагог. А вот и первое испытание. Какие фигуры вы здесь видите? (Ответы) Как называется геометрическая фигура, расположенная в правом верхнем углу? Какого цвета? Как называется геометрическая фигура, расположенная в левом углу? Какого цвета? Она выше или ниже? Найди синюю геометрическую фигуру; Как она называется? В каком углу она расположена? Она больше или меньше…? Назови геометрическую фигуру, расположенную в центре; Какого она цвета?
Молодцы, все справились с заданием, и мы можем продолжать путешествие!
Игра “Найди лишнюю”.
Педагог. Ребята, в этой стране очень забавные человечки. Они все похожи друг на друга, но вот одна из фигур оказалась лишняя, не похожая на остальные. Что это за фигура? (Ответы). Чем она отличается от остальных? (Ответы). Которая по счёту лишняя фигура? (Ответы).
Педагог. Ребята, злые волшебники заколдовали цифры, и они перепутали, кто с кем живет по соседству, поможем им!
«Соседи»
Дети вместе с воспитателем встают в круг. Выбирается ведущий, который бросает мяч (или отдает счетные палочки, сигнальные цифры, и т.д…) по очереди находящимся в кругу называет число от 1 до 10 (или по количеству стоящих). Поймавший мяч должен назвать соседей указанного числа «прямой счёт до 10», «обратный счёт от 10 до 1»
Работа со слайдами
Педагог. Молодцы, все справились с заданием! Мы не будем останавливаться и продолжим спасать жителей математической страны
Педагог. Ребята,
посмотрите, жители этой замечательной страны нам в помощь прислали послания.
Ребята,
посмотрите, жители этой замечательной страны нам в помощь прислали послания.
Воспитатель демонстрирует детям “какие-то загадочные послания” (поочередно показывает чертежи квадрата, треугольника, круга, овала).
Ребята выполняют задания, ведя устный счет:
Задачка от Квадрата
Как-то
вечером к медведю,
На пирог пришли соседи:
Еж, барсук, енот, “косой”,
Волк с плутовкою-лисой.
А медведь никак не мог,
Разделить на всех пирог.
От труда медведь вспотел,
Он считать ведь не умел…
Помоги ему скорей,
Посчитай-ка всех друзей!
Задачка от Круга
Вышла
курочка гулять,
Повела своих цыплят.
7 бежали впереди,
3 осталось позади
Беспокоится их мать
И не может сосчитать.
Задачка от Треугольника
Сколько у трех мышей ушей?
Задачка от Овала
Дружили 4 девочки.
У
каждой девочки по 2 косички.
Сколько всего косичек?
Педагог. А
сейчас давайте немного отдохнём.
А
сейчас давайте немного отдохнём.
Физкультминутка.
Дружно с вами мы считали и про числа рассуждали,
А теперь мы дружно встали, свои косточки размяли.
На счет раз кулак сожмем, на счет два в локтях сожмем.
На счет три — прижмем к плечам, на 4 — к небесам
Хорошо прогнулись, и друг другу улыбнулись
Про пятерку не забудем — добрыми всегда мы будем.
На счет шесть прошу всех сесть.
Числа, я, и вы, друзья, вместе дружная 7-я.
Педагог. Чтобы мы с вами могли идти дальше, нужно выполнить следующее задание: построить домик из счетных палочек.
Игра “Строим домики для цифр”
Педагог. Вот мы с вами и подошли к последнему испытанию, мы расколдовали почти всех, остались заколдованные цифры, которые забыли, в каком они идут порядке. Поможем им?
Игра “По порядку, становись!”
Перед игрой можно посчитать, чтобы дети запомнили свою цифру
Воспитатель раздаёт детям сигнальные карточки от
одного до десяти (или по количеству участников, включая себя), одну берёт себе. Под музыку дети бегают по группе в хаотическом порядке. По сигналу
воспитателя становятся в ряд. Место в ряду соответствует месту числа (надписи
на карточке)” По порядку становись!”
Под музыку дети бегают по группе в хаотическом порядке. По сигналу
воспитателя становятся в ряд. Место в ряду соответствует месту числа (надписи
на карточке)” По порядку становись!”
Можно создать проблемную ситуацию: воспитатель может стать не на то место. Дети вместе с воспитателем проверяют правильность выполнения задания «считают, если что-то не правильно – исправляют ошибку»
Педагог. Мы с вами – молодцы, помогли расколдовать жителей математической страны, они нам очень благодарны и дарят вам вот такие замечательные медальки!
Подведение итогов. Рефлексия вместе с детьми. Вопросы: что мы сегодня вспомнили из того, о чем говорили раньше; где возникли трудности, а где, наоборот, было легко; что запомнилось и хотелось бы повторить еще раз? и т.д.
4 задание ЕГЭ по математике профильного уровня 2023: теория и практика
Русский язык Математика (профиль) Математика (база) Обществознание История Биология Физика Химия Английский язык Информатика Литература
Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18
За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: повышенный.
На решение дается около 5 минут. Уровень сложности: повышенный.
Средний процент выполнения: 86.9%
Ответом к заданию 4 по математике (профильной) может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Посмотреть
Задачи для практики
Задача 1
Чтобы поступить в институт на специальность «Комплексное использование и охрана водных ресурсов», абитуриент должен набрать на ЕГЭ не менее $70$ баллов по каждому из трёх предметов — математике, русскому языку и физике. Чтобы поступить на специальность «Безопасность жизнедеятельности в техносфере», нужно набрать не менее $70$ баллов по каждому из трёх предметов — математике, русскому языку и химии. Вероятность того, что абитуриент Э. получит не менее $70$ баллов по математике, равна $0{,}5$, по русскому языку — $0{,}7$, по физике — $0{,}6$ и по химии — $0{,}3$. Найдите вероятность того, что Э. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Найдите вероятность того, что Э. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решение
Чтобы поступить хотя бы на одну специальность, абитуриенту Э. надо набрать не менее 70 баллов по математике, русскому языку и хотя бы по одному из предметов химия и физика.
Найдём вероятность того, что абитуриент Э. наберёт не менее 70 баллов хотя бы по одному из предметов химия и физика. Сначала отыщем вероятность противоположного события, то есть вероятность того, что абитуриент Э. по обоим этим предметам не наберёт 70 баллов. Результаты экзаменов не зависят друг от друга, вероятность не набрать 70 баллов по физике равна 1 – 0.6 = 0.4, а вероятность не набрать 70 баллов по химия равна 1 – 0.3 = 0.7. Отсюда вероятность того, что абитуриент Э. по обоим этим предметам не наберёт 70 баллов, равна 0.4 · 0.7 = 0.28. Следовательно, вероятность того, что абитуриент Э. наберёт не менее 70 баллов хотя бы по одному из предметов химия и физика, равна 1 – 0.28 = 0.72.
Таким образом, вероятность того, что абитуриент Э. наберёт не менее 70 баллов по математике, русскому языку и хотя бы по одному из предметов химия и физика, равна 0.5 · 0.7 · 0.72 = 0.252.
наберёт не менее 70 баллов по математике, русскому языку и хотя бы по одному из предметов химия и физика, равна 0.5 · 0.7 · 0.72 = 0.252.
Ответ: 0.252
Показать решение
Полный курс
Задача 2
Биатлонист Алексей Антонов пять раз стреляет по мишеням. Вероятность попадания при одном выстреле равна $0{,}7$. Найдите вероятность того, что биатлонист Алексей Антонов один раз попал по мишени, а четыре — промахнулся. Результат округлите до сотых.
Решение
Вероятность промахнуться при одном выстреле равна $1 – 0.7 = 0.3$. Обозначим события.
1. $A_1$ — «Алексей попал по мишени при первом выстреле».
2. $A_2$ — «Алексей попал по мишени при втором выстреле».
3. $A_3$ — «Алексей попал по мишени при третьем выстреле».
4. $A_4$ — «Алексей попал по мишени при четвёртом выстреле».
5. $A_5$ — «Алексей попал по мишени при пятом выстреле».
События ${A_1}↖{-}, {A_2}↖{-}, {A_3}↖{-}, {A_4}↖{-}$ и ${A_5}↖{-}$ — означают, что Алексей промахнулся при соответствующем выстреле. 4 · 0.7 = 0.00567$.
4 · 0.7 = 0.00567$.
Следовательно, искомая вероятность равна $0.00567 · 5 = 0.02835 ≈0.03$.
Ответ: 0.03
Показать решение
Полный курс
Задача 3
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы $4$ очка в двух играх. Если команда выигрывает, она получает $3$ очка, в случае ничьей — $1$ очко, если проигрывает — $0$ очков. Найдите вероятность того, что команде «Ветерок» удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны $0{,}3$.
Решение
Вероятность ничьей в каждой игре равна 1 – 0.3 – 0.3 = 0.4 (из единицы вычитаем вероятность выигрыша и вероятность проигрыша). «Ветерок» выйдет в следующий круг в одном из трёх следующих случаев.
1. «Ветерок» выиграет обе игры. Вероятность этого равна 0.3 · 0.3 = 0.09.
2. «Ветерок» выиграет первую игру и сыграет вничью вторую. Вероятность этого равна 0.3 · 0.4 = 0.12.
Вероятность этого равна 0.3 · 0.4 = 0.12.
3. «Ветерок» сыграет вничью первую игру и выиграет вторую. Вероятность этого равна 0.4 · 0.3 = 0.12.
Искомая вероятность равна 0.09 + 0.12 + 0.12 = 0.33.
Ответ: 0.33
Показать решение
Полный курс
Задача 4
Помещение торгового дома «Светлый» освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна $0{,}6$. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение
Найдём вероятность события «перегорели обе лампы», а затем искомую вероятность.
Вероятность события «перегорела первая лампа» равна вероятности события «перегорела вторая лампа» и равна 0.6. Эти два события независимы, значит, вероятность того, что они наступили оба, равна произведению их вероятностей, то есть равна 0.6 · 0.6 = 0.36. Это вероятность события «перегорели обе лампы».
События «перегорели обе лампы» и «хотя бы одна лампа не перегорела» противоположны, следовательно, сумма их вероятностей равна 1. Значит, вероятность события «хотя бы одна лампа не перегорела» равна 1 – 0.36 = 0.64.
Ответ: 0.64
Показать решение
Полный курс
Задача 5
В ларьке на улице Счастья стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью $0{,}1$ независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение
Найдём вероятность события «оба автомата неисправны», а затем искомую вероятность.
Вероятность события «неисправен первый автомат» равна вероятности события «неcисправен второй автомат» и равна 0,1. Эти два события независимы, значит, вероятность того, что они наступят оба, равна произведению их вероятностей, то есть равна 0.1 · 0.1 = 0.01. Таким образом, мы нашли вероятность события «оба автомата неисправны».
События «оба автомата неисправны» и «хотя бы один автомат исправен» противоположны, следовательно, сумма их вероятностей равна 1. Значит, вероятность события «хотя бы один автомат исправен» равна 1 – 0.01 = 0.99.
Ответ: 0.99
Показать решение
Полный курс
Задача 6
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью $0{,}72$. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью $0{,}6$. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение
По условию вероятность события «шахматист А. выиграет белыми» равна $0{,}72$, вероятность события «шахматист А. выиграет чёрными» равна $0{,}6$. Эти события независимы. Значит, вероятность того, что оба этих события наступят (А. выиграет оба раза) равна произведению вероятностей, то есть равна $0{,}72⋅ 0{,}6=0{,}432$.
Ответ: 0.432
Показать решение
Полный курс
Задача 7
На железнодорожном вокзале $3$ кассира. Каждый из них занят с клиентом с вероятностью $0{,}2$ независимо от других кассиров. Найдите вероятность того, что в случайный момент времени все три кассира заняты одновременно.
Решение
События «первый кассир занят», «второй кассир занят» и «третий кассир занят» по условию независимы. Тогда вероятность их одновременного наступления (вероятность пересечения событий) равна произведению вероятностей этих событий, то есть равна 0.2 · 0.2 · 0.2 = 0.008.
Ответ: 0.008
Показать решение
Полный курс
Задача 8
В магазине сантехники три продавца. Каждый из них занят с клиентом с вероятностью $0{,}7$ независимо от других продавцов. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно.
Решение
События «первый продавец занят», «второй продавец занят» и «третий продавец занят» по условию независимы.
Тогда вероятность их одновременного наступления (вероятность пересечения событий) равна произведению вероятностей этих событий
То есть равна $0.7 · 0.7 · 0.7 = 0.343$
Ответ: 0.343
Показать решение
Полный курс
Задача 9
Вероятность того, что новый электрический чайник прослужит больше года, равна $0{,}93$. Вероятность того, что он прослужит больше двух лет, равна $0{,}84$. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решение
Заметим, что из событий “чайник прослужит меньше года”, “чайник прослужит от 1 до 2 лет” и “чайник прослужит больше двух лет” произойдёт обязательно ровно одно, то есть, говоря математическим языком, они попарно несовместны, а их объединение – достоверное событие. Следовательно, сумма вероятностей этих событий равна 1.
При этом события “чайник прослужит меньше года” и “чайник прослужит больше года” противоположны, поэтому вероятность события “чайник прослужит меньше года” равна 1 – 0.93 = 0.07. Заполним таблицу.
| Событие | Прослужит меньше года | Прослужит от 1 до 2 лет | Прослужит больше двух лет |
| Вероятность | 0.07 | ? | 0.84 |
Отсюда искомая вероятность равна 1 – 0.07 – 0.84 = 0.09.
Ответ: 0.09
Показать решение
Полный курс
Задача 10
На экзамене по биологии студент отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Млекопитающие», равна $0{,}36$. Вероятность того, что это вопрос по теме «Бактерии», равна $0{,}18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене студенту достанется вопрос по одной из этих двух тем.
Решение
Из условия следует, что события A = “достанется вопрос по теме Млекопитающие” и B = “достанется вопрос по теме Бактерии” несовместны. Действительно, нет билетов, относящихся к обоим этим темам одновременно. Событие “достанется вопрос по одной из этих двух тем” – это объединение событий A и B (A $∪$ B). По формуле вероятности объединения несовместных событий получим, что искомая вероятность равна P(A $∪$ B) = P(A) + P(B) = 0.36 + 0.18 = 0.54.
Ответ: 0.54
Показать решение
Полный курс
Задача 11
В торговом центре два одинаковых автомата продают лимонад. Вероятность того, что к концу дня в автомате закончится лимонад, равна $0{,}2$. Вероятность того, что лимонад закончится в обоих автоматах, равна $0{,}09$. Найдите вероятность того, что к концу дня лимонад останется в обоих автоматах.
Решение
По условию вероятность события A =«сладкая вата закончится в первом автомате» равна вероятности события B =«сладкая вата закончится во втором автомате» и равна $0. 2$. Эти два события зависимые.
2$. Эти два события зависимые.
В этом случае воспользуемся формулой $P (A + B) = P (A) + P (B) – P (A B)$.
$P (A + B) = 0.2 + 0.2 – 0.09 = 0.31$. Событие $A + B$ — это событие «сладкая вата закончилась хотя бы в одном автомате». Указанное событие противоположно искомому. Отсюда вероятность события «сладкая вата останется в обоих автоматах» равна $1 – 0.31 = 0.69$.
Ответ: 0.69
Показать решение
Полный курс
Задача 12
Предприниматель закупает для продажи на рынке куриные яйца в двух хозяйствах. $50%$ яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — $40%$ яиц высшей категории. При продаже яиц на рынке оказалось, что всего получилось $42%$ яиц высшей категории. Найдите вероятность того, что яйцо, купленное у предпринимателя, окажется из второго хозяйства.
Решение
Ответ: 0.8
Показать решение
Полный курс
Задача 13
Робин Гуд подошел к столу, на котором лежали 3 его старых лука и 2 новых. Он решил сбить стрелой яблоко с дерева. Робин попадает в цель из своего старого лука с вероятностью $0{,}8$, а из нового — с вероятностью $0{,}3$. Робин случайным образом выбирает один лук. Найдите вероятность того, что Робин промахнётся при стрельбе.
Он решил сбить стрелой яблоко с дерева. Робин попадает в цель из своего старого лука с вероятностью $0{,}8$, а из нового — с вероятностью $0{,}3$. Робин случайным образом выбирает один лук. Найдите вероятность того, что Робин промахнётся при стрельбе.
Решение
Ответ: 0.4
Показать решение
Полный курс
Показать еще
Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.
Включить уведомления
Готовим к ЕГЭ на 85+ баллов и побеждаем лень
Каждый месяц 12 онлайн-занятий в дружелюбной атмосфере + 16 домашних работ с жесткими сроками.
Не готовишься — вылетаешь.
 Подробнее о курсе
Подробнее о курсе10 потрясающих идей для математических проектов на конец года — Mashup Math
Следующий список идей для математических проектов идеально подходит для того, чтобы ваши ученики были заняты в последние недели учебного года (или в любое другое время). Эти задания могут быть адаптированы для всех классов и уровней способностей и включены в мою программу «21 стратегия экономии времени, занятия и идеи, которые должны знать все учителя математики» .
Наступили последние недели учебного года, и найти способы, чтобы ваши дети активно занимались математикой, становится все труднее, чем когда-либо.
Предоставление ученикам работы над проектами, связанными с математикой, — отличный способ удержать их внимание и разбавить монотонность обычной классной рутины.
Следующий список проектных идей можно изменить, чтобы соответствующим образом заинтересовать учащихся математики в начальной и средней школе.
Итак, каким проектом вы собираетесь поделиться со своими детьми?
1.) The Theme Park ProjectДженна через www.musingsfromthemiddleschool.blogspot.com
Описание: Учащиеся используют навыки площади и периметра, чтобы спроектировать план идеального тематического парка.
Изображение с musingsfromthemiddleschool.blogspot.com
2.) The Ultimate Paper Airplane Competitionот Michael на сайте www.thethinkerbuilder.com
Описание: Работая в группах, учащиеся должны спроектировать и построить бумажный самолетик, который выдержит четыре раунда рабочих заданий, включая время зависания и расстояние.
Изображение через www.thethinkerbuilder.com
4. ) Квест-комната в пиратском стиле
) Квест-комната в пиратском стиле от Терезы на сайте www.teacherspayteachers.com
Описание: Ваш класс был захвачен группой отважных пиратов! Они должны использовать свои математические способности, чтобы сбежать.
Изображение с сайта www.gettyimages.com
5.) Парашюты STEMот Amy на сайте www.allabout3rdgrade.com
Описание: Придумайте и сконструируйте парашют, который будет оставаться в воздухе дольше всех.
Изображение с сайта www.allabout3rdgrade.com
ВЫ ищете очень веселые математические головоломки для своих учеников 3-8 классов? Наш бестселлер 9Рабочая тетрадь 0021 101 Daily Math Challenges теперь доступна для скачивания в формате PDF!
6. ) Планируйте отпуск своей мечты
) Планируйте отпуск своей мечты Дженнифер на сайте www.loveteachingkids.com
Описание: Учащиеся работают в группах, используя бюджет, чтобы спланировать все аспекты отпуска своей мечты.
Изображение с www.loveteachingkids.com
7.) Набор «Дроби»от Энтони на www.youtube.com/mashupmath
Описание: Помогите своим детям глубже понять эквивалентные дроби с помощью этого увлекательного практического занятия!
Нажмите здесь, чтобы узнать больше об этом увлекательном занятии!
Изображение через www.mashupmath.com
8.) Преображение экстремальной детской площадкиот Дженнифер на сайте www.teachingtoinspire.com
Описание: Созданные по образцу телешоу, учащиеся отвечают за проектирование экстремальной игровой площадки с использованием геометрических форм, элементов и свойств.
Бесплатно зарегестрироваться
9.) Инфографика «Отражение на конец года»от Brain Waves Instruction
Описание: По мере того, как календарный год подходит к концу, вовлеките своих учащихся в это веселое и творческое личное размышление и задание с инфографикой.
Изображение через www.teacherspayteachers.com
10.) Математические игры на свежем воздухеот www.coffeecupsandcrayons.com
Описание: Свежий воздух и смена обстановки могут быть именно тем, что нужно детям, чтобы увлечься игрой и отработкой математических понятий.
Изображение через www.coffeecupsandcrayons.com
У вас есть еще идеи для веселья и интересных математических проектов, которыми вы могли бы поделиться с нашим сообществом? Поделитесь своими предложениями в разделе комментариев ниже. Подпишитесь на нашу рассылку здесь, чтобы каждую неделю получать больше бесплатных ежедневных ресурсов, уроков и советов по электронной почте.
Подпишитесь на нашу рассылку здесь, чтобы каждую неделю получать больше бесплатных ежедневных ресурсов, уроков и советов по электронной почте.
Энтони — ведущий преподаватель и основатель Mashup Math . Он живет в Денвере, штат Колорадо, а также является партнером YouTube for Education . Следуйте за ним на Twitter в @mashupmath .
Меня интересует…Центр инноваций в преподавании математики
Центр инноваций в преподавании математики – MEP (начальный) Первоначальная разработка этого проекта финансировалась PricewaterhouseCoopers, но с дополнительным финансированием от ESSO, Corus и Garfield Weston. Фундамент. Проект продолжается, и в него вносятся дальнейшие усовершенствования. Фундамент. Проект продолжается, и в него вносятся дальнейшие усовершенствования. |
| Большая часть материала, разработанного для этой инициативы, основана на венгерской серии, отредактированной профессором Сндором Хайду из Института домашних животных в Будапеште и опубликованной Мшаки Книвкиад. Этот
был адаптирован и изменен для школ Великобритании с помощью профессора Тибора Салонтаи и Риты Салонтаи. Благодарим за помощь и сотрудничество наших венгерских коллег в этом проекте. |
| Для доступа почти ко всем материалам требуется Acrobat Reader. Узнайте об этом (что это такое и где это бесплатно!) здесь. |
и рекомендации | |||||||||||||||||||||||
| Сопоставление начальной школы MEP и NEW National Curriculum | |||||||||||||||||||||||
| Коллекция прозрачных пленок OHP для приема, год 1 и год 2 | Коллекция плакатов для приемной, 1-й и 2-й классы | ||||||||||||||||||||||
| Номер строки | |||||||||||||||||||||||
| Карточки с номерами | Знаковые карточки | ||||||||||||||||||||||
| Карточки формы | Карточки с точками | ||||||||||||||||||||||
Размеры больших файлов [в килобайтах] даны в качестве руководства по времени загрузки.
| Приемная | Приемная |
| Планы уроков для | Уроки с 1 по 10 [197] | Уроки с 11 по 20 [174] | Уроки с 21 по 30[242] |
| Копи-мастера для | Уроки с 1 по 10 [1139] | Уроки с 11 по 20 [1332] | Уроки с 21 по 30[2092] |
| Планы уроков для | Уроки с 31 по 40 [182] | Уроки с 41 по 50 [185] | Уроки с 51 по 60 [205] |
| Копи-мастера для | Уроки с 31 по 40 [1114] | Уроки с 41 по 50 [1149] | Уроки с 51 по 60 [1097] |
| Год 1 | Год 1 |
| Цели обучения | Обзор | Факты, которые нужно знать и помнить | Упражнения | Решения | |||||||||||||||
| Учебник 1 | Страницы с 1 по 24 [593] | Страницы с 25 по 40 [277] | Страницы с 41 по 64 [438] | ||||||||||||||||
| Страницы с 65 по 88 [352] | Страницы с 89 по 112 [417] | Страницы со 113 по 140 [526] | |||||||||||||||||
| Практика 1 Ответы | Страницы с 1 по 24 [659] | Страницы с 25 по 40 [302] | Страницы с 41 по 64 [470] | ||||||||||||||||
| Страницы с 65 по 88 [370] | Страницы с 89 по 112 [451] | Страницы со 113 по 140 [576] | |||||||||||||||||
| Планы уроков для | Уроки с 1 по 24 [332] | Уроки с 25 по 40 [170] | Уроки с 41 по 64 [210] | ||||||||||||||||
| Уроки с 65 по 88 [182] | Уроки с 89 по 112 [235] | Уроки с 113 по 140 [287] | |||||||||||||||||
| Копи-мастера для | Уроки с 1 по 24 [354] | Уроки с 25 по 40 [292] | Уроки с 41 по 64 [441] | ||||||||||||||||
| Уроки с 65 по 88 [639] | Уроки с 89 по 112 [816] | Уроки с 113 по 140 [904] | |||||||||||||||||
| Ревизионный материал | Контрольные вопросы [367] | Редакция Ответы [446] | |||||||||||||||||
| Год 2 | Год 2 |
| Цели обучения | Обзор | Факты, которые нужно знать и помнить | Упражнения | Решения | |||||||||||||||
| Учебник 2 | Страницы с 1 по 24 [227] | Страницы с 25 по 40 [1727] | Страницы с 41 по 64 [172] | ||||||||||||||||
| Страницы с 65 по 88 [907] | Страницы с 89 по 112 [238] | Страницы со 113 по 140 [307] | |||||||||||||||||
| Учебник 2 Ответы | Страницы с 1 по 24 [306] | Страницы с 25 по 40 [216] | Страницы с 41 по 64 [217] | ||||||||||||||||
| Страницы с 65 по 88 [736] | Страницы с 89 по 112 [300] | Страницы со 113 по 140 [406] | |||||||||||||||||
| Планы уроков для | Уроки с 1 по 24 [209] | Уроки с 25 по 40 [147] | Уроки с 41 по 64 [211] | ||||||||||||||||
| Уроки с 65 по 88 [329] | Уроки с 89 по 112 [296] | Уроки с 113 по 140 [298] | |||||||||||||||||
| Копи-мастера для | Уроки с 1 по 24 [617] | Уроки с 25 по 40 [408] | Уроки с 41 по 64 [564] | ||||||||||||||||
| Уроки с 65 по 88 [1259] | Уроки с 89 по 112 [660] | Уроки с 113 по 140 [785] | |||||||||||||||||
| Материал ревизии | Вопросы по пересмотру [431] | Редакция Ответы [489] | |||||||||||||||||
| Год 3 | Год 3 |
| Цели обучения | Обзор | Факты, которые нужно знать и помнить | Упражнения | Решения | |||||||||||||||
| Учебник 3 | Страницы с 1 по 24 [271] | Страницы с 25 по 40 [639] | Страницы с 41 по 64 [213] | ||||||||||||||||
| Страницы с 65 по 88 [275] | Страницы с 89 по 112 [357] | Страницы со 113 по 140 [376] | |||||||||||||||||
| Учебник 3 Ответы | Страницы с 1 по 24 [299] | Страницы с 25 по 40 [646] | Страницы с 41 по 64 [423] | ||||||||||||||||
| Страницы с 65 по 88 [275] | Страниц 89по 112 [304] | Страницы со 113 по 140 [243] | |||||||||||||||||
| Планы уроков для | Уроки с 1 по 24 [645] | Уроки с 25 по 40 [429] | Уроки с 41 по 64 [504] | ||||||||||||||||
| Уроки с 65 по 88 [541] | Уроки с 89 по 112 [661] | Уроки с 113 по 140 [674] | |||||||||||||||||
| Копи-мастера на | Уроки с 1 по 24 [1007] | Уроки с 25 по 40 [1073] | Уроки с 41 по 64 [787] | ||||||||||||||||
| Уроки с 65 по 88 [708] | Уроки с 89 по 112 [936] | Уроки с 113 по 140 [1052] | |||||||||||||||||
| Ревизионный материал | Контрольные вопросы [302] | Редакция Ответы [401] | |||||||||||||||||
Если вы используете оригинальные ресурсы 3-го года с книгами Y3a и Y3b, файлы поддержки доступны здесь
| Год 4 | Год 4 |
| Цели обучения | Обзор | Факты, которые нужно знать и помнить | Упражнения | Решения | |||||||||||||||
| Учебник 4a | Страницы с 1 по 30 [150] | Страницы с 31 по 50 [100] | Страницы с 51 по 80 [140] | ||||||||||||||||
| Учебник 4a Ответы | Страницы с 1 по 30 [249] | Страницы с 31 по 50 [181] | Страницы с 51 по 80 [240] | ||||||||||||||||
| Планы уроков для | Уроки с 1 по 30 [480] | Уроки с 31 по 50 [470] | Уроки с 51 по 80 [500] | ||||||||||||||||
| Копи-мастера по | Уроки с 1 по 30 [190] | Уроки с 31 по 50 [300] | Уроки с 51 по 80 [220] | ||||||||||||||||
| Учебник 4b | Страницы с 81 по 110 [170] | Страницы со 111 по 140 [160] | Страницы с 141 по 175 [190] | ||||||||||||||||
| Учебник 4b Ответы | Страницы с 81 по 110 [284] | Страницы со 111 по 140 [281] | Страницы с 141 по 175 [348] | ||||||||||||||||
| Планы уроков для | Уроки с 81 по 110 [550] | Уроки с 111 по 140 [480] | Уроки с 141 по 175 [560] | ||||||||||||||||
| Копи-мастера для | Уроки с 81 по 110 [200] | Уроки с 111 по 140 [150] | Уроки с 141 по 175 [200] | ||||||||||||||||
| Год 5 | Год 5 |
| Цели обучения | Обзор | Факты, которые нужно знать и помнить | Упражнения | Решения | |||||||||||||||
| Учебник 5 | Страницы с 1 по 24 [211] | Страницы с 25 по 40 [367] | Страницы с 41 по 64 [372] | ||||||||||||||||
| Страницы с 65 по 88 [525] | Страницы с 89 по 112 [238] | Страницы со 113 по 140 [573] | |||||||||||||||||
| Учебник 5 ответов | Страницы с 1 по 24 [633] | Страницы с 25 по 40 [3000] | Страницы с 41 по 64 [777] | ||||||||||||||||
| Страницы с 65 по 88 [1350] | Страницы с 89 по 112 [776] | Страницы со 113 по 140 [1227] | |||||||||||||||||
| Планы уроков для | Уроки с 1 по 24 [877] | Уроки с 25 по 40 [605] | Уроки с 41 по 64 [995] | ||||||||||||||||
| Уроки с 65 по 88 [1297] | Уроки с 89 по 112 [801] | Уроки с 113 по 140 [1447] | |||||||||||||||||
| Копи-мастера для | Уроки с 1 по 24 [775] | Уроки с 25 по 40 [1051] | Уроки с 41 по 64 [840] | ||||||||||||||||
| Уроки с 65 по 88 [998] | Уроки с 89 по 112 [681] | Уроки с 113 по 140 [919] | |||||||||||||||||
| Ревизионный материал | Контрольные вопросы [550] | Редакция Ответы [1604] | |||||||||||||||||
| Год 6 | Год 6 |
| Цели обучения | Обзор | Факты, которые нужно знать и помнить | Упражнения | Решения | |||||||||||||||
| Учебник 6a | Страницы с 1 по 30 [260] | Страницы с 31 по 50 [159] | Страницы с 51 по 80 [187] | ||||||||||||||||
| Учебник 6a Ответы | Страницы с 1 по 30 [579] | Страницы с 31 по 50 [729] | Страницы с 51 по 80 [570] | ||||||||||||||||
| Планы уроков для | Уроки с 1 по 30 [506] | Страницы с 31 по 50 [435] | Страницы с 51 по 80 [649] | ||||||||||||||||
| Копи-мастера для | Уроки с 1 по 30 [153] | Страницы с 31 по 50 [145] | Страницы с 51 по 80 [555] | ||||||||||||||||
| Учебник 6b | Страницы с 81 по 110 [164] | Страницы со 111 по 140 [112] | Страницы с 141 по 175 [161] | ||||||||||||||||
| Учебник 6b Ответы | Страницы с 81 по 110 [646] | Страницы со 111 по 140 [503] | Страницы с 141 по 175 [608] | ||||||||||||||||
| Планы уроков для | Уроки с 81 по 110 [654] | Уроки с 111 по 140 [582] | Уроки с 141 по 175 [676] | ||||||||||||||||
| Копи-мастера для | Уроки с 81 по 110 [167] | Уроки с 111 по 140 [57] | Уроки с 141 по 175 [121] | ||||||||||||||||
Южноафриканская версия MEP Primary доступна здесь
Ямайская версия MEP Primary доступна здесь
Испанская версия MEP Primary доступна здесь
Авторское право
Авторские права на все материалы принадлежат создателям.

Материал доступен через CIMT для скачивания и распространения ТОЛЬКО ДЛЯ
НЕКОММЕРЧЕСКИХ ЦЕЛЕЙ.
Задание по математике | Библиотека Университета Ватерлоо
Задания на курсах математики обычно представляют собой список задач, которые необходимо решить. Каждый вопрос может иметь разную сложность и тип, которые отмечаются и возвращаются учащемуся для использования в качестве источника обратной связи.
Задания по математике предназначены для того, чтобы дать возможность «выполнить математику» и закрепить понимание учащимися содержания. Вопросы часто исходят из изученного материала за последнюю неделю, но некоторые вопросы могут потребовать, чтобы учащиеся синтезировали понятия из более раннего периода. Это связано с тем, что изучение математики носит кумулятивный характер; вы постоянно опираетесь на то, чему научились раньше.
Поскольку математические задания обычно используются в качестве контрольной точки для понимания, они, как правило, имеют меньший вес, чем другие оценки с точки зрения оценки, поэтому важно рассматривать их как возможность обучения, а не инструмент для получения максимальных оценок за курс.
Нажмите на временную шкалу для визуального представления временной шкалы. Нажмите на контрольный список, чтобы открыть документ, содержащий элементы контрольного списка для математического задания.
Нажмите на шаги, чтобы развернуть или свернуть. Развернуть все шаги (+)
Шаг 1: понять вопросы Завершено до 30 сентября 2022 г. Процент времени, потраченного на этот шаг: 5%Прочитайте задание после его публикации и поймите вопросы. Прочитайте вопросы заранее, чтобы подготовить свой мозг; слишком много студентов начинают слишком поздно.
- Для некоторых курсов задания выдаются до или по мере изучения содержания, поэтому наличие вопросов в уме при просмотре содержания может помочь вам активно изучить содержание, а также поможет вам узнать, где искать соответствующую информацию. материал в конспектах лекций и/или видео.
 Активное изучение контента означает, что вы задаете себе вопросы по мере изучения, активно следите за своим пониманием темы и предугадываете следующие шаги.
Активное изучение контента означает, что вы задаете себе вопросы по мере изучения, активно следите за своим пониманием темы и предугадываете следующие шаги. - Прочтите все вопросы, чтобы оценить диапазон проверяемого материала, отметьте все, что вам непонятно. Правильное понимание вопроса снижает вероятность застревания.
Самое сложное в общении с математиком – это то, что у него всегда есть проблемы.
– Тендай Читевере
Шаг 2. Сбор материалов и проверка Завершено до 30 сентября 2022 г. Процент времени, потраченного на этот шаг: 15%
- Соберите необходимые материалы (конспекты лекций и/или видео, разделы учебников).
- Изучайте материал (определения, понятия, решаемые задачи и т. д.), пока не освоитесь с ним. Определите связи между концепциями/темами и отработайте дополнительные проблемы. Регулярный просмотр материалов также поможет вам быстро найти нужную информацию, если вы застряли на вопросе.

Шаг 3. Ответьте на вопросы и получите помощь Завершено до 30 сентября 2022 г. Процент времени, потраченного на этот шаг: 70%
Часть A: Попытка решить каждый вопрос
- Попытка решить вопросы, как если бы это был тест. То есть дайте себе определенное количество времени и постарайтесь решить все проблемы. Если вы не можете решить одну, ничего страшного, просто переходите к следующей задаче. Вы вернетесь к этому позже.
- Эмпирическое правило распределения времени: один сложный вопрос может занять значительно больше времени, чем все простые вопросы вместе взятые. Подумайте, сколько времени вам потребовалось, чтобы решить все простые вопросы. На решение одного сложного вопроса может уйти как минимум вдвое больше времени. Попробуйте все простые вопросы как можно скорее, чтобы оценить, сколько времени могут занять остальные.
- Если у вас есть вопросы, которые вы не смогли решить, просмотрите уроки/заметки, чтобы узнать, сможете ли вы понять, чего вам не хватает.
 Затем:
Затем:- Попробуйте сделать перерыв на один день, прежде чем пытаться выполнить их снова, чтобы у вашего разума было время продолжить подсознательную работу.
- Все еще зависает? Проверьте математические задачи: что делать, если вы застряли для получения дополнительных стратегий и советов.
- Отслеживайте нерешенные вопросы и этапы, на которых вы застряли. Не отказывайтесь от незавершенной работы. Ваш инструктор или ассистент могут оказать лучшую помощь, если вы сможете сузить круг вопросов.
Единственный способ выучить математику — заниматься математикой.
– Пол Халмос
Математика не является дедуктивной наукой, это клише. Когда вы пытаетесь доказать теорему, вы не просто перечисляете гипотезы, а затем начинаете рассуждать. То, что вы делаете, это пробы и ошибки, эксперименты, догадки.
– Пол Халмос
Часть B: Получите помощь по нерешенным вопросам
- Посещайте рабочие часы, учебные пособия или онлайн-форум, если он есть в классе.

- Чем раньше вы обратитесь за поддержкой, тем больше времени у вас и инструктора/ассистента будет для последующих бесед.
- Продолжайте работу над нерешенными вопросами. Часто вы можете быть на правильном пути, и инструктор или ассистент могут оказать лучшую помощь, когда они смогут увидеть, что вы пытались сделать.
- Сосредоточьтесь на вопросах, которые помогут сократить разрыв между вашим пониманием и пониманием, необходимым для ответа на вопрос. Такие вопросы, как «Могу ли я получить подсказку по пункту 4?» или «Каков ответ?» обычно не помогают увеличить ваши способности решать проблемы.
- Для вопросов, которые вызвали у вас затруднения, но вы смогли решить их после получения помощи от инструктора или ассистента, убедитесь, что вы полностью понимаете, как найти решение, если аналогичный вопрос задан на тесте.
- Многим студентам полезно учиться вместе. Убедитесь, что вы понимаете ожидания вашего инструктора в отношении групповой работы (если вы не уверены, спросите!).
 Помните о том, сколько вы публикуете о решении задания на доске обсуждений курса, и если вы сомневаетесь, подумайте о публикации в частном порядке. Ознакомьтесь с Стандарты академической честности, ожидаемые на ваших курсах.
Помните о том, сколько вы публикуете о решении задания на доске обсуждений курса, и если вы сомневаетесь, подумайте о публикации в частном порядке. Ознакомьтесь с Стандарты академической честности, ожидаемые на ваших курсах.
Цель обращения за помощью — попытаться найти подход к вопросам, с которыми вы застряли. Из этой дополнительной помощи вы все еще можете не увидеть полной картины того, как решить проблему. Чтобы увидеть это, вам может потребоваться вернуться к , часть A , теперь с учетом предложений инструктора/ассистента.
Я не подвел. Я только что нашел 10 000 способов, которые не работают.
– Томас Алва Эдисон
Шаг 4. Проверьте свои решения Завершено до 30 сентября 2022 г. Процент времени, потраченного на этот шаг: 10%
- Важно, чтобы вы провели некоторое время вдали от своих решений, прежде чем проверять их.
 Для задач, которые вы решили, попытайтесь выяснить, можете ли вы проверить свой собственный ответ, как в тесте (т. е. не ищите ответы в книге или в Интернете).
Для задач, которые вы решили, попытайтесь выяснить, можете ли вы проверить свой собственный ответ, как в тесте (т. е. не ищите ответы в книге или в Интернете). - =Вы можете обратиться за советом к инструктору/ассистенту, но избегайте таких вопросов, как «Правильно ли я это сделал?» Вместо этого спросите себя, задаете ли вы правильные вопросы о своем решении.
- Не забудьте сосредоточиться не только на окончательном ответе, но и на том, как вы его донесли. Спросите себя, сможет ли обычный ученик в классе повторить то, что вы написали.
- Не забудьте указать любые внешние источники, которые вы использовали в своей работе, включая работу, выполненную совместно с другими (если это было разрешено).
Шаг 5. Просмотр отмеченных назначений Завершено до 30 сентября 2022 г. Процент времени, потраченного на этот шаг: 0%
После получения отмеченного задания проверьте неправильные вопросы, а также те, на которые вы ответили правильно. Просмотрите опубликованные решения и прочитайте их критически. Часто существуют разные подходы к проблеме, и вы можете узнать о некоторых из этих новых подходов из этого обзора.
Просмотрите опубликованные решения и прочитайте их критически. Часто существуют разные подходы к проблеме, и вы можете узнать о некоторых из этих новых подходов из этого обзора.
Учебная программа по математике для 12-го класса – Time4Learning
Посмотрите наши демонстрации уроков!
Мы в Time4Learning считаем себя партнерами родителей в обеспечении того, чтобы учащиеся заканчивали среднюю школу с навыками, необходимыми им для успешной учебы на курсах уровня колледжа. Для математики, в частности, это означает предоставление основанной на стандартах программы подготовки к колледжу, которая фокусируется на основных математических понятиях, используя множество различных типов мультимедийных инструментов, чтобы заинтересовать учащихся и пробудить больший интерес к математике.
На этой странице вы узнаете, что должны знать 12-классники по математике, узнаете больше об общих задачах 12-го класса по математике и узнаете, как учебная программа Time4Learning по математике для 12-го класса помогает семьям, обучающимся на дому, достичь своих целей в этот важный год обучения.
- Какой предмет по математике должен сдавать 12-классник?
- Цели для 12-го класса средней школы по математике
- Почему стоит выбрать программу Time4Learning по математике для двенадцатого класса в домашних условиях?
- Дополнительные ресурсы для домашнего обучения 12-го класса
Какие математические курсы должен пройти 12-классник?
Учащимся, планирующим поступить в колледж, рекомендуется 3-4 года изучения математики в старшей школе. К 12-му классу большинство учеников завершат алгебру I, алгебру II и геометрию, поэтому старшеклассники могут захотеть сосредоточиться на курсе математики более высокого уровня, таком как предварительное исчисление или тригонометрия.
Учащиеся, изучающие углубленный курс математики, изучат такие понятия, как:
- Графики экспоненциальных и логарифмических функций
- Распределения вероятностей
- Последовательности, ряды и доказательства по индукции
- Тригонометрические функции, преобразования и обратные функции
- Решение тригонометрических уравнений
- Векторы и векторные операции
Узнайте больше об учебной программе Time4Learning по математике для двенадцатого класса, ознакомившись с объемом и последовательностью занятий для 12-го класса, а также со страницей планов уроков математики для 12-го класса.
Цели для средней школы 12-го класса по математике
Благодаря тому, что карьера в сфере STEM (наука, технология, инженерия и математика) всегда была на высоте, как никогда важно, чтобы старшеклассники поступали в колледж с прочной математической базой. Двенадцатиклассники, изучающие продвинутый курс математики в выпускном классе, получают преимущество в процессе поступления в колледж, особенно если они будут специализироваться в области математики или естественных наук.
Чтобы быть готовым к поступлению в колледж, математическая практика в 12 классе должна быть сосредоточена на развитии таких навыков, как:
- Абстрактные и количественные рассуждения
- Статистическое моделирование
- Стратегическое использование соответствующих инструментов
- Вероятностное моделирование
- Визуализация графиков функций
- Решение систем уравнений
Почему стоит выбрать программу Time4Learning для 12-го класса по математике в домашних условиях?
Учебная программа Time4Learning, основанная на стандартах, охватывает все цели обучения математике для 12-го класса, перечисленные выше, а также многие, многие другие. Курсы продвинутой математики, включенные в нашу учебную программу, развивают критическое мышление и аналитические навыки, которые потребуются учащимся после окончания средней школы.
Курсы продвинутой математики, включенные в нашу учебную программу, развивают критическое мышление и аналитические навыки, которые потребуются учащимся после окончания средней школы.
Некоторые из причин, по которым семьи, обучающиеся на дому, выбирают учебную программу Time4Learning по математике для 12-го класса, включают:
Полная учебная программа
| В качестве дополнения
|
Дополнительные ресурсы для домашнего обучения 12-го класса
Вернуться к обзору учебной программы 12-го класса. Или изучите наши другие ресурсы для двенадцатого класса:
- Учебная программа по математике для двенадцатого класса
- Учебная программа по языкознанию для двенадцатого класса
- Учебная программа по обществознанию для двенадцатого класса
- Как учиться дома в двенадцатом классе
- Прицел и последовательность 12-го класса
- Планы уроков для 12-го класса
Возрастные задачки – ChiliMath
Время от времени мы сталкиваемся со словесными задачками, которые требуют от нас найти взаимосвязь между возрастами разных людей. Проблемы со словами о возрасте обычно включают сравнение возраста двух людей в разные моменты времени, то есть в настоящее время, в прошлом или в будущем.
Этот урок состоит из двух частей. Часть I включает возрастные словесные задачи, которые можно решить с использованием одной переменной , а Часть II содержит возрастные словесные задачи, которые необходимо решить с использованием двух переменных .
Давайте познакомимся с задачами на определение возраста, поработав на нескольких примерах.
ЧАСТЬ I. Решаемые задачи на определение возраста с одной переменной
Пример 1: Таня на 28 лет старше Маркуса. Через 6 лет Таня будет в три раза старше Маркуса. Сколько лет Тане сейчас?
В этой задаче нас просят только найти текущий возраст Тани. Однако проблема также дала нам много другой информации, которая может быть ошеломляющей. Чтобы помочь нам систематизировать важные детали, давайте создадим таблицу, чтобы перечислить то, что мы знаем на данный момент.
Поскольку нам дается только подробная информация об их текущем возрасте и о том, каким они будут через 6 лет, мы продолжим и выделим колонку «Прошлое» серым цветом.
Вы могли заметить, что текущий возраст Тани определяется с помощью возраста Маркуса. Однако настоящий возраст Маркуса в настоящее время неизвестен. Итак, давайте выразим возраст Маркуса, используя переменную x. Поскольку Таня на 28 лет старше Маркуса , то текущий возраст Тани должен быть x+28.
Поскольку Таня на 28 лет старше Маркуса , то текущий возраст Тани должен быть x+28.
Далее заполним колонку Будущее, которая будет состоять из их возраста через 6 лет. Все, что нам нужно сделать, это добавьте 6 к настоящему или текущему возрасту Тани и Маркуса. Таким образом, имеем:
- Таня: \left( {x + 28} \right) {\color{red}+ 6} = x + 34
- Маркус: x {\color{red}+ 6}
Теперь, когда наша таблица заполнена, мы можем продолжить и создать наше уравнение на основе предоставленной информации. Задача гласит следующее:
Через 6 лет Таня будет в три раза старше Маркуса.
Здесь мы пытаемся найти соотношение между их возрастами в будущем. Можно просто сказать, что
Возраст Тани через 6 лет = 3( Возраст Маркуса через 6 лет )
Имея это в виду, мы можем легко построить наше уравнение.
Теперь наш следующий шаг — найти x. Но перед этим вспомним, что наша задача просит нас найти текущий возраст Тани. Поскольку возраст Тани определяется с использованием текущего возраста Маркуса (который равен x), нам нужно сначала найти его возраст, чтобы определить текущий возраст Тани.
Решение:
Теперь, когда у нас есть значение x, давайте узнаем, каков текущий возраст Тани и Маркуса. Мы можем сделать это, просто заменив x на 8.
НАСТОЯЩИЙ ВОЗРАСТ (настоящее время)
- Маркус: x = {\textbf{8}} лет
- Таня: x + 28 = {\color {red}8} + 28 = {\textbf{36}} лет
Возвращаясь к вопросу задачи, сколько сейчас лет Тане?
Ответ: Тане 36 лет.
Проверка ответа:
На данный момент мы уверены, что наш ответ правильный. Но как мы можем быть уверены на 100%? Ну, это всегда хорошая идея, особенно в математике, проверять наши ответы, чтобы быть уверенными, что мы получили правильные значения.
Для этой задачи мы можем просто проверить, соответствует ли наш ответ нашему будущему утверждению. Вы помните это высказывание?
Через 6 лет Таня будет в три раза старше Маркуса.
Нам известен нынешний возраст Маркуса и Тани: 8 и 36 лет соответственно. Следовательно, через 6 лет Маркусу будет 14, а Тане 42 года.
Так через 6 лет Таня будет в три раза старше Маркуса? Ответ: Да .
Пример 2: Брюс на 4 года моложе Гектора. Двадцать лет назад возраст Гектора был на 13 лет больше, чем половина возраста Брюса. Сколько им сейчас лет?
Просто прочитав задачу, мы уже можем сказать, что в ней много информации, которую нам нужно отсортировать, и что эта задача включает в себя дробь. Большинство студентов легко теряются во всей предоставленной информации, не говоря уже о решении уравнений с дробями. Но не волнуйтесь! Пока вы придерживаетесь основных принципов и шагов по решению возрастных задач со словами, у вас все будет хорошо.
В данный момент мы не знаем текущий возраст Брюса или Гектора. Но поскольку возраст Брюса выражается по отношению к возрасту Гектора, наша неизвестная переменная будет основываться на возрасте Гектора. Другими словами,
- Пусть {\textbf{\textit{h}}} = возраст Гектора
- {\textbf{\textit{h} – 4}} = возраст Брюса, поскольку он на 4 года моложе чем Гектор
Давайте организуем все эти важные данные в таблицу. Нам даются сведения только об их настоящем и прошлом (20 лет назад) возрасте, поэтому столбец «Будущее» будет выделен серым цветом.
Двадцать лет назад и Брюс, и Гектор были на 20 лет моложе, поэтому мы вычтем из их текущего возраста 20 .
- Брюс: \left( {h – 4} \right) {\color{red}- 20} = h – 24
- Гектор: h {\color{red}- 20}
Теперь наша таблица готовы, поэтому мы можем приступить к созданию нашего уравнения. Как вы можете видеть в столбце «Прошлое», мы смогли создать алгебраические выражения для возраста Брюса и Гектора 20 лет назад. Но наша проблема также сказала нам, что
Но наша проблема также сказала нам, что
Двадцать лет назад , возраст Гектора был 13 лет больше, чем половина возраста Брюса.
Поскольку возраст Гектора 20 лет назад также на 13 лет больше, чем половина возраста Брюса, мы можем взять эти два алгебраических выражения и приравнять их друг к другу, чтобы составить уравнение.
Возраст Гектора 20 лет назад = \Large{1 \over 2}( Возраст Брюса 20 лет назад )+ 13
Теперь мы готовы найти неизвестную переменную h.
Решение:
Следовательно, настоящий возраст Гектора составляет {\textbf{42}} лет.
С другой стороны, вы можете вспомнить, что текущий возраст Брюса: h – 4. Поскольку h = 42, то текущий возраст Брюса равен 42 – 4 = {\textbf{38}}.
Итак, сколько им сейчас лет?
Ответ: Гектору 42 года и Брюсу 38 лет .
Последним шагом будет проверка наших ответов путем подстановки неизвестных значений в исходное уравнение, чтобы проверить, равна ли каждая часть уравнения другой.
Проверка ответа:
Отлично! Наш ответ проверяет. Это просто показало нам, что если мы возьмем возраст Брюса двадцать лет назад, то есть 18 лет, и разделим его пополам, мы получим 9. Прибавив 13 к этому (9 + 13), мы получим 22, что было возрастом Гектора двадцать лет назад.
Таким образом, мы можем подтвердить, что двадцать лет назад, когда Гектору было 22 года, а Брюсу 18 лет, возраст Гектора был на 13 лет больше, чем половина возраста Брюса.
Пример 3: Стелла на 13 лет моложе Кваме. Через девять лет сумма их возрастов будет равна 43. Найдите настоящий возраст каждого из них.
Эта задача немного отличается от наших предыдущих двух примеров, поскольку нам дана сумма их возрастов за 9 лет. Но сразу же мы видим, что возраст Стеллы определяется возрастом Кваме. Поэтому мы выберем переменную для представления текущего возраста Кваме. В этом случае давайте использовать «k».
- Пусть {\textbf{\textit{k}}} = возраст Кваме
- {\textbf{\textit{k} – 13}} = возраст Стеллы, поскольку она на 13 лет моложе , чем Кваме
Через девять лет Кваме и Стелла станут на девять лет старше. Таким образом, мы просто добавим 9 к их нынешнему возрасту, указанному выше, чтобы показать их будущий возраст.
Таким образом, мы просто добавим 9 к их нынешнему возрасту, указанному выше, чтобы показать их будущий возраст.
- Кваме: k {\color{red}+ 9}
- Стелла: \left( {k – 13} \right) {\color{red}+ 9} = k – 4
Заполним нашу таблицу .
Теперь, когда у нас есть алгебраические выражения для возраста обоих через 9 лет, мы можем добавить этих выражений, чтобы составить наше уравнение. Нам дали следующие данные:
Через девять лет сумма их возрастов будет 43 .
Решение:
Итак, у нас есть,
Вернувшись к нашему столу, k означает возраст Кваме. Но так как наша задача просила нас найти текущий возраст для обоих, давайте еще немного порешаем.
НАСТОЯЩИЙ ВОЗРАСТ (настоящее время)
- Кваме: k = {\textbf{19}} лет
- Стелла: k – 13 = {\color{red}19} – 13 = {\textbf{6} } лет
Ответ: Кваме 19 лет и Стелла 6 лет .
Проверка ответа:
Теперь проверим, действительно ли сумма возрастов Кваме и Стеллы через 9 лет будет равна 43.
- Возраст Кваме через 9 лет: k + 9 = {\color{red}19} + 9 = {\textbf{28}}
- Возраст Стеллы через 9 лет: k – 4 = {\color{red}19} – 4 = {\textbf{15}}
Отлично! Сумма их возрастов через девять лет составляет 43 года, поэтому наши ответы верны.
Пример 4: Мистеру Куку 34 года. Его сын моложе его на 22 года. Через сколько лет возраст мистера Кука будет на 24 года меньше, чем в три раза старше его сына?
Нам уже известен их текущий возраст, поэтому, прежде чем углубляться дальше, давайте начнем заполнять нашу таблицу.
Обратите внимание, что, поскольку сын на 22 года моложе мистера Кука, мы вычли 22 из 34 , чтобы получить текущий возраст его сына, 34 – {\color{red}22} = 12.
Эта задача уникальна, потому что это не спрашивает нас об их возрасте в определенный момент времени, как обычно. Вместо этого он просит нас узнать, сколько лет в будущем возраст мистера Кука будет соответствовать определенному соотношению с возрастом его сына.
Вместо этого он просит нас узнать, сколько лет в будущем возраст мистера Кука будет соответствовать определенному соотношению с возрастом его сына.
Но на данный момент мы не знаем, сколько времени понадобится мистеру Куку, чтобы быть на 24 года меньше, чем в три раза старше его сына. Итак, давайте назначим неизвестную переменную «x» для обозначения количества лет, затем добавим x к обоим их текущим возрастам, чтобы создать алгебраические выражения, которые будут представлять, сколько им будет лет через x лет.
Поскольку возраст мистера Кука через x лет (x + 34) также будет на 24 года меньше, чем в три раза старше его сына , мы можем положить эти два алгебраических выражения равными друг другу, создав таким образом наше уравнение .
Теперь, когда у нас есть уравнение, давайте найдем x.
Решение:
Как вы, возможно, помните, х обозначает количество лет, через которое мистер Кук будет на 24 года меньше, чем в три раза старше своего сына. Следовательно,
Следовательно,
Ответ: Через 11 лет возраст мистера Кука будет на 24 года меньше, чем в три раза старше его сына.
Проверка ответа:
Чтобы проверить правильность нашего ответа, мы должны сначала узнать, сколько лет будет мистеру Куку и его сыну через 11 лет. Подставляя значение x, равное 11, в наши алгебраические выражения, мы получаем:
- Возраст мистера Кукса в 11 лет: x + 34 = {\color{red}11} + 34 = {\textbf{45}}
- Возраст сына в 11 лет: x + 12 = {\color{red} }11} + 12 = {\textbf{23}}
Итак, через 11 лет мистеру Куку будет 45 лет, а его сыну – 23 года.
На этот раз я оставлю вам право проверить, действительно ли за это время его 45-летний возраст будет на 24 года меньше, чем в три раза старше его сына. Если оно удовлетворяет условию, то наш ответ правильный.
Пример 5: Сумма одной пятой возраста Анники четыре года назад и половины ее возраста через шесть лет составляет 33 года. Сколько ей сейчас лет?
Сколько ей сейчас лет?
По сравнению с нашими предыдущими упражнениями, в этой задаче участвует только один человек. Кроме того, вместо сравнения возраста двух людей в определенный момент времени мы будем сравнивать возраст Анники в разные моменты времени, то есть 4 года назад и через 6 лет.
Мы не знаем текущий возраст Анники, поэтому давайте выберем переменную {\textbf{\textit{a}}} для представления этого неизвестного значения. Мы также будем использовать эту переменную для создания алгебраических выражений, которые будут обозначать ее прошлый и будущий возраст.
- Пусть {\textbf{\textit{a}}} = текущий возраст Анники
- {\textbf{\textit{a} – 4}} = возраст Анники 4 года назад
- {\textbf{ \textit{a} + 6}} = возраст Анники через 6 лет
Наша задача также сообщила нам, что если мы добавим \Large{1 \over 5} возраста Анники 4 года назад и \Large{ 1 \over 2} ее возраста через 6 лет , сумма 33 .
Имея эту информацию, нам легко написать наше уравнение.
Наш следующий шаг — найти неизвестную переменную a.
Решение:
Итак, сколько Аннике сейчас лет?
Ответ: Сейчас Аннике 44 года.
Проверка ответа:
Как я уже упоминал ранее, всегда полезно проверить, дали ли вы правильный ответ. Для начала давайте выясним, каковы прошлый и будущий возраст Анники.
- Возраст Анники 4 года назад : a – 4 = {\color{red}44} – 4 = {\textbf{40}}
- Возраст Анники Через 6 лет : a + 6 = {\color{red}44} + 6 = {\textbf{50}}
Теперь, когда мы знаем, сколько ей было лет 4 назад и сколько она будет через 6 лет, мы подставим эти значения в наше исходное уравнение, чтобы увидеть, равны ли обе части уравнения друг другу.
Так и случилось! Мы смогли доказать, что сумма \Large{1 \over 5} возраста Анники 4 года назад и \Large{1 \over 2} ее возраста через 6 лет действительно равна 33.
ЧАСТЬ II: Возраст Word задачи, решаемые с двумя переменными
Пример 6: Сумма возрастов Алии и Харальда составляет 28 лет. Через четыре года Алия будет в три раза старше Харальда. Найдите их настоящий возраст.
Возраст Алии и Харальда не выражается в терминах другого. Итак, для этой задачи мы будем использовать более одной переменной для представления неизвестных значений. Для начала,
- Пусть {\textbf{\textit{a}}} будет возрастом Алии
- Пусть {\textbf{\textit{h}}} будет возрастом Харальда
Так как им будет 4 года старше в течение следующих 4 лет, мы просто должны добавить 4 к их текущему возрасту, чтобы представить их будущие возраста.
Оглядываясь назад на нашу проблему, есть два важных утверждения, которые могут помочь нам найти ответы.
1) Сумма возрастов Алии и Харальда равна 28.
Из этого утверждения мы можем составить следующее уравнение:
2) Через четыре года Алия будет в три раза старше Харальда.
Между тем, приведенное выше утверждение можно перевести в следующее уравнение:
Теперь нам нужно решить два уравнения.
- Уравнение 1: a + h = 28
- Уравнение 2: a + 4 = 3(h + 4)
Сначала мы используем уравнение 4 для
3.
Далее мы заменим a на 28 -h в уравнении 2 .
Отлично! Мы можем найти значения для обеих наших неизвестных переменных, a и h, которые также обозначают нынешний возраст для Алии и Харальда. Итак, у нас есть,
- Настоящий возраст Алии: a = 28 – h = 28 – {\color{red}5} = {\textbf{23}}
- Настоящий возраст Харальда: h = {\textbf{5}}
Ответ: Сейчас Алии 23 года, а Харальду 5 лет.
Проверка ответов:
Я предоставляю вам возможность проверить правильность наших ответов. Но, как вы можете видеть, даже просто используя вычисления в уме, мы уже можем сказать, что сумма возрастов Алии и Харальда равна 28 (23 + 5 = 28), что делает наше первое утверждение верным. Вы можете дополнительно проверить наши ответы, подставив значения a и h в уравнение 2, чтобы проверить, равна ли левая часть уравнения правой, что также делает наше второе утверждение верным.
Вы можете дополнительно проверить наши ответы, подставив значения a и h в уравнение 2, чтобы проверить, равна ли левая часть уравнения правой, что также делает наше второе утверждение верным.
Пример 7: Сумма возрастов Джайи и Нади в три раза больше возраста Нади. Семь лет назад Джайя была в три раза моложе, чем в четыре раза, старше Нади. Сколько им сейчас лет?
Эта проблема аналогична нашему предыдущему примеру. Однако для этого нам не дано точное число для суммы. Сначала нам нужно выяснить каждый из их текущих возрастов, чтобы мы могли определить, какова сумма.
- Пусть {\textbf{\textit{y}}} будет возрастом Джайи
- Пусть {\textbf{\textit{n}}} будет возрастом Нади 9 лет1267
Затем нам нужно вычесть 7 из их текущего возраста, чтобы представить, сколько им было лет семь назад.
Теперь, когда мы организовали наши данные, давайте пройдемся по важным утверждениям, данным в нашей задаче, и превратим каждое из них в уравнение.
1) Сумма возрастов Джайи и Нади в три раза больше возраста Нади.
2) Семь лет назад Джая была в три с лишним раза старше Нади.
Таким образом, наши два уравнения:
- Уравнение 1: y + n = 3n
- Уравнение 2: y – 7 = 4(n – 7) – 3
Решим первое уравнение для 0 и 1003.
Теперь найдем n, используя значение y из уравнения 1. Мы сделаем это, заменив y на 2n в уравнении 2 .
Взяв значения y и n, мы имеем:
- Настоящий возраст Джайи: y = 2n = 2({\color{red}12}) = {\textbf{24}}
- Настоящий возраст Нади: n = {\textbf{12}}
Итак, вернемся к нашей проблеме. Сколько им сейчас лет?
Ответ: Джайе 24 года, а Наде 12 лет.
Проверка ответа:
Чтобы проверить наши ответы, мы заменим значения y и n в уравнении 1 и уравнении 2. Опять же, я оставляю на ваше усмотрение решение обоих уравнений и проверку каждого из них. часть уравнения равна другой. Как только вы закончите со своими решениями, вы увидите, что мы можем доказать, что оба утверждения из нашей задачи верны.
часть уравнения равна другой. Как только вы закончите со своими решениями, вы увидите, что мы можем доказать, что оба утверждения из нашей задачи верны.
Пример 8: Разница в возрасте Пенелопы и ее сына Зака составляет 34 года. Через шесть лет Пенелопа будет в четыре раза старше Зака два года назад. Сколько им сейчас лет?
Легко потеряться во всей предоставленной информации, поэтому сначала мы сосредоточимся на присвоении переменных, которые будут обозначать неизвестные значения.
- Пусть {\textbf{\textit{p}}} будет текущим возрастом Пенелопы
- Пусть {\textbf{\textit{z}}} будет текущим возрастом Зака
Уникальность этой задачи в том, что она включает три разных момента времени. Нам дана не только связь между возрастом Пенелопы и ее сына в настоящее время, но и то, как их возраст через 6 лет соотносится с их возрастом два года назад.
Чтобы показать это, мы вычтем 2 из их возраста сейчас для их возраста 2 года назад, затем добавим 6 к их текущему возрасту для их возраста 6 лет спустя.
Отлично! Теперь у нас есть переменные и алгебраические выражения для представления текущего возраста Пенелопы и Зака, а также их возраста в прошлом и будущем. Двигаясь вперед, давайте рассмотрим важные детали, данные в задаче, и создадим уравнение из каждого утверждения.
1) Разница в возрасте Пенелопы и ее сына Зака составляет 34 года .
Помните, что Пенелопа — мать Зака, поэтому она определенно старше его. Поэтому мы вычитаем возраст Зака из возраста Пенелопы, чтобы найти разницу.
2) Через шесть лет Пенелопе будет в четыре раза больше, чем Заку два года назад.
Вот наши два уравнения:
- Уравнение 1: p – z = 34
- Уравнение 2: p + 6 = 4(z – 2)
Давайте теперь поработаем над уравнением 1 , чтобы найти p.
Затем мы заменим p на 34 + z в уравнении 2 , затем найдем z.
Итак, мы имеем,
- Текущий возраст Пенелопы: p = 34 + z = 34 + ({\color{red}16}) = {\textbf{50}}
- Текущий возраст Зака: z = {\textbf {16}}
Как насчет замены неизвестных значений в нашей таблице, а также выяснения их прошлого и будущего возраста?
Возвращаясь к нашему первоначальному вопросу, сколько им сейчас лет?
Ответ: Сейчас Пенелопе 50 лет, а ее сыну Заку 16 лет.
Математические шалости | Видеоматериалы и рабочие листы по основам математики
Ваш браузер не поддерживает видео HTML5. Вместо этого ссылка на видео.
Проблема с воспроизведением видео? Устранение неполадок
Зарегистрируйтесь $10 на целый год! Войти
Нажмите здесь, чтобы узнать, как включить Javascript.
- Место Значение
- Десятичное разрядное значение
- Числовая линия
- Округление
- Основные неравенства
- Что такое арифметика?
- Порядок операций
- Распределительное свойство в арифметике
- Факторинг
- Простые множители
- Образцы чисел
- Многозначное сложение
- Многозначное вычитание
- Многозначное умножение Pt.
 1
1 - Многозначное умножение Pt. 2
- Базовый дивизион
- Длинный дивизион
- Длинное деление с двузначными делителями
- Десятичная арифметика
- Деление с частичными коэффициентами
- Фракции – это части
- Работа с частями
- дроби это деление
- Типы фракций
- Дроби и десятичные числа
- Преобразование дробей с основанием 10
- Преобразование любой дроби
- Сравнение дробей
- Умножение дробей
- Упрощение дробей
- Сложение и вычитание дробей
- Общий знаменатель: РДРВ
- Общий знаменатель: ЖК-дисплей
- Разделение дробей
- Смешанные номера
- Добавление смешанных номеров
- Вычитание смешанных чисел
- Что такое проценты?
- Проценты и эквивалентные дроби
- Нахождение процента от числа
- Какой это процент?
- Проценты: отсутствующая сумма
- Расчет процентного изменения
- Соотношения и ставки
- Пропорции
- Точки, линии и плоскости
- Основы угла
- Углы и градусы
- Полигоны
- Треугольники
- Четырехугольники
- Периметр
- Область
- Круги: что такое PI?
- Круги: окружность и площадь
- Объем
- Теорема Пифагора
- Среднее, медиана и мода
- Базовая вероятность
- Введение в метрическую систему
- Единицы расстояния
- Измерение расстояния
- Разговорное время
- Отрицательные числа
- Сложение и вычитание целых чисел
- Умножение и деление целых чисел
- Абсолютная величина
- Введение в экспоненты
- Экспоненты и квадратные корни
- Упрощение квадратных корней
- Научная нотация
*Подробнее об экспонентах см.