Задание по математике 3 класс на лето примеры деление умножение: примеры на сложение, вычитание, умножение и деление
примеры на умножение и деление, сложение и вычитание
Ваш ребенок еще только учится в начальной школе, а вы уже задумываетесь о его дальнейшей учебе, развитии и будущем? Это очень похвально. А думали ли вы над тем, что успеваемость ребенка можно улучшить, если заниматься с ним ежедневно по математике всего лишь 15 минут в день дополнительно? И это не выдумки. В материалах этой статьи мы приведем примеры и задачи для школьников начальной школы по математике, а именно, для третьеклассников. (Для удобства решения приведенные ниже задания вы можете распечатать).
Как учить ребенка учиться
Умеет ли ваш ребенок учиться? Уверена, что многих родителей этот вопрос поставил в тупик. А действительно, что значит «уметь учиться»? Когда ваш юный школьник только пошел в школу, после занятий, возможно, он бежал домой и очень хотел сразу же делать уроки. Так бывает, когда дети очень ждут поступления в 1 класс. Но со временем интересы к своевременному выполнению домашнего задания ослабевают и «домашка» становится скучным времяпровождением.
А ведь именно нежелание выполнять домашние задания, готовиться к школьным рефератам, семинарам и викторинам, становится основной причиной того, что ребенок вначале не хочет, а после и не умеет учиться. Пробелы в знаниях могут накапливаться словно снежный ком, снижая успеваемость школьника и убивая в нем желание учиться.
Чтобы школьник учился этой сложной и ответственной науке – учиться – родители должны всячески помогать ему: составить распорядок дня, учить ребенка выполнять домашнее задание наперед, прорешивать или прописывать дополнительные упражнения, чтобы тренировать и руку для письма, и мозг для устного счета. Математике дается детям начального звена сложнее всего, именно поэтому мы и подготовили для школьников 3 класса этот материал.
Примеры по математике на умножение и деление
Еще во втором классе дети выучили таблицу умножения. Если вы сейчас находитесь в полном заблуждении, как выучить с ребенком таблицу умножения, то рекомендуем к ознакомлению следующий материал по ссылке.
Задание 1
Заменить сложение вычитанием в тех примерах, в которых от замены знака ответ не изменится:
5 + 5 + 5 =
1 + 1 + 1 + 1 =
0 + 0 + 0 + 0 + 0 =
8 + 8 + 8 + 8 =
7 + 7 — 7 + 7 =
7 + 7 + 7 — 7 =
14 + 14 =
61 + 61 =
Подсказка:
5 + 5 + 5 = 15, если заменить знак «+» на знак «•», то получится
5 • 5 • 5 = 125. 15 не равно 125. Значит, в первом равенстве заменить знак «+» на знак «•» нельзя.
По аналогии решаем стальные равенства и делаем выводы о возможной или невозможной замене знака «+» на знак «•».
Задание 2
Какие выражения нельзя заменить суммой, чтобы ответ не изменился:
0 • 4 =
1 • 0 =
1 • 1 =
1 • 6 =
0 • 9 =
7 • 0 =
5 • 2 =
2 • 2 =
Подсказка:
Вспомните, каким правилом следует пользоваться при умножении на ноль.
Задание 3
Решите примеры:
45 : 5 + 1 =
45 : 5 • 1 =
543 — 5 • 1 =
(543 — 5) • 1 =
423 + 7 • 0 =
(423 + 7) • 1 =
10 — 0 + 4 =
10 • 0 + 4 =
Задание 4
Из каждого выражения на умножение составьте выражения на деление:
6 • 8 =
7 • 1 =
4 • 0 =
0 • 3 =
4 • 9 =
Подсказка
6 • 8 = 48
48 : 8 = 6
48 : 8 = 6
Задание 5
Какое значение имеют следующие выражение:
а : а =
а : 1 =
0 : а =
а : 0 =
Задание 6
Решите примеры:
(596 + 374) • 1 =
596 + 374 • 1 =
(596 + 374) • 0 =
596 + 374 + 0 =
0 • 320 : 1 =
0 + 320 : 1 =
Обязательно повторите с ребенком правила умножения и деления числа на единицу и умножения или деления числа на ноль, а также особенности деления ноля на любое число. Часто именно в этих примерах дети делают ошибки, которые влекут за собой дальнейшее неправильное решение примеров, выражений и задач.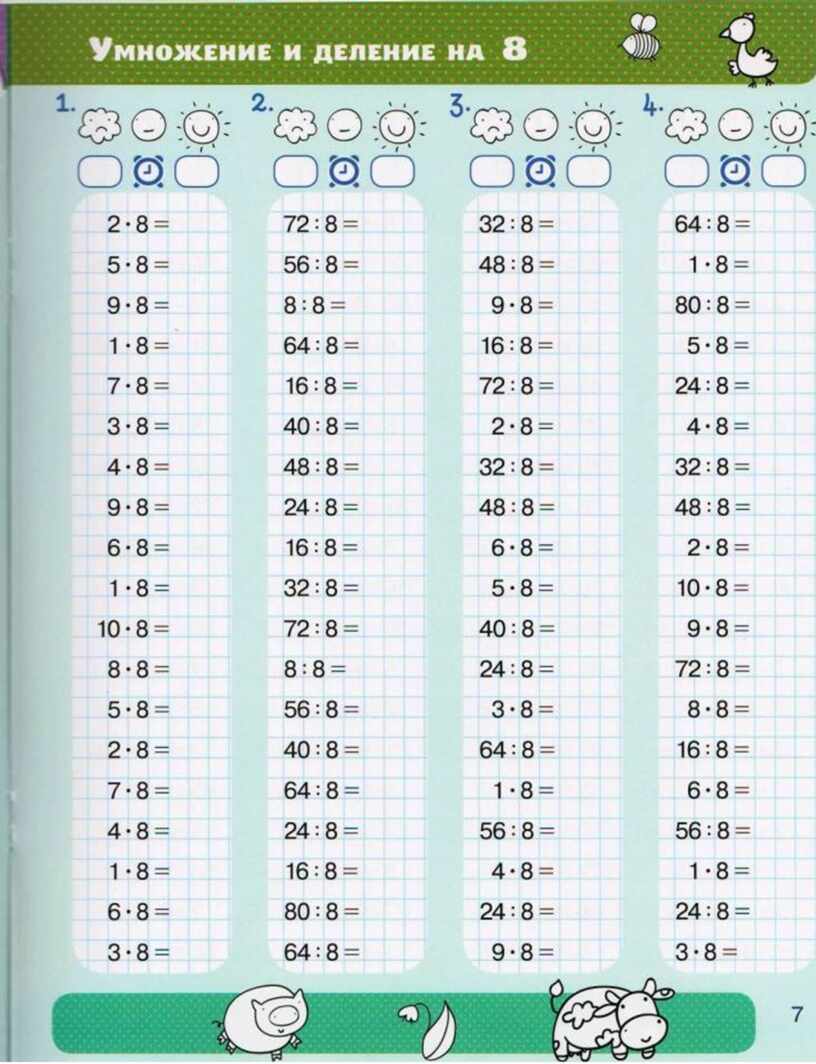
Задание 7 (задача)
В оздоровительный лагерь привезли фрукты: 7 ящиков винограда и 5 ящиков персиков. Масса привезенных персиков составляет 40 килограммов. Какая масса винограда, если ящик винограда на 1 килограмм весит больше, чем ящик персиков.
Решение
Найдем, сколько весит один ящик персиков. Известно, что общая масса персиков составляет 40 кг, а всего ящиков – 5.
Первое действие:
40 : 5 = 8 (кг) весит один ящик персиков.
Теперь найдем, сколько весит один ящик винограда, если известно, что он тяжелее на 1 кг, чем ящик персиков.
Второе действие:
8 + 1 = 9 (кг) весит один ящик винограда.
Теперь находим общую массу всего винограда, если известно, что один ящик весит 9 кг, а всего винограда – 7 ящиков.
Третье действие:
9 • 7 = 63 (кг) – общая масса винограда.
Ответ: масса привезенного винограда составляет 63 кг.
Задание 8
Сосна может расти 600 лет, береза – 350 лет.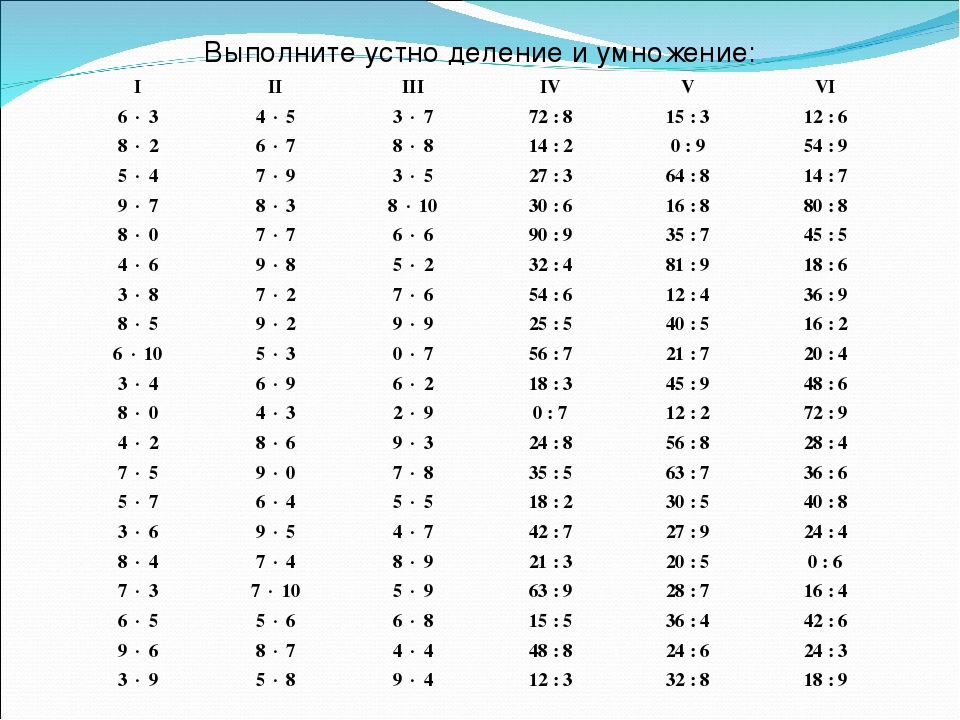 А ива – в 6 раз меньше от сосны. Что может расти дольше береза или ива? И насколько лет?
А ива – в 6 раз меньше от сосны. Что может расти дольше береза или ива? И насколько лет?
Решение
Вначале рассчитаем, сколько лет может расти ива, если известно, что она растет в 6 раз меньше, чем сосна.
Первое действие:
600 : 6 = 100 (лет) может расти ива.
Теперь, когда известно, что ива может расти 100 лет, сравним продолжительность «жизни» березы и ивы. Известно, что береза растет 350 лет, а ива – 100. 350 больше чем 100, значит береза может расти дольше ивы. Чтобы рассчитать, на сколько береза может расти дольше ивы, решаем равенство.
Второе действие:
350 — 100 = 250 (лет) – на столько береза может расти дольше ивы
Ответ: береза может расти дольше ивы на 250 лет.
Важно! Если задачу можно решить несколькими способами, обязательно сообщите об этом ребенку. Пусть потренирует логику и начертит все возможные схем решения задачи, т.е. составить схематическое условие. Ведь правильно составленное условие задачи – это 90% успешного решения.
Задание 9
В понедельник гусеница начала ползти вверх по дереву высотой 9 метров. За день она поднялась вверх на 5 метров, а за ночь – опустилась на 2 метра. На какой день гусеница достигнет верхушки дерева?
Решение
Для начала рассчитаем, на сколько метров поднимается гусеница вверх за один день, с учетом того, что ночью на опускается.
Первое действие:
5 — 2 = 3 (м) гусеница проползает за сутки вверх.
Теперь найдем количеств дней, необходимых на преодоление расстояния 9 метров вверх по дереву.
Второе действие:
9 : 3 = 3 (дня) нужно гусенице, чтобы достичь вершины дерева.
Ответ: 3 дня нужно гусенице, чтобы достичь вершины дерева.
Задание 10
В коробке было 18 килограммов печенья. Сначала из нее взяли 13 килограммов печенья, потом досыпали в 4 раза больше, чем оставалось. Сколько килограммов печенья стало в коробке.
Решение
Сначала найдем, сколько килограммов печенья осталось в коробке, после того, как из нее забрали 13 килограммов.
Первое действие:
18 — 13 = 5 (кг) печенья осталось в коробке
Теперь рассчитаем сколько килограммов печенья досыпали в коробку.
Второе действие:
5 • 4 = 20 (кг) досыпали
Сложим тот вес, который оставался в коробке, и тот, который досыпали, чтобы найти, сколько килограммов печения стало в коробке.
Третье действие:
5 + 20 = 25 (кг) стало
Ответ: 25 килограммов печения стало в коробке.
Задание 11
За лето хозяйка вырастила 208 домашних птиц. Кур и уток было 129, а уток и гусей – 115. Сколько кур, уток и гусей вырастила хозяйка за лето?
Решение
Известно, что кур и уток было 129, а всего птиц – 208. Значит, можно найти количество гусей.
Первое действие:
208 (птиц) – 129 (уток + кур) = 79 гусей
Также известно, что уток и гусей всего 115, значит мы можем найти, сколько было кур.
Второе действие:
208 (птиц) – 115 (уток + гусей) = 93 кур
Теперь, когда мы знаем количество гусей и кур, а также общее количество домашних птиц, мы можем найти количество уток.
Третье действие:
208 — (79 + 93) = 36 уток
Ответ:
Второй вариант решения
Известно, что кур и уток было 129, а всего птиц – 208. Значит, можно найти количество гусей.
Первое действие:
208 (птиц) – 129 (уток + кур) = 79 гусей
Также известно, что уток и гусей всего 115, значит мы можем найти, сколько было уток
Второе действие:
115 (уток + гусей) – 79 (гусей) = 36 уток
Теперь, когда мы знаем количество гусей и уток по отдельности, а также общее количество домашних птиц, мы можем найти количество кур.
Третье действие:
208 – (79 + 36) = 208 – 115 = 93 кур
Ответ: за лето хозяйка вырастила 79 гусей, 93 кур и 36 уток.
Примеры и задачи по математике на сложение и вычитание
Основной задачей заданий и примеров по математике на сложение и вычитание в третьем классе является популяризация математических знаний и идей, поддержка и развитие математических знаний школьников, стимулирование и мотивация учеников в изучении естественно-математический предметов.
Задание 1
Реши уравнения:
Х – 40 = 60
Х + 4 = 61
Х – 16 = 25
Х + 25 = 84
Х – 45 = 251
Х + 56 = 106
Х + 78 = 301
Задание 2
Расставьте скобки так, чтобы ответом выражения в первом случае было 6, а в втором – 2:
12 : 2 + 2 • 2 =
Подсказка
12 : (2 + 2) • 2 = 6
12 : (2 + 2 • 2) = 2
Важно! Некоторые условия составлены таким образом, чтобы ребенок включал логическое мышление. Прорешивая такие задания он мыслит, делает предположения, размышляет, и находит правильное решение задания.
Задание 3
Перевести в одну систему измерения и решить выражения:
1 м – 5 дм =
1 м – 5 см =
6 м 5 дм – 8 дм =
5 см + 5 см =
15 см + 5 дм =
3 дм – 6 см =
3 дм 5 см – 15 см =
1 дм 2 см – 3 см =
1 м 6 дм – 8 дм =
Задание 4
Из каждого выражения произведения отнять 15 и записать новые выражение и решить их:
7 • 3 =
7 • 6 =
7 • 9 =
8 • 6 =
8 • 4 =
3 • 9 =
4 • 4 =
5 • 7 =
Подсказка
Если 7 • 3 = 21, то 21 – 15 = 6
Задание 5
Решить примеры:
7 • 6 + 7 • 4 =
21 : 3 – 6 =
(35 – 28) • 5 =
(68 – 26) : 7 =
7 + (6 : 2) =
3 – 14 : 2 =
60 – 63 : 7 =
81 – 56 : 7 =
50 + 42 : 7 =
Задание 6 (задача)
В шести одинаковых бочонках 24 литра воды. Сколько литров воды в сети таких же бочонках, на сколько литров больше во втором случае, чем в первом?
Сколько литров воды в сети таких же бочонках, на сколько литров больше во втором случае, чем в первом?
Решение
Вначале найдем, сколько воды вмещается в один бочонок.
Первое действие:
24 : 6 = 4 (л) в одном бочонке
Теперь рассчитаем, сколько воды в семи одинаковых бочонках
Второе действие:
4 • 7 = 28 (л) в сети одинаковых бочонках
Найдем ответ на главный вопрос задачи, на сколько литров больше во втором случае, чем в первом.
Третье действие:
28 – 24 = 4 (л) на столько литров больше во втором случае, чем в первом
Ответ: на 4 литра воды больше во втором случае, чем в первом
Задание 7
Отец и сын купили на рынке картошку в 6 одинаковых сетках. Отец принес домой 4 сетки, а сын 2. Всего получилось 18 килограммов картошки. Сколько килограммов принес отец? Сколько килограммов принес сын? На сколько больше килограммов картошки принес отец?
Решение
Рассчитаем, сколько картошки было в одной сетке, если известно, то всего принести 18 килограммов в 6 одинаковых сетках.
Первое действие:
18 : 6 = 3 (кг) в одной сетке.
Теперь узнаем сколько килограммов принес отец и сколько килограммов принес сын.
Второе действие:
3 • 4 = 12 (кг) принес отец
Третье действие:
3 • 2 = 6 (кг) принес сын
Найдем искомую разницу.
Четвертое действие:
12 – 6 = 6 (кг) на столько больше принес отец.
Ответ: Отец принес на 6 килограммов больше картошки, чем сын.
Задание 8
За 5 часов работы двигателя было израсходовано 30 литров бензина. Сколько бензина будет израсходовано за 8 часов работы двигателя. На сколько больше двигатель израсходует бензина за разницу во времени?
Решение
Рассчитаем, сколько бензина расходует двигатель за час своей работы.
Первое действие:
30 : 5 = 6 (л) за один час работы
Рассчитаем, сколько составляет разница во времени?
Второе действие:
8 – 5 = 3 (ч) разница во времени
Теперь можно рассчитать, сколько бензина израсходовано за оставшиеся 3 часа.
Третье действие:
3 • 6 = 18 (л) потрачено за 3 часа.
Ответ: за 3 часа двигатель истратил 18 литров бензина
Второй способ решения
Рассчитаем, сколько бензина расходует двигатель за час своей работы.
Первое действие:
30 : 5 = 6 (л) за один час работы
Рассчитаем, сколько бензина будет израсходовано за 8 часов работы двигателя.
Второе действие:
8 • 6 = 48 (л) израсходовано за 8 часов работы двигателя
Теперь можно рассчитать разницу потраченного топлива.
Третье действие:
48 – 30 = 18 (л) разница потраченного топлива
Ответ: за 3 часа двигатель истратил 18 литров бензина
Важно! Задания на сложение и вычитание не исключают в своем условии или решении возможность других математических действий, например, умножения или деления. Ученик третьего класса уже должен уметь различать в условии требования к сложению и умножению, делению и вычитанию. Именно потому задания по математике для этого класса часто носят смешанный характер.
Задание 9
В двух прудах плавало 56 уток. Когда из первого пруда во второй перелетело 7 уток, то в нем осталось 25. Сколько уток с самого начала плавало во втором пруду?
Решение
Известно, что после того, как из первого пруда улетело 7 уток, в нем осталось 25. Находим количество уток в первом пруду с самого начала.
Первое действие:
7 + 25 = 32 (утки) было в первом пруду.
Теперь можем найти, сколько уток плавало во втором пруду с самого начала.
Второе действие:
56 – 32 = 24 (утки) было во втором пруду.
Ответ: с самого начала во втором пруду было 24 утки.
Задание 10
С первого куста собрали 9 килограммов ягод. Со второго куста собрали на 3 килограммов больше, чем с первого, а с третьего – на 2 килограммов больше, чем со второго. Сколько килограммов ягод собрали с третьего куста? Сколько всего ягод собрали?
Решение
Вначале найдем, сколько килограммов ягод собрали со второго куста.
Первое действие:
9 + 3 = 12 (кг) ягод со второго куста
Теперь определяем, сколько килограммов ягод собрали с третьего куста
Второе действие:
12 + 2 = 14 (кг) год с третьего куста
Когда все составляющие известны, находим ответ на главный вопрос задачи.
Третье действие:
9 + 12 + 14 = 35 (кг) ягод всего
Ответ: всего собрали 35 килограммов ягод.
Вместо заключения
Уделяйте математике достаточно внимания уже с начальной школы. Этот предмет не только тренируем мозг в устном счете, но и умении логически мыслить, развивать смекалку. Постепенно привыкая к выполнению дополнительных и основных заданий, ребенок учится учиться, выполнять требования учителя, грамотно планировать свое время, распределять время для учебы и досуга.
Математические задания для третьеклассников моно составлять самостоятельно по приведенным нами аналогии, это не составит особого труда. Зато ваш ученик сможет больше тренироваться в математике, выполнять задания на каникулах и выходных, а также заниматься дополнительно после школы.
Задания по математике для 3 классак учебникам Моро М.И., “Школа России” и Петерсон Л.Г., “Переспектива”
Дата публикации: .
Домашние задания на темы: “Умножение и деление чисел от 0 до 100”, “Решение текстовых задач”, “Сложение и вычитание числе от 1 до 1000” и др. за 1, 2, 3, 4 четверти
Дополнительные задания по темам:
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать: Домашние задания для 3 класса по учебнику Моро (PDF)
Обучающие пособия и тренажеры для 3 класса в интернет-магазине “Интеграл”
Л.Г. Петерсон
М.И. Моро
Т.Е. Демидовой
Б.П. Гейдмана
Задания для домашних работ для 3 класса (3 четверть)
1. Реши примеры.
| а) 5 * 6 + 64 : 8 = | б) 18 : 9 + 37 * 2= | в) 31 * 3 – 56 : 8 = | г) 70 – 51 : 3 * 4 = |
| д) 9 * 4 – 28 : 7 = | е) 7 * 16 – 80 : 8 = | ж) 11 * 5 – 49 : 7 = | з) 68 – 19 + 30 : 2 = |
2. Реши задачу.
В ящик помещается 12 пачек печенья. Сколько всего пачек печенья помещается в 5 ящиков?3. Реши задачу.
В книжный магазин привезли 88 учебников, которые упакованы в коробки. Сколько коробок с книгами привезли, если в каждой коробке находится 11 учебников?4. Реши примеры.
| а) 17 * 0= | б) 12 : 1= |
| в) 24 * 1 = | г) 21 : 1 = |
| д) 0 * 32 = | е) 0 : 15 = |
5. Реши задачу.
В пекарне из 15 кг муки испекли 45 тортов. Сколько килограмм муки необходимо, чтобы испечь 60 тортов?6. Реши задачу.
На складе находилось 45 кг сахара. Дополнительно привезли 4 мешка по 8 кг сахара в каждом, а затем со склада увезли 10 кг сахара. Сколько килограмм сахара осталось на складе?7. Реши примеры и проверь операцию деления умножением.
| а) 48 : 6 = | б) 12 : 4= |
| в) 24 : 8 = | г) 21 : 7 = |
| д) 15 : 3 = | е) 0 : 15 = |
8. Реши уравнения.
| а) X * 18 = 72 | б) 90 : Y = 30 | в) 21 : X = 3 | г) Y * 6 = 42 |
9. Реши ЗАДАНИЯ по геометрии.
a) Начерти c помощью линейки 3 отрезка. Длина первого отрезка равна 5 см, второй отрезок на 3 см длиннее первого, а третий отрезок в 2 раза короче второго.б) Найди и выпиши все прямые, тупые и острые углы у фигур, изображённых на рисунке.
в) Найди периметр и площадь прямоугольника, изображённого на рисунке.
10. Реши примеры.
| а) 17 * 3 = | б) 52 : 4 = |
| в) 19 * 4 = | г) 48 : 2 = |
| д) 12 * 5 = | е) 69 : 3 = |
| ж) 22 * 3 = | з) 17 * 4 = |
| к) 13 * 5 = | л) 75 : 5 = |
| м) 96 : 4 = | н) 69 : 3 = |
11. Реши задачу.
Школьная бригада собрала в саду 36 кг яблок и 20 кг груш. Весь урожай разложили в ящики по 4 кг. Сколько ящиков понадобилось?Задания для домашней работы для 3 класса (4 четверть)
1. Реши примеры.
| а) 210 * 4 = | б) 840 : 4 = |
| в) 6 * 120 = | г) 660 : 3 = |
| д) 220 * 4 = | е) 490 : 7 = |
| ж) 190 * 3 = | з) 360 : 6 = |
| к) 3 * 280 = | л) 140 : 2 = |
| м) 110 * 7 = | н) 640 : 4 = |
2. Реши примеры.
| а) 970 – 50 = | б) 320 + 50 = |
| в) 520 – 10 = | г) 630 + 90 = |
| д) 320 – 30 = | е) 230 + 90 = |
| ж) 220 – 20 = | з) 590 + 50 = |
3. Реши задачу.
Для ремонта школы привезли 160 мешков цемента и 440 мешков песка. Сколько мешков строительного материала потребовалось для ремонта, если после ремонта осталось 250 мешков?4. Реши задачу.
Фермер вырастил 230 ц картофеля и 140 ц капусты. 360 ц овощей отправили в школьную столовую. Сколько центнеров овощей осталось у фермера?5. Реши уравнения.
а) 7 * х = 490б) у : 9 = 70
в) a – 560 = 120
г) b + 380 = 960
6. Реши задачу.
На автостоянке стояло 84 легковых и несколько грузовых машин, которых было на 63 машины меньше, чем легковых. Во сколько раз грузовых машин меньше, чем легковых стояло на автостоянке?7. Реши примеры столбиком.
| а) 984 – 159 = | б) 523 + 369 = |
| в) 523 – 459 = | г) 374 + 579 = |
| д) 319 – 198 = | е) 130 + 379 = |
8. Реши примеры.
а) 24 * 8 + 336 : 6 + 88 =б) 16 * 9 + 342 : 2 – 146 =
9. Реши задачу.
На продуктовом складе находилось 64 мешка с сахаром и несколько мешков с мукой, которых было на 56 штук меньше, чем мешков с сахаром. Во сколько раз мешков с мукой меньше, чем мешков с сахаром находилось на складе?Задания на сложение
Стр. 1.Дата: __________________ ФИО: _______________________________ Оценка:__________ | ||||||||||||||||
| Сложи 2 числа. Сумма до 100. Повторение. | ||||||||||||||||
| 25 | + | 52 | = | __ | 7 | + | 50 | = | __ | 88 | + | 3 | = | __ | ||
| 19 | + | 11 | = | __ | 46 | + | 7 | = | __ | 56 | + | 0 | = | __ | ||
| 52 | + | 26 | = | __ | 70 | + | 20 | = | __ | 68 | + | 14 | = | __ | ||
| 11 | + | 30 | = | __ | 58 | + | 25 | = | __ | 29 | + | 0 | = | __ | ||
| 10 | + | 50 | = | __ | 51 | + | 19 | = | __ | 11 | + | 1 | = | __ | ||
| 31 | + | 62 | = | __ | 66 | + | 30 | = | __ | 30 | + | 31 | = | __ | ||
| 59 | + | 28 | = | __ | 5 | + | 16 | = | __ | 48 | + | 37 | = | __ | ||
| 70 | + | 5 | = | __ | 16 | + | 71 | = | __ | 59 | + | 20 | = | __ | ||
| 24 | + | 41 | = | __ | 57 | + | 5 | = | __ | 63 | + | 27 | = | __ | ||
| 53 | + | 25 | = | __ | 27 | + | 18 | = | __ | 26 | + | 1 | = | __ | ||
| 5 | + | 31 | = | __ | 18 | + | 29 | = | __ | 23 | + | 54 | = | __ | ||
| 68 | + | 20 | = | __ | 71 | + | 0 | = | __ | 51 | + | 5 | = | __ | ||
Задания на сложение
Стр. 2.Дата: __________________ ФИО: _______________________________ Оценка:__________ | ||||||||||||||||
| Сложи 2 числа. Сумма до 100. Повторение. | ||||||||||||||||
| 2 | + | 51 | = | __ | 67 | + | 5 | = | __ | 98 | + | 1 | = | __ | ||
| 15 | + | 61 | = | __ | 33 | + | 0 | = | __ | 76 | + | 14 | = | __ | ||
| 21 | + | 53 | = | __ | 30 | + | 20 | = | __ | 22 | + | 67 | = | __ | ||
| 28 | + | 21 | = | __ | 55 | + | 36 | = | __ | 9 | + | 58 | = | __ | ||
| 64 | + | 16 | = | __ | 37 | + | 49 | = | __ | 5 | + | 65 | = | __ | ||
| 16 | + | 72 | = | __ | 27 | + | 60 | = | __ | 22 | + | 1 | = | __ | ||
| 11 | + | 44 | = | __ | 26 | + | 23 | = | __ | 49 | + | 37 | = | __ | ||
| 69 | + | 5 | = | __ | 15 | + | 60 | = | __ | 16 | + | 59 | = | __ | ||
| 52 | + | 37 | = | __ | 64 | + | 28 | = | __ | 28 | + | 35 | = | __ | ||
| 57 | + | 8 | = | __ | 50 | + | 15 | = | __ | 20 | + | 5 | = | __ | ||
| 43 | + | 48 | = | __ | 42 | + | 57 | = | __ | 61 | + | 20 | = | __ | ||
| 26 | + | 19 | = | __ | 18 | + | 69 | = | __ | 91 | + | 4 | = | __ | ||
Задания на сложение
Стр. 1.Дата: __________________ ФИО: _______________________________ Оценка:__________ | ||||||||||||||||
| Сложи 2 двузначных числа. | ||||||||||||||||
| 24 | + | 65 | = | __ | 85 | + | 61 | = | __ | 51 | + | 91 | = | __ | ||
| 89 | + | 23 | = | __ | 56 | + | 20 | = | __ | 59 | + | 85 | = | __ | ||
| 54 | + | 10 | = | __ | 52 | + | 89 | = | __ | 40 | + | 48 | = | __ | ||
| 61 | + | 99 | = | __ | 56 | + | 16 | = | __ | 55 | + | 31 | = | __ | ||
| 58 | + | 33 | = | __ | 15 | + | 28 | = | __ | 57 | + | 63 | = | __ | ||
| 21 | + | 25 | = | __ | 68 | + | 14 | = | __ | 48 | + | 47 | = | __ | ||
| 54 | + | 93 | = | __ | 51 | + | 68 | = | __ | 77 | + | 47 | = | __ | ||
| 78 | + | 32 | = | __ | 57 | + | 28 | = | __ | 45 | + | 59 | = | __ | ||
| 63 | + | 57 | = | __ | 66 | + | 13 | = | __ | 23 | + | 11 | = | __ | ||
| 49 | + | 36 | = | __ | 68 | + | 83 | = | __ | 68 | + | 24 | = | __ | ||
| 52 | + | 44 | = | __ | 78 | + | 84 | = | __ | 73 | + | 82 | = | __ | ||
| 70 | + | 42 | = | __ | 94 | + | 31 | = | __ | 79 | + | 55 | = | __ | ||
Задания на сложение
Стр. 2.Дата: __________________ ФИО: _______________________________ Оценка:__________ | ||||||||||||||||
| Сложи 2 двузначных числа. | ||||||||||||||||
| 58 | + | 38 | = | __ | 87 | + | 86 | = | __ | 59 | + | 21 | = | __ | ||
| 19 | + | 16 | = | __ | 77 | + | 56 | = | __ | 84 | + | 12 | = | __ | ||
| 47 | + | 40 | = | __ | 38 | + | 63 | = | __ | 13 | + | 34 | = | __ | ||
| 77 | + | 17 | = | __ | 51 | + | 65 | = | __ | 44 | + | 42 | = | __ | ||
| 18 | + | 37 | = | __ | 64 | + | 89 | = | __ | 81 | + | 36 | = | __ | ||
| 34 | + | 20 | = | __ | 78 | + | 53 | = | __ | 31 | + | 98 | = | __ | ||
| 12 | + | 88 | = | __ | 82 | + | 64 | = | __ | 57 | + | 36 | = | __ | ||
| 43 | + | 99 | = | __ | 99 | + | 74 | = | __ | 73 | + | 78 | = | __ | ||
| 77 | + | 71 | = | __ | 36 | + | 62 | = | __ | 65 | + | 43 | = | __ | ||
| 94 | + | 39 | = | __ | 32 | + | 15 | = | __ | 85 | + | 49 | = | __ | ||
| 14 | + | 50 | = | __ | 34 | + | 74 | = | __ | 29 | + | 27 | = | __ | ||
| 88 | + | 80 | = | __ | 71 | + | 96 | = | __ | 36 | + | 54 | = | __ | ||
Задания на сложение
Стр. 1.Дата: __________________ ФИО: _______________________________ Оценка:__________ | ||||||||||||||
| Сложи три однозначных числа. Повторение. | ||||||||||||||
| 4 | + | 6 | + | 7 | = | __ | 1 | + | 2 | + | 0 | = | __ | |
| 9 | + | 9 | + | 1 | = | __ | 1 | + | 7 | + | 7 | = | __ | |
| 0 | + | 3 | + | 0 | = | __ | 6 | + | 5 | + | 1 | = | __ | |
| 1 | + | 3 | + | 5 | = | __ | 4 | + | 0 | + | 1 | = | __ | |
| 2 | + | 4 | + | 6 | = | __ | 6 | + | 1 | + | 0 | = | __ | |
| 9 | + | 0 | + | 1 | = | __ | 4 | + | 2 | + | 3 | = | __ | |
| 3 | + | 2 | + | 3 | = | __ | 5 | + | 4 | + | 1 | = | __ | |
| 5 | + | 5 | + | 4 | = | __ | 0 | + | 1 | + | 9 | = | __ | |
| 0 | + | 3 | + | 9 | = | __ | 8 | + | 1 | + | 0 | = | __ | |
| 4 | + | 1 | + | 2 | = | __ | 5 | + | 9 | + | 1 | = | __ | |
| 7 | + | 2 | + | 2 | = | __ | 4 | + | 6 | + | 8 | = | __ | |
| 5 | + | 7 | + | 1 | = | __ | 1 | + | 2 | + | 6 | = | __ | |
Задания на сложение
Стр. 2.Дата: __________________ ФИО: _______________________________ Оценка:__________ | ||||||||||||||
| Сложи три однозначных числа. Повторение. | ||||||||||||||
| 9 | + | 4 | + | 7 | = | __ | 3 | + | 8 | + | 5 | = | __ | |
| 2 | + | 1 | + | 7 | = | __ | 4 | + | 4 | + | 4 | = | __ | |
| 9 | + | 4 | + | 7 | = | __ | 6 | + | 8 | + | 5 | = | __ | |
| 7 | + | 5 | + | 8 | = | __ | 3 | + | 7 | + | 3 | = | __ | |
| 8 | + | 0 | + | 5 | = | __ | 3 | + | 6 | + | 6 | = | __ | |
| 2 | + | 0 | + | 0 | = | __ | 1 | + | 3 | + | 8 | = | __ | |
| 7 | + | 9 | + | 5 | = | __ | 3 | + | 8 | + | 3 | = | __ | |
| 5 | + | 0 | + | 6 | = | __ | 6 | + | 1 | + | 1 | = | __ | |
| 8 | + | 8 | + | 6 | = | __ | 2 | + | 2 | + | 0 | = | __ | |
| 7 | + | 1 | + | 8 | = | __ | 4 | + | 0 | + | 2 | = | __ | |
| 0 | + | 6 | + | 9 | = | __ | 9 | + | 7 | + | 5 | = | __ | |
| 1 | + | 5 | + | 0 | = | __ | 5 | + | 4 | + | 2 | = | __ | |
Задания на сложение. Стр.1
Дата: __________________ ФИО: ______________________________ Оценка:__________ | |||||||||
| Сложи два числа в столбик. Сумма до 100. Повторение. | |||||||||
| 22 | 36 | 18 | 40 | 48 | |||||
| + | 7 | + | 3 | + | 23 | + | 1 | + | 2 |
| … | … | … | … | … | |||||
| 36 | 20 | 26 | 13 | 16 | |||||
| + | 2 | + | 4 | + | 19 | + | 2 | + | 20 |
| … | … | … | … | … | |||||
| 1 | 38 | 31 | 29 | 18 | |||||
| + | 24 | + | 8 | + | 17 | + | 2 | + | 13 |
| … | … | … | … | … | |||||
| 21 | 11 | 7 | 36 | 13 | |||||
| + | 0 | + | 2 | + | 39 | + | 10 | + | 15 |
| … | … | … | … | … | |||||
| 27 | 35 | 39 | 31 | 42 | |||||
| + | 10 | + | 14 | + | 11 | + | 5 | + | 1 |
| … | … | … | … | … | |||||
| 19 | 9 | 1 | 12 | 16 | |||||
| + | 23 | + | 38 | + | 34 | + | 8 | + | 21 |
| … | … | … | … | … | |||||
| 14 | 4 | 23 | 18 | 28 | |||||
| + | 13 | + | 0 | + | 9 | + | 17 | + | 22 |
| … | … | … | … | … | |||||
| 38 | 5 | 38 | 14 | 19 | |||||
| + | 7 | + | 5 | + | 8 | + | 24 | + | 7 |
| … | … | … | … | … | |||||
Задания на сложение. Стр.2
Дата: __________________ ФИО: ______________________________ Оценка:__________ | |||||||||
| Сложи два числа в столбик. Сумма до 100. Повторение. | |||||||||
| 11 | 44 | 13 | 40 | 7 | |||||
| + | 21 | + | 3 | + | 7 | + | 4 | + | 40 |
| … | … | … | … | … | |||||
| 9 | 23 | 21 | 37 | 7 | |||||
| + | 32 | + | 9 | + | 21 | + | 4 | + | 5 |
| … | … | … | … | … | |||||
| 3 | 47 | 22 | 10 | 15 | |||||
| + | 28 | + | 2 | + | 15 | + | 20 | + | 5 |
| … | … | … | … | … | |||||
| 9 | 5 | 1 | 19 | 34 | |||||
| + | 40 | + | 18 | + | 8 | + | 15 | + | 15 |
| … | … | … | … | … | |||||
| 31 | 37 | 24 | 36 | 29 | |||||
| + | 1 | + | 4 | + | 0 | + | 9 | + | 18 |
| … | … | … | … | … | |||||
| 14 | 11 | 18 | 33 | 37 | |||||
| + | 15 | + | 24 | + | 28 | + | 15 | + | 4 |
| … | … | … | … | … | |||||
| 39 | 30 | 12 | 19 | 13 | |||||
| + | 11 | + | 12 | + | 14 | + | 19 | + | 13 |
| … | … | … | … | … | |||||
| 39 | 26 | 4 | 15 | 3 | |||||
| + | 4 | + | 0 | + | 32 | + | 22 | + | 42 |
| … | … | … | … | … | |||||
Задания на сложение. Стр.1
Дата: __________________ ФИО: ______________________________ Оценка:__________ | |||||||||
| Сложи в столбик 2 числа (двузначное и однозначное). Повторение. | |||||||||
| 51 | 2 | 13 | 3 | 75 | |||||
| + | 7 | + | 39 | + | 3 | + | 42 | + | 6 |
| … | … | … | … | … | |||||
| 2 | 29 | 4 | 67 | 0 | |||||
| + | 70 | + | 5 | + | 71 | + | 8 | + | 60 |
| … | … | … | … | … | |||||
| 66 | 9 | 97 | 4 | 81 | |||||
| + | 9 | + | 47 | + | 3 | + | 29 | + | 6 |
| … | … | … | … | … | |||||
| 3 | 8 | 8 | 6 | 8 | |||||
| + | 66 | + | 3 | + | 76 | + | 4 | + | 25 |
| … | … | … | … | … | |||||
| 45 | 7 | 40 | 5 | 21 | |||||
| + | 7 | + | 63 | + | 0 | + | 57 | + | 0 |
| … | … | … | … | … | |||||
| 2 | 18 | 3 | 58 | 8 | |||||
| + | 95 | + | 1 | + | 71 | + | 6 | + | 92 |
| … | … | … | … | … | |||||
| 1 | 6 | 59 | 4 | 70 | |||||
| + | 0 | + | 44 | + | 0 | + | 31 | + | 2 |
| … | … | … | … | … | |||||
| 5 | 28 | 6 | 61 | 4 | |||||
| + | 54 | + | 0 | + | 72 | + | 7 | + | 44 |
| … | … | … | … | … | |||||
Задания на сложение. Стр.2
Дата: __________________ ФИО: ______________________________ Оценка:__________ | |||||||||
| Сложи в столбик 2 числа (двузначное и однозначное). Повторение. | |||||||||
| 40 | 1 | 28 | 0 | 79 | |||||
| + | 3 | + | 33 | + | 9 | + | 95 | + | 1 |
| … | … | … | … | … | |||||
| 3 | 21 | 4 | 48 | 6 | |||||
| + | 76 | + | 3 | + | 51 | + | 2 | + | 85 |
| … | … | … | … | … | |||||
| 2 | 9 | 16 | 5 | 74 | |||||
| + | 4 | + | 31 | + | 7 | + | 23 | + | 8 |
| … | … | … | … | … | |||||
| 4 | 61 | 6 | 43 | 8 | |||||
| + | 38 | + | 6 | + | 60 | + | 5 | + | 7 |
| … | … | … | … | … | |||||
| 12 | 2 | 37 | 9 | 21 | |||||
| + | 2 | + | 78 | + | 1 | + | 80 | + | 0 |
| … | … | … | … | … | |||||
| 1 | 12 | 7 | 90 | 2 | |||||
| + | 96 | + | 3 | + | 77 | + | 1 | + | 95 |
| … | … | … | … | … | |||||
| 40 | 5 | 85 | 6 | 5 | |||||
| + | 0 | + | 4 | + | 5 | + | 63 | + | 5 |
| … | … | … | … | … | |||||
| 8 | 44 | 0 | 70 | 1 | |||||
| + | 15 | + | 7 | + | 36 | + | 0 | + | 18 |
| … | … | … | … | … | |||||
Задания на сложение. Стр.1
Дата: __________________ ФИО: ______________________________ Оценка:__________ | |||||||||
| Сложи 3 однозначных числа. Повторение. | |||||||||
| 9 | 5 | 1 | 6 | 9 | |||||
| 7 | 3 | 3 | 3 | 6 | |||||
| + | 4 | + | 8 | + | 1 | + | 3 | + | 5 |
| … | … | … | … | … | |||||
| 2 | 8 | 9 | 2 | 9 | |||||
| 8 | 7 | 8 | 9 | 3 | |||||
| + | 4 | + | 7 | + | 8 | + | 5 | + | 1 |
| … | … | … | … | … | |||||
| 2 | 7 | 4 | 2 | 2 | |||||
| 6 | 3 | 4 | 9 | 8 | |||||
| + | 4 | + | 5 | + | 7 | + | 2 | + | 3 |
| … | … | … | … | … | |||||
| 5 | 2 | 9 | 2 | 9 | |||||
| 7 | 3 | 1 | 9 | 7 | |||||
| + | 5 | + | 7 | + | 9 | + | 8 | + | 9 |
| … | … | … | … | … | |||||
| 5 | 6 | 5 | 7 | 6 | |||||
| 4 | 5 | 1 | 5 | 2 | |||||
| + | 8 | + | 3 | + | 2 | + | 2 | + | 7 |
| … | … | … | … | … | |||||
| 6 | 1 | 7 | 4 | 1 | |||||
| 8 | 7 | 7 | 4 | 1 | |||||
| + | 7 | + | 6 | + | 8 | + | 1 | + | 5 |
| … | … | … | … | … | |||||
Задания на сложение. Стр.2
Дата: __________________ ФИО: ______________________________ Оценка:__________ | |||||||||
| Сложи 3 однозначных числа. | |||||||||
| 7 | 1 | 4 | 1 | 4 | |||||
| 2 | 7 | 9 | 8 | 8 | |||||
| + | 2 | + | 6 | + | 4 | + | 7 | + | 4 |
| … | … | … | … | … | |||||
| 3 | 4 | 6 | 2 | 1 | |||||
| 4 | 2 | 2 | 3 | 7 | |||||
| + | 6 | + | 2 | + | 7 | + | 7 | + | 1 |
| … | … | … | … | … | |||||
| 1 | 1 | 1 | 5 | 6 | |||||
| 9 | 7 | 3 | 1 | 8 | |||||
| + | 5 | + | 4 | + | 8 | + | 5 | + | 8 |
| … | … | … | … | … | |||||
| 7 | 7 | 4 | 3 | 9 | |||||
| 8 | 9 | 4 | 8 | 5 | |||||
| + | 8 | + | 7 | + | 9 | + | 6 | + | 8 |
| … | … | … | … | … | |||||
| 2 | 9 | 6 | 6 | 8 | |||||
| 2 | 2 | 5 | 7 | 6 | |||||
| + | 5 | + | 6 | + | 1 | + | 7 | + | 3 |
| … | … | … | … | … | |||||
| 6 | 5 | 5 | 1 | 4 | |||||
| 3 | 7 | 5 | 1 | 4 | |||||
| + | 4 | + | 5 | + | 1 | + | 1 | + | 2 |
| … | … | … | … | … | |||||
Страница не найдена – Бесплатная электронная библиотека для детей и родителей
Начальная школа, 1-4 классы
О.В. Узорова, Е.А. Нефедова Тренинговая тетрадь содержит 49 задач трёх уровней сложности. В конце
Начальная школа, 1-4 классы
О.И. Крупенчук Эта книга поможет вашим детям научиться читать быстро тексты любой сложности. В
Начальная школа, 1-4 классы
М. В. Беденко Учебное пособие содержит более 500 задач по программе 1 класса. Эти
Начальная школа, 1-4 классы
А.В. Ефимова, М.Р. Гринштейн Данное пособие содержит разноуровневые задания по всем программным темам 3
Начальная школа, 1-4 классы
В.Н. Рудницкая Данное пособие содержит тематические тестовые задания, которые позволят оценить успешность освоения программы
Начальная школа, 1-4 классы
А.В. Ефимова, М.Р. Гринштейн В данной рабочей тетради представлены упражнения для повторения и закрепления
Деление
В данном уроке мы изýчим деление чисел. Деление чисел довольно непростая операция как в освоении, так и в использовании. Рекомендуем набраться терпения, чтобы осилить этот урок до конца.
Что такое деление?
Деление это действие, позволяющее что-либо разделить.
Деление состоит из трёх параметров: делимого, делителя и частного. Делимое это то, что делят. Делитель это число, показывающее на сколько частей нужно разделить делимое. Частное это собственно результат.
Пусть у нас имеются 4 яблока:
Разделим их поровну на двоих друзей. Тогда деление покажет сколько яблок достанется каждому. Нетрудно увидеть, что каждому достанется по два яблока:
Процесс деления четырех яблок на двоих друзей можно описáть следующим выражением:
В этом примере роль делимого играют яблоки. Роль делителя играют двое друзей, показывающих на сколько частей нужно разделить 4 яблока. Роль частного играют два яблока, показывающие сколько досталось каждому.
Говоря о делении, можно рассуждать и по-другому. Вернёмся к предыдущему выражению 4 : 2 = 2. Можно посмотреть на делитель 2 и задать вопрос «сколько двоек в четвёрке?» и ответить: «две двойки». Действительно, если сложить две двойки, то получится число 4
В ситуации с четырьмя яблоками можно задать вопрос «сколько раз два яблока содержатся в четырёх яблоках» и ответить: «два раза».
Чтобы научиться делить, нужно хорошо знать таблицу умножения. Почему же умножения? Ведь мы говорим о делении. Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
Видно, что второе выражение записано в обратном порядке. Если у нас имеются два яблока и мы захотим увеличить их в пять раз, то запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то запишем 10 : 5 = 2
Знак деления выглядит в виде двоеточия : но также можно встретить знак двоеточия и тире ÷
На письме разумнее использовать двоеточие, поскольку оно выглядит аккуратнее.
Деление с остатком
Остаток — это то, что осталось от действия деления неразделённым.
Например, пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Можно проверить это умножением:
(2 × 2) + 1 = 5
Допустим, у нас имеются пять яблок
Разделим их поровну на двоих друзей. Но разделить поровну пять целых яблок не получится. Тогда данное деление покажет, что каждому достанется два яблока, а одно яблоко будет в остатке:
Деление уголком
Когда требуется разделить большое число, то прибегают к такому методу как деление уголком.
Прежде чем делить уголком, человек должен понимать:
- обычное деление маленьких чисел;
- деление с остатком;
- умножение в столбик;
- вычитание в столбик.
Рассмотрим деление уголком на простом примере. Пусть требуется найти значение выражения 9 : 3. Уголком это выражение записывается следующим образом:
Это простой пример. Все знают, что девять разделить на три будет три. Ответ (частное) записывается под правым углом:
Чтобы проверить есть ли остаток от деления, нужно частное умножить на делитель и полученный ответ записать под делимым. Частное в данном случае это 3, делитель тоже 3. Перемножаем эти два числа: 3 × 3 = 9. Получили 9. Записываем эту девятку под делимым:
Теперь от делимого вычитаем девятку, которую мы под ним написали: 9 − 9 = 0. Остаток равен нулю. Проще говоря, остатка нет. На этом деление успешно завершено:
Пример 2. Найти значение выражения 8 : 3
Восемь на три просто-так не разделится. Таблица умножения тоже не поможет. В данном случае будет присутствовать остаток от деления.
Сначала запишем данное выражение уголком:
Теперь надо задать вопрос: «сколько троек в восьмёрке?» В восьмёрке содержится две тройки. Это можно увидеть даже воочию, если мы представим восьмёрку как восемь палочек:
В школе частное подбирается методом подбора. Все мы слышали такие фразы как «берём по одному» , «берём по два» или «берём по три». У нас сейчас как раз такой случай. Мы взяли по два, ответив что в восьмёрке две тройки. Записываем двойку в правом уголке:
Теперь вынимаем остаток. Для этого умножаем частное на делитель (2 на 3) и записываем полученное число под делимым:
Далее из 8 вычитаем 6. Полученное число и будет остатком:
8 : 3 = 2 (2 в остатке)
Проверка: (2 × 3) + 2 = 6 + 2 = 8
Деление многозначного числа на однозначное
Данная тема с первого раза может показаться непонятной. Не спешите отчаиваться и забрасывать обучение. Понимание придёт в любом случае. Если не сразу, то немного позже. Главное не сдаваться и продолжать упорно изучать.
В предыдущих примерах мы делили однозначное число на однозначное, и это не доставляло нам лишних проблем. Сейчас мы займёмся тем, что будем делить многозначное число на однозначное.
Если непонятно, что такое однозначные и многозначные числа, советуем изучить предыдущий урок, который называется умножение.
Чтобы разделить многозначное число на однозначное, нужно сначала посмотреть на первую цифру этого многозначного числа, и проверить больше ли она делителя. Если больше, то разделить, а если нет, то проверить больше ли делителя первые две цифры многозначного числа. Если первые две цифры больше делителя, то разделить, а если нет, то проверить больше ли первые три цифры многозначного числа. И так до тех пор, пока не будет выполнено первое деление.
Сложно? Ни чуть, если мы разберём несколько примеров.
Пример 1. Найти значение выражения 25 : 3
25 это многозначное число, а 3 — однозначное. Применяем правило. Смóтрим на первую цифру многозначного числа. Первая цифра это 2. Два больше, чем три? Нет. Поэтому смóтрим первые две цифры многозначного числа. Первые две цифры образуют число 25. Двадцать пять больше, чем три? Да, больше. Поэтому выполняем деление числа 25 на 3. Записываем уголком данное выражение и начинаем делить:
Сколько троек в числе 25? Если с первого раза ответить сложно, можно заглянуть в таблицу умножения на три. Там необходимо отыскать произведение, которое меньше 25, но очень близко к нему или равно ему. Если найдём такое произведение, то необходимо забрать оттуда множитель, который дал такое произведение:
Это таблица умножения на три. В ней необходимо найти произведение, которое меньше 25, но очень близко к нему или равно ему. Очевидно, что это произведение 24, которое выделено синим. Из этого выражения необходимо забрать множитель, который дал такое произведение. Это множитель 8, который закрашен красным.
Данная восьмёрка и отвечает на вопрос сколько троек в числе 25. Записываем её в правом уголке нашего примера:
Теперь вынимаем остаток. Для этого умножаем частное на делитель (8 на 3) и полученное число записываем под делимым:
Теперь из делимого вычитаем число 24, получим 1. Это и будет остатком:
25 : 3 = 8 (1 в остатке)
(8 × 3) + 1 = 24 + 1 = 25
Последний остаток всегда меньше делителя. Если последний остаток больше делителя это означает, что деление не завершено.
В приведённом примере последним остатком было число 1, а делителем число 3. Единица меньше, чем три, поэтому деление завершено. Последний остаток, меньший делителя, говорит о том, что он не содержит чисел, равных делителю.
В нашем примере, если задать вопрос «сколько троек в единице?», то ответом будет «нисколько», потому что единица не содержит троек, поскольку она меньше тройки.
Пример 2. Разделить 326 на 4.
Смотрим на первую цифру числа 326. Первая цифра это 3. Она больше делителя 4? Нет. Тогда проверяем две цифры делимого. Две цифры делимого образуют число 32. Больше ли оно делителя 4? Да, больше. Поэтому делим. Записываем уголком данное выражение:
Теперь задаём вопрос: «сколько четвёрок в числе 32?». В числе 32 восемь четвёрок. Это можно увидеть в таблице умножения на четыре:
Данная восьмёрка, которая выделена красным отвечает на вопрос сколько четвёрок в числе 32. Записываем её в правом уголке нашего примера:
Теперь умножаем 8 на 4, получаем 32 и записываем это число под делимым. Далее вычитаем это число из 32. Получим 0. Поскольку решение ещё не завершено, ноль не записываем:
Первое число 32 разделили. Осталось разделить оставшуюся 6. Для этого сносим эту шестёрку:
Теперь делим 6 на 4. Для этого задаём вопрос: «сколько четвёрок в шестёрке?» В шестёрке одна четвёрка, это можно увидеть воочию, если представить шестёрку как шесть палочек:
Записываем единицу в правом уголке нашего ответа:
Теперь умножаем нашу единицу на делитель (1 на 4) и записываем полученное число под шестёркой:
Затем из 6 вычитаем 4, получаем число 2, которое является остатком:
Получили 326 : 4 = 81 (2 в остатке)
Проверка: (81 × 4) + 2 = 324 + 2 = 326
Процедура, в которой мы ищем первое число для деления, сравнивая больше ли оно делителя или меньше, называется нахождением первого неполного делимого.
Вернёмся к предыдущему примеру 326 : 4. Первое неполное делимое в данном выражении было число 32, поскольку его мы разделили в первую очередь.
А в примере 25 : 3 первое неполное делимое было 25.
Пример 3. Найти значение выражения 384 : 5
Записываем данное выражение в уголком:
Сначала находим первое неполное делимое. Первая цифра меньше делителя, поэтому проверяем две цифры. Две цифры вместе образуют число 38, которое больше делителя. Это число будет первым неполным делимым. Его и будем в первую очередь делить на делитель:
Сколько пятёрок в числе 38? Если сразу ответить сложно, то можно посмотреть в таблицу умножения на пять и найти произведение, которое меньше 38, но очень близко к нему или равно ему. Найдя такое произведение, нужно забрать оттуда множитель, который будет отвечать на наш вопрос:
Это таблица умножения на пять. Находим произведение, которое меньше 38, но очень близко к нему или равно ему. Очевидно, что это произведение 35, которое выделено синим. Из этого выражения забираем множитель, который дал такое произведение. Это множитель 7, который выделен красным.
Данная семёрка отвечает на вопрос сколько пятёрок в числе 38. Записываем эту семёрку в правом уголке нашего примера:
Умножаем 7 на 5, получаем 35 и записываем его под 38:
Теперь из 38 вычитаем 35, получим 3:
Эта тройка является остатком, которая осталась неразделённой в результате деления 38 на 5. Но видно, что ещё надо разделить и 4. Эту 4 мы снесём и разделим вместе с тройкой:
Видно, что после того, как мы снесли четвёрку, она вместе с тройкой образовала число 34. Это число 34 мы будем делить на 5. Для этого опять задаем вопрос: «сколько пятёрок в числе 34?». Можно снова глянуть в таблицу умножения на пять и найти произведение, которое меньше 34, но очень близко к нему или равно ему:
Видно, что в таблице умножения на пять число 30 меньше нашего 34, но близко к нему. Из этого выражения забираем множитель 6, который отвечает на наш вопрос. Записываем эту шестёрку в правом уголке нашего примера:
Теперь умножаем 6 на 5, получаем 30 и записываем это число под 34:
Теперь из 34 вычитаем 30, получаем 4. Эта четвёрка будет остатком от деления 384 на 5
384 : 5 = 76 (и 4 в остатке)
Проверка: (76 × 5) + 4 = 380 + 4 = 384
Пример 4. Найти значение выражения 8642 : 4
Этот пример немного посложнее. Записываем уголком данное выражение:
Первая цифра 8 больше делителя. Эта восьмёрка будет первым неполным делимым. Делим 8 на 4, получаем 2
Теперь умножаем 2 на 4, получаем 8. Записываем эту восьмёрку под первым неполным делимым:
Вытаскиваем остаток: 8 − 8 = 0. Остаток от деления 8 на 4 это ноль. Ноль не записываем, поскольку решение примера не завершено.
Далее сносим цифру 6 и делим её на делитель, получаем 1
Умножаем 1 на 4, получаем 4. Записываем эту четвёрку под снесённой шестёркой. Затем вынимаем остаток, отняв от шести четыре:
Получили остаток 2. Это остаток, который остался от деления 6 на 4.
Теперь сносим следующую цифру из делимого. Это цифра 4. Эта четвёрка вместе с предыдущим остатком 2 образует число 24. Его делим на делитель. Получим 6
Умножаем 6 на 4, получаем 24. Записываем это число под 24
Вытаскиваем остаток: 24 − 24 = 0. Ноль это остаток от деления 24 на 4. Ноль, как мы уже договорились, не записываем. Далее сносим последнюю цифру 2
Здесь начинается самое интересное. Двойка это последняя цифра, которую мы снесли и которую надо разделить на делитель 4. Но дело в том, что двойка меньше четвёрки, а ведь делимое должно быть больше делителя. Если мы зададим вопрос «сколько четвёрок в двойке?«, то ответом будет ноль, поскольку двойка меньше четвёрки и не может содержать в себе число, бóльшее себя самогó.
Поэтому два разделить на четыре это ноль:
Умножаем 0 на 4, получаем 0. Пишем этот 0 под двойкой:
Теперь находим остаток: 2 − 0 = 2. Двойка это остаток от деления 8642 на 4. Таким образом, пример завершён:
8642 : 4 = 2160 (2 в остатке)
Проверка: (2160 × 4) + 2 = 8640 + 2 = 8642
Деление чисел, у которых на конце 0
Чтобы разделить число, у которого на конце ноль, нужно временно отбросить этот ноль, выполнить обычное деление, и дописать этот ноль в ответе.
Например, разделим 120 : 3
Сколько троек в числе 120? Чтобы ответить на этот вопрос, временно отбрасываем ноль на конце у 120 и делим 12 на 3, получаем 4. И дописываем этот ноль в частном. В итоге получаем 40:
Теперь умножаем частное на делитель (40 на 3), получаем 120. Далее находим остаток: 120 − 120 = 0. Остаток равен нулю. Пример завершён.
120 : 3 = 40
Проверка 40 × 3 = 120.
Такие простые примеры не нуждаются в том, чтобы их решали уголком. Достаточно знать таблицу умножения. Далее просто дописывать нули на конце. Например:
12 : 3 = 4 (делимое без нулей на конце)
120 : 3 = 40 (здесь у делимого один ноль)
1200 : 3 = 400 (здесь у делимого два нуля)
12000 : 3 = 4000 (здесь у делимого три нуля)
В этом способе есть небольшой подвох. Если вы заметили, деля такие числа, мы ссылаемся на таблицу умножения. А представьте, что надо разделить 400 на 5.
Можно рассуждать по старому — отбросить временно все нули и разделить обычные числа. А что будет если отбросить все нули в числе 400? Мы обнаружим, что делим 4 на 5, что недопустимо. В этом случае, надо отбрасывать только один ноль, и делить 40 на 5, а не 4 на 5
Завершаем этот пример, как обычно умножая частное на делитель, и выводя остаток:
Этот способ работает только в том случае, если удаётся гладко применить таблицу умножения. В остальных случаях, придётся искать обходные пути, вычисляя уголком или собирая частное подобно детскому конструктору.
Например, найдём значение выражения 1400 : 5. Здесь отбрасывание нулей нам ничего не даст. Этот пример надо решать уголком или собрать ответ, подобно конструктору. Давайте рассмотрим второй способ.
Что такое 1400? Вспоминаем разряды чисел. 1400 это одна тысяча и четыре сотни:
1000 + 400 = 1400
Можно по-отдельности разделить 1000 на 5 и 400 на 5:
1000 : 5 = 200
400 : 5 = 80
и сложить полученные результаты:
200 + 80 = 280
Итого: 1400 : 5 = 280
Решим этот же пример уголком:
Деление многозначного числа на многозначное
Здесь придётся хорошенько напрячь свой мозговой аппарат и выжать из него по максимуму, потому что разделить многозначное число на многозначное не так то просто.
Принцип деления остаётся тем же что и раньше. Здесь так же надо находить первое неполное делимое. Здесь так же могут присутствовать остатки от деления.
Для начала введём новое понятие — круглое число. Круглым будем называть число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 500, 600, 1000, 13000
Любое число можно превратить в круглое. Для этого первые цифры, образующие старший разряд, оставляют без изменений, а остальные цифры заменяют нулями.
Например, превратим число 19 в круглое число. Первая цифра этого числа 1 образует старший разряд (разряд десятков) — эту цифру оставляем как есть, а оставшуюся 9 заменяем на ноль. В итоге получаем 10
Ещё пример. Превратим число 125 в круглое число. Первая цифра 1 образует старший разряд (разряд сотен) — эту цифру оставляем без изменений, а оставшиеся цифры 25 заменяем нулями. В итоге получаем 100.
Ещё пример. Превратим число 2431 в круглое число. Первая цифра 2 образует старший разряд (разряд тысяч) — эту цифру оставляем без изменений, а остальные цифры 431 заменяем нулями. В итоге получаем 2000.
Ещё пример. Превратим число 13 735 в круглое число. Первые две цифры 13 образуют старший разряд (разряд десятков тысяч) — эти две цифры оставляем без изменений, а остальные цифры 735 заменяем нулями. В итоге получаем 13 000.
Внимание! В дальнейшем понятия круглого числа и перевод любого числа в круглое будут обобщены.
Возвращаемся к делению многозначных чисел на многозначные. Сложность деления таких чисел заключается в том, что частное надо находить методом подбора. Для этого прибегают к различным техникам, например, превращают делимое и делитель в круглые числа.
Пример 1. Найти значение выражения 88 : 12
Записываем данное выражение уголком:
Задаём вопрос сколько чисел 12 в числе 88? С первого раза ответить сложно. Придётся рассуждать.
Со школы мы помним, что частное подбиралось методом угадывания, говоря «берем по два» или «берем по три».
Давайте попробуем угадать частное. К сожалению, его просто так с неба взять нельзя. Это частное должно быть таким, чтобы при его умножении на делитель, получалось число, которое меньше делимого, но очень близко к нему или равно ему.
Давайте предположим, что частное равно 2. Умножаем это частное на делитель 12
Что это нам дало? Полученное число меньше делимого, но близко к нему? Нет. Оно конечно же меньше делимого 88, но очень далеко от него. Значит двойка как частное не подходит.
Пробуем следующее число. Допустим частное равно 5
Полученное число конечно меньше, но оно не близко к делимому 88. Значит пятёрка как частное тоже не подходит.
Попробуем сразу взять по 8
На этот раз полученное число превзошло делимое. А оно должно быть меньше делимого, но очень близким к нему или равным ему. Значит восьмёрка как частное тоже не подходит Попробуем тогда взять по 7
Наконец-то нашли подходящее частное! Умножив частное 7 на делитель 12, мы получили 84, которое меньше делимого, но близко к нему. Теперь находим остаток от деления. Для этого из 88 вычитаем 84, получаем 4.
88 : 12 = 7 (4 в остатке)
Проверка: (12 × 7) + 4 = 84 + 4 = 88
Как видно из примера, на подбор частного уходит драгоценное время. Если мы будем сидеть на контрольной или на экзамене, где каждая минута очень дорогá, этот метод нам явно не поможет.
Чтобы сэкономить время, можно делимое и делитель превратить в круглые числа, а затем осуществить деление этих круглых чисел. Делить круглые числа намного проще и удобнее.
Например, чтобы разделить 90 на 10, достаточно отбросить нули у обоих чисел и разделить 9 на 1. В итоге получим 90 : 10 = 9.
Количество отбрасываемых нулей должно быть строго одинаковым. К примеру, если мы делим 900 на 90, то отбрасываем по нулю от каждого числа, поскольку у числа 900 два нуля, а у 90 только один. Отбросив по нулю от каждого числа, мы получим выражение 90 : 9 = 10. В итоге получаем 900 : 90 = 10.
В делении круглых чисел также нет ничего сложного. Постарайтесь понять это. Если непонятно, изучите этот момент несколько раз. Это очень важно.
Ниже приведено несколько примеров, где делятся круглые числа. Отбрасываемые нули закрашены серым цветом:
800 : 10 = 80 (отбросили по нулю и разделили 80 на 1, получили 80)
800 : 80 = 10 (отбросили по нулю и разделил 80 на 8, получили 10)
900 : 10 = 90 (отбросили по нулю и разделили 90 на 1, получили 90)
400 : 50 = 8 (отбросили по нулю и разделили 40 на 5, получили 8)
320 : 80 = 4 (отбросили по нулю и разделили 32 на 8, получили 4)
Заметно, что всё в конечном итоге свóдится к таблице умножения. Именно поэтому в школе требуют знать её наизусть. Мы тоже этого требуем, хоть и не принуждаем.
Теперь давайте решим предыдущий пример 88 : 12 где мы бились, находя частное методом угадывания.
Для начала превращаем делимое и делитель в круглые числа.
Круглым числом для 88 будет число 80.
А круглым числом для 12 будет число 10.
Теперь делим полученные круглые числа:
80 разделить 10 будет 8. Эту восьмёрку мы пишем в частном:
Теперь проверяем, верно ли подобралось частное. Для этого умножаем частное на делитель (8 на 12). Восьмёрку как частное мы уже проверяли, когда решали этот пример методом угадывания. Она нам не подошла, поскольку после её умножения на делитель, получилось число 96, которое больше делимого. Зато подошло частное 7, которое меньше восьмёрки всего-лишь на единицу.
Отсюда можно сделать вывод, что в выражении 88 : 12 частное, полученное путём превращения делимого и делителя в круглые числа, больше лишь на единицу. Наша с вами задача уменьшить это частное на единицу.
Так и сделаем — уменьшим 8 на единицу: 8 − 1 = 7. Семёрка это частное. Записываем её в правом уголке нашего примера:
Как видно, этим способом мы решили этот пример намного быстрее.
Пример 2. Найти значение выражения 1296 : 144
Записываем уголком данное выражение. Сразу же находим первое неполное делимое. Его образуют все четыре цифры делимого:
Это деление многозначного числа на многозначное. Давайте применим только что изученный метод. Превратим делимое и делитель в круглые числа, а затем разделим их.
Для делимого 1296 круглым числом будет 1000. А для делителя 144 круглым числом будет 100.
Делим 1000 на 100, получим 10. Проверим полученную десятку, умножив её на делитель 144
Десятка не подходит, поскольку при умножении получается число, которое больше делимого.
Попробуем взять по 9, уменьшив десятку на единицу.
Проверяем девятку. Для этого умножаем её на делитель:
Красота! Полученное число оказалось не только ближе к делимому, но и равным ему. Это значит, что деление выполнилось без остатка. Завершаем данный пример, вычитая из 1296 полученное число 1296
1296 : 144 = 9
Проверка: 144 × 9 = 1296
Пример 3. Попробуем решить большой и сложный пример 227 492 : 331
Записываем уголком данное выражение. Сразу же определяем первое неполное делимое. Его образуют первые четыре цифры делимого 2274. Значит сначала будем делить 2274 на 331. Их же превратим в круглые числа.
Для числа 2274 круглым числом будет 2000. А для 331 круглым числом будет 300
Получили 6. Проверим верно ли подобралась эта шестёрка. Для этого, умножим её на делитель 331:
Шестёрка подошла, потому что она отвечает на вопрос сколько чисел 331 в числе 2274. Если бы мы взяли по семь, то получилось бы следующее:
Если бы мы взяли по 7 и проверили эту семёрку, то получили бы 2317, которое больше делимого, а это недопустимо.
Продолжаем решать наш пример. Вычитаем из 2274 число 1986, получаем 288:
288 это остаток от деления 2274 на 331. Далее, чтобы продолжить деление, нужно снести девятку:
Теперь надо разделить 2889 на 331. Превращаем их в круглые числа и делим их. Сразу же проверяем полученное таким способом частное:
Умножив 6 на 331, мы снова получили 1986. Это число должно быть меньше делимого 2889, но близким к нему или равным ему. Но 1986 очень далеко от него. Значит шестёрка, как частное не подходит. Проверим тогда семёрку. Это первый случай, когда нам не помог второй способ, который экономил нам время. Дальнейшее решение придётся проводить методом угадывания частного:
Проверили семёрку. Снова получили число, которое далеко от делимого 2889. Значит семёрка тоже не подходит. Проверим восьмёрку:
Восьмёрка подошла. Она отвечает на вопрос сколько чисел 331 в числе 2889. Если бы мы взяли по девять, то при умножении на делитель, получили бы число 2979, а это уже больше делимого 2889.
Теперь вынимаем остаток от деления 2889 на 331. Для этого от 2889 вычитаем 2648 и получаем 241
241 это остаток от деления 2889 на 331. Чтобы продолжить деление, нужно снести 2 из главного делимого:
Теперь делим 2412 на 331. Возьмём по 7
Теперь находим последний остаток. Для этого из 2412 вычитаем 2317, получаем 95. На этом пример завершается:
227 492 : 331 = 687 (95 в остатке)
Проверка: (331 × 687) + 95= 227 397 + 95 = 227 492
На этом данный урок можно завершить. Не расстраивайтесь, если сразу не научитесь делить числа уголком. Этот навык нарабатывается со временем в сочетании с интенсивными тренировками. Ошибки дело не страшное. Самое главное — понимать.
Отметим, что в данном уроке рассмотрено только деление с остатком. Деление без остатка мы рассмотрим в следующих уроках. Сделано это с целью не усложнять обучение. Как говорится, всему своё время.
Задания для самостоятельного решения
Задание 1. Выполните деление:
Решение:
Задание 2. Выполните деление:
Решение:
Задание 3. Выполните деление:
Решение:
Задание 4. Выполните деление:
Решение:
Задание 5. Выполните деление:
Решение:
Задание 6. Выполните деление:
Решение:
Задание 7. Выполните деление:
Решение:
Задание 8. Выполните деление:
Решение:
Задание 9. Выполните деление:
Решение:
Задание 10. Выполните деление:
Решение:
Задание 11. Выполните деление:
Решение:
Задание 12. Выполните деление:
Решение:
Задание 13. Выполните деление:
Решение:
Задание 14. Выполните деление:
Решение:
Задание 15. Выполните деление:
Решение:
Задание 16. Выполните деление:
Решение:
Задание 17. Выполните деление:
Решение:
Задание 18. Выполните деление:
Решение:
Задание 19. Выполните деление:
Решение:
Задание 20. Выполните деление:
Решение:
Задание 21. Выполните деление:
Решение:
Задание 22. Выполните деление:
Решение:
Задание 23. Выполните деление:
Решение:
Задание 24. Выполните деление:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Проверочная работа по математике “Умножение и деление трёхзначных чисел” 3 класс
Проверочная работа по теме:
«Умножение и деление трёхзначных чисел»
1 – вариант
№1. Реши примеры, делая подробную запись в строчку:
31 · 3= 39 :3=
342 · 2= 84 : 6=
123 · 4= 351 : 3=
№2. Реши примеры, выполняя вычисления в столбик:
32 · 3= 142 · 6= 69 : 3= 864 : 2=
214 · 4= 73 · 3= 408 : 4= 459 :3=
№3. Реши систему неравенств, сделай чертёж и запиши ответ:
х>6
х<11
№4. Реши неравенство, используя решение соответствующего уравнения. Сделай проверку:
в + 53 > 87
№5. Реши задачу. Запиши решение сложным выражением.
В магазин привезли 8 ящиков груш по 32 кг в каждом. Сколько кг груш продали, если осталось 58 кг груш.
№6**Заполни клетки квадрата числами так, чтобы он стал «магическим»:
|
156
|
|
164 |
|
|
158 |
|
|
152
|
|
|
Проверочная работа по теме:
«Умножение и деление трёхзначных чисел»
2 – вариант
№1. Реши примеры, делая подробную запись в строчку:
21 · 3= 69 :3=
243 · 2= 84 : 7=
223 · 4= 357 : 3=
№2. Реши примеры, выполняя вычисления в столбик:
23 · 3= 162 · 6= 96 : 3= 684 : 2=
114 · 4= 83 · 3= 606 : 6= 456 :3=
№3. Реши систему неравенств, сделай чертёж и запиши ответ:
х>7
х<12
№4. Реши неравенство, используя решение соответствующего уравнения. Сделай проверку:
в + 37 < 96
№5. Реши задачу. Запиши решение сложным выражением.
В магазин привезли 7 ящиков груш по 34 кг в каждом. Сколько кг груш продали, если осталось 63 кг груш.
№6**Заполни клетки квадрата числами так, чтобы он стал «магическим»:
|
156
|
|
164 |
|
|
158 |
|
|
152
|
|
|
Урок 30. деление вида а : а, 0 : а – Математика – 3 класс
Математика, 3 класс.
Урок № 30. Деление вида а : а, 0 : а
Перечень вопросов, рассматриваемых в теме:
– как делить выражения вида а : а и 0 : а?
– какие правила используются в случаях деления чисел с 1 и 0?
Глоссарий по теме:
Деление – действие, обратное умножению
Правило – закономерность, устойчивая систематическая взаимосвязь между явлениями, а также высказывание, описывающее эту закономерность.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 84-85.
2. Самсонова Л. Ю. Самостоятельные работы по математике 3 класс. М.: Издательство «Экзамен», 2015 с. 51-52.
3. Рудницкая В.Н. КИМ. ВПР. Математика 3 класс. М.: Издательство «Экзамен», 2018.- с.-36.
Теоретический материал для самостоятельного изучения
Число ноль удивительное во всех отношениях.
Точка, от которой отсчитывают расстояния в Венгрии, отмечена особо. В этом месте (оно находится в центре Будапешта) поставлен памятник нулю. Ни одна другая цифра не удостоилась таких почестей! В Дунайском биосферном заповеднике есть место, называемое «нулевым километром». Так называется место, где Дунай впадает в Чёрное море и откуда начинается отсчёт расстояний на реке.
На острове Анкудинов установлен знак нулевого километра. Отсюда ведется отсчёт длины Дуная, пролегающего по землям десяти государств Европы. Интересно, что Дунай – единственная река в мире, которую измеряют не от истоков, а из дельты.
Также это число удостоилось памятника в городе Мюнхене.
В математике числа 0 и 1 обладают особыми правилами деления и умножения.
Рассмотрим эти правила на примерах.
Найдем значения выражений и пользуясь правилом умножения числа на единицу, составим по одному выражению на деление.
14 : 1 = 14; 17 : 1 = 17;
14 : 14 = 1; 17 : 17 = 1.
Делаем вывод, что если любое число разделить на единицу, получается это же число.
Если ,
то .
Выясним, какое выражение верное.
0 : 5 = 0; 0 : 5 = 5.
Нам известно, что действие умножения связано с действием с деления. 0 разделим на 5. Это значит, надо найти число, при умножении которого на 5 получится 0. Это число ноль. Значит, 0 разделить на 5 равно 0.
x ∙ 5=0, х = 0, следовательно 0 : 5 = 0.
Следовательно, приходим к выводу:
При делении нуля на любое другое число, получается нуль.
Нужно обязательно запомнить: На нуль делить нельзя!
Почему нельзя делить на нуль? Обоснуем свой ответ. (При делении на нуль, например, числа восемь или другого числа, кроме нуля нельзя найти такое число, умножив которое на нуль, получилось бы восемь или другое число).
Задания тренировочного модуля:
1. Соедините пример с правильным ответом.
Правильный ответ:
2. Расставьте выражения в порядке убывания их значений
Правильный ответ:
«3000 примеров по математике. Равенства. Табличное и внетабличное умножение и деление. Два уровня сложности. Ответы. 2-4 классы» Узорова Ольга Васильевна, Нефедова Елена Алексеевна – описание книги | 3000 примеров для начальной школы
Алтайский край
Альметьевск
Ангарск
Астрахань
Белгород
Благовещенск
Богучар
Братск
Брянск
Брянская область
Владивосток
Владимирская область
Волгоград
Волгоградская область
Воронеж
Воронежская область
Грозный
Екатеринбург
Забайкальский край
Ивановская область
Иркутск
Иркутская область
Кабардино-Балкарская Республика
Калач
Калужская
Калужская область
Карачаево-Черкесская Республика
Кемерово
Кемеровская область
Киров
Кострома
Краснодарский край
Красноярск
Красноярский край
Курганская
Курск
Липецк
Лиски
Москва
Московская область
Нижегородская область
Нижний Новгород
Нижний Тагил
Нововоронеж
Новосибирск
Омск
Оренбург
Оренбургская область
Орловская область
Пенза
Пермский край
Пермь
Поворино
Приморский край
Республика Адыгея
Республика Башкортостан
Республика Бурятия
Республика Крым
Республика Мордовия
Республика Северная Осетия — Алания
Республика Татарстан
Республика Тыва
Республика Хакасия
Россошь
Ростов-на-Дону
Ростовская область
Рязань
Самара
Самарская область
Саратов
Саратовская область
Свердловская область
Севастополь
Смоленск
Ставрополь
Ставропольский край
Старый Оскол
Тамбов
Тамбовская область
Тверь
Томск
Тула
Тулун
Тульская область
Тюменская область
Тюмень
Удмуртская Республика
Ульяновск
Ульяновская область
Хабаровск
Ханты-Мансийский автономный округ
Челябинск
Челябинская область
Чувашская Республика
Энгельс
Ямало-Ненецкий автономный округ
Ярославль
Ярославская область
Умножение и деление для 3-го класса по математике
Летняя школа математики для 3-го класса Классная математика: 2-я неделя умножения и деления – Сделайте летнюю математику чем-то, чего стоит ждать! Этот пакет академический, увлекательный и веселый! Он включает в себя полный мини-блок на 1 неделю умножения и деления , который охватывает ключевые концепции математики для 3-го класса. Все предметы оформлены в тематике дорожных путешествий для дополнительного удовольствия. Он был разработан, чтобы сделать изучение основных математических навыков в третьем классе увлекательным и интересным для учащихся, а также простым для учителей в реализации! Этот ресурс идеально подходит для летней школы, репетиторства или дополнительной летней практики по математике для учеников 3-х классов!
Ключевые особенности этой летней математической программы для 3-го класса:
- Пакет включает недельный мини-блок для 3-го класса, предназначенный для летнего обзора концепций умножения и деления в 3-м классе.
- Есть ежедневный рабочий лист (идеально подходит для домашней работы, самостоятельной или дополнительной практики).
- Вся неделя занятий посвящена серфингу для дополнительного удовольствия!
- Пятничная ежедневная практика – это повторение математических навыков третьего класса за неделю; он идеально подходит для использования в качестве экзамена.
- Пакет включает ежедневное задание по математике для 3-го класса по следующему расписанию:
– Понедельник: Партнеры Сравните совместное обучение
– Вторник: Самопроверка по математике Мероприятие Mystery Picture
– Среда: Математическая игра для 3-го класса
– Четверг: Игровое шоу для всего класса
– Пятница: День математической игры для 3-го класса (включены две математические игры)
- Мероприятия высокая вовлеченность, многие из них возглавляются студентами; Это дает учителям время для встреч с небольшими группами, выполнения оценок или выполнения заданий.
- Этот пакет идеально подходит для вовлечения учащихся в академический и увлекательный обзор, который сосредоточен на ключевых математических навыках 3-го класса.
Этот пакет включает в себя все необходимое, чтобы сделать летние занятия математикой в 3-м классе очень увлекательными с небольшой подготовкой учителя! Вы можете использовать занятия в этом наборе в любом порядке и выбирать те, которые хотите использовать со своим классом. Игры можно ламинировать и снова использовать для дополнительного просмотра. Это отличный способ сделать математику в летней школе увлекательной и увлекательной!
Этот пакет скоро будет доступен как часть 5-недельного связанного набора, который включает 5 мини-модулей для недельного обзора математики .Вы сможете приобрести комплект и сэкономить 30% от цены или приобрести единицы по отдельности!
Этот набор доступен как часть 5-недельного связанного набора. Набор экономит 30% от цены покупки каждого набора в отдельности. Если вы хотите приобрести недели по отдельности, щелкните по ссылкам ниже:
Неделя 1: Сложение и вычитание (серфинг-тематика)
Неделя 2: умножение и деление (тематическая поездка)
Неделя 3 : Фракции (тематика бассейна и воды)
Неделя 4: Измерения и геометрия (тематика кемпинга)
Неделя 5: Измерения и решение проблем (тематика пляжа)
Если вы ищете математику для 3-го класса деятельности, ознакомьтесь с этими продуктами:
✔ Математические загадочные картинки с эмодзи: математические навыки для 3-го класса
✔ Распечатайте и играйте в математические игры – 3-й класс
✔ Мега-набор для математических навыков 3-го класса
✔ Мега-карточки по математике для 3-го класса Пакет – все разделы и стандарты
✔ Математические загадочные картинки
✔ 3-й класс Общие экзамены по математике Все стандарты Комплект
✔ Выходные листы по математике – 3-й класс Common Core ll Standards Mega Bundle
✔ 3-й класс Common Core Math Test Prep Все стандарты Mega Bundle
✔ 3-й класс Common Core Math Word Wall и многое другое
✔ 3-й класс Common Core ELA Ultimate Vocabulary Resource
✔ Math Mojo Digital Resources
✔ Мероприятия на конец года
✔ Праздничные и сезонные мероприятия
✔ Подготовка к экзамену по математике
25 математических игр и мероприятий для третьего класса, которые действительно увеличивают веселье
Когда вы переходите в третий класс, математика делает большой шаг вперед.Стандарты Common Core включают, среди прочего, умножение и деление, базовую геометрию и округление. Эти математические игры и задания для третьего класса помогут вашим ученикам овладеть этими ключевыми навыками в увлекательной и увлекательной форме.
1. Считайте точки, чтобы научиться умножению
Умножение – это новый навык для учеников третьего класса математики, но он основан на концепциях, которые они усвоили в более ранних классах. Эта карточная игра помогает им устанавливать связи. Каждый игрок переворачивает две карты, затем рисует сетку и рисует точки на стыках линий.Они считают точки, и тот, у кого больше всего карт, оставляет себе все карты.
Подробнее: Teach Beside Me
2. Пробить отверстия для умножения
Массивы – популярный способ обучения навыкам умножения, и это забавное занятие, в котором используется эта концепция. Вытяните немного макулатуры и вырежьте квадраты или прямоугольники. Затем с помощью дырокола сделайте массивы точек для представления уравнений умножения.
Подробнее: Primary Theme Park
3. Переверните домино и умножьте
В конце концов, детям придется запоминать факты умножения, и эта быстрая и простая игра в домино может помочь.Каждый игрок переворачивает домино и умножает два числа. Тот, у кого больше продукт, получает оба домино.
Подробнее: Веселые игры 4 Обучение
4. Найдите уравнения умножения
Это похоже на поиск слов, но для умножения фактов! Скачайте бесплатные печатные издания по ссылке.
Подробнее: Math Geek Mama
5. Переориентируйте «Угадай, кто»? доска
Еще одна игра на умножение с использованием «Угадай, кто»? игровая доска.(Вы также можете сделать это с фактами разделения.)
Подробнее: Rainbow Sky Creations / Instagram
6. Ремесленное подразделение факт цветы
Это намного веселее, чем карточки! Сделайте цветы для каждого числа и используйте их, чтобы попрактиковаться в делении.
Подробнее: Семья учимся вместе
7. Беги и беги, чтобы попрактиковаться в делении
В математике для третьего класса умножение и деление идут рука об руку. В этой бесплатной игре для печати дети бросают кости, пытаясь первыми правильно ответить на все задачи в одном ряду.Получите распечатку по ссылке.
Подробнее: Дженнифер Финдли
8. Разделяй и властвуй разделительные пары
Think Go Fish, но вместо того, чтобы составлять пары, цель состоит в том, чтобы сопоставить две карты, одна из которых может равномерно разделиться на другую. Например, 8 и 2 являются парой, так как 8 ÷ 2 = 4.
Подробнее: cuppacocoa
9. Найдите недостающий знак
Когда дети выучат все четыре типа арифметики, они смогут работать в обратном порядке, чтобы увидеть, какой знак отсутствует в уравнении.Бесплатная настольная игра для печати по ссылке предлагает им сделать именно это.
Узнать больше: Обманчиво обучающая игра по математике с отсутствующими знаками
10. Используйте стикеры для игры Can You Make It?
Дайте ученикам серию цифр на стикерах вместе с целевым числом. Затем посмотрите, смогут ли они составить уравнение (или несколько уравнений), соответствующее цели.
Подробнее: обучающие игры
11. Представьте округление в карточной игре
Учащиеся третьего класса математики узнают об округлении чисел.В этой карточной игре они переворачивают по две карты каждую и округляют полученное число до ближайшего 10. Тот, чье число больше, сохраняет все карты.
Подробнее: приключения в третьем классе
12. Скатайте и скруглите
Используйте эту бесплатную доску для печати, чтобы играть в Roll It! для большей практики округления. Учащиеся бросают три кубика и складывают их в число. Они округляют до ближайших 10 и отмечают это на своей доске. Цель – первым закончить ряд.
Подробнее: Games 4 Gains
13. Используйте кубики LEGO, чтобы выучить дроби.
Изучая математику в третьем классе, ученики всерьез начинают изучать дроби. Играть с LEGO становится весело! Дети рисуют карточки и используют цветные кубики, чтобы обозначить показанную дробь. Узнайте о других способах использования кубиков LEGO в математике.
Подробнее: JDaniel4’s Mom
14. Подберите пластиковые яйца
Попробуйте другой вид охоты за яйцами, чтобы отработать эквивалентные дроби.Напишите дроби на каждой половине, а затем попросите детей найти их и сопоставить. (Сделайте это сложнее, смешивая цвета!) Ознакомьтесь с другими нашими способами использования пластиковых яиц в классе.
15. Подбор игровых фракций
Возьмите бесплатные карточки для печати по ссылке и постарайтесь найти соответствие между картинками и дробями, которые они представляют.
Узнать больше: Обманчиво образовательное / фракционное совпадение
16. Объявить войну фракций
Каждый игрок переворачивает две карты и выкладывает их дробью.Они решают, какая фракция больше, а все карты остаются у победителя. Сравнивать дроби бывает немного сложно, но если дети сначала начертят их на числовой прямой, они будут практиковать сразу два навыка.
Подробнее: Папка с математическими файлами
17. Мастер, определяющий время с точностью до минуты
Для этой математической игры для третьего класса вам понадобятся многогранные игральные кости. Дети бросают кости и соревнуются, чтобы первыми показать правильное время на своих часах.
Подробнее: Маньяк элементарной математики
18. Подбирайте кубики LEGO, чтобы узнать время
Напишите время различными способами на кубиках LEGO. Затем попросите учащихся посмотреть, как быстро они смогут сопоставить их.
Подробнее: Scholastic
19. Исследуйте периметр и площадь с помощью Array Capture
Геометрия приобретает все большее значение в математике в третьем классе, поскольку учащиеся изучают площадь и периметр. Эта веселая и простая игра охватывает и то, и другое, и все, что вам нужно для игры, – это миллиметровка и несколько кубиков.
Подробнее: Обучение с Джиллиан Старр
20. Нарисуйте периметр людей
Попросите детей нарисовать автопортреты на миллиметровой бумаге, а затем вычислить периметр и площадь своих квартальных людей. Симпатично и весело!
Подробнее: Слово от третьего
21. Создавайте головоломки LEGO, чтобы практиковаться по большей площади и периметру
Задача: соберите головоломку 10 × 10 из кубиков LEGO, чтобы ее могли решить ваши друзья. Попросите детей также определить периметр и площадь каждой части пазла.
Подробнее: Экономные развлечения для мальчиков и девочек
22. Раскрашиваем многоугольное одеяло
Игроки по очереди раскрашивают четыре соединенных треугольника одновременно, зарабатывая очки за форму, которую они создают. Это интересный способ попрактиковаться в многоугольниках.
Подробнее: E для Explore
23. Играть в четырехугольник бинго
Каждый квадрат является прямоугольником, но не все прямоугольники являются квадратами. Разберитесь с причудливыми четырехугольниками в этой бесплатной игре в бинго для печати.
Подробнее: математика у вас есть
24. Прокрутите и добавьте, чтобы построить гистограммы
Сначала ученики бросают кости и складывают два числа, записывая уравнение в столбец правильной суммы. Повторите столько раз, сколько захотите. Затем задавайте вопросы для анализа данных. Какую сумму они выпадали чаще всего? Сколько раз они выполнили наибольший результат, чем наименьший? Это интересный способ просмотреть дополнительные факты и поработать над построением графиков.
Подробнее: первый класс миссис Т.
25.Отгадать математические загадки
Соберите вместе все свои математические навыки третьего класса, чтобы решить эти математические загадки. Получите бесплатный набор для печати по ссылке.
Подробнее: Primary Inspiration
Любите STEM? Вам стоит ознакомиться с этими 27 научными проектами для третьего класса, которые под силу любому учителю.
Plus, когда вы подпишетесь на нашу рассылку, получайте все последние советы и рекомендации по обучению прямо на свой почтовый ящик!
уроков в классе | Математические решения
Черил начала урок с чтения Спагетти и фрикадельки для всех! вслух классу.По сюжету мистер и миссис Комфорт приглашают 32 члена семьи и друзей на встречу и устанавливают восемь квадратных столов, чтобы разместить по четыре человека за каждым, по одному сбоку. По мере того, как приходят гости, у всех есть свои идеи о том, как переставить столы, чтобы группы разного размера могли сидеть вместе. Миссис Комфорт протестует, зная, что позже возникнут проблемы с сиденьем, но ее протесты игнорируются. Вечеринка превращается в веселую смесь переставленных столов, стульев, тарелок, стаканов и еды. Однако в конце концов все сработает, когда миссисВ конце концов, комфорт оказался правильным.
Когда Шерил закончила читать рассказ, она спросила класс: «О чем беспокоилась миссис Комфорт?»
Николь сначала ответила: «Здесь не будет достаточно места, потому что, когда вы складываете столы вместе, вы теряете стулья», – сказала она.
“Что ты имеешь в виду?” – спросила Черил.
«Это как если вы сложите два стола вместе, вы потеряете места там, где они соприкасаются. Это трудно объяснить.” Николь нарисовала в воздухе два стола, указывая на стороны, где они встретились.Черил нарисовала на доске два квадрата, нарисовав стрелку там, где стороны касались друг друга. “Вы имеете в виду потерять стулья здесь?” она спросила. Николь кивнула. (См. Рисунок 1).
Выслушав идеи других студентов о проблеме миссис Комфорт, Черил сказала: «Давайте использовать цветные плитки, чтобы изучить различные способы расстановки всего четырех столов. Начнем всего с четырех столов ».
Черил дала классным указаниям по расстановке квадратных «столов». «Когда плитки соприкасаются, – сказала она, – они должны касаться всей стороны.Прикосновение к частям сторон или только к углам недопустимо ». Она продемонстрировала на диапроекторе. (См. Рисунок 2.)
Шерил также разместила плитки таким образом, чтобы не следовать ее правилу, и попросила учеников объяснить, почему. (См. Рисунок 3.)
Затем она выполнила инструкции. «В своей группе поделитесь плитками, которые я положил на ваш стол, и найдите разные способы расставить четыре плитки. Обязательно следуй моему правилу ». Черил разложила около 70 плиток для каждой группы из четырех учеников.
Пока ученики работали, Черил ходила по классу, наблюдая за учениками и отвечая на вопросы по мере необходимости. Когда у всех была возможность поработать над проблемой, она прервала студентов и попросила их внимания.
«Что вы сделали?» – спросила Черил. «Кто бы хотел описать расположение, чтобы я мог построить его из плитки наверху?»
«Вы можете провести прямую линию», – сообщил Брэндон.
«Как это?» – спросила Черил, складывая четыре плитки в прямоугольник 1 на 4.Брэндон кивнул.
«Сделайте квадрат со всеми четырьмя из них», – сказала Рахиль. Черил построила квадрат из четырех плиток.
«Я сделала тройку и одну», – сказала Николь.
“Что ты имеешь в виду?” – спросила Черил.
«Один маленький столик, как у Натана, – объяснила Николь, – а затем столик 1 на 3».
«Вы можете сделать четыре отдельных стола», – сказал Натан.
«Ты мог бы поставить Т», – сказал Зак. «Положите три в ряд и один под средним».
«Я тоже сделал это, но мой перевернут», – сказал Эрик.
Шерил построила аранжировку Эрика под руководством Зака и указала классу, что когда вы можете перевернуть, повернуть или сдвинуть фигуру, чтобы она точно соответствовала другой фигуре, фигуры совпадают. «Мы будем считать конгруэнтные формы одинаковыми», – пояснила она.
Когда расположение студентов заполнило накладные расходы, Черил спросила: «Что, если бы мы использовали только отдельные прямоугольные столы, сделанные из четырех плиток? Какие формы мы должны удалить? ”
«Я предложил четыре отдельные таблицы, – сказал Натан.
Рифка добавила: «И та, которая похожа на букву Т».
«Вы также должны снять мою», – сказала Николь. “Это не один прямоугольник”.
Когда Малкия предложила убрать квадрат, разговор разгорелся. Некоторые ученики помнили, что квадрат – это прямоугольник, а другие – нет. Черил пояснила: «Квадрат – это особый вид прямоугольника, потому что все его стороны имеют одинаковую длину. Но, как и прямоугольник, квадрат по-прежнему имеет четыре угла в 90 градусов, а противоположные стороны параллельны.”
Шерил хотела убедиться, что ученики умеют маркировать построенные ими прямоугольники. Она нарисовала на доске прямоугольник размером 1 на 4. «Я могу записать это двумя способами», – сказала она и записала под прямоугольником:
Затем Черил нарисовала квадрат 2 на 2 и пометила его.
Черил указала на квадратный стол 2 на 2 и спросила: «Если один человек сидит сбоку от небольшого квадратного стола, и никто не сидит по углам или в щелях между столами, сколько людей может сидеть здесь? ”
«Легко, восемь», – ответила Николь.«Просто сосчитайте по два человека с каждой стороны, умноженные на четыре стороны».
«Когда вы подсчитываете количество людей, которые могут сесть за стол, вы фактически находите его периметр», – объяснила Шерил. «Это потому, что каждый человек сидит по одну сторону от меньшего квадрата и занимает одну единицу длины. Таким образом, периметр прямоугольника 2 на 2 составляет 8 единиц ».
«Периметр стола размером 1 на 4 равен 10», – заметил Эрик.
Черил попросила остальных проверить показания Эрика, а также изобразить периметр нескольких других прямоугольников.Затем она представила другую проблему.
– Давайте вспомним вечеринку мистера и миссис Комфорт, – начала Черил. «Предположим, миссис Комфорт решила, что все 32 человека должны сесть за один большой массивный прямоугольный стол, и она хотела выяснить, сколько маленьких квадратных столов можно арендовать. Посмотрите, сможете ли вы найти все возможные прямоугольные столы разных размеров и форм, на которых могут разместиться 32 человека ».
«Должен ли каждый стол вмещаться ровно 32?» JT хотел знать.
«Да», – ответила Черил.
«Сколько плиток мы используем?» – спросила Малкия.
«Это будет зависеть от столов, которые вы построите», – ответила Черил.
«Можем ли мы работать с партнером?» – спросила Николь.
«Да, – ответила Черил, – но веди свой личный учет».
Больше вопросов не было. Черил дала последнее указание. «Используйте плитки, но нарисуйте свои решения на листе бумаги. Обязательно запишите размеры каждого стола и количество людей, за которыми он может разместиться ».
Наблюдая за детьми
Остаток урока Черил наблюдала за учениками за работой и при необходимости оказывала помощь.
Она наблюдала, как Кэтлин составляла прямоугольник 16 на 2. «Хм, – громко сказала Кэтлин, работая, – давайте посмотрим, 32 человека. Это должно сработать, потому что 16 умножить на 2 будет 32 ». Кэтлин сосредоточенно нахмурилась, считая стороны квадратов. Затем она с удивлением посмотрела на Шерил.
«Я не понимаю», – сказала она. «Я насчитал 36 мест. Но в этом нет смысла, потому что 16 умножить на 2 равно 32. Может, я неправильно посчитал ». Она снова сосчитала стороны.
«Еще 36. Ага». Кэтлин пожала плечами, перемешала 16 плиток обратно в стопку в центре стола и начала строить еще один прямоугольник.
«Что ты делаешь?» – спросила ее Шерил.
«Что ж, я, должно быть, напортачила, потому что первая, которую я сделал, не сработала, поэтому я попробую что-нибудь еще», – ответила Кэтлин.
«Что ты собираешься попробовать?» – спросила Черил.
«Не знаю. Я просто собираюсь повозиться и посмотреть, что будет », – сказала она.
Черил наблюдала, как Кэтлин начала складывать плитки в длинный ряд шириной в один квадрат. Она продолжала считать стороны одну за другой каждый раз, когда добавляла новую плитку.Наконец она улыбнулась.
«Это работает! Этот вмещает 32 человека. Это 1 на 15. А теперь записать это ». Кэтлин начала рисовать прямоугольник на бумаге.
Алекс сидел напротив Кэтлин. «Я тоже нашел это», – сказал он. «Теперь я пробую что-то вдвое».
«О», – ответила Кэтлин и начала строить прямоугольник шириной в четыре квадрата.
Натан подошел к Шерил. «Я не рисую на бумаге прямоугольники, как все, – сказал он. «Вместо этого я решил использовать Xs.Но Люк сказал мне, что это неправильно. Разве я не могу нарисовать крестики, если захочу? ” Натан показал Шерил свою газету.
Черил попросила Натана объяснить, что он сделал. Удовлетворенная тем, что он понимает, что делает, Шерил сказала: «То, что вы сделали, имеет для меня смысл».
Натан вернулся к Люку. «Я сказал вам, что она скажет, что все в порядке», – сказал он.
Черил пошла по классной комнате. К концу периода она увидела, что все студенты нашли некоторые прямоугольники, а некоторые нашли их все.Она попросила детей убрать плитку и собрала их бумаги. Шерил планировала продолжить урок на следующий день.
На следующий день
На следующее утро Черил дала классу возможность подумать над расширением. «Какой самый дешевый способ разместить 32 человека за одним большим прямоугольным столом? А какой самый дорогой способ? Чтобы ответить, некоторым из вас нужно будет найти дополнительные расстановки столов ».
Примерно через 10 минут Черил прервала учеников, чтобы начать обсуждение в классе.«Какие варианты есть у Comforts, чтобы посадить всех 32 человека за один стол?» – спросила Черил. Руки студентов вскинулись.
«У них будет группа, точнее, восемь», – сказала Рэйчел. Большинство студентов кивнули или пробормотали свое согласие.
«Может ли кто-нибудь описать размеры таблиц, которые будут работать?» – спросила Черил. «Я запишу их на доске».
Эрик сообщил: «Один раз-15, 2-раз-14, 3-раз-13, 4-раз-12, 5-раз-11, 6-раз-10, 7-раз-9 и-8-раз-8. . » После того, как Шерил записала размеры, она вернулась и зарисовала каждый соответствующий прямоугольник.
«О, я вижу закономерность!» – сказала Анферни. “Могу я показать это?” Черил кивнула, и Анферни подошла к доске. Она сказала, указывая: «Сверху вниз идет 1, затем 2, затем 3, затем 4, затем 5 и так далее, вплоть до 8».
«А другая сторона идет вниз», – добавила Анн Мария.
«О да, я этого не видела», – сказала Анферни. «Ага, 15, 14, 13 и так далее». Он снова сел.
«Разве список не должен продолжаться?» – спросила Черил. “Разве не следует прямоугольник 9 на 7?” (См. Рисунок 6.)
«Этот у тебя уже есть», – сказала Малкия.
«Да, 9 на 7 и 7 на 9 – это одно и то же, – добавила Николь.
«Все числа после 8-умножить на 8 – это повторения, – сказала Кирстен, – так что вы не можете их сосчитать».
«Давайте подумаем, сколько квадратных столов придется арендовать мистеру и миссис Комфорт на каждый большой прямоугольник», – сказала Шерил. «Сколько им придется арендовать за стол размером 15 на 1?»
«Пятнадцать. Легко, – ответили несколько студентов.
«А как насчет 2 на 14?» Черил продолжила.«Сколько столов придется арендовать Comforts для такой договоренности?»
«Двадцать восемь», – звали многие дети.
«А как насчет расположения 3х13?» – спросила Черил. Класс быстро понял, чем занимается Шерил.
«Вы просто размножаетесь», – сказала Рифка. «Просто сделай это для всех – 28, 39, 48, 55, 60, 63 и 64».
«Что вы заметили в форме столов?» Затем спросила Черил.
Малкия сказала: «Размер 8 на 8 – квадрат, а все остальные – прямоугольники.”
«Но ведь размер 8 на 8 тоже прямоугольник, помнишь?» Эрин напомнила Малкию.
«Смотрите, – сказал Брэндон. «Если они устроят длинный тонкий прямоугольник для 32 человек, то они смогут сделать это всего с 15 столами. Так дешевле всего.
«И они также сэкономили бы место, поскольку 1-умноженный на 15 занимает меньше всего места», – добавил Шарнет.
«Но вам понадобится длинная комната, – добавила Николь, – как для королевского банкета».
Затем Шерил остановила беседу и дала письменное задание оценить мышление каждого ученика.Она написала на доске три вопроса, чтобы дети могли ответить:
- Какие шаблоны вам пригодились в работе?
- Какие расстановки столов наиболее и наименее экономичны?
- Что вы заметили в областях и периметрах выполненных вами мероприятий?
Учащиеся работали над заданием для остальной части класса.
10 советов по развитию математических навыков в 3-м классе
Повседневная жизнь предлагает множество возможностей для изучения и практики важных уроков математики, особенно когда вы привносите чувство веселья и приключений.
Делаем умножение значимым
Часть математики в этом году – это не просто изучение таблиц умножения, но и их освоение. Вот забавный способ помочь: выберите число, которое делится на множество чисел, например 24. Спросите ребенка, какие пары чисел можно умножить на 24 (3 x 8, 6 x 4, 2 x 12 и 1 x 24). ). Используйте фасоль или шоколадную стружку, чтобы сложить их столбцами и рядами (например, 3 ряда по 8 пенсов). Используйте этот рабочий лист, чтобы попрактиковаться в умножении.
Дроби на столе
Во время еды попросите ребенка что-нибудь нарезать (например,г., вафля) на две, три или четыре равных части. Это поможет им понять, что дроби – это равные части одного целого. Затем попробуйте то же самое с двумя объектами: если 4 человека хотят разделить 2 апельсина поровну, сколько получит каждый? Что делать, если у вас есть 3 апельсина? Идея в том, чтобы ваш ребенок понял связь между делением и дробями. Вот как это выглядит с настоящими третьеклассниками.
Верните спортсмена в математику
Если ваш ребенок занимается спортом, помогите ему найти веб-сайт, посвященный любимому виду спорта вашего ребенка.Затем выполните математические вычисления, сосредоточив внимание на четырех операциях. Например: на сколько очков эта команда набрала больше, чем та? На данный момент избегайте всего, что связано со средними или десятичными числами – за исключением 5-го класса. Получите еще 13 советов по математике для 3-го класса!
Fitbit чтение вашего ребенка
Если ваш ребенок любит читать, помогите продемонстрировать огромное количество слов, которые он употребляет, отслеживая их успехи. Составьте таблицу, показывающую, сколько страниц она читает каждый день.Вместе анализируйте данные. В какой день вы читаете больше всего? Примерно сколько страниц вы прочтете на следующей неделе? Получите еще 13 советов по математике для 3-го класса!
Тренируй, но не убивай
Если вы тренируетесь с ребенком в таблице умножения, это может быть очень весело. Сосредоточьтесь на 1–10, но не стесняйтесь подниматься немного выше, если ваш ребенок справится с этим. Если у вашего ребенка возникают проблемы с решением одного из них, помогите ему «аргументировать» его. Например, если 4 умножить на 6 сложно, подумайте 4 умножить на 5 – что это? Было бы 4 умножить на 6 больше или меньше? Почему? Дайте вашему ребенку возможность попрактиковаться с этим рабочим листом.
Добавляем зелень в бакалейную лавку
Если дети заинтересуются стоимостью небольших покупок в магазине, это поможет им освоить математику в третьем классе. В следующий раз, когда вы будете делать покупки, спросите своего ребенка, сколько будет стоить шесть коробок хлопьев, если каждая стоит 3 доллара. Или спросите, сколько буханок хлеба вы можете купить за 16 долларов, если каждая буханка стоит 4 доллара. Вы также можете дать своему ребенку возможность попрактиковаться с помощью этой таблицы значений доллара.
Мера за меру
Умение вычислять площадь двумерной фигуры является ключевым навыком третьего класса.Как помочь? Достаньте измерительную ленту и попросите ребенка выяснить, какой из следующих предметов домашнего обихода имеет наибольшую площадь: экран телевизора, стол, пол в ванной и их кровать. Получите еще 13 советов по математике для 3-го класса!
Решение проблем
Огромный объем высшей математики – это просто решение задач, чистое и простое. Как помочь с этим жизненно важным навыком? Когда ваш ребенок сталкивается с проблемой – в домашней работе или в реальной жизни – не поддавайтесь желанию вскочить и решить ее.Вместо этого спросите Что, по вашему мнению, вам следует попробовать в первую очередь? Самостоятельная работа над задачами поможет вашему ребенку развить навыки решения проблем. См. Все советы по математике для 3-го класса.
Навыки измерения
Измерение и упрощение сопоставления и анализа чисел – это навык, который ваш третьеклассник начал изучать в этом году (и будет использовать больше в будущем). Дайте своему ребенку немного попрактиковаться в реальной жизни. Дайте ребенку рулетку и попросите его определить рост каждого члена семьи – с точностью до четверти дюйма.Затем попросите ребенка нарисовать числа на числовой прямой. Может ли кто-нибудь еще прочитать их таблицу и выяснить, кто самый высокий и насколько? См. Все советы по математике для 3-го класса.
Дробное действие
Вы не хотите, чтобы ваш третий класс забыл то, что он выучил в школе в этом году, особенно дроби. Исследования показывают, что дети теряют знания в течение лета (это называется летней потерей знаний), и это хуже с математикой, чем с чтением. Чтобы предотвратить потерю в обучении, попросите ребенка нарисовать 8 фигур (тренируя свои навыки геометрии), включая один круг и различные правильные многоугольники.Теперь попросите их разделить эти фигуры на фракции равного размера. Произвольно вызывайте что-нибудь – цвет ⅔ формы 1, ⅞ формы 2, ¼ формы 3 и т. Д. Как они это сделали? Чтобы поддерживать у вашего ребенка математические навыки, ознакомьтесь со всеми нашими советами по математике для 3-го класса.
Поделиться в Pinterest
Обновлено: 16 апреля 2020 г.
Заданий на лето
Обведите летние слова в этой головоломке по поиску слов. Список включает в себя август, мяч, пляж, лагерь, друзья, лето, бассейн, на улице и игры.
Детский сад до 2 класса
Зарегистрированные участники могут использовать картотеку Super Teacher Worksheets, чтобы сохранять свои любимые рабочие листы.
Быстрый доступ к наиболее часто используемым файлам И настраиваемым рабочим листам!
Пожалуйста, войдите в свою учетную запись или станьте участником и присоединитесь к нашему сообществу сегодня, чтобы воспользоваться этой полезной функцией.
Эта головоломка с поиском слов на летнюю тематику немного сложнее, чем простая версия, и в ней есть больше слов, которые нужно найти, а также несколько диагоналей.Вот некоторые из слов: отпуск, солнцезащитные очки, спринклер, ночевка, фруктовое мороженое, пикник и лагерь.
Со 2-го по 6-й классы
Приготовьтесь к летним развлечениям, решив эту головоломку с поиском слов на пляжную тематику. Найдите такие слова, как: волны, полотенце, солнечный свет, ракушки, пикник и спасатель.
2–6 классы
Игроки по очереди находят пары чисел, которые в сумме дают до шестнадцати, например 8 + 8, 7 + 9, 10 + 6 и т. Д. В этой игре солнечная графика и летняя тема.
1–3 классы
Вырежьте и переставьте буквы в слове «summertime», чтобы получилось как можно больше уникальных слов.
(Приблизительно 1-3 классы)
1–3 классы
Вырежьте и переставьте буквы в слове «летнее время», чтобы составить как можно больше уникальных слов. Эта версия включает систему подсчета очков.
(Приблизительно для классов 3–6)
3–6 классы
Предложите ученикам найти скрытые изображения в сцене.Это можно использовать как занятие для развлечения или включить в письменное задание.
От детского сада до 3-го класса
Поделки и раскраски
Лето официально начинается 20 или 21 июня каждого года. Вот забавная поделка из короны / шляпы, чтобы отпраздновать этот захватывающий день. ( Мы рекомендуем распечатать этот файл на толстых карточках. Если вы предпочитаете цветную версию файла, нажмите ссылку «ALT» ниже. )
Pre-K – 2nd Grade
Раскрасьте эту летнюю пляжную сцену .На этой фотографии дельфин прыгает, а ребенок строит замок из песка.
От детского сада до 3-го класса
Ученикам понравится использовать цветные карандаши или фломастеры, чтобы раскрасить эту картинку русалки.
Pre-K – 1st Grade
Распечатайте эту раскраску с изображением парусной лодки.
Pre-K – 1 класс
Прочтите стихотворение о летнем времени, а затем ответьте на следующие вопросы для понимания прочитанного.
(Приблизительно 1-3 классы)
1–3 классы
Марк и Ава собирают все необходимое для идеального пикника.Разрушат ли их планы дождевые облака над головой?
1-й класс
Маура очень хочет познакомиться со своими новыми соседями. Она надеется, что девочка ее возраста переедет, и ей будет с кем пообщаться во время летних каникул. Но когда подъезжает движущийся грузовик, Маура узнает, что получит даже больше, чем хотела.
(Приблизительные классы 2–4)
2–4 классы
В этом Интернете учащиеся пишут о вещах, которые они чувствуют, видят, касаются, ощущают на вкус и слышат, когда посещают морской берег.
Со 2-го по 4-й классы
На этой странице есть 16 письменных подсказок на летнюю тематику, из которых ученики могут выбирать.
3–8 классы
Напишите рассказ к картинке. На иллюстрации изображена девушка на пляжном одеяле, читающая книгу.
От детского сада до 4 класса
Двое детей передают друг другу пляжный мяч в бассейне. Напишите творческий рассказ, который будет соответствовать картинке.
2–5 классы
Молодой человек на этой фотографии жарит зефир на костре.
2–5 классы
Свинья плавает в бассейне, а кошка готовится нырнуть.
Опишите свое любимое время года. Расскажите, чем вы любите заниматься в это время года.
От детского сада до 5 класса
Найдите в этом абзаце ошибки, касающиеся кемпинга. Ошибки включают использование заглавных букв, пунктуацию, составные слова и орфографию.
(Приблизительно 2–4 классы)
2–4 классы
Найдите в этом абзаце ошибки, касающиеся бассейна.Включает ошибки в написании заглавных букв, пунктуации, неправильных глаголах и притяжательных существительных.
(Приблизительно 3-5 классов)
3–5 классы
Напишите список слов на лето в алфавитном порядке. В каждом списке слов есть слова, начинающиеся с разных букв. (пример: бассейн, плавание, вода, ныряние)
Рекомендуется для 1 и 2 классов.
От детского сада до 2 класса
Напишите список слов в алфавитном порядке. Этот рабочий лист среднего уровня требует, чтобы учащиеся смотрели на 2-ю, 3-ю или 4-ю букву в каждом слове.(пример: костер, кемпинг, каноэ, s’more, гамак)
Рекомендуется для классов 3 и выше.
3–6 классы
Мероприятия по обучению грамоте в раннем возрасте
С помощью этой мини-книги, выполненной в стиле вырезания и сборки, учащиеся будут практиковаться в чтении слов с долгим гласным звуком е. Длинные слова в этой книге пишутся как ee и ea .
1-й и 2-й классы
«Поймай» светлячков и рассортируй их по семейству словесных банок в этой веселой игре по фонетике для самых маленьких! Это идеальное летнее занятие!
Детский сад и 1 класс
Динамически создаваемые рабочие листы по математикеУчителя, пожалуйста, поделитесь сайтом с родителями во время закрытия школы, чтобы ученики могли продолжать заниматься математикой дома. Math-Aids.Com предоставляет бесплатные рабочие листы по математике для учителей, родителей, студентов и домашних школьников. Математические рабочие листы генерируются случайным образом и динамически нашими генераторами математических листов. Это позволяет мгновенно создавать неограниченное количество математических листов для печати в соответствии с вашими требованиями. Этот сайт является бесплатным для пользователей из-за дохода, получаемого от показа рекламы на сайте. Использование блокировщиков рекламы противоречит нашим условиям использования. Если вы не хотите просматривать рекламу, присоединяйтесь к нашему членскому кабинету, в котором нет рекламы. Веб-сайт содержит более 94 различных математических тем с более чем 1223 уникальными рабочими листами. Гибкость и качество учебников математических рабочих листов делает Math-Aids.Com уникальным ресурсом для людей, желающих создавать и использовать математические рабочие листы. Ключ ответа прилагается к математическим рабочим листам по мере их создания. В каждой математической теме есть несколько различных типов математических листов для решения различных типов задач, над которыми вы можете работать. Мы стремимся создавать лучшие динамические таблицы по математике для наших пользователей. В настоящее время у нас есть рабочие листы по математике по следующим темам: сложение, алгебра 1, алгебра 2, десятичные дроби, деление, оценка, четность и нечетность, экспоненты, семейство фактов, факторы, карточки, дроби, функциональные таблицы, геометрия, график, миллиметровая бумага. , Графики, больше, чем меньше, диаграмма сотен, поля ввода и вывода, целые числа, детский сад, логика, среднее значение и диапазон, измерение, смешанные задачи, деньги, умножение, числовые связи, числовые линии, системы счисления, порядок операций, Шаблоны, процент, размеченное значение, предалгебра, вероятность, свойства, теорема Пифагора, радикалы, отношения, округление, значащие числа, подсчет пропусков, вычитание, определение времени, диаграммы Венна, игры в слова и задачи со словами. Мы добавляем на сайт новые таблицы по математике каждый день, поэтому заходите к нам почаще. Мы будем рады разработать любые рабочие листы по математике, которые могут вам понадобиться для планирования урока. Просто свяжитесь с нами, мы будем рады вам помочь. Учителя и школьники используют рабочие листы по математике на этом веб-сайте, чтобы измерить усвоение детьми основных математических навыков, дать дополнительную практику, выполнить домашнее задание и сэкономить драгоценное время на планирование. Родители используют рабочие листы по математике на этом веб-сайте, чтобы дать своим детям дополнительную практику с необходимыми математическими навыками.Использование заданий по математике во время перерывов и летом позволит детям оставаться в тонусе и подготовиться к предстоящему семестру. Зарегистрируйтесь в зоне для пользователей без рекламы
После того, как вы присоединились, просто нажмите кнопку входа в систему Red Member в верхней части
Быстрая ссылка для всех разделов математического листаЩелкните изображение, чтобы перейти к соответствующему разделу листа математики. | |
Ускоренный курс по математике в 3 классе | Центр талантливой молодежи Джонса Хопкинса
Запишитесь на этот курс
Право на участие: Требуется балл по математике на уровне CTY или Advanced CTY
Предварительные требования: Успешное завершение математики 2 класса или эквивалент
Формат курса: Индивидуально проходимый
Продолжительность курса: Обычно 6 месяцев
Рекомендуемый школьный кредит: Один академический год
Код курса: AG3
Описание курса
Описание
Это полноценный онлайн-курс ускоренной оценки 3 курс математики.Этот курс начинается с обзора математических понятий второго класса, охватывает все темы Общих основных государственных стандартов третьего класса и включает дополнительные темы, чтобы познакомить учащихся с концепциями четвертого класса. Этот курс готовит учащихся к 4 классу математики с отличием.
Уроки проводятся в виде интерактивных видеороликов, интерактивных онлайн-материалов, оцениваемых оценок и проектов. Учащиеся развивают математические рассуждения, изучают навыки критического мышления и приобретают методы решения проблем, чтобы исследовать и изучать математику 3-го класса.
Студентам предоставляются материалы онлайн-курса, такие как видео, заметки, интерактивные веб-страницы и практические задачи с решениями. Студенты проходят курс в своем собственном темпе, и ожидается, что они будут регулярно смотреть видео и просматривать заметки. Каждому студенту назначается инструктор CTY, который будет помогать им во время курса. Студенты могут связаться со своими инструкторами по электронной почте с любыми вопросами или проблемами в любое время. Также можно запланировать онлайн-обзорные сессии один на один для подготовки к оцениваемым экзаменам, которые включают домашнее задание, экзамены по главам, а также промежуточные и заключительные итоги.
Преподаватели используют программное обеспечение виртуального класса, позволяющее использовать видео, голос, текст, совместное использование экрана и интерактивную доску. Студентам настоятельно рекомендуется работать над курсом не менее 1 часа в день 5 дней в неделю (при 6-месячной зачислении) и отправлять своим инструкторам электронные письма не реже одного раза в неделю.
Темы включают:
- Работа с большими числами
- Сложение и вычитание
- Умножение
- Деление
- Введение в дроби
- Введение в десятичные дроби
- Измерение
- Двумерные формы
- Площадь и периметр
- Данные Анализ
Чтобы просмотреть подробный список тем, щелкните вкладку «Список тем».
Необходимые материалы
Для этого курса нет необходимых материалов.
Список тем
Работа с большими числами
- Целые числа до десяти тысяч
- Порядок и округление целых чисел
Сложение и вычитание
- Стратегии сложения
- Стратегии вычитания
- Сложение и вычитание Комбинированные Умножение
- Стратегии умножения
- Свойства умножения
- Факты деления – Часть 1
- Факты деления – Часть 2
- Факторы и умножения
- Определение дроби
- Эквивалент Дроби
- Сравнение и порядок дробей
- Сложение и вычитание дробей
- Десятые, сотые, тысячные доли
- Порядок и округление
- Telli нг Время
- Объем и масса жидкости
- Измерение и длина
- Многоугольники
- Треугольники
- Четырехугольники
- Линия симметрии
- Графики И линейные графики
- Гистограммы
Деление
Введение в дроби
Введение в десятичные дроби
Измерение
Двумерные формы
Площадь и периметр
Анализ данных
Вернуться к началу
Комната поддержки
Комната поддержки
Каждую неделю все учащиеся приглашаются в открытую комнату помощи по элементарной математике для 3 и 4 классов, которую обслуживает постоянно меняющийся состав преподавателей.Студентам предлагается задавать вопросы или просто встречаться с другими онлайн-студентами. Рассматриваемые темы меняются каждую неделю.
Ученики 3 и 4 классов проходят каждый вторник с 19 до 20 часов. E.T.
Образец видео
Образец видео
Технические требования
Для этого курса требуется правильно обслуживаемый компьютер с высокоскоростным доступом в Интернет и современный веб-браузер (например, Chrome или Firefox). Студент должен иметь возможность общаться с инструктором по электронной почте.Посетите страницу “Технические требования и поддержка” для получения более подробной информации.
Виртуальный онлайн-класс Zoom
В этом курсе используется виртуальный онлайн-класс, который можно использовать для общения преподавателя и ученика, если у ученика есть какие-либо вопросы по курсу или учебной программе. Класс работает на стандартных компьютерах с настольным клиентом Zoom, а также на планшетах или портативных компьютерах, поддерживающих приложение Zoom Mobile.

