Задачи на скорость время и расстояние 4 класс с ответами: Подборка задач на путь, скорость и расстояние для 4 класса. | Тренажёр по математике (4 класс) по теме:

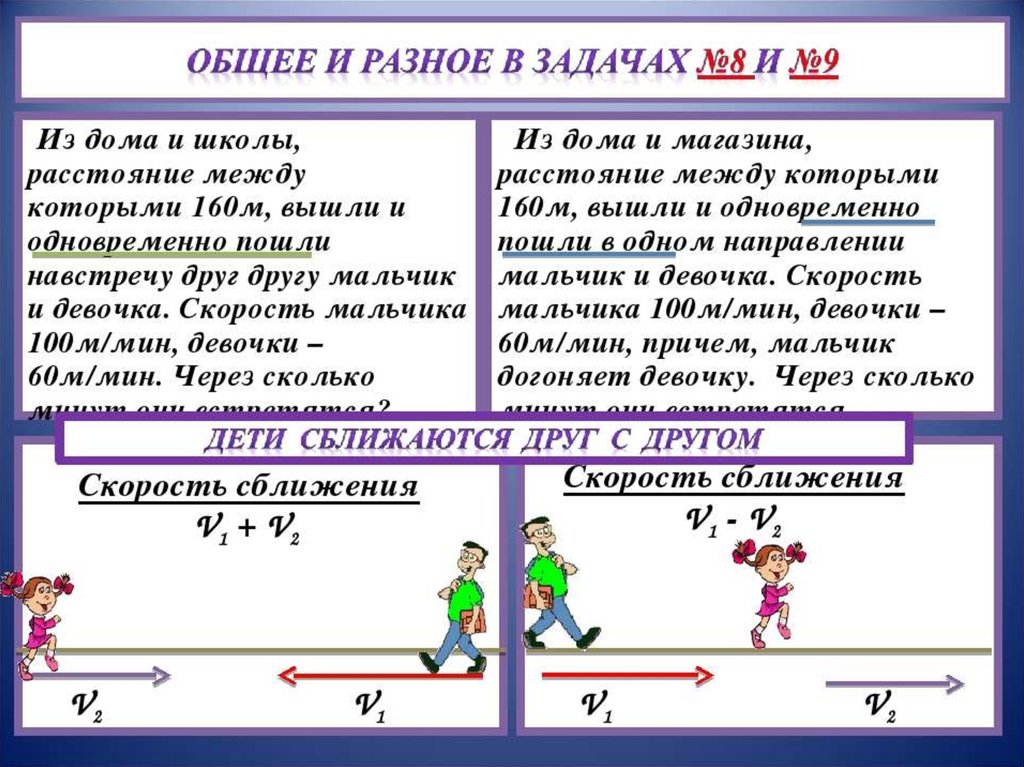
Задачи на встречное движение. Математика 4 класс.



Математика 4 класс

• Математические диктанты
• Тесты
• Нестандартные задачи
• Логические задачи
• Задачи с ответами
• Примеры

Контрольные работы

1 четверть
• Числа, которые больше 1000. Нумерация
• Итоговая контрольная работа за 1 четверть

2 четверть
• Итоговая контрольная работа 1

Итоговая контрольная работа 2

3 четверть
• Контрольная работа 1

Контрольная работа 2

Итоговая контрольная работа

4 четверть
• Деление на двузначное число

Итоговые контрольные работы за курс начальной школы
• Контрольная работа 1

Контрольная работа 2



Задача 1.

Из поселка и города навстречу друг другу, одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость 50 км/час.

Решение:
• 1) 100 : 25 = 4 (часа ехал один автобус)
• 2) 50 * 4 = 200
• Выражение: 50 * (100 : 25) = 200
• Ответ: второй автобус проехал до встречи 200 км.

Задача 2.

Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится чтобы встретиться, если скорость первого 20 км/час, а второго 25 км/час?

Решение:
• 1) 25 + 20 = 45 (сумма скоростей теплоходов)
• 2) 90 : 45 = 2
• Выражение: 90 : (20 + 25) = 2
• Ответ: теплоходы встретятся через 2 часа.

Задача 3.

От двух станций, расстояние между которыми 564 км., одновременно навстречу друг другу вышли два поезда. Скорость одного из них 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?

Решение:
• 1) 63 * 4 = 252 (прошел 1 поезд)
• 2) 564 – 252 =312 (прошел 2 поезд)
• 3) 312 : 4 = 78
• Выражение: (63 * 4 – 252) : 4 = 78
• Ответ: скорость второго поезда 78 км/час.

Задача 4.

Через сколько секунд встретятся две ласточки, летящие на встречу друг другу, если скорость каждой из них 23 метра в секунду, а расстояние между ними 920 м.

Решение:
• 1) 23 * 2 = 46 (сумма скоростей ласточек)
• 2) 920 : 46 = 20
• Выражение: 920 : (23 * 2) = 20
• Ответ: ласточки встретятся через 20 секунд.



Задача 5

С двух поселков, навстречу друг другу выехали одновременно велосипедист и мотоциклист. Скорость мотоциклиста 54 км/час, велосипедиста 16 км/час. Сколько километров проехал мотоциклист до встречи, если велосипедист проехал 48 км?

Решение:
• 1) 48 : 16 = 3 (часа потратил велосипедист)
• 2) 54 * 3 = 162
• Выражение: 54 * (48 : 16) = 162
• Ответ: мотоциклист проехал 162 км.

Задача 6

Две лодки, расстояние между которыми 90 км, начали движение на встречу друг другу. Скорость одной из лодок 10 км /час, другой 8 км/час. Сколько часов понадобится лодкам, чтобы встретится?

Решение:
• 1) 10 + 8 = 18 (скорость двух лодок вместе)
• 2) 90 : 18 = 5
• Выражение: 90 : (10 + 8) = 5
• Ответ: лодки встретятся через 5 часов.

Задача 7

По дорожке, длинна которой 200 метров, навстречу друг другу побежали два мальчика. Один из них бежал со скоростью 5 м/сек. Какова скорость второго мальчика, если встретились они через 20 сек?

Решение:
• 1) 20 * 5 = 100 (метров пробежал первый мальчик)
• 2) 200 – 100 = 100 (метров пробежал второй мальчик)
• 3) 100 : 20 = 5
• Выражение: (200 – 5 * 20) : 20 = 5
• Ответ: скорость второго мальчика 5 км/сек.

Задача 8

Два поезда выехали навстречу друг другу. Скорость одного из них 35 км/час, другого 29 км/час. Какое расстояние между поездами было сначала, если встретились они через 5 часов?

Решение:
• 1) 35 + 29 = 64 (скорсть двух поездов вместе)
• 2) 64 * 5 = 320
• Выражение: (35 + 29) * 5 = 320
• Ответ: расстояние между поездами было 320 км.

Задача 9

Из двух поселков навстречу друг другу выехали два всадника. Скорость одного из них 13 км/час, встретились они через 4 часа. С какой скоростью двигался второй всадник, если расстояние между поселками 100 км.

Решение:
• 1) 13 * 4 = 52 (проехал первый всадник)
• 2) 100 – 52 = 48 (проехал второй всадник)
• 3) 48 : 4 = 12
• Выражение: (100 – 13 * 4) : 4 = 12
• Ответ: скорость второго всадника 12 км/час.





Простые задачи

• Простые задачи на движение

Составные задачи

• Задачи на встречное движение
• Задачи на движение в одном направлении
• Задачи на противоположное движение
• Задачи на нахождение неизвестного по двум разностям
• Задачи на нахождение числа по доле и доли по числу
• Задачи на нахождение площади
• Задачи на сложение и вычитание многозначных чисел
• Задачи на умножение и деление многозначных чисел
• Задачи на приведение к единице и пропорциональное деление
• Задачи на определение цены, количества, стоимости



Тест: Скорость.

Время. Расстояние – Математика 4 класс Тест: Скорость. Время. Расстояние – Математика 4 класс

Английский язык

Астрономия

Белорусский язык

Биология

География

ИЗО

Информатика

История

Итальянский язык

Краеведение

Литература

Математика

Музыка

Немецкий язык

ОБЖ

Обществознание

Окружающий мир

ОРКСЭ

Русский язык

Технология

Физика

Физкультура

Химия

Черчение

Для учителей

Дошкольникам

VIP – доступ

• Предметы
»
• Математика
»
• 4 класс
»
• Скорость. Время. Расстояние

Скорость. Время. Расстояние

Готовимся к контрольной работе

Математика 4 класс | Автор: Елена Владиславовна Танкова | ID: 14124 | Дата: 12.9.2021

Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться

Вопрос № 1

Тройка лошадей пробежала 12 км. По сколько километров пробежала каждая лошадь?

Введите ответ:

Вопрос № 2

Скорость велосипедиста может быть 200 …

км/мин
м/мин
км/ч

Вопрос № 3

Поезд прошел 640 километров за 8 часов двигаясь с одинаковой скоростью. С какой скоростью шёл данный поезд?

Введите ответ:

Вопрос № 4

Используя решение, вставь пропущенные в задаче величины: 30 х 8 = 240 (м)
Пешеход движется со скоростью _______________

8 м/мин
30 м/мин
240 м

Вопрос № 5

39 км/ч = . .. м/ч

390
3900
39000

Вопрос № 6

Чтобы найти время, надо

Введите ответ:

Вопрос № 7

Скорость самолета 16 …

км/ч
м/мин
км/мин

Вопрос № 8

Используя решение, вставь пропущенные в задаче величины.
Какое расстояние он пройдёт за ______________

6 х 3 = 18 (км)

6 ч
18 км
3 ч

Вопрос № 9

Скорость поезда 80 км/ч, а скорость велосипедиста 20 км/ч. На сколько км в час скорость поезда больше, чем скорость велосипедиста?

100 км/ч
60 км/ч
1600 км/ч
4 км/ч

Показать ответы

Получение сертификата
о прохождении теста

Доступно только зарегистрированным пользователям

© TestEdu. ru 2013-2022

E-mail администратора: [email protected]

Скорость, расстояние и время — алгебра среднего уровня

Глава 8. Рациональные выражения

Задачи расстояния, скорости и времени являются стандартным применением линейных уравнений. При решении этих задач используйте соотношение скорость

(скорость или скорость) умножить на время равно расстояние .

[латекс]r\cdot t=d[/латекс]

Например, предположим, что человек должен был двигаться со скоростью 30 км/ч в течение 4 часов. Чтобы найти общее расстояние, умножьте скорость на время или (30 км/ч) (4 ч) = 120 км.

Проблемы, которые нужно решить здесь, будут иметь несколько шагов больше, чем описано выше. Поэтому, чтобы систематизировать информацию в задаче, используйте таблицу. Пример базовой структуры таблицы ниже:

Пример диаграммы расстояния, скорости и времени

Кто или что	Ставка	Время	Расстояние

Третий столбец, расстояние, всегда будет заполняться путем перемножения столбцов скорости и времени. Если указано общее расстояние обоих людей или поездок, поместите эту информацию в столбец расстояния. Теперь используйте эту таблицу, чтобы настроить и решить следующие примеры.

Джоуи и Наташа начинают с одной точки и идут в противоположных направлениях. Джоуи идет на 2 км/ч быстрее, чем Наташа. Через 3 часа расстояние между ними 30 км. С какой скоростью шел каждый?

Кто или что	Ставка	Время	Расстояние
Наташа	[латекс]г[/латекс]	[латекс]\текст{3 ч}[/латекс]	[латекс]\текст{3 ч}(р)[/латекс]
Джои	[латекс]r + 2[/латекс]	[латекс]\текст{3 ч}[/латекс]	[латекс]\текст{3 ч}(г + 2)[/латекс]

Расстояние, пройденное обоими, составляет 30 км. Следовательно, нужно решить уравнение:

[латекс]\begin{array}{rrrrrrl} 3r&+&3(r&+&2)&=&30 \\ 3r&+&3r&+&6&=&30 \\ &&&-&6&&-6 \ \ \hline &&&&\dfrac{6r}{6}&=&\dfrac{24}{6} \\ \\ &&&&&r&=&4 \text{ км/ч} \end{array}[/latex]

Это означает, что Наташа ходит со скоростью 4 км/ч, а Джои ходит со скоростью 6 км/ч.

Ник и Хлоя покинули свой лагерь на каноэ и поплыли вниз по течению со средней скоростью 12 км/ч. Они развернулись и пошли обратно вверх по течению со средней скоростью 4 км/ч. Всего поездка заняла 1 час. Через сколько времени отдыхающие развернулись вниз по течению?

Кто или что	Ставка	Время	Расстояние
Нижестоящий	[латекс]\текст{12 км/ч}[/латекс]	[латекс]т[/латекс]	[латекс]\текст{12 км/ч} (т)[/латекс]
Восходящий поток	[латекс]\текст{4 км/ч}[/латекс]	[латекс](1 – т)[/латекс]	[латекс]\текст{4 км/ч} (1 – т)[/латекс]

Расстояние, пройденное вниз по течению, равно расстоянию, которое они прошли вверх по течению. Таким образом, уравнение, которое нужно решить:

[латекс]\begin{array}{rrlll} 12(t)&=&4(1&-&t) \\ 12t&=&4&-&4t \\ +4t&&&+&4t \\ \ hline \dfrac{16t}{16}&=&\dfrac{4}{16}&& \\ \\ t&=&0.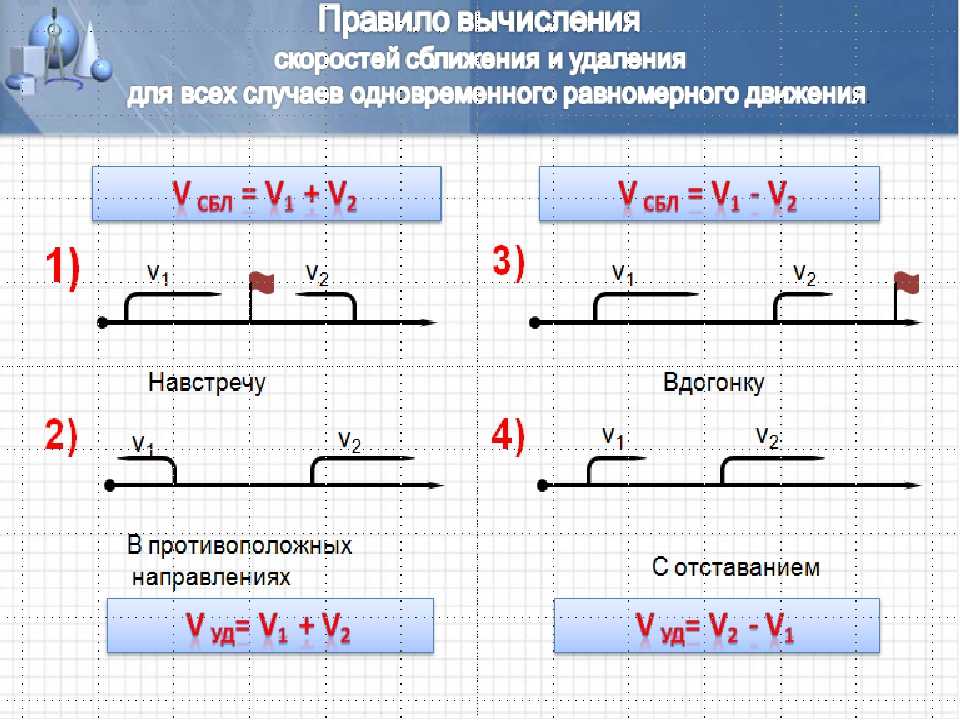 25&& \end{массив}[/latex]

Это означает, что туристы плыли вниз по течению 0,25 часа и 0,75 часа плыли обратно.

Терри выезжает из дома на велосипеде со скоростью 20 км/ч. Через 6 часов Салли уезжает на скутере, чтобы догнать его, двигаясь со скоростью 80 км/ч. Сколько времени ей понадобится, чтобы догнать его?

Кто или что	Ставка	Время	Расстояние
Терри	[латекс]\текст{20 км/ч}[/латекс]	[латекс]т[/латекс]	[латекс]\текст{20 км/ч}(т)[/латекс]
Салли	[латекс]\текст{80 км/ч}[/латекс]	[латекс](т – \текст{6 ч})[/латекс]	[латекс]\текст{80 км/ч}(т – \текст {6 ч})[/латекс]

Расстояние, пройденное обоими, одинаково. Следовательно, нужно решить уравнение:

[латекс]\begin{array}{rrrrr} 20(t)&=&80(t&-&6) \\ 20t&=&80t&-&480 \\ -80t&&-80t&& \\ \ hline \dfrac{-60t}{-60}&=&\dfrac{-480}{-60}&& \\ \\ t&=&8&& \end{array}[/latex]

Это означает, что Терри едет 8 часов, а Салли нужно всего 2 часа, чтобы его догнать.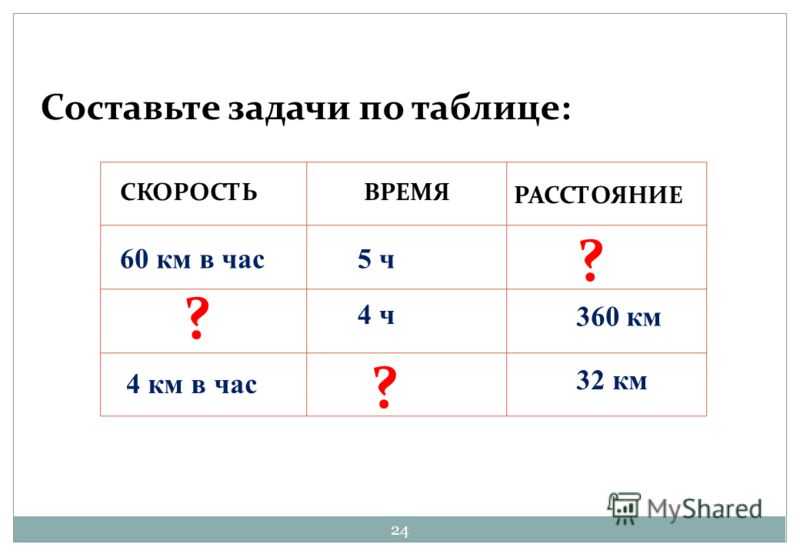

Во время 130-километровой поездки автомобиль двигался со средней скоростью 55 км/ч, а затем снизил скорость до 40 км/ч до конца пути. Поездка заняла 2,5 часа. Сколько времени автомобиль ехал со скоростью 40 км/ч?

Кто или что	Ставка	Время	Расстояние
Пятьдесят пять	[латекс]\текст{55 км/ч}[/латекс]	[латекс]т[/латекс]	[латекс]\текст{55 км/ч}(т)[/латекс]
Сорок	[латекс]\текст{40 км/ч}[/латекс]	[латекс](\текст{2,5 ч}-т)[/латекс]	[латекс]\текст{40 км/ч}(\текст{2,5 ч}-т)[/латекс]

Расстояние, пройденное обоими, составляет 30 км. Таким образом, уравнение, которое нужно решить:

[латекс]\begin{array}{rrrrrrr} 55(t)&+&40(2,5&-&t)&=&130 \\ 55t&+&100&-&40t&=&130 \\ & -&100&&&&-100 \\ \hline &&&&\dfrac{15t}{15}&=&\dfrac{30}{15} \\ \\ &&&&t&=&2 \end{массив}[/latex]

Это означает, что время движения со скоростью 40 км/ч составило 0,5 часа.

Задачи расстояния, времени и скорости имеют несколько вариаций, в которых неизвестные смешиваются между расстоянием, скоростью и временем. Как правило, они включают решение задачи, в которой общее пройденное расстояние используется для равного некоторому расстоянию, или задачи, в которой расстояния, пройденные обеими сторонами, одинаковы. Эти задачи на расстояние, скорость и время будут рассмотрены позже в этом учебнике, где для их решения требуются квадратичные решения.

Для вопросов с 1 по 8 найдите уравнения, необходимые для решения задач. Не решить.

1. A находится в 60 км от B. Автомобиль в A отправляется в B со скоростью 20 км/ч в то же время, что автомобиль в B отправляется в A со скоростью 25 км/ч. Сколько времени пройдет, прежде чем автомобили встретятся?
2. Два автомобиля находятся на расстоянии 276 километров друг от друга и одновременно начинают двигаться навстречу друг другу. Они едут со скоростями, отличающимися на 5 км/ч. Если они встретятся через 6 ч, найдите скорость каждого из них.
3. Два поезда, отправившиеся с одной станции, движутся в противоположных направлениях. Они едут со скоростями 25 и 40 км/ч соответственно. Если они стартуют одновременно, как скоро расстояние между ними составит 195 километров?
4. Два курьера на велосипедах, Джерри и Сьюзен, едут в противоположных направлениях. Если Джерри едет со скоростью 20 км/ч, то с какой скоростью должна ехать Сьюзен, если через 5 часов их разделяет 150 километров?
5. Пассажирский и товарный поезд одновременно отправляются навстречу друг другу из двух точек, удаленных друг от друга на 300 километров. Если скорость пассажирского поезда превышает скорость товарного поезда на 15 км/ч и они встречаются через 4 часа, то какой должна быть скорость каждого из них?
6. Два автомобиля двинулись в одно и то же время в противоположных направлениях из одной и той же точки. Их скорости составляли 25 и 35 км/ч соответственно. Через сколько часов расстояние между ними составило 180 км?
7. Мужчина, имея в своем распоряжении 10 часов, совершил экскурсию на велосипеде, выезжая со скоростью 10 км/ч и возвращаясь пешком со скоростью 3 км/ч. Найдите расстояние, которое он проехал.
8. Человек идет со скоростью 4 км/ч. Какое расстояние он может пройти за город и вернуться обратно на тележке, движущейся со скоростью 20 км/ч, если он должен вернуться домой через 3 часа с момента старта?

Решите вопросы с 9 по 22.

9. Мальчик уезжает из дома на автомобиле со скоростью 28 км/ч и возвращается обратно со скоростью 4 км/ч. Поездка туда и обратно занимает 2 часа. Как далеко он едет?
10. Моторная лодка выходит из гавани и плывет со средней скоростью 15 км/ч к острову. Средняя скорость на обратном пути 10 км/ч. На каком расстоянии от гавани находился остров, если в общей сложности путешествие заняло 5 часов?
11. Семья ехала на курорт со средней скоростью 30 км/ч, а затем возвращалась по той же дороге со средней скоростью 50 км/ч. Найдите расстояние до курорта, если общее время в пути составило 8 часов.
12. В рамках летной подготовки пилот-курсант должен был долететь до аэропорта, а затем вернуться. Средняя скорость до аэропорта составила 90 км/ч, а средняя скорость обратно – 120 км/ч. Найдите расстояние между двумя аэропортами, если общее время полета составило 7 часов.
13. Сэм начинает движение со скоростью 4 км/ч из лагеря на 2 часа раньше Сью, которая едет со скоростью 6 км/ч в том же направлении. Через сколько часов Сью догонит Сэма?
14. Человек едет со скоростью 5 км/ч. Через 6 часов другой человек стартовал с того же места, что и первый, со скоростью 8 км/ч. Когда второй человек догонит первого?
15. Моторная лодка выходит из гавани и плывет со средней скоростью 8 км/ч к маленькому острову. Два часа спустя каютный катер выходит из той же гавани и движется со средней скоростью 16 км/ч к тому же острову. Через сколько часов после отплытия катер с каютами будет рядом с моторной лодкой?
16. Бегун на длинные дистанции стартовал с дистанции со средней скоростью 6 км/ч. Через час второй бегун начал тот же маршрут со средней скоростью 8 км/ч. Через какое время после старта второго бегуна он догонит первого бегуна?
17. Два человека едут в противоположных направлениях со скоростью 20 и 30 км/ч в одно и то же время и из одного и того же места. Через сколько часов расстояние между ними будет 300 км?
18. Два поезда отправляются в одно и то же время из одного и того же места и едут в противоположных направлениях. Если скорость одного из них на 6 км/ч больше, чем скорость другого, и через 4 часа расстояние между ними составляет 168 км, какова скорость каждого из них?
19. Два велосипедиста стартовали из одной точки и едут в противоположных направлениях. Один велосипедист едет в два раза быстрее другого. Через три часа их разделяет 72 километра. Найдите скорость каждого велосипедиста.
20. Два маленьких самолета вылетают из одной точки и летят в противоположных направлениях. Первый самолет летит на 25 км/ч медленнее второго. Через два часа расстояние между самолетами составляет 430 километров. Найдите скорость каждого самолета.
21. Во время 130-километровой поездки автомобиль ехал со средней скоростью 55 км/ч, а затем до конца пути снизил скорость до 40 км/ч. В общей сложности дорога заняла 2,5 часа. Какое время автомобиль ехал со скоростью 40 км/ч?
22. Бегущий со средней скоростью 8 м/с, спринтер добежал до конца дорожки, а затем вернулся к исходной точке со средней скоростью 3 м/с. Спринтеру потребовалось 55 с, чтобы добежать до конца дорожки и вернуться назад. Найдите длину дорожки.

Ключ ответа 8.8

Скорость против скорости

Как расстояние и перемещение имеют совершенно разные значения (несмотря на их сходство), так и скорость и скорость. Скорость — это скалярная величина, которая относится к тому, «как быстро движется объект». Скорость можно рассматривать как скорость, с которой объект преодолевает расстояние. Быстро движущийся объект имеет высокую скорость и преодолевает относительно большое расстояние за короткий промежуток времени. Сравните это с медленно движущимся объектом с низкой скоростью; он покрывает относительно небольшое расстояние за то же время. Объект без движения имеет нулевую скорость.

 

Скорость как векторная величина

Скорость — это векторная величина, которая относится к «скорости, с которой объект меняет свое положение». Представьте себе человека, который быстро движется — один шаг вперед и один шаг назад — и всегда возвращается в исходное исходное положение. Хотя это может привести к безумной активности, это приведет к нулевой скорости. Поскольку человек всегда возвращается в исходное положение, движение никогда не приведет к изменению положения. Поскольку скорость определяется как скорость изменения положения, это движение приводит к нулевой скорости. Если человек в движении хочет максимизировать свою скорость, то этот человек должен приложить все усилия, чтобы максимизировать величину, на которую он смещен от своего исходного положения. Каждый шаг должен быть направлен на то, чтобы продвинуть этого человека дальше от того, с чего он начал. Наверняка человек ни в коем случае не должен менять направления и начинать возвращаться в исходное положение.

Скорость является векторной величиной. Таким образом, скорость равна направлению . При оценке скорости объекта необходимо следить за направлением. Было бы недостаточно сказать, что объект имеет скорость 55 миль в час. Необходимо включить информацию о направлении, чтобы полностью описать скорость объекта. Например, вы должны описать скорость объекта как 55 миль/ч, восток . Это одно из существенных различий между скоростью и скоростью. Скорость является скалярной величиной и не следить за направлением ; скорость является векторной величиной и знает направление .

 

Определение направления вектора скорости

Задача описания направления вектора скорости проста. Направление вектора скорости совпадает с направлением движения объекта. Не имеет значения, ускоряется объект или замедляется. Если объект движется вправо, то его скорость описывается как направленная вправо. Если объект движется вниз, то его скорость описывается как нисходящая. Таким образом, самолет, летящий на запад со скоростью 300 миль/час, имеет скорость 300 миль/час на запад. Обратите внимание, что скорость не имеет направления (это скаляр), а скорость в любой момент времени — это просто значение скорости с направлением.

 

Расчет средней скорости и средней скорости

Когда объект движется, его скорость часто меняется. Например, во время обычной поездки в школу происходит много изменений скорости. Вместо того, чтобы измеритель скорости поддерживал устойчивые показания, стрелка постоянно движется вверх и вниз, отражая остановку и запуск, ускорение и замедление. В один момент машина может двигаться со скоростью 50 миль в час, а в другой момент она может остановиться (т. е. 0 миль в час). Тем не менее, во время поездки в школу человек может проехать в среднем 32 мили в час. Среднюю скорость во время всего движения можно рассматривать как среднее значение всех показаний спидометра. Если бы показания спидометра можно было собирать с интервалом в 1 секунду (или с интервалом в 0,1 секунды, или…), а затем усреднять вместе, можно было бы определить среднюю скорость. Теперь это будет много работы. И, к счастью, есть короткий путь. Читай дальше.

 

Средняя скорость во время движения часто рассчитывается по следующей формуле:

В отличие от этого, средняя скорость часто вычисляется по этой формуле

Давайте начнем реализацию нашего понимания этих формул со следующей задачи:

В: Во время отпуска Лиза Карр преодолела в общей сложности 440 миль. Ее поездка заняла 8 часов. Какова была ее средняя скорость?

Чтобы вычислить ее среднюю скорость, мы просто делим пройденное расстояние на время в пути.

Это было просто! Лиза Карр в среднем разгонялась до 55 миль в час. Возможно, она не двигалась с постоянной скоростью 55 миль в час. Она, несомненно, была остановлена ​​в какой-то момент времени (возможно, для перерыва в ванной или на обед), и, вероятно, в другие моменты времени она двигалась со скоростью 65 миль в час. Тем не менее, она развивала среднюю скорость 55 миль в час. Приведенная выше формула представляет собой сокращенный метод определения средней скорости объекта.

Средняя скорость по сравнению с мгновенной скоростью

Поскольку движущийся объект часто меняет свою скорость в процессе движения, принято различать среднюю скорость и мгновенную скорость. Различие заключается в следующем.

• Мгновенная скорость — скорость в любой заданный момент времени.
• Средняя скорость – среднее значение всех мгновенных скоростей; находится просто по соотношению расстояние/время.

Вы можете думать о мгновенной скорости как о скорости, которую показывает спидометр в любой данный момент времени, а о средней скорости как о среднем значении всех показаний спидометра в ходе поездки. Поскольку задача усреднения показаний спидометра была бы достаточно сложной (а может быть, и опасной), среднюю скорость чаще рассчитывают как отношение расстояния к времени.

Движущиеся объекты не всегда движутся с неустойчивой и меняющейся скоростью. Иногда объект будет двигаться с постоянной скоростью с постоянной скоростью. То есть объект будет преодолевать одно и то же расстояние каждый регулярный интервал времени. Например, бегун по пересеченной местности может бежать с постоянной скоростью 6 м/с по прямой в течение нескольких минут. Если ее скорость постоянна, то расстояние, пройденное за каждую секунду, одинаково. Бегун будет преодолевать расстояние 6 метров каждую секунду. Если бы мы могли измерять ее положение (расстояние от произвольной начальной точки) каждую секунду, то мы бы заметили, что положение меняется на 6 метров каждую секунду. Это будет резко контрастировать с объектом, который меняет свою скорость. Объект с изменяющейся скоростью будет перемещаться на разное расстояние каждую секунду. В приведенных ниже таблицах данных изображены объекты с постоянной и изменяющейся скоростью.

Теперь давайте снова рассмотрим движение этого учителя физики. Учитель физики проходит 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север. Все движение длилось 24 секунды. Определить среднюю скорость и среднюю скорость.

Учитель физики прошел 12 метров за 24 секунды; таким образом, ее средняя скорость составила 0,50 м/с. Однако, поскольку ее перемещение равно 0 м, ее средняя скорость равна 0 м/с. Помните, что смещение относится к изменению положения, а скорость зависит от этого изменения положения. В этом случае движения учителя происходит изменение положения на 0 метров и, следовательно, средняя скорость равна 0 м/с.

Вот еще один пример, аналогичный тому, что мы видели ранее при обсуждении расстояния и смещения. На приведенной ниже диаграмме показано положение лыжника в разное время. В каждый из указанных моментов времени лыжник поворачивается и меняет направление движения. Другими словами, лыжник перемещается из пункта А в пункт В, затем в пункт С и затем в пункт D.

Используйте диаграмму, чтобы определить среднюю скорость и среднюю скорость лыжника в течение этих трех минут. Когда закончите, нажмите кнопку, чтобы просмотреть ответ.

В качестве последнего примера рассмотрим футбольного тренера, расхаживающего взад-вперед вдоль боковой линии. На приведенной ниже диаграмме показаны несколько позиций тренера в разное время. В каждой отмеченной позиции тренер делает «разворот» и движется в обратном направлении. Другими словами, тренер перемещается из позиции A в B, затем в C и затем в D.

Какова средняя скорость и средняя скорость тренера? Когда закончите, нажмите кнопку, чтобы просмотреть ответ.

В заключение, скорость и скорость являются кинематическими величинами, которые имеют совершенно разные определения. Скорость, будучи скалярной величиной, представляет собой скорость, с которой объект преодолевает расстояние. Средняя скорость – это расстояние (скалярная величина) за отношение времени. Скорость не знает направления . С другой стороны, скорость — векторная величина; это с учетом направления . Скорость – это скорость изменения положения. Средняя скорость — это смещение или изменение положения (векторная величина) за отношение времени.

 

Мы хотели бы предложить .