Задачи иллюстрации по математике для дошкольников: картинки для составления задач для дошкольников: 12 тыс изображений найдено в Яндекс.Картинках – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Обучение старших дошкольников решению арифметических задач

Библиографическое описание:

Авсюкевич, Н. И. Обучение старших дошкольников решению арифметических задач / Н. И. Авсюкевич, И. А. Башкатова. — Текст : непосредственный // Вопросы дошкольной педагогики. — 2016. — № 3 (6). — С. 103-105. — URL: https://moluch.ru/th/1/archive/41/1258/ (дата обращения: 17.04.2021).

…За арифметикой, в особенности за арифметическими задачами, всегда признавалась и другая исключительная роль в обучении, а именно развитие сообразительности, смекалки.

А. И. Маркушевич

К моменту поступления в школу дети должны усвоить относительно широкий круг взаимосвязанных знаний о множестве и числе, форме и величине, научиться ориентироваться в пространстве и во времени.

В процессе математического и общего умственного развития детей старшего дошкольного возраста особое внимание уделяется обучению решению и составлению простых арифметических задач. В детском саду проводится подготовительная работа по формированию у детей уверенных навыков вычислений при сложении и вычитании однозначных чисел и быстрых устных вычислений с двузначными числами с целью подготовки их к обучению в начальной школе. Если в школе обучение вычислениям ведется при решении примеров и арифметических задач, то в практике работы дошкольных учреждений принято знакомить детей с арифметическими действиями и простейшими приемами вычисления на основе простых задач, в условии которых отражаются реальные, в основном игровые и бытовые ситуации. В условии задачи указываются связи между данными числами, а также между данными и искомыми. Эти связи и определяют выбор арифметического действия.

Установив эти связи, ребенок довольно легко приходит к пониманию смысла арифметических действий и значения понятий «прибавить», «вычесть», «получится», «останется».

Решая задачи, дети овладевают умением находить зависимость величин.

Вместе с тем задачи являются одним из средств развития у детей логического мышления, смекалки, сообразительности. В работе с задачами совершенствуются умения проводить анализ и синтез, обобщать и конкретизировать, раскрывать основное, выделять главное в тексте задачи и отбрасывать несущественное, второстепенное.

Простые задачи, т. е. задачи, решаемые одним действием, принято делить на следующие группы:

К первой группе относятся простые задачи, при решении которых дети усваивают конкретный смысл каждого из арифметических действий, т. е. какое арифметическое действие соответствует той или иной операции над множествами (сложение или вычитание). Эти задачи на нахождение суммы двух чисел и на нахождение остатка.

Воспитатель формирует представления о действиях сложения и вычитания, одновременно знакомит детей со знаками «+», «-», «=». Таким образом, дети постепенно переходят от действий с конкретными множествами к действиям с числами — решают арифметические задачи и знакомятся с записью модели арифметических действий с помощью математических условных знаков.

Уже на 2–3 занятии, где использовался наглядный материал, детям предлагают решать устные текстовые задачи. Для усвоения алгоритма действия полезны упражнения в самостоятельном составлении задач.

4 + 2 = 6

Ко второй группе относятся простые задачи, при решении которых надо осмысливать связь между компонентами и результатами арифметических действий. Это задачи на нахождение неизвестных компонентов:

а) нахождение первого слагаемого по известным сумме и второму слагаемому.

б) нахождение второго слагаемого по известным сумме и первому слагаемому.

в) нахождение уменьшаемого по известным вычитаемому и разности.

г) нахождение вычитаемого по известным уменьшаемому и разности.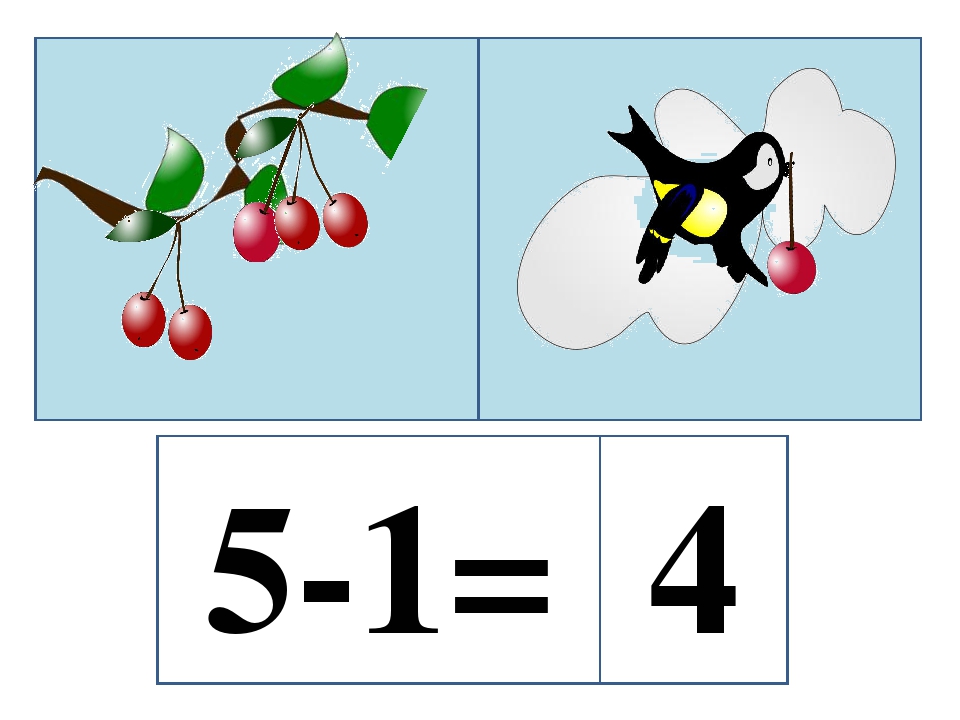

Эти задачи помогают закрепить знания о структуре задачи и развивают умение находить соответствующее арифметическое действие. Чтобы дети лучше запоминали числовые данные, используются карточки с цифрами, а в последствии и со знаками.

9–3 = 6

К третьей группе относятся простые задачи, связанные с понятием разности отношений:

а) увеличение числа на несколько единиц.

б) уменьшение числа на несколько единиц.

В этих задачах арифметические действия как бы подсказаны самим условием задачи. Отношение больше на единицу требует от ребенка увеличения, присчитывания, сложения, отношение меньше на единицу — уменьшения, вычитания.

В зависимости от используемого для составления задач наглядного материала они подразделяются на задачи — драматизации и задачи — иллюстрации. Каждая разновидность этих задач обладает своими особенностями и раскрывает перед детьми те или иные стороны, а также способствует развитию умения отбирать для сюжета задачи необходимый жизненный, бытовой, игровой материал, учит логически мыслить.

Особенность задач-драматизаций состоит в том, что содержание их непосредственно отражает жизнь самих детей, т. е. то, что они только что делали или обычно делают. В задачах-драматизациях наиболее наглядно раскрывается их смысл. Дети начинают понимать, что в задаче всегда отражается конкретная жизнь людей.

Умение вдумываться в соответствие содержания задачи реальной жизни способствуют более глубокому познанию жизни, учит детей рассматривать явления в многообразных связях, включая количественные отношения.

Задачи этого вида особенно ценны на первом этапе обучения: дети учатся составлять задачи про самих себя, рассказывать о действиях друг друга, ставить вопрос для решения, поэтому структура задачи на примере задач — драматизаций наиболее доступна детям.

Особое место в системе наглядных пособий занимают задачи — иллюстрации. В этих задачах при помощи игрушек создается простор для разнообразия сюжетов. Эти задачи развивают воображение, стимулируют память и умение самостоятельно придумывать задачи, а следовательно, подводят к решению и составлению устных задач.

Для иллюстрации задач широко применяются картинки. Основные требования к ним простота сюжета, динамизм содержания и ярко выраженные количественные отношения между объектами.

Сделать задачу-картинку может сам воспитатель. Указанные наглядные пособия способствуют усвоению смысла арифметической задачи и ее структуры.

После того как у детей сформированы представления и некоторые понятия об арифметической задаче, об отношениях между числовыми данными, между условием и вопросом задачи, можно переходить к

ознакомлению спреобразованием прямых задач вобратные. Это помогает усвоить глубже специфику каждого типа задач. Воспитатель объясняет: любую арифметическую задачу можно преобразовать в новую, если полученное искомое считать одним из данных новой задачи, а одно из данных преобразованной задачи считать искомым.

Примерное задание для обучения детей решению задач в уме.

Воспитатель вывешивает карточки с задачами — картинками, на которых с помощью изображенных предметов и арифметических знаков представлены условия четырех задач.

3 груши-1 груша

2 груши+1 груша

2 ягоды+1 ягода

3ягоды-1 ягода

Выберите из четырех задач-картинок ту, решение которой будет соответствовать заданной величине.

1 задание. Задана величина, равная 3 грушам. Какая задача-картинка подходит? Какое действие в этой задаче нужно выполнить?

2 задание. Задана величина, равная 2 ягодам. Какая задача-картинка подходит? Какое действие в этой задаче нужно выполнить?

3 задание. Воспитатель предлагает найти среди разложенных карточек-картинок те, которые соответствуют ответу.

4 задание. Попробуйте придумать похожие задачи по карточкам-картинкам. Дети придумывают условие задачи, рассказывают, как ее надо решить, и с помощью карточек с цифрами и арифметическими знаками выкладывают ответ в пустой клетке карточки-картинки.

Примерное задание для знакомства детей с задачами на отношение «больше (меньше) на несколько единиц».

Задача: «В Машину чашку с чаем мама положила 2 ложки сахара, а в большую папину чашку — на 1 ложку сахара больше. Сколько ложек сахара положила мама в чашку папы?» О чем говорится в этой задаче? Повторите ее условие. О чем спрашивается в этой задаче? Что надо сделать, чтобы решить задачу? В Машиной чашке 2 ложки сахара — это первое множество. Сколько ложек сахара в папиной чашке — неизвестно. Это второе множество. Но известно, что в папиной чашке на 1 ложку сахара больше, чем в Машиной чашке. Надо определить количество сахара во втором множестве. Сахара в папиной чашке столько же, сколько в первом множестве, и еще на одну ложку больше. С помощью какого действия будем решать задачу? Как ответим на вопрос задачи? Запишите в своих тетрадях решение задачи с помощью цифр и арифметических знаков.

Ознакомление с простыми и обратными задачами повышает познавательную активность, развивает способность логически мыслить.

Основные термины (генерируются автоматически): задача, ребенок, ложок сахара, папина чашка, арифметическая задача, действие, какое действие, какая задача-картинка, наглядный материал, примерное задание.

Обучение детей старшего дошкольного возраста решению арифметических задач

ОБУЧЕНИЕ ДЕТЕЙ
СТАРШЕГО ДОШКОЛЬНОГО
ВОЗРАСТА РЕШЕНИЮ
АРИФМЕТИЧЕСКИХ ЗАДАЧ
»
Всякая хорошо решенная
оставляет
Цель: углубитьзадача
и систематизировать
знания педагогов
умственное детей
наслаждение.
по теме «Обучение
старшего дошкольного
Г. Гессе
возраста решению арифметических
задач»
Трудность решения в какой то мере входит в само
понятие задачи: там, где
нет трудности,
нет и задачи.
(Д. Пойа)
2

3. План

• Виды арифметических задач, используемых в
работе с дошкольниками.
• Этапы обучения решению арифметических
задач.
• Структура арифметической задачи.
• Модели записи арифметического действия.
• Алгоритм решения арифметических задач.
• Роль умения решать арифметические задачи
детьми
3
Виды арифметических задач, используемые
в обучении детей старшего дошкольного возраста
I группа – простые задачи: дети усваивают конкретный
смысл
каждого из арифметических действий
(сложение
или
вычитание) – это задачи
на
нахождение суммы двух чисел и на нахождение
остатка.
Пример:
Составьте
свой вариант задачи на нахождении суммы
На столе
красных
яблока и 2 желтых. Сколько
двух
чиселлежало
с опорой3 на
наглядность
всего яблок лежало на столе?
В меню
4
Виды арифметических задач, используемые
в обучении детей старшего дошкольного возраста
II группа – простые задачи: надо осмыслить связь
между
компонентами
и
результатами
арифметических действий – это задачи на нахождение
неизвестных компонентов.

Пример.
Даша и Катя надували шарики. Сколько Катя надула
шариков, если Даша надула 2 шарика, а вместе девочки
надули 5.
В меню
5
Виды арифметических задач, используемые
в обучении детей старшего дошкольного возраста
III группа – простые задачи на разностное сравнение
задачи с вопросом «На сколько больше?»
Пример.
Леша вылепил 6 морковок, а Костя 1 морковку. На сколько
больше вылепил Леша морковок?
Задачи с вопросом «На сколько меньше?»
Пример.
Маша вымыла 4 чашки, а Таня одну чашку. На сколько чашек
меньше вымыла Таня?
В меню
6

7. Виды арифметических задач в зависимости от используемого наглядного материала:

Задачи – драматизации:
отражают жизнь самих детей, т. е. то, что они только
что делали или обычно делают;
дети учатся составлять задачи про самих себя,
рассказывать о действиях друг друга, ставить вопрос
для решения, поэтому структура задачи на примере
задач-драматизаций наиболее доступна детям.
Задачи – иллюстрации (по картинкам, по игрушкам)
служат развитию самостоятельности и накоплению
опыта установления количественных отношений в
различных жизненных ситуациях
Основные требования к картинкам:
Устные
задачи (без опоры на наглядный
-Простота сюжета:
-Динамизм
содержания;
материал)
-Ярко выраженные количественные отношения между объектами
В меню
7

8. Определите вид арифметической задачи

Задача составляется на основе
действий, выполняемых
детьми:
«Нина в одну вазу поставила
пять флажков, а в другую — один
флажок. Сколько флажков
поставила Нина в обе вазы?»
Устная задача
Задача – драматизация
Задача – иллюстрация
В меню
8

9. Определите вид арифметической задачи

Задача – иллюстрация
Устная задача
Задача – драматизация
В меню
9

10. Определите вид арифметической задачи

Устная задача
Три зайчонка, пять ежат
Ходят вместе в детский
сад.

Посчитать мы вас
попросим,
Сколько малышей в
саду?
Задача – иллюстрация
Задача – драматизация
В меню
10

11. Этапы обучения решению арифметических задач

Первый этап — подготовительный. Основная цель этого
этапа — организовать систему упражнений по выполнению
операций над множествами.
Второй этап.
Цель:
научиться составлять задачи;
понимать их отличие от рассказа и загадки;
понимать структуру задачи;
уметь анализировать задачи, устанавливая отношения
между данными и искомым.
Третий этап.
Цель: учить детей формулировать арифметические действия
сложения и вычитания
В меню
11

12. Этапы обучения решению арифметических задач

Подготовительный этап (операции над множествами)
Положите 2 красных кружка, а
ниже положите 4 синих. Сколько
всего кружков вы положили?
Положите 4 красных кружка, а
ниже положите синих на 1 меньше.
Сколько всего кружков вы
положили?
В меню
Отсчитайте 6 грибов,
отними два. Сколько
грибов осталось?
А – 6 грибов,
В – 2 гриба
Круги Эйлера – Венна
12

13. Этапы обучения решению арифметических задач

Второй этап. (упражнения, задания, способствующие
формированию у детей представления об
арифметической задаче и ее структуре)
Задачи – драматизации
Двое детей выполняют действия,
воспитатель комментирует:
У Кости было 7 флажков, Миша
дал ему еще 1 флажок. Сколько стало
флажков у Кости?
д/у «Задай вопрос к задаче»
В меню
д/у «Определи где рассказ, а где
задача»
д/у «Задай вопрос к задаче»
д/у «Выбери верный вопрос к
задаче»
13

14. Структура арифметической задачи:

• Условие
• Вопрос
• Решение
• Ответ
В меню
На аэродроме стояло 5
самолетов. Затем вернулся
ещё один самолёт.
Сколько самолётов стоит на
аэродроме?
5+1=6
На аэродроме стоит 6
самолётов.

15. Определите , являются ли предложенные варианты задачей, аргументируйте свой ответ

Два
Этокольца,
не задача.
дваВконца,
задачеа
посередине
всегда требуется
гвоздик.
Что это?
посчитать.
Решите задачу.
На столе стояло 5
стаканов
В задаче
с молоком.
нет вопроса
Гриша выпил один
стакан.
В меню
Решите задачу.
В задаче нет условия
Сколько птиц на дереве?
Ехал грузовик, вез
мешки с я блоками.
В задаче должно быть
Один мешок упал.
не менее двух чисел.
Сколько мешков
осталось в грузовике?
15

16. Третий этап. Формулировка арифметического действия

Арифметическое действие должно быть сформулировано
полно и правильно.
Упражнять детей в записи и чтении записи арифметического действия
(Читая запись, дети скорее обнаруживают свою ошибку.)
При формулировке арифметического действия можно
считать правильным, когда дети говорят отнять, прибавить, вычесть,
сложить. Слова сложить, вычесть, получится, равняется являются
специальными математическими терминами.
Воспитатель в своей речи должен пользоваться математической
терминологией, постепенно приучая и детей к употреблению этих
слов. (Например, ребенок говорит: «Нужно отнять из пяти яблок
одно», а воспитатель должен уточнить: «Нужно из пяти яблок
вычесть одно яблоко».)
В меню
16

17. Модели записи арифметического действия

• Модель записи действия вычитания:
• Модель записи действия сложения:
В меню
Вперёд
17

18. Алгоритм решения арифметической задачи:

У
В меню
?
>

+
–
Р
Вперёд
О
18

19. Роль умения решать детьми арифметические задачи

Решение задач формирует у детей практические умения,
необходимые каждому человеку в повседневной жизни. Например,
подсчитать стоимость покупки, ремонта квартиры, вычислить, в какое
время надо выйти, чтобы не опоздать на поезд, и т.

п.
Решая задачи, ребенок убеждается, что многие математические
понятия (число, арифметические действия и др.) имеют корни в
реальной жизни, в практике людей.
Через решение задач дети знакомятся с важными в познавательном и
воспитательном отношении фактами.
19

20. Литература

Белошистая А. В.
Формирование и развитие математических способностей
дошкольников: Вопросы теории и практики: Курс лекций для студ.
дошк. факультетов высш. учеб. заведений. — М.: Гуманит. изд.
центр ВЛАДОС, 2003. — 400 с: ил.
Материалы сайта:
http://fatihovalf.ucoz.ru/publ/fatikhova_l_f_obuchenie_resheniju_arif
meticheskikh_zadach_doshkolnikov_s_narusheniem_intellekta/1-1-0-1
Фатихова Л.Ф. Обучение решению арифметических задач
дошкольников с нарушением интеллекта
20

Школьные задачки для дошкольников | Материал по математике (подготовительная группа):

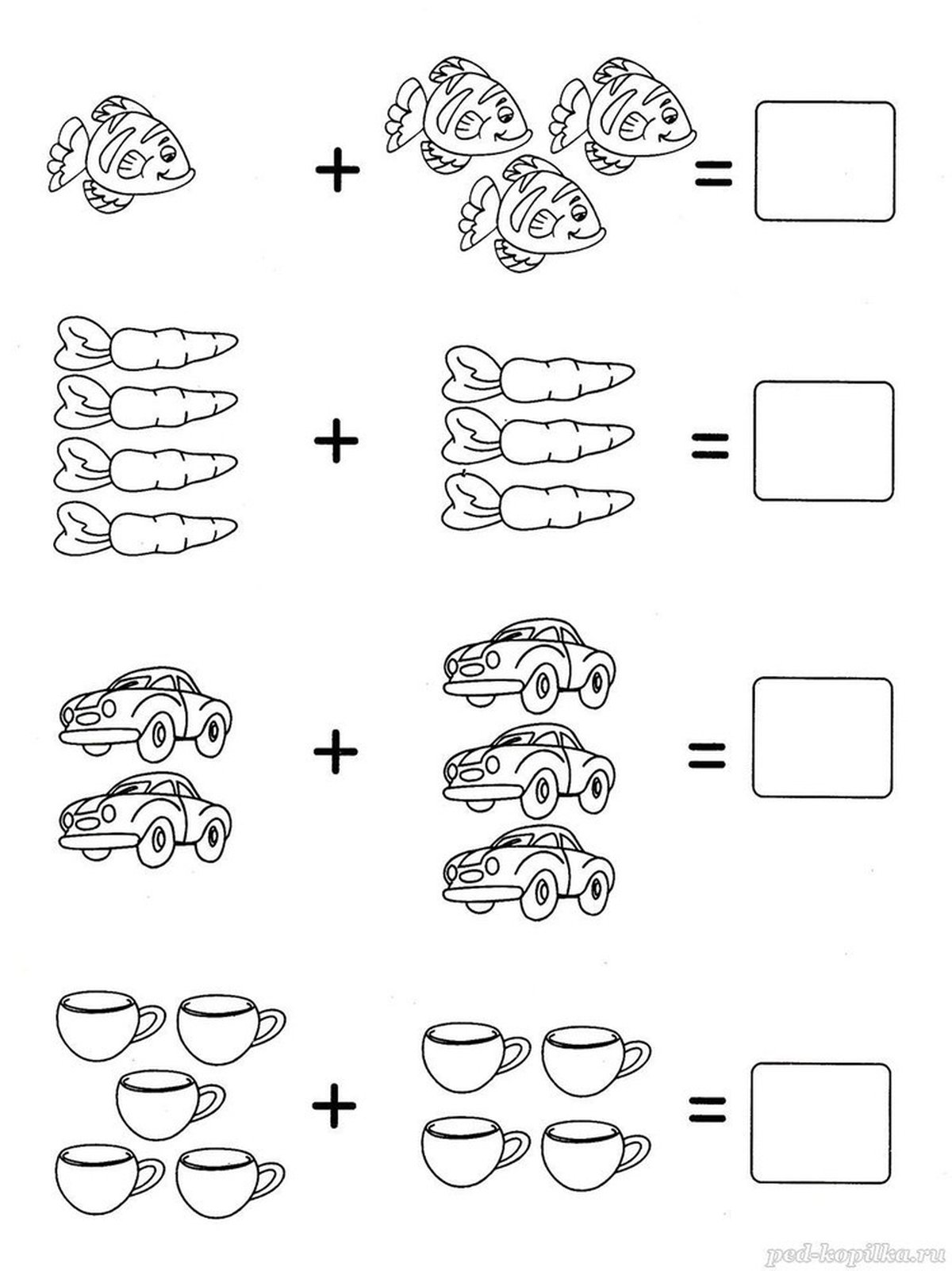
В первом классе у деток иногда обнаруживается такая беда – они не умеют решать простые математические задачи, не понимают, как это делать, не ассоциируют действие с математическим знаком плюс или минус. Чтобы таких проблем в школе избежать, объяснить ребенку решение задач на простых примерах нужно уже в подготовительной группе детского сада, то есть лет в 6. Для начала сопроводите задачи картинками, так будет и нагляднее, и веселее. А чтобы снять напряжение после долгого думания, картинку эту потом раскрасить в соответствии и условием задачи. Чтобы вам (родителю или воспитателю) было проще, мы сделали для вас небольшой сборник задачек на сложение и вычитание. Каждая задачка сопровождается иллюстрацией.

Нужно скачать и распечатать картинку на листе А4 и разрезать пополам, у вас получится 2 листа, на каждом по задачке и раскраске. Сначала предложите ребенку внимательно прочитать условие задачи. Далее – сделать её краткую запись. Написать решение. Записать ответ.

А теперь можно и развлечься, но и развлечение у нас будет полезным, нужно заштриховать разными цветами картинку к задаче. Штриховка отлично развивает мелкую моторику, а мелкая моторика в свою очередь развивает мозг 🙂

Что же такое задача? Это маленькая история с числами. Но не каждая такая история называется задачей. В задаче всегда присутствуют условие и вопрос. В условии говорится, что известно, какие события происходят. А в вопросе говорится, что не известно, что нужно найти.

Алгоритм решения задачи:

прочитай задачу
повтори её текст устно
выдели условие и вопрос
запиши кратко условие и вопрос задачи
запиши действие с числами
найди и запиши ответ задачи
проверь ответ обратным действием

Запомни слова, которые обозначают действие в задачах:

ПЛЮС + пришли, приехали, прибежали, приплыли, принесли, подарили, купили, нашли, добавили.
МИНУС – ушли, уехали, убежали, уплыли, потеряли, продали, забрали, убрали, спрятали

Занимательная математика для дошкольников в детском саду

Дата публикации: 03 апреля 2017.

Занимательные задачки для дошкольников в детском саду

Родителям на заметку

Задачи на смекалку, логические игры, головоломки очень нравятся детям. Они могут долго упражняться, перекладывая фигуры, палочки или кубики с места на место. При этом замечено, что утомление и усталость у детей наступает гораздо позже, чем при решении математических задач. Поэтому воспитатели часто используют такие задания для самостоятельных занятий детей. Математические игры учат малышей обдумывать свои действия, планировать, проявлять настойчивость для достижения цели, а также применять творческий подход.
Для организации занятий занимательной математикой лучше сделать детский уголок, где малышам будут доступы разнообразные игры и пособия. Важно, что бы дети могли их освоить и играть самостоятельно. Давно замечено, что в этом возрасте азы математики усваиваются гораздо легче именно в процессе игры.

Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Занимательные игры на развитие памяти

1. Занимательная игра на развитие памяти “Фотография”

На стол раскладываются различные геометрические фигуры и малышу предлагается выполнить интересное задание. Ребёнок смотрит на расположение фигур секунд 10, а затем отворачивается. Расположение фигур на поверхности меняется. Малыш должен восстановить предыдущее расположение фигур. 2. Игра “Лапки, рожки, хвост”

Сколько ножек у божьей коровки? Сколько лапок у лягушки?

Сколько бабочек на рисунке? Сколько крылышек у бабочек на рисунке?

В лесу живёт три зайчонка. Сколько у них лап? Сколько у них хвостиков? Сколько у них ушей?

3. Занимательные задачки на внимательность и логику

3.1. На столе горело 5 свечей, 2 свечи погасло. Сколько свечей осталось?

3.2. У дуба выросло 4 толстые ветки, на каждой толстой ветке выросло ещё по 2 тонкие ветки. На каждой тонкой ветке висит по одному яблоку. Сколько всего яблок висит на дубе?

3.3. В пакете находится 4 яблока. Как раздать эти яблоки четырём девочкам, чтобы в пакете осталось одно яблоко?

3.4. Если взять лист бумаги, сложить пополам и разрезать, как показано на рисунке, сколько листочков бумаги получится?

3.5. Сколько концов у трёх палок? А у трех с половиной палок?
У Лены было 3 ленты. Одну из них она разрезала пополам. Сколько лент стало у Лены?

4. Занимательные загадки и задания на воображение и логику

4.1. Это длинный фрукт. Когда он не спелый, он зелёный. Если ты хочешь его съесть, ты должен снять с него шкурку. Назови его.

4.2. Она маленькая, красненькая и внутри неё есть косточка. Назови её. Это ягода или фрукт?

4.3. Она не круглая и не гладкая, но очень вкусная и сладкая. Назови её.

4.4. Найди на картинке фрукты и овощи. Назови их.

4.5. Найди на картинке животных и насекомых. Назови их.

5. Занимательные считалки

5.1. Сосчитай предметы на картинках. Соедини линией числа и картинки.

5.2. На какой строке нарисовано 8 карандашей?

5.3. На какой строке нарисовано 5 муравьев?

5.4. На какой строке нарисовано 4 бабочки?

Математика для детей 5-6 лет

Требования современной школьной программы таковы, что к моменту поступления в первый класс у ребенка должны быть сформированы элементарные математические представления. К ним относятся знание цифр и основных знаков, умение считать в пределах десяти и справляться с простыми задачами по математике, в которых детям 5—6 лет необходимо выполнять сложение и вычитание. При этом, как известно, дошколята гораздо быстрее и легче усваивают информацию, которая подается в игровой форме. Специалисты развивающего сайта «Разумейкин» стремились учесть эти факторы при подготовке онлайн-заданий для обучения математике детей 5 лет. Все упражнения представлены в легкой интересной форме.

Раздел «Другие математические представления» знакомит ребенка с основными знаками («больше», «меньше» и «равно») и учит ими пользоваться. С помощью нашего сайта вы сможете легко и продуктивно заниматься. Выполняя задачи по математике, дошкольники 6 лет изучают порядковый счет и основы измерения длины, массы и объема. Ребята учатся понимать и анализировать зависимость результата измерения от величины мерки. Задания в рамках программы онлайн-обучения математике детей 5—6 лет дают представление об основных геометрических фигурах и телах в картинках , а также элементарное понятие о таблицах.

При разработке комплекса упражнений для малышей старшего дошкольного возраста наши специалисты старались сделать их не только максимально понятными и увлекательными, но и действительно полезными в практическом плане. Почти все онлайн-задания по математике для детей 6 лет выстроены в форме игры и имеют подробные объяснения. Найти их можно в обучающем видео перед упражнением. Объяснение к заданиям-тестам в разделе «Математика для дошкольников 5—6 лет» дается также в том случае, если ответ, который вывел ребенок, оказался неправильным или недостаточно полным.

Особенности подачи материала

Для того чтобы процесс обучения математике у детей 6 лет не вызывал затруднений, специалисты развивающего сайта «Разумейкин» подготовили специальные тематические картинки и озвученный текст для каждой задачи. А в отдельных заданиях даже задействуется двигательная сфера. Все упражнения с картинками в разделе «Математика для детей 5 лет» можно выполнить в режиме онлайн.

Каким образом оцениваются результаты?

За выполнение заданий по математике для дошкольников 5 лет на сайте «Разумейкин» предусмотрена целая система поощрений. Мы убеждены, что она позволяет повысить интерес детей к обучению и сформировать положительную мотивацию.

Справляясь с задачами в разделе «Математика для дошкольников 5 лет», малыши получают награду. На нашем сайте предусмотрены медали, кубки, вымпелы и грамоты.

Практически все задания-игры в разделе «Математика для детей 6 лет» оцениваются в зависимости от того, с какой попытки ребенок дал правильный ответ. При необходимости к выполненному упражнению можно вернуться. Сделав задание в разделе «Математика для дошкольников 5—6 лет» повторно, ребенок сможет улучшить прежний результат и получить более высокую награду.

Перед тем как приступить к выполнению упражнений в разделе «Математика для детей 5—6 лет», мы рекомендуем пройти тестирование. Полученные результаты помогут понять, на каких темах потребуется остановиться более детально. Кроме того, родители смогут определить, какие именно задания в разделе «Математика дошкольникам 6 лет» стоит выполнить в первую очередь.

Урок 33. решение текстовых задач – Математика – 1 класс

Математика, 1 класс

Урок № 33. Решение текстовых задач

Перечень вопросов, рассматриваемых на уроке:

Установление взаимосвязи между условием и вопросом задачи.
Таблица сложения чисел первого десятка.
Решение текстовых задач арифметическим способом.
Построение простейших выражений с помощью логических связок и слов.
Решение задач на разностное сравнение.

Глоссарий по теме

Таблица сложения чисел первого десятка.

Решение текстовых задач.

Логические связки, простейшие выражения.

Ключевые слова

Таблица сложения; задачи на разностное сравнение; условие задачи; вопрос задачи; переместительное свойство сложения.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Волкова С. И., Степанова С. В. Математика. Учебник. 1 кл. В 2 ч. Ч. 2.– М.: Просвещение, 2017.–С. 18 – 19.

2. МороМ. И., Волкова С. И. Математика рабочая тетрадь. 1 кл. 2 ч.– М.: Просвещение, – С. 11 – 13.

3. Кац Е.М. Необычная математика. Тетрадь логических заданий для детей 6 – 7лет. – М.: МЦНМО, 2018. – 54 с.

4. Кац Е.М. Необычная математика. Тетрадь логических заданий для детей 7 – 8 лет. – М.: МЦНМО, 2018. – 24 с.

На уроке мы узнаем, как связаны между собой две простые задачи, представленные в одной цепочке. Научимся дополнять условие задачи недостающими данными. Сможем, составлять задания с высказываниями, содержащими логические связки.

Основное содержание урока

Посмотрите на изображение. Что это такое?

Это компоненты задачи, только в неправильном порядке.

Расставьте компоненты задачи верно.

Сначала?

Условие. Потом. Вопрос. Решение. Ответ.

Добавим в таблице ещё один столбик.

Посмотрите на рисунок и составьте условие задачи.

На пруду было 4 утки. К ним прилетели ещё 3.

Задайте вопрос по условию задачи.

Уток в пруду стало больше или меньше?

Уток стало больше.

Значит, каким действием решается эта задача?

Сложением.

Назовите решение задачи.

К четырём прибавить три получится семь уток.

Как записать ответ задачи?

Могут ли компоненты задачи быть расположены в другом порядке?

Не могут.

Тема нашего урока: «Решение текстовых задач».

Посмотрите внимательно на иллюстрации. Подходит ли к ним составленное нами условие?

Условие задачи необходимо поменять.

Составьте условие по первой картинке?

На пруду было четыре утки.

Что произошло потом?

К ним прилетели ещё три утки.

Что случилось дальше?

Две утки улетели.

Задайте вопрос по условию задачи.

Вопрос остаётся прежним. Сколько уток стало?

Давайте решим получившуюся задачу.

Как записать решение, чтобы ответить на вопрос: сколько осталось птиц, когда три утки прилетели?

Мы ответили на вопрос задачи?

Нет, условие изменилось и нужно выполнить ещё одно действие.

Каким действием мы найдём, сколько уток стало после того как улетели две утки?

Вычитанием, так как улетели, значит, количество уменьшилось.

Из семи вычесть два – получится пять уток осталось.

Как будет звучать ответ на вопрос задачи?

Ответ: пять уток осталось.

Почему изменился результат решения задачи?

Потому что изменилось условие задачи.

Какой вывод можно из этого сделать?

Решение задачи и ответ зависят от условия задачи.

Разбор тренировочных заданий.

1. Прочитайте задачу. Выделите синим цветом условие задачи, а красным цветом вопрос задачи.

На осине сидели 2 галки. Прилетели ещё две. Сколько галок стало?

Ответ: На осине сидели 2 галки. Прилетели ещё две. Сколько галок стало?

2. Найдите пару компонентам задачи:

Ответ:

3. Рассмотрите рисунок.

Выберите все высказывания, верные для этого рисунка.

1. На рисунке три воробья и три синицы.

2. Все воробьи смотрят направо.

3. Если птица взлетела, то это синица.

4. У каждой синицы жёлтое брюшко.

Ответ:

1. На рисунке три воробья и три синицы.

2. Все воробьи смотрят направо.

3. Если птица взлетела, то это синица.

4. У каждой синицы жёлтое брюшко.

плюсы и минусы метода Петерсон для дошкольников

Об авторе методики

Людмила Георгиевна Петерсон — российский педагог, математик и доктор педагогических наук. Профессор кафедры начального и дошкольного образования, почётный работник высшего профессионального образования Российской Федерации. В 2002 году Людмилу Петерсон наградили Премией Президента Российской Федерации в области образования.

Источник: mel.fm
‍

Методика Петерсон для дошкольников и младших школьников — это курс математики, который набрал популярность начиная с 1990-х годов. Давайте разберёмся, в чём заключается суть методики Петерсон, разложив программу на преимущества и недостатки.

Плюсы методики Петерсон

1. Программа учит думать самостоятельно

Методика преподавания математики Петерсон отличается от традиционных программ. Обычно учитель объясняет тему, демонстрирует решение, дети копируют способ решения, применяют в заданиях, пишут контрольную и идут дальше.

А у Петерсон ребёнок должен докопаться до решения сам. Так он учится справляться с трудностями и не ориентироваться на готовые шаблоны, а активизировать мозг. Когда додумался до ответа сам, уже не забудешь. Ориентация на понимание, а не зазубривание.

В «Фоксфорде» применяется авторская программа, но курс математики в начальных классах во многом опирается на учебно-методический комплекс Петерсон. Вот что рассказывала на дне открытых дверей Алёна Сергеевна Решетникова, преподаватель математики 1–2 классах начальной онлайн-школы «Фоксфорда»:‍

«За основу берётся деятельностный подход — ребята сами пытаются открыть правило или формулу. Мы вместе к этому приходим. При этом я использую интерактивные задания, яркие презентации и раздаточные материалы, чтобы удерживать внимание юных школьников».

2. Программа опирается на визуализацию

К слову о ярких презентациях — Петерсон считает, что ассоциации и наглядные картинки помогают эффективно усваивать информацию, поэтому учебники снабжены красочными иллюстрациями. Чтобы ребёнку было интересней ориентироваться в материале, вводятся сказочные персонажи — гномы, эльфы, три поросёнка.

3. Подходит всем

Бытует миф, что методика Петерсон в школе подходит только одарённым детям, а ребёнку со средними способностями будет сложно. Ещё ходят слухи, что программа гораздо сложнее традиционной — настолько сложнее, что перейти с другой методики на Петерсон по мере обучения в школе не представляется возможным.

Но это не так. Метод Петерсон, скорее, сложен для родителей — бывает трудно отойти от привычных понятий об обучении и свыкнуться с необычными заданиями. Детям, которые не обременены стереотипами о том, «как должно быть», формат Петерсон нравится.

«Если дети знают математические хитрости, они могут справиться с любой задачкой». Алёна Решетникова

Этим математическим хитростям и другим лайфхакам учат в домашней онлайн-школе «Фоксфорда». Цель наших педагогов — привить любовь к математике и показать, что она не так страшна, как кажется.

4. Учебники удобно оформлены

Помимо визуальных рядов и ярких иллюстраций, учебные пособия по методике преподавания Петерсон составлены так, чтобы ребёнку было увлекательно учиться.

Например, записывать решение задач, примеров, рисовать, соединять фигуры, решать ребусы можно прямо в учебнике — просто вписываешь ответ в нужное окошко. Большое число заданий — сравнить, найти закономерность, решить ребус, раскрасить правильным цветом, закончить узор, объяснить почему так, а не так. И это всё — прямо в пособии.

Обложка учебника по математике Л.Г. Петерсон для 4 класса.
Источник: edvisrb.ru
‍

5. Домашка не занимает много времени

Согласно Петерсон, ученик должен самостоятельно выполнять домашнюю работу за 15–20 минут. Это перекликается с принципами домашней онлайн-школы «Фоксфорда» — здесь учебная нагрузка гораздо меньше, чем в обычной школе, где за домашкой сидят по несколько часов или весь вечер. Как правило, домашка в «Экстернате Фоксфорда» состоит из 5–10 тестовых заданий или нескольких творческих. Если ребёнок был внимателен на уроке, то домашнюю работу он сделает быстро, в среднем, уходит не больше 30–60 минут в средней школе. В начальной тратится ещё меньше времени — в основном ребята закрепляют материал.

<<Блок перелинковки>>

Минусы методики Петерсон

1. В учебнике отсутствует теория

Поколение нынешних родителей привыкло, что в учебнике точных наук сначала идёт теоретический раздел, а затем закрепление материала на практике. У Петерсон всё иначе — теории как таковой нет вообще. В учебнике сразу начинаются практические задачки. Предполагается, что теорию даёт учитель на занятии.

2. Методику убрали из официальной программы

В 2014 году учебники Петерсон исключили из официальной школьной программы — в Минобрнауки посчитали, что они «недостаточно патриотичны». Решение властей вызвало возмущение научного сообщества, учителей и родителей — десятки тысяч людей протестовали и подписывали петиции.

Сейчас учебники по закону могут использоваться в школе, если педагог посчитает нужным, в качестве дополнительных пособий. Но теперь найти учебное заведение, где учат по Петерсон, сложнее. Домашняя онлайн-школа «Фоксфорда» — одна из таких школ.

Источник: freepik.com / @pvproductions
‍

3. Успех обучения зависит от педагога

Эффективность программы сильно опирается на учителя. Он должен уметь вести научную дискуссию, а не просто объяснять тему и давать шаблонные решения. Педагог должен знать, как организовывается работа в группах и строится диалог с учениками. Иногда учителя хотят работать по Петерсон, но просто не знают как.

В начальной онлайн-школе «Фоксфорда» учителя сознательно выбрали методику математики Петерсон — так, по словам Алёны Сергеевны, она перепробовала много программ и остановилась на Петерсон как на самой интересной.

Если педагог не умеет работать по Петерсон, результаты будут плачевные. Дети сидят над домашкой в слезах, а родители разводят руками — из-за непривычного построения учебника помочь ребёнку весьма трудно. Поэтому важно, чтобы педагог знал, как подавать материал по этой методике.

«При работе с 1–2 классом я использую ярких персонажей, увлекательно рассказываю и преподаю материал в формате игры. А ещё регулярно меняю вид деятельности — так малыши не устаю и сохраняют интерес к происходящему». Алёна Решетникова

Резюме

Можно долго спорить о плюсах и минусах Петерсон, но то, что программа отличается от традиционной, — это факт. Главное — чтобы педагог умел работать по такой методике, тогда учёба будет в удовольствие, ведь Петерсон учит думать самостоятельно и докапываться до решений, пособия снабжены иллюстрациями, уровень программы ориентирован на любого ученика, а домашние задания не должны занимать много времени.

В домашней онлайн-школе «Фоксфорда» работают по авторской учебной программе, но курс математики во многом опирается на методику Людмилы Петерсон. А если какой-то темы в курсе не хватает, либо она не раскрывается в полной мере, то учителя подключают пособия и материалы из других систем и методик. Результат — эффективное сбалансированное обучение. Приходите, чтобы составить о программе собственное мнение.

Математика божьих коровок для дошкольников – Обучение маме

На этой неделе мы продолжаем нашу тему ошибок и выполняем некоторые математические задания с некоторыми самодельными божьими коровками!

Для этого вам понадобится коробка для яиц, красная краска, глаза Google и черный маркер. Первый шаг – покрасить коробку для яиц в красный цвет.

Когда она высохнет, разрежьте коробку с яйцами. Затем добавьте глазки и нарисуйте на них антенны.

Для этого задания вам понадобится десять божьих коровок. Вы нарисуете одно черное пятно на первом, два пятна на следующем, три пятна на следующем и продолжите этот узор до числа 10. Цель упражнения – чтобы ваш ребенок посчитал пятна божьей коровки и затем разместите божьих коровок в последовательном порядке от 1 до 10. (Я также помещаю соответствующий номер в каждую коробку с яйцами, чтобы мой ребенок мог проверить его подсчет.)

Перед началом игры спросите своего ребенка, что он знает о божьих коровках.Затем поделитесь с ними несколькими интересными фактами.

Вот то, что я хотел, чтобы мой старший узнал о божьих коровках:

Эти существа на самом деле считаются жуками из-за их твердого панциря
Их красный цвет и черные пятна предупреждают хищников держаться подальше
Количество черных пятен на каждой божьей коровке разное. У некоторых божьих коровок нет пятен, а у некоторых до 24 пятен! Пятна с ними всю жизнь, и они не растут новых пятен.

Затем попросите их подсчитать пятна на каждой божьей коровке.

После того как они посчитают, попросите их расположить божьих коровок в порядке от 1 до 10.

Это было хорошее занятие для моего старшего (которому 3,5 года), потому что он должен был сосредоточиться на подсчете каждой точки и следить за тем, чтобы он не переоценивал точки. Для него было очень хорошей практикой выстраивать божьих коровок в последовательном порядке. Нам нравится включать математические навыки в увлекательные учебные занятия!

Вы, наверное, заметили, что у нас были два размера гуглиевых глаз.Половина из них были крошечными, а другая половина – маленькими глазами. Для следующего упражнения я попросил его разделить божьих коровок на две группы: маленькие глазки и маленькие глазки. После того, как он отсортировал их, я попросил его пересчитать каждую группу, и он обнаружил, что в каждой из них было по 5 божьих коровок.

Это всего лишь несколько упражнений, которые мы проделали с нашими божьими коровками, и я уверен, что буду использовать их для других учебных заданий. У вас есть идеи по использованию этих божьих коровок?

Поделиться – это забота!

Facebook 20
Твиттер
Pinterest 953

Math Play: Как маленькие дети подходят к математике

Четырехлетняя Нита играет с четырьмя куклами из набора из шести. Проходя мимо, ее учитель спрашивает: «А где остальные?» Ее учитель слышит, как Нита говорит: «Эммм … [указывая на каждую куклу] Я называю тебя« одна ». Вы «два», «три» и «четыре». Где твои сестры, пять и шесть? ” Еще минуту она играет с куклами. «О! Тебе шесть? А тебе пять? Ну, пойдем поищем сестер три и четыре». Я тоже должен их найти “.

Нита включила в игру счет, чтобы следить за своими куклами. Мы знаем, что игра важна для развития детей младшего возраста, поэтому неудивительно, что детская игра является источником их первого «предматематического» опыта.

Изучение математики в игре

Дети активно вовлекаются в игру. Преследуя свои собственные цели, они склонны решать проблемы, которые достаточно сложны, чтобы быть увлекательными, но все же не выходят за рамки их возможностей. Привязка к проблеме – разгадывание ее и различные подходы к ней – может привести к эффективному обучению; кроме того, когда несколько детей борются с одной и той же проблемой, они часто придумывают разные подходы, обсуждают различные стратегии и учатся друг у друга. .Эти аспекты игры могут способствовать мышлению и обучению по математике, а также в других областях.

Маленькие дети исследуют узоры и формы, сравнивают размеры и считают. Но как часто они это делают? А что это значит для развития детей? Когда дети изучали детей во время свободной игры, возникло шесть категорий содержания математики.

1. Классификация. Одна девушка, Анна, вынула из контейнера все пластиковые жучки и отсортировала их по типу жуков, а затем по цвету.

2. Изучение звездной величины (описание и сравнение размеров объектов). Когда Брианна принесла газету к столу для художников, чтобы накрыть ее, Эми заметила: «Она недостаточно велика, чтобы накрыть стол».

3. Перечисление (произнесение числовых слов, подсчет, мгновенное распознавание ряда объектов или чтение или запись чисел). Три девочки нарисовали свои семьи и обсудили, сколько у них братьев и сестер и сколько лет их братьям и сестрам.

4.Изучение динамики (складывание, разборка или изучение движений, таких как переворачивание). Несколько девушек превратили глиняный шар в диск, разрезали его и сделали «пиццу».

5. Изучение узора и формы (определение или создание узоров или форм или изучение геометрических свойств). Дженни сделала бусы, создав узор желто-красного цвета.

6. Изучение пространственных отношений (описание или рисование местоположения или направления).Когда Тереза поставила диван в кукольном домике у окна, Кэти переместила его в центр гостиной, сказав: «Диван должен быть перед телевизором».

Диапазон математических исследований, изучаемых во время свободной игры, впечатляет. Мы видим, что бесплатная игра предлагает богатую основу для построения интересной математики. Эти повседневные опыты составляют основу более поздней математики. Позже дети развивают эти идеи. Мы называем этот процесс «математизацией». И мы понимаем, что детям нужны как базовые знания, так и конкретные математические задания.

Play не гарантирует математического развития, но предлагает богатые возможности. Значительные преимущества более вероятны, когда учителя продолжат обучение, вовлекая детей в размышление и представление математических идей, возникших в их игре. Учителя улучшают обучение детей математике, когда они задают вопросы, которые вызывают уточнения, расширения и развитие нового понимания.

Математические блоки: башни обучения

Преимущества блочного строительства глубоки и широки.Строя из кубиков, дети улучшают свои математические, естественные и общие способности к рассуждению. Рассмотрим, как развивается блочное строительство.

Младенцы не проявляют особого интереса к штабелированию. Укладка начинается в 1 год, когда младенцы показывают свое понимание пространственных отношений «на». Отношения «ближайшего окружения» развиваются примерно через полтора года. В 2 года дети ставят каждый следующий кубик на предыдущий или рядом с ним. Похоже, они понимают, что блоки не падают при таком размещении.Дети начинают размышлять и предвкушать. В возрасте от 3 до 4 лет дети регулярно строят вертикальные и горизонтальные элементы здания. Когда их просят построить высокую башню, они используют длинные блоки вертикально, потому что, помимо стремления сделать стабильную башню, их цель – сделать стабильную высокую башню, сначала используя только один блок таким образом, а затем несколько. Через 4 года они могут использовать множественные пространственные отношения, расширяя свои здания в нескольких направлениях и с множеством точек соприкосновения между блоками, демонстрируя гибкость в том, как они строят и интегрируют части конструкции.

Дошкольники используют, по крайней мере на интуитивном уровне, более сложные геометрические концепции, чем большинство детей испытывают в начальной школе, играя в блоки. Например, один дошкольник, Хосе, кладет на коврик двойной блок, два блока – на блок и треугольник – посередине, создавая симметричную структуру.

Представьте дошкольника, который строит нижний этаж блочного дома. Он кладет два длинных квартала вниз, идя в одном направлении.Затем он пытается соединить два конца коротким блоком. Он не достигает, поэтому он перемещает конец одного из длинных блоков, чтобы он достиг. Однако, прежде чем он снова попробует короткий блок, он осторожно регулирует другой конец длинного блока. Он пробует короткий блок. Он тянется. Он быстро ставит много коротких блоков, образуя пол своего дома.

Мы многому научились из этого и других подобных эпизодов. Как и этот маленький мальчик, многие дети интуитивно используют понятия параллельности и перпендикулярности.Мальчик даже, кажется, понимает в своих действиях, что параллельные линии всегда находятся на одинаковом расстоянии друг от друга!

Мы наблюдали, как другие дети регулируют два цилиндра так, чтобы расстояние между ними было равно длине длинного блока. Они оценивают, сколько еще блоков им нужно, чтобы отделать поверхность. По их оценкам, потребовалось восемь блоков, если каждый квадрат четырех размеров был покрыт двумя блоками. Мы знаем многих учителей математики, которые были бы в восторге, если бы их ученики продемонстрировали такое же понимание геометрии, измерений и чисел!

Ритм и паттерны

Дошкольники также занимаются ритмическими и музыкальными паттернами.Они могут добавлять в свой репертуар более сложные, продуманные паттерны, такие как “хлопок, хлопок, пощечина; хлопок, хлопок, пощечина”. Они могут говорить об этих узорах, изображая узор словами. Воспитанникам детского сада нравится придумывать новые движения, соответствующие той же схеме, поэтому хлопки, хлопки в ладоши превращаются в прыжок, прыжок, падение; прыгать, прыгать, падать и вскоре символизируется шаблоном AABAAB. Воспитанники детского сада также могут описывать такие узоры цифрами («два чего-то, потом один чего-то другого»). На самом деле это первые четкие связи между шаблонами, числами и алгеброй.

Дети, которые испытали эти ритмические переживания, намеренно воссоздают и обсуждают шаблоны в своих произведениях искусства. Один четырехлетний ребенок любил знать цвета радуги (ROY G BFV, красный, оранжевый, желтый, зеленый, синий, индиго, фиолетовый) и рисовал радуги, цветы и рисунки, повторяющие эту последовательность несколько раз.

Математика течет сквозь воду Играть

Измерение часто лежит в основе игры в воде или на песчаном столе. Исследователь рассказывает о посещении двух классных комнат в один день и наблюдении за игрой в воде в обоих.Дети наливали воду в каждую комнату, но в одной они также взволнованно наполняли одну и ту же чашку в разные емкости, считая, сколько чашек они могли «уместить» в каждую емкость. Единственная разница между этими двумя классами заключалась в том, что в последнем учитель прошел мимо и небрежно спросил: «Интересно, в каком из них больше всего чашек воды?»

Развертывание математических концепций!

Такие материалы, как песок и пластилин, открывают множество возможностей для математического мышления и рассуждений. Учителя могут предоставить полезные материалы (формочки для печенья), параллельно играть с детьми и задавать вопросы или комментарии относительно форм и количества предметов. Например, они могут сделать несколько копий одной и той же формы в пластилине с помощью форм для лепки или превратить песок или пластилин в разные объекты. Одна учительница сказала двум мальчикам, что она собирается «спрятать» шарик из пластилина, накрыв его плоским предметом и надавив. Мальчики сказали, что мяч все еще был на месте, но когда она подняла его, мяч «исчез».«Это их обрадовало, они скопировали ее действия и обсудили, что мяч находится« в »плоской части.

Математика и манипуляции

Детские игры с манипуляторами, в том числе комбинирование «плоских» блоков для создания картинок и рисунков, а также для решения головоломок, показывают прогресс в развитии, как и построение блоков. Дети сначала не умеют сочетать формы. Они постепенно учатся видеть как отдельные части, так и «целое», и узнают, что части могут составлять целое и при этом оставаться частями.Примерно к 4 годам большинство может решать головоломки методом проб и ошибок и создавать картинки с фигурами, расположенными рядом друг с другом. С опытом они постепенно учатся комбинировать формы, чтобы создавать более крупные формы. Они становятся все более преднамеренными, выстраивая мысленные образы форм и их атрибутов, таких как длина сторон и углы.

Создание концепций с помощью компьютеров

Создание рисунков с фигурами можно выполнять как с помощью строительных блоков, так и с помощью компьютерных фигур. Компьютерные версии обладают тем преимуществом, что предлагают немедленную обратную связь.Например, фигуры могут быть прозрачными, чтобы дети могли видеть загадку под ними. Кроме того, дети часто больше говорят и больше объясняют то, что они делают на компьютере, чем при использовании других материалов. На более высоких уровнях компьютеры позволяют детям разбивать и складывать фигуры способами, невозможными с помощью физических блоков.

Компьютеры также могут облегчить игру. Добавление компьютерного центра не нарушает текущую игру, но облегчает позитивное социальное взаимодействие и сотрудничество.Исследования показывают, что компьютерная деятельность более эффективна в стимулировании вокализации, чем игра с игрушками, а также стимулирует более высокий уровень социальной игры. Кроме того, совместная игра за компьютером аналогична совместной игре в центре блока. Сотрудничество в компьютерном центре может обеспечить контекст для инициирования и поддержания взаимодействия, которое может быть передано и для игры в других областях, особенно для мальчиков.

Драматическая математика

Драматическая игра может быть естественно математической при правильной настройке.В одном исследовании учителя и дети организовали магазин в зоне драматических игр, где продавец заполняет заказы и просит у покупателя деньги (1 доллар за каждую игрушку динозавра).

В одном классе Габи работала продавцом. Тамика вручила ей пять карточек (5 точек и цифра «5») в качестве ее приказа. Габи отсчитала пять игрушечных динозавров.

Учитель (только входящий в зону): Сколько вы купили?

Тамика: Пять.

Учитель: Откуда ты знаешь?

Тамика: Потому что Габи посчитала.(Тамика все еще работала над своими навыками счета и доверяла счету Габи больше, чем ее собственному знанию пяти. Игра позволила ей развить свои знания.)

Жанель: Я получаю большой номер. (Она протянула Габи карты 2 и 5.)

Габи: У меня не так много.

Учитель: Вы можете дать Жанель 2 одного вида и 5 другого.

Пока Габи отсчитывала две отдельные стопки и складывала их в корзину, Джанель отсчитывала доллары.Она неправильно посчитала и дала ей 6 долларов.

Габи: Вам нужно 7 долларов.

Эта постановка драматической игры с помощью учителя «работала» для детей с разным уровнем математического мышления.

Играйте перед решением проблем

Мы видели, как различные виды игр улучшают математическое мышление детей. Исследования также показывают, что если дети играют с предметами до того, как их попросят решить с ними проблемы, они добиваются большего успеха и творчески.Например, в одном исследовании с тремя группами детей от 3 до 5 лет их попросили достать предмет с помощью коротких палок и соединителей. Одной группе разрешили поиграть с палками и соединительными устройствами, одну группу научили, как соединять палки, а одной группе было предложено выполнить задание без предварительной игры или обучения. Первые две группы показали одинаковые результаты и достигли лучших результатов, чем третья группа. Часто группа, которая просто играла с клюшками и соединителями, сначала решала проблему быстрее, чем группа, которую учили их использовать.

Математическая игра

Это подводит нас к последнему увлекательному и обычно упускаемому из виду типу игры: математической игре. Здесь мы не имеем в виду игру, включающую математику – мы говорили об этом на протяжении всей статьи. Мы имеем в виду игру с самой математикой.

Подумайте еще раз о Ните и ее куклах. Когда она назвала их, чтобы идентифицировать «сестер», с которыми она не играла, она использовала математику в своей игре. Но когда она решила переименовать куклы, которые были с ней, с «пять» и «шесть» на «три» и «четыре», она играла с представлением о том, что присвоение номеров коллекции объектов произвольно.Она также считала не только куклы, но и сами счетные слова. Она сосчитала слова «три, четыре» и увидела, что две сестры пропали без вести. Она играла с идеей, что подсчет слов можно считать.

Динамические аспекты компьютеров часто вовлекают детей в математические игры больше, чем физические манипуляции или бумажные материалы. Например, два дошкольника играли с заданиями под названием «Время вечеринки» из проекта «Строительные блоки», в котором они могли выставить любое количество предметов, а компьютер их подсчитывал и маркировал. “У меня есть идея!” – сказала одна девушка, убирая все предметы и перетаскивая салфетки на каждый стул. «Вы должны поставить чашки для всех. Но сначала вы должны сказать мне, сколько чашек это будет». Прежде чем ее подруга начала считать, она прервала его: «И всем нужна одна чашка молока и одна чашка сока!» Девочки сначала усердно работали вместе, пытаясь найти чашки в центре драматургии, но, наконец, сосчитали по два раза на каждой подставке для столовых приборов на экране. Их ответ – изначально 19 – не был точным, но они не расстроились, что их исправили, когда они на самом деле поставили чашки и обнаружили, что им нужно 20.Эти дети играли с математикой в ситуации, с решениями, играя вместе друг с другом.

Математика может быть интересна детям по сути, если они строят идеи во время математической игры.

Развитие математики в повседневной игре

Учителя поддерживают математику в игре, создавая благоприятную среду и надлежащим образом вмешиваясь. Вот что вы можете сделать:

Понаблюдайте за детской игрой. Если вы не видели много новых блочных конструкций, поделитесь книгами, иллюстрирующими различные схемы расположения блоков, или разместите изображения в центре блока.Когда вы видите, как дети сравнивают размеры, предлагайте разные предметы, которые дети могут использовать для измерения своих структур, от кубиков до ниток и линейок.

Вступайте чутко. Полезная стратегия – спросить, развиваются ли социальное взаимодействие и математическое мышление или застопорились. Если они развиваются, просто понаблюдайте и оставьте детей в покое. Позже обсудите этот опыт со всем классом.

Обсудить и уточнить идеи. Каждый из детей может утверждать, что их блочное здание больше.Вы можете видеть, что один ребенок говорит о высоте, а другой – о ширине. Вы можете по-разному прокомментировать, как вы видите здания такими большими, как в примере «У вас очень высокое здание, а здание Криса кажется очень широким».

Запланируйте длинные отрезки времени для игры. Обеспечивает улучшенную среду и материалы, в том числе структурированные материалы, такие как блоки и лего, которые стимулируют математическое мышление.

Дети младшего возраста активно используют математическое мышление и рассуждения в своей игре, особенно если они обладают достаточными знаниями об используемых материалах, если задача понятна и мотивирует, а контекст знаком и удобен.Математику можно легко интегрировать в текущие игры и действия детей, но для этого требуется знающий учитель, который создает благоприятную среду и предлагает соответствующие задачи, предложения, задания и язык. В классах, где учителя внимательны ко всем этим возможностям, детские игры обогащают математические исследования.

Ресурсы для учителей: веб-сайты

Самая важная роль учителей в отношении математики должна заключаться в нахождении частых возможностей помочь детям осмыслить и расширить математику, возникающую в их повседневной деятельности, беседах и играх, а также структурировать среду, которая поддерживает такую деятельность.

1. Из NAEYC, статья, показывающая, как можно разрабатывать математические игры на основе детской литературы. NAEYC также предлагает «Математика для детей младшего возраста: содействие хорошему началу», совместное заявление Национальной ассоциации по образованию детей младшего возраста (NAEYC) и Национального совета учителей математики (NCTM).

2. Из Building Blocks (Национальный научный фонд), идеи по поиску математики и развитию математики с помощью детских занятий.

3. Национальный совет учителей математики (NCTM) предлагает математические стандарты, Принципы и стандарты школьной математики, а также множество мероприятий, программные среды на базе Интернета и видеоролики. “Teachers Corner” NCTM предоставляет информацию о возможностях профессионального развития, ресурсах и многом другом.

4. Центр развития учителей «Математические перспективы» предоставляет преподавателям математики от PreK до 6-го класса инструменты, стратегии и оценки, которые гарантируют, что все учащиеся добьются успеха в изучении математики и смогут использовать математику для решения задач, а также математического мышления .

Веселых математических заданий для дошкольников: Руководство для родителей

Дети начинают развивать свои математические навыки еще в младенчестве, исследуя окружающую среду, и продолжают в дошкольном возрасте.

К тому времени, когда они изучают формальные математические концепции в первом классе, основа успеха уже заложена.

Эти математические задания для дошкольников – отличный способ для родителей поработать над этими навыками дома, сосредоточив внимание на правильных видах деятельности.

Что такое ранняя математика?

Ранняя математика относится к математическим понятиям и навыкам, которые ребенок вырабатывает неформально в течение первых нескольких лет. Их также называют предварительными математическими или начальными навыками счета.

Важно сначала разработать их, прежде чем пытаться вводить слишком сложные концепции.

Когда вы хотите познакомить вашего ребенка с математикой, вы можете сразу же подумать о числах и попытаться научить своего дошкольника считать, узнавать числа и складывать или вычитать их, но на самом деле это одни из более продвинутых ранних математических навыков , которые к вашему 3–4-летнему ребенку не следует торопиться.

Важно сначала понять, как дети учат математические понятия.

Как дети осваивают математические навыки

Три этапа изучения любой математической концепции: конкретный, графический и абстрактный.

Бетонная сцена

На конкретном этапе детям необходимо физически испытать концепцию . Им нужно развить понимание одного предмета, удерживая один блок.

Играя с конкретными предметами, дети формируют представление о том, что может быть одного предмета , нескольких предметов , меньше предметов , предметов больше, и т. Д.

Многие математические процессы происходят, пока ребенок строит башню из кубиков рядом со своим другом.

Подобраны такие понятия, как больше, меньше, еще одно, мало, сколько, много, меньше, убери и добавить на .Дети сравнивают объекты и узнают, что объектам можно присвоить значение.

Живописная сцена

На этапе рисования, который следует за конкретным этапом, дети могут видеть изображение предметов и понимать, что представляет собой реальные предметы.

Например, ребенок может посмотреть на картинку и понять, что 4 листа представляют 4 настоящих листа.

Позже ребенок может увидеть кубик с 4 точками и присвоить ему значение 4, зная, что точки могут гипотетически представлять любой объект.Затем они смогут добавить 4 точки на одном кубике к 3 точкам на другом и сказать, что всего точек 7.

Абстрактная сцена

Это заключительный этап понимания математической концепции. Это означает, что ребенок может посмотреть на сумму, например 4 + 3 , записанные числовыми символами, и добавить их без конкретных предметов или изображений.

Ребенок достаточно повзрослел, чтобы понять, что символы 4 и 3 представляют ряд объектов , которые нужно добавить.

На каком этапе дошкольники?

Дошкольники в основном находятся на бетонной стадии.

Фактически, вплоть до третьего или четвертого класса любой достойный учитель все равно представит новую концепцию конкретным способом, прежде чем перейти к книгам или рабочим листам с примерами для решения.

Когда дети понимают концепцию конкретно, тогда гораздо легче решать абстрактные задачи.

Это означает, что в дошкольном возрасте попытки подтолкнуть ребенка к подсчету изображений предметов или пониманию значения цифровых символов преждевременны и вызовут разочарование.

Вы можете показать своему ребенку числа (например, играть с деревянными числами) или стишки, которые учат счету, но не ожидайте, что ваш ребенок еще поймет значение этих чисел.

Вот краткое изложение этого подхода к обучению:

Как научить дошкольника математике

Лучший способ научить дошкольников математическим навыкам – это их основной способ обучения – игра!

Play – это то, как дошкольники должны учиться абсолютно всему.

Это означает, что в эти ранние годы детям не нужны формальные уроки, рабочие листы и рабочие тетради или что-то еще, что больше похоже на «настоящую работу».

Это может показаться сбивающим с толку, поскольку существует так много официальных программ и рабочих тетрадей, доступных родителям дошкольников. Это заставляет родителей чувствовать, что они должны делать больше и готовить своего ребенка к школе с более формальной деятельностью.

Дошкольное учреждение – это время для неформального обучения.

Когда ваш ребенок получает адекватное неформальное обучение через игру, формальное обучение, естественно, становится легче, когда он к этому готов.

Когда ваш ребенок неадекватно учится в игре и слишком много вынужденных формальных навыков, он страдает позже в школе, когда начинают проявляться пробелы и становится очевидным, что отсутствуют базовые навыки.

Занятия по математике для дошкольников

Любой игровой опыт имеет скрытые возможности для изучения математики.

Научитесь распознавать их и использовать их для осознанного обучения определенным навыкам. Не забудьте ввести новый словарь и постоянно задавать вопросы во время игры.

Введите такие слова, как: тяжелее, легче, длиннее, короче, раньше, позже, больше, меньше, больше, меньше, меньше, лишнее, недостаточно, полностью, слева, другой, полный, пустой, соответствующий, такой же, разные.

Вот список лишь нескольких основных повседневных возможностей, которые можно использовать в качестве идеальных заданий по математике для дошкольников.

Играть с фигурами

Игра с пенопластом или деревянными фигурами знакомит вашего ребенка с основными геометрическими фигурами, а также с их свойствами.

Сделать изображения формы

Вырежьте из цветной бумаги базовые фигуры и сделайте из них рисунок. Дети учатся соединять двухмерные фигуры вместе, чтобы образовывать разные формы.

Пазлы для сборки

Пазлы отлично подходят для развития зрительного восприятия и помогут ребенку понять геометрию.

Играть с Pegboards

Pegboards – еще одно отличное занятие для развития математических навыков.Они развивают понятие чисел и геометрические знания.

Построить форты

Это может показаться не математическим заданием, но строительство фортов и других построек и лазание внутри них – это первый шаг в познании ребенком пространства и формы. Эти ранние игровые сессии просто необходимы!

Использовать манипуляторы

Игра с кубиками, бусинами, лего или фишками – это первый шаг в построении концепции чисел. У детей должна быть возможность ежедневно играть с манипуляторами.

Сделать пироги из грязи

Когда дети играют в песочнице и лепят пироги из глины и другие конструкции, они начинают использовать такие термины, как «Мне нужно сделать еще один», «Есть три торта» или «Я сделал по одному для каждого из нас».

Учимся считать песни

Подсчет песен – это увлекательный способ для маленького ребенка научиться считать вперед и назад. Это называется механическим подсчетом. Они также узнают об увеличении и уменьшении количества песен, таких как «5 зеленых бутылок».

Играть с числами

Пусть ваш ребенок поиграет с поролоновыми, резиновыми, деревянными или пластиковыми цифрами в ванне или на магнитной доске. Поскольку они являются физическими объектами, ваш ребенок может прикоснуться к ним и почувствовать их форму.

Это гораздо более значимо для маленького ребенка, чем просмотр чисел на странице занятия. Со временем они естественным образом научатся узнавать их и понимать, как они сформированы.

Сделайте числа для лепки

Playdough – одно из лучших веществ с удивительными преимуществами.Сделайте еще один шаг к предыдущему заданию и вылепите числа из пластилина. Эта сенсорная деятельность запечатлит числа в уме вашего ребенка гораздо быстрее, чем попытка записать числа на бумаге.

Игра с контейнерами

Когда ваш ребенок играет в песочнице или в ванне, предоставьте емкости разного размера и формы и позвольте ему открыть для себя основы вместимости.

Выпечка – это отличный математический опыт. Пусть ваш ребенок будет участвовать в измерении ингредиентов, чтобы познакомить их с единицами измерения и количествами.

Измерение объектов

Попросите ребенка измерить определенные предметы – например, книгу, стол или комнату – с помощью частей тела, таких как руки или ноги, а затем предметов, например кубика или книги. Дети должны сначала научиться измерять длину с помощью нестандартных предметов, прежде чем они смогут познакомиться со стандартными измерениями.

Разговор о времени

Находите возможности каждый день говорить о времени. Используйте распорядок дня как отправную точку.Обсудите такие понятия, как время дня (утро, день), а также время на часах («Я заберу вас в 12 часов, когда прозвенит школьный звонок»).

Играть с объектами

Дайте ребенку разные предметы и попросите его почувствовать, какие из них тяжелые или легкие, и сравнить вес разных предметов. Сделайте самодельные весы для балансировки и расставьте на них разные предметы домашнего обихода.

Решение проблем

Решение задач может быть самой… эм… проблемной из всех математических задач! Ученикам классов часто сложно представить себе проблемы и то, что они на самом деле означают.

Они часто прибегают к операциям наугад (например, там указано больше , поэтому я должен добавить), не имея представления о том, в чем проблема на самом деле и как при визуализации решение обычно бывает настолько логичным.

Лучший способ подготовить вашего ребенка к решению проблем – это дать возможность безостановочно решать реальные проблемы!

Вы должны научить вашего ребенка развить у него навыки критического мышления.

Необязательно задавать математические задачи, только общие задачи, требующие тренировки мозга и нестандартного мышления!

Позвольте много возможностей:

Собирайте головоломки
Решайте головоломки, такие как головоломки танграм
Разгадывайте загадки
Играйте в игры, требующие мышления
Играйте с игрушками-конструкторами (например.грамм. выясняя, как сделать мост, который не упадет)
Обсудите проблемы и решения во время рассказа
Спросите своего ребенка о решениях повседневных проблем

Надеюсь, вам понравилось читать эту статью, и у вас есть несколько новых идей, которые можно попробовать !

11 Математические приложения и онлайн-инструменты PreK-12, рекомендуемые учителем

Для некоторых учителей математики цифровые инструменты, которые помогают учащимся визуализировать математические концепции, такие как Desmos, или веб-сайты, поощряющие математические дискуссии, такие как Fraction Talks, уже были частью их репертуара до пандемии. Но для других учителей дистанционное обучение подтолкнуло их впервые к изучению математических приложений и онлайн-ресурсов.

Мы поговорили с сотнями преподавателей и проанализировали более 500 комментариев, чтобы узнать, какие математические инструменты они сочли полезными и бесполезными во время дистанционного обучения этой весной и какие из них будут использоваться в новом учебном году.

Практика математических навыков

Ряд математических приложений и онлайн-инструментов могут помочь учащимся развить необходимое базовое понимание арифметических операций, которые им понадобятся в дальнейшем для решения более сложных математических задач, сказали нам учителя математики.

Чтобы помочь младшим школьникам практиковать такие навыки, как счет, сложение и вычитание, Эшли Блэквелдер, координатор начальной школы STEAM в Южной Каролине, настоятельно рекомендует Moose Math, бесплатное приложение для iPhone и iPad. В Moose Math учащиеся играют в математические игры, зарабатывающие очки и помогающие строить город. Blackwelder говорит, что в этом формате легко ориентироваться детям, и он отлично подходит для коротких промежутков времени.

Разработчик учебных программ и инструкций Кэсси Табризи порекомендовала Happy Numbers (до 5-го класса), веб-сайт с подпиской (14 долларов.50 на ученика или 1450 долларов на сайт для начинающих школ), который разбивает математические уравнения, чтобы помочь ученикам понять математические концепции более высокого порядка. Чтобы использовать его, ученики превращаются в персонажей динозавров и решают математические задачи, чтобы вылупить яйца динозавров. Тебризи сказал, что этот веб-сайт полезен, но она рекомендует использовать его в умеренных количествах: ученикам может показаться утомительным, если они практикуют более 10 минут в день.

Учащиеся сражаются с монстрами в образе волшебника на бесплатном игровом веб-сайте Prodigy (1–8 классы) (также доступном в виде приложения для iPhone, iPad, iPod Touch и Android). Дети любят “Вундеркинда”, но в меньшей степени педагоги, потому что они больше основаны на игре. Бриттни Пейдж, учительница пятого класса из Сиэтла, говорит, что, хотя это больше похоже на игру, ей нравится, что она автоматически нацелена на математические концепции, с которыми учащиеся столкнулись при предварительной оценке, и отслеживает, насколько они продвинулись в целевых областях. Большинство учителей предлагают ученикам Prodigy в качестве опции, если они завершают задание раньше срока.

Предоставлено Prodigy

После успешного решения математической задачи питомец ученика произносит заклинание в битве.

Zearn (1–5 классы), бесплатная веб-программа для самостоятельного изучения, согласованная с Eureka Math – бесплатным курсом математики от дошкольного возраста до 12 лет, – начинает типичный урок с веселых разогревающих заданий, таких как сложение сколько яблок съедает мультяшная лиса, чтобы заинтересовать студентов. По мере выполнения программы студенты решают арифметические задачи на время, смотрят обучающие видеоролики по новым концепциям и решают практические задачи. Шеннон МакГрат, инструктор из Вестерн-Спрингс, штат Иллинойс, говорит, что Zearn является хорошей «концептуальной практикой высокого уровня» и дает хорошие отзывы как учителям, так и ученикам, но иногда может прогрессировать слишком медленно для детей, которые быстро усваивают концепции.

Открытые математические задания

Открытые математические задачи – задачи, на которые обычно существует более одного ответа – помогают учащимся развить концептуальное понимание математики, а не зацикливаться на запоминании фактов, – сказали преподаватели математики, с которыми мы разговаривали, которые постоянно упоминали три бесплатных веб-сайта, которые можно использовать для открытых математических задач. .

Open Middle (Pre-K – 12 класс) оставляет части уравнения незаполненными и просит учащихся заполнить их, чтобы они соответствовали действительности. «Мне нравится Open Middle для дистанционного обучения, особенно в сочетании с Google Jamboard, – говорит МакГрат.«Проблемы вдохновляют на исследовательское мышление, игровую игру, творчество и настойчивость».

Предоставлено Мэри Бурасса / Кому не принадлежит

Использование “Кому не принадлежит?” Ученики математики Мэри Бурасса приводят математические аргументы в пользу того, почему каждый график является нечетным.

МакГрат также любит «Не лучше ли математику» (до 12-го класса) для построения сообщества. При использовании сайта учащиеся выбирают между двумя примерами из реальной жизни – например, коробкой шоколадных конфет с пятью рядами и 14 столбцами или коробкой шоколадных конфет с семью строками и девятью столбцами – и должны привести математический аргумент, чтобы подтвердить свой выбор.

Какой из них не принадлежит? (до 12 классов), аналогичный сайт, демонстрирует четыре фигуры, числа или диаграммы и просит учащихся описать, какой из них не принадлежит, используя математический словарь. «Это отлично подходит для начала синхронной дискуссии, так как это считается задачей с низким полом и высоким потолком», – говорит Джозеф Манфре, специалист по математике из Департамента образования Гавайев. Учитель математики средней школы Мэри Бурасса просит своих учеников по математике определить причины, по которым каждый график в наборе из четырех не принадлежит, указав такие характеристики графа, как асимптоты и недифференцируемые точки, а позже ее ученики создают свои собственные наборы WODB.

Задания по богатой математике

Для сложных математических задач – задач, требующих строгости, совместной работы и концептуального мышления – преподаватели математики отметили несколько веб-сайтов.

Предоставлено Брайаном Пенфаундом / Fraction Talks

Студенты используют это изображение из Fraction Talks, чтобы практиковаться в сложении и умножении дробей. Нижняя угловая секция представляет собой ½ x ¼ = ⅛.

Fraction Talks (1–12 классы) – это веб-сайт, заполненный изображениями фигур – например, треугольников внутри треугольников, – которые поощряют математические дискуссии.Просто спросите студентов: «Что вы наблюдаете?» может побудить их рассказать, что и сколько фигур они замечают, задавая вопрос: «Сколько фигур красных или затененных?» побуждает студентов исследовать и понимать дроби. Как только учащиеся получат базовое представление о дробях, они могут приступить к изучению более сложных понятий. Предложив ученикам взглянуть на части фигуры и на то, какие дроби они образовали при объединении, Брайан Пенфаунд помог своим ученикам седьмого и восьмого классов визуализировать сложение и умножение дробей.

Визуальные паттерны (K – 12 класс) показывает начало паттерна – как несколько квадратов в сетке – затем ученикам предлагается составить уравнение, чтобы оно соответствовало паттерну. «Несмотря на то, что есть только один ответ, – говорит Манфре, – вы можете задавать более глубокие вопросы с помощью таких задач и вовлекать студентов в математику в ее более естественной, наглядной форме».

Предоставлено Visual Patterns

Учащимся необходимо определить уравнение для этого шаблона.

Инструменты моделирования

По словам учителей математики, симуляции, такие как манипулирование выражением и наблюдение за изменением в графике, являются отличными инструментами, помогающими учащимся визуализировать математические концепции.

Предоставлено Эшли Тэплин

Эшли Тэплин, специалист по математике среднего звена, попросила своих учеников изобразить, как они себя чувствовали в течение первой недели дистанционного обучения.

Аплеты – простой код с определенной целью – были упомянуты некоторыми учителями как хороший ресурс. Студенты, изучающие статистику Эммы Чиаппетта, используют апплеты с сайта RossmanChance.com, например, для управления и определения шаблонов распределения выборки на графиках. Она создает базовое руководство о том, как использовать апплет, с какими значениями следует изменять, а затем задает вопросы, чтобы студенты критически относились к этим шаблонам. Чиаппетта также использует апплеты Массачусетского технологического института для своих студентов, изучающих линейную алгебру.

Desmos (6–12 классы), веб-сайт с интерактивными математическими упражнениями и графическим калькулятором (также доступный в виде приложения для iPhone, iPad, iPod Touch и Android), – еще один бесплатный инструмент и любимый инструмент учителей, как мы слышали. Хотя может показаться, что социальное и эмоциональное обучение (SEL) и математика не идут рука об руку, учителя интегрировали SEL в уроки математики с помощью Desmos. Например, в первую неделю дистанционного обучения Эшли Тэплин, специалист по математике из Сан-Антонио, штат Техас, попросила своих учеников изобразить, как они себя чувствуют.Таплин говорит, что ей особенно нравится, что учителя могут выполнять свои собственные задания – например, этот, посвященный параболам, и эту сортировку карточек, когда ученики сопоставляют карточки с именем, соответствующим уравнением и правильным графическим представлением функции.

Открытие форм и пространства в дошкольном учреждении

Учителя дошкольных учреждений могут создать среду, в которой дети будут стремиться изучать математику и изучать ее. Они могут предоставить подходящие для развития материалы и возможности, чтобы помочь дошкольникам понять тему.Математика может быть частью распорядка дня, занятий и взаимодействия в дошкольном учреждении.

Общие основные государственные стандарты по математике (CCSSM) написаны для обеспечения того, чтобы учащиеся покидали школу готовыми к работе и поступлению в колледж. В CCSSM содержание детского сада составляет две критических области. Первый представляет собой представление, связь и оперирование целыми числами с наборами объектов. Второй – это описание форм и пространства (NGA Center & CCSSO 2010). К концу детского сада детям необходимо продемонстрировать понимание, анализируя, сравнивая, создавая и составляя эти формы.Воспитатели дошкольных учреждений имеют множество возможностей помочь детям развить понимание форм и пространства.

Распознавать и сравнивать двух- и трехмерные формы

В дошкольных учреждениях дети могут научиться определять и называть круги, треугольники, квадраты, прямоугольники и овалы. Используя такие материалы, как плакаты, кубики, книги и игры, учителя демонстрируют детям различные формы и помогают им анализировать двух- и трехмерные формы различных размеров и ориентации.

Следующие ниже стратегии и упражнения могут помочь дошкольникам научиться распознавать и сравнивать формы.

Определите формы. Познакомьте детей с различными типами треугольников, такими как равносторонний, равнобедренный, разносторонний и правый. Найдя их в классе или на улице, дети могут обвести треугольники цветным скотчем. Например, они могут сделать прямоугольные треугольники красными, а разносторонние треугольники – синими.
Введите математические слова. Создайте стену из математических слов или включите математические слова в существующую стену слов – выделите математические слова цветом, чтобы детям было легче их заметить. Обязательно пишите математические слова на английском и на родном для детей языке. Учителя могут использовать реальные объекты, фотографии и рисунки черными линиями для определения слов.
Сравнить формы. Попросите детей назвать разные размеры одной и той же формы. Например, в классе они могут искать прямоугольники, такие как окна, двери, книги, полки, шкафы, экраны компьютеров, столешницы и тумбочки.Затем помогите детям подумать, сравнивая размеры прямоугольников. Дверь больше, чем тумбочки. Ящики больше книги, но все они прямоугольные. Призовите детей делать то же самое с треугольниками, кругами и другими фигурами.
В чем разница? Объясните разницу между двухмерными (плоскими) формами и трехмерными (твердыми) формами. Чем книга и лист плотной бумаги – одно и то же? Насколько они разные?
Создайте фигуру-пейзаж. Учителя и семьи могут собирать трехмерные объекты, такие как банки, картонные коробки, коробки и шары, для создания очертания формы. Дети могут использовать цилиндры (рулоны бумажных полотенец) в качестве стволов деревьев, сферы (шары) в качестве верхушек деревьев и прямоугольники (коробки с хлопьями) в качестве строений. Учителя и дети могут работать вместе, чтобы обозначить фигуру, подсчитать количество используемых фигур и спланировать дополнения к структуре.
Переходите от трехмерного к двумерному. Дошкольники могут окунуть трехмерные объекты в краски и прижать их к бумаге, чтобы сделать отпечатки.Хорошо подойдут банки, катушки, свечи и стаканы. Дети увидят плоские формы, составляющие стороны предметов.
Открывайте формы на открытом воздухе. Ищите крышки люков, флажки, окна, знаки и другие отличные формы. Работая вместе, дети и учителя могут фотографировать фигуры, маркировать их на фотографиях и собирать фотографии в учебник.
Выучите новый словарный запас. Я n произвожу такие слова, как толстый, тонкий, маленький, большой, длинный, короткий, фасет, слайд, перевернуть и поворачиваю на английском и домашнем языках во время еды и перекусов.Предлагайте закуски разных размеров и поощряйте детей использовать сравнительные слова, когда просят о еде. Я хочу длинную морковку, пожалуйста. Добавьте эти описательные слова к стене слов.
Игровая форма hokey pokey. Пусть каждый дошкольник держит фигуру и помещает ее в круг вместо части тела. Вставьте свой квадрат. Выньте свой квадрат. Сделай хоккей и развернись.
Сыграйте в игру по угадыванию фигур. Предложите дошкольникам играть в парах.Объясните: один ребенок скроет фигуру за спиной, а другой задаст вопросы о фигуре. Есть ли у фигуры три стороны? У формы четыре угла?
Предлагайте задачи с географической зоной. Учителя могут предложить географические доски и географические зоны, чтобы дети могли создавать как можно больше различных форм. Сделайте дополнительную задачу, попросив детей раскрасить фигуры.

Создавайте и разбирайте фигуры

Как только дошкольники смогут правильно определять плоские (квадрат, круг, треугольник, прямоугольник, шестиугольник) и твердые или трехмерные формы (куб, конус, цилиндр, сфера), они готовы создавать, а затем разбирать формы, используя материалы, предоставленные их учителем. .

Создайте форму. Предложите зубочистки, средства для чистки труб, соломинки или палочки для поделок в качестве материалов, которые дети могут использовать для придания форм. Обсудите, какие формы они образуют. Это треугольник. Как можно было превратить его в квадрат?
Создайте новые формы. Дети могут склеить две или более фигур, вырезанных из бумаги, на чистый лист бумаги, чтобы сформировать другие фигуры. Вы склеили два треугольника вместе, чтобы получился прямоугольник.
Создайте твердые формы. Дети могут катать, щипать и манипулировать пластилином или глиной, чтобы сделать две или более фигур. Затем они могут комбинировать свои творения, чтобы создавать новые формы.
Деконструируйте формы. Дети могут научиться формировать трехмерные фигуры. Например, пусть дети смотрят, как вы разрезаете прямоугольные емкости, такие как коробки с хлопьями. Сколько прямоугольников в коробке? Затем попросите детей придумать, как собрать их вместе.
Играйте с танграмами. Имейте под рукой несколько наборов танграмов и карточек с выкройками. Дети могут начать с нанесения загара на каждый узор. Они могут перейти к воссозданию узора на другой поверхности и составлению собственных узоров.
Постройте загадку из шестиугольника. Разрежьте один шестиугольник на трапеции и треугольники. Предложите детям использовать эти части, чтобы заполнить другой шестиугольник того же размера.

Пространственная визуализация

Поощряйте дошкольников скользить, переворачивать или поворачивать фигуры, чтобы способствовать решению проблем и пониманию трансформаций.Эти преобразования имеют решающее значение для развития способностей к пространственной визуализации и понимания геометрии, что включает сопоставление форм посредством визуализации.

Используйте правильные термины. Оборот – это поворот на . Флип – это отражение . Слайд – это перевод .
Отправьте домой карточки с выкройками и танграммы. Поощряйте семьи играть, открывать и называть преобразования дома, когда они дублируют фигурки на карточках. Можете ли вы повернуть треугольник по фигуре? Я видел, как ты сдвинул прямоугольник.
Сыграйте в игру-трансформацию. Дайте детям куклы или мягкие игрушки и укажите на переднюю и заднюю часть каждой игрушки. Назовите направление – переверните куклу, переверните плюшевого мишку на бок – чтобы посмотреть, смогут ли дошкольники продемонстрировать трансформации. После того, как они научатся переворачивать игрушки, попросите детей попрактиковаться с фигурными элементами.
Play Зеркало, Зеркало. Дайте каждому ребенку набор блоков для выкройки и небольшое зеркало. Попросите детей создать дизайн из своих кубиков. Затем попросите их поднести зеркало к каждой стороне рисунка, чтобы увидеть, как оно выглядит в зеркале.

Пространственная ориентация

По мере того как дошкольники учатся определять объекты, они могут использовать словарь пространственной ориентации для описания взаимного расположения объектов. Дошкольники должны понимать и уметь использовать позиционные слова, такие как вверху, внизу, рядом, впереди, позади, рядом, между, на, над, внизу, и внутри .

Сосредоточьтесь на слове в неделю. Введите слово на английском языке и на языках детского дома. Используйте это слово в течение дня в классе, в коридоре и на игровой площадке. Вы сидите рядом с другом. Положите салфетку рядом с тарелкой. Встаньте рядом со своим партнером.
Парный словарь положения и формы. Часы – круг. Он находится рядом с дверью, которая представляет собой прямоугольник.
Создайте книгу. Предложите семьям написать о любимом занятии, используя позиционные слова. Мы проехали рядом с парком, проехали под скоростной автомагистралью, прошли по мосту. Дети могут предоставить иллюстрации.
Используйте фото-примеры. Сфотографируйте детей, демонстрирующих позиционные концепции. Хун стоит под часами. Добавьте фотографии и слова на стену слов.
Играть пространственно, говорит Саймон. Дайте каждому ребенку в небольшой группе мягкую игрушку и поиграйте с Саймоном Сэйсом, используя позиционную лексику. Саймон Сэйс: поставьте животное над головой. Положите животное под стул.
Создайте позиционные полосы препятствий. Поощряйте дошкольников использовать позиционные слова во время игры или переходов. Прежде чем выйти на улицу, поднимитесь по ступенькам, соскользните с горки, перепрыгивайте через конусы и выстраивайтесь рядом с дверью.
Рассказывайте действия с ориентацией. Используйте позиционные слова, чтобы описать, как дети перемещаются с одного места на другое. Вы припарковали свой трехколесный велосипед на детской площадке рядом с окном. Вы прошли под потолочным окном и по ковру, чтобы войти в класс.

Вывод

Учителя дошкольных учреждений могут создавать обстановку и планировать занятия так, чтобы маленькие дети и их семьи одновременно увлекались математикой и занимались ею. Программы могут содержать числовые и геометрические представления с соответствующими словарными терминами. Помимо школьных занятий, дошкольники могут открывать для себя математику и получать от нее удовольствие в своих домах и общинах.

Ресурсы

Копли, Дж. В. 2010. Дети младшего возраста и математика. 2-е изд. Вашингтон, округ Колумбия: NAEYC.
Шиллади, А., изд. 2012. В центре внимания маленькие дети: изучение математики. Вашингтон, округ Колумбия: NAEYC.
Zubrzycki, J. 2011. «Common Core создает проблемы для дошкольных учреждений». Неделя образования 31 (13): 1, 20–21.

Как дети получают пользу от математики

Математика и искусство имеют большое значение. С самого начала они были объединены для создания самых красивых структур, живописи и вневременных фресок.Достаточно взглянуть на парк, чтобы открыть глаза и увидеть, как красиво природа сыграла с математикой.

Знаменитый математик Леонардо Фибоначчи обнаружил самые интересные закономерности в природе. Он был одним из выдающихся математиков, которые популяризировали то, как элементы природы следуют установленному образцу. Такие художники, как Леонардо да Винчи , Пикассо , Кандинский , широко использовали математику в своем искусстве. Удивительно, почему сегодня мы преподаем математику изолированно.

Что происходит, когда математику преподают вместе с искусством?

Art добавляет сенсорный размер к Math. Такие чувства, как прикосновение и слух, связанные с простой математической задачей, стимулируют различные части мозга. Следовательно, это обогащает учебный опыт.
Искусство отлично подходит для практического обучения . Дети узнают гораздо больше, если интегрируют полученные знания в практическую жизнь.
Открытые художественные проекты предлагают детям свободу решать проблемы, делать выводы и пробовать новые идеи. Таким образом, открыв свои умы из из коробки решений.
Дети получают более глубокое понимание своего окружения и навыков критического мышления , когда они работают над математическими художественными проектами. Такие понятия, как симметрия, пространство, формы, легче понять, если их усвоить с помощью искусства.

математических художественных проектов, которые понравятся вашим детям:

1.

Оригами

Оригами – это японское искусство складывания бумаги в разные формы. С помощью этой техники простой лист бумаги можно превратить в трехмерный объект. Дети получают пользу от искусства оригами, поскольку оно требует от них визуализации и понимания. С помощью этого искусства можно легко научить сложным математическим понятиям, таким как пропорции, симметрия, геометрия.

2.

Блочная печать

Переделайте старые блоки, лежащие вокруг дома, с помощью блочной печати.Это простой, но отличный способ научить трехмерным и двумерным объектам. Дайте ребенку немного краски и старые кубики и попросите его напечатать из кубиков домик или кошку.

3.

Коллаж формы

Возьмите старый журнал или поделочную бумагу и вырежьте из него разные формы. Предложите ребенку поиграть с этими фигурами и сделать коллаж. Пусть ее воображение ведет ее. Это прекрасный способ понять формы и их атрибуты.

4.

Shape Craft

Это полезно при обучении количественной оценке и сравнению.Возьмите любую форму и вырежьте ее разных размеров. Попросите ребенка наклеить их, чтобы были видны все вырезы. Для этого ребенок просто должен вставить фигуры в порядке убывания. Но в таком случае заставляет ребенка думать и устраивать. Отлично подходит для пространственного и логического мышления.

5. Номер артикула

Еще одно замечательное занятие, объединяющее математику с искусством и развивающее творческие способности, – это искусство чисел.

Все, что вам нужно, это карандаш и лист. Мы использовали флуоресцентный лист, чтобы добавить изюминку в нашу деятельность.

Попросите ребенка корчить рожи, используя только математические цифры. Возможно, вам придется показать им, нарисовав одно или два лица, прежде чем они начнут свое творческое математическое приключение. Вы также можете настроить его в угадайку. По очереди строите лица, а затем угадывайте числа, использованные для их создания.

Это отличный способ побудить детей увидеть математику вокруг себя. А если у вас есть младший ребенок, который только учит числа, это отличный способ научить распознавать числа.

6.

Арт-узор

Распознавание образов – важная концепция интеллектуального анализа данных. Научите этому своего ребенка с помощью этой несложной поделки-раскраски. Нарисуйте любую картинку и попросите ребенка раскрасить ее разными узорами. Постарайтесь включить в рисунок как можно больше узоров.

Важные математические навыки у детей раннего и раннего возраста

Математические навыки, которым обучают в дошкольном образовании, служат основой, необходимой детям для успешной учебы в начальной школе и за ее пределами.Педагогам следует сосредоточить уроки в раннем детстве вокруг базовых навыков, которые развиваются до продвинутой математики в средней школе и колледже. От дошкольного до окончания начальной школы дети закладывают основу для будущих жизненных навыков.

Базовые математические навыки для дошкольников

Дошкольное образование должно знакомить с простыми математическими понятиями. Знакомя детей с базовой терминологией в раннем детстве, учителя немного упрощают начальное образование, а знакомство с математическими понятиями следует начинать, когда детям исполняется около трех лет.

Закладывая основу для раннего понимания терминологии и концепций, дети готовы применять информацию в классе. Концепции уже понятны, поэтому учителя начальных классов могут сосредоточиться на применении идей.

Хотя дети дошкольного возраста могут еще не быть готовы к практическому изучению математических навыков, они могут получить базовое представление о практике с помощью языка и практики.

Смысл числа

Чувство чисел, или основы изучения чисел, – это первый жизненно важный математический навык, который ребенок должен развить, прежде чем попасть в детский сад.Дети должны научиться считать вперед и назад в раннем детстве, чтобы узнать взаимосвязь между числами в будущем. Чувство чисел – жизненно важный навык, которому воспитатели младшего возраста должны сосредоточиться на обучении до того, как дети дойдут до детского сада.

В то время как классы детского сада изучают основы счета вперед и назад, педагоги дошкольного образования могут заложить более прочную основу, сосредоточив внимание на обучении счету до поступления в начальную школу. Сосредоточившись на чувстве числа, учителя прививают математические навыки, необходимые для будущих концепций и сложных вычислений.

Изучение чисел через изображения или изображения

Дети обладают естественным зрением и могут строить отношения между числами и представленным предметом. По данным Национального центра по делам младенцев, детей ясельного возраста и семей, использование изображений или изображений для прояснения отношений делает использование математики реальным для ребенка.

Дошкольное образование должно быть сосредоточено на представлении чисел с помощью предметов, картинок или даже членов семьи. Например, при обучении основам счета можно использовать изображения яблок или любимых фруктов, чтобы помочь детям понять, что число представляет собой изображенные предметы.

Обучение через изображения или изображения позволит детям установить связь между реальным миром и математическими навыками, которые имеют жизненно важное значение для академической успеваемости. Без связи между жизнью и математикой дети могут запутаться в информации, предоставляемой в классе.

Сложение и вычитание

В то время как дошкольное образование должно вводить понятия, прежде чем приобретать навыки, учителя могут начать с основ сложения и вычитания, прежде чем дети перейдут в начальную школу.Базовые навыки используются в обычных детских взаимодействиях, таких как совместное использование файлов cookie путем вычитания из исходного числа, чтобы обеспечить детям одинаковое количество угощений.

Сосредоточившись на основах сложения и вычитания, учителя могут укрепить основы математических навыков на будущее. В зависимости от возраста детей, основы сложения и вычитания могут ограничивать навыки совместного использования продуктов питания или добавления предметов для игровых действий, которые побуждают детей подсчитывать дополнительные предметы.

По данным Национальной ассоциации образования детей младшего возраста, учителя могут использовать примеры, возникающие во время игр, для обучения идеям сложения или вычитания предметов. Это возможность обучать навыкам без активного создания планов уроков, которые слишком сложны для детской грамотности и знаний.

Математика дошкольного возраста обеспечивает академические строительные блоки

Базовые навыки математики, которые учителя дают в дошкольном образовании, являются строительными блоками для всей академической карьеры.Без изучения простых навыков, таких как чувство чисел, математические концепции и простое применение таких идей, как сложение, дети не готовы перейти в начальное образование. К счастью, маленькие дети могут учиться с удивительной скоростью, и учителя могут применять концепции или математические навыки в обычных детских занятиях.

Присоединяйтесь к Resilient Educator

Подпишитесь на нашу рассылку, чтобы получать контент на свой почтовый ящик. Щелкните или коснитесь кнопки ниже.