Задачи для 3 класса по математике сложные: Задачи по математике 4 класс

Решение задач. 3 класс – презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

63 : 7 · 2 – 6 : 3 · 8 : 4 =
80 – 40 : 8 · 4 – 2 : 2 · 8 =
В книге поместили 24 стихотворения и
8 рассказов. Во сколько раз в книге
стихотворений больше, чем
рассказов?
в 16 раз
в 3 раза
в 4 раза
в 32 раза
В книге поместили 24 стихотворения и
8 рассказов. На сколько в этой книге
стихотворений больше, чем
рассказов?

на 16
на 3
на 4
на 32
На первой полке было 27 книг, на
второй полке – в 3 раза меньше, чем
на первой. Сколько книг на второй
полке?
8 книг
24 книги
9 книг
30 книг
На первой полке было 27 книг, на
второй полке – в 3 раза меньше, чем
на первой. Сколько книг на двух
полках?
57 книг
36 книг
9 книг
30 книг
На первой полке было 9 книг, на
второй полке – в 4 раза больше, чем на
первой. Сколько книг на второй
полке?
5 книг
30 книг
13 книг
36 книг
На первой полке было 9 книг, на
второй полке – в 4 раза больше, чем на
первой. Сколько книг на двух полках?
45 книг
42 книги
22 книги
36 книг
Составь задачу по схеме и
запиши решение.
9 кг
? кг
5 к.
9 кг
45 кг
? к.
? кг
45 кг
5 к.
В магазин
привезли 6 ящиков
яблок,
по 9 кг в каждом.
Сколько
килограммов
яблок привезли в
магазин?
В магазин
привезли 3 ящика
груш,
по 7 кг в каждом.
Сколько
килограммов
груш привезли в
магазин?
Н!
В магазин привезли 6
ящиков яблок, по 9 кг в
каждом, и 3 ящика груш, по
7 кг в каждом. Сколько
всего килограммов фруктов
привезли в магазин?
? кг
1) (·)
9 кг
7 кг
6 ящ.
2)
(·)
? кг
3 ящ.
? кг
3) (+)
1) 9 · 6 = 54 (кг) – яблок
2) 7 · 3 = 21 (кг) – груш
3) 54 + 21 = 75 (кг) – всего
Ответ: 75 кг фруктов
привезли в магазин.
Раз, два, три, четыре, пять –
Все умеем мы считать.
Раз! Подняться, потянуться.
Два! Согнуться, разогнуться.
Три! В ладоши три хлопка,
Головою три кивка.
На четыре – руки шире.
Пять – руками помахать.
Шесть – за парту тихо сесть.
За один день фермер собрал 8
корзин огурцов, по 6 кг в каждой,
и 3 корзины помидоров, по 5 кг в
каждой. Сколько всего кг овощей
собрал фермер в этот день?
6·8
6·8+5·3
5·3
6·8–5·3
Уверены ,что вы
справились с задачами!
Успехов вам!!!

English     Русский Правила

Решаем задачу по математике 3 класс (Петерсон, чтоб ее!): bloha_v_svitere — LiveJournal

?

Category:

• catIsShown({ humanName: ‘образование’ })” data-human-name=”образование”> Образование
• Cancel

Ну как, еще не спите? Вот вам задачка для 3 класса по математике от дражайшей Петерсон (пример б)

Дублирую: заполни проспуски.

17 часов 5 минут – 9 часов 30 минут = 16 часов ? минут Вообще-то тут уже далеко не 16 часов ? минут, а вполне определенные 7 часов 35 минут
А от полученного времени (7 часов 35 минут) невозможно вычесть 9 часов 30 минут.

Или если предлагается из 16 часов ? минут вычесть 9 часрв 30 минут, то минуты к 16 часам мне ставить произвольные?

“Кому бы еще спокойной ночи пожелать?” (с)*

*если не знаете этого анекдота, пишите, расскажу.

Tags: 3 класс, Петерсон, школа

Subscribe

• Помогите решить задачу по математике (3 класс)

  Я очень скромно оцениваю свои математические способности. Но мне кажется, что в условии задачи чего-то не хватает: В одном куске 12 м ткани, а во…

• Очередная петерсонная задача по математике (1 класс)

  Ох уж эта Петерсон и ее учебник по математике для начальной школы! У меня такое ощущение, что она росла на загадках: “Плывут два крокодила. Один…

• Помогите решить задачу по математике (1 класс)

  У меня с логикой плохо. Номер 4 – найти закономерность и вставить пропущенные цифры. Намекните на закономерность, а цифры, может, уже сообразим…

• Помогите решить задачу по математике (3 класс)

  Надо мне взять тэг у antep_fistik “Бурасы Туркие”. Что такое – не знаю, но это очень точно характеризует мое понимание…

• Задача по математике 2-й класс

  Я что-то опять туплю и прошу помощи зала. Задача такая: Андрей забил в три раза больше голов, чем Толя. А Толя на шесть голов больше, чем Андрей.…

• Помогите решить задачу по математике (2 класс)

  С аэродрома поднялось в воздух d пар самолетов, а b самолетов осталось. На сколько больше самолетов осталось, чем улетело? Вариант: b – d*2…

Photo

Hint http://pics.livejournal.com/igrick/pic/000r1edq

• Помогите решить задачу по математике (3 класс)

  Я очень скромно оцениваю свои математические способности. Но мне кажется, что в условии задачи чего-то не хватает: В одном куске 12 м ткани, а во…

• Очередная петерсонная задача по математике (1 класс)

  Ох уж эта Петерсон и ее учебник по математике для начальной школы! У меня такое ощущение, что она росла на загадках: “Плывут два крокодила. Один…

• Помогите решить задачу по математике (1 класс)

  У меня с логикой плохо. Номер 4 – найти закономерность и вставить пропущенные цифры. Намекните на закономерность, а цифры, может, уже сообразим…

• Помогите решить задачу по математике (3 класс)

  Надо мне взять тэг у antep_fistik “Бурасы Туркие”. Что такое – не знаю, но это очень точно характеризует мое понимание…

• Задача по математике 2-й класс

  Я что-то опять туплю и прошу помощи зала. Задача такая: Андрей забил в три раза больше голов, чем Толя. А Толя на шесть голов больше, чем Андрей.…

• Помогите решить задачу по математике (2 класс)

  С аэродрома поднялось в воздух d пар самолетов, а b самолетов осталось. На сколько больше самолетов осталось, чем улетело? Вариант: b – d*2…

Уроки формирующего оценивания

Classroom Challenges — это уроки, которые помогают учителям в формирующем оценивании. Всего 100 уроков, по 20 в каждом классе с 6 по 8 и 40 по теме «Готовность к карьере и колледжу» в 9 классе средней школы и выше. Одни уроки направлены на развитие математических понятий, другие на решение нестандартных задач.

Перед первым использованием этих уроков рекомендуется прочитать Краткое руководство для учителей и администраторов (PDF).

Каждый урок можно загрузить в формате PDF «все в одном» для распечатки, а также вспомогательную презентацию PowerPoint.

В поисках урока

Существует несколько способов навигации:

1. Используйте меню слева для просмотра по оценкам и темам или для поиска по ключевой фразе.
2. Перейдите на вкладку «Стандарты», чтобы найти уроки, связанные с определенным стандартом контента или практикой.
3. Полный комплект уроков указан ниже в алфавитном порядке.

Класс 6

Сложение и вычитание направленных чисел

Создание меры уклона

Проектирование 3D-продуктов: коробки для конфет

Оценка утверждений о числовых операциях

Оценочные утверждения: последовательные суммы

Нахождение факторов и кратных

Интерпретация уравнений

Интерпретация умножения и деления

Максимизация прибыли: продажа супа

Моделирование взаимосвязей: следы заноса автомобиля

Оптимизация покрытия: камеры видеонаблюдения

Представление данных с помощью сгруппированных частотных диаграмм и блочных диаграмм

Представление законов арифметики

Представление изменчивости со средним значением, медианой, модой и диапазоном

Справедливое распределение расходов: поездка в школу

Перевод между дробями, десятичными знаками и процентами

Использование координат для интерпретации и представления данных

Использование пропорциональных рассуждений

Эффективное использование пространства: упаковка грузовика

Использование стандартных алгоритмов для числовых операций

7 класс

Анализ азартных игр

Применение теорем об углах

Классификация пропорциональных и непропорциональных ситуаций

Сравнение данных с использованием статистических показателей

Сравнение стратегий для проблем с пропорциями

Описание и определение четырехугольников

Описание и определение треугольников

Проектирование 3D-продукта в 2D: спортивная сумка

Дизайн: Азартная игра

Рисование в масштабе: сад

Оценка объема: пожиратели денег

Оценка утверждений о вероятности

Нахождение площадей кругов

Увеличение и уменьшение количества на процент

Увеличение площади: золотая лихорадка

Моделирование: горячее и холодное

Представляя: шоссейные гонки

Выборка и оценка: подсчет деревьев

Решение линейных уравнений

Использование положительных и отрицательных чисел в контексте

8 класс

Применение свойств показателей

Построение и решение линейных уравнений

Классификация решений систем уравнений

Сравнение расхода топлива: покупка автомобилей

Сравнение линий и линейных уравнений

Сравнение соотношения цены и качества: бейсбольные майки

Определение линий по точкам, наклонам и уравнениям

Открытие теоремы Пифагора

Оценка длины с использованием экспоненциальной записи

Поиск кратчайшего пути: задача школьного двора

Обобщающие шаблоны: разница двух квадратов

Определение подобных треугольников

Интерпретация и использование данных: установка тарифов на такси

Интерпретация графиков расстояние-время

Сопоставление ситуаций, графиков и линейных уравнений

Моделирование: Изготовление спичек

Представление и объединение преобразований

Выборка и оценка: сколько желейных бобов

Решение линейных уравнений с одной переменной

Перевод между повторяющимися десятичными знаками и дробями

Использование данных: тестирование нового продукта

Средняя школа

Построение и решение сложных уравнений

Вычисление дуг и площадей секторов окружностей

Вычисление объемов составных объектов

Классификация уравнений параллельных и перпендикулярных линий

Классификация рациональных и иррациональных чисел

Вычитание отношений: тени Floodlight

Разработка меры: корреляция

Оценка условий конгруэнтности

Оценка заявлений об расширениях

Оценка утверждений о длине и площади

Оценка утверждений о радикалах

Оценка утверждений о рациональных и иррациональных числах

Обобщающие шаблоны: табличные плитки

Генерация полиномов из шаблонов

Вписывание и описание прямоугольных треугольников

Интерпретация алгебраических выражений

Интерпретация данных: мутить воду

Максимизация прибыли: продажа бумерангов

Моделирование движения: вращающиеся чашки

Моделирование роста населения: наличие котят

Доказательство теоремы Пифагора

Представление 3D-объектов в 2D

Представление условных вероятностей 1

Представление условных вероятностей 2

Представление данных с помощью блочных диаграмм

Представление данных с помощью частотных графиков

Представление функций повседневных ситуаций

Графическое представление неравенств

Представление линейного и экспоненциального роста

Графическое представление многочленов

Представление вероятностей: медицинское тестирование

Графическое представление квадратичных функций

Представление тригонометрических функций

Решение линейных уравнений с двумя переменными

Решение задач с кругами и треугольниками

Решение квадратных уравнений

Сортировка уравнений и тождеств

Сортировка уравнений кругов 1

Сортировка уравнений кругов 2

Преобразование 2D-фигур

5 основных причин, по которым учащиеся испытывают трудности с математикой

• Предыдущий пост
• Следующий пост

6 января 2019 г.

Почему математика такая сложная? Взгляните на наиболее распространенные причины, по которым математика сложна для учащихся

Математика часто считается одним из самых сложных предметов для учащихся. Недавние опросы показывают, что 37% подростков в возрасте 13-17 лет считают математику более сложной, чем другие предметы, что является самым высоким показателем в целом. Итак, если вы задаетесь вопросом: «Почему я так сильно борюсь с математикой?» может быть ряд причин, от проблем со вниманием до пробелов в обучении на прошлых уроках математики или даже просто отсутствия практики. Узнайте о распространенных причинах, по которым учащиеся испытывают затруднения с математикой, и о том, как найти правильную помощь, необходимую для достижения успеха.

Обратитесь к ближайшему врачу-репетитору, чтобы найти репетитора по математике рядом с вами. выполнить несколько последовательных шагов для поиска решения. Это требует активной концентрации на поставленной задаче. При обучении сложным математическим процедурам учащиеся часто теряют концентрацию и отвлекаются во время урока. В результате он или она может пропустить важные этапы в процессе решения задач, а позже испытывать трудности с математикой, пытаясь решить задачи самостоятельно. Возможность вернуться к прежним концепциям, которые ранее были неясны, является одним из основных преимуществ индивидуального подхода Tutor Doctor к обучению.

2) Математика всегда основывается на предыдущих концепциях

Математика основана на последовательном обучении. Если учащийся не полностью понял концепцию предыдущего урока, он, вероятно, будет испытывать затруднения при введении новых концепций. Чтобы сокращать дроби, учащиеся должны сначала знать деление; чтобы заниматься алгеброй, учащиеся должны быть знакомы с многошаговой арифметикой и так далее. К сожалению, многие ученики, у которых проблемы с математикой, чувствуют себя неловко или смущаются, задавая вопросы в классе, когда их учитель уже перешел к следующему уроку. Математические концепции подобны строительным блокам, и всегда необходимо заложить фундамент, прежде чем двигаться вперед. Если фундамента нет, учащийся будет испытывать трудности в классе и может не до конца понять, почему у него проблемы с математикой, когда его сверстники, кажется, продвигаются вперед.

3) Понятия изучены, но не поняты

Часто учащиеся знают, как выполнять операцию путем повторения, но не понимают ее смысла. Например, заучивание таблицы умножения всегда было одним из основных элементов школьной программы. Однако учащийся может знать, что «4 x 4 = 16», только потому, что он или она запомнил это, а не потому, что он полностью понимает концепцию умножения. По этой причине многие учащиеся получают пользу от визуальных представлений, таких как использование небольших предметов (таких как шарики или скрепки) при изучении умножения и деления. Дело в том, что все учащиеся учатся по-разному, и может быть сложно охватить уникальный стиль обучения каждого учащегося в классе. Вот где индивидуальное обучение может действительно помочь тем, у кого проблемы с математикой!

4) Недостаток практики или терпения

Многие учащиеся просто не тратят достаточно времени на изучение математических понятий. Другие учащиеся могут не осознавать, что им нужно больше времени для изучения определенных областей. Иногда учащийся чувствует, что понимает концепцию, но при попытке решить задачу самостоятельно не знает, с чего начать (или в конечном итоге с трудом проходит процесс). Учащиеся часто чувствуют себя уверенно после того, как наблюдают, как их учитель объясняет урок в классе, но обнаруживают, что делать это самостоятельно может быть намного сложнее. К сожалению, не существует быстрого и простого решения для изучения математики — это требует много практики и терпения! Как преподаватели, мы пытаемся конкретно определить области, в которых учащиеся нуждаются в улучшении, и сосредоточиться на устранении этих «пробелов» в обучении.

5) «Когда я буду этим пользоваться?»

Эта классическая линейка любима каждым учителем математики, но, что более важно, отражает мнение многих учащихся о том, что они никогда не будут использовать эти навыки за пределами класса.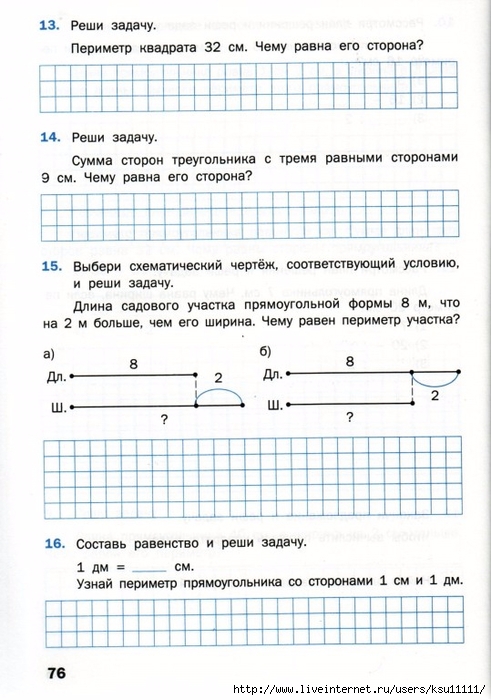 Другими словами, учащимся часто трудно связать математику с реальностью и увидеть, как она применяется в повседневной жизни. Например, учащийся, у которого проблемы с дробями, может иметь проблемы с пониманием того, как преобразовать дробь ½ в десятичную 9.0003 0,50 . Однако тот же студент без проблем понимает, что «полдоллара» равняется 50 центам. Это отличный пример того, с чем студенты иногда сталкиваются, пытаясь справиться с математикой.

Исследования показывают, что математика — одна из немногих дисциплин, доступная всем учащимся, независимо от их природных способностей. Успех в математике — это 1% вдохновения и 99% пота. В то время как природные таланты и способности дадут некоторым ученикам преимущество, математика на самом деле нужна только для практики. Это означает, что каждый может преуспеть в математике, несмотря на то, во что он может верить. Отношение «может сделать» является наиболее важным фактором успеха в математике.

Как мы уже говорили в предыдущих сообщениях блога, типы обучения можно разделить на три категории: визуальные, аудиальные и тактильные.