Задачи 1 класса по математике в два действия: Задачи в два действия | Тренажёр по математике (1 класс) на тему:

Решение задач в два действия, 1 класс, УМК “Школа России”

Этап урока	Деятельность учителя	Деятельность учащихся	Слайдовая презентация
1. Организационный момент	Громко прозвенел звонок. Начинается урок. Наши ушки – на макушке, Глазки широко открыты. Слушаем, запоминаем, Ни минуты не теряем.	Ответы детей.
2. Актуализация знаний	– Ранее мы с вами говорили о том, что математика нужна в жизни каждому человеку. Сегодня она придёт к нам на помощь, когда мы будем выручать героев сказки «Гуси-лебеди». От правильности ваших ответов, от сообразительности будет зависеть окончание сказки. Приготовились. Сказка начинается! – Жили-были мужик да баба. У них была дочка да сынок маленький. Однажды родители уехали, а сестрицу оставили за братом приглядывать, но случилась беда. Налетели гуси-лебеди, да унесли братца к Бабе яге. Трудно одному человеку в беде. Поможем Машеньке освободить братца?  – Бежала, бежала девочка. Вдруг на дороге печка.  – Печка, печка, скажи, куда гуси-лебеди полетели? – А печка говорит: «Расшифруй тему урока – скажу». – Помогите Машеньке решить примеры и расшифровать тему сегодняшнего урока. 1 – О 2 –З 3 – И 4 – А 5 – Е 6 – Д 7 – Ш 8 – Н 9 – Р 10 – Ч 7+2 8-3 3+4 10-5 4+4 9-6 4+1 Р Е Ш Е Н И Е 10-8 2+2 7-1 4+0 6+4 З А Д А Ч	-Да Дети по одному читают и решают примеры.	Слайд 1 Слайд 2 Слайд 3 Слайд 4
3. Постановка темы и цели урока	– Сформулируйте тему урока. – Выберите, чем мы будем заниматься сегодня на уроке? Списывать текст Чётко и ясноизлагать своё мнение Слушать и слышать товарища Решать задачи и примеры – Почему вы выбрали не все предложенные виды деятельности?	– Я думаю, что тема сегодняшнего урока «Решение задач». Дети выбирают нужные виды деятельности. Объясняют.
4. Открытие нового знания 5. Закрепление изученного материала. 6. Итог урока 7. Рефлексия.	– Бежит девочка дальше, а навстречу ей речка. – Реченька, реченька, скажи, куда гуси-лебеди полетели? – А реченька говорит: «Решишь задачи – скажу». – Помогите Машеньке составить и решить задачу. На доске рисунок к задаче: На берегу речки растёт 5 синих цветочков, а красных на 2 меньше. Сколько красных цветочков растёт на берегу? – Поставьте второй вопрос к задаче так, чтобы ответ первой задачи был в условии второй задачи. Сколько всего красных и синих цветочков растёт на берегу? – Могли бы вы сразу ответить на второй вопрос задачи? Почему? Работа с учебником. – На странице 62 учебника прочитайте задачи сегодняшнего урока. – Побежала Машенька дальше, а навстречу ей яблонька. И попросила она познакомить её с новыми задачами. Найдите и прочитайте задачу под номером 1. Запись краткого условия на доске: – Повторите условие задачи. – Повторите вопрос задачи. 1 – 7 ш. ? ш. 2 – ?, на 3 ш. Б -Что нужно знать, чтобы ответить на вопрос задачи? – Сколько шариков на первой проволоке? – Что сказано о числе шариков на второй проволоке? – Можно ли узнать, сколько шариков на второй проволоке? – Каким действием? Запишите первое действие. – Можно ли теперь узнать, сколько шариков на двух проволоках? – Каким действием? Запишите второе действие. – Запишите ответ. – Мы впервые встретились с задачей, решение которой нельзя записать в одно действие. Такие задачи называются составными и решаются в два действия. – Прочитайте в учебнике план решения этой задачи ещё раз. Физкультминутка. – Устала Машенька, давайте и мы вместе с ней отдохнём. Мы ногами топ- топ, Мы руками хлоп – хлоп, А потом прыг – скок И ещё разок. А потом вприсядку, А потом вприсядку, А потом вприсядку, И снова по порядку. Побежим мы по дорожке – Раз, два, три! И похлопаем в ладошки – Раз, два, три! И покрутим головами – Раз, два, три! Все танцуйте вместе с нами – Раз, два, три! -Прочитаем задачу под № 2. – Повторите условие задачи. – Повторите вопрос задачи. 1 – 8 кг ? кг 2 – ?, на 2 кг Б – Можно сразу ответить на вопрос задачи? Что для этого нужно знать? – Можем это узнать? Каким действием? – Теперь можно узнать, сколько всего кг яблок в двух ящиках? Каким действием? – Назовите ответ. – Показала яблонька дорогу к дому Бабы яги. Прибежала Машенька. А там братец Иванушка яблочки собирает и говорит: «Пока яблочки не соберу, никуда не пойду». – Сейчас мы поиграем с вами в игру. Иванушка рассыпал яблочки по всему классу, а вы должны их собрать. Работа по вариантам: первый вариант ищет примеры с ответами 17 и 16, второй вариант с ответами 19, 3,2. Примеры на карточках: 8 + 2 + 7 = 12 – 2 – 7 = 9 + 1 + 6 = 19 – 9 – 8 = 6 + 4 + 9 = 16 – 6 – 7 = 12 – 2 – 8 = 9 + 1 + 7 = 16 – 6 – 7 = 20 – 10 – 8 = 20 – 10 + 7 = 12 – 2 – 1 = 20 – 1 + 0 = 10 + 0 + 6 = 10 + 8 – 2 = – Увидела Баба яга, что дети домой собрались, и говорит: «Так уж и быть, отпущу вас домой, но прежде выполните моё задание.» Задание по выбору учащихся. – Перед вами карточка. На ней 2 задания. Решите задачу по вариантам 1 уровень 2 уровень Реши задачу. На верхней полке 7 книг, а на нижней на 4 книги меньше. Сколько книг на этих двух полках? Реши задачу. На верхней полке 7 книг, а на нижней на 3 книги большеСколько книг на этих двух полках? – С каким видом задач мы познакомились на уроке? – Что вам особенно понравилось на уроке? – Какие были трудности? -А теперь на шкале успешности отметьте, трудно ли вам было решать составные задачи. – Вот и вернулись ребятки домой, а там их ждут родители. Они благодарят вас за помощь. – Оцените своё настроение с помощью яблочек. Раскрасьте их в тот цвет, какое настроение у вас было на уроке.	Дети составляют задачу. Называют решение. Называют решение. – Нет. – Не знакомы с этим видом задач. 1 ребенок читает задачу – Сколько шариков на первой проволоке и на второй. – 7. – На 3 больше. – Да. 1)7 + 3 = 10(ш.) – Да. 2)10 +7= 17(ш.) Ответ: всего 17 шариков. Один человек читает план решения задачи. Дети повторяют движения за учитетелем. 1 ученик читает задачу Разбирают задачу по плану в учебнике. 1)8+2=10(кг) 2)10+8=18(кг) Ответ: всего 18 кг яблок. На доске вывешены яблочки с числами 17, 16, 19, 3, 2. У ребят на местах карточки с примерами. Решают примеры. Первый вариант называют примеры с ответами 16, 17, второй вариант – с ответами 19, 3, 2. Учитель записывает пример под нужным яблочком. Дети решают задачу по вариантам. Отвечают на вопросы Учащиеся ставят крестик там, какого уровня достигли в решении новых задач: красная линия – трудно; середина – не очень; зелёная – легко. Раскрашивают яблочки	Слайд 5 Слайд 6 Слайд 7 Слайд 8 Слайд 9 Слайд 10

задачи в одно действие. Математика 2 класс.

В каждом из тестов нужно правильно выбрать одно из действий: сложение «+» или вычитание «-».

Задание 1

Оля сложила фигуру из 18 кубиков, а Лена из 12. На сколько кубиков больше использовала Оля, чем Лена?

Решение:
• 1) «-».

Задание 2

Олег нарисовал 7 рыцарей и раскрасил их темными цветами, а потом еще 8 рыцарей и раскрасил их светлыми цветами. На сколько больше получилось у Олега светлых рыцарей, чем темных?

Решение:
• 1) «-».

Задание 3

В букете было 7 роз, гвоздик на одну больше. Сколько гвоздик было в букете?

Решение:
• 1) «+».

Задание 4

На столе стояло 6 стаканов и столько же кружек. Сколько кружек и стаканов вместе стояло на столе?

Решение:
• 1) «+».



Задание 5

На одной клумбе росло 12 роз, что на 7 роз больше, чем на другой клумбе. Сколько роз росло на другой клумбе?

Решение:
• 1) «-».

Задание 6

Маша и Света вырезали снежинки. Маша вырезала 11 снежинок, а Света 8. Сколько всего снежинок вырезали девочки?

Решение:
• 1) «+».

Задание 7

В коробке лежало несколько шариков. Красных лежало 8, а зеленых на 4 меньше. Сколько зеленых шариков лежало в коробке?

Решение:
• 1) «-».



Задание 8

На подносе лежало 9 яблок, а груша на 3 меньше. На сколько больше на подносе лежало яблок, чем груш?

Решение:
• 1) «-».

Задание 9

В одном бидоне было 6 литров молока, а в другом на 2 литра меньше. Сколько литров молока было во втором бидоне?

Решение:
• 1) «-».

Задание 10

Маленький ежик принес 6 грибов, а большой еж на 5 грибов больше. Сколько грибов принес большой еж?

Решение:
• 1) «+».

Задание 11

С одного куста винограда собрали 4 кг винограда, а с другого на 3 кг больше. Сколько кг винограда собрали со второго куста?

Решение:
• 1) «+».

Задание 12

До обеда продавец продал 4 коробки печенья, а после обеда на 1 коробку меньше. Сколько коробок печенья было продано после обеда?

Решение:
• 1) «-».

Задание 13

В классе учится 12 мальчиков, а девочек на 3 больше. Сколько девочек учится в классе?

Решение:
• 1) «+».

Задание 14

Саша покрасил 6 метров забора, а его отец на 5 метров больше. Сколько метров забора покрасил отец Саши?

Решение:
• 1) «+».

Задание 15

В одной песочнице играло 7 детей, а в другой на 2 ребенка меньше. Сколько детей играло во второй песочнице?

Решение:
• 1) «-».



Визуальные модели для решения задач в 1-м классе

Когда учащиеся поступают в 1-й класс, они продолжают работать над пониманием математики, используя ранние структуры, такие как журнал «Детский сад», который мы представили на прошлой неделе, но теперь мы начинаем добавлять в смесь визуальные модели!

Давайте подытожим путь развития ребенка через решение задач:

1. В раннем детстве ребенку требуется много соответствующего развитию опыта взаимодействия с реальными объектами в физическом мире.
2. Физический мир запечатлен в количественной картине, которую маленькие дети наблюдают и используют как плацдарм для математических бесед.
3. Мы переходим к более структурированному математическому рабочему коврику, чтобы помочь учащимся связывать числа со словами и слова с числами, используя знакомые ситуации из реальной жизни.
4. Рабочий коврик по математике уступает место официальному математическому журналу в детском саду, в котором используются навыки понимания математики. Он предоставляет учащимся структуру для объяснения своего понимания чисел в реальных ситуациях, которые будут использоваться в начальной школе.

Каждый этап развития основывается на навыках, полученных на предыдущем этапе, поэтому важно, чтобы учащиеся не торопились пройти эти этапы. Цель состоит в том, чтобы научить учащихся почему позади как , чтобы они не просто запоминали процедуры, но и действительно понимали, что происходит при решении задач.

По моему мнению, этот 1-й класс является последним этапом в развитии Math5Littles. После этого не так много строительных лесов, поэтому мы действительно хотим тщательно реализовать все предыдущие этапы решения задач, прежде чем отпустить студентов, потому что мы не хотим, чтобы они начали гадать и проверять. Отправляя учащихся на этот путь развития, мы пытаемся создать прочную основу для визуальных моделей, которые помогут им понять решение проблем.

Как мы учили решать задачи

Когда я преподавал в первом классе, я помню стратегию, которую мы использовали для решения задач, называемую CUBS. метод. Каждая из этих букв обозначала шаг в процессе решения задачи, чтобы учащиеся могли запомнить, что нужно делать: C — обвести цифры, U — подчеркнуть слово, B — выделить операцию, S — решить задачу. Кажется, это простой процесс, который дает детям действительно отличную структуру, чтобы начать понимать, какие слова задают задачи, верно? Но я понял, что эта стратегия не работает в долгосрочной перспективе.

Когда ребенок читал историю о сложении части-целого или вычитании части-целого, бокс и подчеркивание работали отлично. Но когда мы добрались до задач сравнения, все развалилось.

«У Шеннон 5 леденцов, а у Скотта на 4 леденца больше, чем у Шеннон. Сколько их всего вместе?»

Я наблюдал, как студенты следовали этой процедуре с этим типом задач. Они обвели 4 и 5, подчеркнули важную информацию и обвели рамкой слова вместе , что означает добавить, потому что мы все видели T-диаграммы словаря сложения/вычитания – там написано разница , это означает, что мы собираемся вычесть, если вы видите все вместе , мы собираемся добавить . Но эта стратегия дает мне 4, 5 и вместе . Если вы вернетесь к вопросу, то поймете, что ответ не 9.

Как я часто делаю, я спросил себя почему ? Почему не 9? Чтобы расшифровать этот ответ, требуется немного больше понимания прочитанного. Проблема говорит, что у меня было 5 леденцов на палочке. У Скотта было 4 больше, чем меня, а это значит, что у него тоже было 5. Сложив это, у него было 9, а у меня было 5, так что всего было 14.

Почему мы учим детей процедурам, которые они не понимают? Иногда стратегии, которым мы обучаем в математике, являются условными, то есть они работают только для определенного количества детей или определенного периода времени. Затем вам нужно беспокоиться об обучении их тому, как применять это и правилам его применения, и то, что должно было облегчить ученикам, в конечном итоге становится более сложным.

Когда мы начнем работать со стратегиями, я хочу иметь возможность найти эту вертикальную молнию, то есть, если я покажу вам, как эта стратегия может работать в первом классе, она должна работать и по мере того, как ребенок становится старше, чтобы он не каждый год приходится изучать совершенно новый набор стратегий, потому что каждый учитель преподает его по-своему. Честно говоря, метод CUBS, вероятно, сработает для 75% задач в первом классе. Учащиеся решают более сложные задачи на сложение часть-целое, вычитание часть-целое, отсутствующие слагаемые часть-целое, и они начинают решать несколько многошаговых задач, каждая из которых подходит к семейству задач часть-целое, для которых CUBS метод работает хорошо. Но когда вы выходите из этого жанра проблем, он разваливается.

Вот почему даже в журнале «Детский сад» мы используем систему кодирования для наших задач. Учителя и ученики должны начать изучать различные характеристики существующих типов сюжетных задач, что продвинет их вперед.

В журнале Kindergarten мы описали сложение часть-целое, вычитание части-целого, недостающее сложение часть-целое, несколько задач с числами для подростков и смешанный обзор. Дневник очень структурирован, потому что он предназначен для того, чтобы учащиеся думали о том, что они читают в задаче на рассказ: у нас есть рассказ, форма предложения, область быстрого рисования, числовая связь, 10-кадр и вычисление. область. Когда они переходят в 1-й класс, как мы можем убрать некоторые из этих строительных лесов, сохраняя при этом их соответствие уровню развития?

Мы должны быть очень осторожны с тем, как мы совершаем этот переход, потому что очень быстро учащиеся могут перейти к стратегии «обведи числа, вставь слово в рамку», и много раз они просто обращаются к нам, потому что они не знают, что делать. Это проблема со словами, и это сбивает с толку, поэтому они просто добавляют, потому что мы говорим о добавлении этой недели.

Аддитивные задачи на сравнение 

Аддитивные задачи на сравнение, где у меня есть сумма, а у вас та же сумма, но у вас может быть больше или меньше, чем у меня, вводятся после того, как учащиеся потратили некоторое время на работу над многоэтапной частью. целые проблемы.

По моему мнению, этот тип задач представляет собой языковую игру, из-за которой дети сбиваются с толку, пытаясь точно понять, о чем они спрашивают. Итак, мы действительно хотим, чтобы дети сделали шаг назад, чтобы понять проблемы аддитивного сравнения, которые в наших журналах обозначаются кодом AC. Я считаю, что построение этих проблем с помощью кубов unfix — хороший способ начать.

Давайте возьмем такую ​​задачу: у Шеннон есть 10 ручных камней, а у Шерри 4 ручных камня. На сколько камней у Шеннон больше, чем у Шерри?

В некотором смысле может показаться, что это может быть проблема с отсутствующими слагаемыми, но на самом деле мы сравниваем мои любимые камни с любимыми камнями Шерри и спрашиваем, на сколько больше у одного больше, чем у другого. Это действительно требует, чтобы студенты подняли его на конкретный уровень и сделали модель бара с кубами unifix.

Я положил 10 кубиков, чтобы обозначить любимые камни Шеннон, а затем я использую кубики разного цвета, чтобы показать 4 камня Шерри. Затем я хочу сравнить длины этих двух полос и выяснить, в чем на самом деле заключается проблема, а именно в том, промежуток между местом остановки бара Шерри и баром Шеннон. Знак вопроса просит сколько еще у Шеннон?

Иногда язык задачи аддитивного сравнения может быть изменен на противоположный и сказать, на сколько меньше у Шерри? Поскольку это игра слов, которая иногда сбивает учащихся с толку, нам действительно нужно подумать о том, как мы будем учить детей решать подобные задачи.

Визуальные модели для аддитивных задач сравнения

Если бы я выстроил в ряд все программы, с которыми мы работаем, каждая из них имеет немного другое название для визуальных моделей: чертежи моделей, диаграммы лент, модели стержней, единичные стержни. . Мы собираемся называть их визуальными моделями для текстовых задач.

Это не те маленькие быстрые рисунки, которые мы делали в детском саду, потому что по мере взросления учеников и усложнения задач я не смогу нарисовать 13 уточек, а затем еще 9, потому что это займет слишком долго! Вместо этого я хочу поместить его в визуальную модель, в которой есть эти единицы.

Этот первый год обучения является переходным периодом, когда дети переходят от быстрого розыгрыша к тому, что я буду называть пропорциональными полосами, длина отдельных кубов которых представляет величины, о которых мы говорим в задаче. .

Допустим, у Эрин есть 4 книги, но потом она идет в библиотеку и берет еще 3. Каждый куб или квадрат представляет собой книгу, которая помогает детям перейти от быстрого рисования, которое они делали в детском саду, к более формальной структуре. Мы по-прежнему могли поставить крестик в ячейке, чтобы обозначить книги, которые были у Эрин, и кружок в ячейках, чтобы обозначить книги, которые она получила в библиотеке, просто чтобы различать их.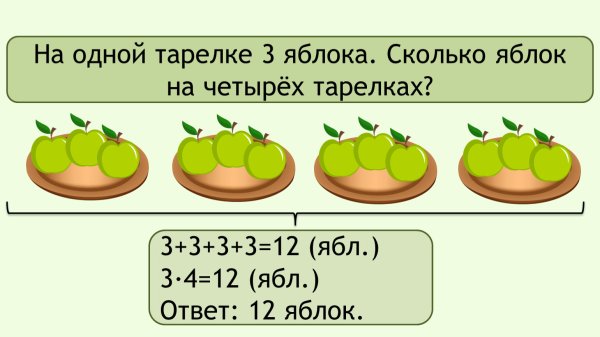 Рисунок — это инструмент понимания, и мы действительно меньше сосредотачиваемся на ответе на вопрос, чем на выяснении того, как его решить. Я думаю, что это самая непонятная часть визуальных моделей.

На прошлой неделе я работал с первоклассником по телефону Zoom, и этот учитель не смог посетить наш семинар в своем кампусе по визуальным моделям. Она, как и большинство учителей, с которыми я работаю, не понимала, почему визуальные модели так важны. Она считала, что ее ученики должны уметь быстро рисовать, и не понимала, зачем им нужно делать коробки. Она сказала мне, что была ярым сторонником поощрения студентов решать задачи разными способами, так зачем ей учить студентов такой процедуре и заставлять их решать текстовые задачи таким образом.

После того, как я показал ей ту же последовательность решения проблем, которую мы проходили в нашем блоге последние несколько недель, она была продана! Я провел ее по пятому классу, чтобы помочь ей понять, почему в 1-м классе мы просим учеников перестать делать быстрые зарисовки и начать использовать визуальную модель, которая имеет линейку единиц измерения с различными частями. Эта пропорциональная модель также является отличным переходом к использованию непропорциональной планки.

Допустим, у меня было 92 драгоценных камня, а у Шерри 45 драгоценных камней. Быстрое рисование явно не сработает для этой задачи, и у меня недостаточно места на бумаге, чтобы нарисовать пропорциональную модель для этих чисел. Но я могу нарисовать более длинную полосу, обозначающую скалы Шеннона, напишите через 92 камня и нарисуйте более короткую полосу, чтобы показать 45 камней Шерри, чтобы я мог видеть пропорциональность.

Когда мы создаем визуальные модели для текстовых задач, самое сложное помнить, что на самом деле это не имеет ничего общего с математикой! На самом деле мы не решаем проблему на модели; мы используем исключительно стратегию понимания прочитанного.

Одно из самых больших заблуждений, с которыми мы столкнулись, когда приступили к развертыванию образцов журналов для 1-го класса, которые я буду использовать в этом видео, заключалось в том, что в строке не указывается итоговая сумма. Если задача требует итоговой суммы, мы представляем ее в визуальной модели знаком вопроса.

Мы также хотим пометить визуальную модель. Например, поставив букву Б над книгами, которые были у Эрин, и буквой Л над книгами, которые она получила в библиотеке.

Весь смысл этого процесса заключается в том, чтобы предоставить учащимся систематический способ решения задач, который не перестает работать после 1-го класса или когда вы начинаете работать над задачами другого типа. На самом деле, эта стратегия распространяется на задачи мультипликативного сравнения и дроби вплоть до соотношений и пропорций в средней школе.

Пошаговое решение проблем

Этот пошаговый контрольный список, который мы используем, помогает учащимся стать более независимыми в этом процессе по мере их продвижения. Мы немного вводим его в детский сад как процесс, в большей степени управляемый учителем, но он также интегрирован в классную комнату первого класса, где дети должны решать пошаговый процесс визуальной модели. Как вы можете видеть в примерах, у нас есть профессор Барбл, объясняющий шаги.

Прочитайте задачу. Затем попросите кого-нибудь прочитать и повторить, и каждый раз, когда будет представлена ​​новая часть математической информации, мы будем вставлять часть. Итак, когда дети читают задачу, они начинают учиться анализировать то, о чем их спрашивают.

Не все первоклассники смогут прочитать задачу-рассказ, но этот процесс моделируется изо дня в день в классе первого класса, так что со временем ребенок станет самостоятельным.

Я буду читать задачку: у Марка 9клубники, 6 из них мелкие. Остальные большие. Сколько клубники крупной?

 

Тогда я вернусь и прочитаю по частям: У Марка 9 клубник . Это новая часть математической информации, поэтому учащиеся будут повторять это утверждение и выделять его или зачеркивать. Студенты также любят говорить кусков! Тогда продолжим чтение: Шесть из них были маленькими. Я остановлюсь, повторю, а ученики говорят кусок! , поскольку они отмечают этот фрагмент в своих журналах. Теперь у нас есть две части математической информации. Продолжим: Остальные были большими . Повторите, а затем кусков! Итак, у нас есть три раздела информации, которую нам дала проблема, которую нам нужно воспроизвести в нашей визуальной модели. Наконец, Сколько ягод клубники больших? Повторите это, а затем кусок!

Медленно и методично решая задачу, учащиеся могут действительно увидеть те разделы, которые они читают, и, переходя к последующим шагам решения задачи, они могут фактически отметить, что они включили все куски информации в свою визуальную модель.

Создать форму предложения. Что такое форма предложения? Проще говоря, это формулировка проблемы в полном предложении. Я не могу вам передать, сколько раз я видел, как ученики решали задачки на рассказы и на самом деле забывали, о чем их спрашивают, потому что они так увлекались арифметикой и выясняли, что они делают! Таким образом, этот шаг удерживает их внимание на том, что на самом деле задает проблема.

В нашей задаче меня спросили, сколько ягод клубники больших? Чтобы выразить это в форме предложения, я бы сказал: У Марка есть ____ большая клубника. я люблю говорить Хмм для ____ , пока мы читаем это вслух.

В детском саду мы предоставляем предложение для учащихся, оставляя пустое место для их ответа. Но в 1-м классе мы убираем часть строительных лесов. Может быть сказано: «Было _____ больших ____», и учащиеся должны заполнить пропуски.

Форма предложения — отличный способ убедиться, что дети понимают то, что читают. Как правило, ученикам первого класса трудно составить предложение, потому что они еще не готовы в своем развитии дать вам полный ответ при чтении. Но учащиеся должны будут составлять предложения со 2-го по 5-й класс, чтобы мы могли быть уверены, что они понимают поставленные задачи, поэтому это действительно отличная практика, чтобы начать в 1-м классе с строительных лесов.

Пропорциональная модель. Начинаем 1 класс с пропорциональной модели. Мы можем построить здесь «кто» или «что», и ученики в конце концов начнут изучать, что входит в эту визуальную модель. В данном случае мы говорим обо всей клубнике Марка, хотя сам вопрос заключается только в том, сколько из них крупных.

В пропорциональной модели вы можете увидеть 9 квадратов. Это проблема с отсутствующим дополнением, поэтому в заголовке будет PWMA вверху, и будет ровно девять квадратов. Некоторые люди могут подумать, что это выдает себя, но помните цель визуальных моделей? Задача состоит не в том, чтобы решить задачу, а в том, чтобы понять, что в ней происходит, поэтому нас больше волнует, сможет ли ученик правильно обозначить рисунок.

В этом примере учащийся подытожит 9 и вычеркнет первую часть задачи, которую мы читали ранее — У Марка девять ягод клубники.

В следующей части говорится: «6 из них маленькие». В шести полях я поставлю шесть крестиков или маленькие кружочки, а вверху напишу маленькими буквами или сокращу s .

Потом написано «остальные большие». Я мог бы пометить эту другую часть ящиков буквой B как большую или написать все слово, если бы захотел. Затем мне нужно поставить вопросительный знак над этим разделом между 9(общее количество ягод клубники) и 6 (количество мелких ягод клубники). Этот раздел представляет собой большую клубнику, и это то, что моя форма предложения напоминает мне, что я ищу.

Технически ученик может просто посмотреть на эту простую пропорциональную модель и сказать: есть 3 большие клубники , потому что она прямо перед ним. Таким образом, некоторые люди могут подумать, что этот дневник слишком прост, но в конце концов студенты укрепляют этот процесс. Они возвращаются к задаче и ставят галочку, когда добавляют крестики или кружочки для шести маленьких ягод клубники. Они выставляют чек, когда говорят о том, чтобы положить большую клубнику. Затем они ставят знак вопроса, чтобы показать, что мы ищем. Есть много деталей, которые мы ищем, чтобы дети взаимодействовали с текстом по математике, чтобы показать понимание.

В некоторых наших школах мы поместим панель единиц внизу страницы. В журнале для 1-го класса, который мы создали для Math5Littles, мы собираемся убрать планку и ввести непропорциональную планку чуть позже в этом году. Нет ничего плохого в том, чтобы иметь модель пропорционального стержня, а затем под ним иметь непропорциональный стержень. В нашем журнале мы планируем показать пропорциональную полосу, а затем ввести оба типа полос, чтобы дети могли видеть взаимосвязь между ними. Если где насчет этой непропорциональной полосы, куда мне ее нарезать, чтобы вставить девятку? И где тогда мой вопросительный знак? он помечен? и т. д.

Неотъемлемыми частями визуальных моделей являются: маркировка кто или что, взятие планки и корректировка ее на основе предоставленной информации, а также запись вопросительного знака. Тогда пора решать!

Расчет. Хотя этот шаг может показаться необязательным, потому что наша примерная задача очень проста, и первоклассникам, после того как они решат так много, она кажется простой, и как учителя, так и ученики могут задаться вопросом, зачем они вообще это делают, но я могу обещать, что эти проблемы станут более сложными, очень быстро. В нашем журнале для 1-го класса мы представим этот взгляд на пропорциональную полосу, а затем перейдем к пропорциональным и непропорциональным моделям, а затем, в конце концов, просто оставим ее пустой и попросим ученика поставить непропорциональную полосу, чтобы увидеть, что они могут развить. эта прогрессия.

Цели для 1-го класса

Цель состоит в том, чтобы к концу первого года обучения учащиеся могли решать задачи с большими числами и непропорциональной планкой. Вы, конечно, не хотите торопиться с этим прогрессом. 1-й класс — это действительно хорошая опора для учеников, чтобы они достигли этой точки независимости, потому что, когда мы добираемся до 2-го класса, мы не делаем много строительных лесов. В предложениях больше открытых окончаний, больше пропусков, и студенты выполняют больше работы.

Кроме того, мы хотим смешать типы задач, которые мы решаем, чтобы дать учащимся время понять их. Вы можете сделать три дня сложения части-целого, чтобы увидеть, смогут ли они получить это под своим поясом. Затем сделайте некоторое вычитание часть-целое, а затем смешайте их, чтобы увидеть, просто ли учащиеся следуют шаблону, где мы складываем сегодня или вычитаем сегодня. Мы хотим знать, что они действительно могут применить то, что изучают. Далее следуют многошаговые задачи, где учащиеся должны складывать, а затем вычитать или наоборот. Дайте учащимся много хорошей практики, а затем снова перемешайте, чтобы увидеть, действительно ли они следуют словам или просто изучают процедуру. Последний тип задач, которые мы будем интегрировать в первый класс, — это аддитивные сравнения.

Видеоуроки

В видеоуроках вы увидите аспекты четырех различных проблем. У некоторых будет полоса пропорциональности, у некоторых будет пропорциональная и непропорциональная, а у некоторых просто ее не будет, чтобы вы могли получить общее представление о том, как это выглядит по ходу дела.

[yotuwp type=”playlist” id=”PL76vNL0J-a405ysBIwEwXfaMp5883yGh5″ ]

Пока вы смотрите видео, подумайте, как вы могли бы настроить это в своем классе, начиная с некоторых примеров задач, которые мы предлагаем в качестве бесплатно скачать сегодня. Скоро мы выпустим полный журнал для 1-го класса, так что следите за обновлениями!

Присоединяйтесь к нам на следующей неделе для решения задач во 2-м классе: С какими проблемами предстоит столкнуться во 2-м классе? Как журналы кодируются? По мере того, как мы начинаем смотреть на то, как кодируются журналы, вы, безусловно, можете использовать эти обучающие видеоролики прямо сейчас в своем классе или на дистанционном обучении, думая о проблемах истории по-другому.

Готовые к работе в классе сложные математические задания, классы K-1

Из математики, грамотность, равенство, многоязычные учащиеся и SEL, оценивание, школьное консультирование, и лидерство в сфере образования, наши книги основаны на исследованиях и написаны экспертами по темам, наиболее актуальным для педагогов сегодня.

 

Поделиться:

Вовлечение учащихся в занятия математикой

Автор: Фрэнсис М. Феннелл, Джеффри Чен Ши, Бет МакКорд Кобетт, Карен С. Карп, Латренда Дуретта Найтен, Делиз Р. Эндрюс

С 56 готовыми к выполнению увлекательными математическими задачами это руководство поможет вашим первоклассникам получить максимально глубокий математический опыт.

информация о продукте

• Уровень обучения: PreK-12
• ISBN: 9781544399102
• Опубликовано: Корвин
• Серия : Серия Corwin Mathematics
• Год: 2021
  
• Количество страниц: 336
  
• Дата публикации: 06 мая 2021 г.

Цена: 37,95 долларов США

Описание

Описание

Подробные планы помощи учащимся начальных классов в углубленном изучении математики 

Вы неустанно работаете над тем, чтобы сделать уроки математики содержательными, сложными, доступными и увлекательными? Вы тратите часы, которых у вас нет, на поиск, адаптацию и создание задач, чтобы предоставить вашим ученикам богатый опыт, дополняющий вашу учебную программу по математике? Помощь прибыла! Готовые сложные математические задания для классов K-1 содержит 56 ориентированных на исследования и стандарты заданий, требующих высокой познавательной способности, которые заставят ваших учащихся заниматься углубленным изучением проблем.

Эти готовые к выполнению увлекательные задания объединяют навыки, концепции и практики, побуждая учащихся рассуждать, решать проблемы, обсуждать, исследовать несколько путей решения, связывать несколько представлений и обосновывать свое мышление. Они помогают учащимся следить за своим мышлением и связывать знания математики, которые они знают, с новыми ситуациями. Другими словами, эти задачи позволяют учащимся по-настоящему заниматься математикой! Это руководство, написанное с учетом сильных сторон и внимательного отношения ко всем учащимся, включает в себя:

• Выполнять уроки на основе задач, ссылаясь на математические стандарты и практики, словарный запас и материалы 
• Загружаемые инструменты планирования, страницы ресурсов для учащихся, продуманные вопросы и подсказки для формирующего оценивания

. • Руководство по подготовке, запуску, содействию и анализу каждой задачи
. • Примечания о доступе и равенстве с упором на сильные стороны учащихся, продуктивную борьбу и дистанционную или альтернативную среду обучения.

Это руководство, содержащее заключительные рекомендации по адаптации или созданию дополнительных сложных задач для ваших учащихся, поможет вам дать всем вашим учащимся максимально глубокий, обогащающий и увлекательный опыт изучения математики.

Автор(ы)

Автор(ы)

Фрэнсис М. Феннелл

Джеффри Чен Ши

Бет МакКорд Кобетт

900 29 Бет МакКорд Кобетт, EdD, is Профессор образования и заместитель декана в Университете Стивенсона, где она руководит, преподает и поддерживает учителей дошкольного, начального и среднего образования в области математического образования. Она бывший классный руководитель, специалист по элементарной математике, адъюнкт-профессор и руководитель университета . Бет также работала директором программы семинаров первого года обучения в Университете Стивенсона. Недавно она завершила трехлетний срок в качестве избранного члена правления Национального совета учителей математики и была бывшим президентом Ассоциации преподавателей математики штата Мэриленд (AMMTE).   Бет руководит профессиональным обучением в области математического образования как на региональном, так и на национальном уровне. Бет является лауреатом премии «Педагог года по математике» Совета учителей математики штата Мэриленд (MCTM) и премии «Выдающиеся выпускники» Университета Джона Хопкинса. Бет также получила премию Роуз Доусон Университета Стивенсона за выдающиеся достижения в области преподавания как в качестве внештатного, так и штатного преподавателя. Бет верит в создание сообщества, основанного на сильных сторонах, со своими учениками, и стремится сделать свое учебное пространство привлекательным, проводить уроки, пробуждающие любопытство и инновации, и культивировать позитивную продуктивную борьбу.

Карен С. Карп

Карен С. Карп — профессор Педагогического факультета Университета Джона Хопкинса. Ранее она была профессором математического образования на факультете дошкольного и начального образования в Университете Луисвилля, где получила Президентскую награду за выдающиеся заслуги в обучении и награду за выдающиеся заслуги за служебную карьеру. Она является бывшим членом совета директоров Национального совета учителей математики (NCTM) и бывшим президентом Ассоциации преподавателей учителей математики (AMTE). Она является членом группы авторов практического руководства What Works Clearinghouse по оказанию помощи учащимся начальной школы, испытывающим трудности с изучением математики, для Института педагогических наук Министерства образования США. Она является автором или соавтором примерно 20 глав книг, 50 статей и 30 книг, в том числе Математика в начальной и средней школе: обучение с развитием , Развитие основных знаний о сложении и вычитании для преподавания математики и Вдохновение девочек к математическому мышлению . Она имеет сертификаты преподавателя в области начального образования, средней математики и специального образования K–12.

Латренда Дюретта Найтен

Латренда Найтен работает преподавателем начальной математической программы в Батон-Руж, штат Луизиана. Она работает педагогом более 30 лет и является активным членом многих профессиональных организаций. В настоящее время она является руководителем группы NCSM Южного региона 2 в Луизиане и секретарем Benjamin Banneker Association, Inc. Латренда также в прошлом была членом Совета директоров NCTM.

Делиз Р. Эндрюс

Делиз Эндрюс является координатором по математике 3-5 государственных школ Линкольна в Линкольне, штат Небраска. За свою карьеру она работала как в сельских, так и в городских районах и преподавала математику ученикам всех возрастов, от детского сада до 8-го класса, математические методы бакалавриата и курсы для учителей математики для выпускников. Делиз является лауреатом Президентской премии за выдающиеся достижения в области преподавания математики и естественных наук, а также научным сотрудником Роберта Нойса. Она также является активным членом NCTM, в прошлом она была членом и председателем Комитета по услугам профессионального развития, членом комитетов региональных конференций и председателем комитета ежегодной конференции в Сент-Луисе, а также куратором профессиональных услуг NCTM.

Отзывы

Отзывы

Это карусель с карточками отзывов. Используйте кнопки «Назад» и «Далее» для навигации.

Название этой книги говорит о ее обещаниях.

Готовые к работе в классе насыщенные математические задачи предлагает учителям большой набор практических задач, чтобы вовлечь учащихся в беглость математики и развитие стратегического мышления — именно то, что ожидают все стандарты математики.

Джей Мактай
Автор и педагог

Эта книга – именно то, что нужно каждому учителю K–1! 56 заданий увлекательны, легко реализуемы и, что наиболее важно, «готовы к работе в классе». Учебные стратегии, представленные в начальных главах, и размышления, подчеркнутые в последней главе, обеспечивают соответствующую основу для учителей маленьких детей. Как опытный учитель K-1, я гарантирую, что воспользуюсь представленными идеями и буду призывать к этому других.

Хуанита Копли
Профессор Эмерита

Как руководитель округа по математике, я ценю эту серию, потому что знаю, что любая задача, которую выберут мои учителя, будет качественной. Я также высоко оцениваю обучение, основанное на исследованиях, представленное в первых нескольких главах, которое поможет моим учителям выбирать, планировать и выполнять задачи, чтобы максимизировать их потенциал.

Брайан Бушарт
Координатор учебной программы по начальной математике

Меган Франке
Временный председатель и профессор педагогики

Основой отличного преподавания математики является высококачественная задача, воплощенная в жизнь благодаря насыщенному взаимодействию. Эти задачи должны быть привлекательными и математически и педагогически генеративными — с интересным содержанием и математических процессов и практик. Эта ценная книга наполнена такими задачами, а также руководством по их планированию и выполнению, а также материалами для максимального удовольствия и пользы для учителей и их учеников.

Дуглас Х. Клементс
Заслуженный профессор университета, председатель Кеннеди по дошкольному обучению и исполнительный директор Института раннего обучения Марсико.

Я настоятельно рекомендую эту книгу, которая представляет собой основанную на исследованиях основу для решения разнообразных задач, которые связаны с предыдущим математическим пониманием, соответствующим контекстом, опытом и ресурсами учащихся и основаны на них, а также связаны с практикой преподавания математики. . Задачи с высокой когнитивной нагрузкой включали поддержку развития важных математических норм, практик и концепций.

Роберт К. Берри, III
Сэмюэл Брейли Грей, профессор математического образования

Эта книга отвечает на часто задаваемый вопрос: «Где я могу найти хорошие задачи?» Авторы собрали коллекцию разнообразных математических задач и дали рекомендации о том, как планировать и проводить уроки, связанные с ними, таким образом, чтобы поддерживать возможности для студенты, чтобы изучать математику с пониманием. Эта книга изменит правила игры для учителей детских садов и первоклассников, которые хотят, чтобы их ученики занимались математикой!

Маргарет (Пег) Смит
Почетный факультет

Найти правильное задание, побуждающее юных учащихся к математическому мышлению и рассуждениям, не всегда легко. Эта впечатляющая книга предлагает различные высококачественные задачи и рассматривает вопросы планирования и реализации. Это бесценный ресурс для всех, кто стремится предоставить полезный опыт для математиков детского сада и первоклассников!

Сьюзи Кэтт
Координатор по математике К–2

Объединив последние исследования с мощным голосом учителя, авторы написали книгу, обязательную к прочтению для каждого учителя математики, который хочет, чтобы их ученики имели более мотивирующий и мощный учебный опыт. Но авторы не просто утверждают, что учителя включают в свое обучение задачи, требующие высокой познавательной способности, — они предпринимают следующие шаги и фактически демонстрируют как планировать, реализовывать и поддерживать эти задачи, чтобы каждый ученик мог по-настоящему участвовать в выполнении математики!

Мэтт Ларсон
Бывший президент

Готовые к работе в классе сложные математические задачи, классы K–1 — это отличный ресурс для учителей, преподавателей и специалистов по профессиональному развитию, которые хотят вовлечь учащихся в математические задачи высокого уровня, требующие интеллектуальных усилий.