Задача на скорость время и расстояние: Задачи на движение
Скорость, время, расстояние. Задачи по математике 3 класс
Задачи для 3 класса
- Математические диктанты
- Комбинаторные задачи
- Нестандартные задачи
- Множество и его элементы
- Способы задания множеств
- Пустое множество
- Диаграмма Венна
- Диаграмма Венна. Часть 2
- Подмножество
- Множество. Задачи
- Скорость, время, расстояние
Числа от 1 до 100
- Сложение и вычитание
- Буквенные выражения
- Единицы длины
Контрольные работы
- Умножение и деление
- Итоговая контрольная работа
- 1 четверть
- 2 четверть
- Контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Контрольная работа 1
- Итоговые контрольные работы 3 класс
- Контрольная работа 1
Тесты.
- Тесты по математике 3 класс
- Табличное умножение и деление чисел
- Особые случаи умножения и деления
Примеры, уравнения
- Примеры
- Уравнения
- Кроссворды
Задание 1
Автомобиль проехал 180 км за 3 часа.С какой скоростью он ехал?
Решение
- Всё время движения автомобиля – 3 часа, а пройденый путь – 180 км. Значит за один час он проезжал 180:3=60. Его скорось 60км/ч
Задание 2
Миша прошол на лыжах 80 м за 20 с,а Игорь 45 м за 15 с. Кто из них шёл быстрее?
РешениеМиша затратил больше времени, чем Иигорь,но он и прошёл больше расстояние. Чтобы узнать, кто шёл быстрее,надо сравнить расстояния которий каждый из ребят проходил за одну секунду: 80:20=4 45:15=3. Миша за одну секунду проходил 4 м, а Игорь только 3 м.Значит, Миша шёл быстрее, или с большей скоростью.
Говорят так: Миша шёл 4 м в секунду,а Игорь 3 м в секунду.
80 : 20 = 4(м), 45 : 15 = 3(м)
Задание 3
- Объясни смысл предложений:
- а) Самолёт летит со скоростью 800 км/ч.
- б) Скорость теплохода 45 км/ч.
- в) Человек идёт со скоростью 4 км/ч.
- г) Меч-рыба развивает скорость 100 км/ч.
- д) Земля движется по орбите со скоростью 30 км/с.
- е) Черепаха ползёт со скоростью 4 м/мин.
- ж) Поезд идёт со скоростью а км/ч. Какие значения может принимать а?
- Можно ли сравнить скорость движения человека со скоростью черепахи?
Решение
- а) Самолёт пролетает за 1 час 800км.
- б) Теплоход проплывает за 1 час 45км.
- в) Человек проходит за 1 час 4км.
- г) Меч-рыба развивает скорость 100 км/ч.
- д) Земля преодолевает расстояние в 30км. за 1 секунду.
- е) Черепаха проползает 4метра за 1 минуту
- ж) а может быть целым положительным числом
- Скорость черепахи можно сравнить со скоростью человека, если выразить эту скорость в одинаковых величинах, например км/ч
Задание 4
- Найди:
- а) Скорость космического корабля, если он пролетел 56 км за 8 с.
- б) Скорость улитки, если она проползла 35 м за 7 ч.
- в) Скорость плота на реке, если он за 4 ч проплыл 16 км.
- г) Скорость автобуса, если он прошёл 120 км за 3 ч.
- д) Скорость велосипедиста, если он проехал 36 км за 2 ч.
Решение
- а) Скорость корабля 7 км/с
- б) Скорость улитки 5м/ч
- в) Скорость плота 4км/ч
- г) Скорость автобуса 40км/ч
- д) Скорость велосипеда 18км/ч
Задание 5
Решение
- Мальчик идет со скоростью 4км/ч
- Велосипедист едет со скоростью 18км/ч
- Электричка едет со оскоростью 90км/ч
- Скорость машины 60км/ч
- Скорость автобуса 45км/ч
- Скорость ракеты 6км/с
- Скорость самолета 900км/ч
Задание 6
Решение
- Волга едет со скоростью 100км/ч
- Жигули едут со скоростью 90км/ч
- Запорожец едет со скоростью 50км/ч
Задание 7
- а) Поезд прошёл 224 км за 4 часа.
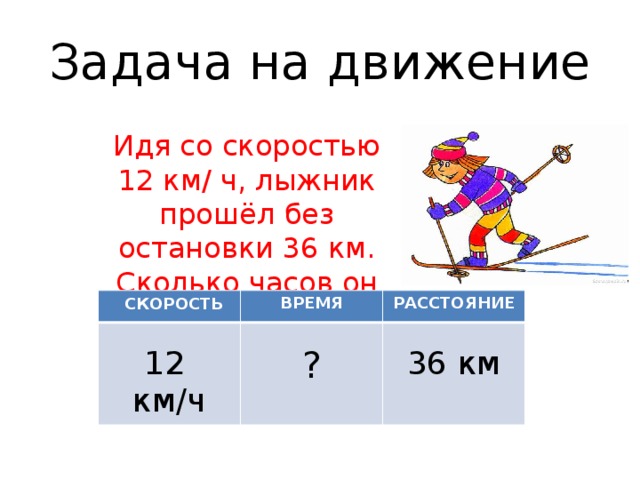
- б) Плот проплыл 27 км за 9 ч, а моторная лодка — 24 км за 2 ч. У кого из них скорость больше и на сколько?
Решение
- а) Скорость вертолета 168км/ч. Скорость поезда – 224 : 4 = 56км/ч, скорость вертолета в 3 раза больше поэтому 56 * 3 = 168.
- б) Скорость больше у моторной лодки на 9км/ч. Скорость плота 3км/ч = 27 : 9. Моторной лодки 12км/ч = 24 : 2. Значит 12-3=9.
Задание 8
| 5 ч 6 мин | 56 мин |
| 9 мин 20 с | 560 с |
| 1 сут. 15 ч | 115 ч |
| 108 мин | 1ч8мин |
| 734с | 7мин 34 с |
| 206ч | 2 сут. 6ч |
Решение:
5 ч 6 мин > 56 мин 9 мин 20 с = 560 с 1 сут. 15 ч
< 115 ч 108 мин > 1ч8мин 734с > 7мин 34 с 206ч > 2 сут. 6ч
Задание 9
- а) Грузовая машина за 8 ч прошла 280 км, а легковая машина это же расстояние — за 4 ч. Во сколько раз скорость грузовой машины меньше скорости легковой?
- б) Велосипедист за 3 ч проехал 57 км, а мотоциклист за 2 ч проехал на 71 км больше. На сколько километров в час скорость велосипедиста меньше скорости мотоциклиста?
Решение
- a) Сначала узнаем скорость грузовика 280 : 8 = 35км/ч. Затем скорость легковой машины 280 : 4 = 70км/ч. Чтобы узнать во сколько раз скорость грузовой машины меньше чем легковой нужно скорость грузовой разделить на скорость легковой: 70 : 35 = 2. Ответ: В 2 раза.
- б) Сначала узнаем скорость велосипедиста 57 : 3 = 19км/ч. Узнаем сколько проехал мотоциклист 57 + 71 = 128км. Узнаем скорость мотоциклиста 128 : 2 = 64км/ч. Узнаем разницу в скорости велосипедиста и мотоциклиста 64 – 19 = 45км/ч. Ответ: 45км/ч.
Задание 10
Придумай задачу, в которой надо найти скорость по известному расстоянию и времени, и реши её.
Решение Задача:
- Из пункта а вышел поезд. Через 4 часа поезд прибыл в пункт б. Какова скорость поезда если расстояние от пункта а до пункта б 360км.
Решение задачи:- 360 : 4 = 90км/ч. Скорость поезда 90км/ч.
Задание 11
Запиши множество делителей и множество кратных числа 14.
Решение
- Множество делителей: 1, 2, 7, 14.
- Множество кратных: 14, 28, 42, 56, 70, 84, 98, 102, 116, 130, 144, и так до бесконечности.
Задание 12
Реши уравнения с комментированием по компонентам действий:
- а) (40 • х): 10 = 28;
- б) у : 9 – 28 = 32;
- в) 39 + 490 : k = 46;
- г) (25 – а) • 7 = 63.
Решение
- а) Сначала узнаем значение выражения в скобках(40 • х) для этого надо 28 * 10 = 280, вычислем значение x = 280 : 40 = 70. x = 70.
- б) Сначала узнаем значение y : 9 для этого 32 + 28 = 60; узнаем значение y для этого 9 * 60 = 540.
- в) Сначала узнаем значение 490 : k для этого 46 – 39 = 7; что бы узнать значение k нужно 490 : 7 = 70. k = 70.
- г) Сначала узнаем значение выражения в скобках(25-а) для этого 63 : 7 = 9; Вычисляем значение а для этого 25 – 9 = 16. а равно 16.
Задание 13
Выполни сложение и вычитание. Сделай проверку:
- а) 547923 + 83699221;
- б) 483567823 + 998430;
- в) 4758036-50854;
- г) 2666990000 – 89607787.
Решение
- а) 84247144; проверка: 84247144 – 83699221 = 547923.
- б) 484566253; проверка: 484566253 – 483567823 = 998430.
- в) 4707182; проверка: 4707182 + 50854 = 4758036.
- г) 2577382213; проверка: 2577382213 + 89607787 = 2666990000.
Задание 14
По двору ходили гуси. Всего у них было 22 ноги. Подошли 3 утёнка и 4 козлёнка. Сколько ног гуляет теперь по двору?
Три утенка – это еще 6 ног, 4 козленка – это еще 16 ног потому что у козленка 4 ноги 4 * 4 =16. Теперь слаживаем все ноги: 22 + 6 + 16 = 44.
Ответ: 44 ноги гуляло по двору.
На странице использованы задачи и задания из книги Л. Г. Петерсон «Математика. 3 класс. Часть3.» 2008г. Ссылка на сайт автора: www.sch3000.ru
Простые задачи
- Задачи на умножение
- Задачи на деление по содержанию и на равные части
- Задачи на 1 действие
Составные задачи
- Задачи на нахождение суммы
- Задачи на нахождение уменьшаемого, вычитаемого, разности
- Задачи на 2 действия
- Задачи на 3 действия
- Задачи на разностное и кратное сравнение
Скорость, время, расстояние – формулы и примеры расчета
Вычислить скорость, время и расстояние часто бывает необходимо в повседневной жизни, когда мы рассчитываем время на дорогу. Все эти величины (время, расстояние и скорость) связаны между собой математической формулой и зная две из них всегда можно найти третью. Мы с вами рассмотрим, что понимается под этими величинами, как их найти, решим несколько задач.
Все эти величины (время, расстояние и скорость) связаны между собой математической формулой и зная две из них всегда можно найти третью. Мы с вами рассмотрим, что понимается под этими величинами, как их найти, решим несколько задач.
Скорость, время и расстояние — это ключевые параметры при решении задач на движение. Эти задачи есть и в ЕГЭ и в ОГЭ по математике. Сегодня мы подробнее остановимся на этих величинах.
Содержание
Расстояние
Расстояние — это физическая величина, означающая длину между двумя объектами. Расстояние обозначается буквой S и измеряется в единицах длины: метрах. Метр — это международно-принятая единица измерения длины. Однако встречаются и другие единицы длины — километр, сантиметр, миллиметр. В этом случае целесообразно перевести единицы длины в международную систему единиц (СИ).
Например: расстояние от Земли до Солнца равно 149 597 870 700 метров.
Расстояние связано со скоростью и временем:
S=v \cdot t
Вот тут таблица длин и их перевода в международную систему единиц — то есть в метры.
| Единицы длины | СИ |
| 1 сантиметр | 0,01 м |
| 1 километр | 1000 м |
| 1 дециметр | 0,1 м |
| 1 миллиметр | 0,001 м |
| 1 микрометр | 1·10-6 м |
| 1 миля | 1609,34 м |
| 1 фут | 0,3048 м |
| 1 ярд | 0,9144 м |
| 1 дюйм | 0,0254 м |
| 1 морская миля | 1852 м |
Время
Время — это физическая величина, которая обозначает непрерывное и необратимое (возможно) движение от прошлого к будущему через настоящее. Это фундаментальная физическая величина, единица измерения времени — секунда. Однако, в задачах могут использоваться и другие единицы времени — часы, минуты, дни.
Время можно найти по формуле:
t=\frac{S}{v}
Ученые о времени
По словам греческого философа Парменида (ок.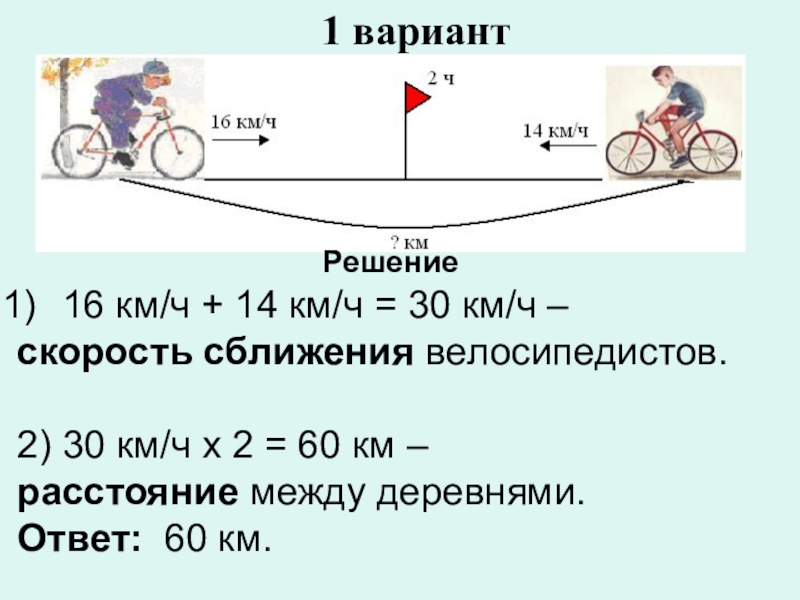 450 г. до н.э.), время и движение были иллюзиями. Его ученик Зенон Элейский разработал два знаменитых парадокса: «Ахиллес и черепаха» и «Парадокс летящей стрелы», чтобы доказать его утверждения. Платон, живший на пару поколений позже, считал, что время создано вместе со вселенной и существует независимо. Он рассматривал время как пустой контейнер, который можно заполнить движущимися вещами и событиями. Его ученик Аристотель считал, что время не существует независимо от событий, но время есть изменение и движение.
450 г. до н.э.), время и движение были иллюзиями. Его ученик Зенон Элейский разработал два знаменитых парадокса: «Ахиллес и черепаха» и «Парадокс летящей стрелы», чтобы доказать его утверждения. Платон, живший на пару поколений позже, считал, что время создано вместе со вселенной и существует независимо. Он рассматривал время как пустой контейнер, который можно заполнить движущимися вещами и событиями. Его ученик Аристотель считал, что время не существует независимо от событий, но время есть изменение и движение.
Аристотель пришел к выводу, что время не состоит из последовательных неделимых моментов «сейчас», как пытался сказать Зенон с помощью своего парадокса стрелы. Согласно Аристотелю, не существует серии моментов «сейчас», потому что такие моменты не могли бы исчезнуть в течение их собственной длительности или в следующий момент «сейчас». Исааку Ньютону (1642–1726) время понадобилось в качестве переменной в его уравнениях, и он начал думать о времени с научной точки зрения. Ньютон поддерживал идею Платона о независимости времени. Он разделил время на абсолютное (математическое) время и относительное (обычное) время.
Ньютон поддерживал идею Платона о независимости времени. Он разделил время на абсолютное (математическое) время и относительное (обычное) время.
Абсолютное время, или продолжительность, является реальным и математическим, и оно течет неуклонно, независимо от чего-либо внешнего. Относительное время кажущееся и является внешней мерой длительности, которая может быть обнаружена органами чувств с помощью движения, которое может быть точным или неточным.
Готфрид Лейбниц (1646–1716) был согласен с Аристотелем и думал, что без событий и перемен не было бы времени. Физик- теоретик Ли Смолин писал в 2010 году, что исследования квантовой гравитации подтверждают, что четырехмерное пространство-время имеет смысл только в том случае, если время реально, фундаментально и даже является единственным аспектом реальности, который мы непосредственно ощущаем.
Скорость
Скорость обозначается буквой — это физическая величина, которая обозначает какое расстояние проходит объект в единицу времени. Единица измерения скорости — м/с. Однако, встречаются также и км/ч и см/с (эти измерения не входят в международную систему единиц измерения). Скорость показывает как быстро изменяется расстояние во времени.
Единица измерения скорости — м/с. Однако, встречаются также и км/ч и см/с (эти измерения не входят в международную систему единиц измерения). Скорость показывает как быстро изменяется расстояние во времени.
Например, выражение 9 м/с означает, что тело за 1 секунду проходит 9 метров. То есть за 1 секунду 9 метров, за 2 секунду еще 9 метров, итого за 2 секунду — 18 метров. В курсе школьной математики мы считаем, что скорость равномерная во времени. То есть тело за равные промежутки времени проходит равные расстояния. То есть 9 м/с означает 9 метров в любую из секунд движения тела. Однако, в реальности движение бывает равномерное и неравномерное. Мы не рассматриваем неравномерное движение в курсе математики (1-6 класс), однако в курсе алгебры элементы кинематики с неравномерным движением рассматриваются.
Еще примеры: скорость 100 км/ч — это прохождение расстояния в 100 километров за 1 час.
Формула скорости
Скорость можно найти через расстояние и время по формуле:
v=\frac{S}{t}
Средняя скорость
Если движение тела можно разбить на несколько участков и в пределах каждого участка скорость тела не меняется, то целесообразно говорить о средней скорости.
Формула средней скорости:
v=\frac{S_{весь \; путь}}{t_{всё \; время}}=\frac{S_1+S_2+…+ S_n}{t_1+t_2+…+ t_n}
То есть средняя скорость это отношение всего пути, ко всему времени.
Скорости сближения и удаления
Понятие скорости ученики изучают еще в 4 классе, а далее это понятие расширяется и уточняется. Вводятся такие понятия как скорость сближения и скорость удаления. Не все педагоги используют эти понятия в своей работе, поскольку эти понятия можно использовать только при решении небольшого класса задач на движение и они ограничивают решение задач и другими условиями (например, если тела удаляются или сближаются не по одной прямой, а по перпендикулярным прямым). И все же, давайте мы уточним, о чем вообще идет речь.
Скорости сближения и удаления
Скорость удаления
Если два тела удаляются друг от друга, двигаясь по одной прямой, то в таких случаях говорят о скорости удаления. То есть скорость удаления характеризует расстояние, которое увеличивается по мере удаления двух тел в единицу времени.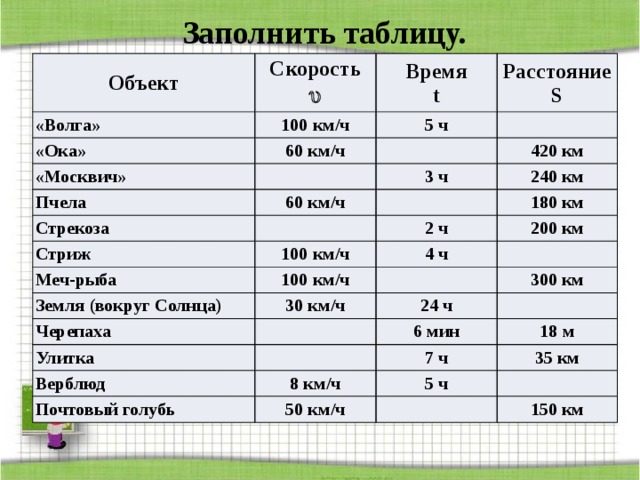
Допустим есть два пешехода, которые удаляются друг от друга, первый пешеход удаляется со скоростью 3 км/ч, а второй пешеход со скоростью 4 км/ч. Тогда скорость удаления будет:
3+4=7 км/ч.
Действительно, расстояние, пройденное первым пешеходом за один час будет 3 километра, а расстояние, пройденное вторым пешеходом за то же время будет 4 километра. Тогда при удалении пешеходов друг от друга расстояние между ними увеличивается на 7 километров в каждый час или наши пешеходы удаляются со скоростью 7 км/ч. Мы должны сложить скорости объектов.
Формула скорости удаления:
v_{удаления}=v_1+v_2
где — скорость одного тела,
— скорость другого тела.
Напомним, что это понятие можно использовать только если тела двигаются в разных направлениях, располагаемых на одной прямой.
Скорость сближения двух тел
Аналогично, рассмотрим ситуацию, если два пешехода двигаются навстречу друг к другу. Один пешеход за один час проходит расстояние 2 км, а второй пешеход за то же время проходит 5 км.
Значит, расстояние между ними будем уменьшаться со скоростью 5+2 = 7 км/ч.
Формула скорости сближения:
v_{сближения}=v_1+v_2
где — скорость одного тела,
— скорость другого тела.
Если один пешеход догоняет другого. То скорость сближения при движении в одном направлении можно определить, если вычесть из большей скорости меньшую.
То есть, если у нас второго пешехода (=3км/ч) догоняет первый пешеход (=5 км/ч), то скорость их сближения будет 2 км/ч:
Формула скорости сближения при движении вдогонку:
v_{сближения}=v_1-v_2
где — скорость одного тела,
— скорость другого тела. При этом
Таблица «скорость, время, расстояние» при решении задач на движение
При решении задач на движение очень удобно пользоваться такой таблицей, в которой три столбца с данными по скорости, времени движения тел и расстоянию, которое они проходят. Эта таблица, кстати помогает легко запомнить формулы скорости, времени и расстояния, если представить что первый столбец — это первый множитель, второй столбец — второй множитель, а третий столбец — произведение.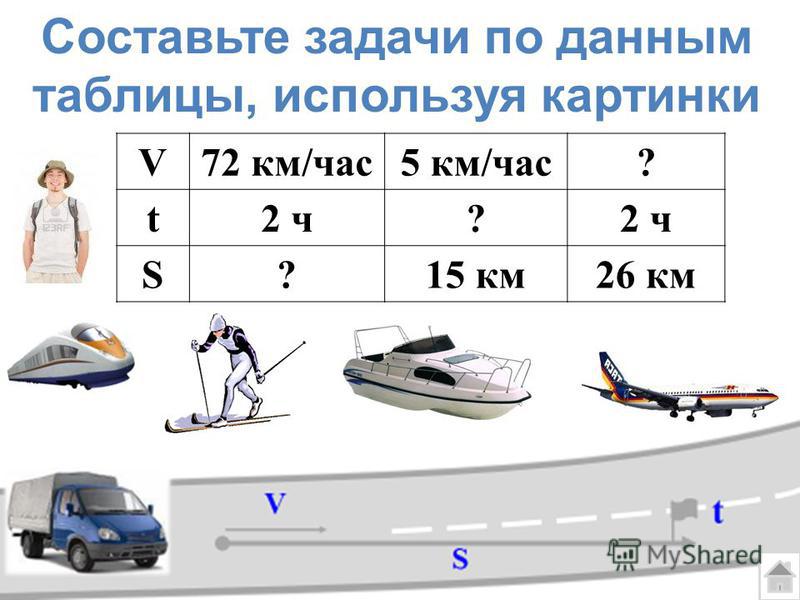
| Скорость, v, м/с | Время, t, с | Расстояние, S, м |
Простой пример, найти скорость велосипедиста, если за 5 часов он прошел 45 километров.
Составляем таблицу и записываем в нее данные:
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км |
| ? | 5 | 45 |
Теперь видно, что неизвестна скорость в первом столбце, значит, неизвестен первый множитель. Чтобы определить неизвестный множитель надо произведение разделить на известный множитель: = 45/5 = 9 км/ч.
Важно! В задачах все единицы измерения должны быть приведены либо к международной системе единиц (метр, секунда, м/с) либо к одним единицам измерения (то есть если в задаче есть и м/с и км/ч можно привести всё либо к м/с (тогда и время в секундах и расстояние в метрах), либо к км/ч (тогда и время в часах будет и расстояние в километрах))
Рассмотрим теперь некоторые примеры решения задач
Примеры задач на движение
Задача 1
Школьник идет домой со скоростью 2 км/ч. Расстояние от школы до дома 1 км. За какое время школьник дойдет до дома?
Расстояние от школы до дома 1 км. За какое время школьник дойдет до дома?
Решение:
Найдем время по формуле: \displaystyle t=\frac{S}{v}=\frac{1}{2}ч.
Школьник дойдет до дома за полчаса.
Ответ: 0,5 ч.
Задача 2
Автомобилист и велосипедист выехали в город из деревни одновременно. Скорость автомобилиста 50 км/ч. Расстояние до города 100 км. Какова скорость велосипедиста, если известно, что он прибыл в город на 8 часов позже автомобилиста?
Рисунок к задаче.
Решение: Составим таблицу
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км | |
| Автомобилист | 50 | 100/50 | 100 |
| Велосипедист | x | 100/x | 100 |
Пусть скорость велосипедиста x. В таблице мы сразу смогли написать соотношения для времени движения. По условию задачи дано, что велосипедист прибыл в город на 8 часов позже автомобилиста.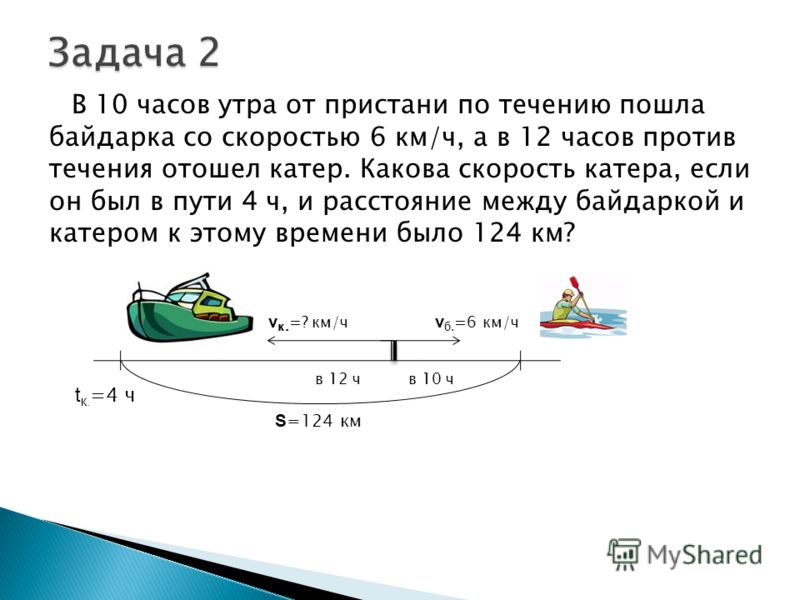 Запишем это:
Запишем это:
\displaystyle \frac{100}{x}-\frac{100}{50}=8
Мы отнимаем от времени, которое потратил велосипедист (он же потратил больше времени) время, которое потратил автомобилист и получаем 8 часов.
Решим полученное уравнение.
\displaystyle \frac{100}{x}-2=8
\displaystyle \frac{100}{x}=10
x=10
Ответ: 10 км/ч
Задача 3
Стрела пролетает 180 метров за 0,05 минуты. Найдите ее скорость.
Решение: прежде чем решать задачу, переведем все единицы в одну систему единиц. Минуты переведем в секунды.
В одной минуте 60 секунд. Значит, чтобы узнать сколько секунд в 0,05 минутах, умножим 0,05 на 60, получим:
0,05 \cdot 60=3 c.
Тогда \displaystyle v= \frac{180}{3}=60 м/с.
Ответ: 60 м/с
Задача 4
Турист прошел лесной участок длиной 10 км со скоростью 5 км/ч, а затем шел по полю 20 км, со скоростью 4 км/ч. Какова средняя скорость туриста?
Решение:
Определим весь путь который прошел турист:
\displaystyle S_{весь \; путь}=S_1+S_2=10+20=30 км.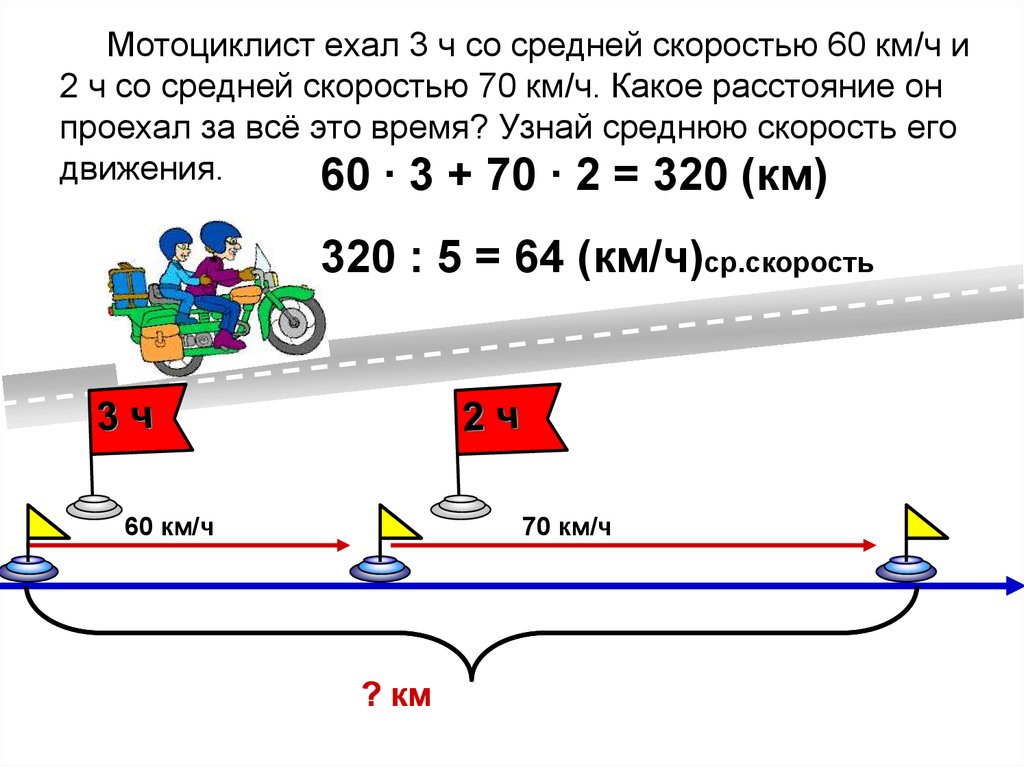
Для прохождения лесного участка турист потратил: \displaystyle t_1= \frac{S_1}{v_1}=\frac{10}{5}=2ч, а на второй участок времени ушло: \displaystyle t_2= \frac{S_2}{v_2}=\frac{20}{4}=5ч
Все время: \displaystyle t_{всё \; время}=t_1+t_2=2+5=7ч
Тогда найдем среднюю скорость:
\displaystyle v_{ср}= \frac{S_{весь \; путь}}{t_{всё \; время}}=\frac{30}{7}=4 \frac{2}{7} км/ч.
Ответ: \displaystyle v_{ср}=4 \frac{2}{7}
Задача 5
Лиса гонится за зайцем. Скорость лисы 20 м/с, а скорость зайца 15 м/с. Догонит ли лиса зайца, если заяц находится на расстоянии 300 метров от безопасного места, а лиса находится на расстоянии 200 метров от зайца?
Рисунок к задаче.
Решение:
Заяц добежит до норы за \displaystyle t= \frac{300}{15}=20 секунд.
Лиса же за 20 секунд пробежит расстояние \displaystyle S= 20 \cdot 20=400 метров.
Лиса не догонит зайца.
Действительно, скорость сближения лисы и зайца:
\displaystyle v=v_{лисы}-v_{зайца}=20-15=5 м/с
То есть, чтобы преодолеть расстояние 200 метров, которое изначально существует между лисой и зайцем, лисе понадобиться \displaystyle t=\frac{200}{5}=40 с
Заяц же уже 20 секунд будет в безопасном месте.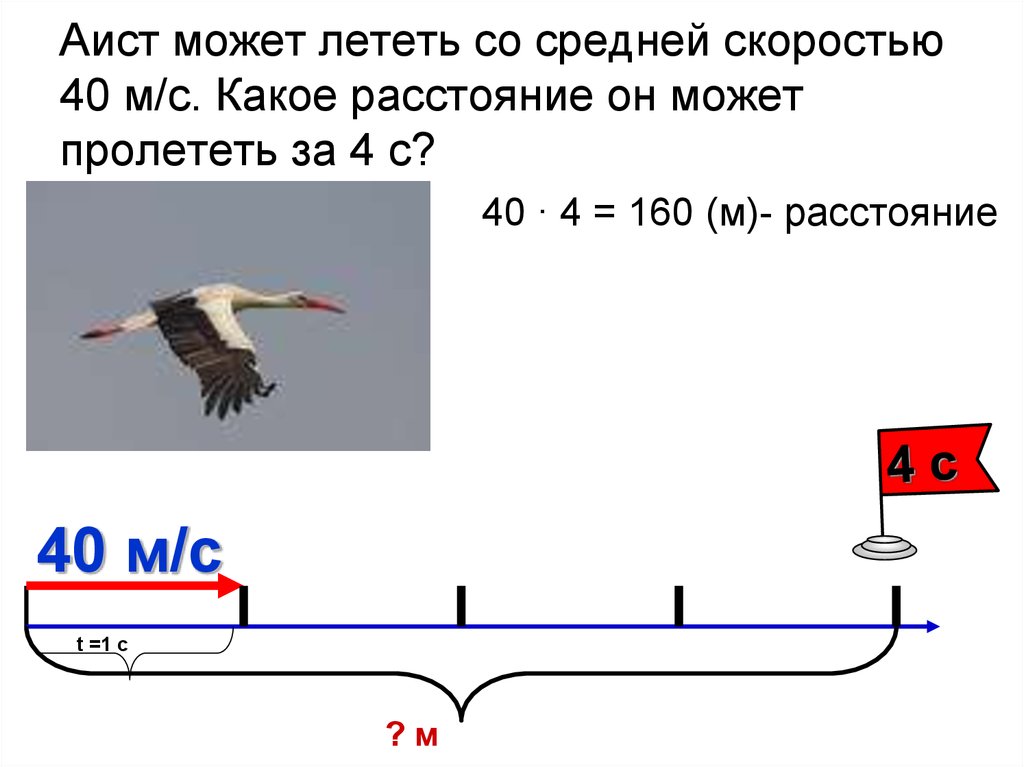
Ответ: лиса зайца не догонит.
Использование скорости времени и расстояния в реальных жизненных ситуациях
Когда дети или обычные люди используют математику для решения реальных жизненных задач, основанных на скорости, времени и расстоянии, они понимают, что математика — это больше, чем задача, которую должен выполнить учитель. ради. Это также дает подросткам важные навыки воздействия на окружающую среду. Расстояние, пройденное движущимся объектом за одну единицу времени, называется его скоростью. Несмотря на то, что понятия скорости, времени и расстояния остаются прежними, типы вопросов, задаваемых в тестах, могут различаться. Скорость, время и расстояние являются тремя наиболее распространенными темами количественных способностей, которые рассматриваются в государственных тестах.
Скорость, время и расстояние, используемые в реальных жизненных ситуациях
Одной из наиболее распространенных тем количественных способностей, задаваемых в государственных тестах, является скорость, время и расстояние. Это одна из тех тем, о которых студенты уже знают до того, как начнут готовиться к конкурсным экзаменам. Хотя понятия скорости, времени и расстояния остаются прежними, типы вопросов, задаваемых в тестах, могут различаться. Большинство поставленных задач из 1-2 слов связаны со скоростью, временем и расстоянием, но кандидатам также следует ожидать вопросов о достаточности данных и интерпретации данных, связанных с темой TDS (время, расстояние и скорость).
Это одна из тех тем, о которых студенты уже знают до того, как начнут готовиться к конкурсным экзаменам. Хотя понятия скорости, времени и расстояния остаются прежними, типы вопросов, задаваемых в тестах, могут различаться. Большинство поставленных задач из 1-2 слов связаны со скоростью, временем и расстоянием, но кандидатам также следует ожидать вопросов о достаточности данных и интерпретации данных, связанных с темой TDS (время, расстояние и скорость).
Задачи, связанные со скоростью, расстоянием и временем, требуют решения для одной из трех переменных при наличии конкретной информации. В этих задачах объекты перемещаются либо с постоянной, либо со средней скоростью.
В большинстве случаев задаются две переменные и запрашивается третья.
Скорость
Термин скорость относится к скорости, с которой что-то или кто-то движется. Мы можем определить среднюю скорость объекта, если знаем пройденное расстояние и время, затраченное на это. Скорость определяется как скорость, с которой движется объект (покрывая определенное расстояние). Поскольку он просто определяет величину, а не направление, это скалярная величина. Формула расчета скорости выглядит следующим образом:
Скорость определяется как скорость, с которой движется объект (покрывая определенное расстояние). Поскольку он просто определяет величину, а не направление, это скалярная величина. Формула расчета скорости выглядит следующим образом:
Скорость = пройденное расстояние/время
Единицы измерения: м/с.
Время
Время — это продолжительность времени, в течение которого происходит действие или событие. Формула времени определяет, сколько времени требуется объекту, чтобы пройти заданное расстояние с определенной скоростью.
Единицей измерения является секунда.
Расстояние
Расстояние между двумя точками — это длина отрезка, соединяющего их. Расстояние между двумя объектами (точками, линиями и т. д.) — это расстояние между ними. Его единица – метр.
Применение скорости, времени и расстояния в реальной жизни
Имея две переменные, учащихся часто просят рассчитать расстояние, скорость или время в пути чего-либо.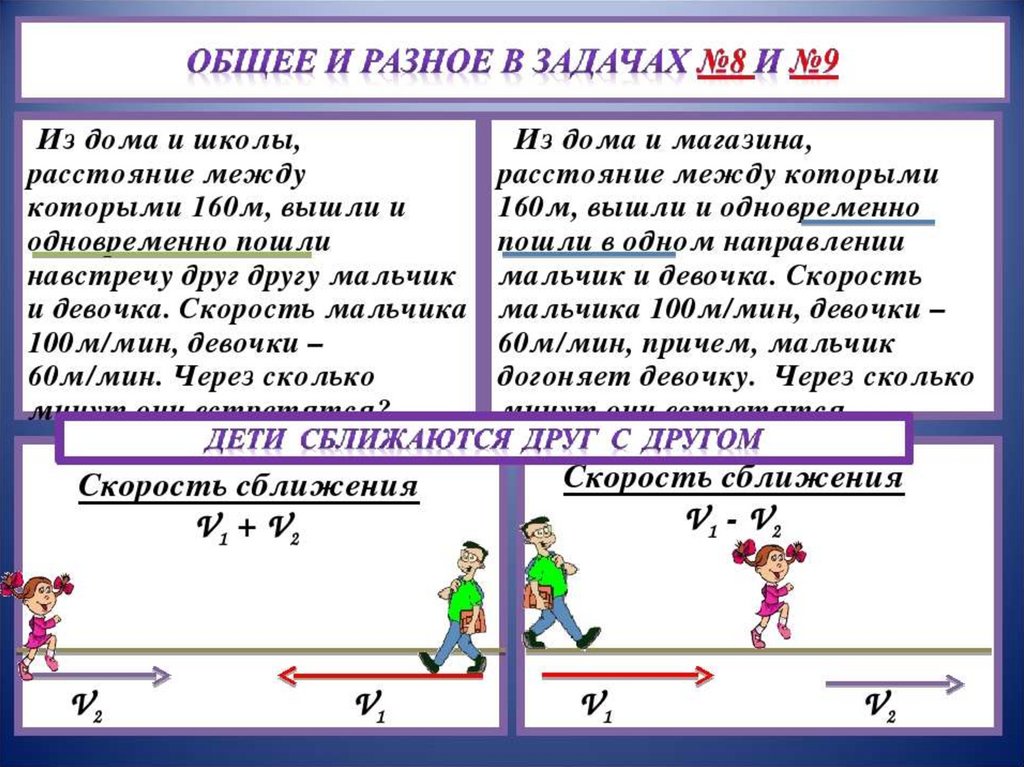 Такие задачи интересно решать, потому что они отражают реальные жизненные обстоятельства многих людей. Например, в запросе может быть указано: Рассчитайте расстояние, пройденное автомобилем за 20 минут с постоянной скоростью 50 км/ч. В большинстве случаев мы вычисляем желаемую величину, используя формулу расстояние-скорость-время.
Такие задачи интересно решать, потому что они отражают реальные жизненные обстоятельства многих людей. Например, в запросе может быть указано: Рассчитайте расстояние, пройденное автомобилем за 20 минут с постоянной скоростью 50 км/ч. В большинстве случаев мы вычисляем желаемую величину, используя формулу расстояние-скорость-время.
Какое значение имеют расстояние, время и скорость?
Значение расстояния, времени и скорости заключается в том, что когда два тела движутся с одинаковой скоростью, расстояния, которые они преодолевают, пропорциональны периодам их движения. Когда s остается постоянным,
Когда два тела движутся с одинаковой скоростью в течение одинакового времени, расстояния, которые они проходят, (прямо) пропорциональны их скоростям. Когда t остается постоянным,
Когда два тела проходят одинаковое расстояние, периоды их движения обратно пропорциональны скорости их движения. Когда d остается постоянным.
Когда два тела проходят мимо друг друга (одно из которых может быть неподвижным), скорость прохождения равна их соответствующим скоростям.
К точечным объектам незначительной длины относятся люди, автомобили, велосипеды, телеграфные столбы и деревья. Когда поезд длины l проходит мимо такого объекта, пройденное расстояние равно длине поезда l.
Заключение
Понятия скорости, расстояния и времени взаимосвязаны. Крайне важно понять общую связь между этими тремя явлениями, чтобы правильно использовать формулы в различных суммах. Когда определены два других фактора, можно использовать несколько формул для расчета любого из них. Скорость, с которой тело перемещается из одного места в другое, называется скоростью. Скорость тела – это расстояние, которое оно проходит за определенное время. Движение объекта в любом направлении определяется как расстояние. Время — это время, за которое объект проходит определенное расстояние. Когда объект проходит одно и то же расстояние за одно и то же время, говорят, что он имеет постоянную скорость; в противном случае он имеет переменную скорость.
Занятие 4.
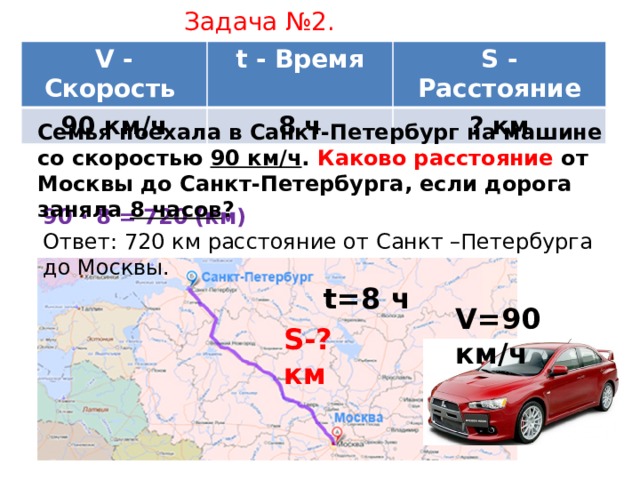 Расстояние, скорость и время
Расстояние, скорость и времяТип инвалидности
- Плохое зрение
- Слепота
- Нарушения слуха
- Неспособность к обучению
- Нарушения подвижности
- Нарушения здоровья
- Психосоциальные нарушения
Учитывайте положение, освещение и потребности учащегося во время презентаций или при использовании текста, манипуляций, прозрачных пленок или других проецируемых изображений.
Запрашивайте и поощряйте учащихся к тому, как наилучшим образом удовлетворить их потребности в обучении.
Предоставьте крупным шрифтом конспекты лекций, раздаточные материалы и рабочие листы.
Чтобы найти говорящие калькуляторы, обратитесь в Национальную федерацию слепых Independence Market Online.
Линейки, транспортиры и другие измерительные инструменты доступны в тактильном и крупном формате в Американской типографии для слепых. Дополнительные измерительные устройства можно найти по адресу Ассистек .
Рассмотрите возможность использования компьютера для писательской деятельности. Предоставьте формат документа, который учащийся может редактировать в электронном виде, например, доступный PDF-файл, документ Word или обычный текстовый документ. Посмотрите видео-презентацию и публикацию «Работаем вместе: компьютеры и люди с сенсорными нарушениями».
Учитывать потребности учащихся с ограниченными возможностями во время инструктажа в лаборатории и собраний по безопасности в лаборатории.
Назначьте групповые занятия, в которых все учащиеся берут на себя ответственность и вносят свой вклад в соответствии со своими способностями.
Используйте несколько форматов — устный, письменный, визуальный, тактильный, электронный — для инструкций и демонстраций.
Для получения общей информации о приспособлениях для учащихся с ограниченными возможностями на уроках естествознания см. документы «Работаем вместе: учителя естественных наук и учащиеся с ограниченными возможностями» и «Уравнение победы: доступ + отношение = успех в математике и естественных науках».
Дополнительные сведения см. в базе знаний AccessSTEM .
Запрашивайте и поощряйте вклад учащихся в том, как наилучшим образом удовлетворить их потребности в обучении.
Дайте четкие словесные описания наглядных пособий, включая видео и печатные материалы, используемые во время презентации.
Чтобы найти калькуляторы для слепых учащихся, обратитесь в Национальную федерацию слепых Independence Market Online или в Американскую типографию для слепых.
Линейки, транспортиры и другие измерительные инструменты доступны в тактильном формате и формате Брайля в Американской типографии для слепых. Дополнительные измерительные устройства можно найти по адресу Ассистек .
Для писательской деятельности предоставить компьютерное оборудование. Предоставьте формат документа, который учащийся может редактировать в электронном виде, например, доступный PDF-файл, документ Word или обычный текстовый документ. Рассмотрим компьютер с оптическим распознаванием символов, голосовым выводом, экраном Брайля и/или рельефным выводом Брайля. Для получения дополнительной информации см. видеопрезентацию и публикацию «Работаем вместе: компьютеры и люди с сенсорными нарушениями» или Доступ к базе знаний STEM .
Для получения дополнительной информации см. видеопрезентацию и публикацию «Работаем вместе: компьютеры и люди с сенсорными нарушениями» или Доступ к базе знаний STEM .
Учитывать потребности учащихся с ограниченными возможностями во время инструктажа в лаборатории и собраний по безопасности в лаборатории.
Назначьте групповые занятия, в которых все учащиеся берут на себя ответственность и вносят свой вклад в соответствии со своими способностями.
Используйте несколько форматов — устный, письменный, визуальный, тактильный, электронный — для инструкций и демонстраций.
Для получения общей информации о приспособлениях для учащихся с ограниченными возможностями на уроках естествознания см. документы «Работаем вместе: учителя естественных наук и учащиеся с ограниченными возможностями» и «Уравнение победы: доступ + отношение = успех в математике и естественных науках».
Дополнительные сведения см. в базе знаний AccessSTEM .
Запрашивайте и поощряйте вклад учащихся в том, как наилучшим образом удовлетворить их потребности в обучении.
Предоставить сурдопереводчика, субтитры в реальном времени и/или FM-систему.
Используйте наглядные пособия, чтобы объяснить учащимся понятия.
Давать письменные задания, лабораторные инструкции и конспекты демонстраций.
Учитывать потребности учащихся с ограниченными возможностями во время инструктажа в лаборатории и собраний по безопасности в лаборатории.
Назначьте групповые занятия, в которых все учащиеся берут на себя ответственность и вносят свой вклад в соответствии со своими способностями.
Используйте несколько форматов — устный, письменный, визуальный, тактильный, электронный — для инструкций и демонстраций.
Для получения общей информации о приспособлениях для учащихся с ограниченными возможностями на уроках естествознания см. документы «Работаем вместе: учителя естественных наук и учащиеся с ограниченными возможностями» и «Уравнение победы: доступ + отношение = успех в математике и естественных науках».
Дополнительные сведения см. в базе знаний AccessSTEM .
в базе знаний AccessSTEM .
Запрашивайте и поощряйте вклад учащихся в том, как наилучшим образом удовлетворить их потребности в обучении.
Некоторым ученикам могут подойти говорящие калькуляторы. Для получения информации о говорящих калькуляторах обратитесь в Independent Living Aids.
При занятиях, требующих письма, рассмотрите возможность использования компьютера. Используйте встроенные функции текстового процессора, такие как проверка орфографии и грамматики. Для получения дополнительной информации см. видеопрезентацию и публикацию «Работаем вместе: компьютеры и люди с ограниченными возможностями обучения».
Максимально сведите к минимуму отвлекающие факторы. Держите дверь в класс закрытой и усадите учащегося с дефицитом внимания подальше от окон и других отвлекающих факторов.
Дайте четкие и конкретные инструкции. Разбивайте большие задачи на более мелкие и давайте указания только для одного или двух действий одновременно.
Учитывать потребности учащихся с ограниченными возможностями во время инструктажа в лаборатории и собраний по безопасности в лаборатории.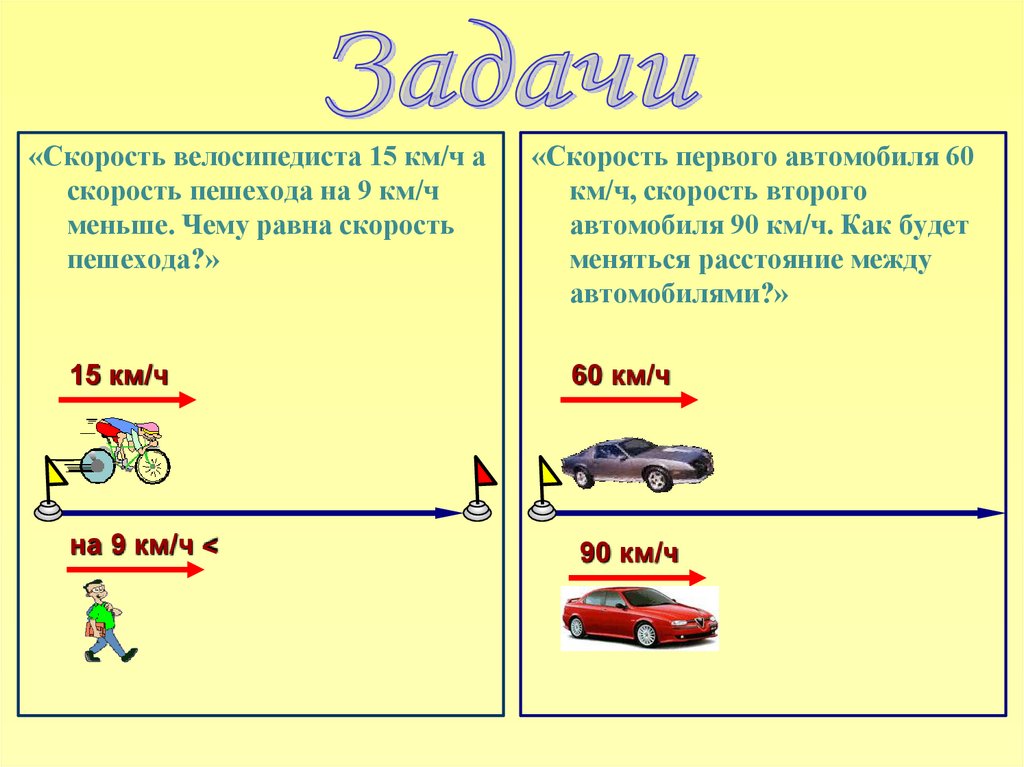
Назначьте групповые занятия, в которых все учащиеся берут на себя ответственность и вносят свой вклад в соответствии со своими способностями.
Используйте несколько форматов — устный, письменный, визуальный, тактильный, электронный — для инструкций и демонстраций.
Для получения общей информации о приспособлениях для учащихся с ограниченными возможностями на уроках естествознания см. документы «Работаем вместе: учителя естественных наук и учащиеся с ограниченными возможностями» и «Уравнение победы: доступ + отношение = успех в математике и естественных науках».
Дополнительные сведения см. в базе знаний AccessSTEM .
Запрашивайте и поощряйте вклад учащихся в том, как наилучшим образом удовлетворить их потребности в обучении.
Убедитесь, что классы и лаборатории находятся в местах, доступных для инвалидных колясок.
Поддерживайте использование учащимся компьютера, оснащенного специальным устройством ввода (например, голосовым вводом, азбукой Морзе, альтернативной клавиатурой), когда это необходимо. Для получения дополнительной информации см. видеопрезентацию и публикацию «Совместная работа: компьютеры и люди с нарушениями подвижности» или базу знаний AccessSTEM .
Для получения дополнительной информации см. видеопрезентацию и публикацию «Совместная работа: компьютеры и люди с нарушениями подвижности» или базу знаний AccessSTEM .
Подумайте о том, чтобы предоставить блокнот.
Учитывать потребности учащихся с ограниченными возможностями во время инструктажа в лаборатории и собраний по безопасности в лаборатории.
Назначьте групповые занятия, в которых все учащиеся берут на себя ответственность и вносят свой вклад в соответствии со своими способностями.
Используйте несколько форматов — устный, письменный, визуальный, тактильный, электронный — для инструкций и демонстраций.
Для получения общей информации о приспособлениях для учащихся с ограниченными возможностями на уроках естествознания см. документы «Работаем вместе: учителя естественных наук и учащиеся с ограниченными возможностями» и «Уравнение победы: доступ + отношение = успех в математике и естественных науках».
Дополнительные сведения см.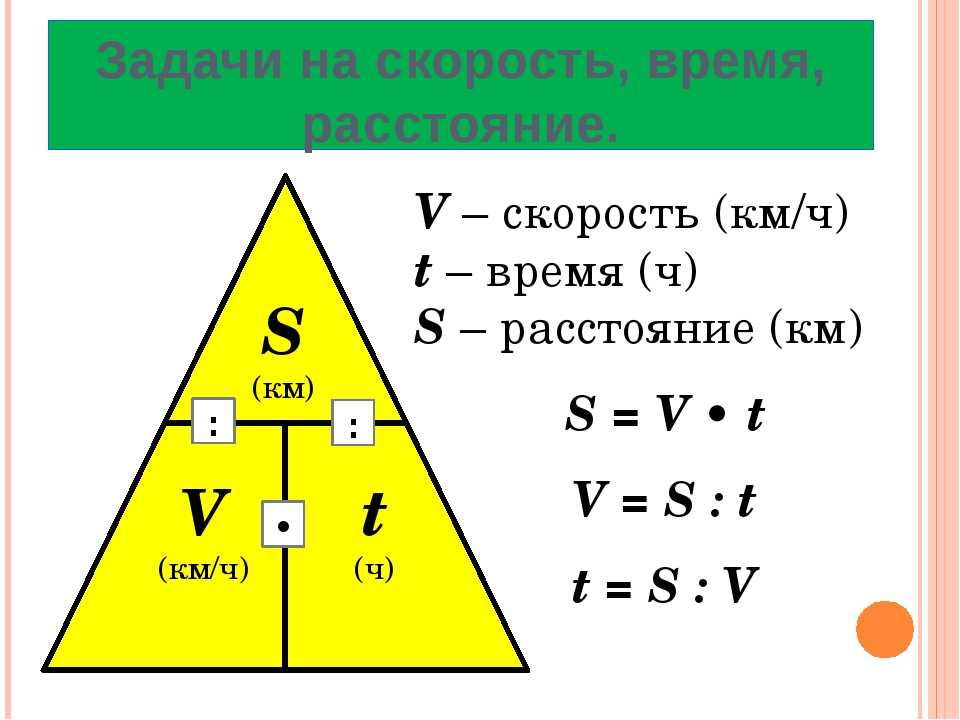 в базе знаний AccessSTEM .
в базе знаний AccessSTEM .
Запрашивайте и поощряйте вклад учащихся в том, как наилучшим образом удовлетворить их потребности в обучении.
Обеспечьте учащимся механизм изучения материала и выполнения заданий, которые они пропустили из-за отсутствия.
Обеспечьте гибкость в расписании и посещаемости.
Поговорите с учащимся и его семьей о любом влиянии занятий в классе на учащегося. Сообщите учащемуся заблаговременно о занятиях в классе, которые могут представлять проблему.
Для получения дополнительной информации см. Ресурсы по инвалидности в Интернете: нарушения здоровья.
Заранее предоставьте классные задания в электронном формате. Избегайте дополнений к заданиям в последнюю минуту.
Используйте электронную почту для облегчения общения и обсуждения в классе.
Подумайте о том, чтобы предоставить блокнот.
Учитывать потребности учащихся с ограниченными возможностями во время инструктажа в лаборатории и собраний по безопасности в лаборатории.
Назначьте групповые занятия, в которых все учащиеся берут на себя ответственность и вносят свой вклад в соответствии со своими способностями.
Используйте несколько форматов — устный, письменный, визуальный, тактильный, электронный — для инструкций и демонстраций.
Для получения общей информации о приспособлениях для учащихся с ограниченными возможностями на уроках естествознания см. документы «Работаем вместе: учителя естественных наук и учащиеся с ограниченными возможностями» и «Уравнение победы: доступ + отношение = успех в математике и естественных науках».
Дополнительные сведения см. в базе знаний AccessSTEM .
Запрашивайте и поощряйте вклад учащихся в том, как наилучшим образом удовлетворить их потребности в обучении.
Установите и соблюдайте расписание занятий и практики. Сообщите учащемуся заранее о любых изменениях в распорядке занятий в классе.
В групповых занятиях назначьте учащегося в группу с поддерживающими сверстниками.