З математики приклади: Упражнения и задачи по математике.

интересные математические задачи и задания

Советы родителям и примеры увлекательных заданий по математике. Занимательные задачи, головоломки, упражнения и тесты с ответами и решениями.

Попробуйте курс ЛогикЛайк в игровой форме!

Выберите возраст для старта

4-5 лет

6-7 лет

1-2 класс

3-5 класс

6-9 класс

15+ для себя

Почему дети и родители выбирают ЛогикЛайк?

ВСЯ ЛОГИКА В ИГРОВОЙ ФОРМЕ!

• Гибкий ум и уверенность Когда дети решают задачи и головоломки на LogicLike, они развивают смекалку и уверенность в своих силах.
• Фундамент для IT Учим грамотно работать с информацией, развиваем логико-математический интеллект, память и мышление.
• Глоток «свежего воздуха» Можно потратить 20-30 минут на себя, пока ребёнок развивается. Кстати, заниматься на ЛогикЛайк интересно и взрослым.

Начать занятия!

Польза занятий логикой и математикой

Элементарные математические представления помогают сформировать в детском саду. Базовые математические способности развивают в школе.

А чтобы ребёнок научился рассуждать логически, мыслить нестандартно — обычных арифметических и геометрических задач недостаточно.

Уже в дошкольном возрасте желательно выработать привычку ежедневно выполнять задания и упражнения на развитие логического мышления.

Благодаря регулярным тренировкам:

• ребёнок учится рассуждать, анализировать и делать правильные выводы;
• развивает сообразительность, память, внимание и интеллект;
• успехи повышают самооценку, интерес к обучению в школе, вдохновляют на победы в математических олимпиадах и конкурсах.

Дети 5-12 лет с удовольствием проходят курс ЛогикЛайк в игровой форме. Тем временем они учатся рассуждать, развивают логику, способности к математике и познавательный интерес.

Математические задачи по возрасту

Заинтересовать дошкольников 5-7 лет, учащихся начальных классов проще всего. Главное — предложить разнообразные занимательные задания, сделать процесс решения задач увлекательным, с элементами игры, и обеспечить умеренную сложность задач.

Примеры заданий по возрасту

• Логика для детей 5-6 лет
• Логика для детей 6-7 лет
• Математика для дошкольников
• 1 класс
• 2 класс
• 3 класс
• 4 класс

К 3-4 классу мотивация у школьника часто снижается.

Родителям важно не упустить этот момент и объяснить ребёнку, зачем вообще заниматься математикой и учиться решать задачи.

Логические и математические примеры

• для дошкольников
• для первоклассников
• примеры для 2 класса
• для 3 класса
• для 4 класса
• примеры для 5 класса

Логико-математические и другие развивающие игры по возрасту

4 – 5 лет

Занимательные задачи по типу

В плане регулярных тренировок в любом возрасте должно быть выполнение заданий минимум 5-7 типов. Это поможет комплексному развитию логики у ребенка, познавательных, творческих и математических способностей.

Среди самых интересных и популярных категорий заданий на логику и смекалку:

• Классические логические задачи. Учат детей анализировать текст, выделять главное, рассуждать и делать выводы.
• Арифметические ребусы. Отличная отработка ключевых мыслительных операций: абстрагирование, анализ и синтез, сравнение и другие.
• Задачи на закономерности, последовательности. Помогают развить аналитические способности и творческое мышление.

Примеры заданий по типу

Логические задачи

Математические ребусы

Задачи на поиск закономерностей

Правда и ложь

Найди лишнее в каждой группе

Магические квадраты

Шахматные задачи для начинающих

Загадки на логику

Головоломки со спичками, перестановки

Ребусы с буквами и цифрами

5 самых старых нерешенных задач Математики о простых числах / Хабр

Математика была предметом, который веками бросал вызов величайшим умам в истории человечества. Пожалуй, одной из наиболее исследуемых областей Математики является изучение простых чисел.

Наши размышления о закономерностях в простых числах привели к некоторым сложнейшим проблемам, нерешенным даже величайшими математическими гениями. Сегодня мы рассмотрим 5 старейших математических задач о простых числах, которые интуитивно понятны старшекласснику, но все еще не доказаны даже после упорных попыток в течение 500-2000 лет.

1. Совершенные числа: существуют ли нечетные совершенные числа? Бесконечны ли четные совершенные числа?

Рассмотрим числа 6, 28, 496, 8128…

Что в них особенного? Если вы не знаете, то я бы посоветовал сделать небольшую паузу и попытаться найти красивое свойство, которым обладают эти числа. 

Двигаемся дальше….

Если посмотреть на собственные делители этих чисел, то нетрудно заметить то самое «красивое» свойство:

Числа, для которых сумма собственных делителей равна самому числу, называются совершенными числами. Самое раннее исследование совершенных чисел затеряно в истории. Однако, мы знаем, что пифагорейцы 525годдон.э. изучали совершенные числа. 

Что мы знаем о таких числах?

• Евклид доказал, что для данного n, если – простое число, то – совершенное число. В качестве упражнения попробуйте доказать это самостоятельно.

Окей, краткий экскурс.

Простые числа Мерсенна: простые числа вида для некоторого n. Мерсенн предположил, что все числа вида простые, когда n простое. (Мы знаем, что это неправда. Например, ).

Открытый вопрос: существует ли бесконечно много простых чисел Мерсенна? На данный момент нам известно 47 простых чисел Мерсенна. 

Как видите, мы знаем о четных совершенных числах и способах их получения еще со времен Евклида около300годдон.э.. Но нам неизвестно, существую ли нечетные совершенные числа!!! насамомделе,прогрессврешенииэтойпроблемыпрактическиотсутствует.

Подводя итог, можно сказать, что изучение совершенных чисел ставит две давние открытые проблемы, а именно «существование нечетных совершенных чисел» и «существование бесконечно большого числа простых чисел Мерсенна».

Евклид (ок. 300 г. до. н. э.) первым доказал то, что простых чисел бесконечно много.

2. Гипотеза о близнецах: простых чисел-близнецов бесконечно много

Простые числа-близнецы — это пара вида (p, p + 2), где p и p + 2 являются простыми числами.

Точное происхождение гипотезы о простых числах-близнецах не установлено. Первая формулировка гипотезы о простых числах-близнецах была дана в 1846 году французским математиком Альфонсом де Полиньяком. Однако греческий математик Евклид дал старейшее из известных доказательств существования бесконечного числа простых чисел. Но он не предполагал, что существует бесконечное число простых чисел-близнецов.

На протяжении 2000 лет в доказательстве этого утверждения практически не было прогресса. 

Что мы знаем!

1. Существует бесконечно много простых пар вида (p, p + k), где k <= 246.

2. Если допустить истинность гипотезы Эллиота — Халберстама (которая, по нашему мнению, верна), то существует бесконечно много простых пар вида (p, p + k), где k <= 6. Это означает, что множество пар простых чисел, отличающихся на 2 (twin-primes), на 4 (cousin-primes) и на 6 (sexy-primes) бесконечно.

Возможно, величайший из ныне живущих математиков, Теренс Тао, активно работает над этой проблемой. Посмотрите это видео, чтобы познакомиться с этим математическим гением и его работой над простыми числами-близнецами. 

3. Какие правильные n-угольники построимы?

Правильный многоугольник считается построимым, если его можно построить с помощью линейки и циркуля. Например, правильный пятиугольник можно построить с помощью линейки и циркуля, а правильный семиугольник нет.

Древние греки знали, как построить правильный многоугольник с 3, 4 и 5 сторонами. Также они умели строить правильные многоугольники с удвоенным числом сторон для данного правильного многоугольника. 

Таким образом, они могли построить правильный n-угольник для n = {3, 6, 12, 24… 4, 8, 16… 5, 10, 20…} и так далее.

Естественно задать вопрос, для каких значений n можно построить правильный многоугольник. Первый реальный результат в решении этой проблемы был получен спустя 2000 лет после того, как древние греки впервые начали её изучать. В 1796 году 19-летний подросток построил правильный 17-угольник. Этим ребенком был не кто иной, как Карл Фридрих Гаусс. Несколько лет спустя Гаусс дал ответ на общую проблему.

Что мы знаем!

Гаусс показал, что правильный n-угольник может быть построен с помощью циркуля и линейки тогда и только тогда, когда n является произведением степени двойки и любого количества различных простых чисел Ферма (включая ни одного).

Простое число Ферма — это простое число вида:

Таким образом, проблема поиска всех построимых многоугольников сводится к нахождению всех простых чисел Ферма. Это отдельная нерешенная проблема. Несколько первых чисел Ферма: 3, 5, 17, 257, 65537, 4294967297…

По состоянию на 2021 год единственными известными простыми числами Ферма являются F0=3, F1=5, F2=17, F3=257, F4=65537.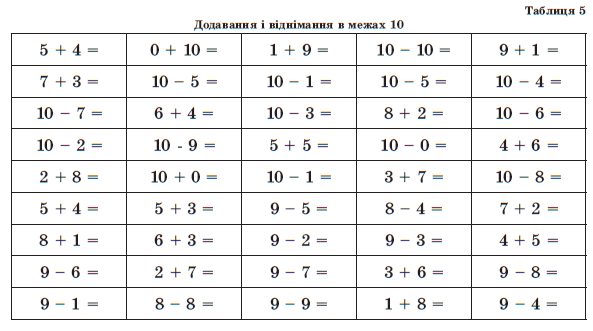

Ферма предположил, что все числа Ферма являются простыми. В 1732 году Эйлер открыл, что F5 делится на 641. С тех пор мы выяснили, что для n = 5, 6…31 числа Ферма составные. Простое число Ферма после F4 неизвестно.

Мы найдем ответ на вопрос о построимых правильных n-угольниках в тот же момент, как только найдем ответ на вопрос о существовании простых чисел Ферма.

4. Гипотеза Гольдбаха (1742)

Сильная гипотеза Гольдбаха:

Каждое чётное число, большее двух, можно представить в виде суммы двух простых чисел.

Слабая гипотеза Гольдбаха:

Каждое нечётное число, большее 5, можно представить в виде суммы трёх простых чисел.

Второе утверждение называется «слабым», потому что в случае истинности «сильной» гипотезы вторая также будет истинной. К сожалению, после значительных усилий поколений математиков, начиная с Эйлера, мы так и не смогли доказать ее.

(Примечание — В 2013 году Харальд Хельфготт опубликовал доказательство слабой гипотезы Гольдбаха.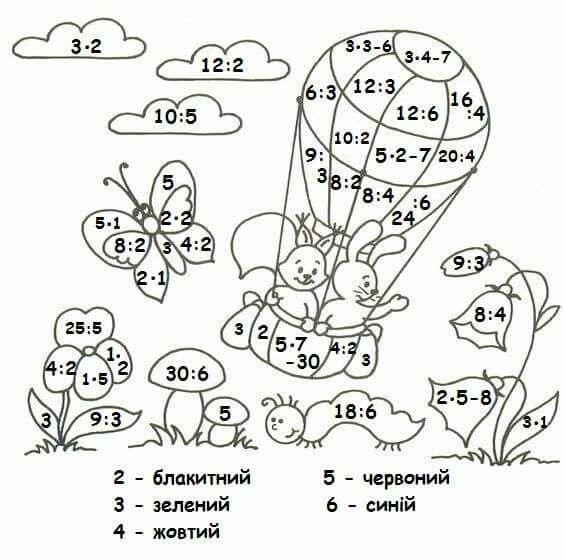 По состоянию на 2018 год доказательство широко принято в математическом сообществе, однако оно еще не было опубликовано в рецензируемом журнале).

В любом случае, все ждут доказательства сильной гипотезы.

Что мы знаем!

1. В 1930 году было доказано, что любое натуральное число больше 1 может быть записано в виде суммы не более чем C простых чисел, где C < 800 000 [Примечание — мы хотим, чтобы C = 2].

2. В последнее десятилетие было показано, что каждое четное число n >= 4 на самом деле является суммой не более чем 6 простых чисел (т.е. С <= 6). Позже результат был улучшен до C <= 4.

Забавный факт — гипотеза Гольдбаха является частью сюжета испанского фильма 2007 года «Западня Ферма«.

Отказ от ответственности: название статьи вводит в заблуждение. После рассказа о 4 нерешенных задачах я хотел бы показать одну математическую проблему (пятая проблема), которая была недавно решена (в 2004 году).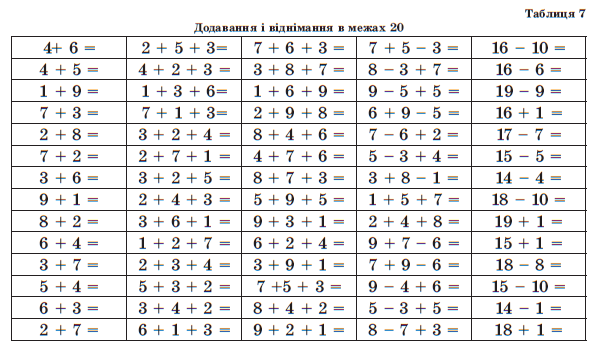

5. Тест простоты числа принадлежит классу P (2004)

Допустим, вам дано число n = 10089886811898868001. Вас спрашивают, простое ли это число. Первое, что вам приходит на ум, так это, 

Алгоритм A — проверить для каждого числа делится ли n на k. Вы можете оптимизировать этот алгоритм, понимая, что если n не является простым, то n будет иметь такой множитель k, что

Алгоритм B — итак, вы проверяется только

Хорошо, но погодите, что такое «P»?

Говорят, что задача находится в «P», если существует «быстрый» алгоритм, который может решить задачу. В нашем случае задача заключается в том, чтобы определить, является ли заданное n простым числом.

Итак, что такое быстрый алгоритм?

Для любой заданной проблемы у нас имеется размер ввода (назовем его x). Для нашей задачи размер ввода — это количество цифр в числе n. Итак, x = 20 для указанного выше n.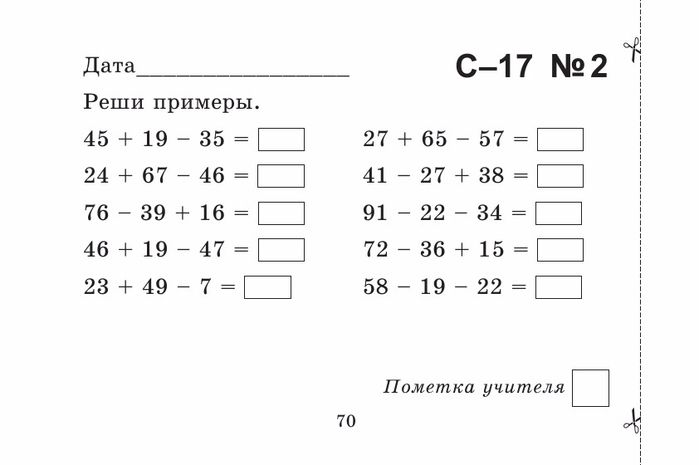 В общем случаем, при заданном n,

Алгоритм называется быстрым (алгоритм с полиномиальным временем), если он решает задачу за f(x) шагов, где f — полиномиальная функция. 

Если взглянуть на вышеупомянутые алгоритмы, то получим, что мы имеем n шагов в алгоритме А и шагов в алгоритме B. 

Итак, размер ввода в нашем случае —

Обозначим – количество шагов в алгоритме для данного размера ввода x.

Для алгоритма А,

Для алгоритма B,

В обоих случаях алгоритмы имеют экспоненциальное время. В течение 400 лет математики пытались выяснить, можно ли решить задачу определения простоты числа за полиномиальное время. Оказывается, что да. Новость об этом распространилась в математическом сообщество (особенно среди теоретиков чисел) в 2004 году, когда об этом объявили профессор и двое его студентов из IITK.

Алгоритм (известный как тест простоты AKS) был опубликован в статье под названием «Primes Is In P«, где показывается, что задача (независимо от того, является ли n простым или нет), может быть решена за ~ шагов. Позже были внесены некоторые улучшения, сократившие время до ~ шагов, также выдвигались предположения, что время можно уменьшить и вовсе до ~ шагов (прим. переводчика — предположение оказалось ложным).

---

Дата-центр ITSOFT — размещение и аренда серверов и стоек в двух дата-центрах в Москве. За последние годы UPTIME 100%. Размещение GPU-ферм и ASIC-майнеров, аренда GPU-серверов, лицензии связи, SSL-сертификаты, администрирование серверов и поддержка сайтов.

Что такое прикладная математика? Перспектива концентратора

Категория Студенческие голоса

Автор

Перрин Прайс Класс 23 года

Автор: 07.07.2021

Статья

Чем отличается чистая математика от прикладной? Не волнуйтесь, если вы не знаете ответа! Я здесь, чтобы помочь объяснить.

Когда я поступил в Гарвард на первом курсе, у меня было некоторое представление о том, что я хочу изучать. Я был студентом, ориентированным на STEM, но я также был любителем музыки и был открыт для изучения новых дисциплин. Математика была тем предметом, который я планировал продолжить, чтобы у меня была прочная основа на уроках естествознания. Затем я узнал, что есть два типа математики, которые я могу изучать: чистая математика и прикладная математика. Поначалу я чувствовал себя немного ошеломленным, потому что никогда раньше не слышал об этом различии; Я думал, что математика — это просто математика! К счастью, и на факультетах математики, и на факультетах прикладной математики есть очень отзывчивые и добрые люди, готовые помочь студентам.

Логистически чистая математика требует 12 курсов (48 кредитов), из которых 8 относятся к математическому факультету и четыре к математике или смежным предметам. Прикладная математика требует 14-15 курсов, в том числе пять курсов в выбранной прикладной области. К счастью, если вы не уверены, что выбрать, но знаете, что хотите изучать математику, многие курсы пересекаются и будут учитываться при выполнении обоих требований по концентрации.

Лето в Гарвардском дворе

Перрин Прайс

Что касается различий между двумя концентрациями, то это довольно интуитивно понятно! По сути, чистая математика фокусируется на абстрактных и теоретических концепциях математики, направленных на доказательство теорем, исследования и открытие новых областей математики. Курсы чистой математики в значительной степени основаны на доказательствах и имеют дело с теоретическими возможностями математики. С другой стороны, прикладная математика фокусируется на способах использования математики. Вот почему все учащиеся выбирают конкретную область применения в рамках своей прикладной математики. Например, многие студенты выбирают экономику в качестве своей области применения и проходят курсы, изучающие механику того, как использовать математику в экономических ситуациях.

Студентам также нравится учиться в библиотеке Уайденера во многих учебных уголках, а также в больших учебных комнатах.

Перрин Прайс

Математика также является междисциплинарной. В прошлом семестре я прошел курс «Прикладная математика 50: введение в прикладную математику». На этом занятии мы узнали о многих различных областях изучения математики, включая такие темы, как эпидемиология, теория игр и теория сетей. Знакомство со многими различными предметами помогло нам всем понять, какие виды процессов и систем может помочь создать математика, а также увидеть, как они могут быть связаны. Многие процессы, которые помогают создавать модели по одному предмету, такие как эпидемиология, также можно использовать таким же образом, чтобы узнать, насколько социально связаны люди. Конец урока завершился окончательным проектом, в котором мы использовали навыки кодирования и математические процессы, о которых мы узнали, для исследования нашей собственной темы. Моя группа решила изучить, как атрибуты популярной музыки в США влияют на их рейтинг в чартах. Было увлекательно сочетать музыку и математику вместе и проводить анализ данных.

Обе концентрации очень полезны для получения широкого и всестороннего понимания математики, что поможет учащимся в работе или в дальнейших академических начинаниях. Математика просто повсюду и служит основой для многих систем, на которые мы полагаемся каждый день и даже можем считать их само собой разумеющимися.

Метки

• Академики
• Студенческая жизнь

Значок книги

Следующая история: Открытое письмо входящему Pre-Frosh

Значок книги

Студенческие голоса

Обзор прикладной математики | Прикладная физика и прикладная математика

Главная > Прикладная математика

Прикладная математика связывает математические концепции и методы с различными областями науки и техники. Целью прикладных математических исследований является не только разумное применение существующих математических инструментов и идей для решения научных задач, но и разработка новой и полезной математики, вдохновленной и управляемой приложениями. С появлением новых вычислительных технологий прикладная математика вышла за рамки своего традиционного стиля и теперь приобретает еще большее значение и новую жизненную силу.

Обзор

Хотя междисциплинарный характер прикладной математики жизненно важен для ее успеха в современной науке и технике, ее уникальная миссия отличает ее от областей, с которыми она связана. По сравнению с чистой математикой прикладной математик больше интересуется проблемами, исходящими из других областей. По сравнению с инженером и ученым-физиком его больше заботит постановка задач и характер решений. По сравнению с ученым-компьютерщиком его больше заботит точность приближений и интерпретация результатов. Излишне говорить, что даже в наш век специализации работа математиков, ученых и инженеров часто пересекается. Прикладная математика по самой своей природе занимала центральное место в этом взаимодействии и оставалась областью увлечения и волнения для активных умов.

Направления карьеры для специальностей прикладной математики

1. Прикладная математика является связующим звеном количественных наук. Его мощные абстракции (алгебраические системы, дифференциальные системы, геометрические описания, распределения вероятностей, дискретные структуры и т. д.) подпитываются всеми другими количественными дисциплинами; его результаты, разработанные в одной области, информируют все другие области, которые разделяют те же абстракции. Таким образом, математики-прикладники могут работать в любой области спектра, от совместной командной работы над приложениями до автономных исследований абстракций, и свободно перемещаться взад и вперед по этому спектру.
2. Прикладные математики и ученые-вычислители необходимы для достижений в области науки и техники от аэродинамики до биомедицины, от геофизики до материаловедения, от квантовой хромодинамики до ранжирования веб-страниц.
3. Учебная программа по прикладной математике в Колумбийском университете легко настраивается с помощью факультативных цепочек или второстепенных предметов в различных приложениях по выбору учащегося.
4. Степень BSE по прикладной математике легко сочетается со степенью магистра за пять лет в Колумбийском университете или, при тщательном планировании и продвинутом размещении, всего за четыре года.
5. Прикладная математика является стратегической специальностью для поступления в профессиональные школы, поскольку в сочетании с соответствующим набором факультативных или дополнительных предметов степень дает количественные знания, необходимые для решения концептуальных задач в области бизнеса, права или медицинских исследований.
6. Прикладная математика является стратегической специальностью для программ докторантуры в области естественных и технических наук.
7. Прикладная математика обеспечивает прочную основу для карьеры, связанной с управлением рисками, областью роста в правительстве и промышленности.