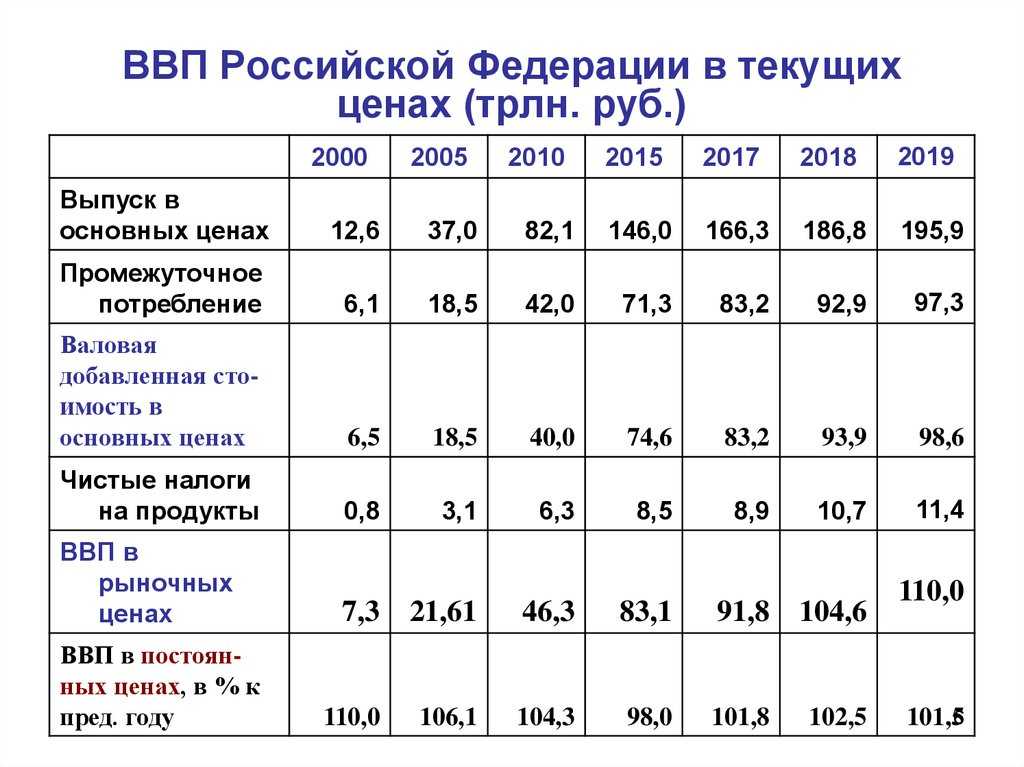
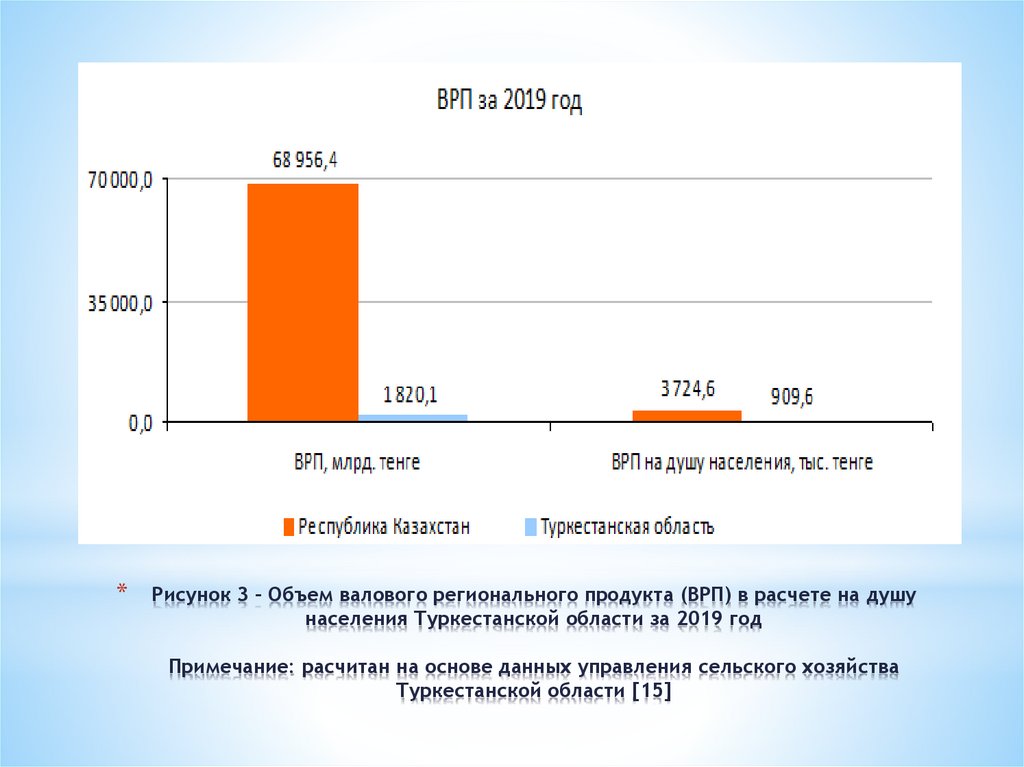
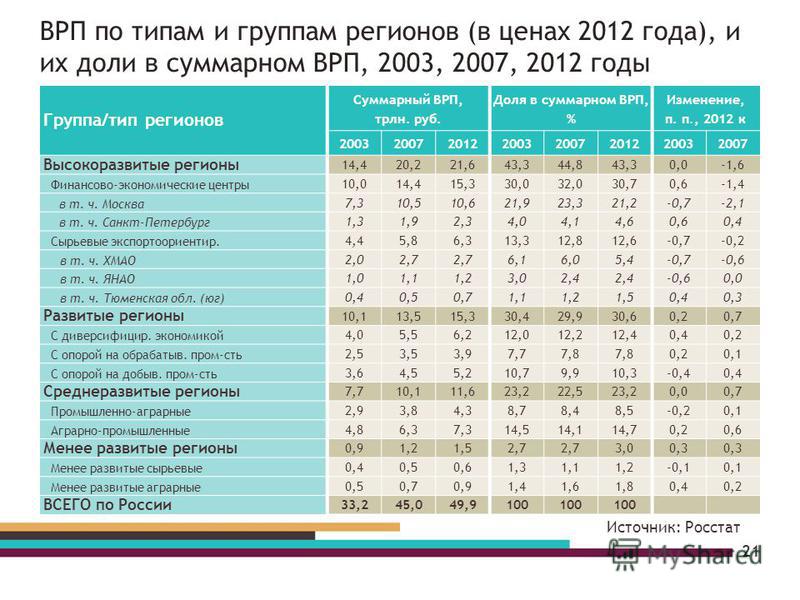
Врп математика 1 класс 2019 год: ВПР за 4 класс по математике
Архивы 1 класс Математика – Начальная школа
1 Математика КИМКомментарии: 0МЦКО Диагностика Математика 1 класс в течение мая 2021 г. Проверочная работа проводится с целью определения уровня усвоения обучающимися первых классов предметного содержания курса математики и выявления элементов содержания, вызывающих наибольшие затруднения. Смотрите также: Проверочная работа по математике для 1-х классов ВСОКО 2020
Читать далее
1 Математика КИМКомментарии: 0Проверочная работа по математике для 1-х классов ВСОКО 2020. Демонстрационный вариант проверочной работы по математике для 1-х классов. Московский центр качества образования. Смотрите также: Эффективная начальная школа Математика 1 класс декабрь 2019
Читать далее
1 Математика КИМКомментарии: 0Эффективная начальная школа Математика 1 класс декабрь 2019 Демоверсия. СПЕЦИФИКАЦИЯ проверочной работы по математике для обучающихся 1-х классов общеобразовательных организаций г. Москвы, участвующих в проекте «Эффективная начальная школа» Смотрите также:
Читать далее
1 Математика КИМКомментарии: 0Итоговая работа по математике для 1 класса 2019 КГКУ РЦОКО.
Оценка образовательных достижений учащихся в конце 1 класса. Демонстрационные варианты. Смотрите также: МЦКО математика 1 класс демоверсия ВСОКО апрель 2019
Читать далее
1 Математика КИМКомментарии: 0МЦКО математика 1 класс демоверсия ВСОКО апрель 2019. Демонстрационный вариант проверочной работы по математике для 1-х классов. Итоговая работа по математике демоверсия апрель 2019 год. скачать Смотрите также: ИТОГОВАЯ РАБОТА ПО МАТЕМАТИКЕ 1 класс Красноярский ЦОКО
Читать далее
1 Математика КИМКомментарии: 0ИТОГОВАЯ РАБОТА ПО МАТЕМАТИКЕ 1 класс Красноярский ЦОКО ДЕМОВЕРСИЯ. Ответы. Демонстрационная версия работы по математике для 1 класса. скачать скачать Смотрите также: Итоговая контрольная работа 1 класс Математика
Читать далее
1 Математика КИМКомментарии: 0Итоговая контрольная работа 1 класс Математика. Варианты по математике с ответами. КИМы по математике 1 класс УМК Школа России. скачать Смотрите также: Контрольная работа «Сложение и вычитание в пределах 10” 1 класс Математика
Читать далее
1 Математика КИМКомментарии: 0Контрольная работа «Сложение и вычитание в пределах 10” 1 класс Математика.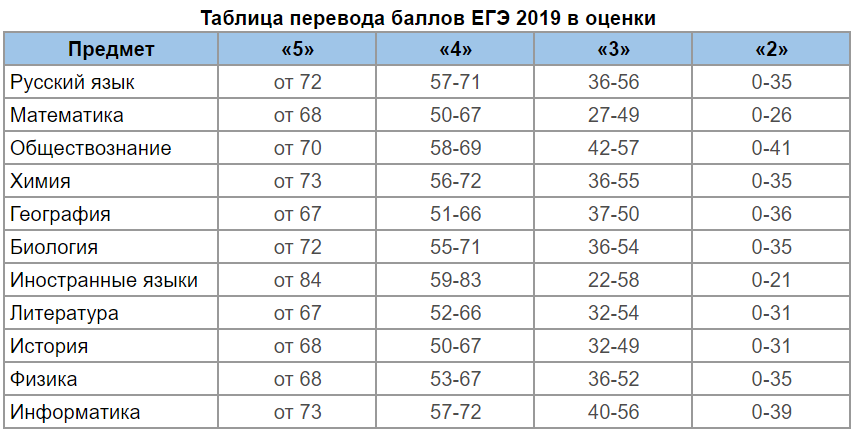
Варианты по математике с ответами. КИМы по математике 1 класс УМК Школа России. Контрольная работа по теме «Сложение и вычитание в пределах 10” скачать Смотрите также: Контрольная работа «Прибавление и вычитание чисел 0-3” 1 класс Математика
Читать далее
1 Математика КИМКомментарии: 0МЦКО Демоверсия Математика 1 класс Эффективная начальная школа. Демонстрационный вариант проверочной работы по МАТЕМАТИКЕ для обучающихся 1-х классов. скачать Смотрите также: Контрольная работа «Прибавление и вычитание чисел 0-3” 1 класс Математика
Читать далее
1 Математика КИМКомментарии: 0Контрольная работа “Прибавление и вычитание чисел 0-3” 1 класс Математика. Варианты по математике с ответами. КИМы по математике 1 класс УМК Школа России. Контрольная работа по теме “Прибавление и вычитание чисел 0, 1, 2, 3”. скачать Смотрите также: Контрольная работа по теме “Числа 1-10” 1 класс Математика
Читать далее
Подготовка к ВПР по математике в начальных классах в 2019 году – статья – Корпорация Российский учебник (издательство Дрофа – Вентана)
Главное о ВПР.
В официальном описании проверочной работы сказано, что она имеет исключительно диагностические цели, следовательно, нельзя использовать результаты ВПР для оценки деятельности учителя, образовательной организации, муниципальных и региональных органов исполнительной власти. В то же время, ВПР имеет определенное значение и для школы, и для учителей: в 2018 году на официальный сайт Рособрнадзора были вывешены номера школ, давших не те результаты, на которые все рассчитывали. Например, было выявлено несоответствие результатов ВПР и результатов ЕГЭ одной и той же школы.
Неудивительно, что учителя начальной школы активно занимаются подготовкой к ВПР. Однако будем помнить, что всероссийская проверочная работа в начальной школе — это не ЕГЭ-2019. Ее результаты во всяком случае не должны влиять на годовую оценку ребенка и его готовность заниматься математикой.
ВПР проверяет не только предметные знания, но и личностные, регулятивные и даже коммуникативные метапредметные результаты, поэтому учителю важно знать, какие именно знания и навыки проверяются в каждом задании.
Типы заданий в 2018-2019 учебном году не изменились, однако выполнить их нужно всего за 45 минут. Верная стратегия — как можно скорее справиться с типовыми заданиями и сэкономить время на логические задачи. При выполнении заданий ученики могут пользоваться черновиком, который не проверяется, а вот калькулятор, учебник, справочники, телефоны — запрещены.
Еще об оценивании: если ребенок получает за ВПР от 16 до 18 баллов, учитель имеет право поставить ему две пятерки, а еще отметить, что это потенциально одаренный ученик, к которому стоит присмотреться и помочь построить индивидуальный маршрут, раскрывающий его математические способности.
Другие материалы по теме:
- ВПР по математике в 6 классе. Подготовка, результаты, анализ
- Демоверсия ОГЭ-2019 по математике
- ВПР в вопросах и ответах
- Методика подготовки к ВПР по математике в 4 классе. Решаем логические и геометрические задачи
- ВПР в вопросах и ответах
Подготовка к ВПР по математике в 4 классе: как не повторить в 2019 году ошибки предыдущих лет
Задание 1.
Найди значение выражения. Это несложное задание успешно выполняют 96% детей. Проверяется знание рациональных приемов вычисления: ошибаются только те, кто плохо усвоил эти приемы или забыл таблицу умножения. Задание можно выполнить и письменно, никто не станет проверять черновик, но жалко тратить много времени на задание второго класса.
Как помочь? Еще раз повторите с детьми все приемы рационального вычисления, тренируйте устный счет. Пусть дети не пугаются, если в задании встретится нетабличное деление или трехзначное число.
Задание 2. Требуется найти значение выражения в 3-4 действия, со скобками или без. Типичная ошибка — неправильный порядок действия или невнимательность. Справляются с этим заданием 89% четвероклассников — что, честно говоря, для типового задания маловато.
Как помочь? Тренируйте внимание, напомните об основных законах вычисления.
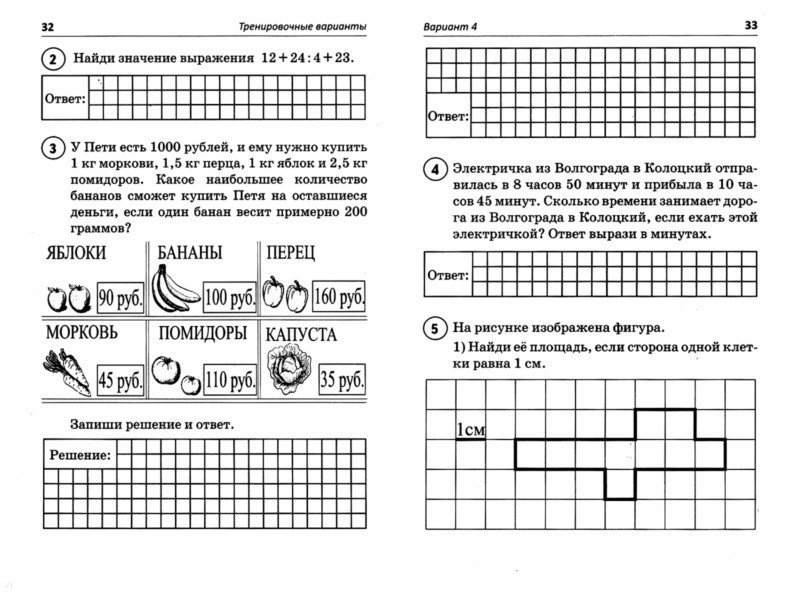
Задание 3. «Рассмотри рисунок и ответь на вопрос».
Это нетиповое задание на внимание и знание жизни. Чтобы его решить, нужно знать (в данном случае) денежные купюры, иметь понятие о цене и стоимости, также важно не обращать внимание на данные, которые даются в задании, но не нужны для решения. Обязательно представить в бланке решение. С этим заданием справляется 86% детей.
Как помочь? Повторите с детьми все величины и наименования, обратите их внимание на оформление решения задачи (действия, наименования, пояснение). Посоветуйте детям, когда они будут заходить в магазины, обращать внимание на цены и тренироваться вычислять стоимость покупок; пусть в этом им помогут родители.
Задание 4. Задача на математические величины. В рассматриваемом варианте — на знание времени: «Во сколько начались занятия, если длились… и закончились…?». Четвероклассников обычно подводит неумение работать с единицами времени, они забывают, что в часе не 100, а 60 минут. Самое главное здесь — понять задачу, представить себе реалистичную жизненную ситуацию.
Как помочь? В течение всего года давайте детям задания на единицы времени, почаще вместе разбирайте практико-ориентированные задачи о расписании, планировании дня и других реалистичных ситуациях, связанных со временем.
В УМК Муравиных для 1-4 классов отрабатываются различные типы заданий на время. Вопрос всегда ставится по-разному: сколько длится урок, во сколько началось занятие, когда был окончен обед и т.д. Задачи на время опасны тем, что, если решать только задачи с типовыми формулировками, ученикам на ВПР будет легко «попасться» на иначе сформулированном вопросе. Чтобы ребята научились совершенно свободно обращаться со временем, полезно давать им задания на определение количества полных часов в том или ином интервале, на часовые пояса, на понимание временного интервала. Важно обращать внимание детей на элементарное понимание величин: какого роста в принципе может быть семилетний мальчик? Сколько может длиться ночной сон человека? Это позволяет оценить, насколько получившийся ответ соответствует здравому смыслу.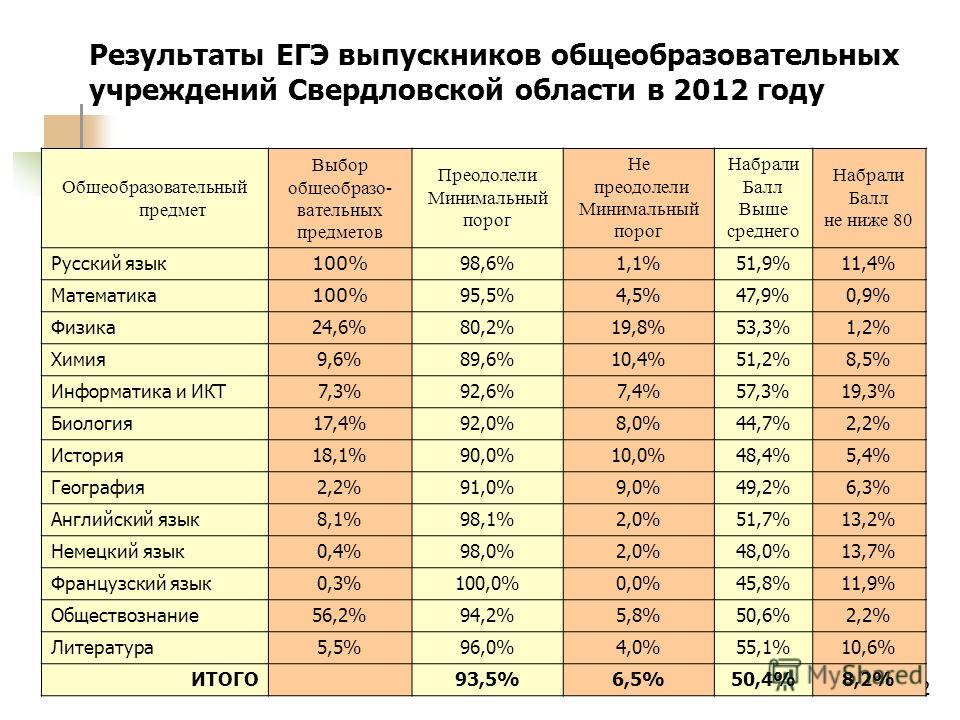
Задание 5. Задание на геометрию: например, найти площадь прямоугольника и провести линию так, чтобы получился квадрат и новый прямоугольник. Здесь самое главное — не пытаться ничего измерять, если нам дана условная единица (обычно одна клетка условно равна сантиметру). Первую часть задания выполняют 59% учеников, и ошибки их бывают связаны с тем, что они путают площадь и периметр. Вторая часть задания, как ни удивительно, дается всего половине детей: ошибки делают из-за недостаточно развитого пространственного мышления и неумения изменять конфигурацию геометрического объекта.
Чем помочь? Такие задания можно освоить, если выполнять их почаще, в том числе и со сложными фигурами. Если вы занимаетесь по УМК Муравиных, задания ВПР покажутся детям простыми: в учебнике им предлагается не просто разделить прямоугольник линией, но и разделить так, чтобы получился прямоугольник определенной площади.
Задание 6. Задача на умение работать с таблицей, читать и интерпретировать данные.
Это может быть распределение призов и медалей у спортивных команд, предпочтения школьников, покупки, результаты контрольной и т.д. Вместо таблицы могут быть даны круговые или столбчатые диаграммы — их ученики тоже не должны испугаться. Ошибки возникают из-за неумения анализировать, а также из-за недостаточного опыта чтения табличных данных.
Как помочь? Поле для решения в бланке контрольной не предложено, однако решение здесь играет большую роль: важен алгоритм, по которому ищется ответ. Например, задан вопрос: кто занял третье место в командном зачете? Решение стандартное: подсчитать число медалей у каждой команды и найти ту, которая имеет третье место.
Задание 7. Типовое задание на письменные приемы вычисления: например, деления в столбик. В некоторых вариантах можно произвести вычисления и устно — но тогда желательна самопроверка. 79% четвероклассников выполняют это задание без ошибок, зато и оценивается оно всего в 1 балл.
Задание 8.
Сложная текстовая задача. В бланке представляем полное решение и ответ. Выполняемость этого задания — не более 50%, опять же по той причине, что задание не типовое и к нему нельзя в полной мере подготовиться. Побеждают те, кто умеет рассуждать и представлять себе ситуацию. Ошибаются те, кто невнимательно читает условие задачи и не видит в нем представленных данных.
Как помочь? Просто решайте как можно больше разнообразных задач на логику. Старайтесь выбирать задачи с&разнообразными формулировками вопросов.
Задание 9. Интересная логическая задача, способная проверить, владеют ли ученики логикой, умеют ли перевести текстовую информацию в удобный наглядный вид. Чтобы решить задачу, нужно составить таблицу или схему и занести на нее все данные: составить расписание, продумать план и т.д. Если таблица составлена, все данные становятся выпуклыми и понятными. Если ответ дан только на один вопрос из двух или трех — это значит, что, скорее всего, ученик не составил таблицу, а нашел ответ случайно, по наитию.
Таких учеников 76%: они дали ответ только на первый вопрос.
Как помочь? Чаще всего такие задачи ученики решают вместе с родителями. В этом нет ничего плохого, но полезнее всего будет, если родители откроют детям путь рассуждения: пусть размышляют вслух вместе с детьми, это гораздо важнее, чем дать правильный ответ.
Задание 10. Задание на пространственное мышление — в основном про асимметрию. Речь может идти об отражении фигуры в зеркале или о выделении симметричных и асимметричных фигур из ряда. Результативность этого задания не слишком высока, и основной причиной ошибок является невнимательность.
Задание 11. Снова логическая задача, в данном варианте даже вполне типовая: о двуногих и четвероногих животных, двухколесных или трехколесных велосипедах и т.д. Подобная задача решается по известному алгоритму (см. видео), однако если ребенок решил ее интуитивно или методом подбора, его ответ все равно будет засчитан.
Как помочь? Дать детям как можно больше известных алгоритмов, но не натаскивать: систематическое решение одинаковых сложных задач может сыграть с ребенком злую шутку.
#ADVERTISING_INSERT#
Национальные баллы групп учащихся и пробелы в баллах
Поделитесь этим результатом:
Тенденции оценок групп учащихся
Более низкие средние баллы для большинства групп учащихся, чем в 2019 году число учащихся в 2022 году было ниже для следующих групп учащихся:
- американских индейцев/коренных жителей Аляски, азиатов, чернокожих, латиноамериканцев, учащихся двух или более рас и белых учащихся;
- учащихся, которые имели право и не имели права на участие в Национальной программе школьных обедов;
- учащихся государственных школ;
- учащихся, посещающих чартерные школы и государственные, нечартерные школы;
- учащихся городских, пригородных, поселковых и сельских школ;
- учащихся, посещающих школы на Северо-Востоке, Среднем Западе, Юге и Западе;
- учащихся, которые были и не были идентифицированы как учащиеся с ограниченными возможностями; и
- студентов, которые были и не были идентифицированы как изучающие английский язык.
Просматривайте тенденции в средних баллах для выбранных групп учащихся, щелкая эскизы в раскрывающихся списках ниже. Прокрутите страницу вниз, чтобы узнать, как процент групп учащихся изменился с течением времени.
Приведенные ниже результаты типа школы включают данные по государственным школам и католическим школам (подкатегория частных школ). В 2022 году результаты для частных школ в целом не соответствовали минимальному уровню участия для отчетности и поэтому не включены сюда. См. дополнительные сведения о годах с доступными данными по типу школы и другим демографическим группам учащихся.
Рисунок Динамика средних показателей NAEP по математике в четвертом классе по отдельным группам учащихся
Загрузка…
Условные обозначения
NAEP Proficient
Связанные с этой темой
- Оценки групп учащихся штата
- Оценки групп учащихся округа
Тенденции разрыва в баллах
Мужчины–Женщины , разрывы в баллах между белыми и черными и белыми и латиноамериканцами по математике в четвертом классе увеличились по сравнению с 2019 годом
).
Среди расовых/этнических групп средний балл по математике у белых четвероклассников был на 29 баллов выше, чем у их чернокожих сверстников (по сравнению с 25 баллами в 2019 году), и на 21 балл выше, чем у их испаноязычных сверстников (по сравнению с 18 баллами в 2019 году).
Посмотреть балл одной группы учащихся …
стрелка внизминус …
–
другой группы учащихся
стрелка внизРисунок Тенденция средних баллов по математике четвертого класса NAEP и разрывы в баллах по расовой/этнической принадлежности
Отобразить как
Отобразить маркеры значимости для:
Линии тренда оценок
Тенденции разрыва 2’96’00’03’05’07’09’11’13’15’17’19’ 22’22< Перетащите, чтобы изменить основные годы >
Загрузка…
Легенда
Линии тренда
Пробелы
Значительная разница в течение года
Нет существенной разницы в течение года
Относится к этой теме 9 0005
- Оценки групп учащихся штата
- Оценки групп учащихся округа
Поделись этим результатом:
Проценты населения группы
Демографические изменения в численности учащихся учащиеся четвертого класса имеют изменены для выбранных групп учащихся.
Например, процент учащихся, которые были идентифицированы как учащиеся с ограниченными возможностями, был выше в 2022 году по сравнению с 2019 годом, как и процент учащихся, которые были идентифицированы как изучающие английский язык. Кроме того, процент учащихся, имеющих право на участие в Национальной программе школьных обедов, и процент посещающих государственные школы были ниже в 2022 году по сравнению с 2019 годом..Подробнее об изменениях в политике отчетности по расе/этнической принадлежности.
Выберите группу учащихся
Раса/этническая принадлежность
стрелка внизРисунок Процентное распределение учащихся четвертого класса по математике NAEP по расе/этнической принадлежности и годам оценки
| Год | Американец Индеец/коренной житель Аляски | Азиат | Азиат/житель тихоокеанских островов | Черный | Латиноамериканец | Коренной гаваец/житель других тихоокеанских островов | Две или более рас | Белый |
|---|---|---|---|---|---|---|---|---|
| 2022 | 901 40 | |||||||
| 2019 | ||||||||
| 2017 | ||||||||
| 2015 | 901 40 | |||||||
| 2013 | ||||||||
| 2011 | 2009 | 901 34 | ||||||
| 2007 | ||||||||
| 2005 | ||||||||
| 2003 | 90 140 | |||||||
| 2000 | 901 40 | |||||||
| 1996 | ||||||||
| 1996 1 | 90 140 | |||||||
| 1992 1 | 901 40 | |||||||
| 1990 1 |
Загрузка.
..
Выберите фокусный год
стрелка внизСвязано с этой темой
- Групповые баллы учащихся штата
- Групповые баллы школьных округов
Следующая страница:
Результаты национального уровня успеваемости ПРИМЕЧАНИЕ. Начиная с оценки 2017 года, результаты NAEP по математике для 4 и 8 классов основаны на цифровой оценке; до 2017 года результаты оценивались с помощью карандаша и бумаги для 4 и 8 классов. В 2019 году впервые проводилась цифровая оценка NAEP по математике в 12 классе. Отчет по математике за 12 класс за 2019 г. включает результаты учащихся, прошедших цифровое оценивание, и учащихся, прошедших бумажное оценивание. Дополнительную информацию см. на странице “О нас”. Шкала математики NAEP колеблется от 0 до 500 в 4 и 8 классах и от 0 до 300 в 12 классе. До 19 лет в оценках NAEP по математике не разрешались поправки.96 на национальном уровне для 4-х и 8-х классов. Результаты не показаны для точек данных, где размеры выборки недостаточны для обеспечения надежной оценки или когда данные недоступны.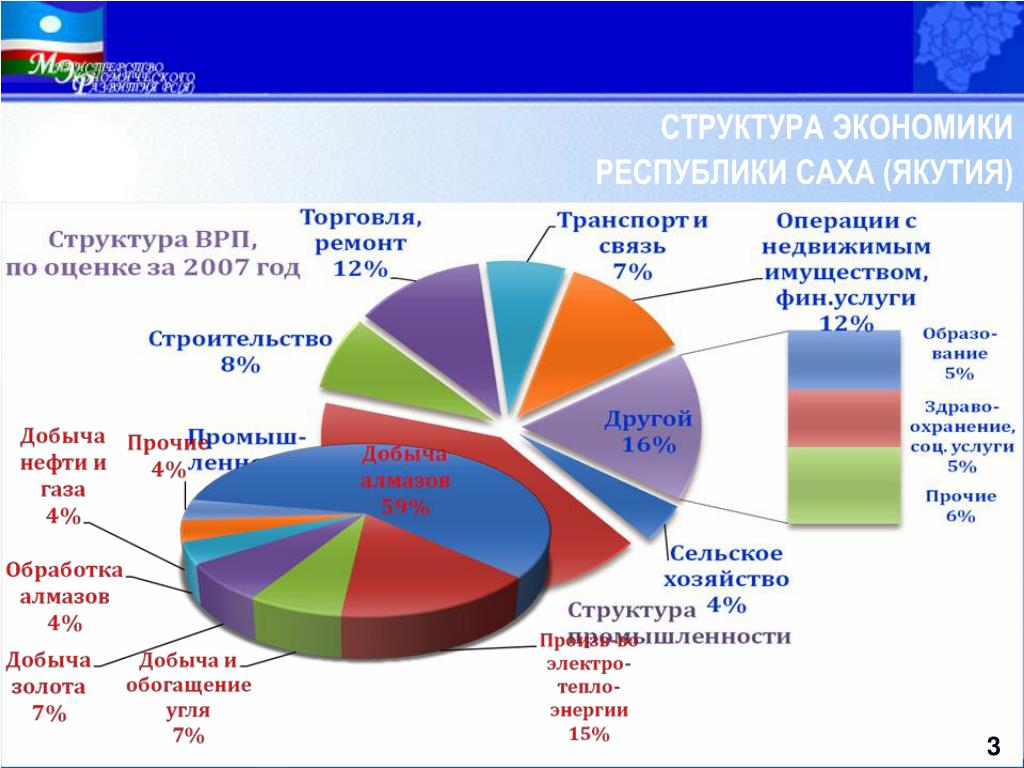
Черный включает афроамериканца, а латиноамериканец включает латиноамериканца. Категории рас исключают латиноамериканское происхождение. В соответствии с новыми стандартами Управления управления и бюджета США для сбора и представления данных о расе / этнической принадлежности, начиная с 2011 года, была собрана дополнительная информация, чтобы результаты можно было сообщать отдельно для азиатских студентов и коренных жителей Гавайев / других тихоокеанских островов. Учащиеся, принадлежащие к двум или более расовым/этническим группам (например, белые и черные), до 2011 года классифицировались как «другие» и относились к «неклассифицированной» категории и классифицировались как «две или более рас». “В 2011 и более поздних годах оценки. Результаты для этих студентов представлены в категории «Две или более гонки» на графиках и в таблицах в этом отчете. Результаты тенденций для «белых», «черных», «латиноамериканцев», «жителей азиатских/тихоокеанских островов» и «двух или более рас», представленные в этом отчете, основаны на переменной расы/этнической принадлежности с 6 категориями, данные доступны начиная с 1990-е.
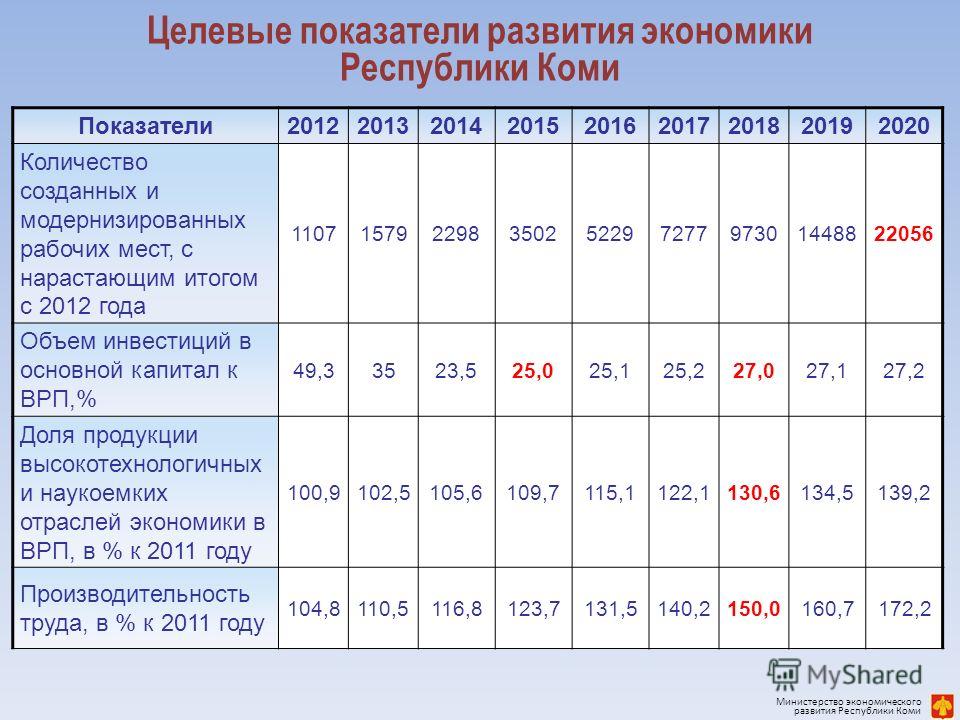Для категории приемлемости Национальной программы школьных обедов (NSLP) результаты сообщались с 2003 года, когда качество данных о соответствии учащихся требованиям для участия в программе улучшилось. Поскольку в 12-м классе информация о соответствии учащихся NSLP может быть занижена, результаты NSLP для 12-го класса не включены в этот отчет. Начиная с 2014–15 учебного года, штаты могли дополнительно классифицировать учащихся как имеющих право на участие в NSLP, включив их в свое Положение о правах сообщества; таким образом, процент учащихся, отнесенных к категории имеющих право на участие, увеличился по сравнению с 2013 годом. Читатели должны с осторожностью интерпретировать результаты тенденций NSLP. Информация о переменной «Право на участие в Национальной программе школьных обедов (NSLP)» основана на доступных школьных записях. Если школьные записи не были доступны, учащийся классифицировался как «Информация недоступна». В категорию «учащиеся с ограниченными возможностями» входят учащиеся, идентифицированные как проходящие индивидуальную программу обучения или защищенные в соответствии с разделом 504 Закона о реабилитации от 1973.
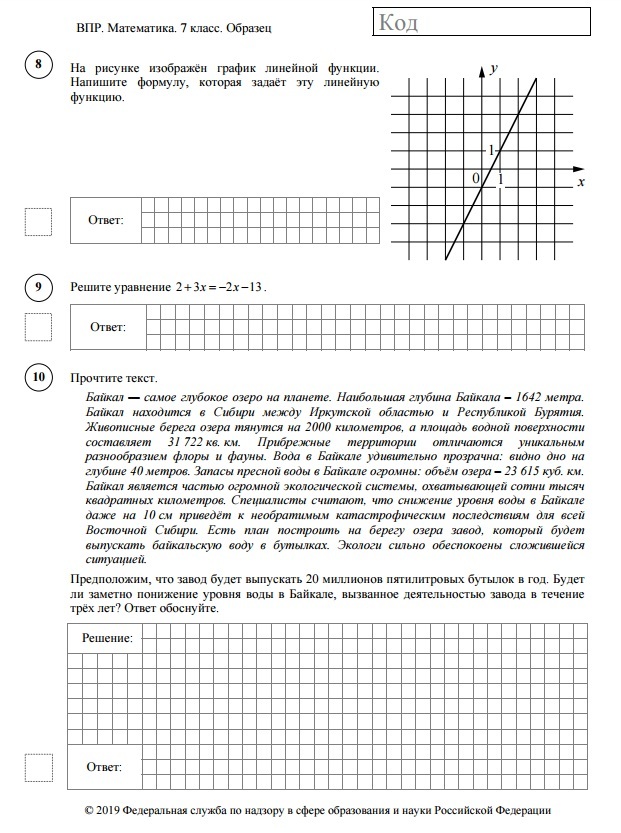Результаты по учащимся с ограниченными возможностями и изучающим английский язык основаны на оцениваемых учащихся и не могут быть обобщены на все такие учащиеся. Дополнительную информацию о переменных группы учащихся см. Детали могут не суммироваться в итоги из-за округления или пропуска категорий. Хотя оценки (например, средние баллы или проценты) показаны в виде округленных чисел, положения точек данных на графике основаны на неокругленных числах. Неокругленные числа использовались для расчета различий между оценками и для теста статистического сравнения, когда оценки сравнивались друг с другом. Не все очевидные различия между оценками являются статистически значимыми.
ИСТОЧНИК: Министерство образования США, Институт педагогических наук, Национальный центр статистики образования, Национальная оценка образовательного прогресса (NAEP), различные годы, 1990–2022 гг. Математические оценки.
Пиратское задание “Математическое уравнение” – О
О пиратском задании “Математическое уравнение”
Мы разработали Pirate Math Equation Quest как расширение программы Pirate Math, разработанной Линн Фукс, доктором философии, и ее коллегами из Университета Вандербильта.
С 2015 по 2019 год мы предлагали учащимся третьего класса, испытывающим трудности с математикой, интенсивную интервенцию со словесными задачами под названием «Квест на математическое уравнение пиратов». Во время квеста «Пиратское математическое уравнение» учащиеся получили подробные инструкции по чтению, интерпретации, настройке и решению текстовых задач с упором на схемы. Студенты также получили моделирование и практику, связанную с пониманием знака равенства и решения уравнений в рамках интервенции словесной задачи.
Мы определили подходящих учащихся, испытывающих трудности с математикой, как тех, кто набрал 13-й процентиль или ниже по шкале задач со словами. В течение 2015-2018 гг. наши первые три когорты учащихся, изучавших задание «Пиратское математическое уравнение: индивидуальное вмешательство в решение словесных задач со схемами сумм, различий и изменений», получали задание на решение словесных задач 3 раза в неделю в течение 16 недель, при этом занятия длились примерно 30 минут.
С нашим последним набором студентов в 2018-2019 гг., мы представили квест «Пиратское математическое уравнение»: задание на решение словесных задач в малых группах со схемами «Общее», «Разница», «Изменение» и «Равные группы» как задание на решение словесных заданий для малых групп, в котором группы из 3–4 учащихся выполняли задание на решение словесных заданий 3 раз в неделю в течение 13 недель, продолжительность сеансов примерно 30 минут. Наша последняя группа студентов также прошла обучение в небольшой группе, посвященное пониманию текстовых проблем в тестах штата Техас на академическую готовность (STAAR). Учащиеся, участвовавшие в квесте «Пиратское математическое уравнение»: вмешательство в малых группах для решения задач со словами в Техасе в рамках оценки академической готовности штата Техас (STAAR) для 3-го класса, занимались решением задач со словами 3 раза в неделю в течение 6 недель, причем занятия длились примерно 30 минут.
Тщательные оценки всех трех итераций квеста «Пиратское математическое уравнение» показали, что учащиеся третьего класса, испытывающие трудности с математикой, продемонстрировали лучшие результаты при решении словесных задач с помощью квеста «Пиратское математическое уравнение» по сравнению с учащимися, которые не участвовали в этом вмешательстве (Пауэлл, Берри и Барнс, 2019 г.
). ).
О нас
Кэтрин А. Берри — руководитель проекта в Центре предотвращения образовательного риска Медоуза Техасского университета в Остине. Она руководит проектом Pirate Math Equation Quest, финансируемым Институтом педагогических наук. Берри получила докторскую степень на факультете специального образования и изучения инвалидности Университета Джорджа Вашингтона. Ранее Берри преподавал ученикам 4-6 классов с высокой степенью нарушения обучаемости в Вашингтоне, округ Колумбия. Исследовательские интересы Берри включают учащихся с особыми трудностями в обучении, решение математических словесных задач, словарный запас по математике, овладение языком, разработку учебных программ, подготовку учителей и искусство. -интегрированная инструкция.
Контакты: [email protected]
Сара Р. Пауэлл — доцент кафедры специального образования Техасского университета в Остине. Пауэлл выступает в качестве главного исследователя гранта Института педагогических наук, который финансирует Pirate Math Equation Quest.