Волшебные квадраты математика: Как решить магический квадрат: учимся решать одну из древнейших задач – Преподавание в начальных классах – Преподавание – Образование, воспитание и обучение

Вступительное слово учителя.

Здравствуйте, ребята. Вы подошли к водопаду чисел. Догадались ли вы, где он находится и в какой стране? (Презентация).

Послушайте музыку воды, а я поведаю вам историю. “Существует предание, согласно которому китайский император Ию, живший примерно 4000-5000 лет до нашей эры, однажды увидел на берегу реки священную черепаху с узором из черных и белых кружков на панцире.

Сообразительный император сразу понял смысл этого рисунка. Черными кружками в этом квадрате изображены (женские) четные числа, белыми - нечетные (мужские) числа.

Чтобы и нам стал понятен смысл, заменим каждую фигуру числом, показывающим, сколько в ней кружков.

В обычной записи он не так эффектен”.

“Символ изображенный на черепахе, китайцы называли Ло Шу (в книге эпохи Мин) и считали магическим – он использовался при заклинаниях. Поэтому квадратные таблицы чисел с тех пор называют магическими квадратами.

Что же в нем магического?

Девять порядковых чисел размещены в девяти клетках квадрата так, что суммы чисел вдоль каждой строки, каждого столбца и каждой из двух диагоналей одинаковы – это основное свойство волшебного квадрата.

Магические квадраты почитались не только в Древнем Китае. Во времена средневековья в Европе свойства магических квадратов тоже считались волшебными. Магические квадраты служили талисманами, защищая тех, кто их носил, от разных бед.

Более поздние сведения о волшебных квадратах, относящиеся к I веку, получены из Индии. Вот один из таких древне индусских памятников почти 2000-летней давности.

Здесь 16 порядковых чисел расположенных в 16 клетках так, что выполняется основное свойство волшебного квадрата – сумма равна 34.

Недаром в ту далекую эпоху суеверий древние индусы, а следом за ними и арабы приписывали этим числовым сочетаниям таинственные и магические свойства.

Вся эта своеобразная мозаика чисел с ее постоянством сумм действительно придает волшебному квадрату “волшебную” силу произведения искусства. И это привлекло внимание не только математиков, но и художников.

В Западную Европу из Индии этот волшебный квадрат проник лишь в начале XVI века и так очаровал выдающегося немецкого художника, гравера и немного математика Альбрехта Дюрера, что художник даже воспроизвел его (в несколько измененном виде) в одной из своих гравюр на меди “Меланхолия” 1514 г.

Интересно, что в нижней строке этого магического квадрата средние числа изображают год создания гравюры – 1514.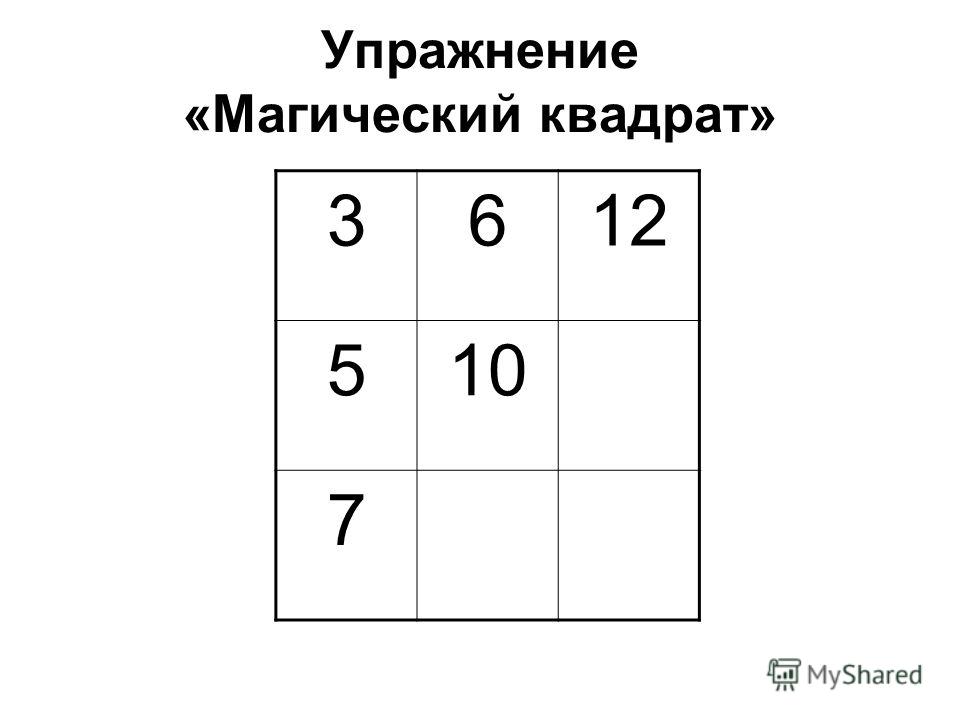 возможно, Дюрер знал этот квадрат, а может быть, начав именно с этих чисел, художник смог найти остальные методом подбора” [1, с.255-271].

Практическая работа

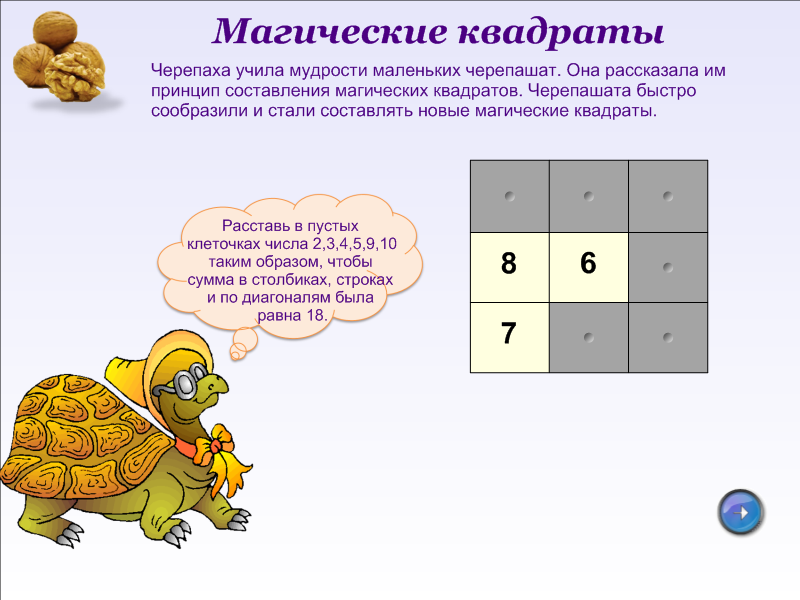
А) – Проверьте основные свойства магического квадрата Дюрера, посчитав суммы по строкам, столбцам и диагоналям.

– Исследуйте другие свойства этого квадрата, посчитав сумму чисел центрального квадрата и каждого из угловых квадратов.

– Впишите в пустые клетки квадрата такие числа, чтобы квадрат стал магическим.

– Восстановите магические квадраты.

Б) – Возьмите квадрат 4х4 и впишите в него числа от 1 до 16 по порядку. Теперь поменяйте местами числа стоящие в противоположных углах квадрата. А затем поменяйте местами числа, стоящие в противоположных углах центрального квадрата. Если вы все сделали правильно, должен получиться магический квадрат. Проверьте.

Итог и награждение.

Молодцы, вы замечательно справились с заданием. На прощание возьмите печенье с сюрпризом.

Литература

1. Кордемский, Б.А. Математическая смекалка. / Б.А. Кордемский. – Государственное издательство технико-теоретической литературы. Москва. 1957. - 575 с.

21.07.2009

Магический квадрат. Интересное из математики

Одной из самых загадочных и популярных математических «головоломок» является знаменитый магический (волшебный) квадрат, который представляет собой табличку с равным количеством столбцов и строк, особенность которой заключается в том, что суммы чисел каждой строки, каждого столбца и каждой диагонали равны — это число называется «магической константой». Классические магические квадраты могут быть нормальными (используются целые числа от 1 и до n2), построенными для всех порядков, кроме второго, а также ассоциативными (сумма двух чисел, расположенных с соблюдением симметрии относительно центра квадрата равна n2 + 1). В том случае, если в «магии» задействованы только числа строк и столбцов, квадрат становится полумагическим.

Помимо классических, существуют нетрадиционные магические квадраты, самым известным из которых считается дьявольский (пандиагональный) магический квадрат. Особенность этого квадрата заключается в том, что к числам основных диагоналей добавляются еще и ломаные, т.е. те диагонали, которые, достигнув края, продолжаются параллельно первому отрезку от противолежащего края квадрата.

Если верить древнекитайской легенде, то первый магический квадрат Ло Шу, содержащий три строки и три столбца, числа которых в сумме составляли 15, был начертан на панцире священной черепахи, обитающей в водах Желтой реки. В Индии известен свой древнейший (XI века) магический квадрат, считающийся «дьявольским», сумма магических чисел которого равна 34. В Европе магический квадрат появился лишь в Средние века благодаря византийскому писателю Мосхопулосу, однако вся слава европейских волшебных квадратов досталась А. Дюреру, который первым придумал и изобразил его в своей гравюре «Меланхолия». Квадрат Дюрера в сумме 34 дает не только по вертикали, горизонтали и по диагонали: Дюрер пошел намного дальше — малые квадраты, составленные из четырех клеточек, расположенных по углам большого, квадрат из четырех клеточек в центре, сумма чисел в угловых клетках, квадраты, имитирующие «ход коня» и пр. — все дает в сумме 34. XYI век добавил в копилку «магии» и астрологии квадраты от 3 до 9 порядков, автором которых стал астролог Корнелий Генрих Агриппа. Благодаря ему магический квадрат с тех пор и поныне является символом магов и чародеев. Последние магические квадраты были построены в начале XX века Генри Дьюдени, Аланом Джонсоном (ими были созданы нетрадиционные магические квадраты, в которых используются не только натуральные числа) и Дж.Манси, который, за небольшим исключением, использовал последовательные простые числа.

Легко ли построить магический квадрат? Ученые считают, что, возможно, существует общий метод, зная который, достаточно просто создать любой магический квадрат, однако, к сожалению, он неизвестен, но, тем не менее, широко распространены частые схемы, авторами которых стали известные математики (Ф. де ла Ир, Л.Эйлер), один из которых — французский геометр А.де ла Лубера — предлагает строить магические квадраты пятого порядка (5×5) следующим образом. После того, как центр верхней строки заняло число 1, все натуральные числа помещаются по порядку снизу вверх в клетки диагоналей справа налево. Достигнув верха квадрата (клетки, соседствующей с единицей), необходимо заняться заполнением диагонали, которая берет начало от нижней клеточки следующего столбца. Оказавшись в пятой клетке второго ряда снизу, заполняется числами диагональ, следующая от первой клетки средней строки. После того, как будет заполнена последняя клетка верхней строки, необходимо спуститься на нижнюю строку и подобным образом продолжить построение магического квадрата.

Поделиться ссылкой

Математическое сокровище: Магический квадрат квадратов Бенджамина Франклина

Автор(ы): 

Сидни Дж. Колпас (Общественный колледж округа Делавэр)

Больший из двух магических квадратов, наиболее связанных с Бенджамином Франклином (1706–1790), был первым опубликовано в «Таблицах и трактатах Джеймса Фергюсона , относительно нескольких искусств и наук» (Лондон, 1767 г. ) и перепечатано годом позже в 38 томе лондонского журнала Gentleman’s Magazine , который действовал с 1731 по 1919 год.22 и нанял таких известных личностей, как Сэмюэл Джонсон.

Джеймс Партон (1822–1891) обсуждал происхождение «Волшебного квадрата квадратов» Бенджамина Франклина 16X16 в своей биографии,

Деятельность ума Франклина была проявляется в его пустяковых развлечениях. Во время сессий Ассамблеи ему приходилось терпеть много скучных часов, сидя на своем месте в качестве клерка, слушая дебаты, в которых он не мог принимать участия. Его друг Логан однажды показал ему французскую книгу «Волшебные квадраты», праздную игру прошлого века. Франклин, который делал эти квадраты в юности, теперь разбавлял утомительную ежедневную сессию, создавая квадраты чрезвычайной сложности, превосходящие все, что когда-либо делалось таким способом. . . .

Это был не самый замечательный из магических квадратов Франклина. Он сделал по одной из 16 ячеек в каждом ряду, которые, помимо того, что обладали свойствами квадрата, приведенными выше (количество, которое прибавлялось, всегда равно 2056), обладали еще и такой замечательной особенностью: в листе бумаги вырезалось квадратное отверстие. такого размера, чтобы вмещать и показывать через него только шестнадцать маленьких квадратов, будучи наложенным на больший квадрат, сумма шестнадцати чисел, проступающая таким образом через отверстие, где бы она ни находилась на большем квадрате, должна была также составлять 2056.

Этот квадрат был выполнен за один вечер. Это вызвало безграничное удивление мистера Логана, которому Франклин отправил его и который назвал его «самым изумительным произведением». Сам Франклин в шутку сказал, что это был «самый волшебно-волшебный из всех магических квадратов, когда-либо созданных каким-либо фокусником». Мистер Логан намекает на эти квадраты в одном из своих писем Питеру Коллинсону из Лондона: «Наш Бенджамин Франклин, безусловно, необыкновенный человек, обладающий исключительным здравым смыслом, но в равной степени скромный.

Обложка The Gentleman’s Magazine , июль 1768 года, из коллекции доктора Сида Колпаса.

«Волшебный квадрат квадратов», Gentleman’s Magazine (июль 1768 г.), стр. 312–313.

Транскрипция страницы 313:

Удивительные свойства чисел, помещенных в Волшебный квадрат квадратов доктора Франклина.

Большой квадрат разделен на 256 маленьких квадратов, в которых все числа от 1 до 256 размещены в 16 столбцах, которые можно рассматривать как по горизонтали, так и по вертикали. Свойства следующие:

1. Сумма 16 чисел в каждом столбце, вертикальном или горизонтальном, равна 2056.
2. Каждая половина столбца, вертикальная и горизонтальная, составляет 1028 или половину 2056.
3. Половина восходящей диагонали, прибавленная к половине нисходящей диагонали, дает 2056; проведя эти полудиагонали от концов любой стороны квадрата к его середине и отсчитав их либо вверх, либо вниз; или сбоку слева направо, или справа налево.
4. То же самое со всеми параллелями полудиагоналей, сколько их можно провести в большом квадрате: для любых двух из них, направленных вверх и вниз, от того места, где они начинаются, до того места, где они заканчиваются, их сумма составит 2056. то же самое вниз и вверх от того, где они начинаются, до того, где они заканчиваются; или то же самое, если взять его боком к середине и снова вернуться к той же стороне.
   Примечание. Один набор этих полудиагоналей и их параллелей проведен на фигуре вверх и вниз. Другой такой набор может быть проведен с любой из трех других сторон.
5. Четыре угловых числа в большом квадрате, добавленные к четырем центральным числам, составляют 1028, равное половине суммы любого вертикального или горизонтального столбца, содержащего 16 чисел, и равное половине диагонали или ее параллели.
6. Если в бумаге прорезать квадратное отверстие (равное по ширине четырем маленьким квадратам), через которое можно увидеть любой из 16 маленьких квадратов в большом квадрате, и положить бумагу на большой квадрат; сумма всех 16 чисел, видимых через отверстие, равна сумме 16 чисел в любой горизонтальной или вертикальной колонке, а именно 2056.

Транскрипция магического квадрата Франклина 16X16. Щелкните эту ссылку, чтобы загрузить файл Excel для использования читателем или учащимся.

Для класса

Попросите учащихся проверить свойства с 1 по 6 с помощью файла Excel. Например:

Свойство 1: Функция Excel =СУММ(B1:B16)  

Ответ: 2056

Свойство 2: Функция Excel =СУММ(B1:B8)  

Ответ: 1028

2 Функция Excel =СУММ(B1+C2+D3+E4+F5+G6+H7+I8+B16+C15+D14+E13+F12+G11+h20+I9)

Ответ: 2056

Свойство 4: Функция Excel =СУММ(B15+C14+D13+E12+F11+G10+H9+I8+J8+K9+L10+M11+N12+O13+P14+Q15)

Ответ: 2056

Свойство 5: Функция Excel =СУММ(B1+Q1+B16+Q16+I8+J8+I9+J9)

Ответ: 1028

Функция Excel =СУММ 6: F1:F4)+СУММ(G1:G4)+СУММ(h2:h5)+СУММ(I1:I4)

Ответ: 2056

Учащиеся также могут исследовать, как составлять магические квадраты (существуют алгоритмы), или учиться больше о работе Франклина над магическими квадратами; одна из лучших книг на эту тему Числа Бенджамина Франклина: незамеченная математическая одиссея Пола К. Паслеса. В американском математическом ежемесячнике было опубликовано множество статей о магических квадратах Франклина, в том числе «Потерянные квадраты доктора Франклина: недостающие квадраты Бена Франклина и секрет магического круга» Паслеса 2001 г. и «Магические квадраты и линейная алгебра» Кристофера Дж. Хенриха. .” Еще одна статья о магических квадратах в Convergence — «Магические квадраты Мануэля Мосхопулоса» П. Г. Брауна.

Ссылки

«Удивительные свойства чисел, помещенных в магический квадрат квадратов доктора Франклина». Журнал джентльмена 38 (июль 1768 г.): 312–313.

Партон, Джеймс. Жизнь и времена Бенджамина Франклина . Том. 1. Бостон: Тикнор и Филдс, 1867.

Паслес, Пол С. Числа Бенджамина Франклина: невоспетая математическая Одиссея. Принстон: Princeton University Press, 2008.

«Журнал для джентльменов». Википедия. https://en.wikipedia.org/wiki/The_Gentleman%27s_Magazine.

Индекс к математическим сокровищам

Сидни Дж. Колпас (Общественный колледж округа Делавэр), «Математическое сокровище: магнитный квадрат квадратов Бенджамина Франклина,« Конвергенция (ноябрь 2019)

Конвергенция

Теги:

Computation Mathematics

Элементарная математика

Элементарная теория чисел

История математики

Развлекательная математика

Магические квадраты, искусство и математика

Магические квадраты — одно из самых увлекательных математических изобретений, а также одно из наиболее отраженных в искусстве, от гравюр Дюрера до храма Святого Семейства Гауди. Это нечто, вдохновленное магическими свойствами — как чисто числовыми, так и гадательными и защитными — которые приписывались им на протяжении всей истории.

Магические квадраты представляют собой числовое расположение натуральных чисел (или целых положительных чисел) в n строках и n столбцах (или, другими словами, порядка n), где вставленные числа идут от 1 до n ² .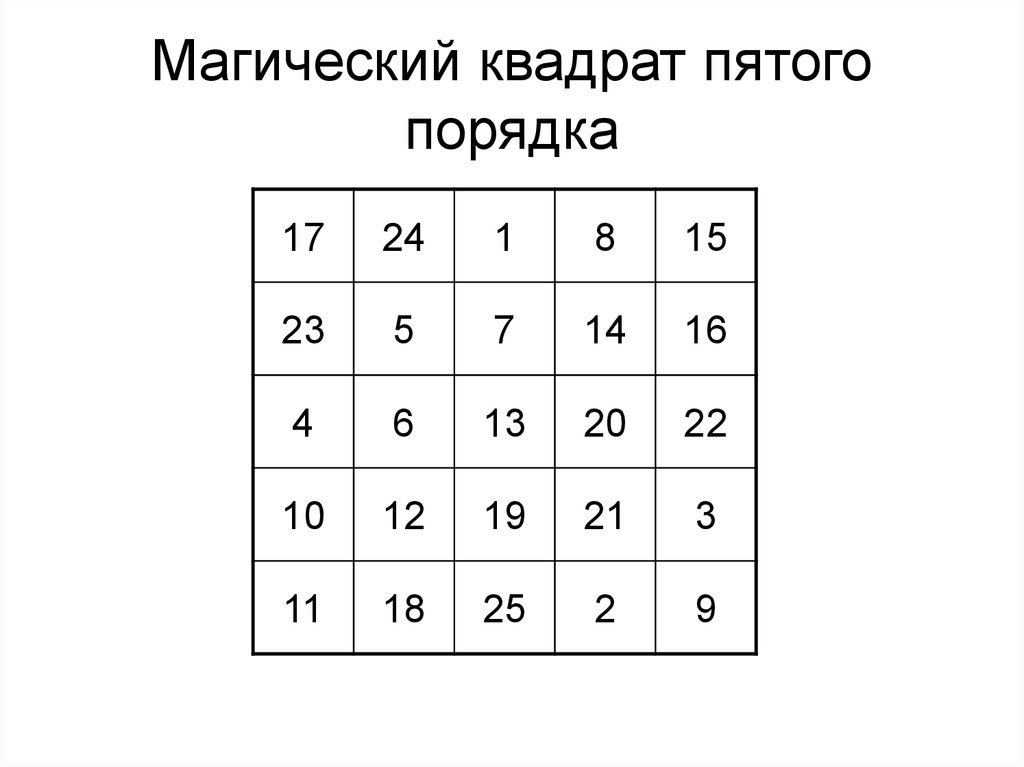 Магия возникает потому, что сумма чисел, присутствующих в каждой строке, в каждом столбце и на каждой главной диагонали, дает один и тот же результат, называемый «магической константой» или «магической суммой».

Вероятно, наиболее известным магическим квадратом является квадрат Альбрехта Дюрера, изображенный на его гравюре Melencolia . Это квадрат четвертого порядка, изобилующий магическими свойствами, поскольку сумма любого из его четырех квадрантов дает также его магическую константу: 34. И то же самое происходит с суммой четырех центральных чисел. Кроме того, центральные клетки нижнего ряда заняты числами 15 и 14, обозначающими дату гравюры: 1514 год.

Со всеми этими подсказками вы сможете завершить магический квадрат Дюрера:

Площадь Ло Шу

Магический квадрат Дюрера, вероятно, является самым известным, а также первым его изображением в Европе, но правда в том, что к тому времени, когда художник представил его, магические квадраты уже имел долгую историю.

Первое упоминание относится к Китаю в 2200 году до н.э. Согласно легендам об Императоре Юй, в Древнем Китае случился огромный потоп. Люди принесли жертвы богу одной из разлившихся рек, реки Луо, и появилась черепаха со странным точечным узором на панцире, квадратом Ло Шу. Это была сетка 3×3, где числа были представлены группами точек.

С дарованными им гадательными и защитными характеристиками, магические квадраты путешествовали из Китая в остальную Азию, а оттуда в Египет, где входили в одежду и украшения в качестве талисманов.

Считается, что первыми, кто углубил и изучил их математические свойства, были арабские ученые и исламский мир, сделавшие их известными в Европе в пятнадцатом веке, где они сразу же проникли благодаря своим предполагаемым магическим свойствам, прежде всего связанным с предсказанием , алхимия и астрология, а позже и чисто математические.

Американский эрудит Бенджамин Франклин также был великим создателем первоклассных магических квадратов. В 1750 году он опубликовал полумагический квадрат 8-го порядка и с магической константой 260. Он называется полумагическим, потому что помимо его обычных атрибутов каждая полустрока и полустолбец в сумме дают 130, т.е. половина магической константы. Более того, сумма четырех углов и четырех центральных квадратов также равна 260. Имея эту информацию, можно составить приведенный ниже магический квадрат:

Примером того, что магические квадраты никогда не теряли своей мистической или божественной сущности, является тот факт, что Антонио Гауди включил его в фасад своего причудливого храма Святого Семейства, посвященного Страсти Иисуса, псевдомагический квадрат 4-го порядка с магической константой 33, возраст Христа. В этом случае это псевдомагия, потому что вместо первых 16 чисел есть два пропущенных (12 и 16) и два, которые повторяются в последовательных ячейках.