Википедия крестики нолики: HTTP 429 – too many requests, слишком много запросов

Квантовые крестики-нолики – frwiki.wiki

Крестики-нолики квант является «обобщение квантовым  » игровой крестики-нолики, в котором удары игроков «  перекрывающие  » выстрелы классической игры. Игра была изобретена Алланом Гоффом и Novatia Labs. По словам автора, игра позволяет ввести понятие квантовой механики без необходимости использования сложных математических инструментов.

Резюме

• 1 принцип
• 2 правила
• 3 Стратегия
  • 3.1 Точное решение
  • 3.2 Стратегические элементы
• 4 См. Также
• 5 ссылки

Принцип

Правила квантовых крестиков-ноликов не особенно сложны, но вводят некоторые механики, незнакомые игрокам; поэтому их изучение является более сложной задачей, чем в большинстве обычных игр. Понимание основы, на которой была изобретена игра, может помочь их усвоить.

Основная цель изобретения квантовых крестиков-ноликов состояла в том, чтобы изучить возможность нанесения удара в двух местах.

В классической физике объект может находиться только в одном месте в любой момент времени, тогда как в квантовой физике математика, используемая для описания квантовой системы, вводит возможность для определенных квантовых частиц находиться в неопределенном состоянии, прежде чем это не определено. путем измерения .

Исследователи, которые изобрели квантовые крестики-нолики, работали над абстрактными квантовыми системами, формальными системами, основополагающие аксиомы которых включают лишь несколько аксиом квантовой механики. Квантовые крестики-нолики стали наиболее тщательно изученной абстрактной квантовой системой и, кроме того, открыли новые интересные направления исследований. Это также оказалось увлекательной игрой с хорошей образовательной ценностью для студентов.

Правила квантовых крестиков-ноликов пытаются отразить несколько явлений квантовых систем:

• Суперпозиция, которая является способностью квантовой частицы находиться в неопределенном состоянии;
• Запутанности, которая представляет собой явление корреляции, которые не участвуют в причинности между различными частями квантовой системы;
• Уменьшение, что означает, что после измерения, квантовая система видит свое восстановленное состояние к одному, что было измерено.

Правила

Второй игрок только что сделал ход O ₈, создав цикл запутанности 3-7-8. Поэтому первый игрок должен выбрать, хочет ли он, чтобы O ₈ было уменьшено в центральном квадрате или в верхнем правом квадрате (в обоих случаях O получит выравнивание).

X решил уменьшить O ₈ в среднем поле, что заставляет все остальные сложности цикла и прикрепленные к ним «призрачные метки» сокращаться по цепочке. X также получает выравнивание, но поскольку максимальный индекс этого (7) выше, чем у выравнивания O (6), O выигрывает на 1 против 1/2.

Квантовые правила крестики-нолики происходят из трех явлений, объясненных выше, путем модификации классического правила крестики-нолики  : количества возможных состояний для движения. Дополнительные правила позволяют указать, когда и как эти штрихи «уменьшаются», чтобы в результате получить классические определенные местоположения крестиков-ноликов.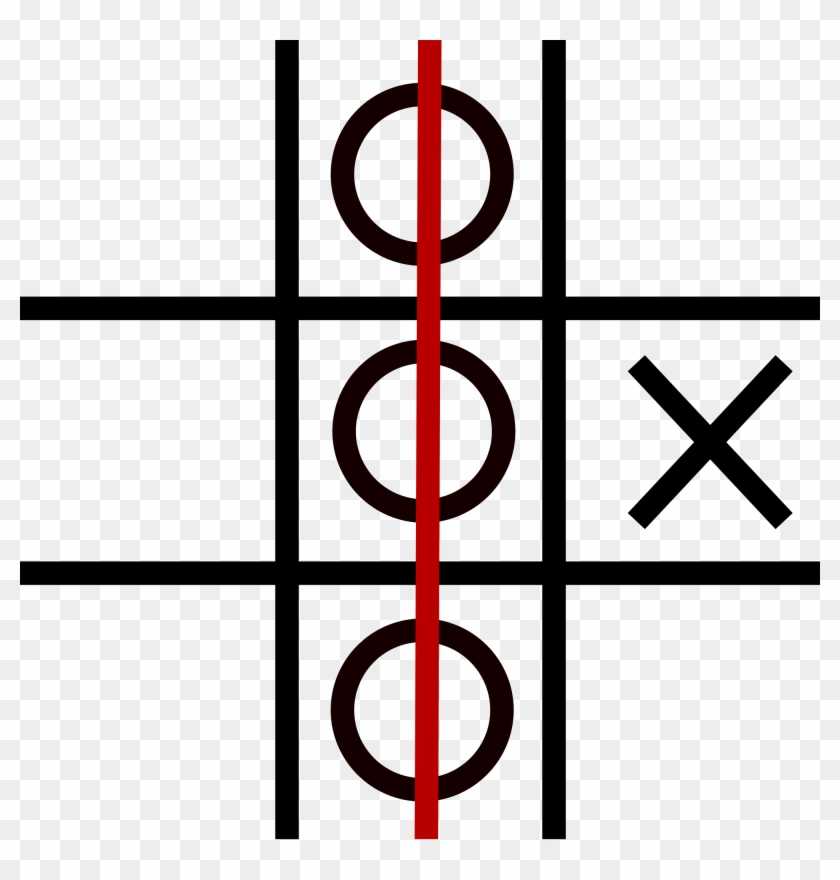

Для каждого хода игрок отмечает два отдельных квадрата своей буквой (X или O) вместо одного, и каждая отметка имеет номер хода в качестве нижнего индекса (от 1, возможно, до 9). Образованные таким образом пары меток называются « жуткими метками» . Если X играет первым, индексы у X нечетные, а у O четные. Две коробки, соединенные парой «призрачных меток», называются «запутанными». Во время игры может быть до восьми «призрачных знаков» в одном квадрате, если он «перепутан» с другими восемью квадратами.

Феномен «редукции» возникает, как только создается цикл запутанности, вызывающий «меру». Это решает игрок, который не несет ответственности за создание цикла (если есть решение, которое необходимо принять). Например, если в начале игры первый игрок решил соединить два ящика, а второй соединяет те же ящики, последний создает цикл, и первый игрок должен выбрать, какой из двух ящиков он хочет. Таким образом, все «призрачные отметки», принадлежащие циклу или связанные с ним, сводятся к окончательным отметкам. Ящики, которые были помечены постоянно, больше не могут содержать новые «призрачные метки».

Первый игрок, которому удастся добиться совмещения (по горизонтали, вертикали или диагонали) трех окончательных отметок, побеждает в игре. Поскольку сокращение может привести к нескольким выравниваниям, существует несколько возможных окончательных конфигураций:

• У одного из игроков коридор, а у другого нет, поэтому он получает очко;
• У одного из игроков два состава, поэтому он набирает два очка;
• У каждого игрока есть состав: тот, чей состав имеет наименьшее максимальное количество очков, получает очко, другой – пол-очка.

Стратегия

Точное решение

На Международной конференции по передовым вычислительным и коммуникационным технологиям 2011 года японские исследователи Такуми Ишизеки и Акихиро Мацуура представили свою работу по вычислительному разрешению квантовых крестиков-ноликов. Их выводы таковы, что первый игрок, следующий идеальной стратегии, не может получить полную победу (1 против 0) или (2 против 0), но может получить половину выигрыша (1 против ½) после девяти ударов, начиная с игры в двух противоположных углах поля.

диагональ.

Изменяя правило игрока, который выбирает меру при сокращении ( т.е. тот, кто создает цикл запутывания, выбирает меру), они заключают, что первый игрок имеет возможность полной победы, начав с двух углов по горизонтали или по вертикали., и полвыигрыш в большинстве других стартовых схем. Из этого они делают вывод, что правило, дающее игроку, не формирующему цикл, выбор меры, позволяет эффективно уравновесить преимущество, данное начинающему игроку.

Стратегические элементы

Смотрите также

• Крестики-нолики

Рекомендации

1. ↑ (in) Аллан Гофф, «  Квантовые крестики-нолики: метафора для обучения суперпозиции в квантовой механике  », Американский журнал физики, вып.  74,
   п ^о  11,Ноябрь 2006 г. , стр.  962-973 ( ISSN  0002-9505, DOI  10.1119 / 1.2213635, читать онлайн )
2. ↑ (in) Такуми Ишизеки и Акихиро Мацуура, «  Решение квантовых крестиков-ноликов  », Международная конференция по передовым вычислительным и коммуникационным технологиям (материалы конференции) ,2011 г.( ISBN  978-981-08-7932-7, читать онлайн )
3. ↑
   (in) Цзя Нин Ли и Энн Сью Чеонг, «  Стратегические идеи из квантовой игры в крестики-нолики  », Journal of Physics, vol.  43, п ^о  45,ноябрь 2010( ISSN  1751-8113, DOI  10. 1088 / 1751-8113 / 43/45/455304 )

<img src=”//fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=”” title=””>

Альтернативные крестики-нолики / Хабр

Однажды на пикнике я заметил математиков, толпящихся возле игры, интереса к которой я ожидал меньше всего: крестики-нолики.

Вы могли и сами заметить, что игра крестики-нолики смертельно скучна. В ней нет места творческой идее или внезапному озарению. Хорошие игроки всегда играют вничью. Игра неизбежно идёт примерно так:

Но математики на пикнике играли в более изощренную версию игры. В каждой из клеток на квадратном поле они нарисовали поле поменьше:

По мере наблюдения я заметил основные правила:

1. Каждый ход делается в одном из маленьких полей.

2. Достигший в маленьком поле расположения трёх одинаковых фигур в ряд выигрывает это поле.

3. Чтобы выиграть игру, необходимо одержать победы в трёх маленьких полях в ряд.

Но чтобы понять самое важное правило, мне потребовалось некоторое время:

Игрок не выбирает одно из девяти маленьких полей, в котором он хочет ходить. Выбор определяется предыдущим ходом вашего оппонента. Клетка в маленьком поле, в которую он сходил — это то маленькое поле, в котором вам предстоит делать ход. (И клетка, в которую вы сходите, в свою очередь определяет, в каком маленьком поле будет ходить ваш оппонент.) К примеру, если я схожу сюда…

Ваш следующий ход вы будете делать сюда…

Это придаёт игре элемент стратегии. Вы не можете позволить себе сфокусироваться на маленьком поле. Вам приходится учитывать то, куда ваш ход отправит вашего оппонента, и куда его следующий ход отправит вас и так далее.

Результат выглядит очень необычно. Игроки могут двигаться случайно, легко пропуская конструкции в две и три одинаковые фигуры в ряд. Но в этом безумии есть порядок — они продумывают свои ходы наперёд, помня о возможности послать оппонента в нетронутую недвижимость. Это, в общем, куда более интересно, чем обычные крестики-нолики.

Необходима пара условностей:

1. Что если мой оппонент отправляет меня в маленькое поле, в котором уже была одержана победа? Это неудачная ситуация. Если там остались незаполненные клетки, вам придётся выбрать одну из них. Хотя повлиять на исход игры в этом поле вы уже не сможете, вы хотя бы определите, где будет ходить ваш оппонент.

2. Что если мой оппонент отправляет меня в заполненное поле? В этом случае, примите наши поздравления — вы можете выбрать для хода любое из полей. (Это означает, что вам следует избегать отсылов вашего оппонента в заполненное поле!)

Когда я вижу, как мои студенты играют в крестики-нолики, я сдерживаю желание закатить глаза и показываю им эту игру. Вы можете поспорить, что игра развивает математические навыки (дедуктивное умозаключение, условное мышление, геометрическая идея подобия), но какая разница? В любом случае игра хороша.

И последнее: я разработал стратегию, которую я скромно назвал Гамбит Орлина. Вы начинаете захватом самой центральной клетки.

Вашему оппоненту придётся поставить нолик в любой из других клеток.

Вновь ходите в центр.

Нолики начинают образовывать ряд.

Опять ходите в центр.

Ваш оппонент образовывает победный ряд, смеясь над вашей глупостью.

Вновь ходите в центр.

Оппонент видит хитрость, на которую вы пошли…

Вновь сходите в центр. Ваш оппонент неохотно понимает, что остановить вас невозможно.

По окончании у крестиков ценой жертвы центрального поля есть наилучшая позиция в других восьми. Это никоим образом не идеальная стратегия. Она стимулирует потерю центрального поля без борьбы. Но вынужденное бесполезное скопление стольких ноликов на одном поле позволяет крестикам взять верх на протяжении остальной игры.

Словом, это альтернативные крестики-нолики. Играйте! Дайте знать, как у вас дела.

Дополнение 18 июня: Частый (и неглупый) вопрос: «Что делать, если в одном из маленьких полей ничья?» Похоже, есть два варианта:

1. Поле считается ни за крестик, ни за нолик. (Так играю я.)

2. Поле считается и за крестик, и за нолик. (Это поможет избегать ничьих, хотя может привести к странной ничье, когда вы и ваш оппонент одерживаете победу одновременно.)

Полагаю, каждый из вариантов работает. Просто убедитесь, что вы и ваш оппонент пришли к соглашению до начала игры, поскольку это влияет на стратегию.

Примечание переводчика: уже есть реализация этой игры для платформы «Андроид».

Крестики-нолики | Brilliant Math & Science Wiki

Сандип Бхардвадж, Джинит Сутар, Иван Косвара, и

способствовал

Содержимое

• Геймплей
• Стратегия
• Смотрите также

Играют два игрока. Им присвоен символ; традиционно один получает X, а другой – O. Начинает один игрок, традиционно игрок X. Каждый игрок, в свою очередь, размещает свой символ на пустом квадрате сетки 3 × 33 × 33 × 3, пытаясь первым создать линию из трех своих символов (горизонтальную, вертикальную или диагональную). Выигрывает тот, кто сделает это первым; если сетка заполнена без результата, это ничья.

При игре в крестики-нолики тактика и стратегия необходимы для победы.

Простейшая тактика — выполнить три в ряд: если два ваших символа выстроились в ряд (по горизонтали, вертикали или диагонали), а оставшаяся клетка пуста, играйте на ней, давая ты победа. Если у вас выстроились два символа, а последний квадрат пуст, это называется угрозой

.

Приведенная выше тактика приводит к тому, что блокирует : если у противника выстроились два своих символа, а оставшаяся клетка пуста, вы должны заблокировать его, сыграв на последней оставшейся клетке.

Учитывая тактику блокирования, вполне естественно подумать о создании двух разных угроз, чтобы противник не мог заблокировать обе одновременно. Это называется вилкой (поскольку она имеет два (или более) направления, как обеденная вилка, разделяющаяся от одной ручки на несколько зубцов; также сравните с вилкой в ​​шахматах, которая должна создавать угрозу в нескольких направлениях).

Хорошо! Теперь пришло время играть в игру:

ааа ббб ссс ддд эээ Либо ааа либо ббб Либо ббб, либо эээ

Предположим, вы играете в крестики-нолики с противником. Вы играете за XXX, а ваш противник играет за OOO.

Игра ведется следующим образом:

Найдите все возможные плитки сетки, на которые вы можете поставить метку XXX, которая поможет вам гарантировать выигрыш при лучшей игре.

Игрок может помешать противнику сделать развилку, если он

1. поставит свою метку на клетку сетки, где можно сделать развилку, или
2. вынуждает противника блокировать его угрозу вместо того, чтобы делать развилку, или
3. мест в центре, если они свободны, что блокирует большинство разветвлений.

Нижний левый угол Верхний правый угол Любой из двух углов Любое из средних мест на стороне Либо среднее пространство слева или справа Либо среднее пространство на верхней или нижней стороне

Вы играете в крестики-нолики. Вы играете за OOO, а ваш противник играет за XXX. Игра выглядит так:

Куда поставить следующий ООО, чтобы уберечь себя от проигрыша?

Да №

Настала очередь X . Может ли O победить?

Примечание: O и X оба воспроизводятся оптимально.

Да Нет

Если ход O\color{#3D99F6}\text{O}O, может ли O\color{#3D99F6}\text{O}O выиграть?

Давай сыграем еще раз:

O Икс Невозможно определить

Два любителя играют в крестики-нолики. Каждый ставит свою отметку: X \color{#D61F06} XX или O \color{#3D99F6}ОО. Мы не знаем, кто начал первым.

После того, как первый игрок поставил свою вторую метку, игроки всегда будут ставить свою метку в строке, которая уже содержит

(a) две свои собственные метки,
(b) две метки его/ее соперника,
(c) , отдавая предпочтение (a) над (b).

Не поставлена ​​только последняя отметка в игре, показанной на рисунке. Кто победит в игре, X \color{#D61F06} XX или O? {\ цвет {# 3D99F6}О}?О?

1 2 3 4 В любом месте

Предположим, вы играете в крестики-нолики с противником. Вы играете за OOO, а ваш противник играет за XXX.

На какое место вы должны сделать свой следующий ход, чтобы проиграть следующий ход независимо от того, где находится следующий ход вашего противника?

• Комбинаторные игры – выигрышные позиции

• ним

• Мышление К-уровня

Цитировать как: Крестики-нолики. Brilliant.org . Извлекаются из https://brilliant. org/wiki/крестики-нолики/

Крестики-нолики | Настольные игры Galore Wiki

Крестики-нолики

Издатель

Римская империя

Год создания

Первый век до н.э.

Возраст

3 года и старше

Количество игроков

2

Время воспроизведения

От 3 до 5 минут

Оцифрованный

Да

Содержание

• 1 Краткое описание
• 2 История
• 3 Как играть
• 4 Ссылки и ссылки

Сводка

Крестики-нолики  (также известная как Крестики-нолики или Xs и Os ) — это игра с бумагой и карандашом для двух игроков, X и O , которые по очереди отмечают ячейки в сетке 3×3. Игрок, которому удается разместить три свои метки в горизонтальном, вертикальном или диагональном ряду, выигрывает игру.

История

В ранний вариант крестиков-ноликов играли в Римской империи примерно в первом веке до нашей эры. Он назывался Терни Лапилли, и вместо того, чтобы иметь любое количество фигур, у каждого игрока было только три, поэтому им приходилось перемещать их на пустые места, чтобы продолжить игру. Маркировка сетки игры была найдена мелом по всему Риму. Однако, согласно книге Клавдии Заславской Крестики-нолики: и другие игры «три в ряд» от Древнего Египта до современного компьютера , Крестики-нолики могут появиться еще в древнем Египте. ^[2]  Еще одна тесно связанная древняя игра — “Моррис трех мужчин “, в которую также играют на простой сетке, и для ее завершения требуется три фигуры в ряд. ^[3]

Другие названия игры более поздние. Первое печатное упоминание о «Крестиках-ноликах», британском названии, появилось в 1864 году. В своем романе «Сможете ли вы простить ее» 1864 года Энтони Троллоп упоминает клерка, играющего в «синицы-тат-нолики». Первое печатное упоминание об игре под названием «крестики-нолики» появилось в 1884 году, но относилось к «детской игре, в которую играют на доске, состоящей в попытке с закрытыми глазами опустить карандаш на одну из цифр на грифельной доске». набор, число попаданий засчитывается». «Крестики-нолики» также могут происходить от «крестики-нолики», названия старой версии игры в нарды, впервые описанной в 1558 году. Переименование крестиков-ноликов в крестики-нолики в США произошло в 20 веке. ^[4]

В 1952 году OXO (или Крестики-нолики ) для компьютера EDSAC стала одной из первых известных видеоигр. Компьютерный игрок мог бы играть в идеальные игры в крестики-нолики против противника-человека.

В 1975 году студенты Массачусетского технологического института также использовали крестики-нолики для демонстрации вычислительной мощности элементов Tinkertoy. Компьютер Tinkertoy, сделанный (почти) только из Tinkertoys, способен отлично играть в крестики-нолики. ^[5]  В настоящее время он выставлен в Музее науки в Бостоне.

Как играть

Цель Tic Tac Toe состоит в том, чтобы получить три в ряд. Вы играете на доске три на три. Первый игрок известен как X, а второй — O.