Веселые геометрические фигуры картинки: Веселые фигуры картинки для оформления геометрические (43 фото) » Юмор, позитив и много смешных картинок

Конкурс рисунков из геометрических фигур. Объемные композиции из простых фигур. Видео: аппликация из геометрических фигур

Веселые и красочные задания для детей “Рисунки из геометрических фигур” являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм: треугольника, круга, овала, квадрата, прямоугольника и трапеции. Все задания предназначены для самостоятельной работы ребенка под наблюдением взрослых. Родитель или педагог должны правильно объяснить ребенку, что он должен сделать в каждом задании.

1. Рисунки из геометрических фигур – Условия к выполнению заданий:

Чтобы начать выполнять задания, скачайте во вложениях бланк, в котором вы найдете 2 типа заданий: рисунки из геометрических фигур для раскрашивания и задание для рисования фигур с помощью логического и образного мышления. Распечатайте скачанную страницу на цветном принтере и дайте ребенку вместе с цветными карандашами или фломастерами.

• В первом задании малышу нужно мысленно соединить каждые две части представленных фигур в одну и нарисовать полученную геометрическую форму в соответствующей клетке. Объясните ребенку, что детали можно поворачивать в уме в разные стороны до тех пор, пока он не получит нужную комбинацию для составления фигуры. Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.
• Во втором задании дети должны правильно назвать фигуры из которых состоят нарисованные картинки. Затем эти картинки нужно раскрасить, используя цвета рядом с геометрическими фигурами. Каждую фигуру нужно раскрасить только в указанный цвет.

Чтобы придать занятию больше энергии и энтузиазма – можно объединить несколько детей в группу и предоставить им выполнение заданий на время. Тот ребенок, который первый выполнит все задания без ошибок, признается победителем. В качестве приза можно повесить его работу на стену достижений (такая стена обязательно должна присутствовать как дома, так и в детском саду).

Скачать задание “Рисунки из геометрических фигур” вы можете во вложениях внизу страницы.

2. Геометрические фигуры в рисунках – 3 задания-раскраски:

Следующее занятие также скрывает основные геометрические фигуры в рисунках. Ребенку нужно найти эти фигуры, назвать их, а затем раскрасить таким образом, чтобы каждой фигуре соответствовал определенный цвет (руководствуясь инструкцией на бланке с заданием).

Во втором задании нужно нарисовать на всех этажах любые геометрические фигуры, но при этом необходимо соблюдать условие: на каждом этаже фигуры должны находиться в разном порядке. В последствии можно это задание видоизменить. Для этого достаточно начертить на бумаге точно такой домик и попросить ребенка заполнить его фигурами так, чтобы в каждом подъезде не встречались одинаковые фигуры (подъезд – вертикальный ряд квадратов).

В третьем задании нужно, руководствуясь стрелками, нарисовать точно такие же геометрические фигуры внутри или снаружи данных фигур.

Не торопите ребенка и не подсказывайте ему, пока он сам вас об этом не попросит. Если у малыша что-то получилось неправильно – вы всегда можете распечатать еще один экземпляр учебного бланка с заданием.

Скачать задание “Геометрические фигуры в рисунках” вы можете во вложениях внизу страницы.

В этом занятии детям опять предстоит отыскать геометрические фигуры среди рисунков. После предыдущих занятий им будет уже легче ориентироваться в знакомых формах, так что, я думаю, оба задания не вызовут у них затруднений.

Второе задание также дает возможность малышу повторить математические знаки и усвоить счет до десяти, так как ему понадобится посчитать количество фигур и поставить знаки “больше” “меньше” между картинками.

Скачать раскраску “Смешные рисунки из фигур” вы можете во вложениях внизу страницы.

Также вам будут полезны и другие материалы по изучению геометрических фигур:

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.

Задания ознакомят ребенка с основными фигурами геометрии – кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.

Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.

Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.

Наложение фигур друг на друга – это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.

Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.

Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.

В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии

Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.

Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.

Выявление индивидуально-типологических различий.

Инструкция к тесту

«Вам нужно нарисовать фигуру человека, составленную из 10 элементов, среди которых могут быть треугольники, круги, квадраты. Вы можете увеличивать или уменьшать эти элементы (геометрические фигуры) в размерах, накладывать друг на друга по мере надобности. Важно, чтобы все эти три элемента в изображении человека присутствовали, а сумма общего количества использованных фигур была равна десяти. Если при рисовании вы использовали большее количество фигур, то нужно зачеркнуть лишнее, если же вами использовано фигур меньше, чем десять, необходимо дорисовать недостающие. Выполните рисунок по данной инструкции».

Материал : испытуемым предлагается три листа бумаги размером 10×10 см, каждый лист нумеруется и подписывается. На листе № 1 выполняется первый пробный рисунок; далее, соответственно, на листе № 2 – второй, на листе № 3 – третий. После выполнения трех рисунков данные обрабатываются. При нарушении инструкции материал не обрабатывается.

Обработка результатов теста

Обработка данных производится следующим образом: подсчитывается количество затраченных в изображении человечка треугольников, кругов и квадратов (по каждому рисунку отдельно), и результат записывается в виде трехзначных чисел, где

• сотни обозначают количество треугольников ,
• десятки – количество кругов ,
• единицы -количество квадратов .

Эти трехзначные цифры составляют так называемую «формулу рисунка», по которой происходит отнесение рисующих к соответствующим типам и подтипам, которые представлены в таблице.

Интерпретация результатов теста

Интерпретация теста основана на том, что геометрические фигуры, используемые в рисунках, различаются по семантике.

Треугольник обычно относят к «острой», «наступательной» фигуре, связанной с мужским началом. Круг – фигура обтекаемая, более созвучна с сочувствием, мягкостью, округлостью, женственностью. Из элементов квадратной формы строить что-либо легче, чем из других, поэтому квадрат , прямоугольник интерпретируются как специфически техническая конструктивная фигура, «технический модуль».

Типы личности

I тип – «руководитель ». Обычно это люди, имеющие склонность к руководящей и организаторской деятельности. Ориентированы на социально-значимые нормы поведения, могут обладать даром хороших рассказчиков, основывающимся на высоком уровне речевого развития. Обладают хорошей адаптацией в социальной сфере, доминирование над другими удерживают в определенных границах.

Формулы рисунков : 901, 910, 802, 811, 820, 703, 712, 721, 730, 604, 613, 622, 631, 640.

• Наиболее жестко доминирование над другими выражено у подтипов 901, 910, 802, 811, 820;
• ситуативно -у 703, 712, 721, 730;
• при воздействии речью на людей – вербальный руководитель или «преподавательский подтип» – 604, 613, 622, 631, 640.

Нужно помнить, что проявление данных качеств зависит от уровня психического развития. При высоком уровне развития индивидуальные черты развиты, реализуемы, достаточно хорошо осознаются. При низком уровне развития могут не выявляться в профессиональной деятельности, а присутствовать ситуативно, хуже, если неадекватно ситуациям. Это относится ко всем характеристикам.

II тип – «ответственный исполнитель » обладает многими чертами типа «руководитель», однако в принятии ответственных решений часто присутствуют колебания.

Данный тип людей более ориентирован на «умение делать дело», высокий профессионализм, обладает высоким чувством ответственности и требовательности к себе и другим, высоко ценит правоту, т.е. характеризуется повышенной чувствительностью к правдивости. Часто они страдают соматическими заболеваниями нервного происхождения как следствие перенапряжения.

Формулы рисунков : 505, 514, 523, 532, 541, 550.

III тип – «тревожно-мнительный » -характеризуется разнообразием способностей и одаренности – от тонких ручных навыков до литературной одаренности. Обычно людям данного типа тесно в рамках одной профессии, они могут поменять ее на совершенно противоположную и неожиданную, иметь также хобби, которое по сути является второй профессией. Физически не переносят беспорядок и грязь. Обычно конфликтуют из-за этого с другими людьми. Отличаются повышенной ранимостью и часто сомневаются в себе. Нуждаются в мягком подбадривании.

Формулы рисунков : 406, 415, 424, 433, 442, 451, 460.

• 415 – «поэтический подтип» – обычно лица, имеющие такую формулу рисунка, обладают поэтической одаренностью;
• 424 – подтип людей, узнаваемых по фразе: «Как это можно плохо работать? Я себе не представляю, как это можно плохо работать». Люди такого типа отличаются особой тщательностью в работе.

IV тип – «ученый ». Эти люди легко абстрагируются от реальности, обладают «концептуальным умом», отличаются способностью разрабатывать «на все» свои теории. Обычно обладают душевным равновесием и рационально продумывают свое поведение.

Формулы рисунков : 307, 316, 325, 334, 343, 352, 361, 370.

• 316 характеризуется способностями создавать теории, по преимуществу глобальные, или осуществлять большую и сложную координационную работу;
• 325 – подтип, характеризующийся большой увлеченностью познания жизни, здоровья, биологическими дисциплинами, медициной.

Представители данного типа часто встречаются среди лиц, занимающихся синтетическими видами искусства: кино, цирк, театрально-зрелищная режиссура, мультипликация и т. д.

V тип – «интуитивный ». Люди этого типа обладают сильной чувствительностью нервной системы, высокой ее истощаемостью.

Легче работают на переключаемости от одной деятельности к другой, обычно выступают «адвокатами меньшинства», за которым стоят новые возможности. Обладают повышенной чувствительностью к новизне. Альтруистичны, часто проявляют заботу о других, обладают хорошими ручными навыками и образным воображением, что дает возможность заниматься техническими видами творчества.

Обычно вырабатывают свои нормы морали, обладают внутренним самоконтролем, т.е. предпочитают самоконтроль, отрицательно реагируя на посягательства, касающиеся их свободы.

Формулы рисунков : 208, 217, 226, 235, 244, 253, 262, 271, 280.

• 235 – часто встречается среди профессиональных психологов или лиц с повышенным интересом к психологии людей;
• 244 – обладает способностью литературного творчества,
• 217 – обладает способностью к изобретательской деятельности;
• 226 – большая потребность в новизне, обычно ставит очень высокие критерии достижений для себя.

VI тип – «изобретатель, конструктор, художник ». Часто встречается среди лиц с «технической жилкой». Это люди, обладающие богатым воображением, пространственным видением, часто занимаются различными видами технического, художественного и интеллектуального творчества. Чаще интравертированы, так же, как интуитивный тип, живут собственными моральными нормами, не приемлют никаких воздействий со стороны, кроме само контроля.

Эмоциональны, одержимы собственными оригинальными идеями.

Формулы рисунков : 109, 118, 127, 136, 145, 019, 028, 037, 046.

• 019 – встречается среди лиц, хорошо владеющих аудиторией;
• 118 – тип с наиболее сильно выраженными конструктивными возможностями и способностью к изобретениям.

VII тип – «эмотивный ». Обладают повышенным сопереживанием по отношению к другим людям, тяжело переживают жестокие кадры фильма, могут надолго быть выбитыми из колеи и быть потрясенными от жестоких событий. Боли и заботы других людей находят у них участие, сопереживание и сочувствие, на которое они тратят много собственной энергии, в результате становится затруднительной реализация их собственных способностей.

Формулы рисунков : 550, 451, 460, 352, 361, 370, 253, 262, 271, 280, 154, 163, 172, 181, 190, 055, 064, 073, 082, 091.

VIII тип – «нечувствительный к переживаниям других ». Обладает противоположной тенденцией эмотивному типу. Обычно не чувствует переживаний других людей или относится к ним с невниманием и даже усиливает давление на людей.

Если это хороший специалист, то он может заставить других делать то, что он считает нужным. Иногда для него характерна «черствость», которая возникает ситуативно, когда в силу каких-либо причин человек замыкается в кругу собственных проблем.

Формулы рисунков : 901, 802, 703, 604, 505, 406, 307, 208, 109.

На Планете геометрических фигур.

Конкурс

(подготовительная к школе группа)

Цель: Расширять представление о космосе. Закреплять знание геометрических фигур. Развивать память, внимание, воображение, творческие способности.

Предварительная работа: Проведение бесед, дидактических игр. Подбор аудиозаписей музыки и звуков. Изготовление сувениров. Придумывание девизов и приветствий команд.

(Под аудиозапись весёлой музыки в зал входят команды. Ведущий представляет членов жюри и капитанов команд.)

Капитан команды «Звёздочки»

Мы звёздочки волшебные –

И я, и он, и ты.

И солнышку лучистому

Подарим мы цветы.

Наш девиз:

Дети (хором) Один за всех, и все за одного.

(Преподносят команде соперников цветы)

Капитан команды «Солнышко»

Мы словно солнышка лучи,

Быстры, красивы, горячи.

И дарим сувениры вам,

Весёлым звёздочкам-друзьям.

Наш девиз:

Дети (хором) Свети всегда, не гасни никогда.

Ведущий. Вот мы и познакомились с командами. Сегодня эти славные ребята отправятся к далёким неизведанным планетам. Перед полётом космонавты должны пройти испытания. Все готовы? (Все!)

Первое задание. Команды должны построить космические корабли, в которых они отправятся в путешествие.

Ведущий в течение одной минуты показывает схему космического корабля, затем дети, используя мягкие модули, в течение пяти минут строят корабли. Жюри оценивает соответствие построек схематическому изображению.

Ведущий. Перед вылетом необходимо проверить знания космонавтов. Чтобы привести корабль в пункт назначения, космонавты должны ориентироваться по карте звёздного неба.

Второе задание. Найдите и покажите созвездие Большой Медведицы и Рыб.

(Члены команд находят на карте звёздного неба созвездия.)

Ведущий. Конкурс капитанов. Вы должны сделать «фотографии» космических объектов: планеты Сатурн и кометы.

Капитан команды «Звёздочки» рисует фломастером комету, капитан команды «Солнышко» – Сатурн.

Ведущий. Мы убедились, что команды готовы отправиться к далёким планетам. Все участники знают, как построить космический корабль, читают звёздные карты, могут распознать созвездия и космические объекты. Пора отправляться в путь. А чтобы в полёте было веселее, спойте песню о дружбе.

Под песню «Дружба крепкая» (муз. Б.Савельева, сл. М. Пляцковского) дети занимают места в построенных ими кораблях. Гаснет свет. Несколько секунд звучит аудиозапись рёва моторов.

Ведущий. Справа по курсу неизвестная планета. Приготовиться к посадке.

Вновь звучит аудиозапись рёва моторов. Воспитатель прикрепляет к шинам плакаты с изображением деревьев, домов, транспортных средств, составленных из геометрических фигур. Зажигается свет. Дети выходят из кораблей.

Ведущий. Вот мы и на поверхности планеты. Обратите внимание, какое здесь всё необычное.

Из-за ширмы выходит инопланетянин (роль исполняет взрослый).

Инопланетянин. Здравствуйте! Кто вы и как попали на нашу планету?

Дети. Здравствуйте! Мы земляне из детского сада «Цветик-семицветик».

Ведущий. Как называется ваша планета?

Инопланетянин. Планета геометрических фигур. Я очень рад, что вы прилетели.

Ведущий. На нашей планете деревья, машины и дома совсем не такие, как у вас.

Инопланетянин. Мне трудно себе представить, что деревья и дома могут выглядеть иначе. Интересно было бы на них взглянуть.

Ведущий. Сейчас девочки нарисуют дома и деревья, а мальчики – различные виды транспорта, и мы подарим эти картины жителям вашей планеты.

(Дети выполняют задания)

Инопланетянин. Спасибо за чудесные рисунки. Наши учёные внимательно изучат эти изображения. А учёным Земли знакомы геометрические фигуры?

Ведущий. Не только учёные, но и дети знают геометрические фигуры и их названия.

Инопланетянин. Сейчас проверим.

(Указывает на плакаты с изображением предметов составленных из геометрических фигур.) Запомните изображения предметов и то, из каких фигур они состоят.

(Дети в течение одной минуты рассматривают плакаты, затем плакаты убирают.)

Найдите на столах геометрические фигуры, из которых состояли предметы на плакатах, и составьте из них такие же изображения.

(Дети выполняют задание)

Ведущий. Обратите внимание – на Планете геометрических фигур нет дорожных знаков.

Инопланетянин. А что такое дорожные знаки?

(Ведущий демонстрирует картинки с изображением светофора и дорожных знаков. )

Как интересно! Некоторые знаки могли бы использоваться для организации движения на дорогах нашей планеты. Помогите мне выбрать знаки, на которых изображены геометрические фигуры.

(Члены команд поочерёдно выбирают такие знаки, рассказывают о том, что они обозначают.)

Ведущий. Наши дети не только много знают, но умеют петь и танцевать. Дети поют песню «Вместе весело шагать» (муз. В.Шаинского, сл. М.Матусовского.) Затем исполняется танец (по выбору музыкального руководителя).

Когда понадобится: для выявления типов личностей: руководитель, исполнитель, ученый, изобретатель и т. п.

ТЕСТ
«Конструктивный рисунок человека из геометрических фигур»

Инструкция

Нарисуйте, пожалуйста, фигуру человека, составленную из 10 элементов, среди которых могут быть треугольники, круги, квадраты. Вы можете увеличивать или уменьшать эти элементы (геометрические фигуры) в размерах, накладывать друг на друга по мере надобности.

Важно, чтобы все эти три элемента в изображении человека присутствовали, а сумма общего количества использованных фигур была равна 10. Если при рисовании вы использовали большее количество фигур, то нужно зачеркнуть лишние, если же вами использовано фигур меньше чем 10, необходимо дорисовать недостающие.

Ключ к тесту «Конструктивный рисунок человека из геометрических фигур»

Описание

Тест «Конструктивный рисунок человека из геометрических фигур» предназначен для выявления индивидуально-типологических различий.

Сотруднику предлагают три листа бумаги размером 10 × 10 см. Каждый лист нумеруется и подписывается. На первом листе выполняется первый пробный рисунок, далее, соответственно, на листе втором – второй, на листе третьем – третий.

Сотруднику необходимо на каждом листе нарисовать фигуру человека, составленную из 10 элементов, среди которых могут быть треугольники, круги, квадраты. Сотрудник может увеличивать или уменьшать эти элементы (геометрические фигуры) в размерах, накладывать друг на друга по мере надобности. Важно, чтобы все эти три элемента в изображении человека присутствовали, а сумма общего количества использованных фигур была равна 10.

Если при рисовании сотрудник использовал большее количество фигур, то ему необходимо зачеркнуть лишние, если же использовал фигур меньше чем 10, ему необходимо дорисовать недостающие.

При нарушении инструкции данные не обрабатываются.

Пример рисунков, сделанных тремя оцениваемыми

Обработка результата

Подсчитайте количество затраченных в изображении человечка треугольников, кругов и квадратов (по каждому рисунку отдельно). Запишите результат в виде трехзначных чисел, где:

• сотни обозначают количество треугольников;
• десятки – количество кругов;
• единицы – количество квадратов.

Эти трехзначные цифры составляют так называемую формулу рисунка, по которой происходит отнесение рисующих к соответствующим типам и подтипам.

Интерпретация результата

Собственные эмпирические исследования, в которых получено и проанализировано более 2000 рисунков, показали, что соотношение различных элементов в конструктивных рисунках не случайно. Анализ позволяет выделить восемь основных типов, которым соответствуют определенные типологические характеристики.

Интерпретация теста основана на том, что геометрические фигуры, использованные в рисунках, различаются по семантике:

• треугольник обычно относят к острой, наступательной фигуре, связанной с мужским началом;
• круг – фигура обтекаемая, более созвучна с сочувствием, мягкостью, округлостью, женственностью;
• квадрат, прямоугольник интерпретируются как специфически техническая конструктивная фигура, технический модуль.

Типология, основанная на предпочтении геометрических фигур, позволяет сформировать своего рода систему индивидуально-типологических различий.

Типы

I тип – руководитель

Формулы рисунков: 901, 910, 802, 811, 820, 703, 712, 721, 730, 604, 613, 622, 631, 640. Наиболее жестко доминирование над другими выражено у подтипов 901, 910, 802, 811, 820; ситуативно – у 703, 712, 721, 730; при воздействии речью на людей – вербальный руководитель или преподавательский подтип – 604, 613, 622, 631, 640.

Обычно это люди, имеющие склонность к руководящей и организаторской деятельности, ориентированные на социально значимые нормы поведения, могут обладать даром хороших рассказчиков, основывающимся на высоком уровне речевого развития. Обладают хорошей адаптацией в социальной сфере, доминирование над другими удерживают в определенных границах.

Нужно помнить, что проявление данных качеств зависит от уровня психического развития. При высоком уровне развития индивидуальные черты развития реализуемы, достаточно хорошо осознаются.

При низком уровне они могут не выявляться в профессиональной деятельности, а присутствовать ситуативно, хуже, если неадекватно ситуациям. Это относится ко всем характеристикам.

II тип – ответственный исполнитель

Формулы рисунков: 505, 514, 523, 532, 541, 550.

Данный тип людей обладает многими чертами типа «руководитель», являясь расположенным к нему, однако в принятии ответственных решений часто присутствуют колебания. Такой человек ориентирован на умение делать дело, высокий профессионализм, обладает высоким чувством ответственности и требовательности к себе и другим, высоко ценит правоту, то есть характеризуется повышенной чувствительностью к правдивости. Часто он страдает соматическими заболеваниями нервного происхождения вследствие перенапряжения.

III тип – тревожно-мнительный

Формулы рисунков: 406, 415, 424, 433, 442, 451, 460.

Данный тип людей характеризуется разнообразием способностей и одаренности – от тонких ручных навыков до литературной одаренности. Обычно этим людям тесно в рамках одной профессии, они могут поменять ее на совершенно противоположную и неожиданную, иметь также хобби, которое по сути является второй профессией. Физически не переносят беспорядка и грязи. Обычно конфликтуют из-за этого с другими людьми. Отличаются повышенной ранимостью и часто сомневаются в себе. Нуждаются в подбадривании.

Кроме этого, 415 – «поэтический подтип» – обычно лица, имеющие такую формулу рисунка, обладают поэтической одаренностью; 424 – подтип людей, узнаваемых по фразе «Как это можно плохо работать? Я себе не представляю, как это можно плохо работать». Люди такого типа отличаются особой тщательностью в работе.

IV тип – ученый

Формулы рисунков: 307, 316, 325, 334, 343, 352, 361, 370.

Эти люди легко абстрагируются от реальности, обладают концептуальным умом, отличаются способностью разрабатывать все свои теории. Обычно обладают душевным равновесием и рационально продумывают свое поведение.

Подтип 316 характеризуется способностью создавать теории, по преимуществу глобальные, или осуществлять большую и сложную координационную работу.

325 – подтип, характеризующийся большой увлеченностью познания жизни, здоровья, биологическими дисциплинами, медициной. Представители этого типа часто встречаются среди лиц, занимающихся синтетическими видами искусства: кино, цирк, театрально-зрелищная режиссура, мультипликация и т. д.

V тип – интуитивный

Формулы рисунков: 208, 217, 226, 235, 244, 253, 262, 271, 280.

Люди этого типа обладают сильной чувствительностью нервной системы, ее высокой истощаемостью. Легче работают на переключаемости от одной деятельности к другой, обычно выступают адвокатами меньшинства. Обладают повышенной чувствительностью к новизне. Альтруистичны, часто проявляют заботу о других, обладают хорошими ручными навыками и образным воображением, что дает им возможность заниматься техническими видами творчества. Обычно вырабатывают свои нормы морали, обладают внутренним самоконтролем, то есть предпочитают самоконтроль, отрицательно реагируя на посягательства, касающиеся их свободы.

235 – часто встречается среди профессиональных психологов или лиц с повышенным интересом к психологии;

244 – обладает способностью к литературному творчеству;

217 – обладает способностью к изобретательской деятельности;

226 – имеет большую потребность в новизне, обычно ставит очень высокие критерии достижений для себя.

VI тип – изобретатель, конструктор, художник

Формулы рисунков: 109, 118, 127, 136, 145, 019, 028, 037, 046.

Часто встречается среди лиц с технической жилкой. Это люди, обладающие богатым воображением, пространственным видением, часто занимаются различными видами технического, художественного и интеллектуального творчества. Чаще интровертированы, так же как интуитивный тип, живут собственными моральными нормами, не приемлют никаких воздействий со стороны, кроме самоконтроля. Эмоциональны, одержимы собственными оригинальными идеями.

Также выделяют особенности следующих подтипов:

019 – встречается среди лиц, хорошо владеющих аудиторией;

118 – тип с наиболее сильно выраженными конструктивными возможностями и способностью к изобретениям.

VII тип – эмотивный

Формулы рисунков: 550, 451, 460, 352, 361, 370, 253, 262, 271, 280, 154, 163, 172, 181, 190, 055, 064, 073, 082, 091.

Обладают повышенным сопереживанием по отношению к другим, тяжело переживают жестокие кадры фильма, могут надолго быть выбитыми из колеи и быть потрясенными от жестоких событий. Боли и заботы других людей находят в них участие, сопереживание и сочувствие, на которое они тратят много собственной энергии, в результате становится затруднительной реализация их собственных способностей.

VIII тип – противоположность эмотивного

Формулы рисунков: 901, 802, 703, 604, 505, 406, 307, 208, 109.

Данный тип людей обладает противоположной тенденцией эмотивному типу. Обычно не чувствует переживаний других людей, или относится к ним с невниманием, или даже усиливает давление на людей. Если это хороший специалист, то он может заставить других делать то, что он считает нужным. Иногда для него характерна черствость, которая возникает ситуативно, когда в силу каких-либо причин человек замыкается в кругу собственных проблем.

Умеете ли вы составлять животных из геометрических фигур?

Никогда не пробовали?

Тогда стоит посмотреть картинки на сайте, где из геометрических фигур сложены разнообразные животные. Предложите эти рисунки своим детям: наверняка они оценят их оригинальность.

Геометрический мир

Во всем, что нас окружает, можно отыскать элементы геометрии.

Стол может быть круглым или квадратным, наши дома – параллелепипеды и т.д. Не наблюдали, как рисуют художники? Они сначала намечают контуры предмета с основой из геометрических фигур, а уж затем проводят вокруг них плавные линии. Они видят мир геометрическим, а ровные или мягкие линии лишь скрывают настоящую суть вещей.

В педагогике для детей дошкольного возраста есть даже целое направление, где ребят учат во всем видеть чистые геометрические фигуры. Это педагогика Марии . Она считала, что чистые геометрические фигуры способствуют лучшему развитию детей и их ориентации в мире. Нельзя сказать, что эта система идеальна, но она нашла своих сторонников.

А теперь давайте вспомним произведения художников эпохи модернизма и постмодернизма. Перед глазами встают картины, наполненные квадратами, треугольниками, кругами, трапециями и всевозможными фигурами, окрашенными в разные цвета. Так живописцы новой эпохи видели мир, и этому должно было основание. Они пытались передать этот мир нетронутым человеческими руками. Их стремлением было показать, что все мы и все предметы вокруг нас состоят из геометрических фигур. Весь наш мир, если присмотреться, — сплошная геометрия.

Как использовать картинки в работе с детьми

Вполне понятно, что встает вопрос: одно дело художники, но зачем детям такое видение мира?

Конечно, картинки с животными из геометрических фигур не ставят целью навязать малышу неординарное видение мира. Однако почему бы ни показать, что и такая трактовка всего, что нас окружает, возможна.

По картинкам можно интересно и увлекательно изучать названия геометрических фигур. От простого показа и повторения ребенок быстро устает и начинает отказываться от занятий, даже если их проводит мама в домашних условиях. Другое дело, если фигуры необходимо отыскать в животных. Тут просыпается неподдельное любопытство.

Когда вы полностью изучите с ребенком названия фигур и их внешний вид, попросите ребенка проявить свое видение мира. Пусть для примера будет взято животное или любой предмет.

Спросите: на какую геометрическую фигуру он похож.

Такие упражнения:

1. — развивают наблюдательность;
2. — совершенствуют логическое и пространственное мышление;
3. — способствуют видению скрытого за внешней оболочкой предмета.

Малыш учится видеть и наблюдать то, что не могут или не умеют видеть другие . Это ли не воспитание художника и творческой личности?

А можно поиграть в обратную игру. Представьте, что вы художники-абстракционисты. Пусть один из вас нарисует что-нибудь, состоящее из геометрических фигур, а другой попытается отгадать, что нарисовано. Живописцы постмодернизма часто зашифровывали свои рисунки на полотне, заполненной квадратами, прямоугольниками, трапециями… такие же головоломки предлагали ранее детские журналы.

Вы и сами можете создать такую головоломку: нужно лишь немного фантазии и взгляд на мир сквозь призму геометрии.

Нажмите на картинку, чтобы скачать эту тетрадку с заданиями для детей бесплатно.
Примеры страниц тетради с аппликациями для детей от 1 года до 3 лет.

«Математическая вертушка»

Участники выставки – конкурса:

Луфиренко Наталья Анатольевна,

воспитатель, высшая квалификационная категория

Баранова Елена Александровна

воспитатель, высшая  квалификационная категория

МАДОУ д/с №146 города Тюмени

       

Дидактическая многофункциональная игра «Волшебная математика»

Цель: Формирование элементарных математических представлений у детей младшего дошкольного возраста через занимательные дидактические игры математического содержания.

Задачи:

• Выделение ярко выраженных признаков конкретных предметов: цвет, форма, величина.
• Формирование представления о числах в пределах 5 на основе действий с конкретными предметными множествами.
• Закрепление умения находить один и много предметов в специально – созданной обстановке, пользоваться словами один, много;
• Формировать пространственные представления «от себя»:  слева, справа, впереди, сзади, вверху, внизу.
• Учить различать и называть геометрические фигуры: круг, квадрат, треугольник, моделировать новые геометрические фигуры из 2-3 деталей.

Описание.

Наша многофункциональная игра «Волшебная математика» состоит из 2 частей: верхней и нижней.

Верхняя часть это игровой маркер из двух полос пластика в виде вертушки, состоящей из 4 отсеков, где живут веселые геометрические фигуры: квадрат – «Квадрик», круг – «Кругляш», треугольник – «Тригубик». В первом отсеке живут квадратные жители – это вязанные кошельки, от большого до малого размера с красивыми застежками, которые можно расстегивать и застегивать,  разного цвета и формы; бумажные квадраты, которые прикрепляются к вертушке прищепками, цифры от 1 до 4 обозначающие углы квадрата.

  Во втором отсеке живут «Кругляши» -это различные картинки, предметы круглой формы,  вязанные фигуры- круги разного цвета и величины.

 Третий отсек включает  геометрические фигуры – треугольники, из которых собираются замечательные картинки.

  В четвертом отсеке живут «Волшебные» фигуры- «Кубарики» разного размера, цвета и прищепки, с помощью которых все крепиться на вертушке и из которых конструируют дети очень интересные фигуры.

 Нижняя часть нашей конструкции представляет мобильный уголок уединения  в группе, который можно складывать. Он состоит из  чехла, который одевается на стол. Сверху он представлен в виде белой скатерти с геометрическими фигурами разного цвета и формы, а «бока» оформлены в виде домика. Дети могут уединиться в домике, а выйдя из него поиграть с детьми в  «Волшебную математику».

Ход игры:

В: Я приглашаю вас в сказку, но не простую, а математическую.
 В некотором волшебном  царстве государстве стояла «Математическая вертушка». И жили в ней три брата – геометрические фигурки: квадрат -«Квадрик», круг-«Кругляш», треугольник – «Трегубик» и у каждого у них была своя комната. Дети дайте познакомимся и поздороваемся с ними. Ребята, какая это фигура? Дети здороваются и называют фигуры.

В: Квадрат – «Квадрик», у него все стороны равны, углы все прямые, он может быть большим и маленьким. Давайте посчитаем сколько сторон у квадрата? Дети считают и рассказывают, что видят перед собой (это волшебные вязанные кошельки разного размера, цифры от 1до 5,картинки квадратов разной формы и цвета.) Рядом с «Квадриком» жил «Кругляш». Ему очень нравились картинки мячей разного цвета и формы, смайлики,  картинки яблок, цветов, ягод, вязанные круги разного цвета и размера.

Посмотрим кто еще в вертушке живет? Какая дети это фигура? (треугольник – Трегубик). «Трегубик» позвал к себе своих братьев «Квадрика» и «Кругляша». Они так веселились, что не заметили, как складываются интересные картинки, давайте поможем им их составить.

И в последней комнате нашей «Вертушки» живут «Кубарики» разного цвета и размера, их можно так переставлять, что получится и  башня, и  домик. В ходе проигрывания,  детям предлагаются следующие игры:

Дидактическая игра «Посчитай, сколько квадратных  кошельков»

Цель: упражнять в счете предметов.

Ход игры: На столе расположены 4- 5   кошельков разного размера. Дети раскладывают кошельки от большого к малому и считают их.

Дидактическая игра   «Узнай форму предмета»

Цель: закрепление знаний о геометрических фигурах.

Ход игры: На столе расположены карточки с геометрическими фигурами: круг, квадрат, треугольник. Воспитатель показывает фигуру маленького размера. Дети должны показать большую такую же фигуру.

Дидактическая игра  «Найди свою комнату в вертушке».

Цель: упражнять в соотнесении предметов по форме с геометрическими образцами и в обобщении предметов по форме.

 Ход игры: На столе лежат разные картинки и предметы, рассмотрите их потрогайте  и найдите ту комнату в вертушке, где будут находится эти предметы и картинки. Расскажите мне, как вы догадались? Какой формы эти предметы?

Дидактическая игра «Что изменилось»

Цель: учить правильно называть фигуры и их пространственное расположение: посередине, вверху, внизу, слева, справа; запоминать расположение фигур.

 Ход игры:

 В: «Сегодня мы будем учиться запоминать, где какая фигура находится. Для этого их нужно назвать по порядку: сначала фигуру, расположенную в центре (посередине), затем вверху, внизу, слева, справа». Вызывает 4-х детей. Они по порядку размещают и называет фигуры, место их расположения. Затем дети становится спиной к вертушке, а воспитатель меняет фигуры, расположенные слева и справа. Дети поворачивается и отгадывает, что изменилось.

Дидактическая игра «Собери картинку из фигур»

Цель: учить правильно называть фигуры, развивать фантазию.

Ход игры: Из геометрических фигур по картинкам собирается дом, черепаха, неваляшка, рыба, машина.

Дидактическая игра «Найди ошибку»

 Цель: анализ геометрических фигур, сравнение и нахождение лишнего.

Ход игры: Детям предлагается проанализировать ряды геометрических фигур и указать на ошибку, предложив вариант исправления с пояснением. Ошибкой может быть круг в ряду квадратов, или фигура красного цвета среди желтых.

Когда дети захотят отдохнуть, уединится, они забираются во внутрь нашей  волшебной вертушки и продолжают играть в ней.

видеоролик организации игры

Поделиться

Сложные математические фигуры. Карточки домана бесплатно, картинки геометрические фигуры, карточки геометрические фигуры, изучаем геометрические фигуры. Фигура тетраэдр: описание

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках. Но обучение будет проходить наиболее эффективно в том случае, если к распечатанному заданию вы добавите еще и различные образцы геометрических фигур. Для этой цели могут подойти такие предметы, как мячики, пирамидки, кубики, надутые воздушные шары (круглые и овальные), кружки для чая (стандартные, в форме цилиндра), апельсины, книги, клубки ниток, квадратные печенья и многое другое – все, что подскажет вам фантазия.

Все перечисленные предметы помогут ребенку понять, что значит объемная геометрическая фигура. Плоские фигуры можно подготовить, вырезав из бумаги нужные геометрические формы, предварительно раскрасив их в разные цвета.

Чем больше различных материалов вы подготовите для занятия, тем интереснее будет ребенку изучать новые для него понятия.

Также вам может понравиться наш онлайн тренажер по математике для 1 класса “Геометрические фигуры”:

Онлайн-тренажер по математике “Геометрические фигуры 1 класс” поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.

Геометрические фигуры и их названия – Проводим занятие с ребенком:

Чтобы легко и непринужденно ребенок смог запомнить геометрические фигуры и их названия, скачайте сначала картинку с заданием во вложениях внизу страницы, распечатайте на цветном принтере и положите на стол вместе с цветными карандашами. Также к этому времени у вас уже должны быть заготовлены различные предметы, которые мы перечисляли ранее.

• 1 этап. Сначала пусть ребенок выполнит задания на распечатанном листе – проговорит вслух названия фигур и раскрасит все картинки.
• 2 этап. Необходимо наглядно показать ребенку отличия объемных фигур от плоских. Для этого разложите все предметы-образцы (как объемные, так и вырезанные из бумаги) и отойдите с ребенком от стола на такое расстояние, с которого хорошо видны все объемные фигуры, но потерялись из виду все плоские образцы. Обратите внимание малыша на этот факт. Пусть он поэкспериментирует, подходя к столу то ближе, то дальше, рассказывая вам о своих наблюдениях.
• 3 этап. Дальше занятие нужно превратить в своеобразную игру. Попросите ребенка, чтобы он внимательно посмотрел вокруг себя и нашел предметы, которые имеют форму каких-либо геометрических фигур. Например, телевизор – прямоугольник, часы – круг и т.д. На каждой найденной фигуре – громко хлопайте в ладоши, чтобы добавить энтузиазма в игру.
• 4 этап. Проведите исследовательскую и наблюдательную работу с теми материалами-образцами, которые вы заготовили к занятию. Например, положите на стол книгу и плоский прямоугольник из бумаги. Предложите ребенку пощупать их, посмотреть на них с разных сторон и рассказать вам свои наблюдения. Таким же образом можно исследовать апельсин и бумажный круг, детскую пирамидку и бумажный треугольник, кубик и бумажный квадрат, воздушный шар овальной формы и овал, вырезанный из бумаги. Список предметов вы можете дополнить сами.
• 5 этап. Положите в непрозрачный пакет различные объемные образцы и попросите ребенка достать на ощупь квадратный предмет, затем круглый, затем прямоугольный и так далее.
• 6 этап. Разложите перед ребенком на столе несколько различных предметов из тех, которые участвуют в занятии. Затем пусть ребенок отвернется на несколько секунд, а вы спрячьте один из предметов. Повернувшись к столу ребенок должен назвать спрятанный предмет и его геометрическую форму.

Скачать геометрические фигуры и их названия – Бланк задания – вы можете во вложениях внизу страницы.

Названия геометрических фигур – Карточки для распечатки

Изучая с малышом геометрические фигуры, вы можете использовать во время занятий карточки для распечатки от Лисёнка Бибуши. Скачайте вложения, распечатайте на цветном принтере бланк с карточками, вырежьте каждую карточку по контуру – и приступайте к обучению. Карточки можно заламинировать, либо наклеить на более плотную бумагу, чтобы сохранить внешний вид картинок, ведь использоваться они будут неоднократно.

Первые шесть карточек дадут вам возможность изучить с ребенком такие фигуры: овал, круг, квадрат, ромб, прямоугольник и треугольник, под каждой фигурой в карточках можно прочесть ее название.

После того, как ребенок запомнил название определенной фигуры, попросите его выполнить следующее: обвести по контуру все имеющиеся на карточке образцы изучаемой фигуры, а затем раскрасить их в цвет основной фигуры, расположенной в верхнем левом углу.

Скачать названия геометрических фигур – Карточки для распечатки – вы можете во вложениях внизу страницы

С помощью следующих шести карточек ребенок сможет познакомиться с такими геометрическими фигурами: параллелограмм, трапеция, пятиугольник, шестиугольник, звезда и сердце. Как и в предыдущем материале под каждой фигурой можно найти ее название.

Чтобы разнообразить занятия с малышом, совмещайте обучение с рисованием – такой метод не даст ребенку переутомиться, и малыш с удовольствием будет продолжать учебу. Следите за тем, чтобы обводя фигуры по черточкам, ребенок не спешил и выполнял задание аккуратно, ведь подобные упражнения не только развивают мелкую моторику, они могут повлиять в дальнейшем на почерк малыша.

Скачать карточки для распечатки с изображением плоских геометрических фигур вы можете во вложениях

В процессе, того, как вы будете изучать с ребенком объемные геометрические фигуры и их названия, используя новые шесть карточек от Бибуши с изображениями куба, цилиндра, конуса, пирамиды, шара и полусферы, приобретите изучаемые фигуры в магазине, либо воспользуйтесь предметами, находящимися в доме, имеющими подобную форму.

Покажите малышу на примерах, как в жизни выглядят объемные фигуры, ребенок должен потрогать и поиграть с ними. Прежде всего, это необходимо для того, чтобы задействовать наглядно – действенное мышление малыша, с помощью которого ребенку проще познавать окружающий мир.

Скачать – Объемные геометрические фигуры и их названия – вы можете во вложениях внизу страницы

Также вам будут полезны и другие материалы по изучению геометрических фигур:

Веселые и красочные задания для детей “Рисунки из геометрических фигур” являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм:

Задания ознакомят ребенка с основными фигурами геометрии – кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.

Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.

Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.

Наложение фигур друг на друга – это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.

Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.

Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.

В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии

Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.

Здесь мы выложили для вас счет до 5 – картинки с математическими заданиями для малышей, благодаря которым ваши дети потренируют не только свои навыки счета, но и умение читать, писать, различать геометрические фигуры, рисовать и раскрашивать.

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.

Цели урока :

• Познавательная : создать условия для ознакомления с понятиями плоские и объёмные геометрические фигуры, расширить представление о видах объёмных фигур, научить определять вид фигуры, сравнивать фигуры.
• Коммуникативная : создать условия для формирования умения работать в парах, группах; воспитание доброжелательного отношения друг к другу; воспитывать у учащихся взаимопомощь, взаимовыручку.
• Регулятивная : создать условия для формирования планировать учебную задачу, выстраивать последовательность необходимых операций, корректировать свою деятельность.
• Личностная : создать условия для развития вычислительных навыков, логического мышления, интереса к математике, формирования познавательных интересов, интеллектуальных способностей учащихся, самостоятельность в приобретении новых знаний и практических умений.

Планируемые результаты:

личностные:

• формирование познавательных интересов, интеллектуальных способностей учащихся; формирование ценностных отношений друг к другу;
  самостоятельность в приобретении новых знаний и практических умений;
• формирование умений воспринимать, перерабатывать полученную информацию, выделять основное содержание.

метапредметные:

• овладение навыками самостоятельного приобретения новых знаний;
• организация учебной деятельности, планирования;
• развитие теоретического мышления на основе формирования умений устанавливать факты.

предметные:

• усвоить понятия плоские и объёмные фигуры, научиться сравнивать фигуры, находить плоские и объёмные фигуры в окружающей действительности, научиться работать с развёрткой.

УУД общенаучные :

• поиск и выделение необходимой информации;
• применение методов информационного поиска, осознанное и произвольное построение речевого высказывания в устной форме.

УУД личностные :

• оценивать свои и чужие поступки;
• проявление доверия, внимательности, доброжелательности;
• умение работать в паре;
• выражать положительное отношение к процессу познания.

Оборудование : учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи, Толковый словарь.

Тип урока : изучение нового материала.

Методы : словесные, исследовательские, наглядные, практические.

Формы работы : фронтальная, групповая, парная, индивидуальная.

1. Организация начала урока.

Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!

2. Актуализация знаний.

Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!

Чтобы дойти до цели, надо прежде всего идти.

Перед вами высказывание, прочитайте. Что означает это высказывание?

(Чтобы чего-то добиться, нужно что-то делать)

И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.

Начнем наш путь к достижению цели сегодняшнего урока.

3. Подготовительная работа.

Посмотрите на экран. Что вы видите? (Геометрические фигуры)

Назовите эти фигуры.

Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)

У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.

По какому признаку вы разделили эти фигуры?

• Плоские и объемные фигуры
• По основаниям объемных фигур

С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?

Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.)

Чему мы должны научиться на уроке?

4. «Открытие» нового знания в практической исследовательской работе.

(Учитель показывает куб и квадрат.)

Чем они похожи?

Можно ли сказать, что это одно и тоже?

Чем же отличается куб от квадрата?

Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)

Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?

! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой. )

Можно ли куб полностью (весь) прижать к парте? Проверим.

Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?

! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)

ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.)

• Можно целиком расположить на одной плоской поверхности.

ОБЪЁМНЫЕ

• занимают определённое пространство,
• возвышаются над плоской поверхностью.

Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.

4. Открытие новых знаний.

1. Назовите фигуры, изображенные на рисунке.

Какую форму имеют основания этих фигур?

Какие еще формы можно увидеть на поверхности куба и призмы?

2. Фигуры и линии на поверхности объемных фигур имеют свои названия.

Предложите свои названия.

Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.

Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.

Работа с тетрадями: чтение нового материала

Соотнесение реальных объектов и объёмных тел.

А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.

Коробка – параллелепипед.

• Яблоко – шар.
• Пирамидка – пирамида.
• Банка – цилиндр.
• Горшок из-под цветка – конус.
• Колпачок – конус.
• Ваза – цилиндр.
• Мяч – шар.

5. Физминутка.

1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.

(Ученики «обхватывают» руками и гладят воображаемый шар.)

А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.

Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.

Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!

6. Групповая работа :

(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку .)
Группа 1. (Для изучения параллелепипеда)

Группа 2. (Для изучения пирамиды)

Группа 3. (Для изучения куба)

7. Решение кроссворда

8. Итог урока. Рефлексия деятельности.

Решение кроссворда в презентации

Что нового вы для себя сегодня открыли?

Все геометрические фигуры можно разделить на объёмные и плоские.

А я узнал названия объёмных фигур

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Геометрия – одна из важнейших компонент математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, а также для эстетического воспитания. Изучение геометрии вносит вклад в развитие логического мышления, формирование навыков доказательства.

В курсе геометрии 7 класса систематизируются знания о простейших геометрических фигурах и их свойствах; вводится понятие равенства фигур; вырабатывается умение доказывать равенство треугольников с помощью изученных признаков; вводится класс задач на построение с помощью циркуля и линейки; вводится одно из важнейших понятий – понятие о параллельных прямых; рассматриваются новые интересные и важные свойства треугольников; рассматривается одна из важнейших теорем в геометрии – теорема о сумме углов треугольника, которая позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный).

На протяжении занятий, особенно при переходе от одной части занятия к другой, смене деятельности встает вопрос о поддержании интереса к занятиям. Таким образом, актуальным становится вопрос о применении на занятиях по геометрии задач, в которых есть условие проблемной ситуации и элементы творчества . Таким образом, целью данного исследования является систематизация заданий геометрического содержания с элементами творчества и проблемных ситуаций.

Объект исследования : Задачи по геометрии с элементами творчества, занимательности и проблемных ситуаций.

Задачи исследования: Проанализировать существующие задачи по геометрии, направленные на развитие логики, воображения и творческого мышления. Показать, как занимательными приемами можно развить интерес к предмету.

Теоретическая и практическая значимость исследования состоит в том, что собранный материал может быть использован в процессе дополнительных занятий по геометрии, а именно на олимпиадах и конкурсах по геометрии.

Объем и структура исследования:

Исследование состоит из введения, двух глав, заключения, библиографического списка, содержит 14 страниц основного машинописного текста, 1 таблицу, 10 рисунков.

Глава 1. ПЛОСКИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

1. 1. Основные геометрические фигуры в архитектуре зданий и сооружений

В окружающем нас мире существует множество материальных предметов разных форм и размеров: жилые дома, детали машин, книги, украшения, игрушки и т. д.

В геометрии вместо слова предмет говорят геометрическая фигура, при этом разделяя геометрические фигуры на плоские и пространственные. В данной работе будет рассмотрен один из интереснейших разделов геометрии – планиметрия, в которой рассматриваются только плоские фигуры. Планиметрия (от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Плоской геометрической фигурой называется такая, все точки которой лежат на одной плоскости. Представление о такой фигуре даёт любой рисунок, сделанный на листе бумаги.

Но прежде, чем рассматривать плоские фигуры, необходимо познакомиться с простыми, но очень важными фигурами, без которых плоские фигуры просто не могут существовать.

Самой простой геометрической фигурой является точка. Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка – это основная фигура для абсолютно всех построений, даже самой высокой сложности. С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии.

Прямая — одно из фундаментальных понятий геометрии.При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии (евклидовой). Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить, как линию, путь вдоль которой равен расстоянию между двумя точками.

Прямые в пространстве могут занимать различные положения, рассмотрим некоторые из них и приведем примеры, встречающиеся в архитектурном облике зданий и сооружений (табл. 1):

Таблица 1

Параллельные прямые	Свойства параллельных прямых
	Если прямые параллельны, то их одноименные проекции параллельны:	Ессентуки, здание грязелечебницы (фото автора)
Пересекающиеся прямые	Свойства пересекающихся прямых	Примеры в архитектуре зданий и сооружений
	Пересекающиеся прямые имеют общую точку, то есть точки пересечения их одноименных проекций лежат на общей линии связи:	Здания «горы» на Тайване https://www.sro-ps.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane
Скрещивающиеся прямые	Свойства скрещивающихся прямых	Примеры в архитектуре зданий и сооружений
	Прямые, не лежащие в одной плоскости и не параллельные между собой, являются скрещивающимися. Ноне является общей линией связи. Если пересекающиеся и параллельные прямые лежат в одной плоскости, то скрещивающиеся прямые лежат в двух параллельных плоскостях.	Робер, Гюбер – Вилла Мадама под Римом https://gallerix.ru/album/Hermitage-10/pic/glrx-172894287

1.2. Плоские геометрические фигуры. Свойства и определения

Наблюдая за формами растений и животных, гор и извилинами рек, за особенностями ландшафта и далекими планетами, человек заимствовал у природы ее правильные формы, размеры и свойства. Материальные потребности побуждали человека строить жилища, изготавливать орудия труда и охоты, лепить из глины посуду и прочее. Все это постепенно способствовало тому, что человек пришел к осознанию основных геометрических понятий.

Четырехугольники:

Параллелограмм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — черта, линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Признаки параллелограмма:

Четырёхугольник является параллелограммом, если выполняется одно из следующих условий: 1. Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник – параллелограмм. 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.

Параллелограмм, у которого все углы прямые, называется прямоугольником.

Параллелограмм, у которого все стороны равны, называется ромбом.

Трапеция— это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

Треугольник — это простейшая геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника , а отрезки — сторонами треугольника. Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звезд используют свойства треугольников. Так возникла наука тригонометрия — наука об измерении треугольников, о выражении сторон через его углы. Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу.

Особенно активно свойства треугольника исследовались в XV-XVI веках. Вот одна из красивейших теорем того времени, принадлежащая Леонарду Эйлеру:

Огромное количество работ по геометрии треугольника, проведенное в XY-XIX веках, создало впечатление, что о треугольнике уже известно все.

Многоуго́льник — это геометрическая фигура, обычно определяемая как замкнутая ломаная.

Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку.

Существует большое количество геометрических фигур, все они отличаются параметрами и свойствами, порой удивляя своими формами.

Чтобы лучше запомнить и отличать плоские фигуры по свойствам и признакам, я придумал геометрическую сказку, которую хотел бы представит вашему вниманию в следующем параграфе.

Глава 2. ЗАДАЧИ-ГОЛОВОЛОМКИ ИЗ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР

2.1.Головоломки на построение сложной фигуры из набора плоских геометрических элементов.

Изучив плоские фигуры, я задумался, а существуют какие-нибудь интересные задачи с плоскими фигурами, которые можно использовать в качестве заданий-игр или заданий-головоломок. И первой задачей, которую я нашел, была головоломка «Танграм».

Это китайская головоломка. В Китае ее называют «чи тао ту», т.е умственная головоломка из семи частей. В Европе название «Танграм» возникло, вероятнее всего, от слова «тань», что означает «китаец» и корня «грамма» (греч. – «буква»).

Для начала необходимо начертить квадрат 10 х10 и разделить его на семь частей: пять треугольников 1-5 , квадрат 6 и параллелограмм 7 . Суть головоломки состоит в том, чтобы, используя все семь частей, сложить фигурки, показанные на рис.3.

Рис.3. Элементы игры «Танграм» и геометрические фигуры

Рис.4. Задания «Танграм»

Особенно интересно составлять из плоских фигур «образные» многоугольники, зная лишь очертания предметов (рис.4). Несколько таких заданий-очертаний я придумал сам и показал эти задания своим одноклассникам, которые с удовольствием принялись разгадывать задания и составили много интересных фигур-многогранников, похожих на очертания предметов окружающего нас мира.

Для развития воображения можно использовать и такие формы занимательных головоломок, как задачи на разрезание и воспроизведение заданных фигур.

Пример 2. Задачи на разрезание (паркетирование) могут показаться, на первый взгляд, весьма многообразными. Однако в большинстве в них используется всего лишь несколько основных типов разрезаний (как правило, те, с помощью которых из одного параллелограмма можно получить другой).

Рассмотрим некоторые приёмы разрезаний. При этом разрезанные фигуры будем называть многоугольниками.

Рис. 5. Приёмы разрезаний

На рис.5 представлены геометрические фигуры, из которых можно собрать различные орнаментальные композиции и составить орнамент своими руками.

Пример 3. Еще одна интересная задача, которую можно самостоятельно придумать и обмениваться с другими учениками, при этом кто больше соберет разрезанные фигуры, тот объявляется победителем. Задач такого типа может быть достаточно много. Для кодирования можно взять все существующие геометрические фигуры, которые разрезаются на три или четыре части.

Рис.6.Примеры задач на разрезание:

—— – воссозданный квадрат; – разрез ножницами;

Основная фигура

2. 2.Равновеликие и равносоставленные фигуры

Рассмотрим еще один интересный прием на разрезание плоских фигур, где основными «героями» разрезаний будут многоугольники. При вычислении площадей многоугольников используется простой прием, называемый методом разбиения.

Вообще многоугольники называются равносоставленными, если, определенным образом разрезав многоугольник F на конечное число частей, можно, располагая эти части иначе, составить из них многоугольник Н.

Отсюда вытекает следующая теорема: равносоставленные многоугольники имеют одинаковую площадь, поэтому они будут считаться равновеликими.

На примере равносоставленных многоугольников можно рассмотреть и такое интересное разрезание, как преобразование «греческого креста» в квадрат (рис.7).

Рис.7. Преобразование «греческого креста»

В случае мозаики (паркета), составленной из греческих крестов, параллелограмм периодов представляет собой квадрат. Мы можем решить задачу, накладывая мозаику, составленную из квадратов, на мозаику, образованную с помощью крестов, так, чтобы при этом конгруэнтные точки одной мозаики совпали с конгруэнтными точками другой (рис. 8).

На рисунке конгруэнтные точки мозаики из крестов, а именно центры крестов, совпадают с конгруэнтными точками «квадратной» мозаики – вершинами квадратов. Параллельно сдвинув квадратную мозаику, мы всегда получим решение задачи. Причем, задача имеет несколько вариантов решений, если при составлении орнамента паркета используется цвет.

Рис.8. Паркет, собранный из греческого креста

Еще один пример равносоставленных фигур можно рассмотреть на примере параллелограмма. Например, параллелограмм равносоставлен с прямоугольником (рис.9).

Этот пример иллюстрирует метод разбиения, состоящий в том, что для вычисления площади многоугольника пытаются разбить его на конечное число частей таким образом, чтобы из этих частей можно было составить более простой многоугольник, площадь которого нам уже известна.

Например, треугольник равносоставлен с параллелограммом, имеющим то же основание и вдвое меньшую высоту. Из этого положения легко выводится формула площади треугольника.

Отметим, что для приведенной выше теоремы справедлива и обратная теорема: если два многоугольника равновелики, то они равносоставлены.

Эту теорему, доказанную в первой половине XIX в. венгерским математиком Ф.Бойяи и немецким офицером и любителем математики П.Гервином, можно представить и в таком виде: если имеется торт в форме многоугольника и многоугольная коробка, совершенно другой формы, но той же площади, то можно так разрезать торт на конечное число кусков (не переворачивая их кремом вниз), что их удастся уложить в эту коробку.

Заключение

В заключении отмечу, что задач на плоские фигуры достаточно представлено в различных источниках, но интерес представили для меня те, на основании которых мне пришлось придумывать свои задачи-головоломки.

Ведь решая такие задачи, можно не просто накопить жизненный опыт, но и приобрести новые знания и умения.

В головоломках при построении действий-ходов используя повороты, сдвиги, переносы на плоскости или их композиции, у меня получились самостоятельно созданные новые образы, например, фигурки-многогранники из игры «Танграм».

Известно, что основным критерием подвижности мышления человека является способность путём воссоздающего и творческого воображения выполнить в установленный отрезок времени определенные действия, а в нашем случае – ходы фигур на плоскости. Поэтому изучение математики и, в частности, геометрии в школе даст мне еще больше знаний, чтобы в дальнейшем применить их в своей будущей профессиональной деятельности.

Библиографический список

1. Павлова, Л.В. Нетрадиционные подходы к обучению черчению: учебное пособие/ Л.В. Павлова. – Нижний Новгород: Изд-во НГТУ, 2002. – 73 с.

2. Энциклопедический словарь юного математика /Сост. А.П. Савин. – М.: Педагогика, 1985. – 352 с.

3.https://www.srops.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane

4.https://www.votpusk.ru/country/dostoprim_info.asp?ID=16053

Приложение 1

Анкета-опросник для одноклассников

1. Знаете ли вы, что такое головоломка «Танграм»?

2. Что такое «греческий крест»?

3. Было бы вам интересно узнать, что такое «Танграм»?

4. Было бы вам интересно узнать, что такое «греческий крест»?

Было опрошено 22 ученика 8 класса. Результаты: 22 ученика не знают, что такое «Танграм» и «греческий крест». 20-ти ученикам было бы интересно узнать о том, как с помощью головоломки “Танграм», состоящая из семи плоских фигур, получить более сложную фигуру. Результаты опроса обобщены на диаграмме.

Приложение 2

Элементы игры «Танграм» и геометрические фигуры

Преобразование «греческого креста»

Маленькие детки готовы учиться везде и всегда. Их юный мозг способен улавливать, анализировать и запоминать столько информации, сколько трудно даже взрослому человеку. То, чему родители должны научить малышей, имеет общепринятые возрастные рамки.

Основные геометрические фигуры и их названия дети должны узнать в возрасте от 3 до 5 лет.

Поскольку все дети разнообучаемы, то эти границы лишь условно приняты в нашей стране.

Геометрия – это наука о формах, размерах и расположении фигур в пространстве. Может создаться впечатление, что это сложно для малышей. Однако предметы изучения этой науки находятся повсюду вокруг нас. Вот почему иметь основные познания в этой области важно и для детей, и для старших.

Чтобы увлечь детей изучением геометрии, можно прибегнуть к веселым картинкам. Дополнительно хорошо бы иметь пособия, которые ребенок сможет потрогать, ощупать, обвести, раскрасить, узнать с закрытыми глазами. Основной принцип любых занятий с детьми – удержание их внимание и развития тяги к предмету с использованием игровых приемов и непринужденной веселой обстановки.

Сочетание нескольких средств восприятия сделает свое дело очень быстро. Воспользуйтесь нашей мини-методичкой, чтобы научить ребенка отличать геометрические фигуры, знать их названия.

Круг – самая первая из всех фигур. В природе вокруг нас многое имеет круглую форму: наша планета, солнце, луна, сердцевина цветка, многие фрукты и овощи, зрачки глаз. Объемный круг – это шар (мячик, клубок)

Начать изучение формы круга с ребенком лучше, рассматривая рисунки, а потом уже подкрепить теорию практикой, дав ребенку подержать что-нибудь круглое в руках.

Квадрат – это фигура, у которой все стороны имеют одинаковую высоту и ширину. Квадратные предметы – кубики, коробки, дом, окно, подушка, табурет и т. п.

Строить из квадратных кубиков всякие домики очень просто. Рисунок квадрата проще сделать на листочке в клетку.

Прямоугольник – родственник квадрата, который отличается тем, что имеет одинаковые противоположные стороны. Так же, как и у квадрата, у прямоугольника все равны 90 градусам.

Можно найти множество предметов, имеющих форму прямоугольника: шкафы, бытовая техника, двери, мебель.

В природе форму треугольника имеют горы и некоторые деревья. Из ближайшего окружения малышей можно привести в пример треугольную крышу дома, различные дорожные знаки.

В форме треугольника были построены некоторые древние сооружения, например храмы и пирамиды.

Овал – это круг, вытянутый с двух сторон. Формой овала обладают, например: яйцо, орехи, многие овощи и фрукты, человеческое лицо, галактики т. д.

Овал в объеме называется эллипсом. Даже Земля сплюснута с полюсов – эллипсовидная.

Ромб

Ромб – тот же квадрат, только вытянутый, т. е. имеет два тупых угла и пару острых.

Изучать ромб можно с помощью наглядных пособий – нарисованной картинки или объемного предмета.

Приемы запоминания

Геометрические фигуры по названиям запомнить несложно. В игру их изучение для детей можно превратить, применив следующие идеи:

• Купите детскую книжку с картинками, в которой будут веселые и красочные рисунки фигур и их аналогии из окружающего мира.

• Нарежьте из разноцветного картона побольше всяких фигурок, заламинируйте их скотчем и используйте как конструктор – очень много интересных сочетаний можно выложить, комбинируя разные фигурки.

• Купите линейку с отверстиями в форме круга, квадрата, треугольника и других – для детей, которые уже дружат с карандашами, рисунки с помощью такой линейки – интереснейшее занятие.

Можно придумать много возможностей научить малышей знать названия геометрических фигур. Все способы хороши: рисунки, игрушки, наблюдения за окружающими предметами. Начните с малого, постепенно усложняя информацию и задания. Вы не ощутите, как пролетит время, а малыш обязательно порадует вас успехами в скором.

Фигура – это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.

Точка – основное понятие геометрии, это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса.

Линия – это множество точек, последовательно расположенных друг за другом. У линии измеряют только длину. Ширины и толщины она не имеет.

Прямая линия – это линия, которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны.

Луч – это часть прямой линии, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону.

Отрезок – это часть прямой линии, ограниченная двумя точками. Отрезок имеет начало и конец, поэтому можно измерить его длину.

Кривая линия – это плавно изгибающаяся линия, которая определяется расположением составляющих её точек.

Ломаная линия – это фигура, которая состоит из отрезков, последовательно соединенных своими концами.

Вершины ломаной – это

1. точка, с которой начинается ломанная,
2. точки, в которых соединяются отрезки, образующие ломаную,
3. точка, которой заканчивается ломанная.

Звенья ломаной – это отрезки, из которых состоит ломаная. Количество звеньев ломаной всегда на 1 меньше, чем количество вершин ломаной.

Незамкнутая линия – это линия, концы которой не соединены вместе.

Замкнутая линия – это линия, концы которой соединены вместе.

Многоугольник – это замкнутая ломанная линия. Вершины ломаной называются вершинами многоугольника, а отрезки – сторонами многоугольника.

Геометрические фигуры — виды с названиями и основные свойства » Kupuk.net

Скопление точек и линий на плоскости образует геометрические фигуры. Их названия зависят от свойств и особенностей. Фигура ограничена линиями и это условие влияет на многообразие форм. Каждый предмет индивидуален, имеет свои предназначения и задачи. Существуют простые и сложные фигуры, различающиеся личными параметрами.

Общая характеристика

Предметы в геометрическом изображении состоят из отдельных частей: точек, линий, лучей, отрезков и вершин. Отдельно взятый предмет имеет свое предназначение.

Основные понятия о составляющих

Когда все точки фигуры принадлежат одной плоскости, она является плоской. К ней относятся отрезок, прямоугольник. Существуют геометрические объекты, не являющиеся разновидностью плоскости, — куб, шар, пирамида, призма.

Минимальным объектом геометрии является точка. Определение того, какой она должна быть известно из школьного математического курса. Учебник характеризует ее как объект, не имеющий измерительных особенностей. Точка (Т) не содержит стандартных свойств: высоты, длины, радиуса, важным является только ее расположение. Обозначается числом или большой заглавной буквой. Например, точка называется D, E, F или 1, 2, 3. Несколько точек бывают отмечены разными цветами или буквами для удобного различия.

Линия состоит из множества точек. Измеряется длина этого составляющего объекта и обозначается маленькими буквами (abc).

Виды линий:

• Замкнутая. Когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
• Разомкнутая. Начало и окончание не соединяются.
• Прямая. Обозначается буквой а или b.
• Ломаная. Заключается в соединенных отрезках не под углом 180 градусов. Линия обозначается перечислением всех вершин.
• Кривая.Отличная от прямой линии.

Задания из школьной программы кажутся школьникам скучными, неинтересным, но эти азы являются основой составления фигур простых и более сложных.

Существуют подвиды прямой линии: пересекающиеся, содержащие общую точку и когда две прямые линии соединяются в одной точке.

Луч в математике представляет часть прямой, имеющей начальную точку, но не имеющую конец. Это продолжение в одну сторону. Если Т разделяет линию пополам — получается два луча. Лучевые линии совпадают, когда расположены на одной прямой, начинаются в точке или направляются в одну сторону.

Отрезок представляет составную часть прямой, ограниченной двумя точками — она имеет начало и конец, поэтому измеряется. Длина отрезка представляет расстояние между его первой и последней точками. Через одну Т проводится бесконечное число линий, а через две — кривые и только одна прямая.

Стандартные объекты

К основным фигурам геометрии на плоскости относятся прямоугольник, треугольник, квадрат, многоугольник и круг. Прямоугольник выглядит как фигура, состоящая из четырех сторон и четырех прямых углов (ПУ). Противоположные стороны равны между собой. В математике прямоугольник обозначается четырьмя латинским заглавными буквами. Все ПУ расположены под 90 градусов. Прямоугольник с равными, одинаковыми сторонами называется квадратом.

Фигура, имеющая 3 стороны и столько же углов (вершин), называется треугольником. Существует классификация этой фигуры по типу У.

Виды треугольника в зависимости от угла (У):

• Прямой. Один У будет прямым, два — менее 90 градусов.
• Острый. Градусная мера больше 0, но меньше 90 гр.
• Тупой. Один У тупой, два других будут острыми.

Геометрическая фигура с углами разной формы называется многоугольником. Его вершины представлены точками, соединяющими отрезками.

Радиус круга — промежуток от середины окружности до любой ее точки. Диаметр — это отрезок, соединяющий две точки окружности, проходящий через ее середину.

Параллелепипед — это призма, у которой основанием является параллелограмм. Когда все ребра параллелепипеда равны, получается куб.

Многогранная фигура, у которой одна грань является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной, называется пирамидой.

Семиугольник (гептагон) — это многоугольник с 7 углами. Многоугольник представляет замкнутую ломанную линию.

Основные фигуры перечислены, но геометрия включает еще сложные объекты, использующиеся в различных областях жизни.

Сложные модели

В сложной геометрии выделяют фигуры с пространственным, плоским и объемным наполнением. Существует понятие геометрического тела, 3D-моделирование и проекция.

Определение тела и пространства

Геометрическое тело (ГТ) представляет часть пространства, отделенное замкнутой поверхностью наружной границы. Это понятие относится к компактному множеству точек, а две из них соединяют отрезком, проходящим внутри границы тела. Внешняя граница ГТ является его гранью, которых может быть несколько. Множество плоских граней определяет вершины и ребра ГТ. Все геометрические тела делятся на многогранники и тела вращения.

Тела вращения — объемные тела, образующиеся из-за вращения плоской фигуры, ограниченной кривой, вокруг оси. Эта ось расположена в той же плоскости. При вращении контуров фигур вокруг собственной оси возникает поверхность вращения, а если вращать заполненные контуры — возникают объекты (шар).

Шар представляет множество точек, расположенных от данной точки на небольшом пространстве. Точка является центром шара, а расстояние ограничено радиусом.

В сферу геометрии входят плоские (двухмерные) и объемные пространственные фигуры (трехмерные).

Плоские фигуры представляют точка, круг, полукруг, окружность, овал, прямоугольник, квадрат, луч, ромб, трапеция.

Существуют двухмерные фигуры (2D), представленные углом, многоугольником, четырехугольником, окружностью, кругом, эллипсом и овалом. Объекты 3D выделены двугранным или многогранным углом. Среди них известны призма, параллелепипед, куб, антипризма, пирамида, тетраэдр икосаэдр, бипирамида, геоид, эллипсоид, сфера шар и другие. Плоские фигуры изучает планиметрия, а объемные — стереометрия.

Объемные фигуры:

• Шар.
• Конус.
• Параллелепипед.
• Цилиндр.
• Сфера.

Конус образуется из треугольника с прямыми углами, при вращении его вокруг одного из катетов. Тороид возникает из замкнутой плоскости (окружности), вращающейся вокруг прямой и не пересекающей ее. Многогранник называется полиэдр, представляет замкнутую поверхность, состоящую из многоугольников.

Виды многогранников:

• Тетраэдер (четырехгранник). Это правильный треугольник.
• Куб (гексаэдр). Грани являются квадратом.
• Октаэдр. Имеется шесть вершин и восемь граней.
• Икосаэдр. Равносторонние треугольники являются гранями. Имеется 12 граней и 12 вершин.
• Додекаэдр. Правильные шестиугольники, имеется 12 граней, 20 вершин.

В школьной программе имеются специальные разделы геометрии, позволяющие распределить знания и не путать их в будущем. Это касается плоских, объемных фигур — одни изучает стереометрия, другие планиметрия.

Познавательные игрушки детям

Геометрия является наукой, которой можно знакомить детей с раннего возраста. Лучше распечатать картинки, геометрические фигуры для детей, затем нарисовать их вместе на чистом листе. Малышу первого года подобное занятие будет не очень интересным и понятным, а у дошкольника вызовет интерес, особенно если объекты изучения будут разноцветными или в необычном исполнении.

Основной материал для обучения детей:

• Яркие карточки с основными фигурами, формами. Шаблоны будут наглядным пособием перед школой.
• Раскраски, прописи, рабочая тетрадь. На каждой странице тетради представлены простейшие графические упражнения и задания. Выполняя их, малыш познакомится с геометрией и узнает названия фигур.
• Специальная детская литература.

Увлекательные, забавные, задорные стихи «Веселая геометрия для малышей» помогут детям быстро познакомиться и усвоить много важной информации о фигурах и размерах предметов. Веселые стишки помогут юному читателю соотнести малопонятные геометрические знания с обыденными предметами обихода. Например, в женской юбке представлена трапеция, в блюдце— круг, а в трубе цилиндр.

Учить детей начинают с плоских фигурок, сделанных из цветной бумаги или фетра. Не нужно ограничивать ребенка в фантазии, ведь он различает фигуры по цветам и форме — треугольник, овал, круг, ромб, квадрат. Увлекательным будет занятие с использованием сортеров, пирамидок из различных геометрических объектов.

Ближе к дошкольному возрасту переходят на объемные фигуры, кубики, конусы, кольца и цилиндры. В школьном возрасте знания накопятся, и дети будут осознанно различать равнобедренный, равносторонний треугольник, три понятия: луч, отрезок, окружность.

Раздел математики геометрия изучает пространственные отношения и формы. Фигура как понятие, рассмотренное во всех учебниках геометрии, является пространственной формой.

Геометрию можно обнаружить везде — в любых окружающих предметах. Это современные здания, архитектурные строения, формы, космическая станция, интерьер квартиры, подводные лодки.

Математические знания являются профессионально важными для современных специальностей: дизайнеров и конструкторов, рабочих и ученых. Без знания основ геометрии невозможно построить здание или отремонтировать квартиру.

Тематическая неделя. Геометрические фигуры — 3 ответов

Такие фигуры мы брали:

пн – круг, квадрат

вт – треугольник, звезда

ср – прямоугольник, ромб

чт – овал, трапеция

пт – повторение, закрепление ))

Наши помощники: литература, пособия, игрушки, самоделки и то, как мы их использовали.

Наклейки, наклейки и еще раз наклейки )) Ванечка их обожает, Анюта наклеет одну-две и убегает (это было в пн, а в пт уже клеит с удовольствием и просит еще) ))

“Веселая геометрия” – замечательное пособие! Наклейки яркие и показательные, задания интересные.

“Геометрические фигуры. Игры с наклейками”. Книжка про то, как на день рождения муравья сходились гости – насекомые. На каждой страничке насекомое, наряд которого нужно украсить геом фигурами. Там маленькая, но милая история про 8 насекомых ))

“Цвета и формы”. Хорошее пособие. Вообще нравятся пособия этой фирмы

И оставшиеся после праздников наклеечки тоже пригодились ))

“Крошка бегемот” Пособие хорошее )

“Формы. Книжка с окошками”. Милая книжица. Я думаю, что окошки любят большинство малышей. Формы и картинки на них: круг, треугольник, прямоугольник, квадрат.

“Моя малышка. Формы”. Книжка малышка. Милая. На каждом развороте фигура и картинки такой формы. Круг, квадрат, треугольник, овал, ромб.

“Геометрические фигуры. Веселые уроки для будущих отличников”. Пособие хорошее.На каждом развороте фигура, на каждой странице маленький стишок, предметы разной формы и задания.

Круг, Полукруг, Овал, Трейгольник, Квадрат, Прямоугольник.

“Это может ваш малыш. Рисуем красками” Здесь можно подобрать задания для изучения круга, квадрата, звезды.

“Формы. Комплект готовых карточек-заданий” Пособие хорошее. Внутри 4 картонных листа. На 2х из них поля с заданиями, еще 2 – карточки.

Первое поле вы видите на фото ниже. На втором поле нужно расставить фигуры по мере убывания их размера.

Блоки Дьенеша – замечательное пособие, можно купить здесь, там же продаются и альбому к нему.

Альбом для работы с блоками

Мягкие пуговички. Вырезала из обивочной ткани для мебели ) Ванечке было не просто с ними справляться, но задание ему понравилось.

Сначала сортировли их, потом надевали – терпения и желания хватило на все! – удивил меня ))

Это уже другие пуговички – пуговицы пришиты на салфетку из фетра, мягкие пуговицы из обивочной ткани для мебели )),

пришитые пуговицы из набора play buttons от elc – они нам еще пригодятся)))

Понравилась Ванечке эта игрушка – приносил мне ее регулярно, играли ))

Как еще мы использовали эти пуговицы. Я спрятала их в муку, а Ванечка просеивал и расставлял пуговицы на соответствующие места на листе с контурами.

Ему так это понравилось, что потом он эти пуговицы искал в гречке, а потом, в другой день, и в других крупах ))

Прыгали по вырезанным из ткани фигурам

Все размазано – прыгают )) Я даже не ожидала такого энтузиазма по поводу этой развлекухи )) Прыгали каждый день (соответсвенно добавляя новые фигуры)

Проговаривали, обводили, разукрашивали

Собирали фигуры из мозаики. Ваня хо-рооо-ший ))

Раскраска – самоделка ))

Пазлы. Вырезала из цветного картона фигуры, разрезала их на несколько частей. Складывали.

Творчество:

Аппликация – цветной картон и клеящий карандаш

Аппликация цв картон + цв бумага + клей пва

Ну куда без расскрасок )) Картинки из “Крошки бегемота”

Штамповали паролоном (круг и квадрат). Геометрические фигуры это напоминало мало, но процесс понравился )))

Аппликация – цв бумага и клеящий карандаш

Аппликация – ткань обивочная + двусторонние липучки

Самоклеющаяся бумага – перламутровая и флюоресцентная.

Что еще мы делали:

собирали пирамидки, башенки и прочее из кубиков

обводили (пытались)) нарисованные пунктиром фигуры

смотрели презентации (их список в конце поста)

искали в окрудающих нс предметах фигуры

Так выгдядит стенка к концу недели. Предметы под картинками – это Ванюшкино изобретение.

В пн мы познакомились с кругом и квадратом и позже я достала пирамидку и кубики, он тут же схватил кольцо и кубик и пытался приставить их к стене.

Я, конечно, очень обрадовалась – стало ясно, что он видит фигуры в окружающих предметах. И вот таким образом решила поддержать его инициативу ))

ТН ББ-шек, которые помогли нам провести нашу ТН:

http://www. babyblog.ru/community/post/igraem/1696277

http://www.babyblog.ru/community/post/igraem/1699275

http://www.babyblog.ru/community/post/igraem/1699276

http://www.babyblog.ru/community/post/igraem/1699758

http://www.babyblog.ru/community/post/igraem/1701586

http://www.babyblog.ru/community/post/igraem/1702512

http://www.babyblog.ru/community/post/igraem/1702512

Спасибо, девочки! ))

Презентации, которые мы смотрели:

http://steshka.ru/prezentaciya-geometricheskie-figury-dlya-detey Геометрические фигуры для детей

http://www.youtube.com/watch?v=xhZAwzlYq5Y Веселая радуга 1

http://www.youtube.com/watch?v=FNDufHPzkSE Baby Einstein – Discovering Shapes (part 1 of 2)

http://www.youtube.com/watch?v=BHMtSZftZhY Baby Einstein – Discovering Shapes (part 2 of 2)

http://www.youtube.com/watch?v=rRewibcaHpg Геометрические фигуры

http://www.youtube.com/watch?v=t5gznkhAYRo&feature=related Учим геометрические фигуры и цвета (1)

http://www. youtube.com/watch?v=8eLlIrDZ4C0 Patrick n friends: Цвета и формы

http://www.youtube.com/watch?v=k_1DK-05Wxw Мультики для самых мал…: Геометрические фигуры

Лэпбук «Веселая геометрия» для детей старшего дошкольного возраста

Лэпбук «Веселая геометрия» составлен для ознакомления и закрепления знаний старших дошкольников о гоеметрических фигурах. Содержаит следующие разделы: Книжка-малышка “Знакомимся с геометрическими фигурами”, “Загадки о геометрических фигурах”, “Загадки о геометрических телах”, “Геометрические сказки”, “Геометрические раскраски”, дидактической игры “Подбери предмет”, “Игротека”. Данное пособие составлено совместно с воспитателем Басовой О.Н. Лэпбук может быть полезен для работы воспитателям, учителям начальных классов. В лэпбуке использованы материалы Сети Интернет.

 

 

СКАЗКИ О ГЕОМЕТРИЧЕСКИХ ФИГУРАХ

«Самый важный».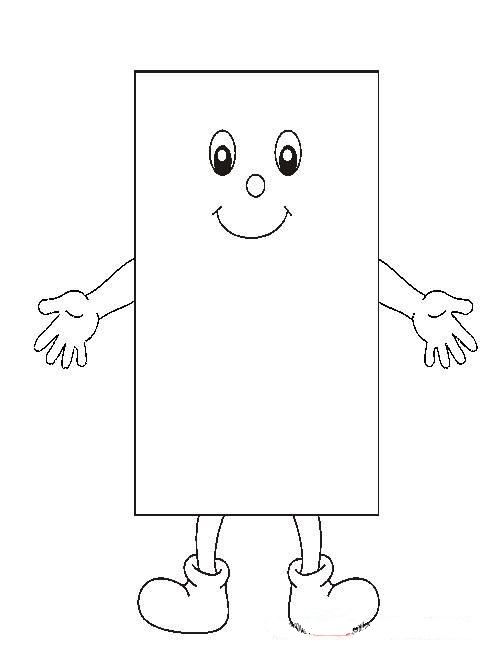

«В одной прекрасной стране, которая называется «Геометрия» жили не тужили разные геометрические фигуры. Жители этой страны всегда друг другу помогали, друг друга выручали, поэтому жили дружно и весело. Но, в одно прекрасное летнее утро треугольник сидел рядом со своим домиком на завалинке (Педагог ставит на наборное полотно геометрическую фигуру треугольник).  Сидел он сидел, думал, думал и решил вдруг, что он самая нужная и важная из геометрических фигур. Обрадовался, вскочил и побежал к другу квадрату (Педагог ставит на наборное полотно геометрическую фигуру квадрат). Стучит в дверь: «Квадрат, открывай. У меня для тебя новость». Посмотри, я самый важный и нужный из фигур. У меня есть три угла. Вот я какой красивый. Квадрат посмотрел на треугольник и сказал: «Нет брат, я самый важный и нужный из фигур. У тебя три угла, а у меня четыре. Спорили, спорили треугольник с квадратом, но так и не о чем не договорились. Решили пойти к прямоугольнику (Педагог ставит на наборное полотно геометрическую фигуру прямоугольник). Подошли они к домику прямоугольника, стучат к нему в дом и просят его: «Рассуди нас, кто главнее»?  Треугольник говорит:«Я главный, у меня три угла». Квадрат говорит: «Я главней. У меня четыре угла». Выслушал их прямоугольник и сказал: «Нет ребята, Вы не правы. Я самый главный. У меня  четыре угла, я самый высокий и красивый». Пуще прежнего друзья рассорились. Никто друг другу уступать не хотел.  Мимо проходил круг, услышал он спор и сказал: «Друзья, не надо спорить и ссориться. Каждая из Вас нужная и важная фигура (Педагог ставит на наборное полотно геометрическую фигуру круг). С давних времен в нашей стране, которая  называется «Геометрия», споров и ссор не было. И с тех пор в этой замечательной стране все фигуры стали жить дружно.

 

 

«Как треугольник и круг познакомились с квадратом».

– Стоит на опушке леса вот такой необычный дом. (Рассматривание, узнавание и называние фигур.)
– Как вы думаете, кто его жители? (Обобщая ответы детей, воспитатель продолжает рассказывать сказку. )
– Жили-были вот в таком доме круг и треугольник. И выглядели они так. (показываем картинку).
Однажды пошли друзья погулять и встретили вот такую фигуру. Узнаете, кто это? (показываем картинку квадрата).
А наши друзья незнакомца не узнали, поэтому испугались, спрятались за куст и думают: «Кто он такой? Стали рассуждать:
– На круг похож? (Нет.) Почему? (У него углы есть.)
– На треугольник похож? (Нет.) Посчитайте углы. (Их четыре.)
Думали-гадали, а потом круг предложил: «Подойдем, спросим, как его зовут и познакомимся».
– Здравствуй, я – круг, у меня нет углов. Я похож на колесо, на солнышко, на тарелку. Я умею катиться.
– А я – треугольник, у меня три угла и я похож на колпак гнома, на крышу домика.
– Здравствуйте, друзья, я очень рад с вами познакомиться и подружиться. Меня зовут квадрат. Смотрите, какой я красивый, все мои стороны одинаковы. А на что я похож, догадайтесь сами. ( Дети предлагают свои варианты.)
– Родом я из большого и дружного семейства четырехугольников, у меня много братьев и сестер. Но сегодня я ушел гулять один и вот заблудился. Не могли бы вы меня приютить на время в своем домике. (Воспитатель подводит детей к мысли, что нужно сконструировать для троих друзей новый домик.) 

«Барон Квадрат».

Давным – давно в мире было много разных волшебных стран. И особым волшебством отличалась страна – Всезнаек! В ней правила мудрая царица Геометрия. В то время из одной страны в другую бродил Лист. Его края были неровными, с множеством загибов, потому что его вырвал из тетради мальчик по имени Веня, и уже долгое время Лист находился в пути. А нашему герою очень хотелось, чтобы все его стороны стали вновь ровными.

Собравшись с силами, Лист отправился к царице Геометрии. Только она могли ему помочь. Лист целых пять дней провел в пути, потому что двигаться он мог только с помощью ветра, а ветреная погода была не каждый день. На шестой день своего пути Лист оказался у дворца самой царицы. Она ласково встретила его, выслушала его просьбу и сказала:

– Хорошо, я помогу тебе, только мне нужны помощники: Карандаш, Линейки и Ножницы.

Хлопнула царица в ладоши три раза и перед ней явились её слуги: Карандаш, Линейки и Ножницы.

– Ну, теперь ты будешь квадратом! – спросила царица Геометрия

– Квадратом? – удивился Лист.

– Да! Да! Квадратом! – убедительно ответила царица Геометрия.

– А что это такое? – спросил Лист.

– Это прямоугольник, у которой все стороны не только ровные, но и равные, – объяснила царица Геометрия.

– Да, мне это подходит, – ответил Лист.

– Тогда все принимайтесь за работу, – сказала царица.

Карандаш чертил ровно. Линейка замеряла стороны так, чтобы все они были одинаковой длины, а ножницы ровно отрезали лишние части. Когда работа была сделана, царица Геометрия объявила:

– Теперь ты превратился в настоящий Квадрат.

Лист обрадовался. Он поблагодарил Карандаша, Линейку и Ножницы, а царица Геометрия велела принести ему зеркало. Он долго смотрелся в него, а потом закричал:

– Квадрат! Квадрат! Ура! У меня теперь все стороны равны!!!

Лист – квадрат поблагодарил царицу Геометрия, а она присвоила ему звание – барона. Барон квадрат пошёл гулять по странам с высоко поднятой головой. Ему очень понравился его внешний вид и звание.

 

«Купец Круг».

У царицы Геометрии в её дворце была потайная комната. И каждый вечер она уединялась в ней для того чтобы… посмотреть в своё волшебное зеркало. В нём она видела всех своих жителей. Но каждый день она подолгу наблюдала за бароном Квадратом. Ей было его очень жалко – он всегда гулял один. У него не было друзей. В её стране он был единственной фигурой.

Однажды вечером царица Геометрия, после наблюдений за бароном Квадратом, вышла погулять в сад. Погода была чудесная! На небе ярко сияла луна и звёзды. Царица Геометрия была очарована видом Луны, и тогда её осенило: а ведь Луна похожа на квадрат, только углы закруглены. Она в один миг достала циркуль и нарисовала круг. Позвала к себе ножницы, велела вырезать фигуру по контуру и нарекла его купцом

 

«Граф Треугольник».

Жизнь в стране Всезнаек шла своим чередом. В ней происходили и хорошие и плохие события. Царица Геометрия следила за всем, но однажды…

Проказник Фокус – Покус решил пошутить над бароном Квадратом. Он притворился его другом и во время очередной встречи разделил его с угла на угол пополам! Квадрат испугался. Он не знал, что ему делать. Но вдруг раздался голос царицы Геометрии:

Не бойся барон Квадрат. Новую фигуру с тремя углами и тремя сторонами я нареку графом треугольником, а ты как был бароном квадратом, так им и останешься. Царица Геометрия наказала Фокуса – Покуса за его злую шутку, но в тоже время была довольна тем, что в её стране появился новый житель.

 

«Полезный прямоугольник».

Прямоугольник все время завидовал Квадрату.
– Я такой неуклюжий, – жаловался он. – Если поднимусь во весь рост, то стану длинным и узким. А если лягу на бок, то буду низким и толстым. 
– А ты всегда остаешься одинаковым, – продолжал он, обращаясь к Квадрату. – И стоя, и сидя, и лежа!
– Да уж, – с гордостью говорил важный Квадрат. – У меня все стороны равны. Не то, что у некоторых: то дылда-дылдой, а то блин-блином.
И Квадрат переворачивался с боку на бок, но его рост и ширина от этого не менялись.
А однажды случилось вот что. Один Человек заблудился в лесу. Он шел наугад сквозь чащу и встретился с Квадратом и Прямоугольником. Поскольку у Квадрата был очень важный вид, то Человек обратился за помощью именно к нему.
– Можно, я заберусь на вас и погляжу, где мой дом? – спросил он у Квадрата.
Человек залез сначала на одну сторону Квадрата. Но ничего не увидел, потому что ему мешали макушки деревьев.
Тогда Человек попросил Квадрат перевернуться и залез на другую сторону. Но, как известно, все стороны у Квадрата одинаковые. Поэтому и на сей раз Человек ничего не увидел из-за деревьев.
– Гражданин Квадрат! – взмолился Человек. – Помогите мне хотя бы через речку перебраться!
Квадрат подошел к речке и попытался дотянуться до другого берега. Но… плюх! Плюхнулся в воду.
– Может, я смогу помочь вам? – предложил Человеку скромный Прямоугольник.
Он встал во весь свой рост. Человек забрался на него и оказался выше деревьев.
Вдалеке он увидел свой дом и наконец понял, куда ему надо идти. Тогда Прямоугольник лег на бок и стал мостом.
Человек перебрался по Прямоугольнику через речку, помог ему подняться и, горячо поблагодарив, отправился домой.
А Квадрат, который сушился на берегу после вынужденного купания, сказал Прямоугольнику:
– Вы, оказывается, полезная фигура!
– Ну, что вы! – скромно улыбнулся Прямоугольник. – Просто мои стороны разной длины: две – длинные, а две – короткие. Иногда это бывает очень удобно.

 

 

«Треугольник и Квадрат».

Жил-был Треугольник. Хотя, по правде сказать, он не столько жил, сколько скучал. Вот так…
С ним по соседству скучал и Квадрат. После того, как ему не удалось помочь Человеку выбраться из леса, он уверовал в свою полную бесполезность. Теперь Квадрат валялся в каком-то овраге и чувствовал себя никому не нужным и ужасно одиноким. Вот таким…
Скучал он, скучал и решил послать письмо Треугольнику. «Дорогой Треугольник! Поодиночке мы ни на что не годимся, – писал он. – А вместе мы уже имеем смысл. Что вы об этом думаете?»
Треугольник ответил ему так: «Уважаемый Квадрат! От скуки я разучился думать. Поэтому почти ничего не думаю. Но мне кажется, что надо жить со смыслом».
И стали они жить со смыслом, то есть вместе. И что же получилось?

 

«Белочка и геометрические фигуры».

Наступила зима. Белочка нашла пустое дупло и решила жить в нем вместе с бельчатами. Но им было холодно в дупле, потому что оно было всегда открыто. В этом же лесу жили два мастера, фигуры Круг и Треугольник. Треугольник был злой и думал о себе, что он самый главный в лесу мастер, а Круг был добрый и веселый. Пошла белочка к фигурам и попросила их сделать для дупла двери. Треугольник сделал дверь треугольную, потому что считал, что самые лучшие двери – треугольные, а все остальные совсем никому не нужны. Поставила белочка треугольную дверь. Но она не закрывала дупло хорошо, так как оно было круглое. Ветер дул в щели, и бельчатам было холодно. Тогда белочка опять пошла к фигурам и попросила сделать другую дверь. Треугольник нахмурился и обиделся. А Круг сделал круглую дверь, которая подошла к дуплу, и всем было тепло. С тех пор Треугольник понял, что все фигуры важны.

Однажды Квадрат и Прямоугольник отправились на прогулку и попали в один двор. Там сидел мальчик и грустил. «Ты почему грустишь?» — спросил его Прямоугольник. «Просто у нас во дворе негде играть», — ответил мальчик. 
И тогда Квадрат и Прямоугольник построили горку.  
Мальчик обрадовался и стал кататься.
«Я понял! — сказал Прямоугольник. — Неважно, какой ты внешне, главное — быть кому-нибудь полезным!»

 

 

 

 

 

ГЕОМЕТРИЧЕСКИЕ РАСКРАСКИ

 

ЗАГАДКИ О ГЕОМЕТРИЧЕСКИХ ТЕЛАХ

 

ЗАГАДКИ О ГЕОМЕТРИЧЕСКИХ ФИГУРАХ И ФОРМАХ

 

 

 

КНИЖКА-МАЛЫШКА «Знакомимся с геометрическими фигурами»

 

Круг

Посмотрите-ка вокруг!

Пальчиком рисуем круг.

Куклы были вместе в ряд,

А теперь в кругу сидят.

Наше солнышко в окне –

Золотой круг в вышине.

Круглый мячик здесь лежит,

В ручки к вам он поспешит.

Треугольник

Треугольник – три угла,

Посмотрите детвора:

Три вершины очень острых –

Треугольник – «остроносый».

Стороны в нем тоже три:

Раз, два, три – ты посмотри.

Треугольник мы рисуем,

Знать теперь его мы будем.

Квадрат

Познакомьтесь, вот квадрат!

Он знакомству очень рад!

В нём угла уже четыре,

Нет его ровнее в мире:

Стороны четыре в нём,

Две скрепляются углом.

Круг в нем может разместиться,

В куб он сможет превратиться.

Ромб

Ромб – фигура непростая,

Две в себе объединяет:

Треугольник раз и два –

Фигура стала вдруг одна.

Четыре в ромбе стороны.

Между собой они равны.

Четыре в ромбе и угла,

Равны между собой по два.

Прямоугольник

Как окно прямоугольник,

Аккуратный, словно школьник.

Он похож дверь, на книжки,

И на ранец у мальчишки.

На автобус, на тетрадку,

На большую шоколадку.

На корыто поросенка

И на фантик у ребенка.

Овал

Вот овальный огуречик,

Из него и человечек

Получиться может ловко:

Ручки, ножки и головка.

Наш овал нам сделать просто:

Круг растянем – больше роста.

Нет углов и нет сторон,

Очень вытянутый он.

 

ИГРОТЕКА

Задание: Посмотри на картинку. Из каких фигур состоят предметы, изображенные предметы. Из представленных фигур найди подходящие и закрой пустые окошки.

 

Задание: Посмотри на картинку. Из каких геометрических фигур она составлена? Попробуй составить такую же картинку.

       

Задание: Посмотри внимательно на фигуры в верхней части карточки. Запомни их цвет. Закрой верхнюю часть карточки и раскрась фигуры в нижней части, также как на верхней.

    

 

 

ДИДАКТИЧЕСКАЯ ИГРА

Игра «Подбери предмет».

Цель: упражнять в умении находить предметы похожие на определенные геометрические фигуры – круг, квадрат, треугольник, овал, ромб, прямоугольник. Из представленных ниже картинок с геометрическими фигурами, необходимо вырезать и заламинировать предметы для игры.

 

 

КАРТИНКИ ДЛЯ ОФОРМЛЕНИЯ ОБЛОЖКИ

Fun Shapes – Bilder und Stockfotos

917.780Bilder

• Bilder
• Fotos
• Grafiken
• Vektoren
• Videos

AlleEssentials

Niedrigster Preis

Signature

Beste Qualität

Durchstöbern Sie 917.780

fun shapes Stock- Фотографии и фотографии. Oder starten Sie eine neuesuche, um noch mehr Stock-Photografie und Bilder zu entdecken.

Большой Затц verschiedenfarbiger векторные иллюстрации в мультяшном плоском дизайне. handgezeichnet abstrakte formen, lustig süß – забавные формы, графика, клипарт, мультфильмы и символы

Большой размер векторных иллюстраций в мультипликационном. ..

Большой размер векторных иллюстраций в мультяшном плоском дизайне. Handgezeichnete abstrakte Formen, lustige niedliche Comic-Charaktere.

kannten sie text auf einer flüssigen trendform mit geometrischen elementen und einem megaphon. vektor-design-banner isoliert für neugier, wissen, quiz-spiele, trivia und andere konzepte – fun shape stock-grafiken, -clipart, -cartoons und -symbole

Kannten Sie Text auf einer flüssigen Trendform mit geometrischen…

Vektor eps10

Satz abstrakter organischer formen und texturen for designlayouts — handgezeichnete vektorelemente – fun shape stock-grafiken, -clipart, -cartoons und -symbole

Satz abstrakter organischer Formen und Texturen for…

геометрическая подложка элемента. grafik минимальный textur für urlaub плакат, карты, социальные сети. abstraktes muster mit kreis- und halbtonpunkten. геометрия-баннер. вектор – забавные формы стоковые графики, -клипарт, -мультфильмы и -символ

геометрическая основа с абстрактными формами элементов. Grafik…

naives nahtloses muster mit abstrakten figuren und formen in leuchtenden regenbogenfarben. адский минималистский zeitgenössisches grafisches bauhaus design. abstrakter Moderner Trendiger Hintergrund. – забавные формы – графика, -клипарт, -мультфильмы и -символы

Naives nahtloses Собрать с абстрактными рисунками и формами в… графика, -клипарт, -мультфильмы и -символ

Satz abstrakter organischer Formen und Texturen für…

круглые абстрактные векторные формы. farbverlauf абстрактный баннер, творческое искусство и элемент графического дизайна – забавные формы, графика, клипарт, мультфильмы и символы

Круглые абстрактные векторные формы. Farbverlauf runde Banner,…

nahtloses muster mit bunten handgezeichneten organischen formen, linien, doodles und elementen – fun shape Stock-grafiken, -clipart, -cartoons und -symbole

nahtloses muster mit bunten handgezeichneten organischen Formen,…

Nahtloses Muster mit bunten handgezeichneten organischen Formen, Linien, Kritzeleien und Elementen. Естественные формы. Векторные тренды Идеальный дизайн для этикеток, флаеров, баннеров, стоффов, этикеток, брендинга, обложек и других материалов.

abstrakte moderne pastelle farbe, schwarze punkte muster mit linien Diagonal auf Weißem Hintergrund. – забавные формы – графика, -клипарт, -мультфильмы и -символы

Abstrakte moderne Pastelle Farbe, schwarze Punkte Muster mit…

пастельные абстрактные формы для фона – забавные формы – графика, -clipart, -cartoons und -symbole

Pastell Abstrakte Formen Hintergrund

reihe von bannern, gotisch mit hashtags. Trendige jungen slang-wörter. vektor-illustration – забавные формы, графика, клипарт, мультфильмы и символы

Reihe von Bannern, Gotisch mit Hashtags. Trendige jungen Slang-Wör

Quadratische Trendvorlagen – веселые формы, графика, клипарт, -мультфильмы и символы

Quadratische Trendvorlagen

Trending quadratische Vorlagen. Bunte Poster mit Zweigen, Blumen, geometrischen Formen und Blättern. Entwerfen Sie Elemente mit Platz für Text. Мультяшный флаг Vektorsammlung isoliert auf weißem Hintergrund

abstrakte moderne gelb, schwarze punkte muster mit linien Diagonal auf Weißem Hintergrund. – забавные формы – графические изображения, -клипарты, -мультфильмы и -символы

Абстрактные современные желтые, черные точки, собранные с линиями…

Быстрые ярлыки и этикетки. вектор handgezeichnete grafiken – забавные формы фондовой графики, -клипарт, -мультфильмы и -символ

Spaß Веркауф Теги и этикетки. Vector handgezeichnete Grafiken

Bearbeitbar in EPS10

structurierte abstraktehintergründe – веселые формы, стоковые графики, -клипарты, -мультфильмы и -символы

Strukturierte abstrakte Hintergründe

Satz bearbeitbarer flacher Vektorillustrationen auf Ebenen. Dieses Bild enthält Schnittmasken.

креативный мультяшный всплеск с геометрическими формами. абстрактный сбор в стиле ретро 80-90er Jahre. векторные иллюстрации пятнистый сбор с линиями и точками. – забавные формы стоковые графики, -клипарт, -мультфильмы и -символ

Креативный мультфильм всплеск Hintergrundfarbe с геометрическими формами.

Creative Cartoon-Farbspritzhintergrund с геометрическими формами. Абстрактные коллекции в стиле ретро от 80er до 90er Jahre.

Абстрактные фоны Trendige Bunte Splash Cartoon Overlay Spot-Muster – Fun Shapes Stock-Grafiken, -Clipart, -Cartoons und -Symbole

Абстрактные фоны Trendige Bunte Splash Cartoon Overlay Spot-M геометрическая форма, линия и точка. 80er-90er Jahre Stil. Vektor-Illustration

Retro-Stil-Banner-Vorlagen-Sammlung – Fun Shapes Stock-Grapiken, -Clipart, -Cartoons und -Symbole

Retro-Stil-Banner-Vorlagen-Sammlung

Sammlung von Bannervorlagen в стиле ретро. 80-90er Jahre trendiger Modehintergrund mit geometrischen Formen. Векториллюстрация. Плакат, Einladung, Grußkarte, Covergestaltung.

bunte handgezeichnete Kreise Hintergrund – забавные формы, графика, клипарт, -мультфильмы и символы.

Bunte handgezeichnete Kreise Hintergrund

. Regenbogenfarbene Kritzeleien.

универсальный шаблон баннера_02 – забавные формы, графика, клипарт, мультфильмы и символы

Universal Banner Template_02

Абстрактное творческое универсальное художественное издание. Необходим для заголовка электронной почты, публикации в социальных сетях, рекламы, обложки событий и объявлений, баннера, фона, торговой марки, визитной карточки, плаката, брошюры и других графических дизайнов.

Креативная векторная иллюстрация – забавные формы, графика, клипарт, мультфильмы и символы

Креативная векторная иллюстрация

Креативная векторная иллюстрация от Kindern Cartoon Farbe Splash Hintergrund. Кунстдизайн трендигер 80er-90er Jahre Stil. Geometrisches Linienformmuster. Abstraktes Konzept Grafik Spielplatz Banner Element.

Красивые фотографии геометрии в природе

Красивые фотографии геометрии в природе Значок поискаУвеличительное стекло. Это означает: «Нажмите, чтобы выполнить поиск». Значок шевронаОн указывает на расширяемый раздел или меню, а иногда и на предыдущие/следующие параметры навигации.ДОМАШНЯЯ СТРАНИЦА

Путешествовать

Значок «Сохранить статью» Значок «Закладка» Значок «Поделиться» Изогнутая стрелка, указывающая вправо.

Скачать приложение

Каждый год в саду появляются миллионы цветов. Ив Херман/Reuters

• Природа – это дом идеальной формы и ярких цветов.
• Если смотреть вблизи, снежинки имеют невероятно совершенную геометрическую форму.
• Круги можно найти на пнях и в океанах, а прямые линии — на пляжах и полях.
• Посетите домашнюю страницу Insider, чтобы узнать больше.

Природа действительно является домом для оптических иллюзий, достопримечательностей и многого другого.

Иногда вы даже можете найти формы, скрытые в природе — радугу, которая представляет собой идеальный полукруг или шестиугольные соты.

Мы собрали фотографии естественных и искусственных форм, которые можно найти во внешнем мире.

Некоторые из них более совершенны, чем другие, но нельзя отрицать, что все эти изображения захватывают дух.

Эти соты недалеко от Кольмара, Франция, имеют идеальную шестиугольную форму, но пчеловодов озадачил оттенок меда в них.

В 2012 году неестественные оттенки повлияли на пчелиные скопления по всему региону Эльзас. Винсент Кесслер/Reuters

Пчеловоды на северо-востоке Франции были встревожены, когда пчелы начали производить мед в оттенках синего и зеленого. В конце концов они приписали мед необычного цвета остаткам из контейнеров с конфетами M&M, которые перерабатываются на биогазовом заводе рядом с ульями.

Эти каплевидные листья происходят от растения алоэ вера.

Растение алоэ. Сабина Хортебуш/Shutterstock

Алоэ вера может помочь при ряде заболеваний, включая солнечные ожоги.

Это пример мозаичного покрытия в Тасмании, Австралия.

Мозаичный тротуар в Тасмании, Австралия. Викимедиа/Джей Джей Харрисон

«Мозаичный тротуар» возникает естественным образом, когда эрозия заставляет плоские поверхности скал образовывать почти идеальные прямоугольники.

Безумно думать, что эту замысловатую паутину, полную форм и форм, создал паук.

Потрясающая паутина в Косово. Хазир Река/Reuters

Эта паутина была найдена в деревне Акарева в Косово.

Эта удивительная двойная радуга появилась после сильных муссонных штормов.

Ниптон-роуд в городе Серчлайт, штат Невада. Джин Блевинс/Reuters

Был замечен в Неваде в 2012 году.

У деревьев идеально круглые кольца.

Кольца деревьев. Игорь Чери/Shutterstock

Дендрохронология, или датировка по годичным кольцам, – это научный метод, в котором эти кольца используются для определения возраста дерева.

На этой фотографии крупным планом показан спил ясеня.

Если смотреть вблизи, снежинки имеют невероятно совершенную геометрическую форму.

Снежинка. Майк Сегар/Reuters

Снежинки с близкого расстояния поистине невероятны.

Если смотреть в безветренный день, когда вода внизу неподвижна, кажется, что Ракотцбрюкке образует идеальный круг благодаря своему отражению.

Мост проходит через озеро Ракоцзе в Габленце, Германия. Лукаш Стефанск/Shutterstock

Построенный во второй половине 19 века, потрясающий Ракоцбрюкке получил свое второе название от старой легенды, согласно которой опасные мосты, такие как этот , были построены дьяволом.

Эти длинные прямоугольные полосы образуют овощное поле в таиландской провинции Патхумтхани.

Фермеры работают в поле. Чайват Субпрасом/Reuters

Это фото было сделано в октябре 2011 года, после того как сильное наводнение накрыло треть страны.

Эта плантация пальмового масла в индонезийской провинции Южная Суматра выглядит как четыре идеальных треугольника сверху.

Эта фотография была сделана в 2010 году. Бовихарта/Рейтер

Индонезия является крупнейшим в мире производителем пальмового масла.

 

На этой недатированной фотографии НАСА показаны Луна, а также границы тропосферы, тропопаузы и атмосферы Земли.

Фотография была сделана экипажем 28-й экспедиции на борту Международной космической станции. НАСА/Рейтер

На этой фотографии тропосфера выделена оранжевым цветом. Это самая нижняя и самая плотная часть атмосферы Земли. Тропосфера резко заканчивается в тропопаузе, которая выглядит на фотографии как резкая граница между оранжевой и синей атмосферой.

Прямые линии пересекают заснеженные поля в Мюлетурнене, недалеко от Берна, Швейцария.

Это похоже на одну холодную верховую езду. Майкл Бухольцер/Reuters

Похоже, ясный холодный день.

Лодочные тропы могут выглядеть как искусство с высоты птичьего полета.

Лодки в океане. Иван Брчич/iStock

Две лодки делают круги в океане недалеко от Хорватии.

Эти сферы не НЛО — на самом деле это облака.

Полуостров Камчатка в России. Михаил Дорогович/Shutterstock

Облака, изображенные выше, называются линзовидными облаками. Когда температура падает достаточно низко, эти стационарные облака часто образуются на нижней стороне горного хребта.

 

На этом фото ровные ряды — это тюки сена, сформированные благодаря трактору.

Поле во Франции. Паскаль Россиньоль/Reuters

Эта фотография была сделана в Кокеле, недалеко от города Кале на севере Франции.

Когда Солнце и Луна выровнялись над Землей в мае 2012 года, Солнце на короткое время превратилось в это кольцо.

Солнечное затмение из начальной школы Хираи Дайни в Токио, Япония. Иссей Като/Reuters 900:02 Солнечное затмение затуманило небо над частями Северной Америки и Азии.

 

Парк Кекенхоф расположен в Лиссе в Нидерландах и считается самым большим цветочным садом в мире. Его чистые границы и яркие цвета поражают.

Каждый год в саду появляются миллионы цветов. Ив Херман/Reuters

В Кёкенхоф работает около 30 садовников. В этом году вы можете совершить поездку по нему виртуально.

Colle des Mees — крупнейшая во Франции солнечная электростанция. На ферме установлено 112 780 солнечных модулей, расположенных на территории почти 500 акров.

Ферма расположена в Les Mees на юге Франции. Жан-Поль Пелисье/Reuters

Солнечные панели производят возобновляемую энергию и обеспечивают мощность 100 МВт.

Эта геометрическая туристическая достопримечательность занимает площадь более 300 акров и расположена в небольшой деревне в Китае.

Аттракцион расположен в Цзуньи в китайской провинции Гуйчжоу. VCG / Getty Images

Местные жители сами построили аттракцион из сорго, а также персиковых и сливовых деревьев менее чем за восемь месяцев.

Рисунок известен как гигантский багуа — восьмигранная диаграмма, символизирующая древнюю китайскую энергетическую карту.

В сентябре 2015 года произошло редкое идеально круглое “суперлуние”.

Тень Земли отбрасывала на Луну красноватое свечение. Мэтт Карди / Getty Images

Суперлуние произошло в результате лунного затмения, совпавшего с ближайшим к Земле полнолунием.

 

Эти нарциссы почти подходят друг к другу.

Нарциссы. Тоби Мелвилл/Reuters

Цветы были замечены на выставке RHS Chelsea Flower Show в Лондоне.

Эти прямоугольные участки составляют региональное предприятие по очистке сточных вод Фресно-Кловис во Фресно, Калифорния.

Региональные очистные сооружения Фресно-Кловис. Люси Николсон/Reuters

Эта фотография была сделана в 2015 году.

Эти круглые формы созданы морским льдом, образующимся над Северным Ледовитым океаном.

Арктические льды истончаются. Кэтрин Хансен/НАСА/Reuters

На фото выше два члена береговой охраны США Хили поднимают грузы, сброшенные на парашютах летом 2011 года.

Красные песчаные дюны Намибии создают красивые формы.

Пустынные дюны. Shutterstock.com

Рябь, создаваемая ветром, создает еще больше узоров.

Читать далее

LoadingЧто-то загружается. Функции Фото Природа

Упражнения с 2D-фигурами для дошкольников, подготовительных классов и детского сада

Изучение 2D-фигур является обязательным для каждого класса дошкольного возраста. Я здесь, чтобы поделиться с вами моими любимыми занятиями по 2D-фигурам! Некоторые учителя могут заниматься темой или разделом с фигурами (например, я), некоторые могут заниматься фигурами на неделю, а некоторые разбрасывать занятия по фигурам в течение всего года. Эти занятия будут работать для всех типов классов и стилей преподавания! Возьмите папку с планом урока, и давайте начнем! Хотите распечатать все формы прямо сейчас? Вы можете найти их в моем разделе Shapes на TPT ЗДЕСЬ.

Этот пост содержит партнерские ссылки.

Манипуляции с фигурами

При настройке деятельности с фигурами первое, что я делаю, — это иду в свой шкаф и достаю все свои игры с фигурами, манипуляции и головоломки. Блоки узоров, файлы cookie и магнитные блоки распределяются по различным школьным центрам. Учащиеся должны играть, манипулировать и создавать фигуры по всему классу, а не только в математическом центре!

Мне очень нравится этот набор для сборки 2D и 3D фигур! Это очень весело и поставляется с карточками форм.

Формы зубочисток

Формы зубочисток — это увлекательный и интерактивный способ изучения фигур! Учащиеся могут делать фигурки из зубочисток и теста для лепки или зефира. Когда вы обучаете своих маленьких учеников фигурам, важно также рассказать о сторонах и вершинах. Используйте эти большие словарные слова! Ощупайте, трогайте и считайте количество сторон и вершин у фигуры. Не забывайте, что у круга нет ни сторон, ни вершин!

В Discovery Center: изучение математики и естественных наук

В центре открытий я настроил таблицу исследования форм. На стене висят плакаты с реальными фотографиями, а задняя часть стола уставлена ​​карточками для построения фигур, манипуляторами и полупрозрачными формами. Сверху есть сортировочная доска с карточками с формами. Это просто доска для плакатов, которую я сделал с помощью скотча. Супер просто! Корзина заполнена реальными предметами и фигурными карточками, которые учащиеся могут сортировать. Эта исследовательская таблица дает учащимся возможность говорить, трогать, чувствовать, строить и манипулировать фигурами со сверстниками или самостоятельно.

Карточки из кубиков! Это крупный план карточек в форме строительных блоков. Учащиеся используют блоки, чтобы создать фигуру на карточке. После того, как тема формы закончена, поместите карточки построения формы в свои манипуляторы или ящики STEM!

Карты формы Geoboard! Я положил эти карты с геобордами в свою корзину с геобордами. Учащиеся могут создавать фигуры с помощью ткацких станков на геоборде. Чтобы представить это занятие, я отложил его на время стола как занятие по прибытии. Также здорово накачать эти маленькие мышцы мелкой моторики!

Формируйте прикрытие! Cover up — это веселая игра, в которой можно потренироваться в подборе формы! Учащиеся крутят спиннер и закрывают соответствующую фигуру. Мне нравятся эти полупрозрачные спиннеры для математических игр. Эта игра есть в моем наборе Shapes. Он бывает четырех разных уровней.

Фигуры нарисуйте это! Это еще одна забавная игра с формами, которую любят мои ученики. Это также отличная возможность поговорить о большем, меньшем и равном. Попробуйте использовать магнитные фишки бинго, чтобы покрыть график, а затем использовать магнитную палочку в конце, чтобы сделать игру еще более захватывающей.

На сенсорном столе

Этот сенсорный стол заполнен фигурными манипуляторами и несколькими формочками для кексов для сортировки. Он имеет бусины в форме пены, цепочки в форме и полупрозрачные формы. Идеально подходит для сортировки, шнуровки и соединения вместе. И, как вы уже догадались, это также отлично подходит для их мелкой моторики!

Переходная активность

Сортировка по форме! Переходные занятия — идеальное время для быстрой оценки или проверки знаний. Перекусываем после музыки и движения. Я всегда планирую переходную деятельность на это время по нескольким причинам. Во-первых, весь класс не выстраивается в очередь, чтобы помыть руки, что просто требует сумасшедшего поведения. Во-вторых, потому что это еще один раз, когда я могу больше учиться! Что я делаю, так это звоню ученику и даю ему карточку для сортировки. Для меня это быстрый и простой способ проверить, знают ли они форму или нет.

В Библиотечном центре

Подносы для письма с формами! Учащиеся могут писать и рисовать фигуры на песке. Этот лоток входит в набор для шнуровки, но вы можете использовать любой небольшой лоток, который у вас есть. Я знаю, что некоторые учителя используют тарелки для пирогов из фольги или детские пластиковые разделенные обеденные тарелки в качестве подносов для письма.

Формируйте мини-книги! После того, как мы вместе делаем мини-книги в небольшой группе или за столом, я кладу их в центр. Они ЛЮБЯТ их делать! Степлеры немного пугают меня с моими маленькими учениками, поэтому я поставила этот бесстеплерный степлер! Это потрясающе!

 Формирует нового читателя! Для деятельности в небольшой группе учащиеся создают свою собственную форму для чтения. После того, как они завершены и мы прочитали их вместе несколько раз, они помещаются в библиотечный центр для чтения студентами.

В Центре искусств

Мои ученики ОБОЖАЮТ подносы для лепки, поэтому я стараюсь делать по одному для каждой темы, которую мы делаем. В этом упражнении они создают монстров в форме пластилина. Учащиеся используют формочки для печенья, чтобы создать тело. Затем добавьте руки, ноги, глаза и волосы, используя нарезанные ершики для труб, маленькие палочки от эскимо, зубочистки и выпученные глаза. Поднос от Долларового дерева.

Коврики в форме пластилина! На этих ковриках учащиеся могут создавать фигурки из пластилина. Они могут придать форму, скатывая змейки из пластилина или формуя тесто.

Отпечатки форм! У него отличная мелкая моторика, и он делает прекрасные произведения искусства для вашего класса. Мы разрезаем трубочки от бумажных полотенец для этого проекта печати кругов.

Мы также печатали деревянными блоками!

Создавайте коллажи! Важно предоставить учащимся задания по созданию новых элементов с использованием фигур. На самом деле, это цель/стандарт обучения во многих штатах. Учащиеся должны уметь манипулировать фигурами, чтобы создавать новые фигуры, объекты или изображения. Коллажи из фигур — идеальное занятие для решения этой учебной задачи.

Коллажи из одной формы! Вы также можете предложить учащимся создавать коллажи из фигур, используя только одну форму. Однажды мои ученики мучились с треугольниками, поэтому мы создали коллажи в форме треугольников. Учащиеся находили треугольные формы, говорили о треугольниках (чем они похожи и чем отличаются) и рисовали с треугольниками!

Драматическая игра

Вы можете изменить центр драматической игры на множество разных вещей для темы формы, но мне больше всего нравится делать пиццерию. В пиццерии есть фигуры. Пицца может быть разной формы и кусочки тоже! Тогда начинки так много разных форм тоже. Вы должны обязательно попробовать!

Превратите изучение форм в УДОВОЛЬСТВИЕ, предоставив своим ученикам практический опыт обучения и игры! Хотите, чтобы все печатные формы 2D Shape были в этом посте? Нажмите ЗДЕСЬ, чтобы получить мой модуль 2D Shapes из моего магазина TPT. Он содержит более 200 страниц карточек для создания фигур (лего, геоборды, палочки для эскимо, зубочистки, тесто для лепки), постеров, ковриков для сортировки, рабочих листов, игр и МНОГОЕ ДРУГОЕ.

Изучение форм — это забавная тема и концепция для маленьких учащихся, и вы можете посмотреть другие забавные занятия с фигурами, нажав на изображение ниже!

Нравятся эти занятия с фигурами? Закрепите это изображение!

Игры Геометрия для Детей Онлайн

Часто Задаваемые Вопросы:

Q1: Какие есть игры по распознаванию 2D фигур?

Ответ:  На веб-сайте SplashLearn есть много игр, посвященных 2D-фигурам, где вы можете проверить свои знания по распознаванию 2D-фигур, их свойствам, а также сравнить их. В SplashLearn вы можете найти «Геометрические игры» на вкладке «Математические игры по темам», чтобы играть в игры с 2D-фигурами.

Q2: Какие свойства есть у двухмерных фигур?

Ответ:  Плоские формы, которые невозможно удержать в руках, являются двумерными. Другие свойства основаны на их сторонах, вершинах и диагоналях. Найдите страницу SplashLearn и найдите «Геометрические игры» на вкладке «Математические игры по темам», чтобы весело провести время, играя в игры с 2D-фигурами и их свойствами.

В3. Как геометрия используется в реальной жизни?

Ответ:  Геометрия означает гео + мера, означающая измерение земли. Геометрия играет очень важную роль в нашей реальной жизни. Начиная с простых 2D и 3D форм, их свойств, он также находит применение в изображениях и графике.

Q4: Какие есть игры с разбиением фигур?

Ответ: Чтобы понять разбиение фигур, нужно знать о фигурах. Существует множество игр по разделению фигур, которые вы можете изучить на веб-сайте SplashLearn. Вы можете найти эти игры в разделе Геометрические игры во вкладке «Математические игры по темам».

В5. Как найти площадь фигуры, используя единичные квадраты?

Ответ: Чтобы найти площадь фигуры с помощью единичных квадратов, вы можете обвести изображение на сетке, состоящей из единичных квадратов. Общее количество квадратов в трассировке формы дает приблизительную площадь в квадратных единицах.

В6. Чем отличаются трехмерные фигуры?

Ответ: Куб, прямоугольный параллелепипед, сфера, цилиндр и конус — вот некоторые из трехмерных фигур. Чтобы изучить свойства 3D-фигур, вы можете посетить страницу SplashLearn и поиграть в веселые игры с 3D-фигурами в разделе игр с геометрией.

В7. Что такое позиционные слова?

Ответ: Слова, описывающие положение объектов, называются позиционными словами. Например, сверху, снизу, по центру, вверх, вниз, вправо, влево, под — все это позиционные слова. Чтобы играть в игры с позиционными словами, вы можете посетить страницу SplashLearn и изучить игры с геометрией.

 

Обзор геометрии

Геометрия — это наука о формах и пространстве. Она считается важной областью математики, поскольку предлагает учащимся более глубокое понимание окружающего мира. Примеры геометрических фигур можно найти как в природе, так и в большинстве областей рукотворного творчества.

Изучение геометрии и пространственного чувства развивает такие понятия и навыки, которые играют важную роль в других областях. Например, область архитектуры требует глубокого понимания геометрических форм и их атрибутов. Геометрическое понимание также оказалось важным в других областях математики. Например, понимание площади и объема включает в себя манипулирование геометрическими фигурами. Кроме того, понимание умножения и деления с использованием массива требует понимания геометрических фигур и фигур.

Дети знакомятся с геометрией и математикой в ​​младших классах школы. Общие основные математические стандарты по геометрии включают введение в геометрию в дошкольном возрасте. Изучение геометрии помогает детям развивать дедуктивные навыки решения задач.

Многие исследования показали, что дети лучше учатся через игры. В последнее время стали популярны математические игры. Одной из наиболее важных причин для введения обучающих игр в математические занятия является волнение и энтузиазм, которые они вызывают у детей. Математические игры позволяют детям испытать успех и удовлетворение и, таким образом, развить уверенность в своих новых навыках. Математическая область геометрии требует визуализации для лучшего понимания.

Развитие геометрии в классах

Детский сад: В детском саду дети учатся определять и описывать двухмерные и трехмерные фигуры. Они способны идентифицировать геометрические фигуры и названия независимо от их ориентации. Они анализируют и сравнивают формы разных размеров и атрибутов. Они также учатся составлять простые фигуры, чтобы формировать более крупные фигуры.

1 класс: В этом классе дети развивают навыки осмысления форм и атрибутов. Они понимают определение основных геометрических фигур. Они анализируют формы по их определяющим атрибутам, таким как количество сторон. Они составляют двухмерные и трехмерные формы для создания более крупных составных форм. Они учатся делить прямоугольники и окружности на равные доли. Они изучают словарный запас, связанный с такими делениями, как четверти, четверти и половинки.

2 класс: Дети учатся определять и рисовать фигуры в соответствии с заданными признаками. Они учатся рисовать фигуры в соответствии с указанным количеством граней или углов геометрии. Они способны идентифицировать кубы, пятиугольники, шестиугольники, четырехугольники и треугольники. Они также учатся разбивать прямоугольник на квадраты одинакового размера. Затем они считают эти квадраты, чтобы определить размер прямоугольника. Дети учатся делить прямоугольники и круги на две-четыре равные части. Они описывают разделенные фигуры, используя такие слова, как половина, треть, третьи, половинки. Они понимают целое как четыре четверти, три трети и две половины.

3 класс: Дети понимают отношения между формами в соответствии с их атрибутами. Они узнают о более крупных формах категорий с общими атрибутами. Например, фигуры с четырьмя сторонами называются четырехугольниками. Они делят фигуры на равные части. Они учатся выражать площадь каждой части как единицу доли целого. Например, они делят фигуру на три равные части и описывают площадь каждой части как 1/3 площади целого. Они также учатся находить площадь и периметр прямоугольника и других многоугольников.

 

 

4 класс: Дети узнают о точках, отрезках, геометрических линиях, лучах и типах углов. Дети определяют их в двухмерных фигурах. Они также узнают о параллельных и перпендикулярных линиях. Они классифицируют фигуры на основе параллельных или перпендикулярных линий. Они также классифицируют фигуры в соответствии с углами заданного размера. Кроме того, они узнают о различных треугольниках в геометрии. Дети также узнают о линии симметрии двухмерной фигуры. Они рисуют линии симметрии и определяют линейно-симметричные фигуры.

5 класс: Дети знакомятся с координатной геометрией. Они учатся отображать точки в системе координат, состоящей из перпендикулярных числовых линий, называемых осями. Они представляют математические задачи, изображая точки на геометрической плоскости. Они также учатся классифицировать простые геометрические фигуры по категориям и подкатегориям на основе геометрических свойств. Например, все квадраты и прямоугольники являются четырехугольниками. Все квадраты являются прямоугольниками. Они учатся классифицировать двумерные фигуры в иерархии.

Изучение геометрии с помощью манипуляций

 

Геометрические понятия можно изучать несколькими способами. Геометрическое обучение можно проводить с помощью манипуляций, конкретных объектов, иллюстраций и диаграмм. Для эффективного понимания у детей должна быть возможность манипулировать твердыми моделями. Изучение геометрии не должно основываться только на картинках и диаграммах. Обучение должно поощрять детей представлять свои собственные математические идеи. Это можно сделать с помощью картинок и конкретных моделей.

Геометрические понятия можно изучить несколькими способами. Геометрическое обучение можно проводить с помощью манипуляций, конкретных объектов, иллюстраций и диаграмм. Для эффективного понимания у детей должна быть возможность манипулировать твердыми моделями. Изучение геометрии не должно основываться только на картинках и диаграммах. Обучение должно поощрять детей представлять свои собственные математические идеи. Это можно сделать с помощью картинок и конкретных моделей.

 

Геометрические тела: 

Это эффективный манипулятор, который можно использовать для обучения детей от дошкольного до второго класса. Детям легче изучать 2D-фигуры, чем 3D-геометрические фигуры. Одна из причин этого заключается в том, что имена трехмерных фигур реже используются в повседневной жизни. Другая причина заключается в том, что в большинстве занятий в классе трехмерные геометрические формы преподаются с помощью рисунков. К сожалению, многие дети не могут понять эти 3D-рисунки. Рисунок сферы выглядит как круг. Это затрудняет понимание разницы между сферой и кругом. Поэтому для обучения детей геометрическим фигурам в 3D отлично подходят геометрические тела.

 

Дети могут трогать, держать и манипулировать этими предметами. Это дает им более четкое представление об атрибутах трехмерных геометрических фигур.

Танграммы: 

Танграммы можно использовать для обучения детей пространственным отношениям. Она подходит для детей от 1 до 4 класса. Это китайская головоломка, состоящая из 7 танов или фигур. Дети должны расположить эти фигуры, чтобы воссоздать заданную форму. Правило головоломки требует, чтобы все фигуры использовались без перекрытия. Игра с танграмами помогает детям улучшить пространственное понимание. Они также узнают о навыках пространственного вращения и связанном с ним словарном запасе. Дети также учатся вычислять площади без изучения формул.

Изучайте геометрию с помощью игр

 

Ниже приведены некоторые интересные геометрические игры: при четном числе игроков. Игра проводится командами, в каждой команде не менее 2 игроков. Перед началом игры чашу наполняют бумажными фишками, на которых написаны разные фигуры. Каждая команда ходит по очереди. Один игрок из команды случайным образом выбирает фишку. Он/она будет читать написанную на нем фигуру, не произнося ее вслух. Затем он или она опишет свойства фигуры члену своей команды. Члены команды должны будут угадать название фигуры. Например. – Если фигура, написанная на фишке, квадратная, то игрок может сказать, что у фигуры 4 стороны и все стороны равны.

Выигрывает команда, угадавшая фигуру за наименьшее количество времени. Эта игра особенно помогает детям запомнить различные характеристики каждой формы. А также приобрести уверенность в плане передачи знаний, полученных ими в рамках изучения геометрии.

Классификация четырехугольников — для 3 класса и выше

Игровой сюжет

Для этого требуется 2 или более игроков. Каждому игроку по очереди нужно толкать колесо для вращения. Когда колесо остановится, стрелка укажет на одну из трех секций колеса. В каждом разделе упоминается геометрический атрибут. Игроку нужно будет упомянуть все имена фигур 2D-геометрии, которые он может связать с этим атрибутом. Например. Если колесо останавливается на «Только одна пара параллельных сторон», он может назвать трапецию правильной формой. Эта игра помогает детям связать свойства с каждой из фигур, а также помогает им визуализировать эти свойства. Игра вызывает здоровую конкуренцию между ними, а также улучшает их обучение геометрическим фигурам.

16 Великолепных математических заданий с картинками на геобордах — раннее обучение

Геоборды — это один из лучших ресурсов. Они прекрасно подходят даже для очень маленьких детей. Одна из моих дочерей могла бы использовать один блестяще, когда она была всего одна. Их можно использовать с этого возраста, пока они вероятно, по крайней мере, восемь или девять. У них развивается отличная мелкая моторика, концентрация внимания, широкий спектр навыков воображения. Но как вы их используете для математика?

Какие есть математические задания на геоборде? Some excellent geoboard math activities include:

1. Symmetry
2. Counting
3. Patterns
4. Pattern snakes
5. Multiple-sided shapes
6. Making pictures with shapes in
7. Поместите на них другие предметы, например крючки для штор или крышки от бутылок
8. Добавьте два количества
9. Создание различных 2D-форм
10. Формирование номеров
11. Сделать формы с определенным количеством сторон
12. Добавление
13. НОМЕР
14. 1. из разных вещей!

Читайте дальше, чтобы услышать полное описание этих мероприятий, воплощенное в жизнь с большим количеством фотографий. Для всего этого я использовал бревенчатую геоборду и большие разноцветные резинки.

1.Симметрия

Симметрия – это сложная концепция для многих детей. их головы вокруг. Часто это лучше всего исследовать, а не слишком много говорили.

Геоборды — отличный способ исследовать симметрия в воображении. Некоторые дети часто делают все, что они делают во всяком случае симметрично. Кажется, у них есть какое-то врожденное желание сделать это.

Идея этого занятия состоит в том, чтобы создать своего рода форма или формы на одной стороне доски. Можешь скопировать с другой стороны? Это легче, если формы касаются друг друга. Сложнее, если они находятся отдельно.

Это простое занятие позволяет им обрести симметрию и посмотреть, что это такое. Если вы хотите узнать больше о симметрии, то я написал подробное руководство из 10 фантастических идей симметрии, которые вы можете посмотреть здесь.

2. Игра «Бросай кости»

Существует так много игр, в которых число связано с количеством, и этот навык является одним из основных математических навыков, в котором детям нужно много практиковаться. еще один центральный навык. Чтобы узнать все о том, что такое переписка один на один, и о лучших способах обучения, ознакомьтесь с этой статьей.

Они также, к счастью, обычно очень любят использовать игральная кость. Особенно, если это какая-то «особая» кость вроде деревянной, которая Мне нравится использовать (выпилить из столба забора).

Просто бросьте кости и попробуйте поставить количество резинок на лог.

Если несколько детей пробуют это одновременно на разных геобордах, то поражает количество различных массивов, которые они могут составить. Число шесть, например, можно представить по-разному.

3.Создание выкроек

Думаю, чем практичнее занятие, тем лучше с узорами. Если это практическое занятие, и дети могут манипулировать предметами в каким-то образом, они с большей вероятностью поймут, что такое шаблон.

Самый простой способ сделать выкройку — использовать два цвета резинок. Поместите один на геоборд каким-то образом, а затем поместите следующий цвет рядом с ним. Например, он может стать синим, зеленым, синим, зеленый и т.д.

Повязки можно надевать любым способом. Они могут быть квадраты или треугольники, или просто линии. Как хочешь.

Если у детей это хорошо получается, то можно расширить эту деятельность, заставив их попробовать более сложные модели. Возможно синий, синий, зеленый, синий, синий, зеленый например.

Или рисунок может состоять из трех или четырех цветов. Действуй!

4. Образец змей

Детям очень нравится все, что связано со змеями, и эти простые змеи прекрасно подходят для обучения моделям. Вы можете использовать свяжите для этих змей маленькие ткацкие ленты или прикрепите к ним цветные резинки большего размера.

Опять же, рекомендуется ограничить детей два цвета. Чем проще, тем лучше, когда вы начинаете с шаблонов.

Поместите полосу ткацкого станка одного цвета между двумя винтами. Затем следуйте за ним другим цветом, затем вернитесь к первому. Вы начнете создавать разноцветную змею, которая может извиваться вокруг геоборда.

• 12 различий между мелкой и крупной моторикой
• Математические игры на открытом воздухе – 50 идей, которые действительно работают!

5. Создавайте фигуры с большим количеством сторон – глупые фигуры

Это отличное задание для развития мелкой моторики, а также отлично подходит для математики, потому что это действительно заставляет их думать. Большие резинки есть идеально подходит для этого – чем больше, тем лучше, потому что тогда вы действительно можете растянуться их по всей доске.

Просто наденьте ленту, а затем начните растягивать ее всевозможными способами по доске. Вы получите гигантскую глупую форму, которая обычно совершенно неправильная.

Когда вы сделали форму, вы можете попытаться сосчитать стороны. Или вы можете попытаться сделать это еще глупее.

Это пробуждает детское чувство глупости, и весело проводить время с формами – отличная вещь.

6. Делать картинки

Это занятие, которым занимаются многие дети. инстинктивно, и тот, в который они действительно могут попасть и попасть в зону.

Вы просто заставляете их делать снимки с резинки, или ленты для станков, или что-то еще, что вы используете.

На изображениях будет много 2D-фигур. Без этого невозможно использовать геоборды. Вы можете говорить о формах, которые они находят и создают на ходу.

Обычные картинки, которые вы увидите, это дома и люди, но, конечно, будут и всякие случайные вещи, и случайнее, тем лучше. Это может быть ракета. Или сани Деда Мороза. Пусть их воображение идет на это.

7. Поместите другие объекты на геоборды

Любые действия, которые вы делаете, определенно могут быть улучшены помещая другие предметы на доски.

Можно использовать крышки от бутылок, чтобы балансировать на винтах, крючки для штор или пробки. Вы можете вплести кусочки шерсти в резинки или добавить простые натуральные материалы, такие как листья, трава или веточки.

Такая игра со свободными частями открыта и во многих отношениях полезна. Если вы хотите узнать, какие материалы вы можете использовать для незакрепленных деталей, посмотрите мою статью о 100 лучших материалах, которые вы можете использовать для этого.

У этого может быть множество целей. Это могло просто быть простым плетением.

Это может быть помощь в создании картины. Бутылка верхушками могут быть два глаза, например, у сделанного ими робота.

Предметы также могут помочь им считать. Например, если бы они сделали треугольник, они могли бы прикрепить по одному крючку для штор на каждый угол объект. Это помогает им затем считать углы и приносит то, что угол находится в более четком фокусе в их сознании.

Вы можете складывать объекты в аранжировки или использовать их как часть узоров.

Возможности поистине безграничны. Это здорово использовать ряд объектов с дочерними элементами в дочернем контексте и просто видеть что они придумывают.

8. Добавление

Отлично поэкспериментировать с добавлением в диапазоне пути реального внедрения знаний детей в этой области.

Почему бы не добавить геоборд?

Возьмите резинки двух цветов и два игральных кубика. Если у вас есть кубики двух цветов, соответствующие резинкам, тогда это действительно сработает хорошо – напр. синий кубик и синие полосы, а также красный кубик и красные полосы.

Затем попросите детей бросить два кубика. Положи это количество полос на доске в некотором роде.

Удивительно видеть творческие способы, которыми они строят массивы!

Затем, когда они наденут их, они смогут подсчитать, сколько вообще много групп. Это действительно визуальное и физическое, смешанное вместе, и просто увлекательный способ изучить дополнение.

Вы можете расширить его, используя числа выше шести на стандартных кубиках, а также используя три кубика и три цвета полос.

9. Создание различных 2D-фигур

Это старая классика и одна из самых популярных деятельность по геоборду.

Можно попробовать сделать треугольник, тыкву, прямоугольник, пятиугольник.

Отличный способ исследовать различные формы. Можно делать фигуры разного размера. Посмотрите, насколько большими или маленькими вы можете их сделать. Простой, но очень интересный способ исследовать эту область.

10. Формирование чисел

В этом упражнении вы используете полосы для создания цифр. Это хороший способ для маленьких детей подумать о том, как формируются числа, а также представляет собой достаточно сложную задачу, чтобы заставить их думать и решать проблемы.

Размышление о формировании чисел в различных контекстах — отличный способ узнать числа. Чтобы прочитать о 16 лучших играх, которые помогут распознавать числа, взгляните на это.

Некоторые цифры проще попытаться создать, чем другие. Номер один, например, не может быть проще. Только одна группа в прямая линия сделает свое дело.

Номер четыре, с другой стороны, требует гораздо больше размышлений, и вполне может потребоваться несколько полос, чтобы выполнить работу.

Эта деятельность потенциально может быть распространена на формирование письма также.

Также вы можете попробовать создать последовательность числа, напр. 1,2,3 на геоборде.

11.Создание фигур с определенным числом сторон

Это задание требует немного творчества и возможность попробовать.

Приятно, в этом кинуть кости. В идеале, если вы есть кости с числами от 3 до 8, тогда это сработает идеально.

Если нет, просто игнорируйте 1 и 2, так как на самом деле они не работать в этой игре. Невозможно создать фигуру с 1 или 2 сторонами на геоборд. Круги и полукруги просто не работают, поэтому лучше начинать с 3.

Идея состоит в том, что вы крутите игральные кости, и на что бы они ни выпали, вы пытаетесь составить фигуру с таким количеством граней.

Например, если выпадет 5, вы попытаетесь составить пятиугольники. Удивительно, сколько разных пятиугольников можно сделать!

Чем больше число, тем больше у вас возможностей для разного количества комбинаций. Когда вы дойдете до 8, количество различные восьмиугольники, которые возможны, ошеломляют!

Если детям трудно сделать эти большие фигуры количество, а затем просто придерживайтесь треугольников и квадратов.

12. Числовые облигации

Числовые облигации — это еще одна вещь, которую хорошо поэкспериментируйте разными способами. Чем больше методов есть в распоряжении детей чтобы помочь им лучше визуализировать числовые связи, а геоборды отлично подходят для это.

Начиная с числовых связей до пяти, почти наверняка путь.

Возьмите ленты двух цветов и расскажите детям что мы можем использовать пять полос на доске одновременно.

Тогда пусть попробуют сделать разные «пятерки». Они будут иметь всевозможные комбинации цветов, например. 4+1, 2+3 и т. д. Они также придумают множество способов размещения связей в массивах. Это могут быть треугольники по всей доске, или квадраты, или мешанина всех видов.

Этот творческий подход к числовым связям действительно оживляет его и делает его чем-то, что вдохновляет их говорить на ходу.

13. Поместите фигуры внутрь фигур

Это отличный способ подумать о размере, и также начинается процесс понимания площади и периметра.

Сделайте небольшую фигуру в середине геоборда. А треугольник — хорошее и простое место для начала.

Затем создайте больший треугольник вокруг первого. Потом снова большая. Продолжайте, пока вы не можете пойти не больше!

Для них здорово видеть, как фигуры становятся больше, и они начинают понимать пространство внутри разных фигур, а также периметр их сторон.

14. Делайте изображения абстрактных форм

Это то, что обычно происходит, если вы просто позволяете дети идут на это без какого-либо направления. Вы получите случайный ассортимент различные абстрактные формы, и это один из лучших способов изучения 2D формы, и просто позволить вашему уму привыкнуть к возможностям в создавая их.

Вероятно, так используется геоборд больше всего, так как маленькие дети должны учиться больше через свои собственные экспериментировать, чем под руководством взрослых.

Дети начнут понимать «квадратность» квадратов и «треугольность» треугольников, если оставить их в покое для поэкспериментируйте и убедитесь сами.

15. Сколько типов треугольников вы можете сделать?

Треугольники отлично подходят в качестве отправной точки для это занятие, но его также определенно можно распространить на фигуры с большим количеством сторон. чем треугольник.

Идея в том, чтобы сказать, что мы постараемся сделать много треугольников, которые выглядят по-разному.

Их действительно так много, что дети могут придумать с.

Экспериментируя, возможно, придут к прямоугольным треугольникам, равнобедренным треугольникам, разносторонним, тупоугольным и всем остальным вариантам.

Они почти наверняка не догадываются, что это это то, что они делают, но они начинают этот процесс в своем уме, и визуализация множества возможных треугольников, существующих в мире.

Геометрия в некоторой степени построена вокруг треугольников, и это простое занятие дает детям прекрасную отправную точку для дальнейшего изучения характеристики.

16.Используйте разные предметы

Мне очень нравится использовать большие цветные резинки для геобордов, но это далеко не единственные варианты.

Ленты для ткацкого станка тоже отличные, их можно купить ленты для ткацких станков в наши дни чрезвычайно дешевы, так как они пришли в упадок в популярность.

Еще одна вещь, которую можно попробовать, это помпоны для волос.

Сочетание разных предметов отлично подходит для детских игр исследование. Кроме того, добавление других объектов для улучшения их опыта тоже здорово. – например, материал или простые незакрепленные детали.

Как сделать геоборд?

Геоборды очень легко сделать, и лишь немногие Нужны навыки рукоделия. Мои любимые геоборды сделаны из больших бревен.

Если вы не можете найти или купить один из них, вы можете используйте небольшое бревно или даже любой обрезк дерева от местного оборудования хранить.

Мне нравится использовать винты на геобордах, предпочтительно с широкими концами, поэтому дети не поранятся, если поставят доску лицом по ошибке!

Однако можно также использовать гвозди, вбитые в древесина. Опять же, используйте гвозди с большими концами и убедитесь, что они хорошо забиты. в лес, а выйти не может.

Мне нравится ставить шурупы ровными рядами, но случайные геоборды тоже хороши. Вы можете просто делать разные вещи на каждом.

Если делать своими руками не для вас, то можно просто купить геоборд. Пластиковые геоборды работают фантастически, и, вероятно, их даже легче хранить. Они легкие и могут быть легко транспортированы.

Заключение

Так почему бы не дать немного математики геобордов деятельность идти!

Геоборды прекрасно подходят для множества ранних навыков геометрии и формы, хотя дети часто не подозревают, что они делая это!

Вы можете использовать их для подсчета, сложения и создания узоры.

Самое главное, геоборды – это весело, а детям просто есть врожденное желание возиться с ними!

Удачи!

Если вам понравилась эта статья, почему бы не попробовать одну из следующих:

• Что такое десятый фрейм? (и 10 способов их использования)
• 21 игра на время для дошкольников (которые действительно работают!)

Recent Posts

ссылка на 17 блестящих игр с парашютом для физкультуры (для всех возрастов)

17 блестящих игр с парашютом для физкультуры (для всех возрастов)

За более чем 12 лет работы в сфере образования я перепробовал сотни упражнений по физкультуре, и одними из моих любимых игр, к которым я снова и снова возвращаюсь, являются игры с парашютом! Имея всего один парашют и. ..

Продолжить чтение

ссылка на 17 фантастических игр с парашютом для средней школы

17 фантастических игр с парашютом для средней школы

Игры с парашютом прекрасно подходят для детей среднего школьного возраста. Они обеспечивают фантастический Я работаю учителем более десяти лет, и за это время испробовал сотни парашютов…

Продолжить чтение

5.529.602 Геометрическая форма Стоковые фото, картинки и изображения

Графические невозможные фигуры. символы круга, квадрата и треугольника с парадоксом Эшера невозможная геометрия геометрическая графика

серый шестиугольник геометрический узор фон вектор

золотой шестиугольник рамка шаблон векторная иллюстрация

геометрический холодный синий многоугольник узор абстрактный фон.

Цветной фоновый вектор дизайна в стиле Мемфис

Набор векторных элементов базовой формы с острыми и закругленными краями.

Коллекция мандал с геометрическим орнаментом. набор этнических логотипов, эмблем, значков, икон, выделенных на белом фоне.

Абстрактный многоцветный геометрический вектор фона

Формирование тел вращения. набор объемных геометрических цветных фигур. объемные геометрические фигуры вращения. векторные иллюстрации

Абстрактный геометрический узор с полосами, линиями. бесшовный векторный фон. черно-белый орнамент

Золотая геометрическая рамка на розовом фоне мазка

Бесшовный серый электронный узор. векторная иллюстрация с шестиугольниками в стиле хай-тек. кибер текстура

Красочный трехмерный рисунок деревянных геометрических фигур на белом фоне с минимальной творческой концепцией.

Фотография деревянной игрушки-сортера для детей с мелкими деревянными деталями в виде геометрических фигур (прямоугольник, квадрат, круг, треугольник), разных цветов на белом изолированном фоне

Геометрические фигуры на деревянном фоне, крупный план. концепция логического мышления

Набор коллекционных рядов из различных трехмерных объемов из акрилового стекла различной геометрической формы. образование изучение физики математика геометрическая концепция, изолированные на белом фоне.

Современный минималистский вектор. логотип геометрической формы. шестиугольники и треугольники, квадратные значки и круглые геометрические значки логотипа векторная иллюстрация

Стикмен иллюстрация детей дошкольного возраста, носящих базовые формы в качестве головных уборов

Подключенная централизованная сеть и центральная сетевая связь бизнес-концепция как группа различных веревок, которые соединяются с центральной точкой как Метафора сети квадратной формы для связи и соединения вместе как прочная опорная структура.

Карта мира абстрактные геометрические фигуры, низкополигональная графика.

Иллюстрация в витражном стиле на тему музыки, форма абстрактной скрипки на геометрическом фоне. современный фон. футуристическая многоугольная форма. низкополигональный минималистичный дизайн для плаката, обложки, брендинга, баннера, плаката.

Абстрактный многоугольный низкополигональный темный фон с соединительными точками и линиями. структура соединения. 3d визуализация

Концепция бизнеса и дизайна – абстрактный геометрический настоящий деревянный цветной куб на фоне деревянного пола, и это не 3D-рендеринг. это символ роста экономики

Золотые геометрические рамки, свадебные пригласительные в форме золотых ромбов. векторные роскошные золотые абстрактные геометрические рамки премиум-класса

Абстрактные 3D-рендеринг геометрических фигур. современный дизайн фона для плаката, обложки, брендинга, баннера, плаката.

Современный геометрический абстрактный фон – круги. шаблон дизайна презентации бизнеса или технологии, шаблон брошюры или флаера, или геометрический векторный веб-баннер

Shape 2d: изучение двухмерных фигур для детей

Мультяшная иллюстрация основных геометрических фигур забавные персонажи для обучения детей

Мультяшная иллюстрация обучающих основных геометрических фигур для детей дошкольного или младшего школьного возраста с изображением животных

Мультяшная иллюстрация основных геометрических фигур веселые персонажи для обучения детей

Фон из геометрических фигур

Сакральная геометрия. алхимия, хипстерские символы

Векторная абстрактная геометрическая форма из серых кубиков.

Фон из геометрических фигур

Синие геометрические абстрактные линии. векторные иллюстрации

Концепция продажи в стиле Мемфис с процентной скидкой на фоне с геометрическими фигурами изолированные векторные иллюстрации

Треугольник Пенроуза многоцветный абстрактный символ – векторные иллюстрации. eps 10

Набор простых фигур в векторе для трассировки. восстановите пунктирную линию и раскрасьте картинку. след игра для детей.

Геометрическая развертка.

Бесшовный абстрактный геометрический узор моды 80-х-90-х годов. его можно использовать в печати, в фоновом режиме веб-сайта и в дизайне ткани.

Набор геометрических кристаллов. геометрические фигуры.

Векторная иллюстрация белая бумага (пустое место для вашего контента) на абстрактном трехмерном геометрическом, многоугольном, треугольном узоре и разноцветном, синем, фиолетовом, желтом и зеленом фоне

Абстрактная геометрическая форма круга с красочной иллюстрацией ветви дерева идеально подходит для творческого разнообразия дизайна . вектор.

Геометрические фигуры, знаки, этикетки и рамки, треугольники, элементы дизайна линии, векторная иллюстрация. абстрактные геометрические фигуры и дизайн геометрических фигур. элемент линейного знака геометрических эзотерических символов.

Набор геометрических кристаллов. геометрические фигуры.

Деревянные геометрические фигуры на миллиметровой бумаге

Векторный бесшовный узор, современная стильная абстрактная текстура.

Бесшовный векторный рисунок со священными золотыми фигурами

Геометрические фигуры — набор из 9 минимальных рисунков

Абстрактный геометрический векторный фон с треугольниками.

Каркас объекта с линиями и точками. абстрактная трехмерная структура соединения. геометрическая форма для дизайна. геометрический элемент решетки, эмблема и значок. соединительная сетка. молекулярная сетка. 3d технологический стиль.

Набор геометрических кристаллов. геометрические фигуры.

Векторный бесшовный геометрический узор с полосатыми треугольниками, абстрактными динамическими формами в черно-белом цвете. ручной обращается фон с пересекающимися линиями в стиле моды 1980-х годов. современный техно-текстильный принт

Абстрактная композиция с текстурированными геометрическими фигурами черного, серого и пастельно-розового цветов. минималистский и современный плакат, брошюра, дизайн карты.

Бесшовный геометрический треугольник. абстрактный геометрический дизайн фона. векторная иллюстрация.

Набор эмблем векторной линейной сакральной геометрии, логотип тонкой линии и знаки духовных геометрических фигур

Набор геометрических фигур, платоновых тел. изолированные на белом фоне. 3d иллюстрация

Набор векторных значков основных геометрических фигур

Векторная современная динамичная композиция из различных округлых форм по цвету и геометрических элементов. абстрактный творческий узор.

Геометрический бесшовный повторяющийся узор с шестиугольниками в пастельных розовых, черных, золотых блестках и текстурой, нарисованной точками.

Круглый геометрический мотив. абстрактный элемент оп-арта в оттенках серого

Геометрическая фигура на белом векторе

Светящиеся геометрические фигуры

Нарисованные кистью треугольники, бесшовный векторный узор пирамиды. черный и желтый, золотой геометрический фон в стиле каракули. абстрактная рисованная текстура. различные треугольные формы с грубыми, неровными краями.

Векторные абстрактные правильные геометрические фигуры – черный на сером фоне

Векторные абстрактные современные шаблоны дизайна логотипа в модном линейном стиле – кубы и ромбы – минимальные геометрические концепции и значки

Геометрическая форма, элемент дизайна. линейный дизайн, нерасширенные штрихи. векторные иллюстрации eps 10

Вектор бесшовные округлые линии текстуры. современный геометрический фон круглой формы. монохромный повторяющийся узор с дугами.

Геометрический абстрактный узор фона из бесшовных квадратов, кругов и ромбовидного треугольника мозаичного образца текстуры.

Абстрактный фон с пирамидами. многоугольные геометрические фигуры.

Яркий красочный акварельный фон с геометрическими фигурами

Набор модных геометрических фигур. набор геометрических фигур, знаков, этикеток и рамок, треугольников, элементов дизайна линии. геометрические фигуры и дизайн геометрических фигур. знак линии элемента геометрический эзотерический.

Абстрактная композиция с текстурированными геометрическими фигурами черного, бирюзово-зеленого и золотого цвета. минималистский и современный плакат, брошюра, дизайн карты.

Коллекция бесшовных геометрических узоров

Синий светящийся спиральный фрактал, сгенерированный компьютером абстрактный фон, 3D-рендеринг монохромный объект с сеткой черных линий, сложной геометрической формы.

Рамка векторного шаблона. форма квадратная. элементы дизайна линии. коллекция коллажей геометрических золотых фигур.

Векторный прозрачный октаэдр. каркасный объект с точками. абстрактная трехмерная структура соединения. геометрическая форма для дизайна. геометрический элемент решетки. молекулярная сетка. 3d технологический стиль с частицей

Лицо думающей женщины, созданное в низкополигональном стиле и с соединенными линиями, трехмерная векторная человеческая голова в оттенках серого, взрыв мозга, который символизирует интеллект и воображение.

Бесшовный фон с геометрическими треугольниками, дизайн 80-х – векторная иллюстрация. ретро группа мемфис. фон из геометрических фигур

Векторный абстрактный бесшовный узор с геометрическими фигурами. ретро стиль мемфис, мода 80-90х годов.

Абстрактный цветочный бесшовный узор с черно-белой линией орнамента в форме сердца, вихрем, геометрической текстурой каракулей. фон с оптическим эффектом декоративной волны.

Цвет модных витых линий, горизонтальный фон, оптическая иллюзия, оптическое искусство, абстрактный фон, волновой дизайн, идеально подходящий для ткани, оберточной бумаги, брошюры, листовки, флаера, абстрактного геометрического элемента

Фон из ярких геометрических фигур

Современный простой геометрический векторный бесшовный узор с текстурой золотой линии на белом фоне. светлые абстрактные обои, яркий фон плитки.

Бесшовный абстрактный геометрический узор моды 80-90-х годов. его можно использовать в печати, в фоновом режиме веб-сайта и в дизайне ткани.

Лошадь в стиле геометрических узоров. вектор eps 10

Набор бесшовных шаблонов. геометрические текстуры с эффектом оптической иллюзии.

Абстрактный многоцветный геометрический фон

Векторный ручной рисунок цветного круга бесшовный узор

Симпатичные маленькие мультяшные дети с основными формами звездного круга для детского образования

3d яркий абстрактный фон

Абстрактные 3d кубики, архитектурная концепция фона

Винтажные одноцветные бесшовные плитки, векторный бесшовный узор.

Бесшовный векторный рисунок. симметричный геометрический фон с ромбами и кругами на синем фоне. декоративный повторяющийся орнамент.

Трехмерные фигуры с примерами предметов из повседневной жизни

Бесшовная сетка. вектор черно-белый фон.