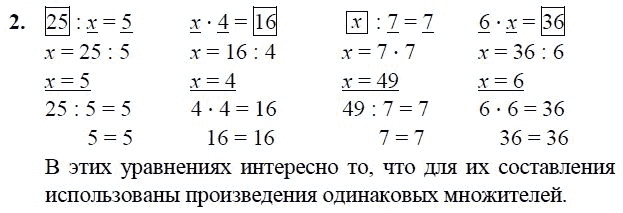Разное

Уравнения математика 3 класс примеры: Уравнения по математике 3 класс

Содержание

Уравнения по математике 3 класс

  • х + 19 = 42
  • x = 42 – 19
  • x = 23
  • 54 + х = 82
  • x = 82 – 54
  • x = 28
  • 9 + у = 15
  • y = 15 – 9
  • y = 6
  • 7 – у = 3
  • y = 7 – 3
  • y = 4
  • с + 6 = 9
  • c = 9 – 6
  • c = 3
  • k + 10 = 30
  • k = 30 – 10
  • k = 20
  • х + 50 = 96
  • x = 96 – 50
  • x = 46
  • х – 25 = 27
  • x = 27 + 25
  • x = 52
  • 42 – х = 18
  • x = 42 – 18
  • x = 24
  • 27 + х = 50
  • x = 50 – 27
  • x = 23
  • х – 28 = 70
  • x = 70 + 28
  • x = 98
  • 63 + х = 90
  • x = 90 – 63
  • x = 27
  • 76 – k = 40
  • k = 76 – 40
  • k = 30
  • х – 16 = 30
  • x = 30 + 16
  • x = 46
  • с + 9 = 12
  • c = 12 – 9
  • c = 3
  • х + 35 = 67
  • x = 67 – 35
  • x = 32

Урок математики по теме “Решение уравнений” (3-й класс)

Цели.

  1. Образовательные:
  • закрепление умений решать уравнения разных видов;
  • совершенствование вычислительных умений и навыков;
  • закрепление приёмов устных вычислительных навыков;
  • закрепление умений решать задачи.
  1. Развивающие:
  • развитие внимания, памяти, математической речи;
  • развитие у учащихся умения выделять главное, существенное в изучаемом материале;
  • формирование умения сравнивать, обобщать изучаемые факты и понятия;
  • развитие самостоятельности мышления;
  • развитие познавательного интереса, творческих способностей, воли, эмоций.
  1. Воспитательные:
  • воспитание культуры поведения;
  • осуществление нравственного воспитания;
  • профилактика утомления (здоровьесбережение).
  1. Организационный момент.

    2. Цель: внешняя и внутренняя подготовка к уроку.

    Ребята, давайте сегодня вспомним все, что мы учили
    Ничего мы не забыли
    Рисуем, чертим, вычисляем
    Математику мы знаем.

  2. Проверка домашнего задания.

Цель: проверка вычислительных навыков умножения и деления, сложения и вычитания, порядок действий в примерах, знание математической терминологии.

1) 81: 9+54: 2=36

63:21+45:9=8

17*3-92:46=49

18*4-72:12=66

  1. Чему равно произведение чисел 4 и 9 (36). Найдите и прочитайте пример с таким ответом.
  2. Прочитайте пример, в ответе которого количество десятков на 5 меньше количества единиц. (49)
  3. Чему равно частное чисел 40 и 5. (8) Прочитайте выражение с таким ответом.
  4. Прочитайте пример, ответ которого записывается одной цифрой.

2) Проверяем задачу. (Посмотрите на экран)

54: 3

– Какой вопрос вы поставили к этому выражению? (сколько листов бумаги в одной тетради)

– Сколько тетрадей получится из 72 листов? (4 тетради)

– Каким действием вы это узнавали? (делением)

– У кого другой ответ?

– Значит, задачу решили правильно.

  1. Подготовка к активной учебной деятельности.

Цель: актуализация опорных знаний и умений, формирование познавательных мотивов.

1.Чистописание.

1) Какое сегодня число? (18 февраля)

Открываем тетради и записываем число.

Дайте характеристику этому числу.

2) Запишите произведение чисел равные 18.

2*9; 3*6; 18*1; 9*2; 6*3; 1*18

Каким свойством умножения вы здесь воспользовались? (переместительным)

Сформулируйте его.

3) Посмотрите на цепочку и продолжите её.

11 17 24 32 41 …

По какому принципу она построена? (сначала число увеличивается на 6, потом на 7, 8 и т.д.)

2. Устный счёт (на карточках).

Приготовьте карточки.

  1. Частное чисел 48 и 8 увеличить на 10
  2. Произведение чисел 20 и 4 уменьшить на 25
  3. 1/10 метра. Сколько это сантиметров?
  4. 12 увеличить в 3 раза
  5. 99 уменьшить в 9 раз
  6. Во сколько раз 80 больше 20
  7. Я задумала число, когда его увеличила в 7 раз, то получила 63. Какое число я задумала?
  8. Найти площадь прямоугольника, если его длина равна 8см, а ширина на 2см меньше.
  9. Половину пути до школы Саша проходит за 12 минут. Сколько времени он потратит на весь путь?
  10. Для игры 18 девочек и 12 мальчиков разделились на 2 команды. Сколько человек было в каждой команде?
  1. Усвоение новых знаний.

Цель: сформировать у учащихся конкретные представления об изучаемом материале, выделить главное, провести обобщение вместе с учащимися, на основе знаний выработать умения.

  1. Посмотрите на экран. Найдите среди следующих записей уравнение.

    2. 48-25=23

    30+х?40

    36:х=12

    х*5

    Прочитайте его.

    Докажите, что это уравнение.

    Что же такое уравнение? (Это равенство, содержащее неизвестное число, которое надо найти)

    Кто догадался, какая тема сегодняшнего урока?

    Тема: “Решение уравнений”

  2. Работа с учебником.

Откройте учебник на с.20

Прочитайте первое уравнение

Что такое 76?(делимое)

Что такое х? (делитель)

Что такое 38? (частное)

Как же найти делитель?

Второе и третье уравнение читаем и разбираем так же.

Ребята, мы вспомнили компоненты действий деления и умножения.

А теперь посмотрите на доску. Перед вами этапы решения уравнения. Но, по-моему, вся последовательность нарушена. Её надо восстановить.

    1. Вспомнить компоненты действия данного уравнения.
    2. Определить неизвестный компонент.
    3. Вспомнить правило нахождения неизвестного компонента.
    4. Применить правило и найти неизвестный компонент.
    5. Записать ответ.
      6.

Мы составили с вами программу действий для решения уравнений, т.

е. по-другому, алгоритм.

А сейчас, используя этот алгоритм, выполним задание №2 с.20. (3 человека у доски)

Проверка с дополнительными вопросами.

Физкультминутка (разговор об осанке)

Раз, два, три, четыре пять
Все умеем мы считать,
Отдыхать умеем тоже.
Руки за спину заложим,
Голову поднимем выше
И легко, легко подышим.
Раз – подняться, потянуться.
Два – согнуть, разогнуться
Три – в ладоши три хлопка,
На четыре – руки шире.
Пять – руками помахать.
Шесть – за парту ровно сесть.

– Почему я часто говорю вам: “Держите спину прямо?”

– Почему человеку нужна хорошая осанка?

1) Чтобы был ровный позвоночник

2) Чтобы хорошо работали внутренние органы и сердце.

3) Чтобы дыхание было глубоким и ровным.

  1. Закрепление знаний.

    2. Цель: организация деятельности учащихся по применению изученных знаний, выделение существенных признаков, конкретизация ЗУН.

    Решение задачи № 5 с.20.

    Что известно в задаче? Что ещё?

    Что значит на каждого? Значит на одного.

    Что нужно узнать?

    Пишем слово “задача” и записываем условие.

    1 чел. – ? по 2б. и по 3б.

    19 чел. – ?

    Посмотрите на краткую запись и скажите, какая это задача? (составная)

    Почему? (два вопросительных знака)

    Из чего состоит составная задача? (из двух простых)

    (два ученика у доски)

    Какой вычислительный приём использовали при решении задачи (умножение суммы на число)

    Как можно умножить сумму на число?

    Какой способ вы считаете в данной задаче рациональным? (1 способ)

  2. Контроль и самопроверка.

    3. Цель: проверка полноты, осознанности и прочности ЗУН, проверка сформированности прочных общих учебных умений.

    Дифференцированная работа – решение уравнений по группам.

    I группа

    Подчеркните уравнения, значения которых равняется 6.

    х*9=54

    12*х=36

    6*х=36

    35: х=5

    24: х=4

    15*х=45

    II группа

    Из данных уравнений подчеркни те, которые решаются делением.

    х: 18=5

    х*11=55

    96: х=16

    52: х=13

    х: 15=6

    15*х=75

    III группа

    Сравни уравнения каждой пары и, не вычисляя, подчеркни те, где значение х будет больше.

    19*х=57

    19*х=76

    40:х=4

    40:х=8

    х:3=18

    х:3=24

    Проверка решения (взаимопроверка)

  3. Домашнее задание

    4. № 8 с. 20, № 1 с. 21

  4. Итог урока.

Цель: дать анализ успешности овладения знаниями и способами деятельности учащихся.

Ребята, давайте вспомним, чем мы занимались на уроке.

Что нового узнали?

Что же такое уравнение?

Понравилось ли вам, как вы работали.

– На доске вы видите лестницу достижений. Каждый из вас должен прикрепить магнит на ту ступеньку, на которую вы сегодня поднялись во время работы на уроке.

См. презентацию.

Уравнения. Математика, 3 класс: уроки, тесты, задания.

Вход Вход Регистрация Начало Новости ТОПы Учебные заведения Предметы Проверочные работы Обновления Переменка Поиск по сайту Отправить отзыв
    org/BreadcrumbList”>
  • Предметы
  • Математика
  • 3 класс

  1. Нахождение неизвестного множителя

  2. Нахождение неизвестного делимого

  3. Нахождение неизвестного делителя

Отправить отзыв Нашёл ошибку? Сообщи нам! Copyright © 2021 ООО ЯКласс Контакты Пользовательское соглашение

Как решать линейные уравнения — формулы и примеры решения простейших уравнений

Понятие уравнения

Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.

В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.


Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядит таках + b = 0, где a и b — действительные числа.

Что поможет в решении:

  • если а не равно нулю, то у уравнения единственный корень: х = -b : а;
  • если а равно нулю — у уравнения нет корней;
  • если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

  • кубические
  • уравнение четвёртой степени
  • иррациональные и рациональные
  • системы линейных алгебраических уравнений

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Как решаем:

  1. Перенесем 6x из левой части в правую. Знак меняем на противоположный, то есть минус.

    6x −5x = 10

  2. Приведем подобные и завершим решение.

    x = 10

Ответ: x = 10.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Как решаем:

  1. Сократим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.

    −4x = 12 | :(−4)
    x = −3

Ответ: x = −3.

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
  1. Раскрываем скобки, если они есть.
  2. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую.
  3. Приводим подобные члены в каждой части уравнения.
  4. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе.

А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Решаем так:

  1. Перенести 1 из левой части в правую со знаком минус.

    6х = 19 — 1

  2. Выполнить вычитание.

    6х = 18

  3. Разделить обе части на общий множитель, то есть 6.

    х = 2

Ответ: х = 2.

Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1.

Решаем так:

  1. Раскрыть скобки

    5х — 15 + 2 = 3х — 2 + 2х — 1

  2. Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены.

    5х — 3х — 2х = – 12 — 1 + 15 — 2

  3. Приведем подобные члены.

    0х = 0

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Решаем так:

  1. Найти неизвестную переменную.

    х = 1/8 : 4

    х = 1/12

Ответ: 1/12 или 0,83. О десятичных дробях можно почитать здесь.

Пример 4. Решить: 4(х + 2) = 6 — 7х.

Решаем так:

  1. 4х + 8 = 6 — 7х
  2. 4х + 7х = 6 — 8
  3. 11х = −2
  4. х = −2 : 11
  5. х = – 0, 18

Ответ: — 0,18.

Пример 5. Решить:

Решаем так:

  2. 3(3х — 4) = 4 · 7х + 24
  3. 9х — 12 = 28х + 24
  4. 9х — 28х = 24 + 12
  5. -19х = 36
  6. х = 36 : (-19)
  7. х = – 36/19

Ответ: 1 17/19.

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

Решаем так:

  1. Раскрыть скобки

    5х — 15 + 2 = 3х — 2 + 2х — 1

  2. Сгруппировать в левой части неизвестные члены, в правой — свободные члены:

    х — х = 4 — 7

  3. Приведем подобные члены.

    0 * х = – 3

Ответ: нет решений.

Пример 7. Решить: 2(х + 3) = 5 — 7х..

Решаем так:

  1. 2х + 6 = 5 — 7х
  2. 2х + 6х = 5 — 7
  3. 8х = −2
  4. х = −2 : 8
  5. х = – 0,25

Ответ: — 0,25.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в современную онлайн-школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. А еще развивающие игры, квесты и головоломки на любой возраст и уровень.

Как решить уравнение 3 класса онлайн

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. В 3 классе школьники учатся решать разнообразные простые уравнения с неизвестными методом перебора с учетом связи членов действиями вычитания/сложения. Для решения таких уравнений главное выучить приоритетность выполнения арифметических операций.

Допустим, дано уравнение следующего вида:

\[64 + d = 82\]

Так же читайте нашу статью “Решить уравнения 3 степени онлайн решателем”

В данном уравнении выполняется такая арифметическая операция как сложение двух чисел, одно из которых неизвестное. Оперируя правилом, которое гласит о том, что чтобы найти неизвестное слагаемое необходимо из суммы вычесть известное слагаемое. Выполним это, сделав перенос неизвестной переменной в левую часть, а числа в правую:

\[d = 82 – 64 \]

Выполнив вычитание, мы получим результат решения нашего уравнения:

\[d = 18\]

Если мы подставим \[18\] на место \[d\] в исходное уравнение, то мы увидим, что левая и правая сторона имеют одинаковое значение, что говорит о правильности полученного ответа.

Где можно решить уравнение онлайн с решением 3 класс?

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Урок математики 3 класс тема: «Уравнения»

Слайды и текст этой онлайн презентации

Слайд 1

Муниципальное бюджетное общеобразовательное учреждение Ярцевская средняя общеобразовательная школа №4 имени Героя Советского Союза О.А.Лосика
Урок математики 3 класс Тема: «Уравнения»
Разработала и провела: учитель начальных классов Клюшина Елена Валентиновна
12. 12.2019

Слайд 2

Реши выражения
90-32 45+45 53-12 72-15 92-18 37+13 26+38 56-38
=58 =90 =41 =57 =74 =50 =64 =18
12.12.2019

Слайд 3

Найдите пропущенное число:
2 +
= 11
+ 11 = 18
15 +
= 17
+ 5 = 13

Слайд 4

Найдите пропущенное число:
13 −
= 7
− 12 = 3
14 −
= 6
− 5 = 13

Слайд 5

Найди уравнения и реши их
18+х 70+х=75 56+х>70 74-30=44 Х- 8=42

Слайд 6

УРАВНЕНИЕ –
математическое
РАВЕНСТВО
с буквой

Слайд 7

Уравнение:
x
5 +
= 14
x = 14 – 5
x = 9
9 – решение уравнения

Слайд 8

Уравнение:
x
5 +
= 14
Проверка:
5 +
= 14
14 = 14

Слайд 9

Уравнение:
z
− 6
= 9
z = 9 + 6
z = 15
15 – решение уравнения

Слайд 10

Уравнение:
z
− 6
= 9
Проверка:
− 6
= 9
9 = 9

Слайд 11

Назовите правильно:
a –
x –
[а]
[икс]
b –
y –
[бэ]
[и́грек]
c –
[цэ]
[зэт]
z –

Слайд 12

Назовите правильно:
d –
[дэ]
k –
[ка]
e –
m –
[эм]
[е]
n –
[эн]
f –
[эф]

Слайд 13

Прочтите правильно:
k = 10
x =12
z =15
f = 19
m = 11
y =14
n = 16
d = 17

Слайд 14

Решите уравнение:
k + 4 = 20
1 + a = 9
k = 16
a = 8
b + 5 = 12
15 – n = 8
b = 7
n = 7
17 – c = 3
m – 16 = 3
c = 14
m = 19

Слайд 15

ИТОГ
Как найти неизвестное слагаемое? Как найти уменьшаемое? Как найти вычитаемое?
МОЛОДЦЫ!

Слайд 16

Памятка
Вспомнить компоненты действия данного уравнения. Определить неизвестный компонент. Вспомнить правило нахождения неизвестного компонента. Применить правило и найти неизвестный компонент. Записать ответ.
12.12.2019

Слайд 17

Список использованных источников:
1. М.И Моро Математика 3 класс, Часть 2. Учебник, Издательство «Просвещение», 2009 год.
2. Анимированные картинки -
http://miranimashek.com
3. Фон для презентации – http://www.pomochnik-vsem.ru
12.12.2019

3 класс. Моро. Учебник №1. Ответы к стр. 7

Числа от 1 до 100


Решение уравнений
Ответы к стр. 7

Будем учится решать уравнения с неизвестным слагаемым, которые подбором решить трудно.

4 + 3 = 7          5 + 4 = 9          3 + 6 = 9
7 – 4 = 3           9 – 5 = 4           9 – 6 = 3
7 – 3 = 4           9 – 4 = 5           9 – 3 = 6

Объясни, что получится, если из суммы двух слагаемых вычесть одно из них.
Закончи вывод.
Чтобы найти неизвестное слагаемое, надо из суммы двух слагаемых вычесть известное слагаемое.

1. Объясни решение уравнения и проверку.
х + 6 = 38          Проверка:
х = 38 – 6           32 + 6 = 38
х = 32                38 = 38
Для решения уравнения – нахождения неизвестного слагаемого – надо из суммы двух слагаемых вычесть известное слагаемое. Находим корень уравнения: х = 32. Для проверки решения подставим найденный корень в уравнение вместо неизвестного слагаемого. Получаем тождество: левая и правая части выражения равны, значит уравнение решено верно.

2. Реши уравнения с объяснением.

х + 18 = 42          Проверка:
х = 42 – 18           24 + 18 = 42
х = 24                  42 = 42

64 + х = 82          Проверка
х = 82 – 64           64 + 18 = 82
х = 18                  82 = 82

3. С одной грядки собрали 20 кг картофеля, а с другой – на 5 кг больше.
Объясни, что узнаешь, выполнив вычисления:

20 + 5      20 + (20 + 5)

20 + 5 = 25 (кг) – картофеля собрали с другой грядки
20 + (20 + 5) = 45 (кг) – картофеля собрали с двух грядок

4. Ваня собрал 8 стаканов малины, а его сестра – на 2 стакана меньше.
Поставь вопрос так, чтобы задача решалась в два действия. Реши её.

Сколько стаканов малины всего собрали дети вместе?
1) 8 – 2 = 6 (с.) – собрала сестра Вани
2) 8 + 6 = 14 (с.) – собрали дети всего вместе
О т в е т: дети собрали 14 стаканов малины.

5. Вычисли, записывая решение столбиком.
75 – 49    64 + 28    93 – 57    56 + 16

    – 75     + 64      – 93     + 56
      49       28        57        16    
      26       92        36        72     

Реши уравнение.
15 + х = 35

х = 35 – 15
х = 20

ЗАДАНИЯ НА ПОЛЯХ
Набери 15

7624
8274
7561
4912

15 = 7 + 6 + 2 = 4 + 8 + 2 + 1 = 7 + 4 + 4 = 9 + 6 = 7 + 5 + 2 + 1     

ГДЗ по математике. Учебник. 3 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.

Математика. 3 класс

3 класс. Моро. Учебник №1. Ответы к стр. 7

4.3 (85.38%) от 130 голосующих

Рабочих листов по уравнениям

Рабочие листы с одношаговым уравнением

Этот набор рабочих листов требует от студентов решения одношаговых уравнений, включающих целые числа, дроби и десятичные дроби, путем выполнения операций сложения, вычитания, умножения или деления. Он также содержит математические загадки, определение стоимости предметов, перевод фраз в одношаговое уравнение и многое другое.

Рабочие листы с двухэтапными уравнениями

Щелкните ссылку, чтобы получить доступ к эксклюзивным рабочим таблицам по решению двухэтапных уравнений, которые включают целые числа, дроби и десятичные дроби.Ряд MCQ, уравнения в геометрии, перевод двухэтапных уравнений и многие другие упражнения доступны для практики.

Рабочие листы с многоступенчатыми уравнениями

Эти рабочие листы требуют от учащихся выполнить несколько шагов для решения уравнений. Используйте знания, полученные при решении одношаговых и двухэтапных уравнений, чтобы решить эти многоступенчатые уравнения. Сюда также включен ряд прикладных задач, основанных на геометрических формах.

Рабочие листы задач по формулам

Загрузите и распечатайте эту огромную коллекцию одношаговых, двухэтапных и многоступенчатых задач по уравнениям со словами, которые включают целые числа, дроби и десятичные дроби.Рабочие листы MCQ представляют собой идеальный инструмент для изучения восприятия учащимся темы.

Рабочие листы перестановки уравнений

Рабочие листы с буквальными уравнениями помогают отточить навыки, такие как перестановка буквальных уравнений, перегруппировка и оценка, включены текстовые задачи, содержащие реальные приложения, и многое другое.

Уравнение рабочего листа

Щелкните здесь, чтобы просмотреть таблицы по уравнению линии. Напишите уравнение прямой в стандартной форме, двухточечной форме, форме с пересечением угла наклона и форме точки с уклоном. Загрузите полный набор рабочих листов по уравнению линии, которые также включают рабочие листы по параллельным и перпендикулярным линиям.

Рабочие листы для построения графиков линейных уравнений

Вы находитесь всего в одном клике от огромной коллекции таблиц по построению графиков линейных уравнений. Постройте точки и нарисуйте линию. Используйте значения x, чтобы заполнить таблицы функций и построить график линии. Рабочие листы MCQ представляют собой идеальный инструмент для проверки знаний учащихся по этой теме.

Рабочие листы по квадратному уравнению

Щелкните ссылку, чтобы просмотреть обширный набор рабочих листов по квадратным уравнениям.Решите квадратные уравнения, разложив на множители, заполнив квадратные, квадратные формулы или методы извлечения квадратного корня. Найдите сумму и произведение корней. Проанализируйте природу корней.

Рабочие листы уравнения абсолютного значения

Используйте эти рабочие листы, чтобы научить своих студентов абсолютному значению целых чисел. Этот модуль включает в себя такие упражнения, как вычисление выражения абсолютного значения для определенного значения, таблицы ввода и вывода, построение графика функции абсолютного значения и решение различных типов уравнений абсолютного значения.

Рабочие листы систем уравнений

Решите эти системы уравнений методом исключения или замены. Уравнения содержат две или три переменные. Уравнение с двумя переменными представляет собой прямые линии, тогда как уравнения с тремя переменными представляют собой плоскость.

Решение простых уравнений (3 из 3)

Мы видели, как решать уравнения, выполняя одно действие с обеими сторонами уравнения. Ниже приведены два примера:

Проблема Решение
п + 17 = 100
Уберите 17 с обеих сторон, чтобы оставить a слева n + 17-17 = 100-17
n + 0 = 83
n = 83
Проблема Решение
6y = 54
Разделите обе стороны на 6 6y ÷ 6 = 54 ÷ 6
y = 9

Иногда возникают задачи, требующие более сложных уравнений. Например, вы хотите купить пальто по цене 100 долларов. У вас есть 40 долларов. Твоя мама сказала тебе, что она потратит любую сумму денег, которую ты сможешь сэкономить, чтобы помочь тебе купить пальто. Сколько нужно сэкономить?

Сумма, необходимая для экономии назовем его
Сумма, которая у вас будет после того, как вы накопите и ваша мама уравновесит
(или удвоит).		 2 x n (или 2n)
Сумма, которая у вас уже есть 40
Необходимая сумма 100
Собираем вместе 2n + 40 = 100

Чтобы решить уравнения типа 2n + 40 = 100, нам нужно «избавиться» от двух вещей: +40 и x2. Нам нужно сделать две вещи, и порядок, в котором мы их делаем, важен. Примеры ниже показывают, что мы можем сделать для решения этих типов уравнений:

2n + 40 = 100
Шаг 1: вычтите 40 из с обеих сторон 2n + 40-40 = 100-40
2n = 60
Шаг 2: Разделите с обеих сторон на 2 2н ÷ 2 = 60 ÷ 2
п = 30

Очень важно, чтобы мы решали уравнения, подобные приведенным на этой странице, путем сложения или вычитания перед делением или умножением.

3n – 7 = 17
Шаг 1: Добавьте 7 к с обеих сторон 3н – 7 + 7 = 17 + 7
3n = 24
Шаг 2: Разделите с обеих сторон на 3 3н ÷ 3 = 24 ÷ 3
п = 8
a / 7 + 8 = 9
Шаг 1: вычтите 8 из с обеих сторон a / 7 + 8-8 = 9-8
a / 7 = 1
Шаг 2: Умножьте с обеих сторон на 7 a / 7 x 7 = 1 x 7
а = 7
b / 2 – 16 = 40
Шаг 1: Добавьте 16 к с обеих сторон b / 2 – 16 + 16 = 40 + 162
b / 2 = 562
Шаг 2: Умножьте с обеих сторон на 2 b / 2 x 2 = 56 x 22
б = 112

Распечатайте приведенные ниже таблицы, чтобы попрактиковаться в решении уравнений в два этапа.

Четыре приведенных выше рабочих листа также включены сюда вместе с другими рабочими листами для решения уравнений.

Определение выражений и уравнений | Предалгебра

Результаты обучения

  • Находить и записывать математические выражения, используя слова и символы
  • Определять и записывать математические уравнения, используя слова и символы
  • Определите разницу между выражением и уравнением
  • Используйте экспоненциальную запись для выражения многократного умножения
  • Записать экспоненциальное выражение в развернутом виде

Определить выражения и уравнения

В чем разница между фразой и предложением в английском языке? Фраза выражает отдельную мысль, которая сама по себе является неполной, а предложение – законченное утверждение.«Очень быстро бежал» – это фраза, а «Футболист бежал очень быстро» – это предложение. В предложении есть подлежащее и глагол.

В алгебре у нас есть выражение и уравнение . Выражение похоже на фразу. Вот несколько примеров выражений и их отношения к словосочетаниям:

Выражение слов Фраза
[латекс] 3 + 5 [/ латекс] [латекс] 3 \ text {plus} 5 [/ латекс] сумма трех и пяти
[латекс] n – 1 [/ латекс] [латекс] н [/ латекс] минус один разница [латекс] н [/ латекс] и одна
[латекс] 6 \ cdot 7 [/ латекс] [латекс] 6 \ text {times} 7 [/ латекс] произведение шести и семи
[латекс] \ frac {x} {y} [/ латекс] [латекс] x [/ латекс] разделить на [латекс] y [/ латекс] частное [латекс] x [/ латекс] и [латекс] y [/ латекс]

Обратите внимание, что фразы не образуют законченное предложение, потому что во фразе нет глагола. Уравнение – это два выражения, соединенных знаком равенства. Когда вы читаете слова, которые символы представляют в уравнении, вы получаете полное предложение на английском языке. Знак равенства дает глагол. Вот несколько примеров уравнений:

Уравнение Приговор
[латекс] 3 + 5 = 8 [/ латекс] Сумма трех и пяти равна восьми.
[латекс] n – 1 = 14 [/ латекс] [латекс] н [/ латекс] минус один равняется четырнадцати.
[латекс] 6 \ cdot 7 = 42 [/ латекс] Произведение шести и семи равно сорока двум.
[латекс] x = 53 [/ латекс] [латекс] х [/ латекс] равен пятидесяти трем.
[латекс] y + 9 = 2y – 3 [/ латекс] [латекс] y [/ latex] плюс девять равно двум [латексу] y [/ latex] минус три.

Выражения и уравнения

Выражение – это число, переменная или комбинация чисел, переменных и символов операций.
Уравнение состоит из двух выражений, соединенных знаком равенства.

пример

Определите, является ли каждое из них выражением или уравнением:

  1. [латекс] 16 – 6 = 10 [/ латекс]
  2. [латекс] 4 \ cdot 2 + 1 [/ латекс]
  3. [латекс] x \ div 25 [/ латекс]
  4. [латекс] y + 8 = 40 [/ латекс]

Решение

1. [латекс] 16 – 6 = 10 [/ латекс] Это уравнение – два выражения соединены знаком равенства.
2. [латекс] 4 \ cdot 2 + 1 [/ латекс] Это выражение – без знака равенства.
3. [латекс] x \ div 25 [/ латекс] Это выражение – без знака равенства.
4. [латекс] y + 8 = 40 [/ латекс] Это уравнение – два выражения соединены знаком равенства.

Упростить выражения с помощью экспонентов

Упростить числовое выражение – значит сделать все возможное.Например, чтобы упростить [латекс] 4 \ cdot 2 + 1 [/ latex], мы сначала умножим [latex] 4 \ cdot 2 [/ latex], чтобы получить [latex] 8 [/ latex], а затем добавить [latex ] 1 [/ latex] чтобы получить [latex] 9 [/ latex]. Хорошая привычка – работать со страницей вниз, записывая каждый шаг процесса под предыдущим. Только что описанный пример будет выглядеть так:

[латекс] 4 \ cdot 2 + 1 [/ латекс]
[латекс] 8 + 1 [/ латекс]
[латекс] 9 [/ латекс]

Предположим, у нас есть выражение [латекс] 2 \ cdot 2 \ cdot 2 \ cdot 2 \ cdot 2 \ cdot 2 \ cdot 2 \ cdot 2 \ cdot 2 [/ latex]. {5} [/ латекс] [латекс] 12 [/ латекс] в пятой степени

пример

Запишите каждое выражение в экспоненциальной форме:

  1. [латекс] 16 \ cdot 16 \ cdot 16 \ cdot 16 \ cdot 16 \ cdot 16 \ cdot 16 [/ латекс]
  2. [латекс] \ text {9} \ cdot \ text {9} \ cdot \ text {9} \ cdot \ text {9} \ cdot \ text {9} [/ latex]
  3. [латекс] x \ cdot x \ cdot x \ cdot x [/ латекс]
  4. [латекс] a \ cdot a \ cdot a \ cdot a \ cdot a \ cdot a \ cdot a \ cdot a [/ латекс]
Показать решение

Решение

1.{4} [/ латекс]
Разверните выражение. [латекс] 3 \ cdot 3 \ cdot 3 \ cdot 3 [/ латекс]
Умножить слева направо. [латекс] 9 \ cdot 3 \ cdot 3 [/ латекс]
[латекс] 27 \ cdot 3 [/ латекс]
Умножить. [латекс] 81 [/ латекс]

Решение простых уравнений

Решая простое уравнение, думайте об уравнении как о балансе, где знак равенства (=) является точкой опоры или центром.Таким образом, если вы делаете что-то с одной стороной уравнения, вы должны сделать то же самое с другой стороной. Выполнение одного и того же действия с обеими сторонами уравнения (скажем, добавление 3 к каждой стороне) сохраняет уравнение сбалансированным.

Решение уравнения – это процесс получения того, что вы ищете, или решения относительно , с одной стороны от знака равенства, и всего остального с другой стороны. Вы действительно сортируете информацию. Если вы решаете для x , вы должны получить x на одной стороне отдельно.

Уравнения сложения и вычитания

Некоторые уравнения включают только сложение и / или вычитание.

Пример 1

Решите для x .

х + 8 = 12

Чтобы решить уравнение x + 8 = 12, вы должны получить x отдельно с одной стороны. Поэтому вычтите 8 с обеих сторон.

Чтобы проверить свой ответ, просто подставьте свой ответ в уравнение:

Пример 2

Решите относительно и .

y – 9 = 25

Чтобы решить это уравнение, вы должны получить y отдельно с одной стороны. Поэтому прибавьте 9 к обеим сторонам.

Для проверки просто замените y на 34:

Пример 3

Решите для x .

х + 15 = 6

Чтобы решить, отнимите 15 с обеих сторон.

Чтобы проверить, просто замените x на –9:

.

Обратите внимание, что в каждом из приведенных выше случаев используются противоположные операции ; то есть, если в уравнении есть сложение, вы вычитаете с каждой стороны.

Уравнения умножения и деления

Некоторые уравнения включают только умножение или деление. Обычно это происходит, когда переменная уже находится на одной стороне уравнения, но существует либо несколько переменных, например 2 x , либо часть переменной, например

.

или

Таким же образом, как при сложении или вычитании, вы можете умножить или разделить обе части уравнения на одно и то же число, , если оно не равно нулю , и уравнение не изменится.

Пример 4

Решите для x .

3 x = 9

Разделите каждую часть уравнения на 3.

Для проверки замените x на 3:

Пример 5

Решите относительно и .

Чтобы решить, умножьте каждую сторону на 5.

Для проверки замените y на 35:

Пример 6

Решите для x .

Чтобы решить, умножьте каждую сторону на.

Или, без отмены,

Обратите внимание, что слева вы обычно не пишете, потому что это всегда отменяется до 1 x или x .

Комбинации операций

Иногда для решения уравнения требуется более одного шага. В большинстве случаев сначала выполните этап сложения или вычитания. Затем, после того, как вы отсортировали переменные в одну сторону, а числа в другую, умножьте или разделите, чтобы получить только одну из переменных (то есть переменную без номера или 1 перед ней: x , а не 2 x ).

Пример 7

Решите для x .

2 x + 4 = 10

Вычтите 4 с обеих сторон, чтобы получить 2 x на одной стороне.

Затем разделите обе стороны на 2, чтобы получить x .

Чтобы проверить, подставьте свой ответ в исходное уравнение:

Пример 8

Решите для x .

5x – 11 = 29

Добавьте 11 с обеих сторон.

Разделите каждую сторону на 5.

Для проверки замените x на 8:

Пример 9

Решите для x .

Вычтем по 6 с каждой стороны.

Умножаем каждую сторону на.

Для проверки замените x на 9:

Пример 10

Решите относительно и .

Добавьте 8 с обеих сторон.

Умножаем каждую сторону на.

Для проверки замените y на –25:

.

Пример 11

Решите для x .

3 x + 2 = x + 4

Вычтем 2 с обеих сторон (то же самое, что прибавить –2).

Вычтите x с обеих сторон.

Обратите внимание, что 3 x – x совпадает с 3 x – 1 x .

Разделите обе стороны на 2.

Для проверки замените x на 1:

Пример 12

Решите относительно и .

5 y + 3 = 2 y + 9

Вычтем 3 с обеих сторон.

Вычтем 2 y с обеих сторон.

Разделите обе стороны на 3.

Для проверки замените y на 2:

Иногда вам нужно упростить каждую сторону (объединить одинаковые термины) перед фактическим запуском процесса сортировки.

Пример 13

Решите для x .

3 x + 4 + 2 = 12 + 3

Во-первых, упростите каждую сторону.

Вычтем 6 с обеих сторон.

Разделите обе стороны на 3.

Для проверки замените x на 3:

Пример 14

Решите для x .

4 x + 2 x + 4 = 5 x + 3 + 11

Упростите каждую сторону.

6 x + 4 = 5 x + 14

Вычтем 4 с обеих сторон.

Вычтите 5 x с обеих сторон.

Для проверки замените x на 10:

.

словарных задач с двумя неизвестными

Пояснение:

Мы можем решить эту проблему, составив алгебраическое уравнение. Мы знаем, что у Ямаркуса двадцать одна монета, но не знаем, сколько у него каждой монеты. Обычно это означает, что нам нужна переменная.Поскольку мы не знаем, сколько у него десятицентовиков, давайте обозначим d как количество десятицентовиков. Если мы хотим найти количество кварталов, мы вычтем количество десятицентовиков из 21, и полученное число будет количеством кварталов. Следовательно, если у Ямаркуса центов, у него должно быть четверти. Мы можем дважды проверить себя. Если мы сложим количество десятицентовиков и четвертаков, мы получим 21.

Теперь единственная другая информация, которая у нас есть, это то, что вместе все 21 монета в сумме составляют 4 доллара.20. Поначалу это может показаться не слишком полезным, но на самом деле позволяет решить проблему. Мы знаем, что каждый цент стоит 10 центов, поэтому каждый цент Джамаркуса составляет 10 центов к его общей сумме в 4,20 доллара. Кроме того, каждый квартал добавляет 25 центов к его общей сумме. Поскольку у Ямаркуса есть десять центов, и каждая стоит 10 центов, общая стоимость его десяти центов составляет всего доллара. Кроме того, поскольку у Ямаркуса есть четвертины стоимостью 25 центов каждая, общая стоимость всех его четвертей равна. Сумма этих двух итогов должна равняться 4 долларам США.20 или 420 центов. Мы можем записать это в виде следующего уравнения.

Затем мы используем свойство распределения для упрощения, умножая 25 как на 21, так и на.

Дальнейшее упрощение получаем

Затем мы хотим объединить похожие термины ( d s)

Затем нам нужно, чтобы все наши переменные были с одной стороны, а все наши константы – с другой, что мы можем сделать, вычитая 525 с обеих сторон.

, что дает

Теперь нам просто нужно разделить обе части на.

, что дает

Это означает, что у Ямаркуса 7 центов. Если вспомнить, что всего у него было 21 монета, то остается 14 четвертей. У Джамаркуса 7 десятицентовиков и 14 четвертей.

Мы можем дважды проверить себя. Семь десятицентовиков составят 0,70 доллара, а 14 кварталов – 3,50 доллара, в результате чего общая сумма будет правильной – 4,20 доллара.

Решение вопросов Word

МНОГО примеров!

В алгебре мы часто задаем словесные вопросы, например:

Пример: Сэм и Алекс играют в теннис.

В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр.

Сколько игр сыграл Алекс?

Как мы их решаем?

Уловка состоит в том, чтобы разбить решение на две части:

Превратите английский в алгебру.

Затем используйте алгебру для решения.

Превращение английского в алгебру

Превратить английский в алгебру помогает:

  • Прочтите сначала все
  • Сделайте набросок , если возможно
  • Назначьте букв для значений
  • Найдите или разработайте формулы

Вам также следует записать , что на самом деле запрашивается для , чтобы вы знали, куда вы собираетесь и когда вы прибыли!

Также ищите ключевые слова:

Когда вы видите Think

сложить, итого, сумма, увеличить, больше, вместе, вместе, плюс, более

 +

минус, меньше, разница, меньше, уменьшено, уменьшено

–

умноженное на произведение, множитель

 ×

разделенное, частное, на, из, соотношение, соотношение, процент, ставка

 ÷
увеличить или уменьшить геометрия
формулы
Скорость, скорость расстояние
формулы
Сколько дней, часов, минут, секунд время

Ясное мышление

Некоторые формулировки могут быть хитрыми, из-за чего трудно думать «правильно», например:

$

Пример: У Сэма на 2 доллара меньше, чем у Алекса.Как это записать в виде уравнения?

  • Пусть S = долларов, у Сэма
  • Пусть A = долларов у Алекса

Теперь … вот что: S – 2 = A

или должно быть: S = A – 2

или должно быть: S = 2 – A

Правильный ответ: S = A – 2

( S – 2 = – распространенная ошибка, так как в вопросе написано «Сэм … на 2 меньше … Алекс»)

Пример: на нашей улице собак вдвое больше, чем кошек.Как это записать в виде уравнения?

  • Пусть D = количество собак
  • Пусть C = количество кошек

Теперь … это то, что: 2D = C

или должно быть: D = 2C

Подумайте внимательно!

Правильный ответ: D = 2C

( 2D = C – распространенная ошибка, так как вопрос написан «дважды … собаки … кошки»)

Примеры

Давайте начнем с очень простого примера , чтобы увидеть, как это делается:

Пример: прямоугольный сад размером 12 на 5 м, какова его площадь?

Превратите английский в алгебру:

Эскиз:

.

Письма:

  • Используйте w для ширины прямоугольника: w = 12 м
  • Используйте h для высоты прямоугольника: h = 5 м

Формула для площади прямоугольника: A = w × h

Нас спрашивают о Районе.

Решить:

A = ш × в = 12 × 5 = 60 м 2

Площадь 60 кв.м .

Теперь попробуем пример сверху страницы:

Пример: Сэм и Алекс играют в теннис. В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр. Сколько игр сыграл Алекс?

Превратите английский в алгебру:

Письма:

  • Используйте S , чтобы узнать, сколько игр Сэм сыграл
  • Используйте A , чтобы узнать, сколько игр Алекс сыграл

Мы знаем, что Сэм сыграл на 4 игры больше, чем Алекс, поэтому: S = A + 4

И мы знаем, что вместе они сыграли 12 игр: S + A = 12

Нас спрашивают, сколько игр сыграл Алекс: A

Решить:

Начать с: S + A = 12

S = A + 4 , поэтому мы можем
заменить S на “A + 4”: (A + 4) + A = 12

Упростить: 2A + 4 = 12

Вычтем 4 с обеих сторон: 2A = 12-4

Упростить: 2A = 8

Разделите обе части на 2: A = 4

Это означает, что Алекс сыграл 4 игры в теннис.

Проверка: Сэм сыграл на 4 игры больше, чем Алекс, поэтому Сэм сыграл 8 игр. Вместе они сыграли 8 + 4 = 12 игр. Да!

Немного более сложный пример:

Пример: Алекс и Сэм также создают таблицы.


Вместе они делают 10 столов за 12 дней.

Алекс, работая в одиночку, может заработать 10 за 30 дней.

Сколько времени потребуется Сэму, работая в одиночку, чтобы сделать 10 столов?

Превратите английский в алгебру:

Письма:

  • Используйте a , чтобы узнать скорость работы Алекса
  • Используйте s для скорости работы Сэма

12 дней Алекса и Сэма – это 10 столов, поэтому: 12a + 12s = 10

30 дней одного Алекса – это тоже 10 столов: 30a = 10

Нас спрашивают, сколько времени потребуется Сэму, чтобы сделать 10 столов.

Решить:

30a = 10 , поэтому ставка Алекса (столов в день): a = 10/30 = 1/3

Начать с: 12a + 12s = 10

Положите “1/3” для a: 12 (1/3) + 12s = 10

Упростить: 4 + 12s = 10

Вычтем 4 с обеих сторон: 12s = 6

Разделите обе стороны на 12: s = 6/12

Упростить: с = 1/2

Это означает, что ставка Сэма составляет половину стола в день (быстрее, чем у Алекса!).

Итак, 10 столов займет у Сэма всего 20 дней.

Интересно, стоит ли Сэму платить больше?

И еще пример “подстановки”:

Пример: Дженна усиленно тренируется, чтобы пройти квалификацию к Национальным играм.

У нее обычный еженедельный распорядок дня, в одни дни она тренируется по пять часов в день, а в другие – по 3 часа в день.

В общей сложности она тренируется 27 часов в семидневную неделю. Сколько дней она тренируется по пять часов?

Письма:

  • Количество «5 часовых» дней: d
  • Количество «3-х часовых» дней: e

Мы знаем, что в неделе семь дней, поэтому: d + e = 7

И она тренируется 27 часов в неделю, из которых d 5 часов в день и e 3 часа в день: 5d + 3e = 27

Нас спрашивают, сколько дней она тренируется по 5 часов: d

Решить:

d + e = 7

Итак: e = 7 – d

Положим в 5d + 3e = 27 5d + 3 (7 − d) = 27

Упростить: 5d + 21 – 3d = 27

Вычтем 21 с обеих сторон: 5d – 3d = 6

Упростить: 2d = 6

Разделим обе части на 2: d = 3

Количество «5 часовых» дней – 3

Проверка : Она тренируется по 5 часов 3 дня в неделю, поэтому она должна тренироваться по 3 часа в день в остальные 4 дня недели.

3 × 5 часов = 15 часов, плюс 4 × 3 часа = 12 часов дает в сумме 27 часов

Некоторые примеры из Geometry:

Пример: круг имеет площадь 12 мм

2 , каков его радиус?

Письма:

  • Используйте A для Area: A = 12 мм 2
  • Используйте r для радиуса

И формула для площади: A = π r 2

У нас спрашивают радиус.

Решить:

Нам нужно переставить формулу, чтобы найти площадь

Начать с: A = π r 2

Поменять местами стороны: π r 2 = A

Разделим обе части на π : r 2 = A / π

Извлечь квадратный корень из обеих частей: r = √ (A / π)

Теперь мы можем использовать формулу: r = √ (12/ π)

И получаем: r = 1.954 (до 3-х мест)

Пример: куб имеет объем 125 мм

3 , какова его площадь поверхности?

Сделайте быстрый набросок:

Письма:

  • Используйте V для Volume
  • Используйте A для Area
  • Используйте s для длины стороны куба

Формулы:

  • Объем куба: В = с 3
  • Площадь куба: A = 6s 2

У нас спрашивают площадь.

Решить:

Первая тренировка s по формуле объема:

Начать с: В = с 3

Поменять местами стороны: s 3 = V

Извлечь кубический корень с обеих сторон: s = ∛ (V )

И получаем: s = ∛ (125 ) = 5

Теперь мы можем рассчитать площадь поверхности:

Начать с: A = 6s 2

И получаем: А = 6 (5) 2

A = 6 × 25 = 150 мм 2

Пример о деньгах:

Пример: Джоэл работает в местной пиццерии.Когда он работает сверхурочно, он зарабатывает в 1¼ раза больше обычного.

Одну неделю Джоэл проработал 40 часов по обычной ставке, а также 12 часов сверхурочно. Если Джоэл заработал за эту неделю 660 долларов, какова его нормальная ставка заработной платы?

Письма:

  • Обычная ставка оплаты труда Джоэла: N $ в час

Формулы:

  • Джоэл работает 40 часов по цене N долларов в час = 40 долларов США
  • Когда Джоэл работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки = 1 доллар.25N в час
  • Джоэл работает 12 часов по цене 1,25 доллара в час = (12 × 1 фунт) = 15 долларов
    • долларов
  • А вместе он заработал 660 долларов, итак:

40N + $ (12 × 1¼N) = 660 $

У нас спрашивают нормальную ставку зарплаты Джоэла в $ N.

Решить:

Начните с 40N + $ (12 × 1¼N) = 660 $

Упростить: 40N + 15N = 660 $

Еще более упростите: 55 долларов США = 660 долларов США

Разделите обе стороны на 55: $ N = 12 $

Итак, обычная ставка оплаты труда Джоэла составляет 12 долларов в час.

Чек

Обычная ставка оплаты труда Джоэла составляет 12 долларов в час, поэтому его сверхурочная ставка составляет 1¼ × 12 долларов в час = 15 долларов в час.Таким образом, его обычная заработная плата 40 × 12 = 480 долларов плюс его сверхурочная работа в размере 12 × 15 долларов = 180 долларов дает нам в общей сложности 660 долларов

.

Подробнее о деньгах на этих двух примерах, связанных со сложным процентом

Пример: Алекс кладет 2000 долларов в банк под 11% годовых. Сколько это будет стоить через 3 года?

Это формула сложных процентов:

Итак, мы будем использовать эти буквы:

  • Текущая стоимость PV = 2000 долларов США
  • Процентная ставка (в десятичном формате): r = 0.11
  • Количество периодов: n = 3
  • Future Value (желаемое значение): FV

Нас спрашивают о будущей стоимости: FV

Решить:

Начать с: FV = PV × (1 + r) n

Добавьте то, что мы знаем: FV = $ 2000 × (1 + 0,11) 3

Вычислить: FV = $ 2000 × 1,367631

Вычислим: FV = 2735 долларов.26 (с точностью до цента)

Пример: Роджер положил 1000 долларов на сберегательный счет. На заработанные деньги ежегодно начислялись проценты по той же ставке. Через девять лет депозит Роджера вырос до 1 551,33 доллара США

Какова была годовая процентная ставка по сберегательному счету?

Формула сложных процентов:

с:

  • Текущая стоимость PV = 1000 долларов США
  • Процентная ставка (желаемое значение):
    • р.
  • Количество периодов: n = 9
  • Будущая стоимость: FV = 1551 доллар.33

Нас спрашивают о процентной ставке: r

Решить:

Начать с: FV = PV × (1 + r) n

Добавьте то, что мы знаем: 1551,33 доллара = 1000 долларов × (1 + r) 9

Стороны обмена: 1000 $ × (1 + r) 9 = 1551,33 $

Разделите обе стороны на 1000: (1 + r) 9 = 1551,33 доллара США / 1000 долларов США

Упростить: (1 + r) 9 = 1.55133

Корень 9-й степени: 1 + r = 1,55133 (1/9)

Вычислить: 1 + r = 1.05

Вычислить: r = 0,05 = 5%

Таким образом, годовая процентная ставка составляет 5%

Чек : 1000 долларов × (1,05) 9 = 1000 долларов × 1,55133 = 1551,33 доллара

И пример вопроса о соотношении:

Пример: В начале года соотношение мальчиков и девочек в классе было 2: 1

Но теперь, полгода спустя, четыре мальчика покинули класс и появились две новые девочки.Соотношение мальчиков и девочек сейчас составляет 4: 3

Сколько всего студентов сейчас?

Письма:

  • Количество мальчиков сейчас: б
  • Количество девочек сейчас: г

Коэффициент текущей ликвидности 4: 3

b г = 4 3

, который можно переставить на 3b = 4g

На начало года насчитывалось (b + 4) мальчиков и (g – 2) девочек, и соотношение составляло 2: 1

б + 4 г – 2 = 2 1

, который может быть преобразован в b + 4 = 2 (g – 2)

Нас спрашивают, сколько всего студентов сейчас: b + g

Решить:

Начать с: b + 4 = 2 (g – 2)

Упростить: b + 4 = 2g – 4

Вычтем 4 с обеих сторон: b = 2g – 8

Умножаем обе стороны на 3 (получаем 3b): 3b = 6g – 24

Запомнить 3b = 4g : 4g = 6g – 24

Вычтем 6g с обеих сторон : −2g = -24

Разделим обе части на −2: g = 12

Всего 12 девушек !

И 3b = 4g , поэтому b = 4g / 3 = 4 × 12/3 = 16 , так что есть 16 мальчиков

Таким образом, сейчас в классе 12 девочек и 16 мальчиков, всего учащихся – 28 человек.

Чек

Сейчас 16 мальчиков и 12 девочек, поэтому соотношение мальчиков и девочек составляет 16: 12 = 4: 3.
В начале года было 20 мальчиков и 10 девочек, поэтому соотношение было 20: 10 = 2: 1

А теперь несколько квадратных уравнений:

Пример: произведение двух последовательных четных целых чисел равно 168. Что такое целые числа?

Последовательные означают один за другим. И это , даже , так что они могут быть 2 и 4, или 4 и 6 и т. Д.

Мы назовем меньшее целое число n , поэтому большее целое число должно быть n + 2

И нам говорят, что произведение (то, что мы получаем после умножения) равно 168, поэтому мы знаем:

п (п + 2) = 168

Нас спрашивают целые числа

Решить:

Начать с: n (n + 2) = 168

Развернуть: n 2 + 2n = 168

Вычтем 168 с обеих сторон: n 2 + 2n – 168 = 0

Это квадратное уравнение, и есть много способов его решить.Используя метод решения квадратного уравнения, мы получаем −14 и 12.

Проверка −14: −14 (−14 + 2) = (−14) × (−12) = 168 ДА

Проверка 12: 12 (12 + 2) = 12 × 14 = 168 ДА

Итак, есть два решения: -14 и -12 – одно, 12 и 14 – другое.

Примечание: мы также могли попробовать «угадать и проверить»:

  • Можно попробовать, скажем, n = 10: 10 (12) = 120 НЕТ (слишком мало)
  • Затем мы могли бы попробовать n = 12: 12 (14) = 168 ДА

Но если мы не вспомним, что умножение двух отрицаний дает положительный результат, мы можем пропустить другое решение (−14) × (−12).

А:

Пример: вы архитектор. Вашему клиенту нужна комната вдвое больше ширины. Им также нужна веранда шириной 3 метра по длинной стороне.

У вашего клиента 56 квадратных метров красивой мраморной плитки для покрытия всей площади.

Какой должна быть длина комнаты?

Давайте сначала сделаем набросок, чтобы все было правильно !:

Письма:

  • длина помещения: л
  • ширина помещения: Вт
  • Общая площадь с верандой: А,

Мы знаем:

  • ширина комнаты равна половине ее длины: W = ½L
  • общая площадь равна (ширина комнаты + 3), умноженная на длину: A = (W + 3) × L = 56

Нас спрашивают о длине комнаты: L

Решить:

Начать с: (Ш + 3) × Д = 56

Заменитель W = ½L : (½L + 3) × L = 56

Упростить: ½L 2 + 3L = 56

Умножьте все члены на 2: L 2 + 6L = 112

Вычесть 112 с обеих сторон : L 2 + 6L – 112 = 0

Это квадратное уравнение , есть много способов его решить, на этот раз воспользуемся факторизацией:

Начать с: L 2 + 6L – 112 = 0

Два числа, которые умножаются, чтобы получить ac = -112,
и сложить, чтобы получить b = 6, 14 и −8: L 2 + 14L – 8L – 112 = 0

Группа: L (L +14) – 8 (L + 14) = 0

Группа: (L – 8) (L + 14) = 0

Итак, L = 8 или -14

Есть два решения квадратного уравнения, но только одно из них возможно, так как длина комнаты не может быть отрицательной!

Итак, длина помещения 8 м

Чек

L = 8, поэтому W = ½L = 4

Итак, площадь прямоугольника = (W + 3) × L = 7 × 8 = 56

Вот и мы…

… Я надеюсь, что эти примеры помогут вам понять, как отвечать на словесные вопросы. А как насчет практики?

задач со словами для алгебраических предложений – ChiliMath

Алгебраическое предложение , записанное в форме уравнения, включает алгебраические выражения (которые содержат переменные, такие как буквы в алфавите), константы и символ равенства. Каждое алгебраическое предложение может содержать комбинацию алгебраических выражений и констант или только два или более алгебраических выражений.Почти всегда слово «есть» в алгебраическом предложении обозначает символ равенства.

В нашем примере выше алгебраическое предложение « Пять больше, чем дважды число равно сорок три » переводится и записывается в форму уравнения: 2x + 5 = 43.

Но прежде чем мы углубимся в решение словесных задач, связанных с алгебраическими предложениями, очень важно, чтобы мы познакомились с тем, как переводить и писать алгебраические выражения.

Алгебраические выражения

Умение писать и переводить алгебраические выражения – основа написания алгебраических предложений.В конце концов, мы будем использовать эти знания для написания алгебраических уравнений, в которых мы решаем значение неизвестной переменной.

Что такое алгебраическое выражение?

Считайте алгебраическое выражение эквивалентом фразы на английском языке. Он не передает законченной мысли, но является важным строительным блоком при построении предложения. Алгебраические выражения состоят из чисел, переменных и арифметических операций.

Давайте кратко рассмотрим некоторые математические фразы, которые были переведены и записаны в алгебраические выражения.

  • сумма числа и 8 \ large {\, \, \, \ to \, \, \, \, {\ color {red} {c + 8}}}
  • 3 меньше числа \ large {\, \, \, \ to \, \, \, \, {\ color {red} {y – 3}}}
  • произведение 45 и m \ large {\, \, \ , \ to \, \, \, \, {\ color {red} {45m}}}
  • число, деленное на 2 \ large {\, \, \, \ to \, \, \, \, \ Large {\ color {red} {x \ over 2}}}

Перевод и написание алгебраических предложений

Если вы научитесь переводить математические фразы в алгебраические выражения, вам будет легко переводить и записывать алгебраические предложения в форме уравнений.

Например, как записать «, разница 16 и k равно семи » в алгебраическое уравнение?

Давайте разберем это алгебраическое предложение.

Вы можете заметить, что мы перевели «разность 16 и k» в алгебраическое выражение 16-k, а затем использовали символ равенства (=) вместо слова «есть».

Как я упоминал в начале этого урока, слово «есть» в алгебраическом предложении большую часть времени означает символ равенства, который имеет место в этом примере.

Следовательно, мы можем записать это алгебраическое предложение в форме уравнения как 16 – k = 7.

Теперь, когда мы уверены в том, что переводим алгебраические предложения и записываем их в формате уравнения, пора сделать еще один шаг вперед. Мы не только переведем и запишем алгебраические предложения в алгебраические уравнения, но и приступим к их решению.

Примеры словесных задач с алгебраическими предложениями

Главный ключ при решении словесных задач с алгебраическими предложениями – это точно перевести алгебраические выражения, затем правильно составить и записать каждое алгебраическое уравнение.Поступая таким образом, мы можем быть уверены, что решаем правильное уравнение и, как результат, получим правильный ответ для каждой проблемы со словом.

Пример 1: Шесть больше семи раз число тридцать четыре. Найдите номер.

Сначала давайте разберем алгебраическое предложение. Важно, чтобы мы идентифицировали и отделяли алгебраические выражения от констант, а также определяли, предполагает ли проблема равенство между терминами.

Для неизвестного значения мы будем использовать \ large {x} в качестве нашей переменной.

Примечание: Поскольку сложение коммутативно, изменение порядка сумм в левой части уравнения не приводит к изменению суммы. Следовательно, мы также можем записать алгебраическое выражение как 7x + 6 или алгебраическое уравнение как 7x + 6 = 34 вместо этого.

Однако для нашего обсуждения мы будем использовать 6 + 7x = 34 в качестве уравнения.

Исходная задача просит нас найти число, которое в данном случае равно \ large {x}. Итак, наш следующий шаг – найти \ large {x} в нашем уравнении, 6 + 7x = 34.

Решение:

Теперь мы оценим значение \ large {x = 4}, чтобы проверить, удовлетворяет ли найденное число исходному алгебраическому предложению.

Помните, что нас просят найти тождество «числа» в нашем алгебраическом предложении, а НЕ значение переменной \ large {x}. Поэтому было бы неправильно говорить, что \ large {x = 4} – это ответ. Это распространенная ошибка, на которую всегда нужно обращать внимание.

Заменим переменную \ large {x} числом 4, чтобы проверить, дает ли алгебраическое выражение в левой части уравнения также 34.

Да, это так! Это означает, что номер 4 – это ответ .

Пример 2: Разница между тройным числом и пятью равна шестнадцати. Найдите номер.

Слово «разница» в нашем алгебраическом предложении сразу дает нам понять, что мы будем использовать операцию вычитания. Но, в отличие от этого, порядок терминов в выражении имеет значение при вычитании. Поэтому мы должны убедиться, что термины в нашем алгебраическом выражении установлены в правильном порядке.

Еще одно ключевое слово – «раз», означающее, что 3 умножается на число, значение которого в настоящее время неизвестно.

На этот раз давайте использовать \ large {g} в качестве нашей переменной. Начните с правильного перевода алгебраического выражения, затем продолжайте писать уравнение.

Теперь, когда у нас есть уравнение, давайте выясним, что такое неизвестное значение, решив переменную \ large {g}.

Решение:

Как обсуждалось в нашем первом примере, важно проверить, делает ли результат нашего решения истинным алгебраическое уравнение.Для этого я предоставлю вам возможность оценить значение \ large {g = 7}. Не забудьте заменить неизвестное значение переменной \ large {g} числом 7, чтобы увидеть, равна ли левая часть уравнения также 16.

Поскольку исходное алгебраическое предложение требует от нас найти число, тогда ответ будет числом 7 .

Пример 3: Число, уменьшенное вдвое, равно четырем. Найдите номер.

Это алгебраическое предложение довольно интересно, потому что у нас есть не одно неизвестное значение, а два! Сначала у нас есть «число» (неизвестное), затем «половина числа», что означает половину неизвестного.

Ключевое слово «половина из» также указывает на умножение чего-либо на половину, в то время как «уменьшение на» говорит нам, что мы будем вычитать один член из другого.

Чтобы упорядочить наши мысли, давайте разберем это алгебраическое предложение на мясо и картошку.

Возможность разбить наше алгебраическое предложение на основные части позволяет нам внимательно прочитать предложение и понять взаимосвязь между его количествами.

После составления алгебраического уравнения следующим шагом будет его решение относительно \ large {m}.

Решение:

Нам нужно вычислить значение \ large {m = 8}, чтобы проверить, соответствует ли полученное нами число нашему алгебраическому уравнению.

Отлично! Значения с обеих сторон уравнения равны друг другу. Следовательно, число 8 является правильным ответом на наше исходное алгебраическое предложение.

Пример 4: Четырехкратная сумма двойного числа и шесть дает тридцать два. Найдите номер.

Присмотревшись, мы видим несколько ключевых слов, которые помогли бы нам преобразовать это алгебраическое предложение в уравнение.

  • умножить на – означает, что мы будем умножать 4 на количество, «сумма двойного числа и шести»
  • сумма – означает, что нам нужно сложить члены «двойное число» и шесть
  • дважды – означает, что число (неизвестное значение) умножается на 2

Имея это в виду, давайте напишем наше алгебраическое уравнение.

Обратите внимание, что мы использовали переменную \ large {d} в нашем уравнении для обозначения неизвестного значения. Теперь давайте продолжим и решим для \ large {d}, а потом проверим, действительно ли полученное нами значение соответствует уравнению.

Решение:

Вычислите значение \ large {d = 1}:

Похоже, все проходит проверку, поэтому ответ на наше алгебраическое предложение – это число 1 .

Пример 5: Две трети суммы, умноженной на три числа и шесть, равны десяти. Какой номер?

Как вы понимаете, эта задача включает дробь и алгебраическое выражение. Ключевое слово «of» указывает на умножение, поэтому оно говорит нам, что нам нужно умножить дробь \ large {2 \ over 3} на сумму двух заданных величин («три раза больше числа» и шесть).

Давайте продолжим и напишем наше алгебраическое уравнение. Мы будем использовать переменную \ large {y} в качестве заполнителя для нашего «числа», значение которого в настоящее время неизвестно.

Отлично! Мы можем преобразовать наше алгебраическое предложение в уравнение. Пришло время решить для \ large {y}, тогда я оставлю это на ваше усмотрение, чтобы вы проверили, соответствует ли число, которое мы находим как значение \ large {y}, алгебраическое уравнение истинным.

Решение:

После того, как вы оцените \ large {y = 3}, вы увидите, что ответ на нашу задачу со словами – это действительно , число 3 .

Пример 6: Двойная разница между числом и тремя на четыре больше, чем число. Найдите номер.

У нас есть пример, который немного отличается от словесных задач, которые мы рассмотрели до сих пор. В этом алгебраическом предложении обе части уравнения содержат алгебраическое выражение. Однако имеющиеся ключевые слова помогут нам правильно преобразовать его в уравнение, поэтому беспокоиться не о чем.

Ключевые слова:

  • дважды – означает, что мы умножим количество (разность числа и трех) на 2
  • разность – говорит нам использовать операцию вычитания между нашим неизвестным значением («числом») и тремя
  • больше – означает, что нам нужно добавить четыре к нашему неизвестному значению

Давайте решим наше неизвестное значение \ large {a}, а затем проверим, что наш результат делает алгебраическое уравнение истинным.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *