Уравнение 4 класс по математике с решением и ответами: Урок математики по теме “Решение уравнений” (4-й класс)
Урок математики по теме “Решение уравнений” (4-й класс)
- Золотова Юлия Михайловна
Разделы: Начальная школа
Класс: 4
Цель: Рассмотреть практические способы решения уравнений, требующих выполнения более одного арифметического действия.
Оборудование урока: компьютерная презентация устного счета, карточки с уравнениями, карточки трех ступеней для самостоятельной работы над задачами, кубик обратной связи
Ход урока
1. Оргмомент
Проверка готовности к уроку. В тетрадях записывается число, классная работа.
2. Устный счет (компьютерная презентация, слайд №1)
Игра «Соревнование улиток»
 Две улитки должны подняться до вершины горы. Кто же из них окажется первой? Наша с вами улитка под №1 слева. Улитка делает шаг, только если мы правильно найдем значение выражения.
Две улитки должны подняться до вершины горы. Кто же из них окажется первой? Наша с вами улитка под №1 слева. Улитка делает шаг, только если мы правильно найдем значение выражения.Вы готовы?
Сигнал к старту уже прозвучал. Повторяем порядок действий и называем правильные значения выражений.
(122 + 18) : 70 = 2
(64 : 8 + 20) : 7 = 4
20 · (26 + 14) : 100 = 8
1 · (30 + 2) – 4 · 4 = 16
5 · 4 + 12 = 32
(400 – 300) – 36 = 64
У нас получился ряд чисел.
2, 4, 8, 16, 32, 64
Какую закономерность в составлении этого ряда заметили? (каждое следующее число увеличено в два раза)
Продолжите этот ряд чисел и назовите не менее трех следующих чисел. (128, 256, 512…)
Молодцы! Мы решали все правильно, поэтому наша улитка на вершине горы.
2 4 8 16 32 64 128 256 512
У Р А В Н Е Н И Е
Что называется уравнением?
Что называется корнем уравнения?
Что значит решить уравнение?
Мы уже умеем решать простые уравнения, а сегодня мы познакомимся с решением сложных уравнений, где надо выполнить несколько арифметических действий.
3. Решение простых уравнений. Подготовка к введению нового материала.
На магнитной доске в произвольном порядке карточки с уравнениями.
На какие группы можно разделить все эти уравнения? (уравнения распределяются в 3 столбика)
1) 7000 – х = 2489
7000 – х = 3489
7000 – х = 1689
Найдите среди них уравнение с наибольшим корнем и решите его (один ученик у доски)
2) 71 : х = 20 + 7
х : 3 = 16 + 11 ( это уравнения, в правой части которых выражение)
Можем ли мы решить уравнения второго столбика?
Решите любое из уравнений, но замените в правой части сумму на разность. Корень уравнения при этом должен остаться прежним. (два ученика у доски)
3) ( 490 – х ) – 250 = 70
Посмотрите на оставшееся уравнение. Легко ли нам его решить? Почему?
Легко ли нам его решить? Почему?
4. Работа над новым материалом. (фронтальная беседа с классом, в ходе которой рассматривается решение уравнения)
( 490 – х ) – 250 = 70
490 – х = 70 + 250
490 – х = 320
х = 170
( 490 – 170 ) – 250 = 70
70 = 70
Ответ: 70
5. Закрепление.
1) Решение уравнения (один из сильных учеников у доски)
5 · а + 500 = 4500 : 5
5 · а + 500 = 900
5 · а = 900 – 500
5 · а = 400
а = 400 : 5
а = 80
5 · 80 + 500 = 900
900 = 900
Ответ: 80
2) № 399
Решите уравнения.
а + 156 = 17 ∙ 20 (1604 – у) – 108 = 800
252 : 36 ∙ х = 560 103300 : (х + 297) = 25 ∙2
Мы решили два новых сложных уравнения. Посмотрите на уравнения, которые перед вами. Все ли они сложные? Какое уравнение лишнее? Почему? Остальные – в левой части выражение в несколько действий. Найдите среди них с таким порядком действий, которое уже встречалось сегодня.
Найдите среди них с таким порядком действий, которое уже встречалось сегодня.
(1604 – у) – 108 = 800
1604 – у = 800 + 108
1604 – у = 908
у = 1604 – 908
у = 696
(1604 – 696) – 108 = 800
800 = 800
Ответ: 696
Уравнение решают в парах. Один ученик на развороте доски для последующей проверки.
6. Решение задачи
Самостоятельная работа по карточкам 3 ступеней. Выполнив задание первой ступени, ученик переходит к выполнению задания второй ступени, затем третьей.( различные способы дифференцированной работы)
| 1 ступень | 2 ступень | 3 ступень |
Школьники должны были высадить 25700 саженцев деревьев. После того, как они высадили часть саженцев, им осталось посадить еще12350 деревьев. Сколько деревьев они уже высадили? Сколько деревьев они уже высадили?Реши задачу, составив уравнение |
Измени задачу так, чтобы она решалась уравнением, в правой части которого было бы выражение. Запиши это уравнение и реши его. |
Школьники должны были высадить 25700 саженцев деревьев. После того, как они высадили несколько саженцев липы и 8580 кленов, им осталось высадить 12350саженцев. Сколько лип они уже посадили? |
Проверка фронтальная
1) 25700 – х = 12350
х = 25700 – 12350
х = 13350
25700 – 13350 = 12350
12350 = 12350
Ответ: 13350 саженцев.
2) 25700 – х = 12000 + 350
3) 25700 – (х + 8580) = 12350
х + 8580 = 25700 – 12350
х + 8580 = 13350
х = 13350 – 8580
х = 4770
25700 – (4770 + 8580) =12350
12350 = 12350
4) А какое еще уравнение можно было составить?
(25700 – х) – 8580 = 12350
Мы решили три задачи, составив три уравнения. Какое уравнение отнесем к сложным? Почему?
Какое уравнение отнесем к сложным? Почему?
7. Домашнее задание.
Рассмотреть, как решались уравнения в учебнике на стр. 106 и решить уравнение в тетради на печатной основе № 44 (а).
Решить задачу № 47. Дополнительное задание: какие еще вопросы можно поставить к этой задаче?
8. Итог урока.
Какие уравнения учились решать на уроке?
Трудно было?
Кому было легко?
Математика в 4-м классе по теме “Решение уравнений. Ознакомление со способом решения задач с помощью уравнения”
Цель: формировать у школьников умение решать уравнения, составлять по данному условию и решать их.
Задачи: развивать умение составлять
уравнения, читать и решать их; научить детей
решать задачи способом составления уравнения;
закреплять понятия “Уравнение”, “корень
уравнения”, “решение уравнения”; воспитывать
аккуратность, коллективизм и взаимопомощь среди
ребят.
Оборудование:
- индивидуальные карточки для вычислительных навыков по (вариантам), учебник математики, индивидуальная тетрадь на печатной основе, плакат – схема задачи, уравнения, музыкальный центр, плакат “Гимнастика для глаз”.
- Н.Б.Истомина Математика 4 класс Издательство “Ассоциация XXI век” Смоленск 2003 г.
- Н.Б.Истомина Тетрадь по математике 2 “Ассоциация XXI век” Смоленск 2005 г.
Ход урока
I. Организационный момент
II. Целеполагание
– Добрый день. Урок математики
– Сегодня, ребята, на уроке мы продолжим развивать умения при составлении уравнения, читать их и решать. И познакомимся со способом решения задач с помощью уравнения.
III. Совершенствование вычислительных навыков
Тема: Внетабличное умножение и деление
Индивидуальные задания по вариантам.
А сейчас мы потренируемся в устных вычислениях, ведь они нам пригодятся в течении всего урока.
Вариант 1:
- Как называются числа при умножении?(множитель, множитель, значение произведения)
- Как найти неизвестный множитель?(Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель, т.е. 60: 5 = 12)
- Смотрим на циферблат. 12 соответствует буква “в” ( Ваш ответ: Всемирный потоп)
Рассказ учителя: в мифологии ряда народов “божья кара”, ниспосланная на человечество и на всё живое на земле. По библейскому мифу, во время всемирного потопа спаслись в ковчеге праведник Ной с семьёй и по паре “от всякой плоти”
Вариант 2:
Смотрим на алгоритм первого ряда. Как найдено
число 19? (171 нужно разделить на 9, получится 19. Это
число соответствует букве “А”. Справа находим
данный ответ и подписываем нужную букву).
Справа находим
данный ответ и подписываем нужную букву).
( Ваш ответ: Пиррова победа)
Рассказ учителя: 302 – 307 года до н. э. царь Эпир воевал на стороне г. Тарента с Римом. Одержал победы при Геракле и Аускулуме, последнюю ценой огромных потерь. Все воины погибли – пиррова победа одержана.
(Дети работают самостоятельно, учитель оказывает индивидуальную помощь).
– У кого получилось?
Для того, чтобы найти свою ошибку проверьте по данному алгоритму.(на доску учитель помещает две таблицы с правильными ответами
IV. Работа в рабочих тетрадях. Повторение об уравнении.
-Я задумала число. Если увеличить его на 300, то получится наибольшее 3х значное число.
-Какое число я задумала?
-Запишите свои записи на доске.
(дети записывают свои варианты: х+300=999, х+300=999, х+300=999),
-Что это? (уравнение)
-Что значит решить уравнение? ( решить уравнение – значит найти такое число, которое нужно записать вместо буквы, чтобы получить верное числовое равенство)
-Как называют это число?( это число называют корнем уравнения)
-Найдите корень уравнения. Чему он равен?
(корень уравнения равен 699)
Чему он равен?
(корень уравнения равен 699)
V. Работа с учебником
Прочитаем задание № 477 стр. 187
– Можно ли утверждать, что значение х во всех уравнениях одинаково:
Х (35+4) = 234
Х (30+9) = 200+34
Х (34+5) = 210+24
– Ваши суждения?(я думаю, что можно утверждать, что значение х во всех уравнениях одинаков)
– Чтобы ваши утверждения подтвердить мы, конечно же, уравнения решим. Наша задача: прочитать уравнение, правильно записать, найти корень уравнения.
1 ряд – первое уравнение, 2ряд – второе, 3ряд – третье уравнение.
Кто желает работать у доски?
( у доски работают три человека, затем они объясняют решение каждого уравнения. Ответ ученика с третьего ряда:
Чтобы решить данное уравнение, нужно его преобразовать
| Х (34 + 5) = 210 + 24 | |
| Х 39 = 234 | получилось простое уравнение с |
| Х = 234 : 39 | неизвестным множителем.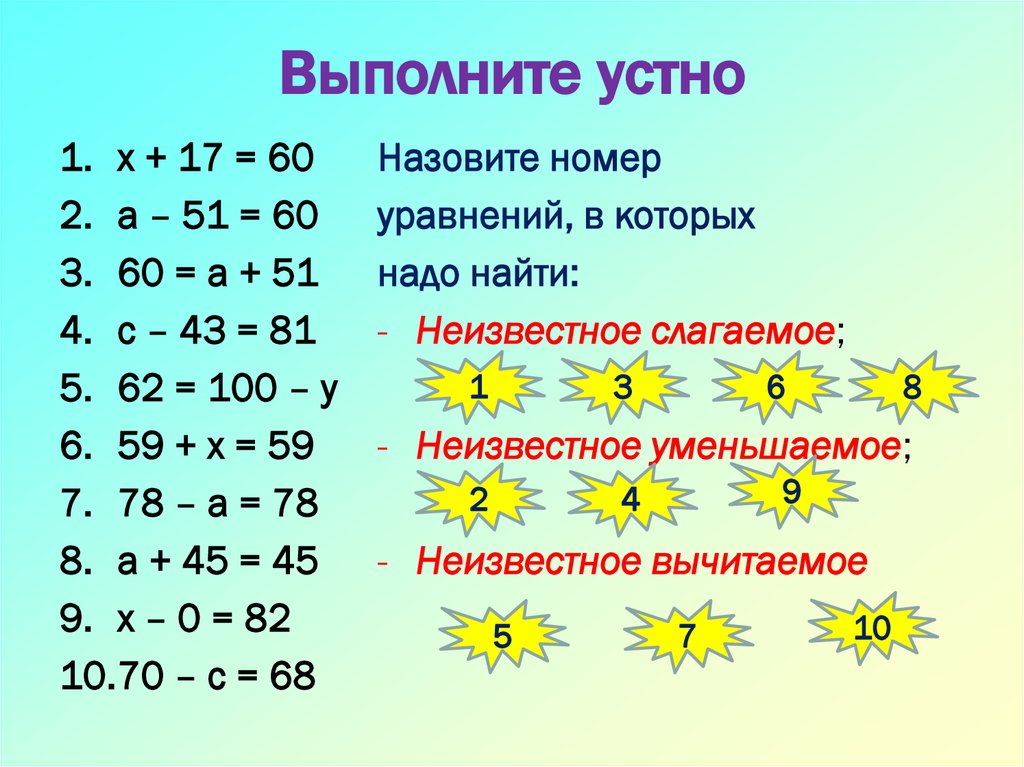 Чтобы Чтобы |
| Х = 6 | найти неизвестный множитель, |
| 6 (34+5) = 210+24 | нужно значение произведения |
| 234 = 234 | разделить на известный множитель |
Корень уравнения равен шести. Теперь вместо х подставляем число шесть и делаем проверку).
– Какой можно сделать вывод? ( утверждения подтвердились, значение х во всех уравнениях одинаково, оно равно шести).
VI. Работа с тетрадью на печатной основе.
Т.с 21 № 58
Прочитайте задание: Подчеркни уравнения, которые имеют одинаковые корни. Реши любое из этих уравнений.
Первый вариант выполняет работу под буквой “б”, второй вариант выполняет работу под буквой “а”,
| а) х: 27 = 120 + 29 х : (3 9) = 130 + 270 х : (9 3) = 400 х : (54 :2) =200 2 |
б) х (47 – 35) = 312 х (40 – 27) = 300 + 12 х (43 – 30) = 290+22 х : 13 = 312 |
Ваша задача: нужно найти уравнения, которые
имеют одинаковые корни и одно из них решить.
– А может кто – то решит уравнение из другого варианта?
Самостоятельная работа
Учитель следит за выполнением задания каждого ученика. Оказывается соответствующая помощь.
Проверка задания первого варианта(мы подчеркнули второе и третье уравнения, корень уравнения равен 24)
Проверка задания второго варианта(мы подчеркнули второе, третье, четвертое уравнения, корень уравнения равен 10800)
Учитель проверяет несколько работ учащихся и выставляет отметки.
VII. Физминутка
1. Гимнастика для глаз
- Ведем глазами по контуру красного круга вправо, затем влево
- Играем глазами (смотрим на красный круг, зеленый, синий и т. Д.)
- Выбрали для себя цвет.(звучит спокойная музыка, ученица читает стихотворение В. Жуковского “Песня”)
VIII. Знакомство со способом решения задач с
помощью уравнения.
Учебник с 187 № 479. Читаем задачу
Наша цель – научиться решать задачи способом составления уравнений.
На доске схема к задаче №479 и варианты уравнения.
Ваша задача – рассмотри схему и выбери уравнения, которые соответствуют данной задачи.
(дети дают разные варианты ответов)
- Перед нами встала проблема, какое же уравнение соответствует схеме?
- Из скольких частей состоит отрезок? (из двух частей).
- Чему равна (как обозначена) первая часть отрезка? (х)
- Чему равна вторая часть отрезка? (12).
- Как обозначить весь отрезок? (х+12)
- А чему равен весь отрезок? (34)
- Какое получится уравнение? (Х+12 = 34)
- Что такое х в этом уравнении? (дети изучающие немецкий язык)
- Что означает 12? (дети изучающие английский язык)
- Что означает 34? (число учеников в классе)
Решение составленного уравнения (1 человек у доски с объяснением)
Х+12 = 34
Х = 34 – 12
Х = 22
22 + 12=34
34 = 34
Ответ: 34 человека изучают немецкий язык.
IX. Закрепление. Т.с.21 №57
Читаем задание. Выбери уравнения, которые соответствуют данной схеме, и реши их.
Задание усложняется – составить условие задачи к данным уравнениям. Учитель контролирует решение задания.
– Какие уравнения вы выбрали к данной схеме?
(уравнения 1, 4; дети составляют условия задачи к данному уравнению, решение данных уравнений в тетради)
Учитель и учащиеся выслушивают ответы детей по составлению и решению задач, выставляются отметки.
X. Рефлексия.
- Чему учились на уроке?
- Что помогает усваивать новый материал?
- Какое задание вызвало у вас наибольший интерес?
- Какое задание вызвало у вас затруднение?
- С какого задания вы бы хотели начать завтрашний день?
– Вы очень хорошо работали на уроке. Спасибо.
Сложные уравнения 4 класс с ответами
А 8 математика
Решить уравнение – значит найти значение неизвестного числа (х, у), при котором равенство будет верным.
Простые уравнения состоят из одного действия.
Сложные уравнения содержат в себе несколько арифметических действий.
Как решать простые уравнения мы подробно рассмотрели в статье «от простого к сложному 2-4 класс»
Сложные уравнения решают, следуя алгоритму:
Упростить уравнение: найти значение той части, выражения, которое можно решить, привести к ответу Перенести неизвестное (х) в одну сторону, цифры в другую, на основе знания нахождения компонентов действий. Проверить (пересчитать) правую и левую часть, они должны быть равны. Перепроверять ребята не любят, это и бывает ошибкой на контрольной или самостоятельной работе.
Приведем примеры сложных уравнений с решениями и ответами:
1) Реши уравнения: (Х + 127) х 12 = 8460 (169 х с) : 35 = 845
Ответ: (Х + 127) х 12 = 8460 (169 х с) : 35 = 845
Х + 127 = 8460:12 169 * с = 845*35
Х + 127 = 705 169 *с = 29575
Х = 705 – 127 С = 29575:169
2) Реши уравнения: 3074 + а : 8 = 3524 Х : 8 – 895 = 779
Ответ: 3074 + а : 8 = 3524 Х : 8 – 895 = 779
А : 8 = 3524-3074 х : 8 = 779 +895
А : 8 = 450 х : 8 = 1674
А = 3600 х = 13392
3) Реши уравнения: с * 215 – 4933 = 63222 (а + 532) * 306 = 290700
Ответ: с * 215 – 4933 = 63222 (а + 532) * 306 = 290700
С * 215 = 63222+4933 а + 532 = 290700 : 306
С * 215 = 68155 а + 532 = 950
4) Реши уравнения: 5890 – а : 4 = 5290 6834 – (Х :245) = 6816
Ответ: 5890 – а : 4 = 5290 6834 – (Х :245) = 6816
5890 – 5290 = а : 4 6834 – 6816 = х : 245
600 = а : 4 18 = х : 245
А = 2400 х = 4410
5) Реши уравнения: 8345 + Х : 716 = 8271 Х : 158 + 106 = 315
Ответ: 8345 + Х : 716 = 8271 Х : 158 + 106 = 315
Х:716 = 8345 – 8271 х : 158 = 315 — 106
X:716 = 74 х: 158 = 209
Х = 716*74 х = 209*158
Х = 52984 х = 33022
6) Реши уравнения: 75 х Х + 8569 = 17869 7 х (5115 – с) = 9156
Ответ: 75 х Х + 8569 = 17869 7 х (5115 – с) = 9156
75 х Х = 17869-8569 5115 – с = 9156 : 7
75 х Х = 9300 5115 – с = 1308
Х = 9300:75 с = 5115 — 1308
7) Реши уравнения: 480 – х : 325 = 396 х : 94 + 36 = 54
Ответ: 480 – х : 325 = 396 х : 94 + 36 = 54
Х : 325 = 480-396 х : 94 = 54-36
Х : 325 = 84 х : 94 = 18
Х = 27300 х = 1692
8) Реши уравнение: y + (127 – 127) = 72782 : 241 х : (160 : 8) = 0
Ответ: y + (127 – 127) = 72782 : 241 х : (160 : 8) = 0
У + 0 = 302 х : 20 = 0
У = 302-0 х = 20 * 0
9) Запиши предложение уравнением и реши его: число 30 увеличили на произведение числа 8 и неизвестного числа и получили 78.
10) Запиши предложение уравнением и реши его: Разность неизвестного числа и 15 уменьшили в 2 раза и получили 20.
Решать с ребенком необходимо до автоматизма, до тех пор пока он не усвоит алгоритм решения сложных уравнений и не сделает это самостоятельно.
Приведем примеры сложных уравнений с решениями и ответами.
Koncpekt. ru
05.11.2017 0:45:01
2017-11-05 00:45:01
Источники:
Https://koncpekt. ru/nachalnye-klassy/konspekty-urokov/matematika-4klass/3771-slozhnye-uravneniya-4-klass-s-otvetami. html
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; }
А 8 математика
Тип 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Тип 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
Источник: ЕГЭ по математике 28.06.2017. Резервный день. Вариант 501 (C часть), Задания 13 (С1) ЕГЭ 2017
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Тип 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19. 06.2013. Основная волна, резервная волна. Центр. Вариант 502, Задания 13 (С1) ЕГЭ 2013
06.2013. Основная волна, резервная волна. Центр. Вариант 502, Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Тип 12 № 502094
Тип 12 № 517739
Б Поскольку отрезку принадлежит единственный корень 2.
Ege. sdamgia. ru
02.07.2017 6:45:09
2017-07-02 06:45:09
Источники:
Https://ege. sdamgia. ru/test? theme=186
Найди значения выражений а-8 и а 10 при а 12, а 20, а 28, а 43. ответ на » /> » /> .
А 8 математика
Найдем значение данных буквенных выражений, для этого подставим значение буквенной переменной, которое нам дано. Для этого будем использовать общепринятое правило записи, если. то.
Получаем:
А — 8, если а = 12, то 12 — 8 = 4
А — 8, если а = 20, то 20 — 8 = 12
А — 8, если а = 28, то 28 — 8 = 20
А — 8, если а = 43, то 43 — 8 =35
А + 10, если а = 12, то 12 + 10 = 22
А + 10, если а = 20, то 20 + 10 = 30
А + 10, если а = 28, то 28 + 10 = 38
А + 10, если а = 43, то 43 + 10 = 53
- Написать правильный и достоверный ответ; Отвечать подробно и ясно, чтобы ответ принес наибольшую пользу; Писать грамотно, поскольку ответы без грамматических, орфографических и пунктуационных ошибок лучше воспринимаются.
- Списывать или копировать что-либо. Высоко ценятся ваши личные, уникальные ответы; Писать не по сути. «Я не знаю». «Думай сам». «Это же так просто» — подобные выражения не приносят пользы; Писать ответ ПРОПИСНЫМИ БУКВАМИ; Материться.
 Это невежливо и неэтично по отношению к другим пользователям.
Это невежливо и неэтично по отношению к другим пользователям.Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Отвечать подробно и ясно, чтобы ответ принес наибольшую пользу;.
Uchi. ru
09.04.2018 17:42:22
2018-04-09 17:42:22
Источники:
Https://uchi. ru/otvety/questions/naydi-znacheniya-vyrazheniy-a-8-i-a-10-pri-a-12-a-20-a-28-a-43
Задачи по математике 4 класс 4 четверть: Контрольные работы по математике для 4 класса за 4 четверть (с ответами по паролю) — ЭкоДом: Дом своими руками
Содержание
Контрольная работа с решениями по математике 4 класс 4 четверть.

Математика 4 класс
Контрольные работы
Вариант 1
1. Выполни деление:
| 288648 : 72 = | 61983 : 97 = |
Решение:
288648 : 72 = 4009 61983 : 97 = 639
2. Реши задачу:
Если в каждом зале помещать по 28 картин, то все картины займут 48 залов. Сколько залов займут все эти картины, если в каждый зал помещать по 24 картины?
Решение:
- 1) 28 * 48 = 1344
- 2) 1344 : 24 = 56
- Ответ: 56 залов.
3. Сравни и поставь знак >, < или = :
| 430 дм … 34 м | 3 т 917 кг … 3 т 719 кг |
Решение:
430 дм > 34 м 3 т 917 кг > 3 т 719 кг
4.
Восстанови пропущенные числа:
Решение:
Вариант 2
1.
 Выполни деление:
Выполни деление:| 25543 : 89 = | 27360 : 38 = |
Решение:
25543 : 89 = 287 27360 : 38 = 720
2. Реши задачу:
Если на каждую страницу помещать 32 строки, то весь текст займет 52 страницы. Сколько страниц займет этот текст, если на каждую страницу помещать 26 строк?
Решение:
- 1) 32 * 52 = 1664
- 2) 1664 : 26 = 64
- Ответ: 64 страницы.
3. Сравни и поставь знак >, < или = :
| 72 т … 720 ц | 4 км 615 м … 4651 м |
72 т = 720 ц 4 км 615 м < 4651 м
4. Восстанови пропущенные числа:
Решение:
Вариант 3
1. Выполни деление:
| 53816 : 56 = | 62652 : 69 = |
Решение:
53816 : 56 = 961 62652 : 69 = 908
2.
 Реши задачу:
Реши задачу:
Если в каждый ряд ставить по 18 стульев, то все стулья уместятся в 24 ряда. Сколько рядов займут все стулья, если в один ряд ставить 16 стульев?
Решение:
- 1) 18 * 24 = 432
- 2) 432 : 16 = 27
- Ответ: 27 рядов.
3. Сравни и поставь знак >, < или = :
| 241 ч … 10 сут. | 320 кг … 32 ц |
Решение:
241 ч > 10 сут. 320 кг = 32 ц
4. Восстанови пропущенные числа:
Решение:
Вариант 4
1. Выполни деление:
| 43992 : 78 = | 13630 : 29 = |
Решение:
43992 : 78 = 564 13630 : 29 = 470
2. Реши задачу:
Если на каждую страницу помещать 12 марок, то все марки займут 52 страницы. Сколько страниц займут эти марки, если на каждую страницу помещать 13 марок?
Сколько страниц займут эти марки, если на каждую страницу помещать 13 марок?
Решение:
- 1) 12 * 52 = 624
- 2) 624 : 13 = 48
- Ответ: 48 страниц.
3. Сравни и поставь знак >, < или = :
| 37 дм2 … 370 см² | 150 мин … 3 ч |
Решение:
37 дм² = 370 см² 150 мин < 3 ч
4. Восстанови пропущенные числа:
Решение:
На странице использованы материалы из книги С. И. Волковой «Математика. Контрольные работы. 1-4 классы» 2008г.
Простые задачи
Составные задачи
Самостоятельные работы и задачи по математике для 4 класса за 1, 2, 3 и 4 четверти по учебнику Моро М.И.
Дата публикации: .
Самостоятельные на темы: «Разряды числа», «Умножение и деление», «Выражения» и пр.
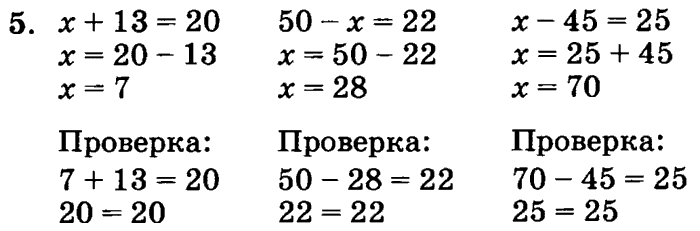
ЗАДАНИЯ по ТЕМАМ:
| – «Нумерация чисел до 1000 и больше 1000.» – «Величины. Сравнение и переводы величин. Общие задачи на величины.» – «Длина, единицы и меры длины, измерение длины.» – «Площадь и периметр, нахождение и расчет площади и периметра.» – «Объем, единицы объема, измерение объема» – «Геометрические задачи» – «Скорость, время,расстояние.» – «Сложение многозначных чисел.» – «Вычитание многозначных чисел.» – «Сложение и вычитание многозначных чисел.» – «Умножение и деление многозначных чисел.» – «Деление многозначных чисел, свойства деления.» – «Дроби, решение дробей, сложение и вычитание дробей.» – «Уравнения, решение уравнений.» – «Устный счет.» – «Логические задачи.» – «Текстовые задачи.» |
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать: Задачи и примеры для самостоятельных работ по математике для 4 класса
1 и 2 четверти (PDF)
3 и 4 четверти (PDF)
Обучающие пособия и тренажеры для 4 класса в интернет-магазине «Интеграл»
М. И. Моро
И. Моро
Л. Г. Петерсон
Б.П.Гейдмана
Т.Е.Демидовой
Самостоятельная работа №1 (1 четверть)
Вариант I.
1. Представьте эти словосочетания в виде числа.
а) Триста пять тысяч сорок девять __________________
б) Пятьдесят три тысячи восемьсот три __________________
в) Четырнадцать тысяч семьсот три __________________
2. Решите примеры.
| а) 198 + 755 = | б) 473 + 97 = | в) 414 + 144 = |
| г) 734 — 267 = | д) 888 — 561 = | е) 873 — 728 = |
| ж) 7 * 9 = | з) 1 * 6 = | к) 9 * 13 = |
| л) 24 : 8 = | м) 21 : 3 = | н) 0 : 7 = |
Вариант II.
1. Представь эти словосочетания в виде числа.
а) Пятьсот сорок тысяч семьдесят __________________
б) Четырнадцать тысяч девяносто восемь __________________
в) Восемь тысяч триста __________________
2. Решите примеры.
| а) 293 + 145 = | б) 289 + 461 = | в) 414 + 580 = |
| г) 534 — 119 = | д) 712 — 245 = | е) 473 — 401 = |
| ж) 17 * 5 = | з) 11 * 6 = | к) 9 * 4 = |
| л) 50 : 5 = | м) 22 : 11 = | н) 0 : 12 = |
Вариант III.
1. Представь эти словосочетания в виде числа.
а) Двадцать три тысячи один __________________
б) Сто тысяч восемьдесят восемь __________________
в) Пятнадцать тысяч триста одиннадцать __________________
2. Решите примеры.
| а) 401 + 98 = | б) 473 + 399 = | в) 554 + 295 = |
| г) 734 — 395 = | д) 643 — 402 = | е) 873 — 556 = |
| ж) 8 * 3 = | з) 11 * 8 = | к) 3 * 14 = |
| л) 3 : 1 = | м) 41 : 41 = | н) 0 : 4 = |
Самостоятельная работа №2 (1 четверть)
Вариант I.
1. Решите примеры.
| а) 2 * 3426 = | б) 3 * 789 = | в) 9 * 657 = | г) 8 * 4895 = |
| д) 2088 : 4 = | е) 2739 : 3 = | ж) 5936 : 2 = | з) 8470 : 5 = |
2. Реши задачу.
Велосипедист проехал 60 километров за 3 часа. Сколько километров он проедет за 7 часов?
Вариант II.
1. Решите примеры.
| а) 5 * 4432 = | б) 6 * 434 = | в) 7 * 668 = | г) 8 * 8764 = |
| е) 6032 : 4 = | ж) 1071 : 3 = | з) 3452 : 2 = | к) 6850 : 5 = |
2. Реши задачу.
Машина проезжает 25 километров за 30 минут. Сколько километров она преодолеет за 4 часа?
Вариант III.
1. Решите примеры.
| а) 5 * 324 = | б) 6 * 6792 = | в) 7 * 4056 = | г) 8 * 3784 = |
| д) 4484 : 4 = | е) 2733 : 3 = | ж) 5962 : 2 = | з) 5965 : 5 = |
2. Реши задачу.
Лыжник пробежал 7 километров за 15 минут. Какое расстояние он пробежит за 1 час 30 минут?
Самостоятельная работа №3 (2 четверть)
Вариант I.
1. Решите примеры.
| а) 4 754 + 37 324 = | б) 3 846 + 65 792 = | в) 74 294 — 4 056 = | г) 8 495 — 7 784 = |
2. Реши:
В первый день школьники собрали 3 т 540 кг яблок. Во второй день – на 300 кг меньше. Весь урожай упаковали в мешки по 30 кг. Сколько мешков понадобилось?
Во второй день – на 300 кг меньше. Весь урожай упаковали в мешки по 30 кг. Сколько мешков понадобилось?
3. Найдите значение выражения: 475 * 8 + (3 745 — 2 495) =
4. Реши:
Машина проехала 450 км со скоростью 90 км/час, затем она проехала ещё 40 минут. Сколько минут она потратила на весь путь?
Вариант II.
1. Решите примеры.
| а) 14 495 + 12 333 = | б) 23 846 + 29 792 = | в) 7 294 — 4 996 = | г) 6 935 — 3 564 = |
2. Реши:
На складе было 3 т 340 кг сахара. Привезли ещё 10 мешков по 45 кг. Сколько кг сахара стало на складе?
3. Найдите значение выражения: 295 * 7 + (9 753 — 1 294) =
4. Реши:
Локомотив проехал 4 часа со скоростью 70 км/ч, затем он снизил скорость на 10 км/час и проехал ещё 2 часа. Сколько км проехал локомотив?
Вариант II.
1. Решите примеры.
| а) 14 394 + 17 394 = | б) 5 436 + 27 452 = | в) 19 234 — 14 396 = | г) 28 885 — 17 724 = |
2. Реши:
Реши:
В школу привезли 1 т 540 кг картофеля. Каждый день в школе съедали по 73 кг. Сколько картофеля осталось через 9 дней?
3. Найдите значение выражения: 389 * 5 + (3 555 — 1 395) =
4. Реши:
Велосипедист проехал 4 часа со скоростью 40 км/ч, затем он проехал ещё 1 час со скоростью 20 км/час. Сколько км преодолел велосипедист?
Самостоятельная работа №4 (2 четверть)
Вариант I.
1. Решите примеры.
| а) 579 * 4 = | б) 921 * 5 = | в) 453 * 9 = | г) 614 * 8 = |
| д) 3 672 : 4 = | ж) 7 488 : 8 = | з) 6 417 : 9 = | к) 4 492 : 2 = |
2. Решите примеры.
| а) 5 932 — 412 * 4 + 3 669 : 3 = | б) 4 290 : (6 — 1) + 2 305 * 7 = |
| в) 6 684 : 6 — 339 + 3 * 289 = | г) 7 * (674 — 278) + 6 777 : 9 = |
3. Решите уравнения.
| а) 3 * 682 = X — 1 301 | б) 6 300 : 6 = Y — 2 455 |
4. Реши:
Реши:
Каждая корова дает примерно 16 литров молока в день. Сколько молока фермер получает за неделю, если у него всего 9 коров?
5. Посмотрите внимательно на рисунок и выпишите.
а) Номера прямоугольных треугольников: _______
б) Номера тупоугольных треугольников: _______
в) Номера остроугольных треугольников: _______
6. На рисунке изображены 2 прямоугольника и квадрат, даны их размеры. Рассчитайте периметры и площади фигур, изображенных на рисунке. Найдите общую площадь всех фигур.
Вариант II.
1. Решите примеры.
| а) 482 * 6 = | б) 412 * 7 = | в) 923 * 2 = | г) 612 * 4 = |
| д) 3 423 : 7 = | е) 4 239 : 9 = | ж) 6 405 : 5 = | з) 4 368 : 2 = |
2. Решите примеры.
| а) 3 456 — 228 * 3 + 7 101 : 9 = | б) 1 548 : (9 — 5) + 921 * 4 = |
| в) 8 816 : 4 — 1 782 + 4 * 1 528 = | г) 9 * (433 — 202) + 4 123 : 7 = |
3. Решите уравнения.
Решите уравнения.
| а) 2 * 597 = X — 4 502 | б) 3 892 : 7 = Y — 2 364 |
4. Реши:
Швея шьёт 18 пар рукавиц за смену. Сколько пар рукавиц сошьёт бригада за 6 дней, если в бригаде работает 7 человек?
5. Посмотрите внимательно на рисунок и выпишите:
1. Номера прямоугольных треугольников: _______
2. Номера тупоугольных треугольников: _______
3. Номера остроугольных треугольников: _______
6. На рисунке изображены один прямоугольник и два квадрата, даны их размеры. Рассчитайте периметры и площади фигур, изображенных на рисунке. Найдите общую площадь всех фигур.
Вариант III.
1. Решите примеры.
| а) 433 * 5 = | б) 6 * 329 = | в) 901 * 3 = | г) 8 * 427 = |
| д) 5 971 : 7 = | ж) 3 384 : 8 = | з) 4 965 : 5 = | к) 4 292 : 2 = |
2. Решите примеры.
| а) 7 543 — 165 * 6 + 3981 : 3 = | б) 4 765 : (2 + 3) + 6 * 763 = |
| 7 865 : 5 — 1 075 + 6 * 763 = | 8 * (397 — 11) + 3 294 : 6 = |
3. Решите уравнения.
Решите уравнения.
| а) 3 * 586 = X — 3 569 | б) 6 309 : 3 = Y — 4 596 |
4. Реши:
Рабочий делает 15 деталей за смену. Сколько деталей сделает бригада за 8 дней, если в бригаде работает 6 человек?
5. Посмотрите внимательно на рисунок и выпишите.
а) Номера прямоугольных треугольников: _______
б) Номера тупоугольных треугольников: _______
в) Номера остроугольных треугольников: _______
6. На рисунке изображены 1 прямоугольник и два квадрата, даны их размеры. Рассчитайте периметры и площади фигур, изображенных на рисунке. Найдите общую площадь всех фигур.
Самостоятельная работа №5 (3 четверть)
Вариант I.
1. Решите примеры.
| а) 67 * 30 = | б) 234 * 63 = |
| в) 542 * 70 = | г) 86 * 25 = |
| д) 750 : 50 = | е) 640 : 80 = |
| ж) 669 : 3 = | з) 138 : 46 = |
2. Реши:
На склад привезли 2 тонны 740 кг крупы, затем увезли 10 мешков по 46 кг крупы в каждом мешке. Сколько крупы осталось на складе?
Сколько крупы осталось на складе?
3. Реши:
С двух пристаней, расстояние между которыми составляет 200 км, на встречу друг другу одновременно отправились 2 катера. Через 5 часов они встретились. С какой скоростью шел первый катер, если скорость второго катера составляла 18 км/час?
4. Найдите значение выражения.
| а) (1 845 * 6 — 219 : 3) — 345 = | б) 45 697 — (3 451 * 6 + 3202 : 2) = |
Вариант II.
1. Решите примеры.
| а) 46 * 30 = | б) 214 * 61 = |
| в) 245 * 30 = | г) 27 * 48 = |
| д) 450 : 50 = | е) 320 : 80 = |
| ж) 483 : 3 = | з) 230 : 46 = |
2. Реши:
В столовую привезли 2580 кг сахара. Каждый день использовали по 55 кг. Сколько кг сахара осталось в столовой через 22 дня?
3. Реши:
Из двух деревень навстречу друг друга вышли два путника. Расстояние между деревнями составляет 84 км. Встретились они через 6 часов. С какой скоростью шел первый путник, если скорость второго – 8 км/час?
С какой скоростью шел первый путник, если скорость второго – 8 км/час?
4. Найдите значение выражения.
| а) (5 672 * 3 — 8 120 : 4) — 2 948 = | б) 19 697 — (6 451 * 2 + 3208 : 2) = |
Вариант III.
1. Решите примеры.
| а) 134 * 70 = | б) 43 * 50 |
| в) 23 * 80 = | г) 186 * 35 = |
| д) 840 : 40 = | е) 990 : 30 = |
| ж) 453 : 3 = | з) 276 : 46 = |
2. Реши:
В мастерскую привезли 3 574 деталей. Для ремонта каждый день использовали 35 деталей. Сколько деталей осталось через 40 дней?
3. Реши:
Из двух городов навстречу друг другу выехали 2 поезда. Расстояние между городами составляет 840 км. Встретились они через 7 часов. С какой скоростью шел первый поезд, если скорость второго – 70 км/час?
4. Найдите значение выражения.
| а) (7 892 — 237 : 3) — 345 * 5 = | б) 15 676 — (4 567 * 6 + 6 788 : 2) = |
Самостоятельная работа №6 ( 4 четверть)
Вариант I.
1. Решите примеры.
| а) 40 584 : 89 = | б) 25 506 : 78 = |
| в) 388 512 : 456 = | г) 119 727 : 159 = |
| д) 241 * 467 = | е) 819 * 178 = |
| ж) 667 * 456 = | з) 417 * 159 = |
2. Переведите из одной единицы измерения в другую.
| а) 8 ч 11 мин = … с | б) 1 т 2 ц 73 кг = … кг |
| в) 1 км 52 м = … дм | г) 28 ч 53 мин = … мин |
3. Реши:
Отряд школьников прошел 20 км. Это составляет четверть пути. Сколько должны пройти школьники?
Вариант II.
1. Решите примеры.
| а) 27 306 : 74 = | б) 8 892 : 12 = |
| в) 118 449 : 123 = | г) 194 768 : 259 = |
| д) 241 * 467 = | е) 819 * 178 = |
| ж) 621 * 628 = | з) 168 * 743 = |
2. Переведите из одной единицы измерения в другую.
| а) 1 ч 15 мин = … с | б) 5 т 6 ц 345 кг = … кг |
| в) 2 км 546 м = … дм | г) 1 сутки 5 ч = … мин |
3. Реши:
Реши:
Турист прошел 15 км. Это составляет треть пути. Сколько должен пройти турист?
Вариант III.
1. Решите примеры.
| а) 229 457 : 269 = | б) 824 328 : 856 = |
| в) 117 819 : 159 = | г) 71 686 : 452 = |
| д) 524 * 409 = | е) 332 * 742 = |
| ж) 226 * 489 = | з) 435 * 721 = |
2. Переведите из одной единицы измерения в другую.
| а) 3 ч 47 мин = … с | б) 12 т 4 ц 23 кг = … кг |
| в) 12 км = … дм | г) 5 ч 13 мин = … мин |
3. Реши:
Пешеход прошел 18 км. Это составляет пятую часть пути. Сколько должен пройти пешеход?
Самостоятельная работа №7 (4 четверть)
Вариант I.
1. Решите примеры.
| а) 2 618 + 8 567 = | б) 25 346 — 5 441 = |
| в) 845 * 18 = | г) 43 776 : 96 = |
2. Найдите значения выражений.
а) 5600 : 70 — 640 : 80 =
б) (123 299 — 22 395) : 2 — 23 * 89 =
3. Реши:
Реши:
Из города одновременно и в одном направлении выехали автомобиль и велосипедист. Скорость автомобиля – 82 км/час, а велосипедиста – 21 км/час. Какое расстояние будет между ними через 3 часа?
Вариант II.
1. Решите примеры.
| а) 6 723 + 16 573 = | б) 53 551 — 897 = |
| в) 715 * 34 = | г) 15 356 : 698 = |
2. Найдите значения выражений.
а) 7200 : 80 + 240 : 80 =
б) ( 16 299 — 2 885 ) : 2 — 23 * 34 =
3. Реши:
Из двух городов одновременно навстречу друг другу выехали грузовик и автомобиль. Скорость грузовика – 48 км/час, а автомобиля – 72 км/час. Через какое время они встретятся, если расстояние между городами составляет 360 км?
Вариант III.
1. Решите примеры.
| а) 3 456 + 17 342 = | б) 51 345 — 945= |
| в) 788 * 43 = | г) 38 340 : 45 = |
2. Найдите значения выражений.
а) 5600 : 70 — 640 : 80 =
б) (123 299 — 22 395) : 2 — 23 * 89 =
3. Реши:
Реши:
Из города одновременно в разных направлениях выехали автомобиль и велосипедист. Скорость автомобиля – 65 км/час, а велосипедиста – 25 км/час. Какое расстояние будет между ними через 3 часа?
Материалы для подготовки к самостоятельным работам
1. Запиши числа, которые содержат:
| 5 | сот. | 9 | дес. | 9 | ед. | = _____ | 1 | сот. | 3 | дес. | 3 | ед. | = _____ | |
| 4 | сот. | 0 | дес. | 3 | ед. | = _____ | 9 | сот. | 4 | дес. | 1 | ед. | = _____ | |
| 0 | сот. | 9 | дес. | 6 | ед. | = _____ | 8 | сот. | 4 | дес.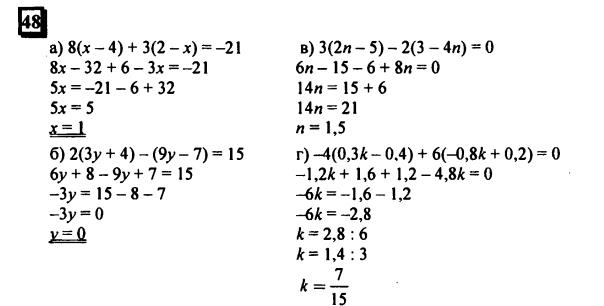 | 1 | ед. | = _____ | |
4. Заполни таблицу.
| g | 457 | 457 | 467 | 447 | 437 | 477 | 487 |
| g+33 | … | … | … | … | … | … | … |
| b | 554 | 453 | 355 | 100 | 274 | 178 | 593 |
| b-24 | … | … | … | … | … | … | … |
| c | 175 | 709 | 532 | 325 | 324 | 387 | 786 |
| c+17 | … | … | … | … | … | … | … |
Заполните таблицу
| Слагаемое | 300 | 255 | 177 | 238 | 312 | 387 | |
| Слагаемое | 557 | 198 | 679 | 411 | 211 | 504 | 236 |
| Сумма | 948 |
Заполните таблицу
| Уменьшаемое | 402 | 744 | 762 | ||||
| Вычитаемое | 191 | 374 | 605 | 305 | 245 | 184 | |
| Разница | 330 | 171 | 195 | 272 | 119 |
4. Вычисли и выполни проверку.
Вычисли и выполни проверку.
| 702 | 451 | 899 | 975 | 237 | |||||
| — | 332 | + | 289 | — | 553 | + | 482 | — | 117 |
| … | … | … | … | … | |||||
| 396 | 204 | 654 | 973 | 832 | |||||
| + | 183 | — | 178 | + | 425 | — | 874 | + | 393 |
| … | … | … | … | … | |||||
4. Вычисли и выполни проверку.
| 219 | 838 | 741 | 343 | 657 | |||||
| — | 114 | — | 729 | — | 126 | — | 340 | — | 572 |
| … | … | … | … | … | |||||
| 238 | 215 | 849 | 477 | 384 | |||||
| — | 136 | — | 104 | — | 216 | — | 388 | — | 302 |
| … | … | … | … | … | |||||
Реши уравнения
| 46 | — | x | = | 28 | y | — | 46 | = | 52 | x | — | 1 | = | 84 | ||
| x | = | … | y | = | … | x | = | … |
Реши уравнения
| 30 | — | x | = | 16 | y | + | 15 | = | 21 | x | — | 42 | = | 69 | ||
| x | = | … | y | = | … | x | = | … |
84. Сколько единиц каждого разряда в числах:
Сколько единиц каждого разряда в числах:
6856, 507, 300 тыс., 16911, 984, 783 тыс., 939, 9658, 404 тыс.?
Что обозначают одинаковые цифры в числах:
1 100
6 6000
13 13000
78 78000
167 167000
257 257000
4 класс, уравнение, решение уравнений, примеры и задачи
Дата публикации: .
Решение уравнений
1. Реши уравнения на сложение и вычитание целых чисел.
| 5456 — х = 2343 | х + 3217 = 7898 | у — 4325 = 346 |
| 9949 — y = 6957 | 1202 — y = 722 | y + 4890 = 8979 |
2. Реши уравнения на умножение и деление целых чисел.
| 45 * х = 225 | х * 18 = 108 | у : 25 = 12 |
| 44 * y = 176 | 224 : y = 32 | y * 40 = 360 |
3. Реши уравнения на сложение и вычитание дробей.
| 3 1⁄8 — х = 2 1⁄8 | х + 4 1⁄3 = 7 3⁄9 | у — 5 8⁄7 = 1⁄14 |
| 12 1⁄15 — y = 1 1⁄5 | 4 1⁄2 — y = 2 1⁄8 | y + 13 1⁄4 = 2 4⁄8 |
4. Реши уравнения на умножение и деление дробей.
Реши уравнения на умножение и деление дробей.
| 45 * х = 225 | х * 17 = 108 | у : 25 = 12 |
| 49 * y = 176 | 224 : y = 32 | y * 40 = 360 |
Текстовые задачи и уравнения
Составь уравнения к задачам и реши их.
1. Автобус проехал 2 часа со скоростью 60 км/час и ещё 3 часа – со скоростью 70 км/час. Какое расстояние проехал автобус за все время?
2. Одновременно в противоположных направлениях из города выехали велосипедист и мотоциклист и продолжили движение в течении 3 часов. Мотоциклист двигался со скоростью 40 км/час, а велосипедист – со скоростью 15 км/час. Сколько километров проехал мотоциклист? Сколько километров проехал велосипедист? На сколько километров мотоциклист проехал больше, чем велосипедист?
3. Из деревни А в село Б вышел пешеход. Через 2 часа он остановился на отдых и отдыхал в течении одного часа. Затем он продолжил свой путь и пришел в село Б через 6 часов после часового отдыха. Какова скорость пешехода, если расстояние между деревней А и селом Б равно Х км?
Какова скорость пешехода, если расстояние между деревней А и селом Б равно Х км?
4. В городе есть 4 улицы: Южная, Северная, Восточная и Западная. На Южной улице живет 10 % от всех жителей города. На Восточной живет на 1 3⁄5 больше, чем на Южной улице. На Северной улице живет в 2 раза больше, чем на Южной улице. Сколько жителей живет на каждой улице, если всего городе зарегистрировано 1 миллион человек?
1. Запиши числа, которые содержат:
| 9 | сот. | 1 | дес. | 2 | ед. | = _____ | 3 | сот. | 0 | дес. | 7 | ед. | = _____ | |
| 6 | сот. | 0 | дес. | 6 | ед. | = _____ | 3 | сот. | 5 | дес. | 0 | ед. | = _____ | |
| 0 | сот. | 5 | дес. | 0 | ед. | = _____ | 9 | сот. | 8 | дес. | 5 | ед. | = _____ | |
4. Заполни таблицу.
| e | 300 | 356 | 353 | 389 | 342 | 384 | 382 |
| e-90 | … | … | … | … | … | … | … |
| f | 451 | 451 | 461 | 441 | 431 | 471 | 481 |
| f+80 | … | … | … | … | … | … | … |
Заполните таблицу
| Слагаемое | 410 | 109 | 358 | ||||
| Слагаемое | 301 | 259 | 758 | 420 | 294 | 273 | 193 |
| Сумма | 772 | 816 | 881 | 689 |
Заполните таблицу
| Уменьшаемое | 161 | 972 | 291 | 494 | 741 | ||
| Вычитаемое | 284 | 216 | 714 | 269 | 161 | ||
| Разница | 32 | 6 | 178 | 33 |
4. Вычисли и выполни проверку.
Вычисли и выполни проверку.
| 458 | 146 | 185 | 164 | 703 | |||||
| — | 132 | + | 15 | — | 50 | + | 10 | — | 58 |
| … | … | … | … | … | |||||
| 773 | 374 | 308 | 659 | 351 | |||||
| + | 241 | — | 214 | + | 247 | — | 487 | + | 220 |
| … | … | … | … | … | |||||
4. Вычисли и выполни проверку.
| 375 | 319 | 782 | 684 | 862 | |||||
| — | 198 | — | 226 | — | 737 | — | 522 | — | 622 |
| … | … | … | … | … | |||||
| 627 | 325 | 777 | 597 | 908 | |||||
| — | 139 | — | 307 | — | 121 | — | 496 | — | 720 |
| … | … | … | … | … | |||||
Реши уравнения
| 9 | + | x | = | 26 | y | + | 26 | = | 68 | x | + | 7 | = | 93 | ||
| x | = | … | y | = | … | x | = | … |
Реши уравнения
| 15 | — | x | = | 8 | y | — | 13 | = | 24 | x | — | 9 | = | 56 | ||
| x | = | … | y | = | … | x | = | … |
Реши уравнения
| 37 | — | x | = | 13 | y | + | 21 | = | 45 | x | — | 32 | = | 58 | ||
| x | = | … | y | = | … | x | = | … |
84. Сколько единиц каждого разряда в числах:
Сколько единиц каждого разряда в числах:
7808, 426, 931 тыс., 21011, 975, 350 тыс., 252, 4919, 628 тыс.?
Контрольные работы по математике 4 класс «Перспектива»
Контрольные работы из пособия «Математика. Методические рекомендации.» Авторы те же, что и у самого учебника математики (Дорофеев и Миракова), по которому учитель ведет уроки, поэтому контрольные синхронно согласуются с пройденной учебной программой.
Контрольная работа №1 предлагается примерно на 21-м уроке, после изучения темы Округление слагаемых. 2-я контрольная на 36 уроке после темы Умножение двузначного числа на двузначное (письменные приемы вычисления). 3-я на 51-м уроке, после деления трехзначного числа на двузначное (писм. приемы) и уроков повторения. 64-й урок — контрольная №4, после задач на нахождение неизвестного по двум разностям. 5-я контрольная на 76-м уроке после сложения и вычитания величин, ч2 учебника. После таблицы единиц дины контрольная №6. За задачами на движение в одном направлении следует проверочная работа №7. На 115 уроке, после задач на движение по реке, идет 8-я контрольная. 9-я после особых случаев умножения и деления многозначных чисел и повторения, затем почти сразу Итоговая.
На 115 уроке, после задач на движение по реке, идет 8-я контрольная. 9-я после особых случаев умножения и деления многозначных чисел и повторения, затем почти сразу Итоговая.
Контрольная работа № 1
Вариант 1
1. Запиши выражения столбиком и выполни действия.
472 + 265 759 – 283 136 · 4 954 : 3
2. Сравни.
8 м 3 дм 1 см и 821 см 36 дм 7 см и 3 м 67 см
3. В 8 одинаковых ящиках лежит 320 кг гвоздей. Сколько килограммов гвоздей лежит в 5 таких же ящиках?
4. Найди значение выражения.
121 + 229 + 117 + 133 + 91
5. Начерти в тетради отрезок АС и отметь точку В, как показано на рисунке. Восстанови прямоугольник ABCD по его диагонали AC и вершине B.
Вариант 2
1. Запиши выражения столбиком и выполни действия.
182 + 569 736 – 485 217 · 3 624 : 4
2. Сравни.
3 м 9 дм 7 см и 387 см 22 дм 7 см и 3 м 27 см
3. В 7 одинаковых мешках 273 кг орехов. Сколько килограммов орехов в 10 таких же мешках?
В 7 одинаковых мешках 273 кг орехов. Сколько килограммов орехов в 10 таких же мешках?
4. Найди значение выражения.
399 + 188 + 151 + 12 + 146
5. Начерти в тетради отрезок КЕ и отметь точку М, как показано на рисунке. Восстанови прямоугольник KOEM по его диагонали КЕ и вершине М.
Контрольная работа № 2
Вариант 1
1. Выполни действия.
5 · (34 · 2) + 228 24 · 30 – 895 : 5
2. Найди среднее арифметическое чисел: 76, 186, 54 и 208.
3. От города до деревни велосипедист ехал 3 ч со скоростью 16 км/ч. Обратно он проехал то же расстояние за 4 ч. С какой скоростью ехал велосипедист на обратном пути?
4. Начерти отрезок АВ = 6 см и отметь на нём середину — точку О. Построй окружность с центром в точке О и радиусом ОА.
Вариант 2
1. Выполни действия.
4 · (6 · 25) – 192 12 · 50 + 207 : 9
2. Найди среднее арифметическое чисел: 113, 368 и 392.
3.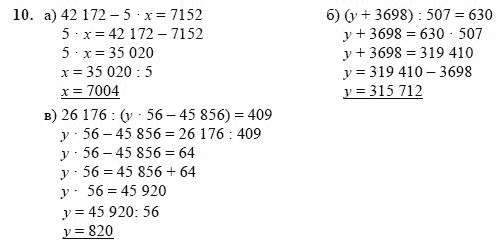 Катер шёл 3 ч по реке со скоростью 24 км/ч. Обратный путь он прошёл со скоростью 18 км/ч. Сколько времени затратил катер на обратный путь?
Катер шёл 3 ч по реке со скоростью 24 км/ч. Обратный путь он прошёл со скоростью 18 км/ч. Сколько времени затратил катер на обратный путь?
4. Начерти отрезок CD = 8 см и отметь на нём середину — точку О. Построй окружность с центром в точке О и радиусом ОC.
Контрольная работа № 3
Вариант 1
1. Сравни.
600 : (4 · 25) и 900 : 30
2. Выполни деление уголком и сделай проверку.
476 : 68
3. В первый день в библиотеку привезли 4 пачки книг, а во второй день привезли ещё 5 таких пачек. Всего в библиотеку за два дня привезли 135 книг. Сколько книг привезли в первый день и сколько — во второй?
4. Начерти в тетради треугольник АВС так, как показано на рисунке. Определи вид треугольника АВС.
Вариант 2
1. Сравни.
1000 : (20 · 5) и 240 : 60
2. Выполни деление уголком и сделай проверку.
456 : 57
3. В палатку привезли 7 ящиков с яблоками и 3 таких же ящика с грушами. Всего привезли 160 кг яблок и груш. Сколько килограммов яблок и сколько килограммов груш привезли в палатку?
Сколько килограммов яблок и сколько килограммов груш привезли в палатку?
4. Начерти в тетради треугольник КМЕ, как показано на рисунке. Определи вид треугольника КМЕ.
Контрольная работа № 4
Вариант 1
1. Запиши цифрами число:
а) сто семьдесят пять тысяч;
б) двадцать тысяч восемьсот три;
в) четыре тысячи четыреста сорок четыре.
2. Сравни.
6 км 90 м и 690 м
6 м 90 см и 62 дм
620 мм и 6 см 2 мм
3. На одной машине привезли 120 кирпичей, а на другой 154 таких же кирпича. Масса кирпичей в первой машине на 136 кг меньше массы кирпичей во второй машине. Найди массу кирпичей в каждой машине.
4. Длины сторон прямоугольника 48 дм и 20 дм. Вычисли периметр и площадь этого прямоугольника.
Вариант 2
1. Запиши цифрами число:
а) двести восемь тысяч;
б) пятьдесят тысяч пятьдесят пять;
в) триста двенадцать тысяч девятьсот шестьдесят один.
2. Сравни.
5 м 8 дм и 580 см
5 дм 8 см и 508 см
5 см 8 мм и 58 мм
3. В одной коробке лежит 36 новогодних шаров, а в другой — 16 таких же шаров. Стоимость шаров в первой коробке на 340 р. больше стоимости шаров во второй коробке. Найди стоимость шаров в каждой коробке.
В одной коробке лежит 36 новогодних шаров, а в другой — 16 таких же шаров. Стоимость шаров в первой коробке на 340 р. больше стоимости шаров во второй коробке. Найди стоимость шаров в каждой коробке.
4. Длины сторон прямоугольника 27 см и 30 см. Вычисли периметр и площадь этого прямоугольника.
Контрольная работа № 5
Вариант 1
1. Выполни действия.
2508 + 137 394
70 025 – 5883
14 592 + 200 356 – 104 087
2. Сравни.
160 кг и 1 ц 60 кг
1600 кг и 16 ц
106 т и 16 000 кг
3. Запиши дроби: а) одна пятая; б) три восьмых; в) семь двадцать четвёртых.
4. Вырази в секундах: а) 7 мин; б) 4 мин 10 с; в) 2 мин 3 с.
5. На машину погрузили 12 бидонов молока по 40 л и 8 бидонов по 30 л. Сколько литров молока погрузили на машину?
Вариант 2
1. Выполни действия.
7261 + 281 109
320 425 – 44 281
613 024 – 28 936 + 19 405
2. Сравни.
305 кг и 3 ц 5 кг
3005 кг и 3 т 5 кг
350 т и 3500 ц
3. Запиши дроби: а) шесть седьмых; б) одна тридцатая; в) две пятнадцатых.
Запиши дроби: а) шесть седьмых; б) одна тридцатая; в) две пятнадцатых.
4. Вырази в секундах: а) 2 мин; б) 3 мин 20 с; в) 5 мин 4 с.
5. Для поездки на экскурсию было выделено 4 автобуса по 48 мест в каждом и 3 автобуса по 60 мест в каждом. Сколько экскурсантов можно посадить в эти автобусы?
Контрольная работа № 6
Вариант 1
1. Выполни действия.
5237 · 4 270 000 : 10 000 + 5048 · 30
2. Сравни.
72 000 м и 72 км
58 000 кг и 58 ц
20 ч и 1200 мин
3. От проволоки длиной 108 м сначала отрезали 1/3 часть, а потом — 3/4 остатка. Сколько метров проволоки отрезали сначала, а сколько — потом?
4. Начерти тупой угол SHT и из его вершины внутри угла проведи луч HC так, чтобы угол SHC был прямым углом.
Вариант 2
1. Выполни действия.
2013 · 7 1567 · 200 – 60 900 : 100
2. Сравни.
500 000 см и 5000 дм
3030 ц и 303 т
50 мин и 320 с
3. В первый день туристы прошли 3/10 всего пути, а во второй день — 1/3 остатка. Сколько километров прошли туристы в первый день и сколько — во второй, если длина всего пути 120 км?
Сколько километров прошли туристы в первый день и сколько — во второй, если длина всего пути 120 км?
4. Начерти тупой угол MND и из его вершины внутри угла проведи луч NF так, чтобы угол MNF был острым углом.
Контрольная работа № 7
Вариант 1
1. Вычисли.
36 · 129 + 36 · 405
2. Из двух городов одновременно навстречу друг другу выехали два мотоциклиста и встретились через 3 ч. Скорость одного мотоциклиста 65 км/ч, а другого 85 км/ч. Найди расстояние между городами. (Реши задачу двумя способами.)
3. Из одного пункта одновременно в одном направлении выехали два автомобиля: первый со скоростью 80 км/ч и второй со скоростью 65 км/ч. Какое расстояние будет между этими автомобилями через 2 ч? (Реши задачу двумя способами.)
Вариант 2
1. Вычисли.
57 · 263 + 57 · 184
2. От двух станций одновременно навстречу друг другу выехали два поезда и встретились через 5 ч. Скорость одного поезда 55 км/ч, а другого 72 км/ч. Найди расстояние между станциями. (Реши задачу двумя способами.)
Найди расстояние между станциями. (Реши задачу двумя способами.)
3. От одной пристани одновременно в противоположных направлениях отправились катер и моторная лодка. Скорость катера 18 км/ч, а скорость моторной лодки 25 км/ч. Какое расстояние будет между катером и моторной лодкой через 4 ч? (Реши задачу двумя способами.)
Контрольная работа № 8
Вариант 1
1. Выполни деление уголком и сделай проверку.
1876 : 7
2. Выполни действия.
382 · 24 – (7049 – 2466)
3. Автобус проехал 3/5 пути, что составляет 141 км. Найди длину всего пути.
4. Пароход проплыл по течению реки 186 км, а против течения 125 км. Сколько времени потребовалось пароходу на весь путь, если его собственная скорость 28 км/ч, а скорость течения 3 км/ч?
Вариант 2
1. Выполни деление уголком и сделай проверку.
2552 : 4
2. Выполни действия.
159 · 36 – (1058 + 2466)
3. Девочка прочитала 5/7 книги, что составляет 125 страниц. Сколько всего страниц в книге?
Сколько всего страниц в книге?
4. Теплоход проплыл против течения 180 км, а по течению 255 км. Сколько времени потребовалось теплоходу на весь путь, если его собственная скорость 48 км/ч, а скорость течения 3 км/ч?
Контрольная работа № 9
Вариант 1
1. Найди значение выражения.
1378 : 53 · 203 – 1278
2. Выполни действия.
35 км 140 м – 6 км 593 м
25 т 180 кг + 13 т 278 кг
2 ч 32 мин – 54 мин
3. Площадь земельного участка прямоугольной формы 96 390 м2. Ширина участка 238 м. Найди длину этого участка.
4. Из двух пунктов, расстояние между которыми 216 км, выехали одновременно навстречу друг другу мотоциклист и велосипедист. Они встретились через 3 ч. Найди скорость мотоциклиста, если скорость велосипедиста 12 км/ч.
Вариант 2
1. Найди значение выражения.
6342 : 21 · 58 – 7516
2. Выполни действия.
12 м 6 дм – 8 м 23 дм
48 ц 23 кг + 7 ц 7 кг
9 мин 36 с – 158 с
3. Площадь земельного участка прямоугольной формы равна 190 320 м2. Длина участка 624 м. Найди ширину этого участка.
Площадь земельного участка прямоугольной формы равна 190 320 м2. Длина участка 624 м. Найди ширину этого участка.
4. Из двух пунктов, расстояние между которыми 600 км, вышли одновременно навстречу друг другу два поезда и встретились через 4 ч. Найди скорость первого поезда, если скорость второго 65 км/ч.
Итоговая контрольная работа за 4 класс
Вариант 1
1. Сравни.
2 т 308 кг и 2380 кг 60 м2 и 60 000 см2
20 ц 17 кг и 2 т 170 кг 3 ч 14 мин и 404 мин
2. Выполни действия.
508 • 208 – 65 960 : 680 – 2567
3. От пристани одновременно отошли пароход и моторная лодка. Через 3 ч моторная лодка была впереди парохода на расстоянии 108 км. Найди скорость моторной лодки, если скорость парохода 24 км/ч.
4. Восстанови квадрат АВСD по его диагонали АС = 6 cм. Построй окружность с центром в точке C и радиусом СВ.
5. Для компота купили 700 г сушёных фруктов: яблок, слив и абрикосов. Яблоки составляют 2/5 всех фруктов, а сливы — 1/4 остатка. Сколько граммов абрикосов купили для компота?
Яблоки составляют 2/5 всех фруктов, а сливы — 1/4 остатка. Сколько граммов абрикосов купили для компота?
Вариант 2
1. Сравни.
4 мин 53 с и 453 с 23 км 5 м и 2305 м
62 ц 2 кг и 6 т 202 кг 40 га и 4000 а
2. Выполни действия.
609 · 309 – 85 440 : 890 – 1085
3. Лыжник стал догонять пешехода, когда расстояние между ними было 960 м, и догнал через 8 мин. Найди скорость лыжника, если скорость пешехода 80 м/мин.
4. Восстанови квадрат АВСD по его диагонали ВD = 4 cм. Построй окружность с центром в точке D и радиусом DC.
5. На свитер купили 900 г шерсти трёх цветов: красного, синего и чёрного. Шерсть красного цвета составляет 3/4 всей купленной шерсти, шерсть синего цвета — 1/3 остатка. Сколько купили шерсти чёрного цвета?
К.р. №1. 4 кл. 1 вар. 1.Из двух городов выехали одновременно навстречу друг другу два мотоциклиста. 2. Реши примеры: 36812 + 42368 800324 – 62831 9038 х 4 62 х 47 972 : 4 252 : 84 3. Вырази одни единицы в другие. 9 мин 6 с = …с 2355 кг= …т…кг 2 ч 45 мин = …мин 584 мм = …см…мм 4. Геометрическая задача. Начерти прямоугольник со сторонами 4 см и 6 см и другой прямоугольник такой же площади. 5*. Расставьте скобки так, чтобы равенства стали верными. 75 + 20 : 5 – 1= 78 75 + 20 : 5 – 1= 18 75 + 20 : 5 – 1= 80 | К.р.№1. 4 кл. 2 вар. 1.Два пловца поплыли одновременно по реке в противоположных направлениях, первый плыл со скоростью 90 м/мин, второй – 40 м/мин. Сколько метров проплывет второй пловец, когда первый проплывет 270 метров? 2.Реши примеры. 692503 + 243497 234006 – 18765 3602 х 6 68 х 45 224 : 32 456 : 8 3. 7 мин 8 с = …с 3 ч 20 мин = …мин 4786 кг = …т …кг 387 мм =…см…мм 4. Геометрическая задача. Начерти два разных прямоугольника, у которых периметры одинаковые – 36 см. 5*. Расставьте скобки так, чтобы равенства стали верными. 80 : 5 + 3 х 5 = 50 80 : 5 + 3 х 5 = 4 80 : 5 + 3 х 5 = 95 |
Контрольная работа №2 в 4 классе I вариант 1. Из двух городов, расстояние между которыми 390 км выехали одновременно навстречу друг другу два мотоциклиста и встретились через 3 часа. Один мотоциклист ехал со скоростью 60 км/ч. Найди скорость другого мотоциклиста. 2. Найди значение выражения: (18370 + 23679) : 7 156 – 96 :(12: 4) : 2 (800035 – 78942) х 6 3. Сравни, поставь знаки <,>,=. 5 км 4 м … 5 км 40 дм 6 т 200 кг … 62000 кг 245 ч … 4 сут 5 ч 4. 84 : а = 6 х 7 5. Найди площадь прямоугольника, если его ширина 4 см, а длина в 2 раза больше. 6. Вместо * вставь знаки арифметических действий: 80 * 20 *600 = 1000 900 * 30 * 30 = 60 | Контрольная работа №2 в 4 классе II вариант 1. Из двух городов, расстояние между которыми 600 км выехали одновременно навстречу друг другу два автомобиля и встретились через 4 часа. Один автомобиль ехал со скоростью 70 км/ч. Найди скорость другого автомобиля. 2. Найди значение выражения: (10283 + 16789) : 9 5 х (125 + 75) : 2 + 80 (200496 – 134597) х 2 3. Сравни, поставь знаки <,>,=. 6 т 20 кг … 6 т 2 ц 20 км 300м … 23000 м 3 сут 10 ч…190 ч 4. Реши уравнение : 3 х в = 87 – 6 5. 6. Вместо * вставь знаки арифметических действий: 40 * 20 * 200 = 1000 600 * 30 * 20 = 40 |
Контрольная работа №3 в 4 классе в 4 четверти, 1 вариант. 1) Велосипедист проехал 24 км со скоростью 8 км\ч. Пешеход потратил на этот путь на 1 час больше. С какой скоростью шел пешеход? 2) 43978 + 120563 2692 х 56 460561 – 387845 17572 : 46 23080 + 714 : 51 х 78 3) а + 459 = 808 в х 48 = 3792 4) 26 м … 260 дм 185 мин…3 ч 9 т 516 кг…9156 кг 3400 см…43 дм 5)* Сколько нужно досок длиной 4 м и шириной 4 дм, чтобы настелить пол в квадратной комнате, сторона которой 8 м? | Контрольная работа №3 в 4 классе в 4 четверти, 2 вариант. 1) Мальчик проплыл 100 м со скоростью 25 м\мин. 2) 700060 – 354769 3429 х 47 654873 + 209618 32870 : 38 13566 : (900 – 56 х16) 3) 3089 – в = 1596 1920 : а = 16 4) 520 ц…52 т 7 км650 м…7560 м 2 ч 5 мин…130 мин 2 м…200 дм 5)* Сколько нужно досок длиной 3 м и шириной 2 дм, чтобы настелить пол в квадратной комнате, сторона которой 6 м? |
Контрольная работа №4 в 4 классе 1 вариант 1. 63027 + 9564 40828 – 32839 5268 х 6 807 х 58 6132 : 14 595690 : 236 2. В магазин привезли 126 пакетов картофеля по 3 кг и столько же кг моркови в сеточках по 2 кг. Сколько сеточек с морковью привезли? 3. Вычисли периметр и площадь прямоугольника, длина которого 60 мм, а ширина вдвое меньше. 4*. Длина одной стороны треугольника 2 дм, другой 25 см, а третьей 250 мм. Определи вид треугольника. 5*. времени? | Контрольная работа №4 в 4 классе 2 вариант 1. 72238 + 8792 60154 – 51457 4057 х 8 803 х 48 5505 : 15 42000 : 175 2. Имеется 168 трехлитровых банок с томатным соком и столько же литров морковного сока в двухлитровых банках. Сколько банок с морковным соком? 3. Вычисли периметр и площадь прямоугольника, ширина которого 30 мм, а длина в 2 раза больше. 4*. Во сколько раз увеличится площадь квадрата, если длину каждой его стороны увеличить в 2 раза? 5*. На покупку 3 кг яблок мама потратила пятую часть своих денег. Сколько кг она могла купить на все деньги? |
Контрольная работа №5 в 4 классе 1 вариант 1. В буфет принесли 7 подносов с пирожными, по 28 пирожных на каждом, и несколько подносов с бутербродами, по 32 бутерброда на каждом. буфет принесли 388 пирожных и бутербродов. Сколько подносов с бутербродами принесли в буфет? 2. 810000 – 654379 472826 : 59 268435 + 345687 7204 х 26 80000 – 4000 х 2 +100 (6200 +800 : 4) 100 3. 16 км 8 м … 16 км 80 дм 2 сут. 3 ч … 123 ч 4900 кг … 49 т 4. Длина прямоугольника равна 8 см, а ширина в 2 раза меньше. Найди его площадь и сумму длин всех его сторон. 5. 600 * 30 * 10 * 5 = 895 6. 1\2 м – 30 см 200 г + 1\5 кг 1\4 ч + 5 мин | Контрольная работа №5 в 4 классе 2 вариант 1. В городе 9 автобусных парков, по 75 автобусов в каждом, несколько троллейбусных парков по 52 троллейбуса в каждом. Сколько троллейбусных парков в городе, если всего в нем 1039 автобусов и троллейбусов? 2. 920000 – 495874 171276 : 84 421937 + 289276 20096 х 49 9000 – 3000 х 3 + 1000 (7400 + 600 : 2) 10 3. 12 км 3 м … 12 км 30 дм 3 сут. 4. Ширина прямоугольника равна 6 см, а длина на 2 см больше. Найди его площадь и сумму длин всех его сторон. 5. 500 * 20 * 10 * 1 = 301 6. 1\5 м – 10 см 400 г + 1\4 кг 1\2 ч + 20 мин |
Контрольная работа №6 в 4 классе 1 вариант 1). Один поезд двигался со скоростью 47 км/ч и проехал 1128 км. Другой поезд двигался со скоростью 49 км/ч и проехал 1813 км. На сколько часов второй поезд был в пути больше, чем первый? 2). (20000 – 3083 х 6) + 73038 : 74 27598 + 695 х 28 : 7 – 6499 56 т 436 кг + 18 т 589 кг 72 км 309 м – 23 км 450 м 3). а х 7 = 560 350 + у = 890 4). Вычисли площадь прямоугольника со сторонами 2 дм и 8 см | Контрольная работа №6 в 4 класе 2 вариант 1). От двух пристаней, находящихся друг от друга на расстоянии 344 км, вышли одновременно навстречу друг другу два парохода. 2). (40000 – 4097 х 9) + 25772 :68 35614 + 785 х 36 : 9 – 8297 78 т 286 кг + 14 т 937 кг 54 км 804 м – 29 км 980 м 3). 900 : у = 20 а – 170= 350 4). Вычисли площадь прямоугольника со сторонами 9 см и 1 дм. |
Контрольные работы по математике 4 класс (1-3 четверть) «Школа России»
1
Вариант 1.
1. Реши задачу.
В овощной ларёк привезли 4 ящика яблок по
50кг в каждом и 3 ящика груш по 60 кг в каждом. Сколько килограммов фруктов
привезли в овощной ларёк?
2. Вычисли значения выражений:
64: (4х2)+14 240+(620-200):7
19х3+27х2 80х3+450-90
3.Вычисли в столбик.
325х3 753-275 762:6
99х8 456+367 972:2
4. Реши уравнения:
Реши уравнения:
Хх5=70 Х:7=12
5.Найти периметр и площадь прямоугольника,
если его длина 10 см, а ширина в 2 раза меньше.
6. Закончи запись:
6м 7дм = ….дм 5см 2мм =
….мм
3ч.=….мин 145мин =
…ч…..мин
Вариант 2.
1.
Реши задачу.
В первый день собрали 6 ящиков клубники по
20 кг в каждом, а во второй день 5 ящиков клубники по 30 кг в каждом. Сколько
всего килограммов клубники собрали за 2 дня?
2.
Вычисли значения
выражений.
56:(7х2)+26 670+(450-300):5
13х4+17х3 90х4+240-70
3.
Вычисли в столбик.
482х2 895-347 819:7
251х3 408+359 536:4
4.
Реши уравнения:
Х:4=21 Хх5=65
5.
Найти периметр и
площадь прямоугольника, если его длина 8 см, а ширина в 2 раза меньше.
6.
Закончи запись:
2м 5дм = ….дм 3см
1мм = ….мм
4ч =….мин
132 мин= …..ч….мин
2
Вариант 1.
1 Запишите числа:
1)7 единиц IV класса
31 единица III класса 907
единиц II класса 36
единиц I класса
2)22
миллиарда 40 миллионов 16 тысяч 20 единиц
3) 118
миллионов 18 тысяч 80 единиц
4)4
миллиарда 217 миллионов 6 тысяч 30 единиц
5) сто
сорок пять тысяч восемь
2. Вычисли:
30 800 :10 30 Х10
620 300 : 100 150 х 100
270 000 :10 000 80 х 1000
3. Представьте число 113 060 в виде суммы разрядных слагаемых.
4. Вычисли по действиям:
245 · 3 + 681 : 3 – 25
5. На складе было 4300 рулонов обоев. Одному магазину отправили 700
На складе было 4300 рулонов обоев. Одному магазину отправили 700
рулонов, второму – на 150 рулонов больше, чем первому. Сколько рулонов обоев
осталось на складе?
Вариант 2.
1. Запишите числа:
1)8
единиц IV класса 72 единицы III класса 307 единиц II класса 5единиц I класса
2)43
миллиарда 60 миллионов 12 тысяч 70 единиц
3)628
миллионов 90 тысяч 80 единиц
4) 2миллиарда
218 миллионов 70 тысяч 8 единиц
5) двести
восемь тысяч сорок два
Вычисли:
40100 :10 500 х 10
190 700 : 100 820 х 100
880 000 :10 000 400 х 1000
3. Представьте число
436 020 в виде суммы разрядных слагаемых.
4. Вычисли по действиям:
245 · 4 + 819 : 3 – 18
5. На складе было 2400 рулонов обоев. Одному магазину отправили
800 рулонов, второму – на 350 рулонов больше, чем первому.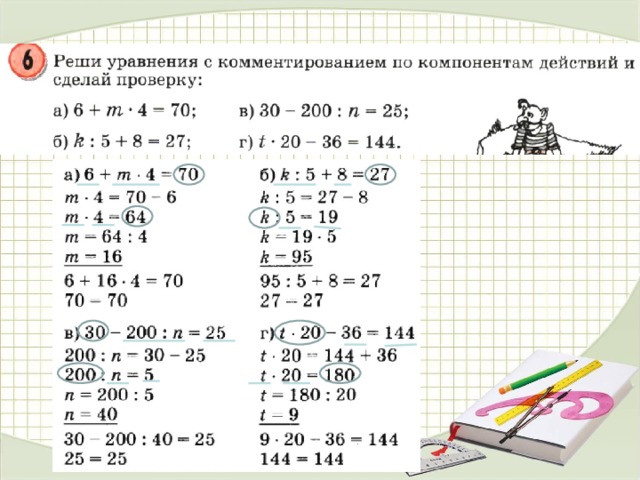 Сколько рулонов
Сколько рулонов
обоев осталось на складе?
Вариант 1.
1 Запишите числа:
1) 6 сот .
тыс. 7. ед тыс. 3 сот
2) 3 ед. II класса 3 ед
. I класса
3 ) 901 ед.
II класса 5 ед. I класса
4) 6 ед. 3
–го разряда 8 ед 2-го разряда
5) Запиши число
123 060 в виде суммы разрядных слагаемых.
2. Сравните числа:
а) 700300…70030
875129….857129
б) Вставьте вместо * подходящие цифры
так, чтобы записи стали верными:
54802 < 5**02
67**3< 67**3
3. Вычислите:
а) 763512
– 500 2360 х 10
600 000
-1 764000 : 100
86759+1
32 х 1000
б) Вставьте
вместо * числа так, чтобы записи стали верными:
7816
=7016+ * 48000+ * = 48010
4. Решите задачу:
Решите задачу:
В одной
пачке 10 книг. В библиотеку принесли 3000 книг. Сколько пачек с книгами
принесли в библиотеку?
5. Решите
задачу:
Что легче
и на сколько килограммов: 8 коробок конфет
по 32 кг в
каждой или 7 коробок вафель по 36 кг в каждой?
Вариант 2.
1 Запишите числа:
1) 6 сот .
тыс. 7 дес. 2 ед.
2) 4 дес. II класса 9 ед . I класса
3 ) 540 ед.
II класса 2 ед. I класса
4) 7 ед. 3
–го разряда 1 ед 2-го разряда
5) Запиши число
215 080 в виде суммы разрядных слагаемых.
2. Сравните числа:
а) 600400…60040 836592….863592
б) Вставьте вместо * подходящие цифры
так, чтобы записи стали верными:
86709 < 8**09 26**1<
26**1
3. Вычислите:
а) 206317
– 300 25800 : 10
30 000
-1 26 х1000
73549+1
84000:100
б)
Вставьте вместо * числа так, чтобы записи стали верными:
8172
=8102+ * 95000+ * = 95430
4. Решите
Решите
задачу:
В одной
коробке 10 пирожных. Сколько коробок понадобиться для упаковки 1000 пирожных?
5. Решите задачу:
Что
тяжелее и на сколько килограммов: 6 мешков муки
по 46 кг в
каждом или 5 мешков риса по 48 кг в каждом?
Вариант 1.
1 Запишите числа:
1) 6 сот .
тыс. 7. ед тыс. 3 сот
2) 3 ед. II класса 3 ед . I класса
3 ) 901 ед.
II класса 5 ед. I класса
4) 6 ед. 3
–го разряда 8 ед 2-го разряда
5) Запиши
число 123 060 в виде суммы разрядных слагаемых.
2. Сравните числа:
а) 700300…70030
875129….857129
б) Вставьте вместо * подходящие цифры
так, чтобы записи стали верными:
54802 < 5**02 67**3<
67**3
3. Вычислите:
а) 763512
– 500 2360 х 10
600 000 -1 764000 : 100
86759+1 32 х 1000
б)
Вставьте вместо * числа так, чтобы записи стали верными:
7816
=7016+ * 48000+ * = 48010
4. Решите
Решите
задачу:
В одной
пачке 10 книг. В библиотеку принесли 3000 книг. Сколько пачек с книгами
принесли в библиотеку?
5. Решите
задачу:
Что легче
и на сколько килограммов: 8 коробок конфет
по 32 кг в
каждой или 7 коробок вафель по 36 кг в каждой?
Вариант 2.
1 Запишите числа:
1) 6 сот .
тыс. 7 дес. 2 ед.
2) 4 дес. II класса 9 ед . I класса
3 ) 540 ед.
II класса 2 ед. I класса
4) 7 ед. 3
–го разряда 1 ед 2-го разряда
5) Запиши
число 215 080 в виде суммы разрядных слагаемых.
2. Сравните числа:
а) 600400…60040
836592….863592
б) Вставьте вместо * подходящие цифры
так, чтобы записи стали верными:
86709 < 8**09 26**1<
26**1
3. Вычислите:
а) 206317
– 300 25800 : 10
30 000
-1 26 х1000
73549+1
84000:100
б)
Вставьте вместо * числа так, чтобы записи стали верными:
8172
=8102+ * 95000+ * = 95430
4. Решите
Решите
задачу:
В одной
коробке 10 пирожных. Сколько коробок понадобиться для упаковки 1000 пирожных?
5. Решите
задачу:
Что
тяжелее и на сколько килограммов: 6 мешков муки
по 46 кг в
каждом или 5 мешков риса по 48 кг в каждом?
Контрольная работа №3
за
1 четверть
Вариант1.
1. Реши задачу по действиям:
С одного участка рабочие собрали 7 мешков
картошки по 35 кг в каждом? Со второго собрали на 124 кг больше. Сколько всего
кг картошки собрали с обоих участков?
2. Вычисли:
64000:1000=
7800х10=
4300х10=
540х1000=
109000:10=
30400:100=
3. Найди
значение выражений:
852 – 214 х 3 + 187 =
736 : 8 + 627 — 567 =
711 : 9 + (506 – 105 х 4 ) =
4. Вставьте
Вставьте
вместо * числа так, чтобы записи стали верными:
4 км2 = * м2
900 см2 = *
дм2
6 см2
20 мм2 = * мм2
5. Решите
задачу:
Найдите площадь и периметр прямоугольника
со сторонами 5 см и 7 см. Начертите квадрат с таким же периметром и найдите его
площадь.
Контрольная
работа №3
за
1 четверть
Вариант 2.
1 Реши задачу по действиям:
У Вани есть 9 наборов открыток по 12 штук
в каждом. У Коли же на 18 открыток меньше. Сколько всего открыток у обоих
ребят?
2. Вычисли:
84000:1000=
9400х10=
5300х100=
280х1000=
207000:10=
10600:100=
3. Найди
Найди
значение выражений:
848 — 146 х 3 + 209 =
665 : 7 + 627 — 458 =
672 : 8 + (801 – 204 х 3) =
4. Вставьте
вместо * числа так, чтобы записи стали верными:
3 км2 = * м2
700 см2 = *
дм2
4 см2
80 мм2 = * мм2
5. Решите
задачу:
Найдите площадь и периметр прямоугольника
со сторонами 4 см и 8 см. Начертите квадрат с таким же периметром и найдите его
площадь.
Контрольная
работа №4
Вариант1.
1. Реши
задачу:
Купили 400 граммов чёрного кофе и 3 пачки чая по 50г. Найдите массу всей покупки.
2. Реши задачу:
Экскурсия
началась в 11 часов 40 минут и закончилась в 13 часов 20 минут. Сколько времени
продолжалась экскурсия?
3. Найди
Найди
значение выражений:
198 х 4 + 852 : 4=
568 : 2 х 4 х 100 =
4. Вырази
в новых единицах
6 543 кг = … т … кг
40
мес. = … г. … мес.
8 765
см = … м … см
185
с = … мин …с
420
мин = …ч
90 000см2
= … м 2
5. Решите задачу:
Стороны прямоугольника – 30 мм и 50 мм. Найди его
площадь, вырази её в см2.
6*. Оля вышла на прогулку на 3 мин раньше, чем Алёша. Алёша вышел на 2
мин позже, чем Саша. Кто из детей вышел раньше всех и на сколько минут?
7.*
Вычисли
22
ч – 5 ч 15 мин =
9 кг 500 г – 6 кг
800 г =
7 м – 6 дм 8 см=
Контрольная
работа №4
Вариант 2.
1 Реши задачу:
Масса пачки чая 50г. Мама купила 4 пачки чая и 500 г. колбасы.
Найдите массу всей покупки.
2. Реши задачу:
Представление
началось в 15 часов 30 минут и закончилось в 17 часов 10 минут. Сколько времени
Сколько времени
продолжалось представление?
3. Найди
значение выражений:
167 х 3 + 432 : 3=
792 : 6 х 5 х 1000=
4. Вырази в новых единицах
7 651 г = … кг … г
52
мес. = … г. … мес.
7
651 см = … м … см
366
с = … мин …с
180
мин = …ч
12 000 000
м2 = … км 2
5. Решите задачу:
Стороны прямоугольника –
60 мм и 40 мм. Найди его площадь, вырази её в см2.
6*. Врач прописал больному 5 уколов – по уколу через каждые полчаса.
Сколько потребуется времени, чтобы сделать все уколы?
7 * Вычисли
23
ч – 4 ч 50 мин =
7
кг 300 г – 5 кг 700 г =
5
м – 4 дм 7 см =
Вариант 1.
1. Решите задачу:
В книге 270 страниц. Мальчик прочитал
эту книгу за три дня. В первый день он прочёл одну третью часть всей книги, во
второй день – 100 страниц. Сколько страниц прочёл мальчик в третий день?
Сколько страниц прочёл мальчик в третий день?
2. Сравните:
5км 206 м …5260 м 1300 мм2
… 13 см2
45 т….45 ц 2
мин 30 с….150 с
3. Вычислите, записывая столбиком:
24798 + 63007 426876
+ 24857
70000 — 24618
302879 — 179243
4 Вычисли, записывая вычисления столбиком:
28 т 640 кг – 9 т 890 км
=
18 кг 360 г + 16 кг 740 г
=
4 ч 40 мин + 55 мин =
5. Решите уравнения:
290 + Х= 640-
260 3 х Х = 87 – 6
6. Решите задачу:
Начерти прямоугольник со
сторонами 3см и 2 см, закрась одну третью часть. Вычисли площадь закрашенной
части.
7 *. Решите задачу:
Зачерпнул Емеля 37 литров
воды в 2 ведра. Пока влезал на пе6чь, пролил 2 литра из первого ведра и 5
литров из второго. Зато воды стало поровну. Сколько литров воды было в каждом
Зато воды стало поровну. Сколько литров воды было в каждом
ведре?
Вариант 2.
1 .Решите задачу:
В магазин привезли 360 кг
сахара. В первый день продали одну третья часть сахара, во второй день- 150 кг.
Сколько кг сахара осталось?
2. Сравните:
2 т 906 кг …2960 кг 1900
см2 … 19 дм2
150 см….150 м 4
ч 30 мин….250 мин
3. Вычислите,
записывая столбиком:
27996 +
50728 321850+ 64008
90000 –
45193 520613 — 318749
4 Вычисли, записывая вычисления столбиком:
38 км 230 м – 8 км 390 м
=
54 кг 120 г + 17 кг 840 г
=
6 мин 20 с + 45 с =
5. Решите уравнения:
400 — Х= 120 +
70 84 : Х = 7 х 3
6. Решите задачу:
Начерти прямоугольник со
сторонами 6 см и 1 см, закрась одну третью часть. Вычисли площадь закрашенной
Вычисли площадь закрашенной
части.
7*. Решите задачу:
В одном бочонке было 20
кг мёда. После того, как Винни –Пух взял из него 2 кг мёда, в нём осталось на 4
кг меньше, чем в другом бочонке. Сколько мёда стало в двух бочонках?
Контрольная работа за 1 полугодие 4 класс.
Вариант 1.
1. Решите задачу:
Из куска ситца длиной 36 метров портниха
сшили 5 платьев и 7 костюмов, причем на каждое платье и на каждый костюм пошло
одинаковое количество ткани. Сколько метров ткани пошло на платья и сколько на
костюмы?
2. Вычислите, записывая
столбиком:
700681
– 23902 280112 + 361754 1762
· 5 34872 : 8
13140 : 6
3. Вычисли,
записывая вычисления столбиком:
11т
823 кг — 6т 748 кг
4ч 40
мин + 1ч 52 мин
4. Решите
Решите
уравнения:
X + 350 = 700 – 230 7000 : Х =7 х 100
5. Решите
задачу:
Начерти прямоугольник с площадью 12 см2 , найди
периметр этого прямоугольника.
6*. Решите
задачу:
Бочка вмещает 84 л воды. Когда бочку налили наполовину и добавили
ещё 7 вёдер воды, бочка заполнилась доверху. Во сколько раз вместимость бочки
больше вместимости ведра?
Контрольная
работа за 1 полугодие 4 класс.
Вариант 2.
1 . Решите задачу:
В магазин привезли 45 кг
картофеля и 20 кг моркови. Всего 13 мешков, причем в каждом мешке овощей было
одинаковое количество. Сколько привезли мешков картофеля и сколько мешков
моркови?
2. Вычислите, записывая
столбиком:
900172
— 10719 598302 +
271908 2764 · 6
58534 : 7 31440 : 4
3. Вычисли,
Вычисли,
записывая вычисления столбиком:
51 км 876 м – 37 км 993
м
5 ч 36 мин + 1ч 42мин
4. Решите
уравнения:
980 – X = 340 + 230 Х :
8 = 800 х 10
5. Решите
задачу:
Начерти прямоугольник с площадью 16 см2 , найди
периметр этого прямоугольника.
6*. Решите задачу:
Бак вмещает 24 л воды. Когда бак налили наполовину и добавили ещё
3 вёдра воды, бак заполнился доверху. Во сколько раз вместимость бака больше
вместимости ведра?
Контрольная
работа №6
Вариант 1.
1. Реши задачу:
Туристы ехали на автобусе 3 часа со скоростью 60 км/ч и шли
пешком 5 часов со скоростью 6 км/ч. Какое расстояние преодолели туристы?
2. Реши задачу:
От двух пристаней навстречу друг другу отправились 2 теплохода.
Расстояние между пристанями равно 180 км. Встретились они через 6 часов. С какой
скоростью шел второй теплоход, если скорость первого была равна
15 км/час?
3. Решите примеры столбиком.
4 1230 · 2
1 263 : 3
603 · 80
1 635 : 5
1 2700 · 4
5 910 : 3
4. Найдите значение выражений:
(15 885 * 6 — 2 230 : 5) — 345 =
62 697 — (2 449 * 7 + 4 524 : 3) =
5. Решите задачу:
Найди периметр
прямоугольника, если известно, что его площадь 7200 дм2 , а
длина – 80 дм.
6* . Вставь пропущенные знаки арифметических
действий и скобки так, чтобы равенство было верным:
6…6…6…6…6…6…6 =
100
Контрольная работа №6
Вариант 2.
1 Реши задачу:
Теплоход
шел по озеру 2 часа со скоростью 42 км/ч, затем 3 часа вверх по реке со
скоростью 40 км/ч. Какой путь прошел теплоход?
Какой путь прошел теплоход?
2. Реши задачу:
Из двух поселков на встречу друг другу вышли два пешехода.
Расстояние между населенными пунктами составляет 48 км. Они встретились через 4
часа. С какой скоростью шел первый пешеход, если скорость второго равна 7
км/час?
3. Решите примеры столбиком.
1 2360 · 4
2 448 : 3
708 · 90
7 528 : 2
3 1600 · 5
8 910 : 9
4. Найдите значение
выражений:
(1845 * 6 — 3240 : 3) — 345 =
45697 — (3451 * 6 + 3202 : 2) =
5. Решите задачу:
Найди периметр
прямоугольника, если известно, что его площадь 4800 дм2 , а
длина – 80 дм.
6* .
Вставь пропущенные знаки арифметических действий и скобки так, чтобы равенство
было верным:
5…5…5…5…5 = 100
Контрольная
работа №7
Вариант 1.
1. Реши задачу:
Из двух городов, расстояние между которыми 390 км, одновременно
навстречу друг другу выехали два мотоциклиста и встретились через 3 часа.
Один мотоциклист ехал со скоростью 60 км/ч. Найдите скорость
другого мотоциклиста.
2. Реши задачу:
Из гаража одновременно в противоположных направлениях вышли две
автомашины. Одна шла со скоростью 50 км/ч, другая — 70 км/ч. Какое расстояние
будет между ними через 4 часа?
3. Решите примеры столбиком.
93650 ·
6 75270 : 30
78240 · 80 205100 : 700
843 · 700 36200 :
40
4. Выполни деление
с остатком:
7360 : 800 11970 : 400
5. Решите задачу:
Школьная спортивная
площадка прямоугольной формы имеет ширину 90 м, а площадь 11 250 м2 .
Найди длину площадки.
6* .
Который теперь час, если
прошедшая часть суток на 4 часа больше оставшейся?
Контрольная
работа №7
Вариант 2.
1 Реши задачу:
Из двух городов, расстояние
между которыми 600 км, одновременно выехали навстречу друг другу два
автомобиля, которые встретились через 4 часа. Один автомобиль ехал со скоростью
70 км/ч. Какова скорость второго автомобиля?
2. Реши задачу:
Автомобиль и мотоцикл выехали одновременно в противоположных
направлениях из одного города. Скорость автомобиля 60 км/ч, мотоцикла – 70
км/ч. Какое расстояние будет между ними через 3 часа?
3. Решите примеры столбиком.
72090 · 7
86240 : 40
8160 · 40
238800 : 600
659 · 600 18240
: 30
4. Выполни деление
с остатком:
4380 : 600 13590 : 300
5. Решите задачу:
Решите задачу:
Площадь пруда
прямоугольной формы 17200 м2 , а его длина 200 м. Найди ширину
пруда.
6* .
Который теперь час, если
прошедшая часть суток на 6 часов меньше оставшейся?
Контрольная
работа №8 за 3 четверть
Вариант 1.
1. Решите задачу.
Из
двух городов, расстояние между которыми 200 км, одновременно в противоположных
направлениях выехали два автомобиля. Скорость одного 65 км/ч, а другого – 75
км/ч. Какое расстояние будет между ними через 2 часа?
2.
Выполните вычисления.
518 · 32 348 · 920
2748 · 56 280 · 840
3. Найди значение выражения:
9000 – 424 · 76 : 4
4. Реши уравнение:
Х + 120 = 4000 : 5
5. Начертите отрезок, длина четвертой части которого равна 2 см 4
мм.
6. Вместо ?
Вместо ?
вставьте знаки арифметических действий так, чтобы равенства стали верными:
80 ? 20 ? 600 = 1 000
900 ? 30 ? 30 = 60
7.* Решите задачу.
Оля вышлана прогулку на 3
минуты раньше, чем Алеша. Алеша вышел на 2 минуты позже, чем Саша. Кто из детей
вышел раньше всех и на сколько минут?
Контрольная
работа №8 за 3 четверть
Вариант 2.
1. Решите задачу.
Из
двух поселков, расстояние между которыми 40 км, одновременно в противоположных
направлениях вышли два пешехода. Скорость одного 5 км/ч, а другого – 6 км/ч.
Какое расстояние будет между ними через 3 часа?
2. Выполните вычисления.
3 489 · 65 234
· 89
623 · 760 420
· 530
3. Найди значение выражения:
8000 — 568 · 14 :
2
4. Реши уравнение:
Х + 970 = 69 · 30
5. Начертите отрезок,
длина третьей части которого равна 3 см 6 мм.
6. Вместо ? вставьте знаки
арифметических действий так, чтобы равенства стали верными:
40 ? 20 ? 200 =
1 000 600 ? 30 ? 20 = 40
7.* Решите задачу.
Врач прописал больному 5
уколов – по уколу через каждые полчаса. Сколько потребуется времени, чтобы
сделать все уколы?
Скачано
с www.znanio.ru
Итоговая контрольная работа — математика — 4 класс
Предлагаю Вашему вниманию 2 итоговые контрольные работы по математике в 4 классе. Каждая контрольная представлена тремя вариантами.
Навыки и умения учащихся после окончания 4 классов
После завершения 4 классов по государственной программе учащиеся должны продемонстрировать следующие умения и навыки :
- Выполнять базовые арифметические операции с многозначными числами от 0 до 1000 000.

- Проверять свои выполненные вычисления.
- Вычислять значение выражений основываясь на особенностях вычисления выражения со скобками и приоритетом выполнения математических операций.
- Уверенно решать задачи в 1-3 действия.
- Выполнять арифметические действия с различными величинами.
- Находить площадь прямоугольника или квадрата.
- Решать простейшие уравнения разных видов на основе взаимосвязи между компонентами.
Итоговая контрольная работа по математике № 1
Вариант I
1. Вычислите
| 38 685 + 295 685 = | 649 483 — 34 586 = |
| 2 382 * 38 = | 44 184 : 56 = |
2. Выполните вычисления:
| 573 853 + 23 596 — 2 592 : 72 * 28 = | 12 м 6 дм 13 см + 8 дм 4 см = |
3. Решите уравнение:
X + 156 = 12 * 25
4. Решите задачу:
Задан участок прямоугольной формы. Вычислите площадь прямоугольника если длина равна 18 метров, а ширина в 3 раза меньше?
Вычислите площадь прямоугольника если длина равна 18 метров, а ширина в 3 раза меньше?
5. Решите задачу:
Можно ли число 450 000 представить как произведение 2 чисел, каждое из которых делится на 100?
Вариант II
1. Вычислите.
| 59 475 + 249 585 = | 384 586 — 234 586 = |
| 2 247 * 24 = | 3 248 : 56 = |
2. Выполните вычисления:
| 589 456 + 21 456 — 2 888 : 38 * 57 = | 3 м 5 дм 78 см + 2 дм 56 см = |
3. Решите уравнение:
X + 342 = 22 * 78
4. Решите задачу:
Задан участок прямоугольной формы. Вычислите площадь прямоугольника если ширина равна 18 метров, а длина в 3 раза больше?
5. Решите задачу:
Можно ли число 580 000 представить как произведение 2 чисел, каждое из которых делится на 100?
Вариант III
1. Вычислите.
| 59 384 + 493 678 = | 502 685 — 293 485 = |
| 4 934 * 27 = | 40 584 : 89 = |
2. Выполните вычисления:
Выполните вычисления:
| 492 679 + 28 523 — 3 465 : 77 * 47 = | 18 м 3 дм 44 см + 12 дм 8 см = |
3. Решите уравнение:
X + 423 = 14 * 67
4. Решите задачу:
Задан участок прямоугольной формы. Вычислите площадь прямоугольника ели длина равна 56 метров, а ширина в 4 раза меньше?
5. Решите задачу:
Можно ли число 720 000 представить как произведение 2 чисел, каждое из которых делится на 100?
Итоговая контрольная работа по математике № 2
Вариант I
1. Решите задачу:
В магазин привезли 72 кг мандарин и разложили в 8 пакетов. Сколько таких пакетов потребуется, если нужно разложить 108 кг мандарин?
2. Решите задачу:
Из точки в противоположном направлении поползли 2 червяка. У первого червяка была скорость 7 см/минуту, а у второго на 1 см/минуту меньше. Какое расстояние будет между ними через 40 минут?
3. Нарисуйте прямоугольник со сторонами 6 и 7 см. Вычислите его площадь и периметр.
Вычислите его площадь и периметр.
4. Решите задачу:
В корзину с яблоками положили 18 груш. За тем половину всех фруктов переложили в ящик. Осталось 4 фрукта. Сколько яблок было в корзине?
Вариант II
1. Решите задачу:
С грядки собрали 56 кг картошки и разложили в 4 мешка. Сколько мешков понадобится, если картошки будет 126 кг?
2. Решите задачу:
Два друга одновременно вышли из домов и пошли по одной и той же улице навстречу друг другу. Скорость первого была 50 м/минуту, а второго на 20 м/ минуту больше. Они встретились через 35 минут. Какое расстояние между домами?
3. Нарисуйте прямоугольник со сторонами 5 и 8 см. Вычислите его площадь и периметр.
4. Решите задачу:
В коробке с карандашами положили 16 ручек, потом половину ручек и карандашей переложили в портфель. Осталось 4 предмета. Сколько карандашей было в коробке?
Вариант III
1. Решите задачу:
Маша собрала 48 кг яблок и сложила это в 8 пакетов. А Петя собрал 72 кг. Сколько таких же пакетов понадобиться Пете?
Сколько таких же пакетов понадобиться Пете?
2. Решите задачу:
Из двух деревень одновременно пешеходы вышли навстречу друг другу. У первого пешехода была скорость 60 м/минуту, а у второго на 15 м/минуту больше. Они встретились через 2 часа. Какое расстояние между деревнями?
3. Нарисуйте квадрат со стороной 4 см. Вычислите его площадь и периметр.
4. Решите задачу:
На полку с мукой поставили 24 пачки крупы. За тем половину всех пакетов убрали. На полке осталось 18 пакетов. Сколько пакетов с мукой всего было на полке?
Файлы для загрузки
Учебная программа по математике для 4-го класса — Общие основные уроки и оценки
Что такое математика для 4-го класса?
4 класс фокусируется на трех ключевых достижениях предыдущих лет: (1) развитие понимания с помощью многозначного умножения и деления; (2) развитие понимания эквивалентности дробей и некоторых случаев сложения, вычитания и умножения дробей; и (3) понимание того, что геометрические фигуры можно анализировать и классифицировать на основе их свойств, включая их угловую меру и симметрию.
Как мы заказывали блоки?
Блок 1, значение разряда, округление, сложение и вычитание , год начинается с основного содержания, на котором основана большая часть оставшихся единиц — разряда. Учащиеся начинают видеть структуру разрядной системы в контексте мультипликативного сравнения — например, 1 тысяча в 10 раз больше, чем 1 сотня. Затем они используют это понимание места для сравнения, округления, сложения и вычитания чисел до 1 000 000.Они также решают многоступенчатые задачи со словами, включая сложение и вычитание, используя округление для оценки обоснованности своих ответов.
В , Блок 2, Многозначное умножение , студенты используют это понимание разряда, чтобы начать развивать понимание многозначного умножения (включая 2-значное, 3-значное и 4-значное на 1-значное, а также как 2-значное умножение на 2-значное). В то время как учащиеся познакомились с идеей мультипликативного сравнения в Блоке 1 в контексте структуры нашей системы разметки, они более глубоко вникают в эти типы задач рассказа в этом блоке. Блок 3, многозначный раздел , аналогично полагается на понимание разряда, чтобы познакомить учащихся с многозначным делением (включая четырехзначное, трехзначное и двузначное на однозначное деление). Учащиеся продолжают работу над многоступенчатыми задачами со словами, работая с остатками, интерпретируя их в контексте задачи.
Блок 3, многозначный раздел , аналогично полагается на понимание разряда, чтобы познакомить учащихся с многозначным делением (включая четырехзначное, трехзначное и двузначное на однозначное деление). Учащиеся продолжают работу над многоступенчатыми задачами со словами, работая с остатками, интерпретируя их в контексте задачи.
В , Блок 4, Углы , студенты получают формальное введение в углы после многих лет неформальной категоризации форм в соответствии с их углами.Учащиеся измеряют углы и находят неизвестные меры углов, а затем используют это более глубокое понимание для классификации форм и изучения симметрии отражения.
В , Блок 5, Эквивалентность дробей и упорядочение учащихся работают с эквивалентностью и сравнением дробей, разрабатывая общий метод генерации эквивалентных дробей и исследуя несколько стратегий для сравнения дробей. Это готовит их к Блок 6, Операции с дробями , где они начинают изучать операции с дробями (а именно сложение, вычитание и умножение на целое число). Студенты также начинают решать задачи со словами, включающие сложение, вычитание и умножение дробей. Затем это распространяется на Блок 7, Десятичные дроби , в котором учащиеся изучают десятичные дроби, которые особенно важны, поскольку они являются расширением системы разметки. Они находят эквивалентные десятичные дроби, складывают и вычитают десятичные дроби (включая десятые и сотые, требующие общего знаменателя) и используют десятичную систему счисления.
Студенты также начинают решать задачи со словами, включающие сложение, вычитание и умножение дробей. Затем это распространяется на Блок 7, Десятичные дроби , в котором учащиеся изучают десятичные дроби, которые особенно важны, поскольку они являются расширением системы разметки. Они находят эквивалентные десятичные дроби, складывают и вычитают десятичные дроби (включая десятые и сотые, требующие общего знаменателя) и используют десятичную систему счисления.
Курс заканчивается блоком 8 , преобразование единиц измерения , в котором студенты применяют большую часть своего понимания четырех операций, а также дробей и десятичных дробей для решения задач со словами, включающих преобразование большей единицы в меньшую единицу в той же системе. .
Этот курс соответствует рамкам учебной программы штата Массачусетс 2017 года, которые включают Общие основные государственные стандарты 2010 года. Кроме того, мы считаем, что ежедневная беглость речи и практическая работа являются важной частью обучения элементарной математике, но не включены в наши математические единицы. Все ученики 4-х классов получают около 45 минут практики в этих областях во время других блоков.
Все ученики 4-х классов получают около 45 минут практики в этих областях во время других блоков.
Онлайн-программа для четвертого класса | Time4Learning
Посмотреть демо наших уроков!
Сомневается ли ваш четвероклассник в ваших решениях, бросает вызов вашему авторитету и выражает мнение, отличное от вашего? Поздравляю! У вас есть независимый ученик.Противоречие ребенка, хотя и расстраивает родителей, может означать что-то весьма положительное для его или ее домашнего обучения. Это означает, что ваш ученик готов взять на себя хотя бы часть бразды правления своим обучением.
Типичный курс обучения для 4-го класса включает в себя языковые искусства, математику, общественные науки и естественные науки. Эта страница содержит информацию о том, чему учатся четвероклассники, как учиться на дому в четвертом классе, на что обращать внимание в программе четвертого класса и многое другое.
Чему учат четвероклассники?
В 4-м классе ученики научатся использовать инструменты исследования для написания отчетов. Они освоят навыки сложения, вычитания, умножения и деления и начнут изучать простую геометрию.
Они освоят навыки сложения, вычитания, умножения и деления и начнут изучать простую геометрию.
Они будут читать и создавать свои собственные диаграммы, графики и таблицы. В этом возрасте ученики четвертых классов начнут понимать сложность природных систем. В этом году ученики 4-х классов будут сосредоточены на всем, от древних цивилизаций до современных экономических принципов в социальных науках.
- Давайте посмотрим на некоторые концепции, которые приобретут четвероклассники в этом году:
- Они будут решать многоступенчатые задачи со словами, используя все четыре операции: сложение, вычитание, умножение и деление.
- Они научатся определять периметр и площадь фигуры путем подсчета единиц.
- Они научатся писать хронологические фрагменты, фрагменты, посвященные причине и следствию, и фрагменты, основанные на личном опыте, при правильном написании часто встречающихся слов.
- Они узнают об изменениях в материи и энергии, а также расширят свои знания о Солнечной системе и Вселенной.

Они узнают о месопотамской, египетской и других древних цивилизациях.
Узнайте больше о том, как Time4Learning может помочь вашим ученикам в достижении их академических целей, просмотрев объем и последовательность занятий для 4-го класса, а также страницы с планами уроков для 4-го класса.
Обзор учебной программы 4-го класса
Типичная учебная программа четвертого класса обеспечивает свободное владение математическими фактами и способствует более высокому уровню понимания прочитанного. Четвероклассники познакомятся с различными древними культурами и цивилизациями, а также расширят свои знания по различным научным темам.
При поиске идеальной учебной программы для 4-го класса примите во внимание следующие рекомендации:
- Представлены ли уроки в понятной и увлекательной форме, чтобы избежать разочарования и мотивировать учащихся учиться?
- Помогают ли концепции учащимся устанавливать связи в реальном мире и понимать, что их окружает?
- Как измеряется прогресс?
- Насколько гибкой является программа, чтобы удовлетворить потребности вашего ребенка, не создавая дополнительной административной работы для родителей?
- Какие есть возможности для повышения квалификации?
- Как в учебной программе учитываются навыки критического мышления и решения проблем?
Поскольку требования к домашнему обучению различаются в зависимости от штата, важно изучить законы своего штата о домашнем обучении, чтобы убедиться, что выбранная вами учебная программа соответствует этим требованиям.
Почему стоит выбрать программу обучения на дому для четвертого класса Time4Learning?
Выбор лучшей программы домашнего обучения для четвероклассника может показаться сложной задачей. Однако обычно правильный выбор — это та программа или сочетание программ, которые наиболее точно соответствуют общим целям домашнего обучения вашей семьи и идеальному стилю обучения вашего ребенка.
Time4Learning популярен во многих семьях, потому что он достаточно разнообразен и гибок, чтобы его можно было использовать с широким спектром стилей домашнего обучения.На протяжении более 16 лет тысячи семей доверяют Time4Learning своей основной учебной программе для домашнего обучения или дополнительной программе повышения квалификации после школы, чтобы обеспечить своим детям отличные результаты в традиционной школьной обстановке.
Ниже приведены лишь некоторые из полезных функций и преимуществ, которыми пользуются семьи при использовании Time4Learning.
В качестве полной учебной программы
| В качестве дополнения
|
Часто задаваемые вопросы о домашнем обучении 4 класс
Какого возраста дети в 4 классе?
Обычно четвероклассникам обычно 9-10 лет. Однако семьи, обучающиеся на дому, часто уделяют меньше внимания согласованию уровней обучения с возрастом, предпочитая использовать уровни обучения для обозначения фактического прогресса в учебе.
Как мне узнать, чему учить в 4 классе?
Прелесть домашнего обучения в том, что ни один план домашнего обучения одной семьи не будет похож на другой.Как учитель вашего ребенка, вы можете выбрать учебный план и объем того, что вы изучаете в этом году. Однако, если ваш ребенок вернется в традиционную школу после обучения на дому, было бы разумно изучить темы, охватываемые основной учебной программой вашего штата, чтобы убедиться, что у вашего ребенка нет значительных пробелов в его / ее образовании.
Что должен знать 4-классник к концу года?
Опять же, цели вашего учебного года на дому зависят от вас. Некоторые из целей для четвероклассников с традиционным образованием включают чтение с более высоким уровнем беглости и выражения, использование простого письменного диалога, навыки многозначной арифметики, понимание структуры местного правительства штата и федерального правительства и распознавание основных источников информации. материя и энергия.
материя и энергия.
Как подготовить ребенка к четвертому классу?
Если вы какое-то время обучались на дому, вы, вероятно, хорошо понимаете сильные и слабые стороны своего ребенка в четвертом классе. Но если домашнее обучение — новое занятие для вас, возможно, вам придется потратить некоторое время на оценку навыков своего ребенка, прежде чем переходить к программе домашнего обучения в четвертом классе.
При подготовке ребенка к четвертому классу вы можете сосредоточиться на:
- Заставить их попрактиковаться в написании часто используемых слов.
- Практика и другие практики их таблицы умножения, сложения, вычитания, умножения и деления.
- Предложить им прочитать книги разных жанров и практиковать правильную пунктуацию.
- Предложите им посмотреть документальные фильмы о научных концепциях, которые они изучили в 4-м классе и которые они начнут изучать в 4-м классе.
Математика 4 класс
Панель приборов
4 класс
Перейти к содержанию
Панель приборов
Авторизоваться
Приборная панель
Календарь
Входящие
История
Помощь
Закрывать
-
Мой Dashboard - Класс 4
NE
- Главная
- Процедуры
- Закрытие
- Банк ресурсов
- Курс 3 класса
- 4 класс G / T
- Курс 5 класса
- Учебная программа 4 класса Сообщество
- Семья и сообщество 4 класса
- Сотрудничество
- Google Drive
Содержание этого курса предлагается по лицензии CC Attribution Non-Commercial Share Alike . Контент этого курса может рассматриваться в рамках этой лицензии, если не указано иное.
Контент этого курса может рассматриваться в рамках этой лицензии, если не указано иное.
Посмотреть ленту курса
В ближайшее время
Просмотр календаря
-
Ничего на следующую неделю
Четвертый класс | Инструменты 4 Учителя NC
Учебная база Введение
Цель этого документа — связать и упорядочить математические идеи, чтобы позволить учителям планировать возможности обучения для учащихся, чтобы развить последовательное понимание математики.Кластеры и последовательность предназначены для того, чтобы помочь учащимся осмыслить связи между математическими идеями и процедурами. Это осмысление происходит сверхурочно. Следовательно, концепции включаются в несколько кластеров с возрастающей глубиной. Они строятся в течение года, начиная с концептуального понимания и переходя к процедурной беглости.
Каждый кластер включает список связанных стандартов контента и диапазон предлагаемой продолжительности. Стандарты указывают на математические ожидания учащихся к концу учебного года.Стандарты вводятся и разрабатываются в течение года, поэтому тот факт, что стандарт контента указан в конкретном кластере, не означает, что он должен быть освоен в кластере. В некоторых кластерах зачеркивание в стандартах контента обозначает часть стандарта этому мы научим позже. В других кластерах появляется полный стандарт, но предложения о предполагаемом фокусе указываются в описании кластера. Поскольку стандарты могут быть включены в кластеры задолго до ожидаемого успеваемости, формирующая оценка является важным инструментом для планирования обучения и отчетности об успеваемости учащихся.Эта оценка естественным образом происходит, когда учителя развивают математическое мышление и рассуждения учащихся, когда они занимаются математикой.
Стандарты указывают на математические ожидания учащихся к концу учебного года.Стандарты вводятся и разрабатываются в течение года, поэтому тот факт, что стандарт контента указан в конкретном кластере, не означает, что он должен быть освоен в кластере. В некоторых кластерах зачеркивание в стандартах контента обозначает часть стандарта этому мы научим позже. В других кластерах появляется полный стандарт, но предложения о предполагаемом фокусе указываются в описании кластера. Поскольку стандарты могут быть включены в кластеры задолго до ожидаемого успеваемости, формирующая оценка является важным инструментом для планирования обучения и отчетности об успеваемости учащихся.Эта оценка естественным образом происходит, когда учителя развивают математическое мышление и рассуждения учащихся, когда они занимаются математикой.
Особые стандарты математической практики указаны для каждого кластера. Перечисленные предложения являются руководством для учителей. Хотя перечисленные практики могут особенно хорошо подходить для содержания кластера, это не означает, что они будут единственными практиками, которые будут использовать студенты. Учащиеся, выполняющие сложные математические задачи, естественно будут заниматься многими математическими практиками, как и математикой.Во время обучения учителя могут наблюдать и решать другие практики, которые учащиеся используют, помимо тех, которые перечислены в кластере.
Учащиеся, выполняющие сложные математические задачи, естественно будут заниматься многими математическими практиками, как и математикой.Во время обучения учителя могут наблюдать и решать другие практики, которые учащиеся используют, помимо тех, которые перечислены в кластере.
Каждый кластер включает раздел под названием «Что такое математика?» который описывает важные концепции и связи в рамках стандартов, необходимых учащимся для понимания и использования математики. Второй раздел под названием «Важные соображения» содержит рекомендации, основанные на прогрессе учащихся, а также идеи и модели для обучения в ситуациях решения проблем.Решение проблем и математические рассуждения определяют, что значит заниматься математикой. Богатые задания (включая задачи со словами) предоставляют учащимся конкретный контекст для использования при знакомстве с новой математикой. Позже работа с такими задачами позволяет учащимся развить понимание и в конечном итоге продемонстрировать мастерство. Богатые задания с множеством точек входа и выхода позволяют естественным образом дифференцировать обучение и доступны для всех студентов.
Богатые задания с множеством точек входа и выхода позволяют естественным образом дифференцировать обучение и доступны для всех студентов.
Первоначальный кластер в каждом классе включает в себя построение математического сообщества.Изучение математики предполагает продуктивную борьбу во время решения проблем и содержательную беседу, когда учащиеся делятся стратегиями и объясняют свое мышление. Это требует от отдельных учащихся математического мышления, веры в то, что они могут учиться и заниматься математикой, поэтому они будут рисковать при решении нестандартных задач. Вместе учащиеся должны публично делиться идеями, критикуя математические идеи со сверстниками и учителем. Безопасное сообщество, в котором ошибки и борьба ценятся как возможности для обучения, очень важны.Математические нормы о том, как учащиеся делают и говорят о математике, должны быть четко установлены таким же образом, как и другие распорядки и ожидания, вводимые в начале учебного года.
Обзор и тесты по математике для 4-х классов | Домашнее задание или утренняя работа | 4 КВАРТАЛ
Описание
Этот ресурс с обзором спирали по математике 4-го класса можно легко использовать в качестве ДОМАШНЕГО ЗАДАНИЯ по математике, УТРЕННЕЙ РАБОТЫ или ЕЖЕДНЕВНОГО ОБЗОРА МАТЕМАТИКИ! Этот ресурс был разработан, чтобы поддерживать актуальность математических концепций в течение всего года и помочь вам легко отслеживать успеваемость учащихся. Все страницы 100% РЕДАКТИРУЕМЫЕ , и их легко дифференцировать, чтобы они соответствовали потребностям ваших учеников.
Все страницы 100% РЕДАКТИРУЕМЫЕ , и их легко дифференцировать, чтобы они соответствовали потребностям ваших учеников.
Получите НАЧАЛО НА ВЕСЬ ГОД! {НАЖМИТЕ ЗДЕСЬ}
☝☝ Ознакомьтесь с превью, чтобы узнать больше и получить 3 БЕСПЛАТНЫХ недели! ☝☝
Эта система спирального обзора также доступна для
Станьте на 100% безбумажным с моей ЦИФРОВОЙ версией GOOGLE Forms! НАЖМИТЕ ЗДЕСЬ
Вам нужно несколько классов или предметов? Посмотрите мой Создайте свой собственный комплект {НАЖМИТЕ ЗДЕСЬ}! С помощью Create Your Own Bundle вы можете выбирать из нескольких предметов и уровней обучения, чтобы сделать идеальный набор для вашего класса!
Что включено…
- 5 недель ежедневных обзоров по спиральной математике
- 5 недель еженедельных викторин по спиральной математике
- PLUS, 3 недели следующего уровня обучения для предварительного просмотра в конце учебного года
- Охватывает 4 ЧЕТВЕРТЬ 4 КЛАССА !!!
- 100% редактируемый в Microsoft Word и Google Docs (также есть в формате PDF)
- КЛЮЧИ ОТВЕТА включены!
- Доступно 2 формата: «Сжатый» формат для экономии бумаги и формат «Больше места», чтобы дать учащимся больше места для демонстрации своих работ.

- Руководство по темпам обучения на весь год по математике
- 3 редактируемых графика для отслеживания успеваемости учащихся (для еженедельных тестов)
- Используйте в качестве ежедневного домашнего задания или утренней работы и проводите викторину в пятницу, чтобы привлечь учащихся к ответственности
✎ Как это работает…
- Студенты заполняют только одну колонку спирального обзора в день с понедельника по четверг.
- Каждую неделю проводится практика по новейшим внедряемым навыкам (см. Руководство по стимуляции в предварительном просмотре) и постоянно пересматриваются ранее обученные навыки.
- В пятницу проведите тест по выровненной спирали, чтобы привлечь учащихся к ответственности за свое обучение и помочь контролировать их успеваемость. (идеально подходит для еженедельных оценок викторин)
❤❤ Почему учителям нравится этот ресурс! ❤❤
- Домашнее / утреннее задание более предсказуемо и легко выполнять.

- Тесты быстро оценивают учащихся каждую неделю, не занимая слишком много времени и не перегружая их.
- Студенты ежедневно знакомятся с множеством стандартов, сохраняя свои навыки на высоком уровне.
- Ежедневные задания значимы и НЕ перегружены.
- Каждую неделю вводится новый стандарт, продолжая пересматриваться.
- Данные викторины помогают определить навыки, которые необходимо переучить.
- Родители ценят последовательность домашнего задания (если оно используется в качестве домашнего задания).
- Учителя могут легко увидеть, где учащиеся по-прежнему постоянно испытывают трудности.
- Вопросы можно легко редактировать в соответствии с потребностями учащихся.
- Учителя считают, что при использовании этого ресурса в течение всего года учащимся практически НЕ нужна подготовка к стандартному тестированию.
- Увеличение количества выполненных домашних заданий! (при использовании в качестве домашнего задания)
Ищете другой класс? {НАЖМИТЕ ссылки ниже, чтобы узнать больше}
✪ Детский сад
✪ 1-й класс
✪ 2-й класс
✪ 3-й класс
✪ 4-й класс
✪ 5-й класс
✪ 6-й класс
✪ 7-й класс
✪ 8-й класс
✪ Алгебра 1
✪ Геометрия
✪ Алгебра 2
☝☝ Ознакомьтесь с превью, чтобы узнать больше и получить 3 БЕСПЛАТНЫХ недели! ☝☝
Использование этого ресурса в качестве ДОМАШНЕГО ЗАДАНИЯ!
Раздайте каждому ученику лист с домашним заданием в понедельник. Они будут заполнять одну колонку каждую ночь (с понедельника по четверг). Вы можете распечатать страницу «Покажи свою работу» на обратной стороне или использовать формат «Больше места».
Они будут заполнять одну колонку каждую ночь (с понедельника по четверг). Вы можете распечатать страницу «Покажи свою работу» на обратной стороне или использовать формат «Больше места».
Каждый день в начале урока я люблю уделять 5-8 минут тому, чтобы быстро просмотреть домашнее задание, выполненное накануне вечером, и прояснить любые вопросы, которые могут возникнуть у моих учеников. Учащиеся используют раздел «Мой прогресс», чтобы следить за своими успехами, и это помогает им нести ответственность за собственное обучение. Мои ученики ценят это время и используют его, чтобы задавать важные вопросы, потому что знают, что на следующий вечер они увидят похожие проблемы при выполнении домашнего задания.
В пятницу я провожу тест по спирали на этой неделе и принимаю его как оценку. Я использую викторину, чтобы понять, где учащиеся все еще испытывают трудности.
** Этот ресурс можно легко использовать как утреннюю работу или разминку.
Дополнительные ресурсы для 4-го класса!
✔ Обзор и викторины по математической спирали 4-го класса
✔ Обзор спирали чтения 4-го класса и викторины
✔ Обзор языковой спирали 4-го класса и викторины
✔ Обзор цифровой математической спирали 4-го класса и викторины
✔ Обзор цифровой спирали чтения 4-го класса и викторины
✔ Спираль цифровых языков для 4-го класса Обзор и викторины
✔ Я МОГУ математические игры
✔ Я МОГУ Грамматические игры
✔ 4-й класс Цифровые Я МОГУ Математические игры
✔ 4-й класс Цифровые Я МОГУ Грамматические игры
✔ Набор материалов по чтению и письму
✔ Универсальный учитель Папка
▼ Увеличивает Сверхмощные Сверхмощные Сверхмощные Сверхмощные Сверхмощные Клавиши
Сверхмощные Сверхмощные Сверхмощные Сверхмощные Клавиатуры Клавиатуры Клавиатуры Клавиатуры Смартфон
ИЩЕТЕ БОЛЬШЕ великих РЕСУРСОВ ???
Загрузите мой БЕСПЛАТНЫЙ Путеводитель по покупкам , чтобы легко просматривать ВСЕ мои ресурсы.
Давайте подключимся!
► ПОДПИСАТЬСЯ на мою рассылку!
► ПОДПИСАТЬСЯ на меня на Учителя платят учителям!
► СЛЕДУЙТЕ за БЛОГОМ One Stop Teacher Shop!
► ПОДПИСАТЬСЯ на меня в Pinterest!
► ПОДПИСАТЬСЯ на меня на Facebook!
►СЛЕДУЙТЕ за мной в Instagram!
Если вы хотите связаться со мной по поводу цен на лицензию для ВСЕЙ школы, округа или округа, напишите мне по адресу [адрес электронной почты защищен]
УСЛОВИЯ ИСПОЛЬЗОВАНИЯ — © One Stop Teacher Shop, Inc.
Этот товар можно загрузить в цифровом виде из моего магазина.
Таким образом, он предназначен для использования только в одном классе. Этот товар также защищен законами об авторском праве. Распространение, редактирование, продажа или размещение этого объекта (или любой его части) в Интернете строго запрещено без предварительного разрешения автора. Нарушения подлежат наказанию в соответствии с Законом об авторском праве в цифровую эпоху. Пожалуйста, свяжитесь со мной, если вы хотите получить особые разрешения!
Пожалуйста, свяжитесь со мной, если вы хотите получить особые разрешения!
Утренняя работа по математике в 4-м классе
Примеры математических навыков Базовые десять концепций 17 — 10 + 7 27 — 20 + 7 Место 34 — 3 десятки и 4 единицы, 29 — 2 десятки и 9 единиц 1 больше, 1 меньше Если задано любое число, Ваш ребенок должен уметь назвать число, которое на 1 больше и на 1 меньше.45 На 1 больше — на 46/1 меньше — 44. На 10 больше, на 10 меньше При любом числе ваш ребенок
Навыки, приобретенные в 4-м классе В 4-м классе определенно будет более быстрый темп обучения, который будет одновременно увлекательным и сложным. для вашего ребенка. Нередко уроки социальных наук, математики, чтения и естествознания проводятся блоками по 30–45 минут.
Этот ресурс «Утренняя работа» для третьеклассников представляет собой всеобъемлющий уникальный тип утренней работы, потому что это полная страница в день (не 1/4 страницы, не 1/2 листа) и включает КАЖДЫЙ 3-й класс. Общий базовый стандарт чтения, языка и математики, а также социальных наук и естественных наук…
Утренние послания 1-го класса наконец-то СДЕЛАНЫ! Хотите узнать больше о том, как появились утренние сообщения? Прочтите этот пост о версии 2-го класса. Чтобы помочь с организацией, мы назначили каждому дню тему: понедельник по математике, вторник с новым семестром, среда Word Power, четверг и смешная пятница.
Чтобы помочь с организацией, мы назначили каждому дню тему: понедельник по математике, вторник с новым семестром, среда Word Power, четверг и смешная пятница.
Бесплатные распечатанные лабиринты и рабочие листы лабиринтов для дошкольных учреждений, детских садов и многого другого! Сотни бесплатных лабиринтов для печати, чтобы бросить вызов своим ученикам и порадовать их.Наши лабиринты бывают разных уровней: легкий, средний и сложный. С лабиринтами для начинающих на нашем уровне MEGA Maze каждый найдет что-то для себя! Тематические лабиринты на Рождество, День Благодарения, Пасху …
Получите неограниченный доступ к 40 000 лучших книг, аудиокниг, видео и многого другого для детей до 12 лет. Попробуйте бесплатно в течение 30 дней.
Math Games позволяет им делать и то, и другое — в школе или дома. Учителя и родители могут создавать индивидуальные задания, которые оценивают или проверяют определенные математические навыки.Мероприятия составлены таким образом, чтобы ученики работали в соответствующем классе. Рабочие листы можно загрузить и распечатать для использования в классе, а задания можно заполнить и автоматически оценить онлайн.
Рабочие листы можно загрузить и распечатать для использования в классе, а задания можно заполнить и автоматически оценить онлайн.
13 июня 2017 г. · Эта таблица привязок четвертого класса идеально подходит для Дня Земли. Мне нравятся все картинки и примеры, которые были включены в «Кекс для учителя». 18. Разрешение конфликтов. Якорные диаграммы хорошо подходят для социально-эмоционального обучения (SEL) и могут использоваться на утренних встречах.
После того, как эта основная концепция валюты установлена, рабочие листы для детского сада и первого класса сосредоточены на подсчете денег, сравнении денежных сумм и простых расчетах.Таблицы денег для 2-го и 3-го классов включают более сложные вычисления, такие как сложение, вычитание, умножение и деление денежных сумм.
Начальная школа / 4 класс
EnVision Math Перевод писем от родителей
Стандарты содержания общих ядер Калифорнии
Обзор :
Четвероклассники используют свои знания о числовом значении, чтобы обобщить до 1 000 000 и научиться округлять многозначные целые числа до любого места. Они плавно складывают и вычитают, используя стандартный алгоритм, а также умножают и делят с помощью многозначных чисел. Четвероклассники расширяют понимание дробей, включая эквивалентность, порядок и простую десятичную запись. Учащиеся измеряют углы и классифицируют геометрические фигуры по линиям (параллельным, перпендикулярным и т. Д.) И углам (прямым, острым, тупым и т. Д.).
Они плавно складывают и вычитают, используя стандартный алгоритм, а также умножают и делят с помощью многозначных чисел. Четвероклассники расширяют понимание дробей, включая эквивалентность, порядок и простую десятичную запись. Учащиеся измеряют углы и классифицируют геометрические фигуры по линиям (параллельным, перпендикулярным и т. Д.) И углам (прямым, острым, тупым и т. Д.).
В частности, ваш ребенок будет…
Операции и алгебраическое мышление
· Используйте сложение, вычитание, умножение и деление с целыми числами для решения задач со словами
· Узнайте о множителях и кратных
· Множители 24: 1, 2, 3, 4, 6, 8, 12
· Кратное 4: 4, 8, 12, 16, 20
· Составить и описать выкройки с предметами и числами
Число и десять операций по основанию
· Понять и использовать числовую стоимость, чтобы обобщить до 1 000 000
· Расширенная форма: 6783 = 6000 + 700 + 80 + 3
· Вычислить с многозначными числами
· Решение задач, связанных с умножением многозначных чисел на двузначные числа
· Многозначные числа делить на однозначный делитель
· Круглые многозначные числа в любое место
Число и операции — дроби
· Понимание эквивалентных дробей и порядок дробей
· Сравните две дроби с разными числителями и разными знаменателями, сделав общие знаменатели
· Сложить и вычесть дроби и смешанные числа с одинаковыми знаменателями
· Понимание десятичной системы счисления дробей
· Сравнить десятичные числа
Измерения и данные
· Решать проблемы с помощью преобразования измерений
· Применить формулы площади и периметра для прямоугольников
· Организуйте и объясните данные с помощью линейного графика
Геометрия
· Определение и измерение углов
· Нарисуйте и обозначьте линии и углы
· Описывать и сортировать фигуры по линиям и углам
· Распознавать линии симметрии
Источник:
Справочник для родителей по общим основным стандартам
См.
ГДЗ. Математика 5 класс Тарасенкова. Уравнения.
Категория: –>> Математика 5 класс Тарасенкова.
Задание: –>> 553 – 569 570 – 586
наверх
|
|
Задание 553.
Какое из чисел 4. 5, 8 и 10 является корнем уравнения:
Решение:
| 1) 5; | 2) 10; | 3) 4. |
Задание 554.
Решите уравнение устно:
Решение:
| 1) 15 + x: = 55, x = 40; | 3) 60 – y = 45, y = 15; | 5) 88 : x = 8, x = 11; |
| 2) х – 22 = 42, x = 64; | 4) у * 12 = 12, y = 1; | 6) у : 10 = 40, y = 400. |
Задание 555.
Можно ли решить уравнение:
| 1) 8x = 0; | 2) 0 : y = 25; | 3) 5х = 5 | 4) 12 : y = 0? |
Решение:
1) x = 0; 2) Не имеет решений; 3) x = 1; 4) Не имеет решений;
Задание 556.
Решите уравнение:
Решение:
1)28 + (45 + х) = 100;
| 11) 121 : (х – 45) = 11;

|
Задание 557.
Решите уравнение:
Решение:
1) 65 + (х + 23) = 105;
| 6) 9х + 50 = 86;

|
Задание 558.
Составьте уравнение, корнем которого является число:
| а) 8; | б) 14. |
Решение:
| а) 2y = 16; | б) x + 7 = 21. |
Задание 559.
Составьте уравнение, корнем которого является число.
| а) 5; | б) 9. |
Решение:
| а) 25 : x = 5; | б) 5x = 45. |
Задание 560.
Некоторое число увеличили на 67 и получили число 109. Найдите это число.
Решение:
- Некоторое число – x.
- x + 67 = 109;
- x = 109 – 67;
- x = 42.
- Ответ: число 42.
Задание 561.
К некоторому числу прибавили 38 и получили число 245. Найдите это число.
Решение:
- x + 38 = 245;
- x = 245 – 38;
- x = 207.

- Ответ: 207.
Задание 562.
Некоторое число увеличили в 24 раза и получили число 1968. Найдите это число.
Решение:
- 24x = 1968;
- x = 1968 : 24;
- x = 82.
- Ответ: 82.
Задание 563.
Некоторое число уменьшили в 18 раз и получили число 378. Найдите это число.
Решение:
- x : 18 = 378;
- x = 378 * 18;
- x = 6804.
- Ответ: 6408.
Задание 564.
Некоторое число уменьшили на 22 и получили число 105. Найдите это число.
Решение:
- x – 22 = 105;
- x = 105 + 22;
- x = 127.
- Ответ: 127.
Задание 565.
Из числа 128 вычли некоторое число и получили 79. Найдите это число.
Решение:
- 128 – x = 79;
- x = 128 – 79;
- x = 49.
- Ответ: 49.
Задание 566.

Составьте и решите уравнение:
- 1) сумма удвоенного числа х и числа 39 равна 81;
- 2) разность чисел 32 и y в 2 раза меньше числа 64;
- 3) частное суммы чисел х и 12 и числа 2 равно 40;
- 4) сумма чисел х и 12 в 3 раза больше числа 15;
- 5) частное разности чисел у и 12 и числа 6 равно 18;
- 6) утроенная разность чисел у и 17 равна 63.
Решение:
- 1) 2x + 39 = 81
- 2x = 81 – 39;
- 2x = 42;
- x = 42 : 2;
- x = 21;
- 2) (32 – y) * 2 = 64
- 32 – y = 64 : 2;
- 32 – y = 32;
- y = 32 – 32;
- y = 0;
- 3) (x + 12) : 2 = 40
- x + 12 = 40 * 2;
- x + 12 = 80;
- x = 80 – 12;
- x = 68;
- 4) (x + 12) : 3 = 15
- x + 12 = 15 * 3;
- x + 12 = 45;
- x = 45 – 12;
- x = 33;
- 5) (y – 12) : 6 = 18
- y – 12 = 18 * 6;
- y – 12 = 108;
- y = 108 + 12;
- y = 120;
- 6) (y – 17) * 3 = 63
- y – 17 = 63 : 3;
- y – 17 = 21;
- y = 21 + 17;
- y = 38;
Задание 567.

Составьте и решите уравнение:
- 1) разность утроенного числа у и числа 41 равна 64;
- 2) сумма чисел 9 и х в 5 раз меньше числа 80;
- 3) частное суммы чисел у и 10 и числа 4 равно 16;
- 4) разность утроенного числа х и числа 17 равна 10.
Решение:
- 1) 3y – 41 = 64
- 3y = 64 + 41;
- 3y = 105;
- y = 105 : 3;
- y = 15;
- 2) (9 + x) * 5 = 80
- 9 + x = 80 : 5;
- 9 + x = 16;
- x = 16 – 9;
- x = 7;
- 3) (y + 10) : 4 = 16
- y + 10 = 16 * 4;
- y + 10 = 64;
- y = 64 – 10;
- y = 54;
- 4) 3x – 17 = 10
- 3x = 10 + 17;
- 3x = 27;
- x = 27 : 3;
- x = 9;
Задание 568.
Некоторое число увеличили на 5 и полученное число удвоили. В результате получили число 22. Найдите неизвестное число.
В результате получили число 22. Найдите неизвестное число.
Решение:
- (x + 5) * 2 = 22;
- x + 5 = 22 : 2;
- x + 5 = 11;
- x = 11 – 5;
- x = 6;
Задание 569.
Некоторое число увеличили в 7 раз и полученное число уменьшили на 54. В результате получили число 100. Найдите неизвестное число.
Решение:
- 7x – 54 = 100;
- 7x = 100 + 54;
- 7x = 154;
- x = 154 : 7;
- x = 22;
Задание: –>> 553 – 569 570 – 586
Конспект урока для 4 класса “Решение задач с помощью уравнений”
Математика 4 класс
Тема: Решение задач с помощью уравнений.
Цель: учить решать задачи алгебраическим способом;
рассмотреть практические способы решения уравнений, требующие выполнения более одного арифметического действия;
закреплять понятия «уравнение», «корень уравнения», «решение уравнения»;
развивать логическое мышление учащихся, вычислительные навыки, речь, память, внимание;
воспитывать трудолюбие и самостоятельность, математическую культуру учащихся.
Тип урока: комбинированный.
Оборудование: карточки-опоры, карточки с задачами, схемами к задачам, карточки для домашней работы.
Ход урока:
1. Организационный этап.
Задачи этапа: обеспечить нормальную обстановку работы и психологическое настроение учащихся.
Время: 1-1,5 мин.
Приветствие, проверка готовности учащихся к уроку, психологический настрой.
– Пожелайте друг другу сегодня на урок что-нибудь доброе и хорошее.
Игра «Я желаю тебе сегодня …» (Можно хором сказать начало фразы, дальше каждый продолжит сам).
В тетрадях записывается число, классная работа.
2. Подготовка учащихся к активному и сознательному усвоению нового материала.
Задачи этапа: организовать целенаправленную познавательную деятельность учащихся; вырабатывать целеустремленность и целенаправленность.
Содержание этапа:
а) опрос.
На доске опорные схемы с прошлого урока: карточки с понятиями «уравнение», «корень уравнения», «решение уравнения».
– Внимательно посмотрите на доску и подумайте, чем мы сегодня будем заниматься на уроке математики?
– Правильно, сегодня на уроке мы продолжим изучение темы «Уравнение», продолжим знакомство с решением задач с помощью уравнений. Перед тем, как начать работу, я бы хотела спросить у вас, какой государственный праздник скоро будет отмечать вся наша страна?
– 16 декабря – День Независимости Республики Казахстан.
– В далеком 1991 году перед нашим Президентом тоже стояла задача со многими неизвестными: как сделать так, чтобы о Казахстане узнали во всем мире как о сильном государстве, в котором созданы условия для свободной жизни всех ее граждан. Как вы думаете, смог ли наш Президент решить эту задачу?
– Об этом говорит тот факт, что в Астане состоялось международное совещание глав государств Европы и Азии. А кто помог нашему Президенту справиться с такой нелегкой задачей?
А кто помог нашему Президенту справиться с такой нелегкой задачей?
– Вот и нам на уроке всем вместе предстоит такая задача – решение уравнений с неизвестными. – Как вы думаете, пригодится ли эта тема вам в будущем?
Обобщение ответов учащихся.
б) Работа по карточкам-опорам:
– Что такое уравнение?
– Что значит, «решить уравнение»?
– Что такое «корень уравнения»?
Методический прием «Идеальный опрос». Ученики сами оценивают степень своей готовности к уроку.
– Кто сегодня чувствует себя готовым на «5»? (Ученики поднимают руку) На «4»? На «3»? Спасибо.
в) Устный счет.
На доске в произвольном порядке карточки с уравнениями.
– На какие группы можно разделить все эти уравнения?
1 группа – 7000-х=2489; 7000-х=3489; 7000-х=1689
– Почему мы выделили именно эти уравнения в первую группу? (Простые уравнения с одинаковым уменьшаемым).
– Можем ли мы их решить?
– Найдите среди них уравнение с наибольшим корнем и решите его. (7000-х=1689)
Один ученик у доски.
2 группа – 81: х=20+7; х:4=16+11 – Это уравнения, в правой части которых есть выражение.
– Можем ли мы решить уравнения второго столбика?
У доски два ученика.
Обратить внимание на алгоритм решения уравнения.
3 группа – (490-х) -250=70
– Посмотрите на оставшееся уравнение. Легко ли нам его решить? Почему?
Решение уравнения с комментированием у доски с использованием методического приема «Показательный ответ» – выбрать ученика, желающего с комментированием решить уравнение на доске.
Оценивание ответа.
Подвижная физминутка.
3. Усвоение новых знаний.
Задачи этапа: дать учащимся конкретное представление об изучаемом материале; добиться в ходе процесса восприятия осознания, осмысления, первичного обобщения и систематизации изучаемого материала; добиться усвоения учащимися способов, путей и средств, приводящих к обобщению знаний; на основе приобретаемых знаний вырабатывать соответствующие умения и навыки; широко использовать воспитательные возможности изучаемого материала.
Содержание этапа:
1) организация внимания.
– На прошлом уроке мы узнали о новом способе решения задач – алгебраическом. Что значит решить задачу алгебраически? (Уравнением)
– Какой еще способ решения задачи вы знаете? (Арифметический).
2) организация учителем усвоения нового.
Решение задачи № 1 по карточке.
Школьники должны были высадить 25700 саженцев деревьев. После того, как они высадили часть саженцев, им осталось посадить еще 12350 деревьев. Сколько деревьев они уже высадили?
Подбор схемы к задаче, решение у доски одним учеником.
25700-х=12350; х=13350
Вывод.
Решение задачи № 2 по карточке.
Школьники должны были высадить 25700 саженцев деревьев. После того, как они посадили несколько саженцев липы и 8580 кленов, им осталось посадить еще 12350 деревьев. Сколько лип они уже посадили?
Сколько лип они уже посадили?
Подбор схемы к задаче, решение у доски одним учеником.
25700-(х+8580) =12350 или (25700-х) -8580=12350; х=4770
Вывод. Сравнение задач.
– Можем ли мы назвать их обратными? (нет, условия похожи, но способы решения разные).
Физминутка – гимнастика для глаз.
6. Проверка усвоения новых знаний, способов и умений деятельности.
Задачи этапа: установление связей и взаимоотношений между фактами, закономерностями, устранение пробелов, если они обнаружены.
Решение задачи № 3 по карточке.
На складе было 912 ц овощей. После того, как несколько центнеров овощей увезли на 9 машинах поровну на каждой, там осталось 552 ц. Сколько центнеров овощей грузили на каждую машину?
Х∙9+552=912; х=40
7. Закрепление нового материала.
Задачи: закрепить ЗУН, необходимые для самостоятельной работы учащихся по новому материалу.
Учебник, с. 118, задача № 6.
Пусть х- количество монет у девочки, тогда…
20∙х=300+700
8. Этап информации учащихся о ДЗ и инструктаж о его выполнении.
– Что на уроке было главным?
– Что было интересным?
– Что нового сегодня узнали?
– Чему учились?
ДЗ – решить задание по карточке.
По выбору: решить 1 задачу и 3 уравнения; или 2 задачи и 1 уравнение.
Если не удается решить задачу алгебраическим способом, можно решить ее арифметически.
1. С одного участка собрали 161 кг свёклы, а с другого 289 кг. Всю свёклу разложили в сетки, по 10 кг в каждую. Сколько потребовалось сеток?
2. На станции из вагона вышли 18 пассажиров, а вошли 12. В вагоне стало 120 пассажиров. Сколько пассажиров было в вагоне первоначально.
3. Дети возвращались из лагеря. Они разместились в 10 автобусах, по 42 человека в каждом. Среди детей было 187 мальчиков, а остальные – девочки. Сколько девочек возвращалось из лагеря?
80 • х – 51 = 429 25 + 70 • х = 375 44 + 91 : х = 45
56 : х = 24 : 3 48 + х• 6 = 60 120 + х • 3 = 375
Решение простых уравнений
Решая простое уравнение, думайте об уравнении как о балансе, где знак равенства (=) является точкой опоры или центром. Таким образом, если вы делаете что-то с одной частью уравнения, вы должны сделать то же самое с другой стороной. Выполняя одно и то же действие с обеими сторонами уравнения (скажем, прибавляя по 3 к каждой стороне), уравнение остается сбалансированным. Решение уравнения – это процесс получения искомого или решения по одну сторону знака равенства, а всего остального по другую. Вы действительно сортируете информацию. Если вы решаете для x , вы должны получить x с одной стороны.
Уравнения сложения и вычитания
Некоторые уравнения включают только сложение и/или вычитание.
Пример 1
Найдите x .
x + 8 = 12
Чтобы решить уравнение x + 8 = 12, вы должны получить x отдельно с одной стороны. Следовательно, вычтите 8 с обеих сторон.
Чтобы проверить свой ответ, просто подставьте его в уравнение:
Пример 2
Найдите y .
г – 9 = 25
Чтобы решить это уравнение, вы должны получить y отдельно с одной стороны. Поэтому прибавьте 9 к обеим сторонам.
Для проверки просто замените y на 34:
Пример 3
Найдите x .
x + 15 = 6
Чтобы решить, вычтите 15 с обеих сторон.
Для проверки просто замените x на –9 :
.
Обратите внимание, что в каждом случае выше используются противоположные операции ; то есть, если в уравнении есть сложение, вы вычитаете из каждой стороны.
Уравнения умножения и деления
Некоторые уравнения включают только умножение или деление. Обычно это происходит, когда переменная уже находится в одной части уравнения, но имеется более одной переменной, например 2 x или часть переменной, например
или
Таким же образом, как при сложении или вычитании, вы можете умножать или делить обе части уравнения на одно и то же число , если оно не равно нулю , и уравнение не изменится.
Пример 4
Найдите x .
3 x = 9
Разделите каждую часть уравнения на 3.
Для проверки замените x на 3:
Пример 5
Найдите y .
Чтобы решить, умножьте каждую сторону на 5.
Для проверки замените y на 35:
Пример 6
Найдите x .
Чтобы решить, умножьте каждую сторону на .
Или без отмены
Обратите внимание, что слева вы обычно не пишете, потому что это всегда отменяется до 1 x или x .
Комбинации операций
Иногда для решения уравнения приходится использовать более одного шага. В большинстве случаев сначала выполните шаг сложения или вычитания. Затем, после того как вы отсортировали переменные с одной стороны, а числа с другой, умножьте или разделите, чтобы получить только одну из переменных (то есть переменную без номера или 1 перед ней: x , а не 2 x ).
Пример 7
Решите для х .
2 x + 4 = 10
Вычтите 4 с обеих сторон, чтобы получить 2 x отдельно с одной стороны.
Затем разделите обе части на 2, чтобы получить x .
Для проверки подставьте свой ответ в исходное уравнение:
Пример 8
Найдите x .
5x – 11 = 29
Добавьте 11 с обеих сторон.
Разделите каждую сторону на 5.
Для проверки замените x на 8:
Пример 9
Найдите x .
Вычтите 6 с каждой стороны.
Умножить каждую сторону на .
Для проверки замените x на 9:
Пример 10
Найдите y .
Добавьте 8 с обеих сторон.
Умножить каждую сторону на .
Для проверки замените y на -25:
Пример 11
Найдите x .
3 x + 2 = x + 4
Вычесть 2 с обеих сторон (то же самое, что добавить -2).
Вычтите x с обеих сторон.
Обратите внимание, что 3 x – x равно 3 x – 1 x .
Разделите обе части на 2.
Для проверки замените x на 1:
Пример 12
Найдите y .
5 у + 3 = 2 у + 9
Вычесть 3 с обеих сторон.
Вычтите 2 y с обеих сторон.
Разделите обе части на 3.
Для проверки замените y на 2:
Иногда вам нужно упростить каждую сторону (объединить одинаковые термины) перед тем, как начать процесс сортировки.
Пример 13
Найти x .
3 x + 4 + 2 = 12 + 3
Во-первых, упростите каждую сторону.
Вычесть 6 с обеих сторон.
Разделите обе части на 3.
Для проверки замените x на 3:
Пример 14
Найдите x .
4 x + 2 x + 4 = 5 x + 3 + 11
Упростите каждую сторону.
6 x + 4 = 5 x + 14
Вычесть 4 с обеих сторон.
Вычтите 5 x с обеих сторон.
Для проверки замените x на 10:
Решение линейных и квадратных уравнений с помощью Пошагового решения математических задач
Решение уравнений является центральной темой алгебры. В этой главе мы изучим некоторые приемы решения уравнений с одной переменной. Для этого мы воспользуемся навыками, полученными при работе с числами и символами алгебры, а также операциями с целыми числами, десятичными дробями и дробями, которые вы изучили в арифметике.
В этой главе мы изучим некоторые приемы решения уравнений с одной переменной. Для этого мы воспользуемся навыками, полученными при работе с числами и символами алгебры, а также операциями с целыми числами, десятичными дробями и дробями, которые вы изучили в арифметике.
УСЛОВНЫЕ И ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Классифицировать уравнение как условное или тождественное.
- Решайте простые уравнения в уме.
- Определите, эквивалентны ли некоторые уравнения.
Уравнение — это утверждение в символах, что два числовых выражения равны.
Уравнения можно разделить на два основных типа:
1. тождество верно для всех значений буквенных и арифметических чисел в нем.
Пример 1 5 x 4 = 20 является тождеством.
Пример 2 2 + 3 = 5 является тождеством.
Пример 3 2x + 3x = 5x является тождеством, поскольку любое значение, подставленное вместо x, даст равенство.
2. Условное уравнение верно только для определенных значений буквенных чисел в нем.
Пример 4 х + 3 = 9верно, только если буквальное число x = 6.
Пример 5 3x – 4 = 11 верно, только если x = 5.
Буквенные числа в уравнении иногда называют переменными .
Поиск значений, которые делают условное уравнение истинным, является одной из основных целей этого текста.
Решение или корень уравнения — это значение переменной или переменных, которые делают уравнение верным утверждением.
Решение или корень называется удовлетворяют уравнению .
Решить уравнение означает найти решение или корень.
Многие уравнения можно решить в уме. Способность решить уравнение в уме будет зависеть от способности манипулировать числами арифметики. Чем лучше вы знаете факты умножения и сложения, тем лучше вы будете решать уравнения в уме.
Пример 6 Решите для x: x + 3 = 7
Решение
Чтобы иметь истинное утверждение, нам нужно значение x, которое при добавлении к 3 даст 7. Наши знания арифметики показывают, что 4 нужное значение. Следовательно, решение уравнения равно x = 4,9.0011
Наши знания арифметики показывают, что 4 нужное значение. Следовательно, решение уравнения равно x = 4,9.0011
| Какое число, добавленное к 3, равно 7? |
Пример 7 Решить для x: x – 5 = 3
Решение
Из какого числа нужно вычесть 5, чтобы получить 3? Снова наш опыт с арифметикой говорит нам, что 8 – 5 = 3. Следовательно, решение будет x = 8.
Пример 8 Решите для x: 3x = 15
Решение
Какое число нужно умножить на 3, чтобы получить 15 ? Наш ответ x = 5.
Решение
На какое число нужно разделить 2, чтобы получить 7? Наш ответ: 14.
Пример 10 Решите для x: 2x – 1 = 5
Решение
Мы должны вычесть 1 из 6, чтобы получить 5. Таким образом, 2x = 6. Тогда x = 3.
Независимо от того, как решается уравнение, всегда следует проверять правильность решения.
Пример 11 Учащийся решил уравнение 5x – 3 = 4x + 2 и нашел ответ x = 6. Правильно это было или нет?
Правильно это было или нет?
Решение
Удовлетворяет ли x = 6 уравнению 5x – 3 = 4x + 2? Чтобы проверить, мы подставляем 6 вместо x в уравнении, чтобы увидеть, получаем ли мы истинное утверждение.
Это неверное утверждение, поэтому ответ x = 6 неверен.
Другой ученик решил то же уравнение и нашел x = 5.
Это верное утверждение, поэтому x = 5 верно.
| Многие студенты думают, что когда они нашли решение уравнения, задача решена. Не так! Последним шагом всегда должна быть проверка решения. |
Не все уравнения можно решить в уме. Теперь мы хотим представить идею, которая представляет собой шаг к упорядоченному процессу решения уравнений.
| Является ли x = 3 решением x – 1 = 2? Является ли x = 3 решением 2x + I = 7? Что можно сказать об уравнениях х – 1 = 2 и 2х + 1 = 7? |
Два уравнения эквивалентны , если они имеют одно и то же решение или решения
Пример 12 3x = 6 и 2x + 1 = 5 эквивалентны, поскольку в обоих случаях x = 2 является решением.
Методы решения уравнений включают процессы преобразования уравнения в эквивалентное уравнение. Если сложное уравнение, такое как 2x – 4 + 3x = 7x + 2 – 4x, можно заменить простым уравнением x = 3, а уравнение x = 3 эквивалентно исходному уравнению, то мы решили уравнение.
Два вопроса теперь становятся очень важными.
- Эквивалентны ли два уравнения?
- Как мы можем заменить одно уравнение другим уравнением, эквивалентным ему?
Ответ на первый вопрос находится с использованием принципа подстановки.
Пример 13 Являются ли 5x + 2 = 6x – 1 и x = 3 эквивалентными уравнениями?
Решение
Ответ на второй вопрос связан с методами решения уравнений, которые будут обсуждаться в нескольких следующих разделах.
Чтобы правильно использовать принцип подстановки, мы должны подставить цифру 3 вместо x везде, где x появляется в уравнении. |
ПРАВИЛО ОТДЕЛЕНИЯ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Используйте правило деления для решения уравнений.
- Решите несколько основных прикладных задач, для решения которых используется правило деления.
Как упоминалось ранее, мы хотим представить упорядоченную процедуру решения уравнений. Эта процедура будет включать в себя четыре основные операции, первая из которых представлена в этом разделе.
Если каждый член уравнения равен , разделенному на на одно и то же ненулевое число, результирующее уравнение будет эквивалентно исходному уравнению.
Чтобы подготовиться к использованию правила деления для решения уравнений, мы должны отметить следующий процесс:
(Обычно мы пишем 1x как x с понятным коэффициентом 1.)
Пример 1 Решить для x: 3x = 10
Решение
Наша цель — получить x = некоторое число. Правило деления позволяет нам делить каждый член 3x = 10 на одно и то же число, и наша цель найти значение x будет означать, что мы делим на 3. Это даст нам коэффициент 1 для x.
Правило деления позволяет нам делить каждый член 3x = 10 на одно и то же число, и наша цель найти значение x будет означать, что мы делим на 3. Это даст нам коэффициент 1 для x.
Проверить: 3x = 10 и x = эти эквивалентные уравнения?
Подставим x в первое уравнение, получим
Уравнения эквивалентны, значит решение верное.
| Всегда проверяйте! |
Пример 2 Найдите x: 5x = 20
Решение
| Обратите внимание, что правило деления не позволяет делить на ноль. Поскольку деление на ноль в математике запрещено, такие выражения, как бессмысленны. |
Пример 3 Решите для x: 8x = 4
Решение
Ошибки иногда делаются в очень простых ситуациях. Не смотрите на эту задачу и придите к x = 2! Не смотрите на эту задачу и придите к x = 2! Обратите внимание, что правило деления позволяет нам делить каждый член уравнения на любое ненулевое число, и полученное уравнение эквивалентно исходному уравнению. Следовательно, мы могли бы разделить каждую часть уравнения на 5 и получить , что эквивалентно исходному уравнению. Однако деление на 5 не помогает найти решение. На какое число нужно поделить, чтобы найти решение? Пример 4 радиус окружности и составляет примерно 3,14. Найдите радиус окружности, если длина окружности равна 40,72 см. Дайте правильный ответ с точностью до двух знаков после запятой. Решение Чтобы решить задачу с использованием формулы, мы сначала используем принцип подстановки.
ПРАВИЛО ВЫЧИТАНИЯЦЕЛИ По завершении этого раздела вы сможете использовать правило вычитания для решения уравнений. Второй шаг к упорядоченной процедуре решения уравнений будет обсуждаться в этом разделе. Вы будете использовать свои знания подобных терминов из главы 1, а также приемы из раздела 9.0421 ПРАВИЛО РАЗДЕЛЕНИЯ . Обратите внимание, как новые идеи в алгебре основываются на предыдущих знаниях. Если из обеих частей уравнения вычесть из одной и той же величины , результирующее уравнение будет эквивалентно исходному уравнению. Пример 1 Найдите x, если x + 7 = 12. Решение Хотя это уравнение легко решить в уме, мы хотим проиллюстрировать правило вычитания. Мы должны думать так: “Я хочу найти х, поэтому мне нужен х сам по себе в одной части уравнения. Но у меня есть х + 7. Поэтому, если я вычту 7 из х + 7, в левой части будет только х.” (Помните, что величина, вычтенная из самой себя, дает ноль.) Но если мы вычтем 7 из одной части уравнения, правило требует, чтобы мы вычли 7 из другой части уравнения. Итак, мы действуем следующим образом:
Пример 2 Решите для x: 5x = 4x + 3 Решение Здесь наше мышление должно действовать таким образом. «Я хочу получить все неизвестные величины с одной стороны уравнения и все арифметические числа с другой, поэтому у меня есть уравнение вида x = некоторое число. Таким образом, мне нужно вычесть Ax из обеих сторон».
Пример 3 Решите для x: 3x + 6 = 2x + 11 Здесь у нас более сложная задача. Сначала вычтите 6 с обеих сторон. Теперь мы должны исключить 2x с правой стороны, вычитая 2x с обеих сторон. Теперь рассмотрим решение, которое требует использования как правила вычитания, так и правила деления.
пример 4
Пример 5 Найдите x: 7x + 1 = 5x + 9 Решение Сначала используем правило вычитания. Тогда правило деления дает нам Пример 6 Периметр (P) прямоугольника находится по формуле P = 2l + 2w, где l обозначает длину, а w обозначает ширину. Чему равна ширина прямоугольника, если его периметр равен 54 см, а длина 15 см? Решение
ПРАВИЛО СЛОЖЕНИЯЦЕЛИ По завершении этого раздела вы сможете использовать правило сложения для решения уравнений. Теперь приступим к следующей операции нашей цели — разработать упорядоченную процедуру решения уравнений. Опять же, мы будем полагаться на предыдущие знания. Если одинаковое количество добавил к обеим частям уравнения, результирующее уравнение будет эквивалентно исходному уравнению. Пример 1 Найдите x, если x – 7 = 2. Решение Как всегда, при решении уравнения мы хотим получить вид «x = некоторое число». Мы видим, что 7 было вычтено из x, поэтому, чтобы получить только x в левой части уравнения, мы добавляем 7 к обеим частям.
Пример 2 Решить для x: 2x – 3 = 6 Решение Помня о нашей цели получить только x, мы видим, что, поскольку 3 вычитается из 2x, мы прибавляем 3 к обеим частям уравнение. Теперь мы должны использовать правило деления.
Пример 3 Найдите x: 3x – 4 = 11 Решение Сначала используем правило сложения. Затем, используя правило деления, мы получаем
Пример 4 Решите для x: 5x = 14 – 2x Решение Здесь наша цель получить только x на одной стороне предполагает удаление 2x справа, поэтому мы добавляем 2x к обеим сторонам уравнение. Затем применим правило деления.
Пример 5 Решите для x: 3x – 2 = 8 – 2x Решение Здесь наша задача более сложная. Мы должны подумать об исключении числа 2 из левой части уравнения, а также lx из правой части, чтобы получить только x с одной стороны. Мы можем сделать любой из них в первую очередь. Если мы решим сначала добавить 2x к обеим сторонам, мы получим Теперь мы добавляем 2 к обеим сторонам. Наконец, правило деления дает
ПРАВИЛО УМНОЖЕНИЯЦЕЛИПо завершении этого раздела вы должны уметь:
Теперь мы подошли к последней из четырех основных операций разработки нашей процедуры решения уравнений. Мы также введем отношение и пропорцию и будем использовать правило умножения для решения пропорций. Если каждый член уравнения равен , умноженному на на одно и то же ненулевое число, результирующее уравнение будет эквивалентно исходному уравнению. В элементарной арифметике одними из самых сложных операций являются операции с дробями. Правило умножения позволяет избежать этих операций при решении уравнения с дробями, найдя эквивалентное уравнение, содержащее только целые числа. Помните, что когда мы умножаем целое число на дробь, мы используем правило Теперь мы готовы решить уравнение с дробями.
Пример 4 Решение Имейте в виду, что мы хотим получить только x в одной части уравнения. Теперь у нас есть эквивалентное уравнение, содержащее только целые числа. Используя правило деления, получаем
Пример 5 Решение
Пример 6 Решение Здесь наша задача такая же, но немного сложнее. У нас есть две фракции, которые нужно устранить. Мы должны умножить каждый член уравнения на число, которое делится и на 3, и на 5. Лучше всего использовать наименьшее из таких чисел, которое, как вы помните, это 9.0421 наименьшее общее кратное . Поэтому мы умножаем на 15.
Пример 7 Решение Наименьшее общее кратное для 8 и 2 равно 8, поэтому мы умножаем каждый член уравнения на 8. Теперь воспользуемся правилом вычитания. Наконец, правило деления дает нам
Решение простых уравнений путем умножения обеих частей на одно и то же число часто встречается при изучении отношений и пропорций. Отношение — это частное двух чисел. Отношение числа x к числу y может быть записано как x:y или . В общем, дробная форма более содержательна и полезна. Таким образом, мы запишем отношение 3 к 4 как . Пропорция — это утверждение о том, что два отношения равны. Пример 8 Решение Нам нужно найти такое значение х, что отношение х к 15 равно отношению 2 к 5.
Пример 9 Какое число x относится к 3 так же, как 6 к 9? Решение Чтобы найти х, сначала запишем пропорцию: Затем умножим каждую часть уравнения на 9. |
Пример 11 Отношение количества женщин к количеству мужчин в классе математики составляет 7 к 8. Если в классе 24 мужчины, сколько женщин в классе?
Решение
| Проверить! |
Пример 12 Два сына должны были разделить наследство в отношении 3 к 5. Если сын, получивший большую долю, получил 20 000 долларов, какова была общая сумма наследства?
Решение
Теперь мы складываем 20 000 долларов + 12 000 долларов, чтобы получить общую сумму 32 000 долларов.
| Проверить! Опять же, будьте внимательны при настройке пропорции. В соотношении 3/5 5 — большая часть. Следовательно, поскольку 20 000 долларов — это большая часть, она также должна появиться в знаменателе. |
Пример 13 Если законодательные требования к вместимости помещения требуют 3 кубических метра воздушного пространства на человека, сколько человек может по закону занимать комнату шириной 6 метров, длиной 8 метров и высотой 3 метра?
Решение
Итак, допустимая вместимость комнаты – 48 человек.
| Это означает, что «1 человек равен 3 кубическим метрам, как x человек соответствует 144 кубическим метрам». Проверьте решение. |
ОБЪЕДИНЕНИЕ ПРАВИЛ ДЛЯ РЕШЕНИЯ УРАВНЕНИЙ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Используйте комбинации различных правил для решения более сложных уравнений.
- Применяйте упорядоченные шаги, описанные в этом разделе, для систематического решения уравнений.
Многие упражнения из предыдущих разделов требовали использования более одного правила в процессе решения. На самом деле вполне возможно, что одна задача может включать все правила
Не существует обязательного процесса решения уравнений, включающего более одного правила, но опыт показывает, что следующий порядок дает более гладкую и безошибочную процедуру.
Первый Удалите дроби, если они есть, умножив каждый член уравнения на наименьшее общее кратное всех знаменателей дробей в уравнении.
Второй Упростите, объединив одинаковые члены с каждой стороны уравнения.
Третий Сложите или вычтите необходимые количества, чтобы получить неизвестное количество с одной стороны и числа арифметики с другой стороны.
Четвертый Разделить на коэффициент неизвестной величины.
Пятый Проверьте свой ответ.
| Помните, коэффициент – это число, умноженное на букву. (То есть в выражении 5x коэффициент равен 5.) |
| Опять же, убедитесь, что каждый член умножить на 3. |
Решение
Умножение каждого члена на 15 дает
Вы можете оставить свой ответ в виде неправильной дроби вместо смешанного числа. Любая форма верна, но форма неправильной дроби будет полезнее для проверки вашего решения.
Обратите внимание, что в этом уравнении четыре члена. |
Пример 3 Продажная цена (S) определенного товара составляла 30 долларов США. Если наценка (М) составила одну пятую стоимости (С), найти стоимость товара. Используйте формулу C + M = S.
Решение
Поскольку маржа составляла одну пятую стоимости, мы можем написать
РЕЗЮМЕ
символы, обозначающие, что два числовых выражения равны.
Процедуры
- Если каждый член уравнения разделить на одно и то же ненулевое число, полученное уравнение будет эквивалентно исходному уравнению.

- Если из обеих частей уравнения вычесть одну и ту же величину, полученное уравнение будет эквивалентно исходному уравнению.
- Если к обеим частям уравнения добавить одну и ту же величину, полученное уравнение будет эквивалентно исходному уравнению.
- Если каждую часть уравнения умножить на одно и то же ненулевое число, полученное уравнение будет эквивалентно исходному уравнению.
- Чтобы решить уравнение, выполните следующие действия:
Шаг 1 Удалите дроби, умножив каждый член на наименьшее общее кратное всех знаменателей в уравнении.
Шаг 2 Объедините одинаковые члены с каждой стороны уравнения.
Шаг 3 Сложите или вычтите члены, чтобы получить неизвестное количество с одной стороны и арифметические числа с другой.
Шаг 4 Разделите каждое слагаемое на коэффициент неизвестной величины.
Шаг 5 Проверьте свой ответ.
Линейные уравнения с одним, нулем или бесконечным числом решений
Рабочие листы по математике для 8 класса
Здесь мы попытаемся найти количество возможных решений любого линейного уравнения.
Теперь рассмотрим каждый из вышеперечисленных случаев отдельно и разберемся в них на примерах.
Линейные уравнения с одним решением
Пример 1: Рассмотрим уравнение 7 x – 35 = 0.
При решении имеем 7 x = 35 или x 5 Верно только линейное уравнение выше. если x = 5 и, следовательно, данное линейное уравнение имеет только одно решение , то есть x = 5.
Пример 2: + 37.
При решении имеем 9 х – 9 – 35 = 8 х + 37.
Собираем одинаковые члены с обеих сторон, перенося их, мы имеем
9х – 8х = 37 + 35 + 9 = 80 что дает х = 80
Приведенное выше линейное уравнение верно, только если x = 80
Следовательно, данное линейное уравнение имеет только одно решение , т. е. x = 80. x не исчезает после решения, и мы говорим, что линейное уравнение будет иметь одно решение если ему удовлетворяет ровно одно значение переменной.
Узнайте больше о линейных уравнениях и других важных темах с репетиторством по математике для 8-го класса на eTutorWorld. Наши опытные преподаватели естественных наук разбивают темы на интерактивные индивидуальные занятия. Мы также предлагаем индивидуальные планы уроков, гибкий график и удобство обучения на дому.
Пример 1: Рассмотрим уравнение 7 x – 35 = 5 x + 2 x – 27.
При решении имеем 7 x – 35 = 7x – 27
Вычитая 7 x с обеих сторон. 7 x – 7 x – 35 = 7 x – 7 x – 27
мы имеем -35 = -27, что является ложным утверждением, поскольку оно не может быть истинным ни для какого значения переменной х.
Следовательно, данное линейное уравнение имеет нулевое решение или число решений равно нулю.
Пример 2: Рассмотрим уравнение 3 ( x + 9) + 21 x = 24 x + 9.
. = 24 x + 9 или 24 x + 27 = 24 x +
Вычитание 24 x с обеих сторон, 24 x – 24 x + 27 = 24 x – 24 x + 9.
У нас есть 27 = 9, что является ложным утверждением, поскольку оно не может быть истинным ни при каком значении переменной 9.0002 х.
Следовательно, данное линейное уравнение не имеет решения или количество решений равно нулю .
Из приведенных выше примеров мы видим, что переменная x исчезает / устраняется, и поэтому мы говорим, что линейное уравнение будет иметь нулевое решение или не будет иметь никакого решения , если оно не может быть удовлетворено ни одним значением переменной или существует не существует ни одного значения переменной, которое делает данное уравнение истинным утверждением.
Линейные уравнения с бесконечными решениями
Пример 1: Рассмотрим уравнение 25 x – 35 = 5 (5 x + 4) – 55.
При решении. + 20 – 55 или 25 x – 35 = 25 x – 35.
Вычитание 25 x с обеих сторон, 25 x – 25 x – 35 = 25 x – 25 x – 35
У нас есть -35 = -35, что является истинным утверждением и будет истинным для любого значения переменной х .
Следовательно, данное линейное уравнение имеет бесконечное число решений или число решений бесконечно.
Пример 2: Рассмотрим уравнение 15 ( x + 9) = 24 x + 9 – (9 x – 126)
Решение Мы имеем 15 x + 144 = 24 х + 9 – 9 х + 126 или 15 х + 144 = 15 х + 144.
Вычитаем 15 х с обеих сторон. 15 x – 15 x +144 = 15 x – 15 x + 144
У нас есть 144 = 144, что является верным утверждением и будет истинным для любого значения переменной x .
Следовательно, данное линейное уравнение имеет бесконечное число решений или число решений бесконечно.
Из приведенных выше примеров мы можем сказать, что линейное уравнение будет иметь бесконечных решения , если оно удовлетворяется любым значением переменной или каждое значение переменной делает данное уравнение верным утверждением.
Контрольная точкаРешите следующие линейные уравнения и определите, имеют ли данные линейные уравнения одно, нулевое или бесконечное число решений.
- 17 х – 75 = 6 + 14 х .
- 3 х – 105 = 4 ( х – 20) – 1 ( х + 5).
- 10 х + 2 7 = 2 (5 х + 99).
- 7 х – 33 + 75 = 6( х + 7) + х.
- 24 х + 60 = 4 ( х – 25).
- 13 х + 10 – 4 х = 4 ( х – 26) + 5 х .

Ключ ответа
- Одно решение, т. е. x = 27.
- Бесконечные решения.
- Нулевое решение.
- Бесконечные решения.
- Одно решение, т. е. x = – 8.
- Нулевое решение.
Узнайте больше о линейных уравнениях и других важных темах с репетиторством по математике для 8-го класса на eTutorWorld. Наши опытные преподаватели естественных наук разбивают темы на интерактивные индивидуальные занятия. Мы также предлагаем индивидуальные планы уроков, гибкий график и удобство обучения на дому.
Персонализированное онлайн-обучение
eTutorWorld предлагает доступное индивидуальное онлайн-обучение для классов K-12, помощь в подготовке к стандартным тестам, таким как SCAT, CogAT, MAP, SSAT, SAT, ACT, ISEE и AP. . Вы можете запланировать уроки онлайн-репетиторства в удобное для вас время с гарантией возврата денег. Первый индивидуальный онлайн-урок всегда БЕСПЛАТНЫЙ, никаких обязательств по покупке, кредитная карта не требуется.
Чтобы получить ответы/решения на любой вопрос или изучить концепции, возьмите БЕСПЛАТНАЯ ПРОБНАЯ ВЕРСИЯ Сессия.
Запись на бесплатную сессию
Кредитная карта не требуется, покупка не обязательна.
Просто запланируйте БЕСПЛАТНОЕ занятие, чтобы встретиться с преподавателем и получить помощь по любой интересующей вас теме!
Стоимость онлайн-обучения
| Пакет репетиторства | Срок действия | Класс (1-12), Колледж |
|---|---|---|
| 5 сеансов | 1 месяц | 124 $ |
| 1 сеанс | 1 месяц | 25 долларов |
| 10 сеансов | 3 месяца | 239 долларов |
| 15 сеансов | 3 месяца | $354 |
| 20 сеансов | 4 месяца | $449 |
| 50 сеансов | 6 месяцев | $1049 |
| 100 сеансов | 12 месяцев | $2049 |
Купить сейчас
Открытые учебники | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Решение уравнений
Что такое уравнение?
Уравнение говорит, что две вещи равны. Он будет иметь знак равенства “=”, например:
| x | − | 2 | = | 4 |
Это уравнение говорит: то, что слева (x − 2), равно тому, что справа (4)
Итак, уравнение похоже на 9Оператор 0421 ” это равно тому ”
Что такое решение?
Решение — это значение, которое мы можем подставить вместо переменной (например, x ), которое делает уравнение истинным .
Пример: x − 2 = 4
Если мы подставим 6 вместо x, мы получим:
6 − 2 = 4
, что верно
Итак, x = 6 является решением.
Как насчет других значений x ?
- Для x=5 мы получаем “5−2=4”, что равно неверно , поэтому x=5 не является решением .
- Для x=9 мы получаем “9−2=4”, что неверно , поэтому x=9 не является решением .
- и т. д.
В этом случае x = 6 — единственное решение.
Вы можете попрактиковаться в решении некоторых анимированных уравнений.
Более одного решения
Может быть более одного решения .
Пример: (x−3)(x−2) = 0
Когда x равно 3, мы получаем:
(3−3)(3−2) = 0 × 1 = 0
, что верно
И когда x равно 2, мы получаем: 1) × 0 = 0
, что также является истинным
. Таким образом, решения:
Приведенный выше набор решений: {2, 3}
Решения везде!
Некоторые уравнения верны для всех допустимых значений и тогда вызываются Тождества
Пример:
sin(−θ) = −sin(θ) является одним из тригонометрических тождествПопробуем θ = 30°:
−sin(30°) = −0,5
Таким образом, верно для θ = 30°
Попробуем θ = 90°:
sin(−90°) = 0 −4 904 = 20 −1 904 904 −sin(90°) = −1
Таким образом, верно также для θ = 90°
Верно ли для все значения θ ? Попробуйте некоторые значения для себя!
Как решить уравнение
Не существует «одного идеального способа» решить все уравнения.
Полезная цель
Но мы часто добиваемся успеха, когда наша цель состоит в том, чтобы получить:
x = что-то
Другими словами, мы хотим переместить все, кроме “x” (или чего-то еще). имя, которое имеет переменная) справа.
Пример: решить 3x−6 = 9
Начните с: 3x−6 = 9
Прибавьте 6 к обеим сторонам: 3x = 9+6
Разделите на 3:x = (9+6)/3
Теперь у нас есть x = что-то ,
, и краткий подсчет показывает, что x = 5
Как головоломка
На самом деле решение уравнения похоже на решение головоломки. И, как и в случае с головоломками, есть вещи, которые мы можем (и не можем) делать.
Вот что мы можем сделать:
- Добавить или вычесть одно и то же значение с обеих сторон
- Удалите любые дроби, умножив каждый член на нижние части
- Разделить каждый член на одно и то же ненулевое значение
- Объединить похожие термины
- Факторинг
- Расширение (противоположное факторингу) также может помочь
- Распознавание шаблона, например разности квадратов
- Иногда мы можем применить функцию к обеим сторонам (например, возвести обе стороны в квадрат)
Пример: Решите √(x/2) = 3
Начните с:√(x/2) = 3
Возведите в квадрат обе стороны:x/2 = 3 2
Вычислите 3 2 = 9:x/2 = 9
Умножьте2 на обе стороны 😡 = 18
И чем больше “трюков” и приемов вы изучите, тем лучше у вас будет получаться.
Специальные уравнения
Существуют специальные способы решения некоторых типов уравнений. Научитесь…
- решать квадратные уравнения
- решать радикальные уравнения
- решить уравнения с синусом, косинусом и тангенсом
Проверьте свои решения
Вы всегда должны проверять, что ваше “решение” действительно является решением.
Как проверить
Возьмите решения и поместите их в исходное уравнение , чтобы увидеть, действительно ли они работают.
Пример: найдите x:
2x x − 3 + 3 = 6 x − 3 (x≠3)
Чтобы избежать деления на ноль, мы сказали x≠3.
Умножим на (x − 3):
2x + 3(x−3) = 6
Перенеси 6 влево:
2x + 3(x−3) − 6 = 0
Расширь и решить:
2x + 3x – 9 – 6 = 0
5x – 15 = 0
5(x – 3) = 0
x – 3 = 0
Это можно решить, если x=3
Проверим:
2 × 3 3 − 3 + 3 = 6 3 − 3
Держись!
Это значит Деление на Ноль!
И вообще, выше мы сказали, что x≠3, так что. ..
..
x = 3 на самом деле не работает, и поэтому:
Существует Нет Решение!
Это было интересно… мы думали что нашли решение, но когда мы посмотрели на вопрос, то обнаружили, что это не разрешено!
Это дает нам моральный урок:
“Решение” дает нам только возможные решения, их нужно проверить!
Советы
- Запишите, где выражение не определено (из-за деления на ноль, квадратного корня из отрицательного числа или по какой-либо другой причине)
- Показать все шаги , чтобы их можно было проверить позже (вы или кто-то другой)
Рабочие листы по алгебре
Добро пожаловать на страницу с рабочими листами по алгебре на сайте Math-Drills.com, где неизвестные часто встречаются, а переменные являются нормой. На этой странице вы найдете рабочие листы по алгебре, предназначенные в основном для учащихся средних школ по таким темам алгебры, как алгебраические выражения, уравнения и графические функции.
Эта страница начинается с рабочих листов с пропущенными числами для младших школьников. Затем мы переходим непосредственно к алгебре, помогая учащимся распознавать и понимать основной язык, связанный с алгеброй. Остальная часть страницы посвящена некоторым основным темам, с которыми вы столкнетесь на уроках алгебры. Помните, что, обучая студентов алгебре, вы помогаете создавать будущих финансовых гениев, инженеров и ученых, которые решат все проблемы нашего мира.
Алгебра намного интереснее, когда вещи более реальны. Решать линейные уравнения намного веселее, когда есть весы с двумя чашами, несколько загадочных мешочков и куча мармеладок. Плитки алгебры используются многими учителями, чтобы помочь учащимся понять различные темы алгебры. И нет ничего лучше набора координатных осей для решения систем линейных уравнений.
Самые популярные рабочие листы по алгебре на этой неделе
Объединение одинаковых терминов и решение простых линейных уравнений ( 1886 просмотров на этой неделе )Использование свойства распределения (ответы не включают показатели степени) ( 1419 просмотров на этой неделе )Перевод алгебраических фраз (простая версия) ) ( 1036 просмотров на этой неделе )Факторизация квадратичных выражений с положительным коэффициентом а, равным 1 ( 842 просмотров на этой неделе )Вычисление одношаговых алгебраических выражений с одной переменной и без экспонент ( 761 просмотр на этой неделе )Свойства и законы чисел Рабочие листы
Коммутативный закон
Закон перестановки или свойство перестановочности утверждают, что вы можете изменить порядок чисел в арифметической задаче и получить тот же результат. В контексте арифметики он работает только с операциями сложения или умножения , но не смешанного сложения и умножения. Например, 3 + 5 = 5 + 3 и 9× 5 = 5 × 9. Увлекательным занятием, которое вы можете использовать в классе, является мозговой штурм нечисловых вещей из повседневной жизни, которые являются коммутативными и некоммутативными. Например, надевание носков является коммутативным, потому что вы можете надеть правый носок, а затем левый, или вы можете надеть левый носок, а затем правый, и вы получите тот же результат. Однако надевать нижнее белье и брюки некоммутативно.
В контексте арифметики он работает только с операциями сложения или умножения , но не смешанного сложения и умножения. Например, 3 + 5 = 5 + 3 и 9× 5 = 5 × 9. Увлекательным занятием, которое вы можете использовать в классе, является мозговой штурм нечисловых вещей из повседневной жизни, которые являются коммутативными и некоммутативными. Например, надевание носков является коммутативным, потому что вы можете надеть правый носок, а затем левый, или вы можете надеть левый носок, а затем правый, и вы получите тот же результат. Однако надевать нижнее белье и брюки некоммутативно.
Коммутативный закон сложения (только числа) Коммутативный закон сложения (некоторые переменные) Коммутативный закон умножения (только числа) Коммутативный закон умножения (некоторые переменные)
Ассоциативный закон
Ассоциативный закон или ассоциативное свойство позволяют изменять группировку операций в арифметической задаче с двумя и более шагами без изменения результата. Порядок чисел остается прежним в ассоциативном законе. Как и в случае с коммутативным законом, он применяется к задачам только на сложение или только на умножение . Лучше всего об этом думать в контексте порядка операций, так как он требует, чтобы сначала были обработаны круглые скобки. Пример ассоциативного закона: (9+ 5) + 6 = 9 + (5 + 6). В этом случае неважно, добавите ли вы сначала 9 + 5 или 5 + 6, вы получите тот же результат. Студенты могут вспомнить несколько примеров из своего опыта, например, класть продукты на поднос во время обеда. Они могли сначала положить на свой поднос молоко и овощи, а затем бутерброд, или они могли начать с овощей и бутерброда, а затем положить молоко. Если их поднос оба раза выглядит одинаково, значит, они смоделировали ассоциативный закон. Чтение книги можно рассматривать как ассоциативное или неассоциативное, поскольку потенциально можно сначала прочитать последние главы и по-прежнему понимать книгу так же, как и тот, кто читает книгу обычным способом.
Порядок чисел остается прежним в ассоциативном законе. Как и в случае с коммутативным законом, он применяется к задачам только на сложение или только на умножение . Лучше всего об этом думать в контексте порядка операций, так как он требует, чтобы сначала были обработаны круглые скобки. Пример ассоциативного закона: (9+ 5) + 6 = 9 + (5 + 6). В этом случае неважно, добавите ли вы сначала 9 + 5 или 5 + 6, вы получите тот же результат. Студенты могут вспомнить несколько примеров из своего опыта, например, класть продукты на поднос во время обеда. Они могли сначала положить на свой поднос молоко и овощи, а затем бутерброд, или они могли начать с овощей и бутерброда, а затем положить молоко. Если их поднос оба раза выглядит одинаково, значит, они смоделировали ассоциативный закон. Чтение книги можно рассматривать как ассоциативное или неассоциативное, поскольку потенциально можно сначала прочитать последние главы и по-прежнему понимать книгу так же, как и тот, кто читает книгу обычным способом.
Ассоциативный закон сложения (только целые числа) Ассоциативный закон умножения (только целые числа)
Обратные отношения с
один пробелРабочие листы с обратными отношениями охватывают предварительные алгебраические навыки, призванные помочь учащимся понять взаимосвязь между умножением и делением, а также связь между сложением и вычитанием.
Сложение и вычитание легко Сложение и вычитание сложнее Все факты умножения и деления от 1 до 18 в цвете (без пробелов) Диапазон умножения и деления от 1 до 9Диапазон умножения и деления от 5 до 12 Умножение и деление Все обратные отношения Диапазон от 2 до 9 Умножение и деление Все обратные отношения Диапазон от 5 до 12 Умножение и деление Все обратные отношения Диапазон от 10 до 25
Обратные отношения с
двумя пробеламиСложение и вычитание (суммы 1-18) Сложение и вычитание, обратные отношения с 1 Сложение и вычитание, обратные отношения с 2 Сложение и вычитание, обратные отношения с 3 Сложение и вычитание, обратные отношения с 4 Сложение и вычитание, обратные отношения с 5 Сложение и вычитание, обратные отношения с 6 Сложение и вычитание, обратные отношения с 7 Сложение и вычитание, обратные отношения с 8 Сложение и вычитание, обратные отношения с 9Сложение и вычитание, обратные отношения с 10 Сложение и вычитание, обратные отношения с 11 Сложение и вычитание, обратные отношения с 12 Сложение и вычитание, обратные отношения с 13 Сложение и вычитание, обратные отношения с 14 Сложение и вычитание, обратные отношения с 15 Сложение и вычитание, обратные отношения с 16 Сложение и вычитание, обратные отношения с 17 Сложение и вычитание, обратные отношения с 18
Пропущенные числа или неизвестные в таблицах уравнений
Пропущенные числа в таблицах уравнений трех типов: пробелы для неизвестных, символы для неизвестных и переменные для неизвестных.
Рабочие листы с отсутствующими числами и
пробелами в качестве неизвестныхВ этих таблицах неизвестное ограничивается ответной частью уравнения, которая может быть слева или справа от знака равенства.
Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 9 ; Пробелы Никогда в позиции ответа ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 9 ; Пробелы в любой позиции ) Отсутствующие числа в уравнениях ( Все операции ; Диапазон от 1 до 20 ; Пробелы никогда не в позиции ответа ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 20 ; Пробелы в любой позиции ) Пропущенные числа в уравнениях ( Только дополнение ; Диапазон от 1 до 9 ; Пробелы никогда не используются в позиции ответа ) Отсутствующие числа в уравнениях ( Добавление только ; Диапазон от 1 до 9 ; Пробелы в любой позиции ) Пропущенные числа в уравнениях ( Дополнение, только ; Диапазон от 1 до 20 ; Пробелы в любой позиции ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 9 ; Пробелы Никогда в позиции ответа ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 9 ; Пробелы в любой позиции ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 20 ; Пробелы в любой позиции ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 9 ; Пробелы никогда не используются в позиции ответа ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 9 ; Заготовки в любом положении ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 20 ; Пробелы в любой позиции ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 9 ; Пробелы никогда в позиции ответа ) Пропущенные числа в уравнениях ( Только раздел ; Диапазон от 1 до 9 ; Пробелы в любой позиции ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 20 ; Пробелы в любой позиции )
Рабочие листы с пропущенными числами и
символами в качестве неизвестныхОтсутствующие числа в уравнениях ( Все операции ; Диапазон от 1 до 9 ; Символы никогда не в позиции ответа ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 9 ; символов в любой позиции ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 20 ; Символы, которые никогда не находятся в позиции ответа ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 20 ; Символы в любой позиции ) Отсутствующие числа в уравнениях ( Только дополнение ; Диапазон от 1 до 9 ; Символы никогда не используются в позиции ответа ) Пропущенные числа в уравнениях ( Дополнение только ; Диапазон от 1 до 9 ; символы в любой позиции ) Отсутствующие числа в уравнениях ( Добавление только ; Диапазон от 1 до 20 ; Символы в любой позиции ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 9 ; Символы никогда не используются в ответной позиции ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 9 ; Символы в любой позиции ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 20 ; символы в любой позиции ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 9 ; Символы никогда не используются в позиции ответа ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 9 ; Символы в любой позиции ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 20 ; Символы в любой позиции ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 9 ; Символы никогда не в позиции ответа ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 9 ; Символы в любой позиции ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 20 ; Символы в любой позиции )
Равенства с
сложением по обеим частям уравнения и символа как неизвестныеРавенства со сложением (от 0 до 9) Символ Неизвестный Равенства со сложением (от 1 до 12) Символ Неизвестные Равенства со сложением (от 1 до 15) Символ Неизвестные Равенства со сложением (от 1 до 25) Символ Неизвестные Равенства со сложением (от 1 до 99) Символ Неизвестный
Рабочие листы с отсутствующими числами с
переменными как неизвестнымиПропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 9 ; Переменные никогда не находятся в позиции ответа ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 9 ; Переменные в любой позиции ) Отсутствующие числа в уравнениях ( Все операции ; Диапазон от 1 до 20 ; Переменные никогда не в позиции ответа ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 20 ; Переменные в любой позиции ) Пропущенные числа в уравнениях ( Только добавление ; Диапазон от 1 до 9 ; Переменные, которые никогда не находятся в позиции ответа ) Отсутствующие числа в уравнениях ( Только добавление ; Диапазон от 1 до 9 ; Переменные в любой позиции ) Отсутствующие числа в уравнениях ( Только добавление ; Диапазон от 1 до 20 ; Переменные в любой позиции ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 9 ; Переменные никогда не находятся в позиции ответа ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 9 ; Переменные в любой позиции ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 20 ; Переменные в любой позиции ) Отсутствующие числа в уравнениях ( Только умножение ; Диапазон от 1 до 9 ; Переменные никогда не в позиции ответа ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 9 ; Переменные в любой позиции ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 20 ; Переменные в любой позиции ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 9 ; Переменные никогда не в позиции ответа ) Отсутствующие числа в уравнениях ( Только деление ; Диапазон от 1 до 9 ; Переменные в любой позиции ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 20 ; Переменные в любой позиции )
Решение простых линейных уравнений
Решение простых линейных уравнений со значениями от от -9 до 9 (неизвестно слева) Решение простых линейных уравнений со значениями от от -99 до 99 (неизвестно слева) Решение простых линейных уравнений со значениями от от -9 до 9 (неизвестно справа или слева) Решение простых линейных уравнений со значениями от от -99 до 99 (неизвестно справа или слева)
Рабочие листы по алгебраическим выражениям
Использование свойства дистрибутива
Свойство дистрибутивности — важный навык в алгебре. Проще говоря, это означает, что вы можете разделить один из множителей умножения на слагаемые, умножить каждое слагаемое отдельно, сложить результаты, и вы получите тот же ответ. Это также полезно в ментальной арифметике, и пример этого должен помочь проиллюстрировать определение. Рассмотрим вопрос 35 × 12. Разделение 12 на 10 + 2 дает нам возможность мысленно решить вопрос, используя распределительное свойство. Сначала умножьте 35 × 10, чтобы получить 350. Во-вторых, умножьте 35 × 2, чтобы получить 70. Наконец, добавьте 350 + 70, чтобы получить 420. В алгебре свойство распределения становится полезным в тех случаях, когда нельзя легко добавить другой множитель перед умножением. Например, в выражении 3(x + 5) нельзя добавить x + 5, не зная значения x. Вместо этого свойство дистрибутивности можно использовать для умножения 3 × x и 3 × 5, чтобы получить 3x + 15,9.0011
Проще говоря, это означает, что вы можете разделить один из множителей умножения на слагаемые, умножить каждое слагаемое отдельно, сложить результаты, и вы получите тот же ответ. Это также полезно в ментальной арифметике, и пример этого должен помочь проиллюстрировать определение. Рассмотрим вопрос 35 × 12. Разделение 12 на 10 + 2 дает нам возможность мысленно решить вопрос, используя распределительное свойство. Сначала умножьте 35 × 10, чтобы получить 350. Во-вторых, умножьте 35 × 2, чтобы получить 70. Наконец, добавьте 350 + 70, чтобы получить 420. В алгебре свойство распределения становится полезным в тех случаях, когда нельзя легко добавить другой множитель перед умножением. Например, в выражении 3(x + 5) нельзя добавить x + 5, не зная значения x. Вместо этого свойство дистрибутивности можно использовать для умножения 3 × x и 3 × 5, чтобы получить 3x + 15,9.0011
Распределительное свойство (ответы не включают показатели степени) Распределительное свойство (некоторые ответы включают показатели степени) Распределительное свойство (все ответы включают показатели степени)
Вычисление алгебраических выраженийВычисление выражений с одной переменной, одним шагом и без экспонент Вычисление выражений с одной переменной и одним шагом Вычисление выражений с одной переменной и двумя шагами Вычисление выражений с двумя переменными и двумя шагами Вычисление выражений с двумя переменными и тремя шагами Вычисление выражений с тремя переменными и четырьмя шагами Вычисление выражений с тремя переменными и пятью шагами
Правила экспоненты и свойства
Практика с
основными правилами экспоненты Как следует из названия, эти рабочие листы содержат только основные вопросы по правилам экспоненты. В каждом вопросе нужно иметь дело только с двумя показателями; сложные перепутанные термины и вещи, с которыми мог бы разобраться более продвинутый студент, остаются в покое. Например, 4 2 равно (2 2 ) 2 = 2 4 , но эти рабочие листы просто оставляют это как 4 2 , поэтому учащиеся могут сосредоточиться на изучении того, как умножать и делить степени более или менее изолированно.
В каждом вопросе нужно иметь дело только с двумя показателями; сложные перепутанные термины и вещи, с которыми мог бы разобраться более продвинутый студент, остаются в покое. Например, 4 2 равно (2 2 ) 2 = 2 4 , но эти рабочие листы просто оставляют это как 4 2 , поэтому учащиеся могут сосредоточиться на изучении того, как умножать и делить степени более или менее изолированно.
Правила смешанной экспоненты (все положительные) Правила смешанной экспоненты (с отрицаниями) Умножение показателей (все положительные) Умножение показателей степени (с отрицательными числами) Умножение одной и той же степени с разными основаниями (все положительные) Умножение одной и той же степени с разными основаниями (с отрицательными числами) Деление показателей с большим показателем в дивиденде (все положительные) Деление показателей с большим показателем в дивиденде (с отрицательными числами) Деление показателей с большим показателем в делителе (все положительные) Деление показателей с большим показателем в делителе (с отрицаниями) Полномочия экспонентов (все положительные) Полномочия экспонент (с отрицаниями)
Линейные выражения и уравнения
Рабочие листы по линейным уравнениям, включая упрощение, построение графиков, оценку и решение систем линейных уравнений.
Знание языка алгебры может помочь извлечь смысл из текстовых задач и ситуаций вне школы. В этих рабочих листах учащимся предлагается преобразовать фразы в алгебраические выражения.
Преобразование алгебраических фраз в выражения (простая версия) Перевод алгебраических фраз в выражения (сложная версия)
Упрощение линейных выражений (объединение одинаковых терминов)Объединение одинаковых терминов часто происходит в алгебре. Студенты могут быть введены в тему и немного попрактиковаться с этими рабочими листами. Планка поднимается с добавлением и вычитанием версий, которые вводят круглые скобки в выражения. Для учащихся, которые хорошо разбираются в дробях, упрощение рабочих листов с простыми алгебраическими дробями представляет собой некоторую проблему по сравнению с другими рабочими листами в этом разделе.
Упрощение линейных выражений с 3 терминами Упрощение линейных выражений с 4 терминами Упрощение линейных выражений с 5 терминами Упрощение линейных выражений с от 6 до 10 терминов Добавление и упрощение линейных выражений Сложение и упрощение линейных выражений с множителями Сложение и упрощение линейных выражений с некоторыми множителями . Вычитание и упрощение линейных выражений Вычитание и упрощение линейных выражений с множителями Вычитание и упрощение линейных выражений с некоторыми множителями Смешанные сложение, вычитание и упрощение линейных выражений Смешанные сложение, вычитание и упрощение линейных выражений с множителями Смешанные сложение, вычитание и упрощение линейных выражений с некоторыми множителями Упрощение простые алгебраические дроби (проще) Упрощение простые алгебраические дроби (сложнее)
Вычитание и упрощение линейных выражений Вычитание и упрощение линейных выражений с множителями Вычитание и упрощение линейных выражений с некоторыми множителями Смешанные сложение, вычитание и упрощение линейных выражений Смешанные сложение, вычитание и упрощение линейных выражений с множителями Смешанные сложение, вычитание и упрощение линейных выражений с некоторыми множителями Упрощение простые алгебраические дроби (проще) Упрощение простые алгебраические дроби (сложнее)
Перепишите линейные уравнения в стандартной форме Преобразование линейных уравнений из 9От стандарта 1342 до формы пересечения с уклоном Преобразование линейных уравнений из Slope-Intercept в стандартную форму Преобразование линейных уравнений между стандартной формой и формой пересечения наклона Переписывание формул (сложение и вычитание; примерно один шаг) Переписывание формул (сложение и вычитание; около двух шагов) Переписывание формул ( умножение и деление ; примерно один шаг)
Определение линейных уравнений из наклонов, точек пересечения с осью Y и точек 90 409 Определите линейное уравнение по наклону и точке пересечения с осью Y Определите линейное уравнение по наклону и точке . Определить линейное уравнение по двум точкам Определение линейного уравнения по двум точкам путем построения графика
Определить линейное уравнение по двум точкам Определение линейного уравнения по двум точкам путем построения графика
Линейное уравнение
ГрафикиПостроение линейных уравнений и чтение существующих графиков дает учащимся визуальное представление, которое очень полезно для понимания концепций наклона и точки пересечения по оси Y.
График Уравнения пересечения наклона Определите уравнение из графика Определите уклон по графику Определите y-пересечения из графика Определите x-перехват из графика Определите наклон и точку пересечения с осью Y на графике Определите наклон и пересечения с графика Определите наклон , точки пересечения и уравнение из графика
Решение линейных уравнений с помощью мармеладок — увлекательное занятие, которое стоит попробовать учащимся, впервые изучающим алгебраические понятия. В идеале вам понадобятся непрозрачные пакеты без массы, но, поскольку это не совсем возможно (часть без массы), здесь есть небольшое условие, которое на самом деле поможет учащимся лучше понять уравнения. Любые сумки, которые вы используете, должны быть сбалансированы с другой стороны уравнения с пустыми.
В идеале вам понадобятся непрозрачные пакеты без массы, но, поскольку это не совсем возможно (часть без массы), здесь есть небольшое условие, которое на самом деле поможет учащимся лучше понять уравнения. Любые сумки, которые вы используете, должны быть сбалансированы с другой стороны уравнения с пустыми.
Вероятно, лучше всего это проиллюстрировать на примере. Давайте использовать 3 x + 2 = 14. Вы можете узнать x как неизвестное, которое на самом деле является количеством мармеладок, которые мы кладем в каждый непрозрачный пакет. 3 в 3 x означает, что нам нужно три мешка. Лучше всего заполнить мешки необходимым количеством мармеладок так, чтобы ученики не видели их, чтобы им действительно пришлось решать уравнение.
С одной стороны двух чашечных весов поместите три пакета с драже размером 90 467 x 90 468 по одному и по два мармеладных драже в каждом, чтобы представить + 2 часть уравнения. На другой стороне весов поместите 14 мармеладных бобов и три пустых мешка, которые, как вы заметите, необходимы для правильного «баланса» уравнения. Теперь самое интересное… если учащиеся удалят две мармеладки с одной стороны уравнения, баланс станет несбалансированным, поэтому им нужно убрать две мармеладки с другой стороны баланса, чтобы сохранить равновесие. Есть желейные бобы необязательно. Цель состоит в том, чтобы изолировать мешки на одной стороне баланса без каких-либо незакрепленных мармеладных бобов, сохраняя баланс уравнения.
Теперь самое интересное… если учащиеся удалят две мармеладки с одной стороны уравнения, баланс станет несбалансированным, поэтому им нужно убрать две мармеладки с другой стороны баланса, чтобы сохранить равновесие. Есть желейные бобы необязательно. Цель состоит в том, чтобы изолировать мешки на одной стороне баланса без каких-либо незакрепленных мармеладных бобов, сохраняя баланс уравнения.
Последним шагом будет разделение драже в одной части уравнения на столько же групп, сколько пакетов. Это, вероятно, даст вам хорошее представление о том, сколько желейных бобов находится в каждом пакете. Если нет, съешьте немного и попробуйте еще раз. Теперь мы понимаем, что это не будет работать для каждого линейного уравнения, так как трудно иметь отрицательные мармеладки, но это еще одна стратегия обучения, которую вы можете использовать для алгебры.
Решение линейных уравнений Вопреки всему, уравнения типа а/ х не являются линейными. Вместо этого они принадлежат другому виду уравнений. Они хороши для их объединения с линейными уравнениями, так как вводят понятие правильных и неправильных ответов для уравнения (то, что позже будет называться областью определения функции). В этом случае неверными ответами для уравнений вида a/ x являются те, у которых знаменатель становится равным 0.
Вместо этого они принадлежат другому виду уравнений. Они хороши для их объединения с линейными уравнениями, так как вводят понятие правильных и неправильных ответов для уравнения (то, что позже будет называться областью определения функции). В этом случае неверными ответами для уравнений вида a/ x являются те, у которых знаменатель становится равным 0.
Объединение одинаковых терминов и решение простых линейных уравнений Решение x = c Линейные уравнения Решение a x = c линейных уравнений, включая отрицательные Решение x /a = c линейных уравнений Решение x /a = c линейных уравнений, включая отрицательные Решение a/ x = c линейных уравнений Решение a/ x = c линейных уравнений, включая отрицательные Решение a x + b = c линейных уравнений Решение x + b = c линейных уравнений, включая отрицательные Решение x – b = c Линейные уравнения Решение a x – b = c линейных уравнений, включая отрицательные Решение a x ± b = c линейных уравнений Решение a x ± b = c линейных уравнений, включая отрицательные Решение x /a ± b = c линейных уравнений Решение x /a ± b = c линейных уравнений, включая отрицательные Решение a/ x ± b = c линейных уравнений Решение a/ x ± b = c линейных уравнений, включая отрицательные Решение различных а/ x ± b = c и x /a ± b = c Линейные уравнения Решение различных a/ x ± b = c и x /a ± b = c линейных уравнений, включая отрицательные Решение линейных уравнений всех типов Решение линейных уравнений всех типов, включая отрицательные
Линейные системы
Решение систем линейных уравненийПростые линейные системы с двумя переменными Простые линейные системы с двумя переменными, включая отрицательные значения Линейные системы с двумя переменными Линейные системы с двумя переменными, включая отрицательные значения Простые линейные системы с тремя переменными; Легкий Простые линейные системы с тремя переменными, включая отрицательные значения Линейные системы с тремя переменными Линейные системы с тремя переменными, включая отрицательные значения
Решение систем линейных уравнений графическим способомРешение линейных систем с помощью графика (только решения в первом квадранте) Решите стандартные линейные системы графически Решите линейные системы пересечения наклона с помощью графика Решите различные линейные системы с помощью графика Определите зависимую линейную систему по графику Идентифицируйте несовместимую линейную систему с помощью графика
Квадратные выражения и уравнения
Квадратные выражения и рабочие листы уравнений, включая коэффициенты умножения, разложение на множители и решение квадратных уравнений.
Упрощение квадратных выражений с 5 членами Упрощение квадратных выражений с 6 членами Упрощение квадратных выражений с 7 членами Упрощение квадратных выражений с 8 членами Упрощение квадратных выражений с помощью 9условия Упрощение квадратных выражений с 10 членами Упрощение квадратных выражений с 5-10 членами
Сложение/вычитание и упрощение квадратных выражений Сложение и упрощение квадратных выражений.
Сложение и упрощение квадратных выражений с помощью множителей.
Добавление и упрощение квадратных выражений с некоторыми множителями.
Вычитание и упрощение квадратных выражений.
Вычитание и упрощение квадратных выражений с помощью множителей.
Вычитание и упрощение квадратных выражений с некоторыми множителями.
Смешанное сложение и вычитание и упрощение квадратных выражений.
Смешанное сложение и вычитание и упрощение квадратных выражений с множителями. Смешанное сложение и вычитание и упрощение квадратных выражений с некоторыми множителями.
Смешанное сложение и вычитание и упрощение квадратных выражений с некоторыми множителями.
Коэффициенты умножения квадратичных чисел с коэффициентами 1 Умножение коэффициентов квадратичных чисел с коэффициентами 1 или -1 Умножение коэффициентов квадратичных чисел с коэффициентами 1 или 2 Умножение коэффициентов квадратичных чисел с коэффициентами 1, -1, 2 или -2 Коэффициенты умножения квадратичных чисел с коэффициентами до 9 Умножение коэффициентов квадратичных чисел с коэффициентами от -9и 9
Разложение квадратичных выражений на множители Рабочие листы по факторингу квадратичных выражений в этом разделе содержат много практических вопросов для студентов, чтобы отточить свои стратегии факторинга. Если вы предпочитаете рабочие листы с квадратными уравнениями, см. следующий раздел. Эти рабочие листы бывают разных уровней, самые простые находятся в начале. Упомянутые ниже коэффициенты «а» являются коэффициентами x 2 член как в общем квадратном выражении: ax 2 + bx + c. В этом разделе также есть рабочие листы для вычисления суммы и произведения и для определения операндов для пар суммы и произведения.
Упомянутые ниже коэффициенты «а» являются коэффициентами x 2 член как в общем квадратном выражении: ax 2 + bx + c. В этом разделе также есть рабочие листы для вычисления суммы и произведения и для определения операндов для пар суммы и произведения.
Разложение на множители квадратных выражений с положительными коэффициентами «а» 1 Факторинг квадратичных выражений с положительными или отрицательными коэффициентами ‘a’ числа 1 Факторинг квадратичных выражений с положительным или отрицательным числом ‘a’ коэффициенты 1 с шагом общего множителя Разложение квадратных выражений с положительными коэффициентами «а» до 4 Разложение квадратичных выражений с положительными или отрицательными коэффициентами ‘a’ до 4 Разложение квадратичных выражений на множители с положительными или отрицательными коэффициентами ‘a’ до 4 с шагом общего множителя Факторинг квадратных выражений с положительными коэффициентами «а» до 5 Факторинг квадратичных выражений с положительными или отрицательными коэффициентами ‘a’ до 5 Разложение квадратичных выражений с положительными или отрицательными коэффициентами ‘a’ до 5 с шагом общего множителя Разложение квадратных выражений с положительными коэффициентами «а» до 9 Разложение квадратичных выражений с положительными или отрицательными коэффициентами ‘a’ до 9 Факторинг квадратных выражений с положительным или Отрицательные ‘a’ коэффициенты до 9 с шагом общего множителя Разложение квадратных выражений с положительными коэффициентами «а» до 81 Факторизация квадратичных выражений с положительными или отрицательными ‘a’ коэффициентами до 81 Факторизация квадратичных выражений с положительными или отрицательными коэффициентами ‘a’ до 81 с шагом общего множителя Вычисление суммы и произведения (диапазон операндов от 0 до 9 ) Вычисление суммы и произведения (диапазон операндов от 1 до 9 ) Вычисление суммы и произведения (диапазон операндов от 0 до 9, включая отрицательные значения ) Вычисление суммы и произведения (диапазон операндов от 1 до 9, включая отрицательные значения ) Вычисление суммы и произведения (диапазон операндов от -20 до 20 ) Вычисление суммы и произведения (диапазон операндов от -99 до 99 ) Определение операндов из пар суммы и произведения (диапазон операндов от 0 до 9 ) Определение операндов из пар суммы и произведения (диапазон операндов от 1 до 9 ) Определение операндов из пар суммы и произведения (диапазон операндов от 0 до 12 ) Определение операндов из пар суммы и произведения (диапазон операндов от 1 до 12 ) Определение операндов из пар суммы и произведения (диапазон операндов от 0 до 9, включая отрицательные значения ) Определение операндов из пар суммы и произведения (диапазон операндов от 1 до 9, включая отрицательные значения ) Определение операндов из пар суммы и произведения (диапазон операндов от -20 до 20 ) Определение операндов из пар суммы и произведения (диапазон операндов от -99 до 99 )
Применяете ли вы метод проб и ошибок, вычисляете квадрат или вычисляете общую квадратичную формулу, эти рабочие листы содержат множество практических вопросов с ответами. В первом разделе рабочие листы включают вопросы, в которых квадратные выражения равны 0. Это делает процесс похожим на разложение квадратных выражений на множители с дополнительным шагом поиска значений x, когда выражение равно 0. Во втором разделе выражения обычно равны чему-то другому, кроме x, поэтому в начале есть дополнительный шаг, чтобы сделать квадратное выражение равным нулю.
В первом разделе рабочие листы включают вопросы, в которых квадратные выражения равны 0. Это делает процесс похожим на разложение квадратных выражений на множители с дополнительным шагом поиска значений x, когда выражение равно 0. Во втором разделе выражения обычно равны чему-то другому, кроме x, поэтому в начале есть дополнительный шаг, чтобы сделать квадратное выражение равным нулю.
Решение квадратных уравнений с положительными коэффициентами «а» числа 1 Решение квадратных уравнений с положительными или отрицательными коэффициентами «а» числа 1 Решение квадратных уравнений с положительными или отрицательными коэффициентами «а» числа 1 с шагом общего множителя Решение квадратных уравнений с положительными коэффициентами «а» до 4 Решение квадратных уравнений с положительными или отрицательными коэффициентами «а» до 4 Решение квадратных уравнений с положительными или отрицательными коэффициентами «а» до 4 с шагом общего множителя Решение квадратных уравнений с положительными коэффициентами «а» до 5 Решение квадратных уравнений с положительными или отрицательными коэффициентами «а» до 5 Решение квадратных уравнений с положительным или Отрицательные ‘a’ коэффициенты до 5 с шагом общего множителя Решение квадратных уравнений с положительными коэффициентами «а» до 9 Решение квадратных уравнений с положительными или отрицательными коэффициентами «а» до 9 Решение квадратных уравнений с положительными или отрицательными коэффициентами «а» до 9 с шагом общего множителя Решение квадратных уравнений с положительными коэффициентами «а» до 81 Решение квадратных уравнений с положительными или отрицательными коэффициентами «а» до 81 Решение квадратных уравнений с положительными или отрицательными коэффициентами «а» до 81 с шагом общего множителя
Решение квадратных уравнений , что равно целому числу (например, ax² + bx + c = d)Решение квадратных уравнений относительно x (коэффициенты «a» равны 1) Решение квадратных уравнений относительно x (коэффициенты “a” равны 1 или -1) Решение квадратных уравнений относительно x (коэффициенты «а» до 4) Решение квадратных уравнений относительно x (коэффициенты “а” между -4 и 4) Решение квадратных уравнений относительно x (коэффициенты «а» до 81) Решение квадратных уравнений относительно x (коэффициенты «а» между -81 и 81)
Прочие полиномиальные и мономиальные выражения и уравнения
Разложение на множители неквадратичных выражений различных уровней сложности.
Сложение и вычитание; 1 переменная; 3 триместра Сложение и вычитание; 1 переменная; 4 срока Сложение и вычитание; 2 переменные; 4 срока Сложение и вычитание; 2 переменные; 5 терминов Сложение и вычитание; 2 переменные; 6 терминов
Упрощающие многочлены , включающие умножение и делениеУмножение и деление; 1 переменная; 3 триместра Умножение и деление; 1 переменная; 4 срока Умножение и деление; 2 переменные; 4 срока Умножение и деление; 2 переменные; 5 терминов
Упрощающие многочлены , которые включают сложение, вычитание, умножение и делениеВсе операции; 1 переменная; 3 триместра Все операции; 1 переменная; 4 срока Все операции; 2 переменные; 4 срока Все операции; 2 переменные; 5 терминов Все операции (вызов)
Факторные выражения, которые
не включают квадратную переменнуюРазложение на множители неквадратичных выражений без квадратов, простых коэффициентов и положительных множителей Разложение на множители неквадратичных выражений без квадратов, простых коэффициентов и отрицательных и положительных множителей Разложение на множители неквадратичных выражений без квадратов, составных коэффициентов и положительных множителей Разложение на множители неквадратичных выражений без квадратов, составных коэффициентов и отрицательных и положительных множителей
Факторные выражения
, которые всегда включают переменную в квадратеФакторинг неквадратичных выражений со всеми квадратами, простыми коэффициентами и положительными множителями Факторинг неквадратичных выражений со всеми квадратами, простыми коэффициентами и отрицательными и положительными множителями Факторинг неквадратичных выражений со всеми квадратами, составными коэффициентами и положительными множителями Факторинг неквадратичных выражений со всеми квадратами, составными коэффициентами и отрицательными и положительными множителями
Факторные выражения
, которые иногда включают квадраты переменныхФакторинг неквадратичных выражений с некоторыми квадратами, простыми коэффициентами и положительными множителями Разложение неквадратичных выражений с некоторыми квадратами, простыми коэффициентами и отрицательными и положительными множителями Факторинг неквадратичных выражений с некоторыми квадратами, составными коэффициентами и положительными множителями Факторинг неквадратичных выражений с некоторыми квадратами, составными коэффициентами и отрицательными и положительными множителями
Умножение многочленов с двумя множителямиУмножение одночлена на двучлен Умножение двух двучленов Умножение одночлена на трехчлен Умножение двучлена на трехчлен Умножение двух трехчленов Умножение двух случайных мон/полиномов
Умножение многочленов с тремя множителямиУмножение одночлена на два двучлена Умножение трех двучленов Умножение двух двучленов на трехчлен Умножение двучлена на два трехчлена Умножение трех трехчленов Умножение трех случайных мон/полиномов
Неравенства, включая графики
Рабочие листы по неравенствам, включая запись неравенства, соответствующего графику, и графическое изображение неравенства на числовой прямой.
 Один из них двигался со скоростью 70 км/ч проехал до встречи 140 км, а другой двигался со скоростью 65 км/ч. Найдите расстояние между городами.
Один из них двигался со скоростью 70 км/ч проехал до встречи 140 км, а другой двигался со скоростью 65 км/ч. Найдите расстояние между городами. . Вырази одни единицы в другие.
. Вырази одни единицы в другие.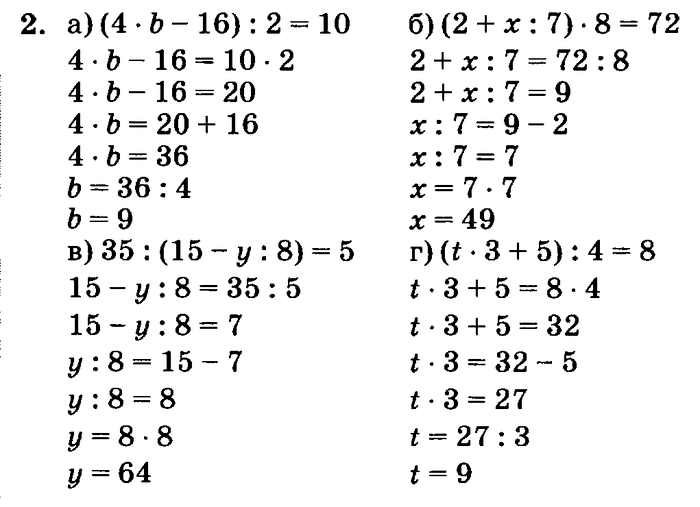 Реши уравнение:
Реши уравнение: Найди площадь прямоугольника, если его длина 9 см, а ширина на 5 см меньше.
Найди площадь прямоугольника, если его длина 9 см, а ширина на 5 см меньше.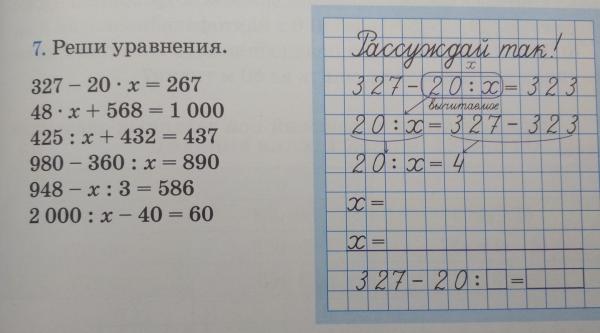 Девочка потратила на одну минуту больше. С какой скоростью плыла девочка?
Девочка потратила на одну минуту больше. С какой скоростью плыла девочка?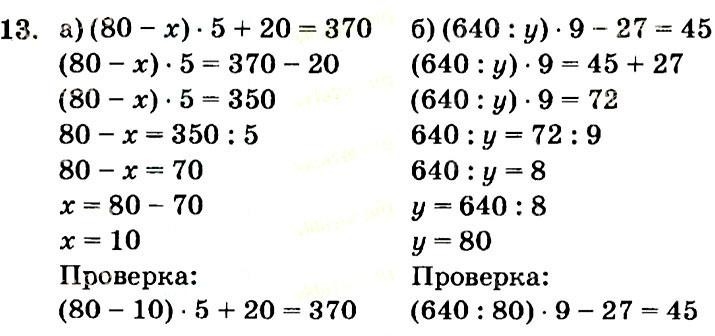 Петя и Митя живут в одном доме. Петя ходит в школу со скоростью 4 км\ч, а Митя со скоростью 6 км\ч. Кто из мальчиков тратит на дорогу меньше
Петя и Митя живут в одном доме. Петя ходит в школу со скоростью 4 км\ч, а Митя со скоростью 6 км\ч. Кто из мальчиков тратит на дорогу меньше Всего в
Всего в 2 ч …182 ч 6800 кг … 68 т
2 ч …182 ч 6800 кг … 68 т Один пароход шел со скоростью 26 км\ч. С какой скоростью шел второй пароход, если они встретились через 8 часов?
Один пароход шел со скоростью 26 км\ч. С какой скоростью шел второй пароход, если они встретились через 8 часов?