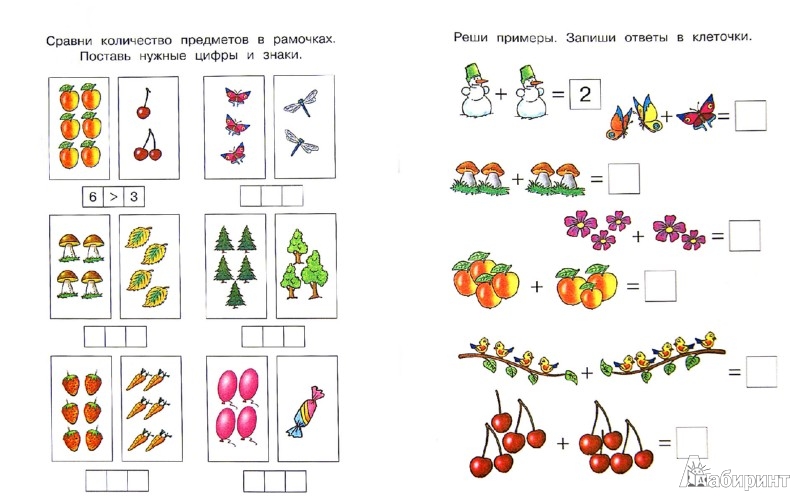
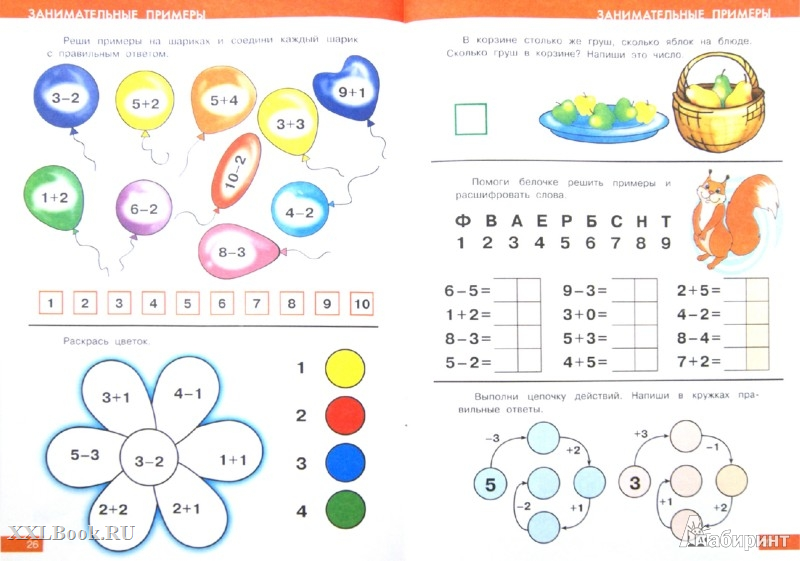
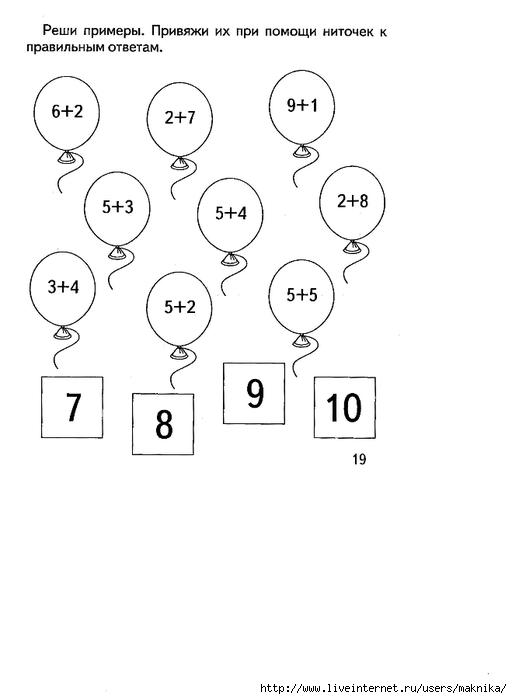
Учимся решать примеры: Книга: “Учимся решать примеры и задачи. Для детей 6-7 лет”. Купить книгу, читать рецензии | ISBN 978-5-699-48804-9

Книга “Учимся решать примеры и задачи: для детей 6-7”

• Книги
  • Художественная литература
  • Нехудожественная литература
  • Детская литература
  • Литература на иностранных языках
  • Путешествия. Хобби. Досуг
  • Книги по искусству
  • Биографии. Мемуары. Публицистика
  • Комиксы. Манга. Графические романы
  • Журналы
  • Печать по требованию
  • Книги с автографом
  • Книги в подарок
  • “Москва” рекомендует

  • Авторы • Серии • Издательства • Жанр
• Электронные книги
  • Русская классика
  • Детективы
  • Экономика
  • Журналы
  • Пособия
  • История
  • Политика
  • Биографии и мемуары
  • Публицистика
• Aудиокниги
  • Электронные аудиокниги
  • CD – диски
• Коллекционные издания
  • Зарубежная проза и поэзия
  • Русская проза и поэзия
  • Детская литература
  • История
  • Искусство
  • Энциклопедии
  • Кулинария. Виноделие
  • Религия, теология
  • Все тематики
• Антикварные книги
  • Детская литература
  • Собрания сочинений
  • Искусство
  • История России до 1917 года
  • Художественная литература.
    Зарубежная
  • Художественная литература. Русская
  • Все тематики
  • Предварительный заказ
  • Прием книг на комиссию
• Подарки
  • Книги в подарок
  • Авторские работы
  • Бизнес-подарки
  • Литературные подарки
  • Миниатюрные издания
  • Подарки детям
  • Подарочные ручки
  • Открытки
  • Календари
  • Все тематики подарков
  • Подарочные сертификаты
  • Подарочные наборы
  • Идеи подарков
• Канцтовары
  • Аксессуары делового человека
  • Необычная канцелярия
  • Бумажно-беловые принадлежности
  • Письменные принадлежности
  • Мелкоофисный товар
  • Для художников
• Услуги
  • Бонусная программа
  • Подарочные сертификаты
  • Доставка по всему миру
  • Корпоративное обслуживание
  • Vip-обслуживание
  • Услуги антикварно-букинистического отдела
  • Подбор и оформление подарков
  • Изготовление эксклюзивных изданий
  • Формирование семейной библиотеки

Расширенный поиск

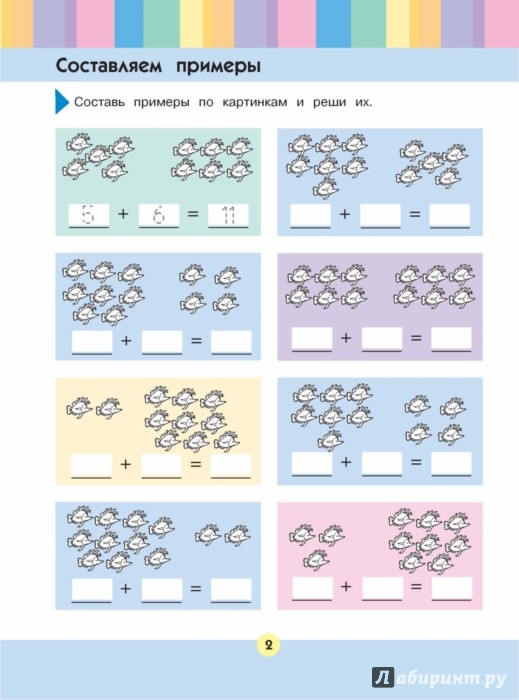
Решаем задачи по математике с ребенком: советы и примеры

1. Почему ребенку сложно выполнять задания по математике?
2. Как научить ребенка решать задачи по математике?
3. Как решать примеры с ребенком?

Математика в начальной школе – это основа для дальнейшей успешной учебы. Чтобы у школьника не возникало проблем со сложными темами в 5-11 классах, ему важно хорошо разобраться с базовыми заданиями по математике. В этот период ребенку необходима помощь и поддержка родителей. 

 

В статье собраны советы, которые помогут объяснить ребенку принцип решения типичных задач и примеров.

Почему ребенку сложно выполнять задания по математике?

 

Не всегда условия урока в школе способствуют качественному усвоению материала. Шум в классе, болтливый сосед по парте не позволяют ребенку сконцентрироваться на теме и проанализировать объяснение учителя.

 

Дома ученик может плохо усваивать материал из-за недостаточного отдыха, большой нагрузки, постоянной усталости. Родителям важно следить за режимом ребенка и в случае перегрузки регулировать расписание. 

 

Существуют и другие причины плохой успеваемости.

Нерегулярные занятия

Нерегулярные занятия также ухудшают понимание школьных предметов. В перерывах между уроками ребенок забывает пройденный материал и вследствие этого плохо разбирается в следующих темах.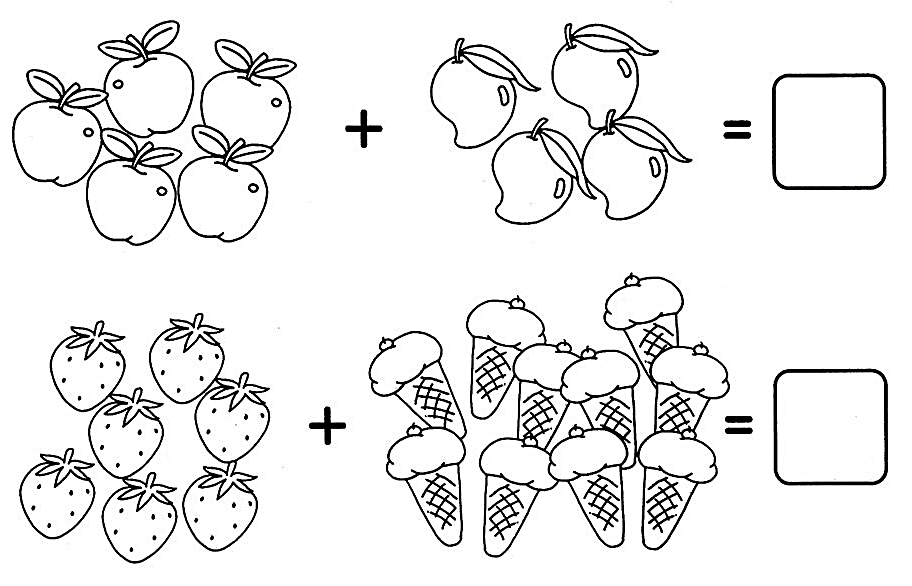  

Недостаток поддержки от родителей

Если у малыша возникают трудности и он замечает недовольство родителей, он теряет уверенность в собственных силах, начинает сомневаться в своей правоте и допускает еще больше ошибок. Взрослым важно с пониманием относиться к проблемам школьника и вместе с ним преодолевать трудности.

Плохое или недостаточное изложение материала

Ученик может не понимать материал из-за недостаточного объяснения. Если в классе много детей, школьный учитель просто не может уделить достаточно времени каждому ребенку. Если проблема кроется в этом, родителям стоит уделить внимание домашним урокам или обратиться за помощью к репетитору по математике.

Невнимательное изучение условия

Проблемы с задачами по математике могут возникать из-за невнимательного изучения условия. Важно просить ученика пересказывать условие задачи своими словами, выписывать из текста все известные числа, объяснять их значение. Особое внимание уделяется вопросу. Часто дети не обдумывают его и потом не знают, что от них требуется.

Непонимание смысла арифметических действий

Ошибки в решении примеров часто случаются из-за непонимания смысла арифметических действий. Если ребенок плохо понял тему на уроке, родителям стоит дома еще раз объяснить ему, что такое сложение, вычитание, умножение и деление.

Отсутствие интереса к дисциплине

Иногда у детей плохая успеваемость по математике из-за отсутствия интереса к дисциплине. В этом случае родителям стоит обсудить со школьным учителем материал, который он подбирает для уроков или самостоятельно находить интересные задания для домашних занятий.

 

Если у взрослых возникают трудности с выбором подходящих задач и примеров, можно обратиться за помощью к репетитору по математике. Педагог составляет график обучения с учетом школьной программы, подбирает задания, исходя из интересов малыша, проводит уроки в комфортном для ребенка темпе и уделяет достаточно времени сложному материалу.

 

Найти репетитора по математике или другой учебной дисциплине можно на сайте BUKI.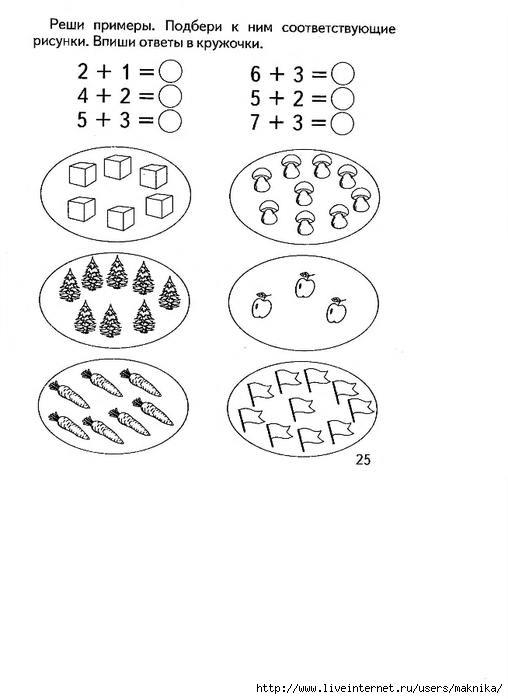

 

Читайте также: Лучшие упражнения и игры для развития памяти у ребенка

Как научить ребенка решать задачи по математике?

Задачи по математике в первом классе – это знакомство ребенка с самим понятием задачи, проблемной ситуацией, которую можно решить математическим методом. 

 

Во втором классе школьник проходит элементарные задачи по нахождению суммы и разности двух чисел, определению неизвестного слагаемого, учится составлять задачи по рисунку или схеме.

 

 

В подобных задачах важно, чтобы ребенок внимательно изучил условие, сделал правильные записи в тетради и понял, сколько действий необходимо выполнить.

 

 

Для начала нужно найти количество чайных роз. Если их на 24 меньше, чем красных, то следует выполнить вычитание и от 57 отнять 24. После этого можно определить общее количество раз, для этого необходимо сложить красные и чайные розы.

 

 

Задачи на движение начинают изучать в третьем классе и традиционно относят к сложным. В них встречается три величины:

• Скорость (v) – это величина, которая обозначает какое расстояние проходит объект за единицу времени, то есть сколько мм, см, дм, м данный объект проходит за секунду, минуту, час, сутки;
• Время (t) – это величина, которая показывает, сколько секунд, часов, дней, недель, лет объект находился в движении;
• Расстояние (S) – тот путь, который проходит герой, измеряется в мм, см, дм, м, км. Это самое большое число из трех величин.

 

Чтобы ребенку было проще решить задачу 3 класса, нужно приучить его к рисованию чертежей или составлению таблиц. Чертежи помогают школьнику понять связь между величинами. К примеру, Баба-Яга летела в ступе 6 часов со скоростью 800 м/час.

 

 

Благодаря визуализации школьник видит, что каждый час Баба-Яга преодолевала расстояние 800 метров и всего она летела 6 часов.

 

Ребенок может тратить много времени на рисование подобной схемы, но если он делает это на черновике, важна не красота, а наглядность.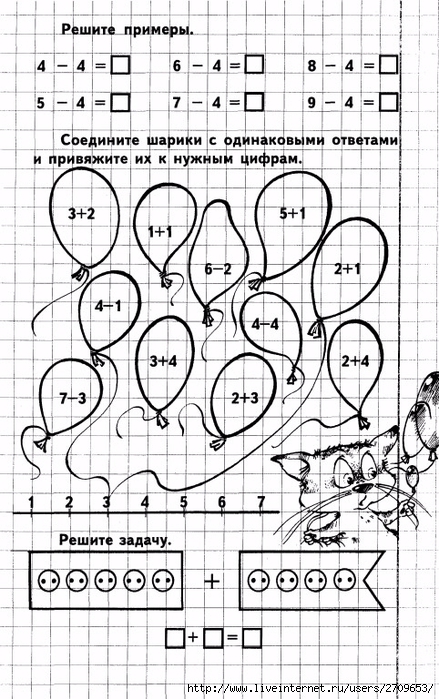 К тому же, домашние тренировки помогут усовершенствовать и ускорить навык черчения, который пригодится и в других сферах жизни.

 

Для решения задач на движение нужно запомнить три формулы.

 

 

Если помнить, что расстояние – это самое большое число, их будет легче выучить.

 

Рассмотрим для примера одну задачу.

 

Добираясь от своей избушки до башни Кощея Бессмертного, Баба-Яга тратит на полет в ступе два часа, если летит по прямой. Каково расстояние до башни Кощея, если скорость ступы с бабушкой 24 километра в час?

 

В начале нужно понять, какие в задачи есть величины. 

t – 2 ч;

v – 24 км/ч;

S – ?

В задаче одно неизвестное, поэтому решаться она будет в одно действие. Для нахождения расстояния используется первая формула.

1. 24×2=48 (км)

Ответ: 48 км. 

Объяснение задач по математике в 4 классе

Большую группу задач по математике в 4 классе составляют задания с дробями. Чтобы без проблем решать задачи по математике с дробями, ребенок должен уметь чертить отрезки. Он уже тренировался это делать в задачах на движение, поэтому у малыша уже должно хорошо получаться.

 

В этом случае ребенок должен начертить отрезок любой длины и разделить его на три части. Три отрезка подразумеваются равными, но если у ребенка они будут неодинаковыми, ничего страшного. 

 

Важно запомнить, что в задачах на дроби важна именно дробь, целое число – вторично. Если нужно найти ⅔ от 18, то нужно сначала обратить внимание именно на ⅔, начертить отрезок любой длины и поделить его на столько частей, сколько указано в знаменателе. Числитель показывает, сколько частей необходимо взять.

 

После проделанной работы можно смотреть на число 18. Когда ученик разделит 18 на 3, он узнает длину одной части отрезка (6 см). Чтобы узнать длину 2 частей из трех, нужно 6 умножить на 2.

 

Читайте также: Как развивать Soft Skills у ребенка

Как решать примеры с ребенком?

Примеры для 1 класса

В первом классе ребенок изучает числа от 1 до 100, решает с ними примеры на сложение и вычитание.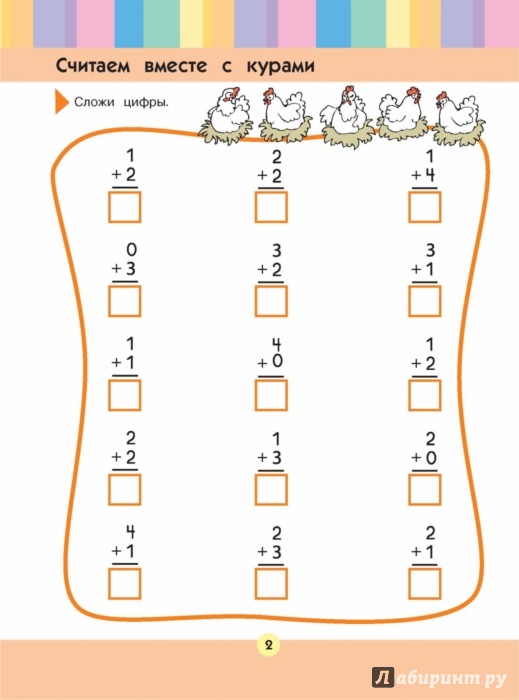 Обычно на этом этапе у ученика не возникает трудностей, но даже если малыш чего-то и не понимает, родители без труда объясняют ему сложные темы. 

 

Чтобы решать простые примеры для 1 класса, школьник должен хорошо считать до 10. Для тренировки этого навыка, родителям нужно запастись любыми предметами, которыми интересуется ребенок. Малыш должен понимать, что состав числа соотносится с определенным количеством реальных объектов. Родители могут показывать, что цифре 5 соответствует пять машинок, а восемь – это восемь яблок. Взрослым нужно просить малыша считать любые объекты – ложки в кухонном ящике, машины на парковке, деревья в саду.

 

Когда учебная программа усложняется, взрослым все сложнее помогать ребенку в учебе. Нижеизложенные советы помогут объяснить малышу, как решить примеры по математике. 

 

В обучении счету до 100 и объяснении смысла сложения/вычитания, важно использовать счетные палочки. С их помощью ребенок увидит на практике, что сложение – это объединение.

Примеры для 2 класса

Во втором классе дети учатся складывать и вычитать двузначные числа столбиком. Ученик должен запомнить, что подобные примеры решаются не слева направо, а справа налево.

 

 

Нужно начинать с младшего десятка, то есть с единиц. 5+1=6, записываем шестерку снизу под единицей. 4+3=7, записывается под тройкой. Этот пример без перехода через десяток.

 

Дети иногда во время решения допускают ошибку и вместо сложения выполняют вычитание. Чтобы этого избежать, нужно научить ученика указывать во время работы пальцем сначала на цифру, с которой он выполняет действие, затем на знак и на вторую цифру.

 

Рассмотрим следующий пример.

 

 

При сложении единиц получается двузначное число. Но так как эта клетка принадлежит единицам, записываем в нее только единицы, то есть цифру, стоящую справа. В числе 10 справа находится 0, поэтому он и будет в ответе справа. А цифру 1 записываем к десяткам, вверху над примером. При сложении основных десятков важно не забыть добавить эту записанную вверху единицу.

 

 

При вычитании двузначных чисел столбиком нужно также начинать действия с единиц, а при работе с примером указывать пальцем на цифры и арифметические знаки.

 

Важно, чтобы ребенок понимал позиционную систему расстановки цифр. Например, в числе 33 вторая 3 – это единицы, а первая – десятки и она обозначает не 3, а 30. Для объяснения этого можно воспользоваться счетными палочками, скрепить три свертка палочек по 10 штук (десятки) и рядом выложить три самостоятельные палочки (единицы).

 

Когда ребенок четко понимает эту связь, ему будет легко решать подобные примеры.

 

Из 0 вычесть 6 не получится, поэтому единицам нужно обратиться к десяткам и занять у них 1. Чтобы не забыть о занятом десятке, над 8 можно поставить точку или написать -1. 

 

Теперь ученик не из 0, о из 10 вычитает 6 и получает 4. В десятках после займа уже не 8, а 7, поэтому нужно из 7 вычесть единицу. Ответом будет 64.

 

В примерах для 2 класса впервые встречается умножение. Важно, чтобы ребенок понял смысл этого арифметического действия. Можно привести любой пример из жизни. 

 

Например, на одном дереве 8 яблок. Сколько яблок на 7 деревьях, если на всех деревьях одинаковое количество яблок? Если использовать сложение, то получится длинный пример 8+8+8+8+8+8+8=56. А если бы деревьев было не 7, а 77, то считать при помощи сложения было бы очень неудобно. Именно для таких случаев подходит умножение.

 

Важно донести до ребенка, что умножением называют специальный способ сложения, при котором определенное число добавляется само к себе несколько раз. Первым в примере будет идти то число, которое повторяется, а вторым – то число, которое указывает на количество повторов.

Примеры в 3 классе

В 3 классе дети знакомятся с уравнениями – равенствами, в которых одно число стало неизвестным. Неизвестное – это число, которое необходимо найти, чтобы решить уравнение. Его обычно обозначают буквами латинского алфавита (х, y, a). Ниже приведен пример решения простого уравнения.

 

 

Обязательной в уравнении является проверка. Во время нее на место неизвестного подставляется 76, выполняется математическое действие и знак равенства в примере ставится только в том случае, если пример решен правильно. В этом варианте проверка будет записана под чертой следующим образом: 72 : 6 = 12, 12=12.

 

Если в легком уравнении такая запись кажется необязательной, то в более сложных уравнениях она пригодится. Поэтому лучше с самого первого уравнения привыкать к правильному алгоритму записи.

Решение примеров в 4 классе

Чтобы ученик в старшей и средней школе мог решать сложные примеры и уравнения, ему нужно хорошо разобраться с дробями в 4 классе.

 

 

Если ученик посмотрит на этот пример, он увидит знакомые арифметические действия – сложение, вычитание и умножение. Но он не найдет привычного деления.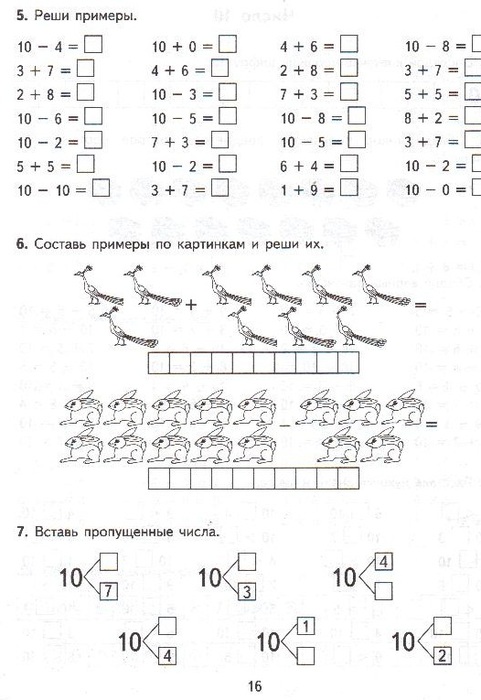 На самом деле оно здесь есть, просто записано непривычным для маленького школьника способом. В старших классах деление записывают не двумя точками, а горизонтальной полоской, которая на рисунке выделена красным цветом.

 

Любая математическая запись, в которой присутствует знак деления в виде черточки называется дробью. В 4 классе ребенку нужно понять это и научиться решать примеры с базовыми, легкими дробями.

 

 

Решение таких примеров для наглядности можно подкреплять историями из жизни. Например, дать ребенку один апельсин и предложить разделить его на две части. После разрезания образуется две половины, то есть ½ и ½.

 

Чтобы понять эту дробь, рассмотрим пример из жизни. Например, в гости пришло 4 друга, а дома есть только три одинаковых пирога.

 

 

Чтобы каждому ребенку досталось одинаковое количество еды, нужно каждый пирог разделить на 4 одинаковые части. Каждый друг заберёт одну часть от каждого пирога.

 

 

Рассмотрим следующую дробь.

 

 

Здесь 2 делится на 3. Для примера разделим два торта между тремя детьми. Каждый торт разрежем на три части и каждому малышу достанется по одной части от каждого торта.

 

Каждая из рассмотренных дробей меньше 1. Верхнее число дроби называют числитель, а нижнее – знаменатель. Знаменатель показывает, на сколько было поделено целое, а числитель – сколько частей целого было взято. 

 

Чтобы маленький школьник хорошо запомнил расположение числителя и знаменателя, можно предложить ему провести ассоциацию с фразой «человек ходит по земле». Человек (числитель) сверху, а земля (знаменатель) – снизу.

 

Если у ребенка возникают проблемы с пониманием дробей, можно предложить ему нарисовать несколько рисунков.

 

 

В этом варианте круг разделен на 4 части, значит в знаменателе будет стоять это число. А в числителе будет стоять 1, потому что именно столько частей взяли из целого круга.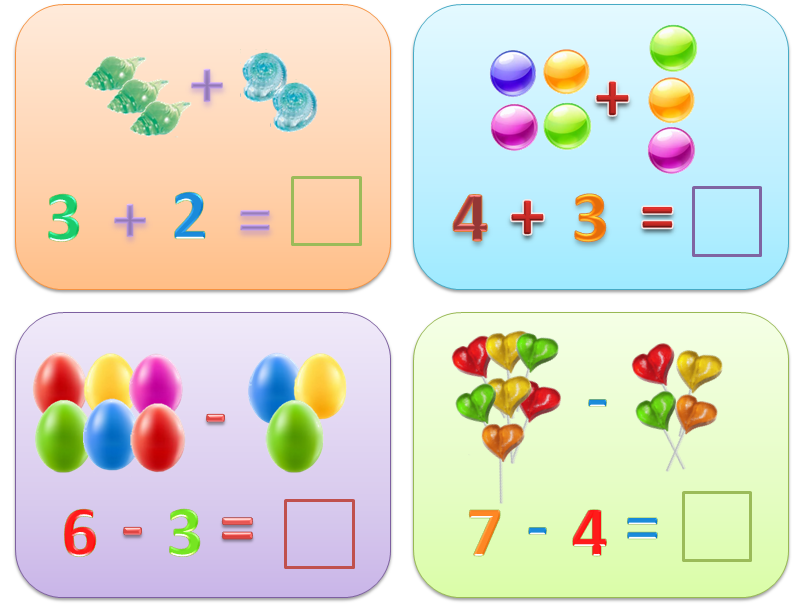

 

Читайте также: Как научить ребенка читать? Пошаговая инструкция и приложения

развивающие игры, упражнения для детей

Содержание статьи

• Правильная база
• Считаем и решаем примеры до 20
• Запоминаем цифры
• Решаем примеры

Когда первые ступени математической науки пройдены, базисные знания о первой десятке цифр усвоены, самое время приступать к обучению дошкольника складыванию и вычитанию чисел второго порядка. Если малыш уже свободно ориентируется в однозначных числах и может работать с первым десятком, различает, что больше и что меньше, знает состав числа, то дальнейшее обучение не составит особого труда.

Самое главное требование – понимать математику. Не заучивать числа как стишок, не считать на пальцах и не подсматривать в тетрадь к своему соседу. Понимание – основа знания.

Правильная база

К сожалению, многие родители учат своих чад считать до 20 слишком быстро, не прививая им понимания сути числительных. Такие дети часто после просьбы посчитать до 20 путаются в цифрах и пропускают их. О решении математических примеров в таком случае не может быть и речи, ведь ребенок не умеет считать. Он лишь механических запомнил порядок слов.

В таком случае родители должны помочь своему малышу освоить счет и сделать особый акцент на первой десятке натуральных чисел.

Именно помощь родителей в обучении дошкольника играет главную роль. Передать свои полномочия учителям и репетиторам не получится – и те, и другие будут давать домашние задания, которые нужно делать дома. Иначе знания, которые не подкреплены практикой, скоро забудутся.

Если малыш никак не заинтересован в понимании числительных, отказывается считать злополучные палочки и черточки – заинтересуйте его.

Можно использовать несколько простых и проверенных способов, чтобы на первых порах заинтересовать ребенка и начать прививать ему знания играючи и в бытовой манере.

1. Дайте ребенку понять, что без знания счета в жизни не обойтись. Объясняйте, где нужна математика, для чего, в какой сфере. Например, строительство домов – необходимость считать расстояния, чтобы дома были ровными и прочными, или правильно рассчитать пропорции для смешивания бетонной смеси, или, например, сколько нужно выпить таблеток, чтобы перестать болеть и не отравиться и т. д.
2. Считайте все подряд: ступеньки в подъезде, голубей, прохожих, скамейки, конфеты, окна в домах, облака. Считайте вместе с малышом, не молчите и называйте числа. Практикуясь, ребенок будет быстро запоминать.
3. Поиграйте в шпионов и найдите спрятавшуюся цифру. Читая книгу или журнал со своим малышом, назовите определенное число и попросите ребенка найти его на открытой странице.
4. Учимся сравнению. Возьмите конфеты, орешки, пуговицы или маленькие игрушки, сложите из них две кучки с разным количеством содержимого и сравнивайте. Пересчитайте и определите, где больше, а где меньше. Научив отличать числа в порядке «больше – меньше», можно учить дошкольника отвечать на вопросы: «Насколько больше/меньше это число?».
5. Учимся понимать прямой и обратный счет. Можно использовать кубики с цифрами или карточки, перемешать их и дать ребенку задание собрать их в правильном порядке.
6. Игра в угадайку. Загадайте число от 1 до 10 и попросите ребенка угадать его с 3 или 5 попыток. Когда он говорит, ориентируйте его направлениями «больше» и «меньше», а потом наградите за усердие.

Развивающие игры пробуждают азарт и интерес к изучению нового. Они – лучший способ привить вашему малышу желание учиться и познавать мир.

Считаем и решаем примеры до 20

Когда счет до 10 был освоен и ребенок стал свободно ориентироваться в первой десятке цифр, наступает время переходить на новый этап и обучаться двузначным числам, считать примеры в пределах 20.

Запоминаем цифры

Чтобы ребенок хорошо запоминал последовательность цифр, лучше всего использовать 20 одинаковых предметов (это даст возможность наглядно все объяснять малышу) или опять же карточки с числами.

В два ряда в количестве 10 штук выкладываем предметы или карточки.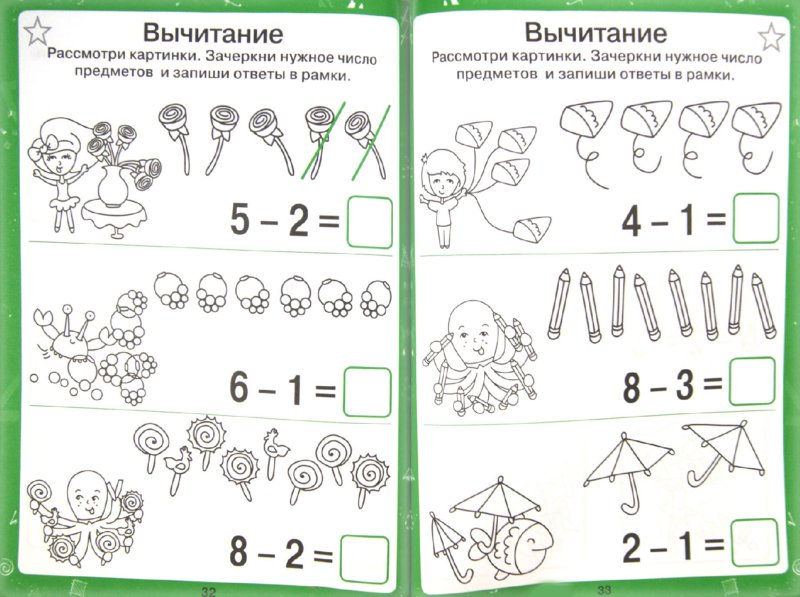 Первая строка – это первый десяток, а вторая – второй десяток.

Выглядеть это будет так:

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20

Поясняем ребенку, что в числах после 10 есть сходство. Визуализируя таким образом числа и десятки, вы поможете ребенку эффективнее запомнить их последовательность и названия. Видим число 11 – говорим «один» и прибавляем окончание «надцать». Так же поступаем и с другими двузначными числами – «три-надцать», «пять-надцать», «шесть-надцать» и т. д.

Работайте с ребенком на повторение, пока он не запомнит названия чисел.

Решаем примеры

Прежде чем приступить к решению примеров и обучению в пределах двадцати, дошкольник должен уяснить такие понятия, как «десятки» и «единицы». Для начального этапа обучения можно использовать кубики, палочки или попробовать учиться на счетах, а потом уже приучать малыша считать в уме. В возрасте 5 или 6 лет он должен уметь считать без помощи пальцев и других посторонних предметов.

Для первых занятий лучше использовать такие упражнения для детей, в которых не нужно совершать вычисления с переходом через десяток. Подойдут примеры, где все математические действия происходят с целым десятком или десятками и с некоторым количеством единиц, которые прибавляются либо вычитаются.

То есть десяток – основа всего примера.

Сложите кубики, палочки или другие предметы, с которыми вы работаете, по порядку в количестве 10 штук. Объясните малышу, что это десяток. Потом попросите прибавить к этому количеству еще несколько предметов, допустим 4. Говорите: «Десять плюс четыре равно четырнадцать». После того, как вы научили ребенка складывать, подобным образом составьте примеры с вычитанием, например:

18-8=10

13-10=3 и т. д.

Следующий этап – вычисления с переходом через десяток. Такие примеры даются ребятам несколько сложнее. Здесь уже понадобятся знания не только целых десятков и отдельных единиц, но и общее представление состава отдельного числа.

• Из чего состоит число 3? Из 1 и 2, или 1 и 1 и 1.
• А что такое 7? Это 1+6= 2+5= 1+1+1+4 и т. д.

Подобным образом поступите со всеми числами, которые знает ребенок, разберите их на составляющие части. Потом эти знания хорошо применить в решении примеров.

Разберем такой пример:

4+9=

Второе слагаемое раскладываем на два составляющих числа, чтобы при сложении с первым слагаемым получить десятку, а потом прибавляем остаток:

4+(6+3)= 10+3=13, т. е. 4+9= 13

Закрепим знания еще несколькими примерами:

5+7=

5+(5+2)= 10+2= 12

или

8+9=

8+(2+7)= 10+7= 17

Таким же образом можно решать примеры с вычитанием:

16-7=

16-(6-1)= 10-1= 9

или

13-8=

13-(3-5)= 10-5= 5

То есть для того чтобы сделать вычисление, раскладываем второе слагаемое таким образом, чтобы при вычитании из первого слагаемого получилась десятка, а потом вычитаем оставшееся число.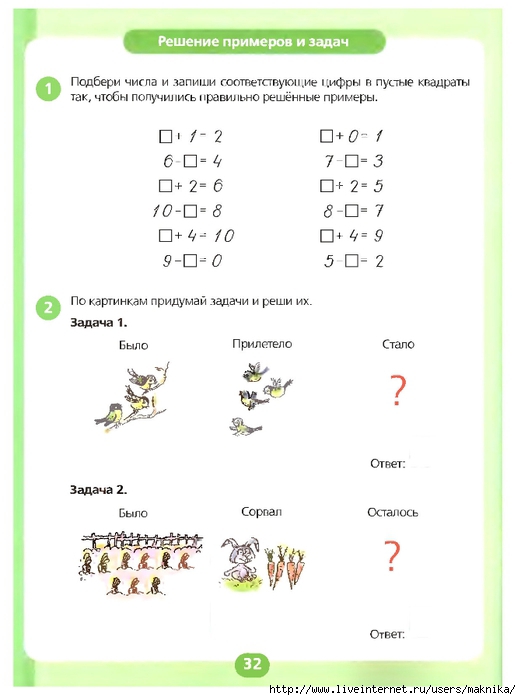

Также удобно показать малышу работу со сложением и вычитанием в столбик. В таких примерах нагляднее видно десятки и единицы, что с чем складывать или вычитать.

Напоследок несколько рекомендаций родителям.

• Во время занятий математикой проявите терпение к своему маленькому ученику и не раздражайтесь от его непонимания, а тем более не кричите.
• Не давите на ребенка и не заставляйте заниматься, если ему не хочется. Отпустите его, ведь он все равно не сконцентрируется. А в следующий раз придумайте, как его заинтересовать занятиями.
• Контролируйте время занятий, не держите малыша часами за решением примера. 10-20 минут должно длиться одно занятие. Дети быстро теряют концентрацию, и долговременные занятия нельзя назвать эффективными.
• На досуге между делом постоянно тренируйтесь с малышом. Когда режете торт, считайте, сколько кусков получилось, когда сервируете стол, посчитайте количество гостей и попросите принести нужное количество тарелок и т. д.

Главное одно – спокойная обстановка, терпение и родительская любовь однажды все равно дадут положительный результат. Не равняйтесь на других, а занимайтесь своим ребенком. Помните, что все дети разные и всем нужен индивидуальный подход.

Обучение с помощью пошаговых решений решенных проблем

Когда неспециалисты изучают новые концепции, для них более эффективно изучать пошаговые решения решенных проблем (рабочие примеры), чем пытаться решать проблемы. Проработанные примеры эффективны только тогда, когда учащиеся сами объясняют решения и когда предоставляется несколько разнообразных проработанных примеров одной и той же концепции. Проработанные примеры наиболее эффективны для неспециалистов (то есть для большинства наших студентов большую часть времени). Эксперты больше выигрывают от попыток решить проблемы, чем от изучения рабочих примеров.

Последствия

• Предоставьте учащимся полностью проработанные примеры и попросите их объяснить решения самостоятельно, задавая учащимся дополнительные вопросы (например: «Почему была использована эта стратегия?», «Какой принцип применяется и почему?») , комментируя решения, определяя ошибку в решении или предлагая учащимся сравнить решения двух противоположных примеров.
  • Рассмотрите возможность использования Lightboard для работы с примерами задач и загрузки видео в Panotpo, где затем можно вставлять контрольные вопросы, которые еще больше вовлекают учащихся в процесс решения. Инструмент цифровой доски, такой как «Объяснить все», также позволит прорабатывать, комментировать и объяснять этапы проблемы в визуальной форме.

• По мере того, как учащиеся становятся более опытными в понимании концепции, ослабляйте поддержку, прося их решать все больше и больше шагов в рамках задачи.
  • Подумайте об использовании Gradescope, который упрощает создание и обновление рубрик для задач, где вы можете изменять элементы, по которым вы оцениваете учащихся, по мере того, как исчезает поддержка для определенных типов задач. В случаях, когда учащиеся работают над вопросами или проблемами на Piazza, преподаватель, желающий избавиться от поддержки, может по-прежнему быстро давать обратную связь учащимся, одобряя публикацию учащегося (т. е. помечая ее как “хорошо”).

Примеры

18.02 Многомерное исчисление | Дени Ору:

22.01 Ядерные науки и техника | Майкл Шорт:

Профессор Майкл Шорт использовал Lightboard для синхронного обучения через Zoom, что дало ему возможность прорабатывать и объяснять проблемы, стоя перед виртуальной аудиторией. Узнайте больше об использовании Lightboard профессором Шортом здесь.

Ссылки

Ключевой ресурс:

• Ренкл, А. (2014). Обучение на рабочих примерах: как подготовить учащихся к осмысленному решению проблем. В VA Benassi, CE Overson и CM Hakala (Eds.). Применение науки обучения в образовании: внедрение психологии в учебную программу.  HTTP (доступен загруженный PDF-файл)

Дополнительно:

• Чи, М., Бассок, М., Льюис, М.В., Райманн, П. , и Глейзер, Р. (1989). Самообъяснения: как учащиеся изучают и используют примеры при обучении решению проблем. Когнитивная наука , 13 (2), 145–182. DOI
• Купер, Г., и Свеллер, Дж. (1987). Влияние получения схемы и автоматизации правил на перенос решения математических задач. Журнал педагогической психологии , 79 (4), 347–362. DOI
• Калюга, С., Чендлер, П., Туовинен, Дж., и Свеллер, Дж. (2001). Когда решение проблем важнее изучения рабочих примеров. Журнал педагогической психологии , 93 (3), 579–588. DOI
• Калюга, С., и Ренкл, А. (2010). Эффект обращения опыта и его учебные последствия: Введение в специальный выпуск. Педагогическая наука , 38 (3), 209–215. ДОИ
• Паас, Ф., и Ван Мерриенбур, Дж. (1994). Вариативность рабочих примеров и передача навыков решения геометрических задач: подход когнитивной нагрузки. Журнал педагогической психологии , 86 (1), 122–133. DOI
• Ренкл, А. (2014). К учебно-ориентированной теории обучения на основе примеров. Когнитивные науки , 38 (1), 1–37. DOI
• Salden, RJCM, Aleven, VAWMM, Renkl, A., & Schwonke, R. (2009). Отработанные примеры и обучение решению проблем: избыточные или синергетические формы поддержки? Темы когнитивных наук , 1 (1), 203–213. DOI
• Шворм, С., и Ренкл, А. (2007). Обучение навыкам аргументации с помощью подсказок на самоочевидных примерах. Журнал педагогической психологии , 99 (2), 285–296. DOI
• Salden, RJCM, Koedinger, KR, Renkl, A., Aleven, V., & McLaren, B.M. (2010). Учет положительного влияния проработанных примеров при решении проблем с помощью наставника. Обзор психологии образования , 22 (4), 379–392. DOI
• Швонке, Р., Ренкл, А., Криг, К., Виттвер, Дж., Алевен, В., и Салден, Р. (2009). Эффект рабочего примера: не артефакт паршивых условий контроля. Компьютеры в человеческом поведении , 25 (2), 258–266. DOI
• Шворм, С., и Ренкл, А. (2007). Обучение навыкам аргументации с помощью подсказок на самоочевидных примерах. Журнал педагогической психологии , 99 (2), 285–296. DOI
• Свеллер, Дж., и Купер, Г.А. (1985). Использование проработанных примеров вместо решения задач при изучении алгебры. Познание и обучение , 2(1), 59–89. DOI

Назад к результатам обучения на основе исследований

Подходы к обучению: решение проблем

Дети закладывают основу для навыков решения проблем посредством развития отношений, активного исследования и социального взаимодействия. В младенчестве дети узнают, что их действия и поведение влияют на других. Например, дети плачут, чтобы сигнализировать о голоде своим опекунам; в свою очередь, их кормят их опекуны. Постоянные реакции воспитателей на попытки детей общаться учат детей самым ранним формам решения проблем. Дети узнают, что у них есть возможность решить проблему, выполнив определенные действия. Дети строят эти знания и переводят их в то, как они взаимодействуют и решают проблемы в будущих ситуациях.

Дети обнаруживают, что их действия и поведение также влияют на объекты. Они узнают, что определенные действия приводят к определенным результатам. Например, дети могут стучать игрушкой снова и снова, замечая звук, который она издает. Такое поведение является преднамеренным и целенаправленным; дети узнают, что у них есть возможность заставить что-то случиться. По мере взросления дети будут экспериментировать с различными способами решения задач, например, по-разному перемещая кусочки головоломки, чтобы правильно их расположить. Они будут использовать метод проб и ошибок, чтобы найти решения задач, над которыми они работают, и использовать навыки общения, чтобы попросить помощи у лиц, осуществляющих уход, или жестикулировать о ней.

К 36 месяцам дети могут уменьшить количество проб и ошибок, которые они используют при решении задач. Их когнитивные навыки развиваются, и они могут использовать логику и рассуждения при решении задач. Повышенное внимание позволяет детям дольше сосредотачиваться при решении задач. Дети по-прежнему зависят от помощи своих опекунов, но, скорее всего, попытаются решить проблему самостоятельно, прежде чем просить кого-то о помощи.

От рождения до 9 месяцев

Дети создают основу для решения проблем посредством активного исследования и социального взаимодействия.

Показатели для детей включают:

• Сосредоточены на привлечении внимания воспитателя с помощью звуков, криков, жестов и мимики опекуном или братом/сестрой
• Сообщает о необходимости помощи с помощью вербальных и/или невербальных сигналов, например, указывая, дотягиваясь, издавая звуки

Стратегии взаимодействия

• Вдумчиво и быстро реагировать на попытки ребенка привлечь внимание
• Предоставить интересные и соответствующие возрасту игрушки и предметы для исследования
• Часто привлекать и взаимодействовать с ребенком в течение дня
7 7
• от месяцев до 18 месяцев

  Дети начинают понимать, что определенные действия и модели поведения могут быть решением проблем и препятствий, с которыми они сталкиваются. Дети также узнают, как привлечь своих опекунов к решению этих проблем.

  Показатели для детей включают:

  • Повторяет действия снова и снова, чтобы понять, как работает объект реагируя одинаково
  • Пробует различные физические стратегии для достижения простых целей, например, дергает за веревочку игрушечный поезд, чтобы пододвинуть его ближе, или ползет, чтобы поймать укатившийся мяч

  Стратегии взаимодействия

  • Продемонстрируйте, как пробовать что-то по-разному, и поощряйте ребенка делать то же самое, например, используя пластиковое ведро в качестве барабана ему или ей достаточно независимости, чтобы пробовать что-то новое
  • Вдумчиво и быстро реагировать на попытки ребенка общаться

  От 16 месяцев до 24 месяцев

  Дети обладают повышенной способностью решать проблемы, с которыми они сталкиваются, используя предметы и подражание. На этом этапе дети могут брать на себя более автономную роль, но в большинстве случаев обращаются к опекунам.

  Показатели для детей включают:

  • Имитирует поведение опекуна для выполнения задачи, например, пытается повернуть дверную ручку пытается вставить фигуру под разными углами, чтобы она поместилась в сортировщике
  • Использует объекты окружающей среды для решения задач, например, использует ведро для перемещения множества книг на другой конец комнаты
  • Использует общение для решения проблем, например, заканчивает клей во время художественного проекта и жестами просит воспитателя еще

  Стратегии взаимодействия

  • Подтверждает и хвалит попытки ребенка найти решения проблем
  • Рассказывает, пока помощь ребенку в поиске решения, например, «Давай попробуем повернуть кусочек пазла вот так»
  • Предоставьте ребенку возможность решать задачи с вашей помощью и без вашей помощи; свести к минимуму вероятность того, что ребенок расстроится
  • Реагировать на коммуникативные усилия ребенка

  От 21 месяца до 36 месяцев

  Дети начинают различать, какие решения работают, с меньшим количеством попыток. Дети становятся все более автономными и сначала пытаются преодолеть препятствия самостоятельно или при ограниченной поддержке со стороны опекунов.

  Показатели для детей включают:

  • При необходимости обращается за помощью к опекуну
  • Начинает решать проблемы с меньшим количеством проб и ошибок
  • Отказывается от помощи, например, зовет на помощь, но затем отталкивает руку
  • Демонстрирует гордость при выполнении задачи
  • Использует все более совершенные навыки при решении проблем, например, использует собственную салфетку, чтобы убрать пролитую жидкость, не обращаясь за помощью к взрослому

  Стратегии взаимодействия

  • Следуйте примеру ребенка и обращайте внимание на его или ее сигналы, когда помогаете в выполнении задачи
  • Разделяйте радость и достижения ребенка
  • Моделируйте и рассказывайте о навыках решения проблем с помощью игры
  • Предоставляйте ребенку блоки непрерывного времени для работы над заданиями
  • Будьте доступны для ребенка и распознавайте, когда ему или ей нужна помощь

  Реальная история

  Себастьян, которому 25 месяцев, занимается мелкой моторикой, предоставленной его опекуном. Он держит большой пластиковый пинцет и пытается использовать его, чтобы поднять большие пушистые шарики с пластиковой тарелки и переместить их в пластиковый стаканчик. Он держит пластиковый пинцет в одной руке и держит тарелку на столе. Он неоднократно пытается использовать одну руку, но не может сжать пинцет достаточно сильно, чтобы взять один из шариков. Себастьян делает паузу, оглядывается и берет мячи большим и указательным пальцами.

  Держа пластиковый пинцет в одной руке и шарик в другой, Себастьян вставляет шарик в пинцет и зажимает его. Он перемещает его к пластиковому стаканчику и бросает его внутрь. Затем он берет еще один пушистый шарик и кладет его в пинцет. Опять же, он крепко сжимает его и переносит в чашку. Себастьян действует таким же образом, пока все пушистые шарики на его тарелке не окажутся в его чашке. Закончив, он выливает содержимое чашки на тарелку и начинает все сначала. Снова успешно завершив процесс, он протягивает полную чашку своему опекуну Марии. Она видит его, улыбается и поднимает два больших пальца вверх. Себастьян берет свою чашку и подходит к ней. Он передает Марии чашку и уходит из-за стола.

  Узнайте, как эта история из реального мира связана с:

  • Саморегуляция: основа развития
    Регулирование внимания
  • Область развития 1: Социальное и эмоциональное развитие
    Я-концепция
  • Физическая область развития 9002 Развитие и здоровье
    Мелкая моторика
  • Область развития 2: Физическое развитие и здоровье
    Перцепция
  • Область развития 4: Когнитивное развитие
    Логика и рассуждения

  В ЭТОМ ПРИМЕРЕ ОСНОВНЫЕ ПОКАЗАНЫ, как дети используют физические пробы и ошибки для решения задач. Первые попытки Себастьяна взять мелкие предметы пинцетом не увенчались успехом. Однако он делает паузу, чтобы подумать о возможных способах работы над этой проблемой, а затем меняет свой процесс. Вместо того, чтобы сжимать пинцет, чтобы схватить мяч, он помещает мяч между пинцетом, а затем зажимает его. Это проще для него, так как он все еще развивает мелкую моторику, необходимую для выполнения этой задачи. Как только он понимает, что ему удалось достичь своей цели, он выполняет эту задачу до тех пор, пока не закончит помещать все шарики со своей тарелки в чашку. Затем он повторяет действие снова и снова. Способность Себастьяна успешно решать проблемы укрепляет его уверенность в себе. Положительное признание Марией его достижений еще больше поддерживает его социальное и эмоциональное развитие. Позитивная самооценка и растущая уверенность в себе очень важны для будущего обучения Себастьяна и общего здорового развития.

  Узнайте, как Решение проблем связано с:

  • Саморегуляция: Основа развития
    Эмоциональная регуляция
  • Саморегуляция: Основа развития
    Регулирование внимания 5 Эмоциональное развитие 2
    7 Развитие Отношения со взрослыми
    • Сфера развития 1: Социальное и эмоциональное развитие
      Я-концепция
    • Сфера развития 4: Когнитивное развитие
      Память
    • Область развития 4: Когнитивное развитие
      Логика и мышление

    Связанные ресурсы

    Следуйте за мной в Твиттере @DavidMoldoff

    Креативность связана с фундаментальными качествами мышления и тем, как мы используем наш банк предыдущего опыта, например гибкость и терпимость к двусмысленности, страху и беспокойству перед неизвестным. Вы обычно подходите к проблеме с разных точек зрения или выбираете одно и то же решение, которое работало в прошлом? В нашем опыте преодоления препятствий мы все сталкиваемся с проблемами, которые кажутся непреодолимыми, невозможными и непрактичными для решения. Одна вещь, которую вы можете сделать, прежде чем делать какие-либо выводы, — это попытаться изменить свою точку зрения. Колледж — это место, где вы можете научиться менять перспективу и решать проблемы, используя методы, которым вы можете научиться. Общение с другими также поможет вам понять и пролить свет на проблему, которую вы, возможно, не видите со своей точки зрения. Там нет правильных или неправильных ответов.

    Перспектива — это то, как вы подходите к проблеме. Увидеть вещи с разных сторон проблемы — хороший способ извлечь из опыта все, что есть. Креативное решение проблем — это навык, который останется с вами на всю оставшуюся жизнь. Каждый сталкивается с препятствиями на своем пути. Если мы заблудимся за рулем автомобиля или велосипеда, у нас есть несколько вариантов. Мы можем остановиться и спросить у кого-нибудь дорогу. Мы можем вытащить карту и посмотреть на ландшафт с того места, где мы находимся. Мы можем позвонить заранее и попросить указатели искать, чтобы помочь нам в нашей попытке вернуться на правильный путь. Каждый подход поможет нам по-разному. Понимание препятствия и того, как к нему подойти, требует терпения. Другими словами, не урод. Сохранение стабильного и сбалансированного обзора препятствия является обязательным. Я всегда ненавидел сдавать анализы. Мои ладони вспотели, голова кружилась, и я всегда сосредотачивался на том, что делать, если потерплю неудачу. Это был личный демон, с которым я сталкивался на протяжении всего своего формального образования, но я выжил. Вот пятнадцать советов о том, как решить проблему:

    1. Укрепить позитивный настрой. Улыбнись. Первое, что вы должны сделать, столкнувшись с трудной проблемой, — начать с позитивного взгляда на нее. Иногда наша первая реакция — бояться неопределенности. Это довольно естественно. Однако с годами я понял, что именно неизвестность дала нам как личностям любопытство, чтобы пробовать новые вещи и стремиться к звездам. Не бойтесь самой проблемы. Посмотрите на это как на возможность узнать что-то новое и проверить свои способности и остроумие. Это нелегко сделать в условиях сжатых сроков и давления, но сохранение позитивного взгляда будет иметь большое значение для того, чтобы сделать каждую проблему немного менее сложной.

    2. Задавайте вопросы, чтобы понять проблему. Помню много курсов, где мои одноклассники сидели на уроках ошарашенные. Во время лекции мы не поняли важного момента, но никто не задал ни одного вопроса. Почему? Во многом это связано со страхом выглядеть глупо. В большинстве случаев я обнаруживаю, что у людей есть те же вопросы, что и у меня, но они по какой-то причине слишком боятся их задать. В любом случае, прежде чем вы сможете решить проблему, вы должны сначала понять ее. Если вам что-то непонятно, задавайте столько вопросов, сколько вам нужно. Не стесняйтесь. Вы не глупы. Глупых вопросов не бывает, есть только те, на которые у вас еще нет ответа.

    3. Будьте непредубежденными. Старая поговорка гласит: «Если у вас есть только молоток, все становится гвоздем». То, как вы поступали в прошлом, может не всегда работать во всех ситуациях. Молотком можно выковыривать гвозди из дерева и втыкать их в дерево, но молотком не следует собирать листья или откручивать ржавые болты. Для этих целей есть лучшие инструменты. В жизни я часто нахожу множество решений одной и той же проблемы. Некоторые из них более эффективны, чем другие. Некоторые из них более подходят, чем другие. Столкнувшись с трудной проблемой, не думайте, что вы знаете ответ с самого начала. Не делайте поспешных выводов. Остановитесь на секунду и найдите время, чтобы понять, в чем на самом деле заключается проблема или вопрос, прежде чем применять решение или ответ. Будьте открыты для всех возможностей. Не думайте, что все это гвоздь.

    4. Смотрите на проблему свысока. Иногда проблема, которую мы пытаемся решить, вовсе не является настоящей проблемой. Это может быть симптомом, а не причиной. Чтобы решить проблему, нам может понадобиться посмотреть на нее свысока. С другой точки зрения мы можем обнаружить, что проблема, на которой мы сосредоточились, на самом деле является частью более крупной проблемы, которая требует совершенно другого подхода. Прежде чем пытаться найти решение, найдите «настоящую» проблему. Как только вы поймете проблему во всей ее полноте и контексте, только тогда вы сможете определить наилучший курс действий.

    5. Полностью определите проблему. Потратьте минуту или две, чтобы определить проблему. При этом сначала определите, в чем проблема не заключается. Изолируйте, в чем проблема. Когда вы досконально разберетесь в проблеме, вы, возможно, уже будете знать, какие инструменты вам нужно применить или какие решения следует избегать, потому что они не подходят. Иногда, столкнувшись с проблемой, мы, естественно, предполагаем, что на самом деле это не так, и тем самым реализуем неправильное решение. Часто более эффективно убедиться, что вы понимаете проблему, ее симптомы и причины, прежде чем продолжить. Спросите что, где, почему, когда, как и кого. Запишите проблему, нарисуйте диаграммы, составьте списки и планы и т. д.

    6. Нарезайте кусочками. Вы бы съели целую пиццу одним глотком? Возможно нет. Точно так же некоторые проблемы просто слишком велики, чтобы их можно было разжевать все сразу. Полезный метод решения сложных проблем — углубляться в детали и продолжать до тех пор, пока каждая часть не станет управляемой. Когда у вас есть набор управляемых частей, решайте каждую по отдельности. Когда данная проблема разбита на мелкие кусочки, легче увидеть шаблоны, симптомы, инструменты и методы, которые необходимо применить, а также действия, которые необходимо предпринять.

    7. Думай логически. Простые проблемы часто не требуют плана действий. Помните Спока из «Звездного пути»? Я Trekkie и смотрел телешоу еще в 60-х. Это изменило мою точку зрения. Спок был логическим противопоставлением Кирку, у которого хватило страсти, наглости и ума, чтобы управлять «Энтерпрайзом». Они работали как команда. Учитывая сложную проблему или проблему, требующую длительного времени, крайне важно иметь действенный план, определяющий, что необходимо сделать. План является хорошим напоминанием о том, что и когда должно произойти, а также средством коммуникации для всех вовлеченных людей. Зависимости должны быть выявлены. Создание плана требует, чтобы вы логически продумали все вопросы и определили все соответствующие проблемы и ограничения.

    8. Найдите сходство. Это похоже на распознавание образов. Я люблю это делать. Всякий раз, когда вы сталкиваетесь с проблемой, спросите себя, имеет ли эта проблема те же характеристики, что и что-то еще, что вы, возможно, решили. Часто проблемы маскируются в своем контексте, но коренная проблема остается той же. Если вы обнаружите, что у вас есть проблема, которая имеет те же характеристики, что и что-то еще, вы можете использовать решение, которое вы применили к этой другой проблеме. Я считаю, что это наиболее полезно в сочетании с предыдущим советом. Когда проблема разбивается на составные части, вы обнаружите, что некоторые из этих частей часто встречаются в других местах.

    9. Ошибки случаются. Решение проблем и совершение ошибок часто идут рука об руку. Иногда, чтобы найти наилучшее решение данной проблемы, нам сначала нужно пройти через сотню плохих решений. Томас Эдисон был мастером этого процесса. На каждое разработанное им изобретение приходилось тысячу неудачных попыток. Самое главное здесь — помнить, что ошибки — это нормально. Не отчаивайтесь. Не расстраивайтесь. Используйте ошибки как ступеньки, чтобы добраться до желаемого решения. Если вы перебрали сотню вариантов безрезультатно, вы нашли сотню способов не делать что-то, а не сотню неудач.

    10. Держите эмоции под контролем. Эмоции или стресс иногда могут влиять на наше мышление и суждения. Не позволяйте им затуманивать ваш разум. В большинстве случаев проблемы лучше всего решать логически. Попробуйте принять рациональное мышление и позвольте своему разуму управлять вашими действиями. Продумайте в уме, в чем проблема, а затем определите шаги, необходимые для разрешения ситуации, прежде чем предпринимать какие-либо действия. Если вы обнаружите, что слишком эмоционально заряжены, сделайте паузу на мгновение и позвольте себе сначала успокоиться. Отойдите от проблемы и, возможно, дайте ей еще один день.

    11. Сосредоточьтесь на конце игры. Это похоже на визуализацию решения. Помните те игры с отслеживанием, которые кто-то давал вам, когда вы были моложе… например, лабиринт? Решение проблем заключается в переходе из одного состояния в другое. Это известно как обход пути решения. Иногда переход от начального состояния к конечному не так очевиден, как понимание того, как конечное состояние может возникнуть из начального состояния. Во многих отношениях это похоже на навигацию по карте — мы можем либо проследить путь от того места, где мы находимся, до того места, куда мы хотим попасть, либо мы можем начать с пункта назначения и двигаться в обратном направлении. Во многих случаях я считаю полезным сосредоточиться на конечном состоянии, а затем работать в обратном направлении. Когда я попаду на знакомую территорию, я смогу связать решение с путем.

    12. Делайте заметки и записывайте свои успехи. Это не было моей сильной стороной; тем не менее, я заставил себя взять блокноты и делать записи. Сегодня у меня есть компьютер, теперь я делаю это с помощью клавиатуры и храню свои мысли в документах. Когда проблема открыта и вы работаете в неизведанном пространстве, будьте бдительны в своих заметках и записывайте свой прогресс. Вести дневник. Несколько месяцев спустя вы можете обнаружить, что заметка, которую вы сделали навскидку, может стать прорывом, который вы ищете. В то время это может быть не сразу очевидно, поэтому записывайте свой прогресс и убедитесь, что вы можете проследить, что вы пробовали, и каковы были результаты.

    13. Проверьте свои предположения. По мере продвижения помните о полученных ответах и ​​сделанных предположениях. Я склонен делать поспешные выводы. Замедлять. Мы все делаем предположения, чтобы попытаться ускорить наш прогресс. Убедитесь, что они логически непротиворечивы и «имеют смысл». Ошибки случаются, так что проверяйте, перепроверяйте и снова проверяйте. Вы не хотите развиваться или полагаться на решение, основанное на неверных ответах и ​​предположениях. Когда вы удовлетворены своим решением, не забудьте протестировать его в различных условиях, а не только в наиболее вероятном сценарии. Только при тщательном тестировании вы можете быть уверены, что ваше решение соответствует первоначальным требованиям.

    14. Если вы не добились успеха, начните сначала. Проблемы и препятствия не всегда решаются с первого, второго или третьего прохода. Это очень похоже на перевод в колледж. Это трудная задача, которую можно решить с моей точки зрения. При решении любой задачи может потребоваться несколько итераций. Тестирование решений часто выявляет пробелы и проблемы, которые не были рассмотрены в ходе проверки и с разных точек зрения. Вы можете отступить и перезапустить любые ранее упомянутые шаги. Решения могут развиваться и улучшаться.

    15. Будьте честны и реалистичны. Один из основных рисков, с которыми мы сталкиваемся при решении проблем, заключается в том, что мы верим в решение больше, чем свидетельствуют факты. Есть суждения, которые должны быть сделаны на основе информации, которая у вас есть или которую вы можете легко обнаружить. Нам нужно быть честными с собой и идеями. Это нормально сделать прыжок веры. Не все визуализированные решения могут быть выражены в цифрах и фактах. В суждении есть ценность. Слишком серьезное или личное отношение к решению может привести к тому, что мы пропустим строгость и тестирование. Это тоже решение. Когда достаточно тестирования? Это не спор о вере. Речь идет о подчеркивании реализма и обоснованного анализа на протяжении всего процесса решения проблемы.

    В зависимости от проблемы, стоимости и уровня усилий, мы должны быть верны требуемому уровню.