Столбиком решать примеры: Онлайн калькулятор. Деление столбиком
Научила примерам в “столбик”
- Форум
- Архив
- Школы, Олимпиады, Вузы
Весь день мучает совесть меня. Выскажите свои мнения пожалуйста. Вчера готовились с сыном к контрольной (2 класс). Я понимаю, что со сложением и вычитанием двухзначных чисел у него прям проблемы. Я решила облегчить ему жизнь, и попробовать показать ему, как можно решить пример сложения и вычитания столбиком. Я очень удивилась, но примеры начал щелкать как орехи.
Но меня очень сильно мучает теперь совесть, что сильно ему облегчила жизнь, что они еще в школе этого не проходили, и что я погорячилась( Вот.. ловлю тапки(
Мы дочери это объяснили в 5 лет – пойду застрелюсь
у вас других забот нет, только вот об этом печалиться?
У нас по программе Петерсон 2 класс уже месяца 2 столбики идут, десятки-сотни В чем криминалЬ?
Ой, а я в 6 лет про столбик объяснила))) Вам тапки, мне зимние сапоги полагаются)))))))))))))
А почему жить надо обязательно трудно?)
И не мучайтесь – это прекрасно, что ребенок стал больше знать. Обратите только внимание, что они теперь все записывают иначе, чем мы раньше, чтобы он правильно (вернее, как требуют) записывал решение.
Обратите только внимание, что они теперь все записывают иначе, чем мы раньше, чтобы он правильно (вернее, как требуют) записывал решение.
Мы уже начали проходить сложение-вычитание в столбик – теперь все подряд только в столбик складываем. Правда, дочь показала, как записывали раньше, так проще
Просто начала переживать, что в школе еще этого не проходили, и могут возникнуть проблемы. Спросила у него, дают ли на контрольных черновики, говорит что нет. А как без черновика справится, не понятно)
криминал в том, что детей учат устному счёту, а складывание а столбик – механические вычисления. поэтому я против такой “помощи”
Потренируйте с ребенком устный счет и перестаньте мучиться совестью
есть у Узоровой замечательные тренажеры, “1000 примеров на сложение”… прорешает, желательно на время – и будет у него все хорошо со счетом. но сначала убедитесь что у ребенка автоматизирован счет с цифрами до 10. не в смысле что он не умеет сложить 5+7. не сомневаюсь что умеет.
Попробуйте давать ребенку примеры и кидать мячик: 7+8? – и смотрите как быстро он вам отвечает. в такой игре задержка на задумывание бросается в глаза. и если она есть, это тема для работы.
2+2 ребенок ответит вам без счета. и 5+5 тоже. вот остальные суммы должны идти в том же темпе.
В том, что ребенок не понял принцип складывания двузначных чисел. И мама вместо того, чтобы объяснить этот принцип, просто научила механически складывать что-то с чем-то. А что с чем, почему и зачем, ребенок так и не разобрался.
Если ребенок при этом понял, что во втором знаке он складывает десятки, а в третьем – сотни (хотя третьего, наверно, пока нет), это очень поможет ему в тренировке устного счета. Они и считают так устно – складывают отдельно десятки и единицы, а потом – между собой (да и взрослые считают аналогично, просто не задумываются об этом).
лучше научите в строчку вычитать и прибавлять, я вот своего первоклашку сдуру научила на свою голову.
В столбик – это ерунда, ничего сложного и в уме потом считать не будет.
после объяснения в столбик, моя устно считает очень быстро. Я сама удивилась, а она сказала, что мысленно себе столбик представляет и всё.
Все зависит от требований учителя. У сына весь первый-второй класс были частые диктанты математические на устный счет (учитель вслух говорит пример, дети пишут только отчет, при этом пример может быть не из одного действия, а из двух и иногда трех), так что столбик оказал бы ему медвежью услугу на тот момент.
Я думаю что ребёнок понял там. А то что он должен моментально отнять в уме 56 – 38 не все сообразят только у кого математический склад ума.
У нас девочка в классе была она моментально корень извлекала из трёх значного числа, о сложении и вычитания я вообще молчу, но из класса она делала это одна. У неё был матем.склад.
У неё был матем.склад.
Правда это не значит, что мы не понимали как делать мы это делали но на бумаге а она в уме. При этом она была не единственной отличницей в математике. более того учитель иногда ставил ей 4 говоря что я просто лмто знаю ты можешь на 5 сейчас просто типа лоботрясничала не думала. Хотя опять же тут с учительницей я не согласна могла бы ей и 5 ставить.
Мы тоже научили дочку считать в столбик из-за проблем с устным счетом. Выдала ей тетрадку с надписью черновик и приказала (!) доставать и пользоваться всегда. Другие дети утверждают, что черновиками пользоваться учительница не разрешает, но моя утверждает, что ей никаких преград не возводят. На днях по программе пошел счет в столбик – моя самая продвинутая
Но на каникулах будем снова развлекаться тренажерами Узоровой
ха. А мы с моей умножали в столбик в начале второго класса сами дома(табл. умножения мы начали в 6 лет учить, по ее желанию). .И что ж теперь нам?Пойти повеситься.
.И что ж теперь нам?Пойти повеситься.
в чём проблема то? вы научили вычитать с переходом через десяток? у нас уже столбики эти проходят с начала 2й четверти начали
Объяснили-отлично. Но сейчас запасайтесь примерами и тренируйте устный счет, иначе ребенок потом попухнет.
Особенно хорошо в несколько действий. Я себе печатаю на листе примеры и дочку тренирую.
Наша учитель слезно просила нас не разрешать детям решать пока дома в столбик, тк потом им же будет тяжелее. То, что во 2 классе они это умеют, это ясно. Мы же умные родители, показываем детям знания
Открыть тему в окнах
Знаменитости в тренде
Как объяснить ребенку деление в столбик, или уголком: простой принцип с примерами
Содержание статьи
- Как правильно делить в столбик?
- Что нужно знать ребенку для понимания деления столбиком?
- Методика обучения детей делению столбиком
- Работа с многозначными числами
- Как объяснить деление с остатком?
Чтобы упростить деление чисел, традиционно используется метод деления в столбик.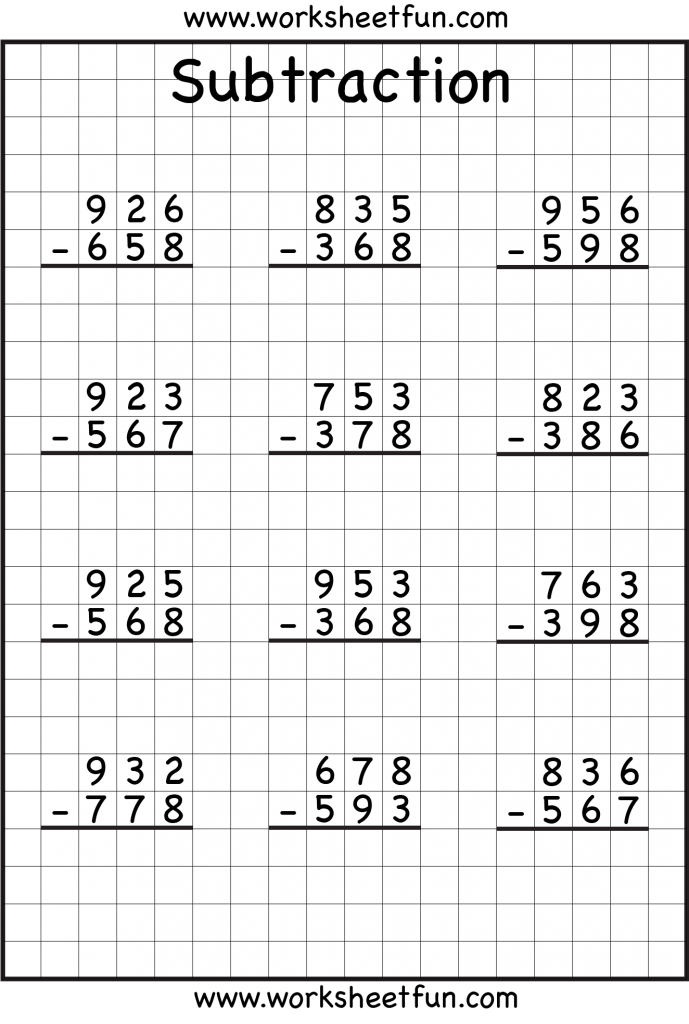 Не все дети понимают принцип с первого раза, а многие взрослые уже успели его забыть. Давайте разберемся, как без лишних слов объяснить ребенку деление «уголком», чтобы он научился решать примеры с двузначными, трехзначными и даже четырехзначными числами.
Не все дети понимают принцип с первого раза, а многие взрослые уже успели его забыть. Давайте разберемся, как без лишних слов объяснить ребенку деление «уголком», чтобы он научился решать примеры с двузначными, трехзначными и даже четырехзначными числами.
Как правильно делить в столбик?
Удобнее рассмотреть сам процесс на несложной иллюстрации (№1).
Как найти частное двух чисел – 35 и 5?
- Пишем числа, участвующие в делении, так:
Делимое в данном случае – 35, делитель – 5. Под делителем пишется частное. - Находим неполное частное. Посмотрим на первую цифру слева. В нашем случае это 3, и оно меньше 5 – значит, добавляем следующую цифру слева и будем работать с этой величиной (у нас 35).
- Определяем, какое количество пятерок (5) поместится в 35. Вспоминаем таблицу умножения и заключаем, что в 35 поместиться 7 пятерок. Значит, в графе частное записываем 7.
- Проверяем правильность действий путем умножения: 7 X 5=35.
 Все верно, решение выполнено точно.
Все верно, решение выполнено точно.
Что нужно знать ребенку для понимания деления столбиком?
Чтобы любимое чадо освоило, как делить уголком (в столбик), нужно два условия:
- отличное знание таблицы умножения;
- умение быстро считать в уме.
В конце 3 класса ученики усваивают, как разделить простые двузначные числа.
При переходе в 4 класс дети учатся делить многозначные числа (больше, чем 100). Также происходит обучение делению уголком чисел с двузначным и трехзначным делителем, решение примеров с остатком.
Методика обучения детей делению столбиком
Если школьник пропустил занятия по математике либо не смог усвоить знания на уроке, то родители должны сами донести до него нужную информацию. Спешка в таком деле неуместна – быстро не значит хорошо. Следует проявить терпение. Деление чисел – простое дело для взрослого, а для школьника задача весьма сложная.
Проверьте знание таблицы умножения.
Если ребенок не умножает «автоматически», позвольте подсматривать в табличку.
Первый пример можно взять простейший, с делением без остатка на однозначное число (как в иллюстрации №1).
Когда малыш понял принцип и успешно справился с несложным заданием, пора научить его делению трехзначных чисел. Выполним пример №2.
Работа с многозначными числами
Задание 2: разделим 372 на 6. Для этого на листке бумаги производим следующие действия:
- Определяем делимое (372) и делитель (6), оформляем запись в уголок:
- Неполное частное в нашем варианте, конечно, 37 (т. к. в 3 не поместится 6 ни разу, берем следующую цифру).
- Считаем, много ли шестерок уместится в 37. Если 36:6, то получим 6. Получившееся 6 пишем в графе «частное», а 36 пишем под делителем.
- Вычитаем из 37-36=1.
 Пишем единичку слева внизу под чертой:
Пишем единичку слева внизу под чертой: - В единичке не поместится ни одной шестерки, значит, берем оставшуюся цифру из делимого (2). Получилось 12. Нужно определить, сколько в 12 поместится 6 (12 больше 6 ровно в два раза). Получаем 2. Записываем в частное получившуюся величину:
Пример решен, можно проверить правильность путем умножения: 62X6=372.
Как объяснить деление с остатком?
Иногда разделить на равные доли невозможно. Легче всего объяснить такую ситуацию школьнику на несложной задаче. Например:
В группе 8 учеников, на обед им выдали 18 ватрушек на подносе. Когда каждый получит по 2 ватрушки (18:8=2 и ост. 2), на подносе останутся лишние 2 штуки. Это и есть остаток.
Решение столбиком с остатком, по математическому правилу, записывается точно так же, как и без него. Разница лишь в том, что в конце остаток будет. В этом варианте правильно прописать количество целых единиц и количество единиц в остатке (пример: 4 целых и 9 в остатке).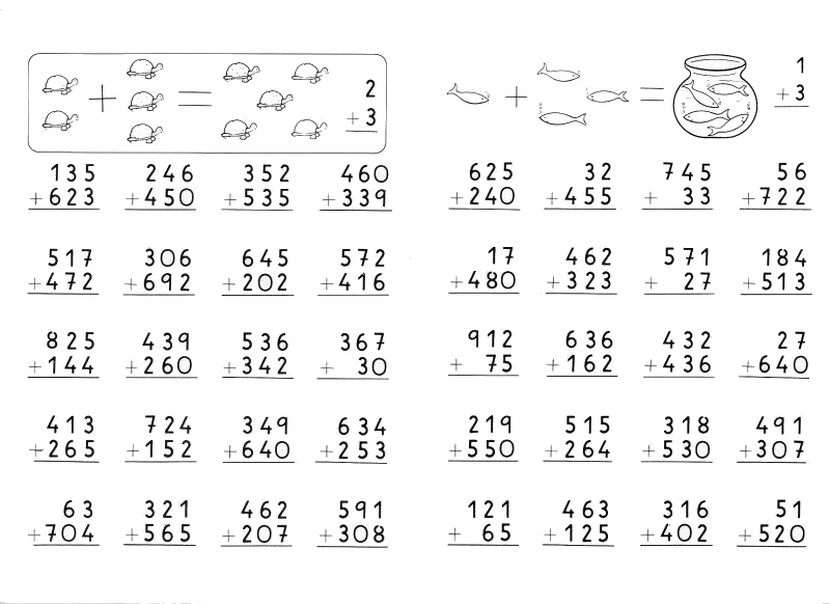.jpg)
Обучение школьника должно проходить поэтапно, от простых примеров к более сложным. Если нет понимания простых действий в делении, значит, нужно повторить информацию еще раз. Постепенно решение примеров начнет происходить быстрее и увереннее. Главное – поверить в силы маленького человека, быть терпеливым, и тогда делить числа методом столбца станет интересным занятием для школьника.
9-Две решенные задачи для анализа стальных колонн.
Содержание
- Две решенные задачи для анализа столбцов.
- Краткое содержание видео включает в себя две Решенные задачи для анализа столбцов.
- Две Решенные задачи для анализа стальных колонн.

- Еще одна решенная задача 13-29 для анализа столбцов.
- Ссылка для значения k на основе различных конечных условий.
Две решенные задачи для анализа столбцов.
Краткое содержание видео включает в себя две Решенные задачи для анализа столбцов.
Мы собираемся продолжить работу с решенными задачами, чтобы выполнить столбцовый анализ, но после внесения некоторых изменений для решенной задачи 13-28 мы назовем эту решенную задачу 13-28а, которая рассматривается с начала видео до времени 4. :53.
Колонка выбрана для новой секции W14x61, Fy 50 KSI. Какова доступная прочность на осевое сжатие в тысячах фунтов? Какое значение из 4 вариантов указано в списке вариантов от A до D?
Опорный корпус колонны – это вариант C, где опора закреплена внизу, а направляющая опора вверху.
Наш kx=ky=1.2 соответствует рекомендациям. Для необходимой информации для W14x61 площадь составляет 17,90 дюйма3.
Ix = 640 дюймов 4, rx = 5,98 дюйма 2, Iy = 107 дюймов 4 и ry = 2,45 дюйма3.
Процедура оценки kx и ky из ранее решенной задачи 14-28 выглядит следующим образом: KyLy=18 футов.
Перейдем непосредственно к таблице 4-1 из книги FE Exam Ref.
У нас наш KyL= 1,2x 15=18 футов, отметьте значение нашего fy 50 ksi, одно замечание, что таблица назначается только при Fy =50 ksi.
Вторая решенная задача начинается с 4:53 до конца видео. Это часть видео с субтитрами и субтитрами на английском языке.
Вы можете щелкнуть любое изображение, чтобы увеличить его, затем нажать маленькую стрелку справа, чтобы просмотреть все остальные изображения в виде слайд-шоу.
Две Решенные задачи для анализа стальных колонн.
Это краткое описание содержания поста.
Две решенные задачи для столбцового анализа, первая задача похожа на решенную задачу 13.28, которую мы решили ранее в предыдущем посте, но на этот раз я изменил размер с W 12×50 на W14x61.
Колонна закреплена на одном конце и имеет направляющий ролик на другом конце, который находится вверху.
Это таблица для различных значений k на основе конечного условия для столбцов. Эта задача взята из распечатанных задач из M Iqbal Book for F E Exam Review.
Сначала мы рассмотрим значения k для шести случаев столбцов с разными условиями окончания.
Это общее положение E-1 кода AISC для графика между Kl/r и Fcr/Fy.
Продолжаем решать ранее решенную задачу 13-28, она будет считаться 13-28а. Но после внесения некоторых изменений для решенной задачи 13-28a столбец выбран как W14x61, Fy – 50 KSI.
Что такое доступная Прочность на осевое сжатие в тысячах фунтов? Какое значение из 4 альтернатив, перечисленных от варианта A до варианта d.
Случай опоры колонны – это случай c, где опора закреплена внизу, а направляемая опора вверху. Наш kx=ky=1,2 соответствует рекомендациям.
Для получения необходимой информации для W14x61 площадь равна 17,90 дюйма 2, значение Ix = 640 дюймов 4, радиус вращения вокруг большой оси rx = 5,98 дюйма 2. Iy = 107 дюймов 4 и ry = 2,45 дюйма 3.
Iy = 107 дюймов 4 и ry = 2,45 дюйма 3.
Процедура заключается в оценке kx и ky. Из предыдущего примера наш KyLy=18 футов.
Перейдем непосредственно к таблице 4.1, Справочная книга экзамена FE. У нас есть KyL = 1,2x 15 = 18 футов, отметьте значение.
Fy составляет 50 тысяч фунтов на квадратный дюйм. Одно замечание, что таблица назначается только при пределе текучести Fy =50 ksi, для других значений используйте таблицу 4-22, с пересечением горизонтальной линии 18′ с вертикальной линией для W14x61.
Мы завершили решение решенной проблемы, изменив раздел на W14x61. Доказать, что Результат из таблицы совпадает с расчетом.
Для традиционного способа расчета. Мы оценим, является ли столбец длинным или коротким, используя формулу для значения (k*l/r), которая даст (4,71sqrt(E/Fy)), даст=4,71sqrt(50000/50)= 113.43. 9(50/36,856)* 50=28,337 тыс.фунтов/кв.дюйм.
r y = 2,45 дюйма 2, для этой секции, но тем не менее, эквивалент k для большой оси x *(L) равен s < ky* ly, поэтому слабая ось контролирует нагрузку, что объясняется следующим образом:
Эквивалент A-Ky=k/(rx/ry)=(1,2/5,98/2,45)=0,4961, затем снова нужно умножить на высоту столбца, которая равна 15, тогда =0,4961*15=7,374 фута. (50/36,856)* 50=28,337 тысяч фунтов на квадратный дюйм
(50/36,856)* 50=28,337 тысяч фунтов на квадратный дюйм
, будет умножено на φ *площадь и будет равно (0,9×17,9×28,337)=457 тыс.фунтов, поэтому вариант b верен. Этот ответ совпадает с ответом, полученным ранее.
Еще одна решенная задача 13-29 для анализа столбцов.
Еще одна решенная задача — 13-29 для столбцового анализа из книги М. Икбала. Указанная колонна имеет высоту 20 футов и закреплена на штырях внизу и вверху, но для направления y есть роликовая опора на средней высоте, но что касается направления x, мы поддерживаем только внизу и вверху.
Сечение имеет размер W10x45, fy=50 тыс.фунтов на кв. дюйм, его управляющий коэффициент гибкости, который составляет K *Lvalue/r, в основном составляет 5 или 65, или 72, или 120.
Решение основано на направлении Y, k принимается равным 1,2.
, в то время как для x высота столбца составляет 20 футов, а k также принимается равным 1,2.
Почему выбрано значение 1,2?
Ссылка для значения k на основе различных конечных условий.

Причину поискал по е фундаменту – Основы машиностроения -включает свободный-свободный, Kl= 1.2L, а навесной-свободный, в нашем случае KL тоже 1.2 .
В направлении y, петля свободна, затем выбирается 1,2 for- k, но длина равна 10 футам, тогда как для k значение x равно 1,2, но длина является общей длиной.
Информация для W10x45 следующая: площадь 13,3 дюйма 2, Ix = 24,8 дюйма 5 и rx = 4,32 дюйма 2, Iy = 53,4 дюйма 3 и ry = 2,01 дюйма 2, это эскиз сечения в направлении Y.
Форма изгиба может быть представлена как сжатие перпендикулярно оси y, форма изгиба для направления x может быть представлена как сжатие перпендикулярно оси x.
Снова мы преобразуем kx в фальшивку или эквивалент с помощью / rx/ ry, kx равно 1,2, см. значения rx,ry.
kx = 1,20 / (4,32/2,01) = 0,558 * 20 = 11,17 футов.
В то время как ky = 1,2, Ky*Ly=1,2*10=12 футов, поскольку эквивалент Kx*Lx < Ky *Ly.
Изгиб контролируется малой осью, тогда управляющий коэффициент гибкости равен (ky*ly/ry).
Ссылаясь на номера опций ky*ly/ry, что даст значение 71,64 почти 72, что является опцией C.
Это pdf-файл, использованный в иллюстрации к этому сообщению.
Следующий пост — Введение в локальную деформацию.
Для внешнего ресурса, это ссылка на этот пост, Concentrally Loaded Compress Members .
Решение задач методом столбцов
В этом уроке мы научимся применять наше понимание метода столбцов для поиска и исправления ошибок и выполнения незавершенных расчетов методом столбцов.
В этом тесте есть изображения без замещающего текста. Пожалуйста, свяжитесь со своим учителем, который сможет помочь вам с аудиоописанием.
Тест:
Прежде чем мы начнем этот урок, давайте посмотрим, что вы можете запомнить из этой темы. Вот быстрый тест!
Q1. Какое уравнение можно использовать для оценки ответа на вопрос: 653 098 – 118 542?653 098 – 118 542650 000 – 120 000600 000 – 200 000653 010 – 118 550
В2. Какие столбцы потребуют перегруппировки при вычитании столбцов: 563 357 – 325 129?
Какие столбцы потребуют перегруппировки при вычитании столбцов: 563 357 – 325 129?Цифры в столбцах единиц и десятков. Цифры в столбцах единиц и сотен. Цифры в столбцах единиц и тысяч. Цифры в столбцах тысяч и десятков тысяч.
Q3. Используйте метод столбца, чтобы вычислить ответ на: 561 998 – 138 422 = 123 576223 576323 576423 576 Q5.Почему моделирование стержней может быть полезным?Моделирование столбцов дает нам возможность нарисовать красивую картинку, соответствующую нашим математическим вопросам. Моделирование столбцов дает нам возможность представлять уравнения по-другому, что может помочь нам решить их. Моделирование столбцов сообщает нам, когда наш ответ неверен. Моделирование помогает нам практиковаться в рисовании прямых линий.
В этом тесте есть изображения без замещающего текста. Пожалуйста, свяжитесь со своим учителем, который сможет помочь вам с аудиоописанием.
Тест:
Прежде чем мы начнем этот урок, давайте посмотрим, что вы можете запомнить из этой темы. Вот быстрый тест!
Вот быстрый тест!
Цифры в столбцах единиц и десятков. Цифры в столбцах единиц и сотен. Цифры в столбцах единиц и тысяч. Цифры в столбцах тысяч и десятков тысяч.
Q3. Используйте метод столбца, чтобы вычислить ответ на: 561 998 – 138 422 =123 576223 576323 576423 576
Q5.Почему моделирование стержней может быть полезным?Моделирование столбцов дает нам возможность нарисовать красивую картинку, соответствующую нашим математическим вопросам. Моделирование столбцов дает нам возможность представлять уравнения по-другому, что может помочь нам решить их. Моделирование столбцов сообщает нам, когда наш ответ неверен. Моделирование помогает нам практиковаться в рисовании прямых линий.
Эти слайды помогут вам выполнить некоторые задания урока. Если вам нужно повторно воспроизвести видео, нажмите значок «Возобновить видео». Если вас попросят добавить ответы на слайды, сначала загрузите или распечатайте рабочий лист. После того, как вы выполнили все задачи, нажмите «Далее» ниже.
Если вам нужно повторно воспроизвести видео, нажмите значок «Возобновить видео». Если вас попросят добавить ответы на слайды, сначала загрузите или распечатайте рабочий лист. После того, как вы выполнили все задачи, нажмите «Далее» ниже.
В этом тесте есть изображения без замещающего текста. Пожалуйста, свяжитесь со своим учителем, который сможет помочь вам с аудиоописанием.
Контрольная работа:
Контрольная работа, которую необходимо выполнить после урока: «Решение задач методом столбцов».
Q1. Выберите приведенное ниже уравнение, которое соответствует этой математической истории: ’87 315 автомобилей были проданы за выходные. 12 872 из этих автомобилей были новыми, а остальные были подержанными. Сколько автомобилей было подержанным?87 315 + 12 87287 315 - 12 87212 872 + 87 31512 872 – 87 315
Q2. Опишите ошибку, допущенную при следующем вычислении: 213 876 – 114 689 = 328 565. Цифры в столбцах не имеют были выровнены правильно. Перегруппировка произошла неправильно более чем в одном столбце. Числа были перепутаны местами при вычитании. Числа были добавлены, а не вычтены.
Числа были перепутаны местами при вычитании. Числа были добавлены, а не вычтены.
Цифры в столбцах выровнены неправильно. Перегруппировка не выполнена правильно более чем в одном столбце .Числа поменялись местами при вычитании.Числа добавлены, а не вычтены.
В4. Какой из следующих методов НЕ является разумным способом проверки того, не сделали ли мы ошибку, используя метод столбца?Используйте обратный метод, чтобы подтвердить свой ответ. Сравните свой ответ с оценкой, чтобы увидеть, похожи ли они. Пересчитайте ответ, используя другой метод. Создайте текстовую задачу с числами, которые вы использовали в своем расчете.
Q5. Какое число отсутствует в следующем уравнении: 435 629 + _________ = 772 345436 716236 716336 716536 716
помочь вам с аудио описанием.
Контрольная работа:
Контрольная работа, которую необходимо выполнить после урока: «Решение задач методом столбцов».
87 315 + 12 87287 315 - 12 87212 872 + 87 31512 872 – 87 315
Q2. Опишите ошибку, допущенную при следующем вычислении: 213 876 – 114 689 = 328 565.Цифры в столбцах не имеют были выровнены правильно. Перегруппировка произошла неправильно более чем в одном столбце. Числа были перепутаны местами при вычитании. Числа были добавлены, а не вычтены.
Q3. Запишите следующий расчет методом столбца и опишите возникшую ошибку: 562 088 – 134 199 = 432 111.Цифры в столбцах выровнены неправильно. Перегруппировка не выполнена правильно более чем в одном столбце .Числа поменялись местами при вычитании.Числа добавлены, а не вычтены.
В4. Какой из следующих методов НЕ является разумным способом проверки того, не сделали ли мы ошибку, используя метод столбца? Используйте обратный метод, чтобы подтвердить свой ответ.