Составные задачи по математике для 2 класса: Составные задачи 2 класс | Учебно-методический материал по математике (2 класс):

Составные задачи на нахождение суммы. Математика 2 класс

Задачи по математике для 2 класса

Задачи на 2 действия.



Задача 1

На одной рубашке 6 пуговиц, на другой на 1 меньше, чем на первой, а на третьей на 4 больше, чем на второй. Сколько пуговиц на третьей рубашке?

Решение
• 6 – 1 = 5
• 5 + 4 = 9
• Ответ: 9

Задача 2

В первом саду растут 4 яблони, во втором на 2 меньше, чем в первом, а в третьем – на 6 больше, чем во втором. Сколько яблонь в третьем саду?

Решение
• 4 – 2 = 2
• 6 + 2 = 8
• Ответ: 8

Задача 3

В первом парке 7 беседок, во втором на 3 меньше, чем в первом, а в третьем на 6 больше, чем во втором. Сколько беседок в третьем парке?

Решение
• 7 – 3 = 4
• 6 + 4 = 10
• Ответ:

Задача 4

В первом городе 6 фонтанов, во втором на 2 меньше, чем в первом, а в третьем на 3 больше, чем во втором. Сколько фонтанов в третьем городе?

Решение
• 6 – 2 = 4
• 3 + 4 = 7
• Ответ:



Задача 5

В одном лесу 15 полян, во втором на 4 меньше, чем в первом, а в третьем на 7 больше, чем во втором. Сколько полян в третьем лесу?

Решение
• 15 – 4 = 11
• 11 + 7 = 18
• Ответ: 18

Задача 6

В первой области 40 городов, во второй на 10 городов меньше, чем в первой, а в третьей на 30 больше, чем во второй.

Сколько городов в тре-тьей области?

Решение
• 40 – 10 = 30
• 30 + 30 = 60
• Ответ: 60

Задача 7

В первом городе 17 парикмахерских, во втором на 5 меньше, чем в первом, а в третьем на 8 больше, чем во втором. Сколько парикмахерских в третьем городе?

Решение
• 17 – 5 = 12
• 12 + 8 =20
• Ответ: 20

Задача 8

В первом отряде 60 человек, во втором на 20 меньше, чем в первом, а в третьем на 40 больше, чем во втором. Сколько человек в третьем отряде?

Решение
• 60 – 20 = 40
• 40 + 40 = 80
• Ответ: 20



Задача 9

В первом цехе работают 50 человек, во втором – на 20 меньше, чем в первом, а в третьем – на 50 больше, чем во втором. Сколько человек работают в третьем цехе?

Решение
• 50 – 20 = 30
• 30 + 50 = 80
• Ответ: 80

Задача 10

В первом озере 14 островков, во втором на 3 меньше, чем в первом, а в третьем на 6 больше, чем во втором. Сколько островков в третьем озере?

Решение
• 14 – 3 = 11
• 11 + 6 = 17
• Ответ: 17

 

На странице использован материал из книги О. В. Узоровой и Е. А. Нефедоваой «300 задач по математике. 2 класс»

Урок математики во 2 классе “Решение задач”

Урок математики во 2 классе

«Решение задач»

 

Дата: 15.05.2019                                                                                  Учитель: Коркач Л. В.

Цель: формирование  умения  решать составные задачи, совершенствовать навыки табличного умножения и деления.

Дидактическая задача: актуализировать умение увеличивать или уменьшать число в несколько раз; закреплять знания табличных случаев умножения и деления; формировать умение решать составные задачи, которые содержат простую задачу на увеличение или уменьшение числа в несколько раз.

Развивающая задача: формировать приёмы умственных действий анализа, синтеза, классификации во время выполнения заданий (№ 3-5)

Ход урока

– Ребята, у нас сегодня необычный урок. К нам пришли гости. Повернитесь и поздоровайтесь с гостями.

Дети кивают головой, потом поворачиваются к учителю.

Позвенел звонок, начинается урок

Все тихонько ровно сели

И соседа не задели!

1. Мотивация учебно-познавательной деятельности учащихся.

– Михаил Васильевич Ломоносов, выдающийся ученый, математик, сказал: «Математику уже затем учить надо, что она ум в порядок приводит».

Как вы понимаете эти слова?

– Правильно. Мы должны быть внимательными, решительными, уверенными в себе и в своих товарищах, усидчивыми. На уроке мы встретимся с трудностями и препятствиями, которые нам надо преодолеть. Мы ведь сильные? Ведь для ученика сила – это его знания. И так, ребята, вперёд!

– Я надеюсь, что сегодня на уроке вы приобретете новые знания и умения.

-Сегодня на уроке вы буде в роли исследователей. Мы будем сравнивать и решать задачи, исследовать зависимость результатов действий умножения и деления от изменения одного из компонентов и исследуем влияние замены одного из компонентов задачи на её решение. Я желаю вам успешной работы!

2. Актуализация опорных знаний и способов действий

1. Устный счет. Игра с мячом на повторение таблицы умножения на 4,5.
2. Задание № 1 (тетрадь «Работаю самостоятельно» с. 98-по вариантам)

3. Формирование умений и навыков. Закрепление изученного.

1. Закрепление знания характера зависимости результата арифметических действий умножения или деления от изменения одного из компонентов.

Задание 2 выполняется с комментированием.

2. Закрепление умения находить число, которое в несколько раз больше или меньше другого числа. Самостоятельное выполнение № 1.

Формирование умения решать составные задачи на примере задач на разностное сравнение или на нахождение суммы, которая содержит увеличение или уменьшение числа в несколько раз.

3. Фронтальное выполнение задания 3.
4. Фронтальное выполнение задания 4.

4. Рефлексия учебно-познавательной деятельности учащихся.

-Что важное вы повторили на уроке? Что закрепили? Чему научились?

5. Объяснение домашнего задания. Оценивание.

Простые и сложные проценты — Математика для нашего мира

Результаты обучения

• Расчет единовременных простых процентов и простых процентов с течением времени
• Определить APY с учетом процентного сценария
• Расчет сложных процентов

Мы должны работать с деньгами каждый день. В то время как балансировка чековой книжки или расчет ежемесячных расходов на эспрессо требует только арифметики, когда мы начинаем копить, планировать выход на пенсию или нуждаемся в кредите, нам нужно больше математики.

 

Простые проценты

Обсуждение процентов начинается с основного долга или суммы, с которой начинается ваш счет. Это может быть стартовая инвестиция или начальная сумма кредита. Проценты в самой простой форме рассчитываются как процент от основной суммы. Например, если вы одолжили 100 долларов у друга и согласны вернуть их с процентной ставкой 5%, то сумма процентов, которую вы заплатите, составит всего 5% от 100: 100 долларов (0,05) = 5 долларов. Общая сумма, которую вы должны будете вернуть, составит 105 долларов США, первоначальная основная сумма плюс проценты.

Простые единовременные проценты

(1)  

Примеры

Друг просит одолжить 300 долларов и соглашается вернуть их в течение 30 дней под 3% годовых. Сколько процентов вы заработаете?

Решение:

(3)   = 300 долларов	основной
г = 0,03	3% ставка
I = 300 долл. США (0,03) = 9 долл. США.	Вы заработаете $9 процентов.

 

В следующем видео подробно рассматривается этот пример.

 

Единовременные простые проценты характерны только для чрезвычайно краткосрочных кредитов.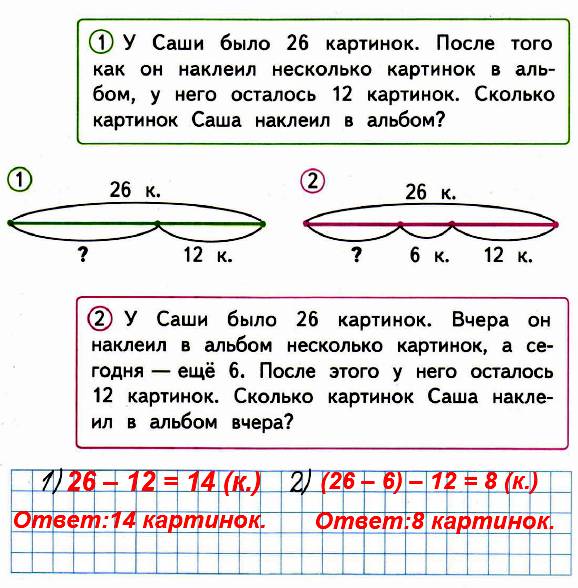

Для более долгосрочных кредитов проценты обычно выплачиваются ежедневно, ежемесячно, ежеквартально или ежегодно. В этом случае проценты будут начисляться регулярно.

Например, облигации представляют собой заем, предоставленный эмитенту облигаций (компании или правительству) вами, держателем облигаций. В обмен на кредит эмитент соглашается платить проценты, часто ежегодно. Облигации имеют срок погашения, когда эмитент выплачивает первоначальную стоимость облигации.

Упражнения

Предположим, ваш город строит новый парк и выпускает облигации, чтобы собрать деньги на его строительство. Вы получаете облигацию на 1000 долларов, по которой выплачивается 5% годовых и срок погашения которой составляет 5 лет. Сколько процентов вы заработаете?
[reveal-answer q=”14596″]Показать решение[/reveal-answer]
[hidden-answer a=”14596″]Каждый год вы будете получать 5% годовых: 1000 долларов (0,05) = 50 долларов в виде процентов. Таким образом, в течение пяти лет вы заработаете в общей сложности 250 долларов в виде процентов.

Когда срок погашения облигации истекает, вы получите обратно 1000 долларов, которые вы первоначально заплатили, в результате чего у вас останется 1250 долларов.[/hidden-answer]

Дальнейшее объяснение решения этого примера можно увидеть здесь.

Мы можем обобщить эту идею простых процентов с течением времени.

Простые проценты с течением времени

(4)  

Единицы измерения (годы, месяцы и т. д.) для времени должны соответствовать периоду времени для процентной ставки.

 

APR – годовая процентная ставка

Процентные ставки обычно указываются в виде годовой процентной ставки (APR) – общая сумма процентов, которые будут выплачены в течение года. Если проценты выплачиваются меньшими временными интервалами, годовая процентная ставка будет разделена.

Например, ежемесячная выплата в размере 6% годовых будет разделена на двенадцать платежей по 0,5%.

Годовая ставка 4%, уплачиваемая ежеквартально, будет разделена на четыре платежа по 1%.

Пример

Казначейские облигации (казначейские облигации) — это облигации, выпущенные федеральным правительством для покрытия его расходов. Предположим, вы получили казначейские облигации на 1000 долларов с годовой ставкой 4%, выплачиваемой раз в полгода, со сроком погашения через 4 года. Сколько процентов вы заработаете?

Решение:

Так как проценты выплачиваются раз в полгода (два раза в год), процентная ставка 4% будет разделена на два платежа по 2%.

(6)   = 1000 долларов	основной
г = 0,02	Ставка 2% за полугодие
т = 8	4 года = 8 полугодий
I = 1000 долларов (0,02) (8) = 160 долларов.	Вы заработаете 160 долларов США в виде процентов за четыре года.

 

В этом видео объясняется решение.

Попробуйте

Щелкните здесь, чтобы попробовать решить эту проблему.

Попробуйте

Кредитная компания взимает проценты в размере 30 долларов США за месячный кредит в размере 500 долларов США. Найдите годовую процентную ставку, которую они взимают.

Решение:

I = $30 процентов
= $500 основной суммы
r = неизвестно
t = 1 месяц

Используя , получаем . Решая, получаем r = 0,06, или 6%. Поскольку время было месячным, это ежемесячный процент. Годовая ставка будет в 12 раз больше: 72% годовых.

Попробуйте

Щелкните здесь, чтобы попробовать решить эту проблему.

Сложные проценты

С простыми процентами мы предполагали, что мы прикарманили проценты, когда мы их получили. На стандартном банковском счете любые проценты, которые мы зарабатываем, автоматически добавляются к нашему балансу, и мы получаем проценты на эти проценты в последующие годы. Это реинвестирование процентов называется начислением сложных процентов .

Предположим, что мы кладем 1000 долларов на банковский счет с ежемесячной процентной ставкой 3%. Как будут расти наши деньги?

Процентная ставка в размере 3% представляет собой годовую процентную ставку (APR) – общую сумму процентов, подлежащих выплате в течение года. Поскольку проценты выплачиваются ежемесячно, каждый месяц мы будем зарабатывать 3% ÷ 12 = 0,25% в месяц.

В первый месяц

• P ₀ = 1000 долларов
• r = 0,0025 (0,25%)
• I = 1000 долл. США (0,0025) = 2,50 долл. США
• A = 1000 долл. США + 2,50 долл. США = 1002,50 долл. США

В первый месяц мы заработаем 2,50 доллара в виде процентов, увеличив баланс нашего счета до 1002,50 доллара.

 

Во втором месяце

• P ₀ = 1002,50 долл. США
• I = 1002,50 долл. США (0,0025) = 2,51 долл. США (округлено)
• A = 1002,50 долл. США + 2,51 долл. США = 1005,01 долл. США

Обратите внимание, что во второй месяц мы заработали больше процентов, чем в первый месяц. Это связано с тем, что мы заработали проценты не только на первоначальные 1000 долларов США, которые мы внесли, но мы также получили проценты на 2,50 доллара США процентов, которые мы заработали в первый месяц. Это ключевое преимущество начисляет проценты.

Подсчет еще нескольких месяцев дает следующее:

Месяц	Начальный баланс	Полученные проценты	Конечный баланс
1	1000. 00	2,50	1002.50
2	1002.50	2,51	1005.01
3	1005.01	2,51	1007.52
4	1007.52	2,52	1010.04
5	1010.04	2,53	1012,57
6	1012,57	2,53	1015.10
7	1015.10	2,54	1017,64
8	1017,64	2,54	1020.18
9	1020.18	2,55	1022.73
10	1022.73	2,56	1025.29
11	1025.29	2,56	1027,85
12	1027,85	2,57	1030.42

Мы хотим упростить процесс расчета сложных процентов, поскольку создание таблицы, подобной приведенной выше, требует много времени. К счастью, математика хорошо подсказывает, как срезать путь. Чтобы найти уравнение, представляющее это, если P _m представляет собой сумму денег через m месяцев, тогда мы могли бы написать рекурсивное уравнение:

P ₀ = 1000 долларов США

P _м = (1+0,0025) P _м-1

Вы, вероятно, знаете, что это рекурсивная форма экспоненциального роста. Если нет, мы проходим шаги, чтобы построить явное уравнение для роста в следующем примере.

Пример

Постройте явное уравнение для роста 1000 долларов, размещенных на банковском счете с процентной ставкой 3%, с ежемесячным начислением сложных процентов.

Решение:

• P ₀ = 1000 долларов
• P ₁ = 1,0025 P ₀ = 1,0025 (1000)
• P ₂ = 1,0025 P ₁ = 1,0025 (1,0025 (1000)) = 1,0025 2(1000)
• P ₃ = 1,0025 P ₂ = 1,0025 (1,00252(1000)) = 1,00253(1000)
• П ₄ = 1,0025 P ₃ = 1,0025 (1,00253(1000)) = 1,00254(1000)

Наблюдая закономерность, мы можем сделать вывод:

• P _м = (1,0025) ^м (1000 долларов США)

Обратите внимание, что 1000 долларов в уравнении были P ₀ , начальной суммой. Мы нашли 1,0025, прибавив единицу к темпу роста, деленному на 12, поскольку мы начисляли сложные проценты 12 раз в год.

 

Обобщая наш результат, мы могли бы написать

 

В этой формуле:

• m — количество периодов начисления процентов (месяцев в нашем примере)
• r это годовая процентная ставка
• k – количество соединений в год.

Посмотрите это видео, чтобы ознакомиться с концепцией сложных процентов.

Хотя эта формула работает нормально, чаще используется формула, включающая количество лет, а не количество периодов начисления сложных процентов. Если N количество лет, тогда м = N k . Это изменение дает нам стандартную формулу сложных процентов.

Сложные проценты

• P _N остаток на счете после N лет.
• P ₀ — начальный баланс счета (также называемый начальным депозитом или основной суммой)
• r – годовая процентная ставка в десятичной форме
• k — количество периодов начисления процентов в одном году.
  • Если начисление производится ежегодно (раз в год), к = 1.
  • Если начисление процентов производится ежеквартально, k = 4.
  • Если начисление процентов производится ежемесячно, к = 12.
  • Если начисление процентов производится ежедневно, k = 365.

Самое важное, что следует помнить об использовании этой формулы, это то, что она предполагает, что мы кладем деньги на счет один раз и оставляем их там, чтобы получать проценты.

В следующем примере показано, как использовать формулу сложных процентов для определения остатка по депозитному сертификату через 20 лет.

Пример

Депозитный сертификат (CD) — это сберегательный инструмент, который предлагают многие банки. Обычно это дает более высокую процентную ставку, но вы не можете получить доступ к своим инвестициям в течение определенного периода времени. Предположим, вы вкладываете 3000 долларов в депозитный сертификат с ежемесячной процентной ставкой 6%. Сколько будет у вас на счету через 20 лет?

Решение:

В этом примере

P 0 = $3000	первоначальный взнос
r = 0,06	6% годовых
к = 12	12 месяцев в 1 году
N = 20	так как мы ищем, сколько у нас будет через 20 лет

Итак (округлите ответ до копейки)

Ниже представлено видео с решением этой задачи.

Давайте сравним сумму денег, заработанную на сложном проценте, с суммой, которую вы заработаете на простых процентах

Годы	Простые проценты (15 долларов США в месяц)	6% ежемесячно начисляется = 0,5% каждый месяц.
5	$3900	4046,55 $
10	4800 $	5458,19 $
15	$5700	7362,28 $
20	6600 $	9930,61 $
25	7500 $	13394,91 $
30	$8400	18067,73 $
35	$9300	24370,65 $

Как видите, в течение длительного периода времени начисление сложных процентов сильно влияет на баланс счета. Вы можете распознать в этом разницу между линейным ростом и экспоненциальным ростом.

Попробуйте

Щелкните здесь, чтобы попробовать решить эту проблему.

 

Оценка степени на калькуляторе Desmos

Когда нам нужно вычислить что-то подобное, достаточно просто умножить. Но когда нам нужно вычислить что-то вроде , было бы очень утомительно вычислять это, умножая на себя раз! Поэтому, чтобы упростить задачу, мы можем использовать возможности наших научных калькуляторов. В этом классе мы используем калькулятор Desmos. Если вы просто хотите возвести число в квадрат, ключ и ² . Если вы хотите возвести число в другую степень, вы используете клавишу a ^b в главном меню.

Для оценки мы должны ввести 1,005 a ^b  240 . Попробуйте — вы должны получить ответ на рисунке ниже:

 

В большинстве научных калькуляторов есть кнопка для экспоненты. Если вы не используете калькулятор Desmos, он обычно помечен следующим образом:

9, , или .

 

Пример

Вы знаете, что через 18 лет вам потребуется 40 000 долларов на образование вашего ребенка. Если ваш счет зарабатывает 4% ежеквартально, сколько вам нужно внести сейчас, чтобы достичь своей цели?

Решение:

В этом примере мы ищем P ₀ .

г = 0,04	4%
к = 4	4 квартала в 1 году
N = 18	Так как мы знаем баланс через 18 лет
P 18 = 40 000 долларов США	Сумма, которую мы имеем за 18 лет

В этом случае нам нужно составить уравнение и найти P ₀ .

(7)  

Таким образом, вам нужно внести 19 539,84 долларов США сейчас, чтобы иметь 40 000 долларов через 18 лет.

Попробуйте

Нажмите здесь, чтобы попробовать решить эту проблему.

 

Округление

Если вы не вводите всю формулу в Desmos, а делаете это по частям, важно быть очень осторожным с округлением при расчетах с показателями степени. В общем, вы хотите сохранить как можно больше десятичных знаков во время вычислений. Убедитесь, что содержит не менее 3 значащих цифр (числа после любых начальных нулей). Округление 0,00012345 до 0,000123 обычно дает «достаточно близкий» ответ, но всегда лучше оставить больше цифр.

Пример

Чтобы понять, почему недопустимость чрезмерного округления так важна, если вы решите не вводить всю формулу сразу в Desmos, предположим, что вы инвестируете 1000 долларов США под 5% годовых, начисляемых ежемесячно в течение 30 лет.

P 0 = 1000 долларов	первоначальный взнос
г = 0,05	5%
к = 12	12 месяцев в 1 году
Н = 30	так как ищем сумму через 30 лет

Если мы сначала вычислим r/k , то получим 0,05/12 = 0,00416666666667

Вот результат округления до различных значений:

р/к округлить до:	Получается P30 :	Ошибка
0,004	4208,59 $	259,15 $
0,0042	4521,45 $	53,71 $
0,00417	4473,09 $	5,35 $
0,004167	4468,28 $	0,54 $
0,0041667	4467,80 $	0,06 $
без округления	4467,74 $

Если вы работаете в банке, вы, конечно, вообще не будете округлять. Для наших целей ответ, который мы получили, округлив до 0,00417, трех значащих цифр, достаточно близок — скидка 5 долларов с 4500 долларов не так уж и плоха. Конечно, сохранение этого четвертого знака после запятой не помешало бы.

Просмотрите следующее для демонстрации этого примера.

 

Использование калькулятора Desmos

 

Во многих случаях можно полностью избежать округления, вводя данные в калькулятор. Например, в приведенном выше примере нам нужно было вычислить

. Мы можем быстро вычислить это на калькуляторе Desmos, введя формулу сразу:

Чтобы ввести это в калькулятор, введите следующее:

1000 * (1 + .05/12) a ^b (12 * 30)

. Теперь вы можете округлить свой окончательный ответ до ближайшего цента.

Attributions

Эта глава содержит материалы, взятые из книги Math in Society (в OpenTextBookStore) Дэвида Липпмана, и используется в соответствии с лицензией CC Attribution-Share Alike 3.0 United States (CC BY-SA 3.0 US).

Эта глава содержит материалы, взятые из Math for the Liberal Arts (о Lumen Learning) компании Lumen Learning, и используется в соответствии с лицензией CC BY: Attribution .

Media Attributions

• Desmos Exponent Entry
• Сложные проценты

Cookie Cutter 3 Act Math Task

• Тема
• Учебная программа Онтарио
• Common Curriculum 9 00006 9000um

Онтарио Согласование по 9 классу1011

Grade 8grade 9grade 10

Выравнивание Ontario по общему выравниванию

CCSS по сравнению с классом

CCSS по стандарту

Решающие проблемы с участием площади составных рисунков

В этом. раздел математической программы Онтарио. В частности, мы рассмотрим площадь составных фигур , включая площадь прямоугольника и площадь круга 9.0020 .

Акт 1. Знакомство с задачей

Приготовление теста для печенья, раскатывание теста и нарезка печенья

В первом акте этой реальной математической задачи мы показываем учащимся видео, на котором тесто для печенья перемешивается и раскатывается скалкой. Затем печенье нарезается с помощью круглой формы для печенья очень особым образом.

После показа видео дайте учащимся время подумать над возможными вопросами, которые мы могли бы задать в этой ситуации.

На наших недавних сессиях профессионального развития MYCI Learning Fair мы получили несколько замечательных вопросов от участвующих учителей, в том числе:

• Сколько еще печенья мы можем испечь из оставшегося теста?
• Какова площадь израсходованного теста?
• Какова площадь гранитной столешницы?
• Сколько еще ингредиентов вам понадобится, если вы утроите рецепт?
• Если этот рецепт служит ____, то что мы должны сделать, чтобы подать 25?
• Сколько стоит 1 печенье?
• Если вы продаете это печенье на распродаже выпечки, сколько вы должны брать, чтобы получать 40% прибыли?
• Сколько калорий в остатках теста?
• Сколько времени ушло на изготовление печенья?
• Коробка какого размера вам нужна для отправки x файлов cookie?
• Коробка какой формы оптимальна для отправки x файлов cookie?
• Какая форма и размеры были бы наиболее эффективными для печенья?

После того, как учащиеся поделятся своими идеями и отметят творческий подход, мы сузим вопрос до:

Сколько еще печенья можно испечь из оставшегося теста?

Акт 2: раскрытие некоторой информации

Размеры формочки для печенья

Попросите учеников провести мозговой штурм, чтобы решить, какая информация им нужна, чтобы определить, сколько еще печенья можно вырезать из оставшегося теста. Я нахожу очень забавным, когда дети делают предположения, используя стратегию высокого / низкого уровня, чтобы установить диапазон, а затем сузить их до конкретного прогноза. Отличный способ вовлечь всех учащихся, независимо от их уровня владения математикой.

После обмена прогнозами и выслушивания того, что учащиеся считают нужным в отношении данной информации, вы можете показать им следующее видео или изображение:

Теперь, когда у учащихся есть информация для работы, они могут к ней приступить! Обмен и празднование различных стратегий решения проблемы действительно может помочь превратить урок в динамичный и инновационный опыт обучения! Я пытаюсь найти действительно «беспорядочное» решение, чтобы отпраздновать потребность студентов в мозговом штурме, написав что угодно и все они думают, а не беспокоятся о том, что их работа представляет собой идеально организованный процесс.

Акт 3: Раскройте ответ

Покажите, сколько дополнительных файлов cookie мы получаем!

После того, как учащиеся разделились, настало время испытать решение этой реальной проблемы:

Если вы предпочитаете показывать изображение вместо видео, вот оно:

Мне очень нравится это задание потому что учащиеся должны придумать ответ: чуть более 3 дополнительных печений из оставшегося теста, в то время как видео акта 3 показывает чуть больше 5. Некоторые большие дискуссии возникают из-за посторонних переменных, которые могут вызвать это. Некоторые учащиеся сразу же заметят во время воспроизведения видео, что тесто для печенья выглядит «тоньше», и поэтому в результате может получиться больше печенья. Другие могут заметить, что некоторые углы прямоугольного теста отсутствовали, и должно получиться менее 3 печенек. Принимая во внимание множество других переменных, это отличная задача, чтобы заставить студентов говорить и участвовать в вашей комнате!

Использовали ли вы резак для печенья в своем классе? Пожалуйста, поделитесь своими результатами в разделе комментариев ниже!

Вы не знакомы с математическими задачами из 3 актов?

Загрузите 2-страничный печатный лист советов по математике 3 Act , чтобы обеспечить себе наилучшее начало своего путешествия, используя математические задачи 3 Act, чтобы пробудить любопытство и стимулировать осмысление в вашем классе математики!

СКАЧАТЬ СОВЕТЫ

Поделитесь со своим учебным сообществом:

Меня зовут Кайл Пирс, и я бывший учитель математики в средней школе. Теперь я консультант по математике K-12 в школьном совете округа Большой Эссекс, где я раскрываю творческие способы пробудить любопытство и стимулировать понимание математики. Читать далее.

Доступ к другим математическим задачам реального мира

← Корзина с тако Дуэль хот-догов →

---

Поиск Еще 3 Act Math Tasks

• Ключевое слово
• Тема
• Учебная программа Онтарио
• Общая базовая учебная программа
• Автор

Поиск:

Класс 1 [Чувство числа и нумерация – NS1, Чувство числа и нумерация – NS3]

Класс 2 [Измерение – M1, Чувство числа и нумерация – NS1, Чувство числа и нумерация – NS2, Чувство числа и нумерация – NS3]

3 класс [Измерение – M1, Чувство числа и нумерация – NS1, Чувство числа и нумерация – NS3]

Класс 4 [Измерение – M1, Числовой смысл и нумерация – NS1, Числовой смысл и нумерация – NS3, Структурирование и алгебра – PA2]

Класс 5 [Измерение – M1, Измерение – M2, Числовой смысл и нумерация – NS1, Число Чувство и нумерация — NS3, построение паттернов и алгебра — PA2]

6 класс [Управление данными и вероятность — DP3, измерение — M1, измерение — M2, числовое чувство и нумерация — NS1, числовое чувство и нумерация — NS2, числовое чувство и нумерация – NS3, Паттерны и алгебра – PA1, Паттерны и алгебра – PA2]

7 класс [Управление данными и вероятность – DP3, Геометрия и пространственное чувство – GS1, Измерение – M1, Измерение – M2, Численное чувство и нумерация – NS1, Числовое чувство и нумерация – NS2, Числовое чувство и нумерация – NS3, Структурирование и Алгебра — PA1, Структурирование и алгебра — PA2]

8 класс [Управление данными и вероятностью — DP1, Управление данными и вероятностью — DP3, Геометрия и пространственное чувство — GS2, Измерение — M1, Измерение — M2, Чувство числа и нумерация — NS1 , Числовой смысл и нумерация – NS2, Числовой смысл и нумерация – NS3, Структурирование и алгебра – PA1, Структурирование и алгебра – PA2]

Класс 9MAP4C [Математические модели – MM1, Математические модели – MM2, Математические модели – MM3]

MAT1LMAT2LMBF3C [Управление данными – DM1, Управление данными – DM2, Геометрия и тригонометрия – GT1, Геометрия и тригонометрия – GT2, Математические модели – MM1 , Математические модели – MM2, Математические модели – MM3]

MCF3M [Экспоненциальные функции – EF2, Квадратичные функции – QF1, Квадратичные функции – QF2, Квадратичные функции – QF3, Тригонометрические функции – TF1, Тригонометрические функции – TF3]

MCR3U [Характеристики функций — CF1, Характеристики функций — CF2, Показательные функции — EF2, Показательные функции — EF3, Тригонометрические функции — TF3]

MCT4C [Показательные функции — EF1, Тригонометрические функции — TF3]

MCV4U [Производные и их приложения — DA2]

MDM4U [Подсчет и вероятность — CP2, Организация данных для анализа — DA2, Распределение вероятностей — PD1, Статистический анализ — SA1, Статистический анализ — SA2]

MEL4EMFM1P [Линейные отношения — LR1, Линейные отношения — LR2, Линейные отношения — LR3, Линейные отношения — LR4, Измерение и геометрия — MG1, Измерение и геометрия — MG2, Измерение и геометрия — MG3, Чувство числа и алгебра — NA1, Число Смысл и алгебра – NA2]

MFM2P [Измерение и тригонометрия – MT1, Измерение и тригонометрия – MT2, Измерение и тригонометрия – MT3, Моделирование линейных отношений – LR1, Моделирование линейных отношений – LR2, Моделирование линейных отношений – LR3, Квадратичные отношения в y = ax^2 + bx + c Форма – QR1, Квадратичные соотношения по y = ax^2 + bx + c Форма – QR2, Квадратичные соотношения по y = ax^2 + bx + c Форма – QR3]

MHF4U [Характеристики функций — CF3, Экспоненциальные и логарифмические функции — EL2, Экспоненциальные и логарифмические функции — EL3]

MPM1D [AG3, Аналитическая геометрия — AG1, Аналитическая геометрия — AG2, LR1, LR2, LR3, MG1, MG2, MG3, NA1, Чувство чисел и алгебра — NA2]

MPM2D [AG1, AG2, AG3, QR2, Квадратичные отношения — QR3, Квадратичные отношения — QR4, T2, T3]

Алгебра [A-CED.