Состав числа до 10 распечатать тренажер: Тренажер – домики на состав числа

Тренажер “Состав числа до 10”

50,00 ₽

Задания на состав числа в пределах 10. Для решения  на компьютере (в Excel без печати).

Количество товара Тренажер “Состав числа до 10”

Артикул: i-13876 Категория: Для учебы Метки: Дошкольники, Состав числа, 1 класс

• Описание
• Детали
• Отзывы (0)

Описание

Тренажер «Состав числа до 10» – это программа, которая формирует задания на состав числа в пределах 10, чтобы решать их на компьютере (не распечатывая). Задания генерируются случайным образом, количество генераций не ограничено.

Программа написана в Excel с помощью макросов. Для решения задания нужно выбрать число, для которого будут формироваться задания

.

При нажатии кнопки «Начать» запускается счетчик, который подсчитывает количество решенных примеров, в том числе  правильных и решенных с ошибкой. При нажатии кнопки «Начать» счетчик обнуляется.
Для удобства внизу карточки есть кнопки с цифрами, которые нужно нажимать при выборе ответа.

Генератор будет полезен как для подготовки к школе, так и для закрепления состава числа учеников 1 класса. Практика счета поможет развить внимательность и закрепить навыки устного счета у детей. Для этого достаточно заниматься 10-15 минут в день.

На сайте также можно скачать программу «Состав числа в пределах 10» для печати в виде домиков.

Другие программы, которые помогут закрепить навыки счета в пределах 10:

• Умная раскраска «Примеры до 10»
• Сложение и вычитание в пределах 10
• Цепочки примеров в пределах 10 (сложение и вычитание)
• Математический лабиринт (состав числа)
• Арифметический маршрут 1 (сложение и вычитание в пределах 10-100)
• Математический диктант для дошкольников

На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.

Вам также будет интересно…

• Главные праздники России

  70,00 ₽В корзину

• Часы для изучения времени детям

  Оценка 5.00 из 5

  70,00 ₽В корзину

• Умная раскраска «Примеры до 10»

  60,00 ₽В корзину

• Состав числа в пределах 10

  50,00 ₽В корзину

• Выучить 12 месяцев

  Оценка 5.00 из 5

  70,00 ₽В корзину

• Тренажер счета в пределах 10

  Оценка 5.00 из 5

  Распродажа! 50,00 ₽ 0,00 ₽ В корзину

• Сложение и вычитание в пределах 10

  Оценка 5.00 из 5

  Распродажа! 50,00 ₽ 0,00 ₽ В корзину

• Сборник заданий для дошкольников

  Распродажа! 545,00 ₽ 320,00 ₽ В корзину

• Арифметический маршрут 1 (сложение и вычитание в пределах 10-100)

  70,00 ₽В корзину

Тренажер «Домики».

Состав числа в пределах 10

Вы можете ознакомиться и скачать презентацию на тему Тренажер «Домики». Состав числа в пределах 10. Доклад-сообщение содержит 91 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

---

Слайд 1

Описание слайда:

---

Слайд 2

Описание слайда:

---

Слайд 3

Описание слайда:

---

Слайд 4

Описание слайда:

---

Слайд 5

Описание слайда:

---

Слайд 6

Описание слайда:

---

Слайд 7

Описание слайда:

---

Слайд 8

Описание слайда:

---

Слайд 9

Описание слайда:

---

Слайд 10

Описание слайда:

---

Слайд 11

Описание слайда:

---

Слайд 12

Описание слайда:

---

Слайд 13

Описание слайда:

---

Слайд 14

Описание слайда:

---

Слайд 15

Описание слайда:

---

Слайд 16

Описание слайда:

---

Слайд 17

Описание слайда:

---

Слайд 18

Описание слайда:

---

Слайд 19

Описание слайда:

---

Слайд 20

Описание слайда:

---

Слайд 21

Описание слайда:

---

Слайд 22

Описание слайда:

---

Слайд 23

Описание слайда:

---

Слайд 24

Описание слайда:

---

Слайд 25

Описание слайда:

---

Слайд 26

Описание слайда:

---

Слайд 27

Описание слайда:

---

Слайд 28

Описание слайда:

---

Слайд 29

Описание слайда:

---

Слайд 30

Описание слайда:

---

Слайд 31

Описание слайда:

---

Слайд 32

Описание слайда:

---

Слайд 33

Описание слайда:

---

Слайд 34

Описание слайда:

---

Слайд 35

Описание слайда:

---

Слайд 36

Описание слайда:

---

Слайд 37

Описание слайда:

---

Слайд 38

Описание слайда:

---

Слайд 39

Описание слайда:

---

Слайд 40

Описание слайда:

---

Слайд 41

Описание слайда:

---

Слайд 42

Описание слайда:

---

Слайд 43

Описание слайда:

---

Слайд 44

Описание слайда:

---

Слайд 45

Описание слайда:

---

Слайд 46

Описание слайда:

---

Слайд 47

Описание слайда:

---

Слайд 48

Описание слайда:

---

Слайд 49

Описание слайда:

---

Слайд 50

Описание слайда:

---

Слайд 51

Описание слайда:

---

Слайд 52

Описание слайда:

---

Слайд 53

Описание слайда:

---

Слайд 54

Описание слайда:

---

Слайд 55

Описание слайда:

---

Слайд 56

Описание слайда:

---

Слайд 57

Описание слайда:

---

Слайд 58

Описание слайда:

---

Слайд 59

Описание слайда:

---

Слайд 60

Описание слайда:

---

Слайд 61

Описание слайда:

---

Слайд 62

Описание слайда:

---

Слайд 63

Описание слайда:

---

Слайд 64

Описание слайда:

---

Слайд 65

Описание слайда:

---

Слайд 66

Описание слайда:

---

Слайд 67

Описание слайда:

---

Слайд 68

Описание слайда:

---

Слайд 69

Описание слайда:

---

Слайд 70

Описание слайда:

---

Слайд 71

Описание слайда:

---

Слайд 72

Описание слайда:

---

Слайд 73

Описание слайда:

---

Слайд 74

Описание слайда:

---

Слайд 75

Описание слайда:

---

Слайд 76

Описание слайда:

---

Слайд 77

Описание слайда:

---

Слайд 78

Описание слайда:

---

Слайд 79

Описание слайда:

---

Слайд 80

Описание слайда:

---

Слайд 81

Описание слайда:

---

Слайд 82

Описание слайда:

---

Слайд 83

Описание слайда:

---

Слайд 84

Описание слайда:

---

Слайд 85

Описание слайда:

---

Слайд 86

Описание слайда:

---

Слайд 87

Описание слайда:

---

Слайд 88

Описание слайда:

---

Слайд 89

Описание слайда:

---

Слайд 90

Описание слайда:

---

Слайд 91

Описание слайда:

---

Что такое линия распознавания символов с магнитными чернилами?

Линия распознавания символов с помощью магнитных чернил (MICR)

Распознавание символов с помощью магнитных чернил (MICR) — это технология, используемая в основном для идентификации и обработки чеков. MICR на чеке — это строка символов, которая появляется в левом нижнем углу чека. Он состоит из трех групп цифр, включая маршрутный номер банка, номер счета клиента и номер чека.

MICR включает в себя (слева направо) девятизначный маршрутный номер, 12-значный номер счета и четырехзначный контрольный номер.

Это называется линией распознавания символов с помощью магнитных чернил в связи с технологией печати, которая позволяет машине считывать, обрабатывать и записывать информацию.

Key Takeaways

• Распознавание символов магнитными чернилами — это строка символов в левом нижнем углу персонального чека, которая включает номер счета, маршрутизации и номера чека.
• Номера MICR предназначены для чтения как отдельными лицами, так и сортировочным оборудованием.
• Их невозможно подделать или скопировать, благодаря использованию магнитных чернил и уникальных шрифтов.
• Преимущества технологии включают повышенную защиту от мошенничества и механизацию обработки чеков.
• MICR был разработан в конце 1950-х годов и в настоящее время используется во всем мире.

Как работает линия распознавания символов с помощью магнитных чернил (MICR)

Линия распознавания символов с помощью магнитных чернил позволяет компьютеру быстро считывать и записывать числа или другую информацию из печатных документов, таких как личный чек. В данном случае эта информация представляет собой контрольный номер, маршрутный номер и номер счета.

Система была разработана Американской ассоциацией банкиров (ABA) в конце 1950-х годов и позже была признана отраслевым стандартом Американским национальным институтом стандартов.

Номер MICR, который иногда путают только с номером счета, напечатан на чеке с использованием магнитных чернил или тонера, менее чем на дюйм выше нижней части документа. Магнитные чернила позволяют компьютеру читать символы, даже если они покрыты подписями, гашениями, банковскими штампами или другими отметками.

Линии MICR помогают автоматизировать клиринг чеков, когда банки отправляют свои чеки в центральные системы обработки в конце дня. Они разработаны таким образом, чтобы их могли легко читать люди, так что информация о проверке может быть легко передана.

Номера обычно печатаются одним из двух специально разработанных шрифтов, называемых E-13B и CMC-7. Оба используются по всему миру, при этом E-13B используется в основном в Северной Америке, Австралии и Великобритании. Шрифт CMC-7 в основном используется в Европе и некоторых частях Южной Америки.

Сканер проверки MICR

Каждый отправленный чек обрабатывается расчетной палатой или банком, или обоими. Они проверяют чек и завершают транзакцию, вычитая правильную сумму с одного счета и зачисляя ее на другой. Один чек может быть обработан несколько раз в разных банках и Федеральных резервных центрах.

Частью этого процесса является считывание идентификационной информации на чеке. Линия MICR механизировала этот процесс. Сканер или компьютеризированная машина для считывания-сортировки используется для обработки информации, напечатанной на чеках магнитным способом, включая маршрутный номер, номер счета и номер чека.

В процессе клиринга чек может считываться несколько раз на очень высоких скоростях. Одно считывание занимает менее 1/1000 секунды, согласно Troy Group, производителю MICR-адаптированных принтеров и сопутствующих товаров.

MICR является причиной того, что чеки имеют такой единый формат. Макет чека и положение данных на нем должны быть размещены жестко, чтобы он мог быть прочитан машинами.

Особые указания

Хотя распознавание символов с помощью магнитных чернил впервые использовалось для печати информации на чеках, эта технология была адаптирована для других приложений.

Различные финансовые документы в США кодируются с помощью технологии MICR. Счета-фактуры по кредитным картам, прямая почтовая рассылка, купоны, используемые для скидок, и оборотные заказы на снятие средств (NOW) также могут использовать эту технологию.

Преимущества линии MICR

Одним из преимуществ линии распознавания символов с помощью магнитных чернил является ее способность упростить использование маршрутного номера для обработки чеков и вычета сумм платежей. Маршрутный номер или маршрутный транзитный номер представляет собой девятизначный числовой код, который банки и другие финансовые учреждения используют для очистки средств и обработки чеков.

Маршрутный номер идентифицирует отделение банка, в котором находится счет, с которого должны быть сняты средства. Банковские переводы и прямые депозиты также часто зависят от номеров маршрутизации.

Обнаружение мошенничества

Борьба с мошенничеством — это постоянная битва в индустрии финансовых услуг. Мошенничество определяется как преднамеренное вводящее в заблуждение действие, направленное на получение преступником незаконной выгоды. Существует целый ряд типов мошенничества, включая налоговое мошенничество, мошенничество с кредитными картами, мошенничество с использованием электронных средств, мошенничество с ценными бумагами и мошенничество с банкротством.

Линия распознавания символов с помощью магнитных чернил затрудняет некоторые формы финансового мошенничества за счет использования защищенных от несанкционированного доступа магнитных чернил и уникальных шрифтов. Таким образом, MICR затрудняет изменение чеков.

Изменение чека обычно влечет за собой изменение имени получателя платежа или суммы чека, или того и другого. Раздел 3-407 Единого коммерческого кодекса (UCC), свода законов о бизнесе, регулирующих финансовые контракты, еще больше разбивает термин «изменение » с девятью статьями, касающимися отдельных аспектов банковского дела и кредитов.

Например, мошенник может попытаться обналичить фотокопию чека через кассира в отделении банка. Фотокопия строки MICR немедленно предупреждает кассира о том, что чек поддельный.

Поскольку технология MICR помогает обнаруживать и предотвращать мошенничество, банки и другие финансовые учреждения используют ее для минимизации потерь.

Маршрутный номер, номер счета и номер чека объединяются для создания уникального идентификатора для каждого чека.

Часто задаваемые вопросы

Что такое номер MICR?

Строка распознавания символов с помощью магнитных чернил (MICR) представляет собой строку символов на чеке, напечатанную с использованием уникальных чернил, которые позволяют считывать символы с помощью считывающего устройства.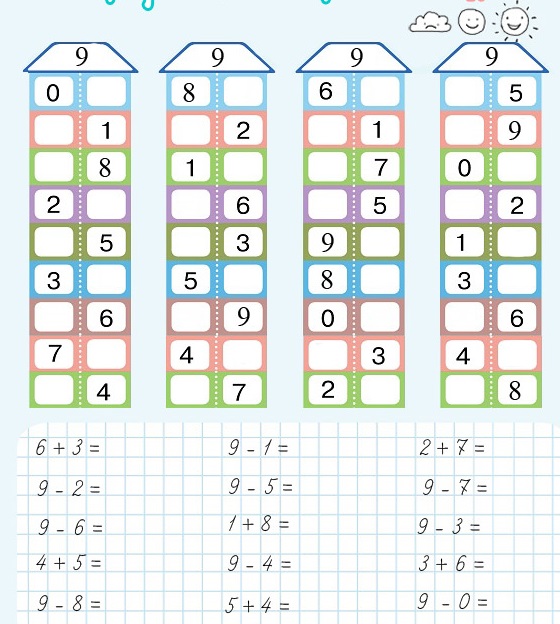 Внедрение процесса считывания-сортировки MICR позволило автоматизировать обработку чеков, затруднив при этом подделку чеков.

Как MICR используется в банках?

Система MICR используется с конца 1950-х годов. Это было заметным улучшением, потому что оно позволило механизировать обработку чеков, усложнив при этом мошенничество с чеками. Банки по всему миру приняли эту систему.

Вот почему формат банковских чеков такой унифицированный. Это должно быть сделано для того, чтобы читатели могли прочитать номера MICR.

Что такое данные MICR на чеке?

Строка символов в нижнем левом углу чека идентифицирует отделение банка, из которого он выдан, номер счета плательщика и номер чека владельца счета в последовательной серии.

Слева в строке отображается следующая информация:

• Девятизначный маршрутный номер, идентифицирующий отделение банка
• 12-значный номер счета, идентифицирующий плательщика.
• Четырехзначный номер чека, указывающий, какой чек из серии использовал владелец счета.

Это выглядит так: 000000000 000000000000 0000

Итог

Распознавание символов с помощью магнитных чернил все еще существует примерно через 70 лет после того, как оно было разработано, потому что оно решило две большие проблемы, с которыми столкнулись банки: обработка чеков должна была быть механизирована, а мошенничество должно было быть затруднено.

Три его компонента, включая маршрутный номер, номер счета и номер чека, вместе являются уникальным идентификатором чека и лица, подписавшего его. Не менее важно и то, что он печатается с использованием специальных чернил и специальных шрифтов, что затрудняет, если не делает невозможным, создание подделок.

python — Генерация списка случайных чисел, сумма которых равна 1

спросил 9 лет, 9 месяцев назад

Изменено 1 год, 2 месяца назад

Просмотрено 108 тысяч раз

• Этот вопрос не является дубликатом Получение N случайных чисел, сумма которых равна M, потому что:
  1. Большинство ответов касаются теории, а не конкретного решения для кодирования в Python для ответа на этот вопрос
  2. Принятый ответ здесь на 5 лет старше, чем один ответ в дубликате, который отвечает на этот вопрос.
  3. Повторяющийся принятый ответ не отвечает на этот вопрос

---

Как составить список из N (скажем, 100) случайных чисел, чтобы их сумма была равна 1?

Я могу составить список случайных чисел с

 r = [random.random() для i в диапазоне (1100)]
 

Как мне изменить это так, чтобы сумма списка равнялась 1 (это для моделирования вероятности).

• питон
• случайный

15

Самое простое решение — взять N случайных значений и разделить их на сумму.

Более общим решением является использование распределения Дирихле. который доступен в numpy.

Путем изменения параметров раздачи можно изменить “случайность” отдельных чисел

 >>> импортировать numpy как np, numpy.random
>>> напечатать np.random.dirichlet (np.ones (10), размер = 1)
[[ 0,01779975 0,14165316 0,01029262 0,168136 0,03061161 0,09046587
   0,19987289 0,13398581 0,03119906 0,17598322]]
>>> напечатать np. random.dirichlet(np.ones(10)/1000.,size=1)
[[ 2,63435230e-115 4,31961290e-209 1.41369771e-212 1.42417285e-188
    0,00000000e+000 5,79841280e-143 0,00000000e+000 9,85329725e-005
    9.99
7e-001 8.37460207e-246]]
>>> напечатать np.random.dirichlet(np.ones(10)*1000.,size=1)
[[ 0,09967689 0,10151585 0,10077575 0,09875282 0,09935606 0,10093678
   0,09517132 0,09891358 0,10206595 0,10283501]]
 

В зависимости от основного параметра распределение Дирихле будет либо давать векторы, все значения которых близки к 1./N, где N — длина вектора, либо давать векторы, где большинство значений векторов будет ~0, и будет одна 1 или что-то среднее между этими возможностями.

РЕДАКТИРОВАТЬ (через 5 лет после первоначального ответа): Еще один полезный факт о распределении Дирихле заключается в том, что вы естественным образом получаете его, если создаете гамма-распределенный набор случайных величин, а затем делите их на их сумму.

17

Лучший способ сделать это — просто составить список из любого количества чисел, а затем разделить их все на сумму. Они совершенно случайны таким образом.

 r = [random.random() для i в диапазоне (1100)]
с = сумма (г)
r = [i/s для i в r]
 

или, как предложил @TomKealy, сохранить сумму и создание в одном цикле:

 rs = []
с = 0
для i в диапазоне (100):
    г = случайный. случайный ()
    с += г
    rs.append(r)
 

Для максимальной производительности используйте numpy :

 import numpy as np
а = np.random.random (100)
а /= а.сум()
 

И вы можете дать случайным числам любое распределение, которое вы хотите, для распределения вероятностей:

 a = np.random.normal(size=100)
а /= а.сум()
 

—- ГРМ —-

 В [52]: %%timeit
    ...: r = [random.random() для i в диапазоне (1100)]
    ...: с = сумма (г)
    ...: r = [i/s для i в r]
   ....:
1000 циклов, лучшее из 3: 231 мкс на цикл
В [53]: %%timeit
   ....: rs = []
   ....: с = 0
   ....: для i в диапазоне (100):
   ....: г = рандом.случайный()
   ....: с += г
   ... .: rs.append(r)
   ....:
10000 циклов, лучший из 3: 39,9 мкс на цикл
В [54]: %%timeit
   ....: а = np.random.random (100)
   ....: а /= а.сумма()
   ....:
10000 циклов, лучший из 3: 21,8 мкс на цикл
 

9

Деление каждого числа на сумму может не дать желаемого распределения. Например, с двумя числами пара x,y = random.random(), random.random() равномерно выбирает точку на квадрате 0<=x<1, 0<=y<1. Деление на сумму «проецирует» эту точку (x, y) на прямую x + y = 1 вдоль линии от (x, y) до начала координат. Точки около (0,5,0,5) будут гораздо более вероятными, чем точки около (0,1,0,9).

Таким образом, для двух переменных x = random.random(), y=1-x дает равномерное распределение вдоль сегмента геометрической прямой.

С 3 переменными вы выбираете случайную точку в кубе и проецируете (радиально, через начало координат), но точки рядом с центром треугольника будут более вероятными, чем точки рядом с вершинами. Полученные точки находятся на треугольнике в плоскости x+y+z. Если вам нужен беспристрастный выбор точек в этом треугольнике, масштабирование бесполезно.

Задача усложняется в n-мерах, но вы можете получить оценку с низкой точностью (но с высокой точностью, для всех вас, поклонников лабораторной науки!) до N, а затем разделив каждое из них на N.

Недавно я придумал алгоритм для небольших n, N. Он должен работать для n = 100 и N = 1 000 000, чтобы давать 6-значные случайные числа. См. мой ответ по адресу:

Создать ограниченные случайные числа?

1

Создайте список, состоящий из 0 и 1, затем добавьте 99 случайных чисел. Отсортируйте список. Последовательные различия будут длинами интервалов, которые в сумме дают 1.

Я не очень хорошо говорю на Python, так что извините меня, если есть более Pythonic способ сделать это. Я надеюсь, что цель ясна:

 случайный импорт
значения = [0,0, 1,0]
для я в диапазоне (99):
    значения.добавлять(случайное.случайное())
значения.sort()
результаты = []
для я в диапазоне (1,101):
    results. append (значения [i] - значения [i-1])
распечатать результаты
 

---

Вот обновленная реализация в Python 3:

 import random
защита сумма_к_одному (n):
    значения = [0.0, 1.0] + [random.random() для _ в диапазоне (n - 1)]
    значения.sort()
    вернуть [значения[i+1] - значения[i] для i в диапазоне (n)]
печать (sum_to_one (100))
 

В дополнение к решению @pjs мы также можем определить функцию с двумя параметрами.

 импортировать numpy как np
по определению сумма_к_х (п, х):
    значения = [0,0, x] + список (np.random.uniform (низкий = 0,0, высокий = x, размер = n-1))
    значения.sort()
    вернуть [значения[i+1] - значения[i] для i в диапазоне (n)]
сумма_к_х(10, 0,6)
Вне:
[0,079058655684546,
 0,04168649034779022,
 0,09897491411670578,
 0,065152293196646,
 0,000544800
2664,
 0,12329662037166766,
 0,09562168167787738,
 0,01641359261155284,
 0,058273232428072474,
 0,020977718663918954]
 

генерирует 100 случайных чисел независимо от диапазона. суммируйте полученные числа, разделите каждое на общее количество.

Если вы хотите иметь минимальный порог для случайно выбранных чисел (т. е. сгенерированные числа должны быть не менее min_thresh ),

 rand_prop = 1 - num_of_values ​​* min_thresh
random_numbers = (np.random.dirichlet (np.ones (10), size = 1) [0] * rand_prop) + min_thresh
 

Просто убедитесь, что у вас есть num_of_values ​​(количество генерируемых значений), чтобы можно было генерировать требуемые числа ( num_values ​​<= 1/min_thesh )

Итак, в основном, мы фиксируем некоторую часть 1 для минимального порога, затем мы создаем случайные числа в другой части. Мы добавляем min_thesh ко всем числам, чтобы получить сумму 1. Например: скажем, вы хотите сгенерировать 3 числа с min_thresh = 0,2. Мы создаем часть для заполнения случайными числами [1 - (0,2x3) = 0,4]. Мы заполним эту часть и добавим 0,2 ко всем значениям, чтобы мы также могли заполнить 0,6.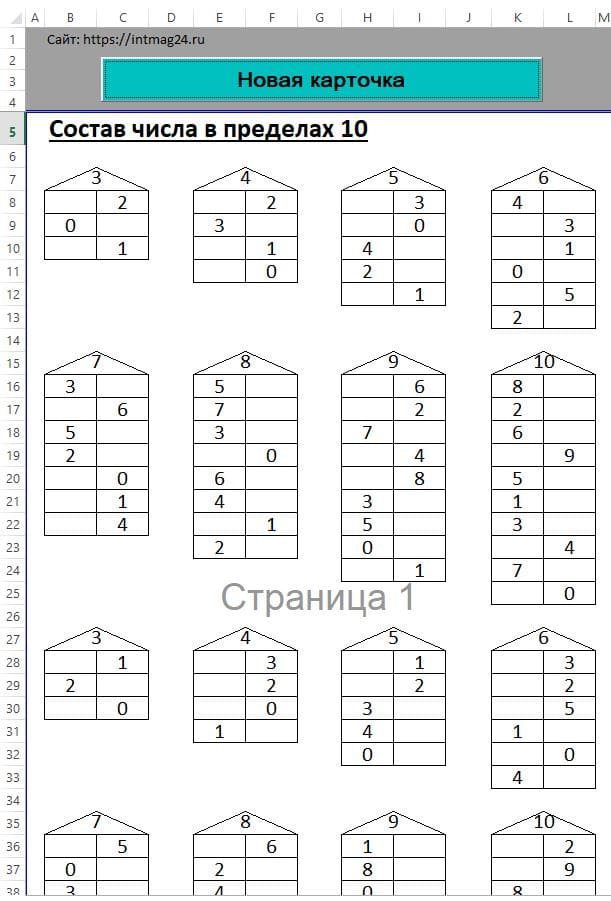

Стандартное масштабирование и сдвиг, используемые в теории генерации случайных чисел. Кредит принадлежит моему другу Джилу Вайшнаву (я не уверен, есть ли у него профиль SO) и @sega_sai.

Альтернативным решением может быть использование random.choice и деление на сумму:

 import random
п = 5
rand_num = [random.choice(range(0,100)) for r in range(n)] # создание случайных целых чисел
rand_num = [i/sum(rand_num) for i in rand_num] # нормализовать их
 

3

Вдохновленный ответом @sega_sai с актуальной и рекомендованной реализацией numpy [март 2022 г.]

 из numpy.random import default_rng
rng = default_rng()
rng.dirichlet (np.ones (10), размер = 1)
>>> массив([[0.01279836, 0,16891858, 0,01136867, 0,17577222, 0,27944229,
        0,06244618, 0,19878224, 0,02481954, 0,01478089, 0,05087103]])
 

Ссылки:

• Документация по случайной выборке Numpy
Документация генератора случайных чисел
• и документация генератора случайных чисел Дирихле

Вы могли бы легко сделать с:

 r. append(1 - sum(r))
 

1

В духе «разделить каждый элемент в списке на сумму списка» это определение создаст список случайных чисел длины = ЧАСТИ, сумма = ИТОГО, с округлением каждого элемента до МЕСТ (или нет):

 случайный импорт
время импорта
ЧАСТИ = 5
ВСЕГО = 10
МЕСТА = 3
def random_sum_split (частей, всего, мест):
    а = []
    для n в диапазоне (частях):
        a.append(случайный.случайный())
    б = сумма (а)
    c = [x/b для x в a]
    д = сумма (с)
    е = с
    если места != Нет:
        e = [округление (x * общее количество мест) для x в c]
    f = e[-(части-1):]
    г = общее количество - сумма (f)
    если места != Нет:
        г = раунд (г, места)
    f.insert(0, г)
    журнал (а)
    журнал (б)
    журнал (с)
    журнал (г)
    журнал (е)
    журнал (f)
    журнал (г)
    возврат f
определить тик():
    если info.tick == 1:
        начало = время.время()
        альфа = random_sum_split (ЧАСТИ, ВСЕГО, МЕСТА)
        бревно('********************')
        log('***** РЕЗУЛЬТАТЫ ******')
        лог('альфа: %s' % альфа)
        log('всего: %. 7f' % сумма(альфа))
        log('детали: %s' % ЧАСТЕЙ)
        журнал('мест: %s' % PLACES)
        конец = время.время()
        log('истекшее: %.7f' % (конец-начало))
 

результат:

 Ожидание...
Успешно сохранено.
[2014-06-13 00:01:00] [0.33561018369775897, 0.4904215932650632, 0.20264927800402832, 0.118862130636748, 0.03107818050878819 ]
[2014-06-13 00:01:00] 1.17862136611
[2014-06-13 00:01:00] [0.28474809073311597, 0.41609766067850096, 0.17193755673414868, 0.10084844382959707, 0.02636824802463 724]
[2014-06-13 00:01:00] 1.0
[2014-06-13 00:01:00] [2,847, 4,161, 1,719, 1,008, 0,264]
[2014-06-13 00:01:00] [2,848, 4,161, 1,719, 1,008, 0,264]
[2014-06-13 00:01:00] 2.848
[2014-06-13 00:01:00] *********************
[2014-06-13 00:01:00] ***** РЕЗУЛЬТАТЫ ******
[2014-06-13 00:01:00] альфа: [2.848, 4.161, 1.719, 1,008, 0,264]
[2014-06-13 00:01:00] всего: 10.0000000
[2014-06-13 00:01:00] частей: 5
[2014-06-13 00:01:00] места: 3
[2014-06-13 00:01:00] прошло: 0,0054131
 

В духе метода pjs:

 a = [0, total] + [random.