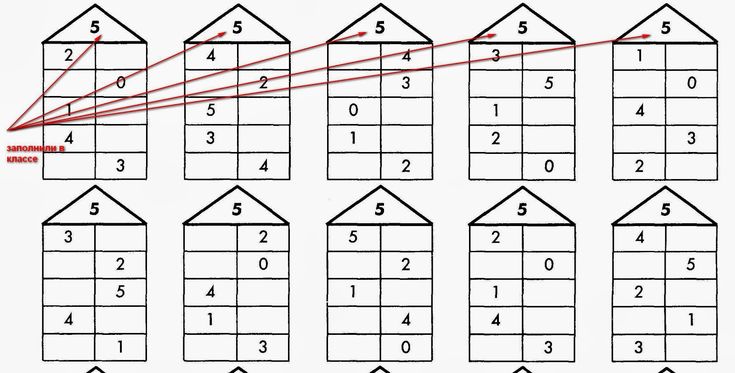
Состав чисел 2 и 3: Состав числа для дошкольников — объяснение состава чисел от 1 до 10

Состав числа из двух чисел

• Предыдущая
• К оглавлению
• Следующая

Главная страница =>библиотека=>оглавление

В плане подготовки детей к деятельности вычисления необходимо познакомить их с составом числа из 2 меньших чисел.
Детей знакомят не только с разложением числа на 2 меньших, но и с получением числа из 2 меньших чисел. Это способствует пониманию детьми особенностей суммы как условного объединения 2 слагаемых.
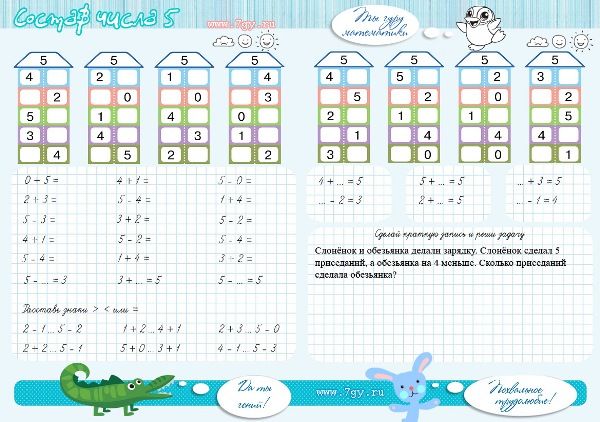
Детям показывают все варианты состава чисел в пределах пятка.
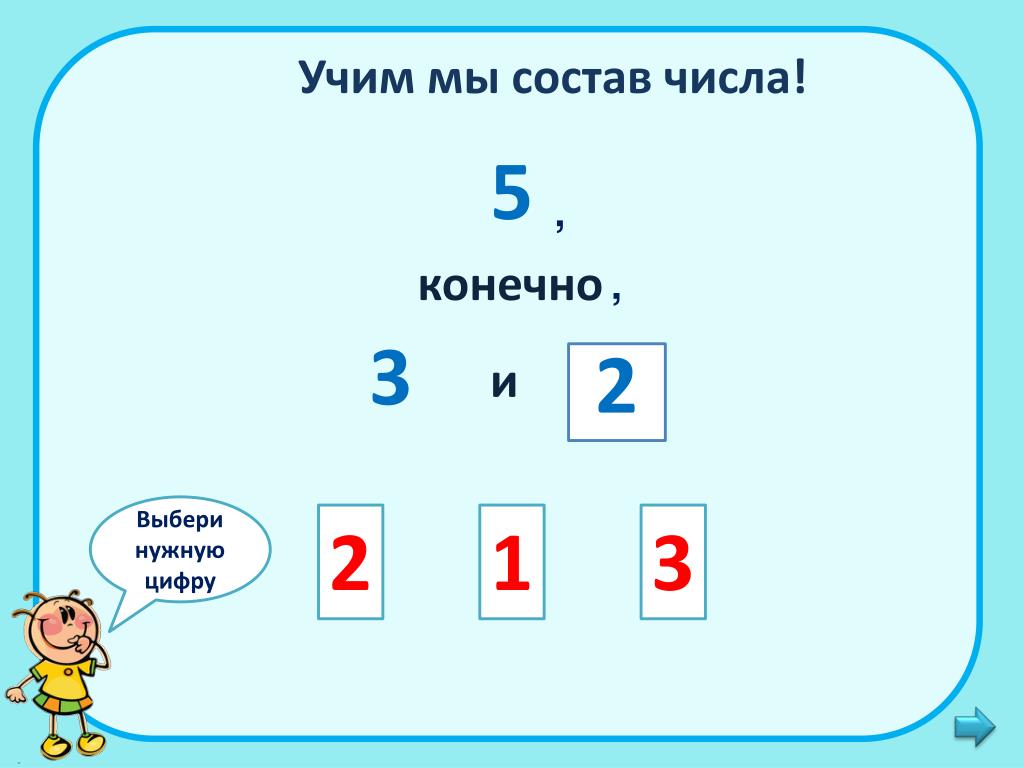
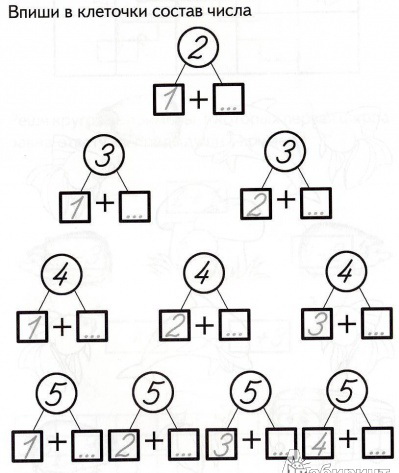
Число 2 — это 1 и 1,
3 —это 2 и 1, 1 и 2,
4 —это 3 и 1, 2 и 2, 1 и 3,
5 — это 4 и 1, 3 и 2, 2 и 3, 1 и 4.
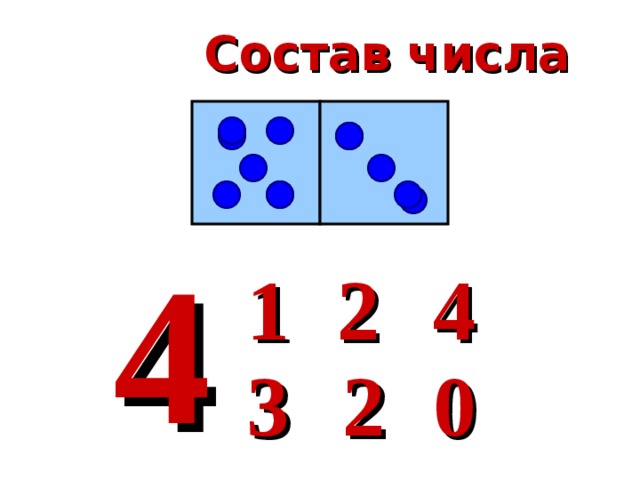
Воспитатель выкладывает на наборном полотне в ряд 3 кружка одного цвета, просит детей сказать, сколько всего кружков, и указывает, что в данном случае группа составлена из 3 кружков красного цвета: 1, 1 и еще 1. «Группу из 3 кружков можно составить и по-другому», — говорит воспитатель и поворачивает третий кружок обратной стороной.

«Как теперь составлена группа?» — спрашивает педагог. Дети отвечают, что группа составлена из 2 кружков красного цвета и 1 кружка синего цвета, а всего — из 3 разноцветных кружков.
Воспитатель делает вывод, что число 3 можно составить из чисел 2 и 1, а 2 и 1 вместе составляют 3. Затем поворачивает обратной стороной второй кружок, и дети рассказывают, что теперь группа составлена из 1 красного и 2 синих кружков.
Обобщая в заключение ответы детей, воспитатель подчеркивает, что число 3 можно составить по-разному: из 2 и 1, из 1 и 2. Данное упражнение наглядно выявляет состав числа, отношение целого и части, поэтому с него целесообразно начинать знакомство детей с составом чисел.
Для закрепления аканий детей о составе числа из 2 меньших чисел используют разнообразные упражнения с предметами и моделями геометрических фигур. Детям предлагают рассказы-задачи, например: «На верхнем проводе сидели 3 ласточки,
1 ласточка пересела на нижний провод. Сколько всего ласточек? Как они теперь сидят? Как они еще могут сидеть?» (Ласточек на наборном полотне пересаживают с провода на провод. ) Или: «Вере подарили 4 карандаша. Она поделилась с Аней. Как она могла разделить карандаши?» С этой же целью дают задания: одному ребенку взять 3 камешка (желудя) в обе руки, а остальным догадаться, сколько камешков у него в каждой руке; разделить группу из 3 (4, 5) игрушек между 2 детьми; нарисовать
2 разновидности фигур, например круги и квадраты, всего 4 фигуры; полезно рассмотреть с детьми числовые фигуры, на которых кружки расчленены на 2 группы.
Выполнив то или иное задание, дети каждый раз рассказывают о том, на какие 2 группы расчленена совокупность, сколько всего предметов в нее входит, и делают обобщение о составе числа из 2 меньших чисел. Например, ребенок говорит: «Я взяла 2 зеленые и 1 желтую ленточку, а всего 3 ленточки. Число 3 можно составить из 2 и 1; 2 и 1 вместе составляют 3».
Важно приучить детей по-разному строить ответы: идти как от частного к общему, так и от общего к частному: «Всего я нарисовал 4 фигуры: 3 квадрата и 1 фигуру овальной формы».
Не менее важно побуждать детей устанавливать отношение между целым и частями, т. е. делать вывод о составе числа: «Число 4 можно составить из 3 и 1; 3 и 1 вместе составляют 4».
Для подведения детей к обобщению им дают такие задания: педагог показывает карточку, на которой изображено от 3 до 5 предметов, но часть их он закрывает и говорит: «На карточке нарисованы 4 зайчика. Угадайте, сколько зайчиков я закрыла». Педагог берет 2 числовые фигуры, одну из них, например с 3 кружками, показывает детям, а вторую поворачивает к ним обратной стороной и спрашивает: «Сколько кружков на перевернутой карточке, если на 2 карточках вместе 5 кружков? Как вы догадались?»
Можно побуждать детей находить в групповой комнате примеры разложения числа на 2 группы. Например, в групповой комнате может оказаться 2 шкафа с игрушками и 1 с пособиями, а всего 3 шкафа; 2 больших мишки и 3 маленьких, а всего 5 мишек и т. п.
Знакомство с составом числа из 2 меньших чисел обеспечивает переход к обучению детей вычислению.

Л.С. Метлина. Математика в детском саду. М.:Просвещение, 1984.

Главная страница =>библиотека=>оглавление

Л.С. Метлина. Математика в детском саду. М.:Просвещение, 1984.

Добавить в закладки:

• Предыдущая
• К оглавлению
• Следующая

Смотрите еще:

• ВЕЛИЧИНА
• ВЕЛИЧИНА
• КОЛИЧЕСТВО И СЧЕТ
• ОБУЧЕНИЕ ДЕТЕЙ ФОРМУЛИРОВКЕ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
• МЕТОДЫ И ПРИЕМЫ ОБУЧЕНИЯ
• ПОДГОТОВИТЕЛЬНАЯ К ШКОЛЕ ГРУППА
• ПРИМЕРНЫЕ КОНСПЕКТЫ ЗАНЯТИИ
• СОСТАВ ЧИСЛА ИЗ 2 ЧИСЕЛ, МЕНЬШИХ ЭТОГО ЧИСЛА
• ПОРЯДКОВОЕ И КОЛИЧЕСТВЕННОЕ ЗНАЧЕНИЕ ЧИСЛА
• ПОКАЗ НЕЗАВИСИМОСТИ ЧИСЛА ПРЕДМЕТОВ ОТ ИХ РАЗМЕРА, ПЛОЩАДИ И ФОРМЫ РАСПОЛОЖЕНИЯ

Конспект урока для 1 класса “Состав числа 3”

Математика 1 класс

Дата:___________________2015г

Подготовил учитель: Шаповалова Н. Т.

Тема: Состав числа 3.

Цели: познакомить учащихся с образованием числа 3 и его графической записью – цифрой 3; продолжать формировать умение детей соотносить числа с соответствующими цифрами; учить писать цифру 3; работать над развитием наблюдательности; прививать детям аккуратность.

Ход урока 1. Организационный момент. 

– Ребята, сегодня урок математики пройдёт под девизом “Больше думай, меньше говори”. Итак, в течение всего урока мы должны думать, а отвлекаться и разговаривать как можно меньше. А теперь давайте поприветствуем друг друга.

1.Этап устного счета.

• 1 2 * 4 5 * 7 8 *

• Назовите число, стоящее за числом 5.

• Назовите число, стоящее перед числом 9.

• Назовите число, стоящее между числами 5 и 7.

• Назовите соседей числа 9.

• Покажите цифру один.

Работа

3. Этап закрепления пройденного материала.

Работа с математическим набором

Выложить 3 треугольника, столько же кругов, квадратов на 2 больше, столько же кругов, кругов на 2 меньше.

 Игра “Скажи наоборот”.

– На прошлом уроке мы изучали число 2. Число 2 символизирует полярность или противопоставление в окружающем мире. Я буду называть слова, а вы будете говорить наоборот. Например, я говорю “хорошо”, а вы отвечаете “плохо”.

У. Свет. ( Тьма)

У. Девочка. (Мальчик)

У. Жизнь. (Смерть)

У. Добро. ( Зло)

У. Вверх. ( Вниз)

У. Правое. (Левое)

У. Прямое. (Кривое)

У. Один.  (Много)

У.  Заполните пропуски.

1*2 2*2 >

( проверка: числовые карточки)

– Как вы рассуждали при поиске знаков действий? Почему выражения записаны в разные столбики?

Игра “Угадай-ка!”

У. Стоит Антошка на одной ножке. Его ищут, а он не откликается. ( Гриб)

У. Покажите цифрой, сколько ножек у гриба.  (Одна)

У. Два конца, два кольца, посередине гвоздик. ( Ножницы)

У. Покажите цифрой, сколько концов у ножниц. Сколько колец у ножниц? Сколько гвоздиков?

4. Физкультминутка.

Солнце глянуло в окошко
Раз, два, три, четыре, пять.
Все мы делаем зарядку,
Надо нам присесть и встать,
Руки вытянем пошире,
1, 2, 3, 4, 5.
И на месте поскакать.
На носок потом на пятку,
Все мы делаем зарядку.

5. Этап усвоения новых знаний.

– Отгадайте загадку

У. У него глаза цветные,
Не глаза, а три огня.
Он по очереди ими,
Сверху смотрит на меня.
Да и как его не знать?
Мы отлично понимаем,
Все, что хочет он сказать.  Светофор.

У. Сколько глаз у светофора? Какого цвета глаза у светофора? Что показывает красный цвет светофора? Что показывает желтый цвет? Что показывает зеленый цвет? Покажите, сколько глаз у светофора.

– Тема сегодняшнего урока – «Состав числа 3». Наша цель познакомиться со всеми способами образования числа 3 и постараться запомнить его состав.

У. Расскажите сами о числе 3 по плану.

План

1. Что у вас в жизни связано с числом 3?
2. Где мы видим, где слышим о числе и цифре 3?
3. Какие художественные произведения связаны с числом 3?

У. Как можно показать число 3?.

– Покажите цифру 3.

Что можно сложить из трех палочек? ( Треугольник, III)

Что можно сложить из четырех палочек? (3)

Практическая работа. На парте должно лежать 3 белых квадрата (1×1 см), одна розовая полоска (1×2 см), одна голубая полоска (1×3 см).

Детям показываю все варианты состава чисел в пределах пятка.

Число 2 – это 1 и 1,
3 – это 2 и 1, 1 и 2,
(4 – это 3 и 1, 2 и 2, 1 и 3, 5 – это 4 и 1, 3 и 2, 2 и 3, 1 и 4.)

Выкладываю на наборном полотне в ряд 3 кружка одного цвета, прошу детей сказать,

– Сколько всего кружков?

( указываю, что в данном случае группа составлена из 3 кружков красного цвета: 1, 1 и еще 1.

– Группу из 3 кружков можно составить и по-другому”, – говорю и поворачиваю третий кружок обратной стороной.

– Как теперь составлена группа?

Дети отвечают, что группа составлена из 2 кружков красного цвета и 1 кружка синего цвета, а всего – из 3 разноцветных кружков.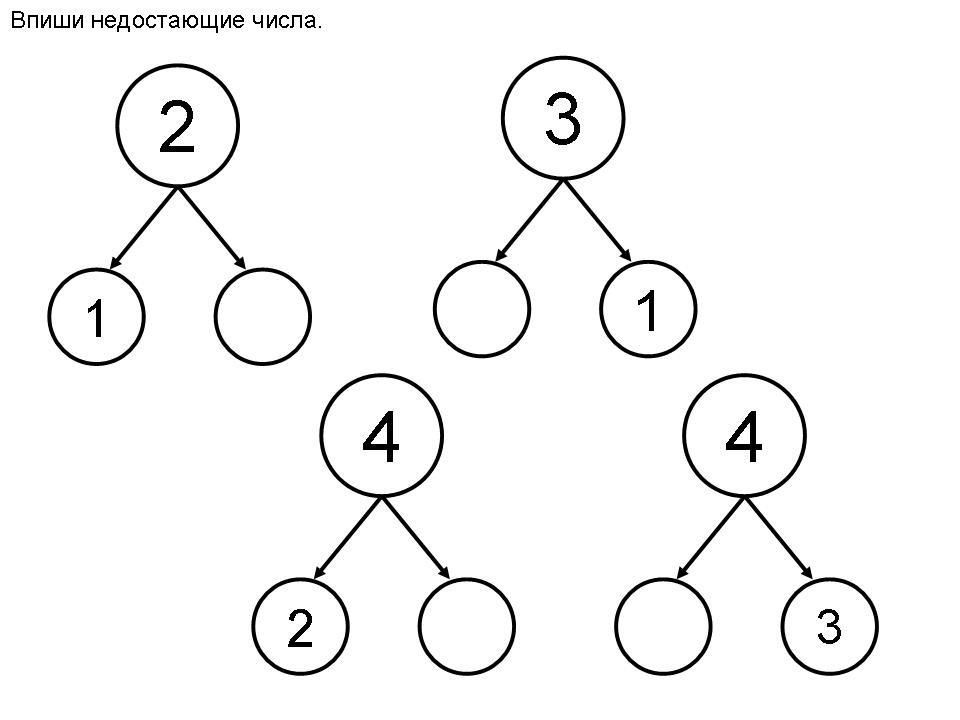

Дети делают вывод, что число 3 можно составить из чисел 2 и 1, а 2 и 1 вместе составляют 3. Затем поворачиваю обратной стороной второй кружок, и дети рассказывают, что теперь группа составлена из 1 красного и 2 синих кружков.

Обобщая в заключение ответы детей, подчеркиваю, что число 3 можно составить по-разному: из 2 и 1, из 1 и 2. Данное упражнение наглядно выявляет состав числа, отношение целого и части, поэтому с него целесообразно начинать знакомство детей с составом чисел.

У. Сравните числа. Ответ обоснуйте с помощью полосок 1 и 2, 2 и 3, 1 и 3.

У. На сколько 1 меньше 2?  

У. Покажите на квадратах 

У. На сколько 1 меньше 3?

Задача на смекалку

Гусятница гнала на рынок гусей,

Старушка какая-то встретилась ей:

– Глаза ослабели , ну просто беда –

Гусей не могу сосчитать никогда:

Двоих за собою передний ведет,

Последний двоих подгоняет вперед,

Один в середине компании всей.

А ну, сосчитай, сколько будет гусей?

6. Гимнастика для глаз (таблица)

7. Этап закрепления новых знаний.

Работа по учебнику

Стр 34 № 3, 4

8. Этап контроля и самоконтроля.

Письмо цифр 1, 2, 3 (самооценка)

Сравнение (сверка с доской)

9. Этап подведения итогов урока.

– Какая у нас была тема урока?

– Что у человека связано с числом и цифрой 3?

– Отгадайте загадку “Трое одним плугом пашут. Что это?”

Заполнение «домиков» (состав числа 3)

10. Этап рефлексии.

– Подойдите к доске и покажите на шкале оценки урока свое отношение к уроку. Сначала подходят те ученики, кому урок понравился, потом те, кому было не очень интересно, затем те, кому на уроке было скучно и неинтересно.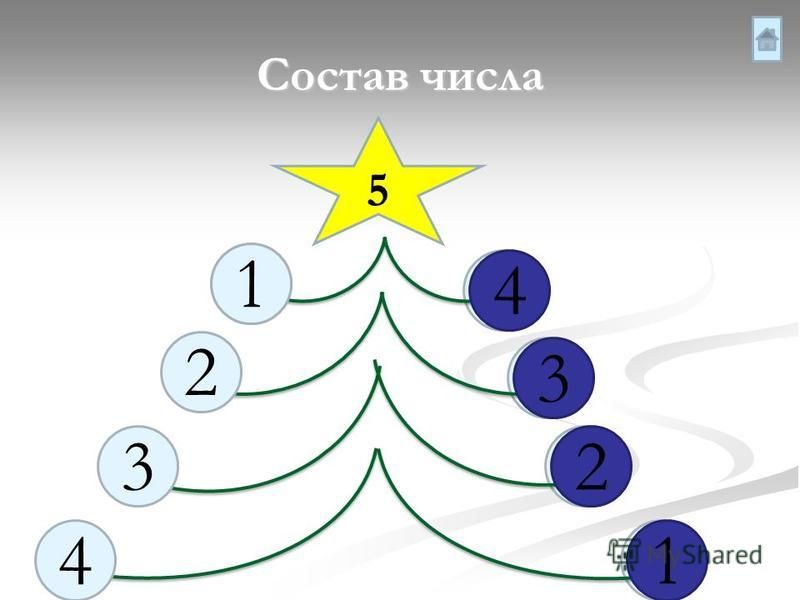

Что такое – состав числа

Что такое состав числа по математике

Давайте разберемся, что такое состав числа? Состав числа — это два числа, сумма которых дает нам исходное число.

Например: 2 + 4 = 6; 6 + 3 = 9; 1 + 1 = 2; 7+ 1 = 8; 8 + 1 = 9; 3 + 3 = 6; 2 + 2 = 4; 6 + 2 = 8; 5 + 1 = 6; 1 + 1 = 2; 1 + 3 = 4; 5 + 4 = 9.

Определим, что такое состав числа

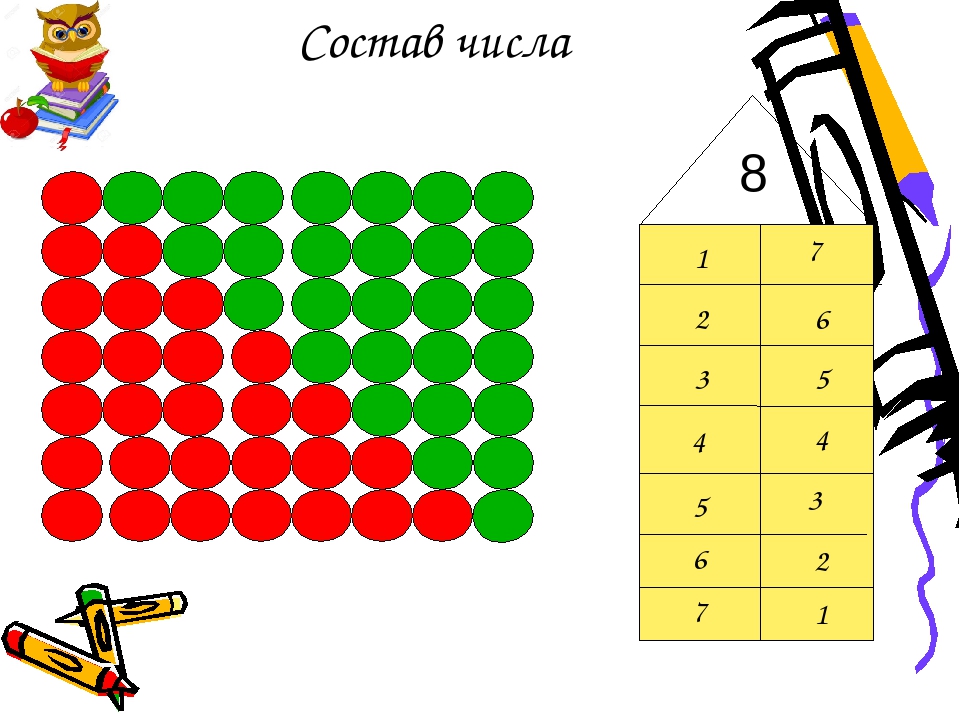
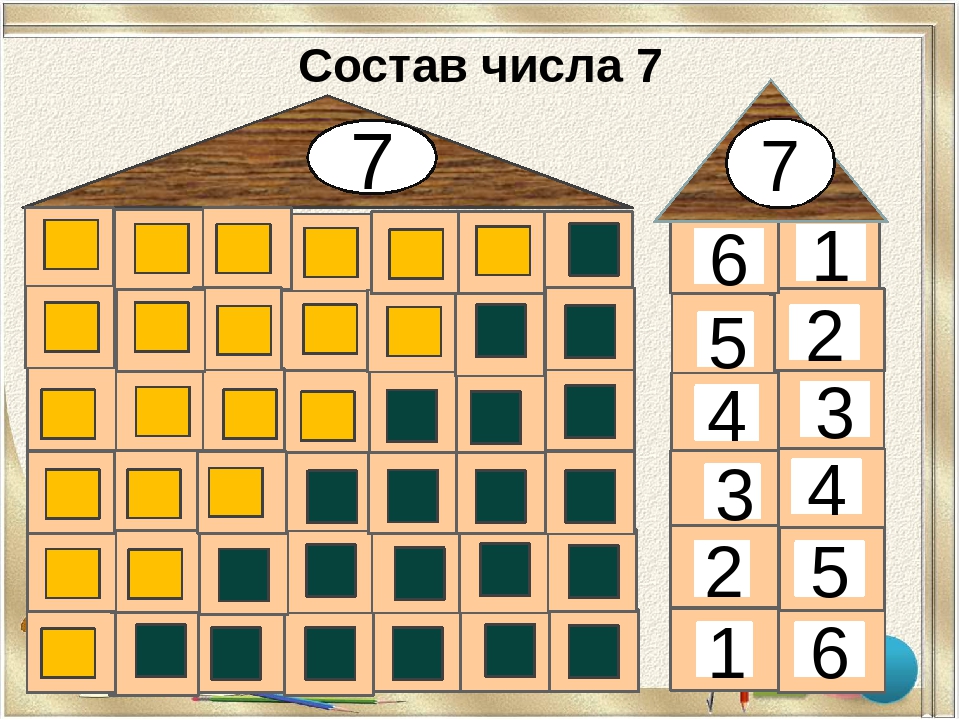
Состав числа – это 2 числа, из которых состоит само число. Например состав числа 7 равен 3 и 4. Также состав числа от 7 может быть равен 2 и 5. Есть и другие варианты.

Другими словами, состав числа – это сумма сотней, десятков, единиц и других составляющих, которое в итоге нам дает само число. Например, число 524 состоит из 5 сотней, 2 десятков и 4 единиц. Каждое число имеет свой класс. Состав числа начинают изучать уже с первого класса. Изначально, детям состав числа объясняют с малых лет на счетных палочках. Так они легче начинают понимать.

Состав числа можно начать обучать ребенка:

На счетных палочках; На бытовых предметах; Использую различные пособия.

Инструкции при изучении состава числа

Для начала, нужно различать значение цифр и чисел. Цифры – это значения, из которых состоит число. Число обозначает количество предметов и так далее. Возьмем на примере 24 конфеты. Число 24 обозначает количество, а само число 24 состоит из цифр 2 и 4. То есть, состав числа 24 равен цифрам 2 и 4.

Для обучения детей состава числа, можно использовать, например счетные палочки. Научим, определят состав числа, например 5. Разделим 5 счетных палочек на 2 палочки и 3 палочки. Разложим палочки по разные стороны. На одной стороне лежит 2 счетные палочки, а на другой 3 счетные палочки. Так начиная с детства, дети изучают состав числа 5, которое например состоит из суммы 2 и 3.

Состав числа — это два числа, сумма которых дает нам исходное число.

Uchi. ru

28.12.2019 6:59:30

2019-12-28 06:59:30

Источники:

Https://uchi. ru/otvety/questions/chto-takoe-sostav-chisla

Состав чисел для дошкольников » /> » /> . keyword { color: red; }

Что такое состав числа по математике

Блог для родителей Помощь Соглашение с пользователем О проекте

—>

Победитель Международного заочного конкурса «Надежда планеты» под эгидой Международной славянской академии наук, образования, искусств и культуры (МСА).

Соглашение с пользователем.

Iqsha. ru

04.10.2020 17:56:42

2020-10-04 17:56:42

Источники:

Https://iqsha. ru/ilove/post/part-numbers-for-preschoolers

Состав числа до 10. Как объяснить ребенку? (Часть 1: состав чисел 2, 3, 4) » /> » /> .keyword { color: red; }

Что такое состав числа по математике

— будет очень хорошо, если к моменту рассмотрения этой темы ребенок уже сможет записывать цифры и числа самостоятельно.

ВАЖНОЕ ЗАМЕЧАНИЕ ВЗРОСЛОМУ: обучение по этой теме нужно проводить постепенно, анализируя предыдущие результаты.

Для того, чтобы объяснить ребенку состав числа, удобно использовать пуговицы, фишки, каштаны или монеты, также необходимы лист бумаги и ручка.

Состав числа 2.

Положите перед ребенком 2 пуговицы и спросите – как можно разложить эти две пуговицы на 2 кучки?

Ответ ребенка: «В каждой кучке будет по одной пуговице».

Подтвердите это и сделайте на листе такую запись:

Покажите эту запись ребенку и скажите, что так мы записали состав числа 2.

Из этой записи видно, что в каждой кучке у нас оказалось по одной пуговице.

Состав числа 3.

Вопрос к ребенку: «На какие две кучки можно разложить три пуговицы?»

Ответ: «В одной кучке одна пуговица, в другой — две».

Можно их также поменять местами.

Сделайте запись на листе и покажите ребенку:

Так мы записали состав числа 3. Поскольку записи повторяют друг друга (просто кучки поменяли местами), вычеркиваем лишнюю запись.

Объяснять эту запись надо так: «Для того, чтобы получить число 3, надо к двум прибавить один. И это нужно запомнить».

Самые простые задания на состав чисел 2 и 3:

Число на крыше здесь указывает, сколько точек должно быть на каждом «этаже». Значит, в левом задании нужно дорисовать одну точку и вписать единицу, в среднем задании нужно дорисовать две точки и вписать двойку, а в последнем задании ребенок должен дорисовать одну точку и вписать единицу.

Если ребенок имеет понятие о сложении и вычитании, из записи состава числа 2 можно сделать такие выводы:

2 – здесь целое, 1 и 1 – части.

Для числа 3 – аналогично.

Здесь 3 – целое, а 1 и 2 – части.

Знание состава числа может помочь и в решении примеров «с окошками».

1 + □ = 2
2 + □ = 3
1 + □ = 3

2 — □ = 1
3 — □ = 2
3 — □ = 1

Материал желательно повторить на следующем занятии. При правильных ответах ребенка можно «двигаться дальше».

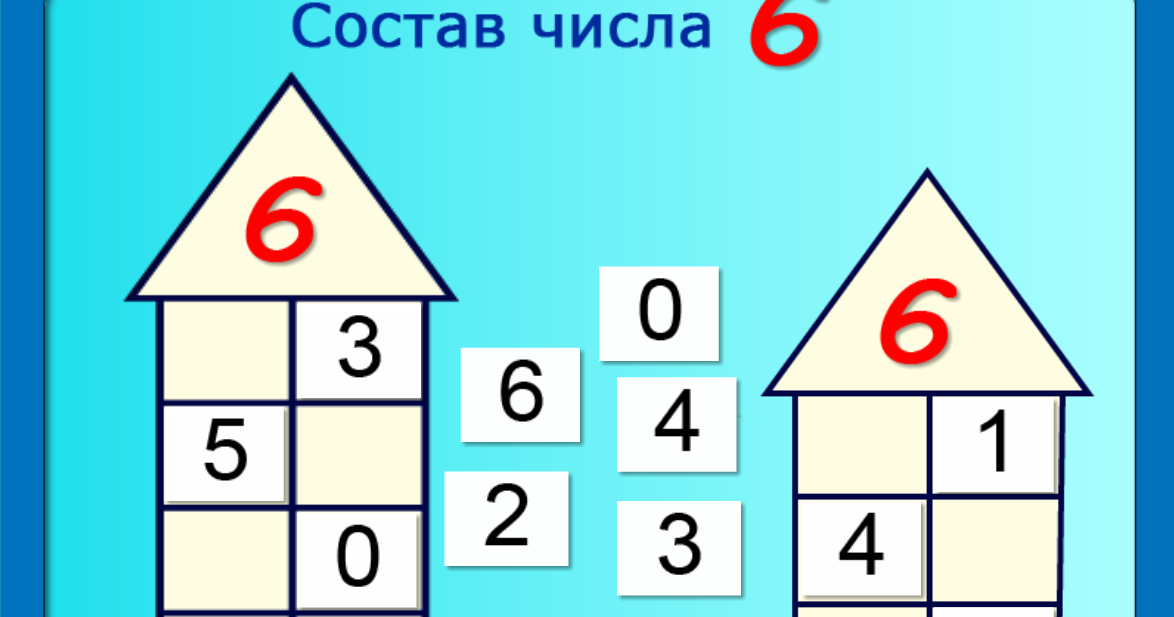
Состав числа 4.

Вопрос ребенку: «На какие две кучки можно разложить 4 пуговицы? Давай будем с тобой откладывать по одной пуговице и делать запись состава числа 4».

Записи в первом столбце и последнем столбце повторяют друг друга. Надо вычеркнуть лишнее:

Эту упрощенную запись числа 4 и нужно запомнить. Из этой записи можно сделать такие выводы:

Предложите ребенку выполнить задание и примеры аналогичные рассмотренным ранее:

Напомним, что число на крыше обозначает сколько точек должно быть нарисовано на каждом «этаже». В левом примере нужно нарисовать 3 точки и вписать число 3.

Числа справа внизу обозначают то количество точек, которое дорисовал ребенок.

На основании состава числа 4 ребенок может решить следующие примеры «с окошками»:

3 + □ = 4
2 + □ = 4
□ + 1 = 4

4 — □ = 3
4 — □ = 1
4 — □ = 2

Если ребенку трудно самостоятельно решать такие примеры, даже имея перед собой подсказки, попробуйте задать ему такие вопросы:

Сколько нужно добавить к трем пуговицам, чтобы стало четыре?

Сколько нужно отложить от четырех пуговиц, чтобы их стало три?

Знания по теме «состав числа» можно закреплять и на прогулке или в других в других обстоятельствах вне учебных занятий.

Число на крыше здесь указывает, сколько точек должно быть на каждом этаже.

Strana-znaek. ru

31.12.2018 14:25:23

2018-12-31 14:25:23

Источники:

Http://strana-znaek. ru/obuchenie-matematike/stati/index. php? ID=81

Комбинации функций

Комбинации функций

Графер Калькулятор Возврат Справка Точечная диаграмма

---

Содержание: Эта страница соответствует § 1.6 (стр. 138) текста.

Предполагаемые проблемы из сообщения

р. 145 #1, 2, 5, 6, 9, 12, 13, 14, 19, 23, 24, 26, 31, 35, 36, 39, 41, 44, 45, 49, 52, 55, 57, 61, 62, 65, 68

Арифметические комбинации

Состав функций

---

Арифметические комбинации

Сумма, разность, произведение и частное двух функций f и g определяются следующим образом.

Сумма	(f + g)(x) = f(x) + g(x)
Разница	(f – g)(x) = f(x) – g(x)
Продукт	(f * г) (х) = f (х) * г (х)
Частное	(f/g)(x) = f(x)/g(x)

Пример 1. Пусть f(x) = x ² + 3x -7 и g(x) = 4x +5.

(f + g)(3) = f(3) + g(3) = 11 + 17 = 28,

(f/g)(2) = f(2)/g(2) = 3/13,

Обратите внимание, что мы могли бы оценить функцию f + g при любом числе, вычисляя f и g по отдельности и добавляя результаты, как мы сделали выше для 3. Однако мы обычно упрощаем формулу для f + g, комбинируя аналогичные члены, затем используйте эту новую формулу для вычисления функции суммы.

(f + g)(x) = f(x) + g(x) = (x ² + 3x -7 ) + (4x +5) = x ² + 7x – 2.

Итак, (f + g)(3) = 3 ² +7*3 -2 = 28, что согласуется с нашим предыдущим ответом.

Примечание о доменах:

Как правило, арифметическая комбинация двух функций f и g при любом x, находящемся в области определения как f, так и g, с одно исключение . Частное f/g не определено при значениях x, где g равно 0.

Например, если f(x) = 2x + 1 и g(x) = x – 3, то доамины f+g, f-g и f*g являются действительными числами. Область определения f/g — это набор всех действительных чисел, кроме 3, поскольку g(3) = 0..

.

Пример 2. Пусть f(x) = x ² – 9 и g(x) = x – 3 . Упрощать формула для f/g.

(f / g)(x) = f(x) / g(x) = (x ² – 9)/(x – 3) = (x + 3)(x – 3)/(x – 3) ) = х + 3.

Существует технический момент, относящийся к этому примеру, который часто игнорируется на уроках предварительного исчисления.

(f/g)(x) равно не равной функции h(x) = x + 3, так как f/g не определена при x = 3, а h является. На самом деле нет ничего плохого в том, чтобы думать о f / g как об одном и том же h, но это разные функции.

92-9)/(x-3) в поле f и введите x+3 в поле ч. В окне расчета введите h(3) и нажмите Enter. Возвращается ответ 6. Теперь оцените f в 3, набрав f(3) и нажав клавишу ввода.

Упражнение 1:

Найдите f + g, f – g, f * g и f / g для f(x) = x ² – 3x + 2, g(x) = x – 2. Примечание: f можно разложить на множители. Мы рассмотрим факторинг многочленов в следующем разделе. Ответ

* часто не пишется для продуктов, поэтому вы увидите, что fg используется для обозначения продукта f*g.

Вернуться к содержанию

Состав функций

Композиция двух функций f и g определяется формулой (f ° g)(x) = f(g(x)).

Пример 3. Пусть f(x) = x ² – x + 1 и g(x) = 3x – 2 .

(f°g)(5) = f(g(5)) = f(13) = 157.

(g ° f)(5) = g(f(5)) = g(21) = 61.

Примечания к составу:

Не путайте состав (f°g) с продуктом (f*g). Композиция (f°g)(x) означает «оценить g в x, затем оценить f в результате g(x)”. Произведение (f*g)(x) означает “оценить f и g в x и умножить результаты».

Композиция не коммутативна. Другими словами, f°g вообще не равно g°f. (см. пример выше.)

В то время как (f ° g)(x) можно вычислить при любом x, вычислив g в x, а затем вычислив f в результате, мы часто желаю упростить формулу композиции.

Пример 4 . Используйте те же функции, что и в последнем примере, f(x) = x ² – x + 1 , и г(х) = 3х – 2 .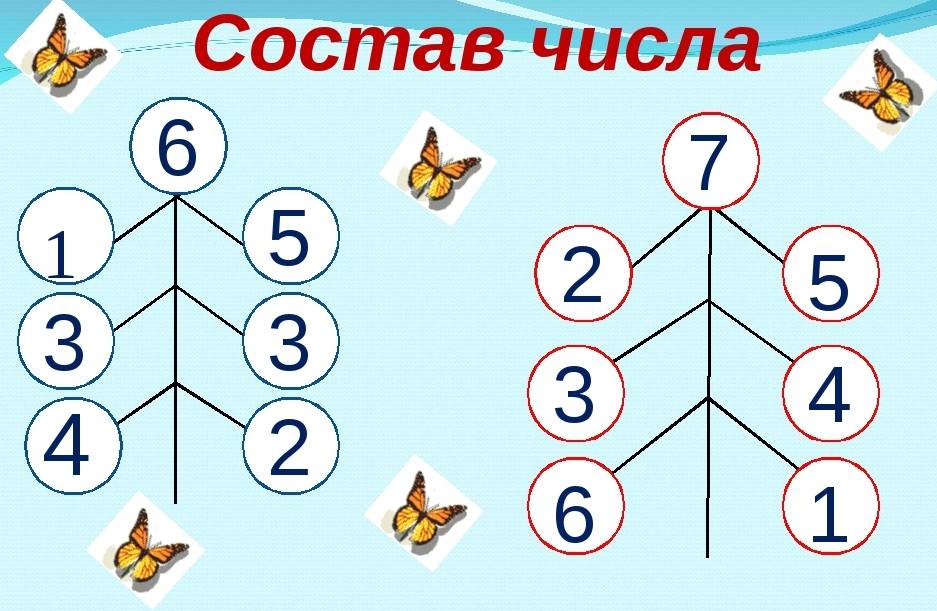

(f°g)(x) = f(3x – 2) = (3x – 2) ² – (3x – 2) + 1 = (9x ² -12x + 4)-(3x-2) +1 = 9x ² – 15х + 7.

(g ° f)(x) = g(x ² – x + 1) = 3(x ² – x + 1) -2 = 3x ² – 3x + 1.

Используя эти формулы, мы получаем те же результаты, что и в предыдущем примере:

(f°g)(5) = 9*25-15*5+7=157.

(г°ж)(5) = 3*25 -3*5 +1 = 61,

Упражнение 2:

Пусть f(x) = x ² -3x + 4 и пусть g(x) = x + 1.

(a) Упростите формулу для f(g(x)).

(b) Проверьте свой ответ с помощью Java-калькулятора следующим образом:

Откройте калькулятор , введите формулы для f и g и в поле h. Введите упрощенный формула для f(g(x)).

В окне вычислений оцените f(g(5)) и h(5). Если формула, которую вы ввели в h, является правильным упрощением f(g(x)), то эти два значения должны совпадать.

Попробуйте провести эксперимент с двумя значениями, отличными от 5.

Вернуться к содержанию

---

Графер Калькулятор Возврат Справка Точечная диаграмма

Примеры композиции функций — Math Insight

Композиция функций — это комбинация двух функций для формирования новой функции. Просто берут выходные данные первой функции и используют их в качестве входных данных для второй функции. Этот процесс работает до тех пор, пока вторая функция будет принимать выходные данные первой функции в качестве своих входных данных (т. е. домен второй функции должен содержать диапазон первой функции). Композицию можно проиллюстрировать, используя метафору функциональной машины, соединяя функциональные машины вместе.

Здесь мы демонстрируем процесс составления функций на ряде примеров.

Пример 1: Функция бабушки

Функция матери $m$ — это функция, которая принимает человека $x$ в качестве входных данных и выводит мать этого человека $m(x)$. Мы можем сформировать бабушкину функцию $g$, скомпоновав материнскую функцию с самой собой. Применение этой комбинированной функции к человеку $x$ выведет мать матери человека $x$, которую мы могли бы обозначить как $g(x) = m(m(x))$. Функция бабушки хорошо определена, потому что диапазон функции матери $m$ — это множество женщин, у которых были дети, и это множество является подмножеством домена функции матери, то есть множества всех людей. У нас не возникнет проблем с применением материнской функции дважды. (Мы проигнорируем проблему происхождения нашего вида и не будем беспокоиться о таких людях, как Адам и Ева).

Пример 2

Пусть $f$ — функция от множества действительных чисел к множеству действительных чисел, которую мы запишем как $f: \R \to \R$. 2}.$$ 92}$. Композиция $f \circ m$ не будет работать, потому что $m$ выводит людей, а $f$ ожидает на входе действительное число. Если вы подумаете о метафоре функциональной машины, люди, выходящие из функциональной машины $m$, застрянут во входной воронке функциональной машины $f$. Точно так же композиция $m \circ f$ не сработает, так как материнская функция $m$ не будет знать, что делать с числами, которые выводит $f$.

Пример 5

Пусть $f$ — функция $f: \R_{\ge 0} \to \R$, где область определения $\R_{\ge 0}$ — множество неотрицательных действительных чисел , $\R_{\ge 0} = \{x \in \R : x \ge 0\}$. Можем ли мы определить композицию $f \circ g$, где $g$ — функция $g: \R \to \R$? Домен $f$ — это неотрицательные действительные числа, но домен $g$ — это целая вещественная строка. Не зная диапазона $g$, мы не можем исключить возможность того, что $g$ может выводить отрицательное число.

Если бы $g(x)$ могло быть отрицательным числом для некоторого входа $x$, то $f$ не знала бы, что делать с входом $g(x)$, и композиция $f \circ g $ не будет определен. 3+1}$ не определяется этим определением $g$. Чтобы сделать эту композицию четко определенной, нам пришлось бы изменить домен $g$ (например, исключить входные данные меньше -1), чтобы убедиться, что она никогда не выводит отрицательное число. 92+1}$ для всех действительных входов $x$.

Функции

\(\def\d{\displaystyle} \def\курс{Математика 228} \ новая команда {\ f} [1] {\ mathfrak # 1} \ новая команда {\ s} [1] {\ mathscr # 1} \def\N{\mathbb N} \def\B{\mathbf{B}} \def\circleA{(-.5,0) круг (1)} \ деф \ Z {\ mathbb Z} \def\circleAlabel{(-1.5,.6) узел[выше]{$A$}} \def\Q{\mathbb Q} \def\circleB{(.5,0) круг (1)} \def\R{\mathbb R} \def\circleBlabel{(1.5,.6) узел[выше]{$B$}} \def\C{\mathbb C} \def\circleC{(0,-1) круг (1)} \def\F{\mathbb F} \def\circleClabel{(.5,-2) узел[справа]{$C$}} \def\А{\mathbb А} \def\twosetbox{(-2,-1.5) прямоугольник (2,1.5)} \ деф \ Х {\ mathbb Х} \def\threesetbox{(-2,-2.5) прямоугольник (2,1.5)} \def\E{\mathbb E} \ деф \ О {\ mathbb О} \def\U{\mathcal U} \def\pow{\mathcal P} \деф\инв{^{-1}} \def\nrml{\triangleleft} \ деф \ ст {:} \ деф \ ~ {\ широкая тильда} \def\rem{\mathcal R} \def\sigalg{$\sigma$-алгебра } \def\Гал{\mbox{Гал}} \def\iff{\leftrightarrow} \def\If{\Leftrightarrow} \ деф \ земля {\ клин} \def\И{\bigwedge} \защита\вход{\вход} \def\AAnd{\d\bigwedge\mkern-18mu\bigwedge} \def\Ви{\bigvee} \def\VVee{\d\Vee\mkern-18mu\Vee} \ деф \ имп {\ стрелка вправо} \def\Imp{\Rightarrow} \def\Fi{\Leftarrow} \def\var{\mbox{var}} \def\Th{\mbox{Th}} \защита\вход{\вход} \def\sat{\mbox{Sat}} \def\con{\mbox{Con}} \def\iffmodels{\bmodels\models} \def\dbland{\bigwedge \!\!\bigwedge} \def\дом{\mbox{дом}} \def\rng{\mbox{диапазон}} \def\isom{\cong} \DeclareMathOperator{\wgt}{wgt} \newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}} \ новая команда {\ va} [1] {\ vtx {выше} {# 1}} \ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}} \ новая команда {\ vr} [1] {\ vtx {право} {# 1}} \ новая команда {\ vl} [1] {\ vtx {слева} {# 1}} \renewcommand{\v}{\vtx{выше}{}} \def\circleA{(-. 5,0) круг (1)} \def\circleAlabel{(-1.5,.6) узел[выше]{$A$}} \def\circleB{(.5,0) круг (1)} \def\circleBlabel{(1.5,.6) узел[выше]{$B$}} \def\circleC{(0,-1) круг (1)} \def\circleClabel{(.5,-2) узел[справа]{$C$}} \def\twosetbox{(-2,-1.4) прямоугольник (2,1.4)} \def\threesetbox{(-2.5,-2.4) прямоугольник (2.5,1.4)} \def\ansfilename{практика-ответы} \def\shadowprops{{fill=black!50,shadow xshift=0.5ex,shadow yshift=0.5ex,path fading={круг с размытым краем 10 процентов}}} \ новая команда {\ hexbox} [3] { \def\x{-cos{30}*\r*#1+cos{30}*#2*\r*2} \def\y{-\r*#1-sin{30}*\r*#1} \рисовать (\х,\у) +(90:\r) — +(30:\r) — +(-30:\r) — +(-90:\r) — +(-150:\r) — +(150: \r) — цикл; \draw (\x,\y) узел{#3}; } \renewcommand{\bar}{\overline} \newcommand{\card}[1]{\left| #1 \справа|} \newcommand{\twoline}[2]{\begin{pmatrix}#1 \\ #2 \end{pmatrix}} \новая команда{\lt}{<} \новая команда{\gt}{>} \newcommand{\amp}{&} \)

¶

Функция — это правило, которое назначает каждому входу ровно один выход. Мы называем выход изображением входа. 2 + 3\text{.}\) Здесь домен и кодовый домен являются одним и тем же набором ( натуральные числа). Правило таково: возьмите ваши входные данные, умножьте их на себя и прибавьте 3. Это работает, потому что мы можем применить это правило к каждому натуральному числу (каждому элементу домена), и результатом всегда будет натуральное число (элемент кодомена) . Однако обратите внимание, что не каждое натуральное число на самом деле является выходом (нет способа получить 0, 1, 2, 5 и т. д.). Набор натуральных чисел равный на самом деле выводит , называется диапазоном функции (в данном случае диапазоном является \(\{3, 4, 7, 12, 19, 28, \ldots\}\text{,}\) все натуральные числа, которые на 3 больше полного квадрата).

Ключевым моментом, который делает правило фактически функцией , является то, что имеется ровно один выход для каждого входа. То есть важно, чтобы правило было хорошим правилом. Какой выход мы назначаем входу 7? Для любой конкретной функции может быть только один ответ.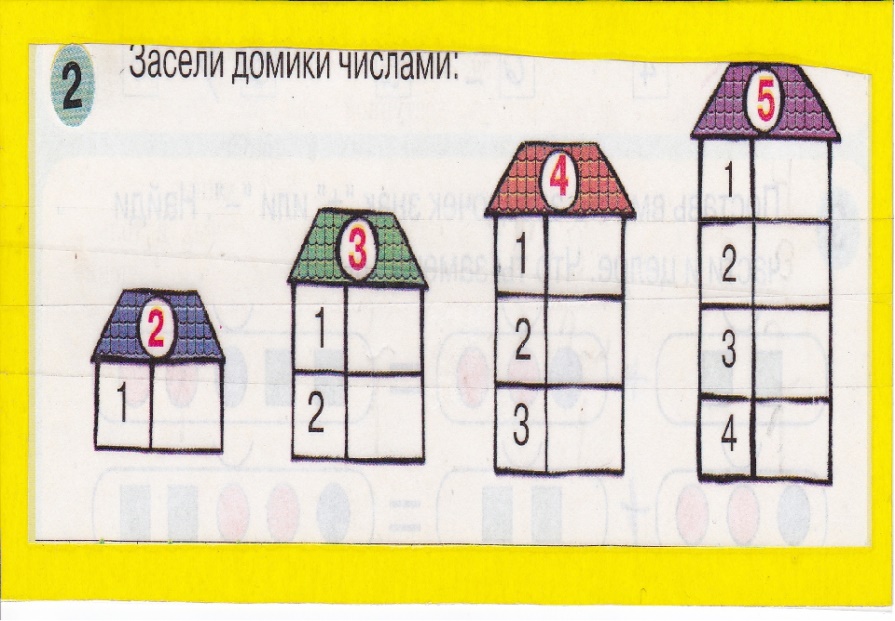

Описание правила может сильно различаться. Мы могли бы просто дать список изображений каждого входа. Вы также можете описать функцию с помощью таблицы или графика или словами.

Пример 0.4.1

Ниже приведены все примеры функций:

1. \(f:\Z \to \Z\), определяемый \(f(n) = 3n\text{.}\) Домен и кодовый домен являются набором целых чисел. Однако диапазон — это только набор целых чисел, кратных 3.
2. \(g: \{1,2,3\} \to \{a,b,c\}\), определяемое как \(g(1) = c\text{,}\) \(g(2) = a\) и \(g(3) = a\text{.}\) Домен — это набор \(\{1,2,3\}\text{,}\) кодовый домен — это набор \( \{a,b,c\}\), а диапазон – это набор \(\{a,c\}\text{.}\) Обратите внимание, что \(g(2)\) и \(g(3) \) являются одним и тем же элементом домена кода. Это нормально, поскольку каждый элемент домена по-прежнему имеет только один выход.

3. \(h:\{1,2,3\} \to \{1,2,3\}\) определяется следующим образом:

   Это означает, что функция \(f\) отправляет 1 в 2, 2 в 1 и 3 в 3: просто следуйте за стрелками.

Стрелочная диаграмма, используемая для определения вышеприведенной функции, может быть очень полезна при визуализации функций. Мы часто будем работать с функциями с 90 117 конечными 90 120 доменами, поэтому такое изображение часто бывает более полезным, чем традиционный график функции. График функции в примере 3 выше будет выглядеть так:

Было бы абсолютно НЕПРАВИЛЬНО соединять точки или пытаться подогнать их под какую-то кривую. В домене всего три элемента. Кривая предполагает, что область содержит весь интервал действительных чисел. Помните, мы больше не занимаемся исчислением!

Поскольку мы так часто будем использовать функции с небольшими доменами и кодоменами, давайте примем некоторые обозначения, с которыми немного легче работать, чем в примерах 2 и 3 выше. Все, что нам нужно, — это какой-то четкий способ обозначения образа каждого элемента в домене. Фактически, написание таблицы значений сработало бы идеально:

\(х\)	0	1	2	3	4
\(f(x)\)	3	3	2	4	1

Мы еще больше упростим это, записав это как матрицу с каждым входом непосредственно над его выходом:

\begin{уравнение*} f = \begin{pmatrix}0 \amp 1 \amp 2\amp 3 \amp 4 \\ 3 \amp 3 \amp 2 \amp 4 \amp 1\end{pmatrix} \end{уравнение*}

Обратите внимание, что это всего лишь обозначения, а не тот тип матрицы, который вы найдете в классе линейной алгебры (например, нет смысла выполнять операции с этими матрицами или уменьшать их по строкам).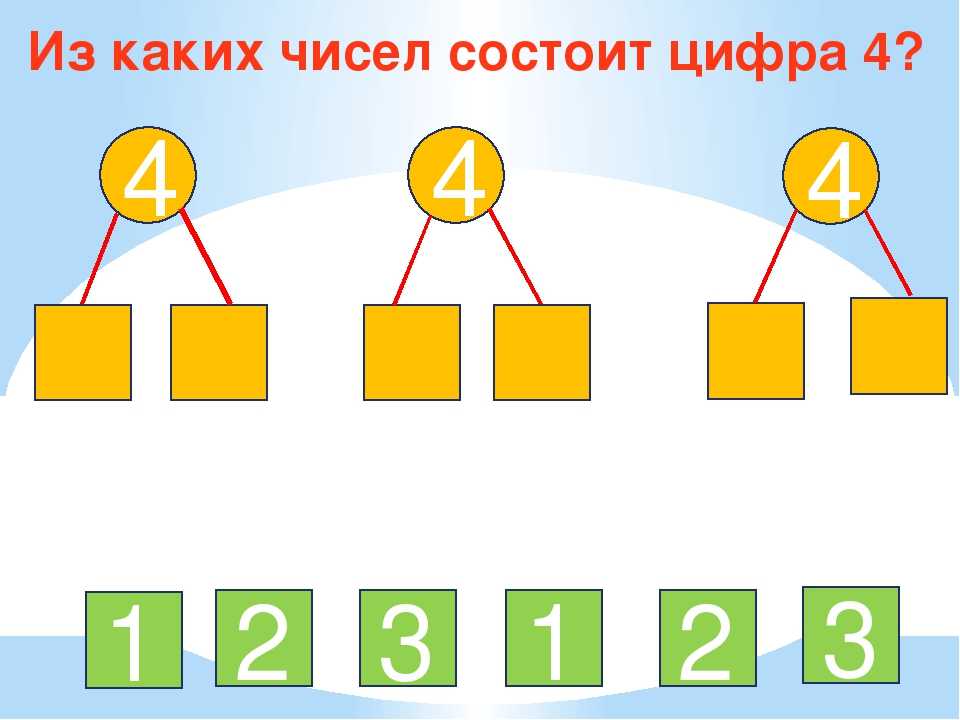

Важно знать, как определить, является ли правило функцией или нет. В этом может помочь рисование стрелочных диаграмм.

Пример 0.4.2

Какая из следующих диаграмм представляет функцию? Пусть \(X = \{1,2,3,4\}\) и \(Y = \{a,b,c,d\}\text{.}\)

Решение

\(f\) — это функция. То же самое и с \(g\text{.}\). Нет проблем с тем, что элемент кодового домена не является изображением какого-либо входа, и нет проблем с тем, что \(a\) из кодового домена является изображением обоих 2 и 3 из домена. Мы могли бы использовать нашу двухстрочную запись, чтобы записать их как

. \begin{уравнение*} f= \begin{pmatrix} 1 \amp 2 \amp 3 \amp 4 \\ d \amp a \amp c \amp b \end{pmatrix} \qquad g = \begin{pmatrix} 1 \amp 2 \amp 3 \amp 4 \\ d \amp a \amp a \amp b \end{pmatrix}. \end{уравнение*}

Однако \(h\) НЕ является функцией. На самом деле он не работает по двум причинам. Во-первых, элемент 1 из домена не был сопоставлен ни с одним элементом из кодового домена. Во-вторых, элемент 2 из домена был сопоставлен более чем с одним элементом из кодового домена (\(a\) и \(c\)). Обратите внимание, что любой из этих проблем достаточно, чтобы сделать правило не функцией. В общем, ни одно из следующих отображений не является функциями:

Также может быть полезно подумать о том, как вы будете писать двухстрочную нотацию для \(h\text{.}\) У нас будет что-то вроде:

\begin{уравнение*} h=\begin{pmatrix} 1 \amp 2 \amp 3 \amp 4 \\ \amp a,c? \amp d \amp b\end{pmatrix}. \end{уравнение*}

Нет ничего ниже 1 (плохо), и нам нужно было поставить более одного объекта под 2 (очень плохо). С правилом, которое на самом деле является функцией, двухстрочная запись всегда будет «работать».

Подраздел Сюръекции, инъекции и биекции

¶

Теперь мы переходим к изучению специальных свойств, которыми могут обладать функции, а могут и не быть.

В приведенных выше примерах вы, возможно, заметили, что иногда есть элементы кодового домена, которые не входят в диапазон.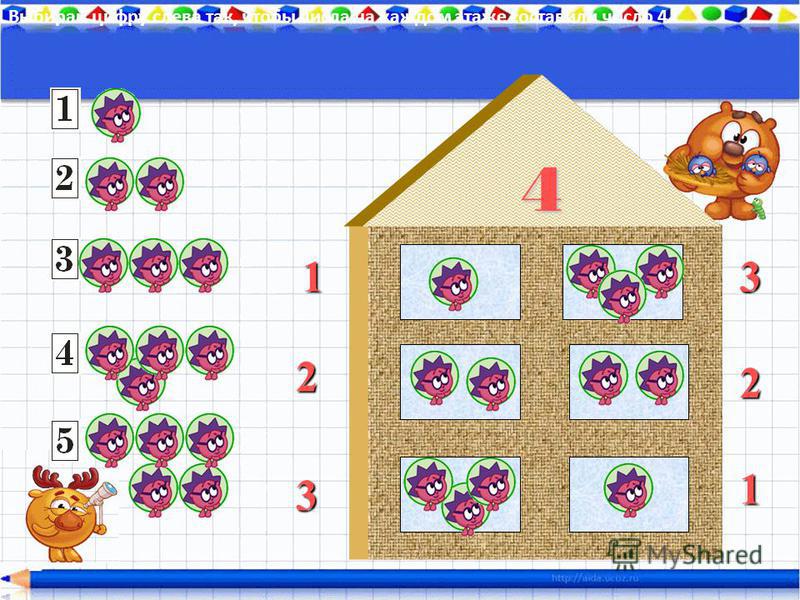 Когда такого рода вещи не бывает (то есть, когда все в кодовом домене находится в диапазоне), мы говорим, что функция на или что функция отображает домен на кодовый домен. Эта терминология должна иметь смысл: функция помещает домен (полностью) поверх кодового домена. Причудливый математический термин для обозначения онтофункции — это сюръекция , и мы говорим, что онтофункция — это сюръективная функция.

На фото:

Пример 0.4.3

Какие функции сюръективны (т. е. онто)?

1. \(f:\Z \to \Z\), определяемый как \(f(n) = 3n\text{.}\)
2. \(g: \{1,2,3\} \to \{a,b,c\}\) определяется как \(g = \begin{pmatrix}1 \amp 2 \amp 3 \\ c \amp а \amp а \end{pmatrix}\text{.}\)

3. \(h:\{1,2,3\} \to \{1,2,3\}\) определяется следующим образом:

Решение

1. \(f\) не сюръективно. В домене кода есть элементы, которые не входят в диапазон. Например, никакое \(n \in \Z\) не отображается в число 1 (правило говорит, что \(\frac{1}{3}\) будет отправлено в 1, но \(\frac{1 {3}\) не входит в домен). На самом деле диапазон функции равен \(3\Z\) (целое число, кратное 3), что не равно \(\Z\text{.}\)
2. \(g\) не сюръективно. Не существует \(x \in \{1,2,3\}\) (домен), для которого \(g(x) = b\text{,}\), поэтому \(b\text{,}\ ), который находится в домене кода, не входит в диапазон. Обратите внимание, что элемент из домена кода «отсутствует» в нижней строке матрицы.
3. \(h\) сюръективно. Каждый элемент кодового домена также находится в этом диапазоне. Ничто в домене кода не пропущено.

Чтобы быть функцией, правило не может назначать один элемент домена двум или более различным элементам домена кода. Однако мы видели, что обратное допустим : функция может назначить один и тот же элемент домена кода двум или более разным элементам домена. Когда это не встречается (то есть, когда каждый элемент кодового домена является изображением не более чем одного элемента домена), тогда мы говорим, что функция взаимно однозначна . Опять же, эта терминология имеет смысл: мы отправляем не более одного элемента из домена одному элементу из домена кода. Один вход на один выход. Причудливый математический термин для взаимно однозначной функции — это число 9.0365 впрыск . Мы называем взаимно однозначными функциями инъективными функциями.

На фото:

Пример 0.4.4

Какие функции являются инъективными (т. е. взаимно однозначными)?

1. \(f:\Z \to \Z\), определяемый как \(f(n) = 3n\text{.}\)
2. \(g: \{1,2,3\} \to \{a,b,c\}\) определяется как \(g = \begin{pmatrix}1 \amp 2 \amp 3 \\ c \amp а \amp а \end{pmatrix}\text{.}\)

3. \(h:\{1,2,3\} \to \{1,2,3\}\) определяется следующим образом:

Решение

1. \(f\) инъективно. Каждому элементу в кодовом домене назначается не более 90 117 и не более 90 120 одного элемента из домена. Если \(x\) кратно трем, то только \(x/3\) отображается в \(x\text{. }\). Если \(x\) не кратно 3, то существует нет ввода, соответствующего выводу \(x\text{.}\)
2. \(g\) не инъективен. Оба входа \(2\) и \(3\) назначаются выходу \(a\text{.}\) Обратите внимание, что есть элемент из кодового домена, который появляется более одного раза в нижней строке матрицы.
3. \(h\) инъективно. Каждый выход является выходом только один раз.

Из приведенных выше примеров должно быть ясно, что существуют функции, которые являются сюръективными, инъективными, обеими или ни одной из них. В случае, когда функция является одновременно взаимно однозначной и на (инъекция и сюръекция), мы говорим, что функция является биекцией или что функция является биективной функцией.

ПодразделОбратное изображение

¶

При обсуждении функций у нас есть обозначения для разговора об элементе домена (скажем, \(x\)) и соответствующем ему элементе в домене кода (мы пишем \(f(x)\text{,}\), который — это образ \(x\)). Также было бы неплохо начать с какого-нибудь элемента кодового домена (скажем, \(y\)) и рассказать о том, какой элемент или элементы (если они есть) из домена являются изображением. Мы могли бы написать «те \(x\) в домене, что \(f(x) = y\text{,}\)», но это слишком много. Вот некоторые обозначения, чтобы сделать нашу жизнь проще.

Предположим, что \(f:X \to Y\) является функцией. Для \(y \in Y\) (элемент кодового домена) мы пишем \(f\inv(y)\) для представления набора всех элементов в домене \(X\), которые отправляются в \(y\text{.}\) То есть \(f\inv(y) = \{x \in X \st f(x) = y\}\text{.}\) Мы говорим, что \( f\inv(y)\) – это полный прообраз \(y\) под \(f\text{.}\)

ВНИМАНИЕ: \(f\inv(y)\) не является обратной функцией! Обратные функции существуют только для биекций, но \(f\inv(y)\) определено для любой функции \(f\text{.}\) Точка: \(f\inv(y)\) – это множество , а не элемент домена.

Пример 0.4.5

Рассмотрим функцию \(f:\{1,2,3,4,5,6\} \to \{a,b,c,d\}\), заданную числом

\begin{уравнение*} f = \begin{pmatrix}1 \amp 2 \amp 3 \amp 4 \amp 5 \amp 6 \\ a \amp a \amp b \amp c \amp c \amp c\end{pmatrix}. \end{уравнение*} 92 = 2\text{.}\) Таких целых чисел нет, поэтому \(g\inv(3) = \emptyset\text{.}\)

Наконец, \(g\inv(10) = \{- 3, 3\}\), так как \(g(-3) = 10\) и \(g(3) = 10\text{.}\)

Так как \(f\inv(y)\) является set, имеет смысл запросить \(\card{f\inv(y)}\text{,}\) количество элементов в домене, которые сопоставляются с \(y\text{.}\)

Пример 0.4.7

Найдите функцию \(f:\{1,2,3,4,5\} \to \N\) такую, что \(\card{f\inv(7)} = 5\text{.}\)

Решение

Есть только одна такая функция. Нам нужно, чтобы пять элементов домена отображались в число \(7 \in \N\text{.}\). Поскольку в домене всего пять элементов, все они должны отображаться в 7. Таким образом,

\begin{уравнение*} f = \begin{pmatrix}1 \amp 2 \amp 3 \amp 4 \amp 5 \\ 7 \amp 7 \amp 7 \amp 7 \amp 7\end{pmatrix}. \end{уравнение*}

Определения функций

• Функция — это правило, которое назначает каждый элемент набора, называемого доменом , ровно одному элементу второго набора, называемого кодовым доменом .

• Обозначение: \(f:X \to Y\) – это наш способ сказать, что функция вызывается \(f\text{,}\) областью определения является множество \(X\text{,}\) и кодовый домен – это набор \(Y\text{.}\)

• Чтобы указать правило для функции с небольшим доменом, используйте двухстрочную нотацию , написав матрицу, в которой каждый выход находится непосредственно под соответствующим входом, например:

  \begin{уравнение*} f = \begin{pmatrix}1 \amp 2 \amp 3 \amp 4 \\ 2 \amp 1 \amp 3 \amp 1 \end{pmatrix}. \end{уравнение*}

• \(f(x) = y\) означает, что элемент \(x\) домена (вход) назначается элементу \(y\) кодомена. Мы говорим, что \(y\) является выходом. В качестве альтернативы мы называем \(y\) изображение \(x\) под \(f\) .

• Диапазон является подмножеством кодового домена. Это набор всех элементов, которые функция присваивает хотя бы одному элементу предметной области. То есть диапазон — это набор всех выходов.

• Функция является инъективной ( инъекцией или взаимно однозначной ), если каждый элемент кодомена является выходом для не более одного элемента из домена.

• Функция является сюръективной ( сюръекция или на ), если каждый элемент кодового домена является результатом по крайней мере одного элемента домена.

• Биекция — это функция, которая одновременно является инъекцией и сюръекцией. Другими словами, если каждый элемент домена кода является выходом , то ровно один элемент домена .

• Изображение элемента \(x\) в домене — это элемент \(y\) в домене кодов, с которым отображается \(x\). То есть образ \(x\) при \(f\) есть \(f(x)\text{.}\)

• полный прообраз элемента \(y\) в домене кодов, записанный как \(f\inv(y)\text{,}\), представляет собой набор всех элементов в домене, которые назначены к \(y\) по функции.

ПодразделУпражнения

¶

1

Выпишите все функции \(f: \{1,2,3\} \to \{a,b\}\) (используя двухстрочную запись). Сколько их там? Сколько инъективных? Сколько сюръективных? Сколько их обоих?

Решение

Имеется 8 различных функций. В двухстрочном обозначении это:

\begin{уравнение*} f = \begin{pmatrix} 1 \amp 2 \amp 3 \\ a \amp a\amp a \end{pmatrix} \quad f = \begin{pmatrix} 1 \amp 2 \amp 3 \\ b \amp b \amp b \end{pmatrix} \end{уравнение*} \begin{уравнение*} f = \begin{pmatrix} 1 \amp 2 \amp 3 \\ a \amp a\amp b \end{pmatrix} \quad f = \begin{pmatrix} 1 \amp 2 \amp 3 \\ a \amp b \amp a \end{pmatrix} \quad f = \begin{pmatrix} 1 \amp 2 \amp 3 \\ b \amp a\amp a \end{pmatrix} \end{уравнение*} \begin{уравнение*} \quad f = \begin{pmatrix} 1 \amp 2 \amp 3 \\ b \amp b \amp a \end{pmatrix} \quad f = \begin{pmatrix} 1 \amp 2 \amp 3 \\ b \ amp a\amp b \end{pmatrix} \quad f = \begin{pmatrix} 1 \amp 2 \amp 3 \\ a \amp b \amp b \end{pmatrix} \end{уравнение*}

Ни одна из функций не является инъективной.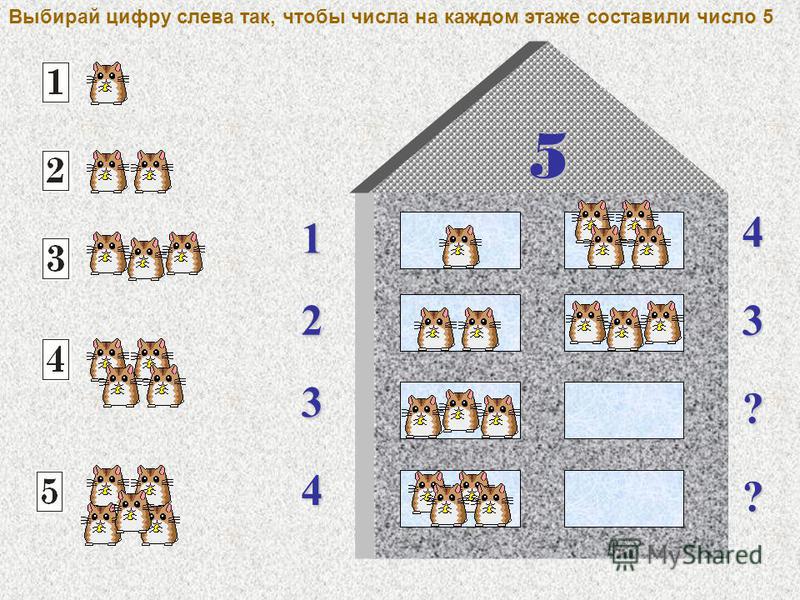 Ровно 6 функций сюръективны. Никакие функции не являются обоими (поскольку здесь нет инъективных функций).

2

Выпишите все функции \(f: \{1,2\} \to \{a,b,c\}\) (в двухстрочном представлении). Сколько их там? Сколько инъективных? Сколько сюръективных? Сколько их обоих?

Решение

Имеется 9 функций: у вас есть выбор из трех выходных данных для \(f(1)\text{,}\) и для каждой у вас есть три варианта выходных данных \(f(2)\text{ .}\) Из этих функций 6 инъективны, 0 сюръективны и 0 являются обеими:

\begin{уравнение*} f = \twoline{1 \amp 2}{a\amp a} \quad f = \twoline{1 \amp 2}{b \amp b} \quad f = \twoline{1 \amp 2}{c \amp в} \end{уравнение*} \begin{уравнение*} f = \twoline{1 \amp 2}{a\amp b} \quad f = \twoline{1 \amp 2}{a \amp c} \quad f = \twoline{1 \amp 2}{b \amp в} \end{уравнение*} \begin{уравнение*} f = \twoline{1 \amp 2}{b \amp a} \quad f = \twoline{1 \amp 2}{c \amp a} \quad f = \twoline{1 \amp 2}{c \amp б} \end{уравнение*}

3

Рассмотрим функцию \(f:\{1,2,3,4,5\} \to \{1,2,3,4\}\), заданную в таблице ниже:

\(х\)	1	2	3	4	5
\(f(x)\)	3	2	4	1	2

1. Является ли \(f\) инъективным? Объяснять.

2. Является ли \(f\) сюръективным? Объяснять.

3. Запишите функцию, используя двухстрочную запись.

4

Рассмотрим функцию \(f:\{1,2,3,4\} \to \{1,2,3,4\}\), представленную на графике ниже.

1. Является ли \(f\) инъективным? Объяснять.

2. Является ли \(f\) сюръективным? Объяснять.

3. Запишите функцию, используя двухстрочную запись.

5

Для каждой приведенной ниже функции определите, является ли функция инъективной и является ли она сюръективной.

1. \(f:\N \to \N\), заданное выражением \(f(n) = n+4\text{.}\)
2. \(f:\Z \to \Z\), заданное выражением \(f(n) = n+4\text{.}\)
3. \(f:\Z \to \Z\), заданное выражением \(f(n) = 5n – 8\text{.}\)
4. \(f:\Z \to \Z\), заданное выражением \(f(n) = \begin{cases}n/2 \amp \text{, если } n \text{ четно} \\ (n+1 )/2 \amp \text{ если } n \text{ нечетно} . \end{cases}\)

Решение

1. \(f\) инъективно, но не сюръективно (поскольку 0, например, никогда не является выходом).
2. \(f\) инъективно и сюръективно. В отличие от предыдущего вопроса, каждое целое число является выходом (целого числа на 4 меньше него).
3. \(f\) инъективно, но не сюръективно (например, 10 не на 8 меньше кратного 5).
4. \(f\) не инъективно, но сюръективно. Каждое целое число является выходом (например, дважды), но некоторые целые числа являются выходом более чем одного входа: \(f(5) = 3 = f(6)\text{.}\)

6

Пусть \(A = \{1,2,3,\ldots,10\}\text{.}\) Рассмотрим функцию \(f:\pow(A) \to \N\), заданную \(f (B) = |B|\text{.}\) То есть \(f\) принимает подмножество \(A\) в качестве входных данных и выводит мощность этого набора.

1. Является ли \(f\) инъективным? Докажите свой ответ.

2. Является ли \(f\) сюръективным? Докажите свой ответ.

3. Найти \(f\inv(1)\text{.}\)

4. Найти \(f\inv(0)\text{.}\)

5. Найти \(f\inv(12)\text{.}\)

Решение

1. \(f\) не является инъективным. Чтобы доказать это, мы должны просто найти два разных элемента домена, которые отображаются на один и тот же элемент кодомена. Поскольку \(f(\{1\}) = 1\) и \(f(\{2\}) = 1\text{,}\), мы видим, что \(f\) не является инъективным.
2. \(f\) не сюръективно. Наибольшее подмножество \(A\) – это само \(A\), а \(|A| = 10\text{.}\) Таким образом, никакое натуральное число больше 10 никогда не будет выходным.
3. \(f\inv(1) = \{\{1\}, \{2\}, \{3\}, \ldots \{10\}\}\) (множество всех одноэлементных подмножеств \(А\)).
4. \(f\inv(0) = \{\emptyset\}\text{.}\) Обратите внимание, было бы неправильно писать \(f\inv(0) = \emptyset\) – это утверждало бы, что существует не является входом, который имеет 0 в качестве выхода.
5. \(f\inv(12) = \emptyset\text{,}\), так как нет подмножеств \(A\) с мощностью 12,

7

Пусть \(A = \{n \in \N \st 0 \le n \le 999\}\) — множество всех чисел, состоящих из трех и менее цифр. Определите функцию \(f:A \to \N\) как \(f(abc) = a+b+c\text{,}\), где \(a\text{,}\) \(b\text {,}\) и \(c\) — это цифры числа в \(A\text{. }\). Например, \(f(253) = 2 + 5 + 3 = 10\text{.} \)

1. Найти \(f\inv(3)\text{.}\)

2. Найти \(f\inv(28)\text{.}\)

3. Является \(f\) инъективным. Объяснять.

4. Является \(f\) сюръективным. Объяснять.

Решение

1. \(f\inv(3) = \{003, 030, 300, 012, 021, 102, 201, 120, 210, 111\}\)
2. \(f\inv(28) = \emptyset\) (поскольку наибольшая сумма трех цифр равна \(9+9+9 = 27\))

3. Часть (а) доказывает, что \(f\) не является инъективным. Выход 3 назначен на 10 различных входов.

4. Часть (b) доказывает, что \(f\) не является сюръективным. Существует элемент домена кода (28), который не назначен никаким входам.

8

Пусть \(f:X\to Y\) — некоторая функция. Предположим, \(3 \in Y\text{.}\) Что вы можете сказать о \(f\inv(3)\), если знаете,

1. \(f\) инъективен? Объяснять.
2. \(f\) сюръективно? Объяснять.
3. \(f\) биективно? Объяснять.

Решение

1. \(|f\inv(3)| \le 1\text{.}\) Другими словами, либо \(f\inv(3)\) — это пустое множество, либо множество, содержащее ровно один элемент. Инъективные функции не могут иметь два элемента из области определения, оба из которых соответствуют 3.
2. \(|f\inv(3)| \ge 1\text{.}\) Другими словами, \(f\inv(3)\) — это множество, содержащее хотя бы один элемент, а возможно, и больше. Сюръективные функции должны иметь какое-то отображение на 3.
3. \(|f\inv(3)| = 1\text{.}\) Существует ровно один элемент из \(X\), который отображается в 3, поэтому \(f\inv(3)\) является набор, содержащий этот один элемент.

9

Найдите множество \(X\) и функцию \(f:X \to \N\) так, чтобы \(f\inv(0) \cup f\inv(1) = X\text{.}\)

Решение

\(X\) действительно может быть любым набором, если \(f(x) = 0\) или \(f(x) = 1\) для каждого \(x \in X\text{. }\ ) Например, \(X = \N\) и \(f(n) = 0\) работают.

10

Какой вывод вы можете сделать о множествах \(X\) и \(Y\), если знаете …

1. есть инъективная функция \(f:X\to Y\text{?}\) Объясните.

2. есть сюръективная функция \(f:X\Y\text{?}\) Объясните.

3. существует биективная функция \(f:X\Y\text{?}\) Объясните.

11

Предположим, что \(f:X \to Y\) является функцией. Что из следующего возможно? Объяснять.

1. \(f\) инъективен, но не сюръективен.
2. \(f\) сюръективно, но не инъективно.
3. \(|X| = |Y|\) и \(f\) инъективно, но не сюръективно.
4. \(|X| = |Y|\) и \(f\) сюръективно, но не инъективно.
5. \(|X| = |Y|\text{,}\) \(X\) и \(Y\) конечны, а \(f\) инъективно, но не сюръективно.
6. \(|X| = |Y|\text{,}\) \(X\) и \(Y\) конечны, а \(f\) сюръективно, но не инъективно.

12

Пусть \(f:X \to Y\) и \(g:Y \to Z\) — функции. Мы можем определить композицию из \(f\) и \(g\) как функцию \(g\circ f:X\to Z\), которой является образ каждого \(x\in X\). \(g(f(x))\text{.}\) То есть подставьте \(x\) в \(f\text{,}\), а затем подставьте результат в \(g\) (точно так же, как композиция по алгебре и вычислениям).

1. Если \(f\) и \(g\) оба инъективны, то должен ли \(g\circ f\) быть инъективным? Объяснять.
2. Если \(f\) и \(g\) оба сюръективны, то должен ли \(g\circ f\) быть сюръективным? Объяснять.
3. Предположим, что \(g\circ f\) инъективен. Что вы можете сказать о \(f\) и \(g\text{?}\)? Объясните.
4. Предположим, что \(g\circ f\) сюръективен. Что вы можете сказать о \(f\) и \(g\text{?}\)? Объясните.

Подсказка

Работа с примерами. Что, если \(f = \twoline{1\amp 2 \amp 3}{a \amp a \amp b}\) и \(g = \twoline{a\amp b \amp c}{5 \amp 6 \ усилитель 7}\текст{?}\)

13

Рассмотрим функцию \(f:\Z \to \Z\), заданную выражением \(f(n) = \begin{cases}n+1 \amp \text{, если }n\text{ четно} \\ n -3 \amp \text{ если }n\text{ нечетное} . \end{cases}\)

1. Является ли \(f\) инъективным? Докажите свой ответ.

2. Является ли \(f\) сюръективным? Докажите свой ответ.

Раствор

1. \(f\) инъективно.

   Доказательство

   Пусть \(x\) и \(y\) элементы области определения \(\Z\text{.}\) Предположим, что \(f(x) = f(y)\text{.}\) Если \ (x\) и \(y\) оба четны, тогда \(f(x) = x+1\) и \(f(y) = y+1\text{.}\) Поскольку \(f( x) = f(y)\text{,}\) имеем \(x + 1 = y + 1\), откуда следует, что \(x = y\text{.}\) Аналогично, если \(x\) и \(y\) оба нечетны, то \(x – 3 = y-3\), так что снова \(x = y\text{.}\) Единственная другая возможность состоит в том, что \(x\) является четным \(у\) нечетно (или наоборот). Но тогда \(x + 1\) было бы нечетным, а \(y – 3\) было бы четным, так что не может быть, чтобы \(f(x) = f(y)\text{.}\) Следовательно, если \ (f(x) = f(y)\), тогда мы имеем \(x = y\text{,}\), что доказывает инъективность \(f\).

2. \(f\) сюръективно.

   Доказательство

   Пусть \(y\) элемент домена кода \(\Z\text{.}\). Мы покажем, что существует элемент \(n\) домена (\(\Z\)) такой, что \ (f(n) = y\text{.}\) Возможны два случая: во-первых, если \(y\) четно, то пусть \(n = y+3\text{.}\) Поскольку \(y \) четно, \(n\) нечетно, поэтому \(f(n) = n-3 = y+3-3 = y\) по желанию. Во-вторых, если \(y\) нечетно, то пусть \(n = y-1\text{.}\) Поскольку \(y\) нечетно, \(n\) четно, поэтому \(f(n ) = n+1 = y-1+1 = y\) по мере необходимости. Поэтому \(f\) сюръективен.

14

В конце семестра учитель выставляет буквенные оценки каждому из своих учеников. Это функция? Если да, то какие множества составляют домен и кодовый домен, и является ли функция инъективной, сюръективной, биективной или ни той, ни другой?

Решение

Да, это функция, если правильно выбрать домен и кодомен. Домен будет набором учеников, а кодовый домен будет набором возможных оценок. Функция почти наверняка не является инъективной, потому что вполне вероятно, что два студента получат одинаковую оценку.