Ш это твердый или мягкий: Звук ш – твердый или мягкий? – Всё о детях – беременность, воспитание, уроки для детей

Содержание

«Согласный, глухой,твёрдый звук [ш].Буквы Ш, ш »

Тема урока:

«Согласный, глухой,

твёрдый звук [ш].

Буквы Ш, ш »

УЧИТЕЛЬ НАЧАЛЬНЫХ КЛАССОВ

АЛОЕВА МАДИНА ХАСАНОВНА

Педагогическая цель	1.Познакомить учащихся с буквами Ш ш; 2.Совершенствовать навыки чтения , работы с текстом; 3.Закрепить знания о звонких и глухих парных согласных; 4.Развивать фонематический слух, внимание, память, речь, мышление;
Тип урока	Изучение нового материала
Планируемые результаты (предметные)	1. Умение выделять в тексте ключевые слова, слова с разделительным мягким знаком; 2.Распростронять и упрощать предложения; 3.Умение работать в паре, в группе; классифицировать слова; понимать смысл предложения.
Личностные результаты	Имеют личностное отношение к полученным знаниям, желание и умение применять их на практике
Универсальные учебные действия	Регулятивные: планируют свое действие в соответствии с поставленной задачей и условиями ее реализации. Познавательные: общеучебные – осознанно и произвольно строят речевые высказывания в устной форме; логические – выполняют фонетический разбор слов. Коммуникативные: умеют в коммуникации строить понятные для партнера высказывания
Основное содержание темы, понятия и термины	Буква Ш ш ; печатная, письменная буквы; предложение; фонетический разбор слов , работа над дикцией «чистоговорка», игра « доскажи словечко», «звуки перепутались»
Образовательные ресурсы	Серии сюжетных картин, предметные картинки, опорная схема, карточки для индивидуальной работы, лента букв, презентация из слайдов, ребусы, электронное приложение к учебнику В. Г. Горецкого, В.А.Кирюшкина, Л.А. Виноградской, учебник «Азбука», поурочные разработки

Ход урока:

I. Организация начала урока

1. Приветствие. Проверка готовности к уроку

2. Ребята, у нас сегодня гости. Поприветствуйте их. Садитесь.

3.А сейчас мы покажем нашим гостям, что мы уже настоящие ученики.

(Учитель начинает стихотворение, а дети отвечают).

Вы пришли сюда… УЧИТЬСЯ.

Не лениться, а … ТРУДИТЬСЯ.

Работать как? … СТАРАТЕЛЬНО.

А слушать как?… ВНИМАТЕЛЬНО.

Если хочешь отвечать… РУКУ НЕ ЗАБУДЬ ПОДНЯТЬ!

Если спросят?. .. НАДО ВСТАТЬ, ГРОМКО, ЧЁТКО ОТВЕЧАТЬ!

II. Включение в учебную деятельность.

1.Игра «Перекличка букв»

( у детей на партах лежат карточки с названиями всех изученных букв)

-Выйдите гласные буквы

-Гласные смягчающие согласные в слиянии.

-Гласные, которые могут обозначать 2 звука.

-Звонкие согласные

-Глухие согласные

-Парные согласные, найдите друг друга.

-Буква не обозначающая звука.

-Для чего она нужна?

-Как вы думаете, существуют ли в русском языке согласные, которые обозначают только твердые согласные звуки?

Правильно вы ответили на мой последний вопрос или нет, вы узнаете по ходу нашего урока, если будете внимательны и старательны.

III. Актуализация знаний.

1. Проведите фонетический разбор слов «деньки», «письмо» (устно).

день-ки -2 слога,2гласных,3согласных,6букв,5звука.

пись-мо-2слога,2гласных,3согласных,6букв,5звука.

2. Проведите фонетический разбор слов (устно) , записанных на доске: пальто коньки клевер сирень (Показ предметных картинок)

-В чем особенность этих слов?

(В них есть гласные звуки, не проверяемые ударением.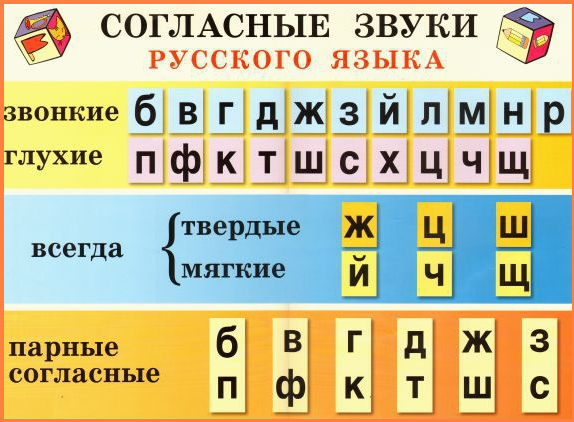 Написание букв в словах нужно запомнить).

3. Составьте с этими словами предложения. Назовите основу этих предложений.

4. Прочитайте текст с доски, соблюдая правильную интонацию и логическое ударение.

Вот бы тебе, заяц, да лисьи зубы!

Вот бы тебе, серый, да волчьи ноги!

Вот бы тебе ,косой, да рысьи когти!

Э-Э-Э, на что мне клыки да когти?

Душа-то у меня все равно заячья.

5. Как автор называет зайца? (серый, косой)

6. В каких случаях мягкий знак бывает разделительным?

(После согласных букв перед гласными И ,Я, Е)

7. Найдите в тексте слова с разделительным мягким знаком.

(Лисьи, волчьи, рысьи, заячья)

-А теперь прочитаем тексты в Азбуке на стр. 14-15

-На обеих страницах найдите слова с мягким знаком. Что они означают?

-На какой вопрос отвечают?

-Эти слова стоят во множественном или в единственном числе.

V. Постановка целей и определение темы урока.

-Как шипит змея? (Ш-ш-ш-ш)

-Как шипит гусь? (Ш-ш-ш-ш)

(Учитель подводит учащихся к тому, чтобы они догадались о целях и теме урока).

VI. Работа по теме урока.

1. Знакомство со звуком [Ш].

-Проведите звуковой анализ слов « шкаф» и «карандаш» по рисункам и схемам слов в красной рамке на стр. 17 «Азбуки».

-Новый звук относится к гласным или согласным звукам? Докажите.

-Это твердый или мягкий звук?

-Звонкий или глухой?

-Внимательно посмотрите на буквы Ш, ш. Что они вам напоминают?

Учитель читает стихотворения

Посмотри на букву Ш-

Буква очень хороша,

Потому что из нее

Можно сделать Е и Ё. (А.Шибаев)

-На что похожа буква «Ш»?

VII. Работа над дикцией.

1. Игра «Доскажи словечко»

Сегодня все ликует!

В руках у детворы

От радости танцуют

Воздушные…(ШАРЫ)

Слышит мишка краем уха,

Как жужжит над ухом муха.

Мишка лапой муху хвать!

Мухи слыхом не слыхать!

Не понять не может мишка,

От чего над ухом… (ШИШКА)

Кот живёт у нас на крыше,

А в чулане живут…(МЫШИ)

Не поедет без бензина

Ни автобус, ни… (МАШИНА)

2. Далее учащиеся проводят фонетический разбор слов:

ШАРЫ-[Ш][А’]-[Р][Ы] ШИШКА-[Ш][Ы’][Ш]-[К][А]

МЫШИ-[М][Ы’]-[Ш][Ы] МАШИНА-[М][А]-[Ш][Ы’]-[Н][А]

3. Сколько букв в слове? Сколько звуков? Сколько слогов? Какой слог ударный?

4. Дайте характеристику звуку [Ш].

Вывод:(звук [Ш] согласный , глухой , твёрдый).

5.Определите место звука [Ш] в словах: шуба, карандаш, шалаш, хорошо, крыша, ушки, крошка, шутка, шиповник , груша, ландыш, машина, камыш, шина.

VIII. Физкультминутка.

Вот бегут машины,

Шуршат своими шинами,

Желтые и красные –

Все такие разные!

IХ. Знакомство с буквами Ш ш.

1.Сравните написание печатных и письменных букв Ш ш.

2.Прочитайте слоги. Повторите чистоговорки чётко (на доске)

ША-ША-ША – Мама моет малыша.

ШУ-ШУ-ШУ – Я письмо пишу.

ШИ-ШИ-ШИ – Зашумели камыши.

АШ-АШ-АШ – У Марины карандаш.

ШО-ШО-ШО – Всем ребятам хорошо.

3.Прочитайте выделенные жирным шрифтом слова на стр. 17.

Учитель читает пословицы под рисунком.

Знай больше, а говори меньше.

Добрая шутка дружбы не рушит.

Поспешишь- людей насмешишь.

4.Как вы понимаете их смысл?

5.Подчеркните букву Ш в пословицах.

6. Может ли шутка разрушить дружбу? Обсудите с другом.

Х. Чтение и анализ текста.

1.Прочитайте текст на стр. 17. Рассмотрите иллюстрацию к нему.

– Как бы вы его озаглавили? Почему?

(Осенний лес. Прогулка в лес. Дети в лесу. Осень.)

2. Ответить на вопросы.

-Какое время года наступило?

-Какие деньки стояли?

-Где горели кисти рябин?

-Что собирали дети в лесу?

-Перескажите прочитанный текст.

-Сравните предложение в учебнике с тем, что придумали вы. Какое из них интереснее?

-Как вы понимаете слово «горели»? (алели, краснели, пылали)

-Найдите основы предложении в этом тексте.

-Объясните написание гласных букв в словах: деньки, ребята, сосновые, еловые.

3. Прочитайте правило внизу на стр. 17.

ШИ ПИШИ С БУКВОЙ И.

В нем говорится, как нужно писать сочетание ШИ. Это нужно помнить всегда при написании текстов.

4. А когда может вырасти шишка на лбу?

Воспитательный момент. Учитель проводит беседу о поведении и правилах безопасности во время перемены, в столовой, в спортивном зале, на лестнице, на улице.

5. Откройте Азбуку на стр. 18. Что нарисовано в верхней части страницы?

-Мы говорим «кисть рябины». Как можно сказать по-другому? (Гроздь рябины).

Гроздь – это когда много ягод как бы связаны воедино, вместе.

-Как называется нижняя часть руки? (Кисть)

-Плоды сосны и ели, кедра как называем? (Шишки).

А в шишках есть орешки?

Как называются плоды сосны , ели и кедра?

шишки сосновые

шишки еловые

шишки кедровые

6. Прочитайте стихотворение В. Берестова «Петушки» на стр.18.

Петушки распетушились,

Но подраться не решились.

Если очень петушиться,

Можно и пера лишиться.

Если и пера лишиться,

Нечем будет петушиться.

-Назовите рифмы. Ребята, каждая строчка имеет одинаковое окончание. Давайте найдем эти слова. ( распетушились – не решились, петушиться -лишиться, лишиться петушиться).

-Найдите и подчеркните сочетание ШИ.

-Когда о детях говорят: «Они распетушились»?

-Как таких детей можно назвать одним словом? (Драчуны).

-Как относятся к драчунам?

7. Повторное чтение с постановкой логического ударения: хором, цепочкой по две строчки, парами.

ХI. Работа по развитию речи. (Использовать электронное приложение к учебнику В.Г. Горецкого, В. А.Кирюшкина, Л.А. Виноградской.)

1.Читаем слоги.

2.Составляем слова.

ДА-ША, МИ-ША, МА-ШИ-НА, ШИ-НА, ШУ-ТЫ.

3.Играем вместе . Прыгаем на лед , если слог с твердым согласным звуком, а если с мягким согласным звуком-то прыгаем в сугроб.

4.Дети рассматривают картинку. Найдите на картинке 6 слов со звуком Ш .

(работа в группе) (шапка, шуба, мешок, шарф, мышки, машинка)

5.Составить по картинкам предложения.

Пришла зимушка-зима. Идет пушистый снег. Елочки одели шубки и шапки. Вот идет дедушка-лесник. У него красный мешок. Лесник нес в мешке подарки. За дедушкой идут мишка и мышки. Дедушка-лесник раздал им подарки. У мишки шары, а у мышат машинка и хлопушка. Мишка повесил шары на елочку. На елке зажглись огоньки. Скоро наступит Новый год. Как хорошо у елки!

6.Смотрим мультфильм.

7. По просмотру фильма рассказать сказку. (2-3 сильных ученика рассказывают сказку)

8. Прочитайте ребусы и укажите место звука [Ш] в слове: в начале, в середине, в конце слова.

шар+ф=шарф ш+утка=шутка ма+шина=машина

9. А сейчас послушайте стихотворение и постарайтесь запомнить слова, в которых пишется буква Ш. Вам нужно будет потом назвать эти слова.

Шла с базара кошка.

У кошки лукошка.

Там подарки свинкам-

Шубки да шапки.

Там подарки уткам-

Тапки и лапки.

Курам – ботинки

Мышкам – картинки.

Ну а вам, малыши,-

Краски и карандаши.

10.Игра «Звуки перепутались» (работа в группе). Каждой группе дается по одной карточке. Найди ошибки.

С другом мы играли в…ЧАШКИ,

Пили чай из белой…ШАШКИ!

Вылезла из норки…ШИШКА,

На неё упала…МЫШКА!

Мы с сестрой посуду…ШИЛИ,

И наряды куклам…МЫЛИ!

Горько плачет бедный…ШАРИК,

Улетел воздушный…ГАРИК!

ХII. Подведение итогов урока.

-В чем секрет буквы Ш?

-Звук [Ш] всегда твердый, не бывает мягким.

-Бывает ли в написанном слове рядом с Ш буквы Ы? Почему?

-Какие игры с буквами, слогами и словами вам больше всего понравились?

Отгадайте загадку

Я и красный, и зеленый,

Я и голубой, и черный.

Только лишь надуй меня,

Улечу я в небеса.

– Да, это воздушные шарики. Они имеют разные цвета, но каждый из вас может выбрать только один шарик.

Я прошу проанализировать вашу работу на уроке. Если вам было интересно, вы легко справлялись с заданиями, вам понравилось работать на уроке и есть, о чем рассказать родителям, друзьям возьмите себе жёлтый шарик

– Если вам что-то не удалось, вам было скучно, или не понравилось работать – возьмите синий шарик.

Возьмите свои шарики за верёвочку и покажите нам свое настроение.

Спасибо за урок. Вы меня очень порадовали работой. Урок окончен.

Д/З:стр.16-18 читать, нарисовать картинку к стихотворению В.Берестова «Петушки»

Конспект урока на тему “Буква Ш, твердый согласный звук [ш]”

Тема: Буква Ш, твердый согласный звук [ш].

Цель: обозначить буквой Ш звук [ш], сопоставлять слоги и слова с буквой ш; слог ши писать с гласной и; вызвать у детей потребность в овладении чтением и письмом; развивать внимание, память, речь; воспитывать аккуратность в работе.

Оборудование: схемы, таблицы, кот Леопольд.

Ход урока.

1. Настрой на урок. Игра «Как живете?»

На доске: «Повторение – мать учения».

– Прочитайте предложения на доске.

– Что это? (пословица)

– Как вы понимаете смысл пословицы?

– И мы начнем урок с повторения.

– Поиграем в игру «Кто, кто в теремочке живет?» (Дети называют изученные буквы. )

– Ребята! На доске столбики слов с изученными буквами. Прочитаем эти слова так:

Первый ряд: Прочитает слова с письменного текста по цепочке, деля их на слоги.

улитка Антон

Тамара Ната

сосны ананас

Роман мыло

томаты лимон

Второй ряд: Найдет, какое из данных слов соответствует одной из схем:

Третий ряд: Сделает звуковой анализ слова лимон.

2. Объяснение нового материала.

– Ребята! Сегодня вы познакомитесь с новым звуком и буквой, которая обозначает этот звук. Будете сопоставлять слоги и слова, развивать внимание, память и речь. Вы научитесь писать новую букву. А поможет нам в этом наш новый друг. Догадайтесь кто? (Открываю рисунок на доске). Конечно, это кот Леопольд. Но он пришел не один. Прочитайте скороговорку и узнаете, о ком идет речь. Обратите внимание на звук, который чаще других встречается в словах.

На доске:

Мышки сушек насушили,

Мышки мышек пригласили.

Мышки сушки кушать стали,

Зубы сразу же сломали.

– Итак, кто явился к нам на урок? (мышки)

Какой одинаковый звук услышали в словах?

– Произносим тихо [ш-ш-ш]

– Какой этот звук? (согласный)

– Еще раз произносим. Твердый звук или мягкий?

– Да, ребята, звук [ш] всегда твердый, мягким он не бывает.

– Ребята! Звук [ш] обозначают буквой (ша) Ш. Хором повторим: «буква ша».

– Кот Леопольд принес нам букву Ш (вывешиваю).

Ш ш – это печатная буква.

Ш ш – это письменная буква.

– А вот Катя расскажет что-то очень важное про букву ш. Ребята, оказывается, есть буквы, которые шипят. Вот их и назвали шипящими. Чтобы хорошо и правильно выговаривать все звуки, особенно шипящие, нужно тренировать свою речь на скороговорках. Прочитаем хором скороговорку. (1-2 вслух в быстром темпе, можно по памяти.)

– Молодцы! Кот Леопольд доволен вами!

Посмотри на букву ша –

Буква очень хороша,

Потому что из нее

Можно сделать я и ё.

– Откройте книжку-малышку.

– Напечатаем букву ш – 3 раза Ш.

– Сравните печатную букву ш с письменной. Где встречали элементы буквы? Напишем строчную букву 5 р. (показываю).

Пишу в рабочей строке и считаю: раз и, два и, три и.

– Напишем в воздухе, по пунктиру.

Физкультминутка.

1,2,3,4 – мышки дернули за гири.

Вдруг раздался страшный гром,

Убежали мышки вон.

– Прочитайте слоги с буквой «ша»: ша шу ше шо. Дополните их до слов (устно).

На доске мыши.

– Выделите слог с буквой Ш. Какой звук слышим после зв. [ш]?

– [ы].

– Какую букву пишем? И.

Запомните: жи-ши пиши с гласной и.

– Ребята! Посмотрите на мышку. Что есть у нее?

хвостик

носик глазки

МЫШКА зубки

усики

ушки

Какие ушки, носик, глазки, зубки?

Ушки маленькие, чуткие, остренькие

Носик черненький

Ротик маленький

Глазки зоркие

Зубки острые, белые

Лапки быстрые

Хвостик длинный

– А какие мышки бывают по характеру? Кто больше назовет слов про мышек со звуком [ш]?

– Назовите слова с звуком [ш]. Вы улыбались, значит, какие мышки? (смешные) Мышки баловались, значит, они … (шалунишки). Делали все быстро (шустрые). Издали звуки (шуршали – шелестели). Слышали громкие звуки – (шумели).

Задание по выбору принес кот Леопольд.

Составить небольшой рассказ про мышек, включая как можно больше слов со звуком [ш].
Слова рассыпались. Построить из них красивое предложение. Составить схему предложения в книжке – малышке.

У, ушки, мышки, серой, чуткие.

У с м ч у.

– Проверяем:

Составляем предложение.

Итоги: Что запомнили про букву Ш?

– Молодцы! Урок закончен.

Конспект урока «Твердый согласный звук [ш], буквы Ш, ш.» | План-конспект урока по чтению (1 класс):

Конспект урока в 1 классе по программе «Школа России»

Тема. Твердый согласный звук [ш], буквы Ш, ш. Сочетание ши.

Тип урока. Решение учебной задачи.

Цель: создать условия для организации деятельности учащихся по ознакомлению со звуком [ш] и буквой Ш, ш.

Задачи:

Предметные:

– организовать деятельность учащихся по изучению и первичному закреплению условного обозначения глухого твердого звука [ш] с помощью печатной буквы;

– обеспечить закрепление умения перекодировать звуковую форму слова в буквенную на основе звуковых моделей слов;

– обеспечить закрепление приема воспроизведения слов вслух на основе его звукобуквенной модели;

– способствовать обогащению словаря учащихся на уроке;

– содействовать активизации словаря учащихся, развитию фонематического слуха и культуры звукопроизношения, развитию познавательного интереса к чтению;

– содействовать воспитанию навыков культуры учебного труда на уроках обучения грамоте.

Личностные УУД: способствовать формированию положительной мотивации к учебной деятельности.

Метапредметные задачи:

Регулятивные: содействовать формированию умения принимать и сохранять учебную задачу; понимать выделенные учителем действия в учебном материале; оценивать совместно с учителем и одноклассниками результат своих действий, вносить соответствующие коррективы.

Познавательные: содействовать развитию умения понимать знаки, символы, модели и схемы, приведенные в учебнике; понимать заданный вопрос, в соответствии с ним строить ответ в устной форме;

Коммуникативные: принимать участие в работе парами и группами, допускать существование различных точек зрения; договариваться, приходить к общему решению; использовать в общении правила вежливости.

Оборудование: компьютер, проектор, колонки, презентация, диск «Обучение грамоте», карточки для работы в группах, учебник «Азбука» (2 часть), картинки (в словах звук [ш], индивидуальные карточки,

Ход урока.

Организационный момент.

Слайд 1.

Прозвенел звонок, урок начинается.

Сегодня к нам на урок пришли гости, давайте повернемся и поприветствуем наших гостей. Садитесь.

Я дарю вам свою улыбку, и вы улыбнитесь друг другу. Подумайте, как хорошо, что мы сегодня все вместе. Мы спокойны, добры, приветливы, ласковы. Мы все здоровы. Глубоко вдохните и выдохните. Выдохните обиду, злость, беспокойство. Забудьте о них. Вдохните в себя свежесть этого дня, радость этого дня, тепло солнечных лучей. Я желаю вам, дорогие ребята, и вам, уважаемые гости, хорошего настроения и бережного отношения друг к другу.

Итак, начинаем урок литературного чтения.

II. Подготовка к работе на основном этапе.

– Перед началом работы проведем разминку речевого аппарата.

1) Дыхательная гимнастика.

«Ароматный цветок»

– Сделайте медленный глубокий вдох носом при плотно сжатых губах и задержите дыхание; на выдохе произнесите фразу: «Какой ароматный цветок».

2) Артикуляционная разминка

«Губы»

– Плотно сжав губы, вытяните их вперед; не разжимая губ, растяните их в улыбке; повторите упражнение 2-3 раза.

3) Упражнение для дикции.

Учитель произносит скороговорку «Мышонку шепчет мышь: «Ты все шуршишь, не спишь?». Дети произносят скороговорку размеренно хором.

III. Усвоение новых знаний и способов действий.

– Назовите звук, который часто повторяется в этой скороговорке. (ш)

– Сформулируйте тему урока.

(на доске вывешивается тема урока)

– Какие цели и задачи мы поставим перед собой на уроке?

(На доске запись: Познакомиться со звуком … и буквой, ….

Учиться отличать …

Учиться читать….)

1. Познакомиться со звуком [ш] и буквой, которая его обозначает.

2. Учиться отличать звук [ш] и букву, которая его обозначает от других звуков и букв.

3. Учиться читать слоги, слова с новой буквой.

– Это и будет планом нашего урока.

– Как вы думаете, для чего нам нужно знакомиться с новыми звуками, буквами?

(Для улучшения дикции, чтобы уметь читать слова с новой буквой).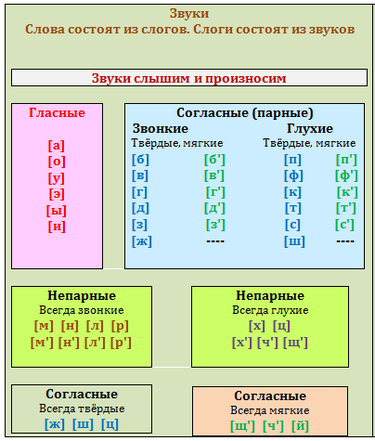

– Какие знания и умения нам потребуются?

(Знания о звуке и букве, умение выделять звук, сравнивать, делать выводы).

IV. Реализация построенного проекта.

Слайд 2

Работа с картинками.

(На доске картинки, все слова на этих картинках начинаются со звука [ш])

– Назовите слова, изображенные на картинках.

– Что общего у всех картинок, изображенных на доске?

– Исключите одну из данных картинок по самостоятельно найденному признаку.

(Слово Шарманщик отвечает на вопрос кто?, а остальные слова отвечают на вопрос что?. Слово Шарманщик обозначает один предмет, а остальные слова – несколько предметов).

– А кто такой шарманщик? (Бродячий музыкант с шарманкой).

(читаем объяснение слова в толковом словаре)

– А что такое шарманка? (Ручной орган).

– Произнесите первый звук в слове Шарманщик. ([ш]).

– Какой это звук: гласный или согласный? Докажите.

(При произнесении звука [ш] воздух встречает препятствие, значит он согласный).

– Какой он: твердый или мягкий? (Твердый).

– Звонкий или глухой?

(При его произнесении слышится только шум, значит он глухой).

– Дайте полную характеристику звуку [ш].

(Согласный, глухой, твердый).

– Подумайте, имеет ли этот звук звонкую пару?

– Как это определить? («Включить» голос).

– Какой согласный является парным глухому согласному звуку [ш]? (Звонкий [ж]).

2. Постановка проблемы, открытие новых знаний.

– Звук [ш] не простой, а с секретом. И секрет этот вы сможете открыть сами, если правильно выполните следующее задание.

(один ученик за компьютером работает над составлением звуковой схемы)

Работа в группах.

– Каждой группе нужно отгадать загадку и составить звуковые схемы отгадок.

1 группа. 2 группа.

На квадратиках доски На четыре ноги

Короли свели полки. Надевали сапоги.

Нет для боя у полков Перед тем как надевать,

Ни патронов, ни штыков. Стали обувь надувать.

(Шахматы) (Шины)

3 группа. 4 группа.

У меня нос колкий, Сижу верхом, не зная на ком,

Как у иголки, Знакомого встречу –

Но не шью, Соскочу, привечу.

А дырявлю только. (Шапка)

(Шило)

– Какой звук [ш] во всех отгадках: твердый или мягкий?

– Может быть, случайно так получилось, что звук [ш] во всех словах твердый? Попробуйте сами подобрать такие слова, в которых звук [ш] произносился бы мягко. (Дети работают в парах).

– Получилось? (Нет).

– Какой вывод можно сделать? (Звук [ш] всегда твердый).

– Вот вы и открыли секрет согласного звука [ш]. Он всегда твердый.

3. Знакомство с новой буквой.

– С новым звуком познакомились. Что дальше по нашему плану мы должны делать?

– Кто знает, как называется буква, которая обозначает звук [ш]?

– Звук [ш] обозначается буквой «ша».

Слайд (диск)

(показ картинки с написанием печатного и письменного вариантов букв, строчной и заглавной)

– Для чего нужна заглавная, строчная буква «ша»?

– Найдите в алфавите букву «ша».

Слайд 3

– На что похожа буква «ша»? Прослушав стихотворении, вы узнаете, с чем сравнили образ буквы «ша» поэты?

(ребята читают стихи и показывают букву)

1. Посмотри на букву Ш – 2. Ах, табуретка хороша!

Буква очень хороша, Перевернул – и буква «ша».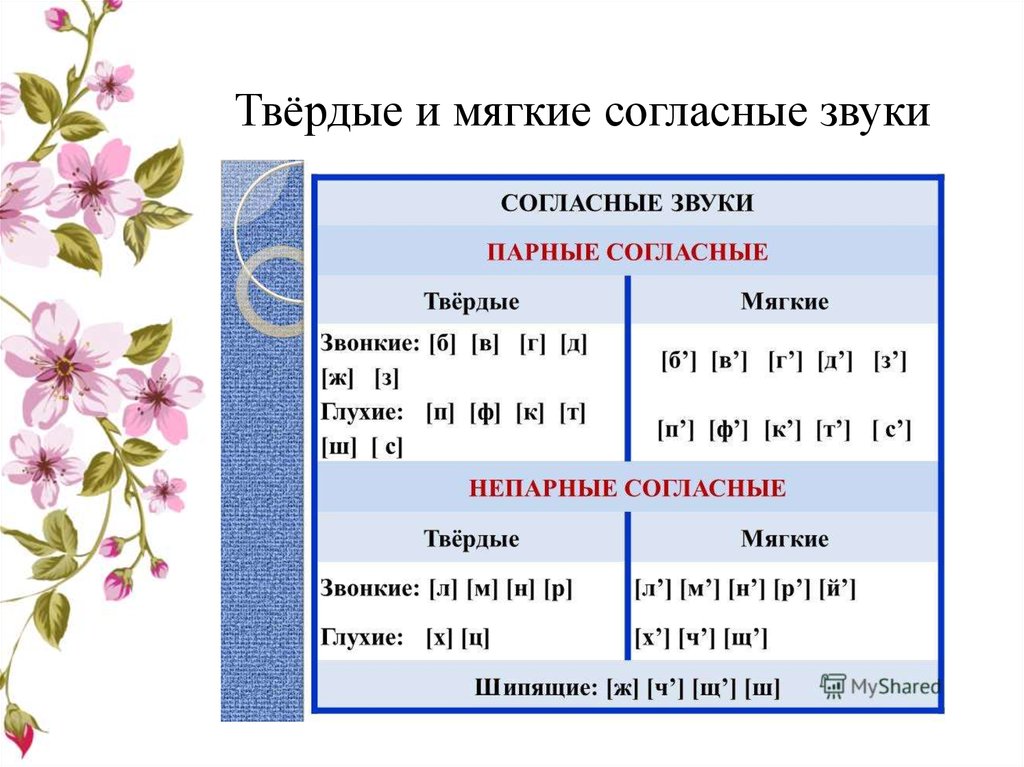

Потому что из нее 3. Шура сено ворошил,

Можно сделать Е и Ё. Вилы в сене позабыл.

– Ребята, выложите на парте букву «ша» из фасоли.

Физкультминутка.

А теперь, ребята, встали!

Быстро руки вверх подняли,

В стороны, вперед, назад,

Повернулись вправо, влево,

Тихо сели, вновь за дело!

– Не поворачивая головы, скажите, картинки с изображением каких предметов вы заметили? В какой части слова находится звук [ш]?

– Еще раз поверните голову вправо, влево. Чем отличаются картинки изображенные справа от картинок изображенных слева? (ед. число, мн. число)

V. Первичное закрепление во внешней речи.

1. Работа с абаками.

– А чтобы прочитать букву «ша», нужно просто назвать звук [ш]. Возьмите абаки.

– Итак, знакомим букву «ша» с гласными буквами: с буквой «а», запишите и прочитайте.

– Знакомим букву «ша» с гласной буквой «о», запишите и прочитайте.

– Знакомим букву «ша» с гласной буквой «у», запишите и прочитайте.

– Знакомим букву «ша» с гласной буквой «е», запишите и прочитайте.

– Как звучит согласный звук [ш]: твердо или мягко? (Твердо).

– Прочитайте еще раз открытый слог. Какое несоответствие вы заметили? (Слышим [э], а пишем «е»).

– Сделайте вывод.

– Знакомим букву «ша» с гласной буквой «и», запишите и прочитайте.

– Как звучит согласный звук [ш]: твердо или мягко? (Твердо).

– Прочитайте еще раз открытый слог. Какое несоответствие вы заметили? (Слышим [ы], а пишем «и»).

– Сделайте вывод.

– Давайте проверим, правильно ли вы сформулировали вывод? Открыли учебник стр. 17.

Слайд 4

– Какие это слоги открытые или закрытые. Докажите.

Чтение слов.

Слайд 5

– Прочитайте слова:

школа Миша

кошка Гриша

– Почему одни слова написаны со строчной буквы, а другие с заглавной?

– По каким признакам мы можем разделить эти слова еще на 2 группы?

(одушевленные и неодушевленные)

– Составьте предложение со словом школа.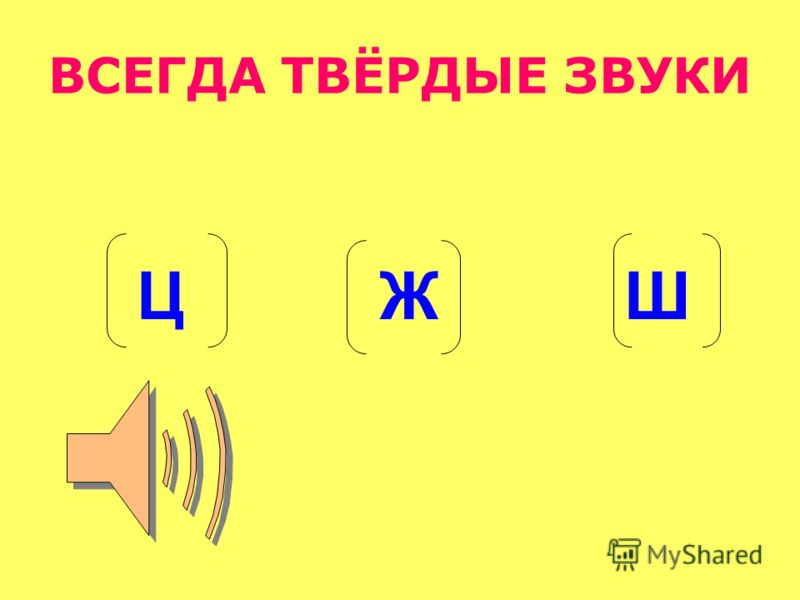

– Сколько слов в вашем предложении?

VI. Самостоятельная работа

Работа по учебнику на с.16

Чтение пословицы и нахождение новой буквы самостоятельно.

– Прочитайте пословицу и отметьте количество букв.

Добрая шутка дружбы не рушит.

– Сколько букв в предложении? (24 буквы)

– Сколько букв «ша» встретилось в предложении? (2)

– В каких словах?

– Прочитаем предложение. Почему так говорят?

– Как вы думаете, может ли шутка разрушить дружбу?

Физкультминутка.

VII. Включение в систему знаний и повторение.

Работа с книгой

Чтение текста с. 17 (по-цепочке).

Выборочное чтение.

– О каком времени года упоминается в рассказе?

– Свой ответ подтвердите предложением из текста. Прочитайте это предложение.

– Какой бывает осень? (золотой, дождливой, поздней)

– Какое слово должно звучать в нашем предложении?

– Что автор говорит нам о рябине? Прочитайте.

– Как вы понимаете слово кисти «горели»? (краснели, алели, пылали)

-Вспомните, какие значения имеет слово кисти?

Слайд 6.(кисти ягод( синоним- грозди), кисти для рисования, кисти рук)

– Что говорится о ребятах?

– Сколько ребят пошли в лес?

– Как вы догадались?

– Придумайте имена детям, которые пошли в лес? Обязательное условие: в словах должен быть звук [ш].

– Какое название вы дадите нашему рассказу?

Индивидуальная работа по карточкам.

– Если вы будете внимательно выполнять упражнения, то у вас обязательно все получится!

Слайд 7.

Карточка 1 (не читающим учащимся)

1. Найди и вычеркни в строчках все буквы «ша».

(Сколько из них строчных, заглавных?)

ОРШПМИКИшИБЮьШЭтМЧБЬсяАЫ

СЦЫФоПАвКЕНцШДИшлРПВШтЭЪХ

Карточка 2 (читающим учащимся)

Найди границы слов и запомни, сколько их спряталось на строке. Как, одним словом назвать все эти предметы?

ГРУШАБРИКОСЛИВАНАНАС

Слайд 8. Проверка

VIII. Итог урока.

– Посмотрите на наш план урока и подведите итог нашей работы.

– Справились мы со своими задачами?

IX. Рефлексия.

Смайлики.

– Оцените свою работу на уроке.

– Я желаю вам успехов и хорошего настроения на весь день!

Буква Ш

: Категория: Ша

Языкознание

Пожалуйста, оцените Оценка 1Оценка 2Оценка 3Оценка 4Оценка 5

Ш, двадцать шестая буква русского алфавита. По начертанию восходит к букве Ш («ша») кириллического (см. Кириллица) и Ш глаголического (см. Глаголица) алфавитов. Цифрового значения «Ш» в кириллице не имела, в глаголице — 800. Соответствующей буквы в греческом алфавите нет. Была введена в славянские азбуки для обозначения звука, отсутствовавшего в греческом языке. По-видимому, восходит к ש древнееврейского квадратного письма или к ሠ (саут) синайского и раннеарабского письма. Буква «ш» обозначает переднеязычный нёбный глухой фрикативный, шипящий звук «ш». Звук «ш» в русском языке может быть кратким и долгим. Краткий — всегда твёрдый — на письме обозначается не только буквами «ш», «шь», а в некоторых случаях и «ж», «жь» («мышка», «мышь», «нож», «рожь»). Долгий мягкий звук «ш» обозначается буквами «щ», «сч», «зч» («щи», «счёты», «возчик»). Долгий твёрдый звук «ш» обозначается буквами «сш», «зш» («нёсший», «вёзший»).

Большая советская энциклопедия.

Ш — двадцать пятая буква русской азбуки, обозначающая собой обыкновенно согласный спирант глухой, переднеязычный, альвеолярный, корональной артикуляции. В большинстве великорусских говоров ш произносится “твердо”, т. е. с надставной трубой широкой, без свойственного “мягким” (палатальным) согласным сужения между средней частью спинки языка и твердым нёбом. Это “твердое” произношение наблюдается и перед узкими нёбными гласными е, и (смягчающими у нас почти все согласные), причем в некоторых говорах, под влиянием твердости ш, гласный и превращается в ы (ср. произношение шыть, шыло вместо шить, шило). В древнерусском ш, напротив, было “мягким”, как это показывают древние написания вроде шюмящь, отсутствие ы после ш (всегда шити и т. д.), а также сохранение древнего ударенного е перед ш (чешешь, тешешь, рядом с причёски, тёс). Написания с ы после ш, свидетельствующие об отвердении ш, начинают появляться в древнерусских памятниках с начала XIV в.: в грамоте рижан в Витебске (около 1300 г.) — слышышь и т. д. Таким образом отвердение ш произошло в течение XIII в., вероятно, во второй его половине. “Мягкое” ш’ осталось только в некоторых немногих говорах, сохранивших вообще “мягкие шипящие”. Кроме того, оно встречается изредка, при известных условиях, и в говорах, представляющих “твердые шипящие”, например, в сочетании ш’ч’, обозначаемом буквой щ (щи = ш’ч’и) или буквами сч (счет = ш’ч’от, считать = ш’ч’итат’ и т. д.), а также в положении между ударенном и и следующим “мягким” (нёбным, палатальным) н’, например, в вишня = в’иш’н’ă, лишний = л’иш’н’ьj и т. д. На былой “мягкости” ш (и соответствующего ему звонкого согласного ж) основано известное орфографическое правило, по которому после ш (и других “шипящих”) нельзя писать ы, а только и. Напротив, позднейшее отвердение шипящих дало основание другой части того же правила, по которой после ш (и ж) пишутся только а и у, никогда я, ю (кроме иностранного брошюра). Параллельной звонкой парой согласного ш является согласный ж, который в немногих редких случаях обозначается знаком ш, например, Вышгород (произносится Выжгърът). Исторически звук ш в большинстве случаев происходит от спирантов с или х, патализованных под влиянием следующего согласного j (пишу = *писj , слышу, душа = *слыхj , *духjа) или нёбных гласных е, и, ь, (дух || душить, душный = , мошка =, слыхать || слышать = и т.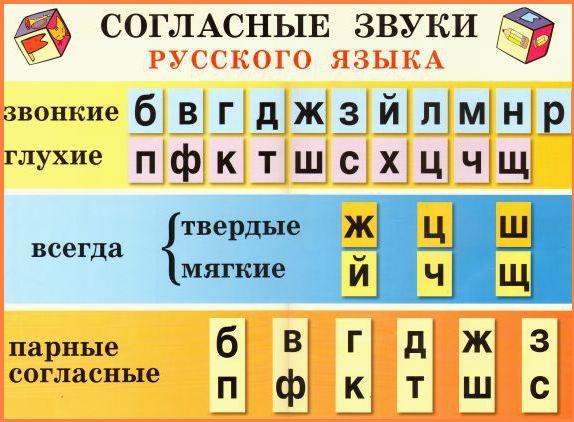 д.). В некоторых случаях звук ш произошел из спирантов с и з, уподобившихся следующим “шипящим” ш и ч. В этом случае этимологический принцип правописания заставляет изображать такое ш знаками тех звуков, из которых оно произошло: говорится шшести, ишшести, но пишется с шести, из шести. Как графический знак, русское ш восходит к старославянскому кириллическому , принадлежащему к тем составным частям славянской азбуки, которые в греческом алфавите отсутствовали и потому были почерпнуты из разных других источников или придуманы ad hoc. Обыкновенно думают, что славянское восходит к еврейской букве , обозначающей подобный же согласный звук.

Энциклопедический словарь. Брокгауза и Ефрона.

Добавить комментарий

4.2: Жесткие и мягкие кислоты и основания

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 274911

Кай Ландскрон
Университет Лихай

Концепция твердых и мягких оснований (HSAB)

Концепция жестких и мягких кислот и оснований (HSAB) может быть задумана как усовершенствование концепции кислот и оснований Льюиса. Его наиболее полезной особенностью является то, что он может делать прогнозы о силе кислотно-основных взаимодействий. Он также может оценить, являются ли взаимодействия более ионными или более ковалентными.

4.2.1 Визуальное представление неполяризованного атома и атома, поляризованного в электрическом поле.

Сначала уточним, что подразумевается под твердым и мягким соответственно. Эти термины относятся к поляризуемости электронов в атоме или молекуле (рис. 4.2.1). Атом мягкий, когда его электроны легко поляризуются. Это означает, что электронное облако легко деформируется в электрическом поле. Легкая деформация согласуется с термином «мягкий». В электрическом поле отрицательно заряженные электроны притягиваются к положительному полюсу электрического поля. Поэтому электронное облако искажается в сторону положительного конца электрического поля, и атом поляризуется. И наоборот, когда электронное облако не поляризуется легко, мы говорим, что атом твердый.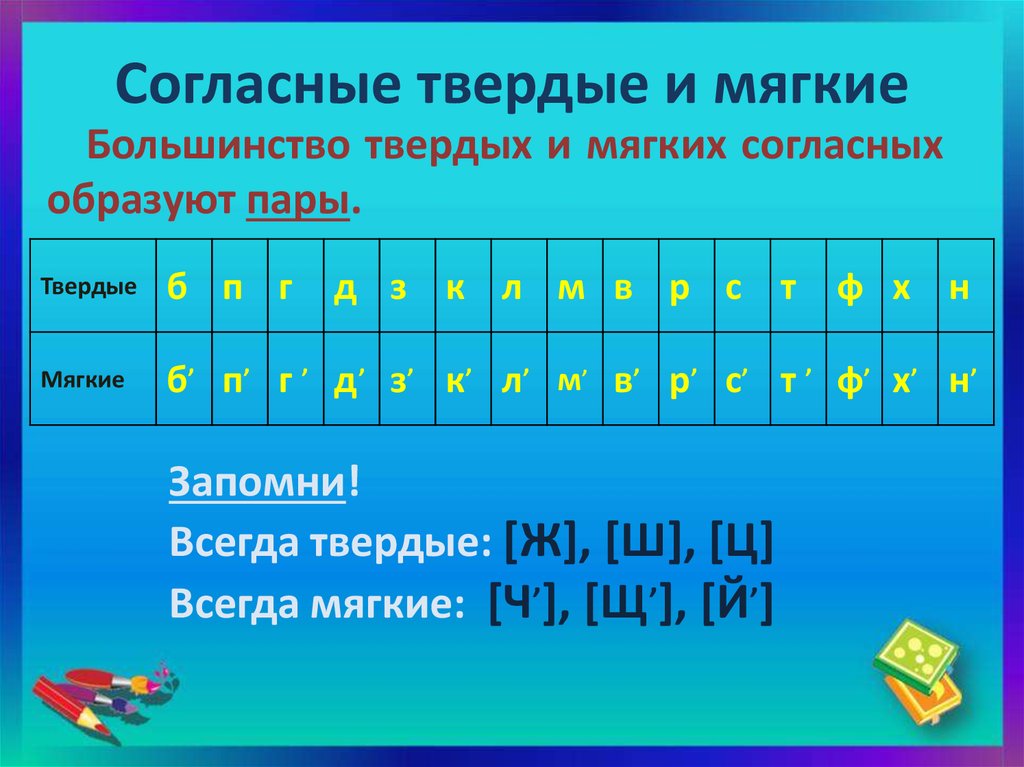 Что же тогда подразумевается под жесткой и мягкой кислотой или основанием? Жесткая или мягкая кислота — это жесткая или мягкая кислота Льюиса, а жесткое или мягкое основание — это жесткое или мягкое основание Льюиса. Как упоминалось ранее, концепция HSAB полезна, потому что она делает утверждения о силе кислотно-основных взаимодействий и, следовательно, прочности связей. Он также может делать утверждения о том, является ли связь более ковалентной или более ионной (рис. 4.2.2).

Рисунок 4.2.2 Взаимосвязь между жесткостью кислот и оснований и силой и характером кислотно-основных взаимодействий

Как правило, жестко-жесткие взаимодействия, то есть взаимодействия между жесткой кислотой и жестким основанием, имеют тенденцию быть сильными. Связь скорее ионная. Мягко-мягкие взаимодействия также имеют тенденцию быть сильными, но они, скорее всего, ковалентны. Жестко-мягкие взаимодействия имеют тенденцию быть слабыми.

Рисунок 4.2.3 Размер донорных атомов влияет на жестко-мягкое поведение

Почему мягко-мягкие и жестко-жесткие взаимодействия сильны, а жестко-мягкие взаимодействия слабы? Чтобы ответить на этот вопрос, мы должны сначала понять, что делает кислоту или основание твердыми или мягкими. В целом можно сказать, что чем более делокализованы электроны, тем мягче частицы. Для отдельного атома или иона это означает, что чем больше атом или ион, тем мягче частицы. Чем больше размер атома, тем более делокализованы его валентные электроны. Размер нейтрального атома определяется его положением в периодической таблице. Как правило, чем выше период, тем мягче атом (рис. 4.2.3).

Рисунок 4.2.4 Влияние заряда на твердо-мягкое поведение

Для ионов также играет роль заряд. Для катионов более высокий положительный заряд делает катион более жестким, для анионов более высокий отрицательный заряд делает анион более мягким (рис. 4.2.4).

Рисунок 4.2.5 Влияние π-связи на жесткость и мягкость

Размер донорно-акцепторного атома — не единственный фактор, определяющий твердость. Также важна способность вида образовывать π-связь. Виды, у которых есть орбитали, подходящие для π-связей, имеют тенденцию быть мягкими, даже если аргументы размера предполагают, что они твердые. Это связано с тем, что π-связь увеличивает делокализацию электронов (рис. 4.2.5).

Например, у переходных металлов есть доступные d-орбитали, которые подходят для π-связи с лигандами, а у щелочных металлов нет. Следовательно, относительно небольшой катион переходного металла, такой как Cu ⁺, мягче, чем крупные ионы щелочного металла, такие как Cs ⁺. Для анионов также важна π-связь. Например, анионы CN ^– являются мягкими основаниями, хотя донорный атом углерода мал, потому что лиганд CN ^– имеет π-орбитали, доступные для π-связи с кислотами Льюиса.

Рисунок 4.2.6 Критерий перекрытия орбит

Итак, вернемся к вопросу: почему взаимодействия мягко-мягкое и жестко-жесткое сильные, а взаимодействия жестко-мягкие слабые? По сути, это сводится к правилу 2 критерия перекрытия орбит (см. главу 3 по теории МО). Две маленькие орбитали обычно имеют хорошее перекрытие, а две большие орбитали также имеют хорошее перекрытие, и поэтому взаимодействие сильное. Однако большие и малые орбитали, как правило, имеют слабое перекрытие орбиталей и, следовательно, слабое связывание.

Теперь к вопросу о том, почему взаимодействия мягко-мягко имеют тенденцию быть более ковалентными, тогда как взаимодействия жестко-жестко имеют тенденцию быть более ионными. Ответ связан с тем фактом, что в меньших атомах разница энергий между атомными орбиталями, как правило, больше, чем в больших атомах. Как следствие, статистически более вероятно, что ВЗМО и НСМО двух мягких видов имеют более близкие энергии по сравнению с двумя твердыми видами. Когда ВЗМО и НСМО кислоты Льюиса и основания Льюиса имеют одинаковую энергию, тогда связь является более ковалентной. Когда они значительно различаются, то связь более ионная.

Рис. 4.2.7 Жестко-жесткие ковалентные взаимодействия в оксиде лития

Проиллюстрируем это двумя качественными примерами. Оксид лития состоит из анионов O ^2- и катионов Li ⁺. Если рассматривать ионную связь между ионами О ^2- и ионами Li ⁺ как крайний случай полярной, дательной связи, то оксид-анион выступает в роли основания Льюиса, а ион Li ⁺ — в роли основания Льюиса. кислота Льюиса. Как можно объяснить высокую ионность? И Li ⁺, и O ^2- — маленькие ионы, поэтому они оба жесткие. Небольшой размер также означает, что разница энергий между атомными орбиталями велика. Из-за этого маловероятно, что высшая занятая атомная орбиталь иона O ^2- имеет такую же энергию, как и низшая незанятая атомная орбиталь иона Li ⁺. Из-за большой разности энергий связывающая МО будет практически полностью локализована на анионе О ^2-, а связь будет ионной (рис. 4.2.7).

Рисунок 4.2.8 Мягко-мягкие ковалентные взаимодействия в иодиде серебра

Примером соединения с сильными мягкими-мягкими взаимодействиями является иодид серебра. Хотя AgI считается ионным соединением, взаимодействия имеют значительно более сильный ковалентный характер. Мягкую природу Ag ⁺ легко понять из того факта, что Ag ⁺ представляет собой ион переходного металла периода 5 с низким положительным зарядом и d-орбиталями, доступными для π-связи. Йод является элементом 6-го периода, поэтому йодид довольно мягкий. Поскольку Ag и I являются элементами периода 5 и 6 соответственно, разница их орбитальной энергии значительно меньше, чем у O и Li, которые являются элементами периода 2. Таким образом, ВЗМО I ^– и НСМО Ag ⁺, естественно, ближе по энергии, что приводит к более ковалентному взаимодействию (рис. 4.2.8).

Мы должны понимать, что к этим соображениям нужно относиться с осторожностью. Например, связи В-О довольно ковалентны, несмотря на то, что и В, и О довольно жесткие. ВЗМО донора и НСМО акцептора твердых частиц не обязательно сильно различаются. Другие параметры, такие как различия в электроотрицательности, также имеют значение, и их необходимо учитывать, чтобы правильно предсказать природу химической связи.

Примеры – Основания

Чтобы получить представление о правильной оценке твердости породы, рассмотрим несколько примеров. Начнем с некоторых основ.

Рисунок 4.2.9 Пример оснований

Какие утверждения о твердости можно сделать для серий F ^– , Cl ^– , Br ^– , I ^– (рис. 4.2.9). Все они представляют собой ионы галогенидов с одинаковым отрицательным зарядом. Размер увеличивается от фторида до хлорида, от бромида до йодида. Таким образом, мягкость должна увеличиваться в том же порядке. Ф ^– – это небольшой ион с небольшим отрицательным зарядом и должен быть твердым, I – очень тяжелый элемент, поэтому I ^– очень мягкий. Cl ^– и Br ^– являются умеренно жесткими и мягкими ионами соответственно.

Рисунок 4.2.10 Пример ряда с донорными атомами O

Далее рассмотрим ряд H ₂ O, OH ^– , O ^{2 –} , CH ₃ O ^– и PhO – . Все виды содержат небольшие донорные атомы O, поэтому все их следует считать жесткими. ОН 9Ион 0052 – несколько мягче, чем H ₂ O из-за отрицательного заряда, который увеличивает размер донорного атома O. По той же причине O ^2- несколько мягче, чем OH ^–. CH ₃ O ^– несколько мягче, чем O ^2- из-за положительного индуктивного эффекта метильной группы. Ион фенолята является самым мягким, потому что отрицательный заряд O может быть делокализован в ароматическом кольце. Делокализация отрицательного заряда приводит к большей поляризуемости и, следовательно, к мягкости. Мы могли бы также подумать о том, если бы F ^–, вероятно, будет тверже или мягче, чем H ₂ O. F немного меньше, чем O, но F несет отрицательный заряд, поэтому случай неоднозначен.

Рисунок 4.2.11 Пример ряда с N донорными атомами

Далее рассмотрим ряды NH ₃ , CH ₃ NH ₂ и PhNH ₂ (рис. 4.2.11). Донорный атом азота представляет собой небольшой малополяризуемый атом, поэтому его следует считать жестким. Однако N несколько больше, чем O, что означает, что NH ₃ несколько мягче, чем H ₂ O. CH ₃ NH ₂ будет немного мягче, чем NH ₃, из-за положительного индуктивного эффекта метильной группы, а анилин будет немного мягче, чем метиламин, потому что о возможности делокализации неподеленной пары при N в ароматическом кольце.

Рисунок 4.2.12 Серия примеров с донорными атомами S

Как насчет H ₂ S, алкилтиолов и диалкилтиолов (4.2.12)? Донорный атом S находится в 3-м периоде и достаточно велик, чтобы считаться мягким. Можно было бы ожидать, что мягкость несколько увеличится по сравнению с H ₂ S на R-SH на R-S-R из-за положительного индуктивного эффекта алкильной группы.

Рисунок 4.2.13 Пример PR ₃

Следующим примером является фосфин общей формулы PR ₃ (4.2.13). Как и сера, фосфор является донорным атомом периода 3, а фосфины обычно мягкие.

Рисунок 4.2.14 Пример серии с донорными атомами C

Наконец, давайте рассмотрим монооксид углерода и цианид (рис. 4.2.14). На первый взгляд эти частицы кажутся твердыми основаниями из-за небольших донорных атомов углерода. Однако на самом деле они довольно мягкие из-за их способности использовать свои π- и π*-орбитали в π-связях с кислотами Льюиса, в частности с ионами переходных металлов. Мы подробнее рассмотрим этот вопрос позже, когда будем подробно обсуждать связи в комплексах переходных металлов.

Пример – Кислоты

Теперь давайте подумаем о жесткости кислот.

Рисунок 4.2.15 Пример ряда катионов щелочных металлов

В ряду H ⁺, Li ⁺, Na ⁺, K ⁺: Это жесткие или мягкие кислоты и как изменяется жесткость в этом ряду (рис. 4.2.15)? Ответ: Все катионы щелочных металлов считаются жесткими кислотами, даже относительно большой катион К ⁺ в 4-м периоде. Это связано с тем, что катионы щелочных металлов имеют только s-валентные орбитали и, следовательно, не имеют орбиталей, подходящих для π-связи. В серии H ⁺ — самая твердая, а K ⁺ — самая мягкая, потому что ионный радиус увеличивается с увеличением периода.

Рисунок 4.2.16 Пример ряда катионов щелочноземельных металлов

Точно так же щелочноземельные металлы Be ² ⁺ , Mg ²⁺ и Ca ² ⁺ являются твердыми катионами с уменьшением жесткости от Be ² ⁺ до Ca ² ⁺ . Из-за заряда 2+ катионы щелочноземельных металлов считаются более твердыми, чем катионы щелочных металлов того же периода, например Be ² ⁺ следует оценивать сложнее, чем Li ⁺ .

Рисунок 4.2.17 Пример серии с бором

В следующей серии BF ₃ , BCl ₃ , B(CH ₃ ) и BH ₃ твердость снижается с BF _{3 3 3} до BH _{3 3} (рис. 4.2.17). BCl ₃ мягче, чем BF ₃, из-за меньшей электроотрицательности Cl по сравнению с F. Более электроотрицательный F забирает больше электронной плотности из бора, делая его меньше и, следовательно, тверже. Из-за положительного индуктивного эффекта B(CH ₃ ) ₃ мягче, чем BCl ₃ . Молекулы BF ₃ и BCl ₃ в целом считаются жесткими кислотами, B(CH ₃ ) ₃ является промежуточным случаем. На первый взгляд может показаться, что BH ₃ тверже, чем B(CH ₃) ₃, тем не менее он действует больше как мягкая кислота, возможно, из-за гидридоподобного характера соединения.

Рисунок 4.2.18 Пример ряда с ионами переходных металлов

Далее рассмотрим ряд ионов переходных металлов Fe ² ⁺, FE ³⁺, CO ² ⁺, CO ³⁺, RH ³ ⁺, IR ³⁺ (фиг. 4.2.18). Эти катионы обладают способностью образовывать π-связь, но из-за более высокого заряда 2+ и 3+ соответственно ни один из них не является мягким. Все катионы периода 4 с зарядом 3+, а именно Fe ³ ⁺ и Co ³ ⁺, являются жесткими кислотами, Fe ² ⁺ и Co ² + ^{Ионы 0053 находятся на границе между жесткими и мягкими из-за их меньшего заряда. Rh ³ ⁺ и Ir ³ ⁺ также находятся на границе. Они имеют более высокий положительный заряд, но находятся в периоде 5 и 6 соответственно. Ожидается, что Rh ³ ⁺ будет более твердым, чем Ir ³ ⁺, потому что он находится в более низком периоде.}

Рисунок 4.2.19 Пример ряда переходных металлов с зарядами 4+

Ti ⁴ ⁺ и Si ⁴ ⁺ — обе жесткие кислоты (рис. 4.2.19). Как правило, все ионы с зарядом +4 и выше являются жесткими кислотами.

Рисунок 4.2.20 Пример ряда ионов переходных металлов 4-го периода

Что можно сказать о последнем ряду Cu ⁺ , Cd ²⁺ , Hg ² ⁺ , Pd ²⁺ 9005 и Pt2253 9005 + (рис. 4.2.20)? Подумай об этом. Все они считаются мягкими кислотами. Cu ⁺ представляет собой элемент с относительно низким периодом 4, но имеет заряд только 1+ и имеет d-орбитали для π-связи. ртутного столба ² ⁺ , Pd ²⁺ и Pt ² ⁺ имеют несколько более высокий заряд 2+, но являются элементами периода 5 и 6, а также имеют d-орбитали для π-связи. Pt ² ⁺ можно было бы ожидать мягче, чем Pd ² ⁺, из-за его более длительного периода.

Количественные меры жесткости

Из предыдущих рассуждений мы видели, что можно делать качественные, а в некоторых случаях и полуколичественные оценки жесткости кислот и оснований, но они не являются количественной мерой жесткости. Шкала твердости, позволяющая количественно измерить твердость, — это концепция абсолютной твердости Пирсона (уравнение 4.2.1).

Уравнение 4.2.1 Уравнение для количественного расчета абсолютной жесткости

Оно связывает жесткость с разницей между энергией ионизации и сродством к электрону в течение 2. количественный расчет мягкости

Затем мягкость определяется как величина, обратная абсолютной твердости (уравнение 4.2.2).

Уравнение 4.2.3 Уравнение электроотрицательности Малликена

Сразу видно, что абсолютная жесткость связана со шкалой электроотрицательности Малликена, которая представляет собой энергию ионизации + сродство к электрону более 2 (4.2. 3).

В чем идея этого определения? Ранее мы качественно обсуждали, что твердые виды, как правило, имеют большие различия в орбитальной энергии, в то время как мягкие виды, как правило, имеют небольшие различия в орбитальных энергиях. Следовательно, имеет смысл определить разницу энергий между самой высокой занятой атомной или молекулярной орбиталью и самой низкой незанятой атомной или молекулярной орбиталью как количественную меру твердости вида (уравнение 4.2.4).

Уравнение 4.2.4 Расширенное уравнение для расчета абсолютной жесткости сродство минус энергия самой низкой незанятой молекулярной или атомной орбитали: EA=-E(LUMO/LUAO). Следовательно, разница между ВЗМО/НОАО и НСМО/ЛУАО такая же, как разница между энергией ионизации и сродством к электрону.

Рисунок 4.2.21 Абсолютная жесткость для катионов щелочных металлов /creativecommons.org/licenses/by-nc-sa/3.0/us/)

Рисунок 4.2.21 иллюстрирует концепцию абсолютной жесткости на примере катионов щелочных металлов.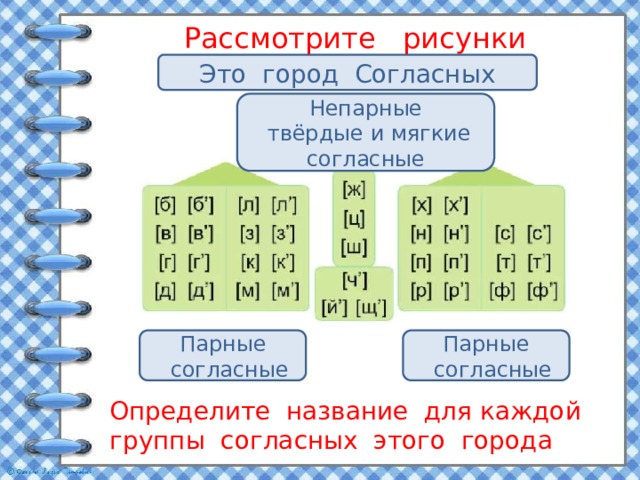 Вы можете видеть, что самые низкие незанятые атомные орбитали довольно близки по энергии, но энергия самой высокой занятой атомной орбитали значительно увеличивается от Li ⁺ в Cs ⁺. Таким образом, энергетические различия уменьшаются от Li ⁺ к Cs ⁺, а абсолютная твердость η составляет всего половину значения. Энергия по оси Y на полпути между энергиями ВЗМО и НСМО минус энергия, связанная с электроотрицательностью Малликена.

Рисунок 4.2.22 Кислоты и основания и их абсолютная жесткость (Атрибуция: R.G. Pearson, Inorg. Chem. 1988, 27, 734) с их жесткостью, рассчитанной на основе энергий ионизации и сродства к электрону. Давайте проверим, соответствуют ли расчетные значения ожиданиям, и посмотрим, какую дополнительную ценность дает концепция абсолютной твердости. Например, мы можем видеть, что Li ⁺ тверже, чем Na ⁺, который тверже, чем K ⁺. Это то, что мы ожидали.

Мы также видим, что мы можем определить относительную твердость, которую невозможно определить с помощью качественного осмотра. Например, мы можем видеть, что Al ³ ⁺ тверже, чем Li ⁺. С точки зрения атомного размера нейтральный Al больше, чем нейтральный Li, и с этой точки зрения Li ⁺ должен быть тверже. С другой стороны, положительный заряд Al выше, чем у Li. С этой точки зрения Al должен быть жестче. При качественном осмотре мы не могли сказать, какой параметр преобладает в общей твердости. Концепция абсолютной жесткости показывает, что (в данном случае) заряд важнее, чем размер нейтрального атома. Точно так же мы не могли решить путем проверки, что Mg ² ⁺ был мягче, чем Li ⁺, потому что аргументы в пользу заряда предполагали, что Mg ² ⁺ тверже, в то время как аргументы о размере нейтрального атома говорили, что Li ⁺ должен быть тверже. Мы видим, что в этом случае размер нейтрального атома оказывает большее влияние, хотя и незначительное. Согласно нашим ожиданиям, Mg ² ⁺ тверже, чем Na ⁺, так как оба иона соседствуют в один и тот же период и, таким образом, очень похожи по атомному радиусу, но Mg имеет более высокий положительный заряд.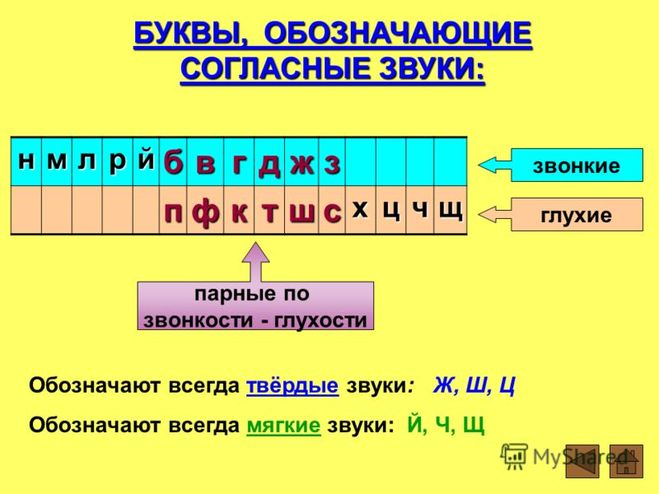 Мы также можем видеть, что Ag ⁺ и Au ⁺ имеют гораздо более низкую твердость, чем K ⁺, которую мы ожидаем. Мы также поняли бы, что Au ⁺ имеет более низкое значение, чем Ag ⁺, потому что эти элементы находятся в одной группе, а Au ⁺ находится в периоде 6, а Ag ⁺ находится в периоде 5.

Ниже Au ⁺ можно увидеть группу нейтральных молекул. Только молекула BF ₃ является кислотой Льюиса, остальные молекулы являются основаниями Льюиса. Мы видим, что BF ₃ имеет относительно высокую твердость, но мягче, чем K ⁺. Из оснований H ₂ O является самым твердым основанием, за ним следует NH ₃, за ним следует PF ₃ _{, за которым следует PH ₃. Это то, что мы ожидали. О является наименьшим донорным атомом, за ним следует N, за которым следует P. PF ₃ тверже, чем PH ₃, из-за более высокой электроотрицательности фтора по сравнению с водородом.}

Последнюю группу составляют анионы галогенидов. По ожиданиям F ^– самые твердые, а I ^– самые мягкие. Мы видим, что Cl ^– имеет более низкое значение твердости, чем PH ₃. Химическое поведение последнего соответствует мягкому основанию, в то время как первое по-прежнему считается относительно твердым основанием. Мы видим, что к абсолютным значениям жесткости тоже нужно относиться с некоторой осторожностью, это не всемогущий метод, на поляризуемость могут влиять и другие факторы, кроме значений энергии ВЗМО и НСМО.

При сравнении трех групп мы видим, что катионы, как правило, имеют самые высокие значения жесткости, за которыми следуют нейтральные молекулы. Анионы, как правило, имеют самые низкие значения. Это означает, что жесткая кислота обычно имеет более высокое значение абсолютной жесткости, чем жесткое основание. Следовательно, чтобы интерпретировать значения значений, мы должны сравнивать только кислоты с кислотами и основания с основаниями.

Концепция HSAB и растворимость

Поскольку концепция HSAB позволяет оценить силу взаимодействия между кислотами Льюиса и основаниями Льюиса, она также может оценить ряд других свойств, вытекающих из этой силы взаимодействия. Например, его можно использовать для оценки растворимости. Когда кислотно-основное взаимодействие Льюиса между катионом и анионом сильное, мы ожидаем низкую растворимость, когда взаимодействие слабое, мы ожидаем высокую растворимость.

Рисунок 4.2.23 Растворимость галогенидов серебра

Например, известно, что растворимость галогенидов серебра в воде увеличивается от AgI до AgBr, затем от AgCl до AgF (рис. 4.2.23). Это соответствует концепции HSAB. Ag ⁺ считается мягким, и, таким образом, он будет наиболее сильно взаимодействовать с самым мягким анионом, йодидом I ^–. Ag ⁺ будет слабее всего взаимодействовать с F ^–, потому что он самый тяжелый.

Рисунок 4.2.24 Растворимость галогенидов лития

Каковы наши ожидания относительно галогенидов лития (рис. 4.2.24)? В этом случае можно было бы ожидать снижения растворимости от LiI к LiBr, к LiCl и к LiF. Почему? Это потому, что Ли ⁺ является жестким катионом, поэтому наиболее сильные взаимодействия должны происходить с F ^– . Следовательно, LiF будет иметь самую низкую растворимость. I ^– является самым мягким анионом, поэтому он должен вступать в самые слабые взаимодействия с Li ⁺. Следовательно, LiI будет иметь самую высокую растворимость. Это то, что мы наблюдаем экспериментально? Экспериментально наибольшая растворимость наблюдается у LiBr, за которым следует LiCl, а затем LiI. LiF имеет самую низкую растворимость. Мы видим, что растворимость LiI не такая, как мы ожидали. Вместо того, чтобы иметь самую высокую растворимость, он имеет вторую самую низкую растворимость. Здесь мы видим ограничения концепции HSAB. Есть и другие факторы, определяющие растворимость, в частности энтальпия сольватации. я ^– имеет очень низкую энтальпию гидратации, что объясняет более низкую, чем ожидалось, растворимость LiI. В некотором смысле концепция HSAB способна объяснить низкую энтальпию гидратации I ^–, поскольку она основана на силе взаимодействия между I ^– и водой. Вода является жесткой кислотой и поэтому слабо взаимодействует с мягким основанием, таким как I ^–. Это может служить объяснением низкой энтальпии гидратации.

Другим хорошим примером, иллюстрирующим влияние энтальпии сольватации на растворимость, является растворимость галогенидов серебра в жидком аммиаке (не в водном аммиаке). На самом деле все наоборот, AgF имеет наименьшую растворимость, а AgI имеет самую высокую растворимость. Взаимодействие HSAB между Ag ⁺ и ионы галогенидов одинаковы независимо от растворителя. Поэтому они не могут служить объяснением. Скорее, мы можем утверждать, что обратные энтальпии сольватации в жидком аммиаке по сравнению с жидкой водой ответственны за обратное поведение. С точки зрения HSAB молекулы аммиака уже значительно мягче молекул воды, поэтому взаимодействия с мягкими анионами становятся значительно сильнее.

Концепция и стабильность HSAB

Концепция HSAB также может быть использована для оценки термодинамической стабильности соединений, например температуры разложения, точки плавления и т. д. Как правило, чем больше кислотно-щелочное взаимодействие, тем выше ожидаемая термодинамическая стабильность. Давайте сделаем пару упражнений, чтобы попрактиковаться в этой концепции.

Рисунок 4.2.25 Термодинамическая стабильность оксидов щелочных металлов

Какой порядок термодинамической стабильности вы ожидаете для оксидов щелочных металлов (рис. 4.2.25)? Ответ: стабильность снижается с увеличением периода щелочного металла. Почему? Оксид-анион считается твердым основанием из-за его относительно небольшого радиуса. Таким образом, самые сильные взаимодействия ожидаются с Li ⁺, который является самым твердым щелочным металлом, и самые слабые взаимодействия можно ожидать для Cs ⁺, который является самым мягким щелочным металлом. Это соответствует экспериментальным наблюдениям. Только Li дает Li ₂ O при сжигании в O ₂ , Na дает пероксид натрия, а остальные щелочные металлы дают супероксиды.

Рис. 4.2.26 Термодинамическая стабильность оксидов щелочноземельных металлов

Мы можем задать тот же вопрос для оксидов щелочноземельных металлов (рис. 4.2.26). Точно так же стабильность BeO является самой высокой, потому что Be имеет самую высокую твердость. BaO имеет самую низкую стабильность, потому что Ba ² ⁺ – самый мягкий щелочноземельный катион. Ba дает пероксид бария вместо оксида бария при сжигании в O ₂ .

Концепция HSAB и кислотность

Концепция HSAB также может объяснить кислотность по Бренстеду. Как?

. 2 Se (рис. 4.2.27). Кислотность по Бренстеду увеличивается от H ₂ от O до H ₂ от S до H ₂ Se. Почему? H ⁺ является жесткой кислотой, и поэтому самые сильные взаимодействия следует ожидать с самым твердым основанием, ионом оксида, а самые слабые взаимодействия следует ожидать с самым мягким основанием, анионом Se ² ^–.

Следовательно, H ₂ Se легче всего теряет протон, что делает ее самой сильной кислотой. Для H ₂ O кислотность наименьшая, потому что взаимодействия между H ⁺ и O ^2- самые большие.

Рис. 4.2.28 Кислотность ряда HClO ₄ в HClO ₃ в HClO ₂ в HClO

Перейдем к несколько более сложному примеру (рис. 4.2.28). Кислотность хлорной кислоты, хлорноватистой кислоты, хлорноватистой кислоты и хлорноватистой кислоты снижается от HClO ₄ до HClO ₃ до HClO ₂ до HClO. В этом случае все протоны связаны с кислородом, поэтому мы не можем рассуждать, как раньше. Однако можно утверждать, что отрицательный заряд анионов кислот наиболее делокализован в случае хлорной кислоты, потому что для хлорной кислоты можно изобразить наибольшее количество резонансных структур. Поскольку отрицательный заряд наиболее делокализован, электрон наиболее поляризуем и, следовательно, наиболее мягок. Для хлорноватистой кислоты мы имеем противоположный случай. Электронная делокализация невозможна, и для аниона гипохлорита можно нарисовать только одну резонансную структуру. Поэтому он самый твердый, сильнее всего взаимодействующий с протоном.

Рисунок 4.2.29 Основность ряда NH ₃ , PH ₃ и AsH ₃

Наконец, давайте подумаем об относительной основности NH ₃ , PH ₃ 1 и AsH ₃ 1 и (рис. 4.2.29)? Атом N — самое твердое основание, и взаимодействия с протонами самые сильные. Следовательно, NH ₃ является самым сильным основанием. AsH ₃ — самое слабое основание, потому что As — самый мягкий атом, наиболее слабо взаимодействующий с протонами.

Доктор Кай Ландскрон (Университет Лихай). Если вам нравится этот учебник, рассмотрите возможность сделать пожертвование для поддержки исследований автора в Университете Лихай: нажмите здесь, чтобы сделать пожертвование.

Эта страница под названием 4. 2: Hard and Soft Acids and Bases распространяется под лицензией CC BY 4.0, ее автором, ремиксом и/или куратором является Кай Ландскрон.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
Кай Ландскрон
Лицензия
СС BY
Версия лицензии
4,0
Метки
1. абсолютная твердость
2. концепция жестких и мягких кислот и оснований
3. твердость
4. HSAB
5. мягкость

Трехмерные изменения мягких и твердых тканей при лечении межчелюстной протрузии

. 2013 г., август; 144(2):218-28.

doi: 10.1016/j.ajodo.2013.03.018.

R Кристиан Солем ¹ , Ричард Мараско, Луис Гитеррес-Пулидо, Иб Нильсен, Сон-Хун Ким, Джеральд Нельсон

Принадлежности

принадлежность

¹ Ортодонт, отделение ортодонтии, кафедра рото-лицевых наук, Калифорнийский университет в Сан-Франциско, Калифорния, США. Ричард.Солем@ucsf.edu

PMID: 233
DOI: 10.1016/j.ajodo.2013.03.018

R Кристиан Солем и др. Am J Orthod Dentofacial Orthop. 2013 авг.

. 2013 г., август; 144(2):218-28.

doi: 10.1016/j.ajodo.2013.03.018.

Авторы

R Кристиан Солем ¹ , Ричард Мараско, Луис Гитеррес-Пулидо, Иб Нильсен, Сон-Хун Ким, Джеральд Нельсон

принадлежность

¹ Ортодонт, отделение ортодонтии, кафедра рото-лицевых наук, Калифорнийский университет в Сан-Франциско, Калифорния, США. Ричард.Солем@ucsf.edu

PMID: 233
DOI: 10.1016/j.ajodo.2013.03.018

Абстрактный

Введение: Выпуклость лица, связанная с бимаксиллярным выпячиванием, распространена во многих популяциях. Скелетная протрузия в сочетании с увеличенной зубоальвеолярной протрузией способствует дисбалансу лицевых мышц и несостоятельности губ, что нежелательно для многих пациентов. В этом исследовании мы оценили взаимосвязь между изменениями мягких и твердых тканей у азиатского населения, прошедшего ортодонтическое лечение.

Методы: Двадцать четыре последовательных взрослых азиатских пациента (средний возраст 24 года) с диагнозом тяжелой двучелюстной зубоальвеолярной протрузии были обследованы с использованием конусно-лучевой компьютерной томографии до и после лечения. Пациентам было проведено удаление 4 первых премоляров с последующей передней ретракцией со скелетной или внутриротовой опорой. Регистрировались серийные конусно-лучевые компьютерные томографы всего основания черепа и ямок. Изменения мягких и твердых тканей определяли с помощью смещения ориентиров и цветового картирования.

Полученные результаты: Ретракция верхней губы была сосредоточена между носогубными складками и спайками. Ретракция нижней губы сопровождалась значительным перераспределением мягких тканей в области погониона. Изменения мягких тканей хорошо коррелировали с регионарной активностью лицевых мышц. Значительные ретракции (2-4 мм) мягких тканей происходили за пределы средней сагиттальной области. Использование скелетной фиксации привело к большей ретракции нижней губы на 1,5 мм по сравнению с внутриротовой фиксацией, с большей ретракцией верхушек корней резцов верхней и нижней челюсти.

Выводы: Глубокие изменения мягких тканей сопровождались ретракцией переднего зубного ряда при обоих методах лечения.

Цитируется

Изменения мягких тканей при скелетной фиксации по сравнению с обычными протоколами фиксации при лечении пациентов с двухчелюстной проклинацией, получавших удаление премоляров: систематический обзор.
Мохан К., Сивараджан С., Лау М.Н., Отман С.А., Файед ММС. Мохан К. и др. Дж Орофак Ортоп. 2022 г., 13 июля. doi: 10.1007/s00056-022-00411-9. Онлайн перед печатью. Дж Орофак Ортоп. 2022. PMID: 35829730 Обзор. Английский.
Трехмерный цифровой анализ изображений точек A и B скелета и мягких тканей после ортодонтического лечения с удалением премоляров у пациентов с двучелюстной протрузией.
Лим Ю.Н., Ян Б.Е., Бьюн С.Х., Йи С.М., Он Ю.В., Пак И.Ю. Лим Ю.Н. и соавт. Биология (Базель). 2022 27 февраля; 11 (3): 381. дои: 10.3390/биология11030381. Биология (Базель). 2022. PMID: 35336755 Бесплатная статья ЧВК.
Удаление или отсутствие удаления в ортодонтических случаях: обзор.
Мапаре С., Мундада Р., Карра А., Агравал С., Махаджан С.Б., Тадавалкар А. Мапар С. и др. Дж. Фарм Биологически активная наука. 13 июня 2021 г. (Приложение 1): S2–S5. doi: 10.4103/jpbs.JPBS_549_20. Epub 2021 5 июня. Дж. Фарм Биологически активная наука. 2021. PMID: 34447032 Бесплатная статья ЧВК. Обзор.
Персонализированная ортодонтия: от сагиттального положения нижних резцов к эстетике профиля лица.
Дервич М. , Минч Л., Митус-Кениг М., Золтовска А., Павловска Е. Дервич М. и соавт. J Pers Med. 2021 22 июля; 11 (8): 692. дои: 10.3390/jpm11080692. J Pers Med. 2021. PMID: 34442336 Бесплатная статья ЧВК.
Сравнение передних альвеолярных параметров верхней и нижней челюсти у афроамериканок и женщин европеоидной расы: ретроспективное пилотное исследование.
Рено Л., Ганди В., Вест С., Гудхимелла С., Джанакираман Н. Рено Л. и др. Imaging Sci Dent. 2021 июнь;51(2):175-185. doi: 10.5624/isd.20200323. Epub 2021 11 марта. Imaging Sci Dent. 2021. PMID: 34235063 Бесплатная статья ЧВК.

Просмотреть все статьи “Цитируется по”

термины MeSH

английских слов, в которых «ch» произносится как «sh»

Есть довольно много английских слов, в которых «ch» произносится как «sh». Я составил список таких слов, которые, надеюсь, будут особенно полезны изучающим английский язык. Он упорядочен от наиболее распространенных до наименее распространенных в современном английском языке (приблизительно), и значение каждого слова объясняется прямо рядом с ним. В самом конце есть также список общеупотребительных имен собственных.

машина /məˈʃiːn/ (mə- блеск ) — это оборудование с подвижными частями.

усы /məˈstɑːʃ/ (mə- staash ) Великобритания, /ˈmʌstæʃ/ ( mʌ -stæsh) или /məˈstæʃ/ (məˈstæʃ/ (məˈstæʃ/ (mə)- 0æ86 stæsh) тип роста волос на лице между ртом и ртом США нос.

повар /ʃef/ ( шеф ) профессиональный старший повар.

шик /ʃiːk/ ( шек ) означает «модный и элегантный».

брошюра /ˈbrəʊʃə/ ( broh -shə) Великобритания, / broʊˈʃʊr/ (broh- shoor ) США представляет собой небольшой буклет, обычно содержащий некоторую сжатую информацию, часто коммерческого типа.

кэш /kæʃ/ (kæsh, то же, что и «наличные») используется в основном в связи с компьютерами, где это означает, что временные данные хранятся таким образом, чтобы к ним можно было быстро получить доступ.

клише /ˈkliːʃeɪ/ ( klee -shei ) Великобритания, /kliːˈʃeɪ/ ( klee- shei ) США — это фраза, которая повторяется так долго, что люди уже не находят ее интересной.

champagne /ʃæmˈpeɪn/ (shæm- peyn ) — французское игристое белое вино.

фисташка /pɪˈstæʃiəʊ/ (pis- tæsh -ee-oh) или /pɪˈstɑːʃiəʊ/ (pis- taash -ee-oh) – вид дерева, известный также своими орехами (которые также известны своими орехами). как «фисташковый»).

парашют /ˈpærəʃuːt/ ( pær -ə-shoot ) — это кусок ткани, используемый для замедления падающих объектов в атмосфере.

фуксия /ˈfjuːʃə/ ( fyoo -shə) – небольшой кустик с цветками характерного цвета, который также называют фуксией.

мачете /məˈʃeti/ (mə- shet -ee) большой тяжелый нож, используемый как инструмент для срезания растительности.

ниша / niːʃ / ( neesh ) или / nɪtʃ / ( nitch ) первоначально относились к полости в стене, обычно используемой для размещения бюста или статуи. В настоящее время его часто используют для обозначения «нишевого рынка», т.е. определенного специфического сегмента рынка.

шофер /ʃɒˈfɜː/ (sho- fə-ə ) или /ˈʃəʊfə/ ( shoh -fə) Великобритания, /ʃoʊˈfɜːr/ , обычно личный водитель автомобиля, США fer богатый или важный.

атташе /əˈtæʃeɪ/ (ə- tæ -shei) Великобритания, /ˌætəˈʃeɪ/ (æ-tə- shei ) США – человек, который работает в посольстве, обычно с особой ответственностью.

шовинист /ˈʃəʊvɪnɪst/ ( шох -вин-ист) Великобритания, /ˈʃoʊvɪnɪst/ ( шох -вин-ист) США изначально означало человека, который был безосновательно и агрессивно патриотичен. Однако в современном английском языке оно используется в основном в связи с мужским шовинизмом — тогда шовинист — это человек, считающий, что мужчины выше женщин.

шарлатан /ˈʃɑːlətən/ ( shaa -lə-tən) Великобритания, /ˈʃɑːrlətən/ ( shaar -lə-tən) США – это человек, который утверждает, что обладает знаниями или не обладает ими. .

люстра /ˌʃændəˈlɪə/ (shæn-də- li -ə) Великобритания, /ˌʃændəˈlɪr/ (shæn-də- lir ) США представляет собой круглую рамку с ветвями, держащими огни или свечи.

шарада /ʃəˈrɑːd/ (shə- raad ) Великобритания, /ʃəˈreɪd/ (shə- reyd ) США – это ситуация, в которой люди притворяются, что что-то верно, хотя это явно не так.

рикошет /ˈrɪkəʃeɪ/ ( rik -ə-shei ), в Великобритании также /ˈrɪkəʃet/ ( rik -ə-shet ) — глагол, означающий «удариться о поверхность и быстро оторваться от нее в под другим углом». При произнесении с /eɪ/ в конце такое же произношение сохраняется и в производных терминах «рикошет» /ˈrɪkəʃeɪd/ ( rik -ə-sheyd) и «рикошетом» /ˈrɪkəʃeɪɪŋ/ ( rik -ə-shei-ing).

chateau /ˈʃætəʊ/ ( shæ -toh) Великобритания, /ʃæˈtoʊ / (shæ- toh ) США — замок или большой загородный дом во Франции. Множественное число — «замки», произносится /ˈʃætəʊz/ ( shæ -toh’z) в Великобритании, /ʃæˈtoʊz/ (shæ- toh’z ) в США.

Душ /duːʃ/ ( doosh ) — это метод промывания внутренней части влагалища женщины струей воды. Душевой мешок – это устройство с мешком, который наполняется жидкостью, используемой для процесса очистки. «Мудак» — это современный сленговый термин, означающий «высокомерный и грубый человек».

лисичка /ˈʃɑːntərel/ ( shaan -tə-rel) или /ˌʃɑːntərel/ (shaan-tə- rel ) — распространенный съедобный желтоватый вид грибов.

рыцарство /ˈʃɪvəlri/ ( shi -vəl-ree ) — вежливое поведение, демонстрирующее чувство чести, особенно со стороны мужчин по отношению к женщинам.

желоб /ʃuːt/ ( Shoot ) — это труба, по которой могут скользить люди или предметы (например, в аквапарке).

шасси /ˈʃæsi/ ( shæ -см.) — внутренняя форма транспортного средства.

сорочка /ʃəˈmiːz/ (shə- meez ) — предмет женского нижнего белья или ночная рубашка.

пирог с заварным кремом /kiːʃ/ ( киш ) — это пирог определенного типа.

фаэтон /ʃeɪz/ ( шейз ) — повозка, запряженная лошадью или лошадьми.

шифон /ˈʃɪfɒn/ ( shi -fon) Великобритания, /ʃɪˈfɑːn/ (shi- faan ) США – это тип тонкой ткани.

стилизация /pæˈstiːʃ/ (pæ- steesh ) — произведение искусства, созданное путем преднамеренного копирования чьего-либо стиля.

склонность к чему-либо .

щегольство /pəˈnæʃ/ (pə- næsh ) или /pæˈnæʃ/ (pæ- næsh ), в США также /pəˈnɑːʃ/ (pə- naash ) или /pæˈnɑːʃ/ (pæ- naash ) — «яркая уверенность в стиле или манерах».

chalet /ˈʃæleɪ/ ( shæ -lei) Великобритания, /ʃæˈleɪ/ (shæ- lei ) США – это определенный тип деревянного дома, обычно строящегося в горных районах.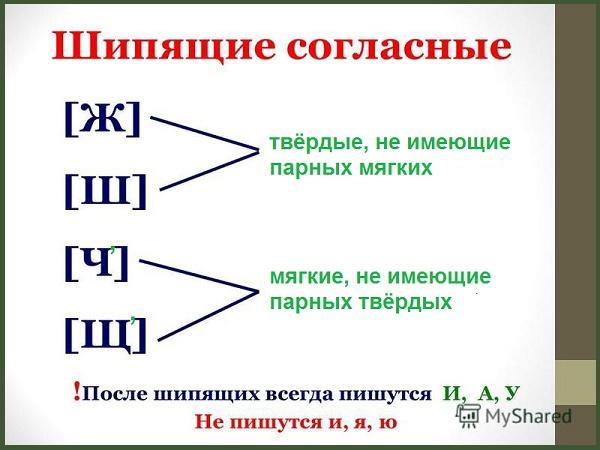

кэш /ˈkæʃeɪ/ ( kæ -shei ) Великобритания, / kæˈʃeɪ/ (kæ- shei ) США; иметь печать означает иметь качество, которым восхищаются другие; например, «ресторан, кажется, теряет свою привлекательность».

chagrin /ˈʃæɡrɪn/ ( shæg -rin)/ Великобритания, /ʃəˈɡrɪn/ (shə- grin ) US обычно используется во фразе «к чьему-то огорчению», что означает «к чьему-то разочарованию»; например, «к его огорчению, ни один из его проектов не увенчался успехом».

chaperone /ˈʃæpərəʊn/ ( shæp -ə-roh’n) Великобритания, /ˈʃæpəroʊn/ ( shæp -ə-roh’n) США – это лицо, которое сопровождает молодых людей) они ведут себя правильно.

ruche /ruːʃ/ ( roosh ) — декоративная складка на одежде или мебели.

вязание крючком /ˈkrəʊʃeɪ/ ( kroh -shei ) Великобритания, /kroʊˈʃeɪ/ (kroh- shei ) США – специфический способ изготовления одежды с помощью специальной толстой иглы.

louche /luːʃ/ ( loosh ) — прилагательное, означающее «сомнительного вкуса или нравственности», но часто в привлекательном смысле (например, «лушный мир театра»).

синель /ʃəˈniːl/ (shə- neel ) — тип ткани.

gauche /ɡəʊʃ/ ( goh’sh ) Великобритания, /ɡoʊʃ/ ( goh’sh ) США — прилагательное, означающее «неуклюжий или лишенный социальных способностей».

Шарлотта /ˈʃɑːlət/ ( shaa -lət) Великобритания, /ˈʃɑːrlət/ ( shaar -lət) США — женское имя. Это также название крупнейшего города американского штата Северная Каролина.

Мишель /mɪˈʃɛl/ (mi- shel ) — женское имя.

Chevrolet /ʃɛvrəˈleɪ/ (shev-rə- lei ) — марка автомобиля.

Chicago / ʃɪˈkːgoʊ / (Shi- KAA -GOH) или / ʃɪˈKɔːOʊ / (SHI- KAW -GOH)- это город в штате США / ɪlɪˈnɔɪ / (IH-H-GOH). ).

Мичиган /ˈmɪʃɪɡən/ ( миль -shi-gn ) — один из штатов США.

Сейшелы /seɪˈʃɛlz/ (sei- shelz ) — островная страна недалеко от Мадагаскара.

Vichy /ˈvɪʃi/ ( vish -ee ) — марка минеральной воды, марка косметики и город во Франции.

Двумерное движение грунта на участке мягкого вязкоупругого слоя/твердого основания в ответ на SH цилиндрические сейсмические волны, излучаемые глубинными и мелкими линейными источниками — I. Теория | Geophysical Journal International

Резюме

Мы рассматриваем, используя теорию (здесь) и соответствующие синтетические сейсмограммы (в сопутствующей статье), сейсмический отклик участка, состоящего из горизонтального, однородного, мягкого вязкоупругого слоя бесконечной поперечной протяженности, лежащего выше, и в сварной контакт с однородным жестко-эластичным субстратом полубесконечной радиальной протяженности. Мы показываем, что для сдвигово-горизонтального движения: (1) связь с модами Лява тем сильнее, чем ближе (в вертикальном направлении) источник (моделируемый линией, предполагаемой лежащей в субстрате) находится к нижней границе мягкий слой, (2) все аномальные особенности (например, большая длительность) сейсмического волнового поля, в том числе и для региональных землетрясений, в первую очередь являются результатом сильного возбуждения мод Лява, (3) 1-D (объемная волна) тип отклика является: нерезонансным, полученным для глубоких источников и обычно характеризующимся относительно короткой продолжительностью, (4) для мелких источников и гипоцентральных расстояний, которые не очень велики, отклик является результатом сложного взаимодействия мод Лява и вкладов объемных волн, что требует числовое описание (приведено в сопутствующей статье).

продолжительность, максимумы интерференции, моды Лява, эффекты региональной трассы, характеристика площадки, положение источника сейсмическая реакция в городской среде (Новикова и Трифунак, 1993; Сингх и Ордаз, 1993; Фаех и Панза, 1994; Фаех, и др., , 1994; Новикова и Трифунак, 1995; Фурумура и Кеннетт, 19).98; Хисада и др. 1988; Шапиро и др. 2000, 2001, 2002; Панза и др. 2001; Карденас и Чавес-Гарсия, 2003 г.; Селеби 2004; Дикарь 2004; Сёдзи и др. 2004; Balendra & Kong 2004),

влияние неоднородностей подстилающего грунта, боковых вариаций нижележащего слоя почвы и застроенной среды на сейсмическую реакцию грунта в различных (особенно городских) местах (Hisada et al. 1988; Faeh & Panza 1994; Фаэх и др. 1994; Романелли 1996; Чен и др. 1998 г.; Фурумура и Кеннет, 1998; Панза и др. 2000а,б; Semblat и др. 2000; Бур 2003; Semblat и др. 2003; Цогка и Виргин, 2003 г. ; Селеби 2004; Сэнди и др. 2004),

анализ реакции поверхностных волн на землю для определения структуры и состава земной коры (Ben-Zion & Aki 1990; Chen et al. 1998; Pollitz 1999; Снайдер 2000; Savage 2004) и зоны подземных разломов (Igel и др. 2002; Jahnke et al. 2002) и

анализ отклика поверхностных волн на земле для выявления очагов землетрясений (Mendiguren 1977; Kanamori & Given 1981; Бен-Цион и Аки, 1990).

Исследование по теме (а) было возобновлено попытками объяснить некоторые загадочные особенности разрушительного землетрясения в Мичоакане, которое произошло в Мехико в 1985 г. (Furumura & Kennett 1998). Помимо того факта, что ответ в центре Мексики значительно различался в пространственном отношении, он был довольно интенсивным и очень длительным (до ∼3 минут) (понятие продолжительности исследуется, например, в Trifunac & Brady 1975; Trifunac & Westermo). 1976 г.) в определенных местах и часто принимал форму квазимонохроматического сигнала с биениями, примечательной особенностью этого землетрясения было то, что столь сильный (в только что упомянутом смысле) отклик мог быть вызван сейсмическим возмущением до сих пор (его эпицентр находился в зоне субдукции у тихоокеанского побережья примерно в 350 км) от города (Chávez-Garcia & Bard 1994; Фаэх и Панза, 1994 г . ; Фаэх и др. 1994; Чавес-Гарсия и др. 1995; Фурумура и Кеннет, 1998). Сингх и Ордаз (1993) отчасти объясняли большую интенсивность и большую продолжительность многолучевым распространением между источником и участком. Эта гипотеза была дополнительно исследована в Chávez-Garcia & Bard (1994), Chávez-Garcia et al. (1995) и Furumura & Kennett (1998), хотя они связаны с распространением поверхностных волн типа Рэлея и Лава, предположительно между источником и входом в бассейн Мехико, через промежуточную кору.

В довольно полном (если не считать пренебрежения затуханием) трехмерном численном исследовании (Шапиро и др. 2000) большая продолжительность и большая амплитуда отклика на различных расстояниях от землетрясений в зоне субдукции в Мексике были приписаны захват сейсмического возмущения аккреционной призмой (клиновидной неоднородностью) земной коры и его последующее распространение до пункта наблюдения. Авторы этой работы позже (Shapiro et al. 2001, 2002), а также Furumura & Kennett (1998) несколько ранее подчеркивал роль поверхностных волн более высокого порядка, которые распространяются в относительно высоком Q слое Трансмексиканского вулканического пояса (TMVB, сложенного низкоскоростной вулканической лавой и туфом, лежащим над высокоскоростным известняком), подстилающим мягкий глиняный бассейн Мехико, вызывающий большой отклик (особенно по продолжительности) в городе. Недавно проведенный анализ (Cárdenas & Chávez-Garcia, 2003) сейсмограмм, зарегистрированных в различных местах центральной Мексики для очагов землетрясений, расположенных в зоне субдукции у побережья Тихого океана, показал, что структура земной коры (включая структуру TMVB) между источник и точки наблюдения действуют как волновод для поверхностных волн, приходящих с расстояний более 200 км, что приводит по необъяснимому механизму к усилению и увеличению продолжительности движения в различных местах, особенно в Мехико. Численные результаты, полученные в более ранних исследованиях (например, Faeh и др. 1994; Faeh & Panza 1994) с достаточно полной двухмерной гибридной моделью пути распространения между источником и бассейном Мехико и воздействия бассейна на падающую волну, также подчеркнули важную роль региональных эффектов пути на аномальный ответ. Трехмерный эквивалент этих численных симуляций, проведенный Furumura & Kennett (1998), подтверждает эти выводы.

Аномальная реакция в других городах, таких как Пекин, Бухарест, Рим и т. д., была подробно изучена, в основном в числовом виде, в рамках проекта ЮНЕСКО-МПГК 414 (Panza и др. 2000b, 2001). Особенности этой реакции объяснялись (как и в более ранней работе Campillo et al. 1989) особенностями параметров источника, региональными эффектами траектории и особенностями распределения и геометрии почвы в городских бассейнах (см. следующий абзац). ). Эти выводы были подтверждены в более позднем исследовании (Boore 2003).

Тема (b) посвящена классу альтернативных или дополнительных (так называемых локальных) парадигм для объяснения сейсмических движений в городских районах, построенных на мягком грунте. Несмотря на то, что аномальный ответ в 1985 в Мехико возник из источника зоны субдукции, эпицентральное расстояние которого составляло около 350 км от города, было обычным делом искать объяснения этой реакции [и других, таких как в Ницце (Semblat et al. 2000, 2003) и Bucharest (Sandi et al. 2004)] путем использования моделей, включающих вертикально распространяющиеся или почти вертикально распространяющиеся плоские волны. Для этого требуется, чтобы глубина очага (известная также как глубина гипоцентра (Novikova & Trifunac, 1995)) была большой, а эпицентральное расстояние от источника до города было довольно небольшим. Хотя оба эти условия на практике часто не выполняются (и, в частности, что касается 1985 Мичоаканское землетрясение), в теоретических/численных исследованиях обычно преобладает вертикально распространяющаяся плоская волна (Balendra & Kong 2004; Sandi et al. 2004; Semblat et al. 2004), по-видимому, потому что это упрощает анализ (еще один Причина в том, что это облегчает сравнение с одномерной моделью нормально падающих плоских волн на вертикально многослойном полупространстве). Это приводит к сосредоточению внимания на том, что происходит в структуре по вертикали под городом, а именно на мягком бассейне, на котором построены сейсмоопасные города. Так, значительное количество исследований (см. Бард и др. 1988; Чавес-Гарсия и Бард, 1994; Semblat и др. 2004, для всесторонних обзоров) исследуют (локальное) влияние мягкого бассейна на падающую волну, но в настоящее время считается, что локальные эффекты объясняют только часть аномального отклика (Chávez-Garcia & Bard 1994; Chávez- Garcia и др. 1995; Panza и др. 2000b, 2001; Cádenas & Chávez-Garcia 2003; Boore 2003). С другой стороны, Hisada et al. (1988) показывают, что положение источника относительно бассейна является решающим фактором для определения отклика грунта в бассейне. Другая идея, которая исследовалась в последние несколько лет, состоит в том, что городские здания при взаимодействии с мягкой почвой и друг с другом также могут усиливать и удлинять продолжительность движения грунта (см. Semblat 9).1261 и др. 2003; Цогка и Виргин, 2003 г.; Boutin & Roussillon 2004 за обзоры по этому вопросу). Большинство этих исследований (включая или исключая здания) указывают на центральную роль поверхностных волн, квалифицируемых либо как локальные поверхностные волны (например, волны Лява) (на краях бассейна или на неоднородностях мягкого грунта) (Bard & Bouchon 1980). ; Bard et al. 1988; Faeh et al. 1994; Boore 2003) или как квази-волны Лява (возбуждаемые у основания зданий и повторно усиливающиеся при взаимодействии с соседними зданиями, Semblat 9).1261 и др. 2003; Цогка и Виргин, 2003 г.; Гроби и др. 2004) в качестве возможного причинного агента аномальной реакции, но мало (Wirgin & Kouoh-Bille 1993), если таковые имеются, теоретических доказательств, подтверждающих эти утверждения.

Тема (c) является классической в сейсмологической геофизике (Ewing et al. 1957). Сейсмические сигналы, связанные с различными типами поверхностных волн (например, волн Лява и Рэлея), часто используются для реконструкции характеристик земной коры, таких как мощность, состав (например, характеристики вертикальной слоистости (Юинг 9). 1261 и др. 1957; Панза 1981; Snieder 2000) и даже латеральные неоднородности (Wirgin 1988; Chen et al. 1998). Совсем недавно (Ben-Zion & Aki 1990; Igel и др. 2002; Jahnke и др. 2002) было показано, что сейсмические источники вблизи зон разломов (FZ, т.е. мягкие почти вертикальные слои, окруженные относительно твердый грунт) возбуждают поверхностные волны (квалифицированные как захваченные) вблизи ЗП, которые распространяются к земле, где их можно обнаружить и использовать для получения информации о физических и геометрических характеристиках ЗП. Для однозначного решения этих обратных задач требуется глубокое понимание того, каким образом сейсмический источник взаимодействует (в частности, насколько точно необходимо знать положение и характеристики источника) с неоднородностями.

Тема (d) также является классической в сейсмологии, основной задачей которой является локализация и определение (например, определение тензора момента) очагов землетрясений (Mendiguren 1977; Kanamori & Given 1981). Поскольку сейсмическая волна, включая ее поверхностные волновые компоненты, распространяется латерально (иногда на большие расстояния) в земной коре и вдоль нее, прежде чем достичь мест измерения на земле, решить обратную задачу трудно, если особенности земной коры (которые могут включать латеральные неоднородность) заранее не известны. В любом случае важно определить влияние ошибок модели земной коры на восстановление положения источника и тензора момента, а для этого необходим соответствующий теоретический анализ.

Приведенное здесь теоретическое исследование (и численное исследование в сопутствующей статье) сосредоточено на вопросах (а) и (б). В отличие от 91 261 обратного рассеяния 91 262 тем (c) и (d) (к которым может быть применен наш анализ), где ответ известен, а среда распространения и/или источник должны быть определены, проблема, с которой мы сталкиваемся здесь речь идет о прямом рассеянии : учитывая источник сейсмических волн и характеристики среды распространения, определить отклик (смещение в частотной и/или временной области) на земле. В частности, нас будет интересовать (обманчиво) простая каноническая задача рассеяния: цилиндрическая импульсная волна ВГ, падающая на мягкий однородный слой, причем последний является горизонтальным, имеет бесконечную поперечную протяженность, ограниченную сверху свободной поверхностью и снизу граница раздела с полупространством, заполненным твердой однородной породой. Вопросы, которые мы рассматриваем и на которые, как мы думаем, можно ответить с помощью такой простой модели, таковы:

(i)
можно ли получить аномальный (в смысле, упомянутом выше в связи с Мичоаканским землетрясением) отклик без какой-либо латеральной неоднородности (возникающей из-за объемных включений или неровностей границ раздела) в подземной среде?
(ii)
каково отношение одномерного к двумерному отклику и насколько адекватно моделировать общий отклик конфигурации его откликом на (почти) вертикально падающую плоскую волну?
(iii)
как глубина фокуса источника влияет на отклик?
В сопутствующей статье (Groby & Wirgin 2005) мы дадим ответы на следующие вопросы (в дополнение к предыдущим, когда будет сочтено необходимым числовое значение):
(iv)
как эпицентральное расстояние повлиять на реакцию?
(v)
как контраст механических свойств между слоем и полупространством влияет на отклик грунта?
(vi)
как толщина слоя влияет на реакцию?
(vii)
как спектральные характеристики падающего импульса влияют на отклик?

Будет показано, что источник, излучающий цилиндрические волны в полностью упругой среде мягкого слоя/твердого полупространства, создает отклик земли, представляющий собой сумму трех слагаемых, соответствующих различным комбинациям двух типов волн в мягком слое (SL) и жесткое полупространство (HHS):

стоячие объемные волны (SBW) в SL и объемные волны (BW) в HHS,
стоячие объемные волны в SL и поверхностные волны (SW) в HHS и
стоячие поверхностные волны (SSW) ) в SL и поверхностных волнах в HHS.

Только волны типа (2) соответствуют модам Лява (на резонансных частотах этих мод), и условия оптимального возбуждения и максимального вклада этих мод будут приведены в явном виде. Теоретически будет показано, что длительная (т. е. аномальная) реакция обычно требует преобладающего вклада по крайней мере одной (обычно низшего порядка) мод Лява в общую реакцию. Волны типа (1) преобладают в ситуации, когда глубина очага велика и обычно не дают длительный отклик , хотя они могут давать сильный (но нормальный) отклик при большом контрасте механических свойств между SL и HHS. Будет показано, что явления биения являются следствием (для импульсивных запросов с преимущественно низкочастотным спектром) интерференции волн типа (1) и типа (2), которые обе приводят к максимумам отклика почти на одной и той же (низкой) частоте. Оказалось, что волны типа (3) вносят незначительный вклад в общий отклик. Большинство этих особенностей переносятся на случай, когда слой имеет потери. Будут обсуждены практические последствия этих результатов в отношении тем (а) и (б).

2 Описание конфигурации

На рис. 1 представлено поперечное сечение (сагиттальная плоскость) типичного голого (т. е. без всех строений) городского участка. Γ _g – земля, предполагаемая плоской и горизонтальной, над которой расположена воздушная среда, предполагаемая вакуумом. Ω ₁ — бесконечная в поперечном направлении область, занятая механически мягким слоем, h — его толщина. Ω ₀ – полубесконечная область (субстрат), занятая механически жесткой средой, а Γ _h плоская горизонтальная поверхность раздела между слоем и субстратом. A OX ₁ x ₂ x ₃ Cartesian Cordinate System прикреплена к этой конфигурации, так что O находится на земле, x 2 2 находится на земле, x 60 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 . ₃ перпендикулярно (сагиттальной) плоскости рисунка. С i _j единичный вектор вдоль положительного x _j оси, заметим, что орты нормали к Γ _g и Γ _h равны i ₂ . Среды заполнения Ω ₀ и Ω ₁ равны M ⁰ и M ¹ соответственно, причем последние предполагаются исходно свободными от напряжений, линейными, изотропными и однородными. Мы предполагаем, что M ⁰ является недиссипативным, а M ¹ обычно (если не указано иное) является диссипативным.

Рисунок 1

Открыть в новой вкладкеСкачать слайд

Конфигурация в разрезе.

Сейсмическое возмущение доставляется на площадку в виде поперечно-горизонтальной (SH) цилиндрической пульсовой волны, излучаемой линейным источником (перпендикулярно сагиттальной плоскости), расположенным на расстоянии x ^с := ( х ^с ₁ , х ^S ₂), с гипотезой, x ^S ₂> H (I. E.E. x 3> H (I.E.E. x3> H (т.е. SH-природа этой волны означает, что связанное с ней движение является строго поперечным (т.е. в направлении x ₃ и не зависит от координаты x ₃). И поляризация ВГ, и инвариантность падающей волны относительно x ₃ сообщаются полям, которые генерируются на площадке в ответ на падающую волну. Таким образом, наш анализ будет иметь дело только с распространением двумерных SH-волн (т.е. волн, зависящих исключительно от двух декартовых координат x ₁ , x ₂ и связанных с движением в x ₃ только направление).

Мы будем заниматься описанием эластодинамического волнового поля на земле (т.е. на Γ _г ) в результате возбуждения площадки цилиндрическими сейсмическими волнами.

3 Основные уравнения

3.

1 Волновые уравнения пространственно-временной области
В обычно неоднородной изотропной упругой или вязкоупругой среде M занимающей , волновое уравнение во временной области для SH-волн имеет вид:
где 2 u 9 компонента смещения в направлении i ₃, f компонента плотности приложенной силы в направлении i ₃ направление, µ дескриптор жесткости Ламе, ρ массовая плотность, t временная переменная, ω угловая частота, ∂ по отношению к t и х = ( х ₁ , х ₂ ). Поскольку наша конфигурация включает две однородные среды, а приложенная сила считается отличной от нуля только в Ω ₀, мы имеем
, где м Обозначают среду (0 для м ⁰ или 1 для М ¹), Δ _{М 0 ), Δ _{М 0 ), Δ _{М 0 ), Δ _{М 0 ), Δ _{М 0 ), Δ _{М 0 ). равным нулю в противном случае, а c ^м – общая комплексная скорость поперечных объемных волн в M ^м , связанная с плотностью и жесткостью соотношением}}}}}}
при том понимании, что ^м (ω); м = 0, 1 константы по отношению к x .
3.2 Представление силы в пространственно-временной области
Во всем последующем мы выбираем силовую функцию линейного источника
где δ( ) — дельта-распределение Дирака, а x ^с обозначает положение линии источник.
3.3 Волновые уравнения в частотной области
Версии волновых уравнений в частотной области получаются путем разложения плотности силы и смещения в интегралы Фурье:
, чтобы получить уравнения Гельмгольца
, где
обычно представляет собой комплексное волновое число в M ^m . На самом деле, из-за допущений, сделанных в разделе 2:
(т. е. k ⁰ действительно),
, где S (ω) — спектр падающего импульса.
3.4 Материальные константы в диссипативной среде
Теперь несколько слов о диссипативной природе слоя. Когда среда M с потерями, волновое число в нем комплексное и может быть записано (опустив пока зависимость от ω) как
, где условно
Теперь обратимся к (7) и отметим, что комплексное k подразумевает комплексное μ, в связи с тем, что плотность массы целесообразно считать действительной величиной. Таким образом, мы пишем
. Чтобы сохранить положительный действительный аспект жесткости для эластичных материалов, мы берем
и выясняем знак мнимой части μ. Подставляя (12) в (7), получаем
Предположим, как это обычно бывает для умеренно диссипативных сред, что |µ″/µ′| ≪ 1, так что разложение в ряд Тейлора [ ] ^−1/2, ограниченное первыми двумя членами, дает
, где по определению
Таким образом, использование (11) и (12) обязательно приводит к
Мы определяем положительную действительную величину, известную как добротность Q , соотношением
и отмечаем, что она бесконечна для среды без потерь, такой как M ⁰ (поскольку в этом случае μ″= 0). Кроме того, комплексное волновое число становится равным
, откуда мы находим
. Возникает вопрос о правильном определении комплексной скорости объемной волны c в M . Мы пишем
и требуем
из-за того, что скорость объемной волны положительна в среде без потерь. У нас есть
, из чего мы видим, что для того, чтобы ℑ k = k ″≥ 0, мы должны иметь
. Остается вопрос о ω-зависимости μ и Q (ω-зависимость k и c следует из зависимости μ и Q ). В сейсмологических приложениях с участием вязкоупругих сред коэффициент качества оказывается либо постоянным, либо слабо меняющейся функцией частоты (Faeh et al. 1994). Предположим, что Q ¹ (ω) = Q ¹ = const, и можно показать (Кьяртанссон, 1979), что это подразумевает
, где: ω _ref — эталонная угловая частота, предпочтительно как можно ближе к нулю, но выбрано здесь по числовым причинам равным 9× 10 ⁻² Гц. Следовательно,
и
. Следует отметить, что хотя Q ¹ является недисперсионным (т. е. не зависит от ω) при данном предположении, фазовая скорость c ¹ равна дисперсионный.
3.5 Граничные и радиационные условия
Считаем, что слой и подложка находятся в сварном контакте так, что перемещения и тангенциальные составляющие тяги непрерывны на границе раздела Γ _h :
Поскольку предполагается, что граница раздела воздух/слой Γ _g (т.е. земля) отделяет вакуум от упругой среды, то тангенциальная составляющая тяги на этой границе должна обращаться в нуль, т.е.
где . Единственность решения задачи прямого рассеяния обеспечивается условием излучения в подложке:
3.6 Постановка краевой задачи (прямого рассеяния)
Задача состоит в определении временного рекорда смещения грунта поле U ¹ ( x _G, T ) (с x _G: = ( x g : = ( x ^{2 ^{1 2^{1 2 ^{1 ^{1 ^{1 ^{1 ^{1). u ¹ ( x _g , ω) via the Fourier transform}}}}}}}}
Note that due to the fact that u ¹ ( x _g , t ) — реальная функция, мы должны иметь
(где символ * обозначает оператор комплексного сопряжения), из которого следует, что
4 Точные решения в частотной области путем разделения переменных
4.1 Предварительные сведения плоские волновые интегральные представления полей, способ разложения и анализа этих интегралов несколько отличается от предыдущих исследований (например, Эттвуд 1951; Коллинз 1960; Харкрайдер 1964; Бен-Менахем и Харкрайдер, 1964, 1970; Туан и Понамги, 1972 г .; Бушон 1982; Апсель и Луко, 1983; Луко и Апсель, 1983; Кеннет 1983; Панза 1985; Ван дер Хейден, 1987 г.
; Дравински и Моссессиан, 1988; Линг и др. 1998 г.; Чжан и др. 2003). Большое количество и разнообразие этих публикаций свидетельствует о богатстве и важности предмета (касающегося как электромагнитных, ультразвуковых, так и сейсмических волн), а также о том, что некоторые черты предмета до сих пор остаются неясными. В первом подклассе этих исследований (обсуждению которого мы посвящаем приложение к сопутствующей статье Groby & Wirgin, 2005) интегралы по плоским волнам (с горизонтальным волновым числом в качестве переменной интегрирования) сводятся к ряду вычетов (т. е. называемые модальными рядами) плюс интегралы отсечения ветвей, последними обычно пренебрегают, если точка от источника до точки наблюдения велика по сравнению с длиной волны. Во втором подклассе вышеупомянутых исследований используются различные устройства для численной эффективной, точной или асимптотической оценки интегралов плоских волн. Третий подход, связанный с так называемым методом Каньяра-де Хоопа (Ван дер Хийден 19). 87), включает в себя получение истории во времени без предварительного явного определения спектра отклика.
Наш вклад по существу двоякий: (1) установить физический смысл членов, входящих в наш выбор разложения интегралов, и (2) проверить численными средствами, когда это возможно, теоретические предсказания и открыть новые особенности реакция земли не сразу проявляется в теоретических формулах. Первая задача решается в настоящей работе, а вторая — в сопутствующей статье (Groby & Wirgin 2005).
4.2 Решения в частотной области при отсутствии слоя и свободной поверхности
При отсутствии слоя и свободной поверхности задача состоит в излучении волны SH от линейного источника в 2- D свободное пространство, занятое однородной средой M ⁰ . Мы называем эту излучаемую волну «падающей волной» и обозначаем ее u ⁱ .
Применяя разделение переменных в декартовой системе координат к уравнению Гельмгольца и используя условие излучения, можно показать, что u ⁱ принимает вид (Morse & Feshbach 1953)
или
где H ⁽¹⁾ ₀ ( ) — функция Ганкеля нулевого порядка для реальный к ₁ . Мы будем использовать в разделе 4.4 форму, принятую u ⁱ в области:
где
4.3 Полевые представления в декартовых координатах для конфигурации, включающей слой и свободную поверхность
При наличии слоя и свободной поверхности падающее поле, описанное в предыдущем разделе, не может распространяться беспрепятственно, т. что путем повторного использования разделения переменных в декартовых координатах и условий излучения мы приходим к представлению полных полей в подложке и слое как
где:1261 B ⁰, A ¹, B ¹ пока не определены.
4.4 Определение коэффициентов дифракции и полей частотной области путем применения граничных условий
Граничное условие свободной поверхности влечет за собой:
откуда
Условие непрерывности смещения приводит к:
тогда как непрерывность тангенциального тягового усилия граничное условие подразумевает:
Решение этой линейной системы уравнений:
, так что решения для полей в частотной области:
Наконец, характеристика земли в частотной области принимает форму:
5 Структура характеристики в частотной области в случае слоя без потерь
5.
1 Частотная характеристика в слое
Когда слой бездиссипативный, т. е. упругий, то μ ¹ является действительным и не зависит от ω, а k ¹ (ω) является действительным ( напомним, что мы предполагали подложку упругой, а это означает, что µ ⁰ действительно и не зависит от ω, а k ⁰ (ω) тоже вещественно). Следовательно, в интегралах предыдущего раздела мы сталкиваемся с интервалами K ₁, через которые K ⁰ ₂ и K ¹ ₂3 – это либо нормейно, ₂3 – это либо нормейно, ₂. Важно отметить, что термины «мягкий слой» и (относительно) «твердый субстрат» имеют в данном контексте следующее значение:
, так что (51) может быть выражено как:
с:
Мы пишем:
, которые вместе с (58) выражают тот факт, что часть (т. поле в слое состоит из суммы стоячих объемных волн (СПВ), каждая из которых представляет собой сумму двух плоских объемных волн, имеющих волновые векторы одинаковой длины.
Таким же образом запишем:
, что вместе с (60) выражает тот факт, что другая часть (т.е. I ¹ ₂ ) поля в слое снова состоит из суммы стоячих объемных волн, каждая из которых является суммой двух плоских объемных волн с волновыми векторами, имеющими одинаковую длину. Обратите внимание, однако, что ни волновые векторы, ни амплитуды этих SBW не являются такими же, как у SBW (далее именуемой SBW1) в I ¹ ₁ (поскольку диапазон интегрирования в последнем отличается от диапазона интегрирования в ). я ¹ ₂). В самом деле, (67) говорит нам, что амплитуды G ¹ ₂ SBW в I ¹ ₂ (далее называемые SBW2) экспоненциально уменьшаются по мере увеличения глубины фокуса (т. s ₂ ) увеличивается, так что SBW2 дают о себе знать тем меньше, чем дальше источник (в вертикальном направлении) от земли . С другой стороны, амплитуды SBW1 являются синусоидальными функциями глубины фокуса, так что SBW1 могут сильно ощущаться в большом количестве мест расположения источников .
Наконец, запишем:
что вместе с (62) выражает тот факт, что третья часть (т.е. волн (SSW), каждая из которых представляет собой сумму двух плоских поверхностных волн с волновыми векторами, имеющими одинаковую длину (заметим, что каждая такая плоская поверхностная волна является неоднородной волной (с комплексным волновым вектором), фаза которой постоянна на x ₁ = константа. и амплитуда которого либо увеличивается, либо уменьшается по мере приближения x ₂ к некоторой горизонтальной поверхности x ₂ = const. ). уравнение (69) говорит нам, что амплитуды G ¹ ₃ ВСП в I ¹ ₃ экспоненциально уменьшаются с увеличением глубины фокуса, так что ВСП тем менее дают о себе знать дальше источник (по вертикали) от земли .
Основной вывод из этого обсуждения заключается в том, что для достаточно больших фокусных глубин источника частотная характеристика в слое по существу определяется выражением I ¹ ₁ и выражается суммой SBW1. Это более или менее соответствует ситуации в квазиодномерном анализе задачи прямого рассеяния, но, как мы увидим далее, ни в коей мере не является верной картиной отклика конфигурации, когда глубина очага источника невелика.
5.2 Частотная характеристика в жестком полупространстве
Мы сосредоточим внимание исключительно на дифрагированном поле в подобласти Ω ⁻ ₀, хотя суть написанного относится ко всему полупространству Ом ₀ . Действуя, как в разделе 5.1, находим:
с:
Пишем:
, что вместе с (71) выражает тот факт, что часть (т. е. I ⁰ ₁ ) полупространство состоит из суммы плоских объемных волн (ОБ). Таким образом, каждому горизонтальному волновому числу k ₁ в интервале [− k ⁰ , k ⁰ ], соответствуют SBW1 в Ω ₁ и BW 2 9,9022 − ^Ω
Таким же образом запишем:
, которые вместе с (73) выражают тот факт, что другая часть (т.е. I ⁰ ₂ ) дифрагированного поля в полупространстве состоит из сумма плоских поверхностных волн (ПВ), далее обозначаемая ПВ2. уравнение (80) говорит нам о том, что амплитуды G ⁰ ₂ SW2 в I ⁰ ₂ экспоненциально уменьшаются с увеличением глубины фокуса, так что SW2 тем меньше дают о себе знать, чем дальше источник (в вертикальном направлении) ) с земли. С другой стороны, амплитуды BW в I ⁰ ₁ являются синусоидальными функциями глубины очага, так что эти BW могут сильно ощущаться при большом разнообразии местоположений источников. Кроме того, отметим, что каждому горизонтальному волновому числу k ₁ in the intervals [− k ¹ , − k ⁰ ] and [ k ⁰ , k ¹ ], correspond a SBW2 in Ω ₁ и SW2 в Ом ⁻ ₀ .
Наконец, пишем:
, что вместе с (75) выражает тот факт, что третья часть (т.е. I ⁰ ₃ ) дифрагированного поля в субстрате состоит из поверхностные волны (далее обозначаемые SW3). уравнение (82) говорит нам о том, что амплитуды G ⁰ ₃ of the SW3 in I ⁰ ₃ decrease exponentially as the focal depth (i. e. h + x ^s ₂ ) increases, so that SW3 дают о себе знать тем меньше, чем дальше источник (по вертикали) от земли. Обратите внимание, однако, что волновые векторы, связанные с SW3, не идентичны тем, которые связаны с SW2, потому что k ₁ охватывает интервал в I ⁰ ₃, который отличается от интервала в I ⁰ ₂ . Кроме того, заметим, что каждому горизонтальному волновому числу k ₁ в интервалах ]−∞, − k ¹ ] и [ k ¹ , ∞[ соответствует ПСВ1 в 2 Ω 1 и SW3 в Ом ⁻ ₀ .
Основной вывод из этого обсуждения заключается в том, что при достаточно большой глубине фокуса источника отклик в частотной области в полупространстве по существу задается как I ⁰ ₁ и выражается суммой BW. Это более или менее соответствует ситуации в квазиодномерном анализе задачи прямого рассеяния, но, как мы увидим далее, ни в коей мере не является верной картиной отклика конфигурации, когда глубина очага источника невелика.
5.3 Амплитуды SBW1
В дальнейшем мы ограничиваем наше внимание полем в мягком слое и, в частности, тремя отдельными типами стоячих волн (SBW1, SBW2, SSW), из которых он состоит. Здесь мы сосредоточимся на общей ВБВ1 и отметим, что ее амплитуда G ¹ ₁ является произведением трех факторов: фактора S (ω), связанного со спектром падающего импульса, геометрического фактора, связанного с местоположением источника (влияние которого уже обсуждалось) , и так называемый коэффициент интерференции F ¹ ₁ . Сначала мы обсудим фактор помех, а затем завершим обсуждение некоторыми замечаниями по поводу S (ω).
Переписываем I ¹ ₁ как
Сделаем замену переменных
и примем определения:
Заметим, что γ > 1 и υ < 1 из-за предыдущих предположений. Затем
, где
Теперь рассмотрим E ¹ ₁ в интервале ζ∈[0, 1]. Поскольку η и ζ действительны, знаменатель в E ¹ ₁ не может обращаться в нуль; однако она достигает минимума при определенных значениях этих параметров. Считаем ζ постоянным и выясняем, при каких значениях η
достигает своего минимума. Необходимое условие:
Существуют три возможности, первая из которых φ=0, но отсюда следует ζ=γ > 1, что противоречит тому, что ζ должно лежать в [0, 1]. Вторая возможность состоит в том, что ψ=υφ; мы рассмотрим этот случай в дальнейшем. Третья возможность: sin (2φη) = 0, откуда φη = n π/2; n = 0, 1, … . Определить, при каких значениях n эти корни соответствуют действительным минимумам | Ф ¹ ₁ (ζ, η)| ⁻² мы должны иметь
Это условие порождает два типа решений в зависимости от знака υ ² φ ² −ψ ² . Первый тип, который мы называем четной объемной волной решения (обозначается верхним индексом Be ), представляет собой:
Пусть ζ ^В — значение ζ, для которого υφ=ψ. Находим
или
, откуда следует, что ζ ^B < 1, а это означает, что вторая возможность (т. е. υφ=ψ) не противоречит ограничению ζ∈[0, 1].
Таким образом, три типа решений, ведущих к минимумам E ¹ ₁, таковы:
Смысл всего этого в том, что η) максимумов для всех значений ζ, что является другим способом сказать, что ∥ E ¹ ₁ ∥ — периодическая функция от η для всех ζ. Период этой функции равен π/φ (даже когда ζ=ζ ^B , потому что константа является периодической функцией с произвольным периодом). Однако в трех случаях (95)–(97) функция принимает разные формы. Фактически,
(i)
для ζ> ζ ^B: ∥ E ¹ ₁ ∥ имеет максимум, равное ψ ^–1 = AT a a aT a a aT a aT a aT a aT a AT a aT a AT a AT a AT a AT a AT a AT a AT a AT a AT AT a AT a AT a AT a AT a AT a AT a AT a AT AT a AT a AT AT a AT a AT AT a AT AT a AT a AT a AT at 9266 = = = 9126 361 26123. и минимумы, равные (υφ) ⁻¹ at η= (2 m + 1)π/2φ,
(ii)
for ζ=ζ ^B :∥ E ¹ ₁ ∥ is a constant равен ψ ⁻¹ = (υφ) ⁻¹ при всех η,
(iii)
) для ζ < ζ ^B : | E ¹ ₁ ∥ имеет минимумы, равные ψ ⁻¹ при η= м π/φ, и максимумы, равные (υφ) ⁻¹ при η= (1 м 9126) п/2ф.
Численный пример поможет оценить относительную важность этих трех типов решений. Напомним, что:
, так что
. Выберем параметры, которые могут быть уместны в контексте тем (а) и (б): кг м ^-3 , с ¹ = 100 м с ^-1 , ρ ¹ = 1000 кг м ^-3 , для которых υ = 0,67 · 10 ⁻² и υγ= 0,67 × 10 ⁻¹ , откуда ζ ^B = 0,995. Таким образом, ∥ E ¹ ₁ ∥ принимает вид функции типа (iii) на большей части интервала [0, 1], фактически при 0 ≤ζ < 0,995. В частности, для объемных волн, волновые векторы которых почти вертикальны (т. е. 0 ≤ ζ ≪ 1), максимум ∥ E ¹ ₁ ∥ равен
, что в данном числовом примере равно 15.
Наименьшая частота (ν=ω/2π), для которой достигается это значение (полученное из η=π/2φ≈π/2γ), равна
и часто называется либо «фундаментальной резонансной частотой Хаскелла» (Bard & Bouchon 1980), либо «одномерной резонансной частотой» (Bard & Bouchon 1985; Semblat et al. 2000) слоя мягкого/твердого грунта. конфигурация субстрата. Однако синусоидальная функция отклика типа E ¹ ₁ не согласуется с резонансным откликом (который велик на резонансных частотах в отсутствие механизма диссипации), который возник бы, например, в контексте возбуждения какого-то структурного режима; на самом деле этот синусоидальный отклик является результатом интерференции волн, поэтому мы назвали F ¹ ₁ «фактор помех». Таким образом, сомнительно, уместно ли использовать термин «резонансы» (Bard 1985; Bard & Bouchon 1980, 1985) в связи с реакцией объемных волн (воплощенной в I ¹) конфигурации.
В завершение обсуждения рассмотрим спектральный фактор S (ω). Очевидно, что если S (ω) = S (η c ⁰ / h ) существенно велико вблизи частот η = (2 м + 1)π/2φ ; m = 0, 1, … , при котором F ¹ ₁ велико, то произведение этих двух функций, воплощенных в I ¹ ₁, будет велико на этих частотах. В частности, если S (ω) = S (η c ⁰ / h ) максимально вблизи низкой частоты η=π/2φ, то отклик будет большим в большом диапазоне горизонтальные волновые числа из-за вклада м = 0 максимум фактора помех E ¹ ₁ . Это неоднократно отмечалось в прошлом (Бард, 1985; Бард и Бушон, 1980, 1985) и называлось «резонансным откликом», хотя (как указывалось в предыдущем абзаце) η = (2 m + 1)π/ 2ф ; m = 0, 1, … не являются резонансными частотами.
5.4 Амплитуды SBW2
Теперь обратим внимание на компоненту SBW2 поля в мягком слое. Отметим, что амплитуда G ¹ ₂ общей SBW2 является произведением трех факторов: фактора S (ω), связанного со спектром падающего импульса, геометрического фактора, связанного с местоположением источника (влияние которого уже обсуждалось), и так называемый фактор интерференции F ¹ ₂ dk ₁ . Здесь мы обсуждаем произведение фактора помех с на (ω), чтобы оценить вклад общего SBW2 в общий отклик в слое и на земле.
We rewrite I ¹ ₂ as
and make the same change of variables as in the previous section, employing the additional definition
Thus
wherein
Let us examine E ¹ ₂ в интервале ζ∈[1, γ]. В отличие от предыдущего случая, здесь знаменатель (в E ¹ ₂ ) может обращаться в нуль для действительных η и ζ, то есть
это не что иное, как дисперсионное соотношение мод Лява . Корни этого соотношения:
, где функция арктангенса определена в [−π/2, π/2] и может быть выражена либо рядом
, либо рядом
. Легко показать, что θ=υφ когда
так, что ζ ^L > 1, как и должно быть для выполнения ограничения ζ∈[1, γ].
Таким образом, три типа решений приводят к нулю в знаменателе F ¹ ₂ : for:
for:
for:
и соответствуют существованию трех типов (четных, нейтральных, нечетных) мод Лява, собственные частоты которых равны η ^Le _{^{1 соответственно.}}
Это означает, что ∥ E ¹ ₂ ∥ имеет регулярно расположенные (в терминах η) максимумы для всех значений ζ, что является другим способом сказать, что ∥ E ¹ ₂ ∥ — периодическая функция от η для всех ζ. Период этой функции равен π/φ (даже когда ζ=ζ ^L, поскольку константа является периодической функцией с произвольным периодом). Однако функция принимает разные формы в трех случаях (111–113). In fact,
(i)
for ζ < ζ ^L : ∥ E ¹ ₂ ∥ has maxima equal to ∞ at η=η ^Le _m,
(II)
для ζ = ζ ^L: ∥ E ¹ ₂ ∥ имеет максимум ∞ AT η = η ^{9122 2 . ,}
(iii)
for ζ > ζ ^L :∥ E ¹ ₂ ∥ has minima equal to ∞ at η=η ^Lo _m .
Численный пример поможет оценить относительную важность этих трех типов решений. Давайте снова выберем: c ⁰ = 1000 m s ⁻¹ , ρ ⁰ = 1500 kg m ⁻³ , c ¹ = 100 m s ⁻¹ , ρ ¹ = 1000 kg m ⁻³ , для которых γ = 10, υ = 0,67 × 10 ⁻² и υγ = 0,67 × 10 ⁻¹ , откуда ζ ^L = 1,0044. Таким образом, | F ¹ ₂ | принимает форму функции типа (iii) для большей части интервала [1, γ], фактически в 1,0044 ≤ζ < 10,
Несколько замечаний по порядку.
Вопреки тому, что можно сделать из таких работ, как Bard & Bouchon (1980, 1985), Bard (1985) и Chávez-Garcia & Bard (1994), отдельные моды Лява не имеют структуры поверхностных волн в слое (а значит, и на земле), поскольку SBW2 фактически являются стоячими объемными волнами; единственная их общая черта с поверхностными волнами (т.е. УВ, которые сосуществуют в твердой подложке при возбуждении мод Лява) — это их фазовая скорость
, при этом можно отметить, что из-за того, что ζ∈[1, γ],
, что означает, что фазовая скорость мод Лява (разделяемая SBW2 в слое и УВ в твердом субстрате) меньше фазовой скорости объемных волн в твердом субстрате,
, в отличие от того, что происходит в В связи с SBW1 возбуждение мод Лява действительно является резонансным процессом, потому что моды Лява на самом деле являются структурными модами конфигурации мягкий слой/твердый субстрат и поскольку отклик, связанный с каждой из этих мод, велик при резонансе в отсутствие диссипации. в обоих носителях конфигурации и
резонансные частоты мод Лява не идентичны частотам, на которых SBW1 достигает своего максимума; например, разность этих частот для м -го преобладающего нечетного типа SBW1 и SBW2 составляет: она может быть близка) к соответствующей ВБВ2 (отметим, что разность в (116) не зависит от м ).
В заключение этого обсуждения мы снова рассмотрим спектральный фактор S (ω). It is obvious that if S (ω) = S (η c ⁰ / h ) is significantly large near the frequencies η ^Lo _m at which E ¹ ₂ велико (бесконечно, если диссипация отсутствует), то произведение этих двух функций, воплощенное в I ¹ ₂ , будет большим на этих частотах. В частности, если S (η c ⁰ / h ) максимальна вблизи низкой частоты η ^Lo ₀ , то отклик будет большим в большом диапазоне горизонтальных волновых чисел. Если S (ω) = S (η c ⁰ / h ) максимально вблизи низкой частоты η ^Lo _{0 9012 ,0052 Lo ₀ не слишком далеко от η ^Bo ₀ , то глобальный отклик может быть еще больше из-за кумулятивного вклада как SBW1, так и SBW2.}
5.5 Амплитуды ВСП
Обратим внимание на ВСП компонент поля в мягком слое. Заметим, что амплитуда G ¹ ₃ общей ВСП является произведением трех факторов: S (ω), связанного со спектром падающего импульса, геометрического фактора, связанного с положением источник (влияние которого уже обсуждалось) и фактор помех Ф ¹ ₃ . Здесь мы обсуждаем произведение фактора помех с на (ω), чтобы оценить вклад общего SSW в общий отклик в слое и на земле.
. Перепишем I ¹ ₃ как
и сделаем ту же замену переменных, что и в предыдущих двух разделах, используя дополнительное определение
, так что
при 0034
[γ, ∞[ и η > 0, sh (χη) ≥ 0 и ch (χη) > 0 при ζ∈[γ, ∞[ что означает, что знаменатель в предыдущей формуле не может обращаться в нуль при действительных η и ζ. Однако он может иметь минимумы для ζ∈[γ, ∞[.
Считаем ζ постоянной величиной и выясняем, при каких значениях η знаменатель E ¹ ₃ имеет минимумы. Для этого требуется, чтобы
Однако [ ]≠ 0, за исключением χ= 0, т. е. для ζ=γ и ∀η. При х = 0 находим | E ¹ ₃ | ⁻¹ =θ, а из того, что sh (χη) ≥ 0 и θ ch (χη) ≥ θ при ζ∈[γ, ∞], заключаем, что | E ¹ ₃ | ⁻¹ ≥θ. Это означает, что ζ=γ соответствует положению минимума | E ¹ ₃ | ⁻¹, и это справедливо для всех η.
Таким образом, | E ¹ ₃ | является монотонно убывающей функцией от ζ для всех ζ∈]γ, ∞[ и достигает своего максимума, равного при ζ=γ для всех η.
Чтобы получить представление о величине этой функции, особенно по отношению к E ¹ ₁ , мы снова рассмотрим числовой пример:0052 0 = 1500 кг M ⁻³, C ¹ = 100 м S ⁻¹, ρ ⁰ = 1000 кг M ^{– 3}, для которого γ = 10, wh. weend max∥
11111111111111111111111111111111111111111111111111.3 , для которого γ = 100053. ¹ ₃ ∥≤ 0,1005, что намного меньше max∥ E ¹ ₁ ∥= 15 для того же набора параметров.
Поскольку максимум E ¹ ₃ достигается на всех частотах (т. е. для всех η), функция спектра S (ω) не влияет на относительный вклад I ¹ ₃ к ответу на землю. Таким образом, чтобы завершить это обсуждение, мы можем сказать, что SSW относительно мало вносит вклад в отклик грунта по сравнению с SBW1 и SBW2, за исключением, возможно, частот, близких к минимумам функций E ¹ ₁ и Е ¹ ₂ .
6 Представление спектров суммарного поля в слое и дифрагированного поля в полупространстве в разрезе полюс-ветвь
Более подробно этот вопрос рассматривается в Приложении B сопроводительного документа (Groby & Wirgin 2005). Здесь мы приведем только основные особенности, опять же предполагая, что среды, заполняющие слой и полупространство, свободны от диссипации и что k ¹ > k ⁰ .
Перепишем (50)–(51) следующим образом (с учетом (40):
где
Из материала раздела 5. 4 видно, что D ( k ₁ , ω) может обращаться в нуль при счетном наборе действительных значений k ₁ (резонансных волновых чисел левовских мод) в интервале [ k ⁰ , k ]. Предположим, что частота такова (то есть мала), что существует только одно такое значение, и назовем его k ^★ ₁ . Тогда подынтегральные выражения в (122)–(123) сингулярны для k ₁ = k * ₁ , что предполагает вычисление соответствующих интегралов с помощью теоремы Коши (Whittaker & Watson 1922; Перевозчик и др. 1983).
Рассмотрим первый из этих двух интегралов. Чтобы применить теорему Коши, мы вычисляем вспомогательный интеграл замкнутого контура (этот контур описан в Приложении B к Groby & Wirgin (2005)) с тем же подынтегральным выражением, что и предыдущий, чей контур содержит действительную k ₁ ось и подходящие ответвления от точки разветвления k ₁ = k ⁰ до k ₁ = ± i ∞. Теорема Коши говорит нам, что вспомогательный интеграл по замкнутому контуру равен 2π i , умноженному на вычет полюса, находящегося внутри пути интегрирования, так что в силу того, что вклад интеграла по полуокружности бесконечного радиуса равен nil, можно найти
, где
и является вкладом от интегралов ветвления (полные выражения этих интегралов см. в Приложении B к Groby & Wirgin 2005).
Аналогично для u ¹ приводит к
Замечание 1 Полюсный вклад в u ^{0 d} (первое слагаемое в правой части (127)) имеет структуру a (типа 912 SW61) поверхностная волна , волновое число которой k ^★ ₁ соответствует фундаментальной моде Любви.
Замечание 2 Амплитуда вклада этого полюса в u ^{0 d} тем больше, чем меньше расстояние источника от нижней границы слоя (напомним, что источник считался лежат в нижнем полупространстве).
Замечание 3 Полюсный вклад в u ¹ (первое слагаемое в правой части (130)) имеет структуру (типа SBW2) стоячей объемной волны с волновым числом k * ₁ — это основной режим Любви.
Замечание 4 Амплитуда вклада этого полюса в u ¹ тем больше, чем меньше расстояние источника от нижней границы слоя.
Замечание 5 Мы не дали явного выражения для вклада с разрезой ветви U ^{0 D} _B до U 1261 до U 1262 0 до U 1261 0 до U 1261 0 до U 111262 до U 111262. b до u ¹ , но в Groby & Wirgin (2005) показано, что все они тем меньше по отношению к полюсному вкладу, чем больше гипоцентральное расстояние; таким образом, для всех гипоцентральных расстояний, за исключением, возможно, очень малых, в отклике земли в частотной области преобладает вклад моды Лява, тогда как на малых гипоцентральных расстояниях что-то еще может мешать модам Лява. Это «что-то еще» было связано с так называемыми «модами» Haskell в представлении SBW1+SBW2+SSW в разделе 5. Мы дадим более точную оценку их влияния в сопутствующей статье (Groby & Wirgin 2005).
7 Комментарии к представлениям отклика грунта SBW1+SBW2+SSW и полюс+ветвь
Хотя теоретический анализ, проведенный в разделе 5, может быть полезен для подчеркивания роли, которую играют различные типы объемных и поверхностных волн I ¹ ₁ , I ¹ ₂ и I ¹ ₃ для частотной характеристики заземления. Другим очевидным недостатком этого анализа является то, что он был ограничен случаем, в котором слой является упругим, но выводы, сделанные для случая упругого слоя, не должны радикально отличаться для случая слабо или умеренно вязкоупругого слоя.
Хотя анализ раздела 6 приводит к кажущемуся простому результату (т. е. для полюсных вкладов), на самом деле мы обычно сталкиваемся с проблемой вычисления интегралов ветвления.
Следовательно, в сопутствующей статье (Groby & Wirgin 2005) мы прибегаем к чисто числовому подходу для оценки I ¹ ₁ , I ¹ _{2 ^{2 ^{3 и ¹ ₃ и их суммы для определения отклика в частотной области на основе конфигурации слоя/подложки. Поскольку физически реалистичные конфигурации включают вязкоупругие слои, мы оцениваем эти интегралы и общую частотную характеристику u ( x _g , ω) в предположении наличия вязкоупругих слоев. После того, как u ( x _g , ω) вычислены, мы определяем временной сигнал u ( x _g ), опять же чисто числовыми средствами 96 9126 1, 9123 34).}}}
В работе Groby & Wirgin (2005) мы также численно оцениваем корни дисперсионного соотношения мод Лява, чтобы определить полюсные вклады, а также интегралы разреза ветвей как для упругого, так и для вязкоупругого слоев. Затем, как и в предыдущем абзаце, мы приступаем к получению временной динамики отклика земли из спектра этого отклика, воплощенного в сумме членов полюса и отсечения ответвления.
Слабость этих по существу численных подходов заключается в трудности распознавания механизмов, лежащих в основе наблюдаемой временной истории отклика земли. Чтобы преодолеть этот недостаток, мы развиваем в следующем разделе (раздел 8) анализ для получения временной диаграммы прямым способом, который, по-видимому, облегчает понимание конкретных особенностей временных характеристик отклика грунта.
8 Прямой анализ временной истории реакции земли
Прежде чем вдаваться в подробности этого анализа, подчеркнем следующие факты: (i) слой в целом неэластичен и (ii) слой мягче субстрата, что в настоящее время означает, что μ ¹ и c ¹ обычно являются сложными и
8.
1 Общие характеристики отклика во временной области на земле
Отправной точкой является (34), где мы делаем замену переменных, описанную в (84) и (85) .
Отклик земли во временной области становится равным
с, в силу (52),
в котором:
Заметим, что с учетом (131),
Изменение порядка интегрирования в (132) и (133) дает
где
Заметим из (134) следует, что α вещественна при |ζ| < 1 и мнимой при |ζ| > 1, или, другими словами:
Для дальнейшего использования мы определяем:
с
Таким образом,
где
с:
ψ вещественны, тогда как υ и β обычно комплексные из-за того, что µ
¹ и k ¹ (и, следовательно, γ) в общем случае комплексные (поскольку слой вообще диссипативный).
Ищем комплекс корней
уравнения
. С определениями:
действительная и мнимая части (151) дают
что представляет собой связанную систему двух нелинейных уравнений с двумя неизвестными а ^Б , б ^Б .
Можно показать, что из этих двух уравнений следует
Замечание 1 . |ζ| ≤ 1, так что d = 0 и (153)–(154) дают
. Это соотношение, определяющее волновые числа так называемых «мод» Haskell, называемых SBW1 в разделе 5, которые, как мы показали, принимают форму объемных (В) волн в субстрате и слое. По этой причине к корням (153)–(154) был добавлен верхний индекс B. В разделе 5.3 было показано, что так называемые четные решения (156) равны
, а так называемые нечетные решения (156) равны
откуда
=ℑ(η ^B β) и β действительно)
Замечание 2 к решениям «режима» Haskell.
Замечание 3 Отсюда следует, что в случае, когда слой является диссипативным , инициализировать итерационную схему получения кейс.
Remark 4 Note that it is not a ^B and b ^B that we are actually looking for, but rather η′ ^B and η″ ^B . У нас есть
, который представляет собой набор двух связанных уравнений для получения η′ ^B и η″ ^B из a ^B и b B. Это показывает, что может быть лучше решать уравнения (153) и (154) напрямую через η’ ^B и η″ ^B .
8.1.2 Комплексные нули числа
Далее рассмотрим, где: ζ и θ действительны, тогда как, как и прежде, v и β обычно комплексные.
Ищем комплекс корней
уравнения
, в котором причина присвоения решениям (164) верхнего индекса ‘ L ’ станет очевидной далее. С определениями:
и c и d , как и ранее, действительная и мнимая части (164) дают
. Мы снова сталкиваемся с задачей решения связанной системы двух уравнений, теперь в терминах из неизвестных а ^л и б ^л . Как и ранее, можно показать, что
Замечание 1 В недиссипативном случае υ и γ вещественны, а β вещественна в силу (135)–(136) и того факта, что в настоящем случай γ≥ |ζ| ≥ 1, так что из уравнений (166) и (167) находим
, что есть не что иное, как дисперсионное соотношение мод Лява в случае недиссипативного слоя в сварном контакте и вышележащего недиссипативного субстрат полубесконечной протяженности .
Один показывает, что другим следствием (166)–(167) является
Другими словами, собственные частоты мод Лява в недиссипативных средах являются реальными .
Действуя, как в разделе 5.4, находим (в отсутствие диссипации):
Замечание 1 Члены с участием d в уравнениях (166) и (166) добавляют небольшое возмущение к собственным частотам (четных (е) и нечетные (о)) формы любви, если принять во внимание (малую) рассеянность.
Примечание 2 См. Примечание 4 раздела 8.1.1.
8.1.3 Комплексные нули числа
Далее рассмотрим, где: ζ и θ действительны, тогда как v и χ обычно комплексные.
Ищем комплекс корней
уравнения
, в котором верхний индекс S присваивается решениям (174) для того, чтобы отличить последние от B и L ‘ решения.
С определениями:
действительная и мнимая части (174) дают
, которое представляет собой связанную систему двух нелинейных уравнений для двух неизвестных a ^S и b ^S . Можно показать, что следствием этих двух уравнений является: есть небольшое количество диссипация члены, содержащие d ≠ 0 в (177)–(178), составляют малое возмущение решений (180)–(181), что предполагает использование бездиссипативных решений в качестве стартовых в итерационной схеме получить решения в случае диссипации.
Примечание 2 См. Примечание 4 раздела 8.1.1.
8.2 Особенности временной характеристики на местности
8.2.1 Приближенное вычисление интеграла по вещественной оси функции, имеющей комплексные полюса
Мы видели в разделе, что отклик во временной области на земле сводится к сумме интегралов типа
где: (i) η заменено на η′, чтобы подчеркнуть тот факт, что эта переменная интегрирования является реальной , and (ii) is of the generic form
The important point is that
it being understood that η _m is a generic designation for η ^Be _m , η ^Bo _m , η ^Le _m , η ^Lo _m , η ^Se _m , and η ^So _м . уравнение (184) предполагает развитие в ряд Тейлора вокруг η=η _m , что дает
или, с учетом (184):
где
Следовательно,
Отсюда следует, что
где η′ ⁰ = 0, η′ ¹ , η′ ² , … , точки на оси η′ такие, что означает, что η′ _m ∈[η2′ 90 м , η′ ^{м +1} ] ; м = 0, 1, 2, ….
Пусть функция Гаусса
Разложение экспоненты в ряд Тейлора дает
, так что
откуда
Если, как предполагается, спектр падающего импульса медленно меняется по сравнению с каждой гауссианой в ряду, мы могу написать
Из-за концентрированного характера гауссиан, если бы пределы каждого интеграла были расширены за пределы интервала [η′ ^m , η′ ^{m +1} ], вклад интегралов расширенного интервала был бы пренебрежимо мала, так что мы можем сделать аппроксимацию
, где (см. (183))
. Сделаем замену переменных
, при этом положим, что η″ _m ≪ϖ, и используем , стр. 302)
(в которой ERF является функцией ошибки, так что), чтобы найти
, так что
, который приближается к
8,3 Оценки
J ¹ ₁, 1112669 9. 9. ³ _{112211123 ³ ₁,} ₁. и j ¹ ₃
Мы имели
, где
Таким образом,
8.
3.1 Вклад U ¹ _{1 на временной земле. и (147) имеем
, в котором
более ясно:
Замечание 1 U ¹ ₁ ( x _G, 112611111111111111111111111111111111111111111111111111111111111112 гг. ¹ ₁ ( x _g , ω), который, как было показано ранее, принимает форму интеграла по переменной ζ (или, что то же самое, по горизонтальному волновому числу k ₁ ), стоячих объемных волн 1-го типа (SBW1) (несколько видоизмененных, когда слой диссипативен). Здесь появляется интеграл того же типа, но подынтегральная функция включает общую волновую функцию вида
, где амплитудная функция равна
. синусоидальная функция пространства и времени, и поскольку аргумент положителен для достаточно больших t , правильно сказать, что общая форма волны представляет собой экспоненциально затухающую синусоиду как функцию временной переменной т для достаточно больших т .
Примечание 2 Скорость затухания может изменяться от линейной функции t для малых t до квадратичной функции t для больших t , и обе эти функции зависят от вертикального расстояния источника от нижней границы слоя, а также на эпицентральном расстоянии (через функции X ₁ и X ₂ ).
Замечание 3 Член вообще мал (а значит, и затухание велико) из-за того, что (η′ ^B _m ) ² мал; единственная ситуация, в которой возможно существование этого члена, — это большие X ₂ , что имеет место при большой глубине фокуса, точнее, когда расстояние по вертикали между источником и нижней границей слоя значительно больше толщины слоя. Это означает, что, как правило, вносит значительный вклад в общую временную динамику только в том случае, если источник относительно глубок и/или велик по какой-либо причине (есть некоторые признаки того, что это может быть в случае большого контраста плотностей и/или объемной волны). скорости между слоем и субстратом). Это указание согласуется с тем, что было обнаружено в отношении SBW1.}
Замечание 4 U ¹ _{1 M} ( x _G, T . горизонтальное волновое число ζ. Общая временная история SBW1 u ¹ ₁ ( x _g , t , ζ) представляет собой сумму за все время этих (четных и нечетных) историй Haskell. Если, как это часто бывает, спектр импульса источника S (ω) такова, что имеет значение только для низких частот, только мода m = 0 Bo дает значительный вклад в , т , ζ).
8.3.2 Вклад
u ¹ ₂ в перемещение грунта во временной области
С учетом (143) и (208) имеем
где 19034

Более явно1261 Замечание 1 U ¹ ₂ ( x _G, T ) – это история времени, соответствующая функции ответа на частоту I ) – это история времени, соответствующая функции ответа на частоту домена I ). _g , ω), который, как было показано ранее, принимает вид интеграла по переменной ζ (или, что то же самое, по горизонтальному волновому числу k ₁ ) стоячих объемных волн 2-го типа (SBW2 ) (несколько видоизменяется, когда слой является диссипативным). Здесь появляется интеграл того же типа, но подынтегральная функция включает волновую функцию общего вида

где амплитудная функция равна

Поскольку η′ ^L _m является действительным, а |η′ ^{L 10052 ^{2 m 2 | ≫ |η′ ^L _m |, множитель в (223) представляет собой синусоидальную функцию пространства и времени, а поскольку аргумент e ^{−[ ]} в (224) положителен для достаточно больших t правильно сказать, что общая форма волны представляет собой синусоиду с экспоненциальным затуханием как функцию временной переменной т для достаточно больших т .}}

Примечание 2 Скорость затухания может изменяться от постоянной относительно t для малых t до квадратичной функции t для больших t ; только малая t функция существенно зависит от вертикального расстояния источника от нижней границы слоя и (в меньшей степени) от эпицентрального расстояния, тогда как большая t функция существенно не зависит ни от глубине очага или эпицентральному расстоянию.

Замечание 3 Член in обычно мал (и поэтому затухание велико) из-за того, что η′ ^L _m положительно и относительно велико; единственная ситуация, в которой возможно существование этого члена, — это малые X ₂ , что имеет место, когда глубина фокуса мала, точнее, когда расстояние по вертикали между источником и нижней границей слоя значительно меньше толщины слоя. Это означает, что он вносит тем больший вклад в общую временную историю, чем ближе источник находится в вертикальном направлении к нижней границе слоя и/или если он по какой-то причине велик. Это указание согласуется с тем, что было обнаружено в отношении SBW2.

Remark 4 U ¹ _{2 m} ( x _g , t , ζ) is the time history corresponding to the m -th order Love mode with приведенное горизонтальное волновое число ζ. Общая временная история SBW2 u ¹ ₂ ( x _g , t , ζ) представляет собой сумму всех этих (четных и нечетных) временных историй режима Любви. Если, как это часто бывает, спектр импульса источника S (ω) такова, что имеет значение только для низких частот, только мода m = 0 Lo дает значительный вклад в , т , ζ).

8.3.3 Вклад u

¹ ₃ во временное смещение грунта

С учетом замечаний в конце раздела 5. 5 вклад u ¹ -3 во время _{3 смещение грунта домена можно считать незначительным.}

8.4 Характеристики временной динамики общего отклика грунта

Материал предыдущих трех разделов показывает, что отклик во временной области принимает форму: ?1262 , H _l функция амплитуды на угловой частоте функция затухания на угловой частоте ω _l , f _l острота резонансного или псевдорезонансного пика на угловой частоте l , ϖ _l угловая частота синусоидального хода вклада резонансного или псевдорезонансного члена на угловой частоте ω _l , ς _l фаза синусоидального изменения вклада резонансного или псевдорезонансного члена на угловой частоте ω _l . Обратите внимание, что резкость составляет 1/ширину на половине высоты пика резонанса в частотной области или псевдорезонансного пика, так что резкость тем больше, чем больше пик напоминает дельта-распределение Дирака.

Используя комплексные представления S _l и H _l :

и обозначения

мы получаем

Рассмотрим случай L = 1. Тогда

просто представляет собой синусоидальную функцию времени с затуханием во времени. Частота синусоиды равна ϖ ₁, а скорость затухания обратно пропорциональна резкости f ₁, т. е. чем меньше резкость, тем меньше длительность сигнала отклика земли. В сопутствующей статье (Groby & Wirgin 2005) мы увидим, что (относительно) кратковременный отклик во временной области обычно получается для глубоких источников, спектр которых таков, что дает доминирующий вклад фундаментального псевдорезонанса Хаскелла. Этот ответ аналогичен тому, который получают при одномерном анализе, и, очевидно, не может объяснить длительные сигналы с биением, которые часто наблюдаются в городских районах, таких как Мехико.

Рассмотрим теперь случай L = 2. Тогда легко показать, что:

представляет собой комбинацию двух амплитудно-модулированных ослабленных во времени синусоидальных сигналов с угловыми частотами несущей . Обратите внимание на то, что период модуляции больше, чем у сигналов несущей.

Примечание 1 Ур. (231) обычно описывает затухающий во времени несущий (синуоидальный) сигнал, проявляющий нерегулярные эффекты биений (из-за функций синусоидальной модуляции).0034

Замечание 2 Если несущая частота близка к фундаментальному резонансу моды Лява и фундаментальному резонансу псевдомоды Хаскелла (ранее было показано, что обе эти частоты близки друг к другу), то мы можем заключить, что отклик преобладает связь с фундаментальным режимом Лава и псевдорежимом Haskell.

Замечание 3 Если, с другой стороны, несущая частота намного больше, чем частота фундаментального резонанса Лява и фундаментального резонанса псевдомоды Хаскелла, то мы можем заключить, что в отклике преобладает связь либо с фундаментальной Режим Лява и псевдомода Хаскелла первого порядка, или к фундаментальной псевдомоде Хаскелла и моде Лява первого порядка (в предположении, что в спектрах преобладают фундаментальный резонанс и резонансы первого порядка и псевдорезонансы).

Замечание 4 Интересная, хотя, возможно, академическая ситуация возникает, когда , и в этом случае мы получаем

, который представляет собой чистый затухающий во времени синусоидальный несущий сигнал угловой частоты ϖ ₊ , амплитудно-модулированный чистой косинусоидальной функцией угловой частоты ϖ ₋ . В сопутствующей статье (Groby & Wirgin 2005) мы увидим, что такие истории времени отклика земли действительно могут иметь место и что они в основном связаны с фундаментальной модой Лава и псевдомодой Хаскелла из-за того, что несущая частота модулированного сигнала близка к резонансным частотам этой моды и псевдомоды.

9 Обсуждение

Теперь мы попытаемся дать ответы на вопросы, поднятые в Разделе 1. Они представлены в сопроводительном документе.

Первый вопрос был: возможно ли получить аномальный отклик без какой-либо латеральной неоднородности в подземной среде?

Изучаемая здесь конфигурация была латерально однородной . Мы показали, что одномерный отклик учитывает только интерференционные эффекты (как воплощено SBW1), но не связь с модами Лява (как воплощено SBW2) в слое, что особенно сильно, когда источник находится в окрестности нижней границы слоя.

Поскольку аномальные эффекты в основном характеризуются большой продолжительностью и явлениями биений в сигналах, ответ на этот вопрос отрицательный, что касается одномерного отклика. Однако, когда контраст свойств материала между слоем и подложкой очень велик, можно получить сигналы достаточно большой длительности (хотя и без биений), которые в основном связаны с одномерным откликом, даже когда источник находится далеко от источника. нижняя граница слоя.

В более общем смысле, то есть когда достигается связь с режимами Любви, ответ на вопрос положительный.

Второй вопрос звучал так: каково отношение одномерного отклика к двумерному и насколько адекватно моделировать общий отклик конфигурации его откликом на (почти) вертикально падающую плоскую волну?

Мы показали, что не только одномерная модель не приводит к резонансным явлениям, но и что действительно резонансные явления, связанные с возбуждением мод Лява, могут быть описаны только полностью двумерной (или трехмерной) моделью. .

Для источника глубоко ниже нижней границы слоя отклик в основном обусловлен вкладом SBW1 (более или менее эквивалентным одномерному отклику), но когда глубина источника близка к глубине На нижней границе слоя волны (SBW2), не включенные в 1-D модель, играют основную роль в общем отклике, поскольку они либо преобладают над 1-D откликом (длительный отклик без биений), либо сочетаются с 1-D D-реакция на подачу сигналов с большой продолжительностью и биениями, которые были выявлены явным образом с помощью прямого анализа во временной области в разделе 8. Эти данные следует учитывать в отношении исследований (например, Sandi 9).1261 и др. 2004), которые пытаются предсказать сейсмическую реакцию городских объектов на основе одномерного анализа.

Третий вопрос был: как глубина фокуса источника влияет на отклик? Ответ на этот вопрос дан в предыдущих двух абзацах. Однако уместно пересмотреть этот вопрос в свете темы (b), касающейся влияния неоднородностей подстилающей почвы, боковых вариаций подстилающего слоя почвы и застроенной среды на сейсмическую реакцию в городских районах. Можно показать (Wirgin, 2002), что волна, падающая на неоднородную среду, порождает дифрагированную волну, которую можно считать излучаемой индуцированных источников (в отличие от активного источника , связанного с первичным сейсмическим возмущением), расположенных в пределах среды. Эти индуцированные источники могут возникать и на границе среды (особенно в концевых точках, углах и неровностях границы), так что края мягкой котловины или грунта без напряжений, включающего здания, лежащие на однородном мягком слое в место, подобное городу, также может представлять собой местонахождение интенсивных индуцированных источников в ответ на падающую сейсмическую волну. Поля, излучаемые всеми этими наведенными источниками, могут быть представлены способом, подобным (при условии сходства базовой геометрии конфигурации) с тем, что используется в настоящей работе, так что многое из того, что было написано и найдено выше, особенно в отношении отклика на активные источники, расположенные снаружи и вблизи мягкого слоя (и, соответственно, наведенные источники, расположенные на расстоянии в пределах или на границах мягкого слоя), следует применять к городским площадкам, построенным на мягких слоях или бассейнах.

Наиболее важным моментом (упомянутым в таких источниках, как Tsogka & Wirgin (2003), неявно подразумеваемым в Igel et al. (2002), Jahnke et al. (2002) и доказанным здесь в отношении активных источников) является следующее: присутствие этих активных или индуцированных источников, расположенных 91 261 вблизи или внутри 91 262 мягкого слоя, лежащего поверх относительно твердого субстрата, позволяет связываться с модами типа Лява, которые могут быть ответственны за часть аномального отклика грунта, наблюдаемого в таких городах, как как Мексика, особенно движение, характеризующееся большой продолжительностью и избиениями.

Естественно, приведенные выше замечания относятся только к рассматриваемому здесь случаю двумерной ВГ-поляризации; будет интересно узнать, переносятся ли они на случай 2-D P-SV , где моды Рэлея–Лэмба играют роль мод Лява, описанных выше. Рассеяние, конечно, может добавить к эффектам увеличения длительности, поскольку его можно отнести к излучению индуцированных источников, но этот вопрос, вероятно, потребует более сложных теоретических моделей и подтверждения с помощью численных исследований (как это делается в таких публикациях, как Furumura и Кеннет 1998).

Ответы на четвертый, пятый, шестой и седьмой вопросы приведены в сопроводительном документе (Groby & Wirgin 2005), в котором будут даны заключительные комментарии по содержанию двух документов.

Благодарности

Это исследование было проведено частично в рамках инициативы Action Concertée Incitative «Prévention des Catastrophes Naturelles» под названием «Взаимодействие «site-ville» et aléa sismique en milieu urbain» Министерства исследований Франции.

Ссылки

Абрамовиц

М.

Стегун

А.

1986

Справочник по математическим функциям,

Дувр

Нью-Йорк

Апсель

Р.Дж.

Луко

1983

О функции Грина для слоистого полупространства. Часть II

Бюлл. сейсм. соц. Являюсь.

931

–

951

Attwood

нержавеющая сталь

1951

Распространение поверхностных волн по плоскому проводнику с покрытием

J. Appl. физ.

504

–

509

Балендра

Т.

Конг

К.Х.

2004

Влияние колебаний грунта в Сингапуре из-за землетрясений в дальней зоне

Proc. 11-я Международная конференция по динамике грунтов и сейсмостойкости

255

–

259

Бард

П.-Ю.

1985

Структурные эффекты места происхождения: основные результаты экспериментальных и теоретических исследований

, в

Génie Parasismique

, стр.

223

–

238

, изд.

Давидовичи

Presses de l’Ecole Nationale des Ponts et Chaussées

Париж

Бард

П.-Ю.

Бушон

М.

1980

Сейсмический отклик заполненных наносами долин. часть 1. Случай падающих SH-волн

Бык. сейсм. соц. Являюсь.

1263

–

1286

Бард

П.-Ю.

Бушон

М.

1985

Двумерный резонанс долин, заполненных наносами

Bull. сейсм. соц. Являюсь.

519

–

541

Бард

П.-Ю.

Eeri

Campillo

Chávez-Garcia

F.J.

Sanchez-Sesma

F. J.

^{10101010134984984984
.
Землетрясение в Мексике 19 сентября 1985 г. – теоретическое исследование крупно- и мелкомасштабных эффектов усиления в долине Мехико
,
Спектры землетрясений
,
4
,
609
–
633
.
Бен-Менахем
А.
Харкрайдер
Д.Г.
,
1964
.
Диаграммы излучения сейсмических волн от захороненных диполярных точечных источников в плоской стратифицированной земле
,
J. geophys. Рез.
,
69
,
2605
–
2620
.
Бен-Цион
Ю.
,
1990
.
Сейсмическое излучение линейного источника SH в латерально-неоднородной зоне плоского разлома
,
Бюлл. сейсм. соц. Являюсь.
,
90
,
971
–
994
.
Бур
Д.М.
,
2003
.
Можно ли предсказать реакцию сайта?
J. Earthquake Engrg.
, отправлено.
Бушон
М.
,
1982
.
Полный синтез сейсмических фаз земной коры на региональном расстоянии
,
J. geophys. Рез.
,
87
(
B3
)
1735
–
1741
4.
Бутен
К.
Руссильон
П.
,
2004
.
Оценка влияния урбанизации на сейсмические реакции
,
Бюлл. сейсм. соц. Являюсь.
,
94
,
251
–
268
.
Кампильо
М.
Гариэль
Х.К.
Санчес-Сесма
Ф.Дж.
Разрушительное движение грунта в Мехико: источник, путь и влияние места во время великих 1985 Мичоаканское землетрясение
,
Bull. сейсм. соц. Являюсь.
,
79
,
1718
–
1735
.
Карденас
М.
Чавес-Гарсия
Ф. Дж.
,
2003
.
Воздействие региональной трассы на распространение сейсмических волн в центральной Мексике
,
Bull. сейсм. соц. Являюсь.
,
93
,
973
–
985
.
Перевозчик
Г.Ф.
Крук
М.
Пирсон
CE
,
1983
.
Функции комплексной переменной
,
Ход Букс, Итака
.
Селеби
М.
,
2004
.
Отклики 14-этажного дома (Анкоридж, Аляска) на дальнее расстояние (Ms = 7,9) Denali (2002) и ближние землетрясения 2002 г.
,
Proc. 11-я Международная конференция по динамике грунтов и сейсмостойкости
, стр.
895
–
900
, ред.
Дулин
Д.
и другие. ,
Stallion Press
,
Беркли
.
Чавес-Гарсия
Ф.Дж.
Бард
П.-Ю.
,
1994
.
Воздействие на местности в Мехико через восемь лет после землетрясений в Мичоакане в сентябре 1985 г.
,
Soil Dyn. Землетрясение англ.
,
13
,
229
–
247
.
Chávez-Garcia
F.J.
Ramos-Martínez
J.
Romero-Jiménez
E.
,
1995
.
Анализ дисперсии поверхностных волн в Мехико
,
Bull. сейсм. соц. Являюсь.
,
85
,
1116
–
1126
.
Чен
К.-Х.
Тенг
Т.-Л.
Гунг
Ю.-К.
,
1998
.
Десятисекундное распространение волн Лява и сильные движения грунта на Тайване
,
J. geophys. Рез.
,
103
(
B9
),
21 253
–
21 273
4 .
Коллинз
Р.Э.
,
1960
.
Полевая теория направленных волн
, Глава 11,
Mc Graw-Hill
,
Нью-Йорк
.
Дравински
М.
Мосесян
Т.К.
,
1988
.
Об оценке функции Грина для гармонических линейных нагрузок в упругом полупространстве
,
J. Num. Мет. инж.
,
26
,
823
–
841
.
Юинг
М.
Джардецки
В.С.
Пресс
Ф.
,
1957
.
Упругие волны в слоистых средах
,
Макгроу Хилл
,
Нью-Йорк
.
Фаэх
Д.
Панза
Г.Ф.
,
1994
.
Реалистическое моделирование наблюдаемых сейсмических движений в сложных осадочных бассейнах
,
Аннал. Геофис.
,
37
,
1771
–
1797
.
Фаэх
Д.
Suhadolc
P.
Mueller
S.
Panza
G.F.
,
1994
.
Гибридный метод оценки движения грунта в осадочных бассейнах: количественное моделирование Мехико
,
Bull. сейсм. соц. Являюсь.
,
84
,
383
–
399
.
Фурумура
Т.
Кеннет
Б.Л.Н.
,
1998
.
О характере региональных сейсмических фаз-III. Влияние неоднородности земной коры на волновое поле субдукционных землетрясений: Мичоакан 1985 г. и Копала, Герреро, Мексика 1995 г.
,
Геофиз. Дж. Междунар.
,
135
,
1060
–
1084
.
Гроби
Ж.-П.
Цогка
К.
Виргин
А.
,
2004
.
A time domain method for modeling viscoelastic SH wave propagation in a city-like environment
,
Proc.11th International Conference on Soil Dynamics &Earthquake Engineering
, pp.
887
–
894
, редакторы
Дулин
Д.
,
Жеребец Пресс
,
Беркли
.
Гроби
Ж.-П.
Wirgin
А.
,
2005
.
Двумерное движение грунта на участке мягкого вязкоупругого слоя/твердого основания в ответ на цилиндрические сейсмические волны SH, излучаемые глубинными и мелкими линейными источниками – II. Численные результаты
,
Геофиз. Дж. Междунар.
, doi: DOI:
arXiv
.
Харкрайдер
Д.Г.
,
1964
.
Поверхностные волны в многослойных упругих средах. часть I: волны Рэлея и Лява от заглубленных источников в многослойном упругом полупространстве
,
Бюлл. сейсм. соц. Являюсь.
,
54
,
627
–
679
.
Харкрайдер
Д.Г.
,
1970
.
Поверхностные волны в многослойных упругих средах. часть II: спектры высших мод и спектральные отношения от точечных источников в плоскослоистых моделях Земли
,
Бык. сейсм. соц. Являюсь.
,
60
,
1937
–
1987
.
Хисада
Ю.
Ямамото
С.
Тани
С.
,
1988
.
Анализ сильных движений грунта на равнинах и впадинах, состоящих из мягких грунтов, с помощью модели разломов и метода граничных элементов
, в
Proc. Девятая Всемирная конференция по сейсмостойкому проектированию
,
Документ 88, Японская ассоциация по предотвращению землетрясений
,
Токио
.
Игель
Х.
Янке
Г.
Бен-Цион
Ю.
,
2002 70014 90.
Численное моделирование направленных волн в зоне разлома: точность и трехмерные эффекты
,
Pure appl. Геофиз.
,
159
,
2067
–
2083
.
Янке
Г.
Игель
Х.
Бен-Цион
Ю.
,
2002 70034 90.
Трехмерные расчеты волн, направленных зонами разломов в различных структурах неправильной формы
,
Геофиз. Дж. Междунар.
,
151
,
416
–
426
.
Канамори
Х.
Дано
Дж.В.
,
1981
.
Использование длиннопериодных поверхностных волн для быстрого определения параметров очагов землетрясений
,
Phys. Планета Земля. Междунар.
,
27
,
8
–
31
.
Кеннет
Б.Л.Н.
,
1983
.
Распространение сейсмических волн в стратифицированных средах
,
Издательство Кембриджского университета
,
Кембридж
.
Кьяртанссон
E.
,
1979
.
Постоянное распространение и затухание волны Q
,
J. geophys. Рез.
,
84
,
4737
–
4748
.
Ли
Д.М.
Дженнингс
П.К.
Хауснер
Г.В.
,
1980
.
Подборка важных записей о сильных землетрясениях
,
Технический отчет Калифорнийский технологический институт EERL-80-01.
Линг
Р.Т.
Scholler
J.D.
Уфимцев
П.Ю.
,
1998
.
Распространение и возбуждение поверхностных волн в поглощающем слое
,
Прог. Электромаг. Рез.
,
19
,
49
–
91
.
Luco
J.E.
Apsel
R.J.
,
1983
.
О функции Грина для слоистого полупространства. часть I
,
Бюлл. сейсм. соц. Являюсь.
,
73
,
909
–
929
.
Мендигурен
Дж.А.
,
1977
.
Инверсия данных о поверхностных волнах в исследованиях механизма источника
,
J. geophys. Рез.
,
82
,
889
–
894
.
Морс
П.М.
Фешбах
Х.
,
1953
.
Методы теоретической физики
,
Макгроу Хилл
,
Нью-Йорк
.
Новикова
Е.И.
Trifunac
M.D.
,
1993
.
Продолжительность сильного землетрясения: физические основы и эмпирические уравнения
,
Технический отчет. Университет Южной Калифорнии, кафедра гражданского строительства, CE 93-02.
Новикова
Е. И.
Трифунак
MD
,
1995
.
Продолжительность сильного землетрясения в зависимости от частоты: обновленные эмпирические уравнения
, Технический отчет. Университет Южной Калифорнии, кафедра гражданского строительства , CE 95-01.
Панза
Г.Ф.
,
1981
.
Разрешающая способность поверхностной сейсмической волны по отношению к структурным моделям земной коры и верхней мантии
, в
Решение обратной задачи геофизической интерпретации
,
стр.
39
–
77
, изд.
Cassinis
R.
,
Пленум
,
Нью-Йорк
.
Панза
Г.Ф.
,
1985
.
Синтетические сейсмограммы: модальное суммирование волн Рэлея
,
Ж. Геофиз.
,
58
,
125
–
145
.
Панза
Г.Ф.
Романелли
Ф.
Ваккари
Ф.
,
2000
.
Реалистическое моделирование волновых форм в латерально-неоднородных неупругих средах методом модального суммирования
,
Геофиз. Дж. Междунар.
,
143
,
340
–
352
.
Панза
Г.Ф.
Романелли
Ф.
Ваккари
Ф.
,
2000
.
Распространение сейсмических волн в латерально-неоднородных неупругих средах: теория и приложения к сейсмическому районированию
,
Успехи геофизики
,
стр.
1
–
95
, ред.
Doolin
D.
Kammerer
A.
Nogami
T.
Seed
R.B.
Towhata
I.
Academic Press
,
New York
.
Панза
Г.Ф.
Ваккари
Ф.
Романелли
Ф.
,
2001
.
Реалистическое моделирование сейсмического воздействия в городских районах: проект ЮНЕСКО-МСГН-МПГК
,
ПАГЕОП
,
158
,
2389
–
2406
4 .
Поллитц
Ф.
,
1999
.
Региональная структура скоростей в Северной Калифорнии по инверсии рассеянных сейсмических поверхностных волн
,
J. geophys. Рез.
,
104
,
15 043
–
15 072
.
Romanelli
F.
Bing
Z.
Vaccari
F.
Panza
G. F.
,
1996
.
Аналитический расчет коэффициентов связи отражения и прохождения волн Лява
,
Геофиз. Дж. Междунар.
,
125
,
132
–
138
.
Санди
Х.
Борча
И.С.
Станку
О.
Станку
М.
,
2004
.
Особенности последовательностей спектров отклика при последовательных землетрясениях средней глубины Вранча
, в
Проц. 11-й Международной конференции по динамике грунтов и сейсмостойкости
, стр.
214
–
221
, ред.
Дулин
Д.
,
Жеребец Пресс
,
Беркли
.
Дикарь
Б.К.
,
2004
. .
Сембла
Ж.-Ф.
Дюваль
А.-М.
Дангла
П.
,
2000
.
Численный анализ усиления сейсмических волн в Ницце (Франция) и сравнение с экспериментами
,
Soil Dynam. Землетрясение англ.
,
19
,
347
–
362
.
Semblat
J.F.
Guéguen
P.
Kham
M.
Бард
П. -Ю.
Дюваль
А.-М.
,
2003
.
Взаимодействие площадки и города в локальном и глобальном масштабах
, в
12-я Европейская конференция по сейсмостойкому проектированию
, документ №. 807 на компакт-диске,
Elsevier
,
Oxford
.
Семблат
Дж.Ф.
Парара
Э.
Кхам
М.
Бард
П.-Ю.
Питилакис
К.
Макра
К.
Раптакис
Д.
,
2004 9.
Эффекты участка: геометрия бассейна и слоистость почвы
, in
Proc. 11-я Международная конференция по динамике грунтов и сейсмостойкости
, стр.
222
–
229
, ред.
Дулин
Д.
,
Stallion Press
,
Беркли
.
Шапиро
Н.М.
Олсен
К.Б.
Сингх
С.К.
,
2000
.
Волноводные эффекты в зонах субдукции: данные трехмерного моделирования
,
Геофиз. Рез. лат.
,
27
,
433
–
436
.
Шапиро
Н.М.
Олсен
К.Б.
Сингх
С.К.
,
2002
.
О продолжительности прихода сейсмических движений в долину Мехико для землетрясений в зоне субдукции
,
Геофиз. Дж. Междунар.
,
151
,
501
–
510
.
Шапиро
Н. М.
Сингх
С.К.
Альмора
Д.
Айала
М.
,
2001
.
Доказательства преобладания высокочастотных поверхностных волн в приозёрной зоне долины Мехико
,
Геофиз. Дж. Междунар.
,
147
,
517
–
527
.
Сёдзи
Ю.
Тании
К.
Камияма
М.
,
2004
.
Исследование длительности и амплитудных характеристик землетрясений
, в
Проц. 11-я Международная конференция по динамике грунтов и сейсмостойкости
, стр.
157
–
164
, ред.
Дулин
Д.
,
Жеребец Пресс
,
Беркли
.
Сингх
С.К.
Ордаз
М.
,
1993
.
О происхождении длинной коды, наблюдаемой в отчетах о сильных движениях дна озера в Мехико
,
Bull. сейсм. соц. Являюсь.
,
83
,
1298
–
1306
.
Снидер
Р.
,
2000
.
Инверсии поверхностных волн регионального масштаба
, в
Сейсмическое моделирование строения Земли
,
стр.
149
–
181
, ред.
Boschi
E.
Ekström
G.
Morelli
A.
Compositori
,
Bologna 90
Trifunac
M.D.
Brady
А.Г.
,
1975
.
Исследование длительности колебаний грунта при сильном землетрясении
,
Бюлл. сейсм. соц. Являюсь.
,
65
,
581
–
626
.
Trifunac
M.D.
Westermo
B.D.
,
1976
.
Зависимость продолжительности подвижек грунта при сильном землетрясении от магнитуды, эпицентрального расстояния, геологических условий на станции регистрации и частоты подвижек
,
Технический отдел. Университет Южной Калифорнии, кафедра гражданского строительства, CE 76-02
.
Цогка
К.
Виргин
А.
,
2003
.
Моделирование сейсмического отклика в идеализированном городе
,
Почва. Динам. Землетрясение англ.
,
23
,
391
–
402
.
Туан
Х.-С.
Понамги
С.Р.
,
1972
.
Возбуждение волн Лява в тонкопленочном слое линейным источником
,
IEEE Trans. Соникс Ультрасон.
, СУ-
19
,
9
–
14
.
Ван дер Хейден
J.H.M.T.
,
1987
.
Распространение нестационарных упругих волн в стратифицированных анизотропных средах
,
Спрингер
,
Нью-Йорк
.
Уиттакер
И.Т.
Ватсон
Г.Н.
,
1922
.
Современный анализ
, главы 5, 6,
Издательство Кембриджского университета
,
Кембридж
.
Wirgin
А.
,
1988
.
Волны любви в плите с шероховатыми границами
,
Последние разработки в области поверхностных акустических волн
, стр.
145
–
155
, ред.
Паркер
Д.Ф.
Можен
Г.А.
Спрингер
,
Берлин
.
Wirgin
А.
,
2002
.
Акустическая визуализация: классические и новые методы для приложений в макрофизике
, в
Рассеяние
, с.
Пайк
Р.
Сабатье
П.
Академик
,
Сан-Диего
.
Wirgin
A.
Kouoh-Bille
L.
,
1993
.
Усиление движения солнц в voisinage d’un groupe de montagnes de profil rectangulaire ou triangulaire soumis à une onde sismique SH
, в
Génie Parasismique et Aspects Vibratoires dans le Génie Civil
, стр. ES28–ES37,
AFPS, Saint-Rémylès-Chevreuse
.
Чжан
Х.-М.
Чен
X.-F.
Чанг
С.
,
2003
.
Эффективный численный метод расчета синтетических сейсмограмм для слоистого полупространства с источниками и приемниками на близких или одинаковых глубинах
,
Чистое приложение. Геофиз.
,
160
,
467
–
486
.
© RAS, 2005 г.
© RAS, 2005 г.
Иноды, жесткие и программные ссылки демистифицируют Esc.sh
Опубликовано 20 марта 2016 г. пользователем ‐ 8 мин чтения
✏ Улучшите эту страницу
Если вы новичок в Linux, скорее всего, вы сами сталкивались с этим вопросом. Что такое жесткая ссылка? И как, черт возьми, это отличается от мягкой ссылки (символической ссылки или символической ссылки). Иногда этот вопрос возникает даже у опытных администраторов Linux.
Большинство из нас знает, что такое символическая ссылка, но сильно смущается, когда мы слышим о «жесткой ссылке». Хотя это не так сложно, позвольте мне объяснить это для вас.
Прежде чем мы узнаем разницу между мягкой и жесткой ссылкой, нам нужно понять несколько основных моментов. Один из них — «Inode»
Что такое Inode и номер Inode?
Inode — это структура данных, представляющая файл или каталог. Номер инода — это уникальный номер, присвоенный иноду. На простом английском это и означает.
Все в системе unix представлено в виде файла (включая обычные файлы, такие как ваши фильмы, документы, аудиофайлы)
Файл хранится в файловой системе (ext3, ext4 и т. д.).
Но когда вы сохраняете файл в файловой системе, вам нужен какой-то механизм идентификации, чтобы вы могли позже получить файл, изменить его или даже удалить. Если нет уникального механизма идентификации, у вас есть файловая система, полная случайных мусорных данных, которые вы не можете идентифицировать или использовать.
Итак, нам нужен способ идентифицировать каждый файл в файловой системе. Для этого мы используем номер inode.
Номер индексного дескриптора файла указывает на индексный дескриптор, соответствующий этому файлу. И каждый индекс представляет собой файл.
Когда я говорю «представлять», я имею в виду, что каждый индекс содержит много информации о файле [размер файла, владелец, группа, права доступа и все такое прочее]
Максимальное ограничение есть количество инодов в файловой системе. Таким образом, вполне возможно, что вы больше не сможете хранить файлы, даже если у вас достаточно места для хранения (правильно, у вас осталось ГБ места для хранения, но у вас есть огромное количество файлов на вашем диске, которые вы израсходовали. все индексные дескрипторы, и вы больше не можете хранить данные. )
Ладно, хватит теории. Давайте посмотрим на некоторые практические вещи, чтобы легко понять индексы и номер индекса.
$ сенсорный файл

Мы используем следующую команду, чтобы увидеть номер инода
$ ls -i файл
797380 файл

Давайте попробуем это с каталогом
$ mkdir dir1
$ ls -id каталог1
797359 дир1

Переключатель «d» используется для отображения описания каталога, а не содержимого каталога
Теперь давайте попробуем изменить содержимое файла и посмотрим, изменится ли номер инода
$ echo "привет" > файл
$ ls -i файл
797380 файл

Нет, номер инода не изменился, а если скопировать файл?
$ cp файл файл1
$ лс -иль
всего 28
797359 drwxr-xr-x 2 мансур мансур 4096 20 марта 13:38 dir1
797380 -rw-r--r-- 1 мансур мансур 12 мар 20 13:40 файл
797385 -rw-r--r-- 1 мансур мансур 12 мар 20 13:40 файл1

Конечно, номер инода для скопированного файла отличается. Как насчет перемещения файла?
$ mv файл файл2
$ ls -i файл2
797380 файл2

Смотрите, номер инода не изменился, изменилось только имя файла.
Итак, теперь вы знаете, что означает индекс и номер индекса. Вернемся к разделу «жесткая и программная ссылка», часть
. Что такое программная ссылка?
Мягкая ссылка также известна как символическая ссылка или символическая ссылка. Как следует из названия, это символическая ссылка на другой файл. Но это не очень хорошее определение.
Символическая ссылка — это файл (да, верно, это другой файл), который содержит информацию о расположении целевого файла или каталога.
Давайте пройдемся по следующим пунктам, чтобы легко понять символическую ссылку
Символическая ссылка — это файл, который указывает на другой файл или каталог
Символическая ссылка не зависит от цели
Если вы удалите символическую ссылку, цель не изменится
Если вы удалите файл, символическая ссылка все еще будет там, но она не будет работать, потому что цель теперь не существует (очевидно)
Хорошо, теперь давайте посмотрим на некоторые реальные примеры с символическими ссылками
Создание символической ссылки
$ ln -s исходный_файл целевая_ссылка

Давайте продолжим и создадим символическую ссылку
$ ls
каталог1 файл1 файл2
$ ln -s файл1 sym_file1

$ лс -л
всего 32
20 мар 13:38 дир1
20 мар 13:40 файл1
20 мар 13:40 файл2
20 марта 14:04 sym_file1 -> файл1

Вы можете видеть, что символическая ссылка «sym_file1» указывает на файл «file1». Теперь давайте проверим номер инода симлинка
$ ls -i sym_file1
797441 sym_file1

Теперь номер инода файла
$ ls -i файл1
797385 файл1

Как видите, номер инода для файла и символической ссылки отличаются. Это означает, что это два разных файла, и один из них (символическая ссылка) указывает
к другому. Довольно просто.
Проверим содержимое ссылки и файла
$ cat sym_file1
привет
$ cat файл1
привет

Они оба одинаковые (правильно)
Как насчет того, чтобы изменить содержимое символической ссылки и посмотреть, изменит ли она оригинал?
$ echo 'до свидания' > sym_file1
$ cat sym_file1
до свидания

$ cat файл1
до свидания

Итак, изменив содержимое символической ссылки, мы фактически изменили исходный файл
Удаление символической ссылки Просто используйте rm для удаления ссылки
$ ls
dir1 file1 file2 sym_file1
$ rm -f sym_file1
$ лс
каталог1 файл1 файл2
$

И вот, вы прошли ускоренный курс по символическим ссылкам и тому, как они работают.
Что же такое жесткая ссылка?
Жесткая ссылка — интересная концепция. Если вы читали приведенное выше объяснение об индексах и номерах индексов, вы должны знать, что каждый файл идентифицируется уникальным номером, называемым номером индекса.
Теперь жесткая ссылка создает ссылку на исходный номер инода. Ну и какая разница?
Думаю будет проще понять на примерах.
Мы создадим жесткую ссылку для файла «файл», но перед этим давайте проверим номер инода для «файла»
$ ls -i файл
797385 файл

Чтобы создать жесткую ссылку, используйте следующий синтаксис:
$ ln file hardlink_file
$ лс
файл dir1 hardlink_file
$ лс -л
всего 28
drwxr-xr-x 2 мансур мансур 4096 20 марта 13:38 dir1
-rw-r--r-- 2 mansoor mansoor 8 мар 20 14:05 файл
-rw-r--r-- 2 мансур мансур 8 мар 20 14:05 hardlink_file

Теперь давайте проверим номер инода новой ссылки
$ ls -i hardlink_file
797385 hardlink_file

Как насчет этого, это тот же номер инода, что и у файла
Давайте создадим еще одну ссылку
$ ln файл hardlink_file2
$ ls -i hardlink_file2
797385 hardlink_file2

Да, опять то же самое. Теперь посмотрим содержимое файлов
$cat file
до свидания
$ cat hardlink_file
до свидания

Что, если мы изменим исходное содержимое файла?
$ echo "привет" > файл
$кошачий файл
всем привет
$ cat hardlink_file
всем привет
$ cat hardlink_file2
всем привет

Изменилось содержимое ссылок (мы ожидали)
Что, если мы изменим ссылку вместо исходного файла?
$ echo "Я изменил" > hardlink_file

$кошачий файл
я изменил
$ cat hardlink_file
я изменил

Изменено содержимое всех из них
Что, если мы удалим исходный файл?
$ rm -f файл
$ лс
dir1 hardlink_file hardlink_file2
$ cat hardlink_file
я изменил

$ cat hardlink_file2
я изменил

$ rm -f файл_жесткой_ссылки2

$ cat hardlink_file
я изменил

Как насчет этого? Как вы заметили, жесткая ссылка все еще здесь. Это основное различие между хардлинком и софтлинком.
Вы можете рассматривать каждый файл как саму жесткую ссылку. Даже если вы удалите жесткую ссылку, файл все равно будет там (если только вы не удаляете
последняя жесткая ссылка )
Итак, что мы узнали о жесткой ссылке? Что ж, жесткая ссылка — это не ссылка на исходный «файл», вместо этого она указывает на исходный индексный дескриптор «файла», что делает его почти похожим на исходный «файл», за исключением имени.
Итак, по этой логике, что, если мы заменим исходный файл другим файлом? Давайте попробуем это, прежде чем подводить итоги.
$ лс
$ эхо "привет" > файл
$ ln жесткая ссылка на файл

$ лс
жесткая ссылка на файл

$ кошка жесткая ссылка
привет

Теперь давайте создадим еще один файл
$ echo "Новый файл" > новый файл

Давайте просто запишем все номера инодов файлов
$ ls -i
797359 файл 797359 жесткая ссылка 797380 новый файл

Как мы и ожидали, жёсткая ссылка и этот файл имели один и тот же номер инода
Теперь давайте заменим «файл» на «новый файл»
$ cp -f новый файл файл
$ лс -я
797359 файл 797359 жесткая ссылка 797380 новый файл

Изменились ли номера инодов? Неа. Давайте проверим содержимое, чтобы увидеть разницу
$ cat файл
Новый файл
$ кошка жесткая ссылка
Новый файл

$ кот новый файл
Новый файл

Ну вот. Таким образом, жесткая ссылка теперь содержит содержимое нового файла. Почему? потому что он все еще указывает на исходный номер инода
а файл с номером инода «797359» имеет содержимое «Новый файл»
Теперь это довольно просто, не так ли?
На этом пост заканчивается. Спасибо за прочтение 😀 хорошего дня.
Руководство по лучшим практикам мультитенантности Kubernetes
Мультитенантность Kubernetes — это тема, которая интересует все больше и больше организаций по мере распространения их использования Kubernetes. Однако, поскольку Kubernetes не является мультиарендной системой как таковой, правильная мультиарендность сопряжена с некоторыми проблемами.
В этой статье я опишу эти проблемы и способы их преодоления, а также некоторые полезные инструменты для мультитенантности Kubernetes. Прежде я объясню, что на самом деле означает мультитенантность Kubernetes, в чем разница между мягкой и жесткой мультитенантностью и почему эта тема сейчас так актуальна.
#What Is Kubernetes Multi-Tenancy
Мультитенантность в Kubernetes означает, что кластер и его плоскость управления совместно используются несколькими пользователями, рабочими нагрузками или приложениями. Это противоположность одиночной аренде, когда только один пользователь использует весь кластер Kubernetes.
Существуют различные типы мультиарендности, от мягкой мультиарендности до жесткой мультиарендности.
#Soft Multi-Tenancy
Мягкая мультиарендность — это форма мультиарендности, которая не имеет строгой изоляции различных пользователей, рабочих нагрузок или приложений. Таким образом, это подходящее решение для доверенных и известных арендаторов, т. е. арендаторов, которые не будут добровольно злоупотреблять друг другом, таких как инженеры в одной организации. Изоляция между пользователями скорее направлена на предотвращение несчастных случаев и не может предотвратить атаки на других арендаторов.
С точки зрения Kubernetes, мягкая мультиарендность обычно связана с простыми пространствами имен Kubernetes, в которых работают отдельные арендаторы. злонамеренного поведения со стороны других арендаторов. Таким образом, в дополнение к доверенным арендаторам его также можно использовать для арендаторов, которым вы не доверяете, таких как множество неподключенных пользователей и людей из разных организаций.
Чтобы реализовать жесткую мультитенантность в Kubernetes, вам потребуется более продвинутая конфигурация пространств имен или виртуальных кластеров (vClusters).
#Мягкая и жесткая мультиарендность
Хотя кажется, что мягкая и жесткая мультиарендность являются разными противоположностями, они скорее являются конечными точками ряда различных реализаций. Некоторые даже утверждают, что идеальной жесткой мультиарендности в Kubernetes не может быть, потому что Kubernetes разработан таким образом, что существует только одна центральная плоскость управления, которая всегда должна использоваться всеми арендаторами, представляющими потенциальную уязвимость.
В целом можно сказать, что жесткая мультиарендность в целом «лучше» (поскольку ее можно использовать для доверенных и ненадежных арендаторов), а мягкую мультиарендность реализовать проще.
#Limitations of Multi-Tenant Kubernetes
Реализуя мультитенантность, вы автоматически вводите «ограничения» для своего кластера Kubernetes, поскольку арендаторы будут технически ограничены по сравнению с пользователями одноарендного кластера и/или арендаторы должны учитывать остальные арендаторы. Примером ограничений мультитенантности на основе пространства имен является то, что арендаторы не могут использовать CRD, устанавливать диаграммы Helm, использующие RBAC, или изменять параметры всего кластера, такие как версия Kubernetes.
Использование виртуальных кластеров смягчает эти ограничения, поскольку арендаторы имеют доступ к настройкам и ресурсам кластера в своих виртуальных кластерах. По этой причине виртуальные кластеры больше похожи на «настоящие» кластеры, чем на пространства имен, поэтому мультиарендность на основе vCluster является формой мультиарендности, которая относительно близка к одноарендной.
Тем не менее, введение любой формы мультиарендности добавляет сложности вашей системе и накладывает некоторые ограничения на арендаторов.
#Reasons For Kubernetes Multi-Tenancy
Теперь вы можете спросить, почему мультитенантность Kubernetes актуальна и почему вы не можете просто использовать вместо нее множество одноарендных кластеров.
Теоретически можно использовать несколько однопользовательских кластеров вместо общего многопользовательского кластера. Некоторые компании действительно делают это в настоящее время, например. чтобы предоставить разработчикам доступ к Kubernetes. Однако такое решение очень неэффективно и поэтому дорого, особенно в больших масштабах.
Это то, что многие организации осознают сейчас, когда внедрение Kubernetes распространяется внутри их организации и все больше инженеров получают доступ к Kubernetes: создание одного кластера на каждого арендатора/пользователя на начальном этапе экспериментов с Kubernetes очень просто и не так дорого. , становится огромной проблемой, если (почти) каждый разработчик в организации получает собственный кластер на более поздних этапах перехода к облачным решениям. Внезапно вы получаете десятки, сотни или даже тысячи кластеров, которые стоят денег (плата за управление кластерами поставщиков общедоступных облаков также начинает иметь большое значение) и нуждаются в эффективном управлении, что далеко не тривиально.
На данном этапе преимущества многопользовательской системы перевешивают ее дополнительные сложности. Просто гораздо проще управлять системой Kubernetes с одним или несколькими кластерами, а совместное использование кластера также более эффективно с точки зрения использования ресурсов, поскольку можно уменьшить избыточность.
Дополнительные сведения по этой теме см. также в моей статье о сравнении отдельных кластеров и общих кластеров.
#Kubernetes Многопользовательская реализация Проблемы
Есть три основные проблемы, с которыми вы столкнетесь при внедрении мультиарендности Kubernetes:
#Управление пользователями
Задача: В большинстве компаний где-то уже есть система управления пользователями для своих инженеров. Это может быть GitHub, Microsoft, Google или любой другой сервис. Поскольку вы не хотите управлять всеми пользователями дважды или даже чаще, вам необходимо включить единый вход (SSO) для вашей системы Kubernetes.
Решение: С помощью dex проекта песочницы CNCF вы можете предоставить арендаторам возможность единого входа. Dex — это поставщик OpenID Connect и OAuth3, который поддерживает различных поставщиков удостоверений, включая LDAP и SAML, и поэтому может использоваться со многими системами управления пользователями. Таким образом, dex — очень хороший вариант для решения проблемы управления пользователями в вашей многопользовательской системе с Kubernetes.
#Fair Resource Sharing
Задача: Поскольку все арендаторы совместно используют одни и те же базовые ресурсы, т. е. сетевые и вычислительные ресурсы, второй задачей является обеспечение справедливого распределения доступных ресурсов между арендаторами. Это важно, потому что вы не хотите, чтобы один арендатор потреблял все или чрезмерное количество ресурсов (случайно или добровольно), в результате чего другие не могли работать. Для этого необходимо убедиться, что у каждого арендатора есть соответствующие лимиты использования.
Решение: Потребление ресурсов арендаторами может быть ограничено в Kubernetes с помощью квот ресурсов. Поскольку пользователи должны указать ограничения ЦП и памяти, если для этих ресурсов включены квоты, имеет смысл также установить интеллектуальные значения по умолчанию через LimitRanges.
#Isolation
Задача: Третья задача — изолировать разных арендаторов друг от друга. Это предотвращает вмешательство жильцов друг в друга. Как описано выше, степень изоляции определяет, есть ли у вас мягкая или жесткая мультиарендность, и должна ли система использоваться только доверенными арендаторами или она также защищена от добровольных атак.
Решение: Пространства имен Kubernetes служат базовой изоляцией для арендаторов. Кроме того, виртуальные кластеры обеспечивают даже большую изоляцию, чем пространства имен, а также предоставляют арендаторам большую гибкость. Другим фактором, который следует учитывать при изоляции арендаторов, является сетевой трафик: сетевые политики должны быть настроены таким образом, чтобы по умолчанию весь трафик был запрещен, а разрешен только трафик в пределах одного и того же пространства имен, интернет-трафик для контейнеров и запросы к DNS. Из-за этого арендаторам гораздо труднее атаковать или мешать друг другу.
#Available Multi-Tenancy Solutions
Уже существуют некоторые полезные решения, которые помогут вам реализовать мультиарендность с помощью Kubernetes. Помимо ранее упомянутого dex, здесь стоит упомянуть киоск и лофт.
#kiosk
kiosk — это мультитенантное расширение с открытым исходным кодом для Kubernetes. Он разработан как легкое, подключаемое и настраиваемое решение для любого кластера Kubernetes и простым способом решает некоторые проблемы с несколькими арендаторами. Это включает в себя разделение учетных записей, ограничение потребления ресурсов на уровне пользователя и шаблоны пространств имен для безопасной изоляции арендаторов и самостоятельной инициализации пространств имен. Хотя он не обеспечивает встроенного управления пользователями, киоск является очень хорошим строительным блоком для разработки собственной многопользовательской системы.
Несмотря на то, что киоск был выпущен всего несколько месяцев назад, он уже включен в руководство EKS Best Practices для мультитенантности от AWS. Подробное руководство по настройке киоска с EKS можно найти здесь.
#Loft
Loft основан на киоске и представляет собой комплексное решение для многопользовательской платформы. Loft можно установить в любой кластер Kubernetes, а затем позволить арендаторам создавать пространства имен и виртуальные кластеры по требованию. Он заботится об управлении пользователями (включая SSO) и изоляции пользователей и позволяет администраторам кластера определять ограничения на использование, поэтому все ранее упомянутые проблемы с несколькими арендаторами решаются. Loft предоставляет некоторые дополнительные функции, такие как спящий режим, который позволяет снизить затраты на облачные вычисления за счет отключения неиспользуемых пространств имен и виртуальных кластеров.
Loft — это коммерческое предложение с уровнем бесплатного пользования, которое также включено в руководство EKS Best Practices Guide для мультитенантности. Хотя изначально он был ориентирован на варианты использования мультитенантной разработки, его также можно использовать для производственных сценариев использования, таких как сегментирование кластера или запуск нескольких экземпляров продукта в общем кластере
#Заключение
проблем, с которыми многие организации сталкиваются в настоящее время по мере внедрения Kubernetes, а решения с одним арендатором становятся все более неосуществимыми.}

«Согласный, глухой,твёрдый звук [ш].Буквы Ш, ш »

Конспект урока на тему “Буква Ш, твердый согласный звук [ш]”

Конспект урока «Твердый согласный звук [ш], буквы Ш, ш.» | План-конспект урока по чтению (1 класс):

Буква Ш

4.2: Жесткие и мягкие кислоты и основания

Концепция твердых и мягких оснований (HSAB)

Примеры – Основания

Пример – Кислоты

Количественные меры жесткости

Концепция HSAB и растворимость

Концепция и стабильность HSAB

Концепция HSAB и кислотность

Трехмерные изменения мягких и твердых тканей при лечении межчелюстной протрузии

принадлежность

Авторы

принадлежность

Абстрактный

Похожие статьи

Цитируется

термины MeSH

английских слов, в которых «ch» произносится как «sh»

Резюме

2 Описание конфигурации

3 Основные уравнения

3.

3.2 Представление силы в пространственно-временной области

3.3 Волновые уравнения в частотной области

3.4 Материальные константы в диссипативной среде

3.5 Граничные и радиационные условия

3.6 Постановка краевой задачи (прямого рассеяния)

4 Точные решения в частотной области путем разделения переменных

4.2 Решения в частотной области при отсутствии слоя и свободной поверхности

4.3 Полевые представления в декартовых координатах для конфигурации, включающей слой и свободную поверхность

4.4 Определение коэффициентов дифракции и полей частотной области путем применения граничных условий

5 Структура характеристики в частотной области в случае слоя без потерь

5.

5.2 Частотная характеристика в жестком полупространстве

5.3 Амплитуды SBW1

5.4 Амплитуды SBW2

5.5 Амплитуды ВСП

6 Представление спектров суммарного поля в слое и дифрагированного поля в полупространстве в разрезе полюс-ветвь

7 Комментарии к представлениям отклика грунта SBW1+SBW2+SSW и полюс+ветвь

8 Прямой анализ временной истории реакции земли

8.

ψ вещественны, тогда как υ и β обычно комплексные из-за того, что µ

8.1.2 Комплексные нули числа

8.1.3 Комплексные нули числа

8.2 Особенности временной характеристики на местности

8.2.1 Приближенное вычисление интеграла по вещественной оси функции, имеющей комплексные полюса

8,3 Оценки

8.

на временной земле. и (147) имеем

8.3.2 Вклад

8.3.3 Вклад u

8.4 Характеристики временной динамики общего отклика грунта

9 Обсуждение

Благодарности

Ссылки

Иноды, жесткие и программные ссылки демистифицируют Esc.sh

Что такое Inode и номер Inode?

. Что такое программная ссылка?

Что же такое жесткая ссылка?

Руководство по лучшим практикам мультитенантности Kubernetes

#What Is Kubernetes Multi-Tenancy

#Soft Multi-Tenancy

#Мягкая и жесткая мультиарендность

#Limitations of Multi-Tenant Kubernetes

#Reasons For Kubernetes Multi-Tenancy

#Kubernetes Многопользовательская реализация Проблемы

#Управление пользователями

#Fair Resource Sharing

#Isolation

#Available Multi-Tenancy Solutions

#kiosk

#Loft

#Заключение

Добавить комментарий Отменить ответ