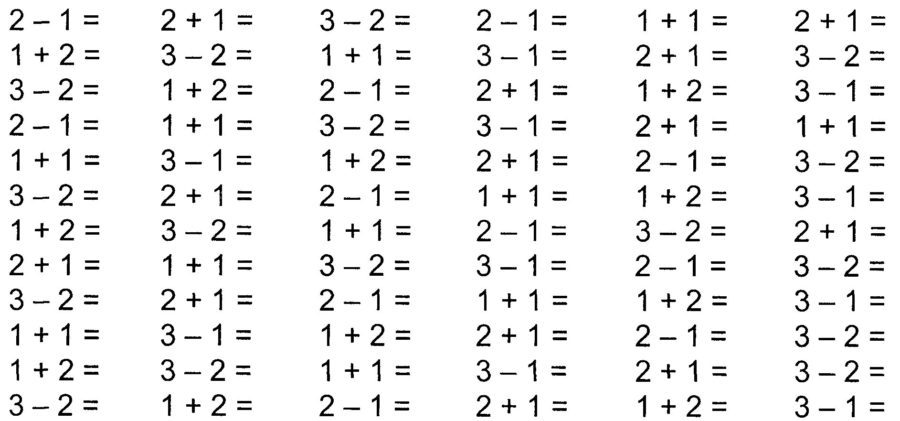Счет до 10 примеры: Математические примеры для детей ” Счет от 1 до 10″
Счет от 6 до 10 (ФГОС), Кузнецова Марта Ивановна . 5000 примеров , Экзамен , 9785377167754 2021г. 94,50р.
Кузнецова Марта Ивановна
Серия: 5000 примеров
94,50р.
Только в магазинах
В наличии в 12 магазинах
Ангарск, ПродаЛитЪ Вертикаль
Ангарск, ПродаЛитЪ Дом Книги
Иркутск, ПродаЛитЪ Детский кварталЪ
Иркутск, ПродаЛитЪ Иркутск-2
Посмотреть все магазины
Цена в магазине может отличаться
от цены, указанной на сайте.
Поделиться ссылкой в:
Издательство:Экзамен
ISBN:978-5-377-16775-4
Штрих-код:9785377167754
Страниц:32
Тип обложки:Мягкая
Год:2021
НДС:10%
Возраст:от 6 лет до 11 лет
Код:822658
Описание
Данное пособие полностью соответствует федеральному государственному образовательному стандарту (второго поколения) для начальной школы.
В книге представлен разнообразный практический материал для изучения, отработки и закрепления навыков вычислений в пределах от 6 до 10. Постепенно усложняющиеся задания научат ребёнка считать от 6 до 10 в прямом и обратном порядке, быстро находить соседей числа, запоминать состав чисел, складывать и вычитать в пределах 10. Книга предназначена первоклассникам для работы в школе и дома, для фронтальной и самостоятельной работы. Пособие является необходимым дополнением к учебникам по математике для 1 класса, рекомендованным Министерством образования и науки Российской Федерации и включённым в Федеральный перечень учебников.
Смотреть все
113,00р.
-20% после регистрации
Тренировочные примеры по русскому языку. 1 класс: Контрольное списывание ФГОС (2023 г.)
Кузнецова Марта Ивановна
113,00р.
-20% после регистрации
Тренировочные примеры по математике. 1 класс: Счет в пределах 20 ФГОС (2023 г.)
Кузнецова Марта Ивановна
113,00р.
-20% после регистрации
Тренировочные примеры по русскому языку. 1 класс: Задания для повторения из закрепления (2023 г.)
Кузнецова Марта Ивановна
-20% после регистрации
Я учусь писать и читать. 1 класс: Рабочая тетрадь (ФГОС) (2022 г.)
Кузнецова Марта Ивановна
377,00р.
-20% после регистрации
Учусь писать без ошибок.
3 класс: Рабочая тетрадь (ФГОС)
(2022 г.)Кузнецова Марта Ивановна
276,00р.
-20% после регистрации
Русский язык. 4 класс: Рабочая тетрадь ФГОС (2022 г.)
Кузнецова Марта Ивановна
402,50р.
-20% после регистрации
Пишем буквы и слова: Для детей 6-7 лет: Рабочая тетрадь ФГОС (2021 г.)
Кузнецова Марта Ивановна
337,00р.
-20% после регистрации
Пишем грамотно. 3 класс: Рабочая тетрадь. В 2-х частях Часть 1 ФП (2021 г.
)Кузнецова Марта Ивановна
110,50р.
-20% после регистрации
Математика. 4 кл.: Самостоятельные работы. Реши задачу! ФГОС (2020 г.)
Кузнецова Марта Ивановна
94,50р.
-20% после регистрации
Тренировочные примеры по русскому языку. 4 кл.: Безударные гласные (2019 г.)
Кузнецова Марта Ивановна
113,00р.
Тренировочные примеры по русскому языку. 3 класс: Задания для повторения и закрепления (2023 г.)
Кузнецова Марта Ивановна
Магазины
398,00р.
Пишем буквы и слова: Для детей 6-7 лет: Рабочая тетрадь ФГОС (2023 г.)
Кузнецова Марта Ивановна
Магазины
113,00р.
Тренировочные примеры по математике. 2-3 классы: Табличное умножение и деление (2023 г.)
Кузнецова Марта Ивановна
Магазины
377,00р.
Учусь писать без ошибок. 2 класс: Рабочая тетрадь (ФГОС) (2022 г.)
Кузнецова Марта Ивановна
Магазины
113,00р.
Тренировочные задачи по математике.
3 класс: Создание условий успешного усвоения материала
(2022 г.)Кузнецова Марта Ивановна
Магазины
113,00р.
Тренировочные примеры по русскому языку. 2 класс: Безударные гласные ФГОС (2022 г.)
Кузнецова Марта Ивановна
Магазины
113,00р.
Тренировочные примеры по математике. 3 класс: Задания для повторения и закрепления (2022 г.)
Кузнецова Марта Ивановна
Магазины
113,00р.
5000 примеров по математике. 2 класс: Задания для повторения и закрепления ФГОС (2022 г.
)Кузнецова Марта Ивановна
Магазины
113,00р.
Тренировочные задачи по математике. 4 класс: Создание условий успешного..ФГОС (2022 г.)
Кузнецова Марта Ивановна
Магазины
113,00р.
Тренировочные примеры по математике. 1 класс: Счет в пределах 10 ФГОС (2022 г.)
Кузнецова Марта Ивановна
Магазины
Смотреть все
Алгебра. 8 кл.: Дидактические материалы (2020 г.)
Жохов В.
И., Макарычев Ю.Н.
Магазины
766,00р.
Репетитор по биологии для старшеклассников и поступающих в вузы (2022 г.)
Шустанова Татьяна Анатольевна
Магазины
203,00р.
Математика. 7-11 классы: Карманный справочник (2022 г.)
Лысенко Ф.Ф.
Магазины
131,00р.Математика. 3 класс: Комплексный тренажер (2022 г.)
Барковская Наталья Францевна
Магазины
172,00р.
-20% после регистрации
Математика. 5 класс: Зачетные работы к учебнику Никольского С.М. ФГОС (к новому ФПУ) (2022 г.)
Ахременкова Вера Игоревна
334,00р.
Биология в инфографике (2022 г.)
Мазур О.Ч.
Магазины
Физика. 7-9 кл.: Справочник ФГОС (2018 г.)
Гормцева О.И.
Магазины
419,00р.
-20% после регистрации
Математическая грамотность. Сборник эталонных заданий: Выпуск 1 Часть 1 (2022 г.
)Ковалева Г.С., Рослова Л.О., Краснянская К.А.
100,00р.
3000 примеров по математике. 1 кл.: Считаем и объясняем. Сложение и вычитание (2021 г.)
Узорова Ольга Васильевна
Магазины
555,00р.
Физика. 10 класс: Базовый уровень. Сборник задач (2022 г.)
Заболотский А.А. Комиссаров В.Ф. Петрова М.
Магазины
94,50р.
Тренировочные примеры по математике. 3 кл.: Счет в пределах 1000 ФГОС (2021 г.)
Кузнецова Марта Ивановна
Магазины
179,50р.
Тренажер по математике. 2 класс ФГОС (2021 г.)
Яценко. И.Ф.
Магазины
153,00р.
География. 5-6 класс: Проверочные работы (2020 г.)
Бондарева М.В. Шидловский И.М.
Магазины
296,50р.
Геометрия. 7-11 кл.: Алгоритмы решения задач (2020 г.)
Виноградова Т.М.
Магазины
322,00р.
Решение задач по химии. 8-11 классы: Решения, методики, советы (2021 г.)
Хомченко И.
Г.
Магазины
150,00р.
Математика. 4-й класс (2020 г.)
Сазонова В.А.
Магазины
81,50р.
Запоминаем таблицу умножения (2019 г.)
.
Магазины
118,00р.
Таблица умножения за 3 дня (2021 г.)
Узорова Ольга Васильевна
Магазины
86,00р.
3000 примеров по математике. 1 класс. Супертренинг. Цепочки примеров.
Три уровня сложности
(2020 г.)Узорова Ольга Васильевна
Магазины
147,00р.
Математика. 3 класс: Тренажер. Учебное пособие (2022 г.)
Коннова Е.
Магазины
Приёмы устного счета для быстрого вычисления в уме
Зачем считать в уме, если решить любую арифметическую задачу можно на калькуляторе. Современная медицина и психология доказывают, что устный счет – это тренаж для серых клеточек. Выполнять такую гимнастику необходимо для развития памяти и математических способностей.
Известно множество приёмов для упрощения вычислений в уме. Все, кто видел знаменитую картину Богданова-Бельского «Устный счёт», всегда удивляются – как крестьянские дети решают такую непростую задачу, как деление суммы из пяти чисел, которые предварительно ещё надо возвести в квадрат?
Оказывается, эти дети – ученики известного педагога-математика Сергея Александровича Рачицкого (он также изображен на картине).
Это не вундеркинды – ученики начальных классов деревенской школы XIX века. Но все они уже знают приёмы упрощения арифметических расчетов и выучили таблицу умножения! Поэтому решить такую задачку этим детишкам вполне под силу!
Секреты устного счёта
Существуют приемы устного счета – простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.
Прибавляем числа 7,8,9
Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.
Примеры:
56+7=56+10-3=63
47+8=47+10-2=55
73+9=73+10-1=82
Быстро складываем двузначные числа
Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».
Примеры:
54+39=54+40-1=93
26+38=26+40-2=64
Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем – единицы.
Пример:
57+32=57+30+2=89
Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:
32+57=32+60-3=89
Складываем в уме трехзначные числа
Быстрый счет и сложение трехзначных чисел – это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.
Пример:
249+533=(200+500)+(40+30)+(9+3)=782
Особенности вычитания: приведение к круглым числам
Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.
Примеры:
67-9=67-10+1=58
576-88=576-100+12=488
Вычитаем в уме трехзначные числа
Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.
Пример:
843-596=843-500-90-6=343-90-6=253-6=247
Умножить и разделить
Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения – это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения – с 11 до 19!
Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:
15*16=15*10+(10*6+5*6)=150+60+30=240
Умножаем и делим на 4, 6, 8, 9
Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.
Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:
-
умножить на 4 – это дважды умножить на 2;
-
умножить на 6 – это значит умножить на 2, а потом на 3;
-
умножить на 8 – это трижды умножить на 2;
-
умножить на 9 – это дважды умножить на 3.
Например:
37*4=(37*2)*2=74*2=148;
412*6=(412*2)·3=824·3=2472
Аналогично:
-
разделить на 4 – это дважды разделить на 2;
-
разделить на 6 – это сначала разделить на 2, а потом на 3;
-
разделить на 8 – это трижды разделить на 2;
-
разделить на 9 – это дважды разделить на 3.
Например:
412:4=(412:2):2=206:2=103
312:6=(312:2):3=156:3=52
Как умножать и делить на 5
Число 5 – это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.
Пример:
326*5=(326*10):2=3260:2=1630
Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.
326:5=(326·2):10=652:10=65,2.
Умножение на 9
Чтобы умножить число на 9, необязательно его дважды умножать на 3.
Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:
37*9=(37*3)*3=111*3=333
или
37*9=37*10 – 37=370-37=333
Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко – это примеры занимательные, так называемые маленькие хитрости.
Счет на пальцах
Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах. Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы – это очень наглядно и удобно. Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием.
Да и загибать пальцы в эпоху айфонов как-то несолидно.
Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:
- Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
- Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.
- Оставшееся количество пальцев слева будет соответствовать десяткам, справа – единицам. В нашем примере – 4 пальца слева и 5 справа. Ответ: 45.
Да, действительно, решение быстрое и наглядное! Но это – из области фокусов. Правило действует только при умножении на 9. А не проще ли, для умножения 5 на 9 выучить таблицу умножения? Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.
Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения.
Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь.
Устный счёт на автомате
-
Во-первых, необходимо хорошо знать состав числа и таблицу умножения.
-
Во-вторых, надо запомнить приемы упрощения расчётов. Как выяснилось, таких математических алгоритмов не так уж много.
-
В-третьих, чтобы приём превратился в удобный навык, надо постоянно проводить краткие «мозговые штурмы» – упражняться в устных вычислениях, используя тот или иной алгоритм.
Тренировки должны быть короткими: решить в уме по 3-4 примера, используя один и тот же приём, затем переходить к следующему. Надо стремиться использовать любую свободную минутку – и полезно, и нескучно. Благодаря простым тренировкам все вычисления со временем будут совершаться молниеносно и без ошибок. Это очень пригодится в жизни и выручит в непростых ситуациях.
Пропустить счет до 10 – Математика с мамой
Что такое Пропустить счет до 10?
Пропустить счет до 10 означает считать десятками, каждый раз прибавляя десять.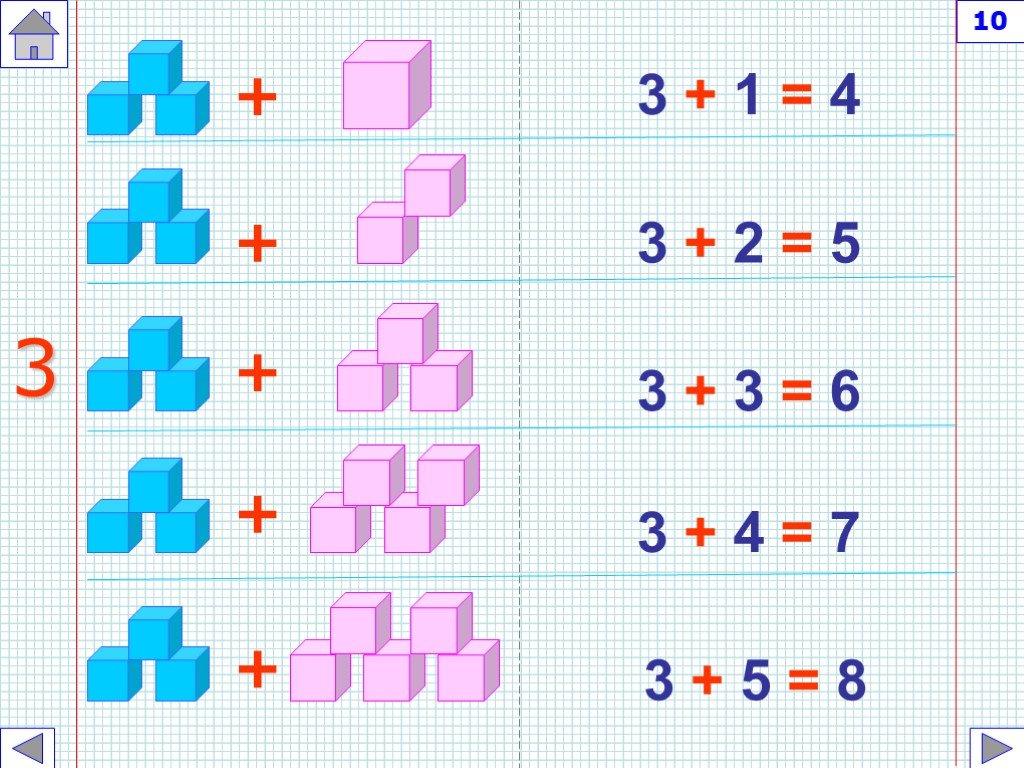
Не произносите числа между ними. Пропустить счет десятками очень важно, потому что это позволяет нам считать быстрее, чем считать единицами.
Например, пропустив счет десятками от нуля, мы получим 10, 20, 30, 40, 50, 60, 70, 80, 90 и 100.
Ниже приведен пример пустой рабочей таблицы гусеницы для подсчета пропусков, которую вы можете использовать, чтобы попрактиковаться в подсчете пропусков. Мы будем считать десятками, чтобы собрать гусеницу, записывая число в каждом сегменте.
Вот готовый пример гусеницы.
Как пропустить счет до 10
Чтобы пропустить счет до 10, добавьте 10, чтобы перейти к следующему числу. Проще всего это сделать, увеличив цифру в десятках числа на 1. Например, пропустим счет десятками от 7, получим 7, 17, 27, 37, 47, 57, 67, 77, 87, 97.
Цифра десятков просто увеличивается с 1 на 2, на 3 и т.д.
Альтернативный метод пропуска подсчета до 10 — использовать числовую сетку до 100 и перемещаться вниз на одну строку каждый раз, когда вы добавляете 10.
Имеем: 7, 17, 27, 37, 47, 57, 67, 77, 87 и 97.
Мы останавливаемся на 97, потому что это последнее число в паттерне перед 100, но мы могли бы продолжать считать, если бы нам было нужно.
Мы видим, что все числа заканчиваются той же цифрой, что и число, с которого мы начали.
Все числа заканчиваются на 7, потому что мы пропускаем счет десятками, начиная с 7.
Мы просто добавляем еще 1 к разряду десятков с каждым добавлением 10.
Счет в десятках от любого числа
Чтобы начать счет десятками с любого числа, прибавьте 10, чтобы перейти к следующему числу. Самый простой способ сделать это — каждый раз увеличивать цифру в столбце десятков на 1. Например, начиная с 1, у нас есть 11, 21, 31, 41, 51, 61, 71, 81 и 91.
Чтобы пропустить счет десятками из любого числа, просто каждый раз добавляйте единицу к разряду десятков. Числа всегда будут заканчиваться одной и той же цифрой в столбце единиц.
Помните, что чтобы добавить 10 в числовую сетку, просто переместитесь на одну клетку вниз.
Вместо того, чтобы начинать с нуля, мы начинаем с «1».
Перемещение на одну клетку вниз по сетке каждый раз добавляет десять. У нас есть:
1, 11, 21, 31, 41, 51, 61, 71, 81 и 91.
Мы могли бы и дальше пропускать счет десятками, если бы это было необходимо.
Мы можем начать с любого числа в числовой сетке и двигаться вниз по столбцу, чтобы пропустить счет десятками. Помните, что эта числовая сетка может быть полезным учебным пособием, помогающим практиковать счет десятками.
Мы можем выбрать любое число в числовой сетке, от которого будем считать десятками.
Например, вот 46. Будем считать десятками от 46.
Мы начнем с 46 и будем двигаться вниз от квадрата к квадрату, каждый раз прибавляя десять.
Снова мы просто увеличиваем цифру десятков на единицу каждый раз от 46 до 56, до 66 и так далее.
Число 46 заканчивается цифрой «6» в столбце единиц измерения, поэтому другие числа в нашем шаблоне счета с пропусками также заканчиваются на «6».
Вот заготовка гусеница-счетчик, которую мы будем собирать вместе, пропускаем счет десятками от 11.
11 заканчивается цифрой единиц «1», поэтому другие числа в шаблоне также будут заканчиваться на «1».
В следующем примере мы считаем десятками, начиная с 3.
Все следующие числа в шаблоне также оканчиваются на 3.
Обучение пропуску счета до 10
Для обучения счету десятками полезно использовать числовую сетку. Чтобы добавить десять в числовую сетку, нужно просто переместиться на одну строку вниз от исходного числа. Используя числовую сетку, можно легче замечать закономерности, показывая, как цифра в столбце десятков каждый раз увеличивается на 1.
Чтобы пропустить счет десятками, продолжайте добавлять десять, чтобы перейти к следующему числу.
Чтобы легко пропустить счет до десяти, каждый раз увеличивайте цифру десятков на единицу. Все числа будут заканчиваться одной и той же цифрой в столбце единиц измерения.
Счет с пропусками — более быстрый способ счета, чем счет единицами.
При первом обучении счету с пропуском до 10 может быть полезно использовать числовую сетку до 100, чтобы помочь визуализировать закономерности в числах.
Начиная с нуля, мы можем добавить десять, чтобы получить 10.
Продолжаем каждый раз прибавлять по 10 и получаем: 20, 30, 40, 50, 60, 70, 80, 90 и 100.
Мы видим, что каждый раз, когда мы прибавляем десять к числу в числовой сетке, мы перемещаемся на одну клетку вниз.
Мы начали с «0» и считали десятками. При пропуске счета на 10 от нуля все числа находятся в таблице десятикратного умножения.
Мы видим шаблон, в котором все числа заканчиваются одной и той же цифрой в столбце единиц. Все числа заканчиваются на ноль.
При обучении счету с пропуском до 10 важно отметить, что добавление десяти к числу каждый раз увеличивает цифру десятков на 1.
Мы можем видеть закономерность в цифрах десятков, увеличивающихся от 1 до 2, до 3 и так далее. 100 это 10 десятков.
Пропустить счет на 10 назад
Чтобы пропустить счет назад на 10, каждый раз вычитайте 10. Вычитание 10 в числовой сетке приводит к перемещению на одну клетку вверх каждый раз. Каждый раз цифра в столбце десятков будет уменьшаться на 1.
Например, из 42, считая в обратном порядке, мы получаем 42, 32, 22, 12 и 2. Цифра в столбце десятков каждый раз уменьшается на 1 от 4 до 3, затем от 2 до 1 и до 0.
Мы можем найти 42 на сетке чисел до 100.
Чтобы вычесть 10 из числовой сетки, мы перемещаемся вверх по сетке к квадрату прямо над числом, в котором мы сейчас находимся.
42 оканчивается на «2», поэтому другие числа в шаблоне также оканчиваются на «2».
Считая в обратном порядке, получаем 42, 32, 22, 12 и 2.
Мы не продолжаем вычитать 10, потому что 2 меньше 10, а на числовой сетке нет других квадратов, показанных выше 2.
Вот еще один пример.
Пропустите обратный счет десятками, начиная со 100, у нас будет 100, 90, 80, 70, 60, 50, 40, 30, 20, 10, 0.
Чтобы пропустить обратный счет десятками, вычтите десять, чтобы перейти к следующему новому числу. Столбец единиц останется прежним, а столбец десятков будет каждый раз уменьшаться на единицу. Все числа будут заканчиваться на одну и ту же цифру.
Мы можем использовать рабочие листы гусеницы с пропуском счета, чтобы попрактиковаться в обратном счете.
Вот пустой пример для пропуска обратного отсчета.
Вот рабочий лист гусеницы, который заполняется пропуском обратного счета десятками.
Мы видим, что числа в рабочем листе гусеницы для обратного счета совпадают с числами для прямого счета. Пропустить счет в обратном направлении может быть полезно для отработки моделей, наблюдаемых при пропуске счета в прямом направлении.
При обучении счету с пропусками важно сначала попрактиковаться в счете в прямом порядке, прежде чем переходить к счету в обратном порядке, используя те же числа.
Вот еще один рабочий лист для подсчета пропусков, в котором мы считаем в обратном порядке десятками от 99.
При обучении счету с пропуском до 10 полезно произносить числа, когда вы считаете вперед и назад, подчеркивая числа, которые остаются неизменными в каждом образце.
В чем смысл подсчета пропусков?
Счет с пропусками помогает нам искать закономерности в числах и лучше понимать относительный размер чисел. Подсчет пропусков — это форма повторного сложения, когда ответы образуют таблицу умножения. Таким образом, подсчёт помогает нам выучить таблицу умножения. Изучение того, как прибавлять и вычитать, пропуская счет вперед и назад, также укрепляет нашу способность выполнять сложение и вычитание.
В общем, пропуск счета укрепляет нашу уверенность при работе с числами. Умножение, деление, сложение и вычитание улучшаются, если сначала научиться пропускать счет вперед и назад на диапазон различных чисел.
Вот пример пропуска обратного счета на 10 из 92.
Мы просто вычитаем десять, чтобы получить каждое число, что равносильно уменьшению цифры десятков на 1 каждый раз.
92 заканчивается цифрой «2» в столбце единиц измерения. Следующие числа в скороговорке также будут заканчиваться на «2», но цифра в столбце десятков каждый раз будет уменьшаться на 1.
Образец, усвоенный в ходе этого процесса, позволяет нам затем научиться вычитать десять из любого числа.
Это помогает нам понять, как разные числа соотносятся друг с другом по размеру.
Счетное число – определение, счет от 1 до 100, таблица счета, примеры начинаются с 1 и заканчиваются в бесконечности. Последовательность подсчета чисел: 1, 2, 3, 4 и так далее. Давайте узнаем о подсчете чисел в деталях.
Что такое счетные числа?
Счетные числа определяются как набор чисел, которые мы используем для подсчета вещей. Счетные числа называются натуральными числами. И эти числа всегда положительные. Счетные числа не включают 0, и по этой причине целые числа нельзя назвать счетными числами.
Примеры счетных чисел: 1, 2, 3, 4, 5 и т. д. Счетные числа используются в повседневной жизни, так как они необходимы для подсчета вещей, предметов, денег и т. д. Следовательно, счетные числа не могут быть десятичными, отрицательными числами, целыми числами или дробями. Счетные числа — это положительные числа, а целые числа содержат как положительные, так и отрицательные числа. Счет чисел может производиться разными способами, например, обратный счет, счет на двойки (2, 4, 6,…), счет на тройки (3, 6, 9).,…), считая по 5 (5, 10, 15,…) и так далее. Основные правила подсчета чисел:
- Счетные числа не включают 0.
- Счетные числа не включают дроби, например, 1/2, 3/4, 5/6 и т. д.
- Счетные числа не включают отрицательные числа, например: -1, -2, -3 и т. д.
- Счетное число не включает десятичные дроби, например: 0,85, 0,67, 3,97 и т. д.
Счетные числа от 1 до 20 1, потому что 0 никогда не включается в счетные числа. Начнем считать числа, а для начала посчитаем числа от 1 до 20 как цифрами, так и прописью.
понимать порядок чисел, повторный счет чисел важен для детей. Это можно сделать в повседневной жизни, просто посчитав все, что валяется в доме. Это включает в себя подсчет книг, денег, печенья или любых счетных вещей. Учат считать числа от 1 до 100, чтобы учащиеся более четко понимали концепцию увеличения чисел и закономерностей. Ниже приведен рабочий лист для подсчета чисел от 1 до 100:
От подсчета дней в году до подсчета конфет, розданных в классе, и так далее. Давайте посмотрим на некоторые примеры подсчета чисел:
