Ряд чисел от 1 до 10 наглядное пособие распечатать: Домики «Состав числа» от 1 до 10, от 11 до 20 — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7 – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Домики «Состав числа» от 1 до 10, от 11 до 20 — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Содержание

Соседи числа — Математические задания для детей

Соседи числа — это математические задания на закрепление знания порядкового счета. В этих заданиях ребенку нужно будет определить соседей для заданных чисел. Для этого ему нужно в уме представить числовой ряд от 0 до 10 и определить какие числа стоят до и после указанного в задании числа.

5.Скачать карточки «Соседи чисел»

Во вложениях внизу страницы вы можете скачать карточки «Соседи чисел» — 2 бланка одним файлом. Распечатать карточки на цветном принтере и получить дополнительное пособие для занятий с ребенком по математике на закрепление темы «Соседи чисел». После распечатки бланков, разрежьте каждый лист на 4 части и у вас получится 8 цветных карточек с заданиями для ваших малышей. Помимо того, что ребенку нужно будет написать в кружочках соседей чисел, ему необходимо дополнительно решить примеры в домиках на закрепление темы «Состав числа».

Карточки «Соседи чисел 2, 4, 6, 8.»

Карточки «Соседи чисел 3, 5, 7, 9.»

4.Помоги животным — Впиши соседей числа.

В четвертом задании ребенку нужно помочь животным: корове, лошадке, свинке, лисичке, овечке, волку, котенку, зайчику и вписать в окошки домиков соседей десяти чисел. После того, как малыш выполнит восемь заданий, попросите его назвать общего соседа чисел 1 и 3, 5 и 7, 8 и 10, 6 и 8, 2 и 4, 3 и 5, 4 и 6, 7 и 9.

Соседи числа — Знаешь ли ты порядковый счет?

В первом задании нарисована деревня, в которой множество домов. Но каждый домик не одинок, он имеет своих соседей. Соседи числа — это и есть соседи каждого домика, который находится в центре. Ребенку нужно определить каждого соседа центрального домика, представив в уме математический числовой ряд до 10, а затем вписать эти числа справа и слева (клетки с точками). Под первым рядом домиков расположены числа, из которых и нужно выбрать соседей. (Хотя можно и не смотреть на эти числа, так как они не являются числовым рядом порядкового счета).

Если у ребенка возникают сложности с заданием и он не может визуально представить себе порядковый счет от 0 до 10, то сделайте ему лист-подсказку, на котором напишите по порядку числа до 10. Пусть ребенок подсматривает в него до тех пор, пока не выучит наизусть.

Во втором задании мы еще раз проверяем навыки счета — здесь нужно посчитать предметы в каждой картинке и обвести соответствующее число.

Скачать задания в картинках — Соседи числа — Знаешь ли ты порядковый счет? — вы можете во вложениях внизу страницы

Найди состав чисел и соседей числа в домиках

В первом задании нарисованы многоэтажные домики, на крыше которых написано число. Ребенку нужно определить состав этого числа, учитывая что одно из чисел уже указано на каждом этаже. Осталось дописать второе число в пустые клетки.

Во втором задании нужно определить соседей числа и вписать в пустые клетки полученные числа. После выполнения задания можно раскрасить картинки.

Скачать задания «Соседи числа» (цветная и черно-белая картинки) вы можете во вложениях внизу страницы.

Числовые домики — Состав чисел от 2 до 9

Следующее пособие поможет малышу закрепить знания состава чисел от 2 до 9 с помощью восьми многоэтажных домиков, в окошки которых ребенок будет вписывать недостающие числа. На домиках сверху написаны числа, состав которых необходимо разместить на каждом этаже в двух окошках. Имея первое слагаемое, изображенное в 1 окошке, ребенку нужно вспомнить и дописать в соседнем — второе.

Рядом с домиками малыш найдет различные предметы, количество которых соответствует цифре, указанной на домике.

Скачать задание — Числовые домики — вы можете во вложениях внизу страницы

Также вы можете скачать и другие математические задания в картинках:

Задания по математике для дошкольников — В картинках

Задания по математике для дошкольников, представленные в этом материале, помогут вам разнообразить свои занятия с детьми, обучая их самым основным математическим понятиям.

Примеры по математике — 1 класс — Распечатать в картинках

Здесь вы можете найти примеры по математике (1 класс), распечатать на принтере и использовать в качестве учебного материала на уроках математики или в детских садах на этапе подготовки к поступлению в школу.

Математические задания для 1 класса — В картинках для печати

Математические задания для 1 класса — это яркие красочные картинки с развивающими упражнениями по математике, включающие в себя разнообразные игровые задания для детей.

Задачи по математике — 1 класс. Распечатать в картинках

Здесь вы найдете увлекательные задачи по математике (1 класс) в картинках, которые научат детей мыслить логически и выполнять простые математические действия.

Разделить поровну предметы — Математические картинки

Здесь вы можете посмотреть и скачать красочные картинки задания, в которых нужно разделить поровну различные предметы. Такие занятия подготавливают детей к одному из сложных математических выражений — делению.

Задания с раскрасками — Порядковый счет до 10

В этих интересных заданиях дети узнают, что такое порядковый счет до 10. А те, кто уже знакомы с этим понятием, могут показать свои знания с помощью данного упражнения.

Устный счет в пределах 10 — Картинки с заданиями

Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках. Данные задания формируют у детей навыки счета и способствуют более эффективному обучению простых математических действий.

Состав числа до 20 — Распечатать числовую таблицу

Здесь вы можете состав числа до 20 распечатать в виде числовой таблицы и дать ребенку для заполнения. Такое занятие прекрасно тренирует навыки счета дошкольников, а также приучает решать примеры до 20.

Названия геометрических фигур — Картинки с заданиями

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.

А еще вы можете поиграть в математические игры онлайн от лисенка Бибуши:

Игра «Счет от 1 до 10 — Посчитай картинки и выбери число»

В этой игре малыш должен посчитать количество предметов на игровом экране и нажать на соответствующее число. После этого он увидит и услышит порядковый счет до данного числа.

Игра «Найди числа на картинке» для малышей от 4 лет

Здесь ребенку нужно быть внимательным, чтобы найти все спрятанные числа на картинке. В игре также используется порядковый счет.

Математическая игра «Найди наибольшее и наименьшее число»

В этой игре ребенку необходимо выбрать среди предложенных чисел самое большое или самое маленькое.

Игра «Сложение и вычитание до 10» — Задачки в картинках

Представляем вашему вниманию еще одну развивающую математическую игру «Сложение и вычитание до 10» для детей раннего возраста от Лисенка Бибуши

Задачи-примеры для малышей в картинках

Математическая онлайн игра «Задачи-примеры для малышей в картинках» состоит из восьми задачек и подойдет детям, которые учатся считать до 10.

Состав чисел первого десятка. Числовые домики.

Согласно школьной программе, первоклашки должны уметь автоматически решать примеры на сложение и вычитание в пределах чисел первого и второго десятков.

Для того, чтобы успешно справиться с поставленными задачами, детки должны знать из чего эти числа состоят . Вся проблема заключается в том, что информация эта — абстрактная и запомнить непоседливому малышу не так просто.

Поэтому преподносить ее нужно в форме увлекательной, наглядной и понятной . Лучше всего для нее подходят так называемые числовые домики — картинки и карточки, созданные специально для освоения дошколятами азов счета.

Мы тоже решили создать на нашем сайте тему «Состав числа до 10 домики» и предложить вамраспечатать картинки и карточки в готовом виде.

Пример карточки:

В конце нашей статьи приведены такие карточки — разного формата и разных авторов.

Также подобные карточки для детей вы можете нарисовать сами . Это совсем не сложно и не требует каких-то особых знаний и талантов. Просто рисуем от руки прямоугольники — многоэтажки на листах бумаги.

Рисуем карточки и объясняем ребенку правила

Как нарисовать числовой домик самому? Да очень просто:

Сначала от руки на чистом листе бумаги изображаем каркас «пятиэтажки», затем делим его на этажи и дорисовываем крышу.
На каждом этаже нужно изобразить по две квартиры (или два окошка). На крыше вместе с ребенком пишем цифру и объясняем малышу, что эта цифра — хозяин домика, который разрешает в нем жить только такому количеству жильцов, которое равно ему самому.
Для «заселения» на первых порах можно использовать счетные палочки — чтобы ребенок не сбился со счета и не запутался.

Помогаем ребенку освоить состав числа до 10 в игре

Помните о том, что маленькие детки очень охотно и быстро учатся на примерах. Поэтому первую карточку вы должны будете заполнить сами . Не забывайте рассуждать вслух о том какая у вас цифра-хозяин и сколько жильцов вам нужно заселить в каждую квартиру, чтобы не нарушать его «правила».

Следующий домик ребенок должен «заселить» сам при вашей помощи. Помогите ему рассуждать и высчитывать сколько жильцов должно быть заселено в каждую квартиру и на каждый этаж.

Закрепляем пройденное

Как помочь ребенку быстрее и легче запомнить состав числа до 10 и научиться считать? Ниже мы приводим еще несколько полезных советов и правил работы с карточками.

Количество жильцов следует менять от этажа к этажу. При этом ребенок активно осваивает новые комбинации чисел. Например, в домике с цифрой-хозяином «6» они будут 1 и 5, 2 и 4, 3 и 3.
Когда ваш малыш будет хорошо ориентироваться в комбинациях, можно переходить от счетных палочек к написанию цифр. Эта задача более трудная, поэтому прибегайте к постоянному повторению и помогайте своему чаду освоиться с новой деятельностью.
Старайтесь постоянно освежать в памяти ребенка игру с карточками. Также старайтесь постепенно усложнять задание, переворачивая одну из карточек чистой стороной вверх и прося ребенка нарисовать этот домик и вспомнить состав числа, которое на нем изображено.
Не забывайте о том, что без регулярного повторения и соответствующей заинтересованности в процессе вашему ребенку будет сложно запомнить пройденный материал.

Ну а для того, чтобы красивые и интересные карточки у вашего малыша всегда были перед глазами, используйте иллюстрации в нашей статье. Все эти красивые и разноцветные картинки можно распечатать и развесить в комнате ребенка, чтобы он постоянно их видел.

Для успешного обучения в начальной школе будет очень полезно, если ребенок еще до поступления в первый класс выучит состав чисел до десяти . Однако дети обычно не любят его заучивать. Другое дело, если превратить процесс обучения в красочную, увлекательную онлайн игру!

В данном разделе мы предлагаем вам развивающие онлайн игры, в которые можно играть совершенно бесплатно и без регистрации на нашем сайте. С ними вы легко выучите состав числа до 10.

Мы предлагаем вам 3 серии онлайн игр , которые последовательно и логично дополняют друг друга.

Прежде всего — это серия онлайн игр «Лампочки» , в которых состав числа показывается наглядно, кроме того, ребенок в конце игры сам может позажигать и посчитать лампочки.

Вы не знаете, как объяснить ребенку, что такое состав числа ? Идите скорее к нам! Представляем вам уникальную серию развивающих онлайн игр «Лампочки», в которые можно играть совершенно бесплатно и без регистрации на нашем сайте. В этих играх наглядно представлен состав числа 5, 6, 7, 8, 9 и 10. Как же учить состав числа? Возьмем, например, онлайн игру «Состав числа 5». На первом слайде мы видим ряд лампочек, которые не горят. Пересчитываем лампочки, и в этом нам помогает игра. Их 5. Затем, на следующем слайде — одна лампочка загорается, и ребенку предлагается посчитать, сколько лампочек из 5 горит, а сколько еще нет, и вставить соответствующие цифры в окошечки. Кнопки с цифрами расположены прямо на экране, что особенно удобно при работе на планшете. Если ребенок ввел цифры правильно, справа появляется ряд примеров, составленных из соответствующих цифр.

На каждом последующем слайде загорается на одну лампочку больше. На последнем слайде учить состав числа еще интересней: ребенок сам может зажигать и гасить любые лампочки, просто кликая по ним левой кнопкой мыши. Таким образом скучное заучивание состава чисел до 10 можно превратить в увлекательную игру.

Далее — развивающие онлайн игры «Числовые домики» . Идея не нова, числовые домики давно используются для изучения состава числа. Но в отличие от числовых домиков, напечатанных на бумаге, используемых в садах и в школах, наши числовые домики интерактивные, в них можно играть снова и снова и тем самым закрепить состав чисел до 10.

И, наконец, третья серия развивающих онлайн игр, направленных на закрепление и автоматизацию состава числа — это математические тренажеры , которые включают примеры и уравнения, помогут довести знание состава числа до автоматизма.

Однако, не забывайте и о других способах заучивания состава числа , так как долгое время находиться перед экраном компьютера ребенку вредно.

Предлагаем вам также серию тренажеров для заучивания состава чисел до 20.

При обучении в 1 классе очень важно твердо выучить состав числа 10.

Он нам пригодится не только для решения примеров в пределах 10, но и в последующем, когда мы начнем работать с двузначными числами, например, при складывании и вычитании с переходом через десяток. При сложении и вычитании столбиком, наконец. Поэтому начинать учить состав числа 10 можно и нужно еще до школы.

Учить состав числа можно разными способами. Самый простой материал для обучения — это собственные руки. Сколько пальцев на двух руках — 10. Зажмите несколько пальцев, и считайте, сколько осталось.

Можно использовать для заучивания состава числа 10 различные счетные материалы — счетные палочки, деревянные бусы и т.д.

Возьмите 10 предметов, и различными способами разделите их на две кучки. Сначала отложите один предмет, затем еще один и т.д., каждый раз считая, сколько осталось.

Вы можете взять также карточки с цифрами, и, сосчитав предметы, выкладывать состав числа с помощью цифр, вы можете скачать карточки с нашего сайта

Один из эффективных способов — наглядно представить состав числа с помощью картинок, так как у детей плохо развито абстрактное мышление, наглядность для них — все. Именно поэтому мы и создали обучающую онлайн игру «Состав числа 10. Лампочки» с интерактивными элементами.

С ней вам будет учить состав числа 10 проще и веселее. Сначала считаем лампочки — сколько горит, а сколько осталось, и нажимаем нужные цифры, следуя заданиям на экране. А затем самостоятельно зажигаем лампочки, нажимая на них, и учим состав числа 10.

Тема: Число 10. Состав числа 10.

Тип урока: Ознакомление с новым материалом.

Познакомить с числом 10 и его составом.
Учить операциям сложения и вычитания в пределах 10 с опорой на его состав.
Закрепить знания составов чисел до 9, действий в пределах 9.
Учить самостоятельности и умению слушать других.
Развивать речь, память, внимание и логическое мышление.

I. Орг. момент.

Прозвенел звонок, начинается урок.

II. Актуализация знаний.

Ребята, посмотрите на доску. В домиках № 7 и № 9 некоторые жильцы получили странное послание. Хотите узнать какое?

Тогда в тетрадях запишите этих жильцов – пропущенные числа в парах состава чисел 7 и 9, а на доске работают двое.

Сейчас расположите числа в порядке убывания, и в соответствии с буквенным кодом прочитайте им послание. Что у вас получилось?

Что такое клад?

Хотите найти математический клад?

Какими качествами должны обладать кладоискатели?

А кто ещё всегда ищет клады?

Откроем учебник на стр. 35 № 8. Посмотрите, пираты нас хотят опередить, они уже на острове. Давайте узнаем, найдут ли они клад, для этого вычислим примеры по стрелкам. Что у вас получилось?

Что заметили? Верно, ответ предыдущего примера становится началом следующего. Такие примеры называются “круговыми”. Ответ последнего должен быть началом всей цепочки:

Где можно было ещё замкнуть круг?

Это нам позволит обогнать пиратов. Пусть они ходят по кругу, а мы пойдём вперёд к цели. Вот и нужное место. Надо копать.

III. Физкультминутка.

Копаем землю и её выбрасываем их ямы (имитация движений под счёт до 9).

IV. Новый материал.

Ну, вот и заветный сундук, но на нём замок. На замке числа. Какие, узнаем, выполнив математический диктант. Все пишут в тетради, а на двое доске. Внимание:

Запишите число, следующее за 7 (8)

Запишите число, предыдущее 5 (4)

Запишите число, стоящее между 6 и 8 (7)

Запишите соседей числа 2 (1 и 3)

Запишите число, стоящее справа от 8 (9)

Запишите число, стоящее слева от 6 (5)

Я задумала число, оно предшествует 3 (2)

Елена Илларьевна задумала число, оно следует за 5 (6)

Проверяем (взаимопроверка) работу на доске.

У нас получился числовой ключ, чтобы им открыть замок, надо числа расположить в порядке возрастания. Пишите и диктуйте: (учитель на доске)

1, 2, 3, 4, 5, 6, 7, 8, 9.

Какое число следует в ряду чисел за 9?

Вот он и наш клад – число 10!

Какая же тема нашего урока?

Чему будем учиться?

Что знаете про число 10?

Число 10 – самое маленькое двузначное число, в записи берутся 2 цифры. Что обозначает цифра 1? Что у человека есть в количестве 1 десятка?

В тетради запишем строчку числа 10. сколько получилось десятков? Кто знает, какое это число?

Нам надо разложить 10 алмазов из нашего клада в 2 мешочка. Как можно это сделать? (В тетради – дети, учитель – на доске)

Что у нас получилось? Какие случаи лишнее? Почему? (По переместительному свойству сложения)

Что будем запоминать? (Хором, по одиночке, с закрытыми глазами)

Кто сможет закончить состав 10 в разбивку? (Учитель – 10 это 8 — ученик – 2,

У дружных кладоискателей всё делится как? Какой случай из состава подойдёт?

V. Физкультминутка
“5 на 5” (5 – прыжков, 5 — хлопков)
VI. Закрепление изученного.
А сейчас, давайте возьмём другие пары из состава 10. Запишите все взаимосвязанные равенства с: 8 + 2 = 10 (I ряд)
7 + 3 = 10 (II ряд)
6 + 4 = 10 (III ряд)
Если затрудняетесь, консультируетесь в паре с соседом. Что у вас получилось?
Что же за взаимосвязанные равенства должны быть? (Переместительное свойство сложения обратные случаи вычитания)
Откроем учебник на стр. 39 № 5. Что нужно сделать? Сравним с объяснением:
1 столбик – с опорой на числовой отрезок.
(10 больше 8, т.к. на числовом отрезке стоит справа, 7 меньше 10, т.к. на числовом отрезке стоит слева)
2 столбик – не вычисляя
(10 + 0 = 10 – 0, т.к. нуль есть ничего,
10 – 2 > 10 – 5, т.к. при одинаковом уменьшаемом чем меньше убираем, тем больше остаётся)

3 столбик – не вычисляя
(3 + 7 = 2 + 8, т.к. первое слагаемое убыло на 1, а второе уменьшилось тоже на 1,
1 + 9 > 5 – 5, т.к. справа число самоуничтожается в 0)
Решим уравнения № 6 (стр 39, по вариантам). Что получилось? Что такое Х?
В тетрадь решим задачи № 7 (стр. 39). Читаем задачу (а). Какая схема на доске подойдёт к этой задаче? Что подпишем? Ведёт решение ученик на доске. (Аналогичная работа над двумя другими задачами.)
VII. Рефлексия.
Что сегодня изучали?
— Игра “Часики”: за 1 минуту вы должны восстановить соседей числа 10 на песочных часиках (у каждого ученика – листок с заданием). Приготовились. Начали. Что получилось?
Встаньте, у кого верные часики.
Хлопните в ладоши, кому было легко выполнить это задание.
Подпрыгните 10 раз, кому было интересно сегодня на уроке.
VIII. Домашнее задание.
В дневниках д/з – стр. 36.
Интерактивная презентация и карточки с аналогичным оформлением по теме «Состав чисел первого десятка. Числовые домики.»
Презентация и карточки подойдут для уроков математики в 1 классе и для занятий с дошкольниками.
Презентация с триггерами.
Закрытые окошки с составным слагаемым открываются по щелчку на любое окошко, в любом порядке.
Переход на следующий слайд по кнопке справа.
Состав чисел 3, 4, 5 – здесь объясняем, закрепляем и повторяем переместительный закон сложения (например, 2+1 и 1+2 одно и то же).
Состав чисел от 4 до 10 представлен двумя вариантами слайдов. На одном слайде за закрытым окошком второе составное слагаемое, на другом слайде – первое составное слагаемое.
Презентация online
Карточки «Числовые домики»
На странице размещены образцы карточек в уменьшенном размере, скачайте карточки архивом в полном размере по ссылке ниже. Для ознакомительного просмотра щелкаем на картинку правой кнопкой мыши, изображение увеличится.
В комплекте с карточками картинки закрытых окошек для вырезания. При индивидуальной работе закрытым окошком можно прикрыть окошко с числом.
Карточки по математике. 1 класс. Состав чисел 1-10. | Учебно-методический материал по математике (1 класс) на тему:
Вставь пропущенные числа.
…2 …. 4……….7 8 9.
Запиши соседей чисел.
….4…. …. 7 …. … 8… …. 5 ….
Сравни.
4+3….2+4 8-3…3+3 10-2….3+4
7-3….2+5 9-3…3+5 7+2….8-2
Заполни таблицу.
Уменьшаемое
7
7
7
7
7
7
7
Вычитаемое
7
2
6
4
1
5
3
Разность
Вставь пропущенные знаки.
7 4 = 3 1 6 = 7 7 1 = 6
7 2 = 5 4 3 = 7 2 5 = 7
В книге 8 рассказов. Юра прочитал 3 рассказа. Сколько рассказов осталось прочитать?
Прочитал –
Осталось –
_________________________
Ответ: ________________________.
* Запиши любое число, которое меньше разности
7 и 4. ___________
Запиши любое число, которое больше разности
2 и 6 ___________
Запиши любое число, которое меньше разности
5 и 3. ___________
Запиши любое число, которое больше разности
10 и 8. ___________
Работа № 11
1. Запиши ответы в строчку.
А. разность чисел 7 и 3.
Б. сумма чисел 3 и 2.
В. число, которое меньше 5 на 4.
Г. увеличь 4 на 4.
Д. уменьши 9 на 7.
Е. на сколько 4 меньше 6.
Ж. на сколько 6 больше 1.
__________________________________________
Заполни таблицу.
Уменьшаемое
9
9
9
9
9
9
9
Вычитаемое
5
3
1
7
Разность
2
4
6
Вставь пропущенные числа, чтобы записи были верными.
5+….=8 4+…=9 2+….=9
…- 6=4 7- …=3 8-….=4
Запиши 3 примера, у которых сумма равна 8.
В маршрутном такси ехали 10 человек. На остановке вышли 5 человек, а вошли 3. Сколько человек едет дальше?
Ответ: _______________________
Работа № 9а
2+2=
8-2=
9-3=
3+2=
6-2=
10-7=
1+2=
4-2=
10-4=
7+2=
10-2=
10-5=
8+2=
8-6=
10-1=
4+2=
6-4=
9-2=
6+2=
10-8=
9-7=
5+2=
4-2=
8-4=
2+1=
5-2=
10-6=
2+5=
7-5=
10-3=
2+8=
3-2=
10-8=
2+1=
9-2=
10-9=
2+2=
7-2=
10-2=
2+7=
9-2=
10-7=
2+6=
5-2=
10-4=
2+3=
6-2=
10-6=
2+4=
6-4=
10-9=
2+0=
2-2=
10-5=
Работа № 11 а.
4+5=
8-5=
6-3=
3+5=
6-5=
10-7=
1+5=
4-4=
10-2=
6+2=
10-5=
10-5=
3+2=
8-5=
10-1=
4+5=
6-5=
9-8=
6+2=
10-8=
9-7=
5+1=
5-2=
8-5=
3+3=
5-3=
9-6=
2+5=
7-5=
10-3=
1+5=
6-5=
10-8=
2+5=
5-4=
10-9=
3+5=
5-2=
10-5=
2+5=
9-5=
10-7=
5+4=
5-4=
10-4=
5+3=
6-5=
10-6=
5+5=
6-4=
10-3=
1+5=
5-5=
10-5=
Запиши ответы в строчку.
А. разность чисел 10 и 5.
Б. сумма чисел 3 и 6.
В. число, которое меньше 8 на 4.
Г. увеличь 6 на 4.
Д. уменьши 9 на 1.
Е. на сколько 5 меньше 8.
Ж. на сколько 6 больше 3.
__________________________________________
Заполни таблицу.
Уменьшаемое
8
8
8
8
8
8
8
Вычитаемое
Разность
3
5
2
4
1
6
7
Сравни.
6+3…..8-4 8-6…1+1 10-3…10-7
7-6……9-8 6-4…5-3 8-5…..9-6
Вставь пропущенные знаки.
8….3=5 9…2=7 7…3=10
6….1=5 5…4=1 2…6=8
Бабушка собрала 9 кг клубники. Из 6 кг сварили компот. Сколько килограммов клубники осталось?
Сварила — __________
Осталось — _________
__________________________
Ответ: _________________________________.
Работа № 12
Запиши ответы в строчку.
А. найди сумму 3 и 6.
Б. на сколько 7 меньше 8.
В. что прибавили к 2, чтобы получить 10.
Г. первое слагаемое – 3, чему равно второе, если сумма равна 6.
Д. найди сумму 2 и 3.
Е. найди разность 8и 5.
______________________________________
Подчеркни примеры с ответом 8.
3+5 10-2 8-4
7-3 3+6 9-6
9-1 1+7 10-6
Вставь подходящее число.
3+4>…. 8-4……
4+6….. 2+3
Заполни таблицу.
Уменьшаемое
9
9
9
5
Вычитаемое
5
3
4
1
3
4
Разность
5
2
4
6
У Кати 5 леденцов и 3 батончика. Сколько конфет у Кати?
Леденцы -__________
Батончики -_________
________________________________
Ответ: _________________________
Работа № 10 а.
2+5=
8-5=
6-3=
3+5=
6-5=
10-7=
1+5=
4-4=
10-2=
5+2=
10-5=
10-5=
3+2=
8-5=
10-1=
4+5=
6-5=
9-8=
6+2=
10-8=
9-7=
5+1=
5-2=
8-5=
2+3=
5-3=
9-6=
2+5=
7-5=
10-3=
5+5=
6-5=
10-8=
2+5=
5-4=
10-9=
1+5=
5-2=
10-5=
3+5=
9-5=
10-7=
5+4=
5-4=
10-4=
5+3=
6-5=
10-6=
5+5=
6-4=
10-3=
1+5=
5-5=
10-5=
Работа № 12 а.
3+3=
3-1=
10-3=
7+3=
6-4=
8-7=
5+2=
4-4=
8-4=
6+2=
2-1=
9-5=
9-3=
8-8=
9-1=
10-2=
6-5=
6-2=
6+1=
10-6=
8-7=
7-6=
4-2=
5-3=
6-2=
5-2=
10-6=
4+5=
7-6=
10-3=
3+4=
8-4=
10-8=
4+1=
9-5=
9-8=
4+2=
10-3=
8-7=
5+5=
10-8=
8-5=
3+2=
10-9=
6-3=
5-1=
6-3=
2-1=
8-2=
8-4=
10-1=
6-1=
9-4=
10-5=
Урок математики 1 класс состав числа 2,3,4.
Размен монет
Психологический настрой
Прозвенел для всех звонок
Начинаем мы урок.
— Руки? Дети: “На месте!”
— Ноги? Дети: “На месте!”
— Локти? Дети: “У края!”
— Спина? Дети: “Прямая!”
Здравствуйте, ребята. Рада вас видеть, садитесь. Сегодня у нас с вами необычный урок, а урок-путешествие. А чтобы узнать, куда мы все вместе отправимся, вам необходимо выполнить задание.
Актуализация опорных знаний:
Поудобнее садитесь,
Не шумите, не вертитесь.
Всё внимательно считайте,
А спрошу вас – отвечайте.
Вам условие понятно?
Это слышать мне приятно.
Математика нас ждет,
Начинаем устный счет.
II. Разминка
Отдых наш физкультминутка.
Занимай свои места.
Раз – присели, два – привстали,
Руки кверху все подняли.
Сели-встали, сели-встали,
Ванькой-встанькой будто стали.
А потом пустились вскачь,
Будто мы упругий мяч.
III. Устный счёт
Мы в лес за наукой сегодня пойдём,
Смекалку, фантазию нашу возьмём,
Дорогой с пути никуда не свернём.
Но чтобы лес нам скорее достичь,
Должны мы подняться по лесенке ввысь.
Счёт до 20 вперёд и обратно.
Сосчитайте от 4 до 12, от 8 до 16.
Сосчитайте от 12 до 3, от 19 до 11.
Назовите последующее число 10, 18.
На сколько последующее число больше предыдущего?
Как получить последующее число?
Назовите предыдущее число 9, 16.
На сколько предыдущее число меньше последующего?
Как получить предыдущее число? (Отнять единицу)
Какое число стоит слева от 13, 18?
Какое число стоит справа от 15, 4?
Назовите соседей числа 13.
Работа над темой урока.
Сегодня на уроке, ребята, вас ожидает много интересных заданий, а помощниками вам будут: внимание, находчивость, смекалка, от каждого потребуется уважение и помощь другу. Улыбнитесь друг другу. Подарите и мне свои улыбки. Спасибо. Ваши улыбки располагают к приятному общению, создают хорошее настроение.
Сегодня к нам на урок пришла гостья. Но сначала мы должны узнать, откуда она. Поставьте цифры в порядке возрастания и расшифруйте слово.
6 2 4
с л е
(лес)
Какое слово получилось?
Из леса к нам прибежала
Не мышь, не птица.
В лесу резвится.
На деревьях живет
И орешки грызет.
Кто это? (Белочка) (надеть маску ученице)
Белочка – хозяюшка
Школу открывает
И лесных зверюшек
Учиться приглашает.
И звери, и птицы
Спешат к нам в класс,
А белочка – учительница
Дает такой наказ:
“Начинаем наш урок,
Повторять мы будем счет
И примеры порешаем
Повторим состав чисел 3,4, 5.
Кто внимательней узнаем”.
— Ребята!
— Как вы думаете, какой же будет тема нашего урока? Какая цель? (Закрепление и обобщение знаний по теме: “Числа 1-5. Состав чисел 2-5”)
Какие числа мы изучали?
— Разложите карточки с цифрами по порядку, начиная с самого маленького числа.
— Назовите числа в обратном порядке, начиная с наибольшего.
— Назовите число, которое при счёте следует за числом 2, 4.
— Назовите число, которое при счёте идёт перед числом 3, 5.
— Назовите число, которое стоит между числами 1 и 3, 3 и 5, 2 и 4.
— Назовите “соседей” числа 4, 2.
— Назовите число, которое стоит справа от 3, 1.
— Назовите число, которое стоит слева от 2, 4.
— Какое число больше: 2 или 3, 1 или 4, 4 или 5.
— Какое число меньше: 3 или 4, 1 или 3, 3 или 5
Игра “Покажи сколько”. Презентация1
На экране предметы. Дети должны показать количество предметов цифрой.
— Назовите предметы одним словом.
Учимся мыслить, рассуждать. (Разгадайте ребус)
Найди ошибку.
Белочка:
За волчишкой еле-еле
Вышел мишка из-за ели.
Он мотает головой
Рассуждает сам с собой.
Медведь:
Есть счетная машинка у меня,
Помогает мне она.
Я примеры все решил,
А проверить нету сил.
Вот ответы перед вами
Вы, друзья, проверьте сами.
5-1=4 2+2=5 3+2=4 6-1=7 5+1=4
Белочка:
Заревел медведь белугой,
Заметался он по кругу.
Медведь:
Ай, машина, ну дела!
Ну, совсем ты не точна!
Белочка:
Не расстраивайся, Мишка,
А учись у ребятишек.
Физкультминутка.
Поработали, ребятки,
А теперь все на зарядку!
Мы сейчас все дружно встанем,
Отдохнем мы на привале,
Влево, вправо повернитесь,
Наклонитесь, поднимитесь.
Руки вверх и руки вбок,
И на месте прыг да скок!
А теперь бежим вприпрыжку,
Молодцы вы, ребятишки.
Замедляем, дети, шаг,
И на месте стой! Вот так!
А теперь мы сядем дружно,
Нам еще работать нужно.
Состав чисел 5, 4, 3.
Учитель надевает перчаточную куклу лисенка
Под кустом сидел
Хитренький лисенок.
Он слушал щебет птичий
И ждал, что в когти попадет
Сама собой добыча.
А мы спрячем птиц в дома,
Но нужно знать состав числа.
(На доске рисунки домиков лисенка и птичек с цифрами)
Ребята! Расселите птичек в дома.
Составьте поезд, решив примеры: Презентация
Всей семьей идут к нам в класс
Летом вдоль дорожки.
Еж – отец, ежиха – мать
И детишки – ежики.
А чтобы быстрее добрались они
Поезд им составим мы.
5-2
2+2
2-1
3-1
3+2
Составьте рассказ по рисунку с вопросом. Составьте схему и решение к задаче.
Ну, ребята, молодцы,
Всем зверятам помогли.
А теперь заданье вам
Я из тетрадочки раздам.
с.14 № 1,2
— Рассмотрите задание. Как вы думаете, какую работу необходимо — А теперь поделитесь своим настроением с окружающими.
— У вас на столе лежат разноцветные отрезки.
Жёлтый — мне было интересно и я доволен своей работой на уроке.
Зелёный – мне понравилось на уроке.
Синий – мне сейчас грустно.
— Жёлтые отрезки – лучи солнышка, зеленые — травка, синие – капли дождя
— Мы с вами хорошо потрудились, сегодня.
— Давайте вернемся к учебным задачам, которые ставили в начале урока.
– Какие задания вы выполнили с удовольствием?
– А есть ли задания, при выполнении которых вы испытывали трудности. Презентация
Продолжите мои предложения:
— Я понял, что…
— Было интересно…
— Было трудно…
— Мне захотелось…
— У меня получилось…
На следующем уроке мы…выполнить в данных заданиях?
Цифры от 0 до 10 для детей. Изучать с детьми цифры нужно в несколько приемов
Как научить малышей понимать цифры? Конечно же, показать ему их наглядно. Наши красочные карточки «Цифры картинки для детей от 1 до 10» и «Таблица для счета от 0 до 10» помогут вашему ребенку быстро запомнить и выучить все цифры.
Существует множество развивающих игр с детьми для изучения счета, которые очень просто сделать своими руками, в их числе и занятия с малышами по обучающим карточкам. Если вы хотите научить ребенка считать, то всегда нужно сначала изучать цифры по картинкам.
Как сделать цифры картинки для детей самим.
Наши цифры картинки адаптированы для печати на листах формата А4. На каждом листе получится 4 карточки с цифрами. Этого размера вполне достаточно, для обучающих занятий.
Карточки для развития ребенка с цифрами можно скачать, вырезать и наклеить на картон. Заниматься по этим картинкам можно и дома и в детском саду.
На каждой картинке, помимо самой цифры, изображены привычные для детей игрушки , поэтому эти развивающие карточки с цифрами прекрасно подойдут для занятий даже с совсем маленькими малышами. По ним он легко научится понимать смысл цифр.
После того как ребенок освоит само понятие цифр и что они обозначают, можно заниматься с ним математикой более углубленно: выучить сложение, вычитание, умножение и деление.
Заходите, скачивайте, распечатывайте цифры развивающие детские карточки и изучайте с ребенком математику.
Развивающие карточки цифры от 1 до 10 для детей
Развивающие карточки цифры от 1 до 10 для детей
Развивающие карточки цифры от 1 до 10 для детей
Развивающие карточки цифры от 1 до 10 для детей
Развивающие карточки цифры от 1 до 10 для детей
Развивающие карточки цифры от 1 до 10 для детей

Развивающие картинки цифры от 1 до 10 для детей
Таблица счета от 1 до 10
Изучать цифры и счет от 1 до 10 с детьми можно еще с помощью развивающих мультфильмов Малышман ТВ
В этом материале вы можете бесплатно скачать замечательную подборку карточек от Лисёнка Бибуши «Цифры от 1 до 10» для печати. Карточки пригодятся родителям, воспитателям детских садов, а также педагогам младших классов для занятий с детьми и обучения ребят счету до 10. Здесь вы найдете 7 наборов карточек, которые находятся в отдельных архивах для скачивания во вложениях внизу страницы.
Во время занятий по карточкам малыши не только познакомятся с цифами от 1 до 10, они будут запоминать, как правильно пишутся цифры, смогут самостоятельно научиться обводить цифры по образцу, а также выполнять различные задания на счет и решать математические примеры.
Образцы карточек для предварительного просмотра мы выложили в ознакомительном материале под описанием. Чтобы не занимать место на странице — мы не стали размещать образцы синих цифр до 10, считаем, что трех цифр будет вполне достаточно для обзора.
Если вас интересуют карточки с числами от 1 до 20, вы можете просто кликнуть по этой ссылке для дальнейшего просмотра и скачивания материалов. Оцените наш труд — не ленитесь писать свои отзывы!
1. «Цифры от 1 до 10» для печати в картинках.
Эти яркие и красочные карточки в картинках с цифрами от 1 до 10 вы можете распечатать на цветном принтере (бумаге формата А-4). Разрежьте каждый бланк на четыре части по указанным линиям — и приступайте к занятиям с ребенком. С помощью данных карточек, вы можете самостоятельно придумывать различные задачи для малышей, например, подобные тем, которые мы разместили на четвертом бланке пособия.
Эти карточки хороши тем, что во время занятий ребенок может совмещать обучение с рисованием. Если вы заметили, что ваш малыш устал и перестал внимательно воспринимать информацию, сделайте перерыв — предложите ребенку раскрасить картинки с цифрой, которую он уже успел выучить. Таким образом, ребенок и отдохнет, и с удовольствием приступит к изучению следующей цифры.
На четвертом бланке вы найдете два задания для малышей на счет, для закрепления пройденного материала. К тому же, во втором задании ребенку предлагается дорисовать узоры на варежках в зеркальном отображении. Такие примеры вы легко сможете составить сами при помощи цифр, картинок и математических знаков, которые распечатаете на странице.
Это пособие пригодится вам уже после того, как ребенок выучит и хорошо запомнит 10 печатных цифр. Чтобы ребенок научился правильно писать прописные цифры, необходимо сначала на наглядном примере продемонстрировать малышу последовательность их написания по стрелочкам. Положите бланк на столике перед ребенком, возьмите ручку или карандаш, и начните обводить первую цифру от указанной точки по направлению стрелочек, затем предложите малышу сделать то же самое. Затем вторую, третью и так далее, в зависимости от того, как быстро ребенок запоминает последовательность написания.
Бланк должен все время быть на виду у ребенка, чтобы он мог в любой момент проверить себя. После того, как малыш запомнил данные правила, можно приступить к седьмому пункту этой страницы, где ребенку нужно обвести цифры по точкам, руководствуясь этим пособием.
4. Карточки с цифрами от 1 до 10 и математическими знаками «плюс» и «минус».
Скачивая четвертый архив, вы получите 2 бланка с цифрами и математическими знаками «плюс» и «минус», которые расположены на листах в рамочках, по 6 штук на каждом. Вырежьте рамочки по линиям и у вас появится замечательный набор карточек для ознакомления ребенка с печатными цифрами и обучения малыша счету до 10.
Ваша основная задача — донести до ребенка, что за цифрами «скрываются» реальные предметы и насколько интересно научиться самостоятельно их пересчитывать.
Во время занятий приводите малышу как можно больше наглядных примеров из окружающей обстановки по счету, ненавязчиво занимайтесь с ним на прогулке, во время еды, игр — сделайте обучение увлекательным и интересным.
5. Скачать цифры от 1 до 10 «Синие». Цифры и их названия.
В пятом архиве находятся 11 карточек с синими цифрами от 1 до 10, начиная с нуля, каждая из которых размещена на отдельной странице. Под каждой цифрой на листе имеется и название цифры. Дополнительно, в наборе карточек мы разместили и математические знаки «плюс», «минус» и «равно».
Во время занятий с малышом при изучении цифр, необходимо направить все усилия на то, чтобы научить ребенка сопоставлять зрительный образ цифры, изображенной на на карточке, с ее количественным значением.
Для распечатки карточек используйте А-4 формат бумаги. Даже если у вас нет цветного принтера, не страшно, при распечатке цифр на черно-белом принтере, цифры станут черного цвета.
6. Карточки «Цифры от 1 до 10» — распечатать каждую цифру на отдельном листе.
В шестом архиве собраны, аналогичные предыдущим, карточки с цифрами и математическими знаками, но уже без названий. Для того, чтобы использовать карточки длительное время, их лучше распечатать на более плотной бумаге, либо заламинировать.
Запоминать цифры ребенку довольно сложно, поэтому процессу обучения необходимо уделить особое внимание, а главное, сделать его увлекательным и интересным. Заниматься нужно постоянно, в игровой форме, с использованием наглядных материалов и предметов. Занимайтесь дома, на улице, в транспорте, магазине, такое обучение, как правило, приносит самые неожиданные результаты и является максимально эффективным.
Если вас интересует полный набор карточек с математическими знаками и символами для составления различных примеров и задач во время занятий с ребенком, перейдите по этой ссылке .
7. Учимся писать цифры по точкам от 0 до 15 по образцу.
После того, как малыш успел познакомится с правильным написанием прописных цифр, предложите ему самостоятельно выполнить данные задания. Здесь ему нужно будет обвести по образцу цифры, начиная с нуля до 15, а также математические знаки «плюс», «минус» и «равно». Проконтролируйте действия ребенка, когда он будет обводить цифры по точкам и проверьте, насколько хорошо он запомнил правила их написания. Бланки с заданиями можно распечатать в любом количестве, поэтому не нужно ругать малыша, если у него с первого раза не будет хорошо получаться чистописание.
Вы также можете воспользоваться нашими прописями для детей с цифрами, раскрасками и картинками для скачивания, если перейдете по этой ссылке
Здесь мы считаем до 20, используя карточки с числами. На каждом листе-карточке расположено число от 1 до 20 и различные предметы, количество которых равняется данному числу. Карточки нужно распечатать и использовать для обучения счету с детьми дошкольного возраста.
Карточки с числами от 1 до 20 — Распечатай и считай
Скачайте карточки с числами во вложениях внизу страницы и распечатайте их на цветном принтере. Затем дайте ребенку для счета. Пусть начинает по порядку — с первого числа. Объясните ему, что количество предметов соответствует написанному числу. Нарисован один персик, значит здесь — число 1. Нарисовано два помидора, значит здесь — число 2. И так далее до 20. С помощью такого занятия ребенок не только потренируется считать, но и основательно закрепит знание цифр от 1 до 20.
Данные карточки пригодятся не только родителям для домашнего обучения детей, но и педагогам в дошкольных учреждениях.
Скачать карточки с числами вы можете во вложениях внизу страницы одним архивом.
Вам могут быть полезны и другие материалы по обучению счету для распечатки:
Здесь вы можете состав числа до 20 распечатать в виде числовой таблицы и дать ребенку для заполнения. Такое занятие прекрасно тренирует навыки счета дошкольников, а также приучает решать примеры до 20.
В этих занимательных задачках мы учимся считать до 20 вместе с героями мультиков и сказок. Дети дошкольного возраста совершенно не любят однообразие и скуку.
В этом материале дети узнают, что такое четные и нечетные числа от 1 до 20 и научатся различать их, выполняя различные задания в картинках.
Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках. Данные задания формируют у детей навыки счета и способствуют более эффективному обучению простых математических действий.
Чтобы дети могли быстро и с интересом освоить счет в пределах 10, мы подготовили для вас веселые раскраски с заданиями. Каждое задание содержит в себе картинки для раскрашивания — это стимулирует ребенка правильно выполнить задание.
Здесь вы можете скачать прописи цифры, распечатать их на принтере и использовать в домашнем обучении для подготовки детей к школе
А также потренируйтесь в математических играх от лисенка Бибуши:
Эта публикация посвящена теме: учим цифры с ребенком. В помощь вам мы разработали карточки с цифрами от 1 до 20, и математические знаки: плюс, минус, равно, умножить и разделить для занятия с детьми постарше. Вам нужно лишь эти карточки — цифры распечатать, вырезать и можете начать обучение малышей.
Если вы хотите, чтобы ваш ребенок быстро освоил математику , научился складывать и вычитать цифры, то с ним нужно как можно раньше начать изучать цифры. Изучение цифр — это основы для занятия математикой. Проводить занятия с ребенком и изучать цифры, можно в процессе игры. На нашем сайте мы предлагаем вам разнообразные варианты развивающих игр с ребенком и обучающий материал к ним.
Если хотите чтобы карточки были прочнее, наклейте их на картон. Яркие большие цифры дети смогут легко запомнить.
По таким карточкам проводить занятия с детьми могут и воспитатели в детском саду и родители дома. Имея такой наглядный материал, научить малыша считать, складывать и вычитать цифры намного проще.
Изучать с детьми цифры нужно в несколько приемов.
1) Сначала, покажите ребенку несколько карточек с первыми цифрами: 0, 1, 2, 3, 4 и 5. Для первого раза ребенку будет достаточно.
2) Каждую цифру с ребенком подробно разберите: покажите как она выглядит, как называется, несколько раз внятно произнесите название цифры, расскажите какая из цифр больше, а какая меньше.
3) Для наглядного примера возьмите любые предметы, например ложки, разложите перед малышом и посчитайте их вместе.
3) На следующем занятии повторите уже изученные цифры и возьмите новые карточки.
4) Когда ребенок освоит счет до 10, можно переходить к цифрам от 11 до 20.
5) Одновременно с изучением цифр, можно начать изучать сложение, затем вычитание и так далее.
Развивающие карточки цифры от 0 до 20 с математическими знаками
Развивающие карточки цифры от 0 до 20 с математическими знаками
Развивающие карточки цифры от 0 до 20 с математическими знаками
Развивающие карточки цифры от 0 до 20 с математическими знаками
Развивающие карточки цифры от 0 до 20 с математическими знаками
Карточка с цифрой 0 распечатать. Изучать с детьми цифры нужно в несколько приемов
Как научить малышей понимать цифры? Конечно же, показать ему их наглядно. Наши красочные карточки «Цифры картинки для детей от 1 до 10» и «Таблица для счета от 0 до 10» помогут вашему ребенку быстро запомнить и выучить все цифры.
Существует множество развивающих игр с детьми для изучения счета, которые очень просто сделать своими руками, в их числе и занятия с малышами по обучающим карточкам. Если вы хотите научить ребенка считать, то всегда нужно сначала изучать цифры по картинкам.
Как сделать цифры картинки для детей самим.
Наши цифры картинки адаптированы для печати на листах формата А4. На каждом листе получится 4 карточки с цифрами. Этого размера вполне достаточно, для обучающих занятий.
Карточки для развития ребенка с цифрами можно скачать, вырезать и наклеить на картон. Заниматься по этим картинкам можно и дома и в детском саду.
На каждой картинке, помимо самой цифры, изображены привычные для детей игрушки , поэтому эти развивающие карточки с цифрами прекрасно подойдут для занятий даже с совсем маленькими малышами. По ним он легко научится понимать смысл цифр.
После того как ребенок освоит само понятие цифр и что они обозначают, можно заниматься с ним математикой более углубленно: выучить сложение, вычитание, умножение и деление.
Заходите, скачивайте, распечатывайте цифры развивающие детские карточки и изучайте с ребенком математику.
Развивающие карточки цифры от 1 до 10 для детей
Развивающие карточки цифры от 1 до 10 для детей
Развивающие карточки цифры от 1 до 10 для детей
Развивающие карточки цифры от 1 до 10 для детей
Развивающие карточки цифры от 1 до 10 для детей
Развивающие карточки цифры от 1 до 10 для детей

Развивающие картинки цифры от 1 до 10 для детей
Таблица счета от 1 до 10
Изучать цифры и счет от 1 до 10 с детьми можно еще с помощью развивающих мультфильмов Малышман ТВ
Здесь мы считаем до 20, используя карточки с числами. На каждом листе-карточке расположено число от 1 до 20 и различные предметы, количество которых равняется данному числу. Карточки нужно распечатать и использовать для обучения счету с детьми дошкольного возраста.
Карточки с числами от 1 до 20 — Распечатай и считай
Скачайте карточки с числами во вложениях внизу страницы и распечатайте их на цветном принтере. Затем дайте ребенку для счета. Пусть начинает по порядку — с первого числа. Объясните ему, что количество предметов соответствует написанному числу. Нарисован один персик, значит здесь — число 1. Нарисовано два помидора, значит здесь — число 2. И так далее до 20. С помощью такого занятия ребенок не только потренируется считать, но и основательно закрепит знание цифр от 1 до 20.
Данные карточки пригодятся не только родителям для домашнего обучения детей, но и педагогам в дошкольных учреждениях.
Скачать карточки с числами вы можете во вложениях внизу страницы одним архивом.
Вам могут быть полезны и другие материалы по обучению счету для распечатки:
Здесь вы можете состав числа до 20 распечатать в виде числовой таблицы и дать ребенку для заполнения. Такое занятие прекрасно тренирует навыки счета дошкольников, а также приучает решать примеры до 20.
В этих занимательных задачках мы учимся считать до 20 вместе с героями мультиков и сказок. Дети дошкольного возраста совершенно не любят однообразие и скуку.
В этом материале дети узнают, что такое четные и нечетные числа от 1 до 20 и научатся различать их, выполняя различные задания в картинках.
Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках. Данные задания формируют у детей навыки счета и способствуют более эффективному обучению простых математических действий.
Чтобы дети могли быстро и с интересом освоить счет в пределах 10, мы подготовили для вас веселые раскраски с заданиями. Каждое задание содержит в себе картинки для раскрашивания — это стимулирует ребенка правильно выполнить задание.
Здесь вы можете скачать прописи цифры, распечатать их на принтере и использовать в домашнем обучении для подготовки детей к школе
А также потренируйтесь в математических играх от лисенка Бибуши:
В этом материале вы можете бесплатно скачать замечательную подборку карточек от Лисёнка Бибуши «Цифры от 1 до 10» для печати. Карточки пригодятся родителям, воспитателям детских садов, а также педагогам младших классов для занятий с детьми и обучения ребят счету до 10. Здесь вы найдете 7 наборов карточек, которые находятся в отдельных архивах для скачивания во вложениях внизу страницы.
Во время занятий по карточкам малыши не только познакомятся с цифами от 1 до 10, они будут запоминать, как правильно пишутся цифры, смогут самостоятельно научиться обводить цифры по образцу, а также выполнять различные задания на счет и решать математические примеры.
Образцы карточек для предварительного просмотра мы выложили в ознакомительном материале под описанием. Чтобы не занимать место на странице — мы не стали размещать образцы синих цифр до 10, считаем, что трех цифр будет вполне достаточно для обзора.
Если вас интересуют карточки с числами от 1 до 20, вы можете просто кликнуть по этой ссылке для дальнейшего просмотра и скачивания материалов. Оцените наш труд — не ленитесь писать свои отзывы!
1. «Цифры от 1 до 10» для печати в картинках.
Эти яркие и красочные карточки в картинках с цифрами от 1 до 10 вы можете распечатать на цветном принтере (бумаге формата А-4). Разрежьте каждый бланк на четыре части по указанным линиям — и приступайте к занятиям с ребенком. С помощью данных карточек, вы можете самостоятельно придумывать различные задачи для малышей, например, подобные тем, которые мы разместили на четвертом бланке пособия.
Эти карточки хороши тем, что во время занятий ребенок может совмещать обучение с рисованием. Если вы заметили, что ваш малыш устал и перестал внимательно воспринимать информацию, сделайте перерыв — предложите ребенку раскрасить картинки с цифрой, которую он уже успел выучить. Таким образом, ребенок и отдохнет, и с удовольствием приступит к изучению следующей цифры.
На четвертом бланке вы найдете два задания для малышей на счет, для закрепления пройденного материала. К тому же, во втором задании ребенку предлагается дорисовать узоры на варежках в зеркальном отображении. Такие примеры вы легко сможете составить сами при помощи цифр, картинок и математических знаков, которые распечатаете на странице.
Это пособие пригодится вам уже после того, как ребенок выучит и хорошо запомнит 10 печатных цифр. Чтобы ребенок научился правильно писать прописные цифры, необходимо сначала на наглядном примере продемонстрировать малышу последовательность их написания по стрелочкам. Положите бланк на столике перед ребенком, возьмите ручку или карандаш, и начните обводить первую цифру от указанной точки по направлению стрелочек, затем предложите малышу сделать то же самое. Затем вторую, третью и так далее, в зависимости от того, как быстро ребенок запоминает последовательность написания.
Бланк должен все время быть на виду у ребенка, чтобы он мог в любой момент проверить себя. После того, как малыш запомнил данные правила, можно приступить к седьмому пункту этой страницы, где ребенку нужно обвести цифры по точкам, руководствуясь этим пособием.
4. Карточки с цифрами от 1 до 10 и математическими знаками «плюс» и «минус».
Скачивая четвертый архив, вы получите 2 бланка с цифрами и математическими знаками «плюс» и «минус», которые расположены на листах в рамочках, по 6 штук на каждом. Вырежьте рамочки по линиям и у вас появится замечательный набор карточек для ознакомления ребенка с печатными цифрами и обучения малыша счету до 10.
Ваша основная задача — донести до ребенка, что за цифрами «скрываются» реальные предметы и насколько интересно научиться самостоятельно их пересчитывать.
Во время занятий приводите малышу как можно больше наглядных примеров из окружающей обстановки по счету, ненавязчиво занимайтесь с ним на прогулке, во время еды, игр — сделайте обучение увлекательным и интересным.
5. Скачать цифры от 1 до 10 «Синие». Цифры и их названия.
В пятом архиве находятся 11 карточек с синими цифрами от 1 до 10, начиная с нуля, каждая из которых размещена на отдельной странице. Под каждой цифрой на листе имеется и название цифры. Дополнительно, в наборе карточек мы разместили и математические знаки «плюс», «минус» и «равно».
Во время занятий с малышом при изучении цифр, необходимо направить все усилия на то, чтобы научить ребенка сопоставлять зрительный образ цифры, изображенной на на карточке, с ее количественным значением.
Для распечатки карточек используйте А-4 формат бумаги. Даже если у вас нет цветного принтера, не страшно, при распечатке цифр на черно-белом принтере, цифры станут черного цвета.
6. Карточки «Цифры от 1 до 10» — распечатать каждую цифру на отдельном листе.
В шестом архиве собраны, аналогичные предыдущим, карточки с цифрами и математическими знаками, но уже без названий. Для того, чтобы использовать карточки длительное время, их лучше распечатать на более плотной бумаге, либо заламинировать.
Запоминать цифры ребенку довольно сложно, поэтому процессу обучения необходимо уделить особое внимание, а главное, сделать его увлекательным и интересным. Заниматься нужно постоянно, в игровой форме, с использованием наглядных материалов и предметов. Занимайтесь дома, на улице, в транспорте, магазине, такое обучение, как правило, приносит самые неожиданные результаты и является максимально эффективным.
Если вас интересует полный набор карточек с математическими знаками и символами для составления различных примеров и задач во время занятий с ребенком, перейдите по этой ссылке .
7. Учимся писать цифры по точкам от 0 до 15 по образцу.
После того, как малыш успел познакомится с правильным написанием прописных цифр, предложите ему самостоятельно выполнить данные задания. Здесь ему нужно будет обвести по образцу цифры, начиная с нуля до 15, а также математические знаки «плюс», «минус» и «равно». Проконтролируйте действия ребенка, когда он будет обводить цифры по точкам и проверьте, насколько хорошо он запомнил правила их написания. Бланки с заданиями можно распечатать в любом количестве, поэтому не нужно ругать малыша, если у него с первого раза не будет хорошо получаться чистописание.
Вы также можете воспользоваться нашими прописями для детей с цифрами, раскрасками и картинками для скачивания, если перейдете по этой ссылке
Рішати приклади 1 клас — litg.ru
Скачать рішати приклади 1 клас djvu
Примеры по математике для 1 класса. Примеры по математике 1 класс. 2. Реши примеры на сложение и вычитание. Тренажеры могут быть использованы для дополнительной работы с первоклассниками учителями и родителями в классе и дома как для индивидуальной, так и коллективной подготовки. Они способствуют автоматизации вычислительных навыков у ребенка, отработке умений складывать, вычитать, сравнивать и решать простые задачи.
Основа математики 1 класса — состав числа. Зная состав числа, а начать следует с домиков, ребенок гораздо быстрее сможет решить абсолютно любой пример на сложение или вычитание. Поэтому составу числа мы отводим целую страницу, кликните по картинке, чтобы посмотреть и скачать тренажеры н.
Цитата сообщения Svetlana-sima Прочитать целикомВ свой цитатник или сообщество! Примеры и задачи по математике.1 класс 1.
2. 3. 4. 5. 6. 7. 8. 9. Отчеты: Посетители Поисковые фразы. Примеры и задачи по математике. 1 класс. Среда, 10 Мая г. + в цитатник. Цитата сообщения Svetlana-sima. Прочитать целиком В свой цитатник или сообщество! Примеры и задачи по математике.1 класс. 1. 2. 3. Роздаткові картки з математики для учнів 1 класу Автор: вчитель початкових класів Ісаєва Ольга Василівна До вашої уваги добірка різноманітних карток з.
Первая часть карточек с задачами для 1 класса на вычисления в пределах Пять задач, решив которые первоклассник научится лучше решать примеры на сложение и вычитание. Карточки по математике на счет в пределах Часть 1.
Обучение будущего школьника счету в пределах 10 – это первый шаг к устному счету. Важно, чтобы ребенок запомнил процессы всех вычислений, как делают это старшие. Второй этап состоит из осваивания. Здесь есть примеры на сложение и вычитание, упражнения на сравнение чисел, математические диктанты и много. Математика 1 класс. Самостоятельные работы. Это книга предназначена для самостоятельных занятий по математике учащимися первого класса.
Здесь есть примеры на сложение и вычитание, упражнения на сравнение чисел, математические диктанты и много задач. Это книга предназначена для самостоятельных занятий по математике учащимися первого класса. Здесь есть примеры на сложение и вычитание, упражнения на сравнение чисел, математические диктанты и много задач. Скачать: litg.ru [,05 Kb] (cкачиваний: ). примеров на 2 листа.
Вариант 2 Страница 1 — Страница 2. Вариант 3 Страница 1 — Страница 2. Вариант 4 Страница 1 — Страница 2. Вариант 5 Страница 1 — Страница 2. Вариант 6 Страница 1 — Страница 2. Вариант 7 Страница 1 — Страница 2. Вариант 8 Страница 1 — Страница 2. Сложение и вычитание в пределах 10, все комбинации. 30 примеров на лист.
djvu, EPUB, rtf, fb2
Похожее:
Урок природознавства 1 клас птахи
Хімія 11 клас профільний рівень буринська величко
Відповіді до практичних робіт з хімії 11 клас
Читання вголос 4 клас іі семестр
Захист вітчизни 11 клас основи самозахисту
Циліндр конус куля 6 клас конспект
Как научить представления чисел | Разобрался
Многие ученики идут в детский сад, уже умея считать. Они могут произносить числа «один, два, три…» и так далее до 10. Но они не всегда понимают, что каждое число, которое они говорят, представляет собой , количество .
Кроме того, их может сбить с толку тот факт, что одно и то же число может быть представлено по-разному — по названию номера («один») и по его цифре («1»). Путаница в отношении различных представлений чисел может затруднить обучение учащихся сложению и вычитанию.
Практика различных способов показа числа может помочь учащимся понять каждое число как количество. Используя эту стратегию, вы будете использовать явное указание обучить трем различным представлениям чисел 1–10: имя числа, число и изображение или набор предметов, показывающих количество.
С этими представлениями учащиеся пройдут серию совместных практических занятий. Стратегия заканчивается оценкой обучения, а также вариантами продолжения практики.
Прокрутите вниз, чтобы получить советы по адаптации этой стратегии для дистанционного обучения.
Поделиться Головоломки с числами
Facebook
Твиттер
Pinterest
Электронное письмо
Копировать ссылку
Текстовое сообщение
Скоро в Google Классе
Задача: Учащиеся идентифицируют число по его письменной цифре, его числовому названию и изображению повторяющихся объектов, показывающих количество.
Уровни оценок (со стандартами):
K (Common Core K.CC.A.3: укажите числа от 0 до 20. Представьте количество предметов с помощью письменной цифры 0–20, где 0 представляет количество объектов.)
K (Common Core K.CC.B.4.A: при подсчете объектов произносите числовые имена в стандартном порядке, сопоставляя каждый объект с одним и только одним числовым именем и каждым имя номера с одним и только одним объектом.)
K (Common Core K.CC.B.4.B: Помните, что последнее указанное число указывает количество подсчитанных предметов. Количество объектов одинаково независимо от их расположения или порядка, в котором они были подсчитаны.)
K (Обычная математическая практика MP2: абстрактное и количественное обоснование.)
Лучше всего использовать для обучения с:
Соберите материалы. Распечатайте головоломку с числами для каждой группы от трех до пяти учеников. Подумайте о том, чтобы вырезать кусочки пазла заранее. Вы можете складывать их вместе или собирать в небольшие пакеты. Печать на карточках или ламинирование частей пазла может облегчить учащимся работу с ними.
Подготовьте набор учетных карточек для цифр 1–10. Напишите по одной цифре на каждой карточке. Подготовьте соответствующий набор для имен номеров.
Разложите небольшие предметы, такие как соломинки, кубики, ластики или счетчики, в группы от 1 до 10. Вы можете сгруппировать объекты в небольшие пластиковые пакеты или чашки, например, пять соломинок в одном пакете или шесть ластиков в чашке.
Совет для учителей: Создайте стену из слов, чтобы поддержать изучающих английский язык (ELL) и других учащихся, которым нужна визуальная поддержка. Наличие числовых имен рядом с написанными цифрами поможет учащимся выучить их как контрольные слова. Если стена слов не подходит, сделайте таблицу привязок достаточно большой, чтобы ее могли видеть все учащиеся.
1. Разогрейте, просмотрев идентификационный номер. Напишите на доске число от 1 до 10 или укажите на число на стене слов или в таблице привязок.Произнесите номер вслух. Попросите учащихся повторить номер. Затем попросите учащихся показать и сосчитать количество пальцев, соответствующее количеству. Смоделируйте правильный ответ. Например, для 3 вы можете смоделировать ответ, подняв три пальца и сказав: «Верно. Это 3. » Затем вслух сосчитайте каждый палец. «Раз два три.»
После нескольких раундов объясните ученикам, что есть много способов представления чисел, и использование пальцев — лишь один из них. Спросите: «Как еще мы можем показать число 3?» Получите разные ответы от студентов.Смоделируйте ответы, написав, рисуя и используя предметы в зависимости от того, что говорят студенты.
2. Модель, представляющая числа по-разному. Сообщите учащимся цель сегодняшнего урока. «Сегодня мы познакомимся с тремя различными способами отображения числа. Вы можете использовать цифру. Вы можете использовать имя номера, которое является словом для номера. Или вы можете использовать картинку или набор предметов ». Попросите учащихся повторить концепцию. Скажите: «Итак, вы можете использовать цифры. Скажите со мной цифра .Вы можете использовать числовое имя. Скажи мне номер , имя . Или вы можете использовать картинку или набор предметов. Скажите со мной картинку или набор предметов ».
Покажите им, как выглядят эти изображения. Например, возьмите карту с цифрой 5 и другую с номером «пять». Затем скажите: «Число 5 можно записать как цифру. Но его также можно записать как слово пять . 5. Пять. Пять — это числовое имя. И это могут показать пять одинаковых объектов.Нарисуйте на доске пять квадратов, считая каждый, пока не дойдете до пяти. «Один два три четыре пять. Пять квадратов. Все они означают одно и то же: 5 (укажите на написанную цифру), 5 (укажите на название числа) и 5 (укажите на квадраты) ».
«Давай попробуем еще раз». Повторите шаги с другим числом из набора 1–10.
Используйте предметы по комнате, чтобы обозначить количество. Вы можете использовать блоки, стойки, мешки с креслами или что-нибудь достаточно большое и яркое, чтобы ученики могли видеть их со своих мест.
3. Практикуйте сопоставление цифр и числовых имен с подсчитываемыми объектами. Прежде чем перейти к работе со всеми числами 1–10 и их представлениями, попросите учащихся попрактиковаться с несколькими числами. Поместите набор предметов перед каждой группой учеников, варьируя количество предметов от группы к группе. Этими объектами могут быть счетчики, блоки, соломинки и т. Д. Один учащийся должен отвечать за отображение объектов, чтобы их могли видеть другие участники.
Затем раздайте учащимся четыре каталожные карточки: две с цифрами и две с соответствующими числовыми именами.Например, если перед группой шесть объектов, они могут получить следующие четыре карты: 1, 6, один, шесть. В группе попросите учащихся решить, какие учетные карточки (одно числовое и одно числовое имя) подходят к набору предметов. Пусть студенты обсудят это и придут к соглашению. Свяжитесь с каждой группой и при необходимости предложите поддержку. Когда все группы примут решение, предложите им поделиться. Пока они поднимают карточки, предложите им произнести число и произнести по буквам название числа: «s-i-x… шесть.”
Перемещайте набор объектов из одной группы в другую и раздайте каждой группе новый набор карточек. Повторите те же действия. После двух раундов, если у каждой группы был успешный матч, переходите к упражнению с числами.
4. Попрактикуйтесь с числами. Раздайте каждой группе набор головоломок с числами (нарезанные заранее или ножницами, если ученики делают наборы). Дайте указания: «Теперь мы будем использовать числовые головоломки, чтобы попрактиковаться в различных способах отображения чисел.Разложите все части головоломки на три стопки: цифры, названия чисел и картинки ».
После того, как ученики составят три стопки, попросите их перемешать каждую стопку так, чтобы ее части не располагались в определенном порядке. Скажите: «Теперь каждый ученик по очереди выбирает один кусок из стопки цифр. Сообщите членам вашей группы номер, который вы выбрали. Вместе группа будет искать совпадающее имя номера и соответствующую карточку с картинкой из двух других стопок, чтобы соответствовать номеру. Продолжайте по очереди складывать части вместе.Когда все части будут объединены в группы по три (цифра, название числа и изображение), поднимите руки, чтобы проверить свою работу ». Смоделируйте, как сделать соответствующий набор, прежде чем ученики начнут.
5. Оценка обучения. Предложите учащимся встретиться с вами один на один за столом с предметами на нем. Дайте каждому учащемуся цифру (учетную карточку или из набора пазлов). Попросите учащихся показать вам соответствующее количество с помощью предметов на столе. Затем попросите их выбрать совпадающее числовое имя из набора учетных карточек или частей головоломки с числами.Попросите учащихся сосчитать предметы и произнести название числа, чтобы показать, что они понимают, что все три представляют собой одно и то же количество. Учащимся, испытывающим трудности с этим заданием, следует дать дополнительные обучение в малых группах сосредоточены на ограниченном наборе чисел, например 1–5, а затем 6–10.
6. Продолжение практики. Дайте студентам возможность продолжать практиковаться в представлении чисел. Попробуйте выполнить следующие упражнения для закрепления знаний:
Сделайте из набора пазлов ожерелья, проделав отверстия с обеих сторон каждого элемента и добавив веревку.Дайте каждому ученику ожерелье. Попросите их встать и найти двух других одноклассников с тем же «номером», но в другой форме.
Используйте стену со словами как способ отметиться с небольшими группами студентов или отдельных лиц. Попросите их определить число, написать название числа и сосчитать предметы.
Покажите номер в любой форме по вашему выбору. Дайте учащимся время подумать, какое это число. Попросите их найти образцы этого числа в комнате.Затем спросите студентов, где еще они могли бы увидеть формы этого числа в своей жизни.
Учащиеся, испытывающие трудности с математикой в младших классах начальной школы, особенно с чувство числа , часто возникают проблемы с переключением между различными представлениями чисел. Им сложно понять, что количество такое же. Непосредственно обучая трем представлениям одного и того же количества, вы можете помочь студентам избежать этой путаницы.
Использование физических объектов и изображений для представления величин помогает студентам практиковать и применять концепции стабильного порядка и индивидуальная переписка.Эти концепции необходимы для понимания сложения, вычитания и сравнения величин.
Совместная учебная деятельность в этой стратегии числовой головоломки дает студентам возможность продемонстрировать и передать свое понимание. Совместное обучение особенно полезно для ELL, потому что они могут находить сверстников более доступными и понятными, чем учителя. Студенты, которые могут быть не готовы выполнить задание самостоятельно, также извлекут выгоду из работы со сверстниками. Иногда сверстники могут предлагать корректирующую обратную связь, на которой другие студенты могут учиться.
Предложите способы, которыми семьи могут практиковать представление чисел дома. Например, семьи могут дать учащимся числовое имя, написанное на небольшом листе бумаги, и попросить их найти это количество предметов. Или семьи могут попросить учащихся пометить набор предметов в доме числовым или числовым названием на листе бумаги, чтобы указать количество.
Играть в игры также отличный способ заниматься числами дома. Настольные игры , как Five Little Monkeys и Hi Ho Cherry-O, представляют количество более чем одним способом.
Сотрудничайте с семьями ваших студентов. Узнайте, какие ресурсы у них есть и что им может понадобиться для поддержки обучения дома.
Проведите весь класс или небольшие группы учащихся по этапам синхронного онлайн-класса или запишите видео для асинхронного обучения. Так или иначе, использовать UDL пока вы планируете урок.
При явном обучении представлений чисел используйте как изображения, так и физические объекты при подсчете каждого числа.Попросите учащихся попрактиковаться в сопоставлении количеств с цифрами и числовыми именами вместе с вами. Предложите им найти и использовать набор из 10 предметов из своего дома, например цветные карандаши, игровые элементы или монеты.
Попросите семьи распечатать числа или написать их от руки. Или предложите им воспользоваться онлайн-игрой на совпадение, например Представляют числа в пределах 10 .
Создать онлайн-карточки, чтобы студенты могли практиковать различные представления чисел.Или покажите семьям, как делать карточки из любой бумаги, которая есть у них дома. Карты можно настроить так, чтобы на одной стороне отображалось имя числа, а на другой — цифры с изображениями объектов (например, точки) для подсчета.
3 НОМЕР: ЧТО ЕСТЬ ЗНАТЬ? | Сложим: помощь детям в изучении математики
классических времен, написал бумагу в форме письма королю своего города, объясняя, как писать такие очень большие числа. Архимед, однако, не зашел так далеко, чтобы изобрести десятичную систему счисления с возможностью неограниченного расширения.
22.
Knuth, 1974, стр. 323.
23.
Steen, 1990. См. Морроу и Кенни, 1998, для получения более подробной информации об алгоритмах.
24.
Точки с многоточием «…» в выражении являются важной частью абстрактной математической записи, компактно обозначающей пропуск необходимых терминов (для достижения м, в данном случае ).
Список литературы
Бер, М.Дж., Харел, Г., Пост, Т., И Леш Р. (1992). Рациональное число, соотношение и пропорция. В D.A.Grouws (Ed.), Справочник по исследованиям по преподаванию и изучению математики (стр. 296–333). Нью-Йорк: Макмиллан.
Bruner, J.S. (1966). К теории обучения . Кембридж, Массачусетс: Belknap Press.
Куоко, А. (Ред.). (2001). Роли представления в школьной математике (Ежегодник Национального совета учителей математики 2001 г.).Рестон, Вирджиния: NCTM.
Дюваль Р. (1999). Представление, видение и визуализация: когнитивные функции в математическом мышлении. Основные вопросы для обучения. В F.Hitt & M.Santos (Eds.), Proceedings of the двадцать первого ежегодного собрания Североамериканского отделения Международной группы психологии математического образования (том 1, стр. 3–26). Колумбус, Огайо: Информационный центр ERIC по естествознанию, математике и экологическому образованию. (ERIC Document Reproduction Service No.ED 433 998).
Фройденталь, Х. (1983). Дидактическая феноменология математических структур . Дордрехт, Нидерланды: Рейдел.
Грино, Дж. Г., и Холл, Р. (1997). Практика репрезентации: изучение репрезентативных форм. Дельта Фи Каппан , 78 , 1–24. Доступно: http://www.pdkintl.org/kappan/kgreeno.htm. [10 июля 2001 г.].
Капут,]. (1987). Системы представлений и математика.В C.Janvier (Ed.), Проблемы представления в преподавании и изучении математики (стр. 19–26). Хиллсдейл, Нью-Джерси: Эрлбаум.
Knuth, D.E. (1974). Информатика и ее отношение к математике. American Mathematical Monthly , 81 , 323–343.
Лакофф, Г., & Нуньес, Р.Э. (1997). Метафорическая структура математики: наброски когнитивных основ математики, основанной на разуме. В Л.D.English (Ed.), Математические рассуждения: аналогии, метафоры и образы (стр. 21–89). Махва, Нью-Джерси: Эрлбаум.
Морроу, Л.Дж., и Кенни, М.Дж. (ред.). (1998). Преподавание и изучение алгоритмов в школьной математике (Ежегодник Национального совета учителей математики 1998 г.). Рестон, Вирджиния: NCTM.
Пимм Д. (1995). Символы и значения в школьной математике . Лондон: Рутледж.
Рассел, Б. (1919). Введение в математическую философию . Нью-Йорк: Макмиллан.
Сфард А. (1997). Комментарий: О метафорических корнях концептуального роста. В L.D. English (Ed.), Математические рассуждения: аналогии, метафоры и изображения (стр. 339–371). Махва, Нью-Джерси: Эрлбаум.
математических трюков — ядро исследования поведенческих наук
Эта веб-страница посвящена
невероятно boffo
идее о том, что математика может быть увлекательной!
Попробуйте эти уловки:
Вот несколько интересных ссылок:
Список для чтения книг по сложной математике, большинство из которых я использовал для этого сайта.
Узнайте об исходном компьютере: Abacus (http://www.ee.ryerson.ca:8080/~elf/abacus/)
Сыграйте в математическую погоню (http://dev.eyecon.com/marcia) — для одного или двух игроков. (Если вы используете Netscape, Не прокручивать страницу вниз, пока загружается .
Играйте в Shoot Balls (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
Играйте в Flippo 24 (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
Проверьте свои знания таблиц умножения (http: // www.fi.uu.nl/wisweb/en/applets/tafels/Welcome.html)
Попробуйте свои силы в оценке (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
Исследуйте геометрию в увлекательной интерактивной форме.
Попробуйте загадку Ханойской башни (http://www.eng.auburn.edu/~fwushan/Hanoi1.html).
Посмотрите, что такое Spriographis (http://www.mainstrike.com/mstservices/handy/Spiro/).
Посмотрите, что такое сет Мандельброта (http://www.franceway.com/java/fractale/mandel_b.htm).
Если вам нужны другие математические задачи , попробуйте новый сайт PBS MATHLINE MATH CHALLENGESsite.Попробуйте, вам понравится. (Но помните, что мы были первыми.)
Трюк с добавлением магии №1
Поразите батраков этим. Все просто. Это эффективно. Он получает их каждый раз.
Спросите свою оценку, чтобы выбрать три (3) различных номеров от 1 до 9.
Скажите ему или ей (или ей или ему) записать три числа рядом друг с другом, наибольшее первое и наименьшее последнее, чтобы получилось одно трехзначное число. Скажите ему / ей, чтобы он не называл вам цифры.
Затем попросите ее или его сформировать новое трехзначное число, поменяв местами цифры, поместив наименьшее первым и наибольшее последнее. И напишите это число прямо под первым числом.
Теперь попросите его или ее вычесть нижнее (и меньшее) трехзначное число из верхнего (и большего) трехзначного числа. Скажите им, чтобы они не рассказывали вам, каков результат.
Теперь у вас есть выбор подытоживания:
Попросите друга сложить три цифры числа, полученного в результате вычитания меньшего из большего трехзначного числа.Затем поразите его или ее, сказав им, какова сумма этих трех чисел. Сумма трехзначного ответа всегда будет 18!
Скажите своему другу, что если он или она скажет вам, какова первая ИЛИ последняя цифра ответа, вы скажете ей или ему, каковы другие две цифры. Это возможно, потому что средняя цифра всегда будет 9, а сумма двух других цифр всегда будет равна 9! Итак, чтобы получить цифру, отличную от средней (то есть 9) и отличную от цифры, которую говорит вам ваш друг, просто вычтите цифру, которую ваш друг говорит вам, из 9, и это неизвестная цифра.
В начало
Магический квадрат № 15
Сумма в каждой строке и столбце в этом магическом квадрате равна 15. Так что сделайте обе диагонали!
В начало
Магический квадрат № 34
Сумма в каждой строке и столбце равна 34 в этом магическом квадрате. Так что сделайте обе диагонали!
1 15 14 4
12 6 7 9
8 10 11 5
13 3 2 16
В начало
Рецепт вашего собственного волшебного квадрата 3 x 3
Вот рецепт создания собственного квадрата с магическим числом 3 х 3. Этот рецепт и оба вышеупомянутых магических квадрата взяты из одной чертовой книги под названием Mathematics for the Million Ланселота Хогбена, опубликованной Norton and Company. Я очень рекомендую это. Вам совсем не нужно много математики, чтобы окунуться в приключение чисел, рассказанное в этой классической книге.
Некоторые необходимые правила и определения:
Пусть буквы a , b и c обозначают целые числа (то есть целые числа).
Всегда выбирайте a , чтобы оно было больше суммы b и c .То есть a > b + c . Это гарантирует, что в магическом квадрате нет отрицательного числа.
Не позволяйте 2 X b = c . Это гарантирует, что вы не получите одинаковый номер в разных ячейках.
Используя формулы в таблице ниже, вы можете составить магические квадраты, в которых сумма строк, столбцов и диагоналей равна 3 X независимо от того, какое значение имеет a .
а + в a + b — c а — б
а — б — в a a + b + c
а + б a — b + c a — c
Чтобы создать первый Магический квадрат # 15, приведенный выше, вы позволяете a быть равным 5, пусть b будет равно 3, и пусть c будет равно 1.Вот еще несколько:
a = 6, b = 3, c = 2
a = 6, b = 3, c = 1
a = 7, b = 3, c = 2
a = 7, b = 4, c = 2
a = 8, b = 6, c = 1
a = 8, b = 5, c = 2
a = 8, b = 4, c = 3
Попробуйте придумать что-нибудь свое.
В начало
Перевернутый магический квадрат
Вот магический квадрат, который не только дает в сумме 264 во всех направлениях, но и делает это, даже когда он перевернут! Если вы мне не верите, посмотрите на него, пока стоите на голове! (Или просто скопируйте его и переверните вверх дном.)
96 11 89 68
88 69 91 16
61 86 18 99
19 98 66 81
В начало
Антимагический квадрат
Вот магический квадрат с максимально возможным количеством различных сумм .
Эта таблица дает 8 различных итогов.
В начало
Выиграйте ставки с этим Magic Square
Хорошо, вот отличный способ выигрывать ставки с помощью магического квадрата. Позвоните другу по телефону. Попросите его или ее взять карандаш и бумагу и поднести их к телефону, чтобы он или она могли записать числа от 1 до 9. Скажите другу, что вы будете по очереди набирать номера от 1 до 9. Никто из вас не может. повторить номер, который вызывает другой.Затем вы оба запишите числа от 1 до 9. Затем, когда ваш друг назовет одно из чисел, он или она обведет это число кружком, и вы тоже. Когда вы произносите число, вы рисуете квадрат вокруг этого числа, и ваш друг делает то же самое. Побеждает тот, кто первым наберет три числа, которые в сумме составляют 15.
Скажите, что вы идете первым, а вы зовете 8. Ваш друг может позвонить 6. Затем вы позвоните 2. Ваш друг зовет 5, а вы зовете 4. Ваш друг зовет 7, а вы звоните 3.Затем вы говорите своему другу, что вы только что выиграли, потому что вы назвали 8, 3 и 4, что в сумме дает 15.
Ваш друг снова захочет сыграть. Итак, на этот раз вы можете поспорить с ним, что выиграете, с условием, что в случае ничьей (когда вы используете числа от 1 до 9, но никто из вас не набирает 15 очков) никто ничего не должен.
Если вы знаете фокус, вы никогда не проиграете и, вероятно, проиграете в большинстве случаев.
Уловки На самом деле трюк основан как на крестиках-ноликах, так и на магическом квадрате.Магический квадрат выглядит так:
Поскольку это магический квадрат, каждая строка, каждый столбец и каждая диагональ в сумме составляют 15. Итак, если у вас есть этот квадрат перед вами с вашим другом по телефону, вы можете поставить крестик в квадратах. номер, который вы вызываете, и букву O в квадратах номеров, которые называет ваш друг. Затем, как и в крестиках-ноликах, вы пытаетесь получить три крестика подряд, потому что они всегда в сумме дают 15.
Итак, в приведенном выше примере, когда вы вызываете 8, вы ставите X в верхнем левом углу.Когда ваш друг говорит 6, вы ставите) в правом верхнем углу. И так далее.
В начало
Математический карточный фокус
Для этого вауера вам понадобится обычная колода карт. Никаких причудливых перетасовок не требуется. Просто выполните следующие простые шаги:
Перемешайте карты, чтобы тщательно перемешать их.
Разложите 36 карт в стопку.
Попросите друга выбрать одну из 36 карточек, посмотреть на нее и запомнить, а затем положить обратно в стопку, не позволяя вам ее увидеть.
Перемешайте 36 карт.
Разложите 36 карточек в 6 рядов по 6 карточек в каждом. Обязательно наносите верхний ряд слева направо. Затем нанесите второй ряд под ним слева направо. И так далее с каждой последующей строкой, лежащей под предыдущей.
Попросите друга взглянуть на карточки и сказать, в каком ряду находится выбранная карта. Запомните, под каким номером находится ряд.
Осторожно возьмите карты в том же порядке, в котором вы их положили .Таким образом, первая карта слева от верхнего ряда находится наверху стопки, а последняя карта справа от нижнего ряда находится внизу стопки.
Теперь выложите карты в 6 рядов по 6 карт в каждом, но на этот раз разложите карту по столбцу за раз . Вместо того, чтобы переходить от одной строки к другой, переходите от одного столбца к следующему. Положите первые шесть карточек в столбец сверху вниз в крайнем левом углу. Затем выложите следующие шесть карт во втором столбце из шести карт справа от первого столбца из шести карт.Продолжайте делать это до тех пор, пока у вас не будет 6 столбцов по 6 карточек в каждом (что выглядит так же, как 6 рядов по 6 карточек в каждом — потому что — это то же самое).
Еще раз спросите друга, в каком ряду находится выбранная карта.
Когда ваш друг говорит вам, в каком ряду находится карта, вы можете сказать, какая именно карта выбрана. Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта находится во втором столбце пятой строки.Это связано с тем, что вы располагаете карточки: то, что было строками в первый раз, во второй раз становится столбцами.
В начало
Калькулятор молний
Вот трюк, чтобы удивлять их каждый раз! Попросите кого-нибудь записать свой номер социального страхования. Затем попросите их переписать его так, чтобы все было перемешано. (Если у них нет номера социального страхования, попросите их записать любые 9 цифр от 1 до 9.) Если есть нули, попросите их заменить их на любое другое число от 1 до 9.Затем попросите их скопировать свои девять чисел в том же порядке рядом с исходными девятью числами. Это даст им номер из 18 цифр, первая половина которого такая же, как и вторая. Затем измените вторую цифру на 7 и измените одиннадцатую цифру (это будет то же число, что и вторая цифра, но во вторых девяти цифрах) также на 7. Затем сделайте ставку на то, что вы сможете сказать им, что останется после деления числа на 7, быстрее, чем они смогут вычислить это вручную.Ответ: 0 — 7 делится на это новое число ровно без остатка!
В начало
Таблицы забавных чисел
Следующие забавные таблицы взяты из одной из моих любимых книг на все времена, Рекреации в теории чисел, , Альберта Х. Байлера, изданной Dover Publications. Эта книга фактически объясняет математические причины, по которым эти уловки работают.
3 х 37 = 111 и 1 + 1 + 1 = 3
6 х 37 = 222 и 2 + 2 + 2 = 6
9 х 37 = 333 и 3 + 3 + 3 = 9
12 х 37 = 444 и 4 + 4 + 4 = 12
15 х 37 = 555 и 5 + 5 + 5 = 15
18 х 37 = 666 и 6 + 6 + 6 = 18
21 х 37 = 777 и 7 + 7 + 7 = 21
24 х 37 = 888 и 8 + 8 + 8 = 24
27 x 37 = 999 и 9 + 9 + 9 = 27
1 х 1 = 1
11 х 11 = 121
111 х 111 = 12321
1111 х 1111 = 1234321
11111 х 11111 = 123454321
111111 х 111111 = 12345654321
1111111 х 1111111 = 1234567654321
11111111 х 11111111 = 123456787654321
111111111 х 111111111 = 12345678987654321
1 х 9 + 2 = 11
12 х 9 + 3 = 111
123 х 9 + 4 = 1111
1234 х 9 + 5 = 11111
12345 х 9 + 6 = 111111
123456 х 9 + 7 = 1111111
1234567 х 9 + 8 = 11111111
12345678 х 9 + 9 = 111111111
123456789 х 9 +10 = 1111111111
9 х 9 + 7 = 88
98 х 9 + 6 = 888
987 х 9 + 5 = 8888
9876 х 9 + 4 = 88888
98765 х 9 + 3 = 888888
987654 х 9 + 2 = 8888888
9876543 х 9 + 1 = 88888888
98765432 х 9 + 0 = 888888888
1 х 8 + 1 = 9
12 х 8 + 2 = 98
123 х 8 + 3 = 987
1234 х 8 + 4 = 9876
12345 х 8 + 5 = 98765
123456 х 8 + 6 = 987654
1234567 х 8 + 7 = 9876543
12345678 х 8 + 8 = 98765432
123456789 х 8 + 9 = 987654321
7 х 7 = 49
67 х 67 = 4489
667 х 667 = 444889
6667 х 6667 = 44448889
66667 x 66667 = 4444488889
666667 x 666667 = 444444888889
6666667 x 6666667 = 44444448888889
и т. п.
4 х 4 = 16
34 х 34 = 1156
334 х 334 = 111556
3334 х 3334 = 11115556
33334 х 33334 = 1111155556
и т.п.
В начало
Знаете ли вы …?
Каждое двузначное число, заканчивающееся на 9, является суммой кратных двух цифр и суммы двух цифр. Таким образом, например, 29 = (2 X 9) + (2 + 9). 2 X 9 = 18. 2 + 9 = 11. 18 + 11 = 29.
40 — уникальное число, потому что при написании «сорок» это единственное число, буквы которого расположены в алфавитном порядке.
Простое число — это целое число больше 1, которое не может делиться равномерно на любое другое целое число, кроме самого себя (и 1). 2, 3, 5, 7, 11, 13 и 17 являются примерами простых чисел.
139 и 149 — первые последовательные простые числа, различающиеся на 10.
69 — единственное число, в квадрате и кубе между ними по одному разу используются все цифры от 0 до 9:
69 ² = 4761 и 69 ³ = 328,509.
Один фунт железа содержит приблизительно 4 891 500 000 000 000 000 000 000 атомов.
Существует около 318 979 564 000 возможных способов сыграть первые четыре хода с каждой стороны в игре в шахматы.
Земля ежедневно проходит более полутора миллионов миль.
В Эйфелевой башне 2 500 000 заклепок.
Если бы все кровеносные сосуды в человеческом теле были проложены встык, они бы растянулись на 100 000 миль.
В начало
Математический трюк на этот год
Предположительно, он будет работать только в 1998 году, но на самом деле одно изменение позволит ему работать в течение любого года.
1. Выберите количество дней в неделю, в которые вы хотели бы выходить (1-7).
2. Умножьте это число на 2.
3. Добавить 5.
4. Умножьте полученную сумму на 50.
5. В 1998 г., если у вас уже был день рождения в этом году, прибавьте 1748. Если нет, добавьте 1747. В 1999 г. просто прибавьте 1 к этим двум числам (поэтому прибавьте 1749, если у вас уже был день рождения, и 1748, если у вас нет). В 2000 году число изменится на 1749 и 1748. И так далее.
6. Вычтите четырехзначный год вашего рождения (19XX).
Результатов:
У вас должно получиться трехзначное число.
Первой цифрой этого числа было количество дней, на которое вы хотите выходить каждую неделю (1-7).
Последние две цифры — ваш возраст.
(Спасибо, что передали мне это, Джуди.)
В начало
Где строка?
В следующий раз, когда вы будете с группой людей и захотите поразить их своими экстрасенсорными способностями, попробуйте это. Пронумеруйте всех в группе от 1 до числа.Возьмите веревку и скажите им привязать ее к пальцу, пока вы выходите из комнаты или поворачиваетесь спиной. Затем скажите, что вы можете сказать им не только, у кого он есть, но и на какой руке и на каком пальце он находится, если они просто сделают для вас простую математику и скажут вам ответы. Затем попросите одного из них ответить на следующие вопросы:
1. Умножьте номер человека со строкой на 2.
2. Добавить 3.
3. Умножьте результат на 5.
4. Если строка справа, добавьте 8.
Если строка слева, добавьте 9.
5. Умножить на 10.
6. Сложите номер пальца (большой палец = 1).
7. Добавить 2.
Попросите их сказать вам ответ. Затем вычтите мысленно 222. Остаток дает ответ, начиная с правой цифры ответа.
Например, предположим, что веревка находится на третьем пальце левой руки Игрока №6:
1. Умножить на 2 = 12.
2. Складываем 3 = 15.
3.Умножить на 5 = 75.
4. Так как строка находится слева, прибавляем 9 = 84.
5. Умножить на 10 = 840.
6. Сложите число пальца (3) = 843.
7. Складываем 2 = 845.
Теперь мысленно вычтите 222 = 623. Правая цифра (3) говорит вам, что строка находится на третьем пальце. Средняя цифра показывает, что он находится слева (правая рука будет = 1). Левая цифра говорит о том, что строка у Игрока №6.
Кстати, когда число людей больше 9, вы получите ЧЕТЫРЕХзначное число, а ДВЕ цифры слева будут номером Игрока.
В чем секрет?
(Это из большой книги Шейлы Энн Барри, Giant Book of Puzzles & Games, . Издана Sterling Publishing Co., Inc., Нью-Йорк, 1978, недавно переиздана в мягкой обложке.)
Следите за новостями, чтобы узнать больше о математических трюках. Они будут добавляться время от времени, поэтому обязательно зарегистрируйтесь еще раз.
Сохранить дату карты | 10 бесплатных образцов
ПРОЧИТАЙТЕ, ЧТО ГОВОРЯТ КЛИЕНТЫ О MINTED СОХРАНИТЕ ДАТЫ:
«Даже благодаря COVID19 я смог создавать и отправлять потрясающие даты сохранения.»- Заказчик из Аризоны, 30.04.2020
«Веб-сайт был очень простым в использовании, и создание Save The Date стало почти легким! Кроме того, я был ДЕЙСТВИТЕЛЬНО впечатлен тем, как быстро они прибыли после заказа!» — Заказчик из Северной Каролины, 18.06.20
«Мне и моему жениху было трудно выбирать между несколькими разными дизайнами, все они были настолько хороши! Нам нравятся открытки Save the Date, которые мы в итоге выбрали, и мы получили много комплиментов от тех, кто их уже получил. »- заказчик из Южной Каролины, 26.03.20
ПРЕЛЮДИЯ НА СВАДЕБНОЕ ПРИГЛАШЕНИЕ
Обручение — это увлекательно, и вы не можете дождаться своего большого дня. Хочется кричать с крыш: «Мы поженимся!» Что ж, мы рекомендуем вам сделать что-нибудь менее опасное и немного более эффективное. Отправьте открытку с указанием даты своим друзьям и родственникам. Свадьба с сохранением даты служит нескольким целям. Смотрите на это не только как на объявление, но и как на мини-приглашение на свадьбу с обещанием более подробной информации.Помня об этом, имейте в виду, что все, кому вы отправляете открытку с сохранением даты, также будут ожидать приглашения на свадьбу. Итак, подготовьте список гостей, потому что пора задать тон для вашего важного дня с помощью первая часть ваших свадебных канцелярских принадлежностей.
Узнать больше ▶ ︎
ПОЧЕМУ НАЧЕНЫ ДЛЯ МОИ СОХРАНЕНИЕ ДАТ?
Отчеканенные изделия создаются с использованием самых свежих дизайнов, и они оживают на нашей роскошной бумаге и с нашими яркими чернилами. Наше сообщество художников и дизайнеров создает одни из самых захватывающих произведений искусства. можно себе представить. Эти дизайны участвуют в конкурсах, которые голосуются одним и тем же сообществом, прежде чем они станут актуальными карточками. Этот процесс открытия нашей платформы для художников из всех слоев общества, а затем Привлечение их к голосованию гарантирует, что самые уникальные и стильные товары попадут на наш сайт.
Мы также стремимся к совершенству в наших процессах печати.Наша бумага была специально разработана нашими партнерами из Mohawk Fine Papers для оптимальной печати фотографий. Эта красивая помолвочная фотография, которую вы использовать на своем Minted, сохраните дату, когда свадебное приглашение появится на любой из наших акций.
ВИДЫ БУМАГИ
Бумага для подписи : Наша золотая стандартная бумага для подписи имеет мягкую кремовую текстуру и не совсем белый цвет. Оптимизированный для печати с высоким разрешением, этот 137 фунт. , Бумага толщиной 17,5 пунктов отлично подходит для фотография.
Гладкая бумага для подписи : Мы взяли нашу бумагу для подписи и придали ей очень полированную отделку, чтобы действительно выделить лучшее на ваших фотографиях. Обратная сторона бумаги имеет такое же хлопковое покрытие, как и наша. подписная бумага. 130 фунтов, толщина 19,3 пункта.
Перламутровая бумага : наша перламутровая бумага придаст вашим свадебным открыткам с сохранением даты немного мерцания.Жемчужная поверхность этой бумаги придает мягкое сияние, элегантное и изысканное. 110 фунтов, толщина 14,5 пункта.
100% переработанная бумага : Мы заботимся об окружающей среде, и вы тоже, поэтому переработанная бумага — отличный выбор. Он сертифицирован FSC и изготовлен из 100% бытовых отходов. Этот тяжелый инвентарь 160 фунтов, толщина 17,5 пункта, гладкая и матовая поверхность.
Doublethick : Для чего-то более тяжелого мы вдвое увеличили размер бумаги для подписи, чтобы будущие невесты могли получить то же качество, на которое они рассчитывали, при вдвое большем весе. 240 фунтов, толщина 35 пунктов.
Triplethick : Сравнимая с музейным картоном, наша бумага Triplethick — самая тяжелая и самая толстая бумага, которую мы производим.Взяв нашу бумагу для подписи и наслоив ее три раза, мы создали роскошный вариант. это практически несгибаемо. 360 фунтов, толщина 54 точки.
Наша бумага не только роскошна и приятна на ощупь, наши печатники также являются мастерами своего дела. Художественная печать бывает разных форм, и Minted использует самые сложные и интересные техники. Мы хотим вашего сохраните дату, чтобы произвести впечатление на ваших получателей.Даже наша стандартная печать дает богатые изображения на кремовой бумаге. Рассмотрите варианты печати, используя приведенное ниже руководство.
ПРОЦЕССЫ ПЕЧАТИ
Плоская печать : Наша стандартная техника печати — это полноцветная цифровая печать с высоким разрешением на выбранной вами бумаге. Качество нашей стандартной печати заметно роскошно, потому что мы хотим Ваш индивидуальный дизайн должен быть максимально красивым.
Высокая печать : Используя старинный печатный станок, слова вдавливаются в бумагу, создавая великолепный эффект тиснения. Эта техника печати придает вашему отпечатку роскошный трехмерный вид.
Foil-Pressed : Мы вдавливаем в бумагу металлическую отделку (похожую на высокую печать), которая добавляет немного блеска вашему сохранению даты. Выберите один из цветов фольги, например золото, серебро, розовое золото, блестящее золото, блестящее серебро, ледяной синий, черный и бронзовый.
Gloss-Press ™ : Новая эксклюзивная эксклюзивная технология печати Minted, отличающаяся красотой и тонкостью глянца, нанесенным тиснением на роскошной бумаге.

НАСТРОЙКА И ПЕРСОНАЛИЗАЦИЯ
Вы и ваш жених — необычная пара, и это будет необычная свадьба — так зачем соглашаться на обычное свидание? Мы предлагаем множество способов настроить и персонализировать вашу свадьбу, сохранив дату, чтобы вы могли отправить объявление, соответствующее вашей личности. Попробуйте один из интересных вариантов отделки для печати, о которых мы упоминали выше, например, фольгу или Gloss-Press ™. Просмотрите нашу подборку магнитов с сохранением даты, чтобы найти уникальный продукт, который смогут увидеть ваши гости. держите в холодильнике до большого дня (и даже после). Мы составили список уникальных магнитных образов.
Есть также более простые способы персонализировать дату сохранения. Большинство наших дизайнов позволяют будущим невестам изменять цвет текста, шрифт и даже сообщение.Вы можете попробовать что-нибудь немного другое, например: «Мы получаем женаты «или» мы связываем себя узами брака «. Или даже самое простое изменение «Сохранить нашу дату ». Нет ничего более персонализированного, чем когда вы добавляете фотографию с помолвки. Вы даже можете найти дизайн, который позволит вам разместить несколько фотографий, щелкнув раскрывающееся меню в наших фильтрах с надписью «Фотографии». Выбрав цифру «0», вы можете просмотреть нашу подборку не-фото и сохранить даты, если это вам больше нравится.
ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ
Что делать, если дата нашей свадьбы изменится? 2020 год был странным, поскольку пары реагируют на ограничения COVID-19 и меняющиеся нормы социального дистанцирования. Микросвадьбы на небольших и уникальных площадках начинают становиться популярной заменой. Minted также предлагает широкий выбор карточек «изменить дату» или объявлений об отсрочке свадьбы, которые можно отправить по почте в список гостей, чтобы держать их в курсе.Вы также можете посоветовать гостям почаще заходить на ваш свадебный веб-сайт, чтобы получить последнюю информацию о вашей свадьбе (даты, место проведения и т. Д.). Мы рекомендуем вам прочитать наш полный пост о планировании свадьбы во время пандемии коронавируса.
Насколько заранее вы рассылаете даты? Большинство невест отправляют их за шесть-восемь месяцев до свадьбы. Однако, если вы планируете свадьбу, вы можете отправить им немного раньше.Попробуйте отправить за 8–12 месяцев заранее даты для свадеб в местах назначения. С другой стороны, не стоит отправлять их слишком рано, так как гости могут выбросить их и вообще забыть о свидании.
Чье имя идет первым? Имя женщины обычно стоит первым на всех предсвадебных бланках. Однако не бойтесь отклоняться от нормы в этой детали. Отложите традиции и выберите, как вас зовут хотел бы пойти первым.Прочтите наш полный список правил этикета и формулировок.
Что мне сказать о сохранении даты? Минимальный объем информации, который вы захотите включить в свое сохранение, — это имена пары и дата предстоящей свадьбы. Большинство людей также указать место проведения свадьбы. Если вы не выбрали место проведения, вы можете просто указать город и штат, и этого будет достаточно, пока гости не получат приглашение.
Можете ли вы попросить RSVP с сохранением даты? Довольно необычно просить RSVP с сохранением даты. Большинство людей проигнорируют это или не ответят на приглашение на свадьбу. Наш предложение было бы оставить его в стороне.
Вы отправляете всем сохраненные даты? Вам нужно будет отправить сохранения только тем людям, которых вы собираетесь пригласить на настоящую свадьбу.Лица, получившие дату сохранения, но не свадьбу приглашение позже будет казаться пренебрежительным.
Сколько стоит распечатать даты с сохранением? Цены на сохранение дат зависят от количества и особенностей. Для начала, вот базовые цены на количество по 100 штук каждого размера, которые мы предлагаем на Minted.
Classic 7 «x 5» : при количестве 100 штук цена за единицу начинается с 1 доллара США.54 штуки
Открытка 6 «x 4,25» : при количестве 100 штук цена за единицу начинается от 1,09 доллара США за штуку.
Petite 6 «x 4,25» : при количестве 100 штук цена начинается от 1,35 доллара США за штуку
Магнит 6 дюймов x 4,25 дюйма : при количестве 100 штук цена за единицу начинается от 2,28 доллара США за штуку
Читать меньше ▶ ︎
60 уникальных идей визиток для профессиональных визиток
В наш век цифровых технологий старомодная визитная карточка по-прежнему актуальна.
Вспомните, когда вы в последний раз встречались с потенциальным клиентом или деловым партнером. Было ли легче вводить в телефон номера телефонов и адреса электронной почты? Или просто обменяться визитками? Последнее, конечно!
Физическая визитка не только позволяет вам установить личную связь при первой встрече с кем-то, но и делает ваш бренд более запоминающимся — если все сделано правильно.
Вот почему мы составили список ярких примеров визиток, которые вдохновят вас и помогут произвести неизгладимое впечатление.
СВЯЗАННО: 50 красивых цветовых комбинаций (и как их применить к вашим дизайнам)
60 привлекательных идей дизайна визиток (по категориям)
Категория №1: Современные идеи для визиток
Категория № 2: Минимальные идеи для визиток
Категория № 3: Креативные идеи для визиток
Категория № 4: Элегантные идеи для визиток
Категория № 5: Идеи винтажных визиток
Категория № 1: Современные идеи визиток
Эти современные идеи визиток модны и современны. Вот почему они идеально подходят для дальновидных компаний, которые хотят попробовать что-то новое, чтобы выделиться.
Вычурно и модно
Через Behance
Если вы ищете что-то столь же модное, но с немного более декоративным чутьем, есть эта визитная карточка веб-дизайнера во множестве стилей, которую также можно использовать для любого другого занятия. Современный и чистый, он демонстрирует внимание дизайнера к цвету и гармоничной композиции.
Изысканный и энергичный
Через Dribbble
Тем, кто ищет чего-то, вызывающего воспоминания об изысканности и элегантности, но при этом энергии и оптимизма, подойдет эта красиво оформленная вертикальная визитная карточка, которая является долгожданным отходом от традиционной горизонтальной карты.
Цветочные и красочные
Через Dribbble
Большинство успешных визитных карточек включают элементы, которые напоминают зрителю об отличном продукте или услуге. В этом случае этот яркий и красочный узор идеально подходит для цветочной компании.
Сияющий и стимулирующий
Через Dribbble
В этой визитной карточке креативного веб-разработчика используется уникальный узор, который привлекает ваше внимание, а затем он сочетается с очень чистым дизайном на противоположной стороне.
Чистый и простой
Через Dribbble
Этот забавный и чистый дизайн визитной карточки эффективен благодаря использованию простых, но привлекательных значков и привлекательной цветовой гамме.
Полужирный и профессиональный
Через Behance
Эта двухцветная визитка для студии 3D-дизайна и анимации эффективно передает индивидуальность бренда: дальновидный, экспериментальный и игривый. Фиолетовый цвет и просверленные отверстия также помогают выделить его из стопки традиционных карточек.
Запоминающийся и уникальный
Через Behance
Эта привлекательная визитная карточка с рельефными деталями из точечного блеска отличается интересными узорами и выбором цветов. Как и любой другой эффективный дизайн, он также передает одно ключевое сообщение бренда: это источник творческого мышления и уникальности.
Прозрачный и прозрачный
Через Pinterest
Еще одна тенденция, которая набирает популярность, — это использование прозрачных или полупрозрачных визитных карточек из специального полимерного пластика, который рассеивает свет при его прохождении.От полупрозрачных открыток до матовых — найдется что-то на любой вкус.
Динамичный и яркий
Через Pinterest
Эта визитная карточка для архитекторов, инженеров или дизайнеров — больше, чем просто лист бумаги — это привлекательная миниатюрная структура, которая напоминает о таких ценностях, как динамизм, креативность и смелость.
Эффективный и заслуживающий внимания
Через Pinterest
Как и другие примеры в этом списке, эта визитная карточка с инструкциями по игре на гитаре максимально использует отведенное небольшое пространство, напоминая потенциальному покупателю о предлагаемых услугах или продуктах.В этом случае использование УФ-пятен (блестящих слоев) в виде разных аккордов — гениальный пример, который может послужить вдохновением для вашей собственной остроумной идеи.
Потрясающе и красиво
Через Pinterest
Эта ретро-визитка из фольги для Absolut — абсолютный хранитель. Яркие цвета, креативные узоры и золотая фольга вместе создают великолепный ретро-образ.
Квадратное и голографическое
Через Pinterest
В отличие от традиционной, эта квадратная визитная карточка отклоняется от нормы не только своей формой, но и использованием голографической кромки фольги.
Белое на белом
Через Pinterest
Еще одна идея для слепой тисненой визитной карточки. Этот пример может вдохновить вас на создание ваших собственных сообщений «белое по белому».
Острый и неповторимый
Через Pinterest
Украинская студия Tough Slate Design создала этот уникальный и оригинальный дизайн для бренда Woodstock Sawmill. Этот дизайн, вдохновленный топографическим ландшафтом региона лесопилки, является уникальным и самобытным.
Современный и игривый
Через Behance
IKEA — это бренд, известный своей игривой и красочной индивидуальностью, поэтому дизайнер Джо Линг задумал создать визитную карточку, отражающую эти ценности. Как и продукты, которыми известна IKEA, карты требуют взаимодействия с другими картами для создания окончательного изображения, в данном случае логотипа IKEA.
Светится в темноте
Через Behance
Если вам кажется, что некоторые из этих идей для визитных карточек немного необычны, обратите внимание на этот светящийся в темноте дизайн.Напечатанная с использованием фосфоресцентных чернил, эта карта эффективно передает смысл, и вы можете позвонить им в любое время дня и ночи.
Красочная окраска краев
Через Dribbble
Еще одна техника печати, которую вы можете использовать, чтобы выделиться, — это красочная окраска краев. Эта визитная карточка социального клуба, отпечатанная на бумаге Muscletone French Paper, уникальна тем, что цвета и материалы работают вместе, чтобы создать более запоминающееся физическое напоминание о бренде.
Креативный плоский дизайн
Через Behance
Тенденции плоского дизайна распространяются и на дизайн визитных карточек, что нашло отражение в этом красочном проекте ребрендинга молодежной программы. Яркий и молодой, дизайн соответствует философии компании, мотивирующей молодежь с помощью танцев, музыки и дизайна.
Категория № 2: Минимальные идеи для визиток
Если вы считаете, что «меньше значит больше», эти минималистичные идеи визиток идеально подходят для вас.Эти визитные карточки с большим количеством белого пространства, чистыми и простыми линиями и успокаивающими цветовыми схемами сделают вашу компанию такой же лаконичной и профессиональной.
Сдержанный и со вкусом
Через Behance
Даже при создании собственных визитных карточек принцип «меньше значит больше» остается хорошим правилом.
Взгляните на эту лаконичную, но запоминающуюся карточку для студии дизайна интерьера. Идеальный подбор цветов, шрифтов и щедрое использование белого пространства сразу бросается в глаза и радует.
Минимальное и геометрическое
Через Behance
Яркие яркие цвета и эстетичные геометрические элементы сочетаются в этой минималистской визитной карточке, которая идеально подходит для начинающего графического дизайнера или художника.
Яркий и цитрусовый
Через Dribbble
Эта игривая открытка цитрусового цвета идеально подходит для тех, кто хочет создать молодой и яркий образ. Выбор цветов и творческое использование шкалы, чтобы название бренда не выделялось на странице, также передают нестандартное мышление.
Простой, но смелый
Через Dribbble
Как и бренд, который он представляет, в этом современном дизайне визитной карточки используются креативные образы, смелые цвета и креативный макет, чтобы привлечь ваше внимание. Его умелое использование белого пространства и теней также делает дизайн популярным.
Красочный и минимальный
Через Dribbble
Этот геометрический и минималистичный дизайн эффективно передает такие ценности, как динамизм, производительность и прогресс.
Абстрактное и возвышенное
Через Behance
В качестве дизайна визитной карточки для центра, продвигающего искусство, это прекрасно продуманный пример эффективного брендинга и дизайна логотипа. Различные вариации форм изобретательно передают миссию и цель центра, вызывая ассоциации с логотипом организации.
Минималистичный и красочный
Источник изображения
Эта минималистичная визитка сочетает в себе иллюстрацию и цвет, создавая изящный игривый дизайн.Благодаря отрицательному пространству и естественным элементам, они работают рука об руку, создавая привлекательную и запоминающуюся визитную карточку.
Веселые и умные
Через Pinterest
Эта уникальная визитная карточка сразу привлекает внимание, поскольку она побуждает зрителей вытащить карточку, чтобы открыть для себя что-то новое. Всего одним взаимодействием они напоминают им о необходимости позаботиться об этой надоедливой полости и звонят стоматологу.
Экологичный и натуральный
Через Pinterest
Еще один пример визитной карточки из экологически чистой крафт-бумаги, этот дизайн выделяется своим чистым, минималистичным и естественным видом.
Простой, но интригующий
Через Behance
Для тех, кто ищет оформленный вручную и минималистичный вид, обратите внимание на этот стильный дизайн для японского ресторана. Его простой, но интригующий дизайн отражает элегантность и загадочность бренда и японской культуры.
Намек на апельсин
Через Dribbble
В современном мире дизайна популярно разумное использование ярких акцентных цветов на приглушенном фоне.Просто взгляните на эту минималистичную карту, которая достигает правильного баланса, разбрызгивая немного апельсина с одной стороны.
Назад к основам
Через Pinterest
Если вы ищете простую корпоративную визитку, без излишеств и цветов, то эта для вас. Он придерживается основ, включая логотип, штамп и контактную информацию.
Категория № 3: Креативные идеи для визиток
Если нормальное — не ваше, то эти креативные идеи визиток обязательно вдохновят вас на создание своей собственной.Это потому, что эти визитки — больше, чем просто листы бумаги.
Вдохновляйтесь вертикальными макетами, всплывающими окнами, вырезами, остроумным юмором, оптическими иллюзиями и другими творческими приемами, использованными в идеях визиток ниже.
Текстура и вибрирующие узоры
Через Dribbble
Эта креативная визитка для высокой печати сочетает в себе черный и металлический серебристый цвет на бумаге кремового цвета. Благодаря так называемому оптическому искусству, создающему иллюзию движения и вибрирующих узоров, этот дизайн обязательно выделит его из кучи других обычных визитных карточек.
Остроумно и с юмором
Через Dribbble
Социальная сеть на основе местоположения Yik Yak создала эти запоминающиеся визитные карточки, которые отходят от нормы: вместо типичной информации о компании они решили создать вариации карточек со своими любимыми цитатами пользователей.
Эффективный макет и типографика
Через Behance
Эта традиционно раскрашенная черно-белая карта, тем не менее, ломает стереотипы, создавая креативный и сильный макет.Он умело использует типографику для создания привлекательного дизайна, заставляющего вас выглядеть дважды.
Творческий и заметный
Через Pinterest
Эта черно-белая высеченная визитка выделяется из стопки прямоугольников 3,5 x 2 не только благодаря своей вертикальной ориентации, но и своей уникальной форме.
Функциональное и оригинальное
Через Dribbble
Один из способов удержать потенциальных клиентов от выбрасывания вашей карты — сделать ее функциональной и полезной.Например, эта подставка в форме шестиугольника может стать неотъемлемой частью чьего-то офисного или домашнего помещения, удерживая ваш бренд в центре внимания.
Игривый и отзывчивый
Через Behance
Еще один творческий способ сделать вашу визитку запоминающейся и функциональной — превратить ее в колоду игральных карт. Таким образом, он с большей вероятностью попадет в чью-то гостиную или обеденный стол.
Умный и изобретательный
Через Pinterest
Если вы ищете другую креативную идею, вот эта забавная складывающаяся трехмерная визитка для транспортной компании.
Рельефный дизайн и вырезы
Через Pinterest
Использование альтернативных материалов — еще один верный способ выделиться. Взгляните на эту вертикальную открытку, напечатанную на нестандартной плотной бумаге. Эта уникальная визитная карточка, выгравированная лазером с индивидуальным рельефным рисунком с вырезами, выглядит почти как тонкая каменная плита.
Развлечения и интерактив
Через Pinterest
Трудно не вспомнить эту визитную карточку, которая умно и эффективно передает уникальное ценностное предложение.Тот факт, что зритель может взаимодействовать с ним, не зная, чего ожидать дальше, делает его особенно запоминающимся.
Милый и непринужденный
Кредит: Дейл Эдвин Мюррей
При правильных обстоятельствах вы также можете использовать милый и неформальный тон, как в этом примере визитной карточки с иллюстрациями. Использование яркого цвета на черно-белой фотографии также делает дизайн заметным и выделяющимся.
Восхитительный и увлекательный
Кредит: Ollibird
Еще один пример успешной маркетинговой идеи — набор визитных карточек мужа и жены, которые идеально дополняют друг друга, как эта пара очаровательных деловых партнеров.
Теплочувствительный и интерактивный
Через Pinterest
Еще один способ выделиться — использовать термочувствительные карты, подобные приведенным выше, созданные для фотографа. Они особенно интерактивны и увлекательны, поскольку позволяют клиентам создавать свои собственные изображения, используя тепло рук или лица. Черный превращается в разные оттенки серого и, наконец, в белый при температуре тела.
Творческий и находчивый
Через Pinterest
Эта восхитительная высеченная визитка позволяет покупателям фактически сделать небольшую скульптуру кролика, используя предоставленные вырезанные детали.Это может быть эффективной идеей для брендов, занимающихся декоративно-прикладным искусством и другими хобби.
Развлечения и игры
Через Pinterest
Эта 3D-визитка для высокой печати для мебельной компании — еще один пример того, как сделать вашу визитку интерактивной и увлекательной.
Хитрый и метафорический
Через Pinterest
Если вы ищете другие идеи для высеченной 3D-визитки, то эта визитка для креативного агентства может дать вам столь необходимое вдохновение.С различными вариантами сообщений, связанных с уникальностью, эта карта стремится буквально «выделиться» из стопки обычных карт.
Использование займов
Через Pinterest
Один из проверенных методов установления связей с потенциальными клиентами — это использовать имя или интересы, которые им больше подходят. Например, ощущение того, что у вас в руках билет на специальное мероприятие в первом ряду, наверняка будет более захватывающим, чем просто визитка в руке.
Умная иллюзия
Через Pinterest
Эта креативная визитная карточка играет с перспективой, чтобы заинтересовать потенциальных клиентов. Линии и необычная форма создают иллюзию трехмерного объекта, который на самом деле является двухмерным.
Категория № 4: Элегантные идеи для визиток
Создайте визитную карточку, которая будет такой же изысканной, роскошной и стильной, как и ваш бизнес. Эти элегантные идеи визиток неподвластны времени и лучше всего подходят для модных брендов, роскошных автомобилей, отелей и аналогичных отраслей.Вдохновитесь идеей вашей любимой элегантной визитки, представленной ниже.
Элегантный и смелый
Через Dribbble
Правильная цветовая гамма может иметь большое значение для создания идеального первого впечатления. Просто взгляните на красивое сочетание синего и золота в этой карточке для компании, занимающейся аэрофотосъемкой.
Имея размеры всего 3,5 x 2 дюйма, он передает многие грани своего бренда: роскошь, элегантность и смелость.
Королевский и роскошный
Через Dribbble
Если вы ищете особенно изысканный дизайн, эта профессионально созданная визитка с тиснением и золотой фольгой — единственная в своем роде.Сочетание золота на черном фоне с рельефными элементами производит неизгладимое впечатление.
Стильный и изысканный
Через Dribbble
Это прекрасное сочетание бирюзы и черного с золотой фольгой — настоящий хит. Как визитная карточка для студии свадебной и портретной фотографии, он прекрасно передает элегантность и яркость в едином дизайне.
Красивая простота
Через Behance
В этом дизайне все выглядит красиво и чисто за счет использования большого количества белого пространства и выделения логотипа за счет лакового покрытия, которое является одним из наиболее распространенных методов печати визитных карточек.
Со вкусом и стильно
Через Behance
Эта открытка, созданная для агентства дизайна интерьеров, сочетает стильное и со вкусом оформленное сочетание шрифтов и цветовых схем, которое, несомненно, послужит источником вдохновения для вас. Как маркетинговый инструмент для компании, ориентированной на эстетику, эта визитная карточка явно превозносит ценности красоты и элегантной простоты.
Гениальный и ловкий
Через Pinterest
В этой саморекламе используется хитроумный трюк с невидимой типографикой, чтобы заставить вас дважды взглянуть: с помощью слепой высокой печати она скрывает сообщение внутри сообщения и в процессе заставляет вас искать на секунду или две дольше.
Элегантный мятный цвет
Через Behance
Эта визитка для розничного интернет-магазина также использует слепую высокую печать и имеет элегантный мятный цвет, который соответствует идентичности бренда и общему внешнему виду.
Категория № 5: Идеи винтажных визиток
Ищете деревенские, винтажные идеи визиток, которые вернут вас в старые добрые времена? Создайте ностальгическую атмосферу вокруг своего бренда с помощью этих идей винтажных визиток. Ниже вы найдете экологически чистые, ретро, органические и аналогичные темы, которые вдохновят вас на создание собственной визитной карточки.
Рустикальный и натуральный
Через Pinterest
Эта визитная карточка из крафт-бумаги подойдет тем, кто ценит экологичность. Его дизайн землистого цвета и текстурированная бумага прекрасно передают идею экологичности.
Старые и старые вещи
Через Dribbble
Конечно, этот список был бы неполным без примера визитки в ретро-винтажном стиле, напоминающей Дикий Запад.
Эта креативная визитная карточка была вручную отшлифована вручную, чтобы придать ей изношенный старинный вид, с использованием слепой высокой печати для создания утонченного и классического вида с одной стороны и трафаретной печати с другой.
Ретро и винтаж
Через Dribbble
Эта впечатляющая черная визитка для высокой печати обязательно привлечет внимание любого. Его использование стильной и пышной типографики с рельефом, которая добавляет приятную дозу текстуры на черном фоне, делает дизайн достойным вау.
Винтажная типографика
Через Pinterest
Эта винтажная визитка для художественной галереи — пример уникального дизайна высокой печати, который подчеркивает дар дизайнера для создания бренда и логотипа.
Натуральные и органические
Через Pinterest
Эта визитная карточка с золотой фольгой для поставщика продуктов идеально отражает слова, которые должны прийти в голову, когда вы думаете о фруктах и овощах: свежие, чистые и натуральные.
Экологичность и бережливость
Через Pinterest
Для тех, кто хочет выделить из толпы, есть экологическая марка-визитка, которую можно напечатать практически на любом типе бумаги или переработанном материале.
Примечание: Это не подойдет для всех видов бизнеса; только те, кто хочет быть очень внимательным к окружающей среде.
Теперь вам
Теперь, когда вы получили много вдохновения для возможных дизайнов, вы можете создавать свои собственные дизайны визиток и макеты, используя бесплатный онлайн-инструмент для создания визуального контента под названием Visme.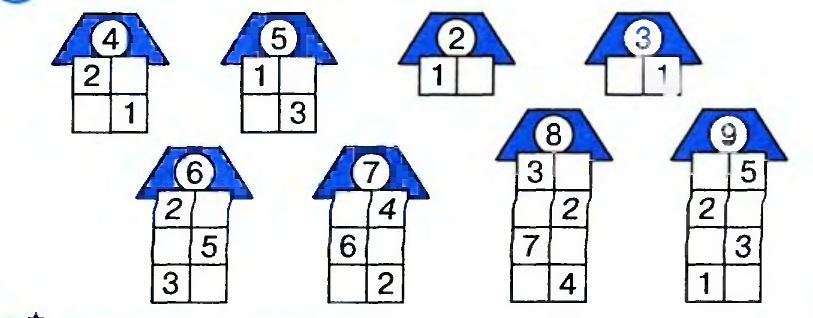 Начните работу с создателем визиток уже сегодня.
И если у вас есть собственные вдохновляющие примеры визитных карточек, которыми вы хотели бы поделиться, не стесняйтесь написать нам строчку ниже, и мы свяжемся с вами.
Часто задаваемые вопросы (FAQ)
В этом разделе мы попытались ответить на некоторые из наиболее часто задаваемых вопросов, касающихся визитных карточек и дизайна визитных карточек. Если у вас есть другие вопросы, не рассмотренные ниже, не стесняйтесь обращаться к нам в разделе комментариев.
Q1. Что должно быть написано на визитке?
Визитная карточка должна включать ваше полное имя, должность, название компании и логотип, веб-сайт, номер телефона, адрес электронной почты и любые другие контактные данные, такие как ваши данные в социальных сетях.
Q2. Что нельзя наносить на визитку?
Не размещайте на визитной карточке устаревшую и ненужную информацию, например старые номера телефонов и физические адреса интернет-компаний. Также убедитесь, что вы не добавляете слишком много текста в виде биографии — делайте это простым и по существу.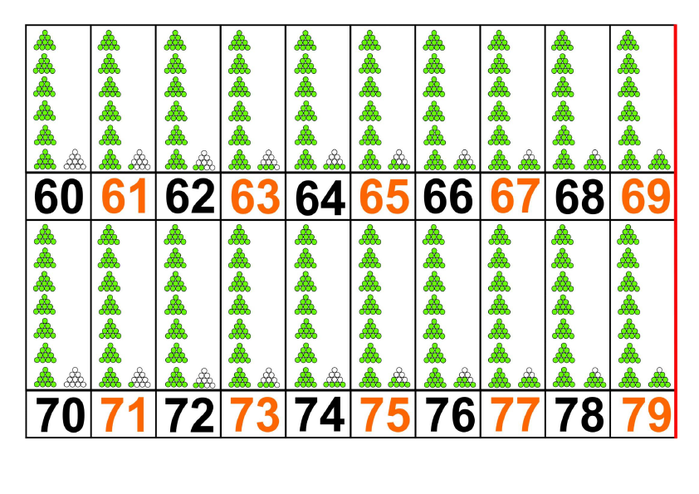
Q3. Как создать хорошую визитку?
Хорошая визитка эффективно использует пространство и принципы дизайна, поэтому может содержать всю важную информацию, не выглядя загроможденной и многословной.
Вы можете создать красивую визитку с помощью профессионально разработанных шаблонов визиток. Просто отредактируйте его, добавив свою информацию, и все готово.
Q4. В чем преимущества визитной карточки?
Визитная карточка — это недорогой и доступный способ продвижения вашего бизнеса, повышения узнаваемости бренда и предоставления потенциальным клиентам возможности связаться с вами.
Визитные карточки
также предлагают индивидуальный подход при передаче потенциальному клиенту, что увеличивает ваши шансы на то, что они с вами свяжутся. То, как вы оформляете свою визитку, также помогает создать и укрепить имидж вашего бренда.
Q5. Стоит ли размещать QR-код на своей визитной карточке?
Да! Добавление QR-кода на вашу визитную карточку — отличный способ привлечь трафик на ваш сайт, заинтриговать потенциальных клиентов и передать больше информации, перенаправляя людей на онлайн-источник, такой как ваш веб-сайт, целевая страница, о странице или странице в социальных сетях.
Q6. В чем разница между визитной карточкой и визитной карточкой?
Разница между визитной карточкой и визитной карточкой заключается в том, что визитная карточка всегда представляет компанию и может также содержать имя и контактные данные человека, который ее раздает.
Визитная карточка, с другой стороны, может выдаваться лицами, не обязательно связанными с бизнесом, и всегда содержит имя и контактную информацию человека, который ее раздает.
Q7.Для чего нужна визитка?
Визитная карточка может служить многим целям: от продвижения вашего бизнеса и повышения узнаваемости бренда до создания имиджа бренда и предоставления возможности потенциальным клиентам связаться с вами.
Q8. Как создать собственную визитку?
Вы можете легко создать свою собственную визитную карточку, используя конструктор визитных карточек Visme. Начните с нуля или настройте один из множества профессионально разработанных шаблонов визиток.
Visme позволяет вам получить доступ к ресурсам дизайна, таким как премиальные шрифты, креативные фоны, значки и формы, QR-коды и многое другое, чтобы создать уникальную и запоминающуюся визитную карточку.
Как использовать золотое сечение в дизайне (с примерами)
Хотите быть на том же творческом уровне, что и Леонардо да Винчи, Сальвадор Дали и дизайнеры Парфенона? Все они объединены одной простой концепцией.
Древние греки были одними из первых, кто открыл способ использовать красивую асимметрию растений, животных, насекомых и других природных структур. Они выразили это математическое явление с помощью греческой буквы фи, но сегодня мы называем это золотым сечением , также известным как божественная пропорция, золотая середина и золотое сечение.
Подобно правилу третей, эту математическую концепцию можно применить к графическому дизайну, чтобы сделать его более привлекательным для зрителя. Золотое сечение немного сложнее, поэтому мы рекомендуем вам сначала прочитать наше руководство по правилу третей, если математика не ваша сильная сторона.
Что такое золотое сечение?
Золотое сечение, вероятно, лучше всего понимать как пропорции 1: 1,618 . Конечно, математическое уравнение здесь намного сложнее.
Само соотношение происходит из последовательности Фибоначчи , естественной последовательности чисел, которые можно найти практически везде в природе, от количества листьев на дереве до спиральной формы морской ракушки. Его также можно найти в известных произведениях искусства и архитектуры и даже в наших собственных лицах.
Последовательность Фибоначчи легко запомнить. Начиная с 0 и 1, прибавьте последний номер последовательности к числу, которое было перед ним, чтобы создать следующее число в последовательности.Так что 0, 1, 1, 2, 3, 5, 8, 13, 21 и так далее до бесконечности. На основе последовательности Фибоначчи греки разработали золотое сечение, чтобы лучше выразить разницу между любыми двумя последовательными числами внутри последовательности.
Золотое сечение неточно, когда дело доходит до последовательности Фибоначчи — разница между двумя числами в последовательности не всегда точно равна золотому сечению, но довольно близко.
Создание золотого прямоугольника
Итак, теперь, когда мы понимаем основные числа в игре, вот более продвинутая техника для более наглядного использования этих чисел.«Золотой прямоугольник» соответствует параметрам золотого сечения, но чем чаще вы делите золотой прямоугольник в соответствии с золотым сечением, тем полезнее он становится.
Давайте начнем с создания прямоугольника с золотыми пропорциями. Чтобы упростить задачу, мы начнем с ширины 1000 пикселей и разделим ее на 1,618, чтобы получить высоту около 618 пикселей.
Теперь добавьте квадрат 618 x 618 с правой стороны холста, оставив прямоугольник 382 x 618 с левой стороны — еще один золотой прямоугольник!
Если вы возьмете этот новый прямоугольник и создадите внутри него еще один квадрат, вы получите еще один золотой прямоугольник в оставшемся пространстве, который затем сможете снова разделить и так далее, и тому подобное.
Обратите внимание, как каждый раз, когда вы делите свой золотой прямоугольник, самая большая разделительная линия изгибается по спирали? Это не случайно — он образует форму «золотой спирали», одной из наиболее распространенных форм, с которыми вы будете иметь дело при работе с золотым сечением.
Визуализация золотого сечения с другими формами
Золотой прямоугольник — самый простой (и, возможно, самый полезный) способ визуализировать золотое сечение, но вы также можете использовать круги и треугольники очень похожим образом.
Например, вы можете создать приблизительную форму золотой спирали из кругов, и эти круги идеально впишутся в систему золотых прямоугольников.
Существует также такое понятие, как «золотой треугольник», равнобедренный треугольник с двумя равными сторонами и одной отличительной стороной, которые находятся в золотой пропорции друг к другу. Когда эти треугольники вложены друг в друга, получается точно такая же форма «золотой спирали».
Золотые пропорции встречаются повсеместно
Золотое сечение — это не просто возвышенная математическая теория; он постоянно проявляется в реальном мире.Хотя многие из наиболее часто цитируемых примеров золотого сечения были развенчаны, их все еще много в природе и в произведениях искусства, созданных руками человека.
Имейте в виду, что золотое сечение основано на иррациональных числах, поэтому многие из этих примеров не соответствуют точно золотому сечению. И даже когда золотое сечение можно найти в произведении искусства, это не обязательно означает, что художник намеренно включил его в какой-то грандиозный дизайн.
Хотя есть те, кто будет утверждать иначе, золотое сечение, вероятно, не обладает какой-либо мистической силой красоты, извлеченной из изначальной ткани вселенной. Но кажется вероятным, что этот вездесущий узор обладает некоторыми эстетически привлекательными свойствами и имеет тенденцию предполагать ощущение естественного баланса и визуальной гармонии.
Использование золотого сечения в графическом дизайне
Фото: Рыба жизни
Построение вашего графического дизайна вокруг золотого прямоугольника или последовательности Фибоначчи требует некоторого настоящего художественного мастерства, но любой дизайнер может использовать это как общее руководство для внесения изменений и улучшений в свой дизайн. Чем больше вы привыкаете к золотому сечению, тем больше вы обнаруживаете, что оно просто показывает вам, где находятся лучшие части вашего дизайна, а не обязательно диктует, как вы должны создавать свой предмет.
Иногда вы обнаруживаете, что золотое сечение идеально подходит для дизайна, а в других случаях вам приходят умные идеи, которые не обязательно соответствуют правилам. Это нормально — из того количества дизайнов, которые вы найдете в мире, которые соответствуют золотому сечению, вы найдете почти такое же количество дизайнов, которые этого не сделают.Это не временное правило; это просто еще один инструмент, который вы можете добавить в набор инструментов своего дизайнера.
Типографика
Самый простой способ начать использовать золотое сечение — внедрить его в элементы типографского графического дизайна. Например, предположим, что вы используете шрифт размером 10 пунктов для основного текста. Используя золотое сечение, вы можете определить лучший размер заголовков, умножив его на 1,618.
Итак, 10 × 1,618 = 16,18, что можно округлить до шрифта 16pt.
Или, скажем, ваш заголовок имеет размер 20 пунктов, и вы хотите найти подходящий размер для основного текста.Поскольку текст заголовка является более крупным элементом, вы должны разделить его на 1,618 вместо умножения.
Таким образом, 20 / 1,618 = 12,36, что можно округлить до 12 пунктов основного текста (или до 13 пунктов, если хотите). В этом вся прелесть золотого сечения — не обязательно быть идеальным.
Размер / обрезка изображений
Естественно, простой способ включить золотое сечение в дизайн — это кадрировать фотографии (или любые другие изображения, которые вы можете использовать) в форме золотого прямоугольника.Опять же, это не означает, что вы всегда должны делать это для на каждую фотографию, но вы можете рассмотреть это для изображения, которое особенно важно для вашего дизайна.
Когда вы кадрируете изображения с учетом золотого сечения (особенно при работе с фотографией), вы также можете использовать золотую спираль в качестве ориентира для композиции кадра. Например, вы можете кадрировать фотографию до золотых пропорций таким образом, чтобы главный фокус изображения находился в центре соответствующей золотой спирали.Это добавляет интереса способом, очень похожим на правило третей, но многие считают его более естественным и эстетичным выбором.
Использование золотого сечения в визуальном дизайне также может быть таким же простым, как применение его к разнице пропорциональных размеров между двумя разными элементами — даже элементами, которые сами по себе не являются «золотыми» формами.
Например, предположим, что в вашем дизайне было изображение шириной 2 дюйма, и вы хотели соединить его с изображением меньшего размера.2-дюймовое изображение, разделенное на 1,618, дает примерно 1,236 дюйма, которые можно безопасно округлить до 1,2 дюйма.
Вы также можете добавить изображение большего размера к дизайну, для чего вам потребуется умножить 2-дюймовую фотографию на золотое сечение, чтобы получить примерно 3,2 дюйма. И теперь у вас есть последовательность Фибоначчи, которая вызывает еще больший интерес, чем раньше.
Дизайн логотипа
Вы также можете использовать золотое сечение, чтобы добавить эстетической привлекательности непосредственно к бренду компании.Даже если сам логотип не имеет формы золотого прямоугольника или треугольника, он все равно может использовать элементы с золотыми пропорциями.
Генеральный план
Еще раз, использование золотой спирали для информирования макета вашего графического дизайна во многом похоже на использование сетки с правилом третей — вы хотите, чтобы фокус дизайна был сосредоточен на спирали, используя золотые прямоугольники в качестве разделительных линий для размещения визуальные элементы. Но в отличие от сетки с правилом третей, вы можете перемещать золотой прямоугольник по своему усмотрению.
В конце концов, если бы вы не могли перемещать золотой прямоугольник, каждый рисунок выглядел бы как золотой прямоугольник или спираль. Вместо этого представьте свой золотой прямоугольник как линейку — он не меняется, но вы можете перемещать его по холсту, чтобы измерить элементы, которые уже есть.
Цифровым дизайнерам приходится работать с более жесткими ограничениями, когда дело доходит до создания макета; в конце концов, они не могут контролировать размер монитора аудитории. Распространенный трюк в веб-дизайне — использовать золотое сечение для разделения пространства между основной частью веб-сайта и боковой панелью.Измеряя пространство, с которым они работают, веб-дизайнеры могут убедиться, что тело в 1,618 раз больше, чем боковая панель, взяв общую ширину холста, разделив ее на 1,618, а затем вычтя это число из общей ширины холст.
Тот же метод можно применить и к полиграфическому дизайну, но вы должны быть осторожны. Веб-дизайнеры работают в горизонтальной среде, а большая часть полиграфического дизайна ориентирована вертикально. Конечно, почти все, что напечатано вертикально, можно распечатать и горизонтально, но у вас не всегда будет такая возможность.
Преимущество работы в печати заключается в том, что размер самого носителя можно измерить по золотому сечению. Однако бывают случаи, когда дизайнеры печати ограничены стандартным размером и не могут использовать настраиваемые параметры печати. К счастью, вы все еще можете применить золотое сечение к макету любого шаблона печати; вам просто нужно быть умным.
Хорошая особенность папок презентаций и других материалов для печати, которые открываются, заключается в том, что они дают вам выровненный по вертикали и горизонтали холст для работы.Всякий раз, когда вы открываете папку с презентацией, объединенная внутренняя часть образует один большой горизонтальный прямоугольник. Таким образом, довольно легко получить элементы интерьера, основанные на золотом сечении, такие как размер и расположение карманов.
Вы также можете реализовать ту же идею боковой панели, которую используют веб-дизайнеры, разместив внутри папки специальную информационную панель. Даже расположение ваших печатных элементов дизайна внутри папки может иметь эстетическую привлекательность для зрителя, если вы разместите их в соответствии с золотой пропорцией.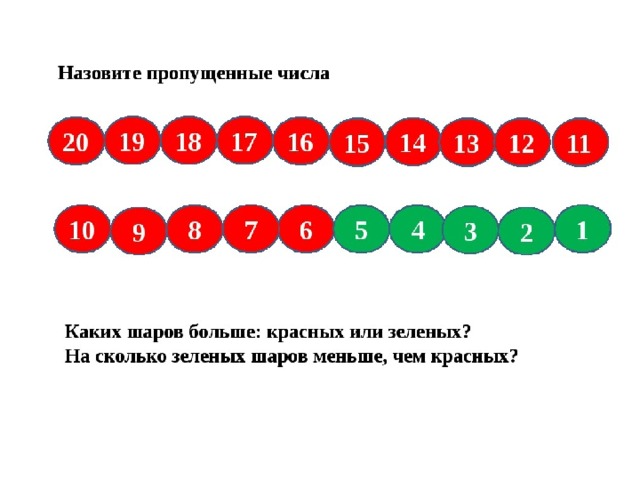
Инструменты золотого сечения
Мы не хотели отпускать вас домой с вечеринки золотого сечения, не взяв с собой несколько подарков. Мы собрали некоторые из лучших инструментов и приложений, которые помогут вам включить золотое сечение в свой дизайн.
Atrise Golden Section — Это удобное дополнение позволяет разместить сетку золотой пропорции прямо над выбранным программным обеспечением для проектирования, что позволит вам измерить дизайн в соответствии с золотым сечением. В новейшей версии Photoshop уже есть встроенные параметры золотого сечения и спирального наложения, но этот инструмент очень полезен, если вы используете старую версию или другую программу.
Golden Calipers — Печать — это физический носитель, поэтому, если вам нравится работать руками, вы можете подобрать пару золотых штангенциркулей — измерительный инструмент, разработанный специально для того, чтобы помочь вам проектировать в соответствии с золотым сечением.
Приложение золотого сечения — За 2,99 доллара в Mac App Store вы можете получить это простое, но эффективное приложение, которое позволяет легко создавать макеты золотого сечения. (Обновление: больше не доступно)
Приложение
Golden Ratio Typography — убедитесь, что ваша типографика пропорциональна, создав столбцы основного текста, соответствующие золотому сечению.
Калькулятор
Phi — Дизайнеры, использующие золотое сечение, часто обнаруживают, что постоянно обращаются к своим калькуляторам. Найдите подходящий продукт, который автоматически рассчитывает золотое сечение.
Phi Matrix — Это компьютерное программное обеспечение для Windows и Mac дает вам возможность применять прямоугольники золотого сечения к любому изображению, которое вы можете создать на своем компьютере с помощью любого программного обеспечения, даже веб-браузера или текстового редактора.
Степень, в которой вы полагаетесь на золотое сечение, зависит от вас, но даже малейшее применение его пропорций может действительно добавить привлекательности вашим дизайнам.Если вы хотите быть более уверенными в своем дизайне, попробуйте измерить его по золотому сечению и правилу третей. Если ваш дизайн удовлетворяет обоим, у вас может быть что-то отличное.
Щелкните изображение ниже, чтобы просмотреть его в полный размер.
Золотое сечение — действительно увлекательная тема, и мы совершенно точно знаем, как часто оно встречается в природе, классическом искусстве, архитектуре, дизайне логотипов и многом другом. Мы хотим увидеть ваши лучшие примеры золотого сечения в действии, поэтому оставьте комментарий ниже с вашими образцами, особенно если это дизайны, которые вы создали сами.
Колледж Композиция CLEP Flashcards | Quizlet
(1) При наблюдении за живым представлением, таким как спектакль или выступление, на каждого отдельного члена аудитории влияет эмоциональная реакция группы на представление. (2) Некоторые исследования показывают, что зрители будут смеяться вместе со смехом других зрителей гораздо чаще, чем они смеялись бы над тем же представлением, если бы смотрели его в одиночку.
(3) По мере того, как в первой половине двадцатого века представления перешли на радио и телевидение, продюсеры хорошо осознавали важную роль этого социального смеха.(4) Ранние радио- и телевизионные комедии транслировались в прямом эфире с реальной аудиторией в студии, чтобы обеспечить реакцию, которая помогала домашней аудитории почувствовать связь с представлением. (5) По мере того, как достижения в области технологий позволили заранее записывать, редактировать и улучшать выступления для последующей трансляции, записанный смех получил более широкое распространение. (6) Это можно назвать «консервированным смехом» или «смехотворной песней».
(7) Песня смеха дает продюсерам возможность создать реакцию аудитории, которая согласуется с законченным отредактированным выступлением.(8) В прямых трансляциях шоу длится от начала до конца без остановки, и живые студийные аудитории получают подлинную, хотя и непредсказуемую реакцию на выступление, точно так же, как аудитория, слушающая или смотрящая дома. (9) Однако в записанном исполнении режиссеры могут остановить сцену, попросить исполнителей переделать определенный сегмент или попросить команду сменить оборудование и начать снова. (10) Такой прерывистый, бессвязный стиль исполнения мешает им поддерживать интерес живой студийной аудитории.(11) Поэтому редакторы часто добавляют записанный смех в окончательную отредактированную версию программы. (12) Подчеркивайте каждую шутку с правильной громкостью, продолжительностью и качеством смеха, чтобы побудить аудиторию дома смеяться в назначенное время. (13) Хотя в некоторых современных телевизионных комедиях не используется смех, многие программы для детей и взрослых в равной степени полагаются на записанный смех, чтобы вызвать у аудитории чувство сопричастности.
В контексте, что из следующего является наилучшей редакцией подчеркнутой части предложения 2 (воспроизведено ниже)?
Некоторые исследования показывают, что зрители будут смеяться вместе со смехом других зрителей гораздо чаще, чем они смеялись бы над тем же представлением, если бы смотрели его в одиночку.
A. Тем не менее, некоторые
B. Тем не менее, некоторые
C. Напротив, некоторые 90 244 D.
Использование наглядных пособий в процессе изучения чисел первого десятка
Курсовая работа
Использование наглядных пособий в процессе изучения чисел первого десятка
Оглавление
Введение
Глава 1. Теоретические основы использования наглядных пособий при изучении математики в начальной школе
Наглядные пособия: классификация, практическое применение
Особенности восприятия младшими школьниками наглядных материалов
Использование наглядных пособий на уроках математики в начальной школе
Глава 2. Экспериментальная работа по использованию наглядных пособий в процессе изучения чисел первого десятка
2.1 Диагностика уровня математического развития детей младшего школьного возраста
2. 2 Организация работы по использованию наглядных пособий в процессе изучения чисел первого десятка
Заключение
Библиография
Приложения
Введение
Одним из важных в работе с младшими школьниками средств является использование наглядности. Изучением и применением методов наглядности занимались Жан-Жак Руссо, Песталоции, К.Д. Ушинский, Л.Н.Толстой, В.П. Вахтеров и др. В методической литературе большое внимание уделяется вопросам использования наглядных средств при обучении младших школьников (работы М. А. Бантовой, Г. В. Бельтюковой, А. С. Пчелко, А. М. Пышкало, Л. Н. Скаткина и др.). Н. Л. Менчинская и М. И. Моро указывают на необходимость самостоятельного оперирования средствами наглядности учащимися начальной школы.
Наглядность это один из компонентов целостной системы обучения, которая может помочь младшему школьнику качественнее усвоить изучаемый материал на более высоком уровне.
Наглядно представленный материал способствует развитию мыслительных операций и всей мыслительной деятельности учащихся, тем самым обеспечивается переход от конкретного к абстрактному в процессе овладения математическими знаниями. Большие возможности дают наглядные средства для развития конструктивной деятельности учащихся (составление различных геометрических фигур по образцу и без образца).
Решению образовательных задач способствует использование различных наглядных средств не только на этапе ознакомления, но и при закреплении знаний, при формировании умений и навыков.
Практика обучения показывает, что при систематическом включении наглядных средств увеличивается самостоятельность учащихся, возрастает их активность, формируется положительное отношение к предмету. Данное обстоятельство является очень важным для обеспечения развития в процессе обучения личности.
Применение средств наглядности способствует решению одной из важнейших задач начального обучения математике – воспитательной. Наглядные средства способствуют формированию материалистического мировоззрении младших школьников. Непосредственно воспринимая множество предметов, пересчитывая число их элементов, объединяя или удаляя части множеств, учащиеся убеждаются в том, что такие математические понятия, как число, арифметическое действие, геометрическая фигуpa взята из окружающей жизни. Наглядно представленный числовой материал расширяет кругозор школьников. Опыт работы школ показывает значительное повышение интереса учащихся к предмету, если учитель привлекает на уроках при изучении различных тем наглядные пособия.
Все это и обусловило актуальность темы исследования.
При изучении психолого-педагогической литературы нами было выявлено противоречие между использованием наглядности на уроках математики в начальной школе и отсутствием в методике преподавания практических рекомендаций по использованию наглядных пособий в процессе изучения чисел первого десятка.
Выявленное противоречие позволило обозначить проблему исследования: проверка возможностей использования наглядных пособий в процессе изучения чисел первого десятка.
Данная проблема позволила сформулировать тему исследования: «Использование наглядных пособий в процессе изучения чисел первого десятка».
Объект исследования: процесс обучения математике в начальной школе.
Предмет исследования: использование средств наглядности на уроках математики начальных классов при изучении чисел первого десятка.
Цель исследования: теоретически обосновать и путем опытно-экспериментальной работы проверить эффективность использования наглядных пособий в процессе изучения чисел первого десятка.
Изучение психолого-педагогической литературы по теме исследования позволило выдвинуть следующую гипотезу: предполагается, что использование различных видов наглядных пособий на уроках математики помогает более эффективно усваивать детьми числа первого десятка, способствует облегчению понимания учебного материала. Вызывает заинтересованность детей.
В соответствии с целью и гипотезой исследования были определены следующие задачи:
1. Проанализировать психолого-педагогическую литературу по проблеме исследования.
2. Рассмотреть понятие, классификацию и практическое применение наглядных пособий на уроках математики в начальной школе.
3. Определить особенности восприятия младшими школьниками наглядных материалов.
4. Экспериментальным путем проверить эффективность использования наглядных пособий в процессе изучения чисел первого десятка.
Теоретико-методологическая основа исследования: методические и научные исследования использования наглядных пособий на уроках математики в начальной школе в трудах М.А. Бантовой, Г.В.Бельтюковой и других, пути и способы практического применения наглядности при изучении чисел в начальной школе в работах М.И.Морро, А.М.Пикало и других.
Для решения поставленных задач и проверки гипотезы были использованы следующие методы исследования: изучение и анализ психолого-педагогической, методической и учебной литературы по проблематике исследования; педагогические наблюдения, беседы, анкетирование учителей и учащихся; проведение педагогического эксперимента, количественная обработка и качественная интерпретация экспериментальных данных, статистическая обработка полученных данных.
Опытно-экспериментальная база исследования: МОУ СОШ №4 города Ишима. В эксперименте участвовали учащиеся 2 «А» и 2 «Б» классов.
Исследование проводилось в три этапа.
Первый этап – постановочный (01.02.10 – 01.03.10) – выбор и осмысление темы. Изучение психолого-педагогической литературы, постановка проблемы, формулировка цели, предмета, объекта, задач исследования, постановка гипотезы.
Второй этап – собственно-исследовательский (02.03.10 – 02.04.10) – разработка комплекса мероприятий и их систематическое проведение, обработка полученных результатов, проверка гипотезы.
Третий этап – интерпретационно-оформительский (03.04.10 – 03.05.10) – обработка и систематизация материала.
Научная новизна исследования: исследования состоит в том, что использование наглядных пособий на уроках математики в начальной школе впервые рассматривается как самостоятельная исследовательская проблема; экспериментально проверена эффективность использования наглядных пособий в процессе изучения чисел первого десятка.
Практическая значимость заключается в том, что выводы и результаты курсовой работы могут быть использованы в учебно-воспитательном процессе общеобразовательных учреждений.
Структура и объем работы: работа состоит из введения, двух глав, заключения, библиографического списка, включающего 39 наименований, приложения.
Общий объем работы 48 страниц компьютерного текста.
Глава 1. Теоретические основы использования наглядных пособий при изучении математики в начальной школе
Наглядные пособия: классификация, практическое применение
В методической литературе большое внимание уделяется вопросам использования наглядных средств при обучении младших школьников (работы М. А. Бантовой, Г. В. Бельтюковой, А. С. Пчелко, А. М. Пышкало, Л. Н. Скаткина и др.). Н. Л. Менчинская и М. И. Моро указывают на необходимость самостоятельного оперирования средствами наглядности учащимися начальной школы. В работах М.И. Земцовой, А. И. Зотова, Ю. А. Кулагина, А. Г. Литвака подчеркивается значение наглядных средств для формирования представлений учащихся.
Наглядное пособие – средство развития выступления, позволяющее воспринимать информацию не только на слух, но и зрительно. Наглядные пособия имеют различное значение. В одних случаях они носят иллюстративный характер. В других – облегчают процесс формирования абстракций.
Выдающийся психолог Л.С.Выготский называл наглядные пособия «психологическим орудием учителя» [7, с.235].
Наглядные средства обучения являются необходимым компонентом учебно-методических комплексов, в которые чаще всего входит учебник, тетрадь с печатной основой и методические указания для учителя.
Наглядные средства в методической литературе принято делить на натуральные и изобразительные. К натуральным средствам относятся различные предметы окружающей действительности, для математики это все, что можно пересчитать. Особенно необходимы натуральные предметы на первых порах, когда у детей только еще формируется понятие о натуральном числе, раскрывается конкретный смысл арифметических действий. Широко используются в начальной школе и изобразительные средства: рисунки, аппликации предметов. Различные изображения предметов включаются по мере накопления у ребенка опыта в оперировании с натуральными объектами. Действия учащихся с предметными картинками способствуют формированию многих математических понятий.
Основные виды наглядных пособий, используемых при обучении в начальной школе [21, с.358]:
Счетные палочки.
Палочки особенно широко используются при формировании понятий о числе и арифметических действиях.
Набор объемных пособий – кубиков и других игрушек.
Большие возможности в работе над математическими задачами открывает применение игрушек (утят, цыплят и других). Они позволяют каждому ученику представить наглядно ситуацию, данную в задаче. Учитель при этом, корригируя деятельность каждого ученика, формирует или уточняет пространственные представления учащихся.
Наборные полотна с картонными трафаретами фигур овощей, листьев, фруктов, животных, птиц и других.
Как показывает практика, при изучении многих тем и на каждом уроке успешно применяются наборные полотна, как демонстрационные, так и индивидуальные.
Трафареты могут быть выполнены из цветного картона, бархатной и другой плотной бумаги. Ко всем наборным полотнам, как демонстрационным, так и индивидуальным, обязательно иметь разрезанные цифры от 0 до 9, карточки со знаками действий сложения и вычитания, равенства и неравенства.
Индивидуальные наборные полотна дают возможность учащемуся оперировать с предметами, не терять на столе разрезные цифры, контролировать свои действия, не сдвигая прикосновением рук трафареты фигур.
Фланелеграф.
Фланелеграф представляет собой доску такого же формата, как и наборное полотно, обтянутую черной фланелью. Трафареты с наклеенными на обратной стороне небольшими кусочками наждачной, бархатной или промокательной бумаги, очень хорошо держатся на начесанной ткани. Удобно в целях экономии времени на уроках применять сразу несколько фланелеграфов, приготовив заранее на каждое из них соответствующие материалу урока задания [33, с.317].
Разрезные цифры и знаки математических действий для наборных полотен.
Наборы разрезных цифр для демонстрационных и индивидуальных полотен дают возможность обучения самостоятельному пользованию средствами наглядности, Разрезные карточки с круглыми числами для изучения нумерации многозначных чисел, изготовлены с расчетом на наложение двух других карточек с круглыми двузначными и однозначными числами. С помощью разрезных цифр и знаков учащиеся могут составить примеры, равенства и неравенства, Большие возможности получают учитель и ученик в иллюстрации проcтых и составных задач, применив фланелеграф или наборные полотна и разрезные цифры.
Сюжетные картины с прорезями.
Для ознакомления с приемами устных вычислений и для решения задач используется, например, четкое изображение деревьев, тарелок, аквариумов, ваз и др. предметов. В прорези вставляются соответственно трафареты грибов, яблок, рыбок, цветов и др. предметов. Для демонстрации нужно брать только специально выполненные с четко выделенными контуром и силуэтом изображения предметов (деревьев), в некоторых случаях – с утрированной четкостью отдельных частей (ветвей), и прорезями для трафаретов (фруктов, птиц) [33, с.198]. Работа с сюжетными картинками позволяет учащимся лучше представить жизненную ситуацию арифметической задачи, дает возможность воспринимать действия учителя с предметами и самостоятельно практически выполнять различные операции над множествами. Выполнение различных упражнений с предметами способствует развитию зрительного восприятия, пространственных представлений, пространственной ориентировки учащихся с различными нарушениями зрения.
Предметные картинки.
Например, поставив одну под другой две картинки с изображениями животных (различных деревьев) и справа числа, означающие продолжительность их жизни, учащимся предлагали составить задачи на разностное или кратное сравнение. Подобные задания позволят расширить тематику при обучении составлению арифметических задач, уточнить при этом предметные представления учащихся.
Плакаты.
Специально изготовленные для восприятия учащимися плакаты с названиями компонентов арифметических действий, примерами, уравнениями, со словами: уехали, улетели, подъехали, купили, подарили, осталось, стало, было, на, больше, меньше. Плакаты должны быть изготовлены с расчетом на выставление их в наборных полотнах, Плакаты для индивидуального использования учащимися выполняются плоским и рельефно-точечным шрифтом.
Таблицы. По назначению таблицы делятся на познавательные, инструктивные, тренировочные и справочные. К познавательным таблицам относятся такие, которые содержат в себе новые сведения и чаще всего используются при объяснении нового материала, например, нумерационная таблица. Нумерационные таблицы следует применять для ознакомления с понятием класса, с названиями разрядов в каждом классе. Данная таблица может в дальнейшем использоваться и как тренировочная. Учащиеся упражняются в чтении и записи многозначных чисел, цифры которых занесены в определенную графу таблицы. Наличие названий разрядов и классов в таблице во многом помогает учащимся ориентироваться в больших числах, правильно их записывать.
Счетные приборы.
Счеты необходимо иметь каждому ученику. Они применяются как при изучении нумерации чисел во всех концентрах, так и при выполнении арифметических действий. Кубики, бруски и доски арифметического ящика используются при обучении счету и изучении нумерации. Счетные приборы дают возможность активизировать деятельность учащихся на уроке, организовать самостоятельную работу. По заданию учителя ученик, к примеру, представляет с помощью счет, кубиков, брусков или абаков двузначное и трехзначное число, что способствует усвоению десятичного состава чисел.
Школьная практика подтверждает эффективность применения таких наглядных пособий, которые четко выражали бы наиболее существенные стороны изучаемого на данном уроке явления, были свободны от излишних деталей, мешающих ученикам сначала вычленить, а затем сгруппировать те же существенные признаки, обобщение которых лежит в основе данного представления или понятия [38, с.339].
Каждое средство наглядности отличается и той специфической функцией, которую оно может выполнять в учебном процессе, обеспечивающем его высокую эффективность. Важным элементом учебного оборудования должны стать комплекты средств вариативной наглядности. Они позволяют во время урока быстро создавать, изменять, разные ситуации с использованием наглядных пособий. Для этого используются наборы иллюстративных материалов или меловых рисунков, чертежей и записей. К числу таких средств относятся магнитная доска и фланелеграф, дидактические возможности которых во многом одинаковы.
В связи с различными дидактическими функциями и возможностями средств наглядности требуется их комплексное применение на уроке. Только в этом случае будет достигнута максимальная эффективность в решении каждой познавательной задачи урока. Комплексное применение различных средств наглядности объясняется тем, что оно обеспечивает совместную работу на уроках различных анализаторов.
Вместе с тем многообразие средств наглядности оправдано лишь в тех случаях, когда требуется раскрыть различные стороны изучаемого явления или предмета, а каждое из этих сторон более убедительно и полно может быть отражена лишь с помощью определенного вида наглядности. Нельзя не согласиться с Ю.К. Бабанским в том, что “чрезмерное увлечение наглядностью ведет к затормаживанию развития абстрактного мышления, без которого невозможно эффективное познание окружающей действительности. Обильное применение наглядности часто рассеивает внимание учащихся, отвлекает от познания главных идей темы, особенно когда речь идет об учащихся не с наглядно-образной, а со словесно-логической памятью” [26, с.110].
Таким образом, наглядные пособия – это средства развития выступления, позволяющее воспринимать информацию не только на слух, но и зрительно. Эффективность применения средств наглядности в учебном процессе зависит не только от педагогически оправданного сочетания на уроке разных его видов, но и от правильного соотношения наглядности и других источников знания, в частности слова учителя.
Наименее эффективным оказывается такое применение средств наглядности, когда оно не используется в качестве одного из источников новых знаний, а служит лишь иллюстрацией к слову учителя. Одна из задач совершенствования учебного процесса состоит в широком использовании на уроках наглядных пособий как самостоятельных источников информации. Это предполагает самостоятельную работу учащихся с различными видами индивидуальных пособий, дидактического материала, проведение предметных уроков, выполнение заданий, основанных на изучении демонстрационных наглядных пособий.
В следующем параграфе мы рассмотрим особенности восприятия наглядных пособий младшими школьниками.
Особенности восприятия младшими школьниками наглядных материалов
Восприятие – процесс отражения человеком предметов и явлений окружающего мира при непосредственном их воздействии на его органы чувств. Для того чтобы воспринимать предметы, воздействующие, например, на глаз человека, воспринимающий уже должен обладать каким – то соответствующим опытом. В восприятии человеком чего–либо огромную роль играет речь – то слово, которым назван предмет.
Ребенок не рождается с готовым умением воспринимать что-либо, даже те простые предметы, которые находятся перед ним. На ранних этапах развития восприятие ребенка не совершенно: образы воспринимаемых объектов отличаются смутностью и не четкостью.
Несмотря на то, что ребенок уже с первых дней своей жизни может смотреть на предметы, рано обнаруживает чувствительность к звукам, в том числе и к голосам людей, его надо систематически учить смотреть, рассматривать, слушать и понимать то, что он воспринимает. Механизм восприятия уже готов, но пользоваться им ребенок еще не умеет [19, с.315].
Пути формирования умения воспринимать и наблюдать могут быть различны. Несмотря на разные методические рекомендации, все исследователи согласны в главном – ребенка следует специально учить восприятию, без чего на долго сохраняете особенности восприятия, которые типичны для самых маленьких детей / слитность, нечеткость /. Поэтому, учитывая особенности младшего школьника, психологи настоятельно рекомендуют, при обучении использовать различные виды дидактического материала и наглядных пособий [15, с.259].
Опираясь на большую доступность маленьким детям чувственного познания, возникает острая необходимость использовать в обучении разные виды наглядных пособий. Использование наглядности позволяет сформировать у ребенка правильное представление о предмете, явлении, законе который он изучает. Как показывают исследования, при использовании наглядных пособий для большего эффекта демонстрируемый предмет или его изображение необходимо комментировать, т. к. всякая наглядность демонстрирует какой-то единичный предмет, но единичное всегда имеет и общие для всех однородных предметов признаки, свои особенные, частные признаки, присущие только данному экземпляру [25, с.157].
Именно комментирование демонстрируемых объектов позволяет детям увидеть в каждом объекте именно то, что является главным и общим для всех данных предметов и, пропуская при этом мелкие частные подробности, и только вопросами и указаниями можно вести глаз ребенка по воспринимаемому объекту. Без речи же наглядность нема.
Кроме того, в речи можно фиксировать не только признаки или части предмета, но и характеризовать особенности каждого единичного предмета. Т.о. сочетание чувственного и словесного необходимо, для того чтобы дети научились в единичном видеть общее, а через части – целое. Однако, в целом ряде исследований подчеркивается, что долго задерживаться на использовании наглядности в обучении уже знакомого материала не следует, так как это задерживает переход ребенка к самостоятельному созданию образа предмета, к обобщению и оперированию отвлеченным содержанием, а следовательно, задерживает развитие у ребенка абстрактного мышления [5, с. 30]
В основе использования технических и аудиовизуальных средств обучения в качестве источника знаний лежат вполне определенные психические процессы. Учитель вводит в класс такие раздражители, которые сильно воздействуют на органы чувств обучающегося, основательно перестраивая все его психические функции. Участвующие в процессе восприятия зрительные и слуховые анализаторы способствуют получению более полных и точных представлений об изучаемых вопросах.
Для успешного обучения важно, чтобы в процессе восприятия участвовало как можно больше видов восприятия. На первом месте по значимости и эффективности в условиях применения технических средств обучения находятся комбинированные зрительно-слуховые виды восприятия, затем следуют зрительные и, наконец, слуховые. Таким образом, одновременное воздействие сложного комплекса раздражителей на разные анализаторы (или как бы их синтетическое воздействие) обладает особой силой, особой эмоциональностью. Поэтому организм обучаемого, воспринимающего информацию с помощью технических средств обучения, находится под воздействием мощного потока качественно необычной информации, создающей эмоциональную основу, на базе которой от чувственного образа легче переходить к логическому мышлению, к абстрагированию.
Вместе с тем психологи указывают, что хотя весь анатомо-физиологический аппарат, необходимый для осуществления процесса восприятия готов к работе уже на первом году жизни ребенка, однако нужна длительная и систематическая работа по обучению детей правильным и рациональным способам чувственного познания окружающей действительности.
Готовность зрительного, слухового и двигательного механизма является лишь возможностью развития осмысленного, целенаправленного и правильного восприятия и наблюдения ребенком как отдельных явлений и предметов, так и целых их компонентов. Таким образом, в процессе обучения следует использовать практические действия самого ребенка, его чувственное познание и речь. При этом необходимо руководить восприятием, упражнять ребенка в анализе предмета с целью его более полного, осмысленного и целостного восприятия [2, с.48].
Известный ученый – психолог Л.С. Выготский различал два уровня развития возможностей ребенка: уровень актуального развития (достигнутый уже уровень развития) и зону ближайшего развития (то, что находится в процессе становления, “завтрашний день” развития) [7, с. 117]. Опираясь на данное положение, можно сказать, что уровнем актуального развития ребенка I класса является наглядно-действенная умственная деятельность, основанная на восприятии выполненных практических операций с предметами, а наглядно-образная, затем словесно-логическая умственная деятельность являются зоной ближайшего развития. Вот почему при обучении детей начальных классов, а особенно I класса необходима четкая последовательность в использовании средств обучения: от действий с конкретными объемными предметами к постепенному переходу к действиям с плоскостным дидактическим материалом (предметным картинкам) и, наконец, к более абстрактным предметам (геометрическим фигурам, знаковым моделям и т.д.) [27, с.105].
Принимая во внимание результаты исследований психологов о том, что у учащихся начальной школы преобладает непроизвольное внимание, что однообразная работа очень быстро утомляет ребенка, а необходимость смены видов деятельности, и эта деятельность часто может и должна быть игровой. Следовательно, обучение ученика первого класса должно быть интересным, радостным, но в то же время обеспечивающим глубокое усвоение программного материала. Одним из главных средств, для достижения этой цели служит широкое и продуманное применение наглядности.
Первоначально младшие школьники лучше запоминают наглядный материал: предметы, которые ребенка окружают и с которыми он взаимодействует, изображения предметов, людей. Продуктивность запоминания такого материала выше, чем запоминания словесного материала. Конкретно-образный характер восприятия и памяти младших школьников проявляется в том, что дети справляются с такими трудными приемами запоминания, как соотнесение, деление на части текста, если при этом есть опора на наглядность, например на соответствующие иллюстрации. Это особенно надо знать и учитывать педагогу при организации учебного процесса.
Результаты исследований по проблеме соотношения роли чувственных и логических компонентов при формировании системы понятий свидетельствуют о том, что именно взаимосвязь предметного содержания знаний, индивидуальных особенностей и аномального фактора определяет характер наглядных пособий. Только на основе работы с дидактическим материалом усваивается конкретный смысл арифметических действий. Учащиеся начальных классов прежде, чем усвоить вычислительные приемы, должны познакомиться с теоретической их основой, со свойствами арифметических действий. Усвоение математической теории в начальной школе проходит при широком использовании наглядных средств.
Наглядно представленный материал способствует развитию мыслительных операций и всей мыслительной деятельности учащихся с нарушениями зрения, тем самым обеспечивается переход от конкретного к абстрактному в процессе овладения математическими знаниями. Большие возможности дают наглядные средства для развития конструктивной деятельности учащихся (составление различных геометрических фигур по образцу и без образца) [10, с.115].
Решению образовательных задач способствует использование различных наглядных средств не только на этапе ознакомления, но и при закреплении знаний, при формировании умений и навыков.
Практика обучения показывает, что при систематическом включении наглядных средств увеличивается самостоятельность учащихся, возрастает их активность, формируется положительное отношение к предмету. Данное обстоятельство является очень важным для обеспечения развития в процессе обучения личности слепого и слабовидящего.
Применение средств наглядности способствует решению одной из важнейших задач начального обучения математике – воспитательной. Наглядные средства способствуют формированию материалистического мировоззрении младших слепых и слабовидящих школьников. Непосредственно воспринимая множество предметов, пересчитывая число их элементов, объединяя или удаляя части множеств, учащиеся убеждаются в том, что такие математические понятия, как число, арифметическое действие, геометрическая фигуpa взяты из окружающей жизни. Наглядно представленный числовой материал, характеризующий результаты выпуска той или иной продукции предприятиями города, района, страны, расширяет кругозор школьников
Таким образом, в младшем школьном возрасте наглядные средства обучения должны точно отражать характерные признаки и свойства объектов, изучаемых в данный момент, т. к. остальное, несущественное отвлекают внимание детей. Поэтому наглядный материал не должен быть чрезмерно броским, пестрым и ярким, при этом пособие должно появляться только в период работы с ним, после чего его следует убирать. В итоге ребенок приобретает богатый чувственный опыт, овладевает умением его расширять и углублять, учится воспринимать окружающий мир в многообразии составляющих его предметов и явлений, использовать это богатство чувственного опыта в своей разнообразной практической и умственной деятельности.
В следующем параграфе мы рассмотрим использование наглядных пособий на уроках математики в начальной школе.
Использование наглядных пособий на уроках математики в начальной школе
Наглядность в обучении способствует тому, что у школьников, благодаря восприятию предметов и процессов окружающего мира, формируются представления, правильно отображающие объективную действительность, и вместе с тем воспринимаемые явления анализируются и обобщаются в связи с учебными задачами.
Использование наглядных средств не только для создания у школьников образных представлений, но и для формирования понятий, для понимания отвлеченных связей и зависимостей — одно из важнейших положений дидактики. Ощущение и понятие — различные ступени единого процесса познания.
Еще Я. А. Коменский выдвинул «золотое правило»: «все, что …можно, предоставлять для восприятия чувствам…» [18, с.57]. Требование, чтобы знания черпались учениками прежде всего из собственных наблюдений, сыграло большую роль в борьбе с догматическим, схоластическим обучением. Однако ограниченность сенсуалистической философии, на которую опирался Коменский, не позволила ему раскрыть принцип наглядности обучения с необходимой полнотой и разносторонностью.
Принцип наглядности был значительно обогащен в трудах Г. Песталоцци. Отстаивая необходимость наглядности в обучении, он считал, что органы чувств сами по себе доставляют нам беспорядочные сведения об окружающем мире. Обучение должно уничтожить беспорядочность в наблюдениях, разграничить предметы, а однородные и близкие снова соединить, то есть сформировать у учащихся понятия.
В современной дидактике понятие наглядности относится к различным видам восприятия (зрительным, слуховым, осязательным и др.). Ни один из видов наглядных пособий не обладает абсолютными преимуществами перед другим. При изучении природы, например, наибольшее значение имеют натуральные объекты и изображения, близкие к натуре, а на уроках грамматики – условные изображения отношений между словами с помощью стрелок, дуг, посредством выделения частей слова разными цветами и т. п. Нередко возникает необходимость использовать различные виды наглядных средств при ознакомлении с одними и теми же вопросами. Например, в курсе истории целесообразно рассматривать предметы, сохранившиеся от изучаемой эпохи, макеты и картины, изображающие соответствующие явления, исторические карты, смотреть кинофильмы и т. д.
Очень важно использовать наглядные средства целенаправленно, не загромождать уроки большим количеством наглядных пособий, ибо это мешает учащимся сосредоточиться и обдумать наиболее существенные вопросы. Такое применение наглядности в обучении не приносит пользы, а скорее вредит и усвоению знаний и развитию школьников.
Когда у учащихся имеются необходимые образные представления, следует использовать их для формирования понятий, для развития отвлеченного мышления учащихся. Это правило относится не только к средним и старшим, но и к начальным классам. Опираясь на восприятие младшими школьниками множеств и отношений между ними, надо уже в 1-м классе постепенно переходить к обобщению наглядных отношений, добиваясь их понимания в отвлеченном плане. Так, проделав умножение и деление на квадратиках или кружочках в пределах двух десятков, следует перейти к уяснению связи между умножением и делением, взаимно обратных отношений между этими арифметическими действиями [28, с.314].
В практике обучения применение наглядных средств сочетается со словом учителя. Способы сочетания слова и средств наглядности при всем их многообразии составляют несколько основных форм. Одна из них характеризуется тем, что при посредстве слова учитель руководит наблюдением, которое ведут учащиеся, а знания о внешнем облике объекта, о его строении, о протекающих процессах школьники получают из наблюдаемых объектов.
Математика изучает не сами предметы и явления окружающей жизни, а “ пространственные формы и количественные отношения действительного мира” ( Ф. Энгельс), поэтому при обучении математике стремятся вычленить именно эти стороны; качественные же признаки предметов становятся несущественными. Часто для изучения математических соотношений и операций используют специально созданные пособия. Такие пособия иногда являются более наглядными, чем сами предметы или ситуации, взятые из окружающей жизни [33, с.52].
На уроках математики осуществляются во взаимосвязи все основные принципы обучения: сознательность, наглядность, систематичность, прочность, учет возрастных возможностей, индивидуальный подход. В обучении математике особую роль играет принцип наглядности.
Несомненно, учебник является основным средством обучения. В настоящее время широко применяется, и хорошо себя зарекомендовали альтернативные учебники М.И. Моро, Л.В. Занкова, Н. Я. Виленкина и других авторов. Школа сама выбирает, какой методике отдать предпочтение, какой автор больше других подходит к их разработанной системе обучения математике.
Правильное использование наглядности на уроках математики способствует формированию четких пространственных и количественных представлений, содержательных понятий, развивает логическое мышление и речь, помогает на основе рассмотрения и анализа конкретных явлений прийти к обобщению, которые затем применяются на практике. Применение различных средств наглядности активизирует учащихся, возбуждает их внимание и тем самым помогает их развитию, способствует более прочному усвоению материала, дает возможность экономить время. Тот факт, что математике присуща большая абстрактность, определяет и характер средств наглядности, и особенности применения их [1, с. 165]. В таких учебных предметах, как естествознание, история, география, наглядные пособия чаще всего используются для показа изучаемых объектов. Чтобы учащиеся могли составить наиболее правильное, наиболее полное представление о животном или растении, о том или ином событии, о природном явлении и т.п., все это необходимо показать в возможно более естественном виде и так, чтобы хорошо были различимы все нужные детали.
В начальном обучении математике используются различные виды наглядных пособий:
Предметы окружающей среды. С первых же дней пребывания детей в школе при обучении их счету и действиям сложения и вычитания, предметы окружающей обстановки могут быть использованы в качестве счетного материала. Таким материалом могут служить книги, тетради, карандаши, счетные палочки и т. д. Отдельные предметы могут быть использованы и в дальнейшем: при ознакомлении учащихся с элементами геометрии. На них можно показывать различные пространственные формы.
Демонстрационные изобразительные пособия. К этому виду наглядных пособий относятся, прежде всего, картины и учебные таблицы с изображением ряда знакомых детям предметов, наборы картинок, картины со вставками, аппликации. Используются как счетный материал, что значительно расширяет возможности учителя при обучении детей счету, или для иллюстрирования задач. К демонстрационным изобразительным пособиям относятся также модели измерительных приборов и инструментов (часовой циферблат, весы), модели мер ( метра, литра), муляжи и макеты хорошо известных детям товаров. Модели используются при изучении мер и обучении измерениям. А муляжи и макеты – как иллюстративный материал при составлении задач. Наконец, к демонстрационным изобразительным пособиям относятся изображения и модели различных геометрических фигур.
Таблицы. Таблицами называют текстовые или числовые записи, располагаемые в определенном порядке. Чаще всего в виде колонок, а также сгруппированные вместе серии рисунков и схем с текстом или без него. Таблицы издаются на больших листах бумаги, наклеенных для удобства пользования на ткань или картон.
Иллюстрации. Под иллюстрациями обычно понимают помещенные в учебнике рисунке и схематические изображения различных предметов и групп предметов. А также планы, чертежи, схемы, таблицы, как и рассмотренные выше наглядные демонстрационные пособия, иллюстрации используются в самых различных случаях. С их помощью наглядно показываются предметы, о которых идет речь, выполняемые действия или разъясняется содержание задачи.
При необходимости иллюстрации к отдельным задачам могут быть сделаны на больших листах бумаги или в виде диапозитивов. В настоящее для каждого класса издаются серии карточек с математическими заданиями, включающие иллюстрации. Эти карточки предназначаются для обучения составлению и решению задач.
Дидактический материал. Для формирования математических понятий, а также для выработки вычислительных, измерительных и графических навыков в начальных классах необходимо использовать разнообразный дидактический материал. Дидактическим материалом по математике называют учебные пособия для самостоятельной работы учащихся, позволяющие индивидуализировать и активизировать процесс обучения. Дидактический материал по математике можно подразделить на [33, с.179]:
а) предметный дидактический материал;
б) дидактический материал в виде карточек с математическими заданиями.
К предметному дидактическому материалу относятся: счетные палочки, наборы разнообразных геометрических фигур, модели монет и т. п. Предметный материал необходимо использовать как при объяснении новых знаний, так и при их закреплении.
Дидактический материал в виде карточек с математическими заданиями обеспечивает приспособление к индивидуальным особенностям учащихся. Некоторые виды карточек позволяют освободить учащихся от переписывания заданий, что дает возможность выполнить больше упражнений. В процессе обучения наглядные пособия используют с различными целями: для ознакомления с новым материалом, для закрепления знаний, умений, навыков, для проверки их усвоения.
Когда наглядное пособие выступает как источник знаний, оно особенно должно подчеркивать существенное то, что является основой для обобщения, а также показывать несущественное, его второстепенное значение.
Знакомя с новым материалом, нужно использовать наглядное пособие с целью конкретизации сообщаемых знаний. В этом случае наглядное пособие выступает как иллюстрация словесных объяснений.
При ознакомлении с новым материалом и особенно при закреплении знаний и умений надо так организовать работу с наглядными пособиями, чтобы учащиеся сами оперировали ими и сопровождали действия соответствующими пояснениями: объединяли множества предметов при изучении сложении, моделировали замкнутые и ломаные незамкнутые линии, пользуясь палочками [31, с.57].
Качество усвоения материала в большинстве случаев значительно повышается, так как в работу включаются различные анализаторы(зрительные, двигательные, речевые, слуховые). При этом дети овладевают не только математическими знаниями. Но и приобретают умения самостоятельно использовать наглядные пособия. Учитель должен всячески поощрять детей к использованию наглядных средств, к самостоятельной работе.
Наглядные пособия иногда используют для проверки знаний и умений учащихся. Это делается так: – чтобы проверить, как усвоили дети понятие многоугольник, можно предложить с помощью палочек сложить многоугольник указанного вида. Используя раздаточный дидактический материал, учитель проверяет умения измерять длину отрезков, площадь, периметр многоугольников и др.
Использование средств наглядности развивает бережное отношение к диалектическому материалу. Красиво оформленное наглядное пособие, выполненное руками учителя, старшеклассников или собственными, сознание того, что им будут пользоваться и другие, заставляет учащихся бережно относиться к нему.
Большое значение имеет изготовление учащимися наглядных пособий: раздаточного материала, трафаретов различных фигур, абаков и других. Данная работа развивает пространственные представления и вооружает школьников с нарушенным зрением практическими навыками.
Применение наглядности на уроках математики дает возможность решать наряду с образовательными, воспитательными, практическими и задачи коррекционные. Наглядные средства в тесном сочетании со словом учителя формируют правильные, четкие представления ученика с дефектами зрения, уточняют имеющиеся представления, развивают его внимание и воображение. Работа с пособиями индивидуального и демонстрационного пользования позволяет учителю осуществлять коррекцию недостатков предметно-практической деятельности учащихся в процессе обучения.
Важным условием эффективности использования наглядных пособий является применение на уроке достаточного и необходимого количества наглядного материала. Если наглядные средства применять там, где этого совсем не требуется, то они играют отрицательную роль, уводя детей в сторону от поставленной задачи. Подобные факты встречаются в практике: например, первоклассник обучается выбору арифметического действия при решении арифметических задач. Если привлечь для этой цели картинку, на которой нарисованы птички, сидящие на ветке и подлетающие к ним, ученик, глядя на эту картинку, находит ответ задачи простым пересчитыванием, не выполняя никакого арифметического действия над числами. Наглядность, использованная в этом случае, не только не помогает, но наоборот, задерживает формирование умения решать задачи, т. е. выбирать действие над числами, данными в условии [27, с.58].
При изучении нумерации чисел в пределах десяти учащиеся должны усвоить способы образования каждого числа, порядок следования чисел, название их. Раскрыть способы образования чисел поможет учащимся оперирование с различным наглядным материалом. Учащиеся выполняют упражнения в присчитывании и отсчитывании предметов по одному. Работу следует осуществлять фронтально, каждый ученик выполняет задание на месте, а в классе слабовидящих одновременно ведется оперирование с предметами у доски. При такой организации развивается самостоятельность в выполнении действий, формируются навыки самоконтроля. Ученик, выполняя определенную операцию с предметами, с самых первых дней учится проверять как конечный, так и промежуточные результаты. Данное обстоятельство является особенно важным для детей с тяжелыми расстройствами зрения в силу ограниченных возможностей зрительного восприятия.
Есть несколько методических условий, выполнение которых обеспечивает успешное использование наглядных средств [21, с.248]:
Хорошее обозрение, которое достигается путем применения соответствующих красок при изготовлении подъемных столиков, экранов подсвечивания, указателей и тому подобное.
Четкое выделение главного, основного при показе иллюстраций, так как они могут содержать и отвлекающие моменты.
Детальное продумывание пояснений, необходимых для выяснения сущности демонстрируемых явлений, а так же для обобщения усвоенной учебной информации.
Привлечение самих учеников к нахождению желаемой информации в наглядном пособии или демонстрационном устройстве, постановка перед ними проблемных заданий наглядного характера.
Из различных видов наглядности – натуральной, изобразительной, символической – широкое применение в обучении математике находит символическая наглядность (чертежи, графики, схемы, таблицы) [32, с. 70]
Изучая математику в начальных классах, младшие школьники усваивают ряд сложных понятий: понятие числа, понятия арифметических действий, законов арифметических действий, понятие уровня, равенства, неравенства и других, которые связаны с отвлеченным, абстрактным мышлением учащихся. К его развитию, к образованию общих математических понятий «надо идти, отправляясь от наглядного обучения, которое опирается на восприятия и ощущения, идущие от предметного, объективного мира, что и называют в школьной практике наглядностью, наглядными пособиями» [32, с. 168].
Знание видов наглядных пособий дает возможность учителю правильно их подбирать и эффективно использовать при обучении, а также изготовлять самому вместе с детьми необходимые наглядные пособия.
На уроке математики интересно проходит работа с перфокартами, которая помогает младшему школьнику лучше усвоить состав чисел первого десятка, изучить приемы сложения и вычитания. Для этой работы заранее для каждого ученика силами родителей и учащихся необходимо сделать карточки. В верхней части карточки – рисунок с изображением, каких – либо предметов и число, состав которого изучается на уроке. В нижней части, в «окошечках» записаны цифры, входящие в состав данного числа, причем дается только одна составная его часть. Другую должны заполнить учащиеся, наложив карточку из своей кассы цифр на пустое «окошечко». Задания могут быть самыми различными.
Например:
Как по-разному можно разложить 9 орехов в 2 кармана?
Сколько надо доложить до 6 орехов, чтобы их стало 9?
Сколько орехов надо взять у 9, чтобы их стало 5?
7 орехов – это 9 без скольких?
9 орехов – это 8 и сколько?
Сколько из 9 орехов ты должен отдать товарищу, чтобы у тебя осталось 4? И т. д.
У каждого ученика имеется целый набор таких карточек на состав чисел 2 -10, и младшие школьники очень любят работать с ними.
Перфокарты можно изготовлять в различных вариантах. Очень интересный вариант – перфокарта в виде домика.
В работе с ней ученики выполняют задания: в прорези «окошечек» вставляют карточки с цифрами, соответствующими составу заданного числа.
Использование наглядности является хорошим средством, стимулирующим деятельность учащихся. Оно не только активизирует мыслительную деятельность детей, повышает их работоспособность, но и воспитывает у них аккуратность, терпение.
Выбирая наглядные пособия, обязательно надо стремиться к тому, чтобы оно способствовало достижению учебно-воспитательной Цели: закреплению и углублению знаний, воспитанию внимания, сообразительности, выдержки.
Таким образом, на уроках математики в начальной школе наглядные пособия используются с различными целями: для ознакомления с новым материалом, для закрепления знаний, умений, навыков, для проверки их усвоения.
Успех учебно-воспитательного процесса зависит и от того, в какой степени учащиеся будут обеспечены необходимыми наглядными пособиями и индивидуальными средствами обучения, активизирующими познавательную деятельность. Многие пособия учителя делают сами, стараясь, чтобы они были достаточно красочными и привлекательными, достаточно крупными, чтобы дети их хорошо видели. Пособие изготавливают таким образом, чтобы служили они не на одном, а на многих уроках в различных вариантах и комбинациях.
Следующая глава будет посвящена экспериментальной работе по использованию наглядных пособий в процессе изучения чисел первого десятка.
Глава 2. Экспериментальная работа по использованию наглядных пособий в процессе изучения чисел первого десятка
2.1 Диагностика уровня математического развития детей младшего школьного возраста
Для проведения экспериментальной работы нами были выбраны 2 «А» и 2 «Б» классы, из которых и сформированы две подгруппы – экспериментальная и контрольная – по 8 человек с приблизительно одинаковым уровнем развития математических представлений.
Вначале была проведена диагностика уровня развития детей по трем разделам программы математического развития:
– Количество;
– Величина;
– Счет, число.
За основу диагностики были взяты, прежде всего, результаты наблюдений за ребенком на уроках, а также диагностические методики, предложенные А.В. Белошистой:
– Сосчитай, сколько здесь кругов (5 кругов расположены в беспорядке).
– Сосчитай, сколько здесь квадратов (4 квадрата расположены в ряд).
– Где фигур больше: там, где 5, или там, где 4?
– Что можно сосчитать в группе? Сосчитай.
– А дома что у тебя можно сосчитать? Вспомни, сосчитай и скажи сколько?
– Возьми круги (4) и квадраты (5). Как узнать, поровну ли их? Или квадратов больше, чем кругов? Какое число больше: 4 или5? Какое число меньше: 5 или 4?
– Ребёнку предлагается посчитать (5) маленьких матрёшек и (5) больших мишек. Каких предметов больше: маленьких матрёшек или больших мишек; Как проверить?
– Ребёнку предлагается посчитать квадраты (4), расположенные по кругу и в линию. Где меньше квадратов: там, где они расположены в линию или по кругу? Как проверить?
– Ребёнку предлагается посчитать грибы (5), расположенные близко и далеко друг к другу. Где грибов больше: там, где они стоят близко или далеко друг от друга?
К высокому уровню развития отнесены те дети, которые владеют навыками сосчитывания предметов (до 8-10), обнаруживают зависимости и отношения между числами. Владеют навыками наложения и приложения предметов с целью доказательства их равенства и неравенства. Устанавливают независимость количества предметов от их расположения в пространстве путём сопоставления, сосчитывания предметов (на одном и том же количестве предметов). Осмысленно отвечают на вопросы, поясняют способ сопоставления, обнаружения соответствия.
Ученики со средним уровнем развития в достаточной степени владеют навыками сосчитывания предметов (до 4-7), пользуясь при этом приёмами наложения и приложения с целью доказательства равенства и неравенства. С помощью взрослого устанавливают независимость количества предметов от их расположения в пространстве. Но затрудняются в высказываниях и пояснениях.
Низкий уровень развития диагностирован у тех учащихся, которые допускают ошибки при сосчитывании предметов (до 3-5), не обнаруживают зависимости и отношений между числами. Плохо владеют приемами наложения и приложения; даже с помощью взрослого с трудом устанавливают независимость количества предметов от их расположения в пространстве.
В результате сравнительного анализа диагностических данных видно, что перед началом эксперимента в обеих группах высокий уровень развития составил 17%, средний – 58%, а низкий – 25%.
Данные об уровне развития представлены в таблице 1.
Таблица 1
Результаты констатирующего этапа эксперимента
Высокий уровень
Для наглядности представим результаты диагностики на рисунке 1.
Рис.1 Результаты констатирующего этапа эксперимента
Наблюдение показало, что учащиеся лучше всего освоили сравнение предметов по величине и групп предметов по количеству. Большинство успешно справляется со сравнением множеств, с сопоставлением элементов одного множества с элементами другого, различают равенство и неравенство групп предметов, составляющих множество.
Наиболее высокий уровень усвоения материала связан у младших школьников с развитием первоначальных представлений о величине предметов контрастных и одинаковых размеров по длине, ширине, высоте, толщине, объему. Также группировка предметов по признакам вырабатывает у учащихся умение сравнивать, осуществлять логические операции классификации.
В процессе разнообразных практических действий с совокупностями дети хорошо усвоили и большинство умеет использовать в речи простые слова и выражения, обозначающие уровень количественных представлений: много, один, по одному, ни одного, совсем нет, мало, такой же, одинаковый, столько же, поровну; столько, сколько; больше, чем; меньше, чем; каждый из, все, всех.
Трудности у большинства испытуемых вызвали навыки устного счета и знакомство с числами. Слабо сформировано понятие о возникновении каждого нового числа путем добавления единицы.
Низкий уровень развития младшие школьники показали также при освоении таких приемов, как сравнение двух чисел, сопоставление, установление равенства и неравенства их. Почти все школьники испытывают трудности в умении отличать порядковый счет от количественного, хотя с порядковым счетом в пределах 1 – 5 справилось большинство учащихся.
Таким образом, на констатирующем этапе эксперимента сформированы две группы детей младшего школьного возраста – экспериментальная и контрольная – с приблизительно равным уровнем развития элементарных математических представлений; заполнены диагностические карты на начало эксперимента; выявлены наиболее слабые показатели уровня математического развития в целом по разделу и по отдельным его частям. Для проверки эффективности использования наглядных пособий в процессе изучения чисел первого десятка нами был проведен формирующий этап эксперимента, о котором пойдет речь в следующем параграфе.
2.2 Организация работы по использованию наглядных пособий в процессе изучения чисел первого десятка
Одним из центральных понятий начального курса математики является понятие натурального числа. Оно трактуется как количественная характеристика класса эквивалентных множеств. Это понятие раскрывается на конкретной основе в результате практического оперирования множествами и величинами. При изучении нумерации натуральное число получает дальнейшее развитие: оно выступает как элемент упорядоченного множества или как член натуральной последовательности. При изучении арифметических действий натуральное число выступает в новом качестве – в качестве объекта, над которым выполняются определенные арифметические действия. Урок представляет собой цепочку последовательных Действий ученика и учителя, направленных на сознательное усвоение знаний, на формирование умений и навыков.
В настоящее время одно из центральных мест в уроке отводится той деятельности учителя и учащихся, которая связана с использованием наглядных пособий, дидактического материала, технических средств обучения. Функции этих средств обучения многообразны, но в основном они заключаются в том, чтобы помогать раскрывать содержание и объем новых понятий, закреплять изучаемый материал, быть средством контроля, обеспечивать активную самостоятельную учебную деятельность учащихся начальной школы.
Система упражнений должна обеспечить наглядную основу формируемого понятия на данном уроке.
Рассмотрим, как можно знакомить учащихся первого класса со связью между суммой и слагаемым, подводя их к выводу индуктивным путем. Используется беседа: «Возьмите четыре синих кружочка, положите к ним три кружочка красных. Сколько получилось? (7) Как узнали? (к 4+3) Давайте запишем. 4+3=7. »
Так в нашем примере учащиеся объединяли два множества кружков и выполняли запись 4+ 3=7. Затем удалить часть множества и снова записать соответствующее арифметическое действие: 7- 3=4 или 7 – 4=3. это и является наглядной основой для «открытия» ими связи: если из суммы вычесть одно из слагаемых, то получим другое слагаемое.
Учитель должен уметь в зависимости от степени подготовленности учащихся своего класса вовремя ограничить применение средств наглядности или заменить ее формы в процессе знаний, формирование умений и навыков.
Самым распространенным видом наглядности является чертеж учителя на доске. Чертеж на доске учитель выполняет постепенно в присутствии учащихся, этим объясняется высокая эффективность его воздействия в процессе обучения. Во время выполнения чертежа учащиеся получают возможность внимательно следить за объяснением учителя, за его пояснениями к чертежу. Заранее выполненный чертеж менее эффективен, хотя и требует меньших затрат времени.
Чертеж используется учителем для ознакомления детей с построением геометрических фигур, составления схем к заданиям и тому подобное.
Эти виды традиционной наглядности просты в графическом отношении, доступны для восприятия, требуют минимальной затраты времени для их создания.
В ходе нашего исследования выдвигалась гипотеза, что систематическое, целенаправленное использование наглядных пособий на уроке повысит качество новых знаний и уровень сформированности умений и навыков.
Работу проводили параллельно в каждом классе с использованием специально подобранными наглядными пособиями. Уроки в контрольной группе – с минимальным набором наглядности.
В конце каждого урока давали самостоятельную работу на закрепление изученного материала. Цель этих самостоятельных работ – проверка качества усвоения знаний, уровня сформированности умений и навыков, отрабатываемых на данном уроке.
После проведения нескольких уроков по данной теме в обеих группах сделали анализ самостоятельных работ, который помог выявить, как влияют наглядные пособия на качество усвоения знаний, умений и навыков.
На примере одного из серии проведенных уроков рассмотрим влияние наглядности на качество знаний, уровень сформированности умений и навыков. Конспекты фрагментов урока с использованием наглядных пособий и с минимальным их использованием, которые можно провести в экспериментальной и контрольной группах даны в нашей работе в приложении.
Тема данных уроков: «Числа 1,2,3,4,5,6.».
В конце каждого из уроков можно провести самостоятельную работу, целью которой является выяснить, как усвоено знание натурального ряда чисел, как сформировано умение сравнивать числа, как понято и усвоено основное свойство натурального ряда чисел.
Самостоятельная работа включала в себя следующие знания:
задание – проверялось знание натурального ряда чисел.
А. Записать число, следующее при счете за числом четыре.
Б. Записать число, предшествующее числу три.
В. записать соседей числа пять.
задание – проверялось, как усвоено основное свойство натурального ряда чисел.
Вычисли:
А. 4+1 В. 5+1
Б. 2+1 Г. 3+1
задание – проверялось умение сравнивать два числа.
>
а. 3…4 б. 2…2 в. 6…5
После проверки работ учащихся обеих групп был сделан поэлементный анализ, в ходе которого выяснилось, что учащиеся в контрольной группе допустили ошибок больше, чем учащиеся в экспериментальной.
Таблица 2
Анализ результатов самостоятельной работы
Фрагменты конспекта урока с использованием наглядных средств обучения.
Тема: Числа 1, 2, 3, 4, 5, 6.
Цели: 1. Формирование понятия числа 6. Познакомить с образованием числа 6, с цифрой 6.
Продолжать обучение счету.
Упражнять в сравнении чисел.
Упражнять в письме цифры 6.
2.Воспитывать усидчивость, дисциплинированность.
3. развивать логическое мышление.
Оборудование: 1. Набор цифр и знаков.
2. Наборное полотно.
3. Касса цифр и букв.
4. Счетные палочки.
5. Набор кубиков
5. Натуральный ряд чисел.
6. Предметные картинки для счета.
Ход урока:
Наглядные пособия, используемые на этапе повторения:
а. Счетный материал для повторения состава чисел:
Положите перед собой 3 красных кружка.
Сколько кружков надо добавить, чтобы получилось 4 кружка?
Положите 3 треугольника, добавьте еще столько, чтобы получилось 5 треугольников.
Положите 5 картинок с огурцами.
Что надо сделать чтобы получилось 4 огурца?
б. Натуральный ряд чисел (на доске, на плакате)
1 2 3 4 5 6 7 8 9 10
Назовите соседей числа 3; 8.
Какое число предшествует при счете числу 6, числу 2, числу 10?
Какое число следует при счете за числом 5, 1, 7?
в. Карточки с цифрами.
г. Сигнальные знаки. Правильно + ; неправильно –
1. 5 – 1 = 4 2. 4 – 2 = 3 3. 4 + 1 = 5
Наглядные пособия, используемые на этапе изучения нового материала:
а. Образование числа 6 (карточки, счетный материал)
Покажите, как имея 5 квадратов, выставленных на наборном полотне сделать так, чтобы их стало 6? (Добавляют еще квадрат)
Давайте запишем пример 5 + 1 = 6
Кто может найти эту цифру ? (Находят карточку с цифрой 6)
б. Кубики.
Составляются столбиком кубики по 5 и 6 штук для сравнения чисел 5 и 6.
Сколько красных кубиков? – 5
А синих? – 6
Каких кубиков больше? – синих
На сколько синих кубиков больше, чем красных? – на один.
А на сколько красных кубиков меньше, чем синих? – на один.
Какое число больше 5 или 6? – 6
Запишем! 6 5
Какое число меньше? – 5
Запишем! 5 6
Наглядные пособия, используемые на этапе закрепления:
а. У Маши 6 яблок (на наборном полотне).
0 + 6 = 6
1 + 5 = 6
2 + 4 = 6
3 + 3 = 6
4 + 2 = 6
5 + 1 = 6
6 + 0 = 6
Закрепляют состав числа 6.
б. На одной тарелке 6 огурцов на другой 5.
Фрагменты конспекта урока с минимальным использованием наглядных средств обучения.
Тема: Числа 1, 2, 3, 4, 5, 6.
Цели: 1. Формирование понятия числа 6. Познакомить с образованием числа 6, с цифрой 6.
2.Воспитывать усидчивость, дисциплинированность.
3. развивать логическое мышление.
Оборудование: 1. Набор цифр и знаков.
2. Наборное полотно.
3. Касса цифр и букв.
4. Счетные палочки.
5. Набор кубиков
5. Натуральный ряд чисел.
6. Предметные картинки для счета.
Ход урока:
1.Повторение устно.
А. Состав числа:
4 это 3 и …
2 и …
б. – Сколько надо прибавить к 3, чтобы получилось 5?
в. – Назовите соседей чисел 4, 7, 9.
Какое число предшествует при счете числу 8, 2, 5?
Какое число следует за 3, 6, 9?
г. Сколько у меня яблок? (картинки) (хором) 3, 5, 1.
2. Изучение нового материала.
а. У меня 5 кружков. Что надо сделать чтобы их стало 6? (добавить еще один)
Запишем 5 + 1 = 6
б. «>», «
5 6 2 1 4 4
3 5 6 6 2 4
3. Закрепление.
6 + 0
5 + 1
4 + 2
3 + 3
2 + 4
1 + 5
0 + 6
Записывают все получившиеся примеры.
После завершения психолого-педагогического эксперимента нами была проведена повторная диагностика уровня развития математических представлений у детей в экспериментальной и контрольной группах и сопоставлены полученные результаты.
Для этой цели в обеих группах использовались те же методики, что и на констатирующем этапе эксперимента, а также наблюдение за изменениями знаний и умений учащихся на занятиях и в блоке совместной деятельности с педагогом.
В результате сравнительного анализа уровня математического развития испытуемых установлено, что в экспериментальной группе за время проведения эксперимента показатели высокого уровня увеличились на 28% (с 17% до 45%) , тогда как в контрольной группе – только 12% (с17% до 29%).
Также выявлено, что показатель низкого уровня развития детей в экспериментальной группе уменьшился на 16% (с 25% до 9%), а в контрольной группе – на 12% (с 25% до 13%).
При изучении диагностических данных по разделам РЭМП можно видеть, что в экспериментальной группе в отличие от контрольной группы за период экспериментальной деятельности по всем разделам наблюдается более значительное улучшение показателей. В экспериментальной группе заметно возрос высокий уровень развития, а изменение низкого уровня близко по показателям к контрольной группе.
Учащиеся экспериментальной группы показали лучшую сформированность общих математических представлений, стали лучше владеть навыками счета, сравнением двух множеств, выраженных смежными числами. У них более развито умение устанавливать равенство и неравенство групп предметов, когда предметы находятся на различном расстоянии друг от друга, когда они различны по величине и т.д. То есть дети экспериментальной группы более приближены к пониманию абстрактного числа.
Кроме того, они используют более разнообразные методы при группировке предметов по признакам, что вырабатывает у детей умение сравнивать, осуществлять логические операции классификации.
В обеих группах – и экспериментальной, и контрольной – у школьников сформировались понятия о порядковом и количественном счете, ими освоены такие приемы, как сравнение двух чисел, сопоставление, установление равенства и неравенства их, счет по осязанию, счет на слух и счет различных движений в пределах 5. Но дети экспериментальной группы лучше овладели приемом отсчитывания предметов из большего количества, а также усвоили значение порядковых числительных. Это говорит об эффективности использования наглядных пособий в процессе изучения младшими школьниками чисел первого десятка.
Таким образом, в результате теоретического изучения данного вопроса и проведенной практической экспериментальной работы можно сделать вывод о том, что более эффективное и рациональное применение наглядных пособий при проведении занятий по развитию элементарных математических представлений у младших школьников позволяет заметно улучшить качество и продуктивность данной работы.
Заключение
Принцип наглядности это один из самых известных и интуитивно понятных принципов обучения, использующийся с древних времен. Закономерное обоснование данного принципа получено сравнительно недавно. В основе его лежат следующие строго зафиксированные научные закономерности: органы чувств человека обладают разной чувствительностью к внешним раздражителям. У большинства людей наибольшей чувствительностью обладают органы зрения, которые «пропускают» в мозг почти в 5 раз больше информации, чем органы слуха, и почти в 13 раз больше, чем тактильные органы.
Наглядность особенно важна в обучении математике ввиду того, что здесь требуется достижение более высокой ступени абстракции, чем в обучении другим предметам, а она содействует развитию абстрактного мышления (при правильном ее применении).
Анализ педагогической и методической литературы позволяет утверждать, что успех обучения во многом зависит от методов обучения с использованием наглядных пособий, что характер наглядных пособий существенно влияет на понимание учебного материала, определяет содержание и структуру урока.
Опора на чувственные образы, ощущения и восприятие ребенка при использовании наглядных пособий создает своеобразную структуру познавательной деятельности ученика. Ребенок мыслит образно, конкретно, и это создает хорошую основу для формирования абстракции и понимания изучаемых теоретических положений при помощи наглядных пособий.
Наглядные пособия одним из главных средств обучения младших школьников на протяжении всего учебно-воспитательного процесса. Использование наглядности на уроках в начальных классах обусловлено психофизиологическими особенностями учащихся данной возрастной группы.
Наглядные пособия по математике делятся на демонстрационные пособия (крупные) и индивидуальные (маленькие). Наглядные пособия подразделяются на две группы: группа средств предметно-образной наглядности и группа средств знаковой наглядности.
Практическое использование наглядных пособий на уроках математики в начальных классах очень широко. Некоторые виды работ с использованием наглядности на уроках математики в начальной школе даны в работе.
В результате работы нами было рассмотрено понятие «наглядные пособия» в психолого-педагогической литературе, определены особенности восприятия младшими школьниками наглядных пособий, выявлены условия использования наглядных пособий в процессе изучения математики в начальной школе.
В ходе исследования был предложен эксперимент. Он был направлен на подтверждение или опровержение гипотезы об эффективности использования наглядных пособий в процессе изучения числе первого десятка.
На констатирующем этапе эксперимента был определен уровень развития математических представлений учащихся двух вторых классов, из которых затем были сформированы экспериментальная и контрольная группы. После проведения уроков с использованием наглядных пособий в обеих классах были обнаружены значимые отличия в уровне сформированности математических представлений. Учащиеся экспериментальной группы, где наглядные пособия использовались в полной мере, показали более высокий уровень развития математических представлений в результате повторной диагностики, чем учащиеся контрольной группы, где наглядные пособия почти не использовались.
Опыт показывает, что после проведения подобных экспериментов действительно оказывается, что систематическое целенаправленное использование наглядных пособий на уроках математики в начальной школе повышает качество усвоения знаний, уровень сформированности умений и навыков.
Таким образом, задачи, поставленные в начале работы, нами были решены, цель исследования достигнута, гипотеза подтверждена.
Библиография
1. Актуальные проблемы методики обучения математике в начальных классах/ под ред. М.И. Моро, А.М. Пышкало. – М.: Педагогика, 1977. – 262 с.
2. Артемов, А.К. Обучение математике [Текст]/А.К.Артемов. – Пенза, 1995. – С.143.
3. Бантова, М.А. Методика преподавания математики в начальных классах. Учеб. пособие для учащихся педучилищ [Текст]/М.А.Бантова. – М.: Просвещение, 1984. – 335 с.
4. Бантова, М.А. Методика преподавания математики в начальных классах [Текст]/М.А.Бантова, Г.В.Бельтюкова. – М.: Просвещение, 1984. – 335 с.
5. Белошистая, А.В. Методика обучения математике в начальной школе: курс лекций: учеб. пособ. для студ. высш. пед. учеб. Заведений [Текст] / А.В.Белошистая. – М.: Гуманит. изд. центр ВЛАДОС, 2005. – С. 80-100.
6. Волошкина, М.И. Активизация познавательной деятельности младших школьников на уроке математики [Текст]/М.И.Волошкина // Начальная школа. – 1992. – № 9/10. – С. 15-18.
7. Выготский, Л.С. Педагогическая психология/ под ред. В.В. Давыдова [Текст] /Л.С.Выготский. – М.: Педагогика, 1991. – 479с.
8. Гальперин, П.Я. К вопросу о формировании начальных математических понятий. Сообщения I – V [Текст]/П.Я.Гальперин, Л.С.Георгиев // Доклады АПН РСФСР, 1960.- № 1.-С. 3,4-6.
9. Жильцова, Т.В. Поурочные разработки по наглядной геометрии: 1 – 4 класс [Текст]/Т.В.Жильцова, Л.А.Обухова. – М.: ВАКО, 2004. – 288с. (В помощь школьному учителю).
10. Иванова, Т.Т. Некоторые визуальные средства на уроках математики [Текст] /Т.Т.Иванова, Н.А.Резник // Начальная школа. – 1995. – № 5. – С.23.
11. Истомина, Н.Б. Активизация учащихся на уроке математики в начальных классах [Текст]/Н.Б.Истомина. – М.:Просвещение, 1986.- С.234.
12. Истомина, Н.Б. Методика обучения математике в начальных классах [Текст]/Н.Б.Истомина. – М.:Издательский центр «Академия», 1998. – 288 с.
13. Истомина, Н.Б. Методика обучения математике в начальных классах: учеб. пособие для студ. сред. и высш. пед. учеб. Заведений [Текст] / Н.Б.Истомина. – М.: Изд. центр «Академия», 1999. – С. 62-63.
14. Истомина, Н.Б. практикум по методике преподавания математики в начальных классах [Текст]/Н.Б.Истомина. – М.:Просвещение, 1986.- С.334.
15. Кабанова, Е.Н.– Меллер. Формирование приемов умственной деятельности и умственное развитие учащихся [Текст]/Е.Н.Кабанова. – М.:Просвещение, 1968.-С. 311.
16. Каган, В.Ф. О свойствах математических понятий [Текст]/В.Ф.Каган. – М.: Наука, 1984. – 144 с.
17. Коджаспирова, Г.М. Технические средства обучения и методика их использования. Учеб. пособие для студ. высш. пед. учеб. Заведений [Текст] / Г.М.Коджаспирова, К.В.Петров.- М.: Академия, 2002.- 256с.
18. Коменский, Я.А. Великая дидактика. Из пед. соч. Т.1[Текст]/Я.А.Коменский. – М.: Педагогика, 1974.- С.217.
19. Люблинская, А.А. Учителю о психологии младшего школьника [Текст] / А.А.Люблинская. – М.: Просвещение, 1986.- 423с.
20. Максимов, В.Г. Педагогическая диагностика в школе: Учеб. пособие для студ. высш. учеб. Заведений [Текст]/В.Г.Максимов. – М.: Издательский центр «Академия», 2002. – 272 с.
21. Моро, М.И. Средства обучения математике в начальных классах: Пособие для учителя [Текст]/М.И.Моро, А.М.Пыткало. – М.:Просвещение, 1981.- С.335.
22. Моро, М.И. Методика обучения математике в 1 – 3 классах. Пособие для учителя [Текст]/М.И.Моро, А.М.Пышкало. М.: Просвещение, 1975. – 304с.
23. Моро, М.И., Пышкало А.М. Средства обучения математике в начальных классах [Текст]/М.И.Моро, А.М.Пышкало. – М.: Просвещение, 1989. – С.315.
24. Петерсон, Л.Г. Математика 2 класс. Методические рекомендации. Пособия для учителей [Текст]/Л.Г.Петерсон. – М.:Просвещение, 1996.- 423 с.
25. Подласый, И.П. Педагогика: Новый курс: Учеб. для студ. высш. учеб. заведений: В 2 кн. [Текст]/И.П.Подласый. – М.: Гуманит. Изд. центр ВЛАДОС, 2001. – Кн. 1: Общие основы. Процесс обучения. – 576 с.
26. Практикум по методике преподавания математики в начальных классах: Учеб. пособие для студентов пед. ин-тов / Н.Б. Истомина, Л.Г. Латохина, Г.Г. Шмырева. – М.: Просвещение, 1986. – С. 38-48.
27. Пышкало, А.М. Средства обучения математике [Текст]/А.М.Пышкало. – М.: Просвещение, 1980.- С.358.
28. Селевко, Г.К. Современные образовательные технологии: Учеб. пособие [Текст]/ Г.К. Селевко. – М.: Народное образование, 1998. – 256 с.
29. Скаткин, Л.Н. Методика начального обучения математики [Текст] / Л.Н.Скаткин. – М.:Просвещние, 1972. – С.217.
30. Смирнова Л.В. Приемы работы при изучении темы «Сложение и вычитание чисел 1-10» [Текст]/В.В.Смирнова // Начальная школа плюс До и После. – 2006. – № 9. – С. 46-48.
31. Смолеусова, Т.В. Наглядные пособия на уроках математики [Текст] / Т.В.Смолеусова // Журнал «Начальная школа» № 4.- 2001.
32. Соколова, А. В. Наглядные средства и их значение для повышения эффективности обучения слабовидящих учащихся младших классов: Методические рекомендации [Текст]/А.В.Соколова. – Л.:Лениздат, 1979.- С.334.
33. Средства обучения математике в начальных классах. Сборник статей. М., 1981.
34. Столяр, А.А. Педагогика математики: Учеб. пособие для физ.-мат.фак. пед . ин-тов [Текст]/А.А.Столяр. – Мн.: Выш.шк., 1986. – 414с.
35. Теоретические основы методики обучения математике в начальных классах: Пособ. для студ. фак. подгот. учителей нач. классов заочн. отделений / Под ред. Н.Б. Истоминой. – М.: Изд-во «Ин-т практической психологии»; НПО «МОДЭК», 1996. – С. 121-132, 136-143.
36. Фаддейчева, Т.И. Обучение устным вычислениям [Текст] / Т.И.Фаддейчева// Начальная школа. – 2003. – № 10. – С.16.
37. Целищева, И.И. Карточки для профилактики и диагностики ошибок в вычислениях [Текст]/И.И.Целищева// Начальная школа плюс До и После. – 2006. – № 2. – С. 50-53.
38. Шергина, В.В. Цвет и форма наглядных пособий [Текст]/В.В.Щергина // Журнал «Начальная школа».- № 5.- 1997.
39. Эрдниев, П.М. Теория и методика обучения математике в начальной школе [Текст]/П.М.Эрдниев, Б.П.Эрдниев. – М.:Просвещение, 1999. – С.23.
Средний уровень
Низкий уровень
17%
58%
25%
Типичные ошибки
Незнание следования чисел в натуральном ряду
Не знание свойств натурального ряда
Не умение сравнивать два натуральных числа
К-во учащихся

К-во учащихся

К-во учащихся

Экспериментальная
группа
3
25
2
17
3
25
Контрольная
группа
7
58
7
58
6
50
Знакомство с числами 2-го десятка. Состав чисел — презентация на Slide-Share.ru 🎓
1
Первый слайд презентации: Знакомство с числами 2-го десятка. Состав чисел

Выполнили: Шарапаева Наталья, Шилова Владлена

Изображение слайда
2
Слайд 2: Математические основы:

Система счисления – это язык для наименования, записи чисел и правила действий над числами. Различают позиционные и непозиционные системы счисления. Наша, естественная система счисления – десятичная – является позиционной Позиционной системой счисления называется такая система, в которой значение каждой цифры в изображении числа зависит от ее положения в ряду других цифр, Положение, занимаемой цифрой при письменном обозначении числа называется разрядом. В данной системе для записи любого числа используется десять знаков, называемых цифрами : 0, 1, 2,3, 4, 5, 6, 7, 8, 9 – это математический алфавит.

Изображение слайда
3
Слайд 3: Математические основы:

Изображение слайда
4
Слайд 4: Математические основы:

Изображение слайда
5
Слайд 5: Знакомство детей с числами 2-го десятка

Чтобы понять эту тему ребенок должен: знать цифры от 0 до 9, знать ряд натуральных чисел, умет 1 этап : знакомство детей с десятком как счетной единицей.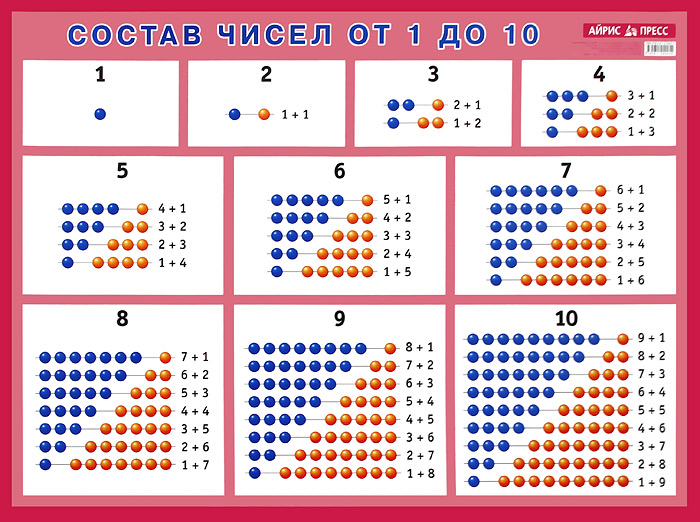 Для этого используют связку из десяти палочек в качестве единицы счета. 2 этап : знакомство с числами второго десятка (от 11 до 20). Знакомство удобно начинать со способа их образования и называния чисел, сопровождая его сначала моделью на палочках, а затем чтением числа по этой модели. Для формирования правильного представления о структуре двузначного числа следует всегда класть десятки слева, а единицы справа. Таким образом ребенок воспринимает правильный образ понятия, без специальных и не всегда понятных объяснений педагога.

Изображение слайда
6
Слайд 6: Знакомство детей с числами 2-го десятка

Задание : положите перед собой 9 палочек, добавьте 1 палочку. Сколько стало? (Десять). Возьмите все палочки в пучок и перетяните резинкой. В пучке десять палочек, и такое количество часто называют десяток. Записывают так: 10. Получили новую единичку измерения – десяток. В старину десяток по-другому называли « дцать ».

Изображение слайда
7
Слайд 7: Образование чисел второго десятка на примере числа «11»

Слово одиннадцать состоит из трёх частей: «один», «на», « дцать ». «ОДИН – НА – ДЦАТЬ» Словом « дцать » в старину называли число десять, поэтому, если одну палочку положить на десять, то получится число одиннадцать. Если к десятку прибавить ещё одну палочку. Сколько палочек станет? Станет одиннадцать палочек. Сколько десятков и единиц в числе одиннадцать? Один десяток и одна единица.

Изображение слайда
8
Слайд 8: Рассмотрим образование других чисел второго десятка

Изображение слайда
9
Слайд 9: Образование числа «20»

Возьмем два десятка палочек. У нас получился ещё один десяток, или дцать. Сколько у нас десятков теперь? Два десятка – двадцать.

Изображение слайда
10
Слайд 10: Сравнение десятков

Сравните два ряда этих чисел и подумайте, чем они отличаются друг от друга. В записи чисел первого ряда присутствует только один значок. То есть, если у нас число один, мы записываем его одной цифрой – 1. Если у нас число два, мы записываем его одной цифрой – 2. Число пять мы записываем одной цифрой – 5. В записи чисел второго ряда присутствуют две цифры. Десять мы записываем двумя цифрами –1 и 0. Двенадцать мы записываем двумя цифрами – 1 и 2. То есть в записи этих чисел мы используем два значка – две цифры. Запишем два ряда чисел.

Изображение слайда
11
Слайд 11: Произношение и запись чисел второго десятка

Когда же мы эти числа записываем, то на первое место мы ставим цифру, которая показывает количество десятков – один десяток, на второе место мы ставим количество свободных единичек, которые мы добавили к десятку. Обратите, внимание на то, что когда мы устно произносим числа второго десятка – десять, одиннадцать, двенадцать, мы сначала называем количество свободных единичек, а потом десяток – дцать.

Изображение слайда
12
Слайд 12: Анализ программы «От рождения до школы»

Содержание образовательной деятельности с детьми 6–7 лет (подготовительная группа) Формирование элементарных математических представлений (Количество, счет) Развивать общие представления о множестве: умение формировать множества по заданным основаниям, видеть составные части множества, в которых предметы отличаются определенными признаками. Упражнять в объединении, дополнении множеств, удалении из множества части или отдельных его частей. Устанавливать отношения между отдельными частями множества, а также целым множеством и каждой его частью на основе счета, составления пар предметов или соединения предметов стрелками. Совершенствовать навыки количественного и порядкового счета в пределах 10. Познакомить со счетом в пределах 20 без операций над числами. Знакомить с числами второго десятка. Закреплять понимание отношений между числами натурального ряда умение увеличивать и уменьшать каждое число на 1 (в пределах 10). Учить называть числа в прямом и обратном порядке (устный счет), последующее и предыдущее число к названному или обозначенному цифрой, определять пропущенное число. Знакомить с составом чисел в пределах 10. Учить раскладывать число на два меньших и составлять из двух меньших большее (в пределах 10, на наглядной основе).

Изображение слайда
13
Слайд 13: Наглядные пособия

Изображение слайда
14
Слайд 14: Наглядные пособия

Изображение слайда
15
Слайд 15: Наглядные пособия

Изображение слайда
16
Слайд 16: Наглядные пособия

Изображение слайда
17
Слайд 17: Усложненные задания (Состав числа )

1. Построение графической, цветовой и числовой модели состава числа 11. Работа с демонстрационным и индивидуальным пособием «Компьютер». Для ограничения 10 кружков на доске нужно провести вертикальную линию, а на парту положить лист бумаги, ограничивающий десяток. В процессе совместной учебной деятельности строится модель числа 11. Учитель прикрепляет полоски при помощи магнитов и рядом записывает равенства, учащиеся размещают полоски на парте (рис. 8).

Изображение слайда
18
Слайд 18: Усложненные задания (Состав числа )

2. Закрепление знаний. Самостоятельная работа в тетради. Учащиеся в тетрадях по клеточкам вычерчивают карандашом модели числа 11 Эта работа дает возможность акцентировать внимание на том, что I слагаемые уменьшаются на 1, а II – увеличиваются на 1, а сумма остается без изменения, и многократно повторить систематизированную информацию, что является необходимым условием запоминания таблицы сложения. Полностью таблица представлена как справочный материал на правом клапане « Суперпапки ».

Изображение слайда
19
Слайд 19: Наглядные материалы

Изображение слайда
20
Слайд 20: Дидактические пособия

Изображение слайда
21
Слайд 21: Дидактические пособия

Татьяна Канашевич : Математика. Числа второго десятка

Изображение слайда
22
Слайд 22: Дидактические наборы

Набор учебных пособий «Изучение счета от 1 до 20» Касса счетных материалов «Учись считать»

Изображение слайда
23
Слайд 23: Прописи/Рабочие тетради

Изображение слайда
24
Слайд 24: Прописи/Рабочие тетради

Изображение слайда
25
Слайд 25: Интегрированные задания

Изображение слайда
26
Слайд 26: ДИДАКТИЧЕСКАЯ ИГРА «НОВОГОДНИЕ ХЛОПОТЫ»

Цель: учить соотносить количество с цифрой; помочь детям закрепить знание состава числа. Как играть: Вариант1 Помоги собрать в дорогу Деда мороза. Надень Снеговику шляпку. Посмотри какая цифра написана на ней. Положи в сани такое же количество подарков. Сколько подарков ты положил в сани? Вариант 2 Помоги собрать в дорогу Деда мороза. Надень Снеговику шляпку. Посмотри какая цифра написана на ней. Положи в сани столько красных и зеленых подарков, чтобы их общее количество соответствовало цифре на шляпке. Сколько подарков ты положил в сани? Сколько красных подарков? Сколько зелёных подарков?

Изображение слайда
27
Слайд 27: ДИДАКТИЧЕСКАЯ ИГРА «АВТОМАСТЕРСКАЯ»

Цель игры: закрепить знание состава числа. Как играть Вариант 1 Почини автомобиль: найди второе колесо для автомобиля, так, чтобы сумма чисел на колёсах была равна числу на автомобиле. Вариант 2 Почини автомобиль: подбери колеса для автомобиля так, чтобы сумма чисел на колёсах была равна числу на автомобиле.

Изображение слайда
28
Слайд 28: Дидактические игры

Эта игра помогает закреплять числа от 1 до 20 и умения складывать и вычитать в пределах 20. Игроки ставят свои фишки на число 1 и по очереди бросают кубик. Ходят на выпавшее количество. Если фишки оказываются на одном поле, то они возвращаются в начало числовой прямой. Чтобы сделать игру, надо распечатать лист. Вырезать и скрепить числовую ленту. Карточки со знаками приклеить на кубик.

Изображение слайда
29
Слайд 29: Художественные средства

От десяти до двадцати, Считать совсем не сложно. Весёлый, лёгкий счёт найти, Всегда для деток можно. Одиннадцать на берегу, Зайчат с мячом играет. Двенадцать месяцев в году, Тринадцать не бывает. Четырнадцать гусей летит, Пятнадцать отдыхают. Шестнадцать дней дождь моросит, И землю заливает. Семнадцать, Вася, съел конфет, А позже шоколадку. Он восемнадцать съесть хотел, Но было слишком сладко. И рой пчелиный прилетел, Пчёл было девятнадцать. Раз двадцать мальчик пожалел… Нельзя с пчелой сражаться!

Изображение слайда
30
Последний слайд презентации: Знакомство с числами 2-го десятка. Состав чисел: Спасибо за внимание!

Изображение слайда
Знакомство с числами 2-го десятка. Состав чисел презентация, доклад, проект
Слайд 1Текст слайда:
Знакомство с числами 2-го десятка. Состав чисел.
Выполнили:
Шарапаева Наталья,
Шилова Владлена
Слайд 2Текст слайда:
Математические основы:
Система счисления – это язык для наименования, записи чисел и правила действий над числами.
Различают позиционные и непозиционные системы счисления.
Наша, естественная система счисления – десятичная – является позиционной
Позиционной системой счисления называется такая система, в которой значение каждой цифры в изображении числа зависит от ее положения в ряду других цифр,
Положение, занимаемой цифрой при письменном обозначении числа называется разрядом.
В данной системе для записи любого числа используется десять знаков, называемых цифрами: 0, 1, 2,3, 4, 5, 6, 7, 8, 9 – это математический алфавит.
Слайд 3Текст слайда:
Математические основы:
Слайд 4Текст слайда:
Математические основы:
Слайд 5Текст слайда:
Знакомство детей с числами 2-го десятка.
Чтобы понять эту тему ребенок должен: знать цифры от 0 до 9, знать ряд натуральных чисел, умет
1 этап: знакомство детей с десятком как счетной единицей. Для этого используют связку из десяти палочек в качестве единицы счета.
2 этап: знакомство с числами второго десятка (от 11 до 20). Знакомство удобно начинать со способа их образования и называния чисел, сопровождая его сначала моделью на палочках, а затем чтением числа по этой модели. Для формирования правильного представления о структуре двузначного числа следует всегда класть десятки слева, а единицы справа. Таким образом ребенок воспринимает правильный образ понятия, без специальных и не всегда понятных объяснений педагога.
Слайд 6Текст слайда:
Знакомство детей с числами 2-го десятка.
Задание: положите перед собой 9 палочек, добавьте 1 палочку. Сколько стало? (Десять). Возьмите все палочки в пучок и перетяните резинкой. В пучке десять палочек, и такое количество часто называют десяток. Записывают так: 10.
Получили новую единичку измерения – десяток. В старину десяток по-другому называли «дцать».
Слайд 7Текст слайда:
Образование чисел второго десятка на примере числа «11»
Слово одиннадцать состоит из трёх частей: «один», «на», «дцать».
«ОДИН – НА – ДЦАТЬ»
Словом «дцать» в старину называли число десять, поэтому, если одну палочку положить на десять, то получится число одиннадцать.
Если к десятку прибавить ещё одну палочку.
Сколько палочек станет?
Станет одиннадцать палочек.
Сколько десятков и единиц в числе одиннадцать?
Один десяток и одна единица.
Слайд 8Текст слайда:
Рассмотрим образование других чисел второго десятка.
Слайд 9Текст слайда:
Образование числа «20»
Возьмем два десятка палочек.
У нас получился ещё один десяток, или дцать. Сколько у нас десятков теперь? Два десятка – двадцать.
Слайд 10Текст слайда:
Сравнение десятков.
Сравните два ряда этих чисел и подумайте, чем они отличаются друг от друга. В записи чисел первого ряда присутствует только один значок. То есть, если у нас число один, мы записываем его одной цифрой – 1. Если у нас число два, мы записываем его одной цифрой – 2. Число пять мы записываем одной цифрой – 5.
В записи чисел второго ряда присутствуют две цифры.
Десять мы записываем двумя цифрами –1 и 0.
Двенадцать мы записываем двумя цифрами – 1 и 2.
То есть в записи этих чисел мы используем два значка – две цифры.
Запишем два ряда чисел.
Слайд 11Текст слайда:
Произношение и запись чисел второго десятка
Когда же мы эти числа записываем, то на первое место мы ставим цифру, которая показывает количество десятков – один десяток, на второе место мы ставим количество свободных единичек, которые мы добавили к десятку.
Обратите, внимание на то, что когда мы устно произносим числа второго десятка – десять, одиннадцать, двенадцать, мы сначала называем количество свободных единичек, а потом десяток – дцать.
Слайд 12Текст слайда:
Анализ программы «От рождения до школы»
Содержание образовательной деятельности с детьми 6–7 лет (подготовительная группа)
Формирование элементарных математических представлений (Количество, счет)
Развивать общие представления о множестве: умение формировать множества по заданным основаниям, видеть составные части множества, в которых предметы отличаются определенными признаками. Упражнять в объединении, дополнении множеств, удалении из множества части или отдельных его частей. Устанавливать отношения между отдельными частями множества, а также целым множеством и каждой его частью на основе счета, составления пар предметов или соединения предметов стрелками.
Совершенствовать навыки количественного и порядкового счета в пределах 10. Познакомить со счетом в пределах 20 без операций над числами. Знакомить с числами второго десятка.
Закреплять понимание отношений между числами натурального ряда умение увеличивать и уменьшать каждое число на 1 (в пределах 10).
Учить называть числа в прямом и обратном порядке (устный счет), последующее и предыдущее число к названному или обозначенному цифрой, определять пропущенное число. Знакомить с составом чисел в пределах 10. Учить раскладывать число на два меньших и составлять из двух меньших большее (в пределах 10, на наглядной основе).
Слайд 13Текст слайда:
Наглядные пособия
Слайд 14Текст слайда:
Наглядные пособия
Слайд 15Текст слайда:
Наглядные пособия
Слайд 16Текст слайда:
Наглядные пособия
Слайд 17Текст слайда:
Усложненные задания (Состав числа )
1. Построение графической, цветовой и числовой модели состава числа 11.
Работа с демонстрационным и индивидуальным пособием «Компьютер». Для ограничения 10 кружков на доске нужно провести вертикальную линию, а на парту положить лист бумаги, ограничивающий десяток. В процессе совместной учебной деятельности строится модель числа 11. Учитель прикрепляет полоски при помощи магнитов и рядом записывает равенства, учащиеся размещают полоски на парте (рис. 8).
Слайд 18Текст слайда:
Усложненные задания (Состав числа )
2. Закрепление знаний. Самостоятельная работа в тетради.
Учащиеся в тетрадях по клеточкам вычерчивают карандашом модели числа 11
Эта работа дает возможность акцентировать внимание на том, что I слагаемые уменьшаются на 1, а II – увеличиваются на 1, а сумма остается без изменения, и многократно повторить систематизированную информацию, что является необходимым условием запоминания таблицы сложения.
Полностью таблица представлена как справочный материал на правом клапане «Суперпапки».
Слайд 19Текст слайда:
Наглядные материалы
Слайд 20Текст слайда:
Дидактические пособия
Слайд 21Текст слайда:
Дидактические пособия
Татьяна Канашевич: Математика. Числа второго десятка
Слайд 22Текст слайда:
Дидактические наборы
Набор учебных пособий «Изучение счета от 1 до 20»
Касса счетных материалов
«Учись считать»
Слайд 23Текст слайда:
Прописи/Рабочие тетради
Слайд 24Текст слайда:
Прописи/Рабочие тетради
Слайд 25Текст слайда:
Интегрированные задания
Слайд 26Текст слайда:
ДИДАКТИЧЕСКАЯ ИГРА «НОВОГОДНИЕ ХЛОПОТЫ»
Цель: учить соотносить количество с цифрой; помочь детям закрепить знание состава числа.
Как играть:
Вариант1 Помоги собрать в дорогу Деда мороза. Надень Снеговику шляпку. Посмотри какая цифра написана на ней. Положи в сани такое же количество подарков. Сколько подарков ты положил в сани?
Вариант 2 Помоги собрать в дорогу Деда мороза. Надень Снеговику шляпку. Посмотри какая цифра написана на ней. Положи в сани столько красных и зеленых подарков, чтобы их общее количество соответствовало цифре на шляпке. Сколько подарков ты положил в сани? Сколько красных подарков? Сколько зелёных подарков?
Слайд 27Текст слайда:
ДИДАКТИЧЕСКАЯ ИГРА «АВТОМАСТЕРСКАЯ»
Цель игры: закрепить знание состава числа.
Как играть
Вариант 1 Почини автомобиль: найди второе колесо для автомобиля, так, чтобы сумма чисел на колёсах была равна числу на автомобиле.
Вариант 2 Почини автомобиль: подбери колеса для автомобиля так, чтобы сумма чисел на колёсах была равна числу на автомобиле.
Слайд 28Текст слайда:
Дидактические игры
Эта игра помогает закреплять числа от 1 до 20 и умения складывать и вычитать в пределах 20. Игроки ставят свои фишки на число 1 и по очереди бросают кубик. Ходят на выпавшее количество. Если фишки оказываются на одном поле, то они возвращаются в начало числовой прямой.
Чтобы сделать игру, надо распечатать лист. Вырезать и скрепить числовую ленту. Карточки со знаками приклеить на кубик.
Слайд 29Текст слайда:
Художественные средства
От десяти до двадцати, Считать совсем не сложно. Весёлый, лёгкий счёт найти, Всегда для деток можно. Одиннадцать на берегу, Зайчат с мячом играет. Двенадцать месяцев в году, Тринадцать не бывает. Четырнадцать гусей летит, Пятнадцать отдыхают. Шестнадцать дней дождь моросит, И землю заливает. Семнадцать, Вася, съел конфет, А позже шоколадку. Он восемнадцать съесть хотел, Но было слишком сладко. И рой пчелиный прилетел, Пчёл было девятнадцать. Раз двадцать мальчик пожалел… Нельзя с пчелой сражаться!
Слайд 30Текст слайда:
Спасибо за внимание!
Использование наглядных пособий на уроках математики в начальной школе
Б. Записать число, предшествующее числу три.
В. записать соседей числа пять.
задание – проверялось, как усвоено основное свойство натурального ряда чисел.
Вычисли:
А. 4+1 В. 5+1
Б. 2+1 Г. 3+1
задание – проверялось умение сравнивать два числа.
> < =
а. 3…4 б. 2…2 в. 6…5
После проверки работ учащихся обеих групп был сделан поэлементный анализ в ходе которого выяснилось, что учащиеся в контрольной группе допустили ошибок больше, чем учащиеся в экспериментальной.
29
Таблица 1 – Анализ результатов самостоятельной работы

Типичные ошибки
Незнание следования чисел в натуральном ряду
Не знание свойств натурального ряда
Не умение сравнивать два натуральных числа
К-во учащихся
%
К-во учащихся
%
К-во учащихся
%
Экспериментальная
группа
3
25
2
17
3
25
Контрольная
группа
7
58
7
58
6
50

Фрагменты конспекта урока с использованием наглядных средств обучения
Тема: Числа 1, 2, 3, 4, 5, 6.
Цели: 1. Формирование понятия числа 6. Познакомить с образованием числа 6, с цифрой 6.
Продолжать обучение счету.
Упражнять в сравнении чисел.
Упражнять в письме цифры 6.
2.Воспитывать усидчивость, дисциплинированность.
30
3. развивать логическое мышление.
Оборудование: 1. Набор цифр и знаков.
2. Наборное полотно.
3. Касса цифр и букв.
4. Счетные палочки.
5. Набор кубиков
5. Натуральный ряд чисел.
6. Предметные картинки для счета.
Ход урока:
Наглядные пособия, используемые на этапе повторения:
а. Счетный материал для повторения состава чисел:
Положите перед собой 3 красных кружка.
Сколько кружков надо добавить, чтобы получилось 4 кружка?
Положите 3 треугольника, добавьте еще столько, чтобы получилось 5 треугольников.
Положите 5 картинок с огурцами.
Что надо сделать чтобы получилось 4 огурца?
б. Натуральный ряд чисел (на доске, на плакате)
1 2 3 4 5 6 7 8 9 10
Назовите соседей числа 3; 8.
Какое число предшествует при счете числу 6, числу 2, числу 10?
Какое число следует при счете за числом 5, 1, 7?
в. Карточки с цифрами.
31
Покажите мне ту цифру, которая соответствует количеству предметов на наборном полотне.
г. Сигнальные знаки. Правильно + ; неправильно –
1. 5 – 1 = 4 2. 4 – 2 = 3 3. 4 + 1 = 5
Наглядные пособия, используемые на этапе изучения нового материала:
а. Образование числа 6 (карточки, счетный материал)
Покажите, как имея 5 квадратов, выставленных на наборном полотне сделать так, чтобы их стало 6? (Добавляют еще квадрат)
Давайте запишем пример 5 + 1 = 6
Кто может найти эту цифру ? (Находят карточку с цифрой 6)
б. Кубики.
Составляются столбиком кубики по 5 и 6 штук для сравнения чисел 5 и 6.
Сколько красных кубиков? – 5
А синих? – 6
Каких кубиков больше? – синих
На сколько синих кубиков больше, чем красных? – на один.
А на сколько красных кубиков меньше, чем синих? – на один.
Какое число больше 5 или 6? – 6
Запишем! 6 5

Какое число меньше? – 5
Запишем! 5 6
Наглядные пособия, используемые на этапе закрепления:
а. У Маши 6 яблок (на наборном полотне).
32
Как их можно разложить в две корзины? (дети раскладывают и каждый раз записывают пример)
0 + 6 = 6
1 + 5 = 6
2 + 4 = 6
3 + 3 = 6
4 + 2 = 6
5 + 1 = 6
6 + 0 = 6
Закрепляют состав числа 6.
б. На одной тарелке 6 огурцов на другой 5.
На какой тарелке огурцов больше? (на первой)
Почему? (потому что 6 > 5)
Фрагменты конспекта урока с минимальным использованием наглядных средств обучения
Тема: Числа 1, 2, 3, 4, 5, 6.
Цели: 1. Формирование понятия числа 6. Познакомить с образованием числа 6, с цифрой 6.
2.Воспитывать усидчивость, дисциплинированность.
3. развивать логическое мышление.
Оборудование: 1. Набор цифр и знаков.
2. Наборное полотно.
33
3. Касса цифр и букв.
4. Счетные палочки.
5. Набор кубиков
5. Натуральный ряд чисел.
6. Предметные картинки для счета.
Ход урока:
1.Повторение устно.
А. Состав числа:
4 это 3 и …
2 и …
б. – Сколько надо прибавить к 3, чтобы получилось 5?
А что надо сделать, чтобы получилось 2?
в. – Назовите соседей чисел 4, 7, 9.
Какое число предшествует при счете числу 8, 2, 5?
Какое число следует за 3, 6, 9?
г. Сколько у меня яблок? (картинки) (хором) 3, 5, 1.
2. Изучение нового материала.
а. У меня 5 кружков. Что надо сделать чтобы их стало 6? (добавить еще один)
Запишем 5 + 1 = 6
Найдите эту цифру в кассе.
б. «>», «<», «=») устный разбор, затем письменно
34
5 6 2 1 4 4

3 5 6 6 2 4
3. Закрепление.
6 + 0
5 + 1
4 + 2
3 + 3
2 + 4
1 + 5
0 + 6
Записывают все получившиеся примеры.

35

Заключение
Итак, наглядность является одним из главных средств обучения младших школьников на протяжении всего учебно-воспитательного процесса. Использование наглядности на уроках в начальных классах обусловлено психофизиологическими особенностями учащихся данной возрастной группы.
Принцип наглядности в обучении используется уже давно. Об его эффективном действии в процессе обучения и воспитания говорил еще великий польский дидактик и ученый Я.А. Коменский, высшим основным принципом обучения признавал наглядность Песталоцци, великий русский педагог Ушинский видел в наглядности одно из условий, которое обеспечивает получение учащимися полноценных знаний, развивает их логическое мышление, широко использовал в своей педагогической деятельности этот принцип Л. Н. Толстой. Принцип наглядности широко используется в обучении младших школьников и в наше время.
Значение средств наглядности в процессе обучения математике младших школьников переоценить трудно. Формирование многих основных математических понятий, таких как: понятие числа, арифметического действия, переместительного закона, понятия больше «на», меньше «на» и других, происходит с использованием различных наглядных пособий. В основе формирования этих понятий лежит взаимнооднозначное соответствие между множествами.
На подготовительном этапе обучения и в начале изучения темы «Нумерация» дети учатся выделять группы предметов на основе определенных практических действий с ними и отмечать, что изменилось (опора наглядно-действенное мышление). Следующий шаг – переход от действий с конкретными предметами к работе по картинкам (переход к
36
наглядно-образному мышлению). Причем здесь обеспечивается постепенность перехода: сначала работа с тремя связанными между собой картинками, наглядно-иллюстрирующими «Что было?», «Что произошло?», «Что стало?», а затем к парным картинкам, показывающим «Что было?», «Что стало?».
Следующий этап – переход к решению задач на основе действий с числами в теме «Сложение и вычитание» переход к словесно-логическому мышлению. В учебнике наблюдается постепенный переход от полной предметной наглядности (когда ответ в задаче находится путем пересчета предметов, изображенных в иллюстрациях) к неполной предметной наглядности (одно из данных задачи выражено числом) и затем – к решению задач, где оба данных представлены в виде чисел, а иллюстрация поясняет лишь сюжет задачи.
Наглядные пособия по математике делятся на демонстрационные пособия (крупные) и индивидуальные (маленькие). Наглядные пособия подразделяются на две группы: группа средств предметно-образной наглядности и группа средств знаковой наглядности.
Практическое использование наглядных пособий на уроках математики в начальных классах очень широко. Некоторые виды работ с использованием наглядности на уроках математики в первом классе даны в работе.
В ходе исследования выдвигалась гипотеза, что систематическое целенаправленное использование наглядных пособий на уроках повысит качество усвоения знаний, уровень сформированности математических умений и навыков.
В ходе исследования был предложен эксперимент. Он был направлен на подтверждение или опровержение гипотезы.
37
Опыт показывает, что после проведения подобных экспериментов действительно оказывается, что систематическое целенаправленное использование наглядных пособий на уроках математики в начальной школе повышает качество усвоения знаний, уровень сформированности умений и навыков.

38
Список литературы :
1. Актуальные проблемы методики обучения математике в начальных классах/ под ред. М.И. Моро, А.М. Пышкало. – М.: Педагогика, 1977.
2. Артемов, А.К. Обучение математике [Текст]/А.К.Артемов. – Пенза, 1995.
3. Бантова, М.А. Методика преподавания математики в начальных классах. Учеб. пособие для учащихся педучилищ [Текст]/М.А.Бантова. – М.: Просвещение, 1984.
4. Бантова, М. А. Методика преподавания математики в начальных классах [Текст]/М.А.Бантова, Г.В.Бельтюкова. – М.: Просвещение, 1984.
5. Белошистая, А.В. Методика обучения математике в начальной школе: курс лекций: учеб. пособ. для студ. высш. пед. учеб. Заведений [Текст] / А.В.Белошистая. – М.: Гуманит. изд. центр ВЛАДОС, 2005.
6. Волошкина, М.И. Активизация познавательной деятельности младших школьников на уроке математики [Текст]/М.И.Волошкина // Начальная школа. – 1992. – № 9/10.
7. Выготский, Л.С. Педагогическая психология/ под ред. В.В. Давыдова [Текст] /Л.С.Выготский. – М.: Педагогика, 1991.
8. Гальперин, П.Я. К вопросу о формировании начальных математических понятий. Сообщения I – V [Текст]/П.Я.Гальперин, Л.С.Георгиев // Доклады АПН РСФСР, 1960.- № 1.
9. Жильцова, Т.В. Поурочные разработки по наглядной геометрии: 1 – 4 класс [Текст]/Т.В.Жильцова, Л.А.Обухова. – М.: ВАКО, 2004. – 288с. (В помощь школьному учителю).
10. Иванова, Т. Т. Некоторые визуальные средства на уроках математики [Текст] /Т.Т.Иванова, Н.А.Резник // Начальная школа. – 1995. – № 5.
История
Дистанционное обучение
Профессиональная переподготовка
Профессиональное обучение
Мастер-классы
Обучение педагогов, воспитателей
Обучение населения
19 июня — День Медицинского работника
Поздравление губернатора Ростовской области с Днем медицинского работника
12 июня — День России
1 июня – Международный день защиты детей
28 мая – Международный день здоровья женщин
12 мая – Международный день медицинской сестры 2022
Наше учреждение начинает свою историю с 1988 года, когда в Ростовской области было создано Ростовское областное училище повышения квалификации работников со средним медицинским и фармацевтическим образованием. В соответствии с постоянно растущими требованиями практического здравоохранения к уровню и качеству подготовки специалистов динамично развивалась материально-техническая база и учебно-методическое обеспечение училища.
В 2004 году произошло переименование РОУПК в государственное образовательное учреждение дополнительного профессионального образования «Центр повышения квалификации специалистов со средним медицинским и фармацевтическим образованием» Ростовской области, а в 2011 году – в государственное бюджетное образовательное учреждение дополнительного профессионального образования Ростовской области «Центр повышения квалификации специалистов со средним медицинским и фармацевтическим образованием»
В настоящее время центр является крупным образовательным учреждением на Юге России, располагающим учебным корпусом площадью 1571 кв.м. и сильной материально-технической базой.
Руководителем центра повышения квалификации является заслуженный врач РФ Димитрова Л.В.
Цель деятельности центра – предоставление образовательных услуг по повышению квалификации на современном и качественном уровне. Ежегодно в центре обучаются свыше 8000 специалистов по 32 специальностям.
Созданы условия для предоставления образовательных услуг:
передовая материально-техническая база,

коллектив с высоким творческим потенциалом,

современные педагогические и здоровьесберегающие технологии в обучении.

Активно ведется модернизация образовательного процесса:
Сформирована единая информационная среда центра

Совершен переход на мультимедийные технологии

Мультимедийное оснащение занятия (используется интерактивная доска, документ-камера и др.) На занятиях по неотложной медицинской помощи слушатели работают с обучающей компьютерной программой по сердечно-легочной реанимации

Проводится компьютерное итоговое тестирование слушателей Мультимедийные презентации имеются в арсенале каждого преподавателя. Пример: разработки Гарликова Н.Н.
Достижением нашего центра является внедрение новейших разработок в учебный процесс:
В области безопасности профессиональной среды медицинских работников

Работа с деструктором игл и портативным автоклавом Новое в лабораторной диагностике (работа с экспресс-анализаторами)
В обучении слушателей по разделу «Скорая и неотложная помощь»

Использование вакуумных шин и проведение массажа сердца при помощи кардиопампа Проведение фельдшерами скорой помощи ИВЛ после интубации трахеи с помощью ларингоскопа
В области сестринских технологий

Освоение технологии забора крови с помощью вакуумных систем Обучение постановке периферических катетеров
Наш вклад в реализацию Приоритетного национального проекта «Здоровье» идет по направлениям:
Формирование здорового образа жизни

Для достижения лучших результатов по этому направлению открыт учебный кабинет «Здоровье»

Демонстрируется аппаратно-программный комплекс «Здоровье-Экспресс» Организована работа по борьбе с табакокурением
Проводятся конкурсы среди слушателей на лучшую творческую работу по пропаганде здорового образа жизни

Победитель конкурса – фильм «Лучезарная улыбка» – цикл «Стоматологическая помощь населению»
Совершенствование оказания медицинской помощи пострадавшим при ДТП

Подготовлено 113 специалистов для оказания помощи пострадавшим на Федеральной трассе М-4
Совершенствование медицинской помощи больным с сердечно-сосудистыми заболеваниями

Подготовлено 422 специалиста для работы в новых сосудистых центрах малоинвазивной хирургии и кардиохирургических отделениях
Особое внимание уделяется сотрудничеству с Международным Комитетом Красного Креста на Северном Кавказе
За пять лет сотрудничества проучилось 74 медицинских работника. Деятельность центра в этом направлении получила высокую оценку руководителя Международного Комитета Красного Креста на Северном Кавказе Мишеля Массона.
Центр повышения квалификации располагает широкими возможностями для предоставления качественных образовательных услуг по обучению специалистов со средним медицинским и фармацевтическим образованием в соответствии с постоянно растущими требованиями практического здравоохранения.

Разработка и поддержка сайта – АО «Региональный межотраслевой центр информации и технологий»
Учебные ресурсы и печатные материалы по числовым рифмам
Рекламные объявления
Посмотреть коллекцию
Пять маленьких обезьянок сидят/качаются на дереве
Реклама
Наглядные пособия This Old Man (Knick Knack Paddywhack) (SB11102)
Набор наглядных пособий для распечатки, сопровождающих детскую песенку This Old Man.
Предварительный просмотр и загрузка
Предварительный просмотр и загрузка
Раскраски This Old Man (Knick Knack Paddywhack).
Предварительный просмотр и загрузка
Наглядные пособия «Счетный зоопарк» (SB10388)
Набор распечатываемых наглядных пособий для сопровождения песни о счете «Счетный зоопарк».
Предварительный просмотр и загрузка
Предварительный просмотр и загрузка
Наглядные пособия «Питер работает одним молотком» (SB11271)
Набор печатных наглядных пособий, сопровождающих числовую рифму «Питер работает одним молотком».
Предварительный просмотр и загрузка
1, 2, 3, 4, 5, Выставочный баннер «Однажды я поймал живую рыбу» (SB7400)
Цветной баннер для показа детских песенок «1, 2, 3, 4, 5, Однажды я поймал живую рыбку».
Предварительный просмотр и загрузка
1, 2, 3, 4, 5, Наглядные пособия «Однажды я поймал рыбу» (SB2072)
Набор наглядных пособий формата А4 для сопровождения известного стихотворения «1, 2, 3, 4, 5, однажды я поймал живую рыбу».
Предварительный просмотр и загрузка
1, 2, 3, 4, 5, Лист с песнями «Однажды я поймал живую рыбку» (SB10735)
Лист со словами популярной детской песенки в простом формате для печати для детей.
Предварительный просмотр и загрузка
Наглядные пособия «Один человек пошел косить» (SB10577)
Набор наглядных пособий для распечатки, сопровождающих счетную песню «Один человек пошел косить».
Предварительный просмотр и загрузка
Листы-раскраски «Один человек пошел косить» (SB10578)
Набор листов-раскрасок формата А4 для сопровождения известной песни «Один человек пошел косить».
Предварительный просмотр и загрузка
Предварительный просмотр и загрузка
1, 2, 3, 4, 5, «Однажды я поймал живую рыбку» Рамки для страниц формата A4 (SB7401)
Рамки для страниц формата A4 в книжной и альбомной ориентации, сопровождающие колодец известный детский стишок. Включает редактируемые шаблоны Microsoft Word, а также изображения JPG изменяемого размера.
Предварительный просмотр и загрузка
Наглядные пособия «Вот улей» (SB3325)
Набор наглядных пособий формата А4 для сопровождения рифмы «Вот улей…».
Предварительный просмотр и загрузка
Предварительный просмотр и загрузка
Баннер дисплея Ten Green Bottles (SB11285)
Распечатанный баннер для настенного дисплея 10 Green Bottles.
Предварительный просмотр и загрузка
СМ. ТАКЖЕ…
1, 2 Наглядные пособия «Пристегни мою обувь» (SB751)
Набор наглядных пособий формата A4 для сопровождения известного стихотворения «Раз, два, пристегни мою обувь».
Предварительный просмотр и загрузка
Одна маленькая, две маленькие птички… Наглядные пособия (SB3319)
Набор наглядных пособий формата А4 для сопровождения числовой рифмы “Одна маленькая… Пять таких маленьких птичек”.
Предварительный просмотр и загрузка
Наглядные пособия «Двенадцать дней Рождества» (SB1121)
Большой набор наглядных материалов для распечатки для пересказа рождественского стихотворения «Двенадцать дней Рождества». Включает в себя текст стихотворения, простые иллюстрации, а также большие числа (в том числе порядковые). Вы можете использовать для упорядочивания действий, подсчета и числа- признание.
Предварительный просмотр и загрузка
Наглядные пособия «Одна картошка, две картофелины» (SB11284)
Набор наглядных материалов для распечатки, сопровождающих числовую рифму «Одна картошка, две картофелины».
Предварительный просмотр и загрузка
Наглядные пособия «Один слон вышел поиграть» (SB1014)
Набор наглядных пособий формата А4 для сопровождения номера- рифма «Один слон вышел поиграть».
Предварительный просмотр и загрузка
Один слон вышел поиграть в паутину и вырезать- Слоны (SB1015)
Набор вырезанных слонов и паутина формата А4 (можно фотокопировать на А3) для детей, чтобы играть в игры со счетом с кубиками, класть из соответствующего количества слонов в Интернете. Идеально подходит для использования с рифмованными наглядными пособиями.
Предварительный просмотр и загрузка
Редактируемые тематические обложки книг Number Rhymes (SB11566)
Редактируемые шаблоны обложек книг Microsoft Word (цветные и черно-белые) для тематических книг Nursery Rhymes.
Предварительный просмотр и загрузка
Плакаты с цифрами «Десять в постели» 10- 0 (SB10030)
Набор плакатов с цифрами формата А4 для сопровождения песни «Десять в постели».
Предварительный просмотр и загрузка
Предварительный просмотр и загрузка
10 in the Bed Bear Cut- Outs (SB2115)
Набор из 10 медвежьих персонажей и кровати (с 10 подушками) для облегчения пересказа числовой рифмы «В постели было десять… ».
Предварительный просмотр и загрузка
Наглядные пособия «Десять зеленых бутылок» (SB11283)
Печатные наглядные пособия для популярной считалки.
Предварительный просмотр и загрузка
СМОТРИТЕ ТАКЖЕ…
Баннер с цифровыми рифмами (SB12180)
Баннер, который печатает более 3 страниц в альбомной ориентации для доски с цифровыми рифмами в классе.
Предварительный просмотр и загрузка
Подпишитесь на нас:
Исследования подтверждают эффективность визуальных средств для привлечения аудитории к электронному обучению
Сейчас мы живем в эпоху визуальной информации, когда визуальный контент играет роль во всех сферах жизни. Поскольку 65 процентов населения являются визуальными учениками, графика играет ключевую роль в вовлечении учащихся в курсы электронного обучения.
Визуальные элементы обобщают содержимое в более мелкие и простые для обработки фрагменты, и при выборе правильных визуальных элементов они обеспечивают большую понятность, чем текстовые пояснения или только аудиозаписи. Кроме того, учащиеся легко связывают эмоции с визуальными элементами, что делает ваши курсы электронного обучения более эффективными и запоминающимися, чем просто добавление текста.
В этом посте мы углубимся в некоторые статистические данные и факты, чтобы еще больше убедиться в том, почему создатели электронного обучения должны использовать визуальные эффекты при создании своих курсов.
И кратковременная, и долговременная память хранят информацию порциями, но первая ограничена. Один из самых простых способов гарантировать, что учащиеся сохранят информацию в своей долговременной памяти, — это сочетать понятия со значимыми изображениями. Наглядные материалы помогают учащимся разобраться в содержании и привлекают внимание, повышая вероятность того, что учащиеся запомнят материал.
По словам доктора Линелла Бермарка , консультанта по вопросам образования, который пишет и говорит о визуальной грамотности: «…если наши слова, концепции, идеи не привязаны к изображению, они войдут в одно ухо, пройдут через мозг и выйти из другого уха. Слова обрабатываются нашей кратковременной памятью, где мы можем сохранить только около семи битов информации (плюс-минус 2) […]. Образы, с другой стороны, попадают прямо в долговременную память, где они остаются неизгладимыми».
Кроме того, этот эффект усиливается со временем. Одно исследование показало, что через три дня пользователь сохранил только 10-20 процентов письменной или устной информации, но почти 65 процентов визуальной информации. Другое исследование показало, что иллюстрированный текст был на девять процентов эффективнее, чем один только текст, при тестировании непосредственного понимания и на 83 процента эффективнее, когда тест откладывался.
Читайте также: Максимальное использование наглядных материалов в электронном обучении: 9 советов и 5 примеров
По данным Альянса визуального обучения:
Мозг может видеть изображения, которые длятся всего 13 миллисекунд.
Наши глаза могут регистрировать 36 000 визуальных сообщений в час.
Мы можем получить представление о визуальной сцене менее чем за 1/10 секунды.
90% информации, передаваемой в мозг, является визуальной.
Визуальные изображения обрабатываются мозгом в 60 000 раз быстрее, чем текст.
40 процентов нервных волокон связаны с сетчаткой
Все это указывает на то, что люди обрабатывают визуальную информацию более эффективно, чем текст. Просто посмотрите сами:
Источник изображения: Блог Uberflip
Принимая все это во внимание, разработчики электронного обучения могут использовать эти знания при разработке своих курсов в своих интересах, включая эффективную графику для облегчения понимания.
Подумайте об этом: какой контент будет лучше структурирован как изображение или видео, а не как маркированный список?
Наглядные материалы улучшают обучение на до 400 процентов . Кроме того, они воздействуют на учащихся на когнитивном уровне и стимулируют воображение, что позволяет пользователям быстрее обрабатывать информацию. Стэнфордский университет Роберт Э. Хорн ясно объяснил эту взаимосвязь: «Когда слова и визуальные элементы тесно переплетены, мы создаем что-то новое и расширяем наш общий интеллект … визуальный язык имеет потенциал для увеличения «человеческой пропускной способности» — способности воспринимать, понимать и более эффективно синтезировать большие объемы новой информации».
Другие исследования обнаружили, что такие визуальные эффекты, как графические организаторы, повышают производительность в таких областях:
• Понимание чтения
• Достижение студентов
• Организация и передача идеи
• показывает, как наш мозг автоматически интерпретирует отношения между объектами, обеспечивая почти мгновенное понимание с минимальными усилиями:
Визуальные эффекты вызывают более быструю и сильную реакцию, чем слова. Они помогают пользователям взаимодействовать с контентом, и такие эмоциональные реакции влияют на запоминание информации. Это связано с тем, что зрительная память кодируется в медиальной височной доле мозга, в том же месте, где обрабатываются эмоции. Мозг устроен таким образом, что визуальные стимулы и эмоциональные реакции легко связываются, и вместе они образуют воспоминания. Негативные визуальные изображения особенно полезны для того, чтобы оставить сильное эмоциональное впечатление.
Даже абстрактные концепции могут выиграть от изображений, если создатели курсов используют визуальные метафоры. Включение визуальных метафор в их курс электронного обучения помогает выражать эмоции, вызывая аналогичную эмоциональную реакцию у учащихся. См. этот пример:
Источник изображения: блог Visual Rhetoric
Около 90 197 40 % учащихся лучше реагируют на визуальную информацию, чем на текст . Просто просмотр изображения позволяет пользователям воссоздать опыт в своем воображении. Профессионалы электронного обучения могут извлечь из этого пользу, рассказывая истории в своих курсах с помощью очаровательных изображений и привлекательных видео.
Важно отметить, что графика также может негативно повлиять на обучение, если она используется не по назначению. Когда на экране появляется графика, не относящаяся к теме, например, используемая в чисто декоративных целях, учащиеся подсознательно пытаются понять сообщение и причину появления изображения.
Ниже приведены примеры изображений, которых создателям курсов всегда следует избегать в визуальном дизайне электронного обучения:
Изображения, которые явно являются стоковыми фотографиями.
Общая графика, демонстрирующая явное отсутствие воображения.
Изображения низкого качества, пикселизированные, с низким разрешением, с чрезмерным сжатием или с неправильным изменением размера.
С другой стороны, хорошо подобранные изображения могут улучшить понимание и понимание, когда разработчики стратегически размещают такую графику в курсе. В отличие от текста, изображения способны обогащать общение и стимулировать эмоциональный отклик. Чтобы использовать наглядные материалы таким образом, чтобы укрепить материал курса и облегчить обучение, необходимо использовать изображения, которые:
Представлять реальные объекты, людей или места.
Упростите сложные или абстрактные идеи.
Мост уже изучил материалы с незнакомыми.
Дизайнеры электронного обучения должны использовать только изображения, которые имеют четкую ценность, в противном случае они в лучшем случае будут отвлекать, а в худшем — создавать у учащихся неправильное впечатление. Это означает исключение всего, что напрямую не поддерживает цели обучения.

Оператор For…Next — Visual Basic
Статья
15.09.2021
9 минут на чтение
Повторяет группу операторов указанное количество раз.
Синтаксис
 Для счетчика [Как тип данных] = от начала до конца [Шаг шага]
    [ заявления ]
    [Продолжить]
    [ заявления ]
    [Выйти для]
    [ заявления ]
Далее [ счетчик ]
 
Детали
Деталь Описание
счетчик Требуется в инструкции For . Числовая переменная. Управляющая переменная для цикла. Дополнительные сведения см. в разделе «Контраргумент» далее в этом разделе.
тип данных Дополнительно. Тип данных счетчика . Дополнительные сведения см. в разделе «Контраргумент» далее в этом разделе.
начало Обязательно. Числовое выражение. Начальное значение счетчика .
конец Обязательно. Числовое выражение. Окончательное значение счетчика .
ступенька Дополнительно. Числовое выражение. Величина, на которую счетчик увеличивается каждый раз в цикле.
заявления По желанию. Один или несколько операторов между For и Next , которые выполняются указанное количество раз.
Продолжить для Дополнительно. Передает управление следующей итерации цикла.
Выход Для Дополнительно. Передает управление из цикла For .
Следующий Обязательно. Завершает определение цикла For .
Примечание
Ключевое слово от до используется в этом операторе для указания диапазона счетчика. Вы также можете использовать это ключевое слово в операторе Select…Case и в объявлениях массивов. Дополнительные сведения об объявлениях массивов см. в разделе Оператор Dim.
Простые примеры
Вы используете структуру For . .. Next , когда хотите повторить набор операторов заданное количество раз.
В следующем примере , индекс , переменная начинается со значения 1 и увеличивается с каждой итерацией цикла, заканчиваясь после того, как значение , индекс , достигает 5.
 Для индекса As Integer = 1 To 5
    Debug.Write(index.ToString & "")
Следующий
Отладка.WriteLine("")
' Вывод: 1 2 3 4 5
 
В следующем примере переменная числа начинается с 2 и уменьшается на 0,25 на каждой итерации цикла, заканчиваясь после того, как значение числа достигает 0. Шаг 9Аргумент 0351 -.25 уменьшает значение на 0,25 на каждой итерации цикла.
 Для числа As Double = от 2 до 0 Шаг -0,25
    Debug.Write(число.ToString & "")
Следующий
Отладка.WriteLine("")
Выход: 2 1,75 1,5 1,25 1 0,75 0,5 0,25 0
 
Совет
Оператор While...End While или оператор Do. ..Loop хорошо работают, когда заранее неизвестно, сколько раз выполнять операторы в цикле. Однако, если вы ожидаете запустить цикл определенное количество раз, Для ... Следующий цикл является лучшим выбором. Вы определяете количество итераций при первом входе в цикл.
Вложение циклов
Вы можете вложить циклы For , поместив один цикл в другой. В следующем примере показаны вложенные структуры For ... Next с разными значениями шага. Внешний цикл создает строку для каждой итерации цикла. Внутренний цикл уменьшает переменную счетчика цикла для каждой итерации цикла.
 Для индекса А = от 1 до 3
    ' Создаем новый StringBuilder, который используется
    ' для эффективного построения строк.
    Dim sb As New System.Text.StringBuilder()
    ' Добавляем в StringBuilder каждое третье число
    ' с 20 до 1 по убыванию.
    Для indexB = 20 To 1 Step -3
        sb.Append(indexB. ToString)
        сб.Добавить(" ")
    Следующий индексB
    ' Отобразить строку.
    Debug.WriteLine(sb.ToString)
Следующий индексA
' Выход:
20 17 14 11 8 5 2
20 17 14 11 8 5 2
20 17 14 11 8 5 2
 
При вложении циклов каждый цикл должен иметь уникальную переменную счетчика .
Вы также можете вкладывать друг в друга различные структуры управления. Дополнительные сведения см. в разделе Вложенные структуры управления.
Exit For and Continue For
Оператор Exit For немедленно выходит из цикла For … Next и передает управление оператору, следующему за оператором Next .
Продолжить 9Оператор 0351 немедленно передает управление следующей итерации цикла. Дополнительные сведения см. в разделе Заявление о продолжении.
В следующем примере показано использование операторов Continue For и Exit For .
 Для индекса Целое число = от 1 до 100000
    ' Если индекс находится между 5 и 7, продолжить
    ' со следующей итерацией. 
    Если индекс >= 5 И также индекс <= 8 Тогда
        Продолжить для
    Конец, если
    ' Показать индекс.
    Debug.Write(index.ToString & "")
    ' Если индекс равен 10, выйти из цикла.
    Если индекс = 10 Тогда
        Выход для
    Конец, если
Следующий
Отладка.WriteLine("")
' Вывод: 1 2 3 4 910
 
Вы можете поместить любое количество операторов Exit For в цикл For … Next . При использовании внутри вложенных циклов For … Next , Exit For выходит из самого внутреннего цикла и передает управление на следующий более высокий уровень вложенности.
Exit For часто используется после оценки некоторого условия (например, в структуре If ... Then ... Else ). Вы можете использовать Exit For для следующих условий:
Продолжение итерации не нужно или невозможно. Это условие может быть вызвано ошибочным значением или запросом на завершение.
A Попытка ... Перехват ... Наконец оператор перехватывает исключение. Вы можете использовать Выход для в конце блока Наконец .
У вас есть бесконечный цикл, который может выполняться большое или даже бесконечное количество раз. Если вы обнаружите такое состояние, вы можете использовать Выход Для выхода из цикла . Дополнительные сведения см. в разделе Оператор Do...Loop.
Техническая реализация
Когда Для ... Запускается следующий цикл , Visual Basic оценивает start , end и step . Visual Basic оценивает эти значения только в этот момент, а затем назначает start счетчику . Перед запуском блока инструкций Visual Basic сравнивает counter с end . Если счетчик уже больше, чем значение end (или меньше, если шаг отрицателен), цикл For завершается, и управление передается оператору, следующему за оператором Next . В противном случае выполняется блок операторов.
Каждый раз, когда Visual Basic встречает оператор Next , он увеличивает счетчик на шаг и возвращается к оператору For . Снова сравнивается счетчик 9от 0351 до end , и снова он либо запускает блок, либо выходит из цикла, в зависимости от результата. Этот процесс продолжается до тех пор, пока счетчик не пройдет end или пока не встретится оператор Exit For .
Цикл не останавливается, пока счетчик не пройдет конец . Если счетчик равен end , цикл продолжается. Сравнение, которое определяет, запускать ли блок, равно counter <= end , если шаг положительный, а счетчик >= конец , если шаг отрицательный.
Если вы измените значение счетчика внутри цикла, ваш код может стать более трудным для чтения и отладки. Изменение значения start , end или step не влияет на значения итерации, которые были определены при первом входе в цикл.
Если вы вкладываете циклы, компилятор сигнализирует об ошибке, если он встречает Следующий оператор внешнего уровня вложенности перед оператором Next внутреннего уровня. Однако компилятор может обнаружить эту ошибку перекрытия, только если вы укажете счетчик в каждом операторе Next .
Аргумент шага
Значение шага может быть как положительным, так и отрицательным. Этот параметр определяет обработку цикла в соответствии со следующей таблицей:
Значение шага Цикл выполняется, если
Положительный или ноль счетчик <= конец
Отрицательный счетчик >= конец
Значение по умолчанию для шага равно 1.
Аргумент счетчика
В следующей таблице указано, определяет ли счетчик новую локальную переменную, которая распространяется на весь For…Next петля. Это определение зависит от того, присутствует ли тип данных и определен ли уже счетчик .
Присутствует ли тип данных ? Счетчик уже определен? Результат (определяет ли счетчик новую локальную переменную, область действия которой распространяется на весь цикл For...Next )
№ Да Нет, потому что счетчик уже определен. Если область действия счетчика не является локальной для процедуры, появляется предупреждение во время компиляции.
№ № Да. Тип данных выводится из выражений start , end и step . Дополнительные сведения о выводе типа см. в разделе Оператор Option Infer и вывод локального типа.
Да Да Да, но только если существующий счетчик переменная определяется вне процедуры. Эта переменная остается отдельной. Если область действия существующей переменной счетчика является локальной для процедуры, возникает ошибка времени компиляции.
Да № Да.
Тип данных счетчика определяет тип итерации, который должен быть одним из следующих типов:
A Byte , SByte , 0 UShort0351 , Short , UInteger , Integer , ULong , Long , Decimal , Single , или 1 .
Перечисление, которое вы объявляете с помощью оператора Enum.
Объект .
Тип T со следующими операторами, где B — это тип, который можно использовать в выражении Boolean .
Общий оператор >= (op1 As T, op2 As T) As B
Общедоступный общий оператор <= (op1 As T, op2 As T) As B
Общедоступный общий оператор — (op1 As T, op2 As T) As T
Общедоступный общий оператор + (op1 As T, op2 As T) As T
Дополнительно можно указать переменную счетчика в операторе Next . Этот синтаксис улучшает читабельность вашей программы, особенно если вы вложили На петель. Необходимо указать переменную, которая появляется в соответствующем операторе For .
Выражения start , end и step могут вычисляться для любого типа данных, который расширяется до типа counter . Если вы используете определяемый пользователем тип для счетчика , вам может потребоваться определить оператор преобразования CType для преобразования типов start , end или step в тип счетчик .
Пример 1
В следующем примере удаляются все элементы из универсального списка. Вместо оператора For Each...Next в примере показан оператор For ... Next , который повторяется в порядке убывания. В примере используется этот метод, поскольку метод removeAt приводит к тому, что элементы после удаленного элемента имеют более низкое значение индекса.
 Dim Lst As New Список (целого числа) из {10, 20, 30, 40}
Для индекса As Integer = lst.Count - от 1 до 0 Step -1
    lst.RemoveAt (индекс)
Следующий
Debug.WriteLine(lst.Count.ToString)
' Вывод: 0
 
Пример 2
В следующем примере выполняется итерация по перечислению, объявленному с помощью оператора Enum.
 Общественные перечисленные млекопитающие
    Баффало
    Газель
    Мангуста
    Носорог
    Кит
Конец перечисления
Публичный подсписокSomeMammals()
    Для млекопитающих As Mammals = Mammals. Gazelle To Mammals.Rhinoceros
        Debug.Write (млекопитающие.ToString и "")
    Следующий
    Отладка.WriteLine("")
    ' Продукт: газель, мангуст, носорог.
Конец сабвуфера
 
Пример 3
В следующем примере параметры инструкции используют класс, который имеет перегруженные операторы для + , - , >= и <= операторы.
 Дистанция частного класса
    Номер публичной собственности () как двойной
    Public Sub New (номер ByVal как двойной)
        Me.Number = число
    Конец сабвуфера
    ' Определить перегруженные операторы для поддержки операторов For...Next.
    Общедоступный общий оператор +(ByVal op1 как расстояние, ByVal op2 как расстояние) как расстояние
        Вернуть новое расстояние (op1.Number + op2.Number)
    Конечный оператор
    Общедоступный общий оператор - (ByVal op1 As Distance, ByVal op2 As Distance) As Distance
        Вернуть новое расстояние (op1.Number - op2. Number)
    Конечный оператор
    Общедоступный общий оператор >=(ByVal op1 As Distance, ByVal op2 As Distance) As Boolean
        Возврат (op1.Number >= op2.Number)
    Конечный оператор
    Общедоступный общий оператор <=(ByVal op1 As Distance, ByVal op2 As Distance) As Boolean
        Возврат (op1.Number <= op2.Number)
    Конечный оператор
Конец класса
Общедоступный подсписок расстояний ()
    Dim distFrom As New Distance(10)
    Dim distTo As New Distance(25)
    Dim distStep As New Distance(4)
    Для dist As Distance = distFrom To distTo Step distStep
        Debug.Write(dist.Number.ToString & "")
    Следующий
    Отладка.WriteLine("")
    ' Вывод: 10 14 18 22
Конец сабвуфера
 
См. также
Список
Петлевые конструкции
Пока... Конец Пока Заявление
Оператор Do...Loop
Вложенные управляющие структуры
Заявление о выходе
Коллекции
Числовые облигации – игры, рабочие листы и как их преподавать
Начальная математика
Помогите своим ученикам узнать числовые связи до 20 и выше с помощью этих идей для уроков, видео и рабочих листов…
по Обучающий провод
Если вы учитель KS1 или KS2 и хотите преподавать числовые связи или освежить память учеников, у нас есть все рабочие листы, песни и онлайн-игры, которые вам нужны, а также советы ведущих экспертов о том, как преподавать эту тему в творческой форме. и памятные способы.
Перейти к разделу: Что такое числовая связь? Номерные листы по связям с облигациями Номерные облигации с 10 рабочим листом Количество Бондс с 20 рабочим листом Номер Бонги 2 Number Bonds с 5 Song Numbers Bonds Number Bonds4 Numbers Bonds. Как обучать числовым связям Использование мятных кремов для обучения числовым связям в KS1 Использование куклы-кенгуру для обучения числовым связям в KS1 Числовые облигации из 6-10 игр в кости для KS1/2 Игра «Очистить колоду» Дополнительные идеи о том, как обучать числовым связям Числовые облигации в играх с числовыми связями Числовые облигации для 10 игр 35 Числовые – основы Количество облигаций до 5 Количество облигаций до 10 Количество облигаций до 20 Количество облигаций до 100 Что такое числовая связь? Связи чисел — это пары чисел, составляющие данное число. Таким образом, они также известны как «пары чисел». Рабочие листы числовых облигаций Ищете распечатанные рабочие листы по числовым облигациям для использования в классе? Мы вас привели в порядок. Количество облигаций до 10 рабочих листов Помогите ученикам попрактиковаться с нашим эксклюзивным набором из 10 рабочих листов. Темы от животных до праздников, от инопланетян до спорта. В бесплатной загрузке вы найдете красочные школьные плакаты, пары карточек и множество иллюстрированных рабочих листов для учеников. Добавляйте сложение и вычитание в смесь с этим набором из 10 рабочих листов, идеально подходящим для KS1. Это четырехстраничный иллюстрированный PDF-файл, содержащий 12 математических задач, предназначенных для того, чтобы помочь учащимся попрактиковаться в связях чисел до 10. Количество облигаций до 20 рабочих листов Помогите учащимся KS1 попрактиковаться в связях чисел до 20 с помощью этого комплекта рабочих листов. Он был создан в соответствии с небольшими этапами математических схем работы «Белая роза» и содержит ряд наглядных примеров, которые помогут ученикам и побудят их к более глубокому мышлению. Номер облигации песни Видеоролики — отличный способ познакомить учащихся с концепцией числовых связей — будьте осторожны, эти запоминающиеся числа застрянут у вас в голове на несколько дней. Номер облигаций на 5 песен Это число Джека Хартмана, связанное с 5 видео, объясняет концепцию с большим энтузиазмом, чем мы когда-либо могли… Номер облигаций на 10 песен Вот еще одно видео с нашим милым другом Джеком — на этот раз это песня Джека Хартмана «Количество бондов к 10». Если вам больше по душе спокойная интерпретация игры Row, Row, Row Your Boat , то вот курс миссис Симм для 1-го класса расскажет вам все, что вам нужно знать о числовых связях до 10: Мы очень усердно работали и практиковали наши числовые связи. Что вы думаете? 👌🏻@crontonceschool @LDSTEducation pic.twitter.com/VJCMnneFvc — Year 1 (@crontony1) 24 января 2019 г. Вот текст полностью, так что ваш класс может попробовать: 9 и 1 - числовые связи, 8 и 2 - друзья, 7 и 3, 6 и 4, 5 и 5 - близнецы. Номер облигации на 20 песен Если бы Джордж Эзра написал песню об облигациях, она бы звучала примерно так. Мы не совсем уверены, какое отношение к чему имеют бананы и спагетти, но вскоре это станет ушным червем, от которого вы просто не сможете избавиться. Как научить числовым связям По словам Джеммы Шервуд, главы математического факультета средней школы Хейбриджа и шестого класса: «Наилучшее понимание чисел достигается, когда учащиеся знают математические факты, такие как числовые связи […] наизусть, потому что они могут затем работать с этими знаниями, что намного проще, чем без них». Национальная учебная программа гласит, что к концу Y2 учащиеся KS1 должны «знать числовые связи до 20 и быть точными в использовании и понимании разрядного значения. Акцент на практике на этом раннем этапе поможет беглости речи». Оценка автоматизма с числовыми связями? L демонстрирует с погремушками. Дети YR развили автоматизм не с помощью карточек, а путем изучения композиции, субитизации, паттерна, структуры и отношений в числах. Внедрение глубокого понимания #EYFS #MasteringNumber pic.twitter.com/9Sasxomh3e — Д-р Дебби Морган CBE (@ThinkingMaths) 18 июня 2022 г. Здесь у нас есть ряд способов помочь учащимся запоминать и рассуждать с числовыми связями до 10 и 20. Использование мятных кремов для обучения числовым связям в KS1 Идея этого урока от Майка Аскью, адъюнкт-профессора педагогики в Университете Монаш, направлена на то, чтобы научить детей KS1 сотрудничать, изучать числовые факты и систематически работать. Подготовка к уроку Перед уроком подготовьте листочки, которые дети потом будут использовать для записи своих результатов. На них показаны массивы квадратов, два на пять, которые достаточно велики, чтобы нарисовать простой «мятный крем»9.0003 Вы должны уместить шесть матриц на листе формата А4, но разрежьте их так, чтобы все они были на отдельных листах. Начать урок Расскажите о коробках со сладостями, которые вы приготовили для друзей на школьных каникулах. Наличие нескольких мятных кремов для детей на вкус также заставит их сесть и обратить внимание! «Каждый год я делаю коробки мятных кремов для семьи и друзей на Рождество. Кто делал или пробовал мятные кремы?» Обсудите эти и другие сладости, которые нравятся детям. Затем поднимите пустой массив, который вы сделали, и скажите: . «Я всегда упаковываю свои мятные кремы в вот такую коробку. Повернитесь к человеку рядом с вами. Договоритесь с этим человеком, сколько кремов я могу положить в коробку». Попросите детей объяснить, откуда они знают, что есть места для 10 кремов, не считая их всех. Кто видел 5+5? Кто видел 5 лотов по 2? Далее, произнесите: Я делаю мятные кремы двух цветов. Некоторые белые, а некоторые зеленые. Я положил немного белого и немного зеленого в каждую коробку. Поговорите со своим партнером, решите, какую коробку кремов сделать и сколько белых и сколько зеленых кремов будет в коробке». Приняв предложения детей, выберите один пример, скажем, 4 зеленых и 6 белых. Попросите детей помочь вам решить, куда положить кремы в коробке, записывая это на линейке по ходу дела. Произнесите: «Обратитесь к своему напарнику. Как вы можете быть уверены, что есть 4 зеленых и 6 белых кремовых?» Пока дети проверяют, правильно ли вы собрали коробку, запишите другое расположение деления 4/6, например: или Покажите детям это второе расположение и попросите партнеров обсудить, другая ли это коробка. Умышленно оставляю здесь вопрос неконкретным — в каком-то смысле отличается тем, что кремы устроены иначе. В другом смысле не отличается тем, что по-прежнему 6 белых и 4 зеленых мяты. Продолжение урока Подведите детей к мысли, что на этом уроке вы будете думать о них как об одной и той же коробке кремов. Коробки будут разными только в том случае, если количество зеленых и белых кремовых разное. Скажи так: «Мне интересно, если я положу в каждую коробку разное количество зеленых и белых кремов, сколько разных коробок получится? Это проблема, которую я хотел бы, чтобы вы помогли мне решить. Я хотел бы сделать как можно больше коробок с двумя видами мятных кремов». Предложите парам еще раз объяснить друг другу проблему и проверьте, все ли понятно, а затем скажите: «Вы будете работать вместе, чтобы записывать разные коробки кремов и брать их по очереди. Вот как — один человек будет записывающим, а другой — выбирающим. Выбирающий скажет, сколько кремов каждого типа положить в коробку, и записывающее устройство быстро нарисует числа каждого типа. Тогда вы поменяетесь местами». Пригласите ребенка стать вашим партнером и покажите, как вы работаете. Парное занятие 1 Пока дети садятся за работу в парах, сконцентрируйтесь на том, чтобы они правильно чередовались и слушали инструкции друг друга. Не позволяйте этой части урока затянуться: как только пары сгенерируют шесть или около того клеток, верните их внимание всем классом к доске. Назад к проблеме Собрав всех вместе, обойдите группы и попросите у них одну из их коробок. Поместите это на доску с помощью Blu-Tack. После того, как каждая пара предложит коробку, спросите класс, думают ли они, что они у вас есть, или есть ли у какой-либо пары еще одна коробка, которой у нас еще нет. Обычно предлагается больше, и неизбежно вы получите несколько коробок, которые выглядят по-разному, но на самом деле содержат одинаковое количество каждого крема. Если этого не происходит, «спроектируйте» это, выбрав и отобразив несколько дубликатов. Теперь, когда выставлено большое количество коробок, попросите детей внимательно посмотреть и проверить, все ли коробки у вас разные. Как только они начнут замечать дубликаты, попросите их поговорить со своим партнером о том, как вы могли бы организовать ящики, чтобы вы могли видеть, есть ли дубликаты и какие недостающие. Работая с их предложениями, заказывайте ящики 1,9; 2,8; 3,7 и так далее. Дубликаты можно размещать друг над другом и оставлять пробелы для любых отсутствующих комбинаций. Разбейте детей на пары, чтобы они продолжили и попытались собрать полный набор коробок. Парное занятие 2 Возвращаясь к задаче, дети будут более организованно проверять наличие дубликатов и недостающих комбинаций. Когда они будут близки к созданию полного набора коробок, предоставьте им сахарную бумагу и клей-карандаши, чтобы они могли «аккуратно» сделать постер из своего набора. (Большинство найдет 9 решений, хотя всего их 11, если вы разрешите поля, которые будут полностью зелеными или полностью белыми). Просмотрите и подумайте Соберите детей вместе, выберите одну или несколько пар, чтобы показать их плакат и рассказать о том, как они организовали свои коробки. Какие закономерности могут увидеть дети? Наконец, поработайте над записью комбинаций, используя соответствующие цифры и символы. Покажите плакаты в классе, чтобы показать ориентиры для пар чисел, составляющих 10. Расширение деятельности Что бывает с тремя видами кремов – белым, розовым и зеленым. Как насчет четырех видов? Что, если сделать коробки по 20 штук? Предположим, что коробки не обязательно должны быть 2 x 5, и что 12 кремов можно упаковать в коробку 2 x 6. Коробки какой другой формы вмещают 12 кремов? А 24 крема? Коробка может иметь более одного слоя. Какие коробки могут вместить 12 кремов? Белые сливки стоят 1 пенс, а зеленые кремы - 2 пенса. Сколько стоит каждый из ящиков? Если у вас есть 20 пенсов, какие различные комбинации зеленого и белого крема вы можете купить? Использование куклы-кенгуру для обучения числовым связям в KS1 Используйте этот урок внештатного консультанта по математике Криса Ингрэма, чтобы помочь своим ученикам KS1 изучить числовые факты и развить навыки решения задач. Знакомство с проблемой Подготовьте нить бус и спрячьте ее в сумке куклы кенгуру. Скажи так: «Сегодня кенгуру спрятала в сумке нитку бус. На нитке 10 бусин. Некоторые красные, а некоторые желтые. Интересно, бусинок больше красных или желтых? Можете ли вы нарисовать картинку или составить числовое выражение, чтобы показать, сколько бусинок может быть красными, а сколько желтыми?» В этот момент покажите детям большую коробку с бусинами и объясните: «Можно использовать синие бусы? Почему бы и нет? Можно ли на нитке 14 бусин? Могут ли все 10 быть желтыми?» Убедитесь, что дети четко понимают, что они собираются составить цепочку из 10 бусин, и что они должны использовать как красные, так и желтые бусины. Решение проблемы Дифференциация довольно проста и определяется тем, подходит ли ребенку исследовать и записывать проблему практически, образно или символически. Кроме того, у вас, вероятно, будут дети, от которых требуется одно решение, тогда как другие дети будут пытаться найти несколько или даже все возможные решения. Группа 1 Используя те же ресурсы, что и вы, попросите детей придумать решение, соответствующее критериям – нить из 10 бусин, часть из которых красного цвета, часть желтого. Это может показаться простым, но наблюдение за детьми в действии показывает, что это больше, чем просто счет. Большинство маленьких детей не знают пары чисел, составляющих 10, поэтому они случайным образом размещают на нитке красные и желтые бусины. Некоторые дети считают общее количество, добавляя каждую бусинку, но большинство, кажется, надевают бусинки до тех пор, пока не станет казаться, что они собрали 10 – после чего они пересчитывают их, чтобы узнать. Если они обнаружат, что бусинок 8 или 11, они, надеюсь, распознают, что их недостаточно/слишком много, и приспособятся соответствующим образом. Однако будет много детей, чья реакция на эту ситуацию будет заключаться в том, чтобы снять все бусы и начать снова, и снова, и снова. Это полезный оценочный пункт, и некоторые тщательные вопросы здесь могут привести детей в правильном направлении. Группа 2 Другие дети также могут решить задачу, используя другие манипуляции. Объясните, что бусинок недостаточно, и предложите ученикам использовать вместо них что-нибудь другое. Признание того, что бусины можно изображать с помощью другого предмета (кубиков, фишек, цветных мишек и т. д.), и что это не повлияет на их способность понять и решить проблему, является большим шагом вперед. Группа 3 Точно так же другие группы могут изобразить решение с помощью краски, цветного карандаша или цветной бумаги. Это требует более сложного процесса, поскольку дети с меньшей вероятностью будут использовать метод проб и ошибок, как группа 1 (возможно, потому, что будут «доказательства» каждой попытки), и гораздо более вероятно, что они будут использовать «расчет на» как способ отслеживание общей суммы по мере их работы. Группа 4 У вас может быть группа детей с более высокими достижениями, которые могут представить свои решения в виде числовых предложений. Если это так, им может быть предложено найти все возможные решения. Будет интересно посмотреть, работают ли дети систематически при составлении упорядоченного списка – и уверены ли они, что открыли все возможности без повторений! Назад к проблеме После того, как дети придумают свое решение (будь то с помощью бисера, красок и т. д.), важно побудить их связать это с исходной задачей. Спросите: «Как ты думаешь, сколько желтых бусинок у кенгуру, и сколько красных бусинок, и сколько всего бусинок?» Если это уместно, вы можете спросить: «Можем ли мы использовать числа, чтобы запомнить вашу идею?» Дети могут предложить написать цифры желтым и красным карандашом или составить числовое предложение. Просмотрите и подумайте Собрать детей вместе после того, как они изучили проблему, — важная часть процесса. Это возможность для кенгуру напомнить детям об исходной задаче, а ученикам представить различные решения, которые они придумали. В этот момент ученики могут подумать, что существует столько решений, сколько детей в классе. Ваша роль состоит в том, чтобы помочь учащимся осмыслить эту информацию. Выберите ребенка, который поделится своим решением, и скажите что-нибудь вроде этого: «Джейк сделал нитку из 3 желтых и 7 красных бусин. У кого-нибудь есть картина или числовое выражение, которое соответствует 3 желтым и 7 красным?» Соберите вместе все презентации с этой комбинацией, а затем перейдите к другому решению. На этом этапе вам придется иметь дело с проблемой коммутативности — хотя 3 + 7 явно эквивалентны 7 + 3, вам нужно обращать внимание на контекст и быть осторожным в использовании языка: равен и совпадает с С какой стороны ни посмотри, есть группа из 10, состоящая из 3 желтых и 7 красных. равно, но не то же, что и Или иметь 3 кошек и 7 собак — это не то же самое, что иметь 3 собак и 7 кошек, хотя в любом случае у вас явно 10 питомцев. Увидеть закономерность Собирая различные решения, начните перечислять их, чтобы дети поняли, что, организуя решения таким образом, вы сможете увидеть появление закономерности: Шаблон дает вам уверенность в том, что вы нашли все возможные решения, а также в выявлении отсутствующих решений или повторений. Некоторые дети с большей вероятностью увидят узор в цветных пятнах, другие найдут узор более четким, если представить его цифрами. Произнесение рисунка вслух нараспев также поможет детям уловить его. Реорганизация бусин так, чтобы они представляли две отдельные группы, облегчит субитизацию или подсчет и поможет позже в сеансе с определением закономерностей. Предоставление практических ресурсов для составления числовых предложений побуждает детей экспериментировать с символической записью как еще одним способом передачи своих идей. Что в сумке? В финале этого урока кенгуру показывает бусины, которые у нее есть в сумке, а дети определяют, есть ли у них подходящее решение. Здесь важно подчеркнуть, что было девять правильных решений проблемы, а не одно. Завтра, а может быть и до конца недели, кенгуру спрячет в сумке еще 10 бусинок – одни красные, другие желтые – а дети смогут использовать другие свои решения, чтобы угадать, что это могут быть. Если вы будете показывать решения и регулярно возвращаться к этому занятию в качестве умственного/устного старта, дети вскоре смогут использовать свои знания для решения задач с пропущенными числами: «У кенгуру в сумке 10 бусинок, одни красные, а остальные желтые. Она даст вам подсказку — она покажет вам все красные бусины, вы можете определить, сколько желтых бусинок? Откуда вы знаете?" Позже вы можете показать детям, как это связано с такими уравнениями, как 3 + [ ] = 10 или 10 – 3 = [ ]. Облигации с номерами из 6-10 игр в кости для KS1/2 Для этого простого задания вам понадобятся игральные кости и несколько цветных карандашей, а также эти бесплатные рабочие листы для игры в кости. Вот как играть: Бросьте кубик Закрасьте количество кружков на кубике Закрасьте другую часть Запишите две части, на которые разбито целое число Очистите колоду Целью этого занятия, проведенного независимым консультантом по вопросам образования Джуди Хорниголд, является помощь учащимся в развитии мгновенного запоминания числовых связей до десяти. Попробуйте это в качестве разминки в начале урока или в конце для повторения или закрепления. Как играть Вам понадобятся четыре набора карт с цифрами от 1 до 9. Перемешайте карты и разложите их лицевой стороной вверх на столе в три ряда по четыре. Игроки по очереди берут пары карт, сумма которых равна 10. Оставшиеся пробелы заполняются картами из оставшейся колоды. Идея состоит в том, чтобы по очереди находить пары, которые составляют 10, как можно быстрее. Другие идеи о том, как преподавать числовые облигации Не возражаете рискнуть хорошенько промокнуть Фредди в Y1? Попробуйте это… Облигации Nerf gun!#StayAtHome #LearnAtHome pic.twitter.com/NNG2CgDri4 — NumBots (Расти) 💎 (@numbots) 27 марта 2020 г. Эта идея от мисс Уорд требует небольшой предварительной подготовки, но фокусируется на конечное число привязывается к 10 инструменту – наши собственные пальцы… Часть первая: 😁Привет от меня и моего супер помощника! Сегодня мы рассмотрели числовые связи до 10 и сделали собственный простой ресурс, который вы можете попробовать дома! 😁 pic.twitter.com/K0KJ8IRk3S — Мисс Уорд (@SomersparkRAW) 26 марта 2020 г. Вам понадобится только чашка и несколько двусторонних фишек, чтобы воссоздать эту простую игру от миссис Бэйли… Учим наши числовые связи до 10 с помощью множества различных занятий! Пришлось кинуть двусторонние жетоны и записать расчет 👍 #Знания pic. twitter.com/g9ZeBo1l7m — Миссис Бэйли 🌟 (@MrsBaillie) 8 февраля 2019 г. Игры с числовыми облигациями Обучение числовым связям до 10 иногда может показаться немного однообразным. Ведь существует лишь небольшое количество комбинаций. Так почему бы не позволить детям заняться чем-нибудь забавным, чтобы либо выучить, либо закрепить свои знания о числовых фактах? Вот подборка бесплатных, простых в использовании онлайн-игр с числовыми связями, которые может попробовать ваш класс. Количество облигаций на 10 игр В этой простой, но удобной игре с десятью рамками есть сетка из 10 ячеек, которые заполняются фишками (или звездами, яблоками или божьими коровками) и спрашивается, сколько их есть или сколько ячеек пусто. Вы также можете перейти на уровень сборки, где дети должны вставить правильное количество фишек. Затем есть «заполнение», когда их спрашивают, сколько еще фишек нужно, чтобы завершить набор из 10. И «добавить», когда у вас есть два набора из 10, которые нужно заполнить правильным количеством фишек, прежде чем суммировать итоги вместе. Изучите числовые облигации до 10 в этой игре «Любопытный Джордж: Музей десятков». Следуйте за ним по музею, где у каждого экспоната должно быть 10 экспонатов, но некоторых не хватает. Задача ваших учеников — помочь Джорджу определить, сколько еще им нужно, чтобы получилось 10. В этой забавной маленькой игре с числовыми облигациями «Одень своего монстра» дети могут одеть своего монстра в различную одежду и аксессуары. Но для этого им нужно будет ответить на вопросы числовых связей до 10. Ряд пронумерованных шаров катится к дыре в этой игре с номером 10, и ваша задача - остановить это. Вы делаете это, запуская свои собственные сферы, чтобы сделать числовые связи 10 и наблюдать, как они исчезают. Это блестяще затягивает. Игры на время В этой быстрой игре «Нажми на кнопку» есть ряд вариантов, которые вы можете попробовать, включая удвоение, половинку, таблицу умножения, факты деления и квадратные числа, а также, конечно же, числовые связи. Даже в числовых облигациях вы можете выбрать числовые облигации до 10, 20 или 100, а затем в них есть разные задачи. С базовым числом, равным 10, детям дается одно число, и они должны выбрать число, которое составит пару, чтобы получить 10. У них есть минута, чтобы получить как можно больше. Еще более простая версия — это игра «Минута безумной математики» (хотя вы можете установить более длительный таймер, если хотите), в которой детям нужно за 60 секунд ответить на как можно больше числовых связей до 10 сумм. Есть опция справки, которая дает вам цветную рамку из 10 для визуальной помощи, и вы также можете проверить и распечатать свои результаты. Еще один вариант системы «Бей по часам», эта игра «Я могу вспомнить все числовые облигации до 10» имеет то преимущество, что в смесь добавляются вопросы на вычитание. Ответьте правильно на последовательные вопросы, чтобы повысить свой уровень, но будьте осторожны, это увеличивает сложность сумм. Продвинутая игра Эта игра с числовыми связями — одна из тех забавных маленьких головоломок, в которые можно играть часами. Идея состоит в том, чтобы соединить числовые связи с 10, расчистив путь между ними. Ваша линия может согнуться один раз, два или шарики могут быть рядом друг с другом (не по диагонали). Просто не забывайте следить за тем, как долго вы играете! Число облигаций – основы Хотите освежить в памяти концепцию числовых связей? Вот что вам нужно знать, в двух словах. Номер облигаций до 5 Числовые связи до 5 — это пары чисел, которые в сумме дают 5. Числовые связи для числа 5: 0 + 5 1 + 4 2 + 3 3 + 2 4 + 1 5 + 0 Количество облигаций от 90 до 30 Числовые связи до 10 — это пары чисел, которые в сумме дают 10. Числовые связи для числа 10: 0 + 10 1 + 9 2 + 8 3 + 7 4 + 6 5 + 5 6 + 4 7 + 3 8 + 2 9 + 1 10 + 0 Номер облигаций до 20 Числовые связи до 20 — это пары чисел, которые в сумме дают 20. Числовые связи до 20: 0 + 20 1 + 19 2 + 18 3 + 17 4 + 16 5 + 15 6 + 14 7 + 13 8 + 12 9 + 11 10 + 10 11 + 9 12 + 8 13 + 7 14 + 6 15 + 5 16 + 4 17 + 3 18 + 2 19 + 1 20 + 0 Число облигаций до 100 Числовые связи до 100 — это пары чисел, которые в сумме дают 100. Вот список числовых связей до 100, если они работают с числами, кратными 10: 0 + 100 10 + 90 20 + 80 30 + 70 40 + 60 50 + 50 60 + 40 70 + 30 80 + 20 90 + 10 100 + 0 Улучшение обучения и помощь в образовательном процессе В этой статье мы обсудим роль наглядных материалов для детей в процессе обучения , мы поделимся некоторыми фактами о том, как дети узнают , и предоставим вам визуальных ресурсов, которые помогут вам в учебном процессе. Давайте начнем с того, что прольем свет на то, почему, по мнению экспертов, наглядные пособия для детей являются важной частью учебного процесса и раннего развития детей в целом. Вас может заинтересовать бесплатная книжка-раскраска GraphicMama: 60+ раскрасок (в формате PDF для печати) Обзор статьи: 1. Как мы запоминаем? 2. Использование наглядных материалов для детей в образовательном процессе 3. Знайте, как дети учатся в вашем классе 4. Примеры наглядных пособий 5. Другие советы по выбору визуального контента для детей 1. Как мы запоминаем? В наши дни мы получаем огромное количество визуальной информации. Сами СМИ признают влияние визуального на аудиальное и все больше полагаются на такой контент. С 1990 г. число изображений в литературе увеличилось на 4000%, в Интернете — на 9900% с 2007 г., а в газетах — на 142%. Статистика показывает, что мы учимся в обычной повседневной жизни следующим образом: 3% через вкус, 3% через обоняние, 6% через осязание, 13% через слух, 75% через зрение мы запоминаем : 10% всего, что мы слышим, 35% всего, что мы видим, и 65% всего, что мы видим и слышим одновременно процесс Но как все это применяются к детям и влияют на их обучение ? Дети со зрением – 50 % их мозга задействованы в обработке зрительных образов, 70 % всех их сенсорных рецепторов находятся в глазах, и они воспринимают изображение за 1/10 секунды. Но не секрет, что дети страдают от информационной перегрузки – они получают в 5 раз больше информации, чем дети 196 , и ежедневно потребляют 34 ГБ информации вне школы. Имея в виду, что дети читают только 28% слов, посещая веб-сайт (например), очень важно включать визуальные эффекты в учебный процесс. Опять же, статистика подтверждает эту точку зрения: цветные изображения увеличивают желание читать на 80%, и понимание повышаются на 95% при использовании изображений рядом с текстом . И последнее, но не менее важное: детей следуют инструкциям с визуальными эффектами на 323 % лучше, чем инструкции только с текстом. Среди других преимуществ использования наглядных материалов для детей: снижение беспокойства, сопротивления изменениям и социальной изоляции, помощь детям с трудным поведением, мотивацией и пониманием, а также помощь в переходных периодах. 3. Узнайте, как дети учатся в вашем классе Психологи различают 3 типа учащихся . Даже в раннем возрасте у нас есть собственный предпочтительный стиль обучения, который остается с нами и во взрослой жизни. 3.1. Визуалы 83% людей учатся, видя. Это люди, которым нравится, когда им что-то показывают, чтобы легче понять информацию. На уроках чаще всего это дети, которые предпочитают сидеть впереди и спокойно наблюдать за всем происходящим. Эти дети любят книжки с картинками, карты и мультфильмы. 3.2. Учащиеся на слух 11% людей учатся на слух. Эти дети обычно любят музыку и обращают внимание на звуки. Они предпочитают говорить им, что делать. Им нравится говорить и слушать разговоры. 3.3. Кинестетические ученики 6% людей учатся, прикасаясь, двигаясь и делая что-то. Зачастую это самые активные дети в классе, и им нужно что-то потрогать и сделать, чтобы понять это. Сложные инструкции могут сбить их с толку. Дети этого типа вроде бы не могут усидеть на месте, но на самом деле запоминают легко и подробно. Конечно, у детей есть предпочтительный стиль обучения, но они часто сочетают разные типы обучения. Поэтому учителя должны уделять внимание каждому из процессов обучения своих учеников. Тем не менее, можно с уверенностью сказать, что большинство в классе очень хорошо отреагируют на обучение с помощью наглядных материалов. 4. Примеры наглядных пособий Существует множество различных наглядных пособий для детей, которые могут помочь учителю объяснить учебный материал, вовлечь детей в учебный процесс и привлечь к участию. Некоторые из них карточки, доски-головоломки, сборники рассказов и временные шкалы. Давайте посмотрим, как вы можете использовать доски «Сначала/Потом» и расписания , например, чтобы помочь детям учиться. 4.1. Доска «Сначала/Потом» Они помогают обучать логической последовательности событий, например, «Сначала вымойте руки, затем поешьте». Они наглядно поясняют пошаговые инструкции. Они также помогают мотивировать детей заниматься менее предпочтительными видами деятельности, зная, что за ними последует более предпочтительное занятие. Сначала/Потом шаблон платы Как сделать такую плату? Вы можете скачать шаблон, который мы сделали для вас здесь, распечатать его и прикрепить свои картинки (или вы также можете найти много мультфильмов на нашем сайте). Покажите детям доску, назовите задания и укажите на картинки. Обычно дети не понимают и не следуют инструкциям с первого раза, но постоянное использование таких досок в учебном процессе даст желаемый эффект. 4.2. Расписание Создание расписания помогает несколькими способами: показывает, какова последовательность предстоящих событий, какие новые действия произойдут, что не происходит, и, таким образом, облегчает тревогу ребенка. Шаблон утреннего расписания Как составить расписание? Используйте максимум 90 197 6-7 визуальных элементов в последовательности, определяйте моменты, когда меняется местоположение или деятельность. Выбирайте символы, которые являются достаточно общими, например, «время обеда», а не конкретное блюдо. До последнего, с точными словами , которые вы будете использовать для обозначения действия. Не забудьте разместить оба изображения на высоте детей, чтобы дети могли прикасаться к ним и использовать их, когда захотят. Установите их на видном месте, чтобы учащиеся могли легко обратиться к ним. Другим полезным инструментом для обучения являются мини-расписания , которые можно использовать и дома, чтобы помочь детям в их повседневных делах – мытье рук, уборка в комнате и т. д. Для максимального эффекта укажите на картинки , чтобы помочь ребенку выучить и подчеркнуть основные слова . Не забудьте! / Сделать Чистый лист бумаги со школьными принадлежностями Наклейки 4.3. Мультфильмы Мультфильмы можно использовать в качестве разогрева или ледокола к уроку, чтобы изменить фокус или начать обсуждение в классе. Вы можете предложить учащимся создавать собственные подписи к предоставленным мультфильмам, сопоставлять подписи с выбранными мультфильмами и анализировать различное культурное и/или социальное поведение. Наконец, можно использовать мультфильмы и попросить детей поразмышлять над событиями, изображенными на картинках. Мы выбрали несколько красивых иллюстраций для детей, которые помогут вам в обучении: 5. Другие советы по выбору визуального контента для детей Вот несколько быстрых советов о том, как выбрать визуальный контент и как к нему подготовиться. их на уроки: Дети общаются и понимают на разных уровнях – определите их уровень Во-первых, используйте реальные объекты и предметы для общения, где это возможно Использование фотографий Используйте цветные картинки и картинки большего размера, когда дети учатся ассоциировать картинку с объектом; позже в процессе включите изображения меньшего размера; перейти к более абстрактному формату, поместив небольшой рисунок рядом с фотографией, чтобы указать, что они представляют одно и то же Через некоторое время показать линейные чертежи До последнего включите написанные слова и цифры Расположите изображения горизонтально – это подготовит ребенка к чтению; некоторым детям легче сканировать по вертикали; Сделайте изображения долговечными — распечатайте на картоне, приклейте к папке с файлами, заламинируйте и т. д. Мы надеемся, что статья была полезна для вас и для улучшения ваших методов обучения и улучшения процесса обучения детей. Напишите нам в разделе комментариев ниже, если у вас есть пожелания и/или вопросы! Набор образовательного клипарта Взгляните на мега-набор образовательного клипарта от GraphicMama. В комплекте 9 упаковок1838 176 образовательных клипартов изображений учителей, учеников, детей, школьных принадлежностей и фонов для образовательных проектов. Эта коллекция поставляется в файлах AI, EPS, PDF и прозрачных PNG, поэтому ее могут легко использовать непрофессионалы. Перейти к загрузке Как преподавать разрядность с помощью связок соломинок Разрядность — важное математическое понятие, которое должны понять учащиеся начальной школы. Они должны усвоить, что значение цифры зависит от ее места в числе. Например, учащиеся должны понимать, что в числе 142 цифра 1 имеет значение 1 сотня. Цифра 4 имеет значение 4 десятка, а цифра 2 имеет значение 2 единицы. Когда учащиеся изо всех сил пытаются понять разрядное значение, это может сдерживать их в понимании более сложных математических концепций. Один из способов помочь учащимся понять значение разряда — использовать манипуляторы, чтобы показать значение каждой цифры. Вы можете сделать это, используя соломинки (или деревянные палочки) и циновку. С помощью этой стратегии вы используете манипулятивные приемы, чтобы явно научить учащихся составлять число. Используя соломинки, они составят многозначное число, показав значение каждой цифры отдельно. Это помогает учащимся установить связь между числами и разрядными значениями. Прокрутите вниз, чтобы найти советы по адаптации этой стратегии для дистанционного обучения. Смотреть: Использование связок для обучения порядковому значению Посмотрите это видео, чтобы узнать, как научить учащихся связывать соломинки или деревянные палочки для рукоделия. Загрузить: Матч с разрядами для печати Распечатайте этот мат с разрядами или научите учащихся рисовать самостоятельно. Матч разрядов — сотни PDF Читать: Как использовать эту стратегию разрядов Задача: Учащиеся будут составлять двузначные (для первого класса) или трехзначные (для второго класса) числа и объясните разрядное значение каждой цифры. Уровни обучения (со стандартами): 1 (Общее ядро 1.NBT.B.2: Понимание того, что две цифры двузначного числа представляют количество десятков и единиц) 2 (Общее ядро 2.NBT.A.1: понимать, что три цифры трехзначного числа представляют количество сотен, десятков и единиц) 1–2 (Common Core Math Practice MP2: Рассуждать абстрактно и количественно; Common Core Math Practice MP5: Стратегически используйте соответствующие инструменты) Лучше всего использовать для обучения с: Весь класс Небольшие группы Индивидуальные Как подготовить: Собрать материалы. Раздайте каждому учащемуся соломинки (или деревянные палочки для рукоделия), резинки и коврик для распечатки. Надевание эластичных лент на соломинки или палочки может быть сложной задачей для учащихся, у которых проблемы с мелкой моторикой. Вы можете предложить своим ученикам варианты того, какие предметы они хотят связать и как они хотят их связать, например, положить 10 мелков в небольшой пакет для закусок или 10 палочек в маленькую чашку, чтобы сформировать связку. Как научить: 1. Потренируйтесь делать связки. Объясните учащимся, что они будут использовать соломинки, чтобы лучше понять разрядное значение. Они будут считать отдельные соломинки «единицами», а связки соломинок группами по 10 штук — «десятками». (Во втором классе они также объединят 10 групп по десяткам, чтобы получились «сотни».) Явно повторите академический словарь, необходимый для урока, например, десятки , единицы , место , и значение . Для изучающих английский язык (ELL): Определите слова, которые имеют более одного значения, например, поместите . Используя картинки или другую поддержку, поделитесь определениями слова. Например, место может означать физическое место, например, парк. Или, если друг говорит: «Освободите мне место на обед», он просит, чтобы вы выделили для него место за столом. Установите связь, что место в месте значение является пятном в числе. Модель, как считать 10 соломинок. Сосчитайте их вслух, а затем свяжите их вместе резинкой, чтобы получилась 1 группа из десяти. Докажите, что 10 единиц равны 1 десятку. Затем попросите учеников сделать то же самое. Предложите им отсчитать 10 соломинок, а затем связать 10 соломинок вместе, чтобы получилась 1 десятка. Затем повторите еще с 10, чтобы сделать вторую связку десятков. Если у учащихся остались соломинки, попросите их посчитать эти соломинки как «единицы», которые нельзя связать. (Для второго класса продолжайте до тех пор, пока учащиеся не смогут сосчитать десятки, чтобы получить 1 сотню.) Вы также можете предложить всем учащимся посмотреть видео о пакетировании, подходящее для учащихся. 2. Составьте число, используя конкретные манипуляции. Скажите учащимся, что они будут использовать соломинки и коврик для разряда, чтобы составить (или «сделать») число. Следуйте последовательности инструкций «конкретно-репрезентативный-абстрактный» (CRA), начиная с конкретного. Начните с просмотра таблицы разрядов и объяснения каждого столбца: сотни, десятки и единицы. Продемонстрируйте, как использовать соломинки на коврике для оценки места. Например, вы можете составить число 24 для первоклассников, поместив 2 пачки по 10 в колонку десятков и 4 единицы в колонку единиц. Для второклассников вы можете составить число 142, сложив 10 связок по 10 в столбец сотен и поместив 4 пачки по 10 в столбец десятков и 2 единицы в столбец единиц. Для ELL: Обеспечьте дополнительную поддержку, используя рамки предложений. Например, для числа 24 вы можете написать на доске и попросить учеников заполнить пропуски: «Число 24 . В числе 24 два десятка . В числе 24 четыре единицы ». Эта визуальная поддержка особенно важна для чисел, которые звучат одинаково, например, 17 и 70. Позвольте учащимся потренироваться делать то же самое с несколькими числами. Дайте им обратную связь, как они работают. Попросите учащихся поделиться своими мыслями со своими одноклассниками после составления каждого числа. Например, вы можете предложить учащимся повернуться и рассказать, что они поместили в каждую колонку для числа 24. 3. Перейти к репрезентативному. После того, как учащиеся научатся составлять числа из конкретных материалов, переходите к репрезентативному уровню понимания. Покажите, как рисовать связки на салфетке. Чтобы представить число 16, нарисуйте 10 вертикальных линий с кружком вокруг них или перечеркните их косой чертой в столбце десятков и 6 вертикальных линий в столбце единиц. Затем представьте то же число с помощью более грубых набросков связок, чтобы показать учащимся, что им не нужно рисовать все линии в связке десятков (или сотен). Поговорите о том, что, хотя вы не видите все 10 линий в своем грубом наброске, вы знаете, что их нужно считать за 10, потому что они связаны с кругом или косой чертой. Затем пусть учащиеся нарисуют связки в соответствующих столбцах на своих ковриках с разрядностью, чтобы составить число. Например, первоклассники могут составить число 53, нарисовав 5 связок по 10 в колонке десятков и 3 единицы в колонке единиц. Во втором классе учащиеся могут составить число 253, используя подобные рисунки. Опять же, предоставьте множество возможностей для практики и обратной связи. Предложите учащимся объяснить свои рисунки и назвать стандартный номер. Учебный совет: Чтобы повторно использовать коврики с позиционными значениями на протяжении всего урока, поместите коврики в карманы для сухостираемых маркеров и попросите учеников использовать маркеры для сухого стирания, которые можно стереть, прежде чем переходить к следующему примеру. 4. Закончите аннотацией. После освоения репрезентативного уровня переходите к абстрактному уровню. На коврике с разрядами попросите учеников составить число, используя только написанные числа — например, 6 десятков и 7 единиц составляют «67» или, для второго класса, 4 сотни, 3 десятка и 6 единиц составляют «436». Разместите на доске рамки предложений, заполнив пробелы для визуальной поддержки: « шесть десятков и семь единиц дает 67 ». Чтобы повысить гибкость, вы можете попробовать менять местами не по порядку. Например, объясните, что число состоит из 7 единиц и 3 десятков, и предложите учащимся показать 37. Если учащиеся испытывают затруднения на абстрактном уровне, позвольте им вернуться к использованию связок, а затем изображений. Подчеркните связь между связанными объектами, репрезентативными изображениями и числовыми символами. Перейдите к абстрактному уровню, как только учащиеся продемонстрируют понимание. Совет преподавателю: Вы можете продолжать практиковать разрядность, находя реальные числа вокруг своих учеников. Во время уроков по другим предметам указывайте на цифры, которые вы видите, например, на пронумерованные страницы в книжке с картинками или почтовый адрес на конверте. Предложите учащимся составить числа по разрядности. Вы также можете предложить учащимся найти двух- или трехзначные числа в своей жизни и принести эти примеры в класс для практики. Поймите: почему эта стратегия работает Некоторые ученики изо всех сил пытаются установить связь между нашей системой счисления с основанием 10 и языком, который мы используем для чисел. Это потому, что язык, который мы используем для чисел, не переводится напрямую. Например, мы пишем «216», а не «200 10 6». Составление чисел с использованием этой стратегии поможет учащимся установить связь между системой счисления и языком. Он показывает им, что число состоит из суммы его частей. Кроме того, учащимся полезно использовать различные модели, в том числе связки соломинок, диски с оценочными значениями и рисунки. Студенты также учатся благодаря поддержке и обратной связи, когда они переходят от конкретных к абстрактным представлениям числа. Улучшение понимания учащимися разряда закладывает основу для будущей работы по математике, включая сложение с перегруппировкой во втором классе и умножение, дроби и десятичные числа в старших классах начальной школы. Расскажите семьям, что учащиеся узнают о ценности места в школе. Это может отличаться от того, как члены семьи учили математику, когда они были моложе. Это потому, что математику сегодня преподают по-другому. Отправляйте домой ресурсы, чтобы помочь семьям укрепить концепцию ценности места. По электронной почте вы можете поделиться статьей, в которой объясняется, как использовать мультисенсорные методы для определения разрядного значения и других математических понятий, а также видео о том, что второклассники узнают о разрядном значении. Вы также можете поделиться этим видео с семьями, чтобы помочь им понять, как их дети учатся составлять и разлагать числа.

	классических времен, написал бумагу в форме письма королю своего города, объясняя, как писать такие очень большие числа. Архимед, однако, не зашел так далеко, чтобы изобрести десятичную систему счисления с возможностью неограниченного расширения.
22.	Knuth, 1974, стр. 323.
23.	Steen, 1990. См. Морроу и Кенни, 1998, для получения более подробной информации об алгоритмах.
24.	Точки с многоточием «…» в выражении являются важной частью абстрактной математической записи, компактно обозначающей пропуск необходимых терминов (для достижения м, в данном случае ).

а + в	a + b — c	а — б
а — б — в	a	a + b + c
а + б	a — b + c	a — c

Средний уровень	Низкий уровень
17%	58%	25%
Типичные ошибки
Незнание следования чисел в натуральном ряду		Не знание свойств натурального ряда		Не умение сравнивать два натуральных числа
К-во учащихся		К-во учащихся		К-во учащихся	
Экспериментальная группа	3	25	2	17	3	25
Контрольная группа	7	58	7	58	6	50


Мультимедийное оснащение занятия (используется интерактивная доска, документ-камера и др.)	На занятиях по неотложной медицинской помощи слушатели работают с обучающей компьютерной программой по сердечно-легочной реанимации

Проводится компьютерное итоговое тестирование слушателей	Мультимедийные презентации имеются в арсенале каждого преподавателя. Пример: разработки Гарликова Н.Н.


Работа с деструктором игл и портативным автоклавом	Новое в лабораторной диагностике (работа с экспресс-анализаторами)


Использование вакуумных шин и проведение массажа сердца при помощи кардиопампа	Проведение фельдшерами скорой помощи ИВЛ после интубации трахеи с помощью ларингоскопа


Освоение технологии забора крови с помощью вакуумных систем	Обучение постановке периферических катетеров


Демонстрируется аппаратно-программный комплекс «Здоровье-Экспресс»	Организована работа по борьбе с табакокурением


Победитель конкурса – фильм «Лучезарная улыбка» – цикл «Стоматологическая помощь населению»

Деталь	Описание
`счетчик`	Требуется в инструкции `For` . Числовая переменная. Управляющая переменная для цикла. Дополнительные сведения см. в разделе «Контраргумент» далее в этом разделе.
`тип данных`	Дополнительно. Тип данных счетчика . Дополнительные сведения см. в разделе «Контраргумент» далее в этом разделе.
`начало`	Обязательно. Числовое выражение. Начальное значение счетчика .
`конец`	Обязательно. Числовое выражение. Окончательное значение счетчика .
`ступенька`	Дополнительно. Числовое выражение. Величина, на которую `счетчик` увеличивается каждый раз в цикле.
`заявления`	По желанию. Один или несколько операторов между `For` и `Next` , которые выполняются указанное количество раз.
`Продолжить для`	Дополнительно. Передает управление следующей итерации цикла.
`Выход Для`	Дополнительно. Передает управление из цикла `For` .
`Следующий`	Обязательно. Завершает определение цикла `For` .

Значение шага	Цикл выполняется, если
Положительный или ноль	`счетчик` <= `конец`
Отрицательный	`счетчик` >= `конец`

Присутствует ли тип данных ?	Счетчик уже определен?	Результат (определяет ли счетчик новую локальную переменную, область действия которой распространяется на весь цикл `For...Next` )
№	Да	Нет, потому что `счетчик` уже определен. Если область действия счетчика не является локальной для процедуры, появляется предупреждение во время компиляции.
№	№	Да. Тип данных выводится из выражений `start` , `end` и `step` . Дополнительные сведения о выводе типа см. в разделе Оператор Option Infer и вывод локального типа.
Да	Да	Да, но только если существующий счетчик переменная определяется вне процедуры. Эта переменная остается отдельной. Если область действия существующей переменной счетчика `является локальной для процедуры, возникает ошибка времени компиляции.`
Да	№	Да.

Домики «Состав числа» от 1 до 10, от 11 до 20 — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Соседи числа — Математические задания для детей

5.Скачать карточки «Соседи чисел»

4.Помоги животным — Впиши соседей числа.

Соседи числа — Знаешь ли ты порядковый счет?

Найди состав чисел и соседей числа в домиках

Числовые домики — Состав чисел от 2 до 9

Состав чисел первого десятка. Числовые домики.

Рисуем карточки и объясняем ребенку правила

Помогаем ребенку освоить состав числа до 10 в игре

Закрепляем пройденное

Презентация online

Карточки «Числовые домики»

Карточки по математике. 1 класс. Состав чисел 1-10. | Учебно-методический материал по математике (1 класс) на тему:

Урок математики 1 класс состав числа 2,3,4.

Цифры от 0 до 10 для детей. Изучать с детьми цифры нужно в несколько приемов

Как сделать цифры картинки для детей самим.

Развивающие карточки цифры от 1 до 10 для детей

Развивающие карточки цифры от 1 до 10 для детей

Развивающие карточки цифры от 1 до 10 для детей

Развивающие карточки цифры от 1 до 10 для детей

Развивающие карточки цифры от 1 до 10 для детей

Развивающие карточки цифры от 1 до 10 для детей

Развивающие картинки цифры от 1 до 10 для детей

Таблица счета от 1 до 10

Изучать цифры и счет от 1 до 10 с детьми можно еще с помощью развивающих мультфильмов Малышман ТВ

1. «Цифры от 1 до 10» для печати в картинках.

4. Карточки с цифрами от 1 до 10 и математическими знаками «плюс» и «минус».

5. Скачать цифры от 1 до 10 «Синие». Цифры и их названия.

6. Карточки «Цифры от 1 до 10» — распечатать каждую цифру на отдельном листе.

7. Учимся писать цифры по точкам от 0 до 15 по образцу.

Карточки с числами от 1 до 20 — Распечатай и считай

Изучать с детьми цифры нужно в несколько приемов.

Развивающие карточки цифры от 0 до 20 с математическими знаками

Развивающие карточки цифры от 0 до 20 с математическими знаками

Развивающие карточки цифры от 0 до 20 с математическими знаками

Развивающие карточки цифры от 0 до 20 с математическими знаками

Развивающие карточки цифры от 0 до 20 с математическими знаками

Карточка с цифрой 0 распечатать. Изучать с детьми цифры нужно в несколько приемов

Как сделать цифры картинки для детей самим.

Развивающие карточки цифры от 1 до 10 для детей

Развивающие карточки цифры от 1 до 10 для детей

Развивающие карточки цифры от 1 до 10 для детей

Развивающие карточки цифры от 1 до 10 для детей

Развивающие карточки цифры от 1 до 10 для детей

Развивающие карточки цифры от 1 до 10 для детей

Развивающие картинки цифры от 1 до 10 для детей

Таблица счета от 1 до 10

Изучать цифры и счет от 1 до 10 с детьми можно еще с помощью развивающих мультфильмов Малышман ТВ

Карточки с числами от 1 до 20 — Распечатай и считай

1. «Цифры от 1 до 10» для печати в картинках.

4. Карточки с цифрами от 1 до 10 и математическими знаками «плюс» и «минус».

5. Скачать цифры от 1 до 10 «Синие». Цифры и их названия.

6. Карточки «Цифры от 1 до 10» — распечатать каждую цифру на отдельном листе.

7. Учимся писать цифры по точкам от 0 до 15 по образцу.

Рішати приклади 1 клас — litg.ru

Как научить представления чисел | Разобрался

3 НОМЕР: ЧТО ЕСТЬ ЗНАТЬ? | Сложим: помощь детям в изучении математики

математических трюков — ядро ​​исследования поведенческих наук

Эта веб-страница посвящена

Попробуйте эти уловки:

Вот несколько интересных ссылок:

Трюк с добавлением магии №1

Магический квадрат № 15

Магический квадрат № 34

Рецепт вашего собственного волшебного квадрата 3 x 3

Перевернутый магический квадрат

Антимагический квадрат

Выиграйте ставки с этим Magic Square

Математический карточный фокус

Калькулятор молний

Таблицы забавных чисел

Знаете ли вы …?

Математический трюк на этот год

Где строка?

Сохранить дату карты | 10 бесплатных образцов

ПРОЧИТАЙТЕ, ЧТО ГОВОРЯТ КЛИЕНТЫ О MINTED СОХРАНИТЕ ДАТЫ:

ПРЕЛЮДИЯ НА СВАДЕБНОЕ ПРИГЛАШЕНИЕ

ПОЧЕМУ НАЧЕНЫ ДЛЯ МОИ СОХРАНЕНИЕ ДАТ?

ВИДЫ БУМАГИ

математических трюков — ядро исследования поведенческих наук