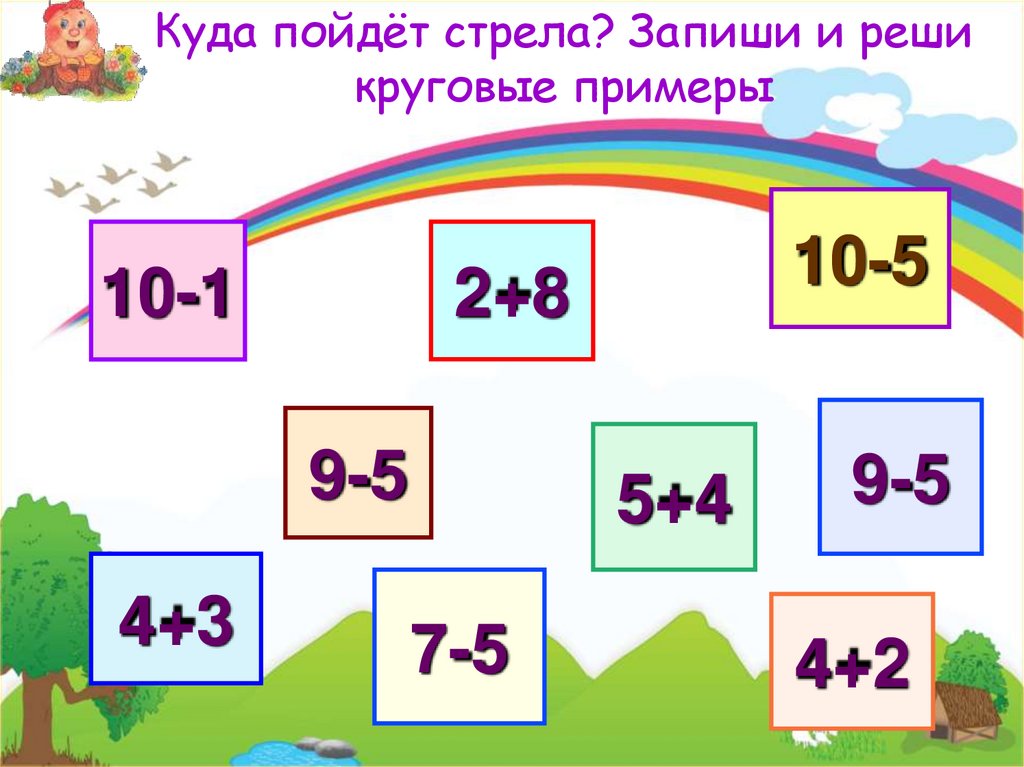
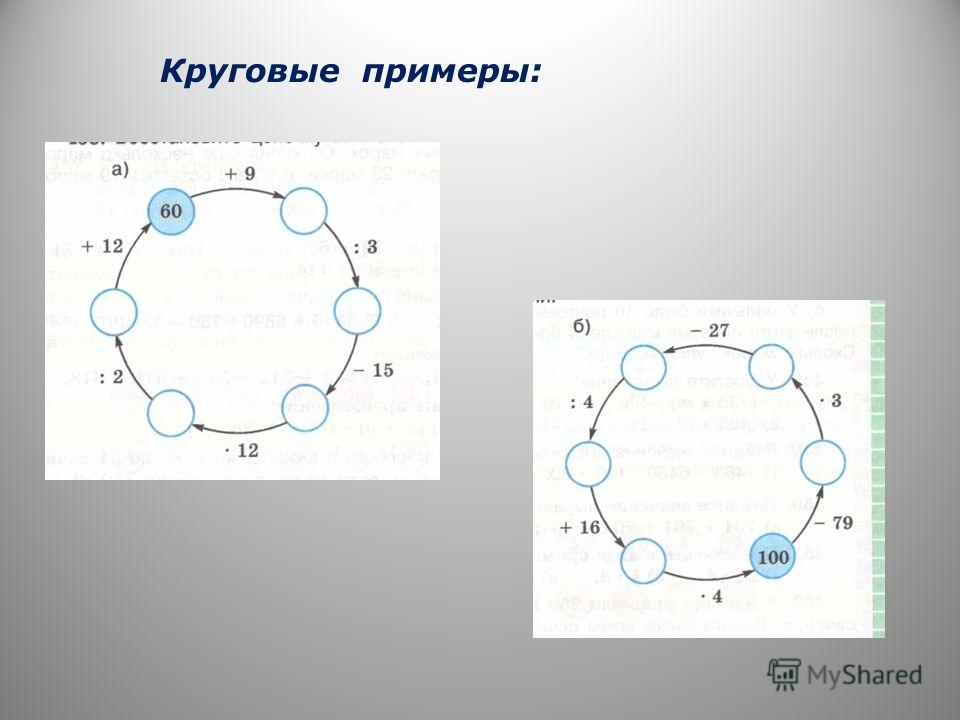
Решить примеры и показать что они круговые: ГДЗ по математике, 2 класс, Моро М.И. Реши примеры. – Рамблер/класс

Игры на уроках математики

Дидактические игры на уроках математики:

1.     Бабочки.

Дидактическая цель: закреплять приемы прибавления и вычитания

Оборудование: рисунки бабочек и цветов.

Содержание: на доске цветы с числом, бабочки группой на другой части доски. Детям предлагают отгадать, на какой цветок сядет бабочка. Для этого они читают примеры на обратной стороне рисунков бабочек и считают его, затем сажают бабочек на цветы.

 

2. Математический футбол.

Дидактическая цель: Формировать навыки сложения и вычитания в пределах  20, 100, 1000 или умножения и деления.

Оборудование: картинки ворот, мячей с примерами.

Содержание: на доске ворота, дети разделились на 2 команды. Выбегают по очереди, берут мяч, с обратной стороны написан пример, если решил правильно – то забил гол. Побеждает тот, кто считает без ошибок и больше забил мячей.

 

3.

Хоккей

Вместо футбола можно детям предложить хоккей

         Примеры записаны на шайбах.

 

       4. Математическая рыбалка

Цель: формировать и закреплять навыки устного счета в 1-4 классах.

Оборудование: рыбки и рыбак

Содержание: играют команды, по очереди берут рыбку и решают пример. Решил правильно – поймал рыбку. Кто больше наловит.

Можно примеры писать с обратной стороны рыбок.

 

      5. Новогодняя елочка

Оборудование: елочка, картинки Деда Мороза и Снегурочки, елочные игрушки.

Цель: Отработка и проверка навыка счета.

Содержание: ученик Снегурочке помогает наряжать елку, если правильно решает пример, записанный на обратной стороне игрушки.

 

6. Поезд.

Дидактическая цель: закрепить порядковое значение числа.

Оборудование: картинки поезда, вагонов, карточки с числами от 10 до20.

Содержание: на доске поезд, вагоны расставлены в беспорядке.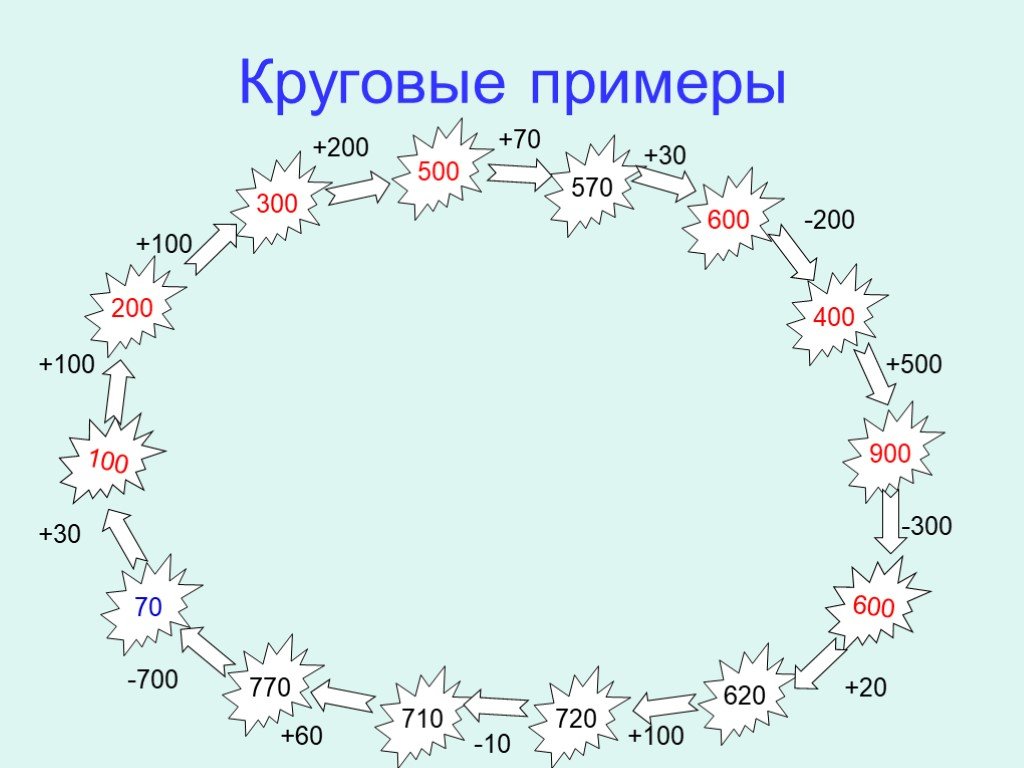 Детям объявляют, что числа заблудились. Дети расставляют цифры, обозначающие числа второго десятка.

 

7. Угадай.

Дидактическая цель: Закрепить знание состава чисел первого десятка.

Содержание: Учитель говорит, что задумала  2 числа, сложила их,  получилось 5. Какие числа сложила? Дети: 0 и 5, 5 и 0, 4  и 1, 1 и 4, 2 и 3, 3 и 2. На первом этапе дети иллюстрируют состав чисел на палочках, на геометрических фигурах.

8. Наоборот.

Дидактическая цель: Развивать речь детей, закреплять понятия толстый, тонкий, широкий, узкий и т. д.

Содержание: Учитель говорит слово, а ребенок противоположное ему. Учитель не называет имен, а бросает мяч.

Дополнение.

Дидактическая цель: Развивать речь детей, включать в активный словарь математические термины.

Оборудование: рисунки ракеты, самолета, вертолета, птицы, бабочки.

Содержание: Учитель на доске размещает картинки  сверху вниз. Разъясняет детям, что надо продолжить предложение (Высоко в небе летит …,ниже ракеты летит …. Самолет летит выше …, ниже вертолета летит …)

9. Составим цветок.

Дидактическая цель: Закрепление состава чисел первого десятка.

Оборудование: лепестки с примерами; стебель с листом, на котором число.

Содержание: На доску крепят  стебли с листом. Лепестки лежат на столе. Выходит ученик и берет лепесток, читает пример  разными способами, решает устно и прикрепляет к нужному стеблю.   Играют дети по командам: сколько цветов,  столько команд.

 

10. Цепочка.

Дидактическая цель: учить преобразовывать одни примеры в другие.

Оборудование: картинки неваляшек, машинок, листьев.

Содержание: картинки размещают по группам, в каждой рисунки двух цветов. Например: 2 зеленых и 3 голубых неваляшки. Один ученик составляет по этой картинке пример на сложение 2+ 3, другой- применяя переместительное свойство 3+2, третий составляет пример на состав чисел 5=3+2, четвертый составляет на вычитание одного из слагаемых 5-3=2, пятый составляет еще пример на вычитание, шестой сравнивает число зеленых неваляшек и  голубых. Затем тоже с другой группой картинок.

 

        11. Поиграем в задачу

Цель: проверить усвоение понятия задача.

Оборудование: карточки.

Содержание: получает карточку ребенок и  должен найти свое место.

 

       12. Лучший космонавт.

Дидактическая цель. Формирование навыков сложения и вычитания.

Содержание игры. Учитель на доске рисует 10 ракет с номерами от 1 до 10. Вызываются сразу 11 учеников. Вокруг стола, где разложены карточки с примерами, дети идут, взявшись за руки, и декламируют: «Ждут нас быстрые ракеты На такую полетим! Для прогулок по планетам. Но в игре один секрет: На какую захотим, Опоздавшим места нет». Как только сказано последнее слово, учитель выдает каждому ученику карточки с примерами, шифрующими номер ракеты, на которой полетит космонавт. Дети решают примеры, определяя номер своей ракеты, и пишут пример под соответствующим номером ракеты.

        13. Составь круговые примеры.

Дидактическая цель. Составление примеров, у которых первый компонент равен ответу предыдущего примера.

 Содержание игры. Учащиеся составляют примеры с ответом, равным первому компоненту следующего примера. Например, на доске даны следующие записи: 7-5=2 2+6=8 8+2=10 10-8=2 Учащиеся составляют цепочку примеров по заданному правилу. Игру можно проводить в любом классе, усложняя задания.

        14. Почтальон.

Дидактическая цель. Закрепление приемов умножения и деления (табличные случаи). Средства обучения. Рисунки домиков, карточки с примерами. Содержание игры. Учитель вызывает к доске учеников, они выбирают карточку с примером, решают, указывают номер дома, квартиры, куда отправлено письмо.

        15. Математическая эстафета.

Дидактическая цель. Обучение навыкам быстрого счёта.

 Содержание игры. Класс разбивается на команды. Для каждой команды учитель пишет примеры. Одновременно от каждой команды к доске вызывается по одному ученику.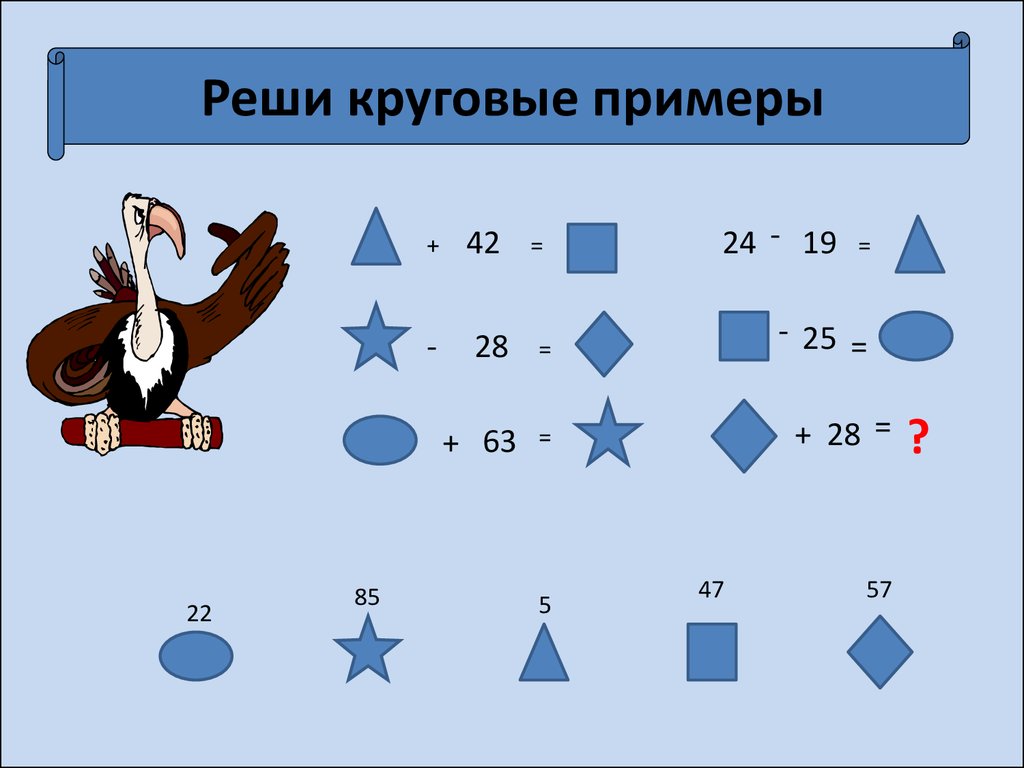 Их задача состоит в том, чтобы правильно и быстро решить соответствующий пример и передать эстафету своему товарищу. Игра продолжается до тех пор, пока ученики каждой команды решат все примеры. Побеждает та команда, которая раньше других правильно решит примеры

         16. Молчанка.

Дидактическая цель. Закрепление навыков устного счёта.

Содержание игры. На доске или карточке записаны числа по кругу, а в центре знак действия. Учитель молча показывает на два числа и на кого-то из учащихся. Тот должен выполнить с ними определённое действие и назвать ответ. Остальные сигнализируют о правильности решения.

 Поезд.

Дидактическая цель. Закрепление навыков устного счёта.

Содержание игры. На доску прикреплены вагоны с числами и знаками действий.  Дети молча считают и называют ответ в конце последнего вагона.

         17.  Кто пришёл в гости?

Дидактическая цель. Формирование навыков сложения и вычитания.

Содержание игры. На доску прикреплены выражения сверху вниз, на обратной стороне которых разрезная картинка с изображением какого-то героя. Дети начиная сверху находят значения выражений и, если решили правильно, переворачивают карточки. В результате получается целая картинка героя, который пришёл сегодня на урок к ребятам.

 

        18.  «Мальчики – Девочки»

Цель: Развитие внимания, быстроты мыслительных операций, памяти.

Описание: По щелчку на экране появляются кружки разного цвета с примерами. 
Задание: Если кружок синего цвета, то ответ хором называют мальчики, если красного – девочки. Выигрывают, те кто меньше допустил ошибок. Если кружок другого цвета , в классе тишина.

        19. «Математическая тучка»

Цель: Развитие внимания, зрительного восприятия, закрепление учебного материала с помощью игровой мотивации.

Описание: На экране изображение тучки и капельки с числом. 
Задание: Дети по вызову учителя выходят к доске и подбирают к тучке пару капельку с таким же числом. Нужно навести курсор на нужную капельку и щёлкнуть.

        20. «Помоги колобку перебраться на другой берег»

Цель: Развитие внимания, зрительного восприятия, закрепление учебного материала с помощью игровой мотивации. 
Описание: на экране примеры на умножение и деление (при желании их можно заменить другими примерами) 
Задание: колобок предлагает пример. Ученик решает, наводит курсор на правильный ответ и щёлкает мышкой. Если пример решён верно, то появляется дощечка через речку. Если пример решён неверно, то дощечка меняет свой цвет.

         21. ЖИВАЯ МАТЕМАТИКА.

У учащихся на груди таблички с цифрами от 0 до 9. Учитель читает примеры. Встаёт ученик, у которого есть цифра-ответ.

Лучше давать примеры на деление, чтобы получались однозначные цифры. В случае двузначного ответа должны встать два ученика.
Проводить игру желательно в конце урока для повышения двигательной активности учащихся. Также можно раздавать по несколько одинаковых цифр, привлекая большее количество детей.

          22. ПРОВЕРЬ СЕБЯ!

Учитель готовит карточки, на которых записаны результаты умножения каких-либо чисел, например 9 и 2 (показывается число 18). Учитель показывает карточку, а ученики записывают пример с таким ответом в тетрадях.

          23. СОРБОНКИ.

Ученик тренируется с сорбонками по 3-5 минут несколько раз в день. Высокая эффективность применения объясняется тремя важными свойствами:
– концентрация внимания ученика только на тех элементах таблицы, которые им не усвоены;
– увеличивается частота тренировок;

– повышение произвольности памяти в процессе игры, что обеспечивает более лёгкое запоминание.
Имея набор таких карточек с записанными примерами (ответы на обратной стороне), ученик может играть в “Угадал – не угадал”. Угадал – карточка ложится в одну сторону, не угадал – в другую. Постепенно остаются карточки только с неусвоенными элементами таблицы, с которыми и продолжает тренироваться ученик.

         24. НЕ ПОДВЕДИ ДРУГА.

К доске выходят одновременно два ученика (возможно и четыре). Учитель читает пример, например 6 * 7, и предлагает составить пример на умножение или деление с такими же числами. Первый ученик составляет примеры на деление, второй – на умножение, записывают на доске. Если примеры составлены и решение верно, поощряют ребят.
В этой игре главное акцентировать внимание на способе нахождения частного по известному произведению и обратно – более прочное усвоение связи компонентов действий.

          25. ТАБЛИЦА ДЛЯ СОСЕДА.
(работа в паре)

Ученики задают по 5-6 примеров на табличное умножение и деление друг другу. После решения примеров проверяются записанные результаты.
Примеры готовятся заранее на карточках. Выигрывает тот, кто решил примеры быстрее и допустил меньше ошибок.

           26. ДЕНЬ И НОЧЬ.

Условия игры: когда учитель произносит слово “Ночь!”, ученики кладут голову на парту и закрывают глаза. В это время учитель читает пример для устного счёта на деление и умножение. Выдерживает небольшую паузу.
Затем учитель говорит “День!”. Дети садятся прямо и те, кто решил пример, поднимает руку и говорит ответ.

          27. ДЕЛИТСЯ – НЕ ДЕЛИТСЯ?

Учитель называет различные числа, а ученики поднимаются руку или хлопают в ладоши, если число делится, например на 3 (или другое) без остатка.

 

28.«ТЕРЕМОК.»

Всем, кто просится пожить в домике, дается задание, например, составить примеры с ответом 3, 4, 5, 6. Дети помогают всем, потому, что хотят, чтобы все житии под одной крышей.

«Составь круговые примеры.»

-составление примеров, у которых первый компонент равен ответу предыдущего примера.

Учитель пишет на доске примеры, у которых задан первый компонент. Учащиеся составляют примеры с ответом, равным первому компоненту следующего примера.

7-5=2      2+6=8     8+2=10                            10-8=2     2+5=7

Учащиеся составляют цепочку примеров по данному образцу.

Числа – перебежчики.

-закрепление знаний о переместительном свойстве сложения.

Вызываются 6 учеников, им раздают карточки с цифрами и знаками. По

Например:    2+8=10     7+1=8     5+4=9

Ведущий предлагает числам перебежать так, чтобы получились другие примеры с таким же ответом.

8+2=10       1+7=8        4+5=9

 

29.«ЗВЕЗДНОЕ НЕБО»

На плакате изображено « звездное небо». Учитель предлагает посчитать звезды на небе, закрывает их тучкой, затем тучку отодвигает и спрашивает: «А сколько теперь звезд?» Дети считают. Учитель останавливает счет и просит детей заглянуть за тучку, чтобы они убедились, что там именно столько звезд, сколько было сказано.

«Полет в космос.»

Винтик и Шпунтик изобрели новую ракету и пригласили вас совершить увлекательное путешествие. Да вот беда. Ракета не может вместить всех желающих. Давайте разделим класс на две команды и выберем от каждой по 5 представителей и по одному капитану. Дается сигнал, и капитаны начинают соревнование. Решив пример, капитаны передают мел следующему игроку команды

Выигрывает та команда, которая быстрее и без ошибок решит примеры. Она и отправляется в космический полет.

«Веселый счет.»

Детям показывает учитель карточки с примерами, а они числом движений дают ответ: « Столько раз ногою топнем (8-4), столько раз руками хлопнем (5+4), мы присядем столько раз (7-4), мы наклонимся сейчас (6-4), мы подпрыгнем ровно столько (10-4). Ай да счет! Игра и только».

 

30.«Составь меню для Робина-Бобина-Барабека.»

Дети отлично знают персонажа произведения С. Маршака Робина-Бобина, который скушал 40 человек, и корову, и быка, и кривого мясника». Наш Робин-Бобин добрый.

 Изменился человек,

Робин-Бобин-Барабек.

Ведь представьте-ка вы сами:

Ест он фрукты с овощами.

10 килограммов он

Вносит за день в рацион.

Что ж при этом он съедает?

Кто из вас скорей узнает?

На плакате – фрукты, овощи. Под каждым рисунком пример на табличное сложение или вычитание в пределах 10. Задача детей: решить примеры и подобрать их пары так, чтобы в ответе было 10. Примеры:

 6-4=                                                       2+6=

 2+7=                                                     10-5=

8-3=                                                      8-7=

                              2+4=                                                       9-6=

                             9-3=                                                      10-6=

Дети не записывают выражения. Они рисуют схематично фрукт или овощ, что им нравится, и в центре пишут ответ.

 

31.«Помогите числам занять свои места по порядку.»

-закрепление знаний о порядке чисел.

1-в.      Учитель расставляет на планке карточки с числами: 0, 1,…, 9, и обращается к детям: «Числа заблудились, помогите им занять свои места». Дети расставляют числа первого десятка по порядку: 0, 1, 2,…10. Учитель спрашивает, сколько понадобилось цифр для обозначения числа 10?

2-в.      Учитель раздает детям карточки с числами первого десятка. По сигналу «Числа, стройтесь по порядку, начиная с меньшего числа: 1, 2..10,

 

32. «Составим поезд»

-обучение детей приемам прибавления и вычитания чисел 2, 3, 4.             

Учитель вызывает к доске 5 девочек. Они образуют поезд из 5 вагонов                   ( цепляются друг за друга – кладут правую руку на плечо впереди стоящего). Затем цепляют еще один вагон ( мальчик ) и еще 1 ( девочка ).                                                                                                                      Учитель записывает пример вида                                                                                                                                                                                                     5+2=7                                                                                                                                                       5+1+1

Дети проговаривают прием прибавления 2.

Затем отцепляются 2 вагона по одному в 2 приема. Ученики записывают и проговаривают прием вычитания 2

5-2=3

5-1-1

Аналогично показываются приемы прибавления и вычитания 3 и 4.

6+3=9           6+3=9

6+1+1+1       6+2+1

 

33.«Маятник»

 -учить детей приему прибавления и вычитания по 1.

Учитель спрашивает детей, кто видел часы с маятником. Просит показать, как покачивается маятник. Что отсчитывает маятник? ( Время  ).

Предлагает детям покачиваться, как маятник, и прибавлять или отнимать по 1.Учитель пишет на доске примеры вида 5+2=  , 7-3=   ,6+4=   , 9-3=   , и т.д. Учащиеся покачиваясь, как маятники, считают, решают пример. Ученики, наклоняясь влево, проговаривают: «5 да 1=6, прибавили1», наклоняясь вправо, продолжают: « 6 да 1=7, прибавили2». Учитель спрашивает: «Сколько всего прибавили?» (2) и  т.д. Учитель задает ритм наклонов взмахом руки.

34. «Белка и грибы»

 -усвоение состава чисел.

   Учитель рассказывает детям о том, что белочка на зиму делает запасы грибов. В одном дупле белочка никогда не хранит свои запасы, а раскладывает их в 2-3 дупла. «Белочка (учитель показывает изображение белочки) каждый день сушила по 7 белых грибов (число можно менять) и раскладывала их в 2 дупла. Поскольку грибов может положить белочка в каждое дупло?

Вопросы. Кто хочет быть белочкой и разложить грибы в дупла? Как белочка могла бы разложить грибы в первый день? Во второй день? В третий день?

 

35.«Математическая рыбалка»

 -закрепление приемов прибавления и вычитания в пределах 10.

На магнитной доске размещаются рыбки, на обратной стороне которых записаны примеры на сложение и вычитание. Учитель поочередно вызывает детей к доске, они «ловят» (снимают) рыбку, читают пример. Все ученики, решившие пример, обозначают ответ цифрой и показывают ее учителю. Кто решит пример раньше всех, тот получит рыбку. Кто больше всех «наловит» рыбок (решит примеры правильно), тот лучший рыболов.

Аналогично проводится игра «Аквариум».

 

36. «Лесная школа»

 -закрепление таблицы сложения.

Вот так чудо из чудес,

Мы попали с вами в лес.

У зверят идет урок.

Волк учитель очень строг.

Кто какой пример решал?

Кто, ребята, отгадал?

Обратная связь. Дети должны по ответу вспомнить пример табличного сложения и вычитания числа 4. Например, ответ:2, пример 6-4;

 

37.«Дополнение»

   -развивать вычислительные навыки.

    Вызываются к доске 2 ученика. Один задает 3 вопроса, другой отвечает, затем меняются ролями. Например, первый говорит: « Я буду называть числа, а ты отвечай, сколько не хватает до 80» (Ученик называет числа 20, 60, 30). Выигрывает тот, кто не сделает ни одной ошибки.

 

38.«Магазин»

  -развивать вычислительные умения.

1-в.   В роли продавца учитель или ученик. На столе учителя товары: карандаши, ручки, тетради, открытки. У детей карточки с числами. Учитель сообщает цены товаров, а учащиеся готовят карточки с числами. Например, ручка стоит 80 тенге. Какими монетами можно за нее заплатить?

2-в.   На красочном плакате или доске размещаются рисунки игрушек, под ними записаны примеры. Чтобы «купить» игрушку, надо решить пример.

 

39. «Парашютисты»

  -отрабатывать навыки счета.

      На доске рисунки парашютов с записанными на них примерами. 80-20;

40+30; т.д. Под рисунками квадраты с заполненными ответами: 60,70.и т.д. Учитель предлагает детям помочь парашютистам приземлиться в заданном квадрате.

 

40. «Молчанка»

   Учитель показывает на числовые данные и знаки действий, учащиеся молча составляют на сложение или вычитание и показывают ответ на карточках. примеры .

 

 

 

 

 

 

 

Закон Кеплера — формулировка законов, рисунки и примеры

Покажем, как применять знание физики в жизни

Начать учиться

«Сижу, никого не трогаю, решаю задания из ЕГЭ, а тут в решении астрономического 24‑го какие-то законы Кеплера. Ничего не понятно, но очень интересно», — так думают многие одиннадцатиклассники, сдающие физику. Рассказываем, как понять эти законы и использовать в решении задачек.

Форма Земли

Сейчас нам сложно представить, что раньше люди верили, будто Земля плоская. У греков, например, плоскость просто парила в воздухе и была окружена ледниками. А в Индии верили, что планета покоится на трех слонах, которые стоят на черепахе. Впрочем, кое-кто до сих пор так думает. Доказательств того, что наша планета на самом деле не плоская — много, но вот вам парочка, чтобы можно было поддержать светскую беседу.

Смена дня и ночи

По представлениям приверженцев плоской Земли, день и ночь сменяются, потому что Луна и Солнце вращаются над Землей — вот как-то так:

Но — упс! — эта модель вызывает целый ряд вопросов:

• Почему длина дня и ночи меняется в течение года?

• Чем объясняется цвет заката и восхода?

• Почему иногда мы можем увидеть Луну и Солнце одновременно?

• Почему Луна и Солнце не появляются каждый раз из одной и той же точки?

• Если нет гравитационного притяжения, почему они вообще крутятся?

Лунные затмения

Если Земля плоская, то непонятно, как объяснить лунные затмения. Чтобы затмение произошло, нужно, чтобы Солнце находилось по одну сторону от диска, а Луна — по другую. Тогда ломается концепция дня и ночи, которую мы описали выше, ведь день и ночь будут наступать для всей Земли одновременно.

Тени

На плоскую Землю свет от Солнца падал бы, как свет от фонаря. То есть высокие объекты в противоположном от Солнца направлении после заката оставались бы в тени.

А на шарообразной Земле небоскребы или горы будут освещены Солнцем после заката или перед рассветом.

Именно это вы увидите, если застанете рассвет или закат в горах — или посмотрите на фотографии.

Окей, Земля все-таки не плоская — с этим разобрались. Но и шаром ее назвать нельзя: Земля имеет форму эллипсоида.

Эллипсоид — это такой приплюснутый шар, в одном из сечений у которого эллипс. Именно по траектории эллипса вращаются все спутники.

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Эллипс

Эллипс — это замкнутая прямая на плоскости, частный случай овала. У эллипса две оси симметрии — горизонтальная и вертикальная, которые состоят из двух полуосей.

А еще у эллипса два фокуса — это такие точки, сумма расстояний от которых до любой точки P(x,y) является постоянной величиной.

Эллипс F1 и F2 — фокусы F1 = ( c ; 0) F2 = (-c ; 0) с — половина расстояния между F1 и F2 a — большая полуось b — малая полуось r1 и r2 — фокальные радиусы

Теперь мы знаем все необходимые понятия, чтобы разобраться, в чем состоят законы Кеплера.

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Первый закон Кеплера

Каждая планета солнечной системы вращается вокруг Солнца по эллипсоидной орбите, в одном из фокусов которого находится Солнце.

Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка B траектории называется перигелием, а точка A, наиболее удаленная от Солнца — афелием.

Первый закон Кеплера достаточно простой, но важный, так как в свое время он сильно продвинул астрономию. До этого открытия астрономы считали, что планеты движутся исключительно по круговым орбитам. Если же наблюдения противоречили этому убеждению, ученые дополняли главное круговое движение малыми кругами, которые планеты описывали вокруг точек основной круговой орбиты. Кеплер получил доступ к огромной базе наблюдений Тихо Браге и, изучив их, перешагнул старые идеи.

Второй закон Кеплера (закон площадей)

Радиус-вектор, соединяющий планету и Солнце, описывает в равные промежутки времени равные площади.

Каждая планета перемещается в плоскости, проходящей через центр Солнца. За равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади. Таким образом, тела движутся вокруг Солнца неравномерно: в перигелии они имеют максимальную скорость, а в афелии — минимальную.

На практике это можно заметить по движению Земли. Ежегодно в начале января наша планета проходит через перигелий и перемещается быстрее. Из-за этого движение Солнца по эклиптике (линии, показывающей путь Солнца по небу) также происходит быстрее, чем в другое время года. В начале июля Земля движется через афелий, из-за чего Солнце по эклиптике перемещается медленнее. Поэтому световой день летом длиннее, чем зимой.

Третий закон Кеплера

Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит.

Согласно третьему закону Кеплера, между периодом обращения планет вокруг Солнца и большими полуосями их орбит устанавливается связь. Этот закон выполняется как для планет, так и для спутников с погрешно­стью менее 1%.

Третий закон Кеплера T1 и T2 — периоды обращения двух планет [c] a1 и a2 — большие полуоси орбит планет [м]

На основании этого закона можно вычис­лить продолжительность года (времени полного оборота вокруг Солнца) любой планеты, если известно ее расстояние до Солнца в афелии.

Также можно проделать обратное — рассчитать орбиту, зная период обращения.

Закон всемирного тяготения

Законы Кеплера — это результаты наблюдений и обобщений. Впоследствии они легли в основу закона всемирного тяготения, который звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения F — сила тяготения [Н] M — масса первого тела (часто планеты) [кг] m — масса второго тела [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6,67 · 10−11м3 · кг−1 · с−2

Ньютон был первым исследователем, который пришел к выводу, что между любыми телами в космосе действуют гравитационные силы, и именно они определяют характер движения этих тел.

Первая и вторая космические скорости

Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля.

В серии книг Дугласа Адамса «‎Автостопом по Галактике»‎ говорится, что летать — это просто промахиваться мимо Земли. Чтобы промахнуться мимо Земли и стать ее искусственным спутником, нужно достичь первой космической скорости 7,9 км/с. Вот как это происходит:

Искусственный спутник Земли — космический летательный аппарат, который вращается вокруг Земли по геоцентрической орбите. Чтобы у него это получалось, аппарат должен иметь начальную скорость, которая равна или больше первой космической.

Первая космическая скорость v1 — первая космическая скорость [м/с] g — ускорение свободного падения на данной планете [м/с2] R — радиус планеты [м] На планете Земля g ≈ 10 м/с2.

Есть еще вторая и третья космические скорости. Вторая космическая скорость — это скорость, которая нужна, чтобы корабль стал искусственным спутником Солнца, а третья — чтобы вылетел за пределы солнечной системы.

Вторая космическая скорость v2 — вторая космическая скорость [м/с] g — ускорение свободного падения на данной планете [м/с2] R — радиус планеты [м] На планете Земля g ≈ 10 м/с2.

Карина Хачатурян

К предыдущей статье

Скорость света

К следующей статье

Явление самоиндукции

Получите индивидуальный план обучения физике на бесплатном вводном уроке

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Использование свойств кругов для решения задач

Результаты обучения

• Найдите длину окружности и площадь круглого объекта, зная его радиус
• Найдите длину окружности и площадь круглого объекта, зная его диаметр
• Рассчитать диаметр круглого объекта, зная его длину окружности

Вы помните свойства кругов из книги «Десятичные числа и дроби вместе»? Мы покажем их здесь снова, чтобы ссылаться на них, когда мы используем их для решения приложений. 9{2}[/латекс]

Помните, что мы приближаем [латекс]\pi [/латекс] к [латекс]3.14[/латекс] или [латекс]\большой\фрак{22}{7}[/латекс] в зависимости от того, является ли радиус круг задается в виде десятичной дроби или дроби. Если вы используете клавишу [latex]\pi [/latex] на своем калькуляторе для выполнения расчетов в этом разделе, ваши ответы будут немного отличаться от показанных ответов. Это связано с тем, что в ключе [latex]\pi [/latex] используется более двух знаков после запятой.

пример

Круглая песочница имеет радиус [латекс]2,5[/латекс] фута. Найдите 1. окружность и 2. площадь песочницы.

Раствор

1. Шаг 1. Прочтите проблему. Нарисуйте рисунок и подпишите его с помощью данной информации.
Шаг 2. Определите , что вы ищете.	длина окружности круга
Шаг 3. Имя. Выберите переменную для ее представления.	Пусть c = длина окружности
Шаг 4. Перевести. Напишите соответствующую формулу Заменитель	[латекс]C=2\pi r[/латекс] [латекс]C=2\pi \влево(2,5\вправо)[/латекс]
Шаг 5. Решите уравнение.	[латекс]C\примерно 2\влево(3,14\вправо)\влево(2,5\вправо)[/латекс] [латекс]C\приблизительно 15\текст{футов}[/латекс]
Шаг 6. Проверка. Имеет ли этот ответ смысл? Да. Если мы нарисуем квадрат вокруг круга, его стороны будут [латекс]5[/латекс] футов (удвоенный радиус), поэтому его периметр будет [латекс]20[/латекс] футов. Это немного больше, чем у круга. окружность, [латекс]15,7[/латекс] футов
Шаг 7. Ответьте на вопрос.	Окружность песочницы составляет [латекс]15,7[/латекс] футов.

“> 9{2}[/латекс]

[латекс]А\ок 19.625\текст{кв. футов}[/латекс]

2. Шаг 1. Прочтите проблему. Нарисуйте рисунок и подпишите его с помощью данной информации.
Шаг 2. Определите , что вы ищете.	площадь круга
Шаг 6. Проверка. Да. Если мы нарисуем квадрат вокруг круга, его стороны будут [латекс]5[/латекс] футов, как показано в части ⓐ. Таким образом, площадь квадрата будет [латекс]25[/латекс] кв. футов. Это немного больше, чем площадь круга, [латекс]19,625[/латекс] кв. футов.
Шаг 7. Ответьте на вопрос.	Площадь круга [латекс]190,625[/латекс] квадратных футов.

 

попробуйте

В следующем видео мы покажем еще один пример того, как найти площадь круга.

Мы обычно видим формулу для длины окружности через радиус [латекс]r[/латекс] окружности:

[латекс]С=2\pi r[/латекс]

круг в два раза больше радиуса, мы могли бы записать формулу для длины окружности в терминах [латекс]\текст{из }d[/латекс].

[латекс]\begin{array}{cccc}& & & C=2\pi r\hfill \\ \text{Используя свойство коммутативности, получаем}\hfill & & & C=\pi \cdot 2r\ hfill \\ \text{Затем подставив}d=2r\hfill & & & C=\pi \cdot d\hfill \\ \text{So}\hfill & & & C=\pi d\hfill \end{массив} [/latex]

Мы будем использовать эту форму окружности, когда нам дана длина диаметра вместо радиуса.

пример

Круглый стол имеет диаметр четыре фута. Какова окружность стола?

Показать решение

 

попробуйте

В следующем видео мы покажем еще два примера того, как найти длину окружности по ее диаметру или радиусу.

пример

Найдите диаметр круга с длиной окружности [латекс]47,1[/латекс] сантиметров.

Показать раствор

 

попробуйте

Обведите примеры с решением – Hitbullseye

Q. 1. Две окружности с одинаковым центром P имеют радиусы 6,5 см и 3,3 см. Через точку A большего круга проведена касательная к меньшему кругу, касающемуся его в точке B. Найдите AC.

A. 8,3 см

B. 11,2 см

C. 5,5 см

D. 16,7 см

Ответ: Вариант B

32 Рекомендуемое действие 012 БЕСПЛАТНЫХ живых мастер-классов от нашего звездного факультета с 20 + многолетний опыт. Зарегистрируйтесь сейчас

Sol :

∠PBC = 90° (касательная перпендикулярна радиусу в точке касания)
So (6.5) ² = (3.3) ² + (BC) ² .
Значит, БК = 5,6. Следовательно, AC = 2 × 5,6 = 11,2 см.

В.2. Найдите площадь круга с центром в (5, 7) и проходящего через (2, 3).

A. 16π

B. 20π

C. 21π

D. 25π

Ответ: Вариант D

Sol : 2, 7) и проходящий через (5, 7) и проходящий через (5, 7) через (5, 7) центр в точке (5, 7).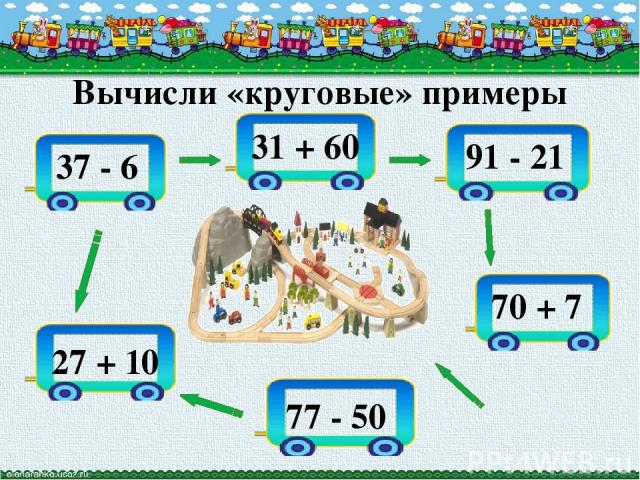 Итак, радиус круга равен r =√(2-5) ² + (3-7) ² = 5. Значит, площадь круга = 25π.

В.3. В круге радиусом 10 A и B являются двумя точками на окружности. Если дуга АВ равна 120°, какова длина отрезка АВ?

А. 10√3;

Б. 10

К. 5√3;

D. Ни один из этих

Ответ: Вариант C

Sol :
Половина треугольника, образованного между A, B и центром круга, будет состоять из 30 – 60 – 90 треугольников. Поскольку 10 (радиус) является гипотенузой этого треугольника, половина AB будет равна 10 × √3/2 = 5√3.

Q.4. AB — хорда окружности с центром O, длина малой дуги AB которой равна 2π метрам. Если ∠AOB = 90°, какова площадь малого сектора AOB?

A. 24πm ²

B. 4πm ²

C. 16πm ²

D. 1πm
7 ^{2 2 2}

043 Ответ: Вариант B

Sol :
Так как центральный угол 90° и длина соответствующей дуги 2π, длина окружности 8π. Значит радиус окружности равен 4 м. Следовательно, площадь сектора равна ¼ × π × 4 ² = 4π м ² .

Q.5. AP касается в точке P окружности с центром O и диаметром BC. Если АР = 20 и АВ = 10, какова длина АО?

A. 25

B. 15

C. 35

D. 20

Ответ: Вариант A

Solr : Предположим, OP =
. Тогда ОА = 10 + r.
In ΔAPO, (10 + r) ² = 400 + r ² .
Решение этого уравнения дает r = 15. Итак, AO = 10 + 15 = 25.

Q.6. На рисунке P, Q и R являются центрами трех окружностей, так что P, Q и R лежат на одной прямой. Каково отношение площади всей заштрихованной области к площади незаштрихованной области?

A. 5:2

B. 17:4

C. 13:3

D. 17:3

Ответ: Вариант C

Sol 3: , то радиусы окружностей P и Q равны 4r и 2r соответственно. Незаштрихованная область 4πr ² – πr ² = 3πr ² . Вся заштрихованная область равна 16πr ² – 3πr ² = 13πr ² . Соотношение 13:3.

Q.7. Хорда АВ окружности радиусом 10,5 см образует в центре окружности угол 120°. Найдите площадь малого сегмента примерно.

A. 62,5 см ²

B. 60,25 см ²

C. 67,7 см ²

15 3 905 см 2902 0012 Ответ: Вариант C

Сол:
Как центральный угол равен 120 °, вы должны быстро понять, что это приведет к равностороннему треугольнику.
Теперь площадь малого сектора: π × (10,5) ² &time’ 120 / 360 = 115,4
Площадь равностороннего треугольника = (10,5) ² × √3/4 = 47,7
Разница двух значений представляет собой площадь малого сегмента (Примечание: это не сектор)
т.е. 115,4 – 47,7 = 67,7 см Макеты, более 75 видео и более 100 тестов по главам. Зарегистрируйтесь сейчас

Q.8. Найдите примерную площадь большого сегмента по информации, приведенной в предыдущем вопросе?

А. 278,5 см ²

В. 242,25 см ²

C. 262 см ²

D. 247 см ²

Ответ: Вариант А

Площадь большого сегмента 3 : 902 3 круг – площадь малый сегмент → × × (10,5) ² = 346,2.
Площадь большого сегмента = 346,2 – 67,7 = 278,5 см ² .

Q.9. Невозможно нарисовать окружность с центром на фиксированной прямой линии М и проходящей через две фиксированные точки Р и Q не на М, если

A. M параллельна PQ

B. M является биссектрисой PQ

C. M перпендикулярна PQ, но не делит ее пополам

D. M не перпендикулярна PQ, но делит ее пополам

Ответ: Вариант С

Sol :
Во всех остальных случаях, кроме (C), можно провести хотя бы одну окружность, лежащую на M и проходящую через P и Q.