Решение задач по математике 3 класс презентация: решение задач в 3 действия | Презентация к уроку по математике (3 класс) на тему:

Презентация “Устный счёт”. Использовать на уроке в 3 классе. Тренировка вычислительных навыков младших школьников. …

Учимся решать задачи при помощи уравнения (3 класс)

Слайды и текст этой онлайн презентации

Слайд 1

Урок – исследование УМК «Перспективная начальная школа»
Тема урока: «Решение задач с помощью уравнений»
МОАУ Усть-Ивановская СОШ Учитель Савченко Г.А.

Слайд 2

Все расселись по местам, никому не тесно, По секрету скажу вам: “Будет интересно!” Будем мы считать, писать, и решать задачи, Чтоб сегодня, как всегда, в руки шла удача. Повторим материал, закрепим умения, Чтобы каждый мог сказать: “Это всё умею я”.

Слайд 3

о будет легко и интересно; о будет трудно, но интересно; о будет трудно и неинтересно
Исследователь -я, м. Человек, который занимается научными исследованиями.

Слайд 4

Ромашка Блума
1
2
3
4
5
6

Слайд 5

1
1. 53 увеличить в 2 раза 2. 90 увеличить на 8 3. На сколько 100 больше 10? 4. 1 + 9 х 9 5. Найти сумму чисел 68 и 6 6. Найти произведение чисел 11 и 6 7. Во сколько раз 500 больше 10? 8. 36 : 6 + 52

Слайд 6

Слайд 7

2
82, 106, 74, 98, 66, 90, 58, 50 Составьте ряд в порядке убывания 106,98, 90, 82, 74, 66, 58, 50

Слайд 8

3
-Посмотрите на последовательность и добавьте ещё 2 числа 106,98, 90, 82, 74, 66, 58, 50, …, … . 42, 34 Какое число лишнее? 106 Что общего во всех этих числах?

Слайд 9

4
Выберите уравнения а)58 х Х=106 б)90 -74 +66 в)Х+50 +98 г) 74 >Х д) Х – 50=82 а) д)

Слайд 10

5
Попробуйте составить задачу по уравнению х – 50 = 82

Слайд 11

6
Тема урока:
Учимся решать задачи с помощью уравнений
Цель урока:
Научиться решать задачи с помощью уравнений

Слайд 12

Многие трудные арифметические задачи легко решаются с помощью уравнений. Если вы освоите искусство составлять уравнение по условию задачи и научитесь их безошибочно решать, то эти задачи будут вам по плечу.

Слайд 13

5 февраля Классная работа
Работа по учебнику с.32 -33

Слайд 14

Задача №79
В одной коробке Число коробок всего

Слайд 15

Х х 9 = 54
Х х 9 = 54 Х = 54 : 9 Х = 6 (ф.) в 1 коробке Ответ: 6

Слайд 16

Не поворачивая головы, двигайте глазами вверх-вниз, вправо-влево. Повторить 5 раз.
Гимнастика для глаз

Слайд 17

Зажмурьтесь посильнее, а затем широко откройте глаза, словно вы чему-то очень удивились. Повторите ещё раз.

Слайд 18

А теперь закройте глаза и расслабьтесь, будто собираетесь спать. Подумайте о чём-нибудь очень приятном.

Слайд 19

Задача № 80
В одной коробке лежит 9 фломастеров. Сколько нужно коробок для 36 фломастеров?   9 х Х = 36  
В одной коробке Число коробок всего
9 х Х = 36 Х = 36 : 9 Х = 4 (к) Ответ: 4

Слайд 20

Задача № 81 или №82
6 : Х = 3
6 : Х = 3 Х = 6 : 3 Х = 2 (р.) купила мама Ответ: 2

Слайд 21

На первой полке стояло 6 банок варенья, а на второй – в 3 раза больше. Сколько банок варенья стояло на второй полке?
Х : 6 = 3
Х : 6 = 3 Х = 3 х 6 Х = 18 (б) на второй полке Ответ: 18

Слайд 22

Задача №83
Длина одной ленточки 90 см, а другой 15 см. Во сколько раз длина первой ленточки больше длины второй?
90 : х = 15
90 : х = 15 Х = 90: 15 Х = 6 (раз) больше Ответ: в 6

Слайд 23

Задача, которую можно решить уравнением:
В нескольких тарелках 32 пирожка, по 8 пирожков на каждой тарелке. Сколько было тарелок? 

Слайд 24

Рефлексия:
Какую цель мы ставили перед собой?
Мы достигли цели?
Что особенно заинтересовало на уроке?
Какая работа понравилась на уроке?
Какая работа вызвала затруднение?
Кем мы были на уроке?
Какое исследование мы проводили?

Слайд 25

В маршрутных листах оцените свою работу.
настроение Задание 1 Зад.2 Зад.3 Зад.4 Зад.5 Зад.6 оцени настроение
Арифметический диктант Работа с числовым рядом Работа с учебником С.32 №79 С.32 №80 С.33 №81 (№82) С. 33 № 83
О О О О О О

Слайд 26

Ребята, просигнальте тем цветом, который соответствует вашему впечатлению от урока.

Слайд 27

Спасибо за работу.

Презентация “Познавательные задачи для устного счёта “О пресмыкающихся и земноводных” в 3 классе

библиотека
материалов

Содержание слайдов

Номер слайда 1

Составитель: Кудашова Светлана Александровна, учитель начальных классов МБОУ «Степноозёрская СОШ»Благовещенского района Алтайского края. Познавательные задачи для устного счёта «О пресмыкающихся и земноводных»3 класс. УМК «Начальная школа 21 века»

Номер слайда 2

Задача № 1 Максимальная длина чёрной мамбы 4 м. Длина вылупившегося детёныша составляет 50 см. Во сколько раз увеличивается длина этой змеи в течение жизни?Ответ: в 8 раз.

Номер слайда 3

Задача № 2 Длина нильского крокодила 6 м, а вылупившегося детёныша 30 см. Во сколько раз взрослая особь больше крокодильчика?Ответ: в 20 раз.

Номер слайда 4

Задача № 3 Чёрная мамба – самая быстрая змея. На короткой дистанции она развивает скорость 23 км/ч. Какое расстояние чёрная мамба преодолеет за 4 часа?Ответ: 92 км.

Номер слайда 5

Задача № 4 Сумчатые квакши вынашивают своих детёнышей в специальных выводковых мешках, которые находятся на спине. У трёх квакш 600 икринок. Сколько икринок вынашивает каждая?Ответ: 200 икринок.

Номер слайда 6

Задача № 5 Масса двух миссисипских аллигаторов 400 кг. Какова масса пяти крокодилов?Ответ: 1000 кг (1т).

Номер слайда 7

Задача № 6 Австралийский короткохвостый сцинк достигает 35 см в длину, а длина цепкохвостого сцинка, который живёт на деревьях, в 2 раза больше.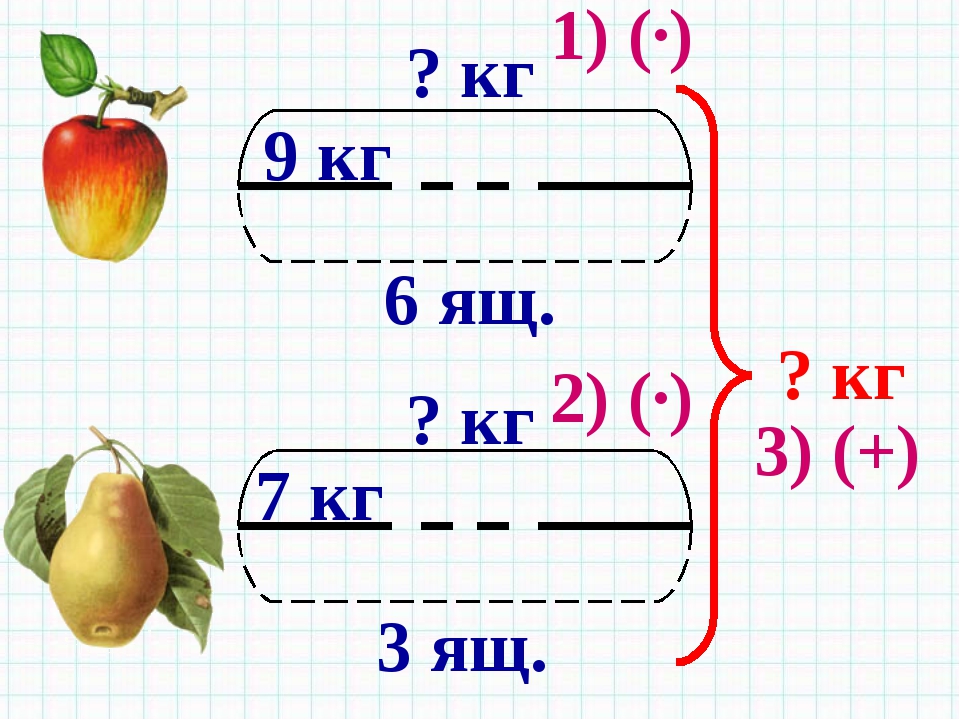 Какова длина цепкохвостого сцинка?Ответ: 70 см.

Номер слайда 8

Задача № 7 Самый маленький хамелеон 5 см в длину, а длина самого крупного из них в 12 раз больше. Чему равна длина самого крупного хамелеона?Ответ: 60 см.

Номер слайда 9

Задача № 8 Зимой в одной подземной норе собирается 30 гремунчиков, чтобы сообща провести зиму, согревая друг друга. Сколько гремунчиков в четырёх норах? В десяти норах?Ответ: 120 гремунчиков, 400 гремунчиков.

Номер слайда 10

Задача № 9 Собственно хвост у удава очень короткий, у многих других змей длина хвоста составляет до половины длины их тела. У трёхметрового удава хвост составляет шестую часть длины. Какой длины хвост у удава?Ответ: 50 см.

Номер слайда 11

Задача № 10 Самка гангского гавиала выкапывает бутылкообразную нору и откладывает в неё 40 яиц. Сколько крокодильчиков родится у четырёх самок? У десяти самок?Ответ: 160 крокодильчиков, 400 крокодильчиков .

Почему математические словесные задачи ТАК трудны для детей младшего школьного возраста?

Большинство детей любят рассказы и даже задачи и головоломки. Так почему же им так трудно решать математические задачи со словами? Я чувствую, что ответ кроется в ТИПАХ словесных задач, которые они решают в самые первые годы школы (1–4 классы).

Эти трудности не начинаются в 1-м классе с таких простых задач, как: На озере пять уток и три на берегу.Сколько всего уток? Часто к учебнику по математике прилагается красивая картинка. Вместо этого, как правило, начиная с 3-го класса многие ученики не могут применять математику даже в самых простых ситуациях, описанных словами.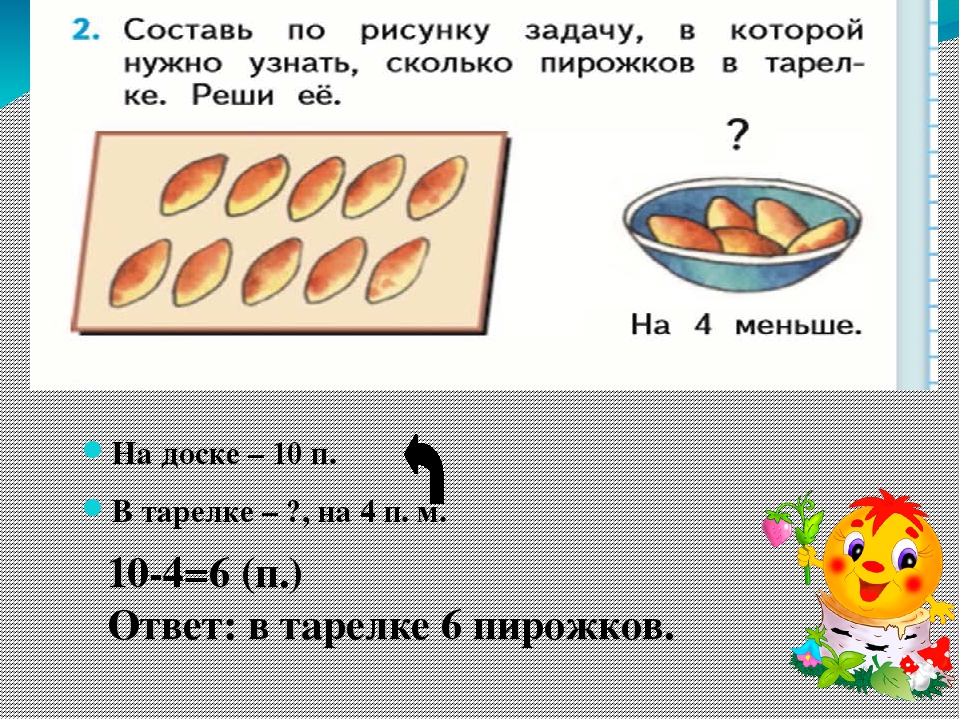

Я чувствую, что все сводится к этому «рецепту» , который используется в МНОЖЕСТВАХ уроков математики:

УРОК X

---

Пояснения и примеры.
Числовые упражнения.
Несколько проблем со словами.

Обратите внимание на следующие характеристики:

• Задачи со словами обычно находятся в конце урока. Таким образом, если нет времени, они пропускаются. Кроме того, поскольку они размещаются последними в уроке, похоже, что они наименее важная часть … верно?
• Очень важно: вы когда-нибудь замечали … Если урок посвящен теме X, то слова «проблемы» также относятся к теме X!

  Например, если тема урока – деление столбиком, то задачи урока, связанные со словами, с большой вероятностью будут решены с помощью деления столбиком.

• Другой общей характеристикой является то, что часто в словарных задачах есть только ДВА числа . Другими словами, это одноэтапные проблемы. (Одноэтапные задачи преобладают в некоторых учебных программах вплоть до 7-го класса!) Таким образом, даже если вы не поняли ни слова в слове «проблема», вы можете решить ее. Просто попробуйте: допустим, на уроке длинного деления обнаружена следующая выдуманная задача. Вы можете это решить?

  La tienda tiene 873 sábanas и 9 различных цветов.Hay la misma cantidad en cada color. ¿Cuántas sábanas de cada color tiene la tienda?

Я думаю, что с годами, когда дети подвергаются таким урокам снова и снова, они как бы понимают, что даже не читать задачу внимательно с умом менее требовательно. Зачем беспокоиться? Просто возьмите два числа и разделите (или умножьте, или сложите, или вычтите) их, и все.

Я не говорю, что такие словесные задачи не нужны в конце уроков по разделению.Я уверен, что у них есть свое место. Но эти простые рутинные задачи заставят студентов усвоить невысказанное «правило» :

«Задачи со словами, найденные в учебниках по математике, решаются с помощью некоторой процедуры или правила, которое вы найдете в начале этого конкретного урока ».

Еще одна трудность состоит в том, что ученики склонны мыслить линейно, , шаг за шагом, и пытаются сопоставить числа и текст в одном и том же порядке. Например, у Джейн было 25 ручек, а она отдала 15.Сколько у нее сейчас? Ответ: 25–15. Тогда, если слово «проблема» не соответствует пошаговому рецепту, они теряются. Например: «После того, как Джейн раздала несколько карт, у нее осталось 17 карт из 30. Сколько карт она отдала?» На этот раз ни один из этих расчетов не даст вам ответа: 17-30, 17 + 30 или 17 × 30.

Что можно сделать?

Анализ элементарных математических задач со словами

Предложите учащимся анализировать текстовые задачи БЕЗ подсчета ответов, чтобы они думали и находили, какая операция необходима для решения каждой задачи.Вот список ситуаций, связанных с определенными операциями:

• Итого делится на такое количество частей / контейнеров, каждая часть имеет одинаковое количество .

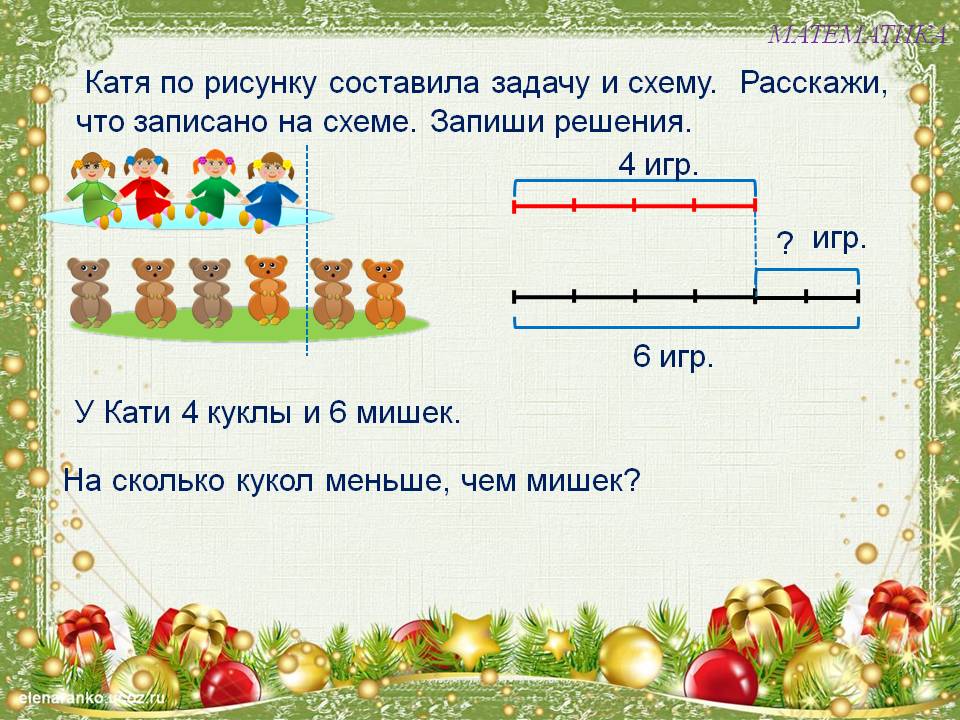
  Это ситуация умножения / деления:
  (количество частей) × (количество в каждой) = всего

  • Если вы знаете, сколько частей и количество в каждой, НЕСКОЛЬКО.
  • Если вы знаете сумму и количество деталей, РАЗДЕЛИТЬ.
  • Если вы знаете общую сумму и сумму в каждом, РАЗДЕЛИТЕ.
  
  
• Итог разделен на неравные группы.

  Это ситуация сложения / вычитания:
  (сумма в группе 1) + (сумма в группе 2) + (сумма в группе 3) + и т. д. = итого.

  • Если вы знаете суммы по группам, но не знаете общую сумму, ДОБАВИТЬ.
  • Если вы знаете общую сумму и суммы во всех группах, кроме одной, ВЫЧИТАЙТЕ. Это противоположно сложению. Вот несколько примеров проблем со словами:

    Из 187 изображений 45 были черно-белыми.Сколько было цветных картинок?

    Тыкв было 57, из них 15 спелых. Сколько еще не созрели?

    Обратите внимание, что НИЧЕГО не уходит и не забирается в этих ситуациях. На самом деле это сложения ситуаций:

    цветных изображения + черно-белые изображения = все изображения

    спелые тыквы + незрелые тыквы = все тыквы

    Тем не менее, они решаются путем вычитания .
  
  


• Что-то уходит или забирают. Это классическая ситуация вычитания.
  У Дженни было 14,56 доллара, и она купила куклу за 2,55 доллара. Сколько денег осталось?
  
• Ситуации «Сколько еще» (= разница) решаются вычитанием. Обратите внимание, что еще раз ничего не «забирают» и не уносят.
  У Джо 24 марки, а у Билла 13. Сколько еще у Джо? .

Вышеупомянутые ситуации охватывают основы того, как четыре операции используются в задачах со словами, которые охватывают большинство типов задач со словами, используемых в 1-4 классах.

См. Также:

Список веб-сайтов, посвященных проблемам со словами и решению проблем

Что можно и чего нельзя делать при обучении решению задач по математике

VDOE :: Ресурсы для профессионального развития

Содержание страницы

Математические стандарты обучения (SOL) Институты

VDOE обеспечивает целевое профессиональное развитие через математические институты. С 2009 года институты, поставившие перед студентами пять целей: научиться решать математические задачи, общаться математически, рассуждать математически, устанавливать математические связи и использовать математические представления для моделирования и интерпретации практических ситуаций, имеют:

• обрисовал в общих чертах изменения стандарта содержания от SOL 2001 по математике до Стандартов обучения по математике 2009 г. (SOL) – 2009;
• поддержали руководителей округов и учителей в реализации программы SOL 2009 по математике – 2009, 2010, 2011, 2012, 2013, 2014;
• проводил обучение по вертикальной содержательной прогрессии и педагогике – 2010, 2014;
• предоставил инструкции по содержанию наиболее проблемных областей – 2010, 2014;
• предоставил ресурсы для профессионального развития, направленные на облегчение понимания математики учащимися посредством решения задач, общения и рассуждений – 2011;
• предоставил ресурсы профессионального развития, ориентированные на использование ресурсов формирующего оценивания для принятия решений по обучению – 2012;
• обеспечил повышение квалификации по анализу и модификации существующих ресурсов для соответствия ожиданиям учащихся от обучения и по содействию решению проблем – 2013; и
• обеспечил профессиональное развитие по развитию способностей учащихся к математическим связям и использованию эффективных и подходящих представлений в математике – 2014.

2014 – Математические связи и использование представлений

Гол

Предоставить учителям возможность повышения квалификации, направленную на развитие способностей учащихся к установлению математических связей и использованию эффективных и подходящих представлений в математике.

Общие ресурсы

• Презентация вступительной сессии (PPT)
• Презентации для фасилитаторов – используются в институтах штата, могут быть изменены для использования фасилитаторами на уровне отделов

Пособия фасилитатора (для групп учителей)

Документы включают встроенные ресурсы.

2013 – Изменение ресурсов для содействия решению проблем и критическому мышлению

Большое спасибо Проекту математической оценки (Copyright 2012 – Ноттингемский университет), который предоставил контент, включенный в эту возможность профессионального развития.

Гол

Предоставить учителям возможность повышения квалификации, направленную на анализ и модификацию существующих ресурсов, чтобы соответствовать ожиданиям учащихся и способствовать решению проблем.

Общие ресурсы

• Учебные презентации на уровне отделов

Руководства для ведущего

Документы включают встроенные ресурсы.

2012 – Использование ресурсов формирующей оценки для принятия решений об обучении

Гол

Предоставить учителям возможность повышения квалификации по использованию ресурсов формирующего оценивания для принятия решений об обучении.

Общие ресурсы

Руководства для ведущего

Документы включают встроенные ресурсы.

2011 – Содействие пониманию математики учащимися посредством акцента на достижении целей процесса для учащихся

Гол

Для улучшения преподавания математики путем предоставления инструкторам районного уровня ресурсов для профессионального развития, направленных на облегчение понимания математики учащимися посредством решения задач, общения и рассуждений.

Общие ресурсы

Ресурсы для профессионального развития

Детский сад – 2 класс

3–5 классы

6–8 классы

9–12 классы

2010 – Внедрение нового содержания и повышение строгости математических стандартов обучения 2009 г.

Ресурсы для профессионального развития

Детский сад – 2 класс

3–5 классы

6-8 классы

9–12 классы

2009 – Обзор изменений в математических стандартах обучения 2001 и 2009 гг.

Начало страницы

Задачи со сложением трехзначных слов – математика для 3-го класса

Как решать задачи со сложением трехзначных слов

Дополнение очень полезно для повседневной жизни.

Представьте, что вы пытаетесь подсчитать свои окончательные очки в соревновании.

Вы заработали 134 балла за написание отчета. Вы также получили 223 балла за презентацию. Сколько очков вы заработали из всех ?

Чтобы выяснить ответ, нам нужно произвести сложение!

Решение проблем со сложением слов

🌟 При решении задач со сложением слов нам нужно выполнить четыре шага .

Во-первых, мы собираем подсказки из проблемы.

Это ключи к разгадке проблемы:

• 134 балла по вашему отчету
• 223 балла за презентацию
• Фраза «во всем» может сказать нам, что нам нужно делать.

Во-вторых, мы, , рисуем картинку , чтобы упорядочить наши подсказки.

Мы можем нарисовать планку и разделить ее на 2 части.

Нам не хватает части или целого?

Нам не хватает всего или целого.

Из словосочетания «всего» мы поняли, что нам нужно делать сложение.

😀 Совет. Вот другие слова и фразы, на которые следует обратить внимание: сколько, сколько всего, всего больше и меньше .

В-третьих, запишите уравнение , чтобы найти ответ на проблему.

Складываем 134 и 223, чтобы получить ответ.

134 + 223 =?

Если сложить эти два числа, мы получим 357.

Наконец, напишите ответное предложение , которое отвечает на вопрос со словом проблема.

Недостаточно просто написать число. Надо сказать, что мы считаем очки!

😀 Совет: вопрос может дать нам подсказку, какое предложение для ответа написать.

Итак, наш ответ предложением для этой задачи:

Вы заработали 357 баллов Всего балла.

Смотри и учись

Отличная работа! 😺

Теперь вы можете переходить к практике.

Практический совет: Приготовьте карандаш и бумагу для работы.Спросите своего родителя или учителя, если их у вас нет.

Вычитание ppt для 3-го класса

Семейства фактов – это взаимосвязанные концепции и факты. Например, с числами 3, 5 и 15 семейство фактов будет: 3 * 5 = 15 5 * 3 = 15 15 ÷ 5 = 3 15 ÷ 3 = 5. Видите связь? Попробуйте свои силы в умножении и делении фактов с помощью нашей веселой распечатываемой математической таблицы для детей «Числовые треугольники».

Откройте каждый из них в приложении PowerPoint для использования с iPad. Вам будут предложены вопросы, которые будут использоваться в качестве математической блок-схемы.Вы также можете открыть с помощью Power Point на компьютере. Выберите «Просмотреть слайд-шоу с начала». Вы можете открыть отдельные главы / темы или Алгебру 1, которая охватывает почти все темы этого года.

Вызов и использование фактов сложения и вычитания до 20, а также получение и использование связанных фактов до 100, например 3 + 7 = 10, 30 + 70 = 100, 10-7 = 3, 100-70 = 30 Сложите и вычтите числа из 100, используя предметы, картинки и мысленно. Поймите, что сложение может выполняться в любом порядке, но вычитание не может

14 января 2018 г. · В блоке 3 «Математика для первого класса» есть 31 практический математический центр и 85 практических страниц, которые помогут обучить, закрепить и освоить базовое вычитание до 20.ПЕРВЫЙ УЧАСТОК МАТЕМАТИКИ СДЕЛАНО УЧАСТНИКАМИ. Ознакомьтесь с другими модулями математики для первоклассников в действии: Модуль 1: Числа до 120. Модуль 2: Дополнение. ЭКОНОМЬТЕ $$$ С НАБОРОМ! ВСЕ 9 БЛОКОВ ВКЛЮЧЕНЫ!

Рабочий лист вертикального вычитания изображений от 0 до 7 Рабочий лист вертикального вычитания изображений от 0 до 8 Стандартные основные государственные стандарты – K.OA.A.1 – Представляют сложение и вычитание с помощью предметов, пальцев, мысленных образов, рисунков, звуков, разыгрывания ситуаций, словесных объяснения, выражения или уравнения.

Игра Subtract-o-poly Эта игра, основанная на популярной монопольной игре, имеет «отличия»! Дети 2-го и 3-го классов смогут улучшить свои навыки с помощью вычитания одной цифры, вычитания двух цифр, вычитания 2 минус 1 цифра и вычитания через нули.

В PowerPoint, презентациях PowerPoint (PPT). 6 класс PPT Четверть 3 Неделя 4–5. Автор Guro Ako Admin.

Задачи из выпущенных тестов для 3-го класса (также охватывает 3.6) 3.8 Учащийся определит путем подсчета стоимость коллекции банкнот и монет, общая стоимость которых составляет 5 долларов США или меньше, сравнит стоимость купюр и монет и сделает менять.

Третий класс – Содержание. Обзор фактов вычитания. Предложения с вычитанием – одна цифра. Вычитание десятков.

Что затрудняет решение математических задач? Изучение роли характеристик словесных задач, понимания текста и арифметических навыков

6 способов помочь учащимся понять математику

Конечная цель обучения математике состоит в том, чтобы учащиеся понимали представленный материал, применяли навыки и вспоминали концепции в будущем. Мало пользы от того, что учащиеся вспомнят формулу или процедуру для подготовки к завтрашнему экзамену, а к следующей неделе забывают основную концепцию. Учителям необходимо сосредоточиться на том, чтобы ученики понимали материал, а не просто запоминали процедуры.

Вот шесть способов научить понимать в классе математики:

1. Создайте эффективный вводный курс.

Первые пять минут урока задают тон всему уроку. В идеале учителя должны начать с того, что поделятся повесткой дня урока, чтобы ученики знали, чего ожидать от того, что будет происходить.Затем учителя могут разместить и сформулировать цель обучения или основной вопрос классу, чтобы учащиеся знали цель и в конце урока могли самостоятельно оценить, была ли цель для них достигнута. Наконец, вводный курс может включать в себя одну или несколько задач для разминки как способ проанализировать и оценить предыдущие знания учащихся при подготовке к ознакомлению с новым материалом. В этом видеоролике показано начало урока седьмого класса, посвященного прямоугольным призмам:

видео

2. Представляйте темы, используя несколько представлений.

Чем больше типов представлений вы можете представить учащимся, обращаясь к их различным стилям обучения, тем с большей вероятностью они действительно поймут представляемую концепцию. Различные представления могут включать использование манипуляторов, показ изображения, рисование проблемы и предложение символического представления. Например, представляя линейные отношения с одним неизвестным, проиллюстрируйте учащимся ту же задачу, что и уравнение, на числовой прямой, словами и картинками.Учащиеся, которые подвергаются воздействию и могут распознать одни и те же отношения, представленные в различных режимах представления, с большей вероятностью будут иметь концептуальное понимание отношений и лучше справляться с оценками (PDF).

3. Решайте проблемы разными способами.

В лучшей обстановке в классе учитель может показать разные способы решения одной и той же проблемы и побудить учеников придумывать свои собственные творческие способы их решения. Чем больше стратегий и подходов используют студенты, тем глубже становится их концептуальное понимание темы.Предоставление учащимся возможности создавать собственные методы решения проблем может заставить учителя нервничать. Что, если мы не будем следовать их логике? Что, если они неверны? Однако стоит рискнуть, чтобы они исследовали. После того, как один, пара или небольшая группа учащихся завершат решение классной задачи одним методом, предложите им поискать альтернативные способы найти такое же правильное решение. Когда учащиеся разрабатывают свои собственные методы, а затем делятся с классом правильными шагами, это очень мощный учебный опыт.На видео ниже показано, как учитель предлагает ученикам несколько способов решить одну и ту же задачу на прямоугольных призмах:

видео

4. Покажите приложение.

В идеальном мире мы всегда сможем продемонстрировать, как каждая концепция может быть применена к реальному миру – и, когда это возможно, это поможет улучшить понимание учащимися. Когда концепция не может быть применена таким образом, мы все равно можем рассказать, как ее можно применить в математике или другой предметной области. Другой вариант – показать, как эта концепция развивалась на протяжении истории математики. Выделите минутку из каждого урока, чтобы показать своим ученикам, где и как математику можно увидеть или использовать в жизни за пределами класса.

5. Предложите учащимся изложить свои соображения.

Студенты должны объяснять свои рассуждения при решении задач. Чтобы учитель мог определить, действительно ли каждый ученик понимает цель урока, каждому ученику необходимо общаться как устно, так и письменно. Предоставив классу десять минут, чтобы обсудить их аргументы друг с другом, изучая при этом несколько способов решения проблем, вы обеспечите отличное взаимодействие и обучение.Не всегда легко заставить учеников говорить в классе, но есть способы их поощрить (PDF).

6. Завершите занятие с аннотацией.

Каждый может заблудиться во время урока, и легко потерять счет времени, пока не прозвенит звонок и урок не закончится. Последние семь минут могут быть самыми важными для того, чтобы студенты поняли учебную цель дня. Вы можете использовать это время для выполнения трех очень важных задач:

• Быстрая формирующая оценка, чтобы определить, сколько было усвоено, например, учащиеся самостоятельно оценивают свой комфорт с концепцией по шкале от 1 до 5. время урока и краткое обсуждение того, где будет проходить урок в следующий раз.
• Предварительный просмотр домашнего задания вместе, чтобы избежать путаницы.

Это лишь некоторые из заданий в конце урока.Есть как минимум 22 дополнительных действия по закрытию. В этом видео показана итоговая фаза того же урока:

видео

В разделе комментариев ниже, пожалуйста, поделитесь своими собственными советами и приемами, которые помогут учащимся понять математику.

PPT – Урок математики: решение проблем в презентации PowerPoint | бесплатно для просмотра

PowerShow.com – ведущий веб-сайт для обмена презентациями и слайд-шоу. Независимо от того, является ли ваше приложение бизнесом, практическими рекомендациями, образованием, медициной, школой, церковью, продажами, маркетингом, онлайн-обучением или просто для развлечения, PowerShow.com – отличный ресурс. И, что лучше всего, большинство его интересных функций бесплатны и просты в использовании.

Вы можете использовать PowerShow. com, чтобы найти и загрузить примеры онлайн-презентаций PowerPoint ppt практически по любой теме, которую вы можете вообразить, чтобы вы могли узнать, как улучшить свои собственные слайды и презентации бесплатно. Или используйте его, чтобы найти и загрузить высококачественные презентации PowerPoint ppt с практическими рекомендациями и иллюстрированными или анимированными слайдами, которые научат вас делать что-то новое, также бесплатно. Или используйте его для загрузки собственных слайдов PowerPoint, чтобы вы могли поделиться ими со своими учителями, классом, студентами, руководителями, сотрудниками, клиентами, потенциальными инвесторами или всем миром.Или используйте его для создания действительно крутых слайд-шоу из фотографий – с двухмерными и трехмерными переходами, анимацией и музыкой на ваш выбор – которыми вы можете поделиться со своими друзьями в Facebook или в кругах Google+. Это тоже бесплатно!

За небольшую плату вы можете получить лучшую в отрасли конфиденциальность в Интернете или публично продвигать свои презентации и слайд-шоу с высокими рейтингами. Но в остальном это бесплатно. Мы даже преобразуем ваши презентации и слайд-шоу в универсальный формат Flash со всей их оригинальной мультимедийной красотой, включая анимацию, эффекты перехода 2D и 3D, встроенную музыку или другой звук или даже видео, встроенное в слайды.Все бесплатно. Большинство презентаций и слайд-шоу на PowerShow.com можно бесплатно просматривать, многие даже можно бесплатно загрузить. (Вы можете выбрать, разрешить ли людям загружать ваши оригинальные презентации PowerPoint и слайд-шоу фотографий за плату или бесплатно или вовсе.) Зайдите на PowerShow.com сегодня – БЕСПЛАТНО. Здесь действительно каждый найдет что-то для себя!

презентации бесплатно. Или используйте его, чтобы найти и загрузить высококачественные презентации PowerPoint ppt с практическими рекомендациями и иллюстрированными или анимированными слайдами, которые научат вас делать что-то новое, также бесплатно.Или используйте его для загрузки собственных слайдов PowerPoint, чтобы вы могли поделиться ими со своими учителями, классом, студентами, руководителями, сотрудниками, клиентами, потенциальными инвесторами или всем миром. Или используйте его для создания действительно крутых слайд-шоу из фотографий – с двухмерными и трехмерными переходами, анимацией и музыкой на ваш выбор – которыми вы можете поделиться со своими друзьями в Facebook или в кругах Google+. Это тоже бесплатно!

За небольшую плату вы можете получить лучшую в отрасли конфиденциальность в Интернете или публично продвигать свои презентации и слайд-шоу с высокими рейтингами.Но в остальном это бесплатно. Мы даже преобразуем ваши презентации и слайд-шоу в универсальный формат Flash со всей их оригинальной мультимедийной красотой, включая анимацию, эффекты перехода 2D и 3D, встроенную музыку или другой звук или даже видео, встроенное в слайды. Все бесплатно. Большинство презентаций и слайд-шоу на PowerShow.com можно бесплатно просматривать, многие даже можно бесплатно загрузить. (Вы можете выбрать, разрешить ли людям загружать ваши оригинальные презентации PowerPoint и слайд-шоу фотографий за плату или бесплатно или вообще.) Посетите PowerShow.