Решение примеров онлайн в столбик: Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком

Калькулятор дробей ОНЛАЙН с решением уравнений в столбик

Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей.

Онлайн калькулятор уравнений с дробями

Дробью в математике называется число, представляющее часть единицы или несколько её частей.

Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.

Дроби бывают правильными и неправильными.

• Правильной называется дробь, у которой числитель меньше знаменателя.
• Неправильная дробь – если у дроби числитель больше знаменателя.

Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть, называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь.

---

Как перевести смешанную дробь в обыкновенную

Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: 

Как перевести обыкновенную дробь в смешанную

Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:

1. Поделить числитель дроби на её знаменатель
2. Результат от деления будет являться целой частью
3. Остаток отделения будет являться числителем

Как перевести обыкновенную дробь в десятичную

Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.

Как перевести десятичную дробь в обыкновенную

Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:

1. Записать дробь в виде десятичная 
2. Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
3. Найти наибольший общий делитель и сократить дробь.

Как перевести дробь в проценты

Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.

Как перевести проценты в дробь

Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.

Сложение дробей

Алгоритм действий при сложении двух дробей такой:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
3. Выполнить сложение дробей путем сложения их числителей.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Вычитание дробей

Алгоритм действий при вычитании двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
3. Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Умножение дробей

Алгоритм действий при умножении двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
3. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
4. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Деление дробей

Алгоритм действий при делении двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
3. Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Калькулятор дробей предоставлен сайтом calcus. ru

Загрузка…

Понравилось? Поделись с друзьями!

Решение больших примеров в столбик калькулятор. Вычитание столбиком

Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться. Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.

Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое – понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.

Алгоритм деления столбиком на двузначное число

Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.

1. Находим первое неполное делимое . Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.

Примеры 76 8:24. Первое неполное делимое 76
265 :53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.

2. Определяем количество цифр в частном . Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого – еще по одной цифре частного.

Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.

265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.

3. Находим цифры в каждом разряде частного . Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.

Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.

4. Находим остаток (если есть).

Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.

Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)

Разбор примеров на деление столбиком на двузначное число

Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.

Найдем значение частного чисел 265 и 53.

Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.

Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.

Значение частного чисел 265 и 53 равно 5.

Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.

Найдем значение частного чисел 184 и 23.

В частном будет однозначное число.

Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.

Значение частного чисел 184 и 23 равно 8.

Рассмотрим более сложные случаи деления.

Найдем значение частного чисел 768 и 24.

Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.

Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.

Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.

Значение частного чисел 768 и 24 равно 32.

Найдем значение частного чисел 15344 и 56.

Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.

Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3).

И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.

Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.

Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.

Значение частного чисел 15344 и 56 равно 274.

Пример на деление с остатком

Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой

Найдем значение частного чисел 15345:56

Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.

Значение частного чисел 15345 и 56 равно 274 (остаток 1).

Деление с нулем в частном

Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.

Найдем значение частного чисел 2870:14

Первое неполное делимое – 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.

Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.

Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.

Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).

70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.

Значение частного чисел 2870 и 14 равно 205.

Деление нужно непременно проверить умножением.

Примеры на деление для самопроверки

Найдите первое неполное делимое и определите количество цифр в частном.

3432:66 2450:98 15145:65 18354:42 17323:17

Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.

1428: 42 30296: 56 254415: 35 16514: 718

Математический-Калькулятор-Онлайн v.1.0

Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.

Решение:

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 – будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
–	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку “корня” производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x 2	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку “возведение в квадрат” производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1 / x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка “%”
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле “Решение” выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение “0”

Алгоритм работы онлайн-калькулятора на примерах

Сложение.

Сложение целых натуральных чисел { 5 + 7 = 12 }

Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }

Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }

Вычитание.

Вычитание целых натуральных чисел { 7 – 5 = 2 }

Вычитание целых натуральных и отрицательных чисел { 5 – (-2) = 7 }

Вычитание десятичных дробных чисел { 6,5 – 1,2 = 4,3 }

Умножение.

Произведение целых натуральных чисел { 3 * 7 = 21 }

Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }

Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }

Деление.

Деление целых натуральных чисел { 27 / 3 = 9 }

Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }

Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }

Извлечение корня из числа.

Извлечение корня из целого числа { корень(9) = 3 }

Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }

Извлечение корня из суммы чисел { корень(56 + 25) = 9 }

Извлечение корня из разницы чисел { корень (32 – 7) = 5 }

Возведение числа в квадрат.

Возведение в квадрат целого числа { (3) 2 = 9 }

Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }

Перевод в десятичные дроби.

Вычисление процентов от числа

Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }

Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }

18% от числа 140 это { 140 * 0,18 = 25,2 }

Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.

• Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
• Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
• Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям

Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.

Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».

Итак, как объяснить ребенку деление столбиком :

• Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
• Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
• Пусть ребенок сам разделит другое число, например, более сложное: 24:4
• Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные

Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.

Начинайте с простого — деление на однозначное число:

Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.

Например, 256 разделить на 4:

• Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
• Спросите у малыша, сколько четверок помещается в двойке — нисколько
• Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
• Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
• Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
• Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
• Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»

Письменное деление на двузначное число

Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.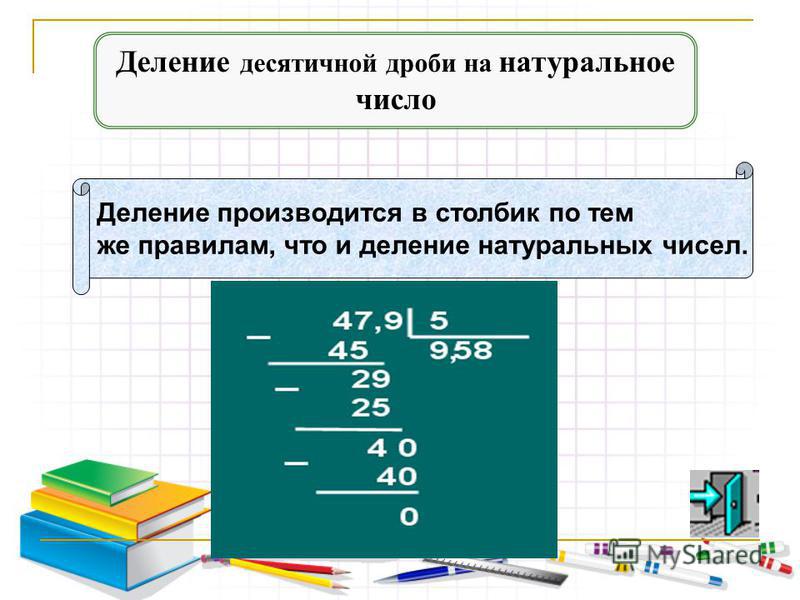

Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.

Выполните вместе такое простое действие: 184:23 — как нужно объяснять:

• Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
• Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8

Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.

Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:

• Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
• Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
• Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
• Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно

Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.

Например:

• Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
• Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
• Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
• Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
• Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
• Запишите 2864 под 2864, получается в разности 0. Ответ 204

Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.

Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.

Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):

• Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
• Делится эта цифра на 8? Правильно — нет. Получается, остаток 3

После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:

• В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
• Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
• Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
• К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
• Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375

Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.

Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.

Алгоритм деления чисел заключается в следующем:

• Сделать прикидку числа, которое будет стоять в ответе
• Найти первое неполное делимое
• Определить число цифр в частном
• Найти цифры в каждом разряде частного
• Найти остаток (если он есть)

По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).

Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:

• 1428:42
• 2924:68
• 30296:56
• 136576:64
• 16514:718

Для закрепления результата можно использовать такие игры на деление:

• «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.

Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.

Видео: Игра арифметика для детей сложение вычитание деление умножение

Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2

Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик) . Также можно встретить название деление уголком . Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .

В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.

Навигация по странице.

Правила записи при делении столбиком

Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.

Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105 , а делителем – 5 5, то их правильная запись при делении в столбик будет такой:

Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.

Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808 на 51 234 (614 808 – шестизначное число, 51 234 – пятизначное число, разница в количестве знаков в записях равна 6−5=1 ) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058 и 4 (здесь разница в количестве знаков равна 4−1=3 ). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:

Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.

Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком

Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.

Пример.

Пусть нам нужно разделить столбиком 8 на 2 .

Решение.

Конечно, мы можем выполнить деление при помощи таблицы умножения , и сразу записать ответ 8:2=4 .

Но нас интересует, как выполнить деление этих чисел столбиком.

Сначала записываем делимое 8 и делитель 2 так, как того требует метод:

Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0 , 1 , 2 , 3 , … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.

Поехали: 2·0=0 ; 2·1=2 ; 2·2=4 ; 2·3=6 ; 2·4=8 . Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4 . При этом запись примет следующий вид:

Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком . Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.

В нашем примере получаем

Теперь перед нами законченная запись деления столбиком числа 8 на 2 . Мы видим, что частное 8:2 равно 4 (и остаток равен 0 ).

Ответ:

8:2=4 .

Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.

Пример.

Разделим столбиком 7 на 3 .

Решение.

На начальном этапе запись выглядит так:

Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3 на 0 , 1 , 2 , 3 и т.д. до того момента, пока не получим число равное или большее, чем делимое 7 . Получаем 3·0=07 (при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6 (оно получено на предпоследнем шаге), а на место неполного частного записываем число 2 (на него проводилось умножение на предпоследнем шаге).

Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7 и 3 будет завершено.

Таким образом, неполное частное равно 2 , и остаток равен 1 .

Ответ:

7:3=2 (ост. 1) .

Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.

Сейчас мы разберем алгоритм деления столбиком . На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288 на однозначное натуральное число 4 . Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.

Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.

Первой слева цифрой в записи делимого 140 288 является цифра 1 . Число 1 меньше, чем делитель 4 , поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14 , с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.

Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.

Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x ). Для этого последовательно умножаем делитель на 0 , 1 , 2 , 3 , … до того момента, пока не получим число x или число больше, чем x . Когда получается число x , то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4 пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).

Умножаем делитель 4 на числа 0 , 1 , 2 , …, пока не получим число, которое равно 14 или больше 14 . Имеем 4·0=014 . Так как на последнем шаге мы получили число 16 , которое больше, чем 14 , то под выделенным числом записываем число 12 , которое получилось на предпоследнем шаге, а на место частного записываем число 3 , так как в предпоследнем пункте умножение проводилось именно на него.


На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.

Нам нужно вычесть столбиком из числа 14 число 12 (для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2 . Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2 меньше делителя 4 , то можно спокойно переходить к следующему пункту.


Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2 по 4 пункты алгоритма.

Под горизонтальной чертой справа от уже имеющейся там цифры 2 записываем цифру 0 , так как именно цифра 0 находится в записи делимого 140 288 в этом столбце. Таким образом, под горизонтальной чертой образуется число 20 .


Это число 20 мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.

Умножаем делитель 4 на 0 , 1 , 2 , …, пока не получим число 20 или число, которое больше, чем 20 . Имеем 4·0=0

Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).


Под горизонтальной линией справа от запомненного места записываем цифру 2 , так как именно она находится в записи делимого 140 288 в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2 .


Число 2 принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4 пунктов алгоритма.

Умножаем делитель на 0 , 1 , 2 и так далее, и сравниваем получающиеся числа с отмеченным числом 2 . Имеем 4·0=02 . Следовательно, под отмеченным числом записываем число 0 (оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0 (на 0 мы проводили умножение на предпоследнем шаге).


Выполняем вычитание столбиком, получаем число 2 под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4 . Так как 2

Под горизонтально чертой справа от числа 2 дописываем цифру 8 (так как она находится в этом столбце в записи делимого 140 288 ). Таким образом, под горизонтальной линией оказывается число 28 .


Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4 пунктов.

Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.

Осталось последний раз провести действия из пунктов 2 , 3 , 4 (предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288 и 4 в столбик:

Обратите внимание, что в самой нижней строчке записано число 0 . Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.

Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288 на однозначное натуральное число 4 , мы видим, что частным является число 35 072 , (а остаток от деления равен нулю, он находится в самой нижней строке).

Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.

Пример.

Выполните деление в столбик, если делимое равно 7 136 , а делителем является однозначное натуральное число 9 .

Решение.

На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида

После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид

Повторив цикл, будем иметь

Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136 и 9

Таким образом, неполное частное равно 792 , а остаток от деления равен 8 .

Ответ:

7 136:9=792 (ост. 8) .

А этот пример демонстрирует, как должно выглядеть деление в столбик.

Пример.

Разделите натуральное число 7 042 035 на однозначное натуральное число 7 .

Решение.

Удобнее всего выполнить деление столбиком.

Ответ:

7 042 035:7=1 006 005 .

Деление столбиком многозначных натуральных чисел

Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел . Это действительно так, так как со 2 по 4 этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.

На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2 , 3 и 4 пункте алгоритма до получения конечного результата.

Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.

Пример.

Выполним деление столбиком многозначных натуральных чисел 5 562 и 206 .

Решение.

Так как в записи делителя 206 участвуют 3 знака, то смотрим на первые 3 цифры слева в записи делимого 5 562 . Эти цифры соответствуют числу 556 . Так как 556 больше, чем делитель 206 , то число 556 принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.

Теперь умножаем делитель 206 на числа 0 , 1 , 2 , 3 , … до того момента, пока не получим число, которое либо равно 556 , либо больше, чем 556 . Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0556 . Так как мы получили число, которое больше числа 556 , то под выделенным числом записываем число 412 (оно было получено на предпоследнем шаге), а на место частного записываем число 2 (так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:

Выполняем вычитание столбиком. Получаем разность 144 , это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.

Под горизонтальной линией справа от имеющегося там числа записываем цифру 2 , так как она находится в записи делимого 5 562 в этом столбце:

Теперь мы работаем с числом 1 442 , выделяем его, и проходим пункты со второго по четвертый еще раз.

Умножаем делитель 206 на 0 , 1 , 2 , 3 , … до получения числа 1 442 или числа, которое больше, чем 1 442 . Поехали: 206·0=0

Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:

Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:

• Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
• Математика. Любые учебники для 5 классов общеобразовательных учреждений.

Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?

Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.

Я уже писала о том, Эта статья может стать для вас полезной.

Осваиваем операцию разделения (деления) на части в игровой форме

На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.

Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.

Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.

Умножаем и делим, используя таблицу умножения

Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.

Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.

Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.

Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!

По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.

Делим столбиком – приведем пример

Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.

Объясняем наглядно

Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.

Шаг 1 . Записываем числа, разделив их «уголком».

Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.

Шаг 3. Переходим к оформлению деления столбиком:

Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.

Записываем результат.

Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.

Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.

Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.

Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.

Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.

Как научить ребенка делению – закрепляем навык

Главное из-за чего у многих школьников возникает проблема с математикой – это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме – необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.

1. «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
2. «Деление. Уровень 4. Рабочая тетрадь» от Kumon
3. «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина – автора обучающих книг-бестселлеров

Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.

Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.

Для того чтобы легко научить ребёнка операции деления нужно:

• Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
• Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.

Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.

Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.

Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт

Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:

Онлайн примеры по математике для 3 класса

Деление в столбик 3 класс петерсон примеры для тренировки по математике

В третьем классе продолжается тренировка навыков счёта в столбик. Ученикам даются примеры с трёхзначными и четырёхзначными числами. Для успешного решения примеров необходима практика: чем больше примеров решает ученик – тем легче ему даётся счёт.

Примеры по математике на сложение, вычитание, умножение и деление можно легко получить с помощью нашего генератора примеров. Бесконечный набор неповторяющихся примеров предназначен для тренировки навыков счёта. Полученные примеры можно применять для домашнего обучения или для школьных работ.

Для успешного решения примеров необходима практика чем больше примеров решает ученик тем легче ему даётся счёт.

Www. primer-online. ru

27.09.2019 18:54:10

2019-09-27 18:54:10

Источники:

Http://www. primer-online. ru/3-klass-primery-online. php

Примеры в столбик | Картотека по математике (3 класс) на тему: | Образовательная социальная сеть » /> » /> .keyword { color: red; }

Деление в столбик 3 класс петерсон примеры для тренировки по математике

По теме: методические разработки, презентации и конспекты

Для самостоятельной работы по математике 3 класс Решение примеров столбиком.

Примеры для решения столбиком 3 класс.

Карточка «примеры столбиком»

Данные карточки можно предложить учащимся для отработки навыков сложения и вычитания столбиком с переходом через десяток.

Самостоятельная работа по математике для 2 класса на тему: «Решение примеров в столбик в пределах 100»

Методический материал разработан для учащихся 2-х классов с нарушением слуха (1 отделение).

Примеры столбиком 2 класс

Примеры столбиком 2 класс.

Карточка по математике «Реши примеры в столбик»

Для отработки деления в столбик.

Карточки по математики — Примеры в столбик

Данны материал позволит закрепить счет столбиком с переходом через десяток 2 класс.

Для самостоятельной работы по математике 3 класс Решение примеров столбиком.

Примеры для решения столбиком 3 класс.

Карточка «примеры столбиком»

Данные карточки можно предложить учащимся для отработки навыков сложения и вычитания столбиком с переходом через десяток.

Самостоятельная работа по математике для 2 класса на тему: «Решение примеров в столбик в пределах 100»

Методический материал разработан для учащихся 2-х классов с нарушением слуха (1 отделение).

Примеры столбиком 2 класс

Примеры столбиком 2 класс.

Карточка по математике «Реши примеры в столбик»

Для отработки деления в столбик.

Карточки по математики — Примеры в столбик

Данны материал позволит закрепить счет столбиком с переходом через десяток 2 класс.

Примеры столбиком 2 класс

Примеры в столбик картотека по математике 3 класс на тему.

Nsportal. ru

23.12.2017 15:22:50

2017-12-23 15:22:50

Источники:

Https://nsportal. ru/nachalnaya-shkola/matematika/2015/06/07/primery-v-stolbik

Для самостоятельной работы по математике 3 класс Решение примеров столбиком. | Тест по математике (3 класс) на тему: | Образовательная социальная сеть » /> » /> .keyword { color: red; }

Деление в столбик 3 класс петерсон примеры для тренировки по математике

По теме: методические разработки, презентации и конспекты

Самостоятельная работа по математике 4 класс.

Деление в столбик на однозначное число. 17 ЯНВАРЯ 2016 ГОДА.

Самостоятельная работа по математике 4 класс. Деление в столбик на однозначное число. В 2 вариантах.

Задачи, примеры, самостоятельные работы по математике

Самостоятельная работа по математике в 1 классе «Прибавить и вычесть числа 1,2, 3. Решение задач»

Самостоятельная работа по математике в 1 классе, II четверть, в двух вариантах, УМК «Школа России».

Задачи и примеры по математике для самостоятельных работ 3-4 класс

Задачи и примеры по математике для самостоятельных работ 3-4 класс.

Самостоятельная работа по математике «Умножение на 2,3. Решение простых текстовых задач» 2 класс, «Перспектива»

Самостоятельная работа по математике «Умножение на 2,3. Решение простых текстовых задач» 2 класс, «Перспектива&quot.

Самостоятельная работа по математике для 2 класса на тему: «Решение примеров в столбик в пределах 100»

Методический материал разработан для учащихся 2-х классов с нарушением слуха (1 отделение).

Технологическая карта по математике на тему: «Самостоятельная работа по теме «Сложение и вычитание столбиком»» 2 класс

Цели деятельности учителя: создание условий для проверки навыка сложения и вычитания в строчку и столбиком;Планируемые результатыПредметные: обладать навыками устного счета, логического мышления. Лично.

Самостоятельная работа по математике 4 класс. Деление в столбик на однозначное число. 17 ЯНВАРЯ 2016 ГОДА.

Самостоятельная работа по математике 4 класс. Деление в столбик на однозначное число. В 2 вариантах.

Задачи, примеры, самостоятельные работы по математике

Самостоятельная работа по математике в 1 классе «Прибавить и вычесть числа 1,2, 3. Решение задач»

Самостоятельная работа по математике в 1 классе, II четверть, в двух вариантах, УМК «Школа России».

Задачи и примеры по математике для самостоятельных работ 3-4 класс

Задачи и примеры по математике для самостоятельных работ 3-4 класс.

Самостоятельная работа по математике «Умножение на 2,3. Решение простых текстовых задач» 2 класс, «Перспектива»

Самостоятельная работа по математике «Умножение на 2,3. Решение простых текстовых задач» 2 класс, «Перспектива&quot.

Самостоятельная работа по математике для 2 класса на тему: «Решение примеров в столбик в пределах 100»

Методический материал разработан для учащихся 2-х классов с нарушением слуха (1 отделение).

Технологическая карта по математике на тему: «Самостоятельная работа по теме «Сложение и вычитание столбиком»» 2 класс

Цели деятельности учителя: создание условий для проверки навыка сложения и вычитания в строчку и столбиком;Планируемые результатыПредметные: обладать навыками устного счета, логического мышления. Лично.

Задачи, примеры, самостоятельные работы по математике

Технологическая карта по математике на тему Самостоятельная работа по теме Сложение и вычитание столбиком 2 класс.

Nsportal. ru

07.12.2020 22:48:43

2020-12-07 22:48:43

Источники:

Https://nsportal. ru/nachalnaya-shkola/matematika/2013/04/18/dlya-samostoyatelnoy-raboty-po-matematike-3-klass-reshenie

7 Проблемы с электронными таблицами Excel и способы их решения

Если вам нужно составить список чего-либо, заманчиво использовать Excel в качестве репозитория по умолчанию: в конце концов, это всего лишь небольшой список элементов для вас или нескольких близких коллег. Возможно, вам нужны более сложные формулы для расчетов или программирование макросов для автоматизации сбора и обработки данных.

К сожалению, простота начала работы в Excel или конкурирующей программе для работы с электронными таблицами также является одной из его самых больших проблем. То, что начинается как небольшой проект в Excel, перерастает во что-то масштабное, и в этот момент вы также можете столкнуться с проблемами скорости и стабильности или даже с проблемой разработки, которую вы не можете решить.

Кроме того, задачи управления большими данными часто сопряжены со значительными проблемами, такими как организация, реализация, классификация файлов, управление базой данных, совместная работа пользователей и многое другое. Все, что нужно, чтобы разрушить структуру базы данных, — это поместить данные в неправильную область, ввести данные непоследовательно или даже заставить двух человек работать над одним листом. Некоторые вещи могут пойти не так, что приведет к временным задержкам и возможной потере данных.

В этой статье объясняются наиболее распространенные проблемы, с которыми сталкиваются пользователи при работе с электронными таблицами Excel, способы их решения и когда лучше сделать решительный шаг и вместо этого переключиться на базу данных.

Проблема № 1: многопользовательское редактирование в Excel

Когда системы Excel органично разрастаются, вы быстро сталкиваетесь с проблемами, когда один пользователь открывает книгу в любой момент времени, а другому сообщается, что она уже открыта . Второй пользователь может отменить, подождать или просмотреть версию только для чтения. Обещание Excel сообщить вам, когда другой человек выходит из книги, — это авантюра, поскольку она не проверяет статус так часто и может никогда не просветить вас. Даже если это произойдет, кто-то другой может войти в систему и открыть файл раньше вас.

Чтобы избежать эффекта «одинокого пользователя», вы можете использовать Excel Online (урезанную веб-версию Excel) или включить функцию Shared Workbooks . Вот краткое руководство о том, как поделиться электронной таблицей.

1. Откройте нужную электронную таблицу и нажмите «Файл» вверху.
2. Затем в меню слева нажмите « Поделиться », чтобы открыть новое окно.
   
3. Теперь введите информацию о пользователе, с которым вы хотите поделиться электронной таблицей.

Примечание: Вы также можете разделить данные на несколько книг, чтобы разные люди работали над разными книгами, не наступая друг другу на пятки.

Проблема № 2: общие книги Excel

Excel Online по умолчанию поддерживает несколько редакторов, но в нем отсутствует значительная часть функций. Служба не претендует ни на что, кроме простейших задач. Хотя функция «Общие рабочие книги» выглядит так, как будто она должна выполнять свою работу, она полна ограничений. Например, вы невозможно создать таблицу или удалить блок ячеек, если книга является общей .

При органическом росте систем Excel возникает проблема, заключающаяся в том, что только один пользователь может одновременно открыть книгу.

Существуют обходные пути для некоторых онлайн-ограничений Excel. Для других это вопрос изменения структуры рабочей книги, а не использования уже настроенной рабочей книги, но этот сценарий часто мешает. В результате невозможно использовать общую книгу так же, как обычную однопользовательскую книгу.

Изменения в общих книгах синхронизируются между пользователями при каждом сохранении книги. Это действие помещается в расписание по времени, например, принудительное сохранение каждые пять минут. Однако накладные расходы на регулярное сохранение и отслеживание изменений каждого пользователя становятся весьма значительными. Книги могут быстро увеличиваться в размерах и создавать нагрузку на вашу сеть, замедляя работу других систем.

Проблема № 3. Связанные книги Excel

Разделение данных по нескольким книгам может решить проблему многопользовательского редактирования. Тем не менее, каждой рабочей книге, скорее всего, потребуются связи между ними, чтобы значения, введенные в одну, использовались в другой . Ссылки между книгами также полезны для хранения отдельных данных в отдельных файлах, а не для отдельных листов в одной книге.

Досадно, что эти ссылки являются еще одним источником разочарования и нестабильности. Они становятся абсолютными, включая полный путь к исходной книге, или относительными, включая разницу между исходным и конечным путями. Хотя это звучит разумно, Excel использует тайные правила, чтобы решить, когда использовать тот или иной тип ссылки и изменить их.

Правила регулируются несколькими параметрами и тем, были ли книги сохранены перед вставкой ссылок. Ссылки также изменяются, когда вы сохраняете книгу или открываете и используете Сохранить как , чтобы создать дубликат, а не копировать файл с помощью проводника. Результатом всей этой путаницы и неопределенности является то, что связи между книгами легко рвутся, а восстановление таких ссылок требует много времени. Никто не получает доступ к затронутым файлам.

Связанные данные обновляются только при открытии файлов, если вы специально не нажмете « Данные > Запросы и подключения > Редактировать ссылки > Обновить значения. » Вот небольшая демонстрация.

1. Откройте нужную электронную таблицу и нажмите «Данные» вверху.
2. Теперь найдите «Запросы и подключения» и нажмите « Редактировать ссылки ».
3. Затем выберите «Обновить значения».

Если ваши ссылки не между двумя рабочими книгами, а охватывают три или более, вы должны открывать все рабочие книги по порядку, гарантируя, что любые процессы обновления данных происходят в правильном порядке, от первой до второй третий. Если вы изменили значение в первой книге и открыл третью, она не увидит никаких изменений, потому что вторая книга не обновила свои значения.

Эта цепочка данных логична, но увеличивает вероятность того, что информация либо неверна, либо что вы попытаетесь открыть книгу, которую уже редактирует кто-то другой.

Конечно, вы можете попытаться вообще избежать связанных книг, но есть вероятность, что вы в конечном итоге будете вводить одни и те же данные более чем в одну книгу, и с этим возникает опасность каждый раз вводить их немного по-разному.

Проблема № 4: Проверка данных Excel

Ошибки могут проникать в данные в любой компьютерной системе: люди неправильно набирают слова или переставляют цифры в числах с монотонной регулярностью. Если ваши данные не проверяются при вводе, у вас будут проблемы.

По умолчанию Excel принимает все, что вводит пользователь. Можно настроить проверку списков поиска, но их сложно поддерживать, в основном, если одно и то же поле используется более чем в одном месте. Если пользователям необходимо вводить идентификационные номера документов или ссылочные номера клиентов без каких-либо проверок, можно легко связать вместе неверные записи, даже не осознавая этого. Целостность данных в системе оказывается фатально скомпрометированной, и любой анализ данных вызывает сомнения.

Возможно, вы уже страдаете от последствий проблем с проверкой данных, не осознавая основной причины. Рассмотрим ситуацию, когда у вас есть список счетов в Excel. Пользователь вводит имя клиента немного по-разному в каждом счете. В результате вы получаете счета на «Jones Ltd», «Jones Limited», «Jonse Ltd» и «joness».

Возможно, вы знаете, что все они относятся к одной и той же компании, но Excel — нет. Любой анализ данных счета, такой как сводная таблица, основанная на клиентах по месяцам, дает несколько результатов, хотя должен быть только один .

Проблема № 5: Навигация в Excel

Навигация по большим книгам затруднена. Вкладки листов в нижней части окна — ужасный механизм для поиска пути, когда их много. Чем больше отображаемых вкладок на экране, тем сложнее найти то, что вам нужно. Вот быстрый способ навигации по листам.

1. В нижней левой части экрана щелкните правой кнопкой мыши «кнопки со стрелками», слева от имен листов, чтобы открыть диалоговое окно « Активировать лист ».
   
2. В списке перечислены только первые 20 листов, прежде чем вам придется прокручивать список. Нет возможности сортировать, группировать или искать нужный лист. Окно должно выглядеть примерно так, как показано ниже.

Проблема № 6: Безопасность Excel

Вы можете повысить безопасность книг Excel, но это чревато проблемами. Защита больше ориентирована на защиту структуры книги, чем данных. Вы можете попытаться заблокировать некоторые листы и ячейки, чтобы запретить пользователям изменять структуру и формулу, но если они могут видеть данные, они обычно могут изменить некоторые из них или все (если только вы не применяете творческий подход к программированию макросов).

Проблема № 7: Проблемы со скоростью работы Excel

Excel — не самое быстрое приложение, а его язык программирования VBA работает медленно по сравнению с более профессиональными языками программирования, такими как C#. Этот сценарий связан с предполагаемым использованием и гибким характером Excel. В конце концов, это табличный движок. Да, Excel VBA может превратиться в сервис, управляющий списками данных, но это не значит, что это лучший выбор для такой работы. Другие приложения лучше подходят для таких задач, главным образом потому, что они специально предназначены для их решения.

Использование базы данных для структурированных данных

Если вы столкнулись с какой-либо из проблем, описанных в этой статье, не игнорируйте их. Существует профессиональный ответ на вопрос о хранении структурированных данных, известный как база данных. Это не должно быть пугающим или дорогим, и оно должно позволить вам логически мыслить о ваших данных, о том, как они связаны друг с другом и как вы с ними взаимодействуете.

Примечание . Если вы переходите от решения для работы с электронными таблицами к базе данных, не рабски дублируйте дизайн электронных таблиц. Воспользуйтесь возможностью сделать его лучше.

Доступны приложения базы данных общего назначения, с помощью которых можно создать индивидуальное решение. В качестве альтернативы вы можете обнаружить, что специализированное приложение базы данных, уже разработанное для ваших целей, дешевле, быстрее в реализации и лучше подходит.

Например, если у вас есть список клиентов и сведения обо всех ваших взаимодействиях с ними, это считается системой управления взаимоотношениями с клиентами (CRM). Несмотря на свое красивое название, CRM-система представляет собой специализированную базу данных. Точно так же пакеты учетных записей, такие как QuickBooks и Sage, являются специализированными базами данных. Если вы не можете найти готовое приложение, отвечающее вашим конкретным потребностям, вы можете создать его самостоятельно или поручить его вашему ИТ-отделу или консультанту.

Наиболее распространенным типом базы данных является реляционная база данных, которая хранит свои данные в таблицах и состоит из строк и столбцов. Каждая строка содержит данные для отдельного элемента. Например, в каждом столбце описывается отдельный атрибут субъекта, например имя клиента или кредитный лимит.

Вам нужно только один раз ввести данные клиента, чтобы создать запись, а затем вы можете использовать ее для любого количества счетов-фактур.

Между таблицами определены отношения, так что, скажем, счет-фактура содержит идентификатор клиента. Этот процесс означает, что вы можете легко найти все счета для конкретного клиента или получить номер телефона клиента из определенного счета. Вам нужно ввести данные клиента только один раз, чтобы создать запись клиента, а затем вы можете использовать ее в любом количестве счетов-фактур без необходимости вводить ее снова. Чтобы создать базу данных, вы должны определить эти таблицы и отношения, а затем определить макеты экрана, которые вы хотите использовать для отображения и редактирования данных.

Существуют десятки приложений для работы с базами данных. Некоторые из них просты в использовании и выполняют всю работу, позволяя настраивать таблицы, экраны ввода данных и отчеты. Другие более полнофункциональны в определенных областях, но требуют других инструментов для выполнения полной работы.

Например, программа может быть надежной при определении таблиц и взаимосвязей и наличии надежных функций анализа и отчетности. Тем не менее, в приложении в конечном итоге отсутствуют какие-либо инструменты для определения экранов ввода данных. Очевидным примером здесь является Microsoft SQL Server. Как и в случае с другими большими системами баз данных, SQL Server заботится о внутренней части и ожидает, что вы будете использовать другой инструмент, например Visual Studio, для разработки внешнего интерфейса.

Какие параметры базы данных вам подходят?

Вариант базы данных № 1: Microsoft Access

Access — один из прародителей настольных баз данных. Его легко использовать, но легко злоупотреблять. Вы можете создавать таблицы, экраны и отчеты с нуля или начинать с шаблона.

Некоторые из шаблонов явно американские и не всегда учат хорошей практике, но они быстро помогут вам начать работу. Экраны и функции программирования могут быть довольно сложными. Вы можете развернуть готовое приложение для других пользователей через свою интрасеть (НЕ Интернет), а не полагаться на общие файловые ресурсы.

База данных Вариант №2: Microsoft SharePoint

SharePoint — это база данных, а также механизм хранения документов. Вы можете использовать его для составления простых списков и связывания их вместе. Конструктор форм немного усложнен, но все же возможна настройка. Способность SharePoint «захватить» список данных, накопленных в Excel, и поместить его в настраиваемый список очень полезна.

Программа делает пользовательский список доступным для всех в вашей сети и позволяет добавить меры безопасности, чтобы ограничить, кто и что может делать с этими данными. Вы можете попросить SharePoint оповещать вас по электронной почте всякий раз, когда кто-то добавляет, редактирует или удаляет записи. Если вы храните данные о людях, элементах календаря или задачах, вы можете синхронизировать эти данные с Outlook.

Вариант базы данных №3: Zoho Creator

Zoho Office — это веб-приложение, включающее базу данных, которая использует функцию перетаскивания для распространения своих форм простым и интуитивно понятным способом. Процесс перетаскивания также используется для программирования взаимодействий и рабочих процессов. Ваши данные и приложения доступны из любого места, а простая защита обеспечивает конфиденциальность ваших данных. Zoho взимает плату за каждого пользователя в месяц, но ограничивает количество записей, которые вы можете хранить по этой установленной цене. Программа стоит дополнительно при хранении большего количества данных или других функций, таких как интеграция с электронной почтой.

Превосходство в Excel

Как видите, Excel предлагает множество функций, но в каждой из них отсутствуют некоторые области. Иногда другое приложение справляется с задачей лучше, особенно если оно разработано специально для этой задачи. В других случаях Excel работает просто отлично, например, для небольших баз данных, если вы знаете, как предотвратить возникновение проблем в первую очередь.

Сравнительные математические задачи

1. x + y = 15 

x – y = 24
Столбец A – (y)
Столбец B – (-5)

1. , если количество в столбце A больше
2. , если количество в столбце B больше
3. , если два количества равны
4. , если невозможно определить, какое количество больше

2. Столбец A – среднее (среднее арифметическое) v,w,y,x и z 
Столбец B – 70

1. , если количество в столбце A больше B больше
2. , если две величины равны
3. если невозможно определить, какое количество больше

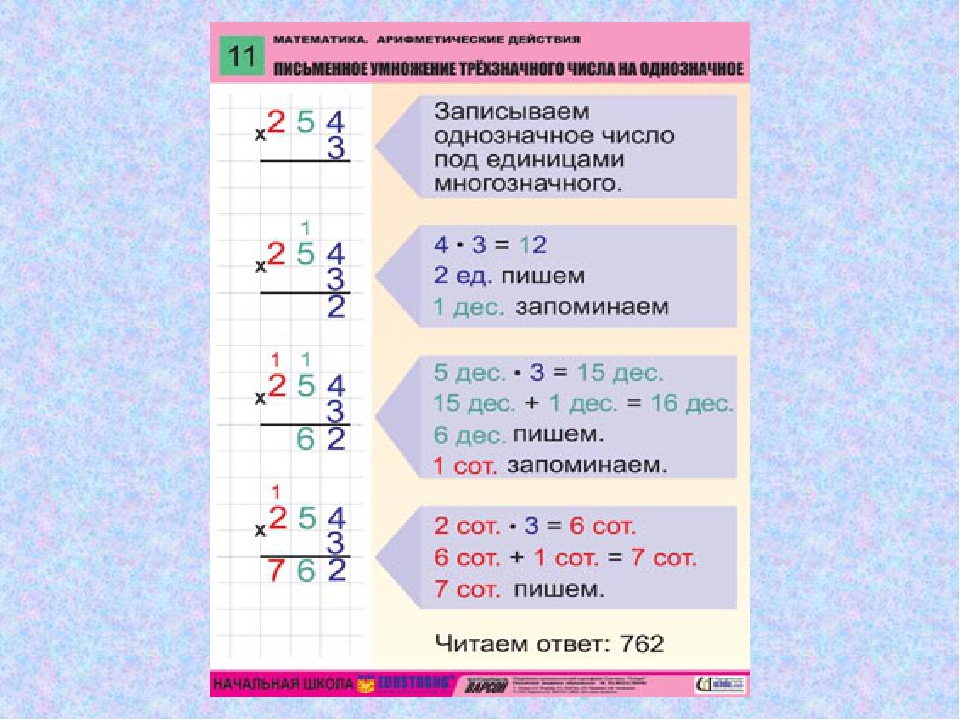3. Заштрихованные на рисунке ниже 65% площади всего круга, каково значение d?
Столбец A – d
Столбец B – 126 градусов

1. если количество в столбце A больше
2. если количество в столбце B больше
3. если два количества равны
9002 определить, какая величина больше

4. Столбец А – Площадь круга радиусом 3 
Столбец Б – Площадь полукруга радиусом 4

1. , если количество в столбце А больше 
2. , если количество в столбце B больше
3. , если два количества равны
4. , если невозможно определить, какое количество больше

5. Сара вызвалась с 9:27 утра. до 12:45
Ян вызвался добровольцем с 9:15 утра. до 12:32
Столбец A – количество времени, которое Сара добровольно вызвалась.
Столбец B — количество времени, которое Ян добровольно вызвался.

1. если количество в столбце А больше
2. если количество в столбце В больше
3. если два количества равны
4. если невозможно определить какое количество больше

6. Если 3. Если 3 % от 360 равно 7,5% от h, что такое h
Столбец A – h
Столбец B – 1634

1. если количество в столбце А больше
2. если количество в столбце Б больше
3. если два количества равны
4. если невозможно определить какое количество больше

7. Столбец А – доля 76 часов в неделю 
Столбец B – Доля 10 часов в сутках

1. , если количество в столбце A больше 
2. , если количество в столбце B больше 
3. , если два количества равны 
4. , если невозможно определить, какое количество больше

8. Столбец А – (x-y)
Столбец Б – 0

1. , если количество в столбце А больше
2. , если количество в столбце В больше
3. если две величины равны
4. если невозможно определить какая величина больше

Столбец А больше

, если количество в столбце B больше

, если два количества равны

, если невозможно определить, какое количество больше

10. Если n>0,
Столбец A – 24/25 от n
Столбец B – 95% от n

1. , если количество в столбце A больше
2. , если количество в столбце B больше
3. , если два количества равны
4. , если невозможно определить, какое количество больше

11. 5 составляет 2/3% от n
Столбец A – n
Столбец B – 15 две величины равны

, если невозможно определить, какая из величин больше

1. A:  Решение системы уравнений дает y  = -4,5. Поскольку -4,5 больше, чем -5, количество в столбце А больше.

2.  A:  Среднее значение может быть представлено как (360°)/5, что равно 72°. Поскольку 72° больше 70°, количество в столбце А больше.

3.  C:  Заштрихованная область представляет собой меру полного угла, которая может быть представлена ​​как 0,65 (360°) или 234°. Таким образом, незаштрихованная площадь, представляющая значение d, равна разности 360° и 234°, или 126°. Это то же значение, что и для столбца B.

4.  A:  Площадь круга с радиусом 3 равна 9п. Площадь полукруга радиусом 4 равна половине 16п, а именно 8п. Таким образом, количество в столбце А больше.

5.  A:  Количество времени, которое Сара предложила, составило 3 часа 18 минут. Количество времени, которое Ян вызвался добровольно, составило 3 часа 17 минут. Таким образом, количество Сары было больше.

6. B: Задача может быть смоделирована как 0,34(360) = 0,075 ч . Решение для ч дает ч = 1632, что меньше 1634. Таким образом, количество в столбце B больше.

7.  A:  Доля 76 часов в неделю может быть представлена ​​соотношением 76/168, что составляет примерно 45%. Доля 10 часов в сутках может быть представлена ​​соотношением 10/24, что составляет примерно 42%. Таким образом, количество в столбце А больше.

8. C:  Поскольку значения x и y одинаковы, разница будет равна 0. Таким образом, количества в столбцах A и B равны.

9.  C:  Значение столбца A может быть записано как 5(6). Значение столбца B может быть записано как 6(5). Оба выражения равны 30, поэтому количества для столбцов A и B равны.

10.  A:  Количество, указанное для столбца A, может быть записано как 0,96 n , что больше, чем 0,95 n . Таким образом, количество для столбца А больше.

11. B: Задача может быть смоделирована как 5 = 0,667 n , где n ˜ 7,5. Поскольку 15 больше 7,5, количество в столбце B больше.

Вычисление определителя матрицы Пошаговое решение математических задач

Введите матрицу и нажмите кнопку Определитель.

Справка

Матрица 5,3,7 2,4,9 3,6,4

Мы знаем, что не каждая система линейных уравнений имеет единственное решение. Иногда система из n уравнений с n переменными не имеет решения или бесконечное множество решений. В этом разделе мы вводим определитель матрица. В следующем разделе мы увидим, что определитель можно использовать определить, имеет ли система уравнений единственное решение.

 Каждой квадратной матрице A соответствует действительное число, называемое определителем А, пишется |А|.

Определитель матрицы 2 x 2 A,

определяется как

ПРИМЕЧАНИЕ Обратите внимание, что матрицы заключены в квадратные скобки, а определители обозначаются вертикальными черточками. Кроме того, матрица представляет собой массив чисел, но ее определитель – одно число.

ОЦЕНКА A 2 X 2 ОПРЕДЕЛИТЕЛЬ

Если

затем

ОПРЕДЕЛИТЕЛЬ А МАТРИЦА 3 X 3

Определитель матрицы 3 x 3 A,

определяется как

Простой метод вычисления определителей 3 X 3 находится путем перестановки и факторизируя термины, данные выше, чтобы получить

Каждая из величин в скобках представляет определитель 2 X 2 матрица, которая является частью матрицы 3 x 3, остающейся, когда строка и столбец множитель исключается, как показано ниже.

Эти определители матриц 2 X 2 называются минорами элемента в матрица 3х3. Символ M _ij представляет определитель матрица, которая получается при удалении строки i и столбца j. Следующий список дает некоторые миноры из матрицы выше.

В матрице 4 x 4 минорами являются определители матриц 3 x 3, а n x Матрица n имеет миноры, которые являются определителями (n – 1) X (n – 1) матрицы.
Чтобы найти определитель матрицы 3 X 3 или больше, сначала выберите любую строку или столбец. Затем необходимо умножить минор каждого элемента в этой строке или столбце. на + l или – 1, в зависимости от того, является ли сумма номеров строк и столбцов числа четные или нечетные. Произведение минора на число + 1 или – l равно называется кофактором .

КОФАКТОР Пусть M _ij будет минором для элемента au в n x n матрице. Кофактор _иж , написано A _ij , это:

Наконец, определитель матрицы n x n находится следующим образом.

ПОИСК ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ
Умножьте каждый элемент в любой строке или столбце матрицы на его коэффициент. сумма этих произведений дает значение определителя. Процесс формирования эта сумма произведений называется расширением по данной строке или столбцу.

ПОИСК КОФАКТОР ЭЛЕМЕНТА
Для матрицы

найдите кофактор каждого из следующих элементов.

(a) 6
Поскольку 6 находится в первой строке и первом столбце матрицы, i = 1 и j = 1.

Кофактор равен (-1) ¹⁺¹ * (-6) = 1 * (-6) = -6.

(b) 3
Здесь i = 2 и j = 3.

Кофактор равен (-1) ²⁺³ * 10 = (-1) * 10 = -10.

(c) 8
Имеем i = 2 и j = l.

Кофактор равен (-1) ²⁺¹ * (-8) = (-1) * (-8) = 8.

 

ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ 3 X 3
Вычисление

2 расширение

2

2 по второму столбцу.

Чтобы найти этот определитель, сначала найдите миноры каждого элемента во втором столбец.

Теперь найдите кофактор каждого из этих миноров.

Определитель находится путем умножения каждого кофактора на соответствующий ему элемент в матрице и нахождение суммы этих произведений.

ПРЕДОСТЕРЕЖЕНИЕ: Будьте очень внимательны и следите за всеми отрицательными знаками при оценивающие детерминанты. Работайте осторожно, записывая каждый шаг, как в Примеры. Пропуск шагов часто приводит к ошибкам в этих вычислениях.

Точно такой же ответ можно найти, используя любую строку или столбец матрицы. Одна из причин, по которой в примере 3 использовался столбец 2, заключается в том, что он содержит элемент 0, так что особо не надо было вычислять М ₃₂ и А ₃₂ выше. Быстро понимаешь, что нули могут быть очень полезны при работе с детерминанты.
Вместо вычисления (-1) ^i+j для заданного элемента выполняется следующее можно использовать шахматные доски для знаков:

Знаки чередуются для каждой строки и столбца, начиная с + в первом строка, позиция первого столбца.