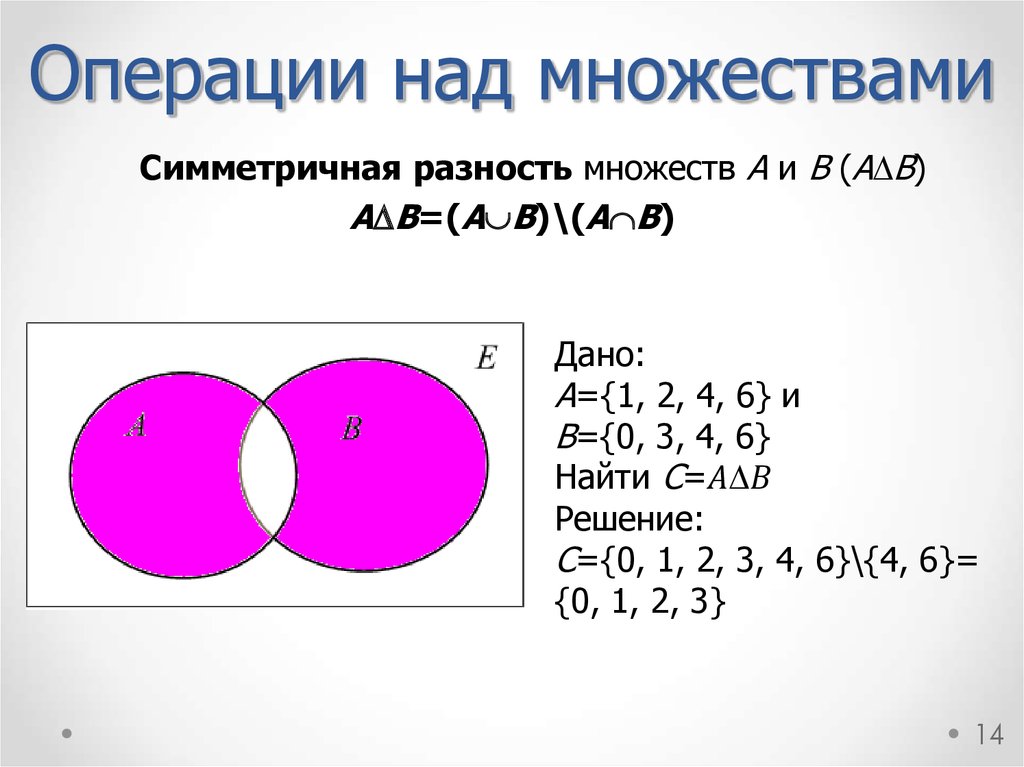
Решение кругов эйлера онлайн: Диаграммы Эйлера-Венна онлайн
Исследовательская работа “Решение логических задач с помощью кругов Эйлера” • Наука и образование ONLINE
Главная Работы на конкурс Предметное образование Физико-математические дисциплины Исследовательская работа «Решение логических задач с помощью кругов Эйлера»
Автор: Борисевич Александра Алексеевна
Место работы/учебы (аффилиация): Кордонская средняя школа Шумилинского района Витебской области Республики Беларусь, 8 класс
Научный руководитель: Борисевич Алеся Александровна
Цель исследования: показать широту применения решений логических задач с помощью кругов Эйлера для привития интереса учащихся к математике.
Задачи исследования:
- Познакомиться с историей возникновения науки комбинаторики.
- Уметь составлять и решать задачи с помощью кругов Эйлера.
- Применять полученные знания в дальнейшем обучении.
- Расширить и углубить представление о практическом значении математики в жизни.
- Уметь работать с научно-познавательной литературой, анализировать, делать выводы.
Гипотеза исследования: Показать, что решение логических задач с помощью кругов Эйлера имеет практическое применение.
Предмет исследования: понятие «Круги Эйлера» и задачи, решаемые с помощью кругов Эйлера.
В результате работы над данной темой я изучила теоретический материал по теме «Круги Эйлера» и пришла к следующим выводам:
- Логические задачи заставляют думать, рассуждать, составлять цепочку действий, последовательность, учат алгоритмизации, что немаловажно в современной жизни. А исследовательские работы учат искать информацию из различных источников (включая и интернет) и обрабатывать её, учат находить из большого материала лишь тот, который необходим.
- Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет показать, что решение логических задач с помощью кругов Эйлера имеет практическое применение. 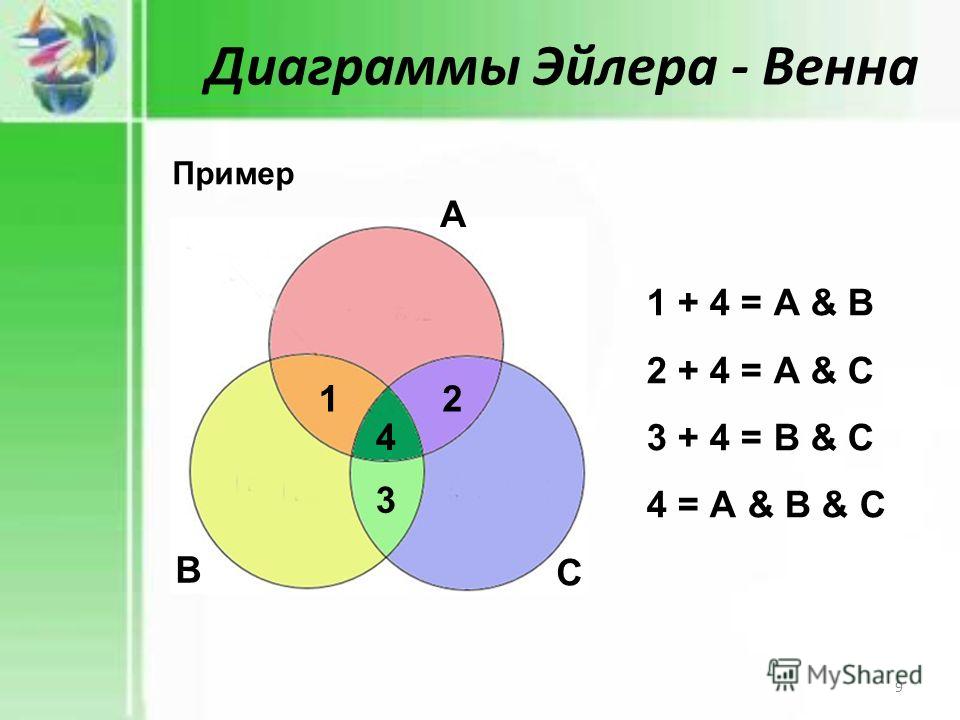Таким образом, моя гипотеза подтвердилась.
- Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными. Автор метода — ученый Леонард Эйлер, говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Я согласна с его словами. Круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
Таким образом, моя гипотеза подтвердилась.Физико-математические дисциплины
Исследовательская работа «Новые типы космических двигателей»
В своей работе я ознакомился и провёл анализ существующих типов космических летательных аппаратов, определил их преимущества и недостатки, сформулировал наглядное и понятное объяснение для каждого из типов, используя различные источники. Космический…
Посмотреть работу
Технические дисциплины, Физико-математические дисциплины
4″>Исследовательская работа «Умный дом»Доступна к просмотру полнотекстовая версия работы
Понятие умный дом появилось не так давно, и для многих его значение до сих пор не понятно. Умный дом – единая система управления светом, розетками, электроприборами, всем чем угодно, что поддерживает систему умный дом. Если говорить более научным язы…
Посмотреть работу
Физико-математические дисциплины
Исследовательская работа на тему «Альтернативные источники энергии»
Доступна к просмотру полнотекстовая версия работы
Мало кто знает, откуда берется энергия, которую мы все используем. Наша страна очень богата полезными ископаемыми и разнообразными ресурсами. Путешествуя по России, невозможно передать словами, насколько она красива. Но сейчас, в век технологий и бол…
Посмотреть работу
Физико-математические дисциплины
4″>Исследовательская работа «Магическое число 7»Введение Цифры очень многое значат в повседневной жизни каждого человека. Особенно меня заинтересовали натуральные числа и их история. А из всего натурального ряда чисел особый интерес вызвала семёрка. И это не случайно. Ещё знаменитый Корнелиус Агр…
Посмотреть работу
Физико-математические дисциплины
Исследовательская работа «Связь математики с экологией»
Наш дом – планета Земля. Она красива, она богата, в ее недрах и на поверхности содержатся огромные сокровища. Но не все люди, к сожалению, по-настоящему любят и берегут природные богатства. Однажды я обратил внимание, что в школьном мусорном ведре оч…
Посмотреть работу
Физико-математические дисциплины
Исследовательская работа «Школьный прогноз погоды»
Гипотеза: возможно создать собственную метеорологическую станцию из подручных средств, которая будет описывать и прогнозировать погоду на данной местности.
Цели: создать метеорологическую станцию, используя подручные средства; описывать и прогнозиров…
Посмотреть работу
Мероприятие завершено
Решение задач с помощью кругов Эйлера
В языке запросов поискового сервера для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение задачи №1
Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б,В).
Из условия задачи следует:
Торты │Пироги = А+Б+В = 12000
Торты & Пироги = Б = 6500
Пироги = Б+В = 7700
Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги.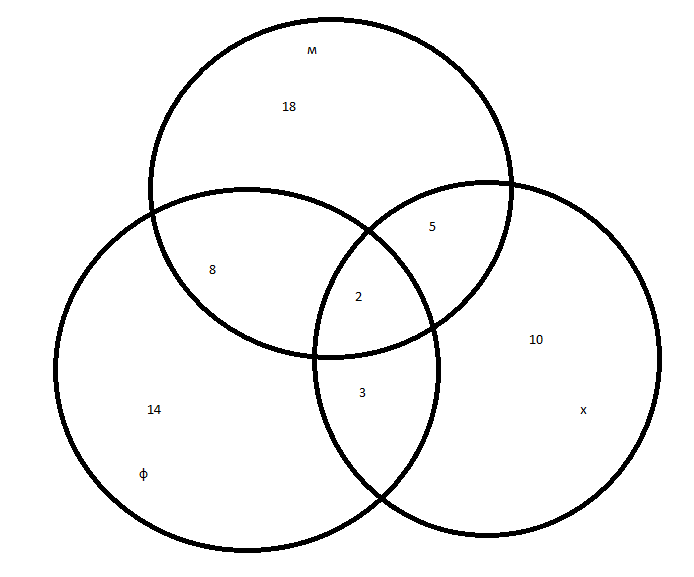
Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300
Сектор А равен 4300, следовательно
Торты = А+Б = 4300+6500 = 10800
Задача №2
В языке запросов поискового сервера для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пироженое & Выпечка | 5100 |
| Пироженое | 9700 |
| Пироженое | Выпечка | 14200 |
Какое количество страниц (в тысячах) будет найдено по запросу Выпечка?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Для решения задачи отобразим множестваПироженых и Выпечек в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б,В).
Из условия задачи следует:
Пироженое & Выпечка = Б = 5100
Пироженое = А+Б = 9700
Пироженое │ Выпечка = А+Б+В = 14200
Чтобы найти количество Выпечки (Выпечка = Б+В), надо найти сектор В, для этого из общего множества (Пироженое │ Выпечка ) отнимем множествоПироженое.
Пироженое │ Выпечка – Пироженное = А+Б+В-(А+Б) = В = 14200–9700 = 4500
Сектор В равен 4500, следовательно Выпечка = Б + В = 4300+5100 = 9400
Задача №3
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
| 1 | спаниели | (терьеры & овчарки) |
| 2 | спаниели | овчарки |
| 3 | спаниели | терьеры | овчарки |
| 4 | терьеры | овчарки |
Решение задачи №3
Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Преобразим условие задачи в виде суммы секторов:
спаниели │(терьеры & овчарки) = Г + Б
спаниели│овчарки = Г + Б + В
спаниели│терьеры│овчарки = А + Б + В + Г
терьеры & овчарки = Б
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4
Задача №4
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.
| 1 | барокко | классицизм | ампир |
| 2 | барокко | классицизм & ампир |
| 3 | классицизм & ампир |
| 4 | барокко | классицизм |
Решение задачи №4
Преобразим условие задачи в виде суммы секторов:
барокко│ классицизм │ампир = А + Б + В + Г
барокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1
Задача №5В таблице приведены запросы к поисковому серверу.
Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.
| 1 | канарейки | терьеры | содержание |
| 2 | канарейки & содержание |
| 3 | канарейки & щеглы & содержание |
| 4 | разведение & содержание & канарейки & щеглы |
Решение задачи №5
Для решения задачи представим запросы в виде кругов Эйлера.
K – канарейки,
Щ – щеглы,
С – содержание,
Р – разведение.
Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.
В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке:
4 3 2 1Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.
Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.
Только при таких условиях мы можем быть уверены, что правильно решили задачу.
Задачи для самостоятельного решения
Задача №6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.
| 1 | принтеры & сканеры & продажа |
| 2 | принтеры & продажа |
| 3 | принтеры | продажа |
| 4 | принтеры | сканеры | продажа |
Задача №7
В таблице приведены запросы к поисковому серверу.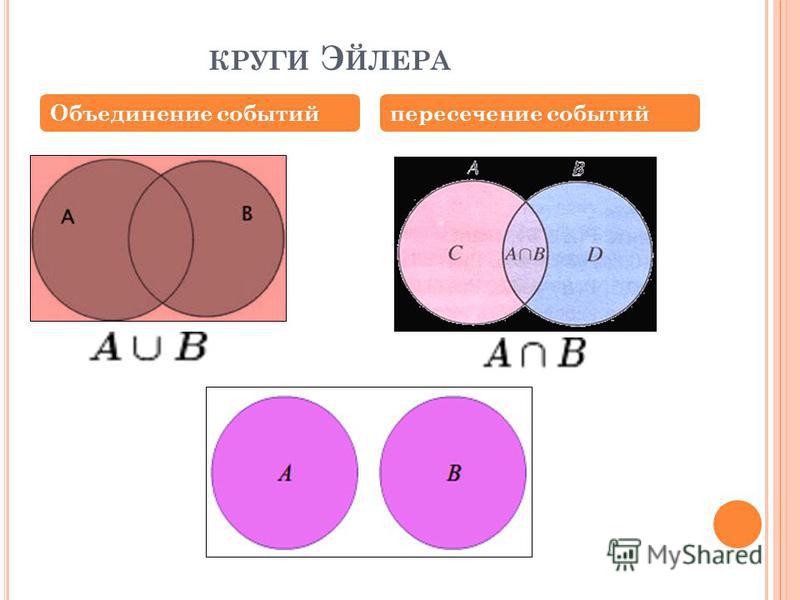
Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.
| 1 | физкультура |
| 2 | физкультура & подтягивания & отжимания |
| 3 | физкультура & подтягивания |
| 4 | физкультура | фитнесс |
| Онлайн-инструмент для построения диаграмм Эйлера
Creately уже используют более 8 миллионов человек и тысячи команд.
ВИЗУАЛИЗИРУЙТЕ
Создавайте диаграммы Эйлера без усилий
Несколько готовых шаблонов для диаграмм Эйлера и диаграмм Венна для различных сценариев, позволяющих быстро приступить к работе.
Предустановленные цветовые темы и расширенные возможности форматирования текста , чтобы легко выделять и обозначать различные контуры и зоны на диаграммах Эйлера.
Рисование от руки и выделение для рисования сложных диаграмм Эйлера с невыпуклыми контурами.
Импортируйте или перетаскивайте изображения , графику и многое другое на холст для создания визуально динамичных диаграмм Эйлера.
Автоматическое рисование с помощью Plus Create . Нарисуйте следующую фигуру и соединитель в правильном положении одним щелчком мыши.
ПОДКЛЮЧАЙТЕ И ОРГАНИЗУЙТЕ
Стройте свои диаграммы
Дополнительные поля данных и пользовательские свойства для отображения подробной информации о том, что содержится в различных зонах диаграммы.
Обширные библиотеки форм для более чем 50 типов диаграмм, графиков и диаграмм для упрощения расширения диаграмм Эйлера дополнительными структурами.
Экспортируйте свои диаграммы в несколько графических форматов , включая PNG, SVG, PDF или JPEGS, для встраивания, печати или совместного использования.
Встроенные инструменты, такие как рамки, режим просмотра и т. д. для удобной организации визуальных элементов на холсте и создания интерактивных презентаций.
СОТРУДНИЧАТЬ
Сотрудничайте с другими в любое время и в любом месте
Курсоры в реальном времени для любого количества участников. Работайте со студентами или коллегами на общем холсте.
Видеоконференцсвязь впилась в платформу, чтобы вы чувствовали себя в одной комнате.
Комментарий с контекстом для обсуждения и последующих действий на одном холсте. Асинхронно!
Автономная синхронизация , чтобы ваша работа всегда синхронизировалась, даже если вы выходите из сети и возвращаетесь.
Что такое диаграмма Эйлера?
Диаграмма Эйлера — это графическое изображение, обычно используемое для иллюстрации отношений между наборами или группами; диаграммы обычно рисуются в виде кругов или овалов, хотя их можно рисовать и в других формах.
Как построить диаграмму Эйлера?
- Включите библиотеку базовых форм Creately или обширную библиотеку шаблонов диаграмм Венна и Эйлера.
- Перетащите круги или любые соответствующие фигуры на холст, чтобы обозначить количество групп, используемых на диаграмме.
- Определите связи между группами и соедините соответствующие фигуры вместе, чтобы визуализировать информацию.
- Продолжайте повторять этот процесс, пока все соответствующие группы не будут отсортированы и связаны соответственно.
- Используйте любую из многочисленных функций дизайна, предлагаемых Creately, для цветового кодирования, выделения и придания вашей диаграмме Эйлера динамичности и презентабельности.
- Завершите работу над диаграммами Эйлера и поделитесь ими с другими в различных графических форматах.
Создайте диаграмму Эйлера
eulerr
Связывайте комбинации, соединяя их с амперсандом (&).
Тип отношений
Непересекающиеся комбинации Союзы
Форма
Круг Эллипс
Случайное семя
напряжение
ошибка диагностики
- Сюжет
- Поместиться
Цвета Список разделенных запятыми
х11
или же
шестнадцатеричные цвета.
Легенда
справа слева вверху внизу
Шрифт
Простой Смелый Курсив Жирный курсив
Бордюры
Твердый Варьируется Никто
Размер точек
Показать количества
Непрозрачность
Ширина (дюймы)
Высота (дюймы)
Сохранить сюжет
пдф png
Диаграммы, пропорциональные площади, с Эйлером
Этот
блестящий
приложение основано на
р
пакет, который я разработал, называется eulerr.
Он генерирует диаграммы Эйлера, пропорциональные площади, используя числовые значения.
процедуры оптимизации.
Диаграммы Эйлера
являются обобщенными диаграммами Венна, для которых выполняется требование
все пересечения присутствуют расслаблены. Они построены
из спецификации установленных отношений, но иногда может
не отображать их должным образом. Например, попробуйте дать
приложение спецификация А = 5, В = 3, С = 1, А и В = 2, АВ и С = 2 чтобы увидеть, что я имею в виду.
Когда это происходит, Эйлер пытается указать на
насколько плохо диаграмма соответствует данным по метрикам стресс а также ошибка диагностики. Последние из них показывают наибольшую разницу в процентах.
точки между спецификацией любой комбинации набора
и его результирующая подгонка. Это максимальное значение ошибка региона, который дается за каждую комбинацию. Этот показатель был
заимствовано из
статья Микаллефа и Питера Роджерса.
Стресс объяснить сложнее, но я советую
заинтересованному читателю читать
Отличная статья Леланда Уилкинсона.
для надлежащего резюме.
Наконец, я многим обязан вышеупомянутый Уилкинсон, а также Бен Фредериксон чьими работами вдохновлялся Эйлер.
Йохан Ларссон
Ограничения в приложении Shiny
Размещенное здесь приложение Shiny не полностью охватывает
все функции, которые предлагает пакет R.
Например, здесь количество наборов ограничено пятью.