Решать примеры по математике: Решебник по математике, решение примеров и задач – Всё о детях – беременность, воспитание, уроки для детей

Содержание

‎App Store: Решать примеры по математике

Описание

Доступ к 40+ обучающим играм co SKIDOS Pass – безопасные и увлекательные игры без рекламы для детей 2-11 лет. 2+ млн детей охотно обучаются с помощью приложений SKIDOS!

Добро пожаловать в SKIDOS! Мы предлагаем разнообразие обучающих игр для детей 2-11 лет. Вы можете оформить подписку на игры SKIDOS с помощью этого приложения, на нашем сайте, или войдя в свой профиль. Подписка SKIDOS обновляется автоматически и действует для 6 пользователей одновременно. Это значит, что 6 детей разного возраста могут играть, учиться и развиваться вместе с нами соответственно своим навыкам и интересам.

—

Smart Boats

Smart Boats – это увлекательная игра по математике и программированию для детей. Захватывающий аркадный игровой процесс заставит возвращаться вновь и вновь за новыми впечатлениями! Ведите большим пальцем по экрану, чтобы провести лодку через океан. Кажется, что просто? Готовы принять вызов? Станьте умным капитаном своей лодки и используйте свои математические навыки и навыки программирования, чтобы направить ее в безопасное место.

—

ДОРОГИЕ РОДИТЕЛИ И УЧИТЕЛЯ,
Приложения SKIDOS – это, в первую очередь, очень веселые игры, в которые дети действительно ЛЮБЯТ играть. Более того, в каждую из них мы интегрировали интерактивный обучающий контент, что позволяет детям развиваться и учиться в увлекательном для них игровом формате.

ПОМОГАЙТЕ СВОИМ ДЕТЯМ УЧИТЬ МАТЕМАТИКУ И ПРОГРАММИРОВАНИЕ
Все игры SKIDOS превращают скучные уроки в интересные задачи, которые соответствуют уровню Вашего ребенка.
В этой обновленной версии мы добавили еще больше игровых интерактивных элементов для детей, чтобы усилить их математические способности. Наши улучшенные вопросы по математике и программированию теперь более визуальные и динамические – для более увлекательного и веселого проведения времени.
Дети любят игры на смартфонах и планшетах. Почему бы не научить их логике, которая используется при создании их любимых игр? Игры SKIDOS на примере очень простых задач покажут, как работают программисты, и, возможно, даже вдохновят вашего ребенка изучать программирование в будущем.

ПЕРСОНАЛИЗИРОВАННОЕ ОБУЧЕНИЕ И ПРАКТИКА

У всех детей разный стиль обучения. Игры SKIDOS дают возможность выбрать предмет (математика или программирование), класс и интересы ребенка. Мы также показываем статистику прогресса.

УЧИМСЯ ПОНИМАТЬ ПРОГРАММИРОВАНИЕ И ЛЮБИТЬ МАТЕМАТИКУ
Обучающие материалы в играх SKIDOS адаптированы под программы обучения по математике и покрывают исчерпывающий список тем.
Задачи включают: понимание цифр, сложение, вычитание, умножение и деление, а также дроби, десятичные дроби, геометрию и многое другое!
Для детей, которые интересуются программированием, мы в SKIDOS разработали уникальный план, который знакомит с концепциями базового программирования и логического мышления.

Все игры SKIDOS соответствуют требованиям COPPA и GDPR и не имеют рекламы третьих сторон.

Информация о подписке:
– Деньги с аккаунта за возобновление подписки снимаются на протяжении 24 часов до окончания текущего периода
– SKIDOS предлагает подписку на месяц, три месяца, полгода и год для 6 пользователей
– Подписка автоматически возобновляется, если за 24 часа до окончания текущего периода пользователь ее не отменит
– Пользователь может управлять подписками и выключить автоматическое возобновление, перейдя в настройки аккаунта после покупки
– Отмена не будет активна пока не закончится платежный цикл
– Любая неиспользованная часть бесплатного пробного периода, если таковая предлагается, будет аннулирована, когда пользователь приобретает подписку.

Наша политика приватности находится здесь http://skidos.com/privacy-policy

Правила использования вы найдете здесь https://skidos.com/terms/”

11 сент. 2021 г.

Версия 5.3 (2)

С радостью представляем Вам обновленную версию игры SKIDOS! Искренне благодарим всех пользователей за предложения – Ваши идеи вдохновляют нас на постоянное совершенствование нашего продукта. Мы в SKIDOS гордимся тем, что помогаем детям становиться более уверенными на пути к познанию нового!
• С подпиской SKIDOS Pass Вы получаете безлимитный доступ к более 40 обучающих игр SKIDOS!
• Мы улучшили дизайн учебных материалов – теперь они более понятны и привлекательны для детей.
• Мы добавили еще больше анимаций-вознаграждений, чтобы отметить правильные ответы на вопросы. Ведь мы понимаем, насколько важно поддерживать наших детей и радоваться их успехам вместе!

• Игра загружается быстрее и работает стабильнее.

• Приложение стало еще более удобным для детей и родителей.

Оценки и отзывы

1 оценка

Разработчик Skidos Learning указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.

Не связанные с пользователем данные

Может вестись сбор следующих данных, которые не связаны с личностью пользователя:

Контактные данные

Пользовательский контент
Данные об использовании
Диагностика

Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Подробнее

Информация

Провайдер: Skidos Learning Private Limited
Размер: 392,2 МБ
Категория: Образование
Возраст: 4+, для детей 9–11 лет
Copyright: © Skidos Labs
Цена: Бесплатно

Сайт разработчика
Поддержка приложения
Политика конфиденциальности

Другие приложения этого разработчика

Говорим о математике на английском ‹ engblog.

Многие считают, что их жизнь никак не связана с математикой и им не нужно разбираться в дебрях данной темы на английском. Но цифры окружают нас везде: номера телефонов, кредитных карт, рейсов, не говоря уже о датах. Сегодняшний материал будет полезен всем: увлеченным энтузиастам математики и далеким от мира точных наук гуманитариям.

Хотелось бы начать с числительных (numerals), ведь это первое, с чем мы сталкиваемся в математическом контексте. Напомню, что числительные бывают двух видов: количественные (отвечают на вопрос «сколько?») и порядковые (отвечают на вопрос «который по счёту?»).

Давайте обратим особое внимание на произношение тех или иных числительных, так как этот, казалось бы, простой момент иногда вызывает замешательство даже у опытных «пользователей» языка.

Тип	Правило	Пример	Особенность
Сотни	And между сотнями и десятками.	“101 (one hundred and* one) Dalmatians” is my favourite cartoon.*	–
Тысячи	And не ставится между тысячами и сотнями.	The population of my village is almost 6500 (six thousand five hundred) people. 1 253 (one thousand two hundred and* fifty-three) candidates passed this exam last year.*	Американцы иногда произносят тысячи и сотни так: 1500 = fifteen hundred = 15 сотен.
Сотни и десятки тысяч	And между сотнями тысяч и десятками тысяч.	The population of Liverpool is 466 415 (four hundred and* sixty-six thousand, four hundred and fifteen) people*.	Американцы используют and намного реже британцев. Так, они сказали бы: 466 415 = four hundred sixty-six thousand, four hundred fifteen .
Миллионы	And не ставится между миллионами и тысячами.	There are 2 629 743 (2 million, 6 hundred and* 29 thousand, 7 hundred and 43) seconds in one month.*	–
Миллиарды	And не ставится между миллиардами и миллионами.	The world population was 5 320 816 000 (5 billion, 3 hundred and* 20 million, 8 hundred and 16 thousand) people in 1990.*	–

Ряд чисел (series of numbers): произнося ряд чисел, из которых состоит банковский счет, номер кредитной карты или телефона, мы называем каждую цифру отдельно. При этом ноль произносится как

oh в британском варианте, и как zero – в американском:

His credit card number is 5368 7208 0944 0699 (five three six eight, seven two oh/zero eight…). – Номер его кредитной карты – 5368 7208 0944 0699.

При этом, если в номере телефона присутствуют две одинаковые цифры, стоящие рядом, говорится, например double nine:

My friend’s number is 2290 4566 (double two nine oh four five double six). – Телефон моего друга – 2290…

Называя десятичные дроби (decimals), мы используем слова nought (британский английский) и zero (американский английский): 10.39 (ten point thirty-nine) – десять целых и тридцать девять сотых. Более подробно ознакомиться с особенностями произношения дробных числительных можно в нашей статье.

Указывая ту или иную дату, мы, конечно же, очень далеки от математики, однако дата – одна из самых популярных сфер употребления числительных. Если вам необходимо освежить в памяти, как именно указываются даты в английском, то советую прочитать статью «Даты и порядковые числительные в английском языке».

И наконец переходим к математическим действиям (mathematical operations): сложению (addition), вычитанию (subtraction), умножению (multiplication) и делению (division).

To add to / to plus – прибавлять.
To minus / to subtract from – вычитать.
To multiply by – умножать.
To divide by – делить.
To equal – равняться

Действие	Пример по-английски	Перевод
Пример: 7 + 8 = 15	7 plus/and 8 equals/is 15. Add 7 to 8 and you’ll get 15.	7 прибавить 8 равняется 15. Прибавь 7 к 8 и получишь 15.
Пример: 23 – 3 = 20	Twenty-three minus three equals/is twenty. If you subtract 3 from 23, the answer is 20.	23 минус 3 будет 20. Если отнимешь 3 от 23, ответ будет 20.
Пример: 6 * 4 = 24	6 multiplied by 4 / 6 times 4 equals/is 24. Multiply 6 by 4 and you’ll get 24.	6 умножить на 4 равно 24. Умножь 6 на 4 и получишь 24.
Пример: 9 ÷ 3 = 3	9 divided by 3 equals/is 3. If you divide 9 by 3, the answer is 3.	9 разделить на 3 равно 3. Если разделить 9 на 3, ответ будет 3.

To do sums / to solve problems – решать примеры, задачи.
He is the best at doing sums in our class. – Он решает примеры лучше всех в нашем классе.
Сommon denominator – общий знаменатель.
The task is to reduce to the common denominator. – Задача – привести к общему знаменателю.
Difference – разность.
The difference of 15 and 10 is 5. – Разность пятнадцати и десяти – пять.
Equation /ɪˈkweɪʒ(ə)n/ – уравнение.
Solve the equation. – Решите уравнение.
Improper fraction – неправильная дробь.
“Improper fractions” are not an easy topic for him. – «Неправильные дроби» – непростая тема для него.
Mixed fraction – смешанная дробь.
He knows exactly what a mixed fraction is. – Он точно знает, что такое смешанная дробь.
Numerator /ˈnjuːməˌreɪtə(r)/ – числитель.
Numerator is the number above the line in a common fraction showing how many of the parts indicated by the denominator are taken. – Числитель – это число над линией простой дроби, показывающее сколько частей, указанных знаменателем, взято.
Quotient /ˈkwəʊʃ(ə)nt/ – частное (при делении).
Quotient is a result obtained by dividing one quantity by another. – Частное – это значение, полученное путем деления некого числа на другое.
Remainder – остаток.
Remainder is the number that is left over in a division in which one quantity does not exactly divide another – Остаток – это число, которое осталось в результате деления, когда одно число не делится на другое без остатка.
Сube root of – корень кубический из.
Find the cube root of 15. – Найдите кубический корень из 15.
Inequality /ˌɪnɪˈkwɒləti/ – неравенство.
Inequality is the relation between two expressions that are not equal. – Неравенство – это соотношение между двумя выражениями, которые не являются одинаковыми.
Equality /ɪˈkwɒləti/ – равенство.
Equality is the condition of being equal in number or amount. – Равенство – это идентичность числа или величины.
Mathematical sign – математический знак.
Minus is an example of a mathematical sign. – Минус – это пример математического знака.
Multiplication table – таблица умножения.
Schoolchildren learn the multiplication table all over the world. – Школьники по всему миру учат таблицу умножения.
Parentheses /pəˈrenθəsɪs/ или round brackets – круглые/овальные скобки.
Parentheses are widely used in mathematics. – Круглые скобки широко используются в математике.
Right angle – прямой угол.
The right angle is 90˚ (degrees). – Прямой угол равняется 90 градусам.

И в завершение статьи хотелось бы предложить вам пройти небольшой тест. Но не волнуйтесь! Это не урок математики! 🙂

Тест

Говорим о математике на английском

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Учим ребенка счету. Задачи и примеры для первого класса по математике

На этом уроке мы научимся решать примеры в несколько действий на сложение и вычитание. Также мы поймем, для чего в примерах ставятся скобки, и в каком порядке решать такие примеры. Полученные знания помогут нам в дальнейшем решать более сложные задачи.

Тема: Знакомство с основными понятиями в математике

Урок: Решение примеров в несколько действий

Необходимо представить следующие действия с помощью математического выражения и решить пример.

На рисунке изображены 4 геометрические фигуры:

После этого добавим еще 2:

Эти действия можно записать следующим математическим выражением:

В результате получили пример в 2 действия: первое действие – сложение, второе действие – тоже сложение.

Примеры в несколько действий решаются по порядку – слева направо, как и выполнялось прибавление фигур.

1-е действие: ;

2-е действие: : .

Ответ: 9

Пример 2:

На рисунке даны 4 геометрические фигуры:

Добавим к этим фигурам еще 3 геометрические фигуры:

Затем уберем 2 фигуры:

Данные действия можно представить с помощью следующего математического выражения:

В результате получили выражение с двумя действиями: первое действие – сложение, второе – вычитание.

1-е действие: ;

2-е действие: : .

Ответ: 5.

Пример 3:

Необходимо решить следующее математическое выражение:

В условии этого примера есть скобки. В математике скобки указывают, что, если они присутствуют в примере, значит, нужно это действие выполнить первым.

Значит, первым действием выполним сложение в скобках , а затем полученный результат вычтем из 7.

1-е действие: ;

2-е действие: .

Ответ: 3.

Если в примере несколько действий, то действия выполняются по порядку – слева направо.

При решении примеров в несколько действий действие в скобках необходимо выполнять в первую очередь, а затем все остальные действия по порядку.

Итак, на этом уроке мы научились решать примеры в несколько действий на сложение и вычитание. Необходимо помнить порядок выполнения действий в примерах без скобочек и с ними.

Список литературы

Александрова Л. А., Мордкович А.Г. Математика 1 класс. – М: Мнемозина, 2012.
Башмаков М.И., Нефедова М.Г. Математика. 1 класс. – М: Астрель, 2012.
Беденко М.В. Математика. 1 класс. – М7: Русское слово, 2012.

Социальная сеть работников образования ().
Учительский портал ().
Myshared.ru ().

Домашнее задание

1. Необходимо представить следующие действия с помощью математического выражения и решить пример.

Тренажеры могут быть использованы для дополнительной работы с первоклассниками учителями и родителями в классе и дома как для индивидуальной, так и коллективной подготовки. Они способствуют автоматизации вычислительных навыков у ребенка, отработке умений складывать, вычитать, сравнивать и решать простые задачи.

Основа математики 1 класса – состав числа. Зная состав числа, а начать следует с домиков, ребенок гораздо быстрее сможет решить абсолютно любой пример на сложение или вычитание. Поэтому составу числа мы отводим целую страницу, кликните по картинке, чтобы

Освоили домики? Теперь можно браться за настоящие примеры на сложение и вычитание сначала в пределах десятка, а затем и в пределах 20.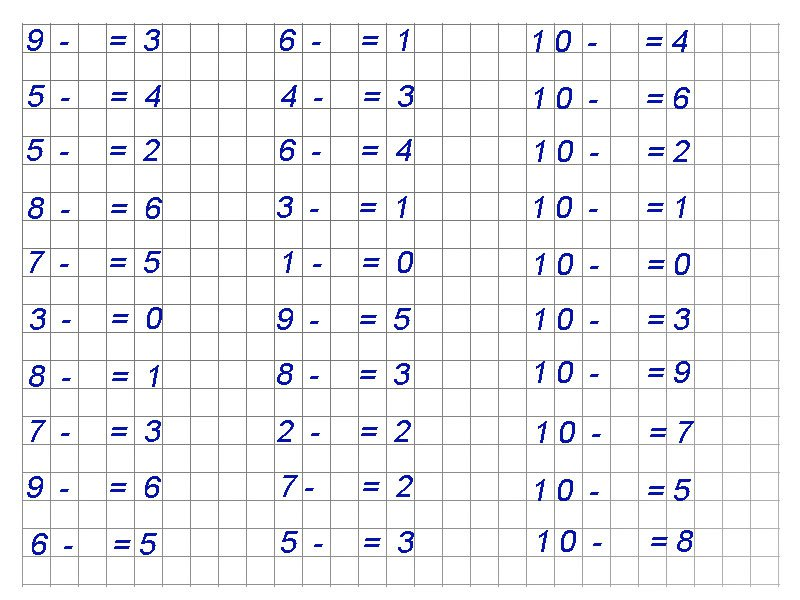

Если есть необходимость повторить всю программу первого класса, начиная с азов, посмотрите тренажеры, размещенные ниже.

Чтобы посмотреть и скачать полную версию тренажера, кликните на картинку.

Примеры по математике за 1 класс

Пособие соответствует ФГОС второго поколения для начальной школы. Каждая работа в пособии рассчитана на недельную нагрузку. Систематическое выполнение заданий закрепит учебные навыки и умения по изучаемым темам курса математики, доведет до автоматизма умение решать задачи, числовые выражения, равенства и неравенства. 12 листов на 12 недель.

Тренажер по математике для 1 класс. Обучение решению задач. А.В.Белошистая

Пособие составлено в соответствии с базовой программой по математике для начальных классов и содержит задания для обучения решению задач в 1 классе. Такие задачи могут использоваться как учителем в школе, так и родителями для обучения и закрепления материала дома.

Математический лабиринт

Необходимо провести дорожку по тем ячейкам, сумма чисел в которых равна 10. Задание развивает не только математические способности, но и внимание, и умение удерживать внимание.

Каждый родитель должен понимать, что высокое качество полученных знаний в первом классе – это возможность в дальнейшем усваивать весь программный материал в школе.

Начиная обучение в школе, нужно научить ребенка решать примеры для первого класса по математике правильно и быстро.

Какие особенности мышления нужно учитывать?

Любые задачи и примеры для первого класса по математике должны быть рассчитаны на работу с наглядным пособием. У ребенка 5-7 лет не развито абстрактное мышление, поэтому работать со сложением и вычитанием в уме ему сложно.

Чтобы помочь малышу понять смысл этих действий, нужно пользоваться счетным материалом. Это могут быть обычные палочки, спички, карандаши. Лучше и интересней ребенку будет решать примеры для первого класса по математике, если условие составить на основе любимых мультипликационных героев.

Такие действия должны и могут делать все родители. Достаточно взять картинки, карточки с любимыми сказочными героями, выстроить машинки, куклы в ряд и составлять примеры на сложение и вычитание. В игре решается любой пример или задача быстро и легко. Постепенно такие действия будут доведены до автоматизма, и ребенок запомнит вычитание и сложение в пределах десятка.

Важно знать! Огромной ошибкой родителей является счет на пальцах. Учить ребенка такому счету нельзя. К середине 1 класса примеры по математике будут иметь несколько действий, в том числе и переход через десяток. Если дома ученик сможет видеть пальцы рук и ног, решать примеры, то в школе такие действия не будут доступны.

Математика (первый класс): примеры

Какие варианты примеров нужно давать детям? В чем секрет быстрого счета?

Во-первых, ученик должен уметь не только складывать или вычитать числа, но и четко понимать понятия «всего», «сумма», «разность». Каждое из этих понятий в последующем будет играть важную роль в решении задач.

Во-вторых, важно заучить наизусть таблицу состава числа. Она в последующем поможет быстро решать примеры первого десятка и складывать или вычитать с переходом через десяток.

Предложите своему ребенку примеры по типу:

2+2; 4+3; 7+3; 8+2; 10-3; 5-2.

Помогают запомнить состав числа примеры такого типа:

… +3=10; 5+… =8; 10-… =7; 8-…=6; … -2=4; 4+…=7.

Дайте ребенку возможность в игре получить знания, запоминать состав числа и складывать, вычитать, развлекаясь.

Первый класс. Математика. Примеры и задачи

Чтобы ученик быстро решал задачи, нужно с ним разобрать все общие понятия, которые в условии будут ключевыми вопросами. Он должен понимать значение фраз «сколько всего», «вместе», «добавить». Они будут требовать сложения имеющихся числовых значений в задаче. В случае наличия фраз «разница», «на сколько больше», «на сколько меньше» – это действие вычитания.

Предложите решение задач в форме игры. Например:

В магазине Дед Мороз купил 5 машин. 1 из них он подарил Саше, вторую – Мише, а все остальные принес вашему малышу. Сколько машин получил ваш ребенок?
Мама принесла домой 2 килограмма конфет, а папа – 3. Сколько всего конфет будет дома?
Лунтик получил от кузнечика Кузи 10 конфет. 5 он отдал Миле, 3 – бабушке Капе. Сколько конфет осталось у Лунтика?

Задачи и примеры для первого класса по математике – это фундамент, который поможет в последующем получать знания и осмысленно их применять в учебе.

Примеры по математике для дошкольников

Контакты

[email protected]

Примеры по математике для дошкольников

Подробности: Автор: Галина; Категория: Подготовка к школе

org/AggregateRating”> Рейтинг: 4 / 5

Пожалуйста, оцените Оценка 1Оценка 2Оценка 3Оценка 4Оценка 5

Школа на пороге. Каким образом быстро активизировать желание заниматься. Проще всего заняться математикой. Детям нравится чёткость и красота математических действий.

У родителей и воспитателей популярны примеры по математике для дошкольников. Дети устали от летнего безделья и с удовольствием решают примеры, придумывают задачки, с удовольствием выполняют поисковые задания. Поставим задачу-минимум.

К школе полезно

научиться выполнять инструкцию;
усвоить количественный и порядковый счёт;
уметь сравнивать числа, понимать БОЛЬШЕ, МЕНЬШЕ;
научиться придумывать задачи;
решать примеры в пределах десятка.

Вспомним цифры

Предложите ребёнку обвести круглый предмет на картоне так, чтобы получилось десять кружков. Пусть вырежет их.

Напишите в каждом цифры от 0 до 9. Сделайте это сами, потому что не все дети знают цифры, часто пишут их зеркально. Сложите в коробочку, чтобы не потерялись. Добавьте к цифрам знаки: плюс, минус, равно, больше (меньше). Этот набор вам пригодится.

Учимся выполнять инструкцию

Возможно, придётся объяснить: рисовать можно в ряд (строчку) или в столбик. Наши задания рассчитаны на рисование предметов в ряд. Работайте в тетрадке в крупную клетку. Поначалу это удобнее.

Варианты заданий

Нарисуй в ряд:

три груши и два яблока;
четыре вишни: первая и последняя из них с листочками;
шесть листочков: три красных, остальные жёлтые;
восемь цветочков: второй, четвёртый и седьмой – синие, остальные – жёлтые;
семь кружков, разных по размеру; раскрась самый большой в синий цвет;
шесть мячиков, чередуя большой и маленький.

Обведи девять клеток. Раскрась их так, чтобы было по три одинаковых.
Нарисуй в уголках листа восемь грибов, чтобы в каждом уголке было поровну.
Нарисуй число (называете любое число) кружками (квадратами, треугольниками, цветочками, домиками, флажками, яблоками, наклонными палочками и прочее). Подбери к нарисованному количеству предметов соответствующую цифру.
Найди цифру 7 (или любую другую). Нарисуй такое же количество предметов. Например, ребёнок нарисовал семь кружков. Спросите: «А если я нарисую вместо кружков столько же груш, это будет правильно?»

Порядковый счёт

Количественный счёт (ответ на вопрос “сколько”) ребята обычно усваивают между делом и закрепляют на занятиях по математике в детском саду. С порядковым (ответ на вопрос “который по счёту”) дело обстоит сложнее. Обычно ему внимания уделяют мало или совсем не уделяют.

Нам поможет познакомиться с порядковым счётом стихотворение Ирины Гуриной, которое так и называется

ПОРЯДКОВЫЙ СЧЁТ

На поляне у реки
Жили-были мотыльки.
Братья разноцветные
Как фантики конфетные.

Первый – красный, как рябина, Словно капелька рубина.	А второй – небесно-синий В белых брызгах, будто иней.	Третий – жёлтый, как лимон, Светом солнца окрылён.

А четвёртый – белоснежный, Лепесток ромашки нежный.	Пятый – рыжий, как лиса, Полосатый, как оса.	В синих точках брат шестой, Бело-красно-золотой.

А седьмой – совсем лиловый, Лишь с полоской бирюзовой.	Брат восьмой – чуть-чуть зелёный, Словно океан солёный.	А девятый – красный в точках, Белых ромбах и кружочках.

	Пёстрый весь, как конфетти, Брат десятый, к нам лети!

Вы можете распечатать картинки наши и выкладывать их по порядку, а можете нарисовать с ребёнком собственные. Возможно, это будет даже лучше. Закрепляя порядковый счёт, расставляйте по порядку любые предметы, например, игрушки. Который по порядку слоник, лисичка…

Сравнение множеств

Не все дети самостоятельно доходят до умения сравнивать числа. Проверьте своего будущего школьника.

Тест

Счётные палочки цветов А и В положите на столе двумя группами по 5 штук. В одной группе палочки должны лежать близко друг к другу, в другой – на небольшом расстоянии. Спросите у ребёнка, каких палочек больше. Если он покажет группу палочек, лежащих на расстоянии, знайте – сравнивать множества он не умеет. Это для будущего школьника плохо. Если скажет правильно, попросите рассказать, а как догадался. Я обычно говорю детям: докажи.

Учимся сравнивать

Можно показать приём выкладывания парами.

Те же палочки двух цветов, пуговицы и прочее выкладываем друг под другом. Тогда ребёнок чётко видит соответствие: чего больше (меньше) и на сколько. Легко сообразить, как сделать поровну.

Предметы надо выкладывать четко друг под другом. Позже от выкладывания переходим к рисованию. Если не получилось нарисовать чёткими парами, пары надо создать, соединяя линиями нарисованные предметы

Придумывание задач

Обычно ребята, посещавшие детский сад, имеют представление о структуре задачи. Но видят сходство (похожесть) задач не все из них. Важно это вот почему. В школе на уроке ученики решают типовые задачи. Домой учитель задаёт похожую. Ребёнок, умеющий сравнивать, рассуждает: «Ага, мы такую задачку в школе решали. Только там было так и так, а здесь эдак». Задачка решается как знакомая. В противном случае она воспринимается как новая. Какую задачку проще решить: известную или новую?

Пример придумывания задачи

У нас есть выражение

3 + 4 = ?

Придумай по нему задачку. Можете дать образец, если не уверены, что чадо понимает, чего вы от него хотите.

Образец.

Условие. Мама дала 3 конфеты дочке и 4 конфеты сыну.

Вопрос. Сколько конфет было у мамы?

А теперь по этому же выражению ребёнок придумывает свою задачку. Меняйте только конфеты на игрушки, тарелки, печенье, зайцев, ёлки ….

Единственное запрещённое действие: нельзя складывать лампочки с апельсинами.

Надоело сложение, переходите к вычитанию. Маму с детьми на что-нибудь другое замените для разнообразия.

Решение примеров

Большинство детей любят играть такую школу. Усаживаем расшалившихся ребят и даём тетрадный листок в клетку со столбиком примеров. Пишем цифры крупно, высотой в две клетки. Детям остаётся только ответ написать. Понаблюдайте, каким способом выполняется задание. Решение на пальцах допустимо. Со временем ребёнок от него откажется.

Варианты предъявления примеров

К заданному числу прибавлять все числа до 10 по порядку (первый ряд).
Меняем слагаемые местами (второй ряд)
Примеры из первого ряда предъявляем вразнобой (ряды 3-5).
Чередуем примеры на сложение и примеры на вычитание. Часто дети, решая примеры на сложение, следующий пример на вычитание тоже решают, как на сложение. Это называется стереотипность внимания. Избавиться от неё многим ребятам сложно. Чередование примеров помогает преодолевать стереотипность внимания.

Сперва математические действия с двойкой, потом с тройкой и так далее.

А потом пишем нашему ученику любые примеры в пределах первого десятка, двух десятков. Покажите приём присчитывания (отсчитывания) по одному. Так легче перейти через десяток.

Сайт Нестандартные дети желает успехов в школе.

Назад
Вперёд

Добавить комментарий

Решить уравнение, Решить задачу по математике

Решить задачу online

Русский English

Сервис для школьников и их родителей, студентов и абитуриентов

Решить задачу сейчас

Решить уравнение сейчас

Посмотрите, как это работает и попробуйте! Вы узнаете как решать любую задачу по математике, например, как решать уравнение…Решить уравнение очень просто!

Экономьте свое время на решении математики Решатель справляется с задачами за секунды. Попробуйте, например, решить уравнение.

Обретите виртуального учителя Подробное решение почти любой задачи. Ощутите, насколько просто решить все задачи из домашнего задания.

Сдайте экзамен или решите контрольную Настоящее спасение для гуманитариев. Вы можете решать задачи или уравнения любой сложности.

Pocket Teacher искусственный интеллект, который 30 лет разрабатывали в МГУ

A
Пошаговый способ решения с подробными комментариями
Решение сложной задачи может быть расписано более чем в 100 шагов. При этом комментарии к решению будут понятны даже школьнику. Например, решить уравнение очень просто за пару секунд.
B
Удобный ввод формул
Все знаки математических операций вводятся по одному клику: корни, степени, дроби, интегралы и т.д.
C
Решение 98% задач
Если сервис не решит вашу задачу – напишите об этом на почту [email protected] Кандидат физико-математических наук пришлет вам решение

Получите онлайн-помощника в решении множества математических дисциплин.

Решить любую задачу, например решить уравнение очень просто!

Решение даже самой сложной задачи займет не более 1 минуты

Уравнения, системы уравнений и неравенства

Иррациональные
Рациональные
Тригонометрические
Логарифмические
Экспоненциальные
С произвольными параметрами
Показательные произвольной сложности

Интегралы

Определенные
Неопределенные

Геометрия

Геометрические задачи можно вводить в текстовом виде

Дифференциальные уравнения

Подробное решение для дифференциальных уравнений
Системы дифференциальных уравнений

Дополнительно

Матрицы – посчитать определитель
Пределы – пока без подробного решения
Текстовые математические задачи

Список разделов математики, которые решает наш сервис, постоянно пополняется

1″/>

Решайте задачи, заданные в текстовом виде

Просто перепишите текст задачи и получите ответ в течение нескольких секунд.

Это работает с задачами по:

Геометрии
Физике скоро
Химии скоро

Pocket Teacher всегда под рукой

Приложение для iOS, Android и удобная мобильная версия

Сервис будет полезен всем, кто сталкивается с математикой

Pocket Teacher показывает не только ответ, но и способ решения. Поэтому он станет для вас настоящим online-репетитором при решении уравнений или задач по математике

Школьникам

Проверит домашнее задание: решите задачи или уравнения и сравните результат
Поможет разобраться в теме, которую вы пропустили или не поняли
Поможет подготовиться к ЕГЭ

Родителям

Проверит решение ребенка
Поможет решить задачу
Сэкономит на репетиторе

Студентам и абитуриентам

Поможет подготовиться к поступлению в ВУЗ и вспомнить пройденный материал
Выручит на контрольной и экзамене
Решит задачи из курсовой
Сэкономит время на решении сложных задач на старших курсах
Станет спасением для тех, у кого математика непрофильный предмет

Наш сервис – один из самых мощных искусственных интеллектов в России и странах СНГ

2s”>73 раздела алгебры
решенных задач
20 разделов геометрии

Как решать Задачи по Математике 5 класс (2017) + Примеры, Таблицы

Существует много причин, по которым ребёнок не может решить задачу по математике 5 класс. В большинстве из них он не виноват, поэтому стоит ему помочь разобраться с проблемой. Задачи не такие трудные, но в связи с появлением дробей и уравнений иногда сложно определить способ и верный путь их решения.

Содержание статьи:

Почему инструкция лучше решебника

В этой инструкции вы сможете найти типовые задачи, которые встречаются в курсах математики за 5 класс и разобранное, подробное, пошаговое решение. Это значительно полезнее книг, так как в них собраны далеко не все задачи, а те решения, которые есть, сжаты до минимума. Поэтому пользоваться решебником — порой не самый лучший выход.

Решебник по математике не всегда может дать исчерпывающую информацию

Как правило, при составлении ответов на свои задачи авторы не расписывают подробности и дают решения не ко всем номерам. Возможно, в расчёт идёт тот факт, что ученик способен справиться самостоятельно. Но вдруг ребёнок пропустил тему, что же тогда делать?

Лучший вариант — посмотреть решение типовых задач с пояснениями каждого действия. В этой инструкции собраны самые распространённые примеры, которые вызывают трудности у детей при решении, а также родителей при попытке объяснить задачу.

Почему важно уметь решать задачи по математике

Математика — точная дисциплина, связанная с вычислениями. Но её часто называют царицей всех наук. Это не просто так. Основное, чему учатся дети — решение конкретно поставленных задач. Это самое важное для развития любого человека.

Для построения правильного ответа на задачу нужно выделить:

главную мысль;
заданное условие;
что требуется найти;
связь между искомым и данным.

Математика — один из самых важных предметов в школьной программе

На основе этого строится логичное решение с использованием условий для получения требуемого результата. Вместе с этим развивается познавательная активность, логические мышление.

Какие бывают задачи по математике в 5-ом классе

В 5-ом классе по математике встречается несколько разновидностей задач. Этот год самый важный для ученика, потому что здесь собраны все базовые условия, которые углублённо решаются в следующие годы обучения. Здесь представлен список самых распространённых задач:

на базовые арифметические действия;
на скорость, время и расстояние;
на движение;
решаемые алгебраическим способом — проценты, дроби, уравнения;
решаемые геометрическим способом — площадь, длина.

Существует немало различных задач и путей их решения

Для грамотного решения всех типов задач можно составить единый алгоритм:

Прочитайте вдумчиво, не торопясь полный текст задачи;
Определите к какому типу она относится;
На основе этого составьте краткое условие или таблицу;
Начните читать каждое предложение отдельно, заполняя таблицу или краткое условие;
Определите вопросом то, что нужно найти;
Выберите вариант решения и составьте выражение, в результате которого получится ответ;
Проверьте правильность и соответствие условию;
Запишите полученный ответ.

Этот алгоритм можно применять ко всем типам задач. В разных заданиях отличаться будут только числа и способ решения.

Далее представлены все типы задач, которые могут встретить пятиклассники в учебниках и задачниках по математике. Все они будут разобраны на двух примерах с подробным разъяснением.

Задачи на сложение, вычитание, умножение и деление

Пример 1

На кухне лежит пакет, в котором 3000 грамм муки. Повар для выпечки из него брал 4 раза муку. В первый раз 250 грамм, во второй 320 грамм, в третий 140 грамм, в четвёртый 690 грамм. Найдите сколько муки осталось в пакете.

Решение

Для начала запишем краткое условие в виде таблицы. Повар брал муку четыре раза, значит для каждого раза делаем по одной строчке.
Всего у нас было 3000 грамм. Это ещё одна строка.
От нас требуют найти остаток, значит — это последняя строка.
Заполняем таблицу. Какой она получится, смотрите ниже.

Таблица 1 — Краткое условие

Условие	Количество
Было	3000
Первый раз	250
Второй раз	320
Третий раз	140
Четвёртый раз	690
Осталось	?

Сделанная таблица наглядно показывает, что для расчёта остатка нужно из 3000 вычесть количество, которое повар забрал всего;
Для этого сложим количество муки, которое повар израсходовал за четыре раза. Получается такое выражение: 250+320+140+690=1400 грамм;
Теперь найдём остаток. Для этого из того, что было, вычтем полученное значение — 1400. Получим выражение: 3000-1400=1600 грамм. Это то, что от нас требовалось — найти сколько осталось муки;
Записываем это в ответ к задаче.

Пример 2

В пассажирском поезде 12 вагонов. В каждом из них по 40 мест. Сколько осталось свободных мест, при условии, что в поездку отправились 352 пассажира?

Решение

Составляем краткое условие. Нагляднее всего будет снова использовать таблицу;
У нас есть количество вагонов — первая строчка. Количество свободных мест в каждом вагоне — вторая строка. Места, которые заняли пассажиры — третья. Сколько осталось мест — четвёртая;
Далее заполняем таблицу числами из условия. Что получилось, смотрите ниже;

Таблица 2 — Условие задачи

Места в вагоне	Количество
Кол-во вагонов	12
Кол-во мест в вагоне	40
Кол-во пассажиров	352
Осталось мест	?

Теперь приступаем к вычислениям. Для начала нам нужно узнать сколько всего свободных мест было в вагонах. Для этого умножим количество вагоном на количество свободных мест в каждом. Получается выражение: 40×12=480;
Для того, чтобы найти сколько осталось свободных мест нужно, из полученного значения вычесть занятые места. Получим выражение: 480-352=128;
Полученное число — это ответ на вопрос из условия задачи. Записываем его.

Задачи на скорость, время, расстояние

Пример 1

За 7 часов теплоход проделал путь в 210 км. Поезд за 4 часа преодолел 420 км. Во сколько раз скорость поезда больше скорости теплохода?

Решение

Записываем краткое условие. В этом типе задач оно немного отличается от стандартного;
У нас есть два объекта — теплоход и поезд. Это значит, что в таблице будет две строки;
Для каждого объекта есть три значения, соответственно, и столбцов будет три;
Заполняем числами таблицу. Что должно получится смотрите ниже;

Таблица 3 — Краткое условие

	Скорость	Время	Расстояние
Теплоход	?	7	210
Поезд	?	3	360

Приступим к поиску неизвестных. Нам нужно узнать скорость у теплохода и поезда. Для этого используется формула — скорость равна результату деления расстояния на время. Математически записывается так — V=S:T;
Подставив числа из условия, получаем выражение для скорости теплохода. 210:7=30 км/ч;
Также поступаем и для расчёта скорости поезда. 360:3=120 км/ч;
Мы нашли все неизвестные и теперь возвращаемся к главному вопросу задачи. Нам нужно определить во сколько раз скорость поезда превышает скорость теплохода;
Для этого делим большее значение на меньшее. Получается: 120:30=4;
В ответ пишем, что скорость теплохода и поезда отличается в 4 раза.

Пример 2

Автомобилист за 4 часа проехал 320 километров. Какой путь проделает автомобиль за 8 часов с той же скоростью?

Решение

Записываем краткое условие. Объект один, значит строка будет одна. Столбцов стандартно три;
Заполняем числа из условия в таблицу. Что получится смотрите ниже;

Таблица 4 — краткое условие

	Скорость	Время	Расстояние
Автомобиль	?	4	320

Ищем неизвестные. В нашем случае нужно найти скорость. Для этого воспользуемся формулой V=S:T. Подставляем числа и получаем: 320:4=80 км/ч;
После того, как стали известны все значения, переходим к главному вопросу задачи — сколько проедет автобус за 8 часов с той же скоростью;
Для расчёта используем формулу S=VT. Подставляем числа и получаем: 80×8=640 км;
Записываем полученное значение в ответ к задаче.

Задачи на движение

Пример 1

Расстояние между двумя городами 125 километров. В одно и то же время выезжают два велосипедиста навстречу. Скорость первого велосипедиста 10 км/ч. Второй едет со скоростью 15 км/ч. Через какое время они встретятся?

Решение

Начинаем с составления краткого условия. Лучше всего оформить в качестве таблицы;
Велосипедиста два— значит нужны 2 строки. Столбцов стандартно 3. Но в этом типе задач у нас будут общие показатели. То есть, расстояние и время всегда одно сразу для всех строк;
Заполняем таблицу числами. Что должно получится смотрите в ниже;

Таблица 5 — краткое условие

	Скорость	Время	Расстояние
1 велосипедист	10	?	125
2 велосипедист	15	?	125

Теперь переходим к расчётам. Логично, что для встречи велосипедисты должны проехать в сумме весь путь. Необязательно одинаковое расстояние, так как оно зависит от скорости каждого из них;
Нам нужно посчитать какое расстояние они преодолевают в час. Для этого сложим скорости первого и второго. Получаем выражение: 10+15=25 км/ч;
Для расчёта времени через которое они встретятся нужно воспользоваться формулой T=S:V. Подставляем числа и получаем выражение: 125:25=5 ч;
Соответственно, велосипедисты пересекутся между собой через 5 часов. Записываем это в ответ.

Пример 2

Расстояние, на котором между собой находятся два города — 600 км. Из них одновременно на встречу друг другу выехали два автомобиля. В пути они встретились через 5 часов. Найдите скорость первого автомобиля, если известно, что второй ехал со скоростью 80 км/ч.

Решение

Составим таблицу, в которой ситуация из условия будет наглядно представлена;
Два автомобиля — две строки. Стандартное количество столбцов — три;
Заполняем числами из условия. Что должно получится, смотрите ниже;

Таблица 6 — краткое условие

	Скорость	Время	Расстояние
1 автомобиль	?	5	600
2 автомобиль	80	5	600

Переходим к расчётам. Для нахождения скорости первого автомобиля нам нужно знать, сколько километров он проехал. Найти это можно, вычтя из общего пути расстояние, которое проехал второй до их встречи;
Используем формулу S=VT. Подставляем числа из таблицы, получаем выражение: 80×5=400 км. Это расстояние прошёл второй автомобиль до встречи с первым. Значит, первый проехал всего: 600-400=200 км;
Теперь можно найти скорость первого автомобиля. Используем формулу V=S:T. Подставляем числа: 200:5=40 км/ч;
Полученное значение — ответ на главный вопрос задачи. Записываем его.

Задачи, решаемые алгебраическим способом

Пример 1

Из цистерны отлили 80 литров молока, в нем осталось на 240 литров больше, чем отлили. Сколько литров молока было в цистерне с самого начала?

Решение

Начинаем с составления краткого условия в виде таблицы. В подобных типовых задачах нужно обозначать неизвестное за «x»;
Потребуются три строки: сколько молока было, сколько его отлили и сколько осталось;
Заполняем числами таблицу;

Таблица 7 — краткое условие задачи

Было	Х
Отлили	80
Осталось	240+80

Приступаем к расчётам. Нам нужно узнать, сколько было молока изначально. Для этого составляем уравнение. От начального количества вычитаем отлитое и получаем остаток;
Математически получаем такую запись: x-80=240+80;
Начинаем решение с того, что считаем всё, что можно посчитать. В данном случае складываем правую часть уравнения. 240+80=320. Теперь уравнение имеет вид: x-80=320;
Теперь находим «x». Используем базовое правило математики и получаем следующее: x=320+80. Считаем правую часть и получаем: x=400;
Возвращаемся к началу и смотрим, что мы обозначили за «x». В этом примере за икс мы взяли объём молока, который был изначально. То есть, изначально было 400 литров молока;
Записываем полученное значение в ответ.

Пример 2

Первое слагаемое на 52 больше второго слагаемого, а второе слагаемое на 14 меньше третьего слагаемого. Сумма трех слагаемых равна 327. Найдите каждое слагаемое.

Решение

Записываем краткое условие в виде таблицы;
Потребуется четыре строки, так как нам дали три слагаемых и их сумму;
Заполняем таблицу числами, обозначив за икс последнее слагаемое. Выбираем третье, потому что от него зависят все остальные;

Таблица 8 — краткое условие задачи

1 слагаемое	(x-14)+52
2 слагаемое	x-14
3 слагаемое	x
Сумма	327

Приступаем к расчётам. Для нахождения слагаемых нужно решить уравнение, после чего число подставить в выражения из таблицы.
Уравнение составляется исходя из условия – три слагаемых и сумма – складываем значения из второго столбца таблицы и приравниваем это к сумме.
Получится такое выражение: (x-14)+52+(x-14)+x=327.
Открываем скобки и упрощаем выражение: 3x+24=327.
Переносим числа в правую часть: 3x=303
Считаем икс: 303:3=101.
Теперь подставляем число 101 в таблицу вместо икса.
Получается третье слагаемое равно 101; второе: 101-14=87; первое: 87+52=139.
Эти числа записываем в ответ. Легко проверить правильность решения просто сложив эти значения. Если пример получается правильный, то и решено всё верно.

Для правильного решения этих типовых задач необходимо ничего не напутать с иксом. Лучше потратить больше времени и сразу всё проверить, чем переделывать задание сначала. Неправильное обозначение повлечёт за собой ошибку на протяжении всего решения

Задачи, решаемые геометрическим способом

Пример 1

В доме 4 двери. Ширина каждой 1 метр, высота — 2 метра. Сколько нужно белил, чтобы покрасить их с обеих сторон, при условии, что на 1 квадратный метр поверхности требуется 100 грамм белил? Ответ дайте в граммах.

Решение

Для решения нужно вычислить площадь каждой двери, которую нужно покрасить. Для этого используем формулу площади прямоугольника – S=ab, где a и b – длины сторон. Подставляем числа из условия и получаем: S=2×1=2 м2;
Далее умножаем площадь на 2, потому что каждую дверь нужно окрасить с двух сторон. Получаем 2×2=4 м2. То есть, покрасочная площадь каждой двери равна 4 квадратным метрам;
Посчитаем общую площадь для всех дверей. Для этого умножаем площадь одной на их количество: 4×4=16 м2;
Главный вопрос задачи — сколько потребуется белил для всех дверей? Чтобы посчитать умножаем количество, требующееся на 1 квадратный метр на всю площадь: 100×16=1600 грамм;
Записываем это значение в ответ.

Пример 2

Площадь прямоугольника 192 квадратных сантиметра, длина одной из сторон — 16 см. Найдите периметр прямоугольника.

Решение

Для начала нужно посчитать другую сторону прямоугольника. Делается это с помощью формулы площади: S=ab, где a и b — длины сторон. Подставляем числа и получаем: 192=16*a. Отсюда получается, что вторая сторона — 12 см;
Для нахождения периметра воспользуемся формулой P=2(a+b). Подставляем числа и получаем: P=2(16+12)=2×28=56 см;
Найденное значение записываем в ответ.

Для решения геометрических задач нужно знать наизусть все формулы площадей и периметров. Без этого не получится даже приступить к решению задания.

Нужен ли ребёнку репетитор по математике в пятом классе?

После перехода в средний этап школы у ребёнка может упасть успеваемость по некоторым предметам, в том числе и по математике. Более того математика — самый проблематичный предмет для детей. Некоторые родители сразу бьют тревогу и ищут репетиторов, чтобы исправить эту ситуацию.

На самом деле, не стоит делать поспешных выводов. Для начала нужно определить причину падения успеваемости. Возможно, некоторые из новых учителей просто халатно относятся к преподнесению нового учебного материала. Другие преподаватели не могут найти особый подход к ребёнку в связи с ограничением по времени.

У многих детей в школе возникают сложности с изучением математики

Это не значит, что ваш ребёнок неспособный к определённым дисциплинам. Попробуйте объяснить ему материал самостоятельно, ведь именно вы знаете своё чадо лучше других. Если и это не помогло, то обращайтесь к помощи репетитора.

Главная задача специалиста — найти персональный подход к каждому ученику. Они смогут максимально эффективно и просто объяснить ребёнку тему в зависимости от особенностей его восприятия и склада ума.

Перед обращением убедитесь, что ухудшение оценок произошло только по нескольким взаимосвязанным предметам, а не в целом. Если успеваемость сильно упала в общем плане, то скорее всего ребёнок ленится. Связано это может быть со скукой на уроках и утратой интереса к учёбе. В таком случае, поговорите с ним, объясните, что это очень важно и пригодится в жизни, приводя аргументы и наглядные примеры.

Конечно, если это связано, например, с пропуском занятий по причине болезни, или в школе неправильно преподносится материал, то стоит задуматься о найме репетитора. Он поможет в кратчайшие сроки улучшить результаты ребёнка.

Как решить проблемы с математикой

Как только у ребёнка появляются проблемы с математикой родители почему-то начинают думать, что причина заключается в плохой предрасположенности к точным наукам. Потому что формулы вроде бы знает, простые примеры решить тоже может, но каждая контрольная и самостоятельная работа превращается в целое испытание для всей семьи. Все сидят в ожидании результатов. Никогда нельзя сказать точно какую оценку получит ребёнок — четвёрку или двойку.

Дети часто получают плохие отметки именно по математике

Также много жалоб по типу: занимаемся все выходные напролёт, учим эту математику, учим, а в итоге всё равно результат прежний. На самом деле, причина такого плохого восприятия — отсутствие адекватных причин заниматься всеми этими цифрами. Большинство родителей сходятся во мнении, что ребёнок просто гуманитарий, главное — литература, история, обществознание, а математика неважна.

Гуманитариям математика не нужна?

Это огромная ошибка, ведь для лучшего восприятия точных наук этому самому «гуманитарию» нужно лишь вдохновение и цель. Отлично будет, если ребёнку объяснить, что математика — это такая же наука, как и любая другая, и она не ограничивается уравнениями и задачами. Это нечто большее. Математика позволяет изменить мышление, воспринимать старые вещи по-новому.

Главная проблема всех гуманитариев, которые имели проблемы с математикой — это логика. Для составления, например, грамотной и структурированной статьи нужно руководствоваться не только правилами русского языка, но и логикой изложения мысли. Все части должны быть связаны между собой, в то же время, должны легко читаться отдельные фрагменты.

Именно логическое мышление в первую очередь развивает математика и воспринимать это нужно, как возможность расширения кругозора и свежего взгляда на старое. Также точные науки помогают дисциплинировать свой ум и комплексно подходить к решению поставленных задач.

Математика — сложный предмет

Самая популярная отговорка заключается в том, что математика — самый сложный предмет из всех. Нет, на самом деле это одна из самых простых и понятных дисциплин. Для сравнения, возьмите наш богатый русский язык.

Мало того, что в нём существует немало правил орфографии, пунктуации, стилистики, так ещё и исключения есть почти в каждом правиле. Вот уж где нужно запоминать «тонну» информации.

В то же время в математике существуют базовые правила, на которых строятся все остальные. То есть, более сложное всегда можно привести к простому. Всё построено на железной логике, и, следуя этим правилам, вы сможете решить задачи, которые казались на первый взгляд непосильными.

Вспомните, как учат всех детей. Для того, чтобы научить их писать, сначала нужно выводить палочки, точки, изгибы. Потом уже буквы, а из букв — простые слова, из слов — предложения.

Начните изучать математику с самых простых уравнений

В математике с самого начала всё объясняется на пальцах или предметах. При этом, за то же самое время, потраченное на русский язык и на математику, прогресс в изучении второй будет больше. Например, считать учатся дети на яблоках, конфетках.

Используйте это и для решения более сложных задач. В пятом классе аналогии привести не составит труда. Это поможет ребёнку ассоциировать вычисления не с сухими числами, а, например, с мандаринами.

Формула спокойствия

Часто плохие оценки становятся причиной ссор между родителями и детьми. Это категорически неправильно. Вместо того, чтобы высказывать ребёнку, что он «ленится», «не думает о будущем» да и в общем «туго соображает», следует отвести от неудачи или помочь исправиться с ней.

Но под помощью подразумевается не «вдалбливание» и «зубрёжка» неинтересных формул и правил. Следует возбудить интерес к теме, которая была плохо воспринята. Да и к тому же поставить правильную цель ребёнку. Не нужно говорить, что от оценок зависит его будущее. Вообще не зацикливайте внимание на оценках.

По исследованиям российских психологов дети, которые хотели стать врачами, инженерами и просто хорошими людьми, быстро повышали свою успеваемость. А те ученики, которым с первого класса «вдалбливают» в голову знания, думали только о том, как не стать худшим в классе, и уделяли своим отметкам слишком большое внимание.

Лучшим вариантом по-прежнему остаются занятия с репетитором. Он сохранит нервы, и вам, и ребёнку. Обеспечивая нужное количество времени на обучение и выбрав правильный подход, ученик станет показывать результаты лучше прежнего. Но, моментально отличником вашего ребёнка это не сделает.

Надеемся, что вы смогли найти решение задач, которое искали. Также для понимания темы рекомендуем посмотреть видео по этой теме от организаторов специальной математической школы федерального уровня «Аристотель».

8.5 Total Score

Решение задач по математике

Некоторые ученики, как пятых, так и других классов, часто сталкиваются с проблемами в изучении математики. В этом случае родителям не стоит впадать в панику. Следует уделить больше внимания детальному разбору примеров и задач. Если это не улучшит успеваемость, есть смысл обратиться за помощью к репетитору.

Простота

Доступность

ПЛЮСЫ

Подробные инструкции помогут разобраться в решении задач и примеров
Для изучения математики можно пользоваться решебниками

МИНУСЫ

Полученных знаний в школе не всегда достаточно для понимания предмета

Добавить отзыв

Решение неравенств с помощью пошагового решения математических задач

В этой главе мы разработаем некоторые приемы, помогающие решать задачи, сформулированные словами. Эти методы включают переписывание задач в виде символов. Например, поставленная задача

«Найдите число, которое при прибавлении к 3 дает 7»

можно записать так:

3 + ? = 7, 3 + n = 7, 3 + x = 1

и т. д., где символы ?, n и x представляют число, которое мы хотим найти. Такие сокращенные версии поставленных задач мы называем уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку показатель степени равен 1. Члены слева от знака равенства составляют левый член уравнения; те, что справа, составляют правый член. Таким образом, в уравнении x + 3 = 7 левая часть равна x + 3, а правая часть равна 7.

РЕШЕНИЕ УРАВНЕНИЙ

Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными. Уравнение:

3 + x = 7

будет ложным, если вместо переменной подставить любое число, кроме 4. Значение переменной, для которой уравнение верно (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.

Пример 1. Определить, является ли значение 3 решением уравнения член.

4(3) – 2 = 3(3) + 1

12 – 2 = 9 + 1

10 = 10

Ответ. 3 это решение.

Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем проверки.

Пример 2 Найдите решение каждого уравнения путем проверки.

а. х + 5 = 12
б. 4 · x = -20

Решения а. 7 является решением, так как 7 + 5 = 12,
b. -5 является решением, поскольку 4(-5) = -20.

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ

В разделе 3.1 мы решили некоторые простые уравнения первой степени путем проверки. Однако решения большинства уравнений не сразу очевидны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.

ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ

Эквивалентные уравнения – это уравнения, имеющие одинаковые решения. Таким образом,

3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5

эквивалентны уравнениям, поскольку 5 является единственным решением каждого из них. Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при проверке, но в уравнении x = 5 решение 5 очевидно при проверке. При решении любого уравнения мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.

Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов генерирования эквивалентных уравнений.

Если к обоим элементам добавляется или вычитается одно и то же количество уравнения, полученное уравнение эквивалентно исходному уравнение.

В символах

a – b, a + c = b + c и a – c = b – c

являются эквивалентными уравнениями.

Пример 1 Напишите уравнение, эквивалентное

x + 3 = 7

путем вычитания 3 из каждого члена.

Решение Вычитание 3 из каждого члена дает

x + 3 – 3 = 7 – 3

или

x = 4

Обратите внимание, что x + 3 = 7 и x = 4 являются эквивалентными уравнениями, поскольку решение одно и то же. для обоих, а именно 4. Следующий пример показывает, как мы можем сгенерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.

Пример 2 Напишите уравнение, эквивалентное

4x- 2-3x = 4 + 6

путем объединения одинаковых терминов, а затем добавления 2 к каждому элементу.

Объединение одинаковых членов дает

x – 2 = 10

Добавление 2 к каждому члену дает

x-2+2 = 10+2

x = 12

Чтобы решить уравнение, мы используем сложение-вычитание свойство преобразовывать данное уравнение в эквивалентное уравнение формы x = a, из которого мы можем найти решение путем проверки.

Пример 3 Решить 2x + 1 = x – 2.

Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому элементу (или вычтем из него 1), мы получим

2x + 1- 1 = x – 2- 1

2x = x – 3

Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим

2x-x = x – 3 – х

х = -3

где решение -3 очевидно.

Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.

Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x – 2. В приведенном выше примере мы можем проверить решение, подставив – 3 вместо x в исходном уравнение

2(-3) + 1 = (-3) – 2

-5 = -5

Симметричное свойство равенства также полезно при решении уравнений. Это свойство указывает

Если a = b, то b = a

Это позволяет нам менять местами члены уравнения в любое время, не заботясь о смене знака. Таким образом,

Если 4 = x + 2, то x + 2 = 4

Если x + 3 = 2x – 5, то 2x – 5 = x + 3

Если d = rt, то rt = d

Может быть несколько различные способы применения вышеуказанного свойства сложения. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.

Пример 4 Решите 2x = 3x – 9. (1)

Решение Если мы сначала прибавим -3x к каждому элементу, мы получим

2x – 3x = 3x – 9 – 3x

-x = -9

где переменная имеет отрицательный коэффициент. Хотя при проверке мы видим, что решение равно 9, поскольку -(9) = -9, мы можем избежать отрицательного коэффициента, добавляя -2x и +9 к каждому члену уравнения (1). В этом случае получаем

2х-2х + 9 = 3х- 9-2х+ 9

9 = х

откуда решение 9очевидно. Если мы хотим, мы можем записать последнее уравнение как x = 9 по симметричному свойству равенства.

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА ДЕЛЕНИЯ

Рассмотрим уравнение

3x = 12

Решением этого уравнения является 4. Также обратите внимание, что если мы разделим каждую часть уравнения на 3, мы получим уравнения

, решение которого также равно 4. В общем случае мы имеем следующее свойство, которое иногда называют свойством деления.

Если оба члена уравнения разделить на одно и то же (отличное от нуля) полученное уравнение эквивалентно исходному уравнению.

В символах

эквивалентны уравнениям.

Пример 1 Напишите уравнение, эквивалентное

-4x = 12

, разделив каждый член на -4.

Решение Деление обоих членов на -4 дает

При решении уравнений мы используем вышеуказанное свойство для получения эквивалентных уравнений, в которых переменная имеет коэффициент 1.

Пример 2 Решите 3y + 2y = 20.

Сначала мы объединяем одинаковые члены, чтобы получить

5y = 20

Затем, разделив каждый член на 5, мы получаем

В следующем примере мы используем сложение – свойство вычитания и свойство деления для решения уравнения.

Пример 3 Решить 4x + 7 = x – 2.

Решение Сначала мы добавляем -x и -7 к каждому члену, чтобы получить

4x + 7 – x – 7 = x – 2 – x – 1

Далее , объединение одинаковых членов дает

3x = -9

Наконец, мы делим каждый член на 3, чтобы получить

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА УМНОЖЕНИЯ

Рассмотрим уравнение

Решение этого уравнения умножая каждый член уравнения на 4, мы получаем уравнения

, решение которых также равно 12. В общем случае мы имеем следующее свойство, которое иногда называют свойством умножения.

Если оба члена уравнения умножить на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.

В символах

a = b и a·c = b·c (c ≠ 0)

являются эквивалентными уравнениями.

Пример 1 Напишите уравнение, эквивалентное

, умножив каждый член на 6.

Решение Умножив каждый член на 6, получим

дроби.

Пример 2 Решить

Решение Сначала умножьте каждый член на 5, чтобы получить

Теперь разделите каждый член на 3,

Пример 3 Решите .

Решение Сначала упростим над дробной чертой, чтобы получить

Затем умножим каждый член на 3, чтобы получить

Наконец, разделив каждый член на 5, получим

ДОПОЛНИТЕЛЬНЫЕ РЕШЕНИЯ 90 все методы, необходимые для решения большинства уравнений первой степени. Нет определенного порядка, в котором следует применять свойства. Любой один или несколько из следующих шагов, перечисленных на странице 102, могут быть подходящими.

Шаги для решения уравнений первой степени:

Объедините одинаковые члены в каждом члене уравнения.
Используя свойство сложения или вычитания, напишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестного в другом.
Объедините одинаковые термины в каждом элементе.
Используйте свойство умножения для удаления дробей.
Используйте свойство Division, чтобы получить коэффициент 1 для переменной.

Пример 1 Решите 5x – 7 = 2x – 4x + 14.

Решение Сначала мы объединяем одинаковые члены, 2x – 4x, чтобы получить

5x – 7 = -2x + 14

Затем мы добавляем +2x и +7 к каждому члену и объединяем одинаковые члены, чтобы получить

5x – 7 + 2x + 7 = -2x + 14 + 2x + 1

7x = 21

Наконец, мы делим каждый член на 7, чтобы получить

В следующем примере мы упрощаем дробную черту перед применением свойств, которые мы изучали.

Пример 2 Решить

Решение Сначала мы объединяем одинаковые члены, 4x – 2x, чтобы получить

Затем мы добавляем -3 к каждому члену и упрощаем

Затем мы умножаем каждый член на 3, чтобы получить

Наконец, мы делим каждый член на 2, чтобы получить

РЕШЕНИЕ ФОРМУЛ

Уравнения, которые включают переменные для измерения двух или более физических величин, называются формулами. Мы можем найти любую переменную в формуле, если известны значения других переменных. Мы подставляем известные значения в формулу и находим неизвестную переменную методами, которые мы использовали в предыдущих разделах.

Пример 1 В формуле d = rt найдите t, если d = 24 и r = 3.

Решение Мы можем найти t, подставив 24 вместо d и 3 вместо r. То есть

d = rt

(24) = (3)t

8 = t

Часто бывает необходимо решать формулы или уравнения, в которых имеется более одной переменной для одной из переменных в терминах другие. Мы используем те же методы, что и в предыдущих разделах.

Пример 2 В формуле d = rt найдите t через r и d.

Решение Мы можем найти t через r и d, разделив оба члена на r, чтобы получить

, откуда по симметричному закону

В приведенном выше примере мы нашли t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.

Пример 3 В уравнении ax + b = c найдите x через a, b и c.

Решение Мы можем найти x, сначала добавив -b к каждому члену, чтобы получить

затем разделив каждый член на a, мы получим

Фактор полинома или выражения с помощью программы «Пошаговое решение математических задач»

Процесс факторизации необходим для упрощения многих алгебраических выражений и является полезный инструмент для решения уравнений более высокой степени. На самом деле процесс факторизации настолько важен, что очень мало алгебры, кроме этого пункта, можно выполнить без его понимания.

В предыдущих главах различие между условий и факторов было подчеркнуто. Вы должны помнить, что члены складываются или вычитаются, а множители умножаются. Далее следуют три важных определения.

Термины встречаются в указанной сумме или разнице. Факторы встречаются в указанном продукте.

Выражение находится в факторизованной форме , только если все выражение является указанным произведением.

Обратите внимание, что в этих примерах мы всегда должны учитывать выражение целиком. Факторы могут состоять из терминов, а термины могут содержать факторы, но факторизованная форма должна соответствовать приведенному выше определению.

Факторинг — это процесс преобразования суммы или разности выражений в произведение факторов.

Обратите внимание, что в этом определении подразумевается, что значение выражения не изменяется – только его форма.

УДАЛЕНИЕ ОБЩИХ ФАКТОРОВ

ЦЕЛИ

По завершении этого раздела вы сможете:

Определите, какие факторы являются общими для всех членов выражения.
Фактор общих факторов.

В предыдущей главе мы умножили такое выражение, как 5(2x + 1), чтобы получить 10x + 5. Обычно факторизация «отменяет» умножение. Каждый член 10x + 5 имеет множитель 5, а 10x + 5 = 5 (2x + 1).

Разложить выражение на множители путем удаления общих множителей, как в примере 1.

3x — наибольший общий множитель всех трех членов.

Затем найдите факторы, общие для всех терминов, и отыщите наибольший из них. Это самый большой общий фактор. В этом случае наибольший общий делитель равен 3x.

Продолжайте, поставив 3x перед скобками.

Члены в скобках находятся путем деления каждого члена исходного выражения на 3x.

Обратите внимание, что это свойство распределения. Это обратный процесс, который мы использовали до сих пор.

Исходное выражение теперь преобразуется в факторизованную форму. Чтобы проверить факторинг, имейте в виду, что факторинг изменяет форму, но не значение выражения. Если ответ правильный, то должно быть верно, что . Умножьте, чтобы увидеть, что это правда. Вторая проверка также необходима для факторинга — мы должны быть уверены, что выражение было полностью факторизовано. Другими словами: «Удалили ли мы все общие факторы? Можем ли мы еще добавить факторы?»

Если бы мы удалили только множитель «3» из 3x ² + 6xy + 9xy ² , ответ был бы

3(x ² + 2xy + 3xy ² ).

Умножая для проверки, мы находим, что ответ на самом деле равен исходному выражению. Однако фактор x по-прежнему присутствует во всех терминах. Следовательно, выражение не является полностью факторизованным.

Это выражение факторизовано, но не полностью.

Чтобы факторинг был правильным, решение должно соответствовать двум критериям:

Должна быть возможность умножить факторизованное выражение и получить исходное выражение.
FВыражение должно быть полностью разложено на .

Пример 2 Коэффициент 12x ³ + 6x ² + 18x.

Решение

На данный момент нет необходимости перечислять факторы каждого термина. Вы должны быть в состоянии мысленно определить наибольший общий множитель. Хорошей процедурой для подражания является продумывание элементов по отдельности. Другими словами, не пытайтесь сразу получить все общие множители, а сначала получите число, а затем каждую соответствующую букву. Например, 6 — это множитель 12, 6 и 18, а x — множитель каждого члена. Отсюда 12x ³ + 6х ² + 18х = 6х(2х ² + х + 3). Умножая, мы получаем оригинал и видим, что члены в скобках не имеют другого общего множителя, поэтому мы знаем, что решение правильное.

Спросите себя: “Каков наибольший общий делитель чисел 12, 6 и 18?”

Затем “Каков наибольший общий делитель x ³ , x ² и x?”

Помните, это проверка, чтобы убедиться, что мы правильно рассчитали.

Снова умножьте в качестве чека.

Снова найдите наибольший общий делитель чисел и каждой буквы в отдельности.

Если выражение нельзя разложить на множители, говорят, что оно простое .

Помните, что 1 всегда является делителем любого выражения.

ФАКТОРИЗАЦИЯ ПО ГРУППИРОВКЕ

ЗАДАЧИ

После заполнения этого раздела вы сможете:

Факторные выражения, когда общий фактор включает более одного термина.
Фактор по группировке.

Расширение идей, представленных в предыдущем разделе, относится к методу факторизации, называемому группировкой .

Во-первых, мы должны отметить, что общий множитель не обязательно должен быть одним термином. Например, в выражении 2y(x + 3) + 5(x + 3) есть два члена. Это 2y(x + 3) и 5(x + 3). В каждом из этих терминов у нас есть множитель (x + 3), состоящий из термов. Этот множитель (x + 3) является общим множителем.

Иногда, когда имеется четыре или более терминов, мы должны вставить один или два промежуточных шага для факторизации.

Решение

Во-первых, обратите внимание, что не все четыре члена в выражении имеют общий делитель, но некоторые из них имеют. Например, мы можем разложить первые два члена на 3, что даст 3(ax + 2y). Если мы разложим a из оставшихся двух членов, мы получим a (ax + 2y). Теперь выражение равно 3(ax + 2y) + a(ax + 2y), и у нас есть общий множитель (ax + 2y), и мы можем разложить как (ax + 2y)(3 + a). Умножая (ax + 2y)(3 + a), мы получаем исходное выражение 3ax + 6y + a ² x + 2ay и убедитесь, что факторинг правильный.

Это пример разложения на множители путем группировки , поскольку мы «сгруппировали» термины по два за раз.

Умножьте (x – y)(a + 2) и посмотрите, получится ли исходное выражение.
Опять умножить как чек.

Иногда члены должны быть сначала переупорядочены, прежде чем можно будет выполнить разложение по группам.

Пример 7 Коэффициент 3ax + 2y + 3ay + 2x.

Решение

Первые два члена не имеют общего делителя, но первый и третий члены имеют, поэтому мы переставим члены так, чтобы третий член располагался после первого. Всегда смотрите вперед, чтобы увидеть порядок, в котором термины могут быть расположены.

Во всех случаях важно убедиться, что коэффициенты в скобках абсолютно одинаковы. Это может потребовать факторизации отрицательного числа или буквы.

Помните, свойство коммутативности позволяет нам переставлять эти термины.
Умножить как чек.

Пример 8 Коэффициент ax – ay – 2x + 2y.

Решение

Обратите внимание, что если мы разложим a из первых двух членов, мы получим a(x – y). Глядя на последние два члена, мы видим, что разложение на множители +2 даст 2(-x + y), но разложение на множители “-2” дает -2(x – y). Мы хотим, чтобы члены в круглых скобках были (x – y), поэтому мы действуем таким образом.

ФАКТОРИЗАЦИЯ ТРЕХНОМОВ

ЦЕЛИ

По завершении этого раздела вы должны уметь:

Умножьте в уме два двучлена.
Разложите на множители трехчлен с коэффициентом первого члена, равным 1.
Найдите делители любого факторизуемого трехчлена.

Большое количество будущих задач будет связано с разложением трехчленов на множители как произведений двух двучленов. В предыдущей главе вы научились умножать многочлены. Теперь мы хотим рассмотреть частный случай умножения двух двучленов и разработать шаблон для этого типа умножения.

Поскольку этот тип умножения очень распространен, полезно иметь возможность найти ответ, не выполняя так много шагов. Давайте посмотрим на шаблон для этого.

Из примера (2x + 3)(3x – 4) = 6x ² + x – 12 обратите внимание, что первый член ответа (6x ² ) получен из произведения двух первых членов множители, то есть (2x)(3x).

Также обратите внимание, что третий член (-12) получен из произведения вторых членов факторов, то есть (+ 3)(-4).

Теперь у нас есть следующая часть шаблона:

Теперь снова взглянув на пример, мы видим, что средний член (+x) получен из суммы двух произведений (2x)(-4) и (3)(3x).

Теперь для любых двух биномов у нас есть следующие четыре произведения:

Первый срок за первым сроком
Внешние условия
Внутренние условия
Последний срок за последним сроком

Эти продукты показаны этим шаблоном.

Когда произведения внешних членов и внутренних членов дают одинаковые члены, их можно объединить, и решение будет трехчленным.

Этот метод умножения двух двучленов иногда называют методом FOIL.
FOIL расшифровывается как First, Outer, Inner, Last.

Это упрощенный метод умножения двух двучленов, и его полезность будет видна, когда мы разложим трехчлены.

Вы должны запомнить эту схему.

Опять же, возможно, запоминание слова ФОЛЬГА поможет.

Этот образец следует не только запомнить, но и научиться переходить от задачи к ответу без каких-либо письменных шагов. Этот умственный процесс умножения необходим, если мы хотим достичь мастерства в факторинге.

Работая над следующими упражнениями, попытайтесь найти правильный ответ, ничего не записывая, кроме самого ответа. Чем больше вы практикуете этот процесс, тем лучше у вас будет факторинг.

Теперь, когда мы установили схему умножения двух двучленов, мы готовы разложить трехчлены на множители. Сначала мы рассмотрим разложение на множители только тех трехчленов, у которых коэффициент первого члена равен 1.

Решение

Поскольку это трехчлен и не имеет общего делителя, мы будем использовать схему умножения для факторизации.

На самом деле мы будем работать в обратном порядке по сравнению с предыдущим упражнением.

Сначала распишите задачу в скобках.

Теперь мы хотим заполнить термины так, чтобы шаблон давал исходный трехчлен при умножении. Первый член прост, поскольку мы знаем, что (x)(x) = x ² .

Помните, произведение первых двух членов двучлена дает первый член трехчлена.

Теперь мы должны найти числа, которые при умножении дают 24 и в то же время складывают, чтобы получить средний член. Обратите внимание, что в каждом из следующих у нас будет правильный первый и последний термин.

Только последний продукт имеет средний член 11x, и правильное решение

Этот метод факторинга называется методом проб и ошибок – по понятным причинам.

Здесь могут быть полезны некоторые числовые факты из арифметики.

Произведение двух нечетных чисел нечетно.
Произведение двух четных чисел четно.
Произведение нечетного и четного числа равно четному.
Сумма двух нечетных чисел четна.
Сумма двух четных чисел четна.
Сумма нечетного и четного числа нечетна.

Следовательно, когда мы факторизуем такое выражение, как x ² + 11x + 24, мы знаем, что произведение двух последних членов бинома должно быть 24, что является четным, а их сумма должна быть равна 11, что является нечетным.
Таким образом, будет работать только нечетное и четное число. Нам даже не нужно пробовать такие комбинации, как 6 и 4 или 2 и 12 и так далее.

Решение

Здесь проблема немного другая. Мы должны найти числа, которые при умножении дают 24 и при этом при сложении дают – 11. Всегда нужно помнить о закономерности. Последний член получается строго путем умножения, а средний член получается, наконец, из суммы. Зная, что произведение двух отрицательных чисел положительно, а сумма двух отрицательных чисел отрицательна, мы получаем

Решение

Здесь мы сталкиваемся с отрицательным числом для третьего слагаемого, и это несколько усложняет задачу. сложно. Поскольку -24 может быть только произведением положительного числа и отрицательного числа, а средний член должен исходить из суммы этих чисел, мы должны мыслить в терминах различия. Мы должны найти числа, произведение которых равно 24 и которые отличаются на 5. Кроме того, большее число должно быть отрицательным, потому что, когда мы складываем положительное и отрицательное число, ответ будет иметь знак большего. Учитывая все это, получаем

Порядок факторов не имеет значения.

по коммутативному закону умножения.

Следующие пункты помогут вам разложить трехчлены на множители:

Когда знак третьего члена положителен, оба знака в множителях должны быть одинаковыми, и они должны быть одинаковыми со знаком среднего члена.
Когда знак последнего члена отрицательный, знаки множителей должны быть разными, а знак большего члена должен быть подобен знаку среднего члена.

В предыдущем упражнении коэффициент каждого из первых слагаемых был равен 1. Когда коэффициент первого слагаемого не равен 1, проблема факторинга значительно усложняется, поскольку число возможностей значительно увеличивается.

Выполнив предыдущий набор упражнений, вы теперь готовы попробовать еще несколько сложных трехчленов.

Обратите внимание, что есть двенадцать способов получить первый и последний члены, но только один из них имеет 17x в качестве среднего члена.

Вы, конечно, могли бы попробовать каждое из них мысленно вместо того, чтобы записывать их.

Есть только один способ получить все три условия:

В этом примере одна из двенадцати возможностей верна. Таким образом, проб и ошибок может занять очень много времени.

Несмотря на то, что используемый метод представляет собой метод угадывания, это должно быть «обоснованное угадывание», в котором мы применяем все наши знания о числах и упражняемся в умственной арифметике. В предыдущем примере мы бы сразу отбросили многие комбинации. Поскольку мы ищем 17x в качестве среднего члена, мы не будем пытаться использовать те возможности, которые умножают 6 на 6, или 3 на 12, или 6 на 12 и т. д., поскольку эти произведения будут больше 17. Кроме того, поскольку 17 нечетно, мы знаем, что это сумма четного числа и нечетного числа. Все эти вещи помогают сократить количество возможных попыток.

Сначала найдите числа, которые дают правильный первый и последний члены трехчлена. Затем добавьте внешний и внутренний продукт, чтобы проверить правильность среднего члена.

Решение

Сначала мы должны проанализировать проблему.

Последний член положительный, поэтому два одинаковых знака.
Средний член отрицательный, поэтому оба знака будут отрицательными.
Множители 6×2 равны x, 2x, 3x, 6x. Делители 15 равны 1, 3, 5, 15.
Исключить как слишком большое произведение 15 на 2x, 3x или 6x. Попробуйте несколько разумных комбинаций.

Это автоматически дало бы слишком большой средний член.

Посмотрите, как сокращается количество возможностей.

Раствор

Анализ:

Последний член отрицательный, поэтому отличается от знаков.
Мы должны найти произведения, отличающиеся на 5 с большим отрицательным числом.
Мы исключаем произведение 4x и 6 как возможно слишком большое.
Попробуйте несколько комбинаций.

Помните, мысленно попробуйте различные возможные комбинации, которые являются разумными. Это процесс факторинга методом проб и ошибок. Вы станете более опытным в этом процессе благодаря практике.

(4x – 3)(x + 2): Здесь средний член равен + 5x, что является правильным числом, но неправильным знаком. Будьте осторожны, чтобы не принять это как решение, а поменяйте знаки так, чтобы большее произведение совпадало по знаку со средним членом.

К тому времени, когда вы закончите следующий набор упражнений, вы должны чувствовать себя гораздо более комфортно при разложении трехчлена на множители.

ОСОБЫЕ СЛУЧАИ В ФАКТОРИНГЕ

ЦЕЛИ

По завершении этого раздела вы должны уметь:

Определите и разложите на множители разности двух полных квадратов.
Определите и разложите на множители совершенный квадратный трехчлен.

В этом разделе мы хотим рассмотреть некоторые частные случаи факторинга, которые часто встречаются в задачах. Если эти особые случаи признаются, факторинг значительно упрощается.

Первый частный случай, который мы обсудим, это разность двух полных квадратов .

Напомним, что при умножении двух двучленов на шаблон средний член получается из суммы двух произведений.

Из нашего опыта работы с числами мы знаем, что сумма двух чисел равна нулю только в том случае, если эти два числа являются отрицательными по отношению друг к другу.

Когда сумма двух чисел равна нулю, одно из чисел называется аддитивным обратным другого.

Например: ( + 3) + (-3) = 0, поэтому + 3 является аддитивной инверсией – 3, также -3 является аддитивной инверсией +3.

В каждом примере средний член равен нулю. Обратите внимание, что если два двучлена умножаются, чтобы получить двучлен (средний член отсутствует), они должны быть в форме (a – b) (a + b).

Правило можно записать как = (a – b)(a + b). Это форма, которую вы найдете наиболее полезной в факторинге.

Чтение этого правила справа налево говорит нам, что если у нас есть проблема для факторизации и если она имеет форму , факторы будут (a – b)(a + b).

Решение

Здесь оба члена являются полными квадратами и разделены знаком минус.

Где a = 5x и b = 4.

Особые случаи действительно облегчают факторинг, но не забудьте признать, что особый случай — это именно то, что является особенным. В этом случае оба члена должны быть полными квадратами, а знак должен быть отрицательным, отсюда «разность двух полных квадратов».

Сумма двух квадратов не разлагается.

Вы также должны быть осторожны, чтобы распознать правильные квадраты. Помните, что совершенные квадратные числа — это числа, квадратные корни которых являются целыми числами. Кроме того, совершенные квадратные показатели четны.

Студенты часто упускают из виду тот факт, что (1) — совершенный квадрат. Таким образом, такое выражение, как x ² – 1, представляет собой разность двух полных квадратов и может быть факторизовано этим методом.

Другим частным случаем факторинга является трехчлен с совершенным квадратом. Заметьте, что возведение бинома в квадрат приводит к этому случаю.

Мы узнаем этот случай, отмечая особенности. Три вещи очевидны.

Первый член — полный квадрат.
Третий член — полный квадрат.
Средний член равен удвоенному произведению квадратного корня из первого и третьего членов.

Для целей факторинга удобнее записать оператор как

Решение

25x ² – это совершенный квадратный главный квадратный корень = 5x.
4 — это совершенный квадратный главный квадратный корень = 2.
20x — удвоенное произведение квадратных корней из 25x ² и
20х = 2(5х)(2).

Чтобы разложить на множители идеальный квадратный трехчлен , сформируйте двучлен из квадратного корня из первого члена, квадратного корня из последнего члена и знака среднего члена и укажите квадрат этого двучлена.

Таким образом, 25x ² + 20x + 4 = (5x + 2) ²

Всегда возводите бином в квадрат, чтобы убедиться, что средний член правильный.

Не частный случай совершенного квадратного трехчлена.

15 ≠ 2(2x)(3)

ДОПОЛНИТЕЛЬНЫЕ КОРРЕКТЫ ДЛЯ ФАКТОРИНГА ПРОБ И ОШИБОК

ЦЕЛИ

По завершении этого раздела вы сможете:

Найдите ключевое число трехчлена.
Используйте номер ключа, чтобы разложить трехчлен на множители.

В этом разделе мы хотим обсудить некоторые упрощения метода проб и ошибок. Они необязательны по двум причинам. Во-первых, некоторые могут предпочесть пропустить эти методы и просто использовать метод проб и ошибок; во-вторых, эти сокращения не всегда практичны для больших чисел. Однако они увеличат скорость и точность для тех, кто их освоит.

Первым шагом в этих сочетаниях клавиш является поиск номер ключа . После того, как вы нашли номер ключа, его можно использовать более чем одним способом.

В разлагаемом на множители трехчлене ключевое число есть произведение коэффициентов первого и третьего членов.

Произведение этих двух чисел является «ключевым числом».

Первое использование номера ключа показано в примере 3.

Решение
Шаг 1 Найдите номер ключа. В этом примере (4)(-10)=-40.
Шаг 2 Найдите множители ключевого числа (-40), которые в сумме дадут коэффициент среднего члена ( + 3). В этом случае (+8)(-5)=-40 и (+8)+(-5)=+3.
Шаг 3 Множители ( + 8) и ( – 5) будут перекрестными произведениями в схеме умножения.

Произведение этих двух чисел является «ключевым числом».

Шаг 4 Используя только внешнее перекрестное произведение, найдите множители первого и третьего членов, которые при умножении дают произведение. В этом примере мы должны найти множители 4×2 и -10, которые при умножении дают +8x. Это 4x от 4×2 и (+2) от (-10).
Поместите эти факторы на первую и последнюю позиции в шаблоне

Есть только один способ сделать это правильно.

Шаг 5 Забудьте номер ключа на этом этапе и вернитесь к исходной проблеме. Поскольку первая и последняя позиции заполнены правильно, теперь необходимо заполнить только две другие позиции.

Опять же, это можно сделать только одним способом.

Мы знаем, что произведение двух первых слагаемых должно давать 4×9.0445 2 и 4x уже на месте. Нет другого выбора, кроме х.

Обратите внимание, что на шаге 4 мы могли бы начать с внутреннего продукта вместо внешнего продукта. Мы получили бы те же коэффициенты.

Наиболее важным является систематический процесс факторинга.

Мы знаем, что произведение двух вторых членов должно быть (-10) и (+2) уже на месте. У нас нет другого выбора, кроме как (- 5).

Помните, что если трехчлен можно разложить на множители, то существует только один возможный набор множителей.

Если не удается найти делителей ключевого числа, сумма которых является коэффициентом при средних членах, то трехчлен является простым и не делит.

Второе использование номера ключа в качестве ярлыка включает факторинг путем группирования. Работает как в примере 5.

Решение
Шаг 1 Найдите число ключа (4)(-10) = -40.
Шаг 2 Найдите множители (-40), которые в сумме дадут коэффициент среднего члена (+3).

Шаги 1 и 2 в этом методе такие же, как и в предыдущем методе.

Шаг 3 Перепишите исходную задачу, разбив средний член на две части, найденные в шаге 2. 8x – 5x = 3x, так что мы можем написать

Шаг 4 Разложите эту задачу из шага 3 по метод группировки, изученный в разделе 8-2

Теперь это становится обычной задачей факторизации по группировке.

Следовательно,

Опять же, существует только одна возможная пара множителей, которые можно получить из данного трехчлена.

Помните, что если шаг 2 невозможен, трехчлен является простым и не может быть разложен на множители.

ПОЛНАЯ ФАКТОРИЗАЦИЯ

ЦЕЛИ

По завершении этого раздела вы сможете разложить трехчлен на множители, выполнив следующие два шага:

Сначала найдите общие факторы.
Разложите на множители оставшийся трехчлен, применяя методы, описанные в этой главе.

Итак, мы изучили все обычные методы факторизации, встречающиеся в элементарной алгебре. Однако вы должны знать, что для решения одной проблемы может потребоваться более одного из этих методов. Помните, что существует две проверки правильности факторинга.

Будут ли множители умножаться, чтобы дать исходную задачу?
Все ли множители простые?

Как только общий множитель найден, вы должны проверить, является ли полученный трехчлен факторизуемым.

Если у трехчлена есть какие-либо общие делители, обычно проще сначала разложить их на множители.

При разложении на множители рекомендуется всегда сначала удалять наибольший общий множитель, а затем, если возможно, факторизовать то, что осталось.

РЕЗЮМЕ

Ключевые слова

Выражение находится в факторизованной форме, только если все выражение является указанным произведением.
Факторинг — это процесс, который превращает сумму или разность условий в произведение факторов.
Простое выражение нельзя разложить на множители.
Наибольший общий делитель — это наибольший общий делитель всех терминов.
Выражение является полностью разложенным на множители , когда дальнейшее разложение на множители невозможно.
Возможность факторизации путем группировки существует, когда выражение содержит четыре или более членов.
Метод FOIL можно использовать для умножения двух двучленов.
Особые случаи факторинга включают разность двух квадратов и трехчленов с совершенными квадратами .
Ключевое число является произведением коэффициентов первого и третьего членов трехчлена.

Процедуры

Чтобы удалить общие делители, найдите наибольший общий делитель и разделите на него каждый член.
Трехчлены можно разложить на множители методом проб и ошибок. При этом используется шаблон для умножения, чтобы найти множители, которые дадут исходный трехчлен.
Для факторизации разницы двух квадратов используйте правило
Чтобы разложить на множители идеальный квадратный трехчлен, сформируйте двучлен с квадратным корнем из первого члена, квадратным корнем из последнего члена и знаком среднего члена и укажите квадрат этого двучлена.
Используйте ключевое число для помощи в определении факторов, сумма которых является коэффициентом среднего члена трехчлена.

‎Photomath в App Store

Описание

Получите математическое приложение, которое поможет вам! Photomath — самая полезная в мире платформа для изучения математики, на которой миллионы учащихся всех уровней ежемесячно проверяют домашние задания, готовятся к тестам и совершают новые математические открытия.

Основные этапы решения и объяснения абсолютно БЕСПЛАТНЫ, но если вы готовы к совершенно новому миру обучения, Photomath Plus предоставляет вам доступ к: задачи на слова и геометрию! Учитесь в своем собственном темпе с материалами, одобренными одними из лучших учителей математики в мире.

МУЛЬТИМЕДИЙНОЕ ОБУЧЕНИЕ
С подробными анимациями искусственного интеллекта и словесными пояснениями, которые помогут вам визуализировать и понять математику в соответствии с вашим стилем обучения.

MATH INSIGHTS
Повысьте уровень своего обучения, понимая, «как» и «почему» решаются математические задачи, или получайте напоминания о забытых терминах и понятиях с помощью нашего встроенного глоссария.

Итак, изучаете ли вы основы арифметики или занимаетесь сложной геометрией, мы поможем вам в этом вместе. Один шаг за раз.

ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
• Бесплатные пошаговые объяснения
• Инструкции по решению задач в формате Word
• Интерактивные графики
• Видеообучение
• Несколько методов решения
• Усовершенствованный научный калькулятор Вещественные и комплексные числа
— Сравнение действительных чисел
— Идентификация чисел
ФУНКЦИИ
— Графики функций (линейные, квадратичные, экспоненциальные и т. д.)
— Свойства функций (область определения, асимптоты и т. д.)
АЛГЕБРА
– Упрощение, разложение на множители и вычисление алгебраических выражений
– Упрощение алгебраических дробей и разложение на неполные дроби
– Решение уравнений и неравенств (линейных, квадратных, экспоненциальных и т. д.)
– Системы уравнений
– Полиномиальное деление
– Биномиальная теорема , Факториалы
– Комбинации, перестановки и вариации
– Матрицы и матричные уравнения
– Детерминанты
– Математическая индукция
ТРИГОНОМЕТРИЯ И УГЛЫ
– Преобразование углов между градусами и радианами
– Преобразование углов между десятичной и DMS формой
– Период тригонометрических функций
– Проверка тригонометрических тождеств
ПОСЛЕДОВАТЕЛЬНОСТИ
– Идентификация последовательностей
– Серия
– Рекурсивная и явная форма
– Тесты на сходимость 9003
– Пределы
– Производные
– Интегралы
– Площадь под кривой
– Идентификация коник
– Вращение коник
– Параметризация кривых
– Идентификация квадратичных поверхностей
– Дифференциальные уравнения
– Касательные линии
– Преобразование между координатами

«Ответ — это не все, что вы получите от этого бесплатного приложения. Photomath также предоставляет пошаговое руководство по решению каждой проблемы». — Huffington Post

«Пошаговое руководство полезно для учащихся, у которых нет доступа к репетитору и у которых возникают проблемы с решением математических задач». — Forbes

«Вирусное видео о новом приложении выглядит как воплощение мечты для всех, у кого проблемы с математикой». — Время
___________________________________________

• Оплата будет снята с вашей учетной записи Apple ID при подтверждении покупки.
• Подписка продлевается автоматически, если она не будет отменена по крайней мере за 24 часа до окончания текущего расчетного периода.
• С вашего аккаунта будет взиматься плата за продление в течение 24 часов до окончания текущего периода.
• Управляйте подпиской или отменяйте ее в настройках своей учетной записи в App Store после покупки.
• Предложения и цены могут быть изменены без предварительного уведомления.

Предложения или вопросы? Напишите нам по адресу support@photomath. com

Веб-сайт: www.photomath.com
TikTok: @photomath
Instagram: @photomath
Facebook: @Photomathapp
Twitter: @Photomath

Условия использования: https://photomath.com /en/termsofuse
Политика конфиденциальности: https://photomath.com/en/privacypolicy

4 сентября 2022 г.

Версия 8.11.0

Уже сентябрь?! Как ты себя чувствуешь? Увлажненный? Готовы на все? Если вы чувствуете, что работа продолжается, не волнуйтесь — мы тоже! Мы полны решимости ВСЕГДА помочь вам, поэтому, если у вас возникла проблема, отсканируйте ее, чтобы мы могли отправить ее нашим экспертам по математике и добавить в приложение! (Глядя на вас, проблемы со словами…) Это довольно интересно, когда работа продолжается, не так ли? Продолжаем двигаться вперед вместе 🙂

Рейтинги и обзоры

573,6 тыс. оценок

Выбор редакции

Время от времени появляется приложение, которое откинет вам волосы назад и заставит вас поверить, что вы живете в научно-фантастическом будущем. Photomath позволяет навести камеру на проблему, и на экране мгновенно появится пошаговое объяснение (и ответ!) Трехзначное умножение? Фотомат получил это. Линейные и квадратные неравенства? Без проблем.

ОЧЕНЬ хороший инструмент для математики.

Хотя есть еще 1 или 2 математических темы, с которыми это приложение пока не может помочь, это ЗАМЕЧАТЕЛЬНОЕ приложение, которое может решить около 90% математических задач, будь то обычная алгебра или уравнения высшего и самого сложного уровня в колледже. Тем не менее, вы хотите, чтобы это приложение было на вашей стороне, когда вы занимаетесь математикой в значительной степени и всеми видами. Его основная функция позволяет вам фотографировать математические уравнения, и, если на снимке случайно оказались части других уравнений, вы можете обрезать их, как только сделаете снимок, и он решит уравнение за вас, как только вы нажимаете кнопку «ОК». В нем также есть калькулятор, где вы можете вручную вводить уравнения и решать их. Это полезно, если вы поняли, что написали уравнение неправильно, потому что вы можете просто перейти прямо к части калькулятора и исправить его, так как все части уравнения, которые приложение увидело на фотографии, сразу же помещаются в калькулятор. Лучшая часть, на мой взгляд, — это последняя функция, где она точно сообщает вам, как она решила уравнение, и даже позволяет вам просматривать каждый шаг и дает вам краткое, но хорошее объяснение того, что происходит на шаге. Если вы также прокрутите вниз, находясь в той же функции, если вы сфотографировали уравнение, которое нужно изобразить в виде графика, вы действительно сможете увидеть уравнение, построенное для вас. Это очень хорошее приложение, и я НАСТОЯТЕЛЬНО рекомендую.

Здравствуйте! Большое спасибо за то, что поделились с нами своими отзывами, мы ценим это! В настоящее время мы формируем пул пользователей, которые считают наше приложение особенно полезным, поскольку мы часто получаем запросы на отзывы от СМИ. Хотели бы вы присоединиться к этому пулу и в конечном итоге получить шанс дать показания для прессы? Напишите нам по адресу [email protected], если у вас есть какие-либо вопросы или если вы рады принять участие.

Идея приложения!!!!Хотите сделать ваше приложение ЛУЧШЕ, прочитайте ЭТО!!

Отлично, это приложение творит чудеса! БАТТТ: Я должен заплатить за это, чтобы научить меня делать это, как Бру. Я думал, вы все зарабатываете на рекламе? Вместо этого у меня есть идея для вас всех. Вместо того, чтобы заставлять людей платить за обучение, но у вас должен быть вариант обучения, но не такой, как тот, который у вас есть сейчас, вариант обучения должен быть вариантом, который учит вас, как это делать, но вместо этого вам действительно нужно решать проблемы. а скорее вы проходите по нему тест и пересдаете его столько раз, сколько хотите! И вы можете заставить людей платить за это, так как это будет «премиум». Вы также можете включить флэш-карты и игры, чтобы помочь понять математический тип!! Люди определенно были бы готовы платить за приложение, которое учит добру!! То, что у вас есть сейчас, мало поможет в обучении, но вместо этого вы можете создать новый, улучшенный и УВЛЕКАТЕЛЬНЫЙ способ изучения математики, тогда вы можете попросить их добавлять баллы к уравнению всякий раз, когда вы правильно отвечаете на вопрос! А затем добавьте аватар, который вы можете настроить, но вам понадобятся монеты, чтобы купить все, что вы хотите, вы можете заработать эти монеты, правильно ответив на математику. Или, по крайней мере, получить 7/10 или больше прав!!! Опять же, это будет основным вашим приложением, как Funner, и учителя могут использовать его как способ обучения и будут платить за программу! Таким образом, добавление этого будет означать БОЛЬШЕ ДЕНЕГ для вашей компании !!! Дайте мне знать, если вы, ребята, используете эту идею, и спасибо за чтение 🥺❤️💕

Привет и спасибо за положительный отзыв! Мы постоянно работаем над улучшением Photomath, поэтому обязательно поделимся вашими предложениями с командой. Не стесняйтесь, напишите нам по адресу [email protected], если у вас есть идеи по улучшению приложения. Ваше здоровье!

Разработчик, Photomath, Inc., указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.

Данные, не связанные с вами

Могут быть собраны следующие данные, но они не связаны с вашей личностью:

Покупки
Расположение
Контактная информация
Пользовательский контент
Идентификаторы
Данные об использовании
Диагностика
Другие данные

Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. Узнать больше

Информация

Продавец: Фотомат, ООО
Размер: 32,5 МБ
Категория: Образование
Возрастной рейтинг: 4+
Цена: Бесплатно

Сайт разработчика
Тех. поддержка
Политика конфиденциальности

Symbolab Math Solver – Пошаговый калькулятор

9{\ квадрат}

\bold{\mathrm{Basic}}

\жирный {\альфа\бета\гамма}

\bold{\mathrm{AB\Gamma}}

\жирный{\sin\cos}

\жирный{\ge\div\стрелка вправо}

\bold{\overline{x}\space\mathbb{C}\forall}

\bold{\sum\space\int\space\product}

\bold{\begin{pmatrix}\square&\square\\\square&\square\end{pmatrix}}

\sqrt{\square}

\nthroot[\msquare]{\square}

\frac{\msquare}{\msquare}

\log_{\msquare}

\пи

\ тета

\infty

\внутр

\frac{d}{dx}

\ле

\cdot 9{\msquare}

\лим

\сумма

\sin

\cos

\ коричневый

детская кроватка

\csc

мс

\альфа	\бета	\гамма	\дельта	\дзета	\эта	\ тета	\йота	\каппа	\лямбда	\мю
\ну	\xi	\пи	\ро	\сигма	\тау	\ипсилон	\фи	\чи	\psi	\омега

А	Б	\Гамма	\Дельта	Е	З	Н	\ Тета	К	\лямбда	М
С	\Xi	\Пи	П	\Сигма	Т	\Ипсилон	\Фи	Х	\пси	\Омега

\sin	\cos	\ коричневый	детская кроватка	мс	\csc	\ш	\кош	\танх		\сеч
\arcsin	Арккос	Арктан	\аркот	\арксек	\arccsc	\arcsinh	\арккош	Арктанх	\арккот	\arcsech

\begin{case}\square\\\square\end{case}

\begin{cases}\square\\\square\\\square\end{cases}

\ne

\дел

\cdot

\раз

> 9{\circ}

\rightarrow

\lпол\квадрат\rпол

\lceil\square\rceil

\overline{\square}

\vec{\square}

\в

\для всех

\ не

\есть

\mathbb{R}

\mathbb{C}

9{”}

\frac{\partial}{\partial x}

(2\раз2)	(2\раз3)	(3\раз3)	(3\раз2)	(4\раз2)	(4\раз3)	(4\4)	(3\4)	(2\4)	(5\х5)
(1\х2)	(1\раз3)	(1\4)	(1\х5)	(1×6)	(2\раз1)	(3\раз1)	(4\раз1)	(5\раз1)	(6\раз1)	(7\раз1)

\mathrm{Радианы}	\mathrm{Градусы}	\квадрат!	(	)	%	\mathrm{очистить}
\arcsin	\sin	\sqrt{\square}	7	8	9	\дел
\арккос	\cos	\лн	4	5	6	\раз
Арктан	\бежевый	\лог	1	2	3	–
\пи	е 9{\ квадрат}	0	“> .	\жирный{=}	+

Математика как комплексное решение задач

Джейкоб Клерляйн и Шина Херви, Generation Ready

К тому времени, когда маленькие дети поступают в школу, они уже находятся на пути к тому, чтобы научиться решать задачи. С самого рождения дети учатся учиться: они реагируют на свое окружение и реакцию окружающих. Это осмысление опыта является непрерывным, рекурсивным процессом. Мы давно знаем, что чтение — это сложная деятельность по решению проблем. Совсем недавно учителя пришли к пониманию того, что повышение математической грамотности — это также сложная деятельность по решению проблем, которая становится более мощной и гибкой, если практиковаться чаще. Проблема в математике — это любая ситуация, которая должна быть решена с помощью математических инструментов, но для которой нет очевидной стратегии. Если путь вперед очевиден, это не проблема — это простое приложение.

Математики всегда понимали, что решение задач занимает центральное место в их дисциплине, потому что без задачи нет математики. Решение проблем играет центральную роль в мышлении педагогов-теоретиков с момента публикации книги Полиа «Как это решить» в 1945 году. Национальный совет учителей математики (NCTM) последовательно выступает за решение проблем для почти 40 лет, в то время как международные тенденции в преподавании математики показали повышенное внимание к решению задач и математическому моделированию, начиная с начала 19 века.90-е. По мере того, как преподаватели во всем мире все больше осознавали, что предоставление опыта решения задач имеет решающее значение для того, чтобы учащиеся могли осмысленно использовать и применять математические знания (Wu and Zhang, 2006), мало что изменилось на школьном уровне в Соединенных Штатах.

«Решение задач — это не только цель изучения математики, но и основное средство для этого».

(NCTM, 2000, стр. 52)

В 2011 году Стандарты Common Core State включили Стандарты процессов NCTM по решению задач, рассуждению и доказательству, общению, представлению и связям в Стандарты математической практики. Для многих учителей математики это был первый раз, когда они должны были объединить сотрудничество учащихся и обсуждение с решением проблем. Эта практика требует обучения совершенно по-другому, поскольку школы перешли от ориентированного на учителя к более диалогическому подходу к преподаванию и обучению. Задача учителей состоит в том, чтобы научить учащихся не только решать задачи, но и изучать математику посредством решения задач. Хотя многие учащиеся могут развить беглость процедур, им часто не хватает глубокого концептуального понимания, необходимого для решения новых задач или установления связей между математическими идеями.

«Однако учебная программа по решению задач требует от учителя другой роли. Вместо того, чтобы руководить уроком, учитель должен предоставить ученикам время для решения проблем, самостоятельного поиска стратегий и решений и научиться оценивать свои собственные результаты. Несмотря на то, что учитель должен присутствовать очень активно, главное внимание в классе должно быть сосредоточено на мыслительных процессах учащихся».

(Burns, 2000, стр. 29)

Обучение решению проблем

Чтобы понять, как учащиеся становятся способными решать задачи, нам нужно взглянуть на теории, лежащие в основе обучения математике. К ним относятся признание аспектов обучения, связанных с развитием, и тот важный факт, что учащиеся активно участвуют в изучении математики посредством «действий, разговоров, размышлений, обсуждений, наблюдений, исследований, слушания и рассуждений» (Copley, 2000, стр. 29). . Концепция совместного конструирования обучения является основой теории. Более того, мы знаем, что каждый студент находится на своем уникальном пути развития.

Убеждения, лежащие в основе эффективного преподавания математики

Самобытность, язык и культура каждого учащегося должны уважаться и цениться.
Каждый учащийся имеет право на доступ к эффективному математическому образованию.
Каждый ученик может стать успешным учеником по математике.

Дети приходят в школу с интуитивным пониманием математики. Учителю необходимо установить связь и опираться на это понимание через опыт, который позволяет учащимся изучать математику и делиться своими идеями в содержательном диалоге с учителем и своими сверстниками.

Обучение происходит в социальных условиях (Выготский, 1978). Учащиеся строят понимание посредством участия в решении проблем и взаимодействия с другими в этих действиях. Благодаря этим социальным взаимодействиям учащиеся чувствуют, что они могут рисковать, пробовать новые стратегии, а также давать и получать обратную связь. Они учатся совместно, когда делятся разными точками зрения или обсуждают способы решения проблемы. Именно через разговоры о проблемах и обсуждение своих идей дети строят знания и осваивают язык, чтобы осмысливать опыт.

Учащиеся приобретают понимание математики и развивают навыки решения задач в результате решения задач, а не непосредственного обучения (Hiebert1997). Роль учителя состоит в том, чтобы создавать проблемы и представлять ситуации, которые обеспечивают форум, на котором может происходить решение проблем.

Почему важно решать проблемы?

Наши учащиеся живут в обществе, основанном на информации и технологиях, где им необходимо уметь критически мыслить о сложных проблемах, а также «анализировать и логически мыслить о новых ситуациях, разрабатывать неопределенные процедуры решения и ясно и убедительно сообщать свое решение другим». (Баруди, 1998). Математическое образование важно не только из-за «роли контролера, которую математика играет в доступе учащихся к образовательным и экономическим возможностям», но и потому, что процессы решения задач и приобретение стратегий решения задач готовят учащихся к жизни после школы (Кобб). и Ходж, 2002).

Важность решения задач при изучении математики исходит из убеждения, что математика в первую очередь связана с рассуждениями, а не с запоминанием. Решение проблем позволяет учащимся развивать понимание и объяснять процессы, используемые для достижения решений, а не запоминать и применять набор процедур. Именно благодаря решению задач учащиеся развивают более глубокое понимание математических концепций, становятся более вовлеченными и ценят актуальность и полезность математики (Wu and Zhang, 2006). Решение задач по математике способствует развитию:

Способность мыслить творчески, критически и логически
Способность структурировать и организовывать
Способность обрабатывать информацию
Удовольствие от интеллектуальной задачи
Навыки решения проблем, которые помогают им исследовать и понимать мир

Решение задач должно лежать в основе всех аспектов преподавания математики, чтобы учащиеся могли ощутить силу математики в окружающем их мире. Этот метод позволяет учащимся рассматривать решение задач как средство построения, оценки и уточнения своих математических теорий и теорий других.

«Проблемные» проблемы

Требования учителя к ученикам очень важны. Учащиеся учатся справляться со сложными проблемами, только столкнувшись с ними. Учащиеся должны иметь возможность работать над сложными задачами, а не над серией простых задач, вытекающих из сложной задачи. Это важно для стимулирования математических рассуждений учащихся и формирования прочных математических знаний 92 523 (Энтони и Уолшоу, 2007). Задача учителей состоит в том, чтобы задачи, которые они ставят, были разработаны для поддержки обучения математике и были подходящими и сложными для всех учащихся. Задачи должны быть достаточно сложными, чтобы вызвать затруднения , но не настолько сложными, чтобы учащиеся не смогли добиться успеха. Учителя, которые понимают это правильно, создают устойчивых решателей проблем, которые знают, что при настойчивости они могут добиться успеха. Задачи должны находиться в «зоне ближайшего развития» учащихся (Выготский 19).68). Эти типы сложных проблем предоставят возможности для обсуждения и обучения.

Учащиеся будут иметь возможность объяснить свои идеи, ответить на идеи других и бросить вызов своему мышлению. Те ученики, которые думают, что математика — это все о «правильном» ответе, нуждаются в поддержке и поощрении, чтобы пойти на риск. Терпимость к трудностям необходима для решения проблем, потому что «застревание» — это неизбежный этап решения практически любой проблемы. Выход из тупика обычно требует времени и включает в себя использование различных подходов. Студенты должны научиться этому на опыте. Эффективных задач:

Доступны и расширяемы
Разрешить отдельным лицам принимать решения
Способствовать обсуждению и общению
Поощряйте оригинальность и изобретательность
Поощряйте «а что, если?» и «а что, если нет?» вопросы
Содержит элемент неожиданности (адаптировано из Ahmed, 1987)

«Учащиеся учатся решать задачи по математике в первую очередь путем «действия, разговора, размышления, обсуждения, наблюдения, исследования, слушания и рассуждений».

(Copley, 2000, стр. 29)

«…когда учащиеся исследуют вместе. Оно становится мини-обществом – сообществом учащихся, занятых математической деятельностью, дискурсом и размышлениями. Учащимся должна быть предоставлена возможность действовать как математики, позволяя, поддерживая и бросая вызов их «математизации» конкретных ситуаций. Сообщество обеспечивает среду, в которой отдельные математические идеи могут быть выражены и проверены на соответствие идеям других… Это позволяет учащимся стать более ясными и уверенными в том, что они знают и понимают».

(Fosnot, 2005, p. 10)

Исследования показывают, что «классы, в которых ориентация последовательно определяет результаты задач с точки зрения ответов, а не мыслительных процессов, связанных с получением ответов, отрицательно влияет на мыслительные процессы и математические тождества. из 92 523 учащихся (Энтони и Уолшоу, 2007 г., стр. 122).

Эффективные учителя формируют у своих учеников хорошие привычки решать проблемы. Их вопросы разработаны, чтобы помочь детям использовать различные стратегии и материалы для решения проблем. Студенты часто хотят начать без плана в виду. Посредством соответствующих вопросов учитель дает учащимся некоторую структуру для начала решения проблемы, не говоря им, что именно делать. В 1945 Полиа опубликовал следующие четыре принципа решения проблем, чтобы помочь учителям помочь своим ученикам.

Понять и изучить проблему
Найдите стратегию
Используйте стратегию для решения проблемы
Оглянитесь назад и подумайте над решением

Решение проблем — это не линейный, а сложный интерактивный процесс. Учащиеся перемещаются вперед и назад между фазами Pólya и между ними. Стандарты Common Core State описывают этот процесс следующим образом:

«Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут точки входа в ее решение. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они отслеживают и оценивают свой прогресс и при необходимости меняют курс». (Стандарты обучения математике нового поколения штата Нью-Йорк, 2017 г.).

Принципы решения проблем Полиа

Понять и изучить проблему
Найдите стратегию
Используйте стратегию для решения проблемы
Оглянитесь назад и подумайте над решением

Учащиеся перемещаются вперед и назад по ходу решения задач.

Цель состоит в том, чтобы учащиеся имели ряд стратегий, которые они используют для решения проблем, и понимали, что может быть более одного решения. Важно понимать, что процесс столь же важен, если не более важен, чем получение решения, поскольку именно в процессе решения учащиеся раскрывают математику. Получение ответа — это не конец процесса. Размышление о стратегиях, используемых для решения проблемы, дает дополнительный опыт обучения. Изучение подхода, используемого для решения одной проблемы, помогает учащимся более комфортно использовать эту стратегию в различных других ситуациях.

При осмыслении идей учащиеся должны иметь возможность работать как самостоятельно, так и совместно. Будут времена, когда учащиеся должны иметь возможность работать самостоятельно, а иногда им нужно будет иметь возможность работать в небольших группах, чтобы они могли делиться идеями и учиться с другими и у них.

Реальность

Эффективные учителя математики создают для учащихся целенаправленный учебный опыт, решая задачи в релевантных и осмысленных контекстах. Хотя текстовые задачи — это способ поместить математику в контекст, он не делает ее автоматически реальной. Задача учителей состоит в том, чтобы давать учащимся задачи, основанные на их опыте реальности, а не просить их приостановить его. Реалистичность не означает, что задачи обязательно связаны с реальным контекстом, скорее они заставляют учащихся думать «настоящим» образом.

Планирование беседы

Планируя и продвигая беседу, учителя могут активно вовлекать учащихся в математическое мышление. На уроках математики, насыщенных дискурсом, учащиеся объясняют и обсуждают стратегии и процессы, которые они используют при решении математических задач, тем самым связывая свой повседневный язык со специальной лексикой математики.

Учащиеся должны понимать, как общаться математически, давать разумные математические объяснения и обосновывать свои решения. Эффективные учителя поощряют своих учеников сообщать свои идеи устно, письменно и с использованием различных представлений. Слушая учеников, учителя могут лучше понять, что знают их ученики, и неправильные представления, которые у них могут быть. Именно заблуждения открывают окно в процесс обучения студентов. Эффективные учителя рассматривают мышление как «процесс понимания», они могут использовать мышление своих учеников как ресурс для дальнейшего обучения. Такие учителя отзывчивы как к своим ученикам, так и к дисциплине математики.

«Сегодня математика требует не только вычислительных навыков, но и способности мыслить и рассуждать математически, чтобы решать новые задачи и изучать новые идеи, с которыми учащиеся столкнутся в будущем. Обучение улучшается в классах, где учащиеся должны оценивать свои собственные идеи и идеи других, им предлагается делать математические предположения и проверять их, а также им помогают развивать свои навыки рассуждения».

(Джон Ван де Валле)

«Капитал. Превосходство в математическом образовании требует справедливости — высоких ожиданий и сильной поддержки для всех учащихся».

(NTCM)

Заключение

То, как учителя организуют обучение в классе, во многом зависит от того, что они знают и думают о математике, а также от того, что они понимают в преподавании и изучении математики. Учителя должны признать, что процессы решения проблем развиваются с течением времени и значительно улучшаются за счет эффективных методов обучения. Роль учителя начинается с выбора подробных задач по решению задач, которые сосредоточены на математике, которую учитель хочет, чтобы их ученики изучали. Подход к решению проблем – это не только способ развития мышления учащихся, но и создание контекста для изучения математических понятий. Решение проблем позволяет учащимся перенести то, что они уже узнали, в незнакомые ситуации. Подход к решению проблем позволяет учащимся активно формировать свои представления о математике и брать на себя ответственность за свое обучение. Задача учителей математики состоит в том, чтобы развивать у учащихся процесс математического мышления наряду со знаниями и создавать возможности для представления даже рутинных математических задач в контексте решения проблем.

Учитывая усилия, предпринятые на сегодняшний день для включения решения задач в качестве неотъемлемой части учебного плана по математике, и ограниченную реализацию в классах, для достижения этой цели потребуется нечто большее, чем риторика. Хотя ценное профессиональное обучение, ресурсы и дополнительное время являются важными шагами, возможно, что решение задач по математике будет цениться только тогда, когда оценка с высокими ставками будет отражать важность решения учащимися сложных задач.

Главная – Фотоматематика

Математика учит, что

получает вас.
Наши пошаговые инструкции помогут вам освоить математику от арифметики до исчисления, чтобы вы могли продолжать совершенствовать свои навыки.
Что мы можем объяснить?
Photomath охватывает широкий спектр математических тем, поэтому мы можем быть вашими товарищами по учебе со второго до старшего класса!
Элементарная математика
Алгебра
Геометрия
Исчисление
Тригонометрия
Статистика
Проблемы со словами
и больше!
Начать обучение
Решение задач с первого дня
Отец изо всех сил пытался помочь своим детям с домашним заданием по математике. Созданное им решение уже помогло миллионам студентов по всему миру.
Еще для родителей
Дамир Сабол
Основатель
Больше, чем просто приложение
В школе один учитель предан десяткам учеников. В Photomath на одного ученика работают десятки учителей.
Фотоматематика в классе
300 млн+
Загрузка приложения
4.7
Рейтинг App Store
Я ставлю этому приложению пять звезд из-за того, насколько оно полезно, когда я не могу обратиться за помощью к своему учителю.
Пошаговые объяснения помогают мне проверить правильность выполнения домашних заданий моими детьми, а приложение разъясняет концепции и улучшает их способность самостоятельно решать задачи.
Раньше я нанимал репетиторов, которые платили более 100 долларов в час, но они часто не преподавали так, чтобы это нашло отклик у моих детей. Пошаговые объяснения Photomath идеально подходят для самостоятельного обучения и экономят мне сотни долларов каждый месяц!
Это замечательное приложение для детей, которое помогает им понять математику. Как родитель, я не слишком много знаю об алгебре, и это помогло мне с домашним заданием моего ребенка.
Я ОБОЖАЮ это приложение. Каждый раз, когда я показываю это студентам, они просто поражены этим (как и я). Тот факт, что он показывает альтернативные способы решения уравнений, открывает большие возможности для обучения, которые могут быть упущены в обычном классе.
Это приложение ЧРЕЗВЫЧАЙНО полезно. Я учусь в 10-м классе, изучаю геометрию 1, поэтому я не знаю, насколько это важно, но для меня это было безумно полезно. 10/10 рекомендую. (Кстати, не бот)
Это помогло мне и моим друзьям сдать 7 и 8 класс, спасибо Photomath
Спасибо, 4 помог мне пройти 7-й класс!
Это приложение помогает мне с одночленами и дробями. Я люблю это приложение.
Я так благодарен, что есть такое приложение, оно заставляет меня думать, что учиться действительно легко и иногда весело.
Помогла мне пройти онлайн-математику 2020-21. Я получил 90+ баллов в основном только с помощью этого приложения. Столько времени сэкономил. Настоятельно рекомендую.
Это приложение очень помогло моей дочери. Просто и ответы хорошо объяснены.
Мне нравится, что есть несколько вариантов выбора, например упрощение или решение практически любого типа проблемы. Я рекомендую щелкнуть кнопку с надписью «Объяснить шаги», потому что она очень хорошо вас учит».
Очень помогает в алгебре, и мне нравится, как она дает все форматы ответов. Она очень хорошо объясняет шаги, чтобы вы могли понять, как решать
Мой сын пошел в среднюю школу, и его математика значительно сложнее. Фотоматематика показывает ему шаги, чтобы получить правильный ответ, и загорелась лампочка.
Помогает мне репетитор! Мне нравится, как это позволяет мне освежить в памяти математику, которую я не делал годами.

‎App Store: Решать примеры по математике

Описание

Оценки и отзывы

Не связанные с пользова­телем данные

Информация

Другие приложения этого разработчика

Вам может понравиться

Говорим о математике на английском ‹ engblog.

Учим ребенка счету. Задачи и примеры для первого класса по математике

Примеры по математике за 1 класс

Тренажер по математике для 1 класс. Обучение решению задач. А.В.Белошистая

Математический лабиринт

Какие особенности мышления нужно учитывать?

Математика (первый класс): примеры

Первый класс. Математика. Примеры и задачи

Примеры по математике для дошкольников

Контакты

Примеры по математике для дошкольников

Вспомним цифры

Учимся выполнять инструкцию

Порядковый счёт

Сравнение множеств

Придумывание задач

Решение примеров

Добавить комментарий

Популярные

Решить уравнение, Решить задачу по математике

Pocket Teacher искусственный интеллект, который 30 лет разрабатывали в МГУ

Получите онлайн-помощника в решении множества математических дисциплин.

Решайте задачи, заданные в текстовом виде

Pocket Teacher всегда под рукой

Сервис будет полезен всем, кто сталкивается с математикой

Наш сервис – один из самых мощных искусственных интеллектов в России и странах СНГ

Как решать Задачи по Математике 5 класс (2017) + Примеры, Таблицы

Почему инструкция лучше решебника

Почему важно уметь решать задачи по математике

Какие бывают задачи по математике в 5-ом классе

Задачи на сложение, вычитание, умножение и деление

Пример 1

Пример 2

Задачи на скорость, время, расстояние

Пример 1

Пример 2

Задачи на движение

Пример 1

Пример 2

Задачи, решаемые алгебраическим способом

Пример 1

Пример 2

Задачи, решаемые геометрическим способом

Пример 1

Пример 2

Нужен ли ребёнку репетитор по математике в пятом классе?

Как решить проблемы с математикой

Гуманитариям математика не нужна?

Математика — сложный предмет

Формула спокойствия

Решение неравенств с помощью пошагового решения математических задач

РЕШЕНИЕ УРАВНЕНИЙ

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА ДЕЛЕНИЯ

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА УМНОЖЕНИЯ

РЕШЕНИЕ ФОРМУЛ

Фактор полинома или выражения с помощью программы «Пошаговое решение математических задач»

УДАЛЕНИЕ ОБЩИХ ФАКТОРОВ

ЦЕЛИ

ФАКТОРИЗАЦИЯ ПО ГРУППИРОВКЕ

ЗАДАЧИ

ФАКТОРИЗАЦИЯ ТРЕХНОМОВ

ЦЕЛИ

ОСОБЫЕ СЛУЧАИ В ФАКТОРИНГЕ

ЦЕЛИ

ДОПОЛНИТЕЛЬНЫЕ КОРРЕКТЫ ДЛЯ ФАКТОРИНГА ПРОБ И ОШИБОК

ЦЕЛИ

ПОЛНАЯ ФАКТОРИЗАЦИЯ

ЦЕЛИ

РЕЗЮМЕ

Ключевые слова

Процедуры

‎Photomath в App Store

Не связанные с пользователем данные