Размеры объемной цифры 1: Цифра 1 на годик своими руками для мальчика: мастер-класс с фото

Как сделать цифру 1 на день рождения своими руками для ребенка

Практически все готово к празднованию первого Дня рождения сына или дочки. Продуман план мероприятия, придумана тематика и подготовлены атрибуты для украшения помещения. Но как же подчеркнуть, что это праздник первой годовщины. А не просто торжество, посвященное ребенку. Здесь на помощь придет непосредственно цифра 1. Причем ее можно использовать в декоре самым неожиданным способом. Но особенно интересно смотрятся большие декоративные цифры. Мы научим, как сделать единичку на день рождения своими руками.

Детский день рождения 1 годик: как использовать цифры

Пусть все вокруг на празднике просто кричит о том, что у вашего малыша сегодня первый День рождения. И в этом помогут не только тематические украшения, наряды, угощения. Но и цифра 1, которую можно использовать различными способами:

1. Обязательно добавьте слова «Мне 1 годик» в праздничную гирлянду. Пусть гости с порога видят, чему посвящен праздник.
2. Можно прикольно сделать свисающие гирлянды с цифрами. Каждую единичку украсьте в соответствии с выбранной тематикой.
3. Для украшения блюд, сладостей, напитков используйте топеры с изображением или в виде единички.
4. Выложите на стене единицу шарами, бантами или сделайте такое украшение из бумаги.
5. В фотозоне обязательно должна присутствовать объемная или плоская цифра, которая в дальнейшем будет напоминать, когда были сделаны фотографии.

И главное, большая декоративная цифра, которая практически станет центральным атрибутом именин. Она может быть миниатюрной или огромной, плоской или объемной.

Такой декор можно легко заказать или купить готовым. Но намного интереснее будет смотреться цифра на День рождения 1 год, сделанная своими руками. Ведь в этом случае можно учесть выбранную тематику, наряд малыша, размеры помещения.

И главное, подготовка любого праздника сближает родных, придает ему особой значимости.

Цифра 1 на день рождения своими руками из шаров

Малыши просто обожают воздушные шарики. Даже совсем крохи приходят в восторг от декора из шаров.

Причем сделать цифру 1 на День рождения из шариков совсем просто.

Предлагаем мастер-класс изготовления цифры 1 из разноцветных шаров.

Подготовим все необходимые заготовки и инструменты. Нам понадобятся голубые шарики до 10 см в диаметре в количестве 52 шт. и 36 зеленых такого же размера. Но лучше купить шары с запасом на случай, если что-то пойдет не так.

Чтобы надуть такое количество шаров, лучше воспользоваться самым простым насосом. Это в разы ускорит процесс. Связывать заготовки будем при помощи лески.

Начинаем процесс изготовления единички с подготовки базовых элементов. Каждый сегмент будет состоять из 4 шаров.

Для этого наполняем воздухом шары при помощи ручного насоса. При этом контролируем размер шаров. Каждый шарик завязываем.

Берем 2 шара одного цвета и связываем их между собой. Делаем еще одну такую заготовку. Две готовых заготовки соединяем между собой, перекручивая. У нас получился базовый сегмент поделки.

Таким же способом делаем зеленый сегмент.

Всего нужно сделать 9 зеленых сегментов и 13 голубых «четверок».

Приступаем к изготовлению основания единички из зеленых шариков. Леску закрепляем на первом сегменте, оборачивая несколько раз между шарами. Теперь к нему прижимаем следующий зеленый сегмент и закрепляем леской. Таким способом соединяем между собой все зеленые «четверки».

Обрезаем леску, и оставшийся хвостик несколько раз завязываем вокруг шаров и прячем.

У нас получилось основание цифры 1.

К центру зеленой полянки привязываем леску, и начинаем крепить синие сегменты. Они будут идти вертикально. Всего закрепим 10 голубых сегментов.

Из оставшихся трех «четверок» делаем носик единичек. Для этого сегменты будем крепить сбоку вертикальной части. Когда все сегменты свяжем, край носика притягиваем к вертикальной части. Леску обрезаем, завязываем и прячем край между шарами.

Наша единичка готова. При желании ее можно украсить шарами другого цвета, из которых легко сделать бабочку, цветы, божью коровку.

Таким же способом можно изготовить цифры в другом дизайнерском исполнении.

Не только практично, но и современно

На самом деле, объемные поделки из проволоки, в частности цифры, становятся все популярнее. Из нее можно создавать и елочные игрушки в форме звезд, шаров и т.п., украшения для сада или для цветов в горшках, из них же получаются очень красивые венки: новогодние из елки, осенние и даже летние из живых цветов.

Все потому, что это наиболее гибкий материал и его можно подобрать к любому дизайну. На проволоку хорошо ложатся глиттер и блестки, прикрепленные на клей. Для венков используется специальный скотч, который позволяет оставить основу вовсе невидимой. Ну а матовая проволока прекрасно сочетается с толстыми нитками природных оттенков, при помощи которых так часто добавляют форму и акценты. И уже нить можно точно украсить чем угодно, в ход идет и краска и дополнительные украшения, те же самые пуговицы, цветы, сосновые шишки и бусины.

Размеры, шаблоны, варианты украшений плоской цифры 1 на день рождения

Оригинально смотрятся плоские единички, которые можно разместить на стене, шторах, просто оперев о другие декоративные элементы.

Достаточно определиться с размером, высотой заготовки и сделать шаблон из бумаги.

Готовый шаблон переносим на картонную основу – обводим контуры карандашом. Вырезаем цифру по контуру.

Картонная заготовка для праздничной единички готова. Декорировать такую заготовку можно всем чем угодно, подбирая дизайн и материал под общий стиль оформления праздника.

Проще всего для украшения плоской цифры использовать шпагат или разноцветные нитки, гофрированную или цветную бумагу, яркую ткань или флористическую пленку, цветы или салфетки.

Такими материалами оборачивают или обклеивают основу.

Чтобы придать украшению дополнительного объема, основу декорируют объемными цветами, помпонами, бантиками.

Как создать цветы для объемной композиции

Для начала нужно сделать сами цветы. Для этого можно использовать любые материалы, приходящиеся вам по вкусу: ткань, бумага, салфетки. Уже из этих материалов вырезаем лепестки разного размера. И постепенно, с самых маленьких начинаем их скреплять, это можно сделать с помощью клея или ниток. Из бусин и проволоки делаем сердцевину.

Есть и другой способ изготовления цветов. Нужно вырезать квадраты одного размера и сложить их стопочкой, потом середину скрепить степлером. Будущим лепесткам нужно предать округлую форму и поднять лепестки вверх, для этого иногда требуется скрепить их ниткой чуть выше крепления степлером.

Такой способ вероятно проще, цветочки получаются чуть менее изящными и теряют немного в индивидуальности, но зато так вы гораздо быстрее и с меньшими усилиями создадите необходимое количество для украшения цифры.

Объемная цифра 1 из картона на День рождения

Но намного интереснее будет смотреться объемная цифра. Ее именинник сможет переставлять, играть с ней. Такая объемная единичка прекрасно впишется и в фотозону, и в дизайн помещения, садовой площадки.

Для ее изготовления можно использовать толстый пенопласт. Но если такого материала нет под рукой, заготовку легко сделать из обычного картона.

Даже если у вас нет больших коробок, можно склеить основу из нескольких частей. Сначала делаем два шаблона самой единички.

В размер вырезаем боковые части и основание цифры.

Заготовки соединяем между собой скотчем.

В итоге должна получиться вот такая объемная цифра из картона.

Не расстраивайтесь, что она не слишком красива.

Все изъяны и неровности будут надежно спрятаны под декоративными элементами. Украсить такую основу можно бумажными зонтиками и цветами, бахромой и фотографиями, фетром и нитками.

Как украсить единичку на День рождения

Предлагаем несколько оригинальных вариантов украшения цифры 1 своими руками из подручных материалов. Сохраните себе эти мастер классы – они обязательно пригодятся для украшения объемных цифр на другие детские праздники.

Цифра 1 в эко-стиле из шпагата , ниток

Очень простой вариант украшения плоской заготовки. Нам понадобится обычный шпагат и клей.

На картон постепенно наносим клей. Обработанный участок оборачиваем шпагатом. Можно делать аккуратные витки, а можно слегка менять угол наклона. Когда обмотаете обклеенный участок, нанесите клей выше и продолжайте наматывать шпагат.

Когда обмотаете всю заготовку, оставьте цифру высохнуть. Практически единичка готова. Но при желании шпагат можно выкрасить акриловыми красками или добавить декоративных элементов.

Но можно изначально использовать не шпагат, а яркие нитки, которыми будем обматывать картонную заготовку.

Цифра 1 из салфеток для мальчика на День рождения

Сделайте для своего малыша самую пушистую цифру на День рождения.

Для этого понадобятся разноцветные салфетки, много салфеток и терпение. Но результат того стоит.

Такой декор выйдет на порядок дешевле, чем готовые цифры.

Покупаем несколько упаковок синих или голубых однотонных салфеток.

Если желаете разбавить синий фон белыми цветами, приобретите соответствующего цвета салфетки. Очень прикольно смотрятся цифры с плавным переходом цвета. В этом случае понадобятся салфетки синего, голубого, небесного и белого цвета.

Чтобы сделать салфетные цветочки, лучше брать однослойные салфетки. Салфетку, не разворачивая, складываем дважды. Разрезать квадраты не обязательно, в дальнейшем все сгибы будут срезаны. Заготовку посередине скрепляем степлером. Можно воспользоваться обычной проволокой, чтобы скрепить основание цветка.

Теперь обрезаем квадрат в размер цветка, чтобы получился ровный круг.

Первый слой салфетки аккуратно собираем вверх, формируя лепестки цветка. Проделываем такую операцию с каждым последующим слоем. Когда поднимете все слои, расправьте все лепестки.

Если хотите сделать более пышный цветок, возьмите две салфетки. Можно также разрезать круглую заготовку на несколько лепестков, не дорезая до основания.

Готовыми цветами украшаем картонную заготовку единички. Лучше это делать при помощи клея в пистолете.

После оклеивания салфеточными цветами получается красивая пышная цифра 1.

Цифра 1 для девочки на День рождения из гофрированной бумаги

Розочки из гофрированной бумаги смотрятся великолепно. Цифра, украшенная такими цветочками, станет шикарным украшением годовасия. Можно фантазировать, экспериментировать с цветом и расположением разноцветных цветов или же просто сделать однотонную единичку.

Понадобится довольно много гофрированной бумаги, а еще времени, чтобы сделать много цветов-заготовок.

Разверните бумагу и нарежьте из нее полосы. Складочки на заготовке должны располагаться поперек. Ширина такой заготовки будет 3,5 см. А вот с длиной определитесь сами. Это может быть и 20, и 50 см. Чем длиннее будет полоса, тем пышнее получится розочка.

Одну из сторон полоски слегка растягиваем и загибаем ее край. За счет растяжки складочек должны получиться красивые волны.

Загибаем краешек и формируем завитушку.

Начинаем собирать сам цветок, для чего придерживая край, начинаем закручивать вокруг основания полоску бумаги.

Когда вся полоса будет свернута, низ цветка нужно прихватить резинкой или ниткой.

Первая розочка готова. Но нужно сделать еще 50, 100 , 300 цветков.

Картонную основу цифры оклеиваем бумагой.

Это поможет скрыть возможные просветы, которые могут получиться при оклеивании.

Готовые цветки приклеиваем к основе при помощи клея ПВА или клеевого термопистолета.

В итоге получается красивейшая декоративная единичка, которая неизменно порадует именинницу.

Другие способы применения гофрированной бумаги

Возиться с розочками из гофрированной бумаги нет времени или желания? Воспользуйтесь более простыми способами, как украсить единичку при ее помощи.

Достаточно нарезать разноцветную гофрированную бумагу на квадраты.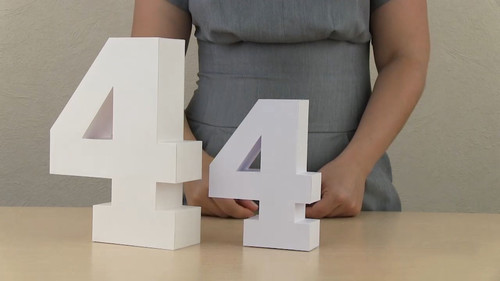

Для этого полосы-заготовки складываем несколько раз и разрезаем по полученным сгибам.

У нас получится много гофрированных квадратов.

Картонную основу смазываем клеем. Берем карандаш и оборачиваем его гофрированной бумагой , чтобы стержень оказался по центру.

Осталось низ цветочка окунуть в клей и приложить к основе, расправить края-лепестки.

Постепенно оклеиваем все стены картонной заготовки. Старайтесь, чтобы лепесточки закрыли всю поверхность цифры.

Но существует способ намного проще.

Нарезаем длинные полосы из гофрированной бумаги разных цветов. По краю каждой полосы делаем надрезы, чтобы получилась бахрома.

Начинаем оклеивать картонную единичку снизу. Приклеиваем первую полосу бахромы, нанеся клей на цельную часть полосы.

Немного отступив, клеем следующую полосу. Следите, чтобы следующая бахрома перекрывала цельный участок предыдущей.

Продолжаем оклеивать всю поверхность единички, меняя цвет полос.

Цифра 1 на День рождения из помпонов

Если есть дома много разноцветных шерстяных ниток, можно использовать их для украшения цифры 1. Только в этот раз будем не обматывать картонную заготовку, а делать из ниток помпоны.

Нам понадобится два кольца, которые по размеру должны быть абсолютно одинаковыми. Их можно вырезать из плотного картона.

Складываем эти кольца вместе. Обматываем постепенно кольца ниткой. Можно взять однотонную нить или нитки разных цветов.

Когда все кольцо будет закрыто нитками, разрезаем нити по внешнему краю круга. На этом этапе нужно быть особенно аккуратным, чтобы заготовка не рассыпалась.

Дополнительной нитью перевязываем все нитки, слегка раздвинув кольца. Убираем картонные кольца и хорошенько встряхиваем полученный помпон.

Делаем столько помпонов из ниток, чтобы их хватило оклеить всю единичку. Таким способом можно украсить как плоскую, так и объемную цифру.

Материалы для изготовления

Если в доме совсем маленький малыш, и вы еще не разжились канцелярскими принадлежностями, советуем немедленно отправиться в магазин для рукодельниц. Создайте заметку в телефоне, чтобы не забыть инструменты, которые необходимо приобрести для будущей поделки:

• Картон Размер картона зависит от размера цифры, которую вы собираетесь смастерить. Для большого количества циферок, планируемых использоваться как реквизит для фотосессии, лучше предпочесть толстый картон А4. если в планах огромные поделки, придется проявить изобретательность и отыскать большие коробки от крупной бытовой техники. Проще всего это сделать, спросив в магазине: обычно продавцы с радостью отдают ненужные упаковки от товара.
• Ножницы Берите удобные ножницы: при резке картона они не должны тереть места соприкосновения с кожей.
• Гофрированная бумага Если в голове еще нет четкого представления, как должна выглядеть ваша цифра, возьмите цвета, которые наиболее приглянутся в магазине. В противном случае подберите материал согласно задумке.
• Бечёвка Приобретите пару мотков бечёвки, если планируемое мероприятие будет проходить в стиле рустик.
• Строительный степлер Степлер понадобится при работе с плотным картоном. Без него создание объемных фигур станет практически невозможным.
• Клеевой пистолет Нужен для скрепления деталей
• Линейки, карандаши, ластики Материалы нужны для конструирования и разметки цифр на листах картона.
• Дополнительные материалы Приобретайте дополнительные материалы при необходимости. К ним относятся: текстиль, бусины (бисер), салфетки и цветная бумага, нитки для вязания, мишура.

Объемная цифра 8 на день рождения девочке | Festima.Ru

✅ Фасадный декор. Архитектурный декор. Облицовка фасада. Отделка фасада. Утепление Фасада. Хотите красивый и теплый фасад с эффектом экономии? Мы вам в этом поможем! С 2009 года наша Мастерская производит качественную, тепло-экономичную и доступную продукцию.  С официальной гарантией 15+ лет.  📌 Производим в Ессентуках доставляем в любую точку России!  ☎ Свяжитесь с нами любым удобным для Вас способом.   Мы готовы предоставить Вам профессиональную консультацию и помочь в выборе материала📝  🔷 Использование наших материалов позволяют Вам экономить на всем сроке эксплуатации на отоплении до 50%, кондиционирование до 50%,  🔷 Срок службы дома увеличивается до 100% из за отсутствия контакта стен с атмосферными и температурными воздействиями.  То есть отсутствие промерзания а следовательно и отсутствие точки росы не допускает в стенах разрушительных процессов. ✅ Наши изделия также существенно снижают нагрузку на стены и фундамент на 99%  📌 Высокая ценность при не высокой цене. Делают наш материал выгодным решением во всех смыслах. 📌 Стоимость элементов декора рассчитывается от размеров и сложности изделий. 📌 Обратитесь к нам любым удобным способом и наши специалисты предоставят подробную консультацию. К вашим услугам команда профессиональных: ✅ дизайнеров ✅ консультантов ✅ мастеров 📌 Работаем качественно и оперативно. 📌 По договору. 📌 Письменная Гарантия 15+лет. Для Вас: ✅ Архитектурные элементы любой сложности и размера. ✅ Индивидуальный подход. ✅ Профессиональный монтаж. ✅ Доставка 🚚 ✅ Шикарный вид вашего фасада. ✅ Удовольствие от работы с профессионалами. 🎦📱📲 Возможна видео-консультация по всем интересующим Вас вопросам. ➡➡➡ ЗВОНИТЕ или пишите на указанный в объявлении номер! 📋 НУЖЕН КАТАЛОГ? ➡ Нажмите на кнопку 💬 [Написать] и напишите слово “каталог”. Характеристики материала: ❗️ Ударопрочный, влагостойкий, долговечный, морозостойкий, экологически безопасный, дополнительная теплоизоляция. ❗️ Состав: Пенополистирол марки ПСБ-С-25Ф, кварцевая/мраморная крошка, полимеры немецкого концерна BASF🇩🇪. Срок службы с покрытием BASF 🇩🇪50 + лет. ❗️ Цвет: можно окрасить в любой цвет. ❗️ Размеры: индивидуальные ❗️ Вес 1 ед., кг: 0,64 ❗️ Легковесность, кг/кв. м: 4,55 ❗️ УФ-устойчивость, балл: 6,4 ❗️ Водопоглащение, %: 0,2 ❗️ Плотность, кг/м3: 25 ❗️ Прочность на изгиб, кг/см2: 0,47 Артикул – 25410B1 ИЗГОТОВИМ ФОРМЫ ЛЮБОЙ СЛОЖНОСТИ С СОХРАНЕНИЕМ УКАЗАННЫХ РАЗМЕРОВ.  С уважением, руководитель ⓂМаксипласт Мастерская Петров Герман 👍 НАС РЕКОМЕНДУЮТ ДРУЗЬЯМ! 👉Переходите в наш профиль, там много интересного👍 Фасадный декор, Архитектурный декор, Клинкер, Гибкий клинкер, Клинкерный кирпич, Клинкерная плитка, гибкий клинкер для фасада, гибкий клинкер монтаж, Теплопанели, Термопанели, Утепление фасадов, Скорлупа, Утепление коммуникаций, Утепление для труб, Изделия из пенопласта, Теплый дом, Объемная реклама, Обрамление окон, Реставрация архитектуры, Декорации, Потолки, Свадебные декорации, Объемные буквы,Фигурная резка пенопласта (пенополистирола), Муляжи товаров из пенопласта, Муляж для торта, надписи из пенопласта,цифры и пенопласта, логотипы, объемная реклама, вывески, фасадный термопанель, фасад цена, утеплять дом, утепление фасада, дом фасад, дом утепление, фасадный декор, фасад декор, декоративный фасад, декоративный элемент, фасадный панель, плитка фасад, дом фасад отделка, панель фасад, облицовка фасада,дом фасад, дом облицовка.

Ремонт и строительство

1.4 Размерный анализ | University Physics Volume 1

Цели обучения

К концу этого раздела вы сможете:

• Находить размерности математического выражения, включающего физические величины.
• Определить, является ли уравнение, включающее физические величины, размерно-согласованным.

Размерность любой физической величины выражает ее зависимость от основных величин как произведение символов (или степеней символов), представляющих основные величины. (Рисунок) перечислены основные величины и символы, используемые для их измерения. Например, говорят, что измерение длины имеет размерность L или L ¹ , измерение массы имеет размерность M или M ¹ , а измерение времени имеет размерность T или T ¹ . Как и единицы, измерения подчиняются правилам алгебры. Таким образом, площадь является произведением двух длин и поэтому имеет размерность L ² , или длину в квадрате. Точно так же объем является произведением трех длин и имеет размерность L

3 , или длину в кубе. Скорость имеет размерность длины во времени, L/T или LT ^–1 . Объемная массовая плотность имеет размерность M/L 3 9{0} [/latex]) называется безразмерным (или иногда «размерностью 1», потому что все, что возведено в нулевую степень, равно единице). Физики часто называют безразмерные величины чистыми числами .

Базовые количества и их размеры

Базовое количество	Символ размера
Длина	л
Масса	М
Время	Т
Текущий	я
Термодинамическая температура	Θ
Количество вещества	Н
Сила света	Дж

Физики часто используют квадратные скобки вокруг символа физической величины, чтобы представить размеры этой величины. Например, если [латекс] r [/латекс] — это радиус цилиндра, а [латекс] h [/латекс] — его высота, то мы пишем [латекс] [г]=\текст{L} [/латекс] и [латекс] [ч]=\текст{L} [/латекс] для указания того, что размеры радиуса и высоты совпадают с размерами длины или L. Аналогично, если мы используем символ [латекс] А [/латекс] для площади поверхности цилиндра и [латекс] V [/латекс] для его объема, то [ 9{-3}. [/latex]

Важность концепции размерности возникает из-за того факта, что любое математическое уравнение, связывающее физические величины, должно быть

размерно-согласованным, что означает, что уравнение должно подчиняться следующим правилам:

• Каждый член выражения должен иметь одинаковые размеры; нет смысла прибавлять или вычитать количества разной размерности (вспомните старую поговорку: «Нельзя складывать яблоки и апельсины»). В частности, выражения по обе стороны равенства в уравнении должны иметь одинаковые размерности.
• Аргументы любых стандартных математических функций, таких как тригонометрические функции (такие как синус и косинус), логарифмы или экспоненциальные функции, которые появляются в уравнении, должны быть безразмерными. Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.

Если какое-либо из этих правил нарушается, уравнение не является размерно-согласованным и не может быть правильной формулировкой физического закона. Этот простой факт можно использовать для проверки опечаток или алгебраических ошибок, чтобы помочь вспомнить различные законы физики и даже предложить форму, которую могут принять новые законы физики. Это последнее использование измерений выходит за рамки этого текста, но вы, несомненно, узнаете об этом позже в своей академической карьере. 9{2} [/латекс] и [латекс] 2\pi r. [/latex] Одно выражение — это длина окружности круга радиусом

r , а другое — его площадь. Но что есть что?

Стратегия

Естественная стратегия — искать информацию, но это может занять время, чтобы найти информацию из авторитетного источника. Кроме того, даже если мы считаем источник авторитетным, мы не должны доверять всему, что читаем. Приятно иметь возможность перепроверить, просто подумав об этом. Кроме того, мы можем оказаться в ситуации, в которой мы не можем найти информацию (например, во время теста). Таким образом, стратегия состоит в том, чтобы найти размерности обоих выражений, используя тот факт, что размерности подчиняются правилам алгебры. Если какое-либо из выражений не имеет таких же размеров, как площадь, то оно не может быть правильным уравнением для площади круга. 9{2} [/latex] имеет размерность площади. Точно так же размерность выражения [латекс] 2\pi r [/латекс] равна

[латекс] [2\pi r]=[2]·[\pi ]·[r]=1·1·\text {L}=\text{L,} [/latex]

, так как константы [latex] 2 [/latex] и [latex] \pi [/latex] безразмерны, а радиус [latex] r [/latex ] — это длина. Мы видим, что [латекс] 2\pi r [/латекс] имеет размерность длины, что означает, что он никак не может быть площадью.

Мы исключаем [латекс] 2\pi r [/латекс], потому что его размеры не соответствуют площади. Мы видим, что [латекс] \pi {r}^{2} [/латекс] согласуется по размерам с областью, поэтому, если нам нужно выбирать между этими двумя выражениями, [латекс] \пи {г}^{2} [/latex] — это то, что нужно выбрать. {2}, [/латекс], то размерные анализ не поможет), но помогает нам запомнить правильную основную форму уравнений. 9{2}\text{/}s). [/latex]

Стратегия

В соответствии с определением размерной согласованности нам необходимо проверить, что каждый член данного уравнения имеет те же размерности, что и другие члены этого уравнения, и что аргументы любых стандартных математических функций безразмерны.

Решение

1. В этом уравнении нет ни тригонометрических, ни логарифмических, ни экспоненциальных функций, поэтому нам достаточно посмотреть на размеры каждого члена, входящего в уравнение. Есть три термина, один в левом выражении и два в выражении справа, поэтому мы рассмотрим каждый по очереди: 9{2}}{s})]=1.\hfill \end{массив} [/latex]

Два термина имеют разные размерности — это означает, что уравнение не является размерно-согласованным. Это уравнение — еще один пример «бессмыслицы».

Значение

Если мы доверяем людям, эти виды размерных проверок могут показаться ненужными. Но, будьте уверены, любой учебник по количественному предмету, такому как физика (включая этот), почти наверняка содержит некоторые уравнения с опечатками. Регулярная проверка уравнений с помощью размерного анализа избавляет нас от необходимости использовать неверное уравнение. Кроме того, проверка размерностей уравнения, которое мы получаем с помощью алгебраических манипуляций, — отличный способ убедиться, что мы не допустили ошибку (или обнаружить ошибку, если она была допущена).

Проверьте свое понимание

Соответствует ли размерность уравнения v = at ?

Показать решение

Еще один момент, о котором следует упомянуть, — это влияние операций исчисления на размерности. Мы видели, что размеры подчиняются правилам алгебры, как и единицы, но что происходит, когда мы берем производную одной физической величины по отношению к другой или интегрируем физическую величину по другой? Производная функции — это просто наклон линии, касательной к ее графику, а наклоны — это отношения, поэтому для физических величин v и t , мы имеем, что размерность производной v по отношению к t есть просто отношение размерности v к размерности t :

[латекс] [ \frac{dv}{dt}]=\frac{[v]}{[t]}. [/latex]

Аналогично, поскольку интегралы представляют собой просто суммы произведений, размерность интеграла

v по отношению к t — это просто размерность v , умноженная на размерность t :

[латекс] [\int vdt]=[v]·[t]. [/latex]

По тем же рассуждениям аналогичные правила справедливы для единиц физических величин, полученных из других величин путем интегрирования или дифференцирования.

Резюме

• Размерность физической величины — это просто выражение основных величин, из которых она получена.
• Все уравнения, выражающие физические законы или принципы, должны быть согласованы по размерам. Этот факт можно использовать как помощь в запоминании физических законов, как способ проверить, возможны ли заявленные соотношения между физическими величинами, и даже для вывода новых физических законов. 9{2}; [/latex] (c) [latex] v=s\text{/}t; [/latex] (d) [latex] a=v\text{/}t. [/latex]

  Показать решение

  Рассмотрим физические величины [латекс] m, [/латекс] [латекс] s, [/латекс] [латекс] v, [/латекс] [латекс] а, [/латекс] и [латекс] t [/латекс ] с размерами [

  м ] = M, [ s ] = L, [ v ] = LT ^–1 , [ a ] = LT ^–2 , и [ 2 t 90 ] T. Предполагая, что каждое из следующих уравнений размерно согласовано, найдите размерность величины в левой части уравнения: (a) F = мА ; б) К = 0,5 mv ² ; в) p = mv ; (г) Вт = мсд ; (e) L = mvr .

  Предположим, что количество [латекс] s [/латекс] — это длина, а количество [латекс] t [/латекс] — это время. Предположим, что количества [латекс] v [/латекс] и [латекс] а [/латекс] определены как v = ds / dt и a = dv / dt . а) Какова размерность числа 9?{–3}, [/latex] и [t] = T. (a) Какова размерность [latex] \int \rho dV? [/latex] (b) Каков размер

  dV / dt ? в) Каков размер [латекс] \rho (dV\text{/}dt)? [/latex]

  Формула длины дуги говорит, что длина [латекс] s [/латекс] дуги, опирающейся на угол [латекс] Ɵ [/латекс] в окружности радиусом [латекс] r [/латекс], определяется выражением уравнение [латекс] s=rƟ. [/latex] Каковы размеры (a) s , (b) r и (c) [latex] \text{Ɵ?} [/latex] 9{0}=1; [/latex] также называется количеством измерения 1 или чистым числом

  Размер ячейки, площадь поверхности и объем

  Размер ячейки, площадь поверхности и объем Размер ячейки: масштабирование Проблемы

  Почему клетки такие маленькие? Ответ на этот вопрос имеет столько же делать с математикой как с биологией. Представьте, что клетка имеет форму примерно куб.

  По мере увеличения размера клетки отношение площади ее поверхности к объему изменения. Площадь поверхности и объем рассчитываются, как показано на рисунок ниже:

   

  площадь стороны равна длина x ширина . Мы можем записать это как A=L*W , а когда стороны одинаковой длины, мы можем написать A=L ²

  Поскольку у куба шесть сторон, давайте также рассчитаем площадь поверхности всей внешней части ячейки как 6 * L ²

  объем куба равен длине x ширине x высота , или V=L*W*H , и когда стороны имеют одинаковую длину, мы можем написать V=L ³

  Вот где становится интересно. Поскольку мы продолжаем удваивать переменную L , от 1 до 2, от 4 до 8, площадь поверхности и объем не увеличиваются с одинаковой скоростью.

  Вопросы :

  1. Перечислите некоторые вещества, проникающие через клеточную мембрану:

  я. ___________________ ii. ___________________ III. ___________________

  2. Почему важно, чтобы клетка имела большую площадь поверхности относительно его объема? (Другими словами, высокая площадь поверхности до соотношение объемов ?)

  3. Представьте, что длина стороны ячейки может быть любого размера. Рассчитайте, что произойдет с отношением площади поверхности к объему, если клетка растет. Единицы здесь могут быть ничего, так как мы просто гипотезы.

  Размер ячейки	Длина стороны Л	Площадь поверхности 6л 2	Объем Л 3	Соотношение SA:V 6л 2 / л 3
  Маленькая ячейка	0,5	6 ( 0,5 ) 2 = 1,5	( 0,5 ) 3 = 0,125	1,5 ÷ 0,125 = 12
  	1	6 ( 1 ) 2 = 6	( 1 ) 3 = 1	6 ÷ 1 = 6
  	2
  	3
  	4
  	5
  	10
  	25
  	50
  Большая ячейка	100

  4. Создайте свой собственный график x-y с помощью Create-A-Graph или Excel, где x — площадь поверхности, а y — объем, и подставьте диапазон значений. Что происходит с отношением площади поверхности к объему при увеличении размера клетки? (Если бы площадь поверхности и объем увеличивались с одинаковой скоростью, линия была бы диагональной с наклоном 1.) Что на самом деле происходит при малых размерах? В промежуточных размерах? В больших размерах? Загрузите электронную таблицу Excel, в которой я провел свои расчеты и создал эти графики: Surface_area_volume_graph.xlsx.

  Рис. 1: Площадь поверхности клетки (SA) в зависимости от объема клетки (V). По мере увеличения размера клетки V увеличивается быстрее, чем SA. Красная пунктирная линия представляет соотношение 1:1.
  Рис. 2: График зависимости длины стороны клетки от отношения площади поверхности к объему. По мере уменьшения размера ячейки до нуля отношение SA:V приближается к бесконечности.

  5. Поскольку транспорт материалов в клетку и из нее возможен только происходит на поверхности клетки, что происходит, когда клетки становятся больше? Как это накладывает ограничение на размер ячейки?

  6. Таким образом масштабируются не только клетки. Целые животные тоже. Изучение размера тела в связи с анатомией, физиологией и поведением называется аллометрией. Для гомеотермных (животных, которые пытаются поддерживать постоянную температуру тела) необходимо производить тепло по мере его потери в окружающую среду, чтобы поддерживать равновесие. Если потеря тепла происходит только на открытых поверхностях, что бы вы предсказали относительно скорости метаболизма на единицу ткани тела крупного животного по сравнению с маленьким?

  7. Возьмите то, что вы знаете об отношении площади поверхности к объему, и попробуйте чтобы объяснить следующий график, который известен как «кривая мыши к слону». Предположим, что скорость метаболизма связана с теплотой производство и что все эти животные пытаются сохранить свое тела нагреваются в одинаковых условиях окружающей среды. Обратите внимание, например что слон имеет массу (и объем) более чем в 1000 раз больше мыши, в то время как скорость ее метаболизма (и теплопродукция) всего лишь примерно в 100 раз больше, чем у мыши. Другими словами, «Почему слон может больше нагреваться? эффективно (на единицу массы), чем мышь?»

  Кривая Броди (1945) от мыши к слону

  8. «Правило Аллена» предсказывает, что эндотермические животные (те, которые регулируют температуру своего тела внутренне) с одинаковым объемом тела должны иметь различную площадь поверхности, предназначенную либо для помощи, либо для препятствия рассеиванию тепла, в зависимости от температуры окружающей среды. Объясните со ссылкой на площадь поверхности и объем. (Подумайте о необходимости удержания тепла в холодном климате или о теплоотдаче в жарком климате и сделайте предсказание о типах телосложения.)

  9. «Правило Бергмана» гласит, что среди видов животных, имеющих глобальное распространение, размер взрослого тела, как правило, самый большой в полярные районы, средние в умеренном климате и наименьшие в тропическом те. Хотя есть исключения, в целом это так. Почему должно быть так?

  10. Контрольный вопрос: В одном из моих любимых старых фильмов о монстрах Их , гигантские муравьи атакуют город. К сожалению, могло никогда не случится. Невероятная сила муравья зависит от его небольшой размер. Увеличьте его даже до человеческого размера, и он рухнет под собственным весом на этих тощих ножках. Объем (и поэтому вес) масштабируется до степени 3, а площадь поверхности (и размер) масштабируйте до степени 2. Создайте график, показывающий, почему гигантский муравей не может разрушить город, а вместо этого рухнет под собственным весом.

  11. Контрольный вопрос: Как показано эмпирически на графике Броуди, мощность пропорциональна массе в степени 0,734, примерно 3/4, однако отношение площади поверхности к объему дает значение только 2/3 или 0,67. Животные в реальном мире работают лучше, чем ожидалось, но животные в реальном мире не полностью полагаются на площадь поверхности для обогрева, охлаждения, газообмена и т.